Transcription

1 211

2

3 1 R *1 n n R n *2 R n = {(x 1,..., x n ) x 1,..., x n R}. R R 2 R 3 R n R n R n D D R n *3 ) (x 1,..., x n ) f(x 1,..., x n ) f D *4 n 2 n = 1 ( ) 1 f D R n f : D R 1.1. (x, y) R 2 f(x, y) = x 2 + y 2 f R 2 : f : R 2 R *5 f : R 2 (x, y) f(x, y) = x 2 + y 2 R *6 f(, ) =, f(1, ) = 1, f( 1, 1) = x y f(x, y)m f(x, y) x y 2 f(, ) = 1.3. x y f(x, y)hpa f(x, y) x y ( ) *1 R R *2 x R x R x *3 D R n D D R n ) 7 4 *4 *5 2 R 2 (x 1, x 2 ) (x, y) f(x, y) x y 2 2 *6 1

4 2 f : D R (D R 2 ) R 3 { ( x, y, f(x, y) ) (x, y) D} f f R 3 2 f : D R c {(x, y) D f(x, y) = c} f c 2 1.2, 1.3 f R 2 f R 2 * xy ( ) (x, y) (, ) f(x, y) = x 2 + y 2 ( ) (x, y) = (, ) : f(, ), f(1, 1), f(1, 2), f(1, 3). f(2, 4), f(3, 6), f(4, 8). f(a, ma) (m, a ) f 1, 2, f(x, y) = x 2 y , 1.3 f 1.2 f f 1-8 3, 4... *7 Scalar field. 2

5 2 2.1 ( ) I R f a I (2.1) lim h f(a + h) f(a) h f a (2.1) f a f (a) I f f 2.1. f : I x f (x) R f(x) = x f x = f(x) = 3 x (x R) f x = f α x α sin 1 f(x) = x + 1 x (x ) 2 (x = ) f α > 1 ( R ) αx α 1 sin 1 f x xα 2 cos 1 x + 1 (x ) 2 (x) = 1 (x = ) 2 f y = f(x) f (x) = dy dx f (x) f (x) f (x) f 2 (2 ) f (x) 3... f (y = f(x)) n f () (x) = f(x) f (n) (x) = dn y dx n ( ) 3

6 2.2 D R 2 2 f : D (x, y) f(x, y) R (a, b) D f (a, b) = lim x h f(a + h, b) f(a, b), h f f(a, b + k) f(a, b) (a, b) = lim y k k f (a, b) ( ) f f (a, b) (a, b) x y f (a, b) x (y ) f D f x f : D (x, y) (x, y) R x D 2 f x f y f y 2.2 ( ). f x 2 d f x = f x, f y = f y f (f(x, y)) x y x 1 f(x, y) x, y f x f(x, y) y x 2.3 f(x, y) f x (x, y), f y (x, y) 4 2 f xx = 2 f x 2 = f x x, f xy = 2 f y x = f y x, f yx = 2 f x y = f x y, f yy = 2 f y 2 = f y y f f(x, y) = x 3 + 3x 2 y + y 2 f x (x, y) = 3x 2 + 6xy, f y (x, y) = 3x 2 + 2y. 4

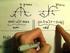
7 2 f xx = 6x + 6y, f xy = 6x, f yx = 6x, f yy = 2 f xy (x y ) f yx (y x ) f xy f yx 2-7 f xy f yx () xy ( ) (x, y) (, ) f(x, y) = x 2 + y 2 ( ) (x, y) = (, ) 2-3 (t, x) 2 u(t, x) ( ) u t 2 u x 2 = ( ) u(t, x) = 1 e x2 4t t ( ) f(x, y) f xx + f yy = f ( ). f(x, y) = log x 2 + y 2, g(x, y) = tan 1 y x. x, y f(x, y, z) f xx + f yy + f zz = f (3 ) F (t) f(x, y, z) = F ( x 2 + y 2 + z 2 ) 3 f F 5

8 2-6 2 f(x, y) f x + f y = x 1 + fx 2 + fy 2 y 1 + fx 2 + fy 2 f ( ) ( ) f(x, y) = log ( x2 + y 2 + x 2 + y 2 1), g(x, y) = log cos x cos y. 2-7 xy(x 2 y 2 ) ( ) (x, y) (, ) f(x, y) = x 2 + y 2 ( ) (x, y) = (, ) 2 2 (cf. 21 7) 2-8 n 2 6

9 3 3.1 ( ) I R 1 f a I lim f(x) = f(a) x a 3.1. f(x) = { 1 (x ) (x = ) lim f(x) = lim x x n = x + f(x) = f(x) = lim f(x) = 1 f() = x { sin 1 x (x ) (x = ) [( 2n + 1 ) 1 [( π], y n = 2n + 3 ) 1 π] (n = 1, 2, 3... ) 2 2 {x n }, {y n } lim x n =, lim y n n n lim f(y n) = 1 lim f(x) n x = lim n f(x n) = 1, 3.2. f a a. ( ) lim f(x) x a ( ( ) ( ) f(a + h) f(a) f(a) = lim f(x) f(a) = lim f(a + h) f(a) = lim x a h h h ( ) ( ) f(a + h) f(a) = lim lim h h h = f (a) =. h ) h C r - I f f I I f I C - f I I f I f f I (f ) f I C 1 -f I f I r f I C r - f r f (r) I f r C r - f C ( ) 7

10 3.3. f I a I a + h I h f(a + h) f(a) = f (a + θh)h ( < θ < 1) θ *8 3.2 f lim f(x, y) = A (x,y) (a,b) (x, y) (a, b) f(x, y) A * (i) lim f(x, y) = lim f(a + h, b + k). (x,y) (a,b) (h,k) (,)) (ii) lim f(a + h, b + k) = A h 2 + k 2 f(a + h, b + k) A (h,k) (,) (iii) lim f(a + h, b + k) = A (h,k) (,) h = r cos θ, k = r sin θ (r > ) r f(a + h, b + k) = f(a + r cos θ, b + r sin θ) A (iv) 2 α(h, k), β(h, k) (v) 2 f lim (x,y) (a,b) lim α(h, k) =, lim β(h, k) = (h,k) (,) f(x, y) = A (h,k) (,) lim f( a + α(h, k), b + β(h, k) ) = A (h,k) (,) lim f(x, y) = A 2 {h n}, {k n } lim f(a+h n, b+k n ) = (x,y) (a,b) n A. (vi) lim f(x, y) = A, 2 {h n}, {k n } (x,y) (a,b) f(a + h n, b + k n ) A 3.5. f(x, y) = 2xy/(x 2 + y 2 ) h n = 1 n, k n = 1 n lim f(h n, k n ) = 1 n h n = 1 n, k n = 1 n lim f(h n, k n ) = 1 lim f(x, y) n (x,y) (,) ( ) ( ) lim lim f(x, y) =, lim lim f(x, y) = x y y x *8 f θ a h a, h θ *9 8

11 f(x, y) = (x 2 y 2 )/(x 2 + y 2 ) (x, y) (, ) ( ) x 2 ( ) lim lim f(x, y) = lim x y x x 2 = 1, lim lim f(x, y) y 2 = lim y x y y 2 = 1 f(x, y) = xy(x 2 y 2 )/(x 2 + y 2 ) (x, y) (, ) x = r cos θ, y = r sin θ ( ) f(x, y) = f(r cos θ, r sin θ) = r 2 cos θ sin θ(cos 2 θ sin 2 θ) = 1 2 r2 sin 2θ cos 2θ = 1 4 r2 sin 4θ sin 4θ 1 r 2 sin 4θ 4 r2 4 ( ) r r2 4 r2 r2 sin 4θ D R 2 2 f (a, b) R 2 lim f(x, y) = f(a, b) (x,y) (a,b) 3.7. (1) R 2 f(x, y) = { 2xy ( ) x 2 +y (x, y) (, ) 2 ( ) (x, y) = (, ) (, ) f (, ) f x (, ) = f y (, ) = (2) R 2 f(x, y) = (, ) { xy(x 2 y 2 ) ( ) x 2 +y (x, y) (, ) 2 ( ) (x, y) = (, ) 3.8. D R 2 f(x, y) (a, b) D A, B (a + h, b + k) D (h, k) ( ) f(a + h, b + k) f(a, b) = Ah + Bk + ε(h, k) h 2 + k 2 lim ε(h, k) = (h,k) (,) 9

12 3.9. f(x, y) (a, b) f (a, b) ( ) A, B A = f x (a, b), B = f y (a, b). ( ) k = ε(h, ) ε(h, ) h h f(a + h, b) f(a, b) h h = B = f y (a, b) = Ah + ε(h, ) h 2 h = A + ε(h, ) h h ε(h, ) h ε(h, ) f(a + h, b) f(a, b) A = lim = f x (a, b). h h 3.1. f (a, b) (a, b). ( ) (h, k) (, ) (1) f (, ) D f D f x, f y D f D. (a, b) D ( ) A = f x (a, b), B = f y (a, b) ε(h, k) ((h, k) (, )) : k ε(h, k) = f(a + h, b + k) f(a, b) f x(a, b)h f y (a, b)k h2 + k 2 F (h) := f(a + h, b + k) f(a, b + k) * 1 f F h F (h) = f x (a + h, b + k), F () = F 3.3 F (h) = F (h) F () = F ( + θh)h = F (θh)h = f x (a + θh, b + k)h ( θ = θ(h, k) 1) θ (θ h k (h, k) ) G(k) = f(a, b + k) f(a, b) k δ G(k) = G (δk)k = f y (a, b + δk)k ( δ = δ(k) 1) ε(h, k) = F (h) + G(k) f x(a, b)h f y (a, b)k h2 + k 2 = ( f x (a + θh, b + k) f x (a, b) ) h h2 + k + ( f y (a, b + δk) f x (a, b) ) k 2 h2 + k 2 *1 := () 1

13 < θ < 1, < δ < 1 θh, δk ((h, k) (, )) h/ h 2 + k 2 1, k/ h 2 + k 2 1 (h, k) (, ) { ( ) (x 2 + y 2 ) sin 1 (x, y) (, ) f(x, y) = x 2 +y 2 ( ) (x, y) = (, ) (, ) f x, f y C r - D R 2 f f D D f I C - f D D f D D f f x, f y D f D C 1 - D f x, f y D f D C 2 -f 2 f xx, f xy, f yx, f yy D D (). D R 2 f 2 2 f xy, f yx, f xy = f yx 2 7 f C 2 - f xy = f yx 3-1 α k { x α sin 1 f(x) = x (x ) (x = ) R C k C k h >, h < C 1 - f(x, y) = x 2 + y 2 (, ) C r - C r - r k C k C - 11

14 D R 2 f(x, y) (a, b) D A, B (a + h, b + k) D (h, k) ( ) f(a + h, b + k) f(a, b) = Ah + Bk + ε(h, k) h 2 + k 2 lim ε(h, k) = (h,k) (,) 4.2. f(x, y) (a, b) f (a, b) ( ) A, B A = f x (a, b), B = f y (a, b) 4.3. D R 2 f(x, y) (a, b) D f (a, b) f(a + h, b + k) f(a, b) f x (a, b)h f y (a, b)k lim = (h,k) (,) h2 + k 2 f(x, y) P = (a, b) ( ) f f (df) P = (a, b), (a, b) x y 2 (df) P f P (x, y) 2 ( f x (x, y), f y (x, y) ) (4.1) df = f ( f x, f ) y 4.4. ϕ(x, y) = x, ψ(x, y) = y dϕ = (1, ), dψ = (, 1) dx = (1, ), dy = (, 1) ( ) 12

15 (4.1) (4.2) df = f f dx + x y dy f P = (a, b) f(a + h, b + k) f(a, b) = (df) P h + ε(h) h h = ( h k), h = h 2 + k 2 lim h ε(h) = (df) P h 1 1 * 11 I 1 x(t), y(t) ( x(t), y(t) ) I R 2 γ : I t γ(t) = ( x(t), y(t) ) R 2. x(t), y(t) * 12 γ γ(t) = ( x(t), y(t) ) γ(t) = dγ dt (t) = ( ẋ(t), ẏ(t) ) ( ) dx dy = (t), dt dt (t) ( x(t), y(t) ) * 13 2 f(x, y) γ(t) = ( x(t), y(t) ) (4.3) F (t) = f ( x(t), y(t) ) f(x, y) γ(t) = ( x(t), y(t) ) (4.3) df dt (t) = f x ( x(t), y(t) )dx dt f ( )dy (t) + x(t), y(t) y dt (t) *11 (x, y) (a, b) (h, k) t (h, k) x = t (x, y) f(x, y) f(x) f(a + h) = (df)ah + ε(h) h, *12 γ *13 velocity speed 13

16 t ε 1(δ) := x(t + δ) x(t) δ ẋ(t), ε 2(δ) := y(t + δ) y(t) δ x, y δ ε j (δ) h(δ) := δ ( ẋ(t) + ε 1 (δ) ), k(δ) := δ ( ẏ(t) + ε 2 (δ) ) ẏ(t) δ h, k f F (t + δ) F (t) = f ( x(t + δ), y(t + δ) ) f ( x(t), y(t) ) = f ( x(t) + h(δ), y(t) + k(δ) ) f ( x(t), y(t) ) = f ( ) f ( ) ( ) x(t), y(t) h(δ) + x(t), y(t) k(δ) + ε h(δ), k(δ) h(δ)2 + k(δ) x y 2 ε(h, k) (h, k) (, ) δ δ 4.6 df dt = f dx x dt + f dy = (df) γ y dt γ v = t (v 1, v 2 ) P = (a, b) γ(t) = t (a+tv 1, b+tv 2 ) = a+tv (a = t (a, b)) γ(t) t = P v γ P 2 f (4.3) F (t) (4.4) F () = f x (a, b)v 1 + f y (a, b)v 2 = (df) p v f P v P = (a, b) f ( ) fx (a, b) grad f P := f y (a, b) f P gradient vector * 14 (4.4) (df) P v = ( (grad f) P ) v f, γ(t) t (4.3) 4-2 (x, y) f(x, y) = x 2 + xy + y γ(t) = ( cos t, sin t ) *14 (df) P 14

17 4-3 P = (a, b) 2 f P (df) P (, ) f P v (df) P v v (grad f ) P v v = t (cos t, sin t) 4-4 P = (a, b) 2 f P (df) P (, ) P f γ(t) = ( x(t), y(t) ) (γ() = P ) t = γ γ() (grad f) P 4-5 f f(x, y) = { 1 (y = x 2 x ). (otherwise) v = t (v 1, v 2 ), f v d dt f ( ) tv 1, tv 2 t= f 15

18 5 () 5.1 ( ( 4.6 )). 2 f(x, y) γ(t) = ( x(t), y(t) ) F (t) = f ( x(t), y(t) ) df dt (t) = f x ( x(t), y(t) )dx dt f ( )dy (t) + x(t), y(t) y dt (t) (). 2 f(x, y) 2 2 x = x(ξ, η), y = y(ξ, η) 2 f(ξ, η) = f ( x(ξ, η), y(ξ, η) ) f ξ f η f ( ) x f ( ) y (ξ, η) = x(ξ, η), y(ξ, η) (ξ, η) + x(ξ, η), y(ξ, η) (ξ, η) x ξ y ξ f ( ) x f ( ) y (ξ, η) = x(ξ, η), y(ξ, η) (ξ, η) + x(ξ, η), y(ξ, η) (ξ, η) x η y η f(ξ, η) f(ξ, η) f(x, y) f () 5.2 f ξ = f x x ξ + f y y ξ, f η = f x x η + f y y η z = f(x, y) = f ( x(ξ, η), y(ξ, η) ) = f(ξ, η) z ξ = z x x ξ + z y y ξ, z η = z x x η + z y y η ( ) 16

19 R m R n m m R m ( 1, 3 ) * 15 D R m F : D R n n D (x 1,..., x m ) R n F (x 1,..., x m ) y = F (x 1,..., x m ) R n n (y 1,..., y n ) y j (x 1,..., x m ) y j (x 1,..., x m ) * 16 F : R m D R n D R m n (5.1) F : R m D (x 1,..., x m ) ( F 1 (x 1,..., x m ),..., F n (x 1,..., x m ) ) R n. F j : D R (j = 1,..., n) D F F F j (j = 1,..., n) F = (F 1,..., F n ) F = (F 1,..., F n ): R m D R n C r - * 17 j F j : D R C r - ( 3 ) 5.4. D R m C 1 - F = (F 1,..., F n ): D R n F 1 x 1... df =..... F n x 1... F 1 x m F n x m (n m ) F differential Jacobian matrix (x 1,..., x m ) D R m F : R m D R n G: R n U R k x D F (x) U, G F : R m D x G ( F (x) ) R k G F : R m D R k F G 5.5. F, G C 1 - d(g F ) = dg df, d(g F )(x) = dg ( F (x) ) df (x) D R m x id D : D x id D (x) = x D *15 47 (1) R m (2) R m {(x 1,..., x m) R m (x 1 ) (x m) 2 < 1} *16 *17 C r - 17

20 D identity map D R m U R m F : D U G: U D G F = id D, F G = id U G F inverse map G = F D = {(r, θ) R 2 r >, π 2 < θ < π 2 } U = {(x, y) R2 x > } ( F : D (r, θ) F (r, θ) = (r cos θ, r sin θ) U, G: U (x, y) x2 + y 2, tan x) 1 y D G = F 1, F = G 1, r >, π 2 < θ < π 2 ( ) G F (r, θ) = G(r cos θ, r sin θ) = r 2 cos 2 θ + r 2 sin 2 1 r sin θ θ, tan = (r, tan 1 tan θ) = (r, θ), r cos θ θ = tan 1 y x π 2 < θ < π 2 cos θ > x > cos tan 1 y x = cos θ = tan 2 θ = tan 2 tan 1 y x sin tan 1 y x = sin θ = cos θ tan θ = x y x2 + y 2 x = = y x2 + y 2. 1 = 1 + y2 x 2 x x2 + y 2 = x x2 + y 2, ( F G(x, y) = F x2 + y 2, tan x) 1 y ( = x2 + y 2 cos tan 1 y x, x 2 + y 2 sin tan x) 1 y = (x, y) (x, y) 5.6 (r, θ) = G(x, y), (r, θ) polar coordinate system * 18 (x, y) Cartesian coordinate system 5.8. F : R m D U R m G = F 1 F F 1 C 1 - df 1 = (df ) 1 d(f 1 ) ( F (x) ) = ( df (x) ) 1 1 m E F 1 F = id D 5.5 df 1 df = E, F F 1 = id U 5.5 df df 1 = E df 1 df ( ) 5.9 (). 5.6 (5.2) x = x(r, θ) = r cos θ, y = y(r, θ) = r sin θ. F : (r, θ) (x, y) ( ) ( ) xr x (5.3) df = θ cos θ r sin θ = sin θ r cos θ *18 θ π < θ < π y r y θ 18

21 G = F 1 : (x, y) (r, θ) r = x 2 + y 2, θ = tan 1 y x (5.4) dg = C 2 - f(x, y) ( ) ( x rx r y = θ x θ y x2 +y 2 y x 2 +y 2 (5.5) z = f = 2 f x f y 2 y x2 +y 2 x x 2 +y 2 Laplacian * 19 f(x, y) (5.2) (r, θ) f f r, θ (5.6) ( 5.2) f x = r f x r + θ f x θ = ( 2 f x 2 = x = x = 2 f y 2 = ( x x2 + y 2 f r x x2 + y 2 ) f r + y 2 x2 + y 23 f r + + 2xy (x 2 + y 2 ) 2 f θ = x2 x 2 + y 2 f rr y2 x 2 + y 2 f rr + x x2 + y 2 f r y x 2 + y 2 f θ y x 2 + y 2 f θ ) x x2 + y 2 f r x x ( x x x2 + y 2 x2 + y f 2 rr ( y x 2 + y 2 2xy x2 + y 23 f rθ + 2xy x2 + y 23 f rθ + x x2 + y 2 f θr y 2 (x 2 + y 2 ) 2 f θθ + x 2 (x 2 + y 2 ) 2 f θθ + ) ( ) y x 2 + y 2 f θ ) y x 2 + y 2 f rθ y x 2 + y 2 f θθ ) y 2 x2 + y 23 f r + x 2 x2 + y 23 f r y f θ x 2 + y 2 x 2xy (x 2 + y 2 ) 2 f θ. 2xy (x 2 + y 2 ) 2 f θ. r = x 2 + y 2 f = f xx + f yy = f rr + 1 r f r + 1 r 2 f θθ ( ) ( ) (5.6) dg = d(f 1 ) = (df ) 1 cos θ sin θ rx r = 1 r sin θ 1 r cos θ = y θ x θ y x = cos θ r 1 r sin θ θ, y = sin θ r + 1 r cos θ θ. *19 19

22 2 f x 2 = cos2 θf rr 2 r cos θ sin θf rθ + 1 r 2 sin2 θf θθ + 1 r sin2 θf r + 2 r 2 sin θ cos θf θ 2 f y 2 = sin2 θf rr + 2 r cos θ sin θf rθ + 1 r 2 cos2 θf θθ + 1 r cos2 θf r 2 r 2 sin θ cos θf θ f(x, y) f = f xx + f yy = f F (t) f(x, y) = F ( x 2 + y 2 ) f(x, y) = tan 1 y x 5-5 c ( = ) ξ = x + ct, η = x ct (t, x) (ξ, η) C 2 - f(t, x) 2 f t 2 c2 2 f x 2 = 4c2 2 f ξ η f tt c 2 f xx = C 2 - f 2 C 2 - F, G f(t, x) = F (x + ct) + G(x ct) f tt = c 2 f xx d Alembert 5-6 f(x, y, z) f = f xx + f yy + f zz x = r cos θ cos ϕ, y = r sin θ cos ϕ, z = r sin ϕ ( r >, π < θ < π, π 2 < ϕ < π ) 2 r x r y r z cos θ cos ϕ sin θ cos ϕ sin ϕ θ x θ y θ z = 1 sin θ 1 cos θ r cos ϕ r cos ϕ ϕ x ϕ y ϕ z 1 r cos θ sin ϕ 1 r sin θ cos ϕ 1 r cos ϕ. f = f rr + 2 r f r + 1 r 2 cos 2 ϕ f θθ + 1 r 2 f ϕϕ 1 r 2 tan ϕf ϕ 2

23 6? ( ) (C - ) 6.1 u(t) 2... u(t) 6.1. A t A u(t) u(t) (6.1) du dt = λu (λ ) k u(t) = ke λt t = t A k Kg t u(t) (6.1) (6.2) u(t ) = k (6.1) (6.2) u(t) = k exp{ λ(t t )} * 2 (6.2) 6.2. m x kx (k > ) mγ dx dt (γ > ) t x(t) (6.3) m d2 x dx +mγ dt2 dt +kx = x = x(t) 2 2 (6.1) 1 t = t (6.4) x(t ) = x, ( ) *2 e X exp(x) dx dt (t ) = v 21

24 6.3. {t t > } f(t) (6.5) f (t) + p t f (t) =, f(1) = α, f (1) = β p, α, β u(t) = 1 ( t 1 p 1 ) + α (p 1 ) β u(t) = β log t + α (p = 1 ) u = u(x, y), 3 w = w(x, y, z) u = 2 u x u y 2, w = 2 w x w y w z 2 (Laplacian) C 2 - u(x, y) (w(x, y, z)) u = ( w = ) () u (w) harmonic function ( ) ( ) w = ρ (ρ = ρ(x, y, z) (x, y, z) ( ) ) w = ρ (ρ ) 6.4. u = u(x, y) F u(x, y) = F ( x 2 + y 2 ) u () (x, y) = (r cos θ, r sin θ) (6.6) u = u rr + 1 r u r + 1 r 2 u θθ u u r θ : u = u(r) * 21 u u rr + 1 r u r = 6.3 u = β log x 2 + y 2 + α (α, β ) *21 u(r) F 22

25 u (.5, x) u (.1, x) u (.15, x) u (.2, x) u (.25, x) u (.3, x) u (.35, x) u (.4, x) u (.45, x) u (.5, x) 1 (c = 1) 6.5. w = w(x, y, z) w = F ( x 2 + y 2 + z 2 ) w = β r + α (α, β ) u(t, x) u x t x (6.7) u t = u c 2 x 2 (1 ) c (6.8) u (t, x) = 1 ) ( 2 πct exp x2 4ct {(t, x) t > } R 2 (6.7) (6.7) C t u (t, x) 2ct ( 2ct) * 22 t u (t, x) dx = lim u (t, x) = t + ) 1 ( 2 πct exp x2 = 1 4ct { (x ) (x = ) t > ( 1) f(x) = { 1 ( 1 2 x 1 2 ) (otherwise) *22 23

26 u(.1, x) u(.2, x) u(.3, x) u(.4, x) u(.5, x) u(.6, x) u(.7, x) u(.8, x) u(.9, x) u(.1, x) 2 (6.9) (c = 1) (6.9) u(t, x) = u (t, x y)f(y) dy u(t, x) (6.7) t f * 23 ( 2) (x, y), t u(t, x, y) u (6.1) u t = c u (c ) (x, y) u = u xx + u yy. u (x, y) u = u(t, x 2 + y 2 ) x = r cos θ, y = r sin θ (6.1) ( u t = c u rr + 1 ) r u r (6.11) u(t, r) = 1 ) ( 4π ct exp r2 4ct u = u(t, x, y, z) u t = c u = 2 x y z 2 *23 24

27 x t u(t, x) u (6.12) 2 u t 2 = c2 2 u x 2 c u(t, x) = F (x + ct) + G(x ct) F, G ( ) 1 ( 5-5) * 24 u tt = c 2 u ( ) ( 137 Cs) 3.17 (6.1) λ () 6-2 (6.3) γ = ω = k/m x(t) = α cos(ωt) + β sin(ωt) (α, β ) (6.4) ( 2-5) 6-4 (6.11) ( ) 6-5 θ e iθ = cos θ + i sin θ (i ) ( ) z = x + iy (x, y ) e z = e x+iy = e x (cos y + i sin y), e z Re e z Im e z (x, y) 6-6 z = x + iy f(z) = z m (m ) Re f(z) (Im f(z)) (x, y) (x, y) *24 25

28 x ( 1 x 1) x = cos y ( y π) y y = cos 1 x x ( 1 x 1) x = sin y ( π 2 y π 2 ) y y = sin 1 x x x = tany ( π 2 < y < π 2 ) y y = tan 1 x cos 1 x, sin 1 x, tan 1 x,, 7.2. cos 1, sin 1, tan 1 arccos, arcsin, arctan tan 1 1 = π 4 + nπ (n ) 7.1 Cos 1 x, Arccos x (7.1) d dx cos 1 x = 1, 1 x 2 d 1 dx sin 1 x =, 1 x 2 d dx tan 1 x = x 2. x = ±1 cos 1 x, sin 1 x (7.1) (7.2) tan 1 x = x cos 1 x + sin 1 x = π 2 1 x 1 + t 2 dt, 1 sin 1 x = dt 1 t 2 (x α ) C x cosh x = ex + e x, sinh x = ex e x, tanh x = sinh x 2 2 cosh x = ex e x e x + e x x hyperbolic cosine, hyperbolic sine, hyperbolic tangent hyperbolic functions ( ) 26

29 7.4. cosh t ht cos ht cosh 2 x sinh 2 x = 1 * 25 ( x(t), y(t) ) = (cosh t, sinh t) (x, y) x 2 y 2 = 1 ( circular functions.) cosh(x + y) = cosh x cosh y + sinh x sinh y, sinh(x + y) = sinh x cosh y + cosh x sinh y, * 26 d d cosh x = sinh x, dx tanh(x + y) = d sinh x = cosh x, dx tanh x + tanh y 1 + tanh x tanh y. u = u, u() = A, u () = B u(t) u(t) = A cosh t + B sinh t dx tanh x = 1 tanh2 x t 1, t 2 1 t 2 + t 4 + ( 1) N t 2N = 1 ( t2 ) N t 2 = t 2 + ( 1)N t 2N t 2 t = x tan 1 x = x dt 1 + t 2 = x 1 3 x3 + + ( 1)N 2N + 1 x2n+1 + R N (x) R N (x) = R N (x) = x x t 2N t 2 dt t 2N t 2 dt x x t 2N+2 dt= x 2N+3 2N + 3 ( (7.3) tan 1 x = x x ( 1)N N 2N + 1 x2n+1 + R N (x) = t 2N x 2 dt = 1 x 2N+3 2N x 2 k= ( x ( 1) N+1 t 2N+2 ) R N (x) = 1 + t 2 dt ) ( 1) k x 2k+1 + R N (x) 2k + 1 x 2N+3 (2N + 3)(1 + x 2 ) R N (x) x 2N+3 2N + 3 *25 cosh 2 x (cosh x) 2 *26 (tanh x) = 1/ cosh 2 x (tan x) = 1 + tan 2 x 27

30 x 1 lim R N(x) = N ( 1 x 1 ) (7.4) tan 1 x = x x3 3 + x5 5 + = k= ( 1) k x 2k+1 2k + 1 ( 1 x 1) (7.4) x = 1, (7.5) π 4 = R N (7.3) R N (1) ) 13 ( 1)N π = 4 ( N + 3 R N, 2 2N + 3 R 4 N 2N R N 1 1 N N ( ) (7.6) (7.3) α = 1 5, β = 1 M π = 4 k= 4( 1) k α k 2k + 1 π 4 = 4 1 tan tan N j= ( 1) j β j 2j R M,N, R M,N 16α2M+1 2M β2N+1 2N + 1 (!) R M,N 1 1 M = 1, N = 2 (7.5) (1 1 ) 7-1 cosh x 1, 1 < tanh x < 1 cosh x sinh x, tanh x y = cosh x, y = sinh x, y = tanh x 2 3 t = tanh u 2 cosh u, sinh u t x 2 y 2 = 1 x y 28

31 A, B A cos t + B sin t r cos(t + α), r sin(t + β) () x 1 x x = cosh y y y y = cosh 1 x cosh 1 x = log ( x + x 2 1 ) sinh 1 x, tanh 1 x sinh 1 x = log ( x + x ), tanh 1 x = 1 2 log 1 + x 1 x 7-2 (7.3) π 5 π 4 = tan tan log x = (x) log x log x cos 1 x, sin 1 x, tan 1 x 7-4 n I n = π/2 cos n x dx n 2 I n = n 1 n I n 2 2m 1 2m 3 π/2 I n = cos n x dx = 2m 2m π (n = 2m), 2 2 2m 2m 2 2m + 1 2m (n = 2m + 1) 3 m sin n x x 2 x = sin θ 1 x u = 1+x 7-6 f(x) = (x 1)(x 2)(x + 4) 2 1/f(x) ( ) 7-7 a, b 1/(x 2 2ax + b) a 2 b =, 1/(x + a) 2 a 2 b > ( ) a 2 b < 1/(1 + u 2 ) 7-8 1/ cos x (= sec x) t = tan x 2 1 cos x = cos x 1 sin 2 x 1 cos x t u = sin x = cosh u x 2 (x) 1 + x 2 1/ 1 + x 2 x = tan θ x = sinh u x 4 1, 1 x 3 1, 1 x

32 7-11 ( R ) 1 1 R R (1 ) 3

33 8 R * 27 (a, b) = {x R a < x < b} ( ) [a, b] = {x R a x b} ( ) (a, b] = {x R a < x b} [a, b) = {x R a x < b} (, a) = {x R x < a} (, a] = {x R x a} (a, ) = {x R a < x} [a, ) = {x R a x}. R = (, ) [a, b] = {x, x 1, x 2,..., x N } a = x < x 1 < < x N = b := max{ x 1 x, x 2 x 1,..., x N x N 1 } I = [a, b] f I = {x, x 1,..., x N } N N (8.1) S (f) := f j x j, S (f) := f j x j, j=1 j=1 x j = x j x j 1 f j :=( [x j 1, x j ] f ), f j :=( [x j 1, x j ] f ) 8.1. I f I I S, S f(x) dx = b I a f(x) dx 8.2. [, 1] f(x) = { 1 (x ) (x ) *27. 31

34 = {x, x 1,..., x N } [x j 1, x j ] N N S (f) = 1(x j x j 1 ) = x N x = 1, S (f) = (x j x j 1 ) = f [, 1] j=1 j= [ 1, 1] f(x) = { 1 (x = ) () [ 1, 1] = {x,..., x N } k = k( ) [x k 1, x k ] f [x k 1, x k ] 1 f S (f) = x k x k 1 ( k = k( ) ), S (f) =. < x k x k 1 S (f) f [ 1, 1] 1 1 f(x) dx = b < a b f(x) dx = a a b f(x) dx 8.4. I = [a, b] f I 8.5 (). I = [a, b] f F (x) = x F I F (x) = f(x) a f(t) dt ( ) f F (x) = f(x) F I f 2 F, G G(x) = F (x) + d { } G(x) F (x) = G (x) F (x) = f(x) f(x) = dx G(x) F (x) I I f 32

35 8.6. I f I a F (x) = x a f(x) dx 8.7. e x2 ( ) x e x2 dx f F (x) F (x) = f(x) dx * I f F I a, b b a f(x) dx = F (b) F (a) ( ) 8.9. [a, b] C 1 - f ( ) b a 1 + {f (x)} 2 dx [a, b] = {x, x 1,..., x N } (x, f(x )), (x 1, f(x 1 )),..., (x N, f(x N )) I = N ( ) 2 f(xj) f(x j 1) 1 + (x j x j 1) x j x j 1 j=1 ξ j f(x j) f(x j 1) x j x j 1 = f (ξ j ) x j 1 < ξ j < x j I = N j=1 1 + (f (ξ j)) 2 (x j x j 1) N F j j, j=1 N I F j j j=1 F (x) = 1 + (f (x)) 2 F j = ( [x j 1, x j] F ), F j = ( [x j 1, x j] F ), j = x j x j 1 F (x) I F (x) a b *28 +C 33

36 8.1. t γ(t) = ( x(t), y(t) ) (a t b) C 1 - b a (dx ) 2 + dt ( ) 2 dy dt dt 8-1 f(x) F (x) b a f(x) dx = F (b) F (a) 8-2 E : x2 a + y2 2 b = 1 (a > b > ) 2 E πab E π 2 4a 1 k 2 sin 2 a2 b t dt, k = 2 a km, km ( 1 x 1 x 2 ) (x ) 43.5 ±.1km 8-3 x 2 y 2 = 1 1 P (x, y) O(, ), A(1, ) OA, OP, AP t/2 P x, y t 8-4 y = x 2 x a 8-5 γ(t) = ( t sin t, 1 cos t ) t 2π x 8-6 R r ( ) ρ = ρ(r)kg/m 3 ρ ρ [, R] 34

37 9 [a, b] [c, d] [a, b] [c, d] = {(x, y) x [a, b], y [c, d]} = {(x, y) a x b, c y d} R 2 [a, b] [c, d] R 2 [a, b] [c, d] (9.1) a = x < x 1 < < x m = b, c = y < y 1 < < y n = d I = [a, b] [c, d] mn I = [a, b] [c, d] = j = 1,..., m k = 1,..., n jk, jk = [x j 1, x j ] [y k 1, y k ] 2 := max{(x 1 x ), (x 2 x 1 ),..., (x m x m 1 ), (y 1 y ),..., (y n y n 1 )} R 2 D R 2 * 29 f 1,..., f n {x R 2 f 1 (x) >,..., f n (x) > } R 2 R 2 {(x, y) x 2 + y 2 < 1} = {(x, y) 1 x 2 y 2 > } R 2 R 2 D R 2 2 D D * 3 R 2 f 1,..., f n {x R 2 f 1 (x),..., f n (x) } R 2 R 2 R 2 D I D I R 2 * * *3 (R n ) *31 R n 35

38 I = [a, b] [c, d] f I (9.1) m j=1 k=1 m f(ξ jk, η jk )(x j+1 x j )(y k+1 y k ) ( ξ jk [x j 1, x j ], η jk [y k 1, y k ]) (ξ jk, η jk ) I f f(x, y) dx dy * 32 D I I R 2 D f f(x, y) = { f(x, y) ( ) (x, y) D ( ) (x, y) D I f f(x, y) dx dy = D I f(x, y) dx dy f D * 33 D R 2 f(x, y) = 1 D D := dx dy D D D R 2 f D Ω f D f 9.1. R 2 D f D f(x, y) dx dy D R 3 D () R m *32 2 *33 D I 36

39 x x = a x = b x ρ(x) (kg/m) b a ρ(x) dx xy D (x, y) D ρ(x, y) (kg/m 2 ) D ρ(x, y) dx dy D (x, y, z) D ρ(x, y, z) (kg/m 3 ) D ρ(x, y, z) dx dy dz I = [a, b] [c, d] R 2 I = (b a)(d c) [a, b] () ϕ(x), ψ(x) ϕ(a) ψ(a), ϕ(b) ψ(b) D := {(x, y) R 2 ϕ(x) y ψ(x), a x b} () R 2 D D = b a [ ] ψ(x) f(x, y) dy dx ϕ(x) [a, b] a = x < x 1 < < x m = b j = [x j 1, x j ] D ϕ(x j 1 ) D j := {(x, y) D, x j } [ ] ψ(xj 1) f(x j, y) dy x j ( x j = x j x j 1 ) j D = {(x, y) x 2 + y 2 1} f(x, y) = x 2 [ 1 ] 1 x 2 x 2 dx dy = D 1 x 2 dy dx 1 x 2 [ 1 ] 1 x 2 = 2 x 2 dy dx 1 = x 2 1 x 2 dx = 4 1 x 2 1 x 2 dx. 37

40 , R 3 1 D D dx dy dz R 4, R

41 D = {(x, y) 3 x y 2 1} R 2 D D := {(x, y) 3 x y 2 1, x, y } D D = 4 D D = 1 dx dy = D 3π/ y 2 dy dx = 1 [ 1 3 y 2 3 ] dy = 3π f(x, y) = 1 x2 a 2 y2 b 2 (a,b ) xy f(x, y) { D = (x, y) x 2 } a 2 + y2 b 2 1 D [x, x + x] [y, y + y] f(x, y) D f(x, y) dx dy = f(x, y) x y D 1 x2 a 2 y2 b 2 dx dy = 2 3 πab 1.3. D = {(x, y, z) z 2 4x, y 2 x x 2 } D D = {(x, y) y 2 x x 2 } D = D dx dy dz = dx dy D 2 x 2 x dz = 4 x dx dy = = 32 D z = f(x, y) ((x, y) D) D R 2 f D C 1 - D [x, x + x] [y, y + y] 3 P = ( x, y, f(x, y) ), Q = ( x + x, y, f(x + x, y) ), R = ( x, y + y, f(x, y + y) ) ( ) 39

42 P Q, P R 2 ( ) P Q P R = ( x,, f(x + x, y) f(x, y)) (, y, f(x, y + y) f(x, y)) ( ) 2 ( ) 2 f(x + x, y) f(x, y) f(x, y + y) f(x, y) = x y x y ( ) 2 ( ) 2 f f 1 + (x, y) + (x, y) x y x y 1 + (f x ) 2 + (f y ) 2 dx dy D ( ) 1-1 R 2 D = [a, b] [c, d] C 2 - F D 2 F dx dy = F (b, d) F (a, d) F (b, c)+f (a, c) x y 1-2 (x 2 + y 2 ) dx dy, D = {(x, y) x + y 1, x, y }, D x D y dx dy D = {(x, y) 1 y x2, 2 x 4} x 2 y dx dy D = {(x, y) x π, y sin x} D xy dx dy D = {(x, y) x, y, x + y 1} D D (x 2 + y 2 + z 2 ) dx dy dz D = {(x, y, z) x, y, z, x + y + z 1}. 1-3 Ω = {(x, y, z) x2 Ω = a 2 + y2 b 2 + z2 } c 2 1 } {(x, y, z) x2 a 2 + y2 b 2 + z4 c 4 1 a, b, c. a, b, c. 1-4 xy D {(x, y) y > } 4

43 xy D x 2π y dx dy D D ( ) ( ) 1 x dx dy, y dx dy D = dx dy D D D D 1-5 xy y = f(x) (a x b) x 2π b a f(x) 1 + ( f (x) ) 2 dx [a, b] f(x) > 1-6 xy C C : γ(t) = ( x(t), y(t) ) (a t b) x(t), y(t) t C 1 - [a, b] y(t) > C x b (dx ) 2 ( ) 2 dy 2π y(t) + dt dt dt C 1 L b a (dx ) 2 x(t) + dt a ( ) 2 dy b dt, y(t) dt a (dx ) 2 ( ) 2 dy + dt dt dt b (dx ) 2 L = + dt a ( dy dt ) 2 dt 41

44 11 R 2 L A : R 2 x X = Ax R 2 (A 2 ) A det A L A L A 1 1 ( ) A L A L A R 2 L A 2 P, Q R 2 l P, Q p, q l L A l L A l = {(1 t)p + tq t R} L A ( (1 t)p + tq ) = (1 t)ap + taq l = {(1 t) p + t q t R} p = Ap, q = Aq OP = p, OQ = q P, Q (1) P Q l P, Q (2) P = Q l P 1 det A L A 1 1 (2) L A R L A l 2 P, Q l 2 R, S l det( P R, P Q) det( P S, P Q) R 2 det 2 2 t (a, b) = P Q n = t ( b, a) (1) det(v, P Q) = (v, n) R 2 (2) n l l R l n P R n ( P R, n) > (1) L A R 2 R 2 L A L A P QRS p = OP, q = OQ P Q {(1 t)p + tq t 1} P, Q P, Q L A P, Q ( )

45 11.5. P QRS det(a, b) a = P Q, b = P R 2. a, b θ (11.1) a b sin θ = a 2 b 2 a 2 b 2 cos 2 θ = a 2 b 2 (a, b) 2. (a, b) a, b a = t (a 1, a 2 ), b = t (b 1, b 2 ) (11.1) L A D det A D D D D = P QRS p, q, r, s a = P Q = q p, b = P R = r p P, Q, R L A P, Q, R P Q = Aq Ap = A(q p) = Aa, P R = Ab D = det(aa, Ab) = det ( A(a, b) ) = det A det(a, b) = det A D. 2 R 2 C 1 - F : R 2 (u, v) F (u, v) = ( x(u, v), y(u, v) ) R 2 ( ) ( ) xu (a, b) x F (a+h, b+k) = F (a, b)+ v (a, b) h + h y u (a, b) y v (a, b) k + k 2 ε(h, k) ε(h, k) as (h, k) (, ) t (h, k) F df ( 5) (h, k) Φ(h, k) := F (a + h, b + k) F (a, b) ( ( ) xu (a, b) x v (a, h y u (a, b) y v (a, b)) k. ( ) (x, y) (u, v) = det xu x v y u y v Jacobian (x, y) (u, v) 43

46 11.7 ( 92 ). xy D uv E F 1 1 f(x, y) dx dy = f ( x(u, v), y(u, v) ) (x, y) (u, v) du dv D E ,7; 95 8, , 12; 11 13, , 2, 3, 4. 44

47 12 ( ) (a, b] f b lim f(x) dx ε + a+ε b a f(x) dx f [a, b) b [a, ) f a f(x) dx M lim f(x) dx M + a a f(x) dx b f(x) dx * ε (, 1) 1 ε 1 x dx = [2 x] 1 ε = 2(1 ε) ε (, 1) 1 1 x dx = lim ε + 2(1 ε) = 2. 1 ε 1 x dx = [log x]1 ε = log 1 log ε = log ε M 1 1 dx = lim log ε +. x ε + M e x dx = [ e x ] M = e M + 1 M M 1 1 x dx = [log x]m 1 = log M 1 e x dx = lim (1 M + e M ) = 1. 1 x dx = lim log M = + M ( ) *34 45

48 12.2. k (, 1) ε (, 1) 1 ε 1 k2 x 2 1 x 2 dx = 1 1 k2 x 2 1 x 2 dx sin 1 (1 ε) 1 k 2 sin 2 t dt (x = sin t) [, π 2 ] ε + * k2 x 2 π 2 1 x 2 dx = 1 k 2 sin 2 t dt f(x) (a, b) b ε2 a+ε 1 f(x) dx ε 1, ε 2 b a f(x) dx * ε 1, ε 2 (, 1) 1 ε2 1+ε 1 [ x 1 x 2 dx = 1 ] 1 ε2 [ 1 2 log(1 ( ) ] 1 ε 2 x2 ) = log(1 x) + log(1 + x) 1+ε 1 2 = 1 ( ) log ε2 + log(2 ε 2 ) log(2 ε 1 ) log ε 1 2 ε x 1 x 2 dx (ε 1, ε 2 ) (, ) 1 ε 1+ε x 1 x 2 dx = [ 1 ( ) ] 1 ε log(1 x) + log(1 + x) = (ε +) 2 1+ε 1+ε x dx = 1 x2 *35 *

49 12.4. I = (a, b] f, g I f(x), g(x) f(x) g(x) (x I), b a g(x) dx b a f(x) dx * ( ). s > e x x s 1 dx Γ(s) = e x x s 1 dx (s > ) 12.6 ( ). p, q B(p, q) = 1 x p 1 (1 x) q 1 dx f(x) [a, b) b 12-2 f(x) (, b] = x α dx, a f(x) dx b 1 f(x) dx x β dx α, β (, 1] [1, + ) m lim x xm e x =. *37 47

50 x > f m (x) := e x (1 + x + 12! x m! ) xm > f m(x) = f m 1 (x) 12-5 s Γ(s + 1) = sγ(s) n Γ(n) = (n 1)!