di-problem.dvi
|
|
|
- しなつ はぎにわ
- 5 years ago
- Views:
Transcription
1 III 005/06/6 by. : : : : : : : : : : : : : : : : : : : : :. : : : : : : : : : : : : : : : : : : : : : : : : : : 3 3. : : : : : : : : : : : : : : 4 4. : : : : : : : : : : : : : : : : : : : : : : 5 5. : : : : : : : : : : : : : : : : : : : : : : 6 6. : : : : : : : : : : : : : : : : : 7 7. : : : : : : : : : : : : : : : : : : : : : 8 8. : : : : : : : 9 9. : : : : : : : : : : : : : : : : : : : : 0 0. : : : : : : : : : : :. sin : : : : : : : : : : : : : :. cos : : : : : : : : : : : : : : 3 3. log ( + ) : : : : : : : : : : : 4 4. : : : : : : : : : : : : : 5 5. e : : : : : : : : : : : : : : : : 6 6. : : : : : : : : : : : : : : 7 7. : : : : : : : : : : : : : : 8. (A): (B): (C):
2 . f () = a y = f () (a; f (a)) y f (a) =f 0 (a)( a) a f 0 (a) y = jj [ ; ] y = a (» a» ) y = jj jj p y = jj y =0 ( ( : ) y = 0 ( : ) (?) ( ) ( ) " " " " " y = p jj =0 y = =3 =0. (A) y = A + B + C (A 6= 0) a; b a + b
3 . dy d = lim y!!0 (Leibniz:646 76) dy d 50 (Cauchy: ) y = f () y dy = df () dy = f 0 () dy ( ) y = d = y = f () dy = f 0 ()d f 0 () dy dy = d dy d d dy dy; d d ; y y y y = f ( + ) f() z = g(y) dz = g 0 (y)dy w = f ()+g(y) dw = f 0 ()d + g 0 (y)dy y = f () y = f () dy = df () =df () y = c (c ) ) dc =(c) 0 d =0d =0 () y = cf () (c ) ) d(cf )=(cf ()) 0 d = cf 0 () d = cdf y! 0 y dy = f( + ) f() f 0 ()d! dy y (3) y = f () +g() ) d(f + g) =(f () +g()) 0 d =(f 0 () +g 0 ()) d = df + dg (4) y = f ()g() ) d(fg)=(f ()g()) 0 d =(f 0 ()g() +f ()g 0 ()) d = gdf + fdg (5) y f = () f f 0 () ) d = d f 0 ()g() f ()g 0 () gdf fdg = d g() g g() g() = g. y = dy = dy d d =(3 +6 ) d.. (A) y = + 3
4 3.. 3 y 5 + y 6 + =0 d( 3 y 5 )+d(y 6 )+d() d() = d(0) d( 3 )y d(y 5 )+6y 5 dy +d 0 d =0d (3 d)y (5y 4 dy) +6y 5 dy +d =0 (3 y 5 +)d +(5 3 y 4 +6y 5 ) dy =0 dy d = 3 y y 4 +6y 5 :. 3 y 5 + y 6 + =0 3 y (5y 4 dy dy )+6y5 d d +=0 dy d. a + y = a d+ydy =0: = 0, y = y 0, d = 0, dy = y y 0 0 ( 0 )+y 0 (y y 0 )=0: 0 + y 0 y = 0 + y 0 = a ( 0 ;y 0 ). 0 = a, y 0 = 0 a = a. = a (a; 0) y y 0 = f 0 ( 0 )( 0 ). y = 3p y 3 = 3y dy = d: = 0, y = y 0, d = 0, dy = y y 0 3y 0 (y y 0) = 0: 3y 0 y = 0: 0 =0,y 0 =0 =0 y y 0 = f 0 ( 0 )( 0 ) 3. (C) y = + 3 y = t, y t t = t 0 t =0,t = ± 4
5 4. s `. ` T T =ß g % s ` T (`) =ß g ` T = T (` + `) T (`): T T (` + `) = = T (`) T (`) r r` + ` = ` + ` ` : ` =0:0` T p T (`) = :0 =:00995 ο 0:0 % dt ß = p d` = g p` T (`)d` ` : d` = ` =0:0` dt =0:0T (`). % 4. (A) r % 5
6 5. f () = a f (a) = a f () <f(a) ( 6= a) f (a). I f () M () I f ()» M () f ( 0 )=M 0 I M = ma f () I f () I m () m =minf () I. f () = a = a 9 f 0 () < 0 ( <a) >= f 0 (a) =0 f () = a f 0 >; () > 0 ( >a) " " f 0 () > 0 f 0 (a) =0 f 0 () < 0 9 ( <a) >= f () = a ( >; >a). f () = a f 0 (a) =0 f 00 (a) < 0 ) f () = a f 00 (a) > 0 ) f () = a f 00 (a) =0 ) 5. (A) I (0; ), (0; ], [0; ), [0; ] 4 f () = ma f () min f () I I p 6. (A), 3, 4, cosh, jj 6
7 6. f () I (a; f (a)), (b; f (b)) f () f () I. f () I f 00 () < 0 (f 00 () > 0) I convave ( ) conve ( ).. y = f () C `: y = a + b lim (f () (a + b)) = 0! C!`. f (), f 0 (), f 00 (), f () 7. (A) e ; 3 ; log ; log ; n lim n log =0;!+0 log : log lim!+ n =0 8. (B) f () = 3 ( 3 + )log ( >0) 9. (C) f () = sin cos () f 0 () > 0(0<<ß). (0 <<ß) () lim f () =0, lim f () =.!+0!ß 0 p p 0. (C) F (t) = t + ( t) + ( + t) (t ) + (0» t» ) () t (0; ) F 00 (t )=0F 00 (t) =0 t = t t = t () t (t ; ) F 0 (t ) = 0 F 0 (+0) = lim F 0 (t) = 0 F 0 (t) = 0 t = 0 t!+0 t = t (3) F (0), F () F (t) (0» t» ) 7
8 7. Rolle. f () [a; b] (a; b) f (a) =f (b) f 0 (c) =0 c (a; b). f () [a; b] (a; b) f 0 f (b) f (a) (c) = c (a; b) b a f (b) f (a). g() = ( a) +f (a) f () b a. f (b) =f (a) +f 0 (c)(b a); a<c<b: f (b) =f (a) +f 0 (( )a + b)(b a); 0 < <: f (a + h) =f (a) +f 0 (a + h)h; b = a + h: f ( + ) =f () +f 0 ( + ) ; 0 < <: c c f(a) = f(b). f () I f () I f 0 () > 0 f 0 () < 0 f 0 () =0 ) f () I ) f () I ) f () k k Cauchy. f (), g() [a; b] (a; b) g 0 () 6= 0 ( (a; b)) f (b) f (a) g(b) g(a) = f 0 (c) g 0 (c) c (a; b). = g(t), y = f (t) (a» t» b) t = a (g(a);f(a)) f (b) f (a) t = b (g(b);f(b)) g(b) g(a). dy fi fi fi f 0 (c) dfi = =c g 0 (c) (g(t);f(t)) (a» t» b) f (b) f (a). F () =f () g() g(b) g(a). (B) p p + () lim! ( + )= lim p p =0k =3; 4; 5;:::! ++ lim (kp + kp )! () sin <( >0) c f(a) = f(b) 8
9 8. 0 0, de l'h^opital. >a lim 0 f 0 () lim!a+0 g 0 () = ` ) lim f ()!a+0 g() = `: lim f!+ () =!+ lim g() =0 f 0 () lim!+ g 0 () = ` )!+ lim f () g() = `:!a+0 f () = lim g() =!a+0. f 0 (e) g 0 (e) f () f (a) = g() g(a) = f () g() (a <e <):. lim, lim!a 0!,. n e () lim! n =! lim () lim! log n = lim! (3) lim!+0 n log = e = lim nn! = = lim nn lim!+0! log = lim n!+0 e e = = lim n(n )n! n! = : (e ) n n =0: = n (n+) = (log ) lim!+0 n n = (4) lim (sin ) log y =(sin) log!+0 lim log y = lim log(sin ) cos = sin = lim =: lim!+0!+0 log!+0 = y = e.!+0 (5) lim! ß (tan ) sec y = (tan ) sec 4 lim! ß log y = lim! ß 4 4 log(tan ) cos = lim! ß 4. (AοB) sec = tan sin 0 : () lim ( +) log! () lim 0 : (3) lim log (4) lim!+0 : (5) lim! 0 0 : (7) lim!0 = lim! ß 4 lim n!+0 n =0: sin = : lim y! ß = e. 4! ß! arctan ß arctan a (6) lim cos (a 6= 0)! a b (a; b > 0) (8) lim! ß sec sin ß a + a + + n a n (a ;:::;a n > 0) n ß arctan ± : (9) lim (0) lim!!0 0 0 : () lim () lim!+0! 0 : (3) lim!+0 (4) lim! log(tan) : (5) lim!+0 log(tan ) 9 p k p + k (k =; 3;:::) a (6) lim (a; b > )! b 3
10 9. f 0 (c) = f (b) f (a) b a (a <c<b) f (b) =f (a) +f 0 (c)(b a) (a <c<b) Taylor. f () [a; b] n (a; b) n c (a; b) f (b) =f (a) +f 0 (a)(b a) + f 00 (a)! (b a) f 000 (a) + (b a) 3 f (n ) (a) + + 3! (n (b )! a)n + R n ; R n = f (n) (c) (b a) n n!. n =. R n. g() = f (b)+f()+f 0 ()(b )+ f 00 () (b ) + f 000 () (b ) 3 +! 3! + f (n ) () (n (b )! )n + K(b ) n g(b) =0 g(a) =0 K g() [a; b]. a<c<b c = a + (b a) (0< <) b = f () =f (a) +f 0 (a)( a) + f 00 (a) f () = a a =0 f () =f (0) + f 0 (0) + f 00 (0)!! ( a) f 000 (a) + ( a) 3 f (n ) (a) + + 3! (n ( )! a)n + R n ; R n () = f (n) (a + ( a)) ( a) n (0 < <); n! f 000 (0) + 3 f (n ) (0) + + 3! (n )! n + R n ; R f (n) ( ) n () = n (0 < <); n! f () Maclaurin 3. (A) 0
11 0. 0 < < (5) ff () e =+! +! + + n (n )! + R n(); R n () = e n! n : () sin = 3 3! + 5 m 5! + +( )m (m )! + R m+(); R m+ () = ( ) m cos( ) m+ : (m +)! (3) cos =! + 4 m + +( )m 4! (m)! + R m+(); R m+ () = ( ) m+ cos( ) m+ : (m +)! (4) log( + ) = + 3 n + +( )n 3 n + R n(); R n () = ( ) n n( + ) n n : ψ! ψ! ψ! ψ! (5) ( + ) ff ff ff =+ + ff + + n ff + R n (); R n () = ( + ) ff n n : n n. ψ! ff ff(ff ) (ff (k )) = ff = n ( ) k k! ψ! n n(n ) (n (k )) = = k k! n! (n k)!k! = nc k R n () = n (5). (5) ff = + = ( ) n n + R n (); R n () =( ) n n : ( + ) n+ (4) = = n + R n (); R n () = n ( ) n+ :. sin sin cos cos 4. (A) 5. (A) 0 < < () sinh = + 3 3! + 5 n + + 5! (n )! + R n+(); R n+ () = () cosh = + 4 4! + 6 n + + 6! (n )! + R n(); R n () = cosh (n +)! n+ : cosh n : (n)!
12 . sin sin = 3 3! ! 7! ( ) n n R n+ : (n )! n cos R n+ =( ) (n + )! n+ (0 < <): () = () = 3 3! (3) = 3 3! + 5 5! (4) = 3 3! ! 7! sin () (4) () (4) sin (4).5 y () () (3) sin
13 . cos cos =! ! 6! + 8 8! ( ) n n R n+ : (n)! R n+ =( ) n+ cos (n +)! n+ (0 < <): () =! () =! + 4 4! (3) =! ! 6! (4) =! ! 6! + 8 8! cos () (4) () (4) cos (4) ().5 y cos - (3) () -.5 3
14 3. log ( + ) log( + ) = R n = ( )n+ n n( + ) n (0 < <): () = () = (3) = (4) = ( ) n n R n : n log( + ) () (4) () (4) log( + ) y (3) () log( + ) (4) () 4
15 4. = n + R n : R n = () = n ( ) n+ (0 < <): () = + (3) = (4) = () (4) () (4) y () ().5 (4) (3)
16 5. e e =+ +! + 3 3! + 4 n + + 4! (n )! + R n: R n = e n n! (0 < <): () = + () = + +! (3) = + +! + 3 3! (4) = + +! + 3 3! + 4 4! e () (4) () (4) e 4 y () () (4) e (3) -4 6
17 6.. lim f () =0, lim g() =0!+0!+0 f () () lim =0f()=o(g()) (! +0)!+0 g() fi fi fi () >0 0 fi f () fi fi fi g() fi» C ( ) f()=o(g()) (! +0) o O Landau.! 0 = O( )=o() = O( )=o() =o() n = O( n )=o( n ) f () = f (0) + f 0 (0) + f 00 (0) = f (0) + f 0 (0) + f 00 (0) + O( 3 )!! = f (0) + f 0 (0) + O( ) f ( + ) = f () +f 0 () + O(( ) ) (! 0) + + f (n ) (0) (n )! n + O( n ) f () =a 0 + a + a + + a n n + O( n+ ) (! +0) f () n. e 3 O( n+ )=o( n ) e =+ +! + 3 3! + O(4 ) (! 0): 6. (A)! 0 ( ) () + + ( 4 ) () log cos ( 4 ) (3) tan ( 3 ) (4) arctan ( 3 ) (5) a ( ) (6) e sin ( 3 ) 7
18 7.! 0 sin = 3 sin sin.! 0 3! + O(5 ) = 3! + O(4 ):! (! 0). =+ + O( ); sin = 3 tan = + 3 tan = O(5 ) + O(4 ) 7. (A)! 0 = 6 + O(5 ); cos = 3 + O(5 )(! 0) O(5 ) + = + O( ); sinh = + 3 tanh = O(4 ) + O(4 ) 6 + O(5 ); cosh =+ 3 + O(5 )(! 0) = O(4 ) 3 + O(5 ):. 0 0 e e sin lim!0 sin (AοB) sin cos () lim = () lim!0!0 = sinh!0 log( + a) (4) lim = a (5) lim!0 (7) lim!0 sin 3 = 6 sin!0 (8) lim cos 9. (AοB) sin () lim!0 3 () lim!0 (3) lim!0 sin + e + log( ) (5) lim (6) lim!0 arctan (7) lim e +! p (9) lim 3 +! tan (3) lim =!0 e a = a!0 = (6) lim = (9) lim!0 p (4) lim!0 log( + ) (8) lim!0 (0) lim! 8 sin cos!0 log( + ) + e e sin sin = p ( + a)( + b) p ( a)( b)
Chap10.dvi
=0. f = 2 +3 { 2 +3 0 2 f = 1 =0 { sin 0 3 f = 1 =0 2 sin 1 0 4 f = 0 =0 { 1 0 5 f = 0 =0 f 3 2 lim = lim 0 0 0 =0 =0. f 0 = 0. 2 =0. 3 4 f 1 lim 0 0 = lim 0 sin 2 cos 1 = lim 0 2 sin = lim =0 0 2 =0.
(1) (2) (3) (4) HB B ( ) (5) (6) (7) 40 (8) (9) (10)
2017 12 9 4 1 30 4 10 3 1 30 3 30 2 1 30 2 50 1 1 30 2 10 (1) (2) (3) (4) HB B ( ) (5) (6) (7) 40 (8) (9) (10) (1) i 23 c 23 0 1 2 3 4 5 6 7 8 9 a b d e f g h i (2) 23 23 (3) 23 ( 23 ) 23 x 1 x 2 23 x
grad φ(p ) φ P grad φ(p ) p P p φ P p l t φ l t = 0 g (0) g (0) (31) grad φ(p ) p grad φ φ (P, φ(p )) xy (x, y) = (ξ(t), η(t)) ( )
2 9 2 5 2.2.3 grad φ(p ) φ P grad φ(p ) p P p φ P p l t φ l t = g () g () (3) grad φ(p ) p grad φ φ (P, φ(p )) y (, y) = (ξ(t), η(t)) ( ) ξ (t) (t) := η (t) grad f(ξ(t), η(t)) (t) g(t) := f(ξ(t), η(t))
I No. sin cos sine, cosine : trigonometric function π : π =.4 : n =, ±, ±, sin + nπ = sin cos + nπ = cos sin = sin : cos = cos :. sin. sin. sin + π si
I 8 No. : No. : No. : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No. : I No. sin cos sine, cosine : trigonometric function π : π =.4 : n =, ±, ±, sin + nπ = sin cos + nπ = cos sin = sin : cos = cos :. sin.
5 36 5................................................... 36 5................................................... 36 5.3..............................
9 8 3............................................. 3.......................................... 4.3............................................ 4 5 3 6 3..................................................
( ) a, b c a 2 + b 2 = c 2. 2 1 2 2 : 2 2 = p q, p, q 2q 2 = p 2. p 2 p 2 2 2 q 2 p, q (QED)
rational number p, p, (q ) q ratio 3.14 = 3 + 1 10 + 4 100 ( ) a, b c a 2 + b 2 = c 2. 2 1 2 2 : 2 2 = p q, p, q 2q 2 = p 2. p 2 p 2 2 2 q 2 p, q (QED) ( a) ( b) a > b > 0 a < nb n A A B B A A, B B A =
I, II 1, A = A 4 : 6 = max{ A, } A A 10 10%
1 2006.4.17. A 3-312 tel: 092-726-4774, e-mail: hara@math.kyushu-u.ac.jp, http://www.math.kyushu-u.ac.jp/ hara/lectures/lectures-j.html Office hours: B A I ɛ-δ ɛ-δ 1. 2. A 1. 1. 2. 3. 4. 5. 2. ɛ-δ 1. ɛ-n
sin cos No. sine, cosine : trigonometric function π : π = 3.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin : odd cos = cos : even.
08 No. : No. : No.3 : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No.0 : No. : sin cos No. sine, cosine : trigonometric function π : π = 3.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin
I No. sin cos sine, cosine : trigonometric function π : π =.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin : odd cos = cos : even.
I 0 No. : No. : No. : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No.0 : I No. sin cos sine, cosine : trigonometric function π : π =.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin : odd
I, II 1, 2 ɛ-δ 100 A = A 4 : 6 = max{ A, } A A 10
1 2007.4.13. A 3-312 tel: 092-726-4774, e-mail: hara@math.kyushu-u.ac.jp, http://www.math.kyushu-u.ac.jp/ hara/lectures/lectures-j.html Office hours: B A I ɛ-δ ɛ-δ 1. 2. A 0. 1. 1. 2. 3. 2. ɛ-δ 1. ɛ-n
[ ] 0.1 lim x 0 e 3x 1 x IC ( 11) ( s114901) 0.2 (1) y = e 2x (x 2 + 1) (2) y = x/(x 2 + 1) 0.3 dx (1) 1 4x 2 (2) e x sin 2xdx (3) sin 2 xdx ( 11) ( s
![[ ] 0.1 lim x 0 e 3x 1 x IC ( 11) ( s114901) 0.2 (1) y = e 2x (x 2 + 1) (2) y = x/(x 2 + 1) 0.3 dx (1) 1 4x 2 (2) e x sin 2xdx (3) sin 2 xdx ( 11) ( s](/thumbs/94/118579915.jpg "[ ] 0.1 lim x 0 e 3x 1 x IC ( 11) ( s114901) 0.2 (1) y = e 2x (x 2 + 1) (2) y = x/(x 2 + 1) 0.3 dx (1) 1 4x 2 (2) e x sin 2xdx (3) sin 2 xdx ( 11) ( s")
[ ]. lim e 3 IC ) s49). y = e + ) ) y = / + ).3 d 4 ) e sin d 3) sin d ) s49) s493).4 z = y z z y s494).5 + y = 4 =.6 s495) dy = 3e ) d dy d = y s496).7 lim ) lim e s49).8 y = e sin ) y = sin e 3) y =
, x R, f (x),, df dx : R R,, f : R R, f(x) ( ).,, f (a) d f dx (a), f (a) d3 f dx 3 (a),, f (n) (a) dn f dx n (a), f d f dx, f d3 f dx 3,, f (n) dn f
,,,,.,,,. R f : R R R a R, f(a + ) f(a) lim 0 (), df dx (a) f (a), f(x) x a, f (a), f(x) x a ( ). y f(a + ) y f(x) f(a+) f(a) f(a + ) f(a) f(a) x a 0 a a + x 0 a a + x y y f(x) 0 : 0, f(a+) f(a)., f(x)
i
i 3 4 4 7 5 6 3 ( ).. () 3 () (3) (4) /. 3. 4/3 7. /e 8. a > a, a = /, > a >. () a >, a =, > a > () a > b, a = b, a < b. c c n a n + b n + c n 3c n..... () /3 () + (3) / (4) /4 (5) m > n, a b >, m > n,
( ) 2.1. C. (1) x 4 dx = 1 5 x5 + C 1 (2) x dx = x 2 dx = x 1 + C = 1 2 x + C xdx (3) = x dx = 3 x C (4) (x + 1) 3 dx = (x 3 + 3x 2 + 3x +
(.. C. ( d 5 5 + C ( d d + C + C d ( d + C ( ( + d ( + + + d + + + + C (5 9 + d + d tan + C cos (sin (6 sin d d log sin + C sin + (7 + + d ( + + + + d log( + + + C ( (8 d 7 6 d + 6 + C ( (9 ( d 6 + 8 d
2009 I 2 II III 14, 15, α β α β l 0 l l l l γ (1) γ = αβ (2) α β n n cos 2k n n π sin 2k n π k=1 k=1 3. a 0, a 1,..., a n α a
009 I II III 4, 5, 6 4 30. 0 α β α β l 0 l l l l γ ) γ αβ ) α β. n n cos k n n π sin k n π k k 3. a 0, a,..., a n α a 0 + a x + a x + + a n x n 0 ᾱ 4. [a, b] f y fx) y x 5. ) Arcsin 4) Arccos ) ) Arcsin
211 kotaro@math.titech.ac.jp 1 R *1 n n R n *2 R n = {(x 1,..., x n ) x 1,..., x n R}. R R 2 R 3 R n R n R n D D R n *3 ) (x 1,..., x n ) f(x 1,..., x n ) f D *4 n 2 n = 1 ( ) 1 f D R n f : D R 1.1. (x,
7. y fx, z gy z gfx dz dx dz dy dy dx. g f a g bf a b fa 7., chain ule Ω, D R n, R m a Ω, f : Ω R m, g : D R l, fω D, b fa, f a g b g f a g f a g bf a
9 203 6 7 WWW http://www.math.meiji.ac.jp/~mk/lectue/tahensuu-203/ 2 8 8 7. 7 7. y fx, z gy z gfx dz dx dz dy dy dx. g f a g bf a b fa 7., chain ule Ω, D R n, R m a Ω, f : Ω R m, g : D R l, fω D, b fa,
( 12 ( ( ( ( Levi-Civita grad div rot ( ( = 4 : 6 3 1 1.1 f(x n f (n (x, d n f(x (1.1 dxn f (2 (x f (x 1.1 f(x = e x f (n (x = e x d dx (fg = f g + fg (1.2 d dx d 2 dx (fg = f g + 2f g + fg 2... d n n
A (1) = 4 A( 1, 4) 1 A 4 () = tan A(0, 0) π A π
4 4.1 4.1.1 A = f() = f() = a f (a) = f() (a, f(a)) = f() (a, f(a)) f(a) = f 0 (a)( a) 4.1 (4, ) = f() = f () = 1 = f (4) = 1 4 4 (4, ) = 1 ( 4) 4 = 1 4 + 1 17 18 4 4.1 A (1) = 4 A( 1, 4) 1 A 4 () = tan
さくらの個別指導 ( さくら教育研究所 ) A a 1 a 2 a 3 a n {a n } a 1 a n n n 1 n n 0 a n = 1 n 1 n n O n {a n } n a n α {a n } α {a
... A a a a 3 a n {a n } a a n n 3 n n n 0 a n = n n n O 3 4 5 6 n {a n } n a n α {a n } α {a n } α α {a n } a n n a n α a n = α n n 0 n = 0 3 4. ()..0.00 + (0.) n () 0. 0.0 0.00 ( 0.) n 0 0 c c c c c
1009.\1.\4.ai
- 1 - E O O O O O O - 2 - E O O O - 3 - O N N N N N N N N N N N N N N N N N N N N N N N E e N N N N N N N N N N N N N N N N N N N N N N N D O O O - 4 - O O O O O O O O N N N N N N N N N N N N N N N N N
1 1. x 1 (1) x 2 + 2x + 5 dx d dx (x2 + 2x + 5) = 2(x + 1) x 1 x 2 + 2x + 5 = x + 1 x 2 + 2x x 2 + 2x + 5 y = x 2 + 2x + 5 dy = 2(x + 1)dx x + 1
. ( + + 5 d ( + + 5 ( + + + 5 + + + 5 + + 5 y + + 5 dy ( + + dy + + 5 y log y + C log( + + 5 + C. ++5 (+ +4 y (+/ + + 5 (y + 4 4(y + dy + + 5 dy Arctany+C Arctan + y ( + +C. + + 5 ( + log( + + 5 Arctan
2009 IA 5 I 22, 23, 24, 25, 26, (1) Arcsin 1 ( 2 (4) Arccos 1 ) 2 3 (2) Arcsin( 1) (3) Arccos 2 (5) Arctan 1 (6) Arctan ( 3 ) 3 2. n (1) ta
009 IA 5 I, 3, 4, 5, 6, 7 6 3. () Arcsin ( (4) Arccos ) 3 () Arcsin( ) (3) Arccos (5) Arctan (6) Arctan ( 3 ) 3. n () tan x (nπ π/, nπ + π/) f n (x) f n (x) fn (x) Arctan x () sin x [nπ π/, nπ +π/] g n
#A A A F, F d F P + F P = d P F, F y P F F x A.1 ( α, 0), (α, 0) α > 0) (x, y) (x + α) 2 + y 2, (x α) 2 + y 2 d (x + α)2 + y 2 + (x α) 2 + y 2 =
#A A A. F, F d F P + F P = d P F, F P F F A. α, 0, α, 0 α > 0, + α +, α + d + α + + α + = d d F, F 0 < α < d + α + = d α + + α + = d d α + + α + d α + = d 4 4d α + = d 4 8d + 6 http://mth.cs.kitmi-it.c.jp/
( ) sin 1 x, cos 1 x, tan 1 x sin x, cos x, tan x, arcsin x, arccos x, arctan x. π 2 sin 1 x π 2, 0 cos 1 x π, π 2 < tan 1 x < π 2 1 (1) (
6 20 ( ) sin, cos, tan sin, cos, tan, arcsin, arccos, arctan. π 2 sin π 2, 0 cos π, π 2 < tan < π 2 () ( 2 2 lim 2 ( 2 ) ) 2 = 3 sin (2) lim 5 0 = 2 2 0 0 2 2 3 3 4 5 5 2 5 6 3 5 7 4 5 8 4 9 3 4 a 3 b
Chap9.dvi
.,. f(),, f(),,.,. () lim 2 +3 2 9 (2) lim 3 3 2 9 (4) lim ( ) 2 3 +3 (5) lim 2 9 (6) lim + (7) lim (8) lim (9) lim (0) lim 2 3 + 3 9 2 2 +3 () lim sin 2 sin 2 (2) lim +3 () lim 2 2 9 = 5 5 = 3 (2) lim
6. Euler x
...............................................................................3......................................... 4.4................................... 5.5......................................
di-problem.dvi
005/05/05 by. I : : : : : : : : : : : : : : : : : : : : : : : : :. II : : : : : : : : : : : : : : : : : : : : : : : : : 3 3. III : : : : : : : : : : : : : : : : : : : : : : : : 4 4. : : : : : : : : : :
5.. z = f(x, y) y y = b f x x g(x) f(x, b) g x ( ) A = lim h 0 g(a + h) g(a) h g(x) a A = g (a) = f x (a, b)
5 partial differentiation (total) differentiation 5. z = f(x, y) (a, b) A = lim h 0 f(a + h, b) f(a, b) h............................................................... ( ) f(x, y) (a, b) x A (a, b) x
x () g(x) = f(t) dt f(x), F (x) 3x () g(x) g (x) f(x), F (x) (3) h(x) = x 3x tf(t) dt.9 = {(x, y) ; x, y, x + y } f(x, y) = xy( x y). h (x) f(x), F (x
[ ] IC. f(x) = e x () f(x) f (x) () lim f(x) lim f(x) x + x (3) lim f(x) lim f(x) x + x (4) y = f(x) ( ) ( s46). < a < () a () lim a log xdx a log xdx ( ) n (3) lim log k log n n n k=.3 z = log(x + y ),
I A A441 : April 21, 2014 Version : Kawahira, Tomoki TA (Kondo, Hirotaka ) Google
I4 - : April, 4 Version :. Kwhir, Tomoki TA (Kondo, Hirotk) Google http://www.mth.ngoy-u.c.jp/~kwhir/courses/4s-biseki.html pdf 4 4 4 4 8 e 5 5 9 etc. 5 6 6 6 9 n etc. 6 6 6 3 6 3 7 7 etc 7 4 7 7 8 5 59
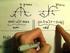
0 = m 2p 1 p = 1/2 p y = 1 m = 1 2 d ( + 1)2 d ( + 1) 2 = d d ( + 1)2 = = 2( + 1) 2 g() 2 f() f() = [g()] 2 = g()g() f f () = [g()g()]
![0 = m 2p 1 p = 1/2 p y = 1 m = 1 2 d ( + 1)2 d ( + 1) 2 = d d ( + 1)2 = = 2( + 1) 2 g() 2 f() f() = [g()] 2 = g()g() f f () = [g()g()]](/thumbs/92/110082312.jpg "0 = m 2p 1 p = 1/2 p y = 1 m = 1 2 d ( + 1)2 d ( + 1) 2 = d d ( + 1)2 = = 2( + 1) 2 g() 2 f() f() = [g()] 2 = g()g() f f () = [g()g()]")
8. 2 1 2 1 2 ma,y u(, y) s.t. p + p y y = m u y y p p y y m u(, y) = y p + p y y = m y ( ) 1 y = (m p ) p y = m p y p p y 2 0 m/p U U() = m p y p p y 2 2 du() d = m p y 2p p y 1 0 = m 2p 1 p = 1/2 p y
1 3 1.1.......................... 3 1............................... 3 1.3....................... 5 1.4.......................... 6 1.5........................ 7 8.1......................... 8..............................
S I. dy fx x fx y fx + C 3 C vt dy fx 4 x, y dy yt gt + Ct + C dt v e kt xt v e kt + C k x v k + C C xt v k 3 r r + dr e kt S Sr πr dt d v } dt k e kt
S I. x yx y y, y,. F x, y, y, y,, y n http://ayapin.film.s.dendai.ac.jp/~matuda n /TeX/lecture.html PDF PS yx.................................... 3.3.................... 9.4................5..............
() x + y + y + x dy dx = 0 () dy + xy = x dx y + x y ( 5) ( s55906) 0.7. (). 5 (). ( 6) ( s6590) 0.8 m n. 0.9 n n A. ( 6) ( s6590) f A (λ) = det(a λi)
0. A A = 4 IC () det A () A () x + y + z = x y z X Y Z = A x y z ( 5) ( s5590) 0. a + b + c b c () a a + b + c c a b a + b + c 0 a b c () a 0 c b b c 0 a c b a 0 0. A A = 7 5 4 5 0 ( 5) ( s5590) () A ()
09-12-15_1203new
12 15 12/15 1/14 E _ GC DC Y FB GA BF Y 2 g g a f Y b b d b b c c b b g a c e b f b - Y b b c a c C A C C Y f g a b c d e - g a b c d c ab ab b g bb fbbd 3 4 1 F B 1 DF C A A A 6 G F A B 5 GA 6 E BF G
ac b 0 r = r a 0 b 0 y 0 cy 0 ac b 0 f(, y) = a + by + cy ac b = 0 1 ac b = 0 z = f(, y) f(, y) 1 a, b, c 0 a 0 f(, y) = a ( ( + b ) ) a y ac b + a y
01 4 17 1.. y f(, y) = a + by + cy + p + qy + r a, b, c 0 y b b 1 z = f(, y) z = a + by + cy z = p + qy + r (, y) z = p + qy + r 1 y = + + 1 y = y = + 1 6 + + 1 ( = + 1 ) + 7 4 16 y y y + = O O O y = y
1007.\1.ai
- 1 - B - 2 - e - 3 - F O f g e f - 4 - O O N N N N N N N N N N N N N N N N N N N N N N N F C - 5 - N N N N N N N N N N N N N N N N N N N N N N N F - 6 - D - 7 - - 8 - - 9 - - 10 - - 11 - - 12 - - 13 -
A B 5 C 9 3.4 7 mm, 89 mm 7/89 = 3.4. π 3 6 π 6 6 = 6 π > 6, π > 3 : π > 3
π 9 3 7 4. π 3................................................. 3.3........................ 3.4 π.................... 4.5..................... 4 7...................... 7..................... 9 3 3. p
e a b a b b a a a 1 a a 1 = a 1 a = e G G G : x ( x =, 8, 1 ) x 1,, 60 θ, ϕ ψ θ G G H H G x. n n 1 n 1 n σ = (σ 1, σ,..., σ N ) i σ i i n S n n = 1,,
01 10 18 ( ) 1 6 6 1 8 8 1 6 1 0 0 0 0 1 Table 1: 10 0 8 180 1 1 1. ( : 60 60 ) : 1. 1 e a b a b b a a a 1 a a 1 = a 1 a = e G G G : x ( x =, 8, 1 ) x 1,, 60 θ, ϕ ψ θ G G H H G x. n n 1 n 1 n σ = (σ 1,
5.. z = f(x, y) y y = b f x x g(x) f(x, b) g x ( ) A = lim h g(a + h) g(a) h g(x) a A = g (a) = f x (a, b)............................................
5 partial differentiation (total) differentiation 5. z = f(x, y) (a, b) A = lim h f(a + h, b) f(a, b) h........................................................... ( ) f(x, y) (a, b) x A (a, b) x (a, b)
untitled
0. =. =. (999). 3(983). (980). (985). (966). 3. := :=. A A. A A. := := 4 5 A B A B A B. A = B A B A B B A. A B A B, A B, B. AP { A, P } = { : A, P } = { A P }. A = {0, }, A, {0, }, {0}, {}, A {0}, {}.
(1) D = [0, 1] [1, 2], (2x y)dxdy = D = = (2) D = [1, 2] [2, 3], (x 2 y + y 2 )dxdy = D = = (3) D = [0, 1] [ 1, 2], 1 {
![(1) D = [0, 1] [1, 2], (2x y)dxdy = D = = (2) D = [1, 2] [2, 3], (x 2 y + y 2 )dxdy = D = = (3) D = [0, 1] [ 1, 2], 1 {](/thumbs/94/118399854.jpg "(1) D = [0, 1] [1, 2], (2x y)dxdy = D = = (2) D = [1, 2] [2, 3], (x 2 y + y 2 )dxdy = D = = (3) D = [0, 1] [ 1, 2], 1 {")
7 4.., ], ], ydy, ], 3], y + y dy 3, ], ], + y + ydy 4, ], ], y ydy ydy y y ] 3 3 ] 3 y + y dy y + 3 y3 5 + 9 3 ] 3 + y + ydy 5 6 3 + 9 ] 3 73 6 y + y + y ] 3 + 3 + 3 3 + 3 + 3 ] 4 y y dy y ] 3 y3 83 3
I y = f(x) a I a x I x = a + x 1 f(x) f(a) x a = f(a + x) f(a) x (11.1) x a x 0 f(x) f(a) f(a + x) f(a) lim = lim x a x a x 0 x (11.2) f(x) x
11 11.1 I y = a I a x I x = a + 1 f(a) x a = f(a +) f(a) (11.1) x a 0 f(a) f(a +) f(a) = x a x a 0 (11.) x = a a f (a) d df f(a) (a) I dx dx I I I f (x) d df dx dx (x) [a, b] x a ( 0) x a (a, b) () [a,
( ) x y f(x, y) = ax
013 4 16 5 54 (03-5465-7040) nkiyono@mail.ecc.u-okyo.ac.jp hp://lecure.ecc.u-okyo.ac.jp/~nkiyono/inde.hml 1.. y f(, y) = a + by + cy + p + qy + r a, b, c 0 y b b 1 z = f(, y) z = a + by + cy z = p + qy
) ] [ h m x + y + + V x) φ = Eφ 1) z E = i h t 13) x << 1) N n n= = N N + 1) 14) N n n= = N N + 1)N + 1) 6 15) N n 3 n= = 1 4 N N + 1) 16) N n 4
![) ] [ h m x + y + + V x) φ = Eφ 1) z E = i h t 13) x << 1) N n n= = N N + 1) 14) N n n= = N N + 1)N + 1) 6 15) N n 3 n= = 1 4 N N + 1) 16) N n 4](/thumbs/92/107866707.jpg ") ] [ h m x + y + + V x) φ = Eφ 1) z E = i h t 13) x << 1) N n n= = N N + 1) 14) N n n= = N N + 1)N + 1) 6 15) N n 3 n= = 1 4 N N + 1) 16) N n 4")
1. k λ ν ω T v p v g k = π λ ω = πν = π T v p = λν = ω k v g = dω dk 1) ) 3) 4). p = hk = h λ 5) E = hν = hω 6) h = h π 7) h =6.6618 1 34 J sec) hc=197.3 MeV fm = 197.3 kev pm= 197.3 ev nm = 1.97 1 3 ev
II 2 II
II 2 II 2005 yugami@cc.utsunomiya-u.ac.jp 2005 4 1 1 2 5 2.1.................................... 5 2.2................................. 6 2.3............................. 6 2.4.................................
1 I p2/30
I I p1/30 1 I p2/30 1 ( ) I p3/30 1 ( ), y = y() d = f() g(y) ( g(y) = f()d) (1) I p4/30 1 ( ), y = y() d = f() g(y) ( g(y) = f()d) (1) g(y) = f()d I p4/30 1 ( ), y = y() d = f() g(y) ( g(y) = f()d) (1)
70 : 20 : A B (20 ) (30 ) 50 1
70 : 0 : A B (0 ) (30 ) 50 1 1 4 1.1................................................ 5 1. A............................................... 6 1.3 B............................................... 7 8.1 A...............................................
f : R R f(x, y) = x + y axy f = 0, x + y axy = 0 y 直線 x+y+a=0 に漸近し 原点で交叉する美しい形をしている x +y axy=0 X+Y+a=0 o x t x = at 1 + t, y = at (a > 0) 1 + t f(x, y
017 8 10 f : R R f(x) = x n + x n 1 + 1, f(x) = sin 1, log x x n m :f : R n R m z = f(x, y) R R R R, R R R n R m R n R m R n R m f : R R f (x) = lim h 0 f(x + h) f(x) h f : R n R m m n M Jacobi( ) m n
1 1 sin cos P (primary) S (secondly) 2 P S A sin(ω2πt + α) A ω 1 ω α V T m T m 1 100Hz m 2 36km 500Hz. 36km 1
sin cos P (primary) S (secondly) 2 P S A sin(ω2πt + α) A ω ω α 3 3 2 2V 3 33+.6T m T 5 34m Hz. 34 3.4m 2 36km 5Hz. 36km m 34 m 5 34 + m 5 33 5 =.66m 34m 34 x =.66 55Hz, 35 5 =.7 485.7Hz 2 V 5Hz.5V.5V V
, 1 ( f n (x))dx d dx ( f n (x)) 1 f n (x)dx d dx f n(x) lim f n (x) = [, 1] x f n (x) = n x x 1 f n (x) = x f n (x) = x 1 x n n f n(x) = [, 1] f n (x
![, 1 ( f n (x))dx d dx ( f n (x)) 1 f n (x)dx d dx f n(x) lim f n (x) = [, 1] x f n (x) = n x x 1 f n (x) = x f n (x) = x 1 x n n f n(x) = [, 1] f n (x](/thumbs/93/113428934.jpg ", 1 ( f n (x))dx d dx ( f n (x)) 1 f n (x)dx d dx f n(x) lim f n (x) = [, 1] x f n (x) = n x x 1 f n (x) = x f n (x) = x 1 x n n f n(x) = [, 1] f n (x")
1 1.1 4n 2 x, x 1 2n f n (x) = 4n 2 ( 1 x), 1 x 1 n 2n n, 1 x n n 1 1 f n (x)dx = 1, n = 1, 2,.. 1 lim 1 lim 1 f n (x)dx = 1 lim f n(x) = ( lim f n (x))dx = f n (x)dx 1 ( lim f n (x))dx d dx ( lim f d
P14・15地域文化祭
2008 1BETSUKAI 2008.10 BETSUKAI 2008.102 3BETSUKAI 2008.10 BETSUKAI 2008.104 5BETSUKAI 2008.10 BETSUKAI 2008.106 7BETSUKAI 2008.10 BETSUKAI 2008.108 9BETSUKAI 2008.10 BETSUKAI 2008.1010 11BETSUKAI 2008.10
IA 2013 : :10722 : 2 : :2 :761 :1 (23-27) : : ( / ) (1 /, ) / e.g. (Taylar ) e x = 1 + x + x xn n! +... sin x = x x3 6 + x5 x2n+1 + (
IA 2013 : :10722 : 2 : :2 :761 :1 23-27) : : 1 1.1 / ) 1 /, ) / e.g. Taylar ) e x = 1 + x + x2 2 +... + xn n! +... sin x = x x3 6 + x5 x2n+1 + 1)n 5! 2n + 1)! 2 2.1 = 1 e.g. 0 = 0.00..., π = 3.14..., 1
応力とひずみ.ppt
in yukawa@numse.nagoya-u.ac.jp 2 3 4 5 x 2 6 Continuum) 7 8 9 F F 10 F L L F L 1 L F L F L F 11 F L F F L F L L L 1 L 2 12 F L F! A A! S! = F S 13 F L L F F n = F " cos# F t = F " sin# S $ = S cos# S S
S I. dy fx x fx y fx + C 3 C dy fx 4 x, y dy v C xt y C v e kt k > xt yt gt [ v dt dt v e kt xt v e kt + C k x v + C C k xt v k 3 r r + dr e kt S dt d
S I.. http://ayapin.film.s.dendai.ac.jp/~matuda /TeX/lecture.html PDF PS.................................... 3.3.................... 9.4................5.............. 3 5. Laplace................. 5....
D xy D (x, y) z = f(x, y) f D (2 ) (x, y, z) f R z = 1 x 2 y 2 {(x, y); x 2 +y 2 1} x 2 +y 2 +z 2 = 1 1 z (x, y) R 2 z = x 2 y
5 5. 2 D xy D (x, y z = f(x, y f D (2 (x, y, z f R 2 5.. z = x 2 y 2 {(x, y; x 2 +y 2 } x 2 +y 2 +z 2 = z 5.2. (x, y R 2 z = x 2 y + 3 (2,,, (, 3,, 3 (,, 5.3 (. (3 ( (a, b, c A : (x, y, z P : (x, y, x
取扱説明書 -詳細版- 液晶プロジェクター CP-AW3019WNJ
B A C D E F K I M L J H G N O Q P Y CB/PB CR/PR COMPONENT VIDEO OUT RS-232C LAN RS-232C LAN LAN BE EF 03 06 00 2A D3 01 00 00 60 00 00 BE EF 03 06 00 BA D2 01 00 00 60 01 00 BE EF 03 06 00 19 D3 02 00
DVIOUT
A. A. A-- [ ] f(x) x = f 00 (x) f 0 () =0 f 00 () > 0= f(x) x = f 00 () < 0= f(x) x = A--2 [ ] f(x) D f 00 (x) > 0= y = f(x) f 00 (x) < 0= y = f(x) P (, f()) f 00 () =0 A--3 [ ] y = f(x) [, b] x = f (y)
高校生の就職への数学II
II O Tped b L A TEX ε . II. 3. 4. 5. http://www.ocn.ne.jp/ oboetene/plan/ 7 9 i .......................................................................................... 3..3...............................
brother.\..2.ai
2004.3 95 pc 2 5 6 7 8 Q SC-370pc 9 HG-2614977766611312 HG-2514977766611329 HG-2414977766611336 HG-2314977766611343 HG-2214977766611350 HG-2114977766611367 TZ-FX2514977766621236 TZ-FX2414977766621229
di-problem.dvi
2005/04/4 by. : : : : : : : : : : : : : : : : : : : : : : : : : : 2 2. : : : : : : : : : : : : : : : : : : : : : : 3 3. : : : : : : : : : : : : : : : : : : : : : : : : : 4 4. : : : : : : : : : : : : :
4 4 4 a b c d a b A c d A a da ad bce O E O n A n O ad bc a d n A n O 5 {a n } S n a k n a n + k S n a a n+ S n n S n n log x x {xy } x, y x + y 7 fx
4 4 5 4 I II III A B C, 5 7 I II A B,, 8, 9 I II A B O A,, Bb, b, Cc, c, c b c b b c c c OA BC P BC OP BC P AP BC n f n x xn e x! e n! n f n x f n x f n x f k x k 4 e > f n x dx k k! fx sin x cos x tan
. sinh x sinh x) = e x e x = ex e x = sinh x 3) y = cosh x, y = sinh x y = e x, y = e x 6 sinhx) coshx) 4 y-axis x-axis : y = cosh x, y = s
. 00 3 9 [] sinh x = ex e x, cosh x = ex + e x ) sinh cosh 4 hyperbolic) hyperbola) = 3 cosh x cosh x) = e x + e x = cosh x ) . sinh x sinh x) = e x e x = ex e x = sinh x 3) y = cosh x, y = sinh x y =
.5 z = a + b + c n.6 = a sin t y = b cos t dy d a e e b e + e c e e e + e 3 s36 3 a + y = a, b > b 3 s363.7 y = + 3 y = + 3 s364.8 cos a 3 s365.9 y =,
[ ] IC. r, θ r, θ π, y y = 3 3 = r cos θ r sin θ D D = {, y ; y }, y D r, θ ep y yddy D D 9 s96. d y dt + 3dy + y = cos t dt t = y = e π + e π +. t = π y =.9 s6.3 d y d + dy d + y = y =, dy d = 3 a, b
r 1 m A r/m i) t ii) m i) t B(t; m) ( B(t; m) = A 1 + r ) mt m ii) B(t; m) ( B(t; m) = A 1 + r ) mt m { ( = A 1 + r ) m } rt r m n = m r m n B
1 1.1 1 r 1 m A r/m i) t ii) m i) t Bt; m) Bt; m) = A 1 + r ) mt m ii) Bt; m) Bt; m) = A 1 + r ) mt m { = A 1 + r ) m } rt r m n = m r m n Bt; m) Aert e lim 1 + 1 n 1.1) n!1 n) e a 1, a 2, a 3,... {a n
untitled
2 (numerical algorithm) 2. = ratio of the circumference to its diameter, number, Ludolph s number... sin, cos =3.45926535... 0 e x2 dx = /2 etc. : 999 : 99 : 974 P.: 973, J.-P.: 200 J. Arndt, Ch. Haenel:
meiji_resume_1.PDF
β β β (q 1,q,..., q n ; p 1, p,..., p n ) H(q 1,q,..., q n ; p 1, p,..., p n ) Hψ = εψ ε k = k +1/ ε k = k(k 1) (x, y, z; p x, p y, p z ) (r; p r ), (θ; p θ ), (ϕ; p ϕ ) ε k = 1/ k p i dq i E total = E
K E N Z U 2012 7 16 HP M. 1 1 4 1.1 3.......................... 4 1.2................................... 4 1.2.1..................................... 4 1.2.2.................................... 5................................
sekibun.dvi
a d = a + a+ (a ), e d = e, sin d = cos, (af() + bg())d = a d = log, cosd = sin, f()d + b g()d d 3 d d d d d d d ( + 3 + )d ( + )d ( 3 )d (e )d ( sin 3 cos)d g ()f (g())d = f(g()) e d e d ( )e d cos d
4................................. 4................................. 4 6................................. 6................................. 9.................................................... 3..3..........................
18 ( ) I II III A B C(100 ) 1, 2, 3, 5 I II A B (100 ) 1, 2, 3 I II A B (80 ) 6 8 I II III A B C(80 ) 1 n (1 + x) n (1) n C 1 + n C
8 ( ) 8 5 4 I II III A B C( ),,, 5 I II A B ( ),, I II A B (8 ) 6 8 I II III A B C(8 ) n ( + x) n () n C + n C + + n C n = 7 n () 7 9 C : y = x x A(, 6) () A C () C P AP Q () () () 4 A(,, ) B(,, ) C(,,
1 I
1 I 3 1 1.1 R x, y R x + y R x y R x, y, z, a, b R (1.1) (x + y) + z = x + (y + z) (1.2) x + y = y + x (1.3) 0 R : 0 + x = x x R (1.4) x R, 1 ( x) R : x + ( x) = 0 (1.5) (x y) z = x (y z) (1.6) x y =
all.dvi
38 5 Cauchy.,,,,., σ.,, 3,,. 5.1 Cauchy (a) (b) (a) (b) 5.1: 5.1. Cauchy 39 F Q Newton F F F Q F Q 5.2: n n ds df n ( 5.1). df n n df(n) df n, t n. t n = df n (5.1) ds 40 5 Cauchy t l n mds df n 5.3: t
C:/KENAR/0p1.dvi
2{3. 53 2{3 [ ] 4 2 1 2 10,15 m 10,10 m 2 2 54 2 III 1{I U 2.4 U r (2.16 F U F =, du dt du dr > 0 du dr < 0 O r 0 r 2.4: 1 m =1:00 10 kg 1:20 10 kgf 8:0 kgf g =9:8 m=s 2 (a) x N mg 2.5: N 2{3. 55 (b) x
M3 x y f(x, y) (= x) (= y) x + y f(x, y) = x + y + *. f(x, y) π y f(x, y) x f(x + x, y) f(x, y) lim x x () f(x,y) x 3 -
M3............................................................................................ 3.3................................................... 3 6........................................... 6..........................................
mugensho.dvi
1 1 f (t) lim t a f (t) = 0 f (t) t a 1.1 (1) lim(t 1) 2 = 0 t 1 (t 1) 2 t 1 (2) lim(t 1) 3 = 0 t 1 (t 1) 3 t 1 2 f (t), g(t) t a lim t a f (t) g(t) g(t) f (t) = o(g(t)) (t a) = 0 f (t) (t 1) 3 1.2 lim
Note.tex 2008/09/19( )
1 20 9 19 2 1 5 1.1........................ 5 1.2............................. 8 2 9 2.1............................. 9 2.2.............................. 10 3 13 3.1.............................. 13 3.2..................................
(ii) (iii) z a = z a =2 z a =6 sin z z a dz. cosh z z a dz. e z dz. (, a b > 6.) (z a)(z b) 52.. (a) dz, ( a = /6.), (b) z =6 az (c) z a =2 53. f n (z
B 4 24 7 9 ( ) :,..,,.,. 4 4. f(z): D C: D a C, 2πi C f(z) dz = f(a). z a a C, ( ). (ii), a D, a U a,r D f. f(z) = A n (z a) n, z U a,r, n= A n := 2πi C f(ζ) dζ, n =,,..., (ζ a) n+, C a D. (iii) U a,r
Gmech08.dvi
51 5 5.1 5.1.1 P r P z θ P P P z e r e, z ) r, θ, ) 5.1 z r e θ,, z r, θ, = r sin θ cos = r sin θ sin 5.1) e θ e z = r cos θ r, θ, 5.1: 0 r
1990 IMO 1990/1/15 1:00-4:00 1 N N N 1, N 1 N 2, N 2 N 3 N 3 2 x x + 52 = 3 x x , A, B, C 3,, A B, C 2,,,, 7, A, B, C
0 9 (1990 1999 ) 10 (2000 ) 1900 1994 1995 1999 2 SAT ACT 1 1990 IMO 1990/1/15 1:00-4:00 1 N 1990 9 N N 1, N 1 N 2, N 2 N 3 N 3 2 x 2 + 25x + 52 = 3 x 2 + 25x + 80 3 2, 3 0 4 A, B, C 3,, A B, C 2,,,, 7,
1 No.1 5 C 1 I III F 1 F 2 F 1 F 2 2 Φ 2 (t) = Φ 1 (t) Φ 1 (t t). = Φ 1(t) t = ( 1.5e 0.5t 2.4e 4t 2e 10t ) τ < 0 t > τ Φ 2 (t) < 0 lim t Φ 2 (t) = 0
1 No.1 5 C 1 I III F 1 F 2 F 1 F 2 2 Φ 2 (t) = Φ 1 (t) Φ 1 (t t). = Φ 1(t) t = ( 1.5e 0.5t 2.4e 4t 2e 10t ) τ < 0 t > τ Φ 2 (t) < 0 lim t Φ 2 (t) = 0 0 < t < τ I II 0 No.2 2 C x y x y > 0 x 0 x > b a dx
i 18 2H 2 + O 2 2H 2 + ( ) 3K
i 18 2H 2 + O 2 2H 2 + ( ) 3K ii 1 1 1.1.................................. 1 1.2........................................ 3 1.3......................................... 3 1.4....................................
a (a + ), a + a > (a + ), a + 4 a < a 4 a,,, y y = + a y = + a, y = a y = ( + a) ( x) + ( a) x, x y,y a y y y ( + a : a ) ( a : a > ) y = (a + ) y = a
[] a x f(x) = ( + a)( x) + ( a)x f(x) = ( a + ) x + a + () x f(x) a a + a > a + () x f(x) a (a + ) a x 4 f (x) = ( + a) ( x) + ( a) x = ( a + a) x + a + = ( a + ) x + a +, () a + a f(x) f(x) = f() = a
熊本県数学問題正解
00 y O x Typed by L A TEX ε ( ) (00 ) 5 4 4 ( ) http://www.ocn.ne.jp/ oboetene/plan/. ( ) (009 ) ( ).. http://www.ocn.ne.jp/ oboetene/plan/eng.html 8 i i..................................... ( )0... (
1
1 1.. ( ) ( ) ( ) (A) E icb φ Et = + cdiva ct (H3) (B) ( ) ct ct ' ctct ' + ' = ' ct ' + ct ' i( ') (H3,H18) 3 (i) cosh Ψ = cosh ΘcoshΩ sinhψ sinhθ sinhω cosh Ψ cosh Θ cosh Ω = sinhψ sinhθ sinhω tanhψ
<4D F736F F D B B83578B6594BB2D834A836F815B82D082C88C60202E646F63>
電気電子数学入門 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/073471 このサンプルページの内容は, 初版 1 刷発行当時のものです. i 14 (tool) [ ] IT ( ) PC (EXCEL) HP() 1 1 4 15 3 010 9 ii 1... 1 1.1 1 1.
0 1-4. 1-5. (1) + b = b +, (2) b = b, (3) + 0 =, (4) 1 =, (5) ( + b) + c = + (b + c), (6) ( b) c = (b c), (7) (b + c) = b + c, (8) ( + b)c = c + bc (9
1-1. 1, 2, 3, 4, 5, 6, 7,, 100,, 1000, n, m m m n n 0 n, m m n 1-2. 0 m n m n 0 2 = 1.41421356 π = 3.141516 1-3. 1 0 1-4. 1-5. (1) + b = b +, (2) b = b, (3) + 0 =, (4) 1 =, (5) ( + b) + c = + (b + c),
( )
18 10 01 ( ) 1 2018 4 1.1 2018............................... 4 1.2 2018......................... 5 2 2017 7 2.1 2017............................... 7 2.2 2017......................... 8 3 2016 9 3.1 2016...............................
007 0 ue ue 6 67 090 b 6666 D 666 0 6 6 0 0 0 4 0 6 7 6 6706 00000 00000 69 000040 000040 0040 0040 000040 000040 0040 0040 674 00000 70 00000 0 00000
EDOGAWA ITY Y @ Y 60 7 66997 00 00 00 00 600 000 000 4900 900 700 000 f 004000 00 000 7f 70g 0 0 007 0 ue ue 6 67 090 b 6666 D 666 0 6 6 0 0 0 4 0 6 7 6 6706 00000 00000 69 000040 000040 0040 0040 000040
4 5.............................................. 5............................................ 6.............................................. 7......................................... 8.3.................................................4.........................................4..............................................4................................................4.3...............................................
HITACHI 液晶プロジェクター CP-AX3505J/CP-AW3005J 取扱説明書 -詳細版- 【技術情報編】
B A C E D 1 3 5 7 9 11 13 15 17 19 2 4 6 8 10 12 14 16 18 H G I F J M N L K Y CB/PB CR/PR COMPONENT VIDEO OUT RS-232C LAN RS-232C LAN LAN BE EF 03 06 00 2A D3 01 00 00 60 00 00 BE EF 03 06 00 BA D2 01
difgeo1.dvi
1 http://matlab0.hwe.oita-u.ac.jp/ matsuo/difgeo.pdf ver.1 8//001 1 1.1 a A. O 1 e 1 ; e ; e e 1 ; e ; e x 1 ;x ;x e 1 ; e ; e X x x x 1 ;x ;x X (x 1 ;x ;x ) 1 1 x x X e e 1 O e x x 1 x x = x 1 e 1 + x
chap1.dvi
1 1 007 1 e iθ = cos θ + isin θ 1) θ = π e iπ + 1 = 0 1 ) 3 11 f 0 r 1 1 ) k f k = 1 + r) k f 0 f k k = 01) f k+1 = 1 + r)f k ) f k+1 f k = rf k 3) 1 ) ) ) 1+r/)f 0 1 1 + r/) f 0 = 1 + r + r /4)f 0 1 f
r III... IV.. grad, div, rot. grad, div, rot 3., B grad, div, rot I, II ɛ-δ web page (
r 8.4.8. 3-3 phone: 9-76-4774, e-mail: hara@math.kyushu-u.ac.jp http://www.math.kyushu-u.ac.jp/~hara/lectures/lectures-j.html Office hours: 4/8 I.. ɛ-n. ɛ-δ 3. 4. II... 3. 4. 5.. r III... IV.. grad, div,
Z: Q: R: C: sin 6 5 ζ a, b
Z: Q: R: C: 3 3 7 4 sin 6 5 ζ 9 6 6............................... 6............................... 6.3......................... 4 7 6 8 8 9 3 33 a, b a bc c b a a b 5 3 5 3 5 5 3 a a a a p > p p p, 3,
微分積分 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. このサンプルページの内容は, 初版 1 刷発行時のものです.
微分積分 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. ttp://www.morikita.co.jp/books/mid/00571 このサンプルページの内容は, 初版 1 刷発行時のものです. i ii 014 10 iii [note] 1 3 iv 4 5 3 6 4 x 0 sin x x 1 5 6 z = f(x, y) 1 y = f(x)
sim0004.dvi
4 : 1 f(x) Z b a dxf(x) (1) ( Double Exponential method=de ) 1 DE N = n T n h h =(b a)=n T n = b a f(a) +f(b) n f + f(a + j b a n )g n j=1 = b a f(a) +f(b) n f + f(a +j b a )g; n n+1 j=1 T n+1 = b a f(a)