. p.1/34
|
|
|
- のぶのすけ ゆきしげ
- 5 years ago
- Views:
Transcription
1 . p.1/34
2 (Optimization) (Mathematical Programming),,. p.2/34
3 p.3/34
4 p.4/34
5 4x + 2y 6, 2x + y 6, x 0, y 0 x, yx + yx, y x + y x + 2y 6, 2x + y 6, x 0, y 0. 2x, y x + y 4x 1, x 2, x 3, x 4 3x 1 + 4x 2 + 2x 3 2x 4 2x 1 + 3x 2 + 4x 3 + x 4 10, 3x 1 + 2x 2 x 3 + 6x 4 8, x 1, x 2, x 3, x 4 :(0). 100, 1000, p.5/34
6 : f(x) (or),: x = (x 1, x 2,..., x n ) S. x j, S : f : x = (x 1,..., x n ), S x f(x) n = 2 S =x, f(x) : f(x) : x* f(x*) f(x) :x (). p.6/34
7 : f(x) (or),: x = (x 1, x 2,..., x n ) S. x j, S : f : x = (x 1,..., x n ), 1.2 (a) (b) (c) =. p.7/34
8 : f(x) (or),: x = (x 1, x 2,..., x n ) S. x j, S : f : x = (x 1,..., x n ), 1.3 S { } S = x R n g j (x) 0 (j = 1, 2,..., p), : h k (x) = 0 (k = 1, 2,..., q), g j h k f,,,. p.8/34
9 (). p.9/34
10 3x, y, z 1, () 3x + 4y + 2z 2x + 3y + 4z 10, 3x + 2y z 8, x 0, y 0, z 0., (), 3x + 4y + 2z 2x + 3y + 4z 10, 3x + 2y z 8, x, y, z :. x + 3x 2 4xy 2y + y 2 + 2z 2 + 4z 2x + 3xy 5y + 4z 2 10, 3x + 2y 2 z 8, x 2 + 3y 2 + 5z p.10/34
11 3x, y, z 2 (), 3x + 4 cos y + 2 log z 2x + 3y 2 + 4z 10, 3e x + 2y z 8, x 0, y 0, z 0.. p.11/34
12 p.12/34
13 LSI. p.13/34
14 2.1 = = mn a ij :j1i c j :jb i :i x j :j : : c 1 x 1 + c 2 x c n x n () a i1 x 1 + a i2 x a in x n b i (i = 1, 2,..., m), x j 0 (j = 1, 2,..., n). =. p.14/34
15 a i :i(/) (i = 1, 2,..., 29) b j :j(/) (j = 1, 2,..., 283) c ij :ij(/) f i :i+(/) S {10,..., 29}: x ij :i j(/) a i f 10 x ij c b ij j (0-1 ) y i = { 1 0. p.15/34
16 p.16/34
17 p.17/34
18 . p.18/34
19 = 32. p.19/34
20 1, x 1 = (x 1 1, x1 2 ), x4 = (x 4 1, x4 2 ) = x i x j = x i x j x 2, x 3, x 4, x 1, x 2, x 3, x 4 x 1 x 1 x 4 = (x 1 1 x 4 1) 2 + (x 1 2 x 4 2) 2 = = 5 (). x 1 1, x 1 2. p.20/34
21 1 = x i x j = x i x j x 2, x 3, x 4, x 1, x 2, x 3, x 4 x 1 n + m+ m. p.21/34
22 x 1 x 2 x 3 a 4 = a 5 = a 6 = a 7 =??? (0,0) (0,1) (1,0) (1,1) x 1 x 2 2 = (x 1 1 x 2 1) 2 + (x 1 2 x 2 2) 2 = x 1 a 4 2 = (x 1 1) 2 + (x 1 2) 2 = p.22/34
23 x 1 x 2 x 3 a 4 = a 5 = a 6 = a 7 =??? (0,0) (0,1) (1,0) (1,1) x 1 x 2 2 = (x 1 1 x 2 1) 2 + (x 1 2 x 2 2) 2 = , x 1 x 3 2 = , x 2 x 3 2 = , x 1 a 4 2 = , x 2 a 5 2 = , x 2 a 7 2 = , x 3 a 6 2 = x 1, x 2, x 3 x 1 x x 3 a p.23/34
24 % : : : :30. p.24/34
25 % : : : :60. p.25/34
26 p.26/34
27 (Linear Program, LP) : 4x 1 + 7x 2 : 5x 1 + 3x 2 21 (1) x 1 + 3x 2 9 (2) x 1 0, x 2 0. nm n = 2, m = 4. (n, m 10, 000). p.27/34
28 (Linear Program, LP) : 4x 1 + 7x 2 : 5x 1 + 3x 2 21 (1) x 1 + 3x 2 9 (2) x 1 0, x x 2 (3,2) 0 0 S (1) (2) 4.2 (a) S= (b) = Dantzig, 1947) x 1. p.28/34
29 3.2 (1947) (1984) S ). p.29/34
30 3.3 (nx 1,..., x n m) : c 1 x c n x n : a i1 x a in x n b i or = b i (i = 1,..., m). n: m:, cont1 40, , , 991 rail4284 1, 092, 610 4, , 372, 358 spal , , , 167, 908 a ij CPLEX xpress-mp CPLEX xpress-mp cont ,389 2,174 2,229 rail ,235 8,928 spal004 4,669 > 200,000. p.30/34
31 p.31/34
32 globallib : 6.3x 5 x x x 3 + x x 6 : 0.820x 2 + x x 6 = 0, 0.98x 4 x 7 (0.01x 5 x 10 + x 4 ) = 0, x 1 x 11 3x 8 = 1.33, x 2 x x 3 + x 6 = 0, x 10 x x 11 = 35.82, x 5 x 12 x 2 ( x x 2 9) = 0, x 8 x x 9 ( x 9 ) 0.325x 7 = 0.574, lbd i x i ubd i (i = 1, 2,..., 14). x 1,..., x n n = 14. x 1,..., x n Sum of Squares of Polynomials). p.32/34
33 globallib : 6.3x 5 x x x 3 + x x 6 : 0.820x 2 + x x 6 = 0, 0.98x 4 x 7 (0.01x 5 x 10 + x 4 ) = 0, x 1 x 11 3x 8 = 1.33, x 2 x x 3 + x 6 = 0, x 10 x x 11 = 35.82, x 5 x 12 x 2 ( x x 2 9) = 0, x 8 x x 9 ( x 9 ) 0.325x 7 = 0.574, lbd i x i ubd i (i = 1, 2,..., 14). 14 ɛ obj ɛ feas ɛ obj ɛ feas 5.6e e ɛ obj = max{1, } () ɛ feas =. p.33/34
34 =() =. p.34/34
AHPを用いた大相撲の新しい番付編成
 5304050 2008/2/15 1 2008/2/15 2 42 2008/2/15 3 2008/2/15 4 195 2008/2/15 5 2008/2/15 6 i j ij >1 ij ij1/>1 i j i 1 ji 1/ j ij 2008/2/15 7 1 =2.01/=0.5 =1.51/=0.67 2008/2/15 8 1 2008/2/15 9 () u ) i i i
5304050 2008/2/15 1 2008/2/15 2 42 2008/2/15 3 2008/2/15 4 195 2008/2/15 5 2008/2/15 6 i j ij >1 ij ij1/>1 i j i 1 ji 1/ j ij 2008/2/15 7 1 =2.01/=0.5 =1.51/=0.67 2008/2/15 8 1 2008/2/15 9 () u ) i i i
( ) () () ( ) () () () ()
 5 1! (Linear Programming, LP) LP OR LP 1.1 1.1.1 1. 2. 3. 4. 4 5. 1000 4 1.1? 1.2 1 1 http://allrecipes.com/ 6 1 1.1 ( ) () 1 0.5 1 0.75 200 () 1.5 1 0.5 1 50 ( ) 2 2 1 30 () 2.25 0.5 2 2.25 30 () 2 100
5 1! (Linear Programming, LP) LP OR LP 1.1 1.1.1 1. 2. 3. 4. 4 5. 1000 4 1.1? 1.2 1 1 http://allrecipes.com/ 6 1 1.1 ( ) () 1 0.5 1 0.75 200 () 1.5 1 0.5 1 50 ( ) 2 2 1 30 () 2.25 0.5 2 2.25 30 () 2 100
最適化手法 第1回 [3mm] 整数計画法 (1) [3mm]
![最適化手法 第1回 [3mm] 整数計画法 (1) [3mm] 最適化手法 第1回 [3mm] 整数計画法 (1) [3mm]](/thumbs/93/112182844.jpg) 1 (1) & 2014 4 9 ( ) (1) 2014 4 9 1 / 39 2013 ( ) (1) 2014 4 9 2 / 39 OR 1 OR 2 OR Excel ( ) (1) 2014 4 9 3 / 39 1 (4 9 ) 2 (4 16 ) 3 (4 23 ) 4 (4 30 ) 5 (5 7 ) 6 (5 14 ) 7 1 (5 21 ) ( ) (1) 2014 4 9 4
1 (1) & 2014 4 9 ( ) (1) 2014 4 9 1 / 39 2013 ( ) (1) 2014 4 9 2 / 39 OR 1 OR 2 OR Excel ( ) (1) 2014 4 9 3 / 39 1 (4 9 ) 2 (4 16 ) 3 (4 23 ) 4 (4 30 ) 5 (5 7 ) 6 (5 14 ) 7 1 (5 21 ) ( ) (1) 2014 4 9 4
OR 2 Excel 2 3.. 4. OK. 1a: Excel2007 Office. Excel2003 1.. 1b. 2.. 3. OK. 2.,,. ツール アドイン 1b: Excel2003 :,.,.,.,,,.,,. 1. Excel2003.
 OR 2 Excel 1 2 2.1 Excel.,. 2.2, x mathematical programming optimization problem, OR 1., 1 : f(x) h i (x) = 0, i = 1,..., m, g j (x) 0, j = 1,..., l, f(x) h i (x) = 0, i = 1,..., m, g j (x) 0, j = 1,...,
OR 2 Excel 1 2 2.1 Excel.,. 2.2, x mathematical programming optimization problem, OR 1., 1 : f(x) h i (x) = 0, i = 1,..., m, g j (x) 0, j = 1,..., l, f(x) h i (x) = 0, i = 1,..., m, g j (x) 0, j = 1,...,
FX ) 2
 (FX) 1 1 2009 12 12 13 2009 1 FX ) 2 1 (FX) 2 1 2 1 2 3 2010 8 FX 1998 1 FX FX 4 1 1 (FX) () () 1998 4 1 100 120 1 100 120 120 100 20 FX 100 100 100 1 100 100 100 1 100 1 100 100 1 100 101 101 100 100
(FX) 1 1 2009 12 12 13 2009 1 FX ) 2 1 (FX) 2 1 2 1 2 3 2010 8 FX 1998 1 FX FX 4 1 1 (FX) () () 1998 4 1 100 120 1 100 120 120 100 20 FX 100 100 100 1 100 100 100 1 100 1 100 100 1 100 101 101 100 100
xyr x y r x y r u u
 xyr x y r x y r u u y a b u a b a b c d e f g u a b c d e g u u e e f yx a b a b a b c a b c a b a b c a b a b c a b c a b c a u xy a b u a b c d a b c d u ar ar a xy u a b c a b c a b p a b a b c a
xyr x y r x y r u u y a b u a b a b c d e f g u a b c d e g u u e e f yx a b a b a b c a b c a b a b c a b a b c a b c a b c a u xy a b u a b c d a b c d u ar ar a xy u a b c a b c a b p a b a b c a
untitled
 20 7 1 22 7 1 1 2 3 7 8 9 10 11 13 14 15 17 18 19 21 22 - 1 - - 2 - - 3 - - 4 - 50 200 50 200-5 - 50 200 50 200 50 200 - 6 - - 7 - () - 8 - (XY) - 9 - 112-10 - - 11 - - 12 - - 13 - - 14 - - 15 - - 16 -
20 7 1 22 7 1 1 2 3 7 8 9 10 11 13 14 15 17 18 19 21 22 - 1 - - 2 - - 3 - - 4 - 50 200 50 200-5 - 50 200 50 200 50 200 - 6 - - 7 - () - 8 - (XY) - 9 - 112-10 - - 11 - - 12 - - 13 - - 14 - - 15 - - 16 -
untitled
 19 1 19 19 3 8 1 19 1 61 2 479 1965 64 1237 148 1272 58 183 X 1 X 2 12 2 15 A B 5 18 B 29 X 1 12 10 31 A 1 58 Y B 14 1 25 3 31 1 5 5 15 Y B 1 232 Y B 1 4235 14 11 8 5350 2409 X 1 15 10 10 B Y Y 2 X 1 X
19 1 19 19 3 8 1 19 1 61 2 479 1965 64 1237 148 1272 58 183 X 1 X 2 12 2 15 A B 5 18 B 29 X 1 12 10 31 A 1 58 Y B 14 1 25 3 31 1 5 5 15 Y B 1 232 Y B 1 4235 14 11 8 5350 2409 X 1 15 10 10 B Y Y 2 X 1 X
a n a n ( ) (1) a m a n = a m+n (2) (a m ) n = a mn (3) (ab) n = a n b n (4) a m a n = a m n ( m > n ) m n 4 ( ) 552
 3 3.0 a n a n ( ) () a m a n = a m+n () (a m ) n = a mn (3) (ab) n = a n b n (4) a m a n = a m n ( m > n ) m n 4 ( ) 55 3. (n ) a n n a n a n 3 4 = 8 8 3 ( 3) 4 = 8 3 8 ( ) ( ) 3 = 8 8 ( ) 3 n n 4 n n
3 3.0 a n a n ( ) () a m a n = a m+n () (a m ) n = a mn (3) (ab) n = a n b n (4) a m a n = a m n ( m > n ) m n 4 ( ) 55 3. (n ) a n n a n a n 3 4 = 8 8 3 ( 3) 4 = 8 3 8 ( ) ( ) 3 = 8 8 ( ) 3 n n 4 n n
f(x) x S (optimal solution) f(x ) (optimal value) f(x) (1) 3 GLPK glpsol -m -d -m glpsol -h -m -d -o -y --simplex ( ) --interior --min --max --check -
 GLPK by GLPK http://mukun mmg.at.infoseek.co.jp/mmg/glpk/ 17 7 5 : update 1 GLPK GNU Linear Programming Kit GNU LP/MIP ILOG AMPL(A Mathematical Programming Language) 1. 2. 3. 2 (optimization problem) X
GLPK by GLPK http://mukun mmg.at.infoseek.co.jp/mmg/glpk/ 17 7 5 : update 1 GLPK GNU Linear Programming Kit GNU LP/MIP ILOG AMPL(A Mathematical Programming Language) 1. 2. 3. 2 (optimization problem) X
( ) ? () 1.1 ( 3 ) j x j 10 j 1 10 j = 1,..., 10 x 1 + x x 10 =
 5 1! (Linear Programming, LP) LP OR LP 1.1 1.1.1 1. 2. 3. 4. 5. ( ) ( ) 1.1 6 1 1.1 ( ) 1 110 2 98 3 85 4 90 5 73 6 62 7 92 8 88 9 79 10 75 1.1.2 4? 900 40 80 120 () 1.1 ( 3 ) j x j 10 j 1 10 j = 1,...,
5 1! (Linear Programming, LP) LP OR LP 1.1 1.1.1 1. 2. 3. 4. 5. ( ) ( ) 1.1 6 1 1.1 ( ) 1 110 2 98 3 85 4 90 5 73 6 62 7 92 8 88 9 79 10 75 1.1.2 4? 900 40 80 120 () 1.1 ( 3 ) j x j 10 j 1 10 j = 1,...,
応力とひずみ.ppt
 in yukawa@numse.nagoya-u.ac.jp 2 3 4 5 x 2 6 Continuum) 7 8 9 F F 10 F L L F L 1 L F L F L F 11 F L F F L F L L L 1 L 2 12 F L F! A A! S! = F S 13 F L L F F n = F " cos# F t = F " sin# S $ = S cos# S S
in yukawa@numse.nagoya-u.ac.jp 2 3 4 5 x 2 6 Continuum) 7 8 9 F F 10 F L L F L 1 L F L F L F 11 F L F F L F L L L 1 L 2 12 F L F! A A! S! = F S 13 F L L F F n = F " cos# F t = F " sin# S $ = S cos# S S
A
 A05-132 2010 2 11 1 1 3 1.1.......................................... 3 1.2..................................... 3 1.3..................................... 3 2 4 2.1............................... 4 2.2
A05-132 2010 2 11 1 1 3 1.1.......................................... 3 1.2..................................... 3 1.3..................................... 3 2 4 2.1............................... 4 2.2
untitled
 186 17 100160250 1 10.1 55 2 18.5 6.9 100 38 17 3.2 17 8.4 45 3.9 53 1.6 22 7.3 100 2.3 31 3.4 47 OR OR 3 1.20.76 63.4 2.16 4 38,937101,118 17 17 17 5 1,765 1,424 854 794 108 839 628 173 389 339 57 6 18613
186 17 100160250 1 10.1 55 2 18.5 6.9 100 38 17 3.2 17 8.4 45 3.9 53 1.6 22 7.3 100 2.3 31 3.4 47 OR OR 3 1.20.76 63.4 2.16 4 38,937101,118 17 17 17 5 1,765 1,424 854 794 108 839 628 173 389 339 57 6 18613
untitled
 1. 3 14 2. 1 12 9 7.1 3. 5 10 17 8 5500 4. 6 11 5. 1 12 101977 1 21 45.31982.9.4 79.71996 / 1997 89.21983 41.01902 6. 7 5 10 2004 30 16.8 37.5 3.3 2004 10.0 7.5 37.0 2004 8. 2 7 9. 6 11 46 37 25 55 10.
1. 3 14 2. 1 12 9 7.1 3. 5 10 17 8 5500 4. 6 11 5. 1 12 101977 1 21 45.31982.9.4 79.71996 / 1997 89.21983 41.01902 6. 7 5 10 2004 30 16.8 37.5 3.3 2004 10.0 7.5 37.0 2004 8. 2 7 9. 6 11 46 37 25 55 10.
() x + y + y + x dy dx = 0 () dy + xy = x dx y + x y ( 5) ( s55906) 0.7. (). 5 (). ( 6) ( s6590) 0.8 m n. 0.9 n n A. ( 6) ( s6590) f A (λ) = det(a λi)
 0. A A = 4 IC () det A () A () x + y + z = x y z X Y Z = A x y z ( 5) ( s5590) 0. a + b + c b c () a a + b + c c a b a + b + c 0 a b c () a 0 c b b c 0 a c b a 0 0. A A = 7 5 4 5 0 ( 5) ( s5590) () A ()
0. A A = 4 IC () det A () A () x + y + z = x y z X Y Z = A x y z ( 5) ( s5590) 0. a + b + c b c () a a + b + c c a b a + b + c 0 a b c () a 0 c b b c 0 a c b a 0 0. A A = 7 5 4 5 0 ( 5) ( s5590) () A ()
70の法則
 70 70 1 / 27 70 1 2 3 4 5 6 2 / 27 70 70 70 X r % = 70 2 r r r 10 72 70 72 70 : 1, 2, 5, 7, 10, 14, 35, 70 72 : 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72 3 / 27 r = 10 70 r = 10 70 1 : X, X 10 = ( X + X
70 70 1 / 27 70 1 2 3 4 5 6 2 / 27 70 70 70 X r % = 70 2 r r r 10 72 70 72 70 : 1, 2, 5, 7, 10, 14, 35, 70 72 : 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72 3 / 27 r = 10 70 r = 10 70 1 : X, X 10 = ( X + X
「産業上利用することができる発明」の審査の運用指針(案)
 1 1.... 2 1.1... 2 2.... 4 2.1... 4 3.... 6 4.... 6 1 1 29 1 29 1 1 1. 2 1 1.1 (1) (2) (3) 1 (4) 2 4 1 2 2 3 4 31 12 5 7 2.2 (5) ( a ) ( b ) 1 3 2 ( c ) (6) 2. 2.1 2.1 (1) 4 ( i ) ( ii ) ( iii ) ( iv)
1 1.... 2 1.1... 2 2.... 4 2.1... 4 3.... 6 4.... 6 1 1 29 1 29 1 1 1. 2 1 1.1 (1) (2) (3) 1 (4) 2 4 1 2 2 3 4 31 12 5 7 2.2 (5) ( a ) ( b ) 1 3 2 ( c ) (6) 2. 2.1 2.1 (1) 4 ( i ) ( ii ) ( iii ) ( iv)
106 4 4.1 1 25.1 25.4 20.4 17.9 21.2 23.1 26.2 1 24 12 14 18 36 42 24 10 5 15 120 30 15 20 10 25 35 20 18 30 12 4.1 7 min. z = 602.5x 1 + 305.0x 2 + 2
 105 4 0 1? 1 LP 0 1 4.1 4.1.1 (intger programming problem) 1 0.5 x 1 = 447.7 448 / / 2 1.1.2 1. 2. 1000 3. 40 4. 20 106 4 4.1 1 25.1 25.4 20.4 17.9 21.2 23.1 26.2 1 24 12 14 18 36 42 24 10 5 15 120 30
105 4 0 1? 1 LP 0 1 4.1 4.1.1 (intger programming problem) 1 0.5 x 1 = 447.7 448 / / 2 1.1.2 1. 2. 1000 3. 40 4. 20 106 4 4.1 1 25.1 25.4 20.4 17.9 21.2 23.1 26.2 1 24 12 14 18 36 42 24 10 5 15 120 30
2009 IA 5 I 22, 23, 24, 25, 26, (1) Arcsin 1 ( 2 (4) Arccos 1 ) 2 3 (2) Arcsin( 1) (3) Arccos 2 (5) Arctan 1 (6) Arctan ( 3 ) 3 2. n (1) ta
 009 IA 5 I, 3, 4, 5, 6, 7 6 3. () Arcsin ( (4) Arccos ) 3 () Arcsin( ) (3) Arccos (5) Arctan (6) Arctan ( 3 ) 3. n () tan x (nπ π/, nπ + π/) f n (x) f n (x) fn (x) Arctan x () sin x [nπ π/, nπ +π/] g n
009 IA 5 I, 3, 4, 5, 6, 7 6 3. () Arcsin ( (4) Arccos ) 3 () Arcsin( ) (3) Arccos (5) Arctan (6) Arctan ( 3 ) 3. n () tan x (nπ π/, nπ + π/) f n (x) f n (x) fn (x) Arctan x () sin x [nπ π/, nπ +π/] g n
応用数学III-4.ppt
 III f x ( ) = 1 f x ( ) = P( X = x) = f ( x) = P( X = x) =! x ( ) b! a, X! U a,b f ( x) =! " e #!x, X! Ex (!) n! ( n! x)!x! " x 1! " x! e"!, X! Po! ( ) n! x, X! B( n;" ) ( ) ! xf ( x) = = n n!! ( n
III f x ( ) = 1 f x ( ) = P( X = x) = f ( x) = P( X = x) =! x ( ) b! a, X! U a,b f ( x) =! " e #!x, X! Ex (!) n! ( n! x)!x! " x 1! " x! e"!, X! Po! ( ) n! x, X! B( n;" ) ( ) ! xf ( x) = = n n!! ( n
 1 1 1 1 1 1 2 f z 2 C 1, C 2 f 2 C 1, C 2 f(c 2 ) C 2 f(c 1 ) z C 1 f f(z) xy uv ( u v ) = ( a b c d ) ( x y ) + ( p q ) (p + b, q + d) 1 (p + a, q + c) 1 (p, q) 1 1 (b, d) (a, c) 2 3 2 3 a = d, c = b
1 1 1 1 1 1 2 f z 2 C 1, C 2 f 2 C 1, C 2 f(c 2 ) C 2 f(c 1 ) z C 1 f f(z) xy uv ( u v ) = ( a b c d ) ( x y ) + ( p q ) (p + b, q + d) 1 (p + a, q + c) 1 (p, q) 1 1 (b, d) (a, c) 2 3 2 3 a = d, c = b
I, II 1, 2 ɛ-δ 100 A = A 4 : 6 = max{ A, } A A 10
 1 2007.4.13. A 3-312 tel: 092-726-4774, e-mail: hara@math.kyushu-u.ac.jp, http://www.math.kyushu-u.ac.jp/ hara/lectures/lectures-j.html Office hours: B A I ɛ-δ ɛ-δ 1. 2. A 0. 1. 1. 2. 3. 2. ɛ-δ 1. ɛ-n
1 2007.4.13. A 3-312 tel: 092-726-4774, e-mail: hara@math.kyushu-u.ac.jp, http://www.math.kyushu-u.ac.jp/ hara/lectures/lectures-j.html Office hours: B A I ɛ-δ ɛ-δ 1. 2. A 0. 1. 1. 2. 3. 2. ɛ-δ 1. ɛ-n
all.dvi
 72 9 Hooke,,,. Hooke. 9.1 Hooke 1 Hooke. 1, 1 Hooke. σ, ε, Young. σ ε (9.1), Young. τ γ G τ Gγ (9.2) X 1, X 2. Poisson, Poisson ν. ν ε 22 (9.) ε 11 F F X 2 X 1 9.1: Poisson 9.1. Hooke 7 Young Poisson G
72 9 Hooke,,,. Hooke. 9.1 Hooke 1 Hooke. 1, 1 Hooke. σ, ε, Young. σ ε (9.1), Young. τ γ G τ Gγ (9.2) X 1, X 2. Poisson, Poisson ν. ν ε 22 (9.) ε 11 F F X 2 X 1 9.1: Poisson 9.1. Hooke 7 Young Poisson G
v v = v 1 v 2 v 3 (1) R = (R ij ) (2) R (R 1 ) ij = R ji (3) 3 R ij R ik = δ jk (4) i=1 δ ij Kronecker δ ij = { 1 (i = j) 0 (i
 1. 1 1.1 1.1.1 1.1.1.1 v v = v 1 v 2 v 3 (1) R = (R ij ) (2) R (R 1 ) ij = R ji (3) R ij R ik = δ jk (4) δ ij Kronecker δ ij = { 1 (i = j) 0 (i j) (5) 1 1.1. v1.1 2011/04/10 1. 1 2 v i = R ij v j (6) [
1. 1 1.1 1.1.1 1.1.1.1 v v = v 1 v 2 v 3 (1) R = (R ij ) (2) R (R 1 ) ij = R ji (3) R ij R ik = δ jk (4) δ ij Kronecker δ ij = { 1 (i = j) 0 (i j) (5) 1 1.1. v1.1 2011/04/10 1. 1 2 v i = R ij v j (6) [
1 n A a 11 a 1n A =.. a m1 a mn Ax = λx (1) x n λ (eigenvalue problem) x = 0 ( x 0 ) λ A ( ) λ Ax = λx x Ax = λx y T A = λy T x Ax = λx cx ( 1) 1.1 Th
 1 n A a 11 a 1n A = a m1 a mn Ax = λx (1) x n λ (eigenvalue problem) x = ( x ) λ A ( ) λ Ax = λx x Ax = λx y T A = λy T x Ax = λx cx ( 1) 11 Th9-1 Ax = λx λe n A = λ a 11 a 12 a 1n a 21 λ a 22 a n1 a n2
1 n A a 11 a 1n A = a m1 a mn Ax = λx (1) x n λ (eigenvalue problem) x = ( x ) λ A ( ) λ Ax = λx x Ax = λx y T A = λy T x Ax = λx cx ( 1) 11 Th9-1 Ax = λx λe n A = λ a 11 a 12 a 1n a 21 λ a 22 a n1 a n2
BayesfiI‡É“ÅfiK‡È−w‘K‡Ì‡½‡ß‡ÌChow-Liu…A…‰…S…−…Y…•
 1 / 21 Kruscal V : w i,j R: w i,j = w j,i i j Kruscal (w i,j 0 ) 1 E {{i, j} i, j V, i i} 2 E {} 3 while(e = ϕ) for w i,j {i, j} E 1 E E\{i, j} 2 G = (V, E {i, j}) = E E {i, j} G {i,j} E w i,j 2 / 21 w
1 / 21 Kruscal V : w i,j R: w i,j = w j,i i j Kruscal (w i,j 0 ) 1 E {{i, j} i, j V, i i} 2 E {} 3 while(e = ϕ) for w i,j {i, j} E 1 E E\{i, j} 2 G = (V, E {i, j}) = E E {i, j} G {i,j} E w i,j 2 / 21 w
.1 A cos 2π 3 sin 2π 3 sin 2π 3 cos 2π 3 T ra 2 deta T ra 2 deta T ra 2 deta a + d 2 ad bc a 2 + d 2 + ad + bc A 3 a b a 2 + bc ba + d c d ca + d bc +
 .1 n.1 1 A T ra A A a b c d A 2 a b a b c d c d a 2 + bc ab + bd ac + cd bc + d 2 a 2 + bc ba + d ca + d bc + d 2 A a + d b c T ra A T ra A 2 A 2 A A 2 A 2 A n A A n cos 2π sin 2π n n A k sin 2π cos 2π
.1 n.1 1 A T ra A A a b c d A 2 a b a b c d c d a 2 + bc ab + bd ac + cd bc + d 2 a 2 + bc ba + d ca + d bc + d 2 A a + d b c T ra A T ra A 2 A 2 A A 2 A 2 A n A A n cos 2π sin 2π n n A k sin 2π cos 2π
2.2 h h l L h L = l cot h (1) (1) L l L l l = L tan h (2) (2) L l 2 l 3 h 2.3 a h a h (a, h)
 1 16 10 5 1 2 2.1 a a a 1 1 1 2.2 h h l L h L = l cot h (1) (1) L l L l l = L tan h (2) (2) L l 2 l 3 h 2.3 a h a h (a, h) 4 2 3 4 2 5 2.4 x y (x,y) l a x = l cot h cos a, (3) y = l cot h sin a (4) h a
1 16 10 5 1 2 2.1 a a a 1 1 1 2.2 h h l L h L = l cot h (1) (1) L l L l l = L tan h (2) (2) L l 2 l 3 h 2.3 a h a h (a, h) 4 2 3 4 2 5 2.4 x y (x,y) l a x = l cot h cos a, (3) y = l cot h sin a (4) h a
Chapter9 9 LDPC sum-product LDPC 9.1 ( ) 9.2 c 1, c 2, {0, 1, } SUM, PROD : {0, 1, } {0, 1, } SUM(c 1, c 2,, c n ) := { c1 + + c n (c n0 (1 n
 9 LDPC sum-product 9.1 9.2 LDPC 9.1 ( ) 9.2 c 1, c 2, {0, 1, } SUM, PROD : {0, 1, } {0, 1, } SUM(c 1, c 2,, c n ) := { c1 + + c n (c n0 (1 n 0 n)) ( ) 0 (N(0 c) > N(1 c)) PROD(c 1, c 2,, c n ) := 1 (N(0
9 LDPC sum-product 9.1 9.2 LDPC 9.1 ( ) 9.2 c 1, c 2, {0, 1, } SUM, PROD : {0, 1, } {0, 1, } SUM(c 1, c 2,, c n ) := { c1 + + c n (c n0 (1 n 0 n)) ( ) 0 (N(0 c) > N(1 c)) PROD(c 1, c 2,, c n ) := 1 (N(0
 3 65 1 4 5 67 1 2 5 5 3 6 68 23 69 2 6 8m 10m 1. 2. 3. 70 66 600km 11 3 16 21 3 0 3m 2m 0 5m 71 11 3 17 0 5 0 0 72 73 74 75 3 76 77 4 78 79 5 80 81 82 83 2 83 . 84 6 a b c d e f g a b c 3 85 16 86 87 7
3 65 1 4 5 67 1 2 5 5 3 6 68 23 69 2 6 8m 10m 1. 2. 3. 70 66 600km 11 3 16 21 3 0 3m 2m 0 5m 71 11 3 17 0 5 0 0 72 73 74 75 3 76 77 4 78 79 5 80 81 82 83 2 83 . 84 6 a b c d e f g a b c 3 85 16 86 87 7
10 1 1 (1) (2) (3) 3 3 1 3 1 3 (4) 2 32 2 (1) 1 1
 10 10 1 1 (1) (2) (3) 3 3 1 3 1 3 (4) 2 32 2 (1) 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 (2) 1 (3) JI S JI S JI S JI S 25 175 J AS 3 (1) 3 70 (2) (3) 100 4 (1)69 (2) (3) (4) (5) (6) (7) (8)70 (9) (10)2 (11)
10 10 1 1 (1) (2) (3) 3 3 1 3 1 3 (4) 2 32 2 (1) 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 (2) 1 (3) JI S JI S JI S JI S 25 175 J AS 3 (1) 3 70 (2) (3) 100 4 (1)69 (2) (3) (4) (5) (6) (7) (8)70 (9) (10)2 (11)
情報理論 第5回 情報量とエントロピー
 5 () ( ) ( ) ( ) p(a) a I(a) p(a) p(a) I(a) p(a) I(a) (2) (self information) p(a) = I(a) = 0 I(a) = 0 I(a) a I(a) = log 2 p(a) = log 2 p(a) bit 2 (log 2 ) (3) I(a) 7 6 5 4 3 2 0 0.5 p(a) p(a) = /2 I(a)
5 () ( ) ( ) ( ) p(a) a I(a) p(a) p(a) I(a) p(a) I(a) (2) (self information) p(a) = I(a) = 0 I(a) = 0 I(a) a I(a) = log 2 p(a) = log 2 p(a) bit 2 (log 2 ) (3) I(a) 7 6 5 4 3 2 0 0.5 p(a) p(a) = /2 I(a)
1 8, : 8.1 1, 2 z = ax + by + c ax by + z c = a b +1 x y z c = 0, (0, 0, c), n = ( a, b, 1). f = n i=1 a ii x 2 i + i<j 2a ij x i x j = ( x, A x), f =
 1 8, : 8.1 1, z = ax + by + c ax by + z c = a b +1 x y z c = 0, (0, 0, c), n = ( a, b, 1). f = a ii x i + i
1 8, : 8.1 1, z = ax + by + c ax by + z c = a b +1 x y z c = 0, (0, 0, c), n = ( a, b, 1). f = a ii x i + i
II Time-stamp: <05/09/30 17:14:06 waki> ii
 II waki@cc.hirosaki-u.ac.jp 18 1 30 II Time-stamp: ii 1 1 1.1.................................................. 1 1.2................................................... 3 1.3..................................................
II waki@cc.hirosaki-u.ac.jp 18 1 30 II Time-stamp: ii 1 1 1.1.................................................. 1 1.2................................................... 3 1.3..................................................
1 I
 1 I 3 1 1.1 R x, y R x + y R x y R x, y, z, a, b R (1.1) (x + y) + z = x + (y + z) (1.2) x + y = y + x (1.3) 0 R : 0 + x = x x R (1.4) x R, 1 ( x) R : x + ( x) = 0 (1.5) (x y) z = x (y z) (1.6) x y =
1 I 3 1 1.1 R x, y R x + y R x y R x, y, z, a, b R (1.1) (x + y) + z = x + (y + z) (1.2) x + y = y + x (1.3) 0 R : 0 + x = x x R (1.4) x R, 1 ( x) R : x + ( x) = 0 (1.5) (x y) z = x (y z) (1.6) x y =
A A = a 41 a 42 a 43 a 44 A (7) 1 (3) A = M 12 = = a 41 (8) a 41 a 43 a 44 (3) n n A, B a i AB = A B ii aa
 1 2 21 2 2 [ ] a 11 a 12 A = a 21 a 22 (1) A = a 11 a 22 a 12 a 21 (2) 3 3 n n A A = n ( 1) i+j a ij M ij i =1 n (3) j=1 M ij A i j (n 1) (n 1) 2-1 3 3 A A = a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33
1 2 21 2 2 [ ] a 11 a 12 A = a 21 a 22 (1) A = a 11 a 22 a 12 a 21 (2) 3 3 n n A A = n ( 1) i+j a ij M ij i =1 n (3) j=1 M ij A i j (n 1) (n 1) 2-1 3 3 A A = a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33
[FX8/FX8C]シリーズカタログ
![[FX8/FX8C]シリーズカタログ [FX8/FX8C]シリーズカタログ](/thumbs/93/112672231.jpg) 2018.6 FX8-120 P - SV 192 1 2 3 1 2 3 4 5 6 6 B 4 5 6 B 0.6±0.1 B +0.05 _0.2 C +0.05 _0.2 D±0.2 6.5 _0.3 0 5.1±0.3 2.45±0.25 (0.4) (0.75) (Ø0.9) t0.2±0.03 w0.25±0.03 (Ø0.6) 2-(C0.2) (1.5) E±0.1 FX8-60P-SV(**)
2018.6 FX8-120 P - SV 192 1 2 3 1 2 3 4 5 6 6 B 4 5 6 B 0.6±0.1 B +0.05 _0.2 C +0.05 _0.2 D±0.2 6.5 _0.3 0 5.1±0.3 2.45±0.25 (0.4) (0.75) (Ø0.9) t0.2±0.03 w0.25±0.03 (Ø0.6) 2-(C0.2) (1.5) E±0.1 FX8-60P-SV(**)
May Copyright 2016 HIROSE ELECTRIC CO., LTD. All Rights Reserved w
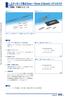 2014.9w FX8-120 P - SV 192 1 2 3 1 2 3 4 5 6 6 B 4 5 6 B 0.6±0.1 B +0.05 _0.2 C +0.05 _0.2 D±0.2 6.5 _0.3 0 5.1±0.3 2.45±0.25 (0.4) (0.75) (Ø0.9) t0.2±0.03 w0.25±0.03 (Ø0.6) 2-(C0.2) (1.5) E±0.1 FX8-60P-SV(92)
2014.9w FX8-120 P - SV 192 1 2 3 1 2 3 4 5 6 6 B 4 5 6 B 0.6±0.1 B +0.05 _0.2 C +0.05 _0.2 D±0.2 6.5 _0.3 0 5.1±0.3 2.45±0.25 (0.4) (0.75) (Ø0.9) t0.2±0.03 w0.25±0.03 (Ø0.6) 2-(C0.2) (1.5) E±0.1 FX8-60P-SV(92)
2 1/2 1/4 x 1 x 2 x 1, x 2 9 3x 1 + 2x 2 9 (1.1) 1/3 RDA 1 15 x /4 RDA 1 6 x /6 1 x 1 3 x 2 15 x (1.2) (1.3) (1.4) 1 2 (1.5) x 1
 1 1 [1] 1.1 1.1. TS 9 1/3 RDA 1/4 RDA 1 1/2 1/4 50 65 3 2 1/15 RDA 2/15 RDA 1/6 RDA 1 1/6 1 1960 2 1/2 1/4 x 1 x 2 x 1, x 2 9 3x 1 + 2x 2 9 (1.1) 1/3 RDA 1 15 x 1 + 2 1/4 RDA 1 6 x 1 1 4 1 1/6 1 x 1 3
1 1 [1] 1.1 1.1. TS 9 1/3 RDA 1/4 RDA 1 1/2 1/4 50 65 3 2 1/15 RDA 2/15 RDA 1/6 RDA 1 1/6 1 1960 2 1/2 1/4 x 1 x 2 x 1, x 2 9 3x 1 + 2x 2 9 (1.1) 1/3 RDA 1 15 x 1 + 2 1/4 RDA 1 6 x 1 1 4 1 1/6 1 x 1 3
弾性定数の対称性について
 () by T. oyama () ij C ij = () () C, C, C () ij ji ij ijlk ij ij () C C C C C C * C C C C C * * C C C C = * * * C C C * * * * C C * * * * * C () * P (,, ) P (,, ) lij = () P (,, ) P(,, ) (,, ) P (, 00,
() by T. oyama () ij C ij = () () C, C, C () ij ji ij ijlk ij ij () C C C C C C * C C C C C * * C C C C = * * * C C C * * * * C C * * * * * C () * P (,, ) P (,, ) lij = () P (,, ) P(,, ) (,, ) P (, 00,
第3章 非線形計画法の基礎
 3 February 25, 2009 1 Armijo Wolfe Newton 2 Newton Lagrange Newton 2 SQP 2 1 2.1 ( ) S R n (n N) f (x) : R n x f R x S f (x ) = min x S R n f (x) (nonlinear programming) x 0 S k = 0, 1, 2, h k R n ɛ k
3 February 25, 2009 1 Armijo Wolfe Newton 2 Newton Lagrange Newton 2 SQP 2 1 2.1 ( ) S R n (n N) f (x) : R n x f R x S f (x ) = min x S R n f (x) (nonlinear programming) x 0 S k = 0, 1, 2, h k R n ɛ k
1.2 y + P (x)y + Q(x)y = 0 (1) y 1 (x), y 2 (x) y 1 (x), y 2 (x) (1) y(x) c 1, c 2 y(x) = c 1 y 1 (x) + c 2 y 2 (x) 3 y 1 (x) y 1 (x) e R P (x)dx y 2
 1 1.1 R(x) = 0 y + P (x)y + Q(x)y = R(x)...(1) y + P (x)y + Q(x)y = 0...(2) 1 2 u(x) v(x) c 1 u(x)+ c 2 v(x) = 0 c 1 = c 2 = 0 c 1 = c 2 = 0 2 0 2 u(x) v(x) u(x) u (x) W (u, v)(x) = v(x) v (x) 0 1 1.2
1 1.1 R(x) = 0 y + P (x)y + Q(x)y = R(x)...(1) y + P (x)y + Q(x)y = 0...(2) 1 2 u(x) v(x) c 1 u(x)+ c 2 v(x) = 0 c 1 = c 2 = 0 c 1 = c 2 = 0 2 0 2 u(x) v(x) u(x) u (x) W (u, v)(x) = v(x) v (x) 0 1 1.2
k m m d2 x i dt 2 = f i = kx i (i = 1, 2, 3 or x, y, z) f i σ ij x i e ij = 2.1 Hooke s law and elastic constants (a) x i (2.1) k m σ A σ σ σ σ f i x
 k m m d2 x i dt 2 = f i = kx i (i = 1, 2, 3 or x, y, z) f i ij x i e ij = 2.1 Hooke s law and elastic constants (a) x i (2.1) k m A f i x i B e e e e 0 e* e e (2.1) e (b) A e = 0 B = 0 (c) (2.1) (d) e
k m m d2 x i dt 2 = f i = kx i (i = 1, 2, 3 or x, y, z) f i ij x i e ij = 2.1 Hooke s law and elastic constants (a) x i (2.1) k m A f i x i B e e e e 0 e* e e (2.1) e (b) A e = 0 B = 0 (c) (2.1) (d) e
II 2 3.,, A(B + C) = AB + AC, (A + B)C = AC + BC. 4. m m A, m m B,, m m B, AB = BA, A,, I. 5. m m A, m n B, AB = B, A I E, 4 4 I, J, K
 II. () 7 F 7 = { 0,, 2, 3, 4, 5, 6 }., F 7 a, b F 7, a b, F 7,. (a) a, b,,. (b) 7., 4 5 = 20 = 2 7 + 6, 4 5 = 6 F 7., F 7,., 0 a F 7, ab = F 7 b F 7. (2) 7, 6 F 6 = { 0,, 2, 3, 4, 5 },,., F 6., 0 0 a F
II. () 7 F 7 = { 0,, 2, 3, 4, 5, 6 }., F 7 a, b F 7, a b, F 7,. (a) a, b,,. (b) 7., 4 5 = 20 = 2 7 + 6, 4 5 = 6 F 7., F 7,., 0 a F 7, ab = F 7 b F 7. (2) 7, 6 F 6 = { 0,, 2, 3, 4, 5 },,., F 6., 0 0 a F
M3 x y f(x, y) (= x) (= y) x + y f(x, y) = x + y + *. f(x, y) π y f(x, y) x f(x + x, y) f(x, y) lim x x () f(x,y) x 3 -
 M3............................................................................................ 3.3................................................... 3 6........................................... 6..........................................
M3............................................................................................ 3.3................................................... 3 6........................................... 6..........................................
OR#5.key
 オペレーションズ リサーチ1 Operations Research 前学期 月曜 3限(3:00-4:30) 8 整数計画モデル Integer Programming 経営A棟106教室 山本芳嗣 筑波大学 大学院 システム情報工学研究科 整数計画問題 2 凸包 最小の凸集合 線形計画問題 変数の整数条件 ctx Ax b x 0 xj は整数 IP LP 3 4 Bx d!!!!!? P NP
オペレーションズ リサーチ1 Operations Research 前学期 月曜 3限(3:00-4:30) 8 整数計画モデル Integer Programming 経営A棟106教室 山本芳嗣 筑波大学 大学院 システム情報工学研究科 整数計画問題 2 凸包 最小の凸集合 線形計画問題 変数の整数条件 ctx Ax b x 0 xj は整数 IP LP 3 4 Bx d!!!!!? P NP
7 27 7.1........................................ 27 7.2.......................................... 28 1 ( a 3 = 3 = 3 a a > 0(a a a a < 0(a a a -1 1 6
 26 11 5 1 ( 2 2 2 3 5 3.1...................................... 5 3.2....................................... 5 3.3....................................... 6 3.4....................................... 7
26 11 5 1 ( 2 2 2 3 5 3.1...................................... 5 3.2....................................... 5 3.3....................................... 6 3.4....................................... 7
untitled
 20010916 22;1017;23;20020108;15;20; 1 N = {1, 2, } Z + = {0, 1, 2, } Z = {0, ±1, ±2, } Q = { p p Z, q N} R = { lim a q n n a n Q, n N; sup a n < } R + = {x R x 0} n = {a + b 1 a, b R} u, v 1 R 2 2 R 3
20010916 22;1017;23;20020108;15;20; 1 N = {1, 2, } Z + = {0, 1, 2, } Z = {0, ±1, ±2, } Q = { p p Z, q N} R = { lim a q n n a n Q, n N; sup a n < } R + = {x R x 0} n = {a + b 1 a, b R} u, v 1 R 2 2 R 3
1 (1) ( i ) 60 (ii) 75 (iii) 315 (2) π ( i ) (ii) π (iii) 7 12 π ( (3) r, AOB = θ 0 < θ < π ) OAB A 2 OB P ( AB ) < ( AP ) (4) 0 < θ < π 2 sin θ
 1 (1) ( i ) 60 (ii) 75 (iii) 15 () ( i ) (ii) 4 (iii) 7 1 ( () r, AOB = θ 0 < θ < ) OAB A OB P ( AB ) < ( AP ) (4) 0 < θ < sin θ < θ < tan θ 0 x, 0 y (1) sin x = sin y (x, y) () cos x cos y (x, y) 1 c
1 (1) ( i ) 60 (ii) 75 (iii) 15 () ( i ) (ii) 4 (iii) 7 1 ( () r, AOB = θ 0 < θ < ) OAB A OB P ( AB ) < ( AP ) (4) 0 < θ < sin θ < θ < tan θ 0 x, 0 y (1) sin x = sin y (x, y) () cos x cos y (x, y) 1 c
Chap9.dvi
 .,. f(),, f(),,.,. () lim 2 +3 2 9 (2) lim 3 3 2 9 (4) lim ( ) 2 3 +3 (5) lim 2 9 (6) lim + (7) lim (8) lim (9) lim (0) lim 2 3 + 3 9 2 2 +3 () lim sin 2 sin 2 (2) lim +3 () lim 2 2 9 = 5 5 = 3 (2) lim
.,. f(),, f(),,.,. () lim 2 +3 2 9 (2) lim 3 3 2 9 (4) lim ( ) 2 3 +3 (5) lim 2 9 (6) lim + (7) lim (8) lim (9) lim (0) lim 2 3 + 3 9 2 2 +3 () lim sin 2 sin 2 (2) lim +3 () lim 2 2 9 = 5 5 = 3 (2) lim
: , 2.0, 3.0, 2.0, (%) ( 2.
 2017 1 2 1.1...................................... 2 1.2......................................... 4 1.3........................................... 10 1.4................................. 14 1.5..........................................
2017 1 2 1.1...................................... 2 1.2......................................... 4 1.3........................................... 10 1.4................................. 14 1.5..........................................
I, II 1, A = A 4 : 6 = max{ A, } A A 10 10%
 1 2006.4.17. A 3-312 tel: 092-726-4774, e-mail: hara@math.kyushu-u.ac.jp, http://www.math.kyushu-u.ac.jp/ hara/lectures/lectures-j.html Office hours: B A I ɛ-δ ɛ-δ 1. 2. A 1. 1. 2. 3. 4. 5. 2. ɛ-δ 1. ɛ-n
1 2006.4.17. A 3-312 tel: 092-726-4774, e-mail: hara@math.kyushu-u.ac.jp, http://www.math.kyushu-u.ac.jp/ hara/lectures/lectures-j.html Office hours: B A I ɛ-δ ɛ-δ 1. 2. A 1. 1. 2. 3. 4. 5. 2. ɛ-δ 1. ɛ-n
i
 i 3 4 4 7 5 6 3 ( ).. () 3 () (3) (4) /. 3. 4/3 7. /e 8. a > a, a = /, > a >. () a >, a =, > a > () a > b, a = b, a < b. c c n a n + b n + c n 3c n..... () /3 () + (3) / (4) /4 (5) m > n, a b >, m > n,
i 3 4 4 7 5 6 3 ( ).. () 3 () (3) (4) /. 3. 4/3 7. /e 8. a > a, a = /, > a >. () a >, a =, > a > () a > b, a = b, a < b. c c n a n + b n + c n 3c n..... () /3 () + (3) / (4) /4 (5) m > n, a b >, m > n,
CALCULUS II (Hiroshi SUZUKI ) f(x, y) A(a, b) 1. P (x, y) A(a, b) A(a, b) f(x, y) c f(x, y) A(a, b) c f(x, y) c f(x, y) c (x a, y b)
 CALCULUS II (Hiroshi SUZUKI ) 16 1 1 1.1 1.1 f(x, y) A(a, b) 1. P (x, y) A(a, b) A(a, b) f(x, y) c f(x, y) A(a, b) c f(x, y) c f(x, y) c (x a, y b) lim f(x, y) = lim f(x, y) = lim f(x, y) = c. x a, y b
CALCULUS II (Hiroshi SUZUKI ) 16 1 1 1.1 1.1 f(x, y) A(a, b) 1. P (x, y) A(a, b) A(a, b) f(x, y) c f(x, y) A(a, b) c f(x, y) c f(x, y) c (x a, y b) lim f(x, y) = lim f(x, y) = lim f(x, y) = c. x a, y b
1 No.1 5 C 1 I III F 1 F 2 F 1 F 2 2 Φ 2 (t) = Φ 1 (t) Φ 1 (t t). = Φ 1(t) t = ( 1.5e 0.5t 2.4e 4t 2e 10t ) τ < 0 t > τ Φ 2 (t) < 0 lim t Φ 2 (t) = 0
 1 No.1 5 C 1 I III F 1 F 2 F 1 F 2 2 Φ 2 (t) = Φ 1 (t) Φ 1 (t t). = Φ 1(t) t = ( 1.5e 0.5t 2.4e 4t 2e 10t ) τ < 0 t > τ Φ 2 (t) < 0 lim t Φ 2 (t) = 0 0 < t < τ I II 0 No.2 2 C x y x y > 0 x 0 x > b a dx
1 No.1 5 C 1 I III F 1 F 2 F 1 F 2 2 Φ 2 (t) = Φ 1 (t) Φ 1 (t t). = Φ 1(t) t = ( 1.5e 0.5t 2.4e 4t 2e 10t ) τ < 0 t > τ Φ 2 (t) < 0 lim t Φ 2 (t) = 0 0 < t < τ I II 0 No.2 2 C x y x y > 0 x 0 x > b a dx
untitled
 ,, 2 2.,, A, PC/AT, MB, 5GB,,,, ( ) MB, GB 2,5,, 8MB, A, MB, GB 2 A,,,? x MB, y GB, A (), x + 2y () 4 (,, ) (hanba@eee.u-ryukyu.ac.jp), A, x + 2y() x y, A, MB ( ) 8 MB ( ) 5GB ( ) ( ), x x x 8 (2) y y
,, 2 2.,, A, PC/AT, MB, 5GB,,,, ( ) MB, GB 2,5,, 8MB, A, MB, GB 2 A,,,? x MB, y GB, A (), x + 2y () 4 (,, ) (hanba@eee.u-ryukyu.ac.jp), A, x + 2y() x y, A, MB ( ) 8 MB ( ) 5GB ( ) ( ), x x x 8 (2) y y
* n x 11,, x 1n N(µ 1, σ 2 ) x 21,, x 2n N(µ 2, σ 2 ) H 0 µ 1 = µ 2 (= µ ) H 1 µ 1 µ 2 H 0, H 1 *2 σ 2 σ 2 0, σ 2 1 *1 *2 H 0 H
 1 1 1.1 *1 1. 1.3.1 n x 11,, x 1n Nµ 1, σ x 1,, x n Nµ, σ H 0 µ 1 = µ = µ H 1 µ 1 µ H 0, H 1 * σ σ 0, σ 1 *1 * H 0 H 0, H 1 H 1 1 H 0 µ, σ 0 H 1 µ 1, µ, σ 1 L 0 µ, σ x L 1 µ 1, µ, σ x x H 0 L 0 µ, σ 0
1 1 1.1 *1 1. 1.3.1 n x 11,, x 1n Nµ 1, σ x 1,, x n Nµ, σ H 0 µ 1 = µ = µ H 1 µ 1 µ H 0, H 1 * σ σ 0, σ 1 *1 * H 0 H 0, H 1 H 1 1 H 0 µ, σ 0 H 1 µ 1, µ, σ 1 L 0 µ, σ x L 1 µ 1, µ, σ x x H 0 L 0 µ, σ 0
newmain.dvi
 数論 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/008142 このサンプルページの内容は, 第 2 版 1 刷発行当時のものです. Daniel DUVERNEY: THÉORIE DES NOMBRES c Dunod, Paris, 1998, This book is published
数論 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/008142 このサンプルページの内容は, 第 2 版 1 刷発行当時のものです. Daniel DUVERNEY: THÉORIE DES NOMBRES c Dunod, Paris, 1998, This book is published
4 4 4 a b c d a b A c d A a da ad bce O E O n A n O ad bc a d n A n O 5 {a n } S n a k n a n + k S n a a n+ S n n S n n log x x {xy } x, y x + y 7 fx
 4 4 5 4 I II III A B C, 5 7 I II A B,, 8, 9 I II A B O A,, Bb, b, Cc, c, c b c b b c c c OA BC P BC OP BC P AP BC n f n x xn e x! e n! n f n x f n x f n x f k x k 4 e > f n x dx k k! fx sin x cos x tan
4 4 5 4 I II III A B C, 5 7 I II A B,, 8, 9 I II A B O A,, Bb, b, Cc, c, c b c b b c c c OA BC P BC OP BC P AP BC n f n x xn e x! e n! n f n x f n x f n x f k x k 4 e > f n x dx k k! fx sin x cos x tan
DVIOUT
 A. A. A-- [ ] f(x) x = f 00 (x) f 0 () =0 f 00 () > 0= f(x) x = f 00 () < 0= f(x) x = A--2 [ ] f(x) D f 00 (x) > 0= y = f(x) f 00 (x) < 0= y = f(x) P (, f()) f 00 () =0 A--3 [ ] y = f(x) [, b] x = f (y)
A. A. A-- [ ] f(x) x = f 00 (x) f 0 () =0 f 00 () > 0= f(x) x = f 00 () < 0= f(x) x = A--2 [ ] f(x) D f 00 (x) > 0= y = f(x) f 00 (x) < 0= y = f(x) P (, f()) f 00 () =0 A--3 [ ] y = f(x) [, b] x = f (y)
1 1.1 ( ). z = a + bi, a, b R 0 a, b 0 a 2 + b 2 0 z = a + bi = ( ) a 2 + b 2 a a 2 + b + b 2 a 2 + b i 2 r = a 2 + b 2 θ cos θ = a a 2 + b 2, sin θ =
 1 1.1 ( ). z = + bi,, b R 0, b 0 2 + b 2 0 z = + bi = ( ) 2 + b 2 2 + b + b 2 2 + b i 2 r = 2 + b 2 θ cos θ = 2 + b 2, sin θ = b 2 + b 2 2π z = r(cos θ + i sin θ) 1.2 (, ). 1. < 2. > 3. ±,, 1.3 ( ). A
1 1.1 ( ). z = + bi,, b R 0, b 0 2 + b 2 0 z = + bi = ( ) 2 + b 2 2 + b + b 2 2 + b i 2 r = 2 + b 2 θ cos θ = 2 + b 2, sin θ = b 2 + b 2 2π z = r(cos θ + i sin θ) 1.2 (, ). 1. < 2. > 3. ±,, 1.3 ( ). A
Part y mx + n mt + n m 1 mt n + n t m 2 t + mn 0 t m 0 n 18 y n n a 7 3 ; x α α 1 7α +t t 3 4α + 3t t x α x α y mx + n
 Part2 47 Example 161 93 1 T a a 2 M 1 a 1 T a 2 a Point 1 T L L L T T L L T L L L T T L L T detm a 1 aa 2 a 1 2 + 1 > 0 11 T T x x M λ 12 y y x y λ 2 a + 1λ + a 2 2a + 2 0 13 D D a + 1 2 4a 2 2a + 2 a
Part2 47 Example 161 93 1 T a a 2 M 1 a 1 T a 2 a Point 1 T L L L T T L L T L L L T T L L T detm a 1 aa 2 a 1 2 + 1 > 0 11 T T x x M λ 12 y y x y λ 2 a + 1λ + a 2 2a + 2 0 13 D D a + 1 2 4a 2 2a + 2 a
III 1 (X, d) d U d X (X, d). 1. (X, d).. (i) d(x, y) d(z, y) d(x, z) (ii) d(x, y) d(z, w) d(x, z) + d(y, w) 2. (X, d). F X.. (1), X F, (2) F 1, F 2 F
 III 1 (X, d) d U d X (X, d). 1. (X, d).. (i) d(x, y) d(z, y) d(x, z) (ii) d(x, y) d(z, w) d(x, z) + d(y, w) 2. (X, d). F X.. (1), X F, (2) F 1, F 2 F F 1 F 2 F, (3) F λ F λ F λ F. 3., A λ λ A λ. B λ λ
III 1 (X, d) d U d X (X, d). 1. (X, d).. (i) d(x, y) d(z, y) d(x, z) (ii) d(x, y) d(z, w) d(x, z) + d(y, w) 2. (X, d). F X.. (1), X F, (2) F 1, F 2 F F 1 F 2 F, (3) F λ F λ F λ F. 3., A λ λ A λ. B λ λ
x, y x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = 15 xy (x y) (x + y) xy (x y) (x y) ( x 2 + xy + y 2) = 15 (x y)
 x, y x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = 15 1 1977 x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = 15 xy (x y) (x + y) xy (x y) (x y) ( x 2 + xy + y 2) = 15 (x y) ( x 2 y + xy 2 x 2 2xy y 2) = 15 (x y) (x + y) (xy
x, y x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = 15 1 1977 x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = 15 xy (x y) (x + y) xy (x y) (x y) ( x 2 + xy + y 2) = 15 (x y) ( x 2 y + xy 2 x 2 2xy y 2) = 15 (x y) (x + y) (xy
微分積分 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. このサンプルページの内容は, 初版 1 刷発行時のものです.
 微分積分 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. ttp://www.morikita.co.jp/books/mid/00571 このサンプルページの内容は, 初版 1 刷発行時のものです. i ii 014 10 iii [note] 1 3 iv 4 5 3 6 4 x 0 sin x x 1 5 6 z = f(x, y) 1 y = f(x)
微分積分 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. ttp://www.morikita.co.jp/books/mid/00571 このサンプルページの内容は, 初版 1 刷発行時のものです. i ii 014 10 iii [note] 1 3 iv 4 5 3 6 4 x 0 sin x x 1 5 6 z = f(x, y) 1 y = f(x)
分散分析・2次元正規分布
 2 II L10(2016-06-30 Thu) : Time-stamp: 2016-06-30 Thu 13:55 JST hig F 2.. http://hig3.net ( ) L10 2 II(2016) 1 / 24 F 2 F L09-Q1 Quiz :F 1 α = 0.05, 2 F 3 H 0, : σ 2 1 /σ2 2 = 1., H 1, σ 2 1 /σ2 2 1. 4
2 II L10(2016-06-30 Thu) : Time-stamp: 2016-06-30 Thu 13:55 JST hig F 2.. http://hig3.net ( ) L10 2 II(2016) 1 / 24 F 2 F L09-Q1 Quiz :F 1 α = 0.05, 2 F 3 H 0, : σ 2 1 /σ2 2 = 1., H 1, σ 2 1 /σ2 2 1. 4
arctan 1 arctan arctan arctan π = = ( ) π = 4 = π = π = π = =
 arctan arctan arctan arctan 2 2000 π = 3 + 8 = 3.25 ( ) 2 8 650 π = 4 = 3.6049 9 550 π = 3 3 30 π = 3.622 264 π = 3.459 3 + 0 7 = 3.4085 < π < 3 + 7 = 3.4286 380 π = 3 + 77 250 = 3.46 5 3.45926 < π < 3.45927
arctan arctan arctan arctan 2 2000 π = 3 + 8 = 3.25 ( ) 2 8 650 π = 4 = 3.6049 9 550 π = 3 3 30 π = 3.622 264 π = 3.459 3 + 0 7 = 3.4085 < π < 3 + 7 = 3.4286 380 π = 3 + 77 250 = 3.46 5 3.45926 < π < 3.45927
,, etc. ( ) [Marti & Stoeckel 04] [Lloyd Smith, Chuang & Munro 90], [Staat & Heitzer 03] worst-case detection [Elishakoff, Haftka & Fang 94] 2 [Cheng
![,, etc. ( ) [Marti & Stoeckel 04] [Lloyd Smith, Chuang & Munro 90], [Staat & Heitzer 03] worst-case detection [Elishakoff, Haftka & Fang 94] 2 [Cheng ,, etc. ( ) [Marti & Stoeckel 04] [Lloyd Smith, Chuang & Munro 90], [Staat & Heitzer 03] worst-case detection [Elishakoff, Haftka & Fang 94] 2 [Cheng](/thumbs/91/107176190.jpg) ( ) ( ) OPTIS 2006 p.1/17 ,, etc. ( ) [Marti & Stoeckel 04] [Lloyd Smith, Chuang & Munro 90], [Staat & Heitzer 03] worst-case detection [Elishakoff, Haftka & Fang 94] 2 [Cheng et al. 02], [Craig et al.
( ) ( ) OPTIS 2006 p.1/17 ,, etc. ( ) [Marti & Stoeckel 04] [Lloyd Smith, Chuang & Munro 90], [Staat & Heitzer 03] worst-case detection [Elishakoff, Haftka & Fang 94] 2 [Cheng et al. 02], [Craig et al.
9 2 1 f(x, y) = xy sin x cos y x y cos y y x sin x d (x, y) = y cos y (x sin x) = y cos y(sin x + x cos x) x dx d (x, y) = x sin x (y cos y) = x sin x
 2009 9 6 16 7 1 7.1 1 1 1 9 2 1 f(x, y) = xy sin x cos y x y cos y y x sin x d (x, y) = y cos y (x sin x) = y cos y(sin x + x cos x) x dx d (x, y) = x sin x (y cos y) = x sin x(cos y y sin y) y dy 1 sin
2009 9 6 16 7 1 7.1 1 1 1 9 2 1 f(x, y) = xy sin x cos y x y cos y y x sin x d (x, y) = y cos y (x sin x) = y cos y(sin x + x cos x) x dx d (x, y) = x sin x (y cos y) = x sin x(cos y y sin y) y dy 1 sin
2012_00表紙
 02 Network Program 05 1 2 3 4 5 6 1 13 60 5,800 06 07 Program 10 12 Program 14 Program 18 20 Program 22 24 Program 25 26 27 28 29 30 31 32 Program 33 34 35 40 Program 41 42 43 44 45 46 Program
02 Network Program 05 1 2 3 4 5 6 1 13 60 5,800 06 07 Program 10 12 Program 14 Program 18 20 Program 22 24 Program 25 26 27 28 29 30 31 32 Program 33 34 35 40 Program 41 42 43 44 45 46 Program
タ 縺29135 タ 縺5 [ y 1 x i R 8 x j 1 7,5 2 x , チ7192, (2) チ41299 f 675
 139ィ 48 1995 3. 753 165, 2 6 86 タ7 9 998917619 4381 縺48 縺55 317832645 タ5 縺4273 971927, 95652539358195 45 チ5197 9 4527259495 2 7545953471 129175253471 9557991 3.9. タ52917652 縺1874ィ 989 95652539358195 45
139ィ 48 1995 3. 753 165, 2 6 86 タ7 9 998917619 4381 縺48 縺55 317832645 タ5 縺4273 971927, 95652539358195 45 チ5197 9 4527259495 2 7545953471 129175253471 9557991 3.9. タ52917652 縺1874ィ 989 95652539358195 45
. p.1/15
 . p./5 [ ] x y y x x y fx) y fx) x y. p.2/5 [ ] x y y x x y fx) y fx) x y y x y x y fx) f y) x f y) f f f f. p.2/5 [ ] x y y x x y fx) y fx) x y y x y x y fx) f y) x f y) f f f f [ ] a > y a x R ). p.2/5
. p./5 [ ] x y y x x y fx) y fx) x y. p.2/5 [ ] x y y x x y fx) y fx) x y y x y x y fx) f y) x f y) f f f f. p.2/5 [ ] x y y x x y fx) y fx) x y y x y x y fx) f y) x f y) f f f f [ ] a > y a x R ). p.2/5
A A p.1/16
 A A p./6 A p.2/6 [ ] x y y x x y fx) y fx) x y A p.3/6 [ ] x y y x x y fx) y fx) x y y x y x y fx) f y) x f y) f f f f A p.3/6 [ ] x y y x x y fx) y fx) x y y x y x y fx) f y) x f y) f f f f [ ] a > y
A A p./6 A p.2/6 [ ] x y y x x y fx) y fx) x y A p.3/6 [ ] x y y x x y fx) y fx) x y y x y x y fx) f y) x f y) f f f f A p.3/6 [ ] x y y x x y fx) y fx) x y y x y x y fx) f y) x f y) f f f f [ ] a > y
カテゴリ変数と独立性の検定
 II L04(2015-05-01 Fri) : Time-stamp: 2015-05-01 Fri 22:28 JST hig 2, Excel 2, χ 2,. http://hig3.net () L04 II(2015) 1 / 20 : L03-S1 Quiz : 1 2 7 3 12 (x = 2) 12 (y = 3) P (X = x) = 5 12 (x = 3), P (Y =
II L04(2015-05-01 Fri) : Time-stamp: 2015-05-01 Fri 22:28 JST hig 2, Excel 2, χ 2,. http://hig3.net () L04 II(2015) 1 / 20 : L03-S1 Quiz : 1 2 7 3 12 (x = 2) 12 (y = 3) P (X = x) = 5 12 (x = 3), P (Y =
Part () () Γ Part ,
 Contents a 6 6 6 6 6 6 6 7 7. 8.. 8.. 8.3. 8 Part. 9. 9.. 9.. 3. 3.. 3.. 3 4. 5 4.. 5 4.. 9 4.3. 3 Part. 6 5. () 6 5.. () 7 5.. 9 5.3. Γ 3 6. 3 6.. 3 6.. 3 6.3. 33 Part 3. 34 7. 34 7.. 34 7.. 34 8. 35
Contents a 6 6 6 6 6 6 6 7 7. 8.. 8.. 8.3. 8 Part. 9. 9.. 9.. 3. 3.. 3.. 3 4. 5 4.. 5 4.. 9 4.3. 3 Part. 6 5. () 6 5.. () 7 5.. 9 5.3. Γ 3 6. 3 6.. 3 6.. 3 6.3. 33 Part 3. 34 7. 34 7.. 34 7.. 34 8. 35
: BV15005
 29 5 26 : BV15005 1 1 1.1............................................. 1 1.2........................................ 1 1.3........................................ 1 2 3 2.1.............................................
29 5 26 : BV15005 1 1 1.1............................................. 1 1.2........................................ 1 1.3........................................ 1 2 3 2.1.............................................
 II 1 3 2 5 3 7 4 8 5 11 6 13 7 16 8 18 2 1 1. x 2 + xy x y (1 lim (x,y (1,1 x 1 x 3 + y 3 (2 lim (x,y (, x 2 + y 2 x 2 (3 lim (x,y (, x 2 + y 2 xy (4 lim (x,y (, x 2 + y 2 x y (5 lim (x,y (, x + y x 3y
II 1 3 2 5 3 7 4 8 5 11 6 13 7 16 8 18 2 1 1. x 2 + xy x y (1 lim (x,y (1,1 x 1 x 3 + y 3 (2 lim (x,y (, x 2 + y 2 x 2 (3 lim (x,y (, x 2 + y 2 xy (4 lim (x,y (, x 2 + y 2 x y (5 lim (x,y (, x + y x 3y
( 28 ) ( ) ( ) 0 This note is c 2016, 2017 by Setsuo Taniguchi. It may be used for personal or classroom purposes, but not for commercial purp
 ( 28) ( ) ( 28 9 22 ) 0 This ote is c 2016, 2017 by Setsuo Taiguchi. It may be used for persoal or classroom purposes, but ot for commercial purposes. i (http://www.stat.go.jp/teacher/c2epi1.htm ) = statistics
( 28) ( ) ( 28 9 22 ) 0 This ote is c 2016, 2017 by Setsuo Taiguchi. It may be used for persoal or classroom purposes, but ot for commercial purposes. i (http://www.stat.go.jp/teacher/c2epi1.htm ) = statistics
December 28, 2018
 e-mail : kigami@i.kyoto-u.ac.jp December 28, 28 Contents 2............................. 3.2......................... 7.3..................... 9.4................ 4.5............. 2.6.... 22 2 36 2..........................
e-mail : kigami@i.kyoto-u.ac.jp December 28, 28 Contents 2............................. 3.2......................... 7.3..................... 9.4................ 4.5............. 2.6.... 22 2 36 2..........................
() n C + n C + n C + + n C n n (3) n C + n C + n C 4 + n C + n C 3 + n C 5 + (5) (6 ) n C + nc + 3 nc n nc n (7 ) n C + nc + 3 nc n nc n (
 3 n nc k+ k + 3 () n C r n C n r nc r C r + C r ( r n ) () n C + n C + n C + + n C n n (3) n C + n C + n C 4 + n C + n C 3 + n C 5 + (4) n C n n C + n C + n C + + n C n (5) k k n C k n C k (6) n C + nc
3 n nc k+ k + 3 () n C r n C n r nc r C r + C r ( r n ) () n C + n C + n C + + n C n n (3) n C + n C + n C 4 + n C + n C 3 + n C 5 + (4) n C n n C + n C + n C + + n C n (5) k k n C k n C k (6) n C + nc
http://www2.math.kyushu-u.ac.jp/~hara/lectures/lectures-j.html 2 N(ε 1 ) N(ε 2 ) ε 1 ε 2 α ε ε 2 1 n N(ɛ) N ɛ ɛ- (1.1.3) n > N(ɛ) a n α < ɛ n N(ɛ) a n
 http://www2.math.kyushu-u.ac.jp/~hara/lectures/lectures-j.html 1 1 1.1 ɛ-n 1 ɛ-n lim n a n = α n a n α 2 lim a n = 1 n a k n n k=1 1.1.7 ɛ-n 1.1.1 a n α a n n α lim n a n = α ɛ N(ɛ) n > N(ɛ) a n α < ɛ
http://www2.math.kyushu-u.ac.jp/~hara/lectures/lectures-j.html 1 1 1.1 ɛ-n 1 ɛ-n lim n a n = α n a n α 2 lim a n = 1 n a k n n k=1 1.1.7 ɛ-n 1.1.1 a n α a n n α lim n a n = α ɛ N(ɛ) n > N(ɛ) a n α < ɛ
No δs δs = r + δr r = δr (3) δs δs = r r = δr + u(r + δr, t) u(r, t) (4) δr = (δx, δy, δz) u i (r + δr, t) u i (r, t) = u i x j δx j (5) δs 2
 No.2 1 2 2 δs δs = r + δr r = δr (3) δs δs = r r = δr + u(r + δr, t) u(r, t) (4) δr = (δx, δy, δz) u i (r + δr, t) u i (r, t) = u i δx j (5) δs 2 = δx i δx i + 2 u i δx i δx j = δs 2 + 2s ij δx i δx j
No.2 1 2 2 δs δs = r + δr r = δr (3) δs δs = r r = δr + u(r + δr, t) u(r, t) (4) δr = (δx, δy, δz) u i (r + δr, t) u i (r, t) = u i δx j (5) δs 2 = δx i δx i + 2 u i δx i δx j = δs 2 + 2s ij δx i δx j
0 (18) /12/13 (19) n Z (n Z ) 5 30 (5 30 ) (mod 5) (20) ( ) (12, 8) = 4
 0 http://homepage3.nifty.com/yakuikei (18) 1 99 3 2014/12/13 (19) 1 100 3 n Z (n Z ) 5 30 (5 30 ) 37 22 (mod 5) (20) 201 300 3 (37 22 5 ) (12, 8) = 4 (21) 16! 2 (12 8 4) (22) (3 n )! 3 (23) 100! 0 1 (1)
0 http://homepage3.nifty.com/yakuikei (18) 1 99 3 2014/12/13 (19) 1 100 3 n Z (n Z ) 5 30 (5 30 ) 37 22 (mod 5) (20) 201 300 3 (37 22 5 ) (12, 8) = 4 (21) 16! 2 (12 8 4) (22) (3 n )! 3 (23) 100! 0 1 (1)
( )
 18 10 01 ( ) 1 2018 4 1.1 2018............................... 4 1.2 2018......................... 5 2 2017 7 2.1 2017............................... 7 2.2 2017......................... 8 3 2016 9 3.1 2016...............................
18 10 01 ( ) 1 2018 4 1.1 2018............................... 4 1.2 2018......................... 5 2 2017 7 2.1 2017............................... 7 2.2 2017......................... 8 3 2016 9 3.1 2016...............................