PowerPoint プレゼンテーション
|
|
|
- ゆきさ ひろき
- 5 years ago
- Views:
Transcription
1 グラフの禁止構造条件について 古谷倫貴 ( 北里大学一般教育部 )
2 話の流れ 1. 禁止部分グラフ a. 問題設定 b. ハミルトン閉路のための禁止部分グラフ c. 完全マッチングのための禁止部分グラフ d. 禁止部分グラフ条件の完全決定の難易 2. 自明な禁止部分グラフ条件 3. 禁止部分グラフ条件の比較
3 問題設定 グラフのある性質 P について,P のための ( 十分 ) 条件として良いものを考えたい. 例えば 完全マッチングを持つ という性質に着目してみる. 完全マッチング : グラフの全頂点を用いる独立辺の集合 グラフに完全マッチングが存在するための有名な必要十分があるが, それについてはとりあえず無視する.
4 問題設定完全マッチングを持たないグラフとは? 奇位数グラフは完全マッチングを持たない 下は完全マッチングを持たない偶位数グラフの無限列 奇数 2k + 1 奇数 K 2m 1 K 2m 1 K 2m 1 K 2k 1 このグラフたちには共通しての形が現れている! ( このグラフを claw という ) 偶位数グラフに claw の構造を 禁止 すれば, 完全マッチングの存在が言える?
5 問題設定 G をグラフとする. S V G について, uv E G u, v S を辺集合とする S 上のグラフ G S を,S で誘導される G の誘導部分グラフという. G がグラフ H と同型な誘導部分グラフを含むとき,H G と書く. H G となるとき,G は H-free であるという. 注意 2 つのグラフ H 1, H 2 に対して,H 1 H 2 が成り立つとき, 任意の H 1 -free グラフは H 2 -free である. 特に,H 1 -free グラフのクラスより,H 2 -free グラフのクラスの方が大きい.
6 問題設定 定理 (Sumner, 1974) 偶位数連結 claw-free グラフは完全マッチングを持つ. ( 証明 ) ある偶位数連結 claw-free グラフ G が完全マッチングを持たないと仮定する. すると 1- 因子定理 (Tutte, 1947) より, ある X V G に対して, が成り立つ. G X の奇位数成分の個数 X + 2 このような X を最小にとると,X の頂点は G X の奇位数連結成分のうち, 少なくとも 3 個と隣接する. claw が誘導部分グラフとして見つかり, 矛盾する.
7 ハミルトン閉路のための禁止部分グラフ グラフが ハミルトン閉路を持つ という性質について, グラフの禁止条件は? ハミルトン閉路 : グラフのすべての頂点を通る閉路 ハミルトン閉路を持つグラフは 2- 連結であるから, 対象のグラフは 2- 連結グラフに限る. 下はハミルトン閉路を持たない 2- 連結グラフの無限列 これらの共通の誘導部分グラフは? (P 3 ) が最大の共通の連結誘導部分グラフ.
8 ハミルトン閉路のための禁止部分グラフ 命題連結 P 3 -free グラフ G は完全グラフである. ( 証明 ) G が完全グラフでないと仮定すると, ある非隣接な 2 頂点が存在する. G は連結であるから, 距離が 2 となる 2 頂点 u, v が存在する. このとき,w N G u N G v について,uwv が誘導 P 3 となる. 命題 2- 連結 P 3 -free グラフはハミルトン閉路を持つ.
9 ハミルトン閉路のための禁止部分グラフ H をいくつかの連結グラフからなる集合とする. グラフ G が, H H, H G を満たすとき,G は H-free であるという. いくつかの連結グラフからなる集合 H 1, H 2 に対して, H 2 H 2, H 1 H 1 s. t. H 1 H 2 が成り立つとき,H 1 H 2 と書く. 注意 H 1 H 2 ならば任意の H 1 -free グラフは H 2 -free である.
10 ハミルトン閉路のための禁止部分グラフ 定理 (Duffus et al., 1981) 2- 連結 claw, N -free グラフはハミルトン閉路を持つ. 定理 (Broesma and Veldman, 1990) 2- 連結 claw, P 6 -free グラフはハミルトン閉路を持つ. 定理 (Bedrossian, 1991) 2- 連結 claw, B 1,2 -free グラフはハミルトン閉路を持つ.
11 ハミルトン閉路のための禁止部分グラフ 定理 (Bedrossian, 1991) 2 つの連結グラフ H 1, H 2 が命題 2- 連結 H 1, H 2 -free グラフはハミルトン閉路を持つ を満たすための必要十分条件は, (1) H 1, H 2 claw, N (2) H 1, H 2 claw, P 6 (3) H 1, H 2 claw, B 1,2 のいずれかとなることである.
12 ハミルトン閉路のための禁止部分グラフ 定理 (Faudree et al., 1995) 2- 連結 claw, Z 3 -free グラフは, 以下の 2 つを除きハミルトン閉路を持つ. 2- 連結 claw, Z 3 -free グラフはハミルトン閉路を持つ という命題は, 反例があるため成り立たない. ( よって Bedrossian の特徴付けに claw, Z 3 は現れない ) しかし, 反例が2 個しか存在しないことが分かっているため, claw, Z 3 はハミルトン閉路のための禁止条件と見なして良さそう.
13 ハミルトン閉路のための禁止部分グラフ 定理 (Faudree and Gould, 1997) 2 つの連結グラフ H 1, H 2 が命題 位数が十分大きい 2- 連結 H 1, H 2 -free グラフはハミルトン閉路を持つ を満たすための必要十分条件は, (1) H 1, H 2 claw, N (2) H 1, H 2 claw, P 6 (3) H 1, H 2 claw, B 1,2 (4) H 1, H 2 claw, Z 3 のいずれかとなることである. 小さい例外グラフを認めて, 今後は 位数が十分大きい という仮定の下で問題を考える.
14 ハミルトン閉路のための禁止部分グラフ 位数が十分大きい 2- 連結 H 1, H 2, H 3 -free グラフはハミルトン閉路を持つ を満たす 3 つの連結グラフ H 1, H 2, H 3 の特徴付けも知られており, 本質的に 12 種類に分類される. (Brousek, 2002; Faudree et al. 2004)
15 ハミルトン閉路のための禁止部分グラフ 禁止するグラフの個数を増やすと, 命題は ( ある意味で ) 強くなる. 定理 (Brousek, 2002) 位数が十分大きい 2- 連結 claw, B 1,3, R -free グラフはハミルトン閉路を持つ. claw, Z 3 claw, B 1,3, R なので, 位数が十分大きい 2- 連結 claw, Z 3 -free グラフはハミルトン閉路を持つ (Faudree et al., 1995) が導かれる.
16 ハミルトン閉路のための禁止部分グラフ 定理 (Fujisawa, 2012) 2 つの連結グラフ H 1, H 2 が命題 位数が十分大きい 3- 連結 H 1, H 2 -free グラフはハミルトン閉路を持つ を満たすならば, ある i 1,2 に対して H i K 1,3 かつ (1)H 3 i P 10 (2)H 3 i は K 3 から 3 本の点素な道を出した位数 12 以下のグラフ (3)2 つの K 3 を長さ 1,3,5,7 いずれかの道で結んだグラフ のいずれかとなる.
17 ハミルトン閉路のための禁止部分グラフ 予想 (Matthews and Sumner, 1984) 4- 連結 claw-free グラフは, ハミルトン閉路を持つ. 定理 (Kaiser and Vrana, 2012) 最小次数 6 以上の 5- 連結 claw-free グラフは, ハミルトン閉路を持つ.
18 ハミルトン閉路のための禁止部分グラフ ( この講演での ) グラフの禁止条件 性質 P に対して, それを見つけるためのグラフの禁止条件を見つけたい. 性質 P の自明な十分条件 ( 完全マッチング : 偶位数, ハミルトン閉路 :2- 連結性 ) は仮定しておく. ただし, より強い仮定 ( ハミルトン閉路について k- 連結 ) を仮定することもある. 対象のグラフは, 位数が十分大きいもののみを考える. 一般に, 禁止するグラフの個数を増やすと考えるべき状況も増えて, 強い命題が得られる.
19 完全マッチングのための禁止部分グラフ 定理 (Sumner, 1974) 偶位数連結 claw-free グラフは完全マッチングを持つ. 定理 (Plummer and Saito, 2005) 連結グラフ H が命題 位数が十分大きい偶位数連結 H-free グラフは完全マッチングを持つ を満たすための必要十分条件は,H claw となることである.
20 完全マッチングのための禁止部分グラフ 定理 (Fujita et al., 2006) 2 つの連結グラフ H 1, H 2 が命題 位数が十分大きい偶位数連結 H 1, H 2 -free グラフは完全マッチングを持つ を満たすための必要十分条件は, H 1, H 2 なることである. claw と
21 完全マッチングのための禁止部分グラフ 定理 (Ota et al., 2010) 3 つの連結グラフ H 1, H 2, H 3 が命題 位数が十分大きい偶位数連結 H 1, H 2, H 3 -free グラフは完全マッチングを持つ を満たすための必要十分条件は, (1) H 1, H 2, H 3 K 1,3 p 4, q 2 (2) H 1, H 2, H 3 K 1,p, Y q, Q 1,r p 4, q 4, r 3 (3) H 1, H 2, H 3 K 1,p, P 4, Q 2,r p 4, r 3 のいずれかとなることである. n 頂点 k 頂点 K n Y n Q k,n
22 完全マッチングのための禁止部分グラフ 定理 (Ota and Sueiro, 2013) 連結グラフの集合 H が命題 位数が十分大きい偶位数連結 H-free グラフは完全マッチングを持つ 禁止条件のを満たすための必要十分条件は, 完全決定 H K 1,p, Y q, W r, Z + i,s 0 i q 2 p 4, q 2, r 2, s 3 となることである. n 頂点 Y n K n m 頂点 K n + W n Z n,m
23 完全マッチングのための禁止部分グラフ 連結度を上げると? 定理 (Sumner, 1975; Plummer and Saito, 2005) k 2 を整数とする. 連結グラフ H が命題 位数が十分大きい偶位数 k- 連結 H-free グラフは完全マッチングを持つ を満たすための必要十分条件は,H K 1,k+1 となることである.
24 完全マッチングのための禁止部分グラフ 定理 (Fujisawa et al., 2011) k 2 を整数とする. 2 つの連結グラフ H 1, H 2 が命題 位数が十分大きい偶位数 k- 連結 H 1, H 2 -free グラフは完全マッチングを持つ を満たすための必要十分条件は, (1) H 1, H 2 K 1,k+1 (2) H 1, H 2 K 1,k+2, F p 1 p k n 頂点 のいずれかとなることである. F n
25 完全マッチングのための禁止部分グラフ 連結度の高いグラフにおいては,star を禁止すれば完全マッチングが存在する. 禁止する star に対して, 連結度を もっと 大きくすると, マッチングに関してより強い性質が得られるのでは? 整数 m 0, n 0 に対し, グラフ G が E m, n を満たすとは, 辺素な任意の 2 つのマッチング M, N E G M = m, N = n について,G が M F かつ F N = なる完全マッチング F = F M,N を持つことである.
26 完全マッチングのための禁止部分グラフ 定理 (Aldred and Plummer, 1999) k 1, m 0, n 0 を,m + n 1 かつ n k 2m+1 満たす整数とするとき, 位数が十分大きい偶位数 k- 連結 K k 2m n+2 -free グラフは E m, n を満たす. 定理 (Egawa and F., 2016) k 4, m 0, n 3 を, k 2m+2 2 n k 2m 1 を 満たす整数とするとき, 位数が十分大きい偶位数 k- 連結 -free グラフは E m, n を満たす. K k m+2 2 n に依存しない禁止条件 2 を
27 禁止部分グラフ条件の完全決定の難易 グラフの禁止条件が,( 自明な必要条件下で ) 完全決定している問題 HIST (F. and Tsuchiya, 2013) HIST: 葉以外の頂点の次数が 3 以上の全域木 0 < t < 1 に対する t-タフ (Ota and Sueiro, 2013) S G が t-タフ S cutset of G, t # of compo. of G S 全域 2- 歩道 (F., 2014) k- 歩道 : 各頂点を高々 k 回通るような歩道
28 禁止部分グラフ条件の完全決定の難易 命題 (Jackson and Wormald, 1990) k 2 を整数とする. グラフ G が全域 k- 歩道を持つならば,G は 1/k - タフである. また, 1/k - タフであるが全域 k- 歩道を持たないグラフの無限列が存在する. 一方で, 1/2 - タフのための禁止条件 と 全域 2- 歩道のための禁止条件 は一致する! 問題グラフの 2 つの ( 強弱のある ) 性質について, それらのための禁止条件が等しいものは他にあるか?
29 禁止部分グラフ条件の完全決定の難易 グラフの禁止条件として, H 1, H 2 -free の形でも未決定の問題 k 3 に対する全域 k- 木 (cf. Ota and Sugiyama, 2010) k- 木 : すべての頂点の次数が k 以下の木 全域部分 Halin グラフ (cf. Chen et al., 2017+) Halin グラフ :HIT の葉を閉路で繋いだ平面グラフ 辺支配閉路 (cf. Chiba, F. and Tsuchiya, 2015, 2016) 辺支配閉路 : 取り除くと孤立点のみが残る閉路 問題グラフの禁止条件を考えるに当たって, 簡単 難しいの違いは何か?
30 自明な禁止部分グラフ条件 禁止部分グラフを考えるとき, 位数が十分大きいことを仮定するのが通常であった. そこに弊害も 定理 (Fujisawa et al., 2013) 5- 連結 claw, K 4 -free グラフは, 正二十面体グラフに限る. 特に 位数 13 以上の 5- 連結 claw, K 4 -free グラフのクラス は ( 空なので ) どのような性質でも満たす. このようなグラフのクラスを考えることは無駄であるが, 禁止条件を考える上では避けられないので, 予め特定しておきたい.
31 自明な禁止部分グラフ条件 k 1 を整数とする. G k を k- 連結グラフ全体からなる集合とする. 連結グラフの集合 H に対して, G k H = G G k G は H-free と定める. 問題 G k H < を満たすような H を決定せよ.
32 自明な禁止部分グラフ条件 定理 (Diestel) 連結グラフの集合 H が G 1 H 必要十分条件は, H K p, P q, K 1,r p 1, q 1, r 1 となることである. < を満たすための ( 必要性の証明 ) K 1,n n 1 は無限集合であるから, ある r 1 に対して K 1,r は H-free でない. よって, H H s. t. H K 1,r となる. したがって,H K 1,r となる. 同様に, K n n 1 と P n n 1 を考えれば, ある p 1, q 1 について H K p と H P q となる.
33 自明な禁止部分グラフ条件 ( 十分性の証明 ) G を連結 K p, P q, K 1,r -free グラフとする. p 2 または q 2 または r = 1 だと,G K 1 となるので, p 3, q 3, r 2 として良い. G は P q -free なので,diam G q 2. x V G を d G x = Δ G を満たす頂点とする. G は K p, K 1,r -free なので,N G x はサイズ p 1 のクリークも, サイズ r の独立集合も含まない. よって Δ G = d G x R p 1, r (R, : ラムゼー数 ). 以上より V G Δ G diam G R p 1, r 1 q 2.
34 自明な禁止部分グラフ条件連結度を上げると? 命題 (Fujisawa et al., 2013) k 1 を整数とする. 連結グラフ H が G k H < を満たすための必要十分条件は,H K 2 となることである.
35 自明な禁止部分グラフ条件 命題 (Fujisawa et al., 2013) k 1 を整数とする. 連結グラフ H 1, H 2 が G k H 1, H 2 < を満たすならば, p 3, 2 r k s. t. H 1, H 2 K p, K 1,r となる. 定理 (Fujisawa et al., 2013) 1 k 6 を整数とする. 連結グラフ H 1, H 2 が G k H 1, H 2 必要十分条件は, < を満たすための (1) H 1, H 2 K p, K 1,2 p 3 (2) H 1, H 2 K 3, K 1,r 3 r k if 3 k 6 (3) H 1, H 2 K 4, K 1,3 if 5 k 6 のいずれかとなることである.
36 自明な禁止部分グラフ条件 定理 (F. and Okubo, 2015) 連結グラフ H 1,, H 4 が G 2 H 1,, H 4 < を満たすための必要十分条件は以下のいずれかとなることである. (1) H 1,, H 4 K 3, P 5, K 2,r r 2 (2) H 1,, H 4 K 3, P 6, K 2,2 (3) H 1,, H 4 1 K 3, P 6, K 2,r, H s r 3, s 2 (4) H 1,, H 4 2 K 3, P 7, K 2,2, H s s 2 (5) H 1,, H 4 K 3, P q, K 2,2, H3 s q 8, s 3 (6) H 1,, H 4 K 3, P q, K 2,r, H4 s q 7, r 2, s 3, q, r 7,2 (7) H 1,, H 4 K p, P 5, K 2,r, H5 s p 4, r 2, s 2 (8) H 1,, H 4 K p, P 6, K 2,2, H5 s p 4, s 2
37 自明な禁止部分グラフ条件 H n 1 H n 2 H n 3 H n 4 H n 5 大抵の場合は禁止するグラフを制限するので, 当初の目的のためにはこの位調べておけば十分.
38 自明な禁止部分グラフ条件 G 3 H 1, H 2, H 3 < について (Egawa and F., 2014; Egawa et al., 2015) H 1, H 2, H 3 の完全な特徴付けには程遠い
39 禁止部分グラフ条件の比較 連結グラフの 2 つの集合 H 1, H 2 について, ほとんど G k H 1 G k H 2 ほとんど G k H 1 = G k H 2 などが分かれば, 禁止条件の問題について, 一方の情報が他方に知見を与える. H 1 H 2 であれば,G k H 1 G k H 2 であったが, それ 以外の状況でも ( ほとんど ) G k H 1 G k H 2 が成り立つ ことはあるか? 問題 G k H 1 G k H 2 < や G k H 1 G k H 2 < を 満たすような H 1, H 2 を決定せよ.
40 禁止部分グラフ条件の比較 G 1 H 1 G 1 H 2 < かつ H 1 H 2 を満たす H 1, H 2 は存在するか? 命題 下のグラフ H 1, H 2 について, G 1 H 1 G 1 H 2 < かつ H 1 H 2 を満たす. H 1 H 2 rep. 十分大のトーラス上 6 正則三角形分割 ( 証明 ) H 1 H 2 は自明. G 1 H 1 G 1 H 2 = H 2, すなわち H 2 を誘導部分グラフに持つ連結 H 1 -free グラフは H 2 のみを示せば良い.
41 禁止部分グラフ条件の比較 G 1 H 1 G 1 H 2 < かつ H 1 H 2 を満たす H 1, H 2 の特徴付けは難しそう 定理 (Fujita et al., 2013) 連結グラフ H 1, H 2 が G 1 H 1 G 1 H 2 < かつH 1 H 2 を満たすならば, 以下が成り立つ. (1)δ H 1 = 1, Δ H 1 = V H 1 1 (2) a 1, a 2 V H 1 s. t. N G a 1 = N G a 2 (3) b 1, b 2 V H 1 s. t. N G b 1 = N G b 2 (4) V H 2 2 V H 1 3 (5)δ H 2 V H 1 2
42 禁止部分グラフ条件の比較 G 1 H 1 G 1 H 2 < を満たす H 1, H 2 は? を満たすための必要十分条件は H 1 = H 2 となることである. 定理 (Fujita et al., 2013) 位数 3 以上の連結グラフ H 1, H 2 が G 1 H 1 G 1 H 2 < ( 必要性の証明 ) 背理法と対称性より H 1 H 2 と仮定する. H 1 = P 3 と仮定すると,G 1 H 1 = K n n 1 となる. H 1 H 2, すなわち H 2 は H 1 -free であるから,H 2 は完全グラフである. このとき, K n n V H 2 G 1 H 1 G 1 H 2 となり, G 1 H 1 G 1 H 2 < に反する. よって H 1 P 3 である.
43 禁止部分グラフ条件の比較 A 1 = H 2 K n n 1 は H 2 -free でない連結グラフの 無限集合であるから,A 1 G 1 G 1 H 2 を満たす. G 1 H 1 G 1 H 2 < であるから, n 1 1, H 2 H 2 s. t. H 1 = H 2 K n1 となる. A 2 = n 1 について同様に考えると, H 2 P n n 2 1, H 2 H 2 s. t. H 1 = H 2 P n2 となる. 特に Δ H 1 = V H 1 1, δ H 1 = 1 となる. また,A 2 の P n の根本の選び方より,δ H 2 V H 1 2.
44 禁止部分グラフ条件の比較 以上より, 以下のようになる. H 1 = x H 2 d H1 x = 1 よって, V H 2 N H2 x V H 1 2 となる. したがって, V H 2 = δ H V H 2 N H2 x 2 V H 1 3. V H 2 > V H 1 であれば H 2 H 1 なので, 同じ議論により V H 1 2 V H 2 3 が得られて矛盾. V H 2 V H 1 であれば V H 1 = V H 2 = 3 と なり,H 1 H 2 より H 1, H 2 = P 3, K 3 となって, 最初 の議論で矛盾.
45 禁止部分グラフ条件の比較 を満たすための必要十分条件は H 1 = H 2 となることである. 定理 (Fujita et al., 2013) k 1 を整数とする. 位数 3 以上の連結グラフ H 1, H 2 が G k H 1 G k H 2 < 定理 (Fujita et al., 2013) 連結グラフ H と H 3 なる連結グラフの集合 H が G 1 H G 1 H < を満たすならば, (1)H H (2)H = K 3 かつ H = 3 のいずれかとなる. G 1 K 3 G 1 K 4,, < G 1 K 3 G 1 K 5,, <
46 禁止部分グラフ条件の比較 ここで, G 1 K 3 G 1 K 4,, < という事実に着目 する. この右側は,K 3 に1 頂点を加えて適当な辺を加えた集合で ある. 一般に, 連結グラフ H に対して,H に 1 頂点 x を加え, x と H を 1 本以上の辺で結んで得られるグラフの集合を H H + と表す. 注意連結グラフ H に対して,G 1 H G 1 H H + = H となる.
47 禁止部分グラフ条件の比較 グラフの禁止条件で重要な,claw に注目する. 注意 + H claw = H 1 H 2 H 3 H 4 H 5 H 6 H 7.
48 禁止部分グラフ条件の比較 定理 (F. and Yokota, 2017+) + 整数 k 1 と H H claw が G k claw G k H < を満たすための必要十分条件は以下のいずれかとなることである. (1)k = 1 かつ, H 1,, H 6 H (2)k = 2 かつ, H 1,, H 6 H または H 1,, H 4, H 7 H (3)k = 3 かつ, H 1,, H 5 H または H 1,, H 4, H 7 H (4)k 4 かつ, H 1, H 2, H 5, H 6 H または H 1, H 2, H 3, H 6, H 7 H または H 1,, H 5 H または H 1,, H 4, H 7 H
49 禁止部分グラフ条件の比較 予想 (Matthews and Sumner, 1984) 4- 連結 claw-free グラフは, ハミルトン閉路を持つ. 定理 (F. and Yokota, 2017+) Matthews-Sumner 予想は, 以下と同値である. (1)4- 連結 H 1, H 2, H 5, H 6 -free グラフはハミルトン閉路を持つ. (2)4- 連結 H 1, H 2, H 3, H 6, H 7 -free グラフはハミルトン閉路を持つ. (3)4- 連結 H 1,, H 5 -free グラフはハミルトン閉路を持つ. (4)4- 連結 H 1,, H 4, H 7 -free グラフはハミルトン閉路を持つ.
50 禁止部分グラフ条件の比較 定理 (Chiba, Fujisawa, F. and Ikarashi, 2017) H 1, H 2, H 3 を位数 3 以上の連結グラフとする. δ H 1 2 であるとき, G 1 H 1, H 2 G 1 H 1, H 3 < を満たすための必要十分条件は (1)H 2 = H 3 (2)H 1 H 2 かつ H 1 H 3 のいずれかを満たすことである. 禁止条件には claw が現れることが多いので,H 1 として claw を考えておくことも重要. より一般に,twin-less( x 1, x 2 s. t. N G x 1 = N G x 2 ) で 考えてみる.
51 禁止部分グラフ条件の比較 G をグラフとする. V G 上の同値関係 ~ を x~y N G x = N G y に よって定める. C G を ~ に関する同値類とし,B G を C 上のグラフで CC E B G C と C の間に G の辺が存在 を満たすものとする. B G
52 禁止部分グラフ条件の比較 グラフ G が点推移的であるとは, 任意の x, y V G に対して, ある自己同型写像 φ で φ x = y を満たすものが存在することである.
53 禁止部分グラフ条件の比較 定理 (Chiba, Fujisawa, F. and Ikarashi, 2017) H 1, H 2, H 3 を位数 3 以上の連結グラフとする. H 1 が twin-less であるとき, G 1 H 1, H 2 G 1 H 1, H 3 < を満たすならば (1)H 2 = H 3 (2)H 1 H 2 かつ H 1 H 3 (3)B H 2 B H 3 が点推移的であり, ある i 2,3 に対して,H i は H 5 i のある 1 点をクリークに置き換えることで得られる. のいずれかとなる.
54 禁止部分グラフ条件の比較 命題下のグラフ H 2, H 3 について, G 1 claw, H 2 G 1 claw, H 3 = かつ G 1 claw, H 3 G 1 claw, H 2 = H 2 である. 特に, G 1 claw, H 2 G 1 claw, H 3 < を満たす. H 2 H 3
55 禁止部分グラフ条件の比較 ここまでは有限個の例外のみを誤差として扱ってきた. しかし次の定理のように, グラフのクラスの差が無限であっても, その表記が簡単であれば考えやすい. 定理 (Olariu, 1988) G 1 G 1 K 3 は, 部集合が 3 個以上の完全多部グラフからなる集合と一致する. 上の定理より,K 3 -free グラフに関する命題は, 部集合が 3 個以上の完全多部グラフをチェックするだけで -free グラフの命題に拡張できる.
56 禁止部分グラフ条件の比較 定理 (Duffus et al., 1981) 2- 連結 claw, N -free グラフはハミルトン閉路を持つ. 定理 (Broesma and Veldman, 1990) 2- 連結 claw, P 6 -free グラフはハミルトン閉路を持つ. 定理 (Bedrossian, 1991) 2- 連結 claw, B 1,2 -free グラフはハミルトン閉路を持つ. 定理 (Faudree et al., 1995) 位数 10 以上の 2- 連結 claw, Z 3 -free グラフは, ハミルトン閉路を持つ.
57 禁止部分グラフ条件の比較 まず,G 1 claw, B 1,2 G 1 claw, N に注目する. 以下のようなグラフが属するため, これは無限集合である. 例 1. m 個の点素なクリーク C, L 1,, L m をとる. ただし C m とする. 2. R 1,, R m を C の点素な部分クリークとする. 3. L i と R i を完全に辺で結ぶ. ( このようなグラフを generalized comb と呼ぶ.) このグラフは claw, B 1,2 -free であるが,N-free でない.
58 禁止部分グラフ条件の比較 定理 (F. and Tsuchiya, 2015) G 1 claw, B 1,2 G 1 claw, N は,generalized comb からなる集合と一致する. 定理 (Duffus et al., 1981) 2- 連結 claw, N -free グラフはハミルトン閉路を持つ. 上の 2 つの定理の系として,Bedrossian の定理 (2- 連結 claw, B 1,2 -free グラフはハミルトン閉路を持つ ) が得られる.
59 禁止部分グラフ条件の比較 G を 2- 連結 claw, B 1,2 -free グラフとする. G が N-free であれば,G は 2- 連結 claw, N -free なのでハミルトン閉路を持つ. G が N-free でなければ,G G 1 claw, B 1,2 となるため,generalized comb である. すると,G にハミルトン閉路が見つかる. G 1 claw, N
60 禁止部分グラフ条件の比較 グラフ G の各頂点を 1 点以上のクリークで置き換えて得られるグラフ全体の集合を A G によって表す. G A G 定理 (Chen, F., Shan, Tsuchiya and Yang, 2017+) G 1 claw, B 1,2 G 1 claw, P 6 = n 6 A P n n 7 A C n
61 禁止部分グラフ条件の比較 定理 (Chen, F., Shan, Tsuchiya and Yang, 2017+) G 1 claw, B 1,2 G 1 claw, P 6 = n 6 A P n n 7 A C n 定理 (Broesma and Veldman, 1990) 2- 連結 claw, P 6 -free グラフはハミルトン閉路を持つ. 上の 2 つの定理の系としても,Bedrossian の定理 (2- 連結 claw, B 1,2 -free グラフはハミルトン閉路を持つ ) が得られる.
62 まとめ グラフの性質 P について,P を満たさないグラフの共通構造を禁止すれば,P のための 本質的 な十分条件が得られる. グラフの問題では, 位数が小さいものが例外になりがちなので, 位数十分大という仮定を加えるのが自然だが, それによって対象のクラスが空になることも 性質 P を満たさない共通構造は似たようなものになることがあるため, 実は本質的に等しい (or 包含関係 ) かも? もう一度, 対象のクラスに目を向けましょう! ご清聴ありがとうございました
グラフ理論における偶奇性の現象
グラフ理論における偶奇性に関連する現象 (3 回目の講義 ) 加納幹雄 (Mikio Kano) 茨城大学名誉教授 講義の概略 1 回目入門的な話証明の多くを演習問題とします 2 回目マッチングと 1- 因子の一般化に関連する話 3 回目因子 = ある条件を満たす全域部分グラフ最近の因子理論のなかで偶奇性に関連するものの紹介 連結グラフ G と G-S の成分 G S S V(G) iso(g-s)=3
<4D F736F F D208C51985F82CD82B682DF82CC88EA95E A>
群論はじめの一歩 (6) 6. 指数 2の定理と2 面体群 命題 H を群 G の部分群とする そして 左剰余類全体 G/ H 右剰 余類全体 \ H G ともに指数 G: H 2 と仮定する このとき H は群 G の正規部分群である すなわち H 注意 ) 集合 A と B があるとき A から B を引いた差集合は A \ B と書かれるが ここで書いた H \ Gは差集合ではなく右剰余類の集合の意味である
Microsoft PowerPoint - DA2_2019.pptx
Johnon のアルゴリズム データ構造とアルゴリズム IⅠ 第 回最大フロー 疎なグラフ, 例えば E O( V lg V ) が仮定できる場合に向いている 隣接リスト表現を仮定する. 実行時間は O( V lg V + V E ). 上記の仮定の下で,Floyd-Warhall アルゴリズムよりも漸近的に高速 Johnon のアルゴリズム : アイデア (I) 辺重みが全部非負なら,Dikra
" 01 JJM 予選 4 番 # 四角形 の辺 上に点 があり, 直線 と は平行である.=,=, =5,=,= のとき, を求めよ. ただし,XY で線分 XY の長さを表すものとする. 辺 と辺 の延長線の交点を, 辺 と辺 の延長線の交点を G とする. 5 四角形 は直線 に関して線対称な
1 " 数学発想ゼミナール # ( 改題 ) 直径を とする半円周上に一定の長さの弦がある. この弦の中点と, 弦の両端の各点から直径 への垂線の足は三角形をつくる. この三角形は二等辺三角形であり, かつその三角形は弦の位置にかかわらず相似であることを示せ. ( 証明 ) 弦の両端を X,Y とし,M を線分 XY の中点,, をそれぞれ X,Y から直径 への垂線の足とする. また,M の直径
学習指導要領
(1 ) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 自然数 整数 有理数 無理数の包含関係など 実 数の構成を理解する ( 例 ) 次の空欄に適当な言葉をいれて, 数の集合を表しなさい 実数の絶対値が実数と対応する点と原点との距離で あることを理解する ( 例 ) 次の値を求めよ (1) () 6 置き換えなどを利用して 三項の無理数の乗法の計
20～22.prt
[ 三クリア W] 辺が等しいことの証明 ( 円周角と弦の関係利用 ) の の二等分線がこの三角形の外接円と交わる点をそれぞれ とするとき 60 ならば であることを証明せよ 60 + + 0 + 0 80-60 60 から ゆえに 等しい長さの弧に対する弦の長さは等しいから [ 三クリア ] 方べきの定理 接線と弦のなす角と円周角を利用 線分 を直径とする円 があり 右の図のように の延長上の点
学習指導要領
(1) 数と式 学習指導要領ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 千早高校学力スタンダード 自然数 整数 有理数 無理数の用語の意味を理解す る ( 例 ) 次の数の中から自然数 整数 有理 数 無理数に分類せよ 3 3,, 0.7, 3,,-, 4 (1) 自然数 () 整数 (3) 有理数 (4) 無理数 自然数 整数 有理数 無理数の包含関係など
オートマトン 形式言語及び演習 1. 有限オートマトンとは 酒井正彦 形式言語 言語とは : 文字列の集合例 : 偶数個の 1 の後に 0 を持つ列からなる集合 {0, 110, 11110,
オートマトン 形式言語及び演習 1 有限オートマトンとは 酒井正彦 wwwtrscssinagoya-uacjp/~sakai/lecture/automata/ 形式言語 言語とは : 文字列の集合例 : 偶数個の 1 の後に 0 を持つ列からなる集合 {0, 110, 11110, } 形式言語 : 数学モデルに基づいて定義された言語 認識機械 : 文字列が該当言語に属するか? 文字列 機械 受理
PowerPoint Presentation
最適化手法 第 回 工学部計数工学科 定兼邦彦 http://researchmap.jp/sada/resources/ 前回の補足 グラフのある点の隣接点をリストで表現すると説明したが, 単に隣接点の集合を持っていると思ってよい. 互いに素な集合のデータ構造でも, 単なる集合と思ってよい. 8 3 4 3 3 4 3 4 E v 重み 3 8 3 4 4 3 {{,},{3,8}} {{3,},{4,}}
<4D F736F F D E4F8E9F82C982A882AF82E98D7397F1>
3 三次における行列 要旨高校では ほとんど 2 2 の正方行列しか扱ってなく 三次の正方行列について考えてみたかったため 数 C で学んだ定理を三次の正方行列に応用して 自分たちで仮説を立てて求めていったら 空間における回転移動を表す行列 三次のケーリー ハミルトンの定理 三次における逆行列を求めたり 仮説をたてることができた. 目的 数 C で学んだ定理を三次の正方行列に応用する 2. 概要目的の到達点として
Microsoft PowerPoint - 10.pptx
m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
学習指導要領
(1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 自然数 整数 有理数 無理数の包含関係など 実数 の構成を理解する ( 例 ) 次の空欄に適当な言葉をいれて, 数の集合を表しなさい ア イ 無理数 整数 ウ 無理数の加法及び減法 乗法公式などを利用した計 算ができる また 分母だけが二項である無理数の 分母の有理化ができる ( 例 1)
学習指導要領
(1) 数と式 ア整式 ( ア ) 式の展開と因数分解二次の乗法公式及び因数分解の公式の理解を深め 式を多面的にみたり目的に応じて式を適切に変形したりすること (ax b)(cx d) acx (ad bc)x bd などの基本的な公式を活用して 二次式の展開や因数分解ができる また 式の置き換えや一文字に着目するなどして 展開 因数分解ができる ( 例 ) 次の問に答えよ (1) (3x a)(4x
Microsoft PowerPoint - 13.ppt [互換モード]
![Microsoft PowerPoint - 13.ppt [互換モード]](/thumbs/98/134838862.jpg "Microsoft PowerPoint - 13.ppt [互換モード]")
13. 近似アルゴリズム 1 13.1 近似アルゴリズムの種類 NP 困難な問題に対しては多項式時間で最適解を求めることは困難であるので 最適解に近い近似解を求めるアルゴリズムが用いられることがある このように 必ずしも厳密解を求めないアルゴリズムは 大きく分けて 2 つの範疇に分けられる 2 ヒューリスティックと近似アルゴリズム ヒュ- リスティクス ( 発見的解法 経験的解法 ) 遺伝的アルゴリズム
2015－2018年度 ２次数学セレクション（整数と数列）解答解説
015 次数学セレクション問題 1 [ 千葉大 文 ] k, m, n を自然数とする 以下の問いに答えよ (1) k を 7 で割った余りが 4 であるとする このとき, k を 3 で割った余りは であることを示せ () 4m+ 5nが 3 で割り切れるとする このとき, mn を 7 で割った余りは 4 ではないことを示せ -1- 015 次数学セレクション問題 [ 九州大 理 ] 以下の問いに答えよ
学習指導要領
(1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 自然数 整数 有理数 無理数 実数のそれぞれの集 合について 四則演算の可能性について判断できる ( 例 ) 下の表において それぞれの数の範囲で四則計算を考えるとき 計算がその範囲で常にできる場合には を 常にできるとは限らない場合には を付けよ ただし 除法では 0 で割ることは考えない
学習指導要領
(1) 数と式 学習指導要領 数と式 (1) 式の計算二次の乗法公式及び因数分解の公式の理解を深め 式を多面的にみたり目的に応じて式を適切に変形したりすること 東京都立町田高等学校学力スタンダード 整式の加法 減法 乗法展開の公式を利用できる 式を1 つの文字におき換えることによって, 式の計算を簡略化することができる 式の形の特徴に着目して変形し, 展開の公式が適用できるようにすることができる 因数分解因数分解の公式を利用できる
Microsoft PowerPoint - 13approx.pptx
I482F 実践的アルゴリズム特論 13,14 回目 : 近似アルゴリズム 上原隆平 (uehara@jaist.ac.jp) ソートの下界の話 比較に基づく任意のソートアルゴリズムはΩ(n log n) 時間の計算時間が必要である 証明 ( 概略 ) k 回の比較で区別できる場合の数は高々 2 k 種類しかない n 個の要素の異なる並べ方は n! 通りある したがって少なくとも k n 2 n!
Microsoft Word - 町田・全 H30学力スタ 別紙１ １年 数学Ⅰ.doc
(1) 数と式 学習指導要領 都立町田高校 学力スタンダード ア 数と集合 ( ア ) 実数 根号を含む式の計算 数を実数まで拡張する意義を理解し 簡単な 循環小数を表す記号を用いて, 分数を循環小数で表 無理数の四則計算をすること すことができる 今まで学習してきた数の体系について整理し, 考察 しようとする 絶対値の意味と記号表示を理解している 根号を含む式の加法, 減法, 乗法の計算ができる
2018年度 筑波大・理系数学
筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ < < とする 放物線 上に 点 (, ), A (ta, ta ), B( - ta, ta ) をとる 三角形 AB の内心の 座標を p とし, 外心の 座標を q とする また, 正の実数 a に対して, 直線 a と放物線 で囲まれた図形の面積を S( a) で表す () p, q を cos を用いて表せ S( p) () S(
2015年度 ２次数学セレクション（整数と数列）
05 次数学セレクション問題 [ 千葉大 文 ] k, m, を自然数とする 以下の問いに答えよ () k を 7 で割った余りが 4 であるとする このとき, k を 3 で割った余りは であることを示せ () 4m+ 5が 3 で割り切れるとする このとき, m を 7 で割った余りは 4 ではないことを示せ -- 05 次数学セレクション問題 [ 九州大 理 ] 以下の問いに答えよ () が正の偶数のとき,
Microsoft PowerPoint - 9.pptx
9/7/8( 水 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 拡大とスカラー倍 行列演算と写像 ( 次変換 拡大後 k 倍 k 倍 k 倍拡大の関係は スカラー倍を用いて次のように表現できる p = (, ' = k ' 拡大前 p ' = ( ', ' = ( k, k 拡大 4 拡大と行列の積 拡大後 k 倍
曲線 = f () は を媒介変数とする自然な媒介変数表示 =,= f () をもつので, これを利用して説明する 以下,f () は定義域で連続であると仮定する 例えば, 直線 =c が曲線 = f () の漸近線になるとする 曲線 = f () 上の点 P(,f ()) が直線 =c に近づくこ
伊伊伊伊伊伊伊伊伊伊 伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊 漸近線の求め方に関する考察 たまい玉井 かつき克樹 伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊 伊伊伊伊伊伊伊伊伊伊. 漸近線についての生徒からの質問 数学において図を使って直感的な説明を与えることは, 理解を深めるのに大いに役立つ
2017年度 金沢大・理系数学
07 金沢大学 ( 理系 前期日程問題 解答解説のページへ 次の問いに答えよ ( 6 z + 7 = 0 を満たす複素数 z をすべて求め, それらを表す点を複素数平面上に図 示せよ ( ( で求めた複素数 z を偏角が小さい方から順に z, z, とするとき, z, z と 積 zz を表す 点が複素数平面上で一直線上にあることを示せ ただし, 偏角は 0 以上 未満とする -- 07 金沢大学
< D8C6082CC90AB8EBF816989A B A>
数 Ⅰ 図形の性質 ( 黄色チャート ) () () () 点 は辺 を : に外分するから :=: :=: であるから :=: == () 点 は辺 を : に内分するから :=:=: = + %= また, 点 は辺 を : に外分するから :=:=: == =+=+= 直線 は の二等分線であるから :=: 直線 は の二等分線であるから :=: 一方, であるから, から, から :=: :=:
学習指導要領
(1) 数と式 学習指導要領ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 第 1 章第 節実数 東高校学力スタンダード 4 実数 (P.3~7) 自然数 整数 有理数 無理数 実数のそれぞれの集 合について 四則演算の可能性について判断できる ( 例 ) 下の表において, それぞれの数の範囲で四則計算を考えるとき, 計算がその範囲で常にできる場合には
2014年度 名古屋大・理系数学
04 名古屋大学 ( 理系 ) 前期日程問題 解答解説のページへ空間内にある半径 の球 ( 内部を含む ) を B とする 直線 と B が交わっており, その交わりは長さ の線分である () B の中心と との距離を求めよ () のまわりに B を 回転してできる立体の体積を求めよ 04 名古屋大学 ( 理系 ) 前期日程問題 解答解説のページへ 実数 t に対して 点 P( t, t ), Q(
Microsoft PowerPoint - DA2_2017.pptx
1// 小テスト内容 データ構造とアルゴリズム IⅠ 第 回単一始点最短路 (I) 1 1 第 章の構成. 単一始点最短路問題 単一始点最短路問題とは 単一始点最短路問題の考え方 単一始点最短路問題を解くつのアルゴリズム ベルマン フォードのアルゴリズム トポロジカル ソートによる解法 ダイクストラのアルゴリズム 1 1 単一始点最短路問題とは 単一始点最短路問題とは 前提 : 重み付き有向グラフ
Microsoft PowerPoint - 9.pptx
9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 行列演算と写像 ( 次変換 3 拡大とスカラー倍 p ' = ( ', ' = ( k, kk p = (, k 倍 k 倍 拡大後 k 倍拡大の関係は スカラー倍を用いて次のように表現できる ' = k ' 拡大前 拡大 4 拡大と行列の積 p ' = ( ', '
Microsoft Word ã‡»ã…«ã‡ªã…¼ã…‹ã…žã…‹ã…³ã†¨åłºæœ›å•¤(佒芤喋çfl�)
Cellulr uo nd heir eigenlues 東洋大学総合情報学部 佐藤忠一 Tdzu So Depren o Inorion Siene nd rs Toyo Uniersiy. まえがき 一次元セルオ-トマトンは数学的には記号列上の行列の固有値問題である 固有値問題の行列はふつう複素数体上の行列である 量子力学における固有値問題も無限次元ではあるが関数環上の行列でその成分は可換環である
Microsoft PowerPoint - ad11-09.pptx
無向グラフと有向グラフ 無向グラフ G=(V, E) 頂点集合 V 頂点の対を表す枝の集合 E e=(u,v) 頂点 u, v は枝 e の端点 f c 0 a 1 e b d 有向グラフ G=(V, E) 頂点集合 V 頂点の順序対を表す枝の集合 E e=(u,v) 頂点 uは枝 eの始点頂点 vは枝 eの終点 f c 0 a 1 e b d グラフのデータ構造 グラフ G=(V, E) を表現するデータ構造
ピタゴラスの定理の証明４
[ 証明 ] この証明を論理的に厳密に行うには 何回か三角形 四角形の合同を証明しなくてはなりません 以下では 直感的な分かりやすさを重視して この証明を行いません 三角形 において であるとする 辺 を一辺とする正方形 を三角形 の外側につくる 辺 を一辺とする正方形 を三角形 の外側につくる 辺 を一辺とする正方形 Fを三角形 の外側につくる 直線 と直線 との交点を J とし 直線 と直線 F
<4D F736F F D208CF68BA48C6F8DCF8A C30342C CFA90B68C6F8DCF8A7782CC8AEE967B92E8979D32288F4390B394C529332E646F63>
2. 厚生経済学の ( 第 ) 基本定理 2 203 年 4 月 7 日 ( 水曜 3 限 )/8 本章では 純粋交換経済において厚生経済学の ( 第 ) 基本定理 が成立することを示す なお より一般的な生産技術のケースについては 4.5 補論 2 で議論する 2. 予算集合と最適消費点 ( 完全 ) 競争市場で達成される資源配分がパレート効率的であることを示すための準備として 個人の最適化行動を検討する
航空機の運動方程式
可制御性 可観測性. 可制御性システムの状態を, 適切な操作によって, 有限時間内に, 任意の状態から別の任意の状態に移動させることができるか否かという特性を可制御性という. 可制御性を有するシステムに対し, システムは可制御である, 可制御なシステム という言い方をする. 状態方程式, 出力方程式が以下で表されるn 次元 m 入力 r 出力線形時不変システム x Ax u y x Du () に対し,
Microsoft PowerPoint - DA2_2018.pptx
1//1 データ構造とアルゴリズム IⅠ 第 回単一始点最短路 (I). 単一始点最短路問題 第 章の構成 単一始点最短路問題とは 単一始点最短路問題の考え方 単一始点最短路問題を解くつのアルゴリズム ベルマン フォードのアルゴリズム トポロジカル ソートによる解法 ダイクストラのアルゴリズム 単一始点最短路問題とは 単一始点最短路問題とは 前提 : 重み付き有向グラフ 特定の開始頂点 から任意の頂点
喨微勃挹稉弑
== 全微分方程式 == 全微分とは 変数の関数 z=f(, ) について,, の増分を Δ, Δ とするとき, z の増分 Δz は Δz z Δ+ z Δ で表されます. この式において, Δ 0, Δ 0 となる極限を形式的に dz= z d+ z d (1) で表し, dz を z の全微分といいます. z は z の に関する偏導関数で, を定数と見なし て, で微分したものを表し, 方向の傾きに対応します.
Math-quarium 練習問題 + 図形の性質 線分 は の二等分線であるから :=:=:=: よって = = = 線分 は の外角の二等分線であるから :=:=:=: よって :=: したがって == 以上から =+=+= 右の図において, 点 は の外心である α,βを求めよ α β 70
Math-quarium 練習問題 + 図形の性質 図形の性質 線分 に対して, 次の点を図示せよ () : に内分する点 () : に外分する点 Q () 7: に外分する点 R () 中点 M () M () Q () () R 右の図において, 線分の長さ を求めよ ただし,R//Q,R//,Q=,=6 とする Q R 6 Q から,:=:6=: より :=: これから,R:=: より :6=:
チェビシェフ多項式の2変数への拡張と公開鍵暗号（ElGamal暗号）への応用
チェビシェフ多項式の 変数への拡張と公開鍵暗号 Ell 暗号 への応用 Ⅰ. チェビシェフ Chbhv Chbhv の多項式 より であるから よって ここで とおくと coθ iθ coθ iθ iθ coθcoθ 4 4 iθ iθ iθ iθ iθ i θ i θ i θ i θ co θ co θ} co θ coθcoθ co θ coθ coθ したがって が成り立つ この漸化式と であることより
Microsoft PowerPoint - 06graph3.ppt [互換モード]
![Microsoft PowerPoint - 06graph3.ppt [互換モード]](/thumbs/100/144239321.jpg "Microsoft PowerPoint - 06graph3.ppt [互換モード]")
I118 グラフとオートマトン理論 Graphs and Automata 担当 : 上原隆平 (Ryuhei UEHARA) uehara@jaist.ac.jp http://www.jaist.ac.jp/~uehara/ 1/20 6.14 グラフにおける探索木 (Search Tree in a Graph) グラフG=(V,E) における探索アルゴリズム : 1. Q:={v { 0 }
2011年度 東京大・文系数学
東京大学 ( 文系 ) 前期日程問題 解答解説のページへ x の 次関数 f( x) = x + x + cx+ d が, つの条件 f () =, f ( ) =, ( x + cx+ d) dx= をすべて満たしているとする このような f( x) の中で定積分 I = { f ( x) } dx を最小にするものを求め, そのときの I の値を求めよ ただし, f ( x) は f ( x)
Microsoft PowerPoint - 2.ppt [互換モード]
![Microsoft PowerPoint - 2.ppt [互換モード]](/thumbs/74/70606453.jpg "Microsoft PowerPoint - 2.ppt [互換モード]")
0 章数学基礎 1 大学では 高校より厳密に議論を行う そのために 議論の議論の対象を明確にする必要がある 集合 ( 定義 ) 集合 物の集まりである集合 X に対して X を構成している物を X の要素または元という 集合については 3 セメスタ開講の 離散数学 で詳しく扱う 2 集合の表現 1. 要素を明示する表現 ( 外延的表現 ) 中括弧で 囲う X = {0,1, 2,3} 慣用的に 英大文字を用いる
Microsoft PowerPoint - H21生物計算化学２.ppt
演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
Microsoft PowerPoint - ppt-7.pptx
テーマ 7: 最小包含円 点集合を包含する半径最小の円 最小包含円問題 問題 : 平面上に n 点の集合が与えられたとき, これらの点をすべて内部に含む半径最小の円を効率よく求める方法を示せ. どの点にも接触しない包含円 すべての点を内部に含む包含円を求める 十分に大きな包含円から始め, 点にぶつかるまで徐々に半径を小さくする 1 点にしか接触しない包含円 現在の中心から周上の点に向けて中心を移動する
2-1 / 語問題 項書換え系 4.0. 準備 (3.1. 項 代入 等価性 ) 定義 3.1.1: - シグネチャ (signature): 関数記号の集合 (Σ と書く ) - それぞれの関数記号は アリティ (arity) と呼ばれる自然数が定められている - Σ (n) : アリ
2-1 / 32 4. 語問題 項書換え系 4.0. 準備 (3.1. 項 代入 等価性 ) 定義 3.1.1: - シグネチャ (signature): 関数記号の集合 (Σ と書く ) - それぞれの関数記号は アリティ (arity) と呼ばれる自然数が定められている - Σ (n) : アリティ n を持つ関数記号からなる Σ の部分集合 例 : 群 Σ G = {e, i, } (e Σ
Microsoft PowerPoint - 10.pptx
0. 固有値とその応用 固有値と固有ベクトル 2 行列による写像から固有ベクトルへ m n A : m n n m 行列によって線形写像 f R R A が表せることを見てきた ここでは 2 次元平面の行列による写像を調べる 2 = 2 A 2 2 とし 写像 まず 単位ベクトルの像を求める u 2 x = v 2 y f : R A R を考える u 2 2 u, 2 2 0 = = v 2 0
2016年度 京都大・文系数学
06 京都大学 ( 文系 ) 前期日程問題 解答解説のページへ xy 平面内の領域の面積を求めよ x + y, x で, 曲線 C : y= x + x -xの上側にある部分 -- 06 京都大学 ( 文系 ) 前期日程問題 解答解説のページへ ボタンを押すと あたり か はずれ のいずれかが表示される装置がある あたり の表示される確率は毎回同じであるとする この装置のボタンを 0 回押したとき,
PowerPoint Presentation
付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
1999年度 センター試験・数学ⅡＢ
99 センター試験数学 Ⅱ 数学 B 問題 第 問 ( 必答問題 ) [] 関数 y cos3x の周期のうち正で最小のものはアイウ 解答解説のページへ 0 x 360 のとき, 関数 y cos3x において, y となる x はエ個, y となる x はオ 個ある また, y sin x と y cos3x のグラフより, 方程式 sin x cos3x は 0 x 360のときカ個の解をもつことがわかる
2015－2017年度 ２次数学セレクション（複素数）解答解説
05 次数学セレクション解答解説 [ 筑波大 ] ( + より, 0 となり, + から, ( (,, よって, の描く図形 C は, 点 を中心とし半径が の円である すなわち, 原 点を通る円となる ( は虚数, は正の実数より, である さて, w ( ( とおくと, ( ( ( w ( ( ( ここで, w は純虚数より, は純虚数となる すると, の描く図形 L は, 点 を通り, 点 と点
Microsoft PowerPoint - DA2_2018.pptx
データ構造とアルゴリズム IⅠ 第 7 回幅優先 / 深さ優先探索 / トポロジカルソート. 基本的グラフアルゴリズム 無向グラフ 個の頂点と7 本の辺からなる無向グラフ 隣接リスト 各頂点に関して, 隣接する ( 直接, 辺で結ばれた ) 頂点集合をリストで表現 無向グラフ G=(V,E),V は頂点集合,E は辺集合.E の要素は頂点のペア {u,} によって表される.{u, } と {, u}
PowerPoint プレゼンテーション
解けない問題 を知ろう 保坂和宏 ( 東京大学 B2) 第 11 回 JOI 春合宿 2012/03/19 概要 計算量に関して P と NP NP 完全 決定不能 いろいろな問題 コンテストにおいて Turing 機械 コンピュータの計算のモデル 計算 を数学的に厳密に扱うためのもの メモリのテープ (0/1 の列 ), ポインタ, 機械の内部状態を持ち, 規則に従って状態遷移をする 本講義では
. 角の二等分線と調和平均 平面上に点 を端点とする線分 と を重ならないようにとる, とし とする の二等分線が線分 と交わる点を とし 点 から に垂直に引いた直線が線分 と交わる点 とする 線分 の長さを求めてみよう 点 から に垂直な直線と および との交点をそれぞれ, Dとする つの直角三
角の二等分線で開くいろいろな平均 札幌旭丘高校中村文則 0. 数直線上に現れるいろいろな平均下図は 数 (, ) の調和平均 相乗平均 相加平均 二乗平均を数直線上に置いたものである, とし 直径 中心 である円を用いていろいろな平均の大小関係を表現するもっとも美しい配置方法であり その証明も容易である Q D E F < 相加平均 > (0), ( ), ( とすると 線分 ) の中点 の座標はである
Microsoft Word - thesis.doc
剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
構造化プログラミングと データ抽象
計算の理論 後半第 3 回 λ 計算と型システム 本日の内容 λ 計算の表現力 ( 前回の復習 ) データの表現 不動点演算子と再帰 λ 計算の重要な性質 チャーチ ロッサー性 簡約戦略 型付き λ 計算 ブール値 組 ブール値と組の表現 true, false を受け取り 対応する要素を返す関数 として表現 T = λt.λf.t F = λt.λf.f if e 1 then e 2 else
2019年度 千葉大・理系数学
9 千葉大学 ( 理系 ) 前期日程問題 解答解説のページへ a, a とし, のとき, a+ a + a - として数列 { a } () のとき a+ a a a - が成り立つことを証明せよ () åai aaa + が成り立つような自然数 を求めよ i を定める -- 9 千葉大学 ( 理系 ) 前期日程問題 解答解説のページへ 三角形 ABC は AB+ AC BCを満たしている また,
Math-Aquarium 例題 図形と計量 図形と計量 1 直角三角形と三角比 P 木の先端を P, 根元を Q とする A 地点の目の位置 A' から 木の先端への仰角が 30,A から 7m 離れた AQB=90 と なる B 地点の目の位置 B' から木の先端への仰角が 45 であ るとき,
図形と計量 直角三角形と三角比 P 木の先端を P, 根元を Q とする 地点の目の位置 ' から 木の先端への仰角が 0, から 7m 離れた Q=90 と なる 地点の目の位置 ' から木の先端への仰角が であ るとき, 木の高さを求めよ ただし, 目の高さを.m とし, Q' を右の図のように定める ' 0 Q' '.m Q 7m 要点 PQ PQ PQ' =x とおき,' Q',' Q' を
2013年度 九州大・理系数学
九州大学 ( 理系 ) 前期日程問題 解答解説のページへ a> とし, つの曲線 y= ( ), y= a ( > ) を順にC, C とする また, C とC の交点 P におけるC の接線をl とする 以下 の問いに答えよ () 曲線 C とy 軸および直線 l で囲まれた部分の面積をa を用いて表せ () 点 P におけるC の接線と直線 l のなす角を ( a) とき, limasin θ(
オートマトンと言語
オートマトンと言語 4 回目 5 月 2 日 ( 水 ) 3 章 ( グラフ ) の続き 授業資料 http://ir.cs.yamanashi.ac.jp/~ysuzuki/public/automaton/ 授業の予定 ( 中間試験まで ) 回数月日 内容 4 月 日オートマトンとは, オリエンテーション 2 4 月 8 日 2 章 ( 数式の記法, スタック,BNF) 3 4 月 25 日 2
2015年度 信州大・医系数学
05 信州大学 ( 医系 ) 前期日程問題 解答解説のページへ 放物線 y = a + b + c ( a > 0) を C とし, 直線 y = -を l とする () 放物線 C が点 (, ) で直線 l と接し, かつ 軸と共有点をもつための a, b, c が満 たす必要十分条件を求めよ () a = 8 のとき, () の条件のもとで, 放物線 C と直線 l および 軸とで囲まれた部
<4D F736F F F696E74202D208AF489BD8A7782C CF97CA82A882DC82AF2E B8CDD8AB B83685D>
幾何学と不変量 数学オリンピックの問題への応用 北海道大学 高等教育推進機構西森敏之 この講演では, 数学の長い歴史の中で見つけられた, 不変量 とよばれるものの考え方を, 実際に数学オリンピックの問題を解きながら, 紹介します 1. ウオーミング アップ まず, 少し脳細胞のウオーミング アップをします 定義 ( 分割合同 ) 平面上の 2 つの多角形 P と Q が分割合同とは, 多角形 P をいくつかの直線で切って小片に分けてから,
Microsoft PowerPoint - DA2_2017.pptx
// データ構造とアルゴリズム IⅠ 第 回単一始点最短路 (II)/ 全点対最短路 トポロジカル ソート順による緩和 トポロジカル ソート順に緩和 閉路のない有向グラフ限定 閉路がないならトポロジカル ソート順に緩和するのがベルマン フォードより速い Θ(V + E) 方針 グラフをトポロジカル ソートして頂点に線形順序を与える ソート順に頂点を選び, その頂点の出辺を緩和する 各頂点は一回だけ選択される
平成 25 年度京都数学オリンピック道場 ( 第 1 回 ) H 正三角形 ABC の外接円の,A を含まない弧 BC 上に点 P をとる. このとき, AP = BP + CP となることを示せ. 解説円周角の定理より, 4APC = 4ABC = 60, であるから, 図のよ
1 正三角形 の外接円の, を含まない弧 上に点 をとる. このとき, = + となることを示せ. 解説円周角の定理より, 4 = 4 = 60, であるから, 図のように直線 上に点 を, 三角形 が正三角形となるようにとることができる. 三角形 と三角形 において, =, = であり, 4 = 4 = 60, - 4 であるから, 辺とその間の角がそれぞれ等しく, 三角形 と三角形 は合同である.
学力スタンダード（様式１）
(1) 数と式 学習指導要領ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 稔ヶ丘高校学力スタンダード 有理数 無理数の定義や実数の分類について理解し ている 絶対値の意味と記号表示を理解している 実数と直線上の点が一対一対応であることを理解 し 実数を数直線上に示すことができる 例 実数 (1) -.5 () π (3) 数直線上の点はどれか答えよ
高ゼミサポSelectⅢ数学Ⅰ_解答.indd
数と式 ⑴ 氏点00 次の式を展開せよ ( 各 6 点 ) ⑴ (a-)(a -a+) ⑵ (x+y+)(x+y-5) 次の式を因数分解せよ (⑴⑵ 各 6 点, ⑶⑷ 各 8 点 ) ⑴ x y+x -x-6y ⑵ x -x - ⑶ a +5b ⑷ (x+y+z+)(x+)+yz 数と式 ⑵ 氏点00 次の問いに答えよ ( 各 6 点 ) ⑴ 次の循環小数を分数で表せ. a-5 = ⑵ 次の等式を満たす実数
2011年度 大阪大・理系数学
0 大阪大学 ( 理系 ) 前期日程問題 解答解説のページへ a a を自然数とする O を原点とする座標平面上で行列 A= a の表す 次変換 を f とする cosθ siθ () >0 および0θ
融合規則 ( もっとも簡単な形, 選言的三段論法 ) ll mm ll mm これについては (ll mm) mmが推論の前提部になり mmであるから mmは常に偽となることがわかり ll mmはllと等しくなることがわかる 機械的には 分配則より (ll mm) mm (ll mm) 0 ll m
知識工学 ( 第 5 回 ) 二宮崇 ( ninomiya@cs.ehime-u.ac.jp ) 論理的エージェント (7 章のつづき ) 証明の戦略その 3 ( 融合法 ) 証明の戦略その 1 やその 2 で証明できたときは たしかにKKKK ααとなることがわかるが なかなか証明できないときや 証明が本当にできないときには KKKK ααが成り立つのか成り立たないのかわからない また どのような証明手続きを踏めば証明できるのか定かではない
DVIOUT-SS_Ma
第 章 微分方程式 ニュートンはリンゴが落ちるのを見て万有引力を発見した という有名な逸話があります 無重力の宇宙船の中ではリンゴは落ちないで静止していることを考えると 重力が働くと始め静止しているものが動き出して そのスピードはどんどん大きくなる つまり速度の変化が現れることがわかります 速度は一般に時間と共に変化します 速度の瞬間的変化の割合を加速度といい で定義しましょう 速度が変化する, つまり加速度がでなくなるためにはその原因があり
DVIOUT-17syoze
平面の合同変換と相似変換 岩瀬順一 要約 : 平面の合同変換と相似変換を論じる いま大学で行列を学び始めている大学一年生を念頭に置いている 高等学校で行列や一次変換を学んでいなくてもよい 1. 写像 定義 1.1 X, Y を集合とする X の各元 x に対し Y のただ一つの元 y を対応させる規則 f を写像とよび,f : X! Y のように書く f によって x に対応する Y の元を f(x)
トポス alg-d 年 5 月 5 日 1 トポス 定義. P, Q: C op Set を関手とする.P が Q の部分関手 ( 記号で P Q と書く ) 自然変換 θ : P Q で 各 a C について θ
トポス alg-d http://alg-d.com/math/kan_extension/ 2018 年 5 月 5 日 1 トポス 定義. P, Q: C op Set を関手とする.P が Q の部分関手 ( 記号で P Q と書く ) 自然変換 θ : P Q で 各 a C について θ a : P a Qa が包含写像になっているもの が存在する. P Q を部分関手とすると, 自然性より,f
調和系工学 ゲーム理論編
ゲーム理論第三部 知的都市基盤工学 5 月 30 日 ( 水 5 限 (6:30~8:0 再掲 : 囚人のジレンマ 囚人のジレンマの利得行列 協調 (Cooperte:C プレイヤー 裏切 (Deect:D ( 協調 = 黙秘 裏切 = 自白 プレイヤー C 3,3 4, D,4, 右がプレイヤー の利得左がプレイヤー の利得 ナッシュ均衡点 プレイヤーの合理的な意思決定の結果 (C,C はナッシュ均衡ではない
2014年度 筑波大・理系数学
筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ f ( x) = x x とする y = f ( x ) のグラフに点 P(, ) から引いた接線は 本あるとする つの接点 A (, f ( )), B(, f ( )), C(, f ( )) を頂点とする三角形の 重心を G とする () + +, + + および を, を用いて表せ () 点 G の座標を, を用いて表せ () 点 G
<8D828D5A838A817C A77425F91E6318FCD2E6D6364>
4 1 平面上のベクトル 1 ベクトルとその演算 例題 1 ベクトルの相等 次の問いに答えよ. ⑴ 右の図 1 は平行四辺形 である., と等しいベクトルをいえ. ⑵ 右の図 2 の中で互いに等しいベクトルをいえ. ただし, すべてのマス目は正方形である. 解 ⑴,= より, =,= より, = ⑵ 大きさと向きの等しいものを調べる. a =d, c = f d e f 1 右の図の長方形 において,
Microsoft Word docx
有限図形の代数的表現について 三角形や星型を式で表現したいという思いから以下のことを 考察をしまし た 有限個の点と辺で 構成される図形を 関数で表現する そのため 基礎 体として 素数の有限体を考える 但し 扱うのは 点の数と辺の数が等しい 特別場合である 先ず P5 のときから 始めることにします. グラフと写像と関数について ( 特別な場合 ) 集合 F {,,,, } について 写像 f :
<4D F736F F D A788EA8E9F95FB92F68EAE>
行列を用いた連立一次方程式の解法 概要私たちは数学 C で一次連立方程式の正方行列を用いた解法を学んだ 今回はこれをベースとし 元一次連立方程式の解法への拡張を目標とした まず 行列の性質から解をもつ条件 不定解の処理を考えた また 逆行列を求める手法は一般的に煩雑である そこでそれ以外に Crmer の定理 掃き出し法などの解法も検証した 今回の研究は発展的で難しかったが 研究を通してより多角的で数学的な思考の一端を学べた.
例 e 指数関数的に減衰する信号を h( a < + a a すると, それらのラプラス変換は, H ( ) { e } e インパルス応答が h( a < ( ただし a >, U( ) { } となるシステムにステップ信号 ( y( のラプラス変換 Y () は, Y ( ) H ( ) X (
第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
Matrix and summation convention Kronecker delta δ ij 1 = 0 ( i = j) ( i j) permutation symbol e ijk = (even permutation) (odd permutation) (othe
Matr ad summato covto Krockr dlta δ ( ) ( ) prmutato symbol k (v prmutato) (odd prmutato) (othrs) gvalu dtrmat dt 6 k rst r s kt opyrght s rsrvd. No part of ths documt may b rproducd for proft. 行列 行 正方行列
<4D F736F F D F90948A F835A E815B8E8E8CB189F090E05F8E6C8D5A>
06 年度大学入試センター試験解説 数学 Ⅱ B 第 問 () 8 より, 5 5 5 6 6 8 ア, イ また, 底の変換公式を用いると, log 7 log log 9 9 log 7 log ウエ, オ (), のグラフは, それぞれ = 89 = 右図のようになり, この つのグラフは 軸に関して対称 ここで, 0, のとき, と log カ のグラフが直線 に関して対称 であることから,
離散数学
離散数学 ブール代数 落合秀也 前回の復習 : 命題計算 キーワード 文 複合文 結合子 命題 恒真 矛盾 論理同値 条件文 重条件文 論法 論理含意 記号 P(p,q,r, ),,,,,,, 2 今日のテーマ : ブール代数 ブール代数 ブール代数と束 そして 順序 加法標準形とカルノー図 3 今日のテーマ : ブール代数 ブール代数 ブール代数と束 そして 順序 加法標準形とカルノー図 4 ブール代数の法則
Microsoft PowerPoint - 3.ppt [互換モード]
![Microsoft PowerPoint - 3.ppt [互換モード]](/thumbs/95/124643964.jpg "Microsoft PowerPoint - 3.ppt [互換モード]")
3. プッシュダウンオートマトンと文脈自由文法 1 3-1. プッシュダウンオートマトン オートマトンはメモリがほとんど無かった この制限を除いた機械を考える 理想的なスタックを利用できるようなオートマトンをプッシュダウンオートマトン (Push Down Automaton,PDA) という 0 1 入力テープ 1 a 1 1 0 1 スタッb 入力テープを一度走査したあと ク2 入力テプを度走査したあと
Microsoft Word - K-ピタゴラス数.doc
- ピタゴラス数の代数と幾何学 津山工業高等専門学校 菅原孝慈 ( 情報工学科 年 ) 野山由貴 ( 情報工学科 年 ) 草地弘幸 ( 電子制御工学科 年 ) もくじ * 第 章ピタゴラス数の幾何学 * 第 章ピタゴラス数の代数学 * 第 3 章代数的極小元の幾何学の考察 * 第 章ピタゴラス数の幾何学的研究の動機 交点に注目すると, つの曲線が直交しているようにみえる. これらは本当に直交しているのだろうか.
DVIOUT-SS_Ma
第 章 テイラー展開 次の図のように関数のグラフをのグラフ ( 積み木のようなものと考えます ) を積み重ねて作ってみましょう ただ単純に足すだけではうまく作れません 色々と削ることが必要になります 次のように半分にしたり, 分のに削らなくてはなりません どうですか? たった枚の積み木を積み重ねただけで, ほぼのグラフに近づきまし たね これから学ぶのがこのテイラー展開のお話です 初等関数の微分 初等関数の微分まずは
二等辺三角形の性質 (2) 次の図の の大きさを求めなさい () = P=Q P=R Q 68 R P (2) (3) 五角形 は正五角形 = F 50 F (4) = = (5) === = 80 2 二等辺三角形の頂角の外角を 底角を y で表すとき y を の式で表しなさい y 2-5-2
三角形 四角形 二等辺三角形の性質 () 二等辺三角形と正三角形 二等辺三角形 2つの辺が等しい三角形( 定義 ) 二等辺三角形の性質定理 二等辺三角形の底角は等しい 定理 2 二等辺三角形の頂点の二等分線は 底辺を直角に2 等分する 正三角形 3 辺が等しい三角形 ( 定義 ) 次の図で 同じ印をつけた辺や角が等しいとき の大きさを求めなさい () (2) (3) 65 40 25 (4) (5)
オートマトン 形式言語及び演習 3. 正規表現 酒井正彦 正規表現とは 正規表現 ( 正則表現, Regular Expression) オートマトン : 言語を定義する機械正規表現 : 言語
オートマトン 形式言語及び演習 3. 酒井正彦 www.trs.css.i.nagoya-u.ac.jp/~sakai/lecture/automata/ とは ( 正則表現, Regular Expression) オートマトン : 言語を定義する機械 : 言語を記号列で定義 - 記述しやすい ( ユーザフレンドリ ) 例 :01 + 10 - UNIX の grep コマンド - UNIX の
Microsoft Word - 数学Ⅰ
() 数と式 ア数と集合 ( ア ) 実数 数を実数まで拡張する意義を理解し 簡単な 無理数の四則計算をすること 自然数 整数 有理数 無理数の包含関係など 実数の構成を理解する ( 例 ) 次の空欄に適当な言葉をいれて, 数の集合を表しなさい イ 整数 ウ ア 無理数 自然数 整数 有理数 無理数 実数のそれぞれ の集合について 四則演算の可能性について判断 できる ( 例 ) 下の表において,
計算幾何学入門 Introduction to Computational Geometry
テーマ 6: ボロノイ図とデローネイ 三角形分割 ボロノイ図, デローネイ三角形分割 ボロノイ図とは 平面上に多数の点が与えられたとき, 平面をどの点に最も近いかという関係で分割したものをボロノイ図 (Voronoi diagram) という. 2 点だけの場合 2 点の垂直 2 等分線による分割 3 点の場合 3 点で決まる三角形の外接円の中心から各辺に引いた垂直線による分割線 2 点からの等距離線
数学の世界
東京女子大学文理学部数学の世界 (2002 年度 ) 永島孝 17 6 行列式の基本法則と効率的な計算法 基本法則 三次以上の行列式についても, 二次の場合と同様な法則がなりたつ ここには三次の場合を例示するが, 四次以上でも同様である 1 単位行列の行列式の値は 1 である すなわち 1 0 0 0 1 0 1 0 0 1 2 二つの列を入れ替えると行列式の値は 1 倍になる 例えば a 13 a
1/10 平成 29 年 3 月 24 日午後 1 時 37 分第 5 章ローレンツ変換と回転 第 5 章ローレンツ変換と回転 Ⅰ. 回転 第 3 章光速度不変の原理とローレンツ変換 では 時間の遅れをローレンツ変換 ct 移動 v相対 v相対 ct - x x - ct = c, x c 2 移動
/ 平成 9 年 3 月 4 日午後 時 37 分第 5 章ローレンツ変換と回転 第 5 章ローレンツ変換と回転 Ⅰ. 回転 第 3 章光速度不変の原理とローレンツ変換 では 時間の遅れをローレンツ変換 t t - x x - t, x 静止静止静止静止 を導いた これを 図の場合に当てはめると t - x x - t t, x t + x x + t t, x (5.) (5.) (5.3) を得る
2017年度 長崎大・医系数学
07 長崎大学 ( 医系 ) 前期日程問題 解答解説のページへ 以下の問いに答えよ () 0 のとき, si + cos の最大値と最小値, およびそのときの の値 をそれぞれ求めよ () e を自然対数の底とする > eの範囲において, 関数 y を考える この両 辺の対数を について微分することにより, y は減少関数であることを示せ また, e< < bのとき, () 数列 { } b の一般項が,
2018年度 神戸大・理系数学
8 神戸大学 ( 理系 ) 前期日程問題 解答解説のページへ t を < t < を満たす実数とする OABC を 辺の長さが の正四面体とする 辺 OA を -t : tに内分する点を P, 辺 OB を t :-tに内分する点を Q, 辺 BC の中点を R とする また a = OA, b = OB, c = OC とする 以下の問いに答えよ () QP と QR をt, a, b, c を用いて表せ
構造化プログラミングと データ抽象
計算の理論 後半第 3 回 λ 計算と型システム 本日の内容 λ 計算の表現力 ( 前回のつづき ) 前回の復習 不動点演算子と再帰 λ 計算の重要な性質 チャーチ ロッサー性 簡約戦略 型付き λ 計算 ブール値 組 ブール値と組の表現 ( 復習 ) true, false を受け取り 対応する要素を返す関数 として表現 T = λt.λf.t F = λt.λf.f if e 1 then e
< 中 3 分野例題付き公式集 > (1)2 の倍数の判定法は 1 の位が 0 又は偶数 ( 例題 )1~5 までの 5 つの数字を使って 3 ケタの数をつくるとき 2 の倍数は何通りできるか (2)5 の倍数の判定法は 1 の位が 0 又は 5 ( 例題 )1~9 までの 9 個の数字を使って 3
() の倍数の判定法は の位が 0 又は偶数 ~ までの つの数字を使って ケタの数をつくるとき の倍数は何通りできるか () の倍数の判定法は の位が 0 又は ~9 までの 9 個の数字を使って ケタの数をつくるとき の倍数は何通りできるか () の倍数の判定法は 下 ケタが 00 又は の倍数 ケタの数 8 が の倍数となるときの 最小の ケタの数は ( 解 ) 一の位の数は の 通り 十の位は一の位の数以外の
数学 ⅡB < 公理 > 公理を論拠に定義を用いて定理を証明する 1 大小関係の公理 順序 (a > b, a = b, a > b 1 つ成立 a > b, b > c a > c 成立 ) 順序と演算 (a > b a + c > b + c (a > b, c > 0 ac > bc) 2 図
数学 Ⅱ < 公理 > 公理を論拠に定義を用いて定理を証明する 大小関係の公理 順序 >, =, > つ成立 >, > > 成立 順序と演算 > + > + >, > > 図形の公理 平行線の性質 錯角 同位角 三角形の合同条件 三角形の合同相似 量の公理 角の大きさ 線分の長さ < 空間における座漂とベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル
母平均 母分散 母標準偏差は, が連続的な場合も含めて, すべての個体の特性値 のすべての実現値 の平均 分散 標準偏差であると考えてよい 有限母集団で が離散的な場合, まさにその意味になるが, そうでない場合も, このように理解してよい 5 母数 母集団から定まる定数のこと 母平均, 母分散,
. 無作為標本. 基本的用語 推測統計における基本的な用語を確認する 母集団 調査の対象になる集団のこと 最終的に, 判断の対象になる集団である 母集団の個体 母集団を構成する つ つのもののこと 母集団は個体の集まりである 個体の特性値 個体の特性を表す数値のこと 身長や体重など 特性値は, 変量ともいう 4 有限母集団と無限母集団 個体の個数が有限の母集団を 有限母集団, 個体の個数が無限の母集団を
紙を折る < 問題 > 長方形の紙を折る このとき 相似形はいくつできるだろうか? 2 個 固定固定固定 固定 2 個 2 個 固定 固定 3 個 3 個 固定 3 個 4 個 4 個
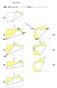紙を折る < 問題 > 長方形の紙を折る このとき 相似形はいくつできるだろうか? 個 固定固定固定 固定 個 個 固定 固定 個 個 固定 個 4 個 4 個 * 隣り合う辺を結んで折るとき 最大 個 * 向かい合う辺を結んで折るとき 最大 4 個 < 問題 > 固定される場合 その位置はどこか? そのときの相似比はいくらか? 返上を移動する場合 その範囲はどうか? 合同になるときはあるか? それはどんなときか?
2 α 2 A α 1 α 5 α 3 α 4 1.2: A 3 π n 4 n 3 n = 3 n 3 n = 2 1 α A 4π α/2π A = 4π α 2π = 2α n = 2 α α 1.3: 2 n = 3,, R 3 α, β, γ S 2,, R,, R 2, R 2 T T
1 I: 1.1 3 1 S 2 = {(x, y, z) : x 2 + y 2 + z 2 = 1} O S 2 S 2 n n O (a) (b) 3 1.1: 3 n A α 1,, α n n α j = (n 2)π + A j=1 n (n 2)π 2 α 2 A α 1 α 5 α 3 α 4 1.2: A 3 π n 4 n 3 n = 3 n 3 n = 2 1 α A 4π α/2π
東邦大学理学部情報科学科 2014 年度 卒業研究論文 コラッツ予想の変形について 提出日 2015 年 1 月 30 日 ( 金 ) 指導教員白柳潔 提出者 山中陽子
東邦大学理学部情報科学科 2014 年度 卒業研究論文 コラッツ予想の変形について 提出日 2015 年 1 月 30 日 ( 金 ) 指導教員白柳潔 提出者 山中陽子 2014 年度東邦大学理学部情報科学科卒業研究 コラッツ予想の変形について 学籍番号 5511104 氏名山中陽子 要旨 コラッツ予想というのは 任意の 0 でない自然数 n をとり n が偶数の場合 n を 2 で割り n が奇数の場合
() ): (1) f(x) g(x) x = x 0 f(x) + g(x) x = x 0 lim f(x) = f(x 0 ), lim g(x) = g(x 0 ) x x 0 x x0 lim {f(x) + g(x)} = f(x 0 ) + g(x 0 ) x x0 lim x x 0
(1) 3 連続関数と逆関数 定義 3.1 y = f (x) のグラフが x = a でつながっているとき f (x) は x = a において連続と いう. 直感的にはこれが わかりやすい x = a では連続 x = b ではグラフがちぎれているので 不連続 定義 3. f (x) が x = a の近くで定義され lim f (x) = f (a) をみたす時 x a f (x) は x =
学習指導要領
(1) 数と式 学習指導要領ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 都立大江戸高校学力スタンダード 平方根の意味を理解し 平方根の計算法則に従って平方根を簡単にすることができる ( 例 1) 次の値を求めよ (1)5 の平方根 () 81 ( 例 ) 次の数を簡単にせよ (1) 5 () 7 1 (3) 49 無理数の加法や減法 乗法公式を利用した計算がで
2014年度 千葉大・医系数学
04 千葉大学 ( 医系 ) 前期日程問題 解答解説のページへ 袋の中に, 赤玉が 3 個, 白玉が 7 個が入っている 袋から玉を無作為に つ取り出し, 色を確認してから, 再び袋に戻すという試行を行う この試行を N 回繰り返したときに, 赤玉を A 回 ( ただし 0 A N) 取り出す確率を p( N, A) とする このとき, 以下の問いに答えよ () 確率 p( N, A) を N と