Microsoft PowerPoint - 03-FEM3D-F.ppt [互換モード]
|
|
|
- すずり しげい
- 4 years ago
- Views:
Transcription
1 有限要素法による 三次元定常熱伝導解析プログラム Fortran 編 中島研吾東京大学情報基盤センター
2 FEM3D 2 対象とする問題 : 三次元定常熱伝導 Z T T=0@Z=z ma Z T z 定常熱伝導 + 発熱 一様な熱伝導率 直方体 T z 一辺長さの立方体 ( 六面体 ) 要素 各方向にX Y Z 個 境界条件 Q z 0 X Y X Y T=0@Z=z ma 体積当たり発熱量は位置 ( メッシュの中心の座標 c c ) に依存 Q z QVOL C C
3 FEM3D 3 対象とする問題 : 三次元定常熱伝導 T T z T z Q z 0 原点から遠い部分が高温 体積当たり発熱量は位置 ( メッシュの中心の座標 ) に依存 Q z C C move
4 FEM3D 有限要素法の処理 支配方程式 ガラーキン法 : 弱形式 要素単位の積分 要素マトリクス生成 全体マトリクス生成 境界条件適用 連立一次方程式
5 FEM3D 5 有限要素法の処理 : プログラム 初期化 制御変数読み込み 座標読み込み 要素生成 (: 節点数 ICELTOT: 要素数 ) 配列初期化 ( 全体マトリクス 要素マトリクス ) 要素 全体マトリクスマッピング (IndeItem) マトリクス生成 要素単位の処理 (do cel= ICELTOT) 要素マトリクス計算 全体マトリクスへの重ね合わせ 境界条件の処理 連立一次方程式 共役勾配法 (CG)
6 FEM3D 6 三次元要素の定式化 三次元熱伝導方程式 ガラーキン法 要素マトリクス生成 プログラムの実行 データ構造 プログラムの構成
7 FEM3D 7 二次元への拡張 : 三角形要素 任意の形状を扱うことができる 特に一次要素は精度が悪く 一部の問題を除いてあまり使用されない
8 FEM3D 二次元への拡張 : 四角形要素 一次元要素と同じ形状関数を 軸に適用することによって 四角形要素の定式化は可能である 三角形と比較して特に低次要素の精度はよい しかしながら 各辺が座標軸に平行な長方形でなければならない 差分法と変わらない 3 このような形状を扱うことができない 2
9 FEM3D 9 アイソパラメトリック要素 (/3) 各要素を 自然座標系 () の正方形要素 [± ±] に変換する 各要素の全体座標系 (global coordnate)() における座標成分を 自然座標系における形状関数 [] ( 従属変数の内挿に使うのと同じ []) を使用して変換する場合 このような要素をアイソパラメトリック要素 (soparametrc element) という
10 アイソパラメトリック要素 (2/3) 2 3 各節点の座標 :( ) ( 2 2 ) ( 3 3 ) ( ) 各節点における温度 :T T 2 T 3 T T T ) ( ) ( ) ( FEM3D 0
11 FEM3D アイソパラメトリック要素 (3/3) 高次の補間関数を使えば 曲線 曲面も扱うことが可能となる そういう意味で 自然座標系 と呼んでいる Sub-Parametrc Super-Parametrc
12 2D 自然座標系の形状関数 (/3) 自然座標系における正方形上の内挿多項式は下式で与えられる : T T T T T T T T T T T T T T T T 3 2 T 各節点での条件より : FEM3D 2
13 2D 自然座標系の形状関数 (2/3) FEM3D T T T T T T T T T T T T T T T T T T T T T T T T T 2 3
14 2D 自然座標系の形状関数 (3/3) 元の式に代入して T について整理すると以下のようになる : ) ( ) ( ) ( ) ( 3 2 形状関数 は以下のようになる : 双一次 (b-lnear) 要素とも呼ばれる 各節点における の値を計算してみよ FEM3D T T T T T
15 FEM3D 5 三次元への拡張 四面体要素 : 二次元における三角形要素 任意の形状を扱うことができる 特に一次要素は精度が悪く 一部の問題を除いてあまり使用されない 高次の四面体要素は広く使用されている 本講義では低次六面体要素 ( アイソパラメトリック要素 ) を使用する tr-lnear 自由度 : 各節点上
16 3D 自然座標系の形状関数 ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( z z T T ) ( ) ( ) ( ) ( FEM3D 6
17 FEM3D 7 三次元要素の定式化 三次元熱伝導方程式 ガラーキン法 要素マトリクス生成 プログラムの実行 データ構造 プログラムの構成
18 ガラーキン法の適用 (/3) 以下のような三次元熱伝導方程式を考慮する ( 熱伝導率一定 ): } { T 要素内の温度分布 ( マトリクス形式 ) 節点における温度を としてある ガラーキン法に従い 重み関数を [] とすると 各要素において以下の積分方程式が得られる : dv Q z T T T T V Q z T T T FEM3D
19 ガラーキン法の適用 (2/3) 三次元のグリーンの定理 前式の 2 階微分の部分に適用 ( 表面積分省略 ): これに以下を代入する : } { } { } { } { z z T T T T V V S dv z B z A B A B A ds n B A dv z B B B A dv T T T dv T T T V z T z T T zz T V FEM3D 9
20 FEM3D 20 ガラーキン法の適用 (3/3) 体積あたり発熱量の項を加えて次式が得られる : Q T T T z z dv Q dv 0 V この式を弱形式 (weak form) と呼ぶ 元の微分方程式では 2 階の微分が含まれていたが 上式では グリーンの定理によって 階微分に低減されている 弱形式によって近似関数 ( 形状関数 内挿関数 ) に対する要求が弱くなっている : すなわち線形関数で2 階微分の効果を記述できる 項が増えただけで 一次元と同じ V
21 境界条件を考慮した弱形式 : 各要素 dv dv dv k V z T z V T V T e ) ( ) ( ) ( ) ( e e e f k dv Q f V T e ) ( FEM3D 2
22 FEM3D 22 要素マトリクス : 行列 j j k j
23 FEM3D 23 要素マトリクス :k j j k j dv T ( e) k T V V T z z dv V dv k j V j j z j z dv
24 D-Part2 2 数値的に積分を実施する方法 台形公式 シンプソンの公式 ガウスの積分公式 ( ガウス=ルジャンドル (Gauss-Legendre) とも呼ばれる 精度良い ) 不定積分を解析的に求めるのではなく 有限な数のサンプル点における値を利用する X X 2 f m d wk f k k
25 D-Part2 25 ガウス積分公式 : 一次元の例シンプソンの公式より精度良い Smpson s f Gauss ( ) sn( ) X h S X X 2 X 3 0 X 2 X 3 2 X h 3 2 X X 3 X f X f X f X S h 2 2 / k f d W k f k f h d
26 D-Part2 26 ガウスの積分公式 無次元化された自然座標系 [-+] を対象とする m 個の積分点を使用すると (2m-) 次の関数までは近似可能 ( 従って 次 2 次の内挿関数 ( 形状関数 ) を使用するときは m=2で十分) f m m 2 m 3 m d w k f k k k 0.00 w 2.00 k wk.00 k 0.00 wk / w 5/ 9 k k k =- =0 =+ k = k =
27 Gaussan Quadrature ガウスの積分公式 自然座標系 () 上で定義 ガウス積分公式が使える ( 三次元 ) k j W W W ) ( k j LM: 方向の積分点数 : 積分点での重み係数 : 積分点の座標値 k k j k j M j L f W W W d d d f I ) ( ) ( FEM3D 27
28 2 Gaussan Quadrature ガウスの積分公式 この組み合わせがよく 使われる 二次元では 点におけるfの値を計算 して足せば良い 三次 元では点
29 29 Gaussan Quadrature ガウスの積分公式 この組み合わせがよく 使われる 二次元では 点におけるfの値を計算 して足せば良い 三次 元では点 I f ( ) d d W W f ( ) m n j j j.0.0 f ( ).0.0 f ( ).0.0 f ( ).0.0 f ( )
30 あとは積分を求めれば良い 自然座標系 () 上で定義 ガウス積分公式が使える ( 三次元 ) しかし 微分が k j W W W ) ( k j LM: 方向の積分点数 : 積分点での重み係数 : 積分点の座標値 k k j k j M j L f W W W d d d f I ) ( ) ( FEM3D 30
31 自然座標系における偏微分 (/) 偏微分の公式より以下のようになる : z z z z z z ) ( ) ( ) ( z は定義より簡単に求められるがを実際の計算で使用する FEM3D 3
32 自然座標系における偏微分 (2/) マトリックス表示すると : z J z z z z J : ヤコビのマトリクス (Jacob matr Jacoban) FEM3D 32
33 自然座標系における偏微分 (3/) の定義より簡単に求められる z z z J J J z z z J J J z z z J J J FEM3D 33
34 自然座標系における偏微分 (/) 従って下記のように偏微分を計算できる ヤコビアン (3 3 行列 ) の逆行列を求める J z z z z FEM3D 3
35 要素単位での積分 V j j j V z j z j j j dv z z dv k j k j FEM3D 35
36 自然座標系での積分 d d d J z z dddz z z dv z z j j j j j j V j j j det j k j FEM3D 36
37 ガウスの積分公式 k k j k j M j L f W W W d d d f I ) ( ) ( d d d J z z j j j det FEM3D 37 j k j
38 FEM3D 3 残りの手順 ここまでで 要素ごとの積分が可能となる あとは : 全体マトリクスへの重ね合わせ 境界条件処理 連立一次方程式を解く 詳細はプログラムの内容を解説しながら説明する
39 要素 全体マトリクス重ね合わせ () () 3 () 2 () () () 3 () 2 () () () 3 () 2 () () 3 () 33 () 32 () 3 () 2 () 23 () 22 () 2 () () 3 () 2 () () () () } { } ]{ [ f f f f k k k k k k k k k k k k k k k k f k (2) (2) 3 (2) 2 (2) (2) (2) 3 (2) 2 (2) (2) (2) 3 (2) 2 (2) (2) 3 (2) 33 (2) 32 (2) 3 (2) 2 (2) 23 (2) 22 (2) 2 (2) (2) 3 (2) 2 (2) (2) (2) (2) } { } ]{ [ f f f f k k k k k k k k k k k k k k k k f k } { } ]{ [ B B B B B B D X X X X D X X X X D X X X X X X D X X X X D X X X X D F K FEM3D 39
40 FEM3D 0 三次元要素の定式化 三次元弾性力学方程式 ガラーキン法 要素マトリクス生成 演習 プログラムの実行 データ構造 プログラムの構成
41 FEM3D 演習 ガウスの積分公式を使用して以下の四角形の面積を求めよ ( プログラムを作って 計算機で計算してください ) V 3 2 :(.0.0) 2:(.0 2.0) 3:( ) :(2.0.0) I V dv det J dd
42 FEM3D 2 ヒント (/2) 座標値によってヤコビアン ( ヤコビの行列 ) を計算 ガウスの積分公式 (n=2) に代入する I m W W j f ( j ) f ( ) dd n j mplct REAL* (A-HO-Z) real* W(2) real* POI(2) W()=.0d0 W(2)=.0d0 POI()= d0 POI(2)= d0 SUM= 0.d0 do jp= 2 do p= 2 FC = F(POI(p)POI(jp)) SUM= SUM + W (p)*w (jp)*fc
43 ヒント (2/2) J J det ) ( ) ( ) ( ) ( 3 2 FEM3D 3
44 FEM3D 三次元要素の定式化 三次元弾性力学方程式 ガラーキン法 要素マトリクス生成 プログラムの実行 データ構造 プログラムの構成
45 FEM3D 5 対象とする問題 : 三次元定常熱伝導 Z T T=0@Z=z ma Z T z 定常熱伝導 + 発熱 一様な熱伝導率 直方体 T z 一辺長さの立方体 ( 六面体 ) 要素 各方向にX Y Z 個 境界条件 Q z 0 X Y X Y T=0@Z=z ma 体積当たり発熱量は位置 ( メッシュの中心の座標 c c ) に依存 Q z QVOL C C
46 FEM3D 6 インストール (Cgwn では *.ee) インストール >$ cd <$P-TOP>/fem3d/src >$ make >$ ls../run/sol sol メッシュジェネレータインストール >$ cd <$P-TOP>/fem3d/run >$ gfortran O3 mgcube.f o mgcube
47 FEM3D 7 計算の流れメッシュ生成 計算 ファイル名称固定 mgcube メッシュジェネレータ cube.0 メッシュファイル sol FEM 本体 IPUT.DAT 制御データ test.np 可視化用出力
48 FEM3D メッシュ生成 (Cgwn では mgcube.ee) Z >$ cd <$P-TOP>/fem3d/run >$./mgcube T=0@Z=z ma X Y Z 各辺長さを訊いてくる このように入れてみる Z >$ ls cube.0 生成を確認 cube.0 X Y X Y
49 FEM3D 9 制御ファイル :IPUT.DAT IPUT.DAT cube.0 fname 2000 ITER.0.0 COD QVOL.0e-0 RESID fname: ITER: COD: QVOL: RESID: メッシュファイル名反復回数上限熱伝導率体積当たり発熱量係数反復法の収束判定値 T Q T z z QVOL C C T z Q z 0
50 FEM3D 50 実行 (Cgwn では sol.ee >$ cd <$P-TOP>/fem3d/run >$./sol >$ ls test.np 生成を確認 test.np
51 FEM3D 5 ParaVew ファイルを開く 図の表示 イメージファイルの保存
52 FEM3D 52 UCD Format (/3) Unstructured Cell Data 要素の種類点線三角形四角形四面体角錐三角柱六面体二次要素線 2 三角形 2 四角形 2 四面体 2 角錐 2 三角柱 2 六面体 2 キーワード pt lne tr quad tet pr prsm he lne2 tr2 quad2 tet2 pr2 prsm2 he2
53 FEM3D 53 UCD Format (2/3) Orgnall for AVS mcroavs Etenson of the UCD fle s np There are two tpes of formats. Onl old tpe can be read b ParaVew.
54 FEM3D 5 UCD Format (3/3): Old Format ( 全節点数 ) ( 全要素数 ) ( 各節点のデータ数 ) ( 各要素のデータ数 ) ( モデルのデータ数 ) ( 節点番号 ) (X 座標 ) (Y 座標 ) (Z 座標 ) ( 節点番号 2) (X 座標 ) (Y 座標 ) (Z 座標 ) ( 要素番号 ) ( 材料番号 ) ( 要素の種類 ) ( 要素を構成する節点のつながり ) ( 要素番号 2) ( 材料番号 ) ( 要素の種類 ) ( 要素を構成する節点のつながり ) ( 要素のデータ成分数 ) ( 成分 の構成数 ) ( 成分 2 の構成数 ) ( 各成分の構成数 ) ( 要素データ成分 のラベル )( 単位 ) ( 要素データ成分 2 のラベル )( 単位 ) ( 各要素データ成分のラベル )( 単位 ) ( 要素番号 ) ( 要素データ ) ( 要素データ 2) ( 要素番号 2) ( 要素データ ) ( 要素データ 2) ( 節点のデータ成分数 ) ( 成分 の構成数 ) ( 成分 2 の構成数 ) ( 各成分の構成数 ) ( 節点データ成分 のラベル )( 単位 ) ( 節点データ成分 2 のラベル )( 単位 ) ( 各節点データ成分のラベル )( 単位 ) ( 節点番号 ) ( 節点データ ) ( 節点データ 2) ( 節点番号 2) ( 節点データ ) ( 節点データ 2)
55 FEM3D 55 三次元要素の定式化 三次元弾性力学方程式 ガラーキン法 要素マトリクス生成 プログラムの実行 データ構造 プログラムの構成
56 FEM3D 56 メッシュファイル構成 :cube.0 番号は から始まっている 節点データ 節点数 節点番号 座標 要素データ 要素数 要素タイプ 要素番号 材料番号 コネクティビティ 節点グループデータ グループ数 グループ内節点数 グループ名 グループ内節点
57 FEM3D 57 cube.0: 節点データ (X=Y=Z=) 25 =5*5*5( 節点数 ) Z T=0@Z=z ma Z X Y X Y 節点 ID X 座標 Y 座標 Z 座標 move
58 FEM3D 5 cube.0: 要素データ (/2) 6 =**( 要素数 ) Z T=0@Z=z ma Z 要素タイプ :36 三次元 六面体 一次 Y X Y X move
59 FEM3D 59 cube.0: 要素データ (2/2) 要素 ID 材料 ID 節点 ID X Z T=0@Z=z ma Z Y X Y
60 FEM3D 60 X=Y=Z= XP=YP=ZP=5 ICELTOT= 6 IODTOT= 25 IBODTOT= 25 k= k= k= k= k=
61 FEM3D 6 cube.0: 節点グループデータ グループ総数 各グループ節点数 ( 累積 ) Z Xmn T=0@Z=z ma Ymn Z Zmn Zma X Y X Y ( 以下使用せず )
62 FEM3D 62 X=Y=Z= XP=YP=ZP=5 ICELTOT= 6 IODTOT= 25 IBODTOT= 25 k= k= k= k= k= Xmn: = Ymn: j= Zmn: k= Zma:k=5
63 FEM3D 63 メッシュ生成 実は技術的には大きな課題 複雑形状 大規模メッシュ 並列化が難しい 市販のメッシュ生成アプリケーション FEMAP CAD データとのインタフェース move
64 FEM3D 6 三次元要素の定式化 三次元弾性力学方程式 ガラーキン法 要素マトリクス生成 プログラムの実行 データ構造 プログラムの構成
65 FEM3D 65 有限要素法の処理 : プログラム 初期化 制御変数読み込み 座標読み込み 要素生成 (: 節点数 E: 要素数 ) 配列初期化 ( 全体マトリクス 要素マトリクス ) 要素 全体マトリクスマッピング (IndeItem) マトリクス生成 要素単位の処理 (do cel= E) 要素マトリクス計算 全体マトリクスへの重ね合わせ 境界条件の処理 連立一次方程式 共役勾配法 (CG)
66 FEM3D 66 test メインプログラム nput_cntl 制御データ入力 nput_grd メッシュファイル入力 fnd_node 節点探索 mat_con0 行列コネクティビティ生成 msort ソート mat_con 行列コネクティビティ生成 mat_ass_man 係数行列生成 jacob ヤコビアン計算 mat_ass_bc 境界条件処理 三次元熱伝導解 析コード heat3d の構成 solve 線形ソルバー制御 output_ucd 可視化処理 cg CG 法計算
67 FEM3D 67 全体処理 program heat3d use solver use pfem_utl mplct REAL*(A-HO-Z) call IPUT_CTL call IPUT_GRID call MAT_CO0 call MAT_CO call MAT_ASS_MAI call MAT_ASS_BC call SOLVE call OUTPUT_UCD end program heat3d
68 FEM3D 6 Global 変数表 :pfem_utl.f(/3) 変数名種別サイズ I/O 内容 fname C (0) I メッシュファイル名 P I I 節点数 ICELTOT I I 要素数 ODGRPtot I I 節点グループ数 XYZ R (3) I 節点座標 ICELOD I (ICELTOT) I 要素コネクティビティ ODGRP_IDEX I (0:ODGRPtot) I 各節点グループに含まれる節点数 ( 累積 ) ODGRP_ITEM I (ODGRP_IDEX(ODG RPTOT) I 節点グループに含まれる節点 ODGRP_AME C0 (ODGRPTOT) I 節点グループ名 LU I O 各節点非対角成分数 PLU I O 非対角成分総数 D R () O 全体行列 : 対角ブロック BX R () O 右辺ベクトル 未知数ベクトル
69 FEM3D 69 Global 変数表 :pfem_utl.f(2/3) 変数名種別サイズ I/O 内容 AMAT R (PLU) O 全体行列 : 非零非対角成分 nde I (0:) O 全体行列 : 非零非対角成分数 tem I (PLU) O 全体行列 : 非零非対角成分 ( 列番号 ) ILU I () O 各節点の非零非対角成分数 IALU I (LU) O 各節点の非零非対角成分数 ( 列番号 ) IWKX I (2) O ワーク用配列 ITER ITERactual I I 反復回数の上限 実際の反復回数 RESID R I 打ち切り誤差 (.e-に設定) pfemiarra I (00) O 諸定数 ( 整数 ) pfemrarra R (00) O 諸定数 ( 実数 )
70 FEM3D 70 Global 変数表 :pfem_utl.f(3/3) 変数名種別サイズ I/O 内容 Oth R I =0.25 PQ PE PT R (22) O 各ガウス積分点における POS WEI R (22) O 各ガウス積分点の座標 重み係数 COL COL2 I (00) O ソート用ワーク配列 SHAPE R (222) O 各ガウス積分点における形状関数 (=~) PX PY PZ R (222) O 各ガウス積分点における ~ ~ z DETJ R (222) O 各ガウス積分点におけるヤコビアン行列式 COD QVOL R I 熱伝導率 体積当たり発熱量係数
71 FEM3D 7 制御ファイル入力 :IPUT_CTL subroutne IPUT_CTL use pfem_utl mplct REAL* (A-HO-Z) open (fle= 'IPUT.DAT' status='unknown') read ('(a0)') fname read (*) ITER read (*) COD QVOL read (*) RESID close () pfemiarra()= ITER pfemrarra()= RESID return end IPUT.DAT cube.0 fname 2000 ITER.0.0 COD QVOL.0e-0 RESID
72 FEM3D 72 メッシュ入力 :IPUT_GRID(/3)!C***!C*** IPUT_GRID!C***!C subroutne IPUT_GRID use pfem_utl mplct REAL* (A-HO-Z) open ( fle= fname status= 'unknown' form= 'formatted')!c!c-- ODE read (*) P= allocate (XYZ(3)) XYZ= 0.d0 do = read (*) (XYZ(kk)kk=3)
73 FEM3D 73 cube.0: 節点データ (X=Y=Z=) 25 = Z T=0@Z=z ma Z X Y X Y XYZ(3) move
74 FEM3D 7 allocate deallocate 関数 (C 言語 ) #nclude <stdo.h> #nclude <stdlb.h> vod* allocate_vector(nt szent m) { vod *a; f ( ( a=(vod * )malloc( m * sze ) ) == ULL ) { fprntf(stdout"error:memor does not enough! n vector n"); et(); } return a; } vod deallocate_vector(vod *a) { free( a ); } vod** allocate_matr(nt szent mnt n) { vod **aa; nt ; f ( ( aa=(vod ** )malloc( m * szeof(vod*) ) ) == ULL ) { fprntf(stdout"error:memor does not enough! aa n matr n"); et(); } f ( ( aa[0]=(vod * )malloc( m * n * sze ) ) == ULL ) { fprntf(stdout"error:memor does not enough! n matr n"); et(); } for(=;<m;++) aa[]=(char*)aa[-]+sze*n; return aa; } vod deallocate_matr(vod **aa) { free( aa ); } allocate を FORTRA 並みに簡単にやるための関数
75 FEM3D 75 メッシュ入力 :IPUT_GRID(2/3)!C!C-- ELEMET read (*) ICELTOT allocate (ICELOD(ICELTOT)) read ('(00)') (TYPE = ICELTOT) do cel= ICELTOT read ('(0025)') IMAT (ICELOD(celk) k=)
76 FEM3D 76 cube.0: 要素データ (/2) 6 = ICELTOT Z T=0@Z=z ma Z 要素タイプ :36 三次元 六面体 一次 Y X Y X move
77 FEM3D 77 cube.0: 要素データ (2/2) MAT ICELOD(cel) X Z T=0@Z=z ma Z Y X Y
78 FEM3D 7 メッシュ入力 :IPUT_GRID(3/3)!C!C-- ODE grp. nfo. read ('(00)') ODGRPtot allocate (ODGRP_IDEX(0:ODGRPtot)ODGRP_AME(ODGRPtot)) ODGRP_IDEX= 0 read ('(00)') (ODGRP_IDEX() = ODGRPtot) nn= ODGRP_IDEX(ODGRPtot) allocate (ODGRP_ITEM(nn)) do k= ODGRPtot S= ODGRP_IDEX(k-) + E= ODGRP_IDEX(k ) read ('(a0)') ODGRP_AME(k) nn= E - S + f (nn.ne.0) then read ('(00)') (ODGRP_ITEM(kk)kk=S E) endf close () return end
79 FEM3D 79 cube.0: 節点グループデータ ODGRPtot ODGTP_IDEX(-) Xmn ODGRP_AME() ODGRP_ITEM(-25) Ymn ODGRP_AME(2) ODGRP_ITEM(26-50) Zmn ODGRP_AME(3) ODGRP_ITEM(5-75) Zma ODGRP_AME() ODGRP_ITEM(76-00)
80 FEM3D 0 test メインプログラム nput_cntl 制御データ入力 nput_grd メッシュファイル入力 fnd_node 節点探索 mat_con0 行列コネクティビティ生成 msort ソート mat_con 行列コネクティビティ生成 mat_ass_man 係数行列生成 jacob ヤコビアン計算 mat_ass_bc 境界条件処理 三次元熱伝導解 析コード heat3d の構成 solve 線形ソルバー制御 output_ucd 可視化処理 cg CG 法計算
81 FEM3D Global 変数表 :pfem_utl.h/f(/3) 変数名種別サイズ I/O 内容 fname C (0) I メッシュファイル名 P I I 節点数 ICELTOT I I 要素数 ODGRPtot I I 節点グループ数 XYZ R (3) I 節点座標 ICELOD I (ICELTOT) I 要素コネクティビティ ODGRP_IDEX I (0:ODGRPtot) I 各節点グループに含まれる節点数 ( 累積 ) ODGRP_ITEM I (ODGRP_IDEX(ODG RPTOT) I 節点グループに含まれる節点 ODGRP_AME C0 (ODGRPTOT) I 節点グループ名 LU I O 各節点非対角成分数 PLU I O 非対角成分総数 D R () O 全体行列 : 対角ブロック BX R () O 右辺ベクトル 未知数ベクトル
82 FEM3D 2 Global 変数表 :pfem_utl.h/f(2/3) 変数名種別サイズ I/O 内容 AMAT R (PLU) O 全体行列 : 非零非対角成分 nde I (0:) O 全体行列 : 非零非対角成分数 tem I (PLU) O 全体行列 : 非零非対角成分 ( 列番号 ) ILU I () O 各節点の非零非対角成分数 IALU I (LU) O 各節点の非零非対角成分数 ( 列番号 ) IWKX I (2) O ワーク用配列 ITER ITERactual I I 反復回数の上限 実際の反復回数 RESID R I 打ち切り誤差 (.e-に設定) pfemiarra I (00) O 諸定数 ( 整数 ) pfemrarra R (00) O 諸定数 ( 実数 )
83 FEM3D 3 Global 変数表 :pfem_utl.h/f(3/3) 変数名種別サイズ I/O 内容 Oth R I =0.25 PQ PE PT R (22) O 各ガウス積分点における POS WEI R (22) O 各ガウス積分点の座標 重み係数 COL COL2 I (00) O ソート用ワーク配列 SHAPE R (222) O 各ガウス積分点における形状関数 (=~) PX PY PZ R (222) O 各ガウス積分点における ~ ~ z DETJ R (222) O 各ガウス積分点におけるヤコビアン行列式 COD QVOL R I 熱伝導率 体積当たり発熱量係数
84 FEM3D マトリクス生成まで 一次元のときは ndetem に関連した情報を簡単に作ることができた 非ゼロ非対角成分の数は2 番号が自分に対して :+と- 三次元の場合はもっと複雑 非ゼロ非対角成分の数は7~26( 現在の形状 ) 実際はもっと複雑 前以て 非ゼロ非対角成分数はわからない move
85 FEM3D 5 マトリクス生成まで 一次元のときは ndetem に関連した情報を簡単に作ることができた 非ゼロ非対角成分の数は2 番号が自分に対して :+と- 三次元の場合はもっと複雑 非ゼロ非対角成分の数は7~26( 現在の形状 ) 実際はもっと複雑 前以て 非ゼロ非対角成分の数はわからない ILU()IALU(LU) を使って非ゼロ非対角成分数を予備的に勘定する
86 FEM3D 6 全体処理 program heat3d use solver use pfem_utl mplct REAL*(A-HO-Z) call IPUT_CTL call IPUT_GRID call MAT_CO0 call MAT_CO call MAT_ASS_MAI call MAT_ASS_BC call SOLVE call OUTPUT_UCD end program heat3d MAT_CO0: IU IALU 生成 MAT_CO: nde tem 生成 とりあえず から始まる節点番号を記憶
87 FEM3D 7 MAT_CO0: 全体構成 do cel= ICELTOT 節点相互の関係から ILUIALU を生成 (FID_ODE)
88 FEM3D 行列コネクティビティ生成 : MAT_CO0(/)!C!C***!C*** MAT_CO0!C***!C subroutne MAT_CO0 use pfem_utl mplct REAL* (A-HO-Z) LU= 26 allocate (ILU() IALU(LU)) ILU= 0 IALU= 0 LU: 各節点における非ゼロ非対角成分の最大数 ( 接続する節点数 ) 今の問題の場合はわかっているので このようにできる 不明の場合の実装 : レポート課題
89 FEM3D 9 行列コネクティビティ生成 : MAT_CO0(/)!C!C***!C*** MAT_CO0!C***!C subroutne MAT_CO0 use pfem_utl mplct REAL* (A-HO-Z) LU= 26 allocate (ILU() IALU(LU)) ILU= 0 IALU= 0 変数名サイズ内容 ILU IALU () (LU) 各節点の非零非対角成分数 各節点の非零非対角成分 ( 列番号 )
90 FEM3D 90 行列コネクティビティ生成 : MAT_CO0(2/): から始まる番号 do cel= ICELTOT n= ICELOD(cel) n2= ICELOD(cel2) n3= ICELOD(cel3) n= ICELOD(cel) n5= ICELOD(cel5) n6= ICELOD(cel6) n7= ICELOD(cel7) n= ICELOD(cel) call FID_TS_ODE (nn2) call FID_TS_ODE (nn3) call FID_TS_ODE (nn) call FID_TS_ODE (nn5) call FID_TS_ODE (nn6) call FID_TS_ODE (nn7) call FID_TS_ODE (nn) call FID_TS_ODE (n2n) call FID_TS_ODE (n2n3) call FID_TS_ODE (n2n) call FID_TS_ODE (n2n5) call FID_TS_ODE (n2n6) call FID_TS_ODE (n2n7) call FID_TS_ODE (n2n) call FID_TS_ODE (n3n) call FID_TS_ODE (n3n2) call FID_TS_ODE (n3n) call FID_TS_ODE (n3n5) call FID_TS_ODE (n3n6) call FID_TS_ODE (n3n7) call FID_TS_ODE (n3n)
91 FEM3D 9 節点探索 :FID_TS_ODE ILUIAU 探索 : 一次元ではこの部分は手動!C!C***!C*** FID_TS_ODE!C***!C subroutne FID_TS_ODE (pp2) do kk= ILU(p) f (p2.eq.ialu(pkk)) return cou= ILU(p) + IALU(pcou)= p2 ILU(p )= cou return end subroutne FID_TS_ODE 変数名サイズ内容 ILU IALU () (LU) 各節点の非零非対角成分数 各節点の非零非対角成分 ( 列番号 )
92 FEM3D 92 節点探索 :FID_TS_ODE 一次元ではこの部分は手動!C!C***!C*** FID_TS_ODE!C***!C subroutne FID_TS_ODE (pp2) do kk= ILU(p) f (p2.eq.ialu(pkk)) return cou= ILU(p) + IALU(pcou)= p2 ILU(p )= cou return 既に IALU に含まれている場合は 次のペアへ end subroutne FID_TS_ODE
93 FEM3D 93 節点探索 :FID_TS_ODE 一次元ではこの部分は手動!C!C***!C*** FID_TS_ODE!C***!C subroutne FID_TS_ODE (pp2) do kk= ILU(p) f (p2.eq.ialu(pkk)) return cou= ILU(p) + IALU(pcou)= p2 ILU(p )= cou return end subroutne FID_TS_ODE IALU に含まれていない場合は ILU に を加えて IALU に格納
94 FEM3D 9 行列コネクティビティ生成 : MAT_CO0(3/) call FID_TS_ODE (nn) call FID_TS_ODE (nn2) call FID_TS_ODE (nn3) call FID_TS_ODE (nn5) call FID_TS_ODE (nn6) call FID_TS_ODE (nn7) call FID_TS_ODE (nn) call FID_TS_ODE (n5n) call FID_TS_ODE (n5n2) call FID_TS_ODE (n5n3) call FID_TS_ODE (n5n) call FID_TS_ODE (n5n6) call FID_TS_ODE (n5n7) call FID_TS_ODE (n5n) call FID_TS_ODE (n6n) call FID_TS_ODE (n6n2) call FID_TS_ODE (n6n3) call FID_TS_ODE (n6n) call FID_TS_ODE (n6n5) call FID_TS_ODE (n6n7) call FID_TS_ODE (n6n) call FID_TS_ODE (n7n) call FID_TS_ODE (n7n2) call FID_TS_ODE (n7n3) call FID_TS_ODE (n7n) call FID_TS_ODE (n7n5) call FID_TS_ODE (n7n6) call FID_TS_ODE (n7n)
95 FEM3D 95 行列コネクティビティ生成 : MAT_CO0(/) call FID_TS_ODE (nn) call FID_TS_ODE (nn2) call FID_TS_ODE (nn3) call FID_TS_ODE (nn) call FID_TS_ODE (nn5) call FID_TS_ODE (nn6) call FID_TS_ODE (nn7) do n= = ILU(n) do k= COL(k)= IALU(nk) call msort (COL COL2 ) do k= - IALU(n-k+)= COL(COL2(k)) 各節点において IALU(k) が小さい番号から大きい番号に並ぶようにソート ( 単純なバブルソート ) せいぜい 00 程度のものをソートする
96 FEM3D 96 CRS 形式への変換 :MAT_CO!C!C***!C*** MAT_CO!C***!C subroutne MAT_CO use pfem_utl mplct REAL* (A-HO-Z) allocate (nde(0:)) nde= 0 do = nde()= nde(-) + ILU() PLU= nde() allocate (tem(plu)) do = do k= ILU() kk = k + nde(-) tem(kk)= IALU(k) deallocate (ILU IALU) end subroutne MAT_CO C nde[ ] nde[0] 0 FORTRA nde(0) 0 k 0 ILU[ k] nde( ) ILU( k) k
97 FEM3D 97 CRS 形式への変換 :MAT_CO!C!C***!C*** MAT_CO!C***!C subroutne MAT_CO use pfem_utl mplct REAL* (A-HO-Z) allocate (nde(0:)) nde= 0 do = nde()= nde(-) + ILU() PLU= nde() allocate (tem(plu)) do = do k= ILU() kk = k + nde(-) tem(kk)= IALU(k) PLU=nde() tem のサイズ非ゼロ非対角成分総数 deallocate (ILU IALU) end subroutne MAT_CO
98 FEM3D 9 CRS 形式への変換 :MAT_CO!C!C***!C*** MAT_CO!C***!C subroutne MAT_CO use pfem_utl mplct REAL* (A-HO-Z) allocate (nde(0:)) nde= 0 do = nde()= nde(-) + ILU() PLU= nde() allocate (tem(plu)) do = do k= ILU() kk = k + nde(-) tem(kk)= IALU(k) tem に から始まる節点番号を記憶 deallocate (ILU IALU) end subroutne MAT_CO
99 FEM3D 99 CRS 形式への変換 :MAT_CO!C!C***!C*** MAT_CO!C***!C subroutne MAT_CO use pfem_utl mplct REAL* (A-HO-Z) allocate (nde(0:)) nde= 0 do = nde()= nde(-) + ILU() PLU= nde() allocate (tem(plu)) do = do k= ILU() kk = k + nde(-) tem(kk)= IALU(k) deallocate (ILU IALU) end subroutne MAT_CO これらはもはや不要
100 FEM3D 00 全体処理 program heat3d use solver use pfem_utl mplct REAL*(A-HO-Z) call IPUT_CTL call IPUT_GRID call MAT_CO0 call MAT_CO call MAT_ASS_MAI call MAT_ASS_BC call SOLVE call OUTPUT_UCD end program heat3d
101 FEM3D 0 MAT_ASS_MAI: 全体構成 do kpn= 2 ガウス積分点番号 ( 方向 ) do jpn= 2 ガウス積分点番号 ( 方向 ) do pn= 2 ガウス積分点番号 ( 方向 ) ガウス積分点 ( 個 ) における形状関数 およびその 自然座標系 における微分の算出 do cel= ICELTOT 要素ループ 節点の座標から ガウス積分点における 形状関数の 全体座標系 における微分 およびヤコビアンを算出 (JACOBI) do e= 局所節点番号 do je= 局所節点番号全体節点番号 :p jp A pjp のtemにおけるアドレス :kk j e do kpn= 2 ガウス積分点番号 ( 方向 ) do jpn= 2 ガウス積分点番号 ( 方向 ) do pn= 2 ガウス積分点番号 ( 方向 ) 要素積分 要素行列成分計算 全体行列への足しこみ e
102 FEM3D 02 係数行列 :MAT_ASS_MAI(/6)!C!C***!C*** MAT_ASS_MAI!C***!C subroutne MAT_ASS_MAI use pfem_utl mplct REAL* (A-HO-Z) nteger(knd=knt) dmenson( ) :: nodlocal allocate (AMAT(PLU)) allocate (B() D() X()) AMAT= 0.d0 係数行列 ( 非零非対角成分 ) B= 0.d0 右辺ベクトル X= 0.d0 未知数ベクトル D= 0.d0 係数行列 ( 対角成分 ) WEI()= D+00 WEI(2)= D+00 POS()= D+00 POS(2)= D+00
103 FEM3D 03 係数行列 :MAT_ASS_MAI(/6)!C!C***!C*** MAT_ASS_MAI!C***!C subroutne MAT_ASS_MAI use pfem_utl mplct REAL* (A-HO-Z) nteger(knd=knt) dmenson( ) :: nodlocal allocate (AMAT(PLU)) allocate (B() D() X()) AMAT= 0.d0 B= 0.d0 X= 0.d0 D= 0.d0 WEI()= D+00 WEI(2)= D+00 POS()= D+00 POS(2)= D+00 POS: WEI: 積分点座標重み係数
104 FEM3D 0 係数行列 :MAT_ASS_MAI(2/6)!C!C-- IIT.!C PQ - st-order dervatve of shape functon b QSI!C PE - st-order dervatve of shape functon b ETA!C PT - st-order dervatve of shape functon b ZET!C do kp= 2 do jp= 2 do p= 2 QP=.d0 + POS(p) QM=.d0 - POS(p) EP=.d0 + POS(jp) EM=.d0 - POS(jp) TP=.d0 + POS(kp) TM=.d0 - POS(kp) SHAPE(pjpkp)= Oth * QM * EM * TM SHAPE(pjpkp2)= Oth * QP * EM * TM SHAPE(pjpkp3)= Oth * QP * EP * TM SHAPE(pjpkp)= Oth * QM * EP * TM SHAPE(pjpkp5)= Oth * QM * EM * TP SHAPE(pjpkp6)= Oth * QP * EM * TP SHAPE(pjpkp7)= Oth * QP * EP * TP SHAPE(pjpkp)= Oth * QM * EP * TP
105 FEM3D 05 係数行列 :MAT_ASS_MAI(2/6)!C!C-- IIT.!C PQ - st-order dervatve of shape functon b QSI!C PE - st-order dervatve of shape functon b ETA!C PT - st-order dervatve of shape functon b ZET!C do kp= 2 do jp= 2 do p= 2 QP=.d0 + POS(p) QM=.d0 - POS(p) EP=.d0 + POS(jp) EM=.d0 - POS(jp) TP=.d0 + POS(kp) TM=.d0 - POS(kp) SHAPE(pjpkp)= Oth * QM * EM * TM SHAPE(pjpkp2)= Oth * QP * EM * TM SHAPE(pjpkp3)= Oth * QP * EP * TM SHAPE(pjpkp)= Oth * QM * EP * TM SHAPE(pjpkp5)= Oth * QM * EM * TP SHAPE(pjpkp6)= Oth * QP * EM * TP SHAPE(pjpkp7)= Oth * QP * EP * TP SHAPE(pjpkp)= Oth * QM * EP * TP QP EP TP k QM j EM j j TMk k k
106 FEM3D 06 係数行列 :MAT_ASS_MAI(2/6)!C!C-- IIT.!C PQ - st-order dervatve of shape functon b QSI!C PE - st-order dervatve of shape functon b ETA!C PT - st-order dervatve of shape functon b ZET!C do kp= 2 do jp= 2 do p= 2 QP=.d0 + POS(p) QM=.d0 - POS(p) EP=.d0 + POS(jp) EM=.d0 - POS(jp) TP=.d0 + POS(kp) TM=.d0 - POS(kp) SHAPE(pjpkp)= Oth * QM * EM * TM SHAPE(pjpkp2)= Oth * QP * EM * TM SHAPE(pjpkp3)= Oth * QP * EP * TM SHAPE(pjpkp)= Oth * QM * EP * TM SHAPE(pjpkp5)= Oth * QM * EM * TP SHAPE(pjpkp6)= Oth * QP * EM * TP SHAPE(pjpkp7)= Oth * QP * EP * TP SHAPE(pjpkp)= Oth * QM * EP * TP
107 FEM3D 07 係数行列 :MAT_ASS_MAI(2/6)!C!C-- IIT.!C PQ - st-order dervatve of shape functon b QSI!C PE - st-order dervatve of shape functon b ETA!C PT - st-order dervatve of shape functon b ZET!C do kp= 2 do jp= 2 do p= 2 QP=.d0 + POS(p) QM=.d0 - POS(p) EP=.d0 + POS(jp) EM=.d0 - POS(jp) TP=.d0 + POS(kp) TM=.d0 - POS(kp) SHAPE(pjpkp)= Oth * QM * EM * TM SHAPE(pjpkp2)= Oth * QP * EM * TM SHAPE(pjpkp3)= Oth * QP * EP * TM SHAPE(pjpkp)= Oth * QM * EP * TM SHAPE(pjpkp5)= Oth * QM * EM * TP SHAPE(pjpkp6)= Oth * QP * EM * TP SHAPE(pjpkp7)= Oth * QP * EP * TP SHAPE(pjpkp)= Oth * QM * EP * TP ) ( ) ( ) ( ) ( 3 2 ) ( ) ( ) ( ) ( 7 6 5
108 FEM3D 0 係数行列 :MAT_ASS_MAI(3/6) PQ(jpkp)= - Oth * EM * TM PQ(jpkp2)= + Oth * EM * TM PQ(jpkp3)= + Oth * EP * TM PQ(jpkp)= - Oth * EP * TM PQ(jpkp5)= - Oth * EM * TP PQ(jpkp6)= + Oth * EM * TP PQ(jpkp7)= + Oth * EP * TP PQ(jpkp)= - Oth * EP * TP PE(pkp)= - Oth * QM * TM PE(pkp2)= - Oth * QP * TM PE(pkp3)= + Oth * QP * TM PE(pkp)= + Oth * QM * TM PE(pkp5)= - Oth * QM * TP PE(pkp6)= - Oth * QP * TP PE(pkp7)= + Oth * QP * TP PE(pkp)= + Oth * QM * TP PT(pjp)= - Oth * QM * EM PT(pjp2)= - Oth * QP * EM PT(pjp3)= - Oth * QP * EP PT(pjp)= - Oth * QM * EP PT(pjp5)= + Oth * QM * EM PT(pjp6)= + Oth * QP * EM PT(pjp7)= + Oth * QP * EP PT(pjp)= + Oth * QM * EP do cel= ICELTOT COD0= COD n= ICELOD(cel) n2= ICELOD(cel2) n3= ICELOD(cel3) n= ICELOD(cel) n5= ICELOD(cel5) n6= ICELOD(cel6) n7= ICELOD(cel7) n= ICELOD(cel) ( j k ) l PQ( j k) ( j k ) PE( k) l ( j k ) PT ( l k j) ( j ) ( j k ) 2 ( j k ) 3 ( j k ) 3 ( j k ) j j j j における形状関数の一階微分 k k k k
109 FEM3D 09 係数行列 :MAT_ASS_MAI(3/6) PQ(jpkp)= - Oth * EM * TM PQ(jpkp2)= + Oth * EM * TM PQ(jpkp3)= + Oth * EP * TM PQ(jpkp)= - Oth * EP * TM PQ(jpkp5)= - Oth * EM * TP PQ(jpkp6)= + Oth * EM * TP PQ(jpkp7)= + Oth * EP * TP PQ(jpkp)= - Oth * EP * TP PE(pkp)= - Oth * QM * TM PE(pkp2)= - Oth * QP * TM PE(pkp3)= + Oth * QP * TM PE(pkp)= + Oth * QM * TM PE(pkp5)= - Oth * QM * TP PE(pkp6)= - Oth * QP * TP PE(pkp7)= + Oth * QP * TP PE(pkp)= + Oth * QM * TP PT(pjp)= - Oth * QM * EM PT(pjp2)= - Oth * QP * EM PT(pjp3)= - Oth * QP * EP PT(pjp)= - Oth * QM * EP PT(pjp5)= + Oth * QM * EM PT(pjp6)= + Oth * QP * EM PT(pjp7)= + Oth * QP * EP PT(pjp)= + Oth * QM * EP do cel= ICELTOT COD0= COD n= ICELOD(cel) n2= ICELOD(cel2) n3= ICELOD(cel3) n= ICELOD(cel) n5= ICELOD(cel5) n6= ICELOD(cel6) n7= ICELOD(cel7) n= ICELOD(cel)
110 FEM3D 0 係数行列 :MAT_ASS_MAI(/6) nodlocal()= n nodlocal(2)= n2 nodlocal(3)= n3 nodlocal()= n nodlocal(5)= n5 nodlocal(6)= n6 nodlocal(7)= n7 nodlocal()= n 節点の節点番号 X= XYZ(n) X2= XYZ(n2) X3= XYZ(n3) X= XYZ(n) X5= XYZ(n5) X6= XYZ(n6) X7= XYZ(n7) X= XYZ(n) Y= XYZ(n2) Y2= XYZ(n22) Y3= XYZ(n32) Y= XYZ(n2) Y5= XYZ(n52) Y6= XYZ(n62) Y7= XYZ(n72) Y= XYZ(n2) QVC= Oth * (X+X2+X3+X+X5+X6+X7+X+ & Y+Y2+Y3+Y+Y5+Y6+Y7+Y) Z= XYZ(n3) Z2= XYZ(n23) Z3= XYZ(n33) Z= XYZ(n3) Z5= XYZ(n53) Z6= XYZ(n63) Z7= XYZ(n73) Z= XYZ(n3) call JACOBI (DETJ PQ PE PT PX PY PZ & & X X2 X3 X X5 X6 X7 X & & Y Y2 Y3 Y Y5 Y6 Y7 Y & & Z Z2 Z3 Z Z5 Z6 Z7 Z )
111 FEM3D 係数行列 :MAT_ASS_MAI(/6) nodlocal()= n nodlocal(2)= n2 nodlocal(3)= n3 nodlocal()= n nodlocal(5)= n5 nodlocal(6)= n6 nodlocal(7)= n7 nodlocal()= n X= XYZ(n) X2= XYZ(n2) X3= XYZ(n3) X= XYZ(n) X5= XYZ(n5) X6= XYZ(n6) X7= XYZ(n7) X= XYZ(n) Y= XYZ(n2) Y2= XYZ(n22) Y3= XYZ(n32) Y= XYZ(n2) Y5= XYZ(n52) Y6= XYZ(n62) Y7= XYZ(n72) Y= XYZ(n2) QVC= Oth * (X+X2+X3+X+X5+X6+X7+X+ & Y+Y2+Y3+Y+Y5+Y6+Y7+Y) Z= XYZ(n3) Z2= XYZ(n23) Z3= XYZ(n33) Z= XYZ(n3) Z5= XYZ(n53) Z6= XYZ(n63) Z7= XYZ(n73) Z= XYZ(n3) 節点の X 座標 節点の Y 座標 節点の Z 座標 call JACOBI (DETJ PQ PE PT PX PY PZ & & X X2 X3 X X5 X6 X7 X & & Y Y2 Y3 Y Y5 Y6 Y7 Y & & Z Z2 Z3 Z Z5 Z6 Z7 Z )
112 FEM3D 2 係数行列 :MAT_ASS_MAI(/6) nodlocal()= n nodlocal(2)= n2 nodlocal(3)= n3 nodlocal()= n nodlocal(5)= n5 nodlocal(6)= n6 nodlocal(7)= n7 nodlocal()= n X= XYZ(n) X2= XYZ(n2) X3= XYZ(n3) X= XYZ(n) X5= XYZ(n5) X6= XYZ(n6) X7= XYZ(n7) X= XYZ(n) Y= XYZ(n2) Y2= XYZ(n22) Y3= XYZ(n32) Y= XYZ(n2) Y5= XYZ(n52) Y6= XYZ(n62) Y7= XYZ(n72) Y= XYZ(n2) QVC= Oth * (X+X2+X3+X+X5+X6+X7+X+ & Y+Y2+Y3+Y+Y5+Y6+Y7+Y) Z= XYZ(n3) Z2= XYZ(n23) Z3= XYZ(n33) Z= XYZ(n3) Z5= XYZ(n53) Z6= XYZ(n63) Z7= XYZ(n73) Z= XYZ(n3) 節点の X 座標 節点の Y 座標 T Q T z QVOL C C T z z 7 3 Q z 0 体積当たり発熱量は位置 ( メッシュの中心の座標 c c ) に依存 call JACOBI (DETJ PQ PE PT PX PY PZ & & X X2 X3 X X5 X6 X7 X & & Y Y2 Y3 Y Y5 Y6 Y7 Y & & Z Z2 Z3 Z Z5 Z6 Z7 Z )
113 FEM3D 3 係数行列 :MAT_ASS_MAI(/6) nodlocal()= n nodlocal(2)= n2 nodlocal(3)= n3 nodlocal()= n nodlocal(5)= n5 nodlocal(6)= n6 nodlocal(7)= n7 nodlocal()= n X= XYZ(n) X2= XYZ(n2) X3= XYZ(n3) X= XYZ(n) X5= XYZ(n5) X6= XYZ(n6) X7= XYZ(n7) X= XYZ(n) Y= XYZ(n2) Y2= XYZ(n22) Y3= XYZ(n32) Y= XYZ(n2) Y5= XYZ(n52) Y6= XYZ(n62) Y7= XYZ(n72) Y= XYZ(n2) QVC= Oth * (X+X2+X3+X+X5+X6+X7+X+ & Y+Y2+Y3+Y+Y5+Y6+Y7+Y) Z= XYZ(n3) Z2= XYZ(n23) Z3= XYZ(n33) Z= XYZ(n3) Z5= XYZ(n53) Z6= XYZ(n63) Z7= XYZ(n73) Z= XYZ(n3) T Q T z QVOL C C QVC C C T z z 7 3 Q z 0 call JACOBI (DETJ PQ PE PT PX PY PZ & & X X2 X3 X X5 X6 X7 X & & Y Y2 Y3 Y Y5 Y6 Y7 Y & & Z Z2 Z3 Z Z5 Z6 Z7 Z )
114 FEM3D 係数行列 :MAT_ASS_MAI(/6) nodlocal()= n nodlocal(2)= n2 nodlocal(3)= n3 nodlocal()= n nodlocal(5)= n5 nodlocal(6)= n6 nodlocal(7)= n7 nodlocal()= n X= XYZ(n) X2= XYZ(n2) X3= XYZ(n3) X= XYZ(n) X5= XYZ(n5) X6= XYZ(n6) X7= XYZ(n7) X= XYZ(n) Y= XYZ(n2) Y2= XYZ(n22) Y3= XYZ(n32) Y= XYZ(n2) Y5= XYZ(n52) Y6= XYZ(n62) Y7= XYZ(n72) Y= XYZ(n2) QVC= Oth * (X+X2+X3+X+X5+X6+X7+X+ & Y+Y2+Y3+Y+Y5+Y6+Y7+Y) Z= XYZ(n3) Z2= XYZ(n23) Z3= XYZ(n33) Z= XYZ(n3) Z5= XYZ(n53) Z6= XYZ(n63) Z7= XYZ(n73) Z= XYZ(n3) call JACOBI (DETJ PQ PE PT PX PY PZ & & X X2 X3 X X5 X6 X7 X & & Y Y2 Y3 Y Y5 Y6 Y7 Y & & Z Z2 Z3 Z Z5 Z6 Z7 Z )
115 FEM3D 5 JACOBI(/) subroutne JACOBI (DETJ PQ PE PT PX PY PZ & & X X2 X3 X X5 X6 X7 X Y Y2 Y3 Y Y5 Y6 Y7 Y & & Z Z2 Z3 Z Z5 Z6 Z7 Z )!C!C calculates JACOBIA & IVERSE JACOBIA!C d/d d/d & d/dz!c mplct REAL* (A-HO-Z) dmenson DETJ(222) dmenson PQ(22) PE(22) PT(22) dmenson PX(222) PY(222) PZ(222) do kp= 2 do jp= 2 do p= 2 PX(pjpkp)=0.d0 PX(pjpkp2)=0.d0 PX(pjpkp3)=0.d0 PX(pjpkp)=0.d0 PX(pjpkp5)=0.d0 PX(pjpkp6)=0.d0 PX(pjpkp7)=0.d0 PX(pjpkp)=0.d0 PY(pjpkp)=0.d0 PY(pjpkp2)=0.d0 PY(pjpkp3)=0.d0 PY(pjpkp)=0.d0 PY(pjpkp5)=0.d0 PY(pjpkp6)=0.d0 PY(pjpkp7)=0.d0 PY(pjpkp)=0.d0 PZ(pjpkp)=0.d0 PZ(pjpkp2)=0.d0 PZ(pjpkp3)=0.d0 PZ(pjpkp)=0.d0 PZ(pjpkp5)=0.d0 PZ(pjpkp6)=0.d0 PZ(pjpkp7)=0.d0 PZ(pjpkp)=0.d0 l l l 入力 z l ~ 出力 l l l det J z 各ガウス積分点 (pjpkp) における値 l l l
116 FEM3D 6 自然座標系における偏微分 (/) 偏微分の公式より以下のようになる : z z z z z z ) ( ) ( ) ( z は定義より簡単に求められるがを実際の計算で使用する
117 FEM3D 7 自然座標系における偏微分 (2/) マトリックス表示すると : z J z z z z J : ヤコビのマトリクス (Jacob matr Jacoban) J J J J J J J J J J
118 FEM3D 自然座標系における偏微分 (3/) の定義より簡単に求められる z z z J J J z z z J J J z z z J J J
119 FEM3D 9!C!C== DETERMIAT of the JACOBIA JACOBI(2/) dxdq = & & + PQ(jpkp) * X + PQ(jpkp2) * X2 & & + PQ(jpkp3) * X3 + PQ(jpkp) * X & & + PQ(jpkp5) * X5 + PQ(jpkp6) * X6 & & + PQ(jpkp7) * X7 + PQ(jpkp) * X dydq = & & + PQ(jpkp) * Y + PQ(jpkp2) * Y2 & & + PQ(jpkp3) * Y3 + PQ(jpkp) * Y & J J2 & + PQ(jpkp5) * Y5 + PQ(jpkp6) * Y6 & & + PQ(jpkp7) * Y7 + PQ(jpkp) * Y dzdq = & J & + PQ(jpkp) * Z + PQ(jpkp2) * Z2 & J 2 J 22 & + PQ(jpkp3) * Z3 + PQ(jpkp) * Z & & + PQ(jpkp5) * Z5 + PQ(jpkp6) * Z6 & J3 J32 & + PQ(jpkp7) * Z7 + PQ(jpkp) * Z dxde = & & + PE(pkp) * X + PE(pkp2) * X2 & & + PE(pkp3) * X3 + PE(pkp) * X & & + PE(pkp5) * X5 + PE(pkp6) * X6 & & + PE(pkp7) * X7 + PE(pkp) * X dyde = & dxdq J & + PE(pkp) * Y + PE(pkp2) * Y2 & & + PE(pkp3) * Y3 + PE(pkp) * Y & & + PE(pkp5) * Y5 + PE(pkp6) * Y6 & & + PE(pkp7) * Y7 + PE(pkp) * Y dydq J2 dzde = & & + PE(pkp) * Z + PE(pkp2) * Z2 & & + PE(pkp3) * Z3 + PE(pkp) * Z & & + PE(pkp5) * Z5 + PE(pkp6) * Z6 & z & + PE(pkp7) * Z7 + PE(pkp) * Z dzdq J3 J J J
120 FEM3D 20 JACOBI(3/) dxdt = & & + PT(pjp) * X + PT(pjp2) * X2 & & + PT(pjp3) * X3 + PT(pjp) * X & & + PT(pjp5) * X5 + PT(pjp6) * X6 & & + PT(pjp7) * X7 + PT(pjp) * X dydt = & & + PT(pjp) * Y + PT(pjp2) * Y2 & & + PT(pjp3) * Y3 + PT(pjp) * Y & & + PT(pjp5) * Y5 + PT(pjp6) * Y6 & & + PT(pjp7) * Y7 + PT(pjp) * Y dzdt = & & + PT(pjp) * Z + PT(pjp2) * Z2 & & + PT(pjp3) * Z3 + PT(pjp) * Z & & + PT(pjp5) * Z5 + PT(pjp6) * Z6 & & + PT(pjp7) * Z7 + PT(pjp) * Z DETJ(pjpkp)= dxdq*(dyde*dzdt-dzde*dydt) + & & dydq*(dzde*dxdt-dxde*dzdt) + & & dzdq*(dxde*dydt-dyde*dxdt)!c!c== IVERSE JACOBIA coef=.d0 / DETJ(pjpkp) a= coef * ( dyde*dzdt - dzde*dydt ) a2= coef * ( dzdq*dydt - dydq*dzdt ) a3= coef * ( dydq*dzde - dzdq*dyde ) a2= coef * ( dzde*dxdt - dxde*dzdt ) a22= coef * ( dxdq*dzdt - dzdq*dxdt ) a23= coef * ( dzdq*dxde - dxdq*dzde ) J J J J 2 3 J J J J J J a3= coef * ( dxde*dydt - dyde*dxdt ) a32= coef * ( dydq*dxdt - dxdq*dydt ) a33= coef * ( dxdq*dyde - dydq*dxde ) DETJ(pjpkp)= dabs(detj(pjpkp))
121 FEM3D 2 自然座標系における偏微分 (/) 従って下記のように偏微分を計算できる ヤコビアン (3 3 行列 ) の逆行列を求める J z z z z
122 FEM3D 22 JACOBI(3/) dxdt = & & + PT(pjp) * X + PT(pjp2) * X2 & & + PT(pjp3) * X3 + PT(pjp) * X & & + PT(pjp5) * X5 + PT(pjp6) * X6 & & + PT(pjp7) * X7 + PT(pjp) * X dydt = & & + PT(pjp) * Y + PT(pjp2) * Y2 & & + PT(pjp3) * Y3 + PT(pjp) * Y & & + PT(pjp5) * Y5 + PT(pjp6) * Y6 & & + PT(pjp7) * Y7 + PT(pjp) * Y dzdt = & & + PT(pjp) * Z + PT(pjp2) * Z2 & & + PT(pjp3) * Z3 + PT(pjp) * Z & & + PT(pjp5) * Z5 + PT(pjp6) * Z6 & & + PT(pjp7) * Z7 + PT(pjp) * Z DETJ(pjpkp)= dxdq*(dyde*dzdt-dzde*dydt) + & & dydq*(dzde*dxdt-dxde*dzdt) + & & dzdq*(dxde*dydt-dyde*dxdt)!c!c== IVERSE JACOBIA coef=.d0 / DETJ(pjpkp) a= coef * ( dyde*dzdt - dzde*dydt ) a2= coef * ( dzdq*dydt - dydq*dzdt ) a3= coef * ( dydq*dzde - dzdq*dyde ) a2= coef * ( dzde*dxdt - dxde*dzdt ) a22= coef * ( dxdq*dzdt - dzdq*dxdt ) a23= coef * ( dzdq*dxde - dxdq*dzde ) a3= coef * ( dxde*dydt - dyde*dxdt ) a32= coef * ( dydq*dxdt - dxdq*dydt ) a33= coef * ( dxdq*dyde - dydq*dxde ) J a a a 2 3 a a a a a a DETJ(pjpkp)= dabs(detj(pjpkp))
123 FEM3D 23 JACOBI(/)!C!C== set the d/dx d/dy & d/dz components PX(pjpkp)= a*pq(jpkp) + a2*pe(pkp) + a3*pt(pjp) PX(pjpkp2)= a*pq(jpkp2) + a2*pe(pkp2) + a3*pt(pjp2) PX(pjpkp3)= a*pq(jpkp3) + a2*pe(pkp3) + a3*pt(pjp3) PX(pjpkp)= a*pq(jpkp) + a2*pe(pkp) + a3*pt(pjp) PX(pjpkp5)= a*pq(jpkp5) + a2*pe(pkp5) + a3*pt(pjp5) PX(pjpkp6)= a*pq(jpkp6) + a2*pe(pkp6) + a3*pt(pjp6) PX(pjpkp7)= a*pq(jpkp7) + a2*pe(pkp7) + a3*pt(pjp7) PX(pjpkp)= a*pq(jpkp) + a2*pe(pkp) + a3*pt(pjp) PY(pjpkp)= a2*pq(jpkp) + a22*pe(pkp) + a23*pt(pjp) PY(pjpkp2)= a2*pq(jpkp2) + a22*pe(pkp2) + a23*pt(pjp2) PY(pjpkp3)= a2*pq(jpkp3) + a22*pe(pkp3) + a23*pt(pjp3) PY(pjpkp)= a2*pq(jpkp) + a22*pe(pkp) + a23*pt(pjp) PY(pjpkp5)= a2*pq(jpkp5) + a22*pe(pkp5) + a23*pt(pjp5) PY(pjpkp6)= a2*pq(jpkp6) + a22*pe(pkp6) + a23*pt(pjp6) PY(pjpkp7)= a2*pq(jpkp7) + a22*pe(pkp7) + a23*pt(pjp7) PY(pjpkp)= a2*pq(jpkp) + a22*pe(pkp) + a23*pt(pjp) PZ(pjpkp)= a3*pq(jpkp) + a32*pe(pkp) + a33*pt(pjp) PZ(pjpkp2)= a3*pq(jpkp2) + a32*pe(pkp2) + a33*pt(pjp2) PZ(pjpkp3)= a3*pq(jpkp3) + a32*pe(pkp3) + a33*pt(pjp3) PZ(pjpkp)= a3*pq(jpkp) + a32*pe(pkp) + a33*pt(pjp) PZ(pjpkp5)= a3*pq(jpkp5) + a32*pe(pkp5) + a33*pt(pjp5) PZ(pjpkp6)= a3*pq(jpkp6) + a32*pe(pkp6) + a33*pt(pjp6) PZ(pjpkp7)= a3*pq(jpkp7) + a32*pe(pkp7) + a33*pt(pjp7) PZ(pjpkp)= a3*pq(jpkp) + a32*pe(pkp) + a33*pt(pjp) a a a a a a a a a z z z z
124 FEM3D 2 係数行列 :MAT_ASS_MAI(5/6)!C!C== COSTRUCT the GLOBAL MATRIX do e= p = nodlocal(e) do je= jp = nodlocal(je) kk= 0 f (jp.ne.p) then S= nde(p-) + E= nde(p ) do k= S E f ( tem(k).eq.jp ) then kk= k et endf endf 全体行列の非対角成分 A p jp kk:tem におけるアドレス p= nodlocal(e) jp= nodlocal(je) 2
125 FEM3D 25 要素マトリクス : 行列 j j k j
126 FEM3D 26 係数行列 :MAT_ASS_MAI(5/6)!C!C== COSTRUCT the GLOBAL MATRIX do e= p = nodlocal(e) do je= jp = nodlocal(je) kk= 0 f (jp.ne.p) then S= nde(p-) + E= nde(p ) do k= S E f ( tem(k).eq.jp ) then kk= k et endf endf 要素マトリクス ( e ~j e ) 全体マトリクス ( p ~j p ) の関係 kk:tem におけるアドレス
127 FEM3D 27 係数行列 :MAT_ASS_MAI(6/6) QV0 = 0.d0 COEFj= 0.d0 do kpn= 2 do jpn= 2 do pn= 2 coef= dabs(detj(pnjpnkpn))*wei(pn)*wei(jpn)*wei(kpn) PX= PX(pnjpnkpne) PY= PY(pnjpnkpne) PZ= PZ(pnjpnkpne) PXj= PX(pnjpnkpnje) PYj= PY(pnjpnkpnje) PZj= PZ(pnjpnkpnje) COEFj= COEFj + coef * COD0 * & (PX*PXj+PY*PYj+PZ*PZj) SH= SHAPE(pnjpnkpne) QV0= QV0 + SH * QVOL * coef f (jp.eq.p) then D(p)= D(p) + COEFj B(p)= B(p) + QV0*QVC else AMAT(kk)= AMAT(kk) + COEFj endf return end j j z z j det J ddd
128 FEM3D 2 係数行列 :MAT_ASS_MAI(6/6) QV0 = 0.d0 COEFj= 0.d0 do kpn= 2 do jpn= 2 do pn= 2 coef= dabs(detj(pnjpnkpn))*wei(pn)*wei(jpn)*wei(kpn) PX= PX(pnjpnkpne) PY= PY(pnjpnkpne) PZ= PZ(pnjpnkpne) PXj= PX(pnjpnkpnje) PYj= PY(pnjpnkpnje) PZj= PZ(pnjpnkpnje) COEFj= COEFj + coef * COD0 * & (PX*PXj+PY*PYj+PZ*PZj) SH= SHAPE(pnjpnkpne) QV0= QV0 + SH * QVOL * coef f (jp.eq.p) then D(p)= D(p) + COEFj B(p)= B(p) + QV0*QVC else AMAT(kk)= AMAT(kk) + COEFj endf return end j I L j M j z f ( ) ddd W W j Wk f ( j k ) k z j det J ddd
129 FEM3D 29 係数行列 :MAT_ASS_MAI(6/6) QV0 = 0.d0 COEFj= 0.d0 do kpn= 2 do jpn= 2 do pn= 2 coef= dabs(detj(pnjpnkpn))*wei(pn)*wei(jpn)*wei(kpn) PX= PX(pnjpnkpne) PY= PY(pnjpnkpne) PZ= PZ(pnjpnkpne) coef W W W det j k J j k PXj= PX(pnjpnkpnje) PYj= PY(pnjpnkpnje) PZj= PZ(pnjpnkpnje) COEFj= COEFj + coef * COD0 * & (PX*PXj+PY*PYj+PZ*PZj) SH= SHAPE(pnjpnkpne) QV0= QV0 + SH * QVOL * coef f (jp.eq.p) then D(p)= D(p) + COEFj B(p)= B(p) + QV0*QVC else AMAT(kk)= AMAT(kk) + COEFj endf return end j I L j M j z f ( ) ddd W W j Wk f ( j k ) k z j det J ddd
130 FEM3D 30 係数行列 :MAT_ASS_MAI(6/6) QV0 = 0.d0 COEFj= 0.d0 do kpn= 2 do jpn= 2 do pn= 2 coef= dabs(detj(pnjpnkpn))*wei(pn)*wei(jpn)*wei(kpn) PX= PX(pnjpnkpne) PY= PY(pnjpnkpne) PZ= PZ(pnjpnkpne) PXj= PX(pnjpnkpnje) PYj= PY(pnjpnkpnje) PZj= PZ(pnjpnkpnje) COEFj= COEFj + coef * COD0 * & (PX*PXj+PY*PYj+PZ*PZj) SH= SHAPE(pnjpnkpne) QV0= QV0 + SH * QVOL * coef f (jp.eq.p) then D(p)= D(p) + COEFj B(p)= B(p) + QV0*QVC else AMAT(kk)= AMAT(kk) + COEFj endf return end j k j j
131 FEM3D 3 係数行列 :MAT_ASS_MAI(6/6) QV0 = 0.d0 COEFj= 0.d0 do kpn= 2 do jpn= 2 do pn= 2 coef= dabs(detj(pnjpnkpn))*wei(pn)*wei(jpn)*wei(kpn) PX= PX(pnjpnkpne) PY= PY(pnjpnkpne) PZ= PZ(pnjpnkpne) PXj= PX(pnjpnkpnje) PYj= PY(pnjpnkpnje) PZj= PZ(pnjpnkpnje) COEFj= COEFj + coef * COD0 * & (PX*PXj+PY*PYj+PZ*PZj) SH= SHAPE(pnjpnkpne) QV0= QV0 + SH * QVOL * coef f (jp.eq.p) then D(p)= D(p) + COEFj B(p)= B(p) + QV0*QVC else AMAT(kk)= AMAT(kk) + COEFj endf return end k ( e) ( e) f ( e) ( e) T f Q dv Q V z QVOL C C QVC C C QV 0 QVOL f ( e) V QV 0QVC T dv
132 FEM3D 32 MAT_ASS_BC: 全体構成 do = 節点ループ ( ディリクレ ) 境界条件を設定する節点をマーク (IWKX) do = 節点ループ f (IWKX().eq.) then マークされた節点だったら対応する右辺ベクトル (B) の成分 対角成分 (D) の成分の修正 ( 行 列 ) do k= nde(-)+ nde() 対応する非零非対角成分 (AMAT) の成分の修正 ( 行 ) endf Z T=0@Z=z ma do = 節点ループ do k= nde (-)+ nde () f (IWKX(tem (k)).eq.) then 対応する非零非対角成分の節点がマークされていたら対応する右辺ベクトル 非零非対角成分 (AMAT) の成分の修正 ( 列 ) endf X Y X Z Y
133 FEM3D 33 境界条件 :MAT_ASS_BC(/2)!C!C== Z=Zma subroutne MAT_ASS_BC use pfem_utl mplct REAL* (A-HO-Z) allocate (IWKX(2)) IWKX= 0 do n= IWKX(n)= 0 b0= - do b0= ODGRPtot f (ODGRP_AME(b0).eq.'Zma') et do b= ODGRP_IDEX(b0-)+ ODGRP_IDEX(b0) n= ODGRP_ITEM(b) IWKX(n)= 節点グループ名が Zma である節点 n において : IWKX(n)= とする
134 FEM3D 3 境界条件 :MAT_ASS_BC(2/2) do n= f (IWKX(n).eq.) then B(n)= 0.d0 D(n)=.d0 S= nde(n-) + E= nde(n ) do k= S E AMAT(k)= 0.d0 endf!c== do n= S= nde(n-) + E= nde(n ) do k= S E f (IWKX(tem(k)).eq.) then AMAT(k)= 0.d0 endf return end
135 FEM3D 35 対象とする問題 : 一次元熱伝導問題 体積当たり一様発熱 Q T Q 0 =0 ( mn ) = ma 一様な : 断面積 A 熱伝導率 体積当たり一様発熱 ( 時間当たり ) QL -3 T - 境界条件 =0 := 0 ( 固定 ) T = ma : 0( 断熱 ) 復習 : 一次元問題 Q
136 FEM3D 36 =0 で成立する方程式 T =0 体積当たり一様発熱 Q T Q 0 =0 ( mn ) = ma 一様な : 断面積 A 熱伝導率 体積当たり一様発熱 ( 時間当たり ) QL -3 T - 境界条件 =0 :=0 ( 固定 ) T = ma : 0( 断熱 ) Q 復習 : 一次元問題
137 FEM3D 37 プログラム :d.f(6/6) !C BOUDARY CODITIOS!C !C===!C!C-- X=Xmn = js= IDEX(-) T =0 対角成分 = 右辺 =0 非対角成分 =0 AMAT(jS+)= 0.d0 DIAG()=.d0 RHS ()= 0.d0!C=== do k= PLU f (ITEM(k).eq.) AMAT(k)= 0.d0 復習 : 一次元問題
138 FEM3D 3 プログラム :d.f(6/6) !C BOUDARY CODITIOS!C !C===!C!C-- X=Xmn = js= IDEX(-) AMAT(jS+)= 0.d0 DIAG()=.d0 RHS ()= 0.d0 T =0 対角成分 = 右辺 =0 非対角成分 =0 ゼロクリア!C=== do k= PLU f (ITEM(k).eq.) AMAT(k)= 0.d0 復習 : 一次元問題
139 FEM3D 39 プログラム :d.f(6/6) !C BOUDARY CODITIOS!C !C===!C!C-- X=Xmn = js= IDEX(-) T =0 対角成分 = 右辺 =0 非対角成分 =0 消去 ゼロクリア AMAT(jS+)= 0.d0 DIAG()=.d0 RHS ()= 0.d0!C=== do k= PLU f (ITEM(k).eq.) AMAT(k)= 0.d0 行列の対称性を保つため 第一種境界条件を適用している節点に対応する 列 を 右辺に移項して消去する ( 今の場合は非対角成分を 0 にするだけで良い ) 復習 : 一次元問題
140 FEM3D 0 第一種境界条件が T 0 の場合!C!C !C BOUDARY CODITIOS!C !C=== 行列の対称性を保つため 第一種境界条件を適用している節点に対応する 列 を 右辺に移項して消去する!C!C-- X=Xmn = js= IDEX(-) Dag j j Inde[ j] Amat k Inde[ j] k Item[ k ] Rhs j AMAT(jS+)= 0.d0 DIAG()=.d0 RHS ()= PHImn!C=== do = do k= IDEX(-)+ IDEX() f (ITEM(k).eq.) then RHS ()= RHS() AMAT(k)*PHImn AMAT(k)= 0.d0 endf 復習 : 一次元問題
141 FEM3D 第一種境界条件が T 0 の場合!C!C !C BOUDARY CODITIOS!C !C=== 行列の対称性を保つため 第一種境界条件を適用している節点に対応する 列 を 右辺に移項して消去する!C!C-- X=Xmn = js= IDEX(-)!C=== Dag AMAT(jS+)= 0.d0 j DIAG()=.d0 RHS ()= PHImn Rhs j do = do k= IDEX(-)+ IDEX() f (ITEM(k).eq.) then RHS ()= RHS() AMAT(k)*PHImn AMAT(k)= 0.d0 endf j Rhs j Inde[ j] k Inde[ j] k k Amat Amat k k s s T Item[ k mn Amat s ] s k Item[ k ] where Item( k s ) 復習 : 一次元問題
142 FEM3D 2 境界条件 :MAT_ASS_BC(2/2) do n= f (IWKX(n).eq.) then B(n)= 0.d0 D(n)=.d0 S= nde(n-) + E= nde(n ) do k= S E AMAT(k)= 0.d0 endf IWKX(n)= となる節点に対して対角成分 = 右辺 =0 非零対角成分 =0 ゼロクリア!C== do n= S= nde(n-) + E= nde(n ) do k= S E f (IWKX(tem(k)).eq.) then AMAT(k)= 0.d0 endf return end ここでやっていることも一次元の時と全く変わらない
143 FEM3D 3 境界条件 :MAT_ASS_BC(2/2)!C== do n= f (IWKX(n).eq.) then B(n)= 0.d0 D(n)=.d0 S= nde(n-) + E= nde(n ) do k= S E AMAT(k)= 0.d0 endf do n= S= nde(n-) + E= nde(n ) do k= S E f (IWKX(tem(k)).eq.) then AMAT(k)= 0.d0 endf return end IWKX(n)= となる節点を非零非対角成分として有している節点に対して 右辺へ移項 当該非零非対角成分 =0 消去 ゼロクリア ここでやっていることも一次元の時と全く変わらない
144 FEM3D test メインプログラム nput_cntl 制御データ入力 nput_grd メッシュファイル入力 fnd_node 節点探索 mat_con0 行列コネクティビティ生成 msort ソート mat_con 行列コネクティビティ生成 mat_ass_man 係数行列生成 jacob ヤコビアン計算 mat_ass_bc 境界条件処理 三次元熱伝導解 析コード heat3d の構成 solve 線形ソルバー制御 output_ucd 可視化処理 cg CG 法計算
145 FEM3D 5 全体処理 program heat3d use solver use pfem_utl mplct REAL*(A-HO-Z) call IPUT_CTL call IPUT_GRID call MAT_CO0 call MAT_CO call MAT_ASS_MAI call MAT_ASS_BC call SOLVE call OUTPUT_UCD end program heat3d
146 FEM3D 6 SOLVE module SOLVER contans subroutne SOLVE use pfem_utl use solver_cg mplct REAL* (A-HO-Z) nteger :: ERROR ICFLAG character(len=char_length) :: BUF data ICFLAG/0/!C!C !C PARAMETERs!C !C=== ITER = pfemiarra() CG 法の最大反復回数 RESID = pfemrarra() CG 法の収束判定値!C===!C!C !C ITERATIVE solver!c !C=== call CG & & ( PLU D AMAT nde tem B X RESID ITER ERROR )!C=== ITERactual= ITER end subroutne SOLVE end module SOLVER
147 FEM3D 7 前処理付き共役勾配法 Precondtoned Conjugate Gradent Method (CG) Compute r (0) = b-[a] (0) for = 2 solve [M]z (-) = r (-) - = r (-) z (-) f = p () = z (0) else 前処理 : 対角スケーリング end - = - / -2 p () = z (-) + - endf q () = [A]p () = - /p () q () () = (-) + p () r () = r (-) - q () check convergence r p (-)
148 FEM3D 対角スケーリング 点ヤコビ前処理 前処理行列として もとの行列の対角成分のみを取り出した行列を前処理行列 [M] とする 対角スケーリング 点ヤコビ (pont-jacob) 前処理 M D D D D solve [M]z (-) = r (-) という場合に逆行列を簡単に求めることができる
149 FEM3D 9 module solver_cg contans CG ソルバー (/6) subroutne CG & & ( PLU D AMAT nde tem B X RESID ITER ERROR) mplct REAL*(A-HO-Z) nclude 'precson.nc' nteger(knd=knt ) ntent(n):: PLU nteger(knd=knt ) ntent(nout):: ITER ERROR real (knd=kreal) ntent(nout):: RESID real(knd=kreal) dmenson() ntent(nout):: B X D real(knd=kreal) dmenson(plu) ntent(nout):: AMAT nteger(knd=knt ) dmenson(0: )ntent(n) :: nde nteger(knd=knt ) dmenson(plu)ntent(n) :: tem real(knd=kreal) dmenson(::) allocatable :: WW nteger(knd=knt) parameter :: R= nteger(knd=knt) parameter :: Z= 2 nteger(knd=knt) parameter :: Q= 2 nteger(knd=knt) parameter :: P= 3 nteger(knd=knt) parameter :: DD= nteger(knd=knt ) :: MAXIT real (knd=kreal) :: TOL W SS
150 FEM3D 50 module solver_cg contans CG ソルバー (/6) WW()= WW(R) {r} WW(2)= WW(Z) {z} WW(2)= mplct REAL*(A-HO-Z) WW(Q) {q} nclude 'precson.nc' WW(3)= WW(P) {p} WW()= WW(DD) /{D} subroutne CG & & ( PLU D AMAT nde tem B X RESID ITER ERROR) nteger(knd=knt ) ntent(n):: PLU nteger(knd=knt ) ntent(nout):: ITER ERROR real (knd=kreal) ntent(nout):: RESID real(knd=kreal) dmenson() ntent(nout):: B X D real(knd=kreal) dmenson(plu) ntent(nout):: AMAT nteger(knd=knt ) dmenson(0: )ntent(n) :: nde nteger(knd=knt ) dmenson(plu)ntent(n) :: tem real(knd=kreal) dmenson(::) allocatable :: WW nteger(knd=knt) parameter :: R= nteger(knd=knt) parameter :: Z= 2 nteger(knd=knt) parameter :: Q= 2 nteger(knd=knt) parameter :: P= 3 nteger(knd=knt) parameter :: DD= nteger(knd=knt ) :: MAXIT real (knd=kreal) :: TOL W SS Compute r (0) = b-[a] (0) for = 2 solve [M]z (-) = r (-) - = r (-) z (-) f = p () = z (0) else - = - / -2 end p () = z (-) + - endf q () = [A]p () = - /p () q () () = (-) + p () r () = r (-) - q () check convergence r p (-)
151 FEM3D 5 CG ソルバー (2/6)!C!C !C IIT.!C !C=== ERROR= 0 allocate (WW()) MAXIT = ITER TOL = RESID X = 0.d0!C===!C !C {r0}= {b} - [A]{n}!C !C=== do j= WW(jDD)=.d0/D(j) WVAL= B(j) - D(j)*X(j) do k= nde(j-)+ nde(j) = tem(k) WVAL= WVAL - AMAT(k)*X() WW(jR)= WVAL WW()= WW(R) {r} WW(2)= WW(Z) {z} WW(2)= WW(Q) {q} WW(3)= WW(P) {p} WW()= WW(DD) /{D} 対角成分の逆数 ( 前処理用 ) その都度 除算をすると効率が悪いため 予め配列に格納
152 FEM3D 52 CG ソルバー (2/6)!C!C !C IIT.!C !C=== ERROR= 0 allocate (WW()) MAXIT = ITER TOL = RESID X = 0.d0!C===!C !C {r0}= {b} - [A]{n}!C !C=== do j= WW(jDD)=.d0/D(j) WVAL= B(j) - D(j)*X(j) do k= nde(j-)+ nde(j) = tem(k) WVAL= WVAL - AMAT(k)*X() WW(jR)= WVAL Compute r (0) = b-[a] (0) for = 2 solve [M]z (-) = r (-) - = r (-) z (-) f = p () = z (0) else - = - / -2 p () = z (-) + - endf q () = [A]p () = - /p () q () () = (-) + p () r () = r (-) - q () check convergence r end p (-)
153 FEM3D 53 CG ソルバー (3/6) BRM20= 0.d0 do = BRM20= BRM20 + B()**2 BRM2= BRM20 BRM2= b 2 あとで収束判定に使用!C=== f (BRM2.eq.0.d0) BRM2=.d0 ITER = 0 do ter= MAXIT!C!C************************************************* Conjugate Gradent Iteraton!C!C !C {z}= [Mnv]{r}!C !C=== do = WW(Z)= WW(R) * WW(DD)!C===
154 FEM3D 5 CG ソルバー (3/6)!C=== BRM20= 0.d0 do = BRM20= BRM20 + B()**2 BRM2= BRM20 f (BRM2.eq.0.d0) BRM2=.d0 ITER = 0 Compute r (0) = b-[a] (0) for = 2 solve [M]z (-) = r (-) - = r (-) z (-) f = p () = z (0) else!c!c !C {z}= [Mnv]{r}!C !C=== do = WW(Z)= WW(R) * WW(DD)!C=== - = - / -2 do ter= MAXIT p () = z (-) +!C - p (-)!C************************************************* Conjugate endf Gradent Iteraton end q () = [A]p () = - /p () q () () = (-) + p () r () = r (-) - q () check convergence r
155 FEM3D 55 CG ソルバー (/6)!C!C !C {RHO}= {r}{z}!c !C=== RHO0= 0.d0 do = RHO0= RHO0 + WW(R)*WW(Z) RHO= RHO0!C===!C !C {p} = {z} f ITER=!C BETA= RHO / RHO otherwse!c !C=== f ( ITER.eq. ) then do = WW(P)= WW(Z) else BETA= RHO / RHO do = WW(P)= WW(Z) + BETA*WW(P) endf!c=== Compute r (0) = b-[a] (0) for = 2 solve [M]z (-) = r (-) - = r (-) z (-) f = p () = z (0) else - = - / -2 p () = z (-) + - endf q () = [A]p () = - /p () q () () = (-) + p () r () = r (-) - q () check convergence r end p (-)
156 FEM3D 56 CG ソルバー (5/6)!C !C {q}= [A]{p}!C !C=== do j= WVAL= D(j)*WW(jP) do k= nde(j-)+ nde(j) = tem(k) WVAL= WVAL + AMAT(k)*WW(P) WW(jQ)= WVAL!C===!C !C ALPHA= RHO / {p}{q}!c !C=== C0= 0.d0 do = C0= C0 + WW(P)*WW(Q) C= C0 ALPHA= RHO / C!C=== Compute r (0) = b-[a] (0) for = 2 solve [M]z (-) = r (-) - = r (-) z (-) f = p () = z (0) else - = - / -2 p () = z (-) + - endf q () = [A]p () = - /p () q () () = (-) + p () r () = r (-) - q () check convergence r end p (-)
157 FEM3D 57 CG ソルバー (6/6)!C!C !C {}= {} + ALPHA*{p}!C {r}= {r} - ALPHA*{q}!C !C=== do = X() = X () + ALPHA * WW(P) WW(R)= WW(R) - ALPHA * WW(Q)!C=== DRM20= 0.d0 do = DRM20= DRM20 + WW(R)**2 DRM2= DRM20 RESID= dsqrt(drm2/brm2)!c=== f ( RESID.le.TOL ) et f ( ITER.eq.MAXIT ) ERROR= -300 RHO = RHO Compute r (0) = b-[a] (0) for = 2 solve [M]z (-) = r (-) - = r (-) z (-) f = p () = z (0) else - = - / -2 p () = z (-) + - endf q () = [A]p () = - /p () q () () = (-) + p () r () = r (-) - q () check convergence r end p (-)
158 FEM3D 5!C!C !C {}= {} + ALPHA*{p}!C {r}= {r} - ALPHA*{q}!C !C=== do = X() = X () + ALPHA * WW(P) WW(R)= WW(R) - ALPHA * WW(Q)!C=== DRM20= 0.d0 do = DRM20= DRM20 + WW(R)**2 DRM2= DRM20 RESID= dsqrt(drm2/brm2)!c=== CG ソルバー (6/6) f ( RESID.le.TOL ) et f ( ITER.eq.MAXIT ) ERROR= -300 RHO = RHO Resd Compute r (0) = b-[a] (0) for = 2 solve [M]z (-) = r (-) - = r (-) z (-) f = p () = z (0) else - = - / -2 p () = z (-) + - endf q () = [A]p () = - /p () q () () = (-) + p () r () = r (-) - q () check convergence r end Dorm2 Borm2 r b A b b p (-) Tol
Microsoft PowerPoint - FEM3D-F [互換モード]
![Microsoft PowerPoint - FEM3D-F [互換モード] Microsoft PowerPoint - FEM3D-F [互換モード]](/thumbs/101/150292954.jpg) 有限要素法による 三次元定常熱伝導解析プログラム Fortran 編 202 年夏季集中講義中島研吾 並列計算プログラミング (66-2057) 先端計算機演習 (66-4009) FEM3D 2 対象とする問題 : 三次元定常熱伝導 Z T T=0@Z=z ma Z T z 定常熱伝導 + 発熱 一様な熱伝導率 直方体 T z 一辺長さの立方体 ( 六面体 ) 要素 各方向にX Y Z 個 境界条件
有限要素法による 三次元定常熱伝導解析プログラム Fortran 編 202 年夏季集中講義中島研吾 並列計算プログラミング (66-2057) 先端計算機演習 (66-4009) FEM3D 2 対象とする問題 : 三次元定常熱伝導 Z T T=0@Z=z ma Z T z 定常熱伝導 + 発熱 一様な熱伝導率 直方体 T z 一辺長さの立方体 ( 六面体 ) 要素 各方向にX Y Z 個 境界条件
Microsoft PowerPoint - 03-FEM3D-C.ppt [互換モード]
![Microsoft PowerPoint - 03-FEM3D-C.ppt [互換モード] Microsoft PowerPoint - 03-FEM3D-C.ppt [互換モード]](/thumbs/101/150293077.jpg) 有限要素法による 三次元定常熱伝導解析プログラム C 言語編 中島研吾東京大学情報基盤センター FEM3D 2 対象とする問題 : 三次元定常熱伝導 Z T T=0@Z= ma Z T 定常熱伝導 + 発熱 一様な熱伝導率 直方体 T 一辺長さの立方体 ( 六面体 ) 要素 各方向にX Y Z 個 境界条件 Q 0 X Y X Y T=0@Z= ma 体積当たり発熱量は位置 ( メッシュの中心の座標
有限要素法による 三次元定常熱伝導解析プログラム C 言語編 中島研吾東京大学情報基盤センター FEM3D 2 対象とする問題 : 三次元定常熱伝導 Z T T=0@Z= ma Z T 定常熱伝導 + 発熱 一様な熱伝導率 直方体 T 一辺長さの立方体 ( 六面体 ) 要素 各方向にX Y Z 個 境界条件 Q 0 X Y X Y T=0@Z= ma 体積当たり発熱量は位置 ( メッシュの中心の座標
Microsoft PowerPoint - FEM3D-C [互換モード]
![Microsoft PowerPoint - FEM3D-C [互換モード] Microsoft PowerPoint - FEM3D-C [互換モード]](/thumbs/94/118221219.jpg) 有限要素法による 三次元定常熱伝導解析プログラム C 言語編 202 年夏季集中講義中島研吾 並列計算プログラミング (66-2057) 先端計算機演習 (66-4009) FEM3D 2 対象とする問題 : 三次元定常熱伝導 Z T T=0@Z= ma Z T 定常熱伝導 + 発熱 一様な熱伝導率 直方体 T 一辺長さの立方体 ( 六面体 ) 要素 各方向にX Y Z 個 境界条件 Q 0 X Y
有限要素法による 三次元定常熱伝導解析プログラム C 言語編 202 年夏季集中講義中島研吾 並列計算プログラミング (66-2057) 先端計算機演習 (66-4009) FEM3D 2 対象とする問題 : 三次元定常熱伝導 Z T T=0@Z= ma Z T 定常熱伝導 + 発熱 一様な熱伝導率 直方体 T 一辺長さの立方体 ( 六面体 ) 要素 各方向にX Y Z 個 境界条件 Q 0 X Y
Microsoft PowerPoint - 3D-FEM-1.ppt [互換モード]
![Microsoft PowerPoint - 3D-FEM-1.ppt [互換モード] Microsoft PowerPoint - 3D-FEM-1.ppt [互換モード]](/thumbs/91/105447131.jpg) 三次元弾性解析コード (/3) プログラムの概要 2 年夏学期 中島研吾 科学技術計算 Ⅰ(482-27) コンピュータ科学特別講義 Ⅰ(48-24) FEM3D-Part 2 対象とする問題 弾性体 Z ヤング率 E ポアソン比 ν U Z Z Z Y Y 直方体 一辺長さの立方体 ( 六面体 ) 要素 各方向に Y Z 個 境界条件 対称条件 U @ U Y @Y U Z @Z 強制変位 U Z
三次元弾性解析コード (/3) プログラムの概要 2 年夏学期 中島研吾 科学技術計算 Ⅰ(482-27) コンピュータ科学特別講義 Ⅰ(48-24) FEM3D-Part 2 対象とする問題 弾性体 Z ヤング率 E ポアソン比 ν U Z Z Z Y Y 直方体 一辺長さの立方体 ( 六面体 ) 要素 各方向に Y Z 個 境界条件 対称条件 U @ U Y @Y U Z @Z 強制変位 U Z
Microsoft PowerPoint - 3D-FEM-2.ppt [互換モード]
![Microsoft PowerPoint - 3D-FEM-2.ppt [互換モード] Microsoft PowerPoint - 3D-FEM-2.ppt [互換モード]](/thumbs/103/159463857.jpg) 三次元弾性解析コード (2/3) マトリクス生成 22 年夏学期 中島研吾 科学技術計算 Ⅰ(482-27) コンピュータ科学特別講義 Ⅰ(48-24) FEM3D-Prt2 2 初期化 有限要素法の処理 : プログラム 制御変数読み込み 座標読み込み 要素生成 (: 節点数 ICELTOT: 要素数 ) 配列初期化 ( 全体マトリクス 要素マトリクス ) 要素 全体マトリクスマッピング (IndeItem)
三次元弾性解析コード (2/3) マトリクス生成 22 年夏学期 中島研吾 科学技術計算 Ⅰ(482-27) コンピュータ科学特別講義 Ⅰ(48-24) FEM3D-Prt2 2 初期化 有限要素法の処理 : プログラム 制御変数読み込み 座標読み込み 要素生成 (: 節点数 ICELTOT: 要素数 ) 配列初期化 ( 全体マトリクス 要素マトリクス ) 要素 全体マトリクスマッピング (IndeItem)
Microsoft PowerPoint - 3D-FEM-1.ppt [互換モード]
![Microsoft PowerPoint - 3D-FEM-1.ppt [互換モード] Microsoft PowerPoint - 3D-FEM-1.ppt [互換モード]](/thumbs/91/105447111.jpg) 三次元弾性解析コード (/3) プログラムの概要 22 年夏学期 中島研吾 科学技術計算 Ⅰ(82-27) コンピュータ科学特別講義 Ⅰ(8-2) FEM3D-Part 2 対象とする問題 弾性体 Z ヤング率 E ポアソン比 ν U Z Z Z Y Y 直方体 一辺長さの立方体 ( 六面体 ) 要素 各方向に Y Z 個 境界条件 対称条件 U @ U Y @Y U Z @Z 強制変位 U Z @ZZ
三次元弾性解析コード (/3) プログラムの概要 22 年夏学期 中島研吾 科学技術計算 Ⅰ(82-27) コンピュータ科学特別講義 Ⅰ(8-2) FEM3D-Part 2 対象とする問題 弾性体 Z ヤング率 E ポアソン比 ν U Z Z Z Y Y 直方体 一辺長さの立方体 ( 六面体 ) 要素 各方向に Y Z 個 境界条件 対称条件 U @ U Y @Y U Z @Z 強制変位 U Z @ZZ
パソコンシミュレータの現状
 第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
Microsoft PowerPoint - 08-pFEM3D-2F.ppt [互換モード]
![Microsoft PowerPoint - 08-pFEM3D-2F.ppt [互換モード] Microsoft PowerPoint - 08-pFEM3D-2F.ppt [互換モード]](/thumbs/82/86518263.jpg) 並列有限要素法による 三次元定常熱伝導解析プログラム (2/2)Fortran 編 中島研吾東京大学情報基盤センター RIKEN AICS HPC Spring School 204 pfem3d-2 2 対象とする問題 : 三次元定常熱伝導 Z x T x T=0@Z=z max y NZ T y z 定常熱伝導 + 発熱 一様な熱伝導率 直方体 T z 一辺長さの立方体 ( 六面体 ) 要素 各方向にNX
並列有限要素法による 三次元定常熱伝導解析プログラム (2/2)Fortran 編 中島研吾東京大学情報基盤センター RIKEN AICS HPC Spring School 204 pfem3d-2 2 対象とする問題 : 三次元定常熱伝導 Z x T x T=0@Z=z max y NZ T y z 定常熱伝導 + 発熱 一様な熱伝導率 直方体 T z 一辺長さの立方体 ( 六面体 ) 要素 各方向にNX
Microsoft PowerPoint - 08-pFEM3D-2F.ppt [互換モード]
![Microsoft PowerPoint - 08-pFEM3D-2F.ppt [互換モード] Microsoft PowerPoint - 08-pFEM3D-2F.ppt [互換モード]](/thumbs/96/126965783.jpg) 並列有限要素法による 三次元定常熱伝導解析プログラム (2/2)Fortran 編 中島研吾東京大学情報基盤センター pfem3d-2 2 対象とする問題 : 三次元定常熱伝導 Z x T x T=0@Z=z max y NZ T y z 定常熱伝導 + 発熱 一様な熱伝導率 直方体 T z 一辺長さ1の立方体 ( 六面体 ) 要素 各方向にNX NY NZ 個 境界条件 Q x, y, z 0 X
並列有限要素法による 三次元定常熱伝導解析プログラム (2/2)Fortran 編 中島研吾東京大学情報基盤センター pfem3d-2 2 対象とする問題 : 三次元定常熱伝導 Z x T x T=0@Z=z max y NZ T y z 定常熱伝導 + 発熱 一様な熱伝導率 直方体 T z 一辺長さ1の立方体 ( 六面体 ) 要素 各方向にNX NY NZ 個 境界条件 Q x, y, z 0 X
Microsoft PowerPoint - FEM3D-C.ppt [互換モード]
![Microsoft PowerPoint - FEM3D-C.ppt [互換モード] Microsoft PowerPoint - FEM3D-C.ppt [互換モード]](/thumbs/69/61300119.jpg) 3D-FEM n C: Stead State Heat Conducton Kengo aajma Informaton echnolog Center Programmng for Parallel Computng (66-2057) Semnar on Advanced Computng (66-009) FEM3D 2 3D Stead-State Heat Conducton Z =0@Z=
3D-FEM n C: Stead State Heat Conducton Kengo aajma Informaton echnolog Center Programmng for Parallel Computng (66-2057) Semnar on Advanced Computng (66-009) FEM3D 2 3D Stead-State Heat Conducton Z =0@Z=
OpenFOAM(R) ソースコード入門 pt1 熱伝導方程式の解法から有限体積法の実装について考える 前編 : 有限体積法の基礎確認 2013/11/17 オープンCAE 富山富山県立大学中川慎二
 OpenFOAM(R) ソースコード入門 pt1 熱伝導方程式の解法から有限体積法の実装について考える 前編 : 有限体積法の基礎確認 2013/11/17 オープンCAE 勉強会 @ 富山富山県立大学中川慎二 * OpenFOAM のソースコードでは, 基礎式を偏微分方程式の形で記述する.OpenFOAM 内部では, 有限体積法を使ってこの微分方程式を解いている. どのようにして, 有限体積法に基づく離散化が実現されているのか,
OpenFOAM(R) ソースコード入門 pt1 熱伝導方程式の解法から有限体積法の実装について考える 前編 : 有限体積法の基礎確認 2013/11/17 オープンCAE 勉強会 @ 富山富山県立大学中川慎二 * OpenFOAM のソースコードでは, 基礎式を偏微分方程式の形で記述する.OpenFOAM 内部では, 有限体積法を使ってこの微分方程式を解いている. どのようにして, 有限体積法に基づく離散化が実現されているのか,
FEM原理講座 (サンプルテキスト)
 サンプルテキスト FEM 原理講座 サイバネットシステム株式会社 8 年 月 9 日作成 サンプルテキストについて 各講師が 講義の内容が伝わりやすいページ を選びました テキストのページは必ずしも連続していません 一部を抜粋しています 幾何光学講座については 実物のテキストではなくガイダンスを掲載いたします 対象とする構造系 物理モデル 連続体 固体 弾性体 / 弾塑性体 / 粘弾性体 / 固体
サンプルテキスト FEM 原理講座 サイバネットシステム株式会社 8 年 月 9 日作成 サンプルテキストについて 各講師が 講義の内容が伝わりやすいページ を選びました テキストのページは必ずしも連続していません 一部を抜粋しています 幾何光学講座については 実物のテキストではなくガイダンスを掲載いたします 対象とする構造系 物理モデル 連続体 固体 弾性体 / 弾塑性体 / 粘弾性体 / 固体
Microsoft PowerPoint - 2_FrontISTRと利用可能なソフトウェア.pptx
 東京大学本郷キャンパス 工学部8号館2階222中会議室 13:30-14:00 FrontISTRと利用可能なソフトウェア 2017年4月28日 第35回FrontISTR研究会 FrontISTRの並列計算ハンズオン 精度検証から並列性能評価まで 観測された物理現象 物理モデル ( 支配方程式 ) 連続体の運動を支配する偏微分方程式 離散化手法 ( 有限要素法, 差分法など ) 代数的な数理モデル
東京大学本郷キャンパス 工学部8号館2階222中会議室 13:30-14:00 FrontISTRと利用可能なソフトウェア 2017年4月28日 第35回FrontISTR研究会 FrontISTRの並列計算ハンズオン 精度検証から並列性能評価まで 観測された物理現象 物理モデル ( 支配方程式 ) 連続体の運動を支配する偏微分方程式 離散化手法 ( 有限要素法, 差分法など ) 代数的な数理モデル
(Microsoft PowerPoint - \221\34613\211\361)
 計算力学 ~ 第 回弾性問題の有限要素解析 (Ⅱ)~ 修士 年後期 ( 選択科目 ) 担当 : 岩佐貴史 講義の概要 全 5 講義. 計算力学概論, ガイダンス. 自然現象の数理モデル化. 行列 場とその演算. 数値計算法 (Ⅰ) 5. 数値計算法 (Ⅱ) 6. 初期値 境界値問題 (Ⅰ) 7. 初期値 境界値問題 (Ⅱ) 8. マトリックス変位法による構造解析 9. トラス構造の有限要素解析. 重み付き残差法と古典的近似解法.
計算力学 ~ 第 回弾性問題の有限要素解析 (Ⅱ)~ 修士 年後期 ( 選択科目 ) 担当 : 岩佐貴史 講義の概要 全 5 講義. 計算力学概論, ガイダンス. 自然現象の数理モデル化. 行列 場とその演算. 数値計算法 (Ⅰ) 5. 数値計算法 (Ⅱ) 6. 初期値 境界値問題 (Ⅰ) 7. 初期値 境界値問題 (Ⅱ) 8. マトリックス変位法による構造解析 9. トラス構造の有限要素解析. 重み付き残差法と古典的近似解法.
Microsoft PowerPoint - 10.pptx
 m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
Microsoft PowerPoint - シミュレーション工学-2010-第1回.ppt
 シミュレーション工学 ( 後半 ) 東京大学人工物工学研究センター 鈴木克幸 CA( Compter Aded geerg ) r. Jaso Lemo (SC, 98) 設計者が解析ツールを使いこなすことにより 設計の評価 設計の質の向上を図る geerg の本質の 計算機による支援 (CA CAM などより広い名前 ) 様々な汎用ソフトの登場 工業製品の設計に不可欠のツール 構造解析 流体解析
シミュレーション工学 ( 後半 ) 東京大学人工物工学研究センター 鈴木克幸 CA( Compter Aded geerg ) r. Jaso Lemo (SC, 98) 設計者が解析ツールを使いこなすことにより 設計の評価 設計の質の向上を図る geerg の本質の 計算機による支援 (CA CAM などより広い名前 ) 様々な汎用ソフトの登場 工業製品の設計に不可欠のツール 構造解析 流体解析
FORTRAN( と C) によるプログラミング 5 ファイル入出力 ここではファイルからデータを読みこんだり ファイルにデータを書き出したりするプログラムを作成してみます はじめに テキスト形式で書かれたデータファイルに書かれているデータを読みこんで配列に代入し 標準出力に書き出すプログラムを作り
 FORTRAN( と C) によるプログラミング 5 ファイル入出力 ここではファイルからデータを読みこんだり ファイルにデータを書き出したりするプログラムを作成してみます はじめに テキスト形式で書かれたデータファイルに書かれているデータを読みこんで配列に代入し 標準出力に書き出すプログラムを作ります FORTRAN の場合 OPEN 文でファイルを開いた後 標準入力の場合と同様に READ 文でデータを読みこみます
FORTRAN( と C) によるプログラミング 5 ファイル入出力 ここではファイルからデータを読みこんだり ファイルにデータを書き出したりするプログラムを作成してみます はじめに テキスト形式で書かれたデータファイルに書かれているデータを読みこんで配列に代入し 標準出力に書き出すプログラムを作ります FORTRAN の場合 OPEN 文でファイルを開いた後 標準入力の場合と同様に READ 文でデータを読みこみます
Microsoft PowerPoint - 10.pptx
 0. 固有値とその応用 固有値と固有ベクトル 2 行列による写像から固有ベクトルへ m n A : m n n m 行列によって線形写像 f R R A が表せることを見てきた ここでは 2 次元平面の行列による写像を調べる 2 = 2 A 2 2 とし 写像 まず 単位ベクトルの像を求める u 2 x = v 2 y f : R A R を考える u 2 2 u, 2 2 0 = = v 2 0
0. 固有値とその応用 固有値と固有ベクトル 2 行列による写像から固有ベクトルへ m n A : m n n m 行列によって線形写像 f R R A が表せることを見てきた ここでは 2 次元平面の行列による写像を調べる 2 = 2 A 2 2 とし 写像 まず 単位ベクトルの像を求める u 2 x = v 2 y f : R A R を考える u 2 2 u, 2 2 0 = = v 2 0
<4D F736F F F696E74202D20906C8D488AC28BAB90DD8C7689F090CD8D488A D91E F1>
 人工環境設計解析工学構造力学と有限要素法 ( 第 回 ) 東京大学新領域創成科学研究科 鈴木克幸 固体力学の基礎方程式 変位 - ひずみの関係 適合条件式 ひずみ - 応力の関係 構成方程式 応力 - 外力の関係 平衡方程式 境界条件 変位規定境界 反力規定境界 境界条件 荷重応力ひずみ変形 場の方程式 Γ t Γ t 平衡方程式構成方程式適合条件式 構造力学の基礎式 ひずみ 一軸 荷重応力ひずみ変形
人工環境設計解析工学構造力学と有限要素法 ( 第 回 ) 東京大学新領域創成科学研究科 鈴木克幸 固体力学の基礎方程式 変位 - ひずみの関係 適合条件式 ひずみ - 応力の関係 構成方程式 応力 - 外力の関係 平衡方程式 境界条件 変位規定境界 反力規定境界 境界条件 荷重応力ひずみ変形 場の方程式 Γ t Γ t 平衡方程式構成方程式適合条件式 構造力学の基礎式 ひずみ 一軸 荷重応力ひずみ変形
行列、ベクトル
 行列 (Mtri) と行列式 (Determinnt). 行列 (Mtri) の演算. 和 差 積.. 行列とは.. 行列の和差 ( 加減算 ).. 行列の積 ( 乗算 ). 転置行列 対称行列 正方行列. 単位行列. 行列式 (Determinnt) と逆行列. 行列式. 逆行列. 多元一次連立方程式のコンピュータによる解法. コンピュータによる逆行列の計算.. 定数項の異なる複数の方程式.. 逆行列の計算
行列 (Mtri) と行列式 (Determinnt). 行列 (Mtri) の演算. 和 差 積.. 行列とは.. 行列の和差 ( 加減算 ).. 行列の積 ( 乗算 ). 転置行列 対称行列 正方行列. 単位行列. 行列式 (Determinnt) と逆行列. 行列式. 逆行列. 多元一次連立方程式のコンピュータによる解法. コンピュータによる逆行列の計算.. 定数項の異なる複数の方程式.. 逆行列の計算
演習2
 神戸市立工業高等専門学校電気工学科 / 電子工学科専門科目 数値解析 2017.6.2 演習 2 山浦剛 (tyamaura@riken.jp) 講義資料ページ h t t p://clim ate.aic s. riken. jp/m embers/yamaura/num erical_analysis. html 曲線の推定 N 次多項式ラグランジュ補間 y = p N x = σ N x x
神戸市立工業高等専門学校電気工学科 / 電子工学科専門科目 数値解析 2017.6.2 演習 2 山浦剛 (tyamaura@riken.jp) 講義資料ページ h t t p://clim ate.aic s. riken. jp/m embers/yamaura/num erical_analysis. html 曲線の推定 N 次多項式ラグランジュ補間 y = p N x = σ N x x
数学の世界
 東京女子大学文理学部数学の世界 (2002 年度 ) 永島孝 17 6 行列式の基本法則と効率的な計算法 基本法則 三次以上の行列式についても, 二次の場合と同様な法則がなりたつ ここには三次の場合を例示するが, 四次以上でも同様である 1 単位行列の行列式の値は 1 である すなわち 1 0 0 0 1 0 1 0 0 1 2 二つの列を入れ替えると行列式の値は 1 倍になる 例えば a 13 a
東京女子大学文理学部数学の世界 (2002 年度 ) 永島孝 17 6 行列式の基本法則と効率的な計算法 基本法則 三次以上の行列式についても, 二次の場合と同様な法則がなりたつ ここには三次の場合を例示するが, 四次以上でも同様である 1 単位行列の行列式の値は 1 である すなわち 1 0 0 0 1 0 1 0 0 1 2 二つの列を入れ替えると行列式の値は 1 倍になる 例えば a 13 a
Microsoft PowerPoint - 08-pFEM3D-2C.ppt [互換モード]
![Microsoft PowerPoint - 08-pFEM3D-2C.ppt [互換モード] Microsoft PowerPoint - 08-pFEM3D-2C.ppt [互換モード]](/thumbs/82/86518317.jpg) 並列有限要素法による 三次元定常熱伝導解析プログラム (2/2)C 言語編 中島研吾東京大学情報基盤センター pfem3d-2 2 対象とする問題 : 三次元定常熱伝導 Z x T x T=0@Z=z max y NZ T y z 定常熱伝導 + 発熱 一様な熱伝導率 直方体 T z 一辺長さの立方体 ( 六面体 ) 要素 各方向にNX NY NZ 個 境界条件 Q x, y, z 0 X NY NX
並列有限要素法による 三次元定常熱伝導解析プログラム (2/2)C 言語編 中島研吾東京大学情報基盤センター pfem3d-2 2 対象とする問題 : 三次元定常熱伝導 Z x T x T=0@Z=z max y NZ T y z 定常熱伝導 + 発熱 一様な熱伝導率 直方体 T z 一辺長さの立方体 ( 六面体 ) 要素 各方向にNX NY NZ 個 境界条件 Q x, y, z 0 X NY NX
09.pptx
 講義内容 数値解析 第 9 回 5 年 6 月 7 日 水 理学部物理学科情報理学コース. 非線形方程式の数値解法. はじめに. 分法. 補間法.4 ニュートン法.4. 多変数問題への応用.4. ニュートン法の収束性. 連立 次方程式の解法. 序論と行列計算の基礎. ガウスの消去法. 重対角行列の場合の解法項目を変更しました.4 LU 分解法.5 特異値分解法.6 共役勾配法.7 反復法.7. ヤコビ法.7.
講義内容 数値解析 第 9 回 5 年 6 月 7 日 水 理学部物理学科情報理学コース. 非線形方程式の数値解法. はじめに. 分法. 補間法.4 ニュートン法.4. 多変数問題への応用.4. ニュートン法の収束性. 連立 次方程式の解法. 序論と行列計算の基礎. ガウスの消去法. 重対角行列の場合の解法項目を変更しました.4 LU 分解法.5 特異値分解法.6 共役勾配法.7 反復法.7. ヤコビ法.7.
Microsoft Word - NumericalComputation.docx
 数値計算入門 武尾英哉. 離散数学と数値計算 数学的解法の中には理論計算では求められないものもある. 例えば, 定積分は, まずは積分 ( 被積分関数の原始関数をみつけること できなければ値を得ることはできない. また, ある関数の所定の値における微分値を得るには, まずその関数の微分ができなければならない. さらに代数方程式の解を得るためには, 解析的に代数方程式を解く必要がある. ところが, これらは必ずしも解析的に導けるとは限らない.
数値計算入門 武尾英哉. 離散数学と数値計算 数学的解法の中には理論計算では求められないものもある. 例えば, 定積分は, まずは積分 ( 被積分関数の原始関数をみつけること できなければ値を得ることはできない. また, ある関数の所定の値における微分値を得るには, まずその関数の微分ができなければならない. さらに代数方程式の解を得るためには, 解析的に代数方程式を解く必要がある. ところが, これらは必ずしも解析的に導けるとは限らない.
GeoFEM開発の経験から
 FrontISTR における並列計算のしくみ < 領域分割に基づく並列 FEM> メッシュ分割 領域分割 領域分割 ( パーティショニングツール ) 全体制御 解析制御 メッシュ hecmw_ctrl.dat 境界条件 材料物性 計算制御パラメータ 可視化パラメータ 領域分割ツール 逐次計算 並列計算 Front ISTR FEM の主な演算 FrontISTR における並列計算のしくみ < 領域分割に基づく並列
FrontISTR における並列計算のしくみ < 領域分割に基づく並列 FEM> メッシュ分割 領域分割 領域分割 ( パーティショニングツール ) 全体制御 解析制御 メッシュ hecmw_ctrl.dat 境界条件 材料物性 計算制御パラメータ 可視化パラメータ 領域分割ツール 逐次計算 並列計算 Front ISTR FEM の主な演算 FrontISTR における並列計算のしくみ < 領域分割に基づく並列
以下 変数の上のドットは時間に関する微分を表わしている (ex. 2 dx d x x, x 2 dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-1) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( x や x, x などがすべて 1 次で なおかつ
 以下 変数の上のドットは時間に関する微分を表わしている (e. d d, dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( や, などがすべて 次で なおかつそれらの係数が定数であるような微分方程式 ) に対して安定性の解析を行ってきた しかしながら 実際には非線形の微分方程式で記述される現象も多く存在する
以下 変数の上のドットは時間に関する微分を表わしている (e. d d, dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( や, などがすべて 次で なおかつそれらの係数が定数であるような微分方程式 ) に対して安定性の解析を行ってきた しかしながら 実際には非線形の微分方程式で記述される現象も多く存在する
テンソル ( その ) テンソル ( その ) スカラー ( 階のテンソル ) スカラー ( 階のテンソル ) 階数 ベクトル ( 階のテンソル ) ベクトル ( 階のテンソル ) 行列表現 シンボリック表現 [ ]
![テンソル ( その ) テンソル ( その ) スカラー ( 階のテンソル ) スカラー ( 階のテンソル ) 階数 ベクトル ( 階のテンソル ) ベクトル ( 階のテンソル ) 行列表現 シンボリック表現 [ ] テンソル ( その ) テンソル ( その ) スカラー ( 階のテンソル ) スカラー ( 階のテンソル ) 階数 ベクトル ( 階のテンソル ) ベクトル ( 階のテンソル ) 行列表現 シンボリック表現 [ ]](/thumbs/93/113587990.jpg) Tsor th-ordr tsor by dcl xprsso m m Lm m k m k L mk kk quott rul by symbolc xprsso Lk X thrd-ordr tsor cotrcto j j Copyrght s rsrvd. No prt of ths documt my b rproducd for proft. テンソル ( その ) テンソル ( その
Tsor th-ordr tsor by dcl xprsso m m Lm m k m k L mk kk quott rul by symbolc xprsso Lk X thrd-ordr tsor cotrcto j j Copyrght s rsrvd. No prt of ths documt my b rproducd for proft. テンソル ( その ) テンソル ( その
情報処理概論(第二日目)
 情報処理概論 工学部物質科学工学科応用化学コース機能物質化学クラス 第 8 回 2005 年 6 月 9 日 前回の演習の解答例 多項式の計算 ( 前半 ): program poly implicit none integer, parameter :: number = 5 real(8), dimension(0:number) :: a real(8) :: x, total integer
情報処理概論 工学部物質科学工学科応用化学コース機能物質化学クラス 第 8 回 2005 年 6 月 9 日 前回の演習の解答例 多項式の計算 ( 前半 ): program poly implicit none integer, parameter :: number = 5 real(8), dimension(0:number) :: a real(8) :: x, total integer
4 月 東京都立蔵前工業高等学校平成 30 年度教科 ( 工業 ) 科目 ( プログラミング技術 ) 年間授業計画 教科 :( 工業 ) 科目 :( プログラミング技術 ) 単位数 : 2 単位 対象学年組 :( 第 3 学年電気科 ) 教科担当者 :( 高橋寛 三枝明夫 ) 使用教科書 :( プロ
 4 東京都立蔵前工業高等学校平成 30 年度教科 ( 工業 ) 科目 ( プログラミング技術 ) 年間授業計画 教科 :( 工業 ) 科目 :( プログラミング技術 ) 単位数 : 2 単位 対象学年組 :( 第 3 学年電気科 ) 教科担当者 :( 高橋寛 三枝明夫 ) 使用教科書 :( プログラミング技術 工業 333 実教出版 ) 共通 : 科目 プログラミング技術 のオリエンテーション プログラミング技術は
4 東京都立蔵前工業高等学校平成 30 年度教科 ( 工業 ) 科目 ( プログラミング技術 ) 年間授業計画 教科 :( 工業 ) 科目 :( プログラミング技術 ) 単位数 : 2 単位 対象学年組 :( 第 3 学年電気科 ) 教科担当者 :( 高橋寛 三枝明夫 ) 使用教科書 :( プログラミング技術 工業 333 実教出版 ) 共通 : 科目 プログラミング技術 のオリエンテーション プログラミング技術は
静的弾性問題の有限要素法解析アルゴリズム
 概要 基礎理論. 応力とひずみおよび平衡方程式. 降伏条件式. 構成式 ( 応力 - ひずみ関係式 ) 有限要素法. 有限要素法の概要. 仮想仕事の原理式と変分原理. 平面ひずみ弾性有限要素法定式化 FEM の基礎方程式平衡方程式. G G G ひずみ - 変位関係式 w w w. kl jkl j D 構成式応力 - ひずみ関係式 ) (. 変位の境界条件力の境界条件境界条件式 t S on V
概要 基礎理論. 応力とひずみおよび平衡方程式. 降伏条件式. 構成式 ( 応力 - ひずみ関係式 ) 有限要素法. 有限要素法の概要. 仮想仕事の原理式と変分原理. 平面ひずみ弾性有限要素法定式化 FEM の基礎方程式平衡方程式. G G G ひずみ - 変位関係式 w w w. kl jkl j D 構成式応力 - ひずみ関係式 ) (. 変位の境界条件力の境界条件境界条件式 t S on V
Microsoft Word - 補論3.2
 補論 3. 多変量 GARC モデル 07//6 新谷元嗣 藪友良 対数尤度関数 3 章 7 節では 変量の対数尤度を求めた ここでは多変量の場合 とくに 変量について対数尤度を求める 誤差項 は平均 0 で 次元の正規分布に従うとする 単純化のため 分散と共分散は時間を通じて一定としよう ( この仮定は後で変更される ) したがって ij から添え字 を除くことができる このとき と の尤度関数は
補論 3. 多変量 GARC モデル 07//6 新谷元嗣 藪友良 対数尤度関数 3 章 7 節では 変量の対数尤度を求めた ここでは多変量の場合 とくに 変量について対数尤度を求める 誤差項 は平均 0 で 次元の正規分布に従うとする 単純化のため 分散と共分散は時間を通じて一定としよう ( この仮定は後で変更される ) したがって ij から添え字 を除くことができる このとき と の尤度関数は
Microsoft PowerPoint - NA03-09black.ppt
 きょうの講義 数値 記号処理 2003.2.6 櫻井彰人 NumSymbol@soft.ae.keo.ac.jp http://www.sakura.comp.ae.keo.ac.jp/ 数値計算手法の定石 多項式近似 ( 復習 )» 誤差と手間の解析も 漸化式» 非線型方程式の求解 数値演算上の誤差 数値計算上の誤差 打ち切り誤差 (truncaton error)» 使う公式を有限項で打ち切る
きょうの講義 数値 記号処理 2003.2.6 櫻井彰人 NumSymbol@soft.ae.keo.ac.jp http://www.sakura.comp.ae.keo.ac.jp/ 数値計算手法の定石 多項式近似 ( 復習 )» 誤差と手間の解析も 漸化式» 非線型方程式の求解 数値演算上の誤差 数値計算上の誤差 打ち切り誤差 (truncaton error)» 使う公式を有限項で打ち切る
12.pptx
 数値解析 第 1 回 15 年 7 月 8 日 水 ) 理学部物理学科情報理学コース 1 講義内容 1. 非線形方程式の数値解法 1.1 はじめに 1. 分法 1.3 補間法 1.4 ニュートン法 1.4.1 多変数問題への応用 1.4. ニュートン法の収束性. 連立 1 次方程式の解法.1 序論と行列計算の基礎. ガウスの消去法.3 3 重対角行列の場合の解法.4 LU 分解法.5 特異値分解法.6
数値解析 第 1 回 15 年 7 月 8 日 水 ) 理学部物理学科情報理学コース 1 講義内容 1. 非線形方程式の数値解法 1.1 はじめに 1. 分法 1.3 補間法 1.4 ニュートン法 1.4.1 多変数問題への応用 1.4. ニュートン法の収束性. 連立 1 次方程式の解法.1 序論と行列計算の基礎. ガウスの消去法.3 3 重対角行列の場合の解法.4 LU 分解法.5 特異値分解法.6
NS NS Scalar turbulence 5 6 FEM NS Mesh (A )
 22 3 2 1 2 2 2 3 3 4 NS 4 4.1 NS............ 5 5 Scalar turbulence 5 6 FEM 5 6.1 NS.................................... 6 6.2 Mes A )................................... 6 6.3.....................................
22 3 2 1 2 2 2 3 3 4 NS 4 4.1 NS............ 5 5 Scalar turbulence 5 6 FEM 5 6.1 NS.................................... 6 6.2 Mes A )................................... 6 6.3.....................................
Microsoft Word - thesis.doc
 剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
有限要素法入門 中島研吾 東京大学情報基盤センター
 有限要素法入門 中島研吾 東京大学情報基盤センター EM-ntro 有限要素法入門 偏微分方程式の数値解法 重み付き残差法 偏微分方程式の数値解法 変分法 EM-ntro 差分法と有限要素法 偏微分方程式の近似解法 全領域を小領域 メッシュ 要素 に分割する 差分法 微分係数を直接近似 Tylor 展開 nte fference Method M Tylor Seres Epnson -!!!! nd
有限要素法入門 中島研吾 東京大学情報基盤センター EM-ntro 有限要素法入門 偏微分方程式の数値解法 重み付き残差法 偏微分方程式の数値解法 変分法 EM-ntro 差分法と有限要素法 偏微分方程式の近似解法 全領域を小領域 メッシュ 要素 に分割する 差分法 微分係数を直接近似 Tylor 展開 nte fference Method M Tylor Seres Epnson -!!!! nd
連立方程式の解法
 連立方程式の解法連立方程式をエクセルを用いて解く方法は以下の 2 種類が考えられます 1) エクセルの行列関数を用いる 2) VBA でヤコビ法やガウスザイデル法を用いる ここでは両方について説明します 1) エクセルの行列関数を用いる方法エクセルは表計算ですから行と列に並んだ数値を扱うのは得意です 連立方程式は次のように行列を用いて表すことができます 連立方程式が行列形式で表されることを考慮して解法を考えてみます
連立方程式の解法連立方程式をエクセルを用いて解く方法は以下の 2 種類が考えられます 1) エクセルの行列関数を用いる 2) VBA でヤコビ法やガウスザイデル法を用いる ここでは両方について説明します 1) エクセルの行列関数を用いる方法エクセルは表計算ですから行と列に並んだ数値を扱うのは得意です 連立方程式は次のように行列を用いて表すことができます 連立方程式が行列形式で表されることを考慮して解法を考えてみます
Fortran 勉強会 第 5 回 辻野智紀
 Fortran 勉強会 第 5 回 辻野智紀 今回のお品書き サブルーチンの分割コンパイル ライブラリ 静的ライブラリ 動的ライブラリ モジュール その前に 以下の URL から STPK ライブラリをインストールしておいて下さい. http://www.gfd-dennou.org/library/davis/stpk 前回参加された方はインストール済みのはず. サブルーチンの分割コンパイル サブルーチンの独立化
Fortran 勉強会 第 5 回 辻野智紀 今回のお品書き サブルーチンの分割コンパイル ライブラリ 静的ライブラリ 動的ライブラリ モジュール その前に 以下の URL から STPK ライブラリをインストールしておいて下さい. http://www.gfd-dennou.org/library/davis/stpk 前回参加された方はインストール済みのはず. サブルーチンの分割コンパイル サブルーチンの独立化
Microsoft PowerPoint - Lec17 [互換モード]
![Microsoft PowerPoint - Lec17 [互換モード] Microsoft PowerPoint - Lec17 [互換モード]](/thumbs/88/115805286.jpg) 情報デザイン専攻 画像情報処理論及び演習 - フィルタ処理 エッジ強調 - 差分法 変分法と平滑化 エッジ S Yoszw: s@re.p 今日の授業内容 www.re.p/rc/yoszw/ecres/e.ml www.re.p/rc/yoszw/ecres/ec7.p. 勾配とエッジの基礎 : 差分法.. plcと拡散方程式の基礎 : 変分法. 第 6 回講義水曜日 限教室 68 吉澤信 s@re.p
情報デザイン専攻 画像情報処理論及び演習 - フィルタ処理 エッジ強調 - 差分法 変分法と平滑化 エッジ S Yoszw: s@re.p 今日の授業内容 www.re.p/rc/yoszw/ecres/e.ml www.re.p/rc/yoszw/ecres/ec7.p. 勾配とエッジの基礎 : 差分法.. plcと拡散方程式の基礎 : 変分法. 第 6 回講義水曜日 限教室 68 吉澤信 s@re.p
数学 ⅡB < 公理 > 公理を論拠に定義を用いて定理を証明する 1 大小関係の公理 順序 (a > b, a = b, a > b 1 つ成立 a > b, b > c a > c 成立 ) 順序と演算 (a > b a + c > b + c (a > b, c > 0 ac > bc) 2 図
 数学 Ⅱ < 公理 > 公理を論拠に定義を用いて定理を証明する 大小関係の公理 順序 >, =, > つ成立 >, > > 成立 順序と演算 > + > + >, > > 図形の公理 平行線の性質 錯角 同位角 三角形の合同条件 三角形の合同相似 量の公理 角の大きさ 線分の長さ < 空間における座漂とベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル
数学 Ⅱ < 公理 > 公理を論拠に定義を用いて定理を証明する 大小関係の公理 順序 >, =, > つ成立 >, > > 成立 順序と演算 > + > + >, > > 図形の公理 平行線の性質 錯角 同位角 三角形の合同条件 三角形の合同相似 量の公理 角の大きさ 線分の長さ < 空間における座漂とベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル
Microsoft PowerPoint - 夏の学校(CFD).pptx
 /9/5 FD( 計算流体力学 ) の基礎理論 性能 運動分野 夏の学校 神戸大学大学院海事科学研究科勝井辰博 流体の質量保存 流体要素内の質量の増加率 [ 単位時間当たりの増加量 ] 単位時間に流体要素に流入する質量 流体要素 Fl lm (orol olm) v ( ) ガウスの定理 v( ) /9/5 = =( ) b=b =(b b b ) b= b = b + b + b アインシュタイン表記
/9/5 FD( 計算流体力学 ) の基礎理論 性能 運動分野 夏の学校 神戸大学大学院海事科学研究科勝井辰博 流体の質量保存 流体要素内の質量の増加率 [ 単位時間当たりの増加量 ] 単位時間に流体要素に流入する質量 流体要素 Fl lm (orol olm) v ( ) ガウスの定理 v( ) /9/5 = =( ) b=b =(b b b ) b= b = b + b + b アインシュタイン表記
例 e 指数関数的に減衰する信号を h( a < + a a すると, それらのラプラス変換は, H ( ) { e } e インパルス応答が h( a < ( ただし a >, U( ) { } となるシステムにステップ信号 ( y( のラプラス変換 Y () は, Y ( ) H ( ) X (
 第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
cp-7. 配列
 cp-7. 配列 (C プログラムの書き方を, パソコン演習で学ぶシリーズ ) https://www.kkaneko.jp/cc/adp/index.html 金子邦彦 1 本日の内容 例題 1. 月の日数配列とは. 配列の宣言. 配列の添え字. 例題 2. ベクトルの内積例題 3. 合計点と平均点例題 4. 棒グラフを描く配列と繰り返し計算の関係例題 5. 行列の和 2 次元配列 2 今日の到達目標
cp-7. 配列 (C プログラムの書き方を, パソコン演習で学ぶシリーズ ) https://www.kkaneko.jp/cc/adp/index.html 金子邦彦 1 本日の内容 例題 1. 月の日数配列とは. 配列の宣言. 配列の添え字. 例題 2. ベクトルの内積例題 3. 合計点と平均点例題 4. 棒グラフを描く配列と繰り返し計算の関係例題 5. 行列の和 2 次元配列 2 今日の到達目標
Microsoft PowerPoint - H21生物計算化学2.ppt
 演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生
 0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
モデリングとは
 コンピュータグラフィックス基礎 第 5 回曲線 曲面の表現 ベジェ曲線 金森由博 学習の目標 滑らかな曲線を扱う方法を学習する パラメトリック曲線について理解する 広く一般的に使われているベジェ曲線を理解する 制御点を入力することで ベジェ曲線を描画するアプリケーションの開発を行えるようになる C++ 言語の便利な機能を使えるようになる 要素数が可変な配列としての std::vector の活用 計算機による曲線の表現
コンピュータグラフィックス基礎 第 5 回曲線 曲面の表現 ベジェ曲線 金森由博 学習の目標 滑らかな曲線を扱う方法を学習する パラメトリック曲線について理解する 広く一般的に使われているベジェ曲線を理解する 制御点を入力することで ベジェ曲線を描画するアプリケーションの開発を行えるようになる C++ 言語の便利な機能を使えるようになる 要素数が可変な配列としての std::vector の活用 計算機による曲線の表現
5-仮想仕事式と種々の応力.ppt
 1 以上, 運動の変数についての話を終える. 次は再び力の変数に戻る. その前に, まず次の話が唐突と思われないように 以下は前置き. 先に, 力の変数と運動の変数には対応関係があって, 適当な内積演算によって仕事量を表す ことを述べた. 実は,Cauchy 応力と速度勾配テンソル ( あるいは変位勾配テンソル ) を用いると, それらの内積は内部仮想仕事を表していて, そして, それは外力がなす仮想仕事に等しいという
1 以上, 運動の変数についての話を終える. 次は再び力の変数に戻る. その前に, まず次の話が唐突と思われないように 以下は前置き. 先に, 力の変数と運動の変数には対応関係があって, 適当な内積演算によって仕事量を表す ことを述べた. 実は,Cauchy 応力と速度勾配テンソル ( あるいは変位勾配テンソル ) を用いると, それらの内積は内部仮想仕事を表していて, そして, それは外力がなす仮想仕事に等しいという
Microsoft PowerPoint - Eigen.pptx
 固有値解析 中島研吾 東京大学情報基盤センター同大学院情報理工学系研究科数理情報学専攻数値解析 ( 科目番号 -58) 行列の固有値問題 べき乗法 対称行列の固有値計算法 : ヤコビ法 A 行列の固有値問題 標準固有値問題 (Stndrd vlue Prolem を満足する と を求める : 固有値 (eigenvlue) : 固有ベクトル (eigenvector) 一般固有値問題 (Generl
固有値解析 中島研吾 東京大学情報基盤センター同大学院情報理工学系研究科数理情報学専攻数値解析 ( 科目番号 -58) 行列の固有値問題 べき乗法 対称行列の固有値計算法 : ヤコビ法 A 行列の固有値問題 標準固有値問題 (Stndrd vlue Prolem を満足する と を求める : 固有値 (eigenvlue) : 固有ベクトル (eigenvector) 一般固有値問題 (Generl
スライド 1
 数値解析 2019 年度前期第 13 週 [7 月 11 日 ] 静岡大学創造科学技術大学院情報科学専攻工学部機械工学科計測情報講座 三浦憲二郎 講義アウトライン [7 月 11 日 ] 関数近似と補間 最小 2 乗近似による関数近似 ラグランジュ補間 T.Kanai, U.Tokyo 関数近似 p.116 複雑な関数を簡単な関数で近似する 関数近似 閉区間 [a,b] で定義された関数 f(x)
数値解析 2019 年度前期第 13 週 [7 月 11 日 ] 静岡大学創造科学技術大学院情報科学専攻工学部機械工学科計測情報講座 三浦憲二郎 講義アウトライン [7 月 11 日 ] 関数近似と補間 最小 2 乗近似による関数近似 ラグランジュ補間 T.Kanai, U.Tokyo 関数近似 p.116 複雑な関数を簡単な関数で近似する 関数近似 閉区間 [a,b] で定義された関数 f(x)
演習1
 神戸市立工業高等専門学校電気工学科 / 電子工学科専門科目 数値解析 2019.5.10 演習 1 山浦剛 (tyamaura@riken.jp) 講義資料ページ http://r-ccs-climate.riken.jp/members/yamaura/numerical_analysis.html Fortran とは? Fortran(= FORmula TRANslation ) は 1950
神戸市立工業高等専門学校電気工学科 / 電子工学科専門科目 数値解析 2019.5.10 演習 1 山浦剛 (tyamaura@riken.jp) 講義資料ページ http://r-ccs-climate.riken.jp/members/yamaura/numerical_analysis.html Fortran とは? Fortran(= FORmula TRANslation ) は 1950
2018年度 東京大・理系数学
 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ関数 f ( ) = + cos (0 < < ) の増減表をつくり, + 0, 0 のと sin きの極限を調べよ 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ n+ 数列 a, a, を, Cn a n = ( n =,, ) で定める n! an qn () n とする を既約分数 an p として表したときの分母
08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ関数 f ( ) = + cos (0 < < ) の増減表をつくり, + 0, 0 のと sin きの極限を調べよ 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ n+ 数列 a, a, を, Cn a n = ( n =,, ) で定める n! an qn () n とする を既約分数 an p として表したときの分母
解析力学B - 第11回: 正準変換
 解析力学 B 第 11 回 : 正準変換 神戸大 : 陰山聡 ホームページ ( 第 6 回から今回までの講義ノート ) http://tinyurl.com/kage2010 2011.01.27 正準変換 バネ問題 ( あえて下手に座標をとった ) ハミルトニアンを考える q 正準方程式は H = p2 2m + k 2 (q l 0) 2 q = H p = p m ṗ = H q = k(q
解析力学 B 第 11 回 : 正準変換 神戸大 : 陰山聡 ホームページ ( 第 6 回から今回までの講義ノート ) http://tinyurl.com/kage2010 2011.01.27 正準変換 バネ問題 ( あえて下手に座標をとった ) ハミルトニアンを考える q 正準方程式は H = p2 2m + k 2 (q l 0) 2 q = H p = p m ṗ = H q = k(q
中学 1 年生 e ライブラリ数学教材一覧 学校図書 ( 株 ) 中学 1 年 数学 文字式式の計算 項と係数 中学 1 年 数学 次式 中学 1 年 数学 項のまとめ方 中学 1 年 数学 次式の加法 中学 1 年 数学 77
 中学 1 年生 e ライブラリ数学教材一覧 学校図書 ( 株 ) 中学 1 年 数学 1 14-20 正の数 負の数正の数 負の数 14- ある基準から考えた量の表現 中学 1 年 数学 14- 正の数 中学 1 年 数学 14- 負の数 中学 1 年 数学 14- 量の基準を表す数 中学 1 年 数学 15- 反対の性質をもつ量の表現 中学 1 年 数学 17- 数直線 中学 1 年 数学 18-19
中学 1 年生 e ライブラリ数学教材一覧 学校図書 ( 株 ) 中学 1 年 数学 1 14-20 正の数 負の数正の数 負の数 14- ある基準から考えた量の表現 中学 1 年 数学 14- 正の数 中学 1 年 数学 14- 負の数 中学 1 年 数学 14- 量の基準を表す数 中学 1 年 数学 15- 反対の性質をもつ量の表現 中学 1 年 数学 17- 数直線 中学 1 年 数学 18-19
<4D F736F F D2097CD8A7793FC96E582BD82ED82DD8A E6318FCD2E646F63>
 - 第 章たわみ角法の基本式 ポイント : たわみ角法の基本式を理解する たわみ角法の基本式を梁の微分方程式より求める 本章では たわみ角法の基本式を導くことにする 基本式の誘導法は各種あるが ここでは 梁の微分方程式を解いて基本式を求める方法を採用する この本で使用する座標系は 右手 右ネジの法則に従った座標を用いる また ひとつの部材では 図 - に示すように部材の左端の 点を原点とし 軸線を
- 第 章たわみ角法の基本式 ポイント : たわみ角法の基本式を理解する たわみ角法の基本式を梁の微分方程式より求める 本章では たわみ角法の基本式を導くことにする 基本式の誘導法は各種あるが ここでは 梁の微分方程式を解いて基本式を求める方法を採用する この本で使用する座標系は 右手 右ネジの法則に従った座標を用いる また ひとつの部材では 図 - に示すように部材の左端の 点を原点とし 軸線を
Microsoft PowerPoint - FEMintro [互換モード]
![Microsoft PowerPoint - FEMintro [互換モード] Microsoft PowerPoint - FEMintro [互換モード]](/thumbs/93/113568989.jpg) 有限要素法入門 年夏季集中講義中島研吾 並列計算プログラミング 66-57 先端計算機演習 66-49 EM-ntro 有限要素法入門 偏微分方程式の数値解法 重み付き残差法 ガウス グリーンの定理 偏微分方程式の数値解法 変分法 EM-ntro 差分法と有限要素法 偏微分方程式の近似解法 全領域を小領域 メッシュ 要素 に分割する 差分法 微分係数を直接近似 Tylor 展開 EM-ntro 差分法
有限要素法入門 年夏季集中講義中島研吾 並列計算プログラミング 66-57 先端計算機演習 66-49 EM-ntro 有限要素法入門 偏微分方程式の数値解法 重み付き残差法 ガウス グリーンの定理 偏微分方程式の数値解法 変分法 EM-ntro 差分法と有限要素法 偏微分方程式の近似解法 全領域を小領域 メッシュ 要素 に分割する 差分法 微分係数を直接近似 Tylor 展開 EM-ntro 差分法
memo
 数理情報工学特論第一 機械学習とデータマイニング 4 章 : 教師なし学習 3 かしまひさし 鹿島久嗣 ( 数理 6 研 ) kashima@mist.i.~ DEPARTMENT OF MATHEMATICAL INFORMATICS 1 グラフィカルモデルについて学びます グラフィカルモデル グラフィカルラッソ グラフィカルラッソの推定アルゴリズム 2 グラフィカルモデル 3 教師なし学習の主要タスクは
数理情報工学特論第一 機械学習とデータマイニング 4 章 : 教師なし学習 3 かしまひさし 鹿島久嗣 ( 数理 6 研 ) kashima@mist.i.~ DEPARTMENT OF MATHEMATICAL INFORMATICS 1 グラフィカルモデルについて学びます グラフィカルモデル グラフィカルラッソ グラフィカルラッソの推定アルゴリズム 2 グラフィカルモデル 3 教師なし学習の主要タスクは
行列の反復解法 1. 点 Jacobi 法 数値解法の重要な概念の一つである反復法を取り上げ 連立一次方程式 Au=b の反復解法を調べる 行列のスペクトル半径と収束行列の定義を与える 行列のスペクトル半径行列 Aの固有値の絶対値の最大値でもって 行列 Aのスペクトル半径 r(a) を与える 収束行
 行列の反復解法 1. 点 Jacobi 法 数値解法の重要な概念の一つである反復法を取り上げ 連立一次方程式 Au=b の反復解法を調べる 行列のスペクトル半径と収束行列の定義を与える 行列のスペクトル半径行列 Aの固有値の絶対値の最大値でもって 行列 Aのスペクトル半径 r(a) を与える 収束行列 B が正方行列で のとき B を収束行列と呼ぶ 定理収束行列のスペクトル半径は である 簡単な証明もし
行列の反復解法 1. 点 Jacobi 法 数値解法の重要な概念の一つである反復法を取り上げ 連立一次方程式 Au=b の反復解法を調べる 行列のスペクトル半径と収束行列の定義を与える 行列のスペクトル半径行列 Aの固有値の絶対値の最大値でもって 行列 Aのスペクトル半径 r(a) を与える 収束行列 B が正方行列で のとき B を収束行列と呼ぶ 定理収束行列のスペクトル半径は である 簡単な証明もし
PowerPoint Presentation
 付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
memo
 計数工学プログラミング演習 ( 第 4 回 ) 2016/05/10 DEPARTMENT OF MATHEMATICA INFORMATICS 1 内容 リスト 疎行列 2 連結リスト (inked ists) オブジェクトをある線形順序に並べて格納するデータ構造 単方向連結リスト (signly linked list) の要素 x キーフィールド key ポインタフィールド next x->next:
計数工学プログラミング演習 ( 第 4 回 ) 2016/05/10 DEPARTMENT OF MATHEMATICA INFORMATICS 1 内容 リスト 疎行列 2 連結リスト (inked ists) オブジェクトをある線形順序に並べて格納するデータ構造 単方向連結リスト (signly linked list) の要素 x キーフィールド key ポインタフィールド next x->next:
Microsoft PowerPoint - 三次元座標測定 ppt
 冗長座標測定機 ()( 三次元座標計測 ( 第 9 回 ) 5 年度大学院講義 6 年 月 7 日 冗長性を持つ 次元座標測定機 次元 辺測量 : 冗長性を出すために つのレーザトラッカを配置し, キャッツアイまでの距離から座標を測定する つのカメラ ( 次元的なカメラ ) とレーザスキャナ : つの角度測定システムによる座標測定 つの回転関節による 次元 自由度多関節機構 高増潔東京大学工学系研究科精密機械工学専攻
冗長座標測定機 ()( 三次元座標計測 ( 第 9 回 ) 5 年度大学院講義 6 年 月 7 日 冗長性を持つ 次元座標測定機 次元 辺測量 : 冗長性を出すために つのレーザトラッカを配置し, キャッツアイまでの距離から座標を測定する つのカメラ ( 次元的なカメラ ) とレーザスキャナ : つの角度測定システムによる座標測定 つの回転関節による 次元 自由度多関節機構 高増潔東京大学工学系研究科精密機械工学専攻
Microsoft Word - 1B2011.doc
 第 14 回モールの定理 ( 単純梁の場合 ) ( モールの定理とは何か?p.11) 例題 下記に示す単純梁の C 点のたわみ角 θ C と, たわみ δ C を求めよ ただし, 部材の曲げ 剛性は材軸に沿って一様で とする C D kn B 1.5m 0.5m 1.0m 解答 1 曲げモーメント図を描く,B 点の反力を求める kn kn 4 kn 曲げモーメント図を描く knm 先に得られた曲げモーメントの値を
第 14 回モールの定理 ( 単純梁の場合 ) ( モールの定理とは何か?p.11) 例題 下記に示す単純梁の C 点のたわみ角 θ C と, たわみ δ C を求めよ ただし, 部材の曲げ 剛性は材軸に沿って一様で とする C D kn B 1.5m 0.5m 1.0m 解答 1 曲げモーメント図を描く,B 点の反力を求める kn kn 4 kn 曲げモーメント図を描く knm 先に得られた曲げモーメントの値を
Microsoft PowerPoint - 講義10改.pptx
 計算機プログラミング ( 後半組 ) Computer Programming (2nd half group) 担当 : 城﨑知至 Instructor: Tomoyuki JOHZAKI 第 9 回ファイルの入出力 Lesson 9 input/output statements 教科書 7.3 章 1 ファイル入出力 : サンプル 1 下記プログラムを outin1.f90 として作成し コンパイル実
計算機プログラミング ( 後半組 ) Computer Programming (2nd half group) 担当 : 城﨑知至 Instructor: Tomoyuki JOHZAKI 第 9 回ファイルの入出力 Lesson 9 input/output statements 教科書 7.3 章 1 ファイル入出力 : サンプル 1 下記プログラムを outin1.f90 として作成し コンパイル実
微分方程式による現象記述と解きかた
 微分方程式による現象記述と解きかた 土木工学 : 公共諸施設 構造物の有用目的にむけた合理的な実現をはかる方法 ( 技術 ) に関する学 橋梁 トンネル ダム 道路 港湾 治水利水施設 安全化 利便化 快適化 合法則的 経済的 自然および人口素材によって作られた 質量保存則 構造物の自然的な性質 作用 ( 外力による応答 ) エネルギー則 の解明 社会的諸現象のうち マスとしての移動 流通 運動量則
微分方程式による現象記述と解きかた 土木工学 : 公共諸施設 構造物の有用目的にむけた合理的な実現をはかる方法 ( 技術 ) に関する学 橋梁 トンネル ダム 道路 港湾 治水利水施設 安全化 利便化 快適化 合法則的 経済的 自然および人口素材によって作られた 質量保存則 構造物の自然的な性質 作用 ( 外力による応答 ) エネルギー則 の解明 社会的諸現象のうち マスとしての移動 流通 運動量則
有限要素法法による弾弾性変形解析 (Gmsh+Calculix)) 海洋エネルギギー研究センター今井 問題断面が1mmx1mm 長さ 20mmm の鋼の一端端を固定 他他端に点荷重重をかけた場場合の先端変変位および最大応力を求求める P Equation Chapter 1 Section 1 l
 有限要素法法による弾弾性変形解析 (Gmsh+Calculix)) 海洋エネルギギー研究センター今井 問題断面が1mmx1mm 長さ 20mmm の鋼の一端端を固定 他他端に点荷重重をかけた場場合の先端変変位および最大応力を求求める P Equation Chapter 1 Section 1 l δ 1 形状の作作成 (Gmsh) c: gmsh test1 フォルダを作る http://geuz.org/gmsh/#
有限要素法法による弾弾性変形解析 (Gmsh+Calculix)) 海洋エネルギギー研究センター今井 問題断面が1mmx1mm 長さ 20mmm の鋼の一端端を固定 他他端に点荷重重をかけた場場合の先端変変位および最大応力を求求める P Equation Chapter 1 Section 1 l δ 1 形状の作作成 (Gmsh) c: gmsh test1 フォルダを作る http://geuz.org/gmsh/#
Chap2
 逆三角関数の微分 Arcsin の導関数を計算する Arcsin I. 初等関数の微積分 sin [, ], [π/, π/] cos sin / (Arcsin ) 計算力の体力をつけよう π/ π/ E. II- 次の関数の導関数を計算せよ () Arccos () Arctan E. I- の解答 不定積分あれこれ () Arccos n log C C (n ) n e e C log (log
逆三角関数の微分 Arcsin の導関数を計算する Arcsin I. 初等関数の微積分 sin [, ], [π/, π/] cos sin / (Arcsin ) 計算力の体力をつけよう π/ π/ E. II- 次の関数の導関数を計算せよ () Arccos () Arctan E. I- の解答 不定積分あれこれ () Arccos n log C C (n ) n e e C log (log
memo
 数理情報工学演習第一 C プログラミング演習 ( 第 5 回 ) 2015/05/11 DEPARTMENT OF MATHEMATICAL INFORMATICS 1 今日の内容 : プロトタイプ宣言 ヘッダーファイル, プログラムの分割 課題 : 疎行列 2 プロトタイプ宣言 3 C 言語では, 関数や変数は使用する前 ( ソースの上のほう ) に定義されている必要がある. double sub(int
数理情報工学演習第一 C プログラミング演習 ( 第 5 回 ) 2015/05/11 DEPARTMENT OF MATHEMATICAL INFORMATICS 1 今日の内容 : プロトタイプ宣言 ヘッダーファイル, プログラムの分割 課題 : 疎行列 2 プロトタイプ宣言 3 C 言語では, 関数や変数は使用する前 ( ソースの上のほう ) に定義されている必要がある. double sub(int
熱伝達の境界条件 (OF-2.1 OF-2.3) 1/7 藤井 15/01/30 熱伝達の境界条件 (OF-2.1 OF-2.3) 目次 1. はじめに 2. 熱伝達の境界条件 (fixedalphatemp) の作成 2-1. 考え方 2-2. fixedalphatemp の作成 3. 作動確認
 1/7 藤井 15/01/30 目次 1. はじめに 2. 熱伝達の境界条件 (fixedalphatemp) の作成 2-1. 考え方 2-2. fixedalphatemp の作成 3. 作動確認 3-1. モデルの作成 3-2. solver 3-3. 境界条件 3-4. 計算結果の確認 4. 計算結果の検証 5. まとめ 1. はじめに 現在 OpenFOAM で laplacianfoam
1/7 藤井 15/01/30 目次 1. はじめに 2. 熱伝達の境界条件 (fixedalphatemp) の作成 2-1. 考え方 2-2. fixedalphatemp の作成 3. 作動確認 3-1. モデルの作成 3-2. solver 3-3. 境界条件 3-4. 計算結果の確認 4. 計算結果の検証 5. まとめ 1. はじめに 現在 OpenFOAM で laplacianfoam
Microsoft Word ã‡»ã…«ã‡ªã…¼ã…‹ã…žã…‹ã…³ã†¨åłºæœ›å•¤(佒芤喋çfl�)
 Cellulr uo nd heir eigenlues 東洋大学総合情報学部 佐藤忠一 Tdzu So Depren o Inorion Siene nd rs Toyo Uniersiy. まえがき 一次元セルオ-トマトンは数学的には記号列上の行列の固有値問題である 固有値問題の行列はふつう複素数体上の行列である 量子力学における固有値問題も無限次元ではあるが関数環上の行列でその成分は可換環である
Cellulr uo nd heir eigenlues 東洋大学総合情報学部 佐藤忠一 Tdzu So Depren o Inorion Siene nd rs Toyo Uniersiy. まえがき 一次元セルオ-トマトンは数学的には記号列上の行列の固有値問題である 固有値問題の行列はふつう複素数体上の行列である 量子力学における固有値問題も無限次元ではあるが関数環上の行列でその成分は可換環である
Microsoft PowerPoint - 1d.ppt [互換モード]
![Microsoft PowerPoint - 1d.ppt [互換モード] Microsoft PowerPoint - 1d.ppt [互換モード]](/thumbs/91/105531336.jpg) 数値計算の基礎 一次元熱伝導方程式の差分法 による解法 年夏季集中講義 中島研吾 並列計算プログラミング 66-57 先端計算機演習 66-49 概要 一次元熱伝導方程式と差分法 連立一次方程式の解法 反復法について 共役勾配法 CG 法 前処理について 共役勾配法を使用した一次元熱伝導解析プログラムについて d d 一次元熱伝導方程式 / 支配方程式 : 簡単のため熱伝導率 BF BF d, @,
数値計算の基礎 一次元熱伝導方程式の差分法 による解法 年夏季集中講義 中島研吾 並列計算プログラミング 66-57 先端計算機演習 66-49 概要 一次元熱伝導方程式と差分法 連立一次方程式の解法 反復法について 共役勾配法 CG 法 前処理について 共役勾配法を使用した一次元熱伝導解析プログラムについて d d 一次元熱伝導方程式 / 支配方程式 : 簡単のため熱伝導率 BF BF d, @,
微分方程式 モデリングとシミュレーション
 1 微分方程式モデリングとシミュレーション 2018 年度 2 質点の運動のモデル化 粒子と粒子に働く力 粒子の運動 粒子の位置の時間変化 粒子の位置の変化の割合 速度 速度の変化の割合 加速度 力と加速度の結び付け Newtonの運動方程式 : 微分方程式 解は 時間の関数としての位置 3 Newton の運動方程式 質点の運動は Newton の運動方程式で記述される 加速度は力に比例する 2
1 微分方程式モデリングとシミュレーション 2018 年度 2 質点の運動のモデル化 粒子と粒子に働く力 粒子の運動 粒子の位置の時間変化 粒子の位置の変化の割合 速度 速度の変化の割合 加速度 力と加速度の結び付け Newtonの運動方程式 : 微分方程式 解は 時間の関数としての位置 3 Newton の運動方程式 質点の運動は Newton の運動方程式で記述される 加速度は力に比例する 2
Microsoft Word - Chap17
 第 7 章化学反応に対する磁場効果における三重項機構 その 7.. 節の訂正 年 7 月 日. 節 章の9ページ の赤枠に記載した説明は間違いであった事に気付いた 以下に訂正する しかし.. 式は 結果的には正しいので安心して下さい 磁場 の存在下でのT 状態のハミルトニアン は ゼーマン項 と時間に依存するスピン-スピン相互作用の項 との和となる..=7.. g S = g S z = S z g
第 7 章化学反応に対する磁場効果における三重項機構 その 7.. 節の訂正 年 7 月 日. 節 章の9ページ の赤枠に記載した説明は間違いであった事に気付いた 以下に訂正する しかし.. 式は 結果的には正しいので安心して下さい 磁場 の存在下でのT 状態のハミルトニアン は ゼーマン項 と時間に依存するスピン-スピン相互作用の項 との和となる..=7.. g S = g S z = S z g
PowerPoint Presentation
 応用数学 Ⅱ (7) 7 連立微分方程式の立て方と解法. 高階微分方程式による解法. ベクトル微分方程式による解法 3. 演算子による解法 連立微分方程式 未知数が複数個あり, 未知数の数だけ微分方程式が与えられている場合, これらを連立微分方程式という. d d 解法 () 高階微分方程式化による解法 つの方程式から つの未知数を消去して, 未知数が つの方程式に変換 のみの方程式にするために,
応用数学 Ⅱ (7) 7 連立微分方程式の立て方と解法. 高階微分方程式による解法. ベクトル微分方程式による解法 3. 演算子による解法 連立微分方程式 未知数が複数個あり, 未知数の数だけ微分方程式が与えられている場合, これらを連立微分方程式という. d d 解法 () 高階微分方程式化による解法 つの方程式から つの未知数を消去して, 未知数が つの方程式に変換 のみの方程式にするために,
スライド 1
 大規模連立一次方程式に対する 高並列前処理技術について 今倉暁筑波大学計算科学研究センター 共同研究者櫻井鉄也 ( 筑波大学 ), 住吉光介 ( 沼津高専 ), 松古栄夫 (KEK) 1 /49 本日のトピック 大規模連立一次方程式 のための ( 前処理付き )Krylov 部分空間法の概略について紹介する. 高並列性を考慮した前処理として, 反復法を用いた重み付き定常反復型前処理を導入し, そのパラメータを最適化手法を提案
大規模連立一次方程式に対する 高並列前処理技術について 今倉暁筑波大学計算科学研究センター 共同研究者櫻井鉄也 ( 筑波大学 ), 住吉光介 ( 沼津高専 ), 松古栄夫 (KEK) 1 /49 本日のトピック 大規模連立一次方程式 のための ( 前処理付き )Krylov 部分空間法の概略について紹介する. 高並列性を考慮した前処理として, 反復法を用いた重み付き定常反復型前処理を導入し, そのパラメータを最適化手法を提案
平成 年 月 7 日 ( 土 第 75 回数学教育実践研究会アスティ 45 ビル F セミナールーム A 札幌医科大学 年 P ab, を正の定数とする 平面上において ( a, を中心とする円 Q 4 C と (, b を中心とする円 C が 原点 O で外接している また P を円 C 上の点と
 平成 年 月 7 日 ( 土 第 75 回数学教育実践研究会アスティ 45 ビル F セミナールーム 微分積分の拡張 変数関数問題へのアプローチ 予選決勝優勝法からラグランジュ未定乗数法 松本睦郎 ( 札幌北高等学校 変数関数の最大値 最小値に関する問題には多様なアプローチ法がある 文字を固定した 予選決勝優勝法, 計算のみで解法する 文字消去法, 微分積分を利用した ラグランジュ未定乗数法 がある
平成 年 月 7 日 ( 土 第 75 回数学教育実践研究会アスティ 45 ビル F セミナールーム 微分積分の拡張 変数関数問題へのアプローチ 予選決勝優勝法からラグランジュ未定乗数法 松本睦郎 ( 札幌北高等学校 変数関数の最大値 最小値に関する問題には多様なアプローチ法がある 文字を固定した 予選決勝優勝法, 計算のみで解法する 文字消去法, 微分積分を利用した ラグランジュ未定乗数法 がある
偏微分方程式、連立1次方程式、乱数
 数値計算法 011/6/8 林田清 大阪大学大学院理学研究科 常微分方程式の応用例 1 Rutherford 散乱 ( 原子核同士の散乱 ; 金の薄膜に α 粒子をあてる ) 1 クーロン力 f= 4 0 r r r Ze y からf cos, si f f f y f f 粒子の 方向 y方向の速度と座標について dv Ze dvy Ze y, 3 3 dt 40m r dt 40m r d dy
数値計算法 011/6/8 林田清 大阪大学大学院理学研究科 常微分方程式の応用例 1 Rutherford 散乱 ( 原子核同士の散乱 ; 金の薄膜に α 粒子をあてる ) 1 クーロン力 f= 4 0 r r r Ze y からf cos, si f f f y f f 粒子の 方向 y方向の速度と座標について dv Ze dvy Ze y, 3 3 dt 40m r dt 40m r d dy
Microsoft PowerPoint - H22制御工学I-2回.ppt
 制御工学 I 第二回ラプラス変換 平成 年 4 月 9 日 /4/9 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
制御工学 I 第二回ラプラス変換 平成 年 4 月 9 日 /4/9 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
Microsoft PowerPoint - 演習1:並列化と評価.pptx
 講義 2& 演習 1 プログラム並列化と性能評価 神戸大学大学院システム情報学研究科横川三津夫 yokokawa@port.kobe-u.ac.jp 2014/3/5 RIKEN AICS HPC Spring School 2014: プログラム並列化と性能評価 1 2014/3/5 RIKEN AICS HPC Spring School 2014: プログラム並列化と性能評価 2 2 次元温度分布の計算
講義 2& 演習 1 プログラム並列化と性能評価 神戸大学大学院システム情報学研究科横川三津夫 yokokawa@port.kobe-u.ac.jp 2014/3/5 RIKEN AICS HPC Spring School 2014: プログラム並列化と性能評価 1 2014/3/5 RIKEN AICS HPC Spring School 2014: プログラム並列化と性能評価 2 2 次元温度分布の計算
< 中 3 分野例題付き公式集 > (1)2 の倍数の判定法は 1 の位が 0 又は偶数 ( 例題 )1~5 までの 5 つの数字を使って 3 ケタの数をつくるとき 2 の倍数は何通りできるか (2)5 の倍数の判定法は 1 の位が 0 又は 5 ( 例題 )1~9 までの 9 個の数字を使って 3
 () の倍数の判定法は の位が 0 又は偶数 ~ までの つの数字を使って ケタの数をつくるとき の倍数は何通りできるか () の倍数の判定法は の位が 0 又は ~9 までの 9 個の数字を使って ケタの数をつくるとき の倍数は何通りできるか () の倍数の判定法は 下 ケタが 00 又は の倍数 ケタの数 8 が の倍数となるときの 最小の ケタの数は ( 解 ) 一の位の数は の 通り 十の位は一の位の数以外の
() の倍数の判定法は の位が 0 又は偶数 ~ までの つの数字を使って ケタの数をつくるとき の倍数は何通りできるか () の倍数の判定法は の位が 0 又は ~9 までの 9 個の数字を使って ケタの数をつくるとき の倍数は何通りできるか () の倍数の判定法は 下 ケタが 00 又は の倍数 ケタの数 8 が の倍数となるときの 最小の ケタの数は ( 解 ) 一の位の数は の 通り 十の位は一の位の数以外の
スライド 1
 数値解析 平成 30 年度前期第 10 週 [6 月 12 日 ] 静岡大学工学研究科機械工学専攻ロボット 計測情報分野創造科学技術大学院情報科学専攻 三浦憲二郎 講義アウトライン [6 月 12 日 ] 連立 1 次方程式の直接解法 ガウス消去法 ( 復習 ) 部分ピボット選択付きガウス消去法 連立 1 次方程式 連立 1 次方程式の重要性 非線形の問題は基本的には解けない. 非線形問題を線形化して解く.
数値解析 平成 30 年度前期第 10 週 [6 月 12 日 ] 静岡大学工学研究科機械工学専攻ロボット 計測情報分野創造科学技術大学院情報科学専攻 三浦憲二郎 講義アウトライン [6 月 12 日 ] 連立 1 次方程式の直接解法 ガウス消去法 ( 復習 ) 部分ピボット選択付きガウス消去法 連立 1 次方程式 連立 1 次方程式の重要性 非線形の問題は基本的には解けない. 非線形問題を線形化して解く.
<4D F736F F D208D5C91A297CD8A7793FC96E591E631308FCD2E646F63>
 第 1 章モールの定理による静定梁のたわみ 1-1 第 1 章モールの定理による静定梁のたわみ ポイント : モールの定理を用いて 静定梁のたわみを求める 断面力の釣合と梁の微分方程式は良く似ている 前章では 梁の微分方程式を直接積分する方法で 静定梁の断面力と変形状態を求めた 本章では 梁の微分方程式と断面力による力の釣合式が類似していることを利用して 微分方程式を直接解析的に解くのではなく 力の釣合より梁のたわみを求める方法を学ぶ
第 1 章モールの定理による静定梁のたわみ 1-1 第 1 章モールの定理による静定梁のたわみ ポイント : モールの定理を用いて 静定梁のたわみを求める 断面力の釣合と梁の微分方程式は良く似ている 前章では 梁の微分方程式を直接積分する方法で 静定梁の断面力と変形状態を求めた 本章では 梁の微分方程式と断面力による力の釣合式が類似していることを利用して 微分方程式を直接解析的に解くのではなく 力の釣合より梁のたわみを求める方法を学ぶ
<4D F736F F F696E74202D D F95C097F D834F E F93FC96E5284D F96E291E85F8DE391E52E >
 SX-ACE 並列プログラミング入門 (MPI) ( 演習補足資料 ) 大阪大学サイバーメディアセンター日本電気株式会社 演習問題の構成 ディレクトリ構成 MPI/ -- practice_1 演習問題 1 -- practice_2 演習問題 2 -- practice_3 演習問題 3 -- practice_4 演習問題 4 -- practice_5 演習問題 5 -- practice_6
SX-ACE 並列プログラミング入門 (MPI) ( 演習補足資料 ) 大阪大学サイバーメディアセンター日本電気株式会社 演習問題の構成 ディレクトリ構成 MPI/ -- practice_1 演習問題 1 -- practice_2 演習問題 2 -- practice_3 演習問題 3 -- practice_4 演習問題 4 -- practice_5 演習問題 5 -- practice_6
8. 自由曲線と曲面の概要 陽関数 陰関数 f x f x x y y y f f x y z g x y z パラメータ表現された 次元曲線 パラメータ表現は xyx 毎のパラメータによる陽関数表現 形状普遍性 座標独立性 曲線上の点を直接に計算可能 多価の曲線も表現可能 gx 低次の多項式は 計
 8. 自由曲線 曲面. 概論. ベジエ曲線 曲面. ベジエ曲線 曲面の数学. OeGLによる実行. URS. スプライン関数. スプライン曲線 曲面. URS 曲線 曲面 4. OeGLによる実行 8. 自由曲線と曲面の概要 陽関数 陰関数 f x f x x y y y f f x y z g x y z パラメータ表現された 次元曲線 パラメータ表現は xyx 毎のパラメータによる陽関数表現 形状普遍性
8. 自由曲線 曲面. 概論. ベジエ曲線 曲面. ベジエ曲線 曲面の数学. OeGLによる実行. URS. スプライン関数. スプライン曲線 曲面. URS 曲線 曲面 4. OeGLによる実行 8. 自由曲線と曲面の概要 陽関数 陰関数 f x f x x y y y f f x y z g x y z パラメータ表現された 次元曲線 パラメータ表現は xyx 毎のパラメータによる陽関数表現 形状普遍性
2014 年 10 月 2 日 本日の講義及び演習 数値シミュレーション 2014 年度第 2 回 偏微分方程式の偏微分項をコンピュータで扱えるようにする 離散化 ( 差分化 ) テイラー展開の利用 1 階微分項に対する差分式 2 階微分項に対する差分式 1 次元熱伝導方程式に適用して差分式を導出
 04 年 0 月 日 本日の講義及び演習 数値シミュレーション 04 年度第 回 偏微分方程式の偏微分項をコンピュータで扱えるようにする 離散化 ( 差分化 テイラー展開の利用 階微分項に対する差分式 階微分項に対する差分式 次元熱伝導方程式に適用して差分式を導出 Ecel を利用した温度変化シミュレーション 永野 ( 熱流体システム研究室 hagao@tc.ac.p 重要! 熱の伝わり方 ( 伝熱モード
04 年 0 月 日 本日の講義及び演習 数値シミュレーション 04 年度第 回 偏微分方程式の偏微分項をコンピュータで扱えるようにする 離散化 ( 差分化 テイラー展開の利用 階微分項に対する差分式 階微分項に対する差分式 次元熱伝導方程式に適用して差分式を導出 Ecel を利用した温度変化シミュレーション 永野 ( 熱流体システム研究室 hagao@tc.ac.p 重要! 熱の伝わり方 ( 伝熱モード
航空機の運動方程式
 オブザーバ 状態フィードバックにはすべての状態変数の値が必要であった. しかしながら, システムの外部から観測できるのは出力だけであり, すべての状態変数が観測できるとは限らない. そこで, 制御対象システムの状態変数を, システムのモデルに基づいてその入出力信号から推定する方法を考える.. オブザーバとは 次元 m 入力 r 出力線形時不変システム x Ax Bu y Cx () の状態変数ベクトル
オブザーバ 状態フィードバックにはすべての状態変数の値が必要であった. しかしながら, システムの外部から観測できるのは出力だけであり, すべての状態変数が観測できるとは限らない. そこで, 制御対象システムの状態変数を, システムのモデルに基づいてその入出力信号から推定する方法を考える.. オブザーバとは 次元 m 入力 r 出力線形時不変システム x Ax Bu y Cx () の状態変数ベクトル
<4D F736F F D208D5C91A297CD8A7793FC96E591E631318FCD2E646F63>
 11-1 第 11 章不静定梁のたわみ ポイント : 基本的な不静定梁のたわみ 梁部材の断面力とたわみ 本章では 不静定構造物として 最も単純でしかも最も大切な両端固定梁の応力解析を行う ここでは 梁の微分方程式を用いて解くわけであるが 前章とは異なり 不静定構造物であるため力の釣合から先に断面力を決定することができない そのため 梁のたわみ曲線と同時に断面力を求めることになる この両端固定梁のたわみ曲線や断面力分布は
11-1 第 11 章不静定梁のたわみ ポイント : 基本的な不静定梁のたわみ 梁部材の断面力とたわみ 本章では 不静定構造物として 最も単純でしかも最も大切な両端固定梁の応力解析を行う ここでは 梁の微分方程式を用いて解くわけであるが 前章とは異なり 不静定構造物であるため力の釣合から先に断面力を決定することができない そのため 梁のたわみ曲線と同時に断面力を求めることになる この両端固定梁のたわみ曲線や断面力分布は
PowerPoint プレゼンテーション
 空間フィルタリング (spatal lterng) 入力画像の対応する画素値だけではなく その周囲 ( 近傍領域 ) の画素も含めた領域内の画素値を用いて 出力画像の対応する画素値を計算する処理 入力画像出力画像入力画像出力画像 画素ごとの濃淡変換 ( 階調処理 ) 領域に基づく濃淡変換 ( 空間フィルタリング ) 空間フィルタ (spatal lter) 線形フィルタ (lnear lter) w
空間フィルタリング (spatal lterng) 入力画像の対応する画素値だけではなく その周囲 ( 近傍領域 ) の画素も含めた領域内の画素値を用いて 出力画像の対応する画素値を計算する処理 入力画像出力画像入力画像出力画像 画素ごとの濃淡変換 ( 階調処理 ) 領域に基づく濃淡変換 ( 空間フィルタリング ) 空間フィルタ (spatal lter) 線形フィルタ (lnear lter) w
ベクトル公式.rtf
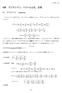 6 章ラプラシアン, ベクトル公式, 定理 6.1 ラプラシアン Laplacian φ はベクトル量である. そこでさらに発散をとると, φ はどういう形になるであろうか? φ = a + a + a φ a + a φ + a φ = φ + φ + φ = 2 φ + 2 φ 2 + 2 φ 2 2 φ = 2 φ 2 + 2 φ 2 + 2 φ 2 = 2 φ したがって,2 階の偏微分演算となる.
6 章ラプラシアン, ベクトル公式, 定理 6.1 ラプラシアン Laplacian φ はベクトル量である. そこでさらに発散をとると, φ はどういう形になるであろうか? φ = a + a + a φ a + a φ + a φ = φ + φ + φ = 2 φ + 2 φ 2 + 2 φ 2 2 φ = 2 φ 2 + 2 φ 2 + 2 φ 2 = 2 φ したがって,2 階の偏微分演算となる.
< BD96CA E B816989A B A>
 数 Ⅱ 平面ベクトル ( 黄色チャート ) () () ~ () " 図 # () () () - - () - () - - () % から %- から - -,- 略 () 求めるベクトルを とする S であるから,k となる実数 k がある このとき k k, であるから k すなわち k$, 求めるベクトルは --,- - -7- - -, から また ',' 7 (),,-,, -, -,
数 Ⅱ 平面ベクトル ( 黄色チャート ) () () ~ () " 図 # () () () - - () - () - - () % から %- から - -,- 略 () 求めるベクトルを とする S であるから,k となる実数 k がある このとき k k, であるから k すなわち k$, 求めるベクトルは --,- - -7- - -, から また ',' 7 (),,-,, -, -,
学習指導要領
 (1) いろいろな式 学習指導要領紅葉川高校学力スタンダードア式と証明展開の公式を用いて 3 乗に関わる式を展開すること ( ア ) 整式の乗法 除法 分数式の計算ができるようにする 三次の乗法公式及び因数分解の公式を理解し そ 3 次の因数分解の公式を理解し それらを用いて因数れらを用いて式の展開や因数分解をすること また 分解することができるようにする 整式の除法や分数式の四則計算について理解し
(1) いろいろな式 学習指導要領紅葉川高校学力スタンダードア式と証明展開の公式を用いて 3 乗に関わる式を展開すること ( ア ) 整式の乗法 除法 分数式の計算ができるようにする 三次の乗法公式及び因数分解の公式を理解し そ 3 次の因数分解の公式を理解し それらを用いて因数れらを用いて式の展開や因数分解をすること また 分解することができるようにする 整式の除法や分数式の四則計算について理解し
kiso2-09.key
 座席指定はありません 計算機基礎実習II 2018 のウェブページか 第9回 ら 以下の課題に自力で取り組んで下さい 計算機基礎実習II 第7回の復習課題(rev07) 第9回の基本課題(base09) 第8回試験の結果 中間試験に関するコメント コンパイルできない不完全なプログラムなど プログラミングに慣れていない あるいは複雑な問題は 要件 をバラして段階的にプログラムを作成する exam08-2.c
座席指定はありません 計算機基礎実習II 2018 のウェブページか 第9回 ら 以下の課題に自力で取り組んで下さい 計算機基礎実習II 第7回の復習課題(rev07) 第9回の基本課題(base09) 第8回試験の結果 中間試験に関するコメント コンパイルできない不完全なプログラムなど プログラミングに慣れていない あるいは複雑な問題は 要件 をバラして段階的にプログラムを作成する exam08-2.c
1999年度 センター試験・数学ⅡB
 99 センター試験数学 Ⅱ 数学 B 問題 第 問 ( 必答問題 ) [] 関数 y cos3x の周期のうち正で最小のものはアイウ 解答解説のページへ 0 x 360 のとき, 関数 y cos3x において, y となる x はエ個, y となる x はオ 個ある また, y sin x と y cos3x のグラフより, 方程式 sin x cos3x は 0 x 360のときカ個の解をもつことがわかる
99 センター試験数学 Ⅱ 数学 B 問題 第 問 ( 必答問題 ) [] 関数 y cos3x の周期のうち正で最小のものはアイウ 解答解説のページへ 0 x 360 のとき, 関数 y cos3x において, y となる x はエ個, y となる x はオ 個ある また, y sin x と y cos3x のグラフより, 方程式 sin x cos3x は 0 x 360のときカ個の解をもつことがわかる
技術者のための構造力学 2014/06/11 1. はじめに 資料 2 節点座標系による傾斜支持節点節点の処理 三好崇夫加藤久人 従来, マトリックス変位法に基づく骨組解析を紹介する教科書においては, 全体座標系に対して傾斜 した斜面上の支持条件を考慮する処理方法として, 一旦, 傾斜支持を無視した
 . はじめに 資料 節点座標系による傾斜支持節点節点の処理 三好崇夫加藤久人 従来, マトリックス変位法に基づく骨組解析を紹介する教科書においては, 全体座標系に対して傾斜 した斜面上の支持条件を考慮する処理方法として, 一旦, 傾斜支持を無視した全体座標系に関する構造 全体の剛性マトリックスを組み立てた後に, 傾斜支持する節点に関して対応する剛性成分を座標変換に よって傾斜方向に回転処理し, その後は通常の全体座標系に対して傾斜していない支持点に対するのと
. はじめに 資料 節点座標系による傾斜支持節点節点の処理 三好崇夫加藤久人 従来, マトリックス変位法に基づく骨組解析を紹介する教科書においては, 全体座標系に対して傾斜 した斜面上の支持条件を考慮する処理方法として, 一旦, 傾斜支持を無視した全体座標系に関する構造 全体の剛性マトリックスを組み立てた後に, 傾斜支持する節点に関して対応する剛性成分を座標変換に よって傾斜方向に回転処理し, その後は通常の全体座標系に対して傾斜していない支持点に対するのと
JSMECM教育認定
 一般社団法人日本機械学会 018/09/6 計算力学技術者 級問題集 ( 固体力学分野 )018 年度版 ( 第 9 版 3 刷 ) P 項目誤正 175 問 -6/ 上 8 行 1 1 sin cos sin cos rs y y xy rs y x xy i 計算力学技術者 級 ( 固体力学分野の有限要素法解析技術者 ) の認定の範囲 認定技術者の技術レベル本認定を取得した技術者は, 基本的な固体力学の問題に対して,
一般社団法人日本機械学会 018/09/6 計算力学技術者 級問題集 ( 固体力学分野 )018 年度版 ( 第 9 版 3 刷 ) P 項目誤正 175 問 -6/ 上 8 行 1 1 sin cos sin cos rs y y xy rs y x xy i 計算力学技術者 級 ( 固体力学分野の有限要素法解析技術者 ) の認定の範囲 認定技術者の技術レベル本認定を取得した技術者は, 基本的な固体力学の問題に対して,
<4D F736F F D E4F8E9F82C982A882AF82E98D7397F1>
 3 三次における行列 要旨高校では ほとんど 2 2 の正方行列しか扱ってなく 三次の正方行列について考えてみたかったため 数 C で学んだ定理を三次の正方行列に応用して 自分たちで仮説を立てて求めていったら 空間における回転移動を表す行列 三次のケーリー ハミルトンの定理 三次における逆行列を求めたり 仮説をたてることができた. 目的 数 C で学んだ定理を三次の正方行列に応用する 2. 概要目的の到達点として
3 三次における行列 要旨高校では ほとんど 2 2 の正方行列しか扱ってなく 三次の正方行列について考えてみたかったため 数 C で学んだ定理を三次の正方行列に応用して 自分たちで仮説を立てて求めていったら 空間における回転移動を表す行列 三次のケーリー ハミルトンの定理 三次における逆行列を求めたり 仮説をたてることができた. 目的 数 C で学んだ定理を三次の正方行列に応用する 2. 概要目的の到達点として
Microsoft Word - スーパーナビ 第6回 数学.docx
 1 ⑴ 与式 =- 5 35 +14 35 =9 35 1 ⑵ 与式 =9-(-5)=9+5=14 1 ⑶ 与式 = 4(a-b)-3(5a-3b) = 8a-4b-15a+9b = -7a+5b 1 1 1 1 ⑷ 与式 =(²+ 1+1²)-{²+(-3+)+(-3) } 1 ⑷ 与式 =(²++1)-(²--6)=²++1-²++6=3+7 1 ⑸ 与式 = - ² + 16 = - +16
1 ⑴ 与式 =- 5 35 +14 35 =9 35 1 ⑵ 与式 =9-(-5)=9+5=14 1 ⑶ 与式 = 4(a-b)-3(5a-3b) = 8a-4b-15a+9b = -7a+5b 1 1 1 1 ⑷ 与式 =(²+ 1+1²)-{²+(-3+)+(-3) } 1 ⑷ 与式 =(²++1)-(²--6)=²++1-²++6=3+7 1 ⑸ 与式 = - ² + 16 = - +16
Microsoft Word - DF-Salford解説09.doc
 Digital Fortran 解説 2009/April 1. プログラム形態とデ - タ構成 最小自乗法プログラム (testlsm.for) m 組の実験データ (x i,y i ) に最も近似する直線式 (y=ax+b) を最小自乗法で決定する 入力データは組数 mと m 組の (x i,y i ) 値 出力データは直線式の係数 a,bとなる 入力データ m=4 (x i,y i ) X=1.50
Digital Fortran 解説 2009/April 1. プログラム形態とデ - タ構成 最小自乗法プログラム (testlsm.for) m 組の実験データ (x i,y i ) に最も近似する直線式 (y=ax+b) を最小自乗法で決定する 入力データは組数 mと m 組の (x i,y i ) 値 出力データは直線式の係数 a,bとなる 入力データ m=4 (x i,y i ) X=1.50
Microsoft PowerPoint - 4.pptx
 while 文 (1) 繰り返しの必要性 while の形式と動作 繰り返しにより平 根を求める ( 演習 ) 繰り返しにより 程式の解を求める ( 課題 ) Hello. をたくさん表示しよう Hello. を画面に 3 回表示するには, 以下で OK. #include int main() { printf("hello. n"); printf("hello. n");
while 文 (1) 繰り返しの必要性 while の形式と動作 繰り返しにより平 根を求める ( 演習 ) 繰り返しにより 程式の解を求める ( 課題 ) Hello. をたくさん表示しよう Hello. を画面に 3 回表示するには, 以下で OK. #include int main() { printf("hello. n"); printf("hello. n");
簡単な検索と整列(ソート)
 フローチャート (2) アルゴリズム論第 2 回講義 2011 年 10 月 7 日 ( 金 ) 反復構造 ( 一定回数のループ処理 ) START 100 回同じ処理を繰り返す お風呂で子供が指をおって数を数える感じ 繰り返し数を記憶する変数をカウンター ( 変数名 I をよく使う ) と呼ぶ カウンターを初期化して, 100 回繰り返したかどうか判定してそうならば終了そうでなければ処理を実行して
フローチャート (2) アルゴリズム論第 2 回講義 2011 年 10 月 7 日 ( 金 ) 反復構造 ( 一定回数のループ処理 ) START 100 回同じ処理を繰り返す お風呂で子供が指をおって数を数える感じ 繰り返し数を記憶する変数をカウンター ( 変数名 I をよく使う ) と呼ぶ カウンターを初期化して, 100 回繰り返したかどうか判定してそうならば終了そうでなければ処理を実行して
応用数学Ⅱ 偏微分方程式(2) 波動方程式(12/13)
 偏微分方程式. 偏微分方程式の形 偏微分 偏導関数 つの独立変数 をもつ関数 があるとき 変数 が一定値をとって だけが変化したとす ると は だけの関数となる このとき を について微分して得られる関数を 関数 の に関する 偏微分係数 略して偏微分 あるいは偏導関数 pil deiie といい 次のように表される についても同様な偏微分を定義できる あるいは あるいは - あるいは あるいは -
偏微分方程式. 偏微分方程式の形 偏微分 偏導関数 つの独立変数 をもつ関数 があるとき 変数 が一定値をとって だけが変化したとす ると は だけの関数となる このとき を について微分して得られる関数を 関数 の に関する 偏微分係数 略して偏微分 あるいは偏導関数 pil deiie といい 次のように表される についても同様な偏微分を定義できる あるいは あるいは - あるいは あるいは -
