Onsager SOLUTION OF THE EIGENWERT PROBLEM (O-29) V = e H A e H B λ max Z 2 Onsager (O-77) (O-82) (O-83) Kramers-Wannier 1 1 Ons
|
|
|
- うまじ たもん
- 4 years ago
- Views:
Transcription
1 Onsager SOLUTION OF THE EIGENWERT PROBLEM O-29 V = e H A e H B λ max Z 2 OnsagerO-77O-82 O-83 2 Kramers-Wannier Onsager * * * * * V self-adjoint V = V /2 V V /2 = V /2 V 2 V /2 = 2 sinh 2H n/2 e 2 H A e H B e 2 H A O-84 V V VV X 0, X,, X n X 0, X,, X n Z 2 r = R ro-68[] expi αz r = cosαz r + i sinαz r = 2! αz r 2 + 4! αz r 4 6! αz r 6 + [ + i αz r 3! αz r 3 + ] 5! αz r 5 + = R r + R r 2! α2 + 4! α4 6! α6 + + i Z r α 3! α3 + 5! α5 + = R r + R r cos α + i Z r sin α O-83 O-83b O-83
2 Z r X r Y r cosαz r = R r + R r cos α 2 sinαz r = Z r sin α 3 Z r X r Y r expαx r = R r + R r cosh α + X r sinh α 4 expαy r = R r + R r cosh α + Y r sinh α 5 expαz r = R r + R r cosh α + Z r sinh α 6 [ X r cosαz r = X r R r + R r 2! α2 + 4! α4 ] 6! α6 + = X r X r + X r 2! α2 + 4! α4 6! α6 + = X r cos α 7 X r sinαz r = X r Z r α 3! α3 + 5! α5 = X r Z r sin α = i Y r sin α 8 Y r cosαz r = Y r cos α 9 Y r sinαz r = Y r Z r sin α = i X sin α 0 X r Y r Z r Onsager X r X r exp n r= iπn r Z r = 2n = n r= n r= [ πn r R r + R r cos + i Z r sin 2n [ R r sin πr 2n + i Z r cos πr ] 2n ] πn r 2n Onsager X r X r ω = rπ/n X r O-68 e iωzr/2 X r e iωzr/2 = { R r sin ω i Z r cos ω 2 2 }X r{ R r sin ω + i Z r cos ω 2 2 } = X r cos ω + Y r sin ω 2 e iωzr/2 Y r e iωzr/2 = { R r sin ω i Z r cos ω 2 2 }Y r{ R r sin ω + i Z r cos ω 2 2 } = X r sin ω Y r cos ω 3 e iωzr/2 Z r e iωzr/2 = { R r sin ω i Z r cos ω 2 2 }Z r{ R r sin ω + i Z r cos ω 2 2 } = Z r 4 2
3 O-86 X r X r X r Onsager P.34 R r + X r Z r X r Y r { R r + X r } X r cos 2ω + Y r sin 2ω{ R r + X r } = X r cos 2ω + Y r sin 2ω 5 { R r + X r }X r sin 2ω Y r cos 2ω{ R r + X r } = X r sin 2ω + Y r cos 2ω 6 { R r + X r }Z r { R r + X r } = Z r 7 Z r Z r V e i αzr X r cos β + Y r sin βe i αzr = X r cos2α + β + Y r sin2α + β O-85 [cosαz r + i sinαz r ]X r cos β + Y r sin β[cosαz r i sinαz r ] = [ R r + R r cos α + i Z r sin α] X r cos β[ R r + R r cos α i Z r sin α] + [ R r + R r cos α + i Z r sin α]y r sin β[ R r + R r cos α i Z r sin α] 8 R r R r 0 = [X r cos 2 α cos β + Z r X r Z r sin 2 α cos β + i Z r X r sin α cos β cos α i X r Z r cos α cos β sin α] + [Y r cos 2 α sin β + Z r Y r Z r sin 2 α sin β + i Z r Y r sin α sin β cos α i Y r Z r cos α sin β sin α] = [X r cos 2 α cos β X r sin 2 α cos β+, Y r sin α cos β cos α + Y r cos α cos β sin α] + [Y r cos 2 α sin β Y r sin 2 α sin β i X r sin α sin β cos α X r cos α sin β sin α] = X r cos 2 α sin 2 α cos β + 2Y r sin α cos β cos α + Y r cos 2 α sin 2 α sin β + 2X r sin α sin β cos α = X r cos 2α cos β sin 2α sin β + Y r sin 2α cos β + cos 2α sin β = X r cos2α cos β + Y r sin2α + β 9 O-85 2α + β = 0 2α + β = π/2 β = 0 β = π/2 X r Y r X r Y r Z r X r = X r cos rπ n + Y r sin rπ n Y r = X r sin rπ n + Y r cos rπ n O-86- O-86-2 Z r = Z r O-86-3 X 0 = X 0, X n = X n, Y 0 = Y n = 0 20 O-85-2 sinrπ/n O-85- cosrπ/n X r = X r cos rπ n + Y r sin rπ n Y r = X r sin rπ n + Y r cos rπ n 2 22 O-73- [2] n A = X0 2 Xr Xn 23 r= 3
4 O-79-[2] 2 22 n B = X 0 2 X r X n 24 r= n = X0 + 2 r= X r cos rπ n Y r sin rπ n + X n O-84 X r X sx 0 = X 0 X n = X n V = 2 sinh 2H n/2 e 2 H X 0 e H P X r e 2 H X n e H X 0 e 2H P X r e H X n e 2 H X 0 e H P X r e 2 H X n = 2 sinh 2H n/2 e 2 H X0 e 2 H X0 e H X 0 e P H Xr e 2H P X r e P H Xr e H X n e 2 H Xn e 2 H Xn [ n ] = 2 sinh 2H n/2 e H X 0 +H X 0 = 2 sinh 2H n/2 e H H X 0 = 2 sinh 2H n/2 e H H X 0 [ n r= [ n r= r= e H X r n r= n e 2H X r e H X r e 2H X r e H X r r= ] e H X r e H +H X n e H X n H X n U r ] e H +H X n O-87 U r = e H X r e 2H X r e H X r 26 U r U r X r X r U r 4 rπ/n = ω r e H X r = Rr + R r cosh H X r sinh H = R r + R r cosh H X r sinh H 27 e 2H X r = R r + R r cosh 2H X r sinh 2H U r = [ R r + R r cosh H X r sinh H ] = R r + R r [cosh 2H + X r cos ω r sinh 2H Y r sin ω r sinh 2H ] 28 { R r + R r [cosh 2H + X r cos ω r sinh 2H Y r sin ω r sinh 2H ]} [ R r + R r cosh H X r sinh H ] = [ R r + R r cosh H X r sinh H ] 2 R r + [ R r + R r cosh H X r sinh H ] 2 R r cosh 2H + [ R r + R r cosh H Xr sinh H ] 2 R r Xr cos ω sinh 2H [ R r + R r cosh H X r sinh H ]Y r sin ω r sinh 2H [ R r + R r cosh H X r sinh H ] 29 R r 0 4
5 23 = [ R r R r R r cosh H X r sinh H + cosh H X r sinh H 2 R 2 r] R r = [ R r + cosh 2 H 2X r cosh H sinh H + X 2 r sinh2 H R r ] R r = [ R r + R r cosh 2H X r sinh 2H ] R r = R r = [ R r + R r cosh 2H X r sinh 2H ]R r cosh 2H = cosh 2H R r cosh 2H X r sinh 2H = [ R r + R r cosh 2H X r sinh 2H ]R r X r cos ω r sinh 2H = R r cosh 2H X r sinh 2H R r X r cos ω r sinh 2H = X r cos ω r sinh 2H cosh 2H R r cos ω r sinh 2H sinh 2H = [ R r + R r cosh H X r sinh H ]Y r sin ω r sinh 2H cosh H X r sinh H = Y r cosh H + X r sinh H sin ω r sinh 2H cosh H X r sinh H = Y r cosh H + X r sinh H cosh H X r sinh H sin ω r sinh 2H = Y r cosh2 H R r sinh 2 H sin ω r sinh 2H = Y r cosh 2 H Y r sinh 2 H sin ω r sinh 2H = Y r sin ω r sinh 2H U r = R r + cosh 2H R r cosh 2H X r sinh 2H + X r cos ω r sinh 2H cosh 2H R r cos ω r sinh 2H sinh 2H Y r sin ω r sinh 2H = R r + R r cosh 2H cosh 2H sinh 2H sinh 2H cos ω r X r sinh 2H cosh 2H cosh 2H sinh 2H cos ω r Y r sin ω r sinh 2H O-87a U r 26 U r U r U r U r = e H X r e 2H X r e H X r 34 T U r = T U r T 35 T = R r + i Z r 36 5
6 T = R r i Z r 37 T T = [ R r + i Z r ][ R r i Z r ] = R r + Zr 2 = R r + R r = Z r Z r = Z r X r X r Z r e H X r e 2H X r e H X r = e H X r e 2H X r e H X r Zr 39 2 R r e H X r e 2H X r e H X r = 0 40 Z r R r + Z r = R r 4 [ R r + i Z r ]e H X r e 2H X r e H X r [ Rr i Z r ] = e H X r e 2H X r e H X r 42 T O-87a O-87aR r X r Y r D E F [ R r i Z r ][ R r DR r EX r F Y r ] = R r + iz r DR r + iez r X r + if Z r Y r = R r + idz r iex r Z r if Y r Z r 43 [ R r + i Z r ] U r [ R r + idz r iex r Z r if Y r Z r ][ R r + i Z r ] = R r DZ 2 r + EX r Z2 r + F Y r Z2 r = R r DR r + EX r + F Y r 44 X r Y r U r O-87a O-89a U r + U r = 2 R r 2sinh 2H cosh 2H cosh 2H sinh 2H cos ω r = 2 R r 2R r cosh γ r 45 cosh γ r 2H 2H ω r [3, 4] OD D ω δ δ γ 2H 2H cosh γ = cosh 2H cosh 2H sinh 2H sinh 2H cos ω O-89a cosh 2H = cosh γ cosh 2H sinh γ sinh 2H cos δ 46 cosh 2H = cosh γ cosh 2H sinh γ sinh 2H cos δ 47 2 Z rx r = X rz r Z rxr = X r Zr Z re H Xr X = Z r n! H Xr n = X n! H Xr n n Z r = X n! H Xr n Z r 6
7 O : O-89a 46 sin ω sinh γ = sin δ sin δ = sinh 2H sinh 2H O-89c sinh γ cos δ = sinh 2H cosh 2H cosh 2H sinh 2H cos ω O-89b O-89c O-89b cot δ = sinh 2H coth 2H cosh 2H cos ω sin ω O-89d 45U + U R r R r = X 2 r 0R r U + U R r χ = χ χ 45 U + U χ = e γr + e γr χ 48 U U U U U e γr e γr R r 0 U + U χ = 2χ 49 U U r R r = X 2 r = X 2 r X r X r U r e γrxr e γrx r X r X r O U r O-87a O-89a O-89b O-89c U r = R r + R r cosh γ r X r sinh γ r cos δ r Y r sinh γ r sin δ r 50 = R r + R r cosh γ r X r cos δ r + Y r sin δ r sinh γ r X r cos δ r + Y r sin δ r O-86 X r+δ X r cos δ + Y r sin δ r = X r cos ω r + Y r sin ω r cos δ r + X r sin ω r + Y r cos ω r sin δ r = X r cosω r + δ r + Y r sinω r + δ r X r+δ 5 7
8 X r+δ X 2 r+δ X r R r 50 Xr+δ = X r cos δ r + Y r sin δ r 2 = Xr 2 R r cosh γ r cos2 δr + Y r 2 sin 2 δr = R r cos 2 δ r + R r sin 2 δ r = R r 52 U r = R r + R r cosh γ r X r+δ sinh γ r 53 R r cosh γ r = X 2 r+δ r + 2! γ2 r + 4! γ2 r + = Xr+δ 2 + 2! γ2 r X 2 r+δ + 4! γ2 r X 4 r+δ r + = X 2 r+δ + X r+δ sinh γ r [ 2! γ2 r X 2 r+δ + 4! γ2 r X 4 r+δ = R r + coshγ r X r+δ 54 ] X r+δ sinh γ r = X r+δγ r + 3! γ3 r + 5! γ5 r + = γ r X r+δ + 3! γ3 r X r+δ + 5! γ5 r X r+δ + = γ r X r+δ + 3! γ3 r X 3 r+δ + 5! γ5 r X 5 r+δ + = sinhγ r X r+δ 55 U r = exp[ γ r X r+δ ] = exp[ γ r X r cos δ r + Y r sin δ r] O-88 U r X r O-88 Y r X r X r O-85 O-85 e i αzr γx r cos β + Y r sin βe i αzr = γ[x r cos2α + β + Y r sin2α + β] 56 γ n X r cos β + Y r sin β n i αzr e = {e i αzr γx r cos β + Y r sin βe i αzr } n = γ n [X r cos2α + β + Y r sin2α + β] n 57 e i αzr exp[ γx r cos β + Y r sin β]e i αzr = exp{ γ[x r cos2α + β + Y r sin2α + β]} 58 X r cos2α + β + Y r sin2α + β 2 22 X r cos2α + β + Y r sin2α + β = X r cos ω r + Y r sin ω r cos2α + β + X r sin ω r + Y r cos ω r sin2α + β = X r cosω r + 2α + β + Y r sinω r + 2α + β = X r cosπ ω r 2α β + Y r sinπ ω r 2α β 59 8
9 58 e i αzr i αzr exp[ γx r cos β +Y r sin β]e = exp{ γ[xr cosπ ω r 2α β+yr sinπ ω r 2α β]} 60 O-88 U r π ω r 2α β = δ r 6 e i αzr i αzr exp[ γx r cos β + Y r sin β]e = exp[ γxr cos δr + Yr sin δr] 62 β = 0 γx r β = π ω r γx r β = 0 α = 2 π ω r δ r e 2 π ωr δ r izr e γrxr e 2 π ωr δ r izr β = π ω r α = 2 δ r = exp[ γxr cos δ r + Y r sin δ r ] 63 e 2 δ r izr e γrx r e 2 δ r izr = exp[ γxr cos δ r + Y r sin δ r ] Y r U r U r exp[ 2 π ω r δ r iz r]u r exp[ 2 π ω r δ r iz r] = exp γ r X r exp 2 δ riz r U r exp 2 δ riz r = exp γ r X r O-90b O-90a rv O-87O-90a O-90br = n n n exp 2 π ω r δr iz r V exp 2 π ω r δr iz r r= X r = 2 sinh 2H n/2 e H H X 0 = 2 sinh 2H n/2 e H H X 0 [ n r= [ n r= r= e 2 π ωr δ r izr U r e 2 π ωr δ r izr ] e H +H X n e γrxr ] e H +H X n n = 2 sinh 2H n/2 exp H H X 0 γ r X r H + H X n r= O-9b exp n r= 2 δ riz r n V exp r= = 2 sinh 2H n/2 e H H X 0 = 2 sinh 2H n/2 e H H X 0 2 δ riz r [ n r= [ n r= e 2 δ r izr U r e 2 δ r izr ] e H +H X n e γrx r ] e H +H X n n = 2 sinh 2H n/2 exp H H X0 γ r Xr H + H X n r= O-9a 9
10 V X r X r V O-9a O-9b X r X r ξ r X r χ λ V O-9b V S 3 S V S, χ = λχ 65 ln λ = n 2 n ln2 sinh 2H + H H ξ 0 γ r ξ r H + H ξ n 66 S = exp r= n 2 π ω r δr iz r r= [2] V λ max X r χ 0 r ξ r = 0r ξ r = n ω = nπ/n = π O-89a 67 cosh γ r = cosh 2H cosh 2H sinh H sinh H cos rπ n 68 cosh γ n = cosh 2H cosh 2H sinh H sinh H cos ω n = cosh 2H cosh 2H + sinh 2H sinh 2H = cosh 2H + H 69 γ n+r = γ n r 70 γ n = 2H + H 7 λ max n ln2 sinh 2H = 2 γ + γ γ 2m n = 2m γ + γ γ 2m + H + H = γ + γ γ 2m + 2 γ n n = 2m + O-93 3 V λ ψ V, ψ = λψ A O-9a O-9b X r X r V S X r X r χ S V S, χ = λχ B O-9b AS B S = e 2 π ωr δ r izr S, V, ψ = S, λψ S V SS, ψ = λs, ψ S V S, S, ψ = λs, ψ χ = S, ψ ψ = S, χ = e 2 π ωr δ r izr, χ ψ = S, χ 0
11 64 n n γ + γ γ 2n = 2γ + γ γ n 2 + γ n = 2γ + γ γ n 2 + 2H + H 72 γ + γ γ 2n = 2γ + γ γ n 73 n λ max 2 n ln2 sinh 2H = 2 n r= γ 2r γ 2r 62 λ max 2 n ln2 sinh 2H = 2 <2r<n cosh cosh 2H cosh 2H sinh H sinh H cos O-93-2r π O-93-2 n λ max B χ 0 ψ max = exp 2 π ω 2r δ2r iz 2r, χ 0 O-96a 4 <2r<n λ max A χ 0 n ψ max = exp, χ 0 r= 2 δ 2r iz 2r O-96b * * * * * 2 O-89acosh 2H / sinh 2H cosh 2H sinh 2H cos ω = cosh 2H cosh 2H cosh 2H cosh 2H cosh γ sinh 2H sinh 2H 2 cosh cosh 2H 46 cosh 2H sinh 2H cos ω = cosh 2H cosh 2H cosh 2H sinh 2H cosh 2H + sinh γ sinh 2H cos δ sinh 2H cosh 2H = sinh 2H cosh2 2H sinh γ cos δ cosh 2H = sinh 2H sinh 2 2H sinh γ cos δ A- = cosh 2H sinh 2H sinh γ cos δ 74 4 S
12 sinh γ cos δ = sinh 2H cosh 2H cosh 2H sinh 2H cos ω O-89b O-89c O-89b sinh 2H sin δ = sinh γ sin ω sinh γ sinh 2H cot δ = sinh 2H cosh 2H cosh 2H sinh 2H cos ω sinh γ sin ω cot δ = sinh 2H coth 2H cosh 2H cos ω sin ω O-89d [] 7 207//5 paper7.pdf [2] 8 207/2/2 paper4.pdf [3] 2 207/2/0 geo 2.pdf [4] 207/0/6 geo S.pdf 2
II No.01 [n/2] [1]H n (x) H n (x) = ( 1) r n! r!(n 2r)! (2x)n 2r. r=0 [2]H n (x) n,, H n ( x) = ( 1) n H n (x). [3] H n (x) = ( 1) n dn x2 e dx n e x2
![II No.01 [n/2] [1]H n (x) H n (x) = ( 1) r n! r!(n 2r)! (2x)n 2r. r=0 [2]H n (x) n,, H n ( x) = ( 1) n H n (x). [3] H n (x) = ( 1) n dn x2 e dx n e x2 II No.01 [n/2] [1]H n (x) H n (x) = ( 1) r n! r!(n 2r)! (2x)n 2r. r=0 [2]H n (x) n,, H n ( x) = ( 1) n H n (x). [3] H n (x) = ( 1) n dn x2 e dx n e x2](/thumbs/101/149159646.jpg) II No.1 [n/] [1]H n x) H n x) = 1) r n! r!n r)! x)n r r= []H n x) n,, H n x) = 1) n H n x) [3] H n x) = 1) n dn x e dx n e x [4] H n+1 x) = xh n x) nh n 1 x) ) d dx x H n x) = H n+1 x) d dx H nx) = nh
II No.1 [n/] [1]H n x) H n x) = 1) r n! r!n r)! x)n r r= []H n x) n,, H n x) = 1) n H n x) [3] H n x) = 1) n dn x e dx n e x [4] H n+1 x) = xh n x) nh n 1 x) ) d dx x H n x) = H n+1 x) d dx H nx) = nh
#A A A F, F d F P + F P = d P F, F y P F F x A.1 ( α, 0), (α, 0) α > 0) (x, y) (x + α) 2 + y 2, (x α) 2 + y 2 d (x + α)2 + y 2 + (x α) 2 + y 2 =
 #A A A. F, F d F P + F P = d P F, F P F F A. α, 0, α, 0 α > 0, + α +, α + d + α + + α + = d d F, F 0 < α < d + α + = d α + + α + = d d α + + α + d α + = d 4 4d α + = d 4 8d + 6 http://mth.cs.kitmi-it.c.jp/
#A A A. F, F d F P + F P = d P F, F P F F A. α, 0, α, 0 α > 0, + α +, α + d + α + + α + = d d F, F 0 < α < d + α + = d α + + α + = d d α + + α + d α + = d 4 4d α + = d 4 8d + 6 http://mth.cs.kitmi-it.c.jp/
量子力学 問題
 3 : 203 : 0. H = 0 0 2 6 0 () = 6, 2 = 2, 3 = 3 3 H 6 2 3 ϵ,2,3 (2) ψ = (, 2, 3 ) ψ Hψ H (3) P i = i i P P 2 = P 2 P 3 = P 3 P = O, P 2 i = P i (4) P + P 2 + P 3 = E 3 (5) i ϵ ip i H 0 0 (6) R = 0 0 [H,
3 : 203 : 0. H = 0 0 2 6 0 () = 6, 2 = 2, 3 = 3 3 H 6 2 3 ϵ,2,3 (2) ψ = (, 2, 3 ) ψ Hψ H (3) P i = i i P P 2 = P 2 P 3 = P 3 P = O, P 2 i = P i (4) P + P 2 + P 3 = E 3 (5) i ϵ ip i H 0 0 (6) R = 0 0 [H,
( ; ) C. H. Scholz, The Mechanics of Earthquakes and Faulting : - ( ) σ = σ t sin 2π(r a) λ dσ d(r a) =
 1 9 8 1 1 1 ; 1 11 16 C. H. Scholz, The Mechanics of Earthquakes and Faulting 1. 1.1 1.1.1 : - σ = σ t sin πr a λ dσ dr a = E a = π λ σ πr a t cos λ 1 r a/λ 1 cos 1 E: σ t = Eλ πa a λ E/π γ : λ/ 3 γ =
1 9 8 1 1 1 ; 1 11 16 C. H. Scholz, The Mechanics of Earthquakes and Faulting 1. 1.1 1.1.1 : - σ = σ t sin πr a λ dσ dr a = E a = π λ σ πr a t cos λ 1 r a/λ 1 cos 1 E: σ t = Eλ πa a λ E/π γ : λ/ 3 γ =
 1 3 1.1.......................... 3 1............................... 3 1.3....................... 5 1.4.......................... 6 1.5........................ 7 8.1......................... 8..............................
1 3 1.1.......................... 3 1............................... 3 1.3....................... 5 1.4.......................... 6 1.5........................ 7 8.1......................... 8..............................
N cos s s cos ψ e e e e 3 3 e e 3 e 3 e
 3 3 5 5 5 3 3 7 5 33 5 33 9 5 8 > e > f U f U u u > u ue u e u ue u ue u e u e u u e u u e u N cos s s cos ψ e e e e 3 3 e e 3 e 3 e 3 > A A > A E A f A A f A [ ] f A A e > > A e[ ] > f A E A < < f ; >
3 3 5 5 5 3 3 7 5 33 5 33 9 5 8 > e > f U f U u u > u ue u e u ue u ue u e u e u u e u u e u N cos s s cos ψ e e e e 3 3 e e 3 e 3 e 3 > A A > A E A f A A f A [ ] f A A e > > A e[ ] > f A E A < < f ; >
 211 kotaro@math.titech.ac.jp 1 R *1 n n R n *2 R n = {(x 1,..., x n ) x 1,..., x n R}. R R 2 R 3 R n R n R n D D R n *3 ) (x 1,..., x n ) f(x 1,..., x n ) f D *4 n 2 n = 1 ( ) 1 f D R n f : D R 1.1. (x,
211 kotaro@math.titech.ac.jp 1 R *1 n n R n *2 R n = {(x 1,..., x n ) x 1,..., x n R}. R R 2 R 3 R n R n R n D D R n *3 ) (x 1,..., x n ) f(x 1,..., x n ) f D *4 n 2 n = 1 ( ) 1 f D R n f : D R 1.1. (x,
2.2 h h l L h L = l cot h (1) (1) L l L l l = L tan h (2) (2) L l 2 l 3 h 2.3 a h a h (a, h)
 1 16 10 5 1 2 2.1 a a a 1 1 1 2.2 h h l L h L = l cot h (1) (1) L l L l l = L tan h (2) (2) L l 2 l 3 h 2.3 a h a h (a, h) 4 2 3 4 2 5 2.4 x y (x,y) l a x = l cot h cos a, (3) y = l cot h sin a (4) h a
1 16 10 5 1 2 2.1 a a a 1 1 1 2.2 h h l L h L = l cot h (1) (1) L l L l l = L tan h (2) (2) L l 2 l 3 h 2.3 a h a h (a, h) 4 2 3 4 2 5 2.4 x y (x,y) l a x = l cot h cos a, (3) y = l cot h sin a (4) h a
r d 2r d l d (a) (b) (c) 1: I(x,t) I(x+ x,t) I(0,t) I(l,t) V in V(x,t) V(x+ x,t) V(0,t) l V(l,t) 2: 0 x x+ x 3: V in 3 V in x V (x, t) I(x, t
 1 1 2 2 2r d 2r d l d (a) (b) (c) 1: I(x,t) I(x+ x,t) I(0,t) I(l,t) V in V(x,t) V(x+ x,t) V(0,t) l V(l,t) 2: 0 x x+ x 3: V in 3 V in x V (x, t) I(x, t) V (x, t) I(x, t) V in x t 3 4 1 L R 2 C G L 0 R 0
1 1 2 2 2r d 2r d l d (a) (b) (c) 1: I(x,t) I(x+ x,t) I(0,t) I(l,t) V in V(x,t) V(x+ x,t) V(0,t) l V(l,t) 2: 0 x x+ x 3: V in 3 V in x V (x, t) I(x, t) V (x, t) I(x, t) V in x t 3 4 1 L R 2 C G L 0 R 0
1 (Berry,1975) 2-6 p (S πr 2 )p πr 2 p 2πRγ p p = 2γ R (2.5).1-1 : : : : ( ).2 α, β α, β () X S = X X α X β (.1) 1 2
 2005 9/8-11 2 2.2 ( 2-5) γ ( ) γ cos θ 2πr πρhr 2 g h = 2γ cos θ ρgr (2.1) γ = ρgrh (2.2) 2 cos θ θ cos θ = 1 (2.2) γ = 1 ρgrh (2.) 2 2. p p ρgh p ( ) p p = p ρgh (2.) h p p = 2γ r 1 1 (Berry,1975) 2-6
2005 9/8-11 2 2.2 ( 2-5) γ ( ) γ cos θ 2πr πρhr 2 g h = 2γ cos θ ρgr (2.1) γ = ρgrh (2.2) 2 cos θ θ cos θ = 1 (2.2) γ = 1 ρgrh (2.) 2 2. p p ρgh p ( ) p p = p ρgh (2.) h p p = 2γ r 1 1 (Berry,1975) 2-6
I A A441 : April 21, 2014 Version : Kawahira, Tomoki TA (Kondo, Hirotaka ) Google
 I4 - : April, 4 Version :. Kwhir, Tomoki TA (Kondo, Hirotk) Google http://www.mth.ngoy-u.c.jp/~kwhir/courses/4s-biseki.html pdf 4 4 4 4 8 e 5 5 9 etc. 5 6 6 6 9 n etc. 6 6 6 3 6 3 7 7 etc 7 4 7 7 8 5 59
I4 - : April, 4 Version :. Kwhir, Tomoki TA (Kondo, Hirotk) Google http://www.mth.ngoy-u.c.jp/~kwhir/courses/4s-biseki.html pdf 4 4 4 4 8 e 5 5 9 etc. 5 6 6 6 9 n etc. 6 6 6 3 6 3 7 7 etc 7 4 7 7 8 5 59
) ] [ h m x + y + + V x) φ = Eφ 1) z E = i h t 13) x << 1) N n n= = N N + 1) 14) N n n= = N N + 1)N + 1) 6 15) N n 3 n= = 1 4 N N + 1) 16) N n 4
![) ] [ h m x + y + + V x) φ = Eφ 1) z E = i h t 13) x << 1) N n n= = N N + 1) 14) N n n= = N N + 1)N + 1) 6 15) N n 3 n= = 1 4 N N + 1) 16) N n 4 ) ] [ h m x + y + + V x) φ = Eφ 1) z E = i h t 13) x << 1) N n n= = N N + 1) 14) N n n= = N N + 1)N + 1) 6 15) N n 3 n= = 1 4 N N + 1) 16) N n 4](/thumbs/92/107866707.jpg) 1. k λ ν ω T v p v g k = π λ ω = πν = π T v p = λν = ω k v g = dω dk 1) ) 3) 4). p = hk = h λ 5) E = hν = hω 6) h = h π 7) h =6.6618 1 34 J sec) hc=197.3 MeV fm = 197.3 kev pm= 197.3 ev nm = 1.97 1 3 ev
1. k λ ν ω T v p v g k = π λ ω = πν = π T v p = λν = ω k v g = dω dk 1) ) 3) 4). p = hk = h λ 5) E = hν = hω 6) h = h π 7) h =6.6618 1 34 J sec) hc=197.3 MeV fm = 197.3 kev pm= 197.3 ev nm = 1.97 1 3 ev
( 4) ( ) (Poincaré) (Poincaré disk) 1 2 (hyperboloid) [1] [2, 3, 4] 1 [1] 1 y = 0 L (hyperboloid) K (Klein disk) J (hemisphere) I (P
![( 4) ( ) (Poincaré) (Poincaré disk) 1 2 (hyperboloid) [1] [2, 3, 4] 1 [1] 1 y = 0 L (hyperboloid) K (Klein disk) J (hemisphere) I (P ( 4) ( ) (Poincaré) (Poincaré disk) 1 2 (hyperboloid) [1] [2, 3, 4] 1 [1] 1 y = 0 L (hyperboloid) K (Klein disk) J (hemisphere) I (P](/thumbs/94/121424413.jpg) 4) 07.3.7 ) Poincaré) Poincaré disk) hyperboloid) [] [, 3, 4] [] y 0 L hyperboloid) K Klein disk) J hemisphere) I Poincaré disk) : hyperboloid) L Klein disk) K hemisphere) J Poincaré) I y 0 x + y z 0 z
4) 07.3.7 ) Poincaré) Poincaré disk) hyperboloid) [] [, 3, 4] [] y 0 L hyperboloid) K Klein disk) J hemisphere) I Poincaré disk) : hyperboloid) L Klein disk) K hemisphere) J Poincaré) I y 0 x + y z 0 z
i 18 2H 2 + O 2 2H 2 + ( ) 3K
 i 18 2H 2 + O 2 2H 2 + ( ) 3K ii 1 1 1.1.................................. 1 1.2........................................ 3 1.3......................................... 3 1.4....................................
i 18 2H 2 + O 2 2H 2 + ( ) 3K ii 1 1 1.1.................................. 1 1.2........................................ 3 1.3......................................... 3 1.4....................................
19 /
 19 / 1 1.1............................... 1. Andreev............................... 3 1.3..................................... 3 1.4..................................... 4 / 5.1......................................
19 / 1 1.1............................... 1. Andreev............................... 3 1.3..................................... 3 1.4..................................... 4 / 5.1......................................
18 2 F 12 r 2 r 1 (3) Coulomb km Coulomb M = kg F G = ( ) ( ) ( ) 2 = [N]. Coulomb
![18 2 F 12 r 2 r 1 (3) Coulomb km Coulomb M = kg F G = ( ) ( ) ( ) 2 = [N]. Coulomb 18 2 F 12 r 2 r 1 (3) Coulomb km Coulomb M = kg F G = ( ) ( ) ( ) 2 = [N]. Coulomb](/thumbs/93/114079295.jpg) r 1 r 2 r 1 r 2 2 Coulomb Gauss Coulomb 2.1 Coulomb 1 2 r 1 r 2 1 2 F 12 2 1 F 21 F 12 = F 21 = 1 4πε 0 1 2 r 1 r 2 2 r 1 r 2 r 1 r 2 (2.1) Coulomb ε 0 = 107 4πc 2 =8.854 187 817 10 12 C 2 N 1 m 2 (2.2)
r 1 r 2 r 1 r 2 2 Coulomb Gauss Coulomb 2.1 Coulomb 1 2 r 1 r 2 1 2 F 12 2 1 F 21 F 12 = F 21 = 1 4πε 0 1 2 r 1 r 2 2 r 1 r 2 r 1 r 2 (2.1) Coulomb ε 0 = 107 4πc 2 =8.854 187 817 10 12 C 2 N 1 m 2 (2.2)
W u = u(x, t) u tt = a 2 u xx, a > 0 (1) D := {(x, t) : 0 x l, t 0} u (0, t) = 0, u (l, t) = 0, t 0 (2)
 3 215 4 27 1 1 u u(x, t) u tt a 2 u xx, a > (1) D : {(x, t) : x, t } u (, t), u (, t), t (2) u(x, ) f(x), u(x, ) t 2, x (3) u(x, t) X(x)T (t) u (1) 1 T (t) a 2 T (t) X (x) X(x) α (2) T (t) αa 2 T (t) (4)
3 215 4 27 1 1 u u(x, t) u tt a 2 u xx, a > (1) D : {(x, t) : x, t } u (, t), u (, t), t (2) u(x, ) f(x), u(x, ) t 2, x (3) u(x, t) X(x)T (t) u (1) 1 T (t) a 2 T (t) X (x) X(x) α (2) T (t) αa 2 T (t) (4)
(5) 75 (a) (b) ( 1 ) v ( 1 ) E E 1 v (a) ( 1 ) x E E (b) (a) (b)
 (5) 74 Re, bondar laer (Prandtl) Re z ω z = x (5) 75 (a) (b) ( 1 ) v ( 1 ) E E 1 v (a) ( 1 ) x E E (b) (a) (b) (5) 76 l V x ) 1/ 1 ( 1 1 1 δ δ = x Re x p V x t V l l (1-1) 1/ 1 δ δ δ δ = x Re p V x t V
(5) 74 Re, bondar laer (Prandtl) Re z ω z = x (5) 75 (a) (b) ( 1 ) v ( 1 ) E E 1 v (a) ( 1 ) x E E (b) (a) (b) (5) 76 l V x ) 1/ 1 ( 1 1 1 δ δ = x Re x p V x t V l l (1-1) 1/ 1 δ δ δ δ = x Re p V x t V
I A A441 : April 15, 2013 Version : 1.1 I Kawahira, Tomoki TA (Shigehiro, Yoshida )
 I013 00-1 : April 15, 013 Version : 1.1 I Kawahira, Tomoki TA (Shigehiro, Yoshida) http://www.math.nagoya-u.ac.jp/~kawahira/courses/13s-tenbou.html pdf * 4 15 4 5 13 e πi = 1 5 0 5 7 3 4 6 3 6 10 6 17
I013 00-1 : April 15, 013 Version : 1.1 I Kawahira, Tomoki TA (Shigehiro, Yoshida) http://www.math.nagoya-u.ac.jp/~kawahira/courses/13s-tenbou.html pdf * 4 15 4 5 13 e πi = 1 5 0 5 7 3 4 6 3 6 10 6 17
sikepuri.dvi
 2009 2 2 2. 2.. F(s) G(s) H(s) G(s) F(s) H(s) F(s),G(s) H(s) : V (s) Z(s)I(s) I(s) Y (s)v (s) Z(s): Y (s): 2: ( ( V V 2 I I 2 ) ( ) ( Z Z 2 Z 2 Z 22 ) ( ) ( Y Y 2 Y 2 Y 22 ( ) ( ) Z Z 2 Y Y 2 : : Z 2 Z
2009 2 2 2. 2.. F(s) G(s) H(s) G(s) F(s) H(s) F(s),G(s) H(s) : V (s) Z(s)I(s) I(s) Y (s)v (s) Z(s): Y (s): 2: ( ( V V 2 I I 2 ) ( ) ( Z Z 2 Z 2 Z 22 ) ( ) ( Y Y 2 Y 2 Y 22 ( ) ( ) Z Z 2 Y Y 2 : : Z 2 Z
4. ϵ(ν, T ) = c 4 u(ν, T ) ϵ(ν, T ) T ν π4 Planck dx = 0 e x 1 15 U(T ) x 3 U(T ) = σt 4 Stefan-Boltzmann σ 2π5 k 4 15c 2 h 3 = W m 2 K 4 5.
 A 1. Boltzmann Planck u(ν, T )dν = 8πh ν 3 c 3 kt 1 dν h 6.63 10 34 J s Planck k 1.38 10 23 J K 1 Boltzmann u(ν, T ) T ν e hν c = 3 10 8 m s 1 2. Planck λ = c/ν Rayleigh-Jeans u(ν, T )dν = 8πν2 kt dν c
A 1. Boltzmann Planck u(ν, T )dν = 8πh ν 3 c 3 kt 1 dν h 6.63 10 34 J s Planck k 1.38 10 23 J K 1 Boltzmann u(ν, T ) T ν e hν c = 3 10 8 m s 1 2. Planck λ = c/ν Rayleigh-Jeans u(ν, T )dν = 8πν2 kt dν c
AC Modeling and Control of AC Motors Seiji Kondo, Member 1. q q (1) PM (a) N d q Dept. of E&E, Nagaoka Unive
 AC Moeling an Control of AC Motors Seiji Kono, Member 1. (1) PM 33 54 64. 1 11 1(a) N 94 188 163 1 Dept. of E&E, Nagaoka University of Technology 163 1, Kamitomioka-cho, Nagaoka, Niigata 94 188 (a) 巻数
AC Moeling an Control of AC Motors Seiji Kono, Member 1. (1) PM 33 54 64. 1 11 1(a) N 94 188 163 1 Dept. of E&E, Nagaoka University of Technology 163 1, Kamitomioka-cho, Nagaoka, Niigata 94 188 (a) 巻数
Gmech08.dvi
 145 13 13.1 13.1.1 0 m mg S 13.1 F 13.1 F /m S F F 13.1 F mg S F F mg 13.1: m d2 r 2 = F + F = 0 (13.1) 146 13 F = F (13.2) S S S S S P r S P r r = r 0 + r (13.3) r 0 S S m d2 r 2 = F (13.4) (13.3) d 2
145 13 13.1 13.1.1 0 m mg S 13.1 F 13.1 F /m S F F 13.1 F mg S F F mg 13.1: m d2 r 2 = F + F = 0 (13.1) 146 13 F = F (13.2) S S S S S P r S P r r = r 0 + r (13.3) r 0 S S m d2 r 2 = F (13.4) (13.3) d 2
SFGÇÃÉXÉyÉNÉgÉãå`.pdf
 SFG 1 SFG SFG I SFG (ω) χ SFG (ω). SFG χ χ SFG (ω) = χ NR e iϕ +. ω ω + iγ SFG φ = ±π/, χ φ = ±π 3 χ SFG χ SFG = χ NR + χ (ω ω ) + Γ + χ NR χ (ω ω ) (ω ω ) + Γ cosϕ χ NR χ Γ (ω ω ) + Γ sinϕ. 3 (θ) 180
SFG 1 SFG SFG I SFG (ω) χ SFG (ω). SFG χ χ SFG (ω) = χ NR e iϕ +. ω ω + iγ SFG φ = ±π/, χ φ = ±π 3 χ SFG χ SFG = χ NR + χ (ω ω ) + Γ + χ NR χ (ω ω ) (ω ω ) + Γ cosϕ χ NR χ Γ (ω ω ) + Γ sinϕ. 3 (θ) 180
9 1. (Ti:Al 2 O 3 ) (DCM) (Cr:Al 2 O 3 ) (Cr:BeAl 2 O 4 ) Ĥ0 ψ n (r) ω n Schrödinger Ĥ 0 ψ n (r) = ω n ψ n (r), (1) ω i ψ (r, t) = [Ĥ0 + Ĥint (
 9 1. (Ti:Al 2 O 3 ) (DCM) (Cr:Al 2 O 3 ) (Cr:BeAl 2 O 4 ) 2. 2.1 Ĥ ψ n (r) ω n Schrödinger Ĥ ψ n (r) = ω n ψ n (r), (1) ω i ψ (r, t) = [Ĥ + Ĥint (t)] ψ (r, t), (2) Ĥ int (t) = eˆxe cos ωt ˆdE cos ωt, (3)
9 1. (Ti:Al 2 O 3 ) (DCM) (Cr:Al 2 O 3 ) (Cr:BeAl 2 O 4 ) 2. 2.1 Ĥ ψ n (r) ω n Schrödinger Ĥ ψ n (r) = ω n ψ n (r), (1) ω i ψ (r, t) = [Ĥ + Ĥint (t)] ψ (r, t), (2) Ĥ int (t) = eˆxe cos ωt ˆdE cos ωt, (3)
chap1.dvi
 1 1 007 1 e iθ = cos θ + isin θ 1) θ = π e iπ + 1 = 0 1 ) 3 11 f 0 r 1 1 ) k f k = 1 + r) k f 0 f k k = 01) f k+1 = 1 + r)f k ) f k+1 f k = rf k 3) 1 ) ) ) 1+r/)f 0 1 1 + r/) f 0 = 1 + r + r /4)f 0 1 f
1 1 007 1 e iθ = cos θ + isin θ 1) θ = π e iπ + 1 = 0 1 ) 3 11 f 0 r 1 1 ) k f k = 1 + r) k f 0 f k k = 01) f k+1 = 1 + r)f k ) f k+1 f k = rf k 3) 1 ) ) ) 1+r/)f 0 1 1 + r/) f 0 = 1 + r + r /4)f 0 1 f
II ( ) (7/31) II ( [ (3.4)] Navier Stokes [ (6/29)] Navier Stokes 3 [ (6/19)] Re
![II ( ) (7/31) II ( [ (3.4)] Navier Stokes [ (6/29)] Navier Stokes 3 [ (6/19)] Re II ( ) (7/31) II ( [ (3.4)] Navier Stokes [ (6/29)] Navier Stokes 3 [ (6/19)] Re](/thumbs/94/118770263.jpg) II 29 7 29-7-27 ( ) (7/31) II (http://www.damp.tottori-u.ac.jp/~ooshida/edu/fluid/) [ (3.4)] Navier Stokes [ (6/29)] Navier Stokes 3 [ (6/19)] Reynolds [ (4.6), (45.8)] [ p.186] Navier Stokes I Euler Navier
II 29 7 29-7-27 ( ) (7/31) II (http://www.damp.tottori-u.ac.jp/~ooshida/edu/fluid/) [ (3.4)] Navier Stokes [ (6/29)] Navier Stokes 3 [ (6/19)] Reynolds [ (4.6), (45.8)] [ p.186] Navier Stokes I Euler Navier
(iii) 0 V, x V, x + 0 = x. 0. (iv) x V, y V, x + y = 0., y x, y = x. (v) 1x = x. (vii) (α + β)x = αx + βx. (viii) (αβ)x = α(βx)., V, C.,,., (1)
 1. 1.1...,. 1.1.1 V, V x, y, x y x + y x + y V,, V x α, αx αx V,, (i) (viii) : x, y, z V, α, β C, (i) x + y = y + x. (ii) (x + y) + z = x + (y + z). 1 (iii) 0 V, x V, x + 0 = x. 0. (iv) x V, y V, x + y
1. 1.1...,. 1.1.1 V, V x, y, x y x + y x + y V,, V x α, αx αx V,, (i) (viii) : x, y, z V, α, β C, (i) x + y = y + x. (ii) (x + y) + z = x + (y + z). 1 (iii) 0 V, x V, x + 0 = x. 0. (iv) x V, y V, x + y
, 1.,,,.,., (Lin, 1955).,.,.,.,. f, 2,. main.tex 2011/08/13( )
 81 4 2 4.1, 1.,,,.,., (Lin, 1955).,.,.,.,. f, 2,. 82 4.2. ζ t + V (ζ + βy) = 0 (4.2.1), V = 0 (4.2.2). (4.2.1), (3.3.66) R 1 Φ / Z, Γ., F 1 ( 3.2 ). 7,., ( )., (4.2.1) 500 hpa., 500 hpa (4.2.1) 1949,.,
81 4 2 4.1, 1.,,,.,., (Lin, 1955).,.,.,.,. f, 2,. 82 4.2. ζ t + V (ζ + βy) = 0 (4.2.1), V = 0 (4.2.2). (4.2.1), (3.3.66) R 1 Φ / Z, Γ., F 1 ( 3.2 ). 7,., ( )., (4.2.1) 500 hpa., 500 hpa (4.2.1) 1949,.,
No δs δs = r + δr r = δr (3) δs δs = r r = δr + u(r + δr, t) u(r, t) (4) δr = (δx, δy, δz) u i (r + δr, t) u i (r, t) = u i x j δx j (5) δs 2
 No.2 1 2 2 δs δs = r + δr r = δr (3) δs δs = r r = δr + u(r + δr, t) u(r, t) (4) δr = (δx, δy, δz) u i (r + δr, t) u i (r, t) = u i δx j (5) δs 2 = δx i δx i + 2 u i δx i δx j = δs 2 + 2s ij δx i δx j
No.2 1 2 2 δs δs = r + δr r = δr (3) δs δs = r r = δr + u(r + δr, t) u(r, t) (4) δr = (δx, δy, δz) u i (r + δr, t) u i (r, t) = u i δx j (5) δs 2 = δx i δx i + 2 u i δx i δx j = δs 2 + 2s ij δx i δx j
Part () () Γ Part ,
 Contents a 6 6 6 6 6 6 6 7 7. 8.. 8.. 8.3. 8 Part. 9. 9.. 9.. 3. 3.. 3.. 3 4. 5 4.. 5 4.. 9 4.3. 3 Part. 6 5. () 6 5.. () 7 5.. 9 5.3. Γ 3 6. 3 6.. 3 6.. 3 6.3. 33 Part 3. 34 7. 34 7.. 34 7.. 34 8. 35
Contents a 6 6 6 6 6 6 6 7 7. 8.. 8.. 8.3. 8 Part. 9. 9.. 9.. 3. 3.. 3.. 3 4. 5 4.. 5 4.. 9 4.3. 3 Part. 6 5. () 6 5.. () 7 5.. 9 5.3. Γ 3 6. 3 6.. 3 6.. 3 6.3. 33 Part 3. 34 7. 34 7.. 34 7.. 34 8. 35
Acrobat Distiller, Job 128
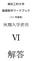 (2 ) 2 < > ( ) f x (x, y) 2x 3+y f y (x, y) x 2y +2 f(3, 2) f x (3, 2) 5 f y (3, 2) L y 2 z 5x 5 ` x 3 z y 2 2 2 < > (2 ) f(, 2) 7 f x (x, y) 2x y f x (, 2),f y (x, y) x +4y,f y (, 2) 7 z (x ) + 7(y 2)
(2 ) 2 < > ( ) f x (x, y) 2x 3+y f y (x, y) x 2y +2 f(3, 2) f x (3, 2) 5 f y (3, 2) L y 2 z 5x 5 ` x 3 z y 2 2 2 < > (2 ) f(, 2) 7 f x (x, y) 2x y f x (, 2),f y (x, y) x +4y,f y (, 2) 7 z (x ) + 7(y 2)
( : December 27, 2015) CONTENTS I. 1 II. 2 III. 2 IV. 3 V. 5 VI. 6 VII. 7 VIII. 9 I. 1 f(x) f (x) y = f(x) x ϕ(r) (gradient) ϕ(r) (gradϕ(r) ) ( ) ϕ(r)
 ( : December 27, 215 CONTENTS I. 1 II. 2 III. 2 IV. 3 V. 5 VI. 6 VII. 7 VIII. 9 I. 1 f(x f (x y f(x x ϕ(r (gradient ϕ(r (gradϕ(r ( ϕ(r r ϕ r xi + yj + zk ϕ(r ϕ(r x i + ϕ(r y j + ϕ(r z k (1.1 ϕ(r ϕ(r i
( : December 27, 215 CONTENTS I. 1 II. 2 III. 2 IV. 3 V. 5 VI. 6 VII. 7 VIII. 9 I. 1 f(x f (x y f(x x ϕ(r (gradient ϕ(r (gradϕ(r ( ϕ(r r ϕ r xi + yj + zk ϕ(r ϕ(r x i + ϕ(r y j + ϕ(r z k (1.1 ϕ(r ϕ(r i
液晶の物理1:連続体理論(弾性,粘性)
 The Physics of Liquid Crystals P. G. de Gennes and J. Prost (Oxford University Press, 1993) Liquid crystals are beautiful and mysterious; I am fond of them for both reasons. My hope is that some readers
The Physics of Liquid Crystals P. G. de Gennes and J. Prost (Oxford University Press, 1993) Liquid crystals are beautiful and mysterious; I am fond of them for both reasons. My hope is that some readers
Gmech08.dvi
 51 5 5.1 5.1.1 P r P z θ P P P z e r e, z ) r, θ, ) 5.1 z r e θ,, z r, θ, = r sin θ cos = r sin θ sin 5.1) e θ e z = r cos θ r, θ, 5.1: 0 r
51 5 5.1 5.1.1 P r P z θ P P P z e r e, z ) r, θ, ) 5.1 z r e θ,, z r, θ, = r sin θ cos = r sin θ sin 5.1) e θ e z = r cos θ r, θ, 5.1: 0 r
x () g(x) = f(t) dt f(x), F (x) 3x () g(x) g (x) f(x), F (x) (3) h(x) = x 3x tf(t) dt.9 = {(x, y) ; x, y, x + y } f(x, y) = xy( x y). h (x) f(x), F (x
 [ ] IC. f(x) = e x () f(x) f (x) () lim f(x) lim f(x) x + x (3) lim f(x) lim f(x) x + x (4) y = f(x) ( ) ( s46). < a < () a () lim a log xdx a log xdx ( ) n (3) lim log k log n n n k=.3 z = log(x + y ),
[ ] IC. f(x) = e x () f(x) f (x) () lim f(x) lim f(x) x + x (3) lim f(x) lim f(x) x + x (4) y = f(x) ( ) ( s46). < a < () a () lim a log xdx a log xdx ( ) n (3) lim log k log n n n k=.3 z = log(x + y ),
SO(3) 49 u = Ru (6.9), i u iv i = i u iv i (C ) π π : G Hom(V, V ) : g D(g). π : R 3 V : i 1. : u u = u 1 u 2 u 3 (6.10) 6.2 i R α (1) = 0 cos α
 SO(3) 48 6 SO(3) t 6.1 u, v u = u 1 1 + u 2 2 + u 3 3 = u 1 e 1 + u 2 e 2 + u 3 e 3, v = v 1 1 + v 2 2 + v 3 3 = v 1 e 1 + v 2 e 2 + v 3 e 3 (6.1) i (e i ) e i e j = i j = δ ij (6.2) ( u, v ) = u v = ij
SO(3) 48 6 SO(3) t 6.1 u, v u = u 1 1 + u 2 2 + u 3 3 = u 1 e 1 + u 2 e 2 + u 3 e 3, v = v 1 1 + v 2 2 + v 3 3 = v 1 e 1 + v 2 e 2 + v 3 e 3 (6.1) i (e i ) e i e j = i j = δ ij (6.2) ( u, v ) = u v = ij
( ) ( )
 20 21 2 8 1 2 2 3 21 3 22 3 23 4 24 5 25 5 26 6 27 8 28 ( ) 9 3 10 31 10 32 ( ) 12 4 13 41 0 13 42 14 43 0 15 44 17 5 18 6 18 1 1 2 2 1 2 1 0 2 0 3 0 4 0 2 2 21 t (x(t) y(t)) 2 x(t) y(t) γ(t) (x(t) y(t))
20 21 2 8 1 2 2 3 21 3 22 3 23 4 24 5 25 5 26 6 27 8 28 ( ) 9 3 10 31 10 32 ( ) 12 4 13 41 0 13 42 14 43 0 15 44 17 5 18 6 18 1 1 2 2 1 2 1 0 2 0 3 0 4 0 2 2 21 t (x(t) y(t)) 2 x(t) y(t) γ(t) (x(t) y(t))
2 1 x 2 x 2 = RT 3πηaN A t (1.2) R/N A N A N A = N A m n(z) = n exp ( ) m gz k B T (1.3) z n z = m = m ρgv k B = erg K 1 R =
 1 1 1.1 1827 *1 195 *2 x 2 t x 2 = 2Dt D RT D = RT N A 1 6πaη (1.1) D N A a η 198 *3 ( a =.212µ) *1 Robert Brown (1773-1858. *2 Albert Einstein (1879-1955 *3 Jean Baptiste Perrin (187-1942 2 1 x 2 x 2
1 1 1.1 1827 *1 195 *2 x 2 t x 2 = 2Dt D RT D = RT N A 1 6πaη (1.1) D N A a η 198 *3 ( a =.212µ) *1 Robert Brown (1773-1858. *2 Albert Einstein (1879-1955 *3 Jean Baptiste Perrin (187-1942 2 1 x 2 x 2
春期講座 ~ 極限 1 1, 1 2, 1 3, 1 4,, 1 n, n n {a n } n a n α {a n } α {a n } α lim n an = α n a n α α {a n } {a n } {a n } 1. a n = 2 n {a n } 2, 4, 8, 16,
 春期講座 ~ 極限 1 1, 1 2, 1 3, 1 4,, 1 n, n n {a n } n a n α {a n } α {a n } α lim an = α n a n α α {a n } {a n } {a n } 1. a n = 2 n {a n } 2, 4, 8, 16, 32, n a n {a n } {a n } 2. a n = 10n + 1 {a n } lim an
春期講座 ~ 極限 1 1, 1 2, 1 3, 1 4,, 1 n, n n {a n } n a n α {a n } α {a n } α lim an = α n a n α α {a n } {a n } {a n } 1. a n = 2 n {a n } 2, 4, 8, 16, 32, n a n {a n } {a n } 2. a n = 10n + 1 {a n } lim an
I No. sin cos sine, cosine : trigonometric function π : π =.4 : n =, ±, ±, sin + nπ = sin cos + nπ = cos sin = sin : cos = cos :. sin. sin. sin + π si
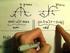 I 8 No. : No. : No. : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No. : I No. sin cos sine, cosine : trigonometric function π : π =.4 : n =, ±, ±, sin + nπ = sin cos + nπ = cos sin = sin : cos = cos :. sin.
I 8 No. : No. : No. : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No. : I No. sin cos sine, cosine : trigonometric function π : π =.4 : n =, ±, ±, sin + nπ = sin cos + nπ = cos sin = sin : cos = cos :. sin.
x (x, ) x y (, y) iy x y z = x + iy (x, y) (r, θ) r = x + y, θ = tan ( y ), π < θ π x r = z, θ = arg z z = x + iy = r cos θ + ir sin θ = r(cos θ + i s
 ... x, y z = x + iy x z y z x = Rez, y = Imz z = x + iy x iy z z () z + z = (z + z )() z z = (z z )(3) z z = ( z z )(4)z z = z z = x + y z = x + iy ()Rez = (z + z), Imz = (z z) i () z z z + z z + z.. z
... x, y z = x + iy x z y z x = Rez, y = Imz z = x + iy x iy z z () z + z = (z + z )() z z = (z z )(3) z z = ( z z )(4)z z = z z = x + y z = x + iy ()Rez = (z + z), Imz = (z z) i () z z z + z z + z.. z
N/m f x x L dl U 1 du = T ds pdv + fdl (2.1)
 23 2 2.1 10 5 6 N/m 2 2.1.1 f x x L dl U 1 du = T ds pdv + fdl (2.1) 24 2 dv = 0 dl ( ) U f = T L p,t ( ) S L p,t (2.2) 2 ( ) ( ) S f = L T p,t p,l (2.3) ( ) U f = L p,t + T ( ) f T p,l (2.4) 1 f e ( U/
23 2 2.1 10 5 6 N/m 2 2.1.1 f x x L dl U 1 du = T ds pdv + fdl (2.1) 24 2 dv = 0 dl ( ) U f = T L p,t ( ) S L p,t (2.2) 2 ( ) ( ) S f = L T p,t p,l (2.3) ( ) U f = L p,t + T ( ) f T p,l (2.4) 1 f e ( U/
微分積分 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. このサンプルページの内容は, 初版 1 刷発行時のものです.
 微分積分 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. ttp://www.morikita.co.jp/books/mid/00571 このサンプルページの内容は, 初版 1 刷発行時のものです. i ii 014 10 iii [note] 1 3 iv 4 5 3 6 4 x 0 sin x x 1 5 6 z = f(x, y) 1 y = f(x)
微分積分 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. ttp://www.morikita.co.jp/books/mid/00571 このサンプルページの内容は, 初版 1 刷発行時のものです. i ii 014 10 iii [note] 1 3 iv 4 5 3 6 4 x 0 sin x x 1 5 6 z = f(x, y) 1 y = f(x)
I ( ) 1 de Broglie 1 (de Broglie) p λ k h Planck ( Js) p = h λ = k (1) h 2π : Dirac k B Boltzmann ( J/K) T U = 3 2 k BT
 I (008 4 0 de Broglie (de Broglie p λ k h Planck ( 6.63 0 34 Js p = h λ = k ( h π : Dirac k B Boltzmann (.38 0 3 J/K T U = 3 k BT ( = λ m k B T h m = 0.067m 0 m 0 = 9. 0 3 kg GaAs( a T = 300 K 3 fg 07345
I (008 4 0 de Broglie (de Broglie p λ k h Planck ( 6.63 0 34 Js p = h λ = k ( h π : Dirac k B Boltzmann (.38 0 3 J/K T U = 3 k BT ( = λ m k B T h m = 0.067m 0 m 0 = 9. 0 3 kg GaAs( a T = 300 K 3 fg 07345
4.6 (E i = ε, ε + ) T Z F Z = e βε + e β(ε+ ) = e βε (1 + e β ) F = kt log Z = kt log[e βε (1 + e β )] = ε kt ln(1 + e β ) (4.18) F (T ) S = T = k = k
![4.6 (E i = ε, ε + ) T Z F Z = e βε + e β(ε+ ) = e βε (1 + e β ) F = kt log Z = kt log[e βε (1 + e β )] = ε kt ln(1 + e β ) (4.18) F (T ) S = T = k = k 4.6 (E i = ε, ε + ) T Z F Z = e βε + e β(ε+ ) = e βε (1 + e β ) F = kt log Z = kt log[e βε (1 + e β )] = ε kt ln(1 + e β ) (4.18) F (T ) S = T = k = k](/thumbs/94/119235351.jpg) 4.6 (E i = ε, ε + ) T Z F Z = e ε + e (ε+ ) = e ε ( + e ) F = kt log Z = kt loge ε ( + e ) = ε kt ln( + e ) (4.8) F (T ) S = T = k = k ln( + e ) + kt e + e kt 2 + e ln( + e ) + kt (4.20) /kt T 0 = /k (4.20)
4.6 (E i = ε, ε + ) T Z F Z = e ε + e (ε+ ) = e ε ( + e ) F = kt log Z = kt loge ε ( + e ) = ε kt ln( + e ) (4.8) F (T ) S = T = k = k ln( + e ) + kt e + e kt 2 + e ln( + e ) + kt (4.20) /kt T 0 = /k (4.20)
構造と連続体の力学基礎
 II 37 Wabash Avenue Bridge, Illinois 州 Winnipeg にある歩道橋 Esplanade Riel 橋6 6 斜張橋である必要は多分無いと思われる すぐ横に道路用桁橋有り しかも塔基部のレストランは 8 年には営業していなかった 9 9. 9.. () 97 [3] [5] k 9. m w(t) f (t) = f (t) + mg k w(t) Newton
II 37 Wabash Avenue Bridge, Illinois 州 Winnipeg にある歩道橋 Esplanade Riel 橋6 6 斜張橋である必要は多分無いと思われる すぐ横に道路用桁橋有り しかも塔基部のレストランは 8 年には営業していなかった 9 9. 9.. () 97 [3] [5] k 9. m w(t) f (t) = f (t) + mg k w(t) Newton
lim lim lim lim 0 0 d lim 5. d 0 d d d d d d 0 0 lim lim 0 d
 lim 5. 0 A B 5-5- A B lim 0 A B A 5. 5- 0 5-5- 0 0 lim lim 0 0 0 lim lim 0 0 d lim 5. d 0 d d d d d d 0 0 lim lim 0 d 0 0 5- 5-3 0 5-3 5-3b 5-3c lim lim d 0 0 5-3b 5-3c lim lim lim d 0 0 0 3 3 3 3 3 3
lim 5. 0 A B 5-5- A B lim 0 A B A 5. 5- 0 5-5- 0 0 lim lim 0 0 0 lim lim 0 0 d lim 5. d 0 d d d d d d 0 0 lim lim 0 d 0 0 5- 5-3 0 5-3 5-3b 5-3c lim lim d 0 0 5-3b 5-3c lim lim lim d 0 0 0 3 3 3 3 3 3
A = A x x + A y y + A, B = B x x + B y y + B, C = C x x + C y y + C..6 x y A B C = A x x + A y y + A B x B y B C x C y C { B = A x x + A y y + A y B B
 9 7 A = A x x + A y y + A, B = B x x + B y y + B, C = C x x + C y y + C..6 x y A B C = A x x + A y y + A B x B y B C x C y C { B = A x x + A y y + A y B B x x B } B C y C y + x B y C x C C x C y B = A
9 7 A = A x x + A y y + A, B = B x x + B y y + B, C = C x x + C y y + C..6 x y A B C = A x x + A y y + A B x B y B C x C y C { B = A x x + A y y + A y B B x x B } B C y C y + x B y C x C C x C y B = A
sin cos No. sine, cosine : trigonometric function π : π = 3.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin : odd cos = cos : even.
 08 No. : No. : No.3 : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No.0 : No. : sin cos No. sine, cosine : trigonometric function π : π = 3.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin
08 No. : No. : No.3 : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No.0 : No. : sin cos No. sine, cosine : trigonometric function π : π = 3.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin
1 1.1 ( ). z = a + bi, a, b R 0 a, b 0 a 2 + b 2 0 z = a + bi = ( ) a 2 + b 2 a a 2 + b + b 2 a 2 + b i 2 r = a 2 + b 2 θ cos θ = a a 2 + b 2, sin θ =
 1 1.1 ( ). z = + bi,, b R 0, b 0 2 + b 2 0 z = + bi = ( ) 2 + b 2 2 + b + b 2 2 + b i 2 r = 2 + b 2 θ cos θ = 2 + b 2, sin θ = b 2 + b 2 2π z = r(cos θ + i sin θ) 1.2 (, ). 1. < 2. > 3. ±,, 1.3 ( ). A
1 1.1 ( ). z = + bi,, b R 0, b 0 2 + b 2 0 z = + bi = ( ) 2 + b 2 2 + b + b 2 2 + b i 2 r = 2 + b 2 θ cos θ = 2 + b 2, sin θ = b 2 + b 2 2π z = r(cos θ + i sin θ) 1.2 (, ). 1. < 2. > 3. ±,, 1.3 ( ). A
z f(z) f(z) x, y, u, v, r, θ r > 0 z = x + iy, f = u + iv C γ D f(z) f(z) D f(z) f(z) z, Rm z, z 1.1 z = x + iy = re iθ = r (cos θ + i sin θ) z = x iy
 z fz fz x, y, u, v, r, θ r > z = x + iy, f = u + iv γ D fz fz D fz fz z, Rm z, z. z = x + iy = re iθ = r cos θ + i sin θ z = x iy = re iθ = r cos θ i sin θ x = z + z = Re z, y = z z = Im z i r = z = z
z fz fz x, y, u, v, r, θ r > z = x + iy, f = u + iv γ D fz fz D fz fz z, Rm z, z. z = x + iy = re iθ = r cos θ + i sin θ z = x iy = re iθ = r cos θ i sin θ x = z + z = Re z, y = z z = Im z i r = z = z
I No. sin cos sine, cosine : trigonometric function π : π =.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin : odd cos = cos : even.
 I 0 No. : No. : No. : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No.0 : I No. sin cos sine, cosine : trigonometric function π : π =.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin : odd
I 0 No. : No. : No. : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No.0 : I No. sin cos sine, cosine : trigonometric function π : π =.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin : odd
nsg04-28/ky208684356100043077
 δ!!! μ μ μ γ UBE3A Ube3a Ube3a δ !!!! α α α α α α α α α α μ μ α β α β β !!!!!!!! μ! Suncus murinus μ Ω! π μ Ω in vivo! μ μ μ!!! ! in situ! in vivo δ δ !!!!!!!!!! ! in vivo Orexin-Arch Orexin-Arch !!
δ!!! μ μ μ γ UBE3A Ube3a Ube3a δ !!!! α α α α α α α α α α μ μ α β α β β !!!!!!!! μ! Suncus murinus μ Ω! π μ Ω in vivo! μ μ μ!!! ! in situ! in vivo δ δ !!!!!!!!!! ! in vivo Orexin-Arch Orexin-Arch !!
II A A441 : October 02, 2014 Version : Kawahira, Tomoki TA (Kondo, Hirotaka )
 II 214-1 : October 2, 214 Version : 1.1 Kawahira, Tomoki TA (Kondo, Hirotaka ) http://www.math.nagoya-u.ac.jp/~kawahira/courses/14w-biseki.html pdf 1 2 1 9 1 16 1 23 1 3 11 6 11 13 11 2 11 27 12 4 12 11
II 214-1 : October 2, 214 Version : 1.1 Kawahira, Tomoki TA (Kondo, Hirotaka ) http://www.math.nagoya-u.ac.jp/~kawahira/courses/14w-biseki.html pdf 1 2 1 9 1 16 1 23 1 3 11 6 11 13 11 2 11 27 12 4 12 11
1 filename=mathformula tex 1 ax 2 + bx + c = 0, x = b ± b 2 4ac, (1.1) 2a x 1 + x 2 = b a, x 1x 2 = c a, (1.2) ax 2 + 2b x + c = 0, x = b ± b 2
 filename=mathformula58.tex ax + bx + c =, x = b ± b 4ac, (.) a x + x = b a, x x = c a, (.) ax + b x + c =, x = b ± b ac. a (.3). sin(a ± B) = sin A cos B ± cos A sin B, (.) cos(a ± B) = cos A cos B sin
filename=mathformula58.tex ax + bx + c =, x = b ± b 4ac, (.) a x + x = b a, x x = c a, (.) ax + b x + c =, x = b ± b ac. a (.3). sin(a ± B) = sin A cos B ± cos A sin B, (.) cos(a ± B) = cos A cos B sin
(ii) (iii) z a = z a =2 z a =6 sin z z a dz. cosh z z a dz. e z dz. (, a b > 6.) (z a)(z b) 52.. (a) dz, ( a = /6.), (b) z =6 az (c) z a =2 53. f n (z
 B 4 24 7 9 ( ) :,..,,.,. 4 4. f(z): D C: D a C, 2πi C f(z) dz = f(a). z a a C, ( ). (ii), a D, a U a,r D f. f(z) = A n (z a) n, z U a,r, n= A n := 2πi C f(ζ) dζ, n =,,..., (ζ a) n+, C a D. (iii) U a,r
B 4 24 7 9 ( ) :,..,,.,. 4 4. f(z): D C: D a C, 2πi C f(z) dz = f(a). z a a C, ( ). (ii), a D, a U a,r D f. f(z) = A n (z a) n, z U a,r, n= A n := 2πi C f(ζ) dζ, n =,,..., (ζ a) n+, C a D. (iii) U a,r
30
 3 ............................................2 2...........................................2....................................2.2...................................2.3..............................
3 ............................................2 2...........................................2....................................2.2...................................2.3..............................
(3) (2),,. ( 20) ( s200103) 0.7 x C,, x 2 + y 2 + ax = 0 a.. D,. D, y C, C (x, y) (y 0) C m. (2) D y = y(x) (x ± y 0), (x, y) D, m, m = 1., D. (x 2 y
 [ ] 7 0.1 2 2 + y = t sin t IC ( 9) ( s090101) 0.2 y = d2 y 2, y = x 3 y + y 2 = 0 (2) y + 2y 3y = e 2x 0.3 1 ( y ) = f x C u = y x ( 15) ( s150102) [ ] y/x du x = Cexp f(u) u (2) x y = xey/x ( 16) ( s160101)
[ ] 7 0.1 2 2 + y = t sin t IC ( 9) ( s090101) 0.2 y = d2 y 2, y = x 3 y + y 2 = 0 (2) y + 2y 3y = e 2x 0.3 1 ( y ) = f x C u = y x ( 15) ( s150102) [ ] y/x du x = Cexp f(u) u (2) x y = xey/x ( 16) ( s160101)
2011de.dvi
 211 ( 4 2 1. 3 1.1............................... 3 1.2 1- -......................... 13 1.3 2-1 -................... 19 1.4 3- -......................... 29 2. 37 2.1................................ 37
211 ( 4 2 1. 3 1.1............................... 3 1.2 1- -......................... 13 1.3 2-1 -................... 19 1.4 3- -......................... 29 2. 37 2.1................................ 37
II (10 4 ) 1. p (x, y) (a, b) ε(x, y; a, b) 0 f (x, y) f (a, b) A, B (6.5) y = b f (x, b) f (a, b) x a = A + ε(x, b; a, b) x a 2 x a 0 A = f x (
 II (1 4 ) 1. p.13 1 (x, y) (a, b) ε(x, y; a, b) f (x, y) f (a, b) A, B (6.5) y = b f (x, b) f (a, b) x a = A + ε(x, b; a, b) x a x a A = f x (a, b) y x 3 3y 3 (x, y) (, ) f (x, y) = x + y (x, y) = (, )
II (1 4 ) 1. p.13 1 (x, y) (a, b) ε(x, y; a, b) f (x, y) f (a, b) A, B (6.5) y = b f (x, b) f (a, b) x a = A + ε(x, b; a, b) x a x a A = f x (a, b) y x 3 3y 3 (x, y) (, ) f (x, y) = x + y (x, y) = (, )
: , 2.0, 3.0, 2.0, (%) ( 2.
 2017 1 2 1.1...................................... 2 1.2......................................... 4 1.3........................................... 10 1.4................................. 14 1.5..........................................
2017 1 2 1.1...................................... 2 1.2......................................... 4 1.3........................................... 10 1.4................................. 14 1.5..........................................
.2 ρ dv dt = ρk grad p + 3 η grad (divv) + η 2 v.3 divh = 0, rote + c H t = 0 dive = ρ, H = 0, E = ρ, roth c E t = c ρv E + H c t = 0 H c E t = c ρv T
 NHK 204 2 0 203 2 24 ( ) 7 00 7 50 203 2 25 ( ) 7 00 7 50 203 2 26 ( ) 7 00 7 50 203 2 27 ( ) 7 00 7 50 I. ( ν R n 2 ) m 2 n m, R = e 2 8πε 0 hca B =.09737 0 7 m ( ν = ) λ a B = 4πε 0ħ 2 m e e 2 = 5.2977
NHK 204 2 0 203 2 24 ( ) 7 00 7 50 203 2 25 ( ) 7 00 7 50 203 2 26 ( ) 7 00 7 50 203 2 27 ( ) 7 00 7 50 I. ( ν R n 2 ) m 2 n m, R = e 2 8πε 0 hca B =.09737 0 7 m ( ν = ) λ a B = 4πε 0ħ 2 m e e 2 = 5.2977
nm (T = K, p = kP a (1atm( )), 1bar = 10 5 P a = atm) 1 ( ) m / m
 .1 1nm (T = 73.15K, p = 101.35kP a (1atm( )), 1bar = 10 5 P a = 0.9863atm) 1 ( ).413968 10 3 m 3 1 37. 1/3 3.34.414 10 3 m 3 6.0 10 3 = 3.7 (109 ) 3 (nm) 3 10 6 = 3.7 10 1 (nm) 3 = (3.34nm) 3 ( P = nrt,
.1 1nm (T = 73.15K, p = 101.35kP a (1atm( )), 1bar = 10 5 P a = 0.9863atm) 1 ( ).413968 10 3 m 3 1 37. 1/3 3.34.414 10 3 m 3 6.0 10 3 = 3.7 (109 ) 3 (nm) 3 10 6 = 3.7 10 1 (nm) 3 = (3.34nm) 3 ( P = nrt,
201711grade1ouyou.pdf
 2017 11 26 1 2 52 3 12 13 22 23 32 33 42 3 5 3 4 90 5 6 A 1 2 Web Web 3 4 1 2... 5 6 7 7 44 8 9 1 2 3 1 p p >2 2 A 1 2 0.6 0.4 0.52... (a) 0.6 0.4...... B 1 2 0.8-0.2 0.52..... (b) 0.6 0.52.... 1 A B 2
2017 11 26 1 2 52 3 12 13 22 23 32 33 42 3 5 3 4 90 5 6 A 1 2 Web Web 3 4 1 2... 5 6 7 7 44 8 9 1 2 3 1 p p >2 2 A 1 2 0.6 0.4 0.52... (a) 0.6 0.4...... B 1 2 0.8-0.2 0.52..... (b) 0.6 0.52.... 1 A B 2
H 0 H = H 0 + V (t), V (t) = gµ B S α qb e e iωt i t Ψ(t) = [H 0 + V (t)]ψ(t) Φ(t) Ψ(t) = e ih0t Φ(t) H 0 e ih0t Φ(t) + ie ih0t t Φ(t) = [
![H 0 H = H 0 + V (t), V (t) = gµ B S α qb e e iωt i t Ψ(t) = [H 0 + V (t)]ψ(t) Φ(t) Ψ(t) = e ih0t Φ(t) H 0 e ih0t Φ(t) + ie ih0t t Φ(t) = [ H 0 H = H 0 + V (t), V (t) = gµ B S α qb e e iωt i t Ψ(t) = [H 0 + V (t)]ψ(t) Φ(t) Ψ(t) = e ih0t Φ(t) H 0 e ih0t Φ(t) + ie ih0t t Φ(t) = [](/thumbs/99/141438442.jpg) 3 3. 3.. H H = H + V (t), V (t) = gµ B α B e e iωt i t Ψ(t) = [H + V (t)]ψ(t) Φ(t) Ψ(t) = e iht Φ(t) H e iht Φ(t) + ie iht t Φ(t) = [H + V (t)]e iht Φ(t) Φ(t) i t Φ(t) = V H(t)Φ(t), V H (t) = e iht V (t)e
3 3. 3.. H H = H + V (t), V (t) = gµ B α B e e iωt i t Ψ(t) = [H + V (t)]ψ(t) Φ(t) Ψ(t) = e iht Φ(t) H e iht Φ(t) + ie iht t Φ(t) = [H + V (t)]e iht Φ(t) Φ(t) i t Φ(t) = V H(t)Φ(t), V H (t) = e iht V (t)e
基礎数学I
 I & II ii ii........... 22................. 25 12............... 28.................. 28.................... 31............. 32.................. 34 3 1 9.................... 1....................... 1............
I & II ii ii........... 22................. 25 12............... 28.................. 28.................... 31............. 32.................. 34 3 1 9.................... 1....................... 1............
grad φ(p ) φ P grad φ(p ) p P p φ P p l t φ l t = 0 g (0) g (0) (31) grad φ(p ) p grad φ φ (P, φ(p )) xy (x, y) = (ξ(t), η(t)) ( )
 2 9 2 5 2.2.3 grad φ(p ) φ P grad φ(p ) p P p φ P p l t φ l t = g () g () (3) grad φ(p ) p grad φ φ (P, φ(p )) y (, y) = (ξ(t), η(t)) ( ) ξ (t) (t) := η (t) grad f(ξ(t), η(t)) (t) g(t) := f(ξ(t), η(t))
2 9 2 5 2.2.3 grad φ(p ) φ P grad φ(p ) p P p φ P p l t φ l t = g () g () (3) grad φ(p ) p grad φ φ (P, φ(p )) y (, y) = (ξ(t), η(t)) ( ) ξ (t) (t) := η (t) grad f(ξ(t), η(t)) (t) g(t) := f(ξ(t), η(t))
II 2 II
 II 2 II 2005 yugami@cc.utsunomiya-u.ac.jp 2005 4 1 1 2 5 2.1.................................... 5 2.2................................. 6 2.3............................. 6 2.4.................................
II 2 II 2005 yugami@cc.utsunomiya-u.ac.jp 2005 4 1 1 2 5 2.1.................................... 5 2.2................................. 6 2.3............................. 6 2.4.................................
H.Haken Synergetics 2nd (1978)
 27 3 27 ) Ising Landau Synergetics Fokker-Planck F-P Landau F-P Gizburg-Landau G-L G-L Bénard/ Hopfield H.Haken Synergetics 2nd (1978) (1) Ising m T T C 1: m h Hamiltonian H = J ij S i S j h i S
27 3 27 ) Ising Landau Synergetics Fokker-Planck F-P Landau F-P Gizburg-Landau G-L G-L Bénard/ Hopfield H.Haken Synergetics 2nd (1978) (1) Ising m T T C 1: m h Hamiltonian H = J ij S i S j h i S
(Bessel) (Legendre).. (Hankel). (Laplace) V = (x, y, z) n (r, θ, ϕ) r n f n (θ, ϕ). f n (θ, ϕ) n f n (θ, ϕ) z = cos θ z θ ϕ n ν. P ν (z), Q ν (z) (Fou
 (Bessel) (Legendre).. (Hankel). (Laplace) V = (x, y, z) n (r, θ, ϕ) r n f n (θ, ϕ). f n (θ, ϕ) n f n (θ, ϕ) z = cos θ z θ ϕ n ν. P ν (z), Q ν (z) (Fourier) (Fourier Bessel).. V ρ(x, y, z) V = 4πGρ G :.
(Bessel) (Legendre).. (Hankel). (Laplace) V = (x, y, z) n (r, θ, ϕ) r n f n (θ, ϕ). f n (θ, ϕ) n f n (θ, ϕ) z = cos θ z θ ϕ n ν. P ν (z), Q ν (z) (Fourier) (Fourier Bessel).. V ρ(x, y, z) V = 4πGρ G :.
O1-1 O1-2 O1-3 O1-4 O1-5 O1-6
 O1-1 O1-2 O1-3 O1-4 O1-5 O1-6 O1-7 O1-8 O1-9 O1-10 O1-11 O1-12 O1-13 O1-14 O1-15 O1-16 O1-17 O1-18 O1-19 O1-20 O1-21 O1-22 O1-23 O1-24 O1-25 O1-26 O1-27 O1-28 O1-29 O1-30 O1-31 O1-32 O1-33 O1-34 O1-35
O1-1 O1-2 O1-3 O1-4 O1-5 O1-6 O1-7 O1-8 O1-9 O1-10 O1-11 O1-12 O1-13 O1-14 O1-15 O1-16 O1-17 O1-18 O1-19 O1-20 O1-21 O1-22 O1-23 O1-24 O1-25 O1-26 O1-27 O1-28 O1-29 O1-30 O1-31 O1-32 O1-33 O1-34 O1-35
1. (8) (1) (x + y) + (x + y) = 0 () (x + y ) 5xy = 0 (3) (x y + 3y 3 ) (x 3 + xy ) = 0 (4) x tan y x y + x = 0 (5) x = y + x + y (6) = x + y 1 x y 3 (
 1 1.1 (1) (1 + x) + (1 + y) = 0 () x + y = 0 (3) xy = x (4) x(y + 3) + y(y + 3) = 0 (5) (a + y ) = x ax a (6) x y 1 + y x 1 = 0 (7) cos x + sin x cos y = 0 (8) = tan y tan x (9) = (y 1) tan x (10) (1 +
1 1.1 (1) (1 + x) + (1 + y) = 0 () x + y = 0 (3) xy = x (4) x(y + 3) + y(y + 3) = 0 (5) (a + y ) = x ax a (6) x y 1 + y x 1 = 0 (7) cos x + sin x cos y = 0 (8) = tan y tan x (9) = (y 1) tan x (10) (1 +
1. z dr er r sinθ dϕ eϕ r dθ eθ dr θ dr dθ r x 0 ϕ r sinθ dϕ r sinθ dϕ y dr dr er r dθ eθ r sinθ dϕ eϕ 2. (r, θ, φ) 2 dr 1 h r dr 1 e r h θ dθ 1 e θ h
 IB IIA 1 1 r, θ, φ 1 (r, θ, φ)., r, θ, φ 0 r
IB IIA 1 1 r, θ, φ 1 (r, θ, φ)., r, θ, φ 0 r
 K E N Z U 2012 7 16 HP M. 1 1 4 1.1 3.......................... 4 1.2................................... 4 1.2.1..................................... 4 1.2.2.................................... 5................................
K E N Z U 2012 7 16 HP M. 1 1 4 1.1 3.......................... 4 1.2................................... 4 1.2.1..................................... 4 1.2.2.................................... 5................................
II Karel Švadlenka * [1] 1.1* 5 23 m d2 x dt 2 = cdx kx + mg dt. c, g, k, m 1.2* u = au + bv v = cu + dv v u a, b, c, d R
![II Karel Švadlenka * [1] 1.1* 5 23 m d2 x dt 2 = cdx kx + mg dt. c, g, k, m 1.2* u = au + bv v = cu + dv v u a, b, c, d R II Karel Švadlenka * [1] 1.1* 5 23 m d2 x dt 2 = cdx kx + mg dt. c, g, k, m 1.2* u = au + bv v = cu + dv v u a, b, c, d R](/thumbs/95/125540821.jpg) II Karel Švadlenka 2018 5 26 * [1] 1.1* 5 23 m d2 x dt 2 = cdx kx + mg dt. c, g, k, m 1.2* 5 23 1 u = au + bv v = cu + dv v u a, b, c, d R 1.3 14 14 60% 1.4 5 23 a, b R a 2 4b < 0 λ 2 + aλ + b = 0 λ =
II Karel Švadlenka 2018 5 26 * [1] 1.1* 5 23 m d2 x dt 2 = cdx kx + mg dt. c, g, k, m 1.2* 5 23 1 u = au + bv v = cu + dv v u a, b, c, d R 1.3 14 14 60% 1.4 5 23 a, b R a 2 4b < 0 λ 2 + aλ + b = 0 λ =
29
 9 .,,, 3 () C k k C k C + C + C + + C 8 + C 9 + C k C + C + C + C 3 + C 4 + C 5 + + 45 + + + 5 + + 9 + 4 + 4 + 5 4 C k k k ( + ) 4 C k k ( k) 3 n( ) n n n ( ) n ( ) n 3 ( ) 3 3 3 n 4 ( ) 4 4 4 ( ) n n
9 .,,, 3 () C k k C k C + C + C + + C 8 + C 9 + C k C + C + C + C 3 + C 4 + C 5 + + 45 + + + 5 + + 9 + 4 + 4 + 5 4 C k k k ( + ) 4 C k k ( k) 3 n( ) n n n ( ) n ( ) n 3 ( ) 3 3 3 n 4 ( ) 4 4 4 ( ) n n
Gauss Gauss ɛ 0 E ds = Q (1) xy σ (x, y, z) (2) a ρ(x, y, z) = x 2 + y 2 (r, θ, φ) (1) xy A Gauss ɛ 0 E ds = ɛ 0 EA Q = ρa ɛ 0 EA = ρea E = (ρ/ɛ 0 )e
 7 -a 7 -a February 4, 2007 1. 2. 3. 4. 1. 2. 3. 1 Gauss Gauss ɛ 0 E ds = Q (1) xy σ (x, y, z) (2) a ρ(x, y, z) = x 2 + y 2 (r, θ, φ) (1) xy A Gauss ɛ 0 E ds = ɛ 0 EA Q = ρa ɛ 0 EA = ρea E = (ρ/ɛ 0 )e z
7 -a 7 -a February 4, 2007 1. 2. 3. 4. 1. 2. 3. 1 Gauss Gauss ɛ 0 E ds = Q (1) xy σ (x, y, z) (2) a ρ(x, y, z) = x 2 + y 2 (r, θ, φ) (1) xy A Gauss ɛ 0 E ds = ɛ 0 EA Q = ρa ɛ 0 EA = ρea E = (ρ/ɛ 0 )e z
 K E N Z U 01 7 16 HP M. 1 1 4 1.1 3.......................... 4 1.................................... 4 1..1..................................... 4 1...................................... 5................................
K E N Z U 01 7 16 HP M. 1 1 4 1.1 3.......................... 4 1.................................... 4 1..1..................................... 4 1...................................... 5................................
°ÌÁê¿ô³ØII
 July 14, 2007 Brouwer f f(x) = x x f(z) = 0 2 f : S 2 R 2 f(x) = f( x) x S 2 3 3 2 - - - 1. X x X U(x) U(x) x U = {U(x) x X} X 1. U(x) A U(x) x 2. A U(x), A B B U(x) 3. A, B U(x) A B U(x) 4. A U(x),
July 14, 2007 Brouwer f f(x) = x x f(z) = 0 2 f : S 2 R 2 f(x) = f( x) x S 2 3 3 2 - - - 1. X x X U(x) U(x) x U = {U(x) x X} X 1. U(x) A U(x) x 2. A U(x), A B B U(x) 3. A, B U(x) A B U(x) 4. A U(x),
Note.tex 2008/09/19( )
 1 20 9 19 2 1 5 1.1........................ 5 1.2............................. 8 2 9 2.1............................. 9 2.2.............................. 10 3 13 3.1.............................. 13 3.2..................................
1 20 9 19 2 1 5 1.1........................ 5 1.2............................. 8 2 9 2.1............................. 9 2.2.............................. 10 3 13 3.1.............................. 13 3.2..................................
untitled
 . x2.0 0.5 0 0.5.0 x 2 t= 0: : x α ij β j O x2 u I = α x j ij i i= 0 y j = + exp( u ) j v J = β y j= 0 j j o = + exp( v ) 0 0 e x p e x p J j I j ij i i o x β α = = = + +.. 2 3 8 x 75 58 28 36 x2 3 3 4
. x2.0 0.5 0 0.5.0 x 2 t= 0: : x α ij β j O x2 u I = α x j ij i i= 0 y j = + exp( u ) j v J = β y j= 0 j j o = + exp( v ) 0 0 e x p e x p J j I j ij i i o x β α = = = + +.. 2 3 8 x 75 58 28 36 x2 3 3 4
I, II 1, A = A 4 : 6 = max{ A, } A A 10 10%
 1 2006.4.17. A 3-312 tel: 092-726-4774, e-mail: hara@math.kyushu-u.ac.jp, http://www.math.kyushu-u.ac.jp/ hara/lectures/lectures-j.html Office hours: B A I ɛ-δ ɛ-δ 1. 2. A 1. 1. 2. 3. 4. 5. 2. ɛ-δ 1. ɛ-n
1 2006.4.17. A 3-312 tel: 092-726-4774, e-mail: hara@math.kyushu-u.ac.jp, http://www.math.kyushu-u.ac.jp/ hara/lectures/lectures-j.html Office hours: B A I ɛ-δ ɛ-δ 1. 2. A 1. 1. 2. 3. 4. 5. 2. ɛ-δ 1. ɛ-n
() x + y + y + x dy dx = 0 () dy + xy = x dx y + x y ( 5) ( s55906) 0.7. (). 5 (). ( 6) ( s6590) 0.8 m n. 0.9 n n A. ( 6) ( s6590) f A (λ) = det(a λi)
 0. A A = 4 IC () det A () A () x + y + z = x y z X Y Z = A x y z ( 5) ( s5590) 0. a + b + c b c () a a + b + c c a b a + b + c 0 a b c () a 0 c b b c 0 a c b a 0 0. A A = 7 5 4 5 0 ( 5) ( s5590) () A ()
0. A A = 4 IC () det A () A () x + y + z = x y z X Y Z = A x y z ( 5) ( s5590) 0. a + b + c b c () a a + b + c c a b a + b + c 0 a b c () a 0 c b b c 0 a c b a 0 0. A A = 7 5 4 5 0 ( 5) ( s5590) () A ()
e a b a b b a a a 1 a a 1 = a 1 a = e G G G : x ( x =, 8, 1 ) x 1,, 60 θ, ϕ ψ θ G G H H G x. n n 1 n 1 n σ = (σ 1, σ,..., σ N ) i σ i i n S n n = 1,,
 01 10 18 ( ) 1 6 6 1 8 8 1 6 1 0 0 0 0 1 Table 1: 10 0 8 180 1 1 1. ( : 60 60 ) : 1. 1 e a b a b b a a a 1 a a 1 = a 1 a = e G G G : x ( x =, 8, 1 ) x 1,, 60 θ, ϕ ψ θ G G H H G x. n n 1 n 1 n σ = (σ 1,
01 10 18 ( ) 1 6 6 1 8 8 1 6 1 0 0 0 0 1 Table 1: 10 0 8 180 1 1 1. ( : 60 60 ) : 1. 1 e a b a b b a a a 1 a a 1 = a 1 a = e G G G : x ( x =, 8, 1 ) x 1,, 60 θ, ϕ ψ θ G G H H G x. n n 1 n 1 n σ = (σ 1,
2000年度『数学展望 I』講義録
 2000 I I IV I II 2000 I I IV I-IV. i ii 3.10 (http://www.math.nagoya-u.ac.jp/ kanai/) 2000 A....1 B....4 C....10 D....13 E....17 Brouwer A....21 B....26 C....33 D....39 E. Sperner...45 F....48 A....53
2000 I I IV I II 2000 I I IV I-IV. i ii 3.10 (http://www.math.nagoya-u.ac.jp/ kanai/) 2000 A....1 B....4 C....10 D....13 E....17 Brouwer A....21 B....26 C....33 D....39 E. Sperner...45 F....48 A....53
2016 ǯ¥Î¡¼¥Ù¥ëʪÍý³Ø¾Þ²òÀ⥻¥ß¥Ê¡¼ Kosterlitz-Thouless ž°Ü¤È Haldane ͽÁÛ
 2016 Kosterlitz-Thouless Haldane Dept. of Phys., Kyushu Univ. 2016 11 29 2016 Figure: D.J.Thouless F D.M.Haldane J.M.Kosterlitz TOPOLOGICAL PHASE TRANSITIONS AND TOPOLOGICAL PHASES OF MATTER ( ) ( ) (Dirac,
2016 Kosterlitz-Thouless Haldane Dept. of Phys., Kyushu Univ. 2016 11 29 2016 Figure: D.J.Thouless F D.M.Haldane J.M.Kosterlitz TOPOLOGICAL PHASE TRANSITIONS AND TOPOLOGICAL PHASES OF MATTER ( ) ( ) (Dirac,
SO(3) 7 = = 1 ( r ) + 1 r r r r ( l ) (5.17) l = 1 ( sin θ ) + sin θ θ θ ϕ (5.18) χ(r)ψ(θ, ϕ) l ψ = αψ (5.19) l 1 = i(sin ϕ θ l = i( cos ϕ θ l 3 = i ϕ
 SO(3) 71 5.7 5.7.1 1 ħ L k l k l k = iϵ kij x i j (5.117) l k SO(3) l z l ± = l 1 ± il = i(y z z y ) ± (z x x z ) = ( x iy) z ± z( x ± i y ) = X ± z ± z (5.118) l z = i(x y y x ) = 1 [(x + iy)( x i y )
SO(3) 71 5.7 5.7.1 1 ħ L k l k l k = iϵ kij x i j (5.117) l k SO(3) l z l ± = l 1 ± il = i(y z z y ) ± (z x x z ) = ( x iy) z ± z( x ± i y ) = X ± z ± z (5.118) l z = i(x y y x ) = 1 [(x + iy)( x i y )
zz + 3i(z z) + 5 = 0 + i z + i = z 2i z z z y zz + 3i (z z) + 5 = 0 (z 3i) (z + 3i) = 9 5 = 4 z 3i = 2 (3i) zz i (z z) + 1 = a 2 {
 04 zz + iz z) + 5 = 0 + i z + i = z i z z z 970 0 y zz + i z z) + 5 = 0 z i) z + i) = 9 5 = 4 z i = i) zz i z z) + = a {zz + i z z) + 4} a ) zz + a + ) z z) + 4a = 0 4a a = 5 a = x i) i) : c Darumafactory
04 zz + iz z) + 5 = 0 + i z + i = z i z z z 970 0 y zz + i z z) + 5 = 0 z i) z + i) = 9 5 = 4 z i = i) zz i z z) + = a {zz + i z z) + 4} a ) zz + a + ) z z) + 4a = 0 4a a = 5 a = x i) i) : c Darumafactory
 1 911 9001030 9:00 A B C D E F G H I J K L M 1A0900 1B0900 1C0900 1D0900 1E0900 1F0900 1G0900 1H0900 1I0900 1J0900 1K0900 1L0900 1M0900 9:15 1A0915 1B0915 1C0915 1D0915 1E0915 1F0915 1G0915 1H0915 1I0915
1 911 9001030 9:00 A B C D E F G H I J K L M 1A0900 1B0900 1C0900 1D0900 1E0900 1F0900 1G0900 1H0900 1I0900 1J0900 1K0900 1L0900 1M0900 9:15 1A0915 1B0915 1C0915 1D0915 1E0915 1F0915 1G0915 1H0915 1I0915
3 filename=quantum-3dim110705a.tex ,2 [1],[2],[3] [3] U(x, y, z; t), p x ˆp x = h i x, p y ˆp y = h i y, p z ˆp z = h
![3 filename=quantum-3dim110705a.tex ,2 [1],[2],[3] [3] U(x, y, z; t), p x ˆp x = h i x, p y ˆp y = h i y, p z ˆp z = h 3 filename=quantum-3dim110705a.tex ,2 [1],[2],[3] [3] U(x, y, z; t), p x ˆp x = h i x, p y ˆp y = h i y, p z ˆp z = h](/thumbs/102/156509212.jpg) filename=quantum-dim110705a.tex 1 1. 1, [1],[],[]. 1980 []..1 U(x, y, z; t), p x ˆp x = h i x, p y ˆp y = h i y, p z ˆp z = h i z (.1) Ĥ ( ) Ĥ = h m x + y + + U(x, y, z; t) (.) z (U(x, y, z; t)) (U(x,
filename=quantum-dim110705a.tex 1 1. 1, [1],[],[]. 1980 []..1 U(x, y, z; t), p x ˆp x = h i x, p y ˆp y = h i y, p z ˆp z = h i z (.1) Ĥ ( ) Ĥ = h m x + y + + U(x, y, z; t) (.) z (U(x, y, z; t)) (U(x,









