RIMS98R2.dvi

RIMS Kokyuroku, vol.084, (999), 45 59. Euler Fourier Euler Fourier S = ( ) n f(n) = e in f(n) (.) I = 0 e ix f(x) dx (.2) Euler Fourier Fourier Euler Euler Fourier Euler Euler Fourier Fourier [5], [6]

(Masatake MORI) 1., $I= \int_{-1}^{1}\frac{dx}{\mathrm{r}_{2-x})(1-\mathcal{i}1}.$ (1.1) $\overline{(2-x)(1-\mathcal{i})^{1}/4(1

1040 1998 143-153 143 (Masatake MORI) 1 $I= \int_{-1}^{1}\frac{dx}{\mathrm{r}_{2-x})(1-\mathcal{i}1}$ (11) $\overline{(2-x)(1-\mathcal{i})^{1}/4(1+x)3/4}$ 1974 [31 8 10 11] $I= \int_{a}^{b}f(\mathcal{i})d_{x}$

211 kotaro@math.titech.ac.jp 1 R *1 n n R n *2 R n = {(x 1,..., x n ) x 1,..., x n R}. R R 2 R 3 R n R n R n D D R n *3 ) (x 1,..., x n ) f(x 1,..., x n ) f D *4 n 2 n = 1 ( ) 1 f D R n f : D R 1.1. (x,

第5章 偏微分方程式の境界値問題

October 5, 2018 1 / 113 4 ( ) 2 / 113 Poisson 5.1 Poisson ( A.7.1) Poisson Poisson 1 (A.6 ) Γ p p N u D Γ D b 5.1.1: = Γ D Γ N 3 / 113 Poisson 5.1.1 d {2, 3} Lipschitz (A.5 ) Γ D Γ N = \ Γ D Γ p Γ N Γ

(iii) 0 V, x V, x + 0 = x. 0. (iv) x V, y V, x + y = 0., y x, y = x. (v) 1x = x. (vii) (α + β)x = αx + βx. (viii) (αβ)x = α(βx)., V, C.,,., (1)

1. 1.1...,. 1.1.1 V, V x, y, x y x + y x + y V,, V x α, αx αx V,, (i) (viii) : x, y, z V, α, β C, (i) x + y = y + x. (ii) (x + y) + z = x + (y + z). 1 (iii) 0 V, x V, x + 0 = x. 0. (iv) x V, y V, x + y

Lebesgue Fubini L p Banach, Hilbert Höld

II (Analysis II) Lebesgue (Applications of Lebesgue Integral Theory) 1 (Seiji HIABA) 1 ( ),,, ( ) 1 1 1.1 1 Lebesgue........................ 1 1.2 2 Fubini...................... 2 2 L p 5 2.1 Banach, Hilbert..............................

微分積分 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. このサンプルページの内容は, 初版 1 刷発行時のものです.

微分積分 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. ttp://www.morikita.co.jp/books/mid/00571 このサンプルページの内容は, 初版 1 刷発行時のものです. i ii 014 10 iii [note] 1 3 iv 4 5 3 6 4 x 0 sin x x 1 5 6 z = f(x, y) 1 y = f(x)

Title 二重指数関数型変数変換を用いたSinc 関数近似 ( 科学技術における数値計算の理論と応用 II) Author(s) 杉原, 正顯 Citation 数理解析研究所講究録 (1997), 990: Issue Date URL

Title 二重指数関数型変数変換を用いたSinc 関数近似 ( 科学技術における数値計算の理論と応用 II) Author(s) 杉原 正顯 Citation 数理解析研究所講究録 (1997) 990 125-134 Issue Date 1997-04 URL http//hdlhandlenet/2433/61094 Right Type Departmental Bulletin Paper

S I. dy fx x fx y fx + C 3 C dy fx 4 x, y dy v C xt y C v e kt k > xt yt gt [ v dt dt v e kt xt v e kt + C k x v + C C k xt v k 3 r r + dr e kt S dt d

S I.. http://ayapin.film.s.dendai.ac.jp/~matuda /TeX/lecture.html PDF PS.................................... 3.3.................... 9.4................5.............. 3 5. Laplace................. 5....

1 1.1 ( ). z = a + bi, a, b R 0 a, b 0 a 2 + b 2 0 z = a + bi = ( ) a 2 + b 2 a a 2 + b + b 2 a 2 + b i 2 r = a 2 + b 2 θ cos θ = a a 2 + b 2, sin θ =

1 1.1 ( ). z = + bi,, b R 0, b 0 2 + b 2 0 z = + bi = ( ) 2 + b 2 2 + b + b 2 2 + b i 2 r = 2 + b 2 θ cos θ = 2 + b 2, sin θ = b 2 + b 2 2π z = r(cos θ + i sin θ) 1.2 (, ). 1. < 2. > 3. ±,, 1.3 ( ). A

I A A441 : April 21, 2014 Version : Kawahira, Tomoki TA (Kondo, Hirotaka ) Google

I4 - : April, 4 Version :. Kwhir, Tomoki TA (Kondo, Hirotk) Google http://www.mth.ngoy-u.c.jp/~kwhir/courses/4s-biseki.html pdf 4 4 4 4 8 e 5 5 9 etc. 5 6 6 6 9 n etc. 6 6 6 3 6 3 7 7 etc 7 4 7 7 8 5 59

) ] [ h m x + y + + V x) φ = Eφ 1) z E = i h t 13) x << 1) N n n= = N N + 1) 14) N n n= = N N + 1)N + 1) 6 15) N n 3 n= = 1 4 N N + 1) 16) N n 4

1. k λ ν ω T v p v g k = π λ ω = πν = π T v p = λν = ω k v g = dω dk 1) ) 3) 4). p = hk = h λ 5) E = hν = hω 6) h = h π 7) h =6.6618 1 34 J sec) hc=197.3 MeV fm = 197.3 kev pm= 197.3 ev nm = 1.97 1 3 ev

Riemann-Stieltjes Poland S. Lojasiewicz [1] An introduction to the theory of real functions, John Wiley & Sons, Ltd., Chichester, 1988.,,,,. Riemann-S

Riemnn-Stieltjes Polnd S. Lojsiewicz [1] An introduction to the theory of rel functions, John Wiley & Sons, Ltd., Chichester, 1988.,,,, Riemnn-Stieltjes 1 2 2 5 3 6 4 Jordn 13 5 Riemnn-Stieltjes 15 6 Riemnn-Stieltjes

z f(z) f(z) x, y, u, v, r, θ r > 0 z = x + iy, f = u + iv C γ D f(z) f(z) D f(z) f(z) z, Rm z, z 1.1 z = x + iy = re iθ = r (cos θ + i sin θ) z = x iy

z fz fz x, y, u, v, r, θ r > z = x + iy, f = u + iv γ D fz fz D fz fz z, Rm z, z. z = x + iy = re iθ = r cos θ + i sin θ z = x iy = re iθ = r cos θ i sin θ x = z + z = Re z, y = z z = Im z i r = z = z

³ÎΨÏÀ

2017 12 12 Makoto Nakashima 2017 12 12 1 / 22 2.1. C, D π- C, D. A 1, A 2 C A 1 A 2 C A 3, A 4 D A 1 A 2 D Makoto Nakashima 2017 12 12 2 / 22 . (,, L p - ). Makoto Nakashima 2017 12 12 3 / 22 . (,, L p

SFGÇÃÉXÉyÉNÉgÉãå`.pdf

SFG 1 SFG SFG I SFG (ω) χ SFG (ω). SFG χ χ SFG (ω) = χ NR e iϕ +. ω ω + iγ SFG φ = ±π/, χ φ = ±π 3 χ SFG χ SFG = χ NR + χ (ω ω ) + Γ + χ NR χ (ω ω ) (ω ω ) + Γ cosϕ χ NR χ Γ (ω ω ) + Γ sinϕ. 3 (θ) 180

Trapezoidal Rule θ = 1/ x n x n 1 t = 1 [f(t n 1, x n 1 ) + f(t n, x n )] (6) 1. dx dt = f(t, x), x(t 0) = x 0 (7) t [t 0, t 1 ] f t [t 0, t 1 ], x x

University of Hyogo 8 8 1 d x(t) =f(t, x(t)), dt (1) x(t 0 ) =x 0 () t n = t 0 + n t x x n n x n x 0 x i i = 0,..., n 1 x n x(t) 1 1.1 1 1 1 0 θ 1 θ x n x n 1 t = θf(t n 1, x n 1 ) + (1 θ)f(t n, x n )

x () g(x) = f(t) dt f(x), F (x) 3x () g(x) g (x) f(x), F (x) (3) h(x) = x 3x tf(t) dt.9 = {(x, y) ; x, y, x + y } f(x, y) = xy( x y). h (x) f(x), F (x

[ ] IC. f(x) = e x () f(x) f (x) () lim f(x) lim f(x) x + x (3) lim f(x) lim f(x) x + x (4) y = f(x) ( ) ( s46). < a < () a () lim a log xdx a log xdx ( ) n (3) lim log k log n n n k=.3 z = log(x + y ),

II No.01 [n/2] [1]H n (x) H n (x) = ( 1) r n! r!(n 2r)! (2x)n 2r. r=0 [2]H n (x) n,, H n ( x) = ( 1) n H n (x). [3] H n (x) = ( 1) n dn x2 e dx n e x2

II No.1 [n/] [1]H n x) H n x) = 1) r n! r!n r)! x)n r r= []H n x) n,, H n x) = 1) n H n x) [3] H n x) = 1) n dn x e dx n e x [4] H n+1 x) = xh n x) nh n 1 x) ) d dx x H n x) = H n+1 x) d dx H nx) = nh

S I. dy fx x fx y fx + C 3 C vt dy fx 4 x, y dy yt gt + Ct + C dt v e kt xt v e kt + C k x v k + C C xt v k 3 r r + dr e kt S Sr πr dt d v } dt k e kt

S I. x yx y y, y,. F x, y, y, y,, y n http://ayapin.film.s.dendai.ac.jp/~matuda n /TeX/lecture.html PDF PS yx.................................... 3.3.................... 9.4................5..............

30

3 ............................................2 2...........................................2....................................2.2...................................2.3..............................

, 1.,,,.,., (Lin, 1955).,.,.,.,. f, 2,. main.tex 2011/08/13( )

81 4 2 4.1, 1.,,,.,., (Lin, 1955).,.,.,.,. f, 2,. 82 4.2. ζ t + V (ζ + βy) = 0 (4.2.1), V = 0 (4.2.2). (4.2.1), (3.3.66) R 1 Φ / Z, Γ., F 1 ( 3.2 ). 7,., ( )., (4.2.1) 500 hpa., 500 hpa (4.2.1) 1949,.,

2000年度『数学展望 I』講義録

2000 I I IV I II 2000 I I IV I-IV. i ii 3.10 (http://www.math.nagoya-u.ac.jp/ kanai/) 2000 A....1 B....4 C....10 D....13 E....17 Brouwer A....21 B....26 C....33 D....39 E. Sperner...45 F....48 A....53

2009 I 2 II III 14, 15, α β α β l 0 l l l l γ (1) γ = αβ (2) α β n n cos 2k n n π sin 2k n π k=1 k=1 3. a 0, a 1,..., a n α a

009 I II III 4, 5, 6 4 30. 0 α β α β l 0 l l l l γ ) γ αβ ) α β. n n cos k n n π sin k n π k k 3. a 0, a,..., a n α a 0 + a x + a x + + a n x n 0 ᾱ 4. [a, b] f y fx) y x 5. ) Arcsin 4) Arccos ) ) Arcsin

n ξ n,i, i = 1,, n S n ξ n,i n 0 R 1,.. σ 1 σ i .10.14.15 0 1 0 1 1 3.14 3.18 3.19 3.14 3.14,. ii 1 1 1.1..................................... 1 1............................... 3 1.3.........................

Z: Q: R: C: sin 6 5 ζ a, b

Z: Q: R: C: 3 3 7 4 sin 6 5 ζ 9 6 6............................... 6............................... 6.3......................... 4 7 6 8 8 9 3 33 a, b a bc c b a a b 5 3 5 3 5 5 3 a a a a p > p p p, 3,

Radiation from moving charges#1 Liénard-Wiechert potential Yuji Chinone 1 Maxwell Maxwell MKS E (x, t) + B (x, t) t = 0 (1) B (x, t) = 0 (2) B (x, t)

Radiation from moving harges# Liénard-Wiehert potential Yuji Chinone Maxwell Maxwell MKS E x, t + B x, t = B x, t = B x, t E x, t = µ j x, t 3 E x, t = ε ρ x, t 4 ε µ ε µ = E B ρ j A x, t φ x, t A x, t

f(x) = f(x ) + α(x)(x x ) α(x) x = x. x = f (y), x = f (y ) y = f f (y) = f f (y ) + α(f (y))(f (y) f (y )) f (y) = f (y ) + α(f (y)) (y y ) ( (2) ) f

22 A 3,4 No.3 () (2) (3) (4), (5) (6) (7) (8) () n x = (x,, x n ), = (,, n ), x = ( (x i i ) 2 ) /2 f(x) R n f(x) = f() + i α i (x ) i + o( x ) α,, α n g(x) = o( x )) lim x g(x) x = y = f() + i α i(x )

2010 II / y = e x y = log x = log e x 2. ( e x ) = e x 3. ( ) log x = 1 x 1.2 Warming Up 1 u = log a M a u = M a 0

2010 II 6 10.11.15/ 10.11.11 1 1 5.6 1.1 1. y = e x y = log x = log e x 2. e x ) = e x 3. ) log x = 1 x 1.2 Warming Up 1 u = log a M a u = M a 0 log a 1 a 1 log a a a r+s log a M + log a N 1 0 a 1 a r

I A A441 : April 15, 2013 Version : 1.1 I Kawahira, Tomoki TA (Shigehiro, Yoshida )

I013 00-1 : April 15, 013 Version : 1.1 I Kawahira, Tomoki TA (Shigehiro, Yoshida) http://www.math.nagoya-u.ac.jp/~kawahira/courses/13s-tenbou.html pdf * 4 15 4 5 13 e πi = 1 5 0 5 7 3 4 6 3 6 10 6 17

1. R n Ω ε G ε 0 Ω ε B n 2 Ωε = with Bu = 0 on Ω ε i=1 x 2 i ε +0 B Bu = u (Dirichlet, D Ω ε ), Bu = u ν (Neumann, N Ω ε ), Ω ε G ( ) / 25

.. IV 2012 10 4 ( ) 2012 10 4 1 / 25 1. R n Ω ε G ε 0 Ω ε B n 2 Ωε = with Bu = 0 on Ω ε i=1 x 2 i ε +0 B Bu = u (Dirichlet, D Ω ε ), Bu = u ν (Neumann, N Ω ε ), Ω ε G ( ) 2012 10 4 2 / 25 1. Ω ε B ε t

18 2 F 12 r 2 r 1 (3) Coulomb km Coulomb M = kg F G = ( ) ( ) ( ) 2 = [N]. Coulomb

r 1 r 2 r 1 r 2 2 Coulomb Gauss Coulomb 2.1 Coulomb 1 2 r 1 r 2 1 2 F 12 2 1 F 21 F 12 = F 21 = 1 4πε 0 1 2 r 1 r 2 2 r 1 r 2 r 1 r 2 (2.1) Coulomb ε 0 = 107 4πc 2 =8.854 187 817 10 12 C 2 N 1 m 2 (2.2)

医系の統計入門第 2 版 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. このサンプルページの内容は, 第 2 版 1 刷発行時のものです.

医系の統計入門第 2 版 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/009192 このサンプルページの内容は, 第 2 版 1 刷発行時のものです. i 2 t 1. 2. 3 2 3. 6 4. 7 5. n 2 ν 6. 2 7. 2003 ii 2 2013 10 iii 1987

#A A A F, F d F P + F P = d P F, F y P F F x A.1 ( α, 0), (α, 0) α > 0) (x, y) (x + α) 2 + y 2, (x α) 2 + y 2 d (x + α)2 + y 2 + (x α) 2 + y 2 =

#A A A. F, F d F P + F P = d P F, F P F F A. α, 0, α, 0 α > 0, + α +, α + d + α + + α + = d d F, F 0 < α < d + α + = d α + + α + = d d α + + α + d α + = d 4 4d α + = d 4 8d + 6 http://mth.cs.kitmi-it.c.jp/

sin cos No. sine, cosine : trigonometric function π : π = 3.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin : odd cos = cos : even.

08 No. : No. : No.3 : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No.0 : No. : sin cos No. sine, cosine : trigonometric function π : π = 3.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin

I No. sin cos sine, cosine : trigonometric function π : π =.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin : odd cos = cos : even.

I 0 No. : No. : No. : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No.0 : I No. sin cos sine, cosine : trigonometric function π : π =.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin : odd

App. of Leb. Integral Theory (S. Hiraba) Lebesgue (X, F, µ) (measure space)., X, 2 X, F 2 X σ (σ-field), i.e., (1) F, (2) A F = A c F, (3)

Lebesgue (Applications of Lebesgue Integral Theory) (Seiji HIABA) 1 1 1.1 1 Lebesgue........................ 1 1.2 2 Fubini...................... 2 2 L p 5 2.1 Banach, Hilbert..............................

1 1 sin cos P (primary) S (secondly) 2 P S A sin(ω2πt + α) A ω 1 ω α V T m T m 1 100Hz m 2 36km 500Hz. 36km 1

sin cos P (primary) S (secondly) 2 P S A sin(ω2πt + α) A ω ω α 3 3 2 2V 3 33+.6T m T 5 34m Hz. 34 3.4m 2 36km 5Hz. 36km m 34 m 5 34 + m 5 33 5 =.66m 34m 34 x =.66 55Hz, 35 5 =.7 485.7Hz 2 V 5Hz.5V.5V V

1. 1 A : l l : (1) l m (m 3) (2) m (3) n (n 3) (4) A α, β γ α β + γ = 2 m l lm n nα nα = lm. α = lm n. m lm 2β 2β = lm β = lm 2. γ l 2. 3

1. 1 A : l l : (1) l m (m 3) (2) m (3) n (n 3) (4) A 2 1 2 1 2 3 α, β γ α β + γ = 2 m l lm n nα nα = lm. α = lm n. m lm 2β 2β = lm β = lm 2. γ l 2. 3 4 P, Q R n = {(x 1, x 2,, x n ) ; x 1, x 2,, x n R}

B [ 0.1 ] x > 0 x 6= 1 f(x) µ 1 1 xn 1 + sin sin x 1 x 1 f(x) := lim. n x n (1) lim inf f(x) (2) lim sup f(x) x 1 0 x 1 0 (

. 28 4 14 [.1 ] x > x 6= 1 f(x) µ 1 1 xn 1 + sin + 2 + sin x 1 x 1 f(x) := lim. 1 + x n (1) lim inf f(x) (2) lim sup f(x) x 1 x 1 (3) lim inf x 1+ f(x) (4) lim sup f(x) x 1+ [.2 ] [, 1] Ω æ x (1) (2) nx(1

(Bessel) (Legendre).. (Hankel). (Laplace) V = (x, y, z) n (r, θ, ϕ) r n f n (θ, ϕ). f n (θ, ϕ) n f n (θ, ϕ) z = cos θ z θ ϕ n ν. P ν (z), Q ν (z) (Fou

(Bessel) (Legendre).. (Hankel). (Laplace) V = (x, y, z) n (r, θ, ϕ) r n f n (θ, ϕ). f n (θ, ϕ) n f n (θ, ϕ) z = cos θ z θ ϕ n ν. P ν (z), Q ν (z) (Fourier) (Fourier Bessel).. V ρ(x, y, z) V = 4πGρ G :.

sim0004.dvi

4 : 1 f(x) Z b a dxf(x) (1) ( Double Exponential method=de ) 1 DE N = n T n h h =(b a)=n T n = b a f(a) +f(b) n f + f(a + j b a n )g n j=1 = b a f(a) +f(b) n f + f(a +j b a )g; n n+1 j=1 T n+1 = b a f(a)

18 I ( ) (1) I-1,I-2,I-3 (2) (3) I-1 ( ) (100 ) θ ϕ θ ϕ m m l l θ ϕ θ ϕ 2 g (1) (2) 0 (3) θ ϕ (4) (3) θ(t) = A 1 cos(ω 1 t + α 1 ) + A 2 cos(ω 2 t + α

18 I ( ) (1) I-1,I-2,I-3 (2) (3) I-1 ( ) (100 ) θ ϕ θ ϕ m m l l θ ϕ θ ϕ 2 g (1) (2) 0 (3) θ ϕ (4) (3) θ(t) = A 1 cos(ω 1 t + α 1 ) + A 2 cos(ω 2 t + α 2 ), ϕ(t) = B 1 cos(ω 1 t + α 1 ) + B 2 cos(ω 2 t

chap03.dvi

99 3 (Coriolis) cm m (free surface wave) 3.1 Φ 2.5 (2.25) Φ 100 3 r =(x, y, z) x y z F (x, y, z, t) =0 ( DF ) Dt = t + Φ F =0 onf =0. (3.1) n = F/ F (3.1) F n Φ = Φ n = 1 F F t Vn on F = 0 (3.2) Φ (3.1)

構造と連続体の力学基礎

II 37 Wabash Avenue Bridge, Illinois 州 Winnipeg にある歩道橋 Esplanade Riel 橋6 6 斜張橋である必要は多分無いと思われる すぐ横に道路用桁橋有り しかも塔基部のレストランは 8 年には営業していなかった 9 9. 9.. () 97 [3] [5] k 9. m w(t) f (t) = f (t) + mg k w(t) Newton

1 3 1.1.......................... 3 1............................... 3 1.3....................... 5 1.4.......................... 6 1.5........................ 7 8.1......................... 8..............................

II ( ) (7/31) II ( [ (3.4)] Navier Stokes [ (6/29)] Navier Stokes 3 [ (6/19)] Re

II 29 7 29-7-27 ( ) (7/31) II (http://www.damp.tottori-u.ac.jp/~ooshida/edu/fluid/) [ (3.4)] Navier Stokes [ (6/29)] Navier Stokes 3 [ (6/19)] Reynolds [ (4.6), (45.8)] [ p.186] Navier Stokes I Euler Navier

untitled

2 : n =1, 2,, 10000 0.5125 0.51 0.5075 0.505 0.5025 0.5 0.4975 0.495 0 2000 4000 6000 8000 10000 2 weak law of large numbers 1. X 1,X 2,,X n 2. µ = E(X i ),i=1, 2,,n 3. σi 2 = V (X i ) σ 2,i=1, 2,,n ɛ>0

‚åŁÎ“·„´Šš‡ðŠp‡¢‡½‹âfi`fiI…A…‰…S…−…Y…•‡ÌMarkovŸA“½fiI›ð’Í

Markov 2009 10 2 Markov 2009 10 2 1 / 25 1 (GA) 2 GA 3 4 Markov 2009 10 2 2 / 25 (GA) (GA) L ( 1) I := {0, 1} L f : I (0, ) M( 2) S := I M GA (GA) f (i) i I Markov 2009 10 2 3 / 25 (GA) ρ(i, j), i, j I

基礎数学I

I & II ii ii........... 22................. 25 12............... 28.................. 28.................... 31............. 32.................. 34 3 1 9.................... 1....................... 1............

36 3 D f(z) D z f(z) z Taylor z D C f(z) z C C f (z) C f(z) f (z) f(z) D C D D z C C 3.: f(z) 3. f (z) f 2 (z) D D D D D f (z) f 2 (z) D D f (z) f 2 (

3 3. D f(z) D D D D D D D D f(z) D f (z) f (z) f(z) D (i) (ii) (iii) f(z) = ( ) n z n = z + z 2 z 3 + n= z < z < z > f (z) = e t(+z) dt Re z> Re z> [ ] f (z) = e t(+z) = (Rez> ) +z +z t= z < f(z) Taylor

9 Feb 2008 NOGUCHI (UT) HDVT 9 Feb / 33

9 Feb 2008 NOGUCHI (UT) HDVT 9 Feb 2008 1 / 33 1 NOGUCHI (UT) HDVT 9 Feb 2008 2 / 33 1 Green-Griffiths (1972) NOGUCHI (UT) HDVT 9 Feb 2008 2 / 33 1 Green-Griffiths (1972) X f : C X f (C) X NOGUCHI (UT)

i

i 3 4 4 7 5 6 3 ( ).. () 3 () (3) (4) /. 3. 4/3 7. /e 8. a > a, a = /, > a >. () a >, a =, > a > () a > b, a = b, a < b. c c n a n + b n + c n 3c n..... () /3 () + (3) / (4) /4 (5) m > n, a b >, m > n,

IA

IA 31 4 11 1 1 4 1.1 Planck.............................. 4 1. Bohr.................................... 5 1.3..................................... 6 8.1................................... 8....................................

TOP URL 1

TOP URL http://amonphys.web.fc.com/ 3.............................. 3.............................. 4.3 4................... 5.4........................ 6.5........................ 8.6...........................7

I, II 1, A = A 4 : 6 = max{ A, } A A 10 10%

1 2006.4.17. A 3-312 tel: 092-726-4774, e-mail: hara@math.kyushu-u.ac.jp, http://www.math.kyushu-u.ac.jp/ hara/lectures/lectures-j.html Office hours: B A I ɛ-δ ɛ-δ 1. 2. A 1. 1. 2. 3. 4. 5. 2. ɛ-δ 1. ɛ-n

1 (Berry,1975) 2-6 p (S πr 2 )p πr 2 p 2πRγ p p = 2γ R (2.5).1-1 : : : : ( ).2 α, β α, β () X S = X X α X β (.1) 1 2

2005 9/8-11 2 2.2 ( 2-5) γ ( ) γ cos θ 2πr πρhr 2 g h = 2γ cos θ ρgr (2.1) γ = ρgrh (2.2) 2 cos θ θ cos θ = 1 (2.2) γ = 1 ρgrh (2.) 2 2. p p ρgh p ( ) p p = p ρgh (2.) h p p = 2γ r 1 1 (Berry,1975) 2-6

master.dvi

4 Maxwell- Boltzmann N 1 4.1 T R R 5 R (Heat Reservor) S E R 20 E 4.2 E E R E t = E + E R E R Ω R (E R ) S R (E R ) Ω R (E R ) = exp[s R (E R )/k] E, E E, E E t E E t E exps R (E t E) exp S R (E t E )

1. 1 BASIC PC BASIC BASIC BASIC Fortran WS PC (1.3) 1 + x 1 x = x = (1.1) 1 + x = (1.2) 1 + x 1 = (1.

Section Title Pages Id 1 3 7239 2 4 7239 3 10 7239 4 8 7244 5 13 7276 6 14 7338 7 8 7338 8 7 7445 9 11 7580 10 10 7590 11 8 7580 12 6 7395 13 z 11 7746 14 13 7753 15 7 7859 16 8 7942 17 8 Id URL http://km.int.oyo.co.jp/showdocumentdetailspage.jsp?documentid=

ohpmain.dvi

fujisawa@ism.ac.jp 1 Contents 1. 2. 3. 4. γ- 2 1. 3 10 5.6, 5.7, 5.4, 5.5, 5.8, 5.5, 5.3, 5.6, 5.4, 5.2. 5.5 5.6 +5.7 +5.4 +5.5 +5.8 +5.5 +5.3 +5.6 +5.4 +5.2 =5.5. 10 outlier 5 5.6, 5.7, 5.4, 5.5, 5.8,

meiji_resume_1.PDF

β β β (q 1,q,..., q n ; p 1, p,..., p n ) H(q 1,q,..., q n ; p 1, p,..., p n ) Hψ = εψ ε k = k +1/ ε k = k(k 1) (x, y, z; p x, p y, p z ) (r; p r ), (θ; p θ ), (ϕ; p ϕ ) ε k = 1/ k p i dq i E total = E

1 filename=mathformula tex 1 ax 2 + bx + c = 0, x = b ± b 2 4ac, (1.1) 2a x 1 + x 2 = b a, x 1x 2 = c a, (1.2) ax 2 + 2b x + c = 0, x = b ± b 2

filename=mathformula58.tex ax + bx + c =, x = b ± b 4ac, (.) a x + x = b a, x x = c a, (.) ax + b x + c =, x = b ± b ac. a (.3). sin(a ± B) = sin A cos B ± cos A sin B, (.) cos(a ± B) = cos A cos B sin

SAMA- SUKU-RU Contents p-adic families of Eisenstein series (modular form) Hecke Eisenstein Eisenstein p T

SAMA- SUKU-RU Contents 1. 1 2. 7.1. p-adic families of Eisenstein series 3 2.1. modular form Hecke 3 2.2. Eisenstein 5 2.3. Eisenstein p 7 3. 7.2. The projection to the ordinary part 9 3.1. The ordinary

Note.tex 2008/09/19( )

1 20 9 19 2 1 5 1.1........................ 5 1.2............................. 8 2 9 2.1............................. 9 2.2.............................. 10 3 13 3.1.............................. 13 3.2..................................

. sinh x sinh x) = e x e x = ex e x = sinh x 3) y = cosh x, y = sinh x y = e x, y = e x 6 sinhx) coshx) 4 y-axis x-axis : y = cosh x, y = s

. 00 3 9 [] sinh x = ex e x, cosh x = ex + e x ) sinh cosh 4 hyperbolic) hyperbola) = 3 cosh x cosh x) = e x + e x = cosh x ) . sinh x sinh x) = e x e x = ex e x = sinh x 3) y = cosh x, y = sinh x y =

III 1 (X, d) d U d X (X, d). 1. (X, d).. (i) d(x, y) d(z, y) d(x, z) (ii) d(x, y) d(z, w) d(x, z) + d(y, w) 2. (X, d). F X.. (1), X F, (2) F 1, F 2 F

III 1 (X, d) d U d X (X, d). 1. (X, d).. (i) d(x, y) d(z, y) d(x, z) (ii) d(x, y) d(z, w) d(x, z) + d(y, w) 2. (X, d). F X.. (1), X F, (2) F 1, F 2 F F 1 F 2 F, (3) F λ F λ F λ F. 3., A λ λ A λ. B λ λ

I No. sin cos sine, cosine : trigonometric function π : π =.4 : n =, ±, ±, sin + nπ = sin cos + nπ = cos sin = sin : cos = cos :. sin. sin. sin + π si

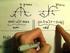I 8 No. : No. : No. : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No. : I No. sin cos sine, cosine : trigonometric function π : π =.4 : n =, ±, ±, sin + nπ = sin cos + nπ = cos sin = sin : cos = cos :. sin.

8.1 Fubini 8.2 Fubini 9 (0%) 10 (50%) Carathéodory 10.3 Fubini 1 Introduction 1 (1) (2) {f n (x)} n=1 [a, b] K > 0 n, x f n (x) K < ( ) x [a

% 100% 1 Introduction 2 (100%) 2.1 2.2 2.3 3 (100%) 3.1 3.2 σ- 4 (100%) 4.1 4.2 5 (100%) 5.1 5.2 5.3 6 (100%) 7 (40%) 8 Fubini (90%) 2007.11.5 1 8.1 Fubini 8.2 Fubini 9 (0%) 10 (50%) 10.1 10.2 Carathéodory

t (x(t), y(t)), a t b (x(a), y(a)) t ( ) ( ) dy s + dt dt dt [a, b] a a t < t 1 < < t n b {(x(t i ), y(t i ))} n i ( s(t) ds ) ( ) dy dt + dt dt ( ) d

1 13 Fall Semester N. Yamada Version:13.9.3 Chapter. Preliminalies (1 3) Chapter 1. (4 16) Chapter. (17 9) Chapter 3. (3 49) Chapter 4. (5 63) Chapter 5. (64 7) Chapter 6. (71 8) 11, ISBN 978-4-535-618-4.

Untitled

II 14 14-7-8 8/4 II (http://www.damp.tottori-u.ac.jp/~ooshida/edu/fluid/) [ (3.4)] Navier Stokes [ 6/ ] Navier Stokes 3 [ ] Reynolds [ (4.6), (45.8)] [ p.186] Navier Stokes I 1 balance law t (ρv i )+ j

tomocci ,. :,,,, Lie,,,, Einstein, Newton. 1 M n C. s, M p. M f, p d ds f = dxµ p ds µ f p, X p = X µ µ p = dxµ ds µ p. µ, X µ.,. p,. T M p.

tomocci 18 7 5...,. :,,,, Lie,,,, Einstein, Newton. 1 M n C. s, M p. M f, p d ds f = dxµ p ds µ f p, X p = X µ µ p = dxµ ds µ p. µ, X µ.,. p,. T M p. M F (M), X(F (M)).. T M p e i = e µ i µ. a a = a i

III ϵ-n ϵ-n lim n a n = α n a n α 1 lim a n = 0 1 n a k n n k= ϵ-n 1.1

III http://www2.mth.kyushu-u.c.jp/~hr/lectures/lectures-j.html 1 1 1.1 ϵ-n ϵ-n lim n = α n n α 1 lim n = 0 1 n k n k=1 0 1.1.7 ϵ-n 1.1.1 n α n n α lim n = α ϵ Nϵ n > Nϵ n α < ϵ 1.1.1 ϵ n > Nϵ n α < ϵ 1.1.2

201711grade1ouyou.pdf

2017 11 26 1 2 52 3 12 13 22 23 32 33 42 3 5 3 4 90 5 6 A 1 2 Web Web 3 4 1 2... 5 6 7 7 44 8 9 1 2 3 1 p p >2 2 A 1 2 0.6 0.4 0.52... (a) 0.6 0.4...... B 1 2 0.8-0.2 0.52..... (b) 0.6 0.52.... 1 A B 2

No δs δs = r + δr r = δr (3) δs δs = r r = δr + u(r + δr, t) u(r, t) (4) δr = (δx, δy, δz) u i (r + δr, t) u i (r, t) = u i x j δx j (5) δs 2

No.2 1 2 2 δs δs = r + δr r = δr (3) δs δs = r r = δr + u(r + δr, t) u(r, t) (4) δr = (δx, δy, δz) u i (r + δr, t) u i (r, t) = u i δx j (5) δs 2 = δx i δx i + 2 u i δx i δx j = δs 2 + 2s ij δx i δx j

(5) 75 (a) (b) ( 1 ) v ( 1 ) E E 1 v (a) ( 1 ) x E E (b) (a) (b)

(5) 74 Re, bondar laer (Prandtl) Re z ω z = x (5) 75 (a) (b) ( 1 ) v ( 1 ) E E 1 v (a) ( 1 ) x E E (b) (a) (b) (5) 76 l V x ) 1/ 1 ( 1 1 1 δ δ = x Re x p V x t V l l (1-1) 1/ 1 δ δ δ δ = x Re p V x t V

x (x, ) x y (, y) iy x y z = x + iy (x, y) (r, θ) r = x + y, θ = tan ( y ), π < θ π x r = z, θ = arg z z = x + iy = r cos θ + ir sin θ = r(cos θ + i s

... x, y z = x + iy x z y z x = Rez, y = Imz z = x + iy x iy z z () z + z = (z + z )() z z = (z z )(3) z z = ( z z )(4)z z = z z = x + y z = x + iy ()Rez = (z + z), Imz = (z z) i () z z z + z z + z.. z

量子力学 問題

3 : 203 : 0. H = 0 0 2 6 0 () = 6, 2 = 2, 3 = 3 3 H 6 2 3 ϵ,2,3 (2) ψ = (, 2, 3 ) ψ Hψ H (3) P i = i i P P 2 = P 2 P 3 = P 3 P = O, P 2 i = P i (4) P + P 2 + P 3 = E 3 (5) i ϵ ip i H 0 0 (6) R = 0 0 [H,

実解析的方法とはどのようなものか

(1) ENCOUNTER with MATHEMATICS 2001 10 26 (2) 1807 J. B. J. Fourier 1 2π f(x) f(x) = n= c n (f) = 1 2π c n (f)e inx (1) π π f(t)e int dt Fourier 2 R f(x) f(x) = F[f](ξ)= 1 2π F [f](ξ)e ixξ dξ f(t)e iξx

( ; ) C. H. Scholz, The Mechanics of Earthquakes and Faulting : - ( ) σ = σ t sin 2π(r a) λ dσ d(r a) =

1 9 8 1 1 1 ; 1 11 16 C. H. Scholz, The Mechanics of Earthquakes and Faulting 1. 1.1 1.1.1 : - σ = σ t sin πr a λ dσ dr a = E a = π λ σ πr a t cos λ 1 r a/λ 1 cos 1 E: σ t = Eλ πa a λ E/π γ : λ/ 3 γ =

III III 2010 PART I 1 Definition 1.1 (, σ-),,,, Borel( ),, (σ-) (M, F, µ), (R, B(R)), (C, B(C)) Borel Definition 1.2 (µ-a.e.), (in µ), (in L 1 (µ)). T

III III 2010 PART I 1 Definition 1.1 (, σ-),,,, Borel( ),, (σ-) (M, F, µ), (R, B(R)), (C, B(C)) Borel Definition 1.2 (µ-a.e.), (in µ), (in L 1 (µ)). Theorem 1.3 (Lebesgue ) lim n f n = f µ-a.e. g L 1 (µ)

H 0 H = H 0 + V (t), V (t) = gµ B S α qb e e iωt i t Ψ(t) = [H 0 + V (t)]ψ(t) Φ(t) Ψ(t) = e ih0t Φ(t) H 0 e ih0t Φ(t) + ie ih0t t Φ(t) = [

3 3. 3.. H H = H + V (t), V (t) = gµ B α B e e iωt i t Ψ(t) = [H + V (t)]ψ(t) Φ(t) Ψ(t) = e iht Φ(t) H e iht Φ(t) + ie iht t Φ(t) = [H + V (t)]e iht Φ(t) Φ(t) i t Φ(t) = V H(t)Φ(t), V H (t) = e iht V (t)e

9 2 1 f(x, y) = xy sin x cos y x y cos y y x sin x d (x, y) = y cos y (x sin x) = y cos y(sin x + x cos x) x dx d (x, y) = x sin x (y cos y) = x sin x

2009 9 6 16 7 1 7.1 1 1 1 9 2 1 f(x, y) = xy sin x cos y x y cos y y x sin x d (x, y) = y cos y (x sin x) = y cos y(sin x + x cos x) x dx d (x, y) = x sin x (y cos y) = x sin x(cos y y sin y) y dy 1 sin

Microsoft Word - 信号処理3.doc

Junji OHTSUBO 2012 FFT FFT SN sin cos x v ψ(x,t) = f (x vt) (1.1) t=0 (1.1) ψ(x,t) = A 0 cos{k(x vt) + φ} = A 0 cos(kx ωt + φ) (1.2) A 0 v=ω/k φ ω k 1.3 (1.2) (1.2) (1.2) (1.1) 1.1 c c = a + ib, a = Re[c],

Macdonald, ,,, Macdonald. Macdonald,,,,,.,, Gauss,,.,, Lauricella A, B, C, D, Gelfand, A,., Heckman Opdam.,,,.,,., intersection,. Macdona

Macdonald, 2015.9.1 9.2.,,, Macdonald. Macdonald,,,,,.,, Gauss,,.,, Lauricella A, B, C, D, Gelfand, A,., Heckman Opdam.,,,.,,., intersection,. Macdonald,, q., Heckman Opdam q,, Macdonald., 1 ,,. Macdonald,

e a b a b b a a a 1 a a 1 = a 1 a = e G G G : x ( x =, 8, 1 ) x 1,, 60 θ, ϕ ψ θ G G H H G x. n n 1 n 1 n σ = (σ 1, σ,..., σ N ) i σ i i n S n n = 1,,

01 10 18 ( ) 1 6 6 1 8 8 1 6 1 0 0 0 0 1 Table 1: 10 0 8 180 1 1 1. ( : 60 60 ) : 1. 1 e a b a b b a a a 1 a a 1 = a 1 a = e G G G : x ( x =, 8, 1 ) x 1,, 60 θ, ϕ ψ θ G G H H G x. n n 1 n 1 n σ = (σ 1,

I-2 (100 ) (1) y(x) y dy dx y d2 y dx 2 (a) y + 2y 3y = 9e 2x (b) x 2 y 6y = 5x 4 (2) Bernoulli B n (n = 0, 1, 2,...) x e x 1 = n=0 B 0 B 1 B 2 (3) co

16 I ( ) (1) I-1 I-2 I-3 (2) I-1 ( ) (100 ) 2l x x = 0 y t y(x, t) y(±l, t) = 0 m T g y(x, t) l y(x, t) c = 2 y(x, t) c 2 2 y(x, t) = g (A) t 2 x 2 T/m (1) y 0 (x) y 0 (x) = g c 2 (l2 x 2 ) (B) (2) (1)

09 8 9 3 Chebyshev 5................................. 5........................................ 5.3............................. 6.4....................................... 8.4...................................

π, R { 2, 0, 3} , ( R),. R, [ 1, 1] = {x R 1 x 1} 1 0 1, [ 1, 1],, 1 0 1,, ( 1, 1) = {x R 1 < x < 1} [ 1, 1] 1 1, ( 1, 1), 1, 1, R A 1

sup inf (ε-δ 4) 2018 1 9 ε-δ,,,, sup inf,,,,,, 1 1 2 3 3 4 4 6 5 7 6 10 6.1............................................. 11 6.2............................... 13 1 R R 5 4 3 2 1 0 1 2 3 4 5 π( R) 2 1 0

simx simxdx, cosxdx, sixdx 6.3 px m m + pxfxdx = pxf x p xf xdx = pxf x p xf x + p xf xdx 7.4 a m.5 fx simxdx 8 fx fx simxdx = πb m 9 a fxdx = πa a =

II 6 ishimori@phys.titech.ac.jp 6.. 5.4.. f Rx = f Lx = fx fx + lim = lim x x + x x f c = f x + x < c < x x x + lim x x fx fx x x = lim x x f c = f x x < c < x cosmx cosxdx = {cosm x + cosm + x} dx = [

V(x) m e V 0 cos x π x π V(x) = x < π, x > π V 0 (i) x = 0 (V(x) V 0 (1 x 2 /2)) n n d 2 f dξ 2ξ d f 2 dξ + 2n f = 0 H n (ξ) (ii) H

199 1 1 199 1 1. Vx) m e V cos x π x π Vx) = x < π, x > π V i) x = Vx) V 1 x /)) n n d f dξ ξ d f dξ + n f = H n ξ) ii) H n ξ) = 1) n expξ ) dn dξ n exp ξ )) H n ξ)h m ξ) exp ξ )dξ = π n n!δ n,m x = Vx)

y = x 4 y = x 8 3 y = x 4 y = x 3. 4 f(x) = x y = f(x) 4 x =,, 3, 4, 5 5 f(x) f() = f() = 3 f(3) = 3 4 f(4) = 4 *3 S S = f() + f() + f(3) + f(4) () *4

Simpson H4 BioS. Simpson 3 3 0 x. β α (β α)3 (x α)(x β)dx = () * * x * * ɛ δ y = x 4 y = x 8 3 y = x 4 y = x 3. 4 f(x) = x y = f(x) 4 x =,, 3, 4, 5 5 f(x) f() = f() = 3 f(3) = 3 4 f(4) = 4 *3 S S = f()

W u = u(x, t) u tt = a 2 u xx, a > 0 (1) D := {(x, t) : 0 x l, t 0} u (0, t) = 0, u (l, t) = 0, t 0 (2)

3 215 4 27 1 1 u u(x, t) u tt a 2 u xx, a > (1) D : {(x, t) : x, t } u (, t), u (, t), t (2) u(x, ) f(x), u(x, ) t 2, x (3) u(x, t) X(x)T (t) u (1) 1 T (t) a 2 T (t) X (x) X(x) α (2) T (t) αa 2 T (t) (4)

2 2 ( Riemann ( 2 ( ( 2 ( (.8.4 (PDF 2

2 ( 28 8 (http://nalab.mind.meiji.ac.jp/~mk/lecture/tahensuu2/ 2 2 ( Riemann ( 2 ( ( 2 ( (.8.4 (PDF http://nalab.mind.meiji.ac.jp/~mk/lecture/tahensuu2/ http://nalab.mind.meiji.ac.jp/~mk/lecture/tahensuu/

2 2 L 5 2. L L L L k.....

L 528 206 2 9 2 2 L 5 2. L........................... 5 2.2 L................................... 7 2............................... 9. L..................2 L k........................ 2 4 I 5 4. I...................................

5 5.1 E 1, E 2 N 1, N 2 E tot N tot E tot = E 1 + E 2, N tot = N 1 + N 2 S 1 (E 1, N 1 ), S 2 (E 2, N 2 ) E 1, E 2 S tot = S 1 + S 2 2 S 1 E 1 = S 2 E

5 5.1 E 1, E 2 N 1, N 2 E tot N tot E tot = E 1 + E 2, N tot = N 1 + N 2 S 1 (E 1, N 1 ), S 2 (E 2, N 2 ) E 1, E 2 S tot = S 1 + S 2 2 S 1 E 1 = S 2 E 2, S 1 N 1 = S 2 N 2 2 (chemical potential) µ S N

1 Introduction 1 (1) (2) (3) () {f n (x)} n=1 [a, b] K > 0 n, x f n (x) K < ( ) x [a, b] lim f n (x) f(x) (1) f(x)? (2) () f(x)? b lim a f n (x)dx = b

1 Introduction 2 2.1 2.2 2.3 3 3.1 3.2 σ- 4 4.1 4.2 5 5.1 5.2 5.3 6 7 8. Fubini,,. 1 1 Introduction 1 (1) (2) (3) () {f n (x)} n=1 [a, b] K > 0 n, x f n (x) K < ( ) x [a, b] lim f n (x) f(x) (1) f(x)?

成長機構

j im πmkt jin jim π mkt j q out j q im π mkt jin j j q out out π mkt π mkt dn dt πmkt dn v( ) Rmax bf dt πmkt R v ( J J ), J J, J J + + T T, J J m + Q+ / kt Q / kt + ( Q Q+ )/ ktm l / ktm J / J, l Q Q

H.Haken Synergetics 2nd (1978)

27 3 27 ) Ising Landau Synergetics Fokker-Planck F-P Landau F-P Gizburg-Landau G-L G-L Bénard/ Hopfield H.Haken Synergetics 2nd (1978) (1) Ising m T T C 1: m h Hamiltonian H = J ij S i S j h i S

第1章 微分方程式と近似解法

April 12, 2018 1 / 52 1.1 ( ) 2 / 52 1.2 1.1 1.1: 3 / 52 1.3 Poisson Poisson Poisson 1 d {2, 3} 4 / 52 1 1.3.1 1 u,b b(t,x) u(t,x) x=0 1.1: 1 a x=l 1.1 1 (0, t T ) (0, l) 1 a b : (0, t T ) (0, l) R, u

Chap11.dvi

. () x 3 + dx () (x )(x ) dx + sin x sin x( + cos x) dx () x 3 3 x + + 3 x + 3 x x + x 3 + dx 3 x + dx 6 x x x + dx + 3 log x + 6 log x x + + 3 rctn ( ) dx x + 3 4 ( x 3 ) + C x () t x t tn x dx x. t x