The Japan Society Sooiety for Industrial 工 and Applied Mathematios Mathematics Li 本応用数理学会論. 文誌 Vol.8,No ,pp 特異な非対称行列を係数とする連立 1 次方程式での各種反
|
|
|
- たかよし あいきょう
- 4 years ago
- Views:
Transcription
1 Li 本応用数理学会論. 文誌 Vol.8No pp 特異な非対称行列を係数とする連立 1 次方程式での各種反復解法の収束特性と流れの数値シミュレシーョンへの応用 堀端康善 株 ) 東芝研究開発センター Solut}on of a SinglllarSystelnof Lineaτ Equations with a Nonsymmetric Coe 田 cient Matrix Using IterativeMethods and it8applica.tion to NulnericalSimula.tion of FluidFlow YasuyoshiHoribata Research& Developm 副 1t Center Toshiba Corporation Abstract.The consiste 皿 cy of a. singular system of h 皿 ea. r equations a. re discussedwhere the coe 缶 cient matrix isllollsymmetr {c a.nd the convergence propeltics of the bicon conjuga jugategradient.te gradient squa.red a 皿 d conjugate residual methods are dis cussed.numerical experiments a. re presented fbra La. pla.ce equa.tion wi もh Neumann boundaly conditions Next the consistency theory of a. sillgular system is applied to numellcal simulatioll of 且 uid 且 ow In order to ensure convelgence of the solution of the pressure equation thispaper proposes the perturbation remqva.i method using the eigenvector of the tra. nsposed coe 冊 cient ma.trixcorresponding to the eige 皿 va lueo. Therma 亅 convection of a Boussinesq Huidiss 三 mulased in a square ca vit y.the pressure equation isso 孟 ved using the proposed method.the convergellee ra.teg.of the iterative methods axe compared.the simulation result isin good a greeernent with a.be 皿 chma. rk solut 三〇 n 1 緒言 特異行列を係数とする連立 1 次方程式. tl c b の整合性と各種反復法による数値解について議論する.A が対称行列である場合について 共役勾配 法の数値解の収束特性は既に議論されている [11 ]. また 全周ノイマン型境界条件をもつボアソン方 程式を離散化してできた 特異な対称行列を係数とする連立 1 次方程式にっいて 各種反復解法で数値実験を行い 収束特性が比較されている [ 16 ]. 本論文は A が非対称行列の場合について論じる. 次に 流れの数値シミュレーションを行うときにあらわれる 圧力についての方程式との関連について考察する. 第 2 章において 特異な非対称行列を係数とする連立 1 次方程式の整合性にっいて論じる. 第 3 章 では 双対共役勾配法 自乗共役勾配法 共役残差法をこの連立 1 次方程式に適用したときの解の収 一 131 一
2 288 凵本応用数理学会論文誌 Vol.8No 束特性を検討する. そして 第 4 章において 簡単なラプラス方程式で数値実験を行い それらの反 復解法の収束特 1 生を実証する. また 比較のため SOR 法についても数値実験する. 最後に 第 5 章 において 流れの数値シミュレーションとの関連について論じ 特異な非対称行列を係数とする連立 1 次方程式の整合化法が 従来使用されて来た非斉次項修正法よりも直接的 簡便 正確な方法であることを示す. そして この整合化法を使って 2 次元正方形キャビティ内自然対流の数値シミュレー ションし また各種反復解法の収束特性を比較する. 2 特異な連立 1 次方程式の整合性 連立 1 次方程式 2.1 ) Ax b について考える. ここで A Rnxn は特異な非対称行列である.Rnxn は実数を成分とする n n 行列の線型空間をあらわす行列 A の階数は n 1 で 固有値 0 はその特性方程式 det.xl 一 A ) 0 の単根であるとする. 但し 1 は単位行列である. 周知のように この連立 1 次方程式が解を持っための必要十分条件は 係数行列 A の階数と拡大係数行列 A A b ) とが一致することである [ 14 ]. A とその転置行列 AT の零空間を使うと この必要十分条件を次のように表現できる. A とその転置行列 AT の零空間をそれぞれ N A ) N AT ) とすると 1>A ) ; span { e } N AT ) ; pan { * } と書ける. ここで e と は それぞれ A と AT の固有値 0 に対応する固有ベクトルである す ると A の値域 R A ) は N A : ) の直交補空間になる. すなわち 実数を成分とする n 項列ベクト ルの線型空間 Rn は部分空間 R A ) と N A τ ) の直和である. Rn R A ) 千 N AT ) そして 連立 1 次方程式は b のときにのみ解を持つ 同様に 随伴方程式 AT π b はゲ e のときにのみ解を持つ. 仮定により固有値 0 が待院方程式 det a;1 A ) 0 の単根であるから 行列 A のジョルダン標準 形は 固有値 0 に対するジョルダン細胞として O 1 ) 0) を一っだけもつ. したがって 行列 AA の階数は行列 A の階数と等しくなり となる. 7 α nk : AA )? αnk A ) n 1 固有ベクトル e と について次の関係が得られる. 定理 [1] 固有ベクトル e と e * は直交しない. e e * ) 0 一 132 一
3 特異な非対称行列を係数とする連立 1 次方程式での各種反復解法の収束特性 289 証明 : e e ) 0 を仮定す る. すると A の値域 R A ) は N AT ) の直交補空間であるから e R A ) となる.N A ) の基底く e > を拡大して Rn の基底く e e1 e2.en _ 1 > を得たとする. このとき < AeiAe2 _ Aen _ i > が R A ) の基底になるから e は Ae1 Ae2.Aen_ 1 の線型結合として表わされる これより 崩 c el + c2e2 + + ctt 一ユ r. ) A e c1 /1e1 + c2ae2 + _ + c _ iae L 1 A + c2ae c. Ae. ) A となる. 一方 んAe o であるから 互いに線型独立な Cle ユ十 C2e 一 Cn _ 1en _ 1 と e は行列 AA の零空間のベクトルになる. したがって 行列 AA の値域 R AA ) の次元は n 2 以下となり 結局 r α 淵舶 ) n 2 となる. これは矛盾である. 口さらに 次の定理を得る. 定理 [2 ] 線型空間 Rn は部分空間 N A ) と R A ) の直和である. Rn N A ) 千 R.A ) 証明 : R.A ) の基底をく i f2... i _ 1 > とする.e fliず 2...fn_ 1 の間に線型関係 C e + Clfl + C2 / C 一 fn 1 があれば これと e * との内積をとると CQ e e ) 0 を得る. 定理 [1 コより e e * ) 0 であるか ら Co 0 となる. したがって 線型関係は Clf + C2 / Cn fn 1 となる. < f1 2_ fn_ 1 > は R A ) の基底だから Cl c2. Cn 1 0 となる. したがっ て ベクトル e f1 f2.. fn 1 は線型独立になり Rn の基底になる. ロ 3 各種反復法の収束特性 反復法を使って特異な連立 1 次方程式 2. 1 ) を解く場合の収束特性にっいて検討する. 3.1 双対共役勾配法 BCG 法 ) 双対共役勾配法を特異な連立 1 次方程式 2.1 ) に適用する. 双対共役勾配法では ムにしたがってベクトル列 Xl x2 _ を求める [6 ]. o と x6 は初期値である. 次のアルゴリズ アルゴリズ厶 1 ro b IXo l r6 b 一 ATxe Po ro : P δ rg ; k : O while IFrkil Odo α k rk rx.)/ APk P :. ) 鰥 +1 Mk + 叫 P た rk rk 一 drkapk ; 噺 1 β た rle +1 rz + 1)1 rk r 蒸 ) 二 rx. 一 katpr Pk + 1 rk fikpkl px. + 1 丁誕 βkp 壽義 :kt 斗.1 一 133 一
4 290 日本応用数理学会論文誌 Vol.8Na21998 このアルゴリズムによって得られるベクトル列 {Pi } と { ri } に対して双対直交性 と共役直交性 丁凱丁ゴ ) o i ゴ ) が成り立っ [ 61. P 菷 4P ゴ ) 0 i ; ゴ ) 定理匚 2 ] から 連立 1 次方程式の解 x は次のように書ける. x y 十 z 但し y 1> A ) z R A ) ここで z は一意的に決まるが y は一意的に決まらない. b R A ) ならば ri R A ) となる. そして 探索ベクトル Pi も R A ) のベクトルであるから h 1 次元の部分空間 R A ) の中で解を探索し z を求めることになる. 定理 [2 ] より e と Pt は線型 独立であるから ベクトル e は探索過程に参入しない. 探索が続く限り 双対直交性から ro rl... ri は線型独立になる. そして 定理 [2 ] より e と ri は線型独立であるから e r rl.. 物は線型独立になる. したがって ある m n 1 で rm o となって解が求まる. 32 自乗共役勾配法 CGS 法 ) 自乗共役勾配法は双対共役勾配法におい 1 r6 re としたものである. 次のアルゴリズムにした がってベクトル列 M1 M2.. を求める [ 15 ]. o は初期値である. アルゴリズム 2 ro b Amo PO ro i k O while α 沁 ; ア和 痢 / APk r j hk + 1 ε た一 ak Ap ) XA + 1 需鞠 + 蝋 e 杜幅 ) 併婦二恥一蝋 e ん嗣 ) β k ro ra: + 1 )1 r Crk ) ex + 1 rk 距んみ +1 Pk + 1ek+1 + β A hk+1 βkpk ) 斥 ; k : 十 1 共役勾配法の場合と同様に b R A ) ならば ある m n 1 で甲 η o と って解が求 NII-Electronic る. 一 134 一 N 工工一 Eleotronio Library
5 特異な非対称行列を係数とする連立 1 次方程式での各種反復解法の収束特性 共役残差法 CR 法 ) 共役残差法では 次のアルゴリズムにしたがってベクトル列 Xl x2 _ を求める [ 13 ].Xo は初期値である. アルゴリズム 3 ro b Axo Po ro ; KlO while l1 副 Odo α k rk APk ) 1 Apk APk ) 記軒 1 コ Ck + α kpic rk + 1 rk akapk βk 一 Ark + 1 APk )/ APk Apk ) Pk + 1 Tk βk Pk k k 十 1 b R A ) ならば ri Pi R A ) となる. したがって 部分空 P7 R A ) の中で解を探索することになり ベクトル e は探索過程に参入しない. この場合 rk APk ) ric Artl ) 0 である限り 探 索を続けることができ rb ri ) の値は単調に減少し続ける. そして 解の成分 z R A ) が求めら れる. 4 ラプラス方程式での数値実験 4.1 連立 1 次方程式 次のラプラス方程式を考えることにする. 解領域は Ω 0 1 ) 2 である. 2 一 i11 Ω 象一 n Ω ここで g は u x ) 二 Ml + x2 が解になるように決める. 格子点が境界付近に集中するように次式に したがって座標囮 x2 ) を座標 ξ1 ξ2 ) へ変換する. β+ 1 ) [β + 1 )/β 一 1 2 ) 亅 ξ1 一 β { 1 1 Kβ 一ト 1 )/β 一. 1 ) 2 ξ1 1 } β + 1 )[ β + 1 )/β 一 2 ].) 亅 ξ? 一 β : 2 { 一 β 一ト 1 ) ノ β 一 1 ) ] 2 一 ξ2 1 } ここで β はパラメータであり β 認 Ll にとることにする. この座標変換によって 解領域 Ω を写像してできた計算領域 Ω O 1 ) 2 上で離散化する. 格子間隔は 1 / 29 にとる. 特異な非対称行列 A R9 OOxgoo を係数とする連立 1 次方程式. 勉 b が得られる. しかしながら この連立 1 次方程 式は擾乱を含み b R A ) となる. 得られた連立 1 次方程式から 次のようにして擾乱を取り除く. 1. 行列 A の転置行列の零空間 N.4T ) のベクトル e を方程式 ATe * o から求める. ベクトル の一つの成分の値を固定してから反復解法を適用すれば容易に求まる. 一 135 一
6 292 日木応用数理学会論文誌 Vol 8No 行列 A の値域 R A ) は N AT ) span { e * } の直交補空間であるから 方程式 Am のベクトル b を R A ) へ射影すると b の右辺 が得られる.b をこの br で置き換える. b 屠卜 b e * )IIIe lj2 ] e * こういうふうにして擾乱を取り除いた連立 1 次方程式 Ax br は br R A ) となり 解をもっ. 擾乱の影響を考察するときは この連立 1 方程式に擾乱 b を加える. そのときの方程式は次の になる. よう Az b ここで b br 十 b 擾乱 b は b r!lle il) e の形で与える. ここで ty の値は 二 7 ]lbrll δ 1 > / i : 歪 0 く δく 1 ) から決める.b と R A ) の間の角度を θ とすると この δ について の関係がある sin θ ilbll11ibll δ 42 数 { 直実験 CRAY Y MP C90 1GFLOPS ) を使う. 擾乱が反復法の収束特性に及ぼす影響を広範囲かつ詳細に考察するため 倍精度実数型の浮動小数点数の演算 計算機イプシロンは約 lo } 29 ) で行う. 双対共役勾配法 自乗共役勾配法 共役残差法 そして比較のため SQR 法 一 136 一
7 特異な非対称行列を係数とする me i fl1 次方程式での各種反復解法の収束特性 コ 丶 ρ 1. リ < ). b 一 0 一 4 一 8 一 12 一 一 number of iterations Fig.1.PBCG fordifferent perturbatio 皿 s. を加えた 全部で 4 種類の反復解法で擾乱のない場合と擾乱を含んだ場合を解く. 初期値は常に Xo. 褐 o にとる. 但し 双対共役勾配法自乗共役勾配法 共役残差法にっいては 収束を加速するため前処理を施す. 前処理には不完全 LDU 分解を使う. すなわち 行列 A を不完全 LDU 分解し て LDU の形にする. 左下三角行列 L と右上三角行列 σ の非対角要素は元の行列 A の対応する要 素に等しくとり 対角行列 D の対角要素だけを計算する [13 亅. そして方程式 LD 一 1 の.4 ゐD 冖 lb の に双対共役勾配法 自乗共役勾配法 共役残差法を適用する. 前処理っき双対共役勾配法 PBCG 法 ) で方程式を解いたときの結果を Fig.1 に示す. 擾乱を除い た方程式では Xi は解に収束する 擾乱があると Xi. はある点まで収束するが途中から残差が増大 し始め っいには発散してしまう. そして 擾乱の大きさが大きいほど早い段階から残差が増大し 始める. これは 次のように説明される. 擾乱が存在するため rk r 毒 ) はある程度以下には小さく ならない. 一方 探索ベクトル Pic と域にそれぞれ擾乱として e とげの成分が入っていようと eg /> A ) N AT ) であるから 五 p 齢露 ) の方は rk r 壽 ) に構わずに小さくなり続ける. その ため ある地点から ak rk r X )1APk pi ) の大きさが擾乱の無い場合よりも大きくなり始め 発散し始める. そして 擾乱の大きさが大きいほど rk の 噌最小値は大きくなるから より早い段階 から発散し始める. 前処理っき自乗共役勾配法 PCGS 法 ) で方程式を解いたときの結果を F 三 g.2 に示す. 前処理っき双対共役勾配法と同様の傾向が得られているが 前処理つき自乗共役勾配法の方が収束速度が速い. また 同じ大きさの擾乱では前処理つき自乗共役勾配法の方がより小さい残差になってから発散を始 める. 前処理っき共役残差法 PCR 法 ) で方程式を解いたときの結果を Fig.3 に示す. 擾舌 L が含まれてい ない場合には Xi は解に収束する. 擾乱が混入している場合には mi は擾乱のない場合と同様にある 点まで収束し続ける. しかし ある点からは反復を続けても残差の大きさはほとんど変化しなくなる. そして 擾乱の大きさが大きいほど より少ない反復回数でより大きい残差に飽和する. これは次の ように説明できる. mi が方程式 Ax br の解に近づくと 残差はハ b 4 鞠 b 酬 le 類 ) に すなわち行列 AT の零空間のベクトルに近づく. そのため rxt Apk ) ATrk ph ) の値は 0 に 近づき )k の値は小さくなり 反復解の改良は止まってしまう. 擾乱の大きさが大きいほど より早い段階で 残差の中で行列 AT の零空間のベクトルが支配的になり 探索が実質的に止まってしまう. 一 137. 一
8 294 )] 本応用数理学会論文誌 Vol.8 No 一 丶 ρ < ) o[ bdo 0 一 4 一 8 一 12 一 16 一 20 一 number of iterations Fig.2 PCGS fordifferent perturbati 皿 s. 0 一 5 丶 皿 の ーガ < ) o[ bdo 一 一 5 一 10 一 15 一 20 一 number of iterations Fig3.PGR.fordifferentperturba. tions. SOR 法で方程式を解いたときの結果を Flg.4 に示す. 加速係数 ω の値としては最適値 ω pt 190 を使用した. 前処理つき共役残差法と同様の傾向が得られている. 次に 擾乱のない方程式について係数行列の特異性を消してから反復解法を適用する. 特異性を消すために 解 x の第 2 成分 :n2 の値を固定して :; 2 O とし 連立 1 次方程式 の第 2 式をこれと入 れ替える そういうふうにして得られた連立 1 次方程式は A x bt となり 係数行列 A は正則である. この連立 1 次方程式を前処理つき双対共役勾配法 前処理っき自乗共役勾配法 前処理つき共役残差法 SOR 法 ω pt 1.98 ) で解き 元の特異な連立 1 次方程式を そのまま解いた場合と比較する. この場合も初期値は Xe ; 端 o にとる. 結果をそれぞれ Fig.5 Fig.6Fig.7Fig.8 に示す. いずれの場合も 特異な連立 1 次方程式をそのまま解く方が 特異性を消去してから解くよりも収束が速い. 一 138 一
9 . 特異な非対称行列を係数とする連立 1 次方程式での各種反復解法の収朿特性 の 丶 ρ < ) o 冖 boo [ 一幣一一一璽 葺 層一一一 number of iterations 600 Fig4.SOR wopt 1.90 ) fbrdsfferent perturba.tions. 至 萋. 乱メ ) ).. b [ 三莖亀島嫋毳 一 2 一 4. ロ6 一 8 一 OI number of iterations 60 Fig 5PBCG fbrthe si 皿 gula. r and nonsingular s ] stenlg. ρ ミ ρ ) 一 [ 蚕醗易 一萋 炉 尭く ) ぎ [ 薫島楞譽 number of iterations 50 Fig.6PCGS forthe singula. r a. nd nonsingular g. } ysterng 一
10 296 目本応用数理学会論文誌 Vol 8 No ρ ρ < ) 三 碧 磊 メ ). 二糞誌易 8 0 一 2 一 4 一 6 一 8 一 number of i 重 erations 150 Fig.7.PCR for the singular and 皿 onsingu ar systems. ニ 互 < ) 葛毎 蚕一 暫 o. メ ). b 莖乱 甥 mmber of iterations 250 Fig.8.SOR forthe singular and nonsingular systems. 5 流れの数値シミュレーションへの応用 5.1 特異な連立 1 次方程式の整合性と圧力についての方程式 非圧縮性流れや低マッハ数流れを数値シミュレーションするとき ノイマン型境界条件をもつ圧力 p についての方程式 一一 S in v 嘉一 G nc を解く必要がある国 このソース関数 3 と墳界値関 ikg との間にガウスの発散定理により 5 1 ) Sd v ff f の関係が成り立っ. ここで レは解の領域 σ は解の領域の境界をなす閉曲線 p/ n は C の法 線方向に沿った p の微分係数である. しかしながら 方程式を離散化した場合 離散化誤差のために Gds 一一 140 一
11 The Japan Society Soolety for Industrial 工 ndustrlal and Applled Applied Mathematlos Mathematics 特異な非対称行列を係数とする連立 1 次方程式での各種反復解法の収束特性 297 一般には式 5.1 ) の積分拘束条件は満たされない. そのため 離散化して得られた連立 1 次方程式を 反復解法で解くと発散してしまうことがある ]. また 流れ場の中のある一点での圧力の値を 規定してから数値解を求めると発散は抑えられるが しばしば解が歪んでしまう [9 10 ]. そのため 通常 非斉次項修正法が使われる [ 非斉次項修正法は ソース 関 iks を 次のように修正する. s * s / v ここで ε 一 ffv s 丿 fc dv G ds S を S * で置き換えると 積分拘束条件は正確に満たされる. しかしながら E を求めるための面積分と線積分を精度よく数値積分するのは非常に煩雑である [ 2 9 ] この問題を特異な連立 1 次方程式の整合陵という観点からみると次のようになる. ノイマン型境界 条件をもっ圧力についての方程式を離散化すると 特異行列を係数とする連立 1 次方程式になる. 式 5.1 ) の積分拘束条件はこの連立 1 次方程式の整合性条件と等価である. この連立 1 次方程式を反復解 法で解いたときに発散するのは 前章で考察したように 連立 1 次方程式の中に擾乱が混入している ためである. また 流れ場の中の基準点での圧力の値を固定してから数値解を求めると 流れ場に基 準点の位置についての依存性がみられるのも 連立 1 次方程式の中に混入している擾乱のためである. 物理空間で等間隔の格子点を使って離散化すると係数行列は対称になるが 一般座標へ座標変換し てから計算空間で等間隔の格子点を使っ て離散化すると係数行列は通常非対称になる. 非対称の場合 には 前章までにおいて論じたように 特異な非対称行列を係数にもつ連立正次方程式を その係数 行列の転置行列の 固有値 0 に対応する固有ベクトルを使って擾乱を取り除いて整合化させると発散 が抑えられる. また 擾乱を取り除くと 基準点で圧力の値を固定しても基準点依存性はなくなる. この連立 1 次方程式の整合化法の方が非斉次項修正法よりも直接的であり である. そしてより簡便で 正確 次元正方形キャビティ内自然対流での数値実験 支配方程式 Fig9 に示した 2 次元正方形キャビティ内自然対流について考える. 上下の壁は断熱壁であり 左一定で TH 305 K Tc 295 K とする. 流体のプラントル数 P7 u /X 右の壁の温度はそれぞれ を O.71 にとる. レイリー数 Ra β9α 甘一 Tc ) D3A u は 106 にとる. ここで β は 300K での体積膨張率 X と v はそれぞれ温度伝導度と動粕性係数 g は重力加速度 D はキャビティの辺の長さである. この自然対流を記述するのに 低マッハ数流れの方程式 [8 を使う. 低マッハ数流れの方程式は次 のようになる. ここでテンソル表示を使い 添字 1 ゴは.7; x 軸のベクトルおよびテンソルの成分 に対応する値 1 2 をとることにする. まず ナビエ ストークス方程式は P 霊占 Pd σ 1ぽ一 ρ 万 τ + 蕊爾 D?t Xid ; σ 2で ρ 万 τ 一 + 冨 ρ 9 一 141 一 NII-Electronic N 工工一 Eleotronlo Llbrary Library
12 298 凵本応用数理学会論文誌 Vol.8No Z T Z 一〇 縛 ldi 1 TH T 一 \ T Z 一〇 〆 X C ー 9 D 一一一一 > Fig.9.Thermal convection in a square cavity と書ける. ここで u w はそれぞれ速度の : z 成分 ρ は密度 Pd は圧力の動力学成分 転ゴは粘性 ストレステンソルで速度から鮪 一 諏 謙一 1 聯 とあらわされる. μ は粕陸係数である. 連続方程式は 1D6 1 Pr 砺 EDt Pr dt 賜 となる. ここで E は単位質量あたりの内部エネル ) e 一 p は流れ場の代表的な圧力である. エネル ギー保存の式は ケ 1 一離 響 ここで 7 は定圧比熱 Cp と定積比熱 Cv の比で 7 Cp / Cv である. qi は熱流束密度で温度丁と熱 伝導度 κ とから となる. 状態方程式は次のようになる. qi 一 κ T 爾 P. r ツー 1 )ρ E 圧力についての方程式はナビエ ストークス方程式から次のように得られる. 5.2 ) 1 ) 一一畠 ここで M. 塞 窪 ) 黔 黔 M 宣ひはそれぞれ Navier Stokes 方程式の z ご成分の移流項 粘性項 重力項の合計をあ らわす 境界では u ; t 疋 0 となることから ナビ エストークス方程式よりノイマン型境界条件伽 G π が得られる. 一 142 一
13 The Japan Society Soolety for Industrial 工 ndustrlal and Applled Applied Mathematlos Mathematics 特異な非対称行列を係数とする連立 1 次方程式での各種反復解法の収束特性 299 Fig10.Grid system 数値シミュレーション 特異な非対称行列を係数にもつ連立 1 次方程式の整合化法を使って圧力にっいての方程式を解き キャビティ内の自然対流を数値シミュレー. 一ションする. 第 4 章では 擾乱が各種反復法の収束特性 に及ぼす影響を広範囲かっ詳細に考察するため rt b Axi の大きさと右辺のベクトル b の大きさの比が 倍精度実数型の浮動小数乾数の演算を採用し 残差 以下になるまで反復を実行し た δ 1]bll /Hbll となるような擾乱 b まで調べた. しかし 流れの数値シミュレーションで は 残差 ri b AXi. の大きさと右辺のベクトル b の大きさの比が 10 1e ま 程度まで収束すれば実用 上十分である. それで CRAY Y MP C90 を使い 単精度実数型の浮動小数点数の演算 計算機イプ シロンは約 ) で行う. 支配方程式を差分化するために の格子点を使う. 解の精度を向上さすため 座標変換を使い Fig10に示すように格子点を境界付近に集める. 差分化により 式 5.2 ) から圧力にっいての連立 1 次方程式 Ax b が得られ る. 係数行列 A R GO は特異な非対称行列になる. 差分化した方程式を MAC 法に類似の方法 [8 亅を使い tx / D2 z 1.08 ]0 4 なる時間刻み幅 t で時間方向に積分する. 静止状態に瞬時に TH Tc の温度差を加える衝撃出発とする. 各時間ステップにおいて圧力についての連立 1 次方程式を解く必要がある. 初期の時間ステップで は この連立 1 次方程式に δ lbll /llbll re 10 5 程度の擾乱 b が混入していた. 第 4 章からわかる ように 擾乱が混入したまま反復解法を使うと 収束する前に解が発散したり 停滞したりする. そ こで 各時問ステップにおいて 整合化法を使ってこの擾乱を除去してから 双対共役勾配法 自乗共役勾配法 共役残差法 2 色 SOR 法 の 4 種類の反復解法で解く. 双対共役勾配法 自乗共役勾配法 共役残差法の前処理には 不完全 LDU 分解に Gustafsson 流の補正を行った MJLDU 分解を用いる [ 131. MJLDU 分解に用いる補正係数 α の値を O.98 とする. 各反復解法において 初期値 Xo を決めるのに 一 143 一 NII-Electronic N 工工一 Eleotronlo Llbrary Library
14 300 日本応用数理学会論文誌 Vol.8No 切唱 O 喟一 邸 〇一順 隔 O O 自 5 口 SOR R & B) PBCG PCR PCGS Fig.11.Average number of itera. も ions 各時間ステップにおいて 初期値 XO を mo 0 にとる 各時問ステップにおいて 一つ前の時間ステップでの圧力を初期値鞠にする の二通りの方法を採用した. そして Il Ami bii /11 b ll く に収束するまで反復を続ける. 時間ステップ数が 10 以上になると 擾乱 b の大きさは常に δ IIbll /1 re であった. どの 反復解法を使っても また初期値鞠の決め方にかかわらず 流体変数は同じ時間的経過を辿り そして時間ステップ数が約 1500 位になると定常状態に到達した. 定常状態に到達するまでの 各反復解法の 1 時間ステップ当たりの平均反復回数と平均 CPU 時間 をそれぞれ Fig.1L Fig.12 に示す. 初期値を常に Xe 数は同数になり Gllstafsso コi 流の補正を行った前処理つきの双対共役勾配法 自乗共役勾配法 共役残差法 および 2 色 SOR 法 u ) 二 ept 1.93 ) でそれぞれ 回であった. 当然各時間ス テップにおいて所要の CPU 時間はほぼ同じ長さになり Gusta.fsson o にすると 各時間ステップにおいて反復回 流の補正を行った前処理つきの 双対共役勾配法 自乗共役勾配法 共役残差法 および 2 色 SOR 法 ω pt 1.93 ) においてそれぞれ ms であった. 一方一つ 前の時間ステップでの圧力を初期値にすると 時間ステッ プが進むにしたがいより少ない反復回数で収束するようになる. これは 定常状態に近づくにしたが い 一っ前の時間ステップでの圧力が連立 1 次方程式の解のより良い近似値になっていくからである. Gustafsson 流の補正を行った前処理つきの双対共役勾配法 自乗共役勾配法 共役残差法 および 2 色 SOR 法 wopt 1.93 ) での平均反復回数はそれぞれ 回であった. また 平均 CPU 時間はそれぞれ ms であった. 初期値記 } の決め方にかかわらず 自乗共役勾配法の 所要 CPU 時間が最短になる. そして 共役残差法 双対共役勾配法 2 色 SOR 法の順番である 係数行列を正則化した場合の収束特性初期値を常に Xo 蕭嬬 o にとった場合の各反復解法の収束特性を調べる. 前述したように この場合の収束特性はどの時間ステップにおいてもほぼ同一になる. したがって 定常状態に到達した後の時間ステップでの すなわち定常状態の速度分布と温度分布から決まる 圧力にっいての連立 ] 一 144 一
15 特異な非対称行列を係数とする連立 1 次方程式での各種反復解法の収束特性 傍邑 60 り葺 P 40 u 20 0SOR R & B ) PBCG PCR PCGS Fig.12.AverageCPU time 次方程式 Ax b について調べることにする. この連立 1 次方程式に混入している擾乱 8 の大きさは である. δ ; llb 闘 /1 bll;2.475 x lo 6 まず ベクトル e * を使ってこの擾乱を除去した後 Gustafsson 流の補正を行った前処理つきの双 対共役勾配法 自乗共役勾配法 共役残差法 および 2 色 SOR 法 w pt 二 1.93 ) で解く. 次に 擾乱を除いた方程式にっいては基準点での圧力を固定しても解は歪まないから 基準点で圧 力を固定して係数行列の特異性を打ち消してから反復解法を使ってみる. 第 1251 番目の成分 1251 が 定義されている格子点を基準点とし その値を 0 に固定して係数行列を正則化してから連立 1 次方程 式 A x bt を解く.Gustafsson 流の補正を行った前処理つきの双対共役勾配法 自乗共役勾配法 共役残差法 および 2 色 SOR?k w pt ) ついて特異なまま扱った場合と正則化した場合の収束特陸の比較をそれぞれ Fig.13 Fig.14Fig15 Fig16に示す 第 4 章の結果と同様に いずれの場合も特異なまま扱った場合の方が収束速度が速いのがわかる 数値シミュレーション結果の検証 どの反復解法を使っても また初期値をどちらの方法で決めてもほとんど同一の定常状態が得られ た. 速度分布と温度分布をそれぞれ Fig.17Fig18 に示す. 温度は? 二 [T と無次元化してある. 得られた定常状態から次のような特徴的な量を計算する. NUONUn 鉛直壁侮 0 ) 上での平均ヌッセルト数 萄 max max axnumin 鉛直壁幕侮 0 ) 上での最大局所ヌッセル ト数 及びその位置 ) 鉛直壁師 0 ) 上での最小局所ヌッセル ト数 及びその位置 ) 鉛直 中線侮 α5 ) 上での最大水平速度成分 及びその位置 ) 水平中線 写 0.5 ) 上での最大鉛直速度成分 及びその位置 ) ここで 座標と速度は次のように無次元化してある. 7 }7 + 距 )12 レ TH Tc ) 記罵 m /D 署 z /D 一 145 一
16 The JapanSociety Society forindustrial Industrial and andappliedmathematics Mathematics 302 H lsc fief M twlgle}ijs}:ra JSa ± Vol. 8No {SmoN-- -4 o-oo-oooo-- ek L'si' ge es a E 1 o o Fig. 13. PBCG number of iterations forthe singular and nonsingll}ar systems for pressure. AF ps)dd 2 o ' rv 1.-.Xts-H-2 vy-ov e.-oo"uaoo-- -4 :L' -6 stse 1uy :- 'z O nurnber of iterations Fig. 14. PCGS for the singulat and llonsingular systems for pressure t'-s.-x D ))b " - ti$-voe -4 :u diss 1u 'Z 8 o -6-8 ge ff. -10 o IOO number of iterations 160 Fig. 15. PCR forthe singular and nonsingular systems for pressure. A-iig$i9.- e"tu-uaoo' NII-Electronic Library
17 特異な非対称行列を係数とする連立 1 次方程式での各種反復解法の収束特性 303 一至 ) 鳥巷 鹽 三ー メ 一 ).. 莖蕊 蒭 亀 點 鹽 L 9.. 曽驢 馬 辱.. 冒.r 辱巳辱 non singular 幽. singular ω P 193 ) number of iterati.ons ω P 嵩 L97 ) Fig.16Red BlackSOR for the singulax a 皿 d nonsingular syg.tems for pressure ttt 1 鹽 一一一 } 一一一辱.. 鹽 畠 L r 一鱒 r 隔亀噛.r 幽. 巳一.. 曾 凾一一. 臨鹽 げ ノー丶 r 9 曹辱一辱嘘 凾一尸 M M 馳 膨篠 ここごここ : 二 :: 二三三三三 i ミ 1 : 翩 lll ::: :1 誉 lllll 三 i 三三淵曲 r 玩 _..._ 9. 二 :: 隔 W ::llllll 常 1::: :::::::::1 ::IIIi ttl LLIIil 曲 鹽幽... lltll.. ili r lh..11 ; lilil. 層... 層... 脚 ::: :: 11 Ul 三藍瀧 1 譱三謡 i 鬢 ; 鱗 11h _ 一一一一一一一一一. tlttilv iill 1 三 :::::: こここごこここ三諺嬲 ; 1 こt:.:: :::::::: ; 111 : ここ 彰二 ll::. 匿隔 鼬 ttf Fig.17.Vel city vect rs. Fig.18.Isotherms.The col 且 tours ra. nge froln 0 5 to O.5 wit 1 a contour interyalof O.1. 一 147 一
18 304 日本応用数理学会論文誌 Vol 8No Tablel.Differences % )betweei1も he solutio 皿 reported i 皿 this paper a 皿 d a benchmark solution Nu 乏 NUmi 質 a. O n[ 毓 Presentr 器 uits de ValllDavis 8.8 董 G.0379 Difference %) a up /x1 wd!x 計算値をベンチマ ーク解 [ 51 と比較すると Table1 のようになる. 誤差が最大になるのは最大局所ヌッ セルト数の位置についてであり 9.0% である.2 番目に大きいのは鉛直中線上での最大水平速度成分にっいてで一 4.8% になる.2 次元正方形キャビティ内自然対流については 既に数多くの数値シミーュレションが行われ ベンチ マーク解と比較されている [ 4 12 ]. それらの中で本論文の結果の誤差は小さい方であり したがって妥当な定常状態がシミュレーションできていると考えられる. 6 結言 旨 特異な非対称行列を係数とする連立 1 次方程式の整合性にっいて論じ 双対共役勾配法 自乗共役 勾配法 共役残差法を適用したときの収束特陸を考察した. 擾乱がなく 整合がとれているとどの反 復解法でも解が得られるこ とを示した. このことを簡単な数値実験で実証した. 擾乱を混入さした数 値実験では 解が発散したり 停滞するのが観測され その理由にっいて考察した. また 擾乱のな い連立 1 次方程式では 特異のままで解く方が 解の一成分の値を固定して係数行列を正則化してから解く場合より収束が速いのがわかった. 次に 特異な非対称行列を係数とする連立 1 次方程式の整合性と 流れの数値シミュレーションと の関連を論じ ノイマン型境界条件をもつ圧力についての方程式を安定に解くために 従来よく使わ れてきた非斉次項修正法の代わりに 係数行列の転置行列の固有値 0 に対応する固有ベクトルを使っ て連立 1 次方程式を整合化させる方法を提案した. 整合化法の方がより直接的で 簡便で 正確であ る. 整合化法を使って 2 次元正方形キャビティ内自然対流を数値シミュレーションし 得られた結果 をベンチマーク解と比較した. 良好な一致が得られ 整合化法の有効性が確認できた. そして 双対 共役勾配法 自乗共役勾配法 共役残差法 および 2 色 SOR 法の所要反復回数と所要 GPU 時間を比 較した. また 圧力についての連立 1 次方程式を特異なまま扱った方が 基準点で圧力の値を固定し て係数行列の特異性を打ち消してから反復解法を使う場合よりも収束速度が速くなるのがわかった. 謝辞 本研究中 山形大学工学部機械システム工学科賈為博士 九州大学大学院数理学研究科田端正 久教授 株 ) アールフロー竹田宏博士から有益な御教示をたまわった. 記して深謝する. 参考文献 国 Anderson D.A.Tannehil1.C. and Pletcher ComputationalFhid Mecb 細 cs and Heat Transfer Hemisphere New York1984. [2 亅 BiringenSand Cook C. On pressurebo 匸 mdary conditions for the l 皿 compressible Navie ト Stokes equations using nollstaggered ハ厂 umer.heat 7b ansfer grids ) 一 148 一
19 特異な非対称行列を係数とする連立 1 次方程式での各種反復解法の収束特性 305 [3 亅 Briley W R.Nulnerical Inethod for predictsng th reedimensional steady viscous fiowinducts J.Comput.Phys ) r41 de Vahl Davis G.and Jones 1.P Natu 凪 lconvection of aiτ in a aquare cavity : acomparison exercise nt.jl IVumer. ル1 etho オ 3 Fluitls ) [ 5 ] de Vahl Davis G. Natural co 皿 vection of air i 皿 a. aquare cavity : abench mark soeution Int. ハ ume? Methods Fluids ) Co 皿 jugate bcrrad ient methods fbr inde 且皿 ite systems LectureNotes ) 73 89Springer V611ag Berlin. 16] Fletcher R Math. [ 7 ] Ghia U Ra 皿 amurti R. and Ghia K.N. Solutionof the Neumd nn pressureproblem j 皿 genetal ortbogonal coordinates using the mul 七 igridtechnique AJAA J ) ] Horibata Y.Numerical simulation of a low Mach number fiowwith a la e temperature va.riation Fluids ) [9 ] 賈為 中村佳朗 保原充 u v p 法による自然対流の数値計算法 ながれ ) [10] 賈為 有限体積 差分法による非圧縮性流の計算法に関する研究 名古屋大学博士論文 [ 11 ] 1aasschieter E.F. Preconditioned conjugate gradientsf{)r solving singular systems.o / Oomput.Appl.Math ) [12 ] Markatos N.C.and Perjcleous K A. Laminal and turbulent natural couvection ina enclosed cavity nt. 訊 HeαtMass 7} ansfer ) [13 ] 村田健郎 名取亮 唐木幸比古 大型数値シミュレーション 第 6 章 岩波書店 東京 [ 141 齋藤正彦 線型代数入門 東大出版会 東京 {IS 亅 Son 皿 eveld P. CGS : a.fastla.nczos type solver {fornonsymmetric linearsystems SIAM J Sci. Sta.tist.Cemput.IO ) [ 16 ] 張紹良 藤野清次 小柳義夫 全周ノイマン型塊界条件をもっボアソン方程式の数値解法 第 5 回数値流体力学シンポジウム講演論文集 1991 ) 堀端康善 正会員 ) 210 川崎市川崎区浮島町 4 1 株 ) 東芝研究開発センター 1979 年東京大学大学院工学系研究科博士課程修了. 工学博士同年 株 ) 東芝入社 現在に至る. 入社後 主として熱と流れの数値シミュレ ション 逆問題の研究に従事 H 本シミュレーション学会 日本数値流体力学会 日本流体力学会 電子情報通信学会 日本気象学会各会員 年 3 月 25 日受付 ) 一 149 一
09.pptx
 講義内容 数値解析 第 9 回 5 年 6 月 7 日 水 理学部物理学科情報理学コース. 非線形方程式の数値解法. はじめに. 分法. 補間法.4 ニュートン法.4. 多変数問題への応用.4. ニュートン法の収束性. 連立 次方程式の解法. 序論と行列計算の基礎. ガウスの消去法. 重対角行列の場合の解法項目を変更しました.4 LU 分解法.5 特異値分解法.6 共役勾配法.7 反復法.7. ヤコビ法.7.
講義内容 数値解析 第 9 回 5 年 6 月 7 日 水 理学部物理学科情報理学コース. 非線形方程式の数値解法. はじめに. 分法. 補間法.4 ニュートン法.4. 多変数問題への応用.4. ニュートン法の収束性. 連立 次方程式の解法. 序論と行列計算の基礎. ガウスの消去法. 重対角行列の場合の解法項目を変更しました.4 LU 分解法.5 特異値分解法.6 共役勾配法.7 反復法.7. ヤコビ法.7.
Microsoft PowerPoint - H21生物計算化学2.ppt
 演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
PowerPoint Presentation
 付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
Microsoft PowerPoint - 10.pptx
 m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
OpenFOAM(R) ソースコード入門 pt1 熱伝導方程式の解法から有限体積法の実装について考える 前編 : 有限体積法の基礎確認 2013/11/17 オープンCAE 富山富山県立大学中川慎二
 OpenFOAM(R) ソースコード入門 pt1 熱伝導方程式の解法から有限体積法の実装について考える 前編 : 有限体積法の基礎確認 2013/11/17 オープンCAE 勉強会 @ 富山富山県立大学中川慎二 * OpenFOAM のソースコードでは, 基礎式を偏微分方程式の形で記述する.OpenFOAM 内部では, 有限体積法を使ってこの微分方程式を解いている. どのようにして, 有限体積法に基づく離散化が実現されているのか,
OpenFOAM(R) ソースコード入門 pt1 熱伝導方程式の解法から有限体積法の実装について考える 前編 : 有限体積法の基礎確認 2013/11/17 オープンCAE 勉強会 @ 富山富山県立大学中川慎二 * OpenFOAM のソースコードでは, 基礎式を偏微分方程式の形で記述する.OpenFOAM 内部では, 有限体積法を使ってこの微分方程式を解いている. どのようにして, 有限体積法に基づく離散化が実現されているのか,
テンソル ( その ) テンソル ( その ) スカラー ( 階のテンソル ) スカラー ( 階のテンソル ) 階数 ベクトル ( 階のテンソル ) ベクトル ( 階のテンソル ) 行列表現 シンボリック表現 [ ]
![テンソル ( その ) テンソル ( その ) スカラー ( 階のテンソル ) スカラー ( 階のテンソル ) 階数 ベクトル ( 階のテンソル ) ベクトル ( 階のテンソル ) 行列表現 シンボリック表現 [ ] テンソル ( その ) テンソル ( その ) スカラー ( 階のテンソル ) スカラー ( 階のテンソル ) 階数 ベクトル ( 階のテンソル ) ベクトル ( 階のテンソル ) 行列表現 シンボリック表現 [ ]](/thumbs/93/113587990.jpg) Tsor th-ordr tsor by dcl xprsso m m Lm m k m k L mk kk quott rul by symbolc xprsso Lk X thrd-ordr tsor cotrcto j j Copyrght s rsrvd. No prt of ths documt my b rproducd for proft. テンソル ( その ) テンソル ( その
Tsor th-ordr tsor by dcl xprsso m m Lm m k m k L mk kk quott rul by symbolc xprsso Lk X thrd-ordr tsor cotrcto j j Copyrght s rsrvd. No prt of ths documt my b rproducd for proft. テンソル ( その ) テンソル ( その
FEM原理講座 (サンプルテキスト)
 サンプルテキスト FEM 原理講座 サイバネットシステム株式会社 8 年 月 9 日作成 サンプルテキストについて 各講師が 講義の内容が伝わりやすいページ を選びました テキストのページは必ずしも連続していません 一部を抜粋しています 幾何光学講座については 実物のテキストではなくガイダンスを掲載いたします 対象とする構造系 物理モデル 連続体 固体 弾性体 / 弾塑性体 / 粘弾性体 / 固体
サンプルテキスト FEM 原理講座 サイバネットシステム株式会社 8 年 月 9 日作成 サンプルテキストについて 各講師が 講義の内容が伝わりやすいページ を選びました テキストのページは必ずしも連続していません 一部を抜粋しています 幾何光学講座については 実物のテキストではなくガイダンスを掲載いたします 対象とする構造系 物理モデル 連続体 固体 弾性体 / 弾塑性体 / 粘弾性体 / 固体
パソコンシミュレータの現状
 第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
Microsoft Word - NumericalComputation.docx
 数値計算入門 武尾英哉. 離散数学と数値計算 数学的解法の中には理論計算では求められないものもある. 例えば, 定積分は, まずは積分 ( 被積分関数の原始関数をみつけること できなければ値を得ることはできない. また, ある関数の所定の値における微分値を得るには, まずその関数の微分ができなければならない. さらに代数方程式の解を得るためには, 解析的に代数方程式を解く必要がある. ところが, これらは必ずしも解析的に導けるとは限らない.
数値計算入門 武尾英哉. 離散数学と数値計算 数学的解法の中には理論計算では求められないものもある. 例えば, 定積分は, まずは積分 ( 被積分関数の原始関数をみつけること できなければ値を得ることはできない. また, ある関数の所定の値における微分値を得るには, まずその関数の微分ができなければならない. さらに代数方程式の解を得るためには, 解析的に代数方程式を解く必要がある. ところが, これらは必ずしも解析的に導けるとは限らない.
untitled
 熱対流現象 山中透 2005 年 3 月 概要 流体を熱源に接触させ, 流体に温度傾度を与えたときを考える. 流体の温度傾度が小さいときは, 熱拡散のみが起こるが, 流体の温度傾度が閾値を越えると, 熱拡散だけでは温度傾度を解消できなくなって不安定となり, 対流が生じる. これをベナール対流とよぶ. ここでは, ベナール対流を記述する非線型方程式の線型安定性の解析によって, 流体が不安定化する条件を求め,
熱対流現象 山中透 2005 年 3 月 概要 流体を熱源に接触させ, 流体に温度傾度を与えたときを考える. 流体の温度傾度が小さいときは, 熱拡散のみが起こるが, 流体の温度傾度が閾値を越えると, 熱拡散だけでは温度傾度を解消できなくなって不安定となり, 対流が生じる. これをベナール対流とよぶ. ここでは, ベナール対流を記述する非線型方程式の線型安定性の解析によって, 流体が不安定化する条件を求め,
Microsoft PowerPoint - 10.pptx
 0. 固有値とその応用 固有値と固有ベクトル 2 行列による写像から固有ベクトルへ m n A : m n n m 行列によって線形写像 f R R A が表せることを見てきた ここでは 2 次元平面の行列による写像を調べる 2 = 2 A 2 2 とし 写像 まず 単位ベクトルの像を求める u 2 x = v 2 y f : R A R を考える u 2 2 u, 2 2 0 = = v 2 0
0. 固有値とその応用 固有値と固有ベクトル 2 行列による写像から固有ベクトルへ m n A : m n n m 行列によって線形写像 f R R A が表せることを見てきた ここでは 2 次元平面の行列による写像を調べる 2 = 2 A 2 2 とし 写像 まず 単位ベクトルの像を求める u 2 x = v 2 y f : R A R を考える u 2 2 u, 2 2 0 = = v 2 0
NS NS Scalar turbulence 5 6 FEM NS Mesh (A )
 22 3 2 1 2 2 2 3 3 4 NS 4 4.1 NS............ 5 5 Scalar turbulence 5 6 FEM 5 6.1 NS.................................... 6 6.2 Mes A )................................... 6 6.3.....................................
22 3 2 1 2 2 2 3 3 4 NS 4 4.1 NS............ 5 5 Scalar turbulence 5 6 FEM 5 6.1 NS.................................... 6 6.2 Mes A )................................... 6 6.3.....................................
行列、ベクトル
 行列 (Mtri) と行列式 (Determinnt). 行列 (Mtri) の演算. 和 差 積.. 行列とは.. 行列の和差 ( 加減算 ).. 行列の積 ( 乗算 ). 転置行列 対称行列 正方行列. 単位行列. 行列式 (Determinnt) と逆行列. 行列式. 逆行列. 多元一次連立方程式のコンピュータによる解法. コンピュータによる逆行列の計算.. 定数項の異なる複数の方程式.. 逆行列の計算
行列 (Mtri) と行列式 (Determinnt). 行列 (Mtri) の演算. 和 差 積.. 行列とは.. 行列の和差 ( 加減算 ).. 行列の積 ( 乗算 ). 転置行列 対称行列 正方行列. 単位行列. 行列式 (Determinnt) と逆行列. 行列式. 逆行列. 多元一次連立方程式のコンピュータによる解法. コンピュータによる逆行列の計算.. 定数項の異なる複数の方程式.. 逆行列の計算
PowerPoint Presentation
 Non-linea factue mechanics き裂先端付近の塑性変形 塑性域 R 破壊進行領域応カ特異場 Ω R R Hutchinson, Rice and Rosengen 全ひずみ塑性理論に基づいた解析 現段階のひずみは 除荷がないとすると現段階の応力で一義的に決まる 単純引張り時の応カーひずみ関係 ( 構成方程式 ): ( ) ( ) n () y y y ここで α,n 定数, /
Non-linea factue mechanics き裂先端付近の塑性変形 塑性域 R 破壊進行領域応カ特異場 Ω R R Hutchinson, Rice and Rosengen 全ひずみ塑性理論に基づいた解析 現段階のひずみは 除荷がないとすると現段階の応力で一義的に決まる 単純引張り時の応カーひずみ関係 ( 構成方程式 ): ( ) ( ) n () y y y ここで α,n 定数, /
線積分.indd
 線積分 線積分 ( n, n, n ) (ξ n, η n, ζ n ) ( n-, n-, n- ) (ξ k, η k, ζ k ) ( k, k, k ) ( k-, k-, k- ) 物体に力 を作用させて位置ベクトル A の点 A から位置ベクトル の点 まで曲線 に沿って物体を移動させたときの仕事 W は 次式で計算された A, A, W : d 6 d+ d+ d@,,, d+ d+
線積分 線積分 ( n, n, n ) (ξ n, η n, ζ n ) ( n-, n-, n- ) (ξ k, η k, ζ k ) ( k, k, k ) ( k-, k-, k- ) 物体に力 を作用させて位置ベクトル A の点 A から位置ベクトル の点 まで曲線 に沿って物体を移動させたときの仕事 W は 次式で計算された A, A, W : d 6 d+ d+ d@,,, d+ d+
<4D F736F F D E4F8E9F82C982A882AF82E98D7397F1>
 3 三次における行列 要旨高校では ほとんど 2 2 の正方行列しか扱ってなく 三次の正方行列について考えてみたかったため 数 C で学んだ定理を三次の正方行列に応用して 自分たちで仮説を立てて求めていったら 空間における回転移動を表す行列 三次のケーリー ハミルトンの定理 三次における逆行列を求めたり 仮説をたてることができた. 目的 数 C で学んだ定理を三次の正方行列に応用する 2. 概要目的の到達点として
3 三次における行列 要旨高校では ほとんど 2 2 の正方行列しか扱ってなく 三次の正方行列について考えてみたかったため 数 C で学んだ定理を三次の正方行列に応用して 自分たちで仮説を立てて求めていったら 空間における回転移動を表す行列 三次のケーリー ハミルトンの定理 三次における逆行列を求めたり 仮説をたてることができた. 目的 数 C で学んだ定理を三次の正方行列に応用する 2. 概要目的の到達点として
(Microsoft PowerPoint - \221\34613\211\361)
 計算力学 ~ 第 回弾性問題の有限要素解析 (Ⅱ)~ 修士 年後期 ( 選択科目 ) 担当 : 岩佐貴史 講義の概要 全 5 講義. 計算力学概論, ガイダンス. 自然現象の数理モデル化. 行列 場とその演算. 数値計算法 (Ⅰ) 5. 数値計算法 (Ⅱ) 6. 初期値 境界値問題 (Ⅰ) 7. 初期値 境界値問題 (Ⅱ) 8. マトリックス変位法による構造解析 9. トラス構造の有限要素解析. 重み付き残差法と古典的近似解法.
計算力学 ~ 第 回弾性問題の有限要素解析 (Ⅱ)~ 修士 年後期 ( 選択科目 ) 担当 : 岩佐貴史 講義の概要 全 5 講義. 計算力学概論, ガイダンス. 自然現象の数理モデル化. 行列 場とその演算. 数値計算法 (Ⅰ) 5. 数値計算法 (Ⅱ) 6. 初期値 境界値問題 (Ⅰ) 7. 初期値 境界値問題 (Ⅱ) 8. マトリックス変位法による構造解析 9. トラス構造の有限要素解析. 重み付き残差法と古典的近似解法.
例 e 指数関数的に減衰する信号を h( a < + a a すると, それらのラプラス変換は, H ( ) { e } e インパルス応答が h( a < ( ただし a >, U( ) { } となるシステムにステップ信号 ( y( のラプラス変換 Y () は, Y ( ) H ( ) X (
 第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
Microsoft PowerPoint - 夏の学校(CFD).pptx
 /9/5 FD( 計算流体力学 ) の基礎理論 性能 運動分野 夏の学校 神戸大学大学院海事科学研究科勝井辰博 流体の質量保存 流体要素内の質量の増加率 [ 単位時間当たりの増加量 ] 単位時間に流体要素に流入する質量 流体要素 Fl lm (orol olm) v ( ) ガウスの定理 v( ) /9/5 = =( ) b=b =(b b b ) b= b = b + b + b アインシュタイン表記
/9/5 FD( 計算流体力学 ) の基礎理論 性能 運動分野 夏の学校 神戸大学大学院海事科学研究科勝井辰博 流体の質量保存 流体要素内の質量の増加率 [ 単位時間当たりの増加量 ] 単位時間に流体要素に流入する質量 流体要素 Fl lm (orol olm) v ( ) ガウスの定理 v( ) /9/5 = =( ) b=b =(b b b ) b= b = b + b + b アインシュタイン表記
行列の反復解法 1. 点 Jacobi 法 数値解法の重要な概念の一つである反復法を取り上げ 連立一次方程式 Au=b の反復解法を調べる 行列のスペクトル半径と収束行列の定義を与える 行列のスペクトル半径行列 Aの固有値の絶対値の最大値でもって 行列 Aのスペクトル半径 r(a) を与える 収束行
 行列の反復解法 1. 点 Jacobi 法 数値解法の重要な概念の一つである反復法を取り上げ 連立一次方程式 Au=b の反復解法を調べる 行列のスペクトル半径と収束行列の定義を与える 行列のスペクトル半径行列 Aの固有値の絶対値の最大値でもって 行列 Aのスペクトル半径 r(a) を与える 収束行列 B が正方行列で のとき B を収束行列と呼ぶ 定理収束行列のスペクトル半径は である 簡単な証明もし
行列の反復解法 1. 点 Jacobi 法 数値解法の重要な概念の一つである反復法を取り上げ 連立一次方程式 Au=b の反復解法を調べる 行列のスペクトル半径と収束行列の定義を与える 行列のスペクトル半径行列 Aの固有値の絶対値の最大値でもって 行列 Aのスペクトル半径 r(a) を与える 収束行列 B が正方行列で のとき B を収束行列と呼ぶ 定理収束行列のスペクトル半径は である 簡単な証明もし
2 図微小要素の流体の流入出 方向の断面の流体の流入出の収支断面 Ⅰ から微小要素に流入出する流体の流量 Q 断面 Ⅰ は 以下のように定式化できる Q 断面 Ⅰ 流量 密度 流速 断面 Ⅰ の面積 微小要素の断面 Ⅰ から だけ移動した断面 Ⅱ を流入出する流体の流量 Q 断面 Ⅱ は以下のように
 3 章 Web に Link 解説 連続式 微分表示 の誘導.64 *4. 連続式連続式は ある領域の内部にある流体の質量の収支が その表面からの流入出の合計と等しくなることを定式化したものであり 流体における質量保存則を示したものである 2. 連続式 微分表示 の誘導図のような微小要素 コントロールボリューム の領域内の流体の増減と外部からの流体の流入出を考えることで定式化できる 微小要素 流入
3 章 Web に Link 解説 連続式 微分表示 の誘導.64 *4. 連続式連続式は ある領域の内部にある流体の質量の収支が その表面からの流入出の合計と等しくなることを定式化したものであり 流体における質量保存則を示したものである 2. 連続式 微分表示 の誘導図のような微小要素 コントロールボリューム の領域内の流体の増減と外部からの流体の流入出を考えることで定式化できる 微小要素 流入
Microsoft Word - 補論3.2
 補論 3. 多変量 GARC モデル 07//6 新谷元嗣 藪友良 対数尤度関数 3 章 7 節では 変量の対数尤度を求めた ここでは多変量の場合 とくに 変量について対数尤度を求める 誤差項 は平均 0 で 次元の正規分布に従うとする 単純化のため 分散と共分散は時間を通じて一定としよう ( この仮定は後で変更される ) したがって ij から添え字 を除くことができる このとき と の尤度関数は
補論 3. 多変量 GARC モデル 07//6 新谷元嗣 藪友良 対数尤度関数 3 章 7 節では 変量の対数尤度を求めた ここでは多変量の場合 とくに 変量について対数尤度を求める 誤差項 は平均 0 で 次元の正規分布に従うとする 単純化のため 分散と共分散は時間を通じて一定としよう ( この仮定は後で変更される ) したがって ij から添え字 を除くことができる このとき と の尤度関数は
数学 t t t t t 加法定理 t t t 倍角公式加法定理で α=β と置く. 三角関数
 . 三角関数 基本関係 t cot c sc c cot sc t 還元公式 t t t t t t cot t cot t 数学 数学 t t t t t 加法定理 t t t 倍角公式加法定理で α=β と置く. 三角関数 数学. 三角関数 5 積和公式 6 和積公式 数学. 三角関数 7 合成 t V v t V v t V V V V VV V V V t V v v 8 べき乗 5 6 6
. 三角関数 基本関係 t cot c sc c cot sc t 還元公式 t t t t t t cot t cot t 数学 数学 t t t t t 加法定理 t t t 倍角公式加法定理で α=β と置く. 三角関数 数学. 三角関数 5 積和公式 6 和積公式 数学. 三角関数 7 合成 t V v t V v t V V V V VV V V V t V v v 8 べき乗 5 6 6
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生
 0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
Microsoft PowerPoint - H22制御工学I-2回.ppt
 制御工学 I 第二回ラプラス変換 平成 年 4 月 9 日 /4/9 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
制御工学 I 第二回ラプラス変換 平成 年 4 月 9 日 /4/9 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
Microsoft Word ã‡»ã…«ã‡ªã…¼ã…‹ã…žã…‹ã…³ã†¨åłºæœ›å•¤(佒芤喋çfl�)
 Cellulr uo nd heir eigenlues 東洋大学総合情報学部 佐藤忠一 Tdzu So Depren o Inorion Siene nd rs Toyo Uniersiy. まえがき 一次元セルオ-トマトンは数学的には記号列上の行列の固有値問題である 固有値問題の行列はふつう複素数体上の行列である 量子力学における固有値問題も無限次元ではあるが関数環上の行列でその成分は可換環である
Cellulr uo nd heir eigenlues 東洋大学総合情報学部 佐藤忠一 Tdzu So Depren o Inorion Siene nd rs Toyo Uniersiy. まえがき 一次元セルオ-トマトンは数学的には記号列上の行列の固有値問題である 固有値問題の行列はふつう複素数体上の行列である 量子力学における固有値問題も無限次元ではあるが関数環上の行列でその成分は可換環である
多次元レーザー分光で探る凝縮分子系の超高速動力学
 波動方程式と量子力学 谷村吉隆 京都大学理学研究科化学専攻 http:theochem.kuchem.kyoto-u.ac.jp TA: 岩元佑樹 iwamoto.y@kuchem.kyoto-u.ac.jp ベクトルと行列の作法 A 列ベクトル c = c c 行ベクトル A = [ c c c ] 転置ベクトル T A = [ c c c ] AA 内積 c AA = [ c c c ] c =
波動方程式と量子力学 谷村吉隆 京都大学理学研究科化学専攻 http:theochem.kuchem.kyoto-u.ac.jp TA: 岩元佑樹 iwamoto.y@kuchem.kyoto-u.ac.jp ベクトルと行列の作法 A 列ベクトル c = c c 行ベクトル A = [ c c c ] 転置ベクトル T A = [ c c c ] AA 内積 c AA = [ c c c ] c =
航空機の運動方程式
 可制御性 可観測性. 可制御性システムの状態を, 適切な操作によって, 有限時間内に, 任意の状態から別の任意の状態に移動させることができるか否かという特性を可制御性という. 可制御性を有するシステムに対し, システムは可制御である, 可制御なシステム という言い方をする. 状態方程式, 出力方程式が以下で表されるn 次元 m 入力 r 出力線形時不変システム x Ax u y x Du () に対し,
可制御性 可観測性. 可制御性システムの状態を, 適切な操作によって, 有限時間内に, 任意の状態から別の任意の状態に移動させることができるか否かという特性を可制御性という. 可制御性を有するシステムに対し, システムは可制御である, 可制御なシステム という言い方をする. 状態方程式, 出力方程式が以下で表されるn 次元 m 入力 r 出力線形時不変システム x Ax u y x Du () に対し,
数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュ
 数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュレーションによって計算してみる 4.1 放物運動一様な重力場における放物運動を考える 一般に質量の物体に作用する力をとすると運動方程式は
数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュレーションによって計算してみる 4.1 放物運動一様な重力場における放物運動を考える 一般に質量の物体に作用する力をとすると運動方程式は
36 th IChO : - 3 ( ) , G O O D L U C K final 1
 36 th ICh - - 5 - - : - 3 ( ) - 169 - -, - - - - - - - G D L U C K final 1 1 1.01 2 e 4.00 3 Li 6.94 4 Be 9.01 5 B 10.81 6 C 12.01 7 N 14.01 8 16.00 9 F 19.00 10 Ne 20.18 11 Na 22.99 12 Mg 24.31 Periodic
36 th ICh - - 5 - - : - 3 ( ) - 169 - -, - - - - - - - G D L U C K final 1 1 1.01 2 e 4.00 3 Li 6.94 4 Be 9.01 5 B 10.81 6 C 12.01 7 N 14.01 8 16.00 9 F 19.00 10 Ne 20.18 11 Na 22.99 12 Mg 24.31 Periodic
4.6: 3 sin 5 sin θ θ t θ 2t θ 4t : sin ωt ω sin θ θ ωt sin ωt 1 ω ω [rad/sec] 1 [sec] ω[rad] [rad/sec] 5.3 ω [rad/sec] 5.7: 2t 4t sin 2t sin 4t
![4.6: 3 sin 5 sin θ θ t θ 2t θ 4t : sin ωt ω sin θ θ ωt sin ωt 1 ω ω [rad/sec] 1 [sec] ω[rad] [rad/sec] 5.3 ω [rad/sec] 5.7: 2t 4t sin 2t sin 4t 4.6: 3 sin 5 sin θ θ t θ 2t θ 4t : sin ωt ω sin θ θ ωt sin ωt 1 ω ω [rad/sec] 1 [sec] ω[rad] [rad/sec] 5.3 ω [rad/sec] 5.7: 2t 4t sin 2t sin 4t](/thumbs/70/62705042.jpg) 1 1.1 sin 2π [rad] 3 ft 3 sin 2t π 4 3.1 2 1.1: sin θ 2.2 sin θ ft t t [sec] t sin 2t π 4 [rad] sin 3.1 3 sin θ θ t θ 2t π 4 3.2 3.1 3.4 3.4: 2.2: sin θ θ θ [rad] 2.3 0 [rad] 4 sin θ sin 2t π 4 sin 1 1
1 1.1 sin 2π [rad] 3 ft 3 sin 2t π 4 3.1 2 1.1: sin θ 2.2 sin θ ft t t [sec] t sin 2t π 4 [rad] sin 3.1 3 sin θ θ t θ 2t π 4 3.2 3.1 3.4 3.4: 2.2: sin θ θ θ [rad] 2.3 0 [rad] 4 sin θ sin 2t π 4 sin 1 1
PowerPoint Presentation
 応用数学 Ⅱ (7) 7 連立微分方程式の立て方と解法. 高階微分方程式による解法. ベクトル微分方程式による解法 3. 演算子による解法 連立微分方程式 未知数が複数個あり, 未知数の数だけ微分方程式が与えられている場合, これらを連立微分方程式という. d d 解法 () 高階微分方程式化による解法 つの方程式から つの未知数を消去して, 未知数が つの方程式に変換 のみの方程式にするために,
応用数学 Ⅱ (7) 7 連立微分方程式の立て方と解法. 高階微分方程式による解法. ベクトル微分方程式による解法 3. 演算子による解法 連立微分方程式 未知数が複数個あり, 未知数の数だけ微分方程式が与えられている場合, これらを連立微分方程式という. d d 解法 () 高階微分方程式化による解法 つの方程式から つの未知数を消去して, 未知数が つの方程式に変換 のみの方程式にするために,
14 化学実験法 II( 吉村 ( 洋 mmol/l の半分だったから さんの測定値は くんの測定値の 4 倍の重みがあり 推定値 としては 0.68 mmol/l その標準偏差は mmol/l 程度ということになる 測定値を 特徴づけるパラメータ t を推定するこの手
 14 化学実験法 II( 吉村 ( 洋 014.6.1. 最小 乗法のはなし 014.6.1. 内容 最小 乗法のはなし...1 最小 乗法の考え方...1 最小 乗法によるパラメータの決定... パラメータの信頼区間...3 重みの異なるデータの取扱い...4 相関係数 決定係数 ( 最小 乗法を語るもう一つの立場...5 実験条件の誤差の影響...5 問題...6 最小 乗法の考え方 飲料水中のカルシウム濃度を
14 化学実験法 II( 吉村 ( 洋 014.6.1. 最小 乗法のはなし 014.6.1. 内容 最小 乗法のはなし...1 最小 乗法の考え方...1 最小 乗法によるパラメータの決定... パラメータの信頼区間...3 重みの異なるデータの取扱い...4 相関係数 決定係数 ( 最小 乗法を語るもう一つの立場...5 実験条件の誤差の影響...5 問題...6 最小 乗法の考え方 飲料水中のカルシウム濃度を
スライド 1
 大規模連立一次方程式に対する 高並列前処理技術について 今倉暁筑波大学計算科学研究センター 共同研究者櫻井鉄也 ( 筑波大学 ), 住吉光介 ( 沼津高専 ), 松古栄夫 (KEK) 1 /49 本日のトピック 大規模連立一次方程式 のための ( 前処理付き )Krylov 部分空間法の概略について紹介する. 高並列性を考慮した前処理として, 反復法を用いた重み付き定常反復型前処理を導入し, そのパラメータを最適化手法を提案
大規模連立一次方程式に対する 高並列前処理技術について 今倉暁筑波大学計算科学研究センター 共同研究者櫻井鉄也 ( 筑波大学 ), 住吉光介 ( 沼津高専 ), 松古栄夫 (KEK) 1 /49 本日のトピック 大規模連立一次方程式 のための ( 前処理付き )Krylov 部分空間法の概略について紹介する. 高並列性を考慮した前処理として, 反復法を用いた重み付き定常反復型前処理を導入し, そのパラメータを最適化手法を提案
Probit , Mixed logit
 Probit, Mixed logit 2016/5/16 スタートアップゼミ #5 B4 後藤祥孝 1 0. 目次 Probit モデルについて 1. モデル概要 2. 定式化と理解 3. 推定 Mixed logit モデルについて 4. モデル概要 5. 定式化と理解 6. 推定 2 1.Probit 概要 プロビットモデルとは. 効用関数の誤差項に多変量正規分布を仮定したもの. 誤差項には様々な要因が存在するため,
Probit, Mixed logit 2016/5/16 スタートアップゼミ #5 B4 後藤祥孝 1 0. 目次 Probit モデルについて 1. モデル概要 2. 定式化と理解 3. 推定 Mixed logit モデルについて 4. モデル概要 5. 定式化と理解 6. 推定 2 1.Probit 概要 プロビットモデルとは. 効用関数の誤差項に多変量正規分布を仮定したもの. 誤差項には様々な要因が存在するため,
経済数学演習問題 2018 年 5 月 29 日 I a, b, c R n に対して a + b + c 2 = a 2 + b 2 + c 2 + 2( a, b) + 2( b, c) + 2( a, c) が成立することを示しましょう.( 線型代数学 教科書 13 ページ 演習 1.17)
 経済数学演習問題 8 年 月 9 日 I a, b, c R n に対して a + b + c a + b + c + a, b + b, c + a, c が成立することを示しましょう. 線型代数学 教科書 ページ 演習.7 II a R n がすべての x R n に対して垂直, すなわち a, x x R n が成立するとします. このとき a となることを示しましょう. 線型代数学 教科書
経済数学演習問題 8 年 月 9 日 I a, b, c R n に対して a + b + c a + b + c + a, b + b, c + a, c が成立することを示しましょう. 線型代数学 教科書 ページ 演習.7 II a R n がすべての x R n に対して垂直, すなわち a, x x R n が成立するとします. このとき a となることを示しましょう. 線型代数学 教科書
Microsoft PowerPoint - 第3回2.ppt
 講義内容 講義内容 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 ベクトルの直交性 3
講義内容 講義内容 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 ベクトルの直交性 3
数学の世界
 東京女子大学文理学部数学の世界 (2002 年度 ) 永島孝 17 6 行列式の基本法則と効率的な計算法 基本法則 三次以上の行列式についても, 二次の場合と同様な法則がなりたつ ここには三次の場合を例示するが, 四次以上でも同様である 1 単位行列の行列式の値は 1 である すなわち 1 0 0 0 1 0 1 0 0 1 2 二つの列を入れ替えると行列式の値は 1 倍になる 例えば a 13 a
東京女子大学文理学部数学の世界 (2002 年度 ) 永島孝 17 6 行列式の基本法則と効率的な計算法 基本法則 三次以上の行列式についても, 二次の場合と同様な法則がなりたつ ここには三次の場合を例示するが, 四次以上でも同様である 1 単位行列の行列式の値は 1 である すなわち 1 0 0 0 1 0 1 0 0 1 2 二つの列を入れ替えると行列式の値は 1 倍になる 例えば a 13 a
Microsoft PowerPoint - 第7章(自然対流熱伝達 )_H27.ppt [互換モード]
![Microsoft PowerPoint - 第7章(自然対流熱伝達 )_H27.ppt [互換モード] Microsoft PowerPoint - 第7章(自然対流熱伝達 )_H27.ppt [互換モード]](/thumbs/94/118222251.jpg) 第 7 章自然対流熱伝達 伝熱工学の基礎 : 伝熱の基本要素 フーリエの法則 ニュートンの冷却則 次元定常熱伝導 : 熱伝導率 熱通過率 熱伝導方程式 次元定常熱伝導 : ラプラスの方程式 数値解析の基礎 非定常熱伝導 : 非定常熱伝導方程式 ラプラス変換 フーリエ数とビオ数 対流熱伝達の基礎 : 熱伝達率 速度境界層と温度境界層 層流境界層と乱流境界層 境界層厚さ 混合平均温度 強制対流熱伝達 :
第 7 章自然対流熱伝達 伝熱工学の基礎 : 伝熱の基本要素 フーリエの法則 ニュートンの冷却則 次元定常熱伝導 : 熱伝導率 熱通過率 熱伝導方程式 次元定常熱伝導 : ラプラスの方程式 数値解析の基礎 非定常熱伝導 : 非定常熱伝導方程式 ラプラス変換 フーリエ数とビオ数 対流熱伝達の基礎 : 熱伝達率 速度境界層と温度境界層 層流境界層と乱流境界層 境界層厚さ 混合平均温度 強制対流熱伝達 :
Microsoft Word - thesis.doc
 剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
<4D F736F F D20824F B CC92E8979D814696CA90CF95AA82C691CC90CF95AA2E646F63>
 1/1 平成 23 年 3 月 24 日午後 6 時 52 分 6 ガウスの定理 : 面積分と体積分 6 ガウスの定理 : 面積分と体積分 Ⅰ. 直交座標系 ガウスの定理は 微分して すぐに積分すると元に戻るというルールを 3 次元積分に適用した定理になります よく知っているのは 簡単化のため 変数が1つの場合は dj ( d ( ににします全微分 = 偏微分 d = d = J ( + C d です
1/1 平成 23 年 3 月 24 日午後 6 時 52 分 6 ガウスの定理 : 面積分と体積分 6 ガウスの定理 : 面積分と体積分 Ⅰ. 直交座標系 ガウスの定理は 微分して すぐに積分すると元に戻るというルールを 3 次元積分に適用した定理になります よく知っているのは 簡単化のため 変数が1つの場合は dj ( d ( ににします全微分 = 偏微分 d = d = J ( + C d です
ଗȨɍɫȮĘർǻ 図 : a)3 次元自由粒子の波数空間におけるエネルギー固有値の分布の様子 b) マクロなサイズの系 L ) における W E) と ΩE) の対応 として与えられる 周期境界条件を満たす波数 kn は kn = πn, L n = 0, ±, ±, 7) となる 長さ L の有限
 : Email: mizushima@mp.es.osaka-u.ac.jp, D38 0 08 5 S = k B ln W ) W n [] [] 5 N. 6 d h m dx ϕ nx) = E n ϕ n x) ) L 5 ϕ n x = 0) = ϕ n x = L) = 0, N k n ϕ n = N sink n x), E n = h k n m 3) k n = nπ, n =,,
: Email: mizushima@mp.es.osaka-u.ac.jp, D38 0 08 5 S = k B ln W ) W n [] [] 5 N. 6 d h m dx ϕ nx) = E n ϕ n x) ) L 5 ϕ n x = 0) = ϕ n x = L) = 0, N k n ϕ n = N sink n x), E n = h k n m 3) k n = nπ, n =,,
スライド タイトルなし
 線形代数 演習 (008 年度版 ) 008/5/6 線形代数 演習 Ⅰ コンピュータ グラフィックス, 次曲面と線形代数指南書第七の巻 直交行列, 実対称行列とその対角化, 次曲線池田勉龍谷大学理工学部数理情報学科 実行列, 正方行列, 実対称行列, 直交行列 a a N A am a MN 実行列 : すべての成分 a が実数である行列 ij ji ij 正方行列 : 行の数と列の数が等しい (
線形代数 演習 (008 年度版 ) 008/5/6 線形代数 演習 Ⅰ コンピュータ グラフィックス, 次曲面と線形代数指南書第七の巻 直交行列, 実対称行列とその対角化, 次曲線池田勉龍谷大学理工学部数理情報学科 実行列, 正方行列, 実対称行列, 直交行列 a a N A am a MN 実行列 : すべての成分 a が実数である行列 ij ji ij 正方行列 : 行の数と列の数が等しい (
ベクトル公式.rtf
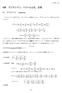 6 章ラプラシアン, ベクトル公式, 定理 6.1 ラプラシアン Laplacian φ はベクトル量である. そこでさらに発散をとると, φ はどういう形になるであろうか? φ = a + a + a φ a + a φ + a φ = φ + φ + φ = 2 φ + 2 φ 2 + 2 φ 2 2 φ = 2 φ 2 + 2 φ 2 + 2 φ 2 = 2 φ したがって,2 階の偏微分演算となる.
6 章ラプラシアン, ベクトル公式, 定理 6.1 ラプラシアン Laplacian φ はベクトル量である. そこでさらに発散をとると, φ はどういう形になるであろうか? φ = a + a + a φ a + a φ + a φ = φ + φ + φ = 2 φ + 2 φ 2 + 2 φ 2 2 φ = 2 φ 2 + 2 φ 2 + 2 φ 2 = 2 φ したがって,2 階の偏微分演算となる.
領域シンポ発表
 1 次元の減衰運動の中の強制振動 ) ( f d d d d d e f e ce ) ( si ) ( 1 ) ( cos ω =ω -γ とおくと 一般解は 外力 f()=f siω の場合 f d d d d si f ce f ce si ) cos( cos si ) cos( この一般解は 1 φ は外力と変位との間の位相差で a 時間が経つと 第 1 項は無視できる この場合の振幅を
1 次元の減衰運動の中の強制振動 ) ( f d d d d d e f e ce ) ( si ) ( 1 ) ( cos ω =ω -γ とおくと 一般解は 外力 f()=f siω の場合 f d d d d si f ce f ce si ) cos( cos si ) cos( この一般解は 1 φ は外力と変位との間の位相差で a 時間が経つと 第 1 項は無視できる この場合の振幅を
Part () () Γ Part ,
 Contents a 6 6 6 6 6 6 6 7 7. 8.. 8.. 8.3. 8 Part. 9. 9.. 9.. 3. 3.. 3.. 3 4. 5 4.. 5 4.. 9 4.3. 3 Part. 6 5. () 6 5.. () 7 5.. 9 5.3. Γ 3 6. 3 6.. 3 6.. 3 6.3. 33 Part 3. 34 7. 34 7.. 34 7.. 34 8. 35
Contents a 6 6 6 6 6 6 6 7 7. 8.. 8.. 8.3. 8 Part. 9. 9.. 9.. 3. 3.. 3.. 3 4. 5 4.. 5 4.. 9 4.3. 3 Part. 6 5. () 6 5.. () 7 5.. 9 5.3. Γ 3 6. 3 6.. 3 6.. 3 6.3. 33 Part 3. 34 7. 34 7.. 34 7.. 34 8. 35
Microsoft PowerPoint - 卒業論文 pptx
 時間に依存するポテンシャルによる 量子状態の変化 龍谷大学理工学部数理情報学科 T966 二正寺章指導教員飯田晋司 目次 はじめに 次元のシュレーディンガー方程式 3 井戸型ポテンシャルの固有エネルギーと固有関数 4 4 中央に障壁のある井戸型ポテンシャルの固有エネルギーと固有関数 3 5 障壁が時間によって変化する場合 7 6 まとめ 5 一次元のシュレディンガー方程式量子力学の基本方程式 ψ (
時間に依存するポテンシャルによる 量子状態の変化 龍谷大学理工学部数理情報学科 T966 二正寺章指導教員飯田晋司 目次 はじめに 次元のシュレーディンガー方程式 3 井戸型ポテンシャルの固有エネルギーと固有関数 4 4 中央に障壁のある井戸型ポテンシャルの固有エネルギーと固有関数 3 5 障壁が時間によって変化する場合 7 6 まとめ 5 一次元のシュレディンガー方程式量子力学の基本方程式 ψ (
数学 ⅡB < 公理 > 公理を論拠に定義を用いて定理を証明する 1 大小関係の公理 順序 (a > b, a = b, a > b 1 つ成立 a > b, b > c a > c 成立 ) 順序と演算 (a > b a + c > b + c (a > b, c > 0 ac > bc) 2 図
 数学 Ⅱ < 公理 > 公理を論拠に定義を用いて定理を証明する 大小関係の公理 順序 >, =, > つ成立 >, > > 成立 順序と演算 > + > + >, > > 図形の公理 平行線の性質 錯角 同位角 三角形の合同条件 三角形の合同相似 量の公理 角の大きさ 線分の長さ < 空間における座漂とベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル
数学 Ⅱ < 公理 > 公理を論拠に定義を用いて定理を証明する 大小関係の公理 順序 >, =, > つ成立 >, > > 成立 順序と演算 > + > + >, > > 図形の公理 平行線の性質 錯角 同位角 三角形の合同条件 三角形の合同相似 量の公理 角の大きさ 線分の長さ < 空間における座漂とベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル
Microsoft Word - 1B2011.doc
 第 14 回モールの定理 ( 単純梁の場合 ) ( モールの定理とは何か?p.11) 例題 下記に示す単純梁の C 点のたわみ角 θ C と, たわみ δ C を求めよ ただし, 部材の曲げ 剛性は材軸に沿って一様で とする C D kn B 1.5m 0.5m 1.0m 解答 1 曲げモーメント図を描く,B 点の反力を求める kn kn 4 kn 曲げモーメント図を描く knm 先に得られた曲げモーメントの値を
第 14 回モールの定理 ( 単純梁の場合 ) ( モールの定理とは何か?p.11) 例題 下記に示す単純梁の C 点のたわみ角 θ C と, たわみ δ C を求めよ ただし, 部材の曲げ 剛性は材軸に沿って一様で とする C D kn B 1.5m 0.5m 1.0m 解答 1 曲げモーメント図を描く,B 点の反力を求める kn kn 4 kn 曲げモーメント図を描く knm 先に得られた曲げモーメントの値を
Microsoft PowerPoint - 9.pptx
 9/7/8( 水 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 拡大とスカラー倍 行列演算と写像 ( 次変換 拡大後 k 倍 k 倍 k 倍拡大の関係は スカラー倍を用いて次のように表現できる p = (, ' = k ' 拡大前 p ' = ( ', ' = ( k, k 拡大 4 拡大と行列の積 拡大後 k 倍
9/7/8( 水 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 拡大とスカラー倍 行列演算と写像 ( 次変換 拡大後 k 倍 k 倍 k 倍拡大の関係は スカラー倍を用いて次のように表現できる p = (, ' = k ' 拡大前 p ' = ( ', ' = ( k, k 拡大 4 拡大と行列の積 拡大後 k 倍
Title 混合体モデルに基づく圧縮性流体と移動する固体の熱連成計算手法 Author(s) 鳥生, 大祐 ; 牛島, 省 Citation 土木学会論文集 A2( 応用力学 ) = Journal of Japan Civil Engineers, Ser. A2 (2017), 73 Issue
 Title 混合体モデルに基づく圧縮性流体と移動する固体の熱連成計算手法 Author(s) 鳥生, 大祐 ; 牛島, 省 Citation 土木学会論文集 A2( 応用力学 ) = Journal of Japan Civil Engineers, Ser. A2 (2017), 73 Issue Date 2017 URL http://hdl.handle.net/2433/229150 Right
Title 混合体モデルに基づく圧縮性流体と移動する固体の熱連成計算手法 Author(s) 鳥生, 大祐 ; 牛島, 省 Citation 土木学会論文集 A2( 応用力学 ) = Journal of Japan Civil Engineers, Ser. A2 (2017), 73 Issue Date 2017 URL http://hdl.handle.net/2433/229150 Right
3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x0 = f x= x0 t f c x f =0 [1] c f 0 x= x 0 x 0 f x= x0 x 2 x 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考
![3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x0 = f x= x0 t f c x f =0 [1] c f 0 x= x 0 x 0 f x= x0 x 2 x 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考 3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x0 = f x= x0 t f c x f =0 [1] c f 0 x= x 0 x 0 f x= x0 x 2 x 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考](/thumbs/103/158269281.jpg) 3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x = f x= x t f c x f = [1] c f x= x f x= x 2 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考える まず 初期時刻 t=t に f =R f exp [ik x ] [3] のような波動を与えたとき どのように時間変化するか調べる
3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x = f x= x t f c x f = [1] c f x= x f x= x 2 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考える まず 初期時刻 t=t に f =R f exp [ik x ] [3] のような波動を与えたとき どのように時間変化するか調べる
Chap2
 逆三角関数の微分 Arcsin の導関数を計算する Arcsin I. 初等関数の微積分 sin [, ], [π/, π/] cos sin / (Arcsin ) 計算力の体力をつけよう π/ π/ E. II- 次の関数の導関数を計算せよ () Arccos () Arctan E. I- の解答 不定積分あれこれ () Arccos n log C C (n ) n e e C log (log
逆三角関数の微分 Arcsin の導関数を計算する Arcsin I. 初等関数の微積分 sin [, ], [π/, π/] cos sin / (Arcsin ) 計算力の体力をつけよう π/ π/ E. II- 次の関数の導関数を計算せよ () Arccos () Arctan E. I- の解答 不定積分あれこれ () Arccos n log C C (n ) n e e C log (log
Microsoft Word - 8章(CI).doc
 8 章配置間相互作用法 : Configuration Interaction () etho [] 化学的精度化学反応の精密な解析をするためには エネルギー誤差は数 ~ kcal/mol 程度に抑えたいものである この程度の誤差内に治まる精度を 化学的精度 と呼ぶことがある He 原子のエネルギーをシュレーディンガー方程式と分子軌道法で計算した結果を示そう He 原子のエネルギー Hartree-Fock
8 章配置間相互作用法 : Configuration Interaction () etho [] 化学的精度化学反応の精密な解析をするためには エネルギー誤差は数 ~ kcal/mol 程度に抑えたいものである この程度の誤差内に治まる精度を 化学的精度 と呼ぶことがある He 原子のエネルギーをシュレーディンガー方程式と分子軌道法で計算した結果を示そう He 原子のエネルギー Hartree-Fock
memo
 数理情報工学特論第一 機械学習とデータマイニング 4 章 : 教師なし学習 3 かしまひさし 鹿島久嗣 ( 数理 6 研 ) kashima@mist.i.~ DEPARTMENT OF MATHEMATICAL INFORMATICS 1 グラフィカルモデルについて学びます グラフィカルモデル グラフィカルラッソ グラフィカルラッソの推定アルゴリズム 2 グラフィカルモデル 3 教師なし学習の主要タスクは
数理情報工学特論第一 機械学習とデータマイニング 4 章 : 教師なし学習 3 かしまひさし 鹿島久嗣 ( 数理 6 研 ) kashima@mist.i.~ DEPARTMENT OF MATHEMATICAL INFORMATICS 1 グラフィカルモデルについて学びます グラフィカルモデル グラフィカルラッソ グラフィカルラッソの推定アルゴリズム 2 グラフィカルモデル 3 教師なし学習の主要タスクは
<4D F736F F F696E74202D20836F CC8A C58B858B4F93B982A882E682D1978E89BA814091B28BC68CA48B E >
 バットの角度 打球軌道および落下地点の関係 T999 和田真迪 担当教員 飯田晋司 目次 1. はじめに. ボールとバットの衝突 -1 座標系 -ボールとバットの衝突の前後でのボールの速度 3. ボールの軌道の計算 4. おわりに参考文献 はじめに この研究テーマにした理由は 好きな野球での小さい頃からの疑問であるバッテングについて 角度が変わればどう打球に変化が起こるのかが大学で学んだ物理と数学んだ物理と数学を使って判明できると思ったから
バットの角度 打球軌道および落下地点の関係 T999 和田真迪 担当教員 飯田晋司 目次 1. はじめに. ボールとバットの衝突 -1 座標系 -ボールとバットの衝突の前後でのボールの速度 3. ボールの軌道の計算 4. おわりに参考文献 はじめに この研究テーマにした理由は 好きな野球での小さい頃からの疑問であるバッテングについて 角度が変わればどう打球に変化が起こるのかが大学で学んだ物理と数学んだ物理と数学を使って判明できると思ったから
A Precise Calculation Method of the Gradient Operator in Numerical Computation with the MPS Tsunakiyo IRIBE and Eizo NAKAZA A highly precise numerical
 A Precise Calculation Method of the Gradient Operator in Numerical Computation with the MPS Tsunakiyo IRIBE and Eizo NAKAZA A highly precise numerical calculation method of the gradient as a differential
A Precise Calculation Method of the Gradient Operator in Numerical Computation with the MPS Tsunakiyo IRIBE and Eizo NAKAZA A highly precise numerical calculation method of the gradient as a differential
<8D828D5A838A817C A77425F91E6318FCD2E6D6364>
 4 1 平面上のベクトル 1 ベクトルとその演算 例題 1 ベクトルの相等 次の問いに答えよ. ⑴ 右の図 1 は平行四辺形 である., と等しいベクトルをいえ. ⑵ 右の図 2 の中で互いに等しいベクトルをいえ. ただし, すべてのマス目は正方形である. 解 ⑴,= より, =,= より, = ⑵ 大きさと向きの等しいものを調べる. a =d, c = f d e f 1 右の図の長方形 において,
4 1 平面上のベクトル 1 ベクトルとその演算 例題 1 ベクトルの相等 次の問いに答えよ. ⑴ 右の図 1 は平行四辺形 である., と等しいベクトルをいえ. ⑵ 右の図 2 の中で互いに等しいベクトルをいえ. ただし, すべてのマス目は正方形である. 解 ⑴,= より, =,= より, = ⑵ 大きさと向きの等しいものを調べる. a =d, c = f d e f 1 右の図の長方形 において,
1 1 H Li Be Na M g B A l C S i N P O S F He N Cl A e K Ca S c T i V C Mn Fe Co Ni Cu Zn Ga Ge As Se B K Rb S Y Z Nb Mo Tc Ru Rh Pd Ag Cd In Sn Sb T e
 No. 1 1 1 H Li Be Na M g B A l C S i N P O S F He N Cl A e K Ca S c T i V C Mn Fe Co Ni Cu Zn Ga Ge As Se B K Rb S Y Z Nb Mo Tc Ru Rh Pd Ag Cd In Sn Sb T e I X e Cs Ba F Ra Hf Ta W Re Os I Rf Db Sg Bh
No. 1 1 1 H Li Be Na M g B A l C S i N P O S F He N Cl A e K Ca S c T i V C Mn Fe Co Ni Cu Zn Ga Ge As Se B K Rb S Y Z Nb Mo Tc Ru Rh Pd Ag Cd In Sn Sb T e I X e Cs Ba F Ra Hf Ta W Re Os I Rf Db Sg Bh
( 慣性抵抗 ) 速度の 2 乗に比例流体中を進む物体は前面にある流体を押しのけて進む. 物 aaa 体の後面には流体が付き従う ( 渦を巻いて ). 前面にある速度 0 の流体が後面に移動して速度 vとなったと考えてよい. この流体の質量は単位時間内に物体が押しのける体積に比例するので,v に比例
 空気抵抗があるときの自由落下 抵抗が速度に比例する場合 1. 絵を描く, 座標と情報, 記号を記入する x F0 v
空気抵抗があるときの自由落下 抵抗が速度に比例する場合 1. 絵を描く, 座標と情報, 記号を記入する x F0 v
, COMPUTATION OF SHALLOW WATER EQUATION WITH HIERARCHICAL QUADTREE GRID SYSTEM 1 2 Hiroyasu YASUDA and Tsuyoshi HOSHINO
 , 2 11 8 COMPUTATION OF SHALLOW WATER EQUATION WITH HIERARCHICAL QUADTREE GRID SYSTEM 1 2 Hiroyasu YASUDA and Tsuyoshi HOSHINO 1 9-2181 2 8 2 9-2181 2 8 Numerical computation of river flows have been employed
, 2 11 8 COMPUTATION OF SHALLOW WATER EQUATION WITH HIERARCHICAL QUADTREE GRID SYSTEM 1 2 Hiroyasu YASUDA and Tsuyoshi HOSHINO 1 9-2181 2 8 2 9-2181 2 8 Numerical computation of river flows have been employed
航空機の運動方程式
 オブザーバ 状態フィードバックにはすべての状態変数の値が必要であった. しかしながら, システムの外部から観測できるのは出力だけであり, すべての状態変数が観測できるとは限らない. そこで, 制御対象システムの状態変数を, システムのモデルに基づいてその入出力信号から推定する方法を考える.. オブザーバとは 次元 m 入力 r 出力線形時不変システム x Ax Bu y Cx () の状態変数ベクトル
オブザーバ 状態フィードバックにはすべての状態変数の値が必要であった. しかしながら, システムの外部から観測できるのは出力だけであり, すべての状態変数が観測できるとは限らない. そこで, 制御対象システムの状態変数を, システムのモデルに基づいてその入出力信号から推定する方法を考える.. オブザーバとは 次元 m 入力 r 出力線形時不変システム x Ax Bu y Cx () の状態変数ベクトル
Matrix and summation convention Kronecker delta δ ij 1 = 0 ( i = j) ( i j) permutation symbol e ijk = (even permutation) (odd permutation) (othe
 Matr ad summato covto Krockr dlta δ ( ) ( ) prmutato symbol k (v prmutato) (odd prmutato) (othrs) gvalu dtrmat dt 6 k rst r s kt opyrght s rsrvd. No part of ths documt may b rproducd for proft. 行列 行 正方行列
Matr ad summato covto Krockr dlta δ ( ) ( ) prmutato symbol k (v prmutato) (odd prmutato) (othrs) gvalu dtrmat dt 6 k rst r s kt opyrght s rsrvd. No part of ths documt may b rproducd for proft. 行列 行 正方行列
以下 変数の上のドットは時間に関する微分を表わしている (ex. 2 dx d x x, x 2 dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-1) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( x や x, x などがすべて 1 次で なおかつ
 以下 変数の上のドットは時間に関する微分を表わしている (e. d d, dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( や, などがすべて 次で なおかつそれらの係数が定数であるような微分方程式 ) に対して安定性の解析を行ってきた しかしながら 実際には非線形の微分方程式で記述される現象も多く存在する
以下 変数の上のドットは時間に関する微分を表わしている (e. d d, dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( や, などがすべて 次で なおかつそれらの係数が定数であるような微分方程式 ) に対して安定性の解析を行ってきた しかしながら 実際には非線形の微分方程式で記述される現象も多く存在する
A
 A04-164 2008 2 13 1 4 1.1.......................................... 4 1.2..................................... 4 1.3..................................... 4 1.4..................................... 5 2
A04-164 2008 2 13 1 4 1.1.......................................... 4 1.2..................................... 4 1.3..................................... 4 1.4..................................... 5 2
計算機シミュレーション
 . 運動方程式の数値解法.. ニュートン方程式の近似速度は, 位置座標 の時間微分で, d と定義されます. これを成分で書くと, d d li li とかけます. 本来は が の極限をとらなければいけませんが, 有限の小さな値とすると 秒後の位置座標は速度を用いて, と近似できます. 同様にして, 加速度は, 速度 の時間微分で, d と定義されます. これを成分で書くと, d d li li とかけます.
. 運動方程式の数値解法.. ニュートン方程式の近似速度は, 位置座標 の時間微分で, d と定義されます. これを成分で書くと, d d li li とかけます. 本来は が の極限をとらなければいけませんが, 有限の小さな値とすると 秒後の位置座標は速度を用いて, と近似できます. 同様にして, 加速度は, 速度 の時間微分で, d と定義されます. これを成分で書くと, d d li li とかけます.
に対して 例 2: に対して 逆行列は常に存在するとは限らない 逆行列が存在する行列を正則行列 (regular matrix) という 正則である 逆行列が存在する 一般に 正則行列 A の逆行列 A -1 も正則であり (A -1 ) -1 =A が成り立つ また 2 つの正則行列 A B の積
 2 逆行列 逆行列の計算は 連立一次方程式を数値的に解くために利用される 気象学の分野では線形系の応答問題を数値的に解くときに用いられることも多い ここでは計算機を用いて逆行列を求める方法を学ぶ 2.1 はじめにたとえば 次のような連立一次方程式を解くことを考える このような 2 元連立一次方程式は 代入法や消去法によって容易に解くことができる 解法をプログラミング言語によって記述することも困難ではない
2 逆行列 逆行列の計算は 連立一次方程式を数値的に解くために利用される 気象学の分野では線形系の応答問題を数値的に解くときに用いられることも多い ここでは計算機を用いて逆行列を求める方法を学ぶ 2.1 はじめにたとえば 次のような連立一次方程式を解くことを考える このような 2 元連立一次方程式は 代入法や消去法によって容易に解くことができる 解法をプログラミング言語によって記述することも困難ではない
1 対 1 対応の演習例題を解いてみた 微分法とその応用 例題 1 極限 微分係数の定義 (2) 関数 f ( x) は任意の実数 x について微分可能なのは明らか f ( 1, f ( 1) ) と ( 1 + h, f ( 1 + h)
 微分法とその応用 例題 1 極限 微分係数の定義 () 関数 ( x) は任意の実数 x について微分可能なのは明らか ( 1, ( 1) ) と ( 1 + h, ( 1 + h) ) の傾き= ( 1 + h ) - ( 1 ) ( 1 + ) - ( 1) = ( 1 + h) - 1 h ( 1) = lim h ( 1 + h) - ( 1) h ( 1, ( 1) ) と ( 1 - h,
微分法とその応用 例題 1 極限 微分係数の定義 () 関数 ( x) は任意の実数 x について微分可能なのは明らか ( 1, ( 1) ) と ( 1 + h, ( 1 + h) ) の傾き= ( 1 + h ) - ( 1 ) ( 1 + ) - ( 1) = ( 1 + h) - 1 h ( 1) = lim h ( 1 + h) - ( 1) h ( 1, ( 1) ) と ( 1 - h,
1/30 平成 29 年 3 月 24 日 ( 金 ) 午前 11 時 25 分第三章フェルミ量子場 : スピノール場 ( 次元あり ) 第三章フェルミ量子場 : スピノール場 フェルミ型 ボーズ量子場のエネルギーは 第二章ボーズ量子場 : スカラー場 の (2.18) より ˆ dp 1 1 =
 / 平成 9 年 月 日 ( 金 午前 時 5 分第三章フェルミ量子場 : スピノール場 ( 次元あり 第三章フェルミ量子場 : スピノール場 フェルミ型 ボーズ量子場のエネルギーは 第二章ボーズ量子場 : スカラー場 の (.8 より ˆ ( ( ( q -, ( ( c ( H c c ë é ù û - Ü + c ( ( - に限る (. である 一方 フェルミ型は 成分をもち その成分を,,,,
/ 平成 9 年 月 日 ( 金 午前 時 5 分第三章フェルミ量子場 : スピノール場 ( 次元あり 第三章フェルミ量子場 : スピノール場 フェルミ型 ボーズ量子場のエネルギーは 第二章ボーズ量子場 : スカラー場 の (.8 より ˆ ( ( ( q -, ( ( c ( H c c ë é ù û - Ü + c ( ( - に限る (. である 一方 フェルミ型は 成分をもち その成分を,,,,
Microsoft PowerPoint rev.pptx
 研究室紹介 卒業研究テーマ紹介 木村拓馬 佐賀大学理工学部知能情報システム学科第 2 研究グループ 第 2 研究グループ -- 木村拓馬 : 卒業研究テーマ紹介 (2016/2/16) 1/15 木村の専門分野 応用数学 ( 数値解析 最適化 ) 内容 : 数学 + 計算機 数学の理論に裏付けされた 良い 計算方法 良さ を計算機で検証する方法について研究 目標は でかい 速い 正確 第 2 研究グループ
研究室紹介 卒業研究テーマ紹介 木村拓馬 佐賀大学理工学部知能情報システム学科第 2 研究グループ 第 2 研究グループ -- 木村拓馬 : 卒業研究テーマ紹介 (2016/2/16) 1/15 木村の専門分野 応用数学 ( 数値解析 最適化 ) 内容 : 数学 + 計算機 数学の理論に裏付けされた 良い 計算方法 良さ を計算機で検証する方法について研究 目標は でかい 速い 正確 第 2 研究グループ
補足 中学で学習したフレミング左手の法則 ( 電 磁 力 ) と関連付けると覚えやすい 電磁力は電流と磁界の外積で表される 力 F 磁 電磁力 F li 右ねじの回転の向き電 li ( l は導線の長さ ) 補足 有向線分とベクトル有向線分 : 矢印の位
 http://totemt.sur.ne.p 外積 ( ベクトル積 ) の活用 ( 面積, 法線ベクトル, 平面の方程式 ) 3 次元空間の つのベクトルの積が つのベクトルを与えるようなベクトルの掛け算 ベクトルの積がベクトルを与えることからベクトル積とも呼ばれる これに対し内積は符号と大きさをもつ量 ( スカラー量 ) を与えるので, スカラー積とも呼ばれる 外積を使うと, 平行四辺形や三角形の面積,
http://totemt.sur.ne.p 外積 ( ベクトル積 ) の活用 ( 面積, 法線ベクトル, 平面の方程式 ) 3 次元空間の つのベクトルの積が つのベクトルを与えるようなベクトルの掛け算 ベクトルの積がベクトルを与えることからベクトル積とも呼ばれる これに対し内積は符号と大きさをもつ量 ( スカラー量 ) を与えるので, スカラー積とも呼ばれる 外積を使うと, 平行四辺形や三角形の面積,
差分スキーム 物理 化学 生物現象には微分方程式でモデル化される例が多い モデルを使って現実の現象をコンピュータ上で再現することをシミュレーション ( 数値シミュレーション コンピュータシミュレーション ) と呼ぶ そのためには 微分方程式をコンピュータ上で計算できる数値スキームで近似することが必要
 差分スキーム 物理 化学 生物現象には微分方程式でモデル化される例が多い モデルを使って現実の現象をコンピュータ上で再現することをシミュレーション ( 数値シミュレーション コンピュータシミュレーション ) と呼ぶ そのためには 微分方程式をコンピュータ上で計算できる数値スキームで近似することが必要になる その一つの方法が微分方程式を差分方程式におき直すことである 微分方程式の差分化 次の 1 次元境界値問題を考える
差分スキーム 物理 化学 生物現象には微分方程式でモデル化される例が多い モデルを使って現実の現象をコンピュータ上で再現することをシミュレーション ( 数値シミュレーション コンピュータシミュレーション ) と呼ぶ そのためには 微分方程式をコンピュータ上で計算できる数値スキームで近似することが必要になる その一つの方法が微分方程式を差分方程式におき直すことである 微分方程式の差分化 次の 1 次元境界値問題を考える
Microsoft Word - 非線形計画法 原稿
 非線形計画法条件付き最適化問題は目的関数と制約条件で示すが この中に一つでも 次式でないものが含まれる問題を総称して非線形計画法いう 非線形計画問題は 多くの分野で研究されているが 複雑性により十分汎用的なものは確立されておらず 限定的なものに限り幾つかの提案がなされている ここでは簡単な解法について紹介する. 制約なし極値問題 単純問題の解法 変数で表される関数 の極値は を解くことによって求められる
非線形計画法条件付き最適化問題は目的関数と制約条件で示すが この中に一つでも 次式でないものが含まれる問題を総称して非線形計画法いう 非線形計画問題は 多くの分野で研究されているが 複雑性により十分汎用的なものは確立されておらず 限定的なものに限り幾つかの提案がなされている ここでは簡単な解法について紹介する. 制約なし極値問題 単純問題の解法 変数で表される関数 の極値は を解くことによって求められる
PowerPoint プレゼンテーション
 米田 戸倉川月 7 限 193~21 西 5-19 応用数学 A 積分定理 Gaussの定理 divbd = B nds Stokesの定理 E bds = E dr Green の定理 g x f y dxdy = fdx + gdy = f e i + ge j dr Gauss の発散定理 S n FdS = Fd 1777-1855 ドイツ Johann arl Friedrich Gauss
米田 戸倉川月 7 限 193~21 西 5-19 応用数学 A 積分定理 Gaussの定理 divbd = B nds Stokesの定理 E bds = E dr Green の定理 g x f y dxdy = fdx + gdy = f e i + ge j dr Gauss の発散定理 S n FdS = Fd 1777-1855 ドイツ Johann arl Friedrich Gauss
大気環境シミュレーション
 第 3 回 (Q) 各自 eelを用いて 次の漸化式 + = の解の初期値依存性を調べよ.は50まで () 0 =.0 () 0 =.5 (3) 0 =.0 締切 04 年 月 6 日 ( 月 ) 夕方まで 提出先 347 室 オーバーフロー失敗ゴメンなさい (Q) 各自 eelを用いて 次の漸化式 + = の解の初期値依存性を調べよ.は50まで () 0 =.330 () 0 =.33 (3) 0
第 3 回 (Q) 各自 eelを用いて 次の漸化式 + = の解の初期値依存性を調べよ.は50まで () 0 =.0 () 0 =.5 (3) 0 =.0 締切 04 年 月 6 日 ( 月 ) 夕方まで 提出先 347 室 オーバーフロー失敗ゴメンなさい (Q) 各自 eelを用いて 次の漸化式 + = の解の初期値依存性を調べよ.は50まで () 0 =.330 () 0 =.33 (3) 0
Microsoft PowerPoint - CSA_B3_EX2.pptx
 Computer Science A Hardware Design Excise 2 Handout V2.01 May 27 th.,2019 CSAHW Computer Science A, Meiji University CSA_B3_EX2.pptx 32 Slides Renji Mikami 1 CSAHW2 ハード演習内容 2.1 二次元空間でのベクトルの直交 2.2 Reserved
Computer Science A Hardware Design Excise 2 Handout V2.01 May 27 th.,2019 CSAHW Computer Science A, Meiji University CSA_B3_EX2.pptx 32 Slides Renji Mikami 1 CSAHW2 ハード演習内容 2.1 二次元空間でのベクトルの直交 2.2 Reserved
: 2005 ( ρ t +dv j =0 r m m r = e E( r +e r B( r T 208 T = d E j 207 ρ t = = = e t δ( r r (t e r r δ( r r (t e r ( r δ( r r (t dv j =
 72 Maxwell. Maxwell e r ( =,,N Maxwell rot E + B t = 0 rot H D t = j dv D = ρ dv B = 0 D = ɛ 0 E H = μ 0 B ρ( r = j( r = N e δ( r r = N e r δ( r r = : 2005 ( 2006.8.22 73 207 ρ t +dv j =0 r m m r = e E(
72 Maxwell. Maxwell e r ( =,,N Maxwell rot E + B t = 0 rot H D t = j dv D = ρ dv B = 0 D = ɛ 0 E H = μ 0 B ρ( r = j( r = N e δ( r r = N e r δ( r r = : 2005 ( 2006.8.22 73 207 ρ t +dv j =0 r m m r = e E(
物性物理学I_2.pptx
 phonon U r U = nαi U ( r nαi + u nαi ) = U ( r nαi ) + () nαi,β j := nαi β j U r nαi r β j > U r nαi r u nαiuβ j + β j β j u β j n α i () nαi,β juβj 調和振動子近似の復習 極 小 値近傍で Tylor展開すると U ( x) = U ( x ) + (
phonon U r U = nαi U ( r nαi + u nαi ) = U ( r nαi ) + () nαi,β j := nαi β j U r nαi r β j > U r nαi r u nαiuβ j + β j β j u β j n α i () nαi,β juβj 調和振動子近似の復習 極 小 値近傍で Tylor展開すると U ( x) = U ( x ) + (
Microsoft PowerPoint - 9.pptx
 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 行列演算と写像 ( 次変換 3 拡大とスカラー倍 p ' = ( ', ' = ( k, kk p = (, k 倍 k 倍 拡大後 k 倍拡大の関係は スカラー倍を用いて次のように表現できる ' = k ' 拡大前 拡大 4 拡大と行列の積 p ' = ( ', '
9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 行列演算と写像 ( 次変換 3 拡大とスカラー倍 p ' = ( ', ' = ( k, kk p = (, k 倍 k 倍 拡大後 k 倍拡大の関係は スカラー倍を用いて次のように表現できる ' = k ' 拡大前 拡大 4 拡大と行列の積 p ' = ( ', '
Microsoft PowerPoint - ロボットの運動学forUpload'C5Q [互換モード]
![Microsoft PowerPoint - ロボットの運動学forUpload'C5Q [互換モード] Microsoft PowerPoint - ロボットの運動学forUpload'C5Q [互換モード]](/thumbs/104/163308363.jpg) ロボットの運動学 順運動学とは 座標系の回転と並進 同次座標変換行列 Denavit-Hartenberg の表記法 多関節ロボットの順運動学 レポート課題 & 中間試験について 逆運動学とは ヤコビアン行列 運動方程式 ( 微分方程式 ) ロボットの運動学 動力学 Equation of motion f ( ( t), ( t), ( t)) τ( t) 姿勢 ( 関節角の組合せ ) Posture
ロボットの運動学 順運動学とは 座標系の回転と並進 同次座標変換行列 Denavit-Hartenberg の表記法 多関節ロボットの順運動学 レポート課題 & 中間試験について 逆運動学とは ヤコビアン行列 運動方程式 ( 微分方程式 ) ロボットの運動学 動力学 Equation of motion f ( ( t), ( t), ( t)) τ( t) 姿勢 ( 関節角の組合せ ) Posture
Chap2.key
 . f( ) V (V V ) V e + V e V V V V ( ) V V ( ) E. - () V (0 ) () V (0 ) () V (0 ) (4) V ( ) E. - () V (0 ) () V (0 ) O r θ ( ) ( ) : (r θ) : { r cos θ r sn θ { r + () V (0 ) (4) V ( ) θ θ arg( ) : π π
. f( ) V (V V ) V e + V e V V V V ( ) V V ( ) E. - () V (0 ) () V (0 ) () V (0 ) (4) V ( ) E. - () V (0 ) () V (0 ) O r θ ( ) ( ) : (r θ) : { r cos θ r sn θ { r + () V (0 ) (4) V ( ) θ θ arg( ) : π π
横浜市環境科学研究所
 周期時系列の統計解析 単回帰分析 io 8 年 3 日 周期時系列に季節調整を行わないで単回帰分析を適用すると, 回帰係数には周期成分の影響が加わる. ここでは, 周期時系列をコサイン関数モデルで近似し単回帰分析によりモデルの回帰係数を求め, 周期成分の影響を検討した. また, その結果を気温時系列に当てはめ, 課題等について考察した. 気温時系列とコサイン関数モデル第 報の結果を利用するので, その一部を再掲する.
周期時系列の統計解析 単回帰分析 io 8 年 3 日 周期時系列に季節調整を行わないで単回帰分析を適用すると, 回帰係数には周期成分の影響が加わる. ここでは, 周期時系列をコサイン関数モデルで近似し単回帰分析によりモデルの回帰係数を求め, 周期成分の影響を検討した. また, その結果を気温時系列に当てはめ, 課題等について考察した. 気温時系列とコサイン関数モデル第 報の結果を利用するので, その一部を再掲する.
03J_sources.key
 Radiation Detection & Measurement (1) (2) (3) (4)1 MeV ( ) 10 9 m 10 7 m 10 10 m < 10 18 m X 10 15 m 10 15 m ......... (isotope)...... (isotone)......... (isobar) 1 1 1 0 1 2 1 2 3 99.985% 0.015% ~0% E
Radiation Detection & Measurement (1) (2) (3) (4)1 MeV ( ) 10 9 m 10 7 m 10 10 m < 10 18 m X 10 15 m 10 15 m ......... (isotope)...... (isotone)......... (isobar) 1 1 1 0 1 2 1 2 3 99.985% 0.015% ~0% E
ギリシャ文字の読み方を教えてください
 埼玉工業大学機械工学学習支援セミナー ( 小西克享 ) 単振り子の振動の近似解と厳密解 -/ テーマ H: 単振り子の振動の近似解と厳密解. 運動方程式図 のように, 質量 m のおもりが糸で吊り下げられている時, おもりには重力 W と糸の張力 が作用しています. おもりは静止した状態なので,W と F は釣り合った状態注 ) になっています. すなわち, W です.W は質量 m と重力加速度
埼玉工業大学機械工学学習支援セミナー ( 小西克享 ) 単振り子の振動の近似解と厳密解 -/ テーマ H: 単振り子の振動の近似解と厳密解. 運動方程式図 のように, 質量 m のおもりが糸で吊り下げられている時, おもりには重力 W と糸の張力 が作用しています. おもりは静止した状態なので,W と F は釣り合った状態注 ) になっています. すなわち, W です.W は質量 m と重力加速度
Microsoft PowerPoint - シミュレーション工学-2010-第1回.ppt
 シミュレーション工学 ( 後半 ) 東京大学人工物工学研究センター 鈴木克幸 CA( Compter Aded geerg ) r. Jaso Lemo (SC, 98) 設計者が解析ツールを使いこなすことにより 設計の評価 設計の質の向上を図る geerg の本質の 計算機による支援 (CA CAM などより広い名前 ) 様々な汎用ソフトの登場 工業製品の設計に不可欠のツール 構造解析 流体解析
シミュレーション工学 ( 後半 ) 東京大学人工物工学研究センター 鈴木克幸 CA( Compter Aded geerg ) r. Jaso Lemo (SC, 98) 設計者が解析ツールを使いこなすことにより 設計の評価 設計の質の向上を図る geerg の本質の 計算機による支援 (CA CAM などより広い名前 ) 様々な汎用ソフトの登場 工業製品の設計に不可欠のツール 構造解析 流体解析
(1.2) T D = 0 T = D = 30 kn 1.2 (1.4) 2F W = 0 F = W/2 = 300 kn/2 = 150 kn 1.3 (1.9) R = W 1 + W 2 = = 1100 N. (1.9) W 2 b W 1 a = 0
 1 1 1.1 1.) T D = T = D = kn 1. 1.4) F W = F = W/ = kn/ = 15 kn 1. 1.9) R = W 1 + W = 6 + 5 = 11 N. 1.9) W b W 1 a = a = W /W 1 )b = 5/6) = 5 cm 1.4 AB AC P 1, P x, y x, y y x 1.4.) P sin 6 + P 1 sin 45
1 1 1.1 1.) T D = T = D = kn 1. 1.4) F W = F = W/ = kn/ = 15 kn 1. 1.9) R = W 1 + W = 6 + 5 = 11 N. 1.9) W b W 1 a = a = W /W 1 )b = 5/6) = 5 cm 1.4 AB AC P 1, P x, y x, y y x 1.4.) P sin 6 + P 1 sin 45
ポリトロープ、対流と輻射、時間尺度
 宇宙物理学 ( 概論 ) 6/6/ 大阪大学大学院理学研究科林田清 ポリトロープ関係式 1+(1/) 圧力と密度の間にP=Kρ という関係が成り立っていると仮定する K とは定数でをポリトロープ指数と呼ぶ 5 = : 非相対論的ガス dlnp 3 断熱変化の場合 断熱指数 γ, と dlnρ 4 = : 相対論的ガス 3 1 = の関係にある γ 1 等温変化の場合は= に相当 一様密度の球は=に相当
宇宙物理学 ( 概論 ) 6/6/ 大阪大学大学院理学研究科林田清 ポリトロープ関係式 1+(1/) 圧力と密度の間にP=Kρ という関係が成り立っていると仮定する K とは定数でをポリトロープ指数と呼ぶ 5 = : 非相対論的ガス dlnp 3 断熱変化の場合 断熱指数 γ, と dlnρ 4 = : 相対論的ガス 3 1 = の関係にある γ 1 等温変化の場合は= に相当 一様密度の球は=に相当
vecrot
 1. ベクトル ベクトル : 方向を持つ量 ベクトルには 1 方向 2 大きさ ( 長さ ) という 2 つの属性がある ベクトルの例 : 物体の移動速度 移動量電場 磁場の強さ風速力トルクなど 2. ベクトルの表現 2.1 矢印で表現される 矢印の長さ : ベクトルの大きさ 矢印の向き : ベクトルの方向 2.2 2 個の点を用いて表現する 始点 () と終点 () を結ぶ半直線の向き : ベクトルの方向
1. ベクトル ベクトル : 方向を持つ量 ベクトルには 1 方向 2 大きさ ( 長さ ) という 2 つの属性がある ベクトルの例 : 物体の移動速度 移動量電場 磁場の強さ風速力トルクなど 2. ベクトルの表現 2.1 矢印で表現される 矢印の長さ : ベクトルの大きさ 矢印の向き : ベクトルの方向 2.2 2 個の点を用いて表現する 始点 () と終点 () を結ぶ半直線の向き : ベクトルの方向
物性物理学I_2.pptx
 The University of Tokyo, Komaba Graduate School of Arts and Sciences I 凝縮系 固体 をデザインする 銅()面上の鉄原子の 量子珊瑚礁 IBM Almaden 許可を得て掲載 www.almaden.ibm.com/vis/stm/imagesstm5.jpg&imgrefurl=http://www.almaden.ibm.com/vis/
The University of Tokyo, Komaba Graduate School of Arts and Sciences I 凝縮系 固体 をデザインする 銅()面上の鉄原子の 量子珊瑚礁 IBM Almaden 許可を得て掲載 www.almaden.ibm.com/vis/stm/imagesstm5.jpg&imgrefurl=http://www.almaden.ibm.com/vis/
C el = 3 2 Nk B (2.14) c el = 3k B C el = 3 2 Nk B
 I ino@hiroshima-u.ac.jp 217 11 14 4 4.1 2 2.4 C el = 3 2 Nk B (2.14) c el = 3k B 2 3 3.15 C el = 3 2 Nk B 3.15 39 2 1925 (Wolfgang Pauli) (Pauli exclusion principle) T E = p2 2m p T N 4 Pauli Sommerfeld
I ino@hiroshima-u.ac.jp 217 11 14 4 4.1 2 2.4 C el = 3 2 Nk B (2.14) c el = 3k B 2 3 3.15 C el = 3 2 Nk B 3.15 39 2 1925 (Wolfgang Pauli) (Pauli exclusion principle) T E = p2 2m p T N 4 Pauli Sommerfeld
様々なミクロ計量モデル†
 担当 : 長倉大輔 ( ながくらだいすけ ) この資料は私の講義において使用するために作成した資料です WEB ページ上で公開しており 自由に参照して頂いて構いません ただし 内容について 一応検証してありますが もし間違いがあった場合でもそれによって生じるいかなる損害 不利益について責任を負いかねますのでご了承ください 間違いは発見次第 継続的に直していますが まだ存在する可能性があります 1 カウントデータモデル
担当 : 長倉大輔 ( ながくらだいすけ ) この資料は私の講義において使用するために作成した資料です WEB ページ上で公開しており 自由に参照して頂いて構いません ただし 内容について 一応検証してありますが もし間違いがあった場合でもそれによって生じるいかなる損害 不利益について責任を負いかねますのでご了承ください 間違いは発見次第 継続的に直していますが まだ存在する可能性があります 1 カウントデータモデル
応用数学A
 応用数学 A 米田 戸倉川月 7 限 1930~2100 西 5-109 V を :x 2 + y 2 + z 2 = 4 で囲まれる内部とする F = ye x xe y + ze z FdV = V e x e y e z F = = 2e z 2e z dv = 2e z 3 23 = 64π 3 e z y x z 4π V n Fd = 1 F nd 2 F nd 法線ベクトル n g x,
応用数学 A 米田 戸倉川月 7 限 1930~2100 西 5-109 V を :x 2 + y 2 + z 2 = 4 で囲まれる内部とする F = ye x xe y + ze z FdV = V e x e y e z F = = 2e z 2e z dv = 2e z 3 23 = 64π 3 e z y x z 4π V n Fd = 1 F nd 2 F nd 法線ベクトル n g x,
2011年度 大阪大・理系数学
 0 大阪大学 ( 理系 ) 前期日程問題 解答解説のページへ a a を自然数とする O を原点とする座標平面上で行列 A= a の表す 次変換 を f とする cosθ siθ () >0 および0θ
0 大阪大学 ( 理系 ) 前期日程問題 解答解説のページへ a a を自然数とする O を原点とする座標平面上で行列 A= a の表す 次変換 を f とする cosθ siθ () >0 および0θ
2011年度 筑波大・理系数学
 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ O を原点とするy 平面において, 直線 y= の を満たす部分をC とする () C 上に点 A( t, ) をとるとき, 線分 OA の垂直二等分線の方程式を求めよ () 点 A が C 全体を動くとき, 線分 OA の垂直二等分線が通過する範囲を求め, それ を図示せよ -- 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ
0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ O を原点とするy 平面において, 直線 y= の を満たす部分をC とする () C 上に点 A( t, ) をとるとき, 線分 OA の垂直二等分線の方程式を求めよ () 点 A が C 全体を動くとき, 線分 OA の垂直二等分線が通過する範囲を求め, それ を図示せよ -- 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ
PowerPoint プレゼンテーション
 電磁波工学 第 5 回平面波の媒質への垂直および射入射と透過 柴田幸司 Bounda Plan Rgon ε μ Rgon Mdum ( ガラスなど ε μ z 平面波の反射と透過 垂直入射の場合 左図に示す様に 平面波が境界面に対して垂直に入射する場合を考える この時の入射波を とすると 入射波は境界において 透過波 と とに分解される この時の透過量を 反射量を Γ とおくと 領域 における媒質の誘電率に対して透過量
電磁波工学 第 5 回平面波の媒質への垂直および射入射と透過 柴田幸司 Bounda Plan Rgon ε μ Rgon Mdum ( ガラスなど ε μ z 平面波の反射と透過 垂直入射の場合 左図に示す様に 平面波が境界面に対して垂直に入射する場合を考える この時の入射波を とすると 入射波は境界において 透過波 と とに分解される この時の透過量を 反射量を Γ とおくと 領域 における媒質の誘電率に対して透過量
<4D F736F F F696E74202D208D E9197BF288CF68A4A B8CDD8AB B83685D>
 離散化手法とスキームの基礎 と選択法 007//6 宇宙航空研究開発機構情報 計算工学センター嶋英志 本講習の目的 基礎的な計算法の性質を述べ 各手法の持つ長所短所を理解することによって 手法の背景を理解した正しい選択に近づくこと クーラン数 風上差分 等の広い範囲の CFD 技術に共通の概念について その意味とイメージを把握すること 本講習の方針 様々な流体方程式の基礎となる移流方程式を用いて色々な計算法の特徴を計算例を示しながら解説する
離散化手法とスキームの基礎 と選択法 007//6 宇宙航空研究開発機構情報 計算工学センター嶋英志 本講習の目的 基礎的な計算法の性質を述べ 各手法の持つ長所短所を理解することによって 手法の背景を理解した正しい選択に近づくこと クーラン数 風上差分 等の広い範囲の CFD 技術に共通の概念について その意味とイメージを把握すること 本講習の方針 様々な流体方程式の基礎となる移流方程式を用いて色々な計算法の特徴を計算例を示しながら解説する
線形代数とは
 線形代数とは 第一回ベクトル 教科書 エクササイズ線形代数 立花俊一 成田清正著 共立出版 必要最低限のことに限る 得意な人には物足りないかもしれません 線形代数とは何をするもの? 線形関係 y 直線 yもも 次式で登場する (( 次の形 ) 線形 ただし 次元の話世の中は 3 次元 [4[ 次元 ] 次元 3 次元 4 次元 はどうやって直線を表すの? ベクトルや行列の概念 y A ベクトルを使うと
線形代数とは 第一回ベクトル 教科書 エクササイズ線形代数 立花俊一 成田清正著 共立出版 必要最低限のことに限る 得意な人には物足りないかもしれません 線形代数とは何をするもの? 線形関係 y 直線 yもも 次式で登場する (( 次の形 ) 線形 ただし 次元の話世の中は 3 次元 [4[ 次元 ] 次元 3 次元 4 次元 はどうやって直線を表すの? ベクトルや行列の概念 y A ベクトルを使うと
<4D F736F F D20824F F6490CF95AA82C696CA90CF95AA2E646F63>
 1/15 平成 3 年 3 月 4 日午後 6 時 49 分 5 ベクトルの 重積分と面積分 5 重積分と面積分 Ⅰ. 重積分 と で 回積分することを 重積分 といいます この 重積分は何を意味しているのでしょう? 通常の積分 (1 重積分 ) では C d 図 1a 1 f d (5.1) 1 f d f ( ) は 図形的には図 1a のように面積を表しています つまり 1 f ( ) を高さとしてプロットすると図
1/15 平成 3 年 3 月 4 日午後 6 時 49 分 5 ベクトルの 重積分と面積分 5 重積分と面積分 Ⅰ. 重積分 と で 回積分することを 重積分 といいます この 重積分は何を意味しているのでしょう? 通常の積分 (1 重積分 ) では C d 図 1a 1 f d (5.1) 1 f d f ( ) は 図形的には図 1a のように面積を表しています つまり 1 f ( ) を高さとしてプロットすると図
19年度一次基礎科目計算問題略解
 9 年度機械科目 ( 計算問題主体 ) 略解 基礎科目の解析の延長としてわかる範囲でトライしてみたものです Coprigh (c) 7 宮田明則技術士事務所 Coprigh (c) 7 宮田明則技術士事務所 Ⅳ- よってから は許容荷重として は直径をロ - プの断面積 Ⅳ- cr E E E I, から Ⅳ- Ⅳ- : q q q q q q q q q で絶対値が最大 で絶対値が最大モーメントはいずれも中央で最大となる
9 年度機械科目 ( 計算問題主体 ) 略解 基礎科目の解析の延長としてわかる範囲でトライしてみたものです Coprigh (c) 7 宮田明則技術士事務所 Coprigh (c) 7 宮田明則技術士事務所 Ⅳ- よってから は許容荷重として は直径をロ - プの断面積 Ⅳ- cr E E E I, から Ⅳ- Ⅳ- : q q q q q q q q q で絶対値が最大 で絶対値が最大モーメントはいずれも中央で最大となる
<4D F736F F F696E74202D20906C8D488AC28BAB90DD8C7689F090CD8D488A D91E F1>
 人工環境設計解析工学構造力学と有限要素法 ( 第 回 ) 東京大学新領域創成科学研究科 鈴木克幸 固体力学の基礎方程式 変位 - ひずみの関係 適合条件式 ひずみ - 応力の関係 構成方程式 応力 - 外力の関係 平衡方程式 境界条件 変位規定境界 反力規定境界 境界条件 荷重応力ひずみ変形 場の方程式 Γ t Γ t 平衡方程式構成方程式適合条件式 構造力学の基礎式 ひずみ 一軸 荷重応力ひずみ変形
人工環境設計解析工学構造力学と有限要素法 ( 第 回 ) 東京大学新領域創成科学研究科 鈴木克幸 固体力学の基礎方程式 変位 - ひずみの関係 適合条件式 ひずみ - 応力の関係 構成方程式 応力 - 外力の関係 平衡方程式 境界条件 変位規定境界 反力規定境界 境界条件 荷重応力ひずみ変形 場の方程式 Γ t Γ t 平衡方程式構成方程式適合条件式 構造力学の基礎式 ひずみ 一軸 荷重応力ひずみ変形
