i s
|
|
|
- えつみ ちゃわんや
- 7 years ago
- Views:
Transcription
1 2 III Copyright c 2 Kazunobu Yoshida. All rights reserved.
2 i s
3 ii
4 ẋ(t) =Ax(t)+bu(t) (1.1) y(t) =cx(t)+du(t) (1.2) (1.1) (1.2) x(t)(n 1) : u(t)(1 1) : y(t)(1 1) : A(n n), b(n 1), c(1 n), d(1 1) u y d = m l b, c B(n m), C(l n)
5 2 1 x C P u 1.1: C u x Cẋ = u (1.3) ẋ = 1 C u (1.4) x y = x (1.5) C θ θ 1 R 1.2: 1.2 θ 1 θ Newton θ 1 C θ 1 = 1 R (θ θ 1 ) (1.6)
6 C R x = θ 1,u= θ,y= θ 1 (1.7) ẋ = 1 CR x + 1 CR u (1.8) y = x (1.9) RC R C v i i vo 1.3: RC Ri + v o = v i (1.1) v o = 1 idt (1.11) C (1.11) v o = 1 C i (1.12) i = C v o (1.13) (1.1) v o = 1 RC (v i v o ) (1.14) x = v o, u = v i (1.15) ẋ = 1 RC x + 1 RC u (1.16) y = x (1.17)
7 4 1 x u m 1.4: 1.4 m u mẍ = u (1.18) x 1 = x, x 2 =ẋ, y = x (1.19) 1 ẋ = x + 1 u (1.2) m y = 1 x (1.21) x = x1 x 2 (1.22) x k m u 1.5: 1
8 mẍ + kx = u (1.23) ẍ = k m x + 1 m u (1.24) x k x 1 = x, x 2 =ẋ, y = x (1.25) ẋ = 1 k m x + 1 u (1.26) m y = 1 x (1.27) RLC R L C v i i vo 1.6: RLC L i + Ri + v o = v i (1.28) v o = 1 idt (1.29) C (1.29) v o = 1 C i (1.3)
9 6 1 i = C v o (1.31) (1.28) LC v o + RC v o + v o = v i (1.32) x 1 = v o, x 2 = v o, u = v i (1.33) ẋ 1 = x 2 ẋ 2 = 1 LC x 1 R C x LC u (1.34) 1 ẋ = 1 LC R x + 1 u (1.35) L LC y 1 y 2 A B k 1 k 2 m 1 m 2 u 1.7: 1.7 A y 1 A m 1 ÿ 1 k 1 y 1 k 2 (y 1 y 2 ) = (1.36) A ÿ 1 = k 1 + k 2 m 1 y 1 + k 2 m 1 y 2 (1.37)
10 B m 2 ÿ 2 k 2 (y 2 y 1 )+u = (1.38) B ÿ 2 = k 2 m 2 y 1 k 2 m 2 y m 2 u (1.39) x 1 = y 1, x 2 = y 2,x 3 =ẏ 1,x 4 =ẏ 2 (1.4) 1 1 ẋ = k 1 + k 2 k 2 x + m 1 m 1 k 2 k 2 m 2 m 2 y = m 2 u (1.41) x (1.42) (1.1) (1.2) h q a C 1.8:
11 q a a C v = 2gh (1.43) g h Cḣ = q fav (1.44) f 1 q q = q h q = fa 2gh (1.45) h q h = h + x, q = q + u (1.46) h,q x, u (1.46) (1.44) x/h h + x = h (1 + x h ) 1/2 h (1 + x 2h ) (1.47) ẋ = 1 CR x + 1 C u (1.48) 1 R = fa g 2h (1.49) x y = x (1.5) 1.9 θ J θ mgl sin θ + u = (1.51)
12 u θ l 1.9: mg J u J = ml 2 θ = g l sin θ + 1 ml 2 u (1.52) θ sin θ θ θ = g l θ + 1 ml 2 u (1.53) x 1 = θ, x 2 = θ, y = θ (1.54) ẋ = 1 g x + 1 u (1.55) l ml 2 y = 1 x (1.56) m 1.2 ẋ(t) = Ax(t)+bu(t) y(t) = cx(t) (1.57) sx(s) x() = AX(s) +bu(s) Y (s) = cx(s) (1.57) (1.58)
13 1 1 x() = G(s) = Y (s) U(s) = c(si A) 1 b (1.59) G(s) U(s) Y (s) (si A) 1 = adj (si A) si A (1.6) G(s) G(s) = cadj (si A)b si A (1.61) G(s) = si A = (1.62) G(s) = cadj (si A)b = (1.63) p R 1 C 1,θ 1 θ R2 C 2,θ 2 1.1: C 1 θ 1 C 2 θ 2 R 1 R 2 θ x 1 = θ 1,x 2 = θ 2
14 h 1 q 1 C 1 a 1 h 2 C 2 a : m mg l θ u 1.12: q x 1 = θ x 2 = θ k 1 k 2 c 1 c 2 5. p
15 s ẋ(t) = Ax(t)+bu(t) y(t) = cx(t) sx(s) x() = AX(s) +bu(s) Y (s) = cx(s) (1.64) (1.65) (si A)X(s) =x() + bu(s) s X(s) =(si A) 1 x() + (si A) 1 bu(s) (1.66) Y (s) =cx(s) =c(si A) 1 x() + c(si A) 1 bu(s) (1.67) ẋ(t) =Ax(t) (1.68) e At := I + At + A 2 t2 t3 + A3 + (1.69) 2! 3! e At (1.68) x(t) =e At x() (1.7) t ẋ(t) =Ae At x() = Ax(t) (1.71) (1.68) e At
16 de At dt 2. e = I = Ae At 3. e At e Aτ = e A(t+τ) 4. (e At ) 1 = e At y(t) ẋ(t) =Ax(t)+bu(t) (1.72) x(t) =e At x() + t y(t) =cx(t) =ce At x() + (1.73) (1.72) e A(t τ) bu(τ )dτ (1.73) t ce A(t τ) bu(τ )dτ (1.74) x(t) =e At v(t) (1.75) ẋ(t) = Ae At v(t)+e At v(t) = Ax(t)+bu(t) e At v(t) =bu(t) v(t) =e At bu(t) dv(t) =e At bu(t)dt t dv(t) = t v(t) v() = e Aτ bu(τ )dτ t e Aτ bu(τ )dτ
17 14 1 v(t) =v() + t x(t) =e At {v() + e Aτ bu(τ )dτ t } e Aτ bu(τ )dτ t = v() = x() t } x(t) = e {x() At + e Aτ bu(τ )dτ s = e At x() + t X(s) =(si A) 1 x() + (si A) 1 bu(s) e A(t τ) bu(τ)dτ (1.76) e At = L 1 (si A) 1 (1.77) e At RC ẋ = 1 RC x + 1 RC u (1.78) RC =1, x() = 1, u(t) =1,t i) s A = 1, b =1 (si A) 1 =(s +1) 1 = 1 s +1 s X(s) = 1 s s +1 1 s = 1 s s 1 s +1 = 1 s 2 s +1 (1.79)
18 x(t) =1 2e t (1.8) ii) e At = L 1 (si A) 1 =L 1 1 = e 1 s +1 x(t) = e t ( 1) + t e (t τ) dτ t = e t + e t e τ dτ = e t + e t (e t 1) = 1 2e t (1.81) p p , ẋ(t) =ax(t) (1.82) x(t) =e at x() (1.83) a (1.82) a< (1.84)
19 16 1 x(t) x(t) x(t) x() x() x() t t t a<( ) a =( ()) a>() 1.13: n ẋ(t) =Ax(t) (1.85) x(t) =e At x() (1.86) A λ 1 λ n A si A = s n + α 1 s n α n 1 s + α n = (1.87) A T (n n) T =v 1, v 2,, v n (1.88) T 1 AT = A = T ΛT 1 e At λ 1 λ 2... λ n = Λ (1.89) e At = e T ΛT 1t = Te Λt T 1 (1.9)
20 e Λt = e λ 1t e λ 2t... e λnt (1.91) (1.83) x(t) e λ1t e λnt x 1 (t) =f 11 e λ 1t + f 12 e λ 2t + + f 1n e λnt f 11 f 1n x() x() lim x(t) = (1.92) t lim t eλ it =, i =1 n (1.93) λ i = a i + jb i, j = 1 (1.93) Re λ i = a i <, i =1 n (1.94) e (a i+jb i )t = e a it e jb it = e a it (cos b i t + j sin b i t) A J 1 = e J1t = e λ 1t Jordan λ 1 1 λ 1 1 λ 1 1 t t 2 /2! 1 t 1
21 18 1 (1.92) t k e λ it lim t k! Re λ i < = (1.95) A λ i Re λ i Maxwell 1875 Routh Strum (1829) Routh 1895 Stodola Hurwitz Hermite (1856) 1914 Lienard Chipart Hurwitz n α s n + α 1 s n α n 1 s + α n =, α > (1.96) s i,i=1 n Re s i <, i =1 n (1.97) Routh
22 : Routh α α 2 α 4 α 6 1 α 1 α 3 α 5 α 7 2 b 1 = α 1α 2 α α 3 b 2 = α 1α 4 α α 5 b 3 = α 1α 6 α α 7 α 1 α 1 α 1 3 c 1 = b 1α 3 α 1 b 2 c 2 = b 1α 5 α 1 b 3 b 1 b 1. n ω α > α n > (1.98) α >, α 1 >,, ω 1 > (1.99) Re (s i ) <, i =1 n (1.1) α 1 α 3 α 5 α 7 α α 2 α 4 α 6 α 1 α 3 α 5 H(n n) = α α 2 α 4 α 1 α α n (1.11)
23 2 1 H i H i α 1 α 3 H 1 = α 1, H 2 =, (1.12) α α α > α n > (1.13) H 1 > H n > (1.14) Re (s i ) <, i =1 n (1.15) 1.3 α > α n > (1.16) H i > i n (1.17) H i > i n (1.18) Re (s i ) <, i =1 n (1.19)
24 x 2 x e 2 e 1 x 1 2.1: 1 x t 2 t 1 2.2: 2
25 22 2 e 1 = 1, e 2 = x = e 1 x 1 + e 2 x 2 = x = t 1 z 1 + t 2 z 2 = 1 e 1 e 2 x 1 x 2 t 1 t 2 z 1 z 2 x t 1, t 2 (2.1) = Ix (2.2) = Tz (2.3) T T (2.4) t 1, t 2 x = Tz T (2.5) n x, z : n T : n n ẋ(t) = Ax(t)+bu(t) y(t) = cx(t) x(t) =Tz(t) (2.6) ẋ(t) =T ż(t) (2.6) T ż(t) = AT z(t)+bu(t) y(t) = ct z(t) ż(t) = Ãz(t)+ bu(t) y(t) = cz(t) (2.7) (2.8) Ã= T 1 AT, b = T 1 b, c = ct (2.9)
26 si à = T 1 (si A)T = T 1 T si A = si A (2.1) 2. c(si Ã) 1 b = ct T 1 (si A)T 1 T 1 b = ct T 1 (si A) 1 TT 1 b = c(si A) 1 b (2.11) 2.2 R.E.Kalman(1959) u(t) x u x 1 x 1 u x 2 x 2 2.3: x() x f t f > u(t), t t f x(t f )=x f b Ab A n 1 b (2.12)
27 24 2 y x 1 x 1 y x 2 x 2 2.4: rank b Ab A n 1 b = n (2.13) u x 1 C 1 x 2 C 2 2.5: u, x 1,x 2 C 1 ẋ 1 = 1 x 1 + u R 1 C 2 ẋ 2 = 1 R 1 x 1 1 R 2 x 2 (2.14) ẋ = a11 a 21 a 22 b1 x + u (2.15)
28 U c = b Ab b1 a 11 b 1 = a 21 b 1 (2.16) rank U c =2 x 1 C 1 u x 2 C 2 2.6: C 1 ẋ 1 = 1 R 1 x 1 C 2 ẋ 2 = 1 R 1 x 1 1 R 2 x 2 + u (2.17) a11 ẋ = x + u a 21 a 22 b 2 (2.18) U c = b Ab = b 2 a 22 b 2 (2.19) rank U c = ẋ = Ax + bu (2.2) (2.2) rank b Ab A n 1 b = n x() = x x(t f )= u(t)
29 26 2 t = x t = t f 2.7: (2.2) t x(t) =e At x + e A(t τ) bu(τ)dτ tf = e At f x + e A(t f τ) bu(τ)dτ e At f x = tf e Aτ bu(τ )dτ (p159) e Aτ = Iφ (τ)+aφ 1 (τ)+ + A n 1 φ n 1 (τ) x = = tf {bφ (τ)+abφ 1 (τ)+ + A n 1 bφ n 1 (τ)}u(τ )dτ b Ab... A n 1 b tf φ (τ) φ 1 (τ). φ n 1 (τ) u(τ)dτ x rank b Ab... A n 1 b = n
30 W t = t e Aτ bb T e AT τ dτ y T W t y = y = y T W t y = = t t τ = y T b = τ τ = y T Ab = y T A 2 b =. y T A n 1 b = y T e Aτ bb T e AT τ ydτ (y T e Aτ b) 2 dτ y T e Aτ b y T b Ab... A n 1 b = u(t) = b T e AT t W 1 t f x W 1 t f x(t f ) = e At f x + e At f tf = e At f x + e At f ( x )= e Aτ b( b T e AT τ )dτ W 1 t f x
31 t f t t f y(t) u(t) x() ẋ(t) =Ax(t) y(t) =cx(t) rank c ca ca 2. ca n 1 = n y(t) =cx 1 (t) =ce At x 1 () y(t) =cx 2 (t) =ce At x 2 () =ce At (x 1 () x 2 ()) z t = cz = t t = caz = ca 2 z =. ca n 1 z =
32 c ca. ca n 1 rank c ca z =, z. ca n 1 <n y x 1 x 1 y x 2 x 2 2.8: a11 A =, c = 1 a 21 a 22 x 1 y = cx = 1 = x 2 x 2 c 1 U o = = ca a 21 a 22
33 3 2 rank U =2 a11 A =, c = a 21 a 22 1 U o = a 11 rank U o =1 1 x u m 2.9: mẍ = u y = x x 1 = x, x 2 =ẋ 1 ẋ = x + u 1/m y = 1 x U o = 1 1 rank U o =2 y =ẋ = 1 U o = 1 rank U o =1
34 x k m u 2.1: mẍ + kx = u x 1 = x, x 2 =ẋ 1 ẋ = x + k/m 1/m y = x = 1 U o = 1 1 x rank U o =2 y =ẋ = 1 U o = 1 k/m rank U o =2 m =1,c=2,k=1, y = x +ẋ 1 ẋ = x u u
35 32 2 k x c m u 2.11: y = 1 1 x 1 1 U o = 1 1 rank U o =1 2.3 A λ i,i=1 n v i,i=1 n Av i = λ i v i x(t) =Tx(t), T = v 1 v 2 v n (2.21) ż(t) =Ãz(t)+ bu(t) (2.22) y(t) = cx(t) (2.23) β 1 Ã = T 1 AT =, b = T 1 β 2 b =. λ 1 λ 2... λ n c = ct = θ 1 θ 2 θ n β n
36 ż i (t) =λ i z i (t)+β i u(t), i =1 n (2.24) y(t) =θ 1 z 1 (t)+θ 2 z 2 (t)+ + θ n z n (t) (2.25) sz 1 = λ 1 Z 1 + β 1 U U + 1 β 1 + s Z 1 λ : Z β 1 + s θ 1 λ 1 Z β 2 + s θ 2 U λ Y Z n + 1 β n + s θ n λ n 2.13:
37 34 2 Ã, b, c : z i (t) : (2.24) (2.25) G(s) = c(si A) 1 b = c(si Ã) 1 b = θ 1β 1 s λ 1 + θ 2β 2 s λ θ nβ n s λ n (2.26) n =2 G(s) = θ 1 θ 2 s 1 1 λ1 λ 2 1 β1 β 2 = θ 1β 1 s λ 1 + θ 2β 2 s λ 2 β i,i=1 n θ i,i=1 n S 1 S 2 u y S 3 S :
38 S 1 : S 2 : S 3 : S 4 : G(s) =c(si A) 1 b = i I β i θ i s λ i I β i,θ i i G(s) = Y (s) U(s) = h 3s 3 + h 2 s + h 1 s 3 + a 3 s 2 + a 2 s + a 1 (2.27) G (s) = Y (s) U(s) = 1 s 3 + a 3 s 2 + a 2 s + a 1 (2.28) Y Y Y (s) =h 1 Y (s)+h 2 sy (s)+h 3 s 2 Y (s) y(t) =h 1 y (t)+h 2 ẏ (t)+h 3 ÿ (t) (2.29) (2.28) (s 3 + a 3 s 2 + a 2 s + a 1 )Y (s) =U(s) t y (3) (t)+a 3ÿ (t)+a 2 ẏ (t)+a 1 y (t) =u(t) y (3) (t) = a 1y (t) a 2 ẏ (t) a 3 ÿ (t)+u(t) (2.3) z 1 = y, z 2 =ẏ, z 3 =ÿ (2.31)
39 36 2 (2.29) (2.3) (2.31) ż 1 = z 2 ż 2 = z 3 ż 3 = a 1 z 1 a 2 z 2 a 3 z 3 + u y = h 1 z 1 + h 2 z 2 + h 3 z 3 Ã b ż 1 1 z 1 ż 2 = 1 z 2 + u ż 3 a 1 a 2 a 3 z 3 1 c y = h 1 h 2 h 3 z 1 z 2 z 3 Ã, b, c sz 1 = Z 2 sz 2 = Z 3 sz 3 = a 1 Z 1 a 2 Z 2 a 3 Z 3 + U Y = h 1 Z 1 + h 2 Z 2 + h 3 Z 3 n G(s) = h ns n h 2 s + h 1 s n + a n s n a 2 s + a 1 Ã = a 1 a 2... a n
40 h 3 h 2 U + Z 1 3 Z 1 2 Z h 1 + s s s + Y a 3 a 2 a : b =., c = 1 h 1 h 2 h n Ã, b, c G(s) = h ns n h 2 s + h 1 s n + a n s n a 2 s + a 1 Ã = a 1 a 2... a n b =., c = h 1 h 2 h n 1
41 38 2 A, b, c Ã, b, c T n =3 Ã = T 1 AT, b = T 1 b, T = t 1 t 2 t 3 AT = T Ã, b = T b = T 1 = t 3 (2.32) A t 1 t 2 t 3 = t 1 t 2 t = a 1 a 2 a 3 a 1 t 3 t 1 a 2 t 3 t 2 a 3 t 3 At 1 = a 1 t 3, At 2 = t 1 a 2 t 3, At 3 = t 2 a 3 t 3 (2.33) (2.32) (2.33) t 3 = b t 2 = At 3 + a 3 t 3 = Ab + a 3 b t 1 = At 2 + a 2 t 3 = A 2 b + a 3 Ab + a 2 b T = = A 2 b + a 3 Ab + a 2 b Ab+ a 3 b b a 2 a 3 1 b Ab A 2 b a n T = U c W = b Ab A n 1 b a 2 a 3 a 4 a n 1 a 3 a 4 a n 1. a n 1. a n 1 1
42 G(s) = Y (s) U(s) = h 3s 2 + h 2 s + h 1 s 3 + a 3 s 2 + a 2 s + a 1 s 3 Y (s) = a 3 s 1 Y (s) a 2 s 2 Y (s) a 1 s 3 Y (s) +h 3 s 1 U(s)+h 2 s 2 U(s)+h 1 s 3 U(s) h 3 h 2 U(s) h Y (s) s Z s s 1 Z 2 Z 3 a 3 a 2 a : ż 1 = a 1 z 3 + h 1 u ż 2 = z 1 a 2 z 3 + h 2 u ż 3 = z 2 a 3 z 3 + h 3 u y = z 3 ż 1 ż 2 ż 3 = y = 1 a 1 1 a 2 1 a 3 z 1 z 2 z 1 z 2 z 3 + h 1 h 2 h 3 u z 3
43 4 2 n... a a 2 1. h à =...., b h 2 = h n 1 a n c = 1 A, b, c Ã, b, c G(s) = θ 1β 1 s λ 1 + θ 2β 2 s λ θ nβ n s λ n
44 ẋ(t) = Ax(t)+bu(t), A(n n), b(n 1) (3.1) y(t) = cx(t), c(1 n) (3.2) x : n u : y : x() x u = f 1 x 1 f 2 x 2 f n x n = fx, f = f 1 f 2 f n (3.3) ẋ =(A bf)x (3.4) u = fx A A bf f A bf ż =(Ã b f)z
45 42 3 Ã = a 1 a 2... a n b =., f = ɛ 1 ɛ 2 ɛ n 1 Ã b f = (a 1 + ɛ 1 ) (a 2 + ɛ 2 )... (a n + ɛ n ) (3.5) si (Ã b f) = s n +(a n + ɛ n )s n 1 + +(a 2 + ɛ 2 )s +(a 1 + ɛ 1 )(3.6) ɛ i µ 1,µ 2,..., µ n (s µ 1 )(s µ 2 ) (s µ n )=s n + d n s n d 2 s + d 1 (3.7) ɛ i = d i a i,i=1 n T T 1 (A bf)t = T 1 AT T 1 bft = Ã b f
46 f = ft, 1 f = ft f = d 1 a 1 d 2 a 2 d n a n T ẋ = Ax + bu, A(n n), b(n n) (3.8) J = {x(t) T Qx(t)+u(t) 2 }dt Q Q = Q T Q (Q, A) 196 R.E.Kalman u (t) u (t) = f x(t) f = b T P P (n n) A T P + PA+ Q Pbb T P = J min J = x() T Px()
47 44 3 DP x(t) u J = x(t) T Px(t) u { û t τ<t+ t u(τ) = u (τ) τ t + t û x(t + t) x(t) u u 3.1: û u(τ) J(û) ={x(t) T Qx(t)+û 2 } t + x(t + t) T Px(t + t) x(t + t) x(t) + x(t) =x(t) +{Ax(t) +bû} t t 2 J(û) = {x T (t)qx(t)+û 2 } t + x(t) T Px(t) +x(t) T (A T P + PA)x(t) t +2ûb T Px(t) t (3.9) J(û) û J(û) û = 2û +2b T Px(t) =
48 û = u (t) = b T Px(t) (3.1) (3.9) J(u ) = x(t) T Px(t) = x(t) T (Q + Pbb T P )x(t) t + x(t) T Px(t) +x(t) T (A T P + PA)x(t) t 2x(t) T Pbb T Px(t) t x(t) T (A T P + PA+ Q Pbb T P )x(t) = A T P + PA+ Q Pbb T P = (3.11) (3.1) P (3.11) J = x(t) T Px(t) > P 3.1 x u m 3.2: m =1, x 1 = x, x 2 =ẋ 1 ẋ = x + u 1 J = (x u 2 )dt min 1 1 A =, b =, Q = 1
49 46 3 A T P + PA+ Q Pbb T P = p11 p 12 p11 p p 12 p 22 p 12 p 22 p11 p 12 p11 p 12 = p 12 p 22 1 p 12 p 22 p p 11 p 12 p 12 1 p 2 12 p 11 p 12 p 22 2p 12 p 2 22 = 1 1 p 2 12 = p 12 =1 (P ) 1 p 2 12 p 12 p 22 p 12 p 22 p 2 = 22 2p 12 p 2 22 = p 22 = 2 (p 22 > 2 ) p 11 p 12 p 22 = p 11 = P = 1 2 f = b T P = = u = f x(t) 3.2 u = fx y(= cx) x x
50 y(t) u(t) n =3 ż 1 = a 1 z 3 + h 1 u ż 2 = z 1 a 2 z 3 + h 2 u ż 3 = z 2 a 3 z 3 + h 3 u (3.12) y = z 3 (3.13) (3.12) (3.13) z 2 = ẏ + a 3 y h 3 u z 1 = ÿ + a 3 ẏ h 3 u + a 2 y h 2 u 2. y(t) u(t) = ẋ = Ax, x() (3.14) (3.14) x(t) =e At x() y(t) =cx(t) =ce At x() (3.15) (3.15) e AT t c T t 1 t1 ( t1 ) e AT t c T y(t)dt = e AT t c T ce At dt x() (3.16) D(t 1 ):= t1 e AT t c T ce At dt (c, A) D(t 1 ), t 1 > D(t 1 ) 1 (3.16) t1 D(t 1 ) 1 e AT t c T y(t)dt = x()
51 x u y ˆx ŷ ẋ = Ax + bu (3.17) ˆx = Aˆx + bu (3.18) e = ˆx x (3.17) (3.18) ė = A(ˆx x) =Ae e(t) =e At e() ˆx(t) =x(t)+e At (ˆx() x()) x() ˆx() = x() ˆx(t) =x(t) x() e At (ˆx() x()) ẋ = Ax + bu (3.19) y = cx (3.2)
52 u y k + ŷ 3.3: (3.19) (3.2) ˆx = Aˆx + bu ŷ = cˆx ˆx = Aˆx + bu + k(y ŷ) = Aˆx + bu + kc(x ˆx) = (A kc)ˆx + bu + ky (3.21) e = ˆx x (3.19) (3.21) ė =(A kc)e A kc (c, A) k A kc (A kc) T = A T c T k T à = A T, b = c T, f = k T A kc à b f (Ã, b) 3.2 (Ã, b) =(c, A)
53 5 3 x k m u 3.4: y = x, m =1, k =1 ( 4, 4) mẍ + kx = u ẍ + x = u x 1 = x, x 2 =ẋ 1 ẋ = x + u 1 1 y = 1 x ˆx =(A kc)ˆx + bu + ky k (A kc) ( 4, 4) 1 k1 k 1 1 A kc = 1 = 1 1 k 2 k 2 s + k 1 1 si (A kc) = 1+k 2 s = s2 + k 1 s +1+k 2 (s +4) 2 = s 2 +8s +16 k 1 =8, k 2 =15
54 ẋ = Ax + Bu, u : m A(n n) B(n m) y = Cx, y : r C(r n) x R n y R r n r G.Gopinath(1971) rank C = r C T = (n n) D D((n r) n) x(t) =Tx(t) (3.22) x(t) =TAT 1 x(t)+tbu(t) (3.23) y(t) =CT 1 x(t) (3.24) I r T = I r C D = C CT 1 = I r x 1 (t) x 2 (t) y(t) =. x r (t) x y(t) x(t) =, z : n r z(t)
55 52 3 A11 A 12 B1 TAT 1 = A 21 A 22, TB = B 2 A 11 (r r), A 12 (r (n r)), A 21 ((n r) r), A 22 ((n r) (n r)) B 1 (r m), B 2 ((n r) m) (3.23) ẏ(t) =A 11 y(t)+a 12 z(t)+b 1 u(t) ż(t) =A 21 y(t)+a 22 z(t)+b 2 u(t) ż(t) =A 22 z(t)+b 2 u(t)+a 21 y(t) (3.25) A 12 z(t) =ẏ(t) A 11 y(t) B 1 u(t) (3.26) (3.25) z(t) (3.26) z(t) n r (C, A) (A 12, A 22 ) x(t) ẑ(t) =A 22 ẑ(t)+b 2 u(t)+a 21 y(t) A 12 z(t) A 12 ẑ(t) G((n r) r) ẑ(t) = A 22 ẑ(t)+b 2 u(t)+a 21 y + G(A 12 z A 12 ẑ(t)) = A 22 ẑ(t)+b 2 u(t)+a 21 y(t)+ga 12 (z(t) ẑ(t)) = (A 22 GA 12 )ẑ(t)+b 2 u(t)+a 21 y(t) +G(ẏ(t) A 11 y(t) B 1 u(t)) (3.27) e(t) =ẑ(t) z(t) (3.25) (3.27) ė(t) = A 22 e(t) GA 12 e(t) = (A 22 GA 12 )e(t) (A 12, A 22 ) G (A 22 GA 12 )
56 (A 22 GA 12 ) ẑ(t) z(t) (3.27) ẏ(t) ẏ(t) z(t) w = z Gy(t) (3.28) (3.27) ŵ(t) = ẑ(t) Gẏ(t) =(A 22 GA 12 )ẑ(t)+b 2 u(t)+a 21 y(t) GA 11 y(t) GB 1 u(t) =(A 22 GA 12 )(ẑ(t) Gy(t)) + (A 22 GA 12 )Gy(t) +B 2 u(t)+a 21 y(t) GA 11 y(t) GB 1 u(t) =(A 22 GA 12 )ŵ(t)+(b 2 GB 1 )u(t) +{(A 22 GA 12 )G + A 21 GA 11 }y(t) w(t) (3.28) z(t) =w(t)+gy(t) (3.22) x(t) =T 1 x(t) =T 1 y(t) z(t) T 1 = H 1 H 2 = T 1 y(t) w(t)+gy(t) x(t) =H 1 y(t)+h 2 (w(t)+gy(t)) = (H 1 + H 2 G)y(t)+H 2 w(t) x(t) ˆx(t) =(H 1 + H 2 G)y(t)+H 2 ŵ(t)
57
58 H.Kwakernaak and R.Sivan: Linear optimal control systems, Wiley- Interscience, W.M.Wonham: Linear multivariable control: a geometric approach, Springer-Verlag, F.R.Gantmacher: The theory of matrices Vol.2, Chelsea Publishing Company, c
4.2.................... 20 4.3.................. 21 4.4 ( )............... 22 4.5 ( )...... 24 4.6 ( )........ 25 4.7 ( )..... 26 5 28 5.1 PID........
version 0.01 : 2004/04/16 1 2 1.1................. 2 1.2.......................... 3 1.3................. 5 1.4............... 6 1.5.............. 7 2 9 2.1........................ 9 2.2......................
08-Note2-web
r(t) t r(t) O v(t) = dr(t) dt a(t) = dv(t) dt = d2 r(t) dt 2 r(t), v(t), a(t) t dr(t) dt r(t) =(x(t),y(t),z(t)) = d 2 r(t) dt 2 = ( dx(t) dt ( d 2 x(t) dt 2, dy(t), dz(t) dt dt ), d2 y(t) dt 2, d2 z(t)
1 No.1 5 C 1 I III F 1 F 2 F 1 F 2 2 Φ 2 (t) = Φ 1 (t) Φ 1 (t t). = Φ 1(t) t = ( 1.5e 0.5t 2.4e 4t 2e 10t ) τ < 0 t > τ Φ 2 (t) < 0 lim t Φ 2 (t) = 0
1 No.1 5 C 1 I III F 1 F 2 F 1 F 2 2 Φ 2 (t) = Φ 1 (t) Φ 1 (t t). = Φ 1(t) t = ( 1.5e 0.5t 2.4e 4t 2e 10t ) τ < 0 t > τ Φ 2 (t) < 0 lim t Φ 2 (t) = 0 0 < t < τ I II 0 No.2 2 C x y x y > 0 x 0 x > b a dx
S I. dy fx x fx y fx + C 3 C dy fx 4 x, y dy v C xt y C v e kt k > xt yt gt [ v dt dt v e kt xt v e kt + C k x v + C C k xt v k 3 r r + dr e kt S dt d
S I.. http://ayapin.film.s.dendai.ac.jp/~matuda /TeX/lecture.html PDF PS.................................... 3.3.................... 9.4................5.............. 3 5. Laplace................. 5....
S I. dy fx x fx y fx + C 3 C vt dy fx 4 x, y dy yt gt + Ct + C dt v e kt xt v e kt + C k x v k + C C xt v k 3 r r + dr e kt S Sr πr dt d v } dt k e kt
S I. x yx y y, y,. F x, y, y, y,, y n http://ayapin.film.s.dendai.ac.jp/~matuda n /TeX/lecture.html PDF PS yx.................................... 3.3.................... 9.4................5..............
214 March 31, 214, Rev.2.1 4........................ 4........................ 5............................. 7............................... 7 1 8 1.1............................... 8 1.2.......................
<4D F736F F D B B83578B6594BB2D834A836F815B82D082C88C60202E646F63>
MATLAB/Simulink による現代制御入門 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/9241 このサンプルページの内容は, 初版 1 刷発行当時のものです. i MATLAB/Simulink MATLAB/Simulink 1. 1 2. 3. MATLAB/Simulink
(3) (2),,. ( 20) ( s200103) 0.7 x C,, x 2 + y 2 + ax = 0 a.. D,. D, y C, C (x, y) (y 0) C m. (2) D y = y(x) (x ± y 0), (x, y) D, m, m = 1., D. (x 2 y
[ ] 7 0.1 2 2 + y = t sin t IC ( 9) ( s090101) 0.2 y = d2 y 2, y = x 3 y + y 2 = 0 (2) y + 2y 3y = e 2x 0.3 1 ( y ) = f x C u = y x ( 15) ( s150102) [ ] y/x du x = Cexp f(u) u (2) x y = xey/x ( 16) ( s160101)
213 March 25, 213, Rev.1.5 4........................ 4........................ 6 1 8 1.1............................... 8 1.2....................... 9 2 14 2.1..................... 14 2.2............................
1.1 ft t 2 ft = t 2 ft+ t = t+ t 2 1.1 d t 2 t + t 2 t 2 = lim t 0 t = lim t 0 = lim t 0 t 2 + 2t t + t 2 t 2 t + t 2 t 2t t + t 2 t 2t + t = lim t 0
A c 2008 by Kuniaki Nakamitsu 1 1.1 t 2 sin t, cos t t ft t t vt t xt t + t xt + t xt + t xt t vt = xt + t xt t t t vt xt + t xt vt = lim t 0 t lim t 0 t 0 vt = dxt ft dft dft ft + t ft = lim t 0 t 1.1
24.15章.微分方程式
m d y dt = F m d y = mg dt V y = dy dt d y dt = d dy dt dt = dv y dt dv y dt = g dv y dt = g dt dt dv y = g dt V y ( t) = gt + C V y ( ) = V y ( ) = C = V y t ( ) = gt V y ( t) = dy dt = gt dy = g t dt
2 1 x 1.1: v mg x (t) = v(t) mv (t) = mg 0 x(0) = x 0 v(0) = v 0 x(t) = x 0 + v 0 t 1 2 gt2 v(t) = v 0 gt t x = x 0 + v2 0 2g v2 2g 1.1 (x, v) θ
1 1 1.1 (Isaac Newton, 1642 1727) 1. : 2. ( ) F = ma 3. ; F a 2 t x(t) v(t) = x (t) v (t) = x (t) F 3 3 3 3 3 3 6 1 2 6 12 1 3 1 2 m 2 1 x 1.1: v mg x (t) = v(t) mv (t) = mg 0 x(0) = x 0 v(0) = v 0 x(t)
mugensho.dvi
1 1 f (t) lim t a f (t) = 0 f (t) t a 1.1 (1) lim(t 1) 2 = 0 t 1 (t 1) 2 t 1 (2) lim(t 1) 3 = 0 t 1 (t 1) 3 t 1 2 f (t), g(t) t a lim t a f (t) g(t) g(t) f (t) = o(g(t)) (t a) = 0 f (t) (t 1) 3 1.2 lim
数学演習：微分方程式
( ) 1 / 21 1 2 3 4 ( ) 2 / 21 x(t)? ẋ + 5x = 0 ( ) 3 / 21 x(t)? ẋ + 5x = 0 x(t) = t 2? ẋ = 2t, ẋ + 5x = 2t + 5t 2 0 ( ) 3 / 21 x(t)? ẋ + 5x = 0 x(t) = t 2? ẋ = 2t, ẋ + 5x = 2t + 5t 2 0 x(t) = sin 5t? ẋ
http://www.ns.kogakuin.ac.jp/~ft13389/lecture/physics1a2b/ pdf I 1 1 1.1 ( ) 1. 30 m µm 2. 20 cm km 3. 10 m 2 cm 2 4. 5 cm 3 km 3 5. 1 6. 1 7. 1 1.2 ( ) 1. 1 m + 10 cm 2. 1 hr + 6400 sec 3. 3.0 10 5 kg
1 y(t)m b k u(t) ẋ = [ 0 1 k m b m x + [ 0 1 m u, x = [ ẏ y (1) y b k m u
( ) LPV( ) 1 y(t)m b k u(t) ẋ = [ 0 1 k m b m x + [ 0 1 m u, x = [ ẏ y (1) y b k m u m 1 m m 2, b 1 b b 2, k 1 k k 2 (2) [m b k ( ) k 0 b m ( ) 2 ẋ = Ax, x(0) 0 (3) (x(t) 0) ( ) V (x) V (x) = x T P x >
December 28, 2018
e-mail : kigami@i.kyoto-u.ac.jp December 28, 28 Contents 2............................. 3.2......................... 7.3..................... 9.4................ 4.5............. 2.6.... 22 2 36 2..........................
IA hara@math.kyushu-u.ac.jp Last updated: January,......................................................................................................................................................................................
p06.dvi
I 6 : 1 (1) u(t) y(t) : n m a n i y (i) = b m i u (i) i=0 i=0 t, y (i) y i (u )., a 0 0, b 0 0. : 2 (2), Laplace, (a 0 s n +a 1 s n 1 + +a n )Y(s) = (b 0 s m + b 1 s m 1 + +b m )U(s),, Y(s) U(s) = b 0s
arma dvi
ARMA 007/05/0 Rev.0 007/05/ Rev.0 007/07/7 3. : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : 3. : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : 3.3 : : : :
c 2006 Yoneda norimasa All rights reserved
LEGO 011242 2006 2 Copyright c 2006 by Yoneda norimasa c 2006 Yoneda norimasa All rights reserved , LEGO,., Matlab Simlink,,., LEGO., 2, 2.,, LEGOMINDSTORMS, LOBOLAB.,,., Matlab,.,,,,,.,,,,, 2.,. i 1
0.,,., m Euclid m m. 2.., M., M R 2 ψ. ψ,, R 2 M.,, (x 1 (),, x m ()) R m. 2 M, R f. M (x 1,, x m ), f (x 1,, x m ) f(x 1,, x m ). f ( ). x i : M R.,,
2012 10 13 1,,,.,,.,.,,. 2?.,,. 1,, 1. (θ, φ), θ, φ (0, π),, (0, 2π). 1 0.,,., m Euclid m m. 2.., M., M R 2 ψ. ψ,, R 2 M.,, (x 1 (),, x m ()) R m. 2 M, R f. M (x 1,, x m ), f (x 1,, x m ) f(x 1,, x m ).
[1.1] r 1 =10e j(ωt+π/4), r 2 =5e j(ωt+π/3), r 3 =3e j(ωt+π/6) ~r = ~r 1 + ~r 2 + ~r 3 = re j(ωt+φ) =(10e π 4 j +5e π 3 j +3e π 6 j )e jωt
![[1.1] r 1 =10e j(ωt+π/4), r 2 =5e j(ωt+π/3), r 3 =3e j(ωt+π/6) ~r = ~r 1 + ~r 2 + ~r 3 = re j(ωt+φ) =(10e π 4 j +5e π 3 j +3e π 6 j )e jωt](/thumbs/101/152334931.jpg "[1.1] r 1 =10e j(ωt+π/4), r 2 =5e j(ωt+π/3), r 3 =3e j(ωt+π/6) ~r = ~r 1 + ~r 2 + ~r 3 = re j(ωt+φ) =(10e π 4 j +5e π 3 j +3e π 6 j )e jωt")
3.4.7 [.] =e j(t+/4), =5e j(t+/3), 3 =3e j(t+/6) ~ = ~ + ~ + ~ 3 = e j(t+φ) =(e 4 j +5e 3 j +3e 6 j )e jt = e jφ e jt cos φ =cos 4 +5cos 3 +3cos 6 =.69 sin φ =sin 4 +5sin 3 +3sin 6 =.9 =.69 +.9 =7.74 [.]
(u(x)v(x)) = u (x)v(x) + u(x)v (x) ( ) u(x) = u (x)v(x) u(x)v (x) v(x) v(x) 2 y = g(t), t = f(x) y = g(f(x)) dy dx dy dx = dy dt dt dx., y, f, g y = f (g(x))g (x). ( (f(g(x)). ). [ ] y = e ax+b (a, b )
chap1.dvi
1 1 007 1 e iθ = cos θ + isin θ 1) θ = π e iπ + 1 = 0 1 ) 3 11 f 0 r 1 1 ) k f k = 1 + r) k f 0 f k k = 01) f k+1 = 1 + r)f k ) f k+1 f k = rf k 3) 1 ) ) ) 1+r/)f 0 1 1 + r/) f 0 = 1 + r + r /4)f 0 1 f
<4D F736F F D B B BB2D834A836F815B82D082C88C602E646F63>
信号処理の基礎 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/081051 このサンプルページの内容は, 初版 1 刷発行時のものです. i AI ii z / 2 3 4 5 6 7 7 z 8 8 iii 2013 3 iv 1 1 1.1... 1 1.2... 2 2 4 2.1...
z z x = y = /x lim y = + x + lim y = x (x a ) a (x a+) lim z z f(z) = A, lim z z g(z) = B () lim z z {f(z) ± g(z)} = A ± B (2) lim {f(z) g(z)} = AB z
Tips KENZOU 28 6 29 sin 2 x + cos 2 x = cos 2 z + sin 2 z = OK... z < z z < R w = f(z) z z w w f(z) w lim z z f(z) = w x x 2 2 f(x) x = a lim f(x) = lim f(x) x a+ x a z z x = y = /x lim y = + x + lim y
x (0, 6, N x 2 (4 + 2(4 + 3 < 6 2 3, a 2 + a 2+ > 0. x (0, 6 si x > 0. (2 cos [0, 6] (0, 6 (cos si < 0. ( 5.4.6 (2 (3 cos 0, cos 3 < 0. cos 0 cos cos
![x (0, 6, N x 2 (4 + 2(4 + 3 < 6 2 3, a 2 + a 2+ > 0. x (0, 6 si x > 0. (2 cos [0, 6] (0, 6 (cos si < 0. ( 5.4.6 (2 (3 cos 0, cos 3 < 0. cos 0 cos cos](/thumbs/39/20131394.jpg "x (0, 6, N x 2 (4 + 2(4 + 3 < 6 2 3, a 2 + a 2+ > 0. x (0, 6 si x > 0. (2 cos [0, 6] (0, 6 (cos si < 0. ( 5.4.6 (2 (3 cos 0, cos 3 < 0. cos 0 cos cos")
6 II 3 6. π 3.459... ( /( π 33 π 00 π 34 6.. ( (a cos π 2 0 π (0, 2 3 π (b z C, m, Z ( ( cos z + π 2 (, si z + π 2 (cos z, si z, 4m, ( si z, cos z, 4m +, (cos z, si z, 4m + 2, (si z, cos z, 4m + 3. (6.
5. [1 ] 1 [], u(x, t) t c u(x, t) x (5.3) ξ x + ct, η x ct (5.4),u(x, t) ξ, η u(ξ, η), ξ t,, ( u(ξ,η) ξ η u(x, t) t ) u(x, t) { ( u(ξ, η) c t ξ ξ { (
![5. [1 ] 1 [], u(x, t) t c u(x, t) x (5.3) ξ x + ct, η x ct (5.4),u(x, t) ξ, η u(ξ, η), ξ t,, ( u(ξ,η) ξ η u(x, t) t ) u(x, t) { ( u(ξ, η) c t ξ ξ { (](/thumbs/92/107866626.jpg "5. [1 ] 1 [], u(x, t) t c u(x, t) x (5.3) ξ x + ct, η x ct (5.4),u(x, t) ξ, η u(ξ, η), ξ t,, ( u(ξ,η) ξ η u(x, t) t ) u(x, t) { ( u(ξ, η) c t ξ ξ { (")
5 5.1 [ ] ) d f(t) + a d f(t) + bf(t) : f(t) 1 dt dt ) u(x, t) c u(x, t) : u(x, t) t x : ( ) ) 1 : y + ay, : y + ay + by : ( ) 1 ) : y + ay, : yy + ay 3 ( ): ( ) ) : y + ay, : y + ay b [],,, [ ] au xx
dynamics-solution2.dvi
1 1. (1) a + b = i +3i + k () a b =5i 5j +3k (3) a b =1 (4) a b = 7i j +1k. a = 14 l =/ 14, m=1/ 14, n=3/ 14 3. 4. 5. df (t) d [a(t)e(t)] =ti +9t j +4k, = d a(t) d[a(t)e(t)] e(t)+ da(t) d f (t) =i +18tj
( ) ( )
20 21 2 8 1 2 2 3 21 3 22 3 23 4 24 5 25 5 26 6 27 8 28 ( ) 9 3 10 31 10 32 ( ) 12 4 13 41 0 13 42 14 43 0 15 44 17 5 18 6 18 1 1 2 2 1 2 1 0 2 0 3 0 4 0 2 2 21 t (x(t) y(t)) 2 x(t) y(t) γ(t) (x(t) y(t))
2019 1 5 0 3 1 4 1.1.................... 4 1.1.1......................... 4 1.1.2........................ 5 1.1.3................... 5 1.1.4........................ 6 1.1.5......................... 6 1.2..........................
３
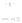- { } / f ( ) e nπ + f( ) = Cne n= nπ / Eucld r e (= N) j = j e e = δj, δj = 0 j r e ( =, < N) r r r { } ε ε = r r r = Ce = r r r e ε = = C = r C r e + CC e j e j e = = ε = r ( r e ) + r e C C 0 r e =
LCR e ix LC AM m k x m x x > 0 x < 0 F x > 0 x < 0 F = k x (k > 0) k x = x(t)
338 7 7.3 LCR 2.4.3 e ix LC AM 7.3.1 7.3.1.1 m k x m x x > 0 x < 0 F x > 0 x < 0 F = k x k > 0 k 5.3.1.1 x = xt 7.3 339 m 2 x t 2 = k x 2 x t 2 = ω 2 0 x ω0 = k m ω 0 1.4.4.3 2 +α 14.9.3.1 5.3.2.1 2 x
x A Aω ẋ ẋ 2 + ω 2 x 2 = ω 2 A 2. (ẋ, ωx) ζ ẋ + iωx ζ ζ dζ = ẍ + iωẋ = ẍ + iω(ζ iωx) dt dζ dt iωζ = ẍ + ω2 x (2.1) ζ ζ = Aωe iωt = Aω cos ωt + iaω sin
2 2.1 F (t) 2.1.1 mẍ + kx = F (t). m ẍ + ω 2 x = F (t)/m ω = k/m. 1 : (ẋ, x) x = A sin ωt, ẋ = Aω cos ωt 1 2-1 x A Aω ẋ ẋ 2 + ω 2 x 2 = ω 2 A 2. (ẋ, ωx) ζ ẋ + iωx ζ ζ dζ = ẍ + iωẋ = ẍ + iω(ζ iωx) dt dζ
4 4 4 a b c d a b A c d A a da ad bce O E O n A n O ad bc a d n A n O 5 {a n } S n a k n a n + k S n a a n+ S n n S n n log x x {xy } x, y x + y 7 fx
4 4 5 4 I II III A B C, 5 7 I II A B,, 8, 9 I II A B O A,, Bb, b, Cc, c, c b c b b c c c OA BC P BC OP BC P AP BC n f n x xn e x! e n! n f n x f n x f n x f k x k 4 e > f n x dx k k! fx sin x cos x tan
M3 x y f(x, y) (= x) (= y) x + y f(x, y) = x + y + *. f(x, y) π y f(x, y) x f(x + x, y) f(x, y) lim x x () f(x,y) x 3 -
M3............................................................................................ 3.3................................................... 3 6........................................... 6..........................................
ばらつき抑制のための確率最適制御
( ) http://wwwhayanuemnagoya-uacjp/ fujimoto/ 2011 3 9 11 ( ) 2011/03/09-11 1 / 46 Outline 1 2 3 4 5 ( ) 2011/03/09-11 2 / 46 Outline 1 2 3 4 5 ( ) 2011/03/09-11 3 / 46 (1/2) r + Controller - u Plant y
7. y fx, z gy z gfx dz dx dz dy dy dx. g f a g bf a b fa 7., chain ule Ω, D R n, R m a Ω, f : Ω R m, g : D R l, fω D, b fa, f a g b g f a g f a g bf a
9 203 6 7 WWW http://www.math.meiji.ac.jp/~mk/lectue/tahensuu-203/ 2 8 8 7. 7 7. y fx, z gy z gfx dz dx dz dy dy dx. g f a g bf a b fa 7., chain ule Ω, D R n, R m a Ω, f : Ω R m, g : D R l, fω D, b fa,
128 3 II S 1, S 2 Φ 1, Φ 2 Φ 1 = { B( r) n( r)}ds S 1 Φ 2 = { B( r) n( r)}ds (3.3) S 2 S S 1 +S 2 { B( r) n( r)}ds = 0 (3.4) S 1, S 2 { B( r) n( r)}ds
127 3 II 3.1 3.1.1 Φ(t) ϕ em = dφ dt (3.1) B( r) Φ = { B( r) n( r)}ds (3.2) S S n( r) Φ 128 3 II S 1, S 2 Φ 1, Φ 2 Φ 1 = { B( r) n( r)}ds S 1 Φ 2 = { B( r) n( r)}ds (3.3) S 2 S S 1 +S 2 { B( r) n( r)}ds
x ( ) x dx = ax
x ( ) x dx = ax 1 dx = a x log x = at + c x(t) = e at C (C = e c ) a > 0 t a < 0 t 0 (at + b ) h dx = lim x(t + h) x(t) h 0 h x(t + h) x(t) h x(t) t x(t + h) x(t) ax(t) h x(t + h) x(t) + ahx(t) 0, h, 2h,
ohp_06nov_tohoku.dvi
2006 11 28 1. (1) ẋ = ax = x(t) =Ce at C C>0 a0 x(t) 0(t )!! 1 0.8 0.6 0.4 0.2 2 4 6 8 10-0.2 (1) a =2 C =1 1. (1) τ>0 (2) ẋ(t) = ax(t τ) 4 2 2 4 6 8 10-2 -4 (2) a =2 τ =1!! 1. (2) A. (2)
i
009 I 1 8 5 i 0 1 0.1..................................... 1 0.................................................. 1 0.3................................. 0.4........................................... 3
2 (2016 3Q N) c = o (11) Ax = b A x = c A n I n n n 2n (A I n ) (I n X) A A X A n A A A (1) (2) c 0 c (3) c A A i j n 1 ( 1) i+j A (i, j) A (i, j) ã i
[ ] (2016 3Q N) a 11 a 1n m n A A = a m1 a mn A a 1 A A = a n (1) A (a i a j, i j ) (2) A (a i ca i, c 0, i ) (3) A (a i a i + ca j, j i, i ) A 1 A 11 0 A 12 0 0 A 1k 0 1 A 22 0 0 A 2k 0 1 0 A 3k 1 A rk
II K116 : January 14, ,. A = (a ij ) ij m n. ( ). B m n, C n l. A = max{ a ij }. ij A + B A + B, AC n A C (1) 1. m n (A k ) k=1,... m n A, A k k
: January 14, 28..,. A = (a ij ) ij m n. ( ). B m n, C n l. A = max{ a ij }. ij A + B A + B, AC n A C (1) 1. m n (A k ) k=1,... m n A, A k k, A. lim k A k = A. A k = (a (k) ij ) ij, A k = (a ij ) ij, i,
1 variation 1.1 imension unit L m M kg T s Q C QT 1 A = C s 1 MKSA F = ma N N = kg m s 1.1 J E = 1 mv W = F x J = kg m s 1 = N m 1.
1.1 1. 1.3.1..3.4 3.1 3. 3.3 4.1 4. 4.3 5.1 5. 5.3 6.1 6. 6.3 7.1 7. 7.3 1 1 variation 1.1 imension unit L m M kg T s Q C QT 1 A = C s 1 MKSA F = ma N N = kg m s 1.1 J E = 1 mv W = F x J = kg m s 1 = N
1990 IMO 1990/1/15 1:00-4:00 1 N N N 1, N 1 N 2, N 2 N 3 N 3 2 x x + 52 = 3 x x , A, B, C 3,, A B, C 2,,,, 7, A, B, C
0 9 (1990 1999 ) 10 (2000 ) 1900 1994 1995 1999 2 SAT ACT 1 1990 IMO 1990/1/15 1:00-4:00 1 N 1990 9 N N 1, N 1 N 2, N 2 N 3 N 3 2 x 2 + 25x + 52 = 3 x 2 + 25x + 80 3 2, 3 0 4 A, B, C 3,, A B, C 2,,,, 7,
23 7 28 i i 1 1 1.1................................... 2 1.2............................... 3 1.2.1.................................... 3 1.2.2............................... 4 1.2.3 SI..............................
v_-3_+2_1.eps
I 9-9 (3) 9 9, x, x (t)+a(t)x (t)+b(t)x(t) = f(t) (9), a(t), b(t), f(t),,, f(t),, a(t), b(t),,, x (t)+ax (t)+bx(t) = (9),, x (t)+ax (t)+bx(t) = f(t) (93), b(t),, b(t) 9 x (t), x (t), x (t)+a(t)x (t)+b(t)x(t)
<4D F736F F D B B83578B6594BB2D834A836F815B82D082C88C60202E646F63>
単純適応制御 SAC サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/091961 このサンプルページの内容は, 初版 1 刷発行当時のものです. 1 2 3 4 5 9 10 12 14 15 A B F 6 8 11 13 E 7 C D URL http://www.morikita.co.jp/support
I ( ) 2019
I ( ) 2019 i 1 I,, III,, 1,,,, III,,,, (1 ) (,,, ), :...,, : NHK... NHK, (YouTube ),!!, manaba http://pen.envr.tsukuba.ac.jp/lec/physics/,, Richard Feynman Lectures on Physics Addison-Wesley,,,, x χ,
II No.01 [n/2] [1]H n (x) H n (x) = ( 1) r n! r!(n 2r)! (2x)n 2r. r=0 [2]H n (x) n,, H n ( x) = ( 1) n H n (x). [3] H n (x) = ( 1) n dn x2 e dx n e x2
![II No.01 [n/2] [1]H n (x) H n (x) = ( 1) r n! r!(n 2r)! (2x)n 2r. r=0 [2]H n (x) n,, H n ( x) = ( 1) n H n (x). [3] H n (x) = ( 1) n dn x2 e dx n e x2](/thumbs/101/149159646.jpg "II No.01 [n/2] [1]H n (x) H n (x) = ( 1) r n! r!(n 2r)! (2x)n 2r. r=0 [2]H n (x) n,, H n ( x) = ( 1) n H n (x). [3] H n (x) = ( 1) n dn x2 e dx n e x2")
II No.1 [n/] [1]H n x) H n x) = 1) r n! r!n r)! x)n r r= []H n x) n,, H n x) = 1) n H n x) [3] H n x) = 1) n dn x e dx n e x [4] H n+1 x) = xh n x) nh n 1 x) ) d dx x H n x) = H n+1 x) d dx H nx) = nh
Note.tex 2008/09/19( )
1 20 9 19 2 1 5 1.1........................ 5 1.2............................. 8 2 9 2.1............................. 9 2.2.............................. 10 3 13 3.1.............................. 13 3.2..................................
( )
18 10 01 ( ) 1 2018 4 1.1 2018............................... 4 1.2 2018......................... 5 2 2017 7 2.1 2017............................... 7 2.2 2017......................... 8 3 2016 9 3.1 2016...............................
2 1 κ c(t) = (x(t), y(t)) ( ) det(c (t), c x (t)) = det (t) x (t) y (t) y = x (t)y (t) x (t)y (t), (t) c (t) = (x (t)) 2 + (y (t)) 2. c (t) =
1 1 1.1 I R 1.1.1 c : I R 2 (i) c C (ii) t I c (t) (0, 0) c (t) c(i) c c(t) 1.1.2 (1) (2) (3) (1) r > 0 c : R R 2 : t (r cos t, r sin t) (2) C f : I R c : I R 2 : t (t, f(t)) (3) y = x c : R R 2 : t (t,
d (K + U) = v [ma F(r)] = (2.4.4) t = t r(t ) = r t 1 r(t 1 ) = r 1 U(r 1 ) U(r ) = t1 t du t1 = t F(r(t)) dr(t) r1 = F dr (2.4.5) r F 2 F ( F) r A r
![d (K + U) = v [ma F(r)] = (2.4.4) t = t r(t ) = r t 1 r(t 1 ) = r 1 U(r 1 ) U(r ) = t1 t du t1 = t F(r(t)) dr(t) r1 = F dr (2.4.5) r F 2 F ( F) r A r](/thumbs/85/92098187.jpg "d (K + U) = v [ma F(r)] = (2.4.4) t = t r(t ) = r t 1 r(t 1 ) = r 1 U(r 1 ) U(r ) = t1 t du t1 = t F(r(t)) dr(t) r1 = F dr (2.4.5) r F 2 F ( F) r A r")
2.4 ( ) U(r) ( ) ( ) U F(r) = x, U y, U = U(r) (2.4.1) z 2 1 K = mv 2 /2 dk = d ( ) 1 2 mv2 = mv dv = v (ma) (2.4.2) ( ) U(r(t)) r(t) r(t) + dr(t) du du = U(r(t) + dr(t)) U(r(t)) = U x = U(r(t)) dr(t)
e a b a b b a a a 1 a a 1 = a 1 a = e G G G : x ( x =, 8, 1 ) x 1,, 60 θ, ϕ ψ θ G G H H G x. n n 1 n 1 n σ = (σ 1, σ,..., σ N ) i σ i i n S n n = 1,,
01 10 18 ( ) 1 6 6 1 8 8 1 6 1 0 0 0 0 1 Table 1: 10 0 8 180 1 1 1. ( : 60 60 ) : 1. 1 e a b a b b a a a 1 a a 1 = a 1 a = e G G G : x ( x =, 8, 1 ) x 1,, 60 θ, ϕ ψ θ G G H H G x. n n 1 n 1 n σ = (σ 1,
x () g(x) = f(t) dt f(x), F (x) 3x () g(x) g (x) f(x), F (x) (3) h(x) = x 3x tf(t) dt.9 = {(x, y) ; x, y, x + y } f(x, y) = xy( x y). h (x) f(x), F (x
[ ] IC. f(x) = e x () f(x) f (x) () lim f(x) lim f(x) x + x (3) lim f(x) lim f(x) x + x (4) y = f(x) ( ) ( s46). < a < () a () lim a log xdx a log xdx ( ) n (3) lim log k log n n n k=.3 z = log(x + y ),
168 13 Maxwell ( H ds = C S rot H = j + D j + D ) ds (13.5) (13.6) Maxwell Ampère-Maxwell (3) Gauss S B 0 B ds = 0 (13.7) S div B = 0 (13.8) (4) Farad
13 Maxwell Maxwell Ampère Maxwell 13.1 Maxwell Maxwell E D H B ε 0 µ 0 (1) Gauss D = ε 0 E (13.1) B = µ 0 H. (13.2) S D = εe S S D ds = ρ(r)dr (13.3) S V div D = ρ (13.4) ρ S V Coulomb (2) Ampère C H =
B ver B
B ver. 2017.02.24 B Contents 1 11 1.1....................... 11 1.1.1............. 11 1.1.2.......................... 12 1.2............................. 14 1.2.1................ 14 1.2.2.......................
CRA3689A
AVIC-DRZ90 AVIC-DRZ80 2 3 4 5 66 7 88 9 10 10 10 11 12 13 14 15 1 1 0 OPEN ANGLE REMOTE WIDE SET UP AVIC-DRZ90 SOURCE OFF AV CONTROL MIC 2 16 17 1 2 0 0 1 AVIC-DRZ90 2 3 4 OPEN ANGLE REMOTE SOURCE OFF
http://www.ike-dyn.ritsumei.ac.jp/ hyoo/wave.html 1 1, 5 3 1.1 1..................................... 3 1.2 5.1................................... 4 1.3.......................... 5 1.4 5.2, 5.3....................
006 11 8 0 3 1 5 1.1..................... 5 1......................... 6 1.3.................... 6 1.4.................. 8 1.5................... 8 1.6................... 10 1.6.1......................
sikepuri.dvi
2009 2 2 2. 2.. F(s) G(s) H(s) G(s) F(s) H(s) F(s),G(s) H(s) : V (s) Z(s)I(s) I(s) Y (s)v (s) Z(s): Y (s): 2: ( ( V V 2 I I 2 ) ( ) ( Z Z 2 Z 2 Z 22 ) ( ) ( Y Y 2 Y 2 Y 22 ( ) ( ) Z Z 2 Y Y 2 : : Z 2 Z
2 0.1 Introduction NMR 70% 1/2
Y. Kondo 2010 1 22 2 0.1 Introduction NMR 70% 1/2 3 0.1 Introduction......................... 2 1 7 1.1.................... 7 1.2............................ 11 1.3................... 12 1.4..........................
f(x) = x (1) f (1) (2) f (2) f(x) x = a y y = f(x) f (a) y = f(x) A(a, f(a)) f(a + h) f(x) = A f(a) A x (3, 3) O a a + h x 1 f(x) x = a
3 3.1 3.1.1 A f(a + h) f(a) f(x) lim f(x) x = a h 0 h f(x) x = a f 0 (a) f 0 (a) = lim h!0 f(a + h) f(a) h = lim x!a f(x) f(a) x a a + h = x h = x a h 0 x a 3.1 f(x) = x x = 3 f 0 (3) f (3) = lim h 0 (
() (, y) E(, y) () E(, y) (3) q ( ) () E(, y) = k q q (, y) () E(, y) = k r r (3).3 [.7 ] f y = f y () f(, y) = y () f(, y) = tan y y ( ) () f y = f y
![() (, y) E(, y) () E(, y) (3) q ( ) () E(, y) = k q q (, y) () E(, y) = k r r (3).3 [.7 ] f y = f y () f(, y) = y () f(, y) = tan y y ( ) () f y = f y](/thumbs/85/92979039.jpg "() (, y) E(, y) () E(, y) (3) q ( ) () E(, y) = k q q (, y) () E(, y) = k r r (3).3 [.7 ] f y = f y () f(, y) = y () f(, y) = tan y y ( ) () f y = f y")
5. [. ] z = f(, y) () z = 3 4 y + y + 3y () z = y (3) z = sin( y) (4) z = cos y (5) z = 4y (6) z = tan y (7) z = log( + y ) (8) z = tan y + + y ( ) () z = 3 8y + y z y = 4 + + 6y () z = y z y = (3) z =
( ) 5. VSS (VIM ) 10. ( ) 11. (ANN ) ( )
1.... ( ) 5. VSS.. 8. 9. (VIM ) 1. ( ) 11. (ANN ) 1. 1. ( ) 1 Lagrange 1..1 Lagrange q, Lagrange D(q)q + C(q; _q)_q + G(q) = (1.1) D(q)q C(q; _q)_q G(q) ( ) D(q) D(q) m ; M < M m (D(q)) (1.) (D(q)) M
曲面のパラメタ表示と接線ベクトル
L11(2011-07-06 Wed) :Time-stamp: 2011-07-06 Wed 13:08 JST hig 1,,. 2. http://hig3.net () (L11) 2011-07-06 Wed 1 / 18 ( ) 1 V = (xy2 ) x + (2y) y = y 2 + 2. 2 V = 4y., D V ds = 2 2 ( ) 4 x 2 4y dy dx =
18 ( ) I II III A B C(100 ) 1, 2, 3, 5 I II A B (100 ) 1, 2, 3 I II A B (80 ) 6 8 I II III A B C(80 ) 1 n (1 + x) n (1) n C 1 + n C
8 ( ) 8 5 4 I II III A B C( ),,, 5 I II A B ( ),, I II A B (8 ) 6 8 I II III A B C(8 ) n ( + x) n () n C + n C + + n C n = 7 n () 7 9 C : y = x x A(, 6) () A C () C P AP Q () () () 4 A(,, ) B(,, ) C(,,
keisoku01.dvi
2.,, Mon, 2006, 401, SAGA, JAPAN Dept. of Mechanical Engineering, Saga Univ., JAPAN 4 Mon, 2006, 401, SAGA, JAPAN Dept. of Mechanical Engineering, Saga Univ., JAPAN 5 Mon, 2006, 401, SAGA, JAPAN Dept.
Excel ではじめる数値解析 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. このサンプルページの内容は, 初版 1 刷発行時のものです.
Excel ではじめる数値解析 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/009631 このサンプルページの内容は, 初版 1 刷発行時のものです. Excel URL http://www.morikita.co.jp/books/mid/009631 i Microsoft Windows
IA
IA 31 4 11 1 1 4 1.1 Planck.............................. 4 1. Bohr.................................... 5 1.3..................................... 6 8.1................................... 8....................................
t = h x z z = h z = t (x, z) (v x (x, z, t), v z (x, z, t)) ρ v x x + v z z = 0 (1) 2-2. (v x, v z ) φ(x, z, t) v x = φ x, v z
I 1 m 2 l k 2 x = 0 x 1 x 1 2 x 2 g x x 2 x 1 m k m 1-1. L x 1, x 2, ẋ 1, ẋ 2 ẋ 1 x = 0 1-2. 2 Q = x 1 + x 2 2 q = x 2 x 1 l L Q, q, Q, q M = 2m µ = m 2 1-3. Q q 1-4. 2 x 2 = h 1 x 1 t = 0 2 1 t x 1 (t)
.. p.2/5
IV. p./5 .. p.2/5 .. 8 >< >: d dt y = a, y + a,2 y 2 + + a,n y n + f (t) d dt y 2 = a 2, y + a 2,2 y 2 + + a 2,n y n + f 2 (t). d dt y n = a n, y + a n,2 y 2 + + a n,n y n + f n (t) (a i,j ) p.2/5 .. 8
2.2 ( y = y(x ( (x 0, y 0 y (x 0 (y 0 = y(x 0 y = y(x ( y (x 0 = F (x 0, y(x 0 = F (x 0, y 0 (x 0, y 0 ( (x 0, y 0 F (x 0, y 0 xy (x, y (, F (x, y ( (
(. x y y x f y = f(x y x y = y(x y x y dx = d dx y(x = y (x = f (x y = y(x x ( (differential equation ( + y 2 dx + xy = 0 dx = xy + y 2 2 2 x y 2 F (x, y = xy + y 2 y = y(x x x xy(x = F (x, y(x + y(x 2
EL-G37
EL-G37 A A A A A A A A A A A A A A GT F543210A CE CA 4 00. 00 23.80 2 015.6250 77.14286 96. 91. 102. 25. 9. 1 700. 2 720. 2.5 7. 20. 25. 220. 400. 4 096. 4.685 0.084 M 125. M 28. M 85.
1 [ 1] (1) MKS? (2) MKS? [ 2] (1) (42.195k) k 2 (2) (3) k/hr [ 3] t = 0 10 ( 1 velocity [/s] 8 4 O
![1 [ 1] (1) MKS? (2) MKS? [ 2] (1) (42.195k) k 2 (2) (3) k/hr [ 3] t = 0 10 ( 1 velocity [/s] 8 4 O](/thumbs/93/114442636.jpg "1 [ 1] (1) MKS? (2) MKS? [ 2] (1) (42.195k) k 2 (2) (3) k/hr [ 3] t = 0 10 ( 1 velocity [/s] 8 4 O")
: 2014 4 10 1 2 2 3 2.1...................................... 3 2.2....................................... 4 2.3....................................... 4 2.4................................ 5 2.5 Free-Body
n=1 1 n 2 = π = π f(z) f(z) 2 f(z) = u(z) + iv(z) *1 f (z) u(x, y), v(x, y) f(z) f (z) = f/ x u x = v y, u y = v x
n= n 2 = π2 6 3 2 28 + 4 + 9 + = π2 6 2 f(z) f(z) 2 f(z) = u(z) + iv(z) * f (z) u(x, y), v(x, y) f(z) f (z) = f/ x u x = v y, u y = v x f x = i f y * u, v 3 3. 3 f(t) = u(t) + v(t) [, b] f(t)dt = u(t)dt
Untitled
http://www.ike-dyn.ritsumei.ac.jp/ hyoo/dynamics.html 1 (i) (ii) 2 (i) (ii) (*) [1] 2 1 3 1.1................................ 3 1.2..................................... 3 2 4 2.1....................................
A(6, 13) B(1, 1) 65 y C 2 A(2, 1) B( 3, 2) C 66 x + 2y 1 = 0 2 A(1, 1) B(3, 0) P 67 3 A(3, 3) B(1, 2) C(4, 0) (1) ABC G (2) 3 A B C P 6
1 1 1.1 64 A6, 1) B1, 1) 65 C A, 1) B, ) C 66 + 1 = 0 A1, 1) B, 0) P 67 A, ) B1, ) C4, 0) 1) ABC G ) A B C P 64 A 1, 1) B, ) AB AB = 1) + 1) A 1, 1) 1 B, ) 1 65 66 65 C0, k) 66 1 p, p) 1 1 A B AB A 67
数値計算：常微分方程式
( ) 1 / 82 1 2 3 4 5 6 ( ) 2 / 82 ( ) 3 / 82 C θ l y m O x mg λ ( ) 4 / 82 θ t C J = ml 2 C mgl sin θ θ C J θ = mgl sin θ = θ ( ) 5 / 82 ω = θ J ω = mgl sin θ ω J = ml 2 θ = ω, ω = g l sin θ = θ ω ( )
K E N Z OU
K E N Z OU 11 1 1 1.1..................................... 1.1.1............................ 1.1..................................................................................... 4 1.........................................
1/68 A. 電気所 ( 発電所, 変電所, 配電塔 ) における変圧器の空き容量一覧 平成 31 年 3 月 6 日現在 < 留意事項 > (1) 空容量は目安であり 系統接続の前には 接続検討のお申込みによる詳細検討が必要となります その結果 空容量が変更となる場合があります (2) 特に記載
1/68 A. 電気所 ( 発電所, 変電所, 配電塔 ) における変圧器の空き容量一覧 平成 31 年 3 月 6 日現在 < 留意事項 > (1) 空容量は目安であり 系統接続の前には 接続検討のお申込みによる詳細検討が必要となります その結果 空容量が変更となる場合があります (2) 特に記載のない限り 熱容量を考慮した空き容量を記載しております その他の要因 ( 電圧や系統安定度など ) で連系制約が発生する場合があります
通信容量制約を考慮したフィードバック制御 - 電子情報通信学会 情報理論研究会（IT） 若手研究者のための講演会
IT 1 2 1 2 27 11 24 15:20 16:05 ( ) 27 11 24 1 / 49 1 1940 Witsenhausen 2 3 ( ) 27 11 24 2 / 49 1940 2 gun director Warren Weaver, NDRC (National Defence Research Committee) Final report D-2 project #2,
入試の軌跡
4 y O x 4 Typed by L A TEX ε ) ) ) 6 4 ) 4 75 ) http://kumamoto.s.xrea.com/plan/.. PDF) Ctrl +L) Ctrl +) Ctrl + Ctrl + ) ) Alt + ) Alt + ) ESC. http://kumamoto.s.xrea.com/nyusi/kumadai kiseki ri i.pdf
c 2009 i
I 2009 c 2009 i 0 1 0.0................................... 1 0.1.............................. 3 0.2.............................. 5 1 7 1.1................................. 7 1.2..............................
I 1
I 1 1 1.1 1. 3 m = 3 1 7 µm. cm = 1 4 km 3. 1 m = 1 1 5 cm 4. 5 cm 3 = 5 1 15 km 3 5. 1 = 36 6. 1 = 8.64 1 4 7. 1 = 3.15 1 7 1 =3 1 7 1 3 π 1. 1. 1 m + 1 cm = 1.1 m. 1 hr + 64 sec = 1 4 sec 3. 3. 1 5 kg
1 1.1 [ 1] velocity [/s] 8 4 (1) MKS? (2) MKS? 1.2 [ 2] (1) (42.195k) k 2 (2) (3) k/hr [ 3] t = 0
![1 1.1 [ 1] velocity [/s] 8 4 (1) MKS? (2) MKS? 1.2 [ 2] (1) (42.195k) k 2 (2) (3) k/hr [ 3] t = 0](/thumbs/93/114340663.jpg "1 1.1 [ 1] velocity [/s] 8 4 (1) MKS? (2) MKS? 1.2 [ 2] (1) (42.195k) k 2 (2) (3) k/hr [ 3] t = 0")
: 2016 4 1 1 2 1.1......................................... 2 1.2................................... 2 2 2 2.1........................................ 2 2.2......................................... 3 2.3.........................................
30 (11/04 )
30 (11/04 ) i, 1,, II I?,,,,,,,,, ( ),,, ϵ δ,,,,, (, ),,,,,, 5 : (1) ( ) () (,, ) (3) ( ) (4) (5) ( ) (1),, (),,, () (3), (),, (4), (1), (3), ( ), (5),,,,,,,, ii,,,,,,,, Richard P. Feynman, The best teaching
24 I ( ) 1. R 3 (i) C : x 2 + y 2 1 = 0 (ii) C : y = ± 1 x 2 ( 1 x 1) (iii) C : x = cos t, y = sin t (0 t 2π) 1.1. γ : [a, b] R n ; t γ(t) = (x
![24 I ( ) 1. R 3 (i) C : x 2 + y 2 1 = 0 (ii) C : y = ± 1 x 2 ( 1 x 1) (iii) C : x = cos t, y = sin t (0 t 2π) 1.1. γ : [a, b] R n ; t γ(t) = (x](/thumbs/94/118744578.jpg "24 I ( ) 1. R 3 (i) C : x 2 + y 2 1 = 0 (ii) C : y = ± 1 x 2 ( 1 x 1) (iii) C : x = cos t, y = sin t (0 t 2π) 1.1. γ : [a, b] R n ; t γ(t) = (x")
24 I 1.1.. ( ) 1. R 3 (i) C : x 2 + y 2 1 = 0 (ii) C : y = ± 1 x 2 ( 1 x 1) (iii) C : x = cos t, y = sin t (0 t 2π) 1.1. γ : [a, b] R n ; t γ(t) = (x 1 (t), x 2 (t),, x n (t)) ( ) ( ), γ : (i) x 1 (t),
2 7 V 7 {fx fx 3 } 8 P 3 {fx fx 3 } 9 V 9 {fx fx f x 2fx } V {fx fx f x 2fx + } V {{a n } {a n } a n+2 a n+ + a n n } 2 V 2 {{a n } {a n } a n+2 a n+
R 3 R n C n V??,?? k, l K x, y, z K n, i x + y + z x + y + z iv x V, x + x o x V v kx + y kx + ky vi k + lx kx + lx vii klx klx viii x x ii x + y y + x, V iii o K n, x K n, x + o x iv x K n, x + x o x
1 1 1 1 1 1 2 f z 2 C 1, C 2 f 2 C 1, C 2 f(c 2 ) C 2 f(c 1 ) z C 1 f f(z) xy uv ( u v ) = ( a b c d ) ( x y ) + ( p q ) (p + b, q + d) 1 (p + a, q + c) 1 (p, q) 1 1 (b, d) (a, c) 2 3 2 3 a = d, c = b
2000年度『数学展望 I』講義録
2000 I I IV I II 2000 I I IV I-IV. i ii 3.10 (http://www.math.nagoya-u.ac.jp/ kanai/) 2000 A....1 B....4 C....10 D....13 E....17 Brouwer A....21 B....26 C....33 D....39 E. Sperner...45 F....48 A....53
I, II 1, A = A 4 : 6 = max{ A, } A A 10 10%
1 2006.4.17. A 3-312 tel: 092-726-4774, e-mail: hara@math.kyushu-u.ac.jp, http://www.math.kyushu-u.ac.jp/ hara/lectures/lectures-j.html Office hours: B A I ɛ-δ ɛ-δ 1. 2. A 1. 1. 2. 3. 4. 5. 2. ɛ-δ 1. ɛ-n
1W II K =25 A (1) office(a439) (2) A4 etc. 12:00-13:30 Cafe David 1 2 TA appointment Cafe D
1W II K200 : October 6, 2004 Version : 1.2, kawahira@math.nagoa-u.ac.jp, http://www.math.nagoa-u.ac.jp/~kawahira/courses.htm TA M1, m0418c@math.nagoa-u.ac.jp TA Talor Jacobian 4 45 25 30 20 K2-1W04-00
211 kotaro@math.titech.ac.jp 1 R *1 n n R n *2 R n = {(x 1,..., x n ) x 1,..., x n R}. R R 2 R 3 R n R n R n D D R n *3 ) (x 1,..., x n ) f(x 1,..., x n ) f D *4 n 2 n = 1 ( ) 1 f D R n f : D R 1.1. (x,