1.500 m X Y m m m m m m m m m m m m N/ N/ ( ) qa N/ N/ 2 2

3.300 m m m m m m 0 m m m 0 m 0 m m m he m T m 1.50 m N/ N

3.300 m 0.500 m 0.300 m 0.300 m 0.300 m 0.500 m 0 m 1.000 m 2.000 m 0 m 0 m 0.300 m 0.300 m -0.200 he 0.400 m T 0.200 m 1.50 m 0.16 2 24.5 N/ 3 18.0 N/ 3 28.0 18.7 18.7 14.0 14.0 X(m) 1.000 2.000 20 Y(m)

he T N/ N/

6.000 1.000 0.800 0.000 0.500 1.500 3.000 1.200 0.000 0.000 0.000 0.000 0.000-0.100 he 1.500 T 0.100 1.50 0.00 2 24.5 N/ 3 18.0 N/ 3 28.0 18.7 18.7 14.0 14.0 X() 20.000 Y() 0.000 (kn/2) 10.000 0.000 kn

untitled

0 ( L CONTENTS 0 . sin(-x-sinx, (-x(x, sin(90-xx,(90-xsinx sin(80-xsinx,(80-x-x ( sin{90-(ωφ}(ωφ. :n :m.0 m.0 n tn. 0 n.0 tn ω m :n.0n tn n.0 tn.0 m c ω sinω c ω c tnω ecω sin ω ω sin c ω c ω tn c tn ω

untitled

9118 154 B-1 B-3 B- 5cm 3cm 5cm 3m18m5.4m.5m.66m1.3m 1.13m 1.134m 1.35m.665m 5 , 4 13 7 56 M 1586.1.18 7.77.9 599.5.8 7 1596.9.5 7.57.75 684.11.9 8.5 165..3 7.9 87.8.11 6.57. 166.6.16 7.57.6 856 6.6.5

untitled

( ) c a sin b c b c a cos a c b c a tan b a b cos sin a c b c a ccos b csin (4) Ma k Mg a (Gal) g(98gal) (Gal) a max (K-E) kh Zck.85.6. 4 Ma g a k a g k D τ f c + σ tanφ σ 3 3 /A τ f3 S S τ A σ /A σ /A

all.dvi

38 5 Cauchy.,,,,., σ.,, 3,,. 5.1 Cauchy (a) (b) (a) (b) 5.1: 5.1. Cauchy 39 F Q Newton F F F Q F Q 5.2: n n ds df n ( 5.1). df n n df(n) df n, t n. t n = df n (5.1) ds 40 5 Cauchy t l n mds df n 5.3: t

untitled

.m 5m :.45.4m.m 3.m.6m (N/mm ).8.6 σ.4 h.m. h.68m h(m) b.35m θ4..5.5.5 -. σ ta.n/mm c 3kN/m 3 w 9.8kN/m 3 -.4 ck 6N/mm -.6 σ -.8 3 () :. 4 5 3.75m :. 7.m :. 874mm 4 865mm mm/ :. 7.m 4.m 4.m 6 7 4. 3.5

(1.2) T D = 0 T = D = 30 kn 1.2 (1.4) 2F W = 0 F = W/2 = 300 kn/2 = 150 kn 1.3 (1.9) R = W 1 + W 2 = = 1100 N. (1.9) W 2 b W 1 a = 0

1 1 1.1 1.) T D = T = D = kn 1. 1.4) F W = F = W/ = kn/ = 15 kn 1. 1.9) R = W 1 + W = 6 + 5 = 11 N. 1.9) W b W 1 a = a = W /W 1 )b = 5/6) = 5 cm 1.4 AB AC P 1, P x, y x, y y x 1.4.) P sin 6 + P 1 sin 45

NETES No.CG V

1 2006 6 NETES No.CG-050001-V 2007 5 2 1 2 1 19 5 1 2 19 8 2 i 1 1 1.1 1 1.2 2 1.3 2 2 3 2.1 3 2.2 8 3 9 3.1 9 3.2 10 3.3 13 3.3.1 13 3.3.2 14 3.3.3 14 3.3.4 16 3.3.5 17 3.3.6 18 3.3.7 21 3.3.8 22 3.4

(1) (kn/m 3 )

1 1 1.1 1.1.1 (1) 1.1 1.2 1.1 (kn/m 3 ) 77 71 24.5 23 21 8.0 22.5 2 1 1.2 N/m 2 2 m 3 m 2000 2200 2500 3000 (2) 1 A B B 1.3 1.5 1.1 T cm 1.1 3 1.3 L m L 4 L > 4 1.0 L 32 + 7 8 1.2 T 4 1 2 5.0 kn/m 2 3.

untitled

PGF 17 6 1 11 1 12 1 2 21 2 22 2 23 3 1 3 1 3 2 3 3 3 4 3 5 4 6 4 2 4 1 4 2 4 3 4 4 4 5 5 3 5 1 5 2 5 5 5 5 4 5 1 5 2 5 3 6 5 6 1 6 2 6 6 6 24 7 1 7 1 7 2 7 3 7 4 8 2 8 1 8 2 8 3 9 4 9 5 9 6 9 3 9 1 9

Ł\”ƒ-2005

第90回日本感染症学会学術講演会抄録（I）

1. z dr er r sinθ dϕ eϕ r dθ eθ dr θ dr dθ r x 0 ϕ r sinθ dϕ r sinθ dϕ y dr dr er r dθ eθ r sinθ dϕ eϕ 2. (r, θ, φ) 2 dr 1 h r dr 1 e r h θ dθ 1 e θ h

IB IIA 1 1 r, θ, φ 1 (r, θ, φ)., r, θ, φ 0 r

4 4 θ X θ P θ 4. 0, 405 P 0 X 405 X P 4. () 60 () 45 () 40 (4) 765 (5) 40 B 60 0 P = 90, = ( ) = X

4 4. 4.. 5 5 0 A P P P X X X X +45 45 0 45 60 70 X 60 X 0 P P 4 4 θ X θ P θ 4. 0, 405 P 0 X 405 X P 4. () 60 () 45 () 40 (4) 765 (5) 40 B 60 0 P 0 0 + 60 = 90, 0 + 60 = 750 0 + 60 ( ) = 0 90 750 0 90 0

(1) 1.1

1 1 1.1 1.1.1 1.1 ( ) ( ) ( ) { ( ) ( ) { ( ) ( ) { ( ) ( ) { ( ) ( ) { ( ) ( ) ( ) ( ) ( ) 2 1 1.1.2 (1) 1.1 1.1 3 (2) 1.2 4 1 (3) 1.3 ( ) ( ) (4) 1.1 5 (5) ( ) 1.4 6 1 (6) 1.5 (7) ( ) (8) 1.1 7 1.1.3

多数アンカー式補強土壁工法

1. (SN ) SS400 ( ) SN400 SM490A ( ) SN490 JIS G 3136:SN -1994 JIS G 3136:SN 1) SN (SNR ) (JIS G 3138-1996) SN SNR490B 1 1SNR490B 2. SN490 SM490A 2) SNR490B SM490 3) 2SNR490B [N/mm 2 ] 185 185 105 [N/mm

1 (Berry,1975) 2-6 p (S πr 2 )p πr 2 p 2πRγ p p = 2γ R (2.5).1-1 : : : : ( ).2 α, β α, β () X S = X X α X β (.1) 1 2

2005 9/8-11 2 2.2 ( 2-5) γ ( ) γ cos θ 2πr πρhr 2 g h = 2γ cos θ ρgr (2.1) γ = ρgrh (2.2) 2 cos θ θ cos θ = 1 (2.2) γ = 1 ρgrh (2.) 2 2. p p ρgh p ( ) p p = p ρgh (2.) h p p = 2γ r 1 1 (Berry,1975) 2-6

Q & A Q A p

Q & A 2004.12 1 Q1. 12 2 A1. 11 3 p.1 1.1 2 Q2. A2. < > [ ] 10 5 15 (p.138) (p.150) (p.176) (p.167 ) 3 1. 4 1.6 1.6.1 (2) (p.6) Q3. 5 1 1:1.0 12 2 1:0.6 1:1.0 1:1.0 1:0.6 1:0.6 1:0.6 1:1.0 1:0.6 ( ) 1:1.0

[Ver. 0.2] 1 2 3 4 5 6 7 1 1.1 1.2 1.3 1.4 1.5 1 1.1 1 1.2 1. (elasticity) 2. (plasticity) 3. (strength) 4. 5. (toughness) 6. 1 1.2 1. (elasticity) } 1 1.2 2. (plasticity), 1 1.2 3. (strength) a < b F

I II III IV V

I II III IV V N/m 2 640 980 50 200 290 440 2m 50 4m 100 100 150 200 290 390 590 150 340 4m 6m 8m 100 170 250 µ = E FRVβ β N/mm 2 N/mm 2 1.1 F c t.1 3 1 1.1 1.1 2 2 2 2 F F b F s F c F t F b F s 3 3 3

第86回日本感染症学会総会学術集会後抄録（I）

κ κ κ κ κ κ μ μ β β β γ α α β β γ α β α α α γ α β β γ μ β β μ μ α ββ β β β β β β β β β β β β β β β β β β γ β μ μ μ μμ μ μ μ μ β β μ μ μ μ μ μ μ μ μ μ μ μ μ μ β

untitled

( 9:: 3:6: (k 3 45 k F m tan 45 k 45 k F m tan S S F m tan( 6.8k tan k F m ( + k tan 373 S S + Σ Σ 3 + Σ os( sin( + Σ sin( os( + sin( os( p z ( γ z + K pzdz γ + K γ K + γ + 9 ( 9 (+ sin( sin { 9 ( } 4

66 σ σ (8.1) σ = 0 0 σd = 0 (8.2) (8.2) (8.1) E ρ d = 0... d = 0 (8.3) d 1 NN K K 8.1 d σd σd M = σd = E 2 d (8.4) ρ 2 d = I M = EI ρ 1 ρ = M EI ρ EI

65 8. K 8 8 7 8 K 6 7 8 K 6 M Q σ (6.4) M O ρ dθ D N d N 1 P Q B C (1 + ε)d M N N h 2 h 1 ( ) B (+) M 8.1: σ = E ρ (E, 1/ρ ) (8.1) 66 σ σ (8.1) σ = 0 0 σd = 0 (8.2) (8.2) (8.1) E ρ d = 0... d = 0 (8.3)

N cos s s cos ψ e e e e 3 3 e e 3 e 3 e

3 3 5 5 5 3 3 7 5 33 5 33 9 5 8 > e > f U f U u u > u ue u e u ue u ue u e u e u u e u u e u N cos s s cos ψ e e e e 3 3 e e 3 e 3 e 3 > A A > A E A f A A f A [ ] f A A e > > A e[ ] > f A E A < < f ; >

LLG-R8.Nisus.pdf

d M d t = γ M H + α M d M d t M γ [ 1/ ( Oe sec) ] α γ γ = gµ B h g g µ B h / π γ g = γ = 1.76 10 [ 7 1/ ( Oe sec) ] α α = λ γ λ λ λ α γ α α H α = γ H ω ω H α α H K K H K / M 1 1 > 0 α 1 M > 0 γ α γ =

untitled

20 3 Copyright (2007) by P.W.R.I. All rights reserved. No part of this book may be reproduced by any means, nor transmitted, nor translated into a machine language without the written permission of the

（１）基礎の設計に関する基本事項

(1) qa 50kN/m 2 qa 13 1113 1 (2) (3) (2) 50 qa 100kN/m 2 13 1113 1 (3) qa 100kN/m 2 qa 120kN/m 2 (1) qa 300kN/m 2 qa 13 1113 1 (2) (2) qa 300 kn/m 2 qa 1000kN/m 2 38 3 50 30 3 /10m 42 1 13 1113 5 6 30

抄録／抄録１　　　　（１）Ｖ

日本内科学会雑誌第98巻第4号

日本内科学会雑誌第97巻第7号

1

GL (a) (b) Ph l P N P h l l Ph Ph Ph Ph l l l l P Ph l P N h l P l .9 αl B βlt D E. 5.5 L r..8 e g s e,e l l W l s l g W W s g l l W W e s g e s g r e l ( s ) l ( l s ) r e l ( s ) l ( l s ) e R e r

ｔｎｂｐ５９－２１＿Ｗｅｂ：Ｐ２／ｋｙ１３２３７９５０９６１０００２９４４

untitled

. 96. 99. ( 000 SIC SIC N88 SIC for Windows95 6 6 3 0 . amano No.008 6. 6.. z σ v σ v γ z (6. σ 0 (a (b 6. (b 0 0 0 6. σ σ v σ σ 0 / v σ v γ z σ σ 0 σ v 0γ z σ / σ ν /( ν, ν ( 0 0.5 0.0 0 v sinφ, φ 0 (6.

16 6 12 1 16 6 23 23 11 16 START 1 Out Ok 1,2 Ok END Out 3 1 1/ H24.2 2 1 L2-1 L2-2 H14.3 3 H9.10 PHC SC 19 1 24 3 18N/mm 2 24N/mm 2 30N/mm 2 25 10 13 12 13 12 11 11 11 11 19 7 25 10 24N 8cm 25(20)mm 45

20 4 20 i 1 1 1.1............................ 1 1.2............................ 4 2 11 2.1................... 11 2.2......................... 11 2.3....................... 19 3 25 3.1.............................

研修コーナー

l l l l l l l l l l l α α β l µ l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l

パーキンソン病治療ガイドライン2002

< B38BD C78F6F97CD97E12D332E786477>

無筋擁壁設計システム Ver4.2 適用基準 土地改良事業計画設計基準 設計 農道 (H7/3) 土地改良事業計画設計基準 設計 水路工 (H26/3) 日本道路協会 道路土工 擁壁工指針 (H24/7) 土木学会 大型ブロック積み擁壁設計 (H6/6) 宅地防災マニュアルの解説 第二次改訂版 (H9/2) 出力例 ブロック積み擁壁の計算書 ( 安定計算および部材断面計算 ) 開発 販売元 ( 株

21 2 26 i 1 1 1.1............................ 1 1.2............................ 3 2 9 2.1................... 9 2.2.......... 9 2.3................... 11 2.4....................... 12 3 15 3.1..........

v v = v 1 v 2 v 3 (1) R = (R ij ) (2) R (R 1 ) ij = R ji (3) 3 R ij R ik = δ jk (4) i=1 δ ij Kronecker δ ij = { 1 (i = j) 0 (i

1. 1 1.1 1.1.1 1.1.1.1 v v = v 1 v 2 v 3 (1) R = (R ij ) (2) R (R 1 ) ij = R ji (3) R ij R ik = δ jk (4) δ ij Kronecker δ ij = { 1 (i = j) 0 (i j) (5) 1 1.1. v1.1 2011/04/10 1. 1 2 v i = R ij v j (6) [

O x y z O ( O ) O (O ) 3 x y z O O x v t = t = 0 ( 1 ) O t = 0 c t r = ct P (x, y, z) r 2 = x 2 + y 2 + z 2 (t, x, y, z) (ct) 2 x 2 y 2 z 2 = 0

9 O y O ( O ) O (O ) 3 y O O v t = t = 0 ( ) O t = 0 t r = t P (, y, ) r = + y + (t,, y, ) (t) y = 0 () ( )O O t (t ) y = 0 () (t) y = (t ) y = 0 (3) O O v O O v O O O y y O O v P(, y,, t) t (, y,, t )

Γ Ec Γ V BIAS THBV3_0401JA THBV3_0402JAa THBV3_0402JAb 1000 800 600 400 50 % 25 % 200 100 80 60 40 20 10 8 6 4 10 % 2.5 % 0.5 % 0.25 % 2 1.0 0.8 0.6 0.4 0.2 0.1 200 300 400 500 600 700 800 1000 1200 14001600

( ) e + e ( ) ( ) e + e () ( ) e e Τ ( ) e e ( ) ( ) () () ( ) ( ) ( ) ( )

n n (n) (n) (n) (n) n n ( n) n n n n n en1, en ( n) nen1 + nen nen1, nen ( ) e + e ( ) ( ) e + e () ( ) e e Τ ( ) e e ( ) ( ) () () ( ) ( ) ( ) ( ) ( n) Τ n n n ( n) n + n ( n) (n) n + n n n n n n n n

1- 擁壁断面の形状 寸法及び荷重の計算 ( 常時 ) フェンス荷重 1 kn/m 1,100 0 上載荷重 10 m kn/ 3, (1) 自重 地表面と水平面とのなす角度 α=0.00 壁背面と鉛直面とのなす角度 θ=.73 擁壁

構造計算例鉄筋コンクリート造擁壁の構造計算例 1 常時 1-1 設計条件 (1) 擁壁の型式及び高さ型式 : 片持梁式鉄筋コンクリート造 L 型擁壁擁壁の高さ :H'=3.00m 擁壁の全高 :H =3.50m () 外力土圧の作用面は縦壁背面とする 上載荷重 : q=10kn/ mフェンス荷重 ( 水平力 ) : 1kN/ m (3) 背面土土質の種類 : 関東ローム土の単位体積重量 :γs=16.0/

さくらの個別指導 ( さくら教育研究所 ) A a 1 a 2 a 3 a n {a n } a 1 a n n n 1 n n 0 a n = 1 n 1 n n O n {a n } n a n α {a n } α {a

... A a a a 3 a n {a n } a a n n 3 n n n 0 a n = n n n O 3 4 5 6 n {a n } n a n α {a n } α {a n } α α {a n } a n n a n α a n = α n n 0 n = 0 3 4. ()..0.00 + (0.) n () 0. 0.0 0.00 ( 0.) n 0 0 c c c c c

Taro11-aマニュアル.jtd

L A m ton m kn t t kn t kn t m m kn ton ton m m m kn/ CK CK = N/mm ca sa a cm kn/ kn/ kn/ kn/ kn/ kn/ kn/ - - kn/m WL % /m - - A c sin cos kn/m kn/m kn/m / - / A A H V H A cos V A sin - - = N/mm P P m

( ) sin 1 x, cos 1 x, tan 1 x sin x, cos x, tan x, arcsin x, arccos x, arctan x. π 2 sin 1 x π 2, 0 cos 1 x π, π 2 < tan 1 x < π 2 1 (1) (

6 20 ( ) sin, cos, tan sin, cos, tan, arcsin, arccos, arctan. π 2 sin π 2, 0 cos π, π 2 < tan < π 2 () ( 2 2 lim 2 ( 2 ) ) 2 = 3 sin (2) lim 5 0 = 2 2 0 0 2 2 3 3 4 5 5 2 5 6 3 5 7 4 5 8 4 9 3 4 a 3 b

PowerPoint プレゼンテーション

003.10.3 003.10.8 Y 1 0031016 B4(4 3 B4,1 M 0 C,Q 0. M,Q 1.- MQ 003/10/16 10/8 Girder BeamColumn Foundation SlabWall Girder BeamColumn Foundation SlabWall 1.-1 5mm 0 kn/m 3 0.05m=0.5 kn/m 60mm 18 kn/m

Part () () Γ Part ,

Contents a 6 6 6 6 6 6 6 7 7. 8.. 8.. 8.3. 8 Part. 9. 9.. 9.. 3. 3.. 3.. 3 4. 5 4.. 5 4.. 9 4.3. 3 Part. 6 5. () 6 5.. () 7 5.. 9 5.3. Γ 3 6. 3 6.. 3 6.. 3 6.3. 33 Part 3. 34 7. 34 7.. 34 7.. 34 8. 35

本文／目次（裏白）

1 1 x y = y(x) y, y,..., y (n) : n y F (x, y, y,..., y (n) ) = 0 n F (x, y, y ) = 0 1 y(x) y y = G(x, y) y, y y + p(x)y = q(x) 1 p(x) q(

1 1 y = y() y, y,..., y (n) : n y F (, y, y,..., y (n) ) = 0 n F (, y, y ) = 0 1 y() 1.1 1 y y = G(, y) 1.1.1 1 y, y y + p()y = q() 1 p() q() (q() = 0) y + p()y = 0 y y + py = 0 y y = p (log y) = p log

3-1. 1) 1-1) =10.92m =18.20m m 2 6,480 3, =30 30kN/m 2 Z=0.9

3-1. 3-2. 3-3. 3-1. 1) 1-1) =10.92m =18.20m 198.74m 2 6,480 3,800 4.5 =30 30kN/m 2 Z=0.9 1-2) G1 G2 G3 G4 1-3) G1 G2 H3 1-4) t = 12 2.5 2) 2-1) No ( ) 1 120 120 2 120 120 3 120 180 360 4 120 150 210 5

(Compton Scattering) Beaming 1 exp [i (k x ωt)] k λ k = 2π/λ ω = 2πν k = ω/c k x ωt ( ω ) k α c, k k x ωt η αβ k α x β diag( + ++) x β = (ct, x) O O x

Compton Scattering Beaming exp [i k x ωt] k λ k π/λ ω πν k ω/c k x ωt ω k α c, k k x ωt η αβ k α x β diag + ++ x β ct, x O O x O O v k α k α β, γ k γ k βk, k γ k + βk k γ k k, k γ k + βk 3 k k 4 k 3 k

A(6, 13) B(1, 1) 65 y C 2 A(2, 1) B( 3, 2) C 66 x + 2y 1 = 0 2 A(1, 1) B(3, 0) P 67 3 A(3, 3) B(1, 2) C(4, 0) (1) ABC G (2) 3 A B C P 6

1 1 1.1 64 A6, 1) B1, 1) 65 C A, 1) B, ) C 66 + 1 = 0 A1, 1) B, 0) P 67 A, ) B1, ) C4, 0) 1) ABC G ) A B C P 64 A 1, 1) B, ) AB AB = 1) + 1) A 1, 1) 1 B, ) 1 65 66 65 C0, k) 66 1 p, p) 1 1 A B AB A 67

Super Build／宅造擁壁 出力例１

宅造擁壁構造計算書 使用プログラム : uper Build/ 宅造擁壁 Ver.1.60 工事名 : 日付 : 設計者名 : 宅地防災マニュアル事例集 015/01/7 UNION YTEM INC. Ⅶ-1 建設地 : L 型擁壁の設計例 壁体背面を荷重面としてとる場合 *** uper Build/ 宅造擁壁 *** 160-999999 [ 宅地防災マニュアル Ⅶ-1] 015/01/7 00:00

(1) (2) (1) (2) 2 3 {a n } a 2 + a 4 + a a n S n S n = n = S n

. 99 () 0 0 0 () 0 00 0 350 300 () 5 0 () 3 {a n } a + a 4 + a 6 + + a 40 30 53 47 77 95 30 83 4 n S n S n = n = S n 303 9 k d 9 45 k =, d = 99 a d n a n d n a n = a + (n )d a n a n S n S n = n(a + a n

6 2 2 x y x y t P P = P t P = I P P P ( ) ( ) ,, ( ) ( ) cos θ sin θ cos θ sin θ, sin θ cos θ sin θ cos θ y x θ x θ P

6 x x 6.1 t P P = P t P = I P P P 1 0 1 0,, 0 1 0 1 cos θ sin θ cos θ sin θ, sin θ cos θ sin θ cos θ x θ x θ P x P x, P ) = t P x)p ) = t x t P P ) = t x = x, ) 6.1) x = Figure 6.1 Px = x, P=, θ = θ P

1. 1 A : l l : (1) l m (m 3) (2) m (3) n (n 3) (4) A α, β γ α β + γ = 2 m l lm n nα nα = lm. α = lm n. m lm 2β 2β = lm β = lm 2. γ l 2. 3

1. 1 A : l l : (1) l m (m 3) (2) m (3) n (n 3) (4) A 2 1 2 1 2 3 α, β γ α β + γ = 2 m l lm n nα nα = lm. α = lm n. m lm 2β 2β = lm β = lm 2. γ l 2. 3 4 P, Q R n = {(x 1, x 2,, x n ) ; x 1, x 2,, x n R}

t θ, τ, α, β S(, 0 P sin(θ P θ S x cos(θ SP = θ P (cos(θ, sin(θ sin(θ P t tan(θ θ 0 cos(θ tan(θ = sin(θ cos(θ ( 0t tan(θ

4 5 ( 5 3 9 4 0 5 ( 4 6 7 7 ( 0 8 3 9 ( 8 t θ, τ, α, β S(, 0 P sin(θ P θ S x cos(θ SP = θ P (cos(θ, sin(θ sin(θ P t tan(θ θ 0 cos(θ tan(θ = sin(θ cos(θ ( 0t tan(θ S θ > 0 θ < 0 ( P S(, 0 θ > 0 ( 60 θ

1 I 1.1 ± e = = - = C C MKSA [m], [Kg] [s] [A] 1C 1A 1 MKSA 1C 1C +q q +q q 1

1 I 1.1 ± e = = - =1.602 10 19 C C MKA [m], [Kg] [s] [A] 1C 1A 1 MKA 1C 1C +q q +q q 1 1.1 r 1,2 q 1, q 2 r 12 2 q 1, q 2 2 F 12 = k q 1q 2 r 12 2 (1.1) k 2 k 2 ( r 1 r 2 ) ( r 2 r 1 ) q 1 q 2 (q 1 q 2

Note.tex 2008/09/19( )

1 20 9 19 2 1 5 1.1........................ 5 1.2............................. 8 2 9 2.1............................. 9 2.2.............................. 10 3 13 3.1.............................. 13 3.2..................................

道路土工擁壁工指針 (H24) に準拠 重力式擁壁の安定計算 ( 盛土土圧対応 ) 正規版 Ver 基本データの入力 2 地形データの入力 3 計算実行 Ver /01/18 Civil Tech 洋洋 本ソフトの概要 機能 道路土工 擁壁工指針 ( 平成 24 年度

道路土工擁壁工指針 (H24) に準拠 重力式擁壁の安定計算 ( 盛土土圧対応 ) 正規版 Ver.1.10 1 基本データの入力 2 地形データの入力 3 計算実行 Ver 1.10 2019/01/18 Civil Tech 洋洋 本ソフトの概要 機能 道路土工 擁壁工指針 ( 平成 24 年度版 ) に準拠して 重力式擁壁の安定計算を行ないます 滑動 転倒 地盤支持力の安定検討を行うことができます

Microsoft Word - 部材規格追記 doc

3 14 10 18 7 20 10 SS SN 21 3 24 4 ... 1... 5... 13 f ck=40n/mm 2 P d1 =60kN/ f ck=40n/mm 2 P d2 =100kN/ f ck=40n/mm 2 P d3 =150kN/ UAUBUC TATBTC DADBDC 115mm 75mm 115mm 75mm 160mm 120mm D13 6.0% l l l

W u = u(x, t) u tt = a 2 u xx, a > 0 (1) D := {(x, t) : 0 x l, t 0} u (0, t) = 0, u (l, t) = 0, t 0 (2)

3 215 4 27 1 1 u u(x, t) u tt a 2 u xx, a > (1) D : {(x, t) : x, t } u (, t), u (, t), t (2) u(x, ) f(x), u(x, ) t 2, x (3) u(x, t) X(x)T (t) u (1) 1 T (t) a 2 T (t) X (x) X(x) α (2) T (t) αa 2 T (t) (4)

6kg 1.1m 1.m.1m.1 l λ ϵ λ l + λ l l l dl dl + dλ ϵ dλ dl dl + dλ dl dl 3 1. JIS 1 6kg 1% 66kg 1 13 σ a1 σ m σ a1 σ m σ m σ a1 f f σ a1 σ a1 σ m f 4

35-8585 7 8 1 I I 1 1.1 6kg 1m P σ σ P 1 l l λ λ l 1.m 1 6kg 1.1m 1.m.1m.1 l λ ϵ λ l + λ l l l dl dl + dλ ϵ dλ dl dl + dλ dl dl 3 1. JIS 1 6kg 1% 66kg 1 13 σ a1 σ m σ a1 σ m σ m σ a1 f f σ a1 σ a1 σ m

http://www.ike-dyn.ritsumei.ac.jp/ hyoo/wave.html 1 1, 5 3 1.1 1..................................... 3 1.2 5.1................................... 4 1.3.......................... 5 1.4 5.2, 5.3....................

all.dvi

5,, Euclid.,..,... Euclid,.,.,, e i (i =,, ). 6 x a x e e e x.:,,. a,,. a a = a e + a e + a e = {e, e, e } a (.) = a i e i = a i e i (.) i= {a,a,a } T ( T ),.,,,,. (.),.,...,,. a 0 0 a = a 0 + a + a 0

I y = f(x) a I a x I x = a + x 1 f(x) f(a) x a = f(a + x) f(a) x (11.1) x a x 0 f(x) f(a) f(a + x) f(a) lim = lim x a x a x 0 x (11.2) f(x) x

11 11.1 I y = a I a x I x = a + 1 f(a) x a = f(a +) f(a) (11.1) x a 0 f(a) f(a +) f(a) = x a x a 0 (11.) x = a a f (a) d df f(a) (a) I dx dx I I I f (x) d df dx dx (x) [a, b] x a ( 0) x a (a, b) () [a,

高等学校学習指導要領

高等学校学習指導要領

I A A441 : April 21, 2014 Version : Kawahira, Tomoki TA (Kondo, Hirotaka ) Google

I4 - : April, 4 Version :. Kwhir, Tomoki TA (Kondo, Hirotk) Google http://www.mth.ngoy-u.c.jp/~kwhir/courses/4s-biseki.html pdf 4 4 4 4 8 e 5 5 9 etc. 5 6 6 6 9 n etc. 6 6 6 3 6 3 7 7 etc 7 4 7 7 8 5 59

日本内科学会雑誌第102巻第4号

B

B YES NO 5 7 6 1 4 3 2 BB BB BB AA AA BB 510J B B A 510J B A A A A A A 510J B A 510J B A A A A A 510J M = σ Z Z = M σ AAA π T T = a ZP ZP = a AAA π B M + M 2 +T 2 M T Me = = 1 + 1 + 2 2 M σ Te = M 2 +T

y = x x R = 0. 9, R = σ $ = y x w = x y x x w = x y α ε = + β + x x x y α ε = + β + γ x + x x x x' = / x y' = y/ x y' =

y x = α + β + ε =,, ε V( ε) = E( ε ) = σ α $ $ β w ( 0) σ = w σ σ y α x ε = + β + w w w w ε / w ( w y x α β ) = α$ $ W = yw βwxw $β = W ( W) ( W)( W) w x x w x x y y = = x W y W x y x y xw = y W = w w

X G P G (X) G BG [X, BG] S 2 2 2 S 2 2 S 2 = { (x 1, x 2, x 3 ) R 3 x 2 1 + x 2 2 + x 2 3 = 1 } R 3 S 2 S 2 v x S 2 x x v(x) T x S 2 T x S 2 S 2 x T x S 2 = { ξ R 3 x ξ } R 3 T x S 2 S 2 x x T x S 2

DVIOUT-HYOU

() P. () AB () AB ³ ³, BA, BA ³ ³ P. A B B A IA (B B)A B (BA) B A ³, A ³ ³ B ³ ³ x z ³ A AA w ³ AA ³ x z ³ x + z +w ³ w x + z +w ½ x + ½ z +w x + z +w x,,z,w ³ A ³ AA I x,, z, w ³ A ³ ³ + + A ³ A A P.

1. 2 P 2 (x, y) 2 x y (0, 0) R 2 = {(x, y) x, y R} x, y R P = (x, y) O = (0, 0) OP ( ) OP x x, y y ( ) x v = y ( ) x 2 1 v = P = (x, y) y ( x y ) 2 (x

. P (, (0, 0 R {(,, R}, R P (, O (0, 0 OP OP, v v P (, ( (, (, { R, R} v (, (, (,, z 3 w z R 3,, z R z n R n.,..., n R n n w, t w ( z z Ke Words:. A P 3 0 B P 0 a. A P b B P 3. A π/90 B a + b c π/ 3. +

集水桝の構造計算(固定版編)V1-正規版.xls

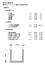集水桝の構造計算 集水桝 3.0.5 3.15 横断方向断面の計算 1. 計算条件 11. 集水桝の寸法 内空幅 B = 3.000 (m) 内空奥行き L =.500 (m) 内空高さ H = 3.150 (m) 側壁厚 T = 0.300 (m) 底版厚 Tb = 0.400 (m) 1. 土質条件 土の単位体積重量 γs = 18.000 (kn/m 3 ) 土の内部摩擦角 φ = 30.000

untitled

.. 3. 3 3. 3 4 3. 5 6 3 7 3.3 9 4. 9 0 6 3 7 0705 φ c d φ d., φ cd, φd. ) O x s + b l cos s s c l / q taφ / q taφ / c l / X + X E + C l w q B s E q q ul q q ul w w q q E E + E E + ul X X + (a) (b) (c)

x () g(x) = f(t) dt f(x), F (x) 3x () g(x) g (x) f(x), F (x) (3) h(x) = x 3x tf(t) dt.9 = {(x, y) ; x, y, x + y } f(x, y) = xy( x y). h (x) f(x), F (x

[ ] IC. f(x) = e x () f(x) f (x) () lim f(x) lim f(x) x + x (3) lim f(x) lim f(x) x + x (4) y = f(x) ( ) ( s46). < a < () a () lim a log xdx a log xdx ( ) n (3) lim log k log n n n k=.3 z = log(x + y ),

2.2 h h l L h L = l cot h (1) (1) L l L l l = L tan h (2) (2) L l 2 l 3 h 2.3 a h a h (a, h)

1 16 10 5 1 2 2.1 a a a 1 1 1 2.2 h h l L h L = l cot h (1) (1) L l L l l = L tan h (2) (2) L l 2 l 3 h 2.3 a h a h (a, h) 4 2 3 4 2 5 2.4 x y (x,y) l a x = l cot h cos a, (3) y = l cot h sin a (4) h a

() n C + n C + n C + + n C n n (3) n C + n C + n C 4 + n C + n C 3 + n C 5 + (5) (6 ) n C + nc + 3 nc n nc n (7 ) n C + nc + 3 nc n nc n (

3 n nc k+ k + 3 () n C r n C n r nc r C r + C r ( r n ) () n C + n C + n C + + n C n n (3) n C + n C + n C 4 + n C + n C 3 + n C 5 + (4) n C n n C + n C + n C + + n C n (5) k k n C k n C k (6) n C + nc

( )

7..-8..8.......................................................................... 4.................................... 3...................................... 3..3.................................. 4.3....................................

TOP URL 1

TOP URL http://amonphys.web.fc.com/ 1 19 3 19.1................... 3 19.............................. 4 19.3............................... 6 19.4.............................. 8 19.5.............................

20 9 19 1 3 11 1 3 111 3 112 1 4 12 6 121 6 122 7 13 7 131 8 132 10 133 10 134 12 14 13 141 13 142 13 143 15 144 16 145 17 15 19 151 1 19 152 20 2 21 21 21 211 21 212 1 23 213 1 23 214 25 215 31 22 33

O1-1 O1-2 O1-3 O1-4 O1-5 O1-6

O1-1 O1-2 O1-3 O1-4 O1-5 O1-6 O1-7 O1-8 O1-9 O1-10 O1-11 O1-12 O1-13 O1-14 O1-15 O1-16 O1-17 O1-18 O1-19 O1-20 O1-21 O1-22 O1-23 O1-24 O1-25 O1-26 O1-27 O1-28 O1-29 O1-30 O1-31 O1-32 O1-33 O1-34 O1-35

r d 2r d l d (a) (b) (c) 1: I(x,t) I(x+ x,t) I(0,t) I(l,t) V in V(x,t) V(x+ x,t) V(0,t) l V(l,t) 2: 0 x x+ x 3: V in 3 V in x V (x, t) I(x, t

1 1 2 2 2r d 2r d l d (a) (b) (c) 1: I(x,t) I(x+ x,t) I(0,t) I(l,t) V in V(x,t) V(x+ x,t) V(0,t) l V(l,t) 2: 0 x x+ x 3: V in 3 V in x V (x, t) I(x, t) V (x, t) I(x, t) V in x t 3 4 1 L R 2 C G L 0 R 0

放射線専門医認定試験（２００９・２０回）／ＨＯＨＳ‐０５（基礎二次）

プログラム

Microsoft Word - CTCWEB講座（4章照査）0419.doc

1912 1914 3 58 16 1 58 2 16 3 4 62 61 4 16 1 16 1914 ( 3) 1955 (30) 1961 (36) 1965 (40) 1970 (45) 1983 (58) 1992 ( 4) 1999 (11) 2004 (16) 2 1 2 3 4 5 6 7 8 9 1 10 2 11 12 13 14 15 16 17 18 19 20 21 22

基礎数学I

I & II ii ii........... 22................. 25 12............... 28.................. 28.................... 31............. 32.................. 34 3 1 9.................... 1....................... 1............

No.004 [1] J. ( ) ( ) (1968) [2] Morse (1997) [3] (1988) 1

No.004 [1] J. ( ) ( ) (1968) [2] Morse (1997) [3] (1988) 1 1 (1) 1.1 X Y f, g : X Y { F (x, 0) = f(x) F (x, 1) = g(x) F : X I Y f g f g F f g 1.2 X Y X Y gf id X, fg id Y f : X Y, g : Y X X Y X Y (2) 1.3

TOP URL 1

TOP URL http://amonphys.web.fc2.com/ 1 30 3 30.1.............. 3 30.2........................... 4 30.3...................... 5 30.4........................ 6 30.5.................................. 8 30.6...............................

... 1... 1... 2... 3... 5... 7... 7... 7... 8... 8... 12... 14... 14... 14... 16... 16... 16... 17... 17... 18... 18... 19... 20... 43... 43... 53... 55... 56... 56... 57 JFE M... 57... 59... 60... 61

70 : 20 : A B (20 ) (30 ) 50 1

70 : 0 : A B (0 ) (30 ) 50 1 1 4 1.1................................................ 5 1. A............................................... 6 1.3 B............................................... 7 8.1 A...............................................

SFGÇÃÉXÉyÉNÉgÉãå`.pdf

SFG 1 SFG SFG I SFG (ω) χ SFG (ω). SFG χ χ SFG (ω) = χ NR e iϕ +. ω ω + iγ SFG φ = ±π/, χ φ = ±π 3 χ SFG χ SFG = χ NR + χ (ω ω ) + Γ + χ NR χ (ω ω ) (ω ω ) + Γ cosϕ χ NR χ Γ (ω ω ) + Γ sinϕ. 3 (θ) 180

振動と波動

Report JS0.5 J Simplicity February 4, 2012 1 J Simplicity HOME http://www.jsimplicity.com/ Preface 2 Report 2 Contents I 5 1 6 1.1..................................... 6 1.2 1 1:................ 7 1.3

x, y x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = 15 xy (x y) (x + y) xy (x y) (x y) ( x 2 + xy + y 2) = 15 (x y)

x, y x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = 15 1 1977 x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = 15 xy (x y) (x + y) xy (x y) (x y) ( x 2 + xy + y 2) = 15 (x y) ( x 2 y + xy 2 x 2 2xy y 2) = 15 (x y) (x + y) (xy