Microsoft Word 浜松TH数3Cロピタルネタ.doc
|
|
|
- ゆきさ ももき
- 5 years ago
- Views:
Transcription
1 ロピタルの定理 で白紙答案撲滅 0. 初めに今回は 数学 Ⅲ が必要な受験生を対象に ロピタルの定理 について解説します. ロピタルの定理は極限を求めるのに強力な定理ですが 極限を求められなくてこれ以上答案を続けられない と言うときに使ってください. 使わずに済むならその方が安全です. 何故ならロピタルの定理を使うと減点すると言う大学の教官が存在するからです.( 何故減点するのか理由は知りません.) 白紙答案を出すよりまし ぐらいのつもりで使って下さい. それで数点でも積み上げて合格ラインに達してくれる受験生がいてくれるのが 本稿の目的です. この定理は内容を正しく記述していない参考書が珍しくなく 証明も全くないか 証明の一部しかないというものがほとんどですので 今回は. ロピタルの定理とは何か. ロピタルの定理の使い方 ~ 標準的な解答との比較. ロピタルの定理の高校数学での証明を解説します.( 高校数学で証明できますよ ). ロピタルの定理とその使い方ロピタルの定理とは次の定理です. ロピタルの定理 関数 () g() は =a(a は実数 ) の近くで定義され微分可能とする. =0 =0 前提 前提 であり が収束するならば 結論がとてもかっこいいですね. 参考書が取り上げ = 結論 たくなるのも当然です. では この内容を順に解説しましょう. まず前提 ですが 数 Ⅲ で扱う関数はこれを満たして いることが普通なので特に気にすることはありません. とした極限を扱うので a で考えますから () や g() が =a で定義されていなくても良いですし =a で微分可能でなくてもかまいません. 次に前提 は は不定形 ( 分子と分母の極 限を別々に考えるだけでは求められない ) ということですね. 私たちが求めるのに苦労する極限は すべて不定 形です ( アタリマエだな ). は 0 0 の不定形 とも言います. その次の がわざわざ下線を引きたくなるぐら い非常に重要ですが ロピタルの定理 を扱っている参 考書の半数ほどはこの前提を書いていません. 例えば =0 =0 ならば = を ロピタルの定理 と称する参考書がありますが この命題は誤りです ( 当然 ロピタルの定理ではない ). 何故ならば 反例が存在するからです. の反例 ()= sin g()= a=0 とすると =0( - () 0 とすればよい ) =0 である. 0 = 0 0 sin = sin =0 0 で 0 ( - sin で 0 とすればよい ) となるが = 0 sin cos 0 となり これは発散 ( 振動 ) する. したがって = は成立しない. 0 0 以上より はの反例である. 誤った命題 を 定理 と呼んではいけませんね.
2 この事に関して面白い入試問題があります. 岐阜薬科大 ( 抜粋. 下線は筆者 ) 不等式 cos<sin<(0<<π) を示し これを用い sin て ()= (0<<π) のとき = + 0 h ( ) h ( ) 0 を示せ. ただし 定理 = (g(0)=0 0 0 h(0)=0)) の使用は その証明をしなければ不可とする この下線部は と同様の の抜けた 誤ったロピ タルの定理 ですね. 出題者の意図はおそらく もしもロピタルの定理を証明して使うような受験生がいたら 自 分で を付け足すかどうかで ロピタルの定理を本 当に理解しているかどうか判断しよう と言うことでしょう.( この問題自体は ロピタルの定理を証明するよりずっと簡単ですよ.) さて ロピタルの定理は の部分を や - にしてもいいですし 前提 を = (or - ) = (or - ) にしてもかまいません.( はそのままですよ ) つまり が± の不定形でもよいのです. この場合も含めて ロピタルの定理 と言います. つまり 書き直せば次のようになります. ロピタルの定理 ( 前提 は省略 ) が不定形 ( 0 0 や ± ) であり が収束するならば = (a は実数でも などでもよい ) 前提 結論. ロピタルの定理の使い方 ~ 標準的な解答との比較ロピタルの定理を使うためのポイントは. 前提 ( または ) と をきちんと確認する sin e. = = などの極限の基本 0 0 公式を示すのには用いないという 点です. 後者については これらの基本公式から微分の公式が得られるのですから当然ですね. 前提 ( または ) は自明なら明記しなくても良い ですが は明記して 私はロピタルの定理を理解 しています と採点する教官にアピールしましょう. 具体的な問題の標準的な解答と それがわからなかった場合のロピタルの定理を用いた解答を比較してもらいましょう 問 log を求めよ. 0 ( 標準的解答 ) ()= log g()= - とおくと (0) =0 g(0)=0 となるから log 0 (0) (0) = = = (0) 0 g (0) 0 g (0) (0) log + 4 log log8 ()= g ()= log であるから (0)= log + log 4 + log8 g (0)=log となり ( 与式 )= (0) (0) = log = log log =. この解答は極限を微分係数に帰着する がポイントで
3 す. この手法をまとめると次のようになります. 極限を微分係数に帰着する手法 微分可能な関数 () g() について (a)=g(a)=0 g (a) 0 であれば ( ) ( a) ( ) a a = = ga ( ) ( a) a これに気づかなければ 白紙答案を作るよりはロピタルの定理でいきましょう. ( ロピタルの定理を用いた解答 ) log ( 与式 )= 0 右辺の分子と分母はともに 0 に収束する log 0 ( ) log + 4 log log8 = log = ( 収束 ) よってロピタルの定理より ( 与式 )= 次の問題は 上記の微分係数を用いる手法が使えないことに注意してください. e + e 問 0 を求めよ. ()=e +e - - g()= とおくと (0)=0 g(0)= 0 となりますから 左記の手法を使って ( ) (0) ( ) ( 与式 )= = 0 0 g (0) 前提 としてみても 右辺の分母の極限は g (0)=0 となりますから うまくいきません. 別の工夫が必要です. ( 標準的解答 ) e e + e ( 与式 )= = 0 0 = e e 気づけばたいしたことのない計算ですが もし気づかなければ ロピタルの定理でどうぞ. ( ロピタルの定理を用いた解答 )( 前提 は自明でしょう ) ( e + e ) e e = 0 0 ( e e ) e + e = = ( 収束 ) 0 ( ) 0 ロピタルの定理より e e 0 = ( 収束 ) とロピタルの定理より e 0 + e = この解答ではロピタルを 回用いていますね. 左記の手法が使えないような極限のときは それ以外のうまい工夫を見つける努力をし ( あるはず!) 見つからなければ応急処置としてロピタルの定理を使ってください.. ロピタルの定理の高校数学での証明いよいよ ロピタルの定理を証明します. 以下では区間 a b を [a b] と表し 区間 a<<b を (a b) と表すことにします. 証明に使うのは 次の単純な定理です. ロルの定理 関数 () は [a b] で連続 (a b) で微分可能とする. このとき (a)=(b) ならば (c)=0 a<c<b この定理の意味することは なだらかな山の頂上 ( あるいは谷底 ) で接線を引いたら 水平である ということですね. これから コーシーの平均値の定理 ( コーシーは有名な数学者 ) と言う定理が示せます.
4 4 コーシーの平均値の定理 関数 () g() は [a b] で連続 (a b) で微分可能とする.g(a) g(b) かつ g () 0(a<<b) ならば () = ( b ) ( a ) a<c<b gb ( ) ga ( ) ( 注. 数学 Ⅲの 平均値の定理 は g()= とした場合になっています ) この定理の図形的な意味は XY 平面上の曲線 C:X=g() Y=() の上に 点 A(g(a) (a)) B(g(b) (b)) をとると C 上のAとBの間の点 P(g(c) (c)) を Pにおける C の接線 ( 傾きが ) と直線 AB( 傾きが ( b) ( a) ) が平行になるようにとれるということで gb ( ) ga ( ) す. コーシーの平均値の定理の証明 XY 平面上に 点 A(g(a) (a)) B(g(b) (b)) をとる.m= ( b ) ( a ) とおくと gb ( ) ga ( ) 直線 AB:Y=m(X-g(a))+(a) Y-{m(X-g(a))+(a)}=0 左辺の (X Y) へ (g() ()) を代入し h()=()-{m(g()-g(a))+(a)} とおく.( 図形的な意味は下図参照 ) h (c)=0 a<c<b より h ()= ()-mg () h (c)=0 より (c)-mg (c)=0 g (c) 0( g () 0(a<<b)) より () = m = ( b ) ( a ) gb ( ) ga ( ) コーシーの平均値の定理を用いて ロピタルの定理を 証明しましょう. 前提 と は仮定し (Ⅰ) =0 =0(a は実数 ) の場合と (Ⅱ) = = の場合を示します.( 前者は容易だが 後者は少し難しい ) 入試の極限に現れるのは この つの場合がほとんどでしょう. いずれの場合も が収束 ( ) している ので g () 0 としてよく コーシーの平均値の定理が使えます. (Ⅰ) の場合のロピタルの定理の証明 (a)=0 g(a)=0 としてよい. a のとき コーシーの平均値の定理より () = ( a ) = ga ( ) となる c が と a の間に存在する. が収束しているので その極限値を l とお く (l は実数 ). のとき c a となり l. h(a)=(a)-{m(g(a)-g(a))+(a)}=0 h(b)=(b)-{m(g(b)-g(a))+(a)} = (b)-{(b)-(a)+(a)}=0 ( 上の図からも h(a)=h(b)=0 は明らかですね ) したがって ロルの定理より したがって =l= (Ⅱ) の場合のロピタルの定理の証明 ( n) < ( ) かつ gn ( ) <
5 5 をみたす最大の整数 n を n () と表すことにする. のとき ( ) かつ とな るから n ( ) となる. ( 注.n() が整数であること には特に意味はない. n ( ) が重要 ) さらに n ( ) が十分大きくなれば ( n ( )) は正と なるから ( n( )) 0 < < ( ) のとき ( ) より 0 となる ( ) ので はさみうちの原理より 同様に コーシーの平均値の定理より ( n( )) = gn ( ( )) ( n( )) = 0 ( ) gn ( ( )) = 0 一方 ( n( )) =l 4 gn ( ( )) ( ) g( ) g( n( )) ( ) ( n( )) = ( ) n ( ( )) gn ( ( )) gn ( ( )) ( ) ( n( )) = ( n( )) gn ( ( )) ( ) ここで とすれば 4より =l= ここまでの証明を読み通せた読者のみなさんは十分力がありますから ロピタルの定理を使う必要はないでしょう ( 逆説的な結論 (^^;). 万が一のときのお守りのつもりでロピタルの定理を知っておいてくださいね. となるc が と n ( ) の間に存在する. ( 注. n ( ) となることと が証明のポイン ト.(n()) は () に比べると十分小さく g(n()) は g() に比べると十分小さいので は を意 味している.) が収束しているので その極限値を l とお く (l は実数 ). のとき n( ) となるので c とな るから () c l. これと より
曲線 = f () は を媒介変数とする自然な媒介変数表示 =,= f () をもつので, これを利用して説明する 以下,f () は定義域で連続であると仮定する 例えば, 直線 =c が曲線 = f () の漸近線になるとする 曲線 = f () 上の点 P(,f ()) が直線 =c に近づくこ
 伊伊伊伊伊伊伊伊伊伊 伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊 漸近線の求め方に関する考察 たまい玉井 かつき克樹 伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊 伊伊伊伊伊伊伊伊伊伊. 漸近線についての生徒からの質問 数学において図を使って直感的な説明を与えることは, 理解を深めるのに大いに役立つ
伊伊伊伊伊伊伊伊伊伊 伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊 漸近線の求め方に関する考察 たまい玉井 かつき克樹 伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊 伊伊伊伊伊伊伊伊伊伊. 漸近線についての生徒からの質問 数学において図を使って直感的な説明を与えることは, 理解を深めるのに大いに役立つ
Microsoft Word - 微分入門.doc
 基本公式 例題 0 定義式 f( ) 数 Ⅲ 微分入門 = の導関数を定義式にもとづいて計算しなさい 基本事項 ( f( ), g( ) が微分可能ならば ) y= f( ) g( ) のとき, y = y= f( ) g( ) h( ) のとき, y = ( f( ), g( ) が微分可能で, g( ) 0 ならば ) f( ) y = のとき, y = g ( ) とくに, y = のとき,
基本公式 例題 0 定義式 f( ) 数 Ⅲ 微分入門 = の導関数を定義式にもとづいて計算しなさい 基本事項 ( f( ), g( ) が微分可能ならば ) y= f( ) g( ) のとき, y = y= f( ) g( ) h( ) のとき, y = ( f( ), g( ) が微分可能で, g( ) 0 ならば ) f( ) y = のとき, y = g ( ) とくに, y = のとき,
2015年度 信州大・医系数学
 05 信州大学 ( 医系 ) 前期日程問題 解答解説のページへ 放物線 y = a + b + c ( a > 0) を C とし, 直線 y = -を l とする () 放物線 C が点 (, ) で直線 l と接し, かつ 軸と共有点をもつための a, b, c が満 たす必要十分条件を求めよ () a = 8 のとき, () の条件のもとで, 放物線 C と直線 l および 軸とで囲まれた部
05 信州大学 ( 医系 ) 前期日程問題 解答解説のページへ 放物線 y = a + b + c ( a > 0) を C とし, 直線 y = -を l とする () 放物線 C が点 (, ) で直線 l と接し, かつ 軸と共有点をもつための a, b, c が満 たす必要十分条件を求めよ () a = 8 のとき, () の条件のもとで, 放物線 C と直線 l および 軸とで囲まれた部
2018年度 東京大・理系数学
 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ関数 f ( ) = + cos (0 < < ) の増減表をつくり, + 0, 0 のと sin きの極限を調べよ 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ n+ 数列 a, a, を, Cn a n = ( n =,, ) で定める n! an qn () n とする を既約分数 an p として表したときの分母
08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ関数 f ( ) = + cos (0 < < ) の増減表をつくり, + 0, 0 のと sin きの極限を調べよ 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ n+ 数列 a, a, を, Cn a n = ( n =,, ) で定める n! an qn () n とする を既約分数 an p として表したときの分母
2010年度 筑波大・理系数学
 00 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ f( x) x ax とおく ただしa>0 とする () f( ) f() となるa の範囲を求めよ () f(x) の極小値が f ( ) 以下になる a の範囲を求めよ () x における f(x) の最小値をa を用いて表せ -- 00 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ つの曲線 C : y six ( 0
00 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ f( x) x ax とおく ただしa>0 とする () f( ) f() となるa の範囲を求めよ () f(x) の極小値が f ( ) 以下になる a の範囲を求めよ () x における f(x) の最小値をa を用いて表せ -- 00 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ つの曲線 C : y six ( 0
2018年度 筑波大・理系数学
 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ < < とする 放物線 上に 点 (, ), A (ta, ta ), B( - ta, ta ) をとる 三角形 AB の内心の 座標を p とし, 外心の 座標を q とする また, 正の実数 a に対して, 直線 a と放物線 で囲まれた図形の面積を S( a) で表す () p, q を cos を用いて表せ S( p) () S(
筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ < < とする 放物線 上に 点 (, ), A (ta, ta ), B( - ta, ta ) をとる 三角形 AB の内心の 座標を p とし, 外心の 座標を q とする また, 正の実数 a に対して, 直線 a と放物線 で囲まれた図形の面積を S( a) で表す () p, q を cos を用いて表せ S( p) () S(
2011年度 大阪大・理系数学
 0 大阪大学 ( 理系 ) 前期日程問題 解答解説のページへ a a を自然数とする O を原点とする座標平面上で行列 A= a の表す 次変換 を f とする cosθ siθ () >0 および0θ
0 大阪大学 ( 理系 ) 前期日程問題 解答解説のページへ a a を自然数とする O を原点とする座標平面上で行列 A= a の表す 次変換 を f とする cosθ siθ () >0 および0θ
数学 Ⅲ 微分法の応用 大学入試問題 ( 教科書程度 ) 1 問 1 (1) 次の各問に答えよ (ⅰ) 極限 を求めよ 年会津大学 ( 前期 ) (ⅱ) 極限値 を求めよ 年愛媛大学 ( 前期 ) (ⅲ) 無限等比級数 が収束するような実数 の範囲と そのときの和を求めよ 年広島市立大学 ( 前期
 数学 Ⅲ 微分法の応用 大学入試問題 ( 教科書程度 )1 問 1 (1) 次の各問に答えよ (ⅰ) 極限 を求めよ 年会津大学 ( 前期 ) (ⅱ) 極限値 を求めよ 年愛媛大学 ( 前期 ) (ⅲ) 無限等比級数 が収束するような実数 の範囲と そのときの和を求めよ 年広島市立大学 ( 前期 ) (2) 次の関数を微分せよ (ⅰ) を正の定数とする (ⅱ) (ⅳ) (ⅵ) ( 解答 )(1) 年群馬大学
数学 Ⅲ 微分法の応用 大学入試問題 ( 教科書程度 )1 問 1 (1) 次の各問に答えよ (ⅰ) 極限 を求めよ 年会津大学 ( 前期 ) (ⅱ) 極限値 を求めよ 年愛媛大学 ( 前期 ) (ⅲ) 無限等比級数 が収束するような実数 の範囲と そのときの和を求めよ 年広島市立大学 ( 前期 ) (2) 次の関数を微分せよ (ⅰ) を正の定数とする (ⅱ) (ⅳ) (ⅵ) ( 解答 )(1) 年群馬大学
2013年度 信州大・医系数学
 03 信州大学 ( 医系 ) 前期日程問題 解答解説のページへ () 式 + + a a a3 を満たす自然数の組 ( a, a, a3) で, a a a3とな るものをすべて求めよ () r を正の有理数とする 式 r + + a a a を満たす自然数の組 ( a, a, a3) で, 3 a a a3となるものは有限個しかないことを証明せよ ただし, そのよう な組が存在しない場合は 0 個とし,
03 信州大学 ( 医系 ) 前期日程問題 解答解説のページへ () 式 + + a a a3 を満たす自然数の組 ( a, a, a3) で, a a a3とな るものをすべて求めよ () r を正の有理数とする 式 r + + a a a を満たす自然数の組 ( a, a, a3) で, 3 a a a3となるものは有限個しかないことを証明せよ ただし, そのよう な組が存在しない場合は 0 個とし,
2014年度 千葉大・医系数学
 04 千葉大学 ( 医系 ) 前期日程問題 解答解説のページへ 袋の中に, 赤玉が 3 個, 白玉が 7 個が入っている 袋から玉を無作為に つ取り出し, 色を確認してから, 再び袋に戻すという試行を行う この試行を N 回繰り返したときに, 赤玉を A 回 ( ただし 0 A N) 取り出す確率を p( N, A) とする このとき, 以下の問いに答えよ () 確率 p( N, A) を N と
04 千葉大学 ( 医系 ) 前期日程問題 解答解説のページへ 袋の中に, 赤玉が 3 個, 白玉が 7 個が入っている 袋から玉を無作為に つ取り出し, 色を確認してから, 再び袋に戻すという試行を行う この試行を N 回繰り返したときに, 赤玉を A 回 ( ただし 0 A N) 取り出す確率を p( N, A) とする このとき, 以下の問いに答えよ () 確率 p( N, A) を N と
喨微勃挹稉弑
 == 全微分方程式 == 全微分とは 変数の関数 z=f(, ) について,, の増分を Δ, Δ とするとき, z の増分 Δz は Δz z Δ+ z Δ で表されます. この式において, Δ 0, Δ 0 となる極限を形式的に dz= z d+ z d (1) で表し, dz を z の全微分といいます. z は z の に関する偏導関数で, を定数と見なし て, で微分したものを表し, 方向の傾きに対応します.
== 全微分方程式 == 全微分とは 変数の関数 z=f(, ) について,, の増分を Δ, Δ とするとき, z の増分 Δz は Δz z Δ+ z Δ で表されます. この式において, Δ 0, Δ 0 となる極限を形式的に dz= z d+ z d (1) で表し, dz を z の全微分といいます. z は z の に関する偏導関数で, を定数と見なし て, で微分したものを表し, 方向の傾きに対応します.
2011年度 筑波大・理系数学
 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ O を原点とするy 平面において, 直線 y= の を満たす部分をC とする () C 上に点 A( t, ) をとるとき, 線分 OA の垂直二等分線の方程式を求めよ () 点 A が C 全体を動くとき, 線分 OA の垂直二等分線が通過する範囲を求め, それ を図示せよ -- 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ
0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ O を原点とするy 平面において, 直線 y= の を満たす部分をC とする () C 上に点 A( t, ) をとるとき, 線分 OA の垂直二等分線の方程式を求めよ () 点 A が C 全体を動くとき, 線分 OA の垂直二等分線が通過する範囲を求め, それ を図示せよ -- 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ
2016年度 九州大・理系数学
 0 九州大学 ( 理系 ) 前期日程問題 解答解説のページへ 座標平面上の曲線 C, C をそれぞれ C : y logx ( x > 0), C : y ( x-)( x- a) とする ただし, a は実数である を自然数とするとき, 曲線 C, C が 点 P, Q で交わり, P, Q の x 座標はそれぞれ, + となっている また, 曲線 C と直線 PQ で囲まれた領域の面積を S,
0 九州大学 ( 理系 ) 前期日程問題 解答解説のページへ 座標平面上の曲線 C, C をそれぞれ C : y logx ( x > 0), C : y ( x-)( x- a) とする ただし, a は実数である を自然数とするとき, 曲線 C, C が 点 P, Q で交わり, P, Q の x 座標はそれぞれ, + となっている また, 曲線 C と直線 PQ で囲まれた領域の面積を S,
Microsoft Word - NumericalComputation.docx
 数値計算入門 武尾英哉. 離散数学と数値計算 数学的解法の中には理論計算では求められないものもある. 例えば, 定積分は, まずは積分 ( 被積分関数の原始関数をみつけること できなければ値を得ることはできない. また, ある関数の所定の値における微分値を得るには, まずその関数の微分ができなければならない. さらに代数方程式の解を得るためには, 解析的に代数方程式を解く必要がある. ところが, これらは必ずしも解析的に導けるとは限らない.
数値計算入門 武尾英哉. 離散数学と数値計算 数学的解法の中には理論計算では求められないものもある. 例えば, 定積分は, まずは積分 ( 被積分関数の原始関数をみつけること できなければ値を得ることはできない. また, ある関数の所定の値における微分値を得るには, まずその関数の微分ができなければならない. さらに代数方程式の解を得るためには, 解析的に代数方程式を解く必要がある. ところが, これらは必ずしも解析的に導けるとは限らない.
DVIOUT-SS_Ma
 第 章 テイラー展開 次の図のように関数のグラフをのグラフ ( 積み木のようなものと考えます ) を積み重ねて作ってみましょう ただ単純に足すだけではうまく作れません 色々と削ることが必要になります 次のように半分にしたり, 分のに削らなくてはなりません どうですか? たった枚の積み木を積み重ねただけで, ほぼのグラフに近づきまし たね これから学ぶのがこのテイラー展開のお話です 初等関数の微分 初等関数の微分まずは
第 章 テイラー展開 次の図のように関数のグラフをのグラフ ( 積み木のようなものと考えます ) を積み重ねて作ってみましょう ただ単純に足すだけではうまく作れません 色々と削ることが必要になります 次のように半分にしたり, 分のに削らなくてはなりません どうですか? たった枚の積み木を積み重ねただけで, ほぼのグラフに近づきまし たね これから学ぶのがこのテイラー展開のお話です 初等関数の微分 初等関数の微分まずは
DVIOUT-SS_Ma
 第 章 微分方程式 ニュートンはリンゴが落ちるのを見て万有引力を発見した という有名な逸話があります 無重力の宇宙船の中ではリンゴは落ちないで静止していることを考えると 重力が働くと始め静止しているものが動き出して そのスピードはどんどん大きくなる つまり速度の変化が現れることがわかります 速度は一般に時間と共に変化します 速度の瞬間的変化の割合を加速度といい で定義しましょう 速度が変化する, つまり加速度がでなくなるためにはその原因があり
第 章 微分方程式 ニュートンはリンゴが落ちるのを見て万有引力を発見した という有名な逸話があります 無重力の宇宙船の中ではリンゴは落ちないで静止していることを考えると 重力が働くと始め静止しているものが動き出して そのスピードはどんどん大きくなる つまり速度の変化が現れることがわかります 速度は一般に時間と共に変化します 速度の瞬間的変化の割合を加速度といい で定義しましょう 速度が変化する, つまり加速度がでなくなるためにはその原因があり
<4D F736F F D F2095A F795AA B B A815B837D839382CC95FB92F68EAE2E646F63>
 1/8 平成 3 年 3 月 4 日午後 6 時 11 分 10 複素微分 : コーシー リーマンの方程式 10 複素微分 : コーシー リーマンの方程式 9 複素微分 : 正則関数 で 正則性は複素数 z の関数 f ( z) の性質として導き出しまし た 複素数 z は つの実数, で表され z i 数 u, v で表され f ( z) u i 複素数 z と つの実数, : z + i + です
1/8 平成 3 年 3 月 4 日午後 6 時 11 分 10 複素微分 : コーシー リーマンの方程式 10 複素微分 : コーシー リーマンの方程式 9 複素微分 : 正則関数 で 正則性は複素数 z の関数 f ( z) の性質として導き出しまし た 複素数 z は つの実数, で表され z i 数 u, v で表され f ( z) u i 複素数 z と つの実数, : z + i + です
05 年度センター試験数学 ⅡB () において,cos q 0 であるから,P ( cos q, sin q) より, 直線 OP を表す方程式は y sin q sin q x cos q cos q x すなわち, (sin q) x - (cos q) y 0 ( ) ク 点 O,P,Q が
 05 年度大学入試センター試験解説 数学 ⅡB 第 問 []() 点間の距離の公式から, OP ( cos q ) + ( sin q ) ( cos q + sin q ) ア PQ { ( cos q + cos 7q ) - cos q } + { ( sin q + sin 7q ) - sin q } cos q + sin q 7 7 イ である また, OQ ( cos q + cos
05 年度大学入試センター試験解説 数学 ⅡB 第 問 []() 点間の距離の公式から, OP ( cos q ) + ( sin q ) ( cos q + sin q ) ア PQ { ( cos q + cos 7q ) - cos q } + { ( sin q + sin 7q ) - sin q } cos q + sin q 7 7 イ である また, OQ ( cos q + cos
2018年度 神戸大・理系数学
 8 神戸大学 ( 理系 ) 前期日程問題 解答解説のページへ t を < t < を満たす実数とする OABC を 辺の長さが の正四面体とする 辺 OA を -t : tに内分する点を P, 辺 OB を t :-tに内分する点を Q, 辺 BC の中点を R とする また a = OA, b = OB, c = OC とする 以下の問いに答えよ () QP と QR をt, a, b, c を用いて表せ
8 神戸大学 ( 理系 ) 前期日程問題 解答解説のページへ t を < t < を満たす実数とする OABC を 辺の長さが の正四面体とする 辺 OA を -t : tに内分する点を P, 辺 OB を t :-tに内分する点を Q, 辺 BC の中点を R とする また a = OA, b = OB, c = OC とする 以下の問いに答えよ () QP と QR をt, a, b, c を用いて表せ
2017年度 金沢大・理系数学
 07 金沢大学 ( 理系 前期日程問題 解答解説のページへ 次の問いに答えよ ( 6 z + 7 = 0 を満たす複素数 z をすべて求め, それらを表す点を複素数平面上に図 示せよ ( ( で求めた複素数 z を偏角が小さい方から順に z, z, とするとき, z, z と 積 zz を表す 点が複素数平面上で一直線上にあることを示せ ただし, 偏角は 0 以上 未満とする -- 07 金沢大学
07 金沢大学 ( 理系 前期日程問題 解答解説のページへ 次の問いに答えよ ( 6 z + 7 = 0 を満たす複素数 z をすべて求め, それらを表す点を複素数平面上に図 示せよ ( ( で求めた複素数 z を偏角が小さい方から順に z, z, とするとき, z, z と 積 zz を表す 点が複素数平面上で一直線上にあることを示せ ただし, 偏角は 0 以上 未満とする -- 07 金沢大学
2019年度 千葉大・理系数学
 9 千葉大学 ( 理系 ) 前期日程問題 解答解説のページへ a, a とし, のとき, a+ a + a - として数列 { a } () のとき a+ a a a - が成り立つことを証明せよ () åai aaa + が成り立つような自然数 を求めよ i を定める -- 9 千葉大学 ( 理系 ) 前期日程問題 解答解説のページへ 三角形 ABC は AB+ AC BCを満たしている また,
9 千葉大学 ( 理系 ) 前期日程問題 解答解説のページへ a, a とし, のとき, a+ a + a - として数列 { a } () のとき a+ a a a - が成り立つことを証明せよ () åai aaa + が成り立つような自然数 を求めよ i を定める -- 9 千葉大学 ( 理系 ) 前期日程問題 解答解説のページへ 三角形 ABC は AB+ AC BCを満たしている また,
<4D F736F F D A CF95AA B B82CC90CF95AA8CF68EAE2E646F63>
 /8 平成 年 月 日午後 時 6 分 複素積分 : コーシーの積分公式 複素積分 : コーシーの積分公式 Ⅰ. 閉じた積分経路と円周 積分しなくても線積分の結果が分かる場合の第 弾です それは ( ( π d は正則関数 d! d 積分経路は を囲む (. になります これを コーシーの積分公式といいます 複素積分 : コーシーの積分定理 -Ⅰ. 線積分の実技での線積分では 半径 r の円 周上の閉じた経路
/8 平成 年 月 日午後 時 6 分 複素積分 : コーシーの積分公式 複素積分 : コーシーの積分公式 Ⅰ. 閉じた積分経路と円周 積分しなくても線積分の結果が分かる場合の第 弾です それは ( ( π d は正則関数 d! d 積分経路は を囲む (. になります これを コーシーの積分公式といいます 複素積分 : コーシーの積分定理 -Ⅰ. 線積分の実技での線積分では 半径 r の円 周上の閉じた経路
< 図形と方程式 > 点間の距離 A x, y, B x, y のとき x y x y : に分ける点 æ ç è A x, y, B x, y のとき 線分 AB を : に分ける点は x x y y, ö ø 注 < のとき外分点 三角形の重心 点 A x, y, B x, y, C x, を頂
 公式集数学 Ⅱ B < 式と証明 > 整式の割り算縦書きの割り算が出来ること f を g で割って 商が Q で余りが R のときは Q g f /////// R f g Q R と書ける 分数式 分母, 分子をそれぞれ因数分解し 約分する 既約分数式 加法, 減法については 分母を通分し分子の計算をする 繁分数式 分母 分子に同じ多項式をかけて 普通の分数式になおす 恒等式 数値代入法 係数比較法
公式集数学 Ⅱ B < 式と証明 > 整式の割り算縦書きの割り算が出来ること f を g で割って 商が Q で余りが R のときは Q g f /////// R f g Q R と書ける 分数式 分母, 分子をそれぞれ因数分解し 約分する 既約分数式 加法, 減法については 分母を通分し分子の計算をする 繁分数式 分母 分子に同じ多項式をかけて 普通の分数式になおす 恒等式 数値代入法 係数比較法
2017年度 千葉大・理系数学
 017 千葉大学 ( 理系 ) 前期日程問題 1 解答解説のページへ n を 4 以上の整数とする 座標平面上で正 n 角形 A1A A n は点 O を中心とする半径 1 の円に内接している a = OA 1, b = OA, c = OA 3, d = OA4 とし, k = cos とおく そして, 線分 A1A3 と線分 AA4 との交点 P は線分 A1A3 を n :1に内分するとする
017 千葉大学 ( 理系 ) 前期日程問題 1 解答解説のページへ n を 4 以上の整数とする 座標平面上で正 n 角形 A1A A n は点 O を中心とする半径 1 の円に内接している a = OA 1, b = OA, c = OA 3, d = OA4 とし, k = cos とおく そして, 線分 A1A3 と線分 AA4 との交点 P は線分 A1A3 を n :1に内分するとする
( 最初の等号は,N =0, 番目は,j= のとき j =0 による ) j>r のときは p =0 から和の上限は r で十分 定義 命題 3 ⑵ 実数 ( 0) に対して, ⑴ =[] []=( 0 または ) =[6]+[] [4] [3] [] =( 0 または ) 実数 に対して, π()
![( 最初の等号は,N =0, 番目は,j= のとき j =0 による ) j>r のときは p =0 から和の上限は r で十分 定義 命題 3 ⑵ 実数 ( 0) に対して, ⑴ =[] []=( 0 または ) =[6]+[] [4] [3] [] =( 0 または ) 実数 に対して, π() ( 最初の等号は,N =0, 番目は,j= のとき j =0 による ) j>r のときは p =0 から和の上限は r で十分 定義 命題 3 ⑵ 実数 ( 0) に対して, ⑴ =[] []=( 0 または ) =[6]+[] [4] [3] [] =( 0 または ) 実数 に対して, π()](/thumbs/85/92025583.jpg) 伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊 伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊 数研通信 70 号を読んで チェビシェフの定理の精密化 と.5 の間に素数がある 伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊 さい才 の 野 せ瀬 いちろう 一郎 伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊 0. はじめに このたび,
伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊 伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊 数研通信 70 号を読んで チェビシェフの定理の精密化 と.5 の間に素数がある 伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊 さい才 の 野 せ瀬 いちろう 一郎 伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊 0. はじめに このたび,
2014年度 九州大・理系数学
 04 九州大学 ( 理系 ) 前期日程問題 解答解説のページへ関数 f ( x) = x-sinx ( 0 x ) を考える 曲線 y = f ( x ) の接線で傾きが となるものを l とする () l の方程式と接点の座標 ( a, b) を求めよ () a は () で求めたものとする 曲線 y = f ( x ), 直線 x = a, および x 軸で囲まれた 領域を, x 軸のまわりに
04 九州大学 ( 理系 ) 前期日程問題 解答解説のページへ関数 f ( x) = x-sinx ( 0 x ) を考える 曲線 y = f ( x ) の接線で傾きが となるものを l とする () l の方程式と接点の座標 ( a, b) を求めよ () a は () で求めたものとする 曲線 y = f ( x ), 直線 x = a, および x 軸で囲まれた 領域を, x 軸のまわりに
2014年度 筑波大・理系数学
 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ f ( x) = x x とする y = f ( x ) のグラフに点 P(, ) から引いた接線は 本あるとする つの接点 A (, f ( )), B(, f ( )), C(, f ( )) を頂点とする三角形の 重心を G とする () + +, + + および を, を用いて表せ () 点 G の座標を, を用いて表せ () 点 G
筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ f ( x) = x x とする y = f ( x ) のグラフに点 P(, ) から引いた接線は 本あるとする つの接点 A (, f ( )), B(, f ( )), C(, f ( )) を頂点とする三角形の 重心を G とする () + +, + + および を, を用いて表せ () 点 G の座標を, を用いて表せ () 点 G
Microsoft Word - 漸化式の解法NEW.DOCX
 閑話休題 漸化式の解法 基本形 ( 等差数列, 等比数列, 階差数列 ) 等差数列 : d 等比数列 : r の一般項を求めよ () 3, 5 () 3, () 5より数列 は, 初項 3, 公差の等差数列であるので 5 3 5 5 () 数列 は, 初項 3, 公比 の等比数列であるので 3 階差数列 : f の一般項を求めよ 3, より のとき k k 3 3 において, を代入すると 33 となるので,は
閑話休題 漸化式の解法 基本形 ( 等差数列, 等比数列, 階差数列 ) 等差数列 : d 等比数列 : r の一般項を求めよ () 3, 5 () 3, () 5より数列 は, 初項 3, 公差の等差数列であるので 5 3 5 5 () 数列 は, 初項 3, 公比 の等比数列であるので 3 階差数列 : f の一般項を求めよ 3, より のとき k k 3 3 において, を代入すると 33 となるので,は
2013年度 九州大・理系数学
 九州大学 ( 理系 ) 前期日程問題 解答解説のページへ a> とし, つの曲線 y= ( ), y= a ( > ) を順にC, C とする また, C とC の交点 P におけるC の接線をl とする 以下 の問いに答えよ () 曲線 C とy 軸および直線 l で囲まれた部分の面積をa を用いて表せ () 点 P におけるC の接線と直線 l のなす角を ( a) とき, limasin θ(
九州大学 ( 理系 ) 前期日程問題 解答解説のページへ a> とし, つの曲線 y= ( ), y= a ( > ) を順にC, C とする また, C とC の交点 P におけるC の接線をl とする 以下 の問いに答えよ () 曲線 C とy 軸および直線 l で囲まれた部分の面積をa を用いて表せ () 点 P におけるC の接線と直線 l のなす角を ( a) とき, limasin θ(
4STEP 数学 Ⅲ( 新課程 ) を解いてみた関数 1 微分法 1 微分係数と導関数微分法 2 導関数の計算 272 ポイント微分法の公式を利用 (1) ( )( )( ) { } ( ) ( )( ) ( )( ) ( ) ( )( )
 微分法 微分係数と導関数微分法 導関数の計算 7 ポイント微分法の公式を利用 () 7 8 別解 [ ] [ ] [ ] 7 8 など () 6 6 など 7 ポイント微分法の公式を利用 () 6 6 6 など () 9 など () þ î ì など () þ î ì þ î ì þ î ì など 7 () () 左辺を で微分すると, 右辺を で微分すると, ( ) ( ) ( ) よって, (
微分法 微分係数と導関数微分法 導関数の計算 7 ポイント微分法の公式を利用 () 7 8 別解 [ ] [ ] [ ] 7 8 など () 6 6 など 7 ポイント微分法の公式を利用 () 6 6 6 など () 9 など () þ î ì など () þ î ì þ î ì þ î ì など 7 () () 左辺を で微分すると, 右辺を で微分すると, ( ) ( ) ( ) よって, (
2015年度 金沢大・理系数学
 05 金沢大学 ( 理系 ) 前期日程問題 解答解説のページへ四面体 OABC において, 3 つのベクトル OA, OB, OC はどの つも互いに垂直で あり, h > 0 に対して, OA, OB, OC h とする 3 点 O, A, B を通る平面上の点 P は, CP が CA と CB のどちらとも垂直となる点であるとする 次の問いに答えよ () OP OA + OB とするとき, と
05 金沢大学 ( 理系 ) 前期日程問題 解答解説のページへ四面体 OABC において, 3 つのベクトル OA, OB, OC はどの つも互いに垂直で あり, h > 0 に対して, OA, OB, OC h とする 3 点 O, A, B を通る平面上の点 P は, CP が CA と CB のどちらとも垂直となる点であるとする 次の問いに答えよ () OP OA + OB とするとき, と
<4D F736F F D20824F B CC92E8979D814696CA90CF95AA82C691CC90CF95AA2E646F63>
 1/1 平成 23 年 3 月 24 日午後 6 時 52 分 6 ガウスの定理 : 面積分と体積分 6 ガウスの定理 : 面積分と体積分 Ⅰ. 直交座標系 ガウスの定理は 微分して すぐに積分すると元に戻るというルールを 3 次元積分に適用した定理になります よく知っているのは 簡単化のため 変数が1つの場合は dj ( d ( ににします全微分 = 偏微分 d = d = J ( + C d です
1/1 平成 23 年 3 月 24 日午後 6 時 52 分 6 ガウスの定理 : 面積分と体積分 6 ガウスの定理 : 面積分と体積分 Ⅰ. 直交座標系 ガウスの定理は 微分して すぐに積分すると元に戻るというルールを 3 次元積分に適用した定理になります よく知っているのは 簡単化のため 変数が1つの場合は dj ( d ( ににします全微分 = 偏微分 d = d = J ( + C d です
高ゼミサポSelectⅢ数学Ⅰ_解答.indd
 数と式 ⑴ 氏点00 次の式を展開せよ ( 各 6 点 ) ⑴ (a-)(a -a+) ⑵ (x+y+)(x+y-5) 次の式を因数分解せよ (⑴⑵ 各 6 点, ⑶⑷ 各 8 点 ) ⑴ x y+x -x-6y ⑵ x -x - ⑶ a +5b ⑷ (x+y+z+)(x+)+yz 数と式 ⑵ 氏点00 次の問いに答えよ ( 各 6 点 ) ⑴ 次の循環小数を分数で表せ. a-5 = ⑵ 次の等式を満たす実数
数と式 ⑴ 氏点00 次の式を展開せよ ( 各 6 点 ) ⑴ (a-)(a -a+) ⑵ (x+y+)(x+y-5) 次の式を因数分解せよ (⑴⑵ 各 6 点, ⑶⑷ 各 8 点 ) ⑴ x y+x -x-6y ⑵ x -x - ⑶ a +5b ⑷ (x+y+z+)(x+)+yz 数と式 ⑵ 氏点00 次の問いに答えよ ( 各 6 点 ) ⑴ 次の循環小数を分数で表せ. a-5 = ⑵ 次の等式を満たす実数
2017年度 長崎大・医系数学
 07 長崎大学 ( 医系 ) 前期日程問題 解答解説のページへ 以下の問いに答えよ () 0 のとき, si + cos の最大値と最小値, およびそのときの の値 をそれぞれ求めよ () e を自然対数の底とする > eの範囲において, 関数 y を考える この両 辺の対数を について微分することにより, y は減少関数であることを示せ また, e< < bのとき, () 数列 { } b の一般項が,
07 長崎大学 ( 医系 ) 前期日程問題 解答解説のページへ 以下の問いに答えよ () 0 のとき, si + cos の最大値と最小値, およびそのときの の値 をそれぞれ求めよ () e を自然対数の底とする > eの範囲において, 関数 y を考える この両 辺の対数を について微分することにより, y は減少関数であることを示せ また, e< < bのとき, () 数列 { } b の一般項が,
2016年度 京都大・文系数学
 06 京都大学 ( 文系 ) 前期日程問題 解答解説のページへ xy 平面内の領域の面積を求めよ x + y, x で, 曲線 C : y= x + x -xの上側にある部分 -- 06 京都大学 ( 文系 ) 前期日程問題 解答解説のページへ ボタンを押すと あたり か はずれ のいずれかが表示される装置がある あたり の表示される確率は毎回同じであるとする この装置のボタンを 0 回押したとき,
06 京都大学 ( 文系 ) 前期日程問題 解答解説のページへ xy 平面内の領域の面積を求めよ x + y, x で, 曲線 C : y= x + x -xの上側にある部分 -- 06 京都大学 ( 文系 ) 前期日程問題 解答解説のページへ ボタンを押すと あたり か はずれ のいずれかが表示される装置がある あたり の表示される確率は毎回同じであるとする この装置のボタンを 0 回押したとき,
Chap2
 逆三角関数の微分 Arcsin の導関数を計算する Arcsin I. 初等関数の微積分 sin [, ], [π/, π/] cos sin / (Arcsin ) 計算力の体力をつけよう π/ π/ E. II- 次の関数の導関数を計算せよ () Arccos () Arctan E. I- の解答 不定積分あれこれ () Arccos n log C C (n ) n e e C log (log
逆三角関数の微分 Arcsin の導関数を計算する Arcsin I. 初等関数の微積分 sin [, ], [π/, π/] cos sin / (Arcsin ) 計算力の体力をつけよう π/ π/ E. II- 次の関数の導関数を計算せよ () Arccos () Arctan E. I- の解答 不定積分あれこれ () Arccos n log C C (n ) n e e C log (log
Microsoft Word - K-ピタゴラス数.doc
 - ピタゴラス数の代数と幾何学 津山工業高等専門学校 菅原孝慈 ( 情報工学科 年 ) 野山由貴 ( 情報工学科 年 ) 草地弘幸 ( 電子制御工学科 年 ) もくじ * 第 章ピタゴラス数の幾何学 * 第 章ピタゴラス数の代数学 * 第 3 章代数的極小元の幾何学の考察 * 第 章ピタゴラス数の幾何学的研究の動機 交点に注目すると, つの曲線が直交しているようにみえる. これらは本当に直交しているのだろうか.
- ピタゴラス数の代数と幾何学 津山工業高等専門学校 菅原孝慈 ( 情報工学科 年 ) 野山由貴 ( 情報工学科 年 ) 草地弘幸 ( 電子制御工学科 年 ) もくじ * 第 章ピタゴラス数の幾何学 * 第 章ピタゴラス数の代数学 * 第 3 章代数的極小元の幾何学の考察 * 第 章ピタゴラス数の幾何学的研究の動機 交点に注目すると, つの曲線が直交しているようにみえる. これらは本当に直交しているのだろうか.
. 角の二等分線と調和平均 平面上に点 を端点とする線分 と を重ならないようにとる, とし とする の二等分線が線分 と交わる点を とし 点 から に垂直に引いた直線が線分 と交わる点 とする 線分 の長さを求めてみよう 点 から に垂直な直線と および との交点をそれぞれ, Dとする つの直角三
 角の二等分線で開くいろいろな平均 札幌旭丘高校中村文則 0. 数直線上に現れるいろいろな平均下図は 数 (, ) の調和平均 相乗平均 相加平均 二乗平均を数直線上に置いたものである, とし 直径 中心 である円を用いていろいろな平均の大小関係を表現するもっとも美しい配置方法であり その証明も容易である Q D E F < 相加平均 > (0), ( ), ( とすると 線分 ) の中点 の座標はである
角の二等分線で開くいろいろな平均 札幌旭丘高校中村文則 0. 数直線上に現れるいろいろな平均下図は 数 (, ) の調和平均 相乗平均 相加平均 二乗平均を数直線上に置いたものである, とし 直径 中心 である円を用いていろいろな平均の大小関係を表現するもっとも美しい配置方法であり その証明も容易である Q D E F < 相加平均 > (0), ( ), ( とすると 線分 ) の中点 の座標はである
公式集 数学 Ⅱ B 頭に入っていますか? 8 和積の公式 A + B A B si A + si B si os A + B A B si A si B os si A + B A B os A + os B os os A + B A B os A os B si si 9 三角関数の合成 si
 公式集 数学 Ⅱ B 頭に入っていますか? < 図形と方程式 > 点間の距離 A x, B x, のとき x x + : に分ける点 A x, B x, のとき 線分 AB を:に分ける点 æ x + x + ö は ç, è + + ø 注 < のとき外分点 直線の方程式 傾き で 点 x, を通る : x 点 x, x, を通る : x 注 分母が のとき は座標軸と平行な直線 x x 4 直線の位置関係
公式集 数学 Ⅱ B 頭に入っていますか? < 図形と方程式 > 点間の距離 A x, B x, のとき x x + : に分ける点 A x, B x, のとき 線分 AB を:に分ける点 æ x + x + ö は ç, è + + ø 注 < のとき外分点 直線の方程式 傾き で 点 x, を通る : x 点 x, x, を通る : x 注 分母が のとき は座標軸と平行な直線 x x 4 直線の位置関係
<4D F736F F D F90948A F835A E815B8E8E8CB189F090E05F8E6C8D5A>
 06 年度大学入試センター試験解説 数学 Ⅱ B 第 問 () 8 より, 5 5 5 6 6 8 ア, イ また, 底の変換公式を用いると, log 7 log log 9 9 log 7 log ウエ, オ (), のグラフは, それぞれ = 89 = 右図のようになり, この つのグラフは 軸に関して対称 ここで, 0, のとき, と log カ のグラフが直線 に関して対称 であることから,
06 年度大学入試センター試験解説 数学 Ⅱ B 第 問 () 8 より, 5 5 5 6 6 8 ア, イ また, 底の変換公式を用いると, log 7 log log 9 9 log 7 log ウエ, オ (), のグラフは, それぞれ = 89 = 右図のようになり, この つのグラフは 軸に関して対称 ここで, 0, のとき, と log カ のグラフが直線 に関して対称 であることから,
1999年度 センター試験・数学ⅡB
 99 センター試験数学 Ⅱ 数学 B 問題 第 問 ( 必答問題 ) [] 関数 y cos3x の周期のうち正で最小のものはアイウ 解答解説のページへ 0 x 360 のとき, 関数 y cos3x において, y となる x はエ個, y となる x はオ 個ある また, y sin x と y cos3x のグラフより, 方程式 sin x cos3x は 0 x 360のときカ個の解をもつことがわかる
99 センター試験数学 Ⅱ 数学 B 問題 第 問 ( 必答問題 ) [] 関数 y cos3x の周期のうち正で最小のものはアイウ 解答解説のページへ 0 x 360 のとき, 関数 y cos3x において, y となる x はエ個, y となる x はオ 個ある また, y sin x と y cos3x のグラフより, 方程式 sin x cos3x は 0 x 360のときカ個の解をもつことがわかる
2018年度 2次数学セレクション(微分と積分)
 08 次数学セレクション問題 [ 東京大 ] > 0 とし, f = x - x とおく () x で f ( x ) が単調に増加するための, についての条件を求めよ () 次の 条件を満たす点 (, b) の動きうる範囲を求め, 座標平面上に図示せよ 条件 : 方程式 f = bは相異なる 実数解をもつ 条件 : さらに, 方程式 f = bの解を < < とすると > である -- 08 次数学セレクション問題
08 次数学セレクション問題 [ 東京大 ] > 0 とし, f = x - x とおく () x で f ( x ) が単調に増加するための, についての条件を求めよ () 次の 条件を満たす点 (, b) の動きうる範囲を求め, 座標平面上に図示せよ 条件 : 方程式 f = bは相異なる 実数解をもつ 条件 : さらに, 方程式 f = bの解を < < とすると > である -- 08 次数学セレクション問題
平成 年 月 7 日 ( 土 第 75 回数学教育実践研究会アスティ 45 ビル F セミナールーム A 札幌医科大学 年 P ab, を正の定数とする 平面上において ( a, を中心とする円 Q 4 C と (, b を中心とする円 C が 原点 O で外接している また P を円 C 上の点と
 平成 年 月 7 日 ( 土 第 75 回数学教育実践研究会アスティ 45 ビル F セミナールーム 微分積分の拡張 変数関数問題へのアプローチ 予選決勝優勝法からラグランジュ未定乗数法 松本睦郎 ( 札幌北高等学校 変数関数の最大値 最小値に関する問題には多様なアプローチ法がある 文字を固定した 予選決勝優勝法, 計算のみで解法する 文字消去法, 微分積分を利用した ラグランジュ未定乗数法 がある
平成 年 月 7 日 ( 土 第 75 回数学教育実践研究会アスティ 45 ビル F セミナールーム 微分積分の拡張 変数関数問題へのアプローチ 予選決勝優勝法からラグランジュ未定乗数法 松本睦郎 ( 札幌北高等学校 変数関数の最大値 最小値に関する問題には多様なアプローチ法がある 文字を固定した 予選決勝優勝法, 計算のみで解法する 文字消去法, 微分積分を利用した ラグランジュ未定乗数法 がある
2016年度 筑波大・理系数学
 06 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ k を実数とする y 平面の曲線 C : y とC : y- + k+ -k が異なる共 有点 P, Q をもつとする ただし点 P, Q の 座標は正であるとする また, 原点を O とする () k のとりうる値の範囲を求めよ () k が () の範囲を動くとき, OPQ の重心 G の軌跡を求めよ () OPQ の面積を S とするとき,
06 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ k を実数とする y 平面の曲線 C : y とC : y- + k+ -k が異なる共 有点 P, Q をもつとする ただし点 P, Q の 座標は正であるとする また, 原点を O とする () k のとりうる値の範囲を求めよ () k が () の範囲を動くとき, OPQ の重心 G の軌跡を求めよ () OPQ の面積を S とするとき,
2011年度 東京工大・数学
 東京工業大学前期日程問題 解答解説のページへ n n を自然数とする 平面上で行列 n( n+ ) n+ の表す 次変換 ( 移動とも いう ) を n とする 次の問いに答えよ () 原点 O(, ) を通る直線で, その直線上のすべての点が n により同じ直線上に移 されるものが 本あることを示し, この 直線の方程式を求めよ () () で得られた 直線と曲線 (3) を求めよ n Sn 6
東京工業大学前期日程問題 解答解説のページへ n n を自然数とする 平面上で行列 n( n+ ) n+ の表す 次変換 ( 移動とも いう ) を n とする 次の問いに答えよ () 原点 O(, ) を通る直線で, その直線上のすべての点が n により同じ直線上に移 されるものが 本あることを示し, この 直線の方程式を求めよ () () で得られた 直線と曲線 (3) を求めよ n Sn 6
以下 変数の上のドットは時間に関する微分を表わしている (ex. 2 dx d x x, x 2 dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-1) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( x や x, x などがすべて 1 次で なおかつ
 以下 変数の上のドットは時間に関する微分を表わしている (e. d d, dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( や, などがすべて 次で なおかつそれらの係数が定数であるような微分方程式 ) に対して安定性の解析を行ってきた しかしながら 実際には非線形の微分方程式で記述される現象も多く存在する
以下 変数の上のドットは時間に関する微分を表わしている (e. d d, dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( や, などがすべて 次で なおかつそれらの係数が定数であるような微分方程式 ) に対して安定性の解析を行ってきた しかしながら 実際には非線形の微分方程式で記述される現象も多く存在する
学習指導要領
 (1) いろいろな式 学習指導要領紅葉川高校学力スタンダードア式と証明展開の公式を用いて 3 乗に関わる式を展開すること ( ア ) 整式の乗法 除法 分数式の計算ができるようにする 三次の乗法公式及び因数分解の公式を理解し そ 3 次の因数分解の公式を理解し それらを用いて因数れらを用いて式の展開や因数分解をすること また 分解することができるようにする 整式の除法や分数式の四則計算について理解し
(1) いろいろな式 学習指導要領紅葉川高校学力スタンダードア式と証明展開の公式を用いて 3 乗に関わる式を展開すること ( ア ) 整式の乗法 除法 分数式の計算ができるようにする 三次の乗法公式及び因数分解の公式を理解し そ 3 次の因数分解の公式を理解し それらを用いて因数れらを用いて式の展開や因数分解をすること また 分解することができるようにする 整式の除法や分数式の四則計算について理解し
<4D F736F F D2094F795AA95FB92F68EAE82CC89F082AB95FB E646F63>
 力学 A 金曜 限 : 松田 微分方程式の解き方 微分方程式の解き方のところが分からなかったという声が多いので プリントにまとめます 数学的に厳密な話はしていないので 詳しくは数学の常微分方程式を扱っているテキストを参照してください また os s は既知とします. 微分方程式の分類 常微分方程式とは 独立変数 と その関数 その有限次の導関数 がみたす方程式 F,,, = のことです 次までの導関数を含む方程式を
力学 A 金曜 限 : 松田 微分方程式の解き方 微分方程式の解き方のところが分からなかったという声が多いので プリントにまとめます 数学的に厳密な話はしていないので 詳しくは数学の常微分方程式を扱っているテキストを参照してください また os s は既知とします. 微分方程式の分類 常微分方程式とは 独立変数 と その関数 その有限次の導関数 がみたす方程式 F,,, = のことです 次までの導関数を含む方程式を
2014年度 信州大・医系数学
 4 信州大学 ( 医系 ) 前期日程問題 解答解説のページへ 3 個の玉が横に 列に並んでいる コインを 回投げて, それが表であれば, そのときに中央にある玉とその左にある玉とを入れ替える また, それが裏であれば, そのときに中央にある玉とその右にある玉とを入れ替える この操作を繰り返す () 最初に中央にあったものが 回後に中央にある確率を求めよ () 最初に右端にあったものが 回後に右端にある確率を求めよ
4 信州大学 ( 医系 ) 前期日程問題 解答解説のページへ 3 個の玉が横に 列に並んでいる コインを 回投げて, それが表であれば, そのときに中央にある玉とその左にある玉とを入れ替える また, それが裏であれば, そのときに中央にある玉とその右にある玉とを入れ替える この操作を繰り返す () 最初に中央にあったものが 回後に中央にある確率を求めよ () 最初に右端にあったものが 回後に右端にある確率を求めよ
ベクトル公式.rtf
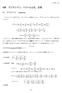 6 章ラプラシアン, ベクトル公式, 定理 6.1 ラプラシアン Laplacian φ はベクトル量である. そこでさらに発散をとると, φ はどういう形になるであろうか? φ = a + a + a φ a + a φ + a φ = φ + φ + φ = 2 φ + 2 φ 2 + 2 φ 2 2 φ = 2 φ 2 + 2 φ 2 + 2 φ 2 = 2 φ したがって,2 階の偏微分演算となる.
6 章ラプラシアン, ベクトル公式, 定理 6.1 ラプラシアン Laplacian φ はベクトル量である. そこでさらに発散をとると, φ はどういう形になるであろうか? φ = a + a + a φ a + a φ + a φ = φ + φ + φ = 2 φ + 2 φ 2 + 2 φ 2 2 φ = 2 φ 2 + 2 φ 2 + 2 φ 2 = 2 φ したがって,2 階の偏微分演算となる.
Chap2.key
 . f( ) V (V V ) V e + V e V V V V ( ) V V ( ) E. - () V (0 ) () V (0 ) () V (0 ) (4) V ( ) E. - () V (0 ) () V (0 ) O r θ ( ) ( ) : (r θ) : { r cos θ r sn θ { r + () V (0 ) (4) V ( ) θ θ arg( ) : π π
. f( ) V (V V ) V e + V e V V V V ( ) V V ( ) E. - () V (0 ) () V (0 ) () V (0 ) (4) V ( ) E. - () V (0 ) () V (0 ) O r θ ( ) ( ) : (r θ) : { r cos θ r sn θ { r + () V (0 ) (4) V ( ) θ θ arg( ) : π π
2017年度 京都大・文系数学
 07 京都大学 ( 文系 ) 前期日程問題 解答解説のページへ 曲線 y= x - 4x+ を C とする 直線 l は C の接線であり, 点 P(, 0) を通るもの とする また, l の傾きは負であるとする このとき, C と l で囲まれた部分の面積 S を求めよ -- 07 京都大学 ( 文系 ) 前期日程問題 解答解説のページへ 次の問いに答えよ ただし, 0.00 < log0
07 京都大学 ( 文系 ) 前期日程問題 解答解説のページへ 曲線 y= x - 4x+ を C とする 直線 l は C の接線であり, 点 P(, 0) を通るもの とする また, l の傾きは負であるとする このとき, C と l で囲まれた部分の面積 S を求めよ -- 07 京都大学 ( 文系 ) 前期日程問題 解答解説のページへ 次の問いに答えよ ただし, 0.00 < log0
2015-2017年度 2次数学セレクション(複素数)解答解説
 05 次数学セレクション解答解説 [ 筑波大 ] ( + より, 0 となり, + から, ( (,, よって, の描く図形 C は, 点 を中心とし半径が の円である すなわち, 原 点を通る円となる ( は虚数, は正の実数より, である さて, w ( ( とおくと, ( ( ( w ( ( ( ここで, w は純虚数より, は純虚数となる すると, の描く図形 L は, 点 を通り, 点 と点
05 次数学セレクション解答解説 [ 筑波大 ] ( + より, 0 となり, + から, ( (,, よって, の描く図形 C は, 点 を中心とし半径が の円である すなわち, 原 点を通る円となる ( は虚数, は正の実数より, である さて, w ( ( とおくと, ( ( ( w ( ( ( ここで, w は純虚数より, は純虚数となる すると, の描く図形 L は, 点 を通り, 点 と点
数学の学び方のヒント
 数学 Ⅱ における微分単元の 指導法の改善に関する研究 2017 年 10 月北数教旭川大会で発表した内容です 北海道札幌国際情報高等学校和田文興 1 Ⅰ. 研究の動機と背景 高校では極限を厳密に定義できず, 曖昧でわかりにくい. 私自身は, はじめて微分と出会ったとき, 極限の考え方等が納得できなかった. y () a h 接線 a 傾き (a) 2 Ⅰ. 研究の動機と背景 微分の指導改善に関する優れた先行研究がいくつかあるが,
数学 Ⅱ における微分単元の 指導法の改善に関する研究 2017 年 10 月北数教旭川大会で発表した内容です 北海道札幌国際情報高等学校和田文興 1 Ⅰ. 研究の動機と背景 高校では極限を厳密に定義できず, 曖昧でわかりにくい. 私自身は, はじめて微分と出会ったとき, 極限の考え方等が納得できなかった. y () a h 接線 a 傾き (a) 2 Ⅰ. 研究の動機と背景 微分の指導改善に関する優れた先行研究がいくつかあるが,
頻出問題の解法 4. 絶対値を含む関数 4.1 絶対値を含む関数 絶対値を含む関数の扱い方関数 X = { X ( X 0 のとき ) X ( X <0 のとき ) であるから, 絶対値の 中身 の符号の変わり目で変数の範囲を場合分けし, 絶対値記号をはずす 例 y= x 2 2 x = x ( x
 頻出問題の解法 4. 絶対値を含む関数 4.1 絶対値を含む関数 絶対値を含む関数の扱い方関数 X = { X ( X 0 のとき ) X ( X
頻出問題の解法 4. 絶対値を含む関数 4.1 絶対値を含む関数 絶対値を含む関数の扱い方関数 X = { X ( X 0 のとき ) X ( X
数学 ⅡB < 公理 > 公理を論拠に定義を用いて定理を証明する 1 大小関係の公理 順序 (a > b, a = b, a > b 1 つ成立 a > b, b > c a > c 成立 ) 順序と演算 (a > b a + c > b + c (a > b, c > 0 ac > bc) 2 図
 数学 Ⅱ < 公理 > 公理を論拠に定義を用いて定理を証明する 大小関係の公理 順序 >, =, > つ成立 >, > > 成立 順序と演算 > + > + >, > > 図形の公理 平行線の性質 錯角 同位角 三角形の合同条件 三角形の合同相似 量の公理 角の大きさ 線分の長さ < 空間における座漂とベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル
数学 Ⅱ < 公理 > 公理を論拠に定義を用いて定理を証明する 大小関係の公理 順序 >, =, > つ成立 >, > > 成立 順序と演算 > + > + >, > > 図形の公理 平行線の性質 錯角 同位角 三角形の合同条件 三角形の合同相似 量の公理 角の大きさ 線分の長さ < 空間における座漂とベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル
長尾谷高等学校レポート 回目 全枚. 関数 f() = について, 次の各問いに答えよ ( 教科書 p6~7, 副読本 p97) () 微分係数 f ( ) を定義に従って求めよ ただし, 求める過程を必ず書くこと () グラフ上の (, ) における接線の傾きを求めよ. 関数 ( ) = 4 f
 長尾谷高等学校レポート 回目 全枚 レポート作成にあたり諸注意. 数学 Ⅲ のレポートは 問題用紙と解答用紙に分かれています この用紙を含め 問題用紙は 提出する必要はありません もし提出用紙の表面に解答が書ききれない場合は 裏面を使用しても構いません ( 裏面の記述方法については後述 ). どの問題も 番号順に問題番号を書くことを忘れないでください また 解けなかった問題は 問題番号を書き 横に
長尾谷高等学校レポート 回目 全枚 レポート作成にあたり諸注意. 数学 Ⅲ のレポートは 問題用紙と解答用紙に分かれています この用紙を含め 問題用紙は 提出する必要はありません もし提出用紙の表面に解答が書ききれない場合は 裏面を使用しても構いません ( 裏面の記述方法については後述 ). どの問題も 番号順に問題番号を書くことを忘れないでください また 解けなかった問題は 問題番号を書き 横に
" 01 JJM 予選 4 番 # 四角形 の辺 上に点 があり, 直線 と は平行である.=,=, =5,=,= のとき, を求めよ. ただし,XY で線分 XY の長さを表すものとする. 辺 と辺 の延長線の交点を, 辺 と辺 の延長線の交点を G とする. 5 四角形 は直線 に関して線対称な
 1 " 数学発想ゼミナール # ( 改題 ) 直径を とする半円周上に一定の長さの弦がある. この弦の中点と, 弦の両端の各点から直径 への垂線の足は三角形をつくる. この三角形は二等辺三角形であり, かつその三角形は弦の位置にかかわらず相似であることを示せ. ( 証明 ) 弦の両端を X,Y とし,M を線分 XY の中点,, をそれぞれ X,Y から直径 への垂線の足とする. また,M の直径
1 " 数学発想ゼミナール # ( 改題 ) 直径を とする半円周上に一定の長さの弦がある. この弦の中点と, 弦の両端の各点から直径 への垂線の足は三角形をつくる. この三角形は二等辺三角形であり, かつその三角形は弦の位置にかかわらず相似であることを示せ. ( 証明 ) 弦の両端を X,Y とし,M を線分 XY の中点,, をそれぞれ X,Y から直径 への垂線の足とする. また,M の直径
2015年度 2次数学セレクション(整数と数列)
 05 次数学セレクション問題 [ 千葉大 文 ] k, m, を自然数とする 以下の問いに答えよ () k を 7 で割った余りが 4 であるとする このとき, k を 3 で割った余りは であることを示せ () 4m+ 5が 3 で割り切れるとする このとき, m を 7 で割った余りは 4 ではないことを示せ -- 05 次数学セレクション問題 [ 九州大 理 ] 以下の問いに答えよ () が正の偶数のとき,
05 次数学セレクション問題 [ 千葉大 文 ] k, m, を自然数とする 以下の問いに答えよ () k を 7 で割った余りが 4 であるとする このとき, k を 3 で割った余りは であることを示せ () 4m+ 5が 3 で割り切れるとする このとき, m を 7 で割った余りは 4 ではないことを示せ -- 05 次数学セレクション問題 [ 九州大 理 ] 以下の問いに答えよ () が正の偶数のとき,
2017年度 信州大・医系数学
 7 信州大学 ( 医系 ) 前期日程問題 解答解説のページへ 座標平面上の点 O(, ), A ( a, a ), B( b, b ), C( b, b) を考える さらに,, に対し, D( acos asi, asi + acos ), E( bcos bsi, bsi + bcos ) とおく () OA = OD を示せ () OA OC = かつ OA OB = OD OE ¹ であるとする
7 信州大学 ( 医系 ) 前期日程問題 解答解説のページへ 座標平面上の点 O(, ), A ( a, a ), B( b, b ), C( b, b) を考える さらに,, に対し, D( acos asi, asi + acos ), E( bcos bsi, bsi + bcos ) とおく () OA = OD を示せ () OA OC = かつ OA OB = OD OE ¹ であるとする
学習指導要領
 (1) 数と式 学習指導要領ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 第 1 章第 節実数 東高校学力スタンダード 4 実数 (P.3~7) 自然数 整数 有理数 無理数 実数のそれぞれの集 合について 四則演算の可能性について判断できる ( 例 ) 下の表において, それぞれの数の範囲で四則計算を考えるとき, 計算がその範囲で常にできる場合には
(1) 数と式 学習指導要領ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 第 1 章第 節実数 東高校学力スタンダード 4 実数 (P.3~7) 自然数 整数 有理数 無理数 実数のそれぞれの集 合について 四則演算の可能性について判断できる ( 例 ) 下の表において, それぞれの数の範囲で四則計算を考えるとき, 計算がその範囲で常にできる場合には
学習指導要領
 (1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 自然数 整数 有理数 無理数の包含関係など 実数 の構成を理解する ( 例 ) 次の空欄に適当な言葉をいれて, 数の集合を表しなさい ア イ 無理数 整数 ウ 無理数の加法及び減法 乗法公式などを利用した計 算ができる また 分母だけが二項である無理数の 分母の有理化ができる ( 例 1)
(1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 自然数 整数 有理数 無理数の包含関係など 実数 の構成を理解する ( 例 ) 次の空欄に適当な言葉をいれて, 数の集合を表しなさい ア イ 無理数 整数 ウ 無理数の加法及び減法 乗法公式などを利用した計 算ができる また 分母だけが二項である無理数の 分母の有理化ができる ( 例 1)
Microsoft PowerPoint - 応用数学8回目.pptx
 8- 次の 標 : 複素関数 ( 正則関数 ) の積分 8- 実関数 : 定積分 講義内容 名城 学理 学部材料機能 学科岩 素顕 複素関数の積分について学ぶ 複素関数の積分 複素積分の性質 周回積分の解法 コーシーの積分定理 コーシーの積分公式 グルサーの公式 - 定義 複素関数の積分 : 線積分 今後の内容 区分的に滑らかな曲線に沿って複素関数の積分を計算する 複素関数の積分の性質に関して議論する
8- 次の 標 : 複素関数 ( 正則関数 ) の積分 8- 実関数 : 定積分 講義内容 名城 学理 学部材料機能 学科岩 素顕 複素関数の積分について学ぶ 複素関数の積分 複素積分の性質 周回積分の解法 コーシーの積分定理 コーシーの積分公式 グルサーの公式 - 定義 複素関数の積分 : 線積分 今後の内容 区分的に滑らかな曲線に沿って複素関数の積分を計算する 複素関数の積分の性質に関して議論する
学習指導要領
 (1) 数と式 学習指導要領ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 千早高校学力スタンダード 自然数 整数 有理数 無理数の用語の意味を理解す る ( 例 ) 次の数の中から自然数 整数 有理 数 無理数に分類せよ 3 3,, 0.7, 3,,-, 4 (1) 自然数 () 整数 (3) 有理数 (4) 無理数 自然数 整数 有理数 無理数の包含関係など
(1) 数と式 学習指導要領ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 千早高校学力スタンダード 自然数 整数 有理数 無理数の用語の意味を理解す る ( 例 ) 次の数の中から自然数 整数 有理 数 無理数に分類せよ 3 3,, 0.7, 3,,-, 4 (1) 自然数 () 整数 (3) 有理数 (4) 無理数 自然数 整数 有理数 無理数の包含関係など
DVIOUT-17syoze
 平面の合同変換と相似変換 岩瀬順一 要約 : 平面の合同変換と相似変換を論じる いま大学で行列を学び始めている大学一年生を念頭に置いている 高等学校で行列や一次変換を学んでいなくてもよい 1. 写像 定義 1.1 X, Y を集合とする X の各元 x に対し Y のただ一つの元 y を対応させる規則 f を写像とよび,f : X! Y のように書く f によって x に対応する Y の元を f(x)
平面の合同変換と相似変換 岩瀬順一 要約 : 平面の合同変換と相似変換を論じる いま大学で行列を学び始めている大学一年生を念頭に置いている 高等学校で行列や一次変換を学んでいなくてもよい 1. 写像 定義 1.1 X, Y を集合とする X の各元 x に対し Y のただ一つの元 y を対応させる規則 f を写像とよび,f : X! Y のように書く f によって x に対応する Y の元を f(x)
2015年度 岡山大・理系数学
 5 岡山大学 ( 理系 ) 前期日程問題 解答解説のページへ を 以上の自然数とし, から までの自然数 k に対して, 番号 k をつけたカードをそれぞれ k 枚用意する これらすべてを箱に入れ, 箱の中から 枚のカードを同時に引くとき, 次の問いに答えよ () 用意したカードは全部で何枚か答えよ () 引いたカード 枚の番号が両方とも k である確率を と k の式で表せ () 引いたカード 枚の番号が一致する確率を
5 岡山大学 ( 理系 ) 前期日程問題 解答解説のページへ を 以上の自然数とし, から までの自然数 k に対して, 番号 k をつけたカードをそれぞれ k 枚用意する これらすべてを箱に入れ, 箱の中から 枚のカードを同時に引くとき, 次の問いに答えよ () 用意したカードは全部で何枚か答えよ () 引いたカード 枚の番号が両方とも k である確率を と k の式で表せ () 引いたカード 枚の番号が一致する確率を
2018試行 共通テスト 数学ⅠA 解答例
 第 1 問 共通テスト ( 試行調査 018) 数学 Ⅰ 数学 A 解答例 [1] (1) 1 のみを要素としてもつ集合が集合 A の部分集合 であることは, C = {1} とおくと, CÌ Aと表される () 命題 x Î, y Î ならば, x+ yîである が偽であることを示すための反例は, x Î かつ y Î かつ x+ yï から探すと, ( x, y ) = (3-3, 3-1),
第 1 問 共通テスト ( 試行調査 018) 数学 Ⅰ 数学 A 解答例 [1] (1) 1 のみを要素としてもつ集合が集合 A の部分集合 であることは, C = {1} とおくと, CÌ Aと表される () 命題 x Î, y Î ならば, x+ yîである が偽であることを示すための反例は, x Î かつ y Î かつ x+ yï から探すと, ( x, y ) = (3-3, 3-1),
学習指導要領
 (1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 自然数 整数 有理数 無理数 実数のそれぞれの集 合について 四則演算の可能性について判断できる ( 例 ) 下の表において それぞれの数の範囲で四則計算を考えるとき 計算がその範囲で常にできる場合には を 常にできるとは限らない場合には を付けよ ただし 除法では 0 で割ることは考えない
(1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 自然数 整数 有理数 無理数 実数のそれぞれの集 合について 四則演算の可能性について判断できる ( 例 ) 下の表において それぞれの数の範囲で四則計算を考えるとき 計算がその範囲で常にできる場合には を 常にできるとは限らない場合には を付けよ ただし 除法では 0 で割ることは考えない
数学 IB まとめ ( 教科書とノートの復習 ) IB ということで計算に関する話題中心にまとめました 理論を知りたい方はのみっちー IA のシケプリを参考にするとよいと思います 河澄教授いわく テストはまんべんなく出すらしいです でも 重積分 ( 特に変数変換使うもの ) 線積分とグリーンの定理は
 数学 IB まとめ ( 教科書とノートの復習 ) IB ということで計算に関する話題中心にまとめました 理論を知りたい方はのみっちー IA のシケプリを参考にするとよいと思います 河澄教授いわく テストはまんべんなく出すらしいです でも 重積分 ( 特に変数変換使うもの ) 線積分とグリーンの定理はほぼ間違いなく出ると思うんで 時間がない人はこのあたりに絞ってやるとよいと思います 多分 前にも書きましたが
数学 IB まとめ ( 教科書とノートの復習 ) IB ということで計算に関する話題中心にまとめました 理論を知りたい方はのみっちー IA のシケプリを参考にするとよいと思います 河澄教授いわく テストはまんべんなく出すらしいです でも 重積分 ( 特に変数変換使うもの ) 線積分とグリーンの定理はほぼ間違いなく出ると思うんで 時間がない人はこのあたりに絞ってやるとよいと思います 多分 前にも書きましたが
2015年度 京都大・理系数学
 05 京都大学 ( 理系 ) 前期日程問題 解答解説のページへ つの関数 y= si( x+ ) と y = six のグラフの 0 x の部分で囲まれる領域 を, x 軸のまわりに 回転させてできる立体の体積を求めよ ただし, x = 0 と x = は領域を囲む線とは考えない -- 05 京都大学 ( 理系 ) 前期日程問題 解答解説のページへ次の つの条件を同時に満たす四角形のうち面積が最小のものの面積を求めよ
05 京都大学 ( 理系 ) 前期日程問題 解答解説のページへ つの関数 y= si( x+ ) と y = six のグラフの 0 x の部分で囲まれる領域 を, x 軸のまわりに 回転させてできる立体の体積を求めよ ただし, x = 0 と x = は領域を囲む線とは考えない -- 05 京都大学 ( 理系 ) 前期日程問題 解答解説のページへ次の つの条件を同時に満たす四角形のうち面積が最小のものの面積を求めよ
例 e 指数関数的に減衰する信号を h( a < + a a すると, それらのラプラス変換は, H ( ) { e } e インパルス応答が h( a < ( ただし a >, U( ) { } となるシステムにステップ信号 ( y( のラプラス変換 Y () は, Y ( ) H ( ) X (
 第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
1 対 1 対応の演習例題を解いてみた 微分法とその応用 例題 1 極限 微分係数の定義 (2) 関数 f ( x) は任意の実数 x について微分可能なのは明らか f ( 1, f ( 1) ) と ( 1 + h, f ( 1 + h)
 微分法とその応用 例題 1 極限 微分係数の定義 () 関数 ( x) は任意の実数 x について微分可能なのは明らか ( 1, ( 1) ) と ( 1 + h, ( 1 + h) ) の傾き= ( 1 + h ) - ( 1 ) ( 1 + ) - ( 1) = ( 1 + h) - 1 h ( 1) = lim h ( 1 + h) - ( 1) h ( 1, ( 1) ) と ( 1 - h,
微分法とその応用 例題 1 極限 微分係数の定義 () 関数 ( x) は任意の実数 x について微分可能なのは明らか ( 1, ( 1) ) と ( 1 + h, ( 1 + h) ) の傾き= ( 1 + h ) - ( 1 ) ( 1 + ) - ( 1) = ( 1 + h) - 1 h ( 1) = lim h ( 1 + h) - ( 1) h ( 1, ( 1) ) と ( 1 - h,
2014年度 センター試験・数学ⅡB
 第 問 解答解説のページへ [] O を原点とする座標平面において, 点 P(, q) を中心とする円 C が, 方程式 y 4 x で表される直線 l に接しているとする () 円 C の半径 r を求めよう 点 P を通り直線 l に垂直な直線の方程式は, y - ア ( x- ) + qなので, P イ から l に引いた垂線と l の交点 Q の座標は ( ( ウ + エ q ), 4 (
第 問 解答解説のページへ [] O を原点とする座標平面において, 点 P(, q) を中心とする円 C が, 方程式 y 4 x で表される直線 l に接しているとする () 円 C の半径 r を求めよう 点 P を通り直線 l に垂直な直線の方程式は, y - ア ( x- ) + qなので, P イ から l に引いた垂線と l の交点 Q の座標は ( ( ウ + エ q ), 4 (
ミクロ経済学・基本講義 第2回
 1 ミクロ経済学基本講義 第 2 回企業行動 Ⅱ りじゅんさいだいか Ⅰ. 利潤最大化生産量の決定 企業の利潤 (π) を式にすると以下のようになる 利潤 (π) = 収入 (R) - 費用 (TC) 費用関数は 生産量と最小費用との関係を表すものですから これを 前提に費用を考えるなら 費用最小化は実現されているといえます では 利潤 (π) はもはや最大化されているのでは? しゅうにゅうかんすうひよう
1 ミクロ経済学基本講義 第 2 回企業行動 Ⅱ りじゅんさいだいか Ⅰ. 利潤最大化生産量の決定 企業の利潤 (π) を式にすると以下のようになる 利潤 (π) = 収入 (R) - 費用 (TC) 費用関数は 生産量と最小費用との関係を表すものですから これを 前提に費用を考えるなら 費用最小化は実現されているといえます では 利潤 (π) はもはや最大化されているのでは? しゅうにゅうかんすうひよう
学習指導要領
 (1 ) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 自然数 整数 有理数 無理数の包含関係など 実 数の構成を理解する ( 例 ) 次の空欄に適当な言葉をいれて, 数の集合を表しなさい 実数の絶対値が実数と対応する点と原点との距離で あることを理解する ( 例 ) 次の値を求めよ (1) () 6 置き換えなどを利用して 三項の無理数の乗法の計
(1 ) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 自然数 整数 有理数 無理数の包含関係など 実 数の構成を理解する ( 例 ) 次の空欄に適当な言葉をいれて, 数の集合を表しなさい 実数の絶対値が実数と対応する点と原点との距離で あることを理解する ( 例 ) 次の値を求めよ (1) () 6 置き換えなどを利用して 三項の無理数の乗法の計
重要例題113
 04_ 高校 数学 Ⅱ 必須基本公式 定理集 数学 Ⅱ 第 章式の計算と方程式 0 商と余り についての整式 A をについての整式 B で割ったときの商を Q, 余りを R とすると, ABQ+R (R の次数 ) > 0
04_ 高校 数学 Ⅱ 必須基本公式 定理集 数学 Ⅱ 第 章式の計算と方程式 0 商と余り についての整式 A をについての整式 B で割ったときの商を Q, 余りを R とすると, ABQ+R (R の次数 ) > 0
学習指導要領
 () いろいろな式 学習指導要領ア式と証明 ( ア ) 整式の乗法 除法 分数式の計算三次の乗法公式及び因数分解の公式を理解し それらを用いて式の展開や因数分解をすること また 整式の除法や分数式の四則計算について理解し 簡単な場合について計算をすること 都立清瀬高校学力スタンダード 変数の 次式の展開や因数分解ができる ( 例 ) 次の式を展開せよ y ( 例 ) 次の式を因数分解せよ 8 7y
() いろいろな式 学習指導要領ア式と証明 ( ア ) 整式の乗法 除法 分数式の計算三次の乗法公式及び因数分解の公式を理解し それらを用いて式の展開や因数分解をすること また 整式の除法や分数式の四則計算について理解し 簡単な場合について計算をすること 都立清瀬高校学力スタンダード 変数の 次式の展開や因数分解ができる ( 例 ) 次の式を展開せよ y ( 例 ) 次の式を因数分解せよ 8 7y
DVIOUT
 3 第 2 章フーリエ級数 23 フーリエ級数展開 これまで 関数 f(x) のフーリエ級数展開に関して 関数の定義区間やフーリエ級数の積分区間を断りなく [, ] に取ってきました これは フーリエ級数を構成する三角関数が基本周期 2 を持つためです すなわち フーリエ級数の各項 cos nx および sin nx (n =1, 2, 3, 4, ) の周期は それぞれ 2, 2 2, 2 3,
3 第 2 章フーリエ級数 23 フーリエ級数展開 これまで 関数 f(x) のフーリエ級数展開に関して 関数の定義区間やフーリエ級数の積分区間を断りなく [, ] に取ってきました これは フーリエ級数を構成する三角関数が基本周期 2 を持つためです すなわち フーリエ級数の各項 cos nx および sin nx (n =1, 2, 3, 4, ) の周期は それぞれ 2, 2 2, 2 3,
横浜市環境科学研究所
 周期時系列の統計解析 単回帰分析 io 8 年 3 日 周期時系列に季節調整を行わないで単回帰分析を適用すると, 回帰係数には周期成分の影響が加わる. ここでは, 周期時系列をコサイン関数モデルで近似し単回帰分析によりモデルの回帰係数を求め, 周期成分の影響を検討した. また, その結果を気温時系列に当てはめ, 課題等について考察した. 気温時系列とコサイン関数モデル第 報の結果を利用するので, その一部を再掲する.
周期時系列の統計解析 単回帰分析 io 8 年 3 日 周期時系列に季節調整を行わないで単回帰分析を適用すると, 回帰係数には周期成分の影響が加わる. ここでは, 周期時系列をコサイン関数モデルで近似し単回帰分析によりモデルの回帰係数を求め, 周期成分の影響を検討した. また, その結果を気温時系列に当てはめ, 課題等について考察した. 気温時系列とコサイン関数モデル第 報の結果を利用するので, その一部を再掲する.
2018年度 岡山大・理系数学
 08 岡山大学 ( 理系 ) 前期日程問題 解答解説のページへ 関数 f ( x) = ( + x) x について, 以下の問いに答えよ () f ( x ) = 0 を満たす x の値を求めよ () 曲線 y = f ( x ) について, 原点を通るすべての接線の方程式を求めよ (3) 曲線 y = f ( x ) について, 原点を通る接線のうち, 接点の x 座標が最大のものを L とする
08 岡山大学 ( 理系 ) 前期日程問題 解答解説のページへ 関数 f ( x) = ( + x) x について, 以下の問いに答えよ () f ( x ) = 0 を満たす x の値を求めよ () 曲線 y = f ( x ) について, 原点を通るすべての接線の方程式を求めよ (3) 曲線 y = f ( x ) について, 原点を通る接線のうち, 接点の x 座標が最大のものを L とする
2014年度 名古屋大・理系数学
 04 名古屋大学 ( 理系 ) 前期日程問題 解答解説のページへ空間内にある半径 の球 ( 内部を含む ) を B とする 直線 と B が交わっており, その交わりは長さ の線分である () B の中心と との距離を求めよ () のまわりに B を 回転してできる立体の体積を求めよ 04 名古屋大学 ( 理系 ) 前期日程問題 解答解説のページへ 実数 t に対して 点 P( t, t ), Q(
04 名古屋大学 ( 理系 ) 前期日程問題 解答解説のページへ空間内にある半径 の球 ( 内部を含む ) を B とする 直線 と B が交わっており, その交わりは長さ の線分である () B の中心と との距離を求めよ () のまわりに B を 回転してできる立体の体積を求めよ 04 名古屋大学 ( 理系 ) 前期日程問題 解答解説のページへ 実数 t に対して 点 P( t, t ), Q(
DVIOUT
 第 3 章 フーリエ変換 3.1 フーリエ積分とフーリエ変換 第 章では 周期を持つ関数のフーリエ級数について学びました この章では 最初に 周期を持つ関数のフーリエ級数を拡張し 周期を持たない ( 一般的な ) 関数のフーリエ級数を導きましょう 具体的には 関数 f(x) を区間 L x L で考え この L を限りなく大きくするというアプローチを取ります (L ) なお ここで扱う関数 f(x)
第 3 章 フーリエ変換 3.1 フーリエ積分とフーリエ変換 第 章では 周期を持つ関数のフーリエ級数について学びました この章では 最初に 周期を持つ関数のフーリエ級数を拡張し 周期を持たない ( 一般的な ) 関数のフーリエ級数を導きましょう 具体的には 関数 f(x) を区間 L x L で考え この L を限りなく大きくするというアプローチを取ります (L ) なお ここで扱う関数 f(x)
微分方程式補足.moc
 Bernoulli( ベルヌーイ ) の微分方程式 ' + P( ) = Q() n ( n 0,) 微分方程式の形の補足 ( 階 ) 注意 : n =0 のときは 階線形微分方程式 n = のときは変数分離形となる 解法 : z = -n とおいて関数 z の微分方程式を解く z' =( - n) -n ' よりこれを元の微分方程 式に代入する - n z' + P() = Q() n 両辺を n
Bernoulli( ベルヌーイ ) の微分方程式 ' + P( ) = Q() n ( n 0,) 微分方程式の形の補足 ( 階 ) 注意 : n =0 のときは 階線形微分方程式 n = のときは変数分離形となる 解法 : z = -n とおいて関数 z の微分方程式を解く z' =( - n) -n ' よりこれを元の微分方程 式に代入する - n z' + P() = Q() n 両辺を n
PowerPoint プレゼンテーション
 - = 4 = 4 = - y = x y = x y = x + 4 y = x 比例は y = ax の形であらわすことができる 4 - 秒後 y = 5 y = 0 (m) 5 秒後 y = 5 5 y = 5 (m) 5 0 = 05 (m) 05 5 = 5 (m/ 秒 ) 4 4 秒後 y = 5 4 y = 80 (m) 5-80 5 4 = 45 (m/ 秒 ) 5 v = 0 5
- = 4 = 4 = - y = x y = x y = x + 4 y = x 比例は y = ax の形であらわすことができる 4 - 秒後 y = 5 y = 0 (m) 5 秒後 y = 5 5 y = 5 (m) 5 0 = 05 (m) 05 5 = 5 (m/ 秒 ) 4 4 秒後 y = 5 4 y = 80 (m) 5-80 5 4 = 45 (m/ 秒 ) 5 v = 0 5
線積分.indd
 線積分 線積分 ( n, n, n ) (ξ n, η n, ζ n ) ( n-, n-, n- ) (ξ k, η k, ζ k ) ( k, k, k ) ( k-, k-, k- ) 物体に力 を作用させて位置ベクトル A の点 A から位置ベクトル の点 まで曲線 に沿って物体を移動させたときの仕事 W は 次式で計算された A, A, W : d 6 d+ d+ d@,,, d+ d+
線積分 線積分 ( n, n, n ) (ξ n, η n, ζ n ) ( n-, n-, n- ) (ξ k, η k, ζ k ) ( k, k, k ) ( k-, k-, k- ) 物体に力 を作用させて位置ベクトル A の点 A から位置ベクトル の点 まで曲線 に沿って物体を移動させたときの仕事 W は 次式で計算された A, A, W : d 6 d+ d+ d@,,, d+ d+
Microsoft Word - 8章(CI).doc
 8 章配置間相互作用法 : Configuration Interaction () etho [] 化学的精度化学反応の精密な解析をするためには エネルギー誤差は数 ~ kcal/mol 程度に抑えたいものである この程度の誤差内に治まる精度を 化学的精度 と呼ぶことがある He 原子のエネルギーをシュレーディンガー方程式と分子軌道法で計算した結果を示そう He 原子のエネルギー Hartree-Fock
8 章配置間相互作用法 : Configuration Interaction () etho [] 化学的精度化学反応の精密な解析をするためには エネルギー誤差は数 ~ kcal/mol 程度に抑えたいものである この程度の誤差内に治まる精度を 化学的精度 と呼ぶことがある He 原子のエネルギーをシュレーディンガー方程式と分子軌道法で計算した結果を示そう He 原子のエネルギー Hartree-Fock
1 1. はじめに ポンスレの閉形定理 Jacobi の証明 June 5, 2013 Akio Arimoto ヤコビは [2] においてポンスレの閉形定理に初等幾何を用いた証明を与え ている 大小 2つの円があり 一方が他方を完全に含んでいるとする 大小 2 円の半径をそれぞれ Rr, とする
![1 1. はじめに ポンスレの閉形定理 Jacobi の証明 June 5, 2013 Akio Arimoto ヤコビは [2] においてポンスレの閉形定理に初等幾何を用いた証明を与え ている 大小 2つの円があり 一方が他方を完全に含んでいるとする 大小 2 円の半径をそれぞれ Rr, とする 1 1. はじめに ポンスレの閉形定理 Jacobi の証明 June 5, 2013 Akio Arimoto ヤコビは [2] においてポンスレの閉形定理に初等幾何を用いた証明を与え ている 大小 2つの円があり 一方が他方を完全に含んでいるとする 大小 2 円の半径をそれぞれ Rr, とする](/thumbs/100/145746324.jpg) . はじめに ポンスレの閉形定理 Jcobi の証明 Jue 5 03 Akio Aimoto ヤコビは [] においてポンスレの閉形定理に初等幾何を用いた証明を与え ている 大小 つの円があり 一方が他方を完全に含んでいるとする 大小 円の半径をそれぞれ とする 中心間の距離を とすれば 0 < + < が成立している 大きい円の周上の点 A から小さい円に接線を引く 接線と大きい円の周上に交わる
. はじめに ポンスレの閉形定理 Jcobi の証明 Jue 5 03 Akio Aimoto ヤコビは [] においてポンスレの閉形定理に初等幾何を用いた証明を与え ている 大小 つの円があり 一方が他方を完全に含んでいるとする 大小 円の半径をそれぞれ とする 中心間の距離を とすれば 0 < + < が成立している 大きい円の周上の点 A から小さい円に接線を引く 接線と大きい円の周上に交わる
学習指導要領
 (1) 数と式 ア整式 ( ア ) 式の展開と因数分解二次の乗法公式及び因数分解の公式の理解を深め 式を多面的にみたり目的に応じて式を適切に変形したりすること (ax b)(cx d) acx (ad bc)x bd などの基本的な公式を活用して 二次式の展開や因数分解ができる また 式の置き換えや一文字に着目するなどして 展開 因数分解ができる ( 例 ) 次の問に答えよ (1) (3x a)(4x
(1) 数と式 ア整式 ( ア ) 式の展開と因数分解二次の乗法公式及び因数分解の公式の理解を深め 式を多面的にみたり目的に応じて式を適切に変形したりすること (ax b)(cx d) acx (ad bc)x bd などの基本的な公式を活用して 二次式の展開や因数分解ができる また 式の置き換えや一文字に着目するなどして 展開 因数分解ができる ( 例 ) 次の問に答えよ (1) (3x a)(4x
p tn tn したがって, 点 の 座標は p p tn tn tn また, 直線 l と直線 p の交点 の 座標は p p tn p tn よって, 点 の座標 (, ) は p p, tn tn と表され p 4p p 4p 4p tn tn tn より, 点 は放物線 4 p 上を動くこと
 567_ 次曲線の三角関数による媒介変数表示 次曲線の三角関数による媒介変数表示 次曲線 ( 放物線 楕円 双曲線 ) の標準形の, についての方程式と, 三角関数による媒介変数表示は次のように対応している.. 放物線 () 4 p (, ) ( ptn, ptn ) (). 楕円. 双曲線 () () (, p p ), tn tn (, ) ( cos, sin ) (, ), tn cos (,
567_ 次曲線の三角関数による媒介変数表示 次曲線の三角関数による媒介変数表示 次曲線 ( 放物線 楕円 双曲線 ) の標準形の, についての方程式と, 三角関数による媒介変数表示は次のように対応している.. 放物線 () 4 p (, ) ( ptn, ptn ) (). 楕円. 双曲線 () () (, p p ), tn tn (, ) ( cos, sin ) (, ), tn cos (,
Phys1_03.key
 物理学1/物理学A 第3回 速度と加速度 速度 加速度 関数の話 やりたいこと : 物体の運動を調べる 物体の位置と速度を調べる これらを時間の関数として表したい 関数とは? ある された変数に対して, 出 の値が決まる対応関係のこと inpu 関数 ( 函数 ) oupu 例 : y(x)=x 2 x=2 を inpu すると y=4 が得られる 時々刻々と変化していく物体の位置 をその時刻とともに記録する
物理学1/物理学A 第3回 速度と加速度 速度 加速度 関数の話 やりたいこと : 物体の運動を調べる 物体の位置と速度を調べる これらを時間の関数として表したい 関数とは? ある された変数に対して, 出 の値が決まる対応関係のこと inpu 関数 ( 函数 ) oupu 例 : y(x)=x 2 x=2 を inpu すると y=4 が得られる 時々刻々と変化していく物体の位置 をその時刻とともに記録する
Microsoft Word - スーパーナビ 第6回 数学.docx
 1 ⑴ 与式 =- 5 35 +14 35 =9 35 1 ⑵ 与式 =9-(-5)=9+5=14 1 ⑶ 与式 = 4(a-b)-3(5a-3b) = 8a-4b-15a+9b = -7a+5b 1 1 1 1 ⑷ 与式 =(²+ 1+1²)-{²+(-3+)+(-3) } 1 ⑷ 与式 =(²++1)-(²--6)=²++1-²++6=3+7 1 ⑸ 与式 = - ² + 16 = - +16
1 ⑴ 与式 =- 5 35 +14 35 =9 35 1 ⑵ 与式 =9-(-5)=9+5=14 1 ⑶ 与式 = 4(a-b)-3(5a-3b) = 8a-4b-15a+9b = -7a+5b 1 1 1 1 ⑷ 与式 =(²+ 1+1²)-{²+(-3+)+(-3) } 1 ⑷ 与式 =(²++1)-(²--6)=²++1-²++6=3+7 1 ⑸ 与式 = - ² + 16 = - +16
教育課程 ( 数学 Ⅲ 数学 C) < ベクトル >( 数 B 数 C) 1 ベクトルの演算 和 差 実数倍については 文字の計算と同様 2 ベクトルの成分表示 平面ベクトル : a x e y e x, ) ( 1 y1 空間ベクトル : a x e y e z e x, y, )
 教育課程 数学 Ⅲ 数学 C < ベクトル > 数 B 数 C ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル : e e, 空間ベクトル : e e e,, 成分での計算ができるようにすること ベクトルの内積 : cos 平面ベクトル :,, のとき 空間ベクトル :,,,, 4 ベクトルの大きさ 平面上 : 空間上 : は 良く用いられる 5 m:
教育課程 数学 Ⅲ 数学 C < ベクトル > 数 B 数 C ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル : e e, 空間ベクトル : e e e,, 成分での計算ができるようにすること ベクトルの内積 : cos 平面ベクトル :,, のとき 空間ベクトル :,,,, 4 ベクトルの大きさ 平面上 : 空間上 : は 良く用いられる 5 m:
パソコンシミュレータの現状
 第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
問 題
 数学 出題のねらい 数と式, 図形, 関数, 資料の活用 の 4 領域について, 基礎的な概念や原理 法則の理解と, それらに基づき, 数学的に考察したり, 表現したり, 処理したりする力をみることをねらいとした () 数と式 では, 数の概念についての理解の程度, 文字を用いた式を処理したり, 文字を用いて式に表現したりする力, 目的に応じて式を変形する力をみるものとした () 図形 では, 平面図形や空間図形についての理解の程度,
数学 出題のねらい 数と式, 図形, 関数, 資料の活用 の 4 領域について, 基礎的な概念や原理 法則の理解と, それらに基づき, 数学的に考察したり, 表現したり, 処理したりする力をみることをねらいとした () 数と式 では, 数の概念についての理解の程度, 文字を用いた式を処理したり, 文字を用いて式に表現したりする力, 目的に応じて式を変形する力をみるものとした () 図形 では, 平面図形や空間図形についての理解の程度,
Microsoft Word - 1B2011.doc
 第 14 回モールの定理 ( 単純梁の場合 ) ( モールの定理とは何か?p.11) 例題 下記に示す単純梁の C 点のたわみ角 θ C と, たわみ δ C を求めよ ただし, 部材の曲げ 剛性は材軸に沿って一様で とする C D kn B 1.5m 0.5m 1.0m 解答 1 曲げモーメント図を描く,B 点の反力を求める kn kn 4 kn 曲げモーメント図を描く knm 先に得られた曲げモーメントの値を
第 14 回モールの定理 ( 単純梁の場合 ) ( モールの定理とは何か?p.11) 例題 下記に示す単純梁の C 点のたわみ角 θ C と, たわみ δ C を求めよ ただし, 部材の曲げ 剛性は材軸に沿って一様で とする C D kn B 1.5m 0.5m 1.0m 解答 1 曲げモーメント図を描く,B 点の反力を求める kn kn 4 kn 曲げモーメント図を描く knm 先に得られた曲げモーメントの値を
<4D F736F F D20824F E B82CC90FC90CF95AA2E646F63>
 1/1 平成 3 年 6 月 11 日午前 1 時 3 分 4 ベクトルの線積分 4 ベクトルの線積分 Ⅰ. 積分の種類 通常の物理で使う積分には 3 種類あります 積分変数の数に応じて 線積分 ( 記号 横(1 重 d, dy, dz d ( ine: 面積分 ( 記号 縦 横 ( 重 線 4 ベクトルの線積分 重積分記号 ddy, dydz, dzdz ds ( Surface: 1 重積分記号
1/1 平成 3 年 6 月 11 日午前 1 時 3 分 4 ベクトルの線積分 4 ベクトルの線積分 Ⅰ. 積分の種類 通常の物理で使う積分には 3 種類あります 積分変数の数に応じて 線積分 ( 記号 横(1 重 d, dy, dz d ( ine: 面積分 ( 記号 縦 横 ( 重 線 4 ベクトルの線積分 重積分記号 ddy, dydz, dzdz ds ( Surface: 1 重積分記号
学習指導要領
 (1) 数と式 学習指導要領ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 都立大江戸高校学力スタンダード 平方根の意味を理解し 平方根の計算法則に従って平方根を簡単にすることができる ( 例 1) 次の値を求めよ (1)5 の平方根 () 81 ( 例 ) 次の数を簡単にせよ (1) 5 () 7 1 (3) 49 無理数の加法や減法 乗法公式を利用した計算がで
(1) 数と式 学習指導要領ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 都立大江戸高校学力スタンダード 平方根の意味を理解し 平方根の計算法則に従って平方根を簡単にすることができる ( 例 1) 次の値を求めよ (1)5 の平方根 () 81 ( 例 ) 次の数を簡単にせよ (1) 5 () 7 1 (3) 49 無理数の加法や減法 乗法公式を利用した計算がで
学習指導要領
 (1) 数と式 学習指導要領 数と式 (1) 式の計算二次の乗法公式及び因数分解の公式の理解を深め 式を多面的にみたり目的に応じて式を適切に変形したりすること 東京都立町田高等学校学力スタンダード 整式の加法 減法 乗法展開の公式を利用できる 式を1 つの文字におき換えることによって, 式の計算を簡略化することができる 式の形の特徴に着目して変形し, 展開の公式が適用できるようにすることができる 因数分解因数分解の公式を利用できる
(1) 数と式 学習指導要領 数と式 (1) 式の計算二次の乗法公式及び因数分解の公式の理解を深め 式を多面的にみたり目的に応じて式を適切に変形したりすること 東京都立町田高等学校学力スタンダード 整式の加法 減法 乗法展開の公式を利用できる 式を1 つの文字におき換えることによって, 式の計算を簡略化することができる 式の形の特徴に着目して変形し, 展開の公式が適用できるようにすることができる 因数分解因数分解の公式を利用できる
学習指導要領
 (1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 絶対値の意味を理解し適切な処理することができる 例題 1-3 の絶対値をはずせ 展開公式 ( a + b ) ( a - b ) = a 2 - b 2 を利用して根号を含む分数の分母を有理化することができる 例題 5 5 + 2 の分母を有理化せよ 実数の整数部分と小数部分の表し方を理解している
(1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 絶対値の意味を理解し適切な処理することができる 例題 1-3 の絶対値をはずせ 展開公式 ( a + b ) ( a - b ) = a 2 - b 2 を利用して根号を含む分数の分母を有理化することができる 例題 5 5 + 2 の分母を有理化せよ 実数の整数部分と小数部分の表し方を理解している
代数 幾何 < ベクトル > 1 ベクトルの演算 和 差 実数倍については 文字の計算と同様 2 ベクトルの成分表示 平面ベクトル : a x e y e x, ) ( 1 y1 空間ベクトル : a x e y e z e x, y, ) ( 1 1 z1
 代数 幾何 < ベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル :, 空間ベクトル : z,, z 成分での計算ができるようにすること ベクトルの内積 : os 平面ベクトル :,, 空間ベクトル :,,,, z z zz 4 ベクトルの大きさ 平面上 : 空間上 : z は 良く用いられる 5 m: に分ける点 : m m 図形への応用
代数 幾何 < ベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル :, 空間ベクトル : z,, z 成分での計算ができるようにすること ベクトルの内積 : os 平面ベクトル :,, 空間ベクトル :,,,, z z zz 4 ベクトルの大きさ 平面上 : 空間上 : z は 良く用いられる 5 m: に分ける点 : m m 図形への応用
