2/ ERATO
|
|
|
- えりか うみのなか
- 7 years ago
- Views:
Transcription
1 , JST, ERATO,
2 2/ ERATO
3 Given n n A 1,..., A N Find P s.t. P A 1 P,..., P A N P A 1 A 2 A N simultaneously P A 1 P P A 2 P P A N P 3/ 36
4 4/ 36
5 5/ 36
6 6/ 36 [Wigner 1931 ]. [de Klerk-Dobre 2011] etc [Arima-Kim-Kojima 2012] etc [Burgdorf-Klep-Povh 2011] [Aiura-Kakimura-Murota 2011] [Gutch-Krumsiek-Theis 2011] [Irving-Sorrentino 2012].
![2012] etc [Burgdorf-Klep-Povh 2011]](/docs-images/58/20055721/images/page_6.jpg "[Aiura-Kakimura-Murota 2011]")
7 7/ 36 [Wigner 1931 ] Hx = ϵx H = α 1 H α N H N H 1,..., H N
8 8/ 36 [Irving-Sorrentino 2012] x(t) = A 1 x(t 1) + + A N x(t N) x(t) t A k k A 1 A 2.
9 [Gatermann-Parrilo 2004], [Murota-Kanno-Kojima-Kojima 2010],... minimize C, X subject to A i, X = b i (i = 1,..., N) X O 7 days 7 mins [de Klerk-Dobre-Pasechnik 2009] 9/ 36
![[Jutten-Herault 1985], [Cardoso-Soulomiac 1993],.](/docs-images/39/20055721/images/10-0.png ".. Y 1 Y 2 Y l Given: Find: n X Y 1,..., Y l W P C P = X = W Y http://www.")
10 [Jutten-Herault 1985], [Cardoso-Soulomiac 1993],... Y 1 Y 2 Y l Given: Find: n X Y 1,..., Y l W P C P = X = W Y 10/ 36
11 11/ 36 [Wigner 1931 ]. [de Klerk-Dobre 2011] etc [Arima-Kim-Kojima 2012] etc [Burgdorf-Klep-Povh 2011] [Aiura-Kakimura-Murota 2011] [Gutch-Krumsiek-Theis 2011] [Irving-Sorrentino 2012].
![2012] etc [Burgdorf-Klep-Povh 2011]](/docs-images/58/20055721/images/page_11.jpg "[Aiura-Kakimura-Murota 2011]")
12 12/ 36
13 13/ 36 SBD = SBD =
14 old new numerical linear algebra Jacobi-like [Bunse-Gerstner, Byers, Mehrmann 1990] JADE [Cardoso-Souloumiacc 1993] [Theis 2007] abstract algebra one-by-one [folklore -1820] The recipe [Schur 1905] MKKKM [Murota-Kanno-Kojima-Kojima MM [Maehara-Murota 2012] 14/ ]
![abstract algebra one-by-one [folklore -1820] The recipe [Schur](/docs-images/58/20055721/images/page_14.jpg "1905] MKKKM [Murota-Kanno-Kojima-Kojima MM [Maehara-Murota 2012]")
15 old new numerical linear algebra Jacobi-like [Bunse-Gerstner, Byers, Mehrmann 1990] JADE [Cardoso-Souloumiacc 1993] [Theis 2007] abstract algebra one-by-one [folklore -1820] The recipe [Schur 1905] MKKKM [Murota-Kanno-Kojima-Kojima MM [Maehara-Murota 2012] 15/ ]
![abstract algebra one-by-one [folklore -1820] The recipe [Schur](/docs-images/58/20055721/images/page_15.jpg "1905] MKKKM [Murota-Kanno-Kojima-Kojima MM [Maehara-Murota 2012]")
16 16/ 36 one-by-one method [ ]. A, X. wlog. X = diag(x 1,..., x n ), AX XA = [(x j x i )a ij ] = O x x y X A X A
17 17/ 36 Jacobi-like method [ ] (Bunse-Gerstner, Byers, Mehrmann 1990) one-by-one minimize [ off(p AP ) + off(p BP ) ] Givens 2 2 Jacobi
18 18/ 36 JADE [ ] (Cardoso, Souloumiac 1993) minimize [ off(p A 1 P ) + + off(p A N P ) ] Jacobi-like method 1 = by Cardoso
19 JADE [ ( )] (Theis 2007) minimize [ off(p A 1 P ) + + off(p A N P ) ] = [Maehara Gutch 2010] 19/ 36
![+ + off(p A N P ) ] =](/docs-images/58/20055721/images/page_19.jpg "[Maehara Gutch 2010] 19/")
20 old new numerical linear algebra Jacobi-like [Bunse-Gerstner, Byers, Mehrmann 1990] JADE [Cardoso-Souloumiacc 1993] [Theis 2007] abstract algebra one-by-one [folklore -1820] Schur lemma [Schur 1905] MKKKM [Murota-Kanno-Kojima-Kojima MM [Maehara-Murota 2012] 20/ ]
![abstract algebra one-by-one [folklore -1820] Schur lemma [Schur](/docs-images/58/20055721/images/page_20.jpg "1905] MKKKM [Murota-Kanno-Kojima-Kojima MM [Maehara-Murota 2012]")
21 A 1,..., A N G Q A j Q = A j (Q G) G Schur - G A j - A j G G Schur lemma: MKKKM, MM: one-by-one 21/ 36
22 22/ 36 Schur lemma (Schur 1905) Q A j Q = A j (Q G) 1. A 1,..., A N G 2. G 3. A 1,..., A N 1930 Wigner cf. Heisenberg 1925
23 [Murota-Kanno-Kojima-Kojima 2010] 23/ 36 Q. 3V 3V (3i + j, 3k + l) k l i j A.
24 24/ 36 MKKKM [Murota-Kanno-Kojima-Kojima 2010, Maehara-Murota 2011] 1. A 1,..., A N cf: one-by-one
25 25/ 36 MKKKM [Murota-Kanno-Kojima-Kojima 2010, Maehara-Murota 2011] cf: one-by-one
26 26/ 36 MKKKM A 1,..., A N Artin-Wedderburn T := A 1,..., A N (M n1 I µ1 ) (M nl I µl ) T M n I µ one-by-one
27 MM [Maehara-Murota 2012] one-by-one X = diag(x 1,..., x n ), AX XA = [(x j x i )a ij ] = O x x X y A 1,..., A N X A 1,..., A N A 27/ 36
28 T := {X A i X X i A = O (i = 1,..., N)} 28/ 36 MM [Maehara-Murota 2012] 1. A i X XA i = O (i = 1,..., N) 2. X Artin-Wedderburn
29 29/ 36 MM [Maehara-Murota 2012] 1. A i X XA i ϵ (i = 1,..., N) 2. X ϵ ϵ
30 / maehara/commdec/ 30/ 36
31 31/ 36 A 1 A 2 A N simultaneously P A 1 P P A 2 P P A N P state of the art: [MM 2012]
32 32/ 36
33 33/ 36 preconditioning
34 A i X XA i = O (i = 1,..., N) X λ i λ j [Dyson index] n n exp( n λ 2 i /4) i<j λ i λ j i.e., λ i λ j cf. λ i λ j 2 34/ 36
35 35/ 36 T T = T 1 T l X T with n 2 k Dyson index ToDo:
36 A 1 A 2 A N simultaneously P A 1 P P A 2 P P A N P state of the art: [MM 2012] ( ) 36/ 36
a a b a b c d e R c d e A a b e a b a b c d a b c d e f a M a b f d a M b a b a M b a M b M M M R M a M b M c a M a R b A a b b a CF a b c a b a M b a b M a M b c a A b a b M b a A b a M b C a M C a M
p _
Index ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap. ap.
index calculus
index calculus 2008 3 8 1 generalized Weil descent p :, E/F p 3 : Y 2 = f(x), where f(x) = X 3 + AX + B, A F p, B F p 3 E(F p 3) 3 : Generalized Weil descent E(F p 4) 2 Index calculus Plain version Double-large-prime
第85 回日本感染症学会総会学術集会後抄録（III）
β β α α α µ µ µ µ α α α α γ αβ α γ α α γ α γ µ µ β β β β β β β β β µ β α µ µ µ β β µ µ µ µ µ µ γ γ γ γ γ γ µ α β γ β β µ µ µ µ µ β β µ β β µ α β β µ µµ β µ µ µ µ µ µ λ µ µ β µ µ µ µ µ µ µ µ
nakata/nakata.html p.1/20
http://www.me.titech.ac.jp/ nakata/nakata.html p.1/20 1-(a). Faybusovich(1997) Linear systems in Jordan algebras and primal-dual interior-point algorithms,, Euclid Jordan p.2/20 Euclid Jordan V Euclid
P-12 P-13 3 4 28 16 00 17 30 P-14 P-15 P-16 4 14 29 17 00 18 30 P-17 P-18 P-19 P-20 P-21 P-22
1 14 28 16 00 17 30 P-1 P-2 P-3 P-4 P-5 2 24 29 17 00 18 30 P-6 P-7 P-8 P-9 P-10 P-11 P-12 P-13 3 4 28 16 00 17 30 P-14 P-15 P-16 4 14 29 17 00 18 30 P-17 P-18 P-19 P-20 P-21 P-22 5 24 28 16 00 17 30 P-23
(1)2004年度 日本地理
1 2 3 4 1 2 3 4 5 6 7 8 9 10 11 12-5.0-5.1-1.4 4.2 8.6 12.4 16.9 19.5 16.6 10.8 3.3-2.0 6.6 16.6 16.6 18.6 21.3 23.8 26.6 28.5 28.2 27.2 24.9 21.7 18.4 22.7 5 1 2 3 4 5 6 7 8 9 10 11 12 2.2 3.5 7.7 11.1
Micro-D 小型高密度角型コネクタ
Micro- 1 2 0.64 1.27 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 2 3 4 5 6 7 8 9 10 11 12 13 1.09 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 3 4 J J
131314 131314 100 16712 1 1 16624 63 4 89 27 3 2 2 1 8 38418 23203 132 252710129 134 24 30201320 136 30 144 30146-18239 23 2 132144 132 64 1322132113261 13413412 1348134212 134622 63013626 1441330 3 11520
1 913 10301200 A B C D E F G H J K L M 1A1030 10 : 45 1A1045 11 : 00 1A1100 11 : 15 1A1115 11 : 30 1A1130 11 : 45 1A1145 12 : 00 1B1030 1B1045 1C1030
1 913 9001030 A B C D E F G H J K L M 9:00 1A0900 9:15 1A0915 9:30 1A0930 9:45 1A0945 10 : 00 1A1000 10 : 15 1B0900 1B0915 1B0930 1B0945 1B1000 1C0900 1C0915 1D0915 1C0930 1C0945 1C1000 1D0930 1D0945 1D1000
人芯経営論 ･･･リーダーシップ考②
2009/12/15 2009/11/17 2009/11/16 2009/10/19 2009/10/15 2009/10/1 2009/9/17 2009/9/1 2009/8/17 2009/8/17 2009/8/14 2009/8/12 2009/7/28 2009/7/17 2009/7/15 2009/6/24 2009/6/18 2009/6/15 2009/5/20 2009/5/15
001 No.3/12 1 1 2 3 4 5 6 4 8 13 27 33 39 001 No.3/12 4 001 No.3/12 5 001 No.3/12 6 001 No.3/12 7 001 8 No.3/12 001 No.3/12 9 001 10 No.3/12 001 No.3/12 11 Index 1 2 3 14 18 21 001 No.3/12 14 001 No.3/12
136 pp p µl µl µl
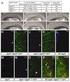135 2006 PCB C 12 H 10-n Cl n n 1 10 CAS No. 42 PCB: 53469-21-9, 54 PCB: 11097-69-1 0.01 mg/m 3 PCB PCB 25 µg/l 136 pp p µl µl µl 137 1 γ 138 1 γ γ γ µl µl µl µl µl µl µl l µl µl µl µl µl l 139 µl µl µl
#2 (IISEC)
#2 (IISEC) 2007 10 6 E Y 2 = F (X) E(F p ) E : Y 2 = F (X) = X 3 + AX + B, A, B F p E(F p ) = {(x, y) F 2 p y2 = F (x)} {P } P : E(F p ) E F p - Given: E/F p : EC, P E(F p ), Q P Find: x Z/NZ s.t. Q =
A11 (1993,1994) 29 A12 (1994) 29 A13 Trefethen and Bau Numerical Linear Algebra (1997) 29 A14 (1999) 30 A15 (2003) 30 A16 (2004) 30 A17 (2007) 30 A18
2013 8 29y, 2016 10 29 1 2 2 Jordan 3 21 3 3 Jordan (1) 3 31 Jordan 4 32 Jordan 4 33 Jordan 6 34 Jordan 8 35 9 4 Jordan (2) 10 41 x 11 42 x 12 43 16 44 19 441 19 442 20 443 25 45 25 5 Jordan 26 A 26 A1
O157 6/23 7/4 6 25 1000 117,050 6 14:00~15:30 1 2 22 22 14:30~15:30 8 12 1 5 20 6 20 10 11 30 9 10 6 1 30 6 6 0 30 6 19 0 3 27 6 20 0 50 1 2 6 4 61 1 6 5 1 2 1 2 6 19 6 4 15 6 1 6 30 6 24 30 59
1 1 36 223 42 14 92 4 3 2 1 4 3 4 3429 13536 5 6 7 8 9 2.4m/ (M) (M) (M) (M) (M) 6.67.3 6.57.2 6.97.6 7.27.8 8.4 5 6 5 6 5 5 74 1,239 0 30 21 ( ) 1,639 3,898 0 1,084 887 2 5 0 2 2 4 22 1 3 1 ( :) 426 1500
1 C 2 C 3 C 4 C 1 C 2 C 3 C
1 e N >. C 40 41 2 >. C 3 >.. C 26 >.. C .mm 4 C 106 e A 107 1 C 2 C 3 C 4 C 1 C 2 C 3 C 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124
平成２４年財政投融資計画ＰＤＦ出後８／０１６‐０３０
24 23 28,707,866 2,317,737 26,390,129 29,289,794 2,899,665 24 23 19,084,525 21,036,598 1952,073 24 23 8,603,613 8,393,427 967,631 925,404 202,440 179,834 217,469 219,963 66,716 64,877 3,160,423 2,951,165
1 2 http://www.japan-shop.jp/ 3 4 http://www.japan-shop.jp/ 5 6 http://www.japan-shop.jp/ 7 2,930mm 2,700 mm 2,950mm 2,930mm 2,950mm 2,700mm 2,930mm 2,950mm 2,700mm 8 http://www.japan-shop.jp/ 9 10 http://www.japan-shop.jp/
第18回海岸シンポジウム報告書
2011.6.25 2011.6.26 L1 2011.6.27 L2 2011.7.6 2011.12.7 2011.10-12 2011.9-10 2012.3.9 23 2012.4, 2013.8.30 2012.6.13 2013.9 2011.7-2011.12-2012.4 2011.12.27 2013.9 1m30 1 2 3 4 5 6 m 5.0m 2.0m -5.0m 1.0m
1 911 34/ 22 1012 2/ 20 69 3/ 22 69 1/ 22 69 3/ 22 69 1/ 22 68 3/ 22 68 1/ 3 8 D 0.0900.129mm 0.1300.179mm 0.1800.199mm 0.1000.139mm 0.1400.409mm 0.4101.199mm 0.0900.139mm 0.1400.269mm 0.2700.289mm
液晶ディスプレイ取説TD-E432/TD-E502/TD-E552/TD-E652/TD-E432D/TD-E502D
1 2 3 4 5 6 7 1 2 3 4 5 6 7 2 2 2 1 1 2 9 10 11 12 13 14 15 16 17 1 8 2 3 4 5 6 7 1 2 3 4 5 6 7 8 9 10 9 11 12 13 13 14 15 16 17 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 1 2 3 4 5 6 7 8 9 11 12
000-.\..
1 1 1 2 3 4 5 6 7 8 9 e e 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 10mm 150mm 60mm 25mm 40mm 30mm 25 26 27 1 28 29 30 31 32 e e e e e e 33 e 34 35 35 e e e e 36 37 38 38 e e 39 e 1 40 e 41 e 42 43
(1519) () 1 ( ) () 1 ( ) - 1 - - 2 - (1531) (25) 5 25,000 (25) 5 30,000 25,000 174 3 323 174 3 323 (1532) () 2 () 2-3 - - 4 - (1533) () 1 (2267)204 () (1)(2) () 1 (2267)204 () (1)(2) (3) (3) 840,000 680,000
[mm] [mm] [mm] 70 60 50 40 30 20 10 1H 0 18 19 20 21 22 23 24 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 1 2 3 4 5 6 7 8 9 10 11 12 60 50 40 30 20 10 0 18 19 20 21 22 23 24 1 2 3 4
0 1-4. 1-5. (1) + b = b +, (2) b = b, (3) + 0 =, (4) 1 =, (5) ( + b) + c = + (b + c), (6) ( b) c = (b c), (7) (b + c) = b + c, (8) ( + b)c = c + bc (9
1-1. 1, 2, 3, 4, 5, 6, 7,, 100,, 1000, n, m m m n n 0 n, m m n 1-2. 0 m n m n 0 2 = 1.41421356 π = 3.141516 1-3. 1 0 1-4. 1-5. (1) + b = b +, (2) b = b, (3) + 0 =, (4) 1 =, (5) ( + b) + c = + (b + c),
Chebyshev Schrödinger Heisenberg H = 1 2m p2 + V (x), m = 1, h = 1 1/36 1 V (x) = { 0 (0 < x < L) (otherwise) ψ n (x) = 2 L sin (n + 1)π x L, n = 0, 1, 2,... Feynman K (a, b; T ) = e i EnT/ h ψ n (a)ψ
J 9229-2887-26 P-A111 9229-2887-24 X-A110 9229-2887-24 106 4 4.1 1 25.1 25.4 20.4 17.9 21.2 23.1 26.2 1 24 12 14 18 36 42 24 10 5 15 120 30 15 20 10 25 35 20 18 30 12 4.1 7 min. z = 602.5x 1 + 305.0x 2 + 2
105 4 0 1? 1 LP 0 1 4.1 4.1.1 (intger programming problem) 1 0.5 x 1 = 447.7 448 / / 2 1.1.2 1. 2. 1000 3. 40 4. 20 106 4 4.1 1 25.1 25.4 20.4 17.9 21.2 23.1 26.2 1 24 12 14 18 36 42 24 10 5 15 120 30
2004 Copyright by Tatsuo Minohara Programming with Mac OS X in Lambda 21 - page 2
Living with Mac OS X in Lambda 21 2004 Copyright by Tatsuo Minohara Programming with Mac OS X in Lambda 21 - page 1 2004 Copyright by Tatsuo Minohara Programming with Mac OS X in Lambda 21 - page 2 2004
MacOSXLambdaJava.aw
Living with Mac OS X in Lambda 21 2005 Copyright by Tatsuo Minohara Programming with Mac OS X in Lambda 21 - page 1 2005 Copyright by Tatsuo Minohara Programming with Mac OS X in Lambda 21 - page 2 2005