FX自己アフリエイトマニュアル

FX ) 2

(FX) 1 1 2009 12 12 13 2009 1 FX ) 2 1 (FX) 2 1 2 1 2 3 2010 8 FX 1998 1 FX FX 4 1 1 (FX) () () 1998 4 1 100 120 1 100 120 120 100 20 FX 100 100 100 1 100 100 100 1 100 1 100 100 1 100 101 101 100 100

キャスティズム.PDF

日本消化器外科学会雑誌第16巻第7号

...h/...r...W001-004

Ver.1.0.1-1512 1. 03 2. 04 3. 05 05 4. 06 07 5. 08 6. 09 10 11 12 14 7. 19 2 1. Plus / 3 2. 1 4 3. Plus 5 4. FX 6 4. 7 5. 1 200 3 8 6. 38 25 16 9 6. 10 6. 11 6. 38 / 12 6. 13 6. 25 14 6. 0 359 15 6. 3

Nobelman 絵文字一覧

Nobelman i-mode EZweb J-SKY 1 88 2 89 3 33 4 32 5 5 F[ 6 6 FZ 7 35 W 8 34 W 9 7 F] W 10 8 F\ W 11 29 FR 12 30 FS 13 64 FU 14 63 FT 15 E697 42 FW 16 E678 70 FV 17 E696 43 FX 18 E6A5 71 FY 19 117 20 E6DA

BLOCK TYPE.indd

.\..*

CirQ045

CirQ 045-3 CirQ 045-4 CirQ 045-5 CirQ 045-6 CirQ 045-7 CirQ 045-8 CirQ 045-9 2007 5 19400m 2007 1 25500m http://otonanokagaku.net/issue/lab/vol5/ index04.html 2007 4 100m PE 8 ( ) () ( )?? CirQ 045-10

+ + + + n S (n) = + + + + n S (n) S (n) S 0 (n) S (n) 6 4 S (n) S (n) 7 S (n) S 4 (n) 8 6 S k (n) 0 7 (k + )S k (n) 8 S 6 (n), S 7 (n), S 8 (n), S 9 (

k k + k + k + + n k 006.7. + + + + n S (n) = + + + + n S (n) S (n) S 0 (n) S (n) 6 4 S (n) S (n) 7 S (n) S 4 (n) 8 6 S k (n) 0 7 (k + )S k (n) 8 S 6 (n), S 7 (n), S 8 (n), S 9 (n), S 0 (n) 9 S (n) S 4

統計学のポイント整理

.. September 17, 2012 1 / 55 n! = n (n 1) (n 2) 1 0! = 1 10! = 10 9 8 1 = 3628800 n k np k np k = n! (n k)! (1) 5 3 5 P 3 = 5! = 5 4 3 = 60 (5 3)! n k n C k nc k = npk k! = n! k!(n k)! (2) 5 3 5C 3 = 5!

17 ( ) II III A B C(100 ) 1, 2, 6, 7 II A B (100 ) 2, 5, 6 II A B (80 ) 8 10 I II III A B C(80 ) 1 a 1 = 1 2 a n+1 = a n + 2n + 1 (n = 1,

17 ( ) 17 5 1 4 II III A B C(1 ) 1,, 6, 7 II A B (1 ), 5, 6 II A B (8 ) 8 1 I II III A B C(8 ) 1 a 1 1 a n+1 a n + n + 1 (n 1,,, ) {a n+1 n } (1) a 4 () a n OA OB AOB 6 OAB AB : 1 P OB Q OP AQ R (1) PQ

春期講座 ~ 極限 1 1, 1 2, 1 3, 1 4,, 1 n, n n {a n } n a n α {a n } α {a n } α lim n an = α n a n α α {a n } {a n } {a n } 1. a n = 2 n {a n } 2, 4, 8, 16,

春期講座 ~ 極限 1 1, 1 2, 1 3, 1 4,, 1 n, n n {a n } n a n α {a n } α {a n } α lim an = α n a n α α {a n } {a n } {a n } 1. a n = 2 n {a n } 2, 4, 8, 16, 32, n a n {a n } {a n } 2. a n = 10n + 1 {a n } lim an

V 0 = + r pv (H) + qv (T ) = + r ps (H) + qs (T ) = S 0 X n+ (T ) = n S n+ (T ) + ( + r)(x n n S n ) = ( + r)x n + n (d r)s n = ( + r)v n + V n+(h) V

I (..2) (0 < d < + r < u) X 0, X X = 0 S + ( + r)(x 0 0 S 0 ) () X 0 = 0, P (X 0) =, P (X > 0) > 0 0 H, T () X 0 = 0, X (H) = 0 us 0 ( + r) 0 S 0 = 0 S 0 (u r) X (T ) = 0 ds 0 ( + r) 0 S 0 = 0 S 0 (d r)

0

G 1 G 2 3 2 3 4 14 f f 0 G G G G a1 GF f 1 1 1 L I H M K J f 1 5 G G G G GG Aa G f 6 G G G Aa G f 1 2 1 2 3 45 C 123 3 4 1234 5 6 7 123 e 8 9 0 1 2 3 4 1 2 3 4 14 f N f f f 1 1 2 12 3 4 5 6 f 3 G G 1 12

FXneo FXneo PC FXneo FX 1 2

FXneo FXneo PC FXneo FX 1 2 FXneo 1. 04 2. 07 PC FX 07 08 09 10 11 13 3. 14 14 19 4. 20 5. 21 3 FXneo 1. 1 4 FXneo 1. 1 1 / 1 5 FXneo 1. 1 2 6 FXneo 2. PC PC FXneo- 2 [ ] 7 FXneo 2. PC 8 FXneo 2. PC 50pips

1 1.1 Excel Excel Excel log 1, log 2, log 3,, log 10 e = ln 10 log cm 1mm 1 10 =0.1mm = f(x) f(x) = n

1 1.1 Excel Excel Excel log 1, log, log,, log e.7188188 ln log 1. 5cm 1mm 1 0.1mm 0.1 4 4 1 4.1 fx) fx) n0 f n) 0) x n n! n + 1 R n+1 x) fx) f0) + f 0) 1! x + f 0)! x + + f n) 0) x n + R n+1 x) n! 1 .

磁性物理学 - 遷移金属化合物磁性のスピンゆらぎ理論

email: [email protected] May 14, 2009 Outline 1. 2. 3. 4. 5. 6. 2 / 262 Today s Lecture: Mode-mode Coupling Theory 100 / 262 Part I Effects of Non-linear Mode-Mode Coupling Effects of Non-linear

1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. !"#$ %&'( )*#$ %&'( +*#$ %&'(,$ -./ 01234 56.7865/ 9 :6:5/ ;$ 5 :6 :6::/ F$ B/ GH :68.7:6B/ I>J> :6::/ KL=34 :65.7:68/

０９　Ｐ１０７〜１１８／木下　〃　芦塚　〃　稲

NK NK NK NK NK NK NK KT M NK NK KT M NK KT VTR SR SR SR SR SR SR KT NK NK FU M M A B C D E NK F G H I J I K M I I S R L L C C NKCL F C J J F M I J NK M M DY NK E E NK D D C D SR E D C C M NK NK SJ KK NK

( )

18 10 01 ( ) 1 2018 4 1.1 2018............................... 4 1.2 2018......................... 5 2 2017 7 2.1 2017............................... 7 2.2 2017......................... 8 3 2016 9 3.1 2016...............................

[FX8/FX8C]シリーズカタログ

2018.6 FX8-120 P - SV 192 1 2 3 1 2 3 4 5 6 6 B 4 5 6 B 0.6±0.1 B +0.05 _0.2 C +0.05 _0.2 D±0.2 6.5 _0.3 0 5.1±0.3 2.45±0.25 (0.4) (0.75) (Ø0.9) t0.2±0.03 w0.25±0.03 (Ø0.6) 2-(C0.2) (1.5) E±0.1 FX8-60P-SV(**)

May Copyright 2016 HIROSE ELECTRIC CO., LTD. All Rights Reserved w

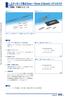2014.9w FX8-120 P - SV 192 1 2 3 1 2 3 4 5 6 6 B 4 5 6 B 0.6±0.1 B +0.05 _0.2 C +0.05 _0.2 D±0.2 6.5 _0.3 0 5.1±0.3 2.45±0.25 (0.4) (0.75) (Ø0.9) t0.2±0.03 w0.25±0.03 (Ø0.6) 2-(C0.2) (1.5) E±0.1 FX8-60P-SV(92)

(2 X Poisso P (λ ϕ X (t = E[e itx ] = k= itk λk e k! e λ = (e it λ k e λ = e eitλ e λ = e λ(eit 1. k! k= 6.7 X N(, 1 ϕ X (t = e 1 2 t2 : Cauchy ϕ X (t

6 6.1 6.1 (1 Z ( X = e Z, Y = Im Z ( Z = X + iy, i = 1 (2 Z E[ e Z ] < E[ Im Z ] < Z E[Z] = E[e Z] + ie[im Z] 6.2 Z E[Z] E[ Z ] : E[ Z ] < e Z Z, Im Z Z E[Z] α = E[Z], Z = Z Z 1 {Z } E[Z] = α = α [ α ]

1 4 2 (1) (B4:B6) (2) (B12:B14) (3) 1 (D4:H4) D5:H243 (4) 240 20 (B8:B10) (5) 240 (B8) 0 1

4 1 4 (1) (2) (3) (4) 1 4 2 (1) (B4:B6) (2) (B12:B14) (3) 1 (D4:H4) D5:H243 (4) 240 20 (B8:B10) (5) 240 (B8) 0 1 4 3 2 2.1 2 Excel 2 (A1:A14 D3:H3 B4,B5,B6) B5 0.035 4 4 2.2 3 1 1 B12: =B5+1 B13: =B12

N/m f x x L dl U 1 du = T ds pdv + fdl (2.1)

23 2 2.1 10 5 6 N/m 2 2.1.1 f x x L dl U 1 du = T ds pdv + fdl (2.1) 24 2 dv = 0 dl ( ) U f = T L p,t ( ) S L p,t (2.2) 2 ( ) ( ) S f = L T p,t p,l (2.3) ( ) U f = L p,t + T ( ) f T p,l (2.4) 1 f e ( U/

取扱説明書 F903i

309 I 1 me51e t 2 a b c d ab cd a b c d t a 3 g t c t cmtpa j 310 g p m7 t m0k g g I 1 me51e me5 c 1 me51ee me2 2 1e e 2 3e 4e1 2 5e17 6e14 7 8e10 I I I I 1 me51e 2 me41 me4 2 e 311 3 1 me51ee pem 2 e

( ) FAS87 FAS FAS87 v = 1 i 1 + i

( ) ( 7 6 ) ( ) 1 6 1 18 FAS87 FAS87 7 1 FAS87 v = 1 i 1 + i 10 14 6 6-1 - 7 73 2 N (m) N L m a N (m) L m a N m a (m) N 73 9 99 18 4-2 - 4 143 2 145 3 37 4 37 4 40 6 40 6 41 10 41 10 13 10 14 4 24 3 145

A 2008 10 (2010 4 ) 1 1 1.1................................. 1 1.2..................................... 1 1.3............................ 3 1.3.1............................. 3 1.3.2..................................

1

0 1 2 OK NG 3 ID 4 CMS 5 CMS 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 [PDF 7KB] [ ] 22 23 (HP ( pt) ) () ( 24 25 ( ) 26 27 28 29 #() URL # # 30 [PDF 7KB] [ ] 31 32 33 34 35 HTML HTML 36 37 38 39 40

閨 , , , 縺05, 縺 縺05, 閨 [

04050900708 000 0. 07050 70, 0 0806 ﾀ07 09 0909080900706009 040080 縺0408 縺0505 00070800060405 ﾀ05 縺040070 090800008080900504040009 09050409080500004040009 050000080908 0000 09080905004090 0508050400 0

1

家族の将来

入試の軌跡

4 y O x 4 Typed by L A TEX ε ) ) ) 6 4 ) 4 75 ) http://kumamoto.s.xrea.com/plan/.. PDF) Ctrl +L) Ctrl +) Ctrl + Ctrl + ) ) Alt + ) Alt + ) ESC. http://kumamoto.s.xrea.com/nyusi/kumadai kiseki ri i.pdf

12 2 E ds = 1 ρdv ε 1 µ D D S S D B d S = 36 E d B l = S d S B d l = S ε E + J d S 4 4 div E = 1 ε ρ div B = rot E = B 1 rot µ E B = ε + J 37 3.2 3.2.

213 12 1 21 5 524 3-5465-74 [email protected] http://lecture.ecc.u-tokyo.ac.jp/~nkiyono/index.html 3 2 1 3.1 ρp, t EP, t BP, t JP, t 35 P t xyz xyz t 4 ε µ D D S S 35 D H D = ε E B = µ H E

1

.1 z = e x +xy y z y 1 1 x 0 1 z x y α β γ z = αx + βy + γ (.1) ax + by + cz = d (.1') a, b, c, d x-y-z (a, b, c). x-y-z 3 (0,

.1.1 Y K L Y = K 1 3 L 3 L K K (K + ) 1 1 3 L 3 K 3 L 3 K 0 (K + K) 1 3 L 3 K 1 3 L 3 lim K 0 K = L (K + K) 1 3 K 1 3 3 lim K 0 K = 1 3 K 3 L 3 z = f(x, y) x y z x-y-z.1 z = e x +xy y 3 x-y ( ) z 0 f(x,

5 1.2, 2, d a V a = M (1.2.1), M, a,,,,, Ω, V a V, V a = V + Ω r. (1.2.2), r i 1, i 2, i 3, i 1, i 2, i 3, A 2, A = 3 A n i n = n=1 da = 3 = n=1 3 n=1

4 1 1.1 ( ) 5 1.2, 2, d a V a = M (1.2.1), M, a,,,,, Ω, V a V, V a = V + Ω r. (1.2.2), r i 1, i 2, i 3, i 1, i 2, i 3, A 2, A = 3 A n i n = n=1 da = 3 = n=1 3 n=1 da n i n da n i n + 3 A ni n n=1 3 n=1

( ) ( ) 1729 (, 2016:17) = = (1) 1 1

1729 1 2016 10 28 1 1729 1111 1111 1729 (1887 1920) (1877 1947) 1729 (, 2016:17) 12 3 1728 9 3 729 1729 = 12 3 + 1 3 = 10 3 + 9 3 (1) 1 1 2 1729 1729 19 13 7 = 1729 = 12 3 + 1 3 = 10 3 + 9 3 13 7 = 91

Im~ ~xplanations (im~; 斎目 ) ~ng dü~

熊本大学学術リポジトリ Kumamoto University Repositor Title 日本における夢研究の展望補遺 (II) : 古代におけるイメ ( 夢 ) の問題 Author(s) 名島, 潤慈 Citation 熊本大学教育実践研究, 12: 63-72 Issue date 1995-02-28 Type URL Departmental Bulletin Paper http://hdl.handle.net/2298/20725

r 1 m A r/m i) t ii) m i) t B(t; m) ( B(t; m) = A 1 + r ) mt m ii) B(t; m) ( B(t; m) = A 1 + r ) mt m { ( = A 1 + r ) m } rt r m n = m r m n B

1 1.1 1 r 1 m A r/m i) t ii) m i) t Bt; m) Bt; m) = A 1 + r ) mt m ii) Bt; m) Bt; m) = A 1 + r ) mt m { = A 1 + r ) m } rt r m n = m r m n Bt; m) Aert e lim 1 + 1 n 1.1) n!1 n) e a 1, a 2, a 3,... {a n

\\Comet\MrAD\マニュ~1\原稿\DSE-

Tempest XGA Pocket FX Model:DSE-001 Multimedia Series PC Video Encoder http://www.ad-techno.com/regist/ FAX:03-5213-5323 Tempest XGA PocketFX Tempest XGA PocketFX Tempest XGA PocketFX Tempest XGA

EOS Kiss F 使用説明書

J J 2 3 6 V U 0 S 0 9 8 3 M M M 1 4 1 2 3 4 5 6 7 8 9 10 5 6 1 2 1 2 3 4 5 6 7 j x 3 4 5 d Z D E S i A s f a 8 q Oy A A A A B 7 6 7 B f x H u b K L B 8 8 9 10 w W d 9 i j s f 7 73 83 1 76 86 10 S x H K

Grushin 2MA16039T

Grushin 2MA1639T 3 2 2 R d Borel α i k (x, bi (x, 1 i d, 1 k N d N α R d b α = α(x := (αk(x i 1 i d, 1 k N b = b(x := (b i (x 1 i d X = (X t t x R d dx t = α(x t db t + b(x t dt ( 3 u t = Au + V u, u(,

1 α X (path) α I = [0, 1] X α(0) = α(1) = p α p (base point) loop α(1) = β(0) X α, β α β : I X (α β)(s) = ( )α β { α(2s) (0 s 1 2 ) β(2s 1) ( 1 2 s 1)

1 α X (path) α I = [0, 1] X α(0) = α(1) = p α p (base point) loop α(1) = β(0) X α, β α β : I X (α β)(s) = ( )α β { α(2s) (0 s 1 2 ) β(2s 1) ( 1 2 s 1) X α α 1 : I X α 1 (s) = α(1 s) ( )α 1 1.1 X p X Ω(p)