Microsoft PowerPoint - 画像工学2007-2印刷用++++
|
|
|
- あまめ いまいだ
- 7 years ago
- Views:
Transcription
1 教室 : OCTOBER 09 画像工学 2007 年度版 Imaging Science and Technolog 画像工学 2007 年度版 2 慶応義塾大学理工学部 教授 中島真人 1
2 ( 例 ) 画像システムとしてのカメラ 入力 f(,) ( 紙に書かれた文字 ) カメラ ( フィルムカメラ デジタルカメラ どちらでも OK ) (u,v) SYSTEM ( フィルム上または CCD 面上の画像 ) 出力 g(,) 画像の場合の伝達関数を OTF という! ( 例 ) 画像システムとしてのカメラ 入力 f(,) ( 紙に書かれた文字 ) カメラ ( フィルムカメラ デジタルカメラ どちらでも OK ) (u,v) SYSTEM 伝達関数 OTF ( Optical Transfer Function ) G ( u, v ) = ( u, v ) F ( u, v ) FT G ( u, v ) g (, ) g (, ) = G, h (, ) =, インパルス応答 ( フィルム上または CCD 面上の画像 ) 出力 g(,) + ( ( u v ) e u + v ) dudv + ( ( u v ) e u + v ) dudv 2
3 ( 例 ) 画像システムとしてのカメラ 入力 f(,) ( 紙に書かれた文字 ) カメラ ( フィルムカメラ デジタルカメラ どちらでも OK ) (u,v) SYSTEM 伝達関数 OTF ( Optical Transfer Function ) G ( u, v ) = ( u, v ) F ( u, v ) FT G ( u, v ) g (, ) 出力 g(,) カメラで撮影された写真 g(,) は 物体 f(,) と伝達関数 (,) のフーリエ逆変換であるインパルス応答 h(,) のコンボリューションによって表される. 言い方を変えると カメラで撮影された写真は h(,) によってボカされたものになっている! と言うことができる. ( フィルム上または CCD 面上の画像 ) 画像の場合のインパルス応答 (OTFのフーリ逆変換) を 点拡がり関数 ( PSF: Point Spread Function ) という. PSF,OTF の求め方 ピンホール (1 画像サイズ ) h(,) PSF δ(,) インパルス FT h (, ) ( u, v ) PSF OTF 3
4 画像空間上空間上でのコンボリューションとは 時間軸上では f(t) h(t) g ( t ) = f ( t ) h ( t ) 画像空間上では f(,) h(,) g (, ) = f (, ) h (, ) 画像空間上空間上でのコンボリューションとは h (,) g (,) f (,) g (, = f ( ), ) h (, ) 4
5 画像空間上空間上でのコンボリューションとは f (,) h (,) g (, ) = f (, ) h (, ) FT FT FT F (u,v) (u,v) G ( u, v ) = F ( u, v ) ( u, v ) 画像空間上空間上でのコンボリューションとは f (,) h (,) g (, ) = f (, ) h (, ) FT FT FT F (u,v) (u,v) G ( u, v ) = F ( u, v ) ( u, v ) 5
6 画像空間上空間上でのコンボリューションとは f (,) h (,) g (, ) = f (, ) h (, ) FT FT FT F (u,v) (u,v) G ( u, v ) = F ( u, v ) ( u, v ) 画像空間上空間上でのコンボリューションとは f (,) h (,) g (, ) = f (, ) h (, ) FT FT FT 両者の違い 何による? F (u,v) (u,v) G ( u, v ) = F ( u, v ) ( u, v ) 6
7 Application.1 [ 画像のボケ補正 ] f (,) g(,) 画像システム (u,v) 撮影した写真がボケてしまった しまった どうしよう? g (, ) = f (, ) h (, ) Convolution 定理 G ( u, v ) = ( u, v ) F ( u, v ) 具体的には δ (,) 1 st step g(,) 画像システム (u,v) h (,) PSF フーリエ変換して 逆数をとる ~. f(,) 2 nd step 逆フィルタ -1 (u,v) G 1 = F FT F ~ f (, ) ボケの取れた取れた画像 7
8 原画像ボケ画像修正画像 PSF 諸君にも簡単にできるので 自分のパソコンで試してみてください ただ 何も考えないでやると はじめは全然駄目かもしれません! その第一の理由は 8
9 その第一の理由は 逆フィルタ : De-convolution Filter G 1 = 1 G X 0 の計算において なる計算をしなければならないところが沢山出てくるのが問題! そこで この計算をする場合には 1 = 1 1/ 2 + Γ を 用いる. これを ウィーナーフィルタ ウィーナーフィルタ という 適当に選んだ小さ目の定数 修正画像 修正画像が 何かもう一つきれいにならない第一の理由は この式が用いられているところにある. 9
10 De-convolution の実空間処理 では... コピーマシン等の実用機でも 実際にこの計算を使うことは可能であろうか? NO! 実用機では Cost-performance が悪くて使えない. De-convolution の実空間処理 Cost-performance 問題とは... (1) メモリ使用量 : 白黒 A4 原稿の情報量 4MB (2) 処理時間 : コピーマシン等では準実時間処理が必至 スキャン g G ボケ G/ f FT IFT 補正 印刷 f 周波数空間での処理はこの部分に時間がかかり過ぎる! 原稿 印刷物 どうせ原稿の読み取り ( スキャン ) に時間が掛かるのだから その間に ボケ補正の処理 を行えば良いい! 逐次的に処理 10
11 ボケとは 原稿上の 1 点の情報が 印刷物上で空間的にばら撒かれる現象である. 原稿 印刷物 そこで 原稿を読み取りながら だいたい数行ずつ処理していくことにする 逐次処理 逐次処理に適した De-convolution 演算 実空間 ( - 空間 ) での処理 g (, ) = f (, ) h(, ) これを外したい! = f (, ) h(, ) d d フーリエ空間 (u-v( 空間 ) で行うように簡単にはいかない. フーリエ変換は 使用しない! ただし その考え方は採用する! 11
12 G 1 = F FT これを 実空間で考えてみよう! g 1 = h f で 良いか? f h 1 h 1 駄目!!! 正解は... [ ] 1 f g F = これを使う! ここで すなわち h F FF [ h ] = 1 1 [ ] 1 G = F 12
13 1 のかたち δ(,) 0-1 (u,v) u h (,) F[ F -1 ] (u,v) u これを De-convolution Window とも言う. 具体的な De-convolution Window の形
14 Piel De-convolution Window (3 3) De-convolution Window ( ここでは 3 3) を 1piel づつ移動しながら畳み込んでいく. スキャン終了と略同じにボケ補正も終了する 年度 画像工学 第 2 回講義 おわり 14
スライド タイトルなし
 次元フーリエ変換 講義内容 空間周波数の概念 次元フーリエ変換代表的な 次元フーリエ変換対 次元離散フーリエ変換 フーリエ変換と逆変換 F.T. j F } ep{ 連続系離散系 } / ep{ N N N j N F F I. F.T. F ただし ここでは絶対値をとって画像化 } / ep{ N N N j F N 順変換逆変換 3 次元フーリエ変換の具体的なイメージ } / ep{ N N N
次元フーリエ変換 講義内容 空間周波数の概念 次元フーリエ変換代表的な 次元フーリエ変換対 次元離散フーリエ変換 フーリエ変換と逆変換 F.T. j F } ep{ 連続系離散系 } / ep{ N N N j N F F I. F.T. F ただし ここでは絶対値をとって画像化 } / ep{ N N N j F N 順変換逆変換 3 次元フーリエ変換の具体的なイメージ } / ep{ N N N
Microsoft PowerPoint - 画像工学2007-5印刷用
 教室 : 4- NOVEMBER 6 画像工学 7 年度版 Imging Scinc nd Tchnolog 画像工学 7 年度版 5 慶応義塾大学理工学部 教授 中島真人 3. 画像のスペクトラム 3-. 画像のフーリエ変換と空間周波数の概念 3-. 簡単な図形のフーリエ変換 3-3. フーリエ変換の重要な性質 3-4. MTF と画像の評価 今週と来週は あまり面白くない. でも 後の講義を理解するために,
教室 : 4- NOVEMBER 6 画像工学 7 年度版 Imging Scinc nd Tchnolog 画像工学 7 年度版 5 慶応義塾大学理工学部 教授 中島真人 3. 画像のスペクトラム 3-. 画像のフーリエ変換と空間周波数の概念 3-. 簡単な図形のフーリエ変換 3-3. フーリエ変換の重要な性質 3-4. MTF と画像の評価 今週と来週は あまり面白くない. でも 後の講義を理解するために,
Microsoft PowerPoint - ip02_01.ppt [互換モード]
![Microsoft PowerPoint - ip02_01.ppt [互換モード] Microsoft PowerPoint - ip02_01.ppt [互換モード]](/thumbs/96/127250376.jpg) 空間周波数 周波数領域での処理 空間周波数 (spatial frquncy) とは 単位長さ当たりの正弦波状の濃淡変化の繰り返し回数を表したもの 正弦波 : y sin( t) 周期 : 周波数 : T f / T 角周波数 : f 画像処理 空間周波数 周波数領域での処理 波形が違うと 周波数も違う 画像処理 空間周波数 周波数領域での処理 画像処理 3 周波数領域での処理 周波数は一つしかない?-
空間周波数 周波数領域での処理 空間周波数 (spatial frquncy) とは 単位長さ当たりの正弦波状の濃淡変化の繰り返し回数を表したもの 正弦波 : y sin( t) 周期 : 周波数 : T f / T 角周波数 : f 画像処理 空間周波数 周波数領域での処理 波形が違うと 周波数も違う 画像処理 空間周波数 周波数領域での処理 画像処理 3 周波数領域での処理 周波数は一つしかない?-
Microsoft PowerPoint - 画像工学2007-8印刷用
 教室 : 14-0 DECEMBER 04 画像工学 007 年度版 Imagng Scnc and Tchnolog 画像工学 007 年度版 8 慶応義塾大学理工学部 教授 中島真人 Drctonal Band-pass Fltr の効果 前回の講義 訂正があります! Huv g v u ここで フィルタの形が間違っていました. Input Imag v Drctonal Band-pass Fltr
教室 : 14-0 DECEMBER 04 画像工学 007 年度版 Imagng Scnc and Tchnolog 画像工学 007 年度版 8 慶応義塾大学理工学部 教授 中島真人 Drctonal Band-pass Fltr の効果 前回の講義 訂正があります! Huv g v u ここで フィルタの形が間違っていました. Input Imag v Drctonal Band-pass Fltr
Microsoft PowerPoint - 第3回2.ppt
 講義内容 講義内容 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 ベクトルの直交性 3
講義内容 講義内容 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 ベクトルの直交性 3
例 e 指数関数的に減衰する信号を h( a < + a a すると, それらのラプラス変換は, H ( ) { e } e インパルス応答が h( a < ( ただし a >, U( ) { } となるシステムにステップ信号 ( y( のラプラス変換 Y () は, Y ( ) H ( ) X (
 第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
画像解析論(2) 講義内容
 画像解析論 画像解析論 東京工業大学長橋宏 主な講義内容 信号処理と画像処理 二次元システムとその表現 二次元システムの特性解析 各種の画像フィルタ 信号処理と画像処理 画像解析論 処理の応答 記憶域 入出力の流れ 信号処理系 実時間性が求められる メモリ容量に対する制限が厳しい オンラインでの対応が厳しく求められる 画像処理系 ある程度の処理時間が許容される 大容量のメモリ使用が容認され易い オフラインでの対応が容認され易い
画像解析論 画像解析論 東京工業大学長橋宏 主な講義内容 信号処理と画像処理 二次元システムとその表現 二次元システムの特性解析 各種の画像フィルタ 信号処理と画像処理 画像解析論 処理の応答 記憶域 入出力の流れ 信号処理系 実時間性が求められる メモリ容量に対する制限が厳しい オンラインでの対応が厳しく求められる 画像処理系 ある程度の処理時間が許容される 大容量のメモリ使用が容認され易い オフラインでの対応が容認され易い
臨床画像技術学Ⅱ
 核医学機器工学概論 2 断層画像 CT( Computed Tomography) を得る方法 1. フィルタ重畳逆投影法 FBP ( Filtered Back Projection ) 2. 逐次近似再構成法 Iterative Reconstruction MLEM (Maximum Likelihood Expectation Maximization) OSEM ( Ordered Subsets
核医学機器工学概論 2 断層画像 CT( Computed Tomography) を得る方法 1. フィルタ重畳逆投影法 FBP ( Filtered Back Projection ) 2. 逐次近似再構成法 Iterative Reconstruction MLEM (Maximum Likelihood Expectation Maximization) OSEM ( Ordered Subsets
第 4 週コンボリューションその 2, 正弦波による分解 教科書 p. 16~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問 1. 以下の図にならって,1 と 2 の δ 関数を図示せよ δ (t) 2
 第 4 週コンボリューションその, 正弦波による分解 教科書 p. 6~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問. 以下の図にならって, と の δ 関数を図示せよ. - - - δ () δ ( ) - - - 図 δ 関数の図示の例 δ ( ) δ ( ) δ ( ) δ ( ) δ ( ) - - - - - - - -
第 4 週コンボリューションその, 正弦波による分解 教科書 p. 6~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問. 以下の図にならって, と の δ 関数を図示せよ. - - - δ () δ ( ) - - - 図 δ 関数の図示の例 δ ( ) δ ( ) δ ( ) δ ( ) δ ( ) - - - - - - - -
PowerPoint Presentation
 付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
EPSON PM-A920 操作ガイド
 h o h l m l m l m l m m h o h o h h h h h h h h h h h h h h h h o h h h h o o o o h o o h h h h o h h h h h h h h h h h h h o o h h h h h h h h h A h B h C D F h G E A h B h C D E h F h E h F h
h o h l m l m l m l m m h o h o h h h h h h h h h h h h h h h h o h h h h o o o o h o o h h h h o h h h h h h h h h h h h h o o h h h h h h h h h A h B h C D F h G E A h B h C D E h F h E h F h
遅延デジタルフィルタの分散型積和演算回路を用いたFPGA実装の検討
 第 回電気学会東京支部栃木 群馬支所合同研究発表会 ETT--7 遅延デジタルフィルタの分散型積和演算回路を用いた FPGA 実装の検討 易茹 * 立岩武徳 ( 群馬大学 ) 浅見幸司 ( 株式会社アドバンテスト ) 小林春夫 ( 群馬大学 ) 発表内容 研究の背景 目的 分散型積和演算回路 実装の検討 まとめ 今後の課題 発表内容 研究の背景 目的 分散型積和演算回路 実装の検討 まとめ 今後の課題
第 回電気学会東京支部栃木 群馬支所合同研究発表会 ETT--7 遅延デジタルフィルタの分散型積和演算回路を用いた FPGA 実装の検討 易茹 * 立岩武徳 ( 群馬大学 ) 浅見幸司 ( 株式会社アドバンテスト ) 小林春夫 ( 群馬大学 ) 発表内容 研究の背景 目的 分散型積和演算回路 実装の検討 まとめ 今後の課題 発表内容 研究の背景 目的 分散型積和演算回路 実装の検討 まとめ 今後の課題
数学 t t t t t 加法定理 t t t 倍角公式加法定理で α=β と置く. 三角関数
 . 三角関数 基本関係 t cot c sc c cot sc t 還元公式 t t t t t t cot t cot t 数学 数学 t t t t t 加法定理 t t t 倍角公式加法定理で α=β と置く. 三角関数 数学. 三角関数 5 積和公式 6 和積公式 数学. 三角関数 7 合成 t V v t V v t V V V V VV V V V t V v v 8 べき乗 5 6 6
. 三角関数 基本関係 t cot c sc c cot sc t 還元公式 t t t t t t cot t cot t 数学 数学 t t t t t 加法定理 t t t 倍角公式加法定理で α=β と置く. 三角関数 数学. 三角関数 5 積和公式 6 和積公式 数学. 三角関数 7 合成 t V v t V v t V V V V VV V V V t V v v 8 べき乗 5 6 6
<B54CB5684E31A4E9C0CBA4E5AA6BC160BEE3B27AA544A5552E706466>
 N1 2 3 1 16 17 18 19 20 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 4 2 38 39 40 41 42 44 45 46 47 48 50 51 52 53 54 55 56 57 58 59 60 61 5 3 62 63 64 65 66 68 69 70 70 72 74 75 76 77 78 80 81 82 83
N1 2 3 1 16 17 18 19 20 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 4 2 38 39 40 41 42 44 45 46 47 48 50 51 52 53 54 55 56 57 58 59 60 61 5 3 62 63 64 65 66 68 69 70 70 72 74 75 76 77 78 80 81 82 83
Microsoft PowerPoint - 6.PID制御.pptx
 プロセス制御工学 6.PID 制御 京都大学 加納学 Division of Process Control & Process Systems Engineering Department of Chemical Engineering, Kyoto University [email protected] http://www-pse.cheme.kyoto-u.ac.jp/~kano/
プロセス制御工学 6.PID 制御 京都大学 加納学 Division of Process Control & Process Systems Engineering Department of Chemical Engineering, Kyoto University [email protected] http://www-pse.cheme.kyoto-u.ac.jp/~kano/
線形システム応答 Linear System response
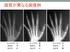 画質が異なる画像例 コントラスト劣 コントラスト優 コントラスト普 鮮鋭性 普 鮮鋭性 優 鮮鋭性 劣 粒状性 普 粒状性 劣 粒状性 優 医用画像の画質 コントラスト, 鮮鋭性, 粒状性の要因が互いに密接に関わり合って形成されている. 比 鮮鋭性 コントラスト 反 反 粒状性 増感紙 - フィルム系での 3 要因の関係 ディジタル画像処理系でもおよそ成り立つ WS u MTFu 画質に影響する因子
画質が異なる画像例 コントラスト劣 コントラスト優 コントラスト普 鮮鋭性 普 鮮鋭性 優 鮮鋭性 劣 粒状性 普 粒状性 劣 粒状性 優 医用画像の画質 コントラスト, 鮮鋭性, 粒状性の要因が互いに密接に関わり合って形成されている. 比 鮮鋭性 コントラスト 反 反 粒状性 増感紙 - フィルム系での 3 要因の関係 ディジタル画像処理系でもおよそ成り立つ WS u MTFu 画質に影響する因子
Microsoft PowerPoint - dm1_5.pptx
 デジタルメディア処理 1 017( 後期 ) 09/6 イントロダクション1 : デジタル画像とは, 量 化と標本化,Dynamic Range 10/03 イントロダクション : デジタルカメラ, 間の視覚, 表 系 10/10 フィルタ処理 1 : トーンカーブ, 線形フィルタ デジタルメディア処理 1 担当 : 井尻敬 10/17 フィルタ処理 : 線形フィルタ, ハーフトーニング 10/4
デジタルメディア処理 1 017( 後期 ) 09/6 イントロダクション1 : デジタル画像とは, 量 化と標本化,Dynamic Range 10/03 イントロダクション : デジタルカメラ, 間の視覚, 表 系 10/10 フィルタ処理 1 : トーンカーブ, 線形フィルタ デジタルメディア処理 1 担当 : 井尻敬 10/17 フィルタ処理 : 線形フィルタ, ハーフトーニング 10/4
Microsoft Word - 知能機械実験・実習プリント_ docx
 018 年 5 月 1 日版 知能機械実験 実習 Ⅳ Ⅳ-1. 制御工学実験 1. 実験概要と目的 ロボットをはじめとするメカトロニクス機器において 高度な動作を実現している背景には 制御技術がある 制御とは 物体の運動を意図した位置や速度で動かす技術である 精度の高い制御を行うためには 正しく制御理論を理解した上に 物体の運動を正しく解析し モデル化する技術や 制御を行うためのパラメータの同定方法を身につける必要がある
018 年 5 月 1 日版 知能機械実験 実習 Ⅳ Ⅳ-1. 制御工学実験 1. 実験概要と目的 ロボットをはじめとするメカトロニクス機器において 高度な動作を実現している背景には 制御技術がある 制御とは 物体の運動を意図した位置や速度で動かす技術である 精度の高い制御を行うためには 正しく制御理論を理解した上に 物体の運動を正しく解析し モデル化する技術や 制御を行うためのパラメータの同定方法を身につける必要がある
2.Picasa3 の実行 デスクトップの をダブルククリック 一番最初の起動の時だけ下記画 面が立ち上がります マイドキュメント マイピクチャ デスクトップのみスキャン にチェックを入れ続行 これはパソコン内部の全画像を検索して Picasa で使用する基本データを作成するものですが 完全スキャン
 Picasa3 を使った写真の整理 写真の整理はエクスプローラーを開いてフォルダの作成から写真の移動やコピーを行うことが望ましいのですが エクスプローラーの操作を覚えられずに写真の整理が進んでいない人のために画像管理ソフト Picasa3 を使った整理方法を説明します なお このソフトは画像に関する多くの機能を持ったものですが 画像整理だけの利用では容量も大きいですからエクスプローラーの使い方をマスターしている人はこのソフトを使う必要はありません
Picasa3 を使った写真の整理 写真の整理はエクスプローラーを開いてフォルダの作成から写真の移動やコピーを行うことが望ましいのですが エクスプローラーの操作を覚えられずに写真の整理が進んでいない人のために画像管理ソフト Picasa3 を使った整理方法を説明します なお このソフトは画像に関する多くの機能を持ったものですが 画像整理だけの利用では容量も大きいですからエクスプローラーの使い方をマスターしている人はこのソフトを使う必要はありません
Microsoft Word - 01マニュアル・入稿原稿p1-112.doc
 4 54 55 56 ( ( 1994 1st stage 2nd stage 2012 57 / 58 365 46.6 120 365 40.4 120 13.0 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 4 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97
4 54 55 56 ( ( 1994 1st stage 2nd stage 2012 57 / 58 365 46.6 120 365 40.4 120 13.0 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 4 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97
スライド 1
 作成 : 群馬大学電気電子教員 電子回路設計 OP アンプ (2) 小林春夫 桑名杏奈 Email: [email protected] Tel: 277-3-788 オフィスアワー : AM9:~AM:( 平日 ) 電気電子棟 (3 号館 )4F 44 室 電子回路設計 授業の内容 第 回講義内容の説明と電子回路設計の基礎知識 第 2 回キルヒホッフ則を用いた回路解析と演習 第 3 回集積回路のデバイス
作成 : 群馬大学電気電子教員 電子回路設計 OP アンプ (2) 小林春夫 桑名杏奈 Email: [email protected] Tel: 277-3-788 オフィスアワー : AM9:~AM:( 平日 ) 電気電子棟 (3 号館 )4F 44 室 電子回路設計 授業の内容 第 回講義内容の説明と電子回路設計の基礎知識 第 2 回キルヒホッフ則を用いた回路解析と演習 第 3 回集積回路のデバイス
インターリーブADCでのタイミングスキュー影響のデジタル補正技術
 1 インターリーブADCでのタイミングスキュー影響のデジタル補正技術 浅見幸司 黒沢烈士 立岩武徳 宮島広行 小林春夫 ( 株 ) アドバンテスト 群馬大学 2 目次 1. 研究背景 目的 2. インターリーブADCの原理 3. チャネル間ミスマッチの影響 3.1. オフセットミスマッチの影響 3.2. ゲインミスマッチの影響 3.3. タイミングスキューの影響 4. 提案手法 4.1. インターリーブタイミングミスマッチ補正フィルタ
1 インターリーブADCでのタイミングスキュー影響のデジタル補正技術 浅見幸司 黒沢烈士 立岩武徳 宮島広行 小林春夫 ( 株 ) アドバンテスト 群馬大学 2 目次 1. 研究背景 目的 2. インターリーブADCの原理 3. チャネル間ミスマッチの影響 3.1. オフセットミスマッチの影響 3.2. ゲインミスマッチの影響 3.3. タイミングスキューの影響 4. 提案手法 4.1. インターリーブタイミングミスマッチ補正フィルタ
振動学特論火曜 1 限 TA332J 藤井康介 6 章スペクトルの平滑化 スペクトルの平滑化とはギザギザした地震波のフーリエ スペクトルやパワ スペクトルでは正確にスペクトルの山がどこにあるかはよく分からない このようなスペクトルから不純なものを取り去って 本当の性質を浮き彫
 6 章スペクトルの平滑化 スペクトルの平滑化とはギザギザした地震波のフーリエ スペクトルやパワ スペクトルでは正確にスペクトルの山がどこにあるかはよく分からない このようなスペクトルから不純なものを取り去って 本当の性質を浮き彫りにするために スペクトルを滑らかにする操作のことをいう 6.1 合積のフーリエ変換スペクトルの平滑化を行う際に必要な 合積とそのフーリエ変換について説明する 6.2 データ
6 章スペクトルの平滑化 スペクトルの平滑化とはギザギザした地震波のフーリエ スペクトルやパワ スペクトルでは正確にスペクトルの山がどこにあるかはよく分からない このようなスペクトルから不純なものを取り去って 本当の性質を浮き彫りにするために スペクトルを滑らかにする操作のことをいう 6.1 合積のフーリエ変換スペクトルの平滑化を行う際に必要な 合積とそのフーリエ変換について説明する 6.2 データ
(Microsoft Word - 10ta320a_\220U\223\256\212w\223\301\230__6\217\315\221O\224\274\203\214\203W\203\201.docx)
 6 章スペクトルの平滑化 スペクトルの平滑化とはフーリエスペクトルやパワ スペクトルのギザギザを取り除き 滑らかにする操作のことをいう ただし 波のもっている本質的なものをゆがめてはいけない 図 6-7 パワ スペクトルの平滑化 6. 合積のフーリエ変換スペクトルの平滑化を学ぶ前に 合積とそのフーリエ変換について説明する 6. データ ウィンドウデータ ウィンドウの定義と特徴について説明する 6.3
6 章スペクトルの平滑化 スペクトルの平滑化とはフーリエスペクトルやパワ スペクトルのギザギザを取り除き 滑らかにする操作のことをいう ただし 波のもっている本質的なものをゆがめてはいけない 図 6-7 パワ スペクトルの平滑化 6. 合積のフーリエ変換スペクトルの平滑化を学ぶ前に 合積とそのフーリエ変換について説明する 6. データ ウィンドウデータ ウィンドウの定義と特徴について説明する 6.3
Microsoft PowerPoint - CSA_B3_EX2.pptx
 Computer Science A Hardware Design Excise 2 Handout V2.01 May 27 th.,2019 CSAHW Computer Science A, Meiji University CSA_B3_EX2.pptx 32 Slides Renji Mikami 1 CSAHW2 ハード演習内容 2.1 二次元空間でのベクトルの直交 2.2 Reserved
Computer Science A Hardware Design Excise 2 Handout V2.01 May 27 th.,2019 CSAHW Computer Science A, Meiji University CSA_B3_EX2.pptx 32 Slides Renji Mikami 1 CSAHW2 ハード演習内容 2.1 二次元空間でのベクトルの直交 2.2 Reserved
Microsoft Word - 第2章 ブロック線図.doc
 NAOSIE: Nagaaki Univriy' Ac il ディジタル制御システム Auhor() 辻, 峰男 Ciaion ディジタル制御システム ; 06 Iu Da 06 URL hp://hdl.handl.n/0069/3686 Righ hi documn i downloadd hp://naoi.lb.nagaaki-u.ac.jp 第 章ブロック線図. インパルス列を用いた z
NAOSIE: Nagaaki Univriy' Ac il ディジタル制御システム Auhor() 辻, 峰男 Ciaion ディジタル制御システム ; 06 Iu Da 06 URL hp://hdl.handl.n/0069/3686 Righ hi documn i downloadd hp://naoi.lb.nagaaki-u.ac.jp 第 章ブロック線図. インパルス列を用いた z
相対性理論入門 1 Lorentz 変換 光がどのような座標系に対しても同一の速さ c で進むことから導かれる座標の一次変換である. (x, y, z, t ) の座標系が (x, y, z, t) の座標系に対して x 軸方向に w の速度で進んでいる場合, 座標系が一次変換で関係づけられるとする
 相対性理論入門 Lorentz 変換 光がどのような座標系に対しても同一の速さ で進むことから導かれる座標の一次変換である. x, y, z, t ) の座標系が x, y, z, t) の座標系に対して x 軸方向に w の速度で進んでいる場合, 座標系が一次変換で関係づけられるとすると, x A x wt) y y z z t Bx + Dt 弨弱弩弨弲弩弨弳弩弨弴弩 が成立する. 図 : 相対速度
相対性理論入門 Lorentz 変換 光がどのような座標系に対しても同一の速さ で進むことから導かれる座標の一次変換である. x, y, z, t ) の座標系が x, y, z, t) の座標系に対して x 軸方向に w の速度で進んでいる場合, 座標系が一次変換で関係づけられるとすると, x A x wt) y y z z t Bx + Dt 弨弱弩弨弲弩弨弳弩弨弴弩 が成立する. 図 : 相対速度
やさしくPDFへ文字入力 v.2.0
 操作マニュアル やさしく PDF へ文字入力 v.2.0 基本操作 目次 1. はじめに 2. やさしく PDF へ文字入力の起動 3. スキャナの設定 4. 原稿の取り込み 4-1. スキャナから 4-2. ファイルから 5. プリンタの設定 6. フィールドの作成 6-1. フィールドの自動作成 6-2. フィールドの手動作成 7. フィールドの設定 8. 文字の入力 9. 印刷 便利な使い方付録
操作マニュアル やさしく PDF へ文字入力 v.2.0 基本操作 目次 1. はじめに 2. やさしく PDF へ文字入力の起動 3. スキャナの設定 4. 原稿の取り込み 4-1. スキャナから 4-2. ファイルから 5. プリンタの設定 6. フィールドの作成 6-1. フィールドの自動作成 6-2. フィールドの手動作成 7. フィールドの設定 8. 文字の入力 9. 印刷 便利な使い方付録
P072-076.indd
 3 STEP0 STEP1 STEP2 STEP3 STEP4 072 3STEP4 STEP3 STEP2 STEP1 STEP0 073 3 STEP0 STEP1 STEP2 STEP3 STEP4 074 3STEP4 STEP3 STEP2 STEP1 STEP0 075 3 STEP0 STEP1 STEP2 STEP3 STEP4 076 3STEP4 STEP3 STEP2 STEP1
3 STEP0 STEP1 STEP2 STEP3 STEP4 072 3STEP4 STEP3 STEP2 STEP1 STEP0 073 3 STEP0 STEP1 STEP2 STEP3 STEP4 074 3STEP4 STEP3 STEP2 STEP1 STEP0 075 3 STEP0 STEP1 STEP2 STEP3 STEP4 076 3STEP4 STEP3 STEP2 STEP1
PowerPoint プレゼンテーション
 ディジタル画像処理 濃度変換 ; 階調処理 2 値化処理 ; しきい値処理 フィルタ処理 画像間演算 データ圧縮 三次元表示 頻度 画像全体で同じ濃度値を持つ画素数を求め, グラフ化したものを濃度ヒストグラムあるいは単にヒストグラム (histogram) という. 横軸は濃淡値 ( 画素値 ), 縦軸にその出現頻度 ( 画素数 ) をとる. Histogram 出現頻度 30 20 0 ヒストグラムの利用法
ディジタル画像処理 濃度変換 ; 階調処理 2 値化処理 ; しきい値処理 フィルタ処理 画像間演算 データ圧縮 三次元表示 頻度 画像全体で同じ濃度値を持つ画素数を求め, グラフ化したものを濃度ヒストグラムあるいは単にヒストグラム (histogram) という. 横軸は濃淡値 ( 画素値 ), 縦軸にその出現頻度 ( 画素数 ) をとる. Histogram 出現頻度 30 20 0 ヒストグラムの利用法
Microsoft PowerPoint - DigitalMedia2_3b.pptx
 Contents デジタルメディア処理 2 の概要 フーリエ級数展開と 離散とその性質 周波数フィルタリング 担当 : 井尻敬 とは ( ) FourierSound.py とは ( ) FourierSound.py 横軸が時間の関数を 横軸が周波数の関数に変換する 法 声周波数 周波数 ( 係数番号 ) 後の関数は元信号に含まれる正弦波の量を す 中央に近いほど低周波, 外ほどが 周波 中央 (
Contents デジタルメディア処理 2 の概要 フーリエ級数展開と 離散とその性質 周波数フィルタリング 担当 : 井尻敬 とは ( ) FourierSound.py とは ( ) FourierSound.py 横軸が時間の関数を 横軸が周波数の関数に変換する 法 声周波数 周波数 ( 係数番号 ) 後の関数は元信号に含まれる正弦波の量を す 中央に近いほど低周波, 外ほどが 周波 中央 (
Microsoft PowerPoint - H22制御工学I-2回.ppt
 制御工学 I 第二回ラプラス変換 平成 年 4 月 9 日 /4/9 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
制御工学 I 第二回ラプラス変換 平成 年 4 月 9 日 /4/9 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
スペクトルに対応する英語はスペクトラム(spectrum)です
 7. ハミング窓とフラットトップ窓の等価ノイズ帯域幅 (ENBW) (1) Hamming 窓 Hamming 窓は次式で表されます MaTX にも関数が用意されています win = 0.54-0.46*cos(2*PI*[k/(N-1)); ただし k=0,1,---,n-1 N=256; K=[0:N-1]; w=0.54-0.46*cos(2*pi*k/(n-1)); mgplot_reset(1);
7. ハミング窓とフラットトップ窓の等価ノイズ帯域幅 (ENBW) (1) Hamming 窓 Hamming 窓は次式で表されます MaTX にも関数が用意されています win = 0.54-0.46*cos(2*PI*[k/(N-1)); ただし k=0,1,---,n-1 N=256; K=[0:N-1]; w=0.54-0.46*cos(2*pi*k/(n-1)); mgplot_reset(1);
 O157 6/23 7/4 6 25 1000 117,050 6 14:00~15:30 1 2 22 22 14:30~15:30 8 12 1 5 20 6 20 10 11 30 9 10 6 1 30 6 6 0 30 6 19 0 3 27 6 20 0 50 1 2 6 4 61 1 6 5 1 2 1 2 6 19 6 4 15 6 1 6 30 6 24 30 59
O157 6/23 7/4 6 25 1000 117,050 6 14:00~15:30 1 2 22 22 14:30~15:30 8 12 1 5 20 6 20 10 11 30 9 10 6 1 30 6 6 0 30 6 19 0 3 27 6 20 0 50 1 2 6 4 61 1 6 5 1 2 1 2 6 19 6 4 15 6 1 6 30 6 24 30 59
<4D F736F F D20907D955C ECA905E939982CC89E6919C B835E82CC93FC8D6582C982C282A282C42E646F63>
 図表 イラスト 写真等の画像データの入稿について 112-0015 東京都文京区目白台 1-9-9 株式会社文化書房博文社 E-Mail: [email protected] http://user.net-web.ne.jp/bunka/index.asp 作成日 :2008 年 3 月 26 日変更日 :2009 年 4 月 8 日変更ヵ所 : Acrobat PDFMaker を使った
図表 イラスト 写真等の画像データの入稿について 112-0015 東京都文京区目白台 1-9-9 株式会社文化書房博文社 E-Mail: [email protected] http://user.net-web.ne.jp/bunka/index.asp 作成日 :2008 年 3 月 26 日変更日 :2009 年 4 月 8 日変更ヵ所 : Acrobat PDFMaker を使った
<4D F736F F D DC58F498D5A814091E6318FCD814089E6919C82C682CD89BD82A92E646F63>
 第 1 章画像とは何か 第 1 章画像とは何か 画像 は英語では image であり 実際に存在する もの を 絵に描いたり カメラで撮影したりしたものである キャンバス フィルム 印画紙などに記録されて 現物が破壊されるなどで存在しなくなっても 遠方にあって直接見ることが不可能であっても 保存 伝送されていつでも どこでも自由に見ることが可能となる 本書で述べる 画像処理 はこの画像を入力とした処理である
第 1 章画像とは何か 第 1 章画像とは何か 画像 は英語では image であり 実際に存在する もの を 絵に描いたり カメラで撮影したりしたものである キャンバス フィルム 印画紙などに記録されて 現物が破壊されるなどで存在しなくなっても 遠方にあって直接見ることが不可能であっても 保存 伝送されていつでも どこでも自由に見ることが可能となる 本書で述べる 画像処理 はこの画像を入力とした処理である
BESEで 高度な設定 とされているオプションは使用しないことを前提とします 点字編集システムでは 図があるページをすべて 図 にすることで 点字がずれないようにしていますので 現時点では 高度な設定 を使うことはお勧めできません (14ページ以降参照) 22 行両面の EdelBook を BES
 BESE を使った編集例 ここで扱う点字データの標準規格は 次のとおりとします ( サピエ図書館 登録点字文書製作 基準 ) より (2) 標準サイズは 1 ページ 18 行 32 マス 両面書きただし グラフィックデータのページは 片面書きとします 基本的な編集例として EdelPaper で作成したグラフィックデータ (1ファイル=1ページ) を BESE で BES に変換して 点字編集システムの
BESE を使った編集例 ここで扱う点字データの標準規格は 次のとおりとします ( サピエ図書館 登録点字文書製作 基準 ) より (2) 標準サイズは 1 ページ 18 行 32 マス 両面書きただし グラフィックデータのページは 片面書きとします 基本的な編集例として EdelPaper で作成したグラフィックデータ (1ファイル=1ページ) を BESE で BES に変換して 点字編集システムの
ワタベウェディング株式会社
 1 2 3 4 140,000 100,000 60,000 20,000 0 0 5 10 15 20 25 30 35 40 45 50 55 60 65 70 5 6 71 2 13 14 7 8 9 10 11 12 1 2 2 point 1 point 2 1 1 3 point 3 4 4 5 6 point 4 point 5 point 6 13 14 15 16 point 17
1 2 3 4 140,000 100,000 60,000 20,000 0 0 5 10 15 20 25 30 35 40 45 50 55 60 65 70 5 6 71 2 13 14 7 8 9 10 11 12 1 2 2 point 1 point 2 1 1 3 point 3 4 4 5 6 point 4 point 5 point 6 13 14 15 16 point 17

















![[商品カタログ]ゼンリン電子地図帳Zi16 [商品カタログ]ゼンリン電子地図帳Zi16](/thumbs/48/24409875.jpg)