4 9, ( ) (3), 3 (3) 7 ( ) Cardano Bombelli de Moivre Euler Gauss Cauchy Abel,
|
|
|
- よりとし ごちょう
- 5 years ago
- Views:
Transcription
1 (7 ) 8 (8 ) pdf
2 4 9, ( ) (3), 3 (3) 7 ( ) Cardano Bombelli de Moivre Euler Gauss Cauchy Abel, Jacobi Weierstrass, Riemann C : () n C... 3
3 Cauchy-Riemann Weierstrass M-test , =Taylor, , Abel, Abel Abel log z log Taylor () e w = z log z z α : R ( ) Cauchy Cauchy Cauchy Cauchy 7. Cauchy
4 8 Green Cauchy, 5 8. Green Green Cauchy, Cauchy Liouville Schwarz... 6 : Laurent,, 6. Laurent Laurent,, () Laurent ,, (residue theorem) Laurent () R 3.3 e iax R 3.4 f(x) dx... 6 π f(x)e iax dx r(cos θ, sin θ)dθ R ( ) : (7)
5 ( ) A 9 A. C... 9 A A.3 Cauchy-Hadamard A A.3. Cauchy-Hadamard A.3.3 Cauchy-Hadamard A.3.4 lim sup n a n A.4... A.5... A.6 Abel... A A B 9 C C. x α C. C.3 (log x) n C.4 (log x) n x α f(x)dx... f(x) dx... 4 g(x)(log x) n dx... 7 f(x)(log x) n dx... 8 C C D 4 D D. tan... 5 D.3 Bernoulli tan... 9 E Cauchy 9 E E E E.3. ( ) E.3. ( ) E.4 Cauchy E.5 Cauchy E E.7 [] (957) VI
6 F Cauchy,, 4 F F F.3 Cauchy, F F G 46 H : ± 6, 8 55 (TODO) ( ).3(p. 4) a n b n = a k b l n n n k+l=n (7 9, ) 57 ( ) 5
7 N = {,, 3, } Z, Q, R, C a, b [a, b] :={( t)a + tb t [, ]} a, b ϕ(t) =( t)a + tb (t [, ]) + ( n n + n ) (6//9 ) 6
8 ( ) (7/9/5 ) ( ). () I, II ( ). Cauchy ( ) f(z) = f(ζ) πi ζ z dζ ( ) c f f(z) = a n (z c) n, a n = f (n) (c) n! C = πi C f(ζ) (ζ z) n+ dζ Taylor ( ) dx x + ( ) =πi Res z + ; i =πi lim(z i) z i z + =πi z + i =πi z=i i = π. (tan dx x 4 + Mathematica ) Cauchy ( []) 4 C C () ( ) Cauchy 7
9 .3.3. Cardano ( ) 3 Cardano (, GerolamoCardano,5 576 ) Ars magna de Rebus Algebraicis (545) 3 ( ) 3 4 ( ) 3 x 3 + px + q = 3 (q /4+p 3 /7 < (Casus irreducibilis) ) Cardano x = 3 q + q 4 + p q q 4 + p3 7 q /4+p 3 /7 Ars Magna (), 4 5 ± 5 ( PDF 67 ) :, 4 5 ± 5 (Ars Magna ) 3 ( ) 3 ( ) Cardano ( ) ( ) 3 ( )., 4 (Cardano ) 5 3 ( ) ( ) 3 8
10 . () f(x) 3, α A, B, C, D f α f(x) =A(x α) 3 + B(x α) + C(x α)+d. () 3 x 3 + ax + bx + c y = x α x 3 + ax + bx + c = y 3 + py + q ( ) α ((p/3) 3 +(q/) 4 ) 3. p, q ( p ) 3 ( q ) () 3 x 3 + px + q = 3 + < 3 ( p ) 3 ( q ) () 3 x 3 + px + q = (3) 3 x 3 + px + q = ( ) ( p ) 3 ( q ) + > 3 4. X 3 + Y 3 + Z 3 3XY Z =(X + Y + Z)(X + Y + Z YZ ZX XY )=(X + Y + Z)(X + ωy + ω Z)(X + ω Y + ωz) ω := + 3i ( p ) 3 ( q ) 5. p, q + > x 3 + px + q = 3 ( : x = 3 q (q ) ( p ) q (q ) ( p ) Cardano 3 ) 3 x, α, β x = α + β α 3 + β 3 = q αβ = p 3 x 3 + px + q = ( x ) ( p ) 3 α 3 + β 3 = q, α 3 β 3 = α, β 3 6. () 5 () p q z 3 + pz + q = 4 := 3 3 [ (p/3) 3 +(q/) ] x 3 + px + q 9
11 .3. Bombelli Bombelli (, RafaelBombelli,56 Bologna 57 Rome ) Algebra (57 ) 3 x 3 =5x +4 ( x =4, ± 3 ) Cardano x = (6/9/ : Bombelli Wikipedia Klein [3], Smith [4] Algebra PDF ).3.3 de Moivre de Moivre (, Abraham de Moivre, 667 Citry-le- François 754 London ) 73 cos nx =cos n n(n ) x sin x cos n n(n )(n )(n 3) x + sin 4 x cos n 4 x, 3 4 sin nx = n sin x cos n n(n )(n ) x sin 3 x cos n 3 x + 3 cos nθ + i sin nθ =(cosθ + i sin θ) n.3.4 Euler Euler Euler 6 Euler (, LeonhardEuler,77 Basel 783 ) Euler e iθ =cosθ + i sin θ ( ) e iθ =cosθ i sin θ cos θ = eiθ + e iθ, sin θ = eiθ e iθ. i de Moivre Euler Euler 5 6 Liesez Euler, Liesez Euler, c est notre maître à tous. Read Euler, read Euler, he is the master of us all
12 .3.5 Gauss Gauss (, Johann Carl Friedrich Gauss, , Brunswick Göttingen ) Gauss 7 Gauss ( ( n ) ) Gauss Cauchy ( [5] ( WWW ) ) (,, ) (Gauss [6] ) Gauss Gauss (8 ) Wessel (, CasparWessel,797 ), Argand (, Jean-Robert Argand, 86 ) ( the Argand plane, an Argand diagram ) Gauss Gauss (a + bi (a, b Z) ).3.6 Cauchy Cauchy (, Augustin Louis Cauchy, , Paris Sceaux ) Cauchy Cauchy Cauchy-Riemann Cauchy Cauchy [7].3.7 Abel, Jacobi Abel (, Niels Henrik Abel, , Frindöe Froland ) ( ) Jacobi (, Carl Gustav Jacob Jacobi, , Potsdam Berlin ) 9 7 d Alembert Gauss Gauss
13 .3.8 Weierstrass, Riemann Weierstrass (, Karl Theodor Wilhelm Weierstrass, , Ostenfelde Berlin ) Riemann (, GeorgFriedrichBernhardRiemann, , Breselenz Selasca ) Cauchy-Riemann, Riemann Riemann, ([5]) ( ) ( [8]).3.9 (a) ( ) (b) 8 n [9]. () ( ) i = (, theimaginaryunit)i a + bi (a b ) (a complex number) a +i a, +bi bi, a +i a + i +i, + i i, +i 8 [9]
14 (a + bi)+(c + di) =(a + c)+(b + d)i, (a + bi) (c + di) =(ac bd)+(ad + bc)i i i () a + i a R C ( ). () i i j JIS () i j ( ) Mathematica I MATLAB i, j i j i j C C = {a + bi a, b R}. (an imaginary number) a + bi (a, b R, b ) a =,b ( + i = ( ) ) z, w, ζ (ζ ) z = x + iy (x, y R) x, y z (real part) (imaginary part) Re z, Imz x =Rez, y =Imz. (Rz, Iz 9 ) =+i, =+i z = x + iy (x, y R) w z zw = w = u + iv (u, v R) (x + iy)(u + iv) = u = x x + y, v = y x + y { xu yv = xv + yu = 9 ( ) 3
15 z w w = 7. x x + y i y x + y x + iy (x, y R) x + iy = x iy x + y. C C z, n z n 8. i n (n Z) 9. ( + i). C C Hamilton ( ) Hamilton C R = {(x, y) x, y R} ( ) () (a, b)(c, d) =(ac bd, ad + bc).. R (a, b)+(c, d) =(a + c, b + d) () (, ), (, ) (x, y) (, ) (x, y) ( ) x (x, y) = x + y, y. x + y..3 (, ) K (, field) () (9) ( ) n z n n z z =( a n z n z z z = z = ), n z z n = z n. 4
16 () ( a, b, c K) (a + b)+c = a +(b + c) () ( K K) ( a K) a + K = K + a = a (3) ( a K) ( a K) a + a = a + a = K (4) ( a, b K) a + b = b + a (5) ( a, b, c K) (ab)c = a(bc) (6) ( K K) ( a K) a K = K a = a (7) ( a K \{ K })( a K) aa = a a = K (8) ( a, b, c K) (a + b)c = ac + bc, a(b + c) =ab + ac (9) ( a, b K) ab = ba (() K (3) K K K C K K ) Q, R C ( ) () ( a, b K) (a b b a) ( ) () ( a, b K) (a b b a a = b) (3) ( a, b, c K) (a b b c a c) (4) ( a, b, c K) (a b a + c b + c) (5) ( a, b K) ( a b ab) [] Hamilton ( ) ( ) ( ) a b b a (a, b R) C i ( ) ( ) I =, J = html 5
17 ( J = I e iθ cos θ sin θ ) sin θ cos θ R[x] (x +) R[x]/(x +) C ( ) 3 ( ).4 Hamilton (William Rowan Hamilton, 85 Dublin 865 Dublin ) (the skew field of Hamilton quaternions) H := {a + bi + cj + dk a, b, c, d R} (843 ) i, j, k i = j = k = ijk = ( ij = ji = k, jk = kj = i, ki = ik = j ) H (a quaternion) Gibbs Heaviside 3 3 [], [].3 : R (i) ( a, b, c R) a>b a + c>b+ c (ii) ( a, b, c R) a>b c> ac > bc z, w d(z,w) d(z,w) = z w () ( ) (d(z,w) = z w ) : C (?) C ( R ) R () C 6
18 .4 ( C, R ) R ( ) R () : O O x y R = {(x, y) x R, y R} (a, b) x a, y b R R ( R ) C = {x + yi x R, y R} R = {(x, y) x R, y R} ϕ: C R, ϕ(x + yi) =(x, y) C C (, thecomplexplane) (the Gauss plane), (the Argand plane, an Argand diagram) R x, y (the real axis), (the imaginary axis).5 ( vs. ) Komplexe Ebene, Komplexe Zahlenebene, Gaußsche Ebene, Gaußsche Zahlenebene complex plane complex number plane ( Google ).5 c C z = c z C c (a square root of c) c c ( ).6 ( ) c C z = c z C c = z =c c = α + βi (α, β R) () z = ( ) α ± +β +α + β α +β α i β (β ) ± α (β = α ) ± αi (β = α<). (() ) 7
19 ( ) z = x + yi (x, y R) z = c (x + yi) = α + βi. (3) x y = α, xy = β (x + yi) = α + βi.7 z =+i z ( ) z = x + iy (x, y R) z = x y +xyi z =+i x y = xy =. xy =y = x. x y = 4x 4 4x =. x R x x = = x = ±. = +. y = x = ± + = ± = ±. + x, y ( ) + z = x + yi = ± + i.. (3) ( β = β ). 3. i ( ) c R x = c x R c x x () c c = c c =. c> c> c c c. c,c c c = c c 4. c,c c c = c c ( ) 8
20 c c := ci ( =i, 3= 3 i) 5. c c c := ci c c = c c c ( ) c c 3 c c c c = c c ( ) c c (a) c c ( ) (b) c c ( ) (c) c c 3 3i 3i ± 3i ± ±.8 ( ) az + bz + c =(a, b, c C, a ) z = b ± b 4ac. a ( az + bz + c = z + b ) = b 4ac a 4a b 4ac b 4ac b 4ac 4a b 4ac ± x + b a a = ± b 4ac. a 3 z := z e i Arg z/ 9
21 .6 z = x + yi (x, y R) x yi z (the complex conjugate of z) z z,w C z = z. z + w = z + w, z w = z w, zw = z w, ( z w ) = z/w = z w. 6. z = x + iy (x, y R) z = x iy (4) x = z + z, y = z z. i (5) Re z = z + z, Im z = z z. i ( z C) z = z z R. (4) x y z z 7. a C \{}, β R az + az + β = ( 9 ).6. n = n =3 ax 3 + bx + cx + d =(a, b, c, d ) x = α + iβ (α, β ) x = α iβ.9 n N, f(z) =a z n + a z n + + a n R[z], c C, f(c) = f(c) =.
22 a j a j = a j z C f(z) =a z n + a z n + + a n z + a n = a z n + a z n + + a n z + a n = a z n + a z n + + a n z + a n = a z n + a z n + + a n z + a n = f (z) f(c) =f(c). f(c) = f (c) =f(c) == f(z) = Q(z) (P (z),q(z) R[z]) f(z) =f (z) P (z) 8. c f(z) m c f(z) m (c f(z) m ).7 z = x + iy (x, y R) z (the absolute value of z, themodulusofz, the magnitute of z) z z = x + iy = x + y R (x, y) () ( ) z = z, z = z. zz = z zz =(x + yi)(x yi) =x y i = x + y = z.. absolute value the maximum modulus principle modulus modulus magnitude ( ) MATLAB ( ) magnitude ( ). zz = z z z = z zz = z z. z z
23 9. c C, β R, β< c zz cz cz + β =. (i) z. z =. (ii) z + w z + w. (iii) zw = z w. ( z = z w w.) a + bi C (a, b) R () (i) (ii) (iii) z = a + ib, w = c + id zw =(ac bd)+(ad + bc)i zw = (ac bd)+(ad + bc)i = (ac bd) +(ad + bc) = a c + b d + a d + b c = (a + b )(c + d ) = a + b c + d = z w. () zz = z zw = zwzw = zwz w = zzww = z w =( z w ) zw = z w..8 () z = x + yi (x, y R) (6) e z =expz := e x (cos y + i sin y) exp: C C ( (6) ) (6) e x z y =(z = x) cos y + i sin y =e z = e x. (7) e z +z = e z e z z = x + y i, z = x + y i e z +z = e x +x (cos(y + y )+i sin(y + y )) = e x e x [cos y cos y sin y sin y + i (sin y cos y +cosy sin y )] = e x e x (cos y + i sin y )(cosy + i sin y ) = e z e z.
24 e z e z = e z+z = e = (8) e z, e z = e z. z z = iθ (θ R) (9) e iθ =cosθ + i sin θ. Euler () e π i = i, e πi =, e 3π i = i, e πi =. () cos θ =Ree iθ, sin θ =Ime iθ. e iθ =cosθ i sin θ () cos θ = eiθ + e iθ, sin θ = eiθ e iθ. i (3) e iθ =, e iθ = e iθ = e. iθ e z = e x cos y + i sin y = e x cos y +sin y = e x (4) e z = e Re z. a xy =(a x ) y e nz =(e z ) n (n Z, z C) n N e z +z + +z n = e z e z e zn (8) n Z.3 ((e z ) n n ) (e x ) y = e xy ( a (a x ) y = a xy ) ( 4. ) ) θ R z = iθ e inθ = ( e iθ) n. (5) cos nθ + i sin nθ =(cosθ + i sin θ) n. de Moivre 3
25 . z () (4) () e z, e = z e z () n Z (e z ) n = e nz (3) e z = e z (4) e z = e Re z. () z C e z = ( k Z) z =kπi. () z,w C e z = e w ( k Z) w = z +kπi.. θ =, π 6, π 4, π 3, π, π 3, 3π 4, 5π 6,π, 3π, π eiθ 3. θ R e iθ =, e iθ = e iθ, = e iθ eiθ.4 cos 5θ, sin5θ cos θ sin θ ( ) ( ) cos 5θ + i sin 5θ = e i5θ = ( e iθ) 5 =(cosθ + i sin θ) 5 =cos 5 θ +5cos 4 θ i sin θ +cos 3 θ i sin θ +cos θ i 3 sin 3 θ +5cosθ i 4 sin 4 θ + i 5 sin 5 θ =cos 5 θ cos 3 θ sin θ +5cosθ sin 4 θ + i ( 5cos 4 θ sin θ cos θ sin 3 θ +sin 5 θ ) cos 5θ =cos 5 θ cos 3 θ sin θ +5cosθ sin 4 θ, sin 5θ =5cos 4 θ sin θ cos θ sin 3 θ +sin 5 θ. 4. cos 3θ, sin3θ cos θ, sinθ.5 cos 5 θ cos kθ, sinkθ (k =,, 3, 4, 5) ( ) ( ) ( ) e cos 5 iθ + e iθ 5 θ = = ( e 5iθ +5e 4iθ e iθ +e 3iθ e iθ +e iθ e 3iθ +5e iθ e 4iθ + e 5iθ) 3 = ( e 5iθ +5e 3iθ +e iθ +e iθ +5e 3iθ + e 5iθ) 3 = ( cos 5θ + 5cos3θ + cos θ) = (cos 5θ +5cos3θ +cosθ). 3 6 (cos 5 θ Fourier ) z C cos z = eiz + e iz, sin z = eiz e iz i (z C) ( ) 4
26 .9 () (x, y) R (6) (x, y) =r(cos θ, sin θ), r, θ R r, θ r (x, y) x + y θ x θ (x, y) (, ) π (r cos θ,r sin θ )=(r cos θ,r sin θ ) (r = r ( k Z) θ θ =kπ). z C (7) z = r (cos θ + i sin θ), r, θ R r, θ (8) z = re iθ, r, θ R r z z = x + y θ θ z π θ z (an argument of z) arg z ( θ z z = re iθ, r = z, θ R ) (7) (8) z r θ z (the polar form of z) ( z z ) θ θ<π π <θ π π θ π <θ π θ z Arg z : Mathematica Arg[z] Arg z.6 Arg ( + i) = π 4, Arg ( i) = π 4, Arg ( +i) =3π 4, Arg ( i) = 3π 4..7 z = i Arg z z = ( ) +( ) =. θ e iθ = z z = + i [, π) θ = 5 4 π,( π, π] θ = 3 4 π.( 5π +nπ (n Z) 4 ) 5
27 z = e i 5π 4, z = e i 3π 4 () π <θ π θ Arg z = 3π 4..8 ( ) (7) (8) (7) ( ) + 3i + ( 3i = cos π 3 + i sin π ) ( cos, sin ) 3 z = re iθ z z = r(cos θ i sin θ) ( ) i, i, 6. z = re iθ z z ( z )., z, z + z, z ( ) : r e iθ r e iθ = r r e i(θ +θ ). (r,r, θ,θ R r r, θ + θ R ) z = r e iθ, z = r e iθ (a) z, z z z ( z z = z z ) (b) z, z z z (b) arg(z z )=argz +argz () arg π arg(z z ) arg z +argz (mod π) 6
28 7. Arg Arg (z z ) = Arg z + Arg z z θ z e iθ z = x+yi (x, y R) ze iθ =(x + yi)(cosθ + i sin θ) =(x cos θ y sin θ)+i (x sin θ + y cos θ) ( )( ) ( ) cos θ sin θ x x cos θ y sin θ = sin θ cos θ y x sin θ + y cos θ 9 (= π ) ei π = i : TikZ. n 7
29 n c z n = c z c n (an n-th root of c) z n = c (binomial equation) ( ) c c c 3 c (a cube root of c) n n = () ( ) (.6) n 3 n (n = m ) ( n ) ( 8, 9 ) 8. c C c = a + bi, z = x + yi (a, b, x, y R) (x + yi) 3 = a + bi ( ) 9. c 4 c ( ), i 4 n n.9 ( n ) n c = ρe iϕ (ρ>, θ R) n n ρe i( ϕ n + π n k) (k =,,,n ) ( n ) n ρ n ( n, n 3 ) ( n ρ r n = ρ, r r ( ) ) z = re iθ (r, θ R) z n = c r n e inθ = ρe iϕ. r n = ρ. r = n ρ. e inθ = e iϕ. 4 nθ ϕ (mod π). ( k Z) nθ ϕ = k π. ( k Z) θ = ϕ n + k π n. c n n ρe i( ϕ n +k π n ) (k Z). 4 cos nθ + i sin nθ = cos ϕ + i sin ϕ cos nθ = cos ϕ sin nθ =sinϕ. 8
30 k π/n k n k n k =,,...,n z n = c (9) z = n ρe i( ϕ n +k π n ) (k =,,...,n ). e i π n n ω 3 z 3 = + 3i ω. ( n ) n n e i π n k (k =,,,n ) ( n ) ω = e i π n ω k (k =,,...,n ).9 c = ρe iϕ n n ρe iϕ/n ω k (k =,,...,n ).9 ρ =,ϕ =. n ω := e i π n z n =(z )(z ω)(z ω ) (z ω n ). (, n ) n n n n = z = e i k π = e ikπ (k =, ) e =,e iπ =. z =(z +)(z ). z = e i( π +k π ) = e i (k+)π (k =, ) e i π = i, e i 3π = i. z +=(z + i)(z i). n =3 z 3 = e i k π 3 (k =,, ) e =,e i π 3 = +i 3 e i 4π 3 = i 3. ( )( ) z 3 =(z )(z + z +)=(z ) z +i 3 z i 3. z 3 = e i( π 3 +k π 3 ) = e i (k+)π 3 e i π 3 = +i 3, e i 3π 3 =, e i 5π 3 = i 3. z 3 +=(z +)(z z +) ± i 3. n =4 z 4 = e i k π 4 = e ik π (k =,,, 3) e =,e i π = i, e iπ =, e i 3π 4 = i. z 4 =(z +)(z ) = (z + i)(z i)(z +)(z ). 9,
31 z 4 = e i( π 4 +k π 4 ) = e i (k+)π 4 e i π 4 = +i, e i 3π 4 e i 7π 4 = i. z 4 +=(z + i)(z i). = +i, e i 5π 4 = i, z = i, z = i z 4 +=z 4 +z + z = ( z + ) ( ) z = (z + )( z + z ) z + ± i, ± i. n =5 z 5 = e ik π 5 (k =,,, 4) e =,e i π 5, e i 4π 5, e i 6π 5, e i 8π 5. z 5 =(z )(z 4 + z 3 + z + z +) z 4 + z 3 + z + z += z + z ++ z + z = ( z + ) + z + z z =. X = z + z X + X = X = ± 5 z + z = + 5 z + z = 5 z +( 5)z += z +(+ 5)z +=. z = ( 5) ± i + 5 4, ( + 5) ± i 5. 4 z 5 = e i( π 5 +k π 5 ) = e i (k+)π 5 (k =,,, 4) e i π 5, e i 3π 5, e i 5π 5 =, e i 7π 5, e i 9π 5. z 5 +=(z +)(z 4 z 3 + z z +) z 4 z 3 + z z += z z + z + z = ( z + ) ( z + ) =. z z 3
32 X = z + z X X = X = ± 5 z + z = + 5 z + z = 5 z ( + 5)z += z ( 5)z +=. z = ( + 5) ± i + 5 4, ( 5) ± i 5. 4 n =6 n =7 z 7 = e ik π 7 (k =,,, 6) e =,e i π 7, e i 4π 7, e i 6π 7, e i 8π 7, e i π 7, e i π 7. z 7 = e i( π 7 +k π 7 ) = e i (k+)π 7 (k =,,, 6) e i π 7, e i 3π 7, e i 5π 7, e i 7π 7 =, e i 9π 7, e i π 7, e i 3π 7. (, ) ( Gauss ) n =8 3., 6 3., 8.3 ( n n ) (.) n c n n c = ( ) ( ).4 ( n ) n Gauss n n n = k F m n =7=F ( 7 5 n n =3, 4, 5, 6, 8,,, 5, 6, 7,,. F m = m + F =3, F =5,F =7,F 3 =57,F 4 =65537 F 5 (F 5 = = () Euler ) 5 cos π 7 = ( ) 7 ( ) 3
33 .5 (sin, cos ) 3,45,6 sin, cos 36,7 sin, cos 8,5 sin, cos 8 5 =3 sin, cos sin, cos n n sin, cos sin, cos (, 38 49, ) 3 sin 3 =3x 4x 3 sin ( [3]). C R z C x := Re z, y := Im z, z := (x, y) z R. z =(x, y) R z := x + iy z C (). z = x + y = z z = x + iy, z = x + iy (x,y,x,y R), z := (x,y ), z := (x,y ) z z = z z. C C C R Bolzano- Weierstrass Weierstrass C {z n } n N n z n N n z n C {z n } c lim z n c = n ε-n z n, c ( ε >)( N N)( n N : n N) z n c <ε x n := Re z n, y n := Im z n, z n := (x n,y n ), a := Re c, b := Im c, c := (a, b) lim z n c = n 3
34 lim x n = a lim y n = b n n lim z n = c lim z n = c n n ( lim x n = a n ) lim y n = b. n ( ) Ω C f :Ω C. f :Ω C (Ω C ) u(x, y) :=Ref(x + iy), v(x, y) :=Imf(x + iy) u, v u v f u, v Ω := { (x, y) R x + iy Ω } u, v : Ω R (Ω Ω C R Ω = Ω.). () f : C C, f(z) =z f(z) =(x + iy) = x y +ixy u(x, y) = x y, v(x, y) =xy. () Ω:=C \{}, f :Ω C, f(z) = z z = x + iy = x iy x u(x, y) = x + y v(x, y) = y x + y. x + y, (3) f : C C, f(z) =e z.(e x+iy = e x (cos y+i sin y)) f(z) =e x+iy = e x (cos y + i sin y) u(x, y) =e x cos y, v(x, y) =e x sin y. 3. f :Ω C f u, v () f(z) =z 3 (z C) () f(z) = z + (z C \ {±i}) (3) f(z) = (eiz + e iz )(z C) ( (3) f(z) =cosz ) 33
35 . c C, r> c r D(c; r) : D(c; r) :={z C z c <r}. Ω C Ω (the closure of Ω) Ω : Ω:={z C ( ε >) D(z; ε) Ω }. Ω C Ω C (an open subset of C) ( z Ω)( ε >) D(z; ε) Ω R n a R n, r> a, r : B(a; r) :={x R n x a <r}. Ω R n Ω : Ω:={x R n ( ε >)B(x; ε) Ω }. Ω R n Ω R n : ( x Ω)( ε >) B(x; ε) Ω..3 () ( ). ( ) Ω C, f :Ω C () c Ω, γ C z c f(z) γ ( ε >)( δ >)( z Ω: z c <δ) f(z) γ <ε lim z c f(z) =γ () c Ω f c lim f(z) =f(c) z c (3) f Ω Ω z f 34
36 u v f f : Ω R ( ) ( ) ( ) a α x c = a + ib (a, b R), γ = α + iβ (α, β R), c =, γ =, z = b β y ( ) ( ) u(z) u(x, y) f(z) =f(x, y) = = v(z) v(x, y) z c = z c = (x a) +(y b), f(z) γ = f(z) γ = (u(x, y) α) +(v(x, y) β) lim f(z) =γ lim f(z) =γ lim z c z c u(x, y) =α lim v(x, y) =β. (x,y) (a,b) (x,y) (a,b) ( ) a f c f c u v c =. b f Ω f Ω u v Ω. f ( ).3 () Ω C, c Ω. f :Ω C, g :Ω C z c lim (f(z)+g(z)) = lim f(z)+limg(z), z c z c z c lim z c lim z c (f(z) g(z)) = lim f(z) lim g(z), z c z c (f(z)g(z)) = lim f(z) lim g(z), z c z c lim f(z) g(z) = z c lim f(z) lim z c ( lim z c g(z) ). g(z) z c ( ) ( [4]) ( 3.7) ε-δ f = u + iv, g = u + iv, fg = u 3 + iv 3 u 3 = u u v v, v 3 = u v + v u u 3, v 3 u, u, v, v.4 () ( ) 35
37 p(z) p(z) f : C C, f(z) =p(z) (z C) C f c (z) =c, f id (z) =z.4 f f p 33. f c, f id ε-δ r(z) r(z) = q(z) p(z),q(z) C[z] p(z) Ω:={z C p(z) } f(z) =r(z) (z Ω) f :Ω C r(z) Ω p(z), q(z) p, q Ω p(z) (z Ω) f = q p.5 f(z) = z {z C z }.6 ( e z ) ( ) ϕ: R R R (x, y) ϕ(x) R R (x, y) ϕ(y) R f (x, y) =e x, f (x, y) =cosy, f 3 (x, y) =siny f, f, f 3 : R R f(z) =e z f f, f f 3 f C e z = z n n! (z C) e z.4.7 (, ) Ω C f :Ω C, c Ω f c f(c + h) f(c) lim h h f (c) f c Ω z f z f Ω (regular,, holomorphic).8 () f c c U ( Ω) f U : U C 36
38 (analytic) ( ) regular holomorphic () ( ) holomorphic (regular ).9 f(z) =γ ( ) z C f(z + h) f(z) lim h h f (z) =. f C f(z) =z z C f(z + h) f(z) lim h h f (z) =. f C =lim h γ γ h =lim h (z + h) z h =lim=. h h =lim=. h h 34. f(z) =z C f (z) =z. Ω C c Ω. f :Ω C g:ω C c f + g, f g, fg, f ( g(c) ) c g (f + g) (c) =f (c)+g (c), (f g) (c) =f (c) g (c), (fg) (c) =f (c)g(c)+f(c)g (c), ( ) f (c) = g(c)f (c) g (c)f(c). g g(c). () k f(z) =z k C f (z) =kz k. () C ( n ) a k z k = k= n n ka k z k = (j +)a j+ z j. k= j= (3) r(z) = q(z) (p(z),q(z) C[z]) Ω:= p(z) {z C p(z) } z r(z) C n n ka k z k = (j +)a j+ z j k= j= 37
39 35.. () ( f f f c f f(c) (f ) (f(c)) = ) f (c).5 Cauchy-Riemann. Ω C f :Ω C f f u v ( ) u x = v y, u y = v x ( ) Cauchy-Riemann (the Cauchy-Riemann equations, the Cauchy-Riemann relations) f u x = v y, u y = v x f c = a + ib (a, b R) u v (a, b) ( ) f (c) =u x (a, b)+iv x (a, b) = i (u y(a, b)+iv y (a, b)) u x (a, b) =v y (a, b), u y (a, b) = v x (a, b). (( ) f = f x = i f y 6 ) f c f (c) =lim h f(c + h) f(c) h h (a) h = h x (h x R) () f(c + h x )=u(a + h x,b)+iv(a + h x,b) f f(c + h x ) f(c) (c) = lim hx h hx R x = lim hx (u(a + h x,b)+iv(a + h x,b)) (u(a, b)+iv(a, b)) = lim hx h x ) ( u(a + hx,b) u(a, b) h x + i v(a + h x,b) v(a, b) h x = u x (a, b)+iv x (a, b). 6 f z x, y f x, f y 38
40 (b) h = ih y (h y R) ( ) f(c + ih y )=u(a, b + h y )+iv(a, b + h y ) f f(c + ih y ) f(c) (c) = lim hx ih hy R y = i lim h y = i lim (u(a, b + h y )+iv(a, b + h y )) (u(a, b)+iv(a, b)) h y h y ) ( u(a, b + hy ) u(a, b) h y + i v(a, b + h y) v(a, b) h y = i (u y(a, b)+iv y (a, b)). f (c) =u x (a, b)+iv x (a, b) = i [u y(a, b)+iv y (a, b)] = v y (a, b) iu y (a, b). u x (a, b) =v y (a, b), v x (a, b) = iu y (a, b). f c ( p, q R) lim f(c + h) f(c) h (p + iq) h = h = h x + ih y (h x,h y R) (p + iq)h =(p + iq)(h x + ih y )=(ph x qh y )+i(ph y + qh x ) f(c + h) f(c) (p + iq) h = [u(a + h x,b+ h y )+iv(a + h x,b+ h y )] [u(a, b)+iv(a, b)] (p + iq) h x + ih y = [u(a + h x,b+ h y ) u(a, b) (ph x qh y )] + i [v(a + h x,b+ h y ) v(a, b) (qh x + ph y )] h x + ih y u(a + h x,b+ h y ) u(a, b) (ph x qh y ) = + i v(a + h x,b+ h y ) v(a, b) (qh x + ph y ) h x + h y h x + h. y u(a + h x,b+ h y ) u(a, b) (ph x qh y ) f c ( p, q R) lim (h x,h y) (,) h x + h y v(a + h x,b+ h y ) v(a, b) (qh x + ph y ) lim = (h x,h y) (,) h x + h y ( p, q R) u v (a, b) u x (a, b) =p, u y (a, b) = q, v x (a, b) =q, v y (a, b) =p. u v (a, b) u x (a, b) =v y (a, b),u y (a, b) = v x (a, b). ( ) ( ) u f = f u x u y = v v x v y 39 =
41 ( f c f (c) =p + iq f (a, b) f p (a, b) = q ) q. p det f (a, b) =u x (a, b) + u y (a, b) = v x (a, b) + v y (a, b) = f (c)..3 (Cauchy-Riemann ) f (c) =p + iq θ f (c) =p + iq = p + q e iθ, ( ) f p q (c) = = ( ) cos θ sin θ p + q. q p sin θ cos θ f(c + h) f(c) f (c)h f(c + h) f(c) f (c)h h h p + q θ () f (c) c () ( f (z) f (conformal mapping) ) : ( ) ( )( ) x y = p q () ( : xy (, ), (, ), (, ), (, ) x y (, ), (p, q), (p q, p + q), ( q, p) ).4 () f :Ω C f c Ω, f (c) =p + iq f : Ω R C det f (a, b). f f(a, b) C f ( f ) (f(x, y)) = (f (x, y)) = p + q q p ( p q x y ) q, p := u x (a, b), q := u y (a, b). p f f(c) f f Cauchy- Riemann Cauchy-Riemann ((, ) (, ) ) (, ) (, ) 4
42 .5 f(z) =z 3 u(x, y) =x 3 3x y, v(x, y) =3x y y 3 u x =3x 3y, u y = 6xy, v x =6xy, v y =3x 3y. Cauchy-Riemann u x = v y, u y = v x f(z) = z u(x, y) = x y xy (x + y, v(x, y) = ) (x + y ) u x = x(3y x ) (x + y ) 3, u y = y(y 3x ) (x + y ) 3, v x = y(3x y ) (x + y ) 3, v y = x(3y x ) (x + y ) 3. Cauchy-Riemann u x = v y, u y = v x f(z) = ez + e z u(x, y) = ex + e x cosh y, v(x, y) = ex e x sinh y u x =sinhx cos y, u y = cosh x sin y, v x =coshx sin y, v y =sinhx cos y. Cauchy-Riemann u x = v y, u y = v x.6 Re z, Imz, z, Arg z, z f(z) =Rez u(x, y) =x, v(x, y) =u x = =v y Cauchy-Riemann f.5. (..9, ) : f = f I R, f : I R f = f No I = R \{} f(x) =(x>), f(x) =(x<) f f = I f = f ( ) 4
43 .7 (, ) Ω R l ( Ω C) (pathwise-connected, arcwise-connected) Ω Ω ( Ω a, b ϕ: [, ] Ω ϕ() = a, ϕ() = b Ω ) () (region) Ω Ω R I I.8 ( ) () R l () ( ) ( ) B.(p. ) Ω R l C Ω a, b Ω C (C ).9 Ω R n u: Ω R u =(u x = u y =) u Ω a, b a b C ϕ: [, ] Ω( ϕ() = a, ϕ() = b) u(ϕ(t)) ( p. 85 ). Ω C ( ) f :Ω C ( z Ω) f (z) = f f u, v f = u =,v = =f (x + yi) =u x (x, y)+iv x (x, y) = i (u y(x, y)+iv y (x, y)) u x = u y = v x = v y =..9 u v f 4
44 . () 39. ( ) f(z) =e z, a =,b =πi f(b) f(a) =f (c)(b a) c. Ω C ( ) f :Ω C () f f () f f Ω :={(x, y) R x + yi Ω} () f u, v u = C ( ) u x = u y =in Ω. Cauchy-Riemann ( ) v x = u y =,v y = u x =in Ω v f = u + iv = u () f = C (C ) C = f =(inω)f C f = C = u + v Cauchy-Riemann uu x +vv x =, uu y +vv y = (in Ω). uu x vu y =, uu y + vu x = (in Ω). ( )( ) ( ) u x u y u = (in u y u x v Ω). ( ) ( ) (x, y) Ω u + v = C u >. v ( ) u x + u y = (in Ω). u x = u y =(in Ω). u () f u, v C 9 Cauchy-Riemann 43
45 .3 ( ) Ω C f :Ω C f u, v u xx (x, y)+u yy (x, y) =, v xx (x, y)+v yy (x, y) = ((x, y) Ω := { (x, y) R x + iy Ω } ) f Ω u v C Cauchy-Riemann u x = v y, u y = v x u xx + u yy = u x x + u y y = v x y + ( v ) = v y x x y v y x =. v C (v ) v xx + v yy = n u(x,...,x n ) ( ) n j= u x j = u (harmonic function) ( ) Laplace Laplace n := ( ) x j= j u = ( ) R Ω u Cauchy-Riemann ( ) v u (a conjugate aharmonic function of u) 4. v u u v ( ) Ω u u () 4. ( ) v u.4 (? ) ( 3 ) Cauchy-Riemann 44
46 u, v C Cauchy-Riemann ( f = f x = i f y ) u, v C ( ) Cauchy-Riemann ( ) ( ) 3 c {a n } n a n (z c) n c (a power series) ( ) ( ) (analytic function) = ( ) 3. a n (z c) n ( z c a n ) 3. ( ) e x,sinx, cosx, logx, (+x) α ( ) Taylor f (n) (a) (f(x) = (x a) n ) x z n! (). a n (z c) n c D(c; ρ) ( ρ + ) ( ) 45
47 ( ) a n (z c) n = a n (z c) n dz = C na n (z c) n = n= a n C (n +)a n+ (z c) n, (z c) n dz = [ ] (z c) n+ b a n. n + a ( C D(c; ρ) a, b C, ) ρ> 3. ( ( ) ) ( ) = ( ) Ω C f :Ω C (Ω ) c Ω D(c; ε) Ω ε> {a n } f(z) = a n (z c) n ( z c <ε) () C A. A. 3. ( c = c ) 3. {a n } n c, z C a n (z c) n z = z z c < z c z C lim a n (z c) n = ( a n : n lim a n =. ) n n= ζ := z c, ζ := z c n a n ζ n ζ = ζ ζ < ζ ζ c = n s := a n, s n := a k s n s s n s n a n = n= n k= n a k a k = s n s n s s =. k= k= 46
48 ( M R)( n N {}) a n (z c) n M. n b n := M z c z c n ( n N {}) a n (z c) n = a n (z c) n z c z c M z c z c {b n } (z c)/(z c) < : b n = M z c / z c. n = b n. ( A.5, p.9, ) a n (z c) n 3. {a n } n c, z C a n (z c) n z = z z c > z c z z c < z c z z 3.3 ( ) {a n } n c C a n (z c) n (i) z = c z (ii) z (iii) ρ z c <ρ z c >ρ ( ) { } A := z C a n (z c) n c A (z = c n a n (z c) n = ) 3 (i) A = {c}. c (ii) A = C. (iii) (i), (ii) 47
49 (iii) (i) z c A \{c}. r := z c c z c <r (ii) z d C \ A. R := z d c z c >R <r <R ρ := r + R c + ρ A z c <ρ r := ρ, R := R c + ρ A z c >ρ r := r, R := ρ z c <r z c >R r r <R R, R r = R r {r n }, {R n } {r n } {R n } n r n <R n, R n r n = R r n. n z c <r n z c >R n {r n } {R n } ρ ρ r > ρ>. z c <ρ z c >ρ (i) ρ =,(ii) ρ = ρ ( ρ ) z c <ρ z c >ρ D(c; ρ) ={z C z c <ρ} ρ ρ =,ρ = D(c;) =, D(c; ) =C 3.4 (,, ) ρ (radius of convergence) {z C z c <ρ} (the circle of convergence) ( ) 3.5 () (c =,a n =) z n z z < z D(; ) = {z C z < }. 48
50 4. ( ) {a n } ρ () 3.6 (, ratio test, d Alembert ) a n (z c) n n a n lim n a n a n+ ( d Alembert 3 ( ) lim = (i ) z c <ρ (ii) z c >ρ ) a n c = lim = ρ z <ρ z >ρ n a n+ z <ρ z <R<ρ R (ρ < R := z + ρ a n R := z + ) lim n a n+ a n a n+ ρ = = ρ ( N N) ( n N: n N) >R ( a n+ < R ). N m an+m z N+m a N+ = a N an+ a N+m z N z m a N a N+ a N+m an z N ( ) m z. R n N b n := a n a n z n an z N ( ) n N z. R a n z n ( n N ) ) an z N n N (n N) ( z R n N a n z n b n, b n = N a n z n + an z N z /R ( ). 3 Jean Le Rond d Alembert (77 Paris 783 Paris ) 49
51 a n z n z >ρ z >R>ρ R (ρ = R := z + ρ a n ) lim = ρ ( N N) ( n N: n N) n a n+ a n <R ( a n+ > R ). a n+ () n N a n z n an z N ( ) n N z. R a n z n a n z n 3.7 (ratio test ) lim n n= a n z n n a n = n a n a n+ = lim n + n n ( = lim + ) =. n n D(; ) = {z C z < }. z n D(; ). n n= z n n! (exp z Taylor ) a n = n! lim n a n a n+ = lim (n +)! n n! C. n!z n. k= = lim n (n +)=. ( ) n (k)! zk (cos z Taylor ) ζ = z k= ( ) k (k)! zk = ( ) n (n)! ζn. ζ a n = ( )n (n)! lim n a n a n+ = lim ((n +))! n (n)! = lim n (n +)(n +)=. ( ) n (ζ ) (n)! ζn ζ ( ) n (k)! zk z. C. k= 5
52 a n a n+ a n+ a n a n ( ) n z ρ ( z <ρ ) ρ 3.8 (Cauchy-Hadamard ) {a n } n c C a n (z c) n ρ =, = () ρ = n lim sup an. n (d Alembert z c <ρ z c >ρ ) {a n } lim sup n a n () () lim sup ( A.3.(p. 95) ) ( ) A z n = z + z 4 + z 9 + (n n= a n =, a n =) n an = lim n Cauchy-Hadamard = 3. ( Cauchy-Hadamard ) {a n } n c C a n (z c) n ρ lim n n an =, = ρ = lim n an. n 5
53 3. n z n, 3 n z n, 3 ( n +3 n ) z n 3 lim n n +3 n n+ +3 n+ = 3 d Alembert a n z n, b n z n R, R <R <R < (a n + b n )z n R 44. a n z n, b n z n R () () (a n + b n )z n R (a n + b n )z n R 3. (6, 7 ) 3.. C ( ( )) K f : K C, {f n } K ( n f n : K C ) {f n } f (K ) (converge pointwise) ( x K) lim f n (x )=f(x ) n 5
54 ( ) 3.3 ( ) f n (x) =tan (nx) (x R, n N) (x>) f(x) = (x =) (x<) x R lim f n (x) = f(x). (x = f n (x) = n lim f n(x) =. x> n nx tan (nx). x< n ) {f n } f (R ) f n f DJ ( 4 ) 3.4 ( (witch s hat), ) n N f n : R R n x ( x< ) n f n (x) := n x +n ( x< ) n n (x < x ) n x R lim f n(x) =. n {f n } f(x) = (R ) ( ) ( ε >) ( N N) ( n N: n N) f n (x) f(x) <ε (a) x : n N f n (x) =N = (b) x> : N> x N N 5 n N f n (x)dx = n n = R R lim f n (x) dx =. n R f(x) dx = lim n f n (x) dx lim f n(x) dx. n R R 4 Fourier 5 : N 53
55 lim f n (x) dx = lim f n(x) dx n K K n {f n } K (term by term integration) 3.5 ( ) K f : K C, {f n } K {f n } f (K ) lim sup f n (x) f(x) = n x K K {a n } n s n (x) := x K a n (x) (K ) n a k (x) {s n } n N (K ) k= f n (x ) f(x ) sup f n (x) f(x) x K ( ) sup f n (x) f(x) =, x R sup f n (x) f(x) = n x R sup f n (x) f(x) = x R () Ω C, f :Ω C,{f n } Ω {f n } Ω f f Ω x Ω ε {f n } Ω f ( N N) ( n N: n N) sup f n (y) f(y) < ε y Ω 3. 6 {f n } f {f n } {f n } f f 54
56 f N Ω ( δ >) ( x Ω: x x <δ) f N (x) f N (x ) < ε 3. x Ω, x x <δ f(x) f(x ) = f(x) f N (x)+f N (x) f N (x )+f N (x ) f(x ) f(x) f N (x) + f N (x) f N (x ) + f N (x ) f(x ) sup y Ω f(y) f N (y) + f N (x) f N (x ) +sup f N (y) f(y) y Ω ε 3 + ε 3 + ε 3 = ε. f x {f n } f x = 3.6 Ω [a, b] 3.7 ( ) [a, b] R {f n } [a, b] n f [a, b] b a f n (x) dx b a b lim n a f n (x) dx = b a f(x) dx. b f(x) dx = b (f n (x) f(x)) dx f n (x) f(x) dx a sup f n (y) f(y) y [a,b] b a dx = sup f n (y) f(y) (b a). y [a,b] a 3.8 R I =[a, b] C {f n } n N () {f n } n N n f I () {f n} n N n g I f I C f = g x [a, b] f n (x) =f n (a)+ x a f n(t) dt 55
57 n f(x) =f(a)+ x a g(t) dt. g f f (x) =g(x). g f C 46. d dx x a g(t) dt = g(x) 3..3 Weierstrass M-test Weierstrass M-test 7 ( ) 3.9 (Weierstrass M-test) Ω {a n } Ω {M n } (i) ( n N) ( x Ω) a n (x) M n. (ii) M n n= a n (x) a n (x) Ω ( n= n= Ω a n (x) Ω ) n= n N, x Ω T n := n M k, S n (x) := n a k (x), s n (x) := n a k (x) k= k= k= x Ω, n, m N ( ) s n (x) s m (x) S n (x) S m (x) T n T m ( ) 7 ( ) ( ) ( ) ( ) ( ) Weierstrass M-test 56
58 {T n } Cauchy x Ω ( ) {S n (x)}, {s n (x)} Cauchy T = lim n T n, ( ) m S(x) = lim n S n (x), s(x) = lim n s n (x) s n (x) s(x) S n (x) S(x) T n T. x Ω sup x Ω s n (x) s(x) sup S n (x) S(x) T n T. x Ω n {S n } S {s n } s Ω ( a n (x) a n (x) n n ) ( 3.3 ) 3. ( ) a n (z c) n ρ <R<ρ R a n (z c) n K := {z C z c R} 3. Weierstrass Mtest c = ρ = ρ> R <r<ρ r (ρ < r = R + ρ, ρ = r = R +) a n z n z = r lim a nr n =. {a n r n } n n N M R. z R M := sup a n r n n N a n z n = a n r n z n M r ( ) n R. r ( ) n R M n := M z K a n z n M n, R<r r Weierstrass M-test a n z n K ( ) 3. ( ) 57 M n
59 D(c; ρ) (D(c; ρ) ) R<ρ {z C z c R} D(c; ρ) D(c; ρ) ( uniformly convergent on every compact set ) 3.3, =Taylor, 3. (, Abel){a n } n c C f(z) = a n (z c) n ρ f D(c; ρ) f (z) = na n (z c) n = n= ρ (n +)a n+ (z c) n (z D(c; ρ)). ( Abel ( A.5) Abel ) c = g(z) := na n z n g(z) ( n lim sup n n= na n z n ) Cauchy-Hadamard nan = n lim n n n lim sup n n an = (/ρ) = ρ. <R<ρ R f D(; R) f (z) =g(z) ε g(z) z R 8 k=n+ k a k R k < ε 3 N N z D(; R) z + h D(; R) h f(z + h) f(z) g(z) h = a n (z + h) n a n z n na n z n h n= N ( ) (z + h) k z k a k kz k (z + h) k z k + a k h h k= k=n+ + ka k z k. k=n+ 8 58
60 ( z k) = kz k h N ( (z + h) k z k a k h k= ( z <R, z + h <R) kz k ) < ε 3. (z + h) k z k = (z + h z) [ (z + h) k +(z + h) k z + +(z + h)z k + z k ] h ( z + h k + z + h k z + + z + h z k + z k ) h kr k (z + h) k z k a k h k=n+ 3 k=n+ f (z) =g(z) ka k z k k=n+ f(z + h) f(z) h k=n+ a k kr k < ε 3. k a k R k < ε 3. g(z) <ε. 3.3 ( ) Cauchy-Hadamard f g Cauchy-Hadamard ( ) 9 a n (z c) n, na n (z c) n ρ, ρ ρ = ρ n= { A = r R r>, } { a n r n <, B = r R r>, n= n a n r n < ( ρ =supa A =(,ρ ) A =(,ρ ] A = ( sup A = ρ )) a n r n n a n r n B A. n= n= <r<ρ r A, r > ρ r A 9 [5] ( Cauchy-Hadamard Cauchy-Hadamard ) } 59
61 { { (A = ) ρ = sup A (A ). ρ (B = ) = sup B (B ). ρ = A =. B A B =. ρ = ρ = ρ. ρ > A (A = B ) ( ) ( r A)( r :<r <r) r B. r ( ) >, lim n n =( N N) ( n N: n N) n n r r n r. n (r/r ) n n a N r n ( r r ) n an r n = a n r n. n a n r n n=n a n r n <. n=n r B (( ) ). B. B A ρ =supb sup A = ρ. ρ <ρ ρ <r <r<ρ r, r r <ρ r A. ( ) r B. ρ =supb r. ρ <r ρ = ρ. ( ) Taylor Taylor ( ) 3.4 ( Taylor ) a n (z c) n f D(c; ρ) a n = f (n) (c). n! f (n) (c) f(z) = (z c) n (z D(c; ρ)). n! D(c; R) k N f (k) (z) = )a n (z c) n k. f (k) (c) =k!a k. n(n ) (n k c C, r>, {a n } n {b n } n n=k a n (z c) n = b n (z c) n ( z c <r) a n = b n (n =,,, ) ( 3.4 z = c (z c) ) 6
62 Taylor Taylor Taylor ( 3 ) 3.5 z z < z z n z = z n ( z < ). D(; ). 3.6 z +4 = 4+z = ( 4 + z ) = 4 ( z = 4 4) ( z ) n ( ) n = n+ zn. z/4 <. z < 4. 4, D(; 4). 3.7 a z a = a ( z/a) = a z a = a ( z n z = a) n a. n+ z/a <. z < a. a, D(; a ). (z a) = n= (z a) = n a n+ zn. = n + a n+ zn. n + a n+ zn. a, D(; a ). 3.8 z + = ( z ) = ( ) z k = ( ) k z k. z < z <, D(; ). k= k= 3 (?) 6
63 ( ) +z =(z i)(z + i) +z = (z i)(z + i) = ( i z i ) = ( ) z + i i i( + iz) i( iz) = ( +iz + ) = [( iz) n +(iz) n ( ) n + ]= i n z n. iz ( ) 3.9 z3 3z z +5 (Taylor ) z 5z +6 f(z) := z3 3z z +5 f(z) z 3 3z z +5 z 5z +6 z 5z +6 z +, 3z 7 f(z) = (z +)(z 5z +6)+3z 7. = z ++ 3z 7 z 5z +6 z 5z z 5z +6=(z )(z 3) 3z 7 z 5z +6 = A z + B z 3 A, B A =,B =. z + Taylor f(z) =z ++ z + z 3. z = z 3 = 3 z z 3 = = z n n+ ( z < ). z n 3 n+ ( z < 3). f(z) =z + = z + z n n+ ( + z 4 + n= z n 3 n+ z n n+ ) = 3 + z z 4 9 z = = z n=, D(; ) n= z 36 ( + n+ 3 n+ 6 ( 3 + z ) 9 + z n 3 n+ n= ( ) z n n= + n+ 3 n+ ( + n+ 3 n+ ) z n. ) z n
64 3.3 ( ) z +3 z +3 = (z ) + 4 = 4 +(z )/4 = 4 ( z ) = 4 4 ( ) n = 4 (z n+ )n. ( ) n (z ) n 4 n (z )/4 < z < 4 4 D(; 4). ( ) 3.3 () {a n } n c C a n (z c) n ρ ρ> f(z) D(c; ρ) F (z) = F (z) := 3.3 ( ) f (z) = a n n + (z c)n+ a n n + zn+ ρ F (z) =f(z), f() = f +z f (z) = +z = ( ) k z k (z D(; )) f(z) = + f() = k= k= ( ) k k + zk+ (z D(; )). f(z) = k= ( ) k k + zk+ (z D(; )). ( f arctan ) 3.33 (a n n a n z n ) n z n n= z n = z = (z ) nz n =(z ). n= 63
65 z n= nz n = n= z (z ). z n ( ) n z n z = z = z + z (z ) (z ) 3. k N n k z n n= 3.34 ( ) f(z) = f() =, f () = ( ) f (z) = f (z) = na n z n, n= n(n )a n z n = n= f(z) a n z n f (z) = f(z), (n +)(n +)a n+ z n. ( n Z : n ) (n +)(n +)a n+ = a n. a n a n+ = (n +)(n +). f() = a =,f () = a = a k = (k N), a k = ( )k (k)! (k =,,, ). f(z) = k= ( ) k (k)! zk. + ( ) f(z) =cosz. ( ) ( ) Gauss x( x)y +(γ (α + β +)x) y αβy = F (α, β; γ; x) Bessel Bessel Bessel J α (x) x y + xy + ( x α ) y = 64
66 () () (3) e z =expz := cos z = cosh z = z n n!, ( ) n (n)! zn, sin z = (n)! zn, sinh z = ( ) n (n )! zn, n= (n )! zn. n= + C z R z R C ( 9.5 ) e z =expz ( e x+iy = e x (cos y + i sin y) ) ( π ) ( ) () 48. z C cos z = eiz + e iz,sinz = eiz e iz i () 49. (e z ) = e z,(cosz) = sin z, (sinz) =cosz ( ) 3.35 e z +z = e z e z ( ) a n b n ( )( ) a n b n = ( k+l=n a k b l ) = e z e z z n z n ( ) = n! n! = zz k l = k!l! k+l=n n n! = n! k!(n k)! zk z n k = = e z +z. k= ( n ) a k b n k k= ( n ) zz k n k k!(n k)! k= n! (z + z ) n 65
67 5. () f(z) =e z f (z) =f(z), f() = c C f(z)f(c z) =f(c) () a, b C e a e b = e a+b 5. (e z ) x, y R e x+iy = e x (cos y + i sin y) () (6) 3.36 ( ) e x = lim (+ x ) n (x R) n n z (4) e z = lim n (+ z n e z e z ( Log z ) (4) e z [6], [7] 5. () sin z = () sin z = () cos(x + yi) =cosx sinh y i sin x cosh y, sin(x + yi) =sinx cosh y + i cos x sinh y ( x, y R x, y C ) ( ) α ( + z) α = z n ( z < ). n ( ( ) α : n ( ) α := n ) n α(α )(α ) (α n +). n! +z =(+z) / ) tan z = log( + z) = ( ) n n + zn+ ( z < ). ( ) n n + zn+ ( z < ). ( ) 66
68 tan z,log(+z) tan x = x dt, log( + x) = t + x dt t + tan z ( tan z = sin z cos z ) 3.4, Abel, Abel ( 3.3) D(c; ρ) {z C z c = ρ} z 3.4. z n z n, n, z n n n= n= z n z < z z = z n n A n := zn n, B n := n n= z = n= B n = n= n= A n = z n = n = B n. z = n A n = z n ( Weierstrass M-test D(; ) n ) z = z n z = n n= n= z n n = n =+ n= z = n= z n n = n= ( ) n ( log ) z = z z 67 n n=
69 3.4. Abel ( A.6 ) ( ) n= z n n z =,z z 3 π 4 = log = + 3. Abel ( ) (, ) n 3.37 (Abel ) {α n } n, {β n } n s n := α k n n α k β k = s n β n + s k (β k β k+ ) k= k= a = s, a k = s k s k= (k ) n α k β k = s β + k= = s β + n (s k s k ) β k = s β + k= n n s k β k s k β k+ = s β + k= k= n n s k β k k= ( n = s (β β )+ s k (β k β k+ )+s n β n k= n = s k (β k β k+ )+s n β n. k= n s k β k k= k= ) ( ) n s k β k + s n β n s β + s k β k+ k= k= 3.38 {α n } n {β n } n α n β n 3 Abel 68
70 s n := n α k ( M R) ( n N) s n M. Abel k= n n αβ k = s k (β k β k+ )+s n β n. k= k= s n β n Mβ n (n ) n s n β n. s k (β k β k+ ) M (β k β k+ ), n M (β k β k+ )=Mβ Mβ n+ Mβ k= n n s k (β k β k+ ) n 3.39 n= k= n α k β k k= z n n z =,z z α n := z n, β n := n n z n = k= z( z n ) z z ( + zn ) z = z {α n } {β n } n= z n n Abel {α n } n, {β n } n m N s n := (n m) n α k β k = s n β n + k=m 3.37 n k=m s k (β k β k+ ) α n β n = n= n k=m α k 69
71 3.4 (Abel (Abel s continuity theorem)) f(z) = a n z n z = R (R >) K { } Ω K := z C z/r z <R, z /R K f Ω K {R} f Ω K {R} lim f(x) =f(r). x [,R) x R (Ω K Mathematica R=; Manipulate[ RegionPlot[ x^ + y^ < R^ && Abs[ - (x + I y)/r]/( - Abs[x + I y]/r) <= K, {x, -, }, {y, -, }], {K,,,.}] K ) 3: R =,K =4.8 Ω K z = R K z Ω K n N ( z ) n α n := a n R n, β :=, fn (z) := R n a k z k k= 7
72 a k z k = α k β k z <R f n (z) = n α k β k, f n (R) = k= β n = ( ) n z <. R n α k. lim n f n (R) =f(r) {f n (R)} n N Cauchy 3 (5) lim β n β n+ = sup n + l>n m, n N, m>n m f m (z) f n (z) = a k z k = s k := k j=n+ k=n+ α j s k = k= f l (R) f n (R) =. ( z n ( R) z ) z/r = R z /R K<. m k=n+ k α j j= α k β k = m k=n+ s k (β k β k+ )+s m β m. n α j = f k (R) f n (R) j= s k = f k (R) f n (R) sup f l (R) f n (R). l>n f m (z) f n (z) sup f l (R) f n (R) l>n ( m k=n+ (K +)sup f l (R) f n (R). l>n β k β k+ + β m lim m f m(z) =f(z) ( {f n (z)} n N Cauchy ) m z f(z) f n (z) (K +)sup f l (R) f n (R). l>n sup f(z) f n (z) (K +)sup f l (R) f n (R). z Ω K l>n (5) {f n } Ω K f 3.4 (Stolz ) Abel α (,π/) α arg(z R) π <α z R (Stolz z R ) f(z) f(r) lim f(z) =f(r). arg(z R) π <α z R z/r z /R = R z < secα R z () 3 ε N n, m N f m (R) f n (R) < ε. sup f l (R) f n (R) ε. l>n 7 )
73 3.43 (Abel ) Abel Niels Henrik Abel (8 89, ). α ( + x) α ( ) ( ) 4 w = z α (α C \ Z) ( Taylor C 33 ) 4. log z 4.. log Taylor () log Taylor ( ) n ( ) n ( ) log ( + x) = n + xn+ = x n ( x < ) n +x = ( x) n = ( ) n x n ( x < ) ( ) n ( ) log ( + z) = z n ( z < ) n log lim log x =+ ( lim log( + x) =+ ) x + x + ( ) x = 33 ( ) n ( ) ( ) log( + z) = z n,(+z) α α = z n, tan ( ) k z = n n k + zk+. n= 7 k=
74 4.. e w = z log log: (, ) R R x e x y R, x (, ) y =logx x = e y. 34 z C \{} 35 z = e w w w = u + iv (u, v R) e w = e u e iv z z = re iθ (r>, θ R) z = e w re iθ = e u e iv r = e u e iθ = e iv. (: re iθ = e u e iv r = e u re iθ = e u e iv e iθ = e iv ) z = e w u =logr v θ (mod π) u =logr ( n Z) v = θ +nπ ( n Z) w =logr + i (θ +nπ). 4. (e w = z ) z C\{} w e w = z z z = re iθ (r>, θ R) w =logr + i (θ +nπ) (n Z) w =log z + i arg z 4. ( ) z e w = z e w = ( e w e w = e w w = e = ) e w = w =log + i arg = nπi (n Z). e w = w =log + i arg = log + nπi (n Z). x> e w = x w =logx +nπi (n Z). nπi e w = w =log + i arg( ) = + (n )πi =(n ) πi (n Z). e w = w =log + i arg( ) = log + (n )πi (n Z). e w = i w =log i + i arg i =+(n +/)πi =(n +/) πi (n Z). e w =i w =log i + i arg(i) =log+(n +/)πi (n Z). x 34 dt log x = t 35 z 73
75 4..3 log z log z e w = z z arg z ( log ( ) ( ) (, π) () ) (i) e w = z w log z :=log z + i arg z =log z + i (θ +nπ) (n Z). z C \{} log z log ( z ) ( ) z log z log z (branch) (ii) π I I =[, π) I =( π, π] ( α R I =[α, α +π) I =(α, α +π].) z C \{} z = re iθ (r>, θ I) r, θ r, θ log z := log r + iθ log: C \{} C {u + iv u R, v I} (a) I =( π, π] log z Log z Log z := log r + iθ, z = re iθ (r>, π <θ π). Log: C \{} C {u + iv u R, π <v π} Log Arg : Log z =log z + i Arg z. Log N := {z C z<} (x z x Im Log z π, z x Im Log z π. lim z x Log z =log x + iπ, Im z> lim z x Log z =log x iπ. Im z< 74
76 z x Log z ) ( ) Mathematica Mathematica Log[] Im Log z Plot3D[Boole[x^+y^<4] Im[Log[x + I y]], {x, -, }, {y, -, }] (Boole[] ) Re Log z log z Im log z C \{z C z } ( ) Ω ( π,π) := {w C π<im w<π} f :Ω ( π,π) C, f(w) =e w (w Ω ( π,π) ) ( ) 36 Log z = f(w) dz dw = ew = z dw dz = z. (6) d dz Log z = z (b) z [, π) ( ) z = re iθ, r>, θ [, π) log z := log r + iθ log: C \{} C ( ) P := {z C z>} C \{z C z } ( ) Ω [,π) := {w C < Im w<π} g :Ω [,π) C, g(w) =e w (w Ω π,π ) z = g(w) dz dw = ew = z dw dz = z. (7) d dz log z = z 36.4 ) 75
77 (ii)-(a) Log (ii)-(b) log log x (, ) log x =Logx = log x. ( log ) (?): (ii)-(a) Log N (ii)-(b) log P 4.3 ( dy/dx = ay ) a dy/dx = ay y = Ce ax (C ) dy y = adx log y = ax + C (C ). y = e ax+c = e C e ax. y = ±e C e ax = C e ax. ±e C C ( ) 37 ( ) 4. z α ( log z ) a, b a b a b (( ) π ) a > (8) a b = e b log a z α 54. a>, b R a b = e b log a z α p(z,α) (p (power) ) z C \{}, α C (9) p(z,α) :=e α log z log z p(z,α) p(z,α) ( ) z z = re iθ (r>, θ R) p(z,α) =e α log z α(log r+i(θ+nπ)) = e (n Z). α R α log r R, α(θ+nπ) R e α log r = ( e log r) α = r α p(z,α) =r α e iαθ e πinα (n Z). e πinα 37 76
78 (a) α Z nα Z e πinα =. p(z,α) =r α e iαθ = ( re iθ) α = z α. ( z α α> α z α < α z ) (b) α Q \ Z (3) α = q p (p N, q Z, p q ) () p(z,α) =r α e iαθ nq πi e p = r α e iαθ ω nq (n Z), ω := e πi/p p q nq p,,..., p p(z,α) =r α e iαθ ω k (k =,,...,p ). z = r α p α = p z p (c) α C \ Q p(z,α) ( ) p(z,α) Mathematica f p[z_, alpha_, maxn_] := Module[{r, t, w}, r = Abs[z]; t = Arg[z]; w = r^alpha*exp[i alpha t]; Table[{Re[w Exp[I n alpha Pi]], Im[w Exp[I n alpha Pi]]}, {n, maxn}]] g8=listplot[p[,/8,8], AspectRatio->Automatic, PlotStyle->{PointSize[.3]}] groota=listplot[p[, Sqrt[], ], AspectRatio -> Automatic] grootb=listplot[p[, Sqrt[], ], AspectRatio -> Automatic] Manipulate[ ListPlot[p[, Sqrt[], n], AspectRatio -> Automatic], {n,, }] : p(, /8), p(, ) ( ), p(, ) ( ) p(z,α) =e α log z z α 77
79 4.4 ( ) ( ) = e πi log( ) = log + i(π +nπ) =(n +)πi (n Z) =( ) / = e log( ) = e (n+)πi = e (n+ )πi = i( ) n = ±i. ( ) α =, z = z = eπi, ω = e πi/ = e πi = =z / = e πi ω k = i ( ) k (k =, ) =±i. 4.5 i i i i = e i π ( π ) ( log i =log + i +nπ = n + ) πi (n Z). (a b = e b log a ) i i = e i log i = e i (n+ )πi = e (n+ )π (n Z). (a) α Z z α (b) α Q \ Z α α = q p (p N, q Z) zα p p p (c) α R \ Q z α : z α = e α log z log z =logr + i(θ +nπ) ( z = re iθ ) α ( z = z / ) 4.3 ( ) 4.6 () sin z = () sin z = ( ) sinz = eiz e iz i () sin z = eiz e iz i ( n Z) ( n Z) = e iz = e iz e iz = iz =log+i( + nπ) z = nπ. sin z = z = nπ (n Z). 78
80 () w := e iz sin z = eiz e iz = e iz e iz =4i w i w =4i w 4iw = w =i ± (i) +=i ± ( 3i = ± ) 3 e iπ/ ( ( n Z) iz =log ± ) 3 + i(π/+nπ) ( ( n Z) z = i log ± ) 3 + π(/+n). sin z = z =(n +/)π i log ( ± 3 ). w C w =sinz z z = i log (iw + ) w. ( ) arcsin z =sin z := i log (iz + ) z, arccos z =cos z := i log (z i ) z = π (iz + i log + ) z, arctan z =tan z := i (log( iz) log( + iz)). ( arcsinh z =sinh z := log z + ) z +, ( arccosh z =cosh z := log z + ) z, arctanh z =tanh z := log +z z. ( arcsinh 38 ) ( log exp z = e log z/ ) 55. cosh(iz) =cosz, sinh(iz) =i sin z. 56. (arcsin z) = z, (arccos z) =, (arctan z z) = +z, (arcsinh z) = z +, (arccosh z) = z, (arctanh z) = z. 38 dx x x + k = log + x + k k > arcsinh x k Mathemaitca ArcSinh[] k log(x + x + k) 79
81 5 ( ) 5. Cauchy 39 log z = z dζ ζ ( : ([5]) WWW ( complex/) 5 ) () C R ().. 3. Cauchy ( ) 39 Ahlfors [8] 8
82 5. ( ) Ω C f :Ω C C : z = ϕ(t) (t [α, β]) Ω C C f (line integral) (3) C f(z) dz := β α f (ϕ(t)) ϕ (t) dt. C 5. Ω C f :Ω C C : z = ϕ(t) (t [α, β]) Ω C β (3) f(z) dz = fds:= f (ϕ(t)) ϕ (t) dt. ( f C C C ds C ) C F (t) :=f (ϕ(t)) ϕ (t) U(t) :=ReF (t), V (t) :=ImF (t) β α F (t) dt = β α α (U(t)+iV (t)) dt := β α β U(t) dt + i V (t) dt α ( Fourier ) β β 57. F :[α, β] C F (t) dt F (t) dt α α 5.3 f(z) =z, C ϕ(θ) =e iθ (θ [,π]) π ( f(z) dz = ) π [ e iθ e ie iθ dθ = i e 3iθ 3iθ dθ = i 3i C ] π = e3πi e 3 = 3 = ( ) t ϕ (t) () (3) ϕ: [α, β] Ω C ϕ: [α, β] Ω {t j } n j= s.t. α = t <t < <t n = β, ϕ I j := [t j,t j ] ϕ j := ϕ Ij I j C tj t j f (ϕ j (t)) ϕ j(t) dt ( [t j,t j ] 4 ) (3) n tj f(z) dz := f (ϕ j (t)) ϕ (t) dt. C t j j= 4 ϕ t = t j (ϕ j (t j) ϕ j+ (t j) ϕ t j )f(ϕ(t))ϕ (t) t = t j 8
83 ( ) 5.5 ( ()) Ω C F :Ω C C Ω C a, b F (z) dz =[F (z)] z=b z=a = F (b) F (a). C C z = ϕ(t) (t [α, β]) ϕ C β β F (z) dz = F (ϕ(t))ϕ d (t) dt = F (ϕ(t))ϕ(t) dt =[F (ϕ(t))]t=β t=α dt C α = F (ϕ(β)) F (ϕ(α)) = F (b) F (a). ϕ C C n tj n F (z) dz = F (ϕ(t))ϕ (t) dt = (F (ϕ (t j )) F (ϕ (t j ))) C t j j= α j= = F (ϕ(t n )) F (ϕ(t )) = F (b) F (a). 5.6 ϕ() =, ϕ(π) =, C ( z 3 3 ) = z [ z 3 f(z) dz = 3 ] z= z= = ( )3 3 3 = Cf. [a, b] R f :[a, b] R f F s.t. F = f. F (x) := b a x a d dx x a f(t) dt = f(x) f(t) dt F f f(x) dx =[F (x)] b a = F (b) F (a) ( 8 b a ) F (x) Dx = F (b) F (a)
84 () () 5.7 ( ) f(z) = z (z Ω:=C \{}), C : z = ϕ(θ) =eiθ (θ [, π]) C f(z) dz =πi. f F f(z) dz = F (ϕ(π)) F (ϕ()) = F () F () = C f F (z) :=logz F (z) =f(z) f Ω := C \{z C z } F (z) =logz =logr + iθ (z = re iθ, θ (, π) ) f <ε< C ε : z = ϕ(θ) =e iθ (θ [ε, π ε]) C ε Ω f(z) dz = F (ϕ(π ε)) F (ϕ(ε)) = (log + i(π ε)) (log + iε) =(π ε)i. C ε ε + πi f(z) dz ( ) n Z, f(z) =z n n F (z) := zn+ n + F (z) =f(z) f(z) dz = F (b) F (a) = bn+ a n+. n + C (n ) () log ( z a z z + ( z + i + ) z i z a ) x =Rez, y =Imz, z, Arg z C 83
85 5.8 ( ) 5.5 (x, z ) ( ) 5. ( ) Riemann : b n f(x) dx = lim f(ξ j ) x j, a x j := x j x j, ξ j [x j,x j ], := max j n (x j x j ). n f(z) dz = lim f(ζ j ) z j. C j= j= z j := z j z j, ( ζ j z j z j, := max j n z j z j. ( ( z j z j z j, z j ) z j, ζ j α = t <t < <t n = β ξ j [t j,t j ] (j =,...,n) z j = ϕ(t j ), ζ j := ϕ(ξ j ) f(ζ j )=f (ϕ(ξ j )), z j = ϕ(t j ) ϕ(t j ) ϕ (ξ j ) t j, t j := t j t j n f(ζ j ) z j j= n f(ϕ(ξ j ))ϕ (ξ j ) t j. j= t f(ϕ(t))ϕ (t) Riemann := max (t j j n t j ) C β C α f (ϕ(t)) ϕ (t)dt n f(z) dz = fds= lim f(ζ j ) z j. (f Riemann ) 84 j=
86 5. () ( ) 5.9 Ω C C : z = ϕ(t) (t [α, β]) Ω ( ϕ: [α, β] Ω ) ϕ {ϕ(t) t [α, β]} C (the image of C) (the spur of C) C C C ϕ C ϕ C C ϕ C ( t [α, β]) ϕ (t) C C [α, β] {t j } n j= [t j,t j ] ϕ ϕ [tj,t j ] C (t j ) C C {t j } n j= [t j,t j ] ϕ ϕ [tj,t j ] C C (closed curve) ϕ(α) =ϕ(β) C (a simple curve) Jordan (a Jordan arc) ( ) ϕ ( t [α, β])( t [α, β]) t t ϕ(t ) ϕ(t ) ( ) ϕ [α, β) ( t [α, β))( t [α, β)) t t ϕ(t ) ϕ(t ) ( ) C C ( ) (Jordan ),3 85
87 5. ( ) c C, r> C : z = ϕ(t) =c + re iθ (θ [, π]) C C C c r {z C z c = r} C z c = r ( ) C : z = ϕ(t) (t [, 4]) t (t [, ]) +i(t ) (t [, ]) z = ϕ(t) := +i (t ) (t [, 3]) i i(t 3) (t [3, 4]) z c =r f(z) dz f(z) dz C C,, + i, i C C i +i O 5: C C 5. (C C) C : z = ϕ(t) (t [α, β]) z = ϕ( t) (t [ β, α]) C C 5.3 ( C, C C + C ) C : z = ϕ (t) (t [α,β ]), C : z = ϕ (t) (t [α,β ]) C C (ϕ (β )=ϕ (α )) { ϕ (t) (t [α,β ]) ϕ(t) := ϕ (t β + α ) (t [β,β + β α ]) C C C + C (C C C + C ) 86
88 6: C = C C + C ( C C C + C ) () (f(z)+g(z)) dz = f(z) dz + g(z) dz. C C C () λf(z) dz = λ f(z) dz. C C (3) f(z) dz f(z) dz. C C (4) f(z) dz = f(z) dz. C C (5) f(z) dz = C +C f(z) dz + C f(z) dz. C (), () (3) F :[α, β] C β α β F (t) dt F (t) dt F (t) =f (ϕ(t)) ϕ (t) C β f(z) dz = β f(ϕ(t))ϕ (t) dt f(ϕ(t))ϕ (t) dt = α (4) z = ϕ( t) (t [ β, α]) dz = ϕ ( t)dt C f(z) dz = α β f(ϕ( t)) ( ϕ ( t))dt = α α β α C f(z) dz. f(ϕ( t))ϕ ( t) dt. s = t t = α s = α, t = β s = β, dt = ds C f(z) dz = β α f(ϕ(s))ϕ (s) ( )ds = f(z) dz. C 87
89 (5) 5.5 C 5.6 C : z = e iθ (θ [,π]), C : z = e iπt (t [, ]), C 3 : z = e iπt (t [, ]), C 4 : z = t + i t (t [, ]) {z C z =, Im z }. (, ) f f(z) dz C j 59. C 5 : z = t + i t (t [, ]) f(z) dz C 5 C 4 f(z) dz 5.5 a b c r ϕ 5.7 ( ) Ω C C Ω C {f n } n N C C C f lim n C f n (z) dz = C f(z) dz. f f n (z) dz f(z) dz f n (z) f(z) dz C C C max f n(ζ) f(ζ) dz. ζ C C dz C n max f n(ζ) f(ζ) C ζ C f n (z) dz f(z) dz (n ). C C 88
90 5.4 : R ( ) f(x, y)dxdy, ( ) P f =, C t Q C f dr = C Ω C fds. f t ds = C Pdx+ Qdy. (Green Green ) C D C C D 4 f dr = rot f dx dy, ( ) D D D Pdx+ Qdy= ( ( ) x rot f =det f =det D (Q x P y ) dx dy. y ) P = Q x P y. Q f u, v f(z) dz = (u + iv)(dx + idy)= (u dx vdy)+i C C C g dz = C gds. C (v dx+ udy). 6 Cauchy Cauchy ( ) 4 Green Gauss Stokes dω = Ω ( M M Stokes ) D = M, C = M = D 89
91 6. Cauchy 4 f(z) dz = 3 (a) f C Ω (b) C Ω C (c) C Ω (f ) C (a) (b) (c) dz =πi z ( Ω=C \{}, f(z) = z, C : z = eiθ (θ [, π])) z = ((a), (b) C f(z) dz = ) (c) C C (Jordan ) Jordan C C ( ) C D C D Jordan C (Jordan ) (i) Ω Ω C Ω Ω C C f(z) dz = C (ii) C 4 ( ) Cauchy 9
92 6. 6. (Goursat, Pringsheim) Ω C f :Ω C Ω f(z) dz =. ( Gray [9] Goursat ( ) [] Pringsheim ) (a) (b) (c) ( az + b a z + bz ), 3 ( : 4 ) M := f(z) dz M = := 4 = 3 4. j ( ) j =,, 3, 4 ( ) f(z) dz = f(z) dz + f(z) dz + f(z) dz + f(z) dz M = f(z) dz f(z) dz j= j. 4 f(z)dz j j M 4 f(z)dz. f(z)dz M 4. : = n N f(z)dz M n 4. n 9
93 ( c C) n = {c}. n N c = Ω f(z)dz = [f(z) (f(c)+f (c)(z c))] dz. n n g(z) f(z)dz = g(z) dz n max n z n g(z) dz. n n dz n L n n n / L n = L n lim z c f(z) f(c) z c lim z c = f (c) g(z) z c =lim f(z) (f(c)+f (c)(z c)) z c z c ε δ> z c <δ g(z) ε z c. c n n n D(c; δ) n max g(z) ε max z c εl n. z n z n M 4 n ε M =. f(z) dz εl n L n = εl n 4 n M εl. 6. ( ) f(z) dz max f(z) dz z n n n f(z) dz L n = L n n f(z) f(c)+f (c)(z c) g(z) f(z) dz = g(z) dz max g(z) dz z n n n n (max f max g ) 9 =
94 f f Taylor max g(z) z n max f (z) L n z c δ n f(z) dz max f (z) L 3 n, z c δ M L3 n M = f ( ) ( ε >) M εl Cauchy 6.3 ( ) 6. f Ω f Ω a Ω f(z) dz = Ω Ω ( ) a a (i) a (ii) a (iii) a 7: a (,, ) (i) ε 3 a ε, ε f(z) dz = f(z) dz + f(z) dz + f(z) dz = f(z) dz. ε ε ε 93 ε
95 ( ε 4ε ) f(z) dz f(z) dz max f(z) dz 4ε max f(z). z ε z ε ε + f(z) dz =. (ii), (iii) (i) 6.4 Cauchy [] ( [] [] ) 6. f f(z) dz = ( j j f(z) dz = j f(z) dz = ) CC C f f(z) dz = Cauchy C 6.5 ( 45 ) 6 ( ) 3 [] ( ) ( ) 6.3 Ω C f :Ω C 3 94
96 (i) f Ω ( F :Ω Cs.t. F = f) (ii) Ω C C f(z) dz = (iii) f Ω (i) (ii) 43 (ii) (i) ( 6.9) (i) (iii) Cauchy 7.4( ) F F f = F (i) (ii) (ii) (iii) Morera ( ) (iii) (ii) Ω=C \{}, f(z) = z ( : f(z) dz =πi ) C (i) (ii) (iii) (iii) (ii) Cauchy Ω (iii) (ii) ( E.) Cauchy ( ) (i), (ii), (iii) 6.6 ( ) 44 (i) f, (ii) f dr =,(iii) rot f =, (i) (ii) (i) ( (ii)) (iii) 6.7 [] (i) (ii) ( ) ( ) 6.8 f (iii) (ii) Ω (i), (ii), (iii) (ii) (i).7(p. 4) C C 43 C f(z) dz = F ( ) F ( ) =. 44 (i), (iii) (ii), (iii) Cauchy 95
97 6.9 ( C ) Ω C f :Ω C Ω C C f(z) dz = C F :Ω CF = f. Ω a Ω z Ω a z Ω C C z F (z) := f(ζ) dζ C z F (z) C z a z Ω C z, C z C := C z +( C z) C (ii) = f(ζ) dζ = f(ζ) dζ f(ζ) dζ C C z F f z Ω ε > D(z; ε) Ω. h <ε h z z + h [z,z + h] Ω C z+h C z +[z,z + h] F (z + h) F (z) = f(ζ)dζ f(ζ)dζ = f(ζ)dζ. C z+[z,z+h] C z [z,z+h] [z,z+h] dζ =[ζ] ζ=z+h ζ=z = h f(z) dζ = f(z)h h [z,z+h] F (z + h) F (z) f(z) = (f(ζ) f(z)) dζ. h h F (z + h) F (z) f(z) h h h [z,z+h] f(ζ) f(z) dζ [z,z+h] max f(ζ) f(z) ζ [z,z+h] C z [z,z+h] dζ = max f(ζ) f(z). ζ [z,z+h] f z h F (z) =f(z). 6.4 Cauchy Cauchy ( E.5 ) 6. () Ω R n C n Ω (simply-connected) Ω Ω 96
98 6. ( Cauchy ) Ω C f :Ω C C Ω C f(z) dz =. C 6. R n, B(a; R) ={x R n x a <R}, (Jordan ) 3 R 3 \{a} R \{a} ( C \{c} ), {z C R < z c <R }, R 3 \ l l, 6.3 Ω () Ω (convex) ( a Ω)( b Ω) [a, b] Ω. () Ω (star-shaped) ( a Ω)( b Ω) [a, b] Ω. Ω a Ω a 6.4 ( ) C, D(c; r), D(c; r), ( ) ( ) () ( C,,, ( ) ) C C \{z C z }, () ( ) C C \{} ( ) 6. () () 97
99 (3) 6.5 Cauchy Cauchy ( ) Cauhcy Cauchy ( ) 6.6 ( ) Ω C f :Ω C f F :Ω C F = f. (f Ω Ω ) ( d x f(t)dt = f(x) dx a ) Ω a Ω z Ω [a, z ] Ω F (z ):= f(z) dz ([a, z ] a z ) [a,z ] F :Ω C F = f Ω z Ω ε D(z ; ε) Ω. < h <ε h z + h Ω. 3 a, z, z + h ( ) Ω( ). () [a, z ]+[z,z + h] [a, z + h] () 6. f(z) dz + f(z) dz f(z) dz =. [a,z ] [z,z +h] F (z + h) F (z )= [z,z +h] [a,z +h] f(z) dz. ( 6.9 ) F (z + h) F (z ) f(z )= f(z) dz dz f(z ) h h [z,z +h] h [z,z +h] = (f(z) f(z )) dz. h F (z + h) F (z ) h f(z ) h [z,z +h] max f(z) f(z ) dz z [z,z +h] [z,z +h] = max z [z,z +h] f(z) f(z ). 98
100 f z h F (z + h) F (z ) lim h h F z F (z )=f(z ). = f(z ). 6. a, z, z + h ( ) Ω 63. ( ) f :Ω C z Ω h f(ζ) dζ f(z) h [z,z+h] ( ) 6.7 ( Cauchy ) Ω C f :Ω C Ω C C f(z) dz = C (f Ω Ω ) C a, b C a = b. f F f(z) dz =[F (z)] b a = F (b) F (a) =. C 6.8 ( Cauchy ) D C f : D C D C C f(z) dz = C (f D D ) 6.9 (/z ) ( Log ) f : C \{} C, f(z) = dz ( : =πi ) Ω:=C \{z C z } z z = z f Ω f Ω dζ F (z) = f(ζ) dζ = (z Ω) ζ [,z] ( Log z z = ) C Ω C f(z)dz =. [,z] C 99
101 45 6. ( z a (33) ) a, c C z c =r { dz z a = πi ( c a <r) ( c a >r). a c >r R := D(c; R) z a r + a c z c = r D(c; R) r <R< a c Cauchy dz z a =. z c =r a c <r ( b) ( ) ( a), ( b) ( a) 8 C, C, C, C,Γ,Γ C + C, C + C z c = r, z a = δ 8: (34) C +C dz z a = C +C dz z a 45 z c = r z a dz z a = δ z c =r z a = dz. Cauchy z a =δ z a f(z) = f(ζ) dζ f πi ζ z C
102 C Γ C Γ z a dz z a =. C Γ C Γ C +Γ C +Γ z a dz z a =. C +Γ C +Γ Γ,Γ dz z a =. (34) C +C C C ( b) z c = r z z a = (z c) (a c) = z c a c z c = a c a c z c = r = (a c) n (z c) n+. < (z ) Weierstrass M-test z c = r 46 z c =r dz z a = z c =r (a c) n (z c) dz = (a c) n πiδ n+ n =πi. ( ( ) n = n = (a c) πi =πi ) ( c) ( []) Green Cauchy 47 D C D f D = D D f(z) dz =. D D := {z C z a >δ, z c <r} D z a C : z c = r C : z a = δ C C D dz = D z c = dz z c =r z a dz z a =δ z a. 64. (34) ( ) 46 Weierstrass M-test 47 Green [] z a
103 7 Cauchy 7. Cauchy 7. ( Cauchy ) c C, R> D := D(c; R) Ω C D Ω f :Ω C z D f(z) = f(ζ) πi ζ c =R ζ z dζ. ( ) ζ c = R C f(ζ) f(z) (ζ Ω \{z}) g(ζ) := ζ z f (z) (ζ = z) g :Ω C Ω \{z} ε D(c; R + ε) Ω D(c; R + ε) Cauchy g(ζ) dζ =. C f(ζ) ζ z dζ = C C f(z) dζ = f(z) ζ z C ( 6. ) πi C f(ζ) dζ = f(z). ζ z dζ ζ z =πif(z). 7. (Cauchy ) ε> f(ζ) ( ) ζ c =R ζ z dζ = f(ζ) ζ z =ε ζ z dζ ζ = z + εe iθ (θ [, π]) f(ζ) πi ζ z =ε ζ z dζ = π f(z + εe iθ ) iεe iθ dθ = π f(z + εe iθ )dθ. πi εe iθ π πi ζ c =R f(ζ) dζ = lim ζ z ε + π f(z + εe iθ )dθ = π f(z)dθ = f(z). π π
104 ( ) 6. Green Cauchy 48 ζ f(ζ) ζ z D := {ζ C ζ z >ε ζ c < R} Ω \{z} f(ζ) = D ζ z dζ = ζ c =R f(ζ) ζ z dζ ζ z =ε f(ζ) ζ z dζ () C C C {f n } C C f f n (z) dz = f(z) dz. lim n n f n (z)dz f(z)dz C C C C C f n (z) f(z) dz sup f n (z) f(z) dz. z C C (analytic function) 7.4 ( ) Ω C f :Ω C c Ω, R>, D(c; R) Ω (35) a n := f(ζ) n+ dζ πi (ζ c) ζ c =R f(z) = a n (z c) n (z D(c; R)). Ω C f :Ω C c Ω, <R, D(c; R) Ω <r<r r (36) a n := f(ζ) n+ dζ πi ζ c =r (ζ c) f(z) = a n (z c) n (z D(c; R)) 48 f 3
105 D := D(c; R), C := D (C ζ = c + Re iθ (θ [, π]), C = {ζ C ζ c = R} ) z D Cauchy r := z c R f(z) = f(ζ) πi ζ c =R ζ z dζ. r< ζ C z c ζ c = r ζ z = (ζ c)+(c z) = ζ c z c ζ c f(z) = πi C f(ζ) ζ c = ζ c ( ) n z c dζ. ζ c f C M := max f(ζ) ζ C f(ζ) ζ c ( ) n z c M ζ c R rn. ( ) n z c. ζ c M n := M R rn M n Weierstrass M-test C f(z) = πi C f(ζ) ζ c ( ) n z c dζ = ζ c ( πi ζ c =R f(ζ) (ζ c) n+ dζ ) (z c) n. f(z) = a n (z c) n. (36) R c R >, D(c; R) Ω R a n R a n = f (n) (c) n! ( ) <R <R, D(c; R ) Ω D = {ζ C R < ζ c <R } ( ) n! πi ζ c =R f(ζ) n! dζ (ζ c) n+ πi ζ c =R f(ζ) dζ =. (ζ c) n+ 4
106 65. ( ) f F = f F F f = F 8 Green Cauchy, Green (Green ) Cauchy ( ([]) ) 8. Green Green (Green ) () (37) Pdx+ Qdy = (Q x P y ) dx dy D D R D ( ) 8. ( ) D D ( ) (a contour integral) L A TEX \oint Green Green D 5
107 8. (( ) Green) R D C C,..., C m C j (j =,...,m) D D C P, Q Pdx+ Qdy = (Q x P y ) dx dy. D D [], [3] 9: D D C + C + C ( Green ) R D (x y ) D C C C D D C P, Q Pdx+ Qdy = (Q x P y ) dx dy. D ( ) [4] 8.3 D D ) (37) 49 D C P, Q (37) D Green D 49 Pdx+ Qdy= (Q x P y )dx dy (37) D j D j 6
108 8. Green Cauchy, Cauchy 8.4 (Green Cauchy ) D C R Green D f f(z) dz =. D D E. f u, v Cauchy-Riemann u x = v y, u y = v x f(z) dz = (u + iv)(dx + idy)= (u dx vdy)+i (v dx+ udy) D D D D = ( v x u y ) dx dy + i (u x v y ) dx dy D D = dx dy + i dx dy =. D D D C C z = ϕ(t) (t [α, β]) ( ) ξ(t) ξ(t) :=Reϕ(t), η(t) :=Imϕ(t), ϕ(t) := η(t) f(z) dz = D = β α β α β = = α D f (ϕ(t)) ϕ (t) dt u (ϕ(t))+iv (ϕ(t)) (ξ (t)+iη(t)) dt β (u (ϕ(t)) ξ (t) v (ϕ(t)) η (t)) dt + i α (u dx vdy)+i D (v dx+ udy). (v (ϕ(t)) η (t)+u (ϕ(t)) ξ (t)) dt 8.5 (Green Cauchy ) D C R Green D f ( a D) f(a) = πi D f(z) z a dz. a D r D(a; r) D <ε<r ε D ε := D \ D(a; ε) D ε Green () 7
109 D ε = D C, C : z a = ε 8.4 = f(z) πi z a dz = f(z) πi z a dz πi D ε D z a =ε f(z) z a dz. πi z a =ε πi D f(z) z a dz = πi z a =ε f(z) z a dz. f(z) dz f(a) z a = π f(a + εe iθ ) dθ f(a) π π = π ( f(a + εe iθ ) f(a) ) dθ π π max f(a + εe iθ ) f(a) π dθ θ [,π] = max f(a + εe iθ ) f(a). θ [,π] π dθ ε πi D f(z) z a dz = f(a). 8.3 ( ) 6 ( (E) ) 8.4 D z a = ε ( 3.4 πi ) 8.6 ( ) C z =cosθ + i sin θ (θ [, π]) z I = z dz f(z) : f(z) = z z = C z (z +)(z ) = z + + z. ε z =+εe iθ (θ [, π]) C,ε, z = +εe iθ (θ [, π]) C,ε ε C, C,ε, C,ε 8
110 D := D { z = x + iy x + y } < z + >ε z >ε D = C C,ε C,ε. D, f D Cauchy ( 8.4) = f(z) dz = f(z) dz f(z) dz f(z) dz. D f(z)dz = C,ε C,ε C dz z + + C,ε,ε dz z,ε =+πi =πi. ( C,ε {z C Re z>} z + Cauchy ) f(z)dz = C,ε C,ε dz z + + C,ε dz z =πi +=πi. I = f(z) dz = f(z)dz + f(z)dz =4πi. C C,ε C,ε u t (x, t) =u xx (x, t) U(x, t) = e x 4t 4πt Fourier 8.7 (Fourier ) h R e (x+ih) dx = π = e x dx. ( R h {x + ih x R} Fourier Fourier ) f(z) =e z (z C) f C R> Γ,R := [ R, R], Γ,R := [R, R + ih], Γ 3,R := [ R + ih, R + ih], Γ 4,R := [ R, R + ih], Γ R := Γ,R +Γ,R Γ 3,R Γ 4,R Γ R C f C Cauchy (38) = f(z)dz = f(z)dz + f(z)dz f(z)dz f(z)dz. Γ R Γ,R Γ,R Γ 3,R Γ 4,R Γ,R z = x (x [ R, R]) dz = dx f(z)dz = Γ,R R f(x) dx = R R R 9 e x dx.
111 R π : R (39) lim e x dx = π. R R Γ 3,R z = x + ih (x [ R, R]) dz = dx Γ 3,R f(z)dz = R R f(x + ih) dx = R R e (x+ih) dx. Γ,R z = R + ith (t [, ]) 5 f(z) = e z = e Re( z ) = e Re( (R+ith) ) = e R +t h e R +h. f(z)dz Γ,R max z Γ,R (4) lim f(z)dz =. R Γ,R R +h f(z) dz e h. Γ,R Γ 4,R z = R + ith (t [, ]) f(z) = e z = e Re( z ) = e Re( ( R+ith) ) = e R +t h e R +h, f(z)dz Γ 4,R max z Γ 4,R (4) lim f(z)dz =. R Γ 4,R R +h f(z) dz e h. Γ 4,R (38) f(z)dz = f(z)dz + f(z)dz f(z)dz Γ 3,R Γ,R Γ,R Γ 4,R R e (x+ih) dx π = R R R R R e x dx π + f(z)dz f(z)dz Γ,R Γ 4,R e x dx π + f(z)dz Γ,R + f(z)dz Γ 4,R. (39), (4), (4) R e (x+ih) dx = π. 5 h> z = R + iy (y [,h]) h < z = R + ith
112 Cauchy (i) ( ) (ii) Cauchy (the Laurent expansion) (residue) Laurent () c f c R >s.t. < z c <Rf c Laurent f(z) = a n (z c) n + a n n= a n = πi ζ c =R a n (z c) n ( < z c <R) f(ζ) (ζ c) n+ dζ (Taylor ) f c Res(f; c) ( ) Res(f; c) :=a f(z) dz. πi z c =R Q Laurent A ζ := ζ z c z c (iii) 9 9. ()
113 9. (, ) c C, f c () c f (zero) f(c) = () c f k N, f(c) =f (c) = = f (k ) (c) = f (k) (c) f c (order) c f k 9. (a) f(z) =sinz mπ (m Z) f(mπ) =sinmπ =, f (mπ) =cosmπ =( ) m mπ f Taylor sin z =( ) m sin(z mπ) =( ) m sin z =(z mπ)g(z), g(z) :=( ) m g(mπ) =( ) m ( ) n (z mπ)n+ (n +)! (b) f(z) =cosz mπ (m Z) f(mπ) =cosmπ = =, f (z) = sin z, f (mπ) = sin mπ =, f (z) = cos z, ( ) n (z mπ)n (n +)! f (mπ) = cos mπ = mπ (m Z) Taylor cos z =cos(z mπ) = cos z =(z mπ) g(z), g(z) := g(mπ) = ( ) n (z mπ)n (n)! n= ( ) n (z mπ)(n ) (n)! 9.3 (k ) c C, f c U k N (i) U g f(z) =(z c) k g(z) (z U) g(c). (ii) f(c) =f (c) = = f (k ) (c) = f (k) (c).
114 k (i) (ii) (ii) = (i) f c c Taylor R >, {a n } s.t. f(z) = a n (z c) n ( z c <R). a n = f (n) (c) a = a = = a k =,a k. n! f(z) = a n (z c) n =(z c) k a n (z c) n k =(z c) k a n+k (z c) n. n=k g(z) := n=k a n+k (z c) n z c <R f(z) =(z c) k g(z), g(c) =a k. (i) = (ii) f(z) =(z c) k g(z), g(c) h(z) :=(z c) k f(z) =g(z)h(z). m k Leibniz m ( ) m f (m) (z) = h (r) (z)g (m r) (z). r r= r k h (r) (c) = m k h (r) (c) =( r m) h (k) (z) k! m ( ) m f (m) (c) = g (m r) (c) = ( m k ), r r= ( ) k f (k) (c) = k!g(c) =k!g(c). k ( Prop. ) 9.4 (k ) f(z) C[z], c C, k N 3 (i) c f(z) k ( f(z) (z c) k k = ) (ii) g(z) C[z] s.t.f(z) =(z c) k g(z) g(c). (iii) f(c) =f (c) = = f (k ) (c) = f (k) (c). ( ) ( ) 3
115 C (c f(z) c f ) c ( ) c c f f(c) = (i) ( n N {}) f (n) (c) =. ( f c ) (ii) ( k N) f(c) =f (c) = = f (k ) (c) =,f (k) (c). 9. ( ) (sin z ) ( ) 9.5 ( (the identity theorem), ) D C ( ) f : D C g : D C c D, {z n } n N (i) lim n z n = c (ii) n N z n D z n c f(z n )=g(z n ) D f = g. ( D f = g (i), (ii) f = g ) f g f g = D ( ε >) D(c; ε) D. 7.4 {a n } n f(z) = a n (z c) n (z D(c; ε)). D(c; ε) f = n a n = n N {} s.t. a n. n k a = a = = a k =, a k. g(z) := f(z) = a n (z c) n =(z c) k n=k a n+k (z c) n z D(c; ε) a n+k (z c) n g(z n )= f(z n) (z n c) k = (z n c) k =. (z D(c; ε)). a k = g(c) = lim n g(z n )= lim n =. 4
116 n a n =. f(z) = (z D(c; ε)). ( ) D := { z D ( n N {})f (n) (z) = }, D := { z D ( n N {})f (n) (z) } () D D = D, D D =. f (n) D 5 D z D ( R >) ( {a n } n N {} C N {} ) ( z D(z ; R)) f(z) = a n (z z ) n. z D n a n = f (n) (z ) =f(z) =(z D(z ; R)). D(z ; R) D n! D c D D. 9.6 D =, D = D. f =ind. 9.6 ( ) D C D D C n D D = D, D D = D D : ( : c c D ϕ(t ) ϕ(t ) D, D ) 9.5 () D D c D, c D ϕ: [, ] Ω, ϕ() = c, ϕ() = c ϕ I := {t [, ] ϕ(t) D }, I := {t [, ] ϕ(t) D } 5 z D D ( δ > ) D(z ; δ ) D. ( n N {}) f (n) (z ). ε := f (n) (z ) ε > f (n) ( δ > ) ( z D : z z <δ ) f (n) (z) f (n) (z ) <ε. f (n) (z) = f (n) (z ) f (n) (z )+f (n) (z) f (n) (z ) f (n) (z ) f (n) (z) >ε ε =. f (n) (z). z D. δ := min{δ,δ } δ > D(z; δ) D. D 5
117 I I =[, ], I I =, I, I. D, D ϕ δ >, δ > s.t.[,δ ] I,[ δ, ] I. t := sup I <t <. t, d := min{t, t } > t I ε (,d)s.t.(t ε,t + ε ) I. t =supi t + ε t I ε (,d)s.t.(t ε,t + ε ) I. I I I 9.7 () c (f(c) = ) ( ε >)( z D D(c; ε) \{c}) f(z). ( ε >)( z D D(c; ε) \{c}) f(z) =. n N < z n c < n, f(z n)= z n D f =ind 9.8 f : C C ( x R) f(x) = ( z C) f(z) = 9.9 ( ) Taylor cos x = ( ) n (n)! xn (x R) ( ) cos z := ( ) n (n)! zn (z C). 9.8 f : C C f(x) =cosx (x R) cos x ( ) 9. ( ()) (4) e x+y = e x e y (x, y R) 6
118 e z+w = e z e w (z,w C) e z E(z), e x ( x R) E(x) =e x 5 y R f : C C f(z) :=E(z + y) E(z)E(y) (z C) E f C z = x R (4) f(z) =f(x) =E(x + y) E(x)E(y) =e x+y e x e y = e x e y e x e y =. ( z C) f(z) =. (43) ( y R)( z C) E(z + y) E(z)E(y) =. z C g : C C g(w) :=E(z + w) E(z)E(w) (w C) g C w = y R (43) g(w) = g(y) = E(z + y) E(z)E(y) =. ( w C) g(w) =. ( z C)( w C) E(z + w) E(z)E(w) =. E(z + w) =E(z)E(w) Ω=C \{x R x } z Ω z Ω z z Ω Log(z z )=Logz +Logz 5 x, y R E(x + yi) :=e x (cos y + i sin y) x R E(x) =e x 7
119 ( (the mean-value property)) Ω C f :Ω C c Ω D(c; r) Ω r> f(c) = π f ( c + re iθ) dθ. π ( z c = r f ) Cauchy z = c f(c) = πi ζ c =r f(ζ) ζ c dζ. ζ = c + re iθ (θ [, π]) f(ζ) πi ζ c =r ζ c dζ = π f(c + re iθ ) ire iθ dθ = π f ( c + re iθ) dθ. πi re iθ π 9. ( ) u = u(x) =u(x,...,x n ) u u = (u ) (Gauss 53 ) f u, v (u(x, y) :=Ref(x + iy), v(x, y) :=Imf(x + iy)) u = v = 9.3 ( (the maximum principle, maximum-modulus theorem)) Ω C f :Ω C z Ω, ( z Ω) f(z) f(z ) ( f(z ) f ) ( C C)( z Ω) f(z) =C. ( ) M := f(z ) Ω ( ε >) D(z ; ε) Ω. ρ := ε/ D(z ; ρ) Ω. <r ρ r f(z )= π π f ( z + re iθ) dθ. M = f(z ) π ( f z + re iθ) π dθ Mdθ= M. π π 53 [5] 3 5 8
120 54 π π f ( z + re iθ) dθ = π π Mdθ. f(z + re iθ ) M θ f ( z + re iθ) f ( z + re iθ) = M (θ [, π]) i.e. f(z) = M ( z z = r). r f(z) = M ( z z ρ).. f D(z ; ρ) : ( C C) f = C on D(z ; ρ). Ω f = C. 9.4 ( ) f f f ( ) f f (/f ) 9.5 ( ) ( ) u 9.4 Liouville 9.6 () C (an entire function) 9.7 ( ) e z, cos z, sinz tan z, Log z, +z 9.8 (Liouville (, Liouville s theorem)) f : C C ( M R) ( z C) f(z) M R {a n,r } f(z) = a n,r z n (z D(; R)). {a n,r } R {a n} f(z) = a n z n (z C). 54 f g on [a, b] b a f(x) dx b ( ) b a f(x) dx = b a g(x) dx f g. a g(x) dx. f g x [a, b] f(x ) <g(x ) b a f(x) dx < 9 b a g(x) dx. f g
121 n N a n = R > Cauchy a n = f(ζ) dζ πi ζn+ a n = πi ζ =R ζ =R f(ζ) ζ n+ dζ π ζ =R ζ =R f(ζ) n+ dζ ζ π ζ =R M dζ. Rn+ dζ =πr Cauchy (44) a n M R n. R a n =(n N). ( z C) f(z) =a. z z 9.9 ( ) n N, {a j } n j= C n+, a, f(z) = a z n + a z n + + a n z + a n ( ε :<ε<)( R R)( z C : z R) ( ε) a z n f(z) ( + ε) a z n. ( z C: z R) f(z) n lim f(z) =. z z f(z) a z =+ a n a z + a a z + + a n a z. n m N f(z) ( z ) lim =. zm z a zn lim z f(z) a z n =. ( ε >) ( R R) ( z C: z R) f(z) a z n f(z) <ε, i.e. ε a z n +ε. 9. n N, {a j } n j= C n+, a,f(z) =a z n + a z n + + a n z + a n ( M R)( M R)( R R)( z C : z R) M z n f(z) M z n. 9.9 ε =/ a z n f(z) 3 a z n ( z R).
122 M := a /, M := 3 a / 9. ( (the fundamental theorem of algebra)) P (z) n P (z) ( ) ( z C) P (z) f(z) := P (z) 9.9 lim P (z) = z ( R R)( z C : z R) P (z). f(z) ( z R). D(; R) ={z C z R} C f Weierstrass f ( M R)( z D(; R)) f(z) M. ( z C) f(z) max {,M}. Liouvillef P n 55 ( ) ( z C) P (z) f(z) := P (z) 9.9 R R ( M >)( R R)( z C : z R ) P (z) M z n. ( ) ( z C : z R) f(z) M z n MR n. f D(; R) z = R ( ) MR f(z) (z C). R n MRn f(z) =. f(z). 9.5 (ratio test (d Alembert ) Cauchy-Hadamard ) 9. Ω C f :Ω C c Ω R := {R > D(c; R) Ω f D(c; R) } f c ρ sup R 55 a z n + a z n + + a n z + a n (a, n ) a z n + a z n + + a n ( )a n = a n = = a = a = a
123 ρ> (Ω D(c; ε) Ω ε> ε D(c; ε) Ω 7.4 f D(c; ε) ρ ε ρ >.) ρ ρ Rρ sup R. R R ε (,R) D(c; R ε) Ω 7.4 f c D(c; R ε) R ε ρ. ε R ρ. sup R ρ. ρ =supr. ρ = f c C C R D(c; R) R R. sup R = ρ =supr. 9.3 () f(z) = Q(z) (P (z),q(z) C[z], P (z) Q(z) P (z) ) P (z) α, α,..., α n Ω:=C\{α,α,...,α n } f j {,,,n} lim f(z) = z = α j z αj (α j f ) c Ω f c min α j c j n () 9.4 ( p. 8) f(x) := +x R x R f x : ( r >)( {a n } n )( x (x r, x + r)) f(x) = x = f(x) = x + x 4 x 6 + = a n (x x n ). ( ) n x n < x < ( ) f(z) = z + = c = min{ i, i } = (z + i)(z i) D(; ) {z C z > } 68. f(z) = c = ( z + ) 9.5 (Bernoulli ) f(z) = (C ) e z = ( n Z)z =nπi f D := C \ n Z {nπi} z e z
124 z C z e z = e z z = n= z n n! = z n n! z n z n g(z) := (n +)! n! = n= z n (n +)!. (z C) g g() = g(z) = z e z = ( n Z \{}) z =nπi. D := C \{nπi n Z, n } = D {}, f(z) := (z D) g(z) f : D C f ( ) z < π {B n } s.t. B n (45) f(z) = n! zn ( z < π). lim f(z) = z = ±πi (z = ) z ±πi (45) π 9. B n Bernoulli (, Euler-Maclaurin, etc.) nk n= n k r 56,tan cot B =, B =, B = 6, B 3 =, B 4 = 3, B 5 =, B 6 = 4, B n ( Cauchy- Hadamard ) Bernoulli () f(z) := z e z B n := f (n) () Bernoulli ( f ) 56 n k = k= n(n + ), n k = k= n(n + )(n + ), 6 Bernoulli k= n ( ) n(n + ) k 3 = k= 3
125 Mathmematica f(z) Taylor Series[z/(Exp[z]-),{z,,}] B n Mathematica Bernoulli, Bernoulli BernoulliB[n], BernoulliB[n, x] Taylor Table[BernoulliB[n],{n,,}] f(z)+ z B B n (n ) ( z ) Bernoulli () f(z) f(z)+z B B = Jacob Bernoulli (655 75) (64 78) (Bernoulli ) ( B n B n ) [] B n (46) z e z + z =+ ( ) n B n (n)! zn n= ( ) n B n > 69. z 9.6 (Bernoulli ) Bernoulli cot, tan, coth : cot z = ( ) k k B k (k)! zk, k= B n z coth z = (n)! n z n, tan z = n= ( Bernoulli tan z = ( Bernoulli ): ( ) n n ( n )B n z n. (n)! n= n ( n )B n z n ) (n)! n i k = i= k j= ( k n )B k+ j j j k + j (n, k N). 4
126 ζ 57 : ζ(k) = k π k n k =( )k+ (k)! n= Euler-Maclaurin : f [,n] C k n n f(i) = f(x)dx + k (f(n) f()) + i= + ( )k k! n B k (x)f (k) (x)dx. j= B k B j j! (k N). ( f (j ) (n) f (j ) () ) B k (x) Bernoulli ( ) B k (x) ( ) Bernoulli [7] 9.7 (cot, tan Taylor ) (45) Bernoulli {B n } (47) (48) cot z = z + ( ) k k B k tan z = k= k= (k)! zk ( ) k k ( k )B k (k)! g(z) := z + f(z) =z + ( < z < π), z k z e z ( z < π). g ( e z/ g(z) = z ez/ + e z/ ) g B =, B k+ = (k =,, ). g(z) =+ k= z cot z = z i eiz + e iz e iz e = iz eiz + iz e iz = iz = g (iz) =+ k= B k (k)! zk. ( + B k (k)! (iz)k =+ ) e iz k= = iz + iz e iz ( ) k k B k (k)! zk. tan z =cotz cotz tan z = ( z + ( ) k k B k (k)! zk z + ( ) k k B k = k= k= ( ) k k B k (k)! ( k )z k = k= k= (k)! (z)k ( ) k k ( k )B k (k)! 57 [6] 8 e z/ e z/ ) z k. 5
127 7. z coth z z = Taylor 9.8 f(z) := z, g(z) := (z )(z ) C \{}, C \{, } f g z < h := f + g z < h z < g(z) g(z) = z + z (h(z) = ) z 9.6 Schwarz ( ) : Laurent,, 6, 7 6, 7. Laurent. ( ) c C, R <R + A(c; R,R ):={z C R < z c <R } c (annulus, annular domain, annular region) A(c; R,R ):={z C R z c R } R = A(c;,R )=D(c; R ) \{c} A(c;,R ) D(c; R ) 6
128 . ( Laurent ) c C, R <R +. f A(c; R,R ) a {a n } n Z C Z (49) f(z) = a n (z c) n + n= a n (z c) n (z A(c; R,R )) R <r <r <R r,r A(c; r,r ) (49) R <r<r r (5) a n = πi z c =r f(z) n+ dz (n Z) (z c) a : f :Ω C A(c; R,R ) Ω. f A(c;R,R ) 3. (, p.8) a n.3 ( ) 3 (z c) n (i) z C \{c} R (, ) {z C z c R } (ii) R (, ) s.t. {z C z c >R} D(c; R) R (R, ) {z C z c R } (iii) z C \{c} (5) m (49) (z c) m+ (5) f(z) (z c) = m+ n= a n (z c) n m (z A(c; R,R )). R <r<r r (.3 ) z c = r Laurent (5) (z c) m+ f(z) πi z c =r (z c) dz = m+ n= a n (z c) n m dz = πi z c =r n= a n δ nm = a m. (49) {a n } ( ) (5) r (49) {a n } r,r R <r <r <R D := A(c; r,r ) f D A(c; R,R ) 7
129 ( 8.5) I := πi ζ c =r f(z) = f(ζ) πi D ζ z dζ (z A(c; r,r )) f(ζ) ζ z f(z) = f(ζ) πi D ζ z dζ, J := πi ζ c =r I Taylor dζ = I + J. f(ζ) ζ z dζ I = a n (z c) n, a n := f(ζ) n+ dζ. πi ζ c =r (ζ z) J ζ c = r ζ c z c = r < ( z c ) ζ z = (ζ c) (z c) = z c (ζ c) n = ζ c (z c) n z c (5) J = πi ζ c =r n= (ζ c) n (z c) n dζ. n= M := max ζ c =r f(ζ) ζ c = r (ζ c) n (z c) f(ζ) n M r ( r ) n z c Weierstrass M-test (5) ζ c = r J = n= πi ζ c =r f(ζ) (ζ c) n+ dζ (z c) n = r,r A(c; R,R ) n= a n (z c) n..4 () (5) D(c; R) Taylor n ( ) () n= a n (z c) n 3 ( ) (i) z C \{c} (ii) R (, + ) z c >R z c <R (iii) z C \{c} 8
130 (i) R =,(iii) R =+ z c >R, z c <R. r>r r {z C z c r} z C \{c} ζ := z c a n (z c) = n n= n= a n ζ n, z c >r ζ < r, z c <r ζ > r, z c = r ζ = r.5 ( Laurent, Laurent ) c C, R <R +, f A(c; R,R ) ( ) f(z) = a n (z c) n + n= a n (z c) n (z A(c; R,R )) {a n } ( ) f A(c; R,R ) Laurent ( ) R = f c (c ) Laurent ( ) a n (z c) n Laurent ( ) ( the principal part) a n= f c (residue) Res(f; c) : Res(f; c) =a. ( : R > ) Laurent 9 Laurent Laurent ( ) ( Laurent ).6 (Laurent Taylor ) f c D(c; R) {a n } n f(z) = a n (z c) n (z D(c; R)) Taylor ( ) a n =(n N) f(z) = a n (z c) n + n= 9 a n (z c) n (z A(c;,R))
131 (A(c;,R) D(c; R) ) Taylor Laurent Laurent f c () Laurent Taylor.7 (Taylor Laurent ) e z = z n n! (z C) f(z) =e z Laurent e z = z n n! (z A(;, + )).8 f : C \{} C f(z) = 3 (z ) (z C \{}) C \{} = A(;, + ) f f Laurent f (53) f(z) = 3 (z ) (z A(;, + )) f Laurent {a n } (53) f(z) = a =3, a n = (n Z \ { }) a n (z ) n + n= a n (z ) n (z A(;, + )) Laurent 3, f Res(f;)=. (z ).9 f : C \{} C f(z) =exp z (z C \{}) C \{} = A(;, + ) exp ζ = n! ζn (ζ C) f(z) =exp z = n! ( ) n =+ z n! n= z n (z A(;, + )). f Laurent (a =,a n = (n N), a n! n =(n N) ( ) ) n! z, Res(f;)= n! =. n= 3
132 . ( ) k (k +)! zk+ k= f(z) = = z f(z) = sin z z sin z = k= k= (z C \{} = A(;, + )) ( ) k (k +)! zk+ (z C) f Laurent ( ) k (k +)! zk = z 3! z + 5! z3 (z A(;, + )). a =, a = 3!, a 3 = 5!,, a k = ( )k (k +)!, n a n =, ( ) k (n, n n =k ) (k +)! a n := (n = ) ( ) ( ) k=. a C f(z) = z a ( ) k (k +)! zk, Res(f;)=. (z C \{a}) (i) c = a f A(c;, + ) f c Laurent f(z) = z a (z A(c;, + )). (ii) c a f D(c; a c ) c Taylor f c Laurent ( f(z) = (z c) n (a c) n+ (z A(c;, a c )). f(z) = z a = (z c) (a c) = a c z c a c ) = a c ( ) n z c a c f A(c; a c, + ) z A(c; a c, + ) z c > a c a c z c < f(z) = (z c) (a c) = z c a c z c 3 = z c ( ) n a c = z c (a c) n (z c) n+.
133 f(z) = n= (a c) n (z c) n (z A(c; a c, + )). f A(c; a c, + ) Laurent.. Ω C f :Ω C, c C c f (an isolated singularity) (54) ( ε >) f A(c;,ε)={z C < z c <ε} {a n } C Z f(z) = a n (z c) n + n= a n (z c) n (z A(c;,ε)) {a n } 3 (i) c f (removable singularity) ( n N) a n = (ii) c f (pole) ( k N)a k ( n N : n>k) a n = k f c (order) c f k (iii) c f ( ) (an essential singularity) ( k N)( n N : n>k) a n c f (regular point) f D(c; ε) z A(c;,ε) < z c <ε.3 ( ) c f (54) f D(c; ε) (f c c ) c 3
134 ( []) (a) () f(z) = z (z C \{}), c =c f f ( ) (b) f D(c; ε) f(z) = (z C \{}), c =c f z f ( ).4 f(z) = 3 (z ) (z C \{}). f f Laurent f(z) = f 3 (z ) ( < z < + ).5 f(z) =exp z (z C \{}). f f Laurent f(z) =+ n! n= z n ( < z < + ) f.6 f(z) = sin z z (z C \{}). f f Laurent f(z) = z 3! z + 5! z3 +( ) k (k +)! zk + ( < z < + ) f.7 f(z) = sin z (z C \{}). z f f Laurent f(z) = 3! z + 5! z4 +( ) k (k +)! zk + ( < z < + ) f 33
135 .8 ( ) Laurent P (z),q(z) C[z], P (z) Q(z) P (z) P (z) α,...,α r, m,...,m r, P (z) a P (z) =a Q(z) P (z) = + r r (z α k ) m k. k= m k k= m= A k,m (z α k ) m, A k,m C Q P Ω:=C \{α,,α r } α k m k Q P (z) Q(z) P P (z) Q(z) () ( : f(z) = z3 ) z c Laurent f(z) = c (z a) m Laurent () m = (i) c = a f(z) = z a = ( < z c < + ). c z c Laurent (ii) c a f(z) = D(c; a c ) c z a f(z) = z a = ( ) = (z c) n ( < z c < a c ) (a c) n+ c Laurent () m> m = Laurent f(z) = (z ) (i) c = c f f(z) = f c Laurent ( < z < + ) (z ) (ii) c = f D(; ) c f z = = ( ) n (z ) n ( z < ). ( ) f(z) = (z ) = = n( ) n (z ) n z n= = (n +)( ) n (z ) n ( z < ). 34
136 f c Laurent ( z < < z < ) Laurent f(z) = A(;, + ) Laurent (z ) z = (z ) + = z + = ( ) n z z z ( ) n = ( < z < + ) (z ) n.9 f(z) = n= ( n)( ) n (z ) n+ = f(z) = { n= (n )( ) n (z ) n ( < z < + ). z + (z ) (z =) f ( f < z < + ) f(z) = { z + (z ) (z =) ( z C f(z) =z + ). f(z) = sin(/z) (z C \ ( { {} nπ })) n Z \{} (n Z \{}) nπ f f Laurent 3 z c lim () c f lim z c f(z) () z c () c f lim z c f(z) = z c (3) c f lim z c f(z) ( z c ) ( ) 35
137 Laurent,, ( ).. ( ) c C R <R R, R A(c; R,R ):={z C R < z c <R } c (an annulus, an annular domain, an annular region) A(c; R,R ):={z C R z c R } Cf: D(c; R) :={z C z c <R}, D(c; R) :={z C z c R}.. (Laurent ) c C, {a n } n Z C Z a n (z c) n + n= a n (z c) n c Laurent ( ) (a) ( 7.4)f : D(c; R) C {a n } n s.t. f(z) = a n (z c) n (z D(c; R)). (b) a n (z c) n ρ ρ, z c <ρ z c >ρ (b) Laurent (.4) f : A(c; R,R ) C {a n } n Z s.t. f(z) = a n (z c) n + n= a n (z c) n (z A(c; R,R )). 36
138 f A(c; R,R ) Laurent R = f c (c ) Laurent ( ) z c C, R<, f {z C R< z c } {a n } n s.t. f(z) =a + a z c + a (z c) + = a n (z c) n (R< z c ).. () a n (z c) n + n= a n (z c) n Laurent Laurent Laurent.3 (Laurent, ) 3 a n (z c) n + n= a n (z c) n (i) R < R s.t. A(c; R,R ) R <r <r <R r,r A(c; r,r ) (ii) R< s.t. z c = R (iii) C (i) R R,(ii) R a n (z c) n R [, ) { } z c <R z c >R a n (z c) R n [, ) { } z c <R n= z c >R R <R Laurent A(c; R,R ) {z C z c < R or z c >R } R = R Laurent {z C z c = R } {z C z c = R } 37
139 R >R Laurent C 7. (i) R, R a n.3 Laurent ( ) Laurent ( Laurent ( ) ).4 ( Laurent ) c C R, R R <R (R R R ) f A(c; R,R ) {a n } n Z s.t. (55) f(z) = a n (z c) n + n= a n (z c) n (R < z c <R ). (55) R <r <r <R r, r A(c; r,r ) ( ) () (55) R <r<r r (56) a n = f(z) dz (n Z). πi z c =r (z c) n+ (55) ( ) f(z) = a n (z c) n n= f(z) = n Z a n (z c) n () m Z (55) (z c) m+ f(z) (z c) = m+ n= a n (z c) n m R <r<r r z c = r f(z) dz = πi z c =r (z c) m+ πi = (56) = n= n= z c =r n= πi a n z c =r a n (z c) n m dz πi a n πiδ nm = a m. (z c) n m dz 38
140 ( ) R <r <r <R r,r z A(c; r,r ) Cauchy ( ) f(z) = πi C : ζ c = r, C : ζ c = r C f(ζ) ζ z dζ πi C f(ζ) ζ z dζ. D := A(c; r,r ), M := max f(ζ) ζ D ( ) Cauchy πi C f(ζ) ζ z dζ = a n (z c) n, a n := πi C f(ζ) (ζ c) n+ dζ. ( ) ζ ζ c = r ζ c z c = r z c < ζ z = (ζ c) (z c) = z c ζ c = ( ) n ζ c = z c z c z c c)n f(ζ)(ζ (z c) n M ( ) n r r z c < Weierstrass M-test (ζ c)n f(ζ) (z c) n C : ζ c = r πi C f(ζ) ζ c dζ = πi = n= C n= πi (ζ c)n f(ζ) (z c) dζ n (ζ c)n f(ζ) (z c) C dζ = n a n := f(ζ)(ζ c) n dζ = πi C πi C f(z) = a n (z c) n + n= n= f(ζ) (ζ c) n= a n (z c) n. n+ dζ. a n (z c) n (z A(c; r,r )). r <r<r r a n = f(ζ) n+ dζ. πi (ζ c) ζ c =r 39 (ζ c) n (z c) n.
141 () r,r r A(c; R,R ).5 ( Laurent, Laurent ) c C, R <R, f A(c; R,R ) (57) f(z) = a n (z c) n + n= a n (z c) n (R < z c <R ) {a n } n Z (57) f A(c; R,R ) Laurent ( ) (the Laurent (series) expansion) Laurent (Laurent series) R = f c ( c ) Laurent (Taylor ) f c D(c; ε) f c Taylor f c ( A(c;,ε) ) Laurent Laurent Taylor Laurent Laurent ( ) Laurent Taylor f(z) = a n (z c) n, a n = f (n) (c) n! (n =,,,...) a n = f(ζ) n+ dζ (n Z) πi (ζ c) ζ c =r a n ( ) a n ( ) f(z) = n= a n (z c) n (R < z c <R ) {a n } f A(c; R,R ) Laurent ( ) 3.6 () () f(z) = C \{} = A(;, ) (z ) Laurent a := 3, a n := (n Z \ { }) 4
142 {a n } f(z) = n= a n (z ) n ( < z < ) () f(z) =exp C \{} = A(;, ) Laurent z exp z Taylor exp ζ = ζ z f(z) =exp z = n! n! ζn (ζ C) ( ) n =+ z A(;, ) Laurent (3) f(z) = sin z z ( < z < ) n! z n n= C \{} = A(;, ) Laurent sin z Taylor z sin z = ( ) n (n +)! zn+ (z C) f(z) = sin z z = ( ) n (n +)! zn = n= ( ) n (n +)! zn + z ( < z < ) f A(;, ) Laurent 7. (), (3) a n f (z a) n A.7 Laurent Laurent f Laurent.7 ( z a Laurent ) f(z) = z a Laurent () f A(a;, ) f a Laurent f(z) f(z) = z a ( < z a < ) f a (A(a;, ) ) Laurent 4
143 () c a f c D(c; a c ) f c Taylor f c ( A(c;, a c ) ) Laurent z a = (z c) (a c) = a c z c a c = ( ) n z c ( (z c)/(a c) < ) a c a c (z c) n = (a c) n+ ( < z c < a c ). (3) c a f A(c; a c, ) Laurent f(z) = z a = (z c) (a c) = z c a c = z c = n= z c ( ) n a c ( (a c)/(z c) < ) z c (a c) n (z c) n ( a c < z c < )..8 ( Laurent Laurent ) f(z) = z(z )(z ) = z z + z f C \{,, } f Laurent () f A(;, ) Laurent z = ( < z < ), z z = z = z n ( z < ), z = z = ( z n z = ) n ( z < ). n+ f(z) = z + z n z n = ( ) z n + n+ n+ z ( < z < ). () f A(;, ) Laurent z = z = ( ) n = ( < z < ). z z z n n= z f(z) = z z n n= z n = n+ 4 z n n+ z n= z n ( < z < ).
144 (3) f A(;, ) Laurent z = z z = z ( ) n = z n z = n+ n= n z n ( < z < ). f(z) = z z + n n= n= ( ) n = z n + z + n = z n n= n=3 n z n ( < z < ). A(;, ) f Laurent.9 (Laurent ) ().4,,. ( ) Ω C c C, f :Ω C () c f (an isolated singularity) ε f {z C < z c <ε} D(c; ε) () c f ε f D(c; ε) () f D(c; ε) {z C < z c <ε} (i) f c (c Ω) (ii) f c c. [] [] ε f D(c; ε) \{c} c f []. : Ω:=C \{}, f :Ω C. () f(z) =z +. () f(z) = sin z z. (3) f(z) = z. (4) f(z) =exp z. 43
145 f Ω Ω f (ε = ) (), () f() = f D(; ) (() () ) ( ) (3) lim f(z) = ( ) z f() f (4) lim (lim z x R x + exp x =, lim x R x exp x = ) ( )f() f f : C C { z + (z ) f(z) := (z =) f ε =f D(; ε) \{} (lim f(z) = =f() ) f z z D(; ε) f f().3 () z = z, sin(/z) sin(/z) = z z C ( { }) Ω:=C \ {} nπ n Z, n f :Ω C f(z) = sin(/z) Ω C f Ω ε n < nπ <εf < z <ε f.4 ( Laurent ) Ω C f :Ω C, c C c f ( ε > ) ( {a n } n Z ) f(z) = a n (z c) n a n + ( < z c <ε) (z c) n n= a n f c Laurent (, theprincipal (z c) n n= part) a f c (the residue of f at c) Res(f; c) Res(f; c) :=a. 44
146 Laurent Taylor Laurent c f ε f D(c; ε) Taylor ( 7.4) A(c;;ε) =D(c; ε) \{c} f c Laurent c f Res(f; c) =.5 (,,, ) Ω C f :Ω C, c C c f ε >, {a n } n Z s.t. f(z) = a n (z c) n + n= a n (z c) n ( < z c <ε) (i) c f (a removable singularity) ( n N) a n = ( c Laurent ) (ii) c f (a pole) ( k N) a k ( n N : n>k)a n = k f c c f k ( c Laurent ) (iii) c f (an essential singularity) ( k N)( n N : n>k) a n ( c Laurent ).6 ( ) f(z) =z + Laurent f(z) =+z ( < z < ). ( a n z n a n ) n= f Res(f;)=. 45
147 f(z) = sin z Laurent z f(z) = ( ) n ( ) n z (n +)! zn+ = (n +)! zn = z 3! + z4 ( < z < ). 5! f Res(f;)=. f(z) = z Laurent f(z) = z ( < z < ). z f(z) =exp z Res(f;)=. Laurent f(z) = n= n! ( ) n = z n! z =+ n z +! z + 3! z + 3 ( < z < ). Res(f;)=. n! zn.7 ( ) f(z) = Q(z) (P (z),q(z) C[z]) P (z) P (z) f P (z) n P (z) n c, c,..., c r f Ω := C \{c,c,...,c r } c i R i := min c i c j R i > j r,j i f < z c i <R i z = c i z c i <R i c,,c r f.8 f(z) = (z C \{3}) 3 4 (z 3) 4 f(z) = (z 3) 4 ( < z 3 < ) 3 Laurent (a 4 =,a n =(n Z \ { 4}) f(z) = a n (z 3) n ) Laurent (z 3) 4 n Z.9 f : C \{,, } C, f(z) = f z (z ) ε = < z <ε f z <ε f f(z) = z + + z z, Laurent z Res(f;)=. 46
148 73. ( p. 84) cos z () z sin z (z =) () z (z =) (z ) 3. ( ) Ω C f :Ω C, c C c f (), () () lim f(z) ( ) z c z c () R (, ], f : D(c; R) C s.t. f(z) = f(z) ( < z c <R). f c c f R >s.t.f < z c <R {a n } s.t. f(z) = a n (z c) n + n= c f f(z) = a n (z c) n ( < z c <R). n N a n =. a n (z c) n ( < z c <R). z = c ( a ) f(z) := a n (z c) n ( z c <R) f : D(c; R) C ( ) z = c lim z c z c f(z) =lim z c z c f(z) = f(c) =a.. c f f D(c; R) f f f(z) ( < z c <R) f(z) := f(z) (z = c) lim z c z c. ( ) Ω C f :Ω C, c C c f f(z) =. lim z c z c 47
149 c f R >, {a n } s.t. f(z) = a n (z c) n a n + ( < z c <R). (z c) n k a k ( n N: n>k) a n = ζ = z c 9.9 f(z) = a n (z c) n + lim z c z c n= k n= a n (z c) n ( < z c <R). a n (z c) n = a. z c, z c ζ k a n k (z c) = n n= n= lim ζ a n ζ n. k a n ζ n =. n= lim f(z) =a + =. z c z c. (Riemann ) c f ε {z C < z c <ε} f c f lim f(z) c f z c z c (Liouville ) f M R s.t. f(z) M ( < z c <ε). f A(c;,ε) {a n } n Z s.t. f(z) = a n (z c) n a n + ( < z c <ε). (z c) n n Z, <r<ε r a n = f(ζ) dζ. πi (ζ c) n+ a n π ζ c =r n N f(ζ) (ζ c) n+ dζ n= ζ c =r M dζ = πr n+ ζ c =r a n M r n = Mrn ( <r<ε). M πr n+ πr = M r n. r a n =(n N). f c c f 48
150 ( 58 ) f A(c;,R) { (z c) f(z) ( < z c <R) g(z) := (z = c) g < z c <R g (c) =lim z c g(z) g(c) z c =lim z c (z c) f(z) z c =lim z c (z c)f(z) = ( f ) g c z c <R : {a n } n s.t. g(z) = a n (z c) n ( z c <R). g(c) =,g (c) =a = a =. g(z) = a n (z c) n =(z c) n= f(z) = n= a n (z c) n =(z c) a n+ (z c) n c f ( < z c <R). a n+ (z c) n ( z c <R)..3 (Casorati-Weierstrass, ) Ω C f :Ω C, c C c f ( ) ( β C)( {z n } n N ) ( n N) z n c lim z n = c lim f(z n )=β. n n ( β = ) f < z c <R β C 59 ( ε >) ( r (,R)) ( z A(c;,r)) f(z) β <ε. n =,, ε = r = n {z n} n N s.t. ( n N) < z n c < n f(z n ) β < n. lim z n = c, n lim f(z n )=β. n 6 ( ε >)( r >)( z A(c;,r)) f(z) β ε. 58 Riemann Liouville Cauchy 59 ε-δ 6 (proof by contradiction, reductio ad absurdum) 49
151 g(z) := f(z) β (z A(c;,r)) ( ) g A(c;,r) c g g(z) ε (z A(c;,r)) Riemann c g B(c; r) g(z) (z A(c;,r)) f(z) =β + g(z) = βg(z)+ g(z) c f (c g c f, c g k c f k ) c f.4 ( lim ) c f (), (), (3) () c f lim f(z) z c z c () c f lim f(z) = z c z c (3) c f lim f(z) lim f(z) = z c z c z c z c 3 ( ).5 f(z) :=exp ( z ) f z f(z) lim f(x) =, x R x lim f(iy) = y R y Casorati-Weierstrass.4 Casorati-Weierstrass ( Ahlfors [8] ).6 (Picard ) c f e C, ( U: c ) v C \{e}, z U s.t. f(z) =v. c 5
152 Picard [8] 74. ( p. 85 ) (), (), (3) () a C \{}, ε >, z A(;,ε)s.t.exp z = a. () {z n } n N s.t. lim n z n = lim n exp z n =. (3) {z n } n N s.t. lim n z n = lim n exp z n =..7 ( p. 85) f a a f (f(z) := z =) sin(/z) (multifunction, multi-valuedfunction) (transcendental branch point) 3 f(z) =Logz z = 75. () f(z) = cos z () f(z) = sin(z3 ) z z( cos z) (3) r> A(c;;r) f : D(c; R) ={z z c <R}, A(c; R,R ):={z R < z c <R }. c f def. R>s.t. f A(c;,R) D(c; R) c f = R>, {a n } s.t. f(z) = a n (z c) n ( < z c <R) n= ( a n a n = f (n) (c) = f(z) dz ( <r<r), n! πi z c =r (z c) n+ < r < r <R A(c; r,r )={z C r z c r } ) c f def. f c Laurent = c f lim f(z) z c z c c f = f(z) f(z) (z A(c;,R)) := f(z) (z = c) D(c; R) lim z c a c c f k def. f c Laurent k n= a n (z c) n, a k c f def. k Ns.t. c f k c f lim f(z) = z c z c c f def. f c Laurent ( ) ( {n N a n } = ) 5
153 .5 Laurent Laurent 9.3 (ii) = (i) Laurent Taylor ( ) Laurent.8 () c f :Ω C, k N (i), (ii) (i) c f k (ii) c U g f(z) = g(z) (z c) k (z U \{c}), g(c). (ii) (U ) (ii) ( R >) ( g : D(c; R) C ) f(z) = g(z) ( < z c <R) g(c). (z c) k (ii) ( g :Ω {c} C ) f(z) = g(z) (z Ω \{c}) g(c). (z c) k ( (z c) k f(z) c ) c f c Laurent R (, + ], {a n } n Z s.t. f(z) = a n (z c) n ( < z c <R). n= (i) = (ii) c f k f(z) = n= k a n (z c) n a k ( n N : n>k) a n =. = a k (z c) k + + a z c + a + a (z c)+a (z c) + (z c) k f(z) =a k + a k+ (z c)+ = a n k (z c) n ( < z c <R) ( < z c <R). ( < z c <R) R g(z) := a n k (z c) n ( z c <R) 5
154 g D(c; R) f(z) = (z c) k f(z) =g(z) ( < z c <R). g(z) (z c) k ( < z c <R) g(c) = n= k a n k (c c) n = a k. (ii)= (i) (ii) R >, g : D(c; R) C s.t. g f(z) = g(z) (z c) k ( < z c <R), g(c). g D(c; R) Taylor {a n } n s.t. g(z) = a n (z c) n = a + a (z c)+a (z c) + ( z c <R). < z c <R z f(z) = g(z) (z c) = a k (z c) + + a k k z c + a k + a k+ (z c)+a k+ (z c) + k = a n+k (z c) n a k n + (z c). n a = g(c) c f k n=.9 ( ) 9.3 c f k f(z) =(z c) k g(z) ( z c <R), g(c) g : D(c; R) C.8 c f k f(z) = g(z) ( < z c <R), g(c) (z c) k g : D(c; R) C.3 P Q c c P k Q(c) c f := Q k P c P k c R P (z) =(z c) k R(z), R(c). g(z) := Q(z) g c g(c) =Q(c) R(z) R(c), f(z) = g(z) (c ).8 c f k (z c) k 53
155 k N, c C, f c c f k c f. f(z) := sinh z sin z ( ) Q(z) :=sinhz, P (z) :=sinz C (sinh z =(expz exp( z))/, sin z =(exp(iz) exp( iz))/(i) Taylor ) c C P (c) = sin c = n Z s.t. c = nπ. P (c) =cosnπ =( ) n c = nπ P (i) n Q(nπ) =sinhnπ (sinhnπ > ) Cor. nπ f = Q/P (ii) P P s.t. P (C OK) P (z) =zp (z), P (z) (< z < ). Q Q s.t. Q (C OK) Q(z) =zq (z). ( < z < ) f(z) = Q(z) P (z) = zq (z) zp (z) = Q (z) P (z). z < f f (residue theorem). ( ). ( (the residue theorem)) D C R Green D D Ω C D Ω c, c,..., c N D f :Ω\{c,,c N } C D f(z) dz =πi N Res(f; c j ). j= f c j Laurent f j f j (z) = k j n= a (j) n (z c j ) n, a(j),,a (j) k j f j C \{c j } D f j (z) dz = D a (j) z c j dz + =πi Res(f; c j ) k j n= D C a (j) n dz =πia(j) (z c j ) n + k j n= 54
156 : (n = Cauchy n k j (z c j ) n ) N g := f f j g Ω \{c,...,c N } g c n ( n N) j= Laurent (g =(f f n )+ j n f j ) c n g g Ω Cauchy = D g(z) dz = D f(z) dz N j= D f j (z) dz = D f(z) dz πi N Res (f; c j ). j= N f(z) dz =πi Res (f; c j ). D j=. ( ) f Laurent g [9] 8.4 N D := D \ D(c j ; ε) j= (ε> ) 8.4 c j c j Γ Cauchy f(z) dz = Γ Cauchy (,3 ) Γ 55
157 . : c j Γ ( ).. Laurent Laurent ({a n } a ).3 f(z) = (z C \{}) f Laurent z (a =,a n =(n ) f(z) = a n z n ( < z < )) Res(f;)=. n=.4 f(z) :=exp z (z C \{}) f(z) = n! ( ) n =+ z z +! z + 3! z + 3 Res(f;)=. Res(zf(z); ) =,Res(z f(z); ) = 3! = 6. f < z c <R 4.6 ( Laurent ) a n = f(ζ) dζ (n Z, <r<r) πi ζ c =r (ζ c) n+ ( ) Res(f; c) =a = πi ζ c =r f(ζ)dζ ( <r<r). 56
158 a (f(ζ)/(ζ c) n+ ) f { (z c) n πi (n = ) dz = (n Z \ { }) z c =R f ( f ).5 Res (f; c) =a Res (3f(z)+cosz; c) ( ) f Res(f; c) Res(f + g; c) =Res(f; c)+res(g; c), Res(λf; c) =λ Res(f; c) ( λ C) ( ) Res (3f(z)+cosz; c) =3Res(f; c)+res(cosz; c) =3a +=3a. ϕ c Res(ϕ; c) =.6 ( Mathematica ) f c n Laurent Series[f[z],{z,c,n}] Series[/(z Sin[z]]),{z,,}] z z z z z z + O(z ) Laurent Laurent.. c f Res(f; c)..7 c f (58) Res(f; c) =lim(z c)f(z). z c z c (c f c f f ) c f R >, {a n } n= s.t. f(z) = a n (z c) n + a z c ( < z c <R). 57
159 (c f a. c f a =.) (z c) (z c)f(z) =a + a (z c)+a (z c) + ( < z c <R). lim(z c)f(z) =a =Res(f; c). z c z c.8 f(z) = z + Res(f; i) f(z) = (z + i)(z i) i f Res(f; i) =lim(z i)f(z) =lim z + i = z + i = z=i i = i. z i z i z i z i (.7 ).9 f(z) = Q(z), P (z) Q(z) c c P (z) P (z) (P (c) = P (c) ) c f (59) Res(f; c) = Q(c) P (c). c P g s.t. g c P (z) =(z c)g(z), g(c). f(z) = Q(z) P (z) = Q(z) (z c)g(z) = h(z) z c, h(z) :=Q(z) g(z). h c c f ( Q(c) Q(c) = ).7 (6) Res(f; c) =lim(z c)f(z) =lim z c z c z c z c (z c)q(z) P (z) =lim z c Q(z) P (z) P (c) z c = Q(c) P (c). P (c) =. f(z) = Res(f; i) z 4 ( ) f(z) = i (z )(z +)(z + i)(z i) Res(f; i) = (z 4 ) = z=i 4i = 3 i 4i 4 = i 4.. n N, f(z) = z n. z = ωk (ω := exp πi, k =,,,n ) n z n ( ( ω k) n = ) Res(f; ω k )= (z n ) z=ω k = z nz n z=ω k = ωk n. 58
160 f Taylor f(z) = a n (z c) n a n = f (n) (c) n!. c f k Res(f; c) =lim z c z c ( ) k d [ (z c) k f(z) ]. (k )! dz c f k R >, {a n } n= k s.t. f(z) = a k (z c) k + + a z c + a + a (z c)+ ( < z c <R). (z c) k f(z) =a k + a (k ) (z c)+ + a (z c) k + a (z c) k + a (z c) k+ + a k ( ) k d [ (z c) k f(z) ] =(k )!a + k! dz! a (z c)+ (k +)! a (z c) +.! z c (k )!.7.3 f(z) = 3 f Res(f;3)= lim z 3 z 3 =lim z 3 z 3 ( d ( )! dz z (z 3) (z +) ) [ (z 3) f(z) ] ( z =lim z 3 z + z 3 (z +) = (3 + ) = 6..4 f(z) =. z = Laurent z sin z f(z) = z Res(f;)=. f 76. f < z <ρ ) (z +) z =lim z 3 (z +) z 3 f( z) =f(z) ( < z <ρ) Res(f;)=.5 c f ϕ c c fϕ Res (fϕ; c) =Res(f; c) ϕ(c). 59
161 c f c g f(z) = g(z) z c f(z)ϕ(z) = g(z)ϕ(z) g(z)ϕ(z) z = c z c gϕ c.7 Res (fϕ; c) =lim z c (z c)f(z)ϕ(z) =lim z c (z c)f(z) lim z c ϕ(z) =Res(f; c)ϕ(c)..6 () f(z) =π cot πz ( ) (.9 ) P (z) :=sinπz, Q(z) :=π cos πz f(z) = Q(z) P (z). P (z) = n Z s.t. z = n. P (z) =Q(z) Q(n) =P (n) =π cos nπ = π( ) n. n f ( : p. 88 ).7 ( pp ) f(z) = Res(f; n) = Q(n) P (n) =. 8z z.8 (c Res(f; c) =a a n ) c f k f(z) = a k (z c) + a (k ) k (z c) + + a k z c + a n (z c) n (a ) a n (6) a n =lim z c z c ( ) n+k d [ (z c) k f(z) ]. (n + k)! dz ( < z c <R) (z c) k f(z) =a k + a (k ) (z c)+a (k ) (z c) + = a n (z c) n+k = a m k (z c) m ( < z c <R) n= k m= g(z) g(z) (z = c ) Taylor m a m k a m k = g(m) (c) m! =lim z c z c ( ) m d [ (z c) k f(z) ]. m! dz m k n..3 6
162 c f or f c (c f ) = Res(f; c) = ( ) k d c f k = Res(f; c) = (k )! lim [ (z c) k f(z) ]. z c dz z c f = Q P, P (c) =,P (c) Res(f; c) = Q(c) P (c) c f ϕ c Res(fϕ; c) =Res(f; c)ϕ(c). c f = Mathematica Mathematica Residue[,{, }] Series[,{,, }] Infinity Apart[ ] Residue[z/((z-)(z-)^3),{z,}] Series[z/((z-)(z-)^3),{z,,}] 3 3. () Cauchy ( ) ( : ) 3. ( ) [3] 6
163 f(x) dx f (6) f(x) dx = lim R,R R R f(x) dx, ( I ( ε >)( R R)( R R : R R)( R R : R R) R I f(x) dx <ε R ) (63) R f(x) dx = lim f(x) dx R R ( ) ( x lim ε + dx lim ( ε ε,ε + x dx + ( ε ε xdx ) x dx + ε x dx ) x dx log ) (63) (a) f ( ) ( + lim ) (b) f(x) dx < 3. (63) 3.3 e iax (6) 3. R f(x) dx C[z] z P (z) C[z] P (z) deg P (z) 6
164 3. P (z),q(z) C[z], f(z) = Q(z),degP(z) deg Q(z)+,( x R) P (x) P (z) f(x) dx =πi Res(f; c). Im c> Im c> f c Im c> ) f(x) dx = πi c Im c< Res(f; c) Res(f; c) = ( ( ) ( M R)( R R)( z C : z R ) P (z) f(z) M z P (z) =a z n + a z n + + a n, a,q(z) =b z m + b z m + + b m, b ( 9.9 ) ( R R)( z C : z R ) P (z) a z n, Q(z) 3 b z m P (z). R := max{,r }, M := 3 b a z R 3 b f(z) z m = 3 b a z n a z m n 3 b a z = M a. ( ) ( : R lim R R f(x) dx = f(x) dx = R lim R,R + f(x) dx ) Γ R : z = x C R : z = Re iθ γ R := Γ R + C R R lim f(x) dx. R + R R f(x) dx (x [ R, R]), (θ [,π]), R f(x) dx = f(z) dz, R Γ R f(z) dz f(z) dz C R C M dz = M R R C R R πr = πm R (R + ). 63
165 R R f(z) dz =πi Res (f; c). γ R Im c> f(x) dx = f(z) dz = f(z) dz f(z) dz Γ R γ R C R =πi Res (f; c) f(z) dz Im c> C R πi Res (f; c) (R + ). Im c> 3.3 I = dx x + = π. tan x x + I = [ tan x ] = π ( π ) = π. 3. P (z) :=z +, Q(z) := P (z),q(z) C[z], deg P (z) ==degq(z)+. x R P (x) =x + += P (x). c P (c) =c += c = ±i. Im c> c = i. 3. ( ) Q I =πi Res P ; i. i f := Q P Res(f; i) =lim(z i)f(z) =lim z i z i z + i = i. Res(f; i) = Q(i) P (i) = z = z=i i. I =πi i = π. 3.4 Mathematica Integrate[/(x^+),{x,-Infinity,Infinity}] Maple int(/(x^+),x=-infinity..infinity) 3.5 I = dx x 4 + = π. x 4 + I P (z) :=z 4 +,Q(z) := 3. ( ) 64
166 c Q P P (c) = c = ei( π 4 +k π 4 ) (k =,,, 3) c = +i, i, +i, i. Im c> c := +i, c := +i. c 4 = P 3. ( ) Q Res P ; c j = Q(c j) P (c j ) = 4c 3 j ( ( ) Q I =πi Res P ; c ( =πi 4 = c j 4c 4 j ( )) Q +Res P ; c ) (c + c )= πi 3. f f(x) dx = 3.6 (Ahlfors [8] p.73)i := I = x x 4 +5x +6 x x 4 +5x +6 dx. = c j 4. i = π. f(x) dx (, ) dx. P (z) :=z 4 +5z +6, Q(z) :=z deg P (z) =4=degQ(z)+, ( x R) P (x) 6 > P (x). c Q P P (c) = (c +)(c +3)= c = ± i, ± 3i. Im c> c = i, 3i. 3. ( Res I = Q(x) P (x) dx = πi ( Q P ; i ) ( Q +Res P ; )) 3i. ( Res f; ) i = Q ( i ) P ( i ) = z 4z 3 +z = z= i ( Res f; ) 3i = Q ( 3i ) P ( 3i ) = z 4z 3 +z = z= 3i z 4z + = z= i z 4z + = z= 3i i i 8+ =, 3i + = 3i. π 5 6 I = πi 3. ( ) 3.7 n N I = dx +x = π n n sin π. n 65
167 3.8 Mathematica Integrate[/(+x^(n)),{x,-Infinity,Infinity}, Assumptions->Element[n,Integers]&& n>] ) (+(e inπ ) n π cosec π n FullSimplidy[] n 3.9 n N I := dx (n )!! = π. ( + x ) n+ (n)!! 3. ( ) Mathematica Integrate[/(+x^)^(n+), {x,-infinity,infinity}, Assumptions-> n>] I = ( πγ n + ) Γ (n +) Γ (x) =xγ (x ) ( Γ n + ) ( = n )( n 3 ) ( Γ (/) = n (n )!! = π, n I = Γ (n +)=n! = (n)!! n π (n )!! π/ n (n)!!/ n = π(n )!!. (n)!! )( n 3 ) π 77. () a I = () a I = (3) a I = (4) a I = (5) a I = (6) a I = dx x + a. ( : π a ) dx x 4 + a dx. ( : π 4 a 3 ) dx (x + a ). ( : π a ) 3 dx x 6 + a 6 dx. ( : π 3a 5 ) x 4 (x + a ) dx. ( : π 4 6a ) 3 x (x 4 + a 4 ) (7) a, n I = 5 π dx. ( : 3 64a ) 9 dx (x + a ). ( : π(n 3)!! n a n (n )!! ) 66
168 dx (8) a, n I = x n + a. ( : π n na n sin π ) n 78. () x x + x 4 +x +9 dx () x dx, a R (Ahlfors p. 73) (x + a ) e iax R f(x)e iax dx Fourier Fourier (F) (F ) f(ξ) := π g(x) := π f(x)e ixξ dx (ξ R), g(ξ)e ixξ dξ (x R) (64) ( a R) e iax = e iax, cos(ax) =Ree iax, sin(ax) =Ime iax 3. P (z),q(z) C[z], f(z) = Q(z),degP(z) deg Q(z)+, ( x R) P (x), P (z) a> (65) Im c> f(x)e iax dx =πi Im c> Res ( f(z)e iaz ; c ). f ( f(z)e iaz ) c Im c> 3. deg P (z) deg Q(z) + 3. deg P (z) deg Q(z)+ a ( a = OK 6 ) γ R =Γ R + C R lim R lim R C R f(z)e iaz dz = π e ar sin θ dθ = R ( <e ar sin θ < Cf. dx x dx x 6, sin x x π e ar sin θ dθ π ) dx ( ) 67
169 3. ( M R)( R R)( z C : z R ) P (z) f(z) M z. A, B R C A,B, : z = x C A,B, : z = B + iy (x [ A, B]), C A,B, : z = x + i(a + B) C A,B, : z = A + iy (y [,A+ B]), (x [ A, B]), (y [,A+ B]), γ A,B = C A,B, + C A,B, + C A,B, + C A,B, P c c <R Im c> γ A,B f(z)e iaz dz =πi Res ( f(z)e iaz ; c ). γ A,B C A,B, f(z)e iaz dz = Im c> B C A,B, z = B + y B A f(z) M z M B. f(x)e iax dx. Re (iaz) = Re[ia(B + iy)] = ay, ( dz = dy ) f(z)e iaz dz C A,B, f(z)e iaz M dz C A,B, B e iaz = e Re(iaz) = e ay A+B C A,B, f(z)e iaz dz C A,B, M aa. C A,B, z = x +(A + B) A + B f(z) M z M A + B. e ay dy M B e ay dy = M ab. Re (iaz) =Re[ia(x + i(a + B))] = a(a + B), e iaz = e Re(iaz) = e a(a+b) ( dz = dx ) f(z)e iaz dz C A,B, f(z)e iaz dz C A,B, 68 M B e a(a+b) dx = Me a(a+b). A + B A
170 B I = lim f(x)e iax dx A,B + A ( ) = lim f(z)e iaz dz f(z)e iaz dz f(z)e iaz dz f(z)e iaz dz A,B + γ A,B C A,B, C A,B, C A,B, =πi Res ( f(z)e iaz ; c ). Im c> a (65) a < 3.3 P (z),q(z) C[z], f(z) = Q(z),degP(z) deg Q(z)+,( x R) P (x), P (z) a< f(x)e iax dx = πi Im c< Res ( f(z)e iaz ; c ) a (66) I = a> 3. I =πi Res e iax x + dx = πe a. ( ) e iaz z + ; i =πi eiaz z = πe a. z=i a = 3. ( 3.3 ) ( ) I =πi Res x + ; i =πi z = π. z=i a< e iax = e iax, a > 3. I = e iax x + dx = e iax x + (66) (66) ( ) e iaz dx = πi Res z + ; i = πi e iaz z = πe a = πe a. z=i cos(ax) x + dx = πe a 3.5 (Mathematica ) Mathematica a Assuming[a>, Integrate[Exp[I a x]/(x^+),{x,-infinity,infinity}] 69
171 3.6 I = x sin x x + dx = π e. sin x =Ime ix I = x sin x x + dx = Im xeix x + dx = Im xe ix x + dx. P (z) :=z +,Q(z) :=z, a := 65 I = ( )) ) z (πi Im Res z + eiz ; i =Im (πi zeiz z = (πie z=i Im i) = π e. 3.7 α> I = (). () a, α I = () a, α I = (3) a, α I = (4) a, α I = x sin αx x 4 + dx = π e α/ sin α. cos αx x + a dx. e aα ( : a ) cos αx π( + aα)e aα dx. ( : ) (x + a ) a 3 cos αx x 4 + a 4 dx. x sin αx x 4 + a πe aα/ ( : a 3 dx. ( : πe aα/ 4 a ( cos aα +sin aα )) sin ab ). x sin x dx (a R) x + a πe a ( : ) 3.4 π r(cos θ, sin θ)dθ r(x, y) x y r(cos θ, sin θ) dθ [, π] ( ) 7
172 3.8 () r(x, y) x, y (67a) π r(cos θ, sin θ) dθ =πi c < Res(f; c). f (67b) f(z) := ( ) z iz r +, z z iz f(z) z = c < f c z < (67a), (67b) z = e iθ (θ [, π]) cos θ = z +/z, sin θ = z /z, dz = ie iθ dθ dθ = dz i iz I := z = e iθ (θ [, π]) I = dz = ie iθ dθ, π cos θ = eiθ + e iθ sin θ = eiθ e iθ i z = r(cos θ, sin θ)dθ dθ = dz iz, = ( z + ) = z +, z z = ( z ) = z i z iz ( ) z + r, z dz z iz iz = f(z) dz. z = z = f I =πi c < Res(f; c). 3. () cos θ = eiθ + e iθ cos θ = eiθ + e iθ = z + z, sin θ = eiθ e iθ i = z + z, sin θ = eiθ e iθ i 7 = z z i = z z i
173 ( ) f(z) := ( z + z iz r, z z ) i f () π dθ 3.9 I := 5 4cosθ ( ) z = e iθ (θ [, ]) J = z = 5 4 z + z iz dz = i dz = i z = (z )(z ) = i πi c < ( = π Res (z )(z ) ; ) = π ( ) = π 3. z = 5z (z +) dz = i dz z = z 5z + ( Res = π lim z π ) (z )(z ) ; c ( z ) (z )(z ) dθ 3. <r<ri := ( R + r Rr cos θ ) ( ) z = e iθ (θ [, π]) I = dz z = R + r Rr z + iz = dz i z = (R + r )z Rr(z +) z dz = i z = Rrz (R + r )z + Rr = i dz z = (Rz r)(rz R). I = i πi ( ) Res (Rz r)(rz R) ; c c < = π lim z r/r z r/r (Rz r)(rz R) = π R ( = π Res r r/r R = (Rz r)(rz R) ; r R π R r. ) 3. a> π dθ a cos θ + a = π a. 3. a> π dθ a +cosθ = π a. 7
174 3.3 e< π dθ ( + e cos θ) = π ( e ). 3/ (Mathematica Integrate[/(+e Cos[x])^,{x,,Pi}, Assumptions->e> && e<] Kepler ) [3] pp () n I = π π cos n θdθ. () n I = π π sin n θdθ. dθ dθ (3) a, b I = a cos θ + b sin. (4) () I = θ 5 4cosθ. π dθ (5) ( ) I = ( <r<r). (6) ( R + r Rr cos θ ) I = π ( ) R + re iθ π dθ Re dθ ( <r<r). (7) I = π R re iθ (R + r Rr cos θ) π dθ ( <r<r). (8) ( ) I = (a >b>). (9) m, r, a + b cos θ R (r <R) I + ij I, J I = π cos mθ R + r Rr cos θ dθ, J = π () a, n I + ij I, J I = π e a cos θ cos (a sin θ nθ) dθ, J = π sin mθ R + r Rr cos θ dθ. e a cos θ sin (a sin θ nθ) dθ. () π(n)! () π(n)! (3) π (4) π π (5) (6) (7) π(r + r ) 4 n (n!) 4 n (n!) ab 3 R r (R r ) 3 π (8) (9) I = π ( r ) m, πa n J = ()I =, J = a b R r R n! 4. a >b + c a, b, c ( : π a b c ) dx a + b cos x + c sin x 5. (Ahlfors [8], p. 73) π/ dx π a +sin, a > ( : x sign a a + a ) 3.5 R ( ) ( ) [a, b] C f b a f(x) x c dx = lim ε,ε + ( c ε a 73 f(x) b x c dx + c+ε ) f(x) x c dx
175 (f(c) ) ( c ε lim ε + a f(x) b x c dx + c+ε b f(x) p.v. a x c dx ) f(x) x c dx Cauchy (the Cauchy principal value) 3.4 a, b > ε a I = b a dx x b dx I =p.v. a x =logb a. dx b x + dx ε x =[log x ] ε a +[log x ]b ε =logε log a +logb log ε =log b a +logε ε ε,ε + ε = ε = ε ε + log b a I I =log b a. f = Q P (P (z),q(z) C[z]) ( x R) P (x) P R f(x) dx f(x)e iax dx ( deg P (z) deg Q(z)+), ( deg P (z) deg Q(z)+) 3.5 P (z),q(z) C[z], f(z) = Q(z), P R P (z) () deg P (z) deg Q(z)+ (68) p.v. f(x) dx =πi Im c> Res(f; c)+πi Im c= Res(f; c). () deg P (z) deg Q(z)+ a> (69) p.v. f(x)e iax dx =πi Res ( f(z)e iaz ; c ) + πi Res ( f(z)e iaz ; c ). Im c> Im c= 74
176 () c <c < <c N D(c j ; ε) ε> R z <R R <c ε, C N + ε<r N Γ ε,r := [ R, c ε]+ [c j + ε, c j+ ε]+[c N + ε, R], C ε,j : z = c j + εe iθ C R : z = Re iθ γ ε,r := Γ ε,r + ( ) j= (θ [, π]), N C ε,j + C R j= (θ [,π]), γ ε,r f(z) dz =πi f(z) dz = f(z) dz γ ε,r Γ ε,r j= R + 3 ε + Γ ε,r f(z) dz = ε + c ε R p.v. f(x) dx + R R p.v. f(x) dx πi 3.6 (Dirichlet ) I = f(x) dx. N j= Im c> Res(f; c). N f(z) dz + f(z) dz C ε,j C R cj+ ε c j +ε f(x) dx + C ε,j f(z) dz πi Res(f; c j ). j= Im c> R c N+ +ε N Res (f; c j )=πi Res(f; c). sin x x dx = sin x x dx. f(x) dx I = p.v. sin x x dx = p.v. Im eix x dx = ( ) Im e ix p.v. x dx. 3.5 () I = ( )) e iz (πi Im Res z ; = Im ( πi e i) = π. 75
177 sin x ( () x e ix dx x dx () ([]) ) 3.6 : 3. ( ) 3. C R +Γ R ( ) ( ) R (7) lim f(x)e iax dx =πi Res(f(z)e iaz ; c) R R Im c> deg P deg Q P (x), Q(x) R[x] deg P (x) =n, m := deg Q(x) P (x) = a x n + + a n (a ),Q(x) =b x m + + a m (b ) n m + ( P (x)e iax = P (x)?? ) n = m + h(x), M R s.t. x f(x) = b a x ( + h(x)), h(x) M x. b a x eiax dx b a x h(x)eiax dx f(x)e iax dx = R R f(x)e iax dx. f(x)e iax dx 76
178 3.6. (7) M R, R [, ) s.t.f(z) P (z) z <R f(z) M z ( z R ). R [R, ) Γ R z = x (x [ R, R]), C R z = Re iθ (θ [,π]) γ R := Γ R + C R P (z) z <R ( γ R ) f(z)e iaz f(z)e iaz γ R f(z)e iaz dz =πi Res(f(z)e iaz ; c) =πi Res(f(z)e iaz ; c). γ R c γ R Im c> C R z = Re iθ (θ [,π]) dz = ire iθ dθ π f(z)e iaz dz = f(re iθ )e iareiθ ire iθ dθ, γ R iare iθ = iar(cos θ + i sin θ) = ar sin θ + iar cos θ, Re [ iare iθ] = ar sin θ, e iareiθ = e Re[iaRe iθ ] = e ar sin θ π f(z)e iaz dz f(re iθ ) e iare iθ ire iθ M dθ γ R R R = M π (7) lim R e ar sin θ dθ. π e ar sin θ dθ = R f(x)e iax dx = lim f(x)e iax dx = R R f(z)e iaz dz Γ R = f(z)e iaz dz f(z)e iaz dz γ R C R =πi Res(f(z)e iaz ; c) f(z)e iaz dz Im c> C R πi Res(f(z)e iaz ; c) (R ) Im c> (7) 3 π e ar sin θ dθ 77
179 (7) [] Lebesgue Lebesgue e ar sin θ { π, lim R dθ = π<, lim R e ar sin θ = e ar sin θ dθ = lim R e ar sin θ dθ = (θ (,π)) (θ =,π) dθ =. = (a.e.) [] (ε-δ ) < δ <π/ π ( π/ δ ) π/ e ar sin θ dθ = e ar sin θ dθ = e ar sin θ dθ + e ar sin θ dθ ( ) π/ δ + e ar sin δ dθ δ ar sin δ δ + πe δ R [3] Jordan 6 (7) sin θ θ π R sin θ Rθ π (73) < π/ e R sin θ dθ R + π/ e Rθ/π dθ = ( θ π ) δ [ π ] π/ R e Rθ/π = π R ( e R ) < π R. 3.7 ( ) π e R sin θ dθ 3.7 ( 3.6 ) I = sin x x dx = π. ( ) f(z) := eiz z, Γ ε,r : z = x C R : z = Re iθ Γ R, ε : z = x C ε : z = εe iθ (x [ε, R]), (θ [,π]), (x [ R, ε]), (θ [,π]), γ ε,r := Γ ε,r + C R +Γ R,ε +( C ε ) 6 Jordan y =sinθ y = θ π Jordan [3] (p. 7) 78
180 ( ) f f γ ε,r ( ) Cauchy ( ) = f(z) dz = f(z) dz + f(z) dz + f(z) dz f(z) dz. γ ε,r Γ ε,r Γ R, ε C R C ε ( ) lim f(z) dz =. R C R C R f(z) dz = (73) π f(z) dz C R Γ R, ε f(z) dz = π e ireiθ Re iθ e ir(cos θ+i sin θ) dθ = π ε R ( ) f(z) dz + f(z) dz = Γ ε,r Γ R, ε π ireiθ dθ = i e ir(cos θ+i sin θ) dθ e R sin θ dθ < π R = π R. e ix ε x dx = e it R R t ( )dt = e it ε t dt R ε e ix R x dx ε e it t R sin x dt =i ε x dx. ( ) lim f(z) dz = iπ ε C ε 63 C ε f(z) dz = π iεe iθ = ε f(z) dz iπ = i C ε ε π π max ζ =ε e i(εeiθ ) εe iθ ( ) e i(εeiθ) n= ζ n n! π iεe iθ dθ = i e i(εeiθ) dθ lim f(z) dz = iπ. C ε ( ), ( ), ( ), ( ) R sin x i ε x dx = f(z)dz + f(z)dz πi + C ε Γ R dθ π max e ζ ζ n = π max ζ =ε ζ =ε n! n= ε n = π n! = π (eε ) (ε ). n= sin x x dx = π. (ε, R ). 63 Cauchy πi C ε 79
181 6. f c C ε : z = c + εe iθ (θ [,π]) f(z) lim dz = πif(c). ε + z c C ε 4 ( Riemann 64 ) Riemann Gauss, Abel, Jacobi, Riemann, Weierstrass 9 ( ) (9 978) Laurent Schwartz (95 ) (distribution) (98 ) (hyperfunction) 5 ( ). ( ) x + y =,xy =4 t t +4= t = ± 4 4 = ± 6 = ± 5 =5± , () D = f(α), C = f (α), B = f (α)/, A = f (3) (α)/6. ( f α Taylor ) () f (α) = 6α +a = α = a
182 3. ( ) 4. X 3 + Y 3 + Z 3 3XY Z =(X + Y + Z)(X + Y + Z YZ ZX XY ) ( ) ( ) ω x + x += (X + ωy + ω Z)(X + ω Y + ωz) =X +(ωy + ω Z + ω Y + ωz)x +(ωy + ω Z)(ω Y + ωz) = X +(ω + ω )(Y + Z)X + ω 3 (Y + Z )+(ω + ω )YZ = X (Y + Z)X +(Y + Z ) YZ = X + Y + Z YZ ZX XY t s 3 = t s 3 t ( ) ( ) 3 t t = 3 t 3 t, 3 t3 = t ( t t 3 3 t ( ) ) α, β ( ) α 3 + β 3 = q, αβ = p 3 Y := α, Z := β x 3 + px + q = x 3 3αβx ( α 3 + β 3) = x 3 3xY Z + Y 3 + Z 3 = x 3 + Y 3 + Z 3 3xY Z x 3 + px + q = =(x + Y + Z)(x + ωy + ω Z)(x + ω Y + ωz). x = (Y + Z), (ωy + ω Z), ( ω Y + ωz ) = α + β,ωα + ω β,ω α + ωβ ( ) α, β ( ) α, β ( ) ( p 3 ( ) α 3 + β 3 = q, α 3 β 3 = 3) A := α 3, B := β 3 (A + B = q, AB = ( p 3 3) ) A, B ( p ) 3 t + qt = 3 t = q ± q p3 = q ± (q 8 ) + ( p 3) 3
183 ( ) t := q (q ) ( p ) 3, t := q (q ) ( p ) 3, + 3 ( ) α := 3 t, β := 3 t α β ( ) α 3 + β 3 = t + t = q, αβ = 3 ( p ) 3 p t t = 3 = 3 3 (( )). α, β ( ),( ) x = α + β () x = 3 q (q ) ( p ) q (q ) ( p ) ( ) α, β ( ) ( ) α, β ( ) ( ) 6. () x 3 + px + q = x = 3 q (q ) ( p ) q (q ) ( p ) 3, ω 3 q (q ) ( p ) ω 3 q (q ) ( p ) 3, ω 3 q (q ) ( p ) ω q (q ) ( p ) () ( q ( ) + p 3 3) =() x ( q ) ( + p ) 3 3 < t, t 3 ( ) α t 3 ( ) αβ = p/3 ) 3 β := p/3 α α 3 + β 3 = α 3 + ( p 3 = t α 3 p3 /7 = = q. ( ) t ( ) α, β ( ) x 3 +px+q = x = α + β,ωα + ω β,ω α + ωβ 8
184 7. ( x y )( ) ( ) y u = x v ( ) ( u x = v y ) ( ) y = x ( x + y x y )( ) x y x = + y x y. x + y 8. i n = (n (mod 4)) i (n (mod 4)) (n (mod 4)) i (n 3 (mod 4)). 9. ( + i) = +i + i =i ( + i) =((+i) ) =(i) = i = 4 ( ) = 4.. (). z = x + iy (x, y R) z = x y = xy = x =,y = ±. z = ±i. ( ) z +=(z + i)(z i) z = z = ±i. ( i ) 3. z = x + iy (x, y R) z = i x y = xy = ( ( (x, y) =±, ). z = ± + i ). 4. z := c, z := c z = c, z, z = c, z. z := z z z, z =(z z ) = z z = c c z = c c. c c = z z = z = c c. 5. c,c < c c > c c c c c c = c i c i = ( c )( c )= c c c c c = c = c c = ( ) =, c c = i i =. 6. (zw = z w ) z = x + iy (x, y R), w = u + iv (u, v R) zw =(x + iy)(u + iv) =xu + x iv + iy u + iy iv =(xu yv)+i(xv + yu), z w =(x iy)(u iv) =xu + x ( iv) iy u iy ( iv) =(xu yv) i(xv + yu) zw =(xu yv) i(xv + yu) =z w. (z/w = z w ) z/w w = z/w w = z z/w = z w. 83
185 7. xy (α, β) R \{(, )}, δ R αx + βy + δ = (α, β) R \{(, )}, δ R αx + βy + δ = xy a = α + iβ (α, β R), z = x + iy (x, y R), γ := δ/ a z +āz = a z + a z =Re(a z) =Re[(α + iβ)(x iy)] = αx +βy. az + az + γ = αx + βy + δ =. a (α, β) (, ). 8. c f(z) m f(c) =f (c) = = f (m ) (c) = f (m) (c) f(c) =f (c) = = f (m ) (c) = f (m) (c) f(z) f(c) =f (c) = = f (m ) (c) = f (m) (c) c f(z) m 9. c, r z c = r. z c = r z c = r (z c)(z c) =r z z c z cz + c c = r z z c z cz + c r =. β = c r β < c. 7. z = z = e i 3π 4 Argz = Argz = 3π z 4 z = e i 3π = e i π Arg (z z )= π (frac3π ( π, π], π ( π, π] ) Arg(z + z )= π 3π = Arg z + Arg z. 8. () 3. WWW PDF 3. WWW PDF 3. 84
186 () z 3 =(x + iy) 3 = x 3 +3x iy +3x (iy) +(iy) 3 = x 3 3xy + i(3x y y 3 ) u(x, y) =x 3 3xy, v(x, y) =3x y y 3. () (3) z + = (x + iy) + = x y ++ixy = u(x, y) = x y + ixy (x y +) +4x y x y + (x y +) +4x y, v(x, y) = xy (x y +) +4x y. ( e iz + e iz) = ( e i(x+iy) + e i(x+iy)) = ( e y e ix + e y e ix) = ( e y (cos x + i sin x)+e y (cos x i sin x) ) =cosx ey + e y + i sin x e y e y =cosxcosh y i sin x sinh y. ( ) ( ) ϕ 38. ϕ = d ϕ dt u(ϕ(t)) = u (ϕ(t))ϕ ϕ (t) =(u x u y ) (t) = ϕ ( ) (t) ϕ ( ) (t) =. ϕ u(ϕ(t)) u(a) =u(ϕ()) = u(ϕ()) = u(b). (t) u 39. f (z) =e z (z C) f(b) f(a) =e πi e = =. f (c)(b a) =e c (πi ) = πie c c C f(b) f(a) f (c)(b a). 4. u x = v y, u y = v x U := v, V := u U x = v x, U y = v y, V x = u x, V y = u y U x = v x = u y = V y, U, V Cauchy-Riemann U x = V y, U y = v y = u x = V x U y = V x 85
187 4. v V u x = v y = V y, u y = v x = V x w := v V w x = w y = w v W (a, b) Ω (x, y) Ω (a, b), (x, y) Ω C v(x, y) =v(a, b)+ (v x dx + v y dy). Cauchy-Riemann v(x, y) =v(a, b)+ C C ( u y dx + u x dx). 45. f(x) f N (x) f N (x ) f N (x ) sup f N (y) f(y) y Ω f N (x ) f(x ) {f n } f f(x) f N (x) x ( x N ) (e z ) = ( ) z n = n! n= nz n n! = n= z n (n )! = z n n! = ez. cos z, sinz ( ) e (cos z) iz + e iz = = ieiz +( i)e iz = i eiz e iz = eiz e iz i =sinz 5. ( ) ()c d (f(z)f(c a)) = (z C) f(z)f(c z) f(z)f(c dz z) =f()f(c ) = f(c) =f(c). () a, b C c = a + b f(z)f(c z) =f(c) (z C) z = a f(a)f(b) =f(c). e a e b = e a+b. 54. () 55. () 56. () 6. [z,z +h] D(z ; ε) Ω [z,z +h] z +th (t [, ]) a [a, z + th] Ω a Ω = [a, z + th] Ω. t [,] 64. c = a c a ρ = c a ρ>. a = c + ρe iφ φ R ρ = c a <rδ := (r ρ)/ δ > D(a; δ) D(c; r). z c = r, z a = δ 86
188 ε< π ε C,ε : z = c + re iθ C,ε : z = a + δe iθ (θ [φ + ε, φ +π ε]), (θ [φ + ε, φ +π ε]), Γ ε : z =[( t)(ρ + δ)+tr] e i(φ+ε) (t [, ]), Γ ε : z =[( t)(ρ + δ)+tr] e i(φ+π ε) (t [, ]), C ε := Γ ε + C,ε Γ ε C,ε C ε ε> Ω:=C \{a + re iφ r } z a ε 65 (Γ =Γ ) dz z a C, C ε dz z a =. C, dz z a =. z c =r z c =r dz z a = z a =δ dz z a dz z a =δ z a =. dz π z a = δe iθ iδeiθ dθ =πi. 66. () 67. () 68. f C \{i, i} f c ρ ρ =min{ i, ( i) } = + = ) z coth z = z ez + e (+ z e z e = z e z = z z e z + e z + z e z = g(z) = B n (n)! n z n. 7. R = ( lim sup n ) ( n an, R = lim sup n ) n a n
189 7. () (3) a n = (n N) ( n)! (n ) ( ) (n )/ (n ) n! a n = (n = ) ( ).j 74. ( : a = re iθ (r>, θ [, π)) exp z = a = reiθ n Z s.t. z n Z s.t. z = =logr + i(θ +nπ) log r + i(θ +nπ) n (), (3) w n =/z n w n ) 78. () 5π () π 6 a ( ) () ( ) 88
190 6. ( ) 6.3 ( ) ( ) ( ) 89
191 () () 66 ([4]) Bolzano-Weierstrass R, R n ( ) Weierstrass A R n 66 9
192 A. C A. (Cauchy ) C (R, R l, C l OK) {a n } Cauchy ( ε >)( N N)( n N : n N)( m N : m N) a n a m <ε A. C (R, R l, C l OK) Cauchy {a n } a ε ε/ >. ( N N) ( n N: n N) a n a < ε. n N, m N n, m N a n a m = a n a + a a m a n a + a a m < ε + ε = ε. {a n } Cauchy C (R, R l, C l OK) Cauchy A.3 R, C, R l, C l C R C l R l R l {x n } R l Cauchy {x n } ( ) {x n } Bolzano-Weierstrass ( a R l )( {x nk } k N : {x n } ) lim x nk = a. k ε {x n } Cauchy ( N N) ( n N: n N) ( m N: m N) x n x m <ε. k N k N n k k N (m n k ) x n x nk <ε. k x n a ε. lim n x n = a {x n } 79. Cauchy 8. R l {x n }, a, c R l, r> lim x n = a, ( n N) x n c <r n a c r ( : x n c <r c r<x n <c+ r {x n }, {y n } lim x n = a, lim y n = b, ( n N) x n y n a b n n c r a c + r ) 9
193 A. ( ) 9% A.4 (Weierstrass M-test (M ), 3.9) K K ( ) a n (z) (z K) {b n } n N n n= a n (z) K (i) ( n N) ( z K) a n (z) b n. (ii) b n n= A.5 () a n {b n } n N n= a n n (i) ( n N) a n b n. (ii) b n n= A.5 A.6 ( ) a n a n n= n= C (Cauchy ) A.7 ( ) a n n s n := n a k, S n := k= n a k k= {S n } A. Cauchy n, m N n >m 9
194 n s n s m = a k k= m a k = k= n k=m+ a k n k=m+ a k = n a k n<m s n s m <S m S n k= m a k = S n S m. k= s n s m S n S m {s n } Cauchy A.3 {s n } a n n ( ) n = n n= 8. n = 8. n= ( ) n {s n } {s n } n N {s n } n N n n= ( ) n n n= Abel log A.7 S n := n a k, T n := k= n b k {T n } k= A. Cauchy n, m N n >m n S n S m = a k k=m+ n k=m+ b k = T n T m. n<m S n S m T m T n S n S m T n T m. {S n } Cauchy A.3 {S n } n a n n a n n b n 93
195 {b n } b n = Mr n b n = M n α ( r<) ( α>) ( ) ( n α 67 ) n= A.8 () {b n } n N b n n= (i) ( n N) b n. (ii) ( M R) ( n N) n b k M. k= ( (i) n b n a n b n (?) (i) (ii) ) n (i) T n := b k {T n } (ii) k= {T n } {T n } b n n A.9 () ( ) X f {ϕ n } n N N N N (f,ϕ n ) f n= (f,ϕ n ) b n = (f,ϕ n ), M = f n= A.8 (f,ϕ n ) f ( Bessel ) n= 67 n n k= k k dx n [ ] x α = dx x α n x α = α α. n α n n dx x α. n k= k α 94
196 A.3 Cauchy-Hadamard ( ) A.3. {a n } lim sup a n R {+, }, n lim inf a n R {, } n {a n } n N {a n } n N n N {a k k n} sup a k =sup{a k k n} k n {a k k } {a k k } {a k k 3} sup k a k sup k a k sup a k. k 3 { } inf a k k n n N inf sup n N k n a k = lim sup n k n a k R { } {a n } n N n N {a k k n} sup a k =sup{a k k n} =+. k n inf sup n N k n a k =+ inf sup n N k n a k = lim sup n k n a k R {, + } {a n } (the limit superior of {a n }) lim sup a n (lim sup n lim a n ) n {a n } (the limit inferior of {a n })liminf a n = lim a n n n {a n } lim sup a n := inf n lim inf n sup n N k n a k = lim sup n k n a k, a n := sup inf a k = lim inf a n N k n n k. k n (sup, inf, ) 95
197 A. {a n } () a lim sup a n = a n (a) ( ε >) ( N N) ( n N: n N) a n <a+ ε (b) ( ε >) ( N N) ( n N: n N ) a n >a ε ( ε a n >a ε n ) () lim sup a n = {a n } n (3) lim sup a n = {a n } n (4) a lim inf n a n = a (a) ( ε >) ( N N) ( n N: n N) a n >a ε (b) ( ε >) ( N N) ( n N: n N ) a n <a+ ε ( ε a n <a+ ε n ) (5) lim inf n a n = {a n } (6) lim inf a n =+ {a n } n () {a n } lim a n = a n ( ε >)( N N)( n N : n N) a ε<a n <a+ ε A. {a n } a R {+, } lim a n = a lim sup n n a n =liminf n a n = a. A. a n =( ) n + n (n N) {a n} lim sup a n =. n 96
198 A.3 () lim inf n a n lim sup a n. n () lim sup( a n )= lim inf a n,liminf ( a n)= lim sup n n n n (3) a n b n lim sup n a n. a n lim sup b n,liminf a n lim inf b n. n n n {a n } a {a n } ( ( ) ) A.4 ( ) () (R ) A R a R a A (an accumulation point) ε >(B(a; ε) \{a}) A a A a A a A () ( ) {a n } a R a {a n } n N (a cluster point, an accumulation point) ε > a n B(a; ε) n n N a n = a a {a n } n N {a n } n N {a n n N} {a} a {a} A.3. Cauchy-Hadamard A.5 ( Cauchy-Hadamard ) λ := lim sup n () λ< n an a n n= () λ>(λ = ) n= (λ =) a n a n n= () λ< λ <µ< µ ( N N) ( n N: n N) n an <µ. a n <µ n. N { a n ( n N ) b n := µ n (n N) 97
199 n N a n b n b n = n= a n n= N k= a k + µn µ. () λ> n a n > n n a n > lim a n = a n n d Alembert A.6 ( d Alembert ) a n a n () λ< () µ> λ := lim sup n a n n= a n n= n= n= a n+ a n+, µ := lim inf a n n a n () a n+ lim sup lim sup n an lim inf n a n n n n an lim inf n (lim sup, lim inf ) { } Cauchy-Hadamard { } lim sup d Alembert n lim sup a n+ an lim inf lim inf a n d Alembert a n+ a n A.3.3 Cauchy-Hadamard A.7 ( Cauchy-Hadamard ) ρ z C lim sup n ρ = n an (z c) n =limsup n n lim sup an. n a n (z c) n ( z c n ) a n = z c lim sup n n an. 98
200 A.5 < > n lim sup an n A.3.4 lim sup n a n a n z n na n z n lim n n n = A.8 k N lim n n n k =. n= a n := n n k log a n = k log n n (n ). a n = e log an e =. z n! Cauchy-Hadamard a n = { (k! =n k N ) ( ) lim sup a n n A.9 {a n }, {b n } b R, X N (i) lim n b n = b. (ii) n X a n = b n, n N \ X a n <b. lim sup a n = b. n ε lim b n = b N n ( n N : n N) b ε<b n <b+ ε. (i) n n N n X a n = b n b ε<a n <b+ ε. n N \ X a n <b. a n <b+ ε (ii) N X N max{n,n } n X a n = b n, b ε<b n b ε<a n. lim sup a n = b. n 99
201 A. {A n }, {k n } lim k n n lim sup k n A n = ka. n ( ) = k(> ), lim sup A n n = A A.4 ( ) A.5 ( ) 68 f n f f n g f n (x) f n (a) = f(x) f(a) = x a x a f n(t) dt g(t) dt f (x) =g(x) () ( ) A. Ω C f n (n N), f, g Ω C n N f n f n Ω {f n} f Ω K {f n} K g f Ω f = g. g ( ) c Ω z Ω c z C C z f n(ζ)dζ = f n (z) f n (c). C z C z γ :[α, β] Ω β β f n(ζ)dζ = f n(γ(t))γ d (t)dt = C z α α dt f n(γ(t))dt =[f n (γ(t))] β α = f n(z) f n (c). 68
202 ( ) C z f n g C z g(ζ)dζ = f(z) f(c). z Ω Ω ε> D(z; ε) Ω < h <ε h f(z + h) f(z) C z+h C z +[z,z + h] ( ) f(z + h) f(z) = f(c)+ g(ζ)dζ C z+h dζ = h [z,z+h] f(z + h) f(z) h ( g(z) = h = h ( ) f(c)+ g(ζ)dζ = g(ζ)dζ. C z [z,z+h] g(ζ)dζ g(z) [z,z+h] [z,z+h] (g(ζ) g(z)) dζ. [z,z+h] ) dζ (f(z + h) f(z)) g(z) h sup g(ζ) g(z) dζ h ζ [z,z+h] [z,z+h] sup g(ζ) g(z). ζ [z,z+h] g h f (z) =g(z). A. a n (z c) n ρ>d(c; ρ) ( ) a n (z c) n = (n +)a n+ (z c) n. ( ρ ) (n +)a n+ (z c) n+ = Cauchy-Hadamard lim sup n n nan = lim n n lim sup n n ( lim n n n = ) na n (z c) n n= n an =limsup n n an. (n +)a n+ (z c) n a n (z c) n
203 n Ω=D(c; ρ), f n (z) = a k (z c) k, f(z) = a n (z c) n, g(z) = k= f n f f n (n +)a n+ (z c) n f n(z) = n n ka k (z c) k = (k +)a k+ (z c) k k= k= Ω K <ρ <ρ D(c; ρ ) f n K g f f = g. ( ) a n (z c) n = (n +)a n+ (z c) n. A.6 Abel () Abel (Abel summation, Abel s transformation, Abel s partial summation) n n n A n := a k a k b k = A n b n + A k (b k b k+ ) k= k= n a k b k = a b + k= n a k b k = A b + k= n = A k (b k b k+ )+A n b n. k= k= n (A k A k )b k = A b + k= [33] 75 n n A k b k A k b k+ k= k=
204 A.3 (Abel (Abel s transformation)) {α n } n, {β n } n (74) ( M R)( n N {}) n α k M, k= (75) β n β n+ <, lim β n = n S = α n β n S A B, k=m+ α k β k A m+ B m+ n A m := sup α k, B m := β k β k+. n m k=m k=m {α n } {β n } {β n } (74) A m M < n n m n m α k = α k α k α k + α k M + M =M k=m k= k= k= k= A m M. n S n := α k β k, σ n := k= n α k S n Abel k= S n = α β + = σ β + n n α k β k = σ β + (σ k σ k )β k k= k= n n σ k β k σ k β k+ = n n σ k β k σ k β k+ k= k= k= k= n = σ k (β k β k+ )+σ n β n. k= σ n β n = σ n β n A β n (n ). n n σ k β k β k+ A β k β k+ A B <. k= k= S = lim n S n S A B. 3
205 k = m + S m+,n := n k=m+ k=m+ α k β k, σ m+,n := α k β k A m+ B m+ n k=m+ k m + α k = σ m+,k σ m+,k, α m+ = σ m+,m+. S m+,n = σ m+,m+ β m+ + = σ m+,m+ β m+ + = = n k=m+ n k=m+ σ m+,k β k n k=m+ n k=m+ n k=m+ α k (σ m+,k σ m+,k ) β k σ m+,k β k σ m+,k β k σ m+,k (β k β k )+σ m+,n β n. n k=m+ σ m+,k β k σ m+,n β n A m+ β n, n k=m+ σ m+,k (β k β k ) lim n S m+,n n k=m+ k=m+ A m+ β k β k lim S m+,n A m+ B m+. n A m+ β k β k = A m+ B m+ A.4 {β n } α n =( ) n α n = e inθ (θ πz) f(z) b z b f(z) f(b) Abel 4
206 A.5 (Abel (Abel s continuity theorem)) f(z) = a n z n z = R (R >) K { } Ω K := z C z/r z <R, z /R K f Ω K {R} f Ω K {R} lim f(x) =f(r). x [,R) x R f n (z) := n a k z k k= sup f(z) f n (z) z Ω K {R} (n ) z = R lim f n (R) =f(r) ( n z ) n z Ω K α n := a n R n, β n := R n n α k = a k R k = f n (R) (n =,,,...) k= k= β n β n+ = ( z R ) n z R = z R z R Abel n N A n+ = K. f(z) f n (z) A n+ B n+ A n+ B KA n+ (z Ω K ). sup m n+ m k=n+ α k = sup m n+ m k=n+ a k R k = sup f m (R) f n (R) m n+ f(z) f n (z) K sup f m (R) f n (R) (z Ω K, n N). m n+ { } sup z Ω K {R} f(z) f n (z) max K sup m n+ f m (R) f n (R), f(r) f n (R). n f n (R) f(r) {f n (R)} n Cauchy n {f n } n N Ω K {R} f 5
207 A.6 (Abel ( A.3) ) a f(x)g(x) dx F (x) := a x a f(x)g(x)dx sup x [a, ) f(t) dt x a f(t) dt a (x [a, )) F (x) =f(x) F, a M := sup F (x) < x [a, ) g (x) dx <, lim x g(x) = F (a) = R a a f(x)g(x) dx = a R a g (x) dx R F (x)g(x) dx =[F (x)g(x)] R a F (x)g (x) dx = F (R)g(R) R a F (x)g (x) dx. F (R)g(R) M g(r) (R ), F (x)g (x) M g (x), f(x)g(x) dx R f(x)g(x) dx M g (x) dx = sup a a x [a, ) c [a, ) f(x)g(x) dx sup x f(t)dt c x [c, ) c a g (x) dx < x a c f(t) dt a g (x) dx. g (x) dx. A.7 IV 69 3 [34] X (654 75)
208 8.. ( ) ( ε-n Cauchy ) n= a n = lim n [35] n k= a k. ( ) Sir Isaac Newton (643 77, Woolsthorpe ). ( ) BrookTaylor(685 73, Middlesex ) 3. () Leonhard Euler (77 783, Basel St Petersburg ) 4. Augustin Louis Cauchy ( , Sceaux ) 8 Cours d analyse (), 5. Niels Henrik Abel (8 89, ), Abel, Abel 6. () Jean-Baptiste-Joseph Fourier (768 83) 7. Karl Theodor Wilhelm Weierstrass (85 897, Westphalia (now Germany) Ostenfelde ), Weierstrass Mtest 7
209 A.8 a n (z c) n ( ) A.7 ( ) f(z) := C \{3} z 3 Taylor ( ) c = D(; ) Taylor f(z) = z 3 = (z ) = ( z ) = ( ) n z (z ) n = ( (z )/ < z D(; )). n+ f D(; ) D := {z C z > } f(z) = z 3 = (z ) = ( ) = z = n= ( ) n = z n (z ) n ( (z ) n z (z ) n+ z < z > ). ( z 3 ) 7.4 A.8 ( ) 3.3(p. 47) 3.(p. 57) A.8 (,.3) a n 3 (z c) n (i) z C \{c} R (, ) {z C z c R } (ii) R (, ) s.t. {z C z c >R} D(c; R) R (R, ) {z C z c R } (iii) z C \{c} ( ) 8
210 ζ = z c c z c = r ζ = r { {z C z c <r} ζ C ζ > } r { {z C z c >r} ζ C ζ < } r a n (z c) = a nζ n. a n n ζ n (i) a n ζ n a n ζ C z C \{c} (z c) n < R < ρ =/R a n ζ n ζ ρ a n (z c) z c n R (ii) < ρ < s.t. a n ζ n ζ <ρ ζ >ρ a n R := /ρ z c >R z c <R (z c) n R <R < R /R < /R = ρ a n ζ n ζ /R a n z c R (z c) n (iii) a n ζ n a n ζ z c (z c) n (i) R =,(iii) R = ( ) A.8 a n R s.t. z c > R z c < R (z c) n R< R a n < (z c) z c n R B 9
211 X (connected) X U, U X = U U U U = U = X, U = U =, U = X X A A A ( V,V : X ) U = A V, U = A V, A = U U, U U = U = U = A X ( ) X X ( x, y X, ϕ: [, ] X s.t. ϕ ϕ() = x, ϕ() = y) R I I ( ) R n R n ( 9.6) B. R n C ( ) R n B. Ω R n Ω a, b Ω Ω := {x Ω a x Ω }, Ω := {x Ω a x Ω } Ω Ω =Ω, Ω Ω =, a Ω. Ω x Ω x Ω Ω ε > s.t. B(x; ε) Ω. B(x; ε) y x a (a x x y ) y Ω. B(x; ε) Ω Ω
212 Ω x Ω x Ω Ω ε > s.t. B(x; ε) Ω. B(x; ε) y x a ( y a y x a x ) y Ω. B(x; ε) Ω Ω Ω Ω =Ω Ω =. a Ω Ω Ω C Ω C Ω C Ω ( B(x; ε) ) C C. x α x α f(x)dx f x α ( <α<) [, ) I = x α f(x) dx z α
213 z α α x α x < z α z α =exp(α log z) a (log z ) ( ) z = re iθ (r>, θ [, π)) log z =logr + i(θ +nπ) (n Z) ( log r log ) z α =exp(α (log r + i(θ +nπ))) = r α e iαθ e iαnπ. α Z n Z nα Z e iαnπ = n α Z ( ) z α = r α = z α. ( z α α ) a x = exp(log x), x α =exp(αlog x) Ω:=C\[, ) log z (, π) z z = re iθ (r>, θ (, π)) log z =logr +iθ. z α := exp (α log z) =exp(α(log r + iθ)) = r α e iαθ. ( ) z α ( α (, )) z = re iθ (r>, θ (, π)) z α = r α e iαθ, z α = z α. z (, ) ( ) (z α ) =(z α ) e παi ( ) C. ( ) f(z) = Q(z), P (z),q(z) C[z], deg P (z) P (z) deg Q(z)+, x (, ) P (x), f <α< x α f(x) dx = πi Res(z α f(z); c). e παi <ε<r,<δ<π ε, R, δ ( ε, δ, R ) C := C + C + C 3 + C 4, C z = te iδ (t [ε, R]), C z = Re iθ (θ [δ, π δ]), C 3 c
214 z = te i(π δ) (t [ε, R]), C 4 z = εe iθ (θ [δ, π δ]), ε, δ, R ( ) z α f(z) dz + z α f(z) dz + z α f(z) dz + z α f(z) dz =πi Res(z α f(z); c). C C C 3 C 4 c C C z α f(z) dz = R ε ( ) R te iδ α f(te iδ ) dt = e iαδ t α f(te iδ ) dt. δ t [ε, R] t α f(te iδ ) t α f(t), e iαδ R z α f(z) dz t α f(t) dt. C ε C π δ z α f(z) dz = (Re iθ ) α f(re iθ ) ire iθ dθ C δ π ε (Re iθ ) α f(re iθ ) ire iθ dθ (δ ). θ = (Re iθ ) α = R α, θ =π (Re iθ ) α = R α e παi ( [, π] ) π π (Re iθ ) α f(re iθ ) ire iθ dθ Rα+ f(re iθ ) dθ R α+ π M R = πm R α (R ). C 3 R z α f(z) dz = (te (π δ)i ) α f(te (π δ)i ) e (π δ)i dt C 3 ε R R = e (π δ)αi e (π δ)i t α f(te (π δ)i ) dt = e παi e (+α)δi t α f(te δi ) dt. δ t [ε, R] t α f(te δi ) t α f(t) R z α f(z) dz e παi t α f(t) dt. C 3 ε C 4 z α f(z) dz = C 4 δ π δ ε (εe iθ ) α f(εe iθ ) iεe iθ dθ π (εe iθ ) α f(εe iθ ) iεe iθ dθ (δ ). θ = (εe iθ ) α = ε α, θ =π (εe iθ ) α = ε α e παi ( [, π] ) π π (εe iθ ) α f(εe iθ ) iεe iθ dθ εα+ f(εe iθ ) dθ ε α+ π M ε =πm ε α (ε ). ( ) δ ε, R t α f(t) dt e παi t α f(t) dt =πi Res(z α f(z); c). c ε t α f(t) dt = πi Res(z α f(z); c). e παi c 3
215 δ C z α f(z) dz R C 3 z α f(z) dz e παi ε t α f(t) dt, R ε t α f(t) dt [ε, R] πi R Res (f(z)logz; c) = f(z)logzdz=( e παi ) f(x)dx +. c C ε,r ( C ε,r ) C. <α< x α +x dx = π sin πα. C. ( <α< ) ( ( ) ( )) x α πi z α z α dx = Res +x e παi +z ; i +Res +z ; i = πi ( ) e παi/ e3παi / e παi i i = π ( e παi/ e 3παi/) π = e παi cos πα. Mathematica, Maple ( Integrate[x^a/(+x^), {x,-infinity,infinity}], integrate(x^a/(+x^),x =-infinity..infinity) ) 7. (Ahlfors p.74) x /3 +x dx ( : π 3 ) C. f(x) dx f ( ) f(x) dx = f(x) dx = πi Im c> Res(f; c) =πi Im c> Res(f; c) f z (, ) (log z) =(logz) +πi 4
216 πi Res (f(z)logz; c) = f(z)logzdz= πi c C ε,r R f(x)dx +. ( C ε,r ) C. () f(z) = Q(z), P (z),q(z) C[z], P (z) deg P (z) deg Q(z)+, x [, ) P (x) f(x) dx = c C\[, ) Res (f(z)logz; c). log Im log (, π) f(z)logz C. ε, δ R 4 f(z)logzdz=πi Res(f(z)logz; c). C j δ j= δ δ π f(z)logzdz C f(z)logzdz C 3 ε c C\[, ) R R C +C 3 f(z)logzdz πi C f(z)logzdz π ε f(t)logtdt, f(t)[logt +πi] dt. R ε f(t) dt. f(re iθ )(log R + iθ) ire iθ dθ, π f(re iθ )(log R + iθ) ire iθ dθ R(log R +π) f(re iθ ) dθ R(log R +π) M R π C 4 ε πi f(t) dt =πi c C\[, ) πi [36] pp.6 63 f(x) dx = f(z)log( z) dz = πi C Res(f(z)logz; c). c f (R ). Res (f(z)log( z); c). 5
217 C C ( ) (?) (principal value) Log ( Log( z) ) f(x) dx = c f Res (f(z); c)log( c). dx C.3 I = x +.(?? ) I = c C\[, ) i, i ( ) log z Res z + ; i C.4 Res ( ) log z z + ; c =lim z i (z i) log z ( ) log z Res z + ; i = lim (z + i) log z z i ( π I = 4 3π 4 I = = c=i, i Res ( ) log z z + ; c. z + = log z z + i = πi/ = π z=i i 4, z + = log z z i = 3πi/ = 3π z= i i 4. ) = π. dx x 3 +. z 3 += z = e πi/3,e πi,e 5πi/3 I = ( ) log z Res z 3 + ; c = c C\[, ) c=e πi/3,e πi,e 5πi 3 ( ) log z Res z 3 + ; c. c 3 = ( ) log z Res z 3 + ; c = log z (z 3 +) z=c = log z 3z = z=c z log z 3. z=c I = 3 (z log z z=e + z log z πi/3 z=e πi + z log z z=e 5πi/3) ( = + 3i π ) 3i i +( ) πi πi = 3π. 9 6
218 C.3 (log x) n g(x)(log x) n dx () Ω={z C Im z>}, g Ω x R g( x) =g(x) R θ [,π] g(re iθ )R log R. g(x)logxdx+ iπ g(x) dx =πi Log z Im(Log z) (, π). C. a> I = log x dx + iπ x + a Im c> log x π log a dx = x + a a. dx =πi Res x + a Res(g(z)Logz; c). ( ) Log z z + a ; ia = π (log a + π ) a i log x π log a dx = x + a a. C.3 a> I = log x (x + a ) dx + iπ C.4 a> I = log x dx + iπ x 4 + a4 C.5 a> I = log x π(log a ) (x + a dx =. ) 4a 3 ( ) Log z dx =πi Res (z + a ) ; ia =πi d ( ) (z ia) Log z dz (z + z ) z=ia z + ia Logz =πi z = (z + ia) 3 z=ia (x + a ) log x π( log a π/) dx = x 4 + a4 4. a 3 dx =πi x 4 + a4 πi Im c> ( Res ( Log z z 4 + a 4 ; aeπi/4 = = π a 3 [ ( log a π )+iπ ] log x x 6 + a dx = π(log a π/ 3). 6 3a 5 ( ) Res() = π loga 3 3a 5 3 π + iπ 7 ) π( log a π i) a 3. ( )) Log z +Res z 4 + a ; 4 ae3πi/4
219 log x 8. (Ahlfors p. 74) dx ( : ) +x C.4 (log x) n ( ) f f(x)(log x) n dx f(x)(logx) n dx (n = C.) x α log C.5 [3] a<b Φ(z) :=Log z a z b z = a, b C \ [a, b] x (a, b) ( lim Log z a ε z b Log z a ) z=x+iε z b = πi z=x iε f [a, b] (C ) D C [a, b] D b f(x) dx = f(z)log z a πi C z b dz. a f [a, b] C f [a, b] x [a, b] b a Φ(z) := f(x) dx = b a b a f(x) = πi C ( πi C dx z x =Logz a z b. f(z) z x dz ) f(z) z x dz dx = f(z)φ(z) dz, πi C C f c R b f(x) dx = Res (f(z)φ(z); c)+ f(z)φ(z) dz. a πi z =R c C\[a,b] 8
220 z Φ(z) =Log z a ( ) f(z) =O (z ) z b z R f(z)φ(z) dz. z =R C.5 f(z) = Q(z), P (z), Q(z) C[z], deg P (z) deg Q(z)+, ( x [a, b]) P (x) P (z) b f(x) dx = ( Res f(z)log z a ) z b ; c. C.6 a c C\[a,b] I = dx x 4 +. Φ(z) =Log z + z. c z4 += c f(z) := z 4 + Res (fφ; c) =Φ(c)Res(f; c) =Φ(c) (z 4 +) =Φ(c) z=c 4c =Φ(c) c 3 4c = cφ(c) 4 4 I = c= +i, +i, i, i Res (f(z)φ(z); c) = ( Log + ) ( ) + π. C.6 a b Γ a,b C.7 (Fresnel ( ) ) f(z) :=exp( z /) C := C + C + C 3, C := Γ,X, C := Γ X,(+i)X, C 3 := Γ (+i)x, (X (, )) cos ( x ) dx = sin ( x ) dx = π 7 ( ) f C = f(z) dz = f(z) dz + f(z) dz + f(z) dz. C C C C 3 f(z) dz = dz + C 3 C C dz. x 7 Augustin-Jean Fresnel (788 87) Fresnel C(x) := sin ( t ) dt x Fresnel x cos ( t ) dt, S(x) := 9
221 C z = x (x [,X]) C f(z) dz = X x/ =t dx = dt C f(z) dz = X/ e x / dx. e t dt C z = X + iy (y [,X]) e (X y +ixy)/ z = y +ixy X, dz = idy e t = π. X f(z) dz = e (X y +ixy)/ idy. C = e (X y )/, (X y )= (X + y)(x y) X(X y) X f(z) dz e (X y )/ dy C = X = X e Xt/ ( )dt = X ( ) e X / X e X(X y)/ dy e Xt/ dt = (X ). [ X e Xt/ ] X C 3 z =(+i)t (t [,X]) z =(+i) t =it, dz =(+i)dt X X ( f(z) dz = e it ( + i)dt =(+i) cos(t ) i sin ( t )) dt. C 3 ( X X ) (+i) cos(t )dt i sin(t )dt = X/ π e t dt+ f(z) dz C (X ). X cos(t ) dt i sin(t ) dt = +i π = i π. cos ( t ) dt = sin ( t ) dt = π. C.8 a R e x +iax dx = e a π. e x cos(ax)dx = e a π, e x sin(ax)dx =.
222 ( ) a = () ( = e x, e x dx < e x +iax ) a > (a < a a ) f(z) :=exp( z ) a >, X> C := Γ X,X, C := Γ X,X+ia, C 3 := Γ X+ia, X+ia, C 4 := Γ X+ia, X, C := C + C + C 3 + C 4 f C = f(z) dz = f(z) dz + f(z) dz + f(z) dz + f(z) dz. C C C C 3 C 4 f(z) dz = f(z) dz + f(z) dz + f(z) dz. C 3 C C C 4 C z = x (x [ X, X]) C f(z) dz = X X e x dx. C z = X + iy (y [,a]) (X + iy) = (X y +ixy) a f(z) dz = exp [ (X y +ixy) ] idy. C X>a y [,a] Re [ (X y +ixy) ] = (X y )= (X + y)(x y) X(X y) X(X a) a f(z) dz [ exp (X y +ixy) ] a dy = e (X y ) dy C a e X(X a) dy = ae X(X a) f(z) dz C 4 (X ). C 3 z = x + ia (x [ X, X]) (X ). exp( z )=exp [ (x + ia) ] =exp [ x + a aix ] = e a e x (cos(ax) i sin(ax)) C 3 f(z) dz = e a ( X e a e x cos(ax)dx i X X ( X X X X ) e x cos(ax)dx i e x sin(ax)dx. X ) X e x sin(ax)dx = e x dx + f(z) dz + f(z) dz X C C 4 π (X ).
223 e x cos(ax)dx = e a π. C.9 n, m N, m<n I = e x sin(ax)dx =. e x e iax dx = e a π. x m +x dx = π/n n sin(mπ/n). ( n ) dx +x = π, dx +x = 4π 5 dx +x = ( dx +x = π 3 3 3, dx +x = π 4, 5 5, dx +x = π 6 3, 5+)π dx, +x = ( 6+ )π. r (, ) 7 x r +x dx = π sin(rπ) dx +x = π 8 4, (r = m/n x n = u ) ( ) f(z) := zm ( + k)πi exp (k =,,...,n ) +zn n ω := exp πi n f ωk+ (k =,,...,n ) ω n =, ω n = R (, ) C := Γ,R, C : z = Re iθ (θ [, π/n]), C 3 := Γ Rω,, C := C + C + C 3 C (C Rω ) f f ω ( ) f(z) dz + f(z) dz + f(z) dz =πi Res(f; ω). C C C 3 ω f Res(f; ω) = zm ( + z n ) z=ω = zm nz n = ωm z=ω nω n = ωm nω n = ωm n. 7
224 C z = x (x [,R]) R R x m f(z) dz = f(x) dx = C +x dx. n C C f(z) dz = π/n f(re iθ ) ire iθ dθ M, R f(z) M/ z ( z R ) R >R π/n f(z) dz f(re iθ ) M π/n Rdθ C R R dθ = πm (R ). nr C 3 z = tω (t [,R]) R R f(z) dz = f(tω ) ω t m ω (m ) dt = ω dt = ω m C 3 +t n ω n ( ) ( ω m ) R x m +x dx + f(z) dz = πi ωm n C n. R x m +x n dx. R C. Γ ( ω m ) x m +x n dx = πiωm n x m πiωm dx = +xn n( ω m ) = π i n(ω m ω m ) = π n sin(mπ/n). ( ) ( q Γ q ) ( q = B p p p, q ) x q = p p +x dx = π p sin (πq/p). B(α, β) =Γ (α)γ (β)/γ (α + β) Γ () = x p = u (76) x q +x p dx = p u q/p +u du. B(p, q) = x = t/( + t) (77) B(p, q) = x p ( x) q dx t p dt ( + t) p+q x q +x dx = ( q p p B p, q ) p 3
225 () x (, ) Γ (x)γ ( x) = C Γ (z) = e γz e z/k z +z/k C. Γ (z)γ ( z) = e γz e γz sin πz = 9. (Ahlfors p. 74) z k= k= π Γ (z)γ ( z) = πz I = π e z/k +z/k k= k= π sin(πx). (γ Euler ) e z/k z/k = z k= (z/k). ( ) ( (z/k) = πz ) (z/k). log sin θdθ= π log. log( + x ) x +α dx ( <α<) ( k= π α sin(απ/) ) D D. f, g c f(c) F := g c f f, g, F D. ( ) f(z) = F (z) = g(z) f(z) a n z n, g(z) = (78) c = b a, c n = b n z n, F(z) = c n z n ( f() ) b n n a k c n k k= a (n N) (78) c n n =,,,... 4
226 g(z) =f(z)f (z) (A + A + A + )(B + B + B + )=A B +(A B +A B )+(A B +A B +A B )+ g(z) = ( )( ) ( n ) A n B n = A k B n k k= ( )( ) ( n ) f(z)f (z) = a n z n c n z n = a k c n k z n. k= b n z n b = a c, b = a c + a c, b = a c + a c + a c,.. b n = a c n +. n a k c n k (n N) k= c = b a, c = b a c a, c = b a c a c a,, c n = b n n a k c n k k= a (n N). D. tan f(z) :=cosz, g(z) :=sinz C f(z) =cosz ( z <π/) z < π F (z) :=tanz = sin z cos z = g(z) f(z) F (z) = Taylor 9.6 c n z n ( z < π ) Bernoulli {B n } z e z = tan z = n= B n n! zn ( ) n n ( n ) B n z n (n)! 5
227 Taylor tan z = z + 3 z3 + 5 z z7 + Bernoulli f f (n) () (n =,,, ) D. (78) cos, sin Taylor cos z = ( ) n (n)! zn, sin z = ( ) n (n +)! zn+ (z C). z <π/ cos z tan z = z 6 z3 + z5 54 z7 + z + 4 z4 7 z6 + = z 6 z + z4 54 z6 + z + 4 z4 7 z6 + ( z <π/). z z 6 z + z4 54 z6 + z + 4 z4 7 z6 + = ( a ) n z n (tan z ) w = z ( (a +a w+a w +a 3 w 3 + ) w + 4 w ) 7 w3 + = 6 w+ w 54 w3 +. a =, a + a = 6, a 4 a + a =, a 7 + a 4 a + a 3 = 54, a =,. a = 6 + a = 3, a = + a a 4 = 5, a 3 = 54 + a a 4 + a 7 = 7 35,. 6
228 tan z = z + 3 z3 + 5 z z7 +. BASIC BASIC BASIC OPTION ARITHMETIC RATIONAL cos, sin Taylor BASIC ^ FACT() 7
229 cotangent.bas OPTION ARITHMETIC RATIONAL DECLARE EXTERNAL SUB INverse DECLARE EXTERNAL SUB conv LET maxn= OPTION BASE DIM c( TO maxn),s( TO maxn),is( TO maxn),cotangent( TO maxn) FOR TO maxn LET c(n)= LET s(n)= NEXT n FOR j= TO maxn/ LET c(*j)=(-)^j/fact(*j) LET s(*j)=(-)^j/fact(*j+) NEXT j PRINT "z/sin(z)" CALL INverse(s,IS,maxn) CALL PRINTc(IS,maxn) PRINT "z cos(z)/sin(z)" CALL CONv(IS,c,cotangent,maxn) CALL printc(cotangent,maxn) END REM EXTERNAL SUB printc(a(),maxn) OPTION ARITHMETIC RATIONAL FOR TO maxn PRINT a(n) NEXT n END SUB REM EXTERNAL SUB INverse(a(),b(),maxn) OPTION ARITHMETIC RATIONAL LET b()=/a() FOR n= TO maxn LET s= FOR k= TO n LET s=s+a(k)*b(n-k) NEXT k LET b(n)=-s/a() NEXT n END sub REM EXTERNAL SUB conv(a(),b(),c(),maxn) OPTION ARITHMETIC RATIONAL FOR TO maxn LET s= FOR j= TO n LET s=s+a(j)*b(n-j) NEXT j LET c(n)=s next n END sub 8
230 OPTION ARITHMETIC RATIONAL LET maxn=4 DIM a( TO maxn+),b( TO maxn) REM sin(z) FOR TO maxn+ LET a(n)= NEXT n FOR j= TO maxn/ LET a(*j+)=(-)^j/fact(*j+) NEXT j REM f(z)=sin(z)/z FOR j= TO maxn+ LET a(j-)=a(j) NEXT j REM /f(z) LET b()=/a() FOR n= TO maxn LET s= FOR k= TO n LET s=s+a(k)*b(n-k) NEXT k LET b(n)=-s/a() NEXT n FOR TO maxn PRINT b(n) NEXT n END D.3 Bernoulli tan 9.5(p. ) () E Cauchy E. Cauchy Cauchy C C C f f(z) dz =. (C f C C f(z) dz =) 9
231 3: f(z) dz = 4: C C f(z) dz 5: C f(z) dz 3
232 : () f C C f(z) dz = C f(z) dz. C 6: f(z) dz = f(z) dz 7: C C f(z) dz = f(z) dz C C 8: : f(z) dz = f(z) dz + f(z) dz C C C 3 () 9: C Cauchy 3
, ( ) 2 (312), 3 (402) Cardano
 214 9 21, 215 4 21 ( ) 2 (312), 3 (42) 5.1.......... 5.2......................................... 6.2.1 Cardano................................... 6.2.2 Bombelli................................... 6.2.3
214 9 21, 215 4 21 ( ) 2 (312), 3 (42) 5.1.......... 5.2......................................... 6.2.1 Cardano................................... 6.2.2 Bombelli................................... 6.2.3
x (x, ) x y (, y) iy x y z = x + iy (x, y) (r, θ) r = x + y, θ = tan ( y ), π < θ π x r = z, θ = arg z z = x + iy = r cos θ + ir sin θ = r(cos θ + i s
 ... x, y z = x + iy x z y z x = Rez, y = Imz z = x + iy x iy z z () z + z = (z + z )() z z = (z z )(3) z z = ( z z )(4)z z = z z = x + y z = x + iy ()Rez = (z + z), Imz = (z z) i () z z z + z z + z.. z
... x, y z = x + iy x z y z x = Rez, y = Imz z = x + iy x iy z z () z + z = (z + z )() z z = (z z )(3) z z = ( z z )(4)z z = z z = x + y z = x + iy ()Rez = (z + z), Imz = (z z) i () z z z + z z + z.. z
z f(z) f(z) x, y, u, v, r, θ r > 0 z = x + iy, f = u + iv C γ D f(z) f(z) D f(z) f(z) z, Rm z, z 1.1 z = x + iy = re iθ = r (cos θ + i sin θ) z = x iy
 z fz fz x, y, u, v, r, θ r > z = x + iy, f = u + iv γ D fz fz D fz fz z, Rm z, z. z = x + iy = re iθ = r cos θ + i sin θ z = x iy = re iθ = r cos θ i sin θ x = z + z = Re z, y = z z = Im z i r = z = z
z fz fz x, y, u, v, r, θ r > z = x + iy, f = u + iv γ D fz fz D fz fz z, Rm z, z. z = x + iy = re iθ = r cos θ + i sin θ z = x iy = re iθ = r cos θ i sin θ x = z + z = Re z, y = z z = Im z i r = z = z
I A A441 : April 15, 2013 Version : 1.1 I Kawahira, Tomoki TA (Shigehiro, Yoshida )
 I013 00-1 : April 15, 013 Version : 1.1 I Kawahira, Tomoki TA (Shigehiro, Yoshida) http://www.math.nagoya-u.ac.jp/~kawahira/courses/13s-tenbou.html pdf * 4 15 4 5 13 e πi = 1 5 0 5 7 3 4 6 3 6 10 6 17
I013 00-1 : April 15, 013 Version : 1.1 I Kawahira, Tomoki TA (Shigehiro, Yoshida) http://www.math.nagoya-u.ac.jp/~kawahira/courses/13s-tenbou.html pdf * 4 15 4 5 13 e πi = 1 5 0 5 7 3 4 6 3 6 10 6 17
(ii) (iii) z a = z a =2 z a =6 sin z z a dz. cosh z z a dz. e z dz. (, a b > 6.) (z a)(z b) 52.. (a) dz, ( a = /6.), (b) z =6 az (c) z a =2 53. f n (z
 B 4 24 7 9 ( ) :,..,,.,. 4 4. f(z): D C: D a C, 2πi C f(z) dz = f(a). z a a C, ( ). (ii), a D, a U a,r D f. f(z) = A n (z a) n, z U a,r, n= A n := 2πi C f(ζ) dζ, n =,,..., (ζ a) n+, C a D. (iii) U a,r
B 4 24 7 9 ( ) :,..,,.,. 4 4. f(z): D C: D a C, 2πi C f(z) dz = f(a). z a a C, ( ). (ii), a D, a U a,r D f. f(z) = A n (z a) n, z U a,r, n= A n := 2πi C f(ζ) dζ, n =,,..., (ζ a) n+, C a D. (iii) U a,r
 Email: kawahiraamath.titech.ac.jp (A=@) 27 2 25 . 2. 3. 4. 5. 3 4 5 ii 5 50 () : (2) R: (3) Q: (4) Z: (5) N: (6) : () α: (2) β: (3) γ, Γ: (4) δ, : (5) ϵ: (6) ζ: (7) η: (8) θ, Θ: (9) ι: (0) κ: () λ, Λ:
Email: kawahiraamath.titech.ac.jp (A=@) 27 2 25 . 2. 3. 4. 5. 3 4 5 ii 5 50 () : (2) R: (3) Q: (4) Z: (5) N: (6) : () α: (2) β: (3) γ, Γ: (4) δ, : (5) ϵ: (6) ζ: (7) η: (8) θ, Θ: (9) ι: (0) κ: () λ, Λ:
No. No. 4 No f(z) z = z z n n sin x x dx = π, π n sin(mπ/n) x m + x n dx = m, n m < n e z, sin z, cos z, log z, z α 4 4 9
 4 4 No. pdf pdf II Fourier No. No. 4 No. 4 4 38 f(z) z = z z n n sin x x dx = π, π n sin(mπ/n) x m + x n dx = m, n m < n e z, sin z, cos z, log z, z α 4 4 9 4 9 i = imaginary unit z = x + iy x, y R x real
4 4 No. pdf pdf II Fourier No. No. 4 No. 4 4 38 f(z) z = z z n n sin x x dx = π, π n sin(mπ/n) x m + x n dx = m, n m < n e z, sin z, cos z, log z, z α 4 4 9 4 9 i = imaginary unit z = x + iy x, y R x real
36 3 D f(z) D z f(z) z Taylor z D C f(z) z C C f (z) C f(z) f (z) f(z) D C D D z C C 3.: f(z) 3. f (z) f 2 (z) D D D D D f (z) f 2 (z) D D f (z) f 2 (
 3 3. D f(z) D D D D D D D D f(z) D f (z) f (z) f(z) D (i) (ii) (iii) f(z) = ( ) n z n = z + z 2 z 3 + n= z < z < z > f (z) = e t(+z) dt Re z> Re z> [ ] f (z) = e t(+z) = (Rez> ) +z +z t= z < f(z) Taylor
3 3. D f(z) D D D D D D D D f(z) D f (z) f (z) f(z) D (i) (ii) (iii) f(z) = ( ) n z n = z + z 2 z 3 + n= z < z < z > f (z) = e t(+z) dt Re z> Re z> [ ] f (z) = e t(+z) = (Rez> ) +z +z t= z < f(z) Taylor
 211 kotaro@math.titech.ac.jp 1 R *1 n n R n *2 R n = {(x 1,..., x n ) x 1,..., x n R}. R R 2 R 3 R n R n R n D D R n *3 ) (x 1,..., x n ) f(x 1,..., x n ) f D *4 n 2 n = 1 ( ) 1 f D R n f : D R 1.1. (x,
211 kotaro@math.titech.ac.jp 1 R *1 n n R n *2 R n = {(x 1,..., x n ) x 1,..., x n R}. R R 2 R 3 R n R n R n D D R n *3 ) (x 1,..., x n ) f(x 1,..., x n ) f D *4 n 2 n = 1 ( ) 1 f D R n f : D R 1.1. (x,
y π π O π x 9 s94.5 y dy dx. y = x + 3 y = x logx + 9 s9.6 z z x, z y. z = xy + y 3 z = sinx y 9 s x dx π x cos xdx 9 s93.8 a, fx = e x ax,. a =
 [ ] 9 IC. dx = 3x 4y dt dy dt = x y u xt = expλt u yt λ u u t = u u u + u = xt yt 6 3. u = x, y, z = x + y + z u u 9 s9 grad u ux, y, z = c c : grad u = u x i + u y j + u k i, j, k z x, y, z grad u v =
[ ] 9 IC. dx = 3x 4y dt dy dt = x y u xt = expλt u yt λ u u t = u u u + u = xt yt 6 3. u = x, y, z = x + y + z u u 9 s9 grad u ux, y, z = c c : grad u = u x i + u y j + u k i, j, k z x, y, z grad u v =
x () g(x) = f(t) dt f(x), F (x) 3x () g(x) g (x) f(x), F (x) (3) h(x) = x 3x tf(t) dt.9 = {(x, y) ; x, y, x + y } f(x, y) = xy( x y). h (x) f(x), F (x
 [ ] IC. f(x) = e x () f(x) f (x) () lim f(x) lim f(x) x + x (3) lim f(x) lim f(x) x + x (4) y = f(x) ( ) ( s46). < a < () a () lim a log xdx a log xdx ( ) n (3) lim log k log n n n k=.3 z = log(x + y ),
[ ] IC. f(x) = e x () f(x) f (x) () lim f(x) lim f(x) x + x (3) lim f(x) lim f(x) x + x (4) y = f(x) ( ) ( s46). < a < () a () lim a log xdx a log xdx ( ) n (3) lim log k log n n n k=.3 z = log(x + y ),
1 : f(z = re iθ ) = u(r, θ) + iv(r, θ). (re iθ ) 2 = r 2 e 2iθ = r 2 cos 2θ + ir 2 sin 2θ r f(z = x + iy) = u(x, y) + iv(x, y). (x + iy) 2 = x 2 y 2 +
 1.3 1.4. (pp.14-27) 1 1 : f(z = re iθ ) = u(r, θ) + iv(r, θ). (re iθ ) 2 = r 2 e 2iθ = r 2 cos 2θ + ir 2 sin 2θ r f(z = x + iy) = u(x, y) + iv(x, y). (x + iy) 2 = x 2 y 2 + i2xy x = 1 y (1 + iy) 2 = 1
1.3 1.4. (pp.14-27) 1 1 : f(z = re iθ ) = u(r, θ) + iv(r, θ). (re iθ ) 2 = r 2 e 2iθ = r 2 cos 2θ + ir 2 sin 2θ r f(z = x + iy) = u(x, y) + iv(x, y). (x + iy) 2 = x 2 y 2 + i2xy x = 1 y (1 + iy) 2 = 1
I, II 1, A = A 4 : 6 = max{ A, } A A 10 10%
 1 2006.4.17. A 3-312 tel: 092-726-4774, e-mail: hara@math.kyushu-u.ac.jp, http://www.math.kyushu-u.ac.jp/ hara/lectures/lectures-j.html Office hours: B A I ɛ-δ ɛ-δ 1. 2. A 1. 1. 2. 3. 4. 5. 2. ɛ-δ 1. ɛ-n
1 2006.4.17. A 3-312 tel: 092-726-4774, e-mail: hara@math.kyushu-u.ac.jp, http://www.math.kyushu-u.ac.jp/ hara/lectures/lectures-j.html Office hours: B A I ɛ-δ ɛ-δ 1. 2. A 1. 1. 2. 3. 4. 5. 2. ɛ-δ 1. ɛ-n
,. Black-Scholes u t t, x c u 0 t, x x u t t, x c u t, x x u t t, x + σ x u t, x + rx ut, x rux, t 0 x x,,.,. Step 3, 7,,, Step 6., Step 4,. Step 5,,.
 9 α ν β Ξ ξ Γ γ o δ Π π ε ρ ζ Σ σ η τ Θ θ Υ υ ι Φ φ κ χ Λ λ Ψ ψ µ Ω ω Def, Prop, Th, Lem, Note, Remark, Ex,, Proof, R, N, Q, C [a, b {x R : a x b} : a, b {x R : a < x < b} : [a, b {x R : a x < b} : a,
9 α ν β Ξ ξ Γ γ o δ Π π ε ρ ζ Σ σ η τ Θ θ Υ υ ι Φ φ κ χ Λ λ Ψ ψ µ Ω ω Def, Prop, Th, Lem, Note, Remark, Ex,, Proof, R, N, Q, C [a, b {x R : a x b} : a, b {x R : a < x < b} : [a, b {x R : a x < b} : a,
n=1 1 n 2 = π = π f(z) f(z) 2 f(z) = u(z) + iv(z) *1 f (z) u(x, y), v(x, y) f(z) f (z) = f/ x u x = v y, u y = v x
 n= n 2 = π2 6 3 2 28 + 4 + 9 + = π2 6 2 f(z) f(z) 2 f(z) = u(z) + iv(z) * f (z) u(x, y), v(x, y) f(z) f (z) = f/ x u x = v y, u y = v x f x = i f y * u, v 3 3. 3 f(t) = u(t) + v(t) [, b] f(t)dt = u(t)dt
n= n 2 = π2 6 3 2 28 + 4 + 9 + = π2 6 2 f(z) f(z) 2 f(z) = u(z) + iv(z) * f (z) u(x, y), v(x, y) f(z) f (z) = f/ x u x = v y, u y = v x f x = i f y * u, v 3 3. 3 f(t) = u(t) + v(t) [, b] f(t)dt = u(t)dt
z f(z) f(z) x, y, u, v, r, θ r > 0 z = x + iy, f = u + iv C γ D f(z) f(z) D f(z) f(z) z, Rm z, z 1.1 z = x + iy = re iθ = r (cos θ + i sin θ) z = x iy
 f f x, y, u, v, r, θ r > = x + iy, f = u + iv C γ D f f D f f, Rm,. = x + iy = re iθ = r cos θ + i sin θ = x iy = re iθ = r cos θ i sin θ x = + = Re, y = = Im i r = = = x + y θ = arg = arctan y x e i =
f f x, y, u, v, r, θ r > = x + iy, f = u + iv C γ D f f D f f, Rm,. = x + iy = re iθ = r cos θ + i sin θ = x iy = re iθ = r cos θ i sin θ x = + = Re, y = = Im i r = = = x + y θ = arg = arctan y x e i =
. sinh x sinh x) = e x e x = ex e x = sinh x 3) y = cosh x, y = sinh x y = e x, y = e x 6 sinhx) coshx) 4 y-axis x-axis : y = cosh x, y = s
 . 00 3 9 [] sinh x = ex e x, cosh x = ex + e x ) sinh cosh 4 hyperbolic) hyperbola) = 3 cosh x cosh x) = e x + e x = cosh x ) . sinh x sinh x) = e x e x = ex e x = sinh x 3) y = cosh x, y = sinh x y =
. 00 3 9 [] sinh x = ex e x, cosh x = ex + e x ) sinh cosh 4 hyperbolic) hyperbola) = 3 cosh x cosh x) = e x + e x = cosh x ) . sinh x sinh x) = e x e x = ex e x = sinh x 3) y = cosh x, y = sinh x y =
I
 I 6 4 10 1 1 1.1............... 1 1................ 1 1.3.................... 1.4............... 1.4.1.............. 1.4................. 1.4.3........... 3 1.4.4.. 3 1.5.......... 3 1.5.1..............
I 6 4 10 1 1 1.1............... 1 1................ 1 1.3.................... 1.4............... 1.4.1.............. 1.4................. 1.4.3........... 3 1.4.4.. 3 1.5.......... 3 1.5.1..............
II No.01 [n/2] [1]H n (x) H n (x) = ( 1) r n! r!(n 2r)! (2x)n 2r. r=0 [2]H n (x) n,, H n ( x) = ( 1) n H n (x). [3] H n (x) = ( 1) n dn x2 e dx n e x2
![II No.01 [n/2] [1]H n (x) H n (x) = ( 1) r n! r!(n 2r)! (2x)n 2r. r=0 [2]H n (x) n,, H n ( x) = ( 1) n H n (x). [3] H n (x) = ( 1) n dn x2 e dx n e x2 II No.01 [n/2] [1]H n (x) H n (x) = ( 1) r n! r!(n 2r)! (2x)n 2r. r=0 [2]H n (x) n,, H n ( x) = ( 1) n H n (x). [3] H n (x) = ( 1) n dn x2 e dx n e x2](/thumbs/101/149159646.jpg) II No.1 [n/] [1]H n x) H n x) = 1) r n! r!n r)! x)n r r= []H n x) n,, H n x) = 1) n H n x) [3] H n x) = 1) n dn x e dx n e x [4] H n+1 x) = xh n x) nh n 1 x) ) d dx x H n x) = H n+1 x) d dx H nx) = nh
II No.1 [n/] [1]H n x) H n x) = 1) r n! r!n r)! x)n r r= []H n x) n,, H n x) = 1) n H n x) [3] H n x) = 1) n dn x e dx n e x [4] H n+1 x) = xh n x) nh n 1 x) ) d dx x H n x) = H n+1 x) d dx H nx) = nh
S I. dy fx x fx y fx + C 3 C dy fx 4 x, y dy v C xt y C v e kt k > xt yt gt [ v dt dt v e kt xt v e kt + C k x v + C C k xt v k 3 r r + dr e kt S dt d
 S I.. http://ayapin.film.s.dendai.ac.jp/~matuda /TeX/lecture.html PDF PS.................................... 3.3.................... 9.4................5.............. 3 5. Laplace................. 5....
S I.. http://ayapin.film.s.dendai.ac.jp/~matuda /TeX/lecture.html PDF PS.................................... 3.3.................... 9.4................5.............. 3 5. Laplace................. 5....
S I. dy fx x fx y fx + C 3 C vt dy fx 4 x, y dy yt gt + Ct + C dt v e kt xt v e kt + C k x v k + C C xt v k 3 r r + dr e kt S Sr πr dt d v } dt k e kt
 S I. x yx y y, y,. F x, y, y, y,, y n http://ayapin.film.s.dendai.ac.jp/~matuda n /TeX/lecture.html PDF PS yx.................................... 3.3.................... 9.4................5..............
S I. x yx y y, y,. F x, y, y, y,, y n http://ayapin.film.s.dendai.ac.jp/~matuda n /TeX/lecture.html PDF PS yx.................................... 3.3.................... 9.4................5..............
Part () () Γ Part ,
 Contents a 6 6 6 6 6 6 6 7 7. 8.. 8.. 8.3. 8 Part. 9. 9.. 9.. 3. 3.. 3.. 3 4. 5 4.. 5 4.. 9 4.3. 3 Part. 6 5. () 6 5.. () 7 5.. 9 5.3. Γ 3 6. 3 6.. 3 6.. 3 6.3. 33 Part 3. 34 7. 34 7.. 34 7.. 34 8. 35
Contents a 6 6 6 6 6 6 6 7 7. 8.. 8.. 8.3. 8 Part. 9. 9.. 9.. 3. 3.. 3.. 3 4. 5 4.. 5 4.. 9 4.3. 3 Part. 6 5. () 6 5.. () 7 5.. 9 5.3. Γ 3 6. 3 6.. 3 6.. 3 6.3. 33 Part 3. 34 7. 34 7.. 34 7.. 34 8. 35
数学の基礎訓練I
 I 9 6 13 1 1 1.1............... 1 1................ 1 1.3.................... 1.4............... 1.4.1.............. 1.4................. 3 1.4.3........... 3 1.4.4.. 3 1.5.......... 3 1.5.1..............
I 9 6 13 1 1 1.1............... 1 1................ 1 1.3.................... 1.4............... 1.4.1.............. 1.4................. 3 1.4.3........... 3 1.4.4.. 3 1.5.......... 3 1.5.1..............
(Bessel) (Legendre).. (Hankel). (Laplace) V = (x, y, z) n (r, θ, ϕ) r n f n (θ, ϕ). f n (θ, ϕ) n f n (θ, ϕ) z = cos θ z θ ϕ n ν. P ν (z), Q ν (z) (Fou
 (Bessel) (Legendre).. (Hankel). (Laplace) V = (x, y, z) n (r, θ, ϕ) r n f n (θ, ϕ). f n (θ, ϕ) n f n (θ, ϕ) z = cos θ z θ ϕ n ν. P ν (z), Q ν (z) (Fourier) (Fourier Bessel).. V ρ(x, y, z) V = 4πGρ G :.
(Bessel) (Legendre).. (Hankel). (Laplace) V = (x, y, z) n (r, θ, ϕ) r n f n (θ, ϕ). f n (θ, ϕ) n f n (θ, ϕ) z = cos θ z θ ϕ n ν. P ν (z), Q ν (z) (Fourier) (Fourier Bessel).. V ρ(x, y, z) V = 4πGρ G :.
2S III IV K A4 12:00-13:30 Cafe David 1 2 TA 1 appointment Cafe David K2-2S04-00 : C
 2S III IV K200 : April 16, 2004 Version : 1.1 TA M2 TA 1 10 2 n 1 ɛ-δ 5 15 20 20 45 K2-2S04-00 : C 2S III IV K200 60 60 74 75 89 90 1 email 3 4 30 A4 12:00-13:30 Cafe David 1 2 TA 1 email appointment Cafe
2S III IV K200 : April 16, 2004 Version : 1.1 TA M2 TA 1 10 2 n 1 ɛ-δ 5 15 20 20 45 K2-2S04-00 : C 2S III IV K200 60 60 74 75 89 90 1 email 3 4 30 A4 12:00-13:30 Cafe David 1 2 TA 1 email appointment Cafe
) ] [ h m x + y + + V x) φ = Eφ 1) z E = i h t 13) x << 1) N n n= = N N + 1) 14) N n n= = N N + 1)N + 1) 6 15) N n 3 n= = 1 4 N N + 1) 16) N n 4
![) ] [ h m x + y + + V x) φ = Eφ 1) z E = i h t 13) x << 1) N n n= = N N + 1) 14) N n n= = N N + 1)N + 1) 6 15) N n 3 n= = 1 4 N N + 1) 16) N n 4 ) ] [ h m x + y + + V x) φ = Eφ 1) z E = i h t 13) x << 1) N n n= = N N + 1) 14) N n n= = N N + 1)N + 1) 6 15) N n 3 n= = 1 4 N N + 1) 16) N n 4](/thumbs/92/107866707.jpg) 1. k λ ν ω T v p v g k = π λ ω = πν = π T v p = λν = ω k v g = dω dk 1) ) 3) 4). p = hk = h λ 5) E = hν = hω 6) h = h π 7) h =6.6618 1 34 J sec) hc=197.3 MeV fm = 197.3 kev pm= 197.3 ev nm = 1.97 1 3 ev
1. k λ ν ω T v p v g k = π λ ω = πν = π T v p = λν = ω k v g = dω dk 1) ) 3) 4). p = hk = h λ 5) E = hν = hω 6) h = h π 7) h =6.6618 1 34 J sec) hc=197.3 MeV fm = 197.3 kev pm= 197.3 ev nm = 1.97 1 3 ev
29
 9 .,,, 3 () C k k C k C + C + C + + C 8 + C 9 + C k C + C + C + C 3 + C 4 + C 5 + + 45 + + + 5 + + 9 + 4 + 4 + 5 4 C k k k ( + ) 4 C k k ( k) 3 n( ) n n n ( ) n ( ) n 3 ( ) 3 3 3 n 4 ( ) 4 4 4 ( ) n n
9 .,,, 3 () C k k C k C + C + C + + C 8 + C 9 + C k C + C + C + C 3 + C 4 + C 5 + + 45 + + + 5 + + 9 + 4 + 4 + 5 4 C k k k ( + ) 4 C k k ( k) 3 n( ) n n n ( ) n ( ) n 3 ( ) 3 3 3 n 4 ( ) 4 4 4 ( ) n n
Z: Q: R: C:
 0 Z: Q: R: C: 3 4 4 4................................ 4 4.................................. 7 5 3 5...................... 3 5......................... 40 5.3 snz) z)........................... 4 6 46 x
0 Z: Q: R: C: 3 4 4 4................................ 4 4.................................. 7 5 3 5...................... 3 5......................... 40 5.3 snz) z)........................... 4 6 46 x
Z: Q: R: C: 3. Green Cauchy
 7 Z: Q: R: C: 3. Green.............................. 3.............................. 5.3................................. 6.4 Cauchy..................... 6.5 Taylor..........................6...............................
7 Z: Q: R: C: 3. Green.............................. 3.............................. 5.3................................. 6.4 Cauchy..................... 6.5 Taylor..........................6...............................
II A A441 : October 02, 2014 Version : Kawahira, Tomoki TA (Kondo, Hirotaka )
 II 214-1 : October 2, 214 Version : 1.1 Kawahira, Tomoki TA (Kondo, Hirotaka ) http://www.math.nagoya-u.ac.jp/~kawahira/courses/14w-biseki.html pdf 1 2 1 9 1 16 1 23 1 3 11 6 11 13 11 2 11 27 12 4 12 11
II 214-1 : October 2, 214 Version : 1.1 Kawahira, Tomoki TA (Kondo, Hirotaka ) http://www.math.nagoya-u.ac.jp/~kawahira/courses/14w-biseki.html pdf 1 2 1 9 1 16 1 23 1 3 11 6 11 13 11 2 11 27 12 4 12 11
2000年度『数学展望 I』講義録
 2000 I I IV I II 2000 I I IV I-IV. i ii 3.10 (http://www.math.nagoya-u.ac.jp/ kanai/) 2000 A....1 B....4 C....10 D....13 E....17 Brouwer A....21 B....26 C....33 D....39 E. Sperner...45 F....48 A....53
2000 I I IV I II 2000 I I IV I-IV. i ii 3.10 (http://www.math.nagoya-u.ac.jp/ kanai/) 2000 A....1 B....4 C....10 D....13 E....17 Brouwer A....21 B....26 C....33 D....39 E. Sperner...45 F....48 A....53
II (10 4 ) 1. p (x, y) (a, b) ε(x, y; a, b) 0 f (x, y) f (a, b) A, B (6.5) y = b f (x, b) f (a, b) x a = A + ε(x, b; a, b) x a 2 x a 0 A = f x (
 II (1 4 ) 1. p.13 1 (x, y) (a, b) ε(x, y; a, b) f (x, y) f (a, b) A, B (6.5) y = b f (x, b) f (a, b) x a = A + ε(x, b; a, b) x a x a A = f x (a, b) y x 3 3y 3 (x, y) (, ) f (x, y) = x + y (x, y) = (, )
II (1 4 ) 1. p.13 1 (x, y) (a, b) ε(x, y; a, b) f (x, y) f (a, b) A, B (6.5) y = b f (x, b) f (a, b) x a = A + ε(x, b; a, b) x a x a A = f x (a, b) y x 3 3y 3 (x, y) (, ) f (x, y) = x + y (x, y) = (, )
I A A441 : April 21, 2014 Version : Kawahira, Tomoki TA (Kondo, Hirotaka ) Google
 I4 - : April, 4 Version :. Kwhir, Tomoki TA (Kondo, Hirotk) Google http://www.mth.ngoy-u.c.jp/~kwhir/courses/4s-biseki.html pdf 4 4 4 4 8 e 5 5 9 etc. 5 6 6 6 9 n etc. 6 6 6 3 6 3 7 7 etc 7 4 7 7 8 5 59
I4 - : April, 4 Version :. Kwhir, Tomoki TA (Kondo, Hirotk) Google http://www.mth.ngoy-u.c.jp/~kwhir/courses/4s-biseki.html pdf 4 4 4 4 8 e 5 5 9 etc. 5 6 6 6 9 n etc. 6 6 6 3 6 3 7 7 etc 7 4 7 7 8 5 59
Tips KENZOU PC no problem 2 1 w = f(z) z 1 w w z w = (z z 0 ) b b w = log (z z 0 ) z = z 0 2π 2 z = z 0 w = z 1/2 z = re iθ θ (z = 0) 0 2π 0
 Tips KENZOU 28 7 6 P no problem 2 w = f(z) z w w z w = (z z ) b b w = log (z z ) z = z 2π 2 z = z w = z /2 z = re iθ θ (z = ) 2π 4π 2 θ θ 2π 4π z r re iθ re i2π = r re i4π = r w r re iθ/2 re iπ = r re
Tips KENZOU 28 7 6 P no problem 2 w = f(z) z w w z w = (z z ) b b w = log (z z ) z = z 2π 2 z = z w = z /2 z = re iθ θ (z = ) 2π 4π 2 θ θ 2π 4π z r re iθ re i2π = r re i4π = r w r re iθ/2 re iπ = r re
2009 I 2 II III 14, 15, α β α β l 0 l l l l γ (1) γ = αβ (2) α β n n cos 2k n n π sin 2k n π k=1 k=1 3. a 0, a 1,..., a n α a
 009 I II III 4, 5, 6 4 30. 0 α β α β l 0 l l l l γ ) γ αβ ) α β. n n cos k n n π sin k n π k k 3. a 0, a,..., a n α a 0 + a x + a x + + a n x n 0 ᾱ 4. [a, b] f y fx) y x 5. ) Arcsin 4) Arccos ) ) Arcsin
009 I II III 4, 5, 6 4 30. 0 α β α β l 0 l l l l γ ) γ αβ ) α β. n n cos k n n π sin k n π k k 3. a 0, a,..., a n α a 0 + a x + a x + + a n x n 0 ᾱ 4. [a, b] f y fx) y x 5. ) Arcsin 4) Arccos ) ) Arcsin
A
 A 2563 15 4 21 1 3 1.1................................................ 3 1.2............................................. 3 2 3 2.1......................................... 3 2.2............................................
A 2563 15 4 21 1 3 1.1................................................ 3 1.2............................................. 3 2 3 2.1......................................... 3 2.2............................................
1 filename=mathformula tex 1 ax 2 + bx + c = 0, x = b ± b 2 4ac, (1.1) 2a x 1 + x 2 = b a, x 1x 2 = c a, (1.2) ax 2 + 2b x + c = 0, x = b ± b 2
 filename=mathformula58.tex ax + bx + c =, x = b ± b 4ac, (.) a x + x = b a, x x = c a, (.) ax + b x + c =, x = b ± b ac. a (.3). sin(a ± B) = sin A cos B ± cos A sin B, (.) cos(a ± B) = cos A cos B sin
filename=mathformula58.tex ax + bx + c =, x = b ± b 4ac, (.) a x + x = b a, x x = c a, (.) ax + b x + c =, x = b ± b ac. a (.3). sin(a ± B) = sin A cos B ± cos A sin B, (.) cos(a ± B) = cos A cos B sin
y = f(x) (x, y : ) w = f(z) (w, z : ) df(x) df(z), f(x)dx dx dz f(z)dz : e iωt = cos(ωt) + i sin(ωt) [ ] : y = f(t) f(ω) = 1 2π f(t)e iωt d
![y = f(x) (x, y : ) w = f(z) (w, z : ) df(x) df(z), f(x)dx dx dz f(z)dz : e iωt = cos(ωt) + i sin(ωt) [ ] : y = f(t) f(ω) = 1 2π f(t)e iωt d y = f(x) (x, y : ) w = f(z) (w, z : ) df(x) df(z), f(x)dx dx dz f(z)dz : e iωt = cos(ωt) + i sin(ωt) [ ] : y = f(t) f(ω) = 1 2π f(t)e iωt d](/thumbs/104/162030620.jpg) 8. y = f(x) (x, y : ) w = f(z) (w, z : ) df(x) df(z), f(x)dx dx dz f(z)dz : e iωt = cos(ωt) + i sin(ωt) [ ] : y = f(t) f(ω) = π f(t)e iωt dt. : ϕ(x, y) x + ϕ(x, y) y = ( ).. . : 3. (z p, e z, sin z, sinh
8. y = f(x) (x, y : ) w = f(z) (w, z : ) df(x) df(z), f(x)dx dx dz f(z)dz : e iωt = cos(ωt) + i sin(ωt) [ ] : y = f(t) f(ω) = π f(t)e iωt dt. : ϕ(x, y) x + ϕ(x, y) y = ( ).. . : 3. (z p, e z, sin z, sinh
.3. (x, x = (, u = = 4 (, x x = 4 x, x 0 x = 0 x = 4 x.4. ( z + z = 8 z, z 0 (z, z = (0, 8, (,, (8, 0 3 (0, 8, (,, (8, 0 z = z 4 z (g f(x = g(
 06 5.. ( y = x x y 5 y 5 = (x y = x + ( y = x + y = x y.. ( Y = C + I = 50 + 0.5Y + 50 r r = 00 0.5Y ( L = M Y r = 00 r = 0.5Y 50 (3 00 0.5Y = 0.5Y 50 Y = 50, r = 5 .3. (x, x = (, u = = 4 (, x x = 4 x,
06 5.. ( y = x x y 5 y 5 = (x y = x + ( y = x + y = x y.. ( Y = C + I = 50 + 0.5Y + 50 r r = 00 0.5Y ( L = M Y r = 00 r = 0.5Y 50 (3 00 0.5Y = 0.5Y 50 Y = 50, r = 5 .3. (x, x = (, u = = 4 (, x x = 4 x,
( z = x 3 y + y ( z = cos(x y ( 8 ( s8.7 y = xe x ( 8 ( s83.8 ( ( + xdx ( cos 3 xdx t = sin x ( 8 ( s84 ( 8 ( s85. C : y = x + 4, l : y = x + a,
 [ ] 8 IC. y d y dx = ( dy dx ( p = dy p y dx ( ( ( 8 ( s8. 3 A A = ( A ( A (3 A P A P AP.3 π y(x = { ( 8 ( s8 x ( π < x x ( < x π y(x π π O π x ( 8 ( s83.4 f (x, y, z grad(f ( ( ( f f f grad(f = i + j
[ ] 8 IC. y d y dx = ( dy dx ( p = dy p y dx ( ( ( 8 ( s8. 3 A A = ( A ( A (3 A P A P AP.3 π y(x = { ( 8 ( s8 x ( π < x x ( < x π y(x π π O π x ( 8 ( s83.4 f (x, y, z grad(f ( ( ( f f f grad(f = i + j
IA 2013 : :10722 : 2 : :2 :761 :1 (23-27) : : ( / ) (1 /, ) / e.g. (Taylar ) e x = 1 + x + x xn n! +... sin x = x x3 6 + x5 x2n+1 + (
 IA 2013 : :10722 : 2 : :2 :761 :1 23-27) : : 1 1.1 / ) 1 /, ) / e.g. Taylar ) e x = 1 + x + x2 2 +... + xn n! +... sin x = x x3 6 + x5 x2n+1 + 1)n 5! 2n + 1)! 2 2.1 = 1 e.g. 0 = 0.00..., π = 3.14..., 1
IA 2013 : :10722 : 2 : :2 :761 :1 23-27) : : 1 1.1 / ) 1 /, ) / e.g. Taylar ) e x = 1 + x + x2 2 +... + xn n! +... sin x = x x3 6 + x5 x2n+1 + 1)n 5! 2n + 1)! 2 2.1 = 1 e.g. 0 = 0.00..., π = 3.14..., 1
 X G P G (X) G BG [X, BG] S 2 2 2 S 2 2 S 2 = { (x 1, x 2, x 3 ) R 3 x 2 1 + x 2 2 + x 2 3 = 1 } R 3 S 2 S 2 v x S 2 x x v(x) T x S 2 T x S 2 S 2 x T x S 2 = { ξ R 3 x ξ } R 3 T x S 2 S 2 x x T x S 2
X G P G (X) G BG [X, BG] S 2 2 2 S 2 2 S 2 = { (x 1, x 2, x 3 ) R 3 x 2 1 + x 2 2 + x 2 3 = 1 } R 3 S 2 S 2 v x S 2 x x v(x) T x S 2 T x S 2 S 2 x T x S 2 = { ξ R 3 x ξ } R 3 T x S 2 S 2 x x T x S 2
 (u(x)v(x)) = u (x)v(x) + u(x)v (x) ( ) u(x) = u (x)v(x) u(x)v (x) v(x) v(x) 2 y = g(t), t = f(x) y = g(f(x)) dy dx dy dx = dy dt dt dx., y, f, g y = f (g(x))g (x). ( (f(g(x)). ). [ ] y = e ax+b (a, b )
(u(x)v(x)) = u (x)v(x) + u(x)v (x) ( ) u(x) = u (x)v(x) u(x)v (x) v(x) v(x) 2 y = g(t), t = f(x) y = g(f(x)) dy dx dy dx = dy dt dt dx., y, f, g y = f (g(x))g (x). ( (f(g(x)). ). [ ] y = e ax+b (a, b )
1/1 lim f(x, y) (x,y) (a,b) ( ) ( ) lim limf(x, y) lim lim f(x, y) x a y b y b x a ( ) ( ) xy x lim lim lim lim x y x y x + y y x x + y x x lim x x 1
 1/5 ( ) Taylor ( 7.1) (x, y) f(x, y) f(x, y) x + y, xy, e x y,... 1 R {(x, y) x, y R} f(x, y) x y,xy e y log x,... R {(x, y, z) (x, y),z f(x, y)} R 3 z 1 (x + y ) z ax + by + c x 1 z ax + by + c y x +
1/5 ( ) Taylor ( 7.1) (x, y) f(x, y) f(x, y) x + y, xy, e x y,... 1 R {(x, y) x, y R} f(x, y) x y,xy e y log x,... R {(x, y, z) (x, y),z f(x, y)} R 3 z 1 (x + y ) z ax + by + c x 1 z ax + by + c y x +
Jacobi, Stieltjes, Gauss : :
 Jacobi, Stieltjes, Gauss : : 28 2 0 894 T. J. Stieltjes [St94a] Recherches sur les fractions continues Stieltjes 0 f(u)du, z + u f(u) > 0, z C z + + a a 2 z + a 3 +..., a p > 0 (a) Vitali (a) Stieltjes
Jacobi, Stieltjes, Gauss : : 28 2 0 894 T. J. Stieltjes [St94a] Recherches sur les fractions continues Stieltjes 0 f(u)du, z + u f(u) > 0, z C z + + a a 2 z + a 3 +..., a p > 0 (a) Vitali (a) Stieltjes
prime number theorem
 For Tutor MeBio ζ Eite by kamei MeBio 7.8.3 : Bernoulli Bernoulli 4 Bernoulli....................................................................................... 4 Bernoulli............................................................................
For Tutor MeBio ζ Eite by kamei MeBio 7.8.3 : Bernoulli Bernoulli 4 Bernoulli....................................................................................... 4 Bernoulli............................................................................
2
 p1 i 2 = 1 i 2 x, y x + iy 2 (x + iy) + (γ + iδ) = (x + γ) + i(y + δ) (x + iy)(γ + iδ) = (xγ yδ) + i(xδ + yγ) i 2 = 1 γ + iδ 0 x + iy γ + iδ xγ + yδ xδ = γ 2 + iyγ + δ2 γ 2 + δ 2 p7 = x 2 +y 2 z z p13
p1 i 2 = 1 i 2 x, y x + iy 2 (x + iy) + (γ + iδ) = (x + γ) + i(y + δ) (x + iy)(γ + iδ) = (xγ yδ) + i(xδ + yγ) i 2 = 1 γ + iδ 0 x + iy γ + iδ xγ + yδ xδ = γ 2 + iyγ + δ2 γ 2 + δ 2 p7 = x 2 +y 2 z z p13
agora04.dvi
 Workbook E-mail: kawahira@math.nagoya-u.ac.jp 2004 8 9, 10, 11 1 2 1 2 a n+1 = pa n + q x = px + q a n better 2 a n+1 = aan+b ca n+d 1 (a, b, c, d) =(p, q, 0, 1) 1 = 0 3 2 2 2 f(z) =z 2 + c a n+1 = a 2
Workbook E-mail: kawahira@math.nagoya-u.ac.jp 2004 8 9, 10, 11 1 2 1 2 a n+1 = pa n + q x = px + q a n better 2 a n+1 = aan+b ca n+d 1 (a, b, c, d) =(p, q, 0, 1) 1 = 0 3 2 2 2 f(z) =z 2 + c a n+1 = a 2
i
 i 3 4 4 7 5 6 3 ( ).. () 3 () (3) (4) /. 3. 4/3 7. /e 8. a > a, a = /, > a >. () a >, a =, > a > () a > b, a = b, a < b. c c n a n + b n + c n 3c n..... () /3 () + (3) / (4) /4 (5) m > n, a b >, m > n,
i 3 4 4 7 5 6 3 ( ).. () 3 () (3) (4) /. 3. 4/3 7. /e 8. a > a, a = /, > a >. () a >, a =, > a > () a > b, a = b, a < b. c c n a n + b n + c n 3c n..... () /3 () + (3) / (4) /4 (5) m > n, a b >, m > n,
III 1 (X, d) d U d X (X, d). 1. (X, d).. (i) d(x, y) d(z, y) d(x, z) (ii) d(x, y) d(z, w) d(x, z) + d(y, w) 2. (X, d). F X.. (1), X F, (2) F 1, F 2 F
 III 1 (X, d) d U d X (X, d). 1. (X, d).. (i) d(x, y) d(z, y) d(x, z) (ii) d(x, y) d(z, w) d(x, z) + d(y, w) 2. (X, d). F X.. (1), X F, (2) F 1, F 2 F F 1 F 2 F, (3) F λ F λ F λ F. 3., A λ λ A λ. B λ λ
III 1 (X, d) d U d X (X, d). 1. (X, d).. (i) d(x, y) d(z, y) d(x, z) (ii) d(x, y) d(z, w) d(x, z) + d(y, w) 2. (X, d). F X.. (1), X F, (2) F 1, F 2 F F 1 F 2 F, (3) F λ F λ F λ F. 3., A λ λ A λ. B λ λ
 21 2 26 i 1 1 1.1............................ 1 1.2............................ 3 2 9 2.1................... 9 2.2.......... 9 2.3................... 11 2.4....................... 12 3 15 3.1..........
21 2 26 i 1 1 1.1............................ 1 1.2............................ 3 2 9 2.1................... 9 2.2.......... 9 2.3................... 11 2.4....................... 12 3 15 3.1..........
CIII CIII : October 4, 2013 Version : 1.1 A A441 Kawahira, Tomoki TA (Takahiro, Wakasa 3 )
 III203 00- III : October 4, 203 Version :. Kawahira, Tomoki TA (Takahiro, Wakasa 3 ) http://www.math.nagoya-u.ac.jp/~kawahira/courses/3w-kansuron.html pdf 0 4 0 0 8 2 0 25 8 5 22 2 6 2 3 2 20 0 7 24 3
III203 00- III : October 4, 203 Version :. Kawahira, Tomoki TA (Takahiro, Wakasa 3 ) http://www.math.nagoya-u.ac.jp/~kawahira/courses/3w-kansuron.html pdf 0 4 0 0 8 2 0 25 8 5 22 2 6 2 3 2 20 0 7 24 3
 ( 12 ( ( ( ( Levi-Civita grad div rot ( ( = 4 : 6 3 1 1.1 f(x n f (n (x, d n f(x (1.1 dxn f (2 (x f (x 1.1 f(x = e x f (n (x = e x d dx (fg = f g + fg (1.2 d dx d 2 dx (fg = f g + 2f g + fg 2... d n n
( 12 ( ( ( ( Levi-Civita grad div rot ( ( = 4 : 6 3 1 1.1 f(x n f (n (x, d n f(x (1.1 dxn f (2 (x f (x 1.1 f(x = e x f (n (x = e x d dx (fg = f g + fg (1.2 d dx d 2 dx (fg = f g + 2f g + fg 2... d n n
 (yx4) 1887-1945 741936 50 1995 1 31 http://kenboushoten.web.fc.com/ OCR TeX 50 yx4 e-mail: yx4.aydx5@gmail.com i Jacobi 1751 1 3 Euler Fagnano 187 9 0 Abel iii 1 1...................................
(yx4) 1887-1945 741936 50 1995 1 31 http://kenboushoten.web.fc.com/ OCR TeX 50 yx4 e-mail: yx4.aydx5@gmail.com i Jacobi 1751 1 3 Euler Fagnano 187 9 0 Abel iii 1 1...................................
I, II 1, 2 ɛ-δ 100 A = A 4 : 6 = max{ A, } A A 10
 1 2007.4.13. A 3-312 tel: 092-726-4774, e-mail: hara@math.kyushu-u.ac.jp, http://www.math.kyushu-u.ac.jp/ hara/lectures/lectures-j.html Office hours: B A I ɛ-δ ɛ-δ 1. 2. A 0. 1. 1. 2. 3. 2. ɛ-δ 1. ɛ-n
1 2007.4.13. A 3-312 tel: 092-726-4774, e-mail: hara@math.kyushu-u.ac.jp, http://www.math.kyushu-u.ac.jp/ hara/lectures/lectures-j.html Office hours: B A I ɛ-δ ɛ-δ 1. 2. A 0. 1. 1. 2. 3. 2. ɛ-δ 1. ɛ-n
W u = u(x, t) u tt = a 2 u xx, a > 0 (1) D := {(x, t) : 0 x l, t 0} u (0, t) = 0, u (l, t) = 0, t 0 (2)
 3 215 4 27 1 1 u u(x, t) u tt a 2 u xx, a > (1) D : {(x, t) : x, t } u (, t), u (, t), t (2) u(x, ) f(x), u(x, ) t 2, x (3) u(x, t) X(x)T (t) u (1) 1 T (t) a 2 T (t) X (x) X(x) α (2) T (t) αa 2 T (t) (4)
3 215 4 27 1 1 u u(x, t) u tt a 2 u xx, a > (1) D : {(x, t) : x, t } u (, t), u (, t), t (2) u(x, ) f(x), u(x, ) t 2, x (3) u(x, t) X(x)T (t) u (1) 1 T (t) a 2 T (t) X (x) X(x) α (2) T (t) αa 2 T (t) (4)
II 2 II
 II 2 II 2005 yugami@cc.utsunomiya-u.ac.jp 2005 4 1 1 2 5 2.1.................................... 5 2.2................................. 6 2.3............................. 6 2.4.................................
II 2 II 2005 yugami@cc.utsunomiya-u.ac.jp 2005 4 1 1 2 5 2.1.................................... 5 2.2................................. 6 2.3............................. 6 2.4.................................
 2 2 MATHEMATICS.PDF 200-2-0 3 2 (p n ), ( ) 7 3 4 6 5 20 6 GL 2 (Z) SL 2 (Z) 27 7 29 8 SL 2 (Z) 35 9 2 40 0 2 46 48 2 2 5 3 2 2 58 4 2 6 5 2 65 6 2 67 7 2 69 2 , a 0 + a + a 2 +... b b 2 b 3 () + b n a
2 2 MATHEMATICS.PDF 200-2-0 3 2 (p n ), ( ) 7 3 4 6 5 20 6 GL 2 (Z) SL 2 (Z) 27 7 29 8 SL 2 (Z) 35 9 2 40 0 2 46 48 2 2 5 3 2 2 58 4 2 6 5 2 65 6 2 67 7 2 69 2 , a 0 + a + a 2 +... b b 2 b 3 () + b n a
.5 z = a + b + c n.6 = a sin t y = b cos t dy d a e e b e + e c e e e + e 3 s36 3 a + y = a, b > b 3 s363.7 y = + 3 y = + 3 s364.8 cos a 3 s365.9 y =,
 [ ] IC. r, θ r, θ π, y y = 3 3 = r cos θ r sin θ D D = {, y ; y }, y D r, θ ep y yddy D D 9 s96. d y dt + 3dy + y = cos t dt t = y = e π + e π +. t = π y =.9 s6.3 d y d + dy d + y = y =, dy d = 3 a, b
[ ] IC. r, θ r, θ π, y y = 3 3 = r cos θ r sin θ D D = {, y ; y }, y D r, θ ep y yddy D D 9 s96. d y dt + 3dy + y = cos t dt t = y = e π + e π +. t = π y =.9 s6.3 d y d + dy d + y = y =, dy d = 3 a, b
( ; ) C. H. Scholz, The Mechanics of Earthquakes and Faulting : - ( ) σ = σ t sin 2π(r a) λ dσ d(r a) =
 1 9 8 1 1 1 ; 1 11 16 C. H. Scholz, The Mechanics of Earthquakes and Faulting 1. 1.1 1.1.1 : - σ = σ t sin πr a λ dσ dr a = E a = π λ σ πr a t cos λ 1 r a/λ 1 cos 1 E: σ t = Eλ πa a λ E/π γ : λ/ 3 γ =
1 9 8 1 1 1 ; 1 11 16 C. H. Scholz, The Mechanics of Earthquakes and Faulting 1. 1.1 1.1.1 : - σ = σ t sin πr a λ dσ dr a = E a = π λ σ πr a t cos λ 1 r a/λ 1 cos 1 E: σ t = Eλ πa a λ E/π γ : λ/ 3 γ =
 4................................. 4................................. 4 6................................. 6................................. 9.................................................... 3..3..........................
4................................. 4................................. 4 6................................. 6................................. 9.................................................... 3..3..........................
1 1 sin cos P (primary) S (secondly) 2 P S A sin(ω2πt + α) A ω 1 ω α V T m T m 1 100Hz m 2 36km 500Hz. 36km 1
 sin cos P (primary) S (secondly) 2 P S A sin(ω2πt + α) A ω ω α 3 3 2 2V 3 33+.6T m T 5 34m Hz. 34 3.4m 2 36km 5Hz. 36km m 34 m 5 34 + m 5 33 5 =.66m 34m 34 x =.66 55Hz, 35 5 =.7 485.7Hz 2 V 5Hz.5V.5V V
sin cos P (primary) S (secondly) 2 P S A sin(ω2πt + α) A ω ω α 3 3 2 2V 3 33+.6T m T 5 34m Hz. 34 3.4m 2 36km 5Hz. 36km m 34 m 5 34 + m 5 33 5 =.66m 34m 34 x =.66 55Hz, 35 5 =.7 485.7Hz 2 V 5Hz.5V.5V V
1 8, : 8.1 1, 2 z = ax + by + c ax by + z c = a b +1 x y z c = 0, (0, 0, c), n = ( a, b, 1). f = n i=1 a ii x 2 i + i<j 2a ij x i x j = ( x, A x), f =
 1 8, : 8.1 1, z = ax + by + c ax by + z c = a b +1 x y z c = 0, (0, 0, c), n = ( a, b, 1). f = a ii x i + i
1 8, : 8.1 1, z = ax + by + c ax by + z c = a b +1 x y z c = 0, (0, 0, c), n = ( a, b, 1). f = a ii x i + i
(3) (2),,. ( 20) ( s200103) 0.7 x C,, x 2 + y 2 + ax = 0 a.. D,. D, y C, C (x, y) (y 0) C m. (2) D y = y(x) (x ± y 0), (x, y) D, m, m = 1., D. (x 2 y
 [ ] 7 0.1 2 2 + y = t sin t IC ( 9) ( s090101) 0.2 y = d2 y 2, y = x 3 y + y 2 = 0 (2) y + 2y 3y = e 2x 0.3 1 ( y ) = f x C u = y x ( 15) ( s150102) [ ] y/x du x = Cexp f(u) u (2) x y = xey/x ( 16) ( s160101)
[ ] 7 0.1 2 2 + y = t sin t IC ( 9) ( s090101) 0.2 y = d2 y 2, y = x 3 y + y 2 = 0 (2) y + 2y 3y = e 2x 0.3 1 ( y ) = f x C u = y x ( 15) ( s150102) [ ] y/x du x = Cexp f(u) u (2) x y = xey/x ( 16) ( s160101)
II 1 II 2012 II Gauss-Bonnet II
 II 1 II 212 II Gauss-Bonnet II 1 1 1.1......................................... 1 1.2............................................ 2 1.3.................................. 3 1.4.............................................
II 1 II 212 II Gauss-Bonnet II 1 1 1.1......................................... 1 1.2............................................ 2 1.3.................................. 3 1.4.............................................
2 2 ( Riemann ( 2 ( ( 2 ( (.8.4 (PDF 2
 2 ( 28 8 (http://nalab.mind.meiji.ac.jp/~mk/lecture/tahensuu2/ 2 2 ( Riemann ( 2 ( ( 2 ( (.8.4 (PDF http://nalab.mind.meiji.ac.jp/~mk/lecture/tahensuu2/ http://nalab.mind.meiji.ac.jp/~mk/lecture/tahensuu/
2 ( 28 8 (http://nalab.mind.meiji.ac.jp/~mk/lecture/tahensuu2/ 2 2 ( Riemann ( 2 ( ( 2 ( (.8.4 (PDF http://nalab.mind.meiji.ac.jp/~mk/lecture/tahensuu2/ http://nalab.mind.meiji.ac.jp/~mk/lecture/tahensuu/
(1) (2) (3) (4) HB B ( ) (5) (6) (7) 40 (8) (9) (10)
 2017 12 9 4 1 30 4 10 3 1 30 3 30 2 1 30 2 50 1 1 30 2 10 (1) (2) (3) (4) HB B ( ) (5) (6) (7) 40 (8) (9) (10) (1) i 23 c 23 0 1 2 3 4 5 6 7 8 9 a b d e f g h i (2) 23 23 (3) 23 ( 23 ) 23 x 1 x 2 23 x
2017 12 9 4 1 30 4 10 3 1 30 3 30 2 1 30 2 50 1 1 30 2 10 (1) (2) (3) (4) HB B ( ) (5) (6) (7) 40 (8) (9) (10) (1) i 23 c 23 0 1 2 3 4 5 6 7 8 9 a b d e f g h i (2) 23 23 (3) 23 ( 23 ) 23 x 1 x 2 23 x
No δs δs = r + δr r = δr (3) δs δs = r r = δr + u(r + δr, t) u(r, t) (4) δr = (δx, δy, δz) u i (r + δr, t) u i (r, t) = u i x j δx j (5) δs 2
 No.2 1 2 2 δs δs = r + δr r = δr (3) δs δs = r r = δr + u(r + δr, t) u(r, t) (4) δr = (δx, δy, δz) u i (r + δr, t) u i (r, t) = u i δx j (5) δs 2 = δx i δx i + 2 u i δx i δx j = δs 2 + 2s ij δx i δx j
No.2 1 2 2 δs δs = r + δr r = δr (3) δs δs = r r = δr + u(r + δr, t) u(r, t) (4) δr = (δx, δy, δz) u i (r + δr, t) u i (r, t) = u i δx j (5) δs 2 = δx i δx i + 2 u i δx i δx j = δs 2 + 2s ij δx i δx j
simx simxdx, cosxdx, sixdx 6.3 px m m + pxfxdx = pxf x p xf xdx = pxf x p xf x + p xf xdx 7.4 a m.5 fx simxdx 8 fx fx simxdx = πb m 9 a fxdx = πa a =
 II 6 ishimori@phys.titech.ac.jp 6.. 5.4.. f Rx = f Lx = fx fx + lim = lim x x + x x f c = f x + x < c < x x x + lim x x fx fx x x = lim x x f c = f x x < c < x cosmx cosxdx = {cosm x + cosm + x} dx = [
II 6 ishimori@phys.titech.ac.jp 6.. 5.4.. f Rx = f Lx = fx fx + lim = lim x x + x x f c = f x + x < c < x x x + lim x x fx fx x x = lim x x f c = f x x < c < x cosmx cosxdx = {cosm x + cosm + x} dx = [
Z: Q: R: C: sin 6 5 ζ a, b
 Z: Q: R: C: 3 3 7 4 sin 6 5 ζ 9 6 6............................... 6............................... 6.3......................... 4 7 6 8 8 9 3 33 a, b a bc c b a a b 5 3 5 3 5 5 3 a a a a p > p p p, 3,
Z: Q: R: C: 3 3 7 4 sin 6 5 ζ 9 6 6............................... 6............................... 6.3......................... 4 7 6 8 8 9 3 33 a, b a bc c b a a b 5 3 5 3 5 5 3 a a a a p > p p p, 3,
..3. Ω, Ω F, P Ω, F, P ). ) F a) A, A,..., A i,... F A i F. b) A F A c F c) Ω F. ) A F A P A),. a) 0 P A) b) P Ω) c) [ ] A, A,..., A i,... F i j A i A
![..3. Ω, Ω F, P Ω, F, P ). ) F a) A, A,..., A i,... F A i F. b) A F A c F c) Ω F. ) A F A P A),. a) 0 P A) b) P Ω) c) [ ] A, A,..., A i,... F i j A i A ..3. Ω, Ω F, P Ω, F, P ). ) F a) A, A,..., A i,... F A i F. b) A F A c F c) Ω F. ) A F A P A),. a) 0 P A) b) P Ω) c) [ ] A, A,..., A i,... F i j A i A](/thumbs/93/112175219.jpg) .. Laplace ). A... i),. ω i i ). {ω,..., ω } Ω,. ii) Ω. Ω. A ) r, A P A) P A) r... ).. Ω {,, 3, 4, 5, 6}. i i 6). A {, 4, 6} P A) P A) 3 6. ).. i, j i, j) ) Ω {i, j) i 6, j 6}., 36. A. A {i, j) i j }.
.. Laplace ). A... i),. ω i i ). {ω,..., ω } Ω,. ii) Ω. Ω. A ) r, A P A) P A) r... ).. Ω {,, 3, 4, 5, 6}. i i 6). A {, 4, 6} P A) P A) 3 6. ).. i, j i, j) ) Ω {i, j) i 6, j 6}., 36. A. A {i, j) i j }.
6. Euler x
 ...............................................................................3......................................... 4.4................................... 5.5......................................
...............................................................................3......................................... 4.4................................... 5.5......................................
(2 X Poisso P (λ ϕ X (t = E[e itx ] = k= itk λk e k! e λ = (e it λ k e λ = e eitλ e λ = e λ(eit 1. k! k= 6.7 X N(, 1 ϕ X (t = e 1 2 t2 : Cauchy ϕ X (t
![(2 X Poisso P (λ ϕ X (t = E[e itx ] = k= itk λk e k! e λ = (e it λ k e λ = e eitλ e λ = e λ(eit 1. k! k= 6.7 X N(, 1 ϕ X (t = e 1 2 t2 : Cauchy ϕ X (t (2 X Poisso P (λ ϕ X (t = E[e itx ] = k= itk λk e k! e λ = (e it λ k e λ = e eitλ e λ = e λ(eit 1. k! k= 6.7 X N(, 1 ϕ X (t = e 1 2 t2 : Cauchy ϕ X (t](/thumbs/67/56612994.jpg) 6 6.1 6.1 (1 Z ( X = e Z, Y = Im Z ( Z = X + iy, i = 1 (2 Z E[ e Z ] < E[ Im Z ] < Z E[Z] = E[e Z] + ie[im Z] 6.2 Z E[Z] E[ Z ] : E[ Z ] < e Z Z, Im Z Z E[Z] α = E[Z], Z = Z Z 1 {Z } E[Z] = α = α [ α ]
6 6.1 6.1 (1 Z ( X = e Z, Y = Im Z ( Z = X + iy, i = 1 (2 Z E[ e Z ] < E[ Im Z ] < Z E[Z] = E[e Z] + ie[im Z] 6.2 Z E[Z] E[ Z ] : E[ Z ] < e Z Z, Im Z Z E[Z] α = E[Z], Z = Z Z 1 {Z } E[Z] = α = α [ α ]
f(x) = f(x ) + α(x)(x x ) α(x) x = x. x = f (y), x = f (y ) y = f f (y) = f f (y ) + α(f (y))(f (y) f (y )) f (y) = f (y ) + α(f (y)) (y y ) ( (2) ) f
 22 A 3,4 No.3 () (2) (3) (4), (5) (6) (7) (8) () n x = (x,, x n ), = (,, n ), x = ( (x i i ) 2 ) /2 f(x) R n f(x) = f() + i α i (x ) i + o( x ) α,, α n g(x) = o( x )) lim x g(x) x = y = f() + i α i(x )
22 A 3,4 No.3 () (2) (3) (4), (5) (6) (7) (8) () n x = (x,, x n ), = (,, n ), x = ( (x i i ) 2 ) /2 f(x) R n f(x) = f() + i α i (x ) i + o( x ) α,, α n g(x) = o( x )) lim x g(x) x = y = f() + i α i(x )
 n ξ n,i, i = 1,, n S n ξ n,i n 0 R 1,.. σ 1 σ i .10.14.15 0 1 0 1 1 3.14 3.18 3.19 3.14 3.14,. ii 1 1 1.1..................................... 1 1............................... 3 1.3.........................
n ξ n,i, i = 1,, n S n ξ n,i n 0 R 1,.. σ 1 σ i .10.14.15 0 1 0 1 1 3.14 3.18 3.19 3.14 3.14,. ii 1 1 1.1..................................... 1 1............................... 3 1.3.........................
zz + 3i(z z) + 5 = 0 + i z + i = z 2i z z z y zz + 3i (z z) + 5 = 0 (z 3i) (z + 3i) = 9 5 = 4 z 3i = 2 (3i) zz i (z z) + 1 = a 2 {
 04 zz + iz z) + 5 = 0 + i z + i = z i z z z 970 0 y zz + i z z) + 5 = 0 z i) z + i) = 9 5 = 4 z i = i) zz i z z) + = a {zz + i z z) + 4} a ) zz + a + ) z z) + 4a = 0 4a a = 5 a = x i) i) : c Darumafactory
04 zz + iz z) + 5 = 0 + i z + i = z i z z z 970 0 y zz + i z z) + 5 = 0 z i) z + i) = 9 5 = 4 z i = i) zz i z z) + = a {zz + i z z) + 4} a ) zz + a + ) z z) + 4a = 0 4a a = 5 a = x i) i) : c Darumafactory
I ( ) 1 de Broglie 1 (de Broglie) p λ k h Planck ( Js) p = h λ = k (1) h 2π : Dirac k B Boltzmann ( J/K) T U = 3 2 k BT
 I (008 4 0 de Broglie (de Broglie p λ k h Planck ( 6.63 0 34 Js p = h λ = k ( h π : Dirac k B Boltzmann (.38 0 3 J/K T U = 3 k BT ( = λ m k B T h m = 0.067m 0 m 0 = 9. 0 3 kg GaAs( a T = 300 K 3 fg 07345
I (008 4 0 de Broglie (de Broglie p λ k h Planck ( 6.63 0 34 Js p = h λ = k ( h π : Dirac k B Boltzmann (.38 0 3 J/K T U = 3 k BT ( = λ m k B T h m = 0.067m 0 m 0 = 9. 0 3 kg GaAs( a T = 300 K 3 fg 07345
[ ] 0.1 lim x 0 e 3x 1 x IC ( 11) ( s114901) 0.2 (1) y = e 2x (x 2 + 1) (2) y = x/(x 2 + 1) 0.3 dx (1) 1 4x 2 (2) e x sin 2xdx (3) sin 2 xdx ( 11) ( s
![[ ] 0.1 lim x 0 e 3x 1 x IC ( 11) ( s114901) 0.2 (1) y = e 2x (x 2 + 1) (2) y = x/(x 2 + 1) 0.3 dx (1) 1 4x 2 (2) e x sin 2xdx (3) sin 2 xdx ( 11) ( s [ ] 0.1 lim x 0 e 3x 1 x IC ( 11) ( s114901) 0.2 (1) y = e 2x (x 2 + 1) (2) y = x/(x 2 + 1) 0.3 dx (1) 1 4x 2 (2) e x sin 2xdx (3) sin 2 xdx ( 11) ( s](/thumbs/94/118579915.jpg) [ ]. lim e 3 IC ) s49). y = e + ) ) y = / + ).3 d 4 ) e sin d 3) sin d ) s49) s493).4 z = y z z y s494).5 + y = 4 =.6 s495) dy = 3e ) d dy d = y s496).7 lim ) lim e s49).8 y = e sin ) y = sin e 3) y =
[ ]. lim e 3 IC ) s49). y = e + ) ) y = / + ).3 d 4 ) e sin d 3) sin d ) s49) s493).4 z = y z z y s494).5 + y = 4 =.6 s495) dy = 3e ) d dy d = y s496).7 lim ) lim e s49).8 y = e sin ) y = sin e 3) y =
main.dvi
 2 f(z) 0 f(z 0 ) lim z!z 0 z 0 z 0 z z 1z = z 0 z 0 1z z z 0 1z 21 22 2 2 (1642-1727) (1646-1716) (1777-1855) (1789-1857) (1826-1866) 18 19 2.1 2.1.1 12 z w w = f (z) (2.1) f(z) z w = f(z) z z 0 w w 0
2 f(z) 0 f(z 0 ) lim z!z 0 z 0 z 0 z z 1z = z 0 z 0 1z z z 0 1z 21 22 2 2 (1642-1727) (1646-1716) (1777-1855) (1789-1857) (1826-1866) 18 19 2.1 2.1.1 12 z w w = f (z) (2.1) f(z) z w = f(z) z z 0 w w 0
newmain.dvi
 数論 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/008142 このサンプルページの内容は, 第 2 版 1 刷発行当時のものです. Daniel DUVERNEY: THÉORIE DES NOMBRES c Dunod, Paris, 1998, This book is published
数論 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/008142 このサンプルページの内容は, 第 2 版 1 刷発行当時のものです. Daniel DUVERNEY: THÉORIE DES NOMBRES c Dunod, Paris, 1998, This book is published
Z[i] Z[i] π 4,1 (x) π 4,3 (x) 1 x (x ) 2 log x π m,a (x) 1 x ϕ(m) log x 1.1 ( ). π(x) x (a, m) = 1 π m,a (x) x modm a 1 π m,a (x) 1 ϕ(m) π(x)
![Z[i] Z[i] π 4,1 (x) π 4,3 (x) 1 x (x ) 2 log x π m,a (x) 1 x ϕ(m) log x 1.1 ( ). π(x) x (a, m) = 1 π m,a (x) x modm a 1 π m,a (x) 1 ϕ(m) π(x) Z[i] Z[i] π 4,1 (x) π 4,3 (x) 1 x (x ) 2 log x π m,a (x) 1 x ϕ(m) log x 1.1 ( ). π(x) x (a, m) = 1 π m,a (x) x modm a 1 π m,a (x) 1 ϕ(m) π(x)](/thumbs/94/118373946.jpg) 3 3 22 Z[i] Z[i] π 4, (x) π 4,3 (x) x (x ) 2 log x π m,a (x) x ϕ(m) log x. ( ). π(x) x (a, m) = π m,a (x) x modm a π m,a (x) ϕ(m) π(x) ϕ(m) x log x ϕ(m) m f(x) g(x) (x α) lim f(x)/g(x) = x α mod m (a,
3 3 22 Z[i] Z[i] π 4, (x) π 4,3 (x) x (x ) 2 log x π m,a (x) x ϕ(m) log x. ( ). π(x) x (a, m) = π m,a (x) x modm a π m,a (x) ϕ(m) π(x) ϕ(m) x log x ϕ(m) m f(x) g(x) (x α) lim f(x)/g(x) = x α mod m (a,
I No. sin cos sine, cosine : trigonometric function π : π =.4 : n =, ±, ±, sin + nπ = sin cos + nπ = cos sin = sin : cos = cos :. sin. sin. sin + π si
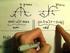 I 8 No. : No. : No. : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No. : I No. sin cos sine, cosine : trigonometric function π : π =.4 : n =, ±, ±, sin + nπ = sin cos + nπ = cos sin = sin : cos = cos :. sin.
I 8 No. : No. : No. : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No. : I No. sin cos sine, cosine : trigonometric function π : π =.4 : n =, ±, ±, sin + nπ = sin cos + nπ = cos sin = sin : cos = cos :. sin.
, x R, f (x),, df dx : R R,, f : R R, f(x) ( ).,, f (a) d f dx (a), f (a) d3 f dx 3 (a),, f (n) (a) dn f dx n (a), f d f dx, f d3 f dx 3,, f (n) dn f
 ,,,,.,,,. R f : R R R a R, f(a + ) f(a) lim 0 (), df dx (a) f (a), f(x) x a, f (a), f(x) x a ( ). y f(a + ) y f(x) f(a+) f(a) f(a + ) f(a) f(a) x a 0 a a + x 0 a a + x y y f(x) 0 : 0, f(a+) f(a)., f(x)
,,,,.,,,. R f : R R R a R, f(a + ) f(a) lim 0 (), df dx (a) f (a), f(x) x a, f (a), f(x) x a ( ). y f(a + ) y f(x) f(a+) f(a) f(a + ) f(a) f(a) x a 0 a a + x 0 a a + x y y f(x) 0 : 0, f(a+) f(a)., f(x)
 4 14 4 14 4 1 1 4 1.1................................................ 4 1............................................. 4 1.3................................................ 5 1.4 1............................................
4 14 4 14 4 1 1 4 1.1................................................ 4 1............................................. 4 1.3................................................ 5 1.4 1............................................
x, y x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = 15 xy (x y) (x + y) xy (x y) (x y) ( x 2 + xy + y 2) = 15 (x y)
 x, y x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = 15 1 1977 x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = 15 xy (x y) (x + y) xy (x y) (x y) ( x 2 + xy + y 2) = 15 (x y) ( x 2 y + xy 2 x 2 2xy y 2) = 15 (x y) (x + y) (xy
x, y x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = 15 1 1977 x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = 15 xy (x y) (x + y) xy (x y) (x y) ( x 2 + xy + y 2) = 15 (x y) ( x 2 y + xy 2 x 2 2xy y 2) = 15 (x y) (x + y) (xy
2.2 ( y = y(x ( (x 0, y 0 y (x 0 (y 0 = y(x 0 y = y(x ( y (x 0 = F (x 0, y(x 0 = F (x 0, y 0 (x 0, y 0 ( (x 0, y 0 F (x 0, y 0 xy (x, y (, F (x, y ( (
 (. x y y x f y = f(x y x y = y(x y x y dx = d dx y(x = y (x = f (x y = y(x x ( (differential equation ( + y 2 dx + xy = 0 dx = xy + y 2 2 2 x y 2 F (x, y = xy + y 2 y = y(x x x xy(x = F (x, y(x + y(x 2
(. x y y x f y = f(x y x y = y(x y x y dx = d dx y(x = y (x = f (x y = y(x x ( (differential equation ( + y 2 dx + xy = 0 dx = xy + y 2 2 2 x y 2 F (x, y = xy + y 2 y = y(x x x xy(x = F (x, y(x + y(x 2
2 2 L 5 2. L L L L k.....
 L 528 206 2 9 2 2 L 5 2. L........................... 5 2.2 L................................... 7 2............................... 9. L..................2 L k........................ 2 4 I 5 4. I...................................
L 528 206 2 9 2 2 L 5 2. L........................... 5 2.2 L................................... 7 2............................... 9. L..................2 L k........................ 2 4 I 5 4. I...................................
数学Ⅱ演習(足助・09夏)
 II I 9/4/4 9/4/2 z C z z z z, z 2 z, w C zw z w 3 z, w C z + w z + w 4 t R t C t t t t t z z z 2 z C re z z + z z z, im z 2 2 3 z C e z + z + 2 z2 + 3! z3 + z!, I 4 x R e x cos x + sin x 2 z, w C e z+w
II I 9/4/4 9/4/2 z C z z z z, z 2 z, w C zw z w 3 z, w C z + w z + w 4 t R t C t t t t t z z z 2 z C re z z + z z z, im z 2 2 3 z C e z + z + 2 z2 + 3! z3 + z!, I 4 x R e x cos x + sin x 2 z, w C e z+w
微分積分 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. このサンプルページの内容は, 初版 1 刷発行時のものです.
 微分積分 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. ttp://www.morikita.co.jp/books/mid/00571 このサンプルページの内容は, 初版 1 刷発行時のものです. i ii 014 10 iii [note] 1 3 iv 4 5 3 6 4 x 0 sin x x 1 5 6 z = f(x, y) 1 y = f(x)
微分積分 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. ttp://www.morikita.co.jp/books/mid/00571 このサンプルページの内容は, 初版 1 刷発行時のものです. i ii 014 10 iii [note] 1 3 iv 4 5 3 6 4 x 0 sin x x 1 5 6 z = f(x, y) 1 y = f(x)
II R n k +1 v 0,, v k k v 1 v 0,, v k v v 0,, v k R n 1 a 0,, a k a 0 v 0 + a k v k v 0 v k k k v 0,, v k σ k σ dimσ = k 1.3. k
 II 231017 1 1.1. R n k +1 v 0,, v k k v 1 v 0,, v k v 0 1.2. v 0,, v k R n 1 a 0,, a k a 0 v 0 + a k v k v 0 v k k k v 0,, v k σ kσ dimσ = k 1.3. k σ {v 0,...,v k } {v i0,...,v il } l σ τ < τ τ σ 1.4.
II 231017 1 1.1. R n k +1 v 0,, v k k v 1 v 0,, v k v 0 1.2. v 0,, v k R n 1 a 0,, a k a 0 v 0 + a k v k v 0 v k k k v 0,, v k σ kσ dimσ = k 1.3. k σ {v 0,...,v k } {v i0,...,v il } l σ τ < τ τ σ 1.4.
Untitled
 II 14 14-7-8 8/4 II (http://www.damp.tottori-u.ac.jp/~ooshida/edu/fluid/) [ (3.4)] Navier Stokes [ 6/ ] Navier Stokes 3 [ ] Reynolds [ (4.6), (45.8)] [ p.186] Navier Stokes I 1 balance law t (ρv i )+ j
II 14 14-7-8 8/4 II (http://www.damp.tottori-u.ac.jp/~ooshida/edu/fluid/) [ (3.4)] Navier Stokes [ 6/ ] Navier Stokes 3 [ ] Reynolds [ (4.6), (45.8)] [ p.186] Navier Stokes I 1 balance law t (ρv i )+ j
7. y fx, z gy z gfx dz dx dz dy dy dx. g f a g bf a b fa 7., chain ule Ω, D R n, R m a Ω, f : Ω R m, g : D R l, fω D, b fa, f a g b g f a g f a g bf a
 9 203 6 7 WWW http://www.math.meiji.ac.jp/~mk/lectue/tahensuu-203/ 2 8 8 7. 7 7. y fx, z gy z gfx dz dx dz dy dy dx. g f a g bf a b fa 7., chain ule Ω, D R n, R m a Ω, f : Ω R m, g : D R l, fω D, b fa,
9 203 6 7 WWW http://www.math.meiji.ac.jp/~mk/lectue/tahensuu-203/ 2 8 8 7. 7 7. y fx, z gy z gfx dz dx dz dy dy dx. g f a g bf a b fa 7., chain ule Ω, D R n, R m a Ω, f : Ω R m, g : D R l, fω D, b fa,
構造と連続体の力学基礎
 II 37 Wabash Avenue Bridge, Illinois 州 Winnipeg にある歩道橋 Esplanade Riel 橋6 6 斜張橋である必要は多分無いと思われる すぐ横に道路用桁橋有り しかも塔基部のレストランは 8 年には営業していなかった 9 9. 9.. () 97 [3] [5] k 9. m w(t) f (t) = f (t) + mg k w(t) Newton
II 37 Wabash Avenue Bridge, Illinois 州 Winnipeg にある歩道橋 Esplanade Riel 橋6 6 斜張橋である必要は多分無いと思われる すぐ横に道路用桁橋有り しかも塔基部のレストランは 8 年には営業していなかった 9 9. 9.. () 97 [3] [5] k 9. m w(t) f (t) = f (t) + mg k w(t) Newton
2011de.dvi
 211 ( 4 2 1. 3 1.1............................... 3 1.2 1- -......................... 13 1.3 2-1 -................... 19 1.4 3- -......................... 29 2. 37 2.1................................ 37
211 ( 4 2 1. 3 1.1............................... 3 1.2 1- -......................... 13 1.3 2-1 -................... 19 1.4 3- -......................... 29 2. 37 2.1................................ 37
.1 1,... ( )
 1 δ( ε )δ 2 f(b) f(a) slope f (c) = f(b) f(a) b a a c b 1 213 3 21. 2 [e-mail] nobuo@math.kyoto-u.ac.jp, [URL] http://www.math.kyoto-u.ac.jp/ nobuo 1 .1 1,... ( ) 2.1....................................
1 δ( ε )δ 2 f(b) f(a) slope f (c) = f(b) f(a) b a a c b 1 213 3 21. 2 [e-mail] nobuo@math.kyoto-u.ac.jp, [URL] http://www.math.kyoto-u.ac.jp/ nobuo 1 .1 1,... ( ) 2.1....................................
 IA hara@math.kyushu-u.ac.jp Last updated: January,......................................................................................................................................................................................
IA hara@math.kyushu-u.ac.jp Last updated: January,......................................................................................................................................................................................
 i 6 3 ii 3 7 8 9 3 6 iii 5 8 5 3 7 8 v...................................................... 5.3....................... 7 3........................ 3.................3.......................... 8 3 35
i 6 3 ii 3 7 8 9 3 6 iii 5 8 5 3 7 8 v...................................................... 5.3....................... 7 3........................ 3.................3.......................... 8 3 35
z z x = y = /x lim y = + x + lim y = x (x a ) a (x a+) lim z z f(z) = A, lim z z g(z) = B () lim z z {f(z) ± g(z)} = A ± B (2) lim {f(z) g(z)} = AB z
 Tips KENZOU 28 6 29 sin 2 x + cos 2 x = cos 2 z + sin 2 z = OK... z < z z < R w = f(z) z z w w f(z) w lim z z f(z) = w x x 2 2 f(x) x = a lim f(x) = lim f(x) x a+ x a z z x = y = /x lim y = + x + lim y
Tips KENZOU 28 6 29 sin 2 x + cos 2 x = cos 2 z + sin 2 z = OK... z < z z < R w = f(z) z z w w f(z) w lim z z f(z) = w x x 2 2 f(x) x = a lim f(x) = lim f(x) x a+ x a z z x = y = /x lim y = + x + lim y
 2016 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 1 16 2 1 () X O 3 (O1) X O, O (O2) O O (O3) O O O X (X, O) O X X (O1), (O2), (O3) (O2) (O3) n (O2) U 1,..., U n O U k O k=1 (O3) U λ O( λ Λ) λ Λ U λ O 0 X 0 (O2) n =
2016 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 1 16 2 1 () X O 3 (O1) X O, O (O2) O O (O3) O O O X (X, O) O X X (O1), (O2), (O3) (O2) (O3) n (O2) U 1,..., U n O U k O k=1 (O3) U λ O( λ Λ) λ Λ U λ O 0 X 0 (O2) n =
18 ( ) I II III A B C(100 ) 1, 2, 3, 5 I II A B (100 ) 1, 2, 3 I II A B (80 ) 6 8 I II III A B C(80 ) 1 n (1 + x) n (1) n C 1 + n C
 8 ( ) 8 5 4 I II III A B C( ),,, 5 I II A B ( ),, I II A B (8 ) 6 8 I II III A B C(8 ) n ( + x) n () n C + n C + + n C n = 7 n () 7 9 C : y = x x A(, 6) () A C () C P AP Q () () () 4 A(,, ) B(,, ) C(,,
8 ( ) 8 5 4 I II III A B C( ),,, 5 I II A B ( ),, I II A B (8 ) 6 8 I II III A B C(8 ) n ( + x) n () n C + n C + + n C n = 7 n () 7 9 C : y = x x A(, 6) () A C () C P AP Q () () () 4 A(,, ) B(,, ) C(,,
