序 本冊子は 2015 年 1 月 5-6 日に行われた統計数理研究所共同利用研究集会 生物に見られる時空間パターンと統計数理: 同調 認知 行動 において行われた統計手法チュートリアル 離散データの確率的トピックモデル ( 統計数理研究所持橋大地 ) の講義録です チュートリアル講義を録音し テー
|
|
|
- うまじ やまがた
- 5 years ago
- Views:
Transcription
1
2 序 本冊子は 2015 年 1 月 5-6 日に行われた統計数理研究所共同利用研究集会 生物に見られる時空間パターンと統計数理: 同調 認知 行動 において行われた統計手法チュートリアル 離散データの確率的トピックモデル ( 統計数理研究所持橋大地 ) の講義録です チュートリアル講義を録音し テープを起こし 講義で用いた該当するスライドと合わせて編集しました なお 講義は一般に話し言葉で語られますが 講義録として読む場合 往々にして同義の書き言葉に変換したほうが読みやすいので 気付いた部分は書き言葉風に直してあります また 講義中は指さしで この式 となっていた部分などは 対応する数式などを明記し 読み物として通用するよう編集しました 本冊子は 持橋氏の講義録音を丹野夕輝 ( 岐阜大学 ) がテープ起こしした上で読みやすいように編集を行った文書を 三村喬生 ( 精神 神経セ ) 長田穣( 東京大 ) 深谷肇一( 統数研 ) がスライドを加えながら再編集し さらに島谷健一郎 ( 統数研 ) が編集 加筆した上で 持橋氏に内容を確認 修正してもらって完成となりました 確率的トピックモデルは 広範な応用可能性を秘めながら 未だ和文教科書はおろか review paper や紹介記事も著しく不足しており 統計数理研究者以外には近寄りがたい手法となっています トピックモデル適用に適した実データを有する非統計数理研究者が独習するさいの いくらかの補助になるよう 本冊子を編集しました なお 冊子中に不適切な表現等が見受けられた場合 それはすべて本研究集会代表の島谷の責任です 目次 序 Introduction スライド 2-8 ナイーブベイズ スライド 9-16 Unigram Mixtures ( ユニグラム混合モデル ) スライド ベイズ推定とディリクレ分布 スライド Probabilistic latent Semantic Indexing (PLSI) スライド Latent Dirichlet Allocation (LDA) スライド 最近の話題から : Geographic Topic Model スライド 編集後記
3 私の専門は統計的自然言語処理という 言葉をあつかう分野です 言葉というのはデータとしては離散データで その扱いにはその特性に応じた統計が必要になります そして トピックモデルというのは もともとは言語処理という統計数理で生まれた手法なのですが 今日では 様々な分野の様々なデータへ適用されるようになっています 生態学でも Valle et al., "Decomposing biodiversity data using the Latent Dirichlet Allocation model, a probabilistic multivariate statistical method". Ecology Letters, 17(12), , 2014 のように使われ始めています なお 私も東大の基礎二という学科にいたせいもあって生態学には関心があり この講義をひとつのきっかけにトピックモデルが日本の生物分野へ適用されていくことになりましたら 望外の喜びというものです
4 離散データは大事です 実際 動物, 植物, 昆虫 バイオ関連の話題など 解析対象に離散データが出てくることは本当にたくさんあります しかし普通の統計解析ではガウス分布などを仮定するため 最初から連続値として取り扱うことが多い そうではなく 離散データそのものに対してまともな統計モデルを作りたいという要求が結構多いのではないかと思います とりわけ データ相互に相関があるとき 例えば生物の例ですと ある種のクジラが観測された場合 見えてはいないが他の種の魚も生息していると考えられます この場合 観測種ごとの観測数のヒストグラムの間は独立でなく 相関があります それをどうやってモデル化していくかというのが 高次元の離散データを扱ううえでの本質的な問題です
5 統計的言語処理の分野では データを Bag of words として表します 言葉というのは テキストがあり テキストに単語が書いてあるというものです Bag of words の考え方では 単語の順番よりも どんな単語が出てくるかの方に着目します 例えば 情報 が 5 回 IT が 2 回 システム が 1 回と出てきたら なんとなく IT 系の文章だとわかります また バッター 監督 ドラフト 打率 などが出てくると野球の話だとわかります この中の バッター と 監督 の間には高い相関があって それをどうとらえていくかが問題になります 言語処理で扱うデータでは 単語の種類は1 万ではおさまらなくて Google などのデータでは 1 千万を簡単に超えるような 超高次元です ここでは言語データを実例として話しますが 例えば生態学では 文書は観測ユニット 単語は生物種で 単語の出現回数はどの種が何回出てきたかという頻度 のように自分が関わっているデータの事例に読み替えて実例を見ていただけると 理解もしやすいことと思います
6 文書を Bag of words としてデータ化するという作業は 行列で表すと簡単にできます 横方向の列 つまり図の W に単語 1 単語 2 と単語の種類をとり 縦方向の行 図の N に一個一個の文書の番号をとり 一個の文書を行 すなわち単語を表す W 次元ベクトルに対応させます 例えば 最初の文書には2 番目の単語が1 回 3 番目の単語が一回出てきています 次の文書には最初の単語が 1 回 しばらく0 回で 最後にまた 1 回ずつです 概して文書を行列表現すると0が多くなります 0が多い行列をスパース ( 疎 ) な行列といいますが そんな行列の扱いが この分野での一つの大きな問題となります
7 上の図は実際のデータの例ですが ご覧のとおり スパースになっています この図は DailyKOS という有名なデータセットの一部で 新聞記事のデータから単語を百個 文章を百個選び その単語の出てきた文書の行に点を入れてあるのですが このように ぽつぽつしたゴマ塩みたいなスパース行列が出てきます 縦の列の中に多く出ている単語がありますが それは例えば日本語の場合では は や が など どの文章にも出てくる単語が対応します 一方 一般の内容的な言葉は出てきたり出てこなかったりするため ほとんどの値は 0 です また 出現したとしても 1 などの小さな数値になりがちです カウントデータとして ポアソン分布のような特徴を示す場合が多くなります
8 このようなデータには 古典的には多変量解析という伝統があると思います しかし 相関分析や回帰分析や判別分析には 問題があります 一つには 一部の変数だけを取り出して分析すること もう一つは 暗黙のうちにこういう解析手法ではガウス分布を仮定することです 本当のデータは離散でかつ非負なのに 無理やりガウス分布に合わせて使ってしまいます それでも カウント数が多ければあまり問題は起こらないのですが 生態学などでは レアな種が 1 回だけ観察されたり 2 回だけ観察されることは普通に見られ かつ そうした情報は重要な意味を持っています そういう情報を 普通の多変量解析では全く無視してしまいます そうではなく 1 回や 2 回という情報までしっかり全部とらえたいというのが 確率的トピックモデルの一番の目標です
9 従来の多変量解析の何が最大の問題かというと 観測データが来たときに 後付けの解析手法になっているという点です 回帰分析や主成分分析は とりあえずガウシアンだという間違った仮定を置いて適当にやるという後付けの解析手法でしかありません そのため そのあとの発展性がない つまり モデルがないので それで解析をやりましたという以上のものがない それに対して そもそも離散で非負の整数の観測データを生み出すような確率モデルを先に考えましょう そのモデルに従って カウントデータは確率論的に出てきたと思うのです そして そのモデルの未知パラメーターを推定します そうすれば より複雑なモデルも作れるし それにより性能も上がるということになります こういう言語処理で統計処理をやるようになったのは大ざっぱに言うと 90 年代の終わりから 2000 年ぐらいで この話の最後に出てくる Latent Dirichlet Allocation model は 2003 年ぐらいに出た話です 今それが非常に複雑なレベルになっていますが たかだかここ 10 年ぐらいの話と思ってかまいません
10 確率的トピックモデルの一番簡単な例は ナイーブベイズです これは有名な例なので 皆さんもネットなどで見たことがある人も多いと思います 電子メールでは 普通のメールに混じって広告などの迷惑メールもいっぱい来るのですが それを分類するという問題を考えます すなわち 普通メールの集合と迷惑メールの集合があったときに 新しいメールをどちらに分類するかという問題です
11 いま カテゴリは 普通メールと迷惑メール ( 広告メール ) の 2 つです そして それぞれで単語の出方が違います 例えば 普通メールでは単語の分布が上の図のようになっているとします 縦軸はある単語が出現する確率を表し すべての単語についての和は 1 になっています このような確率分布を 多項分布といいます それに対して 広告メールでは 例えば 激安 や 特価 や バイアグラ などの単語の出現確率が高く 全然別の分布をしているでしょう 単語の分布が違っており 広告メールは広告メール側の分布から単語をランダムにサンプルしてできたと思い 普通メールは普通メール側の分布から単語をランダムにサンプリングしてできたと思います ここで 単語の選ばれ方は独立と仮定します そしてデータを 単語の順番を無視して 単なる使われた単語のカウント数というベクトルと考えます すると カテゴリ k が決まれば このベクトルが出てくる確率は 一個一個の単語が選ばれる確率を単にかけ算した値になります これが Bag of words (BOW) という仮定です
12 BOW の仮定の下では 普通メールと迷惑メールの生成モデルを簡単に作ることができます まず 普通メールか迷惑メールかの割合をあらわす確率分布 例えば普通メール (k=0) は確率 0.9 迷惑メール (k=1) は確率 0.1 で出てくるという確率分布があり そこから どちらのメールを作るかというカテゴリ k をサンプリングします k として普通メールが選ばれたら p(w 0) という多項分布からランダムにこの単語 この単語 と順に n = 1, 2,, N 番目の単語をサンプリングしてメールを作ります 迷惑メール (k=1) が選ばれたら 迷惑メールの確率分布 p(w 1) から単語を選びます 結局 あるメール ( 文書 : 以下 単語の集合は文書と呼ぶようにします ) が生成される確率はどうなるかというと それは ある文書 d とそのラベル k の対の同時確率となり そこでは まずラベルが決まり それからそのラベルのもとで文書が作られます そのラベルが選ばれる確率を p(k) とし ( ここでは p(k)=[0.9, 0.1] でした ) その k のもとで単語 w が選ばれる確率を p(w k) とすると それらは n 回独立に出てくるので 全体の同時確率は以下の式になります ここで p(k) と p(w k) は本当は未知の パラメータです p(d, k) = p(k) p(w n k) N n=1
13 データがあれば 未知パラメータの値は以下のように推定できます 単純には 単に数えるだけです とても簡単な例ですが 上のようなデータ D があったとします すなわち メールが 3 つ (d 1, d 2, d 3 ) あり 単語の種類は 7 個 (w 1 ~w 7 ) です 最初の二つ (d 1, d 2 ) が普通メールで 最後 (d 3 ) が広告メールです 文章のカテゴリを選ぶ確率 p(k) は 一番ナイーブには 普通メール (k=0) が 2/3 迷惑メール(k=1) が 1/3 と推定できます 普通メールの中でどういう単語が出てくるかの推定は やはり一番ナイーブには 普通メールの中での単語の頻度を単に足して 1 になるように正規化した 以下のような分布になります p(w k = 0) = [0.1, 0.4, 0.1, 0, 0.2, 0.1, 0.1] 迷惑メールのほうの p(w k) は 3 番目のメールの単語のカウントを正規化して 以下のような分布になります p(w k = 1) = [0.2, 0, 0.2, 0.2, 0, 0.4, 0] そうすると 1 個 1 個のメールが生成される確率を計算することができ 例えばメール d 1 の確率は 最初に普通メールである確率が 2/3 で かつ 最初の単語が出てくる確率は 1/10 次に確率 4/10 の単語が 2 回出てくるので 4/10 4/10 次に 1/10 最後に 2/10 が一回掛け算され という確率が求まります
14 さて こんな計算がなんの役に立つかというと それは 新しいメールのカテゴリを分類するときです 与えられた文書 d のカテゴリ k が 0 なのか 1 なのか その確率 p(k d) を p(k) と p(w k) から 計算するのです ところで さきほど求めたのは 同時確率 p(d,k) や p(w k) や p(k) です p(k d) では k が条件を表す記号 の左側にあります k が条件の方にいる条件つき確率ではなく ある d の下で k である確率を知りたいわけです k の位置がひっくり返っているのですが これは最近だとどこかで見たことのある人も多いのではないでしょうか そう ベイズの定理です
15 ベイズの定理では A と B の同時確率は まず B が出て それから B の下で A が出てくるという確 率で書けます p(a, B) = p(a B)p(B) この式から p(a B) は p(a,b) を p(b) で割り算した形で書くことができます p(a B) = p(a, B) p(b) p(a,b) を 先に A が出てそのもとで B が出てくる確率と考えても同じなので p(a, B) = p(b A)p(A) とも書けます この p(a, B) を上に代入します さらに 今は p(a B) では B の下での A の確率の話を しており B の確率 p(b) には関心がないので これは単なる定数ですから 比例式の形にして p(a B) を A と B をひっくり返した p(b A) と p(a) の積で書けることになります p(a B) p(b A)p(A) このように ベイズの定理で 条件付き確率を逆にすることができるわけです
16 今知りたいのは p(k d) ですが 先ほど出てきたモデルのパラメータは p(k) と p(w k) で k の位置が逆です それでも p(k d) を求めたかったら このベイズの定理を使えばよいわけです p(k d) p(d k)p(k) いま カテゴリの出現確率である p(k) はわかっているし カテゴリ k から文書 d が生成される確率 p(d k) は 単語は独立だと思っているので (BOW の仮定 ) 単語の出てくる確率 p(w k) を単にかけ算すれば求まります
17 例えば さきほどからの例で 単語 1 と単語 6 が 1 回だけ出てくる新しい文書が来た場合 これが普通メールか迷惑メールか知りたかったら それぞれの確率を計算します k=0 だという確率は 2/3 (1/10 1/10) に比例しますし k=1 であるという確率は 1/3 (2/10 4/10) に比例します これらを和が 1 になるように正規化すればそれぞれの確率となり それらは 0.2 と 0.8 となっています これが この文書が持っている k の確率分布 事後分布と呼ばれるものです 両者を比べると これはおそらく迷惑メールだろうと推定できます こういうものが実際のメーラーにも入っていて よく使われています
18 これまでの方法では 文書とラベル k の一対一対応があるデータセットを使って k の出現確率 p(k) と ラベルが k の文書に含まれる単語の出現確率分布 p(w k) を推定しておかないと p(k d) が計算できません しかし 一般の文書では こうしたラベル k は与えられていません 文書に最初からこれは 政治 これは スポーツ これは 家庭 というラベルは貼られていたりしないのが普通ですね 次は この場合 どうするか? という話になります
19 Unigram Mixtures ( ユニグラム混合モデル ) という手法があります 先ほどのナイーブベイズの式では ある文書とそのラベル k ではまずラベル k が決まり それからそのラベルのもとでの単語がそれぞれかけ合わされて 確率が決まっているのでした p(d, k) = p(k) p(w n k) ここで もしそもそも k がわからないのなら すべての k について確率の和をとってしまえばよいではないか と考えます これを周辺化といいますが そういう確率モデルを作るのです N n=1 p(d) = p(k) p(w n k) N k n=1 この p(d) は 文書 d が 全てのカテゴリ k を通して生成される確率 です
20 ナイーブベイズに比べて Unigram Mixtures は一般的にあまり知られていないのですが それは これを解こうとすると単に数を数えるだけでは無理で 例えば EM アルゴリズムなどを使わないと解けないからです EM アルゴリズムについてここでは詳しくは説明しませんが 大ざっぱに言うと まず 各文書に初期値 p(k d) を与えます ある文書がどういう kをラベルとして持っているかという 今まさに知りたい値を 最初は適当に設定しておきます それらから 確率分布に関する計算式を使って パラメータ p(k), p(w k) を計算します つまり 先ほどは一個一個の文書が持っている確率分布は既知 言い換えるとデルタ関数のように迷惑メールか普通メールかで 1 か 0 かのどちらかになっているものを仮定したわけですが 一般にはデルタ関数ではなく わからないので何か大ざっぱな初期値を与え そこからパラメータ p(k), p(w k) を推定します すると それらから 先ほどのようにベイズの定理で p(k d) を再推定できます このような操作をぐるぐる回して 交互に推定を繰り返すのです すると ほどなくすべての値が一定の値に収束していきます こういう手法を EM アルゴリズムといいます パラメータ p(k), p(w k) を計算する部分は 基本的に先ほどと同じでデータのカウント数に関する割り算ですが これは多項分布における最尤推定 ( データの確率を最大にするパラメータを求める作業 ) を実行していることに相当します 一般の EM アルゴリズムでは確率の最大化を行うので ここは M-step と呼ばれます 一方 これらのパラメータによる p(k d) の計算は 期待値を求めているので EM アルゴリズムでは E-step と呼ばれます
21 最初の例では 最初の二つが普通メールで最後が迷惑メールだとわかっているとしましたが それを知らずにデータだけ与えられたときに 一個一個のメールをどちらに分類するかという問題を考えます EM アルゴリズムを用いる方法では d 1, d 2, d 3 という3つの文書について 文書 1 は k=0 か k=1 かわからないので ここでは 0.5 を中心に適当に としました (Step 1) d 2 は 0.6 と 0.4 d 3 は 0.4 と 0.6 と やはり適当に置きました この初期値をもとに一回計算し直すと 確率分布が変わりますが k=1 の方が少し大きい値のままなので どうも d 1 は k=1 の確率が高いように思えます (Step 2) 逆に d 2 では k=0 がさらに増えて k=1 が減るので k=0 らしい d 3 では k=0 が減って k=1 が増えるので k=1 らしい こういう風に 少しずつ変わるわけです さらにもう一回計算すると d 1 では大小が逆転し k=0 が増えて k=1 より大きくなっています (Step 3) 他では元から大きかったところがさらに大きく 小さかったところはさらに小さくなっています この操作をぐるぐる回すとこの例では 5 回くらいで収束して 文書 1 はカテゴリ 0 つまり普通メールである確率がほぼ 1 文書 2 が普通メールである確率もほぼ 1 文書 3 は迷惑メールである確率が 1 となっています
22 最初ラベルは与えなかったのですが まるで与えたかのように分類できてしまうのです ただし あくまで各文書があるラベルを持つ確率が 1 に収束するというだけで そのラベルに 普通メール という名前が自動的につくわけではありません 以上が Unigram Mixtures と呼ばれているもので いわゆる K-means という手法とほぼ等価です 何も教えていないのですが 一個一個のテキストあるいは観測データが持っている確率分布を推定できてしまいます これは一番簡単なトピックモデルで 一個一個の文書に潜在トピック つまりこのテキストはこういう話題ですよと決め打ちする 言い換えると真の値があってそれを推定するという 一番簡単なトピックモデルです 先ほどのメールの例でいえば 普通メール 迷惑メールがトピックです 一般的には 政治 とか 経済 とか コンピューター とかトピックがいろいろあるわけです パラメータは 2 種類あり トピックの事前分布 p(k) と そこからどんな単語が出てくるか p(w k) です
23 毎日新聞の 2001 年の新聞記事のデータでは 1 千万個くらい単語があるのですが その 1/10 くらいを使い トピックは 100 個と限定して Unigram Mixtures を適用した場合の結果の例を上に挙げています 分類された各トピックの単語分布の上位特徴語です 特徴語とは 大ざっぱに言うと確率の高いものですね そうすると 例えばトピック 2 は 大体会社経営みたいな内容で トピック 3 は人事に関する内容が目立ちます トピック 4 では国際的な内容でしょうか これは何も経営とか国際に関する言葉を集めるようにプログラムを組んだのではなく Unigram Mixtures というモデルが勝手に学習した結果だという点を留意しておいてください
24 もう少し見てみると トピック 5 では科学のこと トピック 10 では教育問題 トピック 100 は警察の話をしていることがわかります なお ここではトピック数はあらかじめ決めてあり いくつのトピックに分けるべきかという個数を推定しているわけではありません 分けるべき個数自体を推定することもできますが それは難しい話題なので ここでは触れないことにします 今の場合は 100 個と決めてやりました
25 以上で基本的なトピックモデルはできており これを生態データや RNA のシーケンスデータに使うこともできるはずです ただ そういうときしばしば問題になるのが 例えば 100 や 200 といったカウントはいいのですが カウントデータには 1 や 0 などの頻度の低いものも多く それらがそのままでは信用できない場合が多いという点です カウント数 0 の単語に先ほどの手法を使うと当然出る確率は 0 になるのですが そのデータではたまたま 0 だっただけで 本当は確率は 0 ではないのかもしれません つまり データが 0 回だから確率も 0 としたのでは 推定した確率分布自体が信用できなくなるのです 例えば 先ほど迷惑メールでは 出現回数は 単語 1 が 1 回 単語 2 が 0 回 単語 3 が 1 回 数列としては , となっていますが これらを足して割った数値が本当に確率なのでしょうか カウント数を単純に割り算した確率 (p (w)=n(w)/n) はデータの尤度を最大にするので最尤推定量と呼ばれます しかし データのカウント数はたまたま 0 だっただけで 確率が本当に 0 かというと おそらくそういうことではない カウントデータから割り算で算出する最尤推定量は 特にデータが少ない場合 あまり信用できません 言語データでは単語という空間の次元が数万次元あり ほとんどのカウントは 0 で 一個の文書に出てくる単語の数はたかだか数百か多くて 1000 くらいです そんなデータだけからこの数万次元を推定できるわけがなく もっとまじめに確率を考える必要があります
26 そのためにベイズ推定をします 先ほどもナイーブベイズといって ベイズの定理を使った推定をしましたが それとは別に 今一度 もう少し深くベイズの定理を用います ナイーブベイズでは k=0 のときにはどんな単語が出て k=1 のときにはどんな単語が出るか という風に複数個の多項分布を考えました すると あるカテゴリーのデータの中でカウントが 0 のとき そのまま割り算で確率を求めてしまうとその多項分布では確率 0 になってしまいます しかし 他のカテゴリーでは現れている場合が多い 例えば 3 番目の迷惑メールでは 単語 2 単語 5 単語 7 の出現回数はいずれも 0 回です しかし 迷惑メールにこれらの単語が絶対に出ないかというと 例えば単語 2 は普通メールでは文書 1 文書 2 ともに 2 回出現しているのですから 迷惑メールでもそれなりの確率で出現するだろうと思えます 逆に 単語 4 は迷惑メールには 1 回出ていますが 普通メールには出てきていません しかし普通メールに全く出ないと考えるより 低い確率で出てきてもよいとするほうが自然に思えます そこで 確率分布を独立に割り算して決めてしまうのでなく ベイズ的な考え方をしましょう つまり 今 単語の出現頻度という多項分布を考えているのですが その多項分布を生成する分布 [ 事前分布 ] を考えて それによって 多項分布つまりそれぞれの単語の出現確率を直接推定するのではなく 多項分布自体の確率分布 [ 事後分布 ] を推定しようとするのです そのために事前分布として用意する一番簡単な分布が ディリクレ (Dirichlet) 分布と呼ばれるものです
27 例えば カテゴリーが三つの多項分布の場合 まず三角形の内部の点のそれぞれが この多項分布の 3 個の確率を表していると考えます 足して 1 になるような 0 以上の数値の 3 組の集合は 三角形の中に含まれます それを平面に描いたのが上の図です つまり 三面サイコロを考え 1 しか出ないサイコロが三角形の左下の頂点 p=(1,0,0) に相当し 1,2,3 が均等に出るサイコロが三角形の中心 p=(1/3, 1/3, 1/3) に相当すると考えているわけですね 右下の頂点は 3 だけが出るサイコロ 上の頂点は 2 しか出ないサイコロに対応します この 3 角形の中を点が動くことで 全てのサイコロを表現することができます 今あるデータがどのサイコロらしいか の確率分布がディリクレ分布です 文書の単語を出すために 単語の種類と同じ数の面を持つ巨大なサイコロがあると考えると ほぼ 1 しか出ないけれど 少ない確率で 2 や 3 も出る という多項分布や どの値も同じくらいの頻度で出る 多項分布の どれがどのくらいもっともらしいかをディレクレ分布で表現できるわけです カテゴリーが四つの多項分布では 正四面体を考えることになります
28 多項分布 p に対して 以下の式で確率密度関数が定義される確率分布をディリクレ分布といいます k ) p(p a) = Γ( α k Γ (α k ) p k k K k=1 α k 1 最初にガンマ関数を含む謎の定数が付いていますが これは定数なので 確率密度関数の形は後の 部分に比例しています K α p(p a) p k 1 k k=1 今 確率変数は p=(p 1,p 2,...,p K ) で それらは足すと 1 になる数の K 個の組で それらは p k の α k -1 乗の巾乗という形になっています ディリクレ分布は 離散分布におけるガウシアンのようななものと思っていいかもしれません α はハイパーパラメータと呼ばれます 期待値は この α を和が 1 に なるよう正規化した形 α k k α k になり α の総和が 広がりを表す分散のようなものになっています
29 K 個のパラメータ α を変えると いろいろな分布が出てきます 例えば α=(1,1,1) とおくと α k -1=0 ですが p k を 0 乗したら必ず 1 となるため Uniform な分布が作られます α が 1 より大きい値をとると どこかに集中します 逆に 1 より小さい値をとると くぼみが出て端で高くなるような分布になります
30 実際にディリクレ分布から p k たちをランダムにとってみると 例えばすべての α k が 1 に等しい Uniform な分布からとると 得られる多項分布は右上のようにいろいろな形になります 一方 10,10,10, のような中央にピークを持つ分布からとると 得られる多項分布は大ざっぱには一緒で 一様な多項分布になります ( 左上 ) それに対して こういう 0.1,0.1, のときは どこかの値が大きく 他はほとんど 0 のようなものが出てくるはずで 実際やってみると どこかが大きくて他が 0 に近いという多項分布が出てきます
31 ディレクレ分布をどう使うかというと X が何かの観測頻度とします 例えば ある植物 1 が観測 されたのが n 1 回 植物 2 が観測されたのが n 2 回,, 一般に植物 k が n k 回とします (X = (n 1, n 2,, n k,, n K ) この裏には これらの真の確率を表すベクトル p が隠れているはずです この p の X の観 察データを踏まえた事後確率分布 p(p X) は これを逆転して まず事前分布 p(p) があったと考えます この事前分布のもとでデータが生成され それらから事後分布 p(p X) を求めます これは簡単で 一個一個の確率が p k で それが n k 回出てきているので p k の n k 乗がその確率になります それを事 前分布のディレクレ分布に掛け算します 掛け算をすると k 番目は p k の (n k +α k -1) 乗という形になる ので 結局全体では (n k +α k ) という新しいパラメータを持つディリクレ分布になっているだけです その期待値は α k の和が 1 になるように正規化したもので 以下のようになります E[p k X] = n k + α k (n k + α k ) k
32 こうすると たまたま n k が 0 だったとしても E[p k x] には α k が残るので 確率が 0 になることはな く すべてについて穏やかな確率の値が得られます 言い換えると 偶然 k 番目の項目の出現回数 が 0 だった場合 (n k =0) でも 期待値 (n k +α k )/ k(n k + α k ) は 0 になりません このため 全体 的に穏やかな確率が得られます こうした方法をスムージングといいます まとめると 最尤推定では 観察されたカウント数をすべてそのまま正規化して和を 1 にするので すが ここでは k 番目のカウント数 n k に α k というハイパーパラメーターを与え それらを n k +α k のように足し その和が 1 になるように正規化しています 実はそれがベイズ推定になっていて これをディリクレスムージングと言います そのほうが より頑健な推定値になります ナイーブなやり方はカウントに全部 1 を足すというやり方で 1 を足すというのは α k =1 に対応し さきほど示したように これは事前分布が一様分布であることを意味します 言語処理の世界でも 最初の頃 ( どれくらい昔かというと ラプラスが言ったので 18 世紀の終わりくらいです ) は 1 と してたりしたのですが もちろん 1 とすることは良くなくて 正しい値があります それを推定し たい場合は この α k 自体にガンマ分布を置いて さらにベイズでサンプリングをしたりすると正し い値を求められます カテゴリごとに何か小さな値を推定することで 推測性能が良くなることが わかっています
33 質問 今 ディリクレ分布を使ったのは 多項分布のパラメータ p k の分布を求めたいからですか? 答 そうです もともとディリクレ分布の形から それに多項分布の尤度をかけると同じ形で出るわけです p k のべき乗という形です 事前分布が Dir(α) で 事後分布が Dir(α+n) と 同じ形が出てきます なお 絶対にディリクレ分布でないといけないというわけではなく もっと複雑な分布を使ってもかまいません 質問 今のディリクレ分布ではp を表していたと思うのですが ちょっと前の話でカテゴリを迷惑メールとそうでないメールのように いくつか分けていましたね あれをディリクレ分布で表しているのですか? それとも同じカテゴリの中での p のばらつきをディリクレ分布で表しているのでしょうか? 答 両方できます 先ほどのナイーブベイズでは 分布が p(k) と p(w k) の 2 種類あり どちらも多項分布でした どちらでやってもかまいません 片方は最尤推定でもかまいません 質問 モデルを選ぶ p(k) のほうにディリクレ分布を使ってもいいのですか? 答 はい そして そこから単語を出すほうに使ってもいいわけです これはいい質問で それをやらないと Unigram Mixture を動かしてもなかなかうまくいかないという場合は結構あります ディリクレスムージングを入れたソフトを私が書いて プログラムとして公開しています これをダウンロードすると 普通に使えるようになっています
34 これは復習です Bag of Words テキスト = 単語の集合とし その前後関係は考慮に入れず 単語の出現頻度がテキストの特徴を 表現しているという仮定 Unigram Mixtures の生成モデルテキスト d = 1, 2,, D に対し 確率 p(z) でトピック z を採用 トピック z を特徴づける単語の確率分布 p(w z) に従って n 個の単語 w 1, w 2,, w n を抽出
35 さて Unigram mixture の次のステップに進む前に グラフィカルモデルについて説明しておきます 上の図は Unigram Mixture のグラフィカルモデル表現で 黒丸は観測値を表しています 今観測されているのは単語ベクトル w=w 1,, w N だけで その裏に 一個一個の文書ごとにカテゴリ z があり ( 先ほどまでは k と書きましたが いわゆる潜在変数なので z にするほうが多いです ) そのカテゴリから 単語が全部で N 回抽出されています 図の箱は繰返しを表していて 単語 w 1 単語 w 2 単語 w 3 とランダムにサンプリングされているのが全部で N 回あるという意味です そもそも文書が D 個ありますので 同じことが全体で D 回行われています どういうトピック z を選ぶかというパラメーター (λ=p(z)) が一個あり そこから z を選ぶ操作を D 回やり 各 z の中で単語を N 回出す こういうモデルになっています 一方 全ての文書に共通な カテゴリ k からどんな単語が出てくるのですかという分布 p(w k) があり この z が決まったら この分布を使って (k=z として ) 単語 w を出力します 箱は繰返しを表していて 箱の右下に繰り返し回数が書いてあります こういうのがグラフィカルモデルです なお ユニグラムとかナイーブベイズとかいう言葉は最近よく聞かれるのですが 本屋でよく売っているベイズ統計の本は大体このあたりまでで終わっていて それ以上の話題に触れておりません しかし この段階では まだまだ問題があります
36 何が問題かというと 例えばこれは Yahoo ニュースから取ってきたのですが しらせ とか 南極 などは多分 南極観測のようなトピックから出てきていますが この記事はしらせで投票をしたという話なので 衆院選 とか ファックス とか A4 とかも出てきています ところで A4 と 衆院選 と しらせ が一個の確率分布から出てきたとは到底思えない そうではなくて この記事に関する話題は 南極船の話題が 0.6 くらいで 選挙の話題が 0.3 くらいで 他の話題が 0.1 くらい入っているという感じに思えるわけです 一個一個の文書が 複数のトピックにおける単語の確率分布の混合分布になっていると考えられるわけです
37 それが いわゆるトピックモデルというもので 最初に提案されたときには 上のような簡単な形になっていました これは一見簡単に見えますが 文書ごとに それがどういう話題 z を持つかが確率分布になっています つまり 文書 d からどういうトピック z が出てくるかというトピックの分布が文書ごとに一個一個決まっていて その確率分布からまず話題 z を選び 次にそこから単語を出します この操作を全体で N 回繰り返します つまり 一単語ごとに違うトピックがあるのです 先ほどは 一個の文書があったらその話題は全部同じだったのですが このモデルからは一単語ごとに違う話題があるわけです そうすると 先ほどの例では しらせ を出すときには まず 南極トピック を選び 次にそこから しらせ という単語が選ばれたと考える 次に 衆院選 を出した時には まず 選挙トピック が選ばれ そこから 衆院選 という単語が出てきた このように考えられるわけです
38 グラフィカルモデル表現も違ってきます さっきと似ていますが d から z の部分が 図の右に示し たような確率分布 p(z d) になっています これは未知のパラメータなので 推定することになります それからもちろん p(d) や p(w k) も推定します
39 こうしたアイデアに基づく最初のトピックモデルは PLSI と呼ばれるもので これについてはすぐ後で説明しますが 先にその効果を見ておきます これは 前に 1 個の文書はすべて同じ分布から出てきたと考える Unigram Mixture のときの例と同じデータに PLSI を適用した結果の一部なのですが 以前は 頻度の高い上位語の中に を とか の とか する とかいう機能語の類がたくさん入っていました それが PLSI を使うとほとんど除かれるのです 実は Unigram mixture の例でも結構頑張って機能語を除いたのですが 手作業で除くのには限界があり ちゃんと統計的にやらないとうまく動きませんでした それが PLSI を用いると Topic 3 は見事に野球の話ばかり集まっていますし Topic 1 は将棋ですね べつにテキストに トピックは将棋 と書いてあるわけではないのですが モデルが勝手にこうした単語を見つけてまとめてくれるわけです Topic 2 も 原発とか事故とか配管とか 原発事故に関するものですね Topic 4 は 研究 とか 細胞 とか 遺伝子 とか 医学や生物学に関する単語です
40 他のトピックも 何となくどういう話題なのか 想像がつくことと思います
41 さて 生成モデルとして PLSI はどうなっているかというと 全部で D 個の文書があり 文書一個一個について まずインデックスを作り (d~p(d)) このインデックス すなわち文書ごとに単語が N 個あるのですが まず文書が持っている話題分布からトピック z を作り (z~p(z d)) その話題から単語を出す (w~p(w z)) ということをぐるぐる繰り返します つまり確率で書くと ある文書とある単語が共起したのは その裏に z という見えない話題があり それに対して周辺化されているわけですが それは文書をまず選び その文書から話題を選び 話題から単語を選ぶ ということを z に対して和をとったという確率モデルになります
42 今までは一つの文書と一つの単語が共起する確率を考えていましたが ここでは 一つの文書と複 数の単語が共起する確率について考えています それは単に 各文書ごとにすべての単語との共起 確率をかけあわせ さらにそれらをすべての文書についてかけ合せるだけです
43 こうして p(z d) や p(w z) が与えられたら確率的に文書を生成するモデルはできたのですが 問題はこの逆で 文書が沢山与えられたとき それからどうやって p(z d) や p(w z) を推定するかにあります いわゆる逆問題ですね ここで いささかテクニカルになりますが またベイズの定理を使って式を書き直します 特に難解な計算をするわけではありませんが それで Unigram Mixture と同様に EM アルゴリズムを使うことで推定が可能となってしまうのです さきほどから 文書を選ぶ確率 p(d) というのが出ていますが これの意味になんとなく謎めいた印象を受けている人はいませんか?p(d) がちょっと怪しいと気付いた人は鋭い人だと思います そこで 条件付き確率とベイズの定理を使って上のように式を変形します 最後の式はどう解釈されるかというと ある文書 d とその中の単語 w が共起する確率は まず話題 z が先に選ばれます まず z を選び その z から文書と単語が出てきたと思いましょう 最初の p(z) は どんな話題が出やすいかという確率分布を表していて その話題からどんな文書が出やすいのか (p(d z)) あるいはその話題からどんな単語が出やすいのか (p(w z)) が決まってくる ちょっと変形しただけなのですが これでモデルが EM アルゴリズムで解ける形になってしまうのです
44 EM アルゴリズムの手順の詳細は説明しませんが ある程度のイメージを持つために このモデルの下でのデータの対数尤度の式は必要です D は文書の集合 W は単語ベクトルの集合で これらはデータとして与えられます 一方 Z は話題ですが これは未知の潜在変数で 問題はこの推定にあるわけです ですから 推定したいのは p(z), p(d z), p(w z) というパラメータと それぞれの文書の中の各単語がどの話題から選ばれたものなのか という潜在変数 Z です
45 EM アルゴリズムは E-step と M-step に分けられます E-step では 推定したい未知の潜在変数について その期待値を求めます いまのモデルでは 文書 d の中のある単語 w がどのトピックかという確率分布 p(z d,w) の形で求めます これは上のようにして 3 つのパラメータが与えられれば計算できます M ステップでは この期待値の下で対数尤度を最大にするパラメータを求めます そこで テクニカルな話ですが Q 関数というものを作ります
46 Q を最大化したいので これを微分して 0 とおくことで 3 つのパラメータの計算式が得られます ここで n(d, w) は 文書 d の中に単語 w が何回入っているか そのカウント数 要するにデータ を表しています
47 以上の EM アルゴリズムをまとめてみます E-step では 各文書 d の各単語 w について その単語 w はどういう話題から選ばれたらしいかを確率分布の形で推定します この 一個一個の単語がどういう話題に割り当てられたのか がわかっていると ( 期待値という意味で ) それを逆に使うことで ある話題からどういう単語が出やすいかがわかります それが M ステップで それを使って 3つのパラメーターを更新します そうしたら E ステップに戻って もう一回その新しいパラメーターを使って 単語が本当はどういう話題なのかを計算する これをぐるぐる繰り返します この計算は R のようなソフトでもできると思いますが 言語処理では単語の種類の数が数万あり 文書の数も数万とか数十万とか数百万とかあるので R とかでは一年たっても終わらないようです それで普通 C 言語とかでプログラムをゴリゴリ書きます うまく工夫すると 10 時間とか一晩くらいで終わるくらいの計算量です 4 日くらいかかる研究も普通にあります
48 こうして文書 d の各単語 w ごとに潜在的な話題 z を考えるので いわゆるナイーブベイズなどより はるかによいモデルが作れます Unigram Mixture も混合モデルの一種で つまり まず混合比からある話題を選び その話題からテキスト全体を作っているわけです 一方このトピックモデル PLSI では 一個一個の文章ごとにまず混合比 p(z d) を選び この混合比から各単語ごとにトピックを選んで そこから単語を出力します 結局 混合モデルの混合モデルというのがトピックモデルの本質です ただし p(z d) は生成モデルには登場しますが EM を適用する段階で これは逆の p(d z) になっています p(z d) はベイズの定理を使えば p(z)p(d z) に比例するので求められますね この p(d z) というのも少々謎の確率分布ですが この問題はすぐ後で述べます それがそのまま次のステップのモデル LDA へつながっていきます
49 LDA へ進む前に PLSI の性能について 少し触れておきます トピックモデルは言語処理の人にはそれなりに知られてきていますが 他の分野では 多分まだ教科書がないこともあって 1 あまり知られていないと思います Unigram Mixture (UM) と比較してみると PLSI のほうが性能がよいことを示しているのが上の図です 縦軸について しっかりした説明は省きますが モデルの性能の評価の一つで 下に行くほど性能が良いモデルを意味します 赤の DM=Dirichlet Mixtures は今はおいておいて いわゆるナイーブベイズ ( 教師なしナイーブベイズ ) でやると Unigram Mixture は黒い実線ですが 話題の数を増やしていくと性能は良くはなるものの 図のように向上が止まってきます 一方 PLSI や すぐ後で説明するそのベイズ版 LDA では はるかによい性能が出ています ちなみに DM=Dirichlet Mixtures というモデルは 話題は文書ごとに一個ですが 単語にキャッシュがあって 一回出た単語が二回以上出やすくなるという性質をうまくモデル化するものです それを使うと つまり Unigram Mixture にキャッシュを付けると ものすごく性能が良くなるわけです 現状では LDA にキャッシュを入れるともっと性能がよくなるみたいなことがわかりつつあるというのが 今の言語処理の状況です 1 この講演の時点 (2015 年 1 月 ) では まだ日本語の教科書は出版されていなかった
50 PLSI は 99 年頃に出て 統計を知っている人はすごいと思ったわけですが もちろん問題もあります 何が問題かというと 話題の事前分布 p(z) とか 話題ごとの単語の分布 p(w z) を推定するという部分はいいのですが p(d z) がパラメータに入っています これは話題 z からどんな文書 d が選ばれるかの確率ですが この文書 d というよくわからない謎の確率変数が入っています そしてこれは 学習データに比例して増えていきます これはモデルの中に含まれていて 未知パラメータとして推定しないといけません 未知パラメータを導入したことで EM で解けるようになったのですが 推定すべきパラメータ数が膨大になってしまいました そのため しばしば学習データにオーバーフィットして 性能がどんどん悪くなってしまうのです それを解決するためには 焼きなまし (Tempered) 法というのがあって 確率分布の計算をしたときにオーバーフィットしないように β 乗します この β が 1 より小さい値 例えば 1/2 だと をとる形になるので 確率分布がなめらかになるわけです
51 焼きなましでこの β をだんだん 1 に近づけるといった ある意味姑息な方法を使うと β が 1 だとだめなものが β を 0.75 くらいにするとうまくいく みたいな方法が最初のころ取られていました でも こんなアドホックでいいの? という疑問がありました ここでいう アドホック とは オーバーフィットする原因自体を解決することなく 対処療法的に学習し過ぎないようにしていることです
52 そもそも問題は EM で解くということからわかるように PLSI というトピックモデルはベイズではなく 真の生成モデルでもなく 最尤推定をやっているだけなのです 文書ごとの p(d z) をパラメータと思って最尤推定していて p(z d) はパラメータの最尤推定値から求められるのですが これを確率的に生成するようなモデルを考えましょう それには 全体をベイズで書きましょう これが 一番基本的なトピックモデルである Latent Dirichlet Allocation です これが 2001 年から 2003 年ごろの話です
53 基本的な考え方は PLSI と同じで 単語ごとに見えないトピックがあるというものです
54 ではどうすればいいかというと ある文書が持っている話題の分布というものは離散分布なので ディリクレ分布を使ってこれを作る 基本的にはこれだけです このことを簡単に θ と書いていま すが ディリクレ分布を使って作る それだけです
55 そうすると あるテキスト w 1 が持っている話題の分布が上のほうのような感じになっていて それはこのディリクレ分布からランダムにとってきたのだけど それは上の図で θ 1 で指されているあたりからだった w 2 だと下のほうのような感じの分布になっていて それも同じディリクレ分布からランダムにとってきたのだけど こっちは θ 2 で指されているあたりからだった こういうモデルを考えます
56 話題から単語を選ぶ方は こっちは最尤推定をやっても良いのですが これも多項分布なので や はりディリクレ分布から作ることにしましょう たいていの場合 話題より高次元のディリクレ分 布になります
57 全体の生成モデルは 一個一個の文書に対して どういう話題を持っているかという混合比 θ という確率分布 これをまずディリクレ分布からのランダムサンプリングで作ります もし全部で話題が 4 個あるなら 各文書について 4 次元のディリクレ分布からのランダムサンプリングで話題の分布を決めます 次にその多項分布の中から 話題 z をランダムに選びます それから その話題からはどういう単語が出やすいかという多項分布から ランダムに単語を選びます 2 番目の単語についても 同じようにまず混合比の多項分布から話題を決め その話題の多項分布から単語を選びます もし話題 政治 が選ばれたなら 政治 トピックの確率分布から単語をランダムサンプリングします おそらく 法案 とか 国会 とか 議院 などが出やすい確率分布なのでしょう 今とり出した単語が 法案 だったとします 次にまた同じことをして 今度は話題 経済 が選ばれ 経済 トピックから単語を出したとします この操作を N 個ある単語ごとに行います 次の文書に対しては 混合比をディリクレ分布からランダムにサンプリングする作業から始めます これが生成モデルですが もちろん 現実には文書 つまり単語のカウント数というデータがあるだけで この生成過程はわかっていません それをデータから求めるのです
58 グラフィカルモデルでいうと 我々にわかっているのは 出現した単語 w という黒丸だけです この単語の黒丸の裏に見えない話題があって この話題を作る見えない話題分布がある これら全てを推定するという一見無茶に見えることをします なお 話題分布を支配するハイパーパラメーターもあり これも頑張れば推定できます
59 数式で書くと w というのが単語です その裏に一個一個の単語が持っている話題 z n と 文書が持っている話題分布 θ があります ある単語ベクトル w が生成される確率 p(w) は n 個の単語についての n 個の積についての すべての話題の和 (Σ z ) とすべての話題分布の和 (θ についての積分 ) になります θ の分布がディリクレ分布で そこから θ k という話題 k の出る確率が現れ θ k から単語が出てくる パラメーターはディリクレ分布の α と 話題 k から単語 w の出る確率 ( 上では β となっています ) これが全体のパラメーターです こんな尤度をもつモデルの最適化など無理なように思えますが これが実は解けるのです
60 LDA モデルの計算法を説明する前に LDA を適用した時に得られる結果の事例を先に示しておきます 縦の列は それぞれ LDA が求めた話題とその話題の下で選ばれる確率の高い単語です 話題には 単なる番号しか付いていません この結果を見てどういう話題かは人が見て 話題の名前を決めています 例えば話題 1 には Art に関する言葉が多いから Art と名付けました 3 番目には 子供に関する言葉が多いから children にしています 4 番目は教育関係が並んでいるから education にしました Art "Budgets Children Education は モデルではなく図示のために与えた各話題の名前です
61 ここまでですと PLSI の結果と変わらないのですが 実際のテキストの単語ごとに話題があるので テキストを話題で色分けできるのです 例えば この文書の冒頭には William Randolph Hearst Fundation will give $1.25 million to と書いてあります New York Philharmonic と Juilliard School に Foundation をあげましたという話で 音楽関係の話とお金関係の話が混じっているのですが New York Philharmonic とか performing とか Lincoln は音楽関係 ( 赤 ) 緑色のところはお金関係 というように 単語ごとに ( それを選ばせた ) 話題をあてることができるわけです 本当はどの話題かは確率分布として推定されますが ここでは一番事後確率の高かった話題に単語を色づけしています
62 この複雑なモデルをどうやって解くかというと 実はモデルの提唱以来 たくさんの方法が提唱さ れています
63 一番簡単なのは Gibbs サンプラーと呼ばれているもので これだけ紹介します
64
65 図の横軸と縦軸は 2 つの潜在変数 z 1 と z 2 です z 1 と z 2 が特定の値のときにデータが得られる確率 を 等高線状に示しています データの確率が高くなるパラメーターの値を推定するために マル コフ連鎖モンテカルロ法というものを使います
66
67 一個一個の単語 つまりある単語ベクトル w の中の i 番目の単語が持っている話題が k である確率は ベイズでひっくり返すと 上のようになります それが何かというと ある単語が持っている話題の分布は その単語が含まれている文章の中で その話題がどのくらい出てくるかという事前分布と その話題からその単語がどのくらい出てくるかという尤度をかけ合わせた形になります それに従って 一個一個の単語がどういう話題なのかをサンプリングします これがギブスサンプリングです
68 一個一個の単語が観測値で その裏に見えない話題があります 話題を色で分類してあります この黒の単語が持っている話題が青である確率を計算するのですが 青になる確率は この文書の中で青がどのぐらい出てきたかという確率と 青という話題からこの黒い単語はどのぐらい出てくるか この尤度を掛け合わせた形になります それをこの文書という単語の配列に対してサンプリングを回します 通常 計算には一晩くらいかかります
69 人工的に作った文書にギブスサンプリングを実際に行った例をお見せしましょう まず 単語の種類を 25 とし 単語 1, 単語 2,, 単語 25 を横に5つずつ 5 行に並べて表示することにします トピックは 10 個としました 10 個のトピックからそれぞれどんな単語が出てくるかを表すパラメータ β k ={p(w k)} を表すのが 10 個の正方形です 図の黒の部分は単語の出る確率が 0.2 それ以外は 0 を意味します つまり左上のトピックでは 黒の部分は単語 1,6,11,16, 21 なので それらが確率 0.2 ずつ出て 他は 0 という意味です
70 次に このトピックをどういう風に混ぜ合わせて文書を作るかを表す多項分布を ディリクレ分布からランダムに選びます 今 文書を 4 つ作ることにし 一様なディリクレ分布 (Dir(1,1,,1)) からランダムにサンプリングしたところ 右上のような 4 つの多項分布が選ばれたとしましょう この割合に従って 10 個のトピックを混ぜ合わせて単語をサンプリングするので 10 個のトピックをそれぞれの多項分布で混ぜた分布を下に図示しました 一個一個の文書 1 文書 2 文書 3 文書 4が持つ 各単語の出やすさを黒の濃さで表しています もちろん 我々はこの確率分布自体を知っているわけではなくて ここからさらにサンプリングした単語の回数というデータを持っているだけです
71 上がそうやって作った文書の例です この例では 1000 個の文書を作っていて 図にはその最初の 12 個について 25 個の単語がそれぞれ何回出現したかを示しています 横軸が 1 個の文書です 文書 1 では 単語 1 が 10 回 単語 2 が 10 回 単語 3 が 8 回 単語 4 が 12 回 単語 5 が 7 回 という感じで 単語 25 が 13 回出てきています そういった文書が 文書 1 文書 2 文書 3 とたくさん ( 全部で 1000 個 ) あります 我々が知っているのはこれだけです β は教えません そして このカウントデータだけを使って β が本当に復元できるのかを試します つまり β の真の分布は ある 5 個が確率 0.2 で出て他は確率 0 という分布でした もちろん我々は真の β を知りません β を θ で混ぜ合わせ ( 混ぜ合わせ方 θ も知らない ) そこからさらに単語をランダムサンプリングして作ったカウントデータから β を復元できるかテストするのです
72 最初はさっぱりわからないので ひとまずランダムに β を定め そこから少しずつ学習します
73 それで ギブスサンプラーを一回やります 少しきれいになったような たいして変わらないよう な
74 ギブズサンプラーを 3 回やったところです
75
76 16 回で結構きれいになっていて 32 回でかなり真の分布に近づいています 64 回だと もうほぼ復元できています
77
78 10 個のトピックの順番は関係ないので この段階で真の分布はほぼ復元できたといえます
79 データの対数尤度も 最初はだーっと上がっていき 先ほどほぼ正解だった 64 あたりから横ばいに なっています
80 以上が LDA というものです オーバーフィットしないトピックモデルで かつ 完全な生成モデル なので いろいろと拡張することができます それでいて 計算オーダーはほとんどナイーブベイ ズと同じくらいです
81 モデルの性能の比較ですが 今回は特に説明しないことにします
82 最後に Geographic Topic model というのが面白かったので 紹介しようと思います 同じトピックでも 地域によって言葉というものは微妙に違っていて 例えばこの例で Food とは Dinner や Delicious Snack などですけれど サンフランシスコに行くと Food というと Sprouts や Avocados などのほうが結構確率が高い 逆にピッツバーグだと この単語の意味は知らないですが レストランの名前などが多かったりします 全体としては 多分別々のものではなく あくまで Food ですね 大事なのは 地域がサンフランシスコやピッツバーグなどと分かっていれば 地域ごとに単語が出現した回数を数えればよいのですが そもそも どこまでが地域かということがよくわかりません 例えば北海道地域という風に区分できればよいのですが 北海道から東北のここまでが一個のまとまりをもった地域なのかもしれません そうした地域自体をデータから見つけたい そのような問題です
83 方言みたいなものですが データとしては Twitter のツイートを使っているので緯度経度がわかっています 緯度経度からでは領域が見えないわけです まず 地域をガウス混合分布で表現します つまり その地域の中心があり そこから離れるに従ってその地域性は薄れていく このとき 地域ごとのガウス分布は基本となるガウス分布にノイズが加わったものだと仮定します このガウス分布をロジスティック変換して和を 1 にした分布がトピックで それを使って MCMC で学習を動かします どういう地域があるかということと そこからどういう単語が出てくるかの両方を知ろうというのです
84 これは food ではなく basketball 関連らしいのですが 全体としては PISTONS や LAKERS などが出てきます でも Boston だと CELTICS が出てくるし New York だと KNICKS が出てきます 他の例で popular music だと playing, daughter, PEARL が Boston では出てきますが New York では BRONX が出てきます Emoticons ( 顔文字 ) というのは面白くて この haha という笑いマークがアメリカ全土で同じかというとそんなことはなくて ボストンでは図のようなものを使うけれど California では別なものを使い New York ではまた別なものが使われています
85 ガウス混合分布なので この辺り この辺りとたくさんあるんですが そのうちの一部をとってきた例で lol というのは 日本語で言うと ( 笑 ) です ( 笑 ) は 全体的に散らばっています 全国に散らばっているのですが lls(laughing like shit という少し下品な表現 ) があるらしく それはごく一部にしかありません
86 Very は普通の表現で全国にあるのですが カリフォルニアには hella というのがあるらしく それがこういった感じのガウス分布で説明できるようです af というのは 書こうと思いましたが品がないのでやめました odee はなにかの四文字言葉のようです ほかにも色々最近の話を用意してきましたが 今回はこのあたりにしておくのがよいかと思います
87 編集後記 実際のチュートリアルは この後活発な質疑が続き そこからはチュートリアルならではの躍動感が感じ取れると期待できますが テープ起こしの負担は重く また 入門講義としては ナイーブベイズ Unigram Mixture, PLSI, LDA と 1 つずつ 4 つのステップを登ったところがひとつの切れ目になると考え 本講義録はここで打ち切ることにしました トピックモデルについては 佐藤一誠著 トピックモデルによる統計的潜在意味解析 (2015 年 ) 岩田具治著 トピックモデル ( 機械学習プロフェッショナルシリーズ 2015 年 ) のように和文教科書も出版され始めています ただ 統計数理系の読者を満足させる書物になっているため 非統計数理系の研究者が独習するには数式が多く難儀するかもしれません 本講義録は 生物系研究者中心のチュートリアルだったため 計算アルゴリズムの詳細を大胆に割愛し モデルの生成過程やアウトプットの解釈など エンドユーザーにとって最も重要な部分に重点を置いたものとなっています 専門書と合わせて活用することで ぜひこの新しい統計モデルの活用法を覚え 新しいデータ科学の世界を切り拓いていきましょう
様々なミクロ計量モデル†
 担当 : 長倉大輔 ( ながくらだいすけ ) この資料は私の講義において使用するために作成した資料です WEB ページ上で公開しており 自由に参照して頂いて構いません ただし 内容について 一応検証してありますが もし間違いがあった場合でもそれによって生じるいかなる損害 不利益について責任を負いかねますのでご了承ください 間違いは発見次第 継続的に直していますが まだ存在する可能性があります 1 カウントデータモデル
担当 : 長倉大輔 ( ながくらだいすけ ) この資料は私の講義において使用するために作成した資料です WEB ページ上で公開しており 自由に参照して頂いて構いません ただし 内容について 一応検証してありますが もし間違いがあった場合でもそれによって生じるいかなる損害 不利益について責任を負いかねますのでご了承ください 間違いは発見次第 継続的に直していますが まだ存在する可能性があります 1 カウントデータモデル
切片 ( 定数項 ) ダミー 以下の単回帰モデルを考えよう これは賃金と就業年数の関係を分析している : ( 賃金関数 ) ここで Y i = α + β X i + u i, i =1,, n, u i ~ i.i.d. N(0, σ 2 ) Y i : 賃金の対数値, X i : 就業年数. (
 統計学ダミー変数による分析 担当 : 長倉大輔 ( ながくらだいすけ ) 1 切片 ( 定数項 ) ダミー 以下の単回帰モデルを考えよう これは賃金と就業年数の関係を分析している : ( 賃金関数 ) ここで Y i = α + β X i + u i, i =1,, n, u i ~ i.i.d. N(0, σ 2 ) Y i : 賃金の対数値, X i : 就業年数. ( 実際は賃金を就業年数だけで説明するのは現実的はない
統計学ダミー変数による分析 担当 : 長倉大輔 ( ながくらだいすけ ) 1 切片 ( 定数項 ) ダミー 以下の単回帰モデルを考えよう これは賃金と就業年数の関係を分析している : ( 賃金関数 ) ここで Y i = α + β X i + u i, i =1,, n, u i ~ i.i.d. N(0, σ 2 ) Y i : 賃金の対数値, X i : 就業年数. ( 実際は賃金を就業年数だけで説明するのは現実的はない
生命情報学
 生命情報学 5 隠れマルコフモデル 阿久津達也 京都大学化学研究所 バイオインフォマティクスセンター 内容 配列モチーフ 最尤推定 ベイズ推定 M 推定 隠れマルコフモデル HMM Verアルゴリズム EMアルゴリズム Baum-Welchアルゴリズム 前向きアルゴリズム 後向きアルゴリズム プロファイル HMM 配列モチーフ モチーフ発見 配列モチーフ : 同じ機能を持つ遺伝子配列などに見られる共通の文字列パターン
生命情報学 5 隠れマルコフモデル 阿久津達也 京都大学化学研究所 バイオインフォマティクスセンター 内容 配列モチーフ 最尤推定 ベイズ推定 M 推定 隠れマルコフモデル HMM Verアルゴリズム EMアルゴリズム Baum-Welchアルゴリズム 前向きアルゴリズム 後向きアルゴリズム プロファイル HMM 配列モチーフ モチーフ発見 配列モチーフ : 同じ機能を持つ遺伝子配列などに見られる共通の文字列パターン
多変量解析 ~ 重回帰分析 ~ 2006 年 4 月 21 日 ( 金 ) 南慶典
 多変量解析 ~ 重回帰分析 ~ 2006 年 4 月 21 日 ( 金 ) 南慶典 重回帰分析とは? 重回帰分析とは複数の説明変数から目的変数との関係性を予測 評価説明変数 ( 数量データ ) は目的変数を説明するのに有効であるか得られた関係性より未知のデータの妥当性を判断する これを重回帰分析という つまり どんなことをするのか? 1 最小 2 乗法により重回帰モデルを想定 2 自由度調整済寄与率を求め
多変量解析 ~ 重回帰分析 ~ 2006 年 4 月 21 日 ( 金 ) 南慶典 重回帰分析とは? 重回帰分析とは複数の説明変数から目的変数との関係性を予測 評価説明変数 ( 数量データ ) は目的変数を説明するのに有効であるか得られた関係性より未知のデータの妥当性を判断する これを重回帰分析という つまり どんなことをするのか? 1 最小 2 乗法により重回帰モデルを想定 2 自由度調整済寄与率を求め
Probit , Mixed logit
 Probit, Mixed logit 2016/5/16 スタートアップゼミ #5 B4 後藤祥孝 1 0. 目次 Probit モデルについて 1. モデル概要 2. 定式化と理解 3. 推定 Mixed logit モデルについて 4. モデル概要 5. 定式化と理解 6. 推定 2 1.Probit 概要 プロビットモデルとは. 効用関数の誤差項に多変量正規分布を仮定したもの. 誤差項には様々な要因が存在するため,
Probit, Mixed logit 2016/5/16 スタートアップゼミ #5 B4 後藤祥孝 1 0. 目次 Probit モデルについて 1. モデル概要 2. 定式化と理解 3. 推定 Mixed logit モデルについて 4. モデル概要 5. 定式化と理解 6. 推定 2 1.Probit 概要 プロビットモデルとは. 効用関数の誤差項に多変量正規分布を仮定したもの. 誤差項には様々な要因が存在するため,
memo
 数理情報工学特論第一 機械学習とデータマイニング 4 章 : 教師なし学習 3 かしまひさし 鹿島久嗣 ( 数理 6 研 ) kashima@mist.i.~ DEPARTMENT OF MATHEMATICAL INFORMATICS 1 グラフィカルモデルについて学びます グラフィカルモデル グラフィカルラッソ グラフィカルラッソの推定アルゴリズム 2 グラフィカルモデル 3 教師なし学習の主要タスクは
数理情報工学特論第一 機械学習とデータマイニング 4 章 : 教師なし学習 3 かしまひさし 鹿島久嗣 ( 数理 6 研 ) kashima@mist.i.~ DEPARTMENT OF MATHEMATICAL INFORMATICS 1 グラフィカルモデルについて学びます グラフィカルモデル グラフィカルラッソ グラフィカルラッソの推定アルゴリズム 2 グラフィカルモデル 3 教師なし学習の主要タスクは
Microsoft Word - 補論3.2
 補論 3. 多変量 GARC モデル 07//6 新谷元嗣 藪友良 対数尤度関数 3 章 7 節では 変量の対数尤度を求めた ここでは多変量の場合 とくに 変量について対数尤度を求める 誤差項 は平均 0 で 次元の正規分布に従うとする 単純化のため 分散と共分散は時間を通じて一定としよう ( この仮定は後で変更される ) したがって ij から添え字 を除くことができる このとき と の尤度関数は
補論 3. 多変量 GARC モデル 07//6 新谷元嗣 藪友良 対数尤度関数 3 章 7 節では 変量の対数尤度を求めた ここでは多変量の場合 とくに 変量について対数尤度を求める 誤差項 は平均 0 で 次元の正規分布に従うとする 単純化のため 分散と共分散は時間を通じて一定としよう ( この仮定は後で変更される ) したがって ij から添え字 を除くことができる このとき と の尤度関数は
ベイズ統計入門
 ベイズ統計入門 条件付確率 事象 F が起こったことが既知であるという条件の下で E が起こる確率を条件付確率 (codtoal probablt) という P ( E F ) P ( E F ) P( F ) 定義式を変形すると 確率の乗法公式となる ( E F ) P( F ) P( E F ) P( E) P( F E) P 事象の独立 ある事象の生起する確率が 他のある事象が生起するかどうかによって変化しないとき
ベイズ統計入門 条件付確率 事象 F が起こったことが既知であるという条件の下で E が起こる確率を条件付確率 (codtoal probablt) という P ( E F ) P ( E F ) P( F ) 定義式を変形すると 確率の乗法公式となる ( E F ) P( F ) P( E F ) P( E) P( F E) P 事象の独立 ある事象の生起する確率が 他のある事象が生起するかどうかによって変化しないとき
ファイナンスのための数学基礎 第1回 オリエンテーション、ベクトル
 時系列分析 変量時系列モデルとその性質 担当 : 長倉大輔 ( ながくらだいすけ 時系列モデル 時系列モデルとは時系列データを生み出すメカニズムとなるものである これは実際には未知である 私たちにできるのは観測された時系列データからその背後にある時系列モデルを推測 推定するだけである 以下ではいくつかの代表的な時系列モデルを考察する 自己回帰モデル (Auoregressive Model もっとも頻繁に使われる時系列モデルは自己回帰モデル
時系列分析 変量時系列モデルとその性質 担当 : 長倉大輔 ( ながくらだいすけ 時系列モデル 時系列モデルとは時系列データを生み出すメカニズムとなるものである これは実際には未知である 私たちにできるのは観測された時系列データからその背後にある時系列モデルを推測 推定するだけである 以下ではいくつかの代表的な時系列モデルを考察する 自己回帰モデル (Auoregressive Model もっとも頻繁に使われる時系列モデルは自己回帰モデル
EBNと疫学
 推定と検定 57 ( 復習 ) 記述統計と推測統計 統計解析は大きく 2 つに分けられる 記述統計 推測統計 記述統計 観察集団の特性を示すもの 代表値 ( 平均値や中央値 ) や ばらつきの指標 ( 標準偏差など ) 図表を効果的に使う 推測統計 観察集団のデータから母集団の特性を 推定 する 平均 / 分散 / 係数値などの推定 ( 点推定 ) 点推定値のばらつきを調べる ( 区間推定 ) 検定統計量を用いた検定
推定と検定 57 ( 復習 ) 記述統計と推測統計 統計解析は大きく 2 つに分けられる 記述統計 推測統計 記述統計 観察集団の特性を示すもの 代表値 ( 平均値や中央値 ) や ばらつきの指標 ( 標準偏差など ) 図表を効果的に使う 推測統計 観察集団のデータから母集団の特性を 推定 する 平均 / 分散 / 係数値などの推定 ( 点推定 ) 点推定値のばらつきを調べる ( 区間推定 ) 検定統計量を用いた検定
モジュール1のまとめ
 数理統計学 第 0 回 復習 標本分散と ( 標本 ) 不偏分散両方とも 分散 というのが実情 二乗偏差計標本分散 = データ数 (0ページ) ( 標本 ) 不偏分散 = (03 ページ ) 二乗偏差計 データ数 - 分析ではこちらをとることが多い 復習 ここまで 実験結果 ( 万回 ) 平均 50Kg 標準偏差 0Kg 0 人 全体に小さすぎる > mea(jkke) [] 89.4373 標準偏差
数理統計学 第 0 回 復習 標本分散と ( 標本 ) 不偏分散両方とも 分散 というのが実情 二乗偏差計標本分散 = データ数 (0ページ) ( 標本 ) 不偏分散 = (03 ページ ) 二乗偏差計 データ数 - 分析ではこちらをとることが多い 復習 ここまで 実験結果 ( 万回 ) 平均 50Kg 標準偏差 0Kg 0 人 全体に小さすぎる > mea(jkke) [] 89.4373 標準偏差
Excelによる統計分析検定_知識編_小塚明_5_9章.indd
 第7章57766 検定と推定 サンプリングによって得られた標本から, 母集団の統計的性質に対して推測を行うことを統計的推測といいます 本章では, 推測統計の根幹をなす仮説検定と推定の基本的な考え方について説明します 前章までの知識を用いて, 具体的な分析を行います 本章以降の知識は操作編での操作に直接関連していますので, 少し聞きなれない言葉ですが, 帰無仮説 有意水準 棄却域 などの意味を理解して,
第7章57766 検定と推定 サンプリングによって得られた標本から, 母集団の統計的性質に対して推測を行うことを統計的推測といいます 本章では, 推測統計の根幹をなす仮説検定と推定の基本的な考え方について説明します 前章までの知識を用いて, 具体的な分析を行います 本章以降の知識は操作編での操作に直接関連していますので, 少し聞きなれない言葉ですが, 帰無仮説 有意水準 棄却域 などの意味を理解して,
Microsoft PowerPoint - 10.pptx
 m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
数学2 第3回 3次方程式:16世紀イタリア 2005/10/19
 数学 第 9 回方程式とシンメトリ - 010/1/01 数学 #9 010/1/01 1 前回紹介した 次方程式 の解法は どちらかというと ヒラメキ 的なもので 一般的と言えるものではありませんでした というのは 次方程式 の解法を知っても 5 次方程式 の問題に役立てることはできそうもないからです そこで より一般的な別解法はないものかと考えたのがラグランジュという人です ラグランジュの仕事によって
数学 第 9 回方程式とシンメトリ - 010/1/01 数学 #9 010/1/01 1 前回紹介した 次方程式 の解法は どちらかというと ヒラメキ 的なもので 一般的と言えるものではありませんでした というのは 次方程式 の解法を知っても 5 次方程式 の問題に役立てることはできそうもないからです そこで より一般的な別解法はないものかと考えたのがラグランジュという人です ラグランジュの仕事によって
統計学的画像再構成法である
 OSEM アルゴリズムの基礎論 第 1 章 確率 統計の基礎 1.13 最尤推定 やっと本命の最尤推定という言葉が出てきました. お待たせしました. この節はいままでの中で最も長く, 少し難しい内容も出てきます. がんばってください. これが終わるといよいよ本命の MLEM,OSEM の章です. ところで 尤 なる字はあまり見かけませんね. ゆう と読みます. いぬ ではありません!! この意味は
OSEM アルゴリズムの基礎論 第 1 章 確率 統計の基礎 1.13 最尤推定 やっと本命の最尤推定という言葉が出てきました. お待たせしました. この節はいままでの中で最も長く, 少し難しい内容も出てきます. がんばってください. これが終わるといよいよ本命の MLEM,OSEM の章です. ところで 尤 なる字はあまり見かけませんね. ゆう と読みます. いぬ ではありません!! この意味は
文章のトピック 文章には様々なトピックが存在する Cuomo to Push for Broader Ban on Assault Weapons 2012 Was Hottest Year in U.S. History 2
 自然言語処理プログラミング勉強会 7 - トピックモデル Graham Neubig 奈良先端科学技術大学院大学 (NAIST) 1 文章のトピック 文章には様々なトピックが存在する Cuomo to Push for Broader Ban on Assault Weapons 2012 Was Hottest Year in U.S. History 2 文章のトピック 文章には様々なトピックが存在する
自然言語処理プログラミング勉強会 7 - トピックモデル Graham Neubig 奈良先端科学技術大学院大学 (NAIST) 1 文章のトピック 文章には様々なトピックが存在する Cuomo to Push for Broader Ban on Assault Weapons 2012 Was Hottest Year in U.S. History 2 文章のトピック 文章には様々なトピックが存在する
Microsoft PowerPoint - mp11-02.pptx
 数理計画法第 2 回 塩浦昭義情報科学研究科准教授 shioura@dais.is.tohoku.ac.jp http://www.dais.is.tohoku.ac.jp/~shioura/teaching 前回の復習 数理計画とは? 数理計画 ( 復習 ) 数理計画問題とは? 狭義には : 数理 ( 数学 ) を使って計画を立てるための問題 広義には : 与えられた評価尺度に関して最も良い解を求める問題
数理計画法第 2 回 塩浦昭義情報科学研究科准教授 shioura@dais.is.tohoku.ac.jp http://www.dais.is.tohoku.ac.jp/~shioura/teaching 前回の復習 数理計画とは? 数理計画 ( 復習 ) 数理計画問題とは? 狭義には : 数理 ( 数学 ) を使って計画を立てるための問題 広義には : 与えられた評価尺度に関して最も良い解を求める問題
PowerPoint プレゼンテーション
 1/X Chapter 9: Linear correlation Cohen, B. H. (2007). In B. H. Cohen (Ed.), Explaining Psychological Statistics (3rd ed.) (pp. 255-285). NJ: Wiley. 概要 2/X 相関係数とは何か 相関係数の数式 検定 注意点 フィッシャーのZ 変換 信頼区間 相関係数の差の検定
1/X Chapter 9: Linear correlation Cohen, B. H. (2007). In B. H. Cohen (Ed.), Explaining Psychological Statistics (3rd ed.) (pp. 255-285). NJ: Wiley. 概要 2/X 相関係数とは何か 相関係数の数式 検定 注意点 フィッシャーのZ 変換 信頼区間 相関係数の差の検定
Microsoft Word - ミクロ経済学02-01費用関数.doc
 ミクロ経済学の シナリオ 講義の 3 分の 1 の時間で理解させる技術 国際派公務員養成所 第 2 章 生産者理論 生産者の利潤最大化行動について学び 供給曲線の導出プロセスを確認します 2-1. さまざまな費用曲線 (1) 総費用 (TC) 固定費用 (FC) 可変費用 (VC) 今回は さまざまな費用曲線を学んでいきましょう 費用曲線にはまず 総費用曲線があります 総費用 TC(Total Cost)
ミクロ経済学の シナリオ 講義の 3 分の 1 の時間で理解させる技術 国際派公務員養成所 第 2 章 生産者理論 生産者の利潤最大化行動について学び 供給曲線の導出プロセスを確認します 2-1. さまざまな費用曲線 (1) 総費用 (TC) 固定費用 (FC) 可変費用 (VC) 今回は さまざまな費用曲線を学んでいきましょう 費用曲線にはまず 総費用曲線があります 総費用 TC(Total Cost)
C プログラミング演習 1( 再 ) 2 講義では C プログラミングの基本を学び 演習では やや実践的なプログラミングを通して学ぶ
 C プログラミング演習 1( 再 ) 2 講義では C プログラミングの基本を学び 演習では やや実践的なプログラミングを通して学ぶ 今回のプログラミングの課題 次のステップによって 徐々に難易度の高いプログラムを作成する ( 参照用の番号は よくわかる C 言語 のページ番号 ) 1. キーボード入力された整数 10 個の中から最大のものを答える 2. 整数を要素とする配列 (p.57-59) に初期値を与えておき
C プログラミング演習 1( 再 ) 2 講義では C プログラミングの基本を学び 演習では やや実践的なプログラミングを通して学ぶ 今回のプログラミングの課題 次のステップによって 徐々に難易度の高いプログラムを作成する ( 参照用の番号は よくわかる C 言語 のページ番号 ) 1. キーボード入力された整数 10 個の中から最大のものを答える 2. 整数を要素とする配列 (p.57-59) に初期値を与えておき
日心TWS
 2017.09.22 (15:40~17:10) 日本心理学会第 81 回大会 TWS ベイジアンデータ解析入門 回帰分析を例に ベイジアンデータ解析 を体験してみる 広島大学大学院教育学研究科平川真 ベイジアン分析のステップ (p.24) 1) データの特定 2) モデルの定義 ( 解釈可能な ) モデルの作成 3) パラメタの事前分布の設定 4) ベイズ推論を用いて パラメタの値に確信度を再配分ベイズ推定
2017.09.22 (15:40~17:10) 日本心理学会第 81 回大会 TWS ベイジアンデータ解析入門 回帰分析を例に ベイジアンデータ解析 を体験してみる 広島大学大学院教育学研究科平川真 ベイジアン分析のステップ (p.24) 1) データの特定 2) モデルの定義 ( 解釈可能な ) モデルの作成 3) パラメタの事前分布の設定 4) ベイズ推論を用いて パラメタの値に確信度を再配分ベイズ推定
<4D F736F F D2094F795AA95FB92F68EAE82CC89F082AB95FB E646F63>
 力学 A 金曜 限 : 松田 微分方程式の解き方 微分方程式の解き方のところが分からなかったという声が多いので プリントにまとめます 数学的に厳密な話はしていないので 詳しくは数学の常微分方程式を扱っているテキストを参照してください また os s は既知とします. 微分方程式の分類 常微分方程式とは 独立変数 と その関数 その有限次の導関数 がみたす方程式 F,,, = のことです 次までの導関数を含む方程式を
力学 A 金曜 限 : 松田 微分方程式の解き方 微分方程式の解き方のところが分からなかったという声が多いので プリントにまとめます 数学的に厳密な話はしていないので 詳しくは数学の常微分方程式を扱っているテキストを参照してください また os s は既知とします. 微分方程式の分類 常微分方程式とは 独立変数 と その関数 その有限次の導関数 がみたす方程式 F,,, = のことです 次までの導関数を含む方程式を
Microsoft PowerPoint ppt
 情報科学第 07 回データ解析と統計代表値 平均 分散 度数分布表 1 本日の内容 データ解析とは 統計の基礎的な値 平均と分散 度数分布表とヒストグラム 講義のページ 第 7 回のその他の欄に 本日使用する教材があります 171025.xls というファイルがありますので ダウンロードして デスクトップに保存してください 2/45 はじめに データ解析とは この世の中には多くのデータが溢れています
情報科学第 07 回データ解析と統計代表値 平均 分散 度数分布表 1 本日の内容 データ解析とは 統計の基礎的な値 平均と分散 度数分布表とヒストグラム 講義のページ 第 7 回のその他の欄に 本日使用する教材があります 171025.xls というファイルがありますので ダウンロードして デスクトップに保存してください 2/45 はじめに データ解析とは この世の中には多くのデータが溢れています
Microsoft PowerPoint slide2forWeb.ppt [互換モード]
![Microsoft PowerPoint slide2forWeb.ppt [互換モード] Microsoft PowerPoint slide2forWeb.ppt [互換モード]](/thumbs/96/126561931.jpg) 講義内容 9..4 正規分布 ormal dstrbuto ガウス分布 Gaussa dstrbuto 中心極限定理 サンプルからの母集団統計量の推定 不偏推定量について 確率変数, 確率密度関数 確率密度関数 確率密度関数は積分したら. 平均 : 確率変数 分散 : 例 ある場所, ある日時での気温の確率. : 気温, : 気温 が起こる確率 標本平均とのアナロジー 類推 例 人の身長の分布と平均
講義内容 9..4 正規分布 ormal dstrbuto ガウス分布 Gaussa dstrbuto 中心極限定理 サンプルからの母集団統計量の推定 不偏推定量について 確率変数, 確率密度関数 確率密度関数 確率密度関数は積分したら. 平均 : 確率変数 分散 : 例 ある場所, ある日時での気温の確率. : 気温, : 気温 が起こる確率 標本平均とのアナロジー 類推 例 人の身長の分布と平均
カイ二乗フィット検定、パラメータの誤差
 統計的データ解析 008 008.. 林田清 ( 大阪大学大学院理学研究科 ) 問題 C (, ) ( x xˆ) ( y yˆ) σ x πσ σ y y Pabx (, ;,,, ) ˆ y σx σ y = dx exp exp πσx ただし xy ˆ ˆ はyˆ = axˆ+ bであらわされる直線モデル上の点 ( ˆ) ( ˆ ) ( ) x x y ax b y ax b Pabx (,
統計的データ解析 008 008.. 林田清 ( 大阪大学大学院理学研究科 ) 問題 C (, ) ( x xˆ) ( y yˆ) σ x πσ σ y y Pabx (, ;,,, ) ˆ y σx σ y = dx exp exp πσx ただし xy ˆ ˆ はyˆ = axˆ+ bであらわされる直線モデル上の点 ( ˆ) ( ˆ ) ( ) x x y ax b y ax b Pabx (,
Microsoft Word - Time Series Basic - Modeling.doc
 時系列解析入門 モデリング. 確率分布と統計的モデル が確率変数 (radom varable のとき すべての実数 R に対して となる確 率 Prob( が定められる これを の関数とみなして G( Prob ( とあらわすとき G( を確率変数 の分布関数 (probablt dstrbuto ucto と呼 ぶ 時系列解析で用いられる確率変数は通常連続型と呼ばれるもので その分布関数は (
時系列解析入門 モデリング. 確率分布と統計的モデル が確率変数 (radom varable のとき すべての実数 R に対して となる確 率 Prob( が定められる これを の関数とみなして G( Prob ( とあらわすとき G( を確率変数 の分布関数 (probablt dstrbuto ucto と呼 ぶ 時系列解析で用いられる確率変数は通常連続型と呼ばれるもので その分布関数は (
NLMIXED プロシジャを用いた生存時間解析 伊藤要二アストラゼネカ株式会社臨床統計 プログラミング グループグルプ Survival analysis using PROC NLMIXED Yohji Itoh Clinical Statistics & Programming Group, A
 NLMIXED プロシジャを用いた生存時間解析 伊藤要二アストラゼネカ株式会社臨床統計 プログラミング グループグルプ Survival analysis using PROC NLMIXED Yohji Itoh Clinical Statistics & Programming Group, AstraZeneca KK 要旨 : NLMIXEDプロシジャの最尤推定の機能を用いて 指数分布 Weibull
NLMIXED プロシジャを用いた生存時間解析 伊藤要二アストラゼネカ株式会社臨床統計 プログラミング グループグルプ Survival analysis using PROC NLMIXED Yohji Itoh Clinical Statistics & Programming Group, AstraZeneca KK 要旨 : NLMIXEDプロシジャの最尤推定の機能を用いて 指数分布 Weibull
Microsoft PowerPoint - comprog11.pptx
 Outline プログラミング演習第 回エッジを検出する on 3..4 電気通信大学情報理工学部知能機械工学科長井隆行 画像の本質 輝度の境目に情報あり! 画像の微分と 階微分 エッジ検出 画像をぼかす 本日の課題 画像の本質 エッジ抽出 画像の情報は境目にあり! エッジ 輝度が大きく変化しているところ ( 境界 ) 画像の情報はエッジにあり 輝度 人間の視覚系でも特定のエッジの方向に発火するニューロンが見つかっている
Outline プログラミング演習第 回エッジを検出する on 3..4 電気通信大学情報理工学部知能機械工学科長井隆行 画像の本質 輝度の境目に情報あり! 画像の微分と 階微分 エッジ検出 画像をぼかす 本日の課題 画像の本質 エッジ抽出 画像の情報は境目にあり! エッジ 輝度が大きく変化しているところ ( 境界 ) 画像の情報はエッジにあり 輝度 人間の視覚系でも特定のエッジの方向に発火するニューロンが見つかっている
Microsoft PowerPoint - H17-5時限(パターン認識).ppt
 パターン認識早稲田大学講義 平成 7 年度 独 産業技術総合研究所栗田多喜夫 赤穂昭太郎 統計的特徴抽出 パターン認識過程 特徴抽出 認識対象から何らかの特徴量を計測 抽出 する必要がある 認識に有効な情報 特徴 を抽出し 次元を縮小した効率の良い空間を構成する過程 文字認識 : スキャナ等で取り込んだ画像から文字の識別に必要な本質的な特徴のみを抽出 例 文字線の傾き 曲率 面積など 識別 与えられた未知の対象を
パターン認識早稲田大学講義 平成 7 年度 独 産業技術総合研究所栗田多喜夫 赤穂昭太郎 統計的特徴抽出 パターン認識過程 特徴抽出 認識対象から何らかの特徴量を計測 抽出 する必要がある 認識に有効な情報 特徴 を抽出し 次元を縮小した効率の良い空間を構成する過程 文字認識 : スキャナ等で取り込んだ画像から文字の識別に必要な本質的な特徴のみを抽出 例 文字線の傾き 曲率 面積など 識別 与えられた未知の対象を
統計的データ解析
 統計的データ解析 011 011.11.9 林田清 ( 大阪大学大学院理学研究科 ) 連続確率分布の平均値 分散 比較のため P(c ) c 分布 自由度 の ( カイ c 平均値 0, 標準偏差 1の正規分布 に従う変数 xの自乗和 c x =1 が従う分布を自由度 の分布と呼ぶ 一般に自由度の分布は f /1 c / / ( c ) {( c ) e }/ ( / ) 期待値 二乗 ) 分布 c
統計的データ解析 011 011.11.9 林田清 ( 大阪大学大学院理学研究科 ) 連続確率分布の平均値 分散 比較のため P(c ) c 分布 自由度 の ( カイ c 平均値 0, 標準偏差 1の正規分布 に従う変数 xの自乗和 c x =1 が従う分布を自由度 の分布と呼ぶ 一般に自由度の分布は f /1 c / / ( c ) {( c ) e }/ ( / ) 期待値 二乗 ) 分布 c
書式に示すように表示したい文字列をダブルクォーテーション (") の間に書けば良い ダブルクォーテーションで囲まれた文字列は 文字列リテラル と呼ばれる プログラム中では以下のように用いる プログラム例 1 printf(" 情報処理基礎 "); printf("c 言語の練習 "); printf
 情報処理基礎 C 言語についてプログラミング言語は 1950 年以前の機械語 アセンブリ言語 ( アセンブラ ) の開発を始めとして 現在までに非常に多くの言語が開発 発表された 情報処理基礎で習う C 言語は 1972 年にアメリカの AT&T ベル研究所でオペレーションシステムである UNIX を作成するために開発された C 言語は現在使われている多数のプログラミング言語に大きな影響を与えている
情報処理基礎 C 言語についてプログラミング言語は 1950 年以前の機械語 アセンブリ言語 ( アセンブラ ) の開発を始めとして 現在までに非常に多くの言語が開発 発表された 情報処理基礎で習う C 言語は 1972 年にアメリカの AT&T ベル研究所でオペレーションシステムである UNIX を作成するために開発された C 言語は現在使われている多数のプログラミング言語に大きな影響を与えている
Microsoft PowerPoint - e-stat(OLS).pptx
 経済統計学 ( 補足 ) 最小二乗法について 担当 : 小塚匡文 2015 年 11 月 19 日 ( 改訂版 ) 神戸大学経済学部 2015 年度後期開講授業 補足 : 最小二乗法 ( 単回帰分析 ) 1.( 単純 ) 回帰分析とは? 標本サイズTの2 変数 ( ここではXとY) のデータが存在 YをXで説明する回帰方程式を推定するための方法 Y: 被説明変数 ( または従属変数 ) X: 説明変数
経済統計学 ( 補足 ) 最小二乗法について 担当 : 小塚匡文 2015 年 11 月 19 日 ( 改訂版 ) 神戸大学経済学部 2015 年度後期開講授業 補足 : 最小二乗法 ( 単回帰分析 ) 1.( 単純 ) 回帰分析とは? 標本サイズTの2 変数 ( ここではXとY) のデータが存在 YをXで説明する回帰方程式を推定するための方法 Y: 被説明変数 ( または従属変数 ) X: 説明変数
Microsoft PowerPoint - R-stat-intro_12.ppt [互換モード]
![Microsoft PowerPoint - R-stat-intro_12.ppt [互換モード] Microsoft PowerPoint - R-stat-intro_12.ppt [互換モード]](/thumbs/101/151921093.jpg) R で統計解析入門 (12) 生存時間解析 中篇 準備 : データ DEP の読み込み 1. データ DEP を以下からダウンロードする http://www.cwk.zaq.ne.jp/fkhud708/files/dep.csv /fkh /d 2. ダウンロードした場所を把握する ここでは c:/temp とする 3. R を起動し,2. 2 の場所に移動し, データを読み込む 4. データ
R で統計解析入門 (12) 生存時間解析 中篇 準備 : データ DEP の読み込み 1. データ DEP を以下からダウンロードする http://www.cwk.zaq.ne.jp/fkhud708/files/dep.csv /fkh /d 2. ダウンロードした場所を把握する ここでは c:/temp とする 3. R を起動し,2. 2 の場所に移動し, データを読み込む 4. データ
【第一稿】論文執筆のためのワード活用術 (1).docx.docx
 ワード活用マニュアル レポート 論文の作成に欠かせない Word の使い方を勉強しましょう ワードはみんなの味方です 使いこなせればレポート 論文の強い味方になってくれます 就職してからも必要とされるスキルなのでこの機会に基本的なところをおさえちゃいましょう 各セクションの最後に練習問題があるので HP に添付されているワークシート (http://www.tufs.ac.jp/common/library/lc/word_work.docx)
ワード活用マニュアル レポート 論文の作成に欠かせない Word の使い方を勉強しましょう ワードはみんなの味方です 使いこなせればレポート 論文の強い味方になってくれます 就職してからも必要とされるスキルなのでこの機会に基本的なところをおさえちゃいましょう 各セクションの最後に練習問題があるので HP に添付されているワークシート (http://www.tufs.ac.jp/common/library/lc/word_work.docx)
基礎統計
 基礎統計 第 11 回講義資料 6.4.2 標本平均の差の標本分布 母平均の差 標本平均の差をみれば良い ただし, 母分散に依存するため場合分けをする 1 2 3 分散が既知分散が未知であるが等しい分散が未知であり等しいとは限らない 1 母分散が既知のとき が既知 標準化変量 2 母分散が未知であり, 等しいとき 分散が未知であるが, 等しいということは分かっているとき 標準化変量 自由度 の t
基礎統計 第 11 回講義資料 6.4.2 標本平均の差の標本分布 母平均の差 標本平均の差をみれば良い ただし, 母分散に依存するため場合分けをする 1 2 3 分散が既知分散が未知であるが等しい分散が未知であり等しいとは限らない 1 母分散が既知のとき が既知 標準化変量 2 母分散が未知であり, 等しいとき 分散が未知であるが, 等しいということは分かっているとき 標準化変量 自由度 の t
統計学 - 社会統計の基礎 - 正規分布 標準正規分布累積分布関数の逆関数 t 分布正規分布に従うサンプルの平均の信頼区間 担当 : 岸 康人 資料ページ :
 統計学 - 社会統計の基礎 - 正規分布 標準正規分布累積分布関数の逆関数 t 分布正規分布に従うサンプルの平均の信頼区間 担当 : 岸 康人 資料ページ : https://goo.gl/qw1djw 正規分布 ( 復習 ) 正規分布 (Normal Distribution)N (μ, σ 2 ) 別名 : ガウス分布 (Gaussian Distribution) 密度関数 Excel:= NORM.DIST
統計学 - 社会統計の基礎 - 正規分布 標準正規分布累積分布関数の逆関数 t 分布正規分布に従うサンプルの平均の信頼区間 担当 : 岸 康人 資料ページ : https://goo.gl/qw1djw 正規分布 ( 復習 ) 正規分布 (Normal Distribution)N (μ, σ 2 ) 別名 : ガウス分布 (Gaussian Distribution) 密度関数 Excel:= NORM.DIST
ビジネス統計 統計基礎とエクセル分析 正誤表
 ビジネス統計統計基礎とエクセル分析 ビジネス統計スペシャリスト エクセル分析スペシャリスト 公式テキスト正誤表と学習用データ更新履歴 平成 30 年 5 月 14 日現在 公式テキスト正誤表 頁場所誤正修正 6 知識編第 章 -3-3 最頻値の解説内容 たとえば, 表.1 のデータであれば, 最頻値は 167.5cm というたとえば, 表.1 のデータであれば, 最頻値は 165.0cm ということになります
ビジネス統計統計基礎とエクセル分析 ビジネス統計スペシャリスト エクセル分析スペシャリスト 公式テキスト正誤表と学習用データ更新履歴 平成 30 年 5 月 14 日現在 公式テキスト正誤表 頁場所誤正修正 6 知識編第 章 -3-3 最頻値の解説内容 たとえば, 表.1 のデータであれば, 最頻値は 167.5cm というたとえば, 表.1 のデータであれば, 最頻値は 165.0cm ということになります
スライド 1
 データ解析特論第 5 回 ( 全 15 回 ) 2012 年 10 月 30 日 ( 火 ) 情報エレクトロニクス専攻横田孝義 1 をもっとやります 2 第 2 回 3 データマイニングの分野ではマクロ ( 巨視的 ) な視点で全体を捉える能力が求められる 1. コンピュータは数値の集合として全体を把握していますので 意味ある情報として全体を見ることが不得意 2. 逆に人間には もともと空間的に全体像を捉える能力が得意
データ解析特論第 5 回 ( 全 15 回 ) 2012 年 10 月 30 日 ( 火 ) 情報エレクトロニクス専攻横田孝義 1 をもっとやります 2 第 2 回 3 データマイニングの分野ではマクロ ( 巨視的 ) な視点で全体を捉える能力が求められる 1. コンピュータは数値の集合として全体を把握していますので 意味ある情報として全体を見ることが不得意 2. 逆に人間には もともと空間的に全体像を捉える能力が得意
DVIOUT-SS_Ma
 第 章 微分方程式 ニュートンはリンゴが落ちるのを見て万有引力を発見した という有名な逸話があります 無重力の宇宙船の中ではリンゴは落ちないで静止していることを考えると 重力が働くと始め静止しているものが動き出して そのスピードはどんどん大きくなる つまり速度の変化が現れることがわかります 速度は一般に時間と共に変化します 速度の瞬間的変化の割合を加速度といい で定義しましょう 速度が変化する, つまり加速度がでなくなるためにはその原因があり
第 章 微分方程式 ニュートンはリンゴが落ちるのを見て万有引力を発見した という有名な逸話があります 無重力の宇宙船の中ではリンゴは落ちないで静止していることを考えると 重力が働くと始め静止しているものが動き出して そのスピードはどんどん大きくなる つまり速度の変化が現れることがわかります 速度は一般に時間と共に変化します 速度の瞬間的変化の割合を加速度といい で定義しましょう 速度が変化する, つまり加速度がでなくなるためにはその原因があり
Microsoft PowerPoint - sousa pptx
 はじめに 情報機器の操作 ( 第 2 回 ) 産業技術科学科多 知正 htada@kyokyo-u.ac.jp A323 この講義のWWWページ http://teched.kyokyo-u.ac.jp/~htada/class/sousa/ 演習で使うデータ等はここにおいておきます お気に り に登録しておいてください 別に気に ってなくてもしてください 2011/4/19 1 2011/4/19
はじめに 情報機器の操作 ( 第 2 回 ) 産業技術科学科多 知正 htada@kyokyo-u.ac.jp A323 この講義のWWWページ http://teched.kyokyo-u.ac.jp/~htada/class/sousa/ 演習で使うデータ等はここにおいておきます お気に り に登録しておいてください 別に気に ってなくてもしてください 2011/4/19 1 2011/4/19
Microsoft PowerPoint - stat-2014-[9] pptx
![Microsoft PowerPoint - stat-2014-[9] pptx Microsoft PowerPoint - stat-2014-[9] pptx](/thumbs/49/25555771.jpg) 統計学 第 17 回 講義 母平均の区間推定 Part-1 014 年 6 17 ( )6-7 限 担当教員 : 唐渡 広志 ( からと こうじ ) 研究室 : 経済学研究棟 4 階 43 号室 email: kkarato@eco.u-toyama.ac.j website: htt://www3.u-toyama.ac.j/kkarato/ 1 講義の目的 標本平均は正規分布に従うという性質を
統計学 第 17 回 講義 母平均の区間推定 Part-1 014 年 6 17 ( )6-7 限 担当教員 : 唐渡 広志 ( からと こうじ ) 研究室 : 経済学研究棟 4 階 43 号室 email: kkarato@eco.u-toyama.ac.j website: htt://www3.u-toyama.ac.j/kkarato/ 1 講義の目的 標本平均は正規分布に従うという性質を
Microsoft PowerPoint - å®�æ−•è©¦é¨fi3ㆮ対ç�Œ.pptx
 C言語の繰り返し処理 for文と while文と do文 臼杵 潤 0) 準備 変数の加減算 int a, b=10; // a= a = 0; a = a+1; // a= a += 1; // a= // a= a ++; a = a + b; // a= a += b; // a= // a= a --; 下を1行ずつ実行すると それぞれ aの値はどう変わるか 0 1 2 3 13 23 22
C言語の繰り返し処理 for文と while文と do文 臼杵 潤 0) 準備 変数の加減算 int a, b=10; // a= a = 0; a = a+1; // a= a += 1; // a= // a= a ++; a = a + b; // a= a += b; // a= // a= a --; 下を1行ずつ実行すると それぞれ aの値はどう変わるか 0 1 2 3 13 23 22
Information Theory
 前回の復習 講義の概要 chapter 1: 情報を測る... エントロピーの定義 確率変数 X の ( 一次 ) エントロピー M H 1 (X) = p i log 2 p i (bit) i=1 M は実現値の個数,p i は i 番目の実現値が取られる確率 実現値 確率 表 裏 0.5 0.5 H 1 X = 0.5 log 2 0.5 0.5log 2 0.5 = 1bit 1 練習問題の解答
前回の復習 講義の概要 chapter 1: 情報を測る... エントロピーの定義 確率変数 X の ( 一次 ) エントロピー M H 1 (X) = p i log 2 p i (bit) i=1 M は実現値の個数,p i は i 番目の実現値が取られる確率 実現値 確率 表 裏 0.5 0.5 H 1 X = 0.5 log 2 0.5 0.5log 2 0.5 = 1bit 1 練習問題の解答
Microsoft Word - Stattext07.doc
 7 章正規分布 正規分布 (ormal dstrbuto) は 偶発的なデータのゆらぎによって生じる統計学で最も基本的な確率分布です この章では正規分布についてその性質を詳しく見て行きましょう 7. 一般の正規分布正規分布は 平均と分散の つの量によって完全に特徴付けられています 平均 μ 分散 の正規分布は N ( μ, ) 分布とも書かれます ここに N は ormal の頭文字を 表わしています
7 章正規分布 正規分布 (ormal dstrbuto) は 偶発的なデータのゆらぎによって生じる統計学で最も基本的な確率分布です この章では正規分布についてその性質を詳しく見て行きましょう 7. 一般の正規分布正規分布は 平均と分散の つの量によって完全に特徴付けられています 平均 μ 分散 の正規分布は N ( μ, ) 分布とも書かれます ここに N は ormal の頭文字を 表わしています
Microsoft Word - apstattext04.docx
 4 章母集団と指定値との量的データの検定 4.1 検定手順今までは質的データの検定の方法を学んで来ましたが これからは量的データについてよく利用される方法を説明します 量的データでは データの分布が正規分布か否かで検定の方法が著しく異なります この章ではまずデータの分布の正規性を調べる方法を述べ 次にデータの平均値または中央値がある指定された値と違うかどうかの検定方法を説明します 以下の図 4.1.1
4 章母集団と指定値との量的データの検定 4.1 検定手順今までは質的データの検定の方法を学んで来ましたが これからは量的データについてよく利用される方法を説明します 量的データでは データの分布が正規分布か否かで検定の方法が著しく異なります この章ではまずデータの分布の正規性を調べる方法を述べ 次にデータの平均値または中央値がある指定された値と違うかどうかの検定方法を説明します 以下の図 4.1.1
振動学特論火曜 1 限 TA332J 藤井康介 6 章スペクトルの平滑化 スペクトルの平滑化とはギザギザした地震波のフーリエ スペクトルやパワ スペクトルでは正確にスペクトルの山がどこにあるかはよく分からない このようなスペクトルから不純なものを取り去って 本当の性質を浮き彫
 6 章スペクトルの平滑化 スペクトルの平滑化とはギザギザした地震波のフーリエ スペクトルやパワ スペクトルでは正確にスペクトルの山がどこにあるかはよく分からない このようなスペクトルから不純なものを取り去って 本当の性質を浮き彫りにするために スペクトルを滑らかにする操作のことをいう 6.1 合積のフーリエ変換スペクトルの平滑化を行う際に必要な 合積とそのフーリエ変換について説明する 6.2 データ
6 章スペクトルの平滑化 スペクトルの平滑化とはギザギザした地震波のフーリエ スペクトルやパワ スペクトルでは正確にスペクトルの山がどこにあるかはよく分からない このようなスペクトルから不純なものを取り去って 本当の性質を浮き彫りにするために スペクトルを滑らかにする操作のことをいう 6.1 合積のフーリエ変換スペクトルの平滑化を行う際に必要な 合積とそのフーリエ変換について説明する 6.2 データ
Taro-プレミアム第66号PDF.jtd
 ソフトテニス誰でも 10 倍上達しますプレミアム PDF 版 no66 攻め 守りの新機軸 著作制作 :OYA 転載転用禁止です 2013/2/25 編 1, 攻め 守り後衛と対峙する前衛にとっては 相手後衛が攻撃してくるのか 守ってくるのかは とても重要な問題です 相手後衛が攻めてくるのであれば ポジション的に守らなければならないし 相手が守りでくるならば スマッシュを待ったり 飛び出したりする準備をしなければいけません
ソフトテニス誰でも 10 倍上達しますプレミアム PDF 版 no66 攻め 守りの新機軸 著作制作 :OYA 転載転用禁止です 2013/2/25 編 1, 攻め 守り後衛と対峙する前衛にとっては 相手後衛が攻撃してくるのか 守ってくるのかは とても重要な問題です 相手後衛が攻めてくるのであれば ポジション的に守らなければならないし 相手が守りでくるならば スマッシュを待ったり 飛び出したりする準備をしなければいけません
Microsoft Word - 1 color Normalization Document _Agilent version_ .doc
 color 実験の Normalization color 実験で得られた複数のアレイデータを相互比較するためには Normalization( 正規化 ) が必要です 2 つのサンプルを異なる色素でラベル化し 競合ハイブリダイゼーションさせる 2color 実験では 基本的に Dye Normalization( 色素補正 ) が適用されますが color 実験では データの特徴と実験の目的 (
color 実験の Normalization color 実験で得られた複数のアレイデータを相互比較するためには Normalization( 正規化 ) が必要です 2 つのサンプルを異なる色素でラベル化し 競合ハイブリダイゼーションさせる 2color 実験では 基本的に Dye Normalization( 色素補正 ) が適用されますが color 実験では データの特徴と実験の目的 (
スライド 1
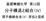 基礎無機化学第 回 分子構造と結合 (IV) 原子価結合法 (II): 昇位と混成 本日のポイント 昇位と混成 s 軌道と p 軌道を混ぜて, 新しい軌道を作る sp 3 混成 : 正四面体型 sp 混成 : 三角形 (p 軌道が つ残る ) sp 混成 : 直線形 (p 軌道が つ残る ) 多重結合との関係炭素などでは以下が基本 ( たまに違う ) 二重結合 sp 混成三重結合 sp 混成 逆に,
基礎無機化学第 回 分子構造と結合 (IV) 原子価結合法 (II): 昇位と混成 本日のポイント 昇位と混成 s 軌道と p 軌道を混ぜて, 新しい軌道を作る sp 3 混成 : 正四面体型 sp 混成 : 三角形 (p 軌道が つ残る ) sp 混成 : 直線形 (p 軌道が つ残る ) 多重結合との関係炭素などでは以下が基本 ( たまに違う ) 二重結合 sp 混成三重結合 sp 混成 逆に,
PowerPoint Presentation
 付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
情報量と符号化
 I. ここでの目的情報量の単位はビットで 2 種の文字を持つ記号の情報量が 1 ビットです ここでは 一般に n 種の文字を持つ記号の情報量を定義します 次に 出現する文字に偏りがある場合の平均情報量を定義します この平均情報量は 記号を適当に 0,1 で符号化する場合の平均符号長にほぼ等しくなることがわかります II. 情報量とは A. bit 情報量の単位としてbitが利用されます 1bitは0か1の情報を運びます
I. ここでの目的情報量の単位はビットで 2 種の文字を持つ記号の情報量が 1 ビットです ここでは 一般に n 種の文字を持つ記号の情報量を定義します 次に 出現する文字に偏りがある場合の平均情報量を定義します この平均情報量は 記号を適当に 0,1 で符号化する場合の平均符号長にほぼ等しくなることがわかります II. 情報量とは A. bit 情報量の単位としてbitが利用されます 1bitは0か1の情報を運びます
次に示す数値の並びを昇順にソートするものとする このソートでは配列の末尾側から操作を行っていく まず 末尾の数値 9 と 8 に着目する 昇順にソートするので この値を交換すると以下の数値の並びになる 次に末尾側から 2 番目と 3 番目の 1
 4. ソート ( 教科書 p.205-p.273) 整列すなわちソートは アプリケーションを作成する際には良く使われる基本的な操作であり 今までに数多くのソートのアルゴリズムが考えられてきた 今回はこれらソートのアルゴリズムについて学習していく ソートとはソートとは与えられたデータの集合をキーとなる項目の値の大小関係に基づき 一定の順序で並べ替える操作である ソートには図 1 に示すように キーの値の小さいデータを先頭に並べる
4. ソート ( 教科書 p.205-p.273) 整列すなわちソートは アプリケーションを作成する際には良く使われる基本的な操作であり 今までに数多くのソートのアルゴリズムが考えられてきた 今回はこれらソートのアルゴリズムについて学習していく ソートとはソートとは与えられたデータの集合をキーとなる項目の値の大小関係に基づき 一定の順序で並べ替える操作である ソートには図 1 に示すように キーの値の小さいデータを先頭に並べる
Microsoft Word - histgram.doc
 1. ヒストグラムと等高線図 データ解析の一つの目的に データ源の分布を求めることがある しかし 最初から特定の分布を仮定して分析を進めることは結構危険 ヒストグラムは1 次元確率分布を推定する一番わかりやすい方法 ヒストグラムで重要なのは区切りの幅 これ次第で結果が変わる Excel では標準アドインソフト ( 分析ツール ) を使うと簡単にヒストグラムが作成できる 1.1 分析ツールを使えるようにする
1. ヒストグラムと等高線図 データ解析の一つの目的に データ源の分布を求めることがある しかし 最初から特定の分布を仮定して分析を進めることは結構危険 ヒストグラムは1 次元確率分布を推定する一番わかりやすい方法 ヒストグラムで重要なのは区切りの幅 これ次第で結果が変わる Excel では標準アドインソフト ( 分析ツール ) を使うと簡単にヒストグラムが作成できる 1.1 分析ツールを使えるようにする
したがって このモデルではの長さをもつ潜在履歴 latent history が存在し 同様に と指標化して扱うことができる 以下では 潜在的に起こりうる履歴を潜在履歴 latent history 実際にデ ータとして記録された履歴を記録履歴 recorded history ということにする M
 Bayesian Inference with ecological applications Chapter 10 Bayesian Inference with ecological applications 輪読会 潜在的な事象を扱うための多項分布モデル Latent Multinomial Models 本章では 記録した頻度データが多項分布に従う潜在的な変数を集約したものと考えられるときの
Bayesian Inference with ecological applications Chapter 10 Bayesian Inference with ecological applications 輪読会 潜在的な事象を扱うための多項分布モデル Latent Multinomial Models 本章では 記録した頻度データが多項分布に従う潜在的な変数を集約したものと考えられるときの
Microsoft PowerPoint - mp11-06.pptx
 数理計画法第 6 回 塩浦昭義情報科学研究科准教授 shioura@dais.is.tohoku.ac.jp http://www.dais.is.tohoku.ac.jp/~shioura/teaching 第 5 章組合せ計画 5.2 分枝限定法 組合せ計画問題 組合せ計画問題とは : 有限個の もの の組合せの中から, 目的関数を最小または最大にする組合せを見つける問題 例 1: 整数計画問題全般
数理計画法第 6 回 塩浦昭義情報科学研究科准教授 shioura@dais.is.tohoku.ac.jp http://www.dais.is.tohoku.ac.jp/~shioura/teaching 第 5 章組合せ計画 5.2 分枝限定法 組合せ計画問題 組合せ計画問題とは : 有限個の もの の組合せの中から, 目的関数を最小または最大にする組合せを見つける問題 例 1: 整数計画問題全般
Microsoft PowerPoint - statistics pptx
 統計学 第 16 回 講義 母平均の区間推定 Part-1 016 年 6 10 ( ) 1 限 担当教員 : 唐渡 広志 ( からと こうじ ) 研究室 : 経済学研究棟 4 階 43 号室 email: kkarato@eco.u-toyama.ac.jp website: http://www3.u-toyama.ac.jp/kkarato/ 1 講義の目的 標本平均は正規分布に従うという性質を
統計学 第 16 回 講義 母平均の区間推定 Part-1 016 年 6 10 ( ) 1 限 担当教員 : 唐渡 広志 ( からと こうじ ) 研究室 : 経済学研究棟 4 階 43 号室 email: kkarato@eco.u-toyama.ac.jp website: http://www3.u-toyama.ac.jp/kkarato/ 1 講義の目的 標本平均は正規分布に従うという性質を
Microsoft PowerPoint - 第3回2.ppt
 講義内容 講義内容 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 ベクトルの直交性 3
講義内容 講義内容 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 ベクトルの直交性 3
Microsoft PowerPoint - 基礎・経済統計6.ppt
 . 確率変数 基礎 経済統計 6 確率分布 事象を数値化したもの ( 事象ー > 数値 の関数 自然に数値されている場合 さいころの目 量的尺度 数値化が必要な場合 質的尺度, 順序的尺度 それらの尺度に数値を割り当てる 例えば, コインの表が出たら, 裏なら 0. 離散確率変数と連続確率変数 確率変数の値 連続値をとるもの 身長, 体重, 実質 GDP など とびとびの値 離散値をとるもの 新生児の性別
. 確率変数 基礎 経済統計 6 確率分布 事象を数値化したもの ( 事象ー > 数値 の関数 自然に数値されている場合 さいころの目 量的尺度 数値化が必要な場合 質的尺度, 順序的尺度 それらの尺度に数値を割り当てる 例えば, コインの表が出たら, 裏なら 0. 離散確率変数と連続確率変数 確率変数の値 連続値をとるもの 身長, 体重, 実質 GDP など とびとびの値 離散値をとるもの 新生児の性別
学習指導要領
 (1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 絶対値の意味を理解し適切な処理することができる 例題 1-3 の絶対値をはずせ 展開公式 ( a + b ) ( a - b ) = a 2 - b 2 を利用して根号を含む分数の分母を有理化することができる 例題 5 5 + 2 の分母を有理化せよ 実数の整数部分と小数部分の表し方を理解している
(1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 絶対値の意味を理解し適切な処理することができる 例題 1-3 の絶対値をはずせ 展開公式 ( a + b ) ( a - b ) = a 2 - b 2 を利用して根号を含む分数の分母を有理化することができる 例題 5 5 + 2 の分母を有理化せよ 実数の整数部分と小数部分の表し方を理解している
第 3 回講義の項目と概要 統計的手法入門 : 品質のばらつきを解析する 平均と標準偏差 (P30) a) データは平均を見ただけではわからない 平均が同じだからといって 同一視してはいけない b) データのばらつきを示す 標準偏差 にも注目しよう c) 平均
 第 3 回講義の項目と概要 016.8.9 1.3 統計的手法入門 : 品質のばらつきを解析する 1.3.1 平均と標準偏差 (P30) a) データは平均を見ただけではわからない 平均が同じだからといって 同一視してはいけない b) データのばらつきを示す 標準偏差 にも注目しよう c) 平均 :AVERAGE 関数, 標準偏差 :STDEVP 関数とSTDEVという関数 1 取得したデータそのものの標準偏差
第 3 回講義の項目と概要 016.8.9 1.3 統計的手法入門 : 品質のばらつきを解析する 1.3.1 平均と標準偏差 (P30) a) データは平均を見ただけではわからない 平均が同じだからといって 同一視してはいけない b) データのばらつきを示す 標準偏差 にも注目しよう c) 平均 :AVERAGE 関数, 標準偏差 :STDEVP 関数とSTDEVという関数 1 取得したデータそのものの標準偏差
分析のステップ Step 1: Y( 目的変数 ) に対する値の順序を確認 Step 2: モデルのあてはめ を実行 適切なモデルの指定 Step 3: オプションを指定し オッズ比とその信頼区間を表示 以下 このステップに沿って JMP の操作をご説明します Step 1: Y( 目的変数 ) の
 JMP によるオッズ比 リスク比 ( ハザード比 ) の算出と注意点 SAS Institute Japan 株式会社 JMP ジャパン事業部 2011 年 10 月改定 1. はじめに 本文書は JMP でロジスティック回帰モデルによるオッズ比 比例ハザードモデルによるリスク比 それぞれに対する信頼区間を求める操作方法と注意点を述べたものです 本文書は JMP 7 以降のバージョンに対応しております
JMP によるオッズ比 リスク比 ( ハザード比 ) の算出と注意点 SAS Institute Japan 株式会社 JMP ジャパン事業部 2011 年 10 月改定 1. はじめに 本文書は JMP でロジスティック回帰モデルによるオッズ比 比例ハザードモデルによるリスク比 それぞれに対する信頼区間を求める操作方法と注意点を述べたものです 本文書は JMP 7 以降のバージョンに対応しております
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生
 0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
はじめに この式を見るとインドの人たちは間髪を入れずに という答が出るそうです インドの小学校の子どもたちは までのかけ算の答をすべて丸暗記しているからです ( 日本では 9 9 までのかけ算の答を九九の暗唱で覚えますね ) そればかりではありません 6
 いちきゅういちきゅう スマッシュ暗算 1 9 1 9 対象 : 小 6 ~ 大人 考える学習をすすめる会 こだま塾 信谷英明 はじめに 1 9 1 9 この式を見るとインドの人たちは間髪を入れずに 3 6 1 という答が出るそうです インドの小学校の子どもたちは 1 9 1 9 までのかけ算の答をすべて丸暗記しているからです ( 日本では 9 9 までのかけ算の答を九九の暗唱で覚えますね ) そればかりではありません
いちきゅういちきゅう スマッシュ暗算 1 9 1 9 対象 : 小 6 ~ 大人 考える学習をすすめる会 こだま塾 信谷英明 はじめに 1 9 1 9 この式を見るとインドの人たちは間髪を入れずに 3 6 1 という答が出るそうです インドの小学校の子どもたちは 1 9 1 9 までのかけ算の答をすべて丸暗記しているからです ( 日本では 9 9 までのかけ算の答を九九の暗唱で覚えますね ) そればかりではありません
SAP11_03
 第 3 回 音声音響信号処理 ( 線形予測分析と自己回帰モデル ) 亀岡弘和 東京大学大学院情報理工学系研究科日本電信電話株式会社 NTT コミュニケーション科学基礎研究所 講義内容 ( キーワード ) 信号処理 符号化 標準化の実用システム例の紹介情報通信の基本 ( 誤り検出 訂正符号 変調 IP) 符号化技術の基本 ( 量子化 予測 変換 圧縮 ) 音声分析 合成 認識 強調 音楽信号処理統計的信号処理の基礎
第 3 回 音声音響信号処理 ( 線形予測分析と自己回帰モデル ) 亀岡弘和 東京大学大学院情報理工学系研究科日本電信電話株式会社 NTT コミュニケーション科学基礎研究所 講義内容 ( キーワード ) 信号処理 符号化 標準化の実用システム例の紹介情報通信の基本 ( 誤り検出 訂正符号 変調 IP) 符号化技術の基本 ( 量子化 予測 変換 圧縮 ) 音声分析 合成 認識 強調 音楽信号処理統計的信号処理の基礎
STEP1 1 案件の選び方 FB 広告であなたが扱うアフィリエイト案件を決めていきます リスティングにしても SEO にしても案件選びは重要ですが FB 広告でアフィリエイトをしていく場合には特にこの案件選びが重要になってきます 詳しくは後述しますが この案件選びを間違ってしまうと いくら広告費を
 STEP1 1 案件の選び方 FB 広告であなたが扱うアフィリエイト案件を決めていきます リスティングにしても SEO にしても案件選びは重要ですが FB 広告でアフィリエイトをしていく場合には特にこの案件選びが重要になってきます 詳しくは後述しますが この案件選びを間違ってしまうと いくら広告費を使っても全然売れない なんてことになりかねませんので 注意してください 案件決定のポイントはしっかり押さえておいてくださいね
STEP1 1 案件の選び方 FB 広告であなたが扱うアフィリエイト案件を決めていきます リスティングにしても SEO にしても案件選びは重要ですが FB 広告でアフィリエイトをしていく場合には特にこの案件選びが重要になってきます 詳しくは後述しますが この案件選びを間違ってしまうと いくら広告費を使っても全然売れない なんてことになりかねませんので 注意してください 案件決定のポイントはしっかり押さえておいてくださいね
不偏推定量
 不偏推定量 情報科学の補足資料 018 年 6 月 7 日藤本祥二 統計的推定 (statistical estimatio) 確率分布が理論的に分かっている標本統計量を利用する 確率分布の期待値の値をそのまま推定値とするのが点推定 ( 信頼度 0%) 点推定に ± で幅を持たせて信頼度を上げたものが区間推定 持たせた幅のことを誤差 (error) と呼ぶ 信頼度 (cofidece level)
不偏推定量 情報科学の補足資料 018 年 6 月 7 日藤本祥二 統計的推定 (statistical estimatio) 確率分布が理論的に分かっている標本統計量を利用する 確率分布の期待値の値をそのまま推定値とするのが点推定 ( 信頼度 0%) 点推定に ± で幅を持たせて信頼度を上げたものが区間推定 持たせた幅のことを誤差 (error) と呼ぶ 信頼度 (cofidece level)
PowerPoint プレゼンテーション
 49 概要 50 は まとめ記事 などの長い文章の方が向いています 本文は 500 文字以上がおすすめです 画像を使って見やすいページを作成しましょう ブログ記事タイトル の特徴 SEO ブログ記事作成の流れ 写真 使い分け 長い文章に最適 ブログ記事タイトル記入 まとめ記事や閲覧者の役に立つ情報など リード文 を書く 目次 使用する機能 通常ブログ機能 アイキャッチ画像文字色変更 リンク追加 自由な画像追加
49 概要 50 は まとめ記事 などの長い文章の方が向いています 本文は 500 文字以上がおすすめです 画像を使って見やすいページを作成しましょう ブログ記事タイトル の特徴 SEO ブログ記事作成の流れ 写真 使い分け 長い文章に最適 ブログ記事タイトル記入 まとめ記事や閲覧者の役に立つ情報など リード文 を書く 目次 使用する機能 通常ブログ機能 アイキャッチ画像文字色変更 リンク追加 自由な画像追加
経営統計学
 5 章基本統計量 3.5 節で量的データの集計方法について簡単に触れ 前章でデータの分布について学びましたが データの特徴をつの数値で示すこともよく行なわれます これは統計量と呼ばれ 主に分布の中心や拡がりなどを表わします この章ではよく利用される分布の統計量を特徴で分類して説明します 数式表示を統一的に行なうために データの個数を 個とし それらを,,, と表わすことにします ここで学ぶ統計量は統計分析の基礎となっており
5 章基本統計量 3.5 節で量的データの集計方法について簡単に触れ 前章でデータの分布について学びましたが データの特徴をつの数値で示すこともよく行なわれます これは統計量と呼ばれ 主に分布の中心や拡がりなどを表わします この章ではよく利用される分布の統計量を特徴で分類して説明します 数式表示を統一的に行なうために データの個数を 個とし それらを,,, と表わすことにします ここで学ぶ統計量は統計分析の基礎となっており
<4D F736F F D E4F8E9F82C982A882AF82E98D7397F1>
 3 三次における行列 要旨高校では ほとんど 2 2 の正方行列しか扱ってなく 三次の正方行列について考えてみたかったため 数 C で学んだ定理を三次の正方行列に応用して 自分たちで仮説を立てて求めていったら 空間における回転移動を表す行列 三次のケーリー ハミルトンの定理 三次における逆行列を求めたり 仮説をたてることができた. 目的 数 C で学んだ定理を三次の正方行列に応用する 2. 概要目的の到達点として
3 三次における行列 要旨高校では ほとんど 2 2 の正方行列しか扱ってなく 三次の正方行列について考えてみたかったため 数 C で学んだ定理を三次の正方行列に応用して 自分たちで仮説を立てて求めていったら 空間における回転移動を表す行列 三次のケーリー ハミルトンの定理 三次における逆行列を求めたり 仮説をたてることができた. 目的 数 C で学んだ定理を三次の正方行列に応用する 2. 概要目的の到達点として
超入門対称座標法 皆様こん は今回の御題は 対称座標法 です この解析手法を解説したものは沢山有りますが ヨクワカラン! というものが多いと思います そこで毎度の事ですが 骨流トンデモ解説擬き を作りました この記載が何かの参考になる事を期待します サイタマ ドズニーランド 大学 SDU 学長鹿の骨
 超入門対称座標法 皆様こん は今回の御題は 対称座標法 です この解析手法を解説したものは沢山有りますが ヨクワカラン! というものが多いと思います そこで毎度の事ですが 骨流トンデモ解説擬き を作りました この記載が何かの参考になる事を期待します サイタマ ドズニーランド 大学 SDU 学長鹿の骨記平成鹿年骨月吉日一説に依ると SDU はさいたまドスケベ大学ではないか? と言う話が有るが あながち間違いでは無い
超入門対称座標法 皆様こん は今回の御題は 対称座標法 です この解析手法を解説したものは沢山有りますが ヨクワカラン! というものが多いと思います そこで毎度の事ですが 骨流トンデモ解説擬き を作りました この記載が何かの参考になる事を期待します サイタマ ドズニーランド 大学 SDU 学長鹿の骨記平成鹿年骨月吉日一説に依ると SDU はさいたまドスケベ大学ではないか? と言う話が有るが あながち間違いでは無い
Microsoft Word - VBA基礎(6).docx
 あるクラスの算数の平均点と理科の平均点を読み込み 総点を計算するプログラムを考えてみましょう 一クラスだけ読み込む場合は test50 のようなプログラムになります プログラムの流れとしては非常に簡単です Sub test50() a = InputBox(" バナナ組の算数の平均点を入力してください ") b = InputBox(" バナナ組の理科の平均点を入力してください ") MsgBox
あるクラスの算数の平均点と理科の平均点を読み込み 総点を計算するプログラムを考えてみましょう 一クラスだけ読み込む場合は test50 のようなプログラムになります プログラムの流れとしては非常に簡単です Sub test50() a = InputBox(" バナナ組の算数の平均点を入力してください ") b = InputBox(" バナナ組の理科の平均点を入力してください ") MsgBox
計算機シミュレーション
 . 運動方程式の数値解法.. ニュートン方程式の近似速度は, 位置座標 の時間微分で, d と定義されます. これを成分で書くと, d d li li とかけます. 本来は が の極限をとらなければいけませんが, 有限の小さな値とすると 秒後の位置座標は速度を用いて, と近似できます. 同様にして, 加速度は, 速度 の時間微分で, d と定義されます. これを成分で書くと, d d li li とかけます.
. 運動方程式の数値解法.. ニュートン方程式の近似速度は, 位置座標 の時間微分で, d と定義されます. これを成分で書くと, d d li li とかけます. 本来は が の極限をとらなければいけませんが, 有限の小さな値とすると 秒後の位置座標は速度を用いて, と近似できます. 同様にして, 加速度は, 速度 の時間微分で, d と定義されます. これを成分で書くと, d d li li とかけます.
ファイナンスのための数学基礎 第1回 オリエンテーション、ベクトル
 春学期統計学 I 記述統計と推測統計 担当 : 長倉大輔 ( ながくらだいすけ ) 1 本日の予定 本日はまず記述統計と推測統計の違い 推測統計学の基本的な構造について説明します 2 記述統計と推測統計 統計学とは? 与えられたデータの背後にある 特性 法則 を 検証 発見 分析 するための手法の開発 その応用などに関わる学問の事です 3 記述統計と推測統計 データの種類 データの種類はおおまかに
春学期統計学 I 記述統計と推測統計 担当 : 長倉大輔 ( ながくらだいすけ ) 1 本日の予定 本日はまず記述統計と推測統計の違い 推測統計学の基本的な構造について説明します 2 記述統計と推測統計 統計学とは? 与えられたデータの背後にある 特性 法則 を 検証 発見 分析 するための手法の開発 その応用などに関わる学問の事です 3 記述統計と推測統計 データの種類 データの種類はおおまかに
Microsoft Word - lec_student-chp3_1-representative
 1. はじめに この節でのテーマ データ分布の中心位置を数値で表す 可視化でとらえた分布の中心位置を数量化する 平均値とメジアン, 幾何平均 この節での到達目標 1 平均値 メジアン 幾何平均の定義を書ける 2 平均値とメジアン, 幾何平均の特徴と使える状況を説明できる. 3 平均値 メジアン 幾何平均を計算できる 2. 特性値 集めたデータを度数分布表やヒストグラムに整理する ( 可視化する )
1. はじめに この節でのテーマ データ分布の中心位置を数値で表す 可視化でとらえた分布の中心位置を数量化する 平均値とメジアン, 幾何平均 この節での到達目標 1 平均値 メジアン 幾何平均の定義を書ける 2 平均値とメジアン, 幾何平均の特徴と使える状況を説明できる. 3 平均値 メジアン 幾何平均を計算できる 2. 特性値 集めたデータを度数分布表やヒストグラムに整理する ( 可視化する )
確率分布 - 確率と計算 1 6 回に 1 回の割合で 1 の目が出るさいころがある. このさいころを 6 回投げたとき,1 度も 1 の目が出ない確率を求めよ. 5 6 /6 6 =15625/46656= (5/6) 6 = ある市の気象観測所での記録では, 毎年雨の降る
 確率分布 - 確率と計算 6 回に 回の割合で の目が出るさいころがある. このさいころを 6 回投げたとき 度も の目が出ない確率を求めよ. 5 6 /6 6 =565/46656=.48 (5/6) 6 =.48 ある市の気象観測所での記録では 毎年雨の降る日と降らない日の割合は概ね :9 で一定している. 前日に発表される予報の精度は 8% で 残りの % は実際とは逆の天気を予報している.
確率分布 - 確率と計算 6 回に 回の割合で の目が出るさいころがある. このさいころを 6 回投げたとき 度も の目が出ない確率を求めよ. 5 6 /6 6 =565/46656=.48 (5/6) 6 =.48 ある市の気象観測所での記録では 毎年雨の降る日と降らない日の割合は概ね :9 で一定している. 前日に発表される予報の精度は 8% で 残りの % は実際とは逆の天気を予報している.
データ解析
 データ解析 ( 前期 ) 最小二乗法 向井厚志 005 年度テキスト 0 データ解析 - 最小二乗法 - 目次 第 回 Σ の計算 第 回ヒストグラム 第 3 回平均と標準偏差 6 第 回誤差の伝播 8 第 5 回正規分布 0 第 6 回最尤性原理 第 7 回正規分布の 分布の幅 第 8 回最小二乗法 6 第 9 回最小二乗法の練習 8 第 0 回最小二乗法の推定誤差 0 第 回推定誤差の計算 第
データ解析 ( 前期 ) 最小二乗法 向井厚志 005 年度テキスト 0 データ解析 - 最小二乗法 - 目次 第 回 Σ の計算 第 回ヒストグラム 第 3 回平均と標準偏差 6 第 回誤差の伝播 8 第 5 回正規分布 0 第 6 回最尤性原理 第 7 回正規分布の 分布の幅 第 8 回最小二乗法 6 第 9 回最小二乗法の練習 8 第 0 回最小二乗法の推定誤差 0 第 回推定誤差の計算 第
Windows10の標準機能だけでデータを完全バックアップする方法 | 【ぱそちき】パソコン初心者に教えたい仕事に役立つPC知識
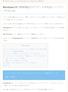 ぱそちき パソコン初心者に教えたい仕事に役立つ PC 知識 Windows10 の標準機能だけでデータを完全バックアッ プする方法 パソコンが急に動かなくなったり 壊れてしまうとパソコンに保存していたテキストや写真などの データも無くなってしまいます このように思いがけない事故からデータを守るには バックアップを取っておくしかありません Windows10のパソコンを使っているなら データをバックアップするのに特別なソフトは必要ありません
ぱそちき パソコン初心者に教えたい仕事に役立つ PC 知識 Windows10 の標準機能だけでデータを完全バックアッ プする方法 パソコンが急に動かなくなったり 壊れてしまうとパソコンに保存していたテキストや写真などの データも無くなってしまいます このように思いがけない事故からデータを守るには バックアップを取っておくしかありません Windows10のパソコンを使っているなら データをバックアップするのに特別なソフトは必要ありません
青焼 1章[15-52].indd
![青焼 1章[15-52].indd 青焼 1章[15-52].indd](/thumbs/86/94313777.jpg) 1 第 1 章統計の基礎知識 1 1 なぜ統計解析が必要なのか? 人間は自分自身の経験にもとづいて 感覚的にものごとを判断しがちである 例えばある疾患に対する標準治療薬の有効率が 50% であったとする そこに新薬が登場し ある医師がその新薬を 5 人の患者に使ったところ 4 人が有効と判定されたとしたら 多くの医師はこれまでの標準治療薬よりも新薬のほうが有効性が高そうだと感じることだろう しかし
1 第 1 章統計の基礎知識 1 1 なぜ統計解析が必要なのか? 人間は自分自身の経験にもとづいて 感覚的にものごとを判断しがちである 例えばある疾患に対する標準治療薬の有効率が 50% であったとする そこに新薬が登場し ある医師がその新薬を 5 人の患者に使ったところ 4 人が有効と判定されたとしたら 多くの医師はこれまでの標準治療薬よりも新薬のほうが有効性が高そうだと感じることだろう しかし
Microsoft PowerPoint - sc7.ppt [互換モード]
![Microsoft PowerPoint - sc7.ppt [互換モード] Microsoft PowerPoint - sc7.ppt [互換モード]](/thumbs/91/107013389.jpg) / 社会調査論 本章の概要 本章では クロス集計表を用いた独立性の検定を中心に方法を学ぶ 1) 立命館大学経済学部 寺脇 拓 2 11 1.1 比率の推定 ベルヌーイ分布 (Bernoulli distribution) 浄水器の所有率を推定したいとする 浄水器の所有の有無を表す変数をxで表し 浄水器をもっている を 1 浄水器をもっていない を 0 で表す 母集団の浄水器を持っている人の割合をpで表すとすると
/ 社会調査論 本章の概要 本章では クロス集計表を用いた独立性の検定を中心に方法を学ぶ 1) 立命館大学経済学部 寺脇 拓 2 11 1.1 比率の推定 ベルヌーイ分布 (Bernoulli distribution) 浄水器の所有率を推定したいとする 浄水器の所有の有無を表す変数をxで表し 浄水器をもっている を 1 浄水器をもっていない を 0 で表す 母集団の浄水器を持っている人の割合をpで表すとすると
Microsoft PowerPoint - 14回パラメータ推定配布用.pptx
 パラメータ推定の理論と実践 BEhavior Study for Transportation Graduate school, Univ. of Yamanashi 山梨大学佐々木邦明 最尤推定法 点推定量を求める最もポピュラーな方法 L n x n i1 f x i 右上の式を θ の関数とみなしたものが尤度関数 データ (a,b) が得られたとき, 全体の平均がいくつとするのがよいか 平均がいくつだったら
パラメータ推定の理論と実践 BEhavior Study for Transportation Graduate school, Univ. of Yamanashi 山梨大学佐々木邦明 最尤推定法 点推定量を求める最もポピュラーな方法 L n x n i1 f x i 右上の式を θ の関数とみなしたものが尤度関数 データ (a,b) が得られたとき, 全体の平均がいくつとするのがよいか 平均がいくつだったら
2014年度 信州大・医系数学
 4 信州大学 ( 医系 ) 前期日程問題 解答解説のページへ 3 個の玉が横に 列に並んでいる コインを 回投げて, それが表であれば, そのときに中央にある玉とその左にある玉とを入れ替える また, それが裏であれば, そのときに中央にある玉とその右にある玉とを入れ替える この操作を繰り返す () 最初に中央にあったものが 回後に中央にある確率を求めよ () 最初に右端にあったものが 回後に右端にある確率を求めよ
4 信州大学 ( 医系 ) 前期日程問題 解答解説のページへ 3 個の玉が横に 列に並んでいる コインを 回投げて, それが表であれば, そのときに中央にある玉とその左にある玉とを入れ替える また, それが裏であれば, そのときに中央にある玉とその右にある玉とを入れ替える この操作を繰り返す () 最初に中央にあったものが 回後に中央にある確率を求めよ () 最初に右端にあったものが 回後に右端にある確率を求めよ
Outlook2010 の メール 連絡先 に関連する内容を解説します 注意 :Outlook2007 と Outlook2010 では 基本操作 基本画面が違うため この資料では Outlook2010 のみで参考にしてください Outlook2010 の画面構成について... 2 メールについて
 Outlook2010 - メール 連絡先など - Outlook2010 の メール 連絡先 に関連する内容を解説します 注意 :Outlook2007 と Outlook2010 では 基本操作 基本画面が違うため この資料では Outlook2010 のみで参考にしてください Outlook2010 の画面構成について... 2 メールについて... 3 画面構成と操作... 3 人物情報ウィンドウ...
Outlook2010 - メール 連絡先など - Outlook2010 の メール 連絡先 に関連する内容を解説します 注意 :Outlook2007 と Outlook2010 では 基本操作 基本画面が違うため この資料では Outlook2010 のみで参考にしてください Outlook2010 の画面構成について... 2 メールについて... 3 画面構成と操作... 3 人物情報ウィンドウ...
Microsoft Word - t30_西_修正__ doc
 反応速度と化学平衡 金沢工業大学基礎教育部西誠 ねらい 化学反応とは分子を構成している原子が組み換り 新しい分子構造を持つことといえます この化学反応がどのように起こるのか どのような速さでどの程度の分子が組み換るのかは 反応の種類や 濃度 温度などの条件で決まってきます そして このような反応の進行方向や速度を正確に予測するために いろいろな数学 物理的な考え方を取り入れて化学反応の理論体系が作られています
反応速度と化学平衡 金沢工業大学基礎教育部西誠 ねらい 化学反応とは分子を構成している原子が組み換り 新しい分子構造を持つことといえます この化学反応がどのように起こるのか どのような速さでどの程度の分子が組み換るのかは 反応の種類や 濃度 温度などの条件で決まってきます そして このような反応の進行方向や速度を正確に予測するために いろいろな数学 物理的な考え方を取り入れて化学反応の理論体系が作られています
<4D F736F F D208C51985F82CD82B682DF82CC88EA95E A>
 群論はじめの一歩 (6) 6. 指数 2の定理と2 面体群 命題 H を群 G の部分群とする そして 左剰余類全体 G/ H 右剰 余類全体 \ H G ともに指数 G: H 2 と仮定する このとき H は群 G の正規部分群である すなわち H 注意 ) 集合 A と B があるとき A から B を引いた差集合は A \ B と書かれるが ここで書いた H \ Gは差集合ではなく右剰余類の集合の意味である
群論はじめの一歩 (6) 6. 指数 2の定理と2 面体群 命題 H を群 G の部分群とする そして 左剰余類全体 G/ H 右剰 余類全体 \ H G ともに指数 G: H 2 と仮定する このとき H は群 G の正規部分群である すなわち H 注意 ) 集合 A と B があるとき A から B を引いた差集合は A \ B と書かれるが ここで書いた H \ Gは差集合ではなく右剰余類の集合の意味である
測量士補 重要事項「標準偏差」
 標準偏差 < 試験合格へのポイント > 士補試験における標準偏差に関する問題は 平成元年が最後の出題となっており それ以来 0 年間に渡って出題された形跡がない このため 受験対策本の中には標準偏差に関して 触れることすら無くなっている物もあるのが現状である しかし平成 0 年度試験において 再び出題が確認されたため ここに解説し過去に出題された問題について触れてみる 標準偏差に関する問題は 基本的にはその公式に当てはめて解けば良いため
標準偏差 < 試験合格へのポイント > 士補試験における標準偏差に関する問題は 平成元年が最後の出題となっており それ以来 0 年間に渡って出題された形跡がない このため 受験対策本の中には標準偏差に関して 触れることすら無くなっている物もあるのが現状である しかし平成 0 年度試験において 再び出題が確認されたため ここに解説し過去に出題された問題について触れてみる 標準偏差に関する問題は 基本的にはその公式に当てはめて解けば良いため
COMET II のプログラミング ここでは機械語レベルプログラミングを学びます 1
 COMET II のプログラミング ここでは機械語レベルプログラミングを学びます 1 ここでは機械命令レベルプログラミングを学びます 機械命令の形式は学びましたね機械命令を並べたプログラムを作ります 2 その前に プログラミング言語について 4 プログラミング言語について 高級言語 (Java とか C とか ) と機械命令レベルの言語 ( アセンブリ言語 ) があります 5 プログラミング言語について
COMET II のプログラミング ここでは機械語レベルプログラミングを学びます 1 ここでは機械命令レベルプログラミングを学びます 機械命令の形式は学びましたね機械命令を並べたプログラムを作ります 2 その前に プログラミング言語について 4 プログラミング言語について 高級言語 (Java とか C とか ) と機械命令レベルの言語 ( アセンブリ言語 ) があります 5 プログラミング言語について
(Microsoft Word - 10ta320a_\220U\223\256\212w\223\301\230__6\217\315\221O\224\274\203\214\203W\203\201.docx)
 6 章スペクトルの平滑化 スペクトルの平滑化とはフーリエスペクトルやパワ スペクトルのギザギザを取り除き 滑らかにする操作のことをいう ただし 波のもっている本質的なものをゆがめてはいけない 図 6-7 パワ スペクトルの平滑化 6. 合積のフーリエ変換スペクトルの平滑化を学ぶ前に 合積とそのフーリエ変換について説明する 6. データ ウィンドウデータ ウィンドウの定義と特徴について説明する 6.3
6 章スペクトルの平滑化 スペクトルの平滑化とはフーリエスペクトルやパワ スペクトルのギザギザを取り除き 滑らかにする操作のことをいう ただし 波のもっている本質的なものをゆがめてはいけない 図 6-7 パワ スペクトルの平滑化 6. 合積のフーリエ変換スペクトルの平滑化を学ぶ前に 合積とそのフーリエ変換について説明する 6. データ ウィンドウデータ ウィンドウの定義と特徴について説明する 6.3
教科書では 同じ割合になっている比は等しい という導入になっているが 2 量の割合は いろいろな表し方ができる という導入に変えている すなわち 2:3 も 4:6 も 6:9 も同じ割合だから等しいという考え方を 2:3 を同じ割合で表すと 4:6 や 6:9 になるという考え方に変えて導入した
 学年 :6 年単元名 :8. 比と比の値 - 割合の表し方を考えよう 1. 単元目標 :( 全 9 時間 ) 2 つの数量の割合を表す方法として 比について理解し 生活や学習で活用する能力を伸ばす 考 表 比の概念をつくる 比の特徴や性質を考える 構造図 線分図を活用して考える 技 知 2 つの数量の関係を調べ 比で表したり 等しい比をつくったりすることができる 比の意味や表し方 比の相等の意味を理解する
学年 :6 年単元名 :8. 比と比の値 - 割合の表し方を考えよう 1. 単元目標 :( 全 9 時間 ) 2 つの数量の割合を表す方法として 比について理解し 生活や学習で活用する能力を伸ばす 考 表 比の概念をつくる 比の特徴や性質を考える 構造図 線分図を活用して考える 技 知 2 つの数量の関係を調べ 比で表したり 等しい比をつくったりすることができる 比の意味や表し方 比の相等の意味を理解する
データ科学2.pptx
 データ科学 多重検定 2 mul%ple test False Discovery Rate 藤博幸 前回の復習 1 多くの検定を繰り返す時には 単純に個々の検定を繰り返すだけでは不十分 5% 有意水準ということは, 1000 回検定を繰り返すと, 50 回くらいは帰無仮説が正しいのに 間違って棄却されてすまうじちがあるということ ex) 1 万個の遺伝子について 正常細胞とガン細胞で それぞれの遺伝子の発現に差があるかどうかを検定
データ科学 多重検定 2 mul%ple test False Discovery Rate 藤博幸 前回の復習 1 多くの検定を繰り返す時には 単純に個々の検定を繰り返すだけでは不十分 5% 有意水準ということは, 1000 回検定を繰り返すと, 50 回くらいは帰無仮説が正しいのに 間違って棄却されてすまうじちがあるということ ex) 1 万個の遺伝子について 正常細胞とガン細胞で それぞれの遺伝子の発現に差があるかどうかを検定
例 e 指数関数的に減衰する信号を h( a < + a a すると, それらのラプラス変換は, H ( ) { e } e インパルス応答が h( a < ( ただし a >, U( ) { } となるシステムにステップ信号 ( y( のラプラス変換 Y () は, Y ( ) H ( ) X (
 第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
スペクトルの用語 1 スペクトル図表は フーリエ変換の終着駅です スペクトル 正確には パワースペクトル ですね この図表は 非常に重要な情報を提供してくれます この内容をきちんと解明しなければいけません まず 用語を検討してみましょう 用語では パワー と スペクトル に分けましょう 次に その意
 ピクトの独り言 フーリエ変換の話し _ その 4 株式会社アイネット スペクトルの用語 1 スペクトル図表は フーリエ変換の終着駅です スペクトル 正確には パワースペクトル ですね この図表は 非常に重要な情報を提供してくれます この内容をきちんと解明しなければいけません まず 用語を検討してみましょう 用語では パワー と スペクトル に分けましょう 次に その意味なり特徴なりを解明しましょう
ピクトの独り言 フーリエ変換の話し _ その 4 株式会社アイネット スペクトルの用語 1 スペクトル図表は フーリエ変換の終着駅です スペクトル 正確には パワースペクトル ですね この図表は 非常に重要な情報を提供してくれます この内容をきちんと解明しなければいけません まず 用語を検討してみましょう 用語では パワー と スペクトル に分けましょう 次に その意味なり特徴なりを解明しましょう
Microsoft Word - ㅎ㇤ㇺå®ı璃ㆨAIã†®æŁ°ç’ƒ.docx
 ベイズの定理から AI の数理 ベイズ更新とロジステック曲線について 松本睦郎 ( 札幌啓成高等学校講師 ) Episode ロジステック曲線 菌やウイルスの増殖数や 人口増加等を表現する曲線の一つにロジステック曲線があります 例 シャーレの中で培養された大腸菌の数について考察する シャーレ内に栄養が十分に存在するとき 菌は栄養を吸収しながら 一定時間ごとに細胞分裂をして増 殖する 菌の数 u u(t)
ベイズの定理から AI の数理 ベイズ更新とロジステック曲線について 松本睦郎 ( 札幌啓成高等学校講師 ) Episode ロジステック曲線 菌やウイルスの増殖数や 人口増加等を表現する曲線の一つにロジステック曲線があります 例 シャーレの中で培養された大腸菌の数について考察する シャーレ内に栄養が十分に存在するとき 菌は栄養を吸収しながら 一定時間ごとに細胞分裂をして増 殖する 菌の数 u u(t)
微分方程式による現象記述と解きかた
 微分方程式による現象記述と解きかた 土木工学 : 公共諸施設 構造物の有用目的にむけた合理的な実現をはかる方法 ( 技術 ) に関する学 橋梁 トンネル ダム 道路 港湾 治水利水施設 安全化 利便化 快適化 合法則的 経済的 自然および人口素材によって作られた 質量保存則 構造物の自然的な性質 作用 ( 外力による応答 ) エネルギー則 の解明 社会的諸現象のうち マスとしての移動 流通 運動量則
微分方程式による現象記述と解きかた 土木工学 : 公共諸施設 構造物の有用目的にむけた合理的な実現をはかる方法 ( 技術 ) に関する学 橋梁 トンネル ダム 道路 港湾 治水利水施設 安全化 利便化 快適化 合法則的 経済的 自然および人口素材によって作られた 質量保存則 構造物の自然的な性質 作用 ( 外力による応答 ) エネルギー則 の解明 社会的諸現象のうち マスとしての移動 流通 運動量則
5. 単元指導目標単元の目標 ( 子どもに事前に知らせる ) 小数 整数の意味を考えよう 小数 整数の計算の仕方を見つけ 計算できるようになろう 子どもに事前に知らせる どうまとめるのか 何を ( どこを ) どうするのか ( 作業 教える 考えさせる ) 何についてまとめるのか 1. 小数 整数の
 学年 :4 年単元名 :13. 小数 整数 小数 整数 1. 単元目標 ( 全 13 時間 ) ( 小数 ) ( 整数 ) ( 小数 ) ( 整数 ) の筆算ができる ( 小数 ) ( 整数 ) ( 小数 ) ( 整数 ) の意味がわかり 筆算の仕方を考えることができる 2. 指導内容 小数 整数の計算の意味とその仕方 (1/10 の位の小数 ) (1,2 位数 ) の筆算 小数 整数の計算の意味とその仕方
学年 :4 年単元名 :13. 小数 整数 小数 整数 1. 単元目標 ( 全 13 時間 ) ( 小数 ) ( 整数 ) ( 小数 ) ( 整数 ) の筆算ができる ( 小数 ) ( 整数 ) ( 小数 ) ( 整数 ) の意味がわかり 筆算の仕方を考えることができる 2. 指導内容 小数 整数の計算の意味とその仕方 (1/10 の位の小数 ) (1,2 位数 ) の筆算 小数 整数の計算の意味とその仕方
Information Theory
 前回の復習 情報をコンパクトに表現するための符号化方式を考える 情報源符号化における基礎的な性質 一意復号可能性 瞬時復号可能性 クラフトの不等式 2 l 1 + + 2 l M 1 ハフマン符号の構成法 (2 元符号の場合 ) D. Huffman 1 前回の練習問題 : ハフマン符号 符号木を再帰的に構成し, 符号を作る A B C D E F 確率 0.3 0.2 0.2 0.1 0.1 0.1
前回の復習 情報をコンパクトに表現するための符号化方式を考える 情報源符号化における基礎的な性質 一意復号可能性 瞬時復号可能性 クラフトの不等式 2 l 1 + + 2 l M 1 ハフマン符号の構成法 (2 元符号の場合 ) D. Huffman 1 前回の練習問題 : ハフマン符号 符号木を再帰的に構成し, 符号を作る A B C D E F 確率 0.3 0.2 0.2 0.1 0.1 0.1
スライド 1
 第 13 章系列データ 2015/9/20 夏合宿 PRML 輪読ゼミ B4 三木真理子 目次 2 1. 系列データと状態空間モデル 2. 隠れマルコフモデル 2.1 定式化とその性質 2.2 最尤推定法 2.3 潜在変数の系列を知るには 3. 線形動的システム この章の目標 : 系列データを扱う際に有効な状態空間モデルのうち 代表的な 2 例である隠れマルコフモデルと線形動的システムの性質を知り
第 13 章系列データ 2015/9/20 夏合宿 PRML 輪読ゼミ B4 三木真理子 目次 2 1. 系列データと状態空間モデル 2. 隠れマルコフモデル 2.1 定式化とその性質 2.2 最尤推定法 2.3 潜在変数の系列を知るには 3. 線形動的システム この章の目標 : 系列データを扱う際に有効な状態空間モデルのうち 代表的な 2 例である隠れマルコフモデルと線形動的システムの性質を知り
Microsoft Word - no11.docx
 3. 関数 3.1 関数関数は数学の関数と同じようなイメージを持つと良いでしょう 例えば三角関数の様に一つの実数値 ( 角度 ) から値を求めますし 対数関数の様に二つの値から一つの値を出すものもあるでしょう これをイメージしてもらえば結構です つまり 何らかの値を渡し それをもとに何かの作業や計算を行い その結果を返すのが関数です C 言語の関数も基本は同じです 0 cos 1 cos(0) =
3. 関数 3.1 関数関数は数学の関数と同じようなイメージを持つと良いでしょう 例えば三角関数の様に一つの実数値 ( 角度 ) から値を求めますし 対数関数の様に二つの値から一つの値を出すものもあるでしょう これをイメージしてもらえば結構です つまり 何らかの値を渡し それをもとに何かの作業や計算を行い その結果を返すのが関数です C 言語の関数も基本は同じです 0 cos 1 cos(0) =
RSS Higher Certificate in Statistics, Specimen A Module 3: Basic Statistical Methods Solutions Question 1 (i) 帰無仮説 : 200C と 250C において鉄鋼の破壊応力の母平均には違いはな
 RSS Higher Certiicate in Statistics, Specimen A Module 3: Basic Statistical Methods Solutions Question (i) 帰無仮説 : 00C と 50C において鉄鋼の破壊応力の母平均には違いはない. 対立仮説 : 破壊応力の母平均には違いがあり, 50C の方ときの方が大きい. n 8, n 7, x 59.6,
RSS Higher Certiicate in Statistics, Specimen A Module 3: Basic Statistical Methods Solutions Question (i) 帰無仮説 : 00C と 50C において鉄鋼の破壊応力の母平均には違いはない. 対立仮説 : 破壊応力の母平均には違いがあり, 50C の方ときの方が大きい. n 8, n 7, x 59.6,
今回のプログラミングの課題 ( 前回の課題で取り上げた )data.txt の要素をソートして sorted.txt というファイルに書出す ソート (sort) とは : 数の場合 小さいものから大きなもの ( 昇順 ) もしくは 大きなものから小さなもの ( 降順 ) になるよう 並び替えること
 C プログラミング演習 1( 再 ) 4 講義では C プログラミングの基本を学び 演習では やや実践的なプログラミングを通して学ぶ 今回のプログラミングの課題 ( 前回の課題で取り上げた )data.txt の要素をソートして sorted.txt というファイルに書出す ソート (sort) とは : 数の場合 小さいものから大きなもの ( 昇順 ) もしくは 大きなものから小さなもの ( 降順
C プログラミング演習 1( 再 ) 4 講義では C プログラミングの基本を学び 演習では やや実践的なプログラミングを通して学ぶ 今回のプログラミングの課題 ( 前回の課題で取り上げた )data.txt の要素をソートして sorted.txt というファイルに書出す ソート (sort) とは : 数の場合 小さいものから大きなもの ( 昇順 ) もしくは 大きなものから小さなもの ( 降順
パソコンシミュレータの現状
 第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
