誤差とは? 真の値からの測定値のズレ 真の値 とは何かが問題 測定値から どのような値を求めたいと考えているのか? ちなみに測定値や推定値からどの範囲に真の値があるかの指標は 不確かさ
|
|
|
- ちえこ いちぬの
- 7 years ago
- Views:
Transcription
1 誤差と統計 画像処理を行う各段階や較正において 真の物理量からのずれが混入する このズレをどう定式化し どう小さくしていくかについて 具体例を交え解説する はずでしたが誤差が大きくなりました 八木雅文 2007/10/09 微改訂版
2 誤差とは? 真の値からの測定値のズレ 真の値 とは何かが問題 測定値から どのような値を求めたいと考えているのか? ちなみに測定値や推定値からどの範囲に真の値があるかの指標は 不確かさ
3 系統誤差とランダム誤差 系統誤差 : 何回やっても同じ量ずれる誤差ランダム誤差 : 毎回再現性のない誤差 機器の目盛りが間違っていて毎回同じ量ずれる 系統誤差機器が不安定で結果に再現性がない ランダム誤差
4 問題設定 データがあった場合 そこから欲しい情報を最も精度良く取り出すにはどうすればよいか? 例えば光赤外の天文データの場合 天体の光 バックグラウンドの光 それに測定の際の雑音が乗って観測される ここから天体の光を取り出すのが整約 解析
5 基本方針 まず生の観測量にはどのような誤差が乗っているのかをモデル化する そのモデルから物理量を求める整約 解析の各段階で 誤差がどのように変化するかを追いかける
6 光の強さ 天球上のある範囲から ある波長範囲の光がどれだけの強さで来ているか つまり ある一定時間にあるエネルギー範囲 (= 波長範囲 ) の光子が観測者側の単位面積をどれだけの数通過するか 単位は光赤外分野では 例えば [erg/sec/cm^2] が良く使われる
7 真の値? 時間変化しないものは 真の値が何かを言うのは簡単 例えば真空中の光速度 ところが 光はミクロな確率過程を経て天体から出てくるため ある 1 秒間に天体から出てくる光の量は別の 1 秒と同じではない つまり観測値は本質的に一定ではない
8 光量の誤差とは? その上で 求めたい 真の値 とは 長時間平均 これはある短時間に観測される光量の 分布の代表値 測光の場合の誤差とは 実際に測定あるいは推定した値がどれだけ精度良くその分布の代表値を求められたかという指標
9 分布と代表値 頻度 分布の代表値として良く使われるのは 平均 中央値 ( メディアン ) 最頻値 ( モード ) など 最頻値 中央値 平均 値
10 確率分布関数 観測量 X: 観測ごとに変わる量 があったとして X=X0 である確率を p(x0) と書ける場合 関数 p(x) が確率分布関数 X が連続量の時 X0-dX/2<X<X0+dX/2 に入る確率が p(x0)dx になるような p(x) が確率密度分布関数
11 サイコロの確率分布 例えば 6 面サイコロ 3 個を振って出た目の和を観測量 X とした時の確率分布関数は以下 X p(x) X p(x) X p(x) 3 1/ / / / / / / / / / / / / / / /216
12 平均 平均 (mean) あるいは期待値は 以下で定義される量 E X =mean= X p X dx もっともタチのいい統計量 ただし 外れ値に抜群に弱い 後述 また平均は線形性を満たす E ax by c =ae X be Y c
13 大数の法則 何回も観測して観測量 X の平均を求めると その値は確率分布 p(x) の平均に近づいていく この性質はメディアンやモードにはない
14 中央値 ( メディアン ) 中央値 (median) は 文字通り分布の中央の値で 以下のように定義できる median 1 p X dx 2 median p X dx 1 2 外れ値に強いが問題もある 後述
15 誤差の評価 一回の測定での誤差は 真の値がわからないと求まらない 測定値の 分布 が何らかの方法でわかっていれば 誤差の典型値 を計算できる 例えば良く使われるのが標準偏差 ( 誤差の二乗平均 )σ などと書かれる 但し σ は正規分布の標準偏差に相当する別の量の場合もある
16 誤差の推定 観測値の母分布がわかる場合 一回の観測値が典型値からどれだけずれるか ( 誤差 ) の分布も推定できて 典型値も求められる 観測値の母分布の関数形はわかるあるいは仮定できるが パラメタが分からない場合 母分布のパラメタを推定
17 誤差と不確かさ なお 測定値が真の値からどれだけずれているか ( 誤差 ) と 測定値からどの範囲に真の値が収まっているか ( 不確かさ ) は 別概念 なのだが 以下ではこの辺りが曖昧に扱われている
18 分散 標準偏差 分散は期待値 E(X) を使って V X = X E X 2 p X dx と書ける 分散の平方根が標準偏差である 分散には以下の性質がある V ax b =a 2 V X b
19 MAD MAD(Median of Absolute Deviation) は 標準偏差に相当する統計量 あまり広く使われてないが 実は便利な量 MAD=Median( X-median ) 各データ点からメディアンを引いた値の絶対値のメディアン 正規分布の場合 MAD= σ
20 サイコロ 3 つの場合 分布の典型値は 10.5 分散はゴリゴリと計算すると 8.75 標準偏差は 2.96 程度 つまり σ=2.96 これが理論から求まる誤差の典型値でこれを略して 誤差 と呼ぶことも多い この場合 3σ の範囲内と言えば 10.5±8.88 である
21 サイコロを振ってみた さて 実際サイコロ 3 つを振ってみた 14,11,14,13,13,13 この 6 回の試行 ( 観測 ) それぞれを X1,X2...X6 とすると 本来の平均 10.5 との差 +3.5,+0.5,+3.5,+2.5,+2.5,+2.5 が 本来の意味での誤差 14,11,14,13,13,13 の平均は 13 標準偏差は 1 これを標本平均 標本標準偏差と呼ぶ
22 まとめ 誤差とは1 回の観測量と 真の値 の差が本来の意味 しかし通常使われるのは 誤差の典型値 の意味であり この典型値として標準偏差が良く用いられる 測光の場合 真の値 とは分布の典型 値である
23 誤差の推定 以下では 1) そもそも誤差はどうなるはずかから考え 誤差の伝播を使って観測量の誤差を推定する ( 限界等級の計算 ) 2) 観測量の統計を考えた上で 解析での誤差の広がりを推定する ( 画像の並行移動 ) を例として挙げる
24 具体例 : 限界等級 撮像データの測光の限界等級とは 天体の測光値 (signal) が 測光誤差 (noise) の何倍かという比 S/N がある一定値 例えば 3 以上の天体が何等か という値である 例えば 28 等の天体が S/N=5 の時 S/N=5 での限界等級が 28 等 という
25 等級誤差と S/N 等級のランダム誤差 Δm と S/N との関係は m= S / N 例えば 0.1 等以下の精度で測光をしたいのであれば S/N>10.86 が必要である
26 限界等級 この場合の限界等級は 測光精度 の意味での限界等級であって 検出限界の意味での限界等級ではない つまり測光精度の意味での限界等級が同じであっても 天体検出の割合が同じであるとは全く限らない 全然別の話
27 という話をしたら 検出の限界はどう推定するのか? と質問されたのですが これを理論から解析的に求めるのは極めて困難 正方形が N 個繋がった図形の数を数えるとかいう数学の未解決問題に関連してたりします こんなペントミノとか
28 S/N の S 露出時間を t システムの透過率を f 天体の光度を L とすると 検出器で検出される信号は形式的に S=f t L ( 単位は光電荷数 ) と書ける
29 S/N の N 測光での大きな誤差源の一つは機器のノイズ ( 読み出し雑音 ) 読み出し雑音は露出時間によらず一定であると考えてよい 1 ピクセルあたりのこの誤差を N1=r と書くことにする 単位は電荷数に換算しておく
30 さらっと書きましたが N1=r と書いたこの意味は ある画素での観測量を X とし 読み出し雑音を δx とした場合に δx の標準偏差が r であるという意味 式で書くとこう E X =0 V X =E X 2 = N1 2 =r 2
31 S/N の N もう一つは測定される電荷の分布の広がり ( ポアソン雑音 ) 素子に溜まった総電荷数を n ピクセル数を A とすると N2= n= S f t A s SKY t A s dark となる この N1,N2 の合成が誤差 N となる
32 何故 N2= n 天体から出てくる光の量は ポアソン分布 に従うと考えられる このポアソン分布とは非常に確率の低い事象について試行を非常に多数行った場合に起きた事象の数の分布であり 二項分布の極限である
33 二項分布 ある確率 p で事象が起きる試行を N 回行ったとき X 回事象が起きる確率分布を二項分布と呼び B(N,p) と書く 平均は Np 分散は Np(1-p) 例えば N=5, p=1/6 の時 (6 面サイコロ 5 個振った時に 1 の目の出る数の確率分布 ) は B(5,1/6) である
34 B N, p X = N C X N C X = B 5, = B 5, = C 5 2 二項分布 N! X! N X! p X 1 p N X 5~ ~0.093
35 平均の計算 ( おまけ ) N E X = X =0 X N C X p X 1 p N X ここでモーメント母関数と呼ばれる以下の関数を導入する N t =E e t X = X=0 N = X =0 e t X N C X N C X = pe t 1 p N p X 1 p N X p e t X 1 p N X
36 平均の計算 ( おまけ ) これを t で微分すると ' t = 一方で N X=0 N ' 0 = X =0 N E X = X =0 X e t X N C X X N C X p X 1 p N X p X 1 p N X ' t =Np e t p e t 1 p N 1 ' 0 = Np X N C X p X 1 p N X = Np
37 分散の計算 ( おまけ ) N V X = X =0 X Np 2 N C X p X 1 p N X 平均同様にモーメント母関数を使うと N ' ' t = X =0 X 2 e t X N C X p X 1 p N X ' ' t = Np e t p e t 1 p N 1 N N 1 p 2 e 2t p e t 1 p N 2 ' ' 0 =Np N 2 p 2 N p 2
38 分散の計算 ( おまけ ) N V X = X=0 X 2 2 Np X Np 2 N C X p X 1 p N X に代入して V X = Np N 2 p 2 Np 2 2 Np Np Np 2 =Np 1 p が導かれる なお (X-Np) 周りの母関数を考えたほうが計算は楽
39 ポアソン分布 平均 E(X)=k 分散 V(X)=k p k x = k x e k x! 二項分布は平均は Np 分散は Np(1-p) だったのだが ポアソン分布は p<<1 の極限なので k=np=np となる 従って標準偏差は k
40 ポアソン分布の和 ポアソン分布に従う X Y という 2 つの変数があったとき 和 X+Y もポアソン分布に従う 二項分布の和は p が等しければ二項分布になるが その他は二項分布には必ずしもならない なお 差 X-Y はポアソン分布には従わない
41 余談 X,Y がポアソン分布なら和 X+Y もポアソン分布に従うのに 何故 X-Y はポアソン分布じゃないのか気になりませんか? 直接の回答じゃないけど以下をどうぞ 自然数 A,B の和 A+B は自然数 さて A-B は自然数??
42 ポアソンの和 今回の場合 天体から出てくる光はポアソン分布に従い 空からの光もポアソンに従っていると考え またダーク電流もポアソン分布に従っていると考える ( ことにする ) この結果この独立な 3 つの量を足した 電荷数 もポアソンに従うと考えて良い ここで中間赤外辺りだと 星から出る光は縮退の影響でポアソンに従わないという指摘を頂き調査中です
43 ポアソン分布の定数倍 ポアソン分布の定数倍はポアソン分布にならない これは要注意 電荷数はポアソン分布に従うが これが FITS になって出てきた値はゲインで割り算されているので ポアソン分布には従わない これが式を電荷数で書いた理由
44 正規分布 別名ガウス分布 誤差は良くこの分布だと仮定される 平均 m 標準偏差 σ の場合 N m, 2 x = 1 x m 2 e ポアソン分布は k が大きければ正規分布で良く近似できる
45 誤差の伝播 さて このように 2 種の誤差源があった場合 その合成に用いられるのが 誤差の伝播の式 一般的には分散 ( 標準偏差 ) が演算によってどのように変わるかをまとめたもの
46 ここでの基本方針 確率変数 X,Y と関数 f(x,y) があった場合 f(x,y) の誤差は 1) 確率変数 X と誤差 δx を求める Y も同様 2) 期待値 E(f(X,Y)) を求める 3) 分散 V(f(X,Y))=E((f(X,Y)-E(f(X,Y))^2) つまり観測値から期待値を引いた二乗平均を求めるという方針で求める
47 誤差の伝播の例 X,Yの平均を, X Y と書き 標準偏差を, とする X Y この時 E(X+Y)= X Y V X Y =E X Y X Y 2 =E X X Y Y 2 =E X X 2 2 E X X Y Y E Y Y 2 = X 2 Y 2 2 E X X Y Y
48 共分散 E X X Y Y ここで出てきたを共分散と呼んで Cov X, Y と書く 共分散が0の時 X Yは独立という 誤差の伝播で変数が独立かどうかは極めて重要 しかし実際のデータでは独立かどうか判断するのは簡単とは限らない
49 測光の S/N V X Y = X 2 Y 2 2Cov X,Y 測光誤差の場合 各ピクセルの読み出し雑音とポアソン雑音は全て独立と考えられるので ピクセル数をAとおくと N 2 =A N 1 2 N 2 2 N = A r 2 S f t A s SKY t A s dark S N = f t L A r 2 t f L A s SKY A s dark
50 測光の S/N S N = t r 2 f t L A r 2 t f L A s SKY A s dark f L A s SKY A s dark S N ~ f L r t t r 2 f L A s SKY A s dark の場合は S N ~ f L f L A s SKY A s dark t
51 しかし 実際には露出時間には上限がある サチり ガイドの影響 宇宙線の増加従って 露出をいくつかに分割して撮ることになる これを足し合わせた結果は 必ずしも総露出時間の平方根で S/N が上がるとは限らない
52 平均とメディアン 分散で N を評価した場合 S/N を最も高くする足し合わせ方は単純平均 しかし 単純平均は外れ値に弱い そこで 複数の露出の足し合わせには sigma-clipped mean や メディアンが用いられる
53 メディアン 例えば 平均 100 分散 20 の観測値のうち 1 つに非常に大きなノイズが乗った場合 113,92,66,10000,104,68,90 これを単純平均を取ると ~1500 一方 median は 92, MAD で σ を推定した上での 3σ-clipped mean は 89 単純平均よりは遥かに良い推定
54 メディアンの誤差 しかし メディアンは単純平均よりも誤差が大きくなる 分散 1 の正規分布の平均とメディアンを比べると N が十分大きいところでは s mean = 1 N s median = 1.25 N
55 メディアンの誤差 N s(median) s(1-clipped) つだけclip された場合とメディアンでは N>4 では clipped の方が誤差が小さい
56 系統誤差の影響 一方 1σ 程度以下の系統誤差 例えば画像の足し合わせではバックグラウンドの引き残りなど に対しては メディアンは引きずられにくいが clipped mean は引きずられる 外れ値が常に大きい側に偏る場合 メディアンは系統的にずれる
57 まとめ 天体からの光の S/N のうち ノイズはポアソン雑音と読み出し雑音の合成であると考えられている 露出時間が長くなると理想的な状態でも S/N は露出時間の平方根でしか上がらない メディアンよりも単純平均や clipped mean の方がランダム誤差は少ない
58 続く? いや この辺で時間切れじゃないかなと
59 画像の並行移動 回転も類似の問題があるのだが ここでは並行移動だけ考える 画像を非整数ピクセルだけ並行移動させたい 例えば位置を合わせて足し合わせる場合など
60 画像の差 ( 余談 ) 画像の差し引きの時は特に精度が必要になる ( 右は 0.2pixel ずれた場合 )
61 並行移動 並行移動の方法として 線形補間のリサンプリングを考える 例えば x 軸方向に -a (0<a<1) だけシフトさせるときは v x' = 1 a v x a v x 1 x x+a x+1
62 実際にシフトさせた 左がシフト前 右は x+0.5, y+0.5 シフト ピクセルあたりのノイズは減っている左 67ADU, 右 43ADU
63 誤差の伝播 各点での誤差を σ とする X 方向だけ考えて v x' = 1 a v x a v x 1 とする 各点の誤差が独立であれば この分散は V 1 a v x a v x 1 = 1 a 2 2 a 2 2 a=0.5 で と小さくなる
64 S/N は上がるのか? 一般的には上がらない S N = f t L A r 2 t f L A s SKY A s dark まず この式を求めた際に 各点での誤差の独立を仮定していたが 並行移動の結果 独立ではなくなる
65 S/N はあがらない また S/N はその天体の光量をどれだけ正しく見積もれたかの指標だと思うと 並行移動によってその天体周りの光量がほとんど変化しない ( 開口の端での出入りだけ ) ので S/N が変わるのはおかしい
66 画像変形に伴う S/N これは単純な線形補間による並行移動の例だが 他の画像変形も行うことによりピクセル当たりのノイズが減る場合が多い しかし 天体全体の光量が同じならば S/N は結果的に変化していないと考えるのが妥当
67 まとめ 画像変形を行うとピクセルあたりの S/N が見かけ上向上して見えることがある しかしこの場合 隣り合ったピクセルとの共分散も高くなり 一定以上の範囲での S/N は向上しない この点は騙されやすいので要注意
統計的データ解析
 統計的データ解析 011 011.11.9 林田清 ( 大阪大学大学院理学研究科 ) 連続確率分布の平均値 分散 比較のため P(c ) c 分布 自由度 の ( カイ c 平均値 0, 標準偏差 1の正規分布 に従う変数 xの自乗和 c x =1 が従う分布を自由度 の分布と呼ぶ 一般に自由度の分布は f /1 c / / ( c ) {( c ) e }/ ( / ) 期待値 二乗 ) 分布 c
統計的データ解析 011 011.11.9 林田清 ( 大阪大学大学院理学研究科 ) 連続確率分布の平均値 分散 比較のため P(c ) c 分布 自由度 の ( カイ c 平均値 0, 標準偏差 1の正規分布 に従う変数 xの自乗和 c x =1 が従う分布を自由度 の分布と呼ぶ 一般に自由度の分布は f /1 c / / ( c ) {( c ) e }/ ( / ) 期待値 二乗 ) 分布 c
基礎統計
 基礎統計 第 11 回講義資料 6.4.2 標本平均の差の標本分布 母平均の差 標本平均の差をみれば良い ただし, 母分散に依存するため場合分けをする 1 2 3 分散が既知分散が未知であるが等しい分散が未知であり等しいとは限らない 1 母分散が既知のとき が既知 標準化変量 2 母分散が未知であり, 等しいとき 分散が未知であるが, 等しいということは分かっているとき 標準化変量 自由度 の t
基礎統計 第 11 回講義資料 6.4.2 標本平均の差の標本分布 母平均の差 標本平均の差をみれば良い ただし, 母分散に依存するため場合分けをする 1 2 3 分散が既知分散が未知であるが等しい分散が未知であり等しいとは限らない 1 母分散が既知のとき が既知 標準化変量 2 母分散が未知であり, 等しいとき 分散が未知であるが, 等しいということは分かっているとき 標準化変量 自由度 の t
カイ二乗フィット検定、パラメータの誤差
 統計的データ解析 008 008.. 林田清 ( 大阪大学大学院理学研究科 ) 問題 C (, ) ( x xˆ) ( y yˆ) σ x πσ σ y y Pabx (, ;,,, ) ˆ y σx σ y = dx exp exp πσx ただし xy ˆ ˆ はyˆ = axˆ+ bであらわされる直線モデル上の点 ( ˆ) ( ˆ ) ( ) x x y ax b y ax b Pabx (,
統計的データ解析 008 008.. 林田清 ( 大阪大学大学院理学研究科 ) 問題 C (, ) ( x xˆ) ( y yˆ) σ x πσ σ y y Pabx (, ;,,, ) ˆ y σx σ y = dx exp exp πσx ただし xy ˆ ˆ はyˆ = axˆ+ bであらわされる直線モデル上の点 ( ˆ) ( ˆ ) ( ) x x y ax b y ax b Pabx (,
Microsoft PowerPoint - 測量学.ppt [互換モード]
![Microsoft PowerPoint - 測量学.ppt [互換モード] Microsoft PowerPoint - 測量学.ppt [互換モード]](/thumbs/92/109082022.jpg) 8/5/ 誤差理論 測定の分類 性格による分類 独立 ( な ) 測定 : 測定値がある条件を満たさなければならないなどの拘束や制約を持たないで独立して行う測定 条件 ( 付き ) 測定 : 三角形の 3 つの内角の和のように, 個々の測定値間に満たすべき条件式が存在する場合の測定 方法による分類 直接測定 : 距離や角度などを機器を用いて直接行う測定 間接測定 : 求めるべき量を直接測定するのではなく,
8/5/ 誤差理論 測定の分類 性格による分類 独立 ( な ) 測定 : 測定値がある条件を満たさなければならないなどの拘束や制約を持たないで独立して行う測定 条件 ( 付き ) 測定 : 三角形の 3 つの内角の和のように, 個々の測定値間に満たすべき条件式が存在する場合の測定 方法による分類 直接測定 : 距離や角度などを機器を用いて直接行う測定 間接測定 : 求めるべき量を直接測定するのではなく,
Microsoft PowerPoint - Inoue-statistics [互換モード]
![Microsoft PowerPoint - Inoue-statistics [互換モード] Microsoft PowerPoint - Inoue-statistics [互換モード]](/thumbs/92/107910528.jpg) 誤差論 神戸大学大学院農学研究科 井上一哉 (Kazuya INOUE) 誤差論 2011 年度前期火曜クラス 1 講義内容 誤差と有効数字 (Slide No.2~8 Text p.76~78) 誤差の分布と標準偏差 (Slide No.9~18 Text p.78~80) 最確値とその誤差 (Slide No.19~25 Text p.80~81) 誤差の伝播 (Slide No.26~32 Text
誤差論 神戸大学大学院農学研究科 井上一哉 (Kazuya INOUE) 誤差論 2011 年度前期火曜クラス 1 講義内容 誤差と有効数字 (Slide No.2~8 Text p.76~78) 誤差の分布と標準偏差 (Slide No.9~18 Text p.78~80) 最確値とその誤差 (Slide No.19~25 Text p.80~81) 誤差の伝播 (Slide No.26~32 Text
様々なミクロ計量モデル†
 担当 : 長倉大輔 ( ながくらだいすけ ) この資料は私の講義において使用するために作成した資料です WEB ページ上で公開しており 自由に参照して頂いて構いません ただし 内容について 一応検証してありますが もし間違いがあった場合でもそれによって生じるいかなる損害 不利益について責任を負いかねますのでご了承ください 間違いは発見次第 継続的に直していますが まだ存在する可能性があります 1 カウントデータモデル
担当 : 長倉大輔 ( ながくらだいすけ ) この資料は私の講義において使用するために作成した資料です WEB ページ上で公開しており 自由に参照して頂いて構いません ただし 内容について 一応検証してありますが もし間違いがあった場合でもそれによって生じるいかなる損害 不利益について責任を負いかねますのでご了承ください 間違いは発見次第 継続的に直していますが まだ存在する可能性があります 1 カウントデータモデル
EBNと疫学
 推定と検定 57 ( 復習 ) 記述統計と推測統計 統計解析は大きく 2 つに分けられる 記述統計 推測統計 記述統計 観察集団の特性を示すもの 代表値 ( 平均値や中央値 ) や ばらつきの指標 ( 標準偏差など ) 図表を効果的に使う 推測統計 観察集団のデータから母集団の特性を 推定 する 平均 / 分散 / 係数値などの推定 ( 点推定 ) 点推定値のばらつきを調べる ( 区間推定 ) 検定統計量を用いた検定
推定と検定 57 ( 復習 ) 記述統計と推測統計 統計解析は大きく 2 つに分けられる 記述統計 推測統計 記述統計 観察集団の特性を示すもの 代表値 ( 平均値や中央値 ) や ばらつきの指標 ( 標準偏差など ) 図表を効果的に使う 推測統計 観察集団のデータから母集団の特性を 推定 する 平均 / 分散 / 係数値などの推定 ( 点推定 ) 点推定値のばらつきを調べる ( 区間推定 ) 検定統計量を用いた検定
不偏推定量
 不偏推定量 情報科学の補足資料 018 年 6 月 7 日藤本祥二 統計的推定 (statistical estimatio) 確率分布が理論的に分かっている標本統計量を利用する 確率分布の期待値の値をそのまま推定値とするのが点推定 ( 信頼度 0%) 点推定に ± で幅を持たせて信頼度を上げたものが区間推定 持たせた幅のことを誤差 (error) と呼ぶ 信頼度 (cofidece level)
不偏推定量 情報科学の補足資料 018 年 6 月 7 日藤本祥二 統計的推定 (statistical estimatio) 確率分布が理論的に分かっている標本統計量を利用する 確率分布の期待値の値をそのまま推定値とするのが点推定 ( 信頼度 0%) 点推定に ± で幅を持たせて信頼度を上げたものが区間推定 持たせた幅のことを誤差 (error) と呼ぶ 信頼度 (cofidece level)
線形システム応答 Linear System response
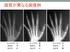 画質が異なる画像例 コントラスト劣 コントラスト優 コントラスト普 鮮鋭性 普 鮮鋭性 優 鮮鋭性 劣 粒状性 普 粒状性 劣 粒状性 優 医用画像の画質 コントラスト, 鮮鋭性, 粒状性の要因が互いに密接に関わり合って形成されている. 比 鮮鋭性 コントラスト 反 反 粒状性 増感紙 - フィルム系での 3 要因の関係 ディジタル画像処理系でもおよそ成り立つ WS u MTFu 画質に影響する因子
画質が異なる画像例 コントラスト劣 コントラスト優 コントラスト普 鮮鋭性 普 鮮鋭性 優 鮮鋭性 劣 粒状性 普 粒状性 劣 粒状性 優 医用画像の画質 コントラスト, 鮮鋭性, 粒状性の要因が互いに密接に関わり合って形成されている. 比 鮮鋭性 コントラスト 反 反 粒状性 増感紙 - フィルム系での 3 要因の関係 ディジタル画像処理系でもおよそ成り立つ WS u MTFu 画質に影響する因子
経営統計学
 5 章基本統計量 3.5 節で量的データの集計方法について簡単に触れ 前章でデータの分布について学びましたが データの特徴をつの数値で示すこともよく行なわれます これは統計量と呼ばれ 主に分布の中心や拡がりなどを表わします この章ではよく利用される分布の統計量を特徴で分類して説明します 数式表示を統一的に行なうために データの個数を 個とし それらを,,, と表わすことにします ここで学ぶ統計量は統計分析の基礎となっており
5 章基本統計量 3.5 節で量的データの集計方法について簡単に触れ 前章でデータの分布について学びましたが データの特徴をつの数値で示すこともよく行なわれます これは統計量と呼ばれ 主に分布の中心や拡がりなどを表わします この章ではよく利用される分布の統計量を特徴で分類して説明します 数式表示を統一的に行なうために データの個数を 個とし それらを,,, と表わすことにします ここで学ぶ統計量は統計分析の基礎となっており
講義「○○○○」
 講義 信頼度の推定と立証 内容. 点推定と区間推定. 指数分布の点推定 区間推定 3. 指数分布 正規分布の信頼度推定 担当 : 倉敷哲生 ( ビジネスエンジニアリング専攻 ) 統計的推測 標本から得られる情報を基に 母集団に関する結論の導出が目的 測定値 x x x 3 : x 母集団 (populaio) 母集団の特性値 統計的推測 標本 (sample) 標本の特性値 分布のパラメータ ( 母数
講義 信頼度の推定と立証 内容. 点推定と区間推定. 指数分布の点推定 区間推定 3. 指数分布 正規分布の信頼度推定 担当 : 倉敷哲生 ( ビジネスエンジニアリング専攻 ) 統計的推測 標本から得られる情報を基に 母集団に関する結論の導出が目的 測定値 x x x 3 : x 母集団 (populaio) 母集団の特性値 統計的推測 標本 (sample) 標本の特性値 分布のパラメータ ( 母数
統計学 - 社会統計の基礎 - 正規分布 標準正規分布累積分布関数の逆関数 t 分布正規分布に従うサンプルの平均の信頼区間 担当 : 岸 康人 資料ページ :
 統計学 - 社会統計の基礎 - 正規分布 標準正規分布累積分布関数の逆関数 t 分布正規分布に従うサンプルの平均の信頼区間 担当 : 岸 康人 資料ページ : https://goo.gl/qw1djw 正規分布 ( 復習 ) 正規分布 (Normal Distribution)N (μ, σ 2 ) 別名 : ガウス分布 (Gaussian Distribution) 密度関数 Excel:= NORM.DIST
統計学 - 社会統計の基礎 - 正規分布 標準正規分布累積分布関数の逆関数 t 分布正規分布に従うサンプルの平均の信頼区間 担当 : 岸 康人 資料ページ : https://goo.gl/qw1djw 正規分布 ( 復習 ) 正規分布 (Normal Distribution)N (μ, σ 2 ) 別名 : ガウス分布 (Gaussian Distribution) 密度関数 Excel:= NORM.DIST
Microsoft PowerPoint - stat-2014-[9] pptx
![Microsoft PowerPoint - stat-2014-[9] pptx Microsoft PowerPoint - stat-2014-[9] pptx](/thumbs/49/25555771.jpg) 統計学 第 17 回 講義 母平均の区間推定 Part-1 014 年 6 17 ( )6-7 限 担当教員 : 唐渡 広志 ( からと こうじ ) 研究室 : 経済学研究棟 4 階 43 号室 email: [email protected] website: htt://www3.u-toyama.ac.j/kkarato/ 1 講義の目的 標本平均は正規分布に従うという性質を
統計学 第 17 回 講義 母平均の区間推定 Part-1 014 年 6 17 ( )6-7 限 担当教員 : 唐渡 広志 ( からと こうじ ) 研究室 : 経済学研究棟 4 階 43 号室 email: [email protected] website: htt://www3.u-toyama.ac.j/kkarato/ 1 講義の目的 標本平均は正規分布に従うという性質を
Microsoft PowerPoint - e-stat(OLS).pptx
 経済統計学 ( 補足 ) 最小二乗法について 担当 : 小塚匡文 2015 年 11 月 19 日 ( 改訂版 ) 神戸大学経済学部 2015 年度後期開講授業 補足 : 最小二乗法 ( 単回帰分析 ) 1.( 単純 ) 回帰分析とは? 標本サイズTの2 変数 ( ここではXとY) のデータが存在 YをXで説明する回帰方程式を推定するための方法 Y: 被説明変数 ( または従属変数 ) X: 説明変数
経済統計学 ( 補足 ) 最小二乗法について 担当 : 小塚匡文 2015 年 11 月 19 日 ( 改訂版 ) 神戸大学経済学部 2015 年度後期開講授業 補足 : 最小二乗法 ( 単回帰分析 ) 1.( 単純 ) 回帰分析とは? 標本サイズTの2 変数 ( ここではXとY) のデータが存在 YをXで説明する回帰方程式を推定するための方法 Y: 被説明変数 ( または従属変数 ) X: 説明変数
Microsoft PowerPoint - 基礎・経済統計6.ppt
 . 確率変数 基礎 経済統計 6 確率分布 事象を数値化したもの ( 事象ー > 数値 の関数 自然に数値されている場合 さいころの目 量的尺度 数値化が必要な場合 質的尺度, 順序的尺度 それらの尺度に数値を割り当てる 例えば, コインの表が出たら, 裏なら 0. 離散確率変数と連続確率変数 確率変数の値 連続値をとるもの 身長, 体重, 実質 GDP など とびとびの値 離散値をとるもの 新生児の性別
. 確率変数 基礎 経済統計 6 確率分布 事象を数値化したもの ( 事象ー > 数値 の関数 自然に数値されている場合 さいころの目 量的尺度 数値化が必要な場合 質的尺度, 順序的尺度 それらの尺度に数値を割り当てる 例えば, コインの表が出たら, 裏なら 0. 離散確率変数と連続確率変数 確率変数の値 連続値をとるもの 身長, 体重, 実質 GDP など とびとびの値 離散値をとるもの 新生児の性別
Kumamoto University Center for Multimedia and Information Technologies Lab. 熊本大学アプリケーション実験 ~ 実環境における無線 LAN 受信電波強度を用いた位置推定手法の検討 ~ InKIAI 宮崎県美郷
 熊本大学アプリケーション実験 ~ 実環境における無線 LAN 受信電波強度を用いた位置推定手法の検討 ~ InKIAI プロジェクト @ 宮崎県美郷町 熊本大学副島慶人川村諒 1 実験の目的 従来 信号の受信電波強度 (RSSI:RecevedSgnal StrengthIndcator) により 対象の位置を推定する手法として 無線 LAN の AP(AccessPont) から受信する信号の減衰量をもとに位置を推定する手法が多く検討されている
熊本大学アプリケーション実験 ~ 実環境における無線 LAN 受信電波強度を用いた位置推定手法の検討 ~ InKIAI プロジェクト @ 宮崎県美郷町 熊本大学副島慶人川村諒 1 実験の目的 従来 信号の受信電波強度 (RSSI:RecevedSgnal StrengthIndcator) により 対象の位置を推定する手法として 無線 LAN の AP(AccessPont) から受信する信号の減衰量をもとに位置を推定する手法が多く検討されている
第 3 回講義の項目と概要 統計的手法入門 : 品質のばらつきを解析する 平均と標準偏差 (P30) a) データは平均を見ただけではわからない 平均が同じだからといって 同一視してはいけない b) データのばらつきを示す 標準偏差 にも注目しよう c) 平均
 第 3 回講義の項目と概要 016.8.9 1.3 統計的手法入門 : 品質のばらつきを解析する 1.3.1 平均と標準偏差 (P30) a) データは平均を見ただけではわからない 平均が同じだからといって 同一視してはいけない b) データのばらつきを示す 標準偏差 にも注目しよう c) 平均 :AVERAGE 関数, 標準偏差 :STDEVP 関数とSTDEVという関数 1 取得したデータそのものの標準偏差
第 3 回講義の項目と概要 016.8.9 1.3 統計的手法入門 : 品質のばらつきを解析する 1.3.1 平均と標準偏差 (P30) a) データは平均を見ただけではわからない 平均が同じだからといって 同一視してはいけない b) データのばらつきを示す 標準偏差 にも注目しよう c) 平均 :AVERAGE 関数, 標準偏差 :STDEVP 関数とSTDEVという関数 1 取得したデータそのものの標準偏差
14 化学実験法 II( 吉村 ( 洋 mmol/l の半分だったから さんの測定値は くんの測定値の 4 倍の重みがあり 推定値 としては 0.68 mmol/l その標準偏差は mmol/l 程度ということになる 測定値を 特徴づけるパラメータ t を推定するこの手
 14 化学実験法 II( 吉村 ( 洋 014.6.1. 最小 乗法のはなし 014.6.1. 内容 最小 乗法のはなし...1 最小 乗法の考え方...1 最小 乗法によるパラメータの決定... パラメータの信頼区間...3 重みの異なるデータの取扱い...4 相関係数 決定係数 ( 最小 乗法を語るもう一つの立場...5 実験条件の誤差の影響...5 問題...6 最小 乗法の考え方 飲料水中のカルシウム濃度を
14 化学実験法 II( 吉村 ( 洋 014.6.1. 最小 乗法のはなし 014.6.1. 内容 最小 乗法のはなし...1 最小 乗法の考え方...1 最小 乗法によるパラメータの決定... パラメータの信頼区間...3 重みの異なるデータの取扱い...4 相関係数 決定係数 ( 最小 乗法を語るもう一つの立場...5 実験条件の誤差の影響...5 問題...6 最小 乗法の考え方 飲料水中のカルシウム濃度を
PowerPoint プレゼンテーション
 1/X Chapter 9: Linear correlation Cohen, B. H. (2007). In B. H. Cohen (Ed.), Explaining Psychological Statistics (3rd ed.) (pp. 255-285). NJ: Wiley. 概要 2/X 相関係数とは何か 相関係数の数式 検定 注意点 フィッシャーのZ 変換 信頼区間 相関係数の差の検定
1/X Chapter 9: Linear correlation Cohen, B. H. (2007). In B. H. Cohen (Ed.), Explaining Psychological Statistics (3rd ed.) (pp. 255-285). NJ: Wiley. 概要 2/X 相関係数とは何か 相関係数の数式 検定 注意点 フィッシャーのZ 変換 信頼区間 相関係数の差の検定
memo
 数理情報工学特論第一 機械学習とデータマイニング 4 章 : 教師なし学習 3 かしまひさし 鹿島久嗣 ( 数理 6 研 ) [email protected].~ DEPARTMENT OF MATHEMATICAL INFORMATICS 1 グラフィカルモデルについて学びます グラフィカルモデル グラフィカルラッソ グラフィカルラッソの推定アルゴリズム 2 グラフィカルモデル 3 教師なし学習の主要タスクは
数理情報工学特論第一 機械学習とデータマイニング 4 章 : 教師なし学習 3 かしまひさし 鹿島久嗣 ( 数理 6 研 ) [email protected].~ DEPARTMENT OF MATHEMATICAL INFORMATICS 1 グラフィカルモデルについて学びます グラフィカルモデル グラフィカルラッソ グラフィカルラッソの推定アルゴリズム 2 グラフィカルモデル 3 教師なし学習の主要タスクは
スライド 1
 計測工学第 12 回以降 測定値の誤差と精度編 2014 年 7 月 2 日 ( 水 )~7 月 16 日 ( 水 ) 知能情報工学科 横田孝義 1 授業計画 4/9 4/16 4/23 5/7 5/14 5/21 5/28 6/4 6/11 6/18 6/25 7/2 7/9 7/16 7/23 2 誤差とその取扱い 3 誤差 = 測定値 真の値 相対誤差 = 誤差 / 真の値 4 誤差 (error)
計測工学第 12 回以降 測定値の誤差と精度編 2014 年 7 月 2 日 ( 水 )~7 月 16 日 ( 水 ) 知能情報工学科 横田孝義 1 授業計画 4/9 4/16 4/23 5/7 5/14 5/21 5/28 6/4 6/11 6/18 6/25 7/2 7/9 7/16 7/23 2 誤差とその取扱い 3 誤差 = 測定値 真の値 相対誤差 = 誤差 / 真の値 4 誤差 (error)
多変量解析 ~ 重回帰分析 ~ 2006 年 4 月 21 日 ( 金 ) 南慶典
 多変量解析 ~ 重回帰分析 ~ 2006 年 4 月 21 日 ( 金 ) 南慶典 重回帰分析とは? 重回帰分析とは複数の説明変数から目的変数との関係性を予測 評価説明変数 ( 数量データ ) は目的変数を説明するのに有効であるか得られた関係性より未知のデータの妥当性を判断する これを重回帰分析という つまり どんなことをするのか? 1 最小 2 乗法により重回帰モデルを想定 2 自由度調整済寄与率を求め
多変量解析 ~ 重回帰分析 ~ 2006 年 4 月 21 日 ( 金 ) 南慶典 重回帰分析とは? 重回帰分析とは複数の説明変数から目的変数との関係性を予測 評価説明変数 ( 数量データ ) は目的変数を説明するのに有効であるか得られた関係性より未知のデータの妥当性を判断する これを重回帰分析という つまり どんなことをするのか? 1 最小 2 乗法により重回帰モデルを想定 2 自由度調整済寄与率を求め
Probit , Mixed logit
 Probit, Mixed logit 2016/5/16 スタートアップゼミ #5 B4 後藤祥孝 1 0. 目次 Probit モデルについて 1. モデル概要 2. 定式化と理解 3. 推定 Mixed logit モデルについて 4. モデル概要 5. 定式化と理解 6. 推定 2 1.Probit 概要 プロビットモデルとは. 効用関数の誤差項に多変量正規分布を仮定したもの. 誤差項には様々な要因が存在するため,
Probit, Mixed logit 2016/5/16 スタートアップゼミ #5 B4 後藤祥孝 1 0. 目次 Probit モデルについて 1. モデル概要 2. 定式化と理解 3. 推定 Mixed logit モデルについて 4. モデル概要 5. 定式化と理解 6. 推定 2 1.Probit 概要 プロビットモデルとは. 効用関数の誤差項に多変量正規分布を仮定したもの. 誤差項には様々な要因が存在するため,
calibT1.dvi
 1 2 flux( ) flux 2.1 flux Flux( flux ) Flux [erg/sec/cm 2 ] erg/sec/cm 2 /Å erg/sec/cm 2 /Hz 1 Flux -2.5 Vega Vega ( Vega +0.03 ) AB cgs F ν [erg/cm 2 /s/hz] m(ab) = 2.5 logf ν 48.6 V-band 2.2 Flux Suprime-Cam
1 2 flux( ) flux 2.1 flux Flux( flux ) Flux [erg/sec/cm 2 ] erg/sec/cm 2 /Å erg/sec/cm 2 /Hz 1 Flux -2.5 Vega Vega ( Vega +0.03 ) AB cgs F ν [erg/cm 2 /s/hz] m(ab) = 2.5 logf ν 48.6 V-band 2.2 Flux Suprime-Cam
<4D F736F F D208EC08CB18C7689E68A E F193F18D8095AA957A C C839395AA957A814590B38B4B95AA957A2E646F63>
 第 4 回二項分布, ポアソン分布, 正規分布 実験計画学 009 年 月 0 日 A. 代表的な分布. 離散分布 二項分布大きさ n の標本で, 事象 Eの起こる確率を p とするとき, そのうち x 個にEが起こる確率 P(x) は二項分布に従う. 例さいころを 0 回振ったときに の出る回数 x の確率分布は二項分布に従う. この場合, n = 0, p = 6 の二項分布になる さいころを
第 4 回二項分布, ポアソン分布, 正規分布 実験計画学 009 年 月 0 日 A. 代表的な分布. 離散分布 二項分布大きさ n の標本で, 事象 Eの起こる確率を p とするとき, そのうち x 個にEが起こる確率 P(x) は二項分布に従う. 例さいころを 0 回振ったときに の出る回数 x の確率分布は二項分布に従う. この場合, n = 0, p = 6 の二項分布になる さいころを
Microsoft PowerPoint - H17-5時限(パターン認識).ppt
 パターン認識早稲田大学講義 平成 7 年度 独 産業技術総合研究所栗田多喜夫 赤穂昭太郎 統計的特徴抽出 パターン認識過程 特徴抽出 認識対象から何らかの特徴量を計測 抽出 する必要がある 認識に有効な情報 特徴 を抽出し 次元を縮小した効率の良い空間を構成する過程 文字認識 : スキャナ等で取り込んだ画像から文字の識別に必要な本質的な特徴のみを抽出 例 文字線の傾き 曲率 面積など 識別 与えられた未知の対象を
パターン認識早稲田大学講義 平成 7 年度 独 産業技術総合研究所栗田多喜夫 赤穂昭太郎 統計的特徴抽出 パターン認識過程 特徴抽出 認識対象から何らかの特徴量を計測 抽出 する必要がある 認識に有効な情報 特徴 を抽出し 次元を縮小した効率の良い空間を構成する過程 文字認識 : スキャナ等で取り込んだ画像から文字の識別に必要な本質的な特徴のみを抽出 例 文字線の傾き 曲率 面積など 識別 与えられた未知の対象を
Microsoft PowerPoint - zairiki_3
 材料力学講義 (3) 応力と変形 Ⅲ ( 曲げモーメント, 垂直応力度, 曲率 ) 今回は, 曲げモーメントに関する, 断面力 - 応力度 - 変形 - 変位の関係について学びます 1 曲げモーメント 曲げモーメント M 静定力学で求めた曲げモーメントも, 仮想的に断面を切ることによって現れる内力です 軸方向力は断面に働く力 曲げモーメント M は断面力 曲げモーメントも, 一つのモーメントとして表しますが,
材料力学講義 (3) 応力と変形 Ⅲ ( 曲げモーメント, 垂直応力度, 曲率 ) 今回は, 曲げモーメントに関する, 断面力 - 応力度 - 変形 - 変位の関係について学びます 1 曲げモーメント 曲げモーメント M 静定力学で求めた曲げモーメントも, 仮想的に断面を切ることによって現れる内力です 軸方向力は断面に働く力 曲げモーメント M は断面力 曲げモーメントも, 一つのモーメントとして表しますが,
ビジネス統計 統計基礎とエクセル分析 正誤表
 ビジネス統計統計基礎とエクセル分析 ビジネス統計スペシャリスト エクセル分析スペシャリスト 公式テキスト正誤表と学習用データ更新履歴 平成 30 年 5 月 14 日現在 公式テキスト正誤表 頁場所誤正修正 6 知識編第 章 -3-3 最頻値の解説内容 たとえば, 表.1 のデータであれば, 最頻値は 167.5cm というたとえば, 表.1 のデータであれば, 最頻値は 165.0cm ということになります
ビジネス統計統計基礎とエクセル分析 ビジネス統計スペシャリスト エクセル分析スペシャリスト 公式テキスト正誤表と学習用データ更新履歴 平成 30 年 5 月 14 日現在 公式テキスト正誤表 頁場所誤正修正 6 知識編第 章 -3-3 最頻値の解説内容 たとえば, 表.1 のデータであれば, 最頻値は 167.5cm というたとえば, 表.1 のデータであれば, 最頻値は 165.0cm ということになります
Microsoft Word - t30_西_修正__ doc
 反応速度と化学平衡 金沢工業大学基礎教育部西誠 ねらい 化学反応とは分子を構成している原子が組み換り 新しい分子構造を持つことといえます この化学反応がどのように起こるのか どのような速さでどの程度の分子が組み換るのかは 反応の種類や 濃度 温度などの条件で決まってきます そして このような反応の進行方向や速度を正確に予測するために いろいろな数学 物理的な考え方を取り入れて化学反応の理論体系が作られています
反応速度と化学平衡 金沢工業大学基礎教育部西誠 ねらい 化学反応とは分子を構成している原子が組み換り 新しい分子構造を持つことといえます この化学反応がどのように起こるのか どのような速さでどの程度の分子が組み換るのかは 反応の種類や 濃度 温度などの条件で決まってきます そして このような反応の進行方向や速度を正確に予測するために いろいろな数学 物理的な考え方を取り入れて化学反応の理論体系が作られています
スライド 1
 データ解析特論第 10 回 ( 全 15 回 ) 2012 年 12 月 11 日 ( 火 ) 情報エレクトロニクス専攻横田孝義 1 終了 11/13 11/20 重回帰分析をしばらくやります 12/4 12/11 12/18 2 前回から回帰分析について学習しています 3 ( 単 ) 回帰分析 単回帰分析では一つの従属変数 ( 目的変数 ) を 一つの独立変数 ( 説明変数 ) で予測する事を考える
データ解析特論第 10 回 ( 全 15 回 ) 2012 年 12 月 11 日 ( 火 ) 情報エレクトロニクス専攻横田孝義 1 終了 11/13 11/20 重回帰分析をしばらくやります 12/4 12/11 12/18 2 前回から回帰分析について学習しています 3 ( 単 ) 回帰分析 単回帰分析では一つの従属変数 ( 目的変数 ) を 一つの独立変数 ( 説明変数 ) で予測する事を考える
1.民営化
 参考資料 最小二乗法 数学的性質 経済統計分析 3 年度秋学期 回帰分析と最小二乗法 被説明変数 の動きを説明変数 の動きで説明 = 回帰分析 説明変数がつ 単回帰 説明変数がつ以上 重回帰 被説明変数 従属変数 係数 定数項傾き 説明変数 独立変数 残差... で説明できる部分 説明できない部分 説明できない部分が小さくなるように回帰式の係数 を推定する有力な方法 = 最小二乗法 最小二乗法による回帰の考え方
参考資料 最小二乗法 数学的性質 経済統計分析 3 年度秋学期 回帰分析と最小二乗法 被説明変数 の動きを説明変数 の動きで説明 = 回帰分析 説明変数がつ 単回帰 説明変数がつ以上 重回帰 被説明変数 従属変数 係数 定数項傾き 説明変数 独立変数 残差... で説明できる部分 説明できない部分 説明できない部分が小さくなるように回帰式の係数 を推定する有力な方法 = 最小二乗法 最小二乗法による回帰の考え方
ii 3.,. 4. F. (), ,,. 8.,. 1. (75% ) (25% ) =9 7, =9 8 (. ). 1.,, (). 3.,. 1. ( ).,.,.,.,.,. ( ) (1 2 )., ( ), 0. 2., 1., 0,.
 23(2011) (1 C104) 5 11 (2 C206) 5 12 http://www.math.is.tohoku.ac.jp/~obata,.,,,.. 1. 2. 3. 4. 5. 6. 7.,,. 1., 2007 ( ). 2. P. G. Hoel, 1995. 3... 1... 2.,,. ii 3.,. 4. F. (),.. 5.. 6.. 7.,,. 8.,. 1. (75%
23(2011) (1 C104) 5 11 (2 C206) 5 12 http://www.math.is.tohoku.ac.jp/~obata,.,,,.. 1. 2. 3. 4. 5. 6. 7.,,. 1., 2007 ( ). 2. P. G. Hoel, 1995. 3... 1... 2.,,. ii 3.,. 4. F. (),.. 5.. 6.. 7.,,. 8.,. 1. (75%
統計学的画像再構成法である
 OSEM アルゴリズムの基礎論 第 1 章 確率 統計の基礎 1.13 最尤推定 やっと本命の最尤推定という言葉が出てきました. お待たせしました. この節はいままでの中で最も長く, 少し難しい内容も出てきます. がんばってください. これが終わるといよいよ本命の MLEM,OSEM の章です. ところで 尤 なる字はあまり見かけませんね. ゆう と読みます. いぬ ではありません!! この意味は
OSEM アルゴリズムの基礎論 第 1 章 確率 統計の基礎 1.13 最尤推定 やっと本命の最尤推定という言葉が出てきました. お待たせしました. この節はいままでの中で最も長く, 少し難しい内容も出てきます. がんばってください. これが終わるといよいよ本命の MLEM,OSEM の章です. ところで 尤 なる字はあまり見かけませんね. ゆう と読みます. いぬ ではありません!! この意味は
Microsoft PowerPoint - statistics pptx
 統計学 第 16 回 講義 母平均の区間推定 Part-1 016 年 6 10 ( ) 1 限 担当教員 : 唐渡 広志 ( からと こうじ ) 研究室 : 経済学研究棟 4 階 43 号室 email: [email protected] website: http://www3.u-toyama.ac.jp/kkarato/ 1 講義の目的 標本平均は正規分布に従うという性質を
統計学 第 16 回 講義 母平均の区間推定 Part-1 016 年 6 10 ( ) 1 限 担当教員 : 唐渡 広志 ( からと こうじ ) 研究室 : 経済学研究棟 4 階 43 号室 email: [email protected] website: http://www3.u-toyama.ac.jp/kkarato/ 1 講義の目的 標本平均は正規分布に従うという性質を
モジュール1のまとめ
 数理統計学 第 0 回 復習 標本分散と ( 標本 ) 不偏分散両方とも 分散 というのが実情 二乗偏差計標本分散 = データ数 (0ページ) ( 標本 ) 不偏分散 = (03 ページ ) 二乗偏差計 データ数 - 分析ではこちらをとることが多い 復習 ここまで 実験結果 ( 万回 ) 平均 50Kg 標準偏差 0Kg 0 人 全体に小さすぎる > mea(jkke) [] 89.4373 標準偏差
数理統計学 第 0 回 復習 標本分散と ( 標本 ) 不偏分散両方とも 分散 というのが実情 二乗偏差計標本分散 = データ数 (0ページ) ( 標本 ) 不偏分散 = (03 ページ ) 二乗偏差計 データ数 - 分析ではこちらをとることが多い 復習 ここまで 実験結果 ( 万回 ) 平均 50Kg 標準偏差 0Kg 0 人 全体に小さすぎる > mea(jkke) [] 89.4373 標準偏差
スライド 1
 データ解析特論重回帰分析編 2017 年 7 月 10 日 ( 月 )~ 情報エレクトロニクスコース横田孝義 1 ( 単 ) 回帰分析 単回帰分析では一つの従属変数 ( 目的変数 ) を 一つの独立変数 ( 説明変数 ) で予測する事を考える 具体的には y = a + bx という回帰直線 ( モデル ) でデータを代表させる このためにデータからこの回帰直線の切片 (a) と傾き (b) を最小
データ解析特論重回帰分析編 2017 年 7 月 10 日 ( 月 )~ 情報エレクトロニクスコース横田孝義 1 ( 単 ) 回帰分析 単回帰分析では一つの従属変数 ( 目的変数 ) を 一つの独立変数 ( 説明変数 ) で予測する事を考える 具体的には y = a + bx という回帰直線 ( モデル ) でデータを代表させる このためにデータからこの回帰直線の切片 (a) と傾き (b) を最小
<4D F736F F D208EC08CB18C7689E68A E F AA957A82C682948C9F92E82E646F63>
 第 7 回 t 分布と t 検定 実験計画学 A.t 分布 ( 小標本に関する平均の推定と検定 ) 前々回と前回の授業では, 標本が十分に大きいあるいは母分散が既知であることを条件に正規分布を用いて推定 検定した. しかし, 母集団が正規分布し, 標本が小さい場合には, 標本分散から母分散を推定するときの不確実さを加味したt 分布を用いて推定 検定しなければならない. t 分布は標本分散の自由度 f(
第 7 回 t 分布と t 検定 実験計画学 A.t 分布 ( 小標本に関する平均の推定と検定 ) 前々回と前回の授業では, 標本が十分に大きいあるいは母分散が既知であることを条件に正規分布を用いて推定 検定した. しかし, 母集団が正規分布し, 標本が小さい場合には, 標本分散から母分散を推定するときの不確実さを加味したt 分布を用いて推定 検定しなければならない. t 分布は標本分散の自由度 f(
ii 2. F. ( ), ,,. 5. G., L., D. ( ) ( ), 2005.,. 6.,,. 7.,. 8. ( ), , (20 ). 1. (75% ) (25% ). 60.,. 2. =8 5, =8 4 (. 1.) 1.,,
 (1 C205) 4 8 27(2015) http://www.math.is.tohoku.ac.jp/~obata,.,,,..,,. 1. 2. 3. 4. 5. 6. 7.... 1., 2014... 2. P. G., 1995.,. 3.,. 4.. 5., 1996... 1., 2007,. ii 2. F. ( ),.. 3... 4.,,. 5. G., L., D. ( )
(1 C205) 4 8 27(2015) http://www.math.is.tohoku.ac.jp/~obata,.,,,..,,. 1. 2. 3. 4. 5. 6. 7.... 1., 2014... 2. P. G., 1995.,. 3.,. 4.. 5., 1996... 1., 2007,. ii 2. F. ( ),.. 3... 4.,,. 5. G., L., D. ( )
測量士補 重要事項「標準偏差」
 標準偏差 < 試験合格へのポイント > 士補試験における標準偏差に関する問題は 平成元年が最後の出題となっており それ以来 0 年間に渡って出題された形跡がない このため 受験対策本の中には標準偏差に関して 触れることすら無くなっている物もあるのが現状である しかし平成 0 年度試験において 再び出題が確認されたため ここに解説し過去に出題された問題について触れてみる 標準偏差に関する問題は 基本的にはその公式に当てはめて解けば良いため
標準偏差 < 試験合格へのポイント > 士補試験における標準偏差に関する問題は 平成元年が最後の出題となっており それ以来 0 年間に渡って出題された形跡がない このため 受験対策本の中には標準偏差に関して 触れることすら無くなっている物もあるのが現状である しかし平成 0 年度試験において 再び出題が確認されたため ここに解説し過去に出題された問題について触れてみる 標準偏差に関する問題は 基本的にはその公式に当てはめて解けば良いため
Microsoft PowerPoint - Statistics[B]
![Microsoft PowerPoint - Statistics[B] Microsoft PowerPoint - Statistics[B]](/thumbs/101/151482563.jpg) 講義の目的 サンプルサイズの大きい標本比率の分布は正規分布で近似できることを理解します 科目コード 130509, 130609, 110225 統計学講義第 19/20 回 2019 年 6 月 25 日 ( 火 )6/7 限 担当教員 : 唐渡広志 ( からと こうじ ) 研究室 : email: website: 経済学研究棟 4 階 432 号室 [email protected]
講義の目的 サンプルサイズの大きい標本比率の分布は正規分布で近似できることを理解します 科目コード 130509, 130609, 110225 統計学講義第 19/20 回 2019 年 6 月 25 日 ( 火 )6/7 限 担当教員 : 唐渡広志 ( からと こうじ ) 研究室 : email: website: 経済学研究棟 4 階 432 号室 [email protected]
PowerPoint プレゼンテーション
 復習 ) 時系列のモデリング ~a. 離散時間モデル ~ y k + a 1 z 1 y k + + a na z n ay k = b 0 u k + b 1 z 1 u k + + b nb z n bu k y k = G z 1 u k = B(z 1 ) A(z 1 u k ) ARMA モデル A z 1 B z 1 = 1 + a 1 z 1 + + a na z n a = b 0
復習 ) 時系列のモデリング ~a. 離散時間モデル ~ y k + a 1 z 1 y k + + a na z n ay k = b 0 u k + b 1 z 1 u k + + b nb z n bu k y k = G z 1 u k = B(z 1 ) A(z 1 u k ) ARMA モデル A z 1 B z 1 = 1 + a 1 z 1 + + a na z n a = b 0
パソコンシミュレータの現状
 第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
統計Ⅰ 第1回 序説~確率
 授業担当 : 徳永伸一 東京医科歯科大学教養部 数学講座 あらためて注意しておきたいこと ( 前期のはじめに注意したこと +α) 後期の授業は今日を含め ( たった )6 回 成績評価は前期試験 + 後期試験で 後期の方が比重が大きいですが前期の出来が悪かった人はハンデがあると思ってください 後期試験の出題範囲には前期授業の内容も含まれます 復習も怠りなく 欠席した場合は次回までに要点の確認を 次回の授業までに授業スライドを
授業担当 : 徳永伸一 東京医科歯科大学教養部 数学講座 あらためて注意しておきたいこと ( 前期のはじめに注意したこと +α) 後期の授業は今日を含め ( たった )6 回 成績評価は前期試験 + 後期試験で 後期の方が比重が大きいですが前期の出来が悪かった人はハンデがあると思ってください 後期試験の出題範囲には前期授業の内容も含まれます 復習も怠りなく 欠席した場合は次回までに要点の確認を 次回の授業までに授業スライドを
第 4 週コンボリューションその 2, 正弦波による分解 教科書 p. 16~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問 1. 以下の図にならって,1 と 2 の δ 関数を図示せよ δ (t) 2
 第 4 週コンボリューションその, 正弦波による分解 教科書 p. 6~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問. 以下の図にならって, と の δ 関数を図示せよ. - - - δ () δ ( ) - - - 図 δ 関数の図示の例 δ ( ) δ ( ) δ ( ) δ ( ) δ ( ) - - - - - - - -
第 4 週コンボリューションその, 正弦波による分解 教科書 p. 6~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問. 以下の図にならって, と の δ 関数を図示せよ. - - - δ () δ ( ) - - - 図 δ 関数の図示の例 δ ( ) δ ( ) δ ( ) δ ( ) δ ( ) - - - - - - - -
データ解析
 データ解析 ( 前期 ) 最小二乗法 向井厚志 005 年度テキスト 0 データ解析 - 最小二乗法 - 目次 第 回 Σ の計算 第 回ヒストグラム 第 3 回平均と標準偏差 6 第 回誤差の伝播 8 第 5 回正規分布 0 第 6 回最尤性原理 第 7 回正規分布の 分布の幅 第 8 回最小二乗法 6 第 9 回最小二乗法の練習 8 第 0 回最小二乗法の推定誤差 0 第 回推定誤差の計算 第
データ解析 ( 前期 ) 最小二乗法 向井厚志 005 年度テキスト 0 データ解析 - 最小二乗法 - 目次 第 回 Σ の計算 第 回ヒストグラム 第 3 回平均と標準偏差 6 第 回誤差の伝播 8 第 5 回正規分布 0 第 6 回最尤性原理 第 7 回正規分布の 分布の幅 第 8 回最小二乗法 6 第 9 回最小二乗法の練習 8 第 0 回最小二乗法の推定誤差 0 第 回推定誤差の計算 第
ファイナンスのための数学基礎 第1回 オリエンテーション、ベクトル
 春学期統計学 I 記述統計と推測統計 担当 : 長倉大輔 ( ながくらだいすけ ) 1 本日の予定 本日はまず記述統計と推測統計の違い 推測統計学の基本的な構造について説明します 2 記述統計と推測統計 統計学とは? 与えられたデータの背後にある 特性 法則 を 検証 発見 分析 するための手法の開発 その応用などに関わる学問の事です 3 記述統計と推測統計 データの種類 データの種類はおおまかに
春学期統計学 I 記述統計と推測統計 担当 : 長倉大輔 ( ながくらだいすけ ) 1 本日の予定 本日はまず記述統計と推測統計の違い 推測統計学の基本的な構造について説明します 2 記述統計と推測統計 統計学とは? 与えられたデータの背後にある 特性 法則 を 検証 発見 分析 するための手法の開発 その応用などに関わる学問の事です 3 記述統計と推測統計 データの種類 データの種類はおおまかに
Microsoft PowerPoint - aep_1.ppt [互換モード]
![Microsoft PowerPoint - aep_1.ppt [互換モード] Microsoft PowerPoint - aep_1.ppt [互換モード]](/thumbs/91/107493198.jpg) 物理計測法特論 No.1 第 1 章 : 信号と雑音 本講義の主題 雑音の性質を理解することで 信号と雑音の大きさが非常に近い状態での信号の測定技術 : 微小信号計測 について学ぶ 講義の Web http://www.g-munu.t.u-tokyo.ac.jp/mio/note/sig_mes/tokuron.html 物理学の基本は実験事実の積み重ねである そして それは何かを測定することから始まる
物理計測法特論 No.1 第 1 章 : 信号と雑音 本講義の主題 雑音の性質を理解することで 信号と雑音の大きさが非常に近い状態での信号の測定技術 : 微小信号計測 について学ぶ 講義の Web http://www.g-munu.t.u-tokyo.ac.jp/mio/note/sig_mes/tokuron.html 物理学の基本は実験事実の積み重ねである そして それは何かを測定することから始まる
Microsoft Word - 補論3.2
 補論 3. 多変量 GARC モデル 07//6 新谷元嗣 藪友良 対数尤度関数 3 章 7 節では 変量の対数尤度を求めた ここでは多変量の場合 とくに 変量について対数尤度を求める 誤差項 は平均 0 で 次元の正規分布に従うとする 単純化のため 分散と共分散は時間を通じて一定としよう ( この仮定は後で変更される ) したがって ij から添え字 を除くことができる このとき と の尤度関数は
補論 3. 多変量 GARC モデル 07//6 新谷元嗣 藪友良 対数尤度関数 3 章 7 節では 変量の対数尤度を求めた ここでは多変量の場合 とくに 変量について対数尤度を求める 誤差項 は平均 0 で 次元の正規分布に従うとする 単純化のため 分散と共分散は時間を通じて一定としよう ( この仮定は後で変更される ) したがって ij から添え字 を除くことができる このとき と の尤度関数は
ファイナンスのための数学基礎 第1回 オリエンテーション、ベクトル
 時系列分析 変量時系列モデルとその性質 担当 : 長倉大輔 ( ながくらだいすけ 時系列モデル 時系列モデルとは時系列データを生み出すメカニズムとなるものである これは実際には未知である 私たちにできるのは観測された時系列データからその背後にある時系列モデルを推測 推定するだけである 以下ではいくつかの代表的な時系列モデルを考察する 自己回帰モデル (Auoregressive Model もっとも頻繁に使われる時系列モデルは自己回帰モデル
時系列分析 変量時系列モデルとその性質 担当 : 長倉大輔 ( ながくらだいすけ 時系列モデル 時系列モデルとは時系列データを生み出すメカニズムとなるものである これは実際には未知である 私たちにできるのは観測された時系列データからその背後にある時系列モデルを推測 推定するだけである 以下ではいくつかの代表的な時系列モデルを考察する 自己回帰モデル (Auoregressive Model もっとも頻繁に使われる時系列モデルは自己回帰モデル
SAP11_03
 第 3 回 音声音響信号処理 ( 線形予測分析と自己回帰モデル ) 亀岡弘和 東京大学大学院情報理工学系研究科日本電信電話株式会社 NTT コミュニケーション科学基礎研究所 講義内容 ( キーワード ) 信号処理 符号化 標準化の実用システム例の紹介情報通信の基本 ( 誤り検出 訂正符号 変調 IP) 符号化技術の基本 ( 量子化 予測 変換 圧縮 ) 音声分析 合成 認識 強調 音楽信号処理統計的信号処理の基礎
第 3 回 音声音響信号処理 ( 線形予測分析と自己回帰モデル ) 亀岡弘和 東京大学大学院情報理工学系研究科日本電信電話株式会社 NTT コミュニケーション科学基礎研究所 講義内容 ( キーワード ) 信号処理 符号化 標準化の実用システム例の紹介情報通信の基本 ( 誤り検出 訂正符号 変調 IP) 符号化技術の基本 ( 量子化 予測 変換 圧縮 ) 音声分析 合成 認識 強調 音楽信号処理統計的信号処理の基礎
解析力学B - 第11回: 正準変換
 解析力学 B 第 11 回 : 正準変換 神戸大 : 陰山聡 ホームページ ( 第 6 回から今回までの講義ノート ) http://tinyurl.com/kage2010 2011.01.27 正準変換 バネ問題 ( あえて下手に座標をとった ) ハミルトニアンを考える q 正準方程式は H = p2 2m + k 2 (q l 0) 2 q = H p = p m ṗ = H q = k(q
解析力学 B 第 11 回 : 正準変換 神戸大 : 陰山聡 ホームページ ( 第 6 回から今回までの講義ノート ) http://tinyurl.com/kage2010 2011.01.27 正準変換 バネ問題 ( あえて下手に座標をとった ) ハミルトニアンを考える q 正準方程式は H = p2 2m + k 2 (q l 0) 2 q = H p = p m ṗ = H q = k(q
Excelによる統計分析検定_知識編_小塚明_1_4章.indd
 第2章 1 変量データのまとめ方 本章では, 記述統計の手法について説明します 具体的には, 得られたデータから表やグラフを作成し, 意昧のある統計量を算出する方法など,1 変量データのまとめ方について学びます 本章から理解を深めるための数式が出てきますが, 必ずしも, これらの式を覚える必要はありません それぞれのデータの性質や統計量の意義を理解することが重要です 円グラフと棒グラフ 1 変量質的データをまとめる方法としてよく使われるグラフは,
第2章 1 変量データのまとめ方 本章では, 記述統計の手法について説明します 具体的には, 得られたデータから表やグラフを作成し, 意昧のある統計量を算出する方法など,1 変量データのまとめ方について学びます 本章から理解を深めるための数式が出てきますが, 必ずしも, これらの式を覚える必要はありません それぞれのデータの性質や統計量の意義を理解することが重要です 円グラフと棒グラフ 1 変量質的データをまとめる方法としてよく使われるグラフは,
代数 幾何 < ベクトル > 1 ベクトルの演算 和 差 実数倍については 文字の計算と同様 2 ベクトルの成分表示 平面ベクトル : a x e y e x, ) ( 1 y1 空間ベクトル : a x e y e z e x, y, ) ( 1 1 z1
 代数 幾何 < ベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル :, 空間ベクトル : z,, z 成分での計算ができるようにすること ベクトルの内積 : os 平面ベクトル :,, 空間ベクトル :,,,, z z zz 4 ベクトルの大きさ 平面上 : 空間上 : z は 良く用いられる 5 m: に分ける点 : m m 図形への応用
代数 幾何 < ベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル :, 空間ベクトル : z,, z 成分での計算ができるようにすること ベクトルの内積 : os 平面ベクトル :,, 空間ベクトル :,,,, z z zz 4 ベクトルの大きさ 平面上 : 空間上 : z は 良く用いられる 5 m: に分ける点 : m m 図形への応用
3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x0 = f x= x0 t f c x f =0 [1] c f 0 x= x 0 x 0 f x= x0 x 2 x 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考
![3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x0 = f x= x0 t f c x f =0 [1] c f 0 x= x 0 x 0 f x= x0 x 2 x 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考 3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x0 = f x= x0 t f c x f =0 [1] c f 0 x= x 0 x 0 f x= x0 x 2 x 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考](/thumbs/103/158269281.jpg) 3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x = f x= x t f c x f = [1] c f x= x f x= x 2 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考える まず 初期時刻 t=t に f =R f exp [ik x ] [3] のような波動を与えたとき どのように時間変化するか調べる
3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x = f x= x t f c x f = [1] c f x= x f x= x 2 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考える まず 初期時刻 t=t に f =R f exp [ik x ] [3] のような波動を与えたとき どのように時間変化するか調べる
Python-statistics5 Python で統計学を学ぶ (5) この内容は山田 杉澤 村井 (2008) R によるやさしい統計学 (
 http://localhost:8888/notebooks/... Python で統計学を学ぶ (5) この内容は山田 杉澤 村井 (2008) R によるやさしい統計学 (http://shop.ohmsha.co.jp/shop /shopdetail.html?brandcode=000000001781&search=978-4-274-06710-5&sort=) を参考にしています
http://localhost:8888/notebooks/... Python で統計学を学ぶ (5) この内容は山田 杉澤 村井 (2008) R によるやさしい統計学 (http://shop.ohmsha.co.jp/shop /shopdetail.html?brandcode=000000001781&search=978-4-274-06710-5&sort=) を参考にしています
統計学の基礎から学ぶ実験計画法ー1
 第 部統計学の基礎と. 統計学とは. 統計学の基本. 母集団とサンプル ( 標本 ). データ (data) 3. 集団の特性を示す統計量 基本的な解析手法 3. 統計量 (statistic) とは 3. 集団を代表する統計量 - 平均値など 3.3 集団のばらつきを表す値 - 平方和 分散 標準偏差 4. ばらつき ( 分布 ) を表す関数 4. 確率密度関数 4. 最も重要な正規分布 4.3
第 部統計学の基礎と. 統計学とは. 統計学の基本. 母集団とサンプル ( 標本 ). データ (data) 3. 集団の特性を示す統計量 基本的な解析手法 3. 統計量 (statistic) とは 3. 集団を代表する統計量 - 平均値など 3.3 集団のばらつきを表す値 - 平方和 分散 標準偏差 4. ばらつき ( 分布 ) を表す関数 4. 確率密度関数 4. 最も重要な正規分布 4.3
Microsoft Word - lec_student-chp3_1-representative
 1. はじめに この節でのテーマ データ分布の中心位置を数値で表す 可視化でとらえた分布の中心位置を数量化する 平均値とメジアン, 幾何平均 この節での到達目標 1 平均値 メジアン 幾何平均の定義を書ける 2 平均値とメジアン, 幾何平均の特徴と使える状況を説明できる. 3 平均値 メジアン 幾何平均を計算できる 2. 特性値 集めたデータを度数分布表やヒストグラムに整理する ( 可視化する )
1. はじめに この節でのテーマ データ分布の中心位置を数値で表す 可視化でとらえた分布の中心位置を数量化する 平均値とメジアン, 幾何平均 この節での到達目標 1 平均値 メジアン 幾何平均の定義を書ける 2 平均値とメジアン, 幾何平均の特徴と使える状況を説明できる. 3 平均値 メジアン 幾何平均を計算できる 2. 特性値 集めたデータを度数分布表やヒストグラムに整理する ( 可視化する )
Microsoft Word - å“Ÿåłžå¸°173.docx
 回帰分析 ( その 3) 経済情報処理 価格弾力性の推定ある商品について その購入量を w 単価を p とし それぞれの変化量を w p で表 w w すことにする この時 この商品の価格弾力性 は により定義される これ p p は p が 1 パーセント変化した場合に w が何パーセント変化するかを示したものである ここで p を 0 に近づけていった極限を考えると d ln w 1 dw dw
回帰分析 ( その 3) 経済情報処理 価格弾力性の推定ある商品について その購入量を w 単価を p とし それぞれの変化量を w p で表 w w すことにする この時 この商品の価格弾力性 は により定義される これ p p は p が 1 パーセント変化した場合に w が何パーセント変化するかを示したものである ここで p を 0 に近づけていった極限を考えると d ln w 1 dw dw
計算機シミュレーション
 . 運動方程式の数値解法.. ニュートン方程式の近似速度は, 位置座標 の時間微分で, d と定義されます. これを成分で書くと, d d li li とかけます. 本来は が の極限をとらなければいけませんが, 有限の小さな値とすると 秒後の位置座標は速度を用いて, と近似できます. 同様にして, 加速度は, 速度 の時間微分で, d と定義されます. これを成分で書くと, d d li li とかけます.
. 運動方程式の数値解法.. ニュートン方程式の近似速度は, 位置座標 の時間微分で, d と定義されます. これを成分で書くと, d d li li とかけます. 本来は が の極限をとらなければいけませんが, 有限の小さな値とすると 秒後の位置座標は速度を用いて, と近似できます. 同様にして, 加速度は, 速度 の時間微分で, d と定義されます. これを成分で書くと, d d li li とかけます.
Microsoft PowerPoint - 資料04 重回帰分析.ppt
 04. 重回帰分析 京都大学 加納学 Division of Process Control & Process Sstems Engineering Department of Chemical Engineering, Koto Universit [email protected] http://www-pse.cheme.koto-u.ac.jp/~kano/ Outline
04. 重回帰分析 京都大学 加納学 Division of Process Control & Process Sstems Engineering Department of Chemical Engineering, Koto Universit [email protected] http://www-pse.cheme.koto-u.ac.jp/~kano/ Outline
Microsoft Word - thesis.doc
 剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
デジカメ天文学実習 < ワークシート : 解説編 > ガリレオ衛星の動きと木星の質量 1. 目的 木星のガリレオ衛星をデジカメで撮影し その動きからケプラーの第三法則と万有引 力の法則を使って, 木星本体の質量を求める 2. ガリレオ衛星の撮影 (1) 撮影の方法 4つのガリレオ衛星の内 一番外側を
 デジカメ天文学実習 < ワークシート : 解説編 > ガリレオ衛星の動きと木星の質量 1. 目的 木星のガリレオ衛星をデジカメで撮影し その動きからケプラーの第三法則と万有引 力の法則を使って, 木星本体の質量を求める 2. ガリレオ衛星の撮影 (1) 撮影の方法 4つのガリレオ衛星の内 一番外側を回るカリストまたはその内側のガニメデが 木星から最も離れる最大離角の日に 200~300mm の望遠レンズ
デジカメ天文学実習 < ワークシート : 解説編 > ガリレオ衛星の動きと木星の質量 1. 目的 木星のガリレオ衛星をデジカメで撮影し その動きからケプラーの第三法則と万有引 力の法則を使って, 木星本体の質量を求める 2. ガリレオ衛星の撮影 (1) 撮影の方法 4つのガリレオ衛星の内 一番外側を回るカリストまたはその内側のガニメデが 木星から最も離れる最大離角の日に 200~300mm の望遠レンズ
ベイズ統計入門
 ベイズ統計入門 条件付確率 事象 F が起こったことが既知であるという条件の下で E が起こる確率を条件付確率 (codtoal probablt) という P ( E F ) P ( E F ) P( F ) 定義式を変形すると 確率の乗法公式となる ( E F ) P( F ) P( E F ) P( E) P( F E) P 事象の独立 ある事象の生起する確率が 他のある事象が生起するかどうかによって変化しないとき
ベイズ統計入門 条件付確率 事象 F が起こったことが既知であるという条件の下で E が起こる確率を条件付確率 (codtoal probablt) という P ( E F ) P ( E F ) P( F ) 定義式を変形すると 確率の乗法公式となる ( E F ) P( F ) P( E F ) P( E) P( F E) P 事象の独立 ある事象の生起する確率が 他のある事象が生起するかどうかによって変化しないとき
画像類似度測定の初歩的な手法の検証
 画像類似度測定の初歩的な手法の検証 島根大学総合理工学部数理 情報システム学科 計算機科学講座田中研究室 S539 森瀧昌志 1 目次 第 1 章序論第 章画像間類似度測定の初歩的な手法について.1 A. 画素値の平均を用いる手法.. 画素値のヒストグラムを用いる手法.3 C. 相関係数を用いる手法.4 D. 解像度を合わせる手法.5 E. 振れ幅のヒストグラムを用いる手法.6 F. 周波数ごとの振れ幅を比較する手法第
画像類似度測定の初歩的な手法の検証 島根大学総合理工学部数理 情報システム学科 計算機科学講座田中研究室 S539 森瀧昌志 1 目次 第 1 章序論第 章画像間類似度測定の初歩的な手法について.1 A. 画素値の平均を用いる手法.. 画素値のヒストグラムを用いる手法.3 C. 相関係数を用いる手法.4 D. 解像度を合わせる手法.5 E. 振れ幅のヒストグラムを用いる手法.6 F. 周波数ごとの振れ幅を比較する手法第
PowerPoint Presentation
 付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュ
 数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュレーションによって計算してみる 4.1 放物運動一様な重力場における放物運動を考える 一般に質量の物体に作用する力をとすると運動方程式は
数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュレーションによって計算してみる 4.1 放物運動一様な重力場における放物運動を考える 一般に質量の物体に作用する力をとすると運動方程式は
コロイド化学と界面化学
 環境表面科学講義 http://res.tagen.tohoku.ac.jp/~liquid/mura/kogi/kaimen/ E-mail: [email protected] 村松淳司 分散と凝集 ( 平衡論的考察! 凝集! van der Waals 力による相互作用! 分散! 静電的反発力 凝集 分散! 粒子表面の電位による反発 分散と凝集 考え方! van der Waals
環境表面科学講義 http://res.tagen.tohoku.ac.jp/~liquid/mura/kogi/kaimen/ E-mail: [email protected] 村松淳司 分散と凝集 ( 平衡論的考察! 凝集! van der Waals 力による相互作用! 分散! 静電的反発力 凝集 分散! 粒子表面の電位による反発 分散と凝集 考え方! van der Waals
自動車感性評価学 1. 二項検定 内容 2 3. 質的データの解析方法 1 ( 名義尺度 ) 2.χ 2 検定 タイプ 1. 二項検定 官能検査における分類データの解析法 識別できるかを調べる 嗜好に差があるかを調べる 2 点比較法 2 点識別法 2 点嗜好法 3 点比較法 3 点識別法 3 点嗜好
 . 内容 3. 質的データの解析方法 ( 名義尺度 ).χ 検定 タイプ. 官能検査における分類データの解析法 識別できるかを調べる 嗜好に差があるかを調べる 点比較法 点識別法 点嗜好法 3 点比較法 3 点識別法 3 点嗜好法 : 点比較法 : 点識別法 配偶法 配偶法 ( 官能評価の基礎と応用 ) 3 A か B かの判定において 回の判定でAが選ばれる回数 kは p の二項分布に従う H :
. 内容 3. 質的データの解析方法 ( 名義尺度 ).χ 検定 タイプ. 官能検査における分類データの解析法 識別できるかを調べる 嗜好に差があるかを調べる 点比較法 点識別法 点嗜好法 3 点比較法 3 点識別法 3 点嗜好法 : 点比較法 : 点識別法 配偶法 配偶法 ( 官能評価の基礎と応用 ) 3 A か B かの判定において 回の判定でAが選ばれる回数 kは p の二項分布に従う H :
Excelによる統計分析検定_知識編_小塚明_5_9章.indd
 第7章57766 検定と推定 サンプリングによって得られた標本から, 母集団の統計的性質に対して推測を行うことを統計的推測といいます 本章では, 推測統計の根幹をなす仮説検定と推定の基本的な考え方について説明します 前章までの知識を用いて, 具体的な分析を行います 本章以降の知識は操作編での操作に直接関連していますので, 少し聞きなれない言葉ですが, 帰無仮説 有意水準 棄却域 などの意味を理解して,
第7章57766 検定と推定 サンプリングによって得られた標本から, 母集団の統計的性質に対して推測を行うことを統計的推測といいます 本章では, 推測統計の根幹をなす仮説検定と推定の基本的な考え方について説明します 前章までの知識を用いて, 具体的な分析を行います 本章以降の知識は操作編での操作に直接関連していますので, 少し聞きなれない言葉ですが, 帰無仮説 有意水準 棄却域 などの意味を理解して,
