殿塚勲 藤原祥史 吉田政春 を観察しながら各面の色の塗り分けをしてゆくと, 色の塗り分けの全体像が理解しやすく, 色の種類の最小解にたどりつくことが分かった この方法によればグローバルな見地から色の塗り分けができ, かつ色の種類が最小であることの見通しを直観的に理解できることがよい点である ここで得
|
|
|
- くうしょう しげい
- 7 years ago
- Views:
Transcription
1 広島工業大学紀要研究編第 44 巻 (2010)pp 論文 準正多面体の構成と色の塗り分け 殿塚勲 * 藤原祥史 * 吉田政春 * Construction and Coloring of Semi-Regular Polyhedrons ( 平成 21 年 10 月 27 日受理 ) Isao TONOZUKA, Yoshifumi FUJIWARA and Masaharu YOSHIDA (Received Oct. 27, 2009) Abstract This paper deals with the coloring of semi-regular polyhedrons. The famous four-color theorem comes into effect for this type of polyhedrons as well as the 2-dimensional maps. The semi-regular polyhedrons are constructed from regular polyhedrons by means of such operations as truncation. In the cource of the constructions of semi-regular polyhedrons from regular polyhedrons, a careful observation leads us a finding of coloring of the semi-regular polyhedrons by use of minimum kind of colors. This method is global, whereas our proposal in the previous report is local. Key Words: semi regular polyhedron, global coloring, four-color theorem, regular polyhedron 1 はじめに前回の報告 [1] では正多面体の塗り分けを, 隣の面同士が同じ色にならないように色を選ぶことを試みた この際, 有名な4 色定理 [2] により多くとも4 色で塗り分けができることを前提とし, 使われる色の種類が最小になるように決めた その結果 の段階になって4 色以内で塗り分けが不可能になったり, あるいは更によい解の存在を知る場合もある ここでは準正多面体の塗り分けを取り上げる 準正多面体はアルキメデスの多面体とも呼ばれ [5] (ⅰ) 有限個の多角形で囲まれた凸多面体である (ⅱ) 各面はすべて辺の長さが等しい正多角形から成る ただし正多面体は除く 正 4 面体正 6 面体正 8 面体正 12 面体正 20 面体 4 色 3 色 2 色 4 色 3 色 (ⅲ) 各頂点での多角錐はすべて, 合同である の条件を満たす 準正多面体を構成するにはすべて正多面体から出発する 正多面体から準正多面体を得るには [5] (1) 切隅 が塗り分けの最小の色の種類であることを示した そこでは隣同士の面が同じ色にならないように塗り分けるアルゴリズムを提案したが, それはある面の色を仮定して隣の面同士が異なるように順々に決めて全体の面の色を決めてゆくもので, いわば局所的な ( ローカルな ) 色の塗り分け方法である したがって順々に色を決めてゆき最後 (2) 中央切り (3) 二重切り (4) 削辺 (5) 捩り切りの5 種類の操作をしながら構成してゆく 上の操作をしながら準正多面体を構成するその途中過程 *** 広島工業大学情報学部知的情報システム学科 259
2 殿塚勲 藤原祥史 吉田政春 を観察しながら各面の色の塗り分けをしてゆくと, 色の塗り分けの全体像が理解しやすく, 色の種類の最小解にたどりつくことが分かった この方法によればグローバルな見地から色の塗り分けができ, かつ色の種類が最小であることの見通しを直観的に理解できることがよい点である ここで得られた塗り分けが色の種類の最小解であるかどうかを判断することは一般には難しい ここでは, 準正多面体に含まれる頂点や辺, 多角形の関係が図 14 の6 種類のどのタイプを含むかにより塗り分けの色の最小種類を判別した なお多面体の名称であるが, 頂点の回りをどのような正多角形で構成しているか, により名づけることにする 例えば正 6 面体の1つの頂点は3つの正四角形でできているので正 6 面体は 444 である 正多面体はすべてこのような表記の仕方が可能であり正 4 面体は 333, 正 8 面体は 3333, 正 12 面体は 555, 正 20 面体は である 準正多面体もこのような表記法が可能であり, それは準正多面体の条件 (ⅲ) による 例えば 388,566,3434 等がある なお正多面体は5 種類であり, 準正多面体の種類は 13 である 但し異性体を入れると 16 種類という見方もあるがここでは基本的な 13 種類の準正多面体をとりあげる 2 正多面体から準正多面体を作る過程 2.1 切隅 操作による準正多面体の構成正多面体の各辺上に2 点を選び, 各面が正多角形になるようにして残りの隅の部分を切りとることにより多面体を作る 出発点としては5 種類すべての正多面体を選ぶことができる 例として立方体 444 から出発して準正多面体 388 を構成する過程を図 1(1)(2)(3)(4) に示す 正 6 面体の 切隅操作 による準正多面体 388 の形成 (444==>( 切隅 )==>388) 正 6 面体 ( 立方体 ) の1つの面の各辺に2 点づつ点を選び, これらを結ぶと正 8 角形になるように点を決める ( 図 1(1)) これを各面について行い6つの正 8 角形の色を正 6 面体の塗り分けを行ったと同様に行うと3 色で可能である ( 図 1(2)) 余った8つの頂点部分の切隅をするとその切り口は正 3 角形であり, これら8つの正 3 角形を第 4 色で塗れば ( 図 1(3)),6つの正 8 角形と8つの正 3 角形とは隣同士には同じ色は現れず, しかもこれが最小の種類の色による塗り分けとなる ( 図 1(4)) 388 の塗り分けには4 色必要 図 1(5) は 388 を2 次元に射影した図 [1] であり, 立体の裏も見え, かつ隣同士の色が異なることが見てとれるが, 面の数は射影のために 1 面だけ少ない 388 の塗り分けに4 色が必要であることは, 図 14(4) タイプ D との比較からこれが最低の色の数であることが分かる 正 6 面体以外の正多面体の 切隅操作 による準正多面体の形成 333==>366 図 2(1) は正四面体から切隅操作で 366 を作った結果であり, 正四面体自身の塗り分けには4 色必要であり, 2 次元射影図の図 2(2) からわかるように 366 でも4 色となる 3333==>466 図 3(1) は正八面体から切隅操作で 466 を作った結果である 正八面体は2 色で塗り分けができるが, 切隅操作で切り口はその2 色とは異なる色が必要なので,466 では3 色が図 3(2) 必要となり, 図 14(1) タイプ A または図 14(5) タイプ E よりこれが最小の色の種類である 555==>31010 正 12 面体の塗り分けにはもともと4 色が必要であり, 切隅操作してできた でも4 色を要する ( 図 4 (1), 図 4(2)) 図 14(4) タイプ D より4 色が最小である 33333==>566 正 20 面体の塗り分けは3 色でできるが, 切隅操作してできた切り口は3 色すべてと面が隣り合わせになるので,4 色が必要となる ( 図 5(1), 図 5(2)) 4 色は図 14(6) タイプ F より最小である 2.2 中央切り 操作による準正多面体の構成切隅では1 辺を3つの部分に分割しているが, さらに切り込みを深くして各辺の中点を結んだ線を結ぶ 444==>3434 正方形の各辺の中点を結ぶと, 各面には面積が半分で 45 度回転した正方形が現れる これらの面は点以外では接していないので同じ色で塗りつぶすことができる ( 図 6(1), 図 6(2)) 切隅された残りの断面は3 角形であり, これも第二の色で塗りつぶすと 3434 は2 色で塗り分けが可能である ( 図 6(3), 図 6(4)) 実際, 各頂点は図 14(2) タイプ B だけから成り立つ 図 6(5) は 3434 の2 次元射影図である 555==>3535 図 7(1) は正 12 面体 (555) から中央切りにより作った 3535 である その作り方は上の 3434 とほぼ同様であ 260
3 準正多面体の構成と色の塗り分け る 各頂点は図 14(2) タイプ B だけから成り立ち, 2 色で塗り分けが可能である 図 7(2) は 3535 の2 次元射影図 2.3 二重切り 操作による準正多面体の構成 444==>468 立方体 (444) の各面に元の面の2 倍の角の正多角形を描く 立方体 (444) から出発するので各面に8 角形が 6 個できるが, 隣の面との間で出来る平行部分が正方形になるように各辺の切り込みを調節し, 同時に立方体の頂点を切り込んでその断面が正 6 角形にすることができる ( 図 8(1) 図 8(2) 図 8(3)) こうして6 面の8 角形を第 1 色, 立方体の辺と同じ個数の 12 面の正方形を第 2 色, 立方体の頂点と同じ枚数の正 6 角形は第 3 色で塗りつぶせば, それらの面は接していないので,3 色で塗り分けができる ( 図 8 (4)) 各頂点は図 14(1) タイプ A または図 14(5) タイプ E から成り立つので最小種類は3 色となる 図 8(5) は 468 の2 次元射影図 555==>4610 正 12 面体の5 角形の各面内に正 10 角形を描き, 隣の面の5 角形との平行線が正方形になるようにする 同時に正 12 面体の各頂点の切り口が正 6 角形になるようにすると準正多面体 4610 ができる 色の塗り分けは上の 468 と同様に3 色でできる 図 9 (1) 図 9(2) は 4610 の2 次元射影図 2.4 削辺 操作による準正多面体の構成 444==>3444 立方体 (444) の各面に元の面よりも小さい面 ( 正方形 ) を描き第 1 色で塗りつぶす 図 10(1), 図 10(2) その大きさは隣の面上の正方形との間でできる平行線で囲われた部分が正方形になるように選ぶ こうして辺を削除してできた正方形には第 2 色を塗る 図 10 (3) 残りは立方体の頂点を切隅した3 角形部分が8 個できるがこれは辺を削除してできた正方形と隣どうしではあるが, はじめに描いた平行線とは隣接していないので, 第 1 色で塗りつぶす 図 10(4) 図 10(5) は 3444 の2 次元射影図 各頂点は図 14(2) タイプ B から成り立ち2 色で塗りつぶしが可能である 555==>3454 正 12 面体の5 角形の各面内により小さな正 5 角形を描き, 第 1 色で塗りつぶす 隣接する5 角形の平行線 で囲われた部分は正方形になるようにしてこれには第 2 色を塗る 正 12 面体の 20 個の頂点を切隅してできた3 角形部分ははじめの正 5 角形とは隣接していないのでこれと同じ第 1 色で塗りつぶす 図 11(1) 3444 と同様に各頂点は図 14(2) タイプ B から成り立ち2 色で塗りつぶしが可能である 図 11(2) は 3454 の2 次元射影図 2.5 捩り切り 操作による準正多面体の構成 444==>33334 立方体の各面内により小さな正方形を捩って配置する [5][6] その配置はその正方形の回りに2つの正三角形を通じて隣の正方形につながるように位置を決める 結果的には正方形の隅の周りに4つの正三角形が回り込むように配置される 各頂点は図 14(3) タイプ C から成り立ち3 色で塗りつぶしが可能である 捩り切りは5 種類の操作の中で最も複雑である 図 12(5) は の2 次元射影図 555 ==> 正 12 面体 555 の正 5 角形の各面上に小さな5 角形を配置し, その正 5 角形の隅の周りに4つの正三角形が回り込むように配置される と同様に各頂点は図 14(3) タイプ C から成り立ち3 色で塗りつぶしが可能である 図 13(2) は の2 次元射影図 3 終わりに 13 種類の準正多面体のすべてに対し最小の色の数での塗り分けを行った [1] とは異なり, 見通しよくグローバルに面の色を決めることができた さらに得られた結果が最小の色の数であるということは頂点や多角形の構造から図 14 のタイプ A,B,C,D,E,F などに分けた各タイプにあてはめて確認ができた すべての準正多面体は Zalgaller の多面体 [3] と呼ばれる 92 種類の多面体に含まれ, その頂点座標などのデータは [4] により計算され公開されている ここでは 13 種類の準正多面体の頂点座標などのデータはこれによらず, ここで述べたような正多面体からの構成により求めたものである 我々は準正多面体を正多面体から構成する過程をすべて 3 次元グラフィックスで作成したが, これは準正多面体の構造を学ぶためのよい教育用教材になると考えている 参考文献 [1] 殿塚勲 村上智秋, 多面体の塗り分け, 広島工業大学紀要, 第 43 巻 pp (2009) 261
4 殿塚勲 藤原祥史 吉田政春 [2] ロビン ウィルソン, 茂木健一郎訳, 四色問題, 新潮社 ( ) [3] 関口次郎, 多面体の数理とグラフィックス, 牧野書店 (1996.2) [4] 小林光夫 鈴木卓治 正多角形を面にもつすべての凸 多面体の頂点座標の計算 電気通信大学紀要, 第 5 巻 (1992),p [5] 一松信, 正多面体を解く, 東海大学出版会 (1983.6) [6] 阿原一志, 数理科学,NO.362,pp54 59(1993), NO.363,pp59 65(1993) 262
5 準正多面体の構成と色の塗り分け 切隅操作による準正多面体の構成 444 ==>388 図 1 1 図 1 2 図 ==>366 図 図 の 2 次元射影図 図 図 の 2 次元射影図 3333==>466 図 図 の 2 次元射影図 263
6 殿塚勲 藤原祥史 吉田政春 555==>31010 図 図 の 2 次元射影図 33333==>566 図 図 の 2 次元図 中央切操作による準正多面体の構成 444==>3434 図 6 1 図 6 2 図 6 3 図 6 4 図
7 準正多面体の構成と色の塗り分け 555==>3535 図 図 の 2 次元射影図 2 重切り操作による準正多面体の構成 444==>468 図 8 1 図 8 2 図 ==>4610 図 8 4 図 8 5 図 図 の 2 次元射影図 265
8 殿塚勲 藤原祥史 吉田政春 削辺操作による準正多面体の構成 444==>3444 図 10 1 図 10 2 図 ==>3454 図 図 図 図 の 2 次元射影図 捩り切り操作による準正多面体の構成 444==> 図 12 1 図 12 2 図
9 準正多面体の構成と色の塗り分け 555==>33335 図 12 4 図 12 5 図 図 の 2 次元射影図 図 14 1 タイプ 図 14 2 タイプ 図 14 3 タイプ 図 14 4 タイプ 図 14 5 タイプ 図 14 6 タイプ 267
10
STEP 数学 Ⅰ を解いてみた から直線 に下ろした垂線の足を H とすると, H in( 80 ) in より, S H in H 同様にして, S in, S in も成り立つ よって, S in 三角形の面積 ヘロンの公式 in in 辺の長
 STEP 数学 Ⅰ を解いてみた http://toitemit.ku.ne.jp 図形と計量 三角形の面積 三角形の面積 の面積を S とすると, S in in in 解説 から直線 に下ろした垂線の足を H とすると, H in より, S H in H STEP 数学 Ⅰ を解いてみた http://toitemit.ku.ne.jp から直線 に下ろした垂線の足を H とすると, H in(
STEP 数学 Ⅰ を解いてみた http://toitemit.ku.ne.jp 図形と計量 三角形の面積 三角形の面積 の面積を S とすると, S in in in 解説 から直線 に下ろした垂線の足を H とすると, H in より, S H in H STEP 数学 Ⅰ を解いてみた http://toitemit.ku.ne.jp から直線 に下ろした垂線の足を H とすると, H in(
20~22.prt
 [ 三クリア W] 辺が等しいことの証明 ( 円周角と弦の関係利用 ) の の二等分線がこの三角形の外接円と交わる点をそれぞれ とするとき 60 ならば であることを証明せよ 60 + + 0 + 0 80-60 60 から ゆえに 等しい長さの弧に対する弦の長さは等しいから [ 三クリア ] 方べきの定理 接線と弦のなす角と円周角を利用 線分 を直径とする円 があり 右の図のように の延長上の点
[ 三クリア W] 辺が等しいことの証明 ( 円周角と弦の関係利用 ) の の二等分線がこの三角形の外接円と交わる点をそれぞれ とするとき 60 ならば であることを証明せよ 60 + + 0 + 0 80-60 60 から ゆえに 等しい長さの弧に対する弦の長さは等しいから [ 三クリア ] 方べきの定理 接線と弦のなす角と円周角を利用 線分 を直径とする円 があり 右の図のように の延長上の点
< D8C6082CC90AB8EBF816989A B A>
 数 Ⅰ 図形の性質 ( 黄色チャート ) () () () 点 は辺 を : に外分するから :=: :=: であるから :=: == () 点 は辺 を : に内分するから :=:=: = + %= また, 点 は辺 を : に外分するから :=:=: == =+=+= 直線 は の二等分線であるから :=: 直線 は の二等分線であるから :=: 一方, であるから, から, から :=: :=:
数 Ⅰ 図形の性質 ( 黄色チャート ) () () () 点 は辺 を : に外分するから :=: :=: であるから :=: == () 点 は辺 を : に内分するから :=:=: = + %= また, 点 は辺 を : に外分するから :=:=: == =+=+= 直線 は の二等分線であるから :=: 直線 は の二等分線であるから :=: 一方, であるから, から, から :=: :=:
< 中 3 分野例題付き公式集 > (1)2 の倍数の判定法は 1 の位が 0 又は偶数 ( 例題 )1~5 までの 5 つの数字を使って 3 ケタの数をつくるとき 2 の倍数は何通りできるか (2)5 の倍数の判定法は 1 の位が 0 又は 5 ( 例題 )1~9 までの 9 個の数字を使って 3
 () の倍数の判定法は の位が 0 又は偶数 ~ までの つの数字を使って ケタの数をつくるとき の倍数は何通りできるか () の倍数の判定法は の位が 0 又は ~9 までの 9 個の数字を使って ケタの数をつくるとき の倍数は何通りできるか () の倍数の判定法は 下 ケタが 00 又は の倍数 ケタの数 8 が の倍数となるときの 最小の ケタの数は ( 解 ) 一の位の数は の 通り 十の位は一の位の数以外の
() の倍数の判定法は の位が 0 又は偶数 ~ までの つの数字を使って ケタの数をつくるとき の倍数は何通りできるか () の倍数の判定法は の位が 0 又は ~9 までの 9 個の数字を使って ケタの数をつくるとき の倍数は何通りできるか () の倍数の判定法は 下 ケタが 00 又は の倍数 ケタの数 8 が の倍数となるときの 最小の ケタの数は ( 解 ) 一の位の数は の 通り 十の位は一の位の数以外の
(Microsoft Word - \213\363\212\324\220}\214`_\220\263\216l\226\312\221\314_.doc)
 立体図形によるによる空間空間の彩り 球 立方体 正四面体の佇まいについて 札幌旭丘高校中村文則 はじめに正三角形 平面上では円とともに図形の代表に位置し, 図形の中に潜む種々の性質は大きな関心をもち扱われる. その正三角形を四面として構成される正四面体もまた煌びやかであり, 空間内では立体図形の主格であり, 正三角形の性質を継承しつつ, 独自に, 球面や他の立体図形との関わりを演出している. それらの佇まいについて調べてみよう.
立体図形によるによる空間空間の彩り 球 立方体 正四面体の佇まいについて 札幌旭丘高校中村文則 はじめに正三角形 平面上では円とともに図形の代表に位置し, 図形の中に潜む種々の性質は大きな関心をもち扱われる. その正三角形を四面として構成される正四面体もまた煌びやかであり, 空間内では立体図形の主格であり, 正三角形の性質を継承しつつ, 独自に, 球面や他の立体図形との関わりを演出している. それらの佇まいについて調べてみよう.
3D の作図ツールについて 3D 画面を表示すると 以下の新しい作図ツールが表示されます より多くのオプションを見るためには ボタンの右下の小さな矢印 をクリックして下さい 28
 GeoGebra5.0Beta には 3D のグラフィックスビューの機能が備わっています これにより 立体図形についても扱うことが出来ます 3.1 3D 画面まず 通常と同じように GeoGebra を起動させましょう そして メニューバーの表示から グラフィックスビュ-3D を選択します ( または Ctrl+Shift+3 でも同様 ) すると グラフィックスビューの隣にグラフィックスビュー 3D
GeoGebra5.0Beta には 3D のグラフィックスビューの機能が備わっています これにより 立体図形についても扱うことが出来ます 3.1 3D 画面まず 通常と同じように GeoGebra を起動させましょう そして メニューバーの表示から グラフィックスビュ-3D を選択します ( または Ctrl+Shift+3 でも同様 ) すると グラフィックスビューの隣にグラフィックスビュー 3D
補足 中学で学習したフレミング左手の法則 ( 電 磁 力 ) と関連付けると覚えやすい 電磁力は電流と磁界の外積で表される 力 F 磁 電磁力 F li 右ねじの回転の向き電 li ( l は導線の長さ ) 補足 有向線分とベクトル有向線分 : 矢印の位
 http://totemt.sur.ne.p 外積 ( ベクトル積 ) の活用 ( 面積, 法線ベクトル, 平面の方程式 ) 3 次元空間の つのベクトルの積が つのベクトルを与えるようなベクトルの掛け算 ベクトルの積がベクトルを与えることからベクトル積とも呼ばれる これに対し内積は符号と大きさをもつ量 ( スカラー量 ) を与えるので, スカラー積とも呼ばれる 外積を使うと, 平行四辺形や三角形の面積,
http://totemt.sur.ne.p 外積 ( ベクトル積 ) の活用 ( 面積, 法線ベクトル, 平面の方程式 ) 3 次元空間の つのベクトルの積が つのベクトルを与えるようなベクトルの掛け算 ベクトルの積がベクトルを与えることからベクトル積とも呼ばれる これに対し内積は符号と大きさをもつ量 ( スカラー量 ) を与えるので, スカラー積とも呼ばれる 外積を使うと, 平行四辺形や三角形の面積,
Microsoft Word - 断面諸量
 応用力学 Ⅱ 講義資料 / 断面諸量 断面諸量 断面 次 次モーメントの定義 図 - に示すような形状を有する横断面を考え その全断面積を とする いま任意に定めた直交座標軸 O-, をとり また図中の斜線部の微小面積要素を d とするとき d, d () で定義される, をそれぞれ与えられた横断面の 軸, 軸に関する断面 次モーメント (geometrcal moment of area) という
応用力学 Ⅱ 講義資料 / 断面諸量 断面諸量 断面 次 次モーメントの定義 図 - に示すような形状を有する横断面を考え その全断面積を とする いま任意に定めた直交座標軸 O-, をとり また図中の斜線部の微小面積要素を d とするとき d, d () で定義される, をそれぞれ与えられた横断面の 軸, 軸に関する断面 次モーメント (geometrcal moment of area) という
2014年度 センター試験・数学ⅡB
 第 問 解答解説のページへ [] O を原点とする座標平面において, 点 P(, q) を中心とする円 C が, 方程式 y 4 x で表される直線 l に接しているとする () 円 C の半径 r を求めよう 点 P を通り直線 l に垂直な直線の方程式は, y - ア ( x- ) + qなので, P イ から l に引いた垂線と l の交点 Q の座標は ( ( ウ + エ q ), 4 (
第 問 解答解説のページへ [] O を原点とする座標平面において, 点 P(, q) を中心とする円 C が, 方程式 y 4 x で表される直線 l に接しているとする () 円 C の半径 r を求めよう 点 P を通り直線 l に垂直な直線の方程式は, y - ア ( x- ) + qなので, P イ から l に引いた垂線と l の交点 Q の座標は ( ( ウ + エ q ), 4 (
例題1 転がり摩擦
 重心 5.. 重心問題解法虎の巻. 半円 分円. 円弧. 扇形. 半球殻 5. 半球体 6. 厚みのある半球殻 7. 三角形 8. 円錐 9. 円錐台. 穴あき板. 空洞のある半球ボール 重心問題解法虎の巻 関西大学工学部物理学教室 齊藤正 重心を求める場合 質点系の重心の求め方が基本 実際の物体では連続体であるので 積分形式で求める場合が多い これらの式は 次元のベクトル形式で書かれている通り つの式は実際には
重心 5.. 重心問題解法虎の巻. 半円 分円. 円弧. 扇形. 半球殻 5. 半球体 6. 厚みのある半球殻 7. 三角形 8. 円錐 9. 円錐台. 穴あき板. 空洞のある半球ボール 重心問題解法虎の巻 関西大学工学部物理学教室 齊藤正 重心を求める場合 質点系の重心の求め方が基本 実際の物体では連続体であるので 積分形式で求める場合が多い これらの式は 次元のベクトル形式で書かれている通り つの式は実際には
Microsoft Word - スーパーナビ 第6回 数学.docx
 1 ⑴ 与式 =- 5 35 +14 35 =9 35 1 ⑵ 与式 =9-(-5)=9+5=14 1 ⑶ 与式 = 4(a-b)-3(5a-3b) = 8a-4b-15a+9b = -7a+5b 1 1 1 1 ⑷ 与式 =(²+ 1+1²)-{²+(-3+)+(-3) } 1 ⑷ 与式 =(²++1)-(²--6)=²++1-²++6=3+7 1 ⑸ 与式 = - ² + 16 = - +16
1 ⑴ 与式 =- 5 35 +14 35 =9 35 1 ⑵ 与式 =9-(-5)=9+5=14 1 ⑶ 与式 = 4(a-b)-3(5a-3b) = 8a-4b-15a+9b = -7a+5b 1 1 1 1 ⑷ 与式 =(²+ 1+1²)-{²+(-3+)+(-3) } 1 ⑷ 与式 =(²++1)-(²--6)=²++1-²++6=3+7 1 ⑸ 与式 = - ² + 16 = - +16
C3 データ可視化とツール
 < 第 3 回 > データ可視化とツール 統計数理研究所 中野純司 [email protected] データ可視化とツール 概要 データサイエンティスト育成クラッシュコース データサイエンティストとしてデータ分析を行う際に必要な可視化の考え方と それを実行するためのフリーソフトウェアを紹介する 1. はじめに 2. 静的なグラフィックス 3. 動的なグラフィックス 4. 対話的なグラフィックス 1.
< 第 3 回 > データ可視化とツール 統計数理研究所 中野純司 [email protected] データ可視化とツール 概要 データサイエンティスト育成クラッシュコース データサイエンティストとしてデータ分析を行う際に必要な可視化の考え方と それを実行するためのフリーソフトウェアを紹介する 1. はじめに 2. 静的なグラフィックス 3. 動的なグラフィックス 4. 対話的なグラフィックス 1.
立体切断⑹-2回切り
 2 回切り問題のポイント 1. 交線を作図する 2つの平面が交わると 必ず直線ができます この直線のことを 交線 ( こうせん ) といいます 2. 体積を求める方法は次の 3 通りのどれか! 1 柱の体積 = 底面積 高さ 1 2 すいの体積 = 底面積 高さ 3 3 柱の斜め切り= 底面積 高さの平均 ただし 高さの平均が使えるのは 底面が円 三角形 正方形 長方形 ひし形 平行四辺形 正偶数角形のときだけ
2 回切り問題のポイント 1. 交線を作図する 2つの平面が交わると 必ず直線ができます この直線のことを 交線 ( こうせん ) といいます 2. 体積を求める方法は次の 3 通りのどれか! 1 柱の体積 = 底面積 高さ 1 2 すいの体積 = 底面積 高さ 3 3 柱の斜め切り= 底面積 高さの平均 ただし 高さの平均が使えるのは 底面が円 三角形 正方形 長方形 ひし形 平行四辺形 正偶数角形のときだけ
二等辺三角形の性質 (2) 次の図の の大きさを求めなさい () = P=Q P=R Q 68 R P (2) (3) 五角形 は正五角形 = F 50 F (4) = = (5) === = 80 2 二等辺三角形の頂角の外角を 底角を y で表すとき y を の式で表しなさい y 2-5-2
 三角形 四角形 二等辺三角形の性質 () 二等辺三角形と正三角形 二等辺三角形 2つの辺が等しい三角形( 定義 ) 二等辺三角形の性質定理 二等辺三角形の底角は等しい 定理 2 二等辺三角形の頂点の二等分線は 底辺を直角に2 等分する 正三角形 3 辺が等しい三角形 ( 定義 ) 次の図で 同じ印をつけた辺や角が等しいとき の大きさを求めなさい () (2) (3) 65 40 25 (4) (5)
三角形 四角形 二等辺三角形の性質 () 二等辺三角形と正三角形 二等辺三角形 2つの辺が等しい三角形( 定義 ) 二等辺三角形の性質定理 二等辺三角形の底角は等しい 定理 2 二等辺三角形の頂点の二等分線は 底辺を直角に2 等分する 正三角形 3 辺が等しい三角形 ( 定義 ) 次の図で 同じ印をつけた辺や角が等しいとき の大きさを求めなさい () (2) (3) 65 40 25 (4) (5)
数学 Ⅲ 無限等比級数の問題解答 問 1 次の無限級数の和を求めよ (1) (5) (2) (6) (7) (3) ( 解 )(1) 初項 < 公比 < の無限等比級数より収束し (4) (2) (3) その和は ( 答 ) であるから 初項 < 公比 となっている よって 収束し その和は よって
 問 1 次の無限級数の和を求めよ (1) (5) (2) (6) (7) (3) ( 解 )(1) 初項 < 公比 < の無限等比級数より収束し (4) (2) (3) その和は であるから 初項 < 公比 となっている よって 収束し その和は よって 収束し その和は < の無限等比級数 であるから 初項 < 公比
問 1 次の無限級数の和を求めよ (1) (5) (2) (6) (7) (3) ( 解 )(1) 初項 < 公比 < の無限等比級数より収束し (4) (2) (3) その和は であるから 初項 < 公比 となっている よって 収束し その和は よって 収束し その和は < の無限等比級数 であるから 初項 < 公比
S02 1 図において = =とする このとき = であることを証明せよ と において = 1 = 2 辺 は共通 より 3 辺 (3 組の辺 ) がそれぞれ等しい よって 合同な三角形の対応する角の大きさは等しい ゆえに = である
 S01 1 図において = =とする このとき であることを証明せよ と において = 1 = 2 辺 は共通 3 1 2 3 より 3 辺 (3 組の辺 ) がそれぞれ等しい よって である S02 1 図において = =とする このとき = であることを証明せよ と において = 1 = 2 辺 は共通 3 1 2 3 より 3 辺 (3 組の辺 ) がそれぞれ等しい よって 合同な三角形の対応する角の大きさは等しい
S01 1 図において = =とする このとき であることを証明せよ と において = 1 = 2 辺 は共通 3 1 2 3 より 3 辺 (3 組の辺 ) がそれぞれ等しい よって である S02 1 図において = =とする このとき = であることを証明せよ と において = 1 = 2 辺 は共通 3 1 2 3 より 3 辺 (3 組の辺 ) がそれぞれ等しい よって 合同な三角形の対応する角の大きさは等しい
学習指導要領
 (1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 絶対値の意味を理解し適切な処理することができる 例題 1-3 の絶対値をはずせ 展開公式 ( a + b ) ( a - b ) = a 2 - b 2 を利用して根号を含む分数の分母を有理化することができる 例題 5 5 + 2 の分母を有理化せよ 実数の整数部分と小数部分の表し方を理解している
(1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 絶対値の意味を理解し適切な処理することができる 例題 1-3 の絶対値をはずせ 展開公式 ( a + b ) ( a - b ) = a 2 - b 2 を利用して根号を含む分数の分母を有理化することができる 例題 5 5 + 2 の分母を有理化せよ 実数の整数部分と小数部分の表し方を理解している
2017年度 金沢大・理系数学
 07 金沢大学 ( 理系 前期日程問題 解答解説のページへ 次の問いに答えよ ( 6 z + 7 = 0 を満たす複素数 z をすべて求め, それらを表す点を複素数平面上に図 示せよ ( ( で求めた複素数 z を偏角が小さい方から順に z, z, とするとき, z, z と 積 zz を表す 点が複素数平面上で一直線上にあることを示せ ただし, 偏角は 0 以上 未満とする -- 07 金沢大学
07 金沢大学 ( 理系 前期日程問題 解答解説のページへ 次の問いに答えよ ( 6 z + 7 = 0 を満たす複素数 z をすべて求め, それらを表す点を複素数平面上に図 示せよ ( ( で求めた複素数 z を偏角が小さい方から順に z, z, とするとき, z, z と 積 zz を表す 点が複素数平面上で一直線上にあることを示せ ただし, 偏角は 0 以上 未満とする -- 07 金沢大学
Microsoft Word - 201hyouka-tangen-1.doc
 数学 Ⅰ 評価規準の作成 ( 単元ごと ) 数学 Ⅰ の目標及び図形と計量について理解させ 基礎的な知識の習得と技能の習熟を図り それらを的確に活用する機能を伸ばすとともに 数学的な見方や考え方のよさを認識できるようにする 評価の観点の趣旨 式と不等式 二次関数及び図形と計量における考え方に関 心をもつとともに 数学的な見方や考え方のよさを認識し それらを事象の考察に活用しようとする 式と不等式 二次関数及び図形と計量における数学的な見
数学 Ⅰ 評価規準の作成 ( 単元ごと ) 数学 Ⅰ の目標及び図形と計量について理解させ 基礎的な知識の習得と技能の習熟を図り それらを的確に活用する機能を伸ばすとともに 数学的な見方や考え方のよさを認識できるようにする 評価の観点の趣旨 式と不等式 二次関数及び図形と計量における考え方に関 心をもつとともに 数学的な見方や考え方のよさを認識し それらを事象の考察に活用しようとする 式と不等式 二次関数及び図形と計量における数学的な見
国語科学習指導案様式(案)
 算数科学習指導案 日時平成 23 年 6 月 5 日 ( 水 ) 5 校時 2 学年第 6 学年 5 名 単元名 対称な形 ( 第 6 学年第 6 時 ) 単元の目標 対称な図形の観察や構成を通して, その意味や性質を理解し, 図形に対する感覚を豊かにする C 図形 (3) ア : 縮図や拡大図について理解することイ : 対称な図形について理解すること 教材について 第 6 学年では, 平面図形を対称という新しい観点から考察し,
算数科学習指導案 日時平成 23 年 6 月 5 日 ( 水 ) 5 校時 2 学年第 6 学年 5 名 単元名 対称な形 ( 第 6 学年第 6 時 ) 単元の目標 対称な図形の観察や構成を通して, その意味や性質を理解し, 図形に対する感覚を豊かにする C 図形 (3) ア : 縮図や拡大図について理解することイ : 対称な図形について理解すること 教材について 第 6 学年では, 平面図形を対称という新しい観点から考察し,
線形代数とは
 線形代数とは 第一回ベクトル 教科書 エクササイズ線形代数 立花俊一 成田清正著 共立出版 必要最低限のことに限る 得意な人には物足りないかもしれません 線形代数とは何をするもの? 線形関係 y 直線 yもも 次式で登場する (( 次の形 ) 線形 ただし 次元の話世の中は 3 次元 [4[ 次元 ] 次元 3 次元 4 次元 はどうやって直線を表すの? ベクトルや行列の概念 y A ベクトルを使うと
線形代数とは 第一回ベクトル 教科書 エクササイズ線形代数 立花俊一 成田清正著 共立出版 必要最低限のことに限る 得意な人には物足りないかもしれません 線形代数とは何をするもの? 線形関係 y 直線 yもも 次式で登場する (( 次の形 ) 線形 ただし 次元の話世の中は 3 次元 [4[ 次元 ] 次元 3 次元 4 次元 はどうやって直線を表すの? ベクトルや行列の概念 y A ベクトルを使うと
平成 25 年度京都数学オリンピック道場 ( 第 1 回 ) H 正三角形 ABC の外接円の,A を含まない弧 BC 上に点 P をとる. このとき, AP = BP + CP となることを示せ. 解説円周角の定理より, 4APC = 4ABC = 60, であるから, 図のよ
 1 正三角形 の外接円の, を含まない弧 上に点 をとる. このとき, = + となることを示せ. 解説円周角の定理より, 4 = 4 = 60, であるから, 図のように直線 上に点 を, 三角形 が正三角形となるようにとることができる. 三角形 と三角形 において, =, = であり, 4 = 4 = 60, - 4 であるから, 辺とその間の角がそれぞれ等しく, 三角形 と三角形 は合同である.
1 正三角形 の外接円の, を含まない弧 上に点 をとる. このとき, = + となることを示せ. 解説円周角の定理より, 4 = 4 = 60, であるから, 図のように直線 上に点 を, 三角形 が正三角形となるようにとることができる. 三角形 と三角形 において, =, = であり, 4 = 4 = 60, - 4 であるから, 辺とその間の角がそれぞれ等しく, 三角形 と三角形 は合同である.
2018年度 筑波大・理系数学
 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ < < とする 放物線 上に 点 (, ), A (ta, ta ), B( - ta, ta ) をとる 三角形 AB の内心の 座標を p とし, 外心の 座標を q とする また, 正の実数 a に対して, 直線 a と放物線 で囲まれた図形の面積を S( a) で表す () p, q を cos を用いて表せ S( p) () S(
筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ < < とする 放物線 上に 点 (, ), A (ta, ta ), B( - ta, ta ) をとる 三角形 AB の内心の 座標を p とし, 外心の 座標を q とする また, 正の実数 a に対して, 直線 a と放物線 で囲まれた図形の面積を S( a) で表す () p, q を cos を用いて表せ S( p) () S(
合同な菱形だけで構成されている多面体を『菱形多面体』と呼びますが、現在存在が確認されている菱形多面体は次の4種類と言われています
 1. はじめに 三次元における白銀比 黄金比の相互補完性および, 準正多面体の双対多面体の白銀化 黄金化 2010 年 6 月 1 日金原博昭 ものの形における基本的な比率となっている黄金比と白銀比は, 従来, 互いに独立した比率であると考えられてきた. しかし筆者は, 菱形十二面体の黄金化および菱形三十面体の白銀化というプロセスに基づき, この二つの比率の間には三次元において密接かつ相互補完的な関係があることを発見した.
1. はじめに 三次元における白銀比 黄金比の相互補完性および, 準正多面体の双対多面体の白銀化 黄金化 2010 年 6 月 1 日金原博昭 ものの形における基本的な比率となっている黄金比と白銀比は, 従来, 互いに独立した比率であると考えられてきた. しかし筆者は, 菱形十二面体の黄金化および菱形三十面体の白銀化というプロセスに基づき, この二つの比率の間には三次元において密接かつ相互補完的な関係があることを発見した.
木村の理論化学小ネタ 体心立方構造 面心立方構造 六方最密構造 剛球の並べ方と最密構造剛球を平面上に の向きに整列させるのに次の 2 つの方法がある 図より,B の方が A より密であることがわかる A B 1
 体心立方構造 面心立方構造 六方最密構造 剛球の並べ方と最密構造剛球を平面上に の向きに整列させるのに次の 2 つの方法がある 図より,B の方が A より密であることがわかる A B 1 体心立方構造 A を土台に剛球を積み重ねる 1 段目 2 2 段目 3 3 段目 他と色で区別した部分は上から見た最小繰り返し単位構造 ( 体心立方構造 ) 4 つまり,1 段目,2 段目,3 段目と順に重ねることにより,
体心立方構造 面心立方構造 六方最密構造 剛球の並べ方と最密構造剛球を平面上に の向きに整列させるのに次の 2 つの方法がある 図より,B の方が A より密であることがわかる A B 1 体心立方構造 A を土台に剛球を積み重ねる 1 段目 2 2 段目 3 3 段目 他と色で区別した部分は上から見た最小繰り返し単位構造 ( 体心立方構造 ) 4 つまり,1 段目,2 段目,3 段目と順に重ねることにより,
解答例 ( 河合塾グループ株式会社 KEI アドバンスが作成しました ) 特別奨学生試験 ( 平成 29 年 12 月 17 日実施 ) 数 学 数学 2= 工 経営情報 国際関係 人文 応用生物 生命健康科 現代教育学部 1 整理して (60 分 100 点 ) (2 3+ 2)(
 解答例 ( 河合塾グループ株式会社 KEI アドバンスが作成しました ) 特別奨学生試験 ( 平成 9 年 月 7 日実施 ) 数 学 数学 = 工 経営情報 国際関係 人文 応用生物 生命健康科 現代教育学部 整理して (60 分 00 点 ) 3+ ( 3+ )( 6 ) ( 与式 ) = = 6 + + 6 (3 + ) すなわち 5 6 (5 6 )(3+ ) = = 3 9 8 = 4 6
解答例 ( 河合塾グループ株式会社 KEI アドバンスが作成しました ) 特別奨学生試験 ( 平成 9 年 月 7 日実施 ) 数 学 数学 = 工 経営情報 国際関係 人文 応用生物 生命健康科 現代教育学部 整理して (60 分 00 点 ) 3+ ( 3+ )( 6 ) ( 与式 ) = = 6 + + 6 (3 + ) すなわち 5 6 (5 6 )(3+ ) = = 3 9 8 = 4 6
<8D828D5A838A817C A77425F91E6318FCD2E6D6364>
 4 1 平面上のベクトル 1 ベクトルとその演算 例題 1 ベクトルの相等 次の問いに答えよ. ⑴ 右の図 1 は平行四辺形 である., と等しいベクトルをいえ. ⑵ 右の図 2 の中で互いに等しいベクトルをいえ. ただし, すべてのマス目は正方形である. 解 ⑴,= より, =,= より, = ⑵ 大きさと向きの等しいものを調べる. a =d, c = f d e f 1 右の図の長方形 において,
4 1 平面上のベクトル 1 ベクトルとその演算 例題 1 ベクトルの相等 次の問いに答えよ. ⑴ 右の図 1 は平行四辺形 である., と等しいベクトルをいえ. ⑵ 右の図 2 の中で互いに等しいベクトルをいえ. ただし, すべてのマス目は正方形である. 解 ⑴,= より, =,= より, = ⑵ 大きさと向きの等しいものを調べる. a =d, c = f d e f 1 右の図の長方形 において,
2013年度 九州大・理系数学
 九州大学 ( 理系 ) 前期日程問題 解答解説のページへ a> とし, つの曲線 y= ( ), y= a ( > ) を順にC, C とする また, C とC の交点 P におけるC の接線をl とする 以下 の問いに答えよ () 曲線 C とy 軸および直線 l で囲まれた部分の面積をa を用いて表せ () 点 P におけるC の接線と直線 l のなす角を ( a) とき, limasin θ(
九州大学 ( 理系 ) 前期日程問題 解答解説のページへ a> とし, つの曲線 y= ( ), y= a ( > ) を順にC, C とする また, C とC の交点 P におけるC の接線をl とする 以下 の問いに答えよ () 曲線 C とy 軸および直線 l で囲まれた部分の面積をa を用いて表せ () 点 P におけるC の接線と直線 l のなす角を ( a) とき, limasin θ(
【】三平方の定理
 FdText 数学 3 年 : 中学 塾用教材 http://www.fdtext.com/txt/ 三角形 x を求めよ (3) (4) (5) (6) (3) (4) (5) (6) [ 解答 ] (1) 34 cm (2) 2 2 cm (3) 13cm (4) 2 7 cm (5) 5 3cm (6) 11 cm - 1 - 次の三角形, 台形の高さ (h) を求めよ (3) (4) (3)
FdText 数学 3 年 : 中学 塾用教材 http://www.fdtext.com/txt/ 三角形 x を求めよ (3) (4) (5) (6) (3) (4) (5) (6) [ 解答 ] (1) 34 cm (2) 2 2 cm (3) 13cm (4) 2 7 cm (5) 5 3cm (6) 11 cm - 1 - 次の三角形, 台形の高さ (h) を求めよ (3) (4) (3)
2018年度 神戸大・理系数学
 8 神戸大学 ( 理系 ) 前期日程問題 解答解説のページへ t を < t < を満たす実数とする OABC を 辺の長さが の正四面体とする 辺 OA を -t : tに内分する点を P, 辺 OB を t :-tに内分する点を Q, 辺 BC の中点を R とする また a = OA, b = OB, c = OC とする 以下の問いに答えよ () QP と QR をt, a, b, c を用いて表せ
8 神戸大学 ( 理系 ) 前期日程問題 解答解説のページへ t を < t < を満たす実数とする OABC を 辺の長さが の正四面体とする 辺 OA を -t : tに内分する点を P, 辺 OB を t :-tに内分する点を Q, 辺 BC の中点を R とする また a = OA, b = OB, c = OC とする 以下の問いに答えよ () QP と QR をt, a, b, c を用いて表せ
図形と証明 1 対頂角 a = b ( 証明 ) a+ c= 180 なので a = c b+ c= 180 なので b = c 1 2 1,2 から a = b a と b のように 交わる直線の向かい合う角を対頂角といいます 等しいことは 当然のように見えますが 証明とは
 図形と証明 1 対頂角 a = b a+ c= 180 なので a = 180 - c b+ c= 180 なので b = 180 - c 1 2 1,2 から a = b a と b のように 交わる直線の向かい合う角を対頂角といいます 等しいことは 当然のように見えますが 証明とは それを筋道立てて説明することです a も b も 角度を使った式で 同じ式になる ということを述べるのが この証明です
図形と証明 1 対頂角 a = b a+ c= 180 なので a = 180 - c b+ c= 180 なので b = 180 - c 1 2 1,2 から a = b a と b のように 交わる直線の向かい合う角を対頂角といいます 等しいことは 当然のように見えますが 証明とは それを筋道立てて説明することです a も b も 角度を使った式で 同じ式になる ということを述べるのが この証明です
Math-Aquarium 例題 図形と計量 図形と計量 1 直角三角形と三角比 P 木の先端を P, 根元を Q とする A 地点の目の位置 A' から 木の先端への仰角が 30,A から 7m 離れた AQB=90 と なる B 地点の目の位置 B' から木の先端への仰角が 45 であ るとき,
 図形と計量 直角三角形と三角比 P 木の先端を P, 根元を Q とする 地点の目の位置 ' から 木の先端への仰角が 0, から 7m 離れた Q=90 と なる 地点の目の位置 ' から木の先端への仰角が であ るとき, 木の高さを求めよ ただし, 目の高さを.m とし, Q' を右の図のように定める ' 0 Q' '.m Q 7m 要点 PQ PQ PQ' =x とおき,' Q',' Q' を
図形と計量 直角三角形と三角比 P 木の先端を P, 根元を Q とする 地点の目の位置 ' から 木の先端への仰角が 0, から 7m 離れた Q=90 と なる 地点の目の位置 ' から木の先端への仰角が であ るとき, 木の高さを求めよ ただし, 目の高さを.m とし, Q' を右の図のように定める ' 0 Q' '.m Q 7m 要点 PQ PQ PQ' =x とおき,' Q',' Q' を
2017年度 神戸大・理系数学
 7 神戸大学 ( 理系 前期日程問題 解答解説のページへ を自然数とする f ( si + とおく < < 4 であることを用い て, 以下の問いに答えよ ( < < のとき, f ( < であることを示せ ( 方程式 f ( は < < の範囲に解をただ つもつことを示せ ( ( における解を とする lim であることを示し, lim を求めよ 7 神戸大学 ( 理系 前期日程問題 解答解説のページへ
7 神戸大学 ( 理系 前期日程問題 解答解説のページへ を自然数とする f ( si + とおく < < 4 であることを用い て, 以下の問いに答えよ ( < < のとき, f ( < であることを示せ ( 方程式 f ( は < < の範囲に解をただ つもつことを示せ ( ( における解を とする lim であることを示し, lim を求めよ 7 神戸大学 ( 理系 前期日程問題 解答解説のページへ
相加平均 相乗平均 調和平均が表す比 台形 の上底 下底 の長さをそれぞれ, とするとき 各平均により 台形の高さ はどのように比に分けられるだろうか 相乗平均は 相似な つの台形になるから台形の高さ を : の 比に分ける また 相加平均は は : の比に分けます 調和平均は 対角線 と の交点を
 台形に潜むいろいろな平均 札幌旭丘高校中村文則 台形に調和平均 相加平均をみる 右図の台形 において = = とする の長さを, を用いて表してみよう = x = y = c とすると であることから : = : より c y = x + y であることから : = : より c x = x + y を辺々加えると x + y c + = より + = x + y c となる ここで = = c =
台形に潜むいろいろな平均 札幌旭丘高校中村文則 台形に調和平均 相加平均をみる 右図の台形 において = = とする の長さを, を用いて表してみよう = x = y = c とすると であることから : = : より c y = x + y であることから : = : より c x = x + y を辺々加えると x + y c + = より + = x + y c となる ここで = = c =
コンピュータグラフィックス基礎 No
 課題 6: モデリング (1) OBJView の動作確認 ( レポートには含めなくてよい ) 次ページ以降の 課題用メモ を参考にして OBJ ファイルを 3D 表示する OBJView を実行し 画面に立体が表示されることを確認するとともに 以下の機能を確認しなさい 左ドラッグによる立体の回転 右ドラッグによる拡大/ 縮小 [v] キーによる頂点の表示 非表示 サンプルに含まれる bunny_3k.obj
課題 6: モデリング (1) OBJView の動作確認 ( レポートには含めなくてよい ) 次ページ以降の 課題用メモ を参考にして OBJ ファイルを 3D 表示する OBJView を実行し 画面に立体が表示されることを確認するとともに 以下の機能を確認しなさい 左ドラッグによる立体の回転 右ドラッグによる拡大/ 縮小 [v] キーによる頂点の表示 非表示 サンプルに含まれる bunny_3k.obj
2 α 2 A α 1 α 5 α 3 α 4 1.2: A 3 π n 4 n 3 n = 3 n 3 n = 2 1 α A 4π α/2π A = 4π α 2π = 2α n = 2 α α 1.3: 2 n = 3,, R 3 α, β, γ S 2,, R,, R 2, R 2 T T
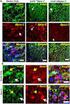 1 I: 1.1 3 1 S 2 = {(x, y, z) : x 2 + y 2 + z 2 = 1} O S 2 S 2 n n O (a) (b) 3 1.1: 3 n A α 1,, α n n α j = (n 2)π + A j=1 n (n 2)π 2 α 2 A α 1 α 5 α 3 α 4 1.2: A 3 π n 4 n 3 n = 3 n 3 n = 2 1 α A 4π α/2π
1 I: 1.1 3 1 S 2 = {(x, y, z) : x 2 + y 2 + z 2 = 1} O S 2 S 2 n n O (a) (b) 3 1.1: 3 n A α 1,, α n n α j = (n 2)π + A j=1 n (n 2)π 2 α 2 A α 1 α 5 α 3 α 4 1.2: A 3 π n 4 n 3 n = 3 n 3 n = 2 1 α A 4π α/2π
2017年度 京都大・文系数学
 07 京都大学 ( 文系 ) 前期日程問題 解答解説のページへ 曲線 y= x - 4x+ を C とする 直線 l は C の接線であり, 点 P(, 0) を通るもの とする また, l の傾きは負であるとする このとき, C と l で囲まれた部分の面積 S を求めよ -- 07 京都大学 ( 文系 ) 前期日程問題 解答解説のページへ 次の問いに答えよ ただし, 0.00 < log0
07 京都大学 ( 文系 ) 前期日程問題 解答解説のページへ 曲線 y= x - 4x+ を C とする 直線 l は C の接線であり, 点 P(, 0) を通るもの とする また, l の傾きは負であるとする このとき, C と l で囲まれた部分の面積 S を求めよ -- 07 京都大学 ( 文系 ) 前期日程問題 解答解説のページへ 次の問いに答えよ ただし, 0.00 < log0
1996 2000 2004 1984 2005 7150 000 9 500 9 4 13 10 95 11 11 12 20002004 9 70
 14 2006 1 Key Words 2002 3 1 2 3 3 1 2 3 1969 1987 69 1996 2000 2004 1984 2005 7150 000 9 500 9 4 13 10 95 11 11 12 20002004 9 70 14 2006 1 15 71 72 1 22 6 32 9 200 6 3 1 2 2000 10 1 2003 10 2005 6 5 4
14 2006 1 Key Words 2002 3 1 2 3 3 1 2 3 1969 1987 69 1996 2000 2004 1984 2005 7150 000 9 500 9 4 13 10 95 11 11 12 20002004 9 70 14 2006 1 15 71 72 1 22 6 32 9 200 6 3 1 2 2000 10 1 2003 10 2005 6 5 4
立命館21_川端先生.indd
 21 119-132 2010 ( ) ' Key Words 119 21 2010 7 1962 2001 2001 2007 1982 1988 1997 2007 1997 1998 1863 1880 1 1998 1998 2001 1599 120 121 1599 1695 8 1695 1714 4 1714 1715 5 1715 100 1812 9 1812 1864 2001
21 119-132 2010 ( ) ' Key Words 119 21 2010 7 1962 2001 2001 2007 1982 1988 1997 2007 1997 1998 1863 1880 1 1998 1998 2001 1599 120 121 1599 1695 8 1695 1714 4 1714 1715 5 1715 100 1812 9 1812 1864 2001
【】 1次関数の意味
 FdText 数学 1 年 : 中学 塾用教材 http://www.fdtext.com/txt/ 直線と角 解答欄に次のものを書き入れよ 1 直線 AB 2 線分 AB 1 2 1 2 右図のように,3 点 A,B,Cがあるとき, 次の図形を書き入れよ 1 直線 AC 2 線分 BC - 1 - 次の図で a, b, c で示された角を A,B,C,D の文字を使って表せ a : b : c :
FdText 数学 1 年 : 中学 塾用教材 http://www.fdtext.com/txt/ 直線と角 解答欄に次のものを書き入れよ 1 直線 AB 2 線分 AB 1 2 1 2 右図のように,3 点 A,B,Cがあるとき, 次の図形を書き入れよ 1 直線 AC 2 線分 BC - 1 - 次の図で a, b, c で示された角を A,B,C,D の文字を使って表せ a : b : c :
ポンスレの定理
 ポンスレの定理. qution Section 定理 有本彰雄 東京都市大学 平成 年 月 4 日 定義. n 角形 P とは 平面上にあるn 個の点の順序列 ( p, p,, pn - ) のことである 各 pk は P の頂点と呼ばれる 記号法を簡単にするため便宜的に p n とする また 線分 p i i pp, i,,,, n - を P の辺と呼ぶ 定義. すべての頂点 p k が曲線 C
ポンスレの定理. qution Section 定理 有本彰雄 東京都市大学 平成 年 月 4 日 定義. n 角形 P とは 平面上にあるn 個の点の順序列 ( p, p,, pn - ) のことである 各 pk は P の頂点と呼ばれる 記号法を簡単にするため便宜的に p n とする また 線分 p i i pp, i,,,, n - を P の辺と呼ぶ 定義. すべての頂点 p k が曲線 C
平成 30 年度 前期選抜学力検査問題 数学 ( 2 時間目 45 分 ) 受検番号氏名 注 意 1 問題は, 表と裏にあります 2 答えは, すべて解答欄に記入しなさい 1 次の (1)~(7) の問いに答えなさい (1) -3 (-6+4) を計算しなさい 表合計 2 次の (1)~(6) の問
 平成 30 年度 前期選抜学力検査問題 数学 ( 2 時間目 45 分 ) 受検番号氏名 注 意 1 問題は, 表と裏にあります 2 答えは, すべて解答欄に記入しなさい 1 次の (1)~(7) の問いに答えなさい (1) -3 (-6+4) を計算しなさい 表合計 2 次の (1)~(6) の問いに答えなさい 合計 (1) 関数 y = x 2 において,x の変域が -2 x 3 のとき, y
平成 30 年度 前期選抜学力検査問題 数学 ( 2 時間目 45 分 ) 受検番号氏名 注 意 1 問題は, 表と裏にあります 2 答えは, すべて解答欄に記入しなさい 1 次の (1)~(7) の問いに答えなさい (1) -3 (-6+4) を計算しなさい 表合計 2 次の (1)~(6) の問いに答えなさい 合計 (1) 関数 y = x 2 において,x の変域が -2 x 3 のとき, y
Microsoft Word - 町田・全 H30学力スタ 別紙1 1年 数学Ⅰ.doc
 (1) 数と式 学習指導要領 都立町田高校 学力スタンダード ア 数と集合 ( ア ) 実数 根号を含む式の計算 数を実数まで拡張する意義を理解し 簡単な 循環小数を表す記号を用いて, 分数を循環小数で表 無理数の四則計算をすること すことができる 今まで学習してきた数の体系について整理し, 考察 しようとする 絶対値の意味と記号表示を理解している 根号を含む式の加法, 減法, 乗法の計算ができる
(1) 数と式 学習指導要領 都立町田高校 学力スタンダード ア 数と集合 ( ア ) 実数 根号を含む式の計算 数を実数まで拡張する意義を理解し 簡単な 循環小数を表す記号を用いて, 分数を循環小数で表 無理数の四則計算をすること すことができる 今まで学習してきた数の体系について整理し, 考察 しようとする 絶対値の意味と記号表示を理解している 根号を含む式の加法, 減法, 乗法の計算ができる
2016年度 筑波大・理系数学
 06 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ k を実数とする y 平面の曲線 C : y とC : y- + k+ -k が異なる共 有点 P, Q をもつとする ただし点 P, Q の 座標は正であるとする また, 原点を O とする () k のとりうる値の範囲を求めよ () k が () の範囲を動くとき, OPQ の重心 G の軌跡を求めよ () OPQ の面積を S とするとき,
06 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ k を実数とする y 平面の曲線 C : y とC : y- + k+ -k が異なる共 有点 P, Q をもつとする ただし点 P, Q の 座標は正であるとする また, 原点を O とする () k のとりうる値の範囲を求めよ () k が () の範囲を動くとき, OPQ の重心 G の軌跡を求めよ () OPQ の面積を S とするとき,
Microsoft PowerPoint - 進化(博物館)2
 Imaginary Cube とその展開 立木秀樹京都大学人間 環境学研究科 京都大学公開講座 進化とは何か? 京都大学総合博物館,2009.10.18 私は 理論計算機科学の研究をしています ( 実数と計算, 位相空間と計算 ) かつては 立体の幾何とも, 模型作りとも, 縁遠いでした きっかけは, 東邦大学 ( 当時 ) の竹内泉氏と共同発表 ( フラクタルおえかき-- 空間の0,1,, 表現
Imaginary Cube とその展開 立木秀樹京都大学人間 環境学研究科 京都大学公開講座 進化とは何か? 京都大学総合博物館,2009.10.18 私は 理論計算機科学の研究をしています ( 実数と計算, 位相空間と計算 ) かつては 立体の幾何とも, 模型作りとも, 縁遠いでした きっかけは, 東邦大学 ( 当時 ) の竹内泉氏と共同発表 ( フラクタルおえかき-- 空間の0,1,, 表現
Taro-1803 平行線と線分の比
 平行線と線分の比 1 4 平行線と線分の比 ポイント : 平行な直線がある つの三角形の線分の比について考える 証明 右の図で で とする (1) は と相似である これを証明しなさい と において から 平行線の ( ) は等しいから 9c = ( ) 1 = ( ) 1, より ( ) がそれぞれ等しいので 相似な図形になるので相似比を利用して () : の相似比を求めなさい 対応する線分の長さを求めることができる
平行線と線分の比 1 4 平行線と線分の比 ポイント : 平行な直線がある つの三角形の線分の比について考える 証明 右の図で で とする (1) は と相似である これを証明しなさい と において から 平行線の ( ) は等しいから 9c = ( ) 1 = ( ) 1, より ( ) がそれぞれ等しいので 相似な図形になるので相似比を利用して () : の相似比を求めなさい 対応する線分の長さを求めることができる
紙を折る < 問題 > 長方形の紙を折る このとき 相似形はいくつできるだろうか? 2 個 固定固定固定 固定 2 個 2 個 固定 固定 3 個 3 個 固定 3 個 4 個 4 個
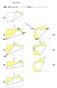 紙を折る < 問題 > 長方形の紙を折る このとき 相似形はいくつできるだろうか? 個 固定固定固定 固定 個 個 固定 固定 個 個 固定 個 4 個 4 個 * 隣り合う辺を結んで折るとき 最大 個 * 向かい合う辺を結んで折るとき 最大 4 個 < 問題 > 固定される場合 その位置はどこか? そのときの相似比はいくらか? 返上を移動する場合 その範囲はどうか? 合同になるときはあるか? それはどんなときか?
紙を折る < 問題 > 長方形の紙を折る このとき 相似形はいくつできるだろうか? 個 固定固定固定 固定 個 個 固定 固定 個 個 固定 個 4 個 4 個 * 隣り合う辺を結んで折るとき 最大 個 * 向かい合う辺を結んで折るとき 最大 4 個 < 問題 > 固定される場合 その位置はどこか? そのときの相似比はいくらか? 返上を移動する場合 その範囲はどうか? 合同になるときはあるか? それはどんなときか?
データ構造とアルゴリズム論
 第 1 章.Java による CG 作成方法 2 学習のねらい 1 先週に続いて Java 言語 (Eclipse 環境における ) を用いて CG( コンピュータグラフィックス ) を作成する方法の基礎を学習する 今回は ( 作成した )CG が自動的に再描画される様にするための処理 ( のプログラミング ) を学習する 今回の学習で Java による CG 作成方法を終了し 次週以降は CG 作成のアルゴリズムの学
第 1 章.Java による CG 作成方法 2 学習のねらい 1 先週に続いて Java 言語 (Eclipse 環境における ) を用いて CG( コンピュータグラフィックス ) を作成する方法の基礎を学習する 今回は ( 作成した )CG が自動的に再描画される様にするための処理 ( のプログラミング ) を学習する 今回の学習で Java による CG 作成方法を終了し 次週以降は CG 作成のアルゴリズムの学
Microsoft Word - ④「図形の拡大と縮小」指導案
 第 6 学年 算数科 ( 習熟度別指導 ) 学習指導案 単元名図形の拡大と縮小 単元の目標 身の回りから縮図や拡大図を見付けようとしたり 縮図や拡大図の作図や構成を進んでしようとす ( 関心 意欲 態度 ) 縮図や拡大図を活用して 実際には測定しにくい長さの求め方を考えることができ( 数学的な考え方 ) 縮図や拡大図の構成や作図をすることができ( 技能 ) 縮図や拡大図の意味や性質について理解することができ
第 6 学年 算数科 ( 習熟度別指導 ) 学習指導案 単元名図形の拡大と縮小 単元の目標 身の回りから縮図や拡大図を見付けようとしたり 縮図や拡大図の作図や構成を進んでしようとす ( 関心 意欲 態度 ) 縮図や拡大図を活用して 実際には測定しにくい長さの求め方を考えることができ( 数学的な考え方 ) 縮図や拡大図の構成や作図をすることができ( 技能 ) 縮図や拡大図の意味や性質について理解することができ
中学 1 年生 e ライブラリ数学教材一覧 学校図書 ( 株 ) 中学 1 年 数学 文字式式の計算 項と係数 中学 1 年 数学 次式 中学 1 年 数学 項のまとめ方 中学 1 年 数学 次式の加法 中学 1 年 数学 77
 中学 1 年生 e ライブラリ数学教材一覧 学校図書 ( 株 ) 中学 1 年 数学 1 14-20 正の数 負の数正の数 負の数 14- ある基準から考えた量の表現 中学 1 年 数学 14- 正の数 中学 1 年 数学 14- 負の数 中学 1 年 数学 14- 量の基準を表す数 中学 1 年 数学 15- 反対の性質をもつ量の表現 中学 1 年 数学 17- 数直線 中学 1 年 数学 18-19
中学 1 年生 e ライブラリ数学教材一覧 学校図書 ( 株 ) 中学 1 年 数学 1 14-20 正の数 負の数正の数 負の数 14- ある基準から考えた量の表現 中学 1 年 数学 14- 正の数 中学 1 年 数学 14- 負の数 中学 1 年 数学 14- 量の基準を表す数 中学 1 年 数学 15- 反対の性質をもつ量の表現 中学 1 年 数学 17- 数直線 中学 1 年 数学 18-19
Microsoft PowerPoint - 10.pptx
 m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
2014年度 千葉大・医系数学
 04 千葉大学 ( 医系 ) 前期日程問題 解答解説のページへ 袋の中に, 赤玉が 3 個, 白玉が 7 個が入っている 袋から玉を無作為に つ取り出し, 色を確認してから, 再び袋に戻すという試行を行う この試行を N 回繰り返したときに, 赤玉を A 回 ( ただし 0 A N) 取り出す確率を p( N, A) とする このとき, 以下の問いに答えよ () 確率 p( N, A) を N と
04 千葉大学 ( 医系 ) 前期日程問題 解答解説のページへ 袋の中に, 赤玉が 3 個, 白玉が 7 個が入っている 袋から玉を無作為に つ取り出し, 色を確認してから, 再び袋に戻すという試行を行う この試行を N 回繰り返したときに, 赤玉を A 回 ( ただし 0 A N) 取り出す確率を p( N, A) とする このとき, 以下の問いに答えよ () 確率 p( N, A) を N と
Microsoft PowerPoint - mp11-02.pptx
 数理計画法第 2 回 塩浦昭義情報科学研究科准教授 [email protected] http://www.dais.is.tohoku.ac.jp/~shioura/teaching 前回の復習 数理計画とは? 数理計画 ( 復習 ) 数理計画問題とは? 狭義には : 数理 ( 数学 ) を使って計画を立てるための問題 広義には : 与えられた評価尺度に関して最も良い解を求める問題
数理計画法第 2 回 塩浦昭義情報科学研究科准教授 [email protected] http://www.dais.is.tohoku.ac.jp/~shioura/teaching 前回の復習 数理計画とは? 数理計画 ( 復習 ) 数理計画問題とは? 狭義には : 数理 ( 数学 ) を使って計画を立てるための問題 広義には : 与えられた評価尺度に関して最も良い解を求める問題
2 ソフトを使っての年賀状作成準備前もって コンピュータ ( PC ) ライブラリ ピクチャ ( マイピクチャ をクリックして空白のところで右クリック 新規作成 フォルダ クリック 新しいフォルダ を右クリック 名前の変更 をクリック 平成 28 年年賀状作成素材 と入力する (1) Photo F
 平成 28 年年賀状作成 1 もっとも簡単な年賀状作成ワードを立ち上げる 差し込み文書 はがき印刷 文面の作成 をクリックして 完了 クリック (Word2007 は 差し込み文書 はがき印刷 文面の作成 をクリックして 完了 をクリック ワード 2003 は ツール はがきと差し込み印刷 はがき印刷 文面の作成 をクリックして 完了 クリック ) Word2010 2013 Word2010 2013
平成 28 年年賀状作成 1 もっとも簡単な年賀状作成ワードを立ち上げる 差し込み文書 はがき印刷 文面の作成 をクリックして 完了 クリック (Word2007 は 差し込み文書 はがき印刷 文面の作成 をクリックして 完了 をクリック ワード 2003 は ツール はがきと差し込み印刷 はがき印刷 文面の作成 をクリックして 完了 クリック ) Word2010 2013 Word2010 2013


