4 次元を見る WITH MATHEMATICA by H.Y 予備知識 : 三角関数 虚数 ( 積分 ) 対象 : 中 3 以上 4 次元の世界を Mathematica のグラフィックの表現力を借りて見ていこう 4 次元を想像することは難しいのではじめに 3 次元の空間図形が 2 次
|
|
|
- あつの やまのかみしゃ
- 5 years ago
- Views:
Transcription
1 4 次元を見る WITH MATHEMATICA by H.Y 予備知識 : 三角関数 虚数 ( 積分 ) 対象 : 中 3 以上 4 次元の世界を Mathematica のグラフィックの表現力を借りて見ていこう 4 次元を想像することは難しいのではじめに 3 次元の空間図形が 2 次元にどう映るかを見 て それを 4 次元に利用することを考える 世界地図で遊ぶ 00はじめに例として地球全体の地図を考えよう 3 次元の中に地球があり 地表面の位置は 緯度と経度で表すことができる これは地表面であれば 2 次元の座標の組で場所を表現できることを意味し 3 次元実数空間 R 3 の中に 2 次元の球面 S 2 があると表す まず 地球儀を地図にすることを考える Mathematica 入力 次の2つのコマンドをshift+enterで入力してみよう 3 次元の図形の表面に Texture を指定することで任意の絵や写真を張り付けることができ る 3 次元の図形は光源の位置や 視点を自由に変えることできる ここでは earth で指定 した衛星四角形の衛星写真を球に張り付ける earth = ;
2 2 4次元を見る.nb ParametricPlot3D[{Sin[θ] Cos[ϕ], Sin[θ] Sin[ϕ], Cos[θ]}, {θ, 0, π}, {ϕ, 0, 2 π}, PlotStyle Directive[Specularity[White, 10], Texture[earth ]], TextureCoordinateFunction ({#5, 1 - #4} &), Lighting "Neutral", Mesh None, Axes False, RotationAction "Clip"] これらを平面つまりR 2 上の地図にしようとすると次に示すように 角度 長さを両方とも に正確に表すことができない よく知られていいるように はじめのユークリッド図法では北極 南極側の面積はとても 大きくなってしまう 00 Mathematica入力 00 Mathematicaのデータベースには数学だけではなく 天文や地理のデータが多くある 次 のコマンドでこれを利用することができる 以下では世界地図を引用し 2つの投影法を用いているが 国別にしたり 別の投影図に したり 国にいろをつけたり 人口などの情報を得ることもできる 以下のコマンドはイ ンターネットにアクセスできないと使えない また 回線によっては時間がかかる
3 4次元を見る.nb 3 GeoGraphics[{}, GeoRange "World", GeoProjection "Equirectangular", GeoGridLines Automatic] GeoGraphics[{}, GeoRange "World", GeoProjection "Albers", GeoGridLines Automatic] 余談になるが地理のパッケージの読み込みとその利用例を少し紹介しておこう 00 Mathematica入力 00 下のれ 例ではWorldPlotのパッケージを読み込み その中の世界地図をgwに入れて 先と 同じようにParametricPlot3D に張り付ける方法である
4 4 4次元を見る.nb << WorldPlot` gw = WorldPlot[{World, RandomColors}] ParametricPlot3D[{Sin[θ] Cos[ϕ], Sin[θ] Sin[ϕ], Cos[θ]}, {θ, 0, π}, {ϕ, 0, 2 π}, PlotStyle Directive[Specularity[White, 10], Texture[gw]], TextureCoordinateFunction ({#5, 1 - #4} &), Lighting "Neutral", Mesh None, Axes False, RotationAction "Clip"] 00 Mathematica入力 00 パッケージを読み込まなくても次のCountryData[]コマンドは標準で使える (Ver10 以下の例では日本の輪郭(Shape),とGDPの1970年から2010年までの推移を表示させた
5 4 次元を見る.n 5 CountryData["Japan", {"Shape", "Mollweide"}] DateListPlot[CountryData["Japan", {{"GDP"}, {1970, 2010}}]] Mathematica 入力 詳しくは Help を参照するとよい また Mathematica のサイトには豊富なデモプログラムがあ り 利用例を学習できる 以下の例はその 1 つで多面体に世界地図を貼りこむことができる
6 6 4 次元を見る.n PolyhedronProjection[polyhedron_] := Module[{pts3D, center, pts2d, proj, pts2dprojected, geographics, plotrange, pts2dscaled, rescale}, rescale[{x_, y_}, {xs_, ys_}] := {Rescale[x, xs], Rescale[y, ys]}; Graphics3D[{ pts3d = First[#]; center = Mean[pts3D]; center = GeoPosition[GeoPositionXYZ[center, Norm[center]]]; pts2d = GeoPosition[GeoPositionXYZ[pts3D, Norm[pts3D[[1]]]]]; proj = {"Gnomonic", "Centering" center}; pts2dprojected = Most /@ GeoGridPosition[pts2D, proj][[1]]; geographics = GeoGraphics[ {Opacity[0], center, GeoPath[pts2D[[1]], CurveClosed True]}, GeoProjection proj, GeoZoomLevel 1]; plotrange = PlotRange /. AbsoluteOptions[geographics, PlotRange]; pts2dscaled = rescale[#, plotrange] & /@ pts2dprojected; {Texture[ImageData[Rasterize[geographics[[1]], "Image"]]], Polygon[pts3D, VertexTextureCoordinates pts2dscaled]}} & /@ N@Normal[PolyhedronData[polyhedron, "Faces"]][[1]], Lighting "Neutral", Boxed False, Method {"ShrinkWrap" True}, ImageSize Small]] PolyhedronProjection["Dodecahedron"] 上の例では 1 面の 5 角形では平面になった地図をみることができるが 全地球の地図を 1 面 で見ることができない もちろん展開図にしてみれば見ることができるがとぎれとぎれになりみにくいであろう そこで 3 次元の中にある球の表面全てをできるだけ スムーズに平坦な平面に写す方法は あるだろうか 鉛筆片手にいろいろ試してほしい 次の節でこの問題をとりあげよう 立体射影 003 次元の立体を2 次元にしてみるには影をみるようにその立体をある方向から見たものを 平面に写す 射影 という操作をする 次の多面体の射影のデモプログラムを見ればすぐ に理解できるだろう
7 4 次元を見る.n 7 Mathematica 入力 WolframのデモのサイトにIzidor Hafner 氏の Three Orthogonal Projections of Polyhedra というプログラムを以下に引用する プログラムの中身の理解は後にして 射影が何なのか実際に実行することで確認してほしい 若干著者によってプログラムを変更してある Manipulate[ Module[{cc, cc1, py1, pyss}, cc1 = With[{cu = PolyhedronData[p, "Faces"], cu1 = PolyhedronData[p, "Edges"]}, {cu[[2, 1]], cu[[1]] // N, cu1[[2, 1]]}]; cc = translate23[{xx, yy, zz}][cc1]; pyss = pys[cc]; py1 = visib2[cc, {0, 100, 0}, pyss]; Column[ {Graphics3D[ {{GrayLevel[0.6], Line[{{0, 0, 0}, {5 + xx, 0, 0}, {5 + xx, 0, 5 + zz}, {0, 0, 5 + zz}, {0, 0, 0}}]}, {GrayLevel[0.6], Line[{{0, 0, 0}, {0, yy + 5, 0}, {0, yy + 5, 5 + zz}, {0, 0, 5 + zz}, {0, 0, 0}}]}, {GrayLevel[0.6], Line[{{0, 0, 0}, {5 + xx, 0, 0}, {5 + xx, 5 + yy, 0}, {0, 5 + yy, 0}, {0, 0, 0}}]}, visib2[cc, {0, 0, 100}, pzs[cc]], visib2[cc, {0, 100, 0}, pys[cc]], visib2[cc, {100, 0, 0}, pxs[cc]], If[shs, show[if[ef 1, Polygon, ClosedLine]][cc], {}]}, ViewPoint {3, 3, 1}, ViewAngle 15 Degree, Boxed False, ImageSize {400, 400}, Lighting "Neutral", SphericalRegion True, PlotRange {{-.5, 4.7}, {-.5, 4.7}, {-2, 4.7}}]}]], {{p, "SquashedDodecahedron", "polyhedron"}, Intersection[PolyhedronData["Convex"], PolyhedronData[ ;; 14]]}, Row[{ "translate ", Column[{ Control@{{xx, 2, Style["x", Italic]}, 1, 3,.001, ImageSize Tiny, Appearance "Labeled"}, Control@{{yy, 2, Style["y", Italic]}, 1, 3,.001, ImageSize Tiny, Appearance "Labeled"}, Control@{{zz, 2, Style["z", Italic]}, 1, 3,.001, ImageSize Tiny, Appearance "Labeled"}
8 8 4 次元を見る.n }], Spacer[20], Control@{{shs, True, "show solid"}, {True, False}}, Spacer[20], Control@{{ef, 1, ""}, {1 "polygon", 2 "line"}, Enabled shs} }], SaveDefinitions True, Initialization { px[r_] := {0, r[[2]], r[[3]]}; py[r_] := {r[[1]], 0, r[[3]]}; pz[r_] := {r[[1]], r[[2]], 0}; pxs[solid_] := {solid[[1]], Map[px, solid[[2]]], solid[[3]]}; pys[solid_] := {solid[[1]], Map[py, solid[[2]]], solid[[3]]}; pzs[solid_] := {solid[[1]], Map[pz, solid[[2]]], solid[[3]]}; show[poly_][solid_] := Map[poly, Map[solid[[2, #]] &, solid[[1]]]]; trans[vec_][r_] := r + vec; translate3[vec_, solid_] := {solid[[1]], Map[trans[vec], solid[[2]]], solid[[3]]}; translate23[vec_][solid_] := translate3[vec, solid]; ClosedLine[a_] := Line[Append[a, First[a]]]; visible[solid_, view_][edge_] := Module[{edges = solid[[3]], vert = solid[[2]], faces = solid[[1]], f = Length[solid[[1]]], fac, normals}, fac = Select[Range[f], Length[Intersection[faces[[#]], edge]] 2 &]; normals = Table[Normalize[ Cross[vert[[faces[[fac[[i]], 2]]]] - vert[[faces[[fac[[i]], 1]]]], vert[[faces[[fac[[i]], 3]]]] - vert[[faces[[fac[[i]], 1]]]]]], {i, 1, 2}]; view.normals[[1]] > view.normals[[2]] > ]; visib2[solid_, viewp_, prsolid_] := Table[{If[! visible[solid, viewp][solid[[3, j]]], Dashed, Thin], Line[Map[prsolid[[2, #]] &, prsolid[[3, j]]]]}, {j, 1, Length[solid[[3]]]}]; }]
9 4 次元を見る.n 9 polyhedron RhombicDodecahedron translate x y z show solid polygon line 単純なプリズムから多面体まで多くの3つの平面への射影図を見ただろう 各壁に写っ た 3 つの射影図はベクトルの 3 つの成分のように独立していてこの 3 つがあれば 3D プリン ターなどで実体化できるわけだ しかしここでは 実際の物体は 1 つなので 3 枚の設計図ではなく 1 枚で表す方法を考えた いのである アイディアは浮かんだだろうか? 球面上の点を平坦な平面に写す方法の1つとして立体射影を紹介する まずは実物を Mathematica で実感してほしい Mathematica 入力 Wolfram のデモのサイトに Erik Mahieu 氏の Inverse Stereographic Projection of Simple Geometric Shapes というプログラムを以下に引用する ここでもプログラムの中身の理解は後にして 立体
10 10 4 次元を見る.n 射影が何なのか実際に実行することで確認してほしい Manipulate Graphics3D[{{GrayLevel[.75], Opacity[.65], Sphere[]}, {Point[{0, 0, -z}]}, {Line[{{0, 0, -z}, {pos 1, pos 2, z}}]}, {Blue, Point /@ (image[r, pos] /.{x_, y_} {x, y, z})}, {Red, Point /@ (inversestereo[#1, z] &) /@ image[r, pos]}}, PlotRange {{-2 - r, 2 + r}, {-2 - r, 2 + r}, {-1.01, 1.01}}, BoxRatios {2 + r, 2 + r, 1}, BoxStyle Dashed, Lighting "Neutral", ViewPoint Dynamic[vp], ImageSize {400, 400}], Style["select an image", Bold], {image, circle, ""}, line, cross, circle, filledcircle, square, filledsquare, SetterBar, {{r,.5, ""}, {.2 "small",.5 "medium", 1 "large"}}, Delimiter, Style["select the projection plane", Bold], {{z, -1, ""}, {-1 " z=-1 ", 1 " z=+1 "}}, Style["move the image around", Bold], {{pos, {1.35, -1.5}, ""}, {-2, -2}, {2, 2}}, Delimiter, Style["choose a viewpoint", Bold], {{vp, {1, -1, 1.25}, ""}, {{1, -1, 1.25} "default", Front "front", Right "right", Top "top"}}, ControlPlacement Left, AutorunSequencing {{4, 10}, {1, 2}, {2, 2}, {3, 2}, {5, 2}}, Initialization ( inversestereo[{x_, y_}, z_] := {4 x, 4 y, z (4 - #)} / (# + 4) &[x^2 + y^2]; line[r_, pos_] := (pos + #1 &) /@ Table[{i, 0}, {i, -50, 50, 0.25}]; cross[r_, pos_] := (pos + #1 &) /@ (r #1.RotationMatrix[π / 4] &) /@ Flatten[{Table[{i, 0}, {i, -1, 1,.1}], Table[{0, i}, {i, -1, 1,.1}]}, 1]; circle[r_, pos_] := (pos + #1 &) /@ Join[r Table[{Cos[γ], Sin[γ]}, {γ, -π, π, π / 24}], {{0, 0}}]; filledcircle[r_, pos_] := Join[circle[r, pos], Select[filledSquare[r, pos], Norm[pos - #1] r &]]; square[r_, pos_] := (pos + #1 &) /@ (r Flatten[Table[#, {i, -1, 1,.25}] & /@ {{i, 1}, {i, -1}, {-1, i}, {1, -i}, {0, 0}}, 1]);
11 4 次元を見る.n 11 filledsquare[r_, pos_] := (pos + #1 &) /@ (r Flatten[Table[Table[{i, j}, {i, -1, 1,.25}], {j, -1, 1,.25}], 1])) select an image small medium large select the projection plane z=-1 z=+1 move the image around choose a viewpoint default front right top 実行してみると z=-1 の北極点 z=1の南極点から球に接している平面に向けて直線が伸びている この直線の球面との交点が赤 接平面との交点が青で示される 球面上の点が円を描けば面白いことに平面上の点も円を描く selectボタンを直線にすると接平面に直線を描く 特別な円が球面上にあることが確認できるだろう また ボタンを選ぶと球面上で直交する直線は接平面でも直交していることがわかる このプログラムでは描画する領域を限っているが無限大まで接平面を広げれば球面上のあらゆる点を接平面に写すことができる? おっと 1 点だけ不可能な点が球面に存在する わかるだろうか? それが直線を始めている極だ しかし この北極 ( 南極 ) を除外すれば接平面に写すことができる この立体射影の方法は1 点の例外をつくるが今回の4 次元を見る方法に使えそうなので少し詳しくみていみよう 図のように半径 1の円でz 軸上の北極をN x 軸上の交点 P, 円周上の交点 P その垂線の足を
12 12 4 次元を見る.n O とする 原点は z 軸と円の接点 O にとる z N P' x P O' O Q1 ここで問題である Pのx 座標をx,P の座標を (x,z ) としてxを円周上の座標 x,z で表してみよ ON:O P =2:z だから三角形の相似から 2 : z' = x : (x - x') x z' = 2 x - 2 x' x (2 - z') = 2 x' (1) x = 2 x' 2 - z' となる さらにP (x,z ) が円周上の点であるから (x') 2 + (z') 2 = 1 (2) が成り立つことに注意する 紙面裏から表に図のO 点にy 軸を作れば3 次元の空間に拡張できる P' を (x',y',z') とすると球面上の極を除いたあらゆる点はx-y 平面上のP(x,y) 写される これが立体射影である P は球面上にあるので x' 2 + y' 2 + z' 2 = 1 (3) が成り立つ 従って3 次元の空間の中で球面上の点はこの式 3に従わなくてはいけないから結局独立した変数は2つしかない その2つの変数が新たに 面 を表すわけだ 式 3という関係があるのでこれを満たす座
13 4次元を見る.nb 13 標表示をθ,ϕの2つで表すことを考えればよい 球面上の点x,y,z から立体射影された平面 が z' {x', y'} (4) のように書ける これは4次元の場合に応用できそうである Q2 半径1の球として 次の図のようにθ, ϕを決めると球上の点p'はどう表されるか考え てみよ 結果は次のようになる これをP としよう x' = Sin[θ] Cos[θ], y' = Sin[θ] Sin[ϕ], z = Cos[θ] (5) P' = {Sin[θ] Cos[ϕ], Sin[θ] Sin[ϕ], Cos[θ]} (6) 自分で各成分を2乗して足してみよ 三角関数の性質をつかうと確かに1になる Mathematica入力 Mathematicaでも簡単に確かめることができる Clear[θ, ϕ]; FullSimplify (Sin[θ] Cos[ϕ])2 + (Sin[θ] Sin[ϕ])2 + (Cos[θ])2 1 次にこの点をMathematicaで表してθ,ϕを自由に変化できるようにしょう はじめに最初の単純な射影は球面上の点が動いたとき 3つの面上にどういう動きになる かイメージを作っておこう Mathematica入力 最初のデモプログラムはやや複雑なので次にシンプルなもので順番に理解していこう
14 14 4 次元を見る.n 次の例では半径 1 の球を薄く表示させてある P は pt に置き換える 赤い小球が球面上を自由に動くと xy,yz,zx 平面に射影された青 黄 緑の点が動く いろ いろ角度を変えて観測してみよう
15 4 次元を見る.n 15 Manipulate[ pt = {Sin[θ] Cos[ϕ], Sin[θ] Sin[ϕ], Cos[θ]}; gp1 = ParametricPlot3D[{Sin[θ] Cos[ϕ], Sin[θ] Sin[ϕ], Cos[θ]}, {θ, 0, π}, {ϕ, 0, 2 π}, PlotStyle Opacity[0.3], Mesh None]; gp2 = Graphics3D[{Red, Sphere[pt, 0.05]}, PlotRange {{-1.2, 1.2}, {-1.2, 1.2}, {-1.2, 1.2}}]; gpx = Graphics3D[{Green, Sphere[{Sin[θ] Cos[ϕ], Sin[θ] Sin[ϕ], 1}, 0.05]}, PlotRange {{-1.2, 1.2}, {-1.2, 1.2}, {-1.2, 1.2}}]; gpy = Graphics3D[{Blue, Sphere[{1, Sin[θ] Sin[ϕ], Cos[θ]}, 0.05]}, PlotRange {{-1.2, 1.2}, {-1.2, 1.2}, {-1.2, 1.2}}]; gpz = Graphics3D[{Yellow, Sphere[{Sin[θ] Cos[ϕ], 1, Cos[θ]}, 0.05]}, PlotRange {{-1.2, 1.2}, {-1.2, 1.2}, {-1.2, 1.2}}]; Show[gp1, gp2, gpx, gpy, gpz], {{θ, π / 3, "θ"}, 0, 2 π, Appearance "Labeled"}, {{ϕ, π / 3, "ϕ"}, 0, 2 π, Appearance "Labeled"}] θ ϕ このように普通の射影では球面上を動く P の影を xy,yz,zx 面からみた様子である
16 16 4 次元を見る.n では次に立体射影を同じように見てみよう Mathematica 入力 原点は中心ではないのでz 成分のみ+1されることに注意する 0で割るとエラーになるのでその補正で微小値入れてある 原点中心のxy 平面を紫の透明色を使うためにHue[ ] を利用している Clear[ps, gss, gs1, gs2] Manipulate[ po = {0, 0, 2}; ps = {Sin[θ] Cos[ϕ], Sin[θ] Sin[ϕ], Cos[θ] + 1}; k = 2 / ( Cos[θ]); pl = {k Sin[θ] Cos[ϕ], k Sin[θ] Sin[ϕ], 0}; rga = 1.2; rgb = 2.2; gs1 = ParametricPlot3D[{Sin[θ] Cos[ϕ], Sin[θ] Sin[ϕ], Cos[θ] + 1}, {θ, 0, π}, {ϕ, 0, 2 π}, PlotStyle Opacity[0.3], Boxed False, Mesh None, Axes None, PlotRange {{-rgb, rgb}, {-rgb, rgb}, {-0.2, rgb}}]; gs2 = Graphics3D[{Red, Sphere[ps, 0.05]}, PlotRange {{-rgb, rgb}, {-rgb, rgb}, {-0.2, rgb}}]; gss = Graphics3D[{Green, Sphere[pl, 0.05]}, PlotRange {{-rgb, rgb}, {-rgb, rgb}, {-0.2, rgb}}]; gsl = Graphics3D[{Blue, Line[{po, pl}]}, PlotRange {{-rgb, rgb}, {-rgb, rgb}, {-0.2, rgb}}]; gsp = Graphics3D[{Hue[2 / 3, 1, 1,.3], Polygon[{{-rgb, rgb, 0}, {rgb, rgb, 0}, {rgb, -rgb, 0}, {-rgb, -rgb, 0}}]}, PlotRange {{-rgb, rgb}, {-rgb, rgb}, {-0.2, rgb}}]; Show[gs1, gs2, gss, gsl, gsp], {{θ, 2 π / 3, "θ"}, 0, 2 π, Appearance "Labeled"}, {{ϕ, 4 π / 3, "ϕ"}, 0, 2 π, Appearance "Labeled"}]
17 4 次元を見る.n 17 θ ϕ 球面上の赤点の動きが立体射影によってxy 平面の緑の動きになることを確かめてほし い 球面上の一点を除く全ての点を平面に写すことができる 球面上での点の動きを線として残せば最初に示したプログラムのようになるわけだ 立体射影がイメージできたらいよいよ次に4 次元の世界にいく とその前にせっかく球上の点を角度をつかって表すことをしたので寄り道をしよう 4 次元球の体積 00この節は積分を用いる 寄り道なので積分を習ってない場合 次の節に飛んでもよい 体積という言葉を拡張して 円板の面積 πr 2 は 2 次元の体積 V 2 とし,V 3 = 4 3 πr3 とする そこで ここでは 4 次元の体積 V 4 を求めてみる 00まずV 2 から始めよう 学校で学んだやり方は x = r cosθ, y = sinθ (7) とすると小さな円輪の 1 部分の面積が rdθ dr となるので次を計算する Mathematica 入力 0 R 0 2 π r dr dθ (8)
18 18 4 次元を見る.n 積分記号はESC int ESC ESC dd ESCで積分変数を次にかく 文字式で積分する時は次のようなコマンドを直接使った方がよい Clear[R, r, θ]; Integrate[r, {r, 0, R}, {θ, 0, 2 π}] π R 2 00ここでは一般化するために断面半径 Dを次のように定義する 2 次元の円は だからこの時の断面半径は D は x 座標になる x をこの x 2 + y 2 = r 2 (9) x = D 2 = ± r 2 - y 2 (10) r 2 - y 2 で置き換えると次のように 1 つ目の積分が簡単に D に置き換わる この場合は {} の中が断面を表し ちょうど x の 2 倍の長さになることに注意して次を得る V 2 = -R R D2 dxdy r 2 -y 2 R = dx dy -R - r 2 -y 2 (11) R = 2 r 2 - y 2 dy -R Mathematica 入力 最後の積分を手計算したらMathematicaで確かめると次の結果が得られる Clear[R, y]; Integrate 2 R 2 - y 2, {y, -R, R} ; Simplify[%, R > 0] π R 2 積分とは簡単にはある区間を細かく刻んで足し合わせることである 断面を刻む数を増やして足し合わせると円板ができる様子をMathematicaで描いてみよう Mathematica 入力 nを増やすと断面の直線の足し合わせで円板ができる 参考のために半径 1の球を薄く表示してある 少しづつ変化させたデータを作る時にはTable[] コマンドを利用する
19 4 次元を見る.n 19 Clear[z, gs, ψ1, ϕ1, θ1]; Manipulate gs1 = ParametricPlot3D[ {Cos[ ϕ1] Sin[θ1], Sin[ϕ1] Sin[θ1], Cos[θ1]}, {ϕ1, 0, 2 π}, {θ1, 0, π}, PlotStyle Opacity[0.2], Mesh None, PlotRange {{-1, 1}, {-1, 1}, {-1, 1}}]; gs2 = Table Graphics3D Hue[Abs[z], 1, 1], Thick, Line 1 - z 2, 0, z, z 2, 0, z, {z, -1, 1, 2 / n} ; Show[gs1, gs2], {{n, 20, "n"}, 1, 100, 1, Appearance "Labeled"} n 55 同じことを3 次元でやろう x 2 + y 2 = r 2 - z 2 (12) よって断面半径を D 3 = ± r 2 - z 2 (13) とおけば今度は {} の中の断面が円板の面積になることに注意する この D 3 を V 2 = πr 2 の Rの中に入れると
20 20 4 次元を見る.n V 3 = -R R D3 dxdy dz = -R R π r 2 - z 2 dz (14) となる このように断面半径と断面をうまくつかうと {} の外を [-R,R] までの積分に置き換えることができる ただし 断面は線になったり面積になったり 体積になったりするわけだ Mathematica 入力 先と同じようにこの様子を断面である円板の足し合わせで表してみよう nを大きくすると球ができることがわかるだろう Clear[gt, z, ψ1, ϕ1, θ1]; Manipulate gt = Table Graphics3D Hue[Abs[z], 1, 1, 0.3], Cylinder {{0, 0, z}, {0, 0, z + 1 / n}}, 1 - z 2, Mesh -> None, {z, -1, 1, 2 / n} ; Show[gt], {{n, 10, "n"}, 4, 40, 1, Appearance "Labeled"} n 40
21 4 次元を見る.n 21 計算と共に積分の操作がイメージできただろうか Mathematica 入力 最後の積分を手計算したらMathematicaで確かめると次の結果が得られる Clear[R, z]; Integrate π R 2 - z 2, {z, -R, R} ; Simplify[%, R > 0] 4 π R 3 3 では同じように V 4 を求めよう x 2 + y 2 + z 2 + w 2 = r 2 x 2 + y 2 + z 2 = r 2 - w 2 D 4 = ± r 2 - w 2 (15) とおけば今度は {} の中の断面が体積になることに注意する この D 4 を V 3 = 4 π R3 のRの中に 3 入れると V 3 = -R R D4 dxdydz dw = -R R 4 π 3 r 2 - w 2 3 dw (16) Mathematica 入力 最後の積分を手計算したら Mathematica で確かめると次の結果が得られる Clear[R, w]; Integrate 4 π 3 R 2 - w 2 3, {w, -R, R} ; Simplify[%, R > 0] π 2 R 次元球の体積が出た! しかもこの調子で この結果を次々に代入していけばn 次元球の 体積も公式化できそうだ 是非チャレンジしてみてほしい では次の節で本題に戻ろう 複素数の組 これまでの学習で 3 次元の球が式 3 を満たしたように 4 次元の空間においても 4 次元球が存在 し 次を満たす x' 2 + y' 2 + z' 2 + w' 2 = 1 (17) この球の表面は S 3 で表され 3 つの変数をもつことが予想される この条件をうまく表すものをみつけるのに複素数を知っておく必要がある
22 22 4 次元を見る.n そこでこの節では簡単に複素数の基礎を学ぶ 複素数は非常に面白く 奥が深い 物理とも密接に関係しているが 今回はその基礎だけに留めておこう 複素数とはzを複素数 x,yを実数とするととすると z = x + i y (18) で表され iを虚数単位といい i 2 = -1 (19) のように2 乗してマイナスになるものまで数の世界を広げるのである 実数は2 乗してマイナスになることはない また 複素数には 共役 と呼ばれる相棒がいて この相棒をかけると必ず実数になる 共役とはiの前の符号を-にしたものだ 数式では次のようにバー z で表す z = x - i y (20) z z = x 2 + y 2 (21) これはMathmaticadでも簡単に確かめることができる Mathematica 入力 虚数単位の入力は ESC ii ESCで行い通常のiとは区別する 共役はConjugate[] というコマンドを用いる ただし3つ目の例で示すように簡素化する時に x,yが実数であることを明示しておく 簡単には4 番目に例のようにしてもよい z1 = x + i y; z2 = x - i y; Simplify[z1 z2] Simplify[z1 Conjugate[z1], {x Reals, y Reals}] Simplify[z1 Conjugate[z1], {x > 0, y > 0}] x 2 + y 2 x 2 + y 2 x 2 + y 2 さて 気が付いた人もいるだろう 複素数の大きさをとると式 17 の内 2 つが出てくるので 2 組の複素数をうまくつかうとよさそうである そして 2 組の複素数には独立した 4 つの実数が入っている これは 4 次元 R 4 を表せそうであ る 複数をイメージしやすいように再び Mathematica のデモプログラムをいくつか見てみよ う Mathematica 入力 00Wolframのデモのサイトに Štefan Porubský 氏の Complex Number
23 4 次元を見る.n 23 というプログラムを以下に引用する ここでもプログラムの中身の理解は後にして 立体射影が何なのか実際に実行することで確認してほしい 著者により若干のプログラムの修正がある これは単純に縦軸を虚数 横軸を実数にして複素数 z=x+iyを表している これを今後複素平面と呼ぶ 複素平面上で共役がどういう関係になるか 考えてみよう 共役関係はちょうど180 の関係であることがわかっただろうか また この表示は複素数が円や回転と関係していそうなこともわかる Manipulate[ r = Norm[xy]; If[r 0, r =.1]; If[showAngle, θ = Arg[xy[[1]] + xy[[2]] i], θ = If[Arg[xy[[1]] + xy[[2]] i] 0, Arg[xy[[1]] + xy[[2]] i], Arg[xy[[1]] + xy[[2]] i] + 2 π]]; Graphics[{{White, Rectangle[{-6, 6}, {6, 8}]}, {Lighter[Yellow, 0.85], Rectangle[{-6, -6}, {6, 6}]}, {Lighter[Black, 0.5], Opacity[0.5], AbsoluteThickness[1], Arrow[{{0, -5}, {0, 5}}], Arrow[{{-5, 0}, {5, 0}}]}, {RGBColor[.6,.73,.36], Opacity[1], AbsoluteThickness[2], Line[{{0, 0}, xy}]}, {RGBColor[.25,.43,.82], Opacity[1], AbsoluteThickness[2], Line[{{xy[[1]], 0}, xy}]}, {RGBColor[.49, 0, 0], Opacity[1], AbsoluteThickness[2], Line[{{0, xy[[2]]}, xy}]}, {Black, Opacity[1], AbsolutePointSize[5], Point[xy]}, {RGBColor[.6,.73,.36], Opacity[0.2], Disk[{0, 0}, r, If[showAngle && θ < 0, {θ, 0}, {0, θ}]]}, {Opacity[0.7], If[showGon, Text[ Style[TraditionalForm[ ToString[PaddedForm[N@Abs[xy[[1]] + I xy[[2]]], {4, 3}]] * Power[e, ToString[PaddedForm[N@ θ, {4, 3}]] <> ToString["i"]]], RGBColor[.25,.43,.82], 14], xy, If[0 θ π, {0, -1}, {0, 1}]], Text[ Style[TraditionalForm[PaddedForm[Chop[N@ xy[[1]] + i xy[[2]]], {4, 3}]], Black, 14], xy, If[0 θ π, {0, -1}, {0, 1}]]]}, {Opacity[0.7], Text[ Style[Row[{"Re(", Style["z", Italic], ") = ", ToString[PaddedForm[N@Chop[Re[xy[[1]] + i xy[[2]]]], {4, 3}]]}], RGBColor[.49, 0, 0], 12], {-5.5, 7.4}, {-1, 0}]},
24 24 4 次元を見る.n {Opacity[0.7], Text[ Style[Row[{"Im(", Style["z", Italic], ") = ", ToString[PaddedForm[N@Chop[Im[xy[[1]] + i xy[[2]]]], {4, 3}]]}], RGBColor[.25,.43,.82], 12], {-5.5, 6.6}, {-1, 0}]}, { Text[ Style[Row[{"abs(", Style["z", Italic], ") = ", ToString[PaddedForm[N@Chop[Abs[xy[[1]] + i xy[[2]]]], {4, 3}]]}], RGBColor[.6,.73,.36], 12], {2, 7.4}, {-1, 0}]}, { Text[ Style[Row[{"arg(", Style["z", Italic], ") = ", ToString[PaddedForm[N@Chop[θ], {4, 3}]]}], RGBColor[.6,.73,.36], 12], {2, 6.6}, {-1, 0}]} }, PlotRange {{-6, 6}, {-6, 6}}, AspectRatio 1, ImageSize 450], {{showangle, True, " 角度の基準 (-π,π]"}, {True, False}}, {{showgon, False, " 指数表示 "}, {True, False}}, {{xy, {-2.001, }}, {-4, -4}, {4, 4}, ControlType Locator, Appearance Style[" ", 12, RGBColor[.6,.73,.36]]}, TrackedSymbols Manipulate]
25 4 次元を見る.n 25 角度の基準 (-π,π] 指数表 i このように複素数は実は原点の周りを回転するベクトルのように表すことができる 2 乗して -1 になるとはちょうど実軸の 1 から出発して 2 回の 90 の回転で実軸上の -1 に写るこ とで これは 180 =π ラジアンの回転である これから複素数の別の表現として 半径 r, 角度 θ[rad] の回転で表すことができて z = r e iθ (22) で表すことができる 例えば大きさが 1 で 3 回で -1 になれば θ= π/3 である これから n 乗根 が簡単にわかることになる Mathematica 入力 さっそく Mathematica で確認しておこう -1 の 3 乗根と 複素平面での 60 の回転を N コマン ドで計算させる
26 26 4 次元を見る.n 3 N -1 N Exp i π i i 同じ複素数を表している さらに n 乗根を大きくしていくと これは n 角形と関係してく ることが複素平面の図形からわかるだろう これも Mathematica のデモに簡単な例があるので確かめてみよう Mathematica 入力 Wolfram のデモのサイトに Germán Alvarado Jiménez 氏の Roots of a Complex Number というプログラムを以下に引用する ここでもプログラムの中身の理解は後にして 立体 射影が何なのか実際に実行することで確認してほしい このプログラムでは Locator を使っているのでマウスでダイレクトに座標を変更できる Manipulate z = aa[[1]] + I aa[[2]]; raices = Table n Abs[z] Cos[(Arg[z] + 2 π k) / n], n Abs[z] Sin[(Arg[z] + 2 π k) / n], {k, 0, n} ; Column Text@Style[RadicalBox[z, n] // DisplayForm, 18], Graphics If circle, Circle {0, 0}, n Abs[z], {}, If[polygon, {Dashed, Red, Line[Append[raices, First@ raices]]}, {}], Red, PointSize[.02], Point[raices], PlotRange 2, AspectRatio Automatic, Axes True, ImageSize {400, 400}, Alignment Center, {polygon, {False, True}}, {circle, {False, True}}, {{n, 2, "n"}, 2, 12, 1, Appearance "Labeled"}, {{aa, {1, 1}}, {-2, -2}, {2, 2}, Locator}, TrackedSymbols :> {polygon, circle, n, aa}
27 4 次元を見る.n 27 polygon circle n i 複素数は z=x+i y のように1つの数に2つの実数の組を持っているので2 成分をもつベクトルz(x,y) と同じように扱うことができる Mathematicaは複素数の実成分と虚成分を取り出すコマンドが用意されていてRe[],Im[] がそうだ Mathematica 入力 実数部分はRe[] 虚数部分はIm[] で取り出す いろいろ試てみよう Clear[z, x, y]; z = 3 + i 4; Re[z] Im[z] 3 4 Mathematica 入力
28 28 4 次元を見る.n θ を実数指定すれば正しく 表示する Clear[z, θ]; z = Cos[θ] + i Sin[θ]; Re[z] Simplify[%, θ > 0] Im[z] Simplify[%, θ > 0] -Im[Sin[θ]] + Re[Cos[θ]] Cos[θ] Im[Cos[θ]] + Re[Sin[θ]] Sin[θ] Mathematica 入力 さて 以下の結果をよーく考えてほしい FullSimplifyを用いると多少時間がかかるが 簡単な関数になるものは簡単にしてくれる Clear[z, θ]; z = Exp[i θ]; Re[z]; FullSimplify[%, θ > 0] Im[z]; FullSimplify[%, θ > 0] Cos[θ] Sin[θ] この結果は e iθ = cosθ + i sinθ (23) であることを表している! これは数学上最も美しい式の1つといわれるEulerの公式である つまり 複素数の世界で指数関数は三角関数にになる 右辺の実成分 虚成分をベクトルの成分とみなせば このベクトルはぐるぐる回転する長さ1のベクトルである Mathematica 入力 ParametircPlotで確かめてみよう
29 4 次元を見る.n 29 Clear[z, θ]; z = Exp[i θ]; ParametricPlot[{Re[z], Im[z]}, {θ, 0, 2 π}] 確かに円になった 改めてこの節の最初のデモに戻って 複素数を指数表示にしていろい ろ試してみるといいだろう 複素数と立体射影 この 2 つの道具が準備できたところで いよいよ次節で本題に戻る Hopf-fibration 問題を確認すると 4 次元のなかの 3 次元球面を表すために式 17 x' 2 + y' 2 + z' 2 + w' 2 = 1 満たすような 3 つの変数を探すことであった さらに立体射影の式 4 からこれを拡張すれば w' {x', y', z'} (24) を考えればよいだろう そこでこれを満たすものの 1 つとして これまで考えてきた 複 素数を用いて次のような 2 つの組を考えよう まず 式 17 を満たすものの 1 つとして これまで考えてきた 複素数を用いて次のような 2 つの組を考えよう Mathematica 入力 ψ は ESC psi ESC で入力する 複素数 z と w は 3 つの変数 θ,ϕ,ψ を持っている
30 30 4 次元を見る.n Clear[z, w, ϕ, θ]; z = Cos[θ] Exp[-i (ψ + ϕ)]; w = Sin[θ] Exp[-i (ψ - ϕ)]; この2つの複素数の実成分と虚成分を考えれば4つの成分をもつことになる これが式 17を満たすかどうか確かめてみよう Mathematica 入力 θ,ϕ,ψ を実数として簡単にする zr = FullSimplify Re[z] 2 + Re[w] 2, {ϕ > 0, ψ > 0, θ > 0} zi = FullSimplify Im[z] 2 + Im[w] 2, {ϕ > 0, ψ > 0, θ > 0} Simplify[zI + zr] Cos[θ] 2 Cos[ϕ + ψ] 2 + Cos[ϕ - ψ] 2 Sin[θ] 2 Sin[θ] 2 Sin[ϕ - ψ] 2 + Cos[θ] 2 Sin[ϕ + ψ] 2 1 実成分 虚成分の大きさの2 乗はθ,ϕ,ψ の関数だがこれを足すと1になる この2 組の複素数の4つの成分が4 次元の空間をつくる はじめに地図を射影してみたように3 次元に射影してみよう ただし 最初は単純に1つの成分をカットし 見えてない部分があることを承知して3 次元の空間に表す 次のプログラムではkという変数を追加して片方の角度の変化を遅らせるようにしている はじめこのkは1としてψの方を変化させ見てみるとよい Mathematica 入力 4つの成分から3つを選んでいる 他にも選び方はあるので自分で変更して試し見るとよい 角度も2πにしてみたりして見てみよ 観測する向きが変わるが他におおきな相違はない
31 4 次元を見る.n 31 Clear[θa, za, wa, ψa, ϕa, ga1, k]; Manipulate[ za = Cos[θa] Exp[-i (ψa + ϕa)]; wa = Sin[θa] Exp[-k i (ψa - ϕa)]; ga1 = ParametricPlot3D[{Re[za], Im[za], Re[wa]}, {θa, 0, π}, {ϕa, 0, π}]; Show[ga1], {{ψa, 0, "ψ"}, 0, 2 π, Appearance "Labeled"}, {{k, 1, "k"}, 0, 1, Appearance "Labeled"}] ψ 0 k 1 最初に実行すると θ や φ の範囲が π までにとってあるので切り口があり 中が見える 次にこれを 2π に変えると閉じた図形がになるが きれいな球には見えない 凸凹が 2 ヶ所あるのがわかるだろう 4 次元球で見えてたでこぼこは 3 次元球になると見え ない これは 3 次元で 1 周することが 4 次元では半周していることに相当するからである 次にこのプログラムのkを変化させてみよう 1 から 0 まで連続的に変化させると 4 次元球をつくっていいた 1 つの変数の影響が少なくな り やがて 3 次元に移行する
32 32 4 次元を見る.n ところがこれでは4 次元の球の全体像を見ているわけではない 全体像を1 点だけ除き 3 次元の空間に表すためには前節の立体射影をつかう 式 24を用いて4 次元を3 次元に立体射影してみる 2 乗した和が1になる4つの変数から3 次元の座標を作り出すわけだ これをHopf 写像という Mathematica 入力 ここでは立体射影の定義を最後のInitializationの中にしている Mnipulateを使い動的な絵を得る時の関数の定義はこうしておくと他と競合しない このプログラムにも先と同じ役割をするkを入れてみた はじめは1に固定してためすとよい
33 4 次元を見る.n 33 Clear[θ, k, zb, wb, ψ, ϕ, x, y, z]; Manipulate zb = Cos[θ] Exp[-i (ψ + ϕ)]; wb = Sin[θ] Exp[-i k (ψ - ϕ)]; ParametricPlot3D[Evaluate[Pj[zb, wb]], {ψ, 0, 2 π}, {ϕ, 0, 2 π}, PlotRange {{-2, 2}, {-2, 2}, {-2, 2}}], {{θ, 3.6, "θ"}, 0, 4 π, Appearance "Labeled"}, {{k, 1, "k"}, 0, 1, Appearance "Labeled"}, 1 Initialization Pj[x_, y_] := {Re[x], Im[x], Im[y]} 1 - Re[y] θ 3.6 k ドーナッツができた! この穴が何に由来しているかわかるだろうか 立体射影が表すこ とができない 1 点が あったことを思い出してほしい ψ,ϕ の範囲を π までにして θ を 3.6 程度にすると最初の図と同じような断面図が得られる ψ,ϕ の範囲を 2π までとると θ の変化で大きさが変わるが 中心軸が一定なドーナツ ( トーラ スという ) が描ける 次に k を変化させると今度は図形の一部が消えていくことがわかるだろう Hopf 写像が
34 34 4 次元を見る.n 4 次元の全体像をほぼ表しているので 1つの変数の影響を小さくするとその面が消えていくわけである この絵だけではなかなかこの立体写像をイメージするのは難しい そこで3 次元の場合の最初のデモでは3 次元の中の球の表面を曲線でたどると 立体射影が同じように曲線で得られた 同じように4 次元の球面上を曲線に沿って進んでいくと立体射影された3 次元内にどんな曲線を描くか見てみよう そのためには変数 ψを固定してみればよい Mathematica 入力 ψを選べるように修正した また 線には色をつけ 参考のために半径 1の球面を表示させた
35 4 次元を見る.n 35 Clear[θ, zc, wc, ψ, ϕ, x, y, z]; Manipulate zc = Cos[θ] Exp[-i (ψ + ϕ)]; wc = Sin[θ] Exp[-i (ψ - ϕ)]; gc1 = ParametricPlot3D[ {Cos[ ϕ1] Sin[θ1], Sin[ϕ1] Sin[θ1], Cos[θ1]}, {ϕ1, 0, 2 π}, {θ1, 0, π}, PlotStyle Opacity[0.5], Mesh None, PlotRange {{-2, 2}, {-2, 2}, {-2, 2}}]; gc2 = ParametricPlot3D[Evaluate[Pj[zc, wc]], {ϕ, 0, 2 π}, PlotRange {{-2, 2}, {-2, 2}, {-2, 2}}, PlotStyle Hue[0.5, 0.8, 1]]; Show[gc1, gc2], {{θ, π / 6, "θ"}, 0, π, Appearance "Labeled"}, {{ψ, π / 2, "ψ"}, 0, π, Appearance "Labeled"}, 1 Initialization Pj[x_, y_] := {Re[x], Im[x], Im[y]} 1 - Re[y] θ ψ 真中の球に絡みながら円輪が回転していく様子からトーラスの表面が想像できる さらにψ,ϕの範囲を上のプログラムはπとしているがこれを2πに変えてみるといい 2πまでの回転で球のまわりを2 回 周っていることがわかるだろう 物理学で全体像を見る時には少し変化させて比べて見るという方法をよくとる
36 36 4 次元を見る.n そこでここでψを固定して 固定したψを少しづつ変化させて見てみよう Mathematica 入力 次のプログラムではψを少しづつ変化させ πだけ全部で変化するようにしてある nを多きすると刻みが小さくなり 全体像が見えてくるが 環境によっては重くなるかもしれない 色も変化するように修正した
37 4 次元を見る.n 37 Clear[θ, zz, wc, ψ1, ϕ, x, y, z]; Manipulate gg1 = ParametricPlot3D[ {Cos[ ϕ1] Sin[θ1], Sin[ϕ1] Sin[θ1], Cos[θ1]}, {ϕ1, 0, 2 π}, {θ1, 0, π}, PlotStyle Opacity[0.2], Mesh None, PlotRange {{-2, 2}, {-2, 2}, {-2, 2}}]; gg2 = Table[ParametricPlot3D[Evaluate[Pj[Cos[θ] zz[ψ1, ϕ], Sin[θ] zz[ψ1, - ϕ]]], {ϕ, 0, 2 π}, PlotRange {{-2, 2}, {-2, 2}, {-2, 2}}, PlotStyle Hue[ψ1 / π, 0.8, 1]], {ψ1, ψ, ψ + π, π / n}]; Show[gg1, gg2], {{n, 4, "n"}, 1, 20, 1, Appearance "Labeled"}, {{θ, π / 6, "θ"}, 0, π, Appearance "Labeled"}, {{ψ, π / 2, "ψ"}, 0, π, Appearance "Labeled"}, 1 Initialization Pj[x_, y_] := {Re[x], Im[x], Im[y]}, 1 - Re[y] zz[ψ_, ϕ_] := Exp[-i (ψ + ϕ)]; n 20 θ ψ n を大きくすると はじめのトーラスの形が浮かびあがる しかし その曲線はねじれて いることがわかる
38 38 4 次元を見る.n さて 4 次元の世界の動きを3 次元の世界で見ることに少しでも興味がもてただろうか 最後に重要な発想の逆転をしてほしい 上の絵には我々にとって身近な3 次元の球面がある どの色の線も4 次元にある球面上を 1 周する 逆にこの曲線と3 次元球の交点が必ず2つあることに注目してほしい 3 次元のこの 点 は4 次元でみるとこの点を突き抜けている円周なのだ この円周上のどの座標も3 次元の球面ではこの2 点を表す 4 次元の世界では3 次元の決まった点を表す座標が無限にあるともいえる この考えは射影の反対でHopf-fibrationという 一般的にファイバーと呼ばれるものだ
<4D F736F F D20824F F6490CF95AA82C696CA90CF95AA2E646F63>
 1/15 平成 3 年 3 月 4 日午後 6 時 49 分 5 ベクトルの 重積分と面積分 5 重積分と面積分 Ⅰ. 重積分 と で 回積分することを 重積分 といいます この 重積分は何を意味しているのでしょう? 通常の積分 (1 重積分 ) では C d 図 1a 1 f d (5.1) 1 f d f ( ) は 図形的には図 1a のように面積を表しています つまり 1 f ( ) を高さとしてプロットすると図
1/15 平成 3 年 3 月 4 日午後 6 時 49 分 5 ベクトルの 重積分と面積分 5 重積分と面積分 Ⅰ. 重積分 と で 回積分することを 重積分 といいます この 重積分は何を意味しているのでしょう? 通常の積分 (1 重積分 ) では C d 図 1a 1 f d (5.1) 1 f d f ( ) は 図形的には図 1a のように面積を表しています つまり 1 f ( ) を高さとしてプロットすると図
<4D F736F F D20824F E B82CC90FC90CF95AA2E646F63>
 1/1 平成 3 年 6 月 11 日午前 1 時 3 分 4 ベクトルの線積分 4 ベクトルの線積分 Ⅰ. 積分の種類 通常の物理で使う積分には 3 種類あります 積分変数の数に応じて 線積分 ( 記号 横(1 重 d, dy, dz d ( ine: 面積分 ( 記号 縦 横 ( 重 線 4 ベクトルの線積分 重積分記号 ddy, dydz, dzdz ds ( Surface: 1 重積分記号
1/1 平成 3 年 6 月 11 日午前 1 時 3 分 4 ベクトルの線積分 4 ベクトルの線積分 Ⅰ. 積分の種類 通常の物理で使う積分には 3 種類あります 積分変数の数に応じて 線積分 ( 記号 横(1 重 d, dy, dz d ( ine: 面積分 ( 記号 縦 横 ( 重 線 4 ベクトルの線積分 重積分記号 ddy, dydz, dzdz ds ( Surface: 1 重積分記号
2018年度 東京大・理系数学
 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ関数 f ( ) = + cos (0 < < ) の増減表をつくり, + 0, 0 のと sin きの極限を調べよ 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ n+ 数列 a, a, を, Cn a n = ( n =,, ) で定める n! an qn () n とする を既約分数 an p として表したときの分母
08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ関数 f ( ) = + cos (0 < < ) の増減表をつくり, + 0, 0 のと sin きの極限を調べよ 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ n+ 数列 a, a, を, Cn a n = ( n =,, ) で定める n! an qn () n とする を既約分数 an p として表したときの分母
2015-2017年度 2次数学セレクション(複素数)解答解説
 05 次数学セレクション解答解説 [ 筑波大 ] ( + より, 0 となり, + から, ( (,, よって, の描く図形 C は, 点 を中心とし半径が の円である すなわち, 原 点を通る円となる ( は虚数, は正の実数より, である さて, w ( ( とおくと, ( ( ( w ( ( ( ここで, w は純虚数より, は純虚数となる すると, の描く図形 L は, 点 を通り, 点 と点
05 次数学セレクション解答解説 [ 筑波大 ] ( + より, 0 となり, + から, ( (,, よって, の描く図形 C は, 点 を中心とし半径が の円である すなわち, 原 点を通る円となる ( は虚数, は正の実数より, である さて, w ( ( とおくと, ( ( ( w ( ( ( ここで, w は純虚数より, は純虚数となる すると, の描く図形 L は, 点 を通り, 点 と点
複素数平面への誘い
 いざな複素数平面への誘い GRS による複素数平面の表現 複素数平面への第一歩 - 複素数モード - 点と複素数 -3 複素数の四則演算 -4 絶対値と偏角, 共役複素数 -5 絶対値と偏角による複素数の表現 複素数平面の変換 4 - 回転移動と相似拡大 - 直線 に関する対称変換 -3 単位円に関する反転変換 -4 複素数平面の変換と曲線 3 入試問題に挑戦 6 3- 陰関数を利用した図形の表示
いざな複素数平面への誘い GRS による複素数平面の表現 複素数平面への第一歩 - 複素数モード - 点と複素数 -3 複素数の四則演算 -4 絶対値と偏角, 共役複素数 -5 絶対値と偏角による複素数の表現 複素数平面の変換 4 - 回転移動と相似拡大 - 直線 に関する対称変換 -3 単位円に関する反転変換 -4 複素数平面の変換と曲線 3 入試問題に挑戦 6 3- 陰関数を利用した図形の表示
GraphicsWithPlotFull.nb Plot[{( 1), ( ),...}, {( ), ( ), ( )}] Plot Plot Cos x Sin x, x, 5 Π, 5 Π, AxesLabel x, y x 1 Plot AxesLabel
![GraphicsWithPlotFull.nb Plot[{( 1), ( ),...}, {( ), ( ), ( )}] Plot Plot Cos x Sin x, x, 5 Π, 5 Π, AxesLabel x, y x 1 Plot AxesLabel GraphicsWithPlotFull.nb Plot[{( 1), ( ),...}, {( ), ( ), ( )}] Plot Plot Cos x Sin x, x, 5 Π, 5 Π, AxesLabel x, y x 1 Plot AxesLabel](/thumbs/81/83602176.jpg) http://yktlab.cis.k.hosei.ac.jp/wiki/ 1(Plot) f x x x 1 1 x x ( )[( 1)_, ( )_, ( 3)_,...]=( ) Plot Plot f x, x, 5, 3 15 10 5 Plot[( ), {( ), ( ), ( )}] D g x x 3 x 3 Plot f x, g x, x, 10, 8 00 100 10 5
http://yktlab.cis.k.hosei.ac.jp/wiki/ 1(Plot) f x x x 1 1 x x ( )[( 1)_, ( )_, ( 3)_,...]=( ) Plot Plot f x, x, 5, 3 15 10 5 Plot[( ), {( ), ( ), ( )}] D g x x 3 x 3 Plot f x, g x, x, 10, 8 00 100 10 5
2018年度 岡山大・理系数学
 08 岡山大学 ( 理系 ) 前期日程問題 解答解説のページへ 関数 f ( x) = ( + x) x について, 以下の問いに答えよ () f ( x ) = 0 を満たす x の値を求めよ () 曲線 y = f ( x ) について, 原点を通るすべての接線の方程式を求めよ (3) 曲線 y = f ( x ) について, 原点を通る接線のうち, 接点の x 座標が最大のものを L とする
08 岡山大学 ( 理系 ) 前期日程問題 解答解説のページへ 関数 f ( x) = ( + x) x について, 以下の問いに答えよ () f ( x ) = 0 を満たす x の値を求めよ () 曲線 y = f ( x ) について, 原点を通るすべての接線の方程式を求めよ (3) 曲線 y = f ( x ) について, 原点を通る接線のうち, 接点の x 座標が最大のものを L とする
PowerPoint Presentation
 付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
応用数学A
 応用数学 A 米田 戸倉川月 7 限 1930~2100 西 5-109 V を :x 2 + y 2 + z 2 = 4 で囲まれる内部とする F = ye x xe y + ze z FdV = V e x e y e z F = = 2e z 2e z dv = 2e z 3 23 = 64π 3 e z y x z 4π V n Fd = 1 F nd 2 F nd 法線ベクトル n g x,
応用数学 A 米田 戸倉川月 7 限 1930~2100 西 5-109 V を :x 2 + y 2 + z 2 = 4 で囲まれる内部とする F = ye x xe y + ze z FdV = V e x e y e z F = = 2e z 2e z dv = 2e z 3 23 = 64π 3 e z y x z 4π V n Fd = 1 F nd 2 F nd 法線ベクトル n g x,
2014年度 名古屋大・理系数学
 04 名古屋大学 ( 理系 ) 前期日程問題 解答解説のページへ空間内にある半径 の球 ( 内部を含む ) を B とする 直線 と B が交わっており, その交わりは長さ の線分である () B の中心と との距離を求めよ () のまわりに B を 回転してできる立体の体積を求めよ 04 名古屋大学 ( 理系 ) 前期日程問題 解答解説のページへ 実数 t に対して 点 P( t, t ), Q(
04 名古屋大学 ( 理系 ) 前期日程問題 解答解説のページへ空間内にある半径 の球 ( 内部を含む ) を B とする 直線 と B が交わっており, その交わりは長さ の線分である () B の中心と との距離を求めよ () のまわりに B を 回転してできる立体の体積を求めよ 04 名古屋大学 ( 理系 ) 前期日程問題 解答解説のページへ 実数 t に対して 点 P( t, t ), Q(
<4D F736F F D20824F B CC92E8979D814696CA90CF95AA82C691CC90CF95AA2E646F63>
 1/1 平成 23 年 3 月 24 日午後 6 時 52 分 6 ガウスの定理 : 面積分と体積分 6 ガウスの定理 : 面積分と体積分 Ⅰ. 直交座標系 ガウスの定理は 微分して すぐに積分すると元に戻るというルールを 3 次元積分に適用した定理になります よく知っているのは 簡単化のため 変数が1つの場合は dj ( d ( ににします全微分 = 偏微分 d = d = J ( + C d です
1/1 平成 23 年 3 月 24 日午後 6 時 52 分 6 ガウスの定理 : 面積分と体積分 6 ガウスの定理 : 面積分と体積分 Ⅰ. 直交座標系 ガウスの定理は 微分して すぐに積分すると元に戻るというルールを 3 次元積分に適用した定理になります よく知っているのは 簡単化のため 変数が1つの場合は dj ( d ( ににします全微分 = 偏微分 d = d = J ( + C d です
Microsoft PowerPoint - 9.pptx
 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 行列演算と写像 ( 次変換 3 拡大とスカラー倍 p ' = ( ', ' = ( k, kk p = (, k 倍 k 倍 拡大後 k 倍拡大の関係は スカラー倍を用いて次のように表現できる ' = k ' 拡大前 拡大 4 拡大と行列の積 p ' = ( ', '
9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 行列演算と写像 ( 次変換 3 拡大とスカラー倍 p ' = ( ', ' = ( k, kk p = (, k 倍 k 倍 拡大後 k 倍拡大の関係は スカラー倍を用いて次のように表現できる ' = k ' 拡大前 拡大 4 拡大と行列の積 p ' = ( ', '
Microsoft PowerPoint - 9.pptx
 9/7/8( 水 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 拡大とスカラー倍 行列演算と写像 ( 次変換 拡大後 k 倍 k 倍 k 倍拡大の関係は スカラー倍を用いて次のように表現できる p = (, ' = k ' 拡大前 p ' = ( ', ' = ( k, k 拡大 4 拡大と行列の積 拡大後 k 倍
9/7/8( 水 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 拡大とスカラー倍 行列演算と写像 ( 次変換 拡大後 k 倍 k 倍 k 倍拡大の関係は スカラー倍を用いて次のように表現できる p = (, ' = k ' 拡大前 p ' = ( ', ' = ( k, k 拡大 4 拡大と行列の積 拡大後 k 倍
2017年度 千葉大・理系数学
 017 千葉大学 ( 理系 ) 前期日程問題 1 解答解説のページへ n を 4 以上の整数とする 座標平面上で正 n 角形 A1A A n は点 O を中心とする半径 1 の円に内接している a = OA 1, b = OA, c = OA 3, d = OA4 とし, k = cos とおく そして, 線分 A1A3 と線分 AA4 との交点 P は線分 A1A3 を n :1に内分するとする
017 千葉大学 ( 理系 ) 前期日程問題 1 解答解説のページへ n を 4 以上の整数とする 座標平面上で正 n 角形 A1A A n は点 O を中心とする半径 1 の円に内接している a = OA 1, b = OA, c = OA 3, d = OA4 とし, k = cos とおく そして, 線分 A1A3 と線分 AA4 との交点 P は線分 A1A3 を n :1に内分するとする
Microsoft Word - Chap11
 第 章 次元回転群とそのリー代数. SO のリー代数. 節でリー代数を定義したが 以下にその定義を再録する なお 多くの教科書に従って本章以降は ep t A の代わりに ep t と書くこととする 定義.. G を 次の線型リー群とすると 任意の実数 t に対して ep t G となる gl C の全体をGのリー代数 またはリー環 という 例えば ep t が 次の特殊直交群 SO の元であれば
第 章 次元回転群とそのリー代数. SO のリー代数. 節でリー代数を定義したが 以下にその定義を再録する なお 多くの教科書に従って本章以降は ep t A の代わりに ep t と書くこととする 定義.. G を 次の線型リー群とすると 任意の実数 t に対して ep t G となる gl C の全体をGのリー代数 またはリー環 という 例えば ep t が 次の特殊直交群 SO の元であれば
2016年度 筑波大・理系数学
 06 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ k を実数とする y 平面の曲線 C : y とC : y- + k+ -k が異なる共 有点 P, Q をもつとする ただし点 P, Q の 座標は正であるとする また, 原点を O とする () k のとりうる値の範囲を求めよ () k が () の範囲を動くとき, OPQ の重心 G の軌跡を求めよ () OPQ の面積を S とするとき,
06 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ k を実数とする y 平面の曲線 C : y とC : y- + k+ -k が異なる共 有点 P, Q をもつとする ただし点 P, Q の 座標は正であるとする また, 原点を O とする () k のとりうる値の範囲を求めよ () k が () の範囲を動くとき, OPQ の重心 G の軌跡を求めよ () OPQ の面積を S とするとき,
2017年度 長崎大・医系数学
 07 長崎大学 ( 医系 ) 前期日程問題 解答解説のページへ 以下の問いに答えよ () 0 のとき, si + cos の最大値と最小値, およびそのときの の値 をそれぞれ求めよ () e を自然対数の底とする > eの範囲において, 関数 y を考える この両 辺の対数を について微分することにより, y は減少関数であることを示せ また, e< < bのとき, () 数列 { } b の一般項が,
07 長崎大学 ( 医系 ) 前期日程問題 解答解説のページへ 以下の問いに答えよ () 0 のとき, si + cos の最大値と最小値, およびそのときの の値 をそれぞれ求めよ () e を自然対数の底とする > eの範囲において, 関数 y を考える この両 辺の対数を について微分することにより, y は減少関数であることを示せ また, e< < bのとき, () 数列 { } b の一般項が,
平成 年 月 7 日 ( 土 第 75 回数学教育実践研究会アスティ 45 ビル F セミナールーム A 札幌医科大学 年 P ab, を正の定数とする 平面上において ( a, を中心とする円 Q 4 C と (, b を中心とする円 C が 原点 O で外接している また P を円 C 上の点と
 平成 年 月 7 日 ( 土 第 75 回数学教育実践研究会アスティ 45 ビル F セミナールーム 微分積分の拡張 変数関数問題へのアプローチ 予選決勝優勝法からラグランジュ未定乗数法 松本睦郎 ( 札幌北高等学校 変数関数の最大値 最小値に関する問題には多様なアプローチ法がある 文字を固定した 予選決勝優勝法, 計算のみで解法する 文字消去法, 微分積分を利用した ラグランジュ未定乗数法 がある
平成 年 月 7 日 ( 土 第 75 回数学教育実践研究会アスティ 45 ビル F セミナールーム 微分積分の拡張 変数関数問題へのアプローチ 予選決勝優勝法からラグランジュ未定乗数法 松本睦郎 ( 札幌北高等学校 変数関数の最大値 最小値に関する問題には多様なアプローチ法がある 文字を固定した 予選決勝優勝法, 計算のみで解法する 文字消去法, 微分積分を利用した ラグランジュ未定乗数法 がある
2011年度 大阪大・理系数学
 0 大阪大学 ( 理系 ) 前期日程問題 解答解説のページへ a a を自然数とする O を原点とする座標平面上で行列 A= a の表す 次変換 を f とする cosθ siθ () >0 および0θ
0 大阪大学 ( 理系 ) 前期日程問題 解答解説のページへ a a を自然数とする O を原点とする座標平面上で行列 A= a の表す 次変換 を f とする cosθ siθ () >0 および0θ
2018年度 筑波大・理系数学
 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ < < とする 放物線 上に 点 (, ), A (ta, ta ), B( - ta, ta ) をとる 三角形 AB の内心の 座標を p とし, 外心の 座標を q とする また, 正の実数 a に対して, 直線 a と放物線 で囲まれた図形の面積を S( a) で表す () p, q を cos を用いて表せ S( p) () S(
筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ < < とする 放物線 上に 点 (, ), A (ta, ta ), B( - ta, ta ) をとる 三角形 AB の内心の 座標を p とし, 外心の 座標を q とする また, 正の実数 a に対して, 直線 a と放物線 で囲まれた図形の面積を S( a) で表す () p, q を cos を用いて表せ S( p) () S(
2017年度 神戸大・理系数学
 7 神戸大学 ( 理系 前期日程問題 解答解説のページへ を自然数とする f ( si + とおく < < 4 であることを用い て, 以下の問いに答えよ ( < < のとき, f ( < であることを示せ ( 方程式 f ( は < < の範囲に解をただ つもつことを示せ ( ( における解を とする lim であることを示し, lim を求めよ 7 神戸大学 ( 理系 前期日程問題 解答解説のページへ
7 神戸大学 ( 理系 前期日程問題 解答解説のページへ を自然数とする f ( si + とおく < < 4 であることを用い て, 以下の問いに答えよ ( < < のとき, f ( < であることを示せ ( 方程式 f ( は < < の範囲に解をただ つもつことを示せ ( ( における解を とする lim であることを示し, lim を求めよ 7 神戸大学 ( 理系 前期日程問題 解答解説のページへ
Microsoft Word - 微分入門.doc
 基本公式 例題 0 定義式 f( ) 数 Ⅲ 微分入門 = の導関数を定義式にもとづいて計算しなさい 基本事項 ( f( ), g( ) が微分可能ならば ) y= f( ) g( ) のとき, y = y= f( ) g( ) h( ) のとき, y = ( f( ), g( ) が微分可能で, g( ) 0 ならば ) f( ) y = のとき, y = g ( ) とくに, y = のとき,
基本公式 例題 0 定義式 f( ) 数 Ⅲ 微分入門 = の導関数を定義式にもとづいて計算しなさい 基本事項 ( f( ), g( ) が微分可能ならば ) y= f( ) g( ) のとき, y = y= f( ) g( ) h( ) のとき, y = ( f( ), g( ) が微分可能で, g( ) 0 ならば ) f( ) y = のとき, y = g ( ) とくに, y = のとき,
木村の物理小ネタ ケプラーの第 2 法則と角運動量保存則 A. 面積速度面積速度とは平面内に定点 O と動点 P があるとき, 定点 O と動点 P を結ぶ線分 OP( 動径 OP という) が単位時間に描く面積を 動点 P の定点 O に
 ケプラーの第 法則と角運動量保存則 A. 面積速度面積速度とは平面内に定点 O と動点 P があるとき, 定点 O と動点 P を結ぶ線分 OP( 動径 OP という が単位時間に描く面積を 動点 P の定点 O に関する面積速度の大きさ という 定点 O まわりを回る面積速度の導き方導き方 A ( x( + D, y( + D v ( q r ( A ( x (, y( 動点 P が xy 座標平面上を時刻
ケプラーの第 法則と角運動量保存則 A. 面積速度面積速度とは平面内に定点 O と動点 P があるとき, 定点 O と動点 P を結ぶ線分 OP( 動径 OP という が単位時間に描く面積を 動点 P の定点 O に関する面積速度の大きさ という 定点 O まわりを回る面積速度の導き方導き方 A ( x( + D, y( + D v ( q r ( A ( x (, y( 動点 P が xy 座標平面上を時刻
第 4 週コンボリューションその 2, 正弦波による分解 教科書 p. 16~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問 1. 以下の図にならって,1 と 2 の δ 関数を図示せよ δ (t) 2
 第 4 週コンボリューションその, 正弦波による分解 教科書 p. 6~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問. 以下の図にならって, と の δ 関数を図示せよ. - - - δ () δ ( ) - - - 図 δ 関数の図示の例 δ ( ) δ ( ) δ ( ) δ ( ) δ ( ) - - - - - - - -
第 4 週コンボリューションその, 正弦波による分解 教科書 p. 6~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問. 以下の図にならって, と の δ 関数を図示せよ. - - - δ () δ ( ) - - - 図 δ 関数の図示の例 δ ( ) δ ( ) δ ( ) δ ( ) δ ( ) - - - - - - - -
2011年度 筑波大・理系数学
 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ O を原点とするy 平面において, 直線 y= の を満たす部分をC とする () C 上に点 A( t, ) をとるとき, 線分 OA の垂直二等分線の方程式を求めよ () 点 A が C 全体を動くとき, 線分 OA の垂直二等分線が通過する範囲を求め, それ を図示せよ -- 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ
0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ O を原点とするy 平面において, 直線 y= の を満たす部分をC とする () C 上に点 A( t, ) をとるとき, 線分 OA の垂直二等分線の方程式を求めよ () 点 A が C 全体を動くとき, 線分 OA の垂直二等分線が通過する範囲を求め, それ を図示せよ -- 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ
Microsoft PowerPoint - 10.pptx
 m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
座標系.rtf
 2 章座標系 場 空間は3 次元なので, ベクトルを表現するには少なくとも3 成分を指定する必要がある. そのために座標系が必要となる. 座標系として最も一般的なものは,,, 成分を使った直角座標系である. しかし, 他にも円柱座標, 球座標, だ円座標, 放物線座標など様々なものがある. 現在までに3 成分で変数分離可能な座標系は11 個あるといわれている (Moon & Spencer, Field
2 章座標系 場 空間は3 次元なので, ベクトルを表現するには少なくとも3 成分を指定する必要がある. そのために座標系が必要となる. 座標系として最も一般的なものは,,, 成分を使った直角座標系である. しかし, 他にも円柱座標, 球座標, だ円座標, 放物線座標など様々なものがある. 現在までに3 成分で変数分離可能な座標系は11 個あるといわれている (Moon & Spencer, Field
Microsoft Word - thesis.doc
 剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
2015年度 岡山大・理系数学
 5 岡山大学 ( 理系 ) 前期日程問題 解答解説のページへ を 以上の自然数とし, から までの自然数 k に対して, 番号 k をつけたカードをそれぞれ k 枚用意する これらすべてを箱に入れ, 箱の中から 枚のカードを同時に引くとき, 次の問いに答えよ () 用意したカードは全部で何枚か答えよ () 引いたカード 枚の番号が両方とも k である確率を と k の式で表せ () 引いたカード 枚の番号が一致する確率を
5 岡山大学 ( 理系 ) 前期日程問題 解答解説のページへ を 以上の自然数とし, から までの自然数 k に対して, 番号 k をつけたカードをそれぞれ k 枚用意する これらすべてを箱に入れ, 箱の中から 枚のカードを同時に引くとき, 次の問いに答えよ () 用意したカードは全部で何枚か答えよ () 引いたカード 枚の番号が両方とも k である確率を と k の式で表せ () 引いたカード 枚の番号が一致する確率を
p tn tn したがって, 点 の 座標は p p tn tn tn また, 直線 l と直線 p の交点 の 座標は p p tn p tn よって, 点 の座標 (, ) は p p, tn tn と表され p 4p p 4p 4p tn tn tn より, 点 は放物線 4 p 上を動くこと
 567_ 次曲線の三角関数による媒介変数表示 次曲線の三角関数による媒介変数表示 次曲線 ( 放物線 楕円 双曲線 ) の標準形の, についての方程式と, 三角関数による媒介変数表示は次のように対応している.. 放物線 () 4 p (, ) ( ptn, ptn ) (). 楕円. 双曲線 () () (, p p ), tn tn (, ) ( cos, sin ) (, ), tn cos (,
567_ 次曲線の三角関数による媒介変数表示 次曲線の三角関数による媒介変数表示 次曲線 ( 放物線 楕円 双曲線 ) の標準形の, についての方程式と, 三角関数による媒介変数表示は次のように対応している.. 放物線 () 4 p (, ) ( ptn, ptn ) (). 楕円. 双曲線 () () (, p p ), tn tn (, ) ( cos, sin ) (, ), tn cos (,
補足 中学で学習したフレミング左手の法則 ( 電 磁 力 ) と関連付けると覚えやすい 電磁力は電流と磁界の外積で表される 力 F 磁 電磁力 F li 右ねじの回転の向き電 li ( l は導線の長さ ) 補足 有向線分とベクトル有向線分 : 矢印の位
 http://totemt.sur.ne.p 外積 ( ベクトル積 ) の活用 ( 面積, 法線ベクトル, 平面の方程式 ) 3 次元空間の つのベクトルの積が つのベクトルを与えるようなベクトルの掛け算 ベクトルの積がベクトルを与えることからベクトル積とも呼ばれる これに対し内積は符号と大きさをもつ量 ( スカラー量 ) を与えるので, スカラー積とも呼ばれる 外積を使うと, 平行四辺形や三角形の面積,
http://totemt.sur.ne.p 外積 ( ベクトル積 ) の活用 ( 面積, 法線ベクトル, 平面の方程式 ) 3 次元空間の つのベクトルの積が つのベクトルを与えるようなベクトルの掛け算 ベクトルの積がベクトルを与えることからベクトル積とも呼ばれる これに対し内積は符号と大きさをもつ量 ( スカラー量 ) を与えるので, スカラー積とも呼ばれる 外積を使うと, 平行四辺形や三角形の面積,
2014年度 千葉大・医系数学
 04 千葉大学 ( 医系 ) 前期日程問題 解答解説のページへ 袋の中に, 赤玉が 3 個, 白玉が 7 個が入っている 袋から玉を無作為に つ取り出し, 色を確認してから, 再び袋に戻すという試行を行う この試行を N 回繰り返したときに, 赤玉を A 回 ( ただし 0 A N) 取り出す確率を p( N, A) とする このとき, 以下の問いに答えよ () 確率 p( N, A) を N と
04 千葉大学 ( 医系 ) 前期日程問題 解答解説のページへ 袋の中に, 赤玉が 3 個, 白玉が 7 個が入っている 袋から玉を無作為に つ取り出し, 色を確認してから, 再び袋に戻すという試行を行う この試行を N 回繰り返したときに, 赤玉を A 回 ( ただし 0 A N) 取り出す確率を p( N, A) とする このとき, 以下の問いに答えよ () 確率 p( N, A) を N と
2015年度 京都大・理系数学
 05 京都大学 ( 理系 ) 前期日程問題 解答解説のページへ つの関数 y= si( x+ ) と y = six のグラフの 0 x の部分で囲まれる領域 を, x 軸のまわりに 回転させてできる立体の体積を求めよ ただし, x = 0 と x = は領域を囲む線とは考えない -- 05 京都大学 ( 理系 ) 前期日程問題 解答解説のページへ次の つの条件を同時に満たす四角形のうち面積が最小のものの面積を求めよ
05 京都大学 ( 理系 ) 前期日程問題 解答解説のページへ つの関数 y= si( x+ ) と y = six のグラフの 0 x の部分で囲まれる領域 を, x 軸のまわりに 回転させてできる立体の体積を求めよ ただし, x = 0 と x = は領域を囲む線とは考えない -- 05 京都大学 ( 理系 ) 前期日程問題 解答解説のページへ次の つの条件を同時に満たす四角形のうち面積が最小のものの面積を求めよ
3D の作図ツールについて 3D 画面を表示すると 以下の新しい作図ツールが表示されます より多くのオプションを見るためには ボタンの右下の小さな矢印 をクリックして下さい 28
 GeoGebra5.0Beta には 3D のグラフィックスビューの機能が備わっています これにより 立体図形についても扱うことが出来ます 3.1 3D 画面まず 通常と同じように GeoGebra を起動させましょう そして メニューバーの表示から グラフィックスビュ-3D を選択します ( または Ctrl+Shift+3 でも同様 ) すると グラフィックスビューの隣にグラフィックスビュー 3D
GeoGebra5.0Beta には 3D のグラフィックスビューの機能が備わっています これにより 立体図形についても扱うことが出来ます 3.1 3D 画面まず 通常と同じように GeoGebra を起動させましょう そして メニューバーの表示から グラフィックスビュ-3D を選択します ( または Ctrl+Shift+3 でも同様 ) すると グラフィックスビューの隣にグラフィックスビュー 3D
Microsoft Word - 201hyouka-tangen-1.doc
 数学 Ⅰ 評価規準の作成 ( 単元ごと ) 数学 Ⅰ の目標及び図形と計量について理解させ 基礎的な知識の習得と技能の習熟を図り それらを的確に活用する機能を伸ばすとともに 数学的な見方や考え方のよさを認識できるようにする 評価の観点の趣旨 式と不等式 二次関数及び図形と計量における考え方に関 心をもつとともに 数学的な見方や考え方のよさを認識し それらを事象の考察に活用しようとする 式と不等式 二次関数及び図形と計量における数学的な見
数学 Ⅰ 評価規準の作成 ( 単元ごと ) 数学 Ⅰ の目標及び図形と計量について理解させ 基礎的な知識の習得と技能の習熟を図り それらを的確に活用する機能を伸ばすとともに 数学的な見方や考え方のよさを認識できるようにする 評価の観点の趣旨 式と不等式 二次関数及び図形と計量における考え方に関 心をもつとともに 数学的な見方や考え方のよさを認識し それらを事象の考察に活用しようとする 式と不等式 二次関数及び図形と計量における数学的な見
Math-Aquarium 例題 図形と計量 図形と計量 1 直角三角形と三角比 P 木の先端を P, 根元を Q とする A 地点の目の位置 A' から 木の先端への仰角が 30,A から 7m 離れた AQB=90 と なる B 地点の目の位置 B' から木の先端への仰角が 45 であ るとき,
 図形と計量 直角三角形と三角比 P 木の先端を P, 根元を Q とする 地点の目の位置 ' から 木の先端への仰角が 0, から 7m 離れた Q=90 と なる 地点の目の位置 ' から木の先端への仰角が であ るとき, 木の高さを求めよ ただし, 目の高さを.m とし, Q' を右の図のように定める ' 0 Q' '.m Q 7m 要点 PQ PQ PQ' =x とおき,' Q',' Q' を
図形と計量 直角三角形と三角比 P 木の先端を P, 根元を Q とする 地点の目の位置 ' から 木の先端への仰角が 0, から 7m 離れた Q=90 と なる 地点の目の位置 ' から木の先端への仰角が であ るとき, 木の高さを求めよ ただし, 目の高さを.m とし, Q' を右の図のように定める ' 0 Q' '.m Q 7m 要点 PQ PQ PQ' =x とおき,' Q',' Q' を
2018年度 神戸大・理系数学
 8 神戸大学 ( 理系 ) 前期日程問題 解答解説のページへ t を < t < を満たす実数とする OABC を 辺の長さが の正四面体とする 辺 OA を -t : tに内分する点を P, 辺 OB を t :-tに内分する点を Q, 辺 BC の中点を R とする また a = OA, b = OB, c = OC とする 以下の問いに答えよ () QP と QR をt, a, b, c を用いて表せ
8 神戸大学 ( 理系 ) 前期日程問題 解答解説のページへ t を < t < を満たす実数とする OABC を 辺の長さが の正四面体とする 辺 OA を -t : tに内分する点を P, 辺 OB を t :-tに内分する点を Q, 辺 BC の中点を R とする また a = OA, b = OB, c = OC とする 以下の問いに答えよ () QP と QR をt, a, b, c を用いて表せ
Chap2.key
 . f( ) V (V V ) V e + V e V V V V ( ) V V ( ) E. - () V (0 ) () V (0 ) () V (0 ) (4) V ( ) E. - () V (0 ) () V (0 ) O r θ ( ) ( ) : (r θ) : { r cos θ r sn θ { r + () V (0 ) (4) V ( ) θ θ arg( ) : π π
. f( ) V (V V ) V e + V e V V V V ( ) V V ( ) E. - () V (0 ) () V (0 ) () V (0 ) (4) V ( ) E. - () V (0 ) () V (0 ) O r θ ( ) ( ) : (r θ) : { r cos θ r sn θ { r + () V (0 ) (4) V ( ) θ θ arg( ) : π π
DVIOUT
 1 体積 1.1 初めに この中では積分は第一基本量 ( 微分幾何 ) を用いて計算する 基本量の 意味を知らなくても別に気にする必要はなく 計算をたどって行けば理解 できるように書いてある 計算するものは球の体積なので カルテシアン 座標 (x-y 座標の畏まった言い方 ) ではなく 球座標を用いるようになる 球座標も x-y 座標と同様に直交座標であるので 扱うのに便利である 通 常は体積などを計算するために座標変換すると
1 体積 1.1 初めに この中では積分は第一基本量 ( 微分幾何 ) を用いて計算する 基本量の 意味を知らなくても別に気にする必要はなく 計算をたどって行けば理解 できるように書いてある 計算するものは球の体積なので カルテシアン 座標 (x-y 座標の畏まった言い方 ) ではなく 球座標を用いるようになる 球座標も x-y 座標と同様に直交座標であるので 扱うのに便利である 通 常は体積などを計算するために座標変換すると
<4D F736F F D A CF95AA B B82CC90CF95AA8CF68EAE2E646F63>
 /8 平成 年 月 日午後 時 6 分 複素積分 : コーシーの積分公式 複素積分 : コーシーの積分公式 Ⅰ. 閉じた積分経路と円周 積分しなくても線積分の結果が分かる場合の第 弾です それは ( ( π d は正則関数 d! d 積分経路は を囲む (. になります これを コーシーの積分公式といいます 複素積分 : コーシーの積分定理 -Ⅰ. 線積分の実技での線積分では 半径 r の円 周上の閉じた経路
/8 平成 年 月 日午後 時 6 分 複素積分 : コーシーの積分公式 複素積分 : コーシーの積分公式 Ⅰ. 閉じた積分経路と円周 積分しなくても線積分の結果が分かる場合の第 弾です それは ( ( π d は正則関数 d! d 積分経路は を囲む (. になります これを コーシーの積分公式といいます 複素積分 : コーシーの積分定理 -Ⅰ. 線積分の実技での線積分では 半径 r の円 周上の閉じた経路
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生
 0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
<4D F736F F D20837D834E B95FB92F68EAE>
 マクスウエルの方程式 Akio Arimoto, Monday, November, 7. イントロ長野 []p.4 に証明抜きで以下のような解説がある 次節以下これを証明していきたいと思う grad f «df d dx =,, rot «( i i), [ ] div «d ( dx dx + dx dx + dx dx ) æ f f f æ f f f rot grad f = rot( df
マクスウエルの方程式 Akio Arimoto, Monday, November, 7. イントロ長野 []p.4 に証明抜きで以下のような解説がある 次節以下これを証明していきたいと思う grad f «df d dx =,, rot «( i i), [ ] div «d ( dx dx + dx dx + dx dx ) æ f f f æ f f f rot grad f = rot( df
測量試補 重要事項
 用地測量面積計算 < 試験合格へのポイント > 座標法による面積計算に関する問題は その出題回数からも定番問題と言えるが 計算自体はさほど難しいものではなく 計算表を作成しその中に数値を当てはめていくことで答えを導くことができる 過去問をしっかりとこなし 計算手順を覚えれば点の取りやすい問題と言える 士補試験に出題される問題は過去の例を見ても 座標が簡単な数値に置き換えることができるようになっている
用地測量面積計算 < 試験合格へのポイント > 座標法による面積計算に関する問題は その出題回数からも定番問題と言えるが 計算自体はさほど難しいものではなく 計算表を作成しその中に数値を当てはめていくことで答えを導くことができる 過去問をしっかりとこなし 計算手順を覚えれば点の取りやすい問題と言える 士補試験に出題される問題は過去の例を見ても 座標が簡単な数値に置き換えることができるようになっている
<4D F736F F D F2095A F795AA B B A815B837D839382CC95FB92F68EAE2E646F63>
 1/8 平成 3 年 3 月 4 日午後 6 時 11 分 10 複素微分 : コーシー リーマンの方程式 10 複素微分 : コーシー リーマンの方程式 9 複素微分 : 正則関数 で 正則性は複素数 z の関数 f ( z) の性質として導き出しまし た 複素数 z は つの実数, で表され z i 数 u, v で表され f ( z) u i 複素数 z と つの実数, : z + i + です
1/8 平成 3 年 3 月 4 日午後 6 時 11 分 10 複素微分 : コーシー リーマンの方程式 10 複素微分 : コーシー リーマンの方程式 9 複素微分 : 正則関数 で 正則性は複素数 z の関数 f ( z) の性質として導き出しまし た 複素数 z は つの実数, で表され z i 数 u, v で表され f ( z) u i 複素数 z と つの実数, : z + i + です
1/10 平成 29 年 3 月 24 日午後 1 時 37 分第 5 章ローレンツ変換と回転 第 5 章ローレンツ変換と回転 Ⅰ. 回転 第 3 章光速度不変の原理とローレンツ変換 では 時間の遅れをローレンツ変換 ct 移動 v相対 v相対 ct - x x - ct = c, x c 2 移動
 / 平成 9 年 3 月 4 日午後 時 37 分第 5 章ローレンツ変換と回転 第 5 章ローレンツ変換と回転 Ⅰ. 回転 第 3 章光速度不変の原理とローレンツ変換 では 時間の遅れをローレンツ変換 t t - x x - t, x 静止静止静止静止 を導いた これを 図の場合に当てはめると t - x x - t t, x t + x x + t t, x (5.) (5.) (5.3) を得る
/ 平成 9 年 3 月 4 日午後 時 37 分第 5 章ローレンツ変換と回転 第 5 章ローレンツ変換と回転 Ⅰ. 回転 第 3 章光速度不変の原理とローレンツ変換 では 時間の遅れをローレンツ変換 t t - x x - t, x 静止静止静止静止 を導いた これを 図の場合に当てはめると t - x x - t t, x t + x x + t t, x (5.) (5.) (5.3) を得る
Chap3.key
 区分求積法. 面積 ( )/ f () > n + n, S 長方形の和集合で近似 n f (n ) リーマン和 f (n ) 区分求積法 リーマン和 S S n n / n n f ()d リーマン積分 ( + ) + S (, f ( )) 微分の心 Zoom In して局所的な性質を調べる 積分の心 Zoom Ou して大域的な性質を調べる 曲線の長さ 領域の面積や体積 ある領域に含まれる物質の質量
区分求積法. 面積 ( )/ f () > n + n, S 長方形の和集合で近似 n f (n ) リーマン和 f (n ) 区分求積法 リーマン和 S S n n / n n f ()d リーマン積分 ( + ) + S (, f ( )) 微分の心 Zoom In して局所的な性質を調べる 積分の心 Zoom Ou して大域的な性質を調べる 曲線の長さ 領域の面積や体積 ある領域に含まれる物質の質量
Microsoft Word - ミクロ経済学02-01費用関数.doc
 ミクロ経済学の シナリオ 講義の 3 分の 1 の時間で理解させる技術 国際派公務員養成所 第 2 章 生産者理論 生産者の利潤最大化行動について学び 供給曲線の導出プロセスを確認します 2-1. さまざまな費用曲線 (1) 総費用 (TC) 固定費用 (FC) 可変費用 (VC) 今回は さまざまな費用曲線を学んでいきましょう 費用曲線にはまず 総費用曲線があります 総費用 TC(Total Cost)
ミクロ経済学の シナリオ 講義の 3 分の 1 の時間で理解させる技術 国際派公務員養成所 第 2 章 生産者理論 生産者の利潤最大化行動について学び 供給曲線の導出プロセスを確認します 2-1. さまざまな費用曲線 (1) 総費用 (TC) 固定費用 (FC) 可変費用 (VC) 今回は さまざまな費用曲線を学んでいきましょう 費用曲線にはまず 総費用曲線があります 総費用 TC(Total Cost)
例題1 転がり摩擦
 重心 5.. 重心問題解法虎の巻. 半円 分円. 円弧. 扇形. 半球殻 5. 半球体 6. 厚みのある半球殻 7. 三角形 8. 円錐 9. 円錐台. 穴あき板. 空洞のある半球ボール 重心問題解法虎の巻 関西大学工学部物理学教室 齊藤正 重心を求める場合 質点系の重心の求め方が基本 実際の物体では連続体であるので 積分形式で求める場合が多い これらの式は 次元のベクトル形式で書かれている通り つの式は実際には
重心 5.. 重心問題解法虎の巻. 半円 分円. 円弧. 扇形. 半球殻 5. 半球体 6. 厚みのある半球殻 7. 三角形 8. 円錐 9. 円錐台. 穴あき板. 空洞のある半球ボール 重心問題解法虎の巻 関西大学工学部物理学教室 齊藤正 重心を求める場合 質点系の重心の求め方が基本 実際の物体では連続体であるので 積分形式で求める場合が多い これらの式は 次元のベクトル形式で書かれている通り つの式は実際には
2014年度 センター試験・数学ⅡB
 第 問 解答解説のページへ [] O を原点とする座標平面において, 点 P(, q) を中心とする円 C が, 方程式 y 4 x で表される直線 l に接しているとする () 円 C の半径 r を求めよう 点 P を通り直線 l に垂直な直線の方程式は, y - ア ( x- ) + qなので, P イ から l に引いた垂線と l の交点 Q の座標は ( ( ウ + エ q ), 4 (
第 問 解答解説のページへ [] O を原点とする座標平面において, 点 P(, q) を中心とする円 C が, 方程式 y 4 x で表される直線 l に接しているとする () 円 C の半径 r を求めよう 点 P を通り直線 l に垂直な直線の方程式は, y - ア ( x- ) + qなので, P イ から l に引いた垂線と l の交点 Q の座標は ( ( ウ + エ q ), 4 (
相関係数と偏差ベクトル
 相関係数と偏差ベクトル 経営統計演習の補足資料 07 年 月 9 日金沢学院大学経営情報学部藤本祥二 相関係数の復習 r = s xy s x s y = = n σ n i= σn i= n σ n i= n σ i= x i xҧ y i തy x i xҧ n σ n i= y i തy x i xҧ x i xҧ y i തy σn i= y i തy 式が長くなるので u, v の文字で偏差を表すことにする
相関係数と偏差ベクトル 経営統計演習の補足資料 07 年 月 9 日金沢学院大学経営情報学部藤本祥二 相関係数の復習 r = s xy s x s y = = n σ n i= σn i= n σ n i= n σ i= x i xҧ y i തy x i xҧ n σ n i= y i തy x i xҧ x i xҧ y i തy σn i= y i തy 式が長くなるので u, v の文字で偏差を表すことにする
2010年度 筑波大・理系数学
 00 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ f( x) x ax とおく ただしa>0 とする () f( ) f() となるa の範囲を求めよ () f(x) の極小値が f ( ) 以下になる a の範囲を求めよ () x における f(x) の最小値をa を用いて表せ -- 00 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ つの曲線 C : y six ( 0
00 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ f( x) x ax とおく ただしa>0 とする () f( ) f() となるa の範囲を求めよ () f(x) の極小値が f ( ) 以下になる a の範囲を求めよ () x における f(x) の最小値をa を用いて表せ -- 00 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ つの曲線 C : y six ( 0
Phys1_03.key
 物理学1/物理学A 第3回 速度と加速度 速度 加速度 関数の話 やりたいこと : 物体の運動を調べる 物体の位置と速度を調べる これらを時間の関数として表したい 関数とは? ある された変数に対して, 出 の値が決まる対応関係のこと inpu 関数 ( 函数 ) oupu 例 : y(x)=x 2 x=2 を inpu すると y=4 が得られる 時々刻々と変化していく物体の位置 をその時刻とともに記録する
物理学1/物理学A 第3回 速度と加速度 速度 加速度 関数の話 やりたいこと : 物体の運動を調べる 物体の位置と速度を調べる これらを時間の関数として表したい 関数とは? ある された変数に対して, 出 の値が決まる対応関係のこと inpu 関数 ( 函数 ) oupu 例 : y(x)=x 2 x=2 を inpu すると y=4 が得られる 時々刻々と変化していく物体の位置 をその時刻とともに記録する
Microsoft Word - 断面諸量
 応用力学 Ⅱ 講義資料 / 断面諸量 断面諸量 断面 次 次モーメントの定義 図 - に示すような形状を有する横断面を考え その全断面積を とする いま任意に定めた直交座標軸 O-, をとり また図中の斜線部の微小面積要素を d とするとき d, d () で定義される, をそれぞれ与えられた横断面の 軸, 軸に関する断面 次モーメント (geometrcal moment of area) という
応用力学 Ⅱ 講義資料 / 断面諸量 断面諸量 断面 次 次モーメントの定義 図 - に示すような形状を有する横断面を考え その全断面積を とする いま任意に定めた直交座標軸 O-, をとり また図中の斜線部の微小面積要素を d とするとき d, d () で定義される, をそれぞれ与えられた横断面の 軸, 軸に関する断面 次モーメント (geometrcal moment of area) という
ポンスレの定理
 ポンスレの定理. qution Section 定理 有本彰雄 東京都市大学 平成 年 月 4 日 定義. n 角形 P とは 平面上にあるn 個の点の順序列 ( p, p,, pn - ) のことである 各 pk は P の頂点と呼ばれる 記号法を簡単にするため便宜的に p n とする また 線分 p i i pp, i,,,, n - を P の辺と呼ぶ 定義. すべての頂点 p k が曲線 C
ポンスレの定理. qution Section 定理 有本彰雄 東京都市大学 平成 年 月 4 日 定義. n 角形 P とは 平面上にあるn 個の点の順序列 ( p, p,, pn - ) のことである 各 pk は P の頂点と呼ばれる 記号法を簡単にするため便宜的に p n とする また 線分 p i i pp, i,,,, n - を P の辺と呼ぶ 定義. すべての頂点 p k が曲線 C
2017年度 金沢大・理系数学
 07 金沢大学 ( 理系 前期日程問題 解答解説のページへ 次の問いに答えよ ( 6 z + 7 = 0 を満たす複素数 z をすべて求め, それらを表す点を複素数平面上に図 示せよ ( ( で求めた複素数 z を偏角が小さい方から順に z, z, とするとき, z, z と 積 zz を表す 点が複素数平面上で一直線上にあることを示せ ただし, 偏角は 0 以上 未満とする -- 07 金沢大学
07 金沢大学 ( 理系 前期日程問題 解答解説のページへ 次の問いに答えよ ( 6 z + 7 = 0 を満たす複素数 z をすべて求め, それらを表す点を複素数平面上に図 示せよ ( ( で求めた複素数 z を偏角が小さい方から順に z, z, とするとき, z, z と 積 zz を表す 点が複素数平面上で一直線上にあることを示せ ただし, 偏角は 0 以上 未満とする -- 07 金沢大学
1 1. はじめに ポンスレの閉形定理 Jacobi の証明 June 5, 2013 Akio Arimoto ヤコビは [2] においてポンスレの閉形定理に初等幾何を用いた証明を与え ている 大小 2つの円があり 一方が他方を完全に含んでいるとする 大小 2 円の半径をそれぞれ Rr, とする
![1 1. はじめに ポンスレの閉形定理 Jacobi の証明 June 5, 2013 Akio Arimoto ヤコビは [2] においてポンスレの閉形定理に初等幾何を用いた証明を与え ている 大小 2つの円があり 一方が他方を完全に含んでいるとする 大小 2 円の半径をそれぞれ Rr, とする 1 1. はじめに ポンスレの閉形定理 Jacobi の証明 June 5, 2013 Akio Arimoto ヤコビは [2] においてポンスレの閉形定理に初等幾何を用いた証明を与え ている 大小 2つの円があり 一方が他方を完全に含んでいるとする 大小 2 円の半径をそれぞれ Rr, とする](/thumbs/100/145746324.jpg) . はじめに ポンスレの閉形定理 Jcobi の証明 Jue 5 03 Akio Aimoto ヤコビは [] においてポンスレの閉形定理に初等幾何を用いた証明を与え ている 大小 つの円があり 一方が他方を完全に含んでいるとする 大小 円の半径をそれぞれ とする 中心間の距離を とすれば 0 < + < が成立している 大きい円の周上の点 A から小さい円に接線を引く 接線と大きい円の周上に交わる
. はじめに ポンスレの閉形定理 Jcobi の証明 Jue 5 03 Akio Aimoto ヤコビは [] においてポンスレの閉形定理に初等幾何を用いた証明を与え ている 大小 つの円があり 一方が他方を完全に含んでいるとする 大小 円の半径をそれぞれ とする 中心間の距離を とすれば 0 < + < が成立している 大きい円の周上の点 A から小さい円に接線を引く 接線と大きい円の周上に交わる
コンピュータグラフィックス第6回
 コンピュータグラフィックス 第 6 回 モデリング技法 1 ~3 次元形状表現 ~ 理工学部 兼任講師藤堂英樹 本日の講義内容 モデリング技法 1 様々な形状モデル 曲線 曲面 2014/11/10 コンピュータグラフィックス 2 CG 制作の主なワークフロー 3DCG ソフトウェアの場合 モデリング カメラ シーン アニメーション テクスチャ 質感 ライティング 画像生成 2014/11/10 コンピュータグラフィックス
コンピュータグラフィックス 第 6 回 モデリング技法 1 ~3 次元形状表現 ~ 理工学部 兼任講師藤堂英樹 本日の講義内容 モデリング技法 1 様々な形状モデル 曲線 曲面 2014/11/10 コンピュータグラフィックス 2 CG 制作の主なワークフロー 3DCG ソフトウェアの場合 モデリング カメラ シーン アニメーション テクスチャ 質感 ライティング 画像生成 2014/11/10 コンピュータグラフィックス
( 表紙 )
 ( 表紙 ) 1 次の各問いに答えなさい. 解答用紙には答えのみ記入すること. ( 48 点 ) (1) U108 -U8 %5U6 + 7 U を計算しなさい. () 15a 7 b 8 &0-5a b 1& - 8 9 ab を計算しなさい. () + y - -5y 6 を計算しなさい. (4) 1 4 5 の 5 枚のカードから 枚を選び, 横に並べて 桁の数を作 るとき, それが の倍数になる確率を求めなさい.
( 表紙 ) 1 次の各問いに答えなさい. 解答用紙には答えのみ記入すること. ( 48 点 ) (1) U108 -U8 %5U6 + 7 U を計算しなさい. () 15a 7 b 8 &0-5a b 1& - 8 9 ab を計算しなさい. () + y - -5y 6 を計算しなさい. (4) 1 4 5 の 5 枚のカードから 枚を選び, 横に並べて 桁の数を作 るとき, それが の倍数になる確率を求めなさい.
1999年度 センター試験・数学ⅡB
 99 センター試験数学 Ⅱ 数学 B 問題 第 問 ( 必答問題 ) [] 関数 y cos3x の周期のうち正で最小のものはアイウ 解答解説のページへ 0 x 360 のとき, 関数 y cos3x において, y となる x はエ個, y となる x はオ 個ある また, y sin x と y cos3x のグラフより, 方程式 sin x cos3x は 0 x 360のときカ個の解をもつことがわかる
99 センター試験数学 Ⅱ 数学 B 問題 第 問 ( 必答問題 ) [] 関数 y cos3x の周期のうち正で最小のものはアイウ 解答解説のページへ 0 x 360 のとき, 関数 y cos3x において, y となる x はエ個, y となる x はオ 個ある また, y sin x と y cos3x のグラフより, 方程式 sin x cos3x は 0 x 360のときカ個の解をもつことがわかる
C 言語第 7 回 掛け算 (multiply number) ìz1 = x1 + iy1 í îz = x + iy 割り算 (devide number) ( )( ) ( ) Þ z z = x + iy x + iy = x x - y y + i y x + x y
 C 言語第 7 回 複素数の使用法 ( シラバス 1 回目 ) 1 1 複素数 複素数 (complex numbers) z は虚数単位 ìi í i = - î 1 を使って つの実数 x, y から z = x + iy と作ります とくに x を z の実数部 (real part): x = Re( z) y を z の虚数部 (imarginary part): y = Im ( z)
C 言語第 7 回 複素数の使用法 ( シラバス 1 回目 ) 1 1 複素数 複素数 (complex numbers) z は虚数単位 ìi í i = - î 1 を使って つの実数 x, y から z = x + iy と作ります とくに x を z の実数部 (real part): x = Re( z) y を z の虚数部 (imarginary part): y = Im ( z)
物性物理学 I( 平山 ) 補足資料 No.6 ( 量子ポイントコンタクト ) 右図のように 2つ物質が非常に小さな接点を介して接触している状況を考えましょう 物質中の電子の平均自由行程に比べて 接点のサイズが非常に小さな場合 この接点を量子ポイントコンタクトと呼ぶことがあります この系で左右の2つ
 物性物理学 I( 平山 ) 補足資料 No.6 ( 量子ポイントコンタクト ) 右図のように つ物質が非常に小さな接点を介して接触している状況を考えましょう 物質中の電子の平均自由行程に比べて 接点のサイズが非常に小さな場合 この接点を量子ポイントコンタクトと呼ぶことがあります この系で左右のつの物質の間に電位差を設けて左から右に向かって電流を流すことを行った場合に接点を通って流れる電流を求めるためには
物性物理学 I( 平山 ) 補足資料 No.6 ( 量子ポイントコンタクト ) 右図のように つ物質が非常に小さな接点を介して接触している状況を考えましょう 物質中の電子の平均自由行程に比べて 接点のサイズが非常に小さな場合 この接点を量子ポイントコンタクトと呼ぶことがあります この系で左右のつの物質の間に電位差を設けて左から右に向かって電流を流すことを行った場合に接点を通って流れる電流を求めるためには
としてもよいし,* を省略し, その代わりにスペースを空けてもよい. In[5]:= 2 3 Out[5]= 6 数値計算 厳密な代数計算 整数および有理数については, 厳密な計算がなされます. In[6]:= Out[6]= In[7]:= Out[7]= 2^
![としてもよいし,* を省略し, その代わりにスペースを空けてもよい. In[5]:= 2 3 Out[5]= 6 数値計算 厳密な代数計算 整数および有理数については, 厳密な計算がなされます. In[6]:= Out[6]= In[7]:= Out[7]= 2^ としてもよいし,* を省略し, その代わりにスペースを空けてもよい. In[5]:= 2 3 Out[5]= 6 数値計算 厳密な代数計算 整数および有理数については, 厳密な計算がなされます. In[6]:= Out[6]= In[7]:= Out[7]= 2^](/thumbs/56/38405467.jpg) Mathematica 入門 はじめに Mathematica は極めて高度かつ有用な機能を有する研究支援統合ソフトウェアです. 理工系学生にとって ( それどころか研究者にとっても ) 非常に便利なツールですから, 基本的な操作方法に慣れておくと, いざというときにとても重宝します. 入力方法 キーボードからの入力 Mathematica では, 数式はすべてキーボードから入力できるようになっています.
Mathematica 入門 はじめに Mathematica は極めて高度かつ有用な機能を有する研究支援統合ソフトウェアです. 理工系学生にとって ( それどころか研究者にとっても ) 非常に便利なツールですから, 基本的な操作方法に慣れておくと, いざというときにとても重宝します. 入力方法 キーボードからの入力 Mathematica では, 数式はすべてキーボードから入力できるようになっています.
untitled
 COM 6 20040920 (Mathematica-1) iijima COM 6 Mathematica (iijima@ae.keio.ac.jp) 1 COM 6 20040920 (Mathematica-1) iijima 1. Mathematica 1.1 1.2 1.3 1.4 2 COM 6 20040920 (Mathematica-1) iijima 1.1 3 COM 6
COM 6 20040920 (Mathematica-1) iijima COM 6 Mathematica (iijima@ae.keio.ac.jp) 1 COM 6 20040920 (Mathematica-1) iijima 1. Mathematica 1.1 1.2 1.3 1.4 2 COM 6 20040920 (Mathematica-1) iijima 1.1 3 COM 6
Microsoft PowerPoint - ip02_01.ppt [互換モード]
![Microsoft PowerPoint - ip02_01.ppt [互換モード] Microsoft PowerPoint - ip02_01.ppt [互換モード]](/thumbs/96/127250376.jpg) 空間周波数 周波数領域での処理 空間周波数 (spatial frquncy) とは 単位長さ当たりの正弦波状の濃淡変化の繰り返し回数を表したもの 正弦波 : y sin( t) 周期 : 周波数 : T f / T 角周波数 : f 画像処理 空間周波数 周波数領域での処理 波形が違うと 周波数も違う 画像処理 空間周波数 周波数領域での処理 画像処理 3 周波数領域での処理 周波数は一つしかない?-
空間周波数 周波数領域での処理 空間周波数 (spatial frquncy) とは 単位長さ当たりの正弦波状の濃淡変化の繰り返し回数を表したもの 正弦波 : y sin( t) 周期 : 周波数 : T f / T 角周波数 : f 画像処理 空間周波数 周波数領域での処理 波形が違うと 周波数も違う 画像処理 空間周波数 周波数領域での処理 画像処理 3 周波数領域での処理 周波数は一つしかない?-
<4D F736F F D2089FC92E82D D4B CF591AA92E882C CA82C982C282A282C42E727466>
 11 Application Note 光測定と単位について 1. 概要 LED の性質を表すには 光の強さ 明るさ等が重要となり これらはその LED をどのようなアプリケーションに使用するかを決定するために必須のものになることが殆どです しかし 測定の方法は多種存在し 何をどのような測定器で測定するかにより 測定結果が異なってきます 本書では光測定とその単位について説明していきます 2. 色とは
11 Application Note 光測定と単位について 1. 概要 LED の性質を表すには 光の強さ 明るさ等が重要となり これらはその LED をどのようなアプリケーションに使用するかを決定するために必須のものになることが殆どです しかし 測定の方法は多種存在し 何をどのような測定器で測定するかにより 測定結果が異なってきます 本書では光測定とその単位について説明していきます 2. 色とは
回転.rtf
 ベクトルの回転の定義は A A rot A ΔS 0 n ΔS (5.) : ounter dl 図 5. ベクトルの回転 であり, 回転量を調べる演算子である. ローテーションA, カールA,Aの回転とも読む. 図 5.のように, 閉曲線 に沿ってベクトル Aの線積分を行うものとする. 線積分はベクトル Aと線素 dl の内積だから, ある大きさ ( スカラー量 ) が得られる. その大きさをもち,
ベクトルの回転の定義は A A rot A ΔS 0 n ΔS (5.) : ounter dl 図 5. ベクトルの回転 であり, 回転量を調べる演算子である. ローテーションA, カールA,Aの回転とも読む. 図 5.のように, 閉曲線 に沿ってベクトル Aの線積分を行うものとする. 線積分はベクトル Aと線素 dl の内積だから, ある大きさ ( スカラー量 ) が得られる. その大きさをもち,
1/30 平成 29 年 3 月 24 日 ( 金 ) 午前 11 時 25 分第三章フェルミ量子場 : スピノール場 ( 次元あり ) 第三章フェルミ量子場 : スピノール場 フェルミ型 ボーズ量子場のエネルギーは 第二章ボーズ量子場 : スカラー場 の (2.18) より ˆ dp 1 1 =
 / 平成 9 年 月 日 ( 金 午前 時 5 分第三章フェルミ量子場 : スピノール場 ( 次元あり 第三章フェルミ量子場 : スピノール場 フェルミ型 ボーズ量子場のエネルギーは 第二章ボーズ量子場 : スカラー場 の (.8 より ˆ ( ( ( q -, ( ( c ( H c c ë é ù û - Ü + c ( ( - に限る (. である 一方 フェルミ型は 成分をもち その成分を,,,,
/ 平成 9 年 月 日 ( 金 午前 時 5 分第三章フェルミ量子場 : スピノール場 ( 次元あり 第三章フェルミ量子場 : スピノール場 フェルミ型 ボーズ量子場のエネルギーは 第二章ボーズ量子場 : スカラー場 の (.8 より ˆ ( ( ( q -, ( ( c ( H c c ë é ù û - Ü + c ( ( - に限る (. である 一方 フェルミ型は 成分をもち その成分を,,,,
2015年度 金沢大・理系数学
 05 金沢大学 ( 理系 ) 前期日程問題 解答解説のページへ四面体 OABC において, 3 つのベクトル OA, OB, OC はどの つも互いに垂直で あり, h > 0 に対して, OA, OB, OC h とする 3 点 O, A, B を通る平面上の点 P は, CP が CA と CB のどちらとも垂直となる点であるとする 次の問いに答えよ () OP OA + OB とするとき, と
05 金沢大学 ( 理系 ) 前期日程問題 解答解説のページへ四面体 OABC において, 3 つのベクトル OA, OB, OC はどの つも互いに垂直で あり, h > 0 に対して, OA, OB, OC h とする 3 点 O, A, B を通る平面上の点 P は, CP が CA と CB のどちらとも垂直となる点であるとする 次の問いに答えよ () OP OA + OB とするとき, と
20~22.prt
 [ 三クリア W] 辺が等しいことの証明 ( 円周角と弦の関係利用 ) の の二等分線がこの三角形の外接円と交わる点をそれぞれ とするとき 60 ならば であることを証明せよ 60 + + 0 + 0 80-60 60 から ゆえに 等しい長さの弧に対する弦の長さは等しいから [ 三クリア ] 方べきの定理 接線と弦のなす角と円周角を利用 線分 を直径とする円 があり 右の図のように の延長上の点
[ 三クリア W] 辺が等しいことの証明 ( 円周角と弦の関係利用 ) の の二等分線がこの三角形の外接円と交わる点をそれぞれ とするとき 60 ならば であることを証明せよ 60 + + 0 + 0 80-60 60 から ゆえに 等しい長さの弧に対する弦の長さは等しいから [ 三クリア ] 方べきの定理 接線と弦のなす角と円周角を利用 線分 を直径とする円 があり 右の図のように の延長上の点
ContourPlot[{x^+y^==,(x-)^+y^==}, {x,-,}, {y,-,}, AspectRatio -> Automatic].. ContourPlot Plot AspectRatio->Automatic.. x a + y = ( ). b ContourPlot[x
![ContourPlot[{x^+y^==,(x-)^+y^==}, {x,-,}, {y,-,}, AspectRatio -> Automatic].. ContourPlot Plot AspectRatio->Automatic.. x a + y = ( ). b ContourPlot[x ContourPlot[{x^+y^==,(x-)^+y^==}, {x,-,}, {y,-,}, AspectRatio -> Automatic].. ContourPlot Plot AspectRatio->Automatic.. x a + y = ( ). b ContourPlot[x](/thumbs/82/86424759.jpg) 3. Mathematica., : f(x) sin x Plot f(x, y) = x + y = ContourPlot f(x, y) > x 4 + (x y ) > RegionPlot (x(t), y(t)) (t sin t, cos t) ParametricPlot r = f(θ) r = sin 4θ PolarPlot.,.. x + y = (x, y). x, y.
3. Mathematica., : f(x) sin x Plot f(x, y) = x + y = ContourPlot f(x, y) > x 4 + (x y ) > RegionPlot (x(t), y(t)) (t sin t, cos t) ParametricPlot r = f(θ) r = sin 4θ PolarPlot.,.. x + y = (x, y). x, y.
LEDの光度調整について
 光測定と単位について 目次 1. 概要 2. 色とは 3. 放射量と測光量 4. 放射束 5. 視感度 6. 放射束と光束の関係 7. 光度と立体角 8. 照度 9. 照度と光束の関係 10. 各単位の関係 11. まとめ 1/6 1. 概要 LED の性質を表すには 光の強さ 明るさ等が重要となり これらはその LED をどのようなアプリケーションに使用するかを決定するために必須のものになることが殆どです
光測定と単位について 目次 1. 概要 2. 色とは 3. 放射量と測光量 4. 放射束 5. 視感度 6. 放射束と光束の関係 7. 光度と立体角 8. 照度 9. 照度と光束の関係 10. 各単位の関係 11. まとめ 1/6 1. 概要 LED の性質を表すには 光の強さ 明るさ等が重要となり これらはその LED をどのようなアプリケーションに使用するかを決定するために必須のものになることが殆どです
公式集 数学 Ⅱ B 頭に入っていますか? 8 和積の公式 A + B A B si A + si B si os A + B A B si A si B os si A + B A B os A + os B os os A + B A B os A os B si si 9 三角関数の合成 si
 公式集 数学 Ⅱ B 頭に入っていますか? < 図形と方程式 > 点間の距離 A x, B x, のとき x x + : に分ける点 A x, B x, のとき 線分 AB を:に分ける点 æ x + x + ö は ç, è + + ø 注 < のとき外分点 直線の方程式 傾き で 点 x, を通る : x 点 x, x, を通る : x 注 分母が のとき は座標軸と平行な直線 x x 4 直線の位置関係
公式集 数学 Ⅱ B 頭に入っていますか? < 図形と方程式 > 点間の距離 A x, B x, のとき x x + : に分ける点 A x, B x, のとき 線分 AB を:に分ける点 æ x + x + ö は ç, è + + ø 注 < のとき外分点 直線の方程式 傾き で 点 x, を通る : x 点 x, x, を通る : x 注 分母が のとき は座標軸と平行な直線 x x 4 直線の位置関係
2017年度 信州大・医系数学
 7 信州大学 ( 医系 ) 前期日程問題 解答解説のページへ 座標平面上の点 O(, ), A ( a, a ), B( b, b ), C( b, b) を考える さらに,, に対し, D( acos asi, asi + acos ), E( bcos bsi, bsi + bcos ) とおく () OA = OD を示せ () OA OC = かつ OA OB = OD OE ¹ であるとする
7 信州大学 ( 医系 ) 前期日程問題 解答解説のページへ 座標平面上の点 O(, ), A ( a, a ), B( b, b ), C( b, b) を考える さらに,, に対し, D( acos asi, asi + acos ), E( bcos bsi, bsi + bcos ) とおく () OA = OD を示せ () OA OC = かつ OA OB = OD OE ¹ であるとする
ベクトルの基礎.rtf
 章ベクトルの表現方法 ベクトルは大きさと方向を持つ量である. 図.に示すように始点 Pから終点 Qに向かう有向線分として で表現する. 大きさは矢印の長さに対応している. Q P 図. ベクトルの表現方法 文字を使ったベクトルの表記方法として, あるいは の表記が用いられるが, このテキストでは太字表示 を採用する. 専門書では太字で書く の表記が一般的であり, 矢印を付ける表記は用いない. なお,
章ベクトルの表現方法 ベクトルは大きさと方向を持つ量である. 図.に示すように始点 Pから終点 Qに向かう有向線分として で表現する. 大きさは矢印の長さに対応している. Q P 図. ベクトルの表現方法 文字を使ったベクトルの表記方法として, あるいは の表記が用いられるが, このテキストでは太字表示 を採用する. 専門書では太字で書く の表記が一般的であり, 矢印を付ける表記は用いない. なお,
例 e 指数関数的に減衰する信号を h( a < + a a すると, それらのラプラス変換は, H ( ) { e } e インパルス応答が h( a < ( ただし a >, U( ) { } となるシステムにステップ信号 ( y( のラプラス変換 Y () は, Y ( ) H ( ) X (
 第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
コンピュータグラフィックス基礎 No
 課題 6: モデリング (1) OBJView の動作確認 ( レポートには含めなくてよい ) 次ページ以降の 課題用メモ を参考にして OBJ ファイルを 3D 表示する OBJView を実行し 画面に立体が表示されることを確認するとともに 以下の機能を確認しなさい 左ドラッグによる立体の回転 右ドラッグによる拡大/ 縮小 [v] キーによる頂点の表示 非表示 サンプルに含まれる bunny_3k.obj
課題 6: モデリング (1) OBJView の動作確認 ( レポートには含めなくてよい ) 次ページ以降の 課題用メモ を参考にして OBJ ファイルを 3D 表示する OBJView を実行し 画面に立体が表示されることを確認するとともに 以下の機能を確認しなさい 左ドラッグによる立体の回転 右ドラッグによる拡大/ 縮小 [v] キーによる頂点の表示 非表示 サンプルに含まれる bunny_3k.obj
解答速報数学 2017 年度大阪医科大学 ( 前期 ) 一般入学試験 1 (1) 0, 8 1 e9 進学塾 0t= $ e e 0t= 11 2e -1 1 = 2 e 0t= -11 dy dx = -2 - t te 3t 2-1 = = ビッグバン dy (2) x
 解答速報数学 07 年度大阪医科大学 ( 前期 ) 一般入学試験 () 0, 8 9 0t= $ - - 0t= - = 0t= - dx = - - t t t - = = () x 軸と平行 dt =- - t t =0. t=0, x=0, y= dx y 軸と平行 dt = t -=0. t=$ U, x=p U, y= - ( 複号同順 ) () t dx = - t - t - より,
解答速報数学 07 年度大阪医科大学 ( 前期 ) 一般入学試験 () 0, 8 9 0t= $ - - 0t= - = 0t= - dx = - - t t t - = = () x 軸と平行 dt =- - t t =0. t=0, x=0, y= dx y 軸と平行 dt = t -=0. t=$ U, x=p U, y= - ( 複号同順 ) () t dx = - t - t - より,
解答例 ( 河合塾グループ株式会社 KEI アドバンスが作成しました ) 特別奨学生試験 ( 平成 29 年 12 月 17 日実施 ) 数 学 数学 2= 工 経営情報 国際関係 人文 応用生物 生命健康科 現代教育学部 1 整理して (60 分 100 点 ) (2 3+ 2)(
 解答例 ( 河合塾グループ株式会社 KEI アドバンスが作成しました ) 特別奨学生試験 ( 平成 9 年 月 7 日実施 ) 数 学 数学 = 工 経営情報 国際関係 人文 応用生物 生命健康科 現代教育学部 整理して (60 分 00 点 ) 3+ ( 3+ )( 6 ) ( 与式 ) = = 6 + + 6 (3 + ) すなわち 5 6 (5 6 )(3+ ) = = 3 9 8 = 4 6
解答例 ( 河合塾グループ株式会社 KEI アドバンスが作成しました ) 特別奨学生試験 ( 平成 9 年 月 7 日実施 ) 数 学 数学 = 工 経営情報 国際関係 人文 応用生物 生命健康科 現代教育学部 整理して (60 分 00 点 ) 3+ ( 3+ )( 6 ) ( 与式 ) = = 6 + + 6 (3 + ) すなわち 5 6 (5 6 )(3+ ) = = 3 9 8 = 4 6
PowerPoint プレゼンテーション
 1 02 グラフゖックで簡単な図形を描く図形描画プログラム 1 今回作成するゕプリケーションの概要 ボタンをクリックすると図形を描くプログラム 行われる動作 [1] ボタンをクリック [2] そのボタンに対する図形を描く これを使用者とコンピュータの関係で描くと [ 使用者 コンピュータ ] ボタンをクリック [ 使用者 コンピュータ ] 図形を描画して見せる 使用者がコンピュータにすること ボタンをクリック
1 02 グラフゖックで簡単な図形を描く図形描画プログラム 1 今回作成するゕプリケーションの概要 ボタンをクリックすると図形を描くプログラム 行われる動作 [1] ボタンをクリック [2] そのボタンに対する図形を描く これを使用者とコンピュータの関係で描くと [ 使用者 コンピュータ ] ボタンをクリック [ 使用者 コンピュータ ] 図形を描画して見せる 使用者がコンピュータにすること ボタンをクリック
数学 Ⅲ 微分法の応用 大学入試問題 ( 教科書程度 ) 1 問 1 (1) 次の各問に答えよ (ⅰ) 極限 を求めよ 年会津大学 ( 前期 ) (ⅱ) 極限値 を求めよ 年愛媛大学 ( 前期 ) (ⅲ) 無限等比級数 が収束するような実数 の範囲と そのときの和を求めよ 年広島市立大学 ( 前期
 数学 Ⅲ 微分法の応用 大学入試問題 ( 教科書程度 )1 問 1 (1) 次の各問に答えよ (ⅰ) 極限 を求めよ 年会津大学 ( 前期 ) (ⅱ) 極限値 を求めよ 年愛媛大学 ( 前期 ) (ⅲ) 無限等比級数 が収束するような実数 の範囲と そのときの和を求めよ 年広島市立大学 ( 前期 ) (2) 次の関数を微分せよ (ⅰ) を正の定数とする (ⅱ) (ⅳ) (ⅵ) ( 解答 )(1) 年群馬大学
数学 Ⅲ 微分法の応用 大学入試問題 ( 教科書程度 )1 問 1 (1) 次の各問に答えよ (ⅰ) 極限 を求めよ 年会津大学 ( 前期 ) (ⅱ) 極限値 を求めよ 年愛媛大学 ( 前期 ) (ⅲ) 無限等比級数 が収束するような実数 の範囲と そのときの和を求めよ 年広島市立大学 ( 前期 ) (2) 次の関数を微分せよ (ⅰ) を正の定数とする (ⅱ) (ⅳ) (ⅵ) ( 解答 )(1) 年群馬大学
DVIOUT-17syoze
 平面の合同変換と相似変換 岩瀬順一 要約 : 平面の合同変換と相似変換を論じる いま大学で行列を学び始めている大学一年生を念頭に置いている 高等学校で行列や一次変換を学んでいなくてもよい 1. 写像 定義 1.1 X, Y を集合とする X の各元 x に対し Y のただ一つの元 y を対応させる規則 f を写像とよび,f : X! Y のように書く f によって x に対応する Y の元を f(x)
平面の合同変換と相似変換 岩瀬順一 要約 : 平面の合同変換と相似変換を論じる いま大学で行列を学び始めている大学一年生を念頭に置いている 高等学校で行列や一次変換を学んでいなくてもよい 1. 写像 定義 1.1 X, Y を集合とする X の各元 x に対し Y のただ一つの元 y を対応させる規則 f を写像とよび,f : X! Y のように書く f によって x に対応する Y の元を f(x)
vecrot
 1. ベクトル ベクトル : 方向を持つ量 ベクトルには 1 方向 2 大きさ ( 長さ ) という 2 つの属性がある ベクトルの例 : 物体の移動速度 移動量電場 磁場の強さ風速力トルクなど 2. ベクトルの表現 2.1 矢印で表現される 矢印の長さ : ベクトルの大きさ 矢印の向き : ベクトルの方向 2.2 2 個の点を用いて表現する 始点 () と終点 () を結ぶ半直線の向き : ベクトルの方向
1. ベクトル ベクトル : 方向を持つ量 ベクトルには 1 方向 2 大きさ ( 長さ ) という 2 つの属性がある ベクトルの例 : 物体の移動速度 移動量電場 磁場の強さ風速力トルクなど 2. ベクトルの表現 2.1 矢印で表現される 矢印の長さ : ベクトルの大きさ 矢印の向き : ベクトルの方向 2.2 2 個の点を用いて表現する 始点 () と終点 () を結ぶ半直線の向き : ベクトルの方向
代数 幾何 < ベクトル > 1 ベクトルの演算 和 差 実数倍については 文字の計算と同様 2 ベクトルの成分表示 平面ベクトル : a x e y e x, ) ( 1 y1 空間ベクトル : a x e y e z e x, y, ) ( 1 1 z1
 代数 幾何 < ベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル :, 空間ベクトル : z,, z 成分での計算ができるようにすること ベクトルの内積 : os 平面ベクトル :,, 空間ベクトル :,,,, z z zz 4 ベクトルの大きさ 平面上 : 空間上 : z は 良く用いられる 5 m: に分ける点 : m m 図形への応用
代数 幾何 < ベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル :, 空間ベクトル : z,, z 成分での計算ができるようにすること ベクトルの内積 : os 平面ベクトル :,, 空間ベクトル :,,,, z z zz 4 ベクトルの大きさ 平面上 : 空間上 : z は 良く用いられる 5 m: に分ける点 : m m 図形への応用
2014年度 筑波大・理系数学
 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ f ( x) = x x とする y = f ( x ) のグラフに点 P(, ) から引いた接線は 本あるとする つの接点 A (, f ( )), B(, f ( )), C(, f ( )) を頂点とする三角形の 重心を G とする () + +, + + および を, を用いて表せ () 点 G の座標を, を用いて表せ () 点 G
筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ f ( x) = x x とする y = f ( x ) のグラフに点 P(, ) から引いた接線は 本あるとする つの接点 A (, f ( )), B(, f ( )), C(, f ( )) を頂点とする三角形の 重心を G とする () + +, + + および を, を用いて表せ () 点 G の座標を, を用いて表せ () 点 G
2016年度 広島大・文系数学
 06 広島大学 ( 文系 ) 前期日程問題 解答解説のページへ a を正の定数とし, 座標平面上において, 円 C : x + y, 放物線 C : y ax + C 上の点 P (, ) を考える - におけるC の接線 l は点 Q( s, t) でC に接してい る 次の問いに答えよ () s, t および a を求めよ () C, l および y 軸で囲まれた部分の面積を求めよ () 円 C
06 広島大学 ( 文系 ) 前期日程問題 解答解説のページへ a を正の定数とし, 座標平面上において, 円 C : x + y, 放物線 C : y ax + C 上の点 P (, ) を考える - におけるC の接線 l は点 Q( s, t) でC に接してい る 次の問いに答えよ () s, t および a を求めよ () C, l および y 軸で囲まれた部分の面積を求めよ () 円 C
<8D828D5A838A817C A77425F91E6318FCD2E6D6364>
 4 1 平面上のベクトル 1 ベクトルとその演算 例題 1 ベクトルの相等 次の問いに答えよ. ⑴ 右の図 1 は平行四辺形 である., と等しいベクトルをいえ. ⑵ 右の図 2 の中で互いに等しいベクトルをいえ. ただし, すべてのマス目は正方形である. 解 ⑴,= より, =,= より, = ⑵ 大きさと向きの等しいものを調べる. a =d, c = f d e f 1 右の図の長方形 において,
4 1 平面上のベクトル 1 ベクトルとその演算 例題 1 ベクトルの相等 次の問いに答えよ. ⑴ 右の図 1 は平行四辺形 である., と等しいベクトルをいえ. ⑵ 右の図 2 の中で互いに等しいベクトルをいえ. ただし, すべてのマス目は正方形である. 解 ⑴,= より, =,= より, = ⑵ 大きさと向きの等しいものを調べる. a =d, c = f d e f 1 右の図の長方形 において,
Microsoft Word - 力学12.doc
 慣性モーメント. 復習 角運動量と角速度 L p υ, L 質点の角運動量 : ( ) ( ) 剛体の角運動量 L ( ) ρ ( ) ( ) d 注 ) この積分は普通の三重積分 d d d ( ) ( ) A B C A C B A B より ベクトル三重積の公式 ( ) ( ) ( )C ( ) L ( ) ( ) R 但し 慣性モーメント (oent of net): I R( ) ρ ;
慣性モーメント. 復習 角運動量と角速度 L p υ, L 質点の角運動量 : ( ) ( ) 剛体の角運動量 L ( ) ρ ( ) ( ) d 注 ) この積分は普通の三重積分 d d d ( ) ( ) A B C A C B A B より ベクトル三重積の公式 ( ) ( ) ( )C ( ) L ( ) ( ) R 但し 慣性モーメント (oent of net): I R( ) ρ ;
発散.rtf
 4 章発散 発散は重要なベクトル演算の一つであり, 定義は A =diva = lim Δv 0 Δv A d (4.) である.Divergence( ダイバージェンス ) ともいう. この意味は, 微小体積 vを取り囲む全表面 ( 閉曲面という ) 上で, 外向きのベクトル法線成分をすべて加えあわせ, 全体としての量を調べるものである. ベクトルAはどのような向きでもかまわないが, 面ベクトルとの内積
4 章発散 発散は重要なベクトル演算の一つであり, 定義は A =diva = lim Δv 0 Δv A d (4.) である.Divergence( ダイバージェンス ) ともいう. この意味は, 微小体積 vを取り囲む全表面 ( 閉曲面という ) 上で, 外向きのベクトル法線成分をすべて加えあわせ, 全体としての量を調べるものである. ベクトルAはどのような向きでもかまわないが, 面ベクトルとの内積
ContourPlot[{x^+y^==,(x-)^+y^==}, {x,-,}, {y,-,}, AspectRatio -> Automatic].5. ContourPlot Plot AspectRatio->Automatic.. x a + y = ( ). b ContourPlot[
![ContourPlot[{x^+y^==,(x-)^+y^==}, {x,-,}, {y,-,}, AspectRatio -> Automatic].5. ContourPlot Plot AspectRatio->Automatic.. x a + y = ( ). b ContourPlot[ ContourPlot[{x^+y^==,(x-)^+y^==}, {x,-,}, {y,-,}, AspectRatio -> Automatic].5. ContourPlot Plot AspectRatio->Automatic.. x a + y = ( ). b ContourPlot[](/thumbs/82/86424576.jpg) 5 3. Mathematica., : f(x) sin x Plot f(x, y) = x + y = ContourPlot f(x, y) > x 4 + (x y ) > RegionPlot (x(t), y(t)) (t sin t, cos t) ParametricPlot r = f(θ) r = sin 4θ PolarPlot.,. 5. x + y = (x, y). x,
5 3. Mathematica., : f(x) sin x Plot f(x, y) = x + y = ContourPlot f(x, y) > x 4 + (x y ) > RegionPlot (x(t), y(t)) (t sin t, cos t) ParametricPlot r = f(θ) r = sin 4θ PolarPlot.,. 5. x + y = (x, y). x,
" 01 JJM 予選 4 番 # 四角形 の辺 上に点 があり, 直線 と は平行である.=,=, =5,=,= のとき, を求めよ. ただし,XY で線分 XY の長さを表すものとする. 辺 と辺 の延長線の交点を, 辺 と辺 の延長線の交点を G とする. 5 四角形 は直線 に関して線対称な
 1 " 数学発想ゼミナール # ( 改題 ) 直径を とする半円周上に一定の長さの弦がある. この弦の中点と, 弦の両端の各点から直径 への垂線の足は三角形をつくる. この三角形は二等辺三角形であり, かつその三角形は弦の位置にかかわらず相似であることを示せ. ( 証明 ) 弦の両端を X,Y とし,M を線分 XY の中点,, をそれぞれ X,Y から直径 への垂線の足とする. また,M の直径
1 " 数学発想ゼミナール # ( 改題 ) 直径を とする半円周上に一定の長さの弦がある. この弦の中点と, 弦の両端の各点から直径 への垂線の足は三角形をつくる. この三角形は二等辺三角形であり, かつその三角形は弦の位置にかかわらず相似であることを示せ. ( 証明 ) 弦の両端を X,Y とし,M を線分 XY の中点,, をそれぞれ X,Y から直径 への垂線の足とする. また,M の直径
ベクトル公式.rtf
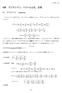 6 章ラプラシアン, ベクトル公式, 定理 6.1 ラプラシアン Laplacian φ はベクトル量である. そこでさらに発散をとると, φ はどういう形になるであろうか? φ = a + a + a φ a + a φ + a φ = φ + φ + φ = 2 φ + 2 φ 2 + 2 φ 2 2 φ = 2 φ 2 + 2 φ 2 + 2 φ 2 = 2 φ したがって,2 階の偏微分演算となる.
6 章ラプラシアン, ベクトル公式, 定理 6.1 ラプラシアン Laplacian φ はベクトル量である. そこでさらに発散をとると, φ はどういう形になるであろうか? φ = a + a + a φ a + a φ + a φ = φ + φ + φ = 2 φ + 2 φ 2 + 2 φ 2 2 φ = 2 φ 2 + 2 φ 2 + 2 φ 2 = 2 φ したがって,2 階の偏微分演算となる.
Microsoft Word - 1B2011.doc
 第 14 回モールの定理 ( 単純梁の場合 ) ( モールの定理とは何か?p.11) 例題 下記に示す単純梁の C 点のたわみ角 θ C と, たわみ δ C を求めよ ただし, 部材の曲げ 剛性は材軸に沿って一様で とする C D kn B 1.5m 0.5m 1.0m 解答 1 曲げモーメント図を描く,B 点の反力を求める kn kn 4 kn 曲げモーメント図を描く knm 先に得られた曲げモーメントの値を
第 14 回モールの定理 ( 単純梁の場合 ) ( モールの定理とは何か?p.11) 例題 下記に示す単純梁の C 点のたわみ角 θ C と, たわみ δ C を求めよ ただし, 部材の曲げ 剛性は材軸に沿って一様で とする C D kn B 1.5m 0.5m 1.0m 解答 1 曲げモーメント図を描く,B 点の反力を求める kn kn 4 kn 曲げモーメント図を描く knm 先に得られた曲げモーメントの値を
Microsoft PowerPoint - 第3回2.ppt
 講義内容 講義内容 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 ベクトルの直交性 3
講義内容 講義内容 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 ベクトルの直交性 3
<4D F736F F D EBF97CD8A B7982D189898F4B A95748E9197BF4E6F31312E646F63>
 土質力学 Ⅰ 及び演習 (B 班 : 小高担当 ) 配付資料 N.11 (6.1.1) モールの応力円 (1) モールの応力円を使う上での3つの約束 1 垂直応力は圧縮を正とし, 軸の右側を正の方向とする 反時計まわりのモーメントを起こさせるせん断応力 の組を正とする 3 物体内で着目する面が,θ だけ回転すると, モールの応力円上では θ 回転する 1とは物理的な実際の作用面とモールの応力円上との回転の方向を一致させるために都合の良い約束である
土質力学 Ⅰ 及び演習 (B 班 : 小高担当 ) 配付資料 N.11 (6.1.1) モールの応力円 (1) モールの応力円を使う上での3つの約束 1 垂直応力は圧縮を正とし, 軸の右側を正の方向とする 反時計まわりのモーメントを起こさせるせん断応力 の組を正とする 3 物体内で着目する面が,θ だけ回転すると, モールの応力円上では θ 回転する 1とは物理的な実際の作用面とモールの応力円上との回転の方向を一致させるために都合の良い約束である
問 1 図 1 の図形を作るプログラムを作成せよ 但し ウィンドウの大きさは と し 座標の関係は図 2 に示すものとする 図 1 作成する図形 原点 (0,0) (280,0) (80,0) (180,0) (260,0) (380,0) (0,160) 図 2 座標関係 問 2
 問 1 図 1 の図形を作るプログラムを作成せよ 但し ウィンドウの大きさは 400 200 と し 座標の関係は図 2 に示すものとする 図 1 作成する図形 原点 (0,0) (280,0) (80,0) (180,0) (260,0) (380,0) (0,160) 図 2 座標関係 問 2 for 文を用いて図 3 の様な図形を描くプログラムを作成せよ 但し ウィンドウのサイズは 300 300
問 1 図 1 の図形を作るプログラムを作成せよ 但し ウィンドウの大きさは 400 200 と し 座標の関係は図 2 に示すものとする 図 1 作成する図形 原点 (0,0) (280,0) (80,0) (180,0) (260,0) (380,0) (0,160) 図 2 座標関係 問 2 for 文を用いて図 3 の様な図形を描くプログラムを作成せよ 但し ウィンドウのサイズは 300 300
スライド 1
 グラフィックスの世界第 3 回 サイバーメディアセンター サイバーコミュニティ研究部門安福健祐 Processing によるアニメーション setup と draw void setup() size(400, 400); void draw() ellipse( mousex,mousey,100,100); void とか setup とか draw とかはじめて見る が出てきてややこしい ellipseは円描く関数でした
グラフィックスの世界第 3 回 サイバーメディアセンター サイバーコミュニティ研究部門安福健祐 Processing によるアニメーション setup と draw void setup() size(400, 400); void draw() ellipse( mousex,mousey,100,100); void とか setup とか draw とかはじめて見る が出てきてややこしい ellipseは円描く関数でした
2016年度 九州大・理系数学
 0 九州大学 ( 理系 ) 前期日程問題 解答解説のページへ 座標平面上の曲線 C, C をそれぞれ C : y logx ( x > 0), C : y ( x-)( x- a) とする ただし, a は実数である を自然数とするとき, 曲線 C, C が 点 P, Q で交わり, P, Q の x 座標はそれぞれ, + となっている また, 曲線 C と直線 PQ で囲まれた領域の面積を S,
0 九州大学 ( 理系 ) 前期日程問題 解答解説のページへ 座標平面上の曲線 C, C をそれぞれ C : y logx ( x > 0), C : y ( x-)( x- a) とする ただし, a は実数である を自然数とするとき, 曲線 C, C が 点 P, Q で交わり, P, Q の x 座標はそれぞれ, + となっている また, 曲線 C と直線 PQ で囲まれた領域の面積を S,
数学 ⅡB < 公理 > 公理を論拠に定義を用いて定理を証明する 1 大小関係の公理 順序 (a > b, a = b, a > b 1 つ成立 a > b, b > c a > c 成立 ) 順序と演算 (a > b a + c > b + c (a > b, c > 0 ac > bc) 2 図
 数学 Ⅱ < 公理 > 公理を論拠に定義を用いて定理を証明する 大小関係の公理 順序 >, =, > つ成立 >, > > 成立 順序と演算 > + > + >, > > 図形の公理 平行線の性質 錯角 同位角 三角形の合同条件 三角形の合同相似 量の公理 角の大きさ 線分の長さ < 空間における座漂とベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル
数学 Ⅱ < 公理 > 公理を論拠に定義を用いて定理を証明する 大小関係の公理 順序 >, =, > つ成立 >, > > 成立 順序と演算 > + > + >, > > 図形の公理 平行線の性質 錯角 同位角 三角形の合同条件 三角形の合同相似 量の公理 角の大きさ 線分の長さ < 空間における座漂とベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル
2011年度 東京工大・数学
 東京工業大学前期日程問題 解答解説のページへ n n を自然数とする 平面上で行列 n( n+ ) n+ の表す 次変換 ( 移動とも いう ) を n とする 次の問いに答えよ () 原点 O(, ) を通る直線で, その直線上のすべての点が n により同じ直線上に移 されるものが 本あることを示し, この 直線の方程式を求めよ () () で得られた 直線と曲線 (3) を求めよ n Sn 6
東京工業大学前期日程問題 解答解説のページへ n n を自然数とする 平面上で行列 n( n+ ) n+ の表す 次変換 ( 移動とも いう ) を n とする 次の問いに答えよ () 原点 O(, ) を通る直線で, その直線上のすべての点が n により同じ直線上に移 されるものが 本あることを示し, この 直線の方程式を求めよ () () で得られた 直線と曲線 (3) を求めよ n Sn 6
2018年度 2次数学セレクション(微分と積分)
 08 次数学セレクション問題 [ 東京大 ] > 0 とし, f = x - x とおく () x で f ( x ) が単調に増加するための, についての条件を求めよ () 次の 条件を満たす点 (, b) の動きうる範囲を求め, 座標平面上に図示せよ 条件 : 方程式 f = bは相異なる 実数解をもつ 条件 : さらに, 方程式 f = bの解を < < とすると > である -- 08 次数学セレクション問題
08 次数学セレクション問題 [ 東京大 ] > 0 とし, f = x - x とおく () x で f ( x ) が単調に増加するための, についての条件を求めよ () 次の 条件を満たす点 (, b) の動きうる範囲を求め, 座標平面上に図示せよ 条件 : 方程式 f = bは相異なる 実数解をもつ 条件 : さらに, 方程式 f = bの解を < < とすると > である -- 08 次数学セレクション問題
