Effect on Phosphorous in Steel for Galvannealing Behavior of Galvanized Steel
|
|
|
- あけなお おおふさ
- 6 years ago
- Views:
Transcription
1 Journal of Surface Analysis Vol.7, o. (00) pp 連載 ( 講義 ) 数値データの取り扱い ~ 四捨五入から検出限界まで ~ 第一回データの丸め方と誤差の基礎 福島整独立行政法人物質 材料研究機構共用基盤部門分析支援ステーション つくば市千現 -- fukushima.sei@nims.go.jp (00 年 5 月 日受理 ) 分析業務にとって, 数字の取り扱いは命である. 有効数字やデータのばらつきは, ほとんどの現場担当者が無意識のうちに正当な方法で処理しているはずであるが, あらためて統計学の用語を目の前にすると自信を無くす人が多い. 本講は, そのような人たちに自信を持たせ, あるいは体系的な知識を学習するための出発点と成ることを意図したものである. 今回は, データの丸め方と, 誤差の最も基礎的な部分について説明する. The handling of numeric data - from round off to detection limit - Ⅰ. How to round the numeric data, and the base of error Sei FUKUSHIMA Materials Analysis Station, Dept. Mat. Infrastructure, IMS, -- Sengen, Tukuba , Japan fukushima.sei@nims.go.jp (Received: May, 00) One of the most important items for the analyst is the handling of the numerical data. The almost analysts handle and treat the numeric data, significant figure or dispersion for example, obtained from the measurement in the correct way unconsciously. However, there are many analysts who lose the self-confidence, when they wish to use the description of the statistical terminology. This lecture is intended giving a starting point for giving the self-confidence and learning a systematic knowledge to such people. In present part of this lecture, the way of rounding of the data and the most basic part of the error will be explained.. はじめに断っておくが, 数字の取り扱いの話は退屈である. 新しい分析法や現場の測定に於ける目からウロコの工夫などのような, 興奮させられる様な話はまず出てこない. それどころか, あー, なんでこんな重箱の隅をつつくような話を なんて思わされる方 が多いであろう. しかし, 現場の分析屋が提出する事実がともすると会社の経営を左右しかねず, その際にもっとも重要なのが 分析結果の数字をどう解釈するか なのだという場合も確かに存在するのだ. そういうケースを, 想像するのも悪くないであろう. 現実の問題として, 故障解析の結果を生産に反映さ Copyright (c) 00 by The Surface Analysis Society of Japan 8
2 Journal of Surface Analysis Vol.7, o. (00) pp せる場合, 分析結果の数字をどう解釈するかが歩留まりを左右するケースは結構多い. さらに, 僅かな歩留まりの差が会社の収益に大きく影響することも, 良くある話だからである. すなわち, いざとなったとき, 分析屋は問題解決のキャスティングボードを握っている場合が確実にあるのだ. その時に, 自分の出した結果から根拠を明確に判断を示せるのは, おそらく分析屋冥利に尽きよう. 言うまでもなく, 分析業務に限らず数値データの取り扱いは, 数字を扱う全ての分野において大変重要である. にもかかわらず, 我が国の教育過程ではそれを比較的重要視してこなかった様に思える. この傾向は世界中でもあるようで, 最近査読を頼まれる分析関係の投稿論文でも, ちょいちょい見かけるようになった. 学術的分野では, 実はその根本である客観性の基本は実験事実の再現性であり, したがって実験結果の数値に対する吟味がもっとも重要なのだが, 安易な成果至上主義はそれを軽視する傾向を助長しているように思えてならない. まあ, 愚痴はとりあえずこの程度に止めよう. 数値データの取り扱いの基礎的な部分は, すでに ISO 化されたものもあるが, 基本的に統計学の基礎と異なるものではない. 数値データの取り扱いの基本は, 平均値とばらつきの取り扱いであることは言うまでもないが, これらについての基本的な ISO には,ISO 575 (98 年改訂 ) があり, それを基にした JIS Z 840 分析 試験の許容差通則 が制定されている. この ISO は,ISO TC-69 "Application of Statistical Method" の中の "Measurement Method and Result" (SC6) により出されたものである. 基本的には, 統計学に基づいた数値データの扱い方を ISO としたと考えて良い. 一方, 検出下限は感度等の議論でも有用であるが, 通常は定量分析を行う作業の しめ の作業と位置づけられる場合が多い. これについては,ISO 843 が存在する. この制定は 997 年 (ISO/TC69 /SC6/WG5) と比較的新しいことから, 基礎概念に対する時代に即した検討が常に行われている事が想像できる. ICP/AES 等での検量線による検出下限の議論は,ISO 095 (996 年 ) として手順が示されている. これについては, 日本では結構批判的な意見も多く, 本稿の執筆時点では対応する JIS は出ていない. 以上について, 図 に簡単にまとめておく. 本講の大部分は, この ISO 575(JIS Z 840) の内容に基づいたものと了解して差し支えない. すなわちここでは データの丸め方 (JIS に基づく ) と有効数字 誤差の扱い方 ( 誤差の伝搬則 ) 異常値の扱い方 ( 棄却検定 ) 測定の繰り返し回数 平均値と区間推定 差及び分散の検定 検量線の作成の各項目について, なるべく公式や例題を用いて説明する. また, 検出下限については,976 年の IUPAC 勧告とその流れを汲んだ ISO 843 (997 年 ) の内容を紹介する. 一方, 表面化学分析 (ISO TC-0) においても, ピーク検出の重要な手順としての検出下限の議論が我が国の提案を出発点として進められている 図 数値処理及び検出下限と関連する ISO 規格 9
3 Journal of Surface Analysis Vol.7, o. (00) pp ことを付け加えておこう. どの項目にしても, 分析現場ではすでに当たり前としてなされていることをおさらいするようなものであるが, まとまった形の資料として提示された例は比較的少ないようであり, 本稿が手順書の参考資料としてでも分析現場のお役に立てれば幸いである.. 生データの取り扱い測定を 回行っただけで得た単独のデータでも, もちろんある程度の結論を得られることは否定しない. しかし, その結論の信憑性 ( 信頼性ではない!) を与えているのは, 測定条件 測定環境に関する情報, 及び経験や理論を根拠とした様々な仮定が存在しているからこそである. 例えば, ある 回の XPS の測定で, 二つの試料 及び に対して, それぞれに対して同じ元素のピークをエネルギー位置でそれぞれ 回ずつ測定して, 信号強度が I, I のデータが得られたとする. この つのデータから, 含有量の大小を判断できるだろうか. 数値処理の言葉で言い換えると, このつの数字に意味のある ( 有為な ) 差があると見なせるだろうか. 例えば, 信号強度のばらつき( 多くは標準偏差を考えているようである ) は, 強度の平方根だから... 等と考えて, 二つの強度に差があるかどうか等を検討しようとするのも, 一つの方針であろう. しかし, その陰には多くの議論が隠れている. まず, 測定値は本当に平均値として扱えるのだろうか? また, その測定の与えるばらつきは, 本当に平均値の平方根に従うと言えるのだろうか. 特に後者は, 大変悩ましい問題を含む. すなわち, 装置の安定度をはじめとして, 試料の均一性, 試料表面の様子 ( なめらかさ, 形状 ) など, 測定に対して理想的な条件であったかどうかで, 大きく変わる ( 通常, ばらつきは数倍程度大きくなってしまう ). 理論的に言うと, ばらつき( 分散 ) が平均値に等しい のは,Poisson 分布の性質から来ている. 電子分光のような粒子計数による計測では, 特に低い計数率の時には信号分布が Poisson 分布に従うのがはっきり分かる. しかし, ある程度平均値の値が大きいと,Poisson 分布は正規分布で近似できることが統計学の教えるところであり, 標準偏差が平均値の平方根で与えられる という理論的な根拠となっているのである. しかし, 分析結果において客観性の高い信頼性 ( 信憑性 ではない) を示すことが分析者に課せ られた使命である. そのためには, 分析法や分析条件, あるいは試料に依存しない, 客観的な信頼性を保証するための共通の手順が必用となってくる. ここに, データ取り扱いに対する標準化の根本的な意義が存在する. したがって, 本講での以下の議論は全て,つの測定に関して常に 複数回の正しい計測 を行っていることを前提としている. それでは, 何回程度の繰り返しをすればよいのか? それについては, いずれ本講の中で触れることにしよう.. 有効数字装置のデータ処理プログラムが出してくる数字に対して, どこまで信用できるか疑ったことはないだろうか? 例えば % で示される結果であると,0.% 程度まで結果を示してくれる場合が多いであろう. この場合なら, 一般に3 桁の結果ということになる (0% を切ると, 桁の表示となるが ). この数字, そのまま信じて良いのだろうか. 3 回程度全く同じ条件で同じ測定を繰り返して結果を出してみると, その目安を得ることが出来る. 3 回とも表示された数値が同じだったのであれば, その実験は少なくとも3 桁の精度を確保している, ( 少なくとも有効桁数は3 桁以上ある ) と言って良い ( しかし, 正確かどうかは保証の限りではない ). 一方,3 回とも結果の数字が違う場合はどう考えるのであろうか. 小数点より上が常に同じ, というのであれば, おそらく 桁の精度はありそうだな と考える. そうでなければ..., ひょっとしたらもっと良い測定条件があるのでは と考えた方がよいかもしれない. 一般に, 数値データは, 有限の桁数で提示される. それでは, その桁 ( 有効数字の桁数 ) はどの様に決めるか.ISO 575 では,3 つの方法を示しているが, そのなかでも田口の方法あるいは Hamaker の方法が推奨されている ( この二つの方法は, ほぼ同じである ). すなわち, 分析精度に相当する測定値の標準偏差 σ M ( 繰り返し測定を行って得られた測定値から得られた平均値を用いて計算された標準偏差でよい ) に対して,σ M /3 の桁を有効数字の桁とする. [ 例 ] 測定値から得られたσ M 0.08 σ M /3 0.03( 小数点第二位までの数字 ) となるので, こ 30
4 Journal of Surface Analysis Vol.7, o. (00) pp 図 有効数字の桁数の決定法の場合の測定値それぞれの数値は小数点以下第三位を丸めればよい. この内容を, 図 にまとめておこう. さらに, このようにして得られた測定値を用いた場合の最終的な平均値と標準偏差の求め方については,95 年に ASTM より出されている Manual on Quality of Materials の勧告を具体的な手順として推奨している. これによれば ( 推奨する であって すべきである ではないことに注意 ) 平均値は, 丸めた測定値より一桁多く示すことを推奨する. 標準偏差は多くても三桁以内で示すことを推奨する ( 三桁で十分 ). 平均値の桁数と比較し, 桁数の少ない方にそろえることを推奨する. 乗算及び除算の結果は, 計算に使用された数値のもっとも小さい桁数に を足したけた数まで求めておくことを推奨する. この内容を, 図 3に示す. 標準偏差は3 桁以内 という点に え と思われる方もおられるとは思うが, もともとデータの各値がかなり大きい場合であると, 標準偏差の値も小数どころかかなり大きくなるという事を想像すれば, 理解できるであろう. 表面分析に限らず一般に機器分析の世界では, ソフトウェアにより数値処理を行った場合,( もちろん測定条件によるものの ) 結果については大体有効数字 桁程度の場合が多い. したがって, ベテランの前でデータを示す場合は,3 桁程度の数字で桁数を揃えておくと良い印象を与えられる ( かも ). これに対して, 重さで分析する場合 ( 湿式分析に於ける重量分析法など ) は, 有効数字が大変大きい. 精密化学天秤の計量限界を思い起こして頂ければ, 容易に理解できよう. したがって, 精度が大変重要な場合, 重量分析は大変有用な手段なのである.. 数値の丸め方さて, 有効数字の桁数 ( 有効桁数 ) が決まったら, データをこれに併せて整えねばならない. これについては, 切り上げや切り捨てももちろん意味があろうが, 最もなじみ深くかつ実用的な方法は 四捨五入 である. 普段の業務でも, なんとなく用いている 四捨五入 であるが, これについても規格があるのだ. ここでは, JIS Z 840 数値の丸めかた を示しておこう. ポイントは, 四捨五入の対象となっている桁の数字が 5 の場合である. n 桁の数字を作ることを考える. (n+) 桁目の数字が 4 以下ならば, 切り捨てる. (n+) 桁目の数字が 6 以上であれば, 切り上げる. (n+) 桁目の数字が 5 の場合であれば, 以下のようにする. (n+) 桁目の数字が無いか 0 のとき,n 桁が偶数ならば切り捨てる. (n+) 桁目の数字が無いか 0 のとき,n 桁が奇数ならば切り上げる. (n+) 桁目の数字が存在して 0 でないときは, 切り上げる. 例えば, 検討の結果, 有効数字は 3 桁であった場合, 上記方法で n3 であるから, 例えば 図 3 有効桁数に数字を整えるための ASTM の勧告 4 桁目の数字が 4 以下ならば, 切り捨てる. [ 例 ]
5 Journal of Surface Analysis Vol.7, o. (00) pp 桁目の数字が 6 以上であれば, 切り上げる. [ 例 ] 桁目の数字が 5 の場合は, 以下のようにする 5 桁目の数字が無いか 0 のとき,3 桁目が偶数ならば切り捨てる. [ 例 ] 桁目の数字が無いか 0 のとき,3 桁目が奇数ならば切り上げる. [ 例 ] 桁目の数字が存在して 0 でないときは, 切り上げる. [ 例 ] 四捨五入したい桁の数字が 5 や 6 の時は, どうするか結構迷うものである. その時の判断として利用して頂ければと考える. また, そのためにも, 測定データの桁数はある程度確保しておき, 結果をまとめるときはきちんと丸めるという習慣をつけておきたいものである. 3. 誤差の扱い方 3. ばらつきと不確かささて, 誤差の大きい測定 と ばらつきの大きい測定 の意味は同じだろうか. このつの表現は, どちらもよく使われるが, おうおうにして混同されている. 単純には, ばらつきは誤差の一要因 と考えれば, 違いがはっきりしよう. ばらつきが大きくても, それから推定された結果が真値に十分近いこともありうるからである ( まあ, 滅多にないが ). このばらつきや誤差を総称して, 不確かさ (uncertainty) と呼ぶ. 実は不確かさの概念も, そう単純ではない.ISO 国際文書 計測における不確かさの表現のガイド [] によれば, まず 不確かさ の定義であるが, この定義では現実に得られる 値のばらつき だけをとらえ, 真の値 については何も言及しない. したがって, 明らかにこの定義だけでは 不確かさ の要因 ( これが パラメータ だと思って良い ) をきちんと特定できない. つまり, どのようなものであれ, ばらつきに影響を与えている要因 ( すなわち, 上記の定義を満たすパラメータ ) なら, 原理的には 不確かさ として用いられる資格がある. では, これをどうやって扱おうとするのか. このガイドにおいて不確かさは, 標準不確かさ 合成標準不確かさ および, 拡張不確かさ の 3つにわけて定義されている. まず, 不確かさとして標準偏差そのものを用いた場合, これを 標準不確かさ と呼ぶ. また, いくつかのばらつきを生ずる要因がわかっていて ( 要するに各パラメータの帰属ができていて ), 測定値がそれぞれの要因によってどう影響を受けているかがわかる ( 要するに, 測定値がばらつきの要因となるものの関数と見なせる ) 場合, それらから計算される不確かさを 合成標準不確かさ と呼ぶ. この場合でも, どの要因一つをとってみても, それから生ずるばらつきは標準偏差の式で計算できるという大前提がある. ところが, 実際の測定では, その他の評価しようのない要因が多い. したがって, 要因の評価しようのない不確かさまで考慮した不確かさの定義が実用上必要となってくる. これが 拡張不確かさ であ る. つまり, 評価しようのない要因を繰り込もうとすると, 式では扱えなくなる. そのため, 合成標準不確かさに対して係数 k をかけ, それを 拡張不確かさ として定義するのである. ガイドによれば,k は一般に ~3 程度の値が取られる. それよりも, もっと重要な点は 測定の結果に付随した, 合理的に測定量に結びつけられ得る値のばらつきを特徴づけるパラメータ. として定義されている. 現実世界では完全な測定はありえず, また真の値も知り得ない. 得られるのは測定の結果としての値のみで, 当然だがその値と 真の値 との距離 ( 誤差 ) も知り得ない. そこで従来からの 知り得ない真の値から誤差だけ隔たった測定値 ( いわゆる精確度 ) という仮想的な考え方を用いずに測定の信頼性を表す ( 規定する ) ために, まず 不確かさ の定義が決められたのだ. すなわち, 実際に得られる不確かさの数値は, 理想的な系もしくは要因をすべて認識した系から得られることはきわめて希であることから, 実際に数値として扱われている不確かさは, 本来拡張不確かさと考えるべきである. ( 筆者の要約 ) という記述があることだ. 推奨もしくは指定された k の値はなく, 大体このぐらいであると言う記述しかない. これがガイドたるゆえんでもあろうか. したがって現場では, 通常の計算で得られる標準偏差は, この 拡張不確かさ 3
6 Journal of Surface Analysis Vol.7, o. (00) pp に相当するものを見ているのだなと認識するのは, 測定結果を解釈する上で必要なことであろう. いずれにせよ, 単に数式の取り扱いだけで十分であれば, 統計学の教科書どおりにやればよく, 国際規格なぞは必要ない. しかし, 実際の現場では, 統計学をそのまま適用するにはあまりに色々と乖離している点があるため, より現場に即した規格やガイドを国際的な合意の下に決めていっているのだということを感じ取って頂ければ, 幸いである. 3. 誤差の用語とそのイメージとは言え, 基本的な話を進めるには, どうしても統計学に戻ってしまう. また不確かさも, 本来は拡張不確かさを用いるべきであろうが, 数式が ( 私にとっても ) 大変複雑であり, それこそ非実用的に見えるので, 標準不確かさの世界でこの後も話を進めよう. さて, 重箱の隅 の一つではあるが, 用語について一言触れておきたい. それは, accuracy である. この用語は, 分野と時代で定義が変わっている. 詳しくは, 例えば文献 [] に簡潔にまとめてあるが, 訳語も 精確さ と 正確さ のつがある. 私のように古い時代の人間は, 正確さ として勉強してきた. しかし, 本講の基本としている ISO 575(99 年 ), あるいは JIS Z 840(99 年 ) では, これは trueness として定義され, 真度 という訳が当てられている. そして, この trueness と precision ( 精度 ) とを総合した概念を accuracy ( 精確さ ) と定義しているのである. しかし, 例えば品質管理用語を定義している JIS Z 80(98 年 ) では昔のままであるし, 計測用語を定義している JIS Z 803(984 年 ) では, 欧文和文 ともにわずかに違った用語が定義されている. さて, この trueness ( 真度 ) と precision ( 精度 ) がどういう関係にあるかというイメージを図 4に示す. 実は, 統計学では 母集団 という概念が大変重要である. 皆さんが 測定する 場合, 統計学では測定データの無限に大きなデータの固まり ( これを 母集団 と呼ぶ) を考え, ここからいくつか抜き出してくる ( サンプリングする ) 事が, 実際の測定に対応すると考えるのである. したがって, 目的とする真の値は, この母集団の平均値が仮定されると言って良い. ただし... ここで気を付けなければならないのは, 母集団の 分布はどんなものか全くわからないので, 図に示す ような左右対称な一つ山の分布 ( ガウス分布, ある いは正規分布と呼ばれる ) が仮定されるのだ, とい う事である. したがって, 母集団の平均値 真の 値 である保証は何処にもない. 母集団の平均値 真の値 が, 真実正しいと誤解している方は結構多 いが, その誤解を捨てないと正しい数値データの取 り扱いは不可能だといって良い. 今まで, このよう な仮定の下に色々な数値が処理されてきたが, 実用 上大きな障害となるような場合はほとんど無く, 現 実と良く即していることが経験的に裏打ちされてき ているため, 統計学は成り立っているのだと思って 頂きたい. ということで, 実際の数値に対して統計学を応用 する目的は, この母集団の平均値や分散を推定する 事である. それによって, 数値を定量的に様々な解 釈に用いる 指標 を得ようとするのが数値処理の 目的である. 3.3 誤差の伝搬則 さて, 概念論ばかりでもつまらないので, 実際に すくに使用できる話をしよう. 実測された数値は, 精度 (precision) と真度 (trueness) の二つを考慮して扱わねばならないの は, ここまでお話ししてきたとおりである. 図 4 に 示すとおり, 実測数値は, その測定を一定の条件で ある定回数だけ繰り返したときに得られるであろう 分布を仮定した場合, その平均値と真の値の差を真 度, 分布の幅 ( 有効数字影響を与えることは先に示 したとおり ) が精度であると考えて良い. 図 4 真度 (trueness) と精度 (precision) 33
7 Journal of Surface Analysis Vol.7, o. (00) pp 測定された数値をそのまま用いるだけでよいので δq δx δy δu δw + あれば話は簡単なのだが, その平均値を用いて何ら q x y u w (6) かの計算を行った結果を用いることも結構多いはず である. すなわち, 平均値とばらつき ( 分散 ) を持 定数積つ数値データ同士について, 平均値を演算した場合に, 結果のばらつきをどう処理すべきだろうか. q Bx (B : 既知の定数 ) (7) これは, 誤差の伝搬則 という形で教科書に出 の時 てくる話である. 公式もいくつか与えられるが, 例えばかけ算やわり算の処理についてもきちんと公式 δ q Bδx (8) を与えている教科書は, 意外に少ない. ここでも, 完全な網羅は難しいので, 具体的な演算に関しては主な公式を示しておくにとどめる. べき乗 また, あまり注意を喚起されることはないが, 以 n q x 下の式のいずれを使う上でも, その前提条件として, (n : 既知の定数 ) (9) それぞれの数値のばらつきが互いに独立かつランダの時ムであること ( 共分散が 0 と出来ること ) がどの教科書にも書かれている. つまり, つの平均値そ q x n q x れぞれをばらつかせている要因は, 互いに無関係で (0) ある という仮定が必要だと言うことだ. さらに注 意すべき事は, 平均値のまわりにばらつきが比較的 以上から, 一変数関数の一般的な計算では コンパクトにまとまっていること ( 分散自体が小さいこと ) である. あまり分散が大きいと, 共分散が q q( x) () 0 という近似の精度が悪くなるということにも注意 しておこう. に対して 式は, 数学で言うところの変分の形で書かれてい dq δ q δx るが, 各式のδ( ナントカ ) には, その ( ナントカ ) の標準偏差を dx () 代入すればよい. あるいは, 例えば数値計算時に平均値 x のまわりの 和と差 誤差として ( u + w) q x y K+ の時 ( δq) ( δx) + K + ( δy) + ( δu) + K( δ w ) δ q δx δy + δu δw () () (3) ( x x) q( x) δq q δ (3) と扱うことが出来る. また, さらに拡張して一般的 な関数においては ( x, K z) q q, に対して (4) 積と商 x K y q u K w の時 δq q δx x δy y δu + u (4) δw + K w (5) ( δq) q q δx δz z かつ q δq δx q δz z (5) (6) で, 議論が出来る. 実は,(6) は実験を考える上で大変重要な点を示 34
8 Journal of Surface Analysis Vol.7, o. (00) pp 唆している. すなわち, 色々なデータを寄せ集めて計算して答えを求めようとする場合, データの中で飛び抜けてばらつきの大きなものが含まれていると, 結果の誤差もそれに含まれてしまうということである. また,(6) のばらつきであるδ( ナントカ ) は, 得られた値をそのまま代入する ( 平均値で割ったりしていない 規格化されていない ) のであるから, 利用する実験データの中で飛び抜けて大きな値を示す種類のもの用いるのであれば, 結果の精度もそのデータが支配してしまうと言うことである. したがって, 複数種類のデータによる計算を必要とする実験の場合, なるべくばらつきも数字の大きさも揃えておくのが, 確からしい結論を得る上で重要であることがわかるであろう. 3.4 平均値の精確さの意味では, 数値の精確さ ( 真の値からのずれ, 及びばらつき ) は, 最終的にどのように考えたら良いであろうか. 統計学の基本にもどると, 図 4を基本にすると, 図 5に示すような考え方が基本になる. すなわち, どんなデータであっても真の値 個が存在するのではなく, 真の値に相当する平均値を与える無限個の要素からなる数値群 ( 母集団 ) があると考える. この数値群は, 様々な要因によるその数値群に固有のばらつきを形成している ( とみなす ). 真の値は, この母集団の平均値と対応させる. これを 母平均 と呼び, 母集団のばらつきを 母分散 と呼ぶ. 母平均 真の値 ではない. 多くは, 正規分布が想定される ( 経験的にほぼ成立 ). したがって, 真の値をどの程度反映しているのか ( どの程度ずれているか ) は, 真の値の代わりに仮定された母平均を用いて, 何らかの論理的根拠に基づいた確率的な表現で表されることになる. 真の値に対する区間推定 や 信頼区間 などの概念はここから生まれる. そうすると, 実際に測定で得られた有限個の数値からなるデータは, 正しくはかられた物であるなら 母集団から無作為に抜き取られたサンプル( 標本 ) ということになる. 我々は, この標本をひねくり回して母集団を推定し, 真の値を知ろうとするのである. したがって, データにより得られた平均値は 標本平均, ばらつきは通常 標本分散 と 呼ばれる. x, x, L, x に対する平均値 x を あるデータ { } 図 5 標本平均 標本分散とそのふるまい x x i (7) で与えたとすると, そのばらつき σ x は (5) より σ x σ x で与えられる. + K + σ x (8) σ x σ x K σ σ x 図 5で示すように, x か L x x つ (7) の微分から るとすれば σ x σ x σ x σ x + K + σ x であ (9) 35
9 Journal of Surface Analysis Vol.7, o. (00) pp これが, 標本平均の誤差 ( 真の値の推定精度と考えればよい. データのばらつきではない ) である. データ点数 が大きければ大きいほど小さくなって, 推定精度が良くなることがわかるであろう. ちなみに, 算術平均 (7) による標本平均を不偏推定値と呼ぶことがあるが, これは各数値との差の二乗が最も小さくなる条件を満足するのが算術平均値であることから来る ( 最尤推定 ). 一方, 標本分散を不偏分散として扱うためには, 標本平均と各数値の差の二乗和を, データ総数から を引いた値で割る必要がある. これは, 以下のようにして示される. 母平均 ( いわば 真の値 ) を μとしたとき, 標本平均と各数値の差の二乗和について ( xi μ) { ( xi x) + ( x μ) } ( xi x) + ( x μ) ( xi x) ( xi x) + ( x μ) + ( x μ) (0) であることから, 分散は二乗和の期待値である関係を用い ( 詳しくは, 統計学の教科書を参照されたい ) (0) 式の両辺の期待値をとれば E ( xi μ) E ( xi x) + ( x μ) E {( xi μ) } E ( xi x) { } + E{ ( x μ) } () { } したがって, σ E ( xi μ ) σ E x び, 次の関係 σ s + σ σ s {( μ) } { }, s E ( xi x) から,() より 及 () となる. これで, 標準偏差を計算するとき, なぜ分母からを引くのかがおわかりになったかと思う. また, 以上の説明から, 測定で得られる分散 ( 標本分散 ) は, 真の値 ( 母平均 ) から求められるはずである値よりも常に若干小さめであることもわかろう. 感覚的に, 標準偏差の値よりも, なんとなく見かけよりもばらつきが大きいような気がする といつも悩んでいる方は, データに関して正常な感覚をお持ちであると言えるのだ. 次回は, 平均値に関する議論をした後に, 検定の話も少々触れる予定である. 参考文献 [] 飯塚幸三監修,ISO 国際文書計測における不確かさの表現のガイド統一される信頼性表現の国際ルール, 日本規格協会 (996). [] 藤森利美著, 分析技術者のための統計的方法第 版,( 社 ) 日本環境測定分析協会, 丸善 (995). 36
EBNと疫学
 推定と検定 57 ( 復習 ) 記述統計と推測統計 統計解析は大きく 2 つに分けられる 記述統計 推測統計 記述統計 観察集団の特性を示すもの 代表値 ( 平均値や中央値 ) や ばらつきの指標 ( 標準偏差など ) 図表を効果的に使う 推測統計 観察集団のデータから母集団の特性を 推定 する 平均 / 分散 / 係数値などの推定 ( 点推定 ) 点推定値のばらつきを調べる ( 区間推定 ) 検定統計量を用いた検定
推定と検定 57 ( 復習 ) 記述統計と推測統計 統計解析は大きく 2 つに分けられる 記述統計 推測統計 記述統計 観察集団の特性を示すもの 代表値 ( 平均値や中央値 ) や ばらつきの指標 ( 標準偏差など ) 図表を効果的に使う 推測統計 観察集団のデータから母集団の特性を 推定 する 平均 / 分散 / 係数値などの推定 ( 点推定 ) 点推定値のばらつきを調べる ( 区間推定 ) 検定統計量を用いた検定
基礎統計
 基礎統計 第 11 回講義資料 6.4.2 標本平均の差の標本分布 母平均の差 標本平均の差をみれば良い ただし, 母分散に依存するため場合分けをする 1 2 3 分散が既知分散が未知であるが等しい分散が未知であり等しいとは限らない 1 母分散が既知のとき が既知 標準化変量 2 母分散が未知であり, 等しいとき 分散が未知であるが, 等しいということは分かっているとき 標準化変量 自由度 の t
基礎統計 第 11 回講義資料 6.4.2 標本平均の差の標本分布 母平均の差 標本平均の差をみれば良い ただし, 母分散に依存するため場合分けをする 1 2 3 分散が既知分散が未知であるが等しい分散が未知であり等しいとは限らない 1 母分散が既知のとき が既知 標準化変量 2 母分散が未知であり, 等しいとき 分散が未知であるが, 等しいということは分かっているとき 標準化変量 自由度 の t
<4D F736F F D208EC08CB18C7689E68A E F AA957A82C682948C9F92E82E646F63>
 第 7 回 t 分布と t 検定 実験計画学 A.t 分布 ( 小標本に関する平均の推定と検定 ) 前々回と前回の授業では, 標本が十分に大きいあるいは母分散が既知であることを条件に正規分布を用いて推定 検定した. しかし, 母集団が正規分布し, 標本が小さい場合には, 標本分散から母分散を推定するときの不確実さを加味したt 分布を用いて推定 検定しなければならない. t 分布は標本分散の自由度 f(
第 7 回 t 分布と t 検定 実験計画学 A.t 分布 ( 小標本に関する平均の推定と検定 ) 前々回と前回の授業では, 標本が十分に大きいあるいは母分散が既知であることを条件に正規分布を用いて推定 検定した. しかし, 母集団が正規分布し, 標本が小さい場合には, 標本分散から母分散を推定するときの不確実さを加味したt 分布を用いて推定 検定しなければならない. t 分布は標本分散の自由度 f(
スライド 1
 データ解析特論第 10 回 ( 全 15 回 ) 2012 年 12 月 11 日 ( 火 ) 情報エレクトロニクス専攻横田孝義 1 終了 11/13 11/20 重回帰分析をしばらくやります 12/4 12/11 12/18 2 前回から回帰分析について学習しています 3 ( 単 ) 回帰分析 単回帰分析では一つの従属変数 ( 目的変数 ) を 一つの独立変数 ( 説明変数 ) で予測する事を考える
データ解析特論第 10 回 ( 全 15 回 ) 2012 年 12 月 11 日 ( 火 ) 情報エレクトロニクス専攻横田孝義 1 終了 11/13 11/20 重回帰分析をしばらくやります 12/4 12/11 12/18 2 前回から回帰分析について学習しています 3 ( 単 ) 回帰分析 単回帰分析では一つの従属変数 ( 目的変数 ) を 一つの独立変数 ( 説明変数 ) で予測する事を考える
スライド 1
 データ解析特論重回帰分析編 2017 年 7 月 10 日 ( 月 )~ 情報エレクトロニクスコース横田孝義 1 ( 単 ) 回帰分析 単回帰分析では一つの従属変数 ( 目的変数 ) を 一つの独立変数 ( 説明変数 ) で予測する事を考える 具体的には y = a + bx という回帰直線 ( モデル ) でデータを代表させる このためにデータからこの回帰直線の切片 (a) と傾き (b) を最小
データ解析特論重回帰分析編 2017 年 7 月 10 日 ( 月 )~ 情報エレクトロニクスコース横田孝義 1 ( 単 ) 回帰分析 単回帰分析では一つの従属変数 ( 目的変数 ) を 一つの独立変数 ( 説明変数 ) で予測する事を考える 具体的には y = a + bx という回帰直線 ( モデル ) でデータを代表させる このためにデータからこの回帰直線の切片 (a) と傾き (b) を最小
RSS Higher Certificate in Statistics, Specimen A Module 3: Basic Statistical Methods Solutions Question 1 (i) 帰無仮説 : 200C と 250C において鉄鋼の破壊応力の母平均には違いはな
 RSS Higher Certiicate in Statistics, Specimen A Module 3: Basic Statistical Methods Solutions Question (i) 帰無仮説 : 00C と 50C において鉄鋼の破壊応力の母平均には違いはない. 対立仮説 : 破壊応力の母平均には違いがあり, 50C の方ときの方が大きい. n 8, n 7, x 59.6,
RSS Higher Certiicate in Statistics, Specimen A Module 3: Basic Statistical Methods Solutions Question (i) 帰無仮説 : 00C と 50C において鉄鋼の破壊応力の母平均には違いはない. 対立仮説 : 破壊応力の母平均には違いがあり, 50C の方ときの方が大きい. n 8, n 7, x 59.6,
Excelによる統計分析検定_知識編_小塚明_5_9章.indd
 第7章57766 検定と推定 サンプリングによって得られた標本から, 母集団の統計的性質に対して推測を行うことを統計的推測といいます 本章では, 推測統計の根幹をなす仮説検定と推定の基本的な考え方について説明します 前章までの知識を用いて, 具体的な分析を行います 本章以降の知識は操作編での操作に直接関連していますので, 少し聞きなれない言葉ですが, 帰無仮説 有意水準 棄却域 などの意味を理解して,
第7章57766 検定と推定 サンプリングによって得られた標本から, 母集団の統計的性質に対して推測を行うことを統計的推測といいます 本章では, 推測統計の根幹をなす仮説検定と推定の基本的な考え方について説明します 前章までの知識を用いて, 具体的な分析を行います 本章以降の知識は操作編での操作に直接関連していますので, 少し聞きなれない言葉ですが, 帰無仮説 有意水準 棄却域 などの意味を理解して,
モジュール1のまとめ
 数理統計学 第 0 回 復習 標本分散と ( 標本 ) 不偏分散両方とも 分散 というのが実情 二乗偏差計標本分散 = データ数 (0ページ) ( 標本 ) 不偏分散 = (03 ページ ) 二乗偏差計 データ数 - 分析ではこちらをとることが多い 復習 ここまで 実験結果 ( 万回 ) 平均 50Kg 標準偏差 0Kg 0 人 全体に小さすぎる > mea(jkke) [] 89.4373 標準偏差
数理統計学 第 0 回 復習 標本分散と ( 標本 ) 不偏分散両方とも 分散 というのが実情 二乗偏差計標本分散 = データ数 (0ページ) ( 標本 ) 不偏分散 = (03 ページ ) 二乗偏差計 データ数 - 分析ではこちらをとることが多い 復習 ここまで 実験結果 ( 万回 ) 平均 50Kg 標準偏差 0Kg 0 人 全体に小さすぎる > mea(jkke) [] 89.4373 標準偏差
Microsoft PowerPoint - statistics pptx
 統計学 第 17 回 講義 母平均の区間推定 Part- 016 年 6 14 ( )3 限 担当教員 : 唐渡 広志 ( からと こうじ ) 研究室 : 経済学研究棟 4 階 43 号室 email: kkarato@eco.u toyama.ac.jp website: http://www3.u toyama.ac.jp/kkarato/ 1 講義の目的 標本平均は正規分布に従うという性質を
統計学 第 17 回 講義 母平均の区間推定 Part- 016 年 6 14 ( )3 限 担当教員 : 唐渡 広志 ( からと こうじ ) 研究室 : 経済学研究棟 4 階 43 号室 email: kkarato@eco.u toyama.ac.jp website: http://www3.u toyama.ac.jp/kkarato/ 1 講義の目的 標本平均は正規分布に従うという性質を
講義「○○○○」
 講義 信頼度の推定と立証 内容. 点推定と区間推定. 指数分布の点推定 区間推定 3. 指数分布 正規分布の信頼度推定 担当 : 倉敷哲生 ( ビジネスエンジニアリング専攻 ) 統計的推測 標本から得られる情報を基に 母集団に関する結論の導出が目的 測定値 x x x 3 : x 母集団 (populaio) 母集団の特性値 統計的推測 標本 (sample) 標本の特性値 分布のパラメータ ( 母数
講義 信頼度の推定と立証 内容. 点推定と区間推定. 指数分布の点推定 区間推定 3. 指数分布 正規分布の信頼度推定 担当 : 倉敷哲生 ( ビジネスエンジニアリング専攻 ) 統計的推測 標本から得られる情報を基に 母集団に関する結論の導出が目的 測定値 x x x 3 : x 母集団 (populaio) 母集団の特性値 統計的推測 標本 (sample) 標本の特性値 分布のパラメータ ( 母数
データ解析
 データ解析 ( 前期 ) 最小二乗法 向井厚志 005 年度テキスト 0 データ解析 - 最小二乗法 - 目次 第 回 Σ の計算 第 回ヒストグラム 第 3 回平均と標準偏差 6 第 回誤差の伝播 8 第 5 回正規分布 0 第 6 回最尤性原理 第 7 回正規分布の 分布の幅 第 8 回最小二乗法 6 第 9 回最小二乗法の練習 8 第 0 回最小二乗法の推定誤差 0 第 回推定誤差の計算 第
データ解析 ( 前期 ) 最小二乗法 向井厚志 005 年度テキスト 0 データ解析 - 最小二乗法 - 目次 第 回 Σ の計算 第 回ヒストグラム 第 3 回平均と標準偏差 6 第 回誤差の伝播 8 第 5 回正規分布 0 第 6 回最尤性原理 第 7 回正規分布の 分布の幅 第 8 回最小二乗法 6 第 9 回最小二乗法の練習 8 第 0 回最小二乗法の推定誤差 0 第 回推定誤差の計算 第
Microsoft PowerPoint - statistics pptx
 統計学 第 16 回 講義 母平均の区間推定 Part-1 016 年 6 10 ( ) 1 限 担当教員 : 唐渡 広志 ( からと こうじ ) 研究室 : 経済学研究棟 4 階 43 号室 email: kkarato@eco.u-toyama.ac.jp website: http://www3.u-toyama.ac.jp/kkarato/ 1 講義の目的 標本平均は正規分布に従うという性質を
統計学 第 16 回 講義 母平均の区間推定 Part-1 016 年 6 10 ( ) 1 限 担当教員 : 唐渡 広志 ( からと こうじ ) 研究室 : 経済学研究棟 4 階 43 号室 email: kkarato@eco.u-toyama.ac.jp website: http://www3.u-toyama.ac.jp/kkarato/ 1 講義の目的 標本平均は正規分布に従うという性質を
第 3 回講義の項目と概要 統計的手法入門 : 品質のばらつきを解析する 平均と標準偏差 (P30) a) データは平均を見ただけではわからない 平均が同じだからといって 同一視してはいけない b) データのばらつきを示す 標準偏差 にも注目しよう c) 平均
 第 3 回講義の項目と概要 016.8.9 1.3 統計的手法入門 : 品質のばらつきを解析する 1.3.1 平均と標準偏差 (P30) a) データは平均を見ただけではわからない 平均が同じだからといって 同一視してはいけない b) データのばらつきを示す 標準偏差 にも注目しよう c) 平均 :AVERAGE 関数, 標準偏差 :STDEVP 関数とSTDEVという関数 1 取得したデータそのものの標準偏差
第 3 回講義の項目と概要 016.8.9 1.3 統計的手法入門 : 品質のばらつきを解析する 1.3.1 平均と標準偏差 (P30) a) データは平均を見ただけではわからない 平均が同じだからといって 同一視してはいけない b) データのばらつきを示す 標準偏差 にも注目しよう c) 平均 :AVERAGE 関数, 標準偏差 :STDEVP 関数とSTDEVという関数 1 取得したデータそのものの標準偏差
ビジネス統計 統計基礎とエクセル分析 正誤表
 ビジネス統計統計基礎とエクセル分析 ビジネス統計スペシャリスト エクセル分析スペシャリスト 公式テキスト正誤表と学習用データ更新履歴 平成 30 年 5 月 14 日現在 公式テキスト正誤表 頁場所誤正修正 6 知識編第 章 -3-3 最頻値の解説内容 たとえば, 表.1 のデータであれば, 最頻値は 167.5cm というたとえば, 表.1 のデータであれば, 最頻値は 165.0cm ということになります
ビジネス統計統計基礎とエクセル分析 ビジネス統計スペシャリスト エクセル分析スペシャリスト 公式テキスト正誤表と学習用データ更新履歴 平成 30 年 5 月 14 日現在 公式テキスト正誤表 頁場所誤正修正 6 知識編第 章 -3-3 最頻値の解説内容 たとえば, 表.1 のデータであれば, 最頻値は 167.5cm というたとえば, 表.1 のデータであれば, 最頻値は 165.0cm ということになります
14 化学実験法 II( 吉村 ( 洋 mmol/l の半分だったから さんの測定値は くんの測定値の 4 倍の重みがあり 推定値 としては 0.68 mmol/l その標準偏差は mmol/l 程度ということになる 測定値を 特徴づけるパラメータ t を推定するこの手
 14 化学実験法 II( 吉村 ( 洋 014.6.1. 最小 乗法のはなし 014.6.1. 内容 最小 乗法のはなし...1 最小 乗法の考え方...1 最小 乗法によるパラメータの決定... パラメータの信頼区間...3 重みの異なるデータの取扱い...4 相関係数 決定係数 ( 最小 乗法を語るもう一つの立場...5 実験条件の誤差の影響...5 問題...6 最小 乗法の考え方 飲料水中のカルシウム濃度を
14 化学実験法 II( 吉村 ( 洋 014.6.1. 最小 乗法のはなし 014.6.1. 内容 最小 乗法のはなし...1 最小 乗法の考え方...1 最小 乗法によるパラメータの決定... パラメータの信頼区間...3 重みの異なるデータの取扱い...4 相関係数 決定係数 ( 最小 乗法を語るもう一つの立場...5 実験条件の誤差の影響...5 問題...6 最小 乗法の考え方 飲料水中のカルシウム濃度を
Microsoft PowerPoint - stat-2014-[9] pptx
![Microsoft PowerPoint - stat-2014-[9] pptx Microsoft PowerPoint - stat-2014-[9] pptx](/thumbs/49/25555771.jpg) 統計学 第 17 回 講義 母平均の区間推定 Part-1 014 年 6 17 ( )6-7 限 担当教員 : 唐渡 広志 ( からと こうじ ) 研究室 : 経済学研究棟 4 階 43 号室 email: kkarato@eco.u-toyama.ac.j website: htt://www3.u-toyama.ac.j/kkarato/ 1 講義の目的 標本平均は正規分布に従うという性質を
統計学 第 17 回 講義 母平均の区間推定 Part-1 014 年 6 17 ( )6-7 限 担当教員 : 唐渡 広志 ( からと こうじ ) 研究室 : 経済学研究棟 4 階 43 号室 email: kkarato@eco.u-toyama.ac.j website: htt://www3.u-toyama.ac.j/kkarato/ 1 講義の目的 標本平均は正規分布に従うという性質を
情報工学概論
 確率と統計 中山クラス 第 11 週 0 本日の内容 第 3 回レポート解説 第 5 章 5.6 独立性の検定 ( カイ二乗検定 ) 5.7 サンプルサイズの検定結果への影響練習問題 (4),(5) 第 4 回レポート課題の説明 1 演習問題 ( 前回 ) の解説 勉強時間と定期試験の得点の関係を無相関検定により調べる. データ入力 > aa
確率と統計 中山クラス 第 11 週 0 本日の内容 第 3 回レポート解説 第 5 章 5.6 独立性の検定 ( カイ二乗検定 ) 5.7 サンプルサイズの検定結果への影響練習問題 (4),(5) 第 4 回レポート課題の説明 1 演習問題 ( 前回 ) の解説 勉強時間と定期試験の得点の関係を無相関検定により調べる. データ入力 > aa
数値計算法
 数値計算法 008 4/3 林田清 ( 大阪大学大学院理学研究科 ) 実験データの統計処理その 誤差について 母集団と標本 平均値と標準偏差 誤差伝播 最尤法 平均値につく誤差 誤差 (Error): 真の値からのずれ 測定誤差 物差しが曲がっていた 測定する対象が室温が低いため縮んでいた g の単位までしかデジタル表示されない計りで g 以下 計りの目盛りを読み取る角度によって値が異なる 統計誤差
数値計算法 008 4/3 林田清 ( 大阪大学大学院理学研究科 ) 実験データの統計処理その 誤差について 母集団と標本 平均値と標準偏差 誤差伝播 最尤法 平均値につく誤差 誤差 (Error): 真の値からのずれ 測定誤差 物差しが曲がっていた 測定する対象が室温が低いため縮んでいた g の単位までしかデジタル表示されない計りで g 以下 計りの目盛りを読み取る角度によって値が異なる 統計誤差
統計的データ解析
 統計的データ解析 011 011.11.9 林田清 ( 大阪大学大学院理学研究科 ) 連続確率分布の平均値 分散 比較のため P(c ) c 分布 自由度 の ( カイ c 平均値 0, 標準偏差 1の正規分布 に従う変数 xの自乗和 c x =1 が従う分布を自由度 の分布と呼ぶ 一般に自由度の分布は f /1 c / / ( c ) {( c ) e }/ ( / ) 期待値 二乗 ) 分布 c
統計的データ解析 011 011.11.9 林田清 ( 大阪大学大学院理学研究科 ) 連続確率分布の平均値 分散 比較のため P(c ) c 分布 自由度 の ( カイ c 平均値 0, 標準偏差 1の正規分布 に従う変数 xの自乗和 c x =1 が従う分布を自由度 の分布と呼ぶ 一般に自由度の分布は f /1 c / / ( c ) {( c ) e }/ ( / ) 期待値 二乗 ) 分布 c
と 測定を繰り返した時のばらつき の和が 全体のばらつき () に対して どれくらいの割合となるかがわかり 測定システムを評価することができる MSA 第 4 版スタディガイド ジャパン プレクサス (010)p.104 では % GRR の値が10% 未満であれば 一般に受容れられる測定システムと
 .5 Gage R&R による解析.5.1 Gage R&Rとは Gage R&R(Gage Repeatability and Reproducibility ) とは 測定システム分析 (MSA: Measurement System Analysis) ともいわれ 測定プロセスを管理または審査するための手法である MSAでは ばらつきの大きさを 変動 という尺度で表し 測定システムのどこに原因があるのか
.5 Gage R&R による解析.5.1 Gage R&Rとは Gage R&R(Gage Repeatability and Reproducibility ) とは 測定システム分析 (MSA: Measurement System Analysis) ともいわれ 測定プロセスを管理または審査するための手法である MSAでは ばらつきの大きさを 変動 という尺度で表し 測定システムのどこに原因があるのか
不偏推定量
 不偏推定量 情報科学の補足資料 018 年 6 月 7 日藤本祥二 統計的推定 (statistical estimatio) 確率分布が理論的に分かっている標本統計量を利用する 確率分布の期待値の値をそのまま推定値とするのが点推定 ( 信頼度 0%) 点推定に ± で幅を持たせて信頼度を上げたものが区間推定 持たせた幅のことを誤差 (error) と呼ぶ 信頼度 (cofidece level)
不偏推定量 情報科学の補足資料 018 年 6 月 7 日藤本祥二 統計的推定 (statistical estimatio) 確率分布が理論的に分かっている標本統計量を利用する 確率分布の期待値の値をそのまま推定値とするのが点推定 ( 信頼度 0%) 点推定に ± で幅を持たせて信頼度を上げたものが区間推定 持たせた幅のことを誤差 (error) と呼ぶ 信頼度 (cofidece level)
<4D F736F F D2090B695A8939D8C768A E F AA957A82C682948C9F92E8>
 第 8 回 t 分布と t 検定 生物統計学 A.t 分布 ( 小標本に関する平均の推定と検定 ) 前々回と前回の授業では, 標本が十分に大きいあるいは母分散が既知であることを条件に正規分布を用いて推定 検定した. しかし, 母集団が正規分布し, 標本が小さい場合には, 標本分散から母分散を推定するときの不確実さを加味したt 分布を用いて推定 検定しなければならない. t 分布は標本分散の自由度 f(
第 8 回 t 分布と t 検定 生物統計学 A.t 分布 ( 小標本に関する平均の推定と検定 ) 前々回と前回の授業では, 標本が十分に大きいあるいは母分散が既知であることを条件に正規分布を用いて推定 検定した. しかし, 母集団が正規分布し, 標本が小さい場合には, 標本分散から母分散を推定するときの不確実さを加味したt 分布を用いて推定 検定しなければならない. t 分布は標本分散の自由度 f(
Microsoft Word - 補論3.2
 補論 3. 多変量 GARC モデル 07//6 新谷元嗣 藪友良 対数尤度関数 3 章 7 節では 変量の対数尤度を求めた ここでは多変量の場合 とくに 変量について対数尤度を求める 誤差項 は平均 0 で 次元の正規分布に従うとする 単純化のため 分散と共分散は時間を通じて一定としよう ( この仮定は後で変更される ) したがって ij から添え字 を除くことができる このとき と の尤度関数は
補論 3. 多変量 GARC モデル 07//6 新谷元嗣 藪友良 対数尤度関数 3 章 7 節では 変量の対数尤度を求めた ここでは多変量の場合 とくに 変量について対数尤度を求める 誤差項 は平均 0 で 次元の正規分布に従うとする 単純化のため 分散と共分散は時間を通じて一定としよう ( この仮定は後で変更される ) したがって ij から添え字 を除くことができる このとき と の尤度関数は
測量士補 重要事項「標準偏差」
 標準偏差 < 試験合格へのポイント > 士補試験における標準偏差に関する問題は 平成元年が最後の出題となっており それ以来 0 年間に渡って出題された形跡がない このため 受験対策本の中には標準偏差に関して 触れることすら無くなっている物もあるのが現状である しかし平成 0 年度試験において 再び出題が確認されたため ここに解説し過去に出題された問題について触れてみる 標準偏差に関する問題は 基本的にはその公式に当てはめて解けば良いため
標準偏差 < 試験合格へのポイント > 士補試験における標準偏差に関する問題は 平成元年が最後の出題となっており それ以来 0 年間に渡って出題された形跡がない このため 受験対策本の中には標準偏差に関して 触れることすら無くなっている物もあるのが現状である しかし平成 0 年度試験において 再び出題が確認されたため ここに解説し過去に出題された問題について触れてみる 標準偏差に関する問題は 基本的にはその公式に当てはめて解けば良いため
<4D F736F F D208EC08CB18C7689E68A E F1939D8C E82E646F63>
 第 5 回統計的推定 実験計画学 A. 統計的推定と検定母集団から無作為抽出した標本から母集団についてなんらかの推論を行う. この場合, 統計から行う推論には統計的 ( ) と統計的 ( ) の 2つがある. 推定統計的に標本の統計量から母集団の母数 ( 母平均, 母標準偏差など ) を推論することを統計的推定という. 例 : 視聴率調査を 200 人に対して行い, 番組 Aの視聴率を推定した. 検定統計的に標本の統計量から母数に関する予想の真偽を検証することを統計的検定という.
第 5 回統計的推定 実験計画学 A. 統計的推定と検定母集団から無作為抽出した標本から母集団についてなんらかの推論を行う. この場合, 統計から行う推論には統計的 ( ) と統計的 ( ) の 2つがある. 推定統計的に標本の統計量から母集団の母数 ( 母平均, 母標準偏差など ) を推論することを統計的推定という. 例 : 視聴率調査を 200 人に対して行い, 番組 Aの視聴率を推定した. 検定統計的に標本の統計量から母数に関する予想の真偽を検証することを統計的検定という.
PowerPoint プレゼンテーション
 1/X Chapter 9: Linear correlation Cohen, B. H. (2007). In B. H. Cohen (Ed.), Explaining Psychological Statistics (3rd ed.) (pp. 255-285). NJ: Wiley. 概要 2/X 相関係数とは何か 相関係数の数式 検定 注意点 フィッシャーのZ 変換 信頼区間 相関係数の差の検定
1/X Chapter 9: Linear correlation Cohen, B. H. (2007). In B. H. Cohen (Ed.), Explaining Psychological Statistics (3rd ed.) (pp. 255-285). NJ: Wiley. 概要 2/X 相関係数とは何か 相関係数の数式 検定 注意点 フィッシャーのZ 変換 信頼区間 相関係数の差の検定
Microsoft Word - lec_student-chp3_1-representative
 1. はじめに この節でのテーマ データ分布の中心位置を数値で表す 可視化でとらえた分布の中心位置を数量化する 平均値とメジアン, 幾何平均 この節での到達目標 1 平均値 メジアン 幾何平均の定義を書ける 2 平均値とメジアン, 幾何平均の特徴と使える状況を説明できる. 3 平均値 メジアン 幾何平均を計算できる 2. 特性値 集めたデータを度数分布表やヒストグラムに整理する ( 可視化する )
1. はじめに この節でのテーマ データ分布の中心位置を数値で表す 可視化でとらえた分布の中心位置を数量化する 平均値とメジアン, 幾何平均 この節での到達目標 1 平均値 メジアン 幾何平均の定義を書ける 2 平均値とメジアン, 幾何平均の特徴と使える状況を説明できる. 3 平均値 メジアン 幾何平均を計算できる 2. 特性値 集めたデータを度数分布表やヒストグラムに整理する ( 可視化する )
カイ二乗フィット検定、パラメータの誤差
 統計的データ解析 008 008.. 林田清 ( 大阪大学大学院理学研究科 ) 問題 C (, ) ( x xˆ) ( y yˆ) σ x πσ σ y y Pabx (, ;,,, ) ˆ y σx σ y = dx exp exp πσx ただし xy ˆ ˆ はyˆ = axˆ+ bであらわされる直線モデル上の点 ( ˆ) ( ˆ ) ( ) x x y ax b y ax b Pabx (,
統計的データ解析 008 008.. 林田清 ( 大阪大学大学院理学研究科 ) 問題 C (, ) ( x xˆ) ( y yˆ) σ x πσ σ y y Pabx (, ;,,, ) ˆ y σx σ y = dx exp exp πσx ただし xy ˆ ˆ はyˆ = axˆ+ bであらわされる直線モデル上の点 ( ˆ) ( ˆ ) ( ) x x y ax b y ax b Pabx (,
Kumamoto University Center for Multimedia and Information Technologies Lab. 熊本大学アプリケーション実験 ~ 実環境における無線 LAN 受信電波強度を用いた位置推定手法の検討 ~ InKIAI 宮崎県美郷
 熊本大学アプリケーション実験 ~ 実環境における無線 LAN 受信電波強度を用いた位置推定手法の検討 ~ InKIAI プロジェクト @ 宮崎県美郷町 熊本大学副島慶人川村諒 1 実験の目的 従来 信号の受信電波強度 (RSSI:RecevedSgnal StrengthIndcator) により 対象の位置を推定する手法として 無線 LAN の AP(AccessPont) から受信する信号の減衰量をもとに位置を推定する手法が多く検討されている
熊本大学アプリケーション実験 ~ 実環境における無線 LAN 受信電波強度を用いた位置推定手法の検討 ~ InKIAI プロジェクト @ 宮崎県美郷町 熊本大学副島慶人川村諒 1 実験の目的 従来 信号の受信電波強度 (RSSI:RecevedSgnal StrengthIndcator) により 対象の位置を推定する手法として 無線 LAN の AP(AccessPont) から受信する信号の減衰量をもとに位置を推定する手法が多く検討されている
<4D F736F F D208EC08CB18C7689E68A E F193F18D8095AA957A C C839395AA957A814590B38B4B95AA957A2E646F63>
 第 4 回二項分布, ポアソン分布, 正規分布 実験計画学 009 年 月 0 日 A. 代表的な分布. 離散分布 二項分布大きさ n の標本で, 事象 Eの起こる確率を p とするとき, そのうち x 個にEが起こる確率 P(x) は二項分布に従う. 例さいころを 0 回振ったときに の出る回数 x の確率分布は二項分布に従う. この場合, n = 0, p = 6 の二項分布になる さいころを
第 4 回二項分布, ポアソン分布, 正規分布 実験計画学 009 年 月 0 日 A. 代表的な分布. 離散分布 二項分布大きさ n の標本で, 事象 Eの起こる確率を p とするとき, そのうち x 個にEが起こる確率 P(x) は二項分布に従う. 例さいころを 0 回振ったときに の出る回数 x の確率分布は二項分布に従う. この場合, n = 0, p = 6 の二項分布になる さいころを
<4D F736F F D AA90CD939D8C7692C789C C F33816A8A6D92E894C52E646F63>
 分析統計概論の参考資料 初心者のための統計学 追加テキスト 精度管理に用いる用語 基本知識 2008 年 6 月 社団法人におい かおり環境協会 1. はじめに臭気に関連する諸データを統計学的に取り扱うための基礎知識の解説書として 初心者のための統計学 が当協会から刊行されている この本は 統計学の基礎的な知識を網羅するとともに 臭気データを統計学的に取り扱うための考え方や事例を解説したもので 臭気データに限らず
分析統計概論の参考資料 初心者のための統計学 追加テキスト 精度管理に用いる用語 基本知識 2008 年 6 月 社団法人におい かおり環境協会 1. はじめに臭気に関連する諸データを統計学的に取り扱うための基礎知識の解説書として 初心者のための統計学 が当協会から刊行されている この本は 統計学の基礎的な知識を網羅するとともに 臭気データを統計学的に取り扱うための考え方や事例を解説したもので 臭気データに限らず
Microsoft PowerPoint - 測量学.ppt [互換モード]
![Microsoft PowerPoint - 測量学.ppt [互換モード] Microsoft PowerPoint - 測量学.ppt [互換モード]](/thumbs/92/109082022.jpg) 8/5/ 誤差理論 測定の分類 性格による分類 独立 ( な ) 測定 : 測定値がある条件を満たさなければならないなどの拘束や制約を持たないで独立して行う測定 条件 ( 付き ) 測定 : 三角形の 3 つの内角の和のように, 個々の測定値間に満たすべき条件式が存在する場合の測定 方法による分類 直接測定 : 距離や角度などを機器を用いて直接行う測定 間接測定 : 求めるべき量を直接測定するのではなく,
8/5/ 誤差理論 測定の分類 性格による分類 独立 ( な ) 測定 : 測定値がある条件を満たさなければならないなどの拘束や制約を持たないで独立して行う測定 条件 ( 付き ) 測定 : 三角形の 3 つの内角の和のように, 個々の測定値間に満たすべき条件式が存在する場合の測定 方法による分類 直接測定 : 距離や角度などを機器を用いて直接行う測定 間接測定 : 求めるべき量を直接測定するのではなく,
ダンゴムシの 交替性転向反応に 関する研究 3A15 今野直輝
 ダンゴムシの 交替性転向反応に 関する研究 3A15 今野直輝 1. 研究の動機 ダンゴムシには 右に曲がった後は左に 左に曲がった後は右に曲がる という交替性転向反応という習性がある 数多くの生物において この習性は見受けられるのだが なかでもダンゴムシやその仲間のワラジムシは その行動が特に顕著であるとして有名である そのため図 1のような道をダンゴムシに歩かせると 前の突き当りでどちらの方向に曲がったかを見ることによって
ダンゴムシの 交替性転向反応に 関する研究 3A15 今野直輝 1. 研究の動機 ダンゴムシには 右に曲がった後は左に 左に曲がった後は右に曲がる という交替性転向反応という習性がある 数多くの生物において この習性は見受けられるのだが なかでもダンゴムシやその仲間のワラジムシは その行動が特に顕著であるとして有名である そのため図 1のような道をダンゴムシに歩かせると 前の突き当りでどちらの方向に曲がったかを見ることによって
Microsoft Word - Stattext12.doc
 章対応のない 群間の量的データの検定. 検定手順 この章ではデータ間に 対 の対応のないつの標本から推定される母集団間の平均値や中央値の比較を行ないます 検定手法は 図. のようにまず正規に従うかどうかを調べます 但し この場合はつの群が共に正規に従うことを調べる必要があります 次に 群とも正規ならば F 検定を用いて等分散であるかどうかを調べます 等分散の場合は t 検定 等分散でない場合はウェルチ
章対応のない 群間の量的データの検定. 検定手順 この章ではデータ間に 対 の対応のないつの標本から推定される母集団間の平均値や中央値の比較を行ないます 検定手法は 図. のようにまず正規に従うかどうかを調べます 但し この場合はつの群が共に正規に従うことを調べる必要があります 次に 群とも正規ならば F 検定を用いて等分散であるかどうかを調べます 等分散の場合は t 検定 等分散でない場合はウェルチ
多変量解析 ~ 重回帰分析 ~ 2006 年 4 月 21 日 ( 金 ) 南慶典
 多変量解析 ~ 重回帰分析 ~ 2006 年 4 月 21 日 ( 金 ) 南慶典 重回帰分析とは? 重回帰分析とは複数の説明変数から目的変数との関係性を予測 評価説明変数 ( 数量データ ) は目的変数を説明するのに有効であるか得られた関係性より未知のデータの妥当性を判断する これを重回帰分析という つまり どんなことをするのか? 1 最小 2 乗法により重回帰モデルを想定 2 自由度調整済寄与率を求め
多変量解析 ~ 重回帰分析 ~ 2006 年 4 月 21 日 ( 金 ) 南慶典 重回帰分析とは? 重回帰分析とは複数の説明変数から目的変数との関係性を予測 評価説明変数 ( 数量データ ) は目的変数を説明するのに有効であるか得られた関係性より未知のデータの妥当性を判断する これを重回帰分析という つまり どんなことをするのか? 1 最小 2 乗法により重回帰モデルを想定 2 自由度調整済寄与率を求め
Microsoft PowerPoint slide2forWeb.ppt [互換モード]
![Microsoft PowerPoint slide2forWeb.ppt [互換モード] Microsoft PowerPoint slide2forWeb.ppt [互換モード]](/thumbs/96/126561931.jpg) 講義内容 9..4 正規分布 ormal dstrbuto ガウス分布 Gaussa dstrbuto 中心極限定理 サンプルからの母集団統計量の推定 不偏推定量について 確率変数, 確率密度関数 確率密度関数 確率密度関数は積分したら. 平均 : 確率変数 分散 : 例 ある場所, ある日時での気温の確率. : 気温, : 気温 が起こる確率 標本平均とのアナロジー 類推 例 人の身長の分布と平均
講義内容 9..4 正規分布 ormal dstrbuto ガウス分布 Gaussa dstrbuto 中心極限定理 サンプルからの母集団統計量の推定 不偏推定量について 確率変数, 確率密度関数 確率密度関数 確率密度関数は積分したら. 平均 : 確率変数 分散 : 例 ある場所, ある日時での気温の確率. : 気温, : 気温 が起こる確率 標本平均とのアナロジー 類推 例 人の身長の分布と平均
Microsoft PowerPoint saitama2.ppt [互換モード]
![Microsoft PowerPoint saitama2.ppt [互換モード] Microsoft PowerPoint saitama2.ppt [互換モード]](/thumbs/96/128502968.jpg) 感度係数について 産業技術総合研究所計測標準研究部門 物性統計科応用統計研究室 城野克広 1 モデル式 そして感度係数 2 不確かさの見積もり例 例ある液体の体積 v を その質量と密度から求めることにした まず 液体の質量を質量計で 5 回反復測定し 測定データ {1., 1., 99.9, 99.7, 1.1 g} を得た 一方液体の密度については
感度係数について 産業技術総合研究所計測標準研究部門 物性統計科応用統計研究室 城野克広 1 モデル式 そして感度係数 2 不確かさの見積もり例 例ある液体の体積 v を その質量と密度から求めることにした まず 液体の質量を質量計で 5 回反復測定し 測定データ {1., 1., 99.9, 99.7, 1.1 g} を得た 一方液体の密度については
Microsoft PowerPoint - Inoue-statistics [互換モード]
![Microsoft PowerPoint - Inoue-statistics [互換モード] Microsoft PowerPoint - Inoue-statistics [互換モード]](/thumbs/92/107910528.jpg) 誤差論 神戸大学大学院農学研究科 井上一哉 (Kazuya INOUE) 誤差論 2011 年度前期火曜クラス 1 講義内容 誤差と有効数字 (Slide No.2~8 Text p.76~78) 誤差の分布と標準偏差 (Slide No.9~18 Text p.78~80) 最確値とその誤差 (Slide No.19~25 Text p.80~81) 誤差の伝播 (Slide No.26~32 Text
誤差論 神戸大学大学院農学研究科 井上一哉 (Kazuya INOUE) 誤差論 2011 年度前期火曜クラス 1 講義内容 誤差と有効数字 (Slide No.2~8 Text p.76~78) 誤差の分布と標準偏差 (Slide No.9~18 Text p.78~80) 最確値とその誤差 (Slide No.19~25 Text p.80~81) 誤差の伝播 (Slide No.26~32 Text
Microsoft Word - Stattext07.doc
 7 章正規分布 正規分布 (ormal dstrbuto) は 偶発的なデータのゆらぎによって生じる統計学で最も基本的な確率分布です この章では正規分布についてその性質を詳しく見て行きましょう 7. 一般の正規分布正規分布は 平均と分散の つの量によって完全に特徴付けられています 平均 μ 分散 の正規分布は N ( μ, ) 分布とも書かれます ここに N は ormal の頭文字を 表わしています
7 章正規分布 正規分布 (ormal dstrbuto) は 偶発的なデータのゆらぎによって生じる統計学で最も基本的な確率分布です この章では正規分布についてその性質を詳しく見て行きましょう 7. 一般の正規分布正規分布は 平均と分散の つの量によって完全に特徴付けられています 平均 μ 分散 の正規分布は N ( μ, ) 分布とも書かれます ここに N は ormal の頭文字を 表わしています
Microsoft Word - thesis.doc
 剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
Microsoft PowerPoint - e-stat(OLS).pptx
 経済統計学 ( 補足 ) 最小二乗法について 担当 : 小塚匡文 2015 年 11 月 19 日 ( 改訂版 ) 神戸大学経済学部 2015 年度後期開講授業 補足 : 最小二乗法 ( 単回帰分析 ) 1.( 単純 ) 回帰分析とは? 標本サイズTの2 変数 ( ここではXとY) のデータが存在 YをXで説明する回帰方程式を推定するための方法 Y: 被説明変数 ( または従属変数 ) X: 説明変数
経済統計学 ( 補足 ) 最小二乗法について 担当 : 小塚匡文 2015 年 11 月 19 日 ( 改訂版 ) 神戸大学経済学部 2015 年度後期開講授業 補足 : 最小二乗法 ( 単回帰分析 ) 1.( 単純 ) 回帰分析とは? 標本サイズTの2 変数 ( ここではXとY) のデータが存在 YをXで説明する回帰方程式を推定するための方法 Y: 被説明変数 ( または従属変数 ) X: 説明変数
母平均 母分散 母標準偏差は, が連続的な場合も含めて, すべての個体の特性値 のすべての実現値 の平均 分散 標準偏差であると考えてよい 有限母集団で が離散的な場合, まさにその意味になるが, そうでない場合も, このように理解してよい 5 母数 母集団から定まる定数のこと 母平均, 母分散,
 . 無作為標本. 基本的用語 推測統計における基本的な用語を確認する 母集団 調査の対象になる集団のこと 最終的に, 判断の対象になる集団である 母集団の個体 母集団を構成する つ つのもののこと 母集団は個体の集まりである 個体の特性値 個体の特性を表す数値のこと 身長や体重など 特性値は, 変量ともいう 4 有限母集団と無限母集団 個体の個数が有限の母集団を 有限母集団, 個体の個数が無限の母集団を
. 無作為標本. 基本的用語 推測統計における基本的な用語を確認する 母集団 調査の対象になる集団のこと 最終的に, 判断の対象になる集団である 母集団の個体 母集団を構成する つ つのもののこと 母集団は個体の集まりである 個体の特性値 個体の特性を表す数値のこと 身長や体重など 特性値は, 変量ともいう 4 有限母集団と無限母集団 個体の個数が有限の母集団を 有限母集団, 個体の個数が無限の母集団を
Microsoft PowerPoint - sc7.ppt [互換モード]
![Microsoft PowerPoint - sc7.ppt [互換モード] Microsoft PowerPoint - sc7.ppt [互換モード]](/thumbs/91/107013389.jpg) / 社会調査論 本章の概要 本章では クロス集計表を用いた独立性の検定を中心に方法を学ぶ 1) 立命館大学経済学部 寺脇 拓 2 11 1.1 比率の推定 ベルヌーイ分布 (Bernoulli distribution) 浄水器の所有率を推定したいとする 浄水器の所有の有無を表す変数をxで表し 浄水器をもっている を 1 浄水器をもっていない を 0 で表す 母集団の浄水器を持っている人の割合をpで表すとすると
/ 社会調査論 本章の概要 本章では クロス集計表を用いた独立性の検定を中心に方法を学ぶ 1) 立命館大学経済学部 寺脇 拓 2 11 1.1 比率の推定 ベルヌーイ分布 (Bernoulli distribution) 浄水器の所有率を推定したいとする 浄水器の所有の有無を表す変数をxで表し 浄水器をもっている を 1 浄水器をもっていない を 0 で表す 母集団の浄水器を持っている人の割合をpで表すとすると
統計学の基礎から学ぶ実験計画法ー1
 第 部統計学の基礎と. 統計学とは. 統計学の基本. 母集団とサンプル ( 標本 ). データ (data) 3. 集団の特性を示す統計量 基本的な解析手法 3. 統計量 (statistic) とは 3. 集団を代表する統計量 - 平均値など 3.3 集団のばらつきを表す値 - 平方和 分散 標準偏差 4. ばらつき ( 分布 ) を表す関数 4. 確率密度関数 4. 最も重要な正規分布 4.3
第 部統計学の基礎と. 統計学とは. 統計学の基本. 母集団とサンプル ( 標本 ). データ (data) 3. 集団の特性を示す統計量 基本的な解析手法 3. 統計量 (statistic) とは 3. 集団を代表する統計量 - 平均値など 3.3 集団のばらつきを表す値 - 平方和 分散 標準偏差 4. ばらつき ( 分布 ) を表す関数 4. 確率密度関数 4. 最も重要な正規分布 4.3
Hara-statistics
 全学共通授業科目 物理学実験平成 3 年度前期測定値の扱い方と誤差論 講義 神戸大学大学院理学研究科物理学専攻原俊雄 測定値を他人に提示するとき なぜ 誤差を考えなければならないのか? なぜ 誤差を測定値に付けなければならないのか? そもそも 誤差とは何か? 人間は 測定により真の値を知ることができるか? 人間は 真の値を知ることはできない 人間は 工夫することによって 限りなく真の値に近づくことができる
全学共通授業科目 物理学実験平成 3 年度前期測定値の扱い方と誤差論 講義 神戸大学大学院理学研究科物理学専攻原俊雄 測定値を他人に提示するとき なぜ 誤差を考えなければならないのか? なぜ 誤差を測定値に付けなければならないのか? そもそも 誤差とは何か? 人間は 測定により真の値を知ることができるか? 人間は 真の値を知ることはできない 人間は 工夫することによって 限りなく真の値に近づくことができる
Microsoft PowerPoint - Statistics[B]
![Microsoft PowerPoint - Statistics[B] Microsoft PowerPoint - Statistics[B]](/thumbs/101/151482563.jpg) 講義の目的 サンプルサイズの大きい標本比率の分布は正規分布で近似できることを理解します 科目コード 130509, 130609, 110225 統計学講義第 19/20 回 2019 年 6 月 25 日 ( 火 )6/7 限 担当教員 : 唐渡広志 ( からと こうじ ) 研究室 : email: website: 経済学研究棟 4 階 432 号室 kkarato@eco.u-toyama.ac.jp
講義の目的 サンプルサイズの大きい標本比率の分布は正規分布で近似できることを理解します 科目コード 130509, 130609, 110225 統計学講義第 19/20 回 2019 年 6 月 25 日 ( 火 )6/7 限 担当教員 : 唐渡広志 ( からと こうじ ) 研究室 : email: website: 経済学研究棟 4 階 432 号室 kkarato@eco.u-toyama.ac.jp
Probit , Mixed logit
 Probit, Mixed logit 2016/5/16 スタートアップゼミ #5 B4 後藤祥孝 1 0. 目次 Probit モデルについて 1. モデル概要 2. 定式化と理解 3. 推定 Mixed logit モデルについて 4. モデル概要 5. 定式化と理解 6. 推定 2 1.Probit 概要 プロビットモデルとは. 効用関数の誤差項に多変量正規分布を仮定したもの. 誤差項には様々な要因が存在するため,
Probit, Mixed logit 2016/5/16 スタートアップゼミ #5 B4 後藤祥孝 1 0. 目次 Probit モデルについて 1. モデル概要 2. 定式化と理解 3. 推定 Mixed logit モデルについて 4. モデル概要 5. 定式化と理解 6. 推定 2 1.Probit 概要 プロビットモデルとは. 効用関数の誤差項に多変量正規分布を仮定したもの. 誤差項には様々な要因が存在するため,
経営統計学
 5 章基本統計量 3.5 節で量的データの集計方法について簡単に触れ 前章でデータの分布について学びましたが データの特徴をつの数値で示すこともよく行なわれます これは統計量と呼ばれ 主に分布の中心や拡がりなどを表わします この章ではよく利用される分布の統計量を特徴で分類して説明します 数式表示を統一的に行なうために データの個数を 個とし それらを,,, と表わすことにします ここで学ぶ統計量は統計分析の基礎となっており
5 章基本統計量 3.5 節で量的データの集計方法について簡単に触れ 前章でデータの分布について学びましたが データの特徴をつの数値で示すこともよく行なわれます これは統計量と呼ばれ 主に分布の中心や拡がりなどを表わします この章ではよく利用される分布の統計量を特徴で分類して説明します 数式表示を統一的に行なうために データの個数を 個とし それらを,,, と表わすことにします ここで学ぶ統計量は統計分析の基礎となっており
Microsoft Word - NumericalComputation.docx
 数値計算入門 武尾英哉. 離散数学と数値計算 数学的解法の中には理論計算では求められないものもある. 例えば, 定積分は, まずは積分 ( 被積分関数の原始関数をみつけること できなければ値を得ることはできない. また, ある関数の所定の値における微分値を得るには, まずその関数の微分ができなければならない. さらに代数方程式の解を得るためには, 解析的に代数方程式を解く必要がある. ところが, これらは必ずしも解析的に導けるとは限らない.
数値計算入門 武尾英哉. 離散数学と数値計算 数学的解法の中には理論計算では求められないものもある. 例えば, 定積分は, まずは積分 ( 被積分関数の原始関数をみつけること できなければ値を得ることはできない. また, ある関数の所定の値における微分値を得るには, まずその関数の微分ができなければならない. さらに代数方程式の解を得るためには, 解析的に代数方程式を解く必要がある. ところが, これらは必ずしも解析的に導けるとは限らない.
Python-statistics5 Python で統計学を学ぶ (5) この内容は山田 杉澤 村井 (2008) R によるやさしい統計学 (
 http://localhost:8888/notebooks/... Python で統計学を学ぶ (5) この内容は山田 杉澤 村井 (2008) R によるやさしい統計学 (http://shop.ohmsha.co.jp/shop /shopdetail.html?brandcode=000000001781&search=978-4-274-06710-5&sort=) を参考にしています
http://localhost:8888/notebooks/... Python で統計学を学ぶ (5) この内容は山田 杉澤 村井 (2008) R によるやさしい統計学 (http://shop.ohmsha.co.jp/shop /shopdetail.html?brandcode=000000001781&search=978-4-274-06710-5&sort=) を参考にしています
Microsoft PowerPoint - データ解析基礎4.ppt [互換モード]
![Microsoft PowerPoint - データ解析基礎4.ppt [互換モード] Microsoft PowerPoint - データ解析基礎4.ppt [互換モード]](/thumbs/91/106398432.jpg) データ解析基礎. 正規分布と相関係数 keyword 正規分布 正規分布の性質 偏差値 変数間の関係を表す統計量 共分散 相関係数 散布図 正規分布 世の中の多くの現象は, 標本数を大きくしていくと, 正規分布に近づいていくことが知られている. 正規分布 データ解析の基礎となる重要な分布 平均と分散によって特徴づけることができる. 平均値 : 分布の中心を表す値 分散 : 分布のばらつきを表す値 正規分布
データ解析基礎. 正規分布と相関係数 keyword 正規分布 正規分布の性質 偏差値 変数間の関係を表す統計量 共分散 相関係数 散布図 正規分布 世の中の多くの現象は, 標本数を大きくしていくと, 正規分布に近づいていくことが知られている. 正規分布 データ解析の基礎となる重要な分布 平均と分散によって特徴づけることができる. 平均値 : 分布の中心を表す値 分散 : 分布のばらつきを表す値 正規分布
Medical3
 Chapter 1 1.4.1 1 元配置分散分析と多重比較の実行 3つの治療法による測定値に有意な差が認められるかどうかを分散分析で調べます この例では 因子が1つだけ含まれるため1 元配置分散分析 one-way ANOVA の適用になります また 多重比較法 multiple comparison procedure を用いて 具体的のどの治療法の間に有意差が認められるかを検定します 1. 分析メニュー
Chapter 1 1.4.1 1 元配置分散分析と多重比較の実行 3つの治療法による測定値に有意な差が認められるかどうかを分散分析で調べます この例では 因子が1つだけ含まれるため1 元配置分散分析 one-way ANOVA の適用になります また 多重比較法 multiple comparison procedure を用いて 具体的のどの治療法の間に有意差が認められるかを検定します 1. 分析メニュー
Microsoft PowerPoint - 基礎・経済統計6.ppt
 . 確率変数 基礎 経済統計 6 確率分布 事象を数値化したもの ( 事象ー > 数値 の関数 自然に数値されている場合 さいころの目 量的尺度 数値化が必要な場合 質的尺度, 順序的尺度 それらの尺度に数値を割り当てる 例えば, コインの表が出たら, 裏なら 0. 離散確率変数と連続確率変数 確率変数の値 連続値をとるもの 身長, 体重, 実質 GDP など とびとびの値 離散値をとるもの 新生児の性別
. 確率変数 基礎 経済統計 6 確率分布 事象を数値化したもの ( 事象ー > 数値 の関数 自然に数値されている場合 さいころの目 量的尺度 数値化が必要な場合 質的尺度, 順序的尺度 それらの尺度に数値を割り当てる 例えば, コインの表が出たら, 裏なら 0. 離散確率変数と連続確率変数 確率変数の値 連続値をとるもの 身長, 体重, 実質 GDP など とびとびの値 離散値をとるもの 新生児の性別
13章 回帰分析
 単回帰分析 つ以上の変数についての関係を見る つの 目的 被説明 変数を その他の 説明 変数を使って 予測しようというものである 因果関係とは限らない ここで勉強すること 最小 乗法と回帰直線 決定係数とは何か? 最小 乗法と回帰直線 これまで 変数の間の関係の深さについて考えてきた 相関係数 ここでは 変数に役割を与え 一方の 説明 変数を用いて他方の 目的 被説明 変数を説明することを考える
単回帰分析 つ以上の変数についての関係を見る つの 目的 被説明 変数を その他の 説明 変数を使って 予測しようというものである 因果関係とは限らない ここで勉強すること 最小 乗法と回帰直線 決定係数とは何か? 最小 乗法と回帰直線 これまで 変数の間の関係の深さについて考えてきた 相関係数 ここでは 変数に役割を与え 一方の 説明 変数を用いて他方の 目的 被説明 変数を説明することを考える
不確かさ 資料 1/8
 不確かさ 資料 /8 天びんの校正の不確かさの目安 表 に 代表的な電子天びんの校正の不確かさ ( 目安 ) 示します 表 校正の不確かさ ( 目安 ) 最小表示 機種 校正ポイント拡張不確かさ ( 風袋なし ) (k=2) 0.00mg BM-20 g 0.09 mg GH-202 50 g 0.7 mg 0.0mg GH-252 00 g 0.3 mg BM-252 00 g 0.29 mg GR-20/GH-20
不確かさ 資料 /8 天びんの校正の不確かさの目安 表 に 代表的な電子天びんの校正の不確かさ ( 目安 ) 示します 表 校正の不確かさ ( 目安 ) 最小表示 機種 校正ポイント拡張不確かさ ( 風袋なし ) (k=2) 0.00mg BM-20 g 0.09 mg GH-202 50 g 0.7 mg 0.0mg GH-252 00 g 0.3 mg BM-252 00 g 0.29 mg GR-20/GH-20
切片 ( 定数項 ) ダミー 以下の単回帰モデルを考えよう これは賃金と就業年数の関係を分析している : ( 賃金関数 ) ここで Y i = α + β X i + u i, i =1,, n, u i ~ i.i.d. N(0, σ 2 ) Y i : 賃金の対数値, X i : 就業年数. (
 統計学ダミー変数による分析 担当 : 長倉大輔 ( ながくらだいすけ ) 1 切片 ( 定数項 ) ダミー 以下の単回帰モデルを考えよう これは賃金と就業年数の関係を分析している : ( 賃金関数 ) ここで Y i = α + β X i + u i, i =1,, n, u i ~ i.i.d. N(0, σ 2 ) Y i : 賃金の対数値, X i : 就業年数. ( 実際は賃金を就業年数だけで説明するのは現実的はない
統計学ダミー変数による分析 担当 : 長倉大輔 ( ながくらだいすけ ) 1 切片 ( 定数項 ) ダミー 以下の単回帰モデルを考えよう これは賃金と就業年数の関係を分析している : ( 賃金関数 ) ここで Y i = α + β X i + u i, i =1,, n, u i ~ i.i.d. N(0, σ 2 ) Y i : 賃金の対数値, X i : 就業年数. ( 実際は賃金を就業年数だけで説明するのは現実的はない
測量試補 重要事項
 重量平均による標高の最確値 < 試験合格へのポイント > 標高の最確値を重量平均によって求める問題である 士補試験では 定番 問題であり 水準測量の計算問題としては この形式か 往復観測の較差と許容範囲 の どちらか または両方がほぼ毎年出題されている 定番の計算問題であるがその難易度は低く 基本的な解き方をマスターしてしまえば 容易に解くことができる ( : 最重要事項 : 重要事項 : 知っておくと良い
重量平均による標高の最確値 < 試験合格へのポイント > 標高の最確値を重量平均によって求める問題である 士補試験では 定番 問題であり 水準測量の計算問題としては この形式か 往復観測の較差と許容範囲 の どちらか または両方がほぼ毎年出題されている 定番の計算問題であるがその難易度は低く 基本的な解き方をマスターしてしまえば 容易に解くことができる ( : 最重要事項 : 重要事項 : 知っておくと良い
統計学 - 社会統計の基礎 - 正規分布 標準正規分布累積分布関数の逆関数 t 分布正規分布に従うサンプルの平均の信頼区間 担当 : 岸 康人 資料ページ :
 統計学 - 社会統計の基礎 - 正規分布 標準正規分布累積分布関数の逆関数 t 分布正規分布に従うサンプルの平均の信頼区間 担当 : 岸 康人 資料ページ : https://goo.gl/qw1djw 正規分布 ( 復習 ) 正規分布 (Normal Distribution)N (μ, σ 2 ) 別名 : ガウス分布 (Gaussian Distribution) 密度関数 Excel:= NORM.DIST
統計学 - 社会統計の基礎 - 正規分布 標準正規分布累積分布関数の逆関数 t 分布正規分布に従うサンプルの平均の信頼区間 担当 : 岸 康人 資料ページ : https://goo.gl/qw1djw 正規分布 ( 復習 ) 正規分布 (Normal Distribution)N (μ, σ 2 ) 別名 : ガウス分布 (Gaussian Distribution) 密度関数 Excel:= NORM.DIST
ファイナンスのための数学基礎 第1回 オリエンテーション、ベクトル
 時系列分析 変量時系列モデルとその性質 担当 : 長倉大輔 ( ながくらだいすけ 時系列モデル 時系列モデルとは時系列データを生み出すメカニズムとなるものである これは実際には未知である 私たちにできるのは観測された時系列データからその背後にある時系列モデルを推測 推定するだけである 以下ではいくつかの代表的な時系列モデルを考察する 自己回帰モデル (Auoregressive Model もっとも頻繁に使われる時系列モデルは自己回帰モデル
時系列分析 変量時系列モデルとその性質 担当 : 長倉大輔 ( ながくらだいすけ 時系列モデル 時系列モデルとは時系列データを生み出すメカニズムとなるものである これは実際には未知である 私たちにできるのは観測された時系列データからその背後にある時系列モデルを推測 推定するだけである 以下ではいくつかの代表的な時系列モデルを考察する 自己回帰モデル (Auoregressive Model もっとも頻繁に使われる時系列モデルは自己回帰モデル
_KyoukaNaiyou_No.4
 理科教科内容指導論 I : 物理分野 物理現象の定量的把握第 4 回 ( 実験 ) データの眺め ~ 統計学の基礎続き 統計のはなし 基礎 応 娯楽 (Best selected business books) 村平 科技連出版社 1836 円 前回の復習と今回以降の 標 東京 学 善 郎 Web サイトより データ ヒストグラム 代表値 ( 平均値 最頻値 中間値 ) 分布の散らばり 集団の分布
理科教科内容指導論 I : 物理分野 物理現象の定量的把握第 4 回 ( 実験 ) データの眺め ~ 統計学の基礎続き 統計のはなし 基礎 応 娯楽 (Best selected business books) 村平 科技連出版社 1836 円 前回の復習と今回以降の 標 東京 学 善 郎 Web サイトより データ ヒストグラム 代表値 ( 平均値 最頻値 中間値 ) 分布の散らばり 集団の分布
横浜市環境科学研究所
 周期時系列の統計解析 単回帰分析 io 8 年 3 日 周期時系列に季節調整を行わないで単回帰分析を適用すると, 回帰係数には周期成分の影響が加わる. ここでは, 周期時系列をコサイン関数モデルで近似し単回帰分析によりモデルの回帰係数を求め, 周期成分の影響を検討した. また, その結果を気温時系列に当てはめ, 課題等について考察した. 気温時系列とコサイン関数モデル第 報の結果を利用するので, その一部を再掲する.
周期時系列の統計解析 単回帰分析 io 8 年 3 日 周期時系列に季節調整を行わないで単回帰分析を適用すると, 回帰係数には周期成分の影響が加わる. ここでは, 周期時系列をコサイン関数モデルで近似し単回帰分析によりモデルの回帰係数を求め, 周期成分の影響を検討した. また, その結果を気温時系列に当てはめ, 課題等について考察した. 気温時系列とコサイン関数モデル第 報の結果を利用するので, その一部を再掲する.
<4D F736F F D208EC08CB18C7689E68A E F193F18D8095AA957A C C839395AA957A814590B38B4B95AA957A2E646F63>
 第 4 回二項分布, ポアソン分布, 正規分布 実験計画学 A. 代表的な分布. 離散分布 二項分布大きさ n の標本で, 事象 Eの起こる確率を p とするとき, そのうち x 個にEが起こる確率 P(x) は二項分布に従う. 例さいころを 0 回振ったときに の出る回数 x の確率分布は二項分布に従う. この場合, n 0, p 6 の二項分布になる さいころを 0 回振ったときに が 0 回出る
第 4 回二項分布, ポアソン分布, 正規分布 実験計画学 A. 代表的な分布. 離散分布 二項分布大きさ n の標本で, 事象 Eの起こる確率を p とするとき, そのうち x 個にEが起こる確率 P(x) は二項分布に従う. 例さいころを 0 回振ったときに の出る回数 x の確率分布は二項分布に従う. この場合, n 0, p 6 の二項分布になる さいころを 0 回振ったときに が 0 回出る
スライド 1
 計測工学第 12 回以降 測定値の誤差と精度編 2014 年 7 月 2 日 ( 水 )~7 月 16 日 ( 水 ) 知能情報工学科 横田孝義 1 授業計画 4/9 4/16 4/23 5/7 5/14 5/21 5/28 6/4 6/11 6/18 6/25 7/2 7/9 7/16 7/23 2 誤差とその取扱い 3 誤差 = 測定値 真の値 相対誤差 = 誤差 / 真の値 4 誤差 (error)
計測工学第 12 回以降 測定値の誤差と精度編 2014 年 7 月 2 日 ( 水 )~7 月 16 日 ( 水 ) 知能情報工学科 横田孝義 1 授業計画 4/9 4/16 4/23 5/7 5/14 5/21 5/28 6/4 6/11 6/18 6/25 7/2 7/9 7/16 7/23 2 誤差とその取扱い 3 誤差 = 測定値 真の値 相対誤差 = 誤差 / 真の値 4 誤差 (error)
ファイナンスのための数学基礎 第1回 オリエンテーション、ベクトル
 春学期統計学 I 記述統計と推測統計 担当 : 長倉大輔 ( ながくらだいすけ ) 1 本日の予定 本日はまず記述統計と推測統計の違い 推測統計学の基本的な構造について説明します 2 記述統計と推測統計 統計学とは? 与えられたデータの背後にある 特性 法則 を 検証 発見 分析 するための手法の開発 その応用などに関わる学問の事です 3 記述統計と推測統計 データの種類 データの種類はおおまかに
春学期統計学 I 記述統計と推測統計 担当 : 長倉大輔 ( ながくらだいすけ ) 1 本日の予定 本日はまず記述統計と推測統計の違い 推測統計学の基本的な構造について説明します 2 記述統計と推測統計 統計学とは? 与えられたデータの背後にある 特性 法則 を 検証 発見 分析 するための手法の開発 その応用などに関わる学問の事です 3 記述統計と推測統計 データの種類 データの種類はおおまかに
Microsoft PowerPoint - R-stat-intro_12.ppt [互換モード]
![Microsoft PowerPoint - R-stat-intro_12.ppt [互換モード] Microsoft PowerPoint - R-stat-intro_12.ppt [互換モード]](/thumbs/101/151921093.jpg) R で統計解析入門 (12) 生存時間解析 中篇 準備 : データ DEP の読み込み 1. データ DEP を以下からダウンロードする http://www.cwk.zaq.ne.jp/fkhud708/files/dep.csv /fkh /d 2. ダウンロードした場所を把握する ここでは c:/temp とする 3. R を起動し,2. 2 の場所に移動し, データを読み込む 4. データ
R で統計解析入門 (12) 生存時間解析 中篇 準備 : データ DEP の読み込み 1. データ DEP を以下からダウンロードする http://www.cwk.zaq.ne.jp/fkhud708/files/dep.csv /fkh /d 2. ダウンロードした場所を把握する ここでは c:/temp とする 3. R を起動し,2. 2 の場所に移動し, データを読み込む 4. データ
様々なミクロ計量モデル†
 担当 : 長倉大輔 ( ながくらだいすけ ) この資料は私の講義において使用するために作成した資料です WEB ページ上で公開しており 自由に参照して頂いて構いません ただし 内容について 一応検証してありますが もし間違いがあった場合でもそれによって生じるいかなる損害 不利益について責任を負いかねますのでご了承ください 間違いは発見次第 継続的に直していますが まだ存在する可能性があります 1 カウントデータモデル
担当 : 長倉大輔 ( ながくらだいすけ ) この資料は私の講義において使用するために作成した資料です WEB ページ上で公開しており 自由に参照して頂いて構いません ただし 内容について 一応検証してありますが もし間違いがあった場合でもそれによって生じるいかなる損害 不利益について責任を負いかねますのでご了承ください 間違いは発見次第 継続的に直していますが まだ存在する可能性があります 1 カウントデータモデル
<4D F736F F D208D A778D5A8A778F4B8E7793B CC A7795D2816A2E646F6378>
 高等学校学習指導要領解説数学統計関係部分抜粋 第 部数学第 2 章各科目第 節数学 Ⅰ 3 内容と内容の取扱い (4) データの分析 (4) データの分析統計の基本的な考えを理解するとともに, それを用いてデータを整理 分析し傾向を把握できるようにする アデータの散らばり四分位偏差, 分散及び標準偏差などの意味について理解し, それらを用いてデータの傾向を把握し, 説明すること イデータの相関散布図や相関係数の意味を理解し,
高等学校学習指導要領解説数学統計関係部分抜粋 第 部数学第 2 章各科目第 節数学 Ⅰ 3 内容と内容の取扱い (4) データの分析 (4) データの分析統計の基本的な考えを理解するとともに, それを用いてデータを整理 分析し傾向を把握できるようにする アデータの散らばり四分位偏差, 分散及び標準偏差などの意味について理解し, それらを用いてデータの傾向を把握し, 説明すること イデータの相関散布図や相関係数の意味を理解し,
untitled
 分析の信頼性を支えるもの データ評価のための統計的方法 確率分布と平均値の推定 検定 田中秀幸 1 はじめに前回は, 統計的手法を適用するために意味のあるデータをどのように取得するのかについて, 母集団と標本について, 期待値 分散 標準偏差について解説した 今回は, 統計的推定 検定の基礎となる確率分布とその確率分布を用いた推定 検定について解説する 2 確率分布 測定データを取得したとき, そのデータのばらつきを視覚的に表すために,
分析の信頼性を支えるもの データ評価のための統計的方法 確率分布と平均値の推定 検定 田中秀幸 1 はじめに前回は, 統計的手法を適用するために意味のあるデータをどのように取得するのかについて, 母集団と標本について, 期待値 分散 標準偏差について解説した 今回は, 統計的推定 検定の基礎となる確率分布とその確率分布を用いた推定 検定について解説する 2 確率分布 測定データを取得したとき, そのデータのばらつきを視覚的に表すために,
Microsoft PowerPoint - 資料04 重回帰分析.ppt
 04. 重回帰分析 京都大学 加納学 Division of Process Control & Process Sstems Engineering Department of Chemical Engineering, Koto Universit manabu@cheme.koto-u.ac.jp http://www-pse.cheme.koto-u.ac.jp/~kano/ Outline
04. 重回帰分析 京都大学 加納学 Division of Process Control & Process Sstems Engineering Department of Chemical Engineering, Koto Universit manabu@cheme.koto-u.ac.jp http://www-pse.cheme.koto-u.ac.jp/~kano/ Outline
青焼 1章[15-52].indd
![青焼 1章[15-52].indd 青焼 1章[15-52].indd](/thumbs/86/94313777.jpg) 1 第 1 章統計の基礎知識 1 1 なぜ統計解析が必要なのか? 人間は自分自身の経験にもとづいて 感覚的にものごとを判断しがちである 例えばある疾患に対する標準治療薬の有効率が 50% であったとする そこに新薬が登場し ある医師がその新薬を 5 人の患者に使ったところ 4 人が有効と判定されたとしたら 多くの医師はこれまでの標準治療薬よりも新薬のほうが有効性が高そうだと感じることだろう しかし
1 第 1 章統計の基礎知識 1 1 なぜ統計解析が必要なのか? 人間は自分自身の経験にもとづいて 感覚的にものごとを判断しがちである 例えばある疾患に対する標準治療薬の有効率が 50% であったとする そこに新薬が登場し ある医師がその新薬を 5 人の患者に使ったところ 4 人が有効と判定されたとしたら 多くの医師はこれまでの標準治療薬よりも新薬のほうが有効性が高そうだと感じることだろう しかし
曲線 = f () は を媒介変数とする自然な媒介変数表示 =,= f () をもつので, これを利用して説明する 以下,f () は定義域で連続であると仮定する 例えば, 直線 =c が曲線 = f () の漸近線になるとする 曲線 = f () 上の点 P(,f ()) が直線 =c に近づくこ
 伊伊伊伊伊伊伊伊伊伊 伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊 漸近線の求め方に関する考察 たまい玉井 かつき克樹 伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊 伊伊伊伊伊伊伊伊伊伊. 漸近線についての生徒からの質問 数学において図を使って直感的な説明を与えることは, 理解を深めるのに大いに役立つ
伊伊伊伊伊伊伊伊伊伊 伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊 漸近線の求め方に関する考察 たまい玉井 かつき克樹 伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊 伊伊伊伊伊伊伊伊伊伊. 漸近線についての生徒からの質問 数学において図を使って直感的な説明を与えることは, 理解を深めるのに大いに役立つ
Microsoft PowerPoint - zairiki_3
 材料力学講義 (3) 応力と変形 Ⅲ ( 曲げモーメント, 垂直応力度, 曲率 ) 今回は, 曲げモーメントに関する, 断面力 - 応力度 - 変形 - 変位の関係について学びます 1 曲げモーメント 曲げモーメント M 静定力学で求めた曲げモーメントも, 仮想的に断面を切ることによって現れる内力です 軸方向力は断面に働く力 曲げモーメント M は断面力 曲げモーメントも, 一つのモーメントとして表しますが,
材料力学講義 (3) 応力と変形 Ⅲ ( 曲げモーメント, 垂直応力度, 曲率 ) 今回は, 曲げモーメントに関する, 断面力 - 応力度 - 変形 - 変位の関係について学びます 1 曲げモーメント 曲げモーメント M 静定力学で求めた曲げモーメントも, 仮想的に断面を切ることによって現れる内力です 軸方向力は断面に働く力 曲げモーメント M は断面力 曲げモーメントも, 一つのモーメントとして表しますが,
統計学 Ⅱ( 章 ( 区間推定のシミュレーション 母平均 μ の区間推定 X ~ N, のとき X T ~ 自由度 1の t分布 1 自由度 -1のt 分布の97.5% 点 :t.975 P t T t この式に T を代入する t.975 母集団
 統計学 Ⅱ(16 11-1 章 11 章母集団パラメータの推定 1. 信頼区間 (1 点推定と区間推定 ( 区間推定のシミュレーション (3 母平均 μの信頼区間 (4 母比率 pの信頼区間 (5 母比率 pのより厳密な信頼区間. 点推定量の特性 (1 標本平均 X の持つ望ましい性質 ( 不偏性 (3 推定量の分散と有効性 (4 平均 乗誤差 MEと最小分散性 (5 一致性 (6 チェビシェフの不等式
統計学 Ⅱ(16 11-1 章 11 章母集団パラメータの推定 1. 信頼区間 (1 点推定と区間推定 ( 区間推定のシミュレーション (3 母平均 μの信頼区間 (4 母比率 pの信頼区間 (5 母比率 pのより厳密な信頼区間. 点推定量の特性 (1 標本平均 X の持つ望ましい性質 ( 不偏性 (3 推定量の分散と有効性 (4 平均 乗誤差 MEと最小分散性 (5 一致性 (6 チェビシェフの不等式
解答のポイント 第 1 章問 1 ポイント仮に1 年生全員の数が 100 人であったとする.100 人全員に数学の試験を課して, それらの 100 人の個人個人の点数が母集団となる. 問 2 ポイント仮に10 人を抽出するとする. 学生に1から 100 までの番号を割り当てたとする. 箱の中に番号札
 解答のポイント 第 1 章問 1 ポイント仮に1 年生全員の数が 100 人であったとする.100 人全員に数学の試験を課して, それらの 100 人の個人個人の点数が母集団となる. 問 2 ポイント仮に10 人を抽出するとする. 学生に1から 100 までの番号を割り当てたとする. 箱の中に番号札を入れまず1 枚取り出す ( 仮に1 番とする ). 最初に1 番の学生を選ぶ. その1 番の札を箱の中に戻し,
解答のポイント 第 1 章問 1 ポイント仮に1 年生全員の数が 100 人であったとする.100 人全員に数学の試験を課して, それらの 100 人の個人個人の点数が母集団となる. 問 2 ポイント仮に10 人を抽出するとする. 学生に1から 100 までの番号を割り当てたとする. 箱の中に番号札を入れまず1 枚取り出す ( 仮に1 番とする ). 最初に1 番の学生を選ぶ. その1 番の札を箱の中に戻し,
Microsoft Word - Stattext13.doc
 3 章対応のある 群間の量的データの検定 3. 検定手順 この章では対応がある場合の量的データの検定方法について学びます この場合も図 3. のように最初に正規に従うかどうかを調べます 正規性が認められた場合は対応がある場合の t 検定 正規性が認められない場合はウィルコクソン (Wlcoxo) の符号付き順位和検定を行ないます 章で述べた検定方法と似ていますが ここでは対応のあるデータ同士を引き算した値を用いて判断します
3 章対応のある 群間の量的データの検定 3. 検定手順 この章では対応がある場合の量的データの検定方法について学びます この場合も図 3. のように最初に正規に従うかどうかを調べます 正規性が認められた場合は対応がある場合の t 検定 正規性が認められない場合はウィルコクソン (Wlcoxo) の符号付き順位和検定を行ないます 章で述べた検定方法と似ていますが ここでは対応のあるデータ同士を引き算した値を用いて判断します
(b) 精密さ 精密度 * precision 測定値のばらつきの程度 標準偏差の大きさに相当する (c) 精度 accuracy 測定結果の正確さと精密さを含めた 測定量の真の値との一致の度合い 補正 correction は 正確さを期すために行われる ( 系統誤差を打ち消すために行われる )
 誤差の話 014.4.4. 内容 誤差の話... 1 正確さ 精密さ 精度... 1 不確かさの表示... 誤差のモデル... 誤差の伝播則... 3 測定の際の注意点 独立でかたよりのない測定の実現... 4 容量分析に見る誤差... 4 問題... 6 誤差の話 正確さ 精密さ 精度 測定値の精確さあるいは不確かさをめぐっては 品質工学の長足の進歩なども背景に この0 年余りの間にさまざまな概念の整理が行われてきた
誤差の話 014.4.4. 内容 誤差の話... 1 正確さ 精密さ 精度... 1 不確かさの表示... 誤差のモデル... 誤差の伝播則... 3 測定の際の注意点 独立でかたよりのない測定の実現... 4 容量分析に見る誤差... 4 問題... 6 誤差の話 正確さ 精密さ 精度 測定値の精確さあるいは不確かさをめぐっては 品質工学の長足の進歩なども背景に この0 年余りの間にさまざまな概念の整理が行われてきた
(.3) 式 z / の計算, alpha( ), sigma( ) から, 値 ( 区間幅 ) を計算 siki.3<-fuctio(, alpha, sigma) elta <- qorm(-alpha/) sigma /sqrt() elta [ 例 ]., 信頼率 として, サイ
![(.3) 式 z / の計算, alpha( ), sigma( ) から, 値 ( 区間幅 ) を計算 siki.3<-fuctio(, alpha, sigma) elta <- qorm(-alpha/) sigma /sqrt() elta [ 例 ]., 信頼率 として, サイ (.3) 式 z / の計算, alpha( ), sigma( ) から, 値 ( 区間幅 ) を計算 siki.3<-fuctio(, alpha, sigma) elta <- qorm(-alpha/) sigma /sqrt() elta [ 例 ]., 信頼率 として, サイ](/thumbs/91/105783221.jpg) 区間推定に基づくサンプルサイズの設計方法 7.7. 株式会社応用数理研究所佐々木俊久 永田靖 サンプルサイズの決め方 朝倉書店 (3) の 章です 原本とおなじ 6 種類を記述していますが 平均値関連 4 つをから4 章とし, 分散の つを 5,6 章に順序を変更しました 推定手順 サンプルサイズの設計方法は, 原本をそのまま引用しています R(S-PLUS) 関数での計算方法および例を追加しました.
区間推定に基づくサンプルサイズの設計方法 7.7. 株式会社応用数理研究所佐々木俊久 永田靖 サンプルサイズの決め方 朝倉書店 (3) の 章です 原本とおなじ 6 種類を記述していますが 平均値関連 4 つをから4 章とし, 分散の つを 5,6 章に順序を変更しました 推定手順 サンプルサイズの設計方法は, 原本をそのまま引用しています R(S-PLUS) 関数での計算方法および例を追加しました.
untitled
 分析の信頼性を支えるもの データ評価のための統計的方法 測定と統計の基礎知識 田中秀幸 1 はじめに 測定とは, ある物理現象をより良く知るために行うものであるが, 測定したデータをどう解釈するかということは案外難しい問題である データを解釈する際に大変有用であるのは統計的手法であり, 適切な統計的手法を取得したデータに適用するとデータの解釈が非常に楽になるだけではなく, データ, グラフを眺めているだけでは見えてこない隠された性質までも明示することができるようになる
分析の信頼性を支えるもの データ評価のための統計的方法 測定と統計の基礎知識 田中秀幸 1 はじめに 測定とは, ある物理現象をより良く知るために行うものであるが, 測定したデータをどう解釈するかということは案外難しい問題である データを解釈する際に大変有用であるのは統計的手法であり, 適切な統計的手法を取得したデータに適用するとデータの解釈が非常に楽になるだけではなく, データ, グラフを眺めているだけでは見えてこない隠された性質までも明示することができるようになる
森林水文 水資源学 2 2. 水文統計 豪雨があった時, 新聞やテレビのニュースで 50 年に一度の大雨だった などと報告されることがある. 今争点となっている川辺川ダムは,80 年に 1 回の洪水を想定して治水計画が立てられている. 畑地かんがいでは,10 年に 1 回の渇水を対象として計画が立て
 . 水文統計 豪雨があった時, 新聞やテレビのニュースで 50 年に一度の大雨だった などと報告されることがある. 今争点となっている川辺川ダムは,80 年に 回の洪水を想定して治水計画が立てられている. 畑地かんがいでは,0 年に 回の渇水を対象として計画が立てられる. このように, 水利構造物の設計や, 治水や利水の計画などでは, 年に 回起こるような降雨事象 ( 最大降雨強度, 最大連続干天日数など
. 水文統計 豪雨があった時, 新聞やテレビのニュースで 50 年に一度の大雨だった などと報告されることがある. 今争点となっている川辺川ダムは,80 年に 回の洪水を想定して治水計画が立てられている. 畑地かんがいでは,0 年に 回の渇水を対象として計画が立てられる. このように, 水利構造物の設計や, 治水や利水の計画などでは, 年に 回起こるような降雨事象 ( 最大降雨強度, 最大連続干天日数など
<4D F736F F F696E74202D A6D82A982B381408AD698418B4B8A E E B8CDD8AB B83685D>
 ISO/TC69 ( 統計的手法の適用 ) で 開発された不確かさに関わる規格 ( 独 ) 産業技術総合研究所 計測標準総合センター 小池昌義 目次 ISO/TC69 統計的方法の適用 TC69 と不確かさ関連 JIS 規格の制定 JIS Z 8404-1(ISO/TS 1748:004) JIS Z 8404-(ISO/TS 1749:004) まとめ ISO/TC69 統計的方法の適用 WG 3:
ISO/TC69 ( 統計的手法の適用 ) で 開発された不確かさに関わる規格 ( 独 ) 産業技術総合研究所 計測標準総合センター 小池昌義 目次 ISO/TC69 統計的方法の適用 TC69 と不確かさ関連 JIS 規格の制定 JIS Z 8404-1(ISO/TS 1748:004) JIS Z 8404-(ISO/TS 1749:004) まとめ ISO/TC69 統計的方法の適用 WG 3:
Microsoft Word - 201hyouka-tangen-1.doc
 数学 Ⅰ 評価規準の作成 ( 単元ごと ) 数学 Ⅰ の目標及び図形と計量について理解させ 基礎的な知識の習得と技能の習熟を図り それらを的確に活用する機能を伸ばすとともに 数学的な見方や考え方のよさを認識できるようにする 評価の観点の趣旨 式と不等式 二次関数及び図形と計量における考え方に関 心をもつとともに 数学的な見方や考え方のよさを認識し それらを事象の考察に活用しようとする 式と不等式 二次関数及び図形と計量における数学的な見
数学 Ⅰ 評価規準の作成 ( 単元ごと ) 数学 Ⅰ の目標及び図形と計量について理解させ 基礎的な知識の習得と技能の習熟を図り それらを的確に活用する機能を伸ばすとともに 数学的な見方や考え方のよさを認識できるようにする 評価の観点の趣旨 式と不等式 二次関数及び図形と計量における考え方に関 心をもつとともに 数学的な見方や考え方のよさを認識し それらを事象の考察に活用しようとする 式と不等式 二次関数及び図形と計量における数学的な見
画像類似度測定の初歩的な手法の検証
 画像類似度測定の初歩的な手法の検証 島根大学総合理工学部数理 情報システム学科 計算機科学講座田中研究室 S539 森瀧昌志 1 目次 第 1 章序論第 章画像間類似度測定の初歩的な手法について.1 A. 画素値の平均を用いる手法.. 画素値のヒストグラムを用いる手法.3 C. 相関係数を用いる手法.4 D. 解像度を合わせる手法.5 E. 振れ幅のヒストグラムを用いる手法.6 F. 周波数ごとの振れ幅を比較する手法第
画像類似度測定の初歩的な手法の検証 島根大学総合理工学部数理 情報システム学科 計算機科学講座田中研究室 S539 森瀧昌志 1 目次 第 1 章序論第 章画像間類似度測定の初歩的な手法について.1 A. 画素値の平均を用いる手法.. 画素値のヒストグラムを用いる手法.3 C. 相関係数を用いる手法.4 D. 解像度を合わせる手法.5 E. 振れ幅のヒストグラムを用いる手法.6 F. 周波数ごとの振れ幅を比較する手法第
Microsoft Word - 操作マニュアル-Excel-2.doc
 Excel プログラム開発の練習マニュアルー 1 ( 関数の学習 ) 作成 2015.01.31 修正 2015.02.04 本マニュアルでは Excel のプログラム開発を行なうに当たって まずは Excel の関数に関する学習 について記述する Ⅰ.Excel の関数に関する学習 1. 初めに Excel は単なる表計算のソフトと思っている方も多いと思います しかし Excel には 一般的に使用する
Excel プログラム開発の練習マニュアルー 1 ( 関数の学習 ) 作成 2015.01.31 修正 2015.02.04 本マニュアルでは Excel のプログラム開発を行なうに当たって まずは Excel の関数に関する学習 について記述する Ⅰ.Excel の関数に関する学習 1. 初めに Excel は単なる表計算のソフトと思っている方も多いと思います しかし Excel には 一般的に使用する
講義ノート p.2 データの視覚化ヒストグラムの作成直感的な把握のために重要入力間違いがないか確認するデータの分布を把握する fig. ヒストグラムの作成 fig. ヒストグラムの出力例 度数分布表の作成 データの度数を把握する 入力間違いが無いかの確認にも便利 fig. 度数分布表の作成
 講義ノート p.1 前回の復習 尺度について数字には情報量に応じて 4 段階の種類がある名義尺度順序尺度 : 質的データ間隔尺度比例尺度 : 量的データ 尺度によって利用できる分析方法に差異がある SPSS での入力の練習と簡単な操作の説明 変数ビューで変数を設定 ( 型や尺度に注意 ) fig. 変数ビュー データビューでデータを入力 fig. データビュー 講義ノート p.2 データの視覚化ヒストグラムの作成直感的な把握のために重要入力間違いがないか確認するデータの分布を把握する
講義ノート p.1 前回の復習 尺度について数字には情報量に応じて 4 段階の種類がある名義尺度順序尺度 : 質的データ間隔尺度比例尺度 : 量的データ 尺度によって利用できる分析方法に差異がある SPSS での入力の練習と簡単な操作の説明 変数ビューで変数を設定 ( 型や尺度に注意 ) fig. 変数ビュー データビューでデータを入力 fig. データビュー 講義ノート p.2 データの視覚化ヒストグラムの作成直感的な把握のために重要入力間違いがないか確認するデータの分布を把握する
第7章
 5. 推定と検定母集団分布の母数を推定する方法と仮説検定の方法を解説する まず 母数を一つの値で推定する点推定について 推定精度としての標準誤差を説明する また 母数が区間に存在することを推定する信頼区間も取り扱う 後半は統計的仮説検定について述べる 検定法の基本的な考え方と正規分布および二項確率についての検定法を解説する 5.1. 点推定先に述べた統計量は対応する母数の推定値である このように母数を一つの値およびベクトルで推定する場合を点推定
5. 推定と検定母集団分布の母数を推定する方法と仮説検定の方法を解説する まず 母数を一つの値で推定する点推定について 推定精度としての標準誤差を説明する また 母数が区間に存在することを推定する信頼区間も取り扱う 後半は統計的仮説検定について述べる 検定法の基本的な考え方と正規分布および二項確率についての検定法を解説する 5.1. 点推定先に述べた統計量は対応する母数の推定値である このように母数を一つの値およびベクトルで推定する場合を点推定
日心TWS
 2017.09.22 (15:40~17:10) 日本心理学会第 81 回大会 TWS ベイジアンデータ解析入門 回帰分析を例に ベイジアンデータ解析 を体験してみる 広島大学大学院教育学研究科平川真 ベイジアン分析のステップ (p.24) 1) データの特定 2) モデルの定義 ( 解釈可能な ) モデルの作成 3) パラメタの事前分布の設定 4) ベイズ推論を用いて パラメタの値に確信度を再配分ベイズ推定
2017.09.22 (15:40~17:10) 日本心理学会第 81 回大会 TWS ベイジアンデータ解析入門 回帰分析を例に ベイジアンデータ解析 を体験してみる 広島大学大学院教育学研究科平川真 ベイジアン分析のステップ (p.24) 1) データの特定 2) モデルの定義 ( 解釈可能な ) モデルの作成 3) パラメタの事前分布の設定 4) ベイズ推論を用いて パラメタの値に確信度を再配分ベイズ推定
0415
 今回の授業の狙い 基本的な統計量を求め 活用できること 章統計量と確率分布のと確率分布の活用 part 統計解析で用いる代表的な確率分布の特徴を 把握すること 統計解析の全体像 統計解析での注意点 ()( サンプリング サンプル 測定 母集団 何らかの意味で同質性が期待できるものの集団 e 日本人男性同じ条件で作った製品 母集団 推定 アクション 事実に基づく判断 データからモノをいう データ解析
今回の授業の狙い 基本的な統計量を求め 活用できること 章統計量と確率分布のと確率分布の活用 part 統計解析で用いる代表的な確率分布の特徴を 把握すること 統計解析の全体像 統計解析での注意点 ()( サンプリング サンプル 測定 母集団 何らかの意味で同質性が期待できるものの集団 e 日本人男性同じ条件で作った製品 母集団 推定 アクション 事実に基づく判断 データからモノをいう データ解析
振動学特論火曜 1 限 TA332J 藤井康介 6 章スペクトルの平滑化 スペクトルの平滑化とはギザギザした地震波のフーリエ スペクトルやパワ スペクトルでは正確にスペクトルの山がどこにあるかはよく分からない このようなスペクトルから不純なものを取り去って 本当の性質を浮き彫
 6 章スペクトルの平滑化 スペクトルの平滑化とはギザギザした地震波のフーリエ スペクトルやパワ スペクトルでは正確にスペクトルの山がどこにあるかはよく分からない このようなスペクトルから不純なものを取り去って 本当の性質を浮き彫りにするために スペクトルを滑らかにする操作のことをいう 6.1 合積のフーリエ変換スペクトルの平滑化を行う際に必要な 合積とそのフーリエ変換について説明する 6.2 データ
6 章スペクトルの平滑化 スペクトルの平滑化とはギザギザした地震波のフーリエ スペクトルやパワ スペクトルでは正確にスペクトルの山がどこにあるかはよく分からない このようなスペクトルから不純なものを取り去って 本当の性質を浮き彫りにするために スペクトルを滑らかにする操作のことをいう 6.1 合積のフーリエ変換スペクトルの平滑化を行う際に必要な 合積とそのフーリエ変換について説明する 6.2 データ
経済統計分析1 イントロダクション
 1 経済統計分析 9 分散分析 今日のおはなし. 検定 statistical test のいろいろ 2 変数の関係を調べる手段のひとつ適合度検定独立性検定分散分析 今日のタネ 吉田耕作.2006. 直感的統計学. 日経 BP. 中村隆英ほか.1984. 統計入門. 東大出版会. 2 仮説検定の手続き 仮説検定のロジック もし帰無仮説が正しければ, 検定統計量が既知の分布に従う 計算された検定統計量の値から,
1 経済統計分析 9 分散分析 今日のおはなし. 検定 statistical test のいろいろ 2 変数の関係を調べる手段のひとつ適合度検定独立性検定分散分析 今日のタネ 吉田耕作.2006. 直感的統計学. 日経 BP. 中村隆英ほか.1984. 統計入門. 東大出版会. 2 仮説検定の手続き 仮説検定のロジック もし帰無仮説が正しければ, 検定統計量が既知の分布に従う 計算された検定統計量の値から,
Microsoft Word - å“Ÿåłžå¸°173.docx
 回帰分析 ( その 3) 経済情報処理 価格弾力性の推定ある商品について その購入量を w 単価を p とし それぞれの変化量を w p で表 w w すことにする この時 この商品の価格弾力性 は により定義される これ p p は p が 1 パーセント変化した場合に w が何パーセント変化するかを示したものである ここで p を 0 に近づけていった極限を考えると d ln w 1 dw dw
回帰分析 ( その 3) 経済情報処理 価格弾力性の推定ある商品について その購入量を w 単価を p とし それぞれの変化量を w p で表 w w すことにする この時 この商品の価格弾力性 は により定義される これ p p は p が 1 パーセント変化した場合に w が何パーセント変化するかを示したものである ここで p を 0 に近づけていった極限を考えると d ln w 1 dw dw
Application Note 光束の評価方法に関して Light Emitting Diode 目次 1. 概要 2. 評価方法 3. 注意事項 4. まとめ This document contains tentative information; the contents may chang
 光束の評価方法に関して 目次 1. 概要 2. 評価方法 3. 注意事項 4. まとめ 1/6 1. 概要 本書では 日亜化学工業株式会社製 LED について積分球にて光束を評価する上での評価方法と注意事項を示します 2. 評価方法 通常 LED の光束を評価する際は積分球を用いて評価を行います 積分球のサイズも数 inch クラスのものから 1inch クラスまでの様々なサイズのものがありますが
光束の評価方法に関して 目次 1. 概要 2. 評価方法 3. 注意事項 4. まとめ 1/6 1. 概要 本書では 日亜化学工業株式会社製 LED について積分球にて光束を評価する上での評価方法と注意事項を示します 2. 評価方法 通常 LED の光束を評価する際は積分球を用いて評価を行います 積分球のサイズも数 inch クラスのものから 1inch クラスまでの様々なサイズのものがありますが
線形システム応答 Linear System response
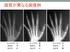 画質が異なる画像例 コントラスト劣 コントラスト優 コントラスト普 鮮鋭性 普 鮮鋭性 優 鮮鋭性 劣 粒状性 普 粒状性 劣 粒状性 優 医用画像の画質 コントラスト, 鮮鋭性, 粒状性の要因が互いに密接に関わり合って形成されている. 比 鮮鋭性 コントラスト 反 反 粒状性 増感紙 - フィルム系での 3 要因の関係 ディジタル画像処理系でもおよそ成り立つ WS u MTFu 画質に影響する因子
画質が異なる画像例 コントラスト劣 コントラスト優 コントラスト普 鮮鋭性 普 鮮鋭性 優 鮮鋭性 劣 粒状性 普 粒状性 劣 粒状性 優 医用画像の画質 コントラスト, 鮮鋭性, 粒状性の要因が互いに密接に関わり合って形成されている. 比 鮮鋭性 コントラスト 反 反 粒状性 増感紙 - フィルム系での 3 要因の関係 ディジタル画像処理系でもおよそ成り立つ WS u MTFu 画質に影響する因子
Microsoft PowerPoint - H21生物計算化学2.ppt
 演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
Microsoft PowerPoint - fuseitei_6
 不静定力学 Ⅱ 骨組の崩壊荷重の計算 不静定力学 Ⅱ では, 最後の問題となりますが, 骨組の崩壊荷重の計算法について学びます 1 参考書 松本慎也著 よくわかる構造力学の基本, 秀和システム このスライドの説明には, 主にこの参考書の説明を引用しています 2 崩壊荷重 構造物に作用する荷重が徐々に増大すると, 構造物内に発生する応力は増加し, やがて, 構造物は荷重に耐えられなくなる そのときの荷重を崩壊荷重あるいは終局荷重という
不静定力学 Ⅱ 骨組の崩壊荷重の計算 不静定力学 Ⅱ では, 最後の問題となりますが, 骨組の崩壊荷重の計算法について学びます 1 参考書 松本慎也著 よくわかる構造力学の基本, 秀和システム このスライドの説明には, 主にこの参考書の説明を引用しています 2 崩壊荷重 構造物に作用する荷重が徐々に増大すると, 構造物内に発生する応力は増加し, やがて, 構造物は荷重に耐えられなくなる そのときの荷重を崩壊荷重あるいは終局荷重という
Microsoft PowerPoint - 10.pptx
 m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
Microsoft PowerPoint - statistics pptx
 統計学 第 回 講義 仮説検定 Part-3 06 年 6 8 ( )3 限 担当教員 唐渡 広志 ( からと こうじ ) 研究室 経済学研究棟 4 階 43 号室 email kkarato@eco.u-toyama.ac.j webite htt://www3.u-toyama.ac.j/kkarato/ 講義の目的 つの 集団の平均 ( 率 ) に差があるかどうかを検定する 法を理解します keyword:
統計学 第 回 講義 仮説検定 Part-3 06 年 6 8 ( )3 限 担当教員 唐渡 広志 ( からと こうじ ) 研究室 経済学研究棟 4 階 43 号室 email kkarato@eco.u-toyama.ac.j webite htt://www3.u-toyama.ac.j/kkarato/ 講義の目的 つの 集団の平均 ( 率 ) に差があるかどうかを検定する 法を理解します keyword:
untitled
 に, 月次モデルの場合でも四半期モデルの場合でも, シミュレーション期間とは無関係に一様に RMSPE を最小にするバンドの設定法は存在しないということである 第 2 は, 表で与えた 2 つの期間及びすべての内生変数を見渡して, 全般的にパフォーマンスのよいバンドの設定法は, 最適固定バンドと最適可変バンドのうちの M 2, Q2 である いずれにしても, 以上述べた 3 つのバンド設定法は若干便宜的なものと言わざるを得ない
に, 月次モデルの場合でも四半期モデルの場合でも, シミュレーション期間とは無関係に一様に RMSPE を最小にするバンドの設定法は存在しないということである 第 2 は, 表で与えた 2 つの期間及びすべての内生変数を見渡して, 全般的にパフォーマンスのよいバンドの設定法は, 最適固定バンドと最適可変バンドのうちの M 2, Q2 である いずれにしても, 以上述べた 3 つのバンド設定法は若干便宜的なものと言わざるを得ない
DVIOUT
 最適レギュレータ 松尾研究室資料 第 最適レギュレータ 節時不変型無限時間最適レギュレータ 状態フィードバックの可能な場合の無限時間問題における最適レギュレータについて確定系について説明する. ここで, レギュレータとは状態量をゼロにするようなコントローラのことである. なぜ, 無限時間問題のみを述べるかという理由は以下のとおりである. 有限時間の最適レギュレータ問題の場合の最適フィードバックゲインは微分方程式の解から構成される時間関数として表現される.
最適レギュレータ 松尾研究室資料 第 最適レギュレータ 節時不変型無限時間最適レギュレータ 状態フィードバックの可能な場合の無限時間問題における最適レギュレータについて確定系について説明する. ここで, レギュレータとは状態量をゼロにするようなコントローラのことである. なぜ, 無限時間問題のみを述べるかという理由は以下のとおりである. 有限時間の最適レギュレータ問題の場合の最適フィードバックゲインは微分方程式の解から構成される時間関数として表現される.
PowerPoint プレゼンテーション
 復習 ) 時系列のモデリング ~a. 離散時間モデル ~ y k + a 1 z 1 y k + + a na z n ay k = b 0 u k + b 1 z 1 u k + + b nb z n bu k y k = G z 1 u k = B(z 1 ) A(z 1 u k ) ARMA モデル A z 1 B z 1 = 1 + a 1 z 1 + + a na z n a = b 0
復習 ) 時系列のモデリング ~a. 離散時間モデル ~ y k + a 1 z 1 y k + + a na z n ay k = b 0 u k + b 1 z 1 u k + + b nb z n bu k y k = G z 1 u k = B(z 1 ) A(z 1 u k ) ARMA モデル A z 1 B z 1 = 1 + a 1 z 1 + + a na z n a = b 0
コロイド化学と界面化学
 環境表面科学講義 http://res.tagen.tohoku.ac.jp/~liquid/mura/kogi/kaimen/ E-mail: mura@tagen.tohoku.ac.jp 村松淳司 分散と凝集 ( 平衡論的考察! 凝集! van der Waals 力による相互作用! 分散! 静電的反発力 凝集 分散! 粒子表面の電位による反発 分散と凝集 考え方! van der Waals
環境表面科学講義 http://res.tagen.tohoku.ac.jp/~liquid/mura/kogi/kaimen/ E-mail: mura@tagen.tohoku.ac.jp 村松淳司 分散と凝集 ( 平衡論的考察! 凝集! van der Waals 力による相互作用! 分散! 静電的反発力 凝集 分散! 粒子表面の電位による反発 分散と凝集 考え方! van der Waals
