平成24年度高知県算数・数学
|
|
|
- かおり うばら
- 7 years ago
- Views:
Transcription
1 平成 4 年度高知県算数 数学思考オリンピック ( 中学校 ) 解答例 問題 1 (1) 1 L 字型の縦の和と横の和を求めると, 左の図のように, アからケまでのうちオだけが 回足したことになる オ =5 なので, ( 縦の和 )+( 横の和 )= =50 縦の和は,50 =5 とわかる アからオのうちア, イ, オが 1,9,5 のときだから, ウ + エ =5-(1+9+5) =10 よって, ウとエの組み合わせは,1 から 9 までで,1,9,5 を用いない合計 10 となる 数の組み合わせである したがって, 答えは と 8,3 と 7,4 と 6 である 答え と 8,3 と 7,4 と 6 1と同じように, 縦の和と横の和の合計は, オだけ 回足した合計オ= x なので, ( 縦の和 )+( 横の和 )= x = x +45 縦の和 = 横の和 = y なので, y x 45 y y x 45 y x 45 答え y x 45 3 オが 4 のとき, より縦に並んだ合計は, しかし, 他の には 1 から 9 の自然数しか入れることがで きないので, 合計が小数になることはあり得ない 4 よって, この場合はできない
2 () 1 左の図のように, 各辺の和を X,Y,Z にすると, X+Y+Z= ア + エ + キア =1, エ =, キ =3,X=Y=Z なので, X+Y+Z= X=51 X=17 よって, 各辺が 17 になる数の組み合わせを考えると答えのようになる 1 と同じように考えると, 各辺の和は, =60 よって,1 つの辺の和は 0 になる 1 ただし, 頂点を除くとなり合った つの数は入れかえが可能 ただし, 頂点を除くとなり合った つの数は入れかえが可能 数の和 17 数の和 0 3 3つの辺の和の合計は,3 3=69 69-( )=4 1,の考えから3つの頂点の合計が4とわかる 1から9のそれぞれ3 数を使って4になるのは, 7,8,9の組み合わせしかないので, それぞれの頂点は,7,8,9とわかる 1,と同じように組み合わせを考えると, 右のような答えになる ただし, 頂点を除くとなり合ったつの数は入れかえが可能 4 3つの頂点の数をA,B,Cとしたとき,3 辺の和の合計は, A+B+C=45+A+B+C 各辺が同じになる には, これが必ず 3 で割りきれなければならない 45 3=15 で 3 で割りきれるので, A+B+C も 3 で割りきれなければならない よって, 各頂点の合計は必ず 3 の倍数になる組み合わせでなければいけないことがわかった
3 問題 (1) 1 ABC の面積を a, ABF の面積を b とすると, a は AC を底辺とし, 頂点 B から垂線を引き, 高さとする三角形 の面積, b は AF を底辺とし, 頂点 B から垂線を引き, 高さとする三角形 の面積といえる 条件より,AC と AF は一直線上にあり,AC=AF である よって, a b また, BDF の面積を c としたとき, b は AB を底辺とし, 頂点 F から垂線を引き, 高さとする三角形 の面積, c は BD を底辺とし, 頂点 F から垂線を引き, 高さとする三角形 の面積といえる よって, b c ここで, a b c ということがわかる 左の図のように, BCD, CDE の面積を, それぞれ d, e とすると, 同様に考えて, a d e 同様に, ACE, AEF の面積を, それぞれ f, g とした ときも, a f g したがって, a b c d e f g となり, DEF= a b c d e f g = a a a a a a a = 7 a である 答え 7 倍 左の図のように, 問題に示されたそれぞれの点を G,H とする と,1 と同様の考えから, ABC と AGB は同じ長さの AC, AG を底辺とし, 同じ頂点 B までの垂線を高さとするので, ABC= AGB= a また, AGB, BGH, HGD の 3 つの三角形を考えた ときも同様で, 全て面積は等しく, a よって, ADG=3a また, 同様に, ADGと GDFを考えたときも, ADG= GDF=3 a, ADF= 6a とわかる 同じように, BDEも CEFも 6a となり, DEF= ABC+ ADF+ BDE+ CEF = a 6a 6a 6a =19 a である 答え 19 倍
4 3 左の図のように, 問題に示されたそれぞれの点を G,H,I,J とすると,1, と同様に, ABC= AGB= BIG= IJG= JDG= a なので, AGD= 4a また, AGD= GHD= HFD= 4a よって, ADF=1a 同じ考え方により, BDE= CEF=1a となり, DEF= ABC+ ADF+ BDE+ CEF = a 1a 1a 1a =37 a である 答え 37 倍 4 1~3をまとめて考えると, 1BC=AB,CE=BC,AF=CAのときは, (-1) 3 +1=7( 倍 ) ADFに含まれる ABCと同じ面積をもつ三角形の数 ADF BDE CEF ABC BC=AB,CE=BC,AF=CAのときは, 3 (3-1) 3+1=19( 倍 ) 3BC=3AB,CE=3BC,AF=3CAのときは, 4 (4-1) 3+1=37( 倍 ) このことから,BC=10AB,CE=10BC,AF=10CA のときは, 11 (11-1) 3+1=331( 倍 ) 答え 331 倍
5 () 1 (1) と同様の考えから, ABC= BPC= CQP= a である よって, BPQ= a また, ACD= DRA= ARS= b であるから, DRS= b したがって, BPQと DRSの面積の和は, a b になる 答え BPQ+ DRS= a b 下の図のように, BCD の面積を d, ABD を e とすると, これまでの考え方より, CQR= d ASP= e とわかる 四角形 PQRS= BPQ+ DRS+ CQR+ ASP+ 四角形 ABCD = a b d e + 四角形 ABCD = a b d e + 四角形 ABCD a b, d e は, それぞれ四角形 ABCDの面積に等しい よって, 四角形 PQRS= 四角形 ABCD+ 四角形 ABCD+ 四角形 ABCD したがって,5 倍である =5 四角形 ABCD 答え 5 倍
6 問題 3 (1) 7 番目は,6 番目の5-1=4 9 番目は,() の8 番目 -1=6-1=5 11 番目は,() の10 番目 -1=7-1=6 答え 7 番目 4 cm 9 番目 5 cm 11 番目 6 cm () 8 番目は,(1) の7 番目 +=4+=6 10 番目は,(1) の9 番目 +=5+=7 1 番目は,(1) の11 番目 +=6+=8 答え 8 番目 6 cm 10 番目 7 cm 1 番目 8 cm (3) 奇数番目を順に見てみると,1 番目 3 番目 5 番目 7 番目 9 番目 1 番の 1 cmから 番進むごとに 1 cmずつ増えている 1 cm cm 3 cm 4 cm 5 cm n 1 そのため, 奇数の n 番目の半径はcmと考えることができる また, 偶数番目を順に見てみると, 番目 4 番目 6 番目 8 番目 10 番目 と, 番の 3 cmから 番進むごとに 1 cmずつ増えている 3cm 4cm 5cm 6cm 7cm (1+) (+) (3+) (4+) (5+) n そのため, 偶数の n 番目の半径は cmと考えることができる
7 (4) (3) で考えたことより, 番目の半径は 17 cm 番目の半径は 16 cm 3 3 番目の半径は 18 cm よって, =67( cm ) 答え 67 cm (5) 円の中心間の距離をまとめると, 次のようになる 1 番目 ~3 番目 番目 ~4 番目 3 番目 ~5 番目 4 番目 ~6 番目 5 番目 ~7 番目 6 番目 ~8 番目 中心間 の距離 = = = = = =19 よって, n 番目と n 番目の距離は, n 7 といえる これが 111 cmとなるので, n n n 104 n 5 答え n 5
二等辺三角形の性質 (2) 次の図の の大きさを求めなさい () = P=Q P=R Q 68 R P (2) (3) 五角形 は正五角形 = F 50 F (4) = = (5) === = 80 2 二等辺三角形の頂角の外角を 底角を y で表すとき y を の式で表しなさい y 2-5-2
 三角形 四角形 二等辺三角形の性質 () 二等辺三角形と正三角形 二等辺三角形 2つの辺が等しい三角形( 定義 ) 二等辺三角形の性質定理 二等辺三角形の底角は等しい 定理 2 二等辺三角形の頂点の二等分線は 底辺を直角に2 等分する 正三角形 3 辺が等しい三角形 ( 定義 ) 次の図で 同じ印をつけた辺や角が等しいとき の大きさを求めなさい () (2) (3) 65 40 25 (4) (5)
三角形 四角形 二等辺三角形の性質 () 二等辺三角形と正三角形 二等辺三角形 2つの辺が等しい三角形( 定義 ) 二等辺三角形の性質定理 二等辺三角形の底角は等しい 定理 2 二等辺三角形の頂点の二等分線は 底辺を直角に2 等分する 正三角形 3 辺が等しい三角形 ( 定義 ) 次の図で 同じ印をつけた辺や角が等しいとき の大きさを求めなさい () (2) (3) 65 40 25 (4) (5)
【】 1次関数の意味
 FdText 数学 1 年 : 中学 塾用教材 http://www.fdtext.com/txt/ 直線と角 解答欄に次のものを書き入れよ 1 直線 AB 2 線分 AB 1 2 1 2 右図のように,3 点 A,B,Cがあるとき, 次の図形を書き入れよ 1 直線 AC 2 線分 BC - 1 - 次の図で a, b, c で示された角を A,B,C,D の文字を使って表せ a : b : c :
FdText 数学 1 年 : 中学 塾用教材 http://www.fdtext.com/txt/ 直線と角 解答欄に次のものを書き入れよ 1 直線 AB 2 線分 AB 1 2 1 2 右図のように,3 点 A,B,Cがあるとき, 次の図形を書き入れよ 1 直線 AC 2 線分 BC - 1 - 次の図で a, b, c で示された角を A,B,C,D の文字を使って表せ a : b : c :
学習の手順
 NAVI 2 MAP 3 ABCD EFGH D F ABCD EFGH CD EH A ABC A BC AD ABC DBA BC//DE x 4 a //b // c x BC//DE EC AD//EF//BC x y AD DB AE EC DE//BC 5 D E AB AC BC 12cm DE 10 AP=PB=BR AQ=CQ BS CS 11 ABCD 1 C AB M BD P
NAVI 2 MAP 3 ABCD EFGH D F ABCD EFGH CD EH A ABC A BC AD ABC DBA BC//DE x 4 a //b // c x BC//DE EC AD//EF//BC x y AD DB AE EC DE//BC 5 D E AB AC BC 12cm DE 10 AP=PB=BR AQ=CQ BS CS 11 ABCD 1 C AB M BD P
【】三平方の定理
 FdText 数学 3 年 : 中学 塾用教材 http://www.fdtext.com/txt/ 三角形 x を求めよ (3) (4) (5) (6) (3) (4) (5) (6) [ 解答 ] (1) 34 cm (2) 2 2 cm (3) 13cm (4) 2 7 cm (5) 5 3cm (6) 11 cm - 1 - 次の三角形, 台形の高さ (h) を求めよ (3) (4) (3)
FdText 数学 3 年 : 中学 塾用教材 http://www.fdtext.com/txt/ 三角形 x を求めよ (3) (4) (5) (6) (3) (4) (5) (6) [ 解答 ] (1) 34 cm (2) 2 2 cm (3) 13cm (4) 2 7 cm (5) 5 3cm (6) 11 cm - 1 - 次の三角形, 台形の高さ (h) を求めよ (3) (4) (3)
<4D F736F F D F90948A F835A E815B8E8E8CB189F090E05F81798D5A97B98CE38F4390B A2E646F63>
 07 年度大学入試センター試験解説 数学 Ⅰ A 第 問 9 のとき, 9 アイ 0 より, 0 であるから, 次に, 解答記号ウを含む等式の右辺を a とおくと, a a a 8 a a a 8 a これが 8 と等しいとき,( 部 ) 0 より, a 0 よって, a ウ ( 注 ) このとき, 8 9 (, より ) 7 エ, オカ また,より, これより, 9 であるから, 6 8 8 すなわち,
07 年度大学入試センター試験解説 数学 Ⅰ A 第 問 9 のとき, 9 アイ 0 より, 0 であるから, 次に, 解答記号ウを含む等式の右辺を a とおくと, a a a 8 a a a 8 a これが 8 と等しいとき,( 部 ) 0 より, a 0 よって, a ウ ( 注 ) このとき, 8 9 (, より ) 7 エ, オカ また,より, これより, 9 であるから, 6 8 8 すなわち,
STEP 数学 Ⅰ を解いてみた から直線 に下ろした垂線の足を H とすると, H in( 80 ) in より, S H in H 同様にして, S in, S in も成り立つ よって, S in 三角形の面積 ヘロンの公式 in in 辺の長
 STEP 数学 Ⅰ を解いてみた http://toitemit.ku.ne.jp 図形と計量 三角形の面積 三角形の面積 の面積を S とすると, S in in in 解説 から直線 に下ろした垂線の足を H とすると, H in より, S H in H STEP 数学 Ⅰ を解いてみた http://toitemit.ku.ne.jp から直線 に下ろした垂線の足を H とすると, H in(
STEP 数学 Ⅰ を解いてみた http://toitemit.ku.ne.jp 図形と計量 三角形の面積 三角形の面積 の面積を S とすると, S in in in 解説 から直線 に下ろした垂線の足を H とすると, H in より, S H in H STEP 数学 Ⅰ を解いてみた http://toitemit.ku.ne.jp から直線 に下ろした垂線の足を H とすると, H in(
比例・反比例 例題編 問題・解答
 中学数学比例 反比例の問題 関数 ( 移行措置による追加 ) 比例 変域 座標 比例のグラフ 比例の式 比例の文章問題 座標と変域 反比例とグラフ 反比例の式 反比例の文章問題 比例と反比例のグラフ * ページ表示 を 見開き でご覧いただきますと 問題とその 答えが見やすくなります * このテキストは家庭学習の補助教材としてのみご利用いただけま す その他 ( 問題の改変 商用など ) の利用はご遠慮くださいま
中学数学比例 反比例の問題 関数 ( 移行措置による追加 ) 比例 変域 座標 比例のグラフ 比例の式 比例の文章問題 座標と変域 反比例とグラフ 反比例の式 反比例の文章問題 比例と反比例のグラフ * ページ表示 を 見開き でご覧いただきますと 問題とその 答えが見やすくなります * このテキストは家庭学習の補助教材としてのみご利用いただけま す その他 ( 問題の改変 商用など ) の利用はご遠慮くださいま
埼玉県学力 学習状況調査 ( 中学校 ) 復習シート第 3 学年数学 組 番 号 名 前 ( 図形 を問う問題 ) 1 レベル 6~8(H28 埼玉県学力 学習状況調査 ) 答え 度 2 レベル 9 10 (H28 埼玉県学力 学習状況調査 ) 答え
 埼玉県学力 学習状況調査 ( 中学校 ) 復習シート第 3 学年数学 組 番 号 名 前 ( 図形 を問う問題 ) 1 レベル 6~8(H28 埼玉県学力 学習状況調査 ) 度 2 レベル 9 10 (H28 埼玉県学力 学習状況調査 ) 3 太郎さんは, 次の問題を考えています 問題右の図で,AO=BO,CO=DOならば, AC=BDであることを証明しなさい D A O B C このとき,(1)
埼玉県学力 学習状況調査 ( 中学校 ) 復習シート第 3 学年数学 組 番 号 名 前 ( 図形 を問う問題 ) 1 レベル 6~8(H28 埼玉県学力 学習状況調査 ) 度 2 レベル 9 10 (H28 埼玉県学力 学習状況調査 ) 3 太郎さんは, 次の問題を考えています 問題右の図で,AO=BO,CO=DOならば, AC=BDであることを証明しなさい D A O B C このとき,(1)
平成 30 年度 前期選抜学力検査問題 数学 ( 2 時間目 45 分 ) 受検番号氏名 注 意 1 問題は, 表と裏にあります 2 答えは, すべて解答欄に記入しなさい 1 次の (1)~(7) の問いに答えなさい (1) -3 (-6+4) を計算しなさい 表合計 2 次の (1)~(6) の問
 平成 30 年度 前期選抜学力検査問題 数学 ( 2 時間目 45 分 ) 受検番号氏名 注 意 1 問題は, 表と裏にあります 2 答えは, すべて解答欄に記入しなさい 1 次の (1)~(7) の問いに答えなさい (1) -3 (-6+4) を計算しなさい 表合計 2 次の (1)~(6) の問いに答えなさい 合計 (1) 関数 y = x 2 において,x の変域が -2 x 3 のとき, y
平成 30 年度 前期選抜学力検査問題 数学 ( 2 時間目 45 分 ) 受検番号氏名 注 意 1 問題は, 表と裏にあります 2 答えは, すべて解答欄に記入しなさい 1 次の (1)~(7) の問いに答えなさい (1) -3 (-6+4) を計算しなさい 表合計 2 次の (1)~(6) の問いに答えなさい 合計 (1) 関数 y = x 2 において,x の変域が -2 x 3 のとき, y
解答例 ( 河合塾グループ株式会社 KEI アドバンスが作成しました ) 特別奨学生試験 ( 平成 29 年 12 月 17 日実施 ) 数 学 数学 2= 工 経営情報 国際関係 人文 応用生物 生命健康科 現代教育学部 1 整理して (60 分 100 点 ) (2 3+ 2)(
 解答例 ( 河合塾グループ株式会社 KEI アドバンスが作成しました ) 特別奨学生試験 ( 平成 9 年 月 7 日実施 ) 数 学 数学 = 工 経営情報 国際関係 人文 応用生物 生命健康科 現代教育学部 整理して (60 分 00 点 ) 3+ ( 3+ )( 6 ) ( 与式 ) = = 6 + + 6 (3 + ) すなわち 5 6 (5 6 )(3+ ) = = 3 9 8 = 4 6
解答例 ( 河合塾グループ株式会社 KEI アドバンスが作成しました ) 特別奨学生試験 ( 平成 9 年 月 7 日実施 ) 数 学 数学 = 工 経営情報 国際関係 人文 応用生物 生命健康科 現代教育学部 整理して (60 分 00 点 ) 3+ ( 3+ )( 6 ) ( 与式 ) = = 6 + + 6 (3 + ) すなわち 5 6 (5 6 )(3+ ) = = 3 9 8 = 4 6
2014年度 センター試験・数学ⅡB
 第 問 解答解説のページへ [] O を原点とする座標平面において, 点 P(, q) を中心とする円 C が, 方程式 y 4 x で表される直線 l に接しているとする () 円 C の半径 r を求めよう 点 P を通り直線 l に垂直な直線の方程式は, y - ア ( x- ) + qなので, P イ から l に引いた垂線と l の交点 Q の座標は ( ( ウ + エ q ), 4 (
第 問 解答解説のページへ [] O を原点とする座標平面において, 点 P(, q) を中心とする円 C が, 方程式 y 4 x で表される直線 l に接しているとする () 円 C の半径 r を求めよう 点 P を通り直線 l に垂直な直線の方程式は, y - ア ( x- ) + qなので, P イ から l に引いた垂線と l の交点 Q の座標は ( ( ウ + エ q ), 4 (
20~22.prt
 [ 三クリア W] 辺が等しいことの証明 ( 円周角と弦の関係利用 ) の の二等分線がこの三角形の外接円と交わる点をそれぞれ とするとき 60 ならば であることを証明せよ 60 + + 0 + 0 80-60 60 から ゆえに 等しい長さの弧に対する弦の長さは等しいから [ 三クリア ] 方べきの定理 接線と弦のなす角と円周角を利用 線分 を直径とする円 があり 右の図のように の延長上の点
[ 三クリア W] 辺が等しいことの証明 ( 円周角と弦の関係利用 ) の の二等分線がこの三角形の外接円と交わる点をそれぞれ とするとき 60 ならば であることを証明せよ 60 + + 0 + 0 80-60 60 から ゆえに 等しい長さの弧に対する弦の長さは等しいから [ 三クリア ] 方べきの定理 接線と弦のなす角と円周角を利用 線分 を直径とする円 があり 右の図のように の延長上の点
Microsoft Word - スーパーナビ 第6回 数学.docx
 1 ⑴ 与式 =- 5 35 +14 35 =9 35 1 ⑵ 与式 =9-(-5)=9+5=14 1 ⑶ 与式 = 4(a-b)-3(5a-3b) = 8a-4b-15a+9b = -7a+5b 1 1 1 1 ⑷ 与式 =(²+ 1+1²)-{²+(-3+)+(-3) } 1 ⑷ 与式 =(²++1)-(²--6)=²++1-²++6=3+7 1 ⑸ 与式 = - ² + 16 = - +16
1 ⑴ 与式 =- 5 35 +14 35 =9 35 1 ⑵ 与式 =9-(-5)=9+5=14 1 ⑶ 与式 = 4(a-b)-3(5a-3b) = 8a-4b-15a+9b = -7a+5b 1 1 1 1 ⑷ 与式 =(²+ 1+1²)-{²+(-3+)+(-3) } 1 ⑷ 与式 =(²++1)-(²--6)=²++1-²++6=3+7 1 ⑸ 与式 = - ² + 16 = - +16
【FdData中間期末過去問題】中学数学1年(比例と反比例の応用/点の移動/速さ)
 FdDt 中間期末過去問題 中学数学 1 年 ( 比例と反比例の応用 / 点の移動 / 速さ ) http://www.fdtet.com/dt/ 水そうの問題 [ 問題 ](2 学期期末 ) 水が 200 l 入る水そうに, 毎分 8 l の割合で水を入れていく 水を入れはじめてから 分後の水の量を y l とするとき, 次の各問いに答えよ (1), y の関係を式に表せ (2) の変域を求めよ
FdDt 中間期末過去問題 中学数学 1 年 ( 比例と反比例の応用 / 点の移動 / 速さ ) http://www.fdtet.com/dt/ 水そうの問題 [ 問題 ](2 学期期末 ) 水が 200 l 入る水そうに, 毎分 8 l の割合で水を入れていく 水を入れはじめてから 分後の水の量を y l とするとき, 次の各問いに答えよ (1), y の関係を式に表せ (2) の変域を求めよ
平成 3 0 年度前期選抜学力検査 数学 ( 1 0 時 ~ 1 0 時 4 5 分, 4 5 分間 ) 問題用紙 注 意 1. 開始 の合図があるまで開いてはいけません 2. 答えは, すべて解答用紙に書きなさい 3. 問題は, からまでで, 6 ページにわたって印刷してあります 4. 開始 の合
 平成 3 0 年度前期選抜学力検査 数学 ( 1 0 時 ~ 1 0 時 4 5 分, 4 5 分間 ) 問題用紙 注 意 1. 開始 の合図があるまで開いてはいけません 2. 答えは, すべて解答用紙に書きなさい 3. 問題は, からまでで, 6 ページにわたって印刷してあります 4. 開始 の合図で, 解答用紙の決められた欄に受検番号を書きなさい 5. 問題を読むとき, 声を出してはいけません
平成 3 0 年度前期選抜学力検査 数学 ( 1 0 時 ~ 1 0 時 4 5 分, 4 5 分間 ) 問題用紙 注 意 1. 開始 の合図があるまで開いてはいけません 2. 答えは, すべて解答用紙に書きなさい 3. 問題は, からまでで, 6 ページにわたって印刷してあります 4. 開始 の合図で, 解答用紙の決められた欄に受検番号を書きなさい 5. 問題を読むとき, 声を出してはいけません
平成 31 年度 前期選抜学力検査問題 数学 ( 2 時間目 45 分 ) 受検番号氏名 注 意 1 問題は, 表と裏にあります 2 答えは, すべて解答欄に記入しなさい 1 次の (1)~(7) の問いに答えなさい (1) 3 (-2 2 ) を計算しなさい 表合計 2 次の (1)~(6) の問
 平成 1 年度 前期選抜学力検査問題 数学 ( 時間目 45 分 ) 受検番号氏名 注 意 1 問題は, 表と裏にあります 答えは, すべて解答欄に記入しなさい 1 次の ~(7) の問いに答えなさい (- ) を計算しなさい 表合計 次の ~(6) の問いに答えなさい 合計 関数 y = x のグラフについて正しいものを, 次のア ~ エからすべて選んで記号を書きなさい アイウエ グラフは原点を通る
平成 1 年度 前期選抜学力検査問題 数学 ( 時間目 45 分 ) 受検番号氏名 注 意 1 問題は, 表と裏にあります 答えは, すべて解答欄に記入しなさい 1 次の ~(7) の問いに答えなさい (- ) を計算しなさい 表合計 次の ~(6) の問いに答えなさい 合計 関数 y = x のグラフについて正しいものを, 次のア ~ エからすべて選んで記号を書きなさい アイウエ グラフは原点を通る
<8D828D5A838A817C A77425F91E6318FCD2E6D6364>
 4 1 平面上のベクトル 1 ベクトルとその演算 例題 1 ベクトルの相等 次の問いに答えよ. ⑴ 右の図 1 は平行四辺形 である., と等しいベクトルをいえ. ⑵ 右の図 2 の中で互いに等しいベクトルをいえ. ただし, すべてのマス目は正方形である. 解 ⑴,= より, =,= より, = ⑵ 大きさと向きの等しいものを調べる. a =d, c = f d e f 1 右の図の長方形 において,
4 1 平面上のベクトル 1 ベクトルとその演算 例題 1 ベクトルの相等 次の問いに答えよ. ⑴ 右の図 1 は平行四辺形 である., と等しいベクトルをいえ. ⑵ 右の図 2 の中で互いに等しいベクトルをいえ. ただし, すべてのマス目は正方形である. 解 ⑴,= より, =,= より, = ⑵ 大きさと向きの等しいものを調べる. a =d, c = f d e f 1 右の図の長方形 において,
PowerPoint プレゼンテーション
 平成 28 年度全国学力 学習状況調査 中学校数学 2 特徴的な問題 A 問題より A B C 垂線の作図方法について理解しているかどうか 3 関連問題 問題番号 問題の概要 全国正答率 三重県 公立 正答率 H24A 4 (1) 角の二等分線の作図の方法で作図された直線がもつ性質として, 正しい記述を選ぶ 58.2% 56.9% H26A 4 (2) 線分の垂直二等分線の作図の方法で作図される直線について,
平成 28 年度全国学力 学習状況調査 中学校数学 2 特徴的な問題 A 問題より A B C 垂線の作図方法について理解しているかどうか 3 関連問題 問題番号 問題の概要 全国正答率 三重県 公立 正答率 H24A 4 (1) 角の二等分線の作図の方法で作図された直線がもつ性質として, 正しい記述を選ぶ 58.2% 56.9% H26A 4 (2) 線分の垂直二等分線の作図の方法で作図される直線について,
埼玉県学力 学習状況調査 ( 中学校 ) 復習シート第 3 学年数学 組 番 号 名 前 ( 数と式 を問う問題 ) 1 次の計算をしなさい レベル 6~8 1 (27x-36y+18) (-9) 答え 2 15x 2 y 5xy 2 3 答え 2 次の各問いに答えなさい レベル 9 10 (1)
 埼玉県学力 学習状況調査 ( 中学校 ) 復習シート第 3 学年数学 組 番 号 名 前 ( 数と式 を問う問題 ) 1 次の計算をしなさい レベル 6~8 1 (27x-36y+18) (-9) 2 15x 2 y 5xy 2 3 2 次の各問いになさい レベル 9 10 (1) 次の等式を の中の文字について解きなさい c=5(a+b) a a= (2) 次の連立方程式を解きなさい 3x 5y
埼玉県学力 学習状況調査 ( 中学校 ) 復習シート第 3 学年数学 組 番 号 名 前 ( 数と式 を問う問題 ) 1 次の計算をしなさい レベル 6~8 1 (27x-36y+18) (-9) 2 15x 2 y 5xy 2 3 2 次の各問いになさい レベル 9 10 (1) 次の等式を の中の文字について解きなさい c=5(a+b) a a= (2) 次の連立方程式を解きなさい 3x 5y
1999年度 センター試験・数学ⅡB
 99 センター試験数学 Ⅱ 数学 B 問題 第 問 ( 必答問題 ) [] 関数 y cos3x の周期のうち正で最小のものはアイウ 解答解説のページへ 0 x 360 のとき, 関数 y cos3x において, y となる x はエ個, y となる x はオ 個ある また, y sin x と y cos3x のグラフより, 方程式 sin x cos3x は 0 x 360のときカ個の解をもつことがわかる
99 センター試験数学 Ⅱ 数学 B 問題 第 問 ( 必答問題 ) [] 関数 y cos3x の周期のうち正で最小のものはアイウ 解答解説のページへ 0 x 360 のとき, 関数 y cos3x において, y となる x はエ個, y となる x はオ 個ある また, y sin x と y cos3x のグラフより, 方程式 sin x cos3x は 0 x 360のときカ個の解をもつことがわかる
< 中 3 分野例題付き公式集 > (1)2 の倍数の判定法は 1 の位が 0 又は偶数 ( 例題 )1~5 までの 5 つの数字を使って 3 ケタの数をつくるとき 2 の倍数は何通りできるか (2)5 の倍数の判定法は 1 の位が 0 又は 5 ( 例題 )1~9 までの 9 個の数字を使って 3
 () の倍数の判定法は の位が 0 又は偶数 ~ までの つの数字を使って ケタの数をつくるとき の倍数は何通りできるか () の倍数の判定法は の位が 0 又は ~9 までの 9 個の数字を使って ケタの数をつくるとき の倍数は何通りできるか () の倍数の判定法は 下 ケタが 00 又は の倍数 ケタの数 8 が の倍数となるときの 最小の ケタの数は ( 解 ) 一の位の数は の 通り 十の位は一の位の数以外の
() の倍数の判定法は の位が 0 又は偶数 ~ までの つの数字を使って ケタの数をつくるとき の倍数は何通りできるか () の倍数の判定法は の位が 0 又は ~9 までの 9 個の数字を使って ケタの数をつくるとき の倍数は何通りできるか () の倍数の判定法は 下 ケタが 00 又は の倍数 ケタの数 8 が の倍数となるときの 最小の ケタの数は ( 解 ) 一の位の数は の 通り 十の位は一の位の数以外の
FdData中間期末数学2年
 中学中間 期末試験問題集( 過去問 ): 数学 年 方程式とグラフ [ 二元一次方程式 ax + by = c のグラフ ] [ 問題 ]( 後期中間 ) 二元一次方程式 x + y = 4 のグラフをかけ http://www.fdtext.com/dat/ [ 解答 ] 方程式の解を座標とする点の全体を, その方程式のグラフという 二元一次方程式 x + y = 4 の解は無数にあるが, 例えば,
中学中間 期末試験問題集( 過去問 ): 数学 年 方程式とグラフ [ 二元一次方程式 ax + by = c のグラフ ] [ 問題 ]( 後期中間 ) 二元一次方程式 x + y = 4 のグラフをかけ http://www.fdtext.com/dat/ [ 解答 ] 方程式の解を座標とする点の全体を, その方程式のグラフという 二元一次方程式 x + y = 4 の解は無数にあるが, 例えば,
2016年度 広島大・文系数学
 06 広島大学 ( 文系 ) 前期日程問題 解答解説のページへ a を正の定数とし, 座標平面上において, 円 C : x + y, 放物線 C : y ax + C 上の点 P (, ) を考える - におけるC の接線 l は点 Q( s, t) でC に接してい る 次の問いに答えよ () s, t および a を求めよ () C, l および y 軸で囲まれた部分の面積を求めよ () 円 C
06 広島大学 ( 文系 ) 前期日程問題 解答解説のページへ a を正の定数とし, 座標平面上において, 円 C : x + y, 放物線 C : y ax + C 上の点 P (, ) を考える - におけるC の接線 l は点 Q( s, t) でC に接してい る 次の問いに答えよ () s, t および a を求めよ () C, l および y 軸で囲まれた部分の面積を求めよ () 円 C
2014年度 九州大・文系数学
 014 九州大学 ( 文系 ) 前期日程問題 1 解答解説のページへ 座標平面上の直線 y =-1 を l 1, 直線 y = 1 を l とし, x 軸上の 点 O(0, 0), A ( a, 0) を考える 点 P( x, y) について, 次の条件を考える d(p, l1 ) PO かつ d(p, l ) PA 1 ただし, d( P, l) は点 P と直線 l の距離である (1) 条件
014 九州大学 ( 文系 ) 前期日程問題 1 解答解説のページへ 座標平面上の直線 y =-1 を l 1, 直線 y = 1 を l とし, x 軸上の 点 O(0, 0), A ( a, 0) を考える 点 P( x, y) について, 次の条件を考える d(p, l1 ) PO かつ d(p, l ) PA 1 ただし, d( P, l) は点 P と直線 l の距離である (1) 条件
平成 31 年度 豊島岡女子学園中学校 < 第 3 回 > 算数 くわしい解説 すぐる学習会 1 (1) イ ア ウ ア = = イ = 1 - = ウ = = (2) 工
 平成 年度 豊島岡女子学園中学校 < 第 回 > 算数 くわしい解説 すぐる学習会 () 2-4 8 5 7 9 4 4 = = 5 7 5 2 4 = - = 5 5 8 = = 5 9 40 (2) 工夫して解く方法もありますが, 普通に計算した方が早くできるのでは 7 5 24 28 0 29 + + + + = + + + + = 2 4 8 2 2 2 2 2 2 2 29 5- = なので,
平成 年度 豊島岡女子学園中学校 < 第 回 > 算数 くわしい解説 すぐる学習会 () 2-4 8 5 7 9 4 4 = = 5 7 5 2 4 = - = 5 5 8 = = 5 9 40 (2) 工夫して解く方法もありますが, 普通に計算した方が早くできるのでは 7 5 24 28 0 29 + + + + = + + + + = 2 4 8 2 2 2 2 2 2 2 29 5- = なので,
FdData中間期末数学3年
 中学中間 期末試験問題集( 過去問 ): 数学 3 年 http://www.fdtext.com/dat/ 相似比と面積比 [ 相似比と面積比 1] [ 問題 ](3 学期 ) 右の図の 2 つの円 A,B について, 次の各問いに答えよ (1) A,B の円の相似比を求めよ (2) A,B の円の面積をそれぞれ求めよ (3) 面積の比を求めよ (1) (2)A B (3) [ 解答 ](1) 7:10
中学中間 期末試験問題集( 過去問 ): 数学 3 年 http://www.fdtext.com/dat/ 相似比と面積比 [ 相似比と面積比 1] [ 問題 ](3 学期 ) 右の図の 2 つの円 A,B について, 次の各問いに答えよ (1) A,B の円の相似比を求めよ (2) A,B の円の面積をそれぞれ求めよ (3) 面積の比を求めよ (1) (2)A B (3) [ 解答 ](1) 7:10
1 1 3 ABCD ABD AC BD E E BD 1 : 2 (1) AB = AD =, AB AD = (2) AE = AB + (3) A F AD AE 2 = AF = AB + AD AF AE = t AC = t AE AC FC = t = (4) ABD ABCD 1 1
 ABCD ABD AC BD E E BD : () AB = AD =, AB AD = () AE = AB + () A F AD AE = AF = AB + AD AF AE = t AC = t AE AC FC = t = (4) ABD ABCD AB + AD AB + 7 9 AD AB + AD AB + 9 7 4 9 AD () AB sin π = AB = ABD AD
ABCD ABD AC BD E E BD : () AB = AD =, AB AD = () AE = AB + () A F AD AE = AF = AB + AD AF AE = t AC = t AE AC FC = t = (4) ABD ABCD AB + AD AB + 7 9 AD AB + AD AB + 9 7 4 9 AD () AB sin π = AB = ABD AD
2014年度 千葉大・医系数学
 04 千葉大学 ( 医系 ) 前期日程問題 解答解説のページへ 袋の中に, 赤玉が 3 個, 白玉が 7 個が入っている 袋から玉を無作為に つ取り出し, 色を確認してから, 再び袋に戻すという試行を行う この試行を N 回繰り返したときに, 赤玉を A 回 ( ただし 0 A N) 取り出す確率を p( N, A) とする このとき, 以下の問いに答えよ () 確率 p( N, A) を N と
04 千葉大学 ( 医系 ) 前期日程問題 解答解説のページへ 袋の中に, 赤玉が 3 個, 白玉が 7 個が入っている 袋から玉を無作為に つ取り出し, 色を確認してから, 再び袋に戻すという試行を行う この試行を N 回繰り返したときに, 赤玉を A 回 ( ただし 0 A N) 取り出す確率を p( N, A) とする このとき, 以下の問いに答えよ () 確率 p( N, A) を N と
<4D F736F F D F90948A F835A E815B8E8E8CB189F090E05F8E6C8D5A>
 06 年度大学入試センター試験解説 数学 Ⅱ B 第 問 () 8 より, 5 5 5 6 6 8 ア, イ また, 底の変換公式を用いると, log 7 log log 9 9 log 7 log ウエ, オ (), のグラフは, それぞれ = 89 = 右図のようになり, この つのグラフは 軸に関して対称 ここで, 0, のとき, と log カ のグラフが直線 に関して対称 であることから,
06 年度大学入試センター試験解説 数学 Ⅱ B 第 問 () 8 より, 5 5 5 6 6 8 ア, イ また, 底の変換公式を用いると, log 7 log log 9 9 log 7 log ウエ, オ (), のグラフは, それぞれ = 89 = 右図のようになり, この つのグラフは 軸に関して対称 ここで, 0, のとき, と log カ のグラフが直線 に関して対称 であることから,
学習指導要領
 (1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 絶対値の意味を理解し適切な処理することができる 例題 1-3 の絶対値をはずせ 展開公式 ( a + b ) ( a - b ) = a 2 - b 2 を利用して根号を含む分数の分母を有理化することができる 例題 5 5 + 2 の分母を有理化せよ 実数の整数部分と小数部分の表し方を理解している
(1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 絶対値の意味を理解し適切な処理することができる 例題 1-3 の絶対値をはずせ 展開公式 ( a + b ) ( a - b ) = a 2 - b 2 を利用して根号を含む分数の分母を有理化することができる 例題 5 5 + 2 の分母を有理化せよ 実数の整数部分と小数部分の表し方を理解している
数学 Ⅲ 無限等比級数の問題解答 問 1 次の無限級数の和を求めよ (1) (5) (2) (6) (7) (3) ( 解 )(1) 初項 < 公比 < の無限等比級数より収束し (4) (2) (3) その和は ( 答 ) であるから 初項 < 公比 となっている よって 収束し その和は よって
 問 1 次の無限級数の和を求めよ (1) (5) (2) (6) (7) (3) ( 解 )(1) 初項 < 公比 < の無限等比級数より収束し (4) (2) (3) その和は であるから 初項 < 公比 となっている よって 収束し その和は よって 収束し その和は < の無限等比級数 であるから 初項 < 公比
問 1 次の無限級数の和を求めよ (1) (5) (2) (6) (7) (3) ( 解 )(1) 初項 < 公比 < の無限等比級数より収束し (4) (2) (3) その和は であるから 初項 < 公比 となっている よって 収束し その和は よって 収束し その和は < の無限等比級数 であるから 初項 < 公比
1990 IMO 1990/1/15 1:00-4:00 1 N N N 1, N 1 N 2, N 2 N 3 N 3 2 x x + 52 = 3 x x , A, B, C 3,, A B, C 2,,,, 7, A, B, C
 0 9 (1990 1999 ) 10 (2000 ) 1900 1994 1995 1999 2 SAT ACT 1 1990 IMO 1990/1/15 1:00-4:00 1 N 1990 9 N N 1, N 1 N 2, N 2 N 3 N 3 2 x 2 + 25x + 52 = 3 x 2 + 25x + 80 3 2, 3 0 4 A, B, C 3,, A B, C 2,,,, 7,
0 9 (1990 1999 ) 10 (2000 ) 1900 1994 1995 1999 2 SAT ACT 1 1990 IMO 1990/1/15 1:00-4:00 1 N 1990 9 N N 1, N 1 N 2, N 2 N 3 N 3 2 x 2 + 25x + 52 = 3 x 2 + 25x + 80 3 2, 3 0 4 A, B, C 3,, A B, C 2,,,, 7,
S02 1 図において = =とする このとき = であることを証明せよ と において = 1 = 2 辺 は共通 より 3 辺 (3 組の辺 ) がそれぞれ等しい よって 合同な三角形の対応する角の大きさは等しい ゆえに = である
 S01 1 図において = =とする このとき であることを証明せよ と において = 1 = 2 辺 は共通 3 1 2 3 より 3 辺 (3 組の辺 ) がそれぞれ等しい よって である S02 1 図において = =とする このとき = であることを証明せよ と において = 1 = 2 辺 は共通 3 1 2 3 より 3 辺 (3 組の辺 ) がそれぞれ等しい よって 合同な三角形の対応する角の大きさは等しい
S01 1 図において = =とする このとき であることを証明せよ と において = 1 = 2 辺 は共通 3 1 2 3 より 3 辺 (3 組の辺 ) がそれぞれ等しい よって である S02 1 図において = =とする このとき = であることを証明せよ と において = 1 = 2 辺 は共通 3 1 2 3 より 3 辺 (3 組の辺 ) がそれぞれ等しい よって 合同な三角形の対応する角の大きさは等しい
05 年度センター試験数学 ⅡB () において,cos q 0 であるから,P ( cos q, sin q) より, 直線 OP を表す方程式は y sin q sin q x cos q cos q x すなわち, (sin q) x - (cos q) y 0 ( ) ク 点 O,P,Q が
 05 年度大学入試センター試験解説 数学 ⅡB 第 問 []() 点間の距離の公式から, OP ( cos q ) + ( sin q ) ( cos q + sin q ) ア PQ { ( cos q + cos 7q ) - cos q } + { ( sin q + sin 7q ) - sin q } cos q + sin q 7 7 イ である また, OQ ( cos q + cos
05 年度大学入試センター試験解説 数学 ⅡB 第 問 []() 点間の距離の公式から, OP ( cos q ) + ( sin q ) ( cos q + sin q ) ア PQ { ( cos q + cos 7q ) - cos q } + { ( sin q + sin 7q ) - sin q } cos q + sin q 7 7 イ である また, OQ ( cos q + cos
埼玉県学力 学習状況調査 ( 中学校 ) 復習シート第 1 学年数学 組 番 号 名 前 ( 数と計算 を問う問題) 1 次の計算をしなさい レベル4~6 (H26 全国学力 学習状況調査 1 (1)) (1) (2) 答え 答え 2 次の計算をしなさい レベル 7 8 (1) (2)
 埼玉県学力 学習状況調査 ( 中学校 ) 復習シート第 1 学年数学 組 番 号 名 前 ( 数と計算 を問う問題) 1 次の計算をしなさい レベル4~6 (H26 全国学力 学習状況調査 1 (1)) (1) (2) 2 次の計算をしなさい レベル 7 8 (1) (2) 0.7 3 3 次の問題になさい レベル 7 8 ア ~ エの中から 計算の結果が より大きくなる式を 2 つ選びましょう ア
埼玉県学力 学習状況調査 ( 中学校 ) 復習シート第 1 学年数学 組 番 号 名 前 ( 数と計算 を問う問題) 1 次の計算をしなさい レベル4~6 (H26 全国学力 学習状況調査 1 (1)) (1) (2) 2 次の計算をしなさい レベル 7 8 (1) (2) 0.7 3 3 次の問題になさい レベル 7 8 ア ~ エの中から 計算の結果が より大きくなる式を 2 つ選びましょう ア
【FdData中間期末過去問題】中学数学2年(連立方程式計算/加減法/代入法/係数決定)
 FdData 中間期末 : 中学数学 年 : 連立方程式計算 [ 元 1 次方程式 / 加減法 / 代入法 / 加減法と代入法 / 分数などのある連立方程式 / A=B=C, 元連立方程式 / 係数の決定 ] [ 数学 年 pdf ファイル一覧 ] 元 1 次方程式 次の方程式ア~カの中から, 元 1 次方程式をすべて選べ ア y = 6 イ x y = 5 ウ xy = 1 エ x + 5 = 9
FdData 中間期末 : 中学数学 年 : 連立方程式計算 [ 元 1 次方程式 / 加減法 / 代入法 / 加減法と代入法 / 分数などのある連立方程式 / A=B=C, 元連立方程式 / 係数の決定 ] [ 数学 年 pdf ファイル一覧 ] 元 1 次方程式 次の方程式ア~カの中から, 元 1 次方程式をすべて選べ ア y = 6 イ x y = 5 ウ xy = 1 エ x + 5 = 9
高ゼミサポSelectⅢ数学Ⅰ_解答.indd
 数と式 ⑴ 氏点00 次の式を展開せよ ( 各 6 点 ) ⑴ (a-)(a -a+) ⑵ (x+y+)(x+y-5) 次の式を因数分解せよ (⑴⑵ 各 6 点, ⑶⑷ 各 8 点 ) ⑴ x y+x -x-6y ⑵ x -x - ⑶ a +5b ⑷ (x+y+z+)(x+)+yz 数と式 ⑵ 氏点00 次の問いに答えよ ( 各 6 点 ) ⑴ 次の循環小数を分数で表せ. a-5 = ⑵ 次の等式を満たす実数
数と式 ⑴ 氏点00 次の式を展開せよ ( 各 6 点 ) ⑴ (a-)(a -a+) ⑵ (x+y+)(x+y-5) 次の式を因数分解せよ (⑴⑵ 各 6 点, ⑶⑷ 各 8 点 ) ⑴ x y+x -x-6y ⑵ x -x - ⑶ a +5b ⑷ (x+y+z+)(x+)+yz 数と式 ⑵ 氏点00 次の問いに答えよ ( 各 6 点 ) ⑴ 次の循環小数を分数で表せ. a-5 = ⑵ 次の等式を満たす実数
Taro-1803 平行線と線分の比
 平行線と線分の比 1 4 平行線と線分の比 ポイント : 平行な直線がある つの三角形の線分の比について考える 証明 右の図で で とする (1) は と相似である これを証明しなさい と において から 平行線の ( ) は等しいから 9c = ( ) 1 = ( ) 1, より ( ) がそれぞれ等しいので 相似な図形になるので相似比を利用して () : の相似比を求めなさい 対応する線分の長さを求めることができる
平行線と線分の比 1 4 平行線と線分の比 ポイント : 平行な直線がある つの三角形の線分の比について考える 証明 右の図で で とする (1) は と相似である これを証明しなさい と において から 平行線の ( ) は等しいから 9c = ( ) 1 = ( ) 1, より ( ) がそれぞれ等しいので 相似な図形になるので相似比を利用して () : の相似比を求めなさい 対応する線分の長さを求めることができる
FdData中間期末数学2年
 中学中間 期末試験問題集( 過去問 ): 数学 2 年 対頂角 同位角と錯角 [ 対頂角 ] [ 問題 ](2 学期中間 ) http://www.fdtext.com/dat/ 右の図で a と c の位置にある角を ( ) という [ 解答 ] 対頂角 右の図で, a= c であることを説明せよ [ 解答 ] a+ b=180, c+ b=180 なので, a+ b= c+ b よって, a=
中学中間 期末試験問題集( 過去問 ): 数学 2 年 対頂角 同位角と錯角 [ 対頂角 ] [ 問題 ](2 学期中間 ) http://www.fdtext.com/dat/ 右の図で a と c の位置にある角を ( ) という [ 解答 ] 対頂角 右の図で, a= c であることを説明せよ [ 解答 ] a+ b=180, c+ b=180 なので, a+ b= c+ b よって, a=
2017年度 長崎大・医系数学
 07 長崎大学 ( 医系 ) 前期日程問題 解答解説のページへ 以下の問いに答えよ () 0 のとき, si + cos の最大値と最小値, およびそのときの の値 をそれぞれ求めよ () e を自然対数の底とする > eの範囲において, 関数 y を考える この両 辺の対数を について微分することにより, y は減少関数であることを示せ また, e< < bのとき, () 数列 { } b の一般項が,
07 長崎大学 ( 医系 ) 前期日程問題 解答解説のページへ 以下の問いに答えよ () 0 のとき, si + cos の最大値と最小値, およびそのときの の値 をそれぞれ求めよ () e を自然対数の底とする > eの範囲において, 関数 y を考える この両 辺の対数を について微分することにより, y は減少関数であることを示せ また, e< < bのとき, () 数列 { } b の一般項が,
数論入門
 数学のかたち 共線問題と共点問題 Masashi Sanae 1 テーマ メネラウスの定理 チェバの定理から 共線問題と共点問題について考える 共線 点が同一直線上に存在 共点 直線が 1 点で交わる 2 内容 I. メネラウスの定理 1. メネラウスの定理とその証明 2. メネラウスの定理の応用 II. 3. チェバの定理とその証明 メネラウスの定理 チェバの定理の逆 1. メネラウスの定理の逆
数学のかたち 共線問題と共点問題 Masashi Sanae 1 テーマ メネラウスの定理 チェバの定理から 共線問題と共点問題について考える 共線 点が同一直線上に存在 共点 直線が 1 点で交わる 2 内容 I. メネラウスの定理 1. メネラウスの定理とその証明 2. メネラウスの定理の応用 II. 3. チェバの定理とその証明 メネラウスの定理 チェバの定理の逆 1. メネラウスの定理の逆
図形と証明 1 対頂角 a = b ( 証明 ) a+ c= 180 なので a = c b+ c= 180 なので b = c 1 2 1,2 から a = b a と b のように 交わる直線の向かい合う角を対頂角といいます 等しいことは 当然のように見えますが 証明とは
 図形と証明 1 対頂角 a = b a+ c= 180 なので a = 180 - c b+ c= 180 なので b = 180 - c 1 2 1,2 から a = b a と b のように 交わる直線の向かい合う角を対頂角といいます 等しいことは 当然のように見えますが 証明とは それを筋道立てて説明することです a も b も 角度を使った式で 同じ式になる ということを述べるのが この証明です
図形と証明 1 対頂角 a = b a+ c= 180 なので a = 180 - c b+ c= 180 なので b = 180 - c 1 2 1,2 から a = b a と b のように 交わる直線の向かい合う角を対頂角といいます 等しいことは 当然のように見えますが 証明とは それを筋道立てて説明することです a も b も 角度を使った式で 同じ式になる ということを述べるのが この証明です
Math-Aquarium 例題 図形と計量 図形と計量 1 直角三角形と三角比 P 木の先端を P, 根元を Q とする A 地点の目の位置 A' から 木の先端への仰角が 30,A から 7m 離れた AQB=90 と なる B 地点の目の位置 B' から木の先端への仰角が 45 であ るとき,
 図形と計量 直角三角形と三角比 P 木の先端を P, 根元を Q とする 地点の目の位置 ' から 木の先端への仰角が 0, から 7m 離れた Q=90 と なる 地点の目の位置 ' から木の先端への仰角が であ るとき, 木の高さを求めよ ただし, 目の高さを.m とし, Q' を右の図のように定める ' 0 Q' '.m Q 7m 要点 PQ PQ PQ' =x とおき,' Q',' Q' を
図形と計量 直角三角形と三角比 P 木の先端を P, 根元を Q とする 地点の目の位置 ' から 木の先端への仰角が 0, から 7m 離れた Q=90 と なる 地点の目の位置 ' から木の先端への仰角が であ るとき, 木の高さを求めよ ただし, 目の高さを.m とし, Q' を右の図のように定める ' 0 Q' '.m Q 7m 要点 PQ PQ PQ' =x とおき,' Q',' Q' を
a (a + ), a + a > (a + ), a + 4 a < a 4 a,,, y y = + a y = + a, y = a y = ( + a) ( x) + ( a) x, x y,y a y y y ( + a : a ) ( a : a > ) y = (a + ) y = a
 [] a x f(x) = ( + a)( x) + ( a)x f(x) = ( a + ) x + a + () x f(x) a a + a > a + () x f(x) a (a + ) a x 4 f (x) = ( + a) ( x) + ( a) x = ( a + a) x + a + = ( a + ) x + a +, () a + a f(x) f(x) = f() = a
[] a x f(x) = ( + a)( x) + ( a)x f(x) = ( a + ) x + a + () x f(x) a a + a > a + () x f(x) a (a + ) a x 4 f (x) = ( + a) ( x) + ( a) x = ( a + a) x + a + = ( a + ) x + a +, () a + a f(x) f(x) = f() = a
p tn tn したがって, 点 の 座標は p p tn tn tn また, 直線 l と直線 p の交点 の 座標は p p tn p tn よって, 点 の座標 (, ) は p p, tn tn と表され p 4p p 4p 4p tn tn tn より, 点 は放物線 4 p 上を動くこと
 567_ 次曲線の三角関数による媒介変数表示 次曲線の三角関数による媒介変数表示 次曲線 ( 放物線 楕円 双曲線 ) の標準形の, についての方程式と, 三角関数による媒介変数表示は次のように対応している.. 放物線 () 4 p (, ) ( ptn, ptn ) (). 楕円. 双曲線 () () (, p p ), tn tn (, ) ( cos, sin ) (, ), tn cos (,
567_ 次曲線の三角関数による媒介変数表示 次曲線の三角関数による媒介変数表示 次曲線 ( 放物線 楕円 双曲線 ) の標準形の, についての方程式と, 三角関数による媒介変数表示は次のように対応している.. 放物線 () 4 p (, ) ( ptn, ptn ) (). 楕円. 双曲線 () () (, p p ), tn tn (, ) ( cos, sin ) (, ), tn cos (,
< D8C6082CC90AB8EBF816989A B A>
 数 Ⅰ 図形の性質 ( 黄色チャート ) () () () 点 は辺 を : に外分するから :=: :=: であるから :=: == () 点 は辺 を : に内分するから :=:=: = + %= また, 点 は辺 を : に外分するから :=:=: == =+=+= 直線 は の二等分線であるから :=: 直線 は の二等分線であるから :=: 一方, であるから, から, から :=: :=:
数 Ⅰ 図形の性質 ( 黄色チャート ) () () () 点 は辺 を : に外分するから :=: :=: であるから :=: == () 点 は辺 を : に内分するから :=:=: = + %= また, 点 は辺 を : に外分するから :=:=: == =+=+= 直線 は の二等分線であるから :=: 直線 は の二等分線であるから :=: 一方, であるから, から, から :=: :=:
3 1 1 BCA ACD HP A AB BC ABC ONP x AM, CN x 30 DM DM! CN CN AM AMD 10 1 AB AC
 3 BCA ACD HP A AB BC ABC ONP x AM, CN x 30 DM DM!CN CN AM AMD 0 AB AC AMD3AMB3030 x x x 0,60,50,30,30 ABCD AC, BD ABD, DBC, BCA, ACD BDA x BDC 80 AB AD ABD sin x sin AD AC ACD sin sin x AC ABC sin AB sin
3 BCA ACD HP A AB BC ABC ONP x AM, CN x 30 DM DM!CN CN AM AMD 0 AB AC AMD3AMB3030 x x x 0,60,50,30,30 ABCD AC, BD ABD, DBC, BCA, ACD BDA x BDC 80 AB AD ABD sin x sin AD AC ACD sin sin x AC ABC sin AB sin
 28 27 8 4 10 17 2 27 8 7 14 00 1 27 8 14 15 00 2 27 8 21 15 00 1 4 5 2 6 1 27 ABCD 6 2 2 5 5 8% 108 100 49 2 13 140 22 12 7 153-8501 19 23 03-5478-1225 27 8 4 (1) (2) (3) (1) (2) (3) (4) (5) (6) (7) (8)
28 27 8 4 10 17 2 27 8 7 14 00 1 27 8 14 15 00 2 27 8 21 15 00 1 4 5 2 6 1 27 ABCD 6 2 2 5 5 8% 108 100 49 2 13 140 22 12 7 153-8501 19 23 03-5478-1225 27 8 4 (1) (2) (3) (1) (2) (3) (4) (5) (6) (7) (8)
測量士補 重要事項 応用測量 点高法による土量計算
 点高法による土量計算 < 試験合格へのポイント > 点高法による土量計算は H9 年度を最後にその出題はない 特に三角形法を用いた土量計算は H 年度が最後の出題であり 26 年ぶりの出題となった 特に公式を覚える必要はないが計算方法を理解することが大切である 1. 点高法による土量計算の方法 点高法による土量計算とは 盛土 ( 又は切土 ) する敷地を長方形 ( 又は三角形 ) に分割し その交点の高さを測り計画高との高低差を求め
点高法による土量計算 < 試験合格へのポイント > 点高法による土量計算は H9 年度を最後にその出題はない 特に三角形法を用いた土量計算は H 年度が最後の出題であり 26 年ぶりの出題となった 特に公式を覚える必要はないが計算方法を理解することが大切である 1. 点高法による土量計算の方法 点高法による土量計算とは 盛土 ( 又は切土 ) する敷地を長方形 ( 又は三角形 ) に分割し その交点の高さを測り計画高との高低差を求め
2015-2017年度 2次数学セレクション(複素数)解答解説
 05 次数学セレクション解答解説 [ 筑波大 ] ( + より, 0 となり, + から, ( (,, よって, の描く図形 C は, 点 を中心とし半径が の円である すなわち, 原 点を通る円となる ( は虚数, は正の実数より, である さて, w ( ( とおくと, ( ( ( w ( ( ( ここで, w は純虚数より, は純虚数となる すると, の描く図形 L は, 点 を通り, 点 と点
05 次数学セレクション解答解説 [ 筑波大 ] ( + より, 0 となり, + から, ( (,, よって, の描く図形 C は, 点 を中心とし半径が の円である すなわち, 原 点を通る円となる ( は虚数, は正の実数より, である さて, w ( ( とおくと, ( ( ( w ( ( ( ここで, w は純虚数より, は純虚数となる すると, の描く図形 L は, 点 を通り, 点 と点
FdData理科3年
 FdData 中間期末 : 中学理科 3 年 : 仕事 [ 仕事の原理 : 斜面 ] [ 仕事の原理 引く力 ] [ 問題 ](2 学期期末 ) 図のような斜面を使って質量 35kg の物体を 3m の高さまで引き上げた ただし, ひもの重さ, 斜面や滑車の摩擦はないものとする また,100g の物体を引き上げるのに必要な力を 1N とする (1) このとき, 物体がされた仕事はいくらか (2) 図のとき,
FdData 中間期末 : 中学理科 3 年 : 仕事 [ 仕事の原理 : 斜面 ] [ 仕事の原理 引く力 ] [ 問題 ](2 学期期末 ) 図のような斜面を使って質量 35kg の物体を 3m の高さまで引き上げた ただし, ひもの重さ, 斜面や滑車の摩擦はないものとする また,100g の物体を引き上げるのに必要な力を 1N とする (1) このとき, 物体がされた仕事はいくらか (2) 図のとき,
FdData中間期末数学1年
 中学中間 期末試験問題集 ( 過去問 ): 数学 年 四則をふくむ式の計算 http://www.fdtext.com/dat/ [ 加減と乗除が混じった計算 ] [ 問題 ]( 前期中間 ) 9+8 (-) [ 解答 ]-7 加減と乗除が混じった式では, 乗除を先に計算する ( +-の順で計算) 9+8 (-) では,8 (-) の部分を先に計算 9+8 (-)9--7 [ 問題 ]( 学期期末
中学中間 期末試験問題集 ( 過去問 ): 数学 年 四則をふくむ式の計算 http://www.fdtext.com/dat/ [ 加減と乗除が混じった計算 ] [ 問題 ]( 前期中間 ) 9+8 (-) [ 解答 ]-7 加減と乗除が混じった式では, 乗除を先に計算する ( +-の順で計算) 9+8 (-) では,8 (-) の部分を先に計算 9+8 (-)9--7 [ 問題 ]( 学期期末
【FdData中間期末過去問題】中学数学1年(負の数/数直線/絶対値/数の大小)
 FdData 中間期末 : 中学数学 年 : 正負の数 [ 正の数 負の数 / 数直線 / 正の数 負の数で量を表す / 絶対値 / 数の大小 / 数直線を使って ] [ 数学 年 pdf ファイル一覧 ] 正の数 負の数 [ 負の数 ] 次の文章中の ( ) に適語を入れよ () +5 や+8 のような 0 より大きい数を ( ) という () - や-7 のような 0 より小さい数を ( ) という
FdData 中間期末 : 中学数学 年 : 正負の数 [ 正の数 負の数 / 数直線 / 正の数 負の数で量を表す / 絶対値 / 数の大小 / 数直線を使って ] [ 数学 年 pdf ファイル一覧 ] 正の数 負の数 [ 負の数 ] 次の文章中の ( ) に適語を入れよ () +5 や+8 のような 0 より大きい数を ( ) という () - や-7 のような 0 より小さい数を ( ) という
2016年度 九州大・理系数学
 0 九州大学 ( 理系 ) 前期日程問題 解答解説のページへ 座標平面上の曲線 C, C をそれぞれ C : y logx ( x > 0), C : y ( x-)( x- a) とする ただし, a は実数である を自然数とするとき, 曲線 C, C が 点 P, Q で交わり, P, Q の x 座標はそれぞれ, + となっている また, 曲線 C と直線 PQ で囲まれた領域の面積を S,
0 九州大学 ( 理系 ) 前期日程問題 解答解説のページへ 座標平面上の曲線 C, C をそれぞれ C : y logx ( x > 0), C : y ( x-)( x- a) とする ただし, a は実数である を自然数とするとき, 曲線 C, C が 点 P, Q で交わり, P, Q の x 座標はそれぞれ, + となっている また, 曲線 C と直線 PQ で囲まれた領域の面積を S,
1 (1) vs. (2) (2) (a)(c) (a) (b) (c) 31 2 (a) (b) (c) LENCHAR
 () 601 1 () 265 OK 36.11.16 20 604 266 601 30.4.5 (1) 91621 3037 (2) 20-12.2 20-13 (3) ex. 2540-64 - LENCHAR 1 (1) vs. (2) (2) 605 50.2.13 41.4.27 10 10 40.3.17 (a)(c) 2 1 10 (a) (b) (c) 31 2 (a) (b) (c)
() 601 1 () 265 OK 36.11.16 20 604 266 601 30.4.5 (1) 91621 3037 (2) 20-12.2 20-13 (3) ex. 2540-64 - LENCHAR 1 (1) vs. (2) (2) 605 50.2.13 41.4.27 10 10 40.3.17 (a)(c) 2 1 10 (a) (b) (c) 31 2 (a) (b) (c)
頻出問題の解法 Check Exercize 1. 四角形 ABCD において 辺 AB, BC,CD, DA の中点をそれぞれ P,Q, R, S とすると 四角形 PQRS は平行四辺形であることを証明せよ 2. AB=2, BC =4,CA=3 である ABC において 辺 BC の中点を M
 第 4 章平面図形 1. 三角形の性質 1-1 平行線と線分の比 平行線と線分の比一般に 平行線において次の定理が成立する 頻出問題の ABC の辺 AB, AC またはその延長上の点を それぞれ D, E とするとき DE BC AD AB = AE DE (= AC BC ) DE BC AD DB = AE EC 中点連結定理上の定理において D, E を辺 AB, AC の中点にとる ABC
第 4 章平面図形 1. 三角形の性質 1-1 平行線と線分の比 平行線と線分の比一般に 平行線において次の定理が成立する 頻出問題の ABC の辺 AB, AC またはその延長上の点を それぞれ D, E とするとき DE BC AD AB = AE DE (= AC BC ) DE BC AD DB = AE EC 中点連結定理上の定理において D, E を辺 AB, AC の中点にとる ABC
2016年度 京都大・文系数学
 06 京都大学 ( 文系 ) 前期日程問題 解答解説のページへ xy 平面内の領域の面積を求めよ x + y, x で, 曲線 C : y= x + x -xの上側にある部分 -- 06 京都大学 ( 文系 ) 前期日程問題 解答解説のページへ ボタンを押すと あたり か はずれ のいずれかが表示される装置がある あたり の表示される確率は毎回同じであるとする この装置のボタンを 0 回押したとき,
06 京都大学 ( 文系 ) 前期日程問題 解答解説のページへ xy 平面内の領域の面積を求めよ x + y, x で, 曲線 C : y= x + x -xの上側にある部分 -- 06 京都大学 ( 文系 ) 前期日程問題 解答解説のページへ ボタンを押すと あたり か はずれ のいずれかが表示される装置がある あたり の表示される確率は毎回同じであるとする この装置のボタンを 0 回押したとき,
2019年度 千葉大・理系数学
 9 千葉大学 ( 理系 ) 前期日程問題 解答解説のページへ a, a とし, のとき, a+ a + a - として数列 { a } () のとき a+ a a a - が成り立つことを証明せよ () åai aaa + が成り立つような自然数 を求めよ i を定める -- 9 千葉大学 ( 理系 ) 前期日程問題 解答解説のページへ 三角形 ABC は AB+ AC BCを満たしている また,
9 千葉大学 ( 理系 ) 前期日程問題 解答解説のページへ a, a とし, のとき, a+ a + a - として数列 { a } () のとき a+ a a a - が成り立つことを証明せよ () åai aaa + が成り立つような自然数 を求めよ i を定める -- 9 千葉大学 ( 理系 ) 前期日程問題 解答解説のページへ 三角形 ABC は AB+ AC BCを満たしている また,
MultiWriter 5650F 活用マニュアル
 1 2 3 4 5 6 7 8 4 9 10 11 12 1 2 3 4 5 6 7 8 9 10 11 12 13 1 2 3 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 1 2 3 a b c 32 33 34 35 2 ± 36 2 2 ± * 37 * 38 39 40 41 42 43 44 45 46 47 1 2 @:./
1 2 3 4 5 6 7 8 4 9 10 11 12 1 2 3 4 5 6 7 8 9 10 11 12 13 1 2 3 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 1 2 3 a b c 32 33 34 35 2 ± 36 2 2 ± * 37 * 38 39 40 41 42 43 44 45 46 47 1 2 @:./
紙を折る < 問題 > 長方形の紙を折る このとき 相似形はいくつできるだろうか? 2 個 固定固定固定 固定 2 個 2 個 固定 固定 3 個 3 個 固定 3 個 4 個 4 個
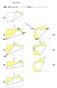 紙を折る < 問題 > 長方形の紙を折る このとき 相似形はいくつできるだろうか? 個 固定固定固定 固定 個 個 固定 固定 個 個 固定 個 4 個 4 個 * 隣り合う辺を結んで折るとき 最大 個 * 向かい合う辺を結んで折るとき 最大 4 個 < 問題 > 固定される場合 その位置はどこか? そのときの相似比はいくらか? 返上を移動する場合 その範囲はどうか? 合同になるときはあるか? それはどんなときか?
紙を折る < 問題 > 長方形の紙を折る このとき 相似形はいくつできるだろうか? 個 固定固定固定 固定 個 個 固定 固定 個 個 固定 個 4 個 4 個 * 隣り合う辺を結んで折るとき 最大 個 * 向かい合う辺を結んで折るとき 最大 4 個 < 問題 > 固定される場合 その位置はどこか? そのときの相似比はいくらか? 返上を移動する場合 その範囲はどうか? 合同になるときはあるか? それはどんなときか?
【FdData中間期末過去問題】中学数学3年(二次方程式応用/係数/数/面積・体積/動点)
 FdData 中間期末 : 中学数学 3 年 : 二次方程式応用 [ 係数の決定 / 整数の問題 / 面積 体積の問題 / 動点の問題 ] [ 数学 3 年 pdf ファイル一覧 ] 係数の決定 [ 係数 a を求める ] 二次方程式 + a = 0 の 1 つの解が 3 であるとき, a の値を求めよ また, もう 1 つの解を求めよ a = = a = 3 = 1 + a = 0 1の解の 1
FdData 中間期末 : 中学数学 3 年 : 二次方程式応用 [ 係数の決定 / 整数の問題 / 面積 体積の問題 / 動点の問題 ] [ 数学 3 年 pdf ファイル一覧 ] 係数の決定 [ 係数 a を求める ] 二次方程式 + a = 0 の 1 つの解が 3 であるとき, a の値を求めよ また, もう 1 つの解を求めよ a = = a = 3 = 1 + a = 0 1の解の 1
2015年度 岡山大・理系数学
 5 岡山大学 ( 理系 ) 前期日程問題 解答解説のページへ を 以上の自然数とし, から までの自然数 k に対して, 番号 k をつけたカードをそれぞれ k 枚用意する これらすべてを箱に入れ, 箱の中から 枚のカードを同時に引くとき, 次の問いに答えよ () 用意したカードは全部で何枚か答えよ () 引いたカード 枚の番号が両方とも k である確率を と k の式で表せ () 引いたカード 枚の番号が一致する確率を
5 岡山大学 ( 理系 ) 前期日程問題 解答解説のページへ を 以上の自然数とし, から までの自然数 k に対して, 番号 k をつけたカードをそれぞれ k 枚用意する これらすべてを箱に入れ, 箱の中から 枚のカードを同時に引くとき, 次の問いに答えよ () 用意したカードは全部で何枚か答えよ () 引いたカード 枚の番号が両方とも k である確率を と k の式で表せ () 引いたカード 枚の番号が一致する確率を
2013年度 九州大・理系数学
 九州大学 ( 理系 ) 前期日程問題 解答解説のページへ a> とし, つの曲線 y= ( ), y= a ( > ) を順にC, C とする また, C とC の交点 P におけるC の接線をl とする 以下 の問いに答えよ () 曲線 C とy 軸および直線 l で囲まれた部分の面積をa を用いて表せ () 点 P におけるC の接線と直線 l のなす角を ( a) とき, limasin θ(
九州大学 ( 理系 ) 前期日程問題 解答解説のページへ a> とし, つの曲線 y= ( ), y= a ( > ) を順にC, C とする また, C とC の交点 P におけるC の接線をl とする 以下 の問いに答えよ () 曲線 C とy 軸および直線 l で囲まれた部分の面積をa を用いて表せ () 点 P におけるC の接線と直線 l のなす角を ( a) とき, limasin θ(
熊本県数学問題正解
 00 y O x Typed by L A TEX ε ( ) (00 ) 5 4 4 ( ) http://www.ocn.ne.jp/ oboetene/plan/. ( ) (009 ) ( ).. http://www.ocn.ne.jp/ oboetene/plan/eng.html 8 i i..................................... ( )0... (
00 y O x Typed by L A TEX ε ( ) (00 ) 5 4 4 ( ) http://www.ocn.ne.jp/ oboetene/plan/. ( ) (009 ) ( ).. http://www.ocn.ne.jp/ oboetene/plan/eng.html 8 i i..................................... ( )0... (
< F2D323289F090E08E9197BF928694E081698E5A A2E6A>
 小学校第 6 学年 算数 B 注 意 1 先生の合図があるまで, 中を開かないでください 2 調査問題は,1 ページから 18 ページまであります 3 解答用紙は, 両面に解答らんがあります 解答は, すべて解答用紙に書きましょう えんぴつ 4 解答は,HBまたはBの黒鉛筆 ( シャープペンシルも可 ) を使い, こく, はっきりと書きましょう また, 消すときは消しゴムできれいに消しましょう 5
小学校第 6 学年 算数 B 注 意 1 先生の合図があるまで, 中を開かないでください 2 調査問題は,1 ページから 18 ページまであります 3 解答用紙は, 両面に解答らんがあります 解答は, すべて解答用紙に書きましょう えんぴつ 4 解答は,HBまたはBの黒鉛筆 ( シャープペンシルも可 ) を使い, こく, はっきりと書きましょう また, 消すときは消しゴムできれいに消しましょう 5
模擬試験問題(第1章~第3章)
 基本情報技術者試験の練習問題 - 第 8 回 この問題は平成 19 年度秋期の問題から抜粋しています 問 1 次のプログラムの説明及びプログラムを読んで, 設問 1,2 に答えよ プログラムの説明 スタックを使って, 実数値を 10 進数字列 ( 文字列 ) に変換する副プログラム FloatFormat である (1) FloatFormat は, 実数 Float の値を 10 進数字列に変換し,
基本情報技術者試験の練習問題 - 第 8 回 この問題は平成 19 年度秋期の問題から抜粋しています 問 1 次のプログラムの説明及びプログラムを読んで, 設問 1,2 に答えよ プログラムの説明 スタックを使って, 実数値を 10 進数字列 ( 文字列 ) に変換する副プログラム FloatFormat である (1) FloatFormat は, 実数 Float の値を 10 進数字列に変換し,
4STEP 数学 B( 新課程 ) を解いてみた 平面上のベクトル 6 ベクトルと図形 59 A 2 B 2 = AB 2 - AA æ 1 2 ö = AB1 + AC1 - ç AA1 + AB1 3 3 è 3 3 ø 1
 平面上のベクトル 6 ベクトルと図形 A B AB AA AB + AC AA + AB AA AB + AC AB AB + AC + AC AB これと A B ¹, AB ¹ より, A B // AB \A B //AB A C A B A B B C 6 解法 AB b, AC とすると, QR AR AQ b QP AP AQ AB + BC b b + ( b ) b b b QR よって,P,
平面上のベクトル 6 ベクトルと図形 A B AB AA AB + AC AA + AB AA AB + AC AB AB + AC + AC AB これと A B ¹, AB ¹ より, A B // AB \A B //AB A C A B A B B C 6 解法 AB b, AC とすると, QR AR AQ b QP AP AQ AB + BC b b + ( b ) b b b QR よって,P,



