Ni PLD GdBa 2 Cu 3 O 7 x 2 6
|
|
|
- としはる うなだ
- 6 years ago
- Views:
Transcription
1 Ni PLD GdBa 2 Cu 3 O 7 x 2 6
2 RE 1 Ba 2 Cu 3 O 7 x GdBa 2 Cu 3 O 7 x IBAD RABiTS PLD GdBCO Ni i
3 TEM TEM J c -d J c -B (c-axis ab-plane) J c -θ J c -B (IBAD ) E-J J c -B IBAD GdBCO J c J c IBAD ii
4 iii
5 1.1 YBCO J c YBCO [] θ J c [] GdBCO YBCO J c [] IBAD [] RABiTS [] GdBCO CeO 2 (a) Y 2 O 3 (b) GdBCO K J c -d (a) I c -d (b) K c-axis J c -B K ab-plane J c -B K ab-plane J c -θ iv
6 K 3 T J c -θ (a)(b) CeO 2 Y 2 O IBAD 77.3 K J c -B IBAD 77.3 K I c -B E= V/m g E= V/m g Y K 1 6 T E-J Y K 1 6 T E-J Y K 1 6 T E-J C K 1 6 T E-J C K 1 6 T E-J C K 1 6 T E-J CeO K J c -B Y 2 O K J c -B CeO K L Y 2 O K L IBAD 77.3 K E-J v
7 Kamerling-Onnes K ( ) T c B c 1957 Badeen Cooper Scherieffer BCS T c 30 K 1986 Johannes G.Bendnortz Karl Alex Muller (La 2 x Ba x CuO 4 ) 30K YBa 2 Cu 3 O 7 x (YBCO) Bi 2 Sr 2 Ca 2 Cu 3 O 10+δ (Bi2223) Magnetic Resonance Imaging(MRI) 1
8 Superconducting Magnetic Energy Strage (SMES) B c B c B c B c B c1 B c2 2 B c2 1 B c 2 B c1 B c2 Lorentz J Loretz F L B F L =J B F L v E E=B v F L F p F L F p F p = J c B J c J c T c B c2 J c T c B c2 J c F p J c 1.2 (JISh7005) 25 K MgB 2 2
9 1.2.1 CuO K CuO 2 CuO 2 Bi2223 REBa 2 Cu 3 O 7 x (RE: Rare Earth) (REBCO) Bi2223 c ab ab CuO 2 km I c = 200 A 2 Km Bi2223 REBCO Bi2223 Bi2223 J c REBCO 1.3 RE 1 Ba 2 Cu 3 O 7 x 1986 J. G. Bednortz K. A. Muller La 2 x Ba x CuO C. W. Chu T c YBCO (4.2 K) REBCO 1.1 Bi2223 J c Nb 3 Sn 3
10 REBCO J c [] REBCO 1.1 YBCO J c [] REBa 2 Cu 3 O 7 x (RE: Rare Earth)(REBCO) RE:BA:Cu 1:2:3 1.2 REBCO YBCO [] REBCO CuO 2 RE CuO 2 2 BaO CuO REBCO CuO 4
![1.2 YBCO [] 1.](/docs-images/102/155442782/images/11-0.jpg "3 θ J c [] 1.3.2 REBCO km J c REBCO 5")
11 1.2 YBCO [] 1.3 θ J c [] REBCO km J c REBCO 5
12 J c Dimos [] Dimos 2 θ SrTiO 3 YBCO θ J c 1.3 Jc G gb Jc θ Jc gb θ=10 θ= J c REBCO J c GdBa 2 Cu 3 O 7 x GdBa 2 Cu 3 O 7 x (GdBCO) YBCO Y Gd REBCO GdBCO 1.4 YBCO [] J c Gd Y T c Nd Y RE 1+x Ba 2 x Cu 3 O 7 δ Pulsed Laser Deposition(PLD) c c J c YBCO 1.4 GdBCO YBCO J c [] 6
13 1.4 REBCO J c REBCO REBCO Ion Beam Assisted Deposition(IBAD) Rolling Assisted Bi-axially Textured Substarte(RABiTS) IBAD 1.5 IBAD IBAD REBCO REBCO J c [] IBAD Y stablized Zr(YSZ) Y 2 O 3 GdZr 2 O 7 (GZO) [] IBAD CeO 2 [] IBAD MgO [] RABiTS 1.6 RABiTS IBAD 2 REBCO RABiTS Ni Ag Cu FCC(Face Center Cubic) [] 7
![1.5 IBAD [] IBAD J c Ni Ni IBAD Hasteoy [] NI W [] RABiTS Cu SS316L](/docs-images/102/155442782/images/14-0.jpg "IBAD 1.")
14 1.5 IBAD [] IBAD J c Ni Ni IBAD Hasteoy [] NI W [] RABiTS Cu SS316L IBAD 1.5 PLD PLD Phisical Vapor Deposition (PVD ) ( ) 2 PLD Chemical Vapor 8
![1.6 RABiTS [] Deposition (CVD ) Metal Organic Deposition (MOD ) 1.6 1.6.1 I c J](/docs-images/102/155442782/images/15-0.jpg "c J c J c Lorentz Lorentz Lorentz F p J c J c B Lorentz F p J c = F p B (1.1) 9")
15 1.6 RABiTS [] Deposition (CVD ) Metal Organic Deposition (MOD ) I c J c J c J c Lorentz Lorentz Lorentz F p J c J c B Lorentz F p J c = F p B (1.1) 9
16 F p J c J c 1.4 Lorentz 1.7 Lorentz Lorentz ( A C) B 1.7 J < J c0 k B T (k B Boltzmann ) U U Arrhenius exp ( U/k B T ) a f a f a f a f ν 0 Lorentz v + ( v + = a f ν 0 exp U ) k B T ν 0 (1.2) ν 0 = ζρ fj c0 2πa f B (1.3) 10
17 1.7 ζ ζ 2π a f ζ = 4 ρ f J c0 Lorentz v ( v = a f ν 0 [exp U ) )] exp ( U k B T k B T (1.4) U Lorentz Maxwell E = Bv ( E = Ba f ν 0 [exp U ) )] exp ( U k B T k B T (1.5) (1.5) 1.1 x F (x) = U 0 2 sin(kx) fx (1.6) 11
18 U 0 /2 k = 2πa f f = JBV (V ) Lorentz x = x 0 x = x 0 F (x) = 0 x 0 = a ( ) f faf 2π cos 1 U 0 π (1.7)?? U U = F (x 0 ) F ( x 0 ) [ ( )] U = U 0 sin cos 1 faf fa ( ) f faf U 0 π π cos 1 U 0 π { ( ) } = U 0 2f 1 2f ( ) 2f U 0 k U 0 k cos 1 (1.8) U 0 k sin(cos 1 (x)) = 1 x 2 k = a f /2π U = 0 2f/U 0 k = 2J c0 BV/U 0 k = 1 J = J c0 ( ) 2f = J j (1.9) U 0 k J c0 j J c0 J c0 ) m ( J c0 = A (1 TTc B γ 1 1 B ) 2 (1.10) B c2 A γ m (1.8) (1.9) k = 2πa f U(j) = U 0 [(1 j 2 ) 1/2 j cos 1 j] (1.11) U (j) U + fa f = U + πu 0 j (1.12) (1.5) [ E = Ba f ν 0 exp U(j) ] [ ( 1 exp πu )] 0j (1.13) k B T k B T 12
19 1.6.3 Lorentz 1.8 U = 0 J c0 Lorentz J B Lorentz Lorentz δ = v/ v J B δf p = 0 (1.14) (1.1) J = J c0 J > J c0 J B δf p B ηv = 0 (1.15) φ 0 φ 0 η (1.1) E = B v J J = J c0 + E ρ f (1.16) Bφ 0 /η = ρ f ρ f E E = ρ f (J J c0 ) (1.17)
20 1.8 Û0 V U 0 = Û0V (1.18) Û0 Labusch α L d i Û 0 = α Ld 2 i 2 (1.19) F p F p = J c0 B = α L d i (1.20) 1.9 d i d i (a) L d d d L L ( ) 1/2 C44 L = α L ( ) 1/2 Baf = (1.21) ζµ 0 J c0 14
21 1.9 L L d d R R R R (a) d < L (b) d > L 1.10 R R = ( C66 α L ) 1/2 (1.22) C 44 C 66 C 44 = B2 µ 0 (1.23) C 66 = B2 c2b 4µ 0 B c2 ( 1 B B c2 ) 2 C 0 66 (1.24) 15
22 C 66 C 66 0 C 66 C66 0 d i a f ζ d i = a f ζ (1.25) d L V = LR 2 (1.26) U 0 = a f 2ζ J c0br 2 L (1.27) R a f R a f R = ga f (1.28) g 2 g 2 (1.22) (1.28) g 2 = C 66 ζj c0 Ba f (1.29) 3 g 2 e = C0 66 ζj c0 Ba f (1.30) g 2 C 66 g 2 g 2 g 2 = g 2 e [ 5kB T 2U e ( )] Baf ν 0 log E c (1.31) 16
23 (1.27) U 0 = 0.835k Bg 2 J 1/2 c0 (1.32) ζ 3/2 B 1/4 1.10(a) d L V V = dr 2 (1.33) U 0 = 4.23g2 k B J c0 d ζb 1/2 (1.34) ζ = 2π [ E cr = Ba f ν 0 exp U(j) ] [ 1 exp K B T ( πu 0j k B T )] ; j < 1 ( = Ba f ν 0 [1 exp πu )] 0 ; j 1 k B T (1.35) E ff = 0; j < 1 = ρ f (J J c0 ); j 1 (1.36) E = (Ecr 2 + Eff) 2 1/2 (1.37) (1.10) U 0 T c (1.10) A f(a) = K exp [ (loga loga m) 2 ] 2σ 2 (1.38) 17
24 K σ 2 A m A A E(J) = 0 Ef(A)dA (1.39) E J J c B 1.7 PLD GdBCO c [] YBCO PLD REBCO I c [] PLD Y Hastelloy Ni [] PLD GdBCO IBAD GdBCO GdBCO 18
25 2 2.1 PLD GdBCO GdBCO PLD GdBCO Ni CeO 2 (60 nm) YSZ(260 nm) CeO 2 (170 nm) Y 2 O 3 (120 nm) PLD GdBCO 2.1 d µm T c d d T c Ni REBCO J c J c 2 PLD RE123 Hastelloy Hastelloy 2 2 IBAD IBAD 19
![2.1 GdBCO 2.1 Specimen Seed layer d [µm] T c [K] Y0.5 0.52 92.4 Y1 1.04 92.6 Y1.5 Y 2 O 3 1.56 92.2 Y2 2.](/docs-images/102/155442782/images/26-0.jpg "08 92.2 Y3 3.12 92.3 C0.5 0.52 92.5 C1 1.04 92.4 C1.5 CeO 2 1.56 92.2 C2 2.08 92.4 C3 3.12 92.9 IBAD 2.60 91.")
26 2.1 GdBCO 2.1 Specimen Seed layer d [µm] T c [K] Y Y Y1.5 Y 2 O Y Y C C C1.5 CeO C C IBAD
27 IBAD 2 FCC FCC Ni Cu Ag Ni Ni Ni W % RABiTS Cu SL316 Ni 2.2 PLD Ni GdBCO GdBCO PLD GdBCO Cu Cu Cu Cu : : =2:1:
28 Ag Ag Ag Ag : : =6:1: posi 4000 rpm C 2 90 C =1:500 22
29 E J R S R S R 2 I 2 I 3 I 1 I 1 = I 2 + I 3 (2.1) V V = R S I 2 + (R V + R 2 + R 3 )I 3 (2.2) R S R 2 + R 3 I 2 0 (2.3) I 1 I 2 (2.4) V V = R S I 2 (2.5) R 1 R 4 V I V I 100 µm 1.0 mm In 23
30 RS R1 R3 R2 R4 V A RV RA 2.2 OXford Instrument 14 T Bi T 0 T 6 T 0 1 T 1 6 T He 77.3 K 0.3 K J c E c = V/m J c θ φ 2.3 n E J E J n (2.6) n E [V/m] n 24
31 TEM Transmission Electron Micrescope(TEM) GdBCO High- Angle Annular Dark-Field transition electron microscopy(haadf) TEM HAADF nm TEM Japan Fine Ceramic Center(JFCC) 25
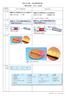
32 第3章 実験結果 3.1 TEM による断面観察 図 3.1(a)(b) に それぞれ種層として CeO2 を用いた試料の断面画像 (a) と Y2 O3 を用 いた試料の断面画像を示す 図 3.1 種層として CeO2 層 (a) 及び Y2 O3 層 (b) を用いて作製した GdBCO コー ト線材の断面画像 図 3.1(a) に示すように 種層として CeO2 を用いた試料では 種層である CeO2 層に 無数の亀裂が発生しているのが確認でき 直上の GdBCO 超伝導層には Gd がリッチに なっているポイントが形成されている また CeO2 層に生じた亀裂には NiO が形成さ 26
33 CeO 2 Gd 2 O 3 CeO 2 CeO 2 Ni CeO 2 CeO 2 3.1(b) 3.1(a) CeO 2 GdBCO Gd Y 2 O 3 Ni Y 2 O 3 Y 2 O 3 CeO 2 J c 3.2 J c -d 3.2(a) J c 3.2(b) I c 3.2(a) Y 2 O 3 J c Y 2 O 3 CeO 2 J c 1 µm J c J c CeO 2 3.2(b) Y 2 O 3 I c 3 µm CeO 2 1 µm 3.3 J c -B (c-axis ab-plane) 3.3(a)(b) c-axis J c -B d Y 2 O 3 J c C1 C2 C3 d J c 27
34 Y 2 O 3 Y 2 O 3 20 J c [GA/m 2 ] CeO I c [A/cm w] 200 CeO K K d [µm] d [µm] K J c -d (a) I c -d (b) J c Y1 Y2 Y3 Y1 Y2 6 T J c d (a) CeO 2 B//c (b) B//c C1 C2 C Y1 Y2 Y3 J c [A/m 2 ] 10 9 J c [A/m 2 ] K B [T] 77.3 K B [T] K c-axis J c -B 3.4(a)(b) ab-plane J c -B 28
35 3.4(a) J c 100 µm 3.4(b) Y1 Y3 CeO (a) CeO 2 B//ab (b) B//ab C1 C2 C Y1 Y2 Y3 J c [A/m 2 ] 10 9 J c [A/m 2 ] K 77.3 K B [T] B [T] 3.4 J c -B 77.3 K ab-plane 3.4 J c -θ 3.5 C1 Y1 1 T 3 T J c 3.5 Y1 C1 J c θ=0 90 J c C1 Y1 c-axis ab-plane C1 C1 Y1 J c 3.6(a) CeO 2 J c 3.6(b) Y 2 O 3 J c 3 T 3.6(a) d θ=
36 T 3 T C1 Y1 J c [GA/m 2 ] K θ [degree] K ab-plane J c -θ 3.6(b) Y1 Y3 CeO 2 d θ= (a) 77.3 K 3T CeO (b) 3 3 Y1 J c [GA/m 2 ] C3 C1 J c [GA/m 2 ] Y K 3 T Y 2 O θ [degree] d [µm] K 3 T J c -θ (a)(b) CeO 2 Y 2 O 3 30
37 3.5 J c -B (IBAD ) 3.7 IBAD GdBCO J c -B (a) I c -B 3.7 IBAD GdBCO J c Y1 c-axis 1 T J c ab-plane Y1 J c ab-plane IBAD Y1 c axis ab plane IBAD Y3 c axis ab plane J c [GA/m 2 ] 10 I c [A/cm w] B [T] 3.7 IBAD 77.3 K J c -B B [T] 3.8 IBAD 77.3 K I c -B 3.8 I c I c Y3 2 J c c-axis ab-plane IBAD Y3 I c 31
38 K A m σ 2 γ g 2 c-axis E-J J c -B 4.1 g E= V/m g 2 g 2 g 2 A 4.1 A m σ 2 γ Y Y Y C C C Y 2 O 3 A m Y1 Y2 Y3 d 32
39 3 3 C1 C2 C3 exp theo exp theo Y1 Y2 Y3 g 2 2 g B [T] B [T] 4.1 E= V/m g E= V/m g 2 σ 2 Y1 Y2 Y3 d CeO 2 A m σ 2 Y 2 O 3 Y 2 O 3 Y1 C1 σ 2 A m Y1 CeO 2 Y 2 O 3 J c 4.2 E-J E-J g 2 [] 33
40 10 2 Y 1 E [V/m] T 2 T 3 T 4 T 5 T 6 T exp Theory E [V/m] Y K exp theo 1 T 2 T 3 T 4 T 5 T 6 T J [A/m 2 ] Y K 1 6 T E-J J [A/m 2 ] Y K 1 6 T E-J E [V/m] Y K exp theo 1 T 2 T 3 T 4 T 5 T 6 T C K exp theo 1 T 2 T 3 T 4 T 5 T 6 T J [A/m 2 ] Y K 1 6 T E-J J [A/m 2 ] C K 1 6 T E-J 4.3 J c -B J c -B 34
41 E [V/m] C K exp theo 1 T 2 T 3 T 4 T 5 T 6 T E [V/m] 10 2 C K T 2 T 3 T 4 T 5 T 6 T J [A/m 2 ] C K 1 6 T E-J J [A/m 2 ] C K 1 6 T E-J E-J J c -B CeO 2 C1 C2 C3 exp theo Y 2 O 3 Y1 Y2 Y3 exp theo J c [A/m 2 ] J c [A/m 2 ] B [T] 4.9 CeO K J c -B 77.3 K B [T] 4.10 Y 2 O K J c -B 35
42 L 4.11 C1 L 3 T C1 d 1.04 µm C2 5 T C3 6 T L d C1 C2 3 T 5 T 3 2 C1 3 T C1 J c C2 C3 C1 C2 C3 J c J c 4.12 Y1 d L 4.5 T L d Y2 Y3 6 T d L Y1 4.5 T 2 Y2 Y3 6 T Y1 Y1 J c Y2 Y3 J c 6 T Y1 Y2 J c µm C1 C2 C3 2.08µm µm Y1 Y2 Y3 2.08µm L [µm] 2 L [µm] µm µm B [T] 4.11 CeO K L B [T] 4.12 Y 2 O K L 36
43 4.5 IBAD GdBCO 4.2 IBAD PLD GdBCO Y1 Y3 g 2 IBAD g IBAD E-J 4.13 IBAD Y1 d σ 2 IBAD Y1 Y3 IBAD Y1 Y3 Y1 IBAD d Y1 d σ 2 d IABD I c I c 4.2 A m σ 2 γ IBAD Y Y
44 E [V/m] IBAD 77.3 K exp theo 0.3 T 0.5 T 0.7 T 1.0 T J [A/m 2 ] 4.13 IBAD 77.3 K E-J 38
45 5 Ni PLD GdBCO E-J 5.1 J c CeO 2 Gd 2 O 3 Y 2 O 3 Y 2 O 3 CeO 2 J c σ 2 Y 2 O 3 CeO 2 CeO 2 TEM CeO 2 Gd 2 O 3 CeO 2 GdBCO 5.2 J c 1 µm J c J c 39
46 1 µm J c J c J c A m σ 2 J c 5.3 IBAD IBAD 2.5 µm J/c 30 GA/m 2 Y1 J c I c -B I c Y3 2 I c IBAD GdBCO σ 2 σ 2 Y1 Y1 IBAD 40
47 41
BaHfO 3 PLD GdBa 2 Cu 3 O 7 δ 24 2 17 1 1 1.1.................................. 1 1.2............................... 2 1.3............................. 2 1.4................................. 3 1.5.........................
2008/02/18 08:40-10:10, 12:50-14:20 14:30-16:00, 16:10-17:40,
008/0/18 08:40-10:10, 1:50-14:0 14:30-16:00, 16:10-17:40, 1pt A 1911 Leiden Heike Kammelingh-Onnes H.Kammelingh Onnes 1907 He 1 4. K H H c T c T H c Hg:40 mt, Pb:80 mt, Sn:30 mt 100 mt I c H c H c H
微分積分 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. このサンプルページの内容は, 初版 1 刷発行時のものです.
微分積分 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. ttp://www.morikita.co.jp/books/mid/00571 このサンプルページの内容は, 初版 1 刷発行時のものです. i ii 014 10 iii [note] 1 3 iv 4 5 3 6 4 x 0 sin x x 1 5 6 z = f(x, y) 1 y = f(x)
医系の統計入門第 2 版 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. このサンプルページの内容は, 第 2 版 1 刷発行時のものです.
医系の統計入門第 2 版 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/009192 このサンプルページの内容は, 第 2 版 1 刷発行時のものです. i 2 t 1. 2. 3 2 3. 6 4. 7 5. n 2 ν 6. 2 7. 2003 ii 2 2013 10 iii 1987
[Ver. 0.2] 1 2 3 4 5 6 7 1 1.1 1.2 1.3 1.4 1.5 1 1.1 1 1.2 1. (elasticity) 2. (plasticity) 3. (strength) 4. 5. (toughness) 6. 1 1.2 1. (elasticity) } 1 1.2 2. (plasticity), 1 1.2 3. (strength) a < b F
TOP URL 1
TOP URL http://amonphys.web.fc.com/ 3.............................. 3.............................. 4.3 4................... 5.4........................ 6.5........................ 8.6...........................7
2000年度『数学展望 I』講義録
2000 I I IV I II 2000 I I IV I-IV. i ii 3.10 (http://www.math.nagoya-u.ac.jp/ kanai/) 2000 A....1 B....4 C....10 D....13 E....17 Brouwer A....21 B....26 C....33 D....39 E. Sperner...45 F....48 A....53
(1.2) T D = 0 T = D = 30 kn 1.2 (1.4) 2F W = 0 F = W/2 = 300 kn/2 = 150 kn 1.3 (1.9) R = W 1 + W 2 = = 1100 N. (1.9) W 2 b W 1 a = 0
1 1 1.1 1.) T D = T = D = kn 1. 1.4) F W = F = W/ = kn/ = 15 kn 1. 1.9) R = W 1 + W = 6 + 5 = 11 N. 1.9) W b W 1 a = a = W /W 1 )b = 5/6) = 5 cm 1.4 AB AC P 1, P x, y x, y y x 1.4.) P sin 6 + P 1 sin 45
1 (Berry,1975) 2-6 p (S πr 2 )p πr 2 p 2πRγ p p = 2γ R (2.5).1-1 : : : : ( ).2 α, β α, β () X S = X X α X β (.1) 1 2
2005 9/8-11 2 2.2 ( 2-5) γ ( ) γ cos θ 2πr πρhr 2 g h = 2γ cos θ ρgr (2.1) γ = ρgrh (2.2) 2 cos θ θ cos θ = 1 (2.2) γ = 1 ρgrh (2.) 2 2. p p ρgh p ( ) p p = p ρgh (2.) h p p = 2γ r 1 1 (Berry,1975) 2-6
The Physics of Atmospheres CAPTER :
The Physics of Atmospheres CAPTER 4 1 4 2 41 : 2 42 14 43 17 44 25 45 27 46 3 47 31 48 32 49 34 41 35 411 36 maintex 23/11/28 The Physics of Atmospheres CAPTER 4 2 4 41 : 2 1 σ 2 (21) (22) k I = I exp(
x () g(x) = f(t) dt f(x), F (x) 3x () g(x) g (x) f(x), F (x) (3) h(x) = x 3x tf(t) dt.9 = {(x, y) ; x, y, x + y } f(x, y) = xy( x y). h (x) f(x), F (x
[ ] IC. f(x) = e x () f(x) f (x) () lim f(x) lim f(x) x + x (3) lim f(x) lim f(x) x + x (4) y = f(x) ( ) ( s46). < a < () a () lim a log xdx a log xdx ( ) n (3) lim log k log n n n k=.3 z = log(x + y ),
量子力学 問題
3 : 203 : 0. H = 0 0 2 6 0 () = 6, 2 = 2, 3 = 3 3 H 6 2 3 ϵ,2,3 (2) ψ = (, 2, 3 ) ψ Hψ H (3) P i = i i P P 2 = P 2 P 3 = P 3 P = O, P 2 i = P i (4) P + P 2 + P 3 = E 3 (5) i ϵ ip i H 0 0 (6) R = 0 0 [H,
. ev=,604k m 3 Debye ɛ 0 kt e λ D = n e n e Ze 4 ln Λ ν ei = 5.6π / ɛ 0 m/ e kt e /3 ν ei v e H + +e H ev Saha x x = 3/ πme kt g i g e n
003...............................3 Debye................. 3.4................ 3 3 3 3. Larmor Cyclotron... 3 3................ 4 3.3.......... 4 3.3............ 4 3.3...... 4 3.3.3............ 5 3.4.........
all.dvi
38 5 Cauchy.,,,,., σ.,, 3,,. 5.1 Cauchy (a) (b) (a) (b) 5.1: 5.1. Cauchy 39 F Q Newton F F F Q F Q 5.2: n n ds df n ( 5.1). df n n df(n) df n, t n. t n = df n (5.1) ds 40 5 Cauchy t l n mds df n 5.3: t
006 11 8 0 3 1 5 1.1..................... 5 1......................... 6 1.3.................... 6 1.4.................. 8 1.5................... 8 1.6................... 10 1.6.1......................
II ( ) (7/31) II ( [ (3.4)] Navier Stokes [ (6/29)] Navier Stokes 3 [ (6/19)] Re
![II ( ) (7/31) II ( [ (3.4)] Navier Stokes [ (6/29)] Navier Stokes 3 [ (6/19)] Re](/thumbs/94/118770263.jpg "II ( ) (7/31) II ( [ (3.4)] Navier Stokes [ (6/29)] Navier Stokes 3 [ (6/19)] Re")
II 29 7 29-7-27 ( ) (7/31) II (http://www.damp.tottori-u.ac.jp/~ooshida/edu/fluid/) [ (3.4)] Navier Stokes [ (6/29)] Navier Stokes 3 [ (6/19)] Reynolds [ (4.6), (45.8)] [ p.186] Navier Stokes I Euler Navier
Note.tex 2008/09/19( )
1 20 9 19 2 1 5 1.1........................ 5 1.2............................. 8 2 9 2.1............................. 9 2.2.............................. 10 3 13 3.1.............................. 13 3.2..................................
高校生の就職への数学II
II O Tped b L A TEX ε . II. 3. 4. 5. http://www.ocn.ne.jp/ oboetene/plan/ 7 9 i .......................................................................................... 3..3...............................
1990 IMO 1990/1/15 1:00-4:00 1 N N N 1, N 1 N 2, N 2 N 3 N 3 2 x x + 52 = 3 x x , A, B, C 3,, A B, C 2,,,, 7, A, B, C
0 9 (1990 1999 ) 10 (2000 ) 1900 1994 1995 1999 2 SAT ACT 1 1990 IMO 1990/1/15 1:00-4:00 1 N 1990 9 N N 1, N 1 N 2, N 2 N 3 N 3 2 x 2 + 25x + 52 = 3 x 2 + 25x + 80 3 2, 3 0 4 A, B, C 3,, A B, C 2,,,, 7,
c 2009 i
I 2009 c 2009 i 0 1 0.0................................... 1 0.1.............................. 3 0.2.............................. 5 1 7 1.1................................. 7 1.2..............................
30
3 ............................................2 2...........................................2....................................2.2...................................2.3..............................
128 3 II S 1, S 2 Φ 1, Φ 2 Φ 1 = { B( r) n( r)}ds S 1 Φ 2 = { B( r) n( r)}ds (3.3) S 2 S S 1 +S 2 { B( r) n( r)}ds = 0 (3.4) S 1, S 2 { B( r) n( r)}ds
127 3 II 3.1 3.1.1 Φ(t) ϕ em = dφ dt (3.1) B( r) Φ = { B( r) n( r)}ds (3.2) S S n( r) Φ 128 3 II S 1, S 2 Φ 1, Φ 2 Φ 1 = { B( r) n( r)}ds S 1 Φ 2 = { B( r) n( r)}ds (3.3) S 2 S S 1 +S 2 { B( r) n( r)}ds
W u = u(x, t) u tt = a 2 u xx, a > 0 (1) D := {(x, t) : 0 x l, t 0} u (0, t) = 0, u (l, t) = 0, t 0 (2)
3 215 4 27 1 1 u u(x, t) u tt a 2 u xx, a > (1) D : {(x, t) : x, t } u (, t), u (, t), t (2) u(x, ) f(x), u(x, ) t 2, x (3) u(x, t) X(x)T (t) u (1) 1 T (t) a 2 T (t) X (x) X(x) α (2) T (t) αa 2 T (t) (4)
.2 ρ dv dt = ρk grad p + 3 η grad (divv) + η 2 v.3 divh = 0, rote + c H t = 0 dive = ρ, H = 0, E = ρ, roth c E t = c ρv E + H c t = 0 H c E t = c ρv T
NHK 204 2 0 203 2 24 ( ) 7 00 7 50 203 2 25 ( ) 7 00 7 50 203 2 26 ( ) 7 00 7 50 203 2 27 ( ) 7 00 7 50 I. ( ν R n 2 ) m 2 n m, R = e 2 8πε 0 hca B =.09737 0 7 m ( ν = ) λ a B = 4πε 0ħ 2 m e e 2 = 5.2977
n ξ n,i, i = 1,, n S n ξ n,i n 0 R 1,.. σ 1 σ i .10.14.15 0 1 0 1 1 3.14 3.18 3.19 3.14 3.14,. ii 1 1 1.1..................................... 1 1............................... 3 1.3.........................
S I. dy fx x fx y fx + C 3 C dy fx 4 x, y dy v C xt y C v e kt k > xt yt gt [ v dt dt v e kt xt v e kt + C k x v + C C k xt v k 3 r r + dr e kt S dt d
S I.. http://ayapin.film.s.dendai.ac.jp/~matuda /TeX/lecture.html PDF PS.................................... 3.3.................... 9.4................5.............. 3 5. Laplace................. 5....
2009 I 2 II III 14, 15, α β α β l 0 l l l l γ (1) γ = αβ (2) α β n n cos 2k n n π sin 2k n π k=1 k=1 3. a 0, a 1,..., a n α a
009 I II III 4, 5, 6 4 30. 0 α β α β l 0 l l l l γ ) γ αβ ) α β. n n cos k n n π sin k n π k k 3. a 0, a,..., a n α a 0 + a x + a x + + a n x n 0 ᾱ 4. [a, b] f y fx) y x 5. ) Arcsin 4) Arccos ) ) Arcsin
4 4 θ X θ P θ 4. 0, 405 P 0 X 405 X P 4. () 60 () 45 () 40 (4) 765 (5) 40 B 60 0 P = 90, = ( ) = X
4 4. 4.. 5 5 0 A P P P X X X X +45 45 0 45 60 70 X 60 X 0 P P 4 4 θ X θ P θ 4. 0, 405 P 0 X 405 X P 4. () 60 () 45 () 40 (4) 765 (5) 40 B 60 0 P 0 0 + 60 = 90, 0 + 60 = 750 0 + 60 ( ) = 0 90 750 0 90 0
2 2 MATHEMATICS.PDF 200-2-0 3 2 (p n ), ( ) 7 3 4 6 5 20 6 GL 2 (Z) SL 2 (Z) 27 7 29 8 SL 2 (Z) 35 9 2 40 0 2 46 48 2 2 5 3 2 2 58 4 2 6 5 2 65 6 2 67 7 2 69 2 , a 0 + a + a 2 +... b b 2 b 3 () + b n a
S I. dy fx x fx y fx + C 3 C vt dy fx 4 x, y dy yt gt + Ct + C dt v e kt xt v e kt + C k x v k + C C xt v k 3 r r + dr e kt S Sr πr dt d v } dt k e kt
S I. x yx y y, y,. F x, y, y, y,, y n http://ayapin.film.s.dendai.ac.jp/~matuda n /TeX/lecture.html PDF PS yx.................................... 3.3.................... 9.4................5..............
18 I ( ) (1) I-1,I-2,I-3 (2) (3) I-1 ( ) (100 ) θ ϕ θ ϕ m m l l θ ϕ θ ϕ 2 g (1) (2) 0 (3) θ ϕ (4) (3) θ(t) = A 1 cos(ω 1 t + α 1 ) + A 2 cos(ω 2 t + α
18 I ( ) (1) I-1,I-2,I-3 (2) (3) I-1 ( ) (100 ) θ ϕ θ ϕ m m l l θ ϕ θ ϕ 2 g (1) (2) 0 (3) θ ϕ (4) (3) θ(t) = A 1 cos(ω 1 t + α 1 ) + A 2 cos(ω 2 t + α 2 ), ϕ(t) = B 1 cos(ω 1 t + α 1 ) + B 2 cos(ω 2 t
m(ẍ + γẋ + ω 0 x) = ee (2.118) e iωt P(ω) = χ(ω)e = ex = e2 E(ω) m ω0 2 ω2 iωγ (2.119) Z N ϵ(ω) ϵ 0 = 1 + Ne2 m j f j ω 2 j ω2 iωγ j (2.120)
2.6 2.6.1 mẍ + γẋ + ω 0 x) = ee 2.118) e iωt Pω) = χω)e = ex = e2 Eω) m ω0 2 ω2 iωγ 2.119) Z N ϵω) ϵ 0 = 1 + Ne2 m j f j ω 2 j ω2 iωγ j 2.120) Z ω ω j γ j f j f j f j sum j f j = Z 2.120 ω ω j, γ ϵω) ϵ
I A A441 : April 15, 2013 Version : 1.1 I Kawahira, Tomoki TA (Shigehiro, Yoshida )
I013 00-1 : April 15, 013 Version : 1.1 I Kawahira, Tomoki TA (Shigehiro, Yoshida) http://www.math.nagoya-u.ac.jp/~kawahira/courses/13s-tenbou.html pdf * 4 15 4 5 13 e πi = 1 5 0 5 7 3 4 6 3 6 10 6 17
Untitled
II 14 14-7-8 8/4 II (http://www.damp.tottori-u.ac.jp/~ooshida/edu/fluid/) [ (3.4)] Navier Stokes [ 6/ ] Navier Stokes 3 [ ] Reynolds [ (4.6), (45.8)] [ p.186] Navier Stokes I 1 balance law t (ρv i )+ j
N/m f x x L dl U 1 du = T ds pdv + fdl (2.1)
23 2 2.1 10 5 6 N/m 2 2.1.1 f x x L dl U 1 du = T ds pdv + fdl (2.1) 24 2 dv = 0 dl ( ) U f = T L p,t ( ) S L p,t (2.2) 2 ( ) ( ) S f = L T p,t p,l (2.3) ( ) U f = L p,t + T ( ) f T p,l (2.4) 1 f e ( U/
Microsoft Word - 11問題表紙（選択）.docx
A B A.70g/cm 3 B.74g/cm 3 B C 70at% %A C B at% 80at% %B 350 C γ δ y=00 x-y ρ l S ρ C p k C p ρ C p T ρ l t l S S ξ S t = ( k T ) ξ ( ) S = ( k T) ( ) t y ξ S ξ / t S v T T / t = v T / y 00 x v S dy dx
1 1.1 ( ). z = a + bi, a, b R 0 a, b 0 a 2 + b 2 0 z = a + bi = ( ) a 2 + b 2 a a 2 + b + b 2 a 2 + b i 2 r = a 2 + b 2 θ cos θ = a a 2 + b 2, sin θ =
1 1.1 ( ). z = + bi,, b R 0, b 0 2 + b 2 0 z = + bi = ( ) 2 + b 2 2 + b + b 2 2 + b i 2 r = 2 + b 2 θ cos θ = 2 + b 2, sin θ = b 2 + b 2 2π z = r(cos θ + i sin θ) 1.2 (, ). 1. < 2. > 3. ±,, 1.3 ( ). A
meiji_resume_1.PDF
β β β (q 1,q,..., q n ; p 1, p,..., p n ) H(q 1,q,..., q n ; p 1, p,..., p n ) Hψ = εψ ε k = k +1/ ε k = k(k 1) (x, y, z; p x, p y, p z ) (r; p r ), (θ; p θ ), (ϕ; p ϕ ) ε k = 1/ k p i dq i E total = E
koji07-01.dvi
2007 I II III 1, 2, 3, 4, 5, 6, 7 5 10 19 (!) 1938 70 21? 1 1 2 1 2 2 1! 4, 5 1? 50 1 2 1 1 2 2 1?? 2 1 1, 2 1, 2 1, 2, 3,... 3 1, 2 1, 3? 2 1 3 1 2 1 1, 2 2, 3? 2 1 3 2 3 2 k,l m, n k,l m, n kn > ml...?
[1] convention Minkovski i Polchinski [2] 1 Clifford Spin 1 2 Euclid Clifford 2 3 Euclid Spin 6 4 Euclid Pin Clifford Spin 10 A 12 B 17 1 Cliffo
![[1] convention Minkovski i Polchinski [2] 1 Clifford Spin 1 2 Euclid Clifford 2 3 Euclid Spin 6 4 Euclid Pin Clifford Spin 10 A 12 B 17 1 Cliffo](/thumbs/101/149329436.jpg "[1] convention Minkovski i Polchinski [2] 1 Clifford Spin 1 2 Euclid Clifford 2 3 Euclid Spin 6 4 Euclid Pin Clifford Spin 10 A 12 B 17 1 Cliffo")
[1] convention Minkovski i Polchinski [2] 1 Clifford Spin 1 2 Euclid Clifford 2 3 Euclid Spin 6 4 Euclid Pin + 8 5 Clifford Spin 10 A 12 B 17 1 Clifford Spin D Euclid Clifford Γ µ, µ = 1,, D {Γ µ, Γ ν
6kg 1.1m 1.m.1m.1 l λ ϵ λ l + λ l l l dl dl + dλ ϵ dλ dl dl + dλ dl dl 3 1. JIS 1 6kg 1% 66kg 1 13 σ a1 σ m σ a1 σ m σ m σ a1 f f σ a1 σ a1 σ m f 4
35-8585 7 8 1 I I 1 1.1 6kg 1m P σ σ P 1 l l λ λ l 1.m 1 6kg 1.1m 1.m.1m.1 l λ ϵ λ l + λ l l l dl dl + dλ ϵ dλ dl dl + dλ dl dl 3 1. JIS 1 6kg 1% 66kg 1 13 σ a1 σ m σ a1 σ m σ m σ a1 f f σ a1 σ a1 σ m
( ) sin 1 x, cos 1 x, tan 1 x sin x, cos x, tan x, arcsin x, arccos x, arctan x. π 2 sin 1 x π 2, 0 cos 1 x π, π 2 < tan 1 x < π 2 1 (1) (
6 20 ( ) sin, cos, tan sin, cos, tan, arcsin, arccos, arctan. π 2 sin π 2, 0 cos π, π 2 < tan < π 2 () ( 2 2 lim 2 ( 2 ) ) 2 = 3 sin (2) lim 5 0 = 2 2 0 0 2 2 3 3 4 5 5 2 5 6 3 5 7 4 5 8 4 9 3 4 a 3 b
i 18 2H 2 + O 2 2H 2 + ( ) 3K
i 18 2H 2 + O 2 2H 2 + ( ) 3K ii 1 1 1.1.................................. 1 1.2........................................ 3 1.3......................................... 3 1.4....................................
SO(2)
TOP URL http://amonphys.web.fc2.com/ 1 12 3 12.1.................................. 3 12.2.......................... 4 12.3............................. 5 12.4 SO(2).................................. 6
36 th IChO : - 3 ( ) , G O O D L U C K final 1
36 th ICh - - 5 - - : - 3 ( ) - 169 - -, - - - - - - - G D L U C K final 1 1 1.01 2 e 4.00 3 Li 6.94 4 Be 9.01 5 B 10.81 6 C 12.01 7 N 14.01 8 16.00 9 F 19.00 10 Ne 20.18 11 Na 22.99 12 Mg 24.31 Periodic
A = A x x + A y y + A, B = B x x + B y y + B, C = C x x + C y y + C..6 x y A B C = A x x + A y y + A B x B y B C x C y C { B = A x x + A y y + A y B B
9 7 A = A x x + A y y + A, B = B x x + B y y + B, C = C x x + C y y + C..6 x y A B C = A x x + A y y + A B x B y B C x C y C { B = A x x + A y y + A y B B x x B } B C y C y + x B y C x C C x C y B = A
20 4 20 i 1 1 1.1............................ 1 1.2............................ 4 2 11 2.1................... 11 2.2......................... 11 2.3....................... 19 3 25 3.1.............................
I A A441 : April 21, 2014 Version : Kawahira, Tomoki TA (Kondo, Hirotaka ) Google
I4 - : April, 4 Version :. Kwhir, Tomoki TA (Kondo, Hirotk) Google http://www.mth.ngoy-u.c.jp/~kwhir/courses/4s-biseki.html pdf 4 4 4 4 8 e 5 5 9 etc. 5 6 6 6 9 n etc. 6 6 6 3 6 3 7 7 etc 7 4 7 7 8 5 59
N cos s s cos ψ e e e e 3 3 e e 3 e 3 e
3 3 5 5 5 3 3 7 5 33 5 33 9 5 8 > e > f U f U u u > u ue u e u ue u ue u e u e u u e u u e u N cos s s cos ψ e e e e 3 3 e e 3 e 3 e 3 > A A > A E A f A A f A [ ] f A A e > > A e[ ] > f A E A < < f ; >
Z: Q: R: C:
0 Z: Q: R: C: 3 4 4 4................................ 4 4.................................. 7 5 3 5...................... 3 5......................... 40 5.3 snz) z)........................... 4 6 46 x
1 1 n 0, 1, 2,, n n 2 a, b a n b n a, b n a b (mod n) 1 1. n = (mod 10) 2. n = (mod 9) n II Z n := {0, 1, 2,, n 1} 1.
1 1 n 0, 1, 2,, n 1 1.1 n 2 a, b a n b n a, b n a b (mod n) 1 1. n = 10 1567 237 (mod 10) 2. n = 9 1567 1826578 (mod 9) n II Z n := {0, 1, 2,, n 1} 1.2 a b a = bq + r (0 r < b) q, r q a b r 2 1. a = 456,
II 2 II
II 2 II 2005 [email protected] 2005 4 1 1 2 5 2.1.................................... 5 2.2................................. 6 2.3............................. 6 2.4.................................
0.1 I I : 0.2 I
1, 14 12 4 1 : 1 436 (445-6585), E-mail : [email protected] 0.1 I I 1. 2. 3. + 10 11 4. 12 1: 0.2 I + 0.3 2 1 109 1 14 3,4 0.6 ( 10 10, 2 11 10, 12/6( ) 3 12 4, 4 14 4 ) 0.6.1 I 1. 2. 3. 0.4 (1)
数学の基礎訓練I
I 9 6 13 1 1 1.1............... 1 1................ 1 1.3.................... 1.4............... 1.4.1.............. 1.4................. 3 1.4.3........... 3 1.4.4.. 3 1.5.......... 3 1.5.1..............
ω 0 m(ẍ + γẋ + ω0x) 2 = ee (2.118) e iωt x = e 1 m ω0 2 E(ω). (2.119) ω2 iωγ Z N P(ω) = χ(ω)e = exzn (2.120) ϵ = ϵ 0 (1 + χ) ϵ(ω) ϵ 0 = 1 +
2.6 2.6.1 ω 0 m(ẍ + γẋ + ω0x) 2 = ee (2.118) e iωt x = e 1 m ω0 2 E(ω). (2.119) ω2 iωγ Z N P(ω) = χ(ω)e = exzn (2.120) ϵ = ϵ 0 (1 + χ) ϵ(ω) ϵ 0 = 1 + Ne2 m j f j ω 2 j ω2 iωγ j (2.121) Z ω ω j γ j f j
2007 5 iii 1 1 1.1.................... 1 2 5 2.1 (shear stress) (shear strain)...... 5 2.1.1...................... 6 2.1.2.................... 6 2.2....................... 7 2.2.1........................
v v = v 1 v 2 v 3 (1) R = (R ij ) (2) R (R 1 ) ij = R ji (3) 3 R ij R ik = δ jk (4) i=1 δ ij Kronecker δ ij = { 1 (i = j) 0 (i
1. 1 1.1 1.1.1 1.1.1.1 v v = v 1 v 2 v 3 (1) R = (R ij ) (2) R (R 1 ) ij = R ji (3) R ij R ik = δ jk (4) δ ij Kronecker δ ij = { 1 (i = j) 0 (i j) (5) 1 1.1. v1.1 2011/04/10 1. 1 2 v i = R ij v j (6) [
QMI_10.dvi
... black body radiation black body black body radiation Gustav Kirchhoff 859 895 W. Wien O.R. Lummer cavity radiation ν ν +dν f T (ν) f T (ν)dν = 8πν2 c 3 kt dν (Rayleigh Jeans) (.) f T (ν) spectral energy
05Mar2001_tune.dvi
2001 3 5 COD 1 1.1 u d2 u + ku =0 (1) dt2 u = a exp(pt) (2) p = ± k (3) k>0k = ω 2 exp(±iωt) (4) k
untitled
(a) (b) (c) (d) (e) (f) (g) (f) (a), (b) 1 He Gleiter 1) 5-25 nm 1/2 Hall-Petch 10 nm Hall-Petch 2) 3) 4) 2 mm 5000% 5) 1(e) 20 µm Pd, Zr 1(f) Fe 6) 10 nm 2 8) Al-- 1,500 MPa 9) 2 Fe 73.5 Si 13.5 B 9 Nb
x = a 1 f (a r, a + r) f(a) r a f f(a) 2 2. (a, b) 2 f (a, b) r f(a, b) r (a, b) f f(a, b)
2011 I 2 II III 17, 18, 19 7 7 1 2 2 2 1 2 1 1 1.1.............................. 2 1.2 : 1.................... 4 1.2.1 2............................... 5 1.3 : 2.................... 5 1.3.1 2.....................................
() x + y + y + x dy dx = 0 () dy + xy = x dx y + x y ( 5) ( s55906) 0.7. (). 5 (). ( 6) ( s6590) 0.8 m n. 0.9 n n A. ( 6) ( s6590) f A (λ) = det(a λi)
0. A A = 4 IC () det A () A () x + y + z = x y z X Y Z = A x y z ( 5) ( s5590) 0. a + b + c b c () a a + b + c c a b a + b + c 0 a b c () a 0 c b b c 0 a c b a 0 0. A A = 7 5 4 5 0 ( 5) ( s5590) () A ()
<4D F736F F D B B83578B6594BB2D834A836F815B82D082C88C602E646F63>
スピントロニクスの基礎 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/077461 このサンプルページの内容は, 初版 1 刷発行時のものです. i 1 2 ii 3 5 4 AMR (anisotropic magnetoresistance effect) GMR (giant magnetoresistance
1. 4cm 16 cm 4cm 20cm 18 cm L λ(x)=ax [kg/m] A x 4cm A 4cm 12 cm h h Y 0 a G 0.38h a b x r(x) x y = 1 h 0.38h G b h X x r(x) 1 S(x) = πr(x) 2 a,b, h,π
![1. 4cm 16 cm 4cm 20cm 18 cm L λ(x)=ax [kg/m] A x 4cm A 4cm 12 cm h h Y 0 a G 0.38h a b x r(x) x y = 1 h 0.38h G b h X x r(x) 1 S(x) = πr(x) 2 a,b, h,π](/thumbs/101/149329485.jpg "1. 4cm 16 cm 4cm 20cm 18 cm L λ(x)=ax [kg/m] A x 4cm A 4cm 12 cm h h Y 0 a G 0.38h a b x r(x) x y = 1 h 0.38h G b h X x r(x) 1 S(x) = πr(x) 2 a,b, h,π")
. 4cm 6 cm 4cm cm 8 cm λ()=a [kg/m] A 4cm A 4cm cm h h Y a G.38h a b () y = h.38h G b h X () S() = π() a,b, h,π V = ρ M = ρv G = M h S() 3 d a,b, h 4 G = 5 h a b a b = 6 ω() s v m θ() m v () θ() ω() dθ()
limit&derivative
- - 7 )................................................................................ 5.................................. 7.. e ).......................... 9 )..........................................
n (1.6) i j=1 1 n a ij x j = b i (1.7) (1.7) (1.4) (1.5) (1.4) (1.7) u, v, w ε x, ε y, ε x, γ yz, γ zx, γ xy (1.8) ε x = u x ε y = v y ε z = w z γ yz
1 2 (a 1, a 2, a n ) (b 1, b 2, b n ) A (1.1) A = a 1 b 1 + a 2 b 2 + + a n b n (1.1) n A = a i b i (1.2) i=1 n i 1 n i=1 a i b i n i=1 A = a i b i (1.3) (1.3) (1.3) (1.1) (ummation convention) a 11 x
1 1 1 1-1 1 1-9 1-3 1-1 13-17 -3 6-4 6 3 3-1 35 3-37 3-3 38 4 4-1 39 4- Fe C TEM 41 4-3 C TEM 44 4-4 Fe TEM 46 4-5 5 4-6 5 5 51 6 5 1 1-1 1991 1,1 multiwall nanotube 1993 singlewall nanotube ( 1,) sp 7.4eV
2 1 7 - TALK ABOUT 21 μ TALK ABOUT 21 Ag As Se 2. 2. 2. Ag As Se 1 2 3 4 5 6 7 8 9 1 1 2 3 4 5 6 7 8 9 1 1 2 3 4 5 6 7 8 9 1 Sb Ga Te 2. Sb 2. Ga 2. Te 1 2 3 4 5 6 7 8 9 1 1 2 3 4 5 6 7 8 9 1 1 2 3 4
all.dvi
72 9 Hooke,,,. Hooke. 9.1 Hooke 1 Hooke. 1, 1 Hooke. σ, ε, Young. σ ε (9.1), Young. τ γ G τ Gγ (9.2) X 1, X 2. Poisson, Poisson ν. ν ε 22 (9.) ε 11 F F X 2 X 1 9.1: Poisson 9.1. Hooke 7 Young Poisson G
1 1 H Li Be Na M g B A l C S i N P O S F He N Cl A e K Ca S c T i V C Mn Fe Co Ni Cu Zn Ga Ge As Se B K Rb S Y Z Nb Mo Tc Ru Rh Pd Ag Cd In Sn Sb T e
No. 1 1 1 H Li Be Na M g B A l C S i N P O S F He N Cl A e K Ca S c T i V C Mn Fe Co Ni Cu Zn Ga Ge As Se B K Rb S Y Z Nb Mo Tc Ru Rh Pd Ag Cd In Sn Sb T e I X e Cs Ba F Ra Hf Ta W Re Os I Rf Db Sg Bh
() 3 3 2 5 3 6 4 2 5 4 2 (; ) () 8 2 4 0 0 2 ex. 3 n n =, 2,, 20 : 3 2 : 9 3 : 27 4 : 8 5 : 243 6 : 729 7 : 287 8 : 656 9 : 9683 0 : 59049 : 7747 2 : 5344 3 : 594323 4 : 4782969 5 : 4348907 6 : 4304672
http://www.ike-dyn.ritsumei.ac.jp/ hyoo/wave.html 1 1, 5 3 1.1 1..................................... 3 1.2 5.1................................... 4 1.3.......................... 5 1.4 5.2, 5.3....................
OHO.dvi
1 Coil D-shaped electrodes ( [1] ) Vacuum chamber Ion source Oscillator 1.1 m e v B F = evb (1) r m v2 = evb r v = erb (2) m r T = 2πr v = 2πm (3) eb v
1. 2 P 2 (x, y) 2 x y (0, 0) R 2 = {(x, y) x, y R} x, y R P = (x, y) O = (0, 0) OP ( ) OP x x, y y ( ) x v = y ( ) x 2 1 v = P = (x, y) y ( x y ) 2 (x
. P (, (0, 0 R {(,, R}, R P (, O (0, 0 OP OP, v v P (, ( (, (, { R, R} v (, (, (,, z 3 w z R 3,, z R z n R n.,..., n R n n w, t w ( z z Ke Words:. A P 3 0 B P 0 a. A P b B P 3. A π/90 B a + b c π/ 3. +