2.6 全微分 重積分 置換積分 ヤコビアン全微分筆者は 全微分をあまり正確には理解していないと自覚しています いくつかの公式は知っていますし それを使うことも出来るのですが 上手ではありません 多次元の時に 具体的なイメージが浮かばないのです ましてや 数学的な証明になるとまったく自信がありません
|
|
|
- よりお よしくに
- 5 years ago
- Views:
Transcription
1 .6 全微分 重積分 置換積分 ヤコビアン全微分筆者は 全微分をあまり正確には理解していないと自覚しています いくつかの公式は知っていますし それを使うことも出来るのですが 上手ではありません 多次元の時に 具体的なイメージが浮かばないのです ましてや 数学的な証明になるとまったく自信がありません 例によって 大雑把にでも 何の話か理解するために 最も簡単な例から考えます 関数が 変数のみで表されている時には 普通の微分も全微分も違いがありません (xx) と書いても良いし 偏微分の記号を使って (xx) = lim ff(xx + Δxx) ff(xx) Δx Δxx = lim ff(xx + Δxx) ff(xx) Δxx Δxx と書いても 実際 何の違いもありません 意味が違ってくるのはff(xx, yy) のように 関数が複数の変数の関数の時です (xx,yy) と (xx,yy) では明らかに意味が違います (xx, yy) ff(xx + Δxx, yy) ff(xx, yy) = lim Δxx Δxx この式は 関数の中に含まれるyyをxxとは独立した 定数のように取り扱って xxで微分するという意味です (xx, yy) の方に どんな意味があるのかと問われると このままでは返答のしようがないのですが たとえば yy = gg(xx) のように yがxxの関数ならば (xx, gg(xx)) = lim Δxx h(xx + Δxx) h(xx, yy) Δxx のように 変数 xxの関数になってしまうから 意味があります しかし yy = gg(xx) で無い場合に この式の意味を問われても 私には返答ができません 全微分も微分なので ある曲面の接線の傾きを考えているのですが 変数ではありませんから 接線というよりは接平面を考えていると捉えたほうが良いでしょう 接線の傾きを考えるよりも x 方向 y 方向に傾きを持った面が 全体としてどんな傾きをもっているか 逆に x 方向 とy 方向にそれぞれ微小分動いたときに その曲面がどのくらい変化するかを考えることだと言ったほうが理解しやすいかもしれません
2 具体的に図に書くと次のようなことです ff(xx, yy) yy Δxx 図 48 全微分の空間的な意味 3 次元空間に ff(xx, yy) があって この場合はff(,) を起点として考えていますが x 方向と y 方向に同時にΔxx Δyy 移動したときに ff(xx, yy) の増加分 Δff(xx, yy) はどのようになるかということです この同時に動かすというのが問題で 小学校以来 計算は丁寧に順番にやるように習っています 同時に動かせるはずがありません この図からも明らかなように 平面という特殊な場合を除くと xxを先に動かすかyyを先に動かすかで 結果は違うでしょう そこで 微分の時にいつも出てくる考え方ですが Δxx Δyyが限りなく小さくなれば 近似的に平面だと考えます これを式で表すと Δff(xx, yy) = lim ff(xx + Δxx, yy + Δyy) ff(xx, yy) Δxx ですが ff(xx, yy + Δyy) + ff(xx, yy + Δyy) を右辺に書き加えて Δff(xx, yy) = lim ff(xx + Δxx, yy + Δyy) ff(xx, yy + Δyy) + ff(xx, yy + Δyy) ff(xx, yy) Δxx,Δyy = lim Δxx,Δyy + Δxx, yy + Δyy) ff(xx, yy + Δyy) ff(xx Δxx + Δxx ff(xx + Δxx, yy) ff(xx, yy) = lim Δxx Δxx Δxx + lim,δyy ff(xx, yy + Δyy) ff(xx, yy) Δyy Δyy ff(xx, yy + Δyy) ff(xx, yy) Δyy Δyy となります 途中 赤字で書いたところの変形 ff(xx + Δxx, yy + Δyy) ff(xx, yy + Δyy) = ff(xx + Δxx, yy) ff(xx, yy) については そんなことはないだろうというツッコミはありそうです しかし Δyyが無限に小さければ 近似的に等式が成り立つでしょう ということで 偏微分の定義で Δ を に書き換えて 微分の式らしくして ff(xx + Δxx, yy) ff(xx, yy) (xx, yy) lim = Δxx Δxx ff(xx, yy + Δyy) ff(xx, yy) (xx, yy) lim =,Δyy Δyy (xx, yy) = (xx, yy) + Δyy xx (xx, yy) Δff(xx, yy)
3 となります これが全微分の公式と言う名前の公式です もっと変数が増えても のようになります (xx, yy, zz) = (xx, yy, zz) + (xx, yy, zz) + (xx, yy, zz) 全微分というものを 式としてどうのように表すのか というのは ありそうな疑問で す 微分を習ったときに たとえば xx = ff(uu) という 変数で表されている関数を変数 uu で 微分する場合 (uu) あるいはと書くと習いました この場合は 変数なのだから 全微 分も = だから 全微分も偏微分も区別がありません しかし 次のような場合には 全微分と偏微分は明らかに違うものです 次のような 変換を考えます 関数と言ってもよいでしょう xx = AAAA 太字で書いたのは このそれぞれが ベクトルないし行列だということです きちんと書けば ということです を考えます もともとの変換式を xx について書けば となります 全微分の公式に従えば ですから xx aa aa aa nn uu xx aa aa aa nn uu = xx nn aa nn aa nn aa nnnn uu nn xx = aa uu + aa uu + + aa nn aa nn xx = xx uu uu + xx uu uu + + xx uu nn uu xx xx xx uu uu xx xx = uu uu nn xx nn xx nn uu uu xx uu nn xx uu nn xx nn nn uu nn と書けます この場合は たまたま 線形になっているので
4 xx uu = aa, xx uu = aa, xx ii uu jj = aa iiii,, xx nn uu nn = aa nnnn ですから xx xx uu uu xx xx uu uu xx nn xx nn uu uu xx uu nn xx aa aa aa nn aa uu nn aa aa nn = = AA xx aa nn aa nn aa nnnn nn uu nn です だから とかけますけれど これは特殊な例です = AA 重積分の考え方分散分析のところで 二項分布から正規分布の確率密度の分布の式を求めるときに 畳み込み法と 重積分について触れたのですが 重積分を取り上げて独立して数学的な説明まではしませんでした 具体的にどういう計算をしているのかは分かったと思うのですが それでも いきなり 積分記号がいくつも重なった重積分で書かれた式を見ると 何を書いているのかとっさに意味が解らずに 腰が引けてしまいます 式は何やら恐ろしげなのですが 多くの場合 式の意味するところはそんなに難しいことではありません そこで 例によって あまり数学的ではないけれど 感覚的にこんなものだという解析をします 始めにやるのは 重積分で書かれていない 普通の積分だって 重積分的に解釈することができるということです これまた例によって 馬鹿馬鹿しいほど簡単なことから考えます 筆者は高等数学を学んだことがないから 簡単なことから考えていかざるを得ないのです 不自由なものです 数学ができる人がうらやましい と言う式です 簡単すぎてかえって意味が解りませんか 雑念なく積分の定義通りに理解すれば十分です xxという変数があって それを小さな部分に分けて作った Δxxをたしあわせる (integrate する ) と言う意味です どこからどこまでたしあわせるのかがこの式ではわかりません たしあわせる範囲が決まっていないということで これは不定積分という形です これまた さらに簡単すぎて具体的に考えると意味が解りませんが
5 = ですから ( この式の意味はxxをxxで微分すればであるということです ) をで積分すればxxです 当たり前のことを 何でわざわざ繰り返して説明しているのかと言われそうですが もう少し付き合ってください ということで この不定積分の答えは = xx + CC ですね CCはxxの積分範囲が決まっていないので どこからたしあわせるかわからないので どこからたしあわせても良いように 定数 CCを付け加えておくということで これを積分定数と呼びます xxの積分範囲をaa xx bbと決めておけば これは定積分になって bb aa = [xx] aa bb = bb aa となります この計算を積分記号を使わないでそのまま表すと ということなのですが これを bb aa nn nn bb aa lim nn nn kk= = Δxxとして書きなおすと lim bb aa Δxx Δxx Δxx kk= aa か bb の直線を 細かく細分化して さらにそれを元通りにたしあわせれば その長さは bb aa に決まっています 人を馬鹿にするなと言われそうです これは 長さですから 幅を持っていません この積分に幅を持たせることを考えます 最初はごく微量の幅を持たせたいので xxと独立し直交している成分を y として Δyだけ幅を持たせます つまり 面積が ΔxxΔyの微小な長方形を考えて これをたしあわせて 面積を求めるということをしたいのです こういう考え方を式に表したのが という式です 微積分ではΔxxΔyの無限小のものをと表すという式の記述における約束やすでに納得されていると思います しかし 重積分の式は 不定積分でいったいどこからどこの範囲で積分するのかわかりません だから 微分式の逆関数として考えれば何らかの意味を考えられるかもしれませんが このままでは 何のことかわかりません そこで 積分する範囲を決めて 定積分とすれば 具体的な意味が発生します
6 D というのが積分範囲です この場合は x-y 平面なのだから aa xx bb, cc yy のよう に積分範囲 D を決めれば これで という式が 具体的な形の面積を意味するこ とになります ここでは aa, bb, cc, ですが もちろん これが範囲を表す ff(aa), ff(bb) のような 数式でもかまいません しかし まず わかりやすい 図 48. 面積と重積分図のような 長方形の面積を求める場合 D の範囲は xx bb, yy です これを計算するとき 普通 yy bb xx xx bb 図 49. 面積の計算手順のように 黄色で表した 微小な長方形の面積を求めて それをたしあわせる つまりxx 方向に積分するということをするでしょう これを重積分で表現すると bb = と言う計算になります bb = [yy] bb = ( ) = [] bb = (aaaa ) = aaaa つまり ff(y) = を y で積分して長さを出して その結果をに Δxx をかけて xx で積分するとい う計算です 小学校で習った長方形の面積は横の長さ 縦の長さだということを難しくいっただけなのです つまり 人間は頭の中で 普通に重積分をしているのです なんだか わかりきったことを言っているようですが でも 確かに重積分を解いているのです この例では yyはxx 独立していて 何の関係もないのですが これを発展させて
7 yy y=αxx + y=αxx bb xx 図 5 平行四辺形の面積と重積分のような平行四辺形について考えます 重積分の式そのものは変わりませんが 積分範囲が違います D の範囲は aa xx bb, αααα yy αααα + です ですから bb = αααα+ αααα bb = () bb = [yy] αααα αααα+ = [] bb = (aaaa ) = aaaa bb = (αααα + αααα) 平行四辺形の体積が底辺 高さだということは 小学校で習いました ですから 計算結果は当然 長方形の場合も平行四辺形の場合も同じです さらに発展させます yy y=βxx y=βxx βb y=αxx + y=αxx bb xx 図 5. 重積分の例 のようなときにどうするかです 全体は部分の総和ですから この場合は
8 yy A SS y=βxx y=βxx βb S 3 S B bb C y=αxx + y=αxx xx 図 5. 図 5 の計算手順 とつの3 角形 (S SS 3 ) とつの平行四辺形 (S ) の3つの部分に分けて計算して 3つをたしあわせればよいでしょう そうすると y=βxxと y=αxx + の交点 A y=βxx βb とy=αxx の交点 B y=αxx + と y=βxx βbの交点 C の座標が必要になります まず それぞれの連立方程式を解きます A について y=βxx y=αxx + を解いて, ββββ B についてを解いて C についてとなります それぞれの面積を計算します ββββ ββ αα, ββββ + ββ αα, y=βxx βb y=αxx y=βxx βb y=αxx + を解いて αααααα ββ αα αααα(bb + ) ββ αα
9 SS について D の範囲は xx SS = βxx = = αxx, αxx yy βxx だから βxx [yy] αxx = (ββ αα)xxxxxx = = (ββ αα) ( ββ αα () ) = (ββ αα) SS について D の範囲は ββββ xx, αxx yy αxx + だから SS = ββββ αxx+ = = ββββ αxx = () SS 3 について D の範囲は ββββ SS 3 = = となるので ββββ+ αxx+ ββββ = [xx] = = ββββ ββββ+ ββββ βxx βb ββββ [yy] αxx αxx+ = ββββ (ββ αα) [xx ] (αxx + αxx) ββββ = ( ββ αα (ββββ ) ) = ββ αα (ββ αα) ββββ+ xx, βxx βb yy αxx + だから ββββ+ ββββ = (α β)xx + + βb αxx+ [yy] βxx βb = ββββ+ ββββ ββββ+ (αxx + βxx + βb)xx = (ββ αα) [xx ] ββββ + ( + βb)[xx] ββββ = + (ββ αα) ββββ ββ αα ββββ ββ αα ββββ + + ( + βb) ββ αα + + βb) ββββββ + ( ββ αα ββ αα = ββββββ + ββββββ + = ββ αα SS = SS + SS + SS 3 = = (ββββ ) + (ββ αα) (ββ αα) + (ββ αα) (ββ αα) ( + ββββββ + ) = ββββββ (ββ αα) ββββ ββ αα ββββ+ = ββ αα ここで この計算結果が正しいことを確認しておきましょう 小学校で習った通りに 底辺かける高さで 平行四辺形の面積を計算します
10 yy y=βxx y=βxxy=αxx βb + H A S 3 C y=αxx S h SS O bb B xx 図 53. 図 5 の面積の重積分を使わない計算手順原点を O とすれば 底辺は OB で 高さは 原点から直線 y=αxx + に下した垂線 (yy = xx) と αα y = αxx + との交点 H と原点との距離 hです H は y=αxx + の連立方程式の解ですから yy = αα xx αxx + = αα xx xx = y = ( + αα ) ( + αα ) H = ( ( + αα ), ( + αα ) ) h = OH = ( + αα ) + ( + αα ) = ( + αα ) ( + αα ) = + αα OB = ββββ ββ αα + αααααα ββ αα = (ββββ) ( + αα ) (ββ αα) = ββββ + αα ββ αα h OB = ββββββ ββ αα 確かに間違いありません これで 式の意味は理解できたと思います しかしこれでは 重積分など使わなくても解ける簡単な問題を わざわざ難しくして解いているようです もう少し 実用的で役に立ちそうなことを考えてみましょう
11 重積分が魅力的な考え方だとわかる最初の例は 立体の体積を求める計算です zz C(,,) B(,,) yy O(,,) A(,,) xx 図 54. 三角錐の体積三角錐の体積は 底面積 高さだから に決まっているだろうと言われてしまえばそれ 3 6 までなのですが そういうことを知らないことにして考えます まず三角形 ABC の平面の式が問題になりますが x + y + z = であることは明らかでしょう ためしに三角形の頂点 A,B,C の座標を入れてみてください ちゃんと成り立っています 3 点で成り立てば 平面はの定義としては十分です つまり z = x y です 一つのやり方としては D の範囲 xx,, yy xx, zz xx yy という3 重積分だとして計算することが考えられます xx xx yy = xx = [zz] xx yy xx = ( xx yy) = ( xx)yy yy = ( xx)yy yy xx xx
12 = ( xx) ( xx) = (( xx) ) = 3 [( xx)3 ] = 6 となるのですが 3 行目の変形のところに注目してください は xx = ( xx yy) ( xx yy) D の範囲は xx,, yy xx という 重積分で表せます こういう問題は ( xx yy) という 重積分として解く方が普通ですたとえば n 個の変数で説明される確率変数 ( たとえば 個々の確率の積としてそれらの同時発生確率を計算する場合を考えてください ) があるとき 同時発生確率をff(xx, xx, xx nn ) のように表して ある範囲内で データが得られる確率を n 重積分で 下記の用の計算することができます 三角錐の計算例で ff(xx, xx, xx nn )xx xx xx nn と計算しようとするときには だと考えれば良いでしょう つまり ffx, yy, zz = xx xx xx nn で表されるn 次元空間の体積 (?) を直接計算しているのですが
13 ( xx yy) と計算するときは xx yy 平面上の D と言う平面図形の上の それぞれの点に ( xx yy) の 高さの柱が立っていて その高さの平面 D で積分しているのです 重積分がその威力を特に発揮するのは このff(xx, xx, xx nn ) の部分が複雑な形をしている場合で 積分を容易にするために しばしば 普通の積分 ( 編積分 ) でも良く出てきた置換積分を使います この置換積分が有効に使われるためには ヤコビアンという概念を導入する必要があります ヤコビアンは 統計検定 のところの 正規分布や t 分布を作る過程で 簡単に触れましたが もう一度 きちんと整理した話をしておきます ヤコビアン xx = AAAA について考えたいのですが 式が大きくなると考えにくいので n= の場合から考えます xx xx = aa aa aa aa uu uu uu uu = aa aa aa aa xx xx aa aa aa aa = aa aa aa aa aa aa aa aa この場合は n がだから この空間の最小の単位として単位平面を考えることができます ここで突然ですが A: (, ) uu C: (, ) O: (, ) B: (, ) 図 55. 単位面積という正方形の面積を考えます もちろん答えはです これを重積分的に解けば D の範囲を xx, xx として uu uu = uu duu = という書き方になります また 簡単なことを難しく表現しました 次に uu
14 xx A : (aa, aa ) C : (aa + aa, aa + aa ) O : (, ) 図 56. 変換と面積の拡大という平行四辺形の面積を考えます このひし形が 次の式による変換によって出来ていることは 理解できるでしょうか xx xx = aa aa aa aa uu uu B : (aa, aa ) xx わかりにくければ 次の計算を確認してください xx xx = aa aa aa = aa xx xx = aa aa aa aa = aa aa xx xx = aa aa aa aa = aa aa xx xx = aa aa aa aa = aa + aa aa + aa ここで 平行四辺形の面積と正方形の面積の比を考えます やり方はいろいろありそうなのですが あまり 面倒な計算はしたくありあません そこで 以前にやった計算の結果をそのまま使うことにします yy y=βxx y=βxx βb y=αxx + h H A SS O S S 3 B bb C xx y=αxx 図 57 ひし形の面積計算
15 平行四辺形 OBCA の面積は ββββββ A:, ββββ, B: ββββ, αααααα, C:ββββ+, αααα(bb+) と知っていますから, ββββ = (aa, aa ), ββββ, αααααα = (aa, aa ) として αα, ββ, bb, を解きます から つづいて から で さらに ββ αα = aa ββββ ββ αα = aa ββ = aa aa ββββ ββ αα = aa αααααα ββ αα = aa α = aa aa β α = aa aa aa aa = aa aa aa aa aa aa ββ αα = aa aa aa aa aa aa aa = aa = aa aa aa aa aa ββββ ββ αα = aa
16 bbaa aa aa aa aa aa aa aa = aa bb = aa aa aa aa aa ββββββ ββ αα = aa aa aa aa aa aa aa aa aa aa aa aa aa aa aa aa aa aa = aa aa aa aa となります ですね aa aa aa aa = aa aa aa aa 以前 行列式とは その変換がもたらす大きさだと説明しました この計算でその実感が持てたでしょうか 極めて微小な正方形を考えます それを xx xx = aa aa aa aa uu uu という変換をしてできた図形の面積は 元の微小な正方形の aa aa aa aa 倍の面積になるとい うことです どんなに複雑な図形でも 微小な正方形が集まってできていると考えれば それを変換してできる図形の面積は 元の図形の面積の aa aa aa aa 倍の面積になるというこ とです これは次元が増えても同じで 微小な立方体を xx aa aa aa 3 uu xx = aa xx 3 aa 3 aa aa 3 aa 3 uu aa 33 uu 3 aa aa aa 3 で変換すると 変換された結果できた3 次元の空間の体積は 元の立方体のaa aa 3 aa aa 3 aa 3 aa 33 倍になるということであり 元の空間の形がどうであれ 変換されてできた空間の体積は aa aa aa 3 元の空間の体積のaa aa 3 aa aa 3 aa 3 倍になるということです 4 次元以上でも同じことが言え aa 33 ますが 日本語でどう表現したらよいのかわかりません 言いたいことはわかると思いま す つまり ならば xx aa aa aa nn uu xx aa aa aa nn uu = xx nn aa nn aa nn aa nnnn uu nn
17 aa aa aa nn aa aa aa nn xx xx xx nn = uu uu uu nn aa nn aa nn aa nnnn ということです ということは当然 微小な図形についてもいえて ならば Δxx aa aa aa nn Δuu Δxx aa aa aa nn Δuu = Δxx nn aa nn aa nn aa nnnn Δuu nn aa aa aa nn aa aa aa nn Δxx Δxx Δxx nn = Δuu Δuu Δuu nn aa nn aa nn aa nnnn です ところで 全微分に戻って考えると = xx xx uu uu xx xx uu uu xx nn xx nn uu uu xx uu nn xx uu nn xx nn uu nn です つまり xx xx uu uu xx xx = uu uu nn xx nn xx nn uu uu xx uu nn xx uu nn xx nn nn uu nn これは aa aa aa nn aa aa aa nn = nn aa nn aa nn aa nnnn nn と言う形になっています 単位になっている正方形を考えたときには φφ (uu, uu nn ) φφ xx = (uu, uu nn ) φφ nn (uu, uu nn ) と書いたときに φφ ii (uu, uu nn ) が 線形 ( 一次の多項式 ) になっているので
18 の全微分が xx aa aa aa nn uu xx aa aa aa nn uu = xx nn aa nn aa nn aa nnnn uu nn になりますが aa aa aa nn aa aa aa nn = nn aa nn aa nn aa nnnn nn φφ ii (uu, uu nn ) が線形でなくても 全微分の結果を 下記のように表せます xx xx uu uu xx xx = uu uu nn xx nn xx nn uu uu xx uu nn xx uu nn xx nn nn uu nn 微小部分がこのような関係であれば これらを寄せ集めて出来た xx xx xx uu uu xx xx = uu uu nn xx nn xx nn uu uu xx uu nn xx uu nn xx nn nn uu nn ならば aa aa aa nn aa aa aa nn nn = nn aa nn aa nn aa nnnn ということですが 無限に小さな単位の関係がこのようになるならば それらを集めでできた複雑な図形というか下記の式で与えられる何かのかたまりの大きさ は ff(xx, xx nn ) xx xx nn 積分記号の D はxxの積分範囲
19 ff(xx, xx nn ) xx xx nn φφ φφ uu uu nn = ff{φφ ii (uu, uu nn ), φφ nn (uu, uu nn )} φφ nn φφ uu uu nn uu nn uu nn で与えられるということです ( 積分記号の D は xx の積分範囲 : は uu の積分範囲 uu nn はヤコビアンと言う名前がついていて JJ φφ のように表します φφ nn φφ nn uu nn uu nn φφ φφ uu 整理して公式的に書けば のとき とすれば ff(xx, xx nn ) φφ (uu, uu nn ) φφ xx = (uu, uu nn ) φφ nn (uu, uu nn ) J φφ = φφ uu xx xx nn = ff{φφ ii (uu, uu nn ), φφ nn (uu, uu nn )} JJ φφ uu uu 式 77 となるということです 全微分 重積分 置換積分 ヤコビアンをまとめて説明すればこのようなことです 実は私たちは このことを小学校 中学校 高校の数学で繰り返し習っています ただ その時は 変数の置換積分の延長で考えていて 全微分 重積分 ヤコビアという言葉を使っていないだけなのです 円の面積は π だと習いましたね 小学校 中学校ではこのことを結構 苦労して教えています 何しろ微積分なしで これを教えるのは至難の業です 高校では積分法の中で置換積分として教わるのですが これが重積分だという説明はしていません おかげで 覚えにくく 説明が技巧的な感じでした まず 高校ではこの問題をどう解いたかを思い出しましょう 重積分が使えないということが前提です
20 θ xx, xx xx xx, xx 図 58. 球の体積計算 ( 直交座標から極座標に変換 ) 太線部の長さを考えて これを xx の範囲で積分すると習いました xx この計算はできないこともないでしょうが めんどうなので xx = cos θθ とおいて これらを使って 下記の変形をして だから xx xx = この過程を重積分で書くと xx = sin θθ = sin θθ = sin θθ = sin θθ cos θθ = cos θθ sin θθ = sin θθ sin θθ = ( cos θθ) cos θθ = [θθ] = xx xx [sin θθ] = ( ) こんな面倒な計算は誰だってやりたくない そこで 気の利いた置換を考えて xx = ll cos θθ y = ll sin θθ とします = cos θθ
21 = ll sin θθ = sin θθ 丁寧にやれば となるので xx = = = ll cos θθ + = cos θθ ll sin θθ + = sin θθ + ll cos θθ θθ = cos sin θθ ll sin θθ ll cos θθ つまり ヤコビアン だから となります = llllllllll cos θθ sin θθ ll sin θθ ll cos θθ = ll(cos θθ sin θθ) = ll JJ φφ = ll 積分範囲は ll, θ π = ll = ll[θθ] = = ll = どうせ置換をするのであれば 初めから極座標で計算する方が楽です Δll ll θθ 図 59. 球の体積 ( 極座標で計算 ) 円周の内 角 θθで切り取られる円弧の長さはll θθです θθの微小分の増加 Δθに伴う長さの増加はllΔ θθです 半径 llの微小な増加分 Δllとして 同時に Δ θθ Δllが同時に増加したときの増加部分はllΔθθΔllの面積を持つ長方形に近似できますからこれを l r, θ πの範囲で重積分します
22 この計算は となります llllllllll llllll = ll[θθ] = = ll = π ところで 直交座標と極座標の計算を比較してみます 極座標の変換は すると xx = ll cos θθ yy = ll sin θθ = cos θθ = ll sin θθ = sin θθ 全微分の公式を使って となるので xx = = = ll cos θθ + = cos θθ ll sin θθ + = sin θθ + ll cos θθ θθ = cos sin θθ ll sin θθ ll cos θθ JJ cos θθ = sin θθ ll sin θθ ll cos θθ = ll(cos θθ sin θθ) = ll
23 重積分の置換積分の公式 ff(xx, xx nn ) に当てはめて考えると だから なので xx xx nn = ff{φφ ii (uu, uu nn ), φφ nn (uu, uu nn )} JJ φφ uu uu xx xx となっていることが確かめられました 置換積分を用いた重積分例 ff(xx, yy) = ff{φφ ii (, θθ), φφ (, θθ)} = = llllllllll = JJ 円の面積の求め方も 重積分を使った上手い計算の例なのですが 残念ながら答えを知っているので あまりありがたみがわかりません 有用性がわかりやすい例を示します y A B y = βxx C y = αxx xx = αyy D xx = ββββ xx 図 6. 重積分の応用例この図で 4つの曲線に囲まれた部分の面積を求めます ここまでの解説に使ったやり方のみでやるならば ひし形の計算と同様に 交点 A(xx aa, yy aa ) B(xx bb, yy bb ) C(xx cc, yy cc ) D(xx, yy ) を求めて 3つの部分に分けて SS について 積分範囲 D を xx aa xx xx bb, xx yy ββ βxx として SS = xx bb βxx βxx = = xx aa [yy] xx = βxx xx xx aa ββ xx aa ββ xx ββ = ββ 3 xx3 3ββ xx3 SS について 積分範囲 D を xx bb xx xx cc, xx ββ yy xx αα として xx bb xx aa xx bb xx bb
24 SS = xx cc xx αα xx αα = = xx bb [yy] xx = xx bb ββ αα ββ xx xx bb xx ββ = 3 αα ββ xx3 SS 3 について 積分範囲 D を xx cc xx xx, αxx yy xx αα として xx cc xx bb xx cc xx cc SS 3 = xx xx αα xx xx αα = = [yy] αxx xx αxx = xx cc xx cc αα ααxx xx = 3 αα xx3 αα 3 xx3 xx cc S = SS + SS + SS 3 = ββ 3 xx3 xx bb 3ββ xx3 + 3 αα xx cc ββ xx3 + 3 αα xx3 αα xx 3 xx3 xx aa xx xx bb cc これを計算すれば 答えは出るには出ますが こんな計算誰もやりたくないでしょう 回で間違えずに計算するのは至難の業です こういう時は置換積分を考えます y = αxx ですから y = βxx xx = ααy xx = ββy xx = uuuu y = vvvv つまり 変数と定数を逆転させて u α vv βの範囲で変動するものとして ββ αα の積分として 計算しようということです をに代入して y vv = uuuu を に代入して ここから y 3 = uuvv xx uu = vvvv xx 3 = vvuu xx cc xx
25 y = uu 3vv 3 xx = uu 3vv 3 y = 3 uu 3 vv 3 y = 3 uu 3vv 3 = 3 uu 3 vv 3 だから = 3 uu 3vv 3 = + = y y + この式を線形代数的な記法で書けば = y y という変換になります ここでヤコビアン ( 変換前の平面の図形と返還後の図形の拡大倍率 ) を知っていれば ヤコビアンは JJ = = y y y y = 3 uu 3 vv 3 3 uu 3vv 3 3 uu 3vv 3 3 uu 3 vv 3 = = 3 なので SS = = JJ αα ββ = JJ = JJ [vv] bb αα ββ αα αα ββ αα = JJ (ββ αα) = JJ (ββ αα)[uu] = JJ (ββ αα) αα ββ ββ ββ αα = (ββ αα) 3 αααα となります この例では 重積分とヤコビアンの有効性が示されていると思います
26 三重積分の典型的な例として 球体の体積を求める例を示します zz y r -r -r r r xx -r 図 6 直交座標での球の表現あまり上手に書けていませんが 黒い色の輪は円ではなくて半径 r の球体を表しています この体積を求めます 球の式は x + yy + zz = です 極座標の取り方は 軸の取り方によって 変わります 南極 北極と緯度経度の取り方が頭の中にあるので 下図のように直交座標の Z 軸を極座標の軸にとるのが普通だと思います zz y θ φ xx 図 6. 極座標で表した球しかし ここでは 直交座標での計算とイメージを合わせるために あえて 次のように座標を取ります 説明の都合上 便宜的にそうするというだけです
27 zz zz y y P ( cos θ,, sin θθ) l θ θ P( cos θ, sin θθ sin φφ, sin θθ cos φφ) φ H ( cos θ, sin θθ sin φφ, ) xx H( cos θ,, ) 図 63. 極座標変換の図という極座標変換の式は です なので 全微分の公式を使って xx = llcosθ y = ll sin θθ sin φφ z = ll sin θθ cos φφ / = cosθ / = ll sin θθ / = / = sin θθ sin φφ / = ll cos θθ sin φφ / = ll sin θθ cos φφ / = sin θθ cos φφ / = llcos θθ cos φφ / = ll sin θθ sin φφ cosθ ll sin θθ = sin θθ sin φφ ll cos θθ sin φφ ll sin θθ cos φφ sin θθ cos φφ llcos θθ cos φφ ll sin θθ sin φφ したがって ヤコビアンは cosθ ll sin θθ [JJ] = sin θθ sin φφ ll cos θθ sin φφ ll sin θθ cos φφ sin θθ cos φφ llcos θθ cos φφ ll sin θθ sin φφ
28 = cosθ ll cos θθ sin φφ ( ll sin θθ sin φφ) + ( ll sin θθ) ll sin θθ cos φφ sin θθ cos φφ cosθ ll sin θθ cos φφ ll cosθ cos φφ ( ll sin θθ) ll sin θθ sin φφ ( ll sin θθ sin φφ) = ll (cos θθ sin φφ sin θθ + sin 3 θθ cos φφ + cos θθ cos φφ sin θθ + sin 3 θθ sin φφ ) = l sin θθ (cos θθ sin φφ θθ + sin θθ cos φφ + cos θθ cos φφ + sin θθ sin φφ ) = ll sin θθ ( cos θθ (sin φφ + cos φφ)+sin θθ(cos φφ + sin φφ)) = ll sin θθ ((sin θθ + cos θθ)(cos φφ + sin φφ)) = ll sin θθ ということを理解したうえで 直交座標 極座標 ヤコビアンを使って解くという3つの方法で球の体積を求めます まず 直交座標からやります 球体ですから = xx + yy + zz という制約で体積を求めます 直交座標で 平面ずつ考えたいので 図 63 をx 軸方向とy 軸方向から見ます z φ O P H y z O P P θ H x Δxx 図 64-. X 軸方向からの図図 64- について この平面上で 破線で描かれた円の面積は この計算は という置換で簡略化されて OP = yy + zz = xx PH = zz = xx yy 図 64- Y 軸方向からの図 xx xx zzzzzz = xx yy xx xx y = xx sin φφ = xx cos φφ xx yy = ( xx )( sin φφ) = xx cos φφ = xx cos φφ xx zzzzzz xx = ( xx ) cos φφφφφφ
29 この式は次の置換で簡略化されます = ( xx ) ( xx ) + cos φφ cos φφ = cos φφ sin φφ = + cos φφ cos φφφφφφ = ( xx ) cos φφφφφφ = xx + cos φφφφφφ xx [φφ] [sin φφ] = xx ( + ) = ( xx ) これは 図 64- の破線で書いた円の面積だから これにxxの微小な幅であるΔxxをかけて 微小な体積として 図 64- の x 軸方向に xx の範囲で積分したものが 求める体積です これはそのまま積分して ( xx ) ( xx ) = xx = [xx] xx3 3 = ( 3 ) = 43 3 極座標でやると, 半径をllとして 図 64- の破線の円の半径はll sin θθで 直交するφの微小な変化量 Δφに対する変化量はll sin θθδφ 一方これと直交するの図 64- の実線の円の半径は llでθθの微小な変化 Δθに対する, 円弧の長さの変化量はllΔθ これらを掛け合わせた ll sin θθδθδφが円周上の面積の微小な変化です この平面に直交 半径の微小な変化 Δllをかけたものが 体積の変化だから これらを 積分範囲で積分すれば 体積になります 積分範囲は φについては一周分だから φ πで θは半周分だから π θ, llは ll です これを重積分で書けば ll sin θθ
30 = ll sin θθ = ll sin θθ = ll [cos θθ] = 4 ll = 4π ll3 3 となります = 4π3 3 ヤコビアンを使って機械的にやろうとすれば = [JJ] D の範囲は r xx, xx yy xx, z xx yy R の範囲は ll, θθ π, φ π = ll sin θθ RR = ll sin θθ = sin θθ = ( [cos θθ] ) = 4π ll = 4π3 3 となります ヤコビアンの良いところは 複雑なものについても頭を悩ます必要がないことです RR ここで 球体の表面積の求め方について 体積の場合と同じく直交座標による重積分 極座標を用いた重積分 ヤコビアンによる計算の計算を比較しておきましょう これは 全微分に対する感覚的な理解を助けると思います まず 座標から直交座標の変換を確認し
31 ておきましょう 球の体積のところでやった極座標系をそのまま使います xx = llcosθ y = ll sin θθ sin φφ z = ll sin θθ cos φφ [JJ] = ll sin θθ 表面積の場合 ll = ( 一定 ) xx + yy + zz = です 直交座標で球体の表面積を求めるのは相当厄介です 頭に描いてもらいたいのはリンゴの皮むきです 一回転剥いたときの リンゴの皮の長さを考えます それから 皮の幅をかけてい回転剥いた時の皮の面積を考えて 最後にそれを全部たしあわせます 極座標と直交座標の関係を示した図を x 軸の方向から見ると zz O φ P H P A B H yy yy Δyy 図 65 X 軸方向から見たベクトルと接線 POHと BPAについて POH BPA だから PB = PA OP PH PH OP = PA PB = Δyyy + zz zz = xx Δy zz これを y 方向に積分しますが 積分範囲は xx y xx です xx xx xx zz マイナスをつけたのは PB を傾きと考えた場合 負の値になるからです この定積分を解くことになりますが
32 ですから と置きます xx = yy + zz y= xx cos φφ z= xx sin φφ π θ π = xx sin φφ = zz xx zz = xx = xx zz xx xx [φφ] = xx この円周の長さに幅をかけるのですが ここでも 下図のような関係になっています P θ 拡大 H θ P zz 図 66. リンゴの皮むき方式による皮の幅 より O θ xx PH OP = P H PP zz = Δxx PP H Δxx PP = Δxx zz これが リンゴの皮むき のたとえにすれば 皮の幅に相当するものですから それを円周の長さとかけた面積は
33 xx Δxx zz = xx ll zz Δxx これを xx の範囲で xx 軸に沿って積分したものが球体の表面積です xx ll zz 再び 三角関数を使った置換積分で計算します だから 変換するまでもなく となります この計算を重積分で書くと xx = cos θθ zz = sin θθ xx = cos θθ = sin θθ = sin θθ xx zz = = xx xx = [xx] = 4 xx zz xx = xx ということです ということを頭に入れておいて 極座標での計算を考えます 極座標でやればもっと簡単です 直交座標の場合と同様に 図 64- の x-z 平面で 破線の線の円の半径は rsin θθ, したがって φを回転させたときにの 微小な回転による増加量は sin θθ Δφ, 一方 図 64- に示した y-z 平面では θをの微小な変化 Δθに対する円弧の長さの変化は で これらは直交しているので これらを同じに変化させた場合の 微小な変化量は sin θθ ΔφΔθである これを 積分範囲を決めて積分すると sin θθθθθθθθθθ = 4π 直交座標での計算と合わせるために 積分範囲を π φφ と移動しておきます 極座標変換のヤコビアンを使って この関係を書いてみると 両者の関係が良くわかります 今のところの結果は 以下の式のようになっています sin θθθθθθθθθθ = xx これを3 重積分の形で無理無理書こうという話です 無理無理やるのだからかなり怪しげな議論です 加える軸は 左辺についてはベクトルの長さllで 右辺についてはxy 平面に直交するz 軸です 工夫しなければならないところはつあって つ目は 左辺の を何 xx
34 かの積分の結果として表さなければならないということです これは比較的簡単で (xx ββ ) = xxだから llllllを加えれば良いことになります 右辺は を加えればよいので αα すが 積分範囲 α βが問題です いろいろな屁理屈はありそうですが とりあえず やってみるという感じで 単位量 =の厚みの体積は 底面の面積と数字的に同じになるか らという理由で を書き加えます llsin θθθθθθθθθθθθθθ = yy xx 右辺の逐次積分の順番を入れ替えておきます 理由はありません 趣味の問題です llsin θθθθθθθθθθθθθθ 左右を入れ替えて 符号も入れ替えます xx xx = xx = llsin θθθθθθθθθθθθθθ xx ここでヤコビアンを使った計算を思い出します xx xx xx yy ff(xx, yy, zz) xx xx yy = ffηη (ll, θθ, φφ), ηη (ll, θθ, φφ), ηη 3 (ll, θθ, φφ)jj ηη xx = ηη (ll, θθ, φφ) = llcosθ yy = ηη (ll, θθ, φφ) = ll sin θθ sin φφ zz = ηη 3 (ll, θθ, φφ) = ll sin θθ cos φφ ( 知っているギリシャ文字の数が限界に近づいていますが なんとか頑張ります ) JJ ηη = ll sin θθ 何がしたいのかと言うと これを xx xx ff(xx, yy, zz) xx xx xx yy xx yy = llsin θθθθθθθθθθθθθθ = ffηη (ll, θθ, φφ), ηη (ll, θθ, φφ), ηη 3 (ll, θθ, φφ)jj ηη このように書きたいのです ff(xx, yy, zz) とffηη (ll, θθ, φφ), ηη (ll, θθ, φφ), ηη 3 (ll, θθ, φφ)をどのようにすれば良いかということなのですが ffηη (ll, θθ, φφ), ηη (ll, θθ, φφ), ηη 3 (ll, θθ, φφ)jj ηη = llsin θθ で
35 だから JJ ηη = ll sin θθ なので つまり xx xx ffηη (ll, θθ, φφ), ηη (ll, θθ, φφ), ηη 3 (ll, θθ, φφ) = ll ff(xx, yy, zz) = xx yy xx yy xx + yy + zz = = ll JJ ηη 多分これで正解だと思いますが 右辺はそのまま変形しただけだからそれで良いとして 左辺がどうなるのか 計算しておきたいところです 最後の から手を付けます xx yy xx yy xx yy z = sin θθ cos φφ = sin θθ sin φφ xx yy = zz xx yy = zz = sin θθ = ( sin θθ sin φφ) = sin θθ [cos φφ] xx yy = sin θθ 次に 番目の積分です 積分範囲にxx しか含まれていないから xxで積分する方が楽ですね xx xx yy xx x = xx xx yy xx cos θθ = cos θθ = π + = πr xx = cosθ = sin θθ sin θθθθθθ = sin θθ π = [θθ] + [sin θθ] 最後に sin θθ = cos θθ = [yy] = 4
36 で確かに正しいことが確認できました 難しい計算ではないのですが 途中錯覚を起こしやすく 途中で結構間違えて混乱します やってみる場合は 落ち着いてやりましょう なんで こんな計算をわざわざしたのかというと xx xx xx yy xx yy = ll JJ ηη という 変換を具体的な像として頭の中に描きたかったのです まず右辺についてみます JJ ηη という倍率を定数と考えてて取り外すと ll ですが これは という直交した3つの長さをかけあわせた 直方体の体積のようではありませんか この微小な直方体を ll 方向に llになるまでたしあわせて llで割ったら で表される 微小な長方形の面積ですね 図に書くと図 67-のようになります xx zz yy 変換 ll 図 67- 直交座標での表面関. 図 67-. 極座標での表面関つまり 図 67- の直交極座標系で赤い楕円 ( 実際には立体的に湾曲した面 ) を極座標系の長方形に変換しているのです 面積や体積の計算をするときには 直交している方が計算しやすいので 空間を極座標系にとって 直交系の湾曲した立体を 直交した立体に変換しているのです 地球上で暮らしている時に 我々は鉛直に建てた柱は並行していると感じていますが これは近似的にそうなのであって 実は図 67- のように並行していません また 平方メートルの床を作ったら それに合わせて天井も 平方メートルの天井を作ります 本当は天井の方が少し大きいはずですね 私たちの頭も 図 67- から図 67- の変換を行っているのです 最後に極座標と直交座標を使って全微分について考えます 重積分の場合とは違って 下の図のように座標系を取って 極座標変換します その方が 微分における傾きが想像しやすいからです
37 zz y θ φ xx 図 68. 球面の傾斜と全微分この変換は xx = ll sin θθ cos φφ yy = ll sin θθ sin φφ zz = llcosθ sin θθ cos φφ ll cosθcos φφ ll sin θθ sin φφ = sin θθ sin φφ llcosθ sin φφ ll sin θθ cos φφ cosθ ll sin θθ ですが から = + = xxxxxx zz xx + yy + zz = = yy xx = zz yy = xx zz = tan θθ (cos φφφφφφ + sin φφφφφφ) ここで ちょっとしたテクニックを使います + yyyyyy ll sin θθ cos φφ + ll sin θθ sin φφφφφφ = = zz llcosθ
38 と + = tan θθ + cos φφ + sin φφ は下図の直角三角形の一つの角 ω に関する cos ωω と sin ωω ですね + ω dy 図 69. 直交する微小な変化と中心角度の関係 これを使えば = tan θθ + (cos φφ cos ωω + sin φφ sin ωω) = tan θθ + cos(φφ ωω) となります つまり φφ = ωωの時 は最小値 tan θθ + φφ = ωω + の時 = φφ = ωω + の時 は最大値 tan θθ + になります 球に上から水を落とすと 上からみて放射状に水が落ちていくのはそのためだと納得できます 球面上で xx 方向にcos ωω 移動し yy 方向にsin ωω 移動すれば 球の中心において x 軸に対してωωの角度の方向に 最大斜度を降下したことになり 反対に 球面上で最大斜度の方向に tan θθ 降下すれば xx 方向にcos ωω 移動し yy 方向にsin ωω 移動することになるということです z φ O P H y z O P P θ H x Δxx 図 64- ( 再掲 ) 図 64-( 再掲 ) 図 64 を見れば そのことは自明なのですが 全微分の公式
39 xx xx xx uu uu xx xx = uu uu nn xx nn xx nn uu uu xx uu nn xx uu nn xx nn nn uu nn この例では = + yy を 極座標変換を媒介して 実感してもらいたかったのです 感覚的に分かったでしょうか
<4D F736F F D20824F F6490CF95AA82C696CA90CF95AA2E646F63>
 1/15 平成 3 年 3 月 4 日午後 6 時 49 分 5 ベクトルの 重積分と面積分 5 重積分と面積分 Ⅰ. 重積分 と で 回積分することを 重積分 といいます この 重積分は何を意味しているのでしょう? 通常の積分 (1 重積分 ) では C d 図 1a 1 f d (5.1) 1 f d f ( ) は 図形的には図 1a のように面積を表しています つまり 1 f ( ) を高さとしてプロットすると図
1/15 平成 3 年 3 月 4 日午後 6 時 49 分 5 ベクトルの 重積分と面積分 5 重積分と面積分 Ⅰ. 重積分 と で 回積分することを 重積分 といいます この 重積分は何を意味しているのでしょう? 通常の積分 (1 重積分 ) では C d 図 1a 1 f d (5.1) 1 f d f ( ) は 図形的には図 1a のように面積を表しています つまり 1 f ( ) を高さとしてプロットすると図
代数 幾何 < ベクトル > 1 ベクトルの演算 和 差 実数倍については 文字の計算と同様 2 ベクトルの成分表示 平面ベクトル : a x e y e x, ) ( 1 y1 空間ベクトル : a x e y e z e x, y, ) ( 1 1 z1
 代数 幾何 < ベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル :, 空間ベクトル : z,, z 成分での計算ができるようにすること ベクトルの内積 : os 平面ベクトル :,, 空間ベクトル :,,,, z z zz 4 ベクトルの大きさ 平面上 : 空間上 : z は 良く用いられる 5 m: に分ける点 : m m 図形への応用
代数 幾何 < ベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル :, 空間ベクトル : z,, z 成分での計算ができるようにすること ベクトルの内積 : os 平面ベクトル :,, 空間ベクトル :,,,, z z zz 4 ベクトルの大きさ 平面上 : 空間上 : z は 良く用いられる 5 m: に分ける点 : m m 図形への応用
<8D828D5A838A817C A77425F91E6318FCD2E6D6364>
 4 1 平面上のベクトル 1 ベクトルとその演算 例題 1 ベクトルの相等 次の問いに答えよ. ⑴ 右の図 1 は平行四辺形 である., と等しいベクトルをいえ. ⑵ 右の図 2 の中で互いに等しいベクトルをいえ. ただし, すべてのマス目は正方形である. 解 ⑴,= より, =,= より, = ⑵ 大きさと向きの等しいものを調べる. a =d, c = f d e f 1 右の図の長方形 において,
4 1 平面上のベクトル 1 ベクトルとその演算 例題 1 ベクトルの相等 次の問いに答えよ. ⑴ 右の図 1 は平行四辺形 である., と等しいベクトルをいえ. ⑵ 右の図 2 の中で互いに等しいベクトルをいえ. ただし, すべてのマス目は正方形である. 解 ⑴,= より, =,= より, = ⑵ 大きさと向きの等しいものを調べる. a =d, c = f d e f 1 右の図の長方形 において,
パソコンシミュレータの現状
 第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
Microsoft Word - 微分入門.doc
 基本公式 例題 0 定義式 f( ) 数 Ⅲ 微分入門 = の導関数を定義式にもとづいて計算しなさい 基本事項 ( f( ), g( ) が微分可能ならば ) y= f( ) g( ) のとき, y = y= f( ) g( ) h( ) のとき, y = ( f( ), g( ) が微分可能で, g( ) 0 ならば ) f( ) y = のとき, y = g ( ) とくに, y = のとき,
基本公式 例題 0 定義式 f( ) 数 Ⅲ 微分入門 = の導関数を定義式にもとづいて計算しなさい 基本事項 ( f( ), g( ) が微分可能ならば ) y= f( ) g( ) のとき, y = y= f( ) g( ) h( ) のとき, y = ( f( ), g( ) が微分可能で, g( ) 0 ならば ) f( ) y = のとき, y = g ( ) とくに, y = のとき,
座標系.rtf
 2 章座標系 場 空間は3 次元なので, ベクトルを表現するには少なくとも3 成分を指定する必要がある. そのために座標系が必要となる. 座標系として最も一般的なものは,,, 成分を使った直角座標系である. しかし, 他にも円柱座標, 球座標, だ円座標, 放物線座標など様々なものがある. 現在までに3 成分で変数分離可能な座標系は11 個あるといわれている (Moon & Spencer, Field
2 章座標系 場 空間は3 次元なので, ベクトルを表現するには少なくとも3 成分を指定する必要がある. そのために座標系が必要となる. 座標系として最も一般的なものは,,, 成分を使った直角座標系である. しかし, 他にも円柱座標, 球座標, だ円座標, 放物線座標など様々なものがある. 現在までに3 成分で変数分離可能な座標系は11 個あるといわれている (Moon & Spencer, Field
<4D F736F F D20824F B CC92E8979D814696CA90CF95AA82C691CC90CF95AA2E646F63>
 1/1 平成 23 年 3 月 24 日午後 6 時 52 分 6 ガウスの定理 : 面積分と体積分 6 ガウスの定理 : 面積分と体積分 Ⅰ. 直交座標系 ガウスの定理は 微分して すぐに積分すると元に戻るというルールを 3 次元積分に適用した定理になります よく知っているのは 簡単化のため 変数が1つの場合は dj ( d ( ににします全微分 = 偏微分 d = d = J ( + C d です
1/1 平成 23 年 3 月 24 日午後 6 時 52 分 6 ガウスの定理 : 面積分と体積分 6 ガウスの定理 : 面積分と体積分 Ⅰ. 直交座標系 ガウスの定理は 微分して すぐに積分すると元に戻るというルールを 3 次元積分に適用した定理になります よく知っているのは 簡単化のため 変数が1つの場合は dj ( d ( ににします全微分 = 偏微分 d = d = J ( + C d です
2013年度 九州大・理系数学
 九州大学 ( 理系 ) 前期日程問題 解答解説のページへ a> とし, つの曲線 y= ( ), y= a ( > ) を順にC, C とする また, C とC の交点 P におけるC の接線をl とする 以下 の問いに答えよ () 曲線 C とy 軸および直線 l で囲まれた部分の面積をa を用いて表せ () 点 P におけるC の接線と直線 l のなす角を ( a) とき, limasin θ(
九州大学 ( 理系 ) 前期日程問題 解答解説のページへ a> とし, つの曲線 y= ( ), y= a ( > ) を順にC, C とする また, C とC の交点 P におけるC の接線をl とする 以下 の問いに答えよ () 曲線 C とy 軸および直線 l で囲まれた部分の面積をa を用いて表せ () 点 P におけるC の接線と直線 l のなす角を ( a) とき, limasin θ(
数学 ⅡB < 公理 > 公理を論拠に定義を用いて定理を証明する 1 大小関係の公理 順序 (a > b, a = b, a > b 1 つ成立 a > b, b > c a > c 成立 ) 順序と演算 (a > b a + c > b + c (a > b, c > 0 ac > bc) 2 図
 数学 Ⅱ < 公理 > 公理を論拠に定義を用いて定理を証明する 大小関係の公理 順序 >, =, > つ成立 >, > > 成立 順序と演算 > + > + >, > > 図形の公理 平行線の性質 錯角 同位角 三角形の合同条件 三角形の合同相似 量の公理 角の大きさ 線分の長さ < 空間における座漂とベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル
数学 Ⅱ < 公理 > 公理を論拠に定義を用いて定理を証明する 大小関係の公理 順序 >, =, > つ成立 >, > > 成立 順序と演算 > + > + >, > > 図形の公理 平行線の性質 錯角 同位角 三角形の合同条件 三角形の合同相似 量の公理 角の大きさ 線分の長さ < 空間における座漂とベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル
2017年度 神戸大・理系数学
 7 神戸大学 ( 理系 前期日程問題 解答解説のページへ を自然数とする f ( si + とおく < < 4 であることを用い て, 以下の問いに答えよ ( < < のとき, f ( < であることを示せ ( 方程式 f ( は < < の範囲に解をただ つもつことを示せ ( ( における解を とする lim であることを示し, lim を求めよ 7 神戸大学 ( 理系 前期日程問題 解答解説のページへ
7 神戸大学 ( 理系 前期日程問題 解答解説のページへ を自然数とする f ( si + とおく < < 4 であることを用い て, 以下の問いに答えよ ( < < のとき, f ( < であることを示せ ( 方程式 f ( は < < の範囲に解をただ つもつことを示せ ( ( における解を とする lim であることを示し, lim を求めよ 7 神戸大学 ( 理系 前期日程問題 解答解説のページへ
2017年度 長崎大・医系数学
 07 長崎大学 ( 医系 ) 前期日程問題 解答解説のページへ 以下の問いに答えよ () 0 のとき, si + cos の最大値と最小値, およびそのときの の値 をそれぞれ求めよ () e を自然対数の底とする > eの範囲において, 関数 y を考える この両 辺の対数を について微分することにより, y は減少関数であることを示せ また, e< < bのとき, () 数列 { } b の一般項が,
07 長崎大学 ( 医系 ) 前期日程問題 解答解説のページへ 以下の問いに答えよ () 0 のとき, si + cos の最大値と最小値, およびそのときの の値 をそれぞれ求めよ () e を自然対数の底とする > eの範囲において, 関数 y を考える この両 辺の対数を について微分することにより, y は減少関数であることを示せ また, e< < bのとき, () 数列 { } b の一般項が,
2018年度 東京大・理系数学
 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ関数 f ( ) = + cos (0 < < ) の増減表をつくり, + 0, 0 のと sin きの極限を調べよ 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ n+ 数列 a, a, を, Cn a n = ( n =,, ) で定める n! an qn () n とする を既約分数 an p として表したときの分母
08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ関数 f ( ) = + cos (0 < < ) の増減表をつくり, + 0, 0 のと sin きの極限を調べよ 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ n+ 数列 a, a, を, Cn a n = ( n =,, ) で定める n! an qn () n とする を既約分数 an p として表したときの分母
2016年度 筑波大・理系数学
 06 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ k を実数とする y 平面の曲線 C : y とC : y- + k+ -k が異なる共 有点 P, Q をもつとする ただし点 P, Q の 座標は正であるとする また, 原点を O とする () k のとりうる値の範囲を求めよ () k が () の範囲を動くとき, OPQ の重心 G の軌跡を求めよ () OPQ の面積を S とするとき,
06 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ k を実数とする y 平面の曲線 C : y とC : y- + k+ -k が異なる共 有点 P, Q をもつとする ただし点 P, Q の 座標は正であるとする また, 原点を O とする () k のとりうる値の範囲を求めよ () k が () の範囲を動くとき, OPQ の重心 G の軌跡を求めよ () OPQ の面積を S とするとき,
2014年度 千葉大・医系数学
 04 千葉大学 ( 医系 ) 前期日程問題 解答解説のページへ 袋の中に, 赤玉が 3 個, 白玉が 7 個が入っている 袋から玉を無作為に つ取り出し, 色を確認してから, 再び袋に戻すという試行を行う この試行を N 回繰り返したときに, 赤玉を A 回 ( ただし 0 A N) 取り出す確率を p( N, A) とする このとき, 以下の問いに答えよ () 確率 p( N, A) を N と
04 千葉大学 ( 医系 ) 前期日程問題 解答解説のページへ 袋の中に, 赤玉が 3 個, 白玉が 7 個が入っている 袋から玉を無作為に つ取り出し, 色を確認してから, 再び袋に戻すという試行を行う この試行を N 回繰り返したときに, 赤玉を A 回 ( ただし 0 A N) 取り出す確率を p( N, A) とする このとき, 以下の問いに答えよ () 確率 p( N, A) を N と
2011年度 大阪大・理系数学
 0 大阪大学 ( 理系 ) 前期日程問題 解答解説のページへ a a を自然数とする O を原点とする座標平面上で行列 A= a の表す 次変換 を f とする cosθ siθ () >0 および0θ
0 大阪大学 ( 理系 ) 前期日程問題 解答解説のページへ a a を自然数とする O を原点とする座標平面上で行列 A= a の表す 次変換 を f とする cosθ siθ () >0 および0θ
2014年度 筑波大・理系数学
 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ f ( x) = x x とする y = f ( x ) のグラフに点 P(, ) から引いた接線は 本あるとする つの接点 A (, f ( )), B(, f ( )), C(, f ( )) を頂点とする三角形の 重心を G とする () + +, + + および を, を用いて表せ () 点 G の座標を, を用いて表せ () 点 G
筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ f ( x) = x x とする y = f ( x ) のグラフに点 P(, ) から引いた接線は 本あるとする つの接点 A (, f ( )), B(, f ( )), C(, f ( )) を頂点とする三角形の 重心を G とする () + +, + + および を, を用いて表せ () 点 G の座標を, を用いて表せ () 点 G
座標軸以外の直線のまわりの回転体の体積 ( バウムクーヘン分割公式 ) の問題の解答 立体の体積の求め方 図 1 の立体の体積 V を求める方法を考えてみる 図 1 図 1 のように 軸の から までの長さを 等分する そして とおく とすると となる 図 1 のように のときの 軸に垂直な平面 に
 立体の体積の求め方 図 1 の立体の体積 V を求める方法を考えてみる 図 1 図 1 のように 軸の から までの長さを 等分する そして とおく とすると となる 図 1 のように のときの 軸に垂直な平面 による立体の断面積を とする 図 1の から までの斜線部分の立体 の体積を とすると, 図 2のように は 底面積 高さ の角柱の体積とみなせる よって 図 2 と表せる ただし とすると,
立体の体積の求め方 図 1 の立体の体積 V を求める方法を考えてみる 図 1 図 1 のように 軸の から までの長さを 等分する そして とおく とすると となる 図 1 のように のときの 軸に垂直な平面 による立体の断面積を とする 図 1の から までの斜線部分の立体 の体積を とすると, 図 2のように は 底面積 高さ の角柱の体積とみなせる よって 図 2 と表せる ただし とすると,
Microsoft Word - 201hyouka-tangen-1.doc
 数学 Ⅰ 評価規準の作成 ( 単元ごと ) 数学 Ⅰ の目標及び図形と計量について理解させ 基礎的な知識の習得と技能の習熟を図り それらを的確に活用する機能を伸ばすとともに 数学的な見方や考え方のよさを認識できるようにする 評価の観点の趣旨 式と不等式 二次関数及び図形と計量における考え方に関 心をもつとともに 数学的な見方や考え方のよさを認識し それらを事象の考察に活用しようとする 式と不等式 二次関数及び図形と計量における数学的な見
数学 Ⅰ 評価規準の作成 ( 単元ごと ) 数学 Ⅰ の目標及び図形と計量について理解させ 基礎的な知識の習得と技能の習熟を図り それらを的確に活用する機能を伸ばすとともに 数学的な見方や考え方のよさを認識できるようにする 評価の観点の趣旨 式と不等式 二次関数及び図形と計量における考え方に関 心をもつとともに 数学的な見方や考え方のよさを認識し それらを事象の考察に活用しようとする 式と不等式 二次関数及び図形と計量における数学的な見
補足 中学で学習したフレミング左手の法則 ( 電 磁 力 ) と関連付けると覚えやすい 電磁力は電流と磁界の外積で表される 力 F 磁 電磁力 F li 右ねじの回転の向き電 li ( l は導線の長さ ) 補足 有向線分とベクトル有向線分 : 矢印の位
 http://totemt.sur.ne.p 外積 ( ベクトル積 ) の活用 ( 面積, 法線ベクトル, 平面の方程式 ) 3 次元空間の つのベクトルの積が つのベクトルを与えるようなベクトルの掛け算 ベクトルの積がベクトルを与えることからベクトル積とも呼ばれる これに対し内積は符号と大きさをもつ量 ( スカラー量 ) を与えるので, スカラー積とも呼ばれる 外積を使うと, 平行四辺形や三角形の面積,
http://totemt.sur.ne.p 外積 ( ベクトル積 ) の活用 ( 面積, 法線ベクトル, 平面の方程式 ) 3 次元空間の つのベクトルの積が つのベクトルを与えるようなベクトルの掛け算 ベクトルの積がベクトルを与えることからベクトル積とも呼ばれる これに対し内積は符号と大きさをもつ量 ( スカラー量 ) を与えるので, スカラー積とも呼ばれる 外積を使うと, 平行四辺形や三角形の面積,
学習指導要領
 (1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 絶対値の意味を理解し適切な処理することができる 例題 1-3 の絶対値をはずせ 展開公式 ( a + b ) ( a - b ) = a 2 - b 2 を利用して根号を含む分数の分母を有理化することができる 例題 5 5 + 2 の分母を有理化せよ 実数の整数部分と小数部分の表し方を理解している
(1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 絶対値の意味を理解し適切な処理することができる 例題 1-3 の絶対値をはずせ 展開公式 ( a + b ) ( a - b ) = a 2 - b 2 を利用して根号を含む分数の分母を有理化することができる 例題 5 5 + 2 の分母を有理化せよ 実数の整数部分と小数部分の表し方を理解している
喨微勃挹稉弑
 == 全微分方程式 == 全微分とは 変数の関数 z=f(, ) について,, の増分を Δ, Δ とするとき, z の増分 Δz は Δz z Δ+ z Δ で表されます. この式において, Δ 0, Δ 0 となる極限を形式的に dz= z d+ z d (1) で表し, dz を z の全微分といいます. z は z の に関する偏導関数で, を定数と見なし て, で微分したものを表し, 方向の傾きに対応します.
== 全微分方程式 == 全微分とは 変数の関数 z=f(, ) について,, の増分を Δ, Δ とするとき, z の増分 Δz は Δz z Δ+ z Δ で表されます. この式において, Δ 0, Δ 0 となる極限を形式的に dz= z d+ z d (1) で表し, dz を z の全微分といいます. z は z の に関する偏導関数で, を定数と見なし て, で微分したものを表し, 方向の傾きに対応します.
<4D F736F F D20824F E B82CC90FC90CF95AA2E646F63>
 1/1 平成 3 年 6 月 11 日午前 1 時 3 分 4 ベクトルの線積分 4 ベクトルの線積分 Ⅰ. 積分の種類 通常の物理で使う積分には 3 種類あります 積分変数の数に応じて 線積分 ( 記号 横(1 重 d, dy, dz d ( ine: 面積分 ( 記号 縦 横 ( 重 線 4 ベクトルの線積分 重積分記号 ddy, dydz, dzdz ds ( Surface: 1 重積分記号
1/1 平成 3 年 6 月 11 日午前 1 時 3 分 4 ベクトルの線積分 4 ベクトルの線積分 Ⅰ. 積分の種類 通常の物理で使う積分には 3 種類あります 積分変数の数に応じて 線積分 ( 記号 横(1 重 d, dy, dz d ( ine: 面積分 ( 記号 縦 横 ( 重 線 4 ベクトルの線積分 重積分記号 ddy, dydz, dzdz ds ( Surface: 1 重積分記号
<4D F736F F D2094F795AA95FB92F68EAE82CC89F082AB95FB E646F63>
 力学 A 金曜 限 : 松田 微分方程式の解き方 微分方程式の解き方のところが分からなかったという声が多いので プリントにまとめます 数学的に厳密な話はしていないので 詳しくは数学の常微分方程式を扱っているテキストを参照してください また os s は既知とします. 微分方程式の分類 常微分方程式とは 独立変数 と その関数 その有限次の導関数 がみたす方程式 F,,, = のことです 次までの導関数を含む方程式を
力学 A 金曜 限 : 松田 微分方程式の解き方 微分方程式の解き方のところが分からなかったという声が多いので プリントにまとめます 数学的に厳密な話はしていないので 詳しくは数学の常微分方程式を扱っているテキストを参照してください また os s は既知とします. 微分方程式の分類 常微分方程式とは 独立変数 と その関数 その有限次の導関数 がみたす方程式 F,,, = のことです 次までの導関数を含む方程式を
2017年度 千葉大・理系数学
 017 千葉大学 ( 理系 ) 前期日程問題 1 解答解説のページへ n を 4 以上の整数とする 座標平面上で正 n 角形 A1A A n は点 O を中心とする半径 1 の円に内接している a = OA 1, b = OA, c = OA 3, d = OA4 とし, k = cos とおく そして, 線分 A1A3 と線分 AA4 との交点 P は線分 A1A3 を n :1に内分するとする
017 千葉大学 ( 理系 ) 前期日程問題 1 解答解説のページへ n を 4 以上の整数とする 座標平面上で正 n 角形 A1A A n は点 O を中心とする半径 1 の円に内接している a = OA 1, b = OA, c = OA 3, d = OA4 とし, k = cos とおく そして, 線分 A1A3 と線分 AA4 との交点 P は線分 A1A3 を n :1に内分するとする
Microsoft PowerPoint - 9.pptx
 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 行列演算と写像 ( 次変換 3 拡大とスカラー倍 p ' = ( ', ' = ( k, kk p = (, k 倍 k 倍 拡大後 k 倍拡大の関係は スカラー倍を用いて次のように表現できる ' = k ' 拡大前 拡大 4 拡大と行列の積 p ' = ( ', '
9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 行列演算と写像 ( 次変換 3 拡大とスカラー倍 p ' = ( ', ' = ( k, kk p = (, k 倍 k 倍 拡大後 k 倍拡大の関係は スカラー倍を用いて次のように表現できる ' = k ' 拡大前 拡大 4 拡大と行列の積 p ' = ( ', '
Microsoft Word - mathtext8.doc
 8 章偏微分と重積分 8. 偏微分とは これまで微分を考える際 関数は f という形で 関数値がつの変数 に依存している場合のみを扱ってきました しかし一般に変数はつとは決まっておらず f のように 複数の変数を持つ関数も考えなければなりません そ こでこの節では今まで学んできた微分を一般化させ 複数の変数に対応した偏微分と呼ばれるものについて説明します これまでの微分を偏微分と区別したいとき 常微分という呼び方を用います
8 章偏微分と重積分 8. 偏微分とは これまで微分を考える際 関数は f という形で 関数値がつの変数 に依存している場合のみを扱ってきました しかし一般に変数はつとは決まっておらず f のように 複数の変数を持つ関数も考えなければなりません そ こでこの節では今まで学んできた微分を一般化させ 複数の変数に対応した偏微分と呼ばれるものについて説明します これまでの微分を偏微分と区別したいとき 常微分という呼び方を用います
20~22.prt
 [ 三クリア W] 辺が等しいことの証明 ( 円周角と弦の関係利用 ) の の二等分線がこの三角形の外接円と交わる点をそれぞれ とするとき 60 ならば であることを証明せよ 60 + + 0 + 0 80-60 60 から ゆえに 等しい長さの弧に対する弦の長さは等しいから [ 三クリア ] 方べきの定理 接線と弦のなす角と円周角を利用 線分 を直径とする円 があり 右の図のように の延長上の点
[ 三クリア W] 辺が等しいことの証明 ( 円周角と弦の関係利用 ) の の二等分線がこの三角形の外接円と交わる点をそれぞれ とするとき 60 ならば であることを証明せよ 60 + + 0 + 0 80-60 60 から ゆえに 等しい長さの弧に対する弦の長さは等しいから [ 三クリア ] 方べきの定理 接線と弦のなす角と円周角を利用 線分 を直径とする円 があり 右の図のように の延長上の点
2011年度 東京工大・数学
 東京工業大学前期日程問題 解答解説のページへ n n を自然数とする 平面上で行列 n( n+ ) n+ の表す 次変換 ( 移動とも いう ) を n とする 次の問いに答えよ () 原点 O(, ) を通る直線で, その直線上のすべての点が n により同じ直線上に移 されるものが 本あることを示し, この 直線の方程式を求めよ () () で得られた 直線と曲線 (3) を求めよ n Sn 6
東京工業大学前期日程問題 解答解説のページへ n n を自然数とする 平面上で行列 n( n+ ) n+ の表す 次変換 ( 移動とも いう ) を n とする 次の問いに答えよ () 原点 O(, ) を通る直線で, その直線上のすべての点が n により同じ直線上に移 されるものが 本あることを示し, この 直線の方程式を求めよ () () で得られた 直線と曲線 (3) を求めよ n Sn 6
2015年度 金沢大・理系数学
 05 金沢大学 ( 理系 ) 前期日程問題 解答解説のページへ四面体 OABC において, 3 つのベクトル OA, OB, OC はどの つも互いに垂直で あり, h > 0 に対して, OA, OB, OC h とする 3 点 O, A, B を通る平面上の点 P は, CP が CA と CB のどちらとも垂直となる点であるとする 次の問いに答えよ () OP OA + OB とするとき, と
05 金沢大学 ( 理系 ) 前期日程問題 解答解説のページへ四面体 OABC において, 3 つのベクトル OA, OB, OC はどの つも互いに垂直で あり, h > 0 に対して, OA, OB, OC h とする 3 点 O, A, B を通る平面上の点 P は, CP が CA と CB のどちらとも垂直となる点であるとする 次の問いに答えよ () OP OA + OB とするとき, と
< BD96CA E B816989A B A>
 数 Ⅱ 平面ベクトル ( 黄色チャート ) () () ~ () " 図 # () () () - - () - () - - () % から %- から - -,- 略 () 求めるベクトルを とする S であるから,k となる実数 k がある このとき k k, であるから k すなわち k$, 求めるベクトルは --,- - -7- - -, から また ',' 7 (),,-,, -, -,
数 Ⅱ 平面ベクトル ( 黄色チャート ) () () ~ () " 図 # () () () - - () - () - - () % から %- から - -,- 略 () 求めるベクトルを とする S であるから,k となる実数 k がある このとき k k, であるから k すなわち k$, 求めるベクトルは --,- - -7- - -, から また ',' 7 (),,-,, -, -,
2015年度 岡山大・理系数学
 5 岡山大学 ( 理系 ) 前期日程問題 解答解説のページへ を 以上の自然数とし, から までの自然数 k に対して, 番号 k をつけたカードをそれぞれ k 枚用意する これらすべてを箱に入れ, 箱の中から 枚のカードを同時に引くとき, 次の問いに答えよ () 用意したカードは全部で何枚か答えよ () 引いたカード 枚の番号が両方とも k である確率を と k の式で表せ () 引いたカード 枚の番号が一致する確率を
5 岡山大学 ( 理系 ) 前期日程問題 解答解説のページへ を 以上の自然数とし, から までの自然数 k に対して, 番号 k をつけたカードをそれぞれ k 枚用意する これらすべてを箱に入れ, 箱の中から 枚のカードを同時に引くとき, 次の問いに答えよ () 用意したカードは全部で何枚か答えよ () 引いたカード 枚の番号が両方とも k である確率を と k の式で表せ () 引いたカード 枚の番号が一致する確率を
Microsoft PowerPoint - 9.pptx
 9/7/8( 水 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 拡大とスカラー倍 行列演算と写像 ( 次変換 拡大後 k 倍 k 倍 k 倍拡大の関係は スカラー倍を用いて次のように表現できる p = (, ' = k ' 拡大前 p ' = ( ', ' = ( k, k 拡大 4 拡大と行列の積 拡大後 k 倍
9/7/8( 水 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 拡大とスカラー倍 行列演算と写像 ( 次変換 拡大後 k 倍 k 倍 k 倍拡大の関係は スカラー倍を用いて次のように表現できる p = (, ' = k ' 拡大前 p ' = ( ', ' = ( k, k 拡大 4 拡大と行列の積 拡大後 k 倍
2014年度 センター試験・数学ⅡB
 第 問 解答解説のページへ [] O を原点とする座標平面において, 点 P(, q) を中心とする円 C が, 方程式 y 4 x で表される直線 l に接しているとする () 円 C の半径 r を求めよう 点 P を通り直線 l に垂直な直線の方程式は, y - ア ( x- ) + qなので, P イ から l に引いた垂線と l の交点 Q の座標は ( ( ウ + エ q ), 4 (
第 問 解答解説のページへ [] O を原点とする座標平面において, 点 P(, q) を中心とする円 C が, 方程式 y 4 x で表される直線 l に接しているとする () 円 C の半径 r を求めよう 点 P を通り直線 l に垂直な直線の方程式は, y - ア ( x- ) + qなので, P イ から l に引いた垂線と l の交点 Q の座標は ( ( ウ + エ q ), 4 (
DVIOUT
 1 体積 1.1 初めに この中では積分は第一基本量 ( 微分幾何 ) を用いて計算する 基本量の 意味を知らなくても別に気にする必要はなく 計算をたどって行けば理解 できるように書いてある 計算するものは球の体積なので カルテシアン 座標 (x-y 座標の畏まった言い方 ) ではなく 球座標を用いるようになる 球座標も x-y 座標と同様に直交座標であるので 扱うのに便利である 通 常は体積などを計算するために座標変換すると
1 体積 1.1 初めに この中では積分は第一基本量 ( 微分幾何 ) を用いて計算する 基本量の 意味を知らなくても別に気にする必要はなく 計算をたどって行けば理解 できるように書いてある 計算するものは球の体積なので カルテシアン 座標 (x-y 座標の畏まった言い方 ) ではなく 球座標を用いるようになる 球座標も x-y 座標と同様に直交座標であるので 扱うのに便利である 通 常は体積などを計算するために座標変換すると
Microsoft PowerPoint - 10.pptx
 m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
Microsoft Word - スーパーナビ 第6回 数学.docx
 1 ⑴ 与式 =- 5 35 +14 35 =9 35 1 ⑵ 与式 =9-(-5)=9+5=14 1 ⑶ 与式 = 4(a-b)-3(5a-3b) = 8a-4b-15a+9b = -7a+5b 1 1 1 1 ⑷ 与式 =(²+ 1+1²)-{²+(-3+)+(-3) } 1 ⑷ 与式 =(²++1)-(²--6)=²++1-²++6=3+7 1 ⑸ 与式 = - ² + 16 = - +16
1 ⑴ 与式 =- 5 35 +14 35 =9 35 1 ⑵ 与式 =9-(-5)=9+5=14 1 ⑶ 与式 = 4(a-b)-3(5a-3b) = 8a-4b-15a+9b = -7a+5b 1 1 1 1 ⑷ 与式 =(²+ 1+1²)-{²+(-3+)+(-3) } 1 ⑷ 与式 =(²++1)-(²--6)=²++1-²++6=3+7 1 ⑸ 与式 = - ² + 16 = - +16
2018年度 2次数学セレクション(微分と積分)
 08 次数学セレクション問題 [ 東京大 ] > 0 とし, f = x - x とおく () x で f ( x ) が単調に増加するための, についての条件を求めよ () 次の 条件を満たす点 (, b) の動きうる範囲を求め, 座標平面上に図示せよ 条件 : 方程式 f = bは相異なる 実数解をもつ 条件 : さらに, 方程式 f = bの解を < < とすると > である -- 08 次数学セレクション問題
08 次数学セレクション問題 [ 東京大 ] > 0 とし, f = x - x とおく () x で f ( x ) が単調に増加するための, についての条件を求めよ () 次の 条件を満たす点 (, b) の動きうる範囲を求め, 座標平面上に図示せよ 条件 : 方程式 f = bは相異なる 実数解をもつ 条件 : さらに, 方程式 f = bの解を < < とすると > である -- 08 次数学セレクション問題
測量試補 重要事項
 用地測量面積計算 < 試験合格へのポイント > 座標法による面積計算に関する問題は その出題回数からも定番問題と言えるが 計算自体はさほど難しいものではなく 計算表を作成しその中に数値を当てはめていくことで答えを導くことができる 過去問をしっかりとこなし 計算手順を覚えれば点の取りやすい問題と言える 士補試験に出題される問題は過去の例を見ても 座標が簡単な数値に置き換えることができるようになっている
用地測量面積計算 < 試験合格へのポイント > 座標法による面積計算に関する問題は その出題回数からも定番問題と言えるが 計算自体はさほど難しいものではなく 計算表を作成しその中に数値を当てはめていくことで答えを導くことができる 過去問をしっかりとこなし 計算手順を覚えれば点の取りやすい問題と言える 士補試験に出題される問題は過去の例を見ても 座標が簡単な数値に置き換えることができるようになっている
2017年度 信州大・医系数学
 7 信州大学 ( 医系 ) 前期日程問題 解答解説のページへ 座標平面上の点 O(, ), A ( a, a ), B( b, b ), C( b, b) を考える さらに,, に対し, D( acos asi, asi + acos ), E( bcos bsi, bsi + bcos ) とおく () OA = OD を示せ () OA OC = かつ OA OB = OD OE ¹ であるとする
7 信州大学 ( 医系 ) 前期日程問題 解答解説のページへ 座標平面上の点 O(, ), A ( a, a ), B( b, b ), C( b, b) を考える さらに,, に対し, D( acos asi, asi + acos ), E( bcos bsi, bsi + bcos ) とおく () OA = OD を示せ () OA OC = かつ OA OB = OD OE ¹ であるとする
Microsoft Word - 1B2011.doc
 第 14 回モールの定理 ( 単純梁の場合 ) ( モールの定理とは何か?p.11) 例題 下記に示す単純梁の C 点のたわみ角 θ C と, たわみ δ C を求めよ ただし, 部材の曲げ 剛性は材軸に沿って一様で とする C D kn B 1.5m 0.5m 1.0m 解答 1 曲げモーメント図を描く,B 点の反力を求める kn kn 4 kn 曲げモーメント図を描く knm 先に得られた曲げモーメントの値を
第 14 回モールの定理 ( 単純梁の場合 ) ( モールの定理とは何か?p.11) 例題 下記に示す単純梁の C 点のたわみ角 θ C と, たわみ δ C を求めよ ただし, 部材の曲げ 剛性は材軸に沿って一様で とする C D kn B 1.5m 0.5m 1.0m 解答 1 曲げモーメント図を描く,B 点の反力を求める kn kn 4 kn 曲げモーメント図を描く knm 先に得られた曲げモーメントの値を
Math-Aquarium 例題 図形と計量 図形と計量 1 直角三角形と三角比 P 木の先端を P, 根元を Q とする A 地点の目の位置 A' から 木の先端への仰角が 30,A から 7m 離れた AQB=90 と なる B 地点の目の位置 B' から木の先端への仰角が 45 であ るとき,
 図形と計量 直角三角形と三角比 P 木の先端を P, 根元を Q とする 地点の目の位置 ' から 木の先端への仰角が 0, から 7m 離れた Q=90 と なる 地点の目の位置 ' から木の先端への仰角が であ るとき, 木の高さを求めよ ただし, 目の高さを.m とし, Q' を右の図のように定める ' 0 Q' '.m Q 7m 要点 PQ PQ PQ' =x とおき,' Q',' Q' を
図形と計量 直角三角形と三角比 P 木の先端を P, 根元を Q とする 地点の目の位置 ' から 木の先端への仰角が 0, から 7m 離れた Q=90 と なる 地点の目の位置 ' から木の先端への仰角が であ るとき, 木の高さを求めよ ただし, 目の高さを.m とし, Q' を右の図のように定める ' 0 Q' '.m Q 7m 要点 PQ PQ PQ' =x とおき,' Q',' Q' を
PowerPoint Presentation
 付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
( 表紙 )
 ( 表紙 ) 1 次の各問いに答えなさい. 解答用紙には答えのみ記入すること. ( 48 点 ) (1) U108 -U8 %5U6 + 7 U を計算しなさい. () 15a 7 b 8 &0-5a b 1& - 8 9 ab を計算しなさい. () + y - -5y 6 を計算しなさい. (4) 1 4 5 の 5 枚のカードから 枚を選び, 横に並べて 桁の数を作 るとき, それが の倍数になる確率を求めなさい.
( 表紙 ) 1 次の各問いに答えなさい. 解答用紙には答えのみ記入すること. ( 48 点 ) (1) U108 -U8 %5U6 + 7 U を計算しなさい. () 15a 7 b 8 &0-5a b 1& - 8 9 ab を計算しなさい. () + y - -5y 6 を計算しなさい. (4) 1 4 5 の 5 枚のカードから 枚を選び, 横に並べて 桁の数を作 るとき, それが の倍数になる確率を求めなさい.
線積分.indd
 線積分 線積分 ( n, n, n ) (ξ n, η n, ζ n ) ( n-, n-, n- ) (ξ k, η k, ζ k ) ( k, k, k ) ( k-, k-, k- ) 物体に力 を作用させて位置ベクトル A の点 A から位置ベクトル の点 まで曲線 に沿って物体を移動させたときの仕事 W は 次式で計算された A, A, W : d 6 d+ d+ d@,,, d+ d+
線積分 線積分 ( n, n, n ) (ξ n, η n, ζ n ) ( n-, n-, n- ) (ξ k, η k, ζ k ) ( k, k, k ) ( k-, k-, k- ) 物体に力 を作用させて位置ベクトル A の点 A から位置ベクトル の点 まで曲線 に沿って物体を移動させたときの仕事 W は 次式で計算された A, A, W : d 6 d+ d+ d@,,, d+ d+
STEP 数学 Ⅰ を解いてみた から直線 に下ろした垂線の足を H とすると, H in( 80 ) in より, S H in H 同様にして, S in, S in も成り立つ よって, S in 三角形の面積 ヘロンの公式 in in 辺の長
 STEP 数学 Ⅰ を解いてみた http://toitemit.ku.ne.jp 図形と計量 三角形の面積 三角形の面積 の面積を S とすると, S in in in 解説 から直線 に下ろした垂線の足を H とすると, H in より, S H in H STEP 数学 Ⅰ を解いてみた http://toitemit.ku.ne.jp から直線 に下ろした垂線の足を H とすると, H in(
STEP 数学 Ⅰ を解いてみた http://toitemit.ku.ne.jp 図形と計量 三角形の面積 三角形の面積 の面積を S とすると, S in in in 解説 から直線 に下ろした垂線の足を H とすると, H in より, S H in H STEP 数学 Ⅰ を解いてみた http://toitemit.ku.ne.jp から直線 に下ろした垂線の足を H とすると, H in(
p tn tn したがって, 点 の 座標は p p tn tn tn また, 直線 l と直線 p の交点 の 座標は p p tn p tn よって, 点 の座標 (, ) は p p, tn tn と表され p 4p p 4p 4p tn tn tn より, 点 は放物線 4 p 上を動くこと
 567_ 次曲線の三角関数による媒介変数表示 次曲線の三角関数による媒介変数表示 次曲線 ( 放物線 楕円 双曲線 ) の標準形の, についての方程式と, 三角関数による媒介変数表示は次のように対応している.. 放物線 () 4 p (, ) ( ptn, ptn ) (). 楕円. 双曲線 () () (, p p ), tn tn (, ) ( cos, sin ) (, ), tn cos (,
567_ 次曲線の三角関数による媒介変数表示 次曲線の三角関数による媒介変数表示 次曲線 ( 放物線 楕円 双曲線 ) の標準形の, についての方程式と, 三角関数による媒介変数表示は次のように対応している.. 放物線 () 4 p (, ) ( ptn, ptn ) (). 楕円. 双曲線 () () (, p p ), tn tn (, ) ( cos, sin ) (, ), tn cos (,
Chap2.key
 . f( ) V (V V ) V e + V e V V V V ( ) V V ( ) E. - () V (0 ) () V (0 ) () V (0 ) (4) V ( ) E. - () V (0 ) () V (0 ) O r θ ( ) ( ) : (r θ) : { r cos θ r sn θ { r + () V (0 ) (4) V ( ) θ θ arg( ) : π π
. f( ) V (V V ) V e + V e V V V V ( ) V V ( ) E. - () V (0 ) () V (0 ) () V (0 ) (4) V ( ) E. - () V (0 ) () V (0 ) O r θ ( ) ( ) : (r θ) : { r cos θ r sn θ { r + () V (0 ) (4) V ( ) θ θ arg( ) : π π
2011年度 筑波大・理系数学
 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ O を原点とするy 平面において, 直線 y= の を満たす部分をC とする () C 上に点 A( t, ) をとるとき, 線分 OA の垂直二等分線の方程式を求めよ () 点 A が C 全体を動くとき, 線分 OA の垂直二等分線が通過する範囲を求め, それ を図示せよ -- 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ
0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ O を原点とするy 平面において, 直線 y= の を満たす部分をC とする () C 上に点 A( t, ) をとるとき, 線分 OA の垂直二等分線の方程式を求めよ () 点 A が C 全体を動くとき, 線分 OA の垂直二等分線が通過する範囲を求め, それ を図示せよ -- 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ
<4D F736F F D E4F8E9F82C982A882AF82E98D7397F1>
 3 三次における行列 要旨高校では ほとんど 2 2 の正方行列しか扱ってなく 三次の正方行列について考えてみたかったため 数 C で学んだ定理を三次の正方行列に応用して 自分たちで仮説を立てて求めていったら 空間における回転移動を表す行列 三次のケーリー ハミルトンの定理 三次における逆行列を求めたり 仮説をたてることができた. 目的 数 C で学んだ定理を三次の正方行列に応用する 2. 概要目的の到達点として
3 三次における行列 要旨高校では ほとんど 2 2 の正方行列しか扱ってなく 三次の正方行列について考えてみたかったため 数 C で学んだ定理を三次の正方行列に応用して 自分たちで仮説を立てて求めていったら 空間における回転移動を表す行列 三次のケーリー ハミルトンの定理 三次における逆行列を求めたり 仮説をたてることができた. 目的 数 C で学んだ定理を三次の正方行列に応用する 2. 概要目的の到達点として
Microsoft PowerPoint - H21生物計算化学2.ppt
 演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
2018年度 筑波大・理系数学
 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ < < とする 放物線 上に 点 (, ), A (ta, ta ), B( - ta, ta ) をとる 三角形 AB の内心の 座標を p とし, 外心の 座標を q とする また, 正の実数 a に対して, 直線 a と放物線 で囲まれた図形の面積を S( a) で表す () p, q を cos を用いて表せ S( p) () S(
筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ < < とする 放物線 上に 点 (, ), A (ta, ta ), B( - ta, ta ) をとる 三角形 AB の内心の 座標を p とし, 外心の 座標を q とする また, 正の実数 a に対して, 直線 a と放物線 で囲まれた図形の面積を S( a) で表す () p, q を cos を用いて表せ S( p) () S(
丛觙形ㆮ隢穓ㆮ亄ç�›å‹ƒç·ı
 三角形の面積は == 三角形の面積の二等分線 == ( 面積 )=( 底辺 ) ( 高さ ) 2 の公式で求められます. 次の図のように, ABC の頂点 A から対辺 BC の中点 ( 真ん中の点,1 対 1 に内分する点 ) D に線分 AD をひくと, ABD と DCA とは, 底辺が等しく, 高さが共通になるから, これら 2 つの三角形の面積は等しくなります.( 高さは底辺と垂直 ( 直角
三角形の面積は == 三角形の面積の二等分線 == ( 面積 )=( 底辺 ) ( 高さ ) 2 の公式で求められます. 次の図のように, ABC の頂点 A から対辺 BC の中点 ( 真ん中の点,1 対 1 に内分する点 ) D に線分 AD をひくと, ABD と DCA とは, 底辺が等しく, 高さが共通になるから, これら 2 つの三角形の面積は等しくなります.( 高さは底辺と垂直 ( 直角
DVIOUT-SS_Ma
 第 章 微分方程式 ニュートンはリンゴが落ちるのを見て万有引力を発見した という有名な逸話があります 無重力の宇宙船の中ではリンゴは落ちないで静止していることを考えると 重力が働くと始め静止しているものが動き出して そのスピードはどんどん大きくなる つまり速度の変化が現れることがわかります 速度は一般に時間と共に変化します 速度の瞬間的変化の割合を加速度といい で定義しましょう 速度が変化する, つまり加速度がでなくなるためにはその原因があり
第 章 微分方程式 ニュートンはリンゴが落ちるのを見て万有引力を発見した という有名な逸話があります 無重力の宇宙船の中ではリンゴは落ちないで静止していることを考えると 重力が働くと始め静止しているものが動き出して そのスピードはどんどん大きくなる つまり速度の変化が現れることがわかります 速度は一般に時間と共に変化します 速度の瞬間的変化の割合を加速度といい で定義しましょう 速度が変化する, つまり加速度がでなくなるためにはその原因があり
平成 年 月 7 日 ( 土 第 75 回数学教育実践研究会アスティ 45 ビル F セミナールーム A 札幌医科大学 年 P ab, を正の定数とする 平面上において ( a, を中心とする円 Q 4 C と (, b を中心とする円 C が 原点 O で外接している また P を円 C 上の点と
 平成 年 月 7 日 ( 土 第 75 回数学教育実践研究会アスティ 45 ビル F セミナールーム 微分積分の拡張 変数関数問題へのアプローチ 予選決勝優勝法からラグランジュ未定乗数法 松本睦郎 ( 札幌北高等学校 変数関数の最大値 最小値に関する問題には多様なアプローチ法がある 文字を固定した 予選決勝優勝法, 計算のみで解法する 文字消去法, 微分積分を利用した ラグランジュ未定乗数法 がある
平成 年 月 7 日 ( 土 第 75 回数学教育実践研究会アスティ 45 ビル F セミナールーム 微分積分の拡張 変数関数問題へのアプローチ 予選決勝優勝法からラグランジュ未定乗数法 松本睦郎 ( 札幌北高等学校 変数関数の最大値 最小値に関する問題には多様なアプローチ法がある 文字を固定した 予選決勝優勝法, 計算のみで解法する 文字消去法, 微分積分を利用した ラグランジュ未定乗数法 がある
例題1 転がり摩擦
 重心 5.. 重心問題解法虎の巻. 半円 分円. 円弧. 扇形. 半球殻 5. 半球体 6. 厚みのある半球殻 7. 三角形 8. 円錐 9. 円錐台. 穴あき板. 空洞のある半球ボール 重心問題解法虎の巻 関西大学工学部物理学教室 齊藤正 重心を求める場合 質点系の重心の求め方が基本 実際の物体では連続体であるので 積分形式で求める場合が多い これらの式は 次元のベクトル形式で書かれている通り つの式は実際には
重心 5.. 重心問題解法虎の巻. 半円 分円. 円弧. 扇形. 半球殻 5. 半球体 6. 厚みのある半球殻 7. 三角形 8. 円錐 9. 円錐台. 穴あき板. 空洞のある半球ボール 重心問題解法虎の巻 関西大学工学部物理学教室 齊藤正 重心を求める場合 質点系の重心の求め方が基本 実際の物体では連続体であるので 積分形式で求める場合が多い これらの式は 次元のベクトル形式で書かれている通り つの式は実際には
vecrot
 1. ベクトル ベクトル : 方向を持つ量 ベクトルには 1 方向 2 大きさ ( 長さ ) という 2 つの属性がある ベクトルの例 : 物体の移動速度 移動量電場 磁場の強さ風速力トルクなど 2. ベクトルの表現 2.1 矢印で表現される 矢印の長さ : ベクトルの大きさ 矢印の向き : ベクトルの方向 2.2 2 個の点を用いて表現する 始点 () と終点 () を結ぶ半直線の向き : ベクトルの方向
1. ベクトル ベクトル : 方向を持つ量 ベクトルには 1 方向 2 大きさ ( 長さ ) という 2 つの属性がある ベクトルの例 : 物体の移動速度 移動量電場 磁場の強さ風速力トルクなど 2. ベクトルの表現 2.1 矢印で表現される 矢印の長さ : ベクトルの大きさ 矢印の向き : ベクトルの方向 2.2 2 個の点を用いて表現する 始点 () と終点 () を結ぶ半直線の向き : ベクトルの方向
学習指導要領
 (1) 数と式 学習指導要領 数と式 (1) 式の計算二次の乗法公式及び因数分解の公式の理解を深め 式を多面的にみたり目的に応じて式を適切に変形したりすること 東京都立町田高等学校学力スタンダード 整式の加法 減法 乗法展開の公式を利用できる 式を1 つの文字におき換えることによって, 式の計算を簡略化することができる 式の形の特徴に着目して変形し, 展開の公式が適用できるようにすることができる 因数分解因数分解の公式を利用できる
(1) 数と式 学習指導要領 数と式 (1) 式の計算二次の乗法公式及び因数分解の公式の理解を深め 式を多面的にみたり目的に応じて式を適切に変形したりすること 東京都立町田高等学校学力スタンダード 整式の加法 減法 乗法展開の公式を利用できる 式を1 つの文字におき換えることによって, 式の計算を簡略化することができる 式の形の特徴に着目して変形し, 展開の公式が適用できるようにすることができる 因数分解因数分解の公式を利用できる
数学の学び方のヒント
 数学 Ⅱ における微分単元の 指導法の改善に関する研究 2017 年 10 月北数教旭川大会で発表した内容です 北海道札幌国際情報高等学校和田文興 1 Ⅰ. 研究の動機と背景 高校では極限を厳密に定義できず, 曖昧でわかりにくい. 私自身は, はじめて微分と出会ったとき, 極限の考え方等が納得できなかった. y () a h 接線 a 傾き (a) 2 Ⅰ. 研究の動機と背景 微分の指導改善に関する優れた先行研究がいくつかあるが,
数学 Ⅱ における微分単元の 指導法の改善に関する研究 2017 年 10 月北数教旭川大会で発表した内容です 北海道札幌国際情報高等学校和田文興 1 Ⅰ. 研究の動機と背景 高校では極限を厳密に定義できず, 曖昧でわかりにくい. 私自身は, はじめて微分と出会ったとき, 極限の考え方等が納得できなかった. y () a h 接線 a 傾き (a) 2 Ⅰ. 研究の動機と背景 微分の指導改善に関する優れた先行研究がいくつかあるが,
学力スタンダード(様式1)
 (1) 数と式 学習指導要領ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 稔ヶ丘高校学力スタンダード 有理数 無理数の定義や実数の分類について理解し ている 絶対値の意味と記号表示を理解している 実数と直線上の点が一対一対応であることを理解 し 実数を数直線上に示すことができる 例 実数 (1) -.5 () π (3) 数直線上の点はどれか答えよ
(1) 数と式 学習指導要領ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 稔ヶ丘高校学力スタンダード 有理数 無理数の定義や実数の分類について理解し ている 絶対値の意味と記号表示を理解している 実数と直線上の点が一対一対応であることを理解 し 実数を数直線上に示すことができる 例 実数 (1) -.5 () π (3) 数直線上の点はどれか答えよ
PowerPoint プレゼンテーション
 - = 4 = 4 = - y = x y = x y = x + 4 y = x 比例は y = ax の形であらわすことができる 4 - 秒後 y = 5 y = 0 (m) 5 秒後 y = 5 5 y = 5 (m) 5 0 = 05 (m) 05 5 = 5 (m/ 秒 ) 4 4 秒後 y = 5 4 y = 80 (m) 5-80 5 4 = 45 (m/ 秒 ) 5 v = 0 5
- = 4 = 4 = - y = x y = x y = x + 4 y = x 比例は y = ax の形であらわすことができる 4 - 秒後 y = 5 y = 0 (m) 5 秒後 y = 5 5 y = 5 (m) 5 0 = 05 (m) 05 5 = 5 (m/ 秒 ) 4 4 秒後 y = 5 4 y = 80 (m) 5-80 5 4 = 45 (m/ 秒 ) 5 v = 0 5
ベクトル公式.rtf
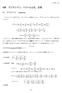 6 章ラプラシアン, ベクトル公式, 定理 6.1 ラプラシアン Laplacian φ はベクトル量である. そこでさらに発散をとると, φ はどういう形になるであろうか? φ = a + a + a φ a + a φ + a φ = φ + φ + φ = 2 φ + 2 φ 2 + 2 φ 2 2 φ = 2 φ 2 + 2 φ 2 + 2 φ 2 = 2 φ したがって,2 階の偏微分演算となる.
6 章ラプラシアン, ベクトル公式, 定理 6.1 ラプラシアン Laplacian φ はベクトル量である. そこでさらに発散をとると, φ はどういう形になるであろうか? φ = a + a + a φ a + a φ + a φ = φ + φ + φ = 2 φ + 2 φ 2 + 2 φ 2 2 φ = 2 φ 2 + 2 φ 2 + 2 φ 2 = 2 φ したがって,2 階の偏微分演算となる.
2018年度 岡山大・理系数学
 08 岡山大学 ( 理系 ) 前期日程問題 解答解説のページへ 関数 f ( x) = ( + x) x について, 以下の問いに答えよ () f ( x ) = 0 を満たす x の値を求めよ () 曲線 y = f ( x ) について, 原点を通るすべての接線の方程式を求めよ (3) 曲線 y = f ( x ) について, 原点を通る接線のうち, 接点の x 座標が最大のものを L とする
08 岡山大学 ( 理系 ) 前期日程問題 解答解説のページへ 関数 f ( x) = ( + x) x について, 以下の問いに答えよ () f ( x ) = 0 を満たす x の値を求めよ () 曲線 y = f ( x ) について, 原点を通るすべての接線の方程式を求めよ (3) 曲線 y = f ( x ) について, 原点を通る接線のうち, 接点の x 座標が最大のものを L とする
学習指導要領
 (1 ) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 自然数 整数 有理数 無理数の包含関係など 実 数の構成を理解する ( 例 ) 次の空欄に適当な言葉をいれて, 数の集合を表しなさい 実数の絶対値が実数と対応する点と原点との距離で あることを理解する ( 例 ) 次の値を求めよ (1) () 6 置き換えなどを利用して 三項の無理数の乗法の計
(1 ) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 自然数 整数 有理数 無理数の包含関係など 実 数の構成を理解する ( 例 ) 次の空欄に適当な言葉をいれて, 数の集合を表しなさい 実数の絶対値が実数と対応する点と原点との距離で あることを理解する ( 例 ) 次の値を求めよ (1) () 6 置き換えなどを利用して 三項の無理数の乗法の計
学習指導要領
 (1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 自然数 整数 有理数 無理数の包含関係など 実数 の構成を理解する ( 例 ) 次の空欄に適当な言葉をいれて, 数の集合を表しなさい ア イ 無理数 整数 ウ 無理数の加法及び減法 乗法公式などを利用した計 算ができる また 分母だけが二項である無理数の 分母の有理化ができる ( 例 1)
(1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 自然数 整数 有理数 無理数の包含関係など 実数 の構成を理解する ( 例 ) 次の空欄に適当な言葉をいれて, 数の集合を表しなさい ア イ 無理数 整数 ウ 無理数の加法及び減法 乗法公式などを利用した計 算ができる また 分母だけが二項である無理数の 分母の有理化ができる ( 例 1)
< 中 3 分野例題付き公式集 > (1)2 の倍数の判定法は 1 の位が 0 又は偶数 ( 例題 )1~5 までの 5 つの数字を使って 3 ケタの数をつくるとき 2 の倍数は何通りできるか (2)5 の倍数の判定法は 1 の位が 0 又は 5 ( 例題 )1~9 までの 9 個の数字を使って 3
 () の倍数の判定法は の位が 0 又は偶数 ~ までの つの数字を使って ケタの数をつくるとき の倍数は何通りできるか () の倍数の判定法は の位が 0 又は ~9 までの 9 個の数字を使って ケタの数をつくるとき の倍数は何通りできるか () の倍数の判定法は 下 ケタが 00 又は の倍数 ケタの数 8 が の倍数となるときの 最小の ケタの数は ( 解 ) 一の位の数は の 通り 十の位は一の位の数以外の
() の倍数の判定法は の位が 0 又は偶数 ~ までの つの数字を使って ケタの数をつくるとき の倍数は何通りできるか () の倍数の判定法は の位が 0 又は ~9 までの 9 個の数字を使って ケタの数をつくるとき の倍数は何通りできるか () の倍数の判定法は 下 ケタが 00 又は の倍数 ケタの数 8 が の倍数となるときの 最小の ケタの数は ( 解 ) 一の位の数は の 通り 十の位は一の位の数以外の
立体切断⑹-2回切り
 2 回切り問題のポイント 1. 交線を作図する 2つの平面が交わると 必ず直線ができます この直線のことを 交線 ( こうせん ) といいます 2. 体積を求める方法は次の 3 通りのどれか! 1 柱の体積 = 底面積 高さ 1 2 すいの体積 = 底面積 高さ 3 3 柱の斜め切り= 底面積 高さの平均 ただし 高さの平均が使えるのは 底面が円 三角形 正方形 長方形 ひし形 平行四辺形 正偶数角形のときだけ
2 回切り問題のポイント 1. 交線を作図する 2つの平面が交わると 必ず直線ができます この直線のことを 交線 ( こうせん ) といいます 2. 体積を求める方法は次の 3 通りのどれか! 1 柱の体積 = 底面積 高さ 1 2 すいの体積 = 底面積 高さ 3 3 柱の斜め切り= 底面積 高さの平均 ただし 高さの平均が使えるのは 底面が円 三角形 正方形 長方形 ひし形 平行四辺形 正偶数角形のときだけ
Math-quarium 練習問題 + 図形の性質 線分 は の二等分線であるから :=:=:=: よって = = = 線分 は の外角の二等分線であるから :=:=:=: よって :=: したがって == 以上から =+=+= 右の図において, 点 は の外心である α,βを求めよ α β 70
 Math-quarium 練習問題 + 図形の性質 図形の性質 線分 に対して, 次の点を図示せよ () : に内分する点 () : に外分する点 Q () 7: に外分する点 R () 中点 M () M () Q () () R 右の図において, 線分の長さ を求めよ ただし,R//Q,R//,Q=,=6 とする Q R 6 Q から,:=:6=: より :=: これから,R:=: より :6=:
Math-quarium 練習問題 + 図形の性質 図形の性質 線分 に対して, 次の点を図示せよ () : に内分する点 () : に外分する点 Q () 7: に外分する点 R () 中点 M () M () Q () () R 右の図において, 線分の長さ を求めよ ただし,R//Q,R//,Q=,=6 とする Q R 6 Q から,:=:6=: より :=: これから,R:=: より :6=:
1 1. はじめに ポンスレの閉形定理 Jacobi の証明 June 5, 2013 Akio Arimoto ヤコビは [2] においてポンスレの閉形定理に初等幾何を用いた証明を与え ている 大小 2つの円があり 一方が他方を完全に含んでいるとする 大小 2 円の半径をそれぞれ Rr, とする
![1 1. はじめに ポンスレの閉形定理 Jacobi の証明 June 5, 2013 Akio Arimoto ヤコビは [2] においてポンスレの閉形定理に初等幾何を用いた証明を与え ている 大小 2つの円があり 一方が他方を完全に含んでいるとする 大小 2 円の半径をそれぞれ Rr, とする 1 1. はじめに ポンスレの閉形定理 Jacobi の証明 June 5, 2013 Akio Arimoto ヤコビは [2] においてポンスレの閉形定理に初等幾何を用いた証明を与え ている 大小 2つの円があり 一方が他方を完全に含んでいるとする 大小 2 円の半径をそれぞれ Rr, とする](/thumbs/100/145746324.jpg) . はじめに ポンスレの閉形定理 Jcobi の証明 Jue 5 03 Akio Aimoto ヤコビは [] においてポンスレの閉形定理に初等幾何を用いた証明を与え ている 大小 つの円があり 一方が他方を完全に含んでいるとする 大小 円の半径をそれぞれ とする 中心間の距離を とすれば 0 < + < が成立している 大きい円の周上の点 A から小さい円に接線を引く 接線と大きい円の周上に交わる
. はじめに ポンスレの閉形定理 Jcobi の証明 Jue 5 03 Akio Aimoto ヤコビは [] においてポンスレの閉形定理に初等幾何を用いた証明を与え ている 大小 つの円があり 一方が他方を完全に含んでいるとする 大小 円の半径をそれぞれ とする 中心間の距離を とすれば 0 < + < が成立している 大きい円の周上の点 A から小さい円に接線を引く 接線と大きい円の周上に交わる
1 対 1 対応の演習例題を解いてみた 微分法とその応用 例題 1 極限 微分係数の定義 (2) 関数 f ( x) は任意の実数 x について微分可能なのは明らか f ( 1, f ( 1) ) と ( 1 + h, f ( 1 + h)
 微分法とその応用 例題 1 極限 微分係数の定義 () 関数 ( x) は任意の実数 x について微分可能なのは明らか ( 1, ( 1) ) と ( 1 + h, ( 1 + h) ) の傾き= ( 1 + h ) - ( 1 ) ( 1 + ) - ( 1) = ( 1 + h) - 1 h ( 1) = lim h ( 1 + h) - ( 1) h ( 1, ( 1) ) と ( 1 - h,
微分法とその応用 例題 1 極限 微分係数の定義 () 関数 ( x) は任意の実数 x について微分可能なのは明らか ( 1, ( 1) ) と ( 1 + h, ( 1 + h) ) の傾き= ( 1 + h ) - ( 1 ) ( 1 + ) - ( 1) = ( 1 + h) - 1 h ( 1) = lim h ( 1 + h) - ( 1) h ( 1, ( 1) ) と ( 1 - h,
Microsoft Word - kogi10ex_main.docx
 機能創造理工学 Ⅱ 期末試験 追試験問題 ( 病欠等による ) 途中の計算を必ず書こう 答えのみでは採点できない 問. 二次元面内を運動する調和振動子のラグランジアン L ( ) ( ) を 極座標, に変換し 極座標でのオイラーラグランジュ方程式を書こう ( 解く必要はない ) 但し, は定数であり また 極座標の定義は cos, sin である 問. 前問において極座標, に共役な一般化運動量,
機能創造理工学 Ⅱ 期末試験 追試験問題 ( 病欠等による ) 途中の計算を必ず書こう 答えのみでは採点できない 問. 二次元面内を運動する調和振動子のラグランジアン L ( ) ( ) を 極座標, に変換し 極座標でのオイラーラグランジュ方程式を書こう ( 解く必要はない ) 但し, は定数であり また 極座標の定義は cos, sin である 問. 前問において極座標, に共役な一般化運動量,
2017年度 金沢大・理系数学
 07 金沢大学 ( 理系 前期日程問題 解答解説のページへ 次の問いに答えよ ( 6 z + 7 = 0 を満たす複素数 z をすべて求め, それらを表す点を複素数平面上に図 示せよ ( ( で求めた複素数 z を偏角が小さい方から順に z, z, とするとき, z, z と 積 zz を表す 点が複素数平面上で一直線上にあることを示せ ただし, 偏角は 0 以上 未満とする -- 07 金沢大学
07 金沢大学 ( 理系 前期日程問題 解答解説のページへ 次の問いに答えよ ( 6 z + 7 = 0 を満たす複素数 z をすべて求め, それらを表す点を複素数平面上に図 示せよ ( ( で求めた複素数 z を偏角が小さい方から順に z, z, とするとき, z, z と 積 zz を表す 点が複素数平面上で一直線上にあることを示せ ただし, 偏角は 0 以上 未満とする -- 07 金沢大学
2014年度 名古屋大・理系数学
 04 名古屋大学 ( 理系 ) 前期日程問題 解答解説のページへ空間内にある半径 の球 ( 内部を含む ) を B とする 直線 と B が交わっており, その交わりは長さ の線分である () B の中心と との距離を求めよ () のまわりに B を 回転してできる立体の体積を求めよ 04 名古屋大学 ( 理系 ) 前期日程問題 解答解説のページへ 実数 t に対して 点 P( t, t ), Q(
04 名古屋大学 ( 理系 ) 前期日程問題 解答解説のページへ空間内にある半径 の球 ( 内部を含む ) を B とする 直線 と B が交わっており, その交わりは長さ の線分である () B の中心と との距離を求めよ () のまわりに B を 回転してできる立体の体積を求めよ 04 名古屋大学 ( 理系 ) 前期日程問題 解答解説のページへ 実数 t に対して 点 P( t, t ), Q(
Microsoft Word - 町田・全 H30学力スタ 別紙1 1年 数学Ⅰ.doc
 (1) 数と式 学習指導要領 都立町田高校 学力スタンダード ア 数と集合 ( ア ) 実数 根号を含む式の計算 数を実数まで拡張する意義を理解し 簡単な 循環小数を表す記号を用いて, 分数を循環小数で表 無理数の四則計算をすること すことができる 今まで学習してきた数の体系について整理し, 考察 しようとする 絶対値の意味と記号表示を理解している 根号を含む式の加法, 減法, 乗法の計算ができる
(1) 数と式 学習指導要領 都立町田高校 学力スタンダード ア 数と集合 ( ア ) 実数 根号を含む式の計算 数を実数まで拡張する意義を理解し 簡単な 循環小数を表す記号を用いて, 分数を循環小数で表 無理数の四則計算をすること すことができる 今まで学習してきた数の体系について整理し, 考察 しようとする 絶対値の意味と記号表示を理解している 根号を含む式の加法, 減法, 乗法の計算ができる
学習指導要領
 (1) いろいろな式 学習指導要領紅葉川高校学力スタンダードア式と証明展開の公式を用いて 3 乗に関わる式を展開すること ( ア ) 整式の乗法 除法 分数式の計算ができるようにする 三次の乗法公式及び因数分解の公式を理解し そ 3 次の因数分解の公式を理解し それらを用いて因数れらを用いて式の展開や因数分解をすること また 分解することができるようにする 整式の除法や分数式の四則計算について理解し
(1) いろいろな式 学習指導要領紅葉川高校学力スタンダードア式と証明展開の公式を用いて 3 乗に関わる式を展開すること ( ア ) 整式の乗法 除法 分数式の計算ができるようにする 三次の乗法公式及び因数分解の公式を理解し そ 3 次の因数分解の公式を理解し それらを用いて因数れらを用いて式の展開や因数分解をすること また 分解することができるようにする 整式の除法や分数式の四則計算について理解し
"éı”ç·ıå½¢ 微勃挹稉弑
 == 1 階線形微分方程式 == 次の形の常微分方程式を1 階線形常微分方程式といいます. '+P()=Q() (1) 方程式 (1) の右辺 : Q() を 0 とおいてできる同次方程式 ( この同次方程式は, 変数分離形になり比較的容易に解けます ) '+P()=0 () の1つの解を とすると, 方程式 (1) の一般解は =( Q() +C) (3) で求められます. 参考書には 上記の の代わりに,
== 1 階線形微分方程式 == 次の形の常微分方程式を1 階線形常微分方程式といいます. '+P()=Q() (1) 方程式 (1) の右辺 : Q() を 0 とおいてできる同次方程式 ( この同次方程式は, 変数分離形になり比較的容易に解けます ) '+P()=0 () の1つの解を とすると, 方程式 (1) の一般解は =( Q() +C) (3) で求められます. 参考書には 上記の の代わりに,
2019 年 6 月 4 日演習問題 I α, β > 0, A > 0 を定数として Cobb-Douglas 型関数 Y = F (K, L) = AK α L β (5) と定義します. (1) F KK, F KL, F LK, F LL を求めましょう. (2) 第 1 象限のすべての点
 09 年 6 月 4 日演習問題 I α, β > 0, A > 0 を定数として Cobb-Douglas 型関数 Y = F K, L) = AK α L β 5) と定義します. ) F KK, F KL, F LK, F LL を求めましょう. ) 第 象限のすべての点 K, L) R ++ に対して F KK K, L) < 0, かつ dethf )K, L) > 0 6) を満たす α,
09 年 6 月 4 日演習問題 I α, β > 0, A > 0 を定数として Cobb-Douglas 型関数 Y = F K, L) = AK α L β 5) と定義します. ) F KK, F KL, F LK, F LL を求めましょう. ) 第 象限のすべての点 K, L) R ++ に対して F KK K, L) < 0, かつ dethf )K, L) > 0 6) を満たす α,
中学 1 年生 e ライブラリ数学教材一覧 学校図書 ( 株 ) 中学 1 年 数学 文字式式の計算 項と係数 中学 1 年 数学 次式 中学 1 年 数学 項のまとめ方 中学 1 年 数学 次式の加法 中学 1 年 数学 77
 中学 1 年生 e ライブラリ数学教材一覧 学校図書 ( 株 ) 中学 1 年 数学 1 14-20 正の数 負の数正の数 負の数 14- ある基準から考えた量の表現 中学 1 年 数学 14- 正の数 中学 1 年 数学 14- 負の数 中学 1 年 数学 14- 量の基準を表す数 中学 1 年 数学 15- 反対の性質をもつ量の表現 中学 1 年 数学 17- 数直線 中学 1 年 数学 18-19
中学 1 年生 e ライブラリ数学教材一覧 学校図書 ( 株 ) 中学 1 年 数学 1 14-20 正の数 負の数正の数 負の数 14- ある基準から考えた量の表現 中学 1 年 数学 14- 正の数 中学 1 年 数学 14- 負の数 中学 1 年 数学 14- 量の基準を表す数 中学 1 年 数学 15- 反対の性質をもつ量の表現 中学 1 年 数学 17- 数直線 中学 1 年 数学 18-19
Microsoft Word - 断面諸量
 応用力学 Ⅱ 講義資料 / 断面諸量 断面諸量 断面 次 次モーメントの定義 図 - に示すような形状を有する横断面を考え その全断面積を とする いま任意に定めた直交座標軸 O-, をとり また図中の斜線部の微小面積要素を d とするとき d, d () で定義される, をそれぞれ与えられた横断面の 軸, 軸に関する断面 次モーメント (geometrcal moment of area) という
応用力学 Ⅱ 講義資料 / 断面諸量 断面諸量 断面 次 次モーメントの定義 図 - に示すような形状を有する横断面を考え その全断面積を とする いま任意に定めた直交座標軸 O-, をとり また図中の斜線部の微小面積要素を d とするとき d, d () で定義される, をそれぞれ与えられた横断面の 軸, 軸に関する断面 次モーメント (geometrcal moment of area) という
学習指導要領
 (1) 数と式 学習指導要領ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 千早高校学力スタンダード 自然数 整数 有理数 無理数の用語の意味を理解す る ( 例 ) 次の数の中から自然数 整数 有理 数 無理数に分類せよ 3 3,, 0.7, 3,,-, 4 (1) 自然数 () 整数 (3) 有理数 (4) 無理数 自然数 整数 有理数 無理数の包含関係など
(1) 数と式 学習指導要領ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 千早高校学力スタンダード 自然数 整数 有理数 無理数の用語の意味を理解す る ( 例 ) 次の数の中から自然数 整数 有理 数 無理数に分類せよ 3 3,, 0.7, 3,,-, 4 (1) 自然数 () 整数 (3) 有理数 (4) 無理数 自然数 整数 有理数 無理数の包含関係など
2018年度 神戸大・理系数学
 8 神戸大学 ( 理系 ) 前期日程問題 解答解説のページへ t を < t < を満たす実数とする OABC を 辺の長さが の正四面体とする 辺 OA を -t : tに内分する点を P, 辺 OB を t :-tに内分する点を Q, 辺 BC の中点を R とする また a = OA, b = OB, c = OC とする 以下の問いに答えよ () QP と QR をt, a, b, c を用いて表せ
8 神戸大学 ( 理系 ) 前期日程問題 解答解説のページへ t を < t < を満たす実数とする OABC を 辺の長さが の正四面体とする 辺 OA を -t : tに内分する点を P, 辺 OB を t :-tに内分する点を Q, 辺 BC の中点を R とする また a = OA, b = OB, c = OC とする 以下の問いに答えよ () QP と QR をt, a, b, c を用いて表せ
線形代数とは
 線形代数とは 第一回ベクトル 教科書 エクササイズ線形代数 立花俊一 成田清正著 共立出版 必要最低限のことに限る 得意な人には物足りないかもしれません 線形代数とは何をするもの? 線形関係 y 直線 yもも 次式で登場する (( 次の形 ) 線形 ただし 次元の話世の中は 3 次元 [4[ 次元 ] 次元 3 次元 4 次元 はどうやって直線を表すの? ベクトルや行列の概念 y A ベクトルを使うと
線形代数とは 第一回ベクトル 教科書 エクササイズ線形代数 立花俊一 成田清正著 共立出版 必要最低限のことに限る 得意な人には物足りないかもしれません 線形代数とは何をするもの? 線形関係 y 直線 yもも 次式で登場する (( 次の形 ) 線形 ただし 次元の話世の中は 3 次元 [4[ 次元 ] 次元 3 次元 4 次元 はどうやって直線を表すの? ベクトルや行列の概念 y A ベクトルを使うと
2015-2017年度 2次数学セレクション(複素数)解答解説
 05 次数学セレクション解答解説 [ 筑波大 ] ( + より, 0 となり, + から, ( (,, よって, の描く図形 C は, 点 を中心とし半径が の円である すなわち, 原 点を通る円となる ( は虚数, は正の実数より, である さて, w ( ( とおくと, ( ( ( w ( ( ( ここで, w は純虚数より, は純虚数となる すると, の描く図形 L は, 点 を通り, 点 と点
05 次数学セレクション解答解説 [ 筑波大 ] ( + より, 0 となり, + から, ( (,, よって, の描く図形 C は, 点 を中心とし半径が の円である すなわち, 原 点を通る円となる ( は虚数, は正の実数より, である さて, w ( ( とおくと, ( ( ( w ( ( ( ここで, w は純虚数より, は純虚数となる すると, の描く図形 L は, 点 を通り, 点 と点
2013年度 信州大・医系数学
 03 信州大学 ( 医系 ) 前期日程問題 解答解説のページへ () 式 + + a a a3 を満たす自然数の組 ( a, a, a3) で, a a a3とな るものをすべて求めよ () r を正の有理数とする 式 r + + a a a を満たす自然数の組 ( a, a, a3) で, 3 a a a3となるものは有限個しかないことを証明せよ ただし, そのよう な組が存在しない場合は 0 個とし,
03 信州大学 ( 医系 ) 前期日程問題 解答解説のページへ () 式 + + a a a3 を満たす自然数の組 ( a, a, a3) で, a a a3とな るものをすべて求めよ () r を正の有理数とする 式 r + + a a a を満たす自然数の組 ( a, a, a3) で, 3 a a a3となるものは有限個しかないことを証明せよ ただし, そのよう な組が存在しない場合は 0 個とし,
破壊の予測
 本日の講義内容 前提 : 微分積分 線形代数が何をしているかはうろ覚え 材料力学は勉強したけど ちょっと 弾性および塑性学は勉強したことが無い ー > ですので 解らないときは質問してください モールの応力円を理解するとともに 応力を 3 次元的に考える FM( 有限要素法 の概略 内部では何を計算しているのか? 3 物が壊れる条件を考える 特に 変形 ( 塑性変形 が発生する条件としてのミーゼス応力とはどのような応力か?
本日の講義内容 前提 : 微分積分 線形代数が何をしているかはうろ覚え 材料力学は勉強したけど ちょっと 弾性および塑性学は勉強したことが無い ー > ですので 解らないときは質問してください モールの応力円を理解するとともに 応力を 3 次元的に考える FM( 有限要素法 の概略 内部では何を計算しているのか? 3 物が壊れる条件を考える 特に 変形 ( 塑性変形 が発生する条件としてのミーゼス応力とはどのような応力か?
曲線 = f () は を媒介変数とする自然な媒介変数表示 =,= f () をもつので, これを利用して説明する 以下,f () は定義域で連続であると仮定する 例えば, 直線 =c が曲線 = f () の漸近線になるとする 曲線 = f () 上の点 P(,f ()) が直線 =c に近づくこ
 伊伊伊伊伊伊伊伊伊伊 伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊 漸近線の求め方に関する考察 たまい玉井 かつき克樹 伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊 伊伊伊伊伊伊伊伊伊伊. 漸近線についての生徒からの質問 数学において図を使って直感的な説明を与えることは, 理解を深めるのに大いに役立つ
伊伊伊伊伊伊伊伊伊伊 伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊 漸近線の求め方に関する考察 たまい玉井 かつき克樹 伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊 伊伊伊伊伊伊伊伊伊伊. 漸近線についての生徒からの質問 数学において図を使って直感的な説明を与えることは, 理解を深めるのに大いに役立つ
31 33
 17 3 31 33 36 38 42 45 47 50 52 54 57 60 74 80 82 88 89 92 98 101 104 106 94 1 252 37 1 2 2 1 252 38 1 15 3 16 6 24 17 2 10 252 29 15 21 20 15 4 15 467,555 14 11 25 15 1 6 15 5 ( ) 41 2 634 640 1 5 252
17 3 31 33 36 38 42 45 47 50 52 54 57 60 74 80 82 88 89 92 98 101 104 106 94 1 252 37 1 2 2 1 252 38 1 15 3 16 6 24 17 2 10 252 29 15 21 20 15 4 15 467,555 14 11 25 15 1 6 15 5 ( ) 41 2 634 640 1 5 252
重要例題113
 04_ 高校 数学 Ⅱ 必須基本公式 定理集 数学 Ⅱ 第 章式の計算と方程式 0 商と余り についての整式 A をについての整式 B で割ったときの商を Q, 余りを R とすると, ABQ+R (R の次数 ) > 0
04_ 高校 数学 Ⅱ 必須基本公式 定理集 数学 Ⅱ 第 章式の計算と方程式 0 商と余り についての整式 A をについての整式 B で割ったときの商を Q, 余りを R とすると, ABQ+R (R の次数 ) > 0
数 IB( 植松 ) 2006 年夏学期解答 ( 兼ノート ) (2007 年のは課題プリでやってしまったので ) 1 (a) 補完公式を使う問題です 補完公式とは n+1 個の点を通る n 次の多項式を求める公式のことです 例 n=3 x y y0 y1 y2 y3 このデータを補
 数 IB( 植松 ) 26 年夏学期解答 ( 兼ノート ) (27 年のは課題プリでやってしまったので ) (a) 補完公式を使う問題です 補完公式とは n+ 個の点を通る n 次の多項式を求める公式のことです 例 n=3 x 2 3 y y y y2 y3 このデータを補完して得られる多項式を y=ax 3 +Bx 2 +Cx+D と置きます データより y = D y = A + B + C +
数 IB( 植松 ) 26 年夏学期解答 ( 兼ノート ) (27 年のは課題プリでやってしまったので ) (a) 補完公式を使う問題です 補完公式とは n+ 個の点を通る n 次の多項式を求める公式のことです 例 n=3 x 2 3 y y y y2 y3 このデータを補完して得られる多項式を y=ax 3 +Bx 2 +Cx+D と置きます データより y = D y = A + B + C +
機構学 平面機構の運動学
 問題 1 静止座標系 - 平面上を運動する節 b 上に2 定点,Bを考える. いま,2 点の座標は(0,0),B(50,0) である. 2 点間の距離は 50 mm, 点の速度が a 150 mm/s, 点 Bの速度の向きが150 である. 以下の問いに答えよ. (1) 点 Bの速度を求めよ. (2) 瞬間中心を求めよ. 節 b a (0,0) b 150 B(50,0) 問題 1(1) 解答 b
問題 1 静止座標系 - 平面上を運動する節 b 上に2 定点,Bを考える. いま,2 点の座標は(0,0),B(50,0) である. 2 点間の距離は 50 mm, 点の速度が a 150 mm/s, 点 Bの速度の向きが150 である. 以下の問いに答えよ. (1) 点 Bの速度を求めよ. (2) 瞬間中心を求めよ. 節 b a (0,0) b 150 B(50,0) 問題 1(1) 解答 b
二次関数 1 二次関数とは ともなって変化する 2 つの数 ( 変数 ) x, y があります x y つの変数 x, y が, 表のように変化するとき y は x の二次関数 といいます また,2 つの変数を式に表すと, 2 y x となりま
 二次関数 二次関数とは ともなって変化する つの数 ( 変数 ) x, y があります y 0 9 6 5 つの変数 x, y が, 表のように変化するとき y は x の二次関数 といいます また, つの変数を式に表すと, x となります < 二次関数の例 > x y 0 7 8 75 x ( 表の上の数 ) を 乗して 倍すると, y ( 表の下の数 ) になります x y 0 - -8-8 -
二次関数 二次関数とは ともなって変化する つの数 ( 変数 ) x, y があります y 0 9 6 5 つの変数 x, y が, 表のように変化するとき y は x の二次関数 といいます また, つの変数を式に表すと, x となります < 二次関数の例 > x y 0 7 8 75 x ( 表の上の数 ) を 乗して 倍すると, y ( 表の下の数 ) になります x y 0 - -8-8 -
二等辺三角形の性質 (2) 次の図の の大きさを求めなさい () = P=Q P=R Q 68 R P (2) (3) 五角形 は正五角形 = F 50 F (4) = = (5) === = 80 2 二等辺三角形の頂角の外角を 底角を y で表すとき y を の式で表しなさい y 2-5-2
 三角形 四角形 二等辺三角形の性質 () 二等辺三角形と正三角形 二等辺三角形 2つの辺が等しい三角形( 定義 ) 二等辺三角形の性質定理 二等辺三角形の底角は等しい 定理 2 二等辺三角形の頂点の二等分線は 底辺を直角に2 等分する 正三角形 3 辺が等しい三角形 ( 定義 ) 次の図で 同じ印をつけた辺や角が等しいとき の大きさを求めなさい () (2) (3) 65 40 25 (4) (5)
三角形 四角形 二等辺三角形の性質 () 二等辺三角形と正三角形 二等辺三角形 2つの辺が等しい三角形( 定義 ) 二等辺三角形の性質定理 二等辺三角形の底角は等しい 定理 2 二等辺三角形の頂点の二等分線は 底辺を直角に2 等分する 正三角形 3 辺が等しい三角形 ( 定義 ) 次の図で 同じ印をつけた辺や角が等しいとき の大きさを求めなさい () (2) (3) 65 40 25 (4) (5)
PowerPoint Presentation
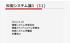 知能システム論 1 (11) 2012.6.20 情報システム学研究科情報メディアシステム学専攻知能システム学講座末廣尚士 13. ロボットアームの逆運動学 ( 幾何的解法 ) 何をしたいか 手首 手先 ツールの3 次元空間での位置や姿勢から それを実現する関節角度を計算する アームソリューション アームの解とも呼ぶ 何のために たとえばビジョンで認識された物をつかむ場合 物の位置 姿勢は3 次元空間で表現されることが普通である
知能システム論 1 (11) 2012.6.20 情報システム学研究科情報メディアシステム学専攻知能システム学講座末廣尚士 13. ロボットアームの逆運動学 ( 幾何的解法 ) 何をしたいか 手首 手先 ツールの3 次元空間での位置や姿勢から それを実現する関節角度を計算する アームソリューション アームの解とも呼ぶ 何のために たとえばビジョンで認識された物をつかむ場合 物の位置 姿勢は3 次元空間で表現されることが普通である
物理演習問題
 < 物理 > =0 問 ビルの高さを, ある速さ ( 初速 をとおく,において等加速度運動の公式より (- : -= t - t : -=- t - t (-, 式よりを消去すると t - t =- t - t ( + - ( + ( - =0 0 t t t t t t ( t + t - ( t - =0 t=t t=t t - 地面 ( t - t t +t 0 より, = 3 図 問 が最高点では速度が
< 物理 > =0 問 ビルの高さを, ある速さ ( 初速 をとおく,において等加速度運動の公式より (- : -= t - t : -=- t - t (-, 式よりを消去すると t - t =- t - t ( + - ( + ( - =0 0 t t t t t t ( t + t - ( t - =0 t=t t=t t - 地面 ( t - t t +t 0 より, = 3 図 問 が最高点では速度が
長尾谷高等学校レポート 回目 全枚. 関数 f() = について, 次の各問いに答えよ ( 教科書 p6~7, 副読本 p97) () 微分係数 f ( ) を定義に従って求めよ ただし, 求める過程を必ず書くこと () グラフ上の (, ) における接線の傾きを求めよ. 関数 ( ) = 4 f
 長尾谷高等学校レポート 回目 全枚 レポート作成にあたり諸注意. 数学 Ⅲ のレポートは 問題用紙と解答用紙に分かれています この用紙を含め 問題用紙は 提出する必要はありません もし提出用紙の表面に解答が書ききれない場合は 裏面を使用しても構いません ( 裏面の記述方法については後述 ). どの問題も 番号順に問題番号を書くことを忘れないでください また 解けなかった問題は 問題番号を書き 横に
長尾谷高等学校レポート 回目 全枚 レポート作成にあたり諸注意. 数学 Ⅲ のレポートは 問題用紙と解答用紙に分かれています この用紙を含め 問題用紙は 提出する必要はありません もし提出用紙の表面に解答が書ききれない場合は 裏面を使用しても構いません ( 裏面の記述方法については後述 ). どの問題も 番号順に問題番号を書くことを忘れないでください また 解けなかった問題は 問題番号を書き 横に
2010年度 筑波大・理系数学
 00 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ f( x) x ax とおく ただしa>0 とする () f( ) f() となるa の範囲を求めよ () f(x) の極小値が f ( ) 以下になる a の範囲を求めよ () x における f(x) の最小値をa を用いて表せ -- 00 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ つの曲線 C : y six ( 0
00 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ f( x) x ax とおく ただしa>0 とする () f( ) f() となるa の範囲を求めよ () f(x) の極小値が f ( ) 以下になる a の範囲を求めよ () x における f(x) の最小値をa を用いて表せ -- 00 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ つの曲線 C : y six ( 0
応用数学A
 応用数学 A 米田 戸倉川月 7 限 1930~2100 西 5-109 V を :x 2 + y 2 + z 2 = 4 で囲まれる内部とする F = ye x xe y + ze z FdV = V e x e y e z F = = 2e z 2e z dv = 2e z 3 23 = 64π 3 e z y x z 4π V n Fd = 1 F nd 2 F nd 法線ベクトル n g x,
応用数学 A 米田 戸倉川月 7 限 1930~2100 西 5-109 V を :x 2 + y 2 + z 2 = 4 で囲まれる内部とする F = ye x xe y + ze z FdV = V e x e y e z F = = 2e z 2e z dv = 2e z 3 23 = 64π 3 e z y x z 4π V n Fd = 1 F nd 2 F nd 法線ベクトル n g x,
数学 IB まとめ ( 教科書とノートの復習 ) IB ということで計算に関する話題中心にまとめました 理論を知りたい方はのみっちー IA のシケプリを参考にするとよいと思います 河澄教授いわく テストはまんべんなく出すらしいです でも 重積分 ( 特に変数変換使うもの ) 線積分とグリーンの定理は
 数学 IB まとめ ( 教科書とノートの復習 ) IB ということで計算に関する話題中心にまとめました 理論を知りたい方はのみっちー IA のシケプリを参考にするとよいと思います 河澄教授いわく テストはまんべんなく出すらしいです でも 重積分 ( 特に変数変換使うもの ) 線積分とグリーンの定理はほぼ間違いなく出ると思うんで 時間がない人はこのあたりに絞ってやるとよいと思います 多分 前にも書きましたが
数学 IB まとめ ( 教科書とノートの復習 ) IB ということで計算に関する話題中心にまとめました 理論を知りたい方はのみっちー IA のシケプリを参考にするとよいと思います 河澄教授いわく テストはまんべんなく出すらしいです でも 重積分 ( 特に変数変換使うもの ) 線積分とグリーンの定理はほぼ間違いなく出ると思うんで 時間がない人はこのあたりに絞ってやるとよいと思います 多分 前にも書きましたが
数学の世界
 東京女子大学文理学部数学の世界 (2002 年度 ) 永島孝 17 6 行列式の基本法則と効率的な計算法 基本法則 三次以上の行列式についても, 二次の場合と同様な法則がなりたつ ここには三次の場合を例示するが, 四次以上でも同様である 1 単位行列の行列式の値は 1 である すなわち 1 0 0 0 1 0 1 0 0 1 2 二つの列を入れ替えると行列式の値は 1 倍になる 例えば a 13 a
東京女子大学文理学部数学の世界 (2002 年度 ) 永島孝 17 6 行列式の基本法則と効率的な計算法 基本法則 三次以上の行列式についても, 二次の場合と同様な法則がなりたつ ここには三次の場合を例示するが, 四次以上でも同様である 1 単位行列の行列式の値は 1 である すなわち 1 0 0 0 1 0 1 0 0 1 2 二つの列を入れ替えると行列式の値は 1 倍になる 例えば a 13 a
経済数学演習問題 2018 年 5 月 29 日 I a, b, c R n に対して a + b + c 2 = a 2 + b 2 + c 2 + 2( a, b) + 2( b, c) + 2( a, c) が成立することを示しましょう.( 線型代数学 教科書 13 ページ 演習 1.17)
 経済数学演習問題 8 年 月 9 日 I a, b, c R n に対して a + b + c a + b + c + a, b + b, c + a, c が成立することを示しましょう. 線型代数学 教科書 ページ 演習.7 II a R n がすべての x R n に対して垂直, すなわち a, x x R n が成立するとします. このとき a となることを示しましょう. 線型代数学 教科書
経済数学演習問題 8 年 月 9 日 I a, b, c R n に対して a + b + c a + b + c + a, b + b, c + a, c が成立することを示しましょう. 線型代数学 教科書 ページ 演習.7 II a R n がすべての x R n に対して垂直, すなわち a, x x R n が成立するとします. このとき a となることを示しましょう. 線型代数学 教科書
Microsoft PowerPoint - ロボットの運動学forUpload'C5Q [互換モード]
![Microsoft PowerPoint - ロボットの運動学forUpload'C5Q [互換モード] Microsoft PowerPoint - ロボットの運動学forUpload'C5Q [互換モード]](/thumbs/104/163308363.jpg) ロボットの運動学 順運動学とは 座標系の回転と並進 同次座標変換行列 Denavit-Hartenberg の表記法 多関節ロボットの順運動学 レポート課題 & 中間試験について 逆運動学とは ヤコビアン行列 運動方程式 ( 微分方程式 ) ロボットの運動学 動力学 Equation of motion f ( ( t), ( t), ( t)) τ( t) 姿勢 ( 関節角の組合せ ) Posture
ロボットの運動学 順運動学とは 座標系の回転と並進 同次座標変換行列 Denavit-Hartenberg の表記法 多関節ロボットの順運動学 レポート課題 & 中間試験について 逆運動学とは ヤコビアン行列 運動方程式 ( 微分方程式 ) ロボットの運動学 動力学 Equation of motion f ( ( t), ( t), ( t)) τ( t) 姿勢 ( 関節角の組合せ ) Posture
