立体切断⑹-2回切り
|
|
|
- ちえこ てらわ
- 7 years ago
- Views:
Transcription
1 2 回切り問題のポイント 1. 交線を作図する 2つの平面が交わると 必ず直線ができます この直線のことを 交線 ( こうせん ) といいます 2. 体積を求める方法は次の 3 通りのどれか! 1 柱の体積 = 底面積 高さ 1 2 すいの体積 = 底面積 高さ 3 3 柱の斜め切り= 底面積 高さの平均 ただし 高さの平均が使えるのは 底面が円 三角形 正方形 長方形 ひし形 平行四辺形 正偶数角形のときだけ 底面が台形のときはダメ! 1
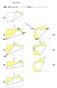
2 ステップ 1 柱の利用 1 図のような 1 辺 6 cmの立方体を D E F を通る平面と A B G を通る平面 で切断し 4 つの立体に分けます ⑴ 3 点 D E F を通る平面と 3 点 A B G を通る平面の交わる線 ( 交線といい ます ) を 次の手順に仕方に従って作図しなさい < 作図のしかた > 1 立方体の表面で 2 つの切り口が交わる交点をさがす 2 1 の 2 点を結ぶ ⑵ 面 EFGH を含む立体の体積を求めなさい 2
3 2 図のような 1 辺 6 cmの立方体を D E F を通る平面と P Q R を通る平面 で切断し 4 つの立体に分けます ただし P Q R は辺のまん中の点です ⑴ D E F を通る平面と P Q R を通る平面の交わる線 ( 交線 ) を作図しなさ い ⑵ G を含む立体の体積を求めなさい 3
4 ステップ 2 すいの利用 3 図のような 1 辺 6 cmの立方体を D E F を通る平面と D B F を通る平 面で切断し 4 つの立体に分けます このとき 3 点 E F H を含む立体の体 積を求めなさい 4
5 4 図のような 1 辺 6 cmの立方体を D E F を通る平面と D A F を通る平面 で切断し 4 つの立体に分けます このとき H を含む立体の体積を求めなさい 5
6 6 5 図のような 1 辺 6 cmの立方体を D P F を通る平面と P Q R を通る平面で切断し 4 つの立体に分けます このとき H を含む立体の体積を求めなさい ただし P Q R は辺のまん中の点です
7 6 図のような 1 辺 6 cmの立方体を D B E を通る平面と P Q R を通る平面 で切断し 4 つの立体に分けます ⑴ 4 つの立体のうち最も小さい立体の体積を求めなさい ⑵ A を含む立体の体積を求めなさい 7
8 8 7 図のような 1 辺 6 cmの立方体を D B E を通る平面と A E G を通る平面で切断し 4 つの立体に分けます このとき 辺 AB を含む立体の体積を求めなさい
9 9 8 図のような 1 辺 6 cmの立方体を D B E を通る平面と A F G を通る平面で切断し 4 つの立体に分けます このとき 辺 AB を含む立体の体積を求めなさい
10 9 図のような 1 辺 6 cmの立方体を D B E を通る平面と A C F を通る平面 で切断し 4 つの立体に分けます ⑴ 辺 AB を含む立体の体積を求めなさい ⑵ G を含む立体の体積を求めなさい 10
11 10 図のような 1 辺 6 cmの立方体を P E G を通る平面と D B E を通る平面 で切断し 4 つの立体に分けます ただし P は辺のまん中の点です ⑴ 4 つの立体のうち 最も小さい立体の体積を求めなさい ⑵ A を含む立体の体積を求めなさい 11
12 ステップ 3 高さ平均の利用 11 図のような 1 辺 6 cmの立方体を D P F を通る平面と D B F を通る 平面で切断し 4 つの立体に分けます このとき 点 E を含む立体の体積を求め なさい ただし P は辺のまん中の点です 12
13 13 12 図のような 1 辺 6 cmの立方体を D P F を通る平面と A E G を通る平面で切断し 4 つの立体に分けます このとき 3 点 E F G を含む立体の体積を求めなさい ただし P は辺のまん中の点です
14 14 13 図のような 1 辺 6 cmの立方体を D P F を通る平面と Q R S を通る平面で切断し 4 つの立体に分けます このとき 点 E を含む立体の体積を求めなさい ただし P Q R S は辺のまん中の点です
15 ステップ 4 延長 14 図のような 1 辺 6 cmの立方体を P E G を通る平面と Q R S を通る平面 で切断し 4 つの立体に分けます このとき 点 F を含む立体の体積を求めなさい ただし P Q R S は辺のまん中の点です 15
16 15 図のような 1 辺 6 cmの立方体を P E G を通る平面と C D E を通る平面 で切断し 4 つの立体に分けます ただし P Q は辺のまん中の点です 点線を 参考に 次の問いに答えなさい ⑴ STの長さを求めなさい ⑵ 三角すいR-EFSの体積を求めなさい ⑶ 4つに分かれた立体のうち 点 Bを含む立体の体積を求めなさい 16
17 16 図のような 1 辺 6 cmの立方体を P E G を通る平面と A C F を通る平面 で切断し 4 つの立体に分けます このとき 点 B を含む立体の体積を求めなさい ただし P は辺のまん中の点です 17
18 17 図のような 1 辺 6 cmの立方体を P E G を通る平面と D Q F を通る平面 で切断し 4 つの立体に分けます このとき 点 B を含む立体の体積を求めなさい ただし P Q は辺のまん中の点です 18
19 18 図のような 1 辺 6 cmの立方体を P E G を通る平面と C Q E を通る平面 で切断し 4 つの立体に分けます このとき B を含む立体の体積を求めなさい ただし P Q は辺のまん中の点です 19
20 20 19 図のような 1 辺 6 cmの立方体を P E G を通る平面と C A Q を通る平面で切断し 4 つの立体に分けます このとき B を含む立体の体積を求めなさい ただし P Q は辺のまん中の点です
21 解答 1 ⑴ 解説参照 ⑵ 54cm3 2 ⑴ 解説参照 ⑵ 81cm3 3 36cm3 4 72cm3 5 90cm3 6 ⑴ 4.5cm3 ⑵ 31.5cm3 7 18cm3 8 18cm3 9 ⑴ 9cm3 ⑵ 153cm3 10 ⑴ 4.5cm3 ⑵ 31.5cm cm cm cm cm3 ( または 8 cm cm3 ) 15 ⑴ 4cm ⑵ 48cm3 ⑶ 39cm cm cm cm cm3 ( または 4 cm cm3 ) 21
22 解説 1 ⑴ 図の が立方体の表面上の交点 この2 点を結ぶ ⑵ 求める立体は 立方体を4 等分したうちの1つ =54( 4 cm3 ) または 斜線部分が底面の三角柱と考えて =54( 2 cm3 ) 2 ⑴ 図の が立方体の表面上の交点 この2 点を結ぶ ⑵ 求める立体は 斜線部分が底面の台形柱 1 (3+6) 3 6=81( 2 cm3 ) 3 求める立体は 斜線部分が底面の三角すい =36( 2 3 cm3 ) 4 求める立体は 斜線部分が底面の四角すい =72( 3 cm3 ) 22
23 5 求める立体 ( 図 1)= 図 2の直方体 図 3の三角すい = = =90( cm3 ) 6 ⑴ 求める立体 ( 図 1) は 斜線部分が底面の三角すい =4.5( 2 3 cm3 ) ⑵ 求める立体 ( 図 2)= 図 3の三角すい 図 1の三角すい = = =31.5( cm3 ) 23
24 7 求める立体は 斜線部分が底面の三角すい =18( 2 3 cm3 ) 8 求める立体は 図 1 図 2の三角すい 図 1の斜線部分を底面と考えると =18( 2 3 cm3 ) 図 2の斜線部分を底面と考えると =18( 2 3 cm3 ) 24
25 9 ⑴ 求める立体は 斜線部分を底面とする三角すい =9( 2 3 cm3 ) ⑵ 求める立体は図 1 図 1の立体は 全体の立方体から図 2の立体を引いたもの 図 2の立体 = 図 3の三角すい+ 図 4の三角すい 図 5の三角すい ( 重なり ) = =63( cm3 ) よって 図 1の立体 = =153( cm3 ) 25
26 10 ⑴ 求める立体 ( 図 1) は 斜線部分を底面とする三角すい 底面の形は図 2のように上から見た図で考えると 底辺が3cm 高さが3 2=1.5( cm ) の直角二等辺三角形 よって =4.5( 2 3 cm3 ) ⑵ 求める立体 ( 図 3)= 図 4の三角すい 図 1の三角すい = =31.5( cm3 ) 26
27 11 求める立体は 斜線部分を底面とする三角柱を斜め に切ったもの 高さの平均を使う =54( 2 3 cm3 ) 12 求める立体は 斜線部分を底面とする三角柱を斜め に切ったもの 高さの平均を使う =36( 2 3 cm3 ) 13 求める立体は 斜線部分を底面とする四角柱を斜め に切ったもの 高さの平均を使う =40.5( 4 cm3 ) 27
28 14 図 2のように 切り口と立方体の1 辺を延長して 大きな三角すいを作る 求める立体 ( 図 1) は 図 2の三角すいから図 3の三角すいを引いたもの 各部分の長さは 図 4のように ピラミッド相似を利用して求める 求める立体 ( 図 1)= 図 2の三角すい 図 3の三角すい = = = =41 ( 8 または )( cm3 ) 28
29 15 ⑴ 延長してちょうちょ相似 相似比 3:3=1:1 ちょうちょ相似 相似比 6:12=1:2 2+1=3 3=6 cm 2=4 cm ⑵ 求める立体は 図 1 図 2の三角すい 図 1の斜線部分を底面と考えると =48( 2 3 cm3 ) 図 2の斜線部分を底面と考えると =48( 2 3 cm3 ) 29
30 ⑶ 求める立体 ( 図 3)= 図 4の三角すい 図 5の三角すい = =48 9 =39( cm3 ) 30
31 16 求める立体 ( 図 1) は 図 2 の三角すいから図 3 の三角すいを引いたもの 図 2 の 4 cmは 下のように ちょうちょ相似を利用して求める 延長してちょうちょ相似 相似比 3:3=1:1 ちょうちょ相似 相似比 6:12=1:2 2+1=3 3=6 cm 2=4 cm 求める立体 ( 図 1)= 図 2の三角すい 図 3の三角すい = =32 9 =23( cm3 ) 31
32 17 求める立体 ( 図 1) は 図 2 の三角すいから図 3 の三角すいを引いたもの 図 2 の 4.8 cmは 下のように ちょうちょ相似を利用して求める 延長してちょうちょ相似 相似比 3:3=1:1 ちょうちょ相似 相似比 3:12=1:4 1+4=5 5=6 cm 2=4.8 cm 求める立体 ( 図 1)= 図 2の三角すい 図 3の三角すい = = =37.08( cm3 ) 32
33 18 求める立体 ( 図 1) は 図 2 の三角すいから図 3 の三角すいを引いたもの 図 2 の 3.6 cmは 下のように ちょうちょ相似を利用して求める 延長してちょうちょ相似 相似比 3:3=1:1 ちょうちょ相似 相似比 9:6=3:2 3+2=5 5=6 cm 3=3.6 cm 求める立体 ( 図 1)= 図 2の三角すい 図 3の三角すい = = =23.4( cm3 ) 33
34 19 求める立体 ( 図 1) は 図 2の立体を2 倍したもの 図 2の立体は 図 3の三角すいから図 4の三角すいを引いたもの 図 3の 4.5 cmは 図 5のように ピラミッド相似を利用して求める 図 2の立体 = 図 3の三角すい 図 4の三角すい = = = ( 8 cm3 ) 求める立体 ( 図 1の立体 )= 2=42 ( 8 4 または )( cm3 ) 34
二等辺三角形の性質 (2) 次の図の の大きさを求めなさい () = P=Q P=R Q 68 R P (2) (3) 五角形 は正五角形 = F 50 F (4) = = (5) === = 80 2 二等辺三角形の頂角の外角を 底角を y で表すとき y を の式で表しなさい y 2-5-2
 三角形 四角形 二等辺三角形の性質 () 二等辺三角形と正三角形 二等辺三角形 2つの辺が等しい三角形( 定義 ) 二等辺三角形の性質定理 二等辺三角形の底角は等しい 定理 2 二等辺三角形の頂点の二等分線は 底辺を直角に2 等分する 正三角形 3 辺が等しい三角形 ( 定義 ) 次の図で 同じ印をつけた辺や角が等しいとき の大きさを求めなさい () (2) (3) 65 40 25 (4) (5)
三角形 四角形 二等辺三角形の性質 () 二等辺三角形と正三角形 二等辺三角形 2つの辺が等しい三角形( 定義 ) 二等辺三角形の性質定理 二等辺三角形の底角は等しい 定理 2 二等辺三角形の頂点の二等分線は 底辺を直角に2 等分する 正三角形 3 辺が等しい三角形 ( 定義 ) 次の図で 同じ印をつけた辺や角が等しいとき の大きさを求めなさい () (2) (3) 65 40 25 (4) (5)
STEP 数学 Ⅰ を解いてみた から直線 に下ろした垂線の足を H とすると, H in( 80 ) in より, S H in H 同様にして, S in, S in も成り立つ よって, S in 三角形の面積 ヘロンの公式 in in 辺の長
 STEP 数学 Ⅰ を解いてみた http://toitemit.ku.ne.jp 図形と計量 三角形の面積 三角形の面積 の面積を S とすると, S in in in 解説 から直線 に下ろした垂線の足を H とすると, H in より, S H in H STEP 数学 Ⅰ を解いてみた http://toitemit.ku.ne.jp から直線 に下ろした垂線の足を H とすると, H in(
STEP 数学 Ⅰ を解いてみた http://toitemit.ku.ne.jp 図形と計量 三角形の面積 三角形の面積 の面積を S とすると, S in in in 解説 から直線 に下ろした垂線の足を H とすると, H in より, S H in H STEP 数学 Ⅰ を解いてみた http://toitemit.ku.ne.jp から直線 に下ろした垂線の足を H とすると, H in(
【】三平方の定理
 FdText 数学 3 年 : 中学 塾用教材 http://www.fdtext.com/txt/ 三角形 x を求めよ (3) (4) (5) (6) (3) (4) (5) (6) [ 解答 ] (1) 34 cm (2) 2 2 cm (3) 13cm (4) 2 7 cm (5) 5 3cm (6) 11 cm - 1 - 次の三角形, 台形の高さ (h) を求めよ (3) (4) (3)
FdText 数学 3 年 : 中学 塾用教材 http://www.fdtext.com/txt/ 三角形 x を求めよ (3) (4) (5) (6) (3) (4) (5) (6) [ 解答 ] (1) 34 cm (2) 2 2 cm (3) 13cm (4) 2 7 cm (5) 5 3cm (6) 11 cm - 1 - 次の三角形, 台形の高さ (h) を求めよ (3) (4) (3)
座標軸以外の直線のまわりの回転体の体積 ( バウムクーヘン分割公式 ) の問題の解答 立体の体積の求め方 図 1 の立体の体積 V を求める方法を考えてみる 図 1 図 1 のように 軸の から までの長さを 等分する そして とおく とすると となる 図 1 のように のときの 軸に垂直な平面 に
 立体の体積の求め方 図 1 の立体の体積 V を求める方法を考えてみる 図 1 図 1 のように 軸の から までの長さを 等分する そして とおく とすると となる 図 1 のように のときの 軸に垂直な平面 による立体の断面積を とする 図 1の から までの斜線部分の立体 の体積を とすると, 図 2のように は 底面積 高さ の角柱の体積とみなせる よって 図 2 と表せる ただし とすると,
立体の体積の求め方 図 1 の立体の体積 V を求める方法を考えてみる 図 1 図 1 のように 軸の から までの長さを 等分する そして とおく とすると となる 図 1 のように のときの 軸に垂直な平面 による立体の断面積を とする 図 1の から までの斜線部分の立体 の体積を とすると, 図 2のように は 底面積 高さ の角柱の体積とみなせる よって 図 2 と表せる ただし とすると,
Microsoft Word - スーパーナビ 第6回 数学.docx
 1 ⑴ 与式 =- 5 35 +14 35 =9 35 1 ⑵ 与式 =9-(-5)=9+5=14 1 ⑶ 与式 = 4(a-b)-3(5a-3b) = 8a-4b-15a+9b = -7a+5b 1 1 1 1 ⑷ 与式 =(²+ 1+1²)-{²+(-3+)+(-3) } 1 ⑷ 与式 =(²++1)-(²--6)=²++1-²++6=3+7 1 ⑸ 与式 = - ² + 16 = - +16
1 ⑴ 与式 =- 5 35 +14 35 =9 35 1 ⑵ 与式 =9-(-5)=9+5=14 1 ⑶ 与式 = 4(a-b)-3(5a-3b) = 8a-4b-15a+9b = -7a+5b 1 1 1 1 ⑷ 与式 =(²+ 1+1²)-{²+(-3+)+(-3) } 1 ⑷ 与式 =(²++1)-(²--6)=²++1-²++6=3+7 1 ⑸ 与式 = - ² + 16 = - +16
< 中 3 分野例題付き公式集 > (1)2 の倍数の判定法は 1 の位が 0 又は偶数 ( 例題 )1~5 までの 5 つの数字を使って 3 ケタの数をつくるとき 2 の倍数は何通りできるか (2)5 の倍数の判定法は 1 の位が 0 又は 5 ( 例題 )1~9 までの 9 個の数字を使って 3
 () の倍数の判定法は の位が 0 又は偶数 ~ までの つの数字を使って ケタの数をつくるとき の倍数は何通りできるか () の倍数の判定法は の位が 0 又は ~9 までの 9 個の数字を使って ケタの数をつくるとき の倍数は何通りできるか () の倍数の判定法は 下 ケタが 00 又は の倍数 ケタの数 8 が の倍数となるときの 最小の ケタの数は ( 解 ) 一の位の数は の 通り 十の位は一の位の数以外の
() の倍数の判定法は の位が 0 又は偶数 ~ までの つの数字を使って ケタの数をつくるとき の倍数は何通りできるか () の倍数の判定法は の位が 0 又は ~9 までの 9 個の数字を使って ケタの数をつくるとき の倍数は何通りできるか () の倍数の判定法は 下 ケタが 00 又は の倍数 ケタの数 8 が の倍数となるときの 最小の ケタの数は ( 解 ) 一の位の数は の 通り 十の位は一の位の数以外の
2015 年度新中学 3 年数学 春休みの課題 3 年組番氏名
 015 年度新中学 3 年数学 春休みの課題 3 年組番氏名 正負の数 (1) 6-1 4 3 を計算しなさい () 6-4 ( -3) を計算しなさい (3) 4+5 ( -6) を計算しなさい 正負の数指数を含む計算 (4) 3-3 - 3 1 を計算しなさい 1 1 3 (5) ( 3- ) + - 4 を計算しなさい (6) 9 5 3 1 - - 3 6 を計算しなさい 3 (7) { (
015 年度新中学 3 年数学 春休みの課題 3 年組番氏名 正負の数 (1) 6-1 4 3 を計算しなさい () 6-4 ( -3) を計算しなさい (3) 4+5 ( -6) を計算しなさい 正負の数指数を含む計算 (4) 3-3 - 3 1 を計算しなさい 1 1 3 (5) ( 3- ) + - 4 を計算しなさい (6) 9 5 3 1 - - 3 6 を計算しなさい 3 (7) { (
Taro-1803 平行線と線分の比
 平行線と線分の比 1 4 平行線と線分の比 ポイント : 平行な直線がある つの三角形の線分の比について考える 証明 右の図で で とする (1) は と相似である これを証明しなさい と において から 平行線の ( ) は等しいから 9c = ( ) 1 = ( ) 1, より ( ) がそれぞれ等しいので 相似な図形になるので相似比を利用して () : の相似比を求めなさい 対応する線分の長さを求めることができる
平行線と線分の比 1 4 平行線と線分の比 ポイント : 平行な直線がある つの三角形の線分の比について考える 証明 右の図で で とする (1) は と相似である これを証明しなさい と において から 平行線の ( ) は等しいから 9c = ( ) 1 = ( ) 1, より ( ) がそれぞれ等しいので 相似な図形になるので相似比を利用して () : の相似比を求めなさい 対応する線分の長さを求めることができる
平成 31 年度 豊島岡女子学園中学校 < 第 3 回 > 算数 くわしい解説 すぐる学習会 1 (1) イ ア ウ ア = = イ = 1 - = ウ = = (2) 工
 平成 年度 豊島岡女子学園中学校 < 第 回 > 算数 くわしい解説 すぐる学習会 () 2-4 8 5 7 9 4 4 = = 5 7 5 2 4 = - = 5 5 8 = = 5 9 40 (2) 工夫して解く方法もありますが, 普通に計算した方が早くできるのでは 7 5 24 28 0 29 + + + + = + + + + = 2 4 8 2 2 2 2 2 2 2 29 5- = なので,
平成 年度 豊島岡女子学園中学校 < 第 回 > 算数 くわしい解説 すぐる学習会 () 2-4 8 5 7 9 4 4 = = 5 7 5 2 4 = - = 5 5 8 = = 5 9 40 (2) 工夫して解く方法もありますが, 普通に計算した方が早くできるのでは 7 5 24 28 0 29 + + + + = + + + + = 2 4 8 2 2 2 2 2 2 2 29 5- = なので,
木村の理論化学小ネタ 体心立方構造 面心立方構造 六方最密構造 剛球の並べ方と最密構造剛球を平面上に の向きに整列させるのに次の 2 つの方法がある 図より,B の方が A より密であることがわかる A B 1
 体心立方構造 面心立方構造 六方最密構造 剛球の並べ方と最密構造剛球を平面上に の向きに整列させるのに次の 2 つの方法がある 図より,B の方が A より密であることがわかる A B 1 体心立方構造 A を土台に剛球を積み重ねる 1 段目 2 2 段目 3 3 段目 他と色で区別した部分は上から見た最小繰り返し単位構造 ( 体心立方構造 ) 4 つまり,1 段目,2 段目,3 段目と順に重ねることにより,
体心立方構造 面心立方構造 六方最密構造 剛球の並べ方と最密構造剛球を平面上に の向きに整列させるのに次の 2 つの方法がある 図より,B の方が A より密であることがわかる A B 1 体心立方構造 A を土台に剛球を積み重ねる 1 段目 2 2 段目 3 3 段目 他と色で区別した部分は上から見た最小繰り返し単位構造 ( 体心立方構造 ) 4 つまり,1 段目,2 段目,3 段目と順に重ねることにより,
< D8C6082CC90AB8EBF816989A B A>
 数 Ⅰ 図形の性質 ( 黄色チャート ) () () () 点 は辺 を : に外分するから :=: :=: であるから :=: == () 点 は辺 を : に内分するから :=:=: = + %= また, 点 は辺 を : に外分するから :=:=: == =+=+= 直線 は の二等分線であるから :=: 直線 は の二等分線であるから :=: 一方, であるから, から, から :=: :=:
数 Ⅰ 図形の性質 ( 黄色チャート ) () () () 点 は辺 を : に外分するから :=: :=: であるから :=: == () 点 は辺 を : に内分するから :=:=: = + %= また, 点 は辺 を : に外分するから :=:=: == =+=+= 直線 は の二等分線であるから :=: 直線 は の二等分線であるから :=: 一方, であるから, から, から :=: :=:
S02 1 図において = =とする このとき = であることを証明せよ と において = 1 = 2 辺 は共通 より 3 辺 (3 組の辺 ) がそれぞれ等しい よって 合同な三角形の対応する角の大きさは等しい ゆえに = である
 S01 1 図において = =とする このとき であることを証明せよ と において = 1 = 2 辺 は共通 3 1 2 3 より 3 辺 (3 組の辺 ) がそれぞれ等しい よって である S02 1 図において = =とする このとき = であることを証明せよ と において = 1 = 2 辺 は共通 3 1 2 3 より 3 辺 (3 組の辺 ) がそれぞれ等しい よって 合同な三角形の対応する角の大きさは等しい
S01 1 図において = =とする このとき であることを証明せよ と において = 1 = 2 辺 は共通 3 1 2 3 より 3 辺 (3 組の辺 ) がそれぞれ等しい よって である S02 1 図において = =とする このとき = であることを証明せよ と において = 1 = 2 辺 は共通 3 1 2 3 より 3 辺 (3 組の辺 ) がそれぞれ等しい よって 合同な三角形の対応する角の大きさは等しい
2015年度 岡山大・理系数学
 5 岡山大学 ( 理系 ) 前期日程問題 解答解説のページへ を 以上の自然数とし, から までの自然数 k に対して, 番号 k をつけたカードをそれぞれ k 枚用意する これらすべてを箱に入れ, 箱の中から 枚のカードを同時に引くとき, 次の問いに答えよ () 用意したカードは全部で何枚か答えよ () 引いたカード 枚の番号が両方とも k である確率を と k の式で表せ () 引いたカード 枚の番号が一致する確率を
5 岡山大学 ( 理系 ) 前期日程問題 解答解説のページへ を 以上の自然数とし, から までの自然数 k に対して, 番号 k をつけたカードをそれぞれ k 枚用意する これらすべてを箱に入れ, 箱の中から 枚のカードを同時に引くとき, 次の問いに答えよ () 用意したカードは全部で何枚か答えよ () 引いたカード 枚の番号が両方とも k である確率を と k の式で表せ () 引いたカード 枚の番号が一致する確率を
<8D828D5A838A817C A77425F91E6318FCD2E6D6364>
 4 1 平面上のベクトル 1 ベクトルとその演算 例題 1 ベクトルの相等 次の問いに答えよ. ⑴ 右の図 1 は平行四辺形 である., と等しいベクトルをいえ. ⑵ 右の図 2 の中で互いに等しいベクトルをいえ. ただし, すべてのマス目は正方形である. 解 ⑴,= より, =,= より, = ⑵ 大きさと向きの等しいものを調べる. a =d, c = f d e f 1 右の図の長方形 において,
4 1 平面上のベクトル 1 ベクトルとその演算 例題 1 ベクトルの相等 次の問いに答えよ. ⑴ 右の図 1 は平行四辺形 である., と等しいベクトルをいえ. ⑵ 右の図 2 の中で互いに等しいベクトルをいえ. ただし, すべてのマス目は正方形である. 解 ⑴,= より, =,= より, = ⑵ 大きさと向きの等しいものを調べる. a =d, c = f d e f 1 右の図の長方形 において,
相加平均 相乗平均 調和平均が表す比 台形 の上底 下底 の長さをそれぞれ, とするとき 各平均により 台形の高さ はどのように比に分けられるだろうか 相乗平均は 相似な つの台形になるから台形の高さ を : の 比に分ける また 相加平均は は : の比に分けます 調和平均は 対角線 と の交点を
 台形に潜むいろいろな平均 札幌旭丘高校中村文則 台形に調和平均 相加平均をみる 右図の台形 において = = とする の長さを, を用いて表してみよう = x = y = c とすると であることから : = : より c y = x + y であることから : = : より c x = x + y を辺々加えると x + y c + = より + = x + y c となる ここで = = c =
台形に潜むいろいろな平均 札幌旭丘高校中村文則 台形に調和平均 相加平均をみる 右図の台形 において = = とする の長さを, を用いて表してみよう = x = y = c とすると であることから : = : より c y = x + y であることから : = : より c x = x + y を辺々加えると x + y c + = より + = x + y c となる ここで = = c =
空間図形の基本問題特集 2 (1) ご機嫌よう 右の図のように 小さい立方体を組み合わせて大きい立方体をつくり 真正面 真上 真横から真っ直ぐに針を通したの 穴があいていない小さい立方体は何個かしら ( 聖園女学院中 ) (2) 図は半径 8cm 高さ 20cm の円柱の 1 4 から 半径 4cm
 空間図形の基本問題特集 1 (1) 右の図は 直方体から半径が 4cm の円柱をくり抜いたものなのよ この立体の体積は何 cm 3 かしら ( 横浜富士見丘学園中等教育学校 ) (2) 右の立方体を 3 つの点 A B C を通る平面で切断したら 切り口はどんな形になるかしら ただし 3 つの点 A B C は それぞれの辺の中点とするわよ ( 横浜女学院中 ) B A C (3) 1 辺が 1cm
空間図形の基本問題特集 1 (1) 右の図は 直方体から半径が 4cm の円柱をくり抜いたものなのよ この立体の体積は何 cm 3 かしら ( 横浜富士見丘学園中等教育学校 ) (2) 右の立方体を 3 つの点 A B C を通る平面で切断したら 切り口はどんな形になるかしら ただし 3 つの点 A B C は それぞれの辺の中点とするわよ ( 横浜女学院中 ) B A C (3) 1 辺が 1cm
平成 30 年度 前期選抜学力検査問題 数学 ( 2 時間目 45 分 ) 受検番号氏名 注 意 1 問題は, 表と裏にあります 2 答えは, すべて解答欄に記入しなさい 1 次の (1)~(7) の問いに答えなさい (1) -3 (-6+4) を計算しなさい 表合計 2 次の (1)~(6) の問
 平成 30 年度 前期選抜学力検査問題 数学 ( 2 時間目 45 分 ) 受検番号氏名 注 意 1 問題は, 表と裏にあります 2 答えは, すべて解答欄に記入しなさい 1 次の (1)~(7) の問いに答えなさい (1) -3 (-6+4) を計算しなさい 表合計 2 次の (1)~(6) の問いに答えなさい 合計 (1) 関数 y = x 2 において,x の変域が -2 x 3 のとき, y
平成 30 年度 前期選抜学力検査問題 数学 ( 2 時間目 45 分 ) 受検番号氏名 注 意 1 問題は, 表と裏にあります 2 答えは, すべて解答欄に記入しなさい 1 次の (1)~(7) の問いに答えなさい (1) -3 (-6+4) を計算しなさい 表合計 2 次の (1)~(6) の問いに答えなさい 合計 (1) 関数 y = x 2 において,x の変域が -2 x 3 のとき, y
測量士補 重要事項 応用測量 点高法による土量計算
 点高法による土量計算 < 試験合格へのポイント > 点高法による土量計算は H9 年度を最後にその出題はない 特に三角形法を用いた土量計算は H 年度が最後の出題であり 26 年ぶりの出題となった 特に公式を覚える必要はないが計算方法を理解することが大切である 1. 点高法による土量計算の方法 点高法による土量計算とは 盛土 ( 又は切土 ) する敷地を長方形 ( 又は三角形 ) に分割し その交点の高さを測り計画高との高低差を求め
点高法による土量計算 < 試験合格へのポイント > 点高法による土量計算は H9 年度を最後にその出題はない 特に三角形法を用いた土量計算は H 年度が最後の出題であり 26 年ぶりの出題となった 特に公式を覚える必要はないが計算方法を理解することが大切である 1. 点高法による土量計算の方法 点高法による土量計算とは 盛土 ( 又は切土 ) する敷地を長方形 ( 又は三角形 ) に分割し その交点の高さを測り計画高との高低差を求め
【算数】テーマ別ポイント集:平面図形ポイント10〜14
 平面図形ポント 0 - 三角形の相似 4 パターン 三角形の相似 4 パターンを覚え 発見できるようになること! 平行線型の相似 この つがほとんど 発見のコツは平行線をさがすこと ピラミッド相似 c x n p 相似比 = : = : n = x : y 単なる辺の比 = : c = : p 相似比とまちがえる生徒が多い y クロス相似 x n 相似比 = : = : n = x : y y 直角三角形の相似
平面図形ポント 0 - 三角形の相似 4 パターン 三角形の相似 4 パターンを覚え 発見できるようになること! 平行線型の相似 この つがほとんど 発見のコツは平行線をさがすこと ピラミッド相似 c x n p 相似比 = : = : n = x : y 単なる辺の比 = : c = : p 相似比とまちがえる生徒が多い y クロス相似 x n 相似比 = : = : n = x : y y 直角三角形の相似
中学 1 年生 e ライブラリ数学教材一覧 学校図書 ( 株 ) 中学 1 年 数学 文字式式の計算 項と係数 中学 1 年 数学 次式 中学 1 年 数学 項のまとめ方 中学 1 年 数学 次式の加法 中学 1 年 数学 77
 中学 1 年生 e ライブラリ数学教材一覧 学校図書 ( 株 ) 中学 1 年 数学 1 14-20 正の数 負の数正の数 負の数 14- ある基準から考えた量の表現 中学 1 年 数学 14- 正の数 中学 1 年 数学 14- 負の数 中学 1 年 数学 14- 量の基準を表す数 中学 1 年 数学 15- 反対の性質をもつ量の表現 中学 1 年 数学 17- 数直線 中学 1 年 数学 18-19
中学 1 年生 e ライブラリ数学教材一覧 学校図書 ( 株 ) 中学 1 年 数学 1 14-20 正の数 負の数正の数 負の数 14- ある基準から考えた量の表現 中学 1 年 数学 14- 正の数 中学 1 年 数学 14- 負の数 中学 1 年 数学 14- 量の基準を表す数 中学 1 年 数学 15- 反対の性質をもつ量の表現 中学 1 年 数学 17- 数直線 中学 1 年 数学 18-19
20~22.prt
 [ 三クリア W] 辺が等しいことの証明 ( 円周角と弦の関係利用 ) の の二等分線がこの三角形の外接円と交わる点をそれぞれ とするとき 60 ならば であることを証明せよ 60 + + 0 + 0 80-60 60 から ゆえに 等しい長さの弧に対する弦の長さは等しいから [ 三クリア ] 方べきの定理 接線と弦のなす角と円周角を利用 線分 を直径とする円 があり 右の図のように の延長上の点
[ 三クリア W] 辺が等しいことの証明 ( 円周角と弦の関係利用 ) の の二等分線がこの三角形の外接円と交わる点をそれぞれ とするとき 60 ならば であることを証明せよ 60 + + 0 + 0 80-60 60 から ゆえに 等しい長さの弧に対する弦の長さは等しいから [ 三クリア ] 方べきの定理 接線と弦のなす角と円周角を利用 線分 を直径とする円 があり 右の図のように の延長上の点
< F2D323289F090E08E9197BF928694E081698E5A A2E6A>
 小学校第 6 学年 算数 B 注 意 1 先生の合図があるまで, 中を開かないでください 2 調査問題は,1 ページから 18 ページまであります 3 解答用紙は, 両面に解答らんがあります 解答は, すべて解答用紙に書きましょう えんぴつ 4 解答は,HBまたはBの黒鉛筆 ( シャープペンシルも可 ) を使い, こく, はっきりと書きましょう また, 消すときは消しゴムできれいに消しましょう 5
小学校第 6 学年 算数 B 注 意 1 先生の合図があるまで, 中を開かないでください 2 調査問題は,1 ページから 18 ページまであります 3 解答用紙は, 両面に解答らんがあります 解答は, すべて解答用紙に書きましょう えんぴつ 4 解答は,HBまたはBの黒鉛筆 ( シャープペンシルも可 ) を使い, こく, はっきりと書きましょう また, 消すときは消しゴムできれいに消しましょう 5
図形と証明 1 対頂角 a = b ( 証明 ) a+ c= 180 なので a = c b+ c= 180 なので b = c 1 2 1,2 から a = b a と b のように 交わる直線の向かい合う角を対頂角といいます 等しいことは 当然のように見えますが 証明とは
 図形と証明 1 対頂角 a = b a+ c= 180 なので a = 180 - c b+ c= 180 なので b = 180 - c 1 2 1,2 から a = b a と b のように 交わる直線の向かい合う角を対頂角といいます 等しいことは 当然のように見えますが 証明とは それを筋道立てて説明することです a も b も 角度を使った式で 同じ式になる ということを述べるのが この証明です
図形と証明 1 対頂角 a = b a+ c= 180 なので a = 180 - c b+ c= 180 なので b = 180 - c 1 2 1,2 から a = b a と b のように 交わる直線の向かい合う角を対頂角といいます 等しいことは 当然のように見えますが 証明とは それを筋道立てて説明することです a も b も 角度を使った式で 同じ式になる ということを述べるのが この証明です
FdData中間期末数学2年
 中学中間 期末試験問題集( 過去問 ): 数学 年 方程式とグラフ [ 二元一次方程式 ax + by = c のグラフ ] [ 問題 ]( 後期中間 ) 二元一次方程式 x + y = 4 のグラフをかけ http://www.fdtext.com/dat/ [ 解答 ] 方程式の解を座標とする点の全体を, その方程式のグラフという 二元一次方程式 x + y = 4 の解は無数にあるが, 例えば,
中学中間 期末試験問題集( 過去問 ): 数学 年 方程式とグラフ [ 二元一次方程式 ax + by = c のグラフ ] [ 問題 ]( 後期中間 ) 二元一次方程式 x + y = 4 のグラフをかけ http://www.fdtext.com/dat/ [ 解答 ] 方程式の解を座標とする点の全体を, その方程式のグラフという 二元一次方程式 x + y = 4 の解は無数にあるが, 例えば,
2014年度 センター試験・数学ⅡB
 第 問 解答解説のページへ [] O を原点とする座標平面において, 点 P(, q) を中心とする円 C が, 方程式 y 4 x で表される直線 l に接しているとする () 円 C の半径 r を求めよう 点 P を通り直線 l に垂直な直線の方程式は, y - ア ( x- ) + qなので, P イ から l に引いた垂線と l の交点 Q の座標は ( ( ウ + エ q ), 4 (
第 問 解答解説のページへ [] O を原点とする座標平面において, 点 P(, q) を中心とする円 C が, 方程式 y 4 x で表される直線 l に接しているとする () 円 C の半径 r を求めよう 点 P を通り直線 l に垂直な直線の方程式は, y - ア ( x- ) + qなので, P イ から l に引いた垂線と l の交点 Q の座標は ( ( ウ + エ q ), 4 (
比例・反比例 例題編 問題・解答
 中学数学比例 反比例の問題 関数 ( 移行措置による追加 ) 比例 変域 座標 比例のグラフ 比例の式 比例の文章問題 座標と変域 反比例とグラフ 反比例の式 反比例の文章問題 比例と反比例のグラフ * ページ表示 を 見開き でご覧いただきますと 問題とその 答えが見やすくなります * このテキストは家庭学習の補助教材としてのみご利用いただけま す その他 ( 問題の改変 商用など ) の利用はご遠慮くださいま
中学数学比例 反比例の問題 関数 ( 移行措置による追加 ) 比例 変域 座標 比例のグラフ 比例の式 比例の文章問題 座標と変域 反比例とグラフ 反比例の式 反比例の文章問題 比例と反比例のグラフ * ページ表示 を 見開き でご覧いただきますと 問題とその 答えが見やすくなります * このテキストは家庭学習の補助教材としてのみご利用いただけま す その他 ( 問題の改変 商用など ) の利用はご遠慮くださいま
平成 31 年度 前期選抜学力検査問題 数学 ( 2 時間目 45 分 ) 受検番号氏名 注 意 1 問題は, 表と裏にあります 2 答えは, すべて解答欄に記入しなさい 1 次の (1)~(7) の問いに答えなさい (1) 3 (-2 2 ) を計算しなさい 表合計 2 次の (1)~(6) の問
 平成 1 年度 前期選抜学力検査問題 数学 ( 時間目 45 分 ) 受検番号氏名 注 意 1 問題は, 表と裏にあります 答えは, すべて解答欄に記入しなさい 1 次の ~(7) の問いに答えなさい (- ) を計算しなさい 表合計 次の ~(6) の問いに答えなさい 合計 関数 y = x のグラフについて正しいものを, 次のア ~ エからすべて選んで記号を書きなさい アイウエ グラフは原点を通る
平成 1 年度 前期選抜学力検査問題 数学 ( 時間目 45 分 ) 受検番号氏名 注 意 1 問題は, 表と裏にあります 答えは, すべて解答欄に記入しなさい 1 次の ~(7) の問いに答えなさい (- ) を計算しなさい 表合計 次の ~(6) の問いに答えなさい 合計 関数 y = x のグラフについて正しいものを, 次のア ~ エからすべて選んで記号を書きなさい アイウエ グラフは原点を通る
1 次関数 1 次関数の式 1 次の表は, ろうそくを燃やした時間 x 分と残りのろうそくの長さ ycm の関係を表しています 次の問いに答えなさい x( 分 ) y(cm ) (1) 上の表のをうめなさい (2) ろうそくは,5 分間に何 cm 短くなっていく
 次関数 次関数の式 次の表は, ろうそくを燃やした時間 分と残りのろうそくの長さ cm の関係を表しています 次の問いに答えなさい ( 分 ) 0 5 0 5 (cm ) 0 () 上の表のをうめなさい () ろうそくは,5 分間に何 cm 短くなっていくか () ろうそくは, 分間に何 cm の割合で短くなっていくか () ろうそくは, 分間に何 cm の割合で短くなっていくか (5) ろうそくの長さ
次関数 次関数の式 次の表は, ろうそくを燃やした時間 分と残りのろうそくの長さ cm の関係を表しています 次の問いに答えなさい ( 分 ) 0 5 0 5 (cm ) 0 () 上の表のをうめなさい () ろうそくは,5 分間に何 cm 短くなっていくか () ろうそくは, 分間に何 cm の割合で短くなっていくか () ろうそくは, 分間に何 cm の割合で短くなっていくか (5) ろうそくの長さ
平成 25 年度京都数学オリンピック道場 ( 第 1 回 ) H 正三角形 ABC の外接円の,A を含まない弧 BC 上に点 P をとる. このとき, AP = BP + CP となることを示せ. 解説円周角の定理より, 4APC = 4ABC = 60, であるから, 図のよ
 1 正三角形 の外接円の, を含まない弧 上に点 をとる. このとき, = + となることを示せ. 解説円周角の定理より, 4 = 4 = 60, であるから, 図のように直線 上に点 を, 三角形 が正三角形となるようにとることができる. 三角形 と三角形 において, =, = であり, 4 = 4 = 60, - 4 であるから, 辺とその間の角がそれぞれ等しく, 三角形 と三角形 は合同である.
1 正三角形 の外接円の, を含まない弧 上に点 をとる. このとき, = + となることを示せ. 解説円周角の定理より, 4 = 4 = 60, であるから, 図のように直線 上に点 を, 三角形 が正三角形となるようにとることができる. 三角形 と三角形 において, =, = であり, 4 = 4 = 60, - 4 であるから, 辺とその間の角がそれぞれ等しく, 三角形 と三角形 は合同である.
【】 1次関数の意味
 FdText 数学 1 年 : 中学 塾用教材 http://www.fdtext.com/txt/ 直線と角 解答欄に次のものを書き入れよ 1 直線 AB 2 線分 AB 1 2 1 2 右図のように,3 点 A,B,Cがあるとき, 次の図形を書き入れよ 1 直線 AC 2 線分 BC - 1 - 次の図で a, b, c で示された角を A,B,C,D の文字を使って表せ a : b : c :
FdText 数学 1 年 : 中学 塾用教材 http://www.fdtext.com/txt/ 直線と角 解答欄に次のものを書き入れよ 1 直線 AB 2 線分 AB 1 2 1 2 右図のように,3 点 A,B,Cがあるとき, 次の図形を書き入れよ 1 直線 AC 2 線分 BC - 1 - 次の図で a, b, c で示された角を A,B,C,D の文字を使って表せ a : b : c :
平成 3 0 年度前期選抜学力検査 数学 ( 1 0 時 ~ 1 0 時 4 5 分, 4 5 分間 ) 問題用紙 注 意 1. 開始 の合図があるまで開いてはいけません 2. 答えは, すべて解答用紙に書きなさい 3. 問題は, からまでで, 6 ページにわたって印刷してあります 4. 開始 の合
 平成 3 0 年度前期選抜学力検査 数学 ( 1 0 時 ~ 1 0 時 4 5 分, 4 5 分間 ) 問題用紙 注 意 1. 開始 の合図があるまで開いてはいけません 2. 答えは, すべて解答用紙に書きなさい 3. 問題は, からまでで, 6 ページにわたって印刷してあります 4. 開始 の合図で, 解答用紙の決められた欄に受検番号を書きなさい 5. 問題を読むとき, 声を出してはいけません
平成 3 0 年度前期選抜学力検査 数学 ( 1 0 時 ~ 1 0 時 4 5 分, 4 5 分間 ) 問題用紙 注 意 1. 開始 の合図があるまで開いてはいけません 2. 答えは, すべて解答用紙に書きなさい 3. 問題は, からまでで, 6 ページにわたって印刷してあります 4. 開始 の合図で, 解答用紙の決められた欄に受検番号を書きなさい 5. 問題を読むとき, 声を出してはいけません
2 ( 178 9)
 ( 1,876.58 km2) 98 ( 11 ) ( 21 ) 4 17 (8 9 ) 28 6 1? H25.12 11,998 489.5 H26.12 13,392 111.6% 565.5 115.5% H27.12 13,828 103.3% 476.8 84.3% H25.12 84 4.5 H26.12 132 157.1% 5 111.1% H27.12 95 72.0 2.56
( 1,876.58 km2) 98 ( 11 ) ( 21 ) 4 17 (8 9 ) 28 6 1? H25.12 11,998 489.5 H26.12 13,392 111.6% 565.5 115.5% H27.12 13,828 103.3% 476.8 84.3% H25.12 84 4.5 H26.12 132 157.1% 5 111.1% H27.12 95 72.0 2.56
 ⑴ ⑵ ⑶ ⑷ A C B ( D Other A C B ( D 1996/2/1 1996/3/1 1996/6/1 1996/8/1 1996/9/1 1997/3/1 1997/5/1 1997/6/1 1997/6/1 1997/6/1 1997/10/1 1997/10/1 1997/10/1 1997/11/1 1997/11/1
⑴ ⑵ ⑶ ⑷ A C B ( D Other A C B ( D 1996/2/1 1996/3/1 1996/6/1 1996/8/1 1996/9/1 1997/3/1 1997/5/1 1997/6/1 1997/6/1 1997/6/1 1997/10/1 1997/10/1 1997/10/1 1997/11/1 1997/11/1
数学 Ⅲ 無限等比級数の問題解答 問 1 次の無限級数の和を求めよ (1) (5) (2) (6) (7) (3) ( 解 )(1) 初項 < 公比 < の無限等比級数より収束し (4) (2) (3) その和は ( 答 ) であるから 初項 < 公比 となっている よって 収束し その和は よって
 問 1 次の無限級数の和を求めよ (1) (5) (2) (6) (7) (3) ( 解 )(1) 初項 < 公比 < の無限等比級数より収束し (4) (2) (3) その和は であるから 初項 < 公比 となっている よって 収束し その和は よって 収束し その和は < の無限等比級数 であるから 初項 < 公比
問 1 次の無限級数の和を求めよ (1) (5) (2) (6) (7) (3) ( 解 )(1) 初項 < 公比 < の無限等比級数より収束し (4) (2) (3) その和は であるから 初項 < 公比 となっている よって 収束し その和は よって 収束し その和は < の無限等比級数 であるから 初項 < 公比
Microsoft Word - 中2数学解答【一問一答i〜n】.doc.pdf
 塾 TV(05 年 4 月版) 一問一答 i-0 式の計算 次の計算をしなさい () xy x y 4 (4) a a 4 ( () ab a b a aaaa aaa a a (7) a a aa a 6a ) ( () x y 4 x y ab 4 x5 y 5 (5) 6 xy 6 xy (6) a b a b 4 6xy 6xy (8) 4 x y xy 4 xxyyy xy (4) ( x
塾 TV(05 年 4 月版) 一問一答 i-0 式の計算 次の計算をしなさい () xy x y 4 (4) a a 4 ( () ab a b a aaaa aaa a a (7) a a aa a 6a ) ( () x y 4 x y ab 4 x5 y 5 (5) 6 xy 6 xy (6) a b a b 4 6xy 6xy (8) 4 x y xy 4 xxyyy xy (4) ( x
2015年度 金沢大・理系数学
 05 金沢大学 ( 理系 ) 前期日程問題 解答解説のページへ四面体 OABC において, 3 つのベクトル OA, OB, OC はどの つも互いに垂直で あり, h > 0 に対して, OA, OB, OC h とする 3 点 O, A, B を通る平面上の点 P は, CP が CA と CB のどちらとも垂直となる点であるとする 次の問いに答えよ () OP OA + OB とするとき, と
05 金沢大学 ( 理系 ) 前期日程問題 解答解説のページへ四面体 OABC において, 3 つのベクトル OA, OB, OC はどの つも互いに垂直で あり, h > 0 に対して, OA, OB, OC h とする 3 点 O, A, B を通る平面上の点 P は, CP が CA と CB のどちらとも垂直となる点であるとする 次の問いに答えよ () OP OA + OB とするとき, と
(Microsoft Word - \213\363\212\324\220}\214`_\220\263\216l\226\312\221\314_.doc)
 立体図形によるによる空間空間の彩り 球 立方体 正四面体の佇まいについて 札幌旭丘高校中村文則 はじめに正三角形 平面上では円とともに図形の代表に位置し, 図形の中に潜む種々の性質は大きな関心をもち扱われる. その正三角形を四面として構成される正四面体もまた煌びやかであり, 空間内では立体図形の主格であり, 正三角形の性質を継承しつつ, 独自に, 球面や他の立体図形との関わりを演出している. それらの佇まいについて調べてみよう.
立体図形によるによる空間空間の彩り 球 立方体 正四面体の佇まいについて 札幌旭丘高校中村文則 はじめに正三角形 平面上では円とともに図形の代表に位置し, 図形の中に潜む種々の性質は大きな関心をもち扱われる. その正三角形を四面として構成される正四面体もまた煌びやかであり, 空間内では立体図形の主格であり, 正三角形の性質を継承しつつ, 独自に, 球面や他の立体図形との関わりを演出している. それらの佇まいについて調べてみよう.
2011年度 東京工大・数学
 東京工業大学前期日程問題 解答解説のページへ n n を自然数とする 平面上で行列 n( n+ ) n+ の表す 次変換 ( 移動とも いう ) を n とする 次の問いに答えよ () 原点 O(, ) を通る直線で, その直線上のすべての点が n により同じ直線上に移 されるものが 本あることを示し, この 直線の方程式を求めよ () () で得られた 直線と曲線 (3) を求めよ n Sn 6
東京工業大学前期日程問題 解答解説のページへ n n を自然数とする 平面上で行列 n( n+ ) n+ の表す 次変換 ( 移動とも いう ) を n とする 次の問いに答えよ () 原点 O(, ) を通る直線で, その直線上のすべての点が n により同じ直線上に移 されるものが 本あることを示し, この 直線の方程式を求めよ () () で得られた 直線と曲線 (3) を求めよ n Sn 6
【FdData中間期末過去問題】中学数学1年(比例と反比例の応用/点の移動/速さ)
 FdDt 中間期末過去問題 中学数学 1 年 ( 比例と反比例の応用 / 点の移動 / 速さ ) http://www.fdtet.com/dt/ 水そうの問題 [ 問題 ](2 学期期末 ) 水が 200 l 入る水そうに, 毎分 8 l の割合で水を入れていく 水を入れはじめてから 分後の水の量を y l とするとき, 次の各問いに答えよ (1), y の関係を式に表せ (2) の変域を求めよ
FdDt 中間期末過去問題 中学数学 1 年 ( 比例と反比例の応用 / 点の移動 / 速さ ) http://www.fdtet.com/dt/ 水そうの問題 [ 問題 ](2 学期期末 ) 水が 200 l 入る水そうに, 毎分 8 l の割合で水を入れていく 水を入れはじめてから 分後の水の量を y l とするとき, 次の各問いに答えよ (1), y の関係を式に表せ (2) の変域を求めよ
2013年度 九州大・理系数学
 九州大学 ( 理系 ) 前期日程問題 解答解説のページへ a> とし, つの曲線 y= ( ), y= a ( > ) を順にC, C とする また, C とC の交点 P におけるC の接線をl とする 以下 の問いに答えよ () 曲線 C とy 軸および直線 l で囲まれた部分の面積をa を用いて表せ () 点 P におけるC の接線と直線 l のなす角を ( a) とき, limasin θ(
九州大学 ( 理系 ) 前期日程問題 解答解説のページへ a> とし, つの曲線 y= ( ), y= a ( > ) を順にC, C とする また, C とC の交点 P におけるC の接線をl とする 以下 の問いに答えよ () 曲線 C とy 軸および直線 l で囲まれた部分の面積をa を用いて表せ () 点 P におけるC の接線と直線 l のなす角を ( a) とき, limasin θ(
中学 3 年数学 ( 東京書籍 ) 単元別コンテンツ一覧 単元ドリル教材解説教材 確認問題ライブラリ (OP) プリント教材 教材数 :17 問題数 : 基本 145, 標準 145, 挑戦 145 多項式と単項式の乗法 除法 式の展開 乗法公式などの問題を収録 解説教材 :6 確認問題 :6 単項
 教材数 :17 問題数 : 基本 145, 標準 145, 挑戦 145 多項式と単項式の乗法 除法 式の展開 乗法公式などの問題を収録 解説教材 :6 確認問題 :6 単項式と多項式の乗除 多項式の乗法などの解説 確認問題 ステープラオリジナル問題を簡単な操作で作成 (OP) 中学校プリントパック単元別プリント 26 枚 多項式多項式の計算 教材数 :8 問題数 : 基本 75, 標準 75, 挑戦
教材数 :17 問題数 : 基本 145, 標準 145, 挑戦 145 多項式と単項式の乗法 除法 式の展開 乗法公式などの問題を収録 解説教材 :6 確認問題 :6 単項式と多項式の乗除 多項式の乗法などの解説 確認問題 ステープラオリジナル問題を簡単な操作で作成 (OP) 中学校プリントパック単元別プリント 26 枚 多項式多項式の計算 教材数 :8 問題数 : 基本 75, 標準 75, 挑戦
PowerPoint プレゼンテーション
 平成 28 年度全国学力 学習状況調査 中学校数学 2 特徴的な問題 A 問題より A B C 垂線の作図方法について理解しているかどうか 3 関連問題 問題番号 問題の概要 全国正答率 三重県 公立 正答率 H24A 4 (1) 角の二等分線の作図の方法で作図された直線がもつ性質として, 正しい記述を選ぶ 58.2% 56.9% H26A 4 (2) 線分の垂直二等分線の作図の方法で作図される直線について,
平成 28 年度全国学力 学習状況調査 中学校数学 2 特徴的な問題 A 問題より A B C 垂線の作図方法について理解しているかどうか 3 関連問題 問題番号 問題の概要 全国正答率 三重県 公立 正答率 H24A 4 (1) 角の二等分線の作図の方法で作図された直線がもつ性質として, 正しい記述を選ぶ 58.2% 56.9% H26A 4 (2) 線分の垂直二等分線の作図の方法で作図される直線について,
⑴ ⑵ ⑶
 - 108 - ⑴ ⑵ ⑶ ⑴ ⑵ ⑶ ⑷ - 110 - ⑴ ⑵ ⑶ - 111 - ⑷ ⑴ ⑸ ⑹ ⑵ ⑶ - 112 - ⑴ ⑵ ⑶ ⑷ ⑴ ⑵ ⑶ ⑷ ⑴ ⑵ - 115 - - 116 - - 117 - - 118 - - 119 - - 120 - ⑴ - ⑴ ⑴ ⑵ ⑴ ⑵ ⑵ ⑴ ⑵ ⑴ ⑵ - 122 - - 123 - ⑴ ⑵ ⑴ ⑵ ⑶ - 124 - ⑷ - 125 -
- 108 - ⑴ ⑵ ⑶ ⑴ ⑵ ⑶ ⑷ - 110 - ⑴ ⑵ ⑶ - 111 - ⑷ ⑴ ⑸ ⑹ ⑵ ⑶ - 112 - ⑴ ⑵ ⑶ ⑷ ⑴ ⑵ ⑶ ⑷ ⑴ ⑵ - 115 - - 116 - - 117 - - 118 - - 119 - - 120 - ⑴ - ⑴ ⑴ ⑵ ⑴ ⑵ ⑵ ⑴ ⑵ ⑴ ⑵ - 122 - - 123 - ⑴ ⑵ ⑴ ⑵ ⑶ - 124 - ⑷ - 125 -
【FdData中間期末過去問題】中学数学3年(二次方程式応用/係数/数/面積・体積/動点)
 FdData 中間期末 : 中学数学 3 年 : 二次方程式応用 [ 係数の決定 / 整数の問題 / 面積 体積の問題 / 動点の問題 ] [ 数学 3 年 pdf ファイル一覧 ] 係数の決定 [ 係数 a を求める ] 二次方程式 + a = 0 の 1 つの解が 3 であるとき, a の値を求めよ また, もう 1 つの解を求めよ a = = a = 3 = 1 + a = 0 1の解の 1
FdData 中間期末 : 中学数学 3 年 : 二次方程式応用 [ 係数の決定 / 整数の問題 / 面積 体積の問題 / 動点の問題 ] [ 数学 3 年 pdf ファイル一覧 ] 係数の決定 [ 係数 a を求める ] 二次方程式 + a = 0 の 1 つの解が 3 であるとき, a の値を求めよ また, もう 1 つの解を求めよ a = = a = 3 = 1 + a = 0 1の解の 1
新中 2 春休みの宿題数学 2 年組番氏名
 新中 春休みの宿題数学 年組番氏名 学年末試験やり直し数学 α 1. 右の図を見て次の (1)~(4) に答えなさい (1) 点 A,B の座標をいいなさい 5 y B () 線分 AB の中点の座標 M を求めなさい A -5 O 5 x (3) 点 A と原点について対称な点 C の座標を求めなさい -5 (4) 点 C が (3) のとき, 四角形 ABCD が平行四辺形となる点 D の座標を求めなさい
新中 春休みの宿題数学 年組番氏名 学年末試験やり直し数学 α 1. 右の図を見て次の (1)~(4) に答えなさい (1) 点 A,B の座標をいいなさい 5 y B () 線分 AB の中点の座標 M を求めなさい A -5 O 5 x (3) 点 A と原点について対称な点 C の座標を求めなさい -5 (4) 点 C が (3) のとき, 四角形 ABCD が平行四辺形となる点 D の座標を求めなさい
FdData中間期末数学3年
 中学中間 期末試験問題集( 過去問 ): 数学 3 年 http://www.fdtext.com/dat/ 相似比と面積比 [ 相似比と面積比 1] [ 問題 ](3 学期 ) 右の図の 2 つの円 A,B について, 次の各問いに答えよ (1) A,B の円の相似比を求めよ (2) A,B の円の面積をそれぞれ求めよ (3) 面積の比を求めよ (1) (2)A B (3) [ 解答 ](1) 7:10
中学中間 期末試験問題集( 過去問 ): 数学 3 年 http://www.fdtext.com/dat/ 相似比と面積比 [ 相似比と面積比 1] [ 問題 ](3 学期 ) 右の図の 2 つの円 A,B について, 次の各問いに答えよ (1) A,B の円の相似比を求めよ (2) A,B の円の面積をそれぞれ求めよ (3) 面積の比を求めよ (1) (2)A B (3) [ 解答 ](1) 7:10
. 角の二等分線と調和平均 平面上に点 を端点とする線分 と を重ならないようにとる, とし とする の二等分線が線分 と交わる点を とし 点 から に垂直に引いた直線が線分 と交わる点 とする 線分 の長さを求めてみよう 点 から に垂直な直線と および との交点をそれぞれ, Dとする つの直角三
 角の二等分線で開くいろいろな平均 札幌旭丘高校中村文則 0. 数直線上に現れるいろいろな平均下図は 数 (, ) の調和平均 相乗平均 相加平均 二乗平均を数直線上に置いたものである, とし 直径 中心 である円を用いていろいろな平均の大小関係を表現するもっとも美しい配置方法であり その証明も容易である Q D E F < 相加平均 > (0), ( ), ( とすると 線分 ) の中点 の座標はである
角の二等分線で開くいろいろな平均 札幌旭丘高校中村文則 0. 数直線上に現れるいろいろな平均下図は 数 (, ) の調和平均 相乗平均 相加平均 二乗平均を数直線上に置いたものである, とし 直径 中心 である円を用いていろいろな平均の大小関係を表現するもっとも美しい配置方法であり その証明も容易である Q D E F < 相加平均 > (0), ( ), ( とすると 線分 ) の中点 の座標はである
2017年度 神戸大・理系数学
 7 神戸大学 ( 理系 前期日程問題 解答解説のページへ を自然数とする f ( si + とおく < < 4 であることを用い て, 以下の問いに答えよ ( < < のとき, f ( < であることを示せ ( 方程式 f ( は < < の範囲に解をただ つもつことを示せ ( ( における解を とする lim であることを示し, lim を求めよ 7 神戸大学 ( 理系 前期日程問題 解答解説のページへ
7 神戸大学 ( 理系 前期日程問題 解答解説のページへ を自然数とする f ( si + とおく < < 4 であることを用い て, 以下の問いに答えよ ( < < のとき, f ( < であることを示せ ( 方程式 f ( は < < の範囲に解をただ つもつことを示せ ( ( における解を とする lim であることを示し, lim を求めよ 7 神戸大学 ( 理系 前期日程問題 解答解説のページへ
紙を折る < 問題 > 長方形の紙を折る このとき 相似形はいくつできるだろうか? 2 個 固定固定固定 固定 2 個 2 個 固定 固定 3 個 3 個 固定 3 個 4 個 4 個
 紙を折る < 問題 > 長方形の紙を折る このとき 相似形はいくつできるだろうか? 個 固定固定固定 固定 個 個 固定 固定 個 個 固定 個 4 個 4 個 * 隣り合う辺を結んで折るとき 最大 個 * 向かい合う辺を結んで折るとき 最大 4 個 < 問題 > 固定される場合 その位置はどこか? そのときの相似比はいくらか? 返上を移動する場合 その範囲はどうか? 合同になるときはあるか? それはどんなときか?
紙を折る < 問題 > 長方形の紙を折る このとき 相似形はいくつできるだろうか? 個 固定固定固定 固定 個 個 固定 固定 個 個 固定 個 4 個 4 個 * 隣り合う辺を結んで折るとき 最大 個 * 向かい合う辺を結んで折るとき 最大 4 個 < 問題 > 固定される場合 その位置はどこか? そのときの相似比はいくらか? 返上を移動する場合 その範囲はどうか? 合同になるときはあるか? それはどんなときか?
2014年度 筑波大・理系数学
 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ f ( x) = x x とする y = f ( x ) のグラフに点 P(, ) から引いた接線は 本あるとする つの接点 A (, f ( )), B(, f ( )), C(, f ( )) を頂点とする三角形の 重心を G とする () + +, + + および を, を用いて表せ () 点 G の座標を, を用いて表せ () 点 G
筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ f ( x) = x x とする y = f ( x ) のグラフに点 P(, ) から引いた接線は 本あるとする つの接点 A (, f ( )), B(, f ( )), C(, f ( )) を頂点とする三角形の 重心を G とする () + +, + + および を, を用いて表せ () 点 G の座標を, を用いて表せ () 点 G
Σ(72回生用数ⅠA教材NO.16~30).spr
 日々の演習 Σ( シグマ ) No. 16 16 ( ) 組 ( ) 番名前 ( ) 1 [ 改訂版 4STEP 数学 Ⅰ 問題 119] 関数 f0x 1 =3x-,g0x 1 =x -3x+1 について, 次の値を求 めよ f001 6 [ 改訂版 4STEP 数学 Ⅰ 例題 16] a は定数とする 関数 y=x -4ax 00(x(1 について, 次の問いに答えよ 最小値 m を求めよ (7)
日々の演習 Σ( シグマ ) No. 16 16 ( ) 組 ( ) 番名前 ( ) 1 [ 改訂版 4STEP 数学 Ⅰ 問題 119] 関数 f0x 1 =3x-,g0x 1 =x -3x+1 について, 次の値を求 めよ f001 6 [ 改訂版 4STEP 数学 Ⅰ 例題 16] a は定数とする 関数 y=x -4ax 00(x(1 について, 次の問いに答えよ 最小値 m を求めよ (7)
2 図形の定義や性質を見いだすための算数的活動を取り入れる 2 枚の長方形, 長方形と三角形,2 枚の三角形を重ねて四角形を作る活動を取り入れ, 向かい合う辺の平行関係に着目させたり, 長さに着目させたりしながら, 四角形を定義できるようにする コンパスや分度器, ものさし等を使って, 四角形の構成
 単元について 指導者 T1 呉市立横路小学校木村智子 T2 呉市立横路小学校末長裕 本単元は, 小学校学習指導要領第 4 学年の目標 (3) 図形を構成要素及びそれらの位置関係に着目して考察し, 平行 四辺形やひし形などの平面図形及び直方体などの立体図形について理解できるようにする, 内容 C(1) ア 直線の平 行や垂直の関係について理解すること イ 平行四辺形, ひし形, 台形について知ること
単元について 指導者 T1 呉市立横路小学校木村智子 T2 呉市立横路小学校末長裕 本単元は, 小学校学習指導要領第 4 学年の目標 (3) 図形を構成要素及びそれらの位置関係に着目して考察し, 平行 四辺形やひし形などの平面図形及び直方体などの立体図形について理解できるようにする, 内容 C(1) ア 直線の平 行や垂直の関係について理解すること イ 平行四辺形, ひし形, 台形について知ること
数学 A 図形の性質発展問題 ( 1) ( 平行線と線分比 ) 3 角形の角の 2 等分線の定理 問 1 ABC の内角 Aの 2 等分線が辺 BCと交わる点を Dとする 内角 Aの外角の 2 等分線が辺 BCの延長線と交わる点を Eとする AB:AC=BD:CD AB:AC=BE:EC が成り立つ
 数学 A 図形の性質発展問題 (1) ( 平行線と線分比 ) 3 角形の角の 2 等分線の定理 問 1 ABC の内角 Aの 2 等分線が辺 BCと交わる点を Dとする 内角 Aの外角の 2 等分線が辺 BCの延長線と交わる点を Eとする AB:AC=BD:CD AB:AC=BE:EC が成り立つことを証明せよ ( 証明 ) 点 Cから辺 ABに平行線を引いて ABの延長線と交わる点を Fとする 点
数学 A 図形の性質発展問題 (1) ( 平行線と線分比 ) 3 角形の角の 2 等分線の定理 問 1 ABC の内角 Aの 2 等分線が辺 BCと交わる点を Dとする 内角 Aの外角の 2 等分線が辺 BCの延長線と交わる点を Eとする AB:AC=BD:CD AB:AC=BE:EC が成り立つことを証明せよ ( 証明 ) 点 Cから辺 ABに平行線を引いて ABの延長線と交わる点を Fとする 点
色塗り⑴
 ステップ 1 塗り分けない ( 隣が同じ色でもいい ) 1 図のような A B C の 3 つの場所を 赤 青 黄の 3 色で塗ります 同じ色を何度使ってもよく 隣り合っている場所を同じ色で塗ってもか まいません このとき 塗り方は全部で何通りあるか 次のように考え ました ( ) にあてはまる数を求めなさい ⑴ A に塗れる色は赤か青か黄の ( ア ⑵ B に塗れる色は赤か青か黄の ( イ ⑶ C
ステップ 1 塗り分けない ( 隣が同じ色でもいい ) 1 図のような A B C の 3 つの場所を 赤 青 黄の 3 色で塗ります 同じ色を何度使ってもよく 隣り合っている場所を同じ色で塗ってもか まいません このとき 塗り方は全部で何通りあるか 次のように考え ました ( ) にあてはまる数を求めなさい ⑴ A に塗れる色は赤か青か黄の ( ア ⑵ B に塗れる色は赤か青か黄の ( イ ⑶ C






