(C) Kazutaka Takahashi 2018
|
|
|
- がんま かんざとばる
- 5 years ago
- Views:
Transcription
1
2 (C) Kazutaka Takahashi 2018
3 i
4 I 11 2 Coulomb Coulomb [ ] Gauss Gauss Gauss Gauss Gauss Gauss [ ] ii
5 Stokes * Poisson * [ ] Poisson ** [ ] ** Cavendish ** II Ohm Ohm Ohm Ampère Ampère iii
6 Biot Savart Lorentz Lorentz Gauss Ampère * * ** Coulomb III Maxwell Maxwell iv
7 12.4 ** ** A (1) 155 B (2) 156 C (3) 157 D (4) 158 v
8
9 Einstein Newton Newton
10 GPS Galilei Newton 6 R. P. Feynman Feynman Global Positioning System Feynman 1965 Nobel J. S. Schwinger 8 III
11 J. Kepler G. Galilei R. Descartes I. Newton Kepler T. Brahe Galilei Descartes Newton Aristotélēs M. Faraday J. C. Maxwell N. L. S. Carnot W. Thomson R. J. E. Clausius 19 Newton Newton
12 Newton 1687 Kepler A. Einstein Hilbert Kepler 16 Kepler Newton 2 4
13 Newton Newton ma = F (1.1) m a F F 2 Kepler Newton (1.1) Kepler Newton (1.1) 17 Newton (1.1) Newton Coulomb 2 electric charge Coulomb 2 18 Newton
14 19 Maxwell 4 E(r, t) = 1 ϵ 0 ρ(r, t) (1.2) B(r, t) = 0 (1.3) E(r, t) + B(r, t) = 0 t (1.4) B(r, t) ϵ 0 µ 0 t E(r, t) = µ 0j(r, t) (1.5) Maxwell Maxwell
15 5 6 9 Maxwell [1] 2000 [2] I 5 7
16 [3] [ ] [2] [4] I II [5] pdf Feynman Jackson 1992 ( )( ) : [1] * 24 **
17 1 I 2 Coulomb Coulomb 3 Gauss II 7 Ohm 8 Ampère Biot Savart Lorentz 9 10 III 11 Faraday 12 Maxwell [ ] 9
18
19 I
20
21 2 Coulomb Coulomb Coulomb Coulomb 2.1 Coulomb Newton Newton universal gravitation 2 r 1 r 2 2 F 12 = G m 1m 2 r 1 r 2 2 r 1 r 2 r 1 r 2 (2.1) 2 mass (2.1) m 1 m G gravitational constant G ( ) ( ) 2 ( ) 2 ma = F ( ) ( ) ( ) 2 G ( ) 3 ( ) 1 ( ) 2 gravitational mass ma = F inertial mass 1 1kg 1m/s 2 1N G N m 2 /kg 2 Newton 1 Newton 13
22 base unit ( ) ( ) 1 dimension 3 (x, y, z) l l = 1.0 cm = 0.01 m l cm ( ) = ( ) ( ) ( ) = ( ) 2 2 r 1 r 2 2 r 1 r Coulomb 0 (2.1) 1 2 r 1 r 2 r 1 r F 21 = G m 1m 2 r 2 r 1 2 r 2 r 1 r 2 r 1 (2.2)
23 2.1: m 1 F 12 m 2 F 21 = F : m F m 1 F 1 m 2 F 2 action-reaction law F 12 = F 21 (2.3) point mass 4 (2.1) superposition principle 2.2 F (r) = i r r i Gmm i r r i 3 (2.4) m r m i r i
24 2 5 vector r = (x, y, z) (2.5) E E = (E x, E y, E z ) (2.6) E x E x E x E x 1 3 ar 1 + br 2 = a(x 1, y 1, z 1 ) + b(x 2, y 2, z 2 ) = (ax 1 + bx 2, ay 1 + by 2, az 1 + bz 2 ) (2.7) a b 2.2 r 1 r 2 = x 1 x 2 + y 1 y 2 + z 1 z 2 (2.8) 1 scalar r = r 2 = x 2 + y 2 + z 2 (2.9) r 2 = r r 1/r r 3 r 2 r equation of motion m d2 r(t) dt 2 = F (r(t)) (2.10)
25 r 2 r(t) t 0 r(t 0 ) t=t0 dr(t) dt Newton Coulomb W. Gilbert Gilbert electricity 17 Newton Coulomb Newton Coulomb Coulomb force q 1 q 2 r 1 r 2 F 12 = k r 1 r 2 2 r 1 r 2 (2.11) Coulomb Coulomb s law 2 2 (2.1) Gm 1 m 2 G q Coulomb (2.11)
26 7 k 8 k ( ) ( ) 2 ( ) 2 = ( ) ( ) 3 ( ) 2 ( ) 2 ma = F m m m k C.-A. de Coulomb [C] 8 k k N m 2 C 2 (2.12) 1C 1kg Coulomb 1C 1C 1kg C kg Coulomb 12 r i i = 1, 2,... q i r q F (r) = kq i q i r r i r r i 3 (2.13) 7 8 k = 1 ϵ 4πϵ (2.1) (2.11)
27 q q 0 ( r r1 F (r) = kqq r r 1 3 r r ) ( 2 r r r 2 3 kqq r 3 r ) r 3 = 0 (2.14) 13 q r 1 q r 2 r Q r r 1 r r q q 1 x 1km y x y x y (2.11) point charge 1 1 Coulomb 1 r 3 V (r) q(r) q(r) = ρ(r) V (r) P.-S. Laplace I Coulomb 19
28 r charge density ρ(r) = lim V (r) 0 q(r) V (r) (2.15) Dirac 17 r q ρ(r) F (r) = kq lim { V (r i)} 0 = kq i ρ(r i ) V (r i ) r r i r r i 3 (2.16a) d 3 r ρ(r ) r r r r 3 (2.16b) r i ρ(r i ) V (r i ) 0 2 volume integral 18 (2.16) 2 r r r q F (r) r q r r F (r) = kq dv (r ) ρ(r ) r r r r 3 = kq dv ρ(r ) r r r r 3 (2.17) d 3 r dv (r ) dv dv r r r d 3 r f(r) = dv f(r) = dx dy dz f(r) (2.18) (2.13) (2.16)
29 Coulomb 2 2 q Coulomb F = qe (2.19) E electric field 19 r E(r) = k d 3 r ρ(r ) r r r r 3 (2.20) field E(r) r E r E : r + = (a, 0, 0) r = ( a, 0, 0) q r = (x, y, z) E(r) = ( r r+ kq r r r r ) r r 3 = x a kq [(x a) 2 + y 2 + z 2 ] 3/2 y z + kq [(x + a) 2 + y 2 + z 2 ] 3/2 x + a y z (2.21a) (2.21b)
30 2.3: z = 0 x y xy z = x = 0 z = 0 y = 0 z = 0 E(x, 0, 0) = E(0, y, 0) = kq x a 3 kq (a 2 + y 2 ) 3/2 x a y 0 kq x + a 3 (2.22) x + a 0 0 (2.23) r + = (a, 0, 0) q r = ( a, 0, 0) q r = (x, y, z) r E(r) = ( r r+ kq r r + 3 r r ) r r 3 = x a kq [(x a) 2 + y 2 + z 2 ] 3/2 y z kq [(x + a) 2 + y 2 + z 2 ] 3/2 x + a y z (2.24a) (2.24b) x = 0 z = 0 kq E(0, y, 0) = (a 2 + y 2 ) 3/2 2a 0 0 (2.25) 21 Gauss 22
31 2.4: x y = 0 z = 0 y x = 0 z = 0 y = 0 z = 0 E(x, 0, 0) = kq x a 3 x a 0 0 kq x + a 3 x + a 0 0 (2.26) xy 2.3 q q x > a x y : 2.5 x x = na n q x y r r = (0, r, 0) na kq E(0, r, 0) = (r 2 + n 2 a 2 ) 3/2 r = n= 0 n= kqr (r 2 + n 2 a 2 ) 3/ (2.27) λ = q/a a 0 q 0 λ linear density (2.15) [2 3] 23 23
32 2.5: 2 2 x x lim af(na) = dx f(x) (2.28) a 0 n= f(x) f a (2.16) V (r i ) 24 r = (0, r, 0) [2 3] E(0, r, 0) = kλ dx r (x 2 + r 2 ) 3/ = 2kλ r (2.29) 2 1 Coulomb 2 3: a 2.6 z = 0 xy 2.7 z z z r = (0, 0, z) z Q λ = Q 2πa 2πa xy x θ 25 adθ 2.8 E z (0, 0, z) = k 2π λadθ 0 2π 1 z a 2 + z 2 (2.30a) (a 2 + z 2 ) 1/2 z (a 2 + z 2 ) 3/2 (2.30b) = k Q dθ 2π 0 z = kq (2.30c) (z 2 + a 2 ) 3/2 2π z a a E z (0, 0, z) kq z 2 (2.31)
33 2.6: 2 3 a 2.7: (a) (b) (c) Q 2 4: 2 xy xy z z z r = (x, y, z) E(r) = 0 0 zf( z ) (2.32) 25
34 2.8: a θ θ + dθ adθ dθ 26 f σ xy 2.9 a a+da da 2 3 Q = 2πσada z de z (r) = 2πkσada (2.33) (z 2 + a 2 ) 3/2 a [ za z E z (r) = 2πkσ da = 2πkσ (z 2 + a 2 ) 3/2 (z 2 + a 2 ) 1/2 0 ] 0 = 2πkσ z z (2.34) z z/ z 2 5: a σ = Q Q 4πa 2 (2.35) 26 z = z 2 f z 2 26
35 2.9: : 2 5 r = (0, 0, r) xy 2.10 z θ dq = Q 4πa 2 2πa sin θadθ = Q sin θdθ (2.36) 2 a sin θ adθ r = (0, 0, r) r a cos θ r = (0, 0, r) z E z (0, 0, r) = kq 2 π 0 r a cos θ dθ sin θ [(r a cos θ) 2 + a 2 sin 2 (2.37) θ] 3/2 [2 6] E z (0, 0, r) = { kq r 2 r a 0 r < a (2.38) r = (0, 0, r) z r = (x, y, z) E(r) = { kq r r 2 r r a 0 r < a (2.39) Q r a
36 symmetry 2 4 z z + z 0 z z z 2.4 [ ] Cartesian coordinate r = x y z (2.40) 3 29 x y z 2.11 polar coordinate x = r sin θ cos φ (2.41) y = r sin θ sin φ (2.42) z = r cos θ (2.43) r = x 2 + y 2 + z 2 (2.44) 28 René Descartes Renatus Cartesius Cartesian 29 28
37 2.11: 3 r (x, y, z) (r, θ, φ) x2 + y tan θ = 2 z tan φ = y x (2.45) (2.46) r θ z φ xy x x y z 30 0 r < (2.47) 0 θ π (2.48) 0 φ < 2π (2.49) 1 e x = 0 0 r = xe x + ye y + ze z (2.50), e y = , e z = (2.51) e x e x = e y e y = e z e z = 1 (2.52) e x e y = e y e x = e y e z = e z e y = e z e x = e x e z = 0 (2.53) e µ e ν = δ µν (µ, ν = x, y, z) (2.54) 30 θ 2π π θ φ φ π
38 µ ν x y z Kronecker Kronecker delta 1 0 δ µν = { 1 µ = ν 0 µ ν (2.55) 1 x y z 3 1 e x e y e z e r e θ e φ e r e r (r) = r e r sin θ cos φ sin θ sin φ cos θ (2.56) r = re r (2.57) [2 11] cos θ cos φ sin φ e θ (r) = cos θ sin φ, e φ(r) = cos φ (2.58) sin θ 0 r = (x, y, z) r = (r, θ, φ) (2.50) (2.57) r = re r + θe θ + φe φ 32 r = (r, θ, φ) f(r) = f(x, y, z) π 2π dv f(r) = dx dy dz f(r) = dr dθ dφ J(r, θ, φ)f(r) (2.59) J(r, θ, φ) = (x, y, z) (r, θ, φ) = r2 sin θ (2.60) 33 f(r) r r dω f(θ, φ) = π 0 dθ 2π 0 dφ sin θ f(θ, φ) (2.61) f θ φ dω 2 Ω
39 2.5 Coulomb Coulomb ρ(r)d 3 r r ρ(r) (2.20) 2 (2.20) (2.32) Coulomb Coulomb k k 31
40 E q F = qe E(r) (2.20) Newton Newton 35 electrostatic field Coulomb 35 32
41 Coulomb [2 1] ( a, 0, 0) q 1 (0, 0, 0) q 2 (2a, 0, 0) q 3 a > 0 (a). (b). 0 (c). (b) [2 2] 2.3 xy f(x, y) dy = f(x, y) (2 2.1) dx [2 3] 2 2 (2.29) 2 2 r = (0, r, 0) [2 4]
42 2.12: [2 8] [2 5] xy a Q z [2 6] (2.37) [2 7] a Q [2 8] 2.12 (a) (b) z = 0 [2 9] (2.8) r 1 r 2 = r 1 r 2 cos θ (2 9.1) θ [2 10] (r, θ, φ) e r e θ e φ (2.58) 34
43 [2 11] cylindrical coordinate (x, y, z) z x y 2 x = ρ cos φ (2 11.1) y = ρ sin φ (2 11.2) (ρ, φ, z) 3 35
44 3 Gauss Gauss Gauss Gauss E(r) r line of electric force [2 2] 33 1 q R E = kq/r 2 2 4πR 2 E = 4πkq (3.1) 4πR 2 R Gauss (3.1) (3.1) (3.1) 1 2 q E E 36
45 3.1: 0 3.2: ds = dsn ds n xy z n 2 E ds = E nds E ds 0 7 S Φ = ds E(r) (3.2) S
46 surface integral ds ds(r) 9 Φ = ds E(r) (3.3) S 10 q S R (3.1) Φ flux of electric force ( ) flux Gauss Gauss Gauss Gauss s law ( S ) = 4πk ( S ) (3.4) S= V ds E(r) = 4πk dv ρ(r) (3.5) V Gauss 12 S V S ds S V S = V 13 V Gauss solid angle 10cm 1cm 2 100m 1cm 2 8 ds Φ ϕ φ π 3 r3 r 4πr 2 38
47 3.3: 1 θ θ r rθ 3.4: r 2 Ω r radian 2 1 1m 1cm 3.3 θ θ r θ rθ θ 0 2π 2π 2πr r θ Ω Ω steradian 14 r Ω r 2 Ω Ω 0 4π 4πr Gauss q V Gauss (3.5) V (3.5) Φ Gauss 14 sr 39
48 3.5 Φ ds ds ds ds ds E(r) = kq ds r 2 (3.6) ds E(r ) = kq ds r 2 (3.7) 0 15 ( ) ds dφ = kq r 2 ds r 2 0 dω = ds r 2 (3.8) = ds r 2 (3.9) Gauss ds r 2 Coulomb 1/r 2 2 Coulomb 3.3 Gauss Gauss Coulomb Gauss 3 1: Gauss a Q 2 5 r E(r) r Gauss 15 Gauss 40
49 3.5: ds r ds r r r ds ds ds 3.6: 3 2 Gauss (3.5) S ds E(r) = 4πr 2 E(r) (3.10) 4πr 2 r a Q 0 { 4πkQ r a 4πk dv ρ(r) = V 0 r < a (3.11) E(r) = { kq r 2 r a 0 r < a (3.12) :
50 2 a πa 2 E(z) πa 2 E( z) = 4πk πa 2 σ (3.13) z E(z) E(z) 2 3 E(z) = 2πkσ z z z ± (3.14) πa 2 E(z + ) πa 2 E(z ) = 0 (3.15) E(z + ) = E(z ) Gauss Coulomb Gauss [1] 3 1 E(r) = E( r ) r r 3 2 (2.32) 25 [2] V S = V [3] Gauss (3.5) [4] [5] V [1] [2] Gauss Gauss [1] 42
51 3.7: r = (x, y, z) dxdydz 3.4 Gauss Gauss (3.5) 1 Gauss 3.7 r 1 dx dy dz (x, y, z) (x + dx, y, z)... (x + dx, y + dy, z + dz) a ā 16 dydz ( ds E(r) dydz E x x + dx, y + dy 2, z + dz ) ( dydz E x x, y + dy 2 2, z + dz ) (3.16a) 2 a,ā dxdydz E x(x, y, z) x (3.16b) 2 E (x, y, z) 1 ( Ex (x, y, z) ds E(r) dxdydz + E y(x, y, z) + E ) z(x, y, z) x y z (3.17) 4πk dv ρ(r) 4πkdxdydz ρ(r) (3.18) 16 43
52 E(r) = 4πkρ(r) (3.19) E(r) divergence E(r) = E x x + E y y + E z z nabla ( = x, y, ) z (3.20) (3.21) (3.19) Gauss r = x 2 + y 2 + z 2 a r > a E(r) = kqr/r 3 ( x E(r) = kq x r 3 + y y r 3 + ) z z r 3 (3.22a) [ ( 3 = kq r 3 + x r x + y r y + z r ) ] 1 z r r 3 (3.22b) [ ( ) ] 3 x 2 = kq r 3 + r + y2 r + z2 3 r r 4 (3.22c) = 0 (3.22d) r < a 0 17 [2 7] 34 [3 5]
53 grad div rot = ( x, y, ) z (3.23) = r = r r ϕ(r) gradient ( ϕ(r) grad ϕ(r) = ϕ(r) = x, ϕ(r) y, ϕ(r) ) z (3.24) (3.25) ϕ(r) E(r) div E(r) = E(r) = E x(r) x + E y(r) y + E z(r) z E(r) rotation ( Ez (r) rot E(r) = E(r) = E y(r), E x(r) E z(r) y z z x, E y(r) E ) x(r) x y (3.26) (3.27) ϕ(r) (x, y, z) (r, θ, φ) 2.4 e r e θ e φ ϕ(r) = ϕ r e r + 1 ϕ r θ e θ + 1 E(r) = 1 r 2 r (r2 E r ) + 1 r sin θ r sin θ ( 1 E(r) = e r r sin θ θ (E φ sin θ) 1 +e φ ( 1 r r (re θ) 1 r ϕ φ e φ (3.28) θ (E θ sin θ) + 1 θ E r r sin θ ) φ E θ r sin θ φ E φ (3.29) ) ( 1 + e θ r sin θ φ E r 1 ) r r (re φ) (3.30) E(r) = E r e r + E θ e θ + E φ e φ 45
54 3.5 Gauss Gauss Gauss Gauss s theorem 18 Gauss S= V ds E(r) = V dv E(r) (3.31) E(r) S S V Gauss divergence theorem Gauss Gauss (3.5) dv E(r) = 4πk V V dv ρ(r) (3.32) V Gauss (3.19) Gauss 0 [3 7] 3.6 [ ] 3 A = A 1 A 2 A 3 = A 1e x + A 2 e y + A 3 e z (3.33) A B inner product scalar product A B = A 1 B 1 + A 2 B 2 + A 3 B 3 (3.34) 19 A B = A B cos θ AB (3.35) [2 9] A A A = A A2 2 + A2 3 θ AB A B A B 0 18 J. C. F. Gauss 1813 M. B. Ostrogradsky dot product 46
55 outer product vector product A 2 B 3 A 3 B 2 A B = A 3 B 1 A 1 B 3 (3.36) A 1 B 2 A 2 B 1 20 A B = A B sin θ AB (3.37) A B A x B y A B z 21 0 A B A B = B A (3.38) A = B A A = 0 (3.39) 0 22 (2.51) 29 e x e y = e z (3.40) e y e z = e x (3.41) e z e x = e y (3.42) x y z x A (B C) = B (C A) = C (A B) (3.43) A (B C) = B(A C) C(A B) (3.44) ( A) = ( A) 2 A (3.45) A B A B C A (B C) (A B) C A (B C) (A B) C 20 cross product
56 3.8: Gauss Φ = ds E(r) S= V q = dv ρ(r) 0 V 3.7 Gauss Gauss Gauss 3.8 Gauss III Gauss
57 II Gauss Gauss Coulomb Coulomb Coulomb Coulomb Gauss Gauss Gauss (3.31) f(x + ) f(x ) = x+ x dx df(x) dx (3.46) Gauss (3.31) 24 Gauss Gauss 2526 Gauss 0 Coulomb 2 2 Coulomb 2 Gauss 24 win win Gauss 5 49
58 3.9: [3 1] r dω Gauss 3.8 [3 1] a Q r E(r) = kq 4πa 2 ds(r 1 r r ) S r r 2 r r (3 1.1) ds r 3.9 r A B dω A B [3 2] Gauss Gauss [3 3] a Gauss σ 50
59 3.10: [3 2] q [3 4] 2 z = a σ z = a σ [3 5] [2 7] 34 Gauss [3 6] a Q ρ(r) E(r) [3 7] Gauss Gauss (3.31) 3.7 [3 8] (a). (A B) = B ( A) A ( B) (3 8.1) (b). (a) (A B) (3 8.2) 51
60 4 Gauss (3.5) 38 (3.19) 44 Coulomb 4.1 work F s W = F s ( ) ( ) = ( ) ( ) 2 ( ) 2 energy 1 2 Coulomb E(r) q C W = dr F (r) = q dr E(r) (4.1) C F (r) = qe(r) 3 line integral C N N C dr E(r) = lim N i=1 C N r i E(r i ) (4.2) q q q q ϕ = dr E(r) (4.3) C
61 [4 1] [4 1] Q 4.1 N r i r i θ i r i l i ϕ = lim = lim N N i=1 N N i=1 rb = dr kq r A r 2 = kq r B kq r A l i kq r 2 i r i kq r 2 i cos θ i (4.4a) (4.4b) (4.4c) (4.4d) l i r i r i = l i cos θ i r A r B r ϕ(r) r A r B ϕ = dr E(r) = ϕ(r B ) ϕ(r A ) (4.5) A B ϕ(r) electric potential electrostatic potential 0 C dr E(r) = 0 (4.6) C 0 0 ϕ(r) 53
62 4.1: Q q A B C C dr E(r) (4.7) C r = r(s) s 0 1 r r(0) r(1) s 1 dr E(r) = ds dr(s) E(r(s)) (4.8) ds dr(s) ds C 0 s (4.7) r = r(s, t) S ds E(r) = 1 0 ds 1 0 dt r(s, t) s r(s, t) t E(r(s, t)) (4.9) 4.2 q E(r) E = kq r r 3 = kq r (4.10) 54
63 1 r = 1 r r = r r 1 r r = r r 1 r 2 = r r 3 (4.11) r r = x 2 + y 2 + z 2 4 E(r) = ϕ(r) (4.12) ϕ(r) = kq r + const. (4.13) 2 r ρ(r) ϕ(r) = k d 3 r ρ(r ) r r + const. (4.14) (4.12) C dr E(r) = dr ϕ(r) (4.15) C 0 s 1 s r(s) dr E(r) = C = ds dr(s) ds ds d ds ϕ(r(s)) ϕ(r(s)) (4.16a) (4.16b) = ϕ(r(1)) ϕ(r(0)) (4.16c) (4.5) r(0) = r(1) (4.6) conservation force q
64 4 1: r + r q (4.14) ( ) 1 ϕ(r) = kq r r (4.17) r r 0 0 r + q r q ( ) 1 ϕ(r) = kq r r + 1 r r (4.18) [4 3] 4 2: a Q E(r) = { kq r r r a 3 0 r < a (4.19) r = r r a ϕ(r) = kq r + C 0 (4.20) C 0 0 C 0 = 0 r < a 0 ϕ(r) = C 1 (4.21) C 1 r = a δ r = a δ r = a + δ ϕ(r) = { kq r r a kq a r < a (4.22) 4 3: xy σ z E z (z) = 2πkσ z z (4.23) ϕ(r) = 2πkσ z + const. (4.24) 0 z = 0 z = const. 56
65 r r (4.5) E(r) r = ϕ(r + r) ϕ(r) = 0 (4.25) r [4 2] (4.6)
66 Coulomb Coulomb Laplace Poisson Poisson Laplace Poisson Coulomb [4 1] Q q 4.2 (a). (r, 0, 0) (r, 0, 0) (b). (r, 0, 0) ( r, 0, 0) (c). (r, 0, 0) ( r, 0, 0) [4 2] (4.6) (4.6) 9 III II 58
67 4.2: [4 1] Q xy (r, 0) q (a). x (b). (c). x y (b) [4 3] 4 1 r + = (a, 0, 0) r = ( a, 0, 0) xy ϕ dy = g(x, y) (4 3.1) dx g [2 2] 33 [4 4] a σ z E(r) ϕ(r) [4 5] 2 (a). x = a y = 0 λ x = a y = 0 λ 0 (b). ϕ xy 59
68 dr E(r) = 0 (5.1) C C 0 C dr dr E(r) 1 1 (5.1) Gauss (3.19) Stokes Stokes theorem 1 C= S dr E(r) = S ds E(r) (5.2) Stokes = r E(r) Stokes E(r) Gauss Stokes W. Thomson Kelvin 1850 G. G. Stokes Stokes H. Hankel 60
69 Stokes S S E(r) = 0 (5.3) E(r) = 0 (5.4) 2 E(r) = ϕ(r) (5.5) ϕ(r) (5.4) (5.4) (5.5) ϕ(r) ϕ(r) = 0 (5.6) ϕ 5.2 S= V ds E(r) = 4πk dv ρ(r) E(r) = 4πkρ(r) (5.7) V dr E(r) = 0 E(r) = 0 (5.8) C V C Gauss Coulomb 3 Gauss Gauss 3 1 Gauss (2.20) 21 Gauss
70 (2.20) Gauss Gauss y E(r) E(r) + C x (5.9) 0 C 2 0 Gauss 2 (5.9) 2 xy C > 0 1 y dr x = 2πr2 (5.10) 0 [5 1] r y x 0 = (5.11) C = 0 Gauss 5.3 Stokes * Stokes dr E(r) = ds E(r) (5.12) C= S S S C C S E(r) r 3 S C 1 1 C S Stokes Gauss V S = V
71 5.1: 5.2: Gauss (5.12) dxe x (r) + dye y (r + dxe x ) dxe x (r + dye y ) dye y (r) ( Ey (r) dxdy E ) x(r) (5.13) x y = dxdy ( E(r)) z (5.14) xy Stokes 5.4 Poisson * (5.5) Gauss (5.7) Poisson Poisson equation 2 ϕ(r) = 4πkρ(r) (5.15) 2 = = 2 x y z Laplacian 2 2 (5.5) Gauss Poisson Poisson 0 2 ϕ(r) = 0 (5.16) Laplace Laplace equation S. D. Poisson Poisson 2 Poisson 5.5 Poisson (4.13) 55 Poisson
72 5.5 [ ] Poisson ** ϕ 1 ϕ 2 Poisson 2 ϕ 1 (r) = 4πkρ(r) (5.17) 2 ϕ 2 (r) = 4πkρ(r) (5.18) 2 (ϕ 1 ϕ 2 ) = 0 (5.19) ϕ 1 ϕ 2 Laplace 0 ϕ 1 = ϕ 2 Poisson Gauss (3.31) 46 E = ϕ ϕ 4 ds ϕ(r) ϕ(r) = dv ( ϕ(r)) 2 + dv ϕ(r) 2 ϕ(r) (5.20) S= V V V Green Green s theorem 5 ϕ = ϕ 1 ϕ dv ( ϕ(r)) 2 = ds ϕ(r) ϕ(r) (5.21) V S= V 0 0 ϕ(r) = 0 (5.22) 0 ϕ(r) 0 ϕ 1 (r) = ϕ 2 (r) ϕ 1 (r) = ϕ 2 (r) [ ] ** q r = r 0 ρ(r) = q 4π 2 1 r r 0 (5.23) (4.13) 55 Poisson (5.15) 4 E ϕ Green 5 ϕ ψ E = ϕ ψ ϕ = ψ ψ 64
73 ( r r 0 = x y z 2 ) 1 (x x0 ) 2 + (y y 0 ) 2 + (z z 0 ) 2 (5.24) 0 0 r = r 0 regularization 2 1 r r 0 ( ) 2 = lim ϵ 0 x y z 2 (5.25) (x x0 ) 2 + (y y 0 ) 2 + (z z 0 ) 2 + ϵ 2 ϵ r = r r r 0 3ϵ 2 = lim ϵ 0 [(x x 0 ) 2 + (y y 0 ) 2 + (z z 0 ) 2 + ϵ 2 ] 5/2 (5.26a) = { 0 r r0 (5.26b) 3 lim ϵ 0 ϵ r = r d 3 r 2 1 = lim r r 0 ϵ 0 = lim ϵ 0 0 4π ϵ 0 = lim d 3 3ϵ 2 r [(r r 0 ) 2 + ϵ 2 ] 5/2 (5.27a) dr 4πr 2 3ϵ 2 (r 2 + ϵ 2 ) 5/2 (5.27b) (5.27c) = 4π (5.27d) 6 1 ρ(r) = q 4π 2 1 r r 0 (5.28) r r 0 0 r = r 0 q Dirac δ 3 (r r 0 ) = 1 4π 2 1 r r 0 (5.29) 0 0 r ρ(r) = qδ 3 (r r 0 ) 6 r = ϵ tan θ 7 Kronecker 8 P. A. M. Dirac 65
74 5.7 Gauss Gauss Stokes 9 Poisson Gauss Poisson 10 Coulomb Poisson 2 I Coulomb II 5.8 [5 1] (5.10) 9 Stokes Stokes
75 5.3: [5 4] C x 0 > a [5 2] 0 0 (5.9) [5 3] C dr E(r) = 0 (5 3.1) C E(r) = 0 (5 3.2) Gauss 43 [5 4] q C 5.3 dr E(r) 0 C 67
76 6 6.1 conductor II Coulomb
77 electrostatic induction 6 1: 6.1 E 0 E σ σ 0 0 = E 0 2πkσ 2πkσ (6.1) σ = E 0 4πk (6.2) E 0 + 2πkσ 2πkσ = E 0 (6.3) electric discharge 69
78 6.1: E 0 6.2: 6.3: 6.4: Gauss E (r) = 4πkσ(r) (6.4) E (r) r Coulomb Gauss S 5 Coulomb 70
79 6 2: 0 q S 1 S 2 S 3 Gauss S 1 ds E(r) = 4πkq (6.5) S 2 ds E(r) = 0 (6.6) S 3 ds E(r) = 4πkq (6.7) S 1 S 3 S q 0 q q electric shielding x < 0 0 earth 0 a r = (a, 0, 0) q x = 0 0 q Gauss q r + = (a, 0, 0) r = ( a, 0, 0) r + q r q x = 0 Laplace 71
80 6.5: x 0 ( ) 1 ϕ(r) = kq (x a)2 + y 2 + z 1 2 (x + a)2 + y 2 + z 2 (6.8) x < 0 ϕ(r) = 0 q ( a, 0, 0) 6.5 method of images σ(y, z) = 1 4πk ϕ(r) x = qa x=0 2π 1 (a 2 + y 2 + z 2 ) 3/2 (6.9) σ σ 72
81 6.6: 6.7: z = ±d/2 z ( z d/2 E z (r) = 2πkσ z d/2 z + d/2 ) = z + d/2 0 z > d 2 4πkσ d 2 < z < d 2 0 z < d 2 (6.10) condenser, capacitor 6 z < d 2 ϕ(r) = 4πkσz + const. (6.11) ϕ ± ϕ + ϕ = 4πkσd (6.12) b a a > b Q Q Gauss r E r = kq r 2 (6.13) ϕ = kq r + const. (6.14) 6 capacitor 1745 E. G. von Kleist 1746 P. van Musschenbroek Leiden jar van Musschenbroek 7 73
82 6.8: p 2 ( 1 ϕ b ϕ a = kq b 1 ) a (6.15) ±Q ±Q Q /Q C = Q ϕ + ϕ (6.16) capacitance 2 C = 1 k ab a b (6.17) a b 2 S σ = Q/S C = 1 S 4πk d (6.18) r + = (0, 0, d/2) q r = (0, 0, d/2) q r x kq E(r) = [ x 2 + y 2 + ( ) z d 2 ] 3/2 y 2 z d 2 kq [ x 2 + y 2 + ( z + d 2 ) 2 ] 3/2 x y z + d 2 (6.19) 74
83 0 asymptotic form r = x 2 + y 2 + z 2 d 8 d/r d Taylor d 0 0 d E(r) kq ( d r 3 e z + 3dz ) r 5 r (6.20) r 3 z r + q r q 9 ( E(r) k p r 3 + 3p r ) r 5 r (6.21) p = q(r + r ) (6.22) ±q electric dipole electric dipole moment p r F 0 10 x f(x) = x + e x (6.23) g(x) = x2 + 1 x + 2 h(x) = 1 + ln x + 1 x (6.24) (6.25) f x g h x 1 f(x) e x (6.26) g(x) x (6.27) h(x) ln x (6.28) x
84 6.9: Cavendish a b a > b (i). (ii). (iii). (ii) 6.5 Cavendish ** Coulomb Coulomb 2 J. Priestley H. Cavendish Maxwell Cavendish 2 2 [6 7] u f Coulomb Coulomb 6.9(i) a b a > b Q σ a = Q 4πa (ii) 0 Coulomb σ a σ b [6 7] ( ) ϕ(r) = 2πσ a f(r + a) f( r a ) ar ( ) + 2πσ b f(r + b) f( r b ) br (6.29) 10 Priestley Coulomb 11 Cavendish Coulomb Ohm Cavendish
85 r ϕ(a) = ϕ(b) ϕ 0 ( ) ϕ 0 = 2πσ a a 2 f(2a) f(0) ϕ 0 = 2πσ a ab + 2πσ b ab ) ( f(a + b) f(a b) ( ) f(a + b) f(a b) ( ) + 2πσ b b 2 f(a + b) f(0) (6.30) (6.31) ϕ 0 σ a σ b ( ) ( ) ( ) pa p ab σ a = ϕ 0 1 2π 1 p ab p b σ b (6.32) p a = f(2a) f(0) f(2b) f(0) f(a + b) f(a b) a 2, p b = b 2, p ab = ab (6.33) (6.32) ( σ a σ b ) = ϕ 0 2π = ϕ 0 2π = ϕ 0 2π ( pa p ab p ab 1 p b ) 1 ( 1 1 ) ( pb p ab p a p b p 2 ab p ab p a ( ) 1 pb p ab p a p b p 2 ab p a p ab ) ( 1 1 ) (6.34a) (6.34b) (6.34c) ϕ 0 f 6.9(iii) 0 (6.29) 0 = 2πσ ap a + 2πσ bp ab (6.35) ϕ(b) = 2πσ ap ab + 2πσ bp b (6.36) σ a σ b σ a = p ab p a σ b (6.37) σ a σ b ( ) p a p2 ab σ b ϕ(b) = 2π ( = 1 p ab p a ( = 1 a b p a ) ϕ 0 f(a + b) f(a b) f(2a) f(0) ) ϕ 0 (6.38a) (6.38b) (6.38c) (iii) (ii) ϕ 0 f 77
86 f Coulomb [6 7] Coulomb u(r) = C R (6.39) (4.13) 55 Coulomb (6.38) ϕ(b) = 0 Coulomb u(r) = C R 1+δ (6.40) δ = 0 Coulomb δ (6.38) [ (a ϕ(b) = 1 a ) 1 δ ( ) ] 1 δ + b a b ϕ 0 b 2a 2a (6.41) δ 0 a b Coulomb Coulomb k 13 Cavendish δ < 1 50 Cavendish Maxwell δ < Gauss [6 3] [6 4]
87 +q q II 15 Wikipedia
88 6.7 [6 1] x = 0 (6.9) [6 2] r r = (a, 0, 0) q a > r (a). 0 r = (a, 0, 0) q a q (b). [6 3] a b (a). E(r) ϕ(r) Q (b). C [6 4] a b [6 5] (a). (6.21) (b). (a) p E 0 (c). (b) r [6 6] (a). (6.21) (b). [6 5](b) 80
89 [6 7] a σ a (a). r r = r ϕ(r) = σ a S a dω(r a ) u( r r a ) (6 7.1) r a u(r) (b). f(r) Ru(R) ϕ(r) = 2πσ ( ) a f(r + a) f( r a ) (6 7.2) ar f(r) = dr Ru(R) (6 7.3) 81
90
91 II
92
93 7 Ohm electric current t r ds J(r, t) ds J(r, t) current density S I(t) I(t) = S ds J(r, t) (7.1) ( ) ( ) 1 ( ) ( ) 2 ( ) 1 Gauss J(r, t) ρ(r, t) V S I(t) = S= V ds J(r, t) (7.2) I(t) Q(t) = dv ρ(r, t) (7.3) V 2 I(t) = d Q(t) (7.4) dt 1 I 2 Gauss Gauss 85
94 7.1: J(r, t) S I(t) d dv ρ(r, t) + ds J(r, t) = 0 (7.5) dt V S= V Gauss (3.31) 46 3 V dv ( ) ρ(r, t) + J(r, t) = 0 (7.6) t Gauss ρ(r, t) + J(r, t) = 0 (7.7) t continuity equation (7.5) (7.7) conservation law E r(t) E(r(t)) = E(r(0)) Q(t) Q(t) III 3 3 (7.7) Gauss Stokes 86
95 7.2: S I = ds J(r) S ρ(r, t) J(r, t) II steady state 1 steady current J(r) = 0 (7.8) J = J(r) (7.8) Gauss ds J(r) = 0 (7.9) S S [7 2] I = ds J(r) (7.10) S S J S I = JS (7.11) (7.10) 87
96 0 7.2 Ohm Ohm Ohm Ohm s law 1826 G. S. Ohm G. R. Kirchhoff 4 voltage V I V = RI (7.12) R electrical resistance Ohm Ohm I V 5 R = ρ l S (7.13) l S ρ electrical resistivity 6 7 (7.11) Ohm V = ρlj (7.14) V V = El (7.15) 8 E Ohm 4 Cavendish
97 Ohm E = ρj (7.16) Ohm E(r) = ρj(r) (7.17) J(r) = σe(r) (7.18) σ = 1/ρ electrical conductivity (7.17) (7.18) Ohm Ohm Ohm 10 0 (7.8) 0 = J(r) = σ E(r) (7.19) Gauss 0 J(r) = 0 (7.20) electromotive force J(r) = σ (E(r) + E emf (r)) (7.21) 2 E emf (r) V emf = dr E emf (r) (7.22) C 12 III 9 Ohm Ohm 12 89
98 7.3 Ohm Ohm + I Ohm Coulomb (!?) 90
99 14 Ohm Ohm ρ v J = ρv (7.23) 15 Ohm m dv dt = qe (7.24) 0 16 m dv dt = q ( E nq σ v ) (7.25) nq 2 /σ Ohm n 0 Ohm 0 17 Ohm [7 1]
100 18 Ohm Ohm Ohm Ohm Coulomb Ohm Ohm Ohm 19 Ohm Ohm Ohm 2 Ohm 20 I Ohm 19 Brown Einstein 20 steady state stationary state steady stationary steady state 21 92
101 7.3: [7 3] N 22 II 7.4 [7 1] ρ(r, t) = ρ 0 (r vt) (7 1.1) v ρ 0 (r) (7.23) [7 2] S (7.10) [7 3] Kirchhoff 7.3 N 0 Kirchhoff Kirchhoff s current law N I i = 0 (7 3.1) i=1 (7.10) I i 22 93
102 [7 4] a b b > a σ Ohm J(r) = σe(r) R [7 5] (7.25) v i (t) = dri(t) dt r i (t) t E 94
103 8 Ampère 8.1 Ampère H. C. Ørsted Ørsted F. Arago A.-M. Ampère Ampère 2 I 1 I 2 r f = 2k m I 1 I 2 r (8.1) 2k m Ampère Ampère force Coulomb 1 Cavendish Coulomb 1785 Poisson 1812 Ohm 1826 Ohm 2 2 Coulomb Coulomb 1750 J. Michell 1760 T. Mayer Coulomb 10 3 J.-B. Biot F. Savart 4 2 (8.2) 95
104 8.1: Ampère d 2 F 12 = k m I 1 I 2 dr 1 dr 2 r 1 r 2 r 1 r 2 3 (8.2) 2 dr 2 1 dr 1 r 1 r 2 (8.1) [8 1] dr 1 dr 2 (8.1) [A] I 1C = 1A s Ampère (8.1) 1m 1m N 1A k m = N A 2 = N s 2 C 2 Coulomb k N m 2 C 2 k m m 2 s 2 2 SI m kg s A MKSA C A A C 5 d 2 F
105 A (B C) = (A C)B (A B)C (8.3) (8.2) ( d 2 F 12 = k m I 1 I 2 [dr 1 dr 2 r ) ] 1 r 2 r 1 r 2 r 1 r 2 3 dr 1 r 1 r 2 3 dr 2 2 r 1 0 C dr 1 (8.4) r 1 r 2 r 1 r 2 3 = 1 dr 1 r1 C r 1 r 2 = 0 (8.5) 0 0 Ampère d 2 F 12 = k m I 1 I 2 dr 1 ( dr 2 r ) 1 r 2 r 1 r 2 3 Ampère H. G. Grassmann 1845 Ampère (8.6) magnetic field (8.6) d 2 F 12 = I 1 dr 1 db (8.7) B static magnetic field 7 db = k m I 2 dr 2 r 1 r 2 r 1 r 2 3 (8.8) r 2 r 1 r 1 8 N A 1 m 1 [T] Tesla electrostatic field magnetostatic field Magnetostatics 8 Ampère 9 B B = µ 0 H = 4πk m H H H 10 97
106 8.3 Biot Savart I r B B(r) = k m I dr r r r r 3 (8.9) C Biot Savart Biot Savart law Biot Savart Ørsted Ampère 11 J(r) B(r) = k m d 3 r J(r ) r r r r 3 (8.10) Idr J(r )d 3 r 0 (8.10) (8.10) (2.20) : z I z r x B(r, 0, 0) = k m I dz e z re x ze z re x ze z 3 = k mi dz r (r 2 + z 2 ) e 3/2 y = 2k mi e y (8.11) r Ampère (r, 0, 0) y 8.2 e φ (r) 8 2: a I xy z (x, y, z) = (ρ cos φ, ρ sin φ, z) 11 98
107 8.2: 8 1 I B 8.3: 8 2 I B B(0, 0, z) = k m I 2π 0 adφ e φ ze z ae ρ ze z ae ρ 3 = k mi 2π 0 dφ a (z 2 + a 2 ) 3/2 (ze ρ + ae z ) (8.12) e φ = ( sin φ, cos φ, 0) e ρ = (cos φ, sin φ, 0) z 8.3 a 2 B(0, 0, z) = 2πk m I (z 2 + a 2 ) e 3/2 z (8.13) z [8 4] 8.5 Lorentz Lorentz Ampère (2.19) 21 (8.7) J (7.23) 91 Idr Idr B ρvdv B = ρdv v B 12 ρdv q qv B 12 (7.23) 91 99
108 m d2 r(t) dt 2 = qe(r(t)) + q dr(t) dt Lorentz Lorentz force 13 B(r(t)) (8.14) : m q m d2 r(t) dt 2 = qe (8.15) E r 0 t = 0 v 0 t = 0 r(t) = qe 2m t2 + v 0 t + r 0 (8.16) 8 4: m d2 r(t) dt 2 = q dr(t) dt 15 dr(t) dt B (8.17) = q m (r(t) r 0) B + v 0 (8.18) r 0 v z dx(t) = q dt m (y(t) y 0)B + v 0x (8.19) dy(t) = q dt m (x(t) x 0)B + v 0y (8.20) dz(t) = v 0z dt (8.21) 13 H. Lorentz Lorentz
109 z z(t) = v 0z t + z 0 (8.22) x y y x d 2 x(t) dt 2 = qb [ q ] m m (x(t) x 0)B + v 0y = q2 B 2 ( m 2 x(t) x 0 m ) qb v 0y (8.23) x(t) x 0 m ( ) ( ) qb qb qb v 0y = C 1 sin m t + C 2 cos m t (8.24) C 1 C 2 r(t) = r 0 dr(t) dt = v 0 t = 0 t=0 1 t = 0 m qb v 0y = C 2 (8.25) v 0x = qb m C 1 (8.26) C 1 = v 0x ω C 2 = v 0y ω ω = qb m (8.27) (8.28) (8.29) (8.19) y(t) x(t) = v 0x ω sin ωt + v 0y ω (1 cos ωt) + x 0 (8.30) y(t) = v 0y ω sin ωt v 0x ω (1 cos ωt) + y 0 (8.31) xy ω Larmor Larmor frequency z ( ) 2 dr(t) = v0 2 (8.32) dt 101
110 8.6 Ampère Biot Savart Lorentz 16 Biot Savart Coulomb Ampère 10 Grassmann 1845 (8.6) 1876 Clausius Grassmann Grassmann 17 Grassmann J. A. Fleming Stokes Grassmann Grassmann 102
111 k m [8 1] Ampère (8.2) (8.1) [8 2] Ampère (8.6) (8.2) [8 3]
112 8.4: [8 3] I I 0 I 0 [8 4] 8 2 [8 5] a b c z a < b < c I I B(r) [8 6] [8 7] [8 8] (8.30) (8.31) f(x, y) = 0 z [8 9] m d2 r(t) dt 2 = qe + q dr(t) dt B (8 9.1) 104
113 0 0 (a). B = 0, E = 0 (b). B = B 0 0 B, E = E E 0 0, r(0) =, r(0) = ,, dr(t) dt = t=0 dr(t) dt = t=0 v E B v 0 [8 10] 2 xy m q v F = m τ v τ (a). E (b). (a) B = Be z x x (c). E = 0 B = Be z 105
114 9 Coulomb Gauss Poisson 9.1 Biot Savart B(r) = k m d 3 r J(r ) r r r r 3 (9.1) Gauss Gauss line of magnetic force S magnetic flux Φ = ds B(r) (9.2) S [Wb] Weber 1Wb = 1T m 2 S 0 Gauss S ds B(r) = 0 (9.3) Gauss B(r) = 0 (9.4) 106
115 (9.1) B(r) = k m d 3 r J(r ) r r r r 3 (9.5) (3 8.1) 51 B(r) = k m d 3 r J(r ) ( r r ) r r r 3 (9.6) r r r r r 3 = r r 1 r r = 0 (9.7) 1 Gauss Gauss Ampère 0 0 C dr B(r) (9.8) C a Ampère dr B(r) = 2πa 2k mi = 4πk m I (9.9) a C I = ds J(r) S C= S dr B(r) = 4πk m S ds J(r) (9.10) 2 1 r = r
116 0 C S Ampère Ampère s law Stokes ds B(r) = 4πk m ds J(r) (9.11) S S S B(r) = 4πk m J(r) (9.12) Ampère (9.1) [9 2] C= S ds B(r) = 0 B(r) = 0 (9.13) S dr B(r) = 4πk m ds J(r) B(r) = 4πk m J(r) (9.14) S S S S= V ds E(r) = 4πk dv ρ(r) E(r) = 4πkρ(r) (9.15) V dr E(r) = 0 E(r) = 0 (9.16) C 0 / / Gauss 9.2 * * Gauss Poisson 108
117 0 ϕ(r) ϕ(r) = 0 0 Gauss Biot Savart 3 B(r) = k m d 3 r J(r 1 ) r (k r r = m d 3 r J(r ) ) r r (9.17) r r 0 A(r) = 0 Gauss B(r) = A(r) (9.18) Gauss 4 A(r) vector potential 5 Biot Savart A(r) = k m d 3 r J(r ) r r (9.19) 3 3 B = 0 Poisson (3.45) 47 B(r) = ( A(r)) = ( A(r)) 2 A(r) (9.20) (9.14) ( A(r)) 2 A(r) = 4πk m J(r) (9.21) Poisson 1 (9.19) (9.21) 1 A(r) = k m d 3 r J(r ) r r = k m d 3 r J(r 1 ) r r r = k m d 3 r J(r 1 ) r r r = k m d 3 r ( r J(r 1 )) r r k m d 3 r J(r ) r r r (9.22a) (9.22b) (9.22c) (9.22d) 3 A ϕ(r) = Aϕ(r) A 4 A (9.18) B = 0 Helmholtz 5 ϕ(r) scalar potential 109
118 r r 1 (7.8) Gauss (3.31) 46 A(r) = k m ds J(r ) r r (9.23) S 0 2 A(r) = 4πk m J(r) (9.24) 3 Poisson B(r) = A(r) (9.25) 2 A(r) = 4πk m J(r) (9.26) ** (9.26) (9.19) A(r) = 0 6 A(r) A (r) = A(r) + A 0 (r), A 0 (r) = 0 (9.27) 0 ϕ(r) ϕ (r) = ϕ(r) + ϕ 0 (r), ϕ 0 (r) = 0 (9.28) ϕ 0 (r) 0 A 0 A 0 (r) = χ(r) (9.29) χ(r) A(r) A (r) = A(r) + χ(r) (9.30) 6 110
119 gauge transformation ϕ(r) A(r) ϕ (r) A (r) gauge invariance A (r) = 0 χ(r) 2 χ(r) = A(r) (9.31) χ(r) 7 Poisson 8 A (r) (9.26) A(r) = 0 (9.26) A(r) = 0 (9.26) (9.19) A(r) = 0 (9.19) : Gauss : Ampère (9.18) (9.19) 7 gauge fixing 8 Poisson 111
120 III 9.4 [9 1] (9.13) (9.14) Biot Savart (9.1) [9 2] (9.1) (9.12) (5.27) 65 [9 3]
121 [9 4] (7.19)
122 10 magnet a I B(r) = k m I dr r r r r 3 (10.1) C C r a 0 B(r) A(r) B(r) = A(r) A(r) dr A(r) = k m I C r r (10.2) r = r r = r 1 r r = = 1 (r r ) 2 1 r2 2r r + r 2 (10.3a) (10.3b) = 1 (10.3c) r 1 2 r r r + r 2 2 r 2 1 r ( ) (10.3d) 1 r r r 2 1 (1 + r ) r r r 2 (10.3e) r 2 A(r) k ( mi dr 1 + r ) r r r 2 C (10.4) 1 B(r) = A(r) A(r) (10.2) 114
123 xy cos θ sin θ r = a sin θ, dr = adθ cos θ (10.5) 0 0 sin θ A(r) k mia r = k mia r 2π 0 y x 0 dθ πa r 2 cos θ 0 [ 1 + a ] r 2 (x cos θ + y sin θ ) (10.6a) (10.6b) = k m ISe z r r 3 (10.6c) S = πa 2 m = ISe z = IS (10.7) S 2 (10.6) B(r) = (k m m r ) r 3 = k m m r r 3 k mm r ( r 3 = k m m r 3 + 3m r ) r r 5 (10.8a) (10.8b) (10.8c) (3 8.2) 51 3 (6.21) 75 magnetic dipole moment m magnetic dipole m = I ds (10.9) S S 10.2 Coulomb 2 115
124 10.1: (a) (b) (c) (d) Coulomb p = qd d 0 1 q q 10.1 r 0 r (6.21) 75 dϕ(r) = k p (r r 0) r r 0 3 (10.10) p = qdr 0 r 0 r r 0 ϕ(r) = kq dr 0 r r 0 3 = kq 1 dr 0 r0 r r 0 = kq C C ( ) 1 r r + 1 r r (10.11) 3 Coulomb 0 magnetic charge Coulomb magnetic potential r 0 m = q m dr 0 ( ) r r 0 ϕ m (r) = k m q m dr 0 C r r 0 3 = k 1 mq m r r + 1 r r ( r r+ B(r) = ϕ m (r) = k m q m r r + 3 r r ) r r 3 Coulomb q m 3 C (10.12) (10.13) 116
125 10.2: 10.3: 10.3 N S N S 4 solenoid magnetic moment [8 3]
126 0 magnetic monopole Gauss (9.4) [10 1] (10.9) m = I r dr (10 1.1) 2 C S C [10 2] (10.8) 7 8 spin 118
127 [10 3] n 119
128
129 III
130
131 11 III 11.1 II Lorentz Lorentz B v q B v qv B 1 0 = qe + qv B (11.1) E = v B (11.2) σ Ohm 11.2 J E + v B = 1 σ J (11.3) V emf = dr v B (11.4) C 1 v 2 (11.3) 7 123
132 11.1: 11.2: ab abcd ab 11.3: dr v v dr v dr (11.4) (3.43) 47 V emf = dr v B (11.5) C 11.3 v dr V emf (t) = d ds B (11.6) dt S(t) 11.2 abcd S(t) (9.2) 106 Lorentz Lorentz S(t) 124
133 II Faraday Lorentz Faraday (11.6) 4 V emf (t) = d ds B(r, t) (11.7) dt S S Faraday electromagnetic induction Faraday Faraday s law of induction 5 [11 2] C 3 J. Henry Faraday Henry [H] 4 B(r, t) V emf (t) Faraday Henry 1830 (11.7) F. E. Neumann 1845 (11.7) E. Lenz Lenz 1834 Lenz Neumann Faraday Neumann 125
134 C= S dr E(r, t) = d dt S ds B(r, t) (11.8) S C C Faraday Stokes (5.12) 62 ds ( E(r, t) + t ) B(r, t) = 0 (11.9) S 6 Faraday E(r, t) + B(r, t) = 0 (11.10) t Faraday 7 Faraday 6 7 Faraday Lorentz 126
135 d V emf (t) = k emf ds B(r, t) (11.11) dt S k emf Faraday E(r, t) + k emf B(r, t) = 0 (11.12) t k emf k m k emf Lorentz (8.14) 100 Lorentz (11.6) k emf 1 principle of relativity k emf = 1 Faraday (11.8) Faraday 11.4 [11 1]
136 11.4: [11 2](a) oa oabcde 11.5: [11 2](b) o abcdo [11 2] (a) (b)
137 12 Maxwell Maxwell ds E(r) = 4πk dv ρ(r) E(r) = 4πkρ(r) (12.1) S= V V dr E(r) = 0 E(r) = 0 (12.2) C ds B(r) = 0 B(r) = 0 (12.3) S dr B(r) = 4πk m ds J(r) B(r) = 4πk m J(r) (12.4) C= S Faraday C= S dr E(r, t) = d dt S S ds B(r, t) E(r, t) + B(r, t) = 0 (12.5) t (12.2) 7 ρ(r, t) + J(r, t) = 0 (12.6) t (12.1) (12.4) t E(r, t) = 4πk ρ(r, t) t (12.7) B(r, t) = 4πk m J(r, t) (12.8)
138 0 E(r, t) = 4πkρ(r, t) (12.9) B(r, t) k m k t E(r, t) = 4πk mj(r, t) (12.10) 2 1 ds E(r, t) = 4πk dv ρ(r, t) (12.11) S= V V ( dr B(r, t) = 4πk m ds J(r, t) + 1 ) E(r, t) (12.12) 4πk t C= S S displacement current J d (r, t) = 1 4πk te(r, t) Maxwell (12.3) (12.2) (12.5) (12.5) E(r, t) + B(r, t) = 0 (12.13) t (12.3) ds B(r, t) = 0 B(r, t) = 0 (12.14) S Faraday (12.5) z < 0 z Q(t) = It Gauss (12.9) E(r, t) = kit r r 3 (12.15) 1 130
139 J d (r, t) = 1 4πk I E(r, t) = t 4π (12.12) r r 3 (12.16) B(r, t) = B(ρ, z, t)e φ (12.17) z ρ z e ρ 0 Gauss (12.14) e z 0 2 z ρ k m I S 2πρB(ρ, z, t) = ds 4πk m I + k m I S ds S r r 3 z > 0 r r 3 z < 0 (12.18) r ρ 2π ds r 3 = ρ dρ z dφ (12.19a) (ρ 2 + z 2 ) 3/2 0 ρ 2 0 dρ 2 = πz (12.19b) 0 (ρ 2 + z 2 ) ( 3/2 ) = 2π z z 1 (12.19c) z ρ2 + z 2 B(ρ, z, t) = k mi ρ ( 1 ) z ρ2 + z 2 (12.20) z > 0 z < 0 z = Maxwell ds E(r, t) = 4πk dv ρ(r, t) (12.21) S= V V dr E(r, t) = d ds B(r, t) C= S dt S (12.22) ds B(r, t) = 0 (12.23) S ( dr B(r, t) = 4πk m ds J(r, t) + 1 ) E(r, t) 4πk t (12.24) C= S 2 [12 1] S 131
140 12.1: z < 0 I Q(t) = It E(r, t) = 4πkρ(r, t) (12.25) E(r, t) + B(r, t) = 0 t (12.26) B(r, t) = 0 (12.27) B(r, t) k m k t E(r, t) = 4πk mj(r, t) (12.28) Maxwell Maxwell equation Maxwell (ρ, J, E, B) 2 Maxwell Maxwell Maxwell 4 (12.28) k m k t E(r, t) = 4πk m J(r, t) = 4πk m ρ(r, t) (12.29) t ( ) E(r, t) 4πkρ(r, t) = 0 (12.30) t 132
141 Maxwell 1 (12.25) 0 2 (12.26) B(r, t) = 0 (12.31) t 3 0 Maxwell 1 3 Maxwell Maxwell (3.45) 47 ( E(r, t)) 2 E(r, t) = B(r, t) (12.32) t ( B(r, t)) 2 B(r, t) = k m k Maxwell E(r, t) + k m k 2 B(r, t) + k m k 0 2 t E(r, t) + 4πk m J(r, t) (12.33) t 2 E(r, t) = 4πk ρ(r, t) 4πk m J(r, t) t (12.34) 2 t 2 B(r, t) = 4πk m J(r, t) (12.35) 2 E(r, t) + k m k 2 B(r, t) + k m k 2 E(r, t) = 0 t2 (12.36) 2 B(r, t) = 0 t2 (12.37) wave equation k v = (12.38) k m 3 133
142 k k m 1/ Maxwell v c m/s 1849 H. Fizeau 1856 R. Kohlrausch W. E. Weber k k m Maxwell v c 4 k k m k = 1 4πϵ 0 (12.39) k m = µ 0 4π ϵ 0 permittivity µ 0 permeability 5 (12.40) ϵ 0 µ 0 = 1 c 2 (12.41) Maxwell 2 Maxwell E(r, t) = 1 ϵ 0 ρ(r, t) (12.42) E(r, t) + B(r, t) = 0 t (12.43) B(r, t) = 0 (12.44) B(r, t) 1 c 2 t E(r, t) = µ 0J(r, t) (12.45) 7 Ohm Maxwell Maxwell t t E(r, t) = 1 ϵ 0 ρ(r, t) (12.46) E(r, t) B(r, t) = 0 t (12.47) B(r, t) = 0 (12.48) B(r, t) + 1 c 2 t E(r, t) = µ 0J(r, t) (12.49) ρ(r, t) = ρ(r, t) (12.50) Faraday 5 134
143 Maxwell J(r, t) = J(r, t) (12.51) E(r, t) = E(r, t) (12.52) B(r, t) = B(r, t) (12.53) 12.3 law of conservation of energy v m q 1 2 mv2 Lorentz 6 v(t) = dr(t) dt ( ) d 1 dt 2 mv2 (t) = mv(t) v(t) (12.54a) = qv(t) (E(r(t), t) + v(t) B(r(t), t)) (12.54b) = qv(t) E(r(t), t) (12.54c) d ( ) 1 dt 2 m ivi 2 (t) = q i v i (t) E(r i (t), t) = dv J(r, t) E(r, t) (12.55) i i (7.23) 91 J(r, t) E(r, t) Maxwell 4 (12.45) ( ) 1 J E = B ϵ 0 µ 0 t E E = ϵ 0 E t E + 1 E B (12.56) µ 0 (3 8.1) 51 E B = B E E B (12.57) 6 Lorentz 135
144 Maxwell 2 (12.43) J E = ϵ 0 E t E + 1 µ 0 B E 1 µ 0 E B = ϵ 0 E t E 1 B µ 0 t B 1 E B µ 0 = ( ϵ0 t 2 E2 + 1 ) B 2 1 E B 2µ 0 µ 0 (12.58a) (12.58b) (12.58c) ( ϵ0 t 2 E2 (r, t) + 1 ) ( ) 1 B 2 (r, t) + E(r, t) B(r, t) = J(r, t) E(r, t) (12.59) 2µ 0 µ 0 (12.55) V ( d ϵ0 dv dt 2 E2 + 1 ) B 2 + dv 1 E B = d 2µ 0 µ 0 dt T (12.60) V T 2 Gauss ( d ϵ0 dv dt 2 E2 + 1 ) B 2 + 1µ0 ds E B = d 2µ 0 dt T (12.61) V 0 E E(t) = dv V V S d (T + E) = 0 (12.62) dt ( ϵ0 2 E2 (r, t) + 1 ) B 2 (r, t) 2µ 0 (12.63) (12.59) E(r, t) + S(r, t) = J(r, t) E(r, t) (12.64) t E(r, t) = ϵ 0 2 E2 (r, t) + 1 2µ 0 B 2 (r, t) (12.65) S(r, t) = 1 µ 0 E(r, t) B(r, t) (12.66) E(r, t) S(r, t) Poynting Poynting vector 7 Poynting (12.64) Poynting J. H. Poynting Pointing 136
145 Poynting (12.64) [12 4] (12 4.1) 12.4 ** I II E(r) = ϕ(r) (12.67) B(r) = A(r) (12.68) ϕ A electromagnetic potential Maxwell (12.44) B(r, t) = A(r, t) (12.69) 2 (12.43) E(r, t) = ϕ(r, t) + Ẽ(r, t) (12.70) 2 Ẽ(r, t) + A(r, t) = 0 (12.71) t Ẽ(r, t) = A(r, t) (12.72) t 137
146 Maxwell 2 3 E(r, t) = ϕ(r, t) A(r, t) t (12.73) B(r, t) = A(r, t) (12.74) ϕ(r) t A(r, t) = 1 ϵ 0 ρ(r, t) (12.75) ( A(r, t)) 2 A(r, t) + 1 c 2 t ϕ(r, t) + 1 c 2 2 t 2 A(r, t) = µ 0J(r, t) (12.76) 2 ϕ(r, t) c 2 t 2 ϕ(r, t) ( 1 t c 2 t 2 A(r, t) + 1 c 2 2 A(r, t) + t2 ) ϕ(r, t) + A(r, t) = 1 ρ(r, t) (12.77) ϵ 0 ( 1 c 2 ϕ(r, t) + A(r, t) t ) = µ 0 J(r, t) (12.78) Maxwell 9 A = 0 1 c 2 ϕ(r, t) + A(r, t) = 0 (12.79) t 8 2 ϕ(r, t) c 2 t 2 ϕ(r, t) = 1 ρ(r, t) ϵ 0 (12.80) 2 A(r, t) c 2 t 2 A(r, t) = µ 0J(r, t) (12.81) (12.74) A(r, t) A (r, t) = A(r, t) + χ(r, t) (12.82) 0 (12.73) ϕ(r, t) ϕ (r, t) = ϕ(r, t) χ(r, t) (12.83) t χ(r, t) (12.79) 12.5 Maxwell 8 Lorenz L. Lorenz Lorentz 138
147 12.2: Maxwell Maxwell Maxwell 12.2 Faraday Faraday Faraday 10 Einstein 139
148 I II Gauss Coulomb Biot Savart Maxwell Maxwell 1 Maxwell 1 2 Newton Newton Maxwell r t 11 0 Maxwell Maxwell
149 12.3: [12 2] V (t) I(t) S 1 S [12 1] e ρ 0 e z [12 2] 12.3 (12.12) S 1 S 2 (6.18) 74 [12 3] Maxwell [12 4] (a). ϵ 0 dv E 2 (r) = 1 dv ρ(r)ϕ(r) (12 4.1) 2 2 V V ϕ(r) (b) V 141
150 ρ = 0 J = 0 Maxwell E(r, t) = 0 (13.1) E(r, t) + B(r, t) = 0 t (13.2) B(r, t) = 0 (13.3) B(r, t) 1 c 2 E(r, t) = 0 t (13.4) 2 E(r, t) + 1 c B(r, t) + 1 c 2 2 E(r, t) = 0 (13.5) t2 B(r, t) = 0 (13.6) t2 Maxwell Maxwell electromagnetic wave 2 Maxwell Maxwell z E(z, t) separation of variables E(z, t) = E 0 Z(z)T (t) (13.7) 142
151 E 0 E 0 ( Z (z)t (t) + 1 ) c 2 Z(z) T (t) = 0 (13.8) Z Z z T T t Z (z) Z(z) + 1 c 2 T (t) T (t) = 0 (13.9) 1 z t 2 t z z t 0 Z (z) Z(z) = C 1 (13.10) 1 T (t) c 2 T (t) = C 1 (13.11) 2 C 1 = k 2 Z (z) = k 2 Z(z) (13.12) T (t) = c 2 k 2 T (t) (13.13) k 2 2 k C 1 < 0 k [13 1] Z(z) = Z 0 sin(kz kz 0 ) (13.14) T (t) = T 0 sin(ckt ckt 0 ) (13.15) 0 4 Z 0 T 0 E 0 E = E 0 sin(k(z z 0 )) sin(ck(t t 0 )) (13.16) 1 k ck c E = 0 ke 0z cos(k(z z 0 )) sin(ck(t t 0 )) = 0 (13.17) z t E 0z = 0 k = 0 E = 0 E 0z = 0 z k k z 1 Fourier 143
152 Maxwell E = E 0x E 0y 0 sin(k(z z 0)) sin(ck(t t 0 )) (13.18) B = 1 c E 0y E 0x 0 cos(k(z z 0)) cos(ck(t t 0 )) (13.19) plain wave z t 2 ξ = z ct η = z + ct ξ η E = 0 (13.20) E(z, t) = E + (ξ) + E (η) = E + (z ct) + E (z + ct) (13.21) E ± 1 E + (z ct) c 2 c E(r, t) = E + (k r ckt) + E (k r + ckt) (13.22) k k E(r, t) = 0 k (E +(k r ckt) + E (k r + ckt) ) = 0 (13.23) E ± E ± k 0 k E(r, t) = 0 (13.24) [13 2] Maxwell E 1 E 2 E 1 + E 2 2 z 144
153 k k ** (13.46) (13.47) ϕ(r) = 1 d 3 r 1 4πϵ 0 r r ρ(r ) (13.25) A(r) = µ 0 d 3 r 1 4π r r J(r ) (13.26) I II ϕ A 5 ( r r ρ ϕ(r, t) = 1 d 3 r 1 4πϵ 0 A(r, t) = µ 0 d 3 r 1 4π r r J r, t r ) r c ( r, t r ) r c (13.27) (13.28) (12.73) (12.74) 138 r r r c r r /c t t r r c 3 Fourier 4 Feynman If it gets difficult in places, well, that s life there is no other way. Feynman Lectures on Physics, Volume II 5 Lorenz 145
154 c retarded potential causality z t = 0 I 8 0 z (ρ, φ, z) E(r, t) = E ρ (ρ, t)e ρ + E φ (ρ, t)e φ + E z (ρ, t)e z (13.29) B(r, t) = B ρ (ρ, t)e ρ + B φ (ρ, t)e φ + B z (ρ, t)e z (13.30) x = ρ cos φ (13.31) y = ρ sin φ (13.32) e ρ = 1 x cos φ ρ y = sin φ, 0 0 e φ = 1 ρ y x 0 = sin φ cos φ 0, e z = (13.33) z ρ E(r) = 0 (13.34) B(r) = µ 0I 2πρ e φ (13.35) 0 7 t = z Gauss ρ 0 Maxwell 1 3 E ρ = 0 (13.36) B ρ = 0 (13.37) 6 (13.39) (13.39) 146
155 13.1: z t l 2 < z < l 2 (13.28) ρ 13.1 l A(r, t) = µ 0I 4π l 2 = c 2 t 2 ρ 2 (13.38) z z < l 2 dz 1 r r e z (13.39) A(r, t) = µ 0I dz 1 4π r r e z (13.40a) = µ 0I 4π = µ 0I 4π z z < l 2 z z < l 2 l/2 l/2 dz 1 ρ2 + (z z ) 2 e z dz 1 ρ2 + z 2 e z = µ [ 0I ( ln ρ2 + z 4π 2 z )] l/2 = µ 0I 4π ln ρ 2 + ( ) l l 2 ρ 2 + ( ) e z l 2 2 l 2 ( = µ 0I 4π ln ct + ) c 2 t 2 ρ 2 e z ct c 2 t 2 ρ 2 l/2 e z (13.40b) (13.40c) (13.40d) (13.40e) (13.40f) B(r, t) = A(r, t) (13.41a) A z = y Az x (13.41b) 0 147
156 = A z ρ e φ = µ 0I ct 2πρ c2 t 2 ρ e 2 φ (13.41c) (13.41d) Maxwell 2 7 A(r, t) E(r, t) = = µ 0I c t 2π c2 t 2 ρ e 2 z (13.42) Maxwell 4 8 z ρ S dr B(r, t) 1 d c 2 ds E(r, t) = µ 0 I (13.43) dt C S C S ρ ct dr B(r, t) = 2πρB φ (ρ, t) = µ 0 I (13.44) c2 t 2 ρ 2 C 1 d c 2 ds E(r, t) = 1 d dt S c 2 dt = µ 0I 2c = µ 0I 2c = µ 0 I d dt d ( dt ρ 0 ρ 2 2πρ dρ E z (ρ, t) dρ 2 0 c2 t 2 ρ 2 (2ct 2 ) c 2 t 2 ρ 2 1 ) ct c2 t 2 ρ 2 (13.45a) (13.45b) (13.45c) (13.45d) Maxwell 4 E(r, t) = µ 0I 2π c c2 t 2 ρ 2 e z (13.46) B(r, t) = µ 0I ct 2πρ c2 t 2 ρ e 2 φ (13.47) ρ 13.2 ρ < ct ρ = ct 0 (13.35) Poynting S(r, t) = 1 µ 0 E(r, t) B(r, t) = µ 0I 2 4π 2 c 2 t ρ(c 2 t 2 ρ 2 ) e ρ (13.48) 13.3 Maxwell 7 Maxwell z =
157 13.2: (13.46) (13.47) ( ): t = t 1, t 2 t 1 < t 2 ρ ( ): ρ = ρ 0 t ρ = ct Maxwell Maxwell Maxwell Maxwell Lorentz Newton 13.2 Einstein 149
158 (12.15) 130 Gauss Gauss 13.4 [13 1] Poynting Poynting k 2 < 0 [13 2] (13.22) k [13 3] r = r t re(r, t) [13 4] ρ(r, t) J(r, t) E(r, t) = k B(r, t) = k m Maxwell d 3 r ρ(r, t) r r r r 3 (13 4.1) d 3 r J(r, t) r r r r 3 (13 4.2) 150
159 Poisson Coulomb Fourier Maxwell Fourier
160 Maxwell E. P. Wigner The unreasonable effectiveness of mathematics in the natural sciences Ohm Maxwell Ohm Ohm 152
161 Newton 4 5 Lorentz Lorentz Coulomb Ampère Faraday Coulomb C. Huygens 6 Newton k
162 19 Einstein Einstein Newton 154
163 A (1) 1. x = a y = 0 λ x = a y = 0 λ [1 1] E(r) ϕ(r) [1 2] xy dy = f(x, y) dx dy = g(x, y) dx f g xy 2. 2 z = a/2 z = a/2 σ σ [2 1] E(r) [2 2] [2 3] b 2b < a ϕ(r) [2 4] [2 5] [2 3] 3. z I m q 155
164 B (2) 1. ρ(r) E(r) [1 1] (a). r = x 2 + y 2 + z 2 : ρ = ρ(r) (b). z : ρ = ρ(x, y) (c). r = x 2 + y 2 : ρ = ρ(r) (d). xy r = x 2 + y 2 : σ = σ(r) [1 2] a E(r) Q 2. z < 0 I Q(t) = It 3. [3 1] [3 1] Maxwell [3 2] Gauss Coulomb [3 3] [3 4] [3 5] 156
165 C (3) 1. xy a x 2 + y 2 a 2 z = 0 Q [1 1] E(r) [1 2] z [1 3] [1 2] 2. R 0 Q [2 1] E(r) [2 2] R 1 R 2 R 0 < R 1 < R 2 Q Q < Q [2 3] [2 2] [2 4] [2 2] ϕ(r) 0 3. [3 1] E(r) = k C dr E(r) = 0 C d 3 r ρ(r ) r r r r 3 [3 2] (a). Gauss (b). Gauss (c). (d). 157
166 D (4) 1. I z [1 1] (ρ, φ, z) B(r) = B ρ (r)e ρ + B φ (r)e φ + B z (r)e z e ρ,φ,z Maxwell (a). B ρ B φ B z ρ (b). B ρ = 0 (c). B z = const. [1 2] Ampère B z = 0 [1 3] 2. oa o ω oabcdeo B oa ocde oa a [2 1] Φ(t) = ds B S(t) S(t) [2 2] bcdeo R Ohm oa ab 3. [3 1] (a). A(r) = 0 (b). B(r) = 0 (c). t C(r, t) + D(r, t) = 0 (d). 2 E(r, t) 1 2 v 2 E(r, t) = 0 t2 [3 2] E B (a). B = 0, 0 (b). E = 0, (c). E B, 0 [3 3] (a). Ampère Maxwell 4 M4 (b). Ohm Maxwell (c). 158
167 Ampère, 95 Ampère, 108 Ampère, 95 Arago, 95 Biot, 95 Biot Savart, 98 Cavendish, 76 Coulomb, 18 Coulomb, 17, 70, 76 Coulomb, 17, 40 Dirac, 65 Faraday, 125 Faraday, 125 Feynman, 2 Fizeau, 134 Fleming, 102 Gauss, 46 Gauss, 46, 86 Gauss, 38, 44, 48, 107 Gilbert, 17 Grassmann, 97, 102 Green, 64 Hankel, 60 Henry, 125 Huygens, 153 Kepler, 4 Kirchhoff, 88 Kirchhoff, 93 Kohlrausch, 134 Kronecker, 30 Laplace, 19 Laplace, 63 Larmor, 101 Lenz, 125 Lorentz, 100 Lorentz, 100, 123 Lorenz, 138 Lorenz, 138, 145 Maxwell, 134 Maxwell, 6, 132, 142 Mayer, 95 Michell, 95 MKSA, 96 Neumann, 125 Newton, 3 Newton, 5 Ohm, 88 Ohm, 88, 123 Ørsted, 95 Ostrogradsky, 46 Poisson, 63 Poisson, 63 Poynting, 136 Poynting, 136 Priestley, 76 Savart, 95 Stokes, 60 Stokes, 60, 62 Thomson, 60 van Musschenbroek, 73 von Kleist, 73 Weber, 134 Wigner, 152,
168 , 146, 149, 106, 60, 16, 52, 135, 135, 35, 45, 47, 45, 60, 15, 18, 13, 89, 123, 72, 28, 18, 96, 111, 111, 138, 111, 45, 55, 1, 73, 137, 15, 116, 116, 115, 115 Coulomb, 116, 117, 14, 52, 114, 117, 106, 124, 15, 13, 97, 13, 13, 106, 16, 46, 109, 137, 145, 39, 118, 97, 108, 65, 71, 32, 61, 53, 69, 71, 75, 52, 54, 23, 127, 117, 28, 20, 14, 118, 146, 87, 87, 28, 97, 65, 88, 53, 55, 5, 17, 21, 20, 85, 75, 115, 75, 88, 88, 89, 74, 36, 57, 38, 142, 137, 145,
169 , 19, 64, 21, 85, 85, 134, 68, 45, 46, 44, 21, 32, 140, 44, 45, 46, 133, 142, 13, 134, 102, 79, 144, 16, 28, 46, 47, 109, 114, 137, 145, 130, 142, 69, 86, 55, 53, 102, 37, 54, 30, 54, 134, 73, 39, 63, 30, 38, 38, 85,
i
 009 I 1 8 5 i 0 1 0.1..................................... 1 0.................................................. 1 0.3................................. 0.4........................................... 3
009 I 1 8 5 i 0 1 0.1..................................... 1 0.................................................. 1 0.3................................. 0.4........................................... 3
18 2 F 12 r 2 r 1 (3) Coulomb km Coulomb M = kg F G = ( ) ( ) ( ) 2 = [N]. Coulomb
![18 2 F 12 r 2 r 1 (3) Coulomb km Coulomb M = kg F G = ( ) ( ) ( ) 2 = [N]. Coulomb 18 2 F 12 r 2 r 1 (3) Coulomb km Coulomb M = kg F G = ( ) ( ) ( ) 2 = [N]. Coulomb](/thumbs/93/114079295.jpg) r 1 r 2 r 1 r 2 2 Coulomb Gauss Coulomb 2.1 Coulomb 1 2 r 1 r 2 1 2 F 12 2 1 F 21 F 12 = F 21 = 1 4πε 0 1 2 r 1 r 2 2 r 1 r 2 r 1 r 2 (2.1) Coulomb ε 0 = 107 4πc 2 =8.854 187 817 10 12 C 2 N 1 m 2 (2.2)
r 1 r 2 r 1 r 2 2 Coulomb Gauss Coulomb 2.1 Coulomb 1 2 r 1 r 2 1 2 F 12 2 1 F 21 F 12 = F 21 = 1 4πε 0 1 2 r 1 r 2 2 r 1 r 2 r 1 r 2 (2.1) Coulomb ε 0 = 107 4πc 2 =8.854 187 817 10 12 C 2 N 1 m 2 (2.2)
120 9 I I 1 I 2 I 1 I 2 ( a) ( b) ( c ) I I 2 I 1 I ( d) ( e) ( f ) 9.1: Ampère (c) (d) (e) S I 1 I 2 B ds = µ 0 ( I 1 I 2 ) I 1 I 2 B ds =0. I 1 I 2
 9 E B 9.1 9.1.1 Ampère Ampère Ampère s law B S µ 0 B ds = µ 0 j ds (9.1) S rot B = µ 0 j (9.2) S Ampère Biot-Savart oulomb Gauss Ampère rot B 0 Ampère µ 0 9.1 (a) (b) I B ds = µ 0 I. I 1 I 2 B ds = µ 0
9 E B 9.1 9.1.1 Ampère Ampère Ampère s law B S µ 0 B ds = µ 0 j ds (9.1) S rot B = µ 0 j (9.2) S Ampère Biot-Savart oulomb Gauss Ampère rot B 0 Ampère µ 0 9.1 (a) (b) I B ds = µ 0 I. I 1 I 2 B ds = µ 0
50 2 I SI MKSA r q r q F F = 1 qq 4πε 0 r r 2 r r r r (2.2 ε 0 = 1 c 2 µ 0 c = m/s q 2.1 r q' F r = 0 µ 0 = 4π 10 7 N/A 2 k = 1/(4πε 0 qq
 49 2 I II 2.1 3 e e = 1.602 10 19 A s (2.1 50 2 I SI MKSA 2.1.1 r q r q F F = 1 qq 4πε 0 r r 2 r r r r (2.2 ε 0 = 1 c 2 µ 0 c = 3 10 8 m/s q 2.1 r q' F r = 0 µ 0 = 4π 10 7 N/A 2 k = 1/(4πε 0 qq F = k r
49 2 I II 2.1 3 e e = 1.602 10 19 A s (2.1 50 2 I SI MKSA 2.1.1 r q r q F F = 1 qq 4πε 0 r r 2 r r r r (2.2 ε 0 = 1 c 2 µ 0 c = 3 10 8 m/s q 2.1 r q' F r = 0 µ 0 = 4π 10 7 N/A 2 k = 1/(4πε 0 qq F = k r
2 1 x 1.1: v mg x (t) = v(t) mv (t) = mg 0 x(0) = x 0 v(0) = v 0 x(t) = x 0 + v 0 t 1 2 gt2 v(t) = v 0 gt t x = x 0 + v2 0 2g v2 2g 1.1 (x, v) θ
 1 1 1.1 (Isaac Newton, 1642 1727) 1. : 2. ( ) F = ma 3. ; F a 2 t x(t) v(t) = x (t) v (t) = x (t) F 3 3 3 3 3 3 6 1 2 6 12 1 3 1 2 m 2 1 x 1.1: v mg x (t) = v(t) mv (t) = mg 0 x(0) = x 0 v(0) = v 0 x(t)
1 1 1.1 (Isaac Newton, 1642 1727) 1. : 2. ( ) F = ma 3. ; F a 2 t x(t) v(t) = x (t) v (t) = x (t) F 3 3 3 3 3 3 6 1 2 6 12 1 3 1 2 m 2 1 x 1.1: v mg x (t) = v(t) mv (t) = mg 0 x(0) = x 0 v(0) = v 0 x(t)
 1 B () Ver 2014 0 2014/10 2015/1 http://www-cr.scphys.kyoto-u.ac.jp/member/tsuru/lecture/... 1. ( ) 2. 3. 3 1 7 1.1..................................................... 7 1.2.............................................
1 B () Ver 2014 0 2014/10 2015/1 http://www-cr.scphys.kyoto-u.ac.jp/member/tsuru/lecture/... 1. ( ) 2. 3. 3 1 7 1.1..................................................... 7 1.2.............................................
 i E B Maxwell Maxwell Newton Newton Schrödinger Newton Maxwell Kepler Maxwell Maxwell B H B ii Newton i 1 1.1.......................... 1 1.2 Coulomb.......................... 2 1.3.........................
i E B Maxwell Maxwell Newton Newton Schrödinger Newton Maxwell Kepler Maxwell Maxwell B H B ii Newton i 1 1.1.......................... 1 1.2 Coulomb.......................... 2 1.3.........................
δ ij δ ij ˆx ˆx ŷ ŷ ẑ ẑ 0, ˆx ŷ ŷ ˆx ẑ, ŷ ẑ ẑ ŷ ẑ, ẑ ˆx ˆx ẑ ŷ, a b a x ˆx + a y ŷ + a z ẑ b x ˆx + b
 23 2 2.1 n n r x, y, z ˆx ŷ ẑ 1 a a x ˆx + a y ŷ + a z ẑ 2.1.1 3 a iˆx i. 2.1.2 i1 i j k e x e y e z 3 a b a i b i i 1, 2, 3 x y z ˆx i ˆx j δ ij, 2.1.3 n a b a i b i a i b i a x b x + a y b y + a z b
23 2 2.1 n n r x, y, z ˆx ŷ ẑ 1 a a x ˆx + a y ŷ + a z ẑ 2.1.1 3 a iˆx i. 2.1.2 i1 i j k e x e y e z 3 a b a i b i i 1, 2, 3 x y z ˆx i ˆx j δ ij, 2.1.3 n a b a i b i a i b i a x b x + a y b y + a z b
( : December 27, 2015) CONTENTS I. 1 II. 2 III. 2 IV. 3 V. 5 VI. 6 VII. 7 VIII. 9 I. 1 f(x) f (x) y = f(x) x ϕ(r) (gradient) ϕ(r) (gradϕ(r) ) ( ) ϕ(r)
 ( : December 27, 215 CONTENTS I. 1 II. 2 III. 2 IV. 3 V. 5 VI. 6 VII. 7 VIII. 9 I. 1 f(x f (x y f(x x ϕ(r (gradient ϕ(r (gradϕ(r ( ϕ(r r ϕ r xi + yj + zk ϕ(r ϕ(r x i + ϕ(r y j + ϕ(r z k (1.1 ϕ(r ϕ(r i
( : December 27, 215 CONTENTS I. 1 II. 2 III. 2 IV. 3 V. 5 VI. 6 VII. 7 VIII. 9 I. 1 f(x f (x y f(x x ϕ(r (gradient ϕ(r (gradϕ(r ( ϕ(r r ϕ r xi + yj + zk ϕ(r ϕ(r x i + ϕ(r y j + ϕ(r z k (1.1 ϕ(r ϕ(r i
I ( ) 1 de Broglie 1 (de Broglie) p λ k h Planck ( Js) p = h λ = k (1) h 2π : Dirac k B Boltzmann ( J/K) T U = 3 2 k BT
 I (008 4 0 de Broglie (de Broglie p λ k h Planck ( 6.63 0 34 Js p = h λ = k ( h π : Dirac k B Boltzmann (.38 0 3 J/K T U = 3 k BT ( = λ m k B T h m = 0.067m 0 m 0 = 9. 0 3 kg GaAs( a T = 300 K 3 fg 07345
I (008 4 0 de Broglie (de Broglie p λ k h Planck ( 6.63 0 34 Js p = h λ = k ( h π : Dirac k B Boltzmann (.38 0 3 J/K T U = 3 k BT ( = λ m k B T h m = 0.067m 0 m 0 = 9. 0 3 kg GaAs( a T = 300 K 3 fg 07345
 http://www.ns.kogakuin.ac.jp/~ft13389/lecture/physics1a2b/ pdf I 1 1 1.1 ( ) 1. 30 m µm 2. 20 cm km 3. 10 m 2 cm 2 4. 5 cm 3 km 3 5. 1 6. 1 7. 1 1.2 ( ) 1. 1 m + 10 cm 2. 1 hr + 6400 sec 3. 3.0 10 5 kg
http://www.ns.kogakuin.ac.jp/~ft13389/lecture/physics1a2b/ pdf I 1 1 1.1 ( ) 1. 30 m µm 2. 20 cm km 3. 10 m 2 cm 2 4. 5 cm 3 km 3 5. 1 6. 1 7. 1 1.2 ( ) 1. 1 m + 10 cm 2. 1 hr + 6400 sec 3. 3.0 10 5 kg
II ( ) (7/31) II ( [ (3.4)] Navier Stokes [ (6/29)] Navier Stokes 3 [ (6/19)] Re
![II ( ) (7/31) II ( [ (3.4)] Navier Stokes [ (6/29)] Navier Stokes 3 [ (6/19)] Re II ( ) (7/31) II ( [ (3.4)] Navier Stokes [ (6/29)] Navier Stokes 3 [ (6/19)] Re](/thumbs/94/118770263.jpg) II 29 7 29-7-27 ( ) (7/31) II (http://www.damp.tottori-u.ac.jp/~ooshida/edu/fluid/) [ (3.4)] Navier Stokes [ (6/29)] Navier Stokes 3 [ (6/19)] Reynolds [ (4.6), (45.8)] [ p.186] Navier Stokes I Euler Navier
II 29 7 29-7-27 ( ) (7/31) II (http://www.damp.tottori-u.ac.jp/~ooshida/edu/fluid/) [ (3.4)] Navier Stokes [ (6/29)] Navier Stokes 3 [ (6/19)] Reynolds [ (4.6), (45.8)] [ p.186] Navier Stokes I Euler Navier
x () g(x) = f(t) dt f(x), F (x) 3x () g(x) g (x) f(x), F (x) (3) h(x) = x 3x tf(t) dt.9 = {(x, y) ; x, y, x + y } f(x, y) = xy( x y). h (x) f(x), F (x
 [ ] IC. f(x) = e x () f(x) f (x) () lim f(x) lim f(x) x + x (3) lim f(x) lim f(x) x + x (4) y = f(x) ( ) ( s46). < a < () a () lim a log xdx a log xdx ( ) n (3) lim log k log n n n k=.3 z = log(x + y ),
[ ] IC. f(x) = e x () f(x) f (x) () lim f(x) lim f(x) x + x (3) lim f(x) lim f(x) x + x (4) y = f(x) ( ) ( s46). < a < () a () lim a log xdx a log xdx ( ) n (3) lim log k log n n n k=.3 z = log(x + y ),
II A A441 : October 02, 2014 Version : Kawahira, Tomoki TA (Kondo, Hirotaka )
 II 214-1 : October 2, 214 Version : 1.1 Kawahira, Tomoki TA (Kondo, Hirotaka ) http://www.math.nagoya-u.ac.jp/~kawahira/courses/14w-biseki.html pdf 1 2 1 9 1 16 1 23 1 3 11 6 11 13 11 2 11 27 12 4 12 11
II 214-1 : October 2, 214 Version : 1.1 Kawahira, Tomoki TA (Kondo, Hirotaka ) http://www.math.nagoya-u.ac.jp/~kawahira/courses/14w-biseki.html pdf 1 2 1 9 1 16 1 23 1 3 11 6 11 13 11 2 11 27 12 4 12 11
Untitled
 II 14 14-7-8 8/4 II (http://www.damp.tottori-u.ac.jp/~ooshida/edu/fluid/) [ (3.4)] Navier Stokes [ 6/ ] Navier Stokes 3 [ ] Reynolds [ (4.6), (45.8)] [ p.186] Navier Stokes I 1 balance law t (ρv i )+ j
II 14 14-7-8 8/4 II (http://www.damp.tottori-u.ac.jp/~ooshida/edu/fluid/) [ (3.4)] Navier Stokes [ 6/ ] Navier Stokes 3 [ ] Reynolds [ (4.6), (45.8)] [ p.186] Navier Stokes I 1 balance law t (ρv i )+ j
 * 1 2014 7 8 *1 iii 1. Newton 1 1.1 Newton........................... 1 1.2............................. 4 1.3................................. 5 2. 9 2.1......................... 9 2.2........................
* 1 2014 7 8 *1 iii 1. Newton 1 1.1 Newton........................... 1 1.2............................. 4 1.3................................. 5 2. 9 2.1......................... 9 2.2........................
 211 kotaro@math.titech.ac.jp 1 R *1 n n R n *2 R n = {(x 1,..., x n ) x 1,..., x n R}. R R 2 R 3 R n R n R n D D R n *3 ) (x 1,..., x n ) f(x 1,..., x n ) f D *4 n 2 n = 1 ( ) 1 f D R n f : D R 1.1. (x,
211 kotaro@math.titech.ac.jp 1 R *1 n n R n *2 R n = {(x 1,..., x n ) x 1,..., x n R}. R R 2 R 3 R n R n R n D D R n *3 ) (x 1,..., x n ) f(x 1,..., x n ) f D *4 n 2 n = 1 ( ) 1 f D R n f : D R 1.1. (x,
46 4 E E E E E 0 0 E E = E E E = ) E =0 2) φ = 3) ρ =0 1) 0 2) E φ E = grad φ E =0 P P φ = E ds 0
 4 4.1 conductor E E E 4.1: 45 46 4 E E E E E 0 0 E E = E E E =0 4.1.1 1) E =0 2) φ = 3) ρ =0 1) 0 2) E φ E = grad φ E =0 P P φ = E ds 0 4.1 47 0 0 3) ε 0 div E = ρ E =0 ρ =0 0 0 a Q Q/4πa 2 ) r E r 0 Gauss
4 4.1 conductor E E E 4.1: 45 46 4 E E E E E 0 0 E E = E E E =0 4.1.1 1) E =0 2) φ = 3) ρ =0 1) 0 2) E φ E = grad φ E =0 P P φ = E ds 0 4.1 47 0 0 3) ε 0 div E = ρ E =0 ρ =0 0 0 a Q Q/4πa 2 ) r E r 0 Gauss
I ( ) 2019
 I ( ) 2019 i 1 I,, III,, 1,,,, III,,,, (1 ) (,,, ), :...,, : NHK... NHK, (YouTube ),!!, manaba http://pen.envr.tsukuba.ac.jp/lec/physics/,, Richard Feynman Lectures on Physics Addison-Wesley,,,, x χ,
I ( ) 2019 i 1 I,, III,, 1,,,, III,,,, (1 ) (,,, ), :...,, : NHK... NHK, (YouTube ),!!, manaba http://pen.envr.tsukuba.ac.jp/lec/physics/,, Richard Feynman Lectures on Physics Addison-Wesley,,,, x χ,
 21 2 26 i 1 1 1.1............................ 1 1.2............................ 3 2 9 2.1................... 9 2.2.......... 9 2.3................... 11 2.4....................... 12 3 15 3.1..........
21 2 26 i 1 1 1.1............................ 1 1.2............................ 3 2 9 2.1................... 9 2.2.......... 9 2.3................... 11 2.4....................... 12 3 15 3.1..........
1 No.1 5 C 1 I III F 1 F 2 F 1 F 2 2 Φ 2 (t) = Φ 1 (t) Φ 1 (t t). = Φ 1(t) t = ( 1.5e 0.5t 2.4e 4t 2e 10t ) τ < 0 t > τ Φ 2 (t) < 0 lim t Φ 2 (t) = 0
 1 No.1 5 C 1 I III F 1 F 2 F 1 F 2 2 Φ 2 (t) = Φ 1 (t) Φ 1 (t t). = Φ 1(t) t = ( 1.5e 0.5t 2.4e 4t 2e 10t ) τ < 0 t > τ Φ 2 (t) < 0 lim t Φ 2 (t) = 0 0 < t < τ I II 0 No.2 2 C x y x y > 0 x 0 x > b a dx
1 No.1 5 C 1 I III F 1 F 2 F 1 F 2 2 Φ 2 (t) = Φ 1 (t) Φ 1 (t t). = Φ 1(t) t = ( 1.5e 0.5t 2.4e 4t 2e 10t ) τ < 0 t > τ Φ 2 (t) < 0 lim t Φ 2 (t) = 0 0 < t < τ I II 0 No.2 2 C x y x y > 0 x 0 x > b a dx
Gauss Gauss ɛ 0 E ds = Q (1) xy σ (x, y, z) (2) a ρ(x, y, z) = x 2 + y 2 (r, θ, φ) (1) xy A Gauss ɛ 0 E ds = ɛ 0 EA Q = ρa ɛ 0 EA = ρea E = (ρ/ɛ 0 )e
 7 -a 7 -a February 4, 2007 1. 2. 3. 4. 1. 2. 3. 1 Gauss Gauss ɛ 0 E ds = Q (1) xy σ (x, y, z) (2) a ρ(x, y, z) = x 2 + y 2 (r, θ, φ) (1) xy A Gauss ɛ 0 E ds = ɛ 0 EA Q = ρa ɛ 0 EA = ρea E = (ρ/ɛ 0 )e z
7 -a 7 -a February 4, 2007 1. 2. 3. 4. 1. 2. 3. 1 Gauss Gauss ɛ 0 E ds = Q (1) xy σ (x, y, z) (2) a ρ(x, y, z) = x 2 + y 2 (r, θ, φ) (1) xy A Gauss ɛ 0 E ds = ɛ 0 EA Q = ρa ɛ 0 EA = ρea E = (ρ/ɛ 0 )e z
B 38 1 (x, y), (x, y, z) (x 1, x 2 ) (x 1, x 2, x 3 ) 2 : x 2 + y 2 = 1. (parameter) x = cos t, y = sin t. y = f(x) r(t) = (x(t), y(t), z(t)), a t b.
 2009 7 9 1 2 2 2 3 6 4 9 5 14 6 18 7 23 8 25 9 26 10 29 11 32 12 35 A 37 1 B 38 1 (x, y), (x, y, z) (x 1, x 2 ) (x 1, x 2, x 3 ) 2 : x 2 + y 2 = 1. (parameter) x = cos t, y = sin t. y = f(x) r(t) = (x(t),
2009 7 9 1 2 2 2 3 6 4 9 5 14 6 18 7 23 8 25 9 26 10 29 11 32 12 35 A 37 1 B 38 1 (x, y), (x, y, z) (x 1, x 2 ) (x 1, x 2, x 3 ) 2 : x 2 + y 2 = 1. (parameter) x = cos t, y = sin t. y = f(x) r(t) = (x(t),
Note.tex 2008/09/19( )
 1 20 9 19 2 1 5 1.1........................ 5 1.2............................. 8 2 9 2.1............................. 9 2.2.............................. 10 3 13 3.1.............................. 13 3.2..................................
1 20 9 19 2 1 5 1.1........................ 5 1.2............................. 8 2 9 2.1............................. 9 2.2.............................. 10 3 13 3.1.............................. 13 3.2..................................
II 2 II
 II 2 II 2005 yugami@cc.utsunomiya-u.ac.jp 2005 4 1 1 2 5 2.1.................................... 5 2.2................................. 6 2.3............................. 6 2.4.................................
II 2 II 2005 yugami@cc.utsunomiya-u.ac.jp 2005 4 1 1 2 5 2.1.................................... 5 2.2................................. 6 2.3............................. 6 2.4.................................
Quz Quz
 http://www.ppl.app.keo.ac.jp/denjk III (1969). (1977). ( ) (1999). (1981). (199). Harry Lass Vector and Tensor Analyss, McGraw-Hll, (195).. Quz Quz II E B / t = Maxwell ρ e E = (1.1) ε E= (1.) B = (1.3)
http://www.ppl.app.keo.ac.jp/denjk III (1969). (1977). ( ) (1999). (1981). (199). Harry Lass Vector and Tensor Analyss, McGraw-Hll, (195).. Quz Quz II E B / t = Maxwell ρ e E = (1.1) ε E= (1.) B = (1.3)
W u = u(x, t) u tt = a 2 u xx, a > 0 (1) D := {(x, t) : 0 x l, t 0} u (0, t) = 0, u (l, t) = 0, t 0 (2)
 3 215 4 27 1 1 u u(x, t) u tt a 2 u xx, a > (1) D : {(x, t) : x, t } u (, t), u (, t), t (2) u(x, ) f(x), u(x, ) t 2, x (3) u(x, t) X(x)T (t) u (1) 1 T (t) a 2 T (t) X (x) X(x) α (2) T (t) αa 2 T (t) (4)
3 215 4 27 1 1 u u(x, t) u tt a 2 u xx, a > (1) D : {(x, t) : x, t } u (, t), u (, t), t (2) u(x, ) f(x), u(x, ) t 2, x (3) u(x, t) X(x)T (t) u (1) 1 T (t) a 2 T (t) X (x) X(x) α (2) T (t) αa 2 T (t) (4)
The Physics of Atmospheres CAPTER :
 The Physics of Atmospheres CAPTER 4 1 4 2 41 : 2 42 14 43 17 44 25 45 27 46 3 47 31 48 32 49 34 41 35 411 36 maintex 23/11/28 The Physics of Atmospheres CAPTER 4 2 4 41 : 2 1 σ 2 (21) (22) k I = I exp(
The Physics of Atmospheres CAPTER 4 1 4 2 41 : 2 42 14 43 17 44 25 45 27 46 3 47 31 48 32 49 34 41 35 411 36 maintex 23/11/28 The Physics of Atmospheres CAPTER 4 2 4 41 : 2 1 σ 2 (21) (22) k I = I exp(
i
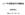 007 0 1 i 0 1 0.1..................................... 1 0.................................................. 1 0.3................................ 3 0.4............................................. 3 1
007 0 1 i 0 1 0.1..................................... 1 0.................................................. 1 0.3................................ 3 0.4............................................. 3 1
(3) (2),,. ( 20) ( s200103) 0.7 x C,, x 2 + y 2 + ax = 0 a.. D,. D, y C, C (x, y) (y 0) C m. (2) D y = y(x) (x ± y 0), (x, y) D, m, m = 1., D. (x 2 y
 [ ] 7 0.1 2 2 + y = t sin t IC ( 9) ( s090101) 0.2 y = d2 y 2, y = x 3 y + y 2 = 0 (2) y + 2y 3y = e 2x 0.3 1 ( y ) = f x C u = y x ( 15) ( s150102) [ ] y/x du x = Cexp f(u) u (2) x y = xey/x ( 16) ( s160101)
[ ] 7 0.1 2 2 + y = t sin t IC ( 9) ( s090101) 0.2 y = d2 y 2, y = x 3 y + y 2 = 0 (2) y + 2y 3y = e 2x 0.3 1 ( y ) = f x C u = y x ( 15) ( s150102) [ ] y/x du x = Cexp f(u) u (2) x y = xey/x ( 16) ( s160101)
I
 I 6 4 10 1 1 1.1............... 1 1................ 1 1.3.................... 1.4............... 1.4.1.............. 1.4................. 1.4.3........... 3 1.4.4.. 3 1.5.......... 3 1.5.1..............
I 6 4 10 1 1 1.1............... 1 1................ 1 1.3.................... 1.4............... 1.4.1.............. 1.4................. 1.4.3........... 3 1.4.4.. 3 1.5.......... 3 1.5.1..............
128 3 II S 1, S 2 Φ 1, Φ 2 Φ 1 = { B( r) n( r)}ds S 1 Φ 2 = { B( r) n( r)}ds (3.3) S 2 S S 1 +S 2 { B( r) n( r)}ds = 0 (3.4) S 1, S 2 { B( r) n( r)}ds
 127 3 II 3.1 3.1.1 Φ(t) ϕ em = dφ dt (3.1) B( r) Φ = { B( r) n( r)}ds (3.2) S S n( r) Φ 128 3 II S 1, S 2 Φ 1, Φ 2 Φ 1 = { B( r) n( r)}ds S 1 Φ 2 = { B( r) n( r)}ds (3.3) S 2 S S 1 +S 2 { B( r) n( r)}ds
127 3 II 3.1 3.1.1 Φ(t) ϕ em = dφ dt (3.1) B( r) Φ = { B( r) n( r)}ds (3.2) S S n( r) Φ 128 3 II S 1, S 2 Φ 1, Φ 2 Φ 1 = { B( r) n( r)}ds S 1 Φ 2 = { B( r) n( r)}ds (3.3) S 2 S S 1 +S 2 { B( r) n( r)}ds
IA
 IA 31 4 11 1 1 4 1.1 Planck.............................. 4 1. Bohr.................................... 5 1.3..................................... 6 8.1................................... 8....................................
IA 31 4 11 1 1 4 1.1 Planck.............................. 4 1. Bohr.................................... 5 1.3..................................... 6 8.1................................... 8....................................
() x + y + y + x dy dx = 0 () dy + xy = x dx y + x y ( 5) ( s55906) 0.7. (). 5 (). ( 6) ( s6590) 0.8 m n. 0.9 n n A. ( 6) ( s6590) f A (λ) = det(a λi)
 0. A A = 4 IC () det A () A () x + y + z = x y z X Y Z = A x y z ( 5) ( s5590) 0. a + b + c b c () a a + b + c c a b a + b + c 0 a b c () a 0 c b b c 0 a c b a 0 0. A A = 7 5 4 5 0 ( 5) ( s5590) () A ()
0. A A = 4 IC () det A () A () x + y + z = x y z X Y Z = A x y z ( 5) ( s5590) 0. a + b + c b c () a a + b + c c a b a + b + c 0 a b c () a 0 c b b c 0 a c b a 0 0. A A = 7 5 4 5 0 ( 5) ( s5590) () A ()
4 2 Rutherford 89 Rydberg λ = R ( n 2 ) n 2 n = n +,n +2, n = Lyman n =2 Balmer n =3 Paschen R Rydberg R = cm 896 Zeeman Zeeman Zeeman Lorentz
 2 Rutherford 2. Rutherford N. Bohr Rutherford 859 Kirchhoff Bunsen 86 Maxwell Maxwell 885 Balmer λ Balmer λ = 364.56 n 2 n 2 4 Lyman, Paschen 3 nm, n =3, 4, 5, 4 2 Rutherford 89 Rydberg λ = R ( n 2 ) n
2 Rutherford 2. Rutherford N. Bohr Rutherford 859 Kirchhoff Bunsen 86 Maxwell Maxwell 885 Balmer λ Balmer λ = 364.56 n 2 n 2 4 Lyman, Paschen 3 nm, n =3, 4, 5, 4 2 Rutherford 89 Rydberg λ = R ( n 2 ) n
 006 11 8 0 3 1 5 1.1..................... 5 1......................... 6 1.3.................... 6 1.4.................. 8 1.5................... 8 1.6................... 10 1.6.1......................
006 11 8 0 3 1 5 1.1..................... 5 1......................... 6 1.3.................... 6 1.4.................. 8 1.5................... 8 1.6................... 10 1.6.1......................
( ) LAN LAN tex ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1
 ( ) LAN LAN tex ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 1 4 2 17 3 Coulomb 23 4 43 5 49 6 51 7 53 8 58 9 66 10 74 11 Lienard-Wiechert potential 78 12 86 13 89 14 Laplace 114 15 138 16 152 17 162 18 166 19 191
( ) LAN LAN tex ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 1 4 2 17 3 Coulomb 23 4 43 5 49 6 51 7 53 8 58 9 66 10 74 11 Lienard-Wiechert potential 78 12 86 13 89 14 Laplace 114 15 138 16 152 17 162 18 166 19 191
S I. dy fx x fx y fx + C 3 C dy fx 4 x, y dy v C xt y C v e kt k > xt yt gt [ v dt dt v e kt xt v e kt + C k x v + C C k xt v k 3 r r + dr e kt S dt d
 S I.. http://ayapin.film.s.dendai.ac.jp/~matuda /TeX/lecture.html PDF PS.................................... 3.3.................... 9.4................5.............. 3 5. Laplace................. 5....
S I.. http://ayapin.film.s.dendai.ac.jp/~matuda /TeX/lecture.html PDF PS.................................... 3.3.................... 9.4................5.............. 3 5. Laplace................. 5....
S I. dy fx x fx y fx + C 3 C vt dy fx 4 x, y dy yt gt + Ct + C dt v e kt xt v e kt + C k x v k + C C xt v k 3 r r + dr e kt S Sr πr dt d v } dt k e kt
 S I. x yx y y, y,. F x, y, y, y,, y n http://ayapin.film.s.dendai.ac.jp/~matuda n /TeX/lecture.html PDF PS yx.................................... 3.3.................... 9.4................5..............
S I. x yx y y, y,. F x, y, y, y,, y n http://ayapin.film.s.dendai.ac.jp/~matuda n /TeX/lecture.html PDF PS yx.................................... 3.3.................... 9.4................5..............
i 18 2H 2 + O 2 2H 2 + ( ) 3K
 i 18 2H 2 + O 2 2H 2 + ( ) 3K ii 1 1 1.1.................................. 1 1.2........................................ 3 1.3......................................... 3 1.4....................................
i 18 2H 2 + O 2 2H 2 + ( ) 3K ii 1 1 1.1.................................. 1 1.2........................................ 3 1.3......................................... 3 1.4....................................
数学の基礎訓練I
 I 9 6 13 1 1 1.1............... 1 1................ 1 1.3.................... 1.4............... 1.4.1.............. 1.4................. 3 1.4.3........... 3 1.4.4.. 3 1.5.......... 3 1.5.1..............
I 9 6 13 1 1 1.1............... 1 1................ 1 1.3.................... 1.4............... 1.4.1.............. 1.4................. 3 1.4.3........... 3 1.4.4.. 3 1.5.......... 3 1.5.1..............
 ( 12 ( ( ( ( Levi-Civita grad div rot ( ( = 4 : 6 3 1 1.1 f(x n f (n (x, d n f(x (1.1 dxn f (2 (x f (x 1.1 f(x = e x f (n (x = e x d dx (fg = f g + fg (1.2 d dx d 2 dx (fg = f g + 2f g + fg 2... d n n
( 12 ( ( ( ( Levi-Civita grad div rot ( ( = 4 : 6 3 1 1.1 f(x n f (n (x, d n f(x (1.1 dxn f (2 (x f (x 1.1 f(x = e x f (n (x = e x d dx (fg = f g + fg (1.2 d dx d 2 dx (fg = f g + 2f g + fg 2... d n n
1 I 1.1 ± e = = - = C C MKSA [m], [Kg] [s] [A] 1C 1A 1 MKSA 1C 1C +q q +q q 1
![1 I 1.1 ± e = = - = C C MKSA [m], [Kg] [s] [A] 1C 1A 1 MKSA 1C 1C +q q +q q 1 1 I 1.1 ± e = = - = C C MKSA [m], [Kg] [s] [A] 1C 1A 1 MKSA 1C 1C +q q +q q 1](/thumbs/94/121802164.jpg) 1 I 1.1 ± e = = - =1.602 10 19 C C MKA [m], [Kg] [s] [A] 1C 1A 1 MKA 1C 1C +q q +q q 1 1.1 r 1,2 q 1, q 2 r 12 2 q 1, q 2 2 F 12 = k q 1q 2 r 12 2 (1.1) k 2 k 2 ( r 1 r 2 ) ( r 2 r 1 ) q 1 q 2 (q 1 q 2
1 I 1.1 ± e = = - =1.602 10 19 C C MKA [m], [Kg] [s] [A] 1C 1A 1 MKA 1C 1C +q q +q q 1 1.1 r 1,2 q 1, q 2 r 12 2 q 1, q 2 2 F 12 = k q 1q 2 r 12 2 (1.1) k 2 k 2 ( r 1 r 2 ) ( r 2 r 1 ) q 1 q 2 (q 1 q 2
 20 4 20 i 1 1 1.1............................ 1 1.2............................ 4 2 11 2.1................... 11 2.2......................... 11 2.3....................... 19 3 25 3.1.............................
20 4 20 i 1 1 1.1............................ 1 1.2............................ 4 2 11 2.1................... 11 2.2......................... 11 2.3....................... 19 3 25 3.1.............................
18 ( ) I II III A B C(100 ) 1, 2, 3, 5 I II A B (100 ) 1, 2, 3 I II A B (80 ) 6 8 I II III A B C(80 ) 1 n (1 + x) n (1) n C 1 + n C
 8 ( ) 8 5 4 I II III A B C( ),,, 5 I II A B ( ),, I II A B (8 ) 6 8 I II III A B C(8 ) n ( + x) n () n C + n C + + n C n = 7 n () 7 9 C : y = x x A(, 6) () A C () C P AP Q () () () 4 A(,, ) B(,, ) C(,,
8 ( ) 8 5 4 I II III A B C( ),,, 5 I II A B ( ),, I II A B (8 ) 6 8 I II III A B C(8 ) n ( + x) n () n C + n C + + n C n = 7 n () 7 9 C : y = x x A(, 6) () A C () C P AP Q () () () 4 A(,, ) B(,, ) C(,,
G:/SHIRAFUJI/テキスト類/EM1999/ALL/em99ps.dvi
 1999 1999 12 17 Contents 1 9 1.1........................ 9 1.2 (Cartesian )..................... 9 1.3........................ 10 1.4............................. 11 1.5............................. 12
1999 1999 12 17 Contents 1 9 1.1........................ 9 1.2 (Cartesian )..................... 9 1.3........................ 10 1.4............................. 11 1.5............................. 12
振動と波動
 Report JS0.5 J Simplicity February 4, 2012 1 J Simplicity HOME http://www.jsimplicity.com/ Preface 2 Report 2 Contents I 5 1 6 1.1..................................... 6 1.2 1 1:................ 7 1.3
Report JS0.5 J Simplicity February 4, 2012 1 J Simplicity HOME http://www.jsimplicity.com/ Preface 2 Report 2 Contents I 5 1 6 1.1..................................... 6 1.2 1 1:................ 7 1.3
 B 1 B.1.......................... 1 B.1.1................. 1 B.1.2................. 2 B.2........................... 5 B.2.1.......................... 5 B.2.2.................. 6 B.2.3..................
B 1 B.1.......................... 1 B.1.1................. 1 B.1.2................. 2 B.2........................... 5 B.2.1.......................... 5 B.2.2.................. 6 B.2.3..................
sin.eps
 9 ( 9 4 7 ) : 3. 3 5 ( ). 3 ( ) (Maxwell).3 (= ) 4.4 x y(x) dy =3 y(x) =3x dx y(x) =3x + y(x) =3x + y(x) =3x + /m OK.5 .6. 5 3 ( ).6 5 5 ( ) +3 m+3kg m 3kg ( ) I(MKA ) m,kg,s(sec),a 4 4 ( ) m kg s 3 A
9 ( 9 4 7 ) : 3. 3 5 ( ). 3 ( ) (Maxwell).3 (= ) 4.4 x y(x) dy =3 y(x) =3x dx y(x) =3x + y(x) =3x + y(x) =3x + /m OK.5 .6. 5 3 ( ).6 5 5 ( ) +3 m+3kg m 3kg ( ) I(MKA ) m,kg,s(sec),a 4 4 ( ) m kg s 3 A
,. Black-Scholes u t t, x c u 0 t, x x u t t, x c u t, x x u t t, x + σ x u t, x + rx ut, x rux, t 0 x x,,.,. Step 3, 7,,, Step 6., Step 4,. Step 5,,.
 9 α ν β Ξ ξ Γ γ o δ Π π ε ρ ζ Σ σ η τ Θ θ Υ υ ι Φ φ κ χ Λ λ Ψ ψ µ Ω ω Def, Prop, Th, Lem, Note, Remark, Ex,, Proof, R, N, Q, C [a, b {x R : a x b} : a, b {x R : a < x < b} : [a, b {x R : a x < b} : a,
9 α ν β Ξ ξ Γ γ o δ Π π ε ρ ζ Σ σ η τ Θ θ Υ υ ι Φ φ κ χ Λ λ Ψ ψ µ Ω ω Def, Prop, Th, Lem, Note, Remark, Ex,, Proof, R, N, Q, C [a, b {x R : a x b} : a, b {x R : a < x < b} : [a, b {x R : a x < b} : a,
() (, y) E(, y) () E(, y) (3) q ( ) () E(, y) = k q q (, y) () E(, y) = k r r (3).3 [.7 ] f y = f y () f(, y) = y () f(, y) = tan y y ( ) () f y = f y
![() (, y) E(, y) () E(, y) (3) q ( ) () E(, y) = k q q (, y) () E(, y) = k r r (3).3 [.7 ] f y = f y () f(, y) = y () f(, y) = tan y y ( ) () f y = f y () (, y) E(, y) () E(, y) (3) q ( ) () E(, y) = k q q (, y) () E(, y) = k r r (3).3 [.7 ] f y = f y () f(, y) = y () f(, y) = tan y y ( ) () f y = f y](/thumbs/85/92979039.jpg) 5. [. ] z = f(, y) () z = 3 4 y + y + 3y () z = y (3) z = sin( y) (4) z = cos y (5) z = 4y (6) z = tan y (7) z = log( + y ) (8) z = tan y + + y ( ) () z = 3 8y + y z y = 4 + + 6y () z = y z y = (3) z =
5. [. ] z = f(, y) () z = 3 4 y + y + 3y () z = y (3) z = sin( y) (4) z = cos y (5) z = 4y (6) z = tan y (7) z = log( + y ) (8) z = tan y + + y ( ) () z = 3 8y + y z y = 4 + + 6y () z = y z y = (3) z =
b3e2003.dvi
 15 II 5 5.1 (1) p, q p = (x + 2y, xy, 1), q = (x 2 + 3y 2, xyz, ) (i) p rotq (ii) p gradq D (2) a, b rot(a b) div [11, p.75] (3) (i) f f grad f = 1 2 grad( f 2) (ii) f f gradf 1 2 grad ( f 2) rotf 5.2
15 II 5 5.1 (1) p, q p = (x + 2y, xy, 1), q = (x 2 + 3y 2, xyz, ) (i) p rotq (ii) p gradq D (2) a, b rot(a b) div [11, p.75] (3) (i) f f grad f = 1 2 grad( f 2) (ii) f f gradf 1 2 grad ( f 2) rotf 5.2
2.5 (Gauss) (flux) v(r)( ) S n S v n v n (1) v n S = v n S = v S, n S S. n n S v S v Minoru TANAKA (Osaka Univ.) I(2012), Sec p. 1/30
 2.5 (Gauss) 2.5.1 (flux) v(r)( ) n v n v n (1) v n = v n = v, n. n n v v I(2012), ec. 2. 5 p. 1/30 i (2) lim v(r i ) i = v(r) d. i 0 i (flux) I(2012), ec. 2. 5 p. 2/30 2.5.2 ( ) ( ) q 1 r 2 E 2 q r 1 E
2.5 (Gauss) 2.5.1 (flux) v(r)( ) n v n v n (1) v n = v n = v, n. n n v v I(2012), ec. 2. 5 p. 1/30 i (2) lim v(r i ) i = v(r) d. i 0 i (flux) I(2012), ec. 2. 5 p. 2/30 2.5.2 ( ) ( ) q 1 r 2 E 2 q r 1 E
V(x) m e V 0 cos x π x π V(x) = x < π, x > π V 0 (i) x = 0 (V(x) V 0 (1 x 2 /2)) n n d 2 f dξ 2ξ d f 2 dξ + 2n f = 0 H n (ξ) (ii) H
 199 1 1 199 1 1. Vx) m e V cos x π x π Vx) = x < π, x > π V i) x = Vx) V 1 x /)) n n d f dξ ξ d f dξ + n f = H n ξ) ii) H n ξ) = 1) n expξ ) dn dξ n exp ξ )) H n ξ)h m ξ) exp ξ )dξ = π n n!δ n,m x = Vx)
199 1 1 199 1 1. Vx) m e V cos x π x π Vx) = x < π, x > π V i) x = Vx) V 1 x /)) n n d f dξ ξ d f dξ + n f = H n ξ) ii) H n ξ) = 1) n expξ ) dn dξ n exp ξ )) H n ξ)h m ξ) exp ξ )dξ = π n n!δ n,m x = Vx)
. ev=,604k m 3 Debye ɛ 0 kt e λ D = n e n e Ze 4 ln Λ ν ei = 5.6π / ɛ 0 m/ e kt e /3 ν ei v e H + +e H ev Saha x x = 3/ πme kt g i g e n
 003...............................3 Debye................. 3.4................ 3 3 3 3. Larmor Cyclotron... 3 3................ 4 3.3.......... 4 3.3............ 4 3.3...... 4 3.3.3............ 5 3.4.........
003...............................3 Debye................. 3.4................ 3 3 3 3. Larmor Cyclotron... 3 3................ 4 3.3.......... 4 3.3............ 4 3.3...... 4 3.3.3............ 5 3.4.........
微分積分 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. このサンプルページの内容は, 初版 1 刷発行時のものです.
 微分積分 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. ttp://www.morikita.co.jp/books/mid/00571 このサンプルページの内容は, 初版 1 刷発行時のものです. i ii 014 10 iii [note] 1 3 iv 4 5 3 6 4 x 0 sin x x 1 5 6 z = f(x, y) 1 y = f(x)
微分積分 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. ttp://www.morikita.co.jp/books/mid/00571 このサンプルページの内容は, 初版 1 刷発行時のものです. i ii 014 10 iii [note] 1 3 iv 4 5 3 6 4 x 0 sin x x 1 5 6 z = f(x, y) 1 y = f(x)
 (u(x)v(x)) = u (x)v(x) + u(x)v (x) ( ) u(x) = u (x)v(x) u(x)v (x) v(x) v(x) 2 y = g(t), t = f(x) y = g(f(x)) dy dx dy dx = dy dt dt dx., y, f, g y = f (g(x))g (x). ( (f(g(x)). ). [ ] y = e ax+b (a, b )
(u(x)v(x)) = u (x)v(x) + u(x)v (x) ( ) u(x) = u (x)v(x) u(x)v (x) v(x) v(x) 2 y = g(t), t = f(x) y = g(f(x)) dy dx dy dx = dy dt dt dx., y, f, g y = f (g(x))g (x). ( (f(g(x)). ). [ ] y = e ax+b (a, b )
No δs δs = r + δr r = δr (3) δs δs = r r = δr + u(r + δr, t) u(r, t) (4) δr = (δx, δy, δz) u i (r + δr, t) u i (r, t) = u i x j δx j (5) δs 2
 No.2 1 2 2 δs δs = r + δr r = δr (3) δs δs = r r = δr + u(r + δr, t) u(r, t) (4) δr = (δx, δy, δz) u i (r + δr, t) u i (r, t) = u i δx j (5) δs 2 = δx i δx i + 2 u i δx i δx j = δs 2 + 2s ij δx i δx j
No.2 1 2 2 δs δs = r + δr r = δr (3) δs δs = r r = δr + u(r + δr, t) u(r, t) (4) δr = (δx, δy, δz) u i (r + δr, t) u i (r, t) = u i δx j (5) δs 2 = δx i δx i + 2 u i δx i δx j = δs 2 + 2s ij δx i δx j
1 variation 1.1 imension unit L m M kg T s Q C QT 1 A = C s 1 MKSA F = ma N N = kg m s 1.1 J E = 1 mv W = F x J = kg m s 1 = N m 1.
 1.1 1. 1.3.1..3.4 3.1 3. 3.3 4.1 4. 4.3 5.1 5. 5.3 6.1 6. 6.3 7.1 7. 7.3 1 1 variation 1.1 imension unit L m M kg T s Q C QT 1 A = C s 1 MKSA F = ma N N = kg m s 1.1 J E = 1 mv W = F x J = kg m s 1 = N
1.1 1. 1.3.1..3.4 3.1 3. 3.3 4.1 4. 4.3 5.1 5. 5.3 6.1 6. 6.3 7.1 7. 7.3 1 1 variation 1.1 imension unit L m M kg T s Q C QT 1 A = C s 1 MKSA F = ma N N = kg m s 1.1 J E = 1 mv W = F x J = kg m s 1 = N
1 filename=mathformula tex 1 ax 2 + bx + c = 0, x = b ± b 2 4ac, (1.1) 2a x 1 + x 2 = b a, x 1x 2 = c a, (1.2) ax 2 + 2b x + c = 0, x = b ± b 2
 filename=mathformula58.tex ax + bx + c =, x = b ± b 4ac, (.) a x + x = b a, x x = c a, (.) ax + b x + c =, x = b ± b ac. a (.3). sin(a ± B) = sin A cos B ± cos A sin B, (.) cos(a ± B) = cos A cos B sin
filename=mathformula58.tex ax + bx + c =, x = b ± b 4ac, (.) a x + x = b a, x x = c a, (.) ax + b x + c =, x = b ± b ac. a (.3). sin(a ± B) = sin A cos B ± cos A sin B, (.) cos(a ± B) = cos A cos B sin
7. y fx, z gy z gfx dz dx dz dy dy dx. g f a g bf a b fa 7., chain ule Ω, D R n, R m a Ω, f : Ω R m, g : D R l, fω D, b fa, f a g b g f a g f a g bf a
 9 203 6 7 WWW http://www.math.meiji.ac.jp/~mk/lectue/tahensuu-203/ 2 8 8 7. 7 7. y fx, z gy z gfx dz dx dz dy dy dx. g f a g bf a b fa 7., chain ule Ω, D R n, R m a Ω, f : Ω R m, g : D R l, fω D, b fa,
9 203 6 7 WWW http://www.math.meiji.ac.jp/~mk/lectue/tahensuu-203/ 2 8 8 7. 7 7. y fx, z gy z gfx dz dx dz dy dy dx. g f a g bf a b fa 7., chain ule Ω, D R n, R m a Ω, f : Ω R m, g : D R l, fω D, b fa,
 215 11 13 1 2 1.1....................... 2 1.2.................... 2 1.3..................... 2 1.4...................... 3 1.5............... 3 1.6........................... 4 1.7.................. 4
215 11 13 1 2 1.1....................... 2 1.2.................... 2 1.3..................... 2 1.4...................... 3 1.5............... 3 1.6........................... 4 1.7.................. 4
I 1
 I 1 1 1.1 1. 3 m = 3 1 7 µm. cm = 1 4 km 3. 1 m = 1 1 5 cm 4. 5 cm 3 = 5 1 15 km 3 5. 1 = 36 6. 1 = 8.64 1 4 7. 1 = 3.15 1 7 1 =3 1 7 1 3 π 1. 1. 1 m + 1 cm = 1.1 m. 1 hr + 64 sec = 1 4 sec 3. 3. 1 5 kg
I 1 1 1.1 1. 3 m = 3 1 7 µm. cm = 1 4 km 3. 1 m = 1 1 5 cm 4. 5 cm 3 = 5 1 15 km 3 5. 1 = 36 6. 1 = 8.64 1 4 7. 1 = 3.15 1 7 1 =3 1 7 1 3 π 1. 1. 1 m + 1 cm = 1.1 m. 1 hr + 64 sec = 1 4 sec 3. 3. 1 5 kg
http://www2.math.kyushu-u.ac.jp/~hara/lectures/lectures-j.html 2 N(ε 1 ) N(ε 2 ) ε 1 ε 2 α ε ε 2 1 n N(ɛ) N ɛ ɛ- (1.1.3) n > N(ɛ) a n α < ɛ n N(ɛ) a n
 http://www2.math.kyushu-u.ac.jp/~hara/lectures/lectures-j.html 1 1 1.1 ɛ-n 1 ɛ-n lim n a n = α n a n α 2 lim a n = 1 n a k n n k=1 1.1.7 ɛ-n 1.1.1 a n α a n n α lim n a n = α ɛ N(ɛ) n > N(ɛ) a n α < ɛ
http://www2.math.kyushu-u.ac.jp/~hara/lectures/lectures-j.html 1 1 1.1 ɛ-n 1 ɛ-n lim n a n = α n a n α 2 lim a n = 1 n a k n n k=1 1.1.7 ɛ-n 1.1.1 a n α a n n α lim n a n = α ɛ N(ɛ) n > N(ɛ) a n α < ɛ
meiji_resume_1.PDF
 β β β (q 1,q,..., q n ; p 1, p,..., p n ) H(q 1,q,..., q n ; p 1, p,..., p n ) Hψ = εψ ε k = k +1/ ε k = k(k 1) (x, y, z; p x, p y, p z ) (r; p r ), (θ; p θ ), (ϕ; p ϕ ) ε k = 1/ k p i dq i E total = E
β β β (q 1,q,..., q n ; p 1, p,..., p n ) H(q 1,q,..., q n ; p 1, p,..., p n ) Hψ = εψ ε k = k +1/ ε k = k(k 1) (x, y, z; p x, p y, p z ) (r; p r ), (θ; p θ ), (ϕ; p ϕ ) ε k = 1/ k p i dq i E total = E
d (K + U) = v [ma F(r)] = (2.4.4) t = t r(t ) = r t 1 r(t 1 ) = r 1 U(r 1 ) U(r ) = t1 t du t1 = t F(r(t)) dr(t) r1 = F dr (2.4.5) r F 2 F ( F) r A r
![d (K + U) = v [ma F(r)] = (2.4.4) t = t r(t ) = r t 1 r(t 1 ) = r 1 U(r 1 ) U(r ) = t1 t du t1 = t F(r(t)) dr(t) r1 = F dr (2.4.5) r F 2 F ( F) r A r d (K + U) = v [ma F(r)] = (2.4.4) t = t r(t ) = r t 1 r(t 1 ) = r 1 U(r 1 ) U(r ) = t1 t du t1 = t F(r(t)) dr(t) r1 = F dr (2.4.5) r F 2 F ( F) r A r](/thumbs/85/92098187.jpg) 2.4 ( ) U(r) ( ) ( ) U F(r) = x, U y, U = U(r) (2.4.1) z 2 1 K = mv 2 /2 dk = d ( ) 1 2 mv2 = mv dv = v (ma) (2.4.2) ( ) U(r(t)) r(t) r(t) + dr(t) du du = U(r(t) + dr(t)) U(r(t)) = U x = U(r(t)) dr(t)
2.4 ( ) U(r) ( ) ( ) U F(r) = x, U y, U = U(r) (2.4.1) z 2 1 K = mv 2 /2 dk = d ( ) 1 2 mv2 = mv dv = v (ma) (2.4.2) ( ) U(r(t)) r(t) r(t) + dr(t) du du = U(r(t) + dr(t)) U(r(t)) = U x = U(r(t)) dr(t)
ma22-9 u ( v w) = u v w sin θê = v w sin θ u cos φ = = 2.3 ( a b) ( c d) = ( a c)( b d) ( a d)( b c) ( a b) ( c d) = (a 2 b 3 a 3 b 2 )(c 2 d 3 c 3 d
 A 2. x F (t) =f sin ωt x(0) = ẋ(0) = 0 ω θ sin θ θ 3! θ3 v = f mω cos ωt x = f mω (t sin ωt) ω t 0 = f ( cos ωt) mω x ma2-2 t ω x f (t mω ω (ωt ) 6 (ωt)3 = f 6m ωt3 2.2 u ( v w) = v ( w u) = w ( u v) ma22-9
A 2. x F (t) =f sin ωt x(0) = ẋ(0) = 0 ω θ sin θ θ 3! θ3 v = f mω cos ωt x = f mω (t sin ωt) ω t 0 = f ( cos ωt) mω x ma2-2 t ω x f (t mω ω (ωt ) 6 (ωt)3 = f 6m ωt3 2.2 u ( v w) = v ( w u) = w ( u v) ma22-9
y π π O π x 9 s94.5 y dy dx. y = x + 3 y = x logx + 9 s9.6 z z x, z y. z = xy + y 3 z = sinx y 9 s x dx π x cos xdx 9 s93.8 a, fx = e x ax,. a =
 [ ] 9 IC. dx = 3x 4y dt dy dt = x y u xt = expλt u yt λ u u t = u u u + u = xt yt 6 3. u = x, y, z = x + y + z u u 9 s9 grad u ux, y, z = c c : grad u = u x i + u y j + u k i, j, k z x, y, z grad u v =
[ ] 9 IC. dx = 3x 4y dt dy dt = x y u xt = expλt u yt λ u u t = u u u + u = xt yt 6 3. u = x, y, z = x + y + z u u 9 s9 grad u ux, y, z = c c : grad u = u x i + u y j + u k i, j, k z x, y, z grad u v =
.5 z = a + b + c n.6 = a sin t y = b cos t dy d a e e b e + e c e e e + e 3 s36 3 a + y = a, b > b 3 s363.7 y = + 3 y = + 3 s364.8 cos a 3 s365.9 y =,
 [ ] IC. r, θ r, θ π, y y = 3 3 = r cos θ r sin θ D D = {, y ; y }, y D r, θ ep y yddy D D 9 s96. d y dt + 3dy + y = cos t dt t = y = e π + e π +. t = π y =.9 s6.3 d y d + dy d + y = y =, dy d = 3 a, b
[ ] IC. r, θ r, θ π, y y = 3 3 = r cos θ r sin θ D D = {, y ; y }, y D r, θ ep y yddy D D 9 s96. d y dt + 3dy + y = cos t dt t = y = e π + e π +. t = π y =.9 s6.3 d y d + dy d + y = y =, dy d = 3 a, b
K E N Z OU
 K E N Z OU 11 1 1 1.1..................................... 1.1.1............................ 1.1..................................................................................... 4 1.........................................
K E N Z OU 11 1 1 1.1..................................... 1.1.1............................ 1.1..................................................................................... 4 1.........................................
 IA hara@math.kyushu-u.ac.jp Last updated: January,......................................................................................................................................................................................
IA hara@math.kyushu-u.ac.jp Last updated: January,......................................................................................................................................................................................
sec13.dvi
 13 13.1 O r F R = m d 2 r dt 2 m r m = F = m r M M d2 R dt 2 = m d 2 r dt 2 = F = F (13.1) F O L = r p = m r ṙ dl dt = m ṙ ṙ + m r r = r (m r ) = r F N. (13.2) N N = R F 13.2 O ˆn ω L O r u u = ω r 1 1:
13 13.1 O r F R = m d 2 r dt 2 m r m = F = m r M M d2 R dt 2 = m d 2 r dt 2 = F = F (13.1) F O L = r p = m r ṙ dl dt = m ṙ ṙ + m r r = r (m r ) = r F N. (13.2) N N = R F 13.2 O ˆn ω L O r u u = ω r 1 1:
2.4 ( ) ( B ) A B F (1) W = B A F dr. A F q dr f(x,y,z) A B Γ( ) Minoru TANAKA (Osaka Univ.) I(2011), Sec p. 1/30
 2.4 ( ) 2.4.1 ( B ) A B F (1) W = B A F dr. A F q dr f(x,y,z) A B Γ( ) I(2011), Sec. 2. 4 p. 1/30 (2) Γ f dr lim f i r i. r i 0 i f i i f r i i i+1 (1) n i r i (3) F dr = lim F i n i r i. Γ r i 0 i n i
2.4 ( ) 2.4.1 ( B ) A B F (1) W = B A F dr. A F q dr f(x,y,z) A B Γ( ) I(2011), Sec. 2. 4 p. 1/30 (2) Γ f dr lim f i r i. r i 0 i f i i f r i i i+1 (1) n i r i (3) F dr = lim F i n i r i. Γ r i 0 i n i
dynamics-solution2.dvi
 1 1. (1) a + b = i +3i + k () a b =5i 5j +3k (3) a b =1 (4) a b = 7i j +1k. a = 14 l =/ 14, m=1/ 14, n=3/ 14 3. 4. 5. df (t) d [a(t)e(t)] =ti +9t j +4k, = d a(t) d[a(t)e(t)] e(t)+ da(t) d f (t) =i +18tj
1 1. (1) a + b = i +3i + k () a b =5i 5j +3k (3) a b =1 (4) a b = 7i j +1k. a = 14 l =/ 14, m=1/ 14, n=3/ 14 3. 4. 5. df (t) d [a(t)e(t)] =ti +9t j +4k, = d a(t) d[a(t)e(t)] e(t)+ da(t) d f (t) =i +18tj
1 (Berry,1975) 2-6 p (S πr 2 )p πr 2 p 2πRγ p p = 2γ R (2.5).1-1 : : : : ( ).2 α, β α, β () X S = X X α X β (.1) 1 2
 2005 9/8-11 2 2.2 ( 2-5) γ ( ) γ cos θ 2πr πρhr 2 g h = 2γ cos θ ρgr (2.1) γ = ρgrh (2.2) 2 cos θ θ cos θ = 1 (2.2) γ = 1 ρgrh (2.) 2 2. p p ρgh p ( ) p p = p ρgh (2.) h p p = 2γ r 1 1 (Berry,1975) 2-6
2005 9/8-11 2 2.2 ( 2-5) γ ( ) γ cos θ 2πr πρhr 2 g h = 2γ cos θ ρgr (2.1) γ = ρgrh (2.2) 2 cos θ θ cos θ = 1 (2.2) γ = 1 ρgrh (2.) 2 2. p p ρgh p ( ) p p = p ρgh (2.) h p p = 2γ r 1 1 (Berry,1975) 2-6
II (10 4 ) 1. p (x, y) (a, b) ε(x, y; a, b) 0 f (x, y) f (a, b) A, B (6.5) y = b f (x, b) f (a, b) x a = A + ε(x, b; a, b) x a 2 x a 0 A = f x (
 II (1 4 ) 1. p.13 1 (x, y) (a, b) ε(x, y; a, b) f (x, y) f (a, b) A, B (6.5) y = b f (x, b) f (a, b) x a = A + ε(x, b; a, b) x a x a A = f x (a, b) y x 3 3y 3 (x, y) (, ) f (x, y) = x + y (x, y) = (, )
II (1 4 ) 1. p.13 1 (x, y) (a, b) ε(x, y; a, b) f (x, y) f (a, b) A, B (6.5) y = b f (x, b) f (a, b) x a = A + ε(x, b; a, b) x a x a A = f x (a, b) y x 3 3y 3 (x, y) (, ) f (x, y) = x + y (x, y) = (, )
: 2005 ( ρ t +dv j =0 r m m r = e E( r +e r B( r T 208 T = d E j 207 ρ t = = = e t δ( r r (t e r r δ( r r (t e r ( r δ( r r (t dv j =
 72 Maxwell. Maxwell e r ( =,,N Maxwell rot E + B t = 0 rot H D t = j dv D = ρ dv B = 0 D = ɛ 0 E H = μ 0 B ρ( r = j( r = N e δ( r r = N e r δ( r r = : 2005 ( 2006.8.22 73 207 ρ t +dv j =0 r m m r = e E(
72 Maxwell. Maxwell e r ( =,,N Maxwell rot E + B t = 0 rot H D t = j dv D = ρ dv B = 0 D = ɛ 0 E H = μ 0 B ρ( r = j( r = N e δ( r r = N e r δ( r r = : 2005 ( 2006.8.22 73 207 ρ t +dv j =0 r m m r = e E(
tomocci ,. :,,,, Lie,,,, Einstein, Newton. 1 M n C. s, M p. M f, p d ds f = dxµ p ds µ f p, X p = X µ µ p = dxµ ds µ p. µ, X µ.,. p,. T M p.
 tomocci 18 7 5...,. :,,,, Lie,,,, Einstein, Newton. 1 M n C. s, M p. M f, p d ds f = dxµ p ds µ f p, X p = X µ µ p = dxµ ds µ p. µ, X µ.,. p,. T M p. M F (M), X(F (M)).. T M p e i = e µ i µ. a a = a i
tomocci 18 7 5...,. :,,,, Lie,,,, Einstein, Newton. 1 M n C. s, M p. M f, p d ds f = dxµ p ds µ f p, X p = X µ µ p = dxµ ds µ p. µ, X µ.,. p,. T M p. M F (M), X(F (M)).. T M p e i = e µ i µ. a a = a i
2 Chapter 4 (f4a). 2. (f4cone) ( θ) () g M. 2. (f4b) T M L P a θ (f4eki) ρ H A a g. v ( ) 2. H(t) ( )
 http://astr-www.kj.yamagata-u.ac.jp/~shibata f4a f4b 2 f4cone f4eki f4end 4 f5meanfp f6coin () f6a f7a f7b f7d f8a f8b f9a f9b f9c f9kep f0a f0bt version feqmo fvec4 fvec fvec6 fvec2 fvec3 f3a (-D) f3b
http://astr-www.kj.yamagata-u.ac.jp/~shibata f4a f4b 2 f4cone f4eki f4end 4 f5meanfp f6coin () f6a f7a f7b f7d f8a f8b f9a f9b f9c f9kep f0a f0bt version feqmo fvec4 fvec fvec6 fvec2 fvec3 f3a (-D) f3b
I A A441 : April 21, 2014 Version : Kawahira, Tomoki TA (Kondo, Hirotaka ) Google
 I4 - : April, 4 Version :. Kwhir, Tomoki TA (Kondo, Hirotk) Google http://www.mth.ngoy-u.c.jp/~kwhir/courses/4s-biseki.html pdf 4 4 4 4 8 e 5 5 9 etc. 5 6 6 6 9 n etc. 6 6 6 3 6 3 7 7 etc 7 4 7 7 8 5 59
I4 - : April, 4 Version :. Kwhir, Tomoki TA (Kondo, Hirotk) Google http://www.mth.ngoy-u.c.jp/~kwhir/courses/4s-biseki.html pdf 4 4 4 4 8 e 5 5 9 etc. 5 6 6 6 9 n etc. 6 6 6 3 6 3 7 7 etc 7 4 7 7 8 5 59
4. ϵ(ν, T ) = c 4 u(ν, T ) ϵ(ν, T ) T ν π4 Planck dx = 0 e x 1 15 U(T ) x 3 U(T ) = σt 4 Stefan-Boltzmann σ 2π5 k 4 15c 2 h 3 = W m 2 K 4 5.
 A 1. Boltzmann Planck u(ν, T )dν = 8πh ν 3 c 3 kt 1 dν h 6.63 10 34 J s Planck k 1.38 10 23 J K 1 Boltzmann u(ν, T ) T ν e hν c = 3 10 8 m s 1 2. Planck λ = c/ν Rayleigh-Jeans u(ν, T )dν = 8πν2 kt dν c
A 1. Boltzmann Planck u(ν, T )dν = 8πh ν 3 c 3 kt 1 dν h 6.63 10 34 J s Planck k 1.38 10 23 J K 1 Boltzmann u(ν, T ) T ν e hν c = 3 10 8 m s 1 2. Planck λ = c/ν Rayleigh-Jeans u(ν, T )dν = 8πν2 kt dν c
II No.01 [n/2] [1]H n (x) H n (x) = ( 1) r n! r!(n 2r)! (2x)n 2r. r=0 [2]H n (x) n,, H n ( x) = ( 1) n H n (x). [3] H n (x) = ( 1) n dn x2 e dx n e x2
![II No.01 [n/2] [1]H n (x) H n (x) = ( 1) r n! r!(n 2r)! (2x)n 2r. r=0 [2]H n (x) n,, H n ( x) = ( 1) n H n (x). [3] H n (x) = ( 1) n dn x2 e dx n e x2 II No.01 [n/2] [1]H n (x) H n (x) = ( 1) r n! r!(n 2r)! (2x)n 2r. r=0 [2]H n (x) n,, H n ( x) = ( 1) n H n (x). [3] H n (x) = ( 1) n dn x2 e dx n e x2](/thumbs/101/149159646.jpg) II No.1 [n/] [1]H n x) H n x) = 1) r n! r!n r)! x)n r r= []H n x) n,, H n x) = 1) n H n x) [3] H n x) = 1) n dn x e dx n e x [4] H n+1 x) = xh n x) nh n 1 x) ) d dx x H n x) = H n+1 x) d dx H nx) = nh
II No.1 [n/] [1]H n x) H n x) = 1) r n! r!n r)! x)n r r= []H n x) n,, H n x) = 1) n H n x) [3] H n x) = 1) n dn x e dx n e x [4] H n+1 x) = xh n x) nh n 1 x) ) d dx x H n x) = H n+1 x) d dx H nx) = nh
x = a 1 f (a r, a + r) f(a) r a f f(a) 2 2. (a, b) 2 f (a, b) r f(a, b) r (a, b) f f(a, b)
 2011 I 2 II III 17, 18, 19 7 7 1 2 2 2 1 2 1 1 1.1.............................. 2 1.2 : 1.................... 4 1.2.1 2............................... 5 1.3 : 2.................... 5 1.3.1 2.....................................
2011 I 2 II III 17, 18, 19 7 7 1 2 2 2 1 2 1 1 1.1.............................. 2 1.2 : 1.................... 4 1.2.1 2............................... 5 1.3 : 2.................... 5 1.3.1 2.....................................
 25 7 18 1 1 1.1 v.s............................. 1 1.1.1.................................. 1 1.1.2................................. 1 1.1.3.................................. 3 1.2................... 3
25 7 18 1 1 1.1 v.s............................. 1 1.1.1.................................. 1 1.1.2................................. 1 1.1.3.................................. 3 1.2................... 3
曲面のパラメタ表示と接線ベクトル
 L11(2011-07-06 Wed) :Time-stamp: 2011-07-06 Wed 13:08 JST hig 1,,. 2. http://hig3.net () (L11) 2011-07-06 Wed 1 / 18 ( ) 1 V = (xy2 ) x + (2y) y = y 2 + 2. 2 V = 4y., D V ds = 2 2 ( ) 4 x 2 4y dy dx =
L11(2011-07-06 Wed) :Time-stamp: 2011-07-06 Wed 13:08 JST hig 1,,. 2. http://hig3.net () (L11) 2011-07-06 Wed 1 / 18 ( ) 1 V = (xy2 ) x + (2y) y = y 2 + 2. 2 V = 4y., D V ds = 2 2 ( ) 4 x 2 4y dy dx =
I A A441 : April 15, 2013 Version : 1.1 I Kawahira, Tomoki TA (Shigehiro, Yoshida )
 I013 00-1 : April 15, 013 Version : 1.1 I Kawahira, Tomoki TA (Shigehiro, Yoshida) http://www.math.nagoya-u.ac.jp/~kawahira/courses/13s-tenbou.html pdf * 4 15 4 5 13 e πi = 1 5 0 5 7 3 4 6 3 6 10 6 17
I013 00-1 : April 15, 013 Version : 1.1 I Kawahira, Tomoki TA (Shigehiro, Yoshida) http://www.math.nagoya-u.ac.jp/~kawahira/courses/13s-tenbou.html pdf * 4 15 4 5 13 e πi = 1 5 0 5 7 3 4 6 3 6 10 6 17
( ; ) C. H. Scholz, The Mechanics of Earthquakes and Faulting : - ( ) σ = σ t sin 2π(r a) λ dσ d(r a) =
 1 9 8 1 1 1 ; 1 11 16 C. H. Scholz, The Mechanics of Earthquakes and Faulting 1. 1.1 1.1.1 : - σ = σ t sin πr a λ dσ dr a = E a = π λ σ πr a t cos λ 1 r a/λ 1 cos 1 E: σ t = Eλ πa a λ E/π γ : λ/ 3 γ =
1 9 8 1 1 1 ; 1 11 16 C. H. Scholz, The Mechanics of Earthquakes and Faulting 1. 1.1 1.1.1 : - σ = σ t sin πr a λ dσ dr a = E a = π λ σ πr a t cos λ 1 r a/λ 1 cos 1 E: σ t = Eλ πa a λ E/π γ : λ/ 3 γ =
Part () () Γ Part ,
 Contents a 6 6 6 6 6 6 6 7 7. 8.. 8.. 8.3. 8 Part. 9. 9.. 9.. 3. 3.. 3.. 3 4. 5 4.. 5 4.. 9 4.3. 3 Part. 6 5. () 6 5.. () 7 5.. 9 5.3. Γ 3 6. 3 6.. 3 6.. 3 6.3. 33 Part 3. 34 7. 34 7.. 34 7.. 34 8. 35
Contents a 6 6 6 6 6 6 6 7 7. 8.. 8.. 8.3. 8 Part. 9. 9.. 9.. 3. 3.. 3.. 3 4. 5 4.. 5 4.. 9 4.3. 3 Part. 6 5. () 6 5.. () 7 5.. 9 5.3. Γ 3 6. 3 6.. 3 6.. 3 6.3. 33 Part 3. 34 7. 34 7.. 34 7.. 34 8. 35
最新耐震構造解析 ( 第 3 版 ) サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. このサンプルページの内容は, 第 3 版 1 刷発行時のものです.
 最新耐震構造解析 ( 第 3 版 ) サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/052093 このサンプルページの内容は, 第 3 版 1 刷発行時のものです. i 3 10 3 2000 2007 26 8 2 SI SI 20 1996 2000 SI 15 3 ii 1 56 6
最新耐震構造解析 ( 第 3 版 ) サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/052093 このサンプルページの内容は, 第 3 版 1 刷発行時のものです. i 3 10 3 2000 2007 26 8 2 SI SI 20 1996 2000 SI 15 3 ii 1 56 6
 A 2008 10 (2010 4 ) 1 1 1.1................................. 1 1.2..................................... 1 1.3............................ 3 1.3.1............................. 3 1.3.2..................................
A 2008 10 (2010 4 ) 1 1 1.1................................. 1 1.2..................................... 1 1.3............................ 3 1.3.1............................. 3 1.3.2..................................
Gmech08.dvi
 51 5 5.1 5.1.1 P r P z θ P P P z e r e, z ) r, θ, ) 5.1 z r e θ,, z r, θ, = r sin θ cos = r sin θ sin 5.1) e θ e z = r cos θ r, θ, 5.1: 0 r
51 5 5.1 5.1.1 P r P z θ P P P z e r e, z ) r, θ, ) 5.1 z r e θ,, z r, θ, = r sin θ cos = r sin θ sin 5.1) e θ e z = r cos θ r, θ, 5.1: 0 r
F S S S S S S S 32 S S S 32: S S rot F ds = F d l (63) S S S 0 F rot F ds = 0 S (63) S rot F S S S S S rot F F (63)
 211 12 1 19 2.9 F 32 32: rot F d = F d l (63) F rot F d = 2.9.1 (63) rot F rot F F (63) 12 2 F F F (63) 33 33: (63) rot 2.9.2 (63) I = [, 1] [, 1] 12 3 34: = 1 2 1 2 1 1 = C 1 + C C 2 2 2 = C 2 + ( C )
211 12 1 19 2.9 F 32 32: rot F d = F d l (63) F rot F d = 2.9.1 (63) rot F rot F F (63) 12 2 F F F (63) 33 33: (63) rot 2.9.2 (63) I = [, 1] [, 1] 12 3 34: = 1 2 1 2 1 1 = C 1 + C C 2 2 2 = C 2 + ( C )
(1) (2) (3) (4) HB B ( ) (5) (6) (7) 40 (8) (9) (10)
 2017 12 9 4 1 30 4 10 3 1 30 3 30 2 1 30 2 50 1 1 30 2 10 (1) (2) (3) (4) HB B ( ) (5) (6) (7) 40 (8) (9) (10) (1) i 23 c 23 0 1 2 3 4 5 6 7 8 9 a b d e f g h i (2) 23 23 (3) 23 ( 23 ) 23 x 1 x 2 23 x
2017 12 9 4 1 30 4 10 3 1 30 3 30 2 1 30 2 50 1 1 30 2 10 (1) (2) (3) (4) HB B ( ) (5) (6) (7) 40 (8) (9) (10) (1) i 23 c 23 0 1 2 3 4 5 6 7 8 9 a b d e f g h i (2) 23 23 (3) 23 ( 23 ) 23 x 1 x 2 23 x
x (x, ) x y (, y) iy x y z = x + iy (x, y) (r, θ) r = x + y, θ = tan ( y ), π < θ π x r = z, θ = arg z z = x + iy = r cos θ + ir sin θ = r(cos θ + i s
 ... x, y z = x + iy x z y z x = Rez, y = Imz z = x + iy x iy z z () z + z = (z + z )() z z = (z z )(3) z z = ( z z )(4)z z = z z = x + y z = x + iy ()Rez = (z + z), Imz = (z z) i () z z z + z z + z.. z
... x, y z = x + iy x z y z x = Rez, y = Imz z = x + iy x iy z z () z + z = (z + z )() z z = (z z )(3) z z = ( z z )(4)z z = z z = x + y z = x + iy ()Rez = (z + z), Imz = (z z) i () z z z + z z + z.. z
 2019 1 5 0 3 1 4 1.1.................... 4 1.1.1......................... 4 1.1.2........................ 5 1.1.3................... 5 1.1.4........................ 6 1.1.5......................... 6 1.2..........................
2019 1 5 0 3 1 4 1.1.................... 4 1.1.1......................... 4 1.1.2........................ 5 1.1.3................... 5 1.1.4........................ 6 1.1.5......................... 6 1.2..........................
.2 ρ dv dt = ρk grad p + 3 η grad (divv) + η 2 v.3 divh = 0, rote + c H t = 0 dive = ρ, H = 0, E = ρ, roth c E t = c ρv E + H c t = 0 H c E t = c ρv T
 NHK 204 2 0 203 2 24 ( ) 7 00 7 50 203 2 25 ( ) 7 00 7 50 203 2 26 ( ) 7 00 7 50 203 2 27 ( ) 7 00 7 50 I. ( ν R n 2 ) m 2 n m, R = e 2 8πε 0 hca B =.09737 0 7 m ( ν = ) λ a B = 4πε 0ħ 2 m e e 2 = 5.2977
NHK 204 2 0 203 2 24 ( ) 7 00 7 50 203 2 25 ( ) 7 00 7 50 203 2 26 ( ) 7 00 7 50 203 2 27 ( ) 7 00 7 50 I. ( ν R n 2 ) m 2 n m, R = e 2 8πε 0 hca B =.09737 0 7 m ( ν = ) λ a B = 4πε 0ħ 2 m e e 2 = 5.2977
untitled
 20010916 22;1017;23;20020108;15;20; 1 N = {1, 2, } Z + = {0, 1, 2, } Z = {0, ±1, ±2, } Q = { p p Z, q N} R = { lim a q n n a n Q, n N; sup a n < } R + = {x R x 0} n = {a + b 1 a, b R} u, v 1 R 2 2 R 3
20010916 22;1017;23;20020108;15;20; 1 N = {1, 2, } Z + = {0, 1, 2, } Z = {0, ±1, ±2, } Q = { p p Z, q N} R = { lim a q n n a n Q, n N; sup a n < } R + = {x R x 0} n = {a + b 1 a, b R} u, v 1 R 2 2 R 3
08-Note2-web
 r(t) t r(t) O v(t) = dr(t) dt a(t) = dv(t) dt = d2 r(t) dt 2 r(t), v(t), a(t) t dr(t) dt r(t) =(x(t),y(t),z(t)) = d 2 r(t) dt 2 = ( dx(t) dt ( d 2 x(t) dt 2, dy(t), dz(t) dt dt ), d2 y(t) dt 2, d2 z(t)
r(t) t r(t) O v(t) = dr(t) dt a(t) = dv(t) dt = d2 r(t) dt 2 r(t), v(t), a(t) t dr(t) dt r(t) =(x(t),y(t),z(t)) = d 2 r(t) dt 2 = ( dx(t) dt ( d 2 x(t) dt 2, dy(t), dz(t) dt dt ), d2 y(t) dt 2, d2 z(t)
II 2 ( )
 II 2 ( 26 1 1 1 3 1.1....................................... 3 1.1.1.............................. 3 1.1.2.............................. 4 1.1.3..................... 5 1.2 : R 3...............................
II 2 ( 26 1 1 1 3 1.1....................................... 3 1.1.1.............................. 3 1.1.2.............................. 4 1.1.3..................... 5 1.2 : R 3...............................
第1章 微分方程式と近似解法
 April 12, 2018 1 / 52 1.1 ( ) 2 / 52 1.2 1.1 1.1: 3 / 52 1.3 Poisson Poisson Poisson 1 d {2, 3} 4 / 52 1 1.3.1 1 u,b b(t,x) u(t,x) x=0 1.1: 1 a x=l 1.1 1 (0, t T ) (0, l) 1 a b : (0, t T ) (0, l) R, u
April 12, 2018 1 / 52 1.1 ( ) 2 / 52 1.2 1.1 1.1: 3 / 52 1.3 Poisson Poisson Poisson 1 d {2, 3} 4 / 52 1 1.3.1 1 u,b b(t,x) u(t,x) x=0 1.1: 1 a x=l 1.1 1 (0, t T ) (0, l) 1 a b : (0, t T ) (0, l) R, u
