Cercignani Shen Kuščer
|
|
|
- ねんたろう こびき
- 5 years ago
- Views:
Transcription
1 Cercignani Shen Kuščer Maxwell Knudsen Grad Nocilla Epstein Cercignani Lampis Lord Knudsen Kuščer
2 2
3 1 Gas Surface Interaction Galilei Darrozes Guiraud 2 elastic collision model specular reflection model f ref ξ[ f ref ξ n, ξ t1, ξ t2 ] f in ξ n, ξ t1, ξ t2, ξ n >. 1 f in f ref ξ n ξ ξ t1 ξ t2 3
4 T w T w 1 f ref ξ σ d 2π exp ξ 2 : σ 3/2 d MT w, ξ, ξ n >. 2 2 σ d ξ n< ξ nf in dξ + ξ n > ξ nf ref dξ σ d 2π ξ n< ξ n f in ξdξ diffuse reflection model perfect/complete accommodation 2 Maxwell Maxwell Maxwell ξ diffuse reflection with incomplete accommodation Lord 7.5 Cercignani Lampis
5 perfect/complete accommodation accommodation coefficient 5 [1] Knudsen T 1 T 2 T 2 T 2 a T 2 T 1 T 2 T 1 [2, 3] ξ φξ ξ n φξf in ξdξ ξ n φξf ref ξdξ αφ; f in ξ n < ξ n >, 4 ξ n φξf in ξdξ ξ n φξσ d MT w ; ξdξ ξ n < ξ n > α φ accommodation coefficient for φ φξ ξ 5
6 φ αφ; f in 1 f ref ξ σ d MT w ; ξ 4 φ 1 2 ξ 2 ξ t1 ξ n 4 3 ξ n ξ 2 f in ξdξ ξ n ξ 2 f ref ξdξ α e f in : ξ n< ξ n>, 5 ξ n ξ 2 f in ξdξ ξ n ξ 2 σ d MT w ; ξdξ ξ n< ξ n> ξ n ξ t1 f in ξdξ ξ n ξ t1 f ref ξdξ α t f in : ξ n< ξ n> ξ n ξ t1 f in ξdξ ξ n ξ t1 σ d MT w ; ξdξ ξ n < ξ n > ξ n ξ t1 f ref ξdξ ξ 1 n >, 6 ξ n ξ t1 f in ξdξ ξ n < ξ n 2 f in ξdξ ξ n 2 f ref ξdξ α p f in : ξ n < ξ n >. 7 ξ n 2 f in ξdξ ξ n 2 σ d MT w ; ξdξ ξ n < ξ n > α e α t α p energy accommodation coefficient[4], accommodation coefficient for energy thermal accommodation coefficient[5] tangential momentum accommodation coefficient[4] accommodation coefficient for tangential momemtum[3] normal momentum accommodation coefficient accommodation coefficient for normal momemtum[3] 3 4 6
7 e tf s tf p tf 1 1 e tf f in ξ n ξ n < 2 ξ 2 f in ξdξ + ξ n ξ n > 2 ξ 2 f ref ξdξ, 8 s tf f in ξ n ξ t1 f in ξdξ + ξ n ξ t1 f ref ξdξ, 9 ξ n < ξ n > p tf f in ξnf 2 in ξdξ + ξnf 2 ref ξdξ, 1 ξ n < ξ n > α e α t α p e tf α ef in ξ n ξ 2 σ d MT w ; ξdξ ξ n ξ 2 f in ξdξ, 11 2 ξ n > ξ n < s tf α t f in ξ n ξ t1 σ d MT w ; ξdξ ξ n ξ t1 f in ξdξ, 12 ξ n > ξ n < p tf [2 α p f in ] ξ n 2 f in ξdξ + α p f in ξ n 2 σ d MT w ; ξdξ, ξ n < ξ n > 13 f in ξ α e α t α p α e α t α p f in Handbuch der Physik Schaaf [6] α e α t α p 6 4 f ref f in 5 α e 6 Schaaf α e α t α p α p Schaaf α t 7
8 ξ ξ n < ξ ξ + dξ ξ n > Rξ ξdξ ξ ξ +dξ ξ n f in ξ dξ Rξ ξdξ ξ n f ref ξdξ ξ n f ref ξ Rξ ξ ξ n f in ξ dξ, ξ n >, 14 ξ n < Rξ ξ R 14 7 R i ii Rξ, ξ, ξ n <, ξ n >, 15 Rξ, ξdξ 1, ξ n <, 16 ξ n > iii reciprocity detailed balance ξ n MT w ; ξ Rξ, ξ ξ n MT w ; ξr ξ, ξ, ξ n <, ξ n >, 17 8 iii 9 iii i iii 17 ξ n < ξ 16 ξ n MT w; ξ Rξ ξ ξ n MT w; ξ dξ, ξ n >, ξ n < 7 Kuščer [7] 8 R Kuščer 1969 [3] 9 iii 8
9 14 R Rξ ξ δξ + ξ n n ξ t, 18 Rξ ξ 2π ξ n MT w ; ξ. 19 ξ t, ξ t1, ξ t2 R 3 δ g ξ n MT w ; ξ Rξ, ξgξ dξ ξ n < ξ n MT w ; ξ δξ + ξ n n ξ t gξ dξ ξ n < ξ n MT w ; ξg ξ n n + ξ t ξ n MT w ; ξ δξ ξ n < n + ξ n δξ t ξ t gξ dξ ξ n MT w ; ξ δ ξ nn + ξ n n + ξ ξ n < t ξ t gξ dξ ξ n MT w ; ξ δ ξ ξ nn + ξ tgξ dξ ξ n < ξ n MT w ; ξ R ξ ξ gξ dξ. ξ n < π F, G : F ξgξ ξ n MT w ; ξdξ, 2 ξ n> 2π 1 1 1,
10 f in ξ σ d MT w ; ξ[1 + ψ in ξ], ξ n <, 22 f ref ξ σ d MT w ; ξ[1 + ψ ref ξ], ξ n >, 23 f in f ref ψ in ψ ref f in f ref ξ n f in ξdξ σ d ξ n MT w ; ξdξ, ξ n< ξ n> ξ n f in ξdξ ξ n f ref ξdξ, ξ n< ξ n> ψ in ψ ref 1 1, ψ in ψ in, 1, 1, ψ ref ψ ref, αφ; ψ in σ d P φ, 1 + ψ in σ d φ, 1 + ψ ref σ d P φ, 1 + ψ in σ d φ, 1 φ, ψ ref 1 P φ φ, 1 + P φ, ψ in. P P F ξ F ξ R 3 F ξ P t F ξ n, ξ t F ξ n, ξ t P t P t P t F, G F, P t G. P P t F ξ n F even P F even P t F even P F even, G F even, P t G P t F even, G φ ξ n φ even φ even ξ n, ξ t φ even ξ n, ξ t. P φ even φ even φ even ξ n, ξ t φ even ξ n, ξ t ξ t P φ even φ even, 1 αφ even ; ψ in αφ even ; ψ in 1 φ even, ψ ref P φ even, ψ in. ψ ref ψ in f ref f in R ξ n f ref ξ ξ n f in ξ Rξ ξdξ, ξ n >, ξ n < 1
11 R ξ n MT w ; ξ[1 + ψ ref ξ] ξ n MT w ; ξ [1 + ψ in ξ ]Rξ ξdξ ξ n < ξ n MT w ; ξ [1 + ψ in ξ ]R ξ ξ dξ ξ n < ξ n MT w ; ξ 1 + ψ in ζr ξ ζdζ, ξ n >, ζ n> ψ ref ξ R ξ ζψ in ζdζ, ξ n >, ζ n > Cercignani R + R 2 R + R 2 A AF ξ : R ξ ζf ζdζ ζ n > ζ n > ζ n MT w ; ζ ξ n MT w ; ξ R ζ ξf ζdζ, ξ n >, [3] ψ ref ψ in Aψ ref ψ in A 2π AF, G ξ n > 2π ξ n> 2π ξ n > 2π F, AG. ζ n > ζ n > ζ n> ζ n > ξ n > R ξ ζf ζdζ ξ n MT w ; ξgξdξ ζ n MT w ; ζ ξ n MT w ; ξ R ζ ξf ζdζ ξ n MT w ; ξgξdξ ζ n MT w ; ζr ζ ξf ζdζ Gξdξ R ζ ξgξdξ ζ n MT w ; ζf ζdζ αφ even ; ψ in αφ even ; ψ in 1 Aφ even, ψ in P t φ even, ψ in. 25 P F even P t F even Cercignani Kuščer [3, 7] 11
12 5.2 Cercignani Cercignani αφ even ; ψ in 25 3 i iii AF even λp t F even F even 1 1 φ even λ φ λ even αφλ even; ψ in αφ λ even; ψ in 1 Aφλ even, ψ in P t φ λ 1 λ, 26 even, ψ in Cercignani Cercignani αφ λ even φ λ even AF even λp t F even R Cercignani φ λ even R Cercignani Lampis AF even λp t F even Shen Kuščer Cercignani Shen Kuščer 25 ψ in φ even + const 12 1 λ 1 F even 1 α 11 Cercignani [3] Cercignani Boltzmann BGK 12 const ψ in 1 12
13 α ij : αφ i even; ψ j in 1 Aφi P t φ i even, ψ j in even, ψ j in, A P t α ij φ 1 even 1 2 ξ 2 ψ 1 in φ1 φ 2 even ξ t1 ψ 2 in φ2 even φ 3 even ξ n ψ 3 in φ3 even 3 3 a E : α 11 1 A 1 2 ξ 2 2, 1 2 ξ ξ 2 2 2, a : α Aξ t 1, ξ t1 ξ t1 2, a : α 33 1 A ξ n π ξ n π 2 2, ξ n, π 2 2 even 2 π 2 a E accommodation coefficient for energy a accommodation coefficient for parallel momentum a accommodation coefficient for normal momentum ψ in α e α t α p ψ in p/σ d T w +ξ v/ ξ 2 / 5 T/T w a E f in T T w + T p σ d T w T T/T w 1 a f in T T w p σ d T w v n v t2 v t1 v t1 v t1 / 1 a f in T T w v t1 v t2 v n v n p σ d T w 1 v n π 2 v n / 1 α e α t a E a Kuščer a E [7] 6 α e α t 13
14 1: [8] Gas Reservoir Source Stage1 2 sample UHV chamber skimmer collimator molecular beam 13 [8, 1] ξ 2 exp ξ u 2 /2RT dξ monoenergetic collimated beam, monochromatic beam thermal beam effusive beam supersonic nozzle beam 14 14
15 ξ 2 exp ξ u 2 /2RT dξ [9] f beam ξdξdω beam R ω beam f in f in ξdξ f beam ξdξdω beam f beam ξδω ω beam dξdω, f beam f in ξ ξ 2 f beam ξ δω ω beam, f ref ξ n f ref ξ, ω Rξ ξ ξ n f in ξ dξ ξ n< Rξ, ω ξ, ωξ ω n f beam ξ δω ω beam dξ dω ω n< Rξ, ω beam ξ, ωξ f beam ξ dξ cosπ θ beam, θ, ϕ ω beam θ beam, ϕ beam D ref D ref ω : ξ 2 ξ n f ref ξ, ωdξ Rξ, ω beam ξ, ωξ ξ 2 f beam ξ dξ dξ cosπ θ beam, 27 u u 15
16 ω n cos θ > ω beam n cos θ beam < D ref ω ξ 3 cos θσ d MT w ; ξdξ 1 RTw π 2π σ d cos θ 1 ξ n f in dξ cos θ π ξ n< 1 ξf beam ξdξ cosπ θ beam cos θ, π i ϕ ii θ cos θ θ D ref ξ n f ref ξ f ref θ D ref cos θ Lambert a 2b a b 2: 15 Lambert n n beam beam
17 7 7.1 Maxwell Maxwell 1 α α f ref ξ 1 αf in ξ n n + ξ t + ασ d MT w ; ξ, ξ n >, 28 2π σ d ξ n f in ξdξ. 29 ξ n < Maxwell α α 1 α α 1 Maxwell 2π Rξ ξ 1 αδξ + ξ n n ξ t + α ξ n MT w ; ξ. 3 i iii Maxwell 2π Aφ even 1 αδ ξ + ζ n n ζ t + α ζ n MT w ; ζ φ even ζdζ ζ n> 1 αp t φ even ξ + α 1, φ even, Aφ even, ψ in 1 α P t φ even, ψ in + α 1, φ even 1, ψ in 1 α P t φ even, ψ in, 25 φ even ψ in αφ even ; ψ in α, 31 17
18 D ref ω 1 α + α Rξ, ω beam ξ, ωξ ξ 2 f beam ξ dξ dξ cosπ θ beam 1 α + α π 1 δξ + ξ n n ξ t ξ ξ 2 f beam ξ dξ dξ cosπ θ beam ξ ξ 2 f beam ξ 2π ξ n MT w ; ξdξ dξ cosπ θ beam ξ 3 f beam ξ dξ cosπ θ beam δω + P t ω beam ξf beam ξdξ cosπ θ beam cos θ. Maxwell cos θ δ 2b 7.2 Knudsen Grad Nocilla Nocilla b f ref ξ σ N 2πRT N exp ξ U N 2, ξ 3/2 n >. 32 2RT N σ N ξ n > ξ n f ref ξdξ ξ n < ξ n f in ξdξ σ N Cu N, T N ξ n f in ξdξ, 33 ξ n < RT N Cu N, T N 2 2π e u N + u N 2 [1 + erfu N] U N / 2RT N u N, v N, w N T N U N U N Knudsen 1911 T N T w Grad 1958 [1] Knudsen Grad Nocilla Rξ ξ Cu N, T N ξ n MT N ; ξ U N, 35 18
19 D ref ω Rξ, ω beam ξ, ωξ ξ 2 f beam ξ dξ dξ cosπ θ beam Cu N, T N ξ n MT N ; ξ U N ξ ξ 2 f beam ξ dξ dξ cosπ θ beam Cu N, T N ξ f 2πRT N 3/2 beam ξ dξ cosπ θ beam ξ 3 exp ξ U Nω ω N 2 + UN 2 1 ω ω N 2 dξ cos θ 2RT N Cu N, T N 2RT N 1/2 ξ f beam ξ dξ cosπ θ beam π 3/2 ζ + u N ω ω N 3 e ζ 2 dζ e u2 N 1 ω ω N 2 cos θ u N ω ω N Cu N, T N RTN ξ f beam ξ dξ cosπ θ beam e u2 N π 2π 1 + u 2 N ω ω N 2 + πu N ω ω N u 2 N ω ω N [1 + erfu Nω ω N ]e u2 N ω ω N 2 cos θ. ω N U N / U N ω ω N cos θ cos θ N +sin θ sin θ N cosϕ ϕ N u N Nicolla [11] α e α t α p 1 Knudsen Grad Nocilla iii iii Knudsen Grad Nocilla 7.3 Epstein Epstein 1967 Maxwell Rξ ξ 2π ξ n MT w ; ξ αξαξ + [1 αξ]δξ + ξ 1, α nn ξ t. αξ αξ 1 ξ i iii Maxwell α ξ α ξ 19
20 δ Cercignani i iii Epstein [3] 2π Rξ ξ ξ n MT w ; ξ[hξh ξ + Kξ, ξ ], ξ n <, ξ n >, 1 1, K, ξ Hξ. 1 1, K, ξ, 1 Kζ, ξ Epstein ζ Bζ K Kζ, ξ Bζδζ P t ξ Epstein K δ 7.4 Cercignani Lampis Cercignani Lampis 1971 i iii i AF even λp t F even Rξ ξ Maxwell λ 1 λ 1 λ 2 1 α ii ξ 2 n ξ t 1 ξ t2 Laguerre Hermite Cercignani Lampis CL [12] 2 p 1 1 q 1 Rξ 1 1 p ξ 2π 2 1 p1 q 2 ξ ξ n ξ n n I 1 p exp ξ2 n + p ξ n p ξ t q ξ t q 2, ξ n >, ξ n <. 36 I I x : 1 2π 2π expx cos ϕdϕ, 2
21 1 Bessel R 2π Rξ ξ ξ n MT w ; ξ Ψ lmn ξ l,m,n p l q m+n Ψ lmn ξ Ψ lmn ξ, 1 ξ 2 l L n H m m! n! 2 m+n 2 ξt1 ξt2 H n 2RTw 2RTw, R L l l Laguerre H m m Hermite Ψ lmn AF even λp t F even p l q m+n Ψ lmn AΨ ijk p i q j+k Ψ ijk AΨ ijk, Ψ lmn p i q j+k δ il δ jm δ kn R 2 i iii ii 2 2 iii Hermite H n x 1 n H n x 2 i Ψ lmn l, m, n p q 1 p q Cercignani Lampis f in Cercignani 1 26 Laguerre Hermite A R A1 1 1, ψ in AΨ 1, ψ in P t Ψ 1, ψ in A 1 2 ξ2 n, ψ in 1 P t 2 ξ2 n, ψ in, AΨ 1, ψ in P t Ψ 1, ψ in Aξ t 1, ψ in P t ξ t1, ψ in, AΨ 2, ψ in P t Ψ 2, ψ in A 1 2 ξ2 t 1, ψ in 1 P t 2 ξ2 t 1, ψ in, 17 L x 1 L 1 x 1 x H x 1 H 1 x 2x H 2 x 2x φ even Ψ 2 Ψ 11 m+n i AF even λp t F even Cercignani Lampis 21
22 φ even Ψ 1 1 ξ2 n 1 p 2 ξ t1 Ψ 1 1 q RTw 1 ξ 2 Ψ 2 2 t1 1 1 q 2 2 ξ t1 ξ t2 Ψ 11 1 q 2 1: Cercignani α Cercignani Lampis p q α n 1 p α t 1 q α e α e ψ in 1 p ξ2 n, ψ in + q 2 ξ t 2, ψ in ξ 2. 37, ψ in α p Cercignani Lampis D ref ω exp Rξ, ω beam ξ, ωξ ξ 2 f beam ξ dξ dξ cosπ θ beam 1 ξ cos θ p 2π 2 1 p1 q 2 I ξ ξ cos θ beam cos θ 1 p ξ2 cos 2 θ + p ξ 2 cos 2 θ beam q2 ξ 2 sin 2 θ beam sin 2 ϕ ϕ beam 2 1 p 2 1 q 2 ξ sin θ qξ sin θ beam cosϕ ϕ beam q 2 ξ ξ 2 f beam ξ dξ dξ 1 cosπ θ beam p ξ ξ 2π 2 1 p1 q 2 I cos θ beam cos θ 1 p exp ξ2 cos 2 θ + p ξ 2 cos 2 θ beam q2 ξ 2 sin 2 θ beam sin 2 ϕ ϕ beam 2 1 p 2 1 q 2 ξ sin θ qξ sin θ beam cosϕ ϕ beam q 2 ξ ξ 3 f beam ξ dξ dξ 2 Cercignani α t.1 α n K ξ ξ2 n 1 2 ξ2 t ξ2 t ξ2 n 1 2 ξ2 t ξ2 t 2 t 1 t 2 cosπ θ beam cos θ. 22
23 191 K [13] [3] Cercignani Cercignani Lampis [3] 36 p q Rξ ξ ξ n 2π 2 w exp p ξ n ξ n wp, qi 1 p 2 ξ2 n + p ξ n 2 1 p ξ t q ξ t q 2 dqdp, ξ n >, ξ n <. wp, q, wp, q1 p1 q 2 dqdp 1, wp, q 1 p 1 1 q 2 1 δp p δq q., Ψ lmn α n α t. Cercignani, α n α t 2 i Ψ lmn 2 Hilbert AF even λp t F even φ i even l,m,n ai lmn Ψ lmn R 2π Rξ ξ ξ n MT w ; ξ λ i φ i RT evenξ φ i evenξ w i 2π ξ n MT w ; ξ λ i a i I RT Ψ Iξ a i J Ψ Jξ w i,i,j 2π ξ n MT w ; ξ b IJ Ψ I ξ Ψ J ξ I,J I J l, m, n b IJ i λi a i I ai J ii p pξ t, ξ t p ξ t, ξ t q qξ n, ξ n q ξ n, ξ n ξ t ξ t ξ n ξ n i iii α n α t 23
24 7.5 Lord Cercignani Lampis CL Lord CL [14] 2 CL p q CL ξ ξ Rξ ξ 2 2RTw π 1 p ξ n p p ξ ξ I ξ ξ 1 exp ξ 2 + p ξ 2. 1 p 2 1 p I Bessel I 1 x x 6π 2π sin 2 θ expx cos θdθ. i iii R ξ n cos θ p p 1 α t 1 p p 1 diffuse elastic reflection 7.6 Knudsen Kuščer 3 Knudsen Knudsen Knudsen T 1 T 2 T 2 Kuščer Knudsen i iii 2 Lord Cercignani Lampis Lord CLL CLL Cercignani Lampis 2 Petek & Kuščer 1979 Lord CL DSMC CL [14] 24
25 iv T in T ref T ref [15] Kuščer Knudsen Knudsen Kuščer Knudsen Fokker Planck CL iv T in T ref ξ n MT ref ; ξ Tref T in ξ n < ξ n MT in ; ξ Rξ ξdξ, 38 i iii Kuščer Fokker Planck t P ξ [ ap ξbp ]. a ξ b 2 P ξ, t δξ ξ P ξ, t 1 [2π 1 e 2t ] exp ξ ξ e t 2 3/2 2 1 e 2t, t ξ t ξ P ξ ξ; t P P ξ n 1 ξ n ; t [2π 1 e 2t ] exp ξ n ξ ne t 2 1/2 2 1 e 2t, 39 P ξ t 1 ξ t ; t 2π 1 e 2t exp ξ t ξ te t e 2t, 4 P ξ ξ; t P ξ n ξ n ; tp ξ t ξ t ; t P 25
26 ξ n exp ξ n 2 P n ξ n ξ n 2 ξ n exp ξ n 2 P n ξ n ξ 2RT n, ξ n >, ξ n <, w P n ξ n ξ n ; tdξ n 1, P n P n ξ n ξ n ; tp ξ t ξ t ; t i iii 5.1 A n A n F ξ n : P n ξ n ζ n ; tf ζ n dζ n, ξ n >, M 1 T w ; ξ n 2π 1/2 exp ξ 2 n/2 2π A n F, G n 2π 2π F, G n : F, A n G n, ξ n M 1 T w ; ξ n F ξ n Gξ n dξ n, ξ n M 1 T w ; ξ n P n ξ n ζ n ; tf ζ n dζ n Gξ n dξ n ξ n M 1 T w ; ξ n ζ n M 1 T w ; ζ n ξ n M 1 T w ; ξ n P n ζ n ξ n ; tf ζ n dζ n Gξ n dξ n ζ n M 1 T w ; ζ n P n ζ n ξ n ; tgξ n dξ n F ζ n dζ n P n A n Fokker Planck t P n ξn [ a n P n ξ n bp n ] : DP n, ξ n >, 41 P n Kuščer t t t t ζ n P n ζ n ξ n ; t e td δξ n ζ n, 42 26
27 A n F, G n 2π A n F, G n dζ n Gζ n ζ n M 1 T w ; ζ n dξ n P n ζ n ξ n ; tf ξ n 2π dζ n Gζ n ζ n M 1 T w ; ζ n dξ n F ξ n [e td δξ n ζ n ] 2π dξ n F ξ n e td dζ n Gζ n ζ n M 1 T w ; ζ n δξ n ζ n 2π dξ n F ξ n e td [Gξ n ξ n M 1 T w ; ξ n ], 2π F, A n G n e td n 1 n! tn D n dξ n Gξ n D[F ξ n ξ n M 1 T w ; ξ n ] dξ n Gξ n e td [F ξ n ξ n M 1 T w ; ξ n ], dξ n F ξ n D[Gξ n ξ n M 1 T w ; ξ n ], D P n A n dξ n GDF ξ n M 1 dξ n F [ a n Gξ n M b Gξ nm 1 ] dξ n F [ a n ξ n M 1 G a n ξ n M 1 G b Gξ nm 1 ] dξ n F [ a n ξ n M 1 G a n ξ n M 1 G ] F b Gξ nm dξ n F b Gξ n M 1 [a n ξ n M 1 F G bξ nm 1 F G ]dξ n 1 2 bm 1 F G [ 1 2 bξ nm 1 F G + a n ξ n M 1 F G ]dξ n, F G a n b a n ξ n M bξ nm 1 a n 1 2 [ db 1 + b ξ ] n, 43 dξ n ξ n Knudsen 38 Rξ ξ P n ξ n ξ n ; tp ξ t ξ t ; t ξ n M 1 T ref ; ξ n 2πRT ref 1 exp ξ t 2 2RT ref, 27
28 Tref dξ T n ξ n M 1 T in ; ξ np n ξ in ξ n < n ξ n 2πRT in 1 dξ t2πrt w 1 1 e 2t 1 exp ξ t e t ξ t e 2t ξ t 2 2RT in Tref dξ T n ξ n M 1 T in ; ξ np n ξ in ξ n < n ξ n 2πRT in 1 2π 1 1 e 2t 1 dξ t ξ t 2 exp 2 1 e 2t T w + T in T w e 2t e t T in 2 T in 1 e 2t [ξ t T w + T in T w e 2t ξ t] 2 Tref ξ t 2 e 2t T ] in e 2t T w + T in T w e 2t dξ T n ξ n M 1 T in ; ξ np n ξ in ξ n < n ξ n 1 2πR[T w + T in T w e 2t ] exp ξ t 2 2R[T w + T in T w e 2t, ] ξ t ξ n M 1 T ref ; ξ n T ref T w + T in T w e 2t, 44 Tref T in ξ n < dξ n ξ n M 1 T in ; ξ np n ξ n ξ n, 42 ξ n M 1 T ref ; ξ n Tref T in Tref ξ n < dξ n ξ n M 1 T in ; ξ ne td δξ n + ξ n e td ξ n M 1 T in ; ξ n, T in T in T ref ξ n M 1 T ref ; ξ n P n ξ n, t ξ n M 1 T in ; ξ n 41 T w T in t ξ 2 n 1 dt ref 1 2RT ref T ref dt Tin T ref ξ n M 1 T ref ; ξ n, T in T ref ξ n M 1 T ref ; ξ n 41 28
29 Tin a n ξ n M 1 T ref ; ξ n + 1 [ Tin ] b ξ n M 1 T ref ; ξ n T ref 2 T ref Tin [ 1 T ref 2 b a n ξ n M 1 T ref ; ξ n + 1 ] ξ 2 b n M 1 T ref ; ξ n Tin T ref 1 2 b a n 1 2 b ξ n RT ref 1 1 2RT ref Tref T w 1 1 2RT ref Tref T w 1 ξ n M 1 T ref ; ξ n ξ n T in bξ 2 T nm 1 T ref ; ξ n ref T [ in ξ b 2 ] ξ n 2b n 1 ξ n M 1 T ref ; ξ n, T ref 2RT ref ξ n 43 b T ref dt ref dt b R Tref 1, T w T ref 44 b 2 43 a n ξn 1 ξn 2 Fokker Planck t P n ξn ξ n ξ n P n + ξn P n : DP n, ξ n >, i iii Knudsen P n ξ n ξ n ; tp ξ t ξ t ; t P 4 P n ξ n x ξ 2 n/2 x F G D[F xgx] dx 1 dx 2 x F G + F G dξ n 2RTw x dξ n x 2 x 1 F G + 2 xf G x 2xF G + 2xF G x F G 2xF G + F G + 2xF G + 2F G + F G x F G 2xF + 1 xf G + 2[2x 1G + 2xG ]F + 1 x x[2x 1G + 2xG ] F, 29
30 2x 1G+2xG G G const xe x D[F x xe x ] 2xF + 1 xf xe x, Laguerre Laguerre L k x Laguerre xy + 1 xy + ky, Laguerre e x F Gdx Hilbert F x k f ktl k x D[F x, t xe x ] 2 t [F x, t xe x ] kf k tl k x xe x, k k df k dt L kx xe x, df k dt 2kf kt f k t const. e 2kt, F xe x 45 ξ n exp 2RTw ξ2 n 2 k ξ 2 n e 2kt L k C k, C k, 2 45 P n δξ n + ξ n t ξ n exp 2RTw ξ2 n 2 k ξ 2 n L k C k ξ 2RT n δξ n +ξ n, ξ n >, ξ n <, w C k ξ n Laguerre L k xl k y e x δx y, k C k ξ n 2 L k ξ n, 2RTw 2 2 3
31 Laguerre k s k L k xl k y 1 1 s exp s 1 s x + y P n ξ n ξ n ; t ξ n exp ξ2 n 2 ξ n 1 1 e 2t exp k ξ 2 n 2 sxy I 1 s, e 2kt L k L k ξ n 2 2 ξ2 n + e 2t ξ n 2 I 2 1 e 2t 2 e t ξ n ξ n 1 e 2t P Rξ ξ n ξ; t 2π 2 1 e 2t 2 I exp e t ξ n ξ n 1 e 2t ξ2 n + e 2t ξ n e 2t ξ t ξ te t e 2t CL p q 2 e 2t α n α t α e α e α n 37 Kuščer CL 1 1 Knudsen 2 T in T ref T ref ξ n M 1 T ref ; ξ n M 1 T ref ; ξ t1 M 1 T ref ; ξ t2 Tref ξ T n MT in ; ξ Rξ ξdξ. in ξ n < Knudsen CL 21., [1] Petek & Kuščer
32 [2] C. Cercignani, Rarefied Gas Dynamics, Cambridge, 2. [3] C. Cercignani, The Boltzmann Equation and Its Applications, Springer, New York, [4] M. N. Kogan, Rarefied Gas Dynamics, Plenum, New York, [5] G. A. Bird, Molecular Gas Dynamics and The Direct Simulation of Gas Flows, Clarendon, Oxford, [6] S. A. Schaaf, Mechanics of rarefied gases, in Handbuch der Physik, Band VIII/2, Springer, Berlin, 1963, pp [7] F. R. W. McCourt, J. J. M. Beenakker, W. E. Köhler, I. Kuščer, Nonequilibrium Phenomena in Polyatomic Gases, Vol. 2, Clarendon, Oxford, [8] G. Attard, C. Barnes, Surfaces, Oxford, Oxford, [9] I. Kinefuchi, H. Yamaguchi, S. Shiozaki, Y. Sakiyama, Y. Matsumoto, Out-of-plane scattering distribution of Nitrogen molecular beam on Graphite 1 surface, in Rarefied Gas Dynamics, AIP, New York, 25, pp [1] H. Grad, Principles of the kinetic theory of gases, in Handbuch der Physik, Band XII, Springer, Berlin, 1958, pp [11] S. Nocilla, The surface re-emission law in free molecule flow, in Rarefied Gas Dynamics, Academic, New York, 1963, pp [12] C. Cercignani, Models for gas surface interactions: Comparison between theory and experiment, in Rarefied Gas Dynamics, Editorice Tecnico Scientifica, Pisa, 1971, pp [13] J. J. Hinchen, W. M. Foley, Scattering of molecular beams by metallic surfaces, in Rarefied Gas Dynamics, Vol. II, Academic, New York, 1966, p [14] R. G. Lord, Some extensions to the Cercignani Lampis gas-surface scattering kernel, Phys. Fluids A, 3, [15] I. Kuščer, J. Mozins, F. Krizanic, The Knudsen model of thermal accomodation, in Rarefied Gas Dynamics, Editorice Tecnico Scientifica, Pisa, 1971, pp
() n C + n C + n C + + n C n n (3) n C + n C + n C 4 + n C + n C 3 + n C 5 + (5) (6 ) n C + nc + 3 nc n nc n (7 ) n C + nc + 3 nc n nc n (
 3 n nc k+ k + 3 () n C r n C n r nc r C r + C r ( r n ) () n C + n C + n C + + n C n n (3) n C + n C + n C 4 + n C + n C 3 + n C 5 + (4) n C n n C + n C + n C + + n C n (5) k k n C k n C k (6) n C + nc
3 n nc k+ k + 3 () n C r n C n r nc r C r + C r ( r n ) () n C + n C + n C + + n C n n (3) n C + n C + n C 4 + n C + n C 3 + n C 5 + (4) n C n n C + n C + n C + + n C n (5) k k n C k n C k (6) n C + nc
30
 3 ............................................2 2...........................................2....................................2.2...................................2.3..............................
3 ............................................2 2...........................................2....................................2.2...................................2.3..............................
5. [1 ] 1 [], u(x, t) t c u(x, t) x (5.3) ξ x + ct, η x ct (5.4),u(x, t) ξ, η u(ξ, η), ξ t,, ( u(ξ,η) ξ η u(x, t) t ) u(x, t) { ( u(ξ, η) c t ξ ξ { (
![5. [1 ] 1 [], u(x, t) t c u(x, t) x (5.3) ξ x + ct, η x ct (5.4),u(x, t) ξ, η u(ξ, η), ξ t,, ( u(ξ,η) ξ η u(x, t) t ) u(x, t) { ( u(ξ, η) c t ξ ξ { ( 5. [1 ] 1 [], u(x, t) t c u(x, t) x (5.3) ξ x + ct, η x ct (5.4),u(x, t) ξ, η u(ξ, η), ξ t,, ( u(ξ,η) ξ η u(x, t) t ) u(x, t) { ( u(ξ, η) c t ξ ξ { (](/thumbs/92/107866626.jpg) 5 5.1 [ ] ) d f(t) + a d f(t) + bf(t) : f(t) 1 dt dt ) u(x, t) c u(x, t) : u(x, t) t x : ( ) ) 1 : y + ay, : y + ay + by : ( ) 1 ) : y + ay, : yy + ay 3 ( ): ( ) ) : y + ay, : y + ay b [],,, [ ] au xx
5 5.1 [ ] ) d f(t) + a d f(t) + bf(t) : f(t) 1 dt dt ) u(x, t) c u(x, t) : u(x, t) t x : ( ) ) 1 : y + ay, : y + ay + by : ( ) 1 ) : y + ay, : yy + ay 3 ( ): ( ) ) : y + ay, : y + ay b [],,, [ ] au xx
W u = u(x, t) u tt = a 2 u xx, a > 0 (1) D := {(x, t) : 0 x l, t 0} u (0, t) = 0, u (l, t) = 0, t 0 (2)
 3 215 4 27 1 1 u u(x, t) u tt a 2 u xx, a > (1) D : {(x, t) : x, t } u (, t), u (, t), t (2) u(x, ) f(x), u(x, ) t 2, x (3) u(x, t) X(x)T (t) u (1) 1 T (t) a 2 T (t) X (x) X(x) α (2) T (t) αa 2 T (t) (4)
3 215 4 27 1 1 u u(x, t) u tt a 2 u xx, a > (1) D : {(x, t) : x, t } u (, t), u (, t), t (2) u(x, ) f(x), u(x, ) t 2, x (3) u(x, t) X(x)T (t) u (1) 1 T (t) a 2 T (t) X (x) X(x) α (2) T (t) αa 2 T (t) (4)
v v = v 1 v 2 v 3 (1) R = (R ij ) (2) R (R 1 ) ij = R ji (3) 3 R ij R ik = δ jk (4) i=1 δ ij Kronecker δ ij = { 1 (i = j) 0 (i
 1. 1 1.1 1.1.1 1.1.1.1 v v = v 1 v 2 v 3 (1) R = (R ij ) (2) R (R 1 ) ij = R ji (3) R ij R ik = δ jk (4) δ ij Kronecker δ ij = { 1 (i = j) 0 (i j) (5) 1 1.1. v1.1 2011/04/10 1. 1 2 v i = R ij v j (6) [
1. 1 1.1 1.1.1 1.1.1.1 v v = v 1 v 2 v 3 (1) R = (R ij ) (2) R (R 1 ) ij = R ji (3) R ij R ik = δ jk (4) δ ij Kronecker δ ij = { 1 (i = j) 0 (i j) (5) 1 1.1. v1.1 2011/04/10 1. 1 2 v i = R ij v j (6) [
1 1.1 ( ). z = a + bi, a, b R 0 a, b 0 a 2 + b 2 0 z = a + bi = ( ) a 2 + b 2 a a 2 + b + b 2 a 2 + b i 2 r = a 2 + b 2 θ cos θ = a a 2 + b 2, sin θ =
 1 1.1 ( ). z = + bi,, b R 0, b 0 2 + b 2 0 z = + bi = ( ) 2 + b 2 2 + b + b 2 2 + b i 2 r = 2 + b 2 θ cos θ = 2 + b 2, sin θ = b 2 + b 2 2π z = r(cos θ + i sin θ) 1.2 (, ). 1. < 2. > 3. ±,, 1.3 ( ). A
1 1.1 ( ). z = + bi,, b R 0, b 0 2 + b 2 0 z = + bi = ( ) 2 + b 2 2 + b + b 2 2 + b i 2 r = 2 + b 2 θ cos θ = 2 + b 2, sin θ = b 2 + b 2 2π z = r(cos θ + i sin θ) 1.2 (, ). 1. < 2. > 3. ±,, 1.3 ( ). A
I ( ) 1 de Broglie 1 (de Broglie) p λ k h Planck ( Js) p = h λ = k (1) h 2π : Dirac k B Boltzmann ( J/K) T U = 3 2 k BT
 I (008 4 0 de Broglie (de Broglie p λ k h Planck ( 6.63 0 34 Js p = h λ = k ( h π : Dirac k B Boltzmann (.38 0 3 J/K T U = 3 k BT ( = λ m k B T h m = 0.067m 0 m 0 = 9. 0 3 kg GaAs( a T = 300 K 3 fg 07345
I (008 4 0 de Broglie (de Broglie p λ k h Planck ( 6.63 0 34 Js p = h λ = k ( h π : Dirac k B Boltzmann (.38 0 3 J/K T U = 3 k BT ( = λ m k B T h m = 0.067m 0 m 0 = 9. 0 3 kg GaAs( a T = 300 K 3 fg 07345
1 No.1 5 C 1 I III F 1 F 2 F 1 F 2 2 Φ 2 (t) = Φ 1 (t) Φ 1 (t t). = Φ 1(t) t = ( 1.5e 0.5t 2.4e 4t 2e 10t ) τ < 0 t > τ Φ 2 (t) < 0 lim t Φ 2 (t) = 0
 1 No.1 5 C 1 I III F 1 F 2 F 1 F 2 2 Φ 2 (t) = Φ 1 (t) Φ 1 (t t). = Φ 1(t) t = ( 1.5e 0.5t 2.4e 4t 2e 10t ) τ < 0 t > τ Φ 2 (t) < 0 lim t Φ 2 (t) = 0 0 < t < τ I II 0 No.2 2 C x y x y > 0 x 0 x > b a dx
1 No.1 5 C 1 I III F 1 F 2 F 1 F 2 2 Φ 2 (t) = Φ 1 (t) Φ 1 (t t). = Φ 1(t) t = ( 1.5e 0.5t 2.4e 4t 2e 10t ) τ < 0 t > τ Φ 2 (t) < 0 lim t Φ 2 (t) = 0 0 < t < τ I II 0 No.2 2 C x y x y > 0 x 0 x > b a dx
2011de.dvi
 211 ( 4 2 1. 3 1.1............................... 3 1.2 1- -......................... 13 1.3 2-1 -................... 19 1.4 3- -......................... 29 2. 37 2.1................................ 37
211 ( 4 2 1. 3 1.1............................... 3 1.2 1- -......................... 13 1.3 2-1 -................... 19 1.4 3- -......................... 29 2. 37 2.1................................ 37
4. ϵ(ν, T ) = c 4 u(ν, T ) ϵ(ν, T ) T ν π4 Planck dx = 0 e x 1 15 U(T ) x 3 U(T ) = σt 4 Stefan-Boltzmann σ 2π5 k 4 15c 2 h 3 = W m 2 K 4 5.
 A 1. Boltzmann Planck u(ν, T )dν = 8πh ν 3 c 3 kt 1 dν h 6.63 10 34 J s Planck k 1.38 10 23 J K 1 Boltzmann u(ν, T ) T ν e hν c = 3 10 8 m s 1 2. Planck λ = c/ν Rayleigh-Jeans u(ν, T )dν = 8πν2 kt dν c
A 1. Boltzmann Planck u(ν, T )dν = 8πh ν 3 c 3 kt 1 dν h 6.63 10 34 J s Planck k 1.38 10 23 J K 1 Boltzmann u(ν, T ) T ν e hν c = 3 10 8 m s 1 2. Planck λ = c/ν Rayleigh-Jeans u(ν, T )dν = 8πν2 kt dν c
phs.dvi
 483F 3 6.........3... 6.4... 7 7.... 7.... 9.5 N (... 3.6 N (... 5.7... 5 3 6 3.... 6 3.... 7 3.3... 9 3.4... 3 4 7 4.... 7 4.... 9 4.3... 3 4.4... 34 4.4.... 34 4.4.... 35 4.5... 38 4.6... 39 5 4 5....
483F 3 6.........3... 6.4... 7 7.... 7.... 9.5 N (... 3.6 N (... 5.7... 5 3 6 3.... 6 3.... 7 3.3... 9 3.4... 3 4 7 4.... 7 4.... 9 4.3... 3 4.4... 34 4.4.... 34 4.4.... 35 4.5... 38 4.6... 39 5 4 5....
 2011 8 26 3 I 5 1 7 1.1 Markov................................ 7 2 Gau 13 2.1.................................. 13 2.2............................... 18 2.3............................ 23 3 Gau (Le vy
2011 8 26 3 I 5 1 7 1.1 Markov................................ 7 2 Gau 13 2.1.................................. 13 2.2............................... 18 2.3............................ 23 3 Gau (Le vy
Hanbury-Brown Twiss (ver. 2.0) van Cittert - Zernike mutual coherence
 Hanbury-Brown Twiss (ver. 2.) 25 4 4 1 2 2 2 2.1 van Cittert - Zernike..................................... 2 2.2 mutual coherence................................. 4 3 Hanbury-Brown Twiss ( ) 5 3.1............................................
Hanbury-Brown Twiss (ver. 2.) 25 4 4 1 2 2 2 2.1 van Cittert - Zernike..................................... 2 2.2 mutual coherence................................. 4 3 Hanbury-Brown Twiss ( ) 5 3.1............................................
(1.2) T D = 0 T = D = 30 kn 1.2 (1.4) 2F W = 0 F = W/2 = 300 kn/2 = 150 kn 1.3 (1.9) R = W 1 + W 2 = = 1100 N. (1.9) W 2 b W 1 a = 0
 1 1 1.1 1.) T D = T = D = kn 1. 1.4) F W = F = W/ = kn/ = 15 kn 1. 1.9) R = W 1 + W = 6 + 5 = 11 N. 1.9) W b W 1 a = a = W /W 1 )b = 5/6) = 5 cm 1.4 AB AC P 1, P x, y x, y y x 1.4.) P sin 6 + P 1 sin 45
1 1 1.1 1.) T D = T = D = kn 1. 1.4) F W = F = W/ = kn/ = 15 kn 1. 1.9) R = W 1 + W = 6 + 5 = 11 N. 1.9) W b W 1 a = a = W /W 1 )b = 5/6) = 5 cm 1.4 AB AC P 1, P x, y x, y y x 1.4.) P sin 6 + P 1 sin 45
Gmech08.dvi
 145 13 13.1 13.1.1 0 m mg S 13.1 F 13.1 F /m S F F 13.1 F mg S F F mg 13.1: m d2 r 2 = F + F = 0 (13.1) 146 13 F = F (13.2) S S S S S P r S P r r = r 0 + r (13.3) r 0 S S m d2 r 2 = F (13.4) (13.3) d 2
145 13 13.1 13.1.1 0 m mg S 13.1 F 13.1 F /m S F F 13.1 F mg S F F mg 13.1: m d2 r 2 = F + F = 0 (13.1) 146 13 F = F (13.2) S S S S S P r S P r r = r 0 + r (13.3) r 0 S S m d2 r 2 = F (13.4) (13.3) d 2
 2019 1 5 0 3 1 4 1.1.................... 4 1.1.1......................... 4 1.1.2........................ 5 1.1.3................... 5 1.1.4........................ 6 1.1.5......................... 6 1.2..........................
2019 1 5 0 3 1 4 1.1.................... 4 1.1.1......................... 4 1.1.2........................ 5 1.1.3................... 5 1.1.4........................ 6 1.1.5......................... 6 1.2..........................
 006 11 8 0 3 1 5 1.1..................... 5 1......................... 6 1.3.................... 6 1.4.................. 8 1.5................... 8 1.6................... 10 1.6.1......................
006 11 8 0 3 1 5 1.1..................... 5 1......................... 6 1.3.................... 6 1.4.................. 8 1.5................... 8 1.6................... 10 1.6.1......................
微分積分 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. このサンプルページの内容は, 初版 1 刷発行時のものです.
 微分積分 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. ttp://www.morikita.co.jp/books/mid/00571 このサンプルページの内容は, 初版 1 刷発行時のものです. i ii 014 10 iii [note] 1 3 iv 4 5 3 6 4 x 0 sin x x 1 5 6 z = f(x, y) 1 y = f(x)
微分積分 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. ttp://www.morikita.co.jp/books/mid/00571 このサンプルページの内容は, 初版 1 刷発行時のものです. i ii 014 10 iii [note] 1 3 iv 4 5 3 6 4 x 0 sin x x 1 5 6 z = f(x, y) 1 y = f(x)
V(x) m e V 0 cos x π x π V(x) = x < π, x > π V 0 (i) x = 0 (V(x) V 0 (1 x 2 /2)) n n d 2 f dξ 2ξ d f 2 dξ + 2n f = 0 H n (ξ) (ii) H
 199 1 1 199 1 1. Vx) m e V cos x π x π Vx) = x < π, x > π V i) x = Vx) V 1 x /)) n n d f dξ ξ d f dξ + n f = H n ξ) ii) H n ξ) = 1) n expξ ) dn dξ n exp ξ )) H n ξ)h m ξ) exp ξ )dξ = π n n!δ n,m x = Vx)
199 1 1 199 1 1. Vx) m e V cos x π x π Vx) = x < π, x > π V i) x = Vx) V 1 x /)) n n d f dξ ξ d f dξ + n f = H n ξ) ii) H n ξ) = 1) n expξ ) dn dξ n exp ξ )) H n ξ)h m ξ) exp ξ )dξ = π n n!δ n,m x = Vx)
 215 11 13 1 2 1.1....................... 2 1.2.................... 2 1.3..................... 2 1.4...................... 3 1.5............... 3 1.6........................... 4 1.7.................. 4
215 11 13 1 2 1.1....................... 2 1.2.................... 2 1.3..................... 2 1.4...................... 3 1.5............... 3 1.6........................... 4 1.7.................. 4
Part () () Γ Part ,
 Contents a 6 6 6 6 6 6 6 7 7. 8.. 8.. 8.3. 8 Part. 9. 9.. 9.. 3. 3.. 3.. 3 4. 5 4.. 5 4.. 9 4.3. 3 Part. 6 5. () 6 5.. () 7 5.. 9 5.3. Γ 3 6. 3 6.. 3 6.. 3 6.3. 33 Part 3. 34 7. 34 7.. 34 7.. 34 8. 35
Contents a 6 6 6 6 6 6 6 7 7. 8.. 8.. 8.3. 8 Part. 9. 9.. 9.. 3. 3.. 3.. 3 4. 5 4.. 5 4.. 9 4.3. 3 Part. 6 5. () 6 5.. () 7 5.. 9 5.3. Γ 3 6. 3 6.. 3 6.. 3 6.3. 33 Part 3. 34 7. 34 7.. 34 7.. 34 8. 35
18 I ( ) (1) I-1,I-2,I-3 (2) (3) I-1 ( ) (100 ) θ ϕ θ ϕ m m l l θ ϕ θ ϕ 2 g (1) (2) 0 (3) θ ϕ (4) (3) θ(t) = A 1 cos(ω 1 t + α 1 ) + A 2 cos(ω 2 t + α
 18 I ( ) (1) I-1,I-2,I-3 (2) (3) I-1 ( ) (100 ) θ ϕ θ ϕ m m l l θ ϕ θ ϕ 2 g (1) (2) 0 (3) θ ϕ (4) (3) θ(t) = A 1 cos(ω 1 t + α 1 ) + A 2 cos(ω 2 t + α 2 ), ϕ(t) = B 1 cos(ω 1 t + α 1 ) + B 2 cos(ω 2 t
18 I ( ) (1) I-1,I-2,I-3 (2) (3) I-1 ( ) (100 ) θ ϕ θ ϕ m m l l θ ϕ θ ϕ 2 g (1) (2) 0 (3) θ ϕ (4) (3) θ(t) = A 1 cos(ω 1 t + α 1 ) + A 2 cos(ω 2 t + α 2 ), ϕ(t) = B 1 cos(ω 1 t + α 1 ) + B 2 cos(ω 2 t
II No.01 [n/2] [1]H n (x) H n (x) = ( 1) r n! r!(n 2r)! (2x)n 2r. r=0 [2]H n (x) n,, H n ( x) = ( 1) n H n (x). [3] H n (x) = ( 1) n dn x2 e dx n e x2
![II No.01 [n/2] [1]H n (x) H n (x) = ( 1) r n! r!(n 2r)! (2x)n 2r. r=0 [2]H n (x) n,, H n ( x) = ( 1) n H n (x). [3] H n (x) = ( 1) n dn x2 e dx n e x2 II No.01 [n/2] [1]H n (x) H n (x) = ( 1) r n! r!(n 2r)! (2x)n 2r. r=0 [2]H n (x) n,, H n ( x) = ( 1) n H n (x). [3] H n (x) = ( 1) n dn x2 e dx n e x2](/thumbs/101/149159646.jpg) II No.1 [n/] [1]H n x) H n x) = 1) r n! r!n r)! x)n r r= []H n x) n,, H n x) = 1) n H n x) [3] H n x) = 1) n dn x e dx n e x [4] H n+1 x) = xh n x) nh n 1 x) ) d dx x H n x) = H n+1 x) d dx H nx) = nh
II No.1 [n/] [1]H n x) H n x) = 1) r n! r!n r)! x)n r r= []H n x) n,, H n x) = 1) n H n x) [3] H n x) = 1) n dn x e dx n e x [4] H n+1 x) = xh n x) nh n 1 x) ) d dx x H n x) = H n+1 x) d dx H nx) = nh
QMI13a.dvi
 I (2013 (MAEDA, Atsutaka) 25 10 15 [ I I [] ( ) 0. (a) (b) Plank Compton de Broglie Bohr 1. (a) Einstein- de Broglie (b) (c) 1 (d) 2. Schrödinger (a) Schrödinger (b) Schrödinger (c) (d) 3. (a) (b) (c)
I (2013 (MAEDA, Atsutaka) 25 10 15 [ I I [] ( ) 0. (a) (b) Plank Compton de Broglie Bohr 1. (a) Einstein- de Broglie (b) (c) 1 (d) 2. Schrödinger (a) Schrödinger (b) Schrödinger (c) (d) 3. (a) (b) (c)
grad φ(p ) φ P grad φ(p ) p P p φ P p l t φ l t = 0 g (0) g (0) (31) grad φ(p ) p grad φ φ (P, φ(p )) xy (x, y) = (ξ(t), η(t)) ( )
 2 9 2 5 2.2.3 grad φ(p ) φ P grad φ(p ) p P p φ P p l t φ l t = g () g () (3) grad φ(p ) p grad φ φ (P, φ(p )) y (, y) = (ξ(t), η(t)) ( ) ξ (t) (t) := η (t) grad f(ξ(t), η(t)) (t) g(t) := f(ξ(t), η(t))
2 9 2 5 2.2.3 grad φ(p ) φ P grad φ(p ) p P p φ P p l t φ l t = g () g () (3) grad φ(p ) p grad φ φ (P, φ(p )) y (, y) = (ξ(t), η(t)) ( ) ξ (t) (t) := η (t) grad f(ξ(t), η(t)) (t) g(t) := f(ξ(t), η(t))
II A A441 : October 02, 2014 Version : Kawahira, Tomoki TA (Kondo, Hirotaka )
 II 214-1 : October 2, 214 Version : 1.1 Kawahira, Tomoki TA (Kondo, Hirotaka ) http://www.math.nagoya-u.ac.jp/~kawahira/courses/14w-biseki.html pdf 1 2 1 9 1 16 1 23 1 3 11 6 11 13 11 2 11 27 12 4 12 11
II 214-1 : October 2, 214 Version : 1.1 Kawahira, Tomoki TA (Kondo, Hirotaka ) http://www.math.nagoya-u.ac.jp/~kawahira/courses/14w-biseki.html pdf 1 2 1 9 1 16 1 23 1 3 11 6 11 13 11 2 11 27 12 4 12 11
応用数学III-4.ppt
 III f x ( ) = 1 f x ( ) = P( X = x) = f ( x) = P( X = x) =! x ( ) b! a, X! U a,b f ( x) =! " e #!x, X! Ex (!) n! ( n! x)!x! " x 1! " x! e"!, X! Po! ( ) n! x, X! B( n;" ) ( ) ! xf ( x) = = n n!! ( n
III f x ( ) = 1 f x ( ) = P( X = x) = f ( x) = P( X = x) =! x ( ) b! a, X! U a,b f ( x) =! " e #!x, X! Ex (!) n! ( n! x)!x! " x 1! " x! e"!, X! Po! ( ) n! x, X! B( n;" ) ( ) ! xf ( x) = = n n!! ( n
 211 kotaro@math.titech.ac.jp 1 R *1 n n R n *2 R n = {(x 1,..., x n ) x 1,..., x n R}. R R 2 R 3 R n R n R n D D R n *3 ) (x 1,..., x n ) f(x 1,..., x n ) f D *4 n 2 n = 1 ( ) 1 f D R n f : D R 1.1. (x,
211 kotaro@math.titech.ac.jp 1 R *1 n n R n *2 R n = {(x 1,..., x n ) x 1,..., x n R}. R R 2 R 3 R n R n R n D D R n *3 ) (x 1,..., x n ) f(x 1,..., x n ) f D *4 n 2 n = 1 ( ) 1 f D R n f : D R 1.1. (x,
1 (Berry,1975) 2-6 p (S πr 2 )p πr 2 p 2πRγ p p = 2γ R (2.5).1-1 : : : : ( ).2 α, β α, β () X S = X X α X β (.1) 1 2
 2005 9/8-11 2 2.2 ( 2-5) γ ( ) γ cos θ 2πr πρhr 2 g h = 2γ cos θ ρgr (2.1) γ = ρgrh (2.2) 2 cos θ θ cos θ = 1 (2.2) γ = 1 ρgrh (2.) 2 2. p p ρgh p ( ) p p = p ρgh (2.) h p p = 2γ r 1 1 (Berry,1975) 2-6
2005 9/8-11 2 2.2 ( 2-5) γ ( ) γ cos θ 2πr πρhr 2 g h = 2γ cos θ ρgr (2.1) γ = ρgrh (2.2) 2 cos θ θ cos θ = 1 (2.2) γ = 1 ρgrh (2.) 2 2. p p ρgh p ( ) p p = p ρgh (2.) h p p = 2γ r 1 1 (Berry,1975) 2-6
Untitled
 II 14 14-7-8 8/4 II (http://www.damp.tottori-u.ac.jp/~ooshida/edu/fluid/) [ (3.4)] Navier Stokes [ 6/ ] Navier Stokes 3 [ ] Reynolds [ (4.6), (45.8)] [ p.186] Navier Stokes I 1 balance law t (ρv i )+ j
II 14 14-7-8 8/4 II (http://www.damp.tottori-u.ac.jp/~ooshida/edu/fluid/) [ (3.4)] Navier Stokes [ 6/ ] Navier Stokes 3 [ ] Reynolds [ (4.6), (45.8)] [ p.186] Navier Stokes I 1 balance law t (ρv i )+ j
,. Black-Scholes u t t, x c u 0 t, x x u t t, x c u t, x x u t t, x + σ x u t, x + rx ut, x rux, t 0 x x,,.,. Step 3, 7,,, Step 6., Step 4,. Step 5,,.
 9 α ν β Ξ ξ Γ γ o δ Π π ε ρ ζ Σ σ η τ Θ θ Υ υ ι Φ φ κ χ Λ λ Ψ ψ µ Ω ω Def, Prop, Th, Lem, Note, Remark, Ex,, Proof, R, N, Q, C [a, b {x R : a x b} : a, b {x R : a < x < b} : [a, b {x R : a x < b} : a,
9 α ν β Ξ ξ Γ γ o δ Π π ε ρ ζ Σ σ η τ Θ θ Υ υ ι Φ φ κ χ Λ λ Ψ ψ µ Ω ω Def, Prop, Th, Lem, Note, Remark, Ex,, Proof, R, N, Q, C [a, b {x R : a x b} : a, b {x R : a < x < b} : [a, b {x R : a x < b} : a,
( ) s n (n = 0, 1,...) n n = δ nn n n = I n=0 ψ = n C n n (1) C n = n ψ α = e 1 2 α 2 n=0 α, β α n n! n (2) β α = e 1 2 α 2 1
 (3.5 3.8) 03032s 2006.7.0 n (n = 0,,...) n n = δ nn n n = I n=0 ψ = n C n n () C n = n ψ α = e 2 α 2 n=0 α, β α n n (2) β α = e 2 α 2 2 β 2 n=0 =0 = e 2 α 2 β n α 2 β 2 n=0 = e 2 α 2 2 β 2 +β α β n α!
(3.5 3.8) 03032s 2006.7.0 n (n = 0,,...) n n = δ nn n n = I n=0 ψ = n C n n () C n = n ψ α = e 2 α 2 n=0 α, β α n n (2) β α = e 2 α 2 2 β 2 n=0 =0 = e 2 α 2 β n α 2 β 2 n=0 = e 2 α 2 2 β 2 +β α β n α!
No δs δs = r + δr r = δr (3) δs δs = r r = δr + u(r + δr, t) u(r, t) (4) δr = (δx, δy, δz) u i (r + δr, t) u i (r, t) = u i x j δx j (5) δs 2
 No.2 1 2 2 δs δs = r + δr r = δr (3) δs δs = r r = δr + u(r + δr, t) u(r, t) (4) δr = (δx, δy, δz) u i (r + δr, t) u i (r, t) = u i δx j (5) δs 2 = δx i δx i + 2 u i δx i δx j = δs 2 + 2s ij δx i δx j
No.2 1 2 2 δs δs = r + δr r = δr (3) δs δs = r r = δr + u(r + δr, t) u(r, t) (4) δr = (δx, δy, δz) u i (r + δr, t) u i (r, t) = u i δx j (5) δs 2 = δx i δx i + 2 u i δx i δx j = δs 2 + 2s ij δx i δx j
 n ξ n,i, i = 1,, n S n ξ n,i n 0 R 1,.. σ 1 σ i .10.14.15 0 1 0 1 1 3.14 3.18 3.19 3.14 3.14,. ii 1 1 1.1..................................... 1 1............................... 3 1.3.........................
n ξ n,i, i = 1,, n S n ξ n,i n 0 R 1,.. σ 1 σ i .10.14.15 0 1 0 1 1 3.14 3.18 3.19 3.14 3.14,. ii 1 1 1.1..................................... 1 1............................... 3 1.3.........................
振動と波動
 Report JS0.5 J Simplicity February 4, 2012 1 J Simplicity HOME http://www.jsimplicity.com/ Preface 2 Report 2 Contents I 5 1 6 1.1..................................... 6 1.2 1 1:................ 7 1.3
Report JS0.5 J Simplicity February 4, 2012 1 J Simplicity HOME http://www.jsimplicity.com/ Preface 2 Report 2 Contents I 5 1 6 1.1..................................... 6 1.2 1 1:................ 7 1.3
量子力学 問題
 3 : 203 : 0. H = 0 0 2 6 0 () = 6, 2 = 2, 3 = 3 3 H 6 2 3 ϵ,2,3 (2) ψ = (, 2, 3 ) ψ Hψ H (3) P i = i i P P 2 = P 2 P 3 = P 3 P = O, P 2 i = P i (4) P + P 2 + P 3 = E 3 (5) i ϵ ip i H 0 0 (6) R = 0 0 [H,
3 : 203 : 0. H = 0 0 2 6 0 () = 6, 2 = 2, 3 = 3 3 H 6 2 3 ϵ,2,3 (2) ψ = (, 2, 3 ) ψ Hψ H (3) P i = i i P P 2 = P 2 P 3 = P 3 P = O, P 2 i = P i (4) P + P 2 + P 3 = E 3 (5) i ϵ ip i H 0 0 (6) R = 0 0 [H,
Z: Q: R: C: sin 6 5 ζ a, b
 Z: Q: R: C: 3 3 7 4 sin 6 5 ζ 9 6 6............................... 6............................... 6.3......................... 4 7 6 8 8 9 3 33 a, b a bc c b a a b 5 3 5 3 5 5 3 a a a a p > p p p, 3,
Z: Q: R: C: 3 3 7 4 sin 6 5 ζ 9 6 6............................... 6............................... 6.3......................... 4 7 6 8 8 9 3 33 a, b a bc c b a a b 5 3 5 3 5 5 3 a a a a p > p p p, 3,
2.2 h h l L h L = l cot h (1) (1) L l L l l = L tan h (2) (2) L l 2 l 3 h 2.3 a h a h (a, h)
 1 16 10 5 1 2 2.1 a a a 1 1 1 2.2 h h l L h L = l cot h (1) (1) L l L l l = L tan h (2) (2) L l 2 l 3 h 2.3 a h a h (a, h) 4 2 3 4 2 5 2.4 x y (x,y) l a x = l cot h cos a, (3) y = l cot h sin a (4) h a
1 16 10 5 1 2 2.1 a a a 1 1 1 2.2 h h l L h L = l cot h (1) (1) L l L l l = L tan h (2) (2) L l 2 l 3 h 2.3 a h a h (a, h) 4 2 3 4 2 5 2.4 x y (x,y) l a x = l cot h cos a, (3) y = l cot h sin a (4) h a
v er.1/ c /(21)
 12 -- 1 1 2009 1 17 1-1 1-2 1-3 1-4 2 2 2 1-5 1 1-6 1 1-7 1-1 1-2 1-3 1-4 1-5 1-6 1-7 c 2011 1/(21) 12 -- 1 -- 1 1--1 1--1--1 1 2009 1 n n α { n } α α { n } lim n = α, n α n n ε n > N n α < ε N {1, 1,
12 -- 1 1 2009 1 17 1-1 1-2 1-3 1-4 2 2 2 1-5 1 1-6 1 1-7 1-1 1-2 1-3 1-4 1-5 1-6 1-7 c 2011 1/(21) 12 -- 1 -- 1 1--1 1--1--1 1 2009 1 n n α { n } α α { n } lim n = α, n α n n ε n > N n α < ε N {1, 1,
December 28, 2018
 e-mail : kigami@i.kyoto-u.ac.jp December 28, 28 Contents 2............................. 3.2......................... 7.3..................... 9.4................ 4.5............. 2.6.... 22 2 36 2..........................
e-mail : kigami@i.kyoto-u.ac.jp December 28, 28 Contents 2............................. 3.2......................... 7.3..................... 9.4................ 4.5............. 2.6.... 22 2 36 2..........................
1 8, : 8.1 1, 2 z = ax + by + c ax by + z c = a b +1 x y z c = 0, (0, 0, c), n = ( a, b, 1). f = n i=1 a ii x 2 i + i<j 2a ij x i x j = ( x, A x), f =
 1 8, : 8.1 1, z = ax + by + c ax by + z c = a b +1 x y z c = 0, (0, 0, c), n = ( a, b, 1). f = a ii x i + i
1 8, : 8.1 1, z = ax + by + c ax by + z c = a b +1 x y z c = 0, (0, 0, c), n = ( a, b, 1). f = a ii x i + i
m(ẍ + γẋ + ω 0 x) = ee (2.118) e iωt P(ω) = χ(ω)e = ex = e2 E(ω) m ω0 2 ω2 iωγ (2.119) Z N ϵ(ω) ϵ 0 = 1 + Ne2 m j f j ω 2 j ω2 iωγ j (2.120)
 2.6 2.6.1 mẍ + γẋ + ω 0 x) = ee 2.118) e iωt Pω) = χω)e = ex = e2 Eω) m ω0 2 ω2 iωγ 2.119) Z N ϵω) ϵ 0 = 1 + Ne2 m j f j ω 2 j ω2 iωγ j 2.120) Z ω ω j γ j f j f j f j sum j f j = Z 2.120 ω ω j, γ ϵω) ϵ
2.6 2.6.1 mẍ + γẋ + ω 0 x) = ee 2.118) e iωt Pω) = χω)e = ex = e2 Eω) m ω0 2 ω2 iωγ 2.119) Z N ϵω) ϵ 0 = 1 + Ne2 m j f j ω 2 j ω2 iωγ j 2.120) Z ω ω j γ j f j f j f j sum j f j = Z 2.120 ω ω j, γ ϵω) ϵ
/ Christopher Essex Radiation and the Violation of Bilinearity in the Thermodynamics of Irreversible Processes, Planet.Space Sci.32 (1984) 1035 Radiat
 / Christopher Essex Radiation and the Violation of Bilinearity in the Thermodynamics of Irreversible Processes, Planet.Space Sci.32 (1984) 1035 Radiation and the Continuing Failure of the Bilinear Formalism,
/ Christopher Essex Radiation and the Violation of Bilinearity in the Thermodynamics of Irreversible Processes, Planet.Space Sci.32 (1984) 1035 Radiation and the Continuing Failure of the Bilinear Formalism,
() x + y + y + x dy dx = 0 () dy + xy = x dx y + x y ( 5) ( s55906) 0.7. (). 5 (). ( 6) ( s6590) 0.8 m n. 0.9 n n A. ( 6) ( s6590) f A (λ) = det(a λi)
 0. A A = 4 IC () det A () A () x + y + z = x y z X Y Z = A x y z ( 5) ( s5590) 0. a + b + c b c () a a + b + c c a b a + b + c 0 a b c () a 0 c b b c 0 a c b a 0 0. A A = 7 5 4 5 0 ( 5) ( s5590) () A ()
0. A A = 4 IC () det A () A () x + y + z = x y z X Y Z = A x y z ( 5) ( s5590) 0. a + b + c b c () a a + b + c c a b a + b + c 0 a b c () a 0 c b b c 0 a c b a 0 0. A A = 7 5 4 5 0 ( 5) ( s5590) () A ()
1. 2 P 2 (x, y) 2 x y (0, 0) R 2 = {(x, y) x, y R} x, y R P = (x, y) O = (0, 0) OP ( ) OP x x, y y ( ) x v = y ( ) x 2 1 v = P = (x, y) y ( x y ) 2 (x
 . P (, (0, 0 R {(,, R}, R P (, O (0, 0 OP OP, v v P (, ( (, (, { R, R} v (, (, (,, z 3 w z R 3,, z R z n R n.,..., n R n n w, t w ( z z Ke Words:. A P 3 0 B P 0 a. A P b B P 3. A π/90 B a + b c π/ 3. +
. P (, (0, 0 R {(,, R}, R P (, O (0, 0 OP OP, v v P (, ( (, (, { R, R} v (, (, (,, z 3 w z R 3,, z R z n R n.,..., n R n n w, t w ( z z Ke Words:. A P 3 0 B P 0 a. A P b B P 3. A π/90 B a + b c π/ 3. +
医系の統計入門第 2 版 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. このサンプルページの内容は, 第 2 版 1 刷発行時のものです.
 医系の統計入門第 2 版 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/009192 このサンプルページの内容は, 第 2 版 1 刷発行時のものです. i 2 t 1. 2. 3 2 3. 6 4. 7 5. n 2 ν 6. 2 7. 2003 ii 2 2013 10 iii 1987
医系の統計入門第 2 版 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/009192 このサンプルページの内容は, 第 2 版 1 刷発行時のものです. i 2 t 1. 2. 3 2 3. 6 4. 7 5. n 2 ν 6. 2 7. 2003 ii 2 2013 10 iii 1987
untitled
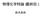 D nucleation 3 3D nucleation Glucose isomerase 10 V / nm s -1 5 0 0 5 10 C - C e / mg ml -1 kinetics µ R K kt kinetics kinetics kinetics r β π µ π r a r s + a s : β: µ πβ µ β s c s c a a r, & exp exp
D nucleation 3 3D nucleation Glucose isomerase 10 V / nm s -1 5 0 0 5 10 C - C e / mg ml -1 kinetics µ R K kt kinetics kinetics kinetics r β π µ π r a r s + a s : β: µ πβ µ β s c s c a a r, & exp exp
..3. Ω, Ω F, P Ω, F, P ). ) F a) A, A,..., A i,... F A i F. b) A F A c F c) Ω F. ) A F A P A),. a) 0 P A) b) P Ω) c) [ ] A, A,..., A i,... F i j A i A
![..3. Ω, Ω F, P Ω, F, P ). ) F a) A, A,..., A i,... F A i F. b) A F A c F c) Ω F. ) A F A P A),. a) 0 P A) b) P Ω) c) [ ] A, A,..., A i,... F i j A i A ..3. Ω, Ω F, P Ω, F, P ). ) F a) A, A,..., A i,... F A i F. b) A F A c F c) Ω F. ) A F A P A),. a) 0 P A) b) P Ω) c) [ ] A, A,..., A i,... F i j A i A](/thumbs/93/112175219.jpg) .. Laplace ). A... i),. ω i i ). {ω,..., ω } Ω,. ii) Ω. Ω. A ) r, A P A) P A) r... ).. Ω {,, 3, 4, 5, 6}. i i 6). A {, 4, 6} P A) P A) 3 6. ).. i, j i, j) ) Ω {i, j) i 6, j 6}., 36. A. A {i, j) i j }.
.. Laplace ). A... i),. ω i i ). {ω,..., ω } Ω,. ii) Ω. Ω. A ) r, A P A) P A) r... ).. Ω {,, 3, 4, 5, 6}. i i 6). A {, 4, 6} P A) P A) 3 6. ).. i, j i, j) ) Ω {i, j) i 6, j 6}., 36. A. A {i, j) i j }.
The Physics of Atmospheres CAPTER :
 The Physics of Atmospheres CAPTER 4 1 4 2 41 : 2 42 14 43 17 44 25 45 27 46 3 47 31 48 32 49 34 41 35 411 36 maintex 23/11/28 The Physics of Atmospheres CAPTER 4 2 4 41 : 2 1 σ 2 (21) (22) k I = I exp(
The Physics of Atmospheres CAPTER 4 1 4 2 41 : 2 42 14 43 17 44 25 45 27 46 3 47 31 48 32 49 34 41 35 411 36 maintex 23/11/28 The Physics of Atmospheres CAPTER 4 2 4 41 : 2 1 σ 2 (21) (22) k I = I exp(
QMI_10.dvi
 ... black body radiation black body black body radiation Gustav Kirchhoff 859 895 W. Wien O.R. Lummer cavity radiation ν ν +dν f T (ν) f T (ν)dν = 8πν2 c 3 kt dν (Rayleigh Jeans) (.) f T (ν) spectral energy
... black body radiation black body black body radiation Gustav Kirchhoff 859 895 W. Wien O.R. Lummer cavity radiation ν ν +dν f T (ν) f T (ν)dν = 8πν2 c 3 kt dν (Rayleigh Jeans) (.) f T (ν) spectral energy
.2 ρ dv dt = ρk grad p + 3 η grad (divv) + η 2 v.3 divh = 0, rote + c H t = 0 dive = ρ, H = 0, E = ρ, roth c E t = c ρv E + H c t = 0 H c E t = c ρv T
 NHK 204 2 0 203 2 24 ( ) 7 00 7 50 203 2 25 ( ) 7 00 7 50 203 2 26 ( ) 7 00 7 50 203 2 27 ( ) 7 00 7 50 I. ( ν R n 2 ) m 2 n m, R = e 2 8πε 0 hca B =.09737 0 7 m ( ν = ) λ a B = 4πε 0ħ 2 m e e 2 = 5.2977
NHK 204 2 0 203 2 24 ( ) 7 00 7 50 203 2 25 ( ) 7 00 7 50 203 2 26 ( ) 7 00 7 50 203 2 27 ( ) 7 00 7 50 I. ( ν R n 2 ) m 2 n m, R = e 2 8πε 0 hca B =.09737 0 7 m ( ν = ) λ a B = 4πε 0ħ 2 m e e 2 = 5.2977
Microsoft Word - 信号処理3.doc
 Junji OHTSUBO 2012 FFT FFT SN sin cos x v ψ(x,t) = f (x vt) (1.1) t=0 (1.1) ψ(x,t) = A 0 cos{k(x vt) + φ} = A 0 cos(kx ωt + φ) (1.2) A 0 v=ω/k φ ω k 1.3 (1.2) (1.2) (1.2) (1.1) 1.1 c c = a + ib, a = Re[c],
Junji OHTSUBO 2012 FFT FFT SN sin cos x v ψ(x,t) = f (x vt) (1.1) t=0 (1.1) ψ(x,t) = A 0 cos{k(x vt) + φ} = A 0 cos(kx ωt + φ) (1.2) A 0 v=ω/k φ ω k 1.3 (1.2) (1.2) (1.2) (1.1) 1.1 c c = a + ib, a = Re[c],
( ) ,
 II 2007 4 0. 0 1 0 2 ( ) 0 3 1 2 3 4, - 5 6 7 1 1 1 1 1) 2) 3) 4) ( ) () H 2.79 10 10 He 2.72 10 9 C 1.01 10 7 N 3.13 10 6 O 2.38 10 7 Ne 3.44 10 6 Mg 1.076 10 6 Si 1 10 6 S 5.15 10 5 Ar 1.01 10 5 Fe 9.00
II 2007 4 0. 0 1 0 2 ( ) 0 3 1 2 3 4, - 5 6 7 1 1 1 1 1) 2) 3) 4) ( ) () H 2.79 10 10 He 2.72 10 9 C 1.01 10 7 N 3.13 10 6 O 2.38 10 7 Ne 3.44 10 6 Mg 1.076 10 6 Si 1 10 6 S 5.15 10 5 Ar 1.01 10 5 Fe 9.00
p = mv p x > h/4π λ = h p m v Ψ 2 Ψ
 II p = mv p x > h/4π λ = h p m v Ψ 2 Ψ Ψ Ψ 2 0 x P'(x) m d 2 x = mω 2 x = kx = F(x) dt 2 x = cos(ωt + φ) mω 2 = k ω = m k v = dx = -ωsin(ωt + φ) dt = d 2 x dt 2 0 y v θ P(x,y) θ = ωt + φ ν = ω [Hz] 2π
II p = mv p x > h/4π λ = h p m v Ψ 2 Ψ Ψ Ψ 2 0 x P'(x) m d 2 x = mω 2 x = kx = F(x) dt 2 x = cos(ωt + φ) mω 2 = k ω = m k v = dx = -ωsin(ωt + φ) dt = d 2 x dt 2 0 y v θ P(x,y) θ = ωt + φ ν = ω [Hz] 2π
H 0 H = H 0 + V (t), V (t) = gµ B S α qb e e iωt i t Ψ(t) = [H 0 + V (t)]ψ(t) Φ(t) Ψ(t) = e ih0t Φ(t) H 0 e ih0t Φ(t) + ie ih0t t Φ(t) = [
![H 0 H = H 0 + V (t), V (t) = gµ B S α qb e e iωt i t Ψ(t) = [H 0 + V (t)]ψ(t) Φ(t) Ψ(t) = e ih0t Φ(t) H 0 e ih0t Φ(t) + ie ih0t t Φ(t) = [ H 0 H = H 0 + V (t), V (t) = gµ B S α qb e e iωt i t Ψ(t) = [H 0 + V (t)]ψ(t) Φ(t) Ψ(t) = e ih0t Φ(t) H 0 e ih0t Φ(t) + ie ih0t t Φ(t) = [](/thumbs/99/141438442.jpg) 3 3. 3.. H H = H + V (t), V (t) = gµ B α B e e iωt i t Ψ(t) = [H + V (t)]ψ(t) Φ(t) Ψ(t) = e iht Φ(t) H e iht Φ(t) + ie iht t Φ(t) = [H + V (t)]e iht Φ(t) Φ(t) i t Φ(t) = V H(t)Φ(t), V H (t) = e iht V (t)e
3 3. 3.. H H = H + V (t), V (t) = gµ B α B e e iωt i t Ψ(t) = [H + V (t)]ψ(t) Φ(t) Ψ(t) = e iht Φ(t) H e iht Φ(t) + ie iht t Φ(t) = [H + V (t)]e iht Φ(t) Φ(t) i t Φ(t) = V H(t)Φ(t), V H (t) = e iht V (t)e
I A A441 : April 21, 2014 Version : Kawahira, Tomoki TA (Kondo, Hirotaka ) Google
 I4 - : April, 4 Version :. Kwhir, Tomoki TA (Kondo, Hirotk) Google http://www.mth.ngoy-u.c.jp/~kwhir/courses/4s-biseki.html pdf 4 4 4 4 8 e 5 5 9 etc. 5 6 6 6 9 n etc. 6 6 6 3 6 3 7 7 etc 7 4 7 7 8 5 59
I4 - : April, 4 Version :. Kwhir, Tomoki TA (Kondo, Hirotk) Google http://www.mth.ngoy-u.c.jp/~kwhir/courses/4s-biseki.html pdf 4 4 4 4 8 e 5 5 9 etc. 5 6 6 6 9 n etc. 6 6 6 3 6 3 7 7 etc 7 4 7 7 8 5 59
5 5.1 E 1, E 2 N 1, N 2 E tot N tot E tot = E 1 + E 2, N tot = N 1 + N 2 S 1 (E 1, N 1 ), S 2 (E 2, N 2 ) E 1, E 2 S tot = S 1 + S 2 2 S 1 E 1 = S 2 E
 5 5.1 E 1, E 2 N 1, N 2 E tot N tot E tot = E 1 + E 2, N tot = N 1 + N 2 S 1 (E 1, N 1 ), S 2 (E 2, N 2 ) E 1, E 2 S tot = S 1 + S 2 2 S 1 E 1 = S 2 E 2, S 1 N 1 = S 2 N 2 2 (chemical potential) µ S N
5 5.1 E 1, E 2 N 1, N 2 E tot N tot E tot = E 1 + E 2, N tot = N 1 + N 2 S 1 (E 1, N 1 ), S 2 (E 2, N 2 ) E 1, E 2 S tot = S 1 + S 2 2 S 1 E 1 = S 2 E 2, S 1 N 1 = S 2 N 2 2 (chemical potential) µ S N
(iii) 0 V, x V, x + 0 = x. 0. (iv) x V, y V, x + y = 0., y x, y = x. (v) 1x = x. (vii) (α + β)x = αx + βx. (viii) (αβ)x = α(βx)., V, C.,,., (1)
 1. 1.1...,. 1.1.1 V, V x, y, x y x + y x + y V,, V x α, αx αx V,, (i) (viii) : x, y, z V, α, β C, (i) x + y = y + x. (ii) (x + y) + z = x + (y + z). 1 (iii) 0 V, x V, x + 0 = x. 0. (iv) x V, y V, x + y
1. 1.1...,. 1.1.1 V, V x, y, x y x + y x + y V,, V x α, αx αx V,, (i) (viii) : x, y, z V, α, β C, (i) x + y = y + x. (ii) (x + y) + z = x + (y + z). 1 (iii) 0 V, x V, x + 0 = x. 0. (iv) x V, y V, x + y
nm (T = K, p = kP a (1atm( )), 1bar = 10 5 P a = atm) 1 ( ) m / m
 .1 1nm (T = 73.15K, p = 101.35kP a (1atm( )), 1bar = 10 5 P a = 0.9863atm) 1 ( ).413968 10 3 m 3 1 37. 1/3 3.34.414 10 3 m 3 6.0 10 3 = 3.7 (109 ) 3 (nm) 3 10 6 = 3.7 10 1 (nm) 3 = (3.34nm) 3 ( P = nrt,
.1 1nm (T = 73.15K, p = 101.35kP a (1atm( )), 1bar = 10 5 P a = 0.9863atm) 1 ( ).413968 10 3 m 3 1 37. 1/3 3.34.414 10 3 m 3 6.0 10 3 = 3.7 (109 ) 3 (nm) 3 10 6 = 3.7 10 1 (nm) 3 = (3.34nm) 3 ( P = nrt,
A B P (A B) = P (A)P (B) (3) A B A B P (B A) A B A B P (A B) = P (B A)P (A) (4) P (B A) = P (A B) P (A) (5) P (A B) P (B A) P (A B) A B P
 1 1.1 (population) (sample) (event) (trial) Ω () 1 1 Ω 1.2 P 1. A A P (A) 0 1 0 P (A) 1 (1) 2. P 1 P 0 1 6 1 1 6 0 3. A B P (A B) = P (A) + P (B) (2) A B A B A 1 B 2 A B 1 2 1 2 1 1 2 2 3 1.3 A B P (A
1 1.1 (population) (sample) (event) (trial) Ω () 1 1 Ω 1.2 P 1. A A P (A) 0 1 0 P (A) 1 (1) 2. P 1 P 0 1 6 1 1 6 0 3. A B P (A B) = P (A) + P (B) (2) A B A B A 1 B 2 A B 1 2 1 2 1 1 2 2 3 1.3 A B P (A
b3e2003.dvi
 15 II 5 5.1 (1) p, q p = (x + 2y, xy, 1), q = (x 2 + 3y 2, xyz, ) (i) p rotq (ii) p gradq D (2) a, b rot(a b) div [11, p.75] (3) (i) f f grad f = 1 2 grad( f 2) (ii) f f gradf 1 2 grad ( f 2) rotf 5.2
15 II 5 5.1 (1) p, q p = (x + 2y, xy, 1), q = (x 2 + 3y 2, xyz, ) (i) p rotq (ii) p gradq D (2) a, b rot(a b) div [11, p.75] (3) (i) f f grad f = 1 2 grad( f 2) (ii) f f gradf 1 2 grad ( f 2) rotf 5.2
3 3.1 R r r + R R r Rr [ ] ˆn(r) = ˆn(r + R) (3.1) R R = r ˆn(r) = ˆn(0) r 0 R = r C nn (r, r ) = C nn (r + R, r + R) = C nn (r r, 0) (3.2) ( 2.2 ) C
![3 3.1 R r r + R R r Rr [ ] ˆn(r) = ˆn(r + R) (3.1) R R = r ˆn(r) = ˆn(0) r 0 R = r C nn (r, r ) = C nn (r + R, r + R) = C nn (r r, 0) (3.2) ( 2.2 ) C 3 3.1 R r r + R R r Rr [ ] ˆn(r) = ˆn(r + R) (3.1) R R = r ˆn(r) = ˆn(0) r 0 R = r C nn (r, r ) = C nn (r + R, r + R) = C nn (r r, 0) (3.2) ( 2.2 ) C](/thumbs/94/119172213.jpg) 3 3.1 R r r + R R r Rr [ ] ˆn(r) = ˆn(r + R) (3.1) R R = r ˆn(r) = ˆn(0) r 0 R = r C nn (r, r ) = C nn (r + R, r + R) = C nn (r r, 0) (3.2) ( 2.2 ) C nn (r r ) = C nn (R(r r )) [2 ] 2 g(r, r ) ˆn(r) ˆn(r
3 3.1 R r r + R R r Rr [ ] ˆn(r) = ˆn(r + R) (3.1) R R = r ˆn(r) = ˆn(0) r 0 R = r C nn (r, r ) = C nn (r + R, r + R) = C nn (r r, 0) (3.2) ( 2.2 ) C nn (r r ) = C nn (R(r r )) [2 ] 2 g(r, r ) ˆn(r) ˆn(r
Hilbert, von Neuman [1, p.86] kt 2 1 [1, 2] 2 2
![Hilbert, von Neuman [1, p.86] kt 2 1 [1, 2] 2 2 Hilbert, von Neuman [1, p.86] kt 2 1 [1, 2] 2 2](/thumbs/91/105692760.jpg) hara@math.kyushu-u.ac.jp 1 1 1.1............................................... 2 1.2............................................. 3 2 3 3 5 3.1............................................. 6 3.2...................................
hara@math.kyushu-u.ac.jp 1 1 1.1............................................... 2 1.2............................................. 3 2 3 3 5 3.1............................................. 6 3.2...................................
II Karel Švadlenka * [1] 1.1* 5 23 m d2 x dt 2 = cdx kx + mg dt. c, g, k, m 1.2* u = au + bv v = cu + dv v u a, b, c, d R
![II Karel Švadlenka * [1] 1.1* 5 23 m d2 x dt 2 = cdx kx + mg dt. c, g, k, m 1.2* u = au + bv v = cu + dv v u a, b, c, d R II Karel Švadlenka * [1] 1.1* 5 23 m d2 x dt 2 = cdx kx + mg dt. c, g, k, m 1.2* u = au + bv v = cu + dv v u a, b, c, d R](/thumbs/95/125540821.jpg) II Karel Švadlenka 2018 5 26 * [1] 1.1* 5 23 m d2 x dt 2 = cdx kx + mg dt. c, g, k, m 1.2* 5 23 1 u = au + bv v = cu + dv v u a, b, c, d R 1.3 14 14 60% 1.4 5 23 a, b R a 2 4b < 0 λ 2 + aλ + b = 0 λ =
II Karel Švadlenka 2018 5 26 * [1] 1.1* 5 23 m d2 x dt 2 = cdx kx + mg dt. c, g, k, m 1.2* 5 23 1 u = au + bv v = cu + dv v u a, b, c, d R 1.3 14 14 60% 1.4 5 23 a, b R a 2 4b < 0 λ 2 + aλ + b = 0 λ =
) ] [ h m x + y + + V x) φ = Eφ 1) z E = i h t 13) x << 1) N n n= = N N + 1) 14) N n n= = N N + 1)N + 1) 6 15) N n 3 n= = 1 4 N N + 1) 16) N n 4
![) ] [ h m x + y + + V x) φ = Eφ 1) z E = i h t 13) x << 1) N n n= = N N + 1) 14) N n n= = N N + 1)N + 1) 6 15) N n 3 n= = 1 4 N N + 1) 16) N n 4 ) ] [ h m x + y + + V x) φ = Eφ 1) z E = i h t 13) x << 1) N n n= = N N + 1) 14) N n n= = N N + 1)N + 1) 6 15) N n 3 n= = 1 4 N N + 1) 16) N n 4](/thumbs/92/107866707.jpg) 1. k λ ν ω T v p v g k = π λ ω = πν = π T v p = λν = ω k v g = dω dk 1) ) 3) 4). p = hk = h λ 5) E = hν = hω 6) h = h π 7) h =6.6618 1 34 J sec) hc=197.3 MeV fm = 197.3 kev pm= 197.3 ev nm = 1.97 1 3 ev
1. k λ ν ω T v p v g k = π λ ω = πν = π T v p = λν = ω k v g = dω dk 1) ) 3) 4). p = hk = h λ 5) E = hν = hω 6) h = h π 7) h =6.6618 1 34 J sec) hc=197.3 MeV fm = 197.3 kev pm= 197.3 ev nm = 1.97 1 3 ev
BGK
 BGK 2009 2 6 i X AGN Eckart [] Landau [2] [3] Israel Stewart Grad moment [4] BGK BGK iii 2 7 2.............................. 7 2................................. 8 2..2......................... 9 2..3
BGK 2009 2 6 i X AGN Eckart [] Landau [2] [3] Israel Stewart Grad moment [4] BGK BGK iii 2 7 2.............................. 7 2................................. 8 2..2......................... 9 2..3
ii p ϕ x, t = C ϕ xe i ħ E t +C ϕ xe i ħ E t ψ x,t ψ x,t p79 やは時間変化しないことに注意 振動 粒子はだいたい このあたりにいる 粒子はだいたい このあたりにいる p35 D.3 Aψ Cϕdx = aψ ψ C Aϕ dx
 i B5 7.8. p89 4. ψ x, tψx, t = ψ R x, t iψ I x, t ψ R x, t + iψ I x, t = ψ R x, t + ψ I x, t p 5.8 π π π F e ix + F e ix + F 3 e 3ix F e ix + F e ix + F 3 e 3ix dx πψ x πψx p39 7. AX = X A [ a b c d x
i B5 7.8. p89 4. ψ x, tψx, t = ψ R x, t iψ I x, t ψ R x, t + iψ I x, t = ψ R x, t + ψ I x, t p 5.8 π π π F e ix + F e ix + F 3 e 3ix F e ix + F e ix + F 3 e 3ix dx πψ x πψx p39 7. AX = X A [ a b c d x
H.Haken Synergetics 2nd (1978)
 27 3 27 ) Ising Landau Synergetics Fokker-Planck F-P Landau F-P Gizburg-Landau G-L G-L Bénard/ Hopfield H.Haken Synergetics 2nd (1978) (1) Ising m T T C 1: m h Hamiltonian H = J ij S i S j h i S
27 3 27 ) Ising Landau Synergetics Fokker-Planck F-P Landau F-P Gizburg-Landau G-L G-L Bénard/ Hopfield H.Haken Synergetics 2nd (1978) (1) Ising m T T C 1: m h Hamiltonian H = J ij S i S j h i S
構造と連続体の力学基礎
 II 37 Wabash Avenue Bridge, Illinois 州 Winnipeg にある歩道橋 Esplanade Riel 橋6 6 斜張橋である必要は多分無いと思われる すぐ横に道路用桁橋有り しかも塔基部のレストランは 8 年には営業していなかった 9 9. 9.. () 97 [3] [5] k 9. m w(t) f (t) = f (t) + mg k w(t) Newton
II 37 Wabash Avenue Bridge, Illinois 州 Winnipeg にある歩道橋 Esplanade Riel 橋6 6 斜張橋である必要は多分無いと思われる すぐ横に道路用桁橋有り しかも塔基部のレストランは 8 年には営業していなかった 9 9. 9.. () 97 [3] [5] k 9. m w(t) f (t) = f (t) + mg k w(t) Newton
TOP URL 1
 TOP URL http://amonphys.web.fc.com/ 3.............................. 3.............................. 4.3 4................... 5.4........................ 6.5........................ 8.6...........................7
TOP URL http://amonphys.web.fc.com/ 3.............................. 3.............................. 4.3 4................... 5.4........................ 6.5........................ 8.6...........................7
* 1 1 (i) (ii) Brückner-Hartree-Fock (iii) (HF, BCS, HFB) (iv) (TDHF,TDHFB) (RPA) (QRPA) (v) (vi) *
 * 1 1 (i) (ii) Brückner-Hartree-Fock (iii) (HF, BCS, HFB) (iv) (TDHF,TDHFB) (RPA) (QRPA) (v) (vi) *1 2004 1 1 ( ) ( ) 1.1 140 MeV 1.2 ( ) ( ) 1.3 2.6 10 8 s 7.6 10 17 s? Λ 2.5 10 10 s 6 10 24 s 1.4 ( m
* 1 1 (i) (ii) Brückner-Hartree-Fock (iii) (HF, BCS, HFB) (iv) (TDHF,TDHFB) (RPA) (QRPA) (v) (vi) *1 2004 1 1 ( ) ( ) 1.1 140 MeV 1.2 ( ) ( ) 1.3 2.6 10 8 s 7.6 10 17 s? Λ 2.5 10 10 s 6 10 24 s 1.4 ( m
ω 0 m(ẍ + γẋ + ω0x) 2 = ee (2.118) e iωt x = e 1 m ω0 2 E(ω). (2.119) ω2 iωγ Z N P(ω) = χ(ω)e = exzn (2.120) ϵ = ϵ 0 (1 + χ) ϵ(ω) ϵ 0 = 1 +
 2.6 2.6.1 ω 0 m(ẍ + γẋ + ω0x) 2 = ee (2.118) e iωt x = e 1 m ω0 2 E(ω). (2.119) ω2 iωγ Z N P(ω) = χ(ω)e = exzn (2.120) ϵ = ϵ 0 (1 + χ) ϵ(ω) ϵ 0 = 1 + Ne2 m j f j ω 2 j ω2 iωγ j (2.121) Z ω ω j γ j f j
2.6 2.6.1 ω 0 m(ẍ + γẋ + ω0x) 2 = ee (2.118) e iωt x = e 1 m ω0 2 E(ω). (2.119) ω2 iωγ Z N P(ω) = χ(ω)e = exzn (2.120) ϵ = ϵ 0 (1 + χ) ϵ(ω) ϵ 0 = 1 + Ne2 m j f j ω 2 j ω2 iωγ j (2.121) Z ω ω j γ j f j
, 1.,,,.,., (Lin, 1955).,.,.,.,. f, 2,. main.tex 2011/08/13( )
 81 4 2 4.1, 1.,,,.,., (Lin, 1955).,.,.,.,. f, 2,. 82 4.2. ζ t + V (ζ + βy) = 0 (4.2.1), V = 0 (4.2.2). (4.2.1), (3.3.66) R 1 Φ / Z, Γ., F 1 ( 3.2 ). 7,., ( )., (4.2.1) 500 hpa., 500 hpa (4.2.1) 1949,.,
81 4 2 4.1, 1.,,,.,., (Lin, 1955).,.,.,.,. f, 2,. 82 4.2. ζ t + V (ζ + βy) = 0 (4.2.1), V = 0 (4.2.2). (4.2.1), (3.3.66) R 1 Φ / Z, Γ., F 1 ( 3.2 ). 7,., ( )., (4.2.1) 500 hpa., 500 hpa (4.2.1) 1949,.,
 [Ver. 0.2] 1 2 3 4 5 6 7 1 1.1 1.2 1.3 1.4 1.5 1 1.1 1 1.2 1. (elasticity) 2. (plasticity) 3. (strength) 4. 5. (toughness) 6. 1 1.2 1. (elasticity) } 1 1.2 2. (plasticity), 1 1.2 3. (strength) a < b F
[Ver. 0.2] 1 2 3 4 5 6 7 1 1.1 1.2 1.3 1.4 1.5 1 1.1 1 1.2 1. (elasticity) 2. (plasticity) 3. (strength) 4. 5. (toughness) 6. 1 1.2 1. (elasticity) } 1 1.2 2. (plasticity), 1 1.2 3. (strength) a < b F
( ) sin 1 x, cos 1 x, tan 1 x sin x, cos x, tan x, arcsin x, arccos x, arctan x. π 2 sin 1 x π 2, 0 cos 1 x π, π 2 < tan 1 x < π 2 1 (1) (
 6 20 ( ) sin, cos, tan sin, cos, tan, arcsin, arccos, arctan. π 2 sin π 2, 0 cos π, π 2 < tan < π 2 () ( 2 2 lim 2 ( 2 ) ) 2 = 3 sin (2) lim 5 0 = 2 2 0 0 2 2 3 3 4 5 5 2 5 6 3 5 7 4 5 8 4 9 3 4 a 3 b
6 20 ( ) sin, cos, tan sin, cos, tan, arcsin, arccos, arctan. π 2 sin π 2, 0 cos π, π 2 < tan < π 2 () ( 2 2 lim 2 ( 2 ) ) 2 = 3 sin (2) lim 5 0 = 2 2 0 0 2 2 3 3 4 5 5 2 5 6 3 5 7 4 5 8 4 9 3 4 a 3 b
x () g(x) = f(t) dt f(x), F (x) 3x () g(x) g (x) f(x), F (x) (3) h(x) = x 3x tf(t) dt.9 = {(x, y) ; x, y, x + y } f(x, y) = xy( x y). h (x) f(x), F (x
 [ ] IC. f(x) = e x () f(x) f (x) () lim f(x) lim f(x) x + x (3) lim f(x) lim f(x) x + x (4) y = f(x) ( ) ( s46). < a < () a () lim a log xdx a log xdx ( ) n (3) lim log k log n n n k=.3 z = log(x + y ),
[ ] IC. f(x) = e x () f(x) f (x) () lim f(x) lim f(x) x + x (3) lim f(x) lim f(x) x + x (4) y = f(x) ( ) ( s46). < a < () a () lim a log xdx a log xdx ( ) n (3) lim log k log n n n k=.3 z = log(x + y ),
I
 I 6 4 10 1 1 1.1............... 1 1................ 1 1.3.................... 1.4............... 1.4.1.............. 1.4................. 1.4.3........... 3 1.4.4.. 3 1.5.......... 3 1.5.1..............
I 6 4 10 1 1 1.1............... 1 1................ 1 1.3.................... 1.4............... 1.4.1.............. 1.4................. 1.4.3........... 3 1.4.4.. 3 1.5.......... 3 1.5.1..............
x (x, ) x y (, y) iy x y z = x + iy (x, y) (r, θ) r = x + y, θ = tan ( y ), π < θ π x r = z, θ = arg z z = x + iy = r cos θ + ir sin θ = r(cos θ + i s
 ... x, y z = x + iy x z y z x = Rez, y = Imz z = x + iy x iy z z () z + z = (z + z )() z z = (z z )(3) z z = ( z z )(4)z z = z z = x + y z = x + iy ()Rez = (z + z), Imz = (z z) i () z z z + z z + z.. z
... x, y z = x + iy x z y z x = Rez, y = Imz z = x + iy x iy z z () z + z = (z + z )() z z = (z z )(3) z z = ( z z )(4)z z = z z = x + y z = x + iy ()Rez = (z + z), Imz = (z z) i () z z z + z z + z.. z
chap1.dvi
 1 1 007 1 e iθ = cos θ + isin θ 1) θ = π e iπ + 1 = 0 1 ) 3 11 f 0 r 1 1 ) k f k = 1 + r) k f 0 f k k = 01) f k+1 = 1 + r)f k ) f k+1 f k = rf k 3) 1 ) ) ) 1+r/)f 0 1 1 + r/) f 0 = 1 + r + r /4)f 0 1 f
1 1 007 1 e iθ = cos θ + isin θ 1) θ = π e iπ + 1 = 0 1 ) 3 11 f 0 r 1 1 ) k f k = 1 + r) k f 0 f k k = 01) f k+1 = 1 + r)f k ) f k+1 f k = rf k 3) 1 ) ) ) 1+r/)f 0 1 1 + r/) f 0 = 1 + r + r /4)f 0 1 f
main.dvi
 6 FIR FIR FIR FIR 6.1 FIR 6.1.1 H(e jω ) H(e jω )= H(e jω ) e jθ(ω) = H(e jω ) (cos θ(ω)+jsin θ(ω)) (6.1) H(e jω ) θ(ω) θ(ω) = KωT, K > 0 (6.2) 6.1.2 6.1 6.1 FIR 123 6.1 H(e jω 1, ω
6 FIR FIR FIR FIR 6.1 FIR 6.1.1 H(e jω ) H(e jω )= H(e jω ) e jθ(ω) = H(e jω ) (cos θ(ω)+jsin θ(ω)) (6.1) H(e jω ) θ(ω) θ(ω) = KωT, K > 0 (6.2) 6.1.2 6.1 6.1 FIR 123 6.1 H(e jω 1, ω
6 6.1 L r p hl = r p (6.1) 1, 2, 3 r =(x, y, z )=(r 1,r 2,r 3 ), p =(p x,p y,p z )=(p 1,p 2,p 3 ) (6.2) hl i = jk ɛ ijk r j p k (6.3) ɛ ijk Levi Civit
 6 6.1 L r p hl = r p (6.1) 1, 2, 3 r =(x, y, z )=(r 1,r 2,r 3 ), p =(p x,p y,p z )=(p 1,p 2,p 3 ) (6.2) hl i = jk ɛ ijk r j p k (6.3) ɛ ijk Levi Civita ɛ 123 =1 0 r p = 2 2 = (6.4) Planck h L p = h ( h
6 6.1 L r p hl = r p (6.1) 1, 2, 3 r =(x, y, z )=(r 1,r 2,r 3 ), p =(p x,p y,p z )=(p 1,p 2,p 3 ) (6.2) hl i = jk ɛ ijk r j p k (6.3) ɛ ijk Levi Civita ɛ 123 =1 0 r p = 2 2 = (6.4) Planck h L p = h ( h
 25 7 18 1 1 1.1 v.s............................. 1 1.1.1.................................. 1 1.1.2................................. 1 1.1.3.................................. 3 1.2................... 3
25 7 18 1 1 1.1 v.s............................. 1 1.1.1.................................. 1 1.1.2................................. 1 1.1.3.................................. 3 1.2................... 3
( ) ( 40 )+( 60 ) Schrödinger 3. (a) (b) (c) yoshioka/education-09.html pdf 1
 2009 1 ( ) ( 40 )+( 60 ) 1 1. 2. Schrödinger 3. (a) (b) (c) http://goofy.phys.nara-wu.ac.jp/ yoshioka/education-09.html pdf 1 1. ( photon) ν λ = c ν (c = 3.0 108 /m : ) ɛ = hν (1) p = hν/c = h/λ (2) h
2009 1 ( ) ( 40 )+( 60 ) 1 1. 2. Schrödinger 3. (a) (b) (c) http://goofy.phys.nara-wu.ac.jp/ yoshioka/education-09.html pdf 1 1. ( photon) ν λ = c ν (c = 3.0 108 /m : ) ɛ = hν (1) p = hν/c = h/λ (2) h
meiji_resume_1.PDF
 β β β (q 1,q,..., q n ; p 1, p,..., p n ) H(q 1,q,..., q n ; p 1, p,..., p n ) Hψ = εψ ε k = k +1/ ε k = k(k 1) (x, y, z; p x, p y, p z ) (r; p r ), (θ; p θ ), (ϕ; p ϕ ) ε k = 1/ k p i dq i E total = E
β β β (q 1,q,..., q n ; p 1, p,..., p n ) H(q 1,q,..., q n ; p 1, p,..., p n ) Hψ = εψ ε k = k +1/ ε k = k(k 1) (x, y, z; p x, p y, p z ) (r; p r ), (θ; p θ ), (ϕ; p ϕ ) ε k = 1/ k p i dq i E total = E
f(x) = f(x ) + α(x)(x x ) α(x) x = x. x = f (y), x = f (y ) y = f f (y) = f f (y ) + α(f (y))(f (y) f (y )) f (y) = f (y ) + α(f (y)) (y y ) ( (2) ) f
 22 A 3,4 No.3 () (2) (3) (4), (5) (6) (7) (8) () n x = (x,, x n ), = (,, n ), x = ( (x i i ) 2 ) /2 f(x) R n f(x) = f() + i α i (x ) i + o( x ) α,, α n g(x) = o( x )) lim x g(x) x = y = f() + i α i(x )
22 A 3,4 No.3 () (2) (3) (4), (5) (6) (7) (8) () n x = (x,, x n ), = (,, n ), x = ( (x i i ) 2 ) /2 f(x) R n f(x) = f() + i α i (x ) i + o( x ) α,, α n g(x) = o( x )) lim x g(x) x = y = f() + i α i(x )
( ) ) ) ) 5) 1 J = σe 2 6) ) 9) 1955 Statistical-Mechanical Theory of Irreversible Processes )
 ( 3 7 4 ) 2 2 ) 8 2 954 2) 955 3) 5) J = σe 2 6) 955 7) 9) 955 Statistical-Mechanical Theory of Irreversible Processes 957 ) 3 4 2 A B H (t) = Ae iωt B(t) = B(ω)e iωt B(ω) = [ Φ R (ω) Φ R () ] iω Φ R (t)
( 3 7 4 ) 2 2 ) 8 2 954 2) 955 3) 5) J = σe 2 6) 955 7) 9) 955 Statistical-Mechanical Theory of Irreversible Processes 957 ) 3 4 2 A B H (t) = Ae iωt B(t) = B(ω)e iωt B(ω) = [ Φ R (ω) Φ R () ] iω Φ R (t)
2000年度『数学展望 I』講義録
 2000 I I IV I II 2000 I I IV I-IV. i ii 3.10 (http://www.math.nagoya-u.ac.jp/ kanai/) 2000 A....1 B....4 C....10 D....13 E....17 Brouwer A....21 B....26 C....33 D....39 E. Sperner...45 F....48 A....53
2000 I I IV I II 2000 I I IV I-IV. i ii 3.10 (http://www.math.nagoya-u.ac.jp/ kanai/) 2000 A....1 B....4 C....10 D....13 E....17 Brouwer A....21 B....26 C....33 D....39 E. Sperner...45 F....48 A....53
IA
 IA 31 4 11 1 1 4 1.1 Planck.............................. 4 1. Bohr.................................... 5 1.3..................................... 6 8.1................................... 8....................................
IA 31 4 11 1 1 4 1.1 Planck.............................. 4 1. Bohr.................................... 5 1.3..................................... 6 8.1................................... 8....................................
note1.dvi
 (1) 1996 11 7 1 (1) 1. 1 dx dy d x τ xx x x, stress x + dx x τ xx x+dx dyd x x τ xx x dyd y τ xx x τ xx x+dx d dx y x dy 1. dx dy d x τ xy x τ x ρdxdyd x dx dy d ρdxdyd u x t = τ xx x+dx dyd τ xx x dyd
(1) 1996 11 7 1 (1) 1. 1 dx dy d x τ xx x x, stress x + dx x τ xx x+dx dyd x x τ xx x dyd y τ xx x τ xx x+dx d dx y x dy 1. dx dy d x τ xy x τ x ρdxdyd x dx dy d ρdxdyd u x t = τ xx x+dx dyd τ xx x dyd
数学Ⅱ演習(足助・09夏)
 II I 9/4/4 9/4/2 z C z z z z, z 2 z, w C zw z w 3 z, w C z + w z + w 4 t R t C t t t t t z z z 2 z C re z z + z z z, im z 2 2 3 z C e z + z + 2 z2 + 3! z3 + z!, I 4 x R e x cos x + sin x 2 z, w C e z+w
II I 9/4/4 9/4/2 z C z z z z, z 2 z, w C zw z w 3 z, w C z + w z + w 4 t R t C t t t t t z z z 2 z C re z z + z z z, im z 2 2 3 z C e z + z + 2 z2 + 3! z3 + z!, I 4 x R e x cos x + sin x 2 z, w C e z+w
1 Abstract 2 3 n a ax 2 + bx + c = 0 (a 0) (1) ( x + b ) 2 = b2 4ac 2a 4a 2 D = b 2 4ac > 0 (1) 2 D = 0 D < 0 x + b 2a = ± b2 4ac 2a b ± b 2
 1 Abstract n 1 1.1 a ax + bx + c = 0 (a 0) (1) ( x + b ) = b 4ac a 4a D = b 4ac > 0 (1) D = 0 D < 0 x + b a = ± b 4ac a b ± b 4ac a b a b ± 4ac b i a D (1) ax + bx + c D 0 () () (015 8 1 ) 1. D = b 4ac
1 Abstract n 1 1.1 a ax + bx + c = 0 (a 0) (1) ( x + b ) = b 4ac a 4a D = b 4ac > 0 (1) D = 0 D < 0 x + b a = ± b 4ac a b ± b 4ac a b a b ± 4ac b i a D (1) ax + bx + c D 0 () () (015 8 1 ) 1. D = b 4ac
( ; ) C. H. Scholz, The Mechanics of Earthquakes and Faulting : - ( ) σ = σ t sin 2π(r a) λ dσ d(r a) =
 1 9 8 1 1 1 ; 1 11 16 C. H. Scholz, The Mechanics of Earthquakes and Faulting 1. 1.1 1.1.1 : - σ = σ t sin πr a λ dσ dr a = E a = π λ σ πr a t cos λ 1 r a/λ 1 cos 1 E: σ t = Eλ πa a λ E/π γ : λ/ 3 γ =
1 9 8 1 1 1 ; 1 11 16 C. H. Scholz, The Mechanics of Earthquakes and Faulting 1. 1.1 1.1.1 : - σ = σ t sin πr a λ dσ dr a = E a = π λ σ πr a t cos λ 1 r a/λ 1 cos 1 E: σ t = Eλ πa a λ E/π γ : λ/ 3 γ =
I-2 (100 ) (1) y(x) y dy dx y d2 y dx 2 (a) y + 2y 3y = 9e 2x (b) x 2 y 6y = 5x 4 (2) Bernoulli B n (n = 0, 1, 2,...) x e x 1 = n=0 B 0 B 1 B 2 (3) co
 16 I ( ) (1) I-1 I-2 I-3 (2) I-1 ( ) (100 ) 2l x x = 0 y t y(x, t) y(±l, t) = 0 m T g y(x, t) l y(x, t) c = 2 y(x, t) c 2 2 y(x, t) = g (A) t 2 x 2 T/m (1) y 0 (x) y 0 (x) = g c 2 (l2 x 2 ) (B) (2) (1)
16 I ( ) (1) I-1 I-2 I-3 (2) I-1 ( ) (100 ) 2l x x = 0 y t y(x, t) y(±l, t) = 0 m T g y(x, t) l y(x, t) c = 2 y(x, t) c 2 2 y(x, t) = g (A) t 2 x 2 T/m (1) y 0 (x) y 0 (x) = g c 2 (l2 x 2 ) (B) (2) (1)
S I. dy fx x fx y fx + C 3 C dy fx 4 x, y dy v C xt y C v e kt k > xt yt gt [ v dt dt v e kt xt v e kt + C k x v + C C k xt v k 3 r r + dr e kt S dt d
 S I.. http://ayapin.film.s.dendai.ac.jp/~matuda /TeX/lecture.html PDF PS.................................... 3.3.................... 9.4................5.............. 3 5. Laplace................. 5....
S I.. http://ayapin.film.s.dendai.ac.jp/~matuda /TeX/lecture.html PDF PS.................................... 3.3.................... 9.4................5.............. 3 5. Laplace................. 5....
数学の基礎訓練I
 I 9 6 13 1 1 1.1............... 1 1................ 1 1.3.................... 1.4............... 1.4.1.............. 1.4................. 3 1.4.3........... 3 1.4.4.. 3 1.5.......... 3 1.5.1..............
I 9 6 13 1 1 1.1............... 1 1................ 1 1.3.................... 1.4............... 1.4.1.............. 1.4................. 3 1.4.3........... 3 1.4.4.. 3 1.5.......... 3 1.5.1..............
main.dvi
 SGC - 70 2, 3 23 ɛ-δ 2.12.8 3 2.92.13 4 2 3 1 2.1 2.102.12 [8][14] [1],[2] [4][7] 2 [4] 1 2009 8 1 1 1.1... 1 1.2... 4 1.3 1... 8 1.4 2... 9 1.5... 12 1.6 1... 16 1.7... 18 1.8... 21 1.9... 23 2 27 2.1
SGC - 70 2, 3 23 ɛ-δ 2.12.8 3 2.92.13 4 2 3 1 2.1 2.102.12 [8][14] [1],[2] [4][7] 2 [4] 1 2009 8 1 1 1.1... 1 1.2... 4 1.3 1... 8 1.4 2... 9 1.5... 12 1.6 1... 16 1.7... 18 1.8... 21 1.9... 23 2 27 2.1
1 filename=mathformula tex 1 ax 2 + bx + c = 0, x = b ± b 2 4ac, (1.1) 2a x 1 + x 2 = b a, x 1x 2 = c a, (1.2) ax 2 + 2b x + c = 0, x = b ± b 2
 filename=mathformula58.tex ax + bx + c =, x = b ± b 4ac, (.) a x + x = b a, x x = c a, (.) ax + b x + c =, x = b ± b ac. a (.3). sin(a ± B) = sin A cos B ± cos A sin B, (.) cos(a ± B) = cos A cos B sin
filename=mathformula58.tex ax + bx + c =, x = b ± b 4ac, (.) a x + x = b a, x x = c a, (.) ax + b x + c =, x = b ± b ac. a (.3). sin(a ± B) = sin A cos B ± cos A sin B, (.) cos(a ± B) = cos A cos B sin
kawa (Spin-Orbit Tomography: Kawahara and Fujii 21,Kawahara and Fujii 211,Fujii & Kawahara submitted) 2 van Cittert-Zernike Appendix A V 2
 Hanbury-Brown Twiss (ver. 1.) 24 2 1 1 1 2 2 2.1 van Cittert - Zernike..................................... 2 2.2 mutual coherence................................. 3 3 Hanbury-Brown Twiss ( ) 4 3.1............................................
Hanbury-Brown Twiss (ver. 1.) 24 2 1 1 1 2 2 2.1 van Cittert - Zernike..................................... 2 2.2 mutual coherence................................. 3 3 Hanbury-Brown Twiss ( ) 4 3.1............................................
Aharonov-Bohm(AB) S 0 1/ 2 1/ 2 S t = 1/ 2 1/2 1/2 1/, (12.1) 2 1/2 1/2 *1 AB ( ) 0 e iθ AB S AB = e iθ, AB 0 θ 2π ϕ = e ϕ (ϕ ) ϕ
 1 13 6 8 3.6.3 - Aharonov-BohmAB) S 1/ 1/ S t = 1/ 1/ 1/ 1/, 1.1) 1/ 1/ *1 AB ) e iθ AB S AB = e iθ, AB θ π ϕ = e ϕ ϕ ) ϕ 1.) S S ) e iθ S w = e iθ 1.3) θ θ AB??) S t = 4 sin θ 1 + e iθ AB e iθ AB + e
1 13 6 8 3.6.3 - Aharonov-BohmAB) S 1/ 1/ S t = 1/ 1/ 1/ 1/, 1.1) 1/ 1/ *1 AB ) e iθ AB S AB = e iθ, AB θ π ϕ = e ϕ ϕ ) ϕ 1.) S S ) e iθ S w = e iθ 1.3) θ θ AB??) S t = 4 sin θ 1 + e iθ AB e iθ AB + e
untitled
 20010916 22;1017;23;20020108;15;20; 1 N = {1, 2, } Z + = {0, 1, 2, } Z = {0, ±1, ±2, } Q = { p p Z, q N} R = { lim a q n n a n Q, n N; sup a n < } R + = {x R x 0} n = {a + b 1 a, b R} u, v 1 R 2 2 R 3
20010916 22;1017;23;20020108;15;20; 1 N = {1, 2, } Z + = {0, 1, 2, } Z = {0, ±1, ±2, } Q = { p p Z, q N} R = { lim a q n n a n Q, n N; sup a n < } R + = {x R x 0} n = {a + b 1 a, b R} u, v 1 R 2 2 R 3
