の強さB または周波数 n を変化させる必要がある NMR 法が要求する磁束密度の空間的, 時間的誤差 (0-8 ~0-9 T 程度 ) は, 超伝導磁石のみでは達成できないので,NMR 装置ではロック ( 磁場の時間変動を修正 ) やシム ( 磁場の空間変動を均一化 ) といった, 装置上の工夫を
|
|
|
- あまめ いさし
- 5 years ago
- Views:
Transcription
1 数式で理解する分析化学 NMR 現象を基礎から振り返る 浅野敦志 数式 数学キーワード複素数, 積分, 指数関数, 三角関数, フーリエ変換, 微分方程式, ベクトル, 内積, 外積 はじめに 単純な NMR スペクトルはすでに, ルーチン的に自動測定できるようになっているが,NMR 現象の基礎的事柄について漠然とではなく, 数式から再認識することは, より高度なスペクトルを観測するために重要であり有意義なことである 本講座では,NMR 共鳴, パルス法, フーリエ変換, ブロッホ (Bloch) 方程式, 緩和, 核オーバーハウザー効果 (nuclear Overhauser effect, NOE) について数式をひも紐解きながら解説する また, NOE に関連して 3 CNMR 法の定量性についても言及する 共鳴とパルス 核磁気モーメントをもつ原子核は, 静磁場中では複数のエネルギー準位に分裂した集団としてみなされる ( 熱平衡状態 ) その準位差間のエネルギーと等しい電磁波を照射することにより, 低いエネルギー状態の原子核が高いエネルギー状態へと遷移する ( 励起状態 ) このときのエネルギー吸収量を観測するのが NMR 分光法である 核磁気モーメントは, 核スピン量子数 ( 単に核スピンという ) に比例するため, 静磁場 (B) と核磁気モーメント (m) の相互作用からなるエネルギー (E, スカラー ) もまた, 核スピン (I, I I) に比例する E - m B - gi B... ( ) ここで g は核種で決まる比例定数 ( 磁気回転比 ), はプランク定数 h の / p 倍 静磁場 B と核スピン I はベクトル量であるので, 式 ( ) の積は内積となる 静磁場 ( 磁束密度を B 0 とする ) は超伝導磁石を用いるの Basic Knowledge of Mathematical Theories of Analytical Chemistry Mathematical Background of NMR Fundamentals. が一般的であり,+z 軸方向が磁場の順方向となる つまり, 要素表記にすれば B(0, 0, B 0 ) と書け, 式 ( ) の内積は B と I の z 軸成分同士の積となる I の z 軸成分 (I z ) は, 磁気量子数 (m-i, -I+,, I-, I) の異なる (I+) 個だけ存在するので, 式 ( ) は E - gi B - g (I x I y I z ) 0 - gmb... 0 ( ) と書ける H 核や 3 C 核のような I/ の核種の場合には,m-/ と / の 種類のエネルギー状態が存在する 一般に, 静磁場と同じ方向に配向する核スピンを I a /, 逆方向に配向する核スピンを I b -/ と表記している a 状態のエネルギー (E a ) は,b 状態のエネルギー (E b ) より若干低い エネルギー準位間のエネルギー差 (DEE b -E a ) は, DE - g ( - ) B 0 - ( - g B 0) gb 0... ( 3 ) となる このエネルギー差 DE に等しい電磁波 (hn 0 ) を照射すると共鳴が起きる すなわち, 次式 ( 4 ) で示される NMR 現象の共鳴条件が得られる gb 0 hn 0 gb 0 pn 0 v... 0 ( 4 ) ここで n 0 は静磁場 B 0 における共鳴周波数 ( または共鳴振動数,s - Hz),v 0 (rad s - ) は共鳴角速度である 現在 NMR 測定に利用されている一般的な静磁場の強さ {9~3 テスラ (T)} では, H 核の共鳴周波数はラジオ波と呼ばれる領域をすでに超えている (400 MHz~ GHz) が,NMR 分光法では慣例でラジオ波と呼ぶ ( H の g は rad s - T - なので,.75 T の静磁場では n s MHz) 低周波数核種ではラジオ波領域 (0~300 MHz) の範囲となり, 照射される電磁波はラジオ波である さて, 式 ( 4 ) の共鳴条件を達成するためには, 磁場 0 B 0 66 ぶんせき
2 の強さB または周波数 n を変化させる必要がある NMR 法が要求する磁束密度の空間的, 時間的誤差 (0-8 ~0-9 T 程度 ) は, 超伝導磁石のみでは達成できないので,NMR 装置ではロック ( 磁場の時間変動を修正 ) やシム ( 磁場の空間変動を均一化 ) といった, 装置上の工夫を施して達成している したがって, 高精度の磁場安定性を要求する高分解能 NMR 実験では, 磁場 B を掃引する方法ではなく, 周波数 n を掃引する方法 (continuous wave, CW 法 ) が適している しかし, 実際には周波数を掃引してはいない 現在では, パルス法という電磁波を矩形的に短時間照射する方法によって, 全観測幅が一気に共鳴条件となるような実験を行っている 初期の NMR 実験では, ラジオ波の周波数を掃引していたが, 現在ではパルス法とフーリエ変換法を組み合わせた手法が確立されている ではなぜパルスを照射することで, 全観測域を式 (4 ) の状態にできるのか? パルスの周波数成分を考えてみることにする 短時間 (ns オーダー ) に電磁波を ON, OFF すると, 電磁波は矩形型 ( パルス波 ) で出力 ( 照射 ) される { 図 (a)} H の化学シフトは,B 0.75 T の静磁場であれば約 0 ppm5000 Hz の範囲に現れるので, この範囲をパルス法で一度に励起できれば良い パルス法を, 鐘を鳴らした時に聞こえる音に例えて考えてみよ う 鐘が観測対象であり, 鐘を鳴らす行為がパルス照射, 聞こえる音が応答である 鐘を鳴らすと空気が振動し, 音が時間とともに空間を伝わる つまり, 横軸を時間にすれば, 一定の振動数で揺れる信号となる 音は時間とともに弱くなるので, 各々の振動数で揺れる信号は時間経過とともに減衰する ( 時間軸の信号, 自由誘導減衰 :free induction decay, FID) 鐘の音色は, 数種類の振動数の音の和から成り立っており, 金属の成分等に依存する 鐘を鳴らす行為は, そのすべての信号 ( 和音 ) を一度に励起したことと同じである 絶対音感のある人は, 和音中の音を区別することが可能だろう つまり, 時間軸の合成波を複数の異なる周波数 ( 異なる音 ) として認識できる これは, 人間の脳が時間軸から周波数軸へ変換 ( フーリエ変換 ) しているためである さて, 図 (a) のように,n 0 MHz の電磁波を t p ns だけパルス照射したとする このときのパルスは次式 ( 5 ) で与えられる f(t) B e pin0t B (cos pn 0 t + i sin pn 0 t)... ( 5 ) ただし,-t p / t t p / と考える それ以外の時間では f(t)0 である 負の時間は存在しないが, 便宜上, パルスの中間地点を起点としてある 電磁波は実数部で cos 波, 虚数部で sin 波を含む B はパルスの磁場強度であり,NMR 信号を励起するために必要な強度である 照射している電磁波は単一の n 0 MHz で振動しているが, パルス状にすることで, 電磁波の周波数成分は単一ではなくなる ただし, その周波数成分全てが磁場強度 B を持つわけではなく,n 0 MHz の周波数のみが磁場強度 B を持ち, その他の周波数は B より磁場強度が弱くなる これを証明するためには, フーリエ変換の知識が必要となる フーリエ変換の詳細は成書に任せることにして ), ここでは定義だけ提示し, 数式を解くことに主眼をおく 式 ( 6 ) がフーリエ変換の定義であり, 時間の関数 f(t ) が周波数 ( 時間の逆数 ) の関数 F(n) に変換される F(n) f f(t)e -pint... ( 6 ) - 式 ( 6 ) に式 ( 5 ) を代入すると, 図 (a): パルスの模式図 ( 右側はオシロスコープ上で見えるパルスの模式図 ),(b): パルスをフーリエ変換し, 周波数軸でプロットしたパルスの周波数特性 ( 縦の点線は 5 ms のパルスの強度 (50 khz) を表し, 横の点線はその時の励起効率 (0.9) を表す ) 化学シフト (d) 差が 5000 Hz の時, 5000 Hz d 500 MHz ppm となり,ppmは500 Hz に相当する F(n) B f-tp/ B e pi(n0 - n)t B [ - n)t tp/ epi(n0 pi(n 0 - n)] -tp/ pi(n 0 - n) - n)tp/ -e -pi(n0-n)tp/ } {epi(n0 B pi(n 0 - n) i sin ( p(n 0 - n) t p ) B t p sin (p(n 0 - n)t p ) p(n 0 - n)t p... ( 7 ) ぶんせき 67
3 となる ここでB t p はパルスの面積を表し { 図 (a)}, 照射したパルスの全パワー ( 磁化を00 % 励起できるパワー ) である また, 式 ( 7 ) の sin x/x の形をした関数を sinc 関数と呼ぶ 図 (b) に式 ( 7 ) を図示した sinc 関数は n 0 を中心とした偶関数であり振動しながら減衰する パルス状にラジオ波を照射すると, 図 (b) に示したように n 0 の単一周波数ではなく, 中心周波数 (n 0 ) から広範囲にある程度の強度の周波数成分が存在する sinc 関数の値が最初に 0 に到達する周波数が /t p Hz であり,t p が短いほど広く有効な周波数成分が存在する つまり, 化学シフトで共鳴周波数が中心周波数からずれていても, 回のパルス実験によりすべての NMR 信号を共鳴させることが可能である ただし, 共鳴させるために必要な強度を持つ周波数成分は, 中心周波数から限られた範囲内である 例えば0 ns のパルス長では, 観測中心から.5 khz 離れても 99.9 % の磁化を励起できるが,5kHz 離れた位置のピーク強度は 99.6 % となる 静磁場の強さが B 0.75 T の場合, H の化学シフトは約 0 ppm 5kHzの範囲 ( 観測中心から ±.5 khz) なので, H の NMR 信号は 0 ns のパルス長でほぼ完全に励起されることが理解できるだろう 直感的にイメージしやすくするため,NMR 信号の共鳴現象は巨視的磁化 (M) と呼ばれるベクトルモデルを用いて説明されることが多い { 図 (a)} 式( 4 ) の共鳴条件を満たすということは, 静磁場方向 (+z 方向 ) を向いている M が,xy 平面へ倒れることと同義と解釈される つまり, 共鳴条件が達成されると M は円運動し て 90 倒れる ( このとき照射したパルスを 90 パルスという ) M が回転する角度 u は, 角速度 v とパルス照射時間 t p により, u v t p pn t p gb t p... ( 8 ) となる { 図 (a), 磁化の運動に関しての詳細は次項参照 } ラジオ波を t p 時間照射して磁化 M が 90 倒れた場合, 式 ( 8 ) に up/ を代入して整理すると n /4t p になる 例えば,90 パルスの長さが 5 ns の場合には, n /( ) s - 50 khz となる { すなわち,n (khz)50/t p (ns) の関係となる } この値は, 中心周波数から励起効率が 90 % となる周波数との差を表している { 図 (b) の点線と青色の曲線の交点 } つまり, 式 ( 7 ) の sinc 関数部分に n 0 -n50 khz と t p s を代入した場合, sin (p(n 0 - n)t p ) p(n 0 - n)t p sin (p ) sin p/4 p p/4 4 p p ( 9 ) と求められるのである このことは,5 ns の 90 パルスは, 中心周波数から ±50 khz の範囲を 90 % 以上の効率で磁化を励起できるという意味を表す 実際には, 99.9 % 程度の励起効率となる範囲までを観測幅に設定するが, 照射ラジオ波の強さとして, 式 ( 8 ) から求められる n 値を記述したり述べたりする つまり, どのぐらいのパワーでラジオ波を照射したのか? という質問に対して, 50 khz のパワー (90 パルスの長さが 5 ns となるパワー ) などと答える 3 シグナルの形 : フーリエ変換法とブロッホ方程式 図 (a):x 軸方向に B の強さのラジオ波を照射したときの回転座標系における巨視的磁化 M の倒れる方向 ( 赤矢印 ) と倒れた角度 u,(b): 外積 (M B) の定義 { ベクトル M と B の外積により ( 右ねじ ( 右回転 ) 方向 :M から B へ青矢印で回転する方向 ) 生ずるトルクの方向と M の回転方向 ( 赤矢印 ) を示している } t の範囲を 0tt p とすると, F(n) B f tp e pi(n0 - n)t B pi(n n) {e pi(n0 - n)tp - } B sin (p(n 0 -n)t p ) -ip(n0 e - n)tp p(n 0 -n) となり,sinc 関数がさらに指数関数で振動する パルスにより励起された磁化は, 時間とともに元の熱平衡状態に戻る パルス NMR 法による信号観測では, パルスにより xy 平面に倒された磁化の時間変化を電気信号として捉える この時間変化は, 磁化が指数関数的に減衰していく過程 (FID) であり, 熱平衡状態に戻る過程とは異なる 巨視的磁化として位相がそろった磁化の核スピン同士の位相の乱れが主原因であり,T 緩和と呼ばれる 一方, 熱平衡状態に戻る過程は T 緩和と呼ばれる 熱平衡状態において xy 平面上に磁化が存在することはないから, 必ず T T が成り立つ パルス NMR 法により観測される FID 信号は, 指数関数的に T 緩和していく磁化である さらに, 化学シフト (n CS n 0 +Dn ) により中心周波数からずれた FID 信号は, そのずれた分 (Dn ) 振動する (n 0 で座標が回 68 ぶんせき
4 転する回転座標系で観測 ) したがって, 次式 (0) で表される関数の FID 信号 f(t) が観測される ( y 軸方向から観測 ) f(t) M cos (pdnt) e -t/t... (0) 式 ( 6 ) のフーリエ変換を行えば, 周波数軸の NMR 信号 { スペクトル, 式 ()} となる F(n) M f cos (pdnt) e -t/t e -pint - M e f -{+pi(n-dn)t/t}t 0 + M e f -{+pi(n+dn)t/t}t 0 0.5MT + 4p (n - Dn) T - i 0.5M p(n -Dn)T + 4p (n - Dn) T 0.5MT + + 4p (n + Dn) T ) 0.5M p(n + Dn)T - i + 4p (n + Dn) T... () ここで, フーリエ変換の時間 t の区間が - から 0 の間は磁化が存在しないため,f(t )0 である 実数部の関数形 /(+n ) は吸収波形であり { 図 3(a, c)}, 虚数部の n/(+n ) は分散波形である { 図 3(b, d)} すなわち, 式 () は n±dn の位置に二つのピークが存在する式となっている 観測している我々が目にするのは実数部であるが, パルスを照射して FID 信号を受信しフーリエ変換をすれば, 強度が 0.5 M の二つのピー クが出現することを式 () は物語っている しかし, 実際にパソコン画面に現れるピークは一つである なぜか? 実は, どちらかがフーリエ変換で現れる偽ピークだからであり, 実際の処理では偽ピークを除去しているからである では, どのようにして除去しているのだろうか? NMR 現象をベクトルモデルで説明する場合,±Dn の位置に観測される二つのピークは,y 軸方向に倒された巨視的磁化の xy 平面上の回転方向の違いとして説明される したがって,x 軸から観測される sin 波の 周期の位相から右回転か左回転かは判断できる ここで sin 波の FID 信号をフーリエ変換してみると, F(n) M f sin (pdnt) e -t/t e -pint - i [ 0.5MT - + 4p (n - Dn) T + i 0.5M p(n -Dn)T + 4p (n - Dn) T 0.5MT + + 4p (n + Dn) T ) 0.5M p(n + Dn)T - i + 4p (n + Dn) T ]... () となる 式 () は, 正負の強度で ±Dn の位置に二つのピークが出現することを示している 偽ピークが負の強度となるので,cos 波のフーリエ変換と sin 波のフーリエ変換との和を求めると, 偽ピークは0 に, 本来のピークは強度 M となって 本のピークとなる sin 波のフーリエ変換の場合には,cos 波に対して虚数部 ( 虚数は観測できないので90 位相がずれている信号を虚数部とする ) を実際のピーク波形とする つまり, 式 () と式 () の [ ] 内の和を求めて式 (3) を得る F(n) T + 4p (n + Dn) T - i M p(n + Dn)T + 4p (n + Dn) T M... (3) 図 3 (a):dn(n CS -n 0 ) で振動する FID をフーリエ変換して得られる実数部のスペクトル,(b): 虚数部 {Dn だけ offresonance にピークが観測される (NMR の横軸は右側が低周波数 },(c):bloch 方程式から得られた M y の onresonance (vv 0 ) の信号,(d): は虚数部 M x を表す ( ただし,T s とした ) 式 (3) の実数部の関数形は, 一般にローレンツ曲線と呼ばれる { 図 3(a)} 次に, この関数形と Bloch 方程式から得られる NMR 信号の形が同じであることを証明しよう Bloch 方程式は, ベクトルモデルを用いた場合の磁化の運動を表した古典的な運動方程式であり, 周波数掃引により得られる NMR 信号を与える 式 (4) に示したように, 巨視的磁化ベクトル M と磁場 B との運動 (dm/) は外積で表される ( 記述を簡略化するため M(t ) を M とした ) 式 (4) の外積は, 磁化 M が磁場 B から受けるトルク ( 力 ) とその方向を表し { 図 (b)},m を B の方向へ右回転した場合の右ねじの進行方向に M が力を受けて, ぶんせき 69
5 倒れることを意味する B から見ると M はB の順方向に対して左回転して xy 平面に倒れる ( 図 ) d M g M B... (4) この式中の磁場 B は, 静磁場 B 0 とラジオ波磁場 B の両方の和であるが, 図 (a) の状態を考えるために回転座標系に変換する 角速度 v 0 で回転する回転座標系に変換することで, 磁化に対する静磁場の影響を考慮せずに済む 実験室座標系の式 (4) は,v を回転ベクトルとすれば, 回転座標系上の磁化の運動 (M/t) と回転運動 (v M) の和として表せる したがって, 回転座標系上の磁化の運動 M/t は t M d M - v M g M ( B + v g )... (5) となる 実際は, 磁化は熱平衡状態へ戻るので, 緩和項を考慮する必要がある T 緩和と T 緩和を考慮すると式 (5) は, t M g M ( B + v g ) - M xi + M y j T - (M z - M 0 )k T... (6) となる ここで i, j, k は単位方向ベクトル 式 (6) をデカルト座標の各 x, y, z 成分に分けて記述してみると 3, t M x g (M y B z - M z B y )+(M y v z - M z v y ) - M x T... (7) t M y g (M z B x - M x B z )+(M z v x - M x v z ) - M y T... (8) t M z g (M x B y - M y B x )+(M x v y - M y v x ) - (M z-m 0 ) T... (9) となる 今,x 軸方向からラジオ波を照射したとすると, g>0 で,gB z gb 0 -v 0, gb x gb -v, B y 0, 回転ベクトル v の成分は z 軸回りの回転のみなので,v x 3 M B (M x M y M z ) (B x B y B z ) M ( x M y M z M x B x B y B z B x ) として,(i, j, k) の各成分は, 赤矢印の積から青矢印の積を引いた値を, 真ん中,3 番目, 最初と並べた順となる つまり,i 要素は M y B z -M z B y,j 要素は M z B x -M x B z,k 要素は M x B y -M y B x となる v y 0,v z v と置ける ( 符号は回転方向を表し, マイナスは左回転 例えば図 (a) のように,B を x 方向の正方向へ照射した場合, 磁化は y 方向の正方向に倒れるので,B から見ると左回転する ) 式(7)~(9) は, t M x (v - v 0 )M y - M x T... (0) t M y - (v - v 0 )M x - v M z - M y T... () t M z v M y - (M z - M 0 ) T... () と書き直される 観測されるスペクトル ( 磁化 ) は, 式 (0)~() をそれぞれ 0 と置いたとき ( 定常状態,t のとき ) の解である 式 (0)~() より M y ( 実数部 ) を求めると, -v T M y M +(v-v 0 ) T + v T T... 0 (3) となる 掃引するラジオ波の強度は, 強すぎると磁化が飽和してしまい 0 となる 強すぎない条件は v T T であり, したがって式 (3) は - v T M y +(v - v 0 ) T T +(v - v 0 ) T T M 0 gb M 0 gb +4p (n - n 0 ) T M... 0 (4) となる この式は中心周波数上 (onresonance, vv 0 ) で観測される信号を表しているが { 図 3(c)}, 信号の形は式 (3) の実数部と同じである このことは, パルス NMR 法で観測されるスペクトルは,Bloch 方程式が想定している CW 法と同じスペクトルの形状を与えることを示している 4 緩和と NOE z 軸方向の磁化 {M z (t ) M z } の時間変化は, 熱平衡状態の磁化 M 0 と励起して t 秒経った後の z 軸方向の磁化 M z (t ) との差に比例する ( 図 4) z 軸方向の磁化の運動だけに注目すれば, d M z - (M z-m 0 ) T... (5) となる 式 (5) は容易に解け, M z M 0 +l e -t/t... (6) となる ここで l は初期条件 ( 実験条件 ) から定まる定数である inversionrecovery 法 ( 反転回復法,80 t 90 パルス ) で T の測定を行ったとすると, 初期条 70 ぶんせき
6 図 4 磁化 M z が時間 t で熱平衡状態に戻る様子を模式的に示した図 ( 左 ) と, 熱平衡値 M 0 と磁化 M z との差を時間 t に対してプロットした図 ( 右 ) 図 5 (a): スピン系 ( H と 3 C) のスピン状態 ( 占有数は線の太さで模式的に表している ) と遷移確率 W の模式図,(b): H ラジオ波照射で H スピンの占有数差を 0 にする様子,(c): 分子運動が速い時の H ラジオ波照射で生じる占有数の様子 ( H スピンの占有数差 ( ) は 0 となり, 3 C の占有数の差 ( ) が大きくなる ) 件 (t0) は M z (0)-M 0 であるから l-m 0 とな り,M z は M z M 0 ( - e -t/t )... (7) と求まる さて, 式 (5) は H の場合には成立する ( ここでは強い同種核間の相互作用は考えない ) が, 3 C の場合はどうだろうか? H から見た場合には 3 C は % しか存在しないので,99 % が H C 結合となり H 3 C 結合は無視できる 一方, 3 C から見ると, H の天然存在比がほぼ 00 % であるため 3 C H の結合は 00 % 存在する したがって 3 C の NMR 緩和は異種核 ( 3 C と H) の スピン系として考える必要がある スピン系のエネルギー準位は,I/ の核種の場合, 一つのスピンが m-/ と / の 種類のエネルギー状態として存在するので,4 種類のエネルギー準位が存在する { 図 5(a)} 3 C 磁化 M C の緩和は,b 状態から a 状態に緩和する 量子遷移 W C が通常起こる過程となるが, 全体としてみると 量子遷移である W C ( 二つ存在 ), 量子遷移であるW,0 量子遷移であるW 0 の 3 種類の遷移によって b 状態から a 状態に緩和する また, 量子遷移の W と 0 量子遷移の W 0 は H スピンも反転してしまう 特に W 0 は, H スピンから見ると 3 C スピンが b 状態から a 状態に戻るとき, 逆に a 状態から b 状態になる したがって 3 C 磁化の静磁場方向への緩和は, 熱平衡状態 (M C0 ) からのずれ (M C -M C0 ) に対して r C W 0 +W C +W /T C が係数として働き, H 磁化の平衡値 M H0 からのずれ (M H -M H0 ) に対しては交差緩和項 s CH W -W 0 が係数として働く ( ここで s CH は H スピンから 3 C スピンへの交差緩和を表す ) したがって, 3 C スピンのトータルとしての 3 C 磁化の時間変化は, dm C - r C (M C - M C0 )-s CH (M H - M H0 )... (8) となる H 磁化の時間変化に対しても同様に次式 (9) が得られる dm H -r H (M H - M H0 )-s HC (M C - M C0 )... (9) 通常, 天然存在比を考慮して 3 C から H への交差緩和項を s HC 0 とすることが多い { つまり式 (5) と同じ } 今, H 核にラジオ波照射 ( H デカップリング ) をして, 3 C 信号を測定する場合を考えよう t0 で H をラジオ波照射し, 3 C 信号の取得中と待ち時間の間照射し続けるとすると { 通常の 3 C{ H} 実験, 図 5(b)}, H 磁化は時間に関係なく a と b の占有数に差が無くなり { 飽和, 図 5(c)},M H (t )M H (0)0 が成り立つ このような状態になると, 3 C の a と b の占有数は逆に増大 { 図 5(c)} し, 3 C 磁化の強度は大きくなる この 3 C 磁化の増大について調べてみよう 3 C の定常状態 (t, dm C /0 が成り立つ ) の磁化を解いてみる 式 (8) に M H (t)0 を代入して dm C /0 とおくと, dm C -r C (M C - M C0 )+s CH M H0 0 g H r C (M C - M C0 )s CH M H0 s CH M C0 g C... (30) となる したがって M C は ぶんせき 7
7 M C M C0 + s CH r C M H0 M C0 ( + s CH r C g H g C ) M C0 (+h)... (3) となり, 元の M C0 の (+h) 倍になることがわかる +h を NOE と言う スピン状態間の遷移確率 W は, スペクトル密度関数 J(v) により記述されるが,J(v) が単一の回転相関時間 (t) で規定される場合 ),NOE は NOE +h + g H g C [{ t - }/ +(v H - v C ) t t { 6t +(v H + v C ) t +(v H - v C ) t + 3t + v C t 6t + }] +(v H + v C ) t... (3) と書き表される 通常, 溶液中の分子運動は非常に速く,(v H +v C )t が成り立つので, 式 (3) から, NOE +h + g H g C... (33) となる 3 C と H の g 値から (g H /g C 3.977), 分子運動が非常に速い場合にはNOE は.988と求められる { 図 5(c) の状態 } したがって, 3 C{ H} 実験では 3 C の強度が最大約 3 倍増大する 逆に分子運動が非常に遅い場合 (v C t ) には,Rg H /g C v H /v C とおいて式 (3) を変形すると, NOE +h + R [ 6(R - ) -(R + ) (R + ) + 3(R - ) (R + ) + 6(R - ) ]... (34) と置け,R3.977 を代入してNOE は.53 と求められる 以上のことより 3 C{ H} 実験では, 3 C の信号強度は分子運動の速さに応じて.53~.988 倍の間で増大することになる さて, 3 C{ H} 実験で inversionrecovery 法を用いて T の測定を行った場合の 3 C 磁化の時間変化を考えてみよう 式 (8) と (30) から, dm C -r C (M C - M C0 )+r C h M C0... (35) となる d/d と置いて演算子法を用いると式 (35) は, (D + r C )M C r C ( + h)m C0... (36) と変形される 式 (36) の一般解は 4, M C l e -rc t + M C0 ( + h)... (37) である ここで l は初期条件により求まる定数 3 C { H} 実験における 80 パルス直後の 3 C 磁化の初期値 M C (0) は,NOE により磁化が増大し,M C (0)-(+ h)m C0 となるので, 式 (37) は M C (+h)m C0 - M C0 ( + h)e -rct (+h)m C0 ( - e -t/tc )... (38) となる この式は式 (7) と同じであるが,NOE の分だけ磁化の強度が増大する NMR は定量性にも優れているが, 定量性を議論するためには, 磁化は励起後, 熱平衡状態に戻る必要がある 熱平衡状態に戻るためには, 次のパルスを照射するまでの待ち時間 (pulse delay) を最低でも 5T 以上に設定する 待ち時間を5T に設定した場合, 磁化は 99.3 % まで回復する { 式 (6) で 90 パルスの場合 l - となり,t5T を代入 式 (7) では %} より精度を要求する定量 NMR の場合には,T の 7~0 倍の待ち時間 ( 磁化の回復率は t7t で %, t 0T で %) を必要とする しかし, 3 C{ H} 実験では NOE の効果が官能基ごとに異なることから, 通常の 3 CNMRスペクトルでは定量性の議論は困難である そのため, 3 CNMR 法で定量性を持たせるために, FID の取り込みの時間 (t acq ) だけ H ラジオ波照射を行い, 待ち時間では行わないという実験を行う (inverse gated H decoupling 法, 図 6 中のパルスプログラム参照 ) この場合, 3 C H のスピン結合によるピーク分裂を回避し,NOE による磁化の増大をなくすることができる ( 待ち時間に照射することで NOE が発生するため ) そのため, 3 C スピン数に比例したピーク強度で観測される しかし,FID 取り込み時間 (t acq ) が長い場合, H ラジオ波照射によりNOE が生じてしまい, 定量性が損なわれることがある 3)4) 特に,45 パルスなどの短いパルスの場合,5T より短い時間の待ち時間でも大丈夫だと考えて実験をすると, 実際には NOE の効果を無視できない場合もある 5) ポリオレフィンを inverse gated H decoupling 法で観測したときの, 3 C 磁化強度の待ち時間依存性を見てみよう 図 6 に, 実測したポリ4 メチル ペンテン (P4MP) の CH 3 基の 3 C ピーク強度の待ち時間依存性を示した 5) この図からわかるように, 励起パルス後のピーク強度の待ち時間依存性は, 待ち時間が短い時が大きく, 待ち時間を長くすると平衡値に減衰していく 予 4 (D + r C )M C r C ( + h)m C0 の一般解は, 右辺 (g(t) とする ) を 0 と置いた時の解 ( 余関数 ) と,g(t ) と余関数との関係から求められる特解の和である (D + r C )M C 0 の余関数は M C l e -rc t 特解( f p ) は余関数の指数部を用いて,f p e -rc (e t rc t g(t)) となる 7 ぶんせき
8 と, M C l e -rc t + h M C0 e -rh r C - t + M C0 r H... (4) となる ここで l は初期条件により求まる定数である FID 取り込み時間 (t acq ) 中に, 3 C 磁化 M C が T C により z 軸方向へ戻っていくので,M C (0) の z 軸方向の大きさ ( 初期条件 ) を,M C (0)zM C0 と置くこととする すると式 (4) は, r C M C M C0 -( - z) e -t/tc T H + h (e -t/th - e -t/tc ) T H - T... (4) C 図 6 P4MP 中の CH 3 基 (T C.6 s) の 3 C ピーク強度の待ち時間依存性 (Inverse gated Hdecouplingシーケンスにて測定, 横軸は Pulse delay) 5) 想される磁化の待ち時間依存性は飽和回復曲線と同様に -e -t/t であり, 待ち時間が長くなると徐々にピーク強度が大きくなると考えられるが, 実際は逆である この現象を説明してみよう FID 取り込み終了直後を t0 とすれば, H 磁化は飽和状態となっていることから M H (0)0 である また, 3 C から H への交差緩和は無視できる (s HC 0) もの として, 式 (9) より M H は, M H M H0 - M H0 e -rh t M H0 (-e -rh t )... (39) と求められる 式 (39) を式 (8) に代入すると, dm C r C (M C - M C0 )-s CH (M H - M H0 ) - r C M C + r C M C0 (h e -rh t + )... (40) となる 式 (36) 同様, 演算子法を用いて式 (40) を解く と変形される ただし,r H /T H, r C /T C を使って式を変形した t acq 中のz 軸の 3 C 磁化の回復は式 (6) と同じ形となる 90 パルス直後の z 軸成分は 0 であり,t acq 後では NOE の効果を考慮して,z(+h)- (+h) exp(-t acq /T C ) となる 45 パルスの場合, パルス直後の z 軸成分は / (+h) M C0 なので,z (+h)-(- )/ (+h) exp(-t acq /T C ) となる 図 6 の実験では,90 パルスと 45 パルスの 種類の励起パルスを用いている 実線は, あらかじめ求めた T C と T H,NOE の値を式 (4) に代入してシミュレーションした結果であり, 実測の測定点を良く再現していることがわかる また, 測定点をより細かく設定すれば, この実験から T C と T H,NOEを求めることも可能である 90 パルス実験の理論曲線を二つに分割して描画してみると, 赤色の曲線で示した前半の -(-z) e -t/tc 項は, 通常は飽和回復 (z0) していく 3 C 磁化が,NOE の効果で増大しているため, 逆に減衰して NOE 前の元の平衡値へ近づく様子を示している また, 青色の曲線で示した後半の 3 項目は, 3 C と H の磁化の緩和時間の差に応じて変化する 3 C 磁化の強度変化を表す FID の取り込み後, H ラジオ波照射を停止すると, H 磁化は式 (39) に従って熱平衡状態に戻る したがって,NOE を確実に除去するためには,FID 取り込み後, 次のパルス照射までの時間 (pulse delay), 最低でも 5T H 待つ必要がある 定量性を求めるためには, 3 C 磁化も熱平衡状態に戻る必要があるため, 実験の繰り返し時間 (recycle delay: 回の積算にトータルでかかる時間 図 6 中のパルスシーケンス参照 ) は少なくとも 5T C 以上でなければならない ( 赤色の曲線 ) 用いたP4MP の CH 3 基の T C は.6 s,t H は.0 s である 図 6 から, パルス長に関係なく磁化が NOE 前の元の平衡値に戻るためには, 少なくとも 0 T H 程度待たないと,inverse gated H decoupling 3 CNMRスペク ぶんせき 73
9 トルの場合でも定量性を議論できないと言える 5) 一般に, 第 3 項 ( 青色の曲線 ) が 0 になると平衡値になるので, 長い方の T の 5 倍以上を pulse delay に設定することで,inverse gated H decoupling 3 CNMRスペクトルで定量性を議論できる 5 おわりに NMR 共鳴条件, パルス, フーリエ変換, 緩和,NOE と,NMR 法の基礎的な事柄について, 数式を紐解きながら説明した 普段何気なく設定しているパラメーターも, このようなバックグラウンドを知ることで理解しながら実験できると思う NMR 法をさらに深く知りたい方は, 広がる NMR の世界 の最終章に挙げた推薦図書をご覧いただければと思う 6) この入門講座が, これからのより良い NMR スペクトルの測定の一助になることを願う 文献 ) J. F. James : ``A student's Guide to Fourier Transforms with applications in physics and engineering'', (995), (Cambridge University Press, New York). ) 齊藤肇, 安藤勲, 内藤晶 : NMR 分光学 基礎と応用, 第 5 章,( 東京化学同人 ). 3) J.H.Noggle,R.E.Schirmer:``TheNuclearOverhauserEffect'', Chapter 6 (97), (Academic Press, Inc., New York and London). 4) D. T. Okamoto, S. L. Cooper, T. W. Root : Macromolecules, 5,303(97). 5) 茂呂ふみか, 佐藤浩子, 恩田光彦 : 第 5 回 NMR 討論会講演要旨集,p. 56 (03). 6) 浅野敦志 : 広がる NMR の世界, 朝倉哲郎編著,p. 70 (0),( コロナ社 ). 浅野敦志 (Atsushi ASANO) 防衛大学校応用科学群応用化学科 ( 横須賀市走水 00) 北海道大学大学院理学研究科高分子学専攻博士後期課程修了 博士 ( 理学 ) 現在の研究テーマ 複合高分子材料, エラストマー材料の固体 NMR 法を用いた構造解析 主な著書と出版社名 広がる NMR の世界 40 人の研究者からの熱いメッセージ ( 共著 ) ( コロナ社 ) 趣味 将棋鑑賞 asanoa@nda.ac.jp 有害物質分析ハンドブック鈴木茂 石井善昭 上堀美和子 長谷川敦子 吉田寧子編集本書は, 有害物質分析の知識 経験のある人が身近にいない, または教えてもらう機会がない方が, 豊富な知識 経験的知見を持った技術者 研究者から集めた分析のコツを知ることができるハンドブックである そのため, 有害物質の現行の分析方法に関する解説だけでなく, 方法の背景にある原理, さらには新しい分析方法開発に取り組むためのノウハウが述べられている 内容 構成は, 本書の活用方法, 有害物質分析方法 ( 定量編 ), 有害物質分析方法 ( 定性編 ), 有害物質分析の知恵 袋となっており, 活用方法 では対象物質の構造, オクタノール / 水分配係数 (P ow ) および分析対象媒体に基づいた分析シナリオの描き方が示されている 分析方法 ( 定量編 ) では新しい分析方法開発の参考となるよう P ow が高い順に掲載されており, 分析方法( 定性編 ) では有害物質のスクリーニング方法と未知の有害物質を検索する最新の方法が紹介されている 知恵袋 では分析方法をつくる際に役立つ分析装置や試料処理などの情報が記され, また知識 経験の断片を提供したコラムも挿入されている 近年, 安全 安心な社会生活の基盤を築くために必須となっている化学物質の特定において, 本書は環境中や廃棄物, 食品および製品 材料に含まれる有害物質の分析方法が具体的 実践的にまとめられており, 有害物質分析を担っている科学者 技術者, それを目指す大学院生や学部生などにぜひ活用していただきたい (ISBN B5 判 83 ページ 8,500 円 + 税 04 年刊 朝倉書店 ) 74 ぶんせき
有機4-有機分析03回配布用
 NMR( 核磁気共鳴 ) の基本原理核スピンと磁気モーメント有機分析化学特論 + 有機化学 4 原子核は正の電荷を持ち その回転 ( スピン ) により磁石としての性質を持つ 外部磁場によって核スピンのエネルギー準位は変わる :Zeeman 分裂 核スピンのエネルギー準位 第 3 回 (2015/04/24) m : 磁気量子数 [+I,, I ] I: スピン量子数 ( 整数 or 半整数 )]
NMR( 核磁気共鳴 ) の基本原理核スピンと磁気モーメント有機分析化学特論 + 有機化学 4 原子核は正の電荷を持ち その回転 ( スピン ) により磁石としての性質を持つ 外部磁場によって核スピンのエネルギー準位は変わる :Zeeman 分裂 核スピンのエネルギー準位 第 3 回 (2015/04/24) m : 磁気量子数 [+I,, I ] I: スピン量子数 ( 整数 or 半整数 )]
Microsoft Word - Chap17
 第 7 章化学反応に対する磁場効果における三重項機構 その 7.. 節の訂正 年 7 月 日. 節 章の9ページ の赤枠に記載した説明は間違いであった事に気付いた 以下に訂正する しかし.. 式は 結果的には正しいので安心して下さい 磁場 の存在下でのT 状態のハミルトニアン は ゼーマン項 と時間に依存するスピン-スピン相互作用の項 との和となる..=7.. g S = g S z = S z g
第 7 章化学反応に対する磁場効果における三重項機構 その 7.. 節の訂正 年 7 月 日. 節 章の9ページ の赤枠に記載した説明は間違いであった事に気付いた 以下に訂正する しかし.. 式は 結果的には正しいので安心して下さい 磁場 の存在下でのT 状態のハミルトニアン は ゼーマン項 と時間に依存するスピン-スピン相互作用の項 との和となる..=7.. g S = g S z = S z g
<4D F736F F F696E74202D2088E B691CC8C7691AA F C82512E B8CDD8AB B83685D>
 前回の復習 医用生体計測磁気共鳴イメージング :2 回目 数理物質科学研究科電子 物理工学専攻巨瀬勝美 203-7-8 NMRとMRI:( 強い ) 静磁場と高周波 ( 磁場 ) を必要とする NMRとMRIの歴史 :952 年と2003 年にノーベル賞 ( 他に2 回 ) 数学的準備 : フーリエ変換 ( 信号の中に, どのような周波数成分が, どれだけ含まれているか ( スペクトル ) を求める方法
前回の復習 医用生体計測磁気共鳴イメージング :2 回目 数理物質科学研究科電子 物理工学専攻巨瀬勝美 203-7-8 NMRとMRI:( 強い ) 静磁場と高周波 ( 磁場 ) を必要とする NMRとMRIの歴史 :952 年と2003 年にノーベル賞 ( 他に2 回 ) 数学的準備 : フーリエ変換 ( 信号の中に, どのような周波数成分が, どれだけ含まれているか ( スペクトル ) を求める方法
2. FLSH の定常状態ここでは磁化の定常状態がどのように作られるのか感覚的につかめるように説明していきます 2.1 磁化ベクトルによる FLSH の定常状態の考察 Fig.3 の磁化ベクトルモデルを使って説明します 1) 縦磁化が定常状態を作っています 大きさを とします 2) 時刻 t=0 に
 グラディエントエコーと定常状態 1. はじめにグラディエントエコーにつきものの定常状態,Bloch 方程式, 信号強度式 とっつきにくいのですが 視覚的に磁化ベクトルを理解すれば分かりやすく 数学も高校生の数学でかなりの部分を理解することができます 今回は adient Echo の代表的な FLSH(GE では SPGR ですね ) と FIEST を主に取り上げて解説したいと思います 1. グラディエントエコーの種類グラディエントエコー型パルスシーケンスには多くの種類がありますが
グラディエントエコーと定常状態 1. はじめにグラディエントエコーにつきものの定常状態,Bloch 方程式, 信号強度式 とっつきにくいのですが 視覚的に磁化ベクトルを理解すれば分かりやすく 数学も高校生の数学でかなりの部分を理解することができます 今回は adient Echo の代表的な FLSH(GE では SPGR ですね ) と FIEST を主に取り上げて解説したいと思います 1. グラディエントエコーの種類グラディエントエコー型パルスシーケンスには多くの種類がありますが
SE法の基礎
 SE 法の基礎 近畿大学医学部奈良病院阪本貴博 本日の内容 Principle of MRI SE 法の基礎 MRI とは SE 法とは 縦緩和と横緩和 TR と TE コントラスト MRI とは Magnetic Resonance Imaging: 核磁気共鳴画像法 MRI に必要な 3 つの要素 N S + + + 静磁場 ( 磁石 ) 水素原子 電波 (RF) 静磁場と電波 (RF) を使って水素原子の様子を画像化している
SE 法の基礎 近畿大学医学部奈良病院阪本貴博 本日の内容 Principle of MRI SE 法の基礎 MRI とは SE 法とは 縦緩和と横緩和 TR と TE コントラスト MRI とは Magnetic Resonance Imaging: 核磁気共鳴画像法 MRI に必要な 3 つの要素 N S + + + 静磁場 ( 磁石 ) 水素原子 電波 (RF) 静磁場と電波 (RF) を使って水素原子の様子を画像化している
第 4 週コンボリューションその 2, 正弦波による分解 教科書 p. 16~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問 1. 以下の図にならって,1 と 2 の δ 関数を図示せよ δ (t) 2
 第 4 週コンボリューションその, 正弦波による分解 教科書 p. 6~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問. 以下の図にならって, と の δ 関数を図示せよ. - - - δ () δ ( ) - - - 図 δ 関数の図示の例 δ ( ) δ ( ) δ ( ) δ ( ) δ ( ) - - - - - - - -
第 4 週コンボリューションその, 正弦波による分解 教科書 p. 6~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問. 以下の図にならって, と の δ 関数を図示せよ. - - - δ () δ ( ) - - - 図 δ 関数の図示の例 δ ( ) δ ( ) δ ( ) δ ( ) δ ( ) - - - - - - - -
DVIOUT
 第 章 離散フーリエ変換 離散フーリエ変換 これまで 私たちは連続関数に対するフーリエ変換およびフーリエ積分 ( 逆フーリエ変換 ) について学んできました この節では フーリエ変換を離散化した離散フーリエ変換について学びましょう 自然現象 ( 音声 ) などを観測して得られる波 ( 信号値 ; 観測値 ) は 通常 電気信号による連続的な波として観測機器から出力されます しかしながら コンピュータはこの様な連続的な波を直接扱うことができないため
第 章 離散フーリエ変換 離散フーリエ変換 これまで 私たちは連続関数に対するフーリエ変換およびフーリエ積分 ( 逆フーリエ変換 ) について学んできました この節では フーリエ変換を離散化した離散フーリエ変換について学びましょう 自然現象 ( 音声 ) などを観測して得られる波 ( 信号値 ; 観測値 ) は 通常 電気信号による連続的な波として観測機器から出力されます しかしながら コンピュータはこの様な連続的な波を直接扱うことができないため
例 e 指数関数的に減衰する信号を h( a < + a a すると, それらのラプラス変換は, H ( ) { e } e インパルス応答が h( a < ( ただし a >, U( ) { } となるシステムにステップ信号 ( y( のラプラス変換 Y () は, Y ( ) H ( ) X (
 第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
機器分析化学 3.核磁気共鳴(NMR)法(1)
 機器分析化学 3. 核磁気共鳴 (NMR) 法 (1) 2011 年度 5. 核磁気共鳴スペクトル法 (Nucler Mgnetic Resonnce:NMR) キーワード原子核磁気共鳴 ⅰ) 原子核 ( 陽子 + 中性子 ) 原子番号 (= 陽子数 ) 質量数 (= 陽子数 + 中性子数 ) もし原子番号も質量数も偶数の場合その原子核はスピンを持たない そうでない場合 ( どちらか あるいは一方が奇数
機器分析化学 3. 核磁気共鳴 (NMR) 法 (1) 2011 年度 5. 核磁気共鳴スペクトル法 (Nucler Mgnetic Resonnce:NMR) キーワード原子核磁気共鳴 ⅰ) 原子核 ( 陽子 + 中性子 ) 原子番号 (= 陽子数 ) 質量数 (= 陽子数 + 中性子数 ) もし原子番号も質量数も偶数の場合その原子核はスピンを持たない そうでない場合 ( どちらか あるいは一方が奇数
Microsoft Word - thesis.doc
 剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
補足 中学で学習したフレミング左手の法則 ( 電 磁 力 ) と関連付けると覚えやすい 電磁力は電流と磁界の外積で表される 力 F 磁 電磁力 F li 右ねじの回転の向き電 li ( l は導線の長さ ) 補足 有向線分とベクトル有向線分 : 矢印の位
 http://totemt.sur.ne.p 外積 ( ベクトル積 ) の活用 ( 面積, 法線ベクトル, 平面の方程式 ) 3 次元空間の つのベクトルの積が つのベクトルを与えるようなベクトルの掛け算 ベクトルの積がベクトルを与えることからベクトル積とも呼ばれる これに対し内積は符号と大きさをもつ量 ( スカラー量 ) を与えるので, スカラー積とも呼ばれる 外積を使うと, 平行四辺形や三角形の面積,
http://totemt.sur.ne.p 外積 ( ベクトル積 ) の活用 ( 面積, 法線ベクトル, 平面の方程式 ) 3 次元空間の つのベクトルの積が つのベクトルを与えるようなベクトルの掛け算 ベクトルの積がベクトルを与えることからベクトル積とも呼ばれる これに対し内積は符号と大きさをもつ量 ( スカラー量 ) を与えるので, スカラー積とも呼ばれる 外積を使うと, 平行四辺形や三角形の面積,
線積分.indd
 線積分 線積分 ( n, n, n ) (ξ n, η n, ζ n ) ( n-, n-, n- ) (ξ k, η k, ζ k ) ( k, k, k ) ( k-, k-, k- ) 物体に力 を作用させて位置ベクトル A の点 A から位置ベクトル の点 まで曲線 に沿って物体を移動させたときの仕事 W は 次式で計算された A, A, W : d 6 d+ d+ d@,,, d+ d+
線積分 線積分 ( n, n, n ) (ξ n, η n, ζ n ) ( n-, n-, n- ) (ξ k, η k, ζ k ) ( k, k, k ) ( k-, k-, k- ) 物体に力 を作用させて位置ベクトル A の点 A から位置ベクトル の点 まで曲線 に沿って物体を移動させたときの仕事 W は 次式で計算された A, A, W : d 6 d+ d+ d@,,, d+ d+
Microsoft PowerPoint - CSA_B3_EX2.pptx
 Computer Science A Hardware Design Excise 2 Handout V2.01 May 27 th.,2019 CSAHW Computer Science A, Meiji University CSA_B3_EX2.pptx 32 Slides Renji Mikami 1 CSAHW2 ハード演習内容 2.1 二次元空間でのベクトルの直交 2.2 Reserved
Computer Science A Hardware Design Excise 2 Handout V2.01 May 27 th.,2019 CSAHW Computer Science A, Meiji University CSA_B3_EX2.pptx 32 Slides Renji Mikami 1 CSAHW2 ハード演習内容 2.1 二次元空間でのベクトルの直交 2.2 Reserved
Microsoft PowerPoint - 第3回2.ppt
 講義内容 講義内容 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 ベクトルの直交性 3
講義内容 講義内容 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 ベクトルの直交性 3
NMR_wakate_ ppt
 NMR 基礎講義 & 2 第 0 回若手 NMR 研究会 2009 年 9 月 4 日 ( 金 )-6 日 ( 日 ) IPC 生産性国際交流センター ( 湘南国際村 ) 大阪大学蛋白質研究所構造プロテオミクス研究系 池上貴久 化学シフトの直積演算子 (product-operator) I " I cos (#t) + I sin (#t) x x y ω : 角速度 (rad/s) z 一周の長さ
NMR 基礎講義 & 2 第 0 回若手 NMR 研究会 2009 年 9 月 4 日 ( 金 )-6 日 ( 日 ) IPC 生産性国際交流センター ( 湘南国際村 ) 大阪大学蛋白質研究所構造プロテオミクス研究系 池上貴久 化学シフトの直積演算子 (product-operator) I " I cos (#t) + I sin (#t) x x y ω : 角速度 (rad/s) z 一周の長さ
1/17 平成 29 年 3 月 25 日 ( 土 ) 午前 11 時 1 分量子力学とクライン ゴルドン方程式 ( 学部 3 年次秋学期向 ) 量子力学とクライン ゴルドン方程式 素粒子の満たす場 y ( x,t) の運動方程式 : クライン ゴルドン方程式 : æ 3 ö ç å è m= 0
 /7 平成 9 年 月 5 日 ( 土 午前 時 分量子力学とクライン ゴルドン方程式 ( 学部 年次秋学期向 量子力学とクライン ゴルドン方程式 素粒子の満たす場 (,t の運動方程式 : クライン ゴルドン方程式 : æ ö ç å è = 0 c + ( t =, 0 (. = 0 ì æ = = = ö æ ö æ ö ç ì =,,,,,,, ç 0 = ç Ñ 0 = ç Ñ 0 Ñ Ñ
/7 平成 9 年 月 5 日 ( 土 午前 時 分量子力学とクライン ゴルドン方程式 ( 学部 年次秋学期向 量子力学とクライン ゴルドン方程式 素粒子の満たす場 (,t の運動方程式 : クライン ゴルドン方程式 : æ ö ç å è = 0 c + ( t =, 0 (. = 0 ì æ = = = ö æ ö æ ö ç ì =,,,,,,, ç 0 = ç Ñ 0 = ç Ñ 0 Ñ Ñ
DVIOUT-SS_Ma
 第 章 微分方程式 ニュートンはリンゴが落ちるのを見て万有引力を発見した という有名な逸話があります 無重力の宇宙船の中ではリンゴは落ちないで静止していることを考えると 重力が働くと始め静止しているものが動き出して そのスピードはどんどん大きくなる つまり速度の変化が現れることがわかります 速度は一般に時間と共に変化します 速度の瞬間的変化の割合を加速度といい で定義しましょう 速度が変化する, つまり加速度がでなくなるためにはその原因があり
第 章 微分方程式 ニュートンはリンゴが落ちるのを見て万有引力を発見した という有名な逸話があります 無重力の宇宙船の中ではリンゴは落ちないで静止していることを考えると 重力が働くと始め静止しているものが動き出して そのスピードはどんどん大きくなる つまり速度の変化が現れることがわかります 速度は一般に時間と共に変化します 速度の瞬間的変化の割合を加速度といい で定義しましょう 速度が変化する, つまり加速度がでなくなるためにはその原因があり
Microsoft PowerPoint - ip02_01.ppt [互換モード]
![Microsoft PowerPoint - ip02_01.ppt [互換モード] Microsoft PowerPoint - ip02_01.ppt [互換モード]](/thumbs/96/127250376.jpg) 空間周波数 周波数領域での処理 空間周波数 (spatial frquncy) とは 単位長さ当たりの正弦波状の濃淡変化の繰り返し回数を表したもの 正弦波 : y sin( t) 周期 : 周波数 : T f / T 角周波数 : f 画像処理 空間周波数 周波数領域での処理 波形が違うと 周波数も違う 画像処理 空間周波数 周波数領域での処理 画像処理 3 周波数領域での処理 周波数は一つしかない?-
空間周波数 周波数領域での処理 空間周波数 (spatial frquncy) とは 単位長さ当たりの正弦波状の濃淡変化の繰り返し回数を表したもの 正弦波 : y sin( t) 周期 : 周波数 : T f / T 角周波数 : f 画像処理 空間周波数 周波数領域での処理 波形が違うと 周波数も違う 画像処理 空間周波数 周波数領域での処理 画像処理 3 周波数領域での処理 周波数は一つしかない?-
Microsoft PowerPoint - 10.pptx
 m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
Microsoft PowerPoint - 多核NMRへの応用_提出版.pptx
 多核 NMR の応用 ~ 19 F NMRを用いた定量分析 ~ 第 1 回定量 NMRクラブ (2012/12/4) 産業技術総合研究所計測標準研究部門有機分析科バイオディカル標準研究室山﨑太一 1 定量 19 FNMR 法の開発目的 フッ素化合物は生化学におけるスクリーニングや材料科学におけるポリマー分析等幅広く用いられている 分子構造解析や酵素活性等の速度論解析に使用 19 FNMR を用いた高精度な定量法開発は重要!
多核 NMR の応用 ~ 19 F NMRを用いた定量分析 ~ 第 1 回定量 NMRクラブ (2012/12/4) 産業技術総合研究所計測標準研究部門有機分析科バイオディカル標準研究室山﨑太一 1 定量 19 FNMR 法の開発目的 フッ素化合物は生化学におけるスクリーニングや材料科学におけるポリマー分析等幅広く用いられている 分子構造解析や酵素活性等の速度論解析に使用 19 FNMR を用いた高精度な定量法開発は重要!
微分方程式による現象記述と解きかた
 微分方程式による現象記述と解きかた 土木工学 : 公共諸施設 構造物の有用目的にむけた合理的な実現をはかる方法 ( 技術 ) に関する学 橋梁 トンネル ダム 道路 港湾 治水利水施設 安全化 利便化 快適化 合法則的 経済的 自然および人口素材によって作られた 質量保存則 構造物の自然的な性質 作用 ( 外力による応答 ) エネルギー則 の解明 社会的諸現象のうち マスとしての移動 流通 運動量則
微分方程式による現象記述と解きかた 土木工学 : 公共諸施設 構造物の有用目的にむけた合理的な実現をはかる方法 ( 技術 ) に関する学 橋梁 トンネル ダム 道路 港湾 治水利水施設 安全化 利便化 快適化 合法則的 経済的 自然および人口素材によって作られた 質量保存則 構造物の自然的な性質 作用 ( 外力による応答 ) エネルギー則 の解明 社会的諸現象のうち マスとしての移動 流通 運動量則
多次元レーザー分光で探る凝縮分子系の超高速動力学
 波動方程式と量子力学 谷村吉隆 京都大学理学研究科化学専攻 http:theochem.kuchem.kyoto-u.ac.jp TA: 岩元佑樹 iwamoto.y@kuchem.kyoto-u.ac.jp ベクトルと行列の作法 A 列ベクトル c = c c 行ベクトル A = [ c c c ] 転置ベクトル T A = [ c c c ] AA 内積 c AA = [ c c c ] c =
波動方程式と量子力学 谷村吉隆 京都大学理学研究科化学専攻 http:theochem.kuchem.kyoto-u.ac.jp TA: 岩元佑樹 iwamoto.y@kuchem.kyoto-u.ac.jp ベクトルと行列の作法 A 列ベクトル c = c c 行ベクトル A = [ c c c ] 転置ベクトル T A = [ c c c ] AA 内積 c AA = [ c c c ] c =
振動学特論火曜 1 限 TA332J 藤井康介 6 章スペクトルの平滑化 スペクトルの平滑化とはギザギザした地震波のフーリエ スペクトルやパワ スペクトルでは正確にスペクトルの山がどこにあるかはよく分からない このようなスペクトルから不純なものを取り去って 本当の性質を浮き彫
 6 章スペクトルの平滑化 スペクトルの平滑化とはギザギザした地震波のフーリエ スペクトルやパワ スペクトルでは正確にスペクトルの山がどこにあるかはよく分からない このようなスペクトルから不純なものを取り去って 本当の性質を浮き彫りにするために スペクトルを滑らかにする操作のことをいう 6.1 合積のフーリエ変換スペクトルの平滑化を行う際に必要な 合積とそのフーリエ変換について説明する 6.2 データ
6 章スペクトルの平滑化 スペクトルの平滑化とはギザギザした地震波のフーリエ スペクトルやパワ スペクトルでは正確にスペクトルの山がどこにあるかはよく分からない このようなスペクトルから不純なものを取り去って 本当の性質を浮き彫りにするために スペクトルを滑らかにする操作のことをいう 6.1 合積のフーリエ変換スペクトルの平滑化を行う際に必要な 合積とそのフーリエ変換について説明する 6.2 データ
数学 t t t t t 加法定理 t t t 倍角公式加法定理で α=β と置く. 三角関数
 . 三角関数 基本関係 t cot c sc c cot sc t 還元公式 t t t t t t cot t cot t 数学 数学 t t t t t 加法定理 t t t 倍角公式加法定理で α=β と置く. 三角関数 数学. 三角関数 5 積和公式 6 和積公式 数学. 三角関数 7 合成 t V v t V v t V V V V VV V V V t V v v 8 べき乗 5 6 6
. 三角関数 基本関係 t cot c sc c cot sc t 還元公式 t t t t t t cot t cot t 数学 数学 t t t t t 加法定理 t t t 倍角公式加法定理で α=β と置く. 三角関数 数学. 三角関数 5 積和公式 6 和積公式 数学. 三角関数 7 合成 t V v t V v t V V V V VV V V V t V v v 8 べき乗 5 6 6
s ss s ss = ε = = s ss s (3) と表される s の要素における s s = κ = κ, =,, (4) jωε jω s は複素比誘電率に相当する物理量であり ここで PML 媒質定数を次のように定義する すなわち κξ をPML 媒質の等価比誘電率 ξ をPML 媒質の
 FDTD 解析法 (Matlab 版 2 次元 PML) プログラム解説 v2.11 1. 概要 FDTD 解析における吸収境界である完全整合層 (Perfectl Matched Laer, PML) の定式化とプログラミングを2 次元 TE 波について解説する PMLは異方性の損失をもつ仮想的な物質であり 侵入して来る電磁波を逃さず吸収する 通常の物質と接する界面でインピーダンスが整合しており
FDTD 解析法 (Matlab 版 2 次元 PML) プログラム解説 v2.11 1. 概要 FDTD 解析における吸収境界である完全整合層 (Perfectl Matched Laer, PML) の定式化とプログラミングを2 次元 TE 波について解説する PMLは異方性の損失をもつ仮想的な物質であり 侵入して来る電磁波を逃さず吸収する 通常の物質と接する界面でインピーダンスが整合しており
Microsoft Word - note02.doc
 年度 物理化学 Ⅱ 講義ノート. 二原子分子の振動. 調和振動子近似 モデル 分子 = 理想的なバネでつながった原子 r : 核間距離, r e : 平衡核間距離, : 変位 ( = r r e ), k f : 力の定数ポテンシャルエネルギー ( ) k V = f (.) 古典運動方程式 [ 振動数 ] 3.3 d kf (.) dt μ : 換算質量 (m, m : 原子, の質量 ) mm
年度 物理化学 Ⅱ 講義ノート. 二原子分子の振動. 調和振動子近似 モデル 分子 = 理想的なバネでつながった原子 r : 核間距離, r e : 平衡核間距離, : 変位 ( = r r e ), k f : 力の定数ポテンシャルエネルギー ( ) k V = f (.) 古典運動方程式 [ 振動数 ] 3.3 d kf (.) dt μ : 換算質量 (m, m : 原子, の質量 ) mm
vecrot
 1. ベクトル ベクトル : 方向を持つ量 ベクトルには 1 方向 2 大きさ ( 長さ ) という 2 つの属性がある ベクトルの例 : 物体の移動速度 移動量電場 磁場の強さ風速力トルクなど 2. ベクトルの表現 2.1 矢印で表現される 矢印の長さ : ベクトルの大きさ 矢印の向き : ベクトルの方向 2.2 2 個の点を用いて表現する 始点 () と終点 () を結ぶ半直線の向き : ベクトルの方向
1. ベクトル ベクトル : 方向を持つ量 ベクトルには 1 方向 2 大きさ ( 長さ ) という 2 つの属性がある ベクトルの例 : 物体の移動速度 移動量電場 磁場の強さ風速力トルクなど 2. ベクトルの表現 2.1 矢印で表現される 矢印の長さ : ベクトルの大きさ 矢印の向き : ベクトルの方向 2.2 2 個の点を用いて表現する 始点 () と終点 () を結ぶ半直線の向き : ベクトルの方向
数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュ
 数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュレーションによって計算してみる 4.1 放物運動一様な重力場における放物運動を考える 一般に質量の物体に作用する力をとすると運動方程式は
数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュレーションによって計算してみる 4.1 放物運動一様な重力場における放物運動を考える 一般に質量の物体に作用する力をとすると運動方程式は
PowerPoint Presentation
 付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
喨微勃挹稉弑
 == 全微分方程式 == 全微分とは 変数の関数 z=f(, ) について,, の増分を Δ, Δ とするとき, z の増分 Δz は Δz z Δ+ z Δ で表されます. この式において, Δ 0, Δ 0 となる極限を形式的に dz= z d+ z d (1) で表し, dz を z の全微分といいます. z は z の に関する偏導関数で, を定数と見なし て, で微分したものを表し, 方向の傾きに対応します.
== 全微分方程式 == 全微分とは 変数の関数 z=f(, ) について,, の増分を Δ, Δ とするとき, z の増分 Δz は Δz z Δ+ z Δ で表されます. この式において, Δ 0, Δ 0 となる極限を形式的に dz= z d+ z d (1) で表し, dz を z の全微分といいます. z は z の に関する偏導関数で, を定数と見なし て, で微分したものを表し, 方向の傾きに対応します.
相対性理論入門 1 Lorentz 変換 光がどのような座標系に対しても同一の速さ c で進むことから導かれる座標の一次変換である. (x, y, z, t ) の座標系が (x, y, z, t) の座標系に対して x 軸方向に w の速度で進んでいる場合, 座標系が一次変換で関係づけられるとする
 相対性理論入門 Lorentz 変換 光がどのような座標系に対しても同一の速さ で進むことから導かれる座標の一次変換である. x, y, z, t ) の座標系が x, y, z, t) の座標系に対して x 軸方向に w の速度で進んでいる場合, 座標系が一次変換で関係づけられるとすると, x A x wt) y y z z t Bx + Dt 弨弱弩弨弲弩弨弳弩弨弴弩 が成立する. 図 : 相対速度
相対性理論入門 Lorentz 変換 光がどのような座標系に対しても同一の速さ で進むことから導かれる座標の一次変換である. x, y, z, t ) の座標系が x, y, z, t) の座標系に対して x 軸方向に w の速度で進んでいる場合, 座標系が一次変換で関係づけられるとすると, x A x wt) y y z z t Bx + Dt 弨弱弩弨弲弩弨弳弩弨弴弩 が成立する. 図 : 相対速度
Microsoft Word - NumericalComputation.docx
 数値計算入門 武尾英哉. 離散数学と数値計算 数学的解法の中には理論計算では求められないものもある. 例えば, 定積分は, まずは積分 ( 被積分関数の原始関数をみつけること できなければ値を得ることはできない. また, ある関数の所定の値における微分値を得るには, まずその関数の微分ができなければならない. さらに代数方程式の解を得るためには, 解析的に代数方程式を解く必要がある. ところが, これらは必ずしも解析的に導けるとは限らない.
数値計算入門 武尾英哉. 離散数学と数値計算 数学的解法の中には理論計算では求められないものもある. 例えば, 定積分は, まずは積分 ( 被積分関数の原始関数をみつけること できなければ値を得ることはできない. また, ある関数の所定の値における微分値を得るには, まずその関数の微分ができなければならない. さらに代数方程式の解を得るためには, 解析的に代数方程式を解く必要がある. ところが, これらは必ずしも解析的に導けるとは限らない.
2018年度 東京大・理系数学
 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ関数 f ( ) = + cos (0 < < ) の増減表をつくり, + 0, 0 のと sin きの極限を調べよ 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ n+ 数列 a, a, を, Cn a n = ( n =,, ) で定める n! an qn () n とする を既約分数 an p として表したときの分母
08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ関数 f ( ) = + cos (0 < < ) の増減表をつくり, + 0, 0 のと sin きの極限を調べよ 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ n+ 数列 a, a, を, Cn a n = ( n =,, ) で定める n! an qn () n とする を既約分数 an p として表したときの分母
画像処理工学
 画像処理工学 画像の空間周波数解析とテクスチャ特徴 フーリエ変換の基本概念 信号波形のフーリエ変換 信号波形を周波数の異なる三角関数 ( 正弦波など ) に分解する 逆に, 周波数の異なる三角関数を重ねあわせることにより, 任意の信号波形を合成できる 正弦波の重ね合わせによる矩形波の表現 フーリエ変換の基本概念 フーリエ変換 次元信号 f (t) のフーリエ変換 変換 ( ω) ( ) ωt F f
画像処理工学 画像の空間周波数解析とテクスチャ特徴 フーリエ変換の基本概念 信号波形のフーリエ変換 信号波形を周波数の異なる三角関数 ( 正弦波など ) に分解する 逆に, 周波数の異なる三角関数を重ねあわせることにより, 任意の信号波形を合成できる 正弦波の重ね合わせによる矩形波の表現 フーリエ変換の基本概念 フーリエ変換 次元信号 f (t) のフーリエ変換 変換 ( ω) ( ) ωt F f
RLC 共振回路 概要 RLC 回路は, ラジオや通信工学, 発信器などに広く使われる. この回路の目的は, 特定の周波数のときに大きな電流を得ることである. 使い方には, 周波数を設定し外へ発する, 外部からの周波数に合わせて同調する, がある. このように, 周波数を扱うことから, 交流を考える
 共振回路 概要 回路は ラジオや通信工学 などに広く使われる この回路の目的は 特定の周波数のときに大きな電流を得ることである 使い方には 周波数を設定し外へ発する 外部からの周波数に合わせて同調する がある このように 周波数を扱うことから 交流を考える 特に ( キャパシタ ) と ( インダクタ ) のそれぞれが 周波数によってインピーダンス *) が変わることが回路解釈の鍵になることに注目する
共振回路 概要 回路は ラジオや通信工学 などに広く使われる この回路の目的は 特定の周波数のときに大きな電流を得ることである 使い方には 周波数を設定し外へ発する 外部からの周波数に合わせて同調する がある このように 周波数を扱うことから 交流を考える 特に ( キャパシタ ) と ( インダクタ ) のそれぞれが 周波数によってインピーダンス *) が変わることが回路解釈の鍵になることに注目する
横浜市環境科学研究所
 周期時系列の統計解析 単回帰分析 io 8 年 3 日 周期時系列に季節調整を行わないで単回帰分析を適用すると, 回帰係数には周期成分の影響が加わる. ここでは, 周期時系列をコサイン関数モデルで近似し単回帰分析によりモデルの回帰係数を求め, 周期成分の影響を検討した. また, その結果を気温時系列に当てはめ, 課題等について考察した. 気温時系列とコサイン関数モデル第 報の結果を利用するので, その一部を再掲する.
周期時系列の統計解析 単回帰分析 io 8 年 3 日 周期時系列に季節調整を行わないで単回帰分析を適用すると, 回帰係数には周期成分の影響が加わる. ここでは, 周期時系列をコサイン関数モデルで近似し単回帰分析によりモデルの回帰係数を求め, 周期成分の影響を検討した. また, その結果を気温時系列に当てはめ, 課題等について考察した. 気温時系列とコサイン関数モデル第 報の結果を利用するので, その一部を再掲する.
Microsoft Word - 中村工大連携教材(最終 ).doc
 音速について考えてみよう! 金沢工業大学 中村晃 ねらい 私たちの身の回りにはいろいろな種類の波が存在する. 体感できる波もあれば, できない波もある. その中で音は体感できる最も身近な波である. 遠くで雷が光ってから雷鳴が届くまで数秒間時間がかかることにより, 音の方が光より伝わるのに時間がかかることも経験していると思う. 高校の物理の授業で音の伝わる速さ ( 音速 ) は約 m/s で, 詳しく述べると
音速について考えてみよう! 金沢工業大学 中村晃 ねらい 私たちの身の回りにはいろいろな種類の波が存在する. 体感できる波もあれば, できない波もある. その中で音は体感できる最も身近な波である. 遠くで雷が光ってから雷鳴が届くまで数秒間時間がかかることにより, 音の方が光より伝わるのに時間がかかることも経験していると思う. 高校の物理の授業で音の伝わる速さ ( 音速 ) は約 m/s で, 詳しく述べると
周期時系列の統計解析 (3) 移動平均とフーリエ変換 nino 2017 年 12 月 18 日 移動平均は, 周期時系列における特定の周期成分の消去や不規則変動 ( ノイズ ) の低減に汎用されている統計手法である. ここでは, 周期時系列をコサイン関数で近似し, その移動平均により周期成分の振幅
 周期時系列の統計解析 3 移動平均とフーリエ変換 io 07 年 月 8 日 移動平均は, 周期時系列における特定の周期成分の消去や不規則変動 ノイズ の低減に汎用されている統計手法である. ここでは, 周期時系列をコサイン関数で近似し, その移動平均により周期成分のがどのように変化するのか等について検討する. また, 気温の実測値に移動平均を適用した結果についてフーリエ変換も併用して考察する. 単純移動平均の計算式移動平均には,
周期時系列の統計解析 3 移動平均とフーリエ変換 io 07 年 月 8 日 移動平均は, 周期時系列における特定の周期成分の消去や不規則変動 ノイズ の低減に汎用されている統計手法である. ここでは, 周期時系列をコサイン関数で近似し, その移動平均により周期成分のがどのように変化するのか等について検討する. また, 気温の実測値に移動平均を適用した結果についてフーリエ変換も併用して考察する. 単純移動平均の計算式移動平均には,
<4D F736F F D2097CD8A7793FC96E582BD82ED82DD8A E6318FCD2E646F63>
 - 第 章たわみ角法の基本式 ポイント : たわみ角法の基本式を理解する たわみ角法の基本式を梁の微分方程式より求める 本章では たわみ角法の基本式を導くことにする 基本式の誘導法は各種あるが ここでは 梁の微分方程式を解いて基本式を求める方法を採用する この本で使用する座標系は 右手 右ネジの法則に従った座標を用いる また ひとつの部材では 図 - に示すように部材の左端の 点を原点とし 軸線を
- 第 章たわみ角法の基本式 ポイント : たわみ角法の基本式を理解する たわみ角法の基本式を梁の微分方程式より求める 本章では たわみ角法の基本式を導くことにする 基本式の誘導法は各種あるが ここでは 梁の微分方程式を解いて基本式を求める方法を採用する この本で使用する座標系は 右手 右ネジの法則に従った座標を用いる また ひとつの部材では 図 - に示すように部材の左端の 点を原点とし 軸線を
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生
 0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
以下 変数の上のドットは時間に関する微分を表わしている (ex. 2 dx d x x, x 2 dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-1) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( x や x, x などがすべて 1 次で なおかつ
 以下 変数の上のドットは時間に関する微分を表わしている (e. d d, dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( や, などがすべて 次で なおかつそれらの係数が定数であるような微分方程式 ) に対して安定性の解析を行ってきた しかしながら 実際には非線形の微分方程式で記述される現象も多く存在する
以下 変数の上のドットは時間に関する微分を表わしている (e. d d, dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( や, などがすべて 次で なおかつそれらの係数が定数であるような微分方程式 ) に対して安定性の解析を行ってきた しかしながら 実際には非線形の微分方程式で記述される現象も多く存在する
第1章 単 位
 H. Hamano,. 長柱の座屈 - 長柱の座屈 長い柱は圧縮荷重によって折れてしまう場合がある. この現象を座屈といい, 座屈するときの荷重を座屈荷重という.. 換算長 長さ の柱に荷重が作用する場合, その支持方法によって, 柱の理論上の長さ L が異なる. 長柱の計算は, この L を用いて行うと都合がよい. この L を換算長 ( あるいは有効長さという ) という. 座屈荷重は一般に,
H. Hamano,. 長柱の座屈 - 長柱の座屈 長い柱は圧縮荷重によって折れてしまう場合がある. この現象を座屈といい, 座屈するときの荷重を座屈荷重という.. 換算長 長さ の柱に荷重が作用する場合, その支持方法によって, 柱の理論上の長さ L が異なる. 長柱の計算は, この L を用いて行うと都合がよい. この L を換算長 ( あるいは有効長さという ) という. 座屈荷重は一般に,
2016年度 京都大・文系数学
 06 京都大学 ( 文系 ) 前期日程問題 解答解説のページへ xy 平面内の領域の面積を求めよ x + y, x で, 曲線 C : y= x + x -xの上側にある部分 -- 06 京都大学 ( 文系 ) 前期日程問題 解答解説のページへ ボタンを押すと あたり か はずれ のいずれかが表示される装置がある あたり の表示される確率は毎回同じであるとする この装置のボタンを 0 回押したとき,
06 京都大学 ( 文系 ) 前期日程問題 解答解説のページへ xy 平面内の領域の面積を求めよ x + y, x で, 曲線 C : y= x + x -xの上側にある部分 -- 06 京都大学 ( 文系 ) 前期日程問題 解答解説のページへ ボタンを押すと あたり か はずれ のいずれかが表示される装置がある あたり の表示される確率は毎回同じであるとする この装置のボタンを 0 回押したとき,
OCW-iダランベールの原理
 講義名連続体力学配布資料 OCW- 第 2 回ダランベールの原理 無機材料工学科准教授安田公一 1 はじめに今回の講義では, まず, 前半でダランベールの原理について説明する これを用いると, 動力学の問題を静力学の問題として解くことができ, さらに, 前回の仮想仕事の原理を適用すると動力学問題も簡単に解くことができるようになる また, 後半では, ダランベールの原理の応用として ラグランジュ方程式の導出を示す
講義名連続体力学配布資料 OCW- 第 2 回ダランベールの原理 無機材料工学科准教授安田公一 1 はじめに今回の講義では, まず, 前半でダランベールの原理について説明する これを用いると, 動力学の問題を静力学の問題として解くことができ, さらに, 前回の仮想仕事の原理を適用すると動力学問題も簡単に解くことができるようになる また, 後半では, ダランベールの原理の応用として ラグランジュ方程式の導出を示す
DVIOUT
 第 3 章 フーリエ変換 3.1 フーリエ積分とフーリエ変換 第 章では 周期を持つ関数のフーリエ級数について学びました この章では 最初に 周期を持つ関数のフーリエ級数を拡張し 周期を持たない ( 一般的な ) 関数のフーリエ級数を導きましょう 具体的には 関数 f(x) を区間 L x L で考え この L を限りなく大きくするというアプローチを取ります (L ) なお ここで扱う関数 f(x)
第 3 章 フーリエ変換 3.1 フーリエ積分とフーリエ変換 第 章では 周期を持つ関数のフーリエ級数について学びました この章では 最初に 周期を持つ関数のフーリエ級数を拡張し 周期を持たない ( 一般的な ) 関数のフーリエ級数を導きましょう 具体的には 関数 f(x) を区間 L x L で考え この L を限りなく大きくするというアプローチを取ります (L ) なお ここで扱う関数 f(x)
スライド 1
 暫定版修正 加筆の可能性あり ( 付録 ) 準備 : 非線形光学効果 (). 絵解き : 第二高調波発生. 基本波の波動方程式 3. 第二高調波の波動方程式 4. 二倍分極振動 : ブランコ 5. 結合波動方程式へ 6. 補足 : 非線形電気感受率 ( 複素数 ) 付録 43 のアプローチ. 分極振動とは振動電場に誘われて伸縮する電気双極子の集団運動. 電気感受率と波動方程式の関係を明らかにする 3.
暫定版修正 加筆の可能性あり ( 付録 ) 準備 : 非線形光学効果 (). 絵解き : 第二高調波発生. 基本波の波動方程式 3. 第二高調波の波動方程式 4. 二倍分極振動 : ブランコ 5. 結合波動方程式へ 6. 補足 : 非線形電気感受率 ( 複素数 ) 付録 43 のアプローチ. 分極振動とは振動電場に誘われて伸縮する電気双極子の集団運動. 電気感受率と波動方程式の関係を明らかにする 3.
レーザー発振の原理
 第 6 章光と原子との相互作用光の吸収と放出前章では 光と相互作用する原子の束縛電子状態は定常状態とは異なるが 定常状態の状態ベクトルで展開して表現できることが示された 原子 個の微視的双極子モーメントの期待値から 巨視的な物質分極が導かれ 我々の観測できるマクロ的な光学定数が関連付けられた 本章では 状態の変化と それに伴う光の吸収と放出について議論する 6. 量子論に基づく A 係数と B 係数分散理論では
第 6 章光と原子との相互作用光の吸収と放出前章では 光と相互作用する原子の束縛電子状態は定常状態とは異なるが 定常状態の状態ベクトルで展開して表現できることが示された 原子 個の微視的双極子モーメントの期待値から 巨視的な物質分極が導かれ 我々の観測できるマクロ的な光学定数が関連付けられた 本章では 状態の変化と それに伴う光の吸収と放出について議論する 6. 量子論に基づく A 係数と B 係数分散理論では
Microsoft PowerPoint - LectureB1_17woAN.pptx
 本講義の範囲 都市防災工学 後半第 回 : 導入 確率過程の基礎 千葉大学大学院工学研究院都市環境システムコース岡野創 http://oko-lb.tu.chib-u.c.jp/oshibousi/. ランダム振動論 地震動を不規則波形 ( 確率過程 ) と捉えて, 構造物の地震応答を評価する理論. 震源モデルによる地震動評価 断層の動きを仮定して, 断層から発せられる地震動を評価する方法 ( 運動学的モデル
本講義の範囲 都市防災工学 後半第 回 : 導入 確率過程の基礎 千葉大学大学院工学研究院都市環境システムコース岡野創 http://oko-lb.tu.chib-u.c.jp/oshibousi/. ランダム振動論 地震動を不規則波形 ( 確率過程 ) と捉えて, 構造物の地震応答を評価する理論. 震源モデルによる地震動評価 断層の動きを仮定して, 断層から発せられる地震動を評価する方法 ( 運動学的モデル
平面波
 平面波 図.に示すように, 波源 ( 送信アンテナあるいは散乱点 ) から遠い位置で, 観測点 Pにおける波の状態を考えてみる. 遠いとは, 波長 λ に比べて距離 が十分大きいことを意味しており, 観測点 Pの近くでは, 等位相面が平面とみなせる状態にある. 平面波とは波の等位相面が平面になっている波のことである. 通信や計測を行うとき, 遠方における波の振舞いは平面波で近似できる. したがって平面波の性質を理解することが最も重要である.
平面波 図.に示すように, 波源 ( 送信アンテナあるいは散乱点 ) から遠い位置で, 観測点 Pにおける波の状態を考えてみる. 遠いとは, 波長 λ に比べて距離 が十分大きいことを意味しており, 観測点 Pの近くでは, 等位相面が平面とみなせる状態にある. 平面波とは波の等位相面が平面になっている波のことである. 通信や計測を行うとき, 遠方における波の振舞いは平面波で近似できる. したがって平面波の性質を理解することが最も重要である.
s とは何か 2011 年 2 月 5 日目次へ戻る 1 正弦波の微分 y=v m sin ωt を時間 t で微分します V m は正弦波の最大値です 合成関数の微分法を用い y=v m sin u u=ωt と置きますと dy dt dy du du dt d du V m sin u d dt
 とは何か 0 年 月 5 日目次へ戻る 正弦波の微分 y= in を時間 で微分します は正弦波の最大値です 合成関数の微分法を用い y= in u u= と置きますと y y in u in u (co u co になります in u の は定数なので 微分後も残ります 合成関数の微分法ですので 最後に u を に戻しています 0[ra] の co 値は [ra] の in 値と同じです その先の角
とは何か 0 年 月 5 日目次へ戻る 正弦波の微分 y= in を時間 で微分します は正弦波の最大値です 合成関数の微分法を用い y= in u u= と置きますと y y in u in u (co u co になります in u の は定数なので 微分後も残ります 合成関数の微分法ですので 最後に u を に戻しています 0[ra] の co 値は [ra] の in 値と同じです その先の角
Microsoft PowerPoint - LectureB1handout.ppt [互換モード]
![Microsoft PowerPoint - LectureB1handout.ppt [互換モード] Microsoft PowerPoint - LectureB1handout.ppt [互換モード]](/thumbs/89/97916837.jpg) 本講義のスコープ 都市防災工学 後半第 回 : イントロダクション 千葉大学大学院工学研究科建築 都市科学専攻都市環境システムコース岡野創 耐震工学の専門家として知っていた方が良いが 敷居が高く 入り口で挫折しがちな分野をいくつか取り上げて説明 ランダム振動論 地震波形に対する構造物応答の理論的把握 減衰と地震応答 エネルギーバランス 地震動の各種スペクトルの相互関係 震源モデル 近年では震源モデルによる地震動予測が良く行われている
本講義のスコープ 都市防災工学 後半第 回 : イントロダクション 千葉大学大学院工学研究科建築 都市科学専攻都市環境システムコース岡野創 耐震工学の専門家として知っていた方が良いが 敷居が高く 入り口で挫折しがちな分野をいくつか取り上げて説明 ランダム振動論 地震波形に対する構造物応答の理論的把握 減衰と地震応答 エネルギーバランス 地震動の各種スペクトルの相互関係 震源モデル 近年では震源モデルによる地震動予測が良く行われている
PowerPoint Presentation
 応用数学 Ⅱ (7) 7 連立微分方程式の立て方と解法. 高階微分方程式による解法. ベクトル微分方程式による解法 3. 演算子による解法 連立微分方程式 未知数が複数個あり, 未知数の数だけ微分方程式が与えられている場合, これらを連立微分方程式という. d d 解法 () 高階微分方程式化による解法 つの方程式から つの未知数を消去して, 未知数が つの方程式に変換 のみの方程式にするために,
応用数学 Ⅱ (7) 7 連立微分方程式の立て方と解法. 高階微分方程式による解法. ベクトル微分方程式による解法 3. 演算子による解法 連立微分方程式 未知数が複数個あり, 未知数の数だけ微分方程式が与えられている場合, これらを連立微分方程式という. d d 解法 () 高階微分方程式化による解法 つの方程式から つの未知数を消去して, 未知数が つの方程式に変換 のみの方程式にするために,
1/10 平成 29 年 3 月 24 日午後 1 時 37 分第 5 章ローレンツ変換と回転 第 5 章ローレンツ変換と回転 Ⅰ. 回転 第 3 章光速度不変の原理とローレンツ変換 では 時間の遅れをローレンツ変換 ct 移動 v相対 v相対 ct - x x - ct = c, x c 2 移動
 / 平成 9 年 3 月 4 日午後 時 37 分第 5 章ローレンツ変換と回転 第 5 章ローレンツ変換と回転 Ⅰ. 回転 第 3 章光速度不変の原理とローレンツ変換 では 時間の遅れをローレンツ変換 t t - x x - t, x 静止静止静止静止 を導いた これを 図の場合に当てはめると t - x x - t t, x t + x x + t t, x (5.) (5.) (5.3) を得る
/ 平成 9 年 3 月 4 日午後 時 37 分第 5 章ローレンツ変換と回転 第 5 章ローレンツ変換と回転 Ⅰ. 回転 第 3 章光速度不変の原理とローレンツ変換 では 時間の遅れをローレンツ変換 t t - x x - t, x 静止静止静止静止 を導いた これを 図の場合に当てはめると t - x x - t t, x t + x x + t t, x (5.) (5.) (5.3) を得る
パソコンシミュレータの現状
 第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
Microsoft Word - 5章摂動法.doc
 5 章摂動法 ( 次の Moller-Plesset (MP) 法のために ) // 水素原子など 電子系を除いては 原子系の Schrödiger 方程式を解析的に解くことはできない 分子系の Schrödiger 方程式の正確な数値解を求めることも困難である そこで Hartree-Fock(H-F) 法を導入した H-F 法は Schrödiger 方程式が与える全エネルギーの 99% を再現することができる優れた近似方法である
5 章摂動法 ( 次の Moller-Plesset (MP) 法のために ) // 水素原子など 電子系を除いては 原子系の Schrödiger 方程式を解析的に解くことはできない 分子系の Schrödiger 方程式の正確な数値解を求めることも困難である そこで Hartree-Fock(H-F) 法を導入した H-F 法は Schrödiger 方程式が与える全エネルギーの 99% を再現することができる優れた近似方法である
2009 年 11 月 16 日版 ( 久家 ) 遠地 P 波の変位波形の作成 遠地 P 波の変位波形 ( 変位の時間関数 ) は 波線理論をもとに P U () t = S()* t E()* t P() t で近似的に計算できる * は畳み込み積分 (convolution) を表す ( 付録
 遠地 波の変位波形の作成 遠地 波の変位波形 ( 変位の時間関数 ) は 波線理論をもとに U () t S() t E() t () t で近似的に計算できる は畳み込み積分 (convolution) を表す ( 付録 参照 ) ここで St () は地震の断層運動によって決まる時間関数 1 E() t は地下構造によって生じる種々の波の到着を与える時間関数 ( ここでは 直達 波とともに 震源そばの地表での反射波や変換波を与える時間関数
遠地 波の変位波形の作成 遠地 波の変位波形 ( 変位の時間関数 ) は 波線理論をもとに U () t S() t E() t () t で近似的に計算できる は畳み込み積分 (convolution) を表す ( 付録 参照 ) ここで St () は地震の断層運動によって決まる時間関数 1 E() t は地下構造によって生じる種々の波の到着を与える時間関数 ( ここでは 直達 波とともに 震源そばの地表での反射波や変換波を与える時間関数
Microsoft PowerPoint - 9.pptx
 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 行列演算と写像 ( 次変換 3 拡大とスカラー倍 p ' = ( ', ' = ( k, kk p = (, k 倍 k 倍 拡大後 k 倍拡大の関係は スカラー倍を用いて次のように表現できる ' = k ' 拡大前 拡大 4 拡大と行列の積 p ' = ( ', '
9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 行列演算と写像 ( 次変換 3 拡大とスカラー倍 p ' = ( ', ' = ( k, kk p = (, k 倍 k 倍 拡大後 k 倍拡大の関係は スカラー倍を用いて次のように表現できる ' = k ' 拡大前 拡大 4 拡大と行列の積 p ' = ( ', '
Microsoft PowerPoint - 9.pptx
 9/7/8( 水 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 拡大とスカラー倍 行列演算と写像 ( 次変換 拡大後 k 倍 k 倍 k 倍拡大の関係は スカラー倍を用いて次のように表現できる p = (, ' = k ' 拡大前 p ' = ( ', ' = ( k, k 拡大 4 拡大と行列の積 拡大後 k 倍
9/7/8( 水 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 拡大とスカラー倍 行列演算と写像 ( 次変換 拡大後 k 倍 k 倍 k 倍拡大の関係は スカラー倍を用いて次のように表現できる p = (, ' = k ' 拡大前 p ' = ( ', ' = ( k, k 拡大 4 拡大と行列の積 拡大後 k 倍
解析力学B - 第11回: 正準変換
 解析力学 B 第 11 回 : 正準変換 神戸大 : 陰山聡 ホームページ ( 第 6 回から今回までの講義ノート ) http://tinyurl.com/kage2010 2011.01.27 正準変換 バネ問題 ( あえて下手に座標をとった ) ハミルトニアンを考える q 正準方程式は H = p2 2m + k 2 (q l 0) 2 q = H p = p m ṗ = H q = k(q
解析力学 B 第 11 回 : 正準変換 神戸大 : 陰山聡 ホームページ ( 第 6 回から今回までの講義ノート ) http://tinyurl.com/kage2010 2011.01.27 正準変換 バネ問題 ( あえて下手に座標をとった ) ハミルトニアンを考える q 正準方程式は H = p2 2m + k 2 (q l 0) 2 q = H p = p m ṗ = H q = k(q
DVIOUT
 最適レギュレータ 松尾研究室資料 第 最適レギュレータ 節時不変型無限時間最適レギュレータ 状態フィードバックの可能な場合の無限時間問題における最適レギュレータについて確定系について説明する. ここで, レギュレータとは状態量をゼロにするようなコントローラのことである. なぜ, 無限時間問題のみを述べるかという理由は以下のとおりである. 有限時間の最適レギュレータ問題の場合の最適フィードバックゲインは微分方程式の解から構成される時間関数として表現される.
最適レギュレータ 松尾研究室資料 第 最適レギュレータ 節時不変型無限時間最適レギュレータ 状態フィードバックの可能な場合の無限時間問題における最適レギュレータについて確定系について説明する. ここで, レギュレータとは状態量をゼロにするようなコントローラのことである. なぜ, 無限時間問題のみを述べるかという理由は以下のとおりである. 有限時間の最適レギュレータ問題の場合の最適フィードバックゲインは微分方程式の解から構成される時間関数として表現される.
2 図微小要素の流体の流入出 方向の断面の流体の流入出の収支断面 Ⅰ から微小要素に流入出する流体の流量 Q 断面 Ⅰ は 以下のように定式化できる Q 断面 Ⅰ 流量 密度 流速 断面 Ⅰ の面積 微小要素の断面 Ⅰ から だけ移動した断面 Ⅱ を流入出する流体の流量 Q 断面 Ⅱ は以下のように
 3 章 Web に Link 解説 連続式 微分表示 の誘導.64 *4. 連続式連続式は ある領域の内部にある流体の質量の収支が その表面からの流入出の合計と等しくなることを定式化したものであり 流体における質量保存則を示したものである 2. 連続式 微分表示 の誘導図のような微小要素 コントロールボリューム の領域内の流体の増減と外部からの流体の流入出を考えることで定式化できる 微小要素 流入
3 章 Web に Link 解説 連続式 微分表示 の誘導.64 *4. 連続式連続式は ある領域の内部にある流体の質量の収支が その表面からの流入出の合計と等しくなることを定式化したものであり 流体における質量保存則を示したものである 2. 連続式 微分表示 の誘導図のような微小要素 コントロールボリューム の領域内の流体の増減と外部からの流体の流入出を考えることで定式化できる 微小要素 流入
Microsoft PowerPoint - H22制御工学I-2回.ppt
 制御工学 I 第二回ラプラス変換 平成 年 4 月 9 日 /4/9 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
制御工学 I 第二回ラプラス変換 平成 年 4 月 9 日 /4/9 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
(Microsoft Word - 10ta320a_\220U\223\256\212w\223\301\230__6\217\315\221O\224\274\203\214\203W\203\201.docx)
 6 章スペクトルの平滑化 スペクトルの平滑化とはフーリエスペクトルやパワ スペクトルのギザギザを取り除き 滑らかにする操作のことをいう ただし 波のもっている本質的なものをゆがめてはいけない 図 6-7 パワ スペクトルの平滑化 6. 合積のフーリエ変換スペクトルの平滑化を学ぶ前に 合積とそのフーリエ変換について説明する 6. データ ウィンドウデータ ウィンドウの定義と特徴について説明する 6.3
6 章スペクトルの平滑化 スペクトルの平滑化とはフーリエスペクトルやパワ スペクトルのギザギザを取り除き 滑らかにする操作のことをいう ただし 波のもっている本質的なものをゆがめてはいけない 図 6-7 パワ スペクトルの平滑化 6. 合積のフーリエ変換スペクトルの平滑化を学ぶ前に 合積とそのフーリエ変換について説明する 6. データ ウィンドウデータ ウィンドウの定義と特徴について説明する 6.3
Microsoft Word - 8章(CI).doc
 8 章配置間相互作用法 : Configuration Interaction () etho [] 化学的精度化学反応の精密な解析をするためには エネルギー誤差は数 ~ kcal/mol 程度に抑えたいものである この程度の誤差内に治まる精度を 化学的精度 と呼ぶことがある He 原子のエネルギーをシュレーディンガー方程式と分子軌道法で計算した結果を示そう He 原子のエネルギー Hartree-Fock
8 章配置間相互作用法 : Configuration Interaction () etho [] 化学的精度化学反応の精密な解析をするためには エネルギー誤差は数 ~ kcal/mol 程度に抑えたいものである この程度の誤差内に治まる精度を 化学的精度 と呼ぶことがある He 原子のエネルギーをシュレーディンガー方程式と分子軌道法で計算した結果を示そう He 原子のエネルギー Hartree-Fock
1/30 平成 29 年 3 月 24 日 ( 金 ) 午前 11 時 25 分第三章フェルミ量子場 : スピノール場 ( 次元あり ) 第三章フェルミ量子場 : スピノール場 フェルミ型 ボーズ量子場のエネルギーは 第二章ボーズ量子場 : スカラー場 の (2.18) より ˆ dp 1 1 =
 / 平成 9 年 月 日 ( 金 午前 時 5 分第三章フェルミ量子場 : スピノール場 ( 次元あり 第三章フェルミ量子場 : スピノール場 フェルミ型 ボーズ量子場のエネルギーは 第二章ボーズ量子場 : スカラー場 の (.8 より ˆ ( ( ( q -, ( ( c ( H c c ë é ù û - Ü + c ( ( - に限る (. である 一方 フェルミ型は 成分をもち その成分を,,,,
/ 平成 9 年 月 日 ( 金 午前 時 5 分第三章フェルミ量子場 : スピノール場 ( 次元あり 第三章フェルミ量子場 : スピノール場 フェルミ型 ボーズ量子場のエネルギーは 第二章ボーズ量子場 : スカラー場 の (.8 より ˆ ( ( ( q -, ( ( c ( H c c ë é ù û - Ü + c ( ( - に限る (. である 一方 フェルミ型は 成分をもち その成分を,,,,
<4D F736F F D20824F B CC92E8979D814696CA90CF95AA82C691CC90CF95AA2E646F63>
 1/1 平成 23 年 3 月 24 日午後 6 時 52 分 6 ガウスの定理 : 面積分と体積分 6 ガウスの定理 : 面積分と体積分 Ⅰ. 直交座標系 ガウスの定理は 微分して すぐに積分すると元に戻るというルールを 3 次元積分に適用した定理になります よく知っているのは 簡単化のため 変数が1つの場合は dj ( d ( ににします全微分 = 偏微分 d = d = J ( + C d です
1/1 平成 23 年 3 月 24 日午後 6 時 52 分 6 ガウスの定理 : 面積分と体積分 6 ガウスの定理 : 面積分と体積分 Ⅰ. 直交座標系 ガウスの定理は 微分して すぐに積分すると元に戻るというルールを 3 次元積分に適用した定理になります よく知っているのは 簡単化のため 変数が1つの場合は dj ( d ( ににします全微分 = 偏微分 d = d = J ( + C d です
Microsoft PowerPoint _量子力学短大.pptx
 . エネルギーギャップとrllouゾーン ブリルアン領域,t_8.. 周期ポテンシャル中の電子とエネルギーギャップ 簡単のため 次元に間隔 で原子が並んでいる結晶を考える 右方向に進行している電子の波は 間隔 で規則正しく並んでいる原子が作る格子によって散乱され 左向きに進行する波となる 波長 λ が の時 r の反射条件 式を満たし 両者の波が互いに強め合い 定在波を作る つまり 式 式を満たす波は
. エネルギーギャップとrllouゾーン ブリルアン領域,t_8.. 周期ポテンシャル中の電子とエネルギーギャップ 簡単のため 次元に間隔 で原子が並んでいる結晶を考える 右方向に進行している電子の波は 間隔 で規則正しく並んでいる原子が作る格子によって散乱され 左向きに進行する波となる 波長 λ が の時 r の反射条件 式を満たし 両者の波が互いに強め合い 定在波を作る つまり 式 式を満たす波は
Microsoft PowerPoint - 10.pptx
 0. 固有値とその応用 固有値と固有ベクトル 2 行列による写像から固有ベクトルへ m n A : m n n m 行列によって線形写像 f R R A が表せることを見てきた ここでは 2 次元平面の行列による写像を調べる 2 = 2 A 2 2 とし 写像 まず 単位ベクトルの像を求める u 2 x = v 2 y f : R A R を考える u 2 2 u, 2 2 0 = = v 2 0
0. 固有値とその応用 固有値と固有ベクトル 2 行列による写像から固有ベクトルへ m n A : m n n m 行列によって線形写像 f R R A が表せることを見てきた ここでは 2 次元平面の行列による写像を調べる 2 = 2 A 2 2 とし 写像 まず 単位ベクトルの像を求める u 2 x = v 2 y f : R A R を考える u 2 2 u, 2 2 0 = = v 2 0
医用工学概論 Medical Engineering (ME) 3年前期の医用工学概論実習と 合わせ、 医療の現場で使用されている 医用機器を正しく安全に使用するために必要な医用工学(ME)の 基礎知識を習得する。
 http://chtgkato3.med.hokudai.ac.jp/kougi/me_practice/ EXCEL でリサージュ曲線のシミュレーションを行う Excel を開いて Aカラムのセル1 に (A1に) t と入力. (Aカラム( 列 ) に時間 ( 秒 ) を入れる ) ツールバーの中央揃えボタンを押すと 文字がセルの中央に配置される. Aカラムのセル2,3,4に (A2 A3 A4
http://chtgkato3.med.hokudai.ac.jp/kougi/me_practice/ EXCEL でリサージュ曲線のシミュレーションを行う Excel を開いて Aカラムのセル1 に (A1に) t と入力. (Aカラム( 列 ) に時間 ( 秒 ) を入れる ) ツールバーの中央揃えボタンを押すと 文字がセルの中央に配置される. Aカラムのセル2,3,4に (A2 A3 A4
RMS(Root Mean Square value 実効値 ) 実効値は AC の電圧と電流両方の値を規定する 最も一般的で便利な値です AC 波形の実効値はその波形から得られる パワーのレベルを示すものであり AC 信号の最も重要な属性となります 実効値の計算は AC の電流波形と それによって
 入門書 最近の数多くの AC 電源アプリケーションに伴う複雑な電流 / 電圧波形のため さまざまな測定上の課題が発生しています このような問題に対処する場合 基本的な測定 使用される用語 それらの関係について理解することが重要になります このアプリケーションノートではパワー測定の基本的な考え方やパワー測定において重要な 以下の用語の明確に定義します RMS(Root Mean Square value
入門書 最近の数多くの AC 電源アプリケーションに伴う複雑な電流 / 電圧波形のため さまざまな測定上の課題が発生しています このような問題に対処する場合 基本的な測定 使用される用語 それらの関係について理解することが重要になります このアプリケーションノートではパワー測定の基本的な考え方やパワー測定において重要な 以下の用語の明確に定義します RMS(Root Mean Square value
Microsoft PowerPoint - aep_1.ppt [互換モード]
![Microsoft PowerPoint - aep_1.ppt [互換モード] Microsoft PowerPoint - aep_1.ppt [互換モード]](/thumbs/91/107493198.jpg) 物理計測法特論 No.1 第 1 章 : 信号と雑音 本講義の主題 雑音の性質を理解することで 信号と雑音の大きさが非常に近い状態での信号の測定技術 : 微小信号計測 について学ぶ 講義の Web http://www.g-munu.t.u-tokyo.ac.jp/mio/note/sig_mes/tokuron.html 物理学の基本は実験事実の積み重ねである そして それは何かを測定することから始まる
物理計測法特論 No.1 第 1 章 : 信号と雑音 本講義の主題 雑音の性質を理解することで 信号と雑音の大きさが非常に近い状態での信号の測定技術 : 微小信号計測 について学ぶ 講義の Web http://www.g-munu.t.u-tokyo.ac.jp/mio/note/sig_mes/tokuron.html 物理学の基本は実験事実の積み重ねである そして それは何かを測定することから始まる
<4D F736F F D20824F F6490CF95AA82C696CA90CF95AA2E646F63>
 1/15 平成 3 年 3 月 4 日午後 6 時 49 分 5 ベクトルの 重積分と面積分 5 重積分と面積分 Ⅰ. 重積分 と で 回積分することを 重積分 といいます この 重積分は何を意味しているのでしょう? 通常の積分 (1 重積分 ) では C d 図 1a 1 f d (5.1) 1 f d f ( ) は 図形的には図 1a のように面積を表しています つまり 1 f ( ) を高さとしてプロットすると図
1/15 平成 3 年 3 月 4 日午後 6 時 49 分 5 ベクトルの 重積分と面積分 5 重積分と面積分 Ⅰ. 重積分 と で 回積分することを 重積分 といいます この 重積分は何を意味しているのでしょう? 通常の積分 (1 重積分 ) では C d 図 1a 1 f d (5.1) 1 f d f ( ) は 図形的には図 1a のように面積を表しています つまり 1 f ( ) を高さとしてプロットすると図
3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x0 = f x= x0 t f c x f =0 [1] c f 0 x= x 0 x 0 f x= x0 x 2 x 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考
![3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x0 = f x= x0 t f c x f =0 [1] c f 0 x= x 0 x 0 f x= x0 x 2 x 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考 3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x0 = f x= x0 t f c x f =0 [1] c f 0 x= x 0 x 0 f x= x0 x 2 x 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考](/thumbs/103/158269281.jpg) 3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x = f x= x t f c x f = [1] c f x= x f x= x 2 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考える まず 初期時刻 t=t に f =R f exp [ik x ] [3] のような波動を与えたとき どのように時間変化するか調べる
3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x = f x= x t f c x f = [1] c f x= x f x= x 2 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考える まず 初期時刻 t=t に f =R f exp [ik x ] [3] のような波動を与えたとき どのように時間変化するか調べる
構造力学Ⅰ第12回
 第 回材の座屈 (0 章 ) p.5~ ( 復習 ) モールの定理 ( 手順 ) 座屈とは 荷重により梁に生じた曲げモーメントをで除して仮想荷重と考える 座屈荷重 偏心荷重 ( 曲げと軸力 ) 断面の核 この仮想荷重に対するある点でのせん断力 たわみ角に相当する曲げモーメント たわみに相当する ( 例 ) 単純梁の支点のたわみ角 : は 図 を仮想荷重と考えたときの 点の支点反力 B は 図 を仮想荷重と考えたときのB
第 回材の座屈 (0 章 ) p.5~ ( 復習 ) モールの定理 ( 手順 ) 座屈とは 荷重により梁に生じた曲げモーメントをで除して仮想荷重と考える 座屈荷重 偏心荷重 ( 曲げと軸力 ) 断面の核 この仮想荷重に対するある点でのせん断力 たわみ角に相当する曲げモーメント たわみに相当する ( 例 ) 単純梁の支点のたわみ角 : は 図 を仮想荷重と考えたときの 点の支点反力 B は 図 を仮想荷重と考えたときのB
学習指導要領
 (1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 絶対値の意味を理解し適切な処理することができる 例題 1-3 の絶対値をはずせ 展開公式 ( a + b ) ( a - b ) = a 2 - b 2 を利用して根号を含む分数の分母を有理化することができる 例題 5 5 + 2 の分母を有理化せよ 実数の整数部分と小数部分の表し方を理解している
(1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 絶対値の意味を理解し適切な処理することができる 例題 1-3 の絶対値をはずせ 展開公式 ( a + b ) ( a - b ) = a 2 - b 2 を利用して根号を含む分数の分母を有理化することができる 例題 5 5 + 2 の分母を有理化せよ 実数の整数部分と小数部分の表し方を理解している
Introduction
 我 日常的関 用 半導体大半 用 近年 化進 小 半導体求 量子 開発活発 開発必要材 料 薄膜半導体必要 材料 期待 物質盛 研究 物質中 今回私黒 物性研究行 黒 次元層状構造 半導体 薄膜半導体 実用期待 物質一 現在 様 実験手法用 物性研究行 物質対 理解深 一方 測定用 研究 行 量子 実現 測定 実験手法非常重要 量子 特 量子 量子状態観測 方法 測定用 材料 物質 測定観測 物性必要
我 日常的関 用 半導体大半 用 近年 化進 小 半導体求 量子 開発活発 開発必要材 料 薄膜半導体必要 材料 期待 物質盛 研究 物質中 今回私黒 物性研究行 黒 次元層状構造 半導体 薄膜半導体 実用期待 物質一 現在 様 実験手法用 物性研究行 物質対 理解深 一方 測定用 研究 行 量子 実現 測定 実験手法非常重要 量子 特 量子 量子状態観測 方法 測定用 材料 物質 測定観測 物性必要
Microsoft PowerPoint - 第06章振幅変調.pptx
 通信システムのモデル コミュニケーション工学 A 第 6 章アナログ変調方式 : 振幅変調 変調の種類振幅変調 () 検波出力の信号対雑音電力比 (S/N) 送信機 送信メッセージ ( 例えば音声 ) をアナログまたはディジタル電気信号に変換. 変調 : 通信路で伝送するのに適した周波数帯の信号波形へ変換. 受信機フィルタで邪魔な雑音を除去し, 処理しやすい電圧まで増幅. 復調 : もとの周波数帯の電気信号波形に変換し,
通信システムのモデル コミュニケーション工学 A 第 6 章アナログ変調方式 : 振幅変調 変調の種類振幅変調 () 検波出力の信号対雑音電力比 (S/N) 送信機 送信メッセージ ( 例えば音声 ) をアナログまたはディジタル電気信号に変換. 変調 : 通信路で伝送するのに適した周波数帯の信号波形へ変換. 受信機フィルタで邪魔な雑音を除去し, 処理しやすい電圧まで増幅. 復調 : もとの周波数帯の電気信号波形に変換し,
Kumamoto University Center for Multimedia and Information Technologies Lab. 熊本大学アプリケーション実験 ~ 実環境における無線 LAN 受信電波強度を用いた位置推定手法の検討 ~ InKIAI 宮崎県美郷
 熊本大学アプリケーション実験 ~ 実環境における無線 LAN 受信電波強度を用いた位置推定手法の検討 ~ InKIAI プロジェクト @ 宮崎県美郷町 熊本大学副島慶人川村諒 1 実験の目的 従来 信号の受信電波強度 (RSSI:RecevedSgnal StrengthIndcator) により 対象の位置を推定する手法として 無線 LAN の AP(AccessPont) から受信する信号の減衰量をもとに位置を推定する手法が多く検討されている
熊本大学アプリケーション実験 ~ 実環境における無線 LAN 受信電波強度を用いた位置推定手法の検討 ~ InKIAI プロジェクト @ 宮崎県美郷町 熊本大学副島慶人川村諒 1 実験の目的 従来 信号の受信電波強度 (RSSI:RecevedSgnal StrengthIndcator) により 対象の位置を推定する手法として 無線 LAN の AP(AccessPont) から受信する信号の減衰量をもとに位置を推定する手法が多く検討されている
木村の物理小ネタ ケプラーの第 2 法則と角運動量保存則 A. 面積速度面積速度とは平面内に定点 O と動点 P があるとき, 定点 O と動点 P を結ぶ線分 OP( 動径 OP という) が単位時間に描く面積を 動点 P の定点 O に
 ケプラーの第 法則と角運動量保存則 A. 面積速度面積速度とは平面内に定点 O と動点 P があるとき, 定点 O と動点 P を結ぶ線分 OP( 動径 OP という が単位時間に描く面積を 動点 P の定点 O に関する面積速度の大きさ という 定点 O まわりを回る面積速度の導き方導き方 A ( x( + D, y( + D v ( q r ( A ( x (, y( 動点 P が xy 座標平面上を時刻
ケプラーの第 法則と角運動量保存則 A. 面積速度面積速度とは平面内に定点 O と動点 P があるとき, 定点 O と動点 P を結ぶ線分 OP( 動径 OP という が単位時間に描く面積を 動点 P の定点 O に関する面積速度の大きさ という 定点 O まわりを回る面積速度の導き方導き方 A ( x( + D, y( + D v ( q r ( A ( x (, y( 動点 P が xy 座標平面上を時刻
PowerPoint プレゼンテーション
 電磁波工学 第 5 回平面波の媒質への垂直および射入射と透過 柴田幸司 Bounda Plan Rgon ε μ Rgon Mdum ( ガラスなど ε μ z 平面波の反射と透過 垂直入射の場合 左図に示す様に 平面波が境界面に対して垂直に入射する場合を考える この時の入射波を とすると 入射波は境界において 透過波 と とに分解される この時の透過量を 反射量を Γ とおくと 領域 における媒質の誘電率に対して透過量
電磁波工学 第 5 回平面波の媒質への垂直および射入射と透過 柴田幸司 Bounda Plan Rgon ε μ Rgon Mdum ( ガラスなど ε μ z 平面波の反射と透過 垂直入射の場合 左図に示す様に 平面波が境界面に対して垂直に入射する場合を考える この時の入射波を とすると 入射波は境界において 透過波 と とに分解される この時の透過量を 反射量を Γ とおくと 領域 における媒質の誘電率に対して透過量
Microsoft PowerPoint - zairiki_3
 材料力学講義 (3) 応力と変形 Ⅲ ( 曲げモーメント, 垂直応力度, 曲率 ) 今回は, 曲げモーメントに関する, 断面力 - 応力度 - 変形 - 変位の関係について学びます 1 曲げモーメント 曲げモーメント M 静定力学で求めた曲げモーメントも, 仮想的に断面を切ることによって現れる内力です 軸方向力は断面に働く力 曲げモーメント M は断面力 曲げモーメントも, 一つのモーメントとして表しますが,
材料力学講義 (3) 応力と変形 Ⅲ ( 曲げモーメント, 垂直応力度, 曲率 ) 今回は, 曲げモーメントに関する, 断面力 - 応力度 - 変形 - 変位の関係について学びます 1 曲げモーメント 曲げモーメント M 静定力学で求めた曲げモーメントも, 仮想的に断面を切ることによって現れる内力です 軸方向力は断面に働く力 曲げモーメント M は断面力 曲げモーメントも, 一つのモーメントとして表しますが,
Techniques for Nuclear and Particle Physics Experiments Energy Loss by Radiation : Bremsstrahlung 制動放射によるエネルギー損失は σ r 2 e = (e 2 mc 2 ) 2 で表される為
 Techniques for Nuclear and Particle Physics Experiments.. Energy Loss by Radiation : Bremsstrahlung 制動放射によるエネルギー損失は σ r e = (e mc ) で表される為 質量に大きく依存する Ex) 電子の次に質量の小さいミューオンの制動放射によるエネルギー損失 m e 0.5 MeV, m
Techniques for Nuclear and Particle Physics Experiments.. Energy Loss by Radiation : Bremsstrahlung 制動放射によるエネルギー損失は σ r e = (e mc ) で表される為 質量に大きく依存する Ex) 電子の次に質量の小さいミューオンの制動放射によるエネルギー損失 m e 0.5 MeV, m
2018/6/12 表面の電子状態 表面に局在する電子状態 表面電子状態表面準位 1. ショックレー状態 ( 準位 ) 2. タム状態 ( 準位 ) 3. 鏡像状態 ( 準位 ) 4. 表面バンドのナローイング 5. 吸着子の状態密度 鏡像力によるポテンシャル 表面からzの位置の電子に働く力とポテン
 表面の電子状態 表面に局在する電子状態 表面電子状態表面準位. ショックレー状態 ( 準位. タム状態 ( 準位 3. 鏡像状態 ( 準位 4. 表面バンドのナローイング 5. 吸着子の状態密度 鏡像力によるポテンシャル 表面からzの位置の電子に働く力とポテンシャル e F z ( z z e V ( z ( Fz dz 4z e V ( z 4z ( z > ( z < のときの電子の運動を考える
表面の電子状態 表面に局在する電子状態 表面電子状態表面準位. ショックレー状態 ( 準位. タム状態 ( 準位 3. 鏡像状態 ( 準位 4. 表面バンドのナローイング 5. 吸着子の状態密度 鏡像力によるポテンシャル 表面からzの位置の電子に働く力とポテンシャル e F z ( z z e V ( z ( Fz dz 4z e V ( z 4z ( z > ( z < のときの電子の運動を考える
三重大学工学部
 反応理論化学 ( その5 6 ポテンシャルエネルギー面と反応経路最も簡単な反応 X + Y X + Y 反応物 ( 生成物 (P X 結合が切断反応系全体のエネルギーは X と Y の Y 結合が形成原子間距離によって変化 r(x と r( Y に対してエネルギーを等高線で表す赤矢印 P:X 結合の切断と Y 結合の形成が同時進行青矢印 P: まず X 結合が切断し次いで Y 結合が形成 谷 X +
反応理論化学 ( その5 6 ポテンシャルエネルギー面と反応経路最も簡単な反応 X + Y X + Y 反応物 ( 生成物 (P X 結合が切断反応系全体のエネルギーは X と Y の Y 結合が形成原子間距離によって変化 r(x と r( Y に対してエネルギーを等高線で表す赤矢印 P:X 結合の切断と Y 結合の形成が同時進行青矢印 P: まず X 結合が切断し次いで Y 結合が形成 谷 X +
Microsoft Word - 1B2011.doc
 第 14 回モールの定理 ( 単純梁の場合 ) ( モールの定理とは何か?p.11) 例題 下記に示す単純梁の C 点のたわみ角 θ C と, たわみ δ C を求めよ ただし, 部材の曲げ 剛性は材軸に沿って一様で とする C D kn B 1.5m 0.5m 1.0m 解答 1 曲げモーメント図を描く,B 点の反力を求める kn kn 4 kn 曲げモーメント図を描く knm 先に得られた曲げモーメントの値を
第 14 回モールの定理 ( 単純梁の場合 ) ( モールの定理とは何か?p.11) 例題 下記に示す単純梁の C 点のたわみ角 θ C と, たわみ δ C を求めよ ただし, 部材の曲げ 剛性は材軸に沿って一様で とする C D kn B 1.5m 0.5m 1.0m 解答 1 曲げモーメント図を描く,B 点の反力を求める kn kn 4 kn 曲げモーメント図を描く knm 先に得られた曲げモーメントの値を
Chap2.key
 . f( ) V (V V ) V e + V e V V V V ( ) V V ( ) E. - () V (0 ) () V (0 ) () V (0 ) (4) V ( ) E. - () V (0 ) () V (0 ) O r θ ( ) ( ) : (r θ) : { r cos θ r sn θ { r + () V (0 ) (4) V ( ) θ θ arg( ) : π π
. f( ) V (V V ) V e + V e V V V V ( ) V V ( ) E. - () V (0 ) () V (0 ) () V (0 ) (4) V ( ) E. - () V (0 ) () V (0 ) O r θ ( ) ( ) : (r θ) : { r cos θ r sn θ { r + () V (0 ) (4) V ( ) θ θ arg( ) : π π
Taro-F25理論 印刷原稿
 第 種理論 A 問題 ( 配点は 問題当たり小問各 点, 計 0 点 ) 問 次の文章は, 真空中の静電界に関する諸法則の微分形に関する記述である 文中の に当てはまるものを解答群の中から選びなさい 図のように, 直交座標系において電界の z 軸成分が零となるような電界について, y 平面の二次元で電位や電界を考える ここで,4 点 (h,0),(0,h), (- h,0),(0,-h) の電位がそれぞれ
第 種理論 A 問題 ( 配点は 問題当たり小問各 点, 計 0 点 ) 問 次の文章は, 真空中の静電界に関する諸法則の微分形に関する記述である 文中の に当てはまるものを解答群の中から選びなさい 図のように, 直交座標系において電界の z 軸成分が零となるような電界について, y 平面の二次元で電位や電界を考える ここで,4 点 (h,0),(0,h), (- h,0),(0,-h) の電位がそれぞれ
PowerPoint プレゼンテーション
 回転型クレーン / 倒立振子の制御 回転型クレーンの制御 状態方程式 コントローラ設計 ( 極配置法 ) コントローラ設計 ( 最適レギュレータ ) 回転型倒立振子の制御 状態方程式 コントローラ設計 コントローラの形式 : 状態フィードバック P-D コントローラ アームの P-D 振子の P-D 目標値 状態フィードバック制御 回転型クレーン コントローラ で 状態フィードバック制御 回転型クレーン
回転型クレーン / 倒立振子の制御 回転型クレーンの制御 状態方程式 コントローラ設計 ( 極配置法 ) コントローラ設計 ( 最適レギュレータ ) 回転型倒立振子の制御 状態方程式 コントローラ設計 コントローラの形式 : 状態フィードバック P-D コントローラ アームの P-D 振子の P-D 目標値 状態フィードバック制御 回転型クレーン コントローラ で 状態フィードバック制御 回転型クレーン
ベクトル公式.rtf
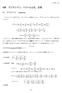 6 章ラプラシアン, ベクトル公式, 定理 6.1 ラプラシアン Laplacian φ はベクトル量である. そこでさらに発散をとると, φ はどういう形になるであろうか? φ = a + a + a φ a + a φ + a φ = φ + φ + φ = 2 φ + 2 φ 2 + 2 φ 2 2 φ = 2 φ 2 + 2 φ 2 + 2 φ 2 = 2 φ したがって,2 階の偏微分演算となる.
6 章ラプラシアン, ベクトル公式, 定理 6.1 ラプラシアン Laplacian φ はベクトル量である. そこでさらに発散をとると, φ はどういう形になるであろうか? φ = a + a + a φ a + a φ + a φ = φ + φ + φ = 2 φ + 2 φ 2 + 2 φ 2 2 φ = 2 φ 2 + 2 φ 2 + 2 φ 2 = 2 φ したがって,2 階の偏微分演算となる.
2016年度 筑波大・理系数学
 06 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ k を実数とする y 平面の曲線 C : y とC : y- + k+ -k が異なる共 有点 P, Q をもつとする ただし点 P, Q の 座標は正であるとする また, 原点を O とする () k のとりうる値の範囲を求めよ () k が () の範囲を動くとき, OPQ の重心 G の軌跡を求めよ () OPQ の面積を S とするとき,
06 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ k を実数とする y 平面の曲線 C : y とC : y- + k+ -k が異なる共 有点 P, Q をもつとする ただし点 P, Q の 座標は正であるとする また, 原点を O とする () k のとりうる値の範囲を求めよ () k が () の範囲を動くとき, OPQ の重心 G の軌跡を求めよ () OPQ の面積を S とするとき,
フィードバック ~ 様々な電子回路の性質 ~ 実験 (1) 目的実験 (1) では 非反転増幅器の増幅率や位相差が 回路を構成する抵抗値や入力信号の周波数によってどのように変わるのかを調べる 実験方法 図 1 のような自由振動回路を組み オペアンプの + 入力端子を接地したときの出力電圧 が 0 と
 フィードバック ~ 様々な電子回路の性質 ~ 実験 (1) 目的実験 (1) では 非反転増幅器の増幅率や位相差が 回路を構成する抵抗値や入力信号の周波数によってどのように変わるのかを調べる 実験方法 図 1 のような自由振動回路を組み オペアンプの + 入力端子を接地したときの出力電圧 が 0 となるように半固定抵抗器を調整する ( ゼロ点調整のため ) 図 1 非反転増幅器 2010 年度版物理工学実験法
フィードバック ~ 様々な電子回路の性質 ~ 実験 (1) 目的実験 (1) では 非反転増幅器の増幅率や位相差が 回路を構成する抵抗値や入力信号の周波数によってどのように変わるのかを調べる 実験方法 図 1 のような自由振動回路を組み オペアンプの + 入力端子を接地したときの出力電圧 が 0 となるように半固定抵抗器を調整する ( ゼロ点調整のため ) 図 1 非反転増幅器 2010 年度版物理工学実験法
Microsoft PowerPoint - DigitalMedia2_3b.pptx
 Contents デジタルメディア処理 2 の概要 フーリエ級数展開と 離散とその性質 周波数フィルタリング 担当 : 井尻敬 とは ( ) FourierSound.py とは ( ) FourierSound.py 横軸が時間の関数を 横軸が周波数の関数に変換する 法 声周波数 周波数 ( 係数番号 ) 後の関数は元信号に含まれる正弦波の量を す 中央に近いほど低周波, 外ほどが 周波 中央 (
Contents デジタルメディア処理 2 の概要 フーリエ級数展開と 離散とその性質 周波数フィルタリング 担当 : 井尻敬 とは ( ) FourierSound.py とは ( ) FourierSound.py 横軸が時間の関数を 横軸が周波数の関数に変換する 法 声周波数 周波数 ( 係数番号 ) 後の関数は元信号に含まれる正弦波の量を す 中央に近いほど低周波, 外ほどが 周波 中央 (
スライド 1
 暫定版修正 加筆の可能性あり ( 付録 ) 電磁波 ( 光 ) の角運動量. 復習 : 電磁波 ( 光 ) のエネルギー. 運動量 角運動量 ( 実空間 ) 3. 軌道 スピン角運動量 4. 円偏光状態 5. 螺旋状態 付録 8 のアプローチ. 本付録では電磁波 ( 光 ) の軌道 スピン角運動量ついて古典的に扱う. スピン角運動量は直線偏光状態では零 円偏光状態では非零 右 左回りで大きさは同じ
暫定版修正 加筆の可能性あり ( 付録 ) 電磁波 ( 光 ) の角運動量. 復習 : 電磁波 ( 光 ) のエネルギー. 運動量 角運動量 ( 実空間 ) 3. 軌道 スピン角運動量 4. 円偏光状態 5. 螺旋状態 付録 8 のアプローチ. 本付録では電磁波 ( 光 ) の軌道 スピン角運動量ついて古典的に扱う. スピン角運動量は直線偏光状態では零 円偏光状態では非零 右 左回りで大きさは同じ
2011年度 筑波大・理系数学
 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ O を原点とするy 平面において, 直線 y= の を満たす部分をC とする () C 上に点 A( t, ) をとるとき, 線分 OA の垂直二等分線の方程式を求めよ () 点 A が C 全体を動くとき, 線分 OA の垂直二等分線が通過する範囲を求め, それ を図示せよ -- 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ
0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ O を原点とするy 平面において, 直線 y= の を満たす部分をC とする () C 上に点 A( t, ) をとるとき, 線分 OA の垂直二等分線の方程式を求めよ () 点 A が C 全体を動くとき, 線分 OA の垂直二等分線が通過する範囲を求め, それ を図示せよ -- 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ
航空機の運動方程式
 可制御性 可観測性. 可制御性システムの状態を, 適切な操作によって, 有限時間内に, 任意の状態から別の任意の状態に移動させることができるか否かという特性を可制御性という. 可制御性を有するシステムに対し, システムは可制御である, 可制御なシステム という言い方をする. 状態方程式, 出力方程式が以下で表されるn 次元 m 入力 r 出力線形時不変システム x Ax u y x Du () に対し,
可制御性 可観測性. 可制御性システムの状態を, 適切な操作によって, 有限時間内に, 任意の状態から別の任意の状態に移動させることができるか否かという特性を可制御性という. 可制御性を有するシステムに対し, システムは可制御である, 可制御なシステム という言い方をする. 状態方程式, 出力方程式が以下で表されるn 次元 m 入力 r 出力線形時不変システム x Ax u y x Du () に対し,
<4D F736F F D FCD B90DB93AE96402E646F63>
 7 章摂動法講義のメモ 式が複雑なので 黒板を何度も修正したし 間違ったことも書いたので メモを置きます 摂動論の式の導出無摂動系 先ず 厳密に解けている Schrödiger 方程式を考える,,,3,... 3,,,3,... は状態を区別する整数であり 状態 はエネルギー順に並んでいる 即ち は基底状態 は励起状態である { m } は相互に規格直交条件が成立する k m k mdx km k
7 章摂動法講義のメモ 式が複雑なので 黒板を何度も修正したし 間違ったことも書いたので メモを置きます 摂動論の式の導出無摂動系 先ず 厳密に解けている Schrödiger 方程式を考える,,,3,... 3,,,3,... は状態を区別する整数であり 状態 はエネルギー順に並んでいる 即ち は基底状態 は励起状態である { m } は相互に規格直交条件が成立する k m k mdx km k
Microsoft PowerPoint - 物情数学C(2012)(フーリエ前半)_up
 年度物理情報工学科 年生秋学期 物理情報数学 C フーリエ解析 (Fourier lysis) 年 月 5 日 フーリエ ( フランス ) (768~83: ナポレオンの時代 ) 歳で Ecole Polyechique ( フランス国立理工科大学 ) の教授 ナポレオンのエジプト遠征に従軍 (798) 87: 任意の関数は三角関数によって級数展開できる という フーリエ級数 の概念を提唱 ( 論文を提出
年度物理情報工学科 年生秋学期 物理情報数学 C フーリエ解析 (Fourier lysis) 年 月 5 日 フーリエ ( フランス ) (768~83: ナポレオンの時代 ) 歳で Ecole Polyechique ( フランス国立理工科大学 ) の教授 ナポレオンのエジプト遠征に従軍 (798) 87: 任意の関数は三角関数によって級数展開できる という フーリエ級数 の概念を提唱 ( 論文を提出
Microsoft Word - 補論3.2
 補論 3. 多変量 GARC モデル 07//6 新谷元嗣 藪友良 対数尤度関数 3 章 7 節では 変量の対数尤度を求めた ここでは多変量の場合 とくに 変量について対数尤度を求める 誤差項 は平均 0 で 次元の正規分布に従うとする 単純化のため 分散と共分散は時間を通じて一定としよう ( この仮定は後で変更される ) したがって ij から添え字 を除くことができる このとき と の尤度関数は
補論 3. 多変量 GARC モデル 07//6 新谷元嗣 藪友良 対数尤度関数 3 章 7 節では 変量の対数尤度を求めた ここでは多変量の場合 とくに 変量について対数尤度を求める 誤差項 は平均 0 で 次元の正規分布に従うとする 単純化のため 分散と共分散は時間を通じて一定としよう ( この仮定は後で変更される ) したがって ij から添え字 を除くことができる このとき と の尤度関数は
Microsoft Word - t30_西_修正__ doc
 反応速度と化学平衡 金沢工業大学基礎教育部西誠 ねらい 化学反応とは分子を構成している原子が組み換り 新しい分子構造を持つことといえます この化学反応がどのように起こるのか どのような速さでどの程度の分子が組み換るのかは 反応の種類や 濃度 温度などの条件で決まってきます そして このような反応の進行方向や速度を正確に予測するために いろいろな数学 物理的な考え方を取り入れて化学反応の理論体系が作られています
反応速度と化学平衡 金沢工業大学基礎教育部西誠 ねらい 化学反応とは分子を構成している原子が組み換り 新しい分子構造を持つことといえます この化学反応がどのように起こるのか どのような速さでどの程度の分子が組み換るのかは 反応の種類や 濃度 温度などの条件で決まってきます そして このような反応の進行方向や速度を正確に予測するために いろいろな数学 物理的な考え方を取り入れて化学反応の理論体系が作られています
学習指導要領
 (1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 自然数 整数 有理数 無理数の包含関係など 実数 の構成を理解する ( 例 ) 次の空欄に適当な言葉をいれて, 数の集合を表しなさい ア イ 無理数 整数 ウ 無理数の加法及び減法 乗法公式などを利用した計 算ができる また 分母だけが二項である無理数の 分母の有理化ができる ( 例 1)
(1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 自然数 整数 有理数 無理数の包含関係など 実数 の構成を理解する ( 例 ) 次の空欄に適当な言葉をいれて, 数の集合を表しなさい ア イ 無理数 整数 ウ 無理数の加法及び減法 乗法公式などを利用した計 算ができる また 分母だけが二項である無理数の 分母の有理化ができる ( 例 1)
