RSA-lecture-2015.pptx
|
|
|
- たつぞう いなくら
- 5 years ago
- Views:
Transcription
1 公開鍵暗号 RSA について 3 年授業 情報ネットワーク 授業スライドより抜粋 豊橋技術科学大学情報 知能工学系梅村恭司 Copyright 2014 Kyoji Umemura ( 出典を明らかにしていただければ 自由に授業 / セミナー等で使っていただいて結構です
2 これからのスライドは下記を参考 に,Java でプログラミングしながら, 作成しました 岡本栄司著, 暗号理論入門 [ 第 2 版 ] 共立出版株式会社
3 RSA 暗号とネットワーク 暗号化と復号の鍵を別にして, かつ, 暗号化の鍵を公開できると便利 計算量という壁を使って, 上記を実現したものの代表が RSA 暗号 これを理解するには, 整数論の知識が必要 : ある整数で割った余りで等しい整数の体系 を扱う
4 Java の BigInteger クラス import java.math.biginteger; x = new BigInteger(" "); System.out.println(x.toString());
5 剰余系 17 = 22 (mod 5) 数を 5 で割ったあまりで比較すれば,17 と 22 は同じ (mod 5) は比較の方法を記述 あまりをとる演算子ではない
6 BigPower のデモ (mod n) で, aのx 乗を計算するプログラム % java BigPower
7 RSA暗号の例 大きな素数2つ(秘密 からnと鍵を二つ生 成する e: encode_key, d: decode_key n= (公開, e=20003 公開, d= 秘密 ベキ乗演算で暗号化 c=me(mod n) ベキ乗演算で復号 m'=cd(mod n) つまりm'=cd=med (mod n) このとき m'=m (mod n) が成立する デモ
8 RSA:n = 10, e = 3, d = 3 暗号化 ( 板書 ) 1 3 = 1 (mod 10) 2 3 = 8 (mod 10) 3 3 = 7 (mod 10) 4 3 = 4 (mod 10) 5 3 = 5 (mod 10) 6 3 = 6 (mod 10) 7 3 = 3 (mod 10) 8 3 = 2 (mod 10) 9 3 = 9 (mod 10)
9 RSA:n = 10, e = 3, d = 3 復号(板書) 13 = 1 (mod 10) 23 = 8 (mod 10) 33 = 7 (mod 10) 43 = 4 (mod 10) 53 = 5 (mod 10) 63 = 6 (mod 10) 73 = 3 (mod 10) 83 = 2 (mod 10) 93 = 9 (mod 10) 13 = 1 (mod 10) 83 = 2 (mod 10) 73 = 3 (mod 10) 43 = 4 (mod 10) 53 = 5 (mod 10) 63 = 6 (mod 10) 33 = 7 (mod 10) 23 = 8 (mod 10) 93 = 9 (mod 10)
10 素朴な疑問 ( 公開 ), 20003( 公開 ), ( 秘密 ) ベキ乗演算で暗号化 ベキ乗演算で復号 どうして 通信できるのか 説明には有限体の知識が必要
11 剰余系 12 = 22 (mod 10) 数を 10 で割ったあまりで比較すれば,12 と 22 は同じ (mod 10) は比較の方法を記述したもの 等しい という関係を修飾している 11
12 a = b (mod n) n で割った余りを問題にするならば,a と b は等しい 直感的にわからなかったら,n=10 とする これは, 整数の一番下の桁で整数を比較することになる
13 a = b (mod n) n で割った余りを問題にするならば,a と b は等しい a; a = a(mod n) 反射律 a; b; a = b(mod n) b = a (mod n) 対称律 a; b; c; a=b(mod n) かつ b=c(mod n) a=c (mod n) 推移律
14 a = b (mod n) n で割った余りを問題にするならば,a と b は等しい 整数は,n 個のグループに分類されるが, そのグループのなまえに,0 から n-1 までの整数を使う これは, グループの名前であることに注意する必要がある
15 加算 a=b (mod n) ならば, z 整数, a+z = b+z (mod n) 直感的にわからなかったら,n=10 とする これは, 整数の一番下の桁で整数を比較することになる グループの名前を求めるには, 通常の加算をして, 下の桁だけを使うことでよい
16 減算 a=b (mod n) ならば, z 整数, a-z = b-z (mod n) 直感的にわからなかったら,n=10 とする これは, 整数の一番下の桁で整数を比較することになる グループの名前を求めるには, 負にならないように 10 を加算することをして, 一番したの桁を使うことでよい
17 乗算 a=b (mod n) ならば, z 整数, z a = z b (mod n) 直感的にわからなかったら,n=10 とする これは, 整数の一番下の桁で整数を比較することになる グループの名前を求めるには, 通常の乗算をして, 一番下の桁だけを使うことでよい
18 逆数 (mod 10) 3 7 = 1 (mod 10) よって,3-1 =7 (mod 10) 注意 逆数は通常の意味と大きく異なる 演習, 下記のxをもとめてみよう x = 1-1 (mod 10) x = 7-1 (mod 10) x = 9-1 (mod 10)
19 逆数 (mod 10) 1 = 1-1 (mod 10) 3 = 7-1 (mod 10) 9 = 9-1 (mod 10) 注意, 0, 及び,10と互いに素でない数, x = 0-1 (mod 10) x = 2-1 (mod 10) x = 5-1 (mod 10) を満たすxは存在しない
20 逆数 : (mod 5) 3 2 = 1 (mod 5) よって,3-1 =2 (mod 5) 注意 逆数は通常の意味と大きく異なる 演習, 下記のxをもとめてみよう x = 1-1 (mod 5) x = 2-1 (mod 5) x = 4-1 (mod 5)
21 逆数 (mod 5) 1 = 1-1 (mod 5) 3 = 2-1 (mod 5) 2 = 3-1 (mod 5) 4 = 4-1 (mod 5) どのように求めた? ( 順番に条件を満たすか検査したと思う ) 注意,x = 0-1 (mod 5) を満たす x は存在しない
22 逆数 (mod 素数 p) n=1, 2,..., p-1について, x = n -1 (mod p) となる,xがある 注意,n 0である x = 0-1 (mod p) を満たすxは存在しない
23 割り算 (mod 素数 p) n=1, 2,..., p-1 について, x = n -1 (mod p) となる,x がある y/n は,y n -1 と考える ( 掛け算の逆演算 ) すると,0 以外の数で割り算した結果が存在する ( 整数はみたさないが, 有理数や実数が満たす性質 : 集合と加算と乗算が 体 である )
24 整数をあまりでグループ分けする グループに名前をつける 5で割ったあまりが0の整数 を "0" と書くことにする "1", "2", "3", "4" も同様, つまり, "1" は,{ 1, 6, 11, 16,... } のグループのこと, グループは5つある 演算は表にできる
25 グループでの足し算と掛け算表
26 負の数 と 逆数 この演算表では, 2 は 3 と考えると考えることができる 2 1 は, 3 と考えることができる
27 有限体 体 とは 数の集合と演算の組合わさったもののである, ある性質をもつものの名前である 体 の重要な性質の一つは, ある数の乗算に逆演算となる数が存在する数が 0 以外には存在することである 逆演算となる数があることが復号で役立つ 有限の集合での 乗算 の体系に 逆数 が存在するのは, 面白い性質 27
28 RSA 暗号の例 ( 再度 ) 大きな素数 2 つ ( 秘密 ) から n と鍵を二つ生成する e: encode_key, d: decode_key n= ( 公開 ), e=20003( 公開 ), d= ( 秘密 ) ベキ乗演算で暗号化 c=m e (mod n) ベキ乗演算で復号 m'=c d (mod n) つまり m'=c d =m ed (mod n) このとき, m'=m (mod n) が成立する 28
29 フェルマーの小定理 pが素数のとき ap-1=1 (mod p) ただし a=1, 2,... p-1 どのような定理か aがどれであっても aをp 1回掛ける ベキ乗す る と1になることが運命付けられている p=5のときを計算してみよう 29
30 p(=5) のときの フェルマーの小定理の確認 p(=5) が素数のとき,a p-1 =1 (mod p) ただし, a=1, 2,... p-1 確認してみる = =4 4= =9 9= =16 16=256 1 注意 :0のときは成立しない =0なので 0 p-1 1 (mod p) 30
31 観測 :p=5 では na の集合と a の集合に 1 対 1 対応が存在する p(=5) は素数 a と n は,1 から p-1 まで整数とする S は 1 から p-1 までの整数の集合とする 任意の a に対し n と an に (mod p) での 1 対 1 対応が存在する
32 観測 :p=5では, 0でないaには, 逆数が存在存在する p(=5) は素数 aは,1からp-1まで整数とする Sは1からp-1までの整数の集合とする 任意のaに対して, an=1 (mod p) となる nが存在する
33 フェルマーの小定理の証明の p は素数とする 準備 (1) a 0 (mod p), x 0 (mod p) である整数 a, x について ax 0 (mod p) つまり a と x が p の倍数でないとき ax も p の倍数でない ax = 0 (mod p) とすると 1 以下 p 1 以下の整数 n があって ax = np 素因数分解するとと a か x が p の倍数であることになり 仮定と矛盾する
34 フェルマーの小定理の証明の準備 (2) pは素数とする aは,1 以上 p-1 以下の整数とする x yは1 以上 p-1 以下の異なる整数とする すると ax ay (mod p) つまり 0でないx,yで異なるx, y をa 倍した結果をpで割った余ま りは異なるということを意味している
35 フェルマーの小定理の証明の準備 (2) pは素数とする aは,1 以上 p-1 以下の整数とする x yは1 以上 p-1 以下の異なる整数とする すると ax ay (mod p) 証明 1. 仮定より (x-y) 0 (mod p), 2. 仮定より a 0 (mod p) 3. よって a(x-y) 0 (mod p) であり ax ay (mod p) となる
36 フェルマーの小定理の証明の p は素数とする 準備 (3) a は,1 から p-1 まで整数とする S は 1 から p-1 までの整数の集合とする T(a)={m n S, m S, m=na (mod p)} なる集合 T(a) を考える すると T(a) = S = p-1 証明 : n ごとに対応する m は異なるので,T(a) の要素の個数は S と同じ p-1 になる
37 フェルマーの小定理の証明の 準備 (4) pは素数とする aは,1からp-1まで整数とする Sは1からp-1までの整数の集合とする T(a)={m n S, m S, m=na (mod p) } とする 任意のaについて,T(a)=S 証明 : 明らかにT(a) Sであり, 一方 T(a) = S
38 フェルマーの小定理の証明の 準備 (5) pを素数とする a, nは,1からp-1まで整数とする S は 1 から p-1 までの整数の集合とする 任意のaに対しあるnが存在して1 = na (mod p) 証明 T(a)={m n S, m S, m=na (mod p) } とする 1 S, より1 T(a), よって, n, 1=na (mod p)
39 フェルマーの定理 ( 実演 ) pが素数のとき a p-1 =1 (mod p) aは 1からp-1まで, どれでも成立する (p= で実験) 39
40 a の集合と anの集合が等しい 0を除いて全部掛け合わせてみる 掛け合わせる対象の集合をSとする S={1,2,..., p-1}
41 n と a n が S 上で 1 対 1 に対応している 全部掛け合わせる n = an(mod p) n T (a) n S n = a p 1 n(mod p) n T (a) n S n = a p 1 n(mod p) n S T(a)=S={1,2,..., p-1} n S n S pが素数なので b n =1 (mod p) となるbが存在するので, それを右から掛けると, 1 = a p 1 (mod p)
42 フェルマーの小定理の系 pが素数 λがp-1の倍数のとき aλ 1=a (mod p) 注意 aが任意の整数で成立 aの制限がないので 使いやすい また 記憶しやすい 42
43 ベキ乗の計算 p の 5 乗 (mod 5) p(=5) が素数のとき,a p =a (mod p) = = =4 4 2= =9 9 3=81 3= = =256 4= aが0のときも成立する 9 乗,13 乗もおなじようにもとにもどる 43
44 フェルマーの小定理の系 ( ) の 証明 pが素数 λがp-1の倍数のとき,a λ+1 =a (mod p) 証明 : ある整数 kをaをpで割ったときの商とする (1)a=kp のとき, 明らかに a λ+1 =k λ+1 p λ+1 =0 (mod p) またa=0 (mod p) よって,a λ+1 =a (mod p) (2)a=kp+b ただし, b {1,2,..., p-1} のとき フェルマの小定理より, b (p-1) =1(mod p) なので, a λ+1 =b λ+1 =b K(p 1)+1 =(b (p 1) ) K b=1 K b (mod p) 一方,a=b (mod p) よって, a λ+1 =a (mod p) 44
45 中国人の剰余定理 pとqが互いに素 最大公約数が1)とする またn=pqとする ある数x, yが x=y (mod p)かつ x=y (mod q)で あれば x=y (mod n) q(=5) p(=2) n(=10) ある数の5で割ったあまりと 奇数 偶数がわかれば 1桁目がわかる
46 中国人の剰余定理 pとqが互いに素でないときは n=pq として, ある数 x, y が x=y (mod p) かつ,x=y (mod q) であっても x=y (mod n) とはいえない q(=4) p(=2) 0 0, 4-2, , 5-3, 7 n(=8)
47 中国人の剰余定理 ( 証明の準備 ) p と q が互いに素 ( 最大公倍数が 1) とする また n=pq とする ある数 z が z=0 (mod p) かつ z=0 (mod q) であれば,z=0 (mod n) である 証明 z は p と q の公倍数である p と q は互いに素なので,p と q の最小公倍数は pq つまり n である よって, ある整数 k に対し z=kn と表現できるので, z=0(mod n) となる
48 中国人の剰余定理 / 証明 pとqが互いに素とする またn=pqとする ある数 x, y が x=y (mod p) かつ,x=y (mod q) とする (x-y) =0 (mod p), かつ (x-y) = 0 (mod q) である よって, (x-y) = 0 (mod n) となる したがって, x = y (mod n)
49 二つの素数に関わる性質 pとqが素数のとき λをp-1とq-1の最小公倍 数とすると 任意の整数K aについてakλ+1=a (mod pq) 49
50 p(=2) と q(=5) が素数のとき λ を p-1 と q-1 の倍数とすると, a λ+1 =a (mod pq) 0 3 = 0 (mod 10) 1 3 = 1 (mod 10) 2 3 = 8 (mod 10) 3 3 = 7 (mod 10) 4 3 = 4 (mod 10) 5 3 = 5 (mod 10) 6 3 = 6 (mod 10) 7 3 = 3 (mod 10) 8 3 = 2 (mod 10) 9 3 = 9 (mod 10) 0 4 = 0 (mod 10) 1 4 = 1 (mod 10) 2 4 = 6 (mod 10) 3 4 = 1 (mod 10) 4 4 = 6 (mod 10) 5 4 = 5 (mod 10) 6 4 = 6 (mod 10) 7 4 = 1 (mod 10) 8 4 = 6 (mod 10) 9 4 = 1 (mod 10) 0 5 = 0 (mod 10) 1 5 = 1 (mod 10) 2 5 = 2 (mod 10) 3 5 = 3 (mod 10) 4 5 = 4(mod 10) 5 5 = 5 (mod 10) 6 5 = 6 (mod 10) 7 5 = 7 (mod 10) 8 5 = 8 (mod 10) 9 5 = 9 (mod 10)
51 二つの素数に関わる性質の証明 p と q が素数のとき λ を p-1 と q-1 の最小公倍数とすると, 任意の整数 K について a Kλ+1 =a (mod pq) 証明 :b=a Kλ+1 とする Kλ は p-1 の倍数であるので ( ) より b=a Kλ+1 =a (mod p) Kλ は q-1 の倍数でもあるので, b=a Kλ+1 =a (mod q) pとqは互いに素であるので, 中国人の剰余定理に 51 より, b=a Kλ+1 =a (mod pq)
52 RSA 暗号 フェルマーの定理 ユークリッドの互除法と拡張これらをつかって, 2つの大きな素数から 上手にn, e, dを生成する n= ( 公開 ), e=20003( 公開 ), d= ( 秘密 ) e: encode, d:decode 52
53 RSA:鍵の生成 大きな素数p, qを決める λをp-1とq-1の最小公倍数とする eをλと互いに素な数として決める ed = 1(mod λ)となる dを求める n(= pq)とeを公開する (他は秘密とする これから 具体的に計算してみる
54 RSA: 鍵の生成 素数 p, q を決める : p=2, q=5
55 RSA: 鍵の生成 素数 p, q を決める : p=2, q=5 λ を p-1 と q-1 の最小公倍数 (= 4 ) とする.
56 RSA: 鍵の生成 素数 p, qを決める : p=2, q=5 λをp-1とq-1の最小公倍数 (=4) とする. eをλと互いに素な数 : たとえば3とする. ( 互いに素 : 最大公約数が 1 であること )
57 RSA: 鍵の生成 素数 p, qを決める : p=2, q=5 λをp-1とq-1の最小公倍数 (=4) とする. eをλ(=4) と互いに素な数 : たとえば 3とする. ( 互いに素 : 最大公約数が1であること ) ed(mod λ)=1となるdをもとめ,d:3とする. 3 3 =1 (mod 4) 注 : ここでは順番にテストしてもとめるが, 効率のよい方法がある
58 RSA:鍵の生成 素数p, qを決める p=2, q=5 λをp-1とq-1の最小公倍数 (4)とする eをλと互いに素な数: 3とする ed(mod λ)=1となるdをもとめ d:3とする 1= 3 3 (mod 4) n = 10, e = 3, d = 3 (注 e: encode, d: decode
59 RSA:n = 10, e = 3, d = 3 暗号化 1 3 = 1 (mod 10) 2 3 = 8 (mod 10) 3 3 = 7 (mod 10) 4 3 = 4 (mod 10) 5 3 = 5 (mod 10) 6 3 = 6 (mod 10) 7 3 = 3 (mod 10) 8 3 = 2 (mod 10) 9 3 = 9 (mod 10)
60 RSA:n = 10, e = 3, d = 3 復号 13 = 1 (mod 10) 23 = 8 (mod 10) 33 = 7 (mod 10) 43 = 4 (mod 10) 53 = 5 (mod 10) 63 = 6 (mod 10) 73 = 3 (mod 10) 83 = 2 (mod 10) 93 = 9 (mod 10) 13 = 1 (mod 10) 83 = 2 (mod 10) 73 = 3 (mod 10) 43 = 4 (mod 10) 53 = 5 (mod 10) 63 = 6 (mod 10) 33 = 7 (mod 10) 23 = 8 (mod 10) 93 = 9 (mod 10)
61 RSA: 鍵の生成 大きな素数 p, q を決める : p=100003, q=100019
62 RSA: 鍵の生成 大きな素数 p, q を決める : p=100003, q= λ を p-1 と q-1 の公倍数 ( ) とする.
63 RSA: 鍵の生成 大きな素数 p, qを決める : p=100003, q= λをp-1とq-1の公倍数 ( ) とする. eをλと互いに素な数 : 20003とする. ( 互いに素 : 最大公約数が 1 であること )
64 RSA: 鍵の生成 大きな素数 p, q を決める : p=100003, q= λ を p-1 と q-1 の公倍数 ( ) とする. e を λ と互いに素な数 : とする. ed=1(mod λ) となる d をもとめ,d: とする. 1= (mod ) ( 注 :e と λ から d を求める方法は, この例のように数が大きいと工夫する必要があることがわかる その方法は後述する )
65 RSA: 鍵の生成 ( 復号の説明の準備 ) 大きな素数 p, q を決める : 秘密 λ を p-1 と q-1 の最小公倍数とする. [ ある a,b が存在して,λ=a(p-1), λ=b(q-1)]...1 e を λ と互いに素な数として決める このとき ed = 1 (mod λ) なる d がもとまる [ ある K が存在して,ed= Kλ+1 ]...2 n(= pq) と e を公開する
66 RSA:鍵の性質 任意の整数m, と任意の整数Kについて mkλ 1=m (mod n) 証明 pとqが素数であり n pqであり λがp-1とq-1の最小公倍数 ① なので を 用いると 任意のKについて mkλ 1=m (mod n)... ③
67 RSA: 送信 受信 c=m e (mod n) で暗号化し c を送る... 4 m'=c d (mod n) で復号し m' を得る... 5
68 RSA暗号:通信ができるわけ m' =cd(mod n) =med(mod n) =m(kλ+1)(mod n) = m (mod n) ⑤ ④ ② ③
69 RSA: 鍵の生成の難しいところ λは大きな数 ( 素数ではない ) λと互いに素なeを求める ed = 1 (mod λ) を満たすdを求める 例 :1= (mod ) λは大きな数そのような数 dは存在するのか eからdを どうやってもとめればよいのか λが大きいと, 順番にdを探すことは不可能
70 RSA: 鍵の生成の難しいところ 逆数を求めるところ ed = 1 (mod λ) を満たす d を求める 例 :1= d (mod ) となる d を求める つまり d を で割った商を -β として, そのときのあまりが 1 になるような d を求める 1=20003 d β を満たす, 整数 d と整数 β を求めたい 整数 という条件は難しい条件である
71 20003 逆数を求める方針 目標 : 整数 d と整数 β で, 1=20003 d β としたい γ(d, β) =20003 d β として, (d, γ, β) の三次元の格子点 ( 座標が整数の点 ) を対象に演算をして, 格子点であることを保証しつつ,γ =1 となる点を求める (1, 20003, 0) と (0, ,1) からスタートする
72 ユークリッドの互除法 お互いに割り算をして, 余りをとっていく 最大公約数を求めることができる 例を板書 ( 次のスライド )
73 u=7, v=5 7, 5 -> 商は1 あまりは7 1 5 = 2 5, 2 -> 商は2 あまりは5 2 2 = 1 2, 1 -> 商は2 あまりは2-2 2 = 0なので その前の数字 1 GCD(7, 5)=1
74 ユークリッド互除法の 操作の準備 d と λ で定まる平面で,(α, αd + βλ, β) の平面は原点を通るので 平面上の 2 点の位置ベクトル p, q に対し 任意の実数 t について p-tq で表される点も 同じ平面にある
75 ユークリッド互除法の 操作の準備 要素が整数の 2 つのベクトル p=(p x, p y, p z ), q=(q x,q y,q z ) があり これが (α, αd + βλ, β) の平面 2 点の位置ベクトルであるとする いま t を p y を q y で割ったときの整数の商であるとすると r = p t q で定まるベクトル r =(r x, r y, r z ) とする r x, r y, r z は整数 r y が 0 でないとき GCD(p y, q y )=GCD(q y, r y ) r は同じ平面上にある点の位置ベクトル
76 ユークリッド互除法の拡張 d と λ から定まる平面で, (α, αd + βλ, β) の関係のある 3 次元空間の平面において,(1, d, 0) と (0,λ,1) からユークリッドの互除法を実行する ( 板書 ) ユークリッドの互除法と同じ動作をして α,β を更新していく 二つ整数 u, v に対し, ある整数 α,β が存在して αd + βλ = GCD(d, λ) となることが示せる
77 u=7, v=5, (α, 7α+5β, β) (1, 7, 0), (0, 5, 1) -> 7 5は1 あまりがある次の点は (1, 2, -1)=(1, 7, 0) 1 (0, 5, 1) (0, 5, 1), (1, 2, -1) -> 5 2は2 あまりがある 次の点は (-2, 1, 3) = (0, 5, 1) 2 (1, 2, -1) (1, 2, -1), (-2, 1, 3) -> 割り切れる 目的地 (-2, 1, 3) に到達 1=GCD(7, 5), (-2) = 1
78 (α, 7α+5β, β) の平面内 α,βは整数 (1, 7, 0), (0, 5, 1) より 操作を開始 (1, 7, 0), (0, 5, 1) -> (1, 2, -1) (0, 5, 1), (1, 2, -1) -> (-2, 1, 3) (-2, 1, 3) は目的地, なぜなら,1 = GCD(7, 5) このとき, 7 (-2) +5 (3) = 1 つまり, 7 (-2) = 1 (mod 5)
79 (α, 3α+4β, β) の平面内 α,βは整数 (0, 4, 1), (1, 3, 0) より 操作を開始 (0, 4, 1), (1, 3, 0) -> (-1, 1, 1) (-1, 1, 1) は目的地, なぜなら,1 = GCD(3, 4) このとき, 3 (-1) +1 (4) = 1 つまり, 3 (-1) = 1 (mod 4), -1 = 3 (mod 4)
80 RSA: 鍵の生成 大きな素数 p, qを決める : p=100003, q= λをp-1とq-1の公倍数 ( ) とする. eをλと互いに素な数 : 20003とする. ed(mod λ)=1となるdをもとめ,d: とする. 1= (mod ) n(= pq= ) と e(=20003) を公開する
81 RSA: まとめ ( 転記 ) 鍵の生成 大きな素数 p, q を決める : 秘密 λ を p-1 と q-1 の最小公倍数とする. e を λ と互いに素な数として決める このとき ed =1(mod λ) なる d がもとまる n(= pq) と e を公開する 送信 :c=m e (mod n) で暗号化し c を送る 受信 :m'=c d (mod n) で復号し m' を得る
2015-2018年度 2次数学セレクション(整数と数列)解答解説
 015 次数学セレクション問題 1 [ 千葉大 文 ] k, m, n を自然数とする 以下の問いに答えよ (1) k を 7 で割った余りが 4 であるとする このとき, k を 3 で割った余りは であることを示せ () 4m+ 5nが 3 で割り切れるとする このとき, mn を 7 で割った余りは 4 ではないことを示せ -1- 015 次数学セレクション問題 [ 九州大 理 ] 以下の問いに答えよ
015 次数学セレクション問題 1 [ 千葉大 文 ] k, m, n を自然数とする 以下の問いに答えよ (1) k を 7 で割った余りが 4 であるとする このとき, k を 3 で割った余りは であることを示せ () 4m+ 5nが 3 で割り切れるとする このとき, mn を 7 で割った余りは 4 ではないことを示せ -1- 015 次数学セレクション問題 [ 九州大 理 ] 以下の問いに答えよ
チェビシェフ多項式の2変数への拡張と公開鍵暗号(ElGamal暗号)への応用
 チェビシェフ多項式の 変数への拡張と公開鍵暗号 Ell 暗号 への応用 Ⅰ. チェビシェフ Chbhv Chbhv の多項式 より であるから よって ここで とおくと coθ iθ coθ iθ iθ coθcoθ 4 4 iθ iθ iθ iθ iθ i θ i θ i θ i θ co θ co θ} co θ coθcoθ co θ coθ coθ したがって が成り立つ この漸化式と であることより
チェビシェフ多項式の 変数への拡張と公開鍵暗号 Ell 暗号 への応用 Ⅰ. チェビシェフ Chbhv Chbhv の多項式 より であるから よって ここで とおくと coθ iθ coθ iθ iθ coθcoθ 4 4 iθ iθ iθ iθ iθ i θ i θ i θ i θ co θ co θ} co θ coθcoθ co θ coθ coθ したがって が成り立つ この漸化式と であることより
2015年度 2次数学セレクション(整数と数列)
 05 次数学セレクション問題 [ 千葉大 文 ] k, m, を自然数とする 以下の問いに答えよ () k を 7 で割った余りが 4 であるとする このとき, k を 3 で割った余りは であることを示せ () 4m+ 5が 3 で割り切れるとする このとき, m を 7 で割った余りは 4 ではないことを示せ -- 05 次数学セレクション問題 [ 九州大 理 ] 以下の問いに答えよ () が正の偶数のとき,
05 次数学セレクション問題 [ 千葉大 文 ] k, m, を自然数とする 以下の問いに答えよ () k を 7 で割った余りが 4 であるとする このとき, k を 3 で割った余りは であることを示せ () 4m+ 5が 3 で割り切れるとする このとき, m を 7 で割った余りは 4 ではないことを示せ -- 05 次数学セレクション問題 [ 九州大 理 ] 以下の問いに答えよ () が正の偶数のとき,
æœ•å¤§å–¬ç´—æŁ°,æœ•å°‘å–¬å•“æŁ°,ã…¦ã…¼ã‡¯ã…ªã……ã…›ã†®äº™éŽ¤æ³Ł
 最大公約数, 最小公倍数, ユークリッドの互除法 最大公約数, 最小公倍数とは つ以上の正の整数に共通な約数 ( 公約数 ) のうち最大のものを最大公約数といいます. と 8 の公約数は,,,,6 で, 6 が最大公約数 つ以上の正の整数の共通な倍数 ( 公倍数 ) のうち最小のものを最小公倍数といいます. と の公倍数は, 6,,8,,... で, 6 が最小公倍数 最大公約数, 最小公倍数の求め方
最大公約数, 最小公倍数, ユークリッドの互除法 最大公約数, 最小公倍数とは つ以上の正の整数に共通な約数 ( 公約数 ) のうち最大のものを最大公約数といいます. と 8 の公約数は,,,,6 で, 6 が最大公約数 つ以上の正の整数の共通な倍数 ( 公倍数 ) のうち最小のものを最小公倍数といいます. と の公倍数は, 6,,8,,... で, 6 が最小公倍数 最大公約数, 最小公倍数の求め方
< 中 3 分野例題付き公式集 > (1)2 の倍数の判定法は 1 の位が 0 又は偶数 ( 例題 )1~5 までの 5 つの数字を使って 3 ケタの数をつくるとき 2 の倍数は何通りできるか (2)5 の倍数の判定法は 1 の位が 0 又は 5 ( 例題 )1~9 までの 9 個の数字を使って 3
 () の倍数の判定法は の位が 0 又は偶数 ~ までの つの数字を使って ケタの数をつくるとき の倍数は何通りできるか () の倍数の判定法は の位が 0 又は ~9 までの 9 個の数字を使って ケタの数をつくるとき の倍数は何通りできるか () の倍数の判定法は 下 ケタが 00 又は の倍数 ケタの数 8 が の倍数となるときの 最小の ケタの数は ( 解 ) 一の位の数は の 通り 十の位は一の位の数以外の
() の倍数の判定法は の位が 0 又は偶数 ~ までの つの数字を使って ケタの数をつくるとき の倍数は何通りできるか () の倍数の判定法は の位が 0 又は ~9 までの 9 個の数字を使って ケタの数をつくるとき の倍数は何通りできるか () の倍数の判定法は 下 ケタが 00 又は の倍数 ケタの数 8 が の倍数となるときの 最小の ケタの数は ( 解 ) 一の位の数は の 通り 十の位は一の位の数以外の
æœ•å¤§å–¬ç´—æŁ°,æœ•å°‘å–¬å•“æŁ°,ã…¦ã…¼ã‡¯ã…ªã……ã…›ã†®äº™éŽ¤æ³Ł
 最大公約数, 最小公倍数, ユークリッドの互除法 最大公約数, 最小公倍数とは つ以上の正の整数に共通な約数 ( 公約数 ) のうち最大のものを最大公約数といいます. 1 と 18 の公約数は, 1,,,6 で, 6 が最大公約数 つ以上の正の整数の共通な倍数 ( 公倍数 ) のうち最小のものを最小公倍数といいます. と の公倍数は, 6,1,18,,... で, 6 が最小公倍数 最大公約数, 最小公倍数の求め方
最大公約数, 最小公倍数, ユークリッドの互除法 最大公約数, 最小公倍数とは つ以上の正の整数に共通な約数 ( 公約数 ) のうち最大のものを最大公約数といいます. 1 と 18 の公約数は, 1,,,6 で, 6 が最大公約数 つ以上の正の整数の共通な倍数 ( 公倍数 ) のうち最小のものを最小公倍数といいます. と の公倍数は, 6,1,18,,... で, 6 が最小公倍数 最大公約数, 最小公倍数の求め方
2018年度 筑波大・理系数学
 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ < < とする 放物線 上に 点 (, ), A (ta, ta ), B( - ta, ta ) をとる 三角形 AB の内心の 座標を p とし, 外心の 座標を q とする また, 正の実数 a に対して, 直線 a と放物線 で囲まれた図形の面積を S( a) で表す () p, q を cos を用いて表せ S( p) () S(
筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ < < とする 放物線 上に 点 (, ), A (ta, ta ), B( - ta, ta ) をとる 三角形 AB の内心の 座標を p とし, 外心の 座標を q とする また, 正の実数 a に対して, 直線 a と放物線 で囲まれた図形の面積を S( a) で表す () p, q を cos を用いて表せ S( p) () S(
Microsoft Word docx
 有限図形の代数的表現について 三角形や星型を式で表現したいという思いから以下のことを 考察をしまし た 有限個の点と辺で 構成される図形を 関数で表現する そのため 基礎 体として 素数の有限体を考える 但し 扱うのは 点の数と辺の数が等しい 特別場合である 先ず P5 のときから 始めることにします. グラフと写像と関数について ( 特別な場合 ) 集合 F {,,,, } について 写像 f :
有限図形の代数的表現について 三角形や星型を式で表現したいという思いから以下のことを 考察をしまし た 有限個の点と辺で 構成される図形を 関数で表現する そのため 基礎 体として 素数の有限体を考える 但し 扱うのは 点の数と辺の数が等しい 特別場合である 先ず P5 のときから 始めることにします. グラフと写像と関数について ( 特別な場合 ) 集合 F {,,,, } について 写像 f :
Microsoft PowerPoint - 9.pptx
 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 行列演算と写像 ( 次変換 3 拡大とスカラー倍 p ' = ( ', ' = ( k, kk p = (, k 倍 k 倍 拡大後 k 倍拡大の関係は スカラー倍を用いて次のように表現できる ' = k ' 拡大前 拡大 4 拡大と行列の積 p ' = ( ', '
9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 行列演算と写像 ( 次変換 3 拡大とスカラー倍 p ' = ( ', ' = ( k, kk p = (, k 倍 k 倍 拡大後 k 倍拡大の関係は スカラー倍を用いて次のように表現できる ' = k ' 拡大前 拡大 4 拡大と行列の積 p ' = ( ', '
線形代数とは
 線形代数とは 第一回ベクトル 教科書 エクササイズ線形代数 立花俊一 成田清正著 共立出版 必要最低限のことに限る 得意な人には物足りないかもしれません 線形代数とは何をするもの? 線形関係 y 直線 yもも 次式で登場する (( 次の形 ) 線形 ただし 次元の話世の中は 3 次元 [4[ 次元 ] 次元 3 次元 4 次元 はどうやって直線を表すの? ベクトルや行列の概念 y A ベクトルを使うと
線形代数とは 第一回ベクトル 教科書 エクササイズ線形代数 立花俊一 成田清正著 共立出版 必要最低限のことに限る 得意な人には物足りないかもしれません 線形代数とは何をするもの? 線形関係 y 直線 yもも 次式で登場する (( 次の形 ) 線形 ただし 次元の話世の中は 3 次元 [4[ 次元 ] 次元 3 次元 4 次元 はどうやって直線を表すの? ベクトルや行列の概念 y A ベクトルを使うと
Microsoft PowerPoint - 9.pptx
 9/7/8( 水 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 拡大とスカラー倍 行列演算と写像 ( 次変換 拡大後 k 倍 k 倍 k 倍拡大の関係は スカラー倍を用いて次のように表現できる p = (, ' = k ' 拡大前 p ' = ( ', ' = ( k, k 拡大 4 拡大と行列の積 拡大後 k 倍
9/7/8( 水 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 拡大とスカラー倍 行列演算と写像 ( 次変換 拡大後 k 倍 k 倍 k 倍拡大の関係は スカラー倍を用いて次のように表現できる p = (, ' = k ' 拡大前 p ' = ( ', ' = ( k, k 拡大 4 拡大と行列の積 拡大後 k 倍
学習指導要領
 (1 ) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 自然数 整数 有理数 無理数の包含関係など 実 数の構成を理解する ( 例 ) 次の空欄に適当な言葉をいれて, 数の集合を表しなさい 実数の絶対値が実数と対応する点と原点との距離で あることを理解する ( 例 ) 次の値を求めよ (1) () 6 置き換えなどを利用して 三項の無理数の乗法の計
(1 ) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 自然数 整数 有理数 無理数の包含関係など 実 数の構成を理解する ( 例 ) 次の空欄に適当な言葉をいれて, 数の集合を表しなさい 実数の絶対値が実数と対応する点と原点との距離で あることを理解する ( 例 ) 次の値を求めよ (1) () 6 置き換えなどを利用して 三項の無理数の乗法の計
Microsoft PowerPoint - 10.pptx
 0. 固有値とその応用 固有値と固有ベクトル 2 行列による写像から固有ベクトルへ m n A : m n n m 行列によって線形写像 f R R A が表せることを見てきた ここでは 2 次元平面の行列による写像を調べる 2 = 2 A 2 2 とし 写像 まず 単位ベクトルの像を求める u 2 x = v 2 y f : R A R を考える u 2 2 u, 2 2 0 = = v 2 0
0. 固有値とその応用 固有値と固有ベクトル 2 行列による写像から固有ベクトルへ m n A : m n n m 行列によって線形写像 f R R A が表せることを見てきた ここでは 2 次元平面の行列による写像を調べる 2 = 2 A 2 2 とし 写像 まず 単位ベクトルの像を求める u 2 x = v 2 y f : R A R を考える u 2 2 u, 2 2 0 = = v 2 0
競技プログラミングと初等整数論入門 67 回生佐竹俊哉 1. はじめに 初めまして satashun と申します 普段はのんびり数学やプログラミングをして楽しんでいます 自分は主にプログラミングの中でも 特に決められた時間の中で問題を解く競技プログラミングというものに興味を持っています そのようなプ
 競技プログラミングと初等整数論入門 67 回生佐竹俊哉 1. はじめに 初めまして satashun と申します 普段はのんびり数学やプログラミングをして楽しんでいます 自分は主にプログラミングの中でも 特に決められた時間の中で問題を解く競技プログラミングというものに興味を持っています そのようなプログラミングコンテストでは プログラムの実行速度が重要であり プログラムを高速化するために数学的知識を要求される問題が出題されることもあるので
競技プログラミングと初等整数論入門 67 回生佐竹俊哉 1. はじめに 初めまして satashun と申します 普段はのんびり数学やプログラミングをして楽しんでいます 自分は主にプログラミングの中でも 特に決められた時間の中で問題を解く競技プログラミングというものに興味を持っています そのようなプログラミングコンテストでは プログラムの実行速度が重要であり プログラムを高速化するために数学的知識を要求される問題が出題されることもあるので
2015-2018年度 2次数学セレクション(整数と数列)解答解説
 05 次数学セレクション解答解説 [ 千葉大 文 ] () k を自然数, l, N を 0 以上の整数とするとき, k l+ l l (i) k= l+ のとき = = 8 = (7+ ) = (7N + ) = 7 N + これより, k を 7 で割った余りは である k l+ l l (ii) k= l+ のとき = = 4 8 = 4(7+ ) = 4(7N + ) = 7 4N + 4
05 次数学セレクション解答解説 [ 千葉大 文 ] () k を自然数, l, N を 0 以上の整数とするとき, k l+ l l (i) k= l+ のとき = = 8 = (7+ ) = (7N + ) = 7 N + これより, k を 7 で割った余りは である k l+ l l (ii) k= l+ のとき = = 4 8 = 4(7+ ) = 4(7N + ) = 7 4N + 4
<8D828D5A838A817C A77425F91E6318FCD2E6D6364>
 4 1 平面上のベクトル 1 ベクトルとその演算 例題 1 ベクトルの相等 次の問いに答えよ. ⑴ 右の図 1 は平行四辺形 である., と等しいベクトルをいえ. ⑵ 右の図 2 の中で互いに等しいベクトルをいえ. ただし, すべてのマス目は正方形である. 解 ⑴,= より, =,= より, = ⑵ 大きさと向きの等しいものを調べる. a =d, c = f d e f 1 右の図の長方形 において,
4 1 平面上のベクトル 1 ベクトルとその演算 例題 1 ベクトルの相等 次の問いに答えよ. ⑴ 右の図 1 は平行四辺形 である., と等しいベクトルをいえ. ⑵ 右の図 2 の中で互いに等しいベクトルをいえ. ただし, すべてのマス目は正方形である. 解 ⑴,= より, =,= より, = ⑵ 大きさと向きの等しいものを調べる. a =d, c = f d e f 1 右の図の長方形 において,
Microsoft PowerPoint - 10.pptx
 m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
Microsoft Word - K-ピタゴラス数.doc
 - ピタゴラス数の代数と幾何学 津山工業高等専門学校 菅原孝慈 ( 情報工学科 年 ) 野山由貴 ( 情報工学科 年 ) 草地弘幸 ( 電子制御工学科 年 ) もくじ * 第 章ピタゴラス数の幾何学 * 第 章ピタゴラス数の代数学 * 第 3 章代数的極小元の幾何学の考察 * 第 章ピタゴラス数の幾何学的研究の動機 交点に注目すると, つの曲線が直交しているようにみえる. これらは本当に直交しているのだろうか.
- ピタゴラス数の代数と幾何学 津山工業高等専門学校 菅原孝慈 ( 情報工学科 年 ) 野山由貴 ( 情報工学科 年 ) 草地弘幸 ( 電子制御工学科 年 ) もくじ * 第 章ピタゴラス数の幾何学 * 第 章ピタゴラス数の代数学 * 第 3 章代数的極小元の幾何学の考察 * 第 章ピタゴラス数の幾何学的研究の動機 交点に注目すると, つの曲線が直交しているようにみえる. これらは本当に直交しているのだろうか.
Microsoft PowerPoint - info09b.ppt
 情報理論と暗号 大久保誠也 静岡県立大学経営情報学部 1/63 はじめに はじめに 先週の課題の補足 現代暗号とは 秘密鍵暗号と公開鍵暗号 RSA 暗号 演習 :RSA 暗号 2/63 先週の演習の解説 3/63 シーザー暗号で行いたいこと シーザー暗号文字ずらすことで暗号化 復号 ex 暗号化 :DOG GRJ ( 各文字を 3 文字分後にずらす ) 復号 :GRJ DOG ( 各文字を 3 文字分前にずらす
情報理論と暗号 大久保誠也 静岡県立大学経営情報学部 1/63 はじめに はじめに 先週の課題の補足 現代暗号とは 秘密鍵暗号と公開鍵暗号 RSA 暗号 演習 :RSA 暗号 2/63 先週の演習の解説 3/63 シーザー暗号で行いたいこと シーザー暗号文字ずらすことで暗号化 復号 ex 暗号化 :DOG GRJ ( 各文字を 3 文字分後にずらす ) 復号 :GRJ DOG ( 各文字を 3 文字分前にずらす
2014年度 千葉大・医系数学
 04 千葉大学 ( 医系 ) 前期日程問題 解答解説のページへ 袋の中に, 赤玉が 3 個, 白玉が 7 個が入っている 袋から玉を無作為に つ取り出し, 色を確認してから, 再び袋に戻すという試行を行う この試行を N 回繰り返したときに, 赤玉を A 回 ( ただし 0 A N) 取り出す確率を p( N, A) とする このとき, 以下の問いに答えよ () 確率 p( N, A) を N と
04 千葉大学 ( 医系 ) 前期日程問題 解答解説のページへ 袋の中に, 赤玉が 3 個, 白玉が 7 個が入っている 袋から玉を無作為に つ取り出し, 色を確認してから, 再び袋に戻すという試行を行う この試行を N 回繰り返したときに, 赤玉を A 回 ( ただし 0 A N) 取り出す確率を p( N, A) とする このとき, 以下の問いに答えよ () 確率 p( N, A) を N と
オートマトン 形式言語及び演習 1. 有限オートマトンとは 酒井正彦 形式言語 言語とは : 文字列の集合例 : 偶数個の 1 の後に 0 を持つ列からなる集合 {0, 110, 11110,
 オートマトン 形式言語及び演習 1 有限オートマトンとは 酒井正彦 wwwtrscssinagoya-uacjp/~sakai/lecture/automata/ 形式言語 言語とは : 文字列の集合例 : 偶数個の 1 の後に 0 を持つ列からなる集合 {0, 110, 11110, } 形式言語 : 数学モデルに基づいて定義された言語 認識機械 : 文字列が該当言語に属するか? 文字列 機械 受理
オートマトン 形式言語及び演習 1 有限オートマトンとは 酒井正彦 wwwtrscssinagoya-uacjp/~sakai/lecture/automata/ 形式言語 言語とは : 文字列の集合例 : 偶数個の 1 の後に 0 を持つ列からなる集合 {0, 110, 11110, } 形式言語 : 数学モデルに基づいて定義された言語 認識機械 : 文字列が該当言語に属するか? 文字列 機械 受理
2016年度 九州大・理系数学
 0 九州大学 ( 理系 ) 前期日程問題 解答解説のページへ 座標平面上の曲線 C, C をそれぞれ C : y logx ( x > 0), C : y ( x-)( x- a) とする ただし, a は実数である を自然数とするとき, 曲線 C, C が 点 P, Q で交わり, P, Q の x 座標はそれぞれ, + となっている また, 曲線 C と直線 PQ で囲まれた領域の面積を S,
0 九州大学 ( 理系 ) 前期日程問題 解答解説のページへ 座標平面上の曲線 C, C をそれぞれ C : y logx ( x > 0), C : y ( x-)( x- a) とする ただし, a は実数である を自然数とするとき, 曲線 C, C が 点 P, Q で交わり, P, Q の x 座標はそれぞれ, + となっている また, 曲線 C と直線 PQ で囲まれた領域の面積を S,
jhs-math3_01-02ans
 因数分解 (1) 因数ある式がいくつかの式の積の形で表されるとき, かけ合わされたそれぞれの式のことをもとの式の因数という 例 ) 多項式 x 2 +( a + b)x + ab は x + a と x + b の積である x 2 +( a + b)x + ab = ( x + a)( x + b) もとの式 このとき,x + a と x + b を x 2 +( a + b)x + ab の因数という
因数分解 (1) 因数ある式がいくつかの式の積の形で表されるとき, かけ合わされたそれぞれの式のことをもとの式の因数という 例 ) 多項式 x 2 +( a + b)x + ab は x + a と x + b の積である x 2 +( a + b)x + ab = ( x + a)( x + b) もとの式 このとき,x + a と x + b を x 2 +( a + b)x + ab の因数という
オートマトン 形式言語及び演習 4. 正規言語の性質 酒井正彦 正規言語の性質 反復補題正規言語が満たす性質 ある与えられた言語が正規言語でないことを証明するために その言語が正規言語であると
 オートマトン 形式言語及び演習 4. 正規言語の性質 酒井正彦 www.trs.css.i.nagoya-u.ac.jp/~sakai/lecture/automata/ 正規言語の性質 正規言語が満たす性質 ある与えられた言語が正規言語でないことを証明するために その言語が正規言語であると仮定してを使い 矛盾を導く 閉包性正規言語を演算により組み合わせて得られる言語が正規言語となる演算について調べる
オートマトン 形式言語及び演習 4. 正規言語の性質 酒井正彦 www.trs.css.i.nagoya-u.ac.jp/~sakai/lecture/automata/ 正規言語の性質 正規言語が満たす性質 ある与えられた言語が正規言語でないことを証明するために その言語が正規言語であると仮定してを使い 矛盾を導く 閉包性正規言語を演算により組み合わせて得られる言語が正規言語となる演算について調べる
<4D F736F F F696E74202D2091E6824F82538FCD8CEB82E88C9F8F6F814592F990B382CC8CB4979D82BB82CC82505F D E95848D8682CC90B69
 第 章 誤り検出 訂正の原理 その ブロック符号とその復号 安達文幸 目次 誤り訂正符号化を用いる伝送系誤り検出符号誤り検出 訂正符号 7, ハミング符号, ハミング符号生成行列, パリティ検査行列の一般形符号の生成行列符号の生成行列とパリティ検査行列の関係符号の訂正能力符号多項式 安達 : コミュニケーション符号理論 安達 : コミュニケーション符号理論 誤り訂正符号化を用いる伝送系 伝送システム
第 章 誤り検出 訂正の原理 その ブロック符号とその復号 安達文幸 目次 誤り訂正符号化を用いる伝送系誤り検出符号誤り検出 訂正符号 7, ハミング符号, ハミング符号生成行列, パリティ検査行列の一般形符号の生成行列符号の生成行列とパリティ検査行列の関係符号の訂正能力符号多項式 安達 : コミュニケーション符号理論 安達 : コミュニケーション符号理論 誤り訂正符号化を用いる伝送系 伝送システム
Fibonacci_square_pdf
 1/81 ページ フィボナッチ数列に現れる平方数 1 と 144 だけであることの証明 フィボナッチ数列と フィボナッチ数列と, 前の 2 つの数を加えると次の数になる という数列です ただし,1 番目と 2 番目の数両方とも 1 です 1, 1, 1 + 1 = 2 ですから,3 番目の数 2 になります 1, 1, 2, 1 + 2 = 3 ですから,4 番目の数 3 です 1, 1, 2, 3,
1/81 ページ フィボナッチ数列に現れる平方数 1 と 144 だけであることの証明 フィボナッチ数列と フィボナッチ数列と, 前の 2 つの数を加えると次の数になる という数列です ただし,1 番目と 2 番目の数両方とも 1 です 1, 1, 1 + 1 = 2 ですから,3 番目の数 2 になります 1, 1, 2, 1 + 2 = 3 ですから,4 番目の数 3 です 1, 1, 2, 3,
> > <., vs. > x 2 x y = ax 2 + bx + c y = 0 2 ax 2 + bx + c = 0 y = 0 x ( x ) y = ax 2 + bx + c D = b 2 4ac (1) D > 0 x (2) D = 0 x (3
 13 2 13.0 2 ( ) ( ) 2 13.1 ( ) ax 2 + bx + c > 0 ( a, b, c ) ( ) 275 > > 2 2 13.3 x 2 x y = ax 2 + bx + c y = 0 2 ax 2 + bx + c = 0 y = 0 x ( x ) y = ax 2 + bx + c D = b 2 4ac (1) D >
13 2 13.0 2 ( ) ( ) 2 13.1 ( ) ax 2 + bx + c > 0 ( a, b, c ) ( ) 275 > > 2 2 13.3 x 2 x y = ax 2 + bx + c y = 0 2 ax 2 + bx + c = 0 y = 0 x ( x ) y = ax 2 + bx + c D = b 2 4ac (1) D >
vecrot
 1. ベクトル ベクトル : 方向を持つ量 ベクトルには 1 方向 2 大きさ ( 長さ ) という 2 つの属性がある ベクトルの例 : 物体の移動速度 移動量電場 磁場の強さ風速力トルクなど 2. ベクトルの表現 2.1 矢印で表現される 矢印の長さ : ベクトルの大きさ 矢印の向き : ベクトルの方向 2.2 2 個の点を用いて表現する 始点 () と終点 () を結ぶ半直線の向き : ベクトルの方向
1. ベクトル ベクトル : 方向を持つ量 ベクトルには 1 方向 2 大きさ ( 長さ ) という 2 つの属性がある ベクトルの例 : 物体の移動速度 移動量電場 磁場の強さ風速力トルクなど 2. ベクトルの表現 2.1 矢印で表現される 矢印の長さ : ベクトルの大きさ 矢印の向き : ベクトルの方向 2.2 2 個の点を用いて表現する 始点 () と終点 () を結ぶ半直線の向き : ベクトルの方向
Microsoft PowerPoint - 2.ppt [互換モード]
![Microsoft PowerPoint - 2.ppt [互換モード] Microsoft PowerPoint - 2.ppt [互換モード]](/thumbs/74/70606453.jpg) 0 章数学基礎 1 大学では 高校より厳密に議論を行う そのために 議論の議論の対象を明確にする必要がある 集合 ( 定義 ) 集合 物の集まりである集合 X に対して X を構成している物を X の要素または元という 集合については 3 セメスタ開講の 離散数学 で詳しく扱う 2 集合の表現 1. 要素を明示する表現 ( 外延的表現 ) 中括弧で 囲う X = {0,1, 2,3} 慣用的に 英大文字を用いる
0 章数学基礎 1 大学では 高校より厳密に議論を行う そのために 議論の議論の対象を明確にする必要がある 集合 ( 定義 ) 集合 物の集まりである集合 X に対して X を構成している物を X の要素または元という 集合については 3 セメスタ開講の 離散数学 で詳しく扱う 2 集合の表現 1. 要素を明示する表現 ( 外延的表現 ) 中括弧で 囲う X = {0,1, 2,3} 慣用的に 英大文字を用いる
Microsoft PowerPoint - while.ppt
 本日の内容 繰り返し計算 while 文, for 文 例題 1. 自然数の和例題 2. 最大公約数の計算例題 3. ベクトルの長さ while 文例題 4. 九九の表 for 文と繰り返しの入れ子例題 5. ド モアブルの公式計算誤差の累積 今日の到達目標 繰り返し (while 文, for 文 ) を使って, 繰り返し計算を行えるようになること ループカウンタとして, 整数の変数を使うこと 今回も,
本日の内容 繰り返し計算 while 文, for 文 例題 1. 自然数の和例題 2. 最大公約数の計算例題 3. ベクトルの長さ while 文例題 4. 九九の表 for 文と繰り返しの入れ子例題 5. ド モアブルの公式計算誤差の累積 今日の到達目標 繰り返し (while 文, for 文 ) を使って, 繰り返し計算を行えるようになること ループカウンタとして, 整数の変数を使うこと 今回も,
重要例題113
 04_ 高校 数学 Ⅱ 必須基本公式 定理集 数学 Ⅱ 第 章式の計算と方程式 0 商と余り についての整式 A をについての整式 B で割ったときの商を Q, 余りを R とすると, ABQ+R (R の次数 ) > 0
04_ 高校 数学 Ⅱ 必須基本公式 定理集 数学 Ⅱ 第 章式の計算と方程式 0 商と余り についての整式 A をについての整式 B で割ったときの商を Q, 余りを R とすると, ABQ+R (R の次数 ) > 0
2011年度 大阪大・理系数学
 0 大阪大学 ( 理系 ) 前期日程問題 解答解説のページへ a a を自然数とする O を原点とする座標平面上で行列 A= a の表す 次変換 を f とする cosθ siθ () >0 および0θ
0 大阪大学 ( 理系 ) 前期日程問題 解答解説のページへ a a を自然数とする O を原点とする座標平面上で行列 A= a の表す 次変換 を f とする cosθ siθ () >0 および0θ
2017年度 京都大・文系数学
 07 京都大学 ( 文系 ) 前期日程問題 解答解説のページへ 曲線 y= x - 4x+ を C とする 直線 l は C の接線であり, 点 P(, 0) を通るもの とする また, l の傾きは負であるとする このとき, C と l で囲まれた部分の面積 S を求めよ -- 07 京都大学 ( 文系 ) 前期日程問題 解答解説のページへ 次の問いに答えよ ただし, 0.00 < log0
07 京都大学 ( 文系 ) 前期日程問題 解答解説のページへ 曲線 y= x - 4x+ を C とする 直線 l は C の接線であり, 点 P(, 0) を通るもの とする また, l の傾きは負であるとする このとき, C と l で囲まれた部分の面積 S を求めよ -- 07 京都大学 ( 文系 ) 前期日程問題 解答解説のページへ 次の問いに答えよ ただし, 0.00 < log0
Microsoft PowerPoint - qcomp.ppt [互換モード]
![Microsoft PowerPoint - qcomp.ppt [互換モード] Microsoft PowerPoint - qcomp.ppt [互換モード]](/thumbs/85/91243661.jpg) 量子計算基礎 東京工業大学 河内亮周 概要 計算って何? 数理科学的に 計算 を扱うには 量子力学を計算に使おう! 量子情報とは? 量子情報に対する演算 = 量子計算 一般的な量子回路の構成方法 計算って何? 計算とは? 計算 = 入力情報から出力情報への変換 入力 計算機構 ( デジタルコンピュータ,etc ) 出力 計算とは? 計算 = 入力情報から出力情報への変換 この関数はどれくらい計算が大変か??
量子計算基礎 東京工業大学 河内亮周 概要 計算って何? 数理科学的に 計算 を扱うには 量子力学を計算に使おう! 量子情報とは? 量子情報に対する演算 = 量子計算 一般的な量子回路の構成方法 計算って何? 計算とは? 計算 = 入力情報から出力情報への変換 入力 計算機構 ( デジタルコンピュータ,etc ) 出力 計算とは? 計算 = 入力情報から出力情報への変換 この関数はどれくらい計算が大変か??
学習指導要領
 (1) 数と式 学習指導要領ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 千早高校学力スタンダード 自然数 整数 有理数 無理数の用語の意味を理解す る ( 例 ) 次の数の中から自然数 整数 有理 数 無理数に分類せよ 3 3,, 0.7, 3,,-, 4 (1) 自然数 () 整数 (3) 有理数 (4) 無理数 自然数 整数 有理数 無理数の包含関係など
(1) 数と式 学習指導要領ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 千早高校学力スタンダード 自然数 整数 有理数 無理数の用語の意味を理解す る ( 例 ) 次の数の中から自然数 整数 有理 数 無理数に分類せよ 3 3,, 0.7, 3,,-, 4 (1) 自然数 () 整数 (3) 有理数 (4) 無理数 自然数 整数 有理数 無理数の包含関係など
2018年度 東京大・理系数学
 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ関数 f ( ) = + cos (0 < < ) の増減表をつくり, + 0, 0 のと sin きの極限を調べよ 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ n+ 数列 a, a, を, Cn a n = ( n =,, ) で定める n! an qn () n とする を既約分数 an p として表したときの分母
08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ関数 f ( ) = + cos (0 < < ) の増減表をつくり, + 0, 0 のと sin きの極限を調べよ 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ n+ 数列 a, a, を, Cn a n = ( n =,, ) で定める n! an qn () n とする を既約分数 an p として表したときの分母
さくらの個別指導 ( さくら教育研究所 ) 1 φ = φ 1 : φ [ ] a [ ] 1 a : b a b b(a + b) b a 2 a 2 = b(a + b). b 2 ( a b ) 2 = a b a/b X 2 X 1 = 0 a/b > 0 2 a
![さくらの個別指導 ( さくら教育研究所 ) 1 φ = φ 1 : φ [ ] a [ ] 1 a : b a b b(a + b) b a 2 a 2 = b(a + b). b 2 ( a b ) 2 = a b a/b X 2 X 1 = 0 a/b > 0 2 a さくらの個別指導 ( さくら教育研究所 ) 1 φ = φ 1 : φ [ ] a [ ] 1 a : b a b b(a + b) b a 2 a 2 = b(a + b). b 2 ( a b ) 2 = a b a/b X 2 X 1 = 0 a/b > 0 2 a](/thumbs/97/131721994.jpg) φ + 5 2 φ : φ [ ] a [ ] a : b a b b(a + b) b a 2 a 2 b(a + b). b 2 ( a b ) 2 a b + a/b X 2 X 0 a/b > 0 2 a b + 5 2 φ φ : 2 5 5 [ ] [ ] x x x : x : x x : x x : x x 2 x 2 x 0 x ± 5 2 x x φ : φ 2 : φ ( )
φ + 5 2 φ : φ [ ] a [ ] a : b a b b(a + b) b a 2 a 2 b(a + b). b 2 ( a b ) 2 a b + a/b X 2 X 0 a/b > 0 2 a b + 5 2 φ φ : 2 5 5 [ ] [ ] x x x : x : x x : x x : x x 2 x 2 x 0 x ± 5 2 x x φ : φ 2 : φ ( )
1999年度 センター試験・数学ⅡB
 99 センター試験数学 Ⅱ 数学 B 問題 第 問 ( 必答問題 ) [] 関数 y cos3x の周期のうち正で最小のものはアイウ 解答解説のページへ 0 x 360 のとき, 関数 y cos3x において, y となる x はエ個, y となる x はオ 個ある また, y sin x と y cos3x のグラフより, 方程式 sin x cos3x は 0 x 360のときカ個の解をもつことがわかる
99 センター試験数学 Ⅱ 数学 B 問題 第 問 ( 必答問題 ) [] 関数 y cos3x の周期のうち正で最小のものはアイウ 解答解説のページへ 0 x 360 のとき, 関数 y cos3x において, y となる x はエ個, y となる x はオ 個ある また, y sin x と y cos3x のグラフより, 方程式 sin x cos3x は 0 x 360のときカ個の解をもつことがわかる
オートマトンと言語
 オートマトンと言語 回目 4 月 8 日 ( 水 ) 章 ( 数式の記法, スタック,BNF 記法 ) 授業資料 http://ir.cs.yamanashi.ac.jp/~ysuzuki/public/automaton/ 授業の予定 ( 中間試験まで ) 回数月日 内容 4 月 日オートマトンとは, オリエンテーション 4 月 8 日 章 ( 数式の記法, スタック,BNF) 3 4 月 5 日
オートマトンと言語 回目 4 月 8 日 ( 水 ) 章 ( 数式の記法, スタック,BNF 記法 ) 授業資料 http://ir.cs.yamanashi.ac.jp/~ysuzuki/public/automaton/ 授業の予定 ( 中間試験まで ) 回数月日 内容 4 月 日オートマトンとは, オリエンテーション 4 月 8 日 章 ( 数式の記法, スタック,BNF) 3 4 月 5 日
Microsoft Word - 補論3.2
 補論 3. 多変量 GARC モデル 07//6 新谷元嗣 藪友良 対数尤度関数 3 章 7 節では 変量の対数尤度を求めた ここでは多変量の場合 とくに 変量について対数尤度を求める 誤差項 は平均 0 で 次元の正規分布に従うとする 単純化のため 分散と共分散は時間を通じて一定としよう ( この仮定は後で変更される ) したがって ij から添え字 を除くことができる このとき と の尤度関数は
補論 3. 多変量 GARC モデル 07//6 新谷元嗣 藪友良 対数尤度関数 3 章 7 節では 変量の対数尤度を求めた ここでは多変量の場合 とくに 変量について対数尤度を求める 誤差項 は平均 0 で 次元の正規分布に従うとする 単純化のため 分散と共分散は時間を通じて一定としよう ( この仮定は後で変更される ) したがって ij から添え字 を除くことができる このとき と の尤度関数は
ベクトル公式.rtf
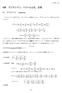 6 章ラプラシアン, ベクトル公式, 定理 6.1 ラプラシアン Laplacian φ はベクトル量である. そこでさらに発散をとると, φ はどういう形になるであろうか? φ = a + a + a φ a + a φ + a φ = φ + φ + φ = 2 φ + 2 φ 2 + 2 φ 2 2 φ = 2 φ 2 + 2 φ 2 + 2 φ 2 = 2 φ したがって,2 階の偏微分演算となる.
6 章ラプラシアン, ベクトル公式, 定理 6.1 ラプラシアン Laplacian φ はベクトル量である. そこでさらに発散をとると, φ はどういう形になるであろうか? φ = a + a + a φ a + a φ + a φ = φ + φ + φ = 2 φ + 2 φ 2 + 2 φ 2 2 φ = 2 φ 2 + 2 φ 2 + 2 φ 2 = 2 φ したがって,2 階の偏微分演算となる.
プログラミング入門1
 プログラミング入門 1 第 5 回 繰り返し (while ループ ) 授業開始前に ログオン後 不要なファイルを削除し て待機してください Java 1 第 5 回 2 参考書について 参考書は自分にあったものをぜひ手元において自習してください 授業の WEB 教材は勉強の入り口へみなさんを案内するのが目的でつくられている これで十分という訳ではない 第 1 回に紹介した本以外にも良書がたくさんある
プログラミング入門 1 第 5 回 繰り返し (while ループ ) 授業開始前に ログオン後 不要なファイルを削除し て待機してください Java 1 第 5 回 2 参考書について 参考書は自分にあったものをぜひ手元において自習してください 授業の WEB 教材は勉強の入り口へみなさんを案内するのが目的でつくられている これで十分という訳ではない 第 1 回に紹介した本以外にも良書がたくさんある
Microsoft PowerPoint - mp11-02.pptx
 数理計画法第 2 回 塩浦昭義情報科学研究科准教授 shioura@dais.is.tohoku.ac.jp http://www.dais.is.tohoku.ac.jp/~shioura/teaching 前回の復習 数理計画とは? 数理計画 ( 復習 ) 数理計画問題とは? 狭義には : 数理 ( 数学 ) を使って計画を立てるための問題 広義には : 与えられた評価尺度に関して最も良い解を求める問題
数理計画法第 2 回 塩浦昭義情報科学研究科准教授 shioura@dais.is.tohoku.ac.jp http://www.dais.is.tohoku.ac.jp/~shioura/teaching 前回の復習 数理計画とは? 数理計画 ( 復習 ) 数理計画問題とは? 狭義には : 数理 ( 数学 ) を使って計画を立てるための問題 広義には : 与えられた評価尺度に関して最も良い解を求める問題
代数 幾何 < ベクトル > 1 ベクトルの演算 和 差 実数倍については 文字の計算と同様 2 ベクトルの成分表示 平面ベクトル : a x e y e x, ) ( 1 y1 空間ベクトル : a x e y e z e x, y, ) ( 1 1 z1
 代数 幾何 < ベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル :, 空間ベクトル : z,, z 成分での計算ができるようにすること ベクトルの内積 : os 平面ベクトル :,, 空間ベクトル :,,,, z z zz 4 ベクトルの大きさ 平面上 : 空間上 : z は 良く用いられる 5 m: に分ける点 : m m 図形への応用
代数 幾何 < ベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル :, 空間ベクトル : z,, z 成分での計算ができるようにすること ベクトルの内積 : os 平面ベクトル :,, 空間ベクトル :,,,, z z zz 4 ベクトルの大きさ 平面上 : 空間上 : z は 良く用いられる 5 m: に分ける点 : m m 図形への応用
Microsoft Word - 微分入門.doc
 基本公式 例題 0 定義式 f( ) 数 Ⅲ 微分入門 = の導関数を定義式にもとづいて計算しなさい 基本事項 ( f( ), g( ) が微分可能ならば ) y= f( ) g( ) のとき, y = y= f( ) g( ) h( ) のとき, y = ( f( ), g( ) が微分可能で, g( ) 0 ならば ) f( ) y = のとき, y = g ( ) とくに, y = のとき,
基本公式 例題 0 定義式 f( ) 数 Ⅲ 微分入門 = の導関数を定義式にもとづいて計算しなさい 基本事項 ( f( ), g( ) が微分可能ならば ) y= f( ) g( ) のとき, y = y= f( ) g( ) h( ) のとき, y = ( f( ), g( ) が微分可能で, g( ) 0 ならば ) f( ) y = のとき, y = g ( ) とくに, y = のとき,
行列、ベクトル
 行列 (Mtri) と行列式 (Determinnt). 行列 (Mtri) の演算. 和 差 積.. 行列とは.. 行列の和差 ( 加減算 ).. 行列の積 ( 乗算 ). 転置行列 対称行列 正方行列. 単位行列. 行列式 (Determinnt) と逆行列. 行列式. 逆行列. 多元一次連立方程式のコンピュータによる解法. コンピュータによる逆行列の計算.. 定数項の異なる複数の方程式.. 逆行列の計算
行列 (Mtri) と行列式 (Determinnt). 行列 (Mtri) の演算. 和 差 積.. 行列とは.. 行列の和差 ( 加減算 ).. 行列の積 ( 乗算 ). 転置行列 対称行列 正方行列. 単位行列. 行列式 (Determinnt) と逆行列. 行列式. 逆行列. 多元一次連立方程式のコンピュータによる解法. コンピュータによる逆行列の計算.. 定数項の異なる複数の方程式.. 逆行列の計算
航空機の運動方程式
 可制御性 可観測性. 可制御性システムの状態を, 適切な操作によって, 有限時間内に, 任意の状態から別の任意の状態に移動させることができるか否かという特性を可制御性という. 可制御性を有するシステムに対し, システムは可制御である, 可制御なシステム という言い方をする. 状態方程式, 出力方程式が以下で表されるn 次元 m 入力 r 出力線形時不変システム x Ax u y x Du () に対し,
可制御性 可観測性. 可制御性システムの状態を, 適切な操作によって, 有限時間内に, 任意の状態から別の任意の状態に移動させることができるか否かという特性を可制御性という. 可制御性を有するシステムに対し, システムは可制御である, 可制御なシステム という言い方をする. 状態方程式, 出力方程式が以下で表されるn 次元 m 入力 r 出力線形時不変システム x Ax u y x Du () に対し,
<4D F736F F D F90948A F835A E815B8E8E8CB189F090E05F81798D5A97B98CE38F4390B A2E646F63>
 07 年度大学入試センター試験解説 数学 Ⅰ A 第 問 9 のとき, 9 アイ 0 より, 0 であるから, 次に, 解答記号ウを含む等式の右辺を a とおくと, a a a 8 a a a 8 a これが 8 と等しいとき,( 部 ) 0 より, a 0 よって, a ウ ( 注 ) このとき, 8 9 (, より ) 7 エ, オカ また,より, これより, 9 であるから, 6 8 8 すなわち,
07 年度大学入試センター試験解説 数学 Ⅰ A 第 問 9 のとき, 9 アイ 0 より, 0 であるから, 次に, 解答記号ウを含む等式の右辺を a とおくと, a a a 8 a a a 8 a これが 8 と等しいとき,( 部 ) 0 より, a 0 よって, a ウ ( 注 ) このとき, 8 9 (, より ) 7 エ, オカ また,より, これより, 9 であるから, 6 8 8 すなわち,
学習指導要領
 (1) 数と式 学習指導要領ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 第 1 章第 節実数 東高校学力スタンダード 4 実数 (P.3~7) 自然数 整数 有理数 無理数 実数のそれぞれの集 合について 四則演算の可能性について判断できる ( 例 ) 下の表において, それぞれの数の範囲で四則計算を考えるとき, 計算がその範囲で常にできる場合には
(1) 数と式 学習指導要領ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 第 1 章第 節実数 東高校学力スタンダード 4 実数 (P.3~7) 自然数 整数 有理数 無理数 実数のそれぞれの集 合について 四則演算の可能性について判断できる ( 例 ) 下の表において, それぞれの数の範囲で四則計算を考えるとき, 計算がその範囲で常にできる場合には
平成 0 年度高校 1 年 ( 中入 ) シラバス予定 授業計画月単元 項目内容時数 10 節三角形への応用数学 Ⅱ 1 章方程式 式と証明 1 節整式 分数式の計算 1 正弦定理 2 余弦定理 三角形の面積 4 空間図形の計量 参 内接円の半径と三角形の面積 発展 ヘロンの公式 1 整式の乗法と因
 平成 0 年度高校 1 年 ( 中入 ) シラバス 科 目 授業時数 教 材 学習到達 目標 時間 / 週 教科書 : Standard( 東京書籍 ), 数学 Ⅱ Standard( 東京書籍 ) 副教材 :Standard Buddy WIDE +A ( 東京書籍 ), 数学 Ⅱ+B( 東京書籍 ) 集合と論証,2 次関数, 図形と計量 ( ) 及び方程式 式の証明, 図形と方程式 ( 数学 Ⅱ)
平成 0 年度高校 1 年 ( 中入 ) シラバス 科 目 授業時数 教 材 学習到達 目標 時間 / 週 教科書 : Standard( 東京書籍 ), 数学 Ⅱ Standard( 東京書籍 ) 副教材 :Standard Buddy WIDE +A ( 東京書籍 ), 数学 Ⅱ+B( 東京書籍 ) 集合と論証,2 次関数, 図形と計量 ( ) 及び方程式 式の証明, 図形と方程式 ( 数学 Ⅱ)
補足 中学で学習したフレミング左手の法則 ( 電 磁 力 ) と関連付けると覚えやすい 電磁力は電流と磁界の外積で表される 力 F 磁 電磁力 F li 右ねじの回転の向き電 li ( l は導線の長さ ) 補足 有向線分とベクトル有向線分 : 矢印の位
 http://totemt.sur.ne.p 外積 ( ベクトル積 ) の活用 ( 面積, 法線ベクトル, 平面の方程式 ) 3 次元空間の つのベクトルの積が つのベクトルを与えるようなベクトルの掛け算 ベクトルの積がベクトルを与えることからベクトル積とも呼ばれる これに対し内積は符号と大きさをもつ量 ( スカラー量 ) を与えるので, スカラー積とも呼ばれる 外積を使うと, 平行四辺形や三角形の面積,
http://totemt.sur.ne.p 外積 ( ベクトル積 ) の活用 ( 面積, 法線ベクトル, 平面の方程式 ) 3 次元空間の つのベクトルの積が つのベクトルを与えるようなベクトルの掛け算 ベクトルの積がベクトルを与えることからベクトル積とも呼ばれる これに対し内積は符号と大きさをもつ量 ( スカラー量 ) を与えるので, スカラー積とも呼ばれる 外積を使うと, 平行四辺形や三角形の面積,
2015年度 京都大・理系数学
 05 京都大学 ( 理系 ) 前期日程問題 解答解説のページへ つの関数 y= si( x+ ) と y = six のグラフの 0 x の部分で囲まれる領域 を, x 軸のまわりに 回転させてできる立体の体積を求めよ ただし, x = 0 と x = は領域を囲む線とは考えない -- 05 京都大学 ( 理系 ) 前期日程問題 解答解説のページへ次の つの条件を同時に満たす四角形のうち面積が最小のものの面積を求めよ
05 京都大学 ( 理系 ) 前期日程問題 解答解説のページへ つの関数 y= si( x+ ) と y = six のグラフの 0 x の部分で囲まれる領域 を, x 軸のまわりに 回転させてできる立体の体積を求めよ ただし, x = 0 と x = は領域を囲む線とは考えない -- 05 京都大学 ( 理系 ) 前期日程問題 解答解説のページへ次の つの条件を同時に満たす四角形のうち面積が最小のものの面積を求めよ
公式集 数学 Ⅱ B 頭に入っていますか? 8 和積の公式 A + B A B si A + si B si os A + B A B si A si B os si A + B A B os A + os B os os A + B A B os A os B si si 9 三角関数の合成 si
 公式集 数学 Ⅱ B 頭に入っていますか? < 図形と方程式 > 点間の距離 A x, B x, のとき x x + : に分ける点 A x, B x, のとき 線分 AB を:に分ける点 æ x + x + ö は ç, è + + ø 注 < のとき外分点 直線の方程式 傾き で 点 x, を通る : x 点 x, x, を通る : x 注 分母が のとき は座標軸と平行な直線 x x 4 直線の位置関係
公式集 数学 Ⅱ B 頭に入っていますか? < 図形と方程式 > 点間の距離 A x, B x, のとき x x + : に分ける点 A x, B x, のとき 線分 AB を:に分ける点 æ x + x + ö は ç, è + + ø 注 < のとき外分点 直線の方程式 傾き で 点 x, を通る : x 点 x, x, を通る : x 注 分母が のとき は座標軸と平行な直線 x x 4 直線の位置関係
メソッドのまとめ
 メソッド (4) 擬似コードテスト技法 http://java.cis.k.hosei.ac.jp/ 授業の前に自己点検以下のことがらを友達に説明できますか? メソッドの宣言とは 起動とは何ですか メソッドの宣言はどのように書きますか メソッドの宣言はどこに置きますか メソッドの起動はどのようにしますか メソッドの仮引数 実引数 戻り値とは何ですか メソッドの起動にあたって実引数はどのようにして仮引数に渡されますか
メソッド (4) 擬似コードテスト技法 http://java.cis.k.hosei.ac.jp/ 授業の前に自己点検以下のことがらを友達に説明できますか? メソッドの宣言とは 起動とは何ですか メソッドの宣言はどのように書きますか メソッドの宣言はどこに置きますか メソッドの起動はどのようにしますか メソッドの仮引数 実引数 戻り値とは何ですか メソッドの起動にあたって実引数はどのようにして仮引数に渡されますか
学習指導要領
 (1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 自然数 整数 有理数 無理数 実数のそれぞれの集 合について 四則演算の可能性について判断できる ( 例 ) 下の表において それぞれの数の範囲で四則計算を考えるとき 計算がその範囲で常にできる場合には を 常にできるとは限らない場合には を付けよ ただし 除法では 0 で割ることは考えない
(1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 自然数 整数 有理数 無理数 実数のそれぞれの集 合について 四則演算の可能性について判断できる ( 例 ) 下の表において それぞれの数の範囲で四則計算を考えるとき 計算がその範囲で常にできる場合には を 常にできるとは限らない場合には を付けよ ただし 除法では 0 で割ることは考えない
漸化式のすべてのパターンを解説しましたー高校数学の達人・河見賢司のサイト
 https://www.hmg-gen.com/tuusin.html https://www.hmg-gen.com/tuusin1.html 1 2 OK 3 4 {a n } (1) a 1 = 1, a n+1 a n = 2 (2) a 1 = 3, a n+1 a n = 2n a n a n+1 a n = ( ) a n+1 a n = ( ) a n+1 a n {a n } 1,
https://www.hmg-gen.com/tuusin.html https://www.hmg-gen.com/tuusin1.html 1 2 OK 3 4 {a n } (1) a 1 = 1, a n+1 a n = 2 (2) a 1 = 3, a n+1 a n = 2n a n a n+1 a n = ( ) a n+1 a n = ( ) a n+1 a n {a n } 1,
2014年度 名古屋大・理系数学
 04 名古屋大学 ( 理系 ) 前期日程問題 解答解説のページへ空間内にある半径 の球 ( 内部を含む ) を B とする 直線 と B が交わっており, その交わりは長さ の線分である () B の中心と との距離を求めよ () のまわりに B を 回転してできる立体の体積を求めよ 04 名古屋大学 ( 理系 ) 前期日程問題 解答解説のページへ 実数 t に対して 点 P( t, t ), Q(
04 名古屋大学 ( 理系 ) 前期日程問題 解答解説のページへ空間内にある半径 の球 ( 内部を含む ) を B とする 直線 と B が交わっており, その交わりは長さ の線分である () B の中心と との距離を求めよ () のまわりに B を 回転してできる立体の体積を求めよ 04 名古屋大学 ( 理系 ) 前期日程問題 解答解説のページへ 実数 t に対して 点 P( t, t ), Q(
様々なミクロ計量モデル†
 担当 : 長倉大輔 ( ながくらだいすけ ) この資料は私の講義において使用するために作成した資料です WEB ページ上で公開しており 自由に参照して頂いて構いません ただし 内容について 一応検証してありますが もし間違いがあった場合でもそれによって生じるいかなる損害 不利益について責任を負いかねますのでご了承ください 間違いは発見次第 継続的に直していますが まだ存在する可能性があります 1 カウントデータモデル
担当 : 長倉大輔 ( ながくらだいすけ ) この資料は私の講義において使用するために作成した資料です WEB ページ上で公開しており 自由に参照して頂いて構いません ただし 内容について 一応検証してありますが もし間違いがあった場合でもそれによって生じるいかなる損害 不利益について責任を負いかねますのでご了承ください 間違いは発見次第 継続的に直していますが まだ存在する可能性があります 1 カウントデータモデル
2014年度 筑波大・理系数学
 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ f ( x) = x x とする y = f ( x ) のグラフに点 P(, ) から引いた接線は 本あるとする つの接点 A (, f ( )), B(, f ( )), C(, f ( )) を頂点とする三角形の 重心を G とする () + +, + + および を, を用いて表せ () 点 G の座標を, を用いて表せ () 点 G
筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ f ( x) = x x とする y = f ( x ) のグラフに点 P(, ) から引いた接線は 本あるとする つの接点 A (, f ( )), B(, f ( )), C(, f ( )) を頂点とする三角形の 重心を G とする () + +, + + および を, を用いて表せ () 点 G の座標を, を用いて表せ () 点 G
DVIOUT-17syoze
 平面の合同変換と相似変換 岩瀬順一 要約 : 平面の合同変換と相似変換を論じる いま大学で行列を学び始めている大学一年生を念頭に置いている 高等学校で行列や一次変換を学んでいなくてもよい 1. 写像 定義 1.1 X, Y を集合とする X の各元 x に対し Y のただ一つの元 y を対応させる規則 f を写像とよび,f : X! Y のように書く f によって x に対応する Y の元を f(x)
平面の合同変換と相似変換 岩瀬順一 要約 : 平面の合同変換と相似変換を論じる いま大学で行列を学び始めている大学一年生を念頭に置いている 高等学校で行列や一次変換を学んでいなくてもよい 1. 写像 定義 1.1 X, Y を集合とする X の各元 x に対し Y のただ一つの元 y を対応させる規則 f を写像とよび,f : X! Y のように書く f によって x に対応する Y の元を f(x)
数学 ⅡB < 公理 > 公理を論拠に定義を用いて定理を証明する 1 大小関係の公理 順序 (a > b, a = b, a > b 1 つ成立 a > b, b > c a > c 成立 ) 順序と演算 (a > b a + c > b + c (a > b, c > 0 ac > bc) 2 図
 数学 Ⅱ < 公理 > 公理を論拠に定義を用いて定理を証明する 大小関係の公理 順序 >, =, > つ成立 >, > > 成立 順序と演算 > + > + >, > > 図形の公理 平行線の性質 錯角 同位角 三角形の合同条件 三角形の合同相似 量の公理 角の大きさ 線分の長さ < 空間における座漂とベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル
数学 Ⅱ < 公理 > 公理を論拠に定義を用いて定理を証明する 大小関係の公理 順序 >, =, > つ成立 >, > > 成立 順序と演算 > + > + >, > > 図形の公理 平行線の性質 錯角 同位角 三角形の合同条件 三角形の合同相似 量の公理 角の大きさ 線分の長さ < 空間における座漂とベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル
学習指導要領
 (1) いろいろな式 学習指導要領紅葉川高校学力スタンダードア式と証明展開の公式を用いて 3 乗に関わる式を展開すること ( ア ) 整式の乗法 除法 分数式の計算ができるようにする 三次の乗法公式及び因数分解の公式を理解し そ 3 次の因数分解の公式を理解し それらを用いて因数れらを用いて式の展開や因数分解をすること また 分解することができるようにする 整式の除法や分数式の四則計算について理解し
(1) いろいろな式 学習指導要領紅葉川高校学力スタンダードア式と証明展開の公式を用いて 3 乗に関わる式を展開すること ( ア ) 整式の乗法 除法 分数式の計算ができるようにする 三次の乗法公式及び因数分解の公式を理解し そ 3 次の因数分解の公式を理解し それらを用いて因数れらを用いて式の展開や因数分解をすること また 分解することができるようにする 整式の除法や分数式の四則計算について理解し
JavaプログラミングⅠ
 Java プログラミング Ⅰ 4 回目演算子 今日の講義で学ぶ内容 演算子とオペランド 式 様々な演算子 代表的な演算子の使用例 演算子とオペランド 演算子 演算の種類です例えば + - * / 掛け算の記号は ではなく *( アスタリスク ) を使います割り算の記号は ではなく /( スラッシュ ) を使います オペランド 演算の対象です例えば 5( 値 ) num( 変数 ) 式 演算子とオペランドの組み合わせにより構成される数式です式は演算結果をもちます
Java プログラミング Ⅰ 4 回目演算子 今日の講義で学ぶ内容 演算子とオペランド 式 様々な演算子 代表的な演算子の使用例 演算子とオペランド 演算子 演算の種類です例えば + - * / 掛け算の記号は ではなく *( アスタリスク ) を使います割り算の記号は ではなく /( スラッシュ ) を使います オペランド 演算の対象です例えば 5( 値 ) num( 変数 ) 式 演算子とオペランドの組み合わせにより構成される数式です式は演算結果をもちます
Taro-再帰関数Ⅰ(公開版).jtd
 再帰関数 Ⅰ 0. 目次 1. 階乗関数 2. 基本演算 2. 1 乗算 2. 2 除算 2. 3 剰余 3. 最大公約数. フィボナッチ関数 5. べき乗関数 5. 1 解法 1 5. 2 解法 2-1 - 1. 階乗関数 再帰関数は 関数の中で自分自身を呼び出す関数をいう 関数を簡潔に定義することができる 階乗関数 f(n) (n 0) を明示的に書くとつぎのようになる 再帰的定義 f(n) =
再帰関数 Ⅰ 0. 目次 1. 階乗関数 2. 基本演算 2. 1 乗算 2. 2 除算 2. 3 剰余 3. 最大公約数. フィボナッチ関数 5. べき乗関数 5. 1 解法 1 5. 2 解法 2-1 - 1. 階乗関数 再帰関数は 関数の中で自分自身を呼び出す関数をいう 関数を簡潔に定義することができる 階乗関数 f(n) (n 0) を明示的に書くとつぎのようになる 再帰的定義 f(n) =
テンソル ( その ) テンソル ( その ) スカラー ( 階のテンソル ) スカラー ( 階のテンソル ) 階数 ベクトル ( 階のテンソル ) ベクトル ( 階のテンソル ) 行列表現 シンボリック表現 [ ]
![テンソル ( その ) テンソル ( その ) スカラー ( 階のテンソル ) スカラー ( 階のテンソル ) 階数 ベクトル ( 階のテンソル ) ベクトル ( 階のテンソル ) 行列表現 シンボリック表現 [ ] テンソル ( その ) テンソル ( その ) スカラー ( 階のテンソル ) スカラー ( 階のテンソル ) 階数 ベクトル ( 階のテンソル ) ベクトル ( 階のテンソル ) 行列表現 シンボリック表現 [ ]](/thumbs/93/113587990.jpg) Tsor th-ordr tsor by dcl xprsso m m Lm m k m k L mk kk quott rul by symbolc xprsso Lk X thrd-ordr tsor cotrcto j j Copyrght s rsrvd. No prt of ths documt my b rproducd for proft. テンソル ( その ) テンソル ( その
Tsor th-ordr tsor by dcl xprsso m m Lm m k m k L mk kk quott rul by symbolc xprsso Lk X thrd-ordr tsor cotrcto j j Copyrght s rsrvd. No prt of ths documt my b rproducd for proft. テンソル ( その ) テンソル ( その
<4D F736F F D208C51985F82CD82B682DF82CC88EA95E A>
 群論はじめの一歩 (6) 6. 指数 2の定理と2 面体群 命題 H を群 G の部分群とする そして 左剰余類全体 G/ H 右剰 余類全体 \ H G ともに指数 G: H 2 と仮定する このとき H は群 G の正規部分群である すなわち H 注意 ) 集合 A と B があるとき A から B を引いた差集合は A \ B と書かれるが ここで書いた H \ Gは差集合ではなく右剰余類の集合の意味である
群論はじめの一歩 (6) 6. 指数 2の定理と2 面体群 命題 H を群 G の部分群とする そして 左剰余類全体 G/ H 右剰 余類全体 \ H G ともに指数 G: H 2 と仮定する このとき H は群 G の正規部分群である すなわち H 注意 ) 集合 A と B があるとき A から B を引いた差集合は A \ B と書かれるが ここで書いた H \ Gは差集合ではなく右剰余類の集合の意味である
2013年度 九州大・理系数学
 九州大学 ( 理系 ) 前期日程問題 解答解説のページへ a> とし, つの曲線 y= ( ), y= a ( > ) を順にC, C とする また, C とC の交点 P におけるC の接線をl とする 以下 の問いに答えよ () 曲線 C とy 軸および直線 l で囲まれた部分の面積をa を用いて表せ () 点 P におけるC の接線と直線 l のなす角を ( a) とき, limasin θ(
九州大学 ( 理系 ) 前期日程問題 解答解説のページへ a> とし, つの曲線 y= ( ), y= a ( > ) を順にC, C とする また, C とC の交点 P におけるC の接線をl とする 以下 の問いに答えよ () 曲線 C とy 軸および直線 l で囲まれた部分の面積をa を用いて表せ () 点 P におけるC の接線と直線 l のなす角を ( a) とき, limasin θ(
Microsoft Word - ‚f’fl.doc
 素数いろいろ H1 下尾知 1 素数 (1) 素数の定義知っているとは思いますが 素数の定義をあらためて確認しましょう 素数 :1およびその数自身の他に約数を有しない正の整数 広辞苑第五版 より例えば 13は1と13と-1と-13でのみ割り切れますが 約数も正の整数ですので -1や-13は13の約数ではありません ゆえに13は素数です 誤解がないために書いておきますが 1 およびその数自身の他に約数を有しない正の整数
素数いろいろ H1 下尾知 1 素数 (1) 素数の定義知っているとは思いますが 素数の定義をあらためて確認しましょう 素数 :1およびその数自身の他に約数を有しない正の整数 広辞苑第五版 より例えば 13は1と13と-1と-13でのみ割り切れますが 約数も正の整数ですので -1や-13は13の約数ではありません ゆえに13は素数です 誤解がないために書いておきますが 1 およびその数自身の他に約数を有しない正の整数
2014年度 東京大・文系数学
 014 東京大学 ( 文系 ) 前期日程問題 1 解答解説のページへ以下の問いに答えよ (1) t を実数の定数とする 実数全体を定義域とする関数 f ( x ) を f ( x) =- x + 8tx- 1x+ t - 17t + 9t-18 と定める このとき, 関数 f ( x ) の最大値を t を用いて表せ () (1) の 関数 f ( x ) の最大値 を g( t ) とする t が
014 東京大学 ( 文系 ) 前期日程問題 1 解答解説のページへ以下の問いに答えよ (1) t を実数の定数とする 実数全体を定義域とする関数 f ( x ) を f ( x) =- x + 8tx- 1x+ t - 17t + 9t-18 と定める このとき, 関数 f ( x ) の最大値を t を用いて表せ () (1) の 関数 f ( x ) の最大値 を g( t ) とする t が
<4D F736F F F696E74202D2088C38D86979D985F82D682CC8FB591D22E >
 08/05/17 IISEC オープンキャンパス模擬授業 (08/06/18 改訂 ) 暗号理論への招待 擬似乱数の話 情報セキュリティ大学院大学有田正剛 0 はじめに 暗号理論の対象 擬似乱数 擬似ランダム関数 一方向性関数 共通鍵暗号 公開鍵暗号 MAC デジタル署名 暗号プロトコル ( 鍵共有 コミットメント ) セキュアシステム / サービス ( 電子投票 オークション ) 暗号理論の目標
08/05/17 IISEC オープンキャンパス模擬授業 (08/06/18 改訂 ) 暗号理論への招待 擬似乱数の話 情報セキュリティ大学院大学有田正剛 0 はじめに 暗号理論の対象 擬似乱数 擬似ランダム関数 一方向性関数 共通鍵暗号 公開鍵暗号 MAC デジタル署名 暗号プロトコル ( 鍵共有 コミットメント ) セキュアシステム / サービス ( 電子投票 オークション ) 暗号理論の目標
<4D F736F F D2094F795AA95FB92F68EAE82CC89F082AB95FB E646F63>
 力学 A 金曜 限 : 松田 微分方程式の解き方 微分方程式の解き方のところが分からなかったという声が多いので プリントにまとめます 数学的に厳密な話はしていないので 詳しくは数学の常微分方程式を扱っているテキストを参照してください また os s は既知とします. 微分方程式の分類 常微分方程式とは 独立変数 と その関数 その有限次の導関数 がみたす方程式 F,,, = のことです 次までの導関数を含む方程式を
力学 A 金曜 限 : 松田 微分方程式の解き方 微分方程式の解き方のところが分からなかったという声が多いので プリントにまとめます 数学的に厳密な話はしていないので 詳しくは数学の常微分方程式を扱っているテキストを参照してください また os s は既知とします. 微分方程式の分類 常微分方程式とは 独立変数 と その関数 その有限次の導関数 がみたす方程式 F,,, = のことです 次までの導関数を含む方程式を
データ解析
 データ解析 ( 前期 ) 最小二乗法 向井厚志 005 年度テキスト 0 データ解析 - 最小二乗法 - 目次 第 回 Σ の計算 第 回ヒストグラム 第 3 回平均と標準偏差 6 第 回誤差の伝播 8 第 5 回正規分布 0 第 6 回最尤性原理 第 7 回正規分布の 分布の幅 第 8 回最小二乗法 6 第 9 回最小二乗法の練習 8 第 0 回最小二乗法の推定誤差 0 第 回推定誤差の計算 第
データ解析 ( 前期 ) 最小二乗法 向井厚志 005 年度テキスト 0 データ解析 - 最小二乗法 - 目次 第 回 Σ の計算 第 回ヒストグラム 第 3 回平均と標準偏差 6 第 回誤差の伝播 8 第 5 回正規分布 0 第 6 回最尤性原理 第 7 回正規分布の 分布の幅 第 8 回最小二乗法 6 第 9 回最小二乗法の練習 8 第 0 回最小二乗法の推定誤差 0 第 回推定誤差の計算 第
2015-2017年度 2次数学セレクション(複素数)解答解説
 05 次数学セレクション解答解説 [ 筑波大 ] ( + より, 0 となり, + から, ( (,, よって, の描く図形 C は, 点 を中心とし半径が の円である すなわち, 原 点を通る円となる ( は虚数, は正の実数より, である さて, w ( ( とおくと, ( ( ( w ( ( ( ここで, w は純虚数より, は純虚数となる すると, の描く図形 L は, 点 を通り, 点 と点
05 次数学セレクション解答解説 [ 筑波大 ] ( + より, 0 となり, + から, ( (,, よって, の描く図形 C は, 点 を中心とし半径が の円である すなわち, 原 点を通る円となる ( は虚数, は正の実数より, である さて, w ( ( とおくと, ( ( ( w ( ( ( ここで, w は純虚数より, は純虚数となる すると, の描く図形 L は, 点 を通り, 点 と点
オートマトン 形式言語及び演習 3. 正規表現 酒井正彦 正規表現とは 正規表現 ( 正則表現, Regular Expression) オートマトン : 言語を定義する機械正規表現 : 言語
 オートマトン 形式言語及び演習 3. 酒井正彦 www.trs.css.i.nagoya-u.ac.jp/~sakai/lecture/automata/ とは ( 正則表現, Regular Expression) オートマトン : 言語を定義する機械 : 言語を記号列で定義 - 記述しやすい ( ユーザフレンドリ ) 例 :01 + 10 - UNIX の grep コマンド - UNIX の
オートマトン 形式言語及び演習 3. 酒井正彦 www.trs.css.i.nagoya-u.ac.jp/~sakai/lecture/automata/ とは ( 正則表現, Regular Expression) オートマトン : 言語を定義する機械 : 言語を記号列で定義 - 記述しやすい ( ユーザフレンドリ ) 例 :01 + 10 - UNIX の grep コマンド - UNIX の
Microsoft PowerPoint - lec4.ppt
 本日の内容 繰り返し計算 while 文, for 文 例題 1. 最大公約数の計算例題 2. 自然数の和 while 文例題 3. フィボナッチ数列例題 4. 自然数の和 for 文例題 5. 九九の表繰り返しの入れ子 今日の到達目標 繰り返し (while 文, for 文 ) を使って, 繰り返し計算を行えるようになること ループカウンタとして, 整数の変数を使うこと 今回も, 見やすいプログラムを書くために,
本日の内容 繰り返し計算 while 文, for 文 例題 1. 最大公約数の計算例題 2. 自然数の和 while 文例題 3. フィボナッチ数列例題 4. 自然数の和 for 文例題 5. 九九の表繰り返しの入れ子 今日の到達目標 繰り返し (while 文, for 文 ) を使って, 繰り返し計算を行えるようになること ループカウンタとして, 整数の変数を使うこと 今回も, 見やすいプログラムを書くために,
Microsoft PowerPoint - C4(反復for).ppt
 C 言語プログラミング 繰返し ( for 文と while 文 ) 例題 (10 個のデータの平均を求める ) 手順 入力データをx1,x2,,x10 として, (x1+x2+x3+x4+x5+x6+x7+x8+x9+x10)/10 を計算する データ数が,1000 個,10000 個, となったらどうする? データ数個分の 変数の宣言, scanf 関数の呼出し, 加算式の記述 が必要 1 総和を求めること
C 言語プログラミング 繰返し ( for 文と while 文 ) 例題 (10 個のデータの平均を求める ) 手順 入力データをx1,x2,,x10 として, (x1+x2+x3+x4+x5+x6+x7+x8+x9+x10)/10 を計算する データ数が,1000 個,10000 個, となったらどうする? データ数個分の 変数の宣言, scanf 関数の呼出し, 加算式の記述 が必要 1 総和を求めること
2018試行 共通テスト 数学ⅠA 解答例
 第 1 問 共通テスト ( 試行調査 018) 数学 Ⅰ 数学 A 解答例 [1] (1) 1 のみを要素としてもつ集合が集合 A の部分集合 であることは, C = {1} とおくと, CÌ Aと表される () 命題 x Î, y Î ならば, x+ yîである が偽であることを示すための反例は, x Î かつ y Î かつ x+ yï から探すと, ( x, y ) = (3-3, 3-1),
第 1 問 共通テスト ( 試行調査 018) 数学 Ⅰ 数学 A 解答例 [1] (1) 1 のみを要素としてもつ集合が集合 A の部分集合 であることは, C = {1} とおくと, CÌ Aと表される () 命題 x Î, y Î ならば, x+ yîである が偽であることを示すための反例は, x Î かつ y Î かつ x+ yï から探すと, ( x, y ) = (3-3, 3-1),
学習指導要領
 (1) 数と式 ア整式 ( ア ) 式の展開と因数分解二次の乗法公式及び因数分解の公式の理解を深め 式を多面的にみたり目的に応じて式を適切に変形したりすること (ax b)(cx d) acx (ad bc)x bd などの基本的な公式を活用して 二次式の展開や因数分解ができる また 式の置き換えや一文字に着目するなどして 展開 因数分解ができる ( 例 ) 次の問に答えよ (1) (3x a)(4x
(1) 数と式 ア整式 ( ア ) 式の展開と因数分解二次の乗法公式及び因数分解の公式の理解を深め 式を多面的にみたり目的に応じて式を適切に変形したりすること (ax b)(cx d) acx (ad bc)x bd などの基本的な公式を活用して 二次式の展開や因数分解ができる また 式の置き換えや一文字に着目するなどして 展開 因数分解ができる ( 例 ) 次の問に答えよ (1) (3x a)(4x
Microsoft PowerPoint - ce07-09b.ppt
 6. フィードバック系の内部安定性キーワード : 内部安定性, 特性多項式 6. ナイキストの安定判別法キーワード : ナイキストの安定判別法 復習 G u u u 制御対象コントローラ u T 閉ループ伝達関数フィードバック制御系 T 相補感度関数 S S T L 開ループ伝達関数 L いま考えているのは どの伝達関数,, T, L? フィードバック系の内部安定性 u 内部安定性 T G だけでは不十分
6. フィードバック系の内部安定性キーワード : 内部安定性, 特性多項式 6. ナイキストの安定判別法キーワード : ナイキストの安定判別法 復習 G u u u 制御対象コントローラ u T 閉ループ伝達関数フィードバック制御系 T 相補感度関数 S S T L 開ループ伝達関数 L いま考えているのは どの伝達関数,, T, L? フィードバック系の内部安定性 u 内部安定性 T G だけでは不十分
学習指導要領
 (1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 自然数 整数 有理数 無理数の包含関係など 実数 の構成を理解する ( 例 ) 次の空欄に適当な言葉をいれて, 数の集合を表しなさい ア イ 無理数 整数 ウ 無理数の加法及び減法 乗法公式などを利用した計 算ができる また 分母だけが二項である無理数の 分母の有理化ができる ( 例 1)
(1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 自然数 整数 有理数 無理数の包含関係など 実数 の構成を理解する ( 例 ) 次の空欄に適当な言葉をいれて, 数の集合を表しなさい ア イ 無理数 整数 ウ 無理数の加法及び減法 乗法公式などを利用した計 算ができる また 分母だけが二項である無理数の 分母の有理化ができる ( 例 1)
20~22.prt
 [ 三クリア W] 辺が等しいことの証明 ( 円周角と弦の関係利用 ) の の二等分線がこの三角形の外接円と交わる点をそれぞれ とするとき 60 ならば であることを証明せよ 60 + + 0 + 0 80-60 60 から ゆえに 等しい長さの弧に対する弦の長さは等しいから [ 三クリア ] 方べきの定理 接線と弦のなす角と円周角を利用 線分 を直径とする円 があり 右の図のように の延長上の点
[ 三クリア W] 辺が等しいことの証明 ( 円周角と弦の関係利用 ) の の二等分線がこの三角形の外接円と交わる点をそれぞれ とするとき 60 ならば であることを証明せよ 60 + + 0 + 0 80-60 60 から ゆえに 等しい長さの弧に対する弦の長さは等しいから [ 三クリア ] 方べきの定理 接線と弦のなす角と円周角を利用 線分 を直径とする円 があり 右の図のように の延長上の点
Microsoft Word - スーパーナビ 第6回 数学.docx
 1 ⑴ 与式 =- 5 35 +14 35 =9 35 1 ⑵ 与式 =9-(-5)=9+5=14 1 ⑶ 与式 = 4(a-b)-3(5a-3b) = 8a-4b-15a+9b = -7a+5b 1 1 1 1 ⑷ 与式 =(²+ 1+1²)-{²+(-3+)+(-3) } 1 ⑷ 与式 =(²++1)-(²--6)=²++1-²++6=3+7 1 ⑸ 与式 = - ² + 16 = - +16
1 ⑴ 与式 =- 5 35 +14 35 =9 35 1 ⑵ 与式 =9-(-5)=9+5=14 1 ⑶ 与式 = 4(a-b)-3(5a-3b) = 8a-4b-15a+9b = -7a+5b 1 1 1 1 ⑷ 与式 =(²+ 1+1²)-{²+(-3+)+(-3) } 1 ⑷ 与式 =(²++1)-(²--6)=²++1-²++6=3+7 1 ⑸ 与式 = - ² + 16 = - +16
Microsoft PowerPoint - 7.pptx
 通信路 (7 章 ) 通信路のモデル 情報 送信者 通信路 受信者 A a,, a b,, b B m = P( b ),, P( b m ) 外乱 ( 雑音 ) n = P( a,, P( a ) n ) 送信情報源 ( 送信アルファベットと生成確率 ) 受信情報源 ( 受信アルファベッと受信確率 ) でもよい 生成確率 ) 受信確率 ) m n 2 イメージ 外乱 ( 雑音 ) により記号 a
通信路 (7 章 ) 通信路のモデル 情報 送信者 通信路 受信者 A a,, a b,, b B m = P( b ),, P( b m ) 外乱 ( 雑音 ) n = P( a,, P( a ) n ) 送信情報源 ( 送信アルファベットと生成確率 ) 受信情報源 ( 受信アルファベッと受信確率 ) でもよい 生成確率 ) 受信確率 ) m n 2 イメージ 外乱 ( 雑音 ) により記号 a
<4D F736F F D E4F8E9F82C982A882AF82E98D7397F1>
 3 三次における行列 要旨高校では ほとんど 2 2 の正方行列しか扱ってなく 三次の正方行列について考えてみたかったため 数 C で学んだ定理を三次の正方行列に応用して 自分たちで仮説を立てて求めていったら 空間における回転移動を表す行列 三次のケーリー ハミルトンの定理 三次における逆行列を求めたり 仮説をたてることができた. 目的 数 C で学んだ定理を三次の正方行列に応用する 2. 概要目的の到達点として
3 三次における行列 要旨高校では ほとんど 2 2 の正方行列しか扱ってなく 三次の正方行列について考えてみたかったため 数 C で学んだ定理を三次の正方行列に応用して 自分たちで仮説を立てて求めていったら 空間における回転移動を表す行列 三次のケーリー ハミルトンの定理 三次における逆行列を求めたり 仮説をたてることができた. 目的 数 C で学んだ定理を三次の正方行列に応用する 2. 概要目的の到達点として
Microsoft Word - 201hyouka-tangen-1.doc
 数学 Ⅰ 評価規準の作成 ( 単元ごと ) 数学 Ⅰ の目標及び図形と計量について理解させ 基礎的な知識の習得と技能の習熟を図り それらを的確に活用する機能を伸ばすとともに 数学的な見方や考え方のよさを認識できるようにする 評価の観点の趣旨 式と不等式 二次関数及び図形と計量における考え方に関 心をもつとともに 数学的な見方や考え方のよさを認識し それらを事象の考察に活用しようとする 式と不等式 二次関数及び図形と計量における数学的な見
数学 Ⅰ 評価規準の作成 ( 単元ごと ) 数学 Ⅰ の目標及び図形と計量について理解させ 基礎的な知識の習得と技能の習熟を図り それらを的確に活用する機能を伸ばすとともに 数学的な見方や考え方のよさを認識できるようにする 評価の観点の趣旨 式と不等式 二次関数及び図形と計量における考え方に関 心をもつとともに 数学的な見方や考え方のよさを認識し それらを事象の考察に活用しようとする 式と不等式 二次関数及び図形と計量における数学的な見
 2 2 MATHEMATICS.PDF 200-2-0 3 2 (p n ), ( ) 7 3 4 6 5 20 6 GL 2 (Z) SL 2 (Z) 27 7 29 8 SL 2 (Z) 35 9 2 40 0 2 46 48 2 2 5 3 2 2 58 4 2 6 5 2 65 6 2 67 7 2 69 2 , a 0 + a + a 2 +... b b 2 b 3 () + b n a
2 2 MATHEMATICS.PDF 200-2-0 3 2 (p n ), ( ) 7 3 4 6 5 20 6 GL 2 (Z) SL 2 (Z) 27 7 29 8 SL 2 (Z) 35 9 2 40 0 2 46 48 2 2 5 3 2 2 58 4 2 6 5 2 65 6 2 67 7 2 69 2 , a 0 + a + a 2 +... b b 2 b 3 () + b n a
学習指導要領
 (1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 絶対値の意味を理解し適切な処理することができる 例題 1-3 の絶対値をはずせ 展開公式 ( a + b ) ( a - b ) = a 2 - b 2 を利用して根号を含む分数の分母を有理化することができる 例題 5 5 + 2 の分母を有理化せよ 実数の整数部分と小数部分の表し方を理解している
(1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 絶対値の意味を理解し適切な処理することができる 例題 1-3 の絶対値をはずせ 展開公式 ( a + b ) ( a - b ) = a 2 - b 2 を利用して根号を含む分数の分母を有理化することができる 例題 5 5 + 2 の分母を有理化せよ 実数の整数部分と小数部分の表し方を理解している
スライド タイトルなし
 線形代数 演習 (008 年度版 ) 008/5/6 線形代数 演習 Ⅰ コンピュータ グラフィックス, 次曲面と線形代数指南書第七の巻 直交行列, 実対称行列とその対角化, 次曲線池田勉龍谷大学理工学部数理情報学科 実行列, 正方行列, 実対称行列, 直交行列 a a N A am a MN 実行列 : すべての成分 a が実数である行列 ij ji ij 正方行列 : 行の数と列の数が等しい (
線形代数 演習 (008 年度版 ) 008/5/6 線形代数 演習 Ⅰ コンピュータ グラフィックス, 次曲面と線形代数指南書第七の巻 直交行列, 実対称行列とその対角化, 次曲線池田勉龍谷大学理工学部数理情報学科 実行列, 正方行列, 実対称行列, 直交行列 a a N A am a MN 実行列 : すべての成分 a が実数である行列 ij ji ij 正方行列 : 行の数と列の数が等しい (
作成時間 40 分 Ecommonsで夏休みの宿題を作ってみた!! 全国の教育者みんなで創る教材データベース すべての ども達に良質な教材を 夏休みの宿題 提出 2019 年 8 26 注意事項 1. 解答は解答 紙に記 すること 2. 解答は ずに 分の で答えること 3. スケジュールを てて,
 作成時間 40 分 Ecommonsで夏休みの宿題を作ってみた!! 全国の教育者みんなで創る教材データベース すべての ども達に良質な教材を 夏休みの宿題 提出 019 年 8 6 注意事項 1. 解答は解答 紙に記 すること. 解答は ずに 分の で答えること 3. スケジュールを てて, 計画的に うこと 4. 丸付けをして提出すること 5. 間違えた箇所は, 直しをすること 6. 提出 を厳守すること
作成時間 40 分 Ecommonsで夏休みの宿題を作ってみた!! 全国の教育者みんなで創る教材データベース すべての ども達に良質な教材を 夏休みの宿題 提出 019 年 8 6 注意事項 1. 解答は解答 紙に記 すること. 解答は ずに 分の で答えること 3. スケジュールを てて, 計画的に うこと 4. 丸付けをして提出すること 5. 間違えた箇所は, 直しをすること 6. 提出 を厳守すること
相対性理論入門 1 Lorentz 変換 光がどのような座標系に対しても同一の速さ c で進むことから導かれる座標の一次変換である. (x, y, z, t ) の座標系が (x, y, z, t) の座標系に対して x 軸方向に w の速度で進んでいる場合, 座標系が一次変換で関係づけられるとする
 相対性理論入門 Lorentz 変換 光がどのような座標系に対しても同一の速さ で進むことから導かれる座標の一次変換である. x, y, z, t ) の座標系が x, y, z, t) の座標系に対して x 軸方向に w の速度で進んでいる場合, 座標系が一次変換で関係づけられるとすると, x A x wt) y y z z t Bx + Dt 弨弱弩弨弲弩弨弳弩弨弴弩 が成立する. 図 : 相対速度
相対性理論入門 Lorentz 変換 光がどのような座標系に対しても同一の速さ で進むことから導かれる座標の一次変換である. x, y, z, t ) の座標系が x, y, z, t) の座標系に対して x 軸方向に w の速度で進んでいる場合, 座標系が一次変換で関係づけられるとすると, x A x wt) y y z z t Bx + Dt 弨弱弩弨弲弩弨弳弩弨弴弩 が成立する. 図 : 相対速度
1/20 平成 29 年 3 月 25 日午前 11 時 7 分第 1 章 :U(N) 群 SU(N) 群 ( 学部 4 年次向 ) 第 1 章 :U(N) 群 SU(N) 群 Ⅰ. 標準模型の素粒子 素粒子の分類図 3 世代 素粒子の標準理論に含まれる素粒子は 素粒子の分類図 から R, G, B
 / 平成 9 年 3 月 5 日午前 時 7 分第 章 :U() 群 SU() 群 ( 学部 4 年次向 ) 第 章 :U() 群 SU() 群 Ⅰ. 標準模型の素粒子 素粒子の分類図 3 世代 素粒子の標準理論に含まれる素粒子は 素粒子の分類図 から R, G, B R, G, B R, G, B u : 5 c :, 6 t :75,e 3 クォーク( quark ) : R, G, B R,
/ 平成 9 年 3 月 5 日午前 時 7 分第 章 :U() 群 SU() 群 ( 学部 4 年次向 ) 第 章 :U() 群 SU() 群 Ⅰ. 標準模型の素粒子 素粒子の分類図 3 世代 素粒子の標準理論に含まれる素粒子は 素粒子の分類図 から R, G, B R, G, B R, G, B u : 5 c :, 6 t :75,e 3 クォーク( quark ) : R, G, B R,
2016年度 筑波大・理系数学
 06 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ k を実数とする y 平面の曲線 C : y とC : y- + k+ -k が異なる共 有点 P, Q をもつとする ただし点 P, Q の 座標は正であるとする また, 原点を O とする () k のとりうる値の範囲を求めよ () k が () の範囲を動くとき, OPQ の重心 G の軌跡を求めよ () OPQ の面積を S とするとき,
06 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ k を実数とする y 平面の曲線 C : y とC : y- + k+ -k が異なる共 有点 P, Q をもつとする ただし点 P, Q の 座標は正であるとする また, 原点を O とする () k のとりうる値の範囲を求めよ () k が () の範囲を動くとき, OPQ の重心 G の軌跡を求めよ () OPQ の面積を S とするとき,
千葉大学 ゲーム論II
 千葉大学ゲーム論 II 第五, 六回 担当 上條良夫 千葉大学ゲーム論 II 第五 六回上條良夫 本日の講義内容 前回宿題の問題 3 の解答 Nash の交渉問題 Nash 解とその公理的特徴づけ 千葉大学ゲーム論 II 第五 六回上條良夫 宿題の問題 3 の解答 ホワイトボードでやる 千葉大学ゲーム論 II 第五 六回上條良夫 3 Nash の二人交渉問題 Nash の二人交渉問題は以下の二つから構成される
千葉大学ゲーム論 II 第五, 六回 担当 上條良夫 千葉大学ゲーム論 II 第五 六回上條良夫 本日の講義内容 前回宿題の問題 3 の解答 Nash の交渉問題 Nash 解とその公理的特徴づけ 千葉大学ゲーム論 II 第五 六回上條良夫 宿題の問題 3 の解答 ホワイトボードでやる 千葉大学ゲーム論 II 第五 六回上條良夫 3 Nash の二人交渉問題 Nash の二人交渉問題は以下の二つから構成される
Microsoft PowerPoint - kyoto
 研究集会 代数系アルゴリズムと言語および計算理論 知識の証明と暗号技術 情報セキュリティ大学大学院学院 有田正剛 1 はじめに 暗号技術の面白さとむずかしさ システムには攻撃者が存在する 条件が整ったときのベストパフォーマンスより 条件が整わないときの安全性 攻撃者は約束事 ( プロトコル ) には従わない 表面上は従っているふり 放置すると 正直者が損をする それを防ぐには 知識の証明 が基本手段
研究集会 代数系アルゴリズムと言語および計算理論 知識の証明と暗号技術 情報セキュリティ大学大学院学院 有田正剛 1 はじめに 暗号技術の面白さとむずかしさ システムには攻撃者が存在する 条件が整ったときのベストパフォーマンスより 条件が整わないときの安全性 攻撃者は約束事 ( プロトコル ) には従わない 表面上は従っているふり 放置すると 正直者が損をする それを防ぐには 知識の証明 が基本手段
解析力学B - 第11回: 正準変換
 解析力学 B 第 11 回 : 正準変換 神戸大 : 陰山聡 ホームページ ( 第 6 回から今回までの講義ノート ) http://tinyurl.com/kage2010 2011.01.27 正準変換 バネ問題 ( あえて下手に座標をとった ) ハミルトニアンを考える q 正準方程式は H = p2 2m + k 2 (q l 0) 2 q = H p = p m ṗ = H q = k(q
解析力学 B 第 11 回 : 正準変換 神戸大 : 陰山聡 ホームページ ( 第 6 回から今回までの講義ノート ) http://tinyurl.com/kage2010 2011.01.27 正準変換 バネ問題 ( あえて下手に座標をとった ) ハミルトニアンを考える q 正準方程式は H = p2 2m + k 2 (q l 0) 2 q = H p = p m ṗ = H q = k(q
Microsoft Word - lec_student-chp3_1-representative
 1. はじめに この節でのテーマ データ分布の中心位置を数値で表す 可視化でとらえた分布の中心位置を数量化する 平均値とメジアン, 幾何平均 この節での到達目標 1 平均値 メジアン 幾何平均の定義を書ける 2 平均値とメジアン, 幾何平均の特徴と使える状況を説明できる. 3 平均値 メジアン 幾何平均を計算できる 2. 特性値 集めたデータを度数分布表やヒストグラムに整理する ( 可視化する )
1. はじめに この節でのテーマ データ分布の中心位置を数値で表す 可視化でとらえた分布の中心位置を数量化する 平均値とメジアン, 幾何平均 この節での到達目標 1 平均値 メジアン 幾何平均の定義を書ける 2 平均値とメジアン, 幾何平均の特徴と使える状況を説明できる. 3 平均値 メジアン 幾何平均を計算できる 2. 特性値 集めたデータを度数分布表やヒストグラムに整理する ( 可視化する )
Microsoft PowerPoint - H21生物計算化学2.ppt
 演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
スライド 1
 暗号入門 教科書 参考書 Oded Goldreich: Foundations of Cryptography, Volume I Basic Tools, Cambridge, 2001 Oded Goldreich: Foundations of Cryptography, Volume II Basic Applications, Cambridge, 2004 J. A. ブーフマン著,
暗号入門 教科書 参考書 Oded Goldreich: Foundations of Cryptography, Volume I Basic Tools, Cambridge, 2001 Oded Goldreich: Foundations of Cryptography, Volume II Basic Applications, Cambridge, 2004 J. A. ブーフマン著,


