Microsoft PowerPoint - DigitalMedia2_2.pptx
|
|
|
- りさこ むらかわ
- 8 years ago
- Views:
Transcription
1 デジタルメディア処理 担当 : 井尻敬 デジタルメディア処理 7( 前期 ) /3 デジタル画像とは : イントロダクション / フィルタ処理 : 画素ごとの濃淡変換 線形フィルタ, 線形フィルタ /7 フィルタ処理 : フーリエ変換, ローパスフィルタ, ハイパスフィルタ 5/ 画像の幾何変換 : アファイン変換 5/8 画像の幾何変換 : 画像の補間, イメージモザイキング 5/5 画像領域分割 : 領域拡張法, 動的輪郭モデル, グラフカット法, 6/ 前半のまとめ ( 約 3 分 ) と中間試験 ( 約 7 分 ) 6/8 特徴検出 : テンプレートマッチング コーナー エッジ検出 6/5 特徴検出 : DoG 特徴量 SIFT 特徴量 ハフ変換 6/ 画像認識 : パターン認識概論, サポートベクタマシン 6/9 画像認識 : ニューラルネットワーク 深層学習 7/6 画像符号化 : 圧縮率, エントロピー, ランレングス符号化,MH 符号化 7/3 画像符号化 : DCT 変換, ウエーブレット変換など 7/ 後半のまとめ ( 約 3 分 ) と期末試験 ( 約 7 分 ) Contents : フィルタ処理 デジタル画像とは ( 復習 ) トーンカーブ 反転, 値化, ポスタリゼーション, ソラリゼーション, ガンマ変換, カラー画像 空間フィルタ ( 線形 ) 平滑化フィルタ, ソーベルフィルタ, ガウシアンフィルタ, ラプラシアンフィルタ 空間フィルタ ( 線形 ) メディアンフィルタ, バイラテラルフィルタ デジタル画像のフィルタリング
2 デジタル画像 : カラー画像 離散値を持つ画素が格 状に並んだデータ 画素 : pixel= picture + element 例 bit bitmap : 各 pixel が (R,G,B) 毎に整数値 [,55] を持つ デジタル画像 : グレースケール画像 離散値を持つ画素が格 状に並んだデータ 画素 : pixel= picture + element 例 8bit bitmap : 各 pixel が整数値 [,55] を持つ 画像 I(i,j) : j 画像 I(i,j) : j i I( i, j) I(i+,j+) : 5 : 6 : 79 : 3 : 5 : 9 i I( i, j) 7 I(i+,j+) 7 原点位置は左下のことも 原点位置は左下のことも 頻度表 ( ヒストグラム ) とは 各階調の画素数を数えた表のこと回転や平 移動に依存しない特徴量 画像処理に頻出 グレースケール画像 RGBカラー画像 ImageJ でヒストグラムを確認してみる. ImageJ 起動. 画像読み込み 3. Menu > analyze > histogram. LiveをOnにすると矩形選択した領域のヒストグラムを確認可能
3 import numpy as np import pylab as plt import cv import itertools # 画像読み込み & グレースケール化 img = cv.imread("imgs/sample.png") img_gry = cv.cvtcolor( img, cv.color_bgrgray ) #histogram 生成 hist = np.zeros(56) for y in range(img_gry.shape[]): for x in range(img_gry.shape[]): hist[ img_gry[y,x] ] += #window を生成して画像を表示 cv.imshow("image", img_gry ) #hist を matplotlib で表示 plt.plot(hist) plt.xlim([,56]) plt.show() ヒストグラムの計算 : histograpm.py デジタル画像のフィルタリング 処理 に対し何らかの計算処理を施し 特定の周波数を持つ信号を強調する 捨てる ( ノイズ除去 ) アーティスティックな効果を得る 画像処理 ( ステレオ視 領域分割 識別器 ) に必要な特徴ベクトルを得る トーンカーブ CToneCurve.exe (C++) Image>Adjust>Window/Level (ImageJ) は 8bit グレースケールとする 各画素の値を異なる値に変換する階調変換関数を考える 階調変換関数をグラフで表現したものをトーンカーブと呼ぶ 55 出 画素値 トーンカーブ 画素値 55
4 トーンカーブは写真編集の基本ツール トーンカーブ : コントラストを上げる GIMP 55 A B C 出 55 ImageJ: 由編集でないのでちょっと違うけど PhotoShop Elements カラーカーブ使いやすいように 由度の限定されたトーンカーブのようなもの Photoshop CS にはトーンカーブがある ( あった ) 領域 A : 出 画素値 となり つぶれ 領域 C : 出 画素値 55 となり び 領域 B : 傾きが より きいため 画素値の取り得る範囲が広がりコントラストが上がる画素値は離散値であるため出 ヒストグラムは び びに トーンカーブ : コントラストをさげる トーンカーブ : 特殊効果 ネガポジ反転 値化 55 出 55 ポスタリゼーション 閾値より下は 閾値以上は 55 ソラリゼーション 傾きが より さいため 出 画素値の取り得る範囲が縮まり コントラストが下がる 元画像 出 の 数を極端に減らす 実装が間に合わず 書きで曲線を与えました 本来は関数で与えるべき 上記のような曲線を指定
5 元画像 トーンカーブ : ガンマ補正 次のトーンカーブを利 した濃淡変換をガンマ変換と呼ぶ : 値 [,55] : 出 値 [,55] : パラメータ ( >) =. =/3..5. =.5 3. RGB 各チャンネルにガンマ補正を適 トーンカーブ : カラー画像への適 カラー画像をトーンカーブで編集するとき RGBの各チャンネルにトーンカーブの画素値変換を適 YCbCr Colorに変換し輝度値成分 (Y) のみに変換を適 その他 R G Y RGB color YCbCr color 輝度 / み / み B Cb Cr 画像出 デバイスには 出力値 入力値 と う関係があり この特性を補正する 的で上記の関数が いられていた これを画像の補正に利 したのがガンマ変換 トーンカーブ : カラー画像への適 トーンカーブ : カラー画像への適 γ=.3 のガンマ変換 RGB 各チャンネル YCbCr の輝度 Y のみ γ=.3 のガンマ変換 RGB 各チャンネル YCbCr の輝度 Y のみ
6 トーンカーブ : カラー画像への適 トーンカーブ : まとめ トーンカーブ : 各画素の輝度値 を変換する階調変換関数 画像の 栄えの編集に利 される キーワード : コントラスト変換 ネガポジ反転 ポスタリゼーション ソラリゼーション 値化 ガンマ補正 55 ポスタリゼーション RGB 各チャンネル YCbCr の輝度 Y のみ (Cb Cr の階調数は減らない ) 出 画素値 画素値 55 import numpy as np import cv import itertools def myconvolve(srcimg, filter) : H = srcimg.shape[] W = srcimg.shape[] R = int(filter.shape[] / ) trgtimg = np.zeros(srcimg.shape) Convolution.py 線形フィルタの計算 for v, u in itertools.product(range(,h-),range(,w-)): pix =. for vv, uu in itertools.product(range(-r,r+),range(-r,r+)) : pix += filter[r + vv][r + uu] * srcimg[v+vv][u+uu] trgtimg[v][u] = min(55,max(,abs(pix))) return np.uint8(trgtimg) img = cv.imread("imgs/lenacolcd.png") img = cv.cvtcolor( img, cv.color_bgrgray ) filter_smooth = np.array( [[,, ],[.,.,.],[.,.,.]])/9. filter_sobelv = np.array( [[-.,-.,-.],[.,.,.],[.,.,.]]) filter_sobelh = np.array( [[-.,.,.],[-.,.,.],[-.,.,.]]) img_smooth = myconvolve(img, filter_smooth ) img_sobelv = myconvolve(img, filter_sobelv ) img_sobelh = myconvolve(img, filter_sobelh ) 空間フィルタ ( 線形 ) cv.imshow("original ", img ) cv.imshow("img_smooth", img_smooth ) cv.imshow("img_sovelv", img_sobelv ) cv.imshow("img_sovelh", img_sobelh ) cv.waitkey()
7 線形フィルタの例 線形フィルタの例 ぼかす 先鋭化 エッジ抽出横 向縦 向 空間フィルタとは 空間フィルタとは周囲の情報を利 して画素値を決めるフィルタ 空間フィルタは 線形フィルタと 線形フィルタに分けられる トーンカーブ : 出 画素 Iʼ(i,j) を求めるのに 画素 I(i.j) のみを利 : I(i,j) I(i,j) 出 画像 : Iʼ(i,j) Iʼ(i,j) 空間フィルタ : 出 画素 Iʼ(i,j) を求めるのに 画素 I(i.j) の周囲画素も利 : I(i,j) I(i,j) 出 画像 : Iʼ(i,j) Iʼ (i,j) 線形フィルタとは 出 画素値を周囲画素の重み付和で計算するフィルタ,,, (i,j) Iʼ (i,j) 出 画像 h(i,j) フィルタ (i,j) I(i,j)
8 線形フィルタの例 D 線形フィルタの例 D 平滑化したい! 平滑化したい! /3 /3 /3 /3 /3 / 周囲 3 ピクセルの平均を取る 周囲 3 ピクセルの平均を取る 端ははみ出すので値をコピー ( ほかの 法もある ) 線形フィルタの例 D 線形フィルタの例 D もっと平滑化したい! エッジ ( 変化の きい部分 ) を検出したい / / / / / 周囲 5 ピクセルの平均を取る 右と左のピクセルの差をとる 端ははみ出すので値をコピー ( ほかの 法もある )
9 線形フィルタ : 平滑化 9 5 LinaerFilter.exe (C++) convolution.py (python) Process>Filters>Convolve (ImageJ) 線形フィルタ : 特定 向の平滑化 線形フィルタ : ガウシアンフィルタ 6 係数をガウス分布に近づけ中央ほど強い重みに 画像の出典 [CG Arts 協会ディジタル画像処理 ] 図 5.8, 5.9
10 線形フィルタ : ガウシアンフィルタ ガウス関数 D exp ガウス関数 D, exp = = 68.3% 95.% 99.7% これを重みにして線形フィルタをしたいさすがに 3x3 は精度が悪くない?? 68.3% 95.% 99.7% 線形フィルタ : ガウシアンフィルタ 線形フィルタ : 微分 標準偏差 σ の きなガウス関数の畳み込みを計算するとき 3 3 や 5 5 の窓では精度が悪い 精度を出すには窓の半径を 3σ 程度にすべき ( 計算時間はかかる ) (3σ) (3σ) (,), 例 ) σ = 5 pixel のガウシアンフィルタ Window size は 3 3 が適当 関数, の 軸, 軸 向の偏微分は以下の通り定義され,, lim,, lim,, 点, における 軸, 軸 向の関数, の傾きを与える. また,, の勾配, は 次元ベクトルであり,,,, 点, において, の増加が 番 きくなる 向を す 微分の復習. 丈夫ですよね? 練習., 上記の関数の (,), (,3) における勾配を計算し さらに図 せよ
11 線形フィルタ : 微分 線形フィルタ : 微分 I(u,v) 次元関数 z= f(x,y) の x 向偏微分 v v u I x I(x) グレースケール画像 I(u,v) は, さ関数 z = I(u,v) と なせるなので関数 I(u,v) の勾配 ( 微分 ) は計算できそう v, lim,, 画像 z=i(i,j) の横 向偏微分 ( 近似 ),,,,,,, (a) (b) (c) - - 正値 :, 負値 : で可視化 -/ / I(u,v) の勾配は, 画像の変化の きい 向を表す 画像の出典 [Ijiri et al 3, Eurographics] h = pitch ( 画素サイズ ) = と近似 (a) (b) (c) 線形フィルタ : 微分 -/ /, 横方向微分 線形フィルタ : 微分 前述の単純なフィルタはノイズにも鋭敏に反応する ノイズを押さえつつエッジを検出するフィルタが必要横 向微分 : 横 向微分し縦 向平滑化する縦 向微分 : 縦 向微分し横 向平滑化する, 教科書図 5.6 微分フィルタには画像のエッジで強く応答する -/ /, 縦方向微分 Prewitt filter Sobel filter - - -
12 元画像 フィルタ処理 右の7x7 画像に対して. 横 向 Sobelフィルタを適 せよ. 縦 向 Sobelフィルタを適 せよ 3. ガウシアンフィルタを適 せよ 微分フィルタの正値を可視化 Sobel フィルタではノイズが削減されているのが分かる 横 Sobel 縦 Sobel ガウシアン 線形フィルタ : 階微分フィルタ 線形フィルタ : ラプラシアンフィルタ 関数, の 階偏微分は, 以下の通り定義される, lim,,, 画像 I(i,j) の 階偏微分の近似は,,, - - 関数, のラプラシアン,,,, = - * + - * = - * 画像, のラプラシアン,, 出典 [CGArts 協会, デジタル画像処理図 5.6] ラプラシアンフィルタ * は convolution 向に依存しないエッジが 度で得られるエッジをまたぎ正負の対が現れる なら [-+] が現れる
13 線形フィルタ : 先鋭化フィルタ 回微分に関するラプラシアンフィルタを改良すると画像のエッジを強調する先鋭化フィルタが設計できる? まとめ : 空間フィルタ ( 線形 ) 出 画素値を周囲画素の重み付和で計算するフィルタ,,, 平滑化フィルタ ガウシアンフィルタ 先鋭化フィルタ /9 /9 /9 /9 /9 /9 /9 /9 /9 /6 /6 /6 /6 /6 /6 /6 /6 /6? [CGArts 協会, デジタル画像処理 ] 図 5.6, Sobelフィルタ ( 横 ) Sobelフィルタ ( 縦 ) ラプラシアンフィルタ
Microsoft PowerPoint - dm1_3.pptx
 スケジュール 9/6 イントロダクション : デジタル画像とは, 量 化と標本化,Dynamic Range /3 イントロダクション : デジタルカメラ, 間の視覚, 表 系 / フィルタ処理 : トーンカーブ, 線形フィルタ デジタルメディア処理 担当 : 井尻敬 /7 フィルタ処理 : 線形フィルタ, ハーフトーニング / フィルタ処理 3 : 離散フーリエ変換と周波数フィルタリング /7 前半のまとめと中間試験
スケジュール 9/6 イントロダクション : デジタル画像とは, 量 化と標本化,Dynamic Range /3 イントロダクション : デジタルカメラ, 間の視覚, 表 系 / フィルタ処理 : トーンカーブ, 線形フィルタ デジタルメディア処理 担当 : 井尻敬 /7 フィルタ処理 : 線形フィルタ, ハーフトーニング / フィルタ処理 3 : 離散フーリエ変換と周波数フィルタリング /7 前半のまとめと中間試験
Microsoft PowerPoint - DigitalMedia2_12.pptx
 デジタルメディア処理 2 2017( 前期 ) デジタルメディア処理 2 担当 : 井尻敬 4/13 デジタル画像とは : イントロダクション 4/20 フィルタ処理 1 : 画素ごとの濃淡変換 線形フィルタ, 線形フィルタ 4/27 フィルタ処理 2 : フーリエ変換, ローパスフィルタ, ハイパスフィルタ 5/11 画像の幾何変換 1 : アファイン変換 5/18 画像の幾何変換 2 : 画像の補間,
デジタルメディア処理 2 2017( 前期 ) デジタルメディア処理 2 担当 : 井尻敬 4/13 デジタル画像とは : イントロダクション 4/20 フィルタ処理 1 : 画素ごとの濃淡変換 線形フィルタ, 線形フィルタ 4/27 フィルタ処理 2 : フーリエ変換, ローパスフィルタ, ハイパスフィルタ 5/11 画像の幾何変換 1 : アファイン変換 5/18 画像の幾何変換 2 : 画像の補間,
PowerPoint プレゼンテーション
 空間フィルタリング (spatal lterng) 入力画像の対応する画素値だけではなく その周囲 ( 近傍領域 ) の画素も含めた領域内の画素値を用いて 出力画像の対応する画素値を計算する処理 入力画像出力画像入力画像出力画像 画素ごとの濃淡変換 ( 階調処理 ) 領域に基づく濃淡変換 ( 空間フィルタリング ) 空間フィルタ (spatal lter) 線形フィルタ (lnear lter) w
空間フィルタリング (spatal lterng) 入力画像の対応する画素値だけではなく その周囲 ( 近傍領域 ) の画素も含めた領域内の画素値を用いて 出力画像の対応する画素値を計算する処理 入力画像出力画像入力画像出力画像 画素ごとの濃淡変換 ( 階調処理 ) 領域に基づく濃淡変換 ( 空間フィルタリング ) 空間フィルタ (spatal lter) 線形フィルタ (lnear lter) w
Microsoft PowerPoint - comprog11.pptx
 Outline プログラミング演習第 回エッジを検出する on 3..4 電気通信大学情報理工学部知能機械工学科長井隆行 画像の本質 輝度の境目に情報あり! 画像の微分と 階微分 エッジ検出 画像をぼかす 本日の課題 画像の本質 エッジ抽出 画像の情報は境目にあり! エッジ 輝度が大きく変化しているところ ( 境界 ) 画像の情報はエッジにあり 輝度 人間の視覚系でも特定のエッジの方向に発火するニューロンが見つかっている
Outline プログラミング演習第 回エッジを検出する on 3..4 電気通信大学情報理工学部知能機械工学科長井隆行 画像の本質 輝度の境目に情報あり! 画像の微分と 階微分 エッジ検出 画像をぼかす 本日の課題 画像の本質 エッジ抽出 画像の情報は境目にあり! エッジ 輝度が大きく変化しているところ ( 境界 ) 画像の情報はエッジにあり 輝度 人間の視覚系でも特定のエッジの方向に発火するニューロンが見つかっている
Microsoft PowerPoint - dm1_5.pptx
 デジタルメディア処理 1 017( 後期 ) 09/6 イントロダクション1 : デジタル画像とは, 量 化と標本化,Dynamic Range 10/03 イントロダクション : デジタルカメラ, 間の視覚, 表 系 10/10 フィルタ処理 1 : トーンカーブ, 線形フィルタ デジタルメディア処理 1 担当 : 井尻敬 10/17 フィルタ処理 : 線形フィルタ, ハーフトーニング 10/4
デジタルメディア処理 1 017( 後期 ) 09/6 イントロダクション1 : デジタル画像とは, 量 化と標本化,Dynamic Range 10/03 イントロダクション : デジタルカメラ, 間の視覚, 表 系 10/10 フィルタ処理 1 : トーンカーブ, 線形フィルタ デジタルメディア処理 1 担当 : 井尻敬 10/17 フィルタ処理 : 線形フィルタ, ハーフトーニング 10/4
Microsoft PowerPoint - dm1kadai.pptx
 デジタルメディア処理 1 担当 : 井尻敬 提出 法 : 共有フォルダに dm1 学籍番号 というフォルダを作成し, その中にソースコードの ったファイルを置く. フォルダ名は全て半. フォルダ名の例 : dm2al150999 課題雛形 : http://takashiijiri.com/classes/dm2018_1/dm1exer.zip 出 : 課題ではを受け取り, 画像またはファイルを保存するプログラムを作る.
デジタルメディア処理 1 担当 : 井尻敬 提出 法 : 共有フォルダに dm1 学籍番号 というフォルダを作成し, その中にソースコードの ったファイルを置く. フォルダ名は全て半. フォルダ名の例 : dm2al150999 課題雛形 : http://takashiijiri.com/classes/dm2018_1/dm1exer.zip 出 : 課題ではを受け取り, 画像またはファイルを保存するプログラムを作る.
l10
 ノイズ除去と画像の強調 画質改善 第4章 pp.101~136 入力画像にはさまざまな 雑音 と 歪み が含まれている 画質劣化 の要因を取り除く 画像を見やすくする 有用な情報を抽出しやすく強調する ことは 画像処理の最も重要な役割の一つ 目的 人間にとって見やすい画像を作る 画像の解析や認識にとって 特徴抽出が容易に行えるための 前処理 preprocessing) ノイズ除去と画像の強調 ノイズ除去と画像の強調
ノイズ除去と画像の強調 画質改善 第4章 pp.101~136 入力画像にはさまざまな 雑音 と 歪み が含まれている 画質劣化 の要因を取り除く 画像を見やすくする 有用な情報を抽出しやすく強調する ことは 画像処理の最も重要な役割の一つ 目的 人間にとって見やすい画像を作る 画像の解析や認識にとって 特徴抽出が容易に行えるための 前処理 preprocessing) ノイズ除去と画像の強調 ノイズ除去と画像の強調
Microsoft PowerPoint - DigitalMedia2_3b.pptx
 Contents デジタルメディア処理 2 の概要 フーリエ級数展開と 離散とその性質 周波数フィルタリング 担当 : 井尻敬 とは ( ) FourierSound.py とは ( ) FourierSound.py 横軸が時間の関数を 横軸が周波数の関数に変換する 法 声周波数 周波数 ( 係数番号 ) 後の関数は元信号に含まれる正弦波の量を す 中央に近いほど低周波, 外ほどが 周波 中央 (
Contents デジタルメディア処理 2 の概要 フーリエ級数展開と 離散とその性質 周波数フィルタリング 担当 : 井尻敬 とは ( ) FourierSound.py とは ( ) FourierSound.py 横軸が時間の関数を 横軸が周波数の関数に変換する 法 声周波数 周波数 ( 係数番号 ) 後の関数は元信号に含まれる正弦波の量を す 中央に近いほど低周波, 外ほどが 周波 中央 (
目次. はじめに デジタル画像のビット数 図形認識に用いた画像と方法 ハフ変換 検出方法と画像について TIFF 画像 RAW 画像データ フィルタ処理 平滑化
 205 年度卒業研究論文 画像と図形のエッジ検出について 岡山理科大学総合情報学部情報科学科 I2I00 小名川薫儀 I2I0 渡邊貴裕 目次. はじめに... 2. デジタル画像のビット数... 2 3. 図形認識に用いた画像と方法... 2 3.. ハフ変換... 2. 検出方法と画像について... 3.. TIFF 画像... 3.2. RAW 画像データ... 3 5. フィルタ処理...
205 年度卒業研究論文 画像と図形のエッジ検出について 岡山理科大学総合情報学部情報科学科 I2I00 小名川薫儀 I2I0 渡邊貴裕 目次. はじめに... 2. デジタル画像のビット数... 2 3. 図形認識に用いた画像と方法... 2 3.. ハフ変換... 2. 検出方法と画像について... 3.. TIFF 画像... 3.2. RAW 画像データ... 3 5. フィルタ処理...
Microsoft PowerPoint - CV04.ppt [互換モード]
![Microsoft PowerPoint - CV04.ppt [互換モード] Microsoft PowerPoint - CV04.ppt [互換モード]](/thumbs/101/149709049.jpg) コンピュータビジョン特論 Advanced Computer Vision 第 4 回 画像特徴 ( 点 直線 領域 ) の検出と識別 -1 画質の改善エッジの検出 濃度ヒストグラム (Histogram) 画素数 8 6 4 2 濃度ヒストグラム (Histogram) は 画像の濃度値を横軸に その濃度値を持つ画素数を縦軸に取った ヒストグラム 19 38 57 76 95 114 133 152
コンピュータビジョン特論 Advanced Computer Vision 第 4 回 画像特徴 ( 点 直線 領域 ) の検出と識別 -1 画質の改善エッジの検出 濃度ヒストグラム (Histogram) 画素数 8 6 4 2 濃度ヒストグラム (Histogram) は 画像の濃度値を横軸に その濃度値を持つ画素数を縦軸に取った ヒストグラム 19 38 57 76 95 114 133 152
Microsoft PowerPoint - Lec15 [互換モード]
![Microsoft PowerPoint - Lec15 [互換モード] Microsoft PowerPoint - Lec15 [互換モード]](/thumbs/91/106545378.jpg) 情報デザイン専攻 画像情報処理論及び演習 II 周波数分解 FFT Gaussian フィルタと周波数分解 今日の授業内容 www.riken.jp/brict/yoshizawa/lectures/index.html www.riken.jp/brict/yoshizawa/lectures/lec5.pdf. 前回 前々回の復習 レポートの説明. 第 3, 回講義水曜日 限教室 68 吉澤信
情報デザイン専攻 画像情報処理論及び演習 II 周波数分解 FFT Gaussian フィルタと周波数分解 今日の授業内容 www.riken.jp/brict/yoshizawa/lectures/index.html www.riken.jp/brict/yoshizawa/lectures/lec5.pdf. 前回 前々回の復習 レポートの説明. 第 3, 回講義水曜日 限教室 68 吉澤信
Microsoft PowerPoint - ip02_01.ppt [互換モード]
![Microsoft PowerPoint - ip02_01.ppt [互換モード] Microsoft PowerPoint - ip02_01.ppt [互換モード]](/thumbs/96/127250376.jpg) 空間周波数 周波数領域での処理 空間周波数 (spatial frquncy) とは 単位長さ当たりの正弦波状の濃淡変化の繰り返し回数を表したもの 正弦波 : y sin( t) 周期 : 周波数 : T f / T 角周波数 : f 画像処理 空間周波数 周波数領域での処理 波形が違うと 周波数も違う 画像処理 空間周波数 周波数領域での処理 画像処理 3 周波数領域での処理 周波数は一つしかない?-
空間周波数 周波数領域での処理 空間周波数 (spatial frquncy) とは 単位長さ当たりの正弦波状の濃淡変化の繰り返し回数を表したもの 正弦波 : y sin( t) 周期 : 周波数 : T f / T 角周波数 : f 画像処理 空間周波数 周波数領域での処理 波形が違うと 周波数も違う 画像処理 空間周波数 周波数領域での処理 画像処理 3 周波数領域での処理 周波数は一つしかない?-
PowerPoint プレゼンテーション
 ディジタル画像処理 濃度変換 ; 階調処理 2 値化処理 ; しきい値処理 フィルタ処理 画像間演算 データ圧縮 三次元表示 頻度 画像全体で同じ濃度値を持つ画素数を求め, グラフ化したものを濃度ヒストグラムあるいは単にヒストグラム (histogram) という. 横軸は濃淡値 ( 画素値 ), 縦軸にその出現頻度 ( 画素数 ) をとる. Histogram 出現頻度 30 20 0 ヒストグラムの利用法
ディジタル画像処理 濃度変換 ; 階調処理 2 値化処理 ; しきい値処理 フィルタ処理 画像間演算 データ圧縮 三次元表示 頻度 画像全体で同じ濃度値を持つ画素数を求め, グラフ化したものを濃度ヒストグラムあるいは単にヒストグラム (histogram) という. 横軸は濃淡値 ( 画素値 ), 縦軸にその出現頻度 ( 画素数 ) をとる. Histogram 出現頻度 30 20 0 ヒストグラムの利用法
認識行動システム論
 05/5/ レポートメールエラー インタラクティブシステム論第 7 回 梶本裕之 Twitter ID kajimoto ハッシュタグ #ninshiki 第 5 回分のレポートメールがエラーになった可能性があります.( メールボックスのサイズオーバー ) 再度送信してください. 日程 4/9 イントロダクション 4/6 Scilab の紹介 ( 西 6 号館 3 階 PC ルーム ) 4/3 出張により休講
05/5/ レポートメールエラー インタラクティブシステム論第 7 回 梶本裕之 Twitter ID kajimoto ハッシュタグ #ninshiki 第 5 回分のレポートメールがエラーになった可能性があります.( メールボックスのサイズオーバー ) 再度送信してください. 日程 4/9 イントロダクション 4/6 Scilab の紹介 ( 西 6 号館 3 階 PC ルーム ) 4/3 出張により休講
「情報」って何だ!?
 画像処理システム論 Image Media Systems 加藤俊一 Toshi KATO 感性の強化 人間の感性的な行動 知覚を支援 演奏支援 虫眼鏡 電子的メガネ ( 画像強調 雑音除去 ) 仮想現実感への応用 ( 建築設計支援 ) 感性の強化 電子的メガネ ( 画像強調 雑音除去 ) 生体から学ぶべきメカニズム (1) 明暗順応 : 明るさの変化に対する調節機構 側抑制 : 視野の中の明暗の微小変化を局所的に検出
画像処理システム論 Image Media Systems 加藤俊一 Toshi KATO 感性の強化 人間の感性的な行動 知覚を支援 演奏支援 虫眼鏡 電子的メガネ ( 画像強調 雑音除去 ) 仮想現実感への応用 ( 建築設計支援 ) 感性の強化 電子的メガネ ( 画像強調 雑音除去 ) 生体から学ぶべきメカニズム (1) 明暗順応 : 明るさの変化に対する調節機構 側抑制 : 視野の中の明暗の微小変化を局所的に検出
画像解析論(2) 講義内容
 画像解析論 画像解析論 東京工業大学長橋宏 主な講義内容 信号処理と画像処理 二次元システムとその表現 二次元システムの特性解析 各種の画像フィルタ 信号処理と画像処理 画像解析論 処理の応答 記憶域 入出力の流れ 信号処理系 実時間性が求められる メモリ容量に対する制限が厳しい オンラインでの対応が厳しく求められる 画像処理系 ある程度の処理時間が許容される 大容量のメモリ使用が容認され易い オフラインでの対応が容認され易い
画像解析論 画像解析論 東京工業大学長橋宏 主な講義内容 信号処理と画像処理 二次元システムとその表現 二次元システムの特性解析 各種の画像フィルタ 信号処理と画像処理 画像解析論 処理の応答 記憶域 入出力の流れ 信号処理系 実時間性が求められる メモリ容量に対する制限が厳しい オンラインでの対応が厳しく求められる 画像処理系 ある程度の処理時間が許容される 大容量のメモリ使用が容認され易い オフラインでの対応が容認され易い
Microsoft PowerPoint - pr_12_template-bs.pptx
 12 回パターン検出と画像特徴 テンプレートマッチング 領域分割 画像特徴 テンプレート マッチング 1 テンプレートマッチング ( 図形 画像などの ) 型照合 Template Matching テンプレートと呼ばれる小さな一部の画像領域と同じパターンが画像全体の中に存在するかどうかを調べる方法 画像内にある対象物体の位置検出 物体数のカウント 物体移動の検出などに使われる テンプレートマッチングの計算
12 回パターン検出と画像特徴 テンプレートマッチング 領域分割 画像特徴 テンプレート マッチング 1 テンプレートマッチング ( 図形 画像などの ) 型照合 Template Matching テンプレートと呼ばれる小さな一部の画像領域と同じパターンが画像全体の中に存在するかどうかを調べる方法 画像内にある対象物体の位置検出 物体数のカウント 物体移動の検出などに使われる テンプレートマッチングの計算
tottori2013-print.key
 1 / 152 3 / 152 2 / 152 4 / 152 5 / 152 7 / 152 6 / 152 8 / 152 9 / 152 11 / 152 Red: [R,G,B] = [255,0,0] Yellow [R,G,B] = [255, 255, 0] Magenta [R,G,B] = [255, 0, 255] W [R,G,B] = [ Green: [R,G,B] = [0,
1 / 152 3 / 152 2 / 152 4 / 152 5 / 152 7 / 152 6 / 152 8 / 152 9 / 152 11 / 152 Red: [R,G,B] = [255,0,0] Yellow [R,G,B] = [255, 255, 0] Magenta [R,G,B] = [255, 0, 255] W [R,G,B] = [ Green: [R,G,B] = [0,
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生
 0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
スライド タイトルなし
 次元フーリエ変換 講義内容 空間周波数の概念 次元フーリエ変換代表的な 次元フーリエ変換対 次元離散フーリエ変換 フーリエ変換と逆変換 F.T. j F } ep{ 連続系離散系 } / ep{ N N N j N F F I. F.T. F ただし ここでは絶対値をとって画像化 } / ep{ N N N j F N 順変換逆変換 3 次元フーリエ変換の具体的なイメージ } / ep{ N N N
次元フーリエ変換 講義内容 空間周波数の概念 次元フーリエ変換代表的な 次元フーリエ変換対 次元離散フーリエ変換 フーリエ変換と逆変換 F.T. j F } ep{ 連続系離散系 } / ep{ N N N j N F F I. F.T. F ただし ここでは絶対値をとって画像化 } / ep{ N N N j F N 順変換逆変換 3 次元フーリエ変換の具体的なイメージ } / ep{ N N N
内容梗概近年 液晶用ガラスはテレビやパソコンディスプレイ スマートフォンなど 様々な分野で使用されている 液晶用ガラスの欠損を検出するためには 欠損検出の精度の高さが重要である そのほかでは 劣化などの問題で認識しにくい甲骨文字の解読が必要である 甲骨文字を切り出し 鮮明化することが未解読資料の解読
 学士論文 OpenCV を用いたフィルタ処理の実現と応用 氏名 : 麻生啓太学籍番号 : 2260100001-0 担当教員 : 山崎勝弘教授提出日 : 2014 年 2 月 20 日 立命館大学理工学部電子情報デザイン学科 内容梗概近年 液晶用ガラスはテレビやパソコンディスプレイ スマートフォンなど 様々な分野で使用されている 液晶用ガラスの欠損を検出するためには 欠損検出の精度の高さが重要である
学士論文 OpenCV を用いたフィルタ処理の実現と応用 氏名 : 麻生啓太学籍番号 : 2260100001-0 担当教員 : 山崎勝弘教授提出日 : 2014 年 2 月 20 日 立命館大学理工学部電子情報デザイン学科 内容梗概近年 液晶用ガラスはテレビやパソコンディスプレイ スマートフォンなど 様々な分野で使用されている 液晶用ガラスの欠損を検出するためには 欠損検出の精度の高さが重要である
Microsoft Word - 卒論レジュメ_最終_.doc
 指紋認証のマニューシャ抽出について 澤見研究室 I02I036 兼信雄一 I02I093 柳楽和信 I02I142 吉田寛孝 1. はじめに近年, キャッシュカードや暗証番号が盗用され, 現金が引き出されるような事件が相次いでいる. これらの対向策として人間の体の一部を認証の鍵として利用する生体認証に注目が集まっている. そこで我々は, 生体認証で最も歴史がある指紋認証技術に着目した. 指紋認証方式は,2
指紋認証のマニューシャ抽出について 澤見研究室 I02I036 兼信雄一 I02I093 柳楽和信 I02I142 吉田寛孝 1. はじめに近年, キャッシュカードや暗証番号が盗用され, 現金が引き出されるような事件が相次いでいる. これらの対向策として人間の体の一部を認証の鍵として利用する生体認証に注目が集まっている. そこで我々は, 生体認証で最も歴史がある指紋認証技術に着目した. 指紋認証方式は,2
スライド 1
 医用画像処理学 (4) ( 教科書 pp.104-122) 有村秀孝 種々の濃度変換曲線 255 y=255 - x 0 I ディスプレイの電気 - 光変換特性 org _ out CI org _ in I out ( I org _ C in 1 ) フィラデルフィア (Philadelphia) はアメリカ合衆国ペンシルバニア州南東部にある都市 フィラデルフィア郡の全域を占めるペンシルバニア州最大の都市である
医用画像処理学 (4) ( 教科書 pp.104-122) 有村秀孝 種々の濃度変換曲線 255 y=255 - x 0 I ディスプレイの電気 - 光変換特性 org _ out CI org _ in I out ( I org _ C in 1 ) フィラデルフィア (Philadelphia) はアメリカ合衆国ペンシルバニア州南東部にある都市 フィラデルフィア郡の全域を占めるペンシルバニア州最大の都市である
Microsoft PowerPoint - 第3回2.ppt
 講義内容 講義内容 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 ベクトルの直交性 3
講義内容 講義内容 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 ベクトルの直交性 3
Microsoft Word - 卒業論文.doc
 006 年度卒業研究 画像補間法を用いた拡大画像の比較 岡山理科大学総合情報学部情報科学科 澤見研究室 I03I04 兼安俊治 I03I050 境永 目次 はじめに ラスタ画像 3 画像補間法 3. ニアレストネイバー法 3. バイリニア法 3.3 バイキュービック法 4 DCT を用いた拡大画像手法 5 FIR 法 6 評価 6. SNR 6. PSNR 7 実験 7. 主観評価 7. 客観評価
006 年度卒業研究 画像補間法を用いた拡大画像の比較 岡山理科大学総合情報学部情報科学科 澤見研究室 I03I04 兼安俊治 I03I050 境永 目次 はじめに ラスタ画像 3 画像補間法 3. ニアレストネイバー法 3. バイリニア法 3.3 バイキュービック法 4 DCT を用いた拡大画像手法 5 FIR 法 6 評価 6. SNR 6. PSNR 7 実験 7. 主観評価 7. 客観評価
スライド 1
 知能制御システム学 画像処理の基礎 (2) OpenCV による基本的な例 東北大学大学院情報科学研究科鏡慎吾 swk(at)ic.is.tohoku.ac.jp 2010.07.06 局所処理の例 空間フィルタリング 注目点の近傍 ( 典型的には 3x3 画素,5x5 画素,... など ) の画素値から, 出力 G x,y を定める { F i,j }, (i, j) Neighbor(x,y)
知能制御システム学 画像処理の基礎 (2) OpenCV による基本的な例 東北大学大学院情報科学研究科鏡慎吾 swk(at)ic.is.tohoku.ac.jp 2010.07.06 局所処理の例 空間フィルタリング 注目点の近傍 ( 典型的には 3x3 画素,5x5 画素,... など ) の画素値から, 出力 G x,y を定める { F i,j }, (i, j) Neighbor(x,y)
ディジタル信号処理
 ディジタルフィルタの設計法. 逆フィルター. 直線位相 FIR フィルタの設計. 窓関数法による FIR フィルタの設計.5 時間領域での FIR フィルタの設計 3. アナログフィルタを基にしたディジタル IIR フィルタの設計法 I 4. アナログフィルタを基にしたディジタル IIR フィルタの設計法 II 5. 双 次フィルタ LI 離散時間システムの基礎式の証明 [ ] 4. ] [ ]*
ディジタルフィルタの設計法. 逆フィルター. 直線位相 FIR フィルタの設計. 窓関数法による FIR フィルタの設計.5 時間領域での FIR フィルタの設計 3. アナログフィルタを基にしたディジタル IIR フィルタの設計法 I 4. アナログフィルタを基にしたディジタル IIR フィルタの設計法 II 5. 双 次フィルタ LI 離散時間システムの基礎式の証明 [ ] 4. ] [ ]*
Analog signal 標本化 量子化 Digital signal 定理に基づく sampling 間隔の決定 f Δx max = 1 2 Δx 1 2 f max 標本化間隔 等号が成り立つとき周波数 従わないとエリアシングエラー (aliasing error) が生じる ( 折り返し雑
 画像処理工学 Computer Image Processing pixel dpi picture cell picture element 画像の最小単位 ppi pixel per inch 1 インチ当たりの画素数. 画像の解像度の単位. dot per inch 1 インチ当たりの点の数. 主にプリンタやスキャナなどの解像度の単位として使われる. bps bit per second 1
画像処理工学 Computer Image Processing pixel dpi picture cell picture element 画像の最小単位 ppi pixel per inch 1 インチ当たりの画素数. 画像の解像度の単位. dot per inch 1 インチ当たりの点の数. 主にプリンタやスキャナなどの解像度の単位として使われる. bps bit per second 1
画像工学入門
 セグメンテーション 講義内容 閾値法,k-mean 法 領域拡張法 SNAK 法 P タイル法 モード法 P タイル法 画像内で対象物の占める面積 (P パーセント ) があらかじめわかっているとき, 濃度ヒストグラムを作成し, 濃度値の累積分布が全体の P パーセントとなる濃度値を見つけ, この値を閾値とする. モード法 画像の輝度ヒストグラムを調べ その分布のモード ( 頻値輝度 ) 間の谷をしきい値とする
セグメンテーション 講義内容 閾値法,k-mean 法 領域拡張法 SNAK 法 P タイル法 モード法 P タイル法 画像内で対象物の占める面積 (P パーセント ) があらかじめわかっているとき, 濃度ヒストグラムを作成し, 濃度値の累積分布が全体の P パーセントとなる濃度値を見つけ, この値を閾値とする. モード法 画像の輝度ヒストグラムを調べ その分布のモード ( 頻値輝度 ) 間の谷をしきい値とする
スライド 1
 5.5.2 画像の間引き 5.1 線形変換 5.2 アフィン変換 5.3 同次座標 5.4 平面射影変換 5.5 再標本化 1. 画素数の減少による表現能力の低下 画像の縮小 変形を行う際 結果画像の 画素数 < 入力画像の 画素数 ( 画素の密度 ) ( 画素の密度 ) になることがある この場合 結果画像の表現力 < 入力画像の表現力 ( 情報量 ) ( 情報量 ) 結果的に 情報の損失が生じる!
5.5.2 画像の間引き 5.1 線形変換 5.2 アフィン変換 5.3 同次座標 5.4 平面射影変換 5.5 再標本化 1. 画素数の減少による表現能力の低下 画像の縮小 変形を行う際 結果画像の 画素数 < 入力画像の 画素数 ( 画素の密度 ) ( 画素の密度 ) になることがある この場合 結果画像の表現力 < 入力画像の表現力 ( 情報量 ) ( 情報量 ) 結果的に 情報の損失が生じる!
画像処理工学
 画像処理工学 画像の空間周波数解析とテクスチャ特徴 フーリエ変換の基本概念 信号波形のフーリエ変換 信号波形を周波数の異なる三角関数 ( 正弦波など ) に分解する 逆に, 周波数の異なる三角関数を重ねあわせることにより, 任意の信号波形を合成できる 正弦波の重ね合わせによる矩形波の表現 フーリエ変換の基本概念 フーリエ変換 次元信号 f (t) のフーリエ変換 変換 ( ω) ( ) ωt F f
画像処理工学 画像の空間周波数解析とテクスチャ特徴 フーリエ変換の基本概念 信号波形のフーリエ変換 信号波形を周波数の異なる三角関数 ( 正弦波など ) に分解する 逆に, 周波数の異なる三角関数を重ねあわせることにより, 任意の信号波形を合成できる 正弦波の重ね合わせによる矩形波の表現 フーリエ変換の基本概念 フーリエ変換 次元信号 f (t) のフーリエ変換 変換 ( ω) ( ) ωt F f
PowerPoint Presentation
 付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
例 e 指数関数的に減衰する信号を h( a < + a a すると, それらのラプラス変換は, H ( ) { e } e インパルス応答が h( a < ( ただし a >, U( ) { } となるシステムにステップ信号 ( y( のラプラス変換 Y () は, Y ( ) H ( ) X (
 第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
適応フィルタのSIMD最適化
 茂木和洋 @ まるも製作所 今回は省略 初めての方は #1 の資料を参照 適応フィルタとは 適応フィルタの問題点 ( 速度面で ) SIMD 比較命令でマスク処理 ベンチマーク 固定のフィルタではなく 入力値によって処理を変更し 最適な結果を求める 例 基準値との差異を閾値と比較して 参照画素として使うか使わないかを切り替える 最小自乗法でフィッティングしてフィルタ係数自体を動的に作成する 他いろいろ
茂木和洋 @ まるも製作所 今回は省略 初めての方は #1 の資料を参照 適応フィルタとは 適応フィルタの問題点 ( 速度面で ) SIMD 比較命令でマスク処理 ベンチマーク 固定のフィルタではなく 入力値によって処理を変更し 最適な結果を求める 例 基準値との差異を閾値と比較して 参照画素として使うか使わないかを切り替える 最小自乗法でフィッティングしてフィルタ係数自体を動的に作成する 他いろいろ
Microsoft Word 年度卒業研究.1.doc
 006 年度卒業研究 アンシャープ処理 ( ディジタル画像の強調処理 ) 岡山理科大学 総合情報学部 情報科学科 澤見研究室 I03I054 澤田慧 I03I055 柴田勇輝 目次 1 はじめに ディジタル画像の強調処理 3 強調処理の種類 3.1 ヒストグラム均等化法 (HE) 3. コンボリューション処理 (Convolution) 3.3 アンシャープ処理 (Unsharp) 4 アンシャープ処理の実現
006 年度卒業研究 アンシャープ処理 ( ディジタル画像の強調処理 ) 岡山理科大学 総合情報学部 情報科学科 澤見研究室 I03I054 澤田慧 I03I055 柴田勇輝 目次 1 はじめに ディジタル画像の強調処理 3 強調処理の種類 3.1 ヒストグラム均等化法 (HE) 3. コンボリューション処理 (Convolution) 3.3 アンシャープ処理 (Unsharp) 4 アンシャープ処理の実現
Microsoft PowerPoint - Lec11 [互換モード]
![Microsoft PowerPoint - Lec11 [互換モード] Microsoft PowerPoint - Lec11 [互換モード]](/thumbs/88/114651022.jpg) 第 11 回講義水曜日 1 限教室 6215 情報デザイン専攻 画像情報処理論及び演習 I - 画像合成 類推 - Poisson Image Analogy 吉澤信 [email protected], 非常勤講師 大妻女子大学社会情報学部 1 2 今日の授業内容 www.riken.jp/brict/yoshizawa/lectures/index.html www.riken.jp/brict/yoshizawa/lectures/lec11.pdf
第 11 回講義水曜日 1 限教室 6215 情報デザイン専攻 画像情報処理論及び演習 I - 画像合成 類推 - Poisson Image Analogy 吉澤信 [email protected], 非常勤講師 大妻女子大学社会情報学部 1 2 今日の授業内容 www.riken.jp/brict/yoshizawa/lectures/index.html www.riken.jp/brict/yoshizawa/lectures/lec11.pdf
目次 1 はじめに ラスタ画像 bit 数による差 画像拡大と画像補間法 ニアレストネイバー法 バイリニア法 バイキュービック法 Lanczos(n) 法 拡大画像の比
 2015 年度卒業研究論文 画像補間法による拡大 岡山理科大学総合情報学部情報科学科 I12I061 田中宏美 I12I063 仲陽美 目次 1 はじめに... 1 2 ラスタ画像... 1 2.1 bit 数による差... 2 3 画像拡大と画像補間法... 2 3.1 ニアレストネイバー法... 2 3.2 バイリニア法... 4 3.3 バイキュービック法... 6 3.4 Lanczos(n)
2015 年度卒業研究論文 画像補間法による拡大 岡山理科大学総合情報学部情報科学科 I12I061 田中宏美 I12I063 仲陽美 目次 1 はじめに... 1 2 ラスタ画像... 1 2.1 bit 数による差... 2 3 画像拡大と画像補間法... 2 3.1 ニアレストネイバー法... 2 3.2 バイリニア法... 4 3.3 バイキュービック法... 6 3.4 Lanczos(n)
スライド 1
 CNN を用いた弱教師学習による画像領域分割 下田和, 柳井啓司 電気通信大学 大学院情報理工学 研究科 総合情報学専攻 c 2015 UEC Tokyo. Convolutional Neural Network CNN クラス分類タスクにおいてトップの精度 CNN の応用 ( 物体位置の認識 ) 物体検出 物体に BB を付与 領域分割 ピクセル単位の認識 CNN を用いた領域分割 CNN による完全教師ありのセグメンテーション
CNN を用いた弱教師学習による画像領域分割 下田和, 柳井啓司 電気通信大学 大学院情報理工学 研究科 総合情報学専攻 c 2015 UEC Tokyo. Convolutional Neural Network CNN クラス分類タスクにおいてトップの精度 CNN の応用 ( 物体位置の認識 ) 物体検出 物体に BB を付与 領域分割 ピクセル単位の認識 CNN を用いた領域分割 CNN による完全教師ありのセグメンテーション
Microsoft PowerPoint - SPECTPETの原理2012.ppt [互換モード]
![Microsoft PowerPoint - SPECTPETの原理2012.ppt [互換モード] Microsoft PowerPoint - SPECTPETの原理2012.ppt [互換モード]](/thumbs/94/121508518.jpg) 22 年国家試験解答 1,5 フーリエ変換は線形変換 FFT はデータ数に 2 の累乗数を要求するが DFT は任意のデータ数に対応 123I-IMP Brain SPECT FBP with Ramp filter 123I-IMP Brain SPECT FBP with Shepp&Logan filter 99mTc-MIBI Myocardial SPECT における ストリークアーチファクト
22 年国家試験解答 1,5 フーリエ変換は線形変換 FFT はデータ数に 2 の累乗数を要求するが DFT は任意のデータ数に対応 123I-IMP Brain SPECT FBP with Ramp filter 123I-IMP Brain SPECT FBP with Shepp&Logan filter 99mTc-MIBI Myocardial SPECT における ストリークアーチファクト
file:///N|/ncs/サービス技術課/e-learning/社内検図用/販促用/32-35/ope35ver3.02.html
 QSS-35 シリーズ Ver. 3.02 新機能の説明 (1) 17 インチ液晶モニター ( オプション ) に対応しました (2) QSS-35 型で使用されている USB 操作キーボード ( オプション ) を QSS-Kids でも使用できるようにしました QSS-Kids で USB 操作キーボードを使用する場合は QSS-Kids の 機能 オプション登録 画面で USB キーボード を選択します
QSS-35 シリーズ Ver. 3.02 新機能の説明 (1) 17 インチ液晶モニター ( オプション ) に対応しました (2) QSS-35 型で使用されている USB 操作キーボード ( オプション ) を QSS-Kids でも使用できるようにしました QSS-Kids で USB 操作キーボードを使用する場合は QSS-Kids の 機能 オプション登録 画面で USB キーボード を選択します
様々なミクロ計量モデル†
 担当 : 長倉大輔 ( ながくらだいすけ ) この資料は私の講義において使用するために作成した資料です WEB ページ上で公開しており 自由に参照して頂いて構いません ただし 内容について 一応検証してありますが もし間違いがあった場合でもそれによって生じるいかなる損害 不利益について責任を負いかねますのでご了承ください 間違いは発見次第 継続的に直していますが まだ存在する可能性があります 1 カウントデータモデル
担当 : 長倉大輔 ( ながくらだいすけ ) この資料は私の講義において使用するために作成した資料です WEB ページ上で公開しており 自由に参照して頂いて構いません ただし 内容について 一応検証してありますが もし間違いがあった場合でもそれによって生じるいかなる損害 不利益について責任を負いかねますのでご了承ください 間違いは発見次第 継続的に直していますが まだ存在する可能性があります 1 カウントデータモデル
画像類似度測定の初歩的な手法の検証
 画像類似度測定の初歩的な手法の検証 島根大学総合理工学部数理 情報システム学科 計算機科学講座田中研究室 S539 森瀧昌志 1 目次 第 1 章序論第 章画像間類似度測定の初歩的な手法について.1 A. 画素値の平均を用いる手法.. 画素値のヒストグラムを用いる手法.3 C. 相関係数を用いる手法.4 D. 解像度を合わせる手法.5 E. 振れ幅のヒストグラムを用いる手法.6 F. 周波数ごとの振れ幅を比較する手法第
画像類似度測定の初歩的な手法の検証 島根大学総合理工学部数理 情報システム学科 計算機科学講座田中研究室 S539 森瀧昌志 1 目次 第 1 章序論第 章画像間類似度測定の初歩的な手法について.1 A. 画素値の平均を用いる手法.. 画素値のヒストグラムを用いる手法.3 C. 相関係数を用いる手法.4 D. 解像度を合わせる手法.5 E. 振れ幅のヒストグラムを用いる手法.6 F. 周波数ごとの振れ幅を比較する手法第
OpenFOAM(R) ソースコード入門 pt1 熱伝導方程式の解法から有限体積法の実装について考える 前編 : 有限体積法の基礎確認 2013/11/17 オープンCAE 富山富山県立大学中川慎二
 OpenFOAM(R) ソースコード入門 pt1 熱伝導方程式の解法から有限体積法の実装について考える 前編 : 有限体積法の基礎確認 2013/11/17 オープンCAE 勉強会 @ 富山富山県立大学中川慎二 * OpenFOAM のソースコードでは, 基礎式を偏微分方程式の形で記述する.OpenFOAM 内部では, 有限体積法を使ってこの微分方程式を解いている. どのようにして, 有限体積法に基づく離散化が実現されているのか,
OpenFOAM(R) ソースコード入門 pt1 熱伝導方程式の解法から有限体積法の実装について考える 前編 : 有限体積法の基礎確認 2013/11/17 オープンCAE 勉強会 @ 富山富山県立大学中川慎二 * OpenFOAM のソースコードでは, 基礎式を偏微分方程式の形で記述する.OpenFOAM 内部では, 有限体積法を使ってこの微分方程式を解いている. どのようにして, 有限体積法に基づく離散化が実現されているのか,
遅延デジタルフィルタの分散型積和演算回路を用いたFPGA実装の検討
 第 回電気学会東京支部栃木 群馬支所合同研究発表会 ETT--7 遅延デジタルフィルタの分散型積和演算回路を用いた FPGA 実装の検討 易茹 * 立岩武徳 ( 群馬大学 ) 浅見幸司 ( 株式会社アドバンテスト ) 小林春夫 ( 群馬大学 ) 発表内容 研究の背景 目的 分散型積和演算回路 実装の検討 まとめ 今後の課題 発表内容 研究の背景 目的 分散型積和演算回路 実装の検討 まとめ 今後の課題
第 回電気学会東京支部栃木 群馬支所合同研究発表会 ETT--7 遅延デジタルフィルタの分散型積和演算回路を用いた FPGA 実装の検討 易茹 * 立岩武徳 ( 群馬大学 ) 浅見幸司 ( 株式会社アドバンテスト ) 小林春夫 ( 群馬大学 ) 発表内容 研究の背景 目的 分散型積和演算回路 実装の検討 まとめ 今後の課題 発表内容 研究の背景 目的 分散型積和演算回路 実装の検討 まとめ 今後の課題
Microsoft PowerPoint - Lec21 [互換モード]
![Microsoft PowerPoint - Lec21 [互換モード] Microsoft PowerPoint - Lec21 [互換モード]](/thumbs/39/20064041.jpg) 情 報 デザイン 専 攻 画 像 情 報 処 理 論 及 び 演 習 II 計 算 Photography Artistic Stylization HDR 画 像 NPR 今 日 の 授 業 内 容 www.riken.jp/brict/yoshizawa/lectures/index.html www.riken.jp/brict/yoshizawa/lectures/lec21.pdf 1.
情 報 デザイン 専 攻 画 像 情 報 処 理 論 及 び 演 習 II 計 算 Photography Artistic Stylization HDR 画 像 NPR 今 日 の 授 業 内 容 www.riken.jp/brict/yoshizawa/lectures/index.html www.riken.jp/brict/yoshizawa/lectures/lec21.pdf 1.
パソコンシミュレータの現状
 第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
Signal Processing Toolbox
 Signal Processing Toolbox 信号処理 解析およびアルゴリズム開発の実行 Signal Processing Toolbox は アナログおよびデジタル信号処理 (DSP) の業界標準アルゴリズムを提供 します この Toolbox を使用すると 時間領域および周波数領域での信号の可視化 スペクトル解析 における FFT の計算 FIR および IIR フィルターの設計 コンボリューション
Signal Processing Toolbox 信号処理 解析およびアルゴリズム開発の実行 Signal Processing Toolbox は アナログおよびデジタル信号処理 (DSP) の業界標準アルゴリズムを提供 します この Toolbox を使用すると 時間領域および周波数領域での信号の可視化 スペクトル解析 における FFT の計算 FIR および IIR フィルターの設計 コンボリューション
Microsoft PowerPoint - 04_yokota.ppt
 VCAD 理研シンポジュウム VCAT: 実在するものからの VCAD データの創出 理化学研究所 VCAD システム研究プログラム生物研究基盤構築チーム横田秀夫 VCAT 各種 CT データから VCAD への形状情報 & 材料情報の受け渡し 形状情報 ( ボクセルデータ 表面データ ) 材料情報 ( ボクセル毎の推定物性値 ) ボクセルデータからの特定領域抽出機能 抽出領域の編集ソフトウエア 抽出領域の確認機能
VCAD 理研シンポジュウム VCAT: 実在するものからの VCAD データの創出 理化学研究所 VCAD システム研究プログラム生物研究基盤構築チーム横田秀夫 VCAT 各種 CT データから VCAD への形状情報 & 材料情報の受け渡し 形状情報 ( ボクセルデータ 表面データ ) 材料情報 ( ボクセル毎の推定物性値 ) ボクセルデータからの特定領域抽出機能 抽出領域の編集ソフトウエア 抽出領域の確認機能
PowerPoint プレゼンテーション
 20150528 信号処理システム特論 本日の内容 適応フィルタ ( 時間領域 ) 適応アルゴリズム (LMS,NLMS,RLS) 適応フィルタの応用例 適応処理 非適応処理 : 状況によらずいつでも同じ処理 適応処理 : 状況に応じた適切な処理 高度な適応処理の例 雑音抑圧, 音響エコーキャンセラ, 騒音制御など 時間領域の適応フィルタ 誤差信号 与えられた手順に従ってフィルタ係数を更新し 自動的に所望の信号を得るフィルタ
20150528 信号処理システム特論 本日の内容 適応フィルタ ( 時間領域 ) 適応アルゴリズム (LMS,NLMS,RLS) 適応フィルタの応用例 適応処理 非適応処理 : 状況によらずいつでも同じ処理 適応処理 : 状況に応じた適切な処理 高度な適応処理の例 雑音抑圧, 音響エコーキャンセラ, 騒音制御など 時間領域の適応フィルタ 誤差信号 与えられた手順に従ってフィルタ係数を更新し 自動的に所望の信号を得るフィルタ
Microsoft PowerPoint - H22制御工学I-2回.ppt
 制御工学 I 第二回ラプラス変換 平成 年 4 月 9 日 /4/9 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
制御工学 I 第二回ラプラス変換 平成 年 4 月 9 日 /4/9 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
Microsoft Word - 簡単な計算と作図.doc
 エクセルを用いた簡単な技術計算と作図について 画像処理 Ⅰ 配付資料 ( 岡山理科大学澤見英男 2006 年作成 ) 表計算ソフト エクセル を用いた簡単な技術計算と作図について紹介します 例として正弦波の標本化と周波数特性の計算を取り上げることにします (1) 正弦波の描画先ず表計算ソフト エクセル を立ち上げます 以下の様な表示が現れます この中のA 列を横座標軸 ( 工学単位 ; 度 ) に割り当てます
エクセルを用いた簡単な技術計算と作図について 画像処理 Ⅰ 配付資料 ( 岡山理科大学澤見英男 2006 年作成 ) 表計算ソフト エクセル を用いた簡単な技術計算と作図について紹介します 例として正弦波の標本化と周波数特性の計算を取り上げることにします (1) 正弦波の描画先ず表計算ソフト エクセル を立ち上げます 以下の様な表示が現れます この中のA 列を横座標軸 ( 工学単位 ; 度 ) に割り当てます
Microsoft Word - SKY操作マニュアル.doc
 2. 使用方法 SKY の使用方法について説明する前に 画面構成について説明する SKY は図 c-2 に示すようにシングルインターフェースドキュメント (SDI) で作成しており 図 3 に示すメニュバーに機能拡張処理を実行可能な項目を作成している また メニューの構成を図 4 に示すとおり 1ファイル 2イメージ 3 設定 4フィルタの4つの大きな項目に分かれる 1 図 2 SKY のメイン画面
2. 使用方法 SKY の使用方法について説明する前に 画面構成について説明する SKY は図 c-2 に示すようにシングルインターフェースドキュメント (SDI) で作成しており 図 3 に示すメニュバーに機能拡張処理を実行可能な項目を作成している また メニューの構成を図 4 に示すとおり 1ファイル 2イメージ 3 設定 4フィルタの4つの大きな項目に分かれる 1 図 2 SKY のメイン画面
スライド 1
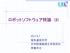 (8) 2017.6.7 電気通信大学大学院情報理工学研究科末廣尚士 9. ロボットアームの逆運動学 ( 幾何 学的 ( 解析的 ) 解法 ) 何をしたいか 手首, 手先, ツールの 3 次元空間での位置や姿勢から, それを実現する関節角度を計算する. アームソリューション, アームの解とも呼ぶ 何のために たとえばビジョンで認識された物をつかむ場合, 物の位置 姿勢は 3 次元空間で表現されることが普通である.
(8) 2017.6.7 電気通信大学大学院情報理工学研究科末廣尚士 9. ロボットアームの逆運動学 ( 幾何 学的 ( 解析的 ) 解法 ) 何をしたいか 手首, 手先, ツールの 3 次元空間での位置や姿勢から, それを実現する関節角度を計算する. アームソリューション, アームの解とも呼ぶ 何のために たとえばビジョンで認識された物をつかむ場合, 物の位置 姿勢は 3 次元空間で表現されることが普通である.
Microsoft PowerPoint - multi_media05-dct_jpeg [互換モード]
![Microsoft PowerPoint - multi_media05-dct_jpeg [互換モード] Microsoft PowerPoint - multi_media05-dct_jpeg [互換モード]](/thumbs/66/54949554.jpg) マルチメディア工学 マルチメディアデータの解析データ圧縮 : 離散コサイン変換と JPEG マルチメディア工学 : 講義計画 イントロダクション コンピュータグラフィックス (Computer Graphics: CG) マルチメディアデータの解析 佐藤嘉伸 大阪大学大学院医学系研究科放射線統合医学講座 [email protected] u.ac.jp http://www.image.med.osaka
マルチメディア工学 マルチメディアデータの解析データ圧縮 : 離散コサイン変換と JPEG マルチメディア工学 : 講義計画 イントロダクション コンピュータグラフィックス (Computer Graphics: CG) マルチメディアデータの解析 佐藤嘉伸 大阪大学大学院医学系研究科放射線統合医学講座 [email protected] u.ac.jp http://www.image.med.osaka
FEM原理講座 (サンプルテキスト)
 サンプルテキスト FEM 原理講座 サイバネットシステム株式会社 8 年 月 9 日作成 サンプルテキストについて 各講師が 講義の内容が伝わりやすいページ を選びました テキストのページは必ずしも連続していません 一部を抜粋しています 幾何光学講座については 実物のテキストではなくガイダンスを掲載いたします 対象とする構造系 物理モデル 連続体 固体 弾性体 / 弾塑性体 / 粘弾性体 / 固体
サンプルテキスト FEM 原理講座 サイバネットシステム株式会社 8 年 月 9 日作成 サンプルテキストについて 各講師が 講義の内容が伝わりやすいページ を選びました テキストのページは必ずしも連続していません 一部を抜粋しています 幾何光学講座については 実物のテキストではなくガイダンスを掲載いたします 対象とする構造系 物理モデル 連続体 固体 弾性体 / 弾塑性体 / 粘弾性体 / 固体
モデリングとは
 コンピュータグラフィックス基礎 第 5 回曲線 曲面の表現 ベジェ曲線 金森由博 学習の目標 滑らかな曲線を扱う方法を学習する パラメトリック曲線について理解する 広く一般的に使われているベジェ曲線を理解する 制御点を入力することで ベジェ曲線を描画するアプリケーションの開発を行えるようになる C++ 言語の便利な機能を使えるようになる 要素数が可変な配列としての std::vector の活用 計算機による曲線の表現
コンピュータグラフィックス基礎 第 5 回曲線 曲面の表現 ベジェ曲線 金森由博 学習の目標 滑らかな曲線を扱う方法を学習する パラメトリック曲線について理解する 広く一般的に使われているベジェ曲線を理解する 制御点を入力することで ベジェ曲線を描画するアプリケーションの開発を行えるようになる C++ 言語の便利な機能を使えるようになる 要素数が可変な配列としての std::vector の活用 計算機による曲線の表現
構造力学Ⅰ第12回
 第 回材の座屈 (0 章 ) p.5~ ( 復習 ) モールの定理 ( 手順 ) 座屈とは 荷重により梁に生じた曲げモーメントをで除して仮想荷重と考える 座屈荷重 偏心荷重 ( 曲げと軸力 ) 断面の核 この仮想荷重に対するある点でのせん断力 たわみ角に相当する曲げモーメント たわみに相当する ( 例 ) 単純梁の支点のたわみ角 : は 図 を仮想荷重と考えたときの 点の支点反力 B は 図 を仮想荷重と考えたときのB
第 回材の座屈 (0 章 ) p.5~ ( 復習 ) モールの定理 ( 手順 ) 座屈とは 荷重により梁に生じた曲げモーメントをで除して仮想荷重と考える 座屈荷重 偏心荷重 ( 曲げと軸力 ) 断面の核 この仮想荷重に対するある点でのせん断力 たわみ角に相当する曲げモーメント たわみに相当する ( 例 ) 単純梁の支点のたわみ角 : は 図 を仮想荷重と考えたときの 点の支点反力 B は 図 を仮想荷重と考えたときのB
Microsoft PowerPoint - 画像工学2007-2印刷用++++
 教室 : 14-202 OCTOBER 09 画像工学 2007 年度版 Imaging Science and Technolog 画像工学 2007 年度版 2 慶応義塾大学理工学部 教授 中島真人 1 ( 例 ) 画像システムとしてのカメラ 入力 f(,) ( 紙に書かれた文字 ) カメラ ( フィルムカメラ デジタルカメラ どちらでも OK ) (u,v) SYSTEM ( フィルム上または
教室 : 14-202 OCTOBER 09 画像工学 2007 年度版 Imaging Science and Technolog 画像工学 2007 年度版 2 慶応義塾大学理工学部 教授 中島真人 1 ( 例 ) 画像システムとしてのカメラ 入力 f(,) ( 紙に書かれた文字 ) カメラ ( フィルムカメラ デジタルカメラ どちらでも OK ) (u,v) SYSTEM ( フィルム上または
Microsoft PowerPoint - 画像工学2007-8印刷用
 教室 : 14-0 DECEMBER 04 画像工学 007 年度版 Imagng Scnc and Tchnolog 画像工学 007 年度版 8 慶応義塾大学理工学部 教授 中島真人 Drctonal Band-pass Fltr の効果 前回の講義 訂正があります! Huv g v u ここで フィルタの形が間違っていました. Input Imag v Drctonal Band-pass Fltr
教室 : 14-0 DECEMBER 04 画像工学 007 年度版 Imagng Scnc and Tchnolog 画像工学 007 年度版 8 慶応義塾大学理工学部 教授 中島真人 Drctonal Band-pass Fltr の効果 前回の講義 訂正があります! Huv g v u ここで フィルタの形が間違っていました. Input Imag v Drctonal Band-pass Fltr
す 局所領域 ωk において 線形変換に用いる係数 (ak 画素の係数 (ak bk ) を算出し 入力画像の信号成分を bk ) は次式のコスト関数 E を最小化するように最適化 有さない画素に対して 式 (2) より画素値を算出する される これにより 低解像度な画像から補間によるアップサ E(
 IR E-mail: [email protected] Abstract IR RGB ( ) IR IR IR RGB RGB PSNR 1 Time-Of- Flight(TOF)[1] Kinect [2] TOF LED TOF [3] [6] [4][5] 2 [6] RGB ( ) Infrared(IR) IR 2 2.1 1 す 局所領域 ωk において 線形変換に用いる係数 (ak
IR E-mail: [email protected] Abstract IR RGB ( ) IR IR IR RGB RGB PSNR 1 Time-Of- Flight(TOF)[1] Kinect [2] TOF LED TOF [3] [6] [4][5] 2 [6] RGB ( ) Infrared(IR) IR 2 2.1 1 す 局所領域 ωk において 線形変換に用いる係数 (ak
連続講座 断層映像法の基礎第 32 回 : 篠原広行 他 断層映像法の基礎 第 32 回 ML-EM 法と OS-EM 法 篠原広行 1) 桑山潤 1) 小川亙 1) 2) 橋本雄幸 1) 首都大学東京人間健康科学研究科放射線科学域 2) 横浜創英短期大学情報学科 はじめに第 31 回では繰り返しを
 断層映像法の基礎 第 32 回 ML-EM 法と OS-EM 法 篠原広行 1) 桑山潤 1) 小川亙 1) 2) 橋本雄幸 1) 首都大学東京人間健康科学研究科放射線科学域 2) 横浜創英短期大学情報学科 はじめに第 31 回では繰り返しを利用して徐々に解に近づけていく方法を紹介した 本稿ではその繰り返しを使った方法で最も多く使われている ML-EM 法と OS-EM 法について解説する また その方法を利用した数値シミュレーションの結果についても紹介する
断層映像法の基礎 第 32 回 ML-EM 法と OS-EM 法 篠原広行 1) 桑山潤 1) 小川亙 1) 2) 橋本雄幸 1) 首都大学東京人間健康科学研究科放射線科学域 2) 横浜創英短期大学情報学科 はじめに第 31 回では繰り返しを利用して徐々に解に近づけていく方法を紹介した 本稿ではその繰り返しを使った方法で最も多く使われている ML-EM 法と OS-EM 法について解説する また その方法を利用した数値シミュレーションの結果についても紹介する
Microsoft Word - 犬飼.doc
 2004 年度卒業研究 肌色抽出について 岡山理科大学 総合情報学部 情報科学科 澤見研究室 I01I013 犬飼芳久 目次 1 はじめに 2 2 色空間に注目した肌色抽出手法 2.1 肌色抽出の手法について 2.2 色空間について 2.2.1 RGB 2.2.2 XYZ 2.2.3 L*a*b* 2.2.4 YCbCr 2.2.5 YIQ 2.2.6 HSV 2.2.7 修正 HSV 2.3 画素分布における検討
2004 年度卒業研究 肌色抽出について 岡山理科大学 総合情報学部 情報科学科 澤見研究室 I01I013 犬飼芳久 目次 1 はじめに 2 2 色空間に注目した肌色抽出手法 2.1 肌色抽出の手法について 2.2 色空間について 2.2.1 RGB 2.2.2 XYZ 2.2.3 L*a*b* 2.2.4 YCbCr 2.2.5 YIQ 2.2.6 HSV 2.2.7 修正 HSV 2.3 画素分布における検討
スライド 1
 Athena による 動径構造関数の導出 ー実践 ZnO 結晶の解析ー Athena の位置づけ Athena 測定データの解析 ( データの読込みからフーリエ変換まで ) Artemis EXAFS データへのモデルフィッテング Hephaestus 各元素のデータベース ( 吸収端や蛍光線のエネルギー 吸収係数の計算機能など ) Outline 最新のAthenaを入手する Athenaの起動と測定データの読み込み
Athena による 動径構造関数の導出 ー実践 ZnO 結晶の解析ー Athena の位置づけ Athena 測定データの解析 ( データの読込みからフーリエ変換まで ) Artemis EXAFS データへのモデルフィッテング Hephaestus 各元素のデータベース ( 吸収端や蛍光線のエネルギー 吸収係数の計算機能など ) Outline 最新のAthenaを入手する Athenaの起動と測定データの読み込み
学生 23 省メモリ指向一枚超解像 アーキテクチャとその FPGA 実装 北海道大学大学院情報科学研究科 大平貴徳 真田祐樹 築田聡史 五十嵐正樹 池辺将之 浅井哲也 本村真人 1
 学生 23 省メモリ指向一枚超解像 アーキテクチャとその FPGA 実装 北海道大学大学院情報科学研究科 大平貴徳 真田祐樹 築田聡史 五十嵐正樹 池辺将之 浅井哲也 本村真人 1 研究背景 映像機器の高機能化に伴う映像の高解像化 ーレティナディスプレイー 4K ハイビジョンテレビ 低解像度の映像コンテンツが数多く存在 4K テレビ 解像度を高める研究 ( 超解像 ) ー高速ー低コストー解像度の精度
学生 23 省メモリ指向一枚超解像 アーキテクチャとその FPGA 実装 北海道大学大学院情報科学研究科 大平貴徳 真田祐樹 築田聡史 五十嵐正樹 池辺将之 浅井哲也 本村真人 1 研究背景 映像機器の高機能化に伴う映像の高解像化 ーレティナディスプレイー 4K ハイビジョンテレビ 低解像度の映像コンテンツが数多く存在 4K テレビ 解像度を高める研究 ( 超解像 ) ー高速ー低コストー解像度の精度
Slide 1
 ハンズオン受講の為の準備講座 これから始める人の為の ディープラーニング基礎講座 村上真奈 NVIDIA CUDA & Deep Learning Solution Architect NVIDIA Corporation 1 機械学習とディープラーニングの関係 AGENDA ディープラーニングとは? ニューラルネットワークの構造 ディープラーニングの学習とは 畳み込みニューラルネットワーク 午後に予定しているハンズオンの為の基礎講座ディープラーニングをこれから始める方を対象に基礎概念や用語の解説を行います
ハンズオン受講の為の準備講座 これから始める人の為の ディープラーニング基礎講座 村上真奈 NVIDIA CUDA & Deep Learning Solution Architect NVIDIA Corporation 1 機械学習とディープラーニングの関係 AGENDA ディープラーニングとは? ニューラルネットワークの構造 ディープラーニングの学習とは 畳み込みニューラルネットワーク 午後に予定しているハンズオンの為の基礎講座ディープラーニングをこれから始める方を対象に基礎概念や用語の解説を行います
Kumamoto University Center for Multimedia and Information Technologies Lab. 熊本大学アプリケーション実験 ~ 実環境における無線 LAN 受信電波強度を用いた位置推定手法の検討 ~ InKIAI 宮崎県美郷
 熊本大学アプリケーション実験 ~ 実環境における無線 LAN 受信電波強度を用いた位置推定手法の検討 ~ InKIAI プロジェクト @ 宮崎県美郷町 熊本大学副島慶人川村諒 1 実験の目的 従来 信号の受信電波強度 (RSSI:RecevedSgnal StrengthIndcator) により 対象の位置を推定する手法として 無線 LAN の AP(AccessPont) から受信する信号の減衰量をもとに位置を推定する手法が多く検討されている
熊本大学アプリケーション実験 ~ 実環境における無線 LAN 受信電波強度を用いた位置推定手法の検討 ~ InKIAI プロジェクト @ 宮崎県美郷町 熊本大学副島慶人川村諒 1 実験の目的 従来 信号の受信電波強度 (RSSI:RecevedSgnal StrengthIndcator) により 対象の位置を推定する手法として 無線 LAN の AP(AccessPont) から受信する信号の減衰量をもとに位置を推定する手法が多く検討されている
画像参照画像送り 5 画像下部に再生ボタンが表示されます 再生ボタンをクリックすると 自動コマ送りされます 1
 画像参照画像送り 画像参照の画像送り方法について説明します 画像上にカーソルを表示した状態で マウスのホイールボタンでスクロールする またはマウスの左ボタンで上下にドラックすると アクティブなシリーズの画像送りができます 1 カルテ タブや 画像 レポート タブから 画像アイコンをクリックします 画像が表示されます 3 画像が切り替わって表示されます シリーズの位置はバー上の で表示されます 2 画像上にカーソルを表示した状態で
画像参照画像送り 画像参照の画像送り方法について説明します 画像上にカーソルを表示した状態で マウスのホイールボタンでスクロールする またはマウスの左ボタンで上下にドラックすると アクティブなシリーズの画像送りができます 1 カルテ タブや 画像 レポート タブから 画像アイコンをクリックします 画像が表示されます 3 画像が切り替わって表示されます シリーズの位置はバー上の で表示されます 2 画像上にカーソルを表示した状態で
MATLABを使用した‘胃腫瘍性病変’ のデジタル画像処理
 MATLAB を使用した 胃腫瘍性病変 のデジタル画像処理 日本文理大学医療専門学校診療放射線学科 ( 大分大学大学院工学研究科博士前期課程 ) 長野宣道 1 目的 胃 X 線写真の自動診断支援 (Computer aided diagnosis : 以後 CAD) の研究を行う上で MATLAB を使用し処理しやすいプログラムを選択 決定する目的で試験的に処理法と処理画像を比較検討した. 元画像ポジ反転画像キャニー法
MATLAB を使用した 胃腫瘍性病変 のデジタル画像処理 日本文理大学医療専門学校診療放射線学科 ( 大分大学大学院工学研究科博士前期課程 ) 長野宣道 1 目的 胃 X 線写真の自動診断支援 (Computer aided diagnosis : 以後 CAD) の研究を行う上で MATLAB を使用し処理しやすいプログラムを選択 決定する目的で試験的に処理法と処理画像を比較検討した. 元画像ポジ反転画像キャニー法
Microsoft PowerPoint - 時系列解析(11)_講義用.pptx
 時系列解析 () ボラティリティ 時変係数 AR モデル 東京 学数理 情報教育研究センター 北川源四郎 概要. 分散 定常モデル : 線形化 正規近似. 共分散 定常モデル : 時変係数モデル 3. 線形 ガウス型状態空間モデル 分散 共分散 定常 3 地震波 経 5 定常時系列のモデル 4. 平均 定常 トレンド, 季節調整. 分散 定常 線形 ガウスモデル ( カルマンフィルタ ) で推定するためには
時系列解析 () ボラティリティ 時変係数 AR モデル 東京 学数理 情報教育研究センター 北川源四郎 概要. 分散 定常モデル : 線形化 正規近似. 共分散 定常モデル : 時変係数モデル 3. 線形 ガウス型状態空間モデル 分散 共分散 定常 3 地震波 経 5 定常時系列のモデル 4. 平均 定常 トレンド, 季節調整. 分散 定常 線形 ガウスモデル ( カルマンフィルタ ) で推定するためには
また おすすめはしませんが C: Program Files Adobe Adobe After Effects [version] Support Files Plug-ins に配置することによって After Effects からのみ使用できます macos の場合 /Library/Appl
![また おすすめはしませんが C: Program Files Adobe Adobe After Effects [version] Support Files Plug-ins に配置することによって After Effects からのみ使用できます macos の場合 /Library/Appl また おすすめはしませんが C: Program Files Adobe Adobe After Effects [version] Support Files Plug-ins に配置することによって After Effects からのみ使用できます macos の場合 /Library/Appl](/thumbs/89/98423442.jpg) Fast Camera Lens Blur User Guide 高速なブラー グローをあなたに 動作環境 OS : Windows / Mac Adobe After Effects / Premiere Pro CS6 - CC 2018 実際に動作を確認した環境については 最後の動作確認環境をご覧ください インストール方法 Windows の場合 C: Program Files Adobe
Fast Camera Lens Blur User Guide 高速なブラー グローをあなたに 動作環境 OS : Windows / Mac Adobe After Effects / Premiere Pro CS6 - CC 2018 実際に動作を確認した環境については 最後の動作確認環境をご覧ください インストール方法 Windows の場合 C: Program Files Adobe
読取革命Lite かんたん入門ガイド
 かんたん入門ガイド かんたん入門ガイドは 読取革命 Lite の基本的な操作手順を記載しています 紙 Word INDEX はじめに 2 困ったときには 2 操作の流れ 3 アプリケーションの起動 3 画像の読み込み 4 認識結果をWordへ転送 6 手動で領域枠を作成する 8 領域枠について 10 文字の認識率向上ポイント 11 画像 認識結果 P1008-20310 はじめに このたびは 日本語
かんたん入門ガイド かんたん入門ガイドは 読取革命 Lite の基本的な操作手順を記載しています 紙 Word INDEX はじめに 2 困ったときには 2 操作の流れ 3 アプリケーションの起動 3 画像の読み込み 4 認識結果をWordへ転送 6 手動で領域枠を作成する 8 領域枠について 10 文字の認識率向上ポイント 11 画像 認識結果 P1008-20310 はじめに このたびは 日本語
