PowerPoint プレゼンテーション
|
|
|
- まさとし つちた
- 7 years ago
- Views:
Transcription
1 空間フィルタリング (spatal lterng) 入力画像の対応する画素値だけではなく その周囲 ( 近傍領域 ) の画素も含めた領域内の画素値を用いて 出力画像の対応する画素値を計算する処理 入力画像出力画像入力画像出力画像 画素ごとの濃淡変換 ( 階調処理 ) 領域に基づく濃淡変換 ( 空間フィルタリング )
2 空間フィルタ (spatal lter) 線形フィルタ (lnear lter) w w m nhm n g nw mw ( ): 入力画像 g ( ): 出力画像 h (m n): フィルタ係数を表す配列 (w+) (w+): フィルタの大きさ () 非線形フィルタ (nonlnear lter) () 式にあてはまらない処理をともなうフィルタ 畳み込み積分コンボリューション フィルタ カーネル オペレータ ( 演算子 ) 重み係数行列 などとも呼ばれる フィルタサイズ d
3 ( ) a d g b e h c (3 ) ( ) フィルタサイズ3 3 (w = のとき ) のフィルタ h(m n) 重み係数 画素の位置を表す座標はアドレスとしてその画素の番地を示すもの (7 ) = 画像処理とは あるルールに従って画素値 ( ) を別の値に置き換える処理のこと 空間フィルタリングは フィルタを用いて画素ごとに (pel b pel) で積和演算を行う. フィルタの原点 ( フィルタの中心 ) を注目画素 ( ) と重ねて積和演算を行う. フィルタは マスク オペレータ ( 演算子 ) カーネルなどとも呼ばれる. 注目画素が ( 3) のとき g(3) = a+ b+ c+ d+ e+ + g+ h+
4 線形フィルタの計算例 フィルタ フィルタの原点 ( 青い四角 ) 積和 5 (-)+5 (-)+5 (-) +5 (-)+ + (-) + (-)+ (-) + (-) = フィルタの原点を注目画素に合わせて重ね ( 緑の四角 ) 重なった位置どうしで フィルタの係数と入力画素値を掛け算し さらにその結果をすべて足し合わせる. ( コンボリューション : 畳み込み ) 注目画素 ( ) ( 赤い四角 ) ( ) 入力画像 出力画像
5 フィルタリングの目的 機能 平滑化 (smoothng) 画像になめらかな濃淡変化を与える処理 画像に含まれるノイズなどの不要な濃淡変動を軽減する エッジ抽出 (edge etracton) 画像中の明るさが急に変化する部分 ( エッジ ) を取り出す処理 画像中から特徴や図形を検出したりするための前処理として利用される 鮮鋭化 (sharpenng) 平滑化フィルタ 元の画像の濃淡を残したままエッジを強調する処理 画像中のエッジを強調することで画像の鮮鋭性を改善する
6 フィルタリング処理画像 入力 平滑化 鮮鋭化 エッジ抽出
7 移動平均フィルタ (averagng lter) フィルタを移動させながら つぎつぎに局所的な平均値を求めるため移動平均フィルタと呼ばれる. 単に平均化フィルタとも言う. フィルタサイズが大きいほど また 繰り返すほど 平滑化の度合いが増す = 3 3 の移動平均フィルタ の移動平均フィルタ
8 移動平均による平滑化 g() = ( ) =8 = g()= ( ) =7 =3 ( ) 処理 3 3 入力画像 () 出力画像 g() 濃度プロファイル 3
9 ( ) 入力画像 () 加重平均フィルタ (weghted averagng lter) 単純な平均ではなく フィルタの原点 ( 通常は中央 ) に近いほど大きな重みを付けた平均化フィルタ. 単純な平均化フィルタに比べ よりなめらかで自然な平均化の効果が期待できる. 中心画素 注目画素 移動平均フィルタ 周辺画素よりも中心画素により大きな重みをかける. 各フィルタの係数は すべて足すと になるように正規化する. これは 平滑化後の画像の明るさの平均を一定に保つために重要である の加重平均フィルタ 3 3 の加重平均フィルタ
10 . ガウシアンフィルタ (Gaussan lter) フィルタ係数の重みを平均 分散 σ のガウス分布 (Gaussan dstrbuton) に近づけた加重平均フィルタフィルタサイズ (w + )(w + ) の場合 σ = w/ とするのが一つの目安 - h g ep 次元ガウス分布の式とグラフの例 (w = σ = w/ = 5) のガウシアンカーネル のガウシアンカーネル
11 5 5 回 回 7 7 回 入力画像 回 3 回 7 7 回 移動平均 フィルタの 処理例 回 5 回 回
12 統計フィルタ (statstcs lter) ごま雑音 : 黒い粒状雑音塩雑音 : 白い粒状雑音 フィルタ領域内の最大値 最小値 中央値 平均値 分散などの統計量を出力値とするフィルタ. 特に順序に関係する統計値を出力するフィルタは順序統計フィルタ (order-statstcs lter) とも呼ばれ ごま塩雑音の除去に優れている 平均フィルタ (mean lter) 分散フィルタ (varance lter) 最大値フィルタ (ma lter) 最小値フィルタ (mn lter) 中央値フィルタ (medan lter) 近傍領域の画素値を順番に並び替え その特定の順番の値で 注目画素の画素値を置き換える 順序統計フィルタ 入力画像 平均画像 分散画像最大値画像最小値画像中央値画像
13 メディアンフィルタ (medan lter) ( 中間値フィルタ 中央値フィルタ ) 非線形フィルタ 入力画像 スパイク状雑音 ( ごま塩雑音 ) 変化の激しい孤立画素 ( スパイク状雑音 ) を抑制する 処理画像
14 局所領域における濃淡レベルの中央値 (medan) を出力するフィルタである. エッジや線が保存されやすく スパイク状雑音 ( ごま塩雑音 ) の除去に優れる. 6 ( ) g( ) フィルタサイズ3 3の場合 () = : { } g() = (3) = : { 5 5} g(3) = (5) = 5 : { 5 5} g(5) = (3) = : { 5 5 5} g(3) =
15 メディアンフィルタ の効果 移動平均フィルタ メディアンフィルタ ごま塩雑音を伴う入力画像
16 連続関数の微分 ( ) lm h 微小な変化分 d d h h d d ( ) h h + 接線の傾き 関数 () が微分可能であれば h + ( 右側微分 ) の場合も h ( 左側微分 ) の場合も その極限値は等しくなる
17 ディジタル画像における微分 ディジタル画像の場合には 微分は注目画素と隣接画素との差分で置き換えられる. ただし 隣接画素を右側にとるか 左側にとるかによって 一般に差分値は異なる ( ) (+) () ( ) () ( ) 右側差分 左側差分 横方向の差分 Δ 縦方向の差分 Δ
18 微分フィルタ R L R L U D U D
19 微分フィルタの出力画像 入力画像 横方向の差分画像 Δ 縦方向の差分画像 Δ エッジ強度画像 G mag ( 勾配の大きさ ) 各画素における横方向の差分 : 各画素における縦方向の差分 : D ( ) D ( ) 画素値の勾配の大きさ : G mag ( ) 画素値の勾配の方向 : G dr ( ) G mag ( ) ( ) G dr tan ( ) ( ) 微分フィルタは エッジの強度 ( 濃度勾配の大きさ ) とエッジの方向 ( 濃度勾配の方向 ) の つ出力する
20 微分フィルタの改良 効果 : 画像の濃淡が急激に変化するエッジ部分を検出できる欠点 : 画像に含まれるノイズに対しても敏感に反応する傾向にある 展望 : できるだけノイズを抑えながらエッジを抽出したい対策 : 微分と平滑化を組み合わせる 横方向の微分と縦方向の平滑化の組み合わせ 入力画像 出力画像 縦方向の微分と横方向の平滑化の組み合わせ 入力画像 出力画像
21 Prewtt lter プリューウィットフィルタプレヴィットフィルタ 横方向の微分フィルタ 縦 3 画素の平均フィルタ Prewtt lter( 横方向 ) 縦方向の微分フィルタ 横 3 画素の平均フィルタ Prewtt lter ( 縦方向 )
22 Sobel lter ソーベルフィルタゾーベルフィルタ 横方向の微分フィルタ 縦 3 画素の加重平均フィルタ Sobel lter ( 横方向 ) 縦方向の微分フィルタ 横 3 画素の加重平均フィルタ Sobel lter ( 縦方向 )
23 微分フィルタ vs. ソーベルフィルタ 微分フィルタのエッジ強度画像 ( 拡大 ) ソーベルフィルタのエッジ強度画像 ( 拡大 )
24 次微分とラプラシアン 次微分は 微分を 回繰り返すこと ラプラシアンは 階微分の作用素であり 次元の直交座標系では次のように定義される 関数 ( ) のラプラシアンは次式で定義される X 軸方向の 次微分 画像は 次元の直交座標系 Y 軸方向の 次微分
25 連続関数の 次微分 ( ) 関数 () d d d d d d 次微分 次微分
26 次微分の意味するところ d d d d dr d d d d d d d d d d 谷底のような勾配山頂のような勾配平坦ラプラシアンが意味しているのは
27 画像の 次微分 ( 差分 ) とラプラシアン 横方向の 次微分 縦方向の 次微分 ラプラシアン
28 ラプラシアンフィルタ (Laplacan lter) つの 次微分の差 次微分フィルタ ( 横方向 ) + 次微分フィルタ ( 縦方向 ) ラプラシアンフィルタ
29 ラプラシアンフィルタの処理結果 入力画像処理画像処理画像 次微分フィルタはエッジの強度のみを出力する ラプラシアンフィルタラプラシアンフィルタ ( 変形版 )
30 ゼロ交差 (zero crossng) 画素値 画素値 画素値 ゼロ交差点 原画像 次微分 次微分
31 鮮鋭化の考え方 原画像 鮮鋭化画像 g 次微分 = g ( 原画像 )-( 次微分画像 ) = 鮮鋭化画像 5
32 鮮鋭化フィルタ (sharpenng lter) 入力画像を表すフィルタ 鮮鋭化フィルタ ( 近傍 ) 入力画像を表すフィルタ ラプラシアンフィルタ 鮮鋭化フィルタ (8 近傍 ) ラプラシアンフィルタ ( 変形版 )
33 年国家試験問題 3 3 の空間フィルタを示す エッジの抽出に用いるのはどれか つ選べ ただし 数字は重み係数を示す
34 年国家試験問題 スパイク状ノイズの除去に効果的なのはどれか. Sobel フィルタ. ハイパスフィルタ 3. メディアンフィルタ. ガウシアンフィルタ 5. ラプラシアンフィルタ
35 年国家試験問題 5 5 の画素から構成される画像を図 A に示す 図に B に示す加重平均フィルタで処理した後の太枠で囲まれた部分の画素値はどれか ただし 図 A の数値は各画素値を示す 図 A 図 B
36 年国家試験問題 デジタル画像処理のおけるエッジ検出フィルタはどれか. ソーベルフィルタ. 加重平均フィルタ 3. 移動平均フィルタ. ガウシアンフィルタ 5. メディアンフィルタ
37 8 年国家試験問題 画像が最も平滑化される空間フィルタはどれか ただし 数字は重み係数を示す
38 7 年国家試験問題 3 3 の空間フィルタを示す. 画像の鮮鋭化に用いるのはどれか ただし 数字は重み係数を示す
Microsoft PowerPoint - comprog11.pptx
 Outline プログラミング演習第 回エッジを検出する on 3..4 電気通信大学情報理工学部知能機械工学科長井隆行 画像の本質 輝度の境目に情報あり! 画像の微分と 階微分 エッジ検出 画像をぼかす 本日の課題 画像の本質 エッジ抽出 画像の情報は境目にあり! エッジ 輝度が大きく変化しているところ ( 境界 ) 画像の情報はエッジにあり 輝度 人間の視覚系でも特定のエッジの方向に発火するニューロンが見つかっている
Outline プログラミング演習第 回エッジを検出する on 3..4 電気通信大学情報理工学部知能機械工学科長井隆行 画像の本質 輝度の境目に情報あり! 画像の微分と 階微分 エッジ検出 画像をぼかす 本日の課題 画像の本質 エッジ抽出 画像の情報は境目にあり! エッジ 輝度が大きく変化しているところ ( 境界 ) 画像の情報はエッジにあり 輝度 人間の視覚系でも特定のエッジの方向に発火するニューロンが見つかっている
l10
 ノイズ除去と画像の強調 画質改善 第4章 pp.101~136 入力画像にはさまざまな 雑音 と 歪み が含まれている 画質劣化 の要因を取り除く 画像を見やすくする 有用な情報を抽出しやすく強調する ことは 画像処理の最も重要な役割の一つ 目的 人間にとって見やすい画像を作る 画像の解析や認識にとって 特徴抽出が容易に行えるための 前処理 preprocessing) ノイズ除去と画像の強調 ノイズ除去と画像の強調
ノイズ除去と画像の強調 画質改善 第4章 pp.101~136 入力画像にはさまざまな 雑音 と 歪み が含まれている 画質劣化 の要因を取り除く 画像を見やすくする 有用な情報を抽出しやすく強調する ことは 画像処理の最も重要な役割の一つ 目的 人間にとって見やすい画像を作る 画像の解析や認識にとって 特徴抽出が容易に行えるための 前処理 preprocessing) ノイズ除去と画像の強調 ノイズ除去と画像の強調
Microsoft PowerPoint - CV04.ppt [互換モード]
![Microsoft PowerPoint - CV04.ppt [互換モード] Microsoft PowerPoint - CV04.ppt [互換モード]](/thumbs/101/149709049.jpg) コンピュータビジョン特論 Advanced Computer Vision 第 4 回 画像特徴 ( 点 直線 領域 ) の検出と識別 -1 画質の改善エッジの検出 濃度ヒストグラム (Histogram) 画素数 8 6 4 2 濃度ヒストグラム (Histogram) は 画像の濃度値を横軸に その濃度値を持つ画素数を縦軸に取った ヒストグラム 19 38 57 76 95 114 133 152
コンピュータビジョン特論 Advanced Computer Vision 第 4 回 画像特徴 ( 点 直線 領域 ) の検出と識別 -1 画質の改善エッジの検出 濃度ヒストグラム (Histogram) 画素数 8 6 4 2 濃度ヒストグラム (Histogram) は 画像の濃度値を横軸に その濃度値を持つ画素数を縦軸に取った ヒストグラム 19 38 57 76 95 114 133 152
Microsoft PowerPoint - dm1_3.pptx
 スケジュール 9/6 イントロダクション : デジタル画像とは, 量 化と標本化,Dynamic Range /3 イントロダクション : デジタルカメラ, 間の視覚, 表 系 / フィルタ処理 : トーンカーブ, 線形フィルタ デジタルメディア処理 担当 : 井尻敬 /7 フィルタ処理 : 線形フィルタ, ハーフトーニング / フィルタ処理 3 : 離散フーリエ変換と周波数フィルタリング /7 前半のまとめと中間試験
スケジュール 9/6 イントロダクション : デジタル画像とは, 量 化と標本化,Dynamic Range /3 イントロダクション : デジタルカメラ, 間の視覚, 表 系 / フィルタ処理 : トーンカーブ, 線形フィルタ デジタルメディア処理 担当 : 井尻敬 /7 フィルタ処理 : 線形フィルタ, ハーフトーニング / フィルタ処理 3 : 離散フーリエ変換と周波数フィルタリング /7 前半のまとめと中間試験
PowerPoint プレゼンテーション
 ディジタル画像処理 濃度変換 ; 階調処理 2 値化処理 ; しきい値処理 フィルタ処理 画像間演算 データ圧縮 三次元表示 頻度 画像全体で同じ濃度値を持つ画素数を求め, グラフ化したものを濃度ヒストグラムあるいは単にヒストグラム (histogram) という. 横軸は濃淡値 ( 画素値 ), 縦軸にその出現頻度 ( 画素数 ) をとる. Histogram 出現頻度 30 20 0 ヒストグラムの利用法
ディジタル画像処理 濃度変換 ; 階調処理 2 値化処理 ; しきい値処理 フィルタ処理 画像間演算 データ圧縮 三次元表示 頻度 画像全体で同じ濃度値を持つ画素数を求め, グラフ化したものを濃度ヒストグラムあるいは単にヒストグラム (histogram) という. 横軸は濃淡値 ( 画素値 ), 縦軸にその出現頻度 ( 画素数 ) をとる. Histogram 出現頻度 30 20 0 ヒストグラムの利用法
目次. はじめに デジタル画像のビット数 図形認識に用いた画像と方法 ハフ変換 検出方法と画像について TIFF 画像 RAW 画像データ フィルタ処理 平滑化
 205 年度卒業研究論文 画像と図形のエッジ検出について 岡山理科大学総合情報学部情報科学科 I2I00 小名川薫儀 I2I0 渡邊貴裕 目次. はじめに... 2. デジタル画像のビット数... 2 3. 図形認識に用いた画像と方法... 2 3.. ハフ変換... 2. 検出方法と画像について... 3.. TIFF 画像... 3.2. RAW 画像データ... 3 5. フィルタ処理...
205 年度卒業研究論文 画像と図形のエッジ検出について 岡山理科大学総合情報学部情報科学科 I2I00 小名川薫儀 I2I0 渡邊貴裕 目次. はじめに... 2. デジタル画像のビット数... 2 3. 図形認識に用いた画像と方法... 2 3.. ハフ変換... 2. 検出方法と画像について... 3.. TIFF 画像... 3.2. RAW 画像データ... 3 5. フィルタ処理...
Microsoft PowerPoint - DigitalMedia2_2.pptx
 デジタルメディア処理 担当 : 井尻敬 デジタルメディア処理 7( 前期 ) /3 デジタル画像とは : イントロダクション / フィルタ処理 : 画素ごとの濃淡変換 線形フィルタ, 線形フィルタ /7 フィルタ処理 : フーリエ変換, ローパスフィルタ, ハイパスフィルタ 5/ 画像の幾何変換 : アファイン変換 5/8 画像の幾何変換 : 画像の補間, イメージモザイキング 5/5 画像領域分割
デジタルメディア処理 担当 : 井尻敬 デジタルメディア処理 7( 前期 ) /3 デジタル画像とは : イントロダクション / フィルタ処理 : 画素ごとの濃淡変換 線形フィルタ, 線形フィルタ /7 フィルタ処理 : フーリエ変換, ローパスフィルタ, ハイパスフィルタ 5/ 画像の幾何変換 : アファイン変換 5/8 画像の幾何変換 : 画像の補間, イメージモザイキング 5/5 画像領域分割
画像解析論(2) 講義内容
 画像解析論 画像解析論 東京工業大学長橋宏 主な講義内容 信号処理と画像処理 二次元システムとその表現 二次元システムの特性解析 各種の画像フィルタ 信号処理と画像処理 画像解析論 処理の応答 記憶域 入出力の流れ 信号処理系 実時間性が求められる メモリ容量に対する制限が厳しい オンラインでの対応が厳しく求められる 画像処理系 ある程度の処理時間が許容される 大容量のメモリ使用が容認され易い オフラインでの対応が容認され易い
画像解析論 画像解析論 東京工業大学長橋宏 主な講義内容 信号処理と画像処理 二次元システムとその表現 二次元システムの特性解析 各種の画像フィルタ 信号処理と画像処理 画像解析論 処理の応答 記憶域 入出力の流れ 信号処理系 実時間性が求められる メモリ容量に対する制限が厳しい オンラインでの対応が厳しく求められる 画像処理系 ある程度の処理時間が許容される 大容量のメモリ使用が容認され易い オフラインでの対応が容認され易い
Microsoft PowerPoint - ip02_01.ppt [互換モード]
![Microsoft PowerPoint - ip02_01.ppt [互換モード] Microsoft PowerPoint - ip02_01.ppt [互換モード]](/thumbs/96/127250376.jpg) 空間周波数 周波数領域での処理 空間周波数 (spatial frquncy) とは 単位長さ当たりの正弦波状の濃淡変化の繰り返し回数を表したもの 正弦波 : y sin( t) 周期 : 周波数 : T f / T 角周波数 : f 画像処理 空間周波数 周波数領域での処理 波形が違うと 周波数も違う 画像処理 空間周波数 周波数領域での処理 画像処理 3 周波数領域での処理 周波数は一つしかない?-
空間周波数 周波数領域での処理 空間周波数 (spatial frquncy) とは 単位長さ当たりの正弦波状の濃淡変化の繰り返し回数を表したもの 正弦波 : y sin( t) 周期 : 周波数 : T f / T 角周波数 : f 画像処理 空間周波数 周波数領域での処理 波形が違うと 周波数も違う 画像処理 空間周波数 周波数領域での処理 画像処理 3 周波数領域での処理 周波数は一つしかない?-
スライド 1
 医用画像処理学 (4) ( 教科書 pp.104-122) 有村秀孝 種々の濃度変換曲線 255 y=255 - x 0 I ディスプレイの電気 - 光変換特性 org _ out CI org _ in I out ( I org _ C in 1 ) フィラデルフィア (Philadelphia) はアメリカ合衆国ペンシルバニア州南東部にある都市 フィラデルフィア郡の全域を占めるペンシルバニア州最大の都市である
医用画像処理学 (4) ( 教科書 pp.104-122) 有村秀孝 種々の濃度変換曲線 255 y=255 - x 0 I ディスプレイの電気 - 光変換特性 org _ out CI org _ in I out ( I org _ C in 1 ) フィラデルフィア (Philadelphia) はアメリカ合衆国ペンシルバニア州南東部にある都市 フィラデルフィア郡の全域を占めるペンシルバニア州最大の都市である
ディジタル信号処理
 ディジタルフィルタの設計法. 逆フィルター. 直線位相 FIR フィルタの設計. 窓関数法による FIR フィルタの設計.5 時間領域での FIR フィルタの設計 3. アナログフィルタを基にしたディジタル IIR フィルタの設計法 I 4. アナログフィルタを基にしたディジタル IIR フィルタの設計法 II 5. 双 次フィルタ LI 離散時間システムの基礎式の証明 [ ] 4. ] [ ]*
ディジタルフィルタの設計法. 逆フィルター. 直線位相 FIR フィルタの設計. 窓関数法による FIR フィルタの設計.5 時間領域での FIR フィルタの設計 3. アナログフィルタを基にしたディジタル IIR フィルタの設計法 I 4. アナログフィルタを基にしたディジタル IIR フィルタの設計法 II 5. 双 次フィルタ LI 離散時間システムの基礎式の証明 [ ] 4. ] [ ]*
Microsoft PowerPoint - 第3回2.ppt
 講義内容 講義内容 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 ベクトルの直交性 3
講義内容 講義内容 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 ベクトルの直交性 3
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生
 0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
Microsoft PowerPoint - pr_12_template-bs.pptx
 12 回パターン検出と画像特徴 テンプレートマッチング 領域分割 画像特徴 テンプレート マッチング 1 テンプレートマッチング ( 図形 画像などの ) 型照合 Template Matching テンプレートと呼ばれる小さな一部の画像領域と同じパターンが画像全体の中に存在するかどうかを調べる方法 画像内にある対象物体の位置検出 物体数のカウント 物体移動の検出などに使われる テンプレートマッチングの計算
12 回パターン検出と画像特徴 テンプレートマッチング 領域分割 画像特徴 テンプレート マッチング 1 テンプレートマッチング ( 図形 画像などの ) 型照合 Template Matching テンプレートと呼ばれる小さな一部の画像領域と同じパターンが画像全体の中に存在するかどうかを調べる方法 画像内にある対象物体の位置検出 物体数のカウント 物体移動の検出などに使われる テンプレートマッチングの計算
0 スペクトル 時系列データの前処理 法 平滑化 ( スムージング ) と微分 明治大学理 学部応用化学科 データ化学 学研究室 弘昌
 0 スペクトル 時系列データの前処理 法 平滑化 ( スムージング ) と微分 明治大学理 学部応用化学科 データ化学 学研究室 弘昌 スペクトルデータの特徴 1 波 ( 波数 ) が近いと 吸光度 ( 強度 ) の値も似ている ノイズが含まれる 吸光度 ( 強度 ) の極大値 ( ピーク ) 以外のデータも重要 時系列データの特徴 2 時刻が近いと プロセス変数の値も似ている ノイズが含まれる プロセス変数の極大値
0 スペクトル 時系列データの前処理 法 平滑化 ( スムージング ) と微分 明治大学理 学部応用化学科 データ化学 学研究室 弘昌 スペクトルデータの特徴 1 波 ( 波数 ) が近いと 吸光度 ( 強度 ) の値も似ている ノイズが含まれる 吸光度 ( 強度 ) の極大値 ( ピーク ) 以外のデータも重要 時系列データの特徴 2 時刻が近いと プロセス変数の値も似ている ノイズが含まれる プロセス変数の極大値
内容梗概近年 液晶用ガラスはテレビやパソコンディスプレイ スマートフォンなど 様々な分野で使用されている 液晶用ガラスの欠損を検出するためには 欠損検出の精度の高さが重要である そのほかでは 劣化などの問題で認識しにくい甲骨文字の解読が必要である 甲骨文字を切り出し 鮮明化することが未解読資料の解読
 学士論文 OpenCV を用いたフィルタ処理の実現と応用 氏名 : 麻生啓太学籍番号 : 2260100001-0 担当教員 : 山崎勝弘教授提出日 : 2014 年 2 月 20 日 立命館大学理工学部電子情報デザイン学科 内容梗概近年 液晶用ガラスはテレビやパソコンディスプレイ スマートフォンなど 様々な分野で使用されている 液晶用ガラスの欠損を検出するためには 欠損検出の精度の高さが重要である
学士論文 OpenCV を用いたフィルタ処理の実現と応用 氏名 : 麻生啓太学籍番号 : 2260100001-0 担当教員 : 山崎勝弘教授提出日 : 2014 年 2 月 20 日 立命館大学理工学部電子情報デザイン学科 内容梗概近年 液晶用ガラスはテレビやパソコンディスプレイ スマートフォンなど 様々な分野で使用されている 液晶用ガラスの欠損を検出するためには 欠損検出の精度の高さが重要である
画像処理工学
 画像処理工学 画像の空間周波数解析とテクスチャ特徴 フーリエ変換の基本概念 信号波形のフーリエ変換 信号波形を周波数の異なる三角関数 ( 正弦波など ) に分解する 逆に, 周波数の異なる三角関数を重ねあわせることにより, 任意の信号波形を合成できる 正弦波の重ね合わせによる矩形波の表現 フーリエ変換の基本概念 フーリエ変換 次元信号 f (t) のフーリエ変換 変換 ( ω) ( ) ωt F f
画像処理工学 画像の空間周波数解析とテクスチャ特徴 フーリエ変換の基本概念 信号波形のフーリエ変換 信号波形を周波数の異なる三角関数 ( 正弦波など ) に分解する 逆に, 周波数の異なる三角関数を重ねあわせることにより, 任意の信号波形を合成できる 正弦波の重ね合わせによる矩形波の表現 フーリエ変換の基本概念 フーリエ変換 次元信号 f (t) のフーリエ変換 変換 ( ω) ( ) ωt F f
Microsoft Word - 卒論レジュメ_最終_.doc
 指紋認証のマニューシャ抽出について 澤見研究室 I02I036 兼信雄一 I02I093 柳楽和信 I02I142 吉田寛孝 1. はじめに近年, キャッシュカードや暗証番号が盗用され, 現金が引き出されるような事件が相次いでいる. これらの対向策として人間の体の一部を認証の鍵として利用する生体認証に注目が集まっている. そこで我々は, 生体認証で最も歴史がある指紋認証技術に着目した. 指紋認証方式は,2
指紋認証のマニューシャ抽出について 澤見研究室 I02I036 兼信雄一 I02I093 柳楽和信 I02I142 吉田寛孝 1. はじめに近年, キャッシュカードや暗証番号が盗用され, 現金が引き出されるような事件が相次いでいる. これらの対向策として人間の体の一部を認証の鍵として利用する生体認証に注目が集まっている. そこで我々は, 生体認証で最も歴史がある指紋認証技術に着目した. 指紋認証方式は,2
PowerPoint Presentation
 付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
Microsoft Word - 1B2011.doc
 第 14 回モールの定理 ( 単純梁の場合 ) ( モールの定理とは何か?p.11) 例題 下記に示す単純梁の C 点のたわみ角 θ C と, たわみ δ C を求めよ ただし, 部材の曲げ 剛性は材軸に沿って一様で とする C D kn B 1.5m 0.5m 1.0m 解答 1 曲げモーメント図を描く,B 点の反力を求める kn kn 4 kn 曲げモーメント図を描く knm 先に得られた曲げモーメントの値を
第 14 回モールの定理 ( 単純梁の場合 ) ( モールの定理とは何か?p.11) 例題 下記に示す単純梁の C 点のたわみ角 θ C と, たわみ δ C を求めよ ただし, 部材の曲げ 剛性は材軸に沿って一様で とする C D kn B 1.5m 0.5m 1.0m 解答 1 曲げモーメント図を描く,B 点の反力を求める kn kn 4 kn 曲げモーメント図を描く knm 先に得られた曲げモーメントの値を
パソコンシミュレータの現状
 第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
「情報」って何だ!?
 画像処理システム論 Image Media Systems 加藤俊一 Toshi KATO 感性の強化 人間の感性的な行動 知覚を支援 演奏支援 虫眼鏡 電子的メガネ ( 画像強調 雑音除去 ) 仮想現実感への応用 ( 建築設計支援 ) 感性の強化 電子的メガネ ( 画像強調 雑音除去 ) 生体から学ぶべきメカニズム (1) 明暗順応 : 明るさの変化に対する調節機構 側抑制 : 視野の中の明暗の微小変化を局所的に検出
画像処理システム論 Image Media Systems 加藤俊一 Toshi KATO 感性の強化 人間の感性的な行動 知覚を支援 演奏支援 虫眼鏡 電子的メガネ ( 画像強調 雑音除去 ) 仮想現実感への応用 ( 建築設計支援 ) 感性の強化 電子的メガネ ( 画像強調 雑音除去 ) 生体から学ぶべきメカニズム (1) 明暗順応 : 明るさの変化に対する調節機構 側抑制 : 視野の中の明暗の微小変化を局所的に検出
Microsoft PowerPoint - SPECTPETの原理2012.ppt [互換モード]
![Microsoft PowerPoint - SPECTPETの原理2012.ppt [互換モード] Microsoft PowerPoint - SPECTPETの原理2012.ppt [互換モード]](/thumbs/94/121508518.jpg) 22 年国家試験解答 1,5 フーリエ変換は線形変換 FFT はデータ数に 2 の累乗数を要求するが DFT は任意のデータ数に対応 123I-IMP Brain SPECT FBP with Ramp filter 123I-IMP Brain SPECT FBP with Shepp&Logan filter 99mTc-MIBI Myocardial SPECT における ストリークアーチファクト
22 年国家試験解答 1,5 フーリエ変換は線形変換 FFT はデータ数に 2 の累乗数を要求するが DFT は任意のデータ数に対応 123I-IMP Brain SPECT FBP with Ramp filter 123I-IMP Brain SPECT FBP with Shepp&Logan filter 99mTc-MIBI Myocardial SPECT における ストリークアーチファクト
スライド タイトルなし
 次元フーリエ変換 講義内容 空間周波数の概念 次元フーリエ変換代表的な 次元フーリエ変換対 次元離散フーリエ変換 フーリエ変換と逆変換 F.T. j F } ep{ 連続系離散系 } / ep{ N N N j N F F I. F.T. F ただし ここでは絶対値をとって画像化 } / ep{ N N N j F N 順変換逆変換 3 次元フーリエ変換の具体的なイメージ } / ep{ N N N
次元フーリエ変換 講義内容 空間周波数の概念 次元フーリエ変換代表的な 次元フーリエ変換対 次元離散フーリエ変換 フーリエ変換と逆変換 F.T. j F } ep{ 連続系離散系 } / ep{ N N N j N F F I. F.T. F ただし ここでは絶対値をとって画像化 } / ep{ N N N j F N 順変換逆変換 3 次元フーリエ変換の具体的なイメージ } / ep{ N N N
<4D F736F F D208D5C91A297CD8A7793FC96E591E631308FCD2E646F63>
 第 1 章モールの定理による静定梁のたわみ 1-1 第 1 章モールの定理による静定梁のたわみ ポイント : モールの定理を用いて 静定梁のたわみを求める 断面力の釣合と梁の微分方程式は良く似ている 前章では 梁の微分方程式を直接積分する方法で 静定梁の断面力と変形状態を求めた 本章では 梁の微分方程式と断面力による力の釣合式が類似していることを利用して 微分方程式を直接解析的に解くのではなく 力の釣合より梁のたわみを求める方法を学ぶ
第 1 章モールの定理による静定梁のたわみ 1-1 第 1 章モールの定理による静定梁のたわみ ポイント : モールの定理を用いて 静定梁のたわみを求める 断面力の釣合と梁の微分方程式は良く似ている 前章では 梁の微分方程式を直接積分する方法で 静定梁の断面力と変形状態を求めた 本章では 梁の微分方程式と断面力による力の釣合式が類似していることを利用して 微分方程式を直接解析的に解くのではなく 力の釣合より梁のたわみを求める方法を学ぶ
スライド 1
 5.5.2 画像の間引き 5.1 線形変換 5.2 アフィン変換 5.3 同次座標 5.4 平面射影変換 5.5 再標本化 1. 画素数の減少による表現能力の低下 画像の縮小 変形を行う際 結果画像の 画素数 < 入力画像の 画素数 ( 画素の密度 ) ( 画素の密度 ) になることがある この場合 結果画像の表現力 < 入力画像の表現力 ( 情報量 ) ( 情報量 ) 結果的に 情報の損失が生じる!
5.5.2 画像の間引き 5.1 線形変換 5.2 アフィン変換 5.3 同次座標 5.4 平面射影変換 5.5 再標本化 1. 画素数の減少による表現能力の低下 画像の縮小 変形を行う際 結果画像の 画素数 < 入力画像の 画素数 ( 画素の密度 ) ( 画素の密度 ) になることがある この場合 結果画像の表現力 < 入力画像の表現力 ( 情報量 ) ( 情報量 ) 結果的に 情報の損失が生じる!
Microsoft PowerPoint - DigitalMedia2_3b.pptx
 Contents デジタルメディア処理 2 の概要 フーリエ級数展開と 離散とその性質 周波数フィルタリング 担当 : 井尻敬 とは ( ) FourierSound.py とは ( ) FourierSound.py 横軸が時間の関数を 横軸が周波数の関数に変換する 法 声周波数 周波数 ( 係数番号 ) 後の関数は元信号に含まれる正弦波の量を す 中央に近いほど低周波, 外ほどが 周波 中央 (
Contents デジタルメディア処理 2 の概要 フーリエ級数展開と 離散とその性質 周波数フィルタリング 担当 : 井尻敬 とは ( ) FourierSound.py とは ( ) FourierSound.py 横軸が時間の関数を 横軸が周波数の関数に変換する 法 声周波数 周波数 ( 係数番号 ) 後の関数は元信号に含まれる正弦波の量を す 中央に近いほど低周波, 外ほどが 周波 中央 (
Microsoft Word - NumericalComputation.docx
 数値計算入門 武尾英哉. 離散数学と数値計算 数学的解法の中には理論計算では求められないものもある. 例えば, 定積分は, まずは積分 ( 被積分関数の原始関数をみつけること できなければ値を得ることはできない. また, ある関数の所定の値における微分値を得るには, まずその関数の微分ができなければならない. さらに代数方程式の解を得るためには, 解析的に代数方程式を解く必要がある. ところが, これらは必ずしも解析的に導けるとは限らない.
数値計算入門 武尾英哉. 離散数学と数値計算 数学的解法の中には理論計算では求められないものもある. 例えば, 定積分は, まずは積分 ( 被積分関数の原始関数をみつけること できなければ値を得ることはできない. また, ある関数の所定の値における微分値を得るには, まずその関数の微分ができなければならない. さらに代数方程式の解を得るためには, 解析的に代数方程式を解く必要がある. ところが, これらは必ずしも解析的に導けるとは限らない.
Microsoft Word 年度卒業研究.1.doc
 006 年度卒業研究 アンシャープ処理 ( ディジタル画像の強調処理 ) 岡山理科大学 総合情報学部 情報科学科 澤見研究室 I03I054 澤田慧 I03I055 柴田勇輝 目次 1 はじめに ディジタル画像の強調処理 3 強調処理の種類 3.1 ヒストグラム均等化法 (HE) 3. コンボリューション処理 (Convolution) 3.3 アンシャープ処理 (Unsharp) 4 アンシャープ処理の実現
006 年度卒業研究 アンシャープ処理 ( ディジタル画像の強調処理 ) 岡山理科大学 総合情報学部 情報科学科 澤見研究室 I03I054 澤田慧 I03I055 柴田勇輝 目次 1 はじめに ディジタル画像の強調処理 3 強調処理の種類 3.1 ヒストグラム均等化法 (HE) 3. コンボリューション処理 (Convolution) 3.3 アンシャープ処理 (Unsharp) 4 アンシャープ処理の実現
図 5 一次微分 図 6 コントラスト変化に伴う微分プロファイルの変化 価し, 合否判定を行う. 3. エッジ検出の原理ここでは, 一般的なエッジ検出の処理内容と, それぞれの処理におけるパラメータについて述べる. 3.1 濃度投影検出線と直交する方向に各画素をスキャンし, その濃度平均値を検出線上
 The Principles of Edge Detection, and Its Application to Image Measurement/ Junichi SUGANO ヴィスコ テクノロジーズ株式会社開発本部研究部菅野純一 1. はじめに画像処理におけるエッジとは, 対象物と背景の境界点を指しており, この境界点が連なることで対象物の輪郭を形成する. 対象物の輪郭を拡大してみると, レンズボケにより明から暗または暗から明へ濃度値が連続的に変化していることがわかる.
The Principles of Edge Detection, and Its Application to Image Measurement/ Junichi SUGANO ヴィスコ テクノロジーズ株式会社開発本部研究部菅野純一 1. はじめに画像処理におけるエッジとは, 対象物と背景の境界点を指しており, この境界点が連なることで対象物の輪郭を形成する. 対象物の輪郭を拡大してみると, レンズボケにより明から暗または暗から明へ濃度値が連続的に変化していることがわかる.
Microsoft PowerPoint - dm1_5.pptx
 デジタルメディア処理 1 017( 後期 ) 09/6 イントロダクション1 : デジタル画像とは, 量 化と標本化,Dynamic Range 10/03 イントロダクション : デジタルカメラ, 間の視覚, 表 系 10/10 フィルタ処理 1 : トーンカーブ, 線形フィルタ デジタルメディア処理 1 担当 : 井尻敬 10/17 フィルタ処理 : 線形フィルタ, ハーフトーニング 10/4
デジタルメディア処理 1 017( 後期 ) 09/6 イントロダクション1 : デジタル画像とは, 量 化と標本化,Dynamic Range 10/03 イントロダクション : デジタルカメラ, 間の視覚, 表 系 10/10 フィルタ処理 1 : トーンカーブ, 線形フィルタ デジタルメディア処理 1 担当 : 井尻敬 10/17 フィルタ処理 : 線形フィルタ, ハーフトーニング 10/4
Microsoft PowerPoint - dm1kadai.pptx
 デジタルメディア処理 1 担当 : 井尻敬 提出 法 : 共有フォルダに dm1 学籍番号 というフォルダを作成し, その中にソースコードの ったファイルを置く. フォルダ名は全て半. フォルダ名の例 : dm2al150999 課題雛形 : http://takashiijiri.com/classes/dm2018_1/dm1exer.zip 出 : 課題ではを受け取り, 画像またはファイルを保存するプログラムを作る.
デジタルメディア処理 1 担当 : 井尻敬 提出 法 : 共有フォルダに dm1 学籍番号 というフォルダを作成し, その中にソースコードの ったファイルを置く. フォルダ名は全て半. フォルダ名の例 : dm2al150999 課題雛形 : http://takashiijiri.com/classes/dm2018_1/dm1exer.zip 出 : 課題ではを受け取り, 画像またはファイルを保存するプログラムを作る.
目次 1 はじめに ラスタ画像 bit 数による差 画像拡大と画像補間法 ニアレストネイバー法 バイリニア法 バイキュービック法 Lanczos(n) 法 拡大画像の比
 2015 年度卒業研究論文 画像補間法による拡大 岡山理科大学総合情報学部情報科学科 I12I061 田中宏美 I12I063 仲陽美 目次 1 はじめに... 1 2 ラスタ画像... 1 2.1 bit 数による差... 2 3 画像拡大と画像補間法... 2 3.1 ニアレストネイバー法... 2 3.2 バイリニア法... 4 3.3 バイキュービック法... 6 3.4 Lanczos(n)
2015 年度卒業研究論文 画像補間法による拡大 岡山理科大学総合情報学部情報科学科 I12I061 田中宏美 I12I063 仲陽美 目次 1 はじめに... 1 2 ラスタ画像... 1 2.1 bit 数による差... 2 3 画像拡大と画像補間法... 2 3.1 ニアレストネイバー法... 2 3.2 バイリニア法... 4 3.3 バイキュービック法... 6 3.4 Lanczos(n)
線形システム応答 Linear System response
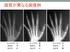 画質が異なる画像例 コントラスト劣 コントラスト優 コントラスト普 鮮鋭性 普 鮮鋭性 優 鮮鋭性 劣 粒状性 普 粒状性 劣 粒状性 優 医用画像の画質 コントラスト, 鮮鋭性, 粒状性の要因が互いに密接に関わり合って形成されている. 比 鮮鋭性 コントラスト 反 反 粒状性 増感紙 - フィルム系での 3 要因の関係 ディジタル画像処理系でもおよそ成り立つ WS u MTFu 画質に影響する因子
画質が異なる画像例 コントラスト劣 コントラスト優 コントラスト普 鮮鋭性 普 鮮鋭性 優 鮮鋭性 劣 粒状性 普 粒状性 劣 粒状性 優 医用画像の画質 コントラスト, 鮮鋭性, 粒状性の要因が互いに密接に関わり合って形成されている. 比 鮮鋭性 コントラスト 反 反 粒状性 増感紙 - フィルム系での 3 要因の関係 ディジタル画像処理系でもおよそ成り立つ WS u MTFu 画質に影響する因子
スライド 1
 知能制御システム学 画像処理の基礎 (2) OpenCV による基本的な例 東北大学大学院情報科学研究科鏡慎吾 swk(at)ic.is.tohoku.ac.jp 2010.07.06 局所処理の例 空間フィルタリング 注目点の近傍 ( 典型的には 3x3 画素,5x5 画素,... など ) の画素値から, 出力 G x,y を定める { F i,j }, (i, j) Neighbor(x,y)
知能制御システム学 画像処理の基礎 (2) OpenCV による基本的な例 東北大学大学院情報科学研究科鏡慎吾 swk(at)ic.is.tohoku.ac.jp 2010.07.06 局所処理の例 空間フィルタリング 注目点の近傍 ( 典型的には 3x3 画素,5x5 画素,... など ) の画素値から, 出力 G x,y を定める { F i,j }, (i, j) Neighbor(x,y)
画像工学入門
 セグメンテーション 講義内容 閾値法,k-mean 法 領域拡張法 SNAK 法 P タイル法 モード法 P タイル法 画像内で対象物の占める面積 (P パーセント ) があらかじめわかっているとき, 濃度ヒストグラムを作成し, 濃度値の累積分布が全体の P パーセントとなる濃度値を見つけ, この値を閾値とする. モード法 画像の輝度ヒストグラムを調べ その分布のモード ( 頻値輝度 ) 間の谷をしきい値とする
セグメンテーション 講義内容 閾値法,k-mean 法 領域拡張法 SNAK 法 P タイル法 モード法 P タイル法 画像内で対象物の占める面積 (P パーセント ) があらかじめわかっているとき, 濃度ヒストグラムを作成し, 濃度値の累積分布が全体の P パーセントとなる濃度値を見つけ, この値を閾値とする. モード法 画像の輝度ヒストグラムを調べ その分布のモード ( 頻値輝度 ) 間の谷をしきい値とする
Microsoft PowerPoint - 9.pptx
 9/7/8( 水 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 拡大とスカラー倍 行列演算と写像 ( 次変換 拡大後 k 倍 k 倍 k 倍拡大の関係は スカラー倍を用いて次のように表現できる p = (, ' = k ' 拡大前 p ' = ( ', ' = ( k, k 拡大 4 拡大と行列の積 拡大後 k 倍
9/7/8( 水 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 拡大とスカラー倍 行列演算と写像 ( 次変換 拡大後 k 倍 k 倍 k 倍拡大の関係は スカラー倍を用いて次のように表現できる p = (, ' = k ' 拡大前 p ' = ( ', ' = ( k, k 拡大 4 拡大と行列の積 拡大後 k 倍
スライド 1
 知能制御システム学 画像追跡 (1) 特徴点の検出と追跡 東北大学大学院情報科学研究科鏡慎吾 swk(at)ic.is.tohoku.ac.jp 2008.07.07 今日の内容 前回までの基本的な画像処理の例を踏まえて, ビジュアルサーボシステムの構成要素となる画像追跡の代表的手法を概説する 画像上の ある点 の追跡 オプティカルフローの拘束式 追跡しやすい点 (Harris オペレータ ) Lucas-Kanade
知能制御システム学 画像追跡 (1) 特徴点の検出と追跡 東北大学大学院情報科学研究科鏡慎吾 swk(at)ic.is.tohoku.ac.jp 2008.07.07 今日の内容 前回までの基本的な画像処理の例を踏まえて, ビジュアルサーボシステムの構成要素となる画像追跡の代表的手法を概説する 画像上の ある点 の追跡 オプティカルフローの拘束式 追跡しやすい点 (Harris オペレータ ) Lucas-Kanade
Microsoft Word - 卒業論文.doc
 006 年度卒業研究 画像補間法を用いた拡大画像の比較 岡山理科大学総合情報学部情報科学科 澤見研究室 I03I04 兼安俊治 I03I050 境永 目次 はじめに ラスタ画像 3 画像補間法 3. ニアレストネイバー法 3. バイリニア法 3.3 バイキュービック法 4 DCT を用いた拡大画像手法 5 FIR 法 6 評価 6. SNR 6. PSNR 7 実験 7. 主観評価 7. 客観評価
006 年度卒業研究 画像補間法を用いた拡大画像の比較 岡山理科大学総合情報学部情報科学科 澤見研究室 I03I04 兼安俊治 I03I050 境永 目次 はじめに ラスタ画像 3 画像補間法 3. ニアレストネイバー法 3. バイリニア法 3.3 バイキュービック法 4 DCT を用いた拡大画像手法 5 FIR 法 6 評価 6. SNR 6. PSNR 7 実験 7. 主観評価 7. 客観評価
多次元レーザー分光で探る凝縮分子系の超高速動力学
 波動方程式と量子力学 谷村吉隆 京都大学理学研究科化学専攻 http:theochem.kuchem.kyoto-u.ac.jp TA: 岩元佑樹 [email protected] ベクトルと行列の作法 A 列ベクトル c = c c 行ベクトル A = [ c c c ] 転置ベクトル T A = [ c c c ] AA 内積 c AA = [ c c c ] c =
波動方程式と量子力学 谷村吉隆 京都大学理学研究科化学専攻 http:theochem.kuchem.kyoto-u.ac.jp TA: 岩元佑樹 [email protected] ベクトルと行列の作法 A 列ベクトル c = c c 行ベクトル A = [ c c c ] 転置ベクトル T A = [ c c c ] AA 内積 c AA = [ c c c ] c =
<4D F736F F D DC58F498D5A814091E6318FCD814089E6919C82C682CD89BD82A92E646F63>
 第 1 章画像とは何か 第 1 章画像とは何か 画像 は英語では image であり 実際に存在する もの を 絵に描いたり カメラで撮影したりしたものである キャンバス フィルム 印画紙などに記録されて 現物が破壊されるなどで存在しなくなっても 遠方にあって直接見ることが不可能であっても 保存 伝送されていつでも どこでも自由に見ることが可能となる 本書で述べる 画像処理 はこの画像を入力とした処理である
第 1 章画像とは何か 第 1 章画像とは何か 画像 は英語では image であり 実際に存在する もの を 絵に描いたり カメラで撮影したりしたものである キャンバス フィルム 印画紙などに記録されて 現物が破壊されるなどで存在しなくなっても 遠方にあって直接見ることが不可能であっても 保存 伝送されていつでも どこでも自由に見ることが可能となる 本書で述べる 画像処理 はこの画像を入力とした処理である
線積分.indd
 線積分 線積分 ( n, n, n ) (ξ n, η n, ζ n ) ( n-, n-, n- ) (ξ k, η k, ζ k ) ( k, k, k ) ( k-, k-, k- ) 物体に力 を作用させて位置ベクトル A の点 A から位置ベクトル の点 まで曲線 に沿って物体を移動させたときの仕事 W は 次式で計算された A, A, W : d 6 d+ d+ d@,,, d+ d+
線積分 線積分 ( n, n, n ) (ξ n, η n, ζ n ) ( n-, n-, n- ) (ξ k, η k, ζ k ) ( k, k, k ) ( k-, k-, k- ) 物体に力 を作用させて位置ベクトル A の点 A から位置ベクトル の点 まで曲線 に沿って物体を移動させたときの仕事 W は 次式で計算された A, A, W : d 6 d+ d+ d@,,, d+ d+
す 局所領域 ωk において 線形変換に用いる係数 (ak 画素の係数 (ak bk ) を算出し 入力画像の信号成分を bk ) は次式のコスト関数 E を最小化するように最適化 有さない画素に対して 式 (2) より画素値を算出する される これにより 低解像度な画像から補間によるアップサ E(
 IR E-mail: [email protected] Abstract IR RGB ( ) IR IR IR RGB RGB PSNR 1 Time-Of- Flight(TOF)[1] Kinect [2] TOF LED TOF [3] [6] [4][5] 2 [6] RGB ( ) Infrared(IR) IR 2 2.1 1 す 局所領域 ωk において 線形変換に用いる係数 (ak
IR E-mail: [email protected] Abstract IR RGB ( ) IR IR IR RGB RGB PSNR 1 Time-Of- Flight(TOF)[1] Kinect [2] TOF LED TOF [3] [6] [4][5] 2 [6] RGB ( ) Infrared(IR) IR 2 2.1 1 す 局所領域 ωk において 線形変換に用いる係数 (ak
1 対 1 対応の演習例題を解いてみた 微分法とその応用 例題 1 極限 微分係数の定義 (2) 関数 f ( x) は任意の実数 x について微分可能なのは明らか f ( 1, f ( 1) ) と ( 1 + h, f ( 1 + h)
 微分法とその応用 例題 1 極限 微分係数の定義 () 関数 ( x) は任意の実数 x について微分可能なのは明らか ( 1, ( 1) ) と ( 1 + h, ( 1 + h) ) の傾き= ( 1 + h ) - ( 1 ) ( 1 + ) - ( 1) = ( 1 + h) - 1 h ( 1) = lim h ( 1 + h) - ( 1) h ( 1, ( 1) ) と ( 1 - h,
微分法とその応用 例題 1 極限 微分係数の定義 () 関数 ( x) は任意の実数 x について微分可能なのは明らか ( 1, ( 1) ) と ( 1 + h, ( 1 + h) ) の傾き= ( 1 + h ) - ( 1 ) ( 1 + ) - ( 1) = ( 1 + h) - 1 h ( 1) = lim h ( 1 + h) - ( 1) h ( 1, ( 1) ) と ( 1 - h,
Analog signal 標本化 量子化 Digital signal 定理に基づく sampling 間隔の決定 f Δx max = 1 2 Δx 1 2 f max 標本化間隔 等号が成り立つとき周波数 従わないとエリアシングエラー (aliasing error) が生じる ( 折り返し雑
 画像処理工学 Computer Image Processing pixel dpi picture cell picture element 画像の最小単位 ppi pixel per inch 1 インチ当たりの画素数. 画像の解像度の単位. dot per inch 1 インチ当たりの点の数. 主にプリンタやスキャナなどの解像度の単位として使われる. bps bit per second 1
画像処理工学 Computer Image Processing pixel dpi picture cell picture element 画像の最小単位 ppi pixel per inch 1 インチ当たりの画素数. 画像の解像度の単位. dot per inch 1 インチ当たりの点の数. 主にプリンタやスキャナなどの解像度の単位として使われる. bps bit per second 1
講義「○○○○」
 講義 信頼度の推定と立証 内容. 点推定と区間推定. 指数分布の点推定 区間推定 3. 指数分布 正規分布の信頼度推定 担当 : 倉敷哲生 ( ビジネスエンジニアリング専攻 ) 統計的推測 標本から得られる情報を基に 母集団に関する結論の導出が目的 測定値 x x x 3 : x 母集団 (populaio) 母集団の特性値 統計的推測 標本 (sample) 標本の特性値 分布のパラメータ ( 母数
講義 信頼度の推定と立証 内容. 点推定と区間推定. 指数分布の点推定 区間推定 3. 指数分布 正規分布の信頼度推定 担当 : 倉敷哲生 ( ビジネスエンジニアリング専攻 ) 統計的推測 標本から得られる情報を基に 母集団に関する結論の導出が目的 測定値 x x x 3 : x 母集団 (populaio) 母集団の特性値 統計的推測 標本 (sample) 標本の特性値 分布のパラメータ ( 母数
Microsoft PowerPoint - H22制御工学I-2回.ppt
 制御工学 I 第二回ラプラス変換 平成 年 4 月 9 日 /4/9 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
制御工学 I 第二回ラプラス変換 平成 年 4 月 9 日 /4/9 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュ
 数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュレーションによって計算してみる 4.1 放物運動一様な重力場における放物運動を考える 一般に質量の物体に作用する力をとすると運動方程式は
数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュレーションによって計算してみる 4.1 放物運動一様な重力場における放物運動を考える 一般に質量の物体に作用する力をとすると運動方程式は
PowerPoint プレゼンテーション
 復習 ) 時系列のモデリング ~a. 離散時間モデル ~ y k + a 1 z 1 y k + + a na z n ay k = b 0 u k + b 1 z 1 u k + + b nb z n bu k y k = G z 1 u k = B(z 1 ) A(z 1 u k ) ARMA モデル A z 1 B z 1 = 1 + a 1 z 1 + + a na z n a = b 0
復習 ) 時系列のモデリング ~a. 離散時間モデル ~ y k + a 1 z 1 y k + + a na z n ay k = b 0 u k + b 1 z 1 u k + + b nb z n bu k y k = G z 1 u k = B(z 1 ) A(z 1 u k ) ARMA モデル A z 1 B z 1 = 1 + a 1 z 1 + + a na z n a = b 0
テンソル ( その ) テンソル ( その ) スカラー ( 階のテンソル ) スカラー ( 階のテンソル ) 階数 ベクトル ( 階のテンソル ) ベクトル ( 階のテンソル ) 行列表現 シンボリック表現 [ ]
![テンソル ( その ) テンソル ( その ) スカラー ( 階のテンソル ) スカラー ( 階のテンソル ) 階数 ベクトル ( 階のテンソル ) ベクトル ( 階のテンソル ) 行列表現 シンボリック表現 [ ] テンソル ( その ) テンソル ( その ) スカラー ( 階のテンソル ) スカラー ( 階のテンソル ) 階数 ベクトル ( 階のテンソル ) ベクトル ( 階のテンソル ) 行列表現 シンボリック表現 [ ]](/thumbs/93/113587990.jpg) Tsor th-ordr tsor by dcl xprsso m m Lm m k m k L mk kk quott rul by symbolc xprsso Lk X thrd-ordr tsor cotrcto j j Copyrght s rsrvd. No prt of ths documt my b rproducd for proft. テンソル ( その ) テンソル ( その
Tsor th-ordr tsor by dcl xprsso m m Lm m k m k L mk kk quott rul by symbolc xprsso Lk X thrd-ordr tsor cotrcto j j Copyrght s rsrvd. No prt of ths documt my b rproducd for proft. テンソル ( その ) テンソル ( その
画像類似度測定の初歩的な手法の検証
 画像類似度測定の初歩的な手法の検証 島根大学総合理工学部数理 情報システム学科 計算機科学講座田中研究室 S539 森瀧昌志 1 目次 第 1 章序論第 章画像間類似度測定の初歩的な手法について.1 A. 画素値の平均を用いる手法.. 画素値のヒストグラムを用いる手法.3 C. 相関係数を用いる手法.4 D. 解像度を合わせる手法.5 E. 振れ幅のヒストグラムを用いる手法.6 F. 周波数ごとの振れ幅を比較する手法第
画像類似度測定の初歩的な手法の検証 島根大学総合理工学部数理 情報システム学科 計算機科学講座田中研究室 S539 森瀧昌志 1 目次 第 1 章序論第 章画像間類似度測定の初歩的な手法について.1 A. 画素値の平均を用いる手法.. 画素値のヒストグラムを用いる手法.3 C. 相関係数を用いる手法.4 D. 解像度を合わせる手法.5 E. 振れ幅のヒストグラムを用いる手法.6 F. 周波数ごとの振れ幅を比較する手法第
Microsoft PowerPoint - DigitalMedia2_12.pptx
 デジタルメディア処理 2 2017( 前期 ) デジタルメディア処理 2 担当 : 井尻敬 4/13 デジタル画像とは : イントロダクション 4/20 フィルタ処理 1 : 画素ごとの濃淡変換 線形フィルタ, 線形フィルタ 4/27 フィルタ処理 2 : フーリエ変換, ローパスフィルタ, ハイパスフィルタ 5/11 画像の幾何変換 1 : アファイン変換 5/18 画像の幾何変換 2 : 画像の補間,
デジタルメディア処理 2 2017( 前期 ) デジタルメディア処理 2 担当 : 井尻敬 4/13 デジタル画像とは : イントロダクション 4/20 フィルタ処理 1 : 画素ごとの濃淡変換 線形フィルタ, 線形フィルタ 4/27 フィルタ処理 2 : フーリエ変換, ローパスフィルタ, ハイパスフィルタ 5/11 画像の幾何変換 1 : アファイン変換 5/18 画像の幾何変換 2 : 画像の補間,
連続講座 断層映像法の基礎第 32 回 : 篠原広行 他 断層映像法の基礎 第 32 回 ML-EM 法と OS-EM 法 篠原広行 1) 桑山潤 1) 小川亙 1) 2) 橋本雄幸 1) 首都大学東京人間健康科学研究科放射線科学域 2) 横浜創英短期大学情報学科 はじめに第 31 回では繰り返しを
 断層映像法の基礎 第 32 回 ML-EM 法と OS-EM 法 篠原広行 1) 桑山潤 1) 小川亙 1) 2) 橋本雄幸 1) 首都大学東京人間健康科学研究科放射線科学域 2) 横浜創英短期大学情報学科 はじめに第 31 回では繰り返しを利用して徐々に解に近づけていく方法を紹介した 本稿ではその繰り返しを使った方法で最も多く使われている ML-EM 法と OS-EM 法について解説する また その方法を利用した数値シミュレーションの結果についても紹介する
断層映像法の基礎 第 32 回 ML-EM 法と OS-EM 法 篠原広行 1) 桑山潤 1) 小川亙 1) 2) 橋本雄幸 1) 首都大学東京人間健康科学研究科放射線科学域 2) 横浜創英短期大学情報学科 はじめに第 31 回では繰り返しを利用して徐々に解に近づけていく方法を紹介した 本稿ではその繰り返しを使った方法で最も多く使われている ML-EM 法と OS-EM 法について解説する また その方法を利用した数値シミュレーションの結果についても紹介する
構造力学Ⅰ第12回
 第 回材の座屈 (0 章 ) p.5~ ( 復習 ) モールの定理 ( 手順 ) 座屈とは 荷重により梁に生じた曲げモーメントをで除して仮想荷重と考える 座屈荷重 偏心荷重 ( 曲げと軸力 ) 断面の核 この仮想荷重に対するある点でのせん断力 たわみ角に相当する曲げモーメント たわみに相当する ( 例 ) 単純梁の支点のたわみ角 : は 図 を仮想荷重と考えたときの 点の支点反力 B は 図 を仮想荷重と考えたときのB
第 回材の座屈 (0 章 ) p.5~ ( 復習 ) モールの定理 ( 手順 ) 座屈とは 荷重により梁に生じた曲げモーメントをで除して仮想荷重と考える 座屈荷重 偏心荷重 ( 曲げと軸力 ) 断面の核 この仮想荷重に対するある点でのせん断力 たわみ角に相当する曲げモーメント たわみに相当する ( 例 ) 単純梁の支点のたわみ角 : は 図 を仮想荷重と考えたときの 点の支点反力 B は 図 を仮想荷重と考えたときのB
例 e 指数関数的に減衰する信号を h( a < + a a すると, それらのラプラス変換は, H ( ) { e } e インパルス応答が h( a < ( ただし a >, U( ) { } となるシステムにステップ信号 ( y( のラプラス変換 Y () は, Y ( ) H ( ) X (
 第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
Microsoft PowerPoint - H17-5時限(パターン認識).ppt
 パターン認識早稲田大学講義 平成 7 年度 独 産業技術総合研究所栗田多喜夫 赤穂昭太郎 統計的特徴抽出 パターン認識過程 特徴抽出 認識対象から何らかの特徴量を計測 抽出 する必要がある 認識に有効な情報 特徴 を抽出し 次元を縮小した効率の良い空間を構成する過程 文字認識 : スキャナ等で取り込んだ画像から文字の識別に必要な本質的な特徴のみを抽出 例 文字線の傾き 曲率 面積など 識別 与えられた未知の対象を
パターン認識早稲田大学講義 平成 7 年度 独 産業技術総合研究所栗田多喜夫 赤穂昭太郎 統計的特徴抽出 パターン認識過程 特徴抽出 認識対象から何らかの特徴量を計測 抽出 する必要がある 認識に有効な情報 特徴 を抽出し 次元を縮小した効率の良い空間を構成する過程 文字認識 : スキャナ等で取り込んだ画像から文字の識別に必要な本質的な特徴のみを抽出 例 文字線の傾き 曲率 面積など 識別 与えられた未知の対象を
Microsoft Word - 補論3.2
 補論 3. 多変量 GARC モデル 07//6 新谷元嗣 藪友良 対数尤度関数 3 章 7 節では 変量の対数尤度を求めた ここでは多変量の場合 とくに 変量について対数尤度を求める 誤差項 は平均 0 で 次元の正規分布に従うとする 単純化のため 分散と共分散は時間を通じて一定としよう ( この仮定は後で変更される ) したがって ij から添え字 を除くことができる このとき と の尤度関数は
補論 3. 多変量 GARC モデル 07//6 新谷元嗣 藪友良 対数尤度関数 3 章 7 節では 変量の対数尤度を求めた ここでは多変量の場合 とくに 変量について対数尤度を求める 誤差項 は平均 0 で 次元の正規分布に従うとする 単純化のため 分散と共分散は時間を通じて一定としよう ( この仮定は後で変更される ) したがって ij から添え字 を除くことができる このとき と の尤度関数は
tottori2013-print.key
 1 / 152 3 / 152 2 / 152 4 / 152 5 / 152 7 / 152 6 / 152 8 / 152 9 / 152 11 / 152 Red: [R,G,B] = [255,0,0] Yellow [R,G,B] = [255, 255, 0] Magenta [R,G,B] = [255, 0, 255] W [R,G,B] = [ Green: [R,G,B] = [0,
1 / 152 3 / 152 2 / 152 4 / 152 5 / 152 7 / 152 6 / 152 8 / 152 9 / 152 11 / 152 Red: [R,G,B] = [255,0,0] Yellow [R,G,B] = [255, 255, 0] Magenta [R,G,B] = [255, 0, 255] W [R,G,B] = [ Green: [R,G,B] = [0,
Probit , Mixed logit
 Probit, Mixed logit 2016/5/16 スタートアップゼミ #5 B4 後藤祥孝 1 0. 目次 Probit モデルについて 1. モデル概要 2. 定式化と理解 3. 推定 Mixed logit モデルについて 4. モデル概要 5. 定式化と理解 6. 推定 2 1.Probit 概要 プロビットモデルとは. 効用関数の誤差項に多変量正規分布を仮定したもの. 誤差項には様々な要因が存在するため,
Probit, Mixed logit 2016/5/16 スタートアップゼミ #5 B4 後藤祥孝 1 0. 目次 Probit モデルについて 1. モデル概要 2. 定式化と理解 3. 推定 Mixed logit モデルについて 4. モデル概要 5. 定式化と理解 6. 推定 2 1.Probit 概要 プロビットモデルとは. 効用関数の誤差項に多変量正規分布を仮定したもの. 誤差項には様々な要因が存在するため,
第 4 週コンボリューションその 2, 正弦波による分解 教科書 p. 16~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問 1. 以下の図にならって,1 と 2 の δ 関数を図示せよ δ (t) 2
 第 4 週コンボリューションその, 正弦波による分解 教科書 p. 6~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問. 以下の図にならって, と の δ 関数を図示せよ. - - - δ () δ ( ) - - - 図 δ 関数の図示の例 δ ( ) δ ( ) δ ( ) δ ( ) δ ( ) - - - - - - - -
第 4 週コンボリューションその, 正弦波による分解 教科書 p. 6~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問. 以下の図にならって, と の δ 関数を図示せよ. - - - δ () δ ( ) - - - 図 δ 関数の図示の例 δ ( ) δ ( ) δ ( ) δ ( ) δ ( ) - - - - - - - -
統計的データ解析
 統計的データ解析 011 011.11.9 林田清 ( 大阪大学大学院理学研究科 ) 連続確率分布の平均値 分散 比較のため P(c ) c 分布 自由度 の ( カイ c 平均値 0, 標準偏差 1の正規分布 に従う変数 xの自乗和 c x =1 が従う分布を自由度 の分布と呼ぶ 一般に自由度の分布は f /1 c / / ( c ) {( c ) e }/ ( / ) 期待値 二乗 ) 分布 c
統計的データ解析 011 011.11.9 林田清 ( 大阪大学大学院理学研究科 ) 連続確率分布の平均値 分散 比較のため P(c ) c 分布 自由度 の ( カイ c 平均値 0, 標準偏差 1の正規分布 に従う変数 xの自乗和 c x =1 が従う分布を自由度 の分布と呼ぶ 一般に自由度の分布は f /1 c / / ( c ) {( c ) e }/ ( / ) 期待値 二乗 ) 分布 c
カイ二乗フィット検定、パラメータの誤差
 統計的データ解析 008 008.. 林田清 ( 大阪大学大学院理学研究科 ) 問題 C (, ) ( x xˆ) ( y yˆ) σ x πσ σ y y Pabx (, ;,,, ) ˆ y σx σ y = dx exp exp πσx ただし xy ˆ ˆ はyˆ = axˆ+ bであらわされる直線モデル上の点 ( ˆ) ( ˆ ) ( ) x x y ax b y ax b Pabx (,
統計的データ解析 008 008.. 林田清 ( 大阪大学大学院理学研究科 ) 問題 C (, ) ( x xˆ) ( y yˆ) σ x πσ σ y y Pabx (, ;,,, ) ˆ y σx σ y = dx exp exp πσx ただし xy ˆ ˆ はyˆ = axˆ+ bであらわされる直線モデル上の点 ( ˆ) ( ˆ ) ( ) x x y ax b y ax b Pabx (,
Microsoft PowerPoint - ad11-09.pptx
 無向グラフと有向グラフ 無向グラフ G=(V, E) 頂点集合 V 頂点の対を表す枝の集合 E e=(u,v) 頂点 u, v は枝 e の端点 f c 0 a 1 e b d 有向グラフ G=(V, E) 頂点集合 V 頂点の順序対を表す枝の集合 E e=(u,v) 頂点 uは枝 eの始点頂点 vは枝 eの終点 f c 0 a 1 e b d グラフのデータ構造 グラフ G=(V, E) を表現するデータ構造
無向グラフと有向グラフ 無向グラフ G=(V, E) 頂点集合 V 頂点の対を表す枝の集合 E e=(u,v) 頂点 u, v は枝 e の端点 f c 0 a 1 e b d 有向グラフ G=(V, E) 頂点集合 V 頂点の順序対を表す枝の集合 E e=(u,v) 頂点 uは枝 eの始点頂点 vは枝 eの終点 f c 0 a 1 e b d グラフのデータ構造 グラフ G=(V, E) を表現するデータ構造
Microsoft PowerPoint - 資料04 重回帰分析.ppt
 04. 重回帰分析 京都大学 加納学 Division of Process Control & Process Sstems Engineering Department of Chemical Engineering, Koto Universit [email protected] http://www-pse.cheme.koto-u.ac.jp/~kano/ Outline
04. 重回帰分析 京都大学 加納学 Division of Process Control & Process Sstems Engineering Department of Chemical Engineering, Koto Universit [email protected] http://www-pse.cheme.koto-u.ac.jp/~kano/ Outline
2 図微小要素の流体の流入出 方向の断面の流体の流入出の収支断面 Ⅰ から微小要素に流入出する流体の流量 Q 断面 Ⅰ は 以下のように定式化できる Q 断面 Ⅰ 流量 密度 流速 断面 Ⅰ の面積 微小要素の断面 Ⅰ から だけ移動した断面 Ⅱ を流入出する流体の流量 Q 断面 Ⅱ は以下のように
 3 章 Web に Link 解説 連続式 微分表示 の誘導.64 *4. 連続式連続式は ある領域の内部にある流体の質量の収支が その表面からの流入出の合計と等しくなることを定式化したものであり 流体における質量保存則を示したものである 2. 連続式 微分表示 の誘導図のような微小要素 コントロールボリューム の領域内の流体の増減と外部からの流体の流入出を考えることで定式化できる 微小要素 流入
3 章 Web に Link 解説 連続式 微分表示 の誘導.64 *4. 連続式連続式は ある領域の内部にある流体の質量の収支が その表面からの流入出の合計と等しくなることを定式化したものであり 流体における質量保存則を示したものである 2. 連続式 微分表示 の誘導図のような微小要素 コントロールボリューム の領域内の流体の増減と外部からの流体の流入出を考えることで定式化できる 微小要素 流入
14 化学実験法 II( 吉村 ( 洋 mmol/l の半分だったから さんの測定値は くんの測定値の 4 倍の重みがあり 推定値 としては 0.68 mmol/l その標準偏差は mmol/l 程度ということになる 測定値を 特徴づけるパラメータ t を推定するこの手
 14 化学実験法 II( 吉村 ( 洋 014.6.1. 最小 乗法のはなし 014.6.1. 内容 最小 乗法のはなし...1 最小 乗法の考え方...1 最小 乗法によるパラメータの決定... パラメータの信頼区間...3 重みの異なるデータの取扱い...4 相関係数 決定係数 ( 最小 乗法を語るもう一つの立場...5 実験条件の誤差の影響...5 問題...6 最小 乗法の考え方 飲料水中のカルシウム濃度を
14 化学実験法 II( 吉村 ( 洋 014.6.1. 最小 乗法のはなし 014.6.1. 内容 最小 乗法のはなし...1 最小 乗法の考え方...1 最小 乗法によるパラメータの決定... パラメータの信頼区間...3 重みの異なるデータの取扱い...4 相関係数 決定係数 ( 最小 乗法を語るもう一つの立場...5 実験条件の誤差の影響...5 問題...6 最小 乗法の考え方 飲料水中のカルシウム濃度を
<4D F736F F D FCD B90DB93AE96402E646F63>
 7 章摂動法講義のメモ 式が複雑なので 黒板を何度も修正したし 間違ったことも書いたので メモを置きます 摂動論の式の導出無摂動系 先ず 厳密に解けている Schrödiger 方程式を考える,,,3,... 3,,,3,... は状態を区別する整数であり 状態 はエネルギー順に並んでいる 即ち は基底状態 は励起状態である { m } は相互に規格直交条件が成立する k m k mdx km k
7 章摂動法講義のメモ 式が複雑なので 黒板を何度も修正したし 間違ったことも書いたので メモを置きます 摂動論の式の導出無摂動系 先ず 厳密に解けている Schrödiger 方程式を考える,,,3,... 3,,,3,... は状態を区別する整数であり 状態 はエネルギー順に並んでいる 即ち は基底状態 は励起状態である { m } は相互に規格直交条件が成立する k m k mdx km k
断面の諸量
 断面の諸量 建設システム工学科高谷富也 断面 次モーメント 定義 G d G d 座標軸の平行移動 断面 次モーメント 軸に平行な X Y 軸に関する断面 次モーメント G X G Y を求める X G d d d Y 0 0 G 0 G d d d 0 0 G 0 重心 軸に関する断面 次モーメントを G G とし 軸に平行な座標軸 X Y の原点が断面の重心に一致するものとする G G, G G
断面の諸量 建設システム工学科高谷富也 断面 次モーメント 定義 G d G d 座標軸の平行移動 断面 次モーメント 軸に平行な X Y 軸に関する断面 次モーメント G X G Y を求める X G d d d Y 0 0 G 0 G d d d 0 0 G 0 重心 軸に関する断面 次モーメントを G G とし 軸に平行な座標軸 X Y の原点が断面の重心に一致するものとする G G, G G
Microsoft PowerPoint - 画像工学2007-8印刷用
 教室 : 14-0 DECEMBER 04 画像工学 007 年度版 Imagng Scnc and Tchnolog 画像工学 007 年度版 8 慶応義塾大学理工学部 教授 中島真人 Drctonal Band-pass Fltr の効果 前回の講義 訂正があります! Huv g v u ここで フィルタの形が間違っていました. Input Imag v Drctonal Band-pass Fltr
教室 : 14-0 DECEMBER 04 画像工学 007 年度版 Imagng Scnc and Tchnolog 画像工学 007 年度版 8 慶応義塾大学理工学部 教授 中島真人 Drctonal Band-pass Fltr の効果 前回の講義 訂正があります! Huv g v u ここで フィルタの形が間違っていました. Input Imag v Drctonal Band-pass Fltr
数学の学び方のヒント
 数学 Ⅱ における微分単元の 指導法の改善に関する研究 2017 年 10 月北数教旭川大会で発表した内容です 北海道札幌国際情報高等学校和田文興 1 Ⅰ. 研究の動機と背景 高校では極限を厳密に定義できず, 曖昧でわかりにくい. 私自身は, はじめて微分と出会ったとき, 極限の考え方等が納得できなかった. y () a h 接線 a 傾き (a) 2 Ⅰ. 研究の動機と背景 微分の指導改善に関する優れた先行研究がいくつかあるが,
数学 Ⅱ における微分単元の 指導法の改善に関する研究 2017 年 10 月北数教旭川大会で発表した内容です 北海道札幌国際情報高等学校和田文興 1 Ⅰ. 研究の動機と背景 高校では極限を厳密に定義できず, 曖昧でわかりにくい. 私自身は, はじめて微分と出会ったとき, 極限の考え方等が納得できなかった. y () a h 接線 a 傾き (a) 2 Ⅰ. 研究の動機と背景 微分の指導改善に関する優れた先行研究がいくつかあるが,
<4D F736F F D208CF68BA48C6F8DCF8A C30342C CFA90B68C6F8DCF8A7782CC8AEE967B92E8979D32288F4390B394C529332E646F63>
 2. 厚生経済学の ( 第 ) 基本定理 2 203 年 4 月 7 日 ( 水曜 3 限 )/8 本章では 純粋交換経済において厚生経済学の ( 第 ) 基本定理 が成立することを示す なお より一般的な生産技術のケースについては 4.5 補論 2 で議論する 2. 予算集合と最適消費点 ( 完全 ) 競争市場で達成される資源配分がパレート効率的であることを示すための準備として 個人の最適化行動を検討する
2. 厚生経済学の ( 第 ) 基本定理 2 203 年 4 月 7 日 ( 水曜 3 限 )/8 本章では 純粋交換経済において厚生経済学の ( 第 ) 基本定理 が成立することを示す なお より一般的な生産技術のケースについては 4.5 補論 2 で議論する 2. 予算集合と最適消費点 ( 完全 ) 競争市場で達成される資源配分がパレート効率的であることを示すための準備として 個人の最適化行動を検討する
応用数学Ⅱ 偏微分方程式(2) 波動方程式(12/13)
 偏微分方程式. 偏微分方程式の形 偏微分 偏導関数 つの独立変数 をもつ関数 があるとき 変数 が一定値をとって だけが変化したとす ると は だけの関数となる このとき を について微分して得られる関数を 関数 の に関する 偏微分係数 略して偏微分 あるいは偏導関数 pil deiie といい 次のように表される についても同様な偏微分を定義できる あるいは あるいは - あるいは あるいは -
偏微分方程式. 偏微分方程式の形 偏微分 偏導関数 つの独立変数 をもつ関数 があるとき 変数 が一定値をとって だけが変化したとす ると は だけの関数となる このとき を について微分して得られる関数を 関数 の に関する 偏微分係数 略して偏微分 あるいは偏導関数 pil deiie といい 次のように表される についても同様な偏微分を定義できる あるいは あるいは - あるいは あるいは -
Microsoft PowerPoint - zairiki_3
 材料力学講義 (3) 応力と変形 Ⅲ ( 曲げモーメント, 垂直応力度, 曲率 ) 今回は, 曲げモーメントに関する, 断面力 - 応力度 - 変形 - 変位の関係について学びます 1 曲げモーメント 曲げモーメント M 静定力学で求めた曲げモーメントも, 仮想的に断面を切ることによって現れる内力です 軸方向力は断面に働く力 曲げモーメント M は断面力 曲げモーメントも, 一つのモーメントとして表しますが,
材料力学講義 (3) 応力と変形 Ⅲ ( 曲げモーメント, 垂直応力度, 曲率 ) 今回は, 曲げモーメントに関する, 断面力 - 応力度 - 変形 - 変位の関係について学びます 1 曲げモーメント 曲げモーメント M 静定力学で求めた曲げモーメントも, 仮想的に断面を切ることによって現れる内力です 軸方向力は断面に働く力 曲げモーメント M は断面力 曲げモーメントも, 一つのモーメントとして表しますが,
振動学特論火曜 1 限 TA332J 藤井康介 6 章スペクトルの平滑化 スペクトルの平滑化とはギザギザした地震波のフーリエ スペクトルやパワ スペクトルでは正確にスペクトルの山がどこにあるかはよく分からない このようなスペクトルから不純なものを取り去って 本当の性質を浮き彫
 6 章スペクトルの平滑化 スペクトルの平滑化とはギザギザした地震波のフーリエ スペクトルやパワ スペクトルでは正確にスペクトルの山がどこにあるかはよく分からない このようなスペクトルから不純なものを取り去って 本当の性質を浮き彫りにするために スペクトルを滑らかにする操作のことをいう 6.1 合積のフーリエ変換スペクトルの平滑化を行う際に必要な 合積とそのフーリエ変換について説明する 6.2 データ
6 章スペクトルの平滑化 スペクトルの平滑化とはギザギザした地震波のフーリエ スペクトルやパワ スペクトルでは正確にスペクトルの山がどこにあるかはよく分からない このようなスペクトルから不純なものを取り去って 本当の性質を浮き彫りにするために スペクトルを滑らかにする操作のことをいう 6.1 合積のフーリエ変換スペクトルの平滑化を行う際に必要な 合積とそのフーリエ変換について説明する 6.2 データ
Matrix and summation convention Kronecker delta δ ij 1 = 0 ( i = j) ( i j) permutation symbol e ijk = (even permutation) (odd permutation) (othe
 Matr ad summato covto Krockr dlta δ ( ) ( ) prmutato symbol k (v prmutato) (odd prmutato) (othrs) gvalu dtrmat dt 6 k rst r s kt opyrght s rsrvd. No part of ths documt may b rproducd for proft. 行列 行 正方行列
Matr ad summato covto Krockr dlta δ ( ) ( ) prmutato symbol k (v prmutato) (odd prmutato) (othrs) gvalu dtrmat dt 6 k rst r s kt opyrght s rsrvd. No part of ths documt may b rproducd for proft. 行列 行 正方行列
Microsoft PowerPoint - Lec15 [互換モード]
![Microsoft PowerPoint - Lec15 [互換モード] Microsoft PowerPoint - Lec15 [互換モード]](/thumbs/91/106545378.jpg) 情報デザイン専攻 画像情報処理論及び演習 II 周波数分解 FFT Gaussian フィルタと周波数分解 今日の授業内容 www.riken.jp/brict/yoshizawa/lectures/index.html www.riken.jp/brict/yoshizawa/lectures/lec5.pdf. 前回 前々回の復習 レポートの説明. 第 3, 回講義水曜日 限教室 68 吉澤信
情報デザイン専攻 画像情報処理論及び演習 II 周波数分解 FFT Gaussian フィルタと周波数分解 今日の授業内容 www.riken.jp/brict/yoshizawa/lectures/index.html www.riken.jp/brict/yoshizawa/lectures/lec5.pdf. 前回 前々回の復習 レポートの説明. 第 3, 回講義水曜日 限教室 68 吉澤信
4STEP 数学 Ⅲ( 新課程 ) を解いてみた関数 1 微分法 1 微分係数と導関数微分法 2 導関数の計算 272 ポイント微分法の公式を利用 (1) ( )( )( ) { } ( ) ( )( ) ( )( ) ( ) ( )( )
 微分法 微分係数と導関数微分法 導関数の計算 7 ポイント微分法の公式を利用 () 7 8 別解 [ ] [ ] [ ] 7 8 など () 6 6 など 7 ポイント微分法の公式を利用 () 6 6 6 など () 9 など () þ î ì など () þ î ì þ î ì þ î ì など 7 () () 左辺を で微分すると, 右辺を で微分すると, ( ) ( ) ( ) よって, (
微分法 微分係数と導関数微分法 導関数の計算 7 ポイント微分法の公式を利用 () 7 8 別解 [ ] [ ] [ ] 7 8 など () 6 6 など 7 ポイント微分法の公式を利用 () 6 6 6 など () 9 など () þ î ì など () þ î ì þ î ì þ î ì など 7 () () 左辺を で微分すると, 右辺を で微分すると, ( ) ( ) ( ) よって, (
解析力学B - 第11回: 正準変換
 解析力学 B 第 11 回 : 正準変換 神戸大 : 陰山聡 ホームページ ( 第 6 回から今回までの講義ノート ) http://tinyurl.com/kage2010 2011.01.27 正準変換 バネ問題 ( あえて下手に座標をとった ) ハミルトニアンを考える q 正準方程式は H = p2 2m + k 2 (q l 0) 2 q = H p = p m ṗ = H q = k(q
解析力学 B 第 11 回 : 正準変換 神戸大 : 陰山聡 ホームページ ( 第 6 回から今回までの講義ノート ) http://tinyurl.com/kage2010 2011.01.27 正準変換 バネ問題 ( あえて下手に座標をとった ) ハミルトニアンを考える q 正準方程式は H = p2 2m + k 2 (q l 0) 2 q = H p = p m ṗ = H q = k(q
Microsoft Word - thesis.doc
 剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
Microsoft Word - 犬飼.doc
 2004 年度卒業研究 肌色抽出について 岡山理科大学 総合情報学部 情報科学科 澤見研究室 I01I013 犬飼芳久 目次 1 はじめに 2 2 色空間に注目した肌色抽出手法 2.1 肌色抽出の手法について 2.2 色空間について 2.2.1 RGB 2.2.2 XYZ 2.2.3 L*a*b* 2.2.4 YCbCr 2.2.5 YIQ 2.2.6 HSV 2.2.7 修正 HSV 2.3 画素分布における検討
2004 年度卒業研究 肌色抽出について 岡山理科大学 総合情報学部 情報科学科 澤見研究室 I01I013 犬飼芳久 目次 1 はじめに 2 2 色空間に注目した肌色抽出手法 2.1 肌色抽出の手法について 2.2 色空間について 2.2.1 RGB 2.2.2 XYZ 2.2.3 L*a*b* 2.2.4 YCbCr 2.2.5 YIQ 2.2.6 HSV 2.2.7 修正 HSV 2.3 画素分布における検討
<4D F736F F D2097CD8A7793FC96E582BD82ED82DD8A E6318FCD2E646F63>
 - 第 章たわみ角法の基本式 ポイント : たわみ角法の基本式を理解する たわみ角法の基本式を梁の微分方程式より求める 本章では たわみ角法の基本式を導くことにする 基本式の誘導法は各種あるが ここでは 梁の微分方程式を解いて基本式を求める方法を採用する この本で使用する座標系は 右手 右ネジの法則に従った座標を用いる また ひとつの部材では 図 - に示すように部材の左端の 点を原点とし 軸線を
- 第 章たわみ角法の基本式 ポイント : たわみ角法の基本式を理解する たわみ角法の基本式を梁の微分方程式より求める 本章では たわみ角法の基本式を導くことにする 基本式の誘導法は各種あるが ここでは 梁の微分方程式を解いて基本式を求める方法を採用する この本で使用する座標系は 右手 右ネジの法則に従った座標を用いる また ひとつの部材では 図 - に示すように部材の左端の 点を原点とし 軸線を
破壊の予測
 本日の講義内容 前提 : 微分積分 線形代数が何をしているかはうろ覚え 材料力学は勉強したけど ちょっと 弾性および塑性学は勉強したことが無い ー > ですので 解らないときは質問してください モールの応力円を理解するとともに 応力を 3 次元的に考える FM( 有限要素法 の概略 内部では何を計算しているのか? 3 物が壊れる条件を考える 特に 変形 ( 塑性変形 が発生する条件としてのミーゼス応力とはどのような応力か?
本日の講義内容 前提 : 微分積分 線形代数が何をしているかはうろ覚え 材料力学は勉強したけど ちょっと 弾性および塑性学は勉強したことが無い ー > ですので 解らないときは質問してください モールの応力円を理解するとともに 応力を 3 次元的に考える FM( 有限要素法 の概略 内部では何を計算しているのか? 3 物が壊れる条件を考える 特に 変形 ( 塑性変形 が発生する条件としてのミーゼス応力とはどのような応力か?
