微分積分学2
|
|
|
- あいね いさやま
- 5 years ago
- Views:
Transcription
1 ver
2
3 f f G f fx df x fx dx fx, y f G f x, y, z z fx, y G f fx, y fx, y fx, y x a y ψy fa, y y b x φx fx, b x φx fx, y f x, b x y ψy fx, y f a, y y fx, y R x, y a x b, c y d fx, y G f xy R f x, y, z z fx, y, x, y R i
4 fx, y dxdy R G f x, y, fx, y T C T T f f + x, y + x, y dxdy x y R C S A A n ds V V S A S A diva V A n ds diva dxdydz S V S Ω Ω C X X C X rotx Stokes X t C ds rotx n ds C Green R 3 Ω S ii
5 C ω C ω Ω Ω C ω C Green Green S S V V ω dω Stokes z fx, y Gnuplot c Thomas Williams, Collin Kelley and many others. Mathematica c Wolfram Research, Inc. OPTION 6 4 iii
6 iv
7 ivergence Theorem Green Green Stokes v
8 vi
9 ɛ δ ,, Gamma Beta vii
10 viii
11 4 4. A. R fx, y fx, y Γ f a, Γ f b, fa, b R 3 a, b. fx fx, y fx, y y 3 x, y R 3 <x<3, 3 <y<3 x yz z y 3 z z y x x y fx, y x y x + y fx, y x x, y R
12 y fx xy x y + z fx. x a + y x b x a + y + z b. x 4az x z x 4az z x + y 4az z 3 x a y x y b. x a y + z b x + z a y b. x y.
13 3 B. R fx, y α C α a, b fa, b α C α α fx, y x 3 + y 3 3xy 4.8 B. R 3 fx, y, z α S α a, b, c fa, b, c α S α α fx, y, z x + y + z α a, b, c fa, b, c α α C. R 3 x, y, z R x, y z x r cos θ, y r sin θ, z r, θ R, z R y z r θ x 3
14 Helicoid x r cos θ y r sin θ z θ Helix x 4cosθ y 4sinθ z θ r 4, π θ π. π θ π.. R 3 γ γ xt, yt, zt R 3 a t b, xt, yt, zt a t b Helix S S xu, v, yu, v, zu, v R 3 u, v, xu, v, yu, v, zu, v u, v x u cos v y u sin v z cosv <u, <v<. R S : x + y z x S z x z x + y.5 O,,
15 x a + y b z c x a cos u + vasin u y b sin u vbcos u <u,v< z cv x a y b z x u y bv bu a <u,v< z v + vu a fx, y, z x + y + z +3 6x + y T x, y, z R 3 x + y + z +3 6x + y x + y + z +3 4 x + y x + y + z. T x, y, z, R 3 C x, y, R 3 x + y 4 C yz- y +z z
16 4. R fx, y A. lim fx, y x,y a,b x, y a, b a, b a, b x, y a, b fx, y α lim fx, y α lim fx, y α fx, y α x, y a, b x,y a,b x a,y b α x, y a, b fx, y lim x,y a,b lim x,y a,b lim fx, y α, lim x,y a,b fx, y +gx, y γfx, y gx, y β 4. x,y a,b α + β γα γ 3 lim x,y a,b 4 lim x,y a,b fx, y gx, y αβ fx, y gx, y α β β. a, b fx, y R fx, y lim x,y a,b a, b fx, y fa, b lim fx, y fa, b x,y a,b lim x,y a,b fx, y fa, b lim x,y a,b fx, y a, b. fx, y fx, y R x, y fx, y fx, y fx, y fx, y fx, y y x x, y R x 6
17 lim fx, y lim y x,y +,y x,y +,y x lim fx, y lim y x,y,y x,y,y x y > y < y > y < lim fx, y x,y,y z y/x z y fx, y y // x fx, y x y x + y x, y R x + y R \, x, y r cos θ, r sin θ, lim fx, y lim x,y, x,y, x y x + y r 4 cos θ sin θ lim lim r cos θ sin θ r r r lim fx, y x,y, fx, y, fx, y R fx, y x, y, fx, y x, y,, lim fx, y f, x,y, z x y x + y // z y x R fx, y, gx, y fx, y+gx, y, fx, y gx, y, fx, ygx, y fx, y gx, y x, y gx, y fx, y R fx, y fx, y x, y R I φt I φfx, y. pt qt R J t J pt, qt fpt, qt J. 7
18 4. fx, y x y x + y O, R. fx, y tan y x R 3 R 3 z cos θ r B. R x n,y n n,, R x, y xn x +y n y. lim n R K K x n,y n n,, R x,y x,y K. [a, b] [c, d] [a, b] [c, d] x n,y n n,, R x,y x n,y n [a, b] [c, d] a x n b, c y n d n,, a x b, c y d n,, x,y [a, b] [c, d] // y. R a, b a, b r r a, b x, y R x a +y b r a, b r a, b x n,y n n,, R x,y x ra, b x a +y b x x n +y y n + x n a +y n b x n x +y n y + r r n x a +y b r x,y r a, b // 8
19 4. 5.,. R K fx, y K K x,y K x, y fx, y fx,y fx, y fx,y x, y K. K x, y K x, y fx, y fx,y fx, y fx,y x, y K. R O O x,y x,y r r x,y x, y x x +y y <r O. R x,y r r x,y x, y x x +y y <r R R a, b c, d y tx,y x,y rx,y x,y r x,y x,y x s x x +y y <r x, y t < r s t x,y x, y x x +y y <t x, y x x +y y x x +y y + x x +y y <t+ s<r t x,y x, y x x +y y <t r x,y. y R r x,y x 9
20 R R a, b c, d R Ω Ω x, y, x,y x,y, x,y Ω γ : [, ] Ω, γ x,y γ x,y. ɛ δ R x n,y n n,, R x, y lim xn x +y n y n ɛ N n n N x n x +y n y < ɛ x n,y n x, y ɛ N n n N x n x +y n y ɛ n fx, y x, y fx, y x,y ɛ δ x, y x x +y y < δ fx, y fx,y < ɛ ɛ δ x δ,y δ xδ x +y δ y < δ fx δ,y δ fx,y ɛ.
21 R K fx, y K ɛ δ x, y, x,y K x x +y y < δ fx, y fx,y < ɛ R fx, y x, y, a, b fa, b >. : δ> : x a +y b fa, b <δ fx, y. δ x a +y b fa, b <δ fx, y 3 R R R p, q, p,q fp, q, fp,q R... Bolzano-Weierstrass R K x n,y n n x nk, y nk k K fx, y K fx, y K n fx n,y n >n x n,y n K x n,y n K n x nk,y nk k lim k x n k,y nk x,y K fx,y lim fx n k,y nk <fx,y < k fx, y K V fx, y x, y K R.. sup V fxn,y n V n x n,y n n K
22 K x nk,y nk k fx, y sup V V lim x n k,y nk x, y K k fx, y lim k fx n k,y nk lim n fx n,y n sup V fx, y fx,y x, y K. max fx, y fx,y supv x,y K x,y K fx, y K //. R K fx, y K ɛ n K x n,y n, x n,y n xn x n +y n y n < n fx n,y n fx n,y n ɛ n,, Bolzano-Weierstrass x n,y n, x n,y n n x nk,y nk, x n k,y n k x k,y k, x k,y k k x k x k +y k y k < k K fx k,y k fx k,y k ɛ k,, lim x k,y k x,y, lim k k x k,y kx,y lim x k x k k +y k y k x x +y y x,y x,y lim fx n,y n fx n,y n fx,y fx,y ɛ> k K fx, y K //
23 4.3 A. z fx, y a, b R fa + h, b fa, b lim h h fx, y a, b x a, b x f x a, b fa, b + h fa, b lim h h fx, y a, b y a, b y f y a, b fx, y R a, b x f x a, b f x x, y f x x, y fx, y x fx, y R a, b y f y a, b f y x, y f y x, y fx, y y fx, y x y 3 + x +5y, gx, y e xy +sinx +y f x x, y xy 3 +, f y x, y 3x y +5 g x x, y ye xy +cosx +y, g y x, y xe xy +cosx + y B. fx, y, gx, y x 4. fx, y+gx, y fx, y+ gx, y x x x αfx, y α fx, y α x x 3 fx, y gx, y x 4 gx, y x fx, y gx, y+fx, y gx, y x fx, y x fx, y gx, y fx, y xgx, y. x gx, y gx, y 3
24 fx, y, gx, y y fx, y f x x, y x f xx x, y fx, y. x f x x, y y f xy x, y fx, y. y x f y x, y x f yx x, y fx, y. x y f y x, y y f yy x, y fx, y. y f xx x, y x f xxx x, y 3 fx, y. x3 f xx x, y y f xxy x, y 3 fx, y. y x 4.3 fx, y x 3 3xy + y 3 fx, y xy x + y 3 fx, y exy e x + e y 4 fx, y logx + y 5 fx, y x y 6 fx, y tan y x x> 7 fx, y cos x y> 8 fx, y x + y x +y x + y fx, y x y 3 + x +5y, gx, y e xy +sinx +y 3 fx, y, z fx,x,,x n fx, y, z f x a, b, c, f y a, b, c, f z a, b, c, fx, y, z αx + βy + γz +λxy +μyz +νzx C. z fx, y S S Pa, b, fa, b R 3 π a : x a π b : y b S π b S π b x t y b z ft, b t R R 3 4
25 π b : y b x t C b : z ft, b t R π b C b Pa, b, fa, b π b fx, y y y b fx, b x ϕx fx, b C b Pa, b, fa, b z ϕx fx, b x a ϕ a a, b fx, y x fa + h, b fa, b f x a, b lim ϕ a. h h C b Pa, b, fa, b, R 3 x t y b z f x a, bt a+fa, b t R S π a S π a R 3 x a y t z fa, t t R π a : x a y t C a : z fa, t t R π a C a Pa, b, fa, b π a fx, y x x a fa, y y ψy fa, y C a Pa, b, fa, b z ψy fa, y y b ψ b a, b fx, y y fa, b + h fa, b f y a, b lim ψ b h h C a Pa, b, fa, b, R 3 x a y t z f y a, bt b+fa, b t R 5
26 4.4 A. R 3 a, b, c R 3 ax + by + cz d x,y,z x x + ta : y y + tb t R. z z + tc abc : x x a y y b z z c R 3 a, b, c,, x,y,z ax x +by y +cz z, ax + by + cz ax + by + cz. r> x + y + z r x,y,z Hint. x,y,z 3 R 3 O x + y + z 6,, x + y + z 6,,,, : x + y +z 6. 6
27 B. fx, y R C f x x, y, f y x, y c fa, b, α f x a, b, β f y a, b a, b z fx, y Pa, b, c Pa, b, c P h a + h, b, fa + h, b P k a, b + k, fa, b + k hk P, P h, P k π h,k π h,k : z c fa + h, b fa, b x a+ h fa, b + k fa, b y b. k h, k P h, P k P π h,k T P T P : z c f x a, bx a +f y a, by b T p T P z fx, y Pa, b, c z fx, y x a T P : y b +s +t s, t R z c α β π h,k lp z fx, y Pa, b, c z fx, y l P l P : x a tf x a, b y b tf y a, b z c t t R. z fx, y Pa, b, c l P x a α α l P : y b + t β t R, N P β z c N P f x a, bf y a, b l P l P : x a f x a, b y b f y a, b z c. 7
28 R 3 O x + y + z 6,,,, z 6 x y,, x z x x, y 6 x y, z y yx, y 6 x y z x,, z y,.,, z x y, z x y +3. // z 4 z x + y,, z x x, y x, z y x, y y, z x,, z y,. x y z x + y,, : z x +y, z z x +y. // 5 gx, y e x y 3 z gx, y a, b, ga, b a, b,.6 z e -x -y 3 y C. R 3 γ γt xt, yt, zt R 3 a t b, xt, yt, zt a t b C x γ γt, γt + h l h X x, y, z R 3 h l h : X γt+s γt + h γt h γt + h γt h <s< R 3 h 8
29 γ γt + h γt t lim h h xt + h xt yt + h yt zt + h zt lim, lim, lim h h h h h h x t, y t, z t R 3 γ t γ γt T T γ γt l T : X x, y, z R 3 x xt+sx t y yt+sy t s R z zt+sz t l T : X γt +st s R, T γ t x t, y t, z t. 4.3 C. 6 x +y +z tan δ x+z Px, y, z <δ < π P xy Q O P δ POQ δx, y, z P T P xt,yt,zt xy P δ POQ δt x <, y, z > x z O P Q y. R 3 Aa,a,a 3, Bb,b,b 3 R 3 θ A B a b + a b + a 3 b 3 A B cos θ, A B a b 3 a 3 b, a 3 b a b 3, a b a b R 3. A B A a a b 3 a 3 b +a a 3 b a b 3 +a 3 a b a b A B B b a b 3 a 3 b +b a 3 b a b 3 +b 3 a b a b 9
30 A B A, B π sa+tb s, t R A B π π Xx, y, z A B X A B Cc,c,c 3 π π C sa+tb+c s, t R π C Xx, y, z A B X C S R 3 S Xu, v xu, v, yu, v, zu, v R 3 u, v, xu, v, yu, v, zu, v u, v R C S Xu,v xu,v, yu,v, zu,v R 3 u,v T : S x xu,v +sx u u,v +tx v u,v y yu,v +sy u u,v +ty v u,v z zu,v +sz u u,v +tz v u,v s, t R. X u u,v x u u,v,y u u,v,z u u,v R 3 X v u,v x v u,v,y v u,v,z v u,v R 3 T : X Xu,v +sx u u,v +tx v u,v s, t R. T S fx, y z fx, y S γt S Xu, v xu, v, yu, v, zu, v R 3 u, v γt Xu + at, v + bt R 3 t< ɛ γ γ γ d dt Xu + at, v + bt t ax u u,v +bx v u,v,ay u u,v +by v u,v, az u u,v +bz v u, v ax u u,v +bx u u, v R 3.
31 γ γ l T : X γ + tγ Xu,v +tax u u, v +tbx u u,v t R. γ γ l T T T S T S S Xu,v xu,v, yu,v, zu,v R 3 u,v T : X Xu,v +sx u u,v +tx v u,v s, t R N X u u,v X v u,v y u u,v y v u,v z u u,v z v u,v, z u u,v z v u,v x u u,v x v u,v, x u u,v x v u,v y u u,v y v u,v l N : X Xu,v +t N t R C. x u cos v Helicoid y u sin v z v u, <v< fx, y R C z fx, y Xx, y x, y, fx, y R 3 x, y B. S : z fx, y x, y. S : Xx, y x, y, fx, y R 3 x, y
32 4.5 A. qx, y Ax +Bxy+Cy A, B, C a, b, ϕt qat, bt t R ϕ t, ϕ t B. z - fa,b α h + β k fx, y R C f x x, y, f y x, y α f x a, b, β f y a, b a, b a,b,fa,b z fx, y ɛh, k fa + h, b + k fa, b αh βk h + k h, k, fa + h, b + k fa, b+αh + βk + h + k ɛh, k lim ɛh, k h,k, fx, y a, b a, b fx, y a, b, fa, b fx, y fa, b z fa, b f x a, bx a+f y a, by b dz f x a, bdx + f y a, bdy df f x x, ydx + f y x, ydy fx, y fx, y C xt, yt d dt fxt,yt f xxt,ytx t+f y xt,yty t fxt,yt 3 z fx, y C x ϕu, v y ψu, v
33 z fϕu, v,ψu, v z u z x x u + z y y u z v z x x v + z y y v, z u z x z v z x fϕu, v,ψu, v u fϕu, v,ψu, v v x u + z y x v + z y y u y v. f v ϕu, v,ψu, v ϕu, + f v ϕu, v,ψu, v ψu, x u y u f v ϕu, v,ψu, v ϕu, + f v ϕu, v,ψu, v ψu, x v y v. // x ϕu, v y ψu, v u, v- x, y- T T :u, v x, y ϕu, v, ψu, v. T x ϕu, v y ψu, v ϕu, v u ψu, v u Jacobian, ϕu, v v ψu, v v ϕ, ψ u, v x, y u, v J T u, v 4 F :r, s u, v λr, s, μr, s G :u, v x, y ϕu, v, ψu, v G F : r, s x, y ϕλr, s,μr, s, ψλr, s,μr, s x, y r, s x, y u, v u, v r, s, J G F J G J F 3 ϕ r ϕ u λ r + ϕ v μ r ϕ s ϕ u λ s + ϕ v μ s ψ r ψ u λ r + ψ v μ r ψ s ψ u λ s + ψ v μ s ϕ r ψ r ϕ s ψ s ϕ u ψ u ϕ v ψ v λ r μ r λ s μ s // 3
34 C. z fx, y C x r cos θ, y r sin θ z zr, θ zr cos θ, y r sin θ z r z x x r + z y y r z x cos θ + z y sin θ z θ z x x θ + z y y θ z x r sin θ+z y r cos θ. z r z θ cos θ r sin θ z x cos θ sin θ r sin θ rcos θ z y z x z y z r z θ sin θ rcos θ z x z r r x + z θ θ x z y z r r y + z θ θ y, r x r y θ x θ y z x z y cos θ sin θ z r z θ sin θ r cos θ r r x cosθ, r y sinθ θ x sin θ, θ y cos θ r r r tan y x > x x + y θ π +tan y x x< r x x x + y x r cosθ, r y y x + y y r sinθ z r z θ. θ x y x + y x y x + y y r sin θ r, θ y x + y x x x + y x r cos θ r //. z x +z y z r + r z θ z x +z y z r cos θ z θ sin θ + z r sin θ + z θ cos θ zr + r r r z θ. 4
35 . fx, y C h, k,, Δf fx + h, y + k fx, y Δf fx + h, y + k fx, y + k+fx, y + k fx, y y + k x ϕx fx, y + k fx + h, y + k fx, y + k ϕx + h ϕx ϕ x + θ hh hf x x + θ h, y + k x y ψy fx, y fx, y + k fx, y ψy + k ψy ψ y + θ kk kf y x, y + θ k Δf fx + h, y + k fx, y + k+fx, y + k fx, y hf x x + θ h, y + k+kf y x, y + θ k < θ, θ < ɛ f x x + θ h, y + k f x x, y ɛ f y x, y + θ k f y x, y Δf hf x x, y+kf y x, y+hɛ + kɛ. Cauchy-Schwarz dz f x x,y dx + f y x,y dy x,y,fx,y hɛ + kɛ h + k ɛ + ɛ f x x, y f y x, y lim ɛ lim ɛ h,k, h,k, lim h,k, ɛ + ɛ, hɛ + kɛ lim h,k, h + k a b α f x a, b β f y a, b // fa + h, b + k fa, b αh βk h + k h, k, 5
36 fx, y C xt, yt ϕt fxt,yt x xt, y yt h xt + δ xt, k yt + δ yt α f x x, y, β f y x, y ϕt + δ ϕt fxt + δ,yt + δ fxt,yt fx + h, y + k fx, y ϕt + δ ϕt αh βk δ xt, yt h lim δ δ x t fx + h, y + k fx, y αh βk h + k h + k δ k lim δ δ y t h + k lim x δ δ t + y t <. ϕt + δ ϕt αh βk lim δ δ // fx + h, y + k fx, y αh βk lim δ h + k ϕt + δ ϕt αh βk lim δ δ ϕt + δ ϕt h lim α lim δ δ δ δ β lim k δ δ ϕt + δ ϕt lim αx t βy t δ δ ϕ ϕt + δ ϕt t lim αx t+βy t δ δ. n n fx,x,,x n C n x t, x t,,x n t d dt fx t,x t,,x n t n f xi x t,x t,,x n t x it. i 6
37 4.5 fx, y C f y x, y fx, y ϕx fx, y x fx, y C xf x x, y yf y x, y xy z fx, y xy u Hint. u xy, v y uv zu, v f v,v 3 fx, y C xf y x, y yf x x, y x, y, z fx, y r x + y 4 ux, y C u xy x, y ux, y fx+gy 5 t> ftx ty t m fx, y fx, y m fx, y, R C fx, y m xf x x, y+yf y x, y mfx, y af x a, b+bf y a, b mfa, b a, b R 6 x + y xy x + y 3 x y 4 x + y 3 e y x x + y 7 xy x, y, fx, y x + y x, y, R, y z x z fx, y 8 fx, y x y x + y 4. R C 7
38 4.6 A. fx, y f x x, y, f y x, y, f xy x, y, f yx x, y f xy x, y f yx x, y f xyx x, y f yxx x, y f xxy x, y 4 f x y 4 f x x y y 4 f x y x y 4 f x y y x 4 f y x y x 4 f y y x x 4 f y x. fx, y n n k k n fx, y C n fx, y fx, y C 4.5 B. n n n x i fx, y n i y y n i fx, y i,,,n i x B. fx, y e x cos y f xx x, y, f yy x, y z e x cos y z y Δfx, y f xx x, y+f yy x, y x Δ x + y Laplacian z Δfx, y fx, y x x + y, ex cos y, e x sin y, tan y x, log x + y. y x z log p x.5 +y.5 +log p x.75 +y.7 +log p x.75 +y.9. 8
39 z fx, y C x r cos θ, y r sin θ z xx + z yy z rr + z r r + z θθ r. x z x z r r z θ 4.5 C. y z y z r r + z θ y r x r z xx z rr r x + z rθ θ x x r + z y r r 3 z θrr x + z θθ θ x y r z xy θ r 4 x z rr r z xy rθ r 3 + z y θθ r 4 + z y r r 3 + z xy θ r 4 z yy z rr r y + z rθ θ y y r + z r r 3 +z θrr y + z θθ θ y x r + z θ y z rr r +z xy rθ r 3 + z x θθ r 4 + z x r r 3 z xy θ r 4. x z xx + z yy z rr r + z y rr r + z y θθ r 4 + z x θθ r 4 + z y r r 3 + z r x xy r 4 x r 3 z rr + z r r + z θθ r. // C. u fx, y, z C x ρ cos ϕ, y ρ sin ϕ, z z <ρ, ϕ<π, <z< 4.5 C. u x + u y + u z u uϕ +u ρ + ρ z. u xx + u yy + u zz u ρρ + u ρ ρ + u ϕϕ ρ + u zz. 3 u fx, y, z C x r sin θ cos ϕ, y r sin θ sin ϕ, z r cos θ <r, θ π, ϕ<π z, θ ϕ u x +u y +u z u r + uθ + uϕ. r r sin θ y r x 9
40 u xx + u yy + u zz u rr + u θθ r + u ϕϕ r sin θ +u r r +cotθ u θ r r r ru + r sin θ u + sin θ θ θ r r r u r + r sin θ θ sin θ u θ u ϕ r sin θ + r sin θ u ϕ. r x + y + z, θ cos z r, ϕ cos x x + y r x x r, r y y r, r z z r xz θ x r x + y, θ yz y r x + y, ϕ x y x + y, ϕ x y x + y, ϕ z. θ z x + y x u x u r r + u xz θ r x + y u y ϕ x + y, y u y u r r + u yz θ r x + y + u x ϕ x + y, z u z u r r u x + y θ r u x + u y + u z u r + uθ + uϕ. ϕ r r sin θ r ϕ π y x x ρ cos ϕ, y ρ sin ϕ, z z <ρ, ϕ<π, <z< uρ, ϕ, z u xx + u yy + u zz u ρρ + u ρ ρ + u ϕϕ ρ + u zz. ρ r sin θ, z r cos θ, ϕ ϕ <r, <θ<π, ϕ<π ur, θ, ϕ u ρρ + u zz u rr + u r r + u θθ r u ρ ρ cos θ u r sin θ + u θ r sin θ r u xx + u yy + u zz u rr + u r r + u θθ r + u r r +cotθ u θ r + u ϕϕ r sin θ u rr + u r r + u θθ r +cotθ u θ r + u ϕϕ r sin θ r r ru + r sin θ r r r u r θ + r sin θ 3 sin θ u θ θ sin θ u θ + r sin θ + r sin θ u r r +cotθ u θ r u ϕ u ϕ. //
41 Δ x + y + z fx, y, z. Laplacian Δfx, y, z, sin 3x sin 4y sinh 5z. x + y + z. fx, y f xy x, y, f yx x, y x,y h, k,, Δfx + h, y + k fx + h, y fx,y + k+fx,y y, y + k ϕx fx, y + k fx, y ϕx Δϕx + h ϕx ϕ x f x x, y + k f x x, y Δ ϕ x + θ h h f x x + θ h, y + k f x x + θ h, y h < θ < f xy x, y y ψy f x x + θ h, y ψ y f xy x + θ h, y Δψy + k ψy h ψ y + θ k kh f xy x + θh, y + θ k hk < θ < Δ f xy x, y lim h,k, hk f xyx,y x,x + h ϕy fx + h, y fx,y Δ ϕy + k ϕy ϕ y + θ k k f y x + h, y + θ k f yx,y + θ k k < θ < x ψx f y x, y + θ k ψ x f yx x, y + θ k Δ ψx + h ψx k ψ x + θ h hk f yx x + θ h, y + θ k hk < θ < f yx x, y lim h,k, Δ hk f yxx,y // f xy x,y lim h,k, Δ hk f yxx,y 3
42 4.6 z xx, z xy,z yx,z yy : z R x y α z tan x + y t fx, t A coskx + ωt+bcoskx ωt A, B, k, ω R z f xx + k f x z cosx +4t+3cosx 4t 3 C fζ gζ c k ux, t fkx + ct+gkx ct u xx c u tt * ft ϕx, y fϕx,y fϕx,y x f ϕx, y ϕx, y, x fϕx,y y f ϕx, y ϕx, y. y 4 u xx c u tt C ux, t Hint: ξ x + ct, η x ct z ux, t z ξη 5 ux, y, t x +y 4πkt e 4kt k z ux, y, t t u t kδu r z r e 4t 4πt 3
43 6 r x + y + z x r, y r, Δ r z r x + y + z r 7 F x, y, z r x + y + z fr F x, y, z fr ΔF x, y, z Δfr f r+ r f r fr r α α R, log r Δfr 8 fx C ux, y, z, t f x + y + z ct x + y + z z t c ux, y, z, t u t c Δu u c cosr t z r <r<π, π <t<π r 9 C fζ gζ c λ, μ, ν λ + μ + ν ux, y, z, t fλx + μy + νz + ct+gλx + μy + νz ct u t c Δu u λ, μ λ + μ ux, y cosλx + μy Δu u k, λ, μ λ + μ z cosx + y z y ux, y, t e kt cosλx + μy u t kδu x 33
44 4.7 B. Taylor Maclaurin fx, y R C n 4.6 A <p n p p fx, y p fx, y x p, x p y,, p fx, y x p i y i,, p fx, y x y p, p fx, y y p p h, k p pc i h p i k i p fx, y x p i y i h x + k pfx, y a, b y i h x + k pfa, b h y x + k pfx, p [ y y xa, pc i h p i k i p f ] yb x p i y i a, b p C i p! i!p i! i fx, y R C n a, b, x, y fx, y fa, b+ x a x +y b fa, b+ x a y! x +y b fa, b+ y + x a n! x y +y b n fa, b+rn R n x a n! x +y b nfa + θx a,b+ θy b < θ< y T n x, y n p x a p! x +y b pfa, b fx, y a, b n y Taylor fx, y T n x, y R n a, b x, y a+θx a,b+θy b < θ< Lagrange fx, y, R C n,, x, y fx, y f, + x x + y f, + x y! x + y f, + y + x n! x + y n f, + Rn y R n x n! x + y nfθx, θy < θ < y 34
45 fx, y x, y a, b C R n lim R n fx, y a, b, n fx, y x a n! x +y b nfa, b. y n fx, y h x + k fx, y hf x x, y+kf y x, y, y h x y + k fx, y h f xx x, y+hkf xy x, y+k f yy x, y, h x y + k 3fx, y h 3 f xx x, y+3h kf xxy x, y+3hk f xyy x, y+k 3 f yyy x, y,. fx, y x + y xy x, y, Taylor f x x, y x y, f y x, y y x f xx x, y, f xy x, y, f yy x, y f xxx x, y f xxy x, y f xyy x, y f yyy x, y fx, y +x + y + x x y + y! +x + y + x x y + y, R.. fx, y e x+y x, y, Taylor e x+y +x + y + x + y! + + x + yn n! + θx + θyn n! p+q fx, y fx, y e x+y x p y q p, q,,, x k! x + y kf, x + y k y k! k,,. fx, y +x + y+! x + x + y yn R n n! θx + θyn R n < θ <. n! C. fx, y a, b C n t F t fa+ht, b+kt F t C n 35
46 F p t h x + k pfa + ht, b + kt p,,,n y p F p t h x + k y pfx, ip y i pc i h p i k i p fx, y x p i y i x a + ht, y b + kt F p t h x + k pfx, y y xa+ht, h yb+kt x y + k pfa + ht, b + kt F t fa + ht, b + kt F t hf x a + ht, b + kt+kf y a + ht, b + kt d h dt F t x + k fx, y y 4.5 xa+ht, yb+kt p F p t h x + k y pfx, y xa+ht, yb+kt F p+ t d dt F p t h x + k h y x y + k pfx, y xa+ht, yb+kt h x y + k p+fx, xa+ht, y yb+kt //. Taylor fx, y C n a, b h, k,, t F t fa + th, b + tk t F t Taylor F t F + F t + F t + + F n! n! tn + F n θt t n < θ < n! 36
47 F p F F + F + F! F n θ F p t fa + h, b + k fa, b+ + + F n n! h x + k pfa + ht, b + kt y + F n θ n! h x + k pfa, b p,,,n y h x + k nfa + θh, b + θk y t F h + n! h x + k y fa, b+! x + k y n fa, b+ n! h h x + k y x + k fa, b+ y nfa + θh, b + θk < θ < x, y a + h, b + k h x a, k y b fx, y fa, b+ x a x +y b fa, b+ x a y! x +y b fa, b+ y + x a n! x +y b n fa, b+rn y R n x a n! x +y b nfa + θx a,b+ θy b < θ < y 4.7 fx, y x 3 + y 3 3xy x,y 3 Taylor fx, y e x cos y x,y Taylor 3 fx, y e ax sin by a, b x,y π Taylor 4 ϕx x a C n, ψy y b C n fx, y ϕxψy a, b C n h x + k pfx, p y pc i h p i k i ϕ p i xψ i y y i 37
48 4.8 A. A fx, y x, y x,y δ x x +y y <δ, x, y A fx,y fx, y A fx, y x, y x,y δ x x +y y <δ, x, y A fx,y fx, y O fx, y fx, y A fx, y x, y x,y fx, y x, y x,y fx, y e x y fx, y e r z z e x y r x + y y fx, y x, y, f, x fx, y x + y x + y + fx, y z fx, y gx, y 6 x + y +x + y 3 38
49 z fx, y z y z y x x z gx, y B. z qx, y αx +βxy + γy α qx, y α x + β α y αγ β + α α>, β αγ < qx, y, α<, β αγ < qx, y, α, β αγ > q, y y x β αγ > α > qx, αx > x q βy, αy αy αγ β < y, qx, y qx, x +xy +3y q, fx, y x,y R ϕx fx, y x x ψy fx,y y y f x x,y f y x,y x,y fx, y fx, y f xx x, y f xy x, y Hx, y fx, y Hesse f yx x, y f yy x, y, fx, y C x,y R fx, y f x x,y f y x,y 39
50 f xy x,y f xx x,y f yy x,y Hx,y f xx x,y >, < fx,y f xx x,y <, < fx,y 3 > fx,y 4 fx, y x 3 + y 3 3xy z z x 3 + y 3 3xy f x x, y f y x, y x, y f xx x, y, f xy x, y, f yy x, y 3 fx, y f x x, y 3x y f y x, y 3y x x, y,,,. f xx 6x, f xy 3, f yy 6y. y x 3 fxy f xxf yy 9 36xy x, y, 9> f, x, y, <, f x, 6 > f, 4.8 fx, y xy + a x + a y a> z z y y x x z x 4 + y 4 +x y x +y z xy + a x + a y 4
51 z x 4 + y 4 +x y x +y 3 z x 3 +3xy 3x 3y +4 4 fx, y xy e x y 5 fx, y cosx + y +sinx +siny x, y <π 6 z x +4xy + y z 3x y z π 4 fx, y x +4xy + y. fx, y, xt, yt C ϕt fxt,yt ϕ t f x xt,ytx t+f y xt,yty t ϕ t f xx xt,ytx t +f xy xt,ytx ty t+f yy xt,yty t + f x xt,ytx t+f y xt,yty t x xt, y yt f x x,y f y x,y f xx x,y f xy x,y f xx x,y f yy z,y < x t,y t, ϕ f x x,y x + f y x,y y ϕ f xx x,y x +f xy x,y x y + f yy x,y y B. ϕt t t a, b, ϕt fx + at, y + bt t fx, y C x,y R f x x,y f y x,y f xy x,y f xx x,y f yy x,y fx, y C x, y f xy x, y f xx x, yf yy x, y f xx x, y 4
52 x,y f xy x,y f xx x,y f yy x,y f xx x,y x, y x,y x, y f xx x,y δ x,y > x,y < f xx x,y > fxx x,y < x x +y y <δ x, y >, x x +y y <δ x, y <, x x +y y <δ f xx x, y >. x x +y y <δ f xx x, y <. x, y x + a, y + b < x x +y y a + b <δ ϕt fx + at, y + bt t x,y < f xx x,y > ϕ f x x,y a + f y x,y b ϕ t f xx x + at, y + bt a +f xy x + at, y + bt ab +f yy x + at, y + bt b > t ϕ t t ϕt t fx, y ϕ ϕ fx,y fx,y x,y < f xx x,y < fx,y x,y > f xx x,y > α f xx x,y >, β f xy x,y, γ f yy x,y B. ϕt fx + αt, y t ϕ f x x,y α ϕ α α > ϕ t t t x,y fx, y > x, y ϕt fx βt, y + αt ϕ f x x,y β +f y x,y α ϕ α β +β βα + γα α β + αγ < ϕ t t t x,y fx, y < x, y fx,y // 4
53 4.9 A. fx, y R ϕx fx, ϕx 4.5 f y x, ϕx d dx fx, ϕx f xx, ϕx + f y x, ϕxϕ x ϕ x f xx, ϕx f y x, ϕx fx, y x + y fx, y y x y x f xx, y f y x, y x y x. x yx fx, y x + yx d x + yx x +yy dx y x y x y x x fx, y R C fa, b, f y a, b a, b a I R ϕx,, 3 b ϕa fx, ϕx and f y x, ϕx x I 3 ϕx C, ϕ x f xx, ϕx f y x, ϕx x I. zf x,y z z fx, y z y ϕx 4 fx, y C p ϕx C p 43
54 fx, y, z R 3 C fa, b, c, f z a, b, c a, b, c a, b R R ϕx, y,, 3 c ϕa, b fx, y, ϕx, y and f z x, y, ϕx, y x, y R 3 ϕx, y C, ϕ x x, y f xx, y, ϕx, y f z x, y, ϕx, y, ϕ yx, y f yx, y, ϕx, y f z x, y, ϕx, y x, y R. 4 fx, y C p ϕx, y C p fx, y C fx, y, f y x, y y ϕx y f xxfy f xy f x f y + f yy fx fy 3 ϕ x ϕ x f xxx, ϕx f y x, ϕx. B. C fx, y fx,y f x x,y f y x,y x,y y ϕx C ϕx ϕ x ϕ x f xxx,y f y x,y ϕ x f xx x,y x ϕ x ϕx ϕ x y ϕx 44
55 fx, y x 3 + y 3 3xy, f y x, y y ϕx ϕ x x, y ϕx ϕ x x 3 ϕ x x,y ϕx 4 ϕx escarte x 3 + y 3 3xy f x x, y 3x 3y 3x y, f y x, y 3y 3x 3y x, f xx x, y 6x ϕ x f xx, ϕx f y x, ϕx ϕx x ϕx x ϕx x x ϕx y x f x x, y fx, y y ϕx y x x 6 x 3 x 3 x 3 f x x, y x, 3 x y, f y x,y x 3,y x f xx x, y 6x ϕ x f xxx,y f y x,y 6x 3y 3x x 3. 4 x 3 f y 3, >, ϕ 3 < ϕx x y 3 4 y ϕx. // escarte x 3t +t 3, y 3t t +t3 C. R 3 C fx, y, z Px,y,z fx,y,z α α S α a, b, c fa, b, c α f z x,y,z x,y,z fx, y, ϕx, y C z φx, y φx, φ y, f x, f y, f x,f y,f z f z f z f z 45
56 S α Px,y,z T P x x f x x,y,z +y y f y x,y,z +z z f z x,y,z. l P x x tf x x,y,z l P : y y tf y x,y,z t R z z tf z x,y,z 4.9 x + y x y Bernoulli Lemniscate fx, y x + y x y, f y x, y y ϕx ϕ x x, y ϕx ϕ x x 3 ϕ x x, y ϕx 4 ϕx a> 4x 4-4a x +a y y fx, y 4x 4 4a x + a y, f y x, y y ϕx ϕx x 3 fx, y x x xy +y, f y x, y y ϕx ϕx 4 x a + y b + z c Px,y,z T P l P 46
57 . fx, y R C fa, b, f y a, b a, b fx, y z fx, y a, b y- a, b K x, y a δ x a + δ, b ɛ y b + ɛ δ, ɛ > a [a δ, a + δ] y fa,y [b ɛ, b + ɛ] fa,y [b ɛ, b + ɛ] x [a δ, a + δ] y fx, y [b ɛ, b + ɛ] y ϕx fx, y a, b K z fx, y z y ϕx f y a, b > f y x, y η ɛ f y x, y > a η x a + η, b ɛ y b + ɛ x a fa, y d dy fa, y f ya, y >. fa, y [b ɛ, b+ɛ] fa, b ɛ <fa, b <fa, b + ɛ y f x, y b+ε b K b-ε a-η a-δ a a+δ a+η x fx, y δ< η fx, b ɛ <, fx, b + ɛ > a δ x a + δ δ ɛ a, b K x, y a δ x a + δ, b ɛ y b + ɛ δ, ɛ > x a δ, a + δ y fx, y d dy fx, y f yx, y > 47
58 fx, y [ b ɛ, b + ɛ] fx, b ɛ < <fx, b + ɛ fx, y y b ɛ, b+ɛ y ϕx a I a δ, a + δ ϕx, b ϕa fx, ϕx and f y x, ϕx x I. ϕx x a ϕx ɛ δ ϕa ɛ<ϕx <ϕa+ɛ a δ<x<a+ δ ϕx a a δ, a + δ a b ϕa ϕx a,b 3 ϕx 4.7 B. Taylor fx + h, y + k fx, y+hf x x + θh, y + θk+kf y x + θh, y + θk < θ < y ϕx, y+ k ϕx + h fx + h, ϕx + h fx, ϕx + hf x x + θh, y + θk+kf y x + θh, y + θk < θ < ϕx + h ϕx h k h f xx + θh, y + θk f y x + θh, y + θk f xx, y f y x, y h 4 y ϕx ϕ x f xx, ϕx f y x, ϕx fx, y C f xx, ϕx f y x, ϕx C ϕ x f xxx, ϕxf y x, ϕx f xy x, ϕxf x x, ϕxf y x, ϕx + f yy x, ϕxf x x, ϕx f y x, ϕx A. ϕx C fx, y C p ϕx C p // 48
59 4. C. fx, y, gx, y C gx, y fx, y gx,y x,y fx,y g y x,y x y ϕx y ϕx gx, ϕx ϕ x g xx, ϕx g y x, ϕx x,y gx, y x, y y ϕx fx,y z fx, ϕx z fx, ϕx dz dx f xx, ϕx f y x, ϕx g xx, ϕx g y x, ϕx f x x,y g y x,y f y x,y g x x,y λ f yx,y g y x,y f xx,y λg x x,y f y x,x,y y λg y x,y λ Lagrange Lagrange fx, y, gx, y C gx, y fx, y λ x, y f x x, y λg x x, y f y x, y λg y x, y g y x, y x,y y ϕx C ϕx d dx fx, ϕx xx f x x,y f y x,y g xx,y g y x,y g y x, y x, y fx, y x,y fx,y 49
60 x + y fx, y x + y Lagrange gx, y x + y. gx, y f x x, y λg x x, y f y x, y λg y x, y, x + y 4λx λy λ λ 3 λ ± x 4λ ± 6 y λ ± 6 x 4λx+y λy x + y λx + y x + y λ fx, y x + y x, y 6, 6 λ 3 x, y 6, 6 λ 3 // - x 4. a + y fx, y x + y b 8x + y fx, y x + y 3 x + y xy x y + fx, y xy x + y xy x y + x + y x y
61 4 ϕx, y x xy + y, z x + y x xy + y x + y + 3 x + y sin x +siny π 6 x, y 7π 6 3 z x + y.. C. 3. fx, y, z, gx, y, z C gx, y, z fx, y, z λ x, y, z f x x, y, z λg x x, y, z f y x, y, z λg y x, y, z f z x, y, z λg z x, y, z g z x, y, z x,y,z z ϕx,y C ϕx, y x fx, y, ϕx, y f x x,y,z f z x,y,z xx,yy g xx,y g z x,y y fx, y, ϕx, y f y x,y,z f z x,y,z xx,yy g yx,y,z g z x,y,z g z x, y, z x, y, z fx, y, z fx,y,z x,y,z x a + y b + z a, b, c >, xyz c 5
62 4.. V ΦU U u,v x Φ,y Φu,v u,v x,yφu,v uv- C Φ: x xu, v, y yu, v x, y Ju, v u, v u, v u,v x,y Φu,v u,v U x,y V Φ U V Φ : V U C Ju, v Ju, v u,v x,y Φu,v u,v r r u,v r u,v r u,v u, v u u +v v r. Ju, v Ju, v r u,v m m min Ju, v u, v r u,v >. r u,v M > x u u, v M, x v u, v M, y u u, v M, y v u, v M u, v r u,v r u,v m ɛ ɛ M δ u, v, u,v r u,v max u u, v v <δ x u u, v x u u,v < ɛ M, x vu, v x v u,v < ɛ M y u u, v y u u,v < ɛ M, y vu, v y v u,v < ɛ M r u,v r u,v R 4 C xu, v, yu, v Ku,v,u,v x u u,v y v u,v x v u,v y u u,v max u u, v v <δ Ku,v,u,v Ju,v <ɛ. 5
63 max u u, v v <δ Ku,v,u,v Ju,v xu u,v y v u,v x v u,v y u u,v x u u,v y v u,v x v u,v y u u,v x u u,v x u u,v y v u,v x v u,v x v u,v y u u,v M x u u,v x u u,v + M x v u,v x v u,v < M ɛ M + M ɛ M ɛ u,v, u,v r u,v Ku,v,u,v Ju,v <ɛ<m Ku,v,u,v > Ju,v ɛ>ju,v m> r u,v r u,v Ku,v,u,v > Φ r u,v r u,v u, v, u,v Φu, v Φu,v x, y u,v, u,v r u,v xu,v xu, v x u u,v u u+x v u,v v v yu,v yu, v y u u,v u u+y v u,v v v u u, v v x u u,v y v u,v x v u,v y u u,v Ku,v,u,v > u,vu, v Φ r u,v U r u,v V ΦU Φ : V U V x,y Φ U r u,v u,v U x,y Φu,v ρ min xu, v x +yu, v y u, v U > U r u,v u,v r x,y ρ ρ x,y ρ x,y x,y ρ x,y x,y Φ U μu, v xu, v x +yu, v y u, v U U μ μu,v <ρ u,v U x u u,v xu,v x +y u u,v yu,v y x v u,v xu,v x +y v u,v yu,v y x u u,v y v u,v x v u,v y u u,v Ju,v > xu,v x yu,v y Φu,v x,y x,y V ρ x,y V ΦU V ΦU // Φ Φ C 53
64 54
65 5 5. A. R [a, b] [c, d] x, y R a x b, c y d fx, y fx, y M R x, y fx, y M M fx, y M R [a, b] [c, d] n m a a <a <a < <a m <a m b Δ : c c <c <c < <c n <c n d. R i,j [a i,a i ] [c j,c j ] ξ ij,η ij : a i ξ ij a i μ : b j η ij b j i,,,m, j,,,n. Δ μ RΔ,μ fξ ij,η ij a i a i c j c j i m, j n R i,j R RΔ,μ fξ ij,η ij a i a i c j c j Mb ad c i m, j n Δ Δ Δ max δ i,j δ i,j a i a i +c j c j i,j Δ Δ RΔ,μ fx, y dxdy lim RΔ,μ fx, y R R Δ fx, y R fx, y > x, y R fx, y dxdy z fx, y R. R 55
66 fx, y R [a, b] [c, d] f fx, y x, y x, y x, y f x, y dxdy R f x, y R f x, y dxdy R fx, y dxdy f x, y dxdy R. fx, y x, y χ x, y x, y χ x, y dxdy R χ x, y dxdy R X X R [a, b] [c, d] R i,j Δ Δ : a a <a <a < <a m <a m b c c <c <c < <c n <c n d, R i,j [a i,a i ] [c j,c j ]. X R i,j bδ a i a i c j c j X R i,j R, lim bδ Δ fx, y R [a, b] [c, d] fx, y R B. fx, y, gx, y E 56
67 3 fx, y+gx, y dxdy αfx, y dxdy α fx, y dxdy fx, y dxdy + gx, y dxdy. fx, y dxdy α. fx, y dxdy. 4 E E E fx, y dxdy fx, y dxdy + fx, y dxdy. E E fx, y R [a, b] [c, d] y [c, d] x fx, y [a, b] y R b a fx, y dxdy fx, y dx [c, d] d c b a fx, y dx dy. 3 ϕ x ϕ x a x b x, y R a x b, ϕ x y ϕ x fx, y ϕx ϕ x fx, y dy a x b [a, b] fx, y dxdy b ϕx a ϕ x fx, y dy dx y y ϕ x y ϕ x a b x 3 α y α y c y d x, y R c y d, α y x α y fx, y d y x α y x α y αy α y fx, y dx c y d [c, d] fx, y dxdy d αy c α y fx, y dx dy c x 57
68 fx, y R d b b d fx, y dxdy fx, y dx dy R c a a c fx, y dy dx. fx, y R [a, b] [c, d] f fx, y x, y x, y x, y f x, y R R Δ Δ Δ f x, y RΔ,μ lim RΔ,μ Δ lim RΔ,μ RΔ,μ Δ Cauchy ɛ δ Δ, Δ <δ RΔ,μ RΔ,μ <ɛ lim RΔ,μ Δ, Δ RΔ,μ. Δ,μ R K fx, y K R K fx, y K ɛ δ x, y, x,y K x x +y y < δ fx, y fx,y < ɛ 4. 58
69 M max x, y fx, y max x, y R f x, y < R [a, b] [c, d] mn R ij [a i,a i ] [c j,c j ] a a <a <a < <a m <a m b Δ : c c <c <c < <c n <c n d. R b ad c R, R ij a i a i c j c j R ij i,j R i,j R R ij s ij,t ij a i s ij a i μ : c j t ij c j i,,,m, j,,,n. RΔ,μ f s ij,t ij a i a i c j c j i,j i,j f s ij,t ij R ij, R i,j R i,j RΔ,μ i,j f s ij,t ij R ij M R ij M R. i,j R [a, b] [c, d] f x, y RΔ,μ I R ij [a i,a i ] [c j,c j ] s ij, t ij : a i s ij a i μ : c j t ij c j i,,,m, j,,,n. Δ μ RΔ, μ i,j f s ij, t ij R ij RΔ, μ RΔ,μ i,j A f s ij, t ij f s ij,t ij R ij f s ij, t ij f s ij,t ij R ij + B f s ij, t ij f s ij,t ij R ij. 59
70 A f s ij, t ij f s ij,t ij R ij R ij f s ij, t ij f s ij,t ij R ij B R ij fx, y ɛ < M δ x, y, x, ỹ x x +y ỹ < δ fx, y f x, ỹ < ɛ Δ Δ <δ fx, y f x, y f x, y f s ij, t ij f s ij,t ij <ɛ R ij R ij M s ij, t ij, s ij,t ij R \ s ij, t ij R \, s ij,t ij f s ij, t ij f s ij,t ij M f s ij, t ij f s ij,t ij R ij < ɛ R ij R ɛ. B B f s ij, t ij f s ij,t ij R ij A R ij R ij A R i,j f s ij, t ij f s ij,t ij M A a i a i c j c j bδ f s ij, t ij f s ij,t ij R ij M A R ij MbΔ. RΔ, μ RΔ,μ f s ij, t ij f s ij,t ij R ij < MbΔ + R ɛ. i,j II, [a, b] [c, d] Δ Δ Δ Δ 6
71 Δ : a ã < ã < ã < < ã p < ã p b c c < c < c < < c q < c q d, Δ Δ <δ. R k,l [ã k, ã k ] [ c l, c l ] s kl, t kl : ã i s ij ã i μ : c j t ij c j i,,,p, j,,,q. R k,l ã k ã k c l c l R kl Δ μ R Δ, μ f s kl, t kl R kl k,l R [a, b] [c, d] Δ Δ RΔ,μ Δ Δ RΔ,μ f s ij,t ij a i a i c j c j f s ij,t ij ã k ã k c l c l i,j i,j a i <ã k a i,c j < c l c j Δ R ij R Δ, μ RΔ,μ i,j a i <ã k a i,c j < c l c j A a i <ã k a i,c j < c l c j + B f s kl, t kl f s ij,t ij R kl f s kl, t kl f s ij,t ij R kl f s kl, t kl f s ij,t ij R kl. A a i <ã k a i,c j < c l c j R ij R ij B Δ Δ <δ fx, y f x, y R kl R ij f s kl, t kl f s ij,t ij <ɛ f s kl, t kl f s ij,t ij Rkl < ɛ R ij R ɛ. B a i <ã k a i,c j < c l c j R ij R kl R ij. I Δ Δ <δ R ij R kl f s kl, t kl f s ij,t ij M f s kl, t kl f s ij,t ij R kl A a i <ã k a i,c j < c l c j M A M A a i <ã k a i,c j < c l c j R ij Mb Δ. Rkl B 6
72 R Δ, μ RΔ,μ i,j f s ij, t ij R ij k,l f s kl, t kl R kl < MbΔ + R ɛ. III R [a, b] [c, d] Δ Δ Δ, Δ <δ R Δ Δ R Δ Δ μ c j c l c l c j y RΔ,μ a i a i x R Δ,μ, Δ,μ RΔ,μ, RΔ,μ I II RΔ,μ RΔ,μ RΔ,μ RΔ,μ + RΔ,μ RΔ,μ MbΔ+MbΔ + R ɛ. R ij R ij a i a i c j c j bδ Δ A R i,j I, II II lim bδ lim Δ Δ bδ ɛ // lim RΔ,μ Δ, Δ RΔ,μ ã k ã k y b a fx, y dx [c, d] [c, d] Δ y t j Δ y : c c <c <c < <c n <c n d, c j t j c j j,,,n fx, y dxdy b fx, t j dx c j c j [a,b] [c,d] j a R [a, b] [c, d] Δ Δ RΔ,μ [c, d] Δ y t j a a <a <a < <a m <a m b Δ : c c <c <c < <c n <c n d 6
73 R i,j [a i,a i ] [c j,c j ] s i,t j a i s i a i μ : c j t j c j i,,,m, j,,,n. RΔ,μ i,j fs i,t j a i a i c j c j fx, y R ɛ δ Δ <δ fx, y dxdy RΔ,μ < ɛ R Δ Δ <δ RΔ,μ i,j j j fs i,t j a i a i c j c j b a + j b a fx, t j dx c j c j fs i,t j a i a i i fx, t j dx c j c j + j b a R j fx, t j dx c j c j b a fx, t j dx c j c j, R j i fs i,t j a i a i. fx, y dxdy b fx, t j dx c j c j R j a fx, y dxdy RΔ,μ+ b R j R j a fx, y dxdy RΔ,μ + b R j R < ɛ + R j j b a fx, t j dx c j c j j a fx, t j dx fx, t j dx c j c j c j c j [c, d] Δ y Δ y maxc j c j < δ j Δ x maxa i a i R j fs i,t j a i a i [a, b] i i fx, t j ɛ δ x < δ Δ x <δ x R j b a fx, t j dx < ɛ d c [a, b] [c, d] Δ Δ max a i a i +c j c j < δx + δ i,j 4 <δ 63
74 Δ y < δ fx, y dxdy b fx, t j dx c j c j R j a < ɛ + b R j fx, t j dx c j c j < ɛ j a + j ɛ d c c j c j ɛ ϕy R fx, y dxdy // lim Δ y j b a b a fx, y dx c y d [c, d] fx, t j dx c j c j d c b a fx, y dx dy ϕ x ϕ x a x b x, y R a x b, ϕ x y ϕ x fx, y C,C L a, L b C x, y R y ϕ x, C x, y R y ϕ x L a a, y ϕ a y ϕ a,l b b, y ϕ b y ϕ b [a, b] ϕ x, ϕ x d max a x b ϕ x c min a x b ϕ x R [a, b] [c, d], C C L a L b. ϕ x ϕ x [a, b] ɛ δ [a, b] x, x x x < δ ϕ x ϕ x < ɛ ɛ δ [a, b] x x < δ ϕ x ϕ x < ɛ δ minδ,δ [a, b] x, x x x < δ ϕ x ϕ x, ϕ x ϕ x < ɛ 64
75 R [a, b] [c, d] R i,j Δ Δ : a a <a <a < <a m <a m b c c <c <c < <c n <c n d, R i,j [a i,a i ] [c j,c j ]. R i,j bδ R i,j a i a i c j c j Δ ɛ Δ <δmin δ, y C L a L b R ij a i a i c j c j δd c. R i,j L a L b ɛ a i a i C x i R ij C R ij C R ij ɛ +δ, a i x a i a i a i <δ δ ϕ x ϕ a i <ɛ. x, ϕ x ai x a i [ ϕ a i ɛ, ϕ a i +ɛ ]. ɛ [a i,a i ] [ϕ a i ɛ, ϕ a i +ɛ] δ R i,j ɛ +δ i R ij C R ij ɛ +δ a i a i c j c j b a4ɛ +4δ 6b aɛ δ ɛ R i,j C C ɛ δ Δ <δ bδ a i a i c j c j δd c+6b aɛ 6b a+d c ɛ R i,j ɛ lim bδ Δ f x, y R b d fx, y dxdy f x, y dy dx a c b a ϕ x ϕ x fx, y dy dx. // 3 ϕx ϕx ϕ x fx, y dy a x b 65
76 5. A. : b a dx qx px fx, y dy b qx a px fx, y dy dx b qx a px fx, y dydx b a qx px fx, y dy dx, d c dy sy ry fx, y dx d c sy ry fx, y dx dy d sy c ry fx, y dxdy d c sy ry fx, y dx dy. px, qx a x b, ry, sy c y c. b a xy dxdy. z y b a b a b [ x y ] a xy dxdy xy dx dy dy b b a y [ a y ] b dy a b 4. // a x x,y,z,x + y + z z V V x y dxdy, x, y x, y, x + y.. y x y dxdy x y dxdy [ yx x y y y dy dy [ y 3 ] // x ] y dy y 66
77 3 a, b > b a x + y dxdy xy dxdy, x, y x a, y bx a 3 xy dxdy, x, y bx x a, y b a 4 x x x + ydydx [ ] x x + ydydx 3 x + y 3 dx x 3 3 x dx [ x ] dx x // y, x B... x x, y x, y x fx, y dy dx fx, y dx dy y x fx, y dydx fx, y dydx y fx, y dxdy. y e x3 dxdy π sin x e cos y dydx. e x3 dxdy y x e x3 dydx [ e x x 3 e x3 dx 3 ] [ye x3] x dx e. 3 π sin x e cos y dydx π π sin y e cos y dxdy π [xe cos y] sin y dy [ ] π sin ye cos y dy e cos y e. 67
78 3 x + ye y dxdy,. x + ye y dxdy x, y x, x y. x x + ye y dy dx x te t x dt dx [te t x] x x t x + y e t x dt dx y x x [e t x] x dx [ x x +e x dx x e x] e. //, 5. x dx x fx, ydy ft t R x ds s ftdt x ftx tdt x R x dx fx, ydy x t x, x x s 3 F x, y [a, b] [c, d] C fx, y F x, y x y d b c a fx, y dxdy F b, d F b, c F a, d+f a, c 4 R K x, y a x a, b y b R x a y dxdy b x, y, z z x a y b, x, y R z y x 68
79 5.3 A. C x xu, v, y yu, v uv- K xy : xu, v, yu, v R u, v K. fx, y fx, y dxdy fxu, v,yu, v x, y y v K u, v dudv x, y u, v K x u a b ad bc x au + bv, y cu + dv uv- c d K u, v R u, v xy a b abs. ad bc c d dxdy x, y u, v dudv ad bc dudv ad bc K K xr, θ r cos θ, yr, θ r sin θ r >, θ R x, y r, θ x r y r x θ y θ cos θ sin θ r sin θ rcos θ r. B. xy dxdy x, y R x + y 4, x, y. y x r cos θ, r sin θ R r, θ π π θ r xy dxdy π [ r 4 4 ] [ 3 sin θ r cos θ 4 drdθ ] π 5 8. π r 3 dr sin θ dθ 69
80 3 x, y R x, y, x + y e x y dxdy xu, v uv, yu, v u v u, v R uv, u v R u, v e x y dxdy x, y u, v dv x u y u x v y v e u x, y u, v dudv [ e u udu e u u y v u v u ] x e u ududv u. e u du e + [ e u] v u e. 4 <a< : a x + y α dxdy x + y α α dxdy x + y α π a π a x + y α [ r r α α ] drdθ π α [ ] r drdθ π log r a dxdy. a π a α α π log a.. 5 fx, y 4x +4xy +4y 4x 4y + x, y, z R 3 fx, y z V x HINT. fx, y 6 + y + x y
81 π <α<β π C C : r fθ α θ β r cos θ, r sin θ R : r fθ, α θ β y θ β C θ α β fθ dθ. α xy rθ- K r, θ R r fθ, α θ β x dxdy rdrdθ β fθ rdrdθ β K α α [ r ] fθ dθ β α fθ dθ. // 5.3 fx x C x +y f x +y dxdy π f f Cardioid r a + cos θ θ π 3 Lemniscate x + y a x y a> x + y a x y 4 Rhodonea n N, a > r a sin nθ θ< π n r sin5θ 5 : x + y a 4 a x y dxdy. 7
82 5.4. C Φ: x xu, v, y yu, v uv- K xy K Ju, v ; xu, v, yu, v R u, v K. fx, y fx, y dxdy fxu, v,yu, v x, y u, v dudv. K x, y u, v K R [a, b] [c, d]. xu, v yu, v R L xu, v <L, yu, v <L u, v R L L + E [ L, L] [ L, L] E E. ΦR R Φ Φ:R C R R Φ R α R α [a + α, b α] [c + α, d α] R R α α ΦR α α Φ R α ρ α α ρ α min x x +y y : x, y, x,y α > a M > x u u, v M, x v u, v M, y u u, v M, y v u, v M u, v R..4 R R [a,b ] [c,d ] R b a d c R k < d c b a <k ΦR 4M K R K k + k 7
83 .4 K k + k δ b a +d c b a d c + d c b a R K R ΦR u, v, u,v R xu,v xu, v xu,v xu, v +xu, v xu, v x u ξ, v u u+x v u, ηv v ξ, v, u, η R x u ξ, v u u + x v u, ηv v M u u +v v M δ max xu, v min u,v R xu, v M δ. u,v R u, v, u,v R i,j yu,v yu, v M δ max yu, v min u,v R yu, v M δ. u,v R ΦR M δ δ K R ΦR 4M K R //.5 R R α [a + α, b α] [c + α, d α] R α> \ α ΦR \ ΦR α ΦR \ R α M R R α.5 R\R α R A [a, a+α] [c, d], B[b α, b] [c, d], C [a + α, b α] [c, c + α], [a + α, b α] [d α, d] R \ R α A B C A < < A i A A A na.4 ΦA i 4M 5 A i M A i ΦA M A B, C, ΦR \ R α M R \ R α // R b ad c R, R α b a αd c α R α.5 R \ R α R R α αb a + d c α R \ R α αb a + d c α α 73
84 \ α ΦR \ R α α Φ R ΦR \ R α.6 ΦR fx, y fx, y E f fx, y x, y x, y x, y. E fx, y dxdy f x, y dxdy E 5. A. R Δ : a a <a < <a m b c c <c < <c n d. Δ P i,j a i,c j i,,,m, j,,,n Δ Δ max δ i,j, δ i,j a i a i +c j c j i,j R i,j [a i,a i ] [c j,c j ] : R Δ i,j P i,j, P i,j, P i,j R i,j P i,j, P i,j, P i,j R i,j R Δ i,j R i,j. Q i,j ΦP i,j xa i,c j,ya i,c j Φ R R Δ i,j,r i,j R R Δ i,j R i,j ΦR ΦR Δ i,j i,j i,j i,j i,j ΦR i,j. Q i-,j Qi,j P i-,j P i-,j- P i,j P i,j- Φ Q i-,j- Q i,j- Q i,j ΦP i,j Q i,j, Q i,j, Q i,j Q i-,j Q i,j T Δ i,j Q i,j, Q i,j, Q i,j T i,j Δ T i,j Ti,j T Δ Ti,j Δ Ti,j i,j i,j Q i-,j- Q i,j- 74
85 T Δ i,j ΦΔ i,j RΔ i,j x xa i,c j + xa i,c j xa i,c j a i a i u a i + xa i,c j xa i,c j c j c j v c j y ya i,c j + ya i,c j ya i,c j u a i + ya i,c j ya i,c j v c j. a i a i c j c j R Δ i,j u, v a i u a i,c j v c j + c j c j u a i a i a i T i,j Φ i,j R i,j x xa i,c j + xa i,c j xa i,c j a i a i u a i + xa i,c j xa i,c j c j c j v c j y ya i,c j + ya i,c j ya i,c j u a i + ya i,c j ya i,c j v c j. a i a i c j c j R i,j u, v a i u a i,c j v c j + c j c j u a i a i a i Φ Δ i,j xa i,c j xa i,c j x u ξ i,j,c j, a i a i ya i,c j ya i,c j y u ξ a i a i,j,c j, i Φ Δ i,j Φ Δ i,j : xa i,c j xa i,c j c j c j x v a i,η i,j ya i,c j ya i,c j y v a i,η c j c i,j j ξ i,j,ξ i,j a i,a i, η i,j,η i,j c j,c j x xa i,c j +x u ξ i,j,c j u a i + x v a i,η i,j v c j y ya i,c j +y u ξ i,j,c j u a i + y v a i,η i,j v c j Φ i,j Φ i,j : x xa i,c j +x u μ i,j,c j u a i + x v a i,ν i,j v c j y ya i,c j +y u μ i,j,c ju a i + y v a i,ν i,j v c j μ i,j,μ i,j a i,a i, ν i,j,ν i,j c j,c j R i,j a i a i c j c j R i,j R b ad c R i,j R i,j R i,j R i,j R Δ i,j RΔ i,j R i,j Ti,j Δ Δ Ti,j, T i,j Ti,j, R i,j fx, y R fu, v fxu, v,yu, v fai,c j fxa i,c j,ya i,c j. 75
86 lim fai,c j Ja i,c j R Δ i,j + fa i,c j Ja i,c j Ri,j Δ i,j fxu, v,yu, v Ju, v dudv, R lim fai,c j Ti,j Δ + fa i,c j Ti,j Δ i,j lim fai,c j Ja i,c j R Δ i,j + fa i,c j Ja i,c j R i,j Δ i,j 3 fx, y lim Δ i,j fai,c j T Δ i,j + fa i,c j T i,j,, 3 fx, y dxdy. fu, v Ju, v R R 5., 4.. ɛ δ 3 fa i,c j Ja i,c j R Δ i,j + fa i,c j Ja i,c j R i,j fa i,c j Ja i,c j + fa i,c j Ja i,c j R i,j fp i,j,q i,j Jp i,j,q i,j R i,j p i,j,q i,j R i,j fai,c j Ja i,c j R Δ i,j + fa i,c j Ja i,c j Ri,j lim Δ i,j lim Δ i,j fp i,j,q i,j Jp i,j,q i,j R i,j R fxu, v,yu, v Ju, v dudv. Ti,j, Δ Ti,j Φxu, v,yu, v R C b R ɛ ɛ 4M δ u, v, u,v R max u u, v v <δ x u u, v x u u,v < ɛ 4M, x vu, v x v u,v < ɛ 4M y u u, v y u u,v < ɛ 4M, y vu, v y v u,v < ɛ 4M R C xu, v, yu, v Ju, u,u,v,v,v x u u,vy v u, v x v u, v y u u,v u, u,u,v,v,v R [a, b] [a, b] [a, b] [c, d] [c, d] [c, d] R 6 max u u, u u, v v, v v <δ Ju, u,u,v,v,v Ju, u, u, v, v, v <ɛ. 76
87 a b max u u, u u, v v, v v <δ Ju, u,u,v,v,v Ju, u, u, v, v, v Ju, u,u,v,v,v Ju, v x u u,vy v u, v x v u, v y u u,v x u u, vy v u, v x v u, vy u u, v x u u,vy v u, v x u u, vy v u, v x v u, v y u u,v x v u, vy u u, v x u u,v y v u, v y v u, v + x u u,v x u u, v y v u, v x v u, v y u u,v y u u, v + x v u, v x v u, v y u u, v M y v u, v y v u, v + M x u u,v x u u, v +M y u u,v y u u, v + M x v u, v x v u, v < M ɛ 4M + M ɛ 4M + M ɛ 4M + M ɛ ɛ // 4M Ju, v R Ju, v Ju, v R Ju, v > u, v R Ju, v < u, v R Ju, v R m m min Ju, v >. u,v R ɛ ɛ < m ɛ b δ c max u u, u u, v v, v v <δ Ju, u,u,v,v,v Ju, u, u, v, v, v <ɛ Ju, u,u,v,v,v >. max u u, u u, v v, v v <δ Ju, u,u,v,v,v Ju, u, u, v, v, v > ɛ m Ju, u,u,v,v,v > Ju, u, u, v, v, v m Ju, v m. R Δ Δ <δ< x i,j, y i,j Q i,j ΦP i,j xa i,c j,ya i,c j Φ Δ i,j T i,j Δ Δ Ti,j : T Δ i,j x i,j x i,j y i,j y i,j x i,j x i,j y i,j y i,j x uξ i,j,c j y v a i,η i,j x v a i,η i,j y u ξ i,j,c j a i a i c j c j x u ξ i,j,c j y v a i,η i,j x va i,η i,j y u ξ i,j,c j R Δ i,j c Ja i,ξ i,j,ξ i,j,c j,η i,j,η i,j R Δ i,j. ɛ Δ i,j Ja i,ξ i,j,ξ i,j,c j,η i,j,η i,j Ja i,c j 77
88 Ti,j Δ Ja i,c j +ɛ Δ i,j R Δ i,j Ti,j Ti,j x i,j x i,j y i,j y i,j x i,j x i,j y i,j y i,j x uμ i,j,c j y v a i,ν i,j x va i,ν i,j y u μ i,j,c j a i a i c j c j xu μ i,j,c j y v a i,ν i,j x va i,ν i,j y u μ i,j,c j a i a i c j c j Ja i,μ i,j,μ i,j,c j,ν i,j,ν i,j R i,j Ja i,c j +ɛ i,j R i,j ɛ i,j Ja i,μ i,j,μ i,j,c j,ν i,j,ν i,j Ja i,c j. ɛ Δ i,j a i,ξ i,j,ξ i,j [a i,a i ],c j,η i,j,η i,j [c j,c j ] c ɛ Δ i,j Ja i,ξ i,j,ξ i,j,c j,η i,j,η i,j Ja i,c j Ja i,ξ i,j,ξ i,j,c j,η i,j,η i,j Ja i,a i,a i,c j,c j,c j <ɛ T i,j ɛ i,j <ɛ. d fx, y ΦR V fai,c j Ti,j Δ + fa i,c j Ti,j i,j V max fx, y < x,y + fai,c j ɛ Δ i,j R Δ i,j + fa i,c j ɛ i,j R i,j i,j fai,c j Ja i,c j R Δ i,j + fa i,c j Ja i,c j R i,j i,j fai,c j ɛ Δ i,j R Δ i,j + fa i,c j ɛ i,j Ri,j V ɛ Δ i,j R Δ i,j + V ɛ i,j R i,j i,j i,j < Vɛ i,j R Δ i,j + R i,j V R ɛ ɛ> V R ɛ lim fai,c j Ti,j Δ + fa i,c j Ti,j Δ i,j lim fai,c j Ja i,c j R Δ i,j + fa i,c j Ja i,c j R i,j Δ i,j 3.6 fx, y dxdy f x, y dxdy lim fai,c j Ti,j Δ + fa i,c j Ti,j E Δ i,j 78
89 f x, y dxdy E E T Δ Ti,j Δ Ti,j i,j i,j ΦR ΦR Δ i,j ΦR i,j i,j i,j Φ:R C Ti,j, Δ Ti,j i,j ΦR \ ΦR \ R <i<m, <j<n P i,j R \ R Q i,j ΦP i,j xa i,c j,ya i,c j \. R A,, A,, A,, A,,, 3 A, A, A, A, A, A, A, A, p,q, A, A, p,q A, A, r,s, A, A, r,s p q p q > r s r s > A, A, A, A, A, A, A, A, A, A, A, A, A, A, A, A, A, A, A, A, p,q, A, A, p,q, p q p q > A, A, A, A, A, 3 A, A, A, A, A, A, A, A, p,q, A, A, p,q, p q p q > A, A, A, A, A, A, A, r,s p, q, A, A, r,s r s r s > A,A, A, A, A, r,s, A, A, r,s p, q r s r s > A,A, A, 79
90 Δ <δ Ju, u,u,v,v,v > max u u, u u, v v, v v < Δ c Ti,j Δ Ja i,ξ i,j,ξ i,j,c j,η i,j,η i,j R Δ i,j xi,j x i,j y i,j y i,j x i,j x i,j y i,j y i,j > T i,j Ja i,μ i,j,μ i,j,c j,ν i,j,ν i,j R i,j xi,j x i,j y i,j y i,j x i,j x i,j y i,j y i,j > 3 T Δ Ti,j Δ Ti,j T Δ Ti,j Δ + Ti,j i,j i,j i,j T Δ T Δ P, P, P m, P m, P m,n P m,n P,n P,n P, Ti,j Δ T i,j T Δ T Δ \ T Δ <i<m, <j<n T Δ T Δ Φ R ΦR i, ΦR m,j ΦR i,n ΦR,j i,,m j,,n i,,m j,,n Φ R x, y R R R i,j u, v R i,j R Φu, v xu, v,yu, v x, y u, v R Δ i,j R u, v R i,j R x,y Φ Δ i,ju, v T Δ x,y Φ i,ju, v T Δ u, v R Δ i,j R Φu, v xu, v,yu, v x, y r i,j,r i,j a i,a i s i,j s i,j c j,c j x xu, v xa i,c j +x u r i,j,s i,j u a i +x v r i,j,s i,j v c j y yu, v ya i,c j +y u r i,j,s i,j u a i +y v r i,j,s i,j v c j Φu, v Φ Δ x x i,ju, v y y x u r i,j,s i,j x u ξ i,j,c j x v r i,j,s i,j x v a i,η i,j u a i y u r i,j,s i,j y uξ i,j,c j y v r i,j,s i,j y va i,η i,j v c j 8
91 b Δ <δ x x +y y < ɛ u a i 4M +v c j ɛ 4M δ ɛ Δ i,j. 4M ɛ< T Δ Δ <δ< E T Δ E \ T Δ α δ δ<ρ α.3 R α [a+α, b+α] [c α, d α] R α ΦR α α Φ R α ρ α T Δ T Δ α α T Δ \ T Δ \ α \ T Δ \ α ΦR \ R α lim Δ \ α lim \ T Δ. Δ E \ T Δ E Δ E s E T Δ E \ T Δ s E s. E s E s E s x s,y s E s s f x s,y s E s f x s,y s E s + s i,j fai,c j Ti,j Δ + fa i,c j Ti,j f x, y E f x, y E \ \ TΔ lim Δ E lim Δ f x s,y s E s s f x, y dxdy lim f x s,y s E s + Δ s i,j lim fai,c j T Δ Δ i,j fai,c j Ti,j Δ + fa i,c j Ti,j i,j + fa i,c j T i,j K ΦK C Φ K K Ω C Φ Ω K Ω Ω. 8
92 M > x u u, v M, x v u, v M, y u u, v M, y v u, v M u, v Ω. Ω A [p, q] [r, s] q ps r A.4 A k < s r <k ΦA q p 4M K A K k + k K K K R [a, b] [c, d] R i,j a a <a <a < <a m <a m b Δ : c c <c <c < <c n <c n d, R i,j [a i,a i ] [c j,c j ] bδ K R i,j a i a i c j c j lim bδ Δ R R Φ Φ R K R i,j ΦR i,j < c j c j a i a i < i m, j n M bδ fx, y E f fx, y x, y x, y x, y. E E f x, y dxdy i,j ΦR i,j i m, j n i,j i,j fx, y dxdy. fx, y dxdy lim fx, y dxdy + fx, y dxdy Δ i,j i,j i,j i,j lim fxu, v,yu, v x, y Δ R i,j K R i,j u, v dudv fxu, v,yu, v x, y u, v dudv // K 8
93 5.5 n n n,, n n 5.5 C. x + y x + y dxdy, n x, y <x, y x. x, y n x, y x y z /n n,, x n,, n n x + y n x + y dxdy dx n n n+ x x x + y + y dy. x + y n n x x x x + y dy x x dy y + x dt +t tan π 4, y [ ] x x + y dy logx + y log. n x + y x + y dxdy x + y x dxdy lim + y n n π 4 + log dx ɛ π 4 + log. n x + y π x dxdy lim + y n 4 + n log π n 4 + log. // I a <a I I a x + y dxdy, a : a x + y y I 3 a I a x + y dxdy, : <x + y 3 x + y dxdy 3 a a x π a r 3 rdrdθπ [ 3 4 r 4 3 ] a 3π a
94 I dxdy lim 3 x + y a I a 3π lim a a 4 3π 3. //. Technics y dxdy R e x n x, y x, y, x + y n y dxdy n e x x ɛ > n ɛ x, y x, y, ɛ x + y n n e x R e x y dxdy lim ɛ π lim ɛ y dxdy lim n e x y dxdy lim n ɛ ] n [ e r x +y n e x lim π ɛ ɛ ɛ π n ɛ z n e r rdrdθ lim e ɛ e n π 4 e n. y dxdy lim 4 n n e x ɛ π dθ n ɛ y e r rdr y dxdy lim π. n π e n E n x, y x n, y n y dxdy n e dx x. E n e x n n E n e x y dxdy e x e y dxdy n n n 3 e x y dxdy e y n e x dx dy π e x y dxdy lim R n lim 4 e x y dxdy lim n E n n R n z e y dy n e x dx π x, y n n e x y dxdy n x n. e x dx e dx x e x dx e x dx R y 84
95 4 σ> μ R log x +y μ πx + y σ e σ R dxdy z log x +y πx + y e <x<, <y< Gamma Beta Gamma Beta t u, Γx t cos θ, Bx, y e t t x dt ΓxΓy Γx + y Bx, y. dt udu Γ Γx e u u x du dt cosθ sin θ Beta Bx, y t x t y dt π cos x θ sin y θdθ n E n ΓxΓy 4 e u u x du e v v y dv 4 lim e u v u x v y dudv n E n 4 e u v u x v y dudv u, v 4 lim e r r x+y cos x θ sin y θdrdθ n n π 4 cos x θ sin x θdθ e r r x+y dr Bx, yγx + y. // 5.5 Gamma Beta Γ π π e x dx 3 x e ax dx π 4 a 3 a> n n n,, n n n n i n 85
96 n i n i n n n+ i, n i i. n fx, y lim n fx, y dxdy n 5.6 A. 5. R 3 V fx, y, z fx, y, z dxdydz dxdy R 3 V V dxdydz V V V B x, y R 3 x + y + z B dxdydz x x x y x y dxdydz x x y dz dy dx x x y π x dx 4π 3. R 3 z c c R c x, y R x, y, c z Az V dxdydz b a z a c b dxdy a z b z dxdy dz b c <a<b< a Az dz. B. K x, y, z x 3 + y 3 + z 3 a 3 a > 86
97 z [, a] xy x 3 + y 3 a 3 z 3 3. x 3 +y 3 a 3 z 3 K V a V dxdydz K z a sin 3 t 3π 4 π 9π 4 a3 π dxdy 3 8 π a 3 3 z 3 x 3 +y 3 a 3 z 3 a 3 a 3 sin t 3 3a sin t cos t dt 9π π 4 a3 a 3 dxdy dz 8 π a 3 3 z 3 dz cos 7 t sin tdt π cos 7 tdt cos 9 tdt 9π 4 a πa3. // xy y fx a x b x V V π b a fx dx. 3 xy x +y a R a>r> x V y a+ R x R x R x y a R x R x R x V π R R R a + R x R dx π a R x dx 4πa R x dx R [ 4πa x R x + R sin x ] R R C. R 4πa πr π R a. n n C Φ : x x u,u,u 3,x x u,u,u 3, x 3 x 3 u,u,u 3 R 3 K R 3 x u,u,u 3,x u,u,u 3,x 3 u,u,u 3 R 3 u,u,u 3 K R 87
98 fx,x,x 3 dx dx dx 3 K fu,u,u 3 x,x,x 3 u,u,u 3 du du du 3 fu,u,u 3 fx u,u,u 3, x u,u,u 3, x 3 u,u,u 3 x,x,x 3 u,u,u 3 x x x u u u 3 x x x u u u 3 x 3 x 3 x 3 u u u 3 Φ Jacobian, 3 x, y, z r, θ, ϕ x r sin θ cos ϕ, y r sin θ sin ϕ, z r cos θ x, y, z r, θ, ϕ x r x θ x ϕ y r y θ y ϕ z r z θ z ϕ r sin θ r >, θ [, π], ϕ R. sin θ cos ϕ rcos θ cos ϕ r sin θ sin ϕ sin θ cos ϕ cos θ cos ϕ sin ϕ sin θ sin ϕ rcos θ sin ϕ rsin θ cos ϕ r sin θ sin θ sin ϕ cos θ sin ϕ cos ϕ cos θ r sin θ cos θ sin θ r sin θ sin ϕ cos θ sin ϕ sin θ sin ϕ cos θ sin θ cos ϕ sin θ cos ϕ cos θ cos ϕ cos θ sin θ r sin θ sin ϕ +cos ϕ r sin θ. x, y R 3 x + y + z 4, x, y, z xdxdydz π π π r 3 dr [ r 4 ] [ cos θ 4 r sin θ cos ϕr sin θdrdθdϕ π sin θdθ ] π [ sin ϕ cos ϕdϕ ] π 4 π 4 π. 5.6 a > x + y a y + z a 88
99 a x + y ax a > 3 z x + y x y a a > z 4 z x + y x + y ax a > z 5 z x + y x + y ax a > z 6 Cardioid r a + cos θ π θ π x x +y +z 7 p > p dxdydz 4 x + y + z + p 5 R x +y +z dxdy 3 x + y + z p dxdydz 5 R 3 e R3 p 8 R> a R x a x +y +z R a x + y + z dxdydz 3 9 R 3 r, θ, z θ u x + y + z + p 5 x +y +z dxdydz x + y + z p dxdydz 4πR3 3 a R a 4πa 3 r a a<r. + z b r, θ, z,u, τ u S u<π S S R 3 xyz x +acos ρ cos θ b sin ρ sin θ cos θ y +acos ρ cos θ b sin ρ sin θ sin θ z a cos ρ sin θ + b sin ρ cos θ θ<π, ρ<π. x + y z θ τ y <a<b<a+ b< S Ω x 89
100 5.7 A. R 3 xy R 3 π : ax + by + cz d c T T AT xy K AK AT cosγ AK γ π xy π N a, b, c π xy γ π z N z ν,, c γ < π cos γ N ν N ν c N x π ax+byd T K γ N N a + b + c AT AK cos γ N AK. c y c π : z d a c x b y T AT xy c K a + b + c dxdy zx c + zy +dxdy K K AK dxdy K R 3 A a,a,a 3, B b,b,b 3 R 3 Cc,c,c 3 R 3 π X x, y, z x a u + b v + c, y a u + b v + c, z a 3 u + b 3 v + c 3 u, v R. π N A B a b 3 a 3 b,a 3 b a b 3,a b a b a b π a 3 b 3 x c a b a 3 b 3 y c + a b a b z c 3. π A B a b a b π T T Xu, v ua + vb + C a u b, c v d 9
101 T xy K ua + vb + c,ua + vb + c a u b, c v d x a u + b v, y a u + b v R [a, b] [c, d] R K ua + vb,ua + vb a u b, c v d AK K AK a b a b R R b ad c R. 5.3 A. π N N X u X v A B a b 3 a 3 b,a 3 b a b 3,a b a b AT A B AK A B R a b a b R X u X v dudv. R 3 S Φ Φu, v xu, v, yu, v, zu, v R 3 u, v, xu, v, yu, v, zu, v u, v R C y u y v Φ u u, v Φ v u, v, z u z v, x u x v. z u z v S T R T ΦR T AT Φ u u, v Φ v u, v dudv Φ u u, v Φ v u, v y u u, v y v u, v z u u, v z v u, v R x u x v y u y v z u u, v z v u, v + x u u, v x v u, v x u u, v x v u, v + y u u, v y v u, v z fx, y R R C Φx, y, fx, y x, y S : z fx, y Φ x x, y Φ y x, y f x x, y + f y x, y + S T AT xy K AT f x x, y + f y x, y +dxdy K. 9
102 B. z a x y S x, y x + y a S 4 x z x a x y, z y y a x y fx x, y + f y x, y + S a S x +y a π π a a a x y S π a a x y dxdy [ a r ] a dθ a π π π a a x y dxdy π π [ a r ] a dθ a π π π a dθ πa. π a a a r rdrdθ a a r rdrdθ 3 dθ 3πa. // C. z a x y x, y x + y ax x z x a x y,z y y y a x y fx x, y + f y x, y a + a x y θ r cos θ, r sin θ π <θ π,r acos θ a x S a π π a π π a a x y dxdy [ a r ] a cos θ π a cos θ dθ a π π sin θ dθ π a. // a a r rdrdθ sin θ dθ 3 z x + y x, y x + y fx x, y + f y x, y + +4x +4y S π S +4x +4y dxdy +4r rdrdθ π π dθ +4r rdr π[ +4r 3 ] 3 8 π // π 9
103 . S Φu, v xu, v, yu, v, zu, v R 3 u, v T R [a, b] [c, d] T ΦR R R i,j [a i,a i ] [c j,c j ] Δ: a a <a < <a m b c c <c < <c n d P i,j a i,c j R : R Δ i,j P i,j, P i,j, P i,j R i,j P i,j, P i,j, P i,j R i,j R Δ i,j R i,j R R i,j. i,j T Q i,j Φa i,c j T Δ i,j Q i,j, Q i,j, Q i,j T i,j Q i,j, Q i,j, Q i,j R i,j a i a i c j c j R i,j R R i,j R 3 Ti,j Δ Δ ATi,j, R i,j R Δ i,j RΔ i,j R i,j R i,j R i,j T i,j ATi,j S Φ T Δ i,j T i,j AT Δ i,j > AT i,j > T Δ i,j T i,j. T Δ i,j T Δ i,j i,j T i,j AT Δ AT Δ ATi,j Δ +AT i,j i,j Ti,j Δ x, y, z ΦΔ i,j u, v RΔ i,j Φ Δ i,ju, v Φa i,c j + Φa i,c j Φa i,c j a i a i u a i + Φa i,c j Φa i,c j c j c j v c j. x xa i,c j + xa i,c j xa i,c j u a i + xa i,c j xa i,c j v c j a i a i c j c j y ya i,c j + ya i,c j ya i,c j u a i + ya i,c j ya i,c j v c j a i a i c j c j z za i,c j + za i,c j za i,c j a i a i u a i + za i,c j za i,c j c j c j v c j. 93
II A A441 : October 02, 2014 Version : Kawahira, Tomoki TA (Kondo, Hirotaka )
 II 214-1 : October 2, 214 Version : 1.1 Kawahira, Tomoki TA (Kondo, Hirotaka ) http://www.math.nagoya-u.ac.jp/~kawahira/courses/14w-biseki.html pdf 1 2 1 9 1 16 1 23 1 3 11 6 11 13 11 2 11 27 12 4 12 11
II 214-1 : October 2, 214 Version : 1.1 Kawahira, Tomoki TA (Kondo, Hirotaka ) http://www.math.nagoya-u.ac.jp/~kawahira/courses/14w-biseki.html pdf 1 2 1 9 1 16 1 23 1 3 11 6 11 13 11 2 11 27 12 4 12 11
II (10 4 ) 1. p (x, y) (a, b) ε(x, y; a, b) 0 f (x, y) f (a, b) A, B (6.5) y = b f (x, b) f (a, b) x a = A + ε(x, b; a, b) x a 2 x a 0 A = f x (
 II (1 4 ) 1. p.13 1 (x, y) (a, b) ε(x, y; a, b) f (x, y) f (a, b) A, B (6.5) y = b f (x, b) f (a, b) x a = A + ε(x, b; a, b) x a x a A = f x (a, b) y x 3 3y 3 (x, y) (, ) f (x, y) = x + y (x, y) = (, )
II (1 4 ) 1. p.13 1 (x, y) (a, b) ε(x, y; a, b) f (x, y) f (a, b) A, B (6.5) y = b f (x, b) f (a, b) x a = A + ε(x, b; a, b) x a x a A = f x (a, b) y x 3 3y 3 (x, y) (, ) f (x, y) = x + y (x, y) = (, )
v er.1/ c /(21)
 12 -- 1 1 2009 1 17 1-1 1-2 1-3 1-4 2 2 2 1-5 1 1-6 1 1-7 1-1 1-2 1-3 1-4 1-5 1-6 1-7 c 2011 1/(21) 12 -- 1 -- 1 1--1 1--1--1 1 2009 1 n n α { n } α α { n } lim n = α, n α n n ε n > N n α < ε N {1, 1,
12 -- 1 1 2009 1 17 1-1 1-2 1-3 1-4 2 2 2 1-5 1 1-6 1 1-7 1-1 1-2 1-3 1-4 1-5 1-6 1-7 c 2011 1/(21) 12 -- 1 -- 1 1--1 1--1--1 1 2009 1 n n α { n } α α { n } lim n = α, n α n n ε n > N n α < ε N {1, 1,
5.. z = f(x, y) y y = b f x x g(x) f(x, b) g x ( ) A = lim h 0 g(a + h) g(a) h g(x) a A = g (a) = f x (a, b)
 5 partial differentiation (total) differentiation 5. z = f(x, y) (a, b) A = lim h 0 f(a + h, b) f(a, b) h............................................................... ( ) f(x, y) (a, b) x A (a, b) x
5 partial differentiation (total) differentiation 5. z = f(x, y) (a, b) A = lim h 0 f(a + h, b) f(a, b) h............................................................... ( ) f(x, y) (a, b) x A (a, b) x
 II 1 3 2 5 3 7 4 8 5 11 6 13 7 16 8 18 2 1 1. x 2 + xy x y (1 lim (x,y (1,1 x 1 x 3 + y 3 (2 lim (x,y (, x 2 + y 2 x 2 (3 lim (x,y (, x 2 + y 2 xy (4 lim (x,y (, x 2 + y 2 x y (5 lim (x,y (, x + y x 3y
II 1 3 2 5 3 7 4 8 5 11 6 13 7 16 8 18 2 1 1. x 2 + xy x y (1 lim (x,y (1,1 x 1 x 3 + y 3 (2 lim (x,y (, x 2 + y 2 x 2 (3 lim (x,y (, x 2 + y 2 xy (4 lim (x,y (, x 2 + y 2 x y (5 lim (x,y (, x + y x 3y
I, II 1, A = A 4 : 6 = max{ A, } A A 10 10%
 1 2006.4.17. A 3-312 tel: 092-726-4774, e-mail: hara@math.kyushu-u.ac.jp, http://www.math.kyushu-u.ac.jp/ hara/lectures/lectures-j.html Office hours: B A I ɛ-δ ɛ-δ 1. 2. A 1. 1. 2. 3. 4. 5. 2. ɛ-δ 1. ɛ-n
1 2006.4.17. A 3-312 tel: 092-726-4774, e-mail: hara@math.kyushu-u.ac.jp, http://www.math.kyushu-u.ac.jp/ hara/lectures/lectures-j.html Office hours: B A I ɛ-δ ɛ-δ 1. 2. A 1. 1. 2. 3. 4. 5. 2. ɛ-δ 1. ɛ-n
1/1 lim f(x, y) (x,y) (a,b) ( ) ( ) lim limf(x, y) lim lim f(x, y) x a y b y b x a ( ) ( ) xy x lim lim lim lim x y x y x + y y x x + y x x lim x x 1
 1/5 ( ) Taylor ( 7.1) (x, y) f(x, y) f(x, y) x + y, xy, e x y,... 1 R {(x, y) x, y R} f(x, y) x y,xy e y log x,... R {(x, y, z) (x, y),z f(x, y)} R 3 z 1 (x + y ) z ax + by + c x 1 z ax + by + c y x +
1/5 ( ) Taylor ( 7.1) (x, y) f(x, y) f(x, y) x + y, xy, e x y,... 1 R {(x, y) x, y R} f(x, y) x y,xy e y log x,... R {(x, y, z) (x, y),z f(x, y)} R 3 z 1 (x + y ) z ax + by + c x 1 z ax + by + c y x +
40 6 y mx x, y 0, 0 x 0. x,y 0,0 y x + y x 0 mx x + mx m + m m 7 sin y x, x x sin y x x. x sin y x,y 0,0 x 0. 8 x r cos θ y r sin θ x, y 0, 0, r 0. x,
 9.. x + y + 0. x,y, x,y, x r cos θ y r sin θ xy x y x,y 0,0 4. x, y 0, 0, r 0. xy x + y r 0 r cos θ sin θ r cos θ sin θ θ 4 y mx x, y 0, 0 x 0. x,y 0,0 x x + y x 0 x x + mx + m m x r cos θ 5 x, y 0, 0,
9.. x + y + 0. x,y, x,y, x r cos θ y r sin θ xy x y x,y 0,0 4. x, y 0, 0, r 0. xy x + y r 0 r cos θ sin θ r cos θ sin θ θ 4 y mx x, y 0, 0 x 0. x,y 0,0 x x + y x 0 x x + mx + m m x r cos θ 5 x, y 0, 0,
x () g(x) = f(t) dt f(x), F (x) 3x () g(x) g (x) f(x), F (x) (3) h(x) = x 3x tf(t) dt.9 = {(x, y) ; x, y, x + y } f(x, y) = xy( x y). h (x) f(x), F (x
 [ ] IC. f(x) = e x () f(x) f (x) () lim f(x) lim f(x) x + x (3) lim f(x) lim f(x) x + x (4) y = f(x) ( ) ( s46). < a < () a () lim a log xdx a log xdx ( ) n (3) lim log k log n n n k=.3 z = log(x + y ),
[ ] IC. f(x) = e x () f(x) f (x) () lim f(x) lim f(x) x + x (3) lim f(x) lim f(x) x + x (4) y = f(x) ( ) ( s46). < a < () a () lim a log xdx a log xdx ( ) n (3) lim log k log n n n k=.3 z = log(x + y ),
1 8, : 8.1 1, 2 z = ax + by + c ax by + z c = a b +1 x y z c = 0, (0, 0, c), n = ( a, b, 1). f = n i=1 a ii x 2 i + i<j 2a ij x i x j = ( x, A x), f =
 1 8, : 8.1 1, z = ax + by + c ax by + z c = a b +1 x y z c = 0, (0, 0, c), n = ( a, b, 1). f = a ii x i + i
1 8, : 8.1 1, z = ax + by + c ax by + z c = a b +1 x y z c = 0, (0, 0, c), n = ( a, b, 1). f = a ii x i + i
(3) (2),,. ( 20) ( s200103) 0.7 x C,, x 2 + y 2 + ax = 0 a.. D,. D, y C, C (x, y) (y 0) C m. (2) D y = y(x) (x ± y 0), (x, y) D, m, m = 1., D. (x 2 y
 [ ] 7 0.1 2 2 + y = t sin t IC ( 9) ( s090101) 0.2 y = d2 y 2, y = x 3 y + y 2 = 0 (2) y + 2y 3y = e 2x 0.3 1 ( y ) = f x C u = y x ( 15) ( s150102) [ ] y/x du x = Cexp f(u) u (2) x y = xey/x ( 16) ( s160101)
[ ] 7 0.1 2 2 + y = t sin t IC ( 9) ( s090101) 0.2 y = d2 y 2, y = x 3 y + y 2 = 0 (2) y + 2y 3y = e 2x 0.3 1 ( y ) = f x C u = y x ( 15) ( s150102) [ ] y/x du x = Cexp f(u) u (2) x y = xey/x ( 16) ( s160101)
 211 kotaro@math.titech.ac.jp 1 R *1 n n R n *2 R n = {(x 1,..., x n ) x 1,..., x n R}. R R 2 R 3 R n R n R n D D R n *3 ) (x 1,..., x n ) f(x 1,..., x n ) f D *4 n 2 n = 1 ( ) 1 f D R n f : D R 1.1. (x,
211 kotaro@math.titech.ac.jp 1 R *1 n n R n *2 R n = {(x 1,..., x n ) x 1,..., x n R}. R R 2 R 3 R n R n R n D D R n *3 ) (x 1,..., x n ) f(x 1,..., x n ) f D *4 n 2 n = 1 ( ) 1 f D R n f : D R 1.1. (x,
y π π O π x 9 s94.5 y dy dx. y = x + 3 y = x logx + 9 s9.6 z z x, z y. z = xy + y 3 z = sinx y 9 s x dx π x cos xdx 9 s93.8 a, fx = e x ax,. a =
 [ ] 9 IC. dx = 3x 4y dt dy dt = x y u xt = expλt u yt λ u u t = u u u + u = xt yt 6 3. u = x, y, z = x + y + z u u 9 s9 grad u ux, y, z = c c : grad u = u x i + u y j + u k i, j, k z x, y, z grad u v =
[ ] 9 IC. dx = 3x 4y dt dy dt = x y u xt = expλt u yt λ u u t = u u u + u = xt yt 6 3. u = x, y, z = x + y + z u u 9 s9 grad u ux, y, z = c c : grad u = u x i + u y j + u k i, j, k z x, y, z grad u v =
微分積分 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. このサンプルページの内容は, 初版 1 刷発行時のものです.
 微分積分 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. ttp://www.morikita.co.jp/books/mid/00571 このサンプルページの内容は, 初版 1 刷発行時のものです. i ii 014 10 iii [note] 1 3 iv 4 5 3 6 4 x 0 sin x x 1 5 6 z = f(x, y) 1 y = f(x)
微分積分 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. ttp://www.morikita.co.jp/books/mid/00571 このサンプルページの内容は, 初版 1 刷発行時のものです. i ii 014 10 iii [note] 1 3 iv 4 5 3 6 4 x 0 sin x x 1 5 6 z = f(x, y) 1 y = f(x)
x = a 1 f (a r, a + r) f(a) r a f f(a) 2 2. (a, b) 2 f (a, b) r f(a, b) r (a, b) f f(a, b)
 2011 I 2 II III 17, 18, 19 7 7 1 2 2 2 1 2 1 1 1.1.............................. 2 1.2 : 1.................... 4 1.2.1 2............................... 5 1.3 : 2.................... 5 1.3.1 2.....................................
2011 I 2 II III 17, 18, 19 7 7 1 2 2 2 1 2 1 1 1.1.............................. 2 1.2 : 1.................... 4 1.2.1 2............................... 5 1.3 : 2.................... 5 1.3.1 2.....................................
5.. z = f(x, y) y y = b f x x g(x) f(x, b) g x ( ) A = lim h g(a + h) g(a) h g(x) a A = g (a) = f x (a, b)............................................
 5 partial differentiation (total) differentiation 5. z = f(x, y) (a, b) A = lim h f(a + h, b) f(a, b) h........................................................... ( ) f(x, y) (a, b) x A (a, b) x (a, b)
5 partial differentiation (total) differentiation 5. z = f(x, y) (a, b) A = lim h f(a + h, b) f(a, b) h........................................................... ( ) f(x, y) (a, b) x A (a, b) x (a, b)
K E N Z OU
 K E N Z OU 11 1 1 1.1..................................... 1.1.1............................ 1.1..................................................................................... 4 1.........................................
K E N Z OU 11 1 1 1.1..................................... 1.1.1............................ 1.1..................................................................................... 4 1.........................................
DVIOUT
 A. A. A-- [ ] f(x) x = f 00 (x) f 0 () =0 f 00 () > 0= f(x) x = f 00 () < 0= f(x) x = A--2 [ ] f(x) D f 00 (x) > 0= y = f(x) f 00 (x) < 0= y = f(x) P (, f()) f 00 () =0 A--3 [ ] y = f(x) [, b] x = f (y)
A. A. A-- [ ] f(x) x = f 00 (x) f 0 () =0 f 00 () > 0= f(x) x = f 00 () < 0= f(x) x = A--2 [ ] f(x) D f 00 (x) > 0= y = f(x) f 00 (x) < 0= y = f(x) P (, f()) f 00 () =0 A--3 [ ] y = f(x) [, b] x = f (y)
 ( 12 ( ( ( ( Levi-Civita grad div rot ( ( = 4 : 6 3 1 1.1 f(x n f (n (x, d n f(x (1.1 dxn f (2 (x f (x 1.1 f(x = e x f (n (x = e x d dx (fg = f g + fg (1.2 d dx d 2 dx (fg = f g + 2f g + fg 2... d n n
( 12 ( ( ( ( Levi-Civita grad div rot ( ( = 4 : 6 3 1 1.1 f(x n f (n (x, d n f(x (1.1 dxn f (2 (x f (x 1.1 f(x = e x f (n (x = e x d dx (fg = f g + fg (1.2 d dx d 2 dx (fg = f g + 2f g + fg 2... d n n
,. Black-Scholes u t t, x c u 0 t, x x u t t, x c u t, x x u t t, x + σ x u t, x + rx ut, x rux, t 0 x x,,.,. Step 3, 7,,, Step 6., Step 4,. Step 5,,.
 9 α ν β Ξ ξ Γ γ o δ Π π ε ρ ζ Σ σ η τ Θ θ Υ υ ι Φ φ κ χ Λ λ Ψ ψ µ Ω ω Def, Prop, Th, Lem, Note, Remark, Ex,, Proof, R, N, Q, C [a, b {x R : a x b} : a, b {x R : a < x < b} : [a, b {x R : a x < b} : a,
9 α ν β Ξ ξ Γ γ o δ Π π ε ρ ζ Σ σ η τ Θ θ Υ υ ι Φ φ κ χ Λ λ Ψ ψ µ Ω ω Def, Prop, Th, Lem, Note, Remark, Ex,, Proof, R, N, Q, C [a, b {x R : a x b} : a, b {x R : a < x < b} : [a, b {x R : a x < b} : a,
i
 i 3 4 4 7 5 6 3 ( ).. () 3 () (3) (4) /. 3. 4/3 7. /e 8. a > a, a = /, > a >. () a >, a =, > a > () a > b, a = b, a < b. c c n a n + b n + c n 3c n..... () /3 () + (3) / (4) /4 (5) m > n, a b >, m > n,
i 3 4 4 7 5 6 3 ( ).. () 3 () (3) (4) /. 3. 4/3 7. /e 8. a > a, a = /, > a >. () a >, a =, > a > () a > b, a = b, a < b. c c n a n + b n + c n 3c n..... () /3 () + (3) / (4) /4 (5) m > n, a b >, m > n,
= M + M + M + M M + =.,. f = < ρ, > ρ ρ. ρ f. = ρ = = ± = log 4 = = = ± f = k k ρ. k
 7 b f n f} d = b f n f d,. 5,. [ ] ɛ >, n ɛ + + n < ɛ. m. n m log + < n m. n lim sin kπ sin kπ } k π sin = n n n. k= 4 f, y = r + s, y = rs f rs = f + r + sf y + rsf yy + f y. f = f =, f = sin. 5 f f =.
7 b f n f} d = b f n f d,. 5,. [ ] ɛ >, n ɛ + + n < ɛ. m. n m log + < n m. n lim sin kπ sin kπ } k π sin = n n n. k= 4 f, y = r + s, y = rs f rs = f + r + sf y + rsf yy + f y. f = f =, f = sin. 5 f f =.
No δs δs = r + δr r = δr (3) δs δs = r r = δr + u(r + δr, t) u(r, t) (4) δr = (δx, δy, δz) u i (r + δr, t) u i (r, t) = u i x j δx j (5) δs 2
 No.2 1 2 2 δs δs = r + δr r = δr (3) δs δs = r r = δr + u(r + δr, t) u(r, t) (4) δr = (δx, δy, δz) u i (r + δr, t) u i (r, t) = u i δx j (5) δs 2 = δx i δx i + 2 u i δx i δx j = δs 2 + 2s ij δx i δx j
No.2 1 2 2 δs δs = r + δr r = δr (3) δs δs = r r = δr + u(r + δr, t) u(r, t) (4) δr = (δx, δy, δz) u i (r + δr, t) u i (r, t) = u i δx j (5) δs 2 = δx i δx i + 2 u i δx i δx j = δs 2 + 2s ij δx i δx j
notekiso1_09.dvi
 39 3 3.1 2 Ax 1,y 1 Bx 2,y 2 x y fx, y z fx, y x 1,y 1, 0 x 1,y 1,fx 1,y 1 x 2,y 2, 0 x 2,y 2,fx 2,y 2 A s I fx, yds lim fx i,y i Δs. 3.1.1 Δs 0 x i,y i N Δs 1 I lim Δx 2 +Δy 2 0 x 1 fx i,y i Δx i 2 +Δy
39 3 3.1 2 Ax 1,y 1 Bx 2,y 2 x y fx, y z fx, y x 1,y 1, 0 x 1,y 1,fx 1,y 1 x 2,y 2, 0 x 2,y 2,fx 2,y 2 A s I fx, yds lim fx i,y i Δs. 3.1.1 Δs 0 x i,y i N Δs 1 I lim Δx 2 +Δy 2 0 x 1 fx i,y i Δx i 2 +Δy
( ) ( )
 20 21 2 8 1 2 2 3 21 3 22 3 23 4 24 5 25 5 26 6 27 8 28 ( ) 9 3 10 31 10 32 ( ) 12 4 13 41 0 13 42 14 43 0 15 44 17 5 18 6 18 1 1 2 2 1 2 1 0 2 0 3 0 4 0 2 2 21 t (x(t) y(t)) 2 x(t) y(t) γ(t) (x(t) y(t))
20 21 2 8 1 2 2 3 21 3 22 3 23 4 24 5 25 5 26 6 27 8 28 ( ) 9 3 10 31 10 32 ( ) 12 4 13 41 0 13 42 14 43 0 15 44 17 5 18 6 18 1 1 2 2 1 2 1 0 2 0 3 0 4 0 2 2 21 t (x(t) y(t)) 2 x(t) y(t) γ(t) (x(t) y(t))
B 38 1 (x, y), (x, y, z) (x 1, x 2 ) (x 1, x 2, x 3 ) 2 : x 2 + y 2 = 1. (parameter) x = cos t, y = sin t. y = f(x) r(t) = (x(t), y(t), z(t)), a t b.
 2009 7 9 1 2 2 2 3 6 4 9 5 14 6 18 7 23 8 25 9 26 10 29 11 32 12 35 A 37 1 B 38 1 (x, y), (x, y, z) (x 1, x 2 ) (x 1, x 2, x 3 ) 2 : x 2 + y 2 = 1. (parameter) x = cos t, y = sin t. y = f(x) r(t) = (x(t),
2009 7 9 1 2 2 2 3 6 4 9 5 14 6 18 7 23 8 25 9 26 10 29 11 32 12 35 A 37 1 B 38 1 (x, y), (x, y, z) (x 1, x 2 ) (x 1, x 2, x 3 ) 2 : x 2 + y 2 = 1. (parameter) x = cos t, y = sin t. y = f(x) r(t) = (x(t),
 i 6 3 ii 3 7 8 9 3 6 iii 5 8 5 3 7 8 v...................................................... 5.3....................... 7 3........................ 3.................3.......................... 8 3 35
i 6 3 ii 3 7 8 9 3 6 iii 5 8 5 3 7 8 v...................................................... 5.3....................... 7 3........................ 3.................3.......................... 8 3 35
S I. dy fx x fx y fx + C 3 C dy fx 4 x, y dy v C xt y C v e kt k > xt yt gt [ v dt dt v e kt xt v e kt + C k x v + C C k xt v k 3 r r + dr e kt S dt d
 S I.. http://ayapin.film.s.dendai.ac.jp/~matuda /TeX/lecture.html PDF PS.................................... 3.3.................... 9.4................5.............. 3 5. Laplace................. 5....
S I.. http://ayapin.film.s.dendai.ac.jp/~matuda /TeX/lecture.html PDF PS.................................... 3.3.................... 9.4................5.............. 3 5. Laplace................. 5....
Untitled
 II 14 14-7-8 8/4 II (http://www.damp.tottori-u.ac.jp/~ooshida/edu/fluid/) [ (3.4)] Navier Stokes [ 6/ ] Navier Stokes 3 [ ] Reynolds [ (4.6), (45.8)] [ p.186] Navier Stokes I 1 balance law t (ρv i )+ j
II 14 14-7-8 8/4 II (http://www.damp.tottori-u.ac.jp/~ooshida/edu/fluid/) [ (3.4)] Navier Stokes [ 6/ ] Navier Stokes 3 [ ] Reynolds [ (4.6), (45.8)] [ p.186] Navier Stokes I 1 balance law t (ρv i )+ j
III No (i) (ii) (iii) (iv) (v) (vi) x 2 3xy + 2 lim. (x,y) (1,0) x 2 + y 2 lim (x,y) (0,0) lim (x,y) (0,0) lim (x,y) (0,0) 5x 2 y x 2 + y 2. xy x2 + y
 III No (i) (ii) (iii) (iv) (v) (vi) x 2 3xy + 2. (x,y) (1,0) x 2 + y 2 5x 2 y x 2 + y 2. xy x2 + y 2. 2x + y 3 x 2 + y 2 + 5. sin(x 2 + y 2 ). x 2 + y 2 sin(x 2 y + xy 2 ). xy (i) (ii) (iii) 2xy x 2 +
III No (i) (ii) (iii) (iv) (v) (vi) x 2 3xy + 2. (x,y) (1,0) x 2 + y 2 5x 2 y x 2 + y 2. xy x2 + y 2. 2x + y 3 x 2 + y 2 + 5. sin(x 2 + y 2 ). x 2 + y 2 sin(x 2 y + xy 2 ). xy (i) (ii) (iii) 2xy x 2 +
Part () () Γ Part ,
 Contents a 6 6 6 6 6 6 6 7 7. 8.. 8.. 8.3. 8 Part. 9. 9.. 9.. 3. 3.. 3.. 3 4. 5 4.. 5 4.. 9 4.3. 3 Part. 6 5. () 6 5.. () 7 5.. 9 5.3. Γ 3 6. 3 6.. 3 6.. 3 6.3. 33 Part 3. 34 7. 34 7.. 34 7.. 34 8. 35
Contents a 6 6 6 6 6 6 6 7 7. 8.. 8.. 8.3. 8 Part. 9. 9.. 9.. 3. 3.. 3.. 3 4. 5 4.. 5 4.. 9 4.3. 3 Part. 6 5. () 6 5.. () 7 5.. 9 5.3. Γ 3 6. 3 6.. 3 6.. 3 6.3. 33 Part 3. 34 7. 34 7.. 34 7.. 34 8. 35
S I. dy fx x fx y fx + C 3 C vt dy fx 4 x, y dy yt gt + Ct + C dt v e kt xt v e kt + C k x v k + C C xt v k 3 r r + dr e kt S Sr πr dt d v } dt k e kt
 S I. x yx y y, y,. F x, y, y, y,, y n http://ayapin.film.s.dendai.ac.jp/~matuda n /TeX/lecture.html PDF PS yx.................................... 3.3.................... 9.4................5..............
S I. x yx y y, y,. F x, y, y, y,, y n http://ayapin.film.s.dendai.ac.jp/~matuda n /TeX/lecture.html PDF PS yx.................................... 3.3.................... 9.4................5..............
7. y fx, z gy z gfx dz dx dz dy dy dx. g f a g bf a b fa 7., chain ule Ω, D R n, R m a Ω, f : Ω R m, g : D R l, fω D, b fa, f a g b g f a g f a g bf a
 9 203 6 7 WWW http://www.math.meiji.ac.jp/~mk/lectue/tahensuu-203/ 2 8 8 7. 7 7. y fx, z gy z gfx dz dx dz dy dy dx. g f a g bf a b fa 7., chain ule Ω, D R n, R m a Ω, f : Ω R m, g : D R l, fω D, b fa,
9 203 6 7 WWW http://www.math.meiji.ac.jp/~mk/lectue/tahensuu-203/ 2 8 8 7. 7 7. y fx, z gy z gfx dz dx dz dy dy dx. g f a g bf a b fa 7., chain ule Ω, D R n, R m a Ω, f : Ω R m, g : D R l, fω D, b fa,
i
 009 I 1 8 5 i 0 1 0.1..................................... 1 0.................................................. 1 0.3................................. 0.4........................................... 3
009 I 1 8 5 i 0 1 0.1..................................... 1 0.................................................. 1 0.3................................. 0.4........................................... 3
A
 A 2563 15 4 21 1 3 1.1................................................ 3 1.2............................................. 3 2 3 2.1......................................... 3 2.2............................................
A 2563 15 4 21 1 3 1.1................................................ 3 1.2............................................. 3 2 3 2.1......................................... 3 2.2............................................
D xy D (x, y) z = f(x, y) f D (2 ) (x, y, z) f R z = 1 x 2 y 2 {(x, y); x 2 +y 2 1} x 2 +y 2 +z 2 = 1 1 z (x, y) R 2 z = x 2 y
 5 5. 2 D xy D (x, y z = f(x, y f D (2 (x, y, z f R 2 5.. z = x 2 y 2 {(x, y; x 2 +y 2 } x 2 +y 2 +z 2 = z 5.2. (x, y R 2 z = x 2 y + 3 (2,,, (, 3,, 3 (,, 5.3 (. (3 ( (a, b, c A : (x, y, z P : (x, y, x
5 5. 2 D xy D (x, y z = f(x, y f D (2 (x, y, z f R 2 5.. z = x 2 y 2 {(x, y; x 2 +y 2 } x 2 +y 2 +z 2 = z 5.2. (x, y R 2 z = x 2 y + 3 (2,,, (, 3,, 3 (,, 5.3 (. (3 ( (a, b, c A : (x, y, z P : (x, y, x
() x + y + y + x dy dx = 0 () dy + xy = x dx y + x y ( 5) ( s55906) 0.7. (). 5 (). ( 6) ( s6590) 0.8 m n. 0.9 n n A. ( 6) ( s6590) f A (λ) = det(a λi)
 0. A A = 4 IC () det A () A () x + y + z = x y z X Y Z = A x y z ( 5) ( s5590) 0. a + b + c b c () a a + b + c c a b a + b + c 0 a b c () a 0 c b b c 0 a c b a 0 0. A A = 7 5 4 5 0 ( 5) ( s5590) () A ()
0. A A = 4 IC () det A () A () x + y + z = x y z X Y Z = A x y z ( 5) ( s5590) 0. a + b + c b c () a a + b + c c a b a + b + c 0 a b c () a 0 c b b c 0 a c b a 0 0. A A = 7 5 4 5 0 ( 5) ( s5590) () A ()
W u = u(x, t) u tt = a 2 u xx, a > 0 (1) D := {(x, t) : 0 x l, t 0} u (0, t) = 0, u (l, t) = 0, t 0 (2)
 3 215 4 27 1 1 u u(x, t) u tt a 2 u xx, a > (1) D : {(x, t) : x, t } u (, t), u (, t), t (2) u(x, ) f(x), u(x, ) t 2, x (3) u(x, t) X(x)T (t) u (1) 1 T (t) a 2 T (t) X (x) X(x) α (2) T (t) αa 2 T (t) (4)
3 215 4 27 1 1 u u(x, t) u tt a 2 u xx, a > (1) D : {(x, t) : x, t } u (, t), u (, t), t (2) u(x, ) f(x), u(x, ) t 2, x (3) u(x, t) X(x)T (t) u (1) 1 T (t) a 2 T (t) X (x) X(x) α (2) T (t) αa 2 T (t) (4)
M3 x y f(x, y) (= x) (= y) x + y f(x, y) = x + y + *. f(x, y) π y f(x, y) x f(x + x, y) f(x, y) lim x x () f(x,y) x 3 -
 M3............................................................................................ 3.3................................................... 3 6........................................... 6..........................................
M3............................................................................................ 3.3................................................... 3 6........................................... 6..........................................
201711grade1ouyou.pdf
 2017 11 26 1 2 52 3 12 13 22 23 32 33 42 3 5 3 4 90 5 6 A 1 2 Web Web 3 4 1 2... 5 6 7 7 44 8 9 1 2 3 1 p p >2 2 A 1 2 0.6 0.4 0.52... (a) 0.6 0.4...... B 1 2 0.8-0.2 0.52..... (b) 0.6 0.52.... 1 A B 2
2017 11 26 1 2 52 3 12 13 22 23 32 33 42 3 5 3 4 90 5 6 A 1 2 Web Web 3 4 1 2... 5 6 7 7 44 8 9 1 2 3 1 p p >2 2 A 1 2 0.6 0.4 0.52... (a) 0.6 0.4...... B 1 2 0.8-0.2 0.52..... (b) 0.6 0.52.... 1 A B 2
Acrobat Distiller, Job 128
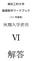 (2 ) 2 < > ( ) f x (x, y) 2x 3+y f y (x, y) x 2y +2 f(3, 2) f x (3, 2) 5 f y (3, 2) L y 2 z 5x 5 ` x 3 z y 2 2 2 < > (2 ) f(, 2) 7 f x (x, y) 2x y f x (, 2),f y (x, y) x +4y,f y (, 2) 7 z (x ) + 7(y 2)
(2 ) 2 < > ( ) f x (x, y) 2x 3+y f y (x, y) x 2y +2 f(3, 2) f x (3, 2) 5 f y (3, 2) L y 2 z 5x 5 ` x 3 z y 2 2 2 < > (2 ) f(, 2) 7 f x (x, y) 2x y f x (, 2),f y (x, y) x +4y,f y (, 2) 7 z (x ) + 7(y 2)
.1 z = e x +xy y z y 1 1 x 0 1 z x y α β γ z = αx + βy + γ (.1) ax + by + cz = d (.1') a, b, c, d x-y-z (a, b, c). x-y-z 3 (0,
 .1.1 Y K L Y = K 1 3 L 3 L K K (K + ) 1 1 3 L 3 K 3 L 3 K 0 (K + K) 1 3 L 3 K 1 3 L 3 lim K 0 K = L (K + K) 1 3 K 1 3 3 lim K 0 K = 1 3 K 3 L 3 z = f(x, y) x y z x-y-z.1 z = e x +xy y 3 x-y ( ) z 0 f(x,
.1.1 Y K L Y = K 1 3 L 3 L K K (K + ) 1 1 3 L 3 K 3 L 3 K 0 (K + K) 1 3 L 3 K 1 3 L 3 lim K 0 K = L (K + K) 1 3 K 1 3 3 lim K 0 K = 1 3 K 3 L 3 z = f(x, y) x y z x-y-z.1 z = e x +xy y 3 x-y ( ) z 0 f(x,
.3. (x, x = (, u = = 4 (, x x = 4 x, x 0 x = 0 x = 4 x.4. ( z + z = 8 z, z 0 (z, z = (0, 8, (,, (8, 0 3 (0, 8, (,, (8, 0 z = z 4 z (g f(x = g(
 06 5.. ( y = x x y 5 y 5 = (x y = x + ( y = x + y = x y.. ( Y = C + I = 50 + 0.5Y + 50 r r = 00 0.5Y ( L = M Y r = 00 r = 0.5Y 50 (3 00 0.5Y = 0.5Y 50 Y = 50, r = 5 .3. (x, x = (, u = = 4 (, x x = 4 x,
06 5.. ( y = x x y 5 y 5 = (x y = x + ( y = x + y = x y.. ( Y = C + I = 50 + 0.5Y + 50 r r = 00 0.5Y ( L = M Y r = 00 r = 0.5Y 50 (3 00 0.5Y = 0.5Y 50 Y = 50, r = 5 .3. (x, x = (, u = = 4 (, x x = 4 x,
untitled
 20010916 22;1017;23;20020108;15;20; 1 N = {1, 2, } Z + = {0, 1, 2, } Z = {0, ±1, ±2, } Q = { p p Z, q N} R = { lim a q n n a n Q, n N; sup a n < } R + = {x R x 0} n = {a + b 1 a, b R} u, v 1 R 2 2 R 3
20010916 22;1017;23;20020108;15;20; 1 N = {1, 2, } Z + = {0, 1, 2, } Z = {0, ±1, ±2, } Q = { p p Z, q N} R = { lim a q n n a n Q, n N; sup a n < } R + = {x R x 0} n = {a + b 1 a, b R} u, v 1 R 2 2 R 3
 http://www.ns.kogakuin.ac.jp/~ft13389/lecture/physics1a2b/ pdf I 1 1 1.1 ( ) 1. 30 m µm 2. 20 cm km 3. 10 m 2 cm 2 4. 5 cm 3 km 3 5. 1 6. 1 7. 1 1.2 ( ) 1. 1 m + 10 cm 2. 1 hr + 6400 sec 3. 3.0 10 5 kg
http://www.ns.kogakuin.ac.jp/~ft13389/lecture/physics1a2b/ pdf I 1 1 1.1 ( ) 1. 30 m µm 2. 20 cm km 3. 10 m 2 cm 2 4. 5 cm 3 km 3 5. 1 6. 1 7. 1 1.2 ( ) 1. 1 m + 10 cm 2. 1 hr + 6400 sec 3. 3.0 10 5 kg
II 2 II
 II 2 II 2005 yugami@cc.utsunomiya-u.ac.jp 2005 4 1 1 2 5 2.1.................................... 5 2.2................................. 6 2.3............................. 6 2.4.................................
II 2 II 2005 yugami@cc.utsunomiya-u.ac.jp 2005 4 1 1 2 5 2.1.................................... 5 2.2................................. 6 2.3............................. 6 2.4.................................
 n ξ n,i, i = 1,, n S n ξ n,i n 0 R 1,.. σ 1 σ i .10.14.15 0 1 0 1 1 3.14 3.18 3.19 3.14 3.14,. ii 1 1 1.1..................................... 1 1............................... 3 1.3.........................
n ξ n,i, i = 1,, n S n ξ n,i n 0 R 1,.. σ 1 σ i .10.14.15 0 1 0 1 1 3.14 3.18 3.19 3.14 3.14,. ii 1 1 1.1..................................... 1 1............................... 3 1.3.........................
Fubini
 3............................... 3................................ 5.3 Fubini........................... 7.4.............................5..........................6.............................. 3.7..............................
3............................... 3................................ 5.3 Fubini........................... 7.4.............................5..........................6.............................. 3.7..............................
1 No.1 5 C 1 I III F 1 F 2 F 1 F 2 2 Φ 2 (t) = Φ 1 (t) Φ 1 (t t). = Φ 1(t) t = ( 1.5e 0.5t 2.4e 4t 2e 10t ) τ < 0 t > τ Φ 2 (t) < 0 lim t Φ 2 (t) = 0
 1 No.1 5 C 1 I III F 1 F 2 F 1 F 2 2 Φ 2 (t) = Φ 1 (t) Φ 1 (t t). = Φ 1(t) t = ( 1.5e 0.5t 2.4e 4t 2e 10t ) τ < 0 t > τ Φ 2 (t) < 0 lim t Φ 2 (t) = 0 0 < t < τ I II 0 No.2 2 C x y x y > 0 x 0 x > b a dx
1 No.1 5 C 1 I III F 1 F 2 F 1 F 2 2 Φ 2 (t) = Φ 1 (t) Φ 1 (t t). = Φ 1(t) t = ( 1.5e 0.5t 2.4e 4t 2e 10t ) τ < 0 t > τ Φ 2 (t) < 0 lim t Φ 2 (t) = 0 0 < t < τ I II 0 No.2 2 C x y x y > 0 x 0 x > b a dx
 20 4 20 i 1 1 1.1............................ 1 1.2............................ 4 2 11 2.1................... 11 2.2......................... 11 2.3....................... 19 3 25 3.1.............................
20 4 20 i 1 1 1.1............................ 1 1.2............................ 4 2 11 2.1................... 11 2.2......................... 11 2.3....................... 19 3 25 3.1.............................
..3. Ω, Ω F, P Ω, F, P ). ) F a) A, A,..., A i,... F A i F. b) A F A c F c) Ω F. ) A F A P A),. a) 0 P A) b) P Ω) c) [ ] A, A,..., A i,... F i j A i A
![..3. Ω, Ω F, P Ω, F, P ). ) F a) A, A,..., A i,... F A i F. b) A F A c F c) Ω F. ) A F A P A),. a) 0 P A) b) P Ω) c) [ ] A, A,..., A i,... F i j A i A ..3. Ω, Ω F, P Ω, F, P ). ) F a) A, A,..., A i,... F A i F. b) A F A c F c) Ω F. ) A F A P A),. a) 0 P A) b) P Ω) c) [ ] A, A,..., A i,... F i j A i A](/thumbs/93/112175219.jpg) .. Laplace ). A... i),. ω i i ). {ω,..., ω } Ω,. ii) Ω. Ω. A ) r, A P A) P A) r... ).. Ω {,, 3, 4, 5, 6}. i i 6). A {, 4, 6} P A) P A) 3 6. ).. i, j i, j) ) Ω {i, j) i 6, j 6}., 36. A. A {i, j) i j }.
.. Laplace ). A... i),. ω i i ). {ω,..., ω } Ω,. ii) Ω. Ω. A ) r, A P A) P A) r... ).. Ω {,, 3, 4, 5, 6}. i i 6). A {, 4, 6} P A) P A) 3 6. ).. i, j i, j) ) Ω {i, j) i 6, j 6}., 36. A. A {i, j) i j }.
II No.01 [n/2] [1]H n (x) H n (x) = ( 1) r n! r!(n 2r)! (2x)n 2r. r=0 [2]H n (x) n,, H n ( x) = ( 1) n H n (x). [3] H n (x) = ( 1) n dn x2 e dx n e x2
![II No.01 [n/2] [1]H n (x) H n (x) = ( 1) r n! r!(n 2r)! (2x)n 2r. r=0 [2]H n (x) n,, H n ( x) = ( 1) n H n (x). [3] H n (x) = ( 1) n dn x2 e dx n e x2 II No.01 [n/2] [1]H n (x) H n (x) = ( 1) r n! r!(n 2r)! (2x)n 2r. r=0 [2]H n (x) n,, H n ( x) = ( 1) n H n (x). [3] H n (x) = ( 1) n dn x2 e dx n e x2](/thumbs/101/149159646.jpg) II No.1 [n/] [1]H n x) H n x) = 1) r n! r!n r)! x)n r r= []H n x) n,, H n x) = 1) n H n x) [3] H n x) = 1) n dn x e dx n e x [4] H n+1 x) = xh n x) nh n 1 x) ) d dx x H n x) = H n+1 x) d dx H nx) = nh
II No.1 [n/] [1]H n x) H n x) = 1) r n! r!n r)! x)n r r= []H n x) n,, H n x) = 1) n H n x) [3] H n x) = 1) n dn x e dx n e x [4] H n+1 x) = xh n x) nh n 1 x) ) d dx x H n x) = H n+1 x) d dx H nx) = nh
(1) (2) (3) (4) HB B ( ) (5) (6) (7) 40 (8) (9) (10)
 2017 12 9 4 1 30 4 10 3 1 30 3 30 2 1 30 2 50 1 1 30 2 10 (1) (2) (3) (4) HB B ( ) (5) (6) (7) 40 (8) (9) (10) (1) i 23 c 23 0 1 2 3 4 5 6 7 8 9 a b d e f g h i (2) 23 23 (3) 23 ( 23 ) 23 x 1 x 2 23 x
2017 12 9 4 1 30 4 10 3 1 30 3 30 2 1 30 2 50 1 1 30 2 10 (1) (2) (3) (4) HB B ( ) (5) (6) (7) 40 (8) (9) (10) (1) i 23 c 23 0 1 2 3 4 5 6 7 8 9 a b d e f g h i (2) 23 23 (3) 23 ( 23 ) 23 x 1 x 2 23 x
2000年度『数学展望 I』講義録
 2000 I I IV I II 2000 I I IV I-IV. i ii 3.10 (http://www.math.nagoya-u.ac.jp/ kanai/) 2000 A....1 B....4 C....10 D....13 E....17 Brouwer A....21 B....26 C....33 D....39 E. Sperner...45 F....48 A....53
2000 I I IV I II 2000 I I IV I-IV. i ii 3.10 (http://www.math.nagoya-u.ac.jp/ kanai/) 2000 A....1 B....4 C....10 D....13 E....17 Brouwer A....21 B....26 C....33 D....39 E. Sperner...45 F....48 A....53
II 1 II 2012 II Gauss-Bonnet II
 II 1 II 212 II Gauss-Bonnet II 1 1 1.1......................................... 1 1.2............................................ 2 1.3.................................. 3 1.4.............................................
II 1 II 212 II Gauss-Bonnet II 1 1 1.1......................................... 1 1.2............................................ 2 1.3.................................. 3 1.4.............................................
2 1 κ c(t) = (x(t), y(t)) ( ) det(c (t), c x (t)) = det (t) x (t) y (t) y = x (t)y (t) x (t)y (t), (t) c (t) = (x (t)) 2 + (y (t)) 2. c (t) =
 1 1 1.1 I R 1.1.1 c : I R 2 (i) c C (ii) t I c (t) (0, 0) c (t) c(i) c c(t) 1.1.2 (1) (2) (3) (1) r > 0 c : R R 2 : t (r cos t, r sin t) (2) C f : I R c : I R 2 : t (t, f(t)) (3) y = x c : R R 2 : t (t,
1 1 1.1 I R 1.1.1 c : I R 2 (i) c C (ii) t I c (t) (0, 0) c (t) c(i) c c(t) 1.1.2 (1) (2) (3) (1) r > 0 c : R R 2 : t (r cos t, r sin t) (2) C f : I R c : I R 2 : t (t, f(t)) (3) y = x c : R R 2 : t (t,
I A A441 : April 21, 2014 Version : Kawahira, Tomoki TA (Kondo, Hirotaka ) Google
 I4 - : April, 4 Version :. Kwhir, Tomoki TA (Kondo, Hirotk) Google http://www.mth.ngoy-u.c.jp/~kwhir/courses/4s-biseki.html pdf 4 4 4 4 8 e 5 5 9 etc. 5 6 6 6 9 n etc. 6 6 6 3 6 3 7 7 etc 7 4 7 7 8 5 59
I4 - : April, 4 Version :. Kwhir, Tomoki TA (Kondo, Hirotk) Google http://www.mth.ngoy-u.c.jp/~kwhir/courses/4s-biseki.html pdf 4 4 4 4 8 e 5 5 9 etc. 5 6 6 6 9 n etc. 6 6 6 3 6 3 7 7 etc 7 4 7 7 8 5 59
 21 2 26 i 1 1 1.1............................ 1 1.2............................ 3 2 9 2.1................... 9 2.2.......... 9 2.3................... 11 2.4....................... 12 3 15 3.1..........
21 2 26 i 1 1 1.1............................ 1 1.2............................ 3 2 9 2.1................... 9 2.2.......... 9 2.3................... 11 2.4....................... 12 3 15 3.1..........
http://www2.math.kyushu-u.ac.jp/~hara/lectures/lectures-j.html 2 N(ε 1 ) N(ε 2 ) ε 1 ε 2 α ε ε 2 1 n N(ɛ) N ɛ ɛ- (1.1.3) n > N(ɛ) a n α < ɛ n N(ɛ) a n
 http://www2.math.kyushu-u.ac.jp/~hara/lectures/lectures-j.html 1 1 1.1 ɛ-n 1 ɛ-n lim n a n = α n a n α 2 lim a n = 1 n a k n n k=1 1.1.7 ɛ-n 1.1.1 a n α a n n α lim n a n = α ɛ N(ɛ) n > N(ɛ) a n α < ɛ
http://www2.math.kyushu-u.ac.jp/~hara/lectures/lectures-j.html 1 1 1.1 ɛ-n 1 ɛ-n lim n a n = α n a n α 2 lim a n = 1 n a k n n k=1 1.1.7 ɛ-n 1.1.1 a n α a n n α lim n a n = α ɛ N(ɛ) n > N(ɛ) a n α < ɛ
f(x) = f(x ) + α(x)(x x ) α(x) x = x. x = f (y), x = f (y ) y = f f (y) = f f (y ) + α(f (y))(f (y) f (y )) f (y) = f (y ) + α(f (y)) (y y ) ( (2) ) f
 22 A 3,4 No.3 () (2) (3) (4), (5) (6) (7) (8) () n x = (x,, x n ), = (,, n ), x = ( (x i i ) 2 ) /2 f(x) R n f(x) = f() + i α i (x ) i + o( x ) α,, α n g(x) = o( x )) lim x g(x) x = y = f() + i α i(x )
22 A 3,4 No.3 () (2) (3) (4), (5) (6) (7) (8) () n x = (x,, x n ), = (,, n ), x = ( (x i i ) 2 ) /2 f(x) R n f(x) = f() + i α i (x ) i + o( x ) α,, α n g(x) = o( x )) lim x g(x) x = y = f() + i α i(x )
meiji_resume_1.PDF
 β β β (q 1,q,..., q n ; p 1, p,..., p n ) H(q 1,q,..., q n ; p 1, p,..., p n ) Hψ = εψ ε k = k +1/ ε k = k(k 1) (x, y, z; p x, p y, p z ) (r; p r ), (θ; p θ ), (ϕ; p ϕ ) ε k = 1/ k p i dq i E total = E
β β β (q 1,q,..., q n ; p 1, p,..., p n ) H(q 1,q,..., q n ; p 1, p,..., p n ) Hψ = εψ ε k = k +1/ ε k = k(k 1) (x, y, z; p x, p y, p z ) (r; p r ), (θ; p θ ), (ϕ; p ϕ ) ε k = 1/ k p i dq i E total = E
III 1 (X, d) d U d X (X, d). 1. (X, d).. (i) d(x, y) d(z, y) d(x, z) (ii) d(x, y) d(z, w) d(x, z) + d(y, w) 2. (X, d). F X.. (1), X F, (2) F 1, F 2 F
 III 1 (X, d) d U d X (X, d). 1. (X, d).. (i) d(x, y) d(z, y) d(x, z) (ii) d(x, y) d(z, w) d(x, z) + d(y, w) 2. (X, d). F X.. (1), X F, (2) F 1, F 2 F F 1 F 2 F, (3) F λ F λ F λ F. 3., A λ λ A λ. B λ λ
III 1 (X, d) d U d X (X, d). 1. (X, d).. (i) d(x, y) d(z, y) d(x, z) (ii) d(x, y) d(z, w) d(x, z) + d(y, w) 2. (X, d). F X.. (1), X F, (2) F 1, F 2 F F 1 F 2 F, (3) F λ F λ F λ F. 3., A λ λ A λ. B λ λ
 23 7 28 i i 1 1 1.1................................... 2 1.2............................... 3 1.2.1.................................... 3 1.2.2............................... 4 1.2.3 SI..............................
23 7 28 i i 1 1 1.1................................... 2 1.2............................... 3 1.2.1.................................... 3 1.2.2............................... 4 1.2.3 SI..............................
x (x, ) x y (, y) iy x y z = x + iy (x, y) (r, θ) r = x + y, θ = tan ( y ), π < θ π x r = z, θ = arg z z = x + iy = r cos θ + ir sin θ = r(cos θ + i s
 ... x, y z = x + iy x z y z x = Rez, y = Imz z = x + iy x iy z z () z + z = (z + z )() z z = (z z )(3) z z = ( z z )(4)z z = z z = x + y z = x + iy ()Rez = (z + z), Imz = (z z) i () z z z + z z + z.. z
... x, y z = x + iy x z y z x = Rez, y = Imz z = x + iy x iy z z () z + z = (z + z )() z z = (z z )(3) z z = ( z z )(4)z z = z z = x + y z = x + iy ()Rez = (z + z), Imz = (z z) i () z z z + z z + z.. z
i 18 2H 2 + O 2 2H 2 + ( ) 3K
 i 18 2H 2 + O 2 2H 2 + ( ) 3K ii 1 1 1.1.................................. 1 1.2........................................ 3 1.3......................................... 3 1.4....................................
i 18 2H 2 + O 2 2H 2 + ( ) 3K ii 1 1 1.1.................................. 1 1.2........................................ 3 1.3......................................... 3 1.4....................................
r 1 m A r/m i) t ii) m i) t B(t; m) ( B(t; m) = A 1 + r ) mt m ii) B(t; m) ( B(t; m) = A 1 + r ) mt m { ( = A 1 + r ) m } rt r m n = m r m n B
 1 1.1 1 r 1 m A r/m i) t ii) m i) t Bt; m) Bt; m) = A 1 + r ) mt m ii) Bt; m) Bt; m) = A 1 + r ) mt m { = A 1 + r ) m } rt r m n = m r m n Bt; m) Aert e lim 1 + 1 n 1.1) n!1 n) e a 1, a 2, a 3,... {a n
1 1.1 1 r 1 m A r/m i) t ii) m i) t Bt; m) Bt; m) = A 1 + r ) mt m ii) Bt; m) Bt; m) = A 1 + r ) mt m { = A 1 + r ) m } rt r m n = m r m n Bt; m) Aert e lim 1 + 1 n 1.1) n!1 n) e a 1, a 2, a 3,... {a n
変 位 変位とは 物体中のある点が変形後に 別の点に異動したときの位置の変化で あり ベクトル量である 変位には 物体の変形の他に剛体運動 剛体変位 が含まれている 剛体変位 P(x, y, z) 平行移動と回転 P! (x + u, y + v, z + w) Q(x + d x, y + dy,
 変 位 変位とは 物体中のある点が変形後に 別の点に異動したときの位置の変化で あり ベクトル量である 変位には 物体の変形の他に剛体運動 剛体変位 が含まれている 剛体変位 P(x, y, z) 平行移動と回転 P! (x + u, y + v, z + w) Q(x + d x, y + dy, z + dz) Q! (x + d x + u + du, y + dy + v + dv, z +
変 位 変位とは 物体中のある点が変形後に 別の点に異動したときの位置の変化で あり ベクトル量である 変位には 物体の変形の他に剛体運動 剛体変位 が含まれている 剛体変位 P(x, y, z) 平行移動と回転 P! (x + u, y + v, z + w) Q(x + d x, y + dy, z + dz) Q! (x + d x + u + du, y + dy + v + dv, z +
, = = 7 6 = 42, =
 http://www.ss.u-tokai.ac.jp/~mahoro/2016autumn/alg_intro/ 1 1 2016.9.26, http://www.ss.u-tokai.ac.jp/~mahoro/2016autumn/alg_intro/ 1.1 1 214 132 = 28258 2 + 1 + 4 1 + 3 + 2 = 7 6 = 42, 4 + 2 = 6 2 + 8
http://www.ss.u-tokai.ac.jp/~mahoro/2016autumn/alg_intro/ 1 1 2016.9.26, http://www.ss.u-tokai.ac.jp/~mahoro/2016autumn/alg_intro/ 1.1 1 214 132 = 28258 2 + 1 + 4 1 + 3 + 2 = 7 6 = 42, 4 + 2 = 6 2 + 8
f(x,y) (x,y) x (x,y), y (x,y) f(x,y) x y f x (x,y),f y (x,y) B p.1/14
 B p.1/14 f(x,y) (x,y) x (x,y), y (x,y) f(x,y) x y f x (x,y),f y (x,y) B p.1/14 f(x,y) (x,y) x (x,y), y (x,y) f(x,y) x y f x (x,y),f y (x,y) f(x 1,...,x n ) (x 1 x 0,...,x n 0), (x 1,...,x n ) i x i f xi
B p.1/14 f(x,y) (x,y) x (x,y), y (x,y) f(x,y) x y f x (x,y),f y (x,y) B p.1/14 f(x,y) (x,y) x (x,y), y (x,y) f(x,y) x y f x (x,y),f y (x,y) f(x 1,...,x n ) (x 1 x 0,...,x n 0), (x 1,...,x n ) i x i f xi
2011de.dvi
 211 ( 4 2 1. 3 1.1............................... 3 1.2 1- -......................... 13 1.3 2-1 -................... 19 1.4 3- -......................... 29 2. 37 2.1................................ 37
211 ( 4 2 1. 3 1.1............................... 3 1.2 1- -......................... 13 1.3 2-1 -................... 19 1.4 3- -......................... 29 2. 37 2.1................................ 37
 2016 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 1 16 2 1 () X O 3 (O1) X O, O (O2) O O (O3) O O O X (X, O) O X X (O1), (O2), (O3) (O2) (O3) n (O2) U 1,..., U n O U k O k=1 (O3) U λ O( λ Λ) λ Λ U λ O 0 X 0 (O2) n =
2016 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 1 16 2 1 () X O 3 (O1) X O, O (O2) O O (O3) O O O X (X, O) O X X (O1), (O2), (O3) (O2) (O3) n (O2) U 1,..., U n O U k O k=1 (O3) U λ O( λ Λ) λ Λ U λ O 0 X 0 (O2) n =
6. Euler x
 ...............................................................................3......................................... 4.4................................... 5.5......................................
...............................................................................3......................................... 4.4................................... 5.5......................................
Note.tex 2008/09/19( )
 1 20 9 19 2 1 5 1.1........................ 5 1.2............................. 8 2 9 2.1............................. 9 2.2.............................. 10 3 13 3.1.............................. 13 3.2..................................
1 20 9 19 2 1 5 1.1........................ 5 1.2............................. 8 2 9 2.1............................. 9 2.2.............................. 10 3 13 3.1.............................. 13 3.2..................................
 X G P G (X) G BG [X, BG] S 2 2 2 S 2 2 S 2 = { (x 1, x 2, x 3 ) R 3 x 2 1 + x 2 2 + x 2 3 = 1 } R 3 S 2 S 2 v x S 2 x x v(x) T x S 2 T x S 2 S 2 x T x S 2 = { ξ R 3 x ξ } R 3 T x S 2 S 2 x x T x S 2
X G P G (X) G BG [X, BG] S 2 2 2 S 2 2 S 2 = { (x 1, x 2, x 3 ) R 3 x 2 1 + x 2 2 + x 2 3 = 1 } R 3 S 2 S 2 v x S 2 x x v(x) T x S 2 T x S 2 S 2 x T x S 2 = { ξ R 3 x ξ } R 3 T x S 2 S 2 x x T x S 2
Chap11.dvi
 . () x 3 + dx () (x )(x ) dx + sin x sin x( + cos x) dx () x 3 3 x + + 3 x + 3 x x + x 3 + dx 3 x + dx 6 x x x + dx + 3 log x + 6 log x x + + 3 rctn ( ) dx x + 3 4 ( x 3 ) + C x () t x t tn x dx x. t x
. () x 3 + dx () (x )(x ) dx + sin x sin x( + cos x) dx () x 3 3 x + + 3 x + 3 x x + x 3 + dx 3 x + dx 6 x x x + dx + 3 log x + 6 log x x + + 3 rctn ( ) dx x + 3 4 ( x 3 ) + C x () t x t tn x dx x. t x
I A A441 : April 15, 2013 Version : 1.1 I Kawahira, Tomoki TA (Shigehiro, Yoshida )
 I013 00-1 : April 15, 013 Version : 1.1 I Kawahira, Tomoki TA (Shigehiro, Yoshida) http://www.math.nagoya-u.ac.jp/~kawahira/courses/13s-tenbou.html pdf * 4 15 4 5 13 e πi = 1 5 0 5 7 3 4 6 3 6 10 6 17
I013 00-1 : April 15, 013 Version : 1.1 I Kawahira, Tomoki TA (Shigehiro, Yoshida) http://www.math.nagoya-u.ac.jp/~kawahira/courses/13s-tenbou.html pdf * 4 15 4 5 13 e πi = 1 5 0 5 7 3 4 6 3 6 10 6 17
( : December 27, 2015) CONTENTS I. 1 II. 2 III. 2 IV. 3 V. 5 VI. 6 VII. 7 VIII. 9 I. 1 f(x) f (x) y = f(x) x ϕ(r) (gradient) ϕ(r) (gradϕ(r) ) ( ) ϕ(r)
 ( : December 27, 215 CONTENTS I. 1 II. 2 III. 2 IV. 3 V. 5 VI. 6 VII. 7 VIII. 9 I. 1 f(x f (x y f(x x ϕ(r (gradient ϕ(r (gradϕ(r ( ϕ(r r ϕ r xi + yj + zk ϕ(r ϕ(r x i + ϕ(r y j + ϕ(r z k (1.1 ϕ(r ϕ(r i
( : December 27, 215 CONTENTS I. 1 II. 2 III. 2 IV. 3 V. 5 VI. 6 VII. 7 VIII. 9 I. 1 f(x f (x y f(x x ϕ(r (gradient ϕ(r (gradϕ(r ( ϕ(r r ϕ r xi + yj + zk ϕ(r ϕ(r x i + ϕ(r y j + ϕ(r z k (1.1 ϕ(r ϕ(r i
50 2 I SI MKSA r q r q F F = 1 qq 4πε 0 r r 2 r r r r (2.2 ε 0 = 1 c 2 µ 0 c = m/s q 2.1 r q' F r = 0 µ 0 = 4π 10 7 N/A 2 k = 1/(4πε 0 qq
 49 2 I II 2.1 3 e e = 1.602 10 19 A s (2.1 50 2 I SI MKSA 2.1.1 r q r q F F = 1 qq 4πε 0 r r 2 r r r r (2.2 ε 0 = 1 c 2 µ 0 c = 3 10 8 m/s q 2.1 r q' F r = 0 µ 0 = 4π 10 7 N/A 2 k = 1/(4πε 0 qq F = k r
49 2 I II 2.1 3 e e = 1.602 10 19 A s (2.1 50 2 I SI MKSA 2.1.1 r q r q F F = 1 qq 4πε 0 r r 2 r r r r (2.2 ε 0 = 1 c 2 µ 0 c = 3 10 8 m/s q 2.1 r q' F r = 0 µ 0 = 4π 10 7 N/A 2 k = 1/(4πε 0 qq F = k r
 4................................. 4................................. 4 6................................. 6................................. 9.................................................... 3..3..........................
4................................. 4................................. 4 6................................. 6................................. 9.................................................... 3..3..........................
CALCULUS II (Hiroshi SUZUKI ) f(x, y) A(a, b) 1. P (x, y) A(a, b) A(a, b) f(x, y) c f(x, y) A(a, b) c f(x, y) c f(x, y) c (x a, y b)
 CALCULUS II (Hiroshi SUZUKI ) 16 1 1 1.1 1.1 f(x, y) A(a, b) 1. P (x, y) A(a, b) A(a, b) f(x, y) c f(x, y) A(a, b) c f(x, y) c f(x, y) c (x a, y b) lim f(x, y) = lim f(x, y) = lim f(x, y) = c. x a, y b
CALCULUS II (Hiroshi SUZUKI ) 16 1 1 1.1 1.1 f(x, y) A(a, b) 1. P (x, y) A(a, b) A(a, b) f(x, y) c f(x, y) A(a, b) c f(x, y) c f(x, y) c (x a, y b) lim f(x, y) = lim f(x, y) = lim f(x, y) = c. x a, y b
webkaitou.dvi
 ( c Akir KANEKO) ).. m. l s = lθ m d s dt = mg sin θ d θ dt = g l sinθ θ l θ mg. d s dt xy t ( d x dt, d y dt ) t ( mg sin θ cos θ, sin θ sin θ). (.) m t ( d x dt, d y dt ) = t ( mg sin θ cos θ, mg sin
( c Akir KANEKO) ).. m. l s = lθ m d s dt = mg sin θ d θ dt = g l sinθ θ l θ mg. d s dt xy t ( d x dt, d y dt ) t ( mg sin θ cos θ, sin θ sin θ). (.) m t ( d x dt, d y dt ) = t ( mg sin θ cos θ, mg sin
mugensho.dvi
 1 1 f (t) lim t a f (t) = 0 f (t) t a 1.1 (1) lim(t 1) 2 = 0 t 1 (t 1) 2 t 1 (2) lim(t 1) 3 = 0 t 1 (t 1) 3 t 1 2 f (t), g(t) t a lim t a f (t) g(t) g(t) f (t) = o(g(t)) (t a) = 0 f (t) (t 1) 3 1.2 lim
1 1 f (t) lim t a f (t) = 0 f (t) t a 1.1 (1) lim(t 1) 2 = 0 t 1 (t 1) 2 t 1 (2) lim(t 1) 3 = 0 t 1 (t 1) 3 t 1 2 f (t), g(t) t a lim t a f (t) g(t) g(t) f (t) = o(g(t)) (t a) = 0 f (t) (t 1) 3 1.2 lim
1W II K =25 A (1) office(a439) (2) A4 etc. 12:00-13:30 Cafe David 1 2 TA appointment Cafe D
 1W II K200 : October 6, 2004 Version : 1.2, kawahira@math.nagoa-u.ac.jp, http://www.math.nagoa-u.ac.jp/~kawahira/courses.htm TA M1, m0418c@math.nagoa-u.ac.jp TA Talor Jacobian 4 45 25 30 20 K2-1W04-00
1W II K200 : October 6, 2004 Version : 1.2, kawahira@math.nagoa-u.ac.jp, http://www.math.nagoa-u.ac.jp/~kawahira/courses.htm TA M1, m0418c@math.nagoa-u.ac.jp TA Talor Jacobian 4 45 25 30 20 K2-1W04-00
f : R R f(x, y) = x + y axy f = 0, x + y axy = 0 y 直線 x+y+a=0 に漸近し 原点で交叉する美しい形をしている x +y axy=0 X+Y+a=0 o x t x = at 1 + t, y = at (a > 0) 1 + t f(x, y
 017 8 10 f : R R f(x) = x n + x n 1 + 1, f(x) = sin 1, log x x n m :f : R n R m z = f(x, y) R R R R, R R R n R m R n R m R n R m f : R R f (x) = lim h 0 f(x + h) f(x) h f : R n R m m n M Jacobi( ) m n
017 8 10 f : R R f(x) = x n + x n 1 + 1, f(x) = sin 1, log x x n m :f : R n R m z = f(x, y) R R R R, R R R n R m R n R m R n R m f : R R f (x) = lim h 0 f(x + h) f(x) h f : R n R m m n M Jacobi( ) m n
<4D F736F F D B B83578B6594BB2D834A836F815B82D082C88C60202E646F63>
 電気電子数学入門 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/073471 このサンプルページの内容は, 初版 1 刷発行当時のものです. i 14 (tool) [ ] IT ( ) PC (EXCEL) HP() 1 1 4 15 3 010 9 ii 1... 1 1.1 1 1.
電気電子数学入門 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/073471 このサンプルページの内容は, 初版 1 刷発行当時のものです. i 14 (tool) [ ] IT ( ) PC (EXCEL) HP() 1 1 4 15 3 010 9 ii 1... 1 1.1 1 1.
( z = x 3 y + y ( z = cos(x y ( 8 ( s8.7 y = xe x ( 8 ( s83.8 ( ( + xdx ( cos 3 xdx t = sin x ( 8 ( s84 ( 8 ( s85. C : y = x + 4, l : y = x + a,
 [ ] 8 IC. y d y dx = ( dy dx ( p = dy p y dx ( ( ( 8 ( s8. 3 A A = ( A ( A (3 A P A P AP.3 π y(x = { ( 8 ( s8 x ( π < x x ( < x π y(x π π O π x ( 8 ( s83.4 f (x, y, z grad(f ( ( ( f f f grad(f = i + j
[ ] 8 IC. y d y dx = ( dy dx ( p = dy p y dx ( ( ( 8 ( s8. 3 A A = ( A ( A (3 A P A P AP.3 π y(x = { ( 8 ( s8 x ( π < x x ( < x π y(x π π O π x ( 8 ( s83.4 f (x, y, z grad(f ( ( ( f f f grad(f = i + j
II ( ) (7/31) II ( [ (3.4)] Navier Stokes [ (6/29)] Navier Stokes 3 [ (6/19)] Re
![II ( ) (7/31) II ( [ (3.4)] Navier Stokes [ (6/29)] Navier Stokes 3 [ (6/19)] Re II ( ) (7/31) II ( [ (3.4)] Navier Stokes [ (6/29)] Navier Stokes 3 [ (6/19)] Re](/thumbs/94/118770263.jpg) II 29 7 29-7-27 ( ) (7/31) II (http://www.damp.tottori-u.ac.jp/~ooshida/edu/fluid/) [ (3.4)] Navier Stokes [ (6/29)] Navier Stokes 3 [ (6/19)] Reynolds [ (4.6), (45.8)] [ p.186] Navier Stokes I Euler Navier
II 29 7 29-7-27 ( ) (7/31) II (http://www.damp.tottori-u.ac.jp/~ooshida/edu/fluid/) [ (3.4)] Navier Stokes [ (6/29)] Navier Stokes 3 [ (6/19)] Reynolds [ (4.6), (45.8)] [ p.186] Navier Stokes I Euler Navier
2S III IV K A4 12:00-13:30 Cafe David 1 2 TA 1 appointment Cafe David K2-2S04-00 : C
 2S III IV K200 : April 16, 2004 Version : 1.1 TA M2 TA 1 10 2 n 1 ɛ-δ 5 15 20 20 45 K2-2S04-00 : C 2S III IV K200 60 60 74 75 89 90 1 email 3 4 30 A4 12:00-13:30 Cafe David 1 2 TA 1 email appointment Cafe
2S III IV K200 : April 16, 2004 Version : 1.1 TA M2 TA 1 10 2 n 1 ɛ-δ 5 15 20 20 45 K2-2S04-00 : C 2S III IV K200 60 60 74 75 89 90 1 email 3 4 30 A4 12:00-13:30 Cafe David 1 2 TA 1 email appointment Cafe
2009 IA 5 I 22, 23, 24, 25, 26, (1) Arcsin 1 ( 2 (4) Arccos 1 ) 2 3 (2) Arcsin( 1) (3) Arccos 2 (5) Arctan 1 (6) Arctan ( 3 ) 3 2. n (1) ta
 009 IA 5 I, 3, 4, 5, 6, 7 6 3. () Arcsin ( (4) Arccos ) 3 () Arcsin( ) (3) Arccos (5) Arctan (6) Arctan ( 3 ) 3. n () tan x (nπ π/, nπ + π/) f n (x) f n (x) fn (x) Arctan x () sin x [nπ π/, nπ +π/] g n
009 IA 5 I, 3, 4, 5, 6, 7 6 3. () Arcsin ( (4) Arccos ) 3 () Arcsin( ) (3) Arccos (5) Arctan (6) Arctan ( 3 ) 3. n () tan x (nπ π/, nπ + π/) f n (x) f n (x) fn (x) Arctan x () sin x [nπ π/, nπ +π/] g n
) ] [ h m x + y + + V x) φ = Eφ 1) z E = i h t 13) x << 1) N n n= = N N + 1) 14) N n n= = N N + 1)N + 1) 6 15) N n 3 n= = 1 4 N N + 1) 16) N n 4
![) ] [ h m x + y + + V x) φ = Eφ 1) z E = i h t 13) x << 1) N n n= = N N + 1) 14) N n n= = N N + 1)N + 1) 6 15) N n 3 n= = 1 4 N N + 1) 16) N n 4 ) ] [ h m x + y + + V x) φ = Eφ 1) z E = i h t 13) x << 1) N n n= = N N + 1) 14) N n n= = N N + 1)N + 1) 6 15) N n 3 n= = 1 4 N N + 1) 16) N n 4](/thumbs/92/107866707.jpg) 1. k λ ν ω T v p v g k = π λ ω = πν = π T v p = λν = ω k v g = dω dk 1) ) 3) 4). p = hk = h λ 5) E = hν = hω 6) h = h π 7) h =6.6618 1 34 J sec) hc=197.3 MeV fm = 197.3 kev pm= 197.3 ev nm = 1.97 1 3 ev
1. k λ ν ω T v p v g k = π λ ω = πν = π T v p = λν = ω k v g = dω dk 1) ) 3) 4). p = hk = h λ 5) E = hν = hω 6) h = h π 7) h =6.6618 1 34 J sec) hc=197.3 MeV fm = 197.3 kev pm= 197.3 ev nm = 1.97 1 3 ev
I 1
 I 1 1 1.1 1. 3 m = 3 1 7 µm. cm = 1 4 km 3. 1 m = 1 1 5 cm 4. 5 cm 3 = 5 1 15 km 3 5. 1 = 36 6. 1 = 8.64 1 4 7. 1 = 3.15 1 7 1 =3 1 7 1 3 π 1. 1. 1 m + 1 cm = 1.1 m. 1 hr + 64 sec = 1 4 sec 3. 3. 1 5 kg
I 1 1 1.1 1. 3 m = 3 1 7 µm. cm = 1 4 km 3. 1 m = 1 1 5 cm 4. 5 cm 3 = 5 1 15 km 3 5. 1 = 36 6. 1 = 8.64 1 4 7. 1 = 3.15 1 7 1 =3 1 7 1 3 π 1. 1. 1 m + 1 cm = 1.1 m. 1 hr + 64 sec = 1 4 sec 3. 3. 1 5 kg
2.4 ( ) ( B ) A B F (1) W = B A F dr. A F q dr f(x,y,z) A B Γ( ) Minoru TANAKA (Osaka Univ.) I(2011), Sec p. 1/30
 2.4 ( ) 2.4.1 ( B ) A B F (1) W = B A F dr. A F q dr f(x,y,z) A B Γ( ) I(2011), Sec. 2. 4 p. 1/30 (2) Γ f dr lim f i r i. r i 0 i f i i f r i i i+1 (1) n i r i (3) F dr = lim F i n i r i. Γ r i 0 i n i
2.4 ( ) 2.4.1 ( B ) A B F (1) W = B A F dr. A F q dr f(x,y,z) A B Γ( ) I(2011), Sec. 2. 4 p. 1/30 (2) Γ f dr lim f i r i. r i 0 i f i i f r i i i+1 (1) n i r i (3) F dr = lim F i n i r i. Γ r i 0 i n i
24 I ( ) 1. R 3 (i) C : x 2 + y 2 1 = 0 (ii) C : y = ± 1 x 2 ( 1 x 1) (iii) C : x = cos t, y = sin t (0 t 2π) 1.1. γ : [a, b] R n ; t γ(t) = (x
![24 I ( ) 1. R 3 (i) C : x 2 + y 2 1 = 0 (ii) C : y = ± 1 x 2 ( 1 x 1) (iii) C : x = cos t, y = sin t (0 t 2π) 1.1. γ : [a, b] R n ; t γ(t) = (x 24 I ( ) 1. R 3 (i) C : x 2 + y 2 1 = 0 (ii) C : y = ± 1 x 2 ( 1 x 1) (iii) C : x = cos t, y = sin t (0 t 2π) 1.1. γ : [a, b] R n ; t γ(t) = (x](/thumbs/94/118744578.jpg) 24 I 1.1.. ( ) 1. R 3 (i) C : x 2 + y 2 1 = 0 (ii) C : y = ± 1 x 2 ( 1 x 1) (iii) C : x = cos t, y = sin t (0 t 2π) 1.1. γ : [a, b] R n ; t γ(t) = (x 1 (t), x 2 (t),, x n (t)) ( ) ( ), γ : (i) x 1 (t),
24 I 1.1.. ( ) 1. R 3 (i) C : x 2 + y 2 1 = 0 (ii) C : y = ± 1 x 2 ( 1 x 1) (iii) C : x = cos t, y = sin t (0 t 2π) 1.1. γ : [a, b] R n ; t γ(t) = (x 1 (t), x 2 (t),, x n (t)) ( ) ( ), γ : (i) x 1 (t),
1. (8) (1) (x + y) + (x + y) = 0 () (x + y ) 5xy = 0 (3) (x y + 3y 3 ) (x 3 + xy ) = 0 (4) x tan y x y + x = 0 (5) x = y + x + y (6) = x + y 1 x y 3 (
 1 1.1 (1) (1 + x) + (1 + y) = 0 () x + y = 0 (3) xy = x (4) x(y + 3) + y(y + 3) = 0 (5) (a + y ) = x ax a (6) x y 1 + y x 1 = 0 (7) cos x + sin x cos y = 0 (8) = tan y tan x (9) = (y 1) tan x (10) (1 +
1 1.1 (1) (1 + x) + (1 + y) = 0 () x + y = 0 (3) xy = x (4) x(y + 3) + y(y + 3) = 0 (5) (a + y ) = x ax a (6) x y 1 + y x 1 = 0 (7) cos x + sin x cos y = 0 (8) = tan y tan x (9) = (y 1) tan x (10) (1 +
6kg 1.1m 1.m.1m.1 l λ ϵ λ l + λ l l l dl dl + dλ ϵ dλ dl dl + dλ dl dl 3 1. JIS 1 6kg 1% 66kg 1 13 σ a1 σ m σ a1 σ m σ m σ a1 f f σ a1 σ a1 σ m f 4
 35-8585 7 8 1 I I 1 1.1 6kg 1m P σ σ P 1 l l λ λ l 1.m 1 6kg 1.1m 1.m.1m.1 l λ ϵ λ l + λ l l l dl dl + dλ ϵ dλ dl dl + dλ dl dl 3 1. JIS 1 6kg 1% 66kg 1 13 σ a1 σ m σ a1 σ m σ m σ a1 f f σ a1 σ a1 σ m
35-8585 7 8 1 I I 1 1.1 6kg 1m P σ σ P 1 l l λ λ l 1.m 1 6kg 1.1m 1.m.1m.1 l λ ϵ λ l + λ l l l dl dl + dλ ϵ dλ dl dl + dλ dl dl 3 1. JIS 1 6kg 1% 66kg 1 13 σ a1 σ m σ a1 σ m σ m σ a1 f f σ a1 σ a1 σ m
I ( ) 1 de Broglie 1 (de Broglie) p λ k h Planck ( Js) p = h λ = k (1) h 2π : Dirac k B Boltzmann ( J/K) T U = 3 2 k BT
 I (008 4 0 de Broglie (de Broglie p λ k h Planck ( 6.63 0 34 Js p = h λ = k ( h π : Dirac k B Boltzmann (.38 0 3 J/K T U = 3 k BT ( = λ m k B T h m = 0.067m 0 m 0 = 9. 0 3 kg GaAs( a T = 300 K 3 fg 07345
I (008 4 0 de Broglie (de Broglie p λ k h Planck ( 6.63 0 34 Js p = h λ = k ( h π : Dirac k B Boltzmann (.38 0 3 J/K T U = 3 k BT ( = λ m k B T h m = 0.067m 0 m 0 = 9. 0 3 kg GaAs( a T = 300 K 3 fg 07345
untitled
 0.1 1 vector.tex 20010412;20;23;25;28 0507;09 19;0917-19;22;23;1017;1127;1204; 20020108;15; 20061107; 0 1 0.1............................................. 1 0.2....................................... 2
0.1 1 vector.tex 20010412;20;23;25;28 0507;09 19;0917-19;22;23;1017;1127;1204; 20020108;15; 20061107; 0 1 0.1............................................. 1 0.2....................................... 2
1 (Berry,1975) 2-6 p (S πr 2 )p πr 2 p 2πRγ p p = 2γ R (2.5).1-1 : : : : ( ).2 α, β α, β () X S = X X α X β (.1) 1 2
 2005 9/8-11 2 2.2 ( 2-5) γ ( ) γ cos θ 2πr πρhr 2 g h = 2γ cos θ ρgr (2.1) γ = ρgrh (2.2) 2 cos θ θ cos θ = 1 (2.2) γ = 1 ρgrh (2.) 2 2. p p ρgh p ( ) p p = p ρgh (2.) h p p = 2γ r 1 1 (Berry,1975) 2-6
2005 9/8-11 2 2.2 ( 2-5) γ ( ) γ cos θ 2πr πρhr 2 g h = 2γ cos θ ρgr (2.1) γ = ρgrh (2.2) 2 cos θ θ cos θ = 1 (2.2) γ = 1 ρgrh (2.) 2 2. p p ρgh p ( ) p p = p ρgh (2.) h p p = 2γ r 1 1 (Berry,1975) 2-6
1 2 1 No p. 111 p , 4, 2, f (x, y) = x2 y x 4 + y. 2 (1) y = mx (x, y) (0, 0) f (x, y). m. (2) y = ax 2 (x, y) (0, 0) f (x,
 No... p. p. 3, 4,, 5.... f (, y) y 4 + y. () y m (, y) (, ) f (, y). m. () y a (, y) (, ) f (, y). a. (3) lim f (, y). (,y) (,)... (, y) (, ). () f (, y) a + by, a, b. + y () f (, y) 4 + y + y 3 + y..3.
No... p. p. 3, 4,, 5.... f (, y) y 4 + y. () y m (, y) (, ) f (, y). m. () y a (, y) (, ) f (, y). a. (3) lim f (, y). (,y) (,)... (, y) (, ). () f (, y) a + by, a, b. + y () f (, y) 4 + y + y 3 + y..3.
IA 2013 : :10722 : 2 : :2 :761 :1 (23-27) : : ( / ) (1 /, ) / e.g. (Taylar ) e x = 1 + x + x xn n! +... sin x = x x3 6 + x5 x2n+1 + (
 IA 2013 : :10722 : 2 : :2 :761 :1 23-27) : : 1 1.1 / ) 1 /, ) / e.g. Taylar ) e x = 1 + x + x2 2 +... + xn n! +... sin x = x x3 6 + x5 x2n+1 + 1)n 5! 2n + 1)! 2 2.1 = 1 e.g. 0 = 0.00..., π = 3.14..., 1
IA 2013 : :10722 : 2 : :2 :761 :1 23-27) : : 1 1.1 / ) 1 /, ) / e.g. Taylar ) e x = 1 + x + x2 2 +... + xn n! +... sin x = x x3 6 + x5 x2n+1 + 1)n 5! 2n + 1)! 2 2.1 = 1 e.g. 0 = 0.00..., π = 3.14..., 1
