単純パラエルミート対称空間の等長変換群について (新しい変換群論とその周辺)
|
|
|
- ひろと ちとく
- 6 years ago
- Views:
Transcription
1 数理解析研究所講究録第 2016 巻 2017 年 単純パラエルミート対称空間の等長変換群について 東京理科大学大学院理学研究科 Dl 下川拓哉 Takuya Shimokawa Graduate School of Science Mathematics Tokyo University of Science 1 初めに 本稿の内容は杉本恭司氏 ( 東京理科大学大学院理学研究科 ) との共同研究 [Sh Su] に基づいている 本研究の 目的は パラエルミート対称空間 (GlH $\sigma$i g) のある類に対して その等長変換群 Isom(GlH g) を完全に決定 することである 本稿では その決定方法と一例を紹介する ここでパラエルミート対称空間とは S Kaneyuki M Kozai[Ka Kozl により導入された一葉双曲面の高次元 化である より正確には エルミート対称空間が不変複素構造と それと両立する不変エルミート計量とを同時 に持つアフィン対称空間であるのに対し パラエルミート対称空間とは G 不変パラ複素構造 I と それと両立 する G 不変パラエルミート計量 g とを同時に持つアフィン対称空間 (GlH $\sigma$ ) である 前者の計量がケーラー 計量になるのと同様に 後者の計量もパラケーラー計量になる その一方で 前者がリーマン計量であるのに対 し 後者はニュートラル計量であることには注意が必要となる (cf 注意 1 余談 1) ところで パラエルミート対称空間に対してその等長変換群 Isom(GlH g) を決定することにはどのような意 味があるだろうか 例えば F C Klein によれば幾何学とは集合に対する変換群の作用によって不変な性質を研 究する学問であり ユークリッド幾何学はユークリッド空間鰹における合同変換により変わらない性質を取り 扱う分野である ここでの合同変換とはユークリッド計量に関する等長変換のことで そのため ユークリッド 計量に関する等長変換群を決定することはユークリッド幾何学を決定することを意味している 擬リーマン幾 何学においては対象となる空間 ( 集合 ) がその都度変わってしまうが それは大した問題ではないだろう つま り擬リーマン幾何学における問題は 擬リーマン多様体 (M g) を固定しようとも M 上には他の計量 \tilde{g} が自由に 許容され得り g とは無関係な幾何学が同一の M 上に展開されてしまうことである 本研究に視点を戻せば 今 回の目的はアフィン対称空間 (GlH $\sigma$ ) のある類に対して GlH 上の G 不変パラ複素構造 I と両立する の G 不変パラエルミート計量 g が織り成す幾何学を決定することと言える この目的を達成するにあたり I と両立する 任意の G 不変パラエルミート計量が 0 でない実数倍の差を除いてキリング形式から誘導される ことを加えて示している (cf 定理 1) これにより 今回においては計量を変えることにより生じる幾何学の差異 は存在しない つまり本研究 パラエルミート対称空間 (GlH $\sigma$ I g) に対してその等長変換群 Isom(GlH g) を 決定すること は G/H 上の G 不変パラ複素構造 I と両立する 任意の G 不変パラエルミート計量 \tilde{g} が織り 成す幾何学を決定することを意味しているのである 特定 2 パラエルミート対称空間 パラエルミート対称空間とは PLibermann により確立されたパラ複素構造とパラエルミート計量とを K Nomizu により紹介されたアフィン対称空間上に導入した概念である 初めにその定義を復習しておこう : 定義 1(S Kaneyuki M Kozai [Ka Koz] p86 87) (GlH a) をアフィン対称空間 1 を G/H の G 不変 (1 1) テ ンソル場 g を G/H の G 不変擬リーマン計量とする このとき (GlH $\sigma$i g) がパラエルミート対称空間である :\Leftrightarrow (1) I^{2}=\mathrm{i}\mathrm{d}_{X(G/H)} (2) \dim T_{p}^{+}(G/H)=\dim T_{p}^{-}(G/H) (3) [IX ly]-i[ix Y]-I[X IY]+[X \mathrm{y}]=0 (4) g(ix Y)+g(X I\mathrm{Y})=0 \forall p\in G/H \forall X Y\in \mathrm{x}(g/h) ここで T_{p}^{\pm}(G/H) は接空間 Tp(GlH) における Ip の \pm 1 固有空間 X(G/H) は G/H のベクトル場全体である
2 143 注意 1 (1) g はパラケーラー計量になる すなわち $\omega$ : X(G/H)\times X(G/H)\rightarrow C^{\infty}(G/H) (X \mathrm{y})\mapsto g(x I\mathrm{Y}) は G/H のシンプレクティック形式である (cf [Ka Koz] p86) (2) g } よニュートラル計量 ( 符号数が (qq) と表せる擬リーマン計量 ) である ここで 具体的なパラエルミート対称空間の例を挙げる この例は 最も基本的なパラエルミート対称空間の例であろう なお パラ複素構造 I が G のリー代数 \mathfrak{g} の元 Z により導入されていること パラエルミート計量 g が \mathrm{g} のキリング形式 Bg (X Y)=4\mathrm{T}\mathrm{r}(XY) for X \mathrm{y}\in \mathfrak{g} により定められていることに留意したい : 例 1( 一葉双曲面 ) G:=SL(2 \mathbb{r}) とおく いまより パラエルミート対称空間 (GlH $\sigma$i g) を構成する (1 回帰的自己同型写像 ) G の回帰的自己同型写像を次で定義しよう : $\sigma$:=\mathrm{a}\mathrm{d}\mathrm{i}_{11} ここで Ad b(a):=bab^{-1} for a\in G b:2\times 2 行列 I_{1\downarrow}:=\left(\begin{array}{ll}-1 & 0\\0 & 1\end{array}\right) このとき 固定点集合 G^{ $\sigma$} は次の通りである : G`=S(GL(1\mathbb{R})\times GL(1 \mathbb{r}))=\{\left(\begin{array}{ll}x & 0\\0 & 1/x\end{array}\right) x\in \mathbb{r}\backslash \{0\}\} よって H:=S(GL(1\mathbb{R})\times GL(1\mathrm{R})) と定めると (GlH $\sigma$ ) は 1つのアフィン対称空間になる ( 一葉双曲面 cf 図 1) (2 パラ複素構造 ) いま 原点 0 における接空間 T_{o}(G/H) は そこで T_{o}(G/H)=\{\left(\begin{array}{ll}0 & y-z\\y+z & 0\end{array}\right) yz\in \mathbb{r}\} Z=\displaystyle \frac{1}{2}\left(\begin{array}{ll}\mathrm{l} & 0\\0 & -1\end{array}\right) とおくと ad Z は T_{o}(G/H) の回帰的自己同型写像であり 従って 0 におけるパラ複素構造 I が次で定まる: I_{o}:=\mathrm{a}\mathrm{d}Z 図 1 一葉双曲面 このとき T_{0}(G/H) 上で I_{o}\circ Adh =\mathrm{a}\mathrm{d}h\circ I_{o} for all h\in H なので I_{o} は G/H 上のパラ複素構造 I へと拡張さ れる (3 パラエルミート計量 ) 原点 0 におけるパラエルミート計量 g を以下のように定めよう : g_{0}(x Y):=4\mathrm{T}\mathrm{r}(XY) for X \mathrm{y}\in T_{o}(G/H) 実際 g_{0}(i_{0}x \mathrm{y})=-g_{0}(x I_{0}Y) for all X Y\in T_{o}(G/H) より q はちと両立していることがわかる さらに g_{0}( \mathrm{a}\mathrm{d}h(x)ad h(y)) =g_{0}(x Y) for all X Y\in T_{o}(G/H) h\in H を満足するため g_{0} は (GlH I ) 上のパラエルミー ト計量に拡張される 以上により パラエルミート対称空間 (GlH $\sigma$i g) が構成された 次に パラエルミート対称空間における基本的な性質を紹介しよう それは概効果的半単純パラエルミート対 称空間があるリー代数の元により特徴づけられるということである : 命題 1 G を連結半単純リー群 (GlH $\sigma$ Ig) を概効果的パラエルミート対称空間 \mathfrak{g} を G のリー代数 そして \mathfrak{h} \mathfrak{m} をそれぞれの微分写像 $\sigma$ による 1-1 固有空間とする 加えて $\theta$ を $\sigma$_{*} と可換な \mathrm{g} のカルタン対合 \mathfrak{k}
3 144 \mathfrak{p} をそれぞれ $\theta$ による 1-1 固有空間とおく 1 (cf S Kaneyuki M Kozai [Ka Koz] p89 92) 以下の条件を満たす Z\in 3(\mathfrak{h})\cap \mathfrak{p} が一意的に存在する : C_{G}(Z)_{0}\subset H\subset C_{G}(Z) \mathfrak{h}=\mathrm{c}_{\mathfrak{g}}(z)=\mathrm{g}_{0} \mathfrak{m}=\mathrm{g}_{-1}\oplus \mathfrak{g}_{1} I_{o}=\mathrm{a}\mathrm{d}_{\mathfrak{m}}Z ($\tau$_{*}=\exp\sqrt{-1} $\pi$ ad Z ここで \mathfrak{z}(\mathfrak{h}) は \mathfrak{y} の中心 C_{G}(Z) は Z の G における中心化群 C_{G}(Z)_{0} はその単位連結成分 \mathfrak{g}_{ $\lambda$} は \mathrm{a}\mathrm{d}z の $\lambda$ 固有空間 2 (cf [Ka Koz] p92) C_{G}(Z)_{0}\subset\overline{H} なる C_{G}(Z) の任意の部分群 \overline{h} に対し \overline{i}_{h^{-}} を $\lambda$_{1}\mathrm{a}\mathrm{d}_{\mathfrak{m}}z の G 不変拡張 \overline{g}_{h^{-}} を $\lambda$2b \mathfrak{g} \mathfrak{m}\times \mathfrak{m} の G 不変拡張 ただし $\lambda$_{1}=\pm 1 $\lambda$_{2}\in \mathbb{r}\backslash \{0\} B_{\mathfrak{g}} は \mathfrak{g} のキリング形式とする このとき (GlH $\sigma$\overline{i}_{h^{-}}\overline{g}_{h^{-}}) はパラエルミート対称空間になる 3 (cf S S Koh [KOh] p306) 特に \mathfrak{g} がある複素単純リー代数の実形であるとき \mathfrak{z}(\mathfrak{y})=\mathbb{r}z いま 概効果的半単純パラエルミート対称空間 (GlH $\sigma$i g) が与えられると 命題 により特別な元 Z が存在し H I などが特徴づけられ 空間 (GlH $\sigma$ ) にはキリング形式 Bg により誘導される計量 \overline{g} が必ず許容さ れる これは I と両立する g とは無関係なパラエルミート計量である 従って g に関する等長変換群のみを決 定したとしても I と両立する別のパラエルミート計量 例えば \overline{g} に対してはその結果は流用できず 普遍性に 乏しい結果と言える そこで 空間 (GlH $\sigma$ ) に対して G 不変パラ複素構造 I を与えたとき I と両立する \mathrm{r} 任意 の G 不変パラエルミート計量に対して等長変換群の構造を共通とする十分条件を考えたい このとき 命題 1 3 を用いることで次の結果を得る : 定理 1 (GlH $\sigma$i g) をパラエルミート対称空間 \mathrm{g} を G のリー代数とし それはある複素単純リー代数の実形 と仮定する また \mathfrak{m} を $\sigma$ の微分写像 $\sigma$ による -1 固有空間とおく このとき 1 と両立する任意の G 不変パラ エルミート計量は 0 ではない実数倍を除いて \mathrm{g} のキリング形式 Bg から誘導される よって特に \exists $\lambda$\in \mathbb{r}\backslash \{0\}\mathrm{s}\mathrm{t} g は $\lambda$ B_{\mathrm{g}} _{\mathfrak{n} $\tau$\times \mathfrak{m}} の G 不変拡張 注意 2 定理 1により G のリー代数 \mathfrak{g} がある複素単純リー代数の実形となっているパラエルミート対称空間 (GlH $\sigma$ I g) の等長変換群を考察するとき その計量としては $\lambda$ B_{\mathrm{g}} _{\mathfrak{m}\times \mathfrak{m}} の G 不変拡張として誘導される計量 \overline{g} だけを考えればよい 同時に g( 従って \overline{g}) をパラエルミート計量とする G/H 上のパラ複素構造は 命題 1 によ り \pm I のみである 余談 1 9 はある複素単純リー代数の実形 という仮定は比較的重い条件と言える これは リーマン計量で ( もローレンツ計量でも ) ない擬リーマン計量 であるニュートラル計量 (cf 注意 1-(2)) を制御することが一般に難しいことに起因する 例えば存在非存在に目を向けると リーマン計量は多様体がパラコンパクトという位相的性質を伴えば必ず存在するのに対して リーマン計量ではない擬リーマン計量 は たとえコンパクトや向きづけ可能 単連結といった仮定を課しても存在する ( あるいはしない ) とは限らない リーマン計量でもローレンツ計量でもない擬リーマン計量 の場合 このような問題はより複雑になる *1 1 なお N Steenrod はコンパクト連結多様体について少なくとも 4 次元まではさほどの努力なく判別できるだろうと著書で綴っている ( その一方で 複素射影平面 CP^{2} がニュートラル計量を許容するか否かを興味ある問題とし その場では明言しなかった ([St] p ))
4 いま 等長変換群の決定 (GlH $\sigma$i g) をパラエルミート対称空間 \mathfrak{g} を G のリー代数 そしてそれはある複素単純リー代数の実形と仮定する 加えて \mathfrak{y} \mathfrak{m} をそれぞれの微分写像 $\sigma$ による 1-1 固有空間 Z を命題 1により定まる元とする 今回は パラエルミート対称空間が随伴表現の双曲軌道として実現されている場合を考えよう すなわち H=C_{G}(Z) を仮定する また G の中心は自明とする *2 定理 2 \mathrm{a}\mathrm{u}\mathrm{t}(\mathfrak{g}z)^{\neq}:=\{ $\phi$\in \mathrm{a}\mathrm{u}\mathrm{t}(\mathrm{g}) $\phi$(z)=\pm Z\} \mathrm{j}\mathrm{n}\mathrm{t}(\mathfrak{g}z)^{+}=\mathrm{a}\mathrm{u}\mathrm{t}(\mathfrak{g}z)^{+}\cap \mathrm{i}\mathrm{n}\mathrm{t}(\mathrm{g}) とおくとき Isom(GlH g) /\mathrm{i}\mathrm{s}\mathrm{o}\mathrm{m}(g/h g)_{0}\cong(\mathrm{a}\mathrm{u}\mathrm{t}(\mathfrak{g}z)^{+}\mathrm{u}\mathrm{a}\mathrm{u}\mathrm{t}(\mathrm{g}z)^{-})/\mathrm{i}\mathrm{n}\mathrm{t}(\mathfrak{g}z)^{+} 注意 3 $\tau$ を G の G/H への作用とする つまり $\tau$_{a}(bh):=abh for a b\in G すると Isom(GlH g)0=$\tau$_{g}= \{$\tau$_{a} a\in G\} が成り立つ 従って Isom(GlH g) を単に決定するよりIsom(GlH g) /\mathrm{i}\mathrm{s}\mathrm{o}\mathrm{m}(g/h g)_{0} を決定する方が有用な結果である (cf 例 2) なお Isom(GlH g) /\mathrm{i}\mathrm{s}\mathrm{o}\mathrm{m}(g/h g)_{0} は有限群である 定理 2により 等長変換群はリー代数の自己同型群に帰着される 従って 残る問題は Z の計算方法であるが Z の性質を追及することにより 勝手に 与えたワイル領域の中のある元 2に Z を移すことが可能となる 定理 3 $\xi$ を \mathrm{g} の 1 つのカルタン対合 \mathfrak{k} \mathrm{p} をそれぞれ $\xi$ による 1-1 固有空間 \mathfrak{a} を \mathrm{p} 内の 1 つの極大可換部分 空間 $\Delta$ を (\mathfrak{g} a) に関する制限ルート系 $\Pi$ を $\Delta$ の基本系 $\gamma$ を最大ルート とそれぞれおく このとき 以下が成 り立つ : 1 $\gamma$(\tilde{z})=1\hslash^{1} つ Isom (G/H g)/\mathrm{i}\mathrm{s}\mathrm{o}\mathrm{m}(g/h g)0\cong(\mathrm{a}\mathrm{u}\mathrm{t}(\mathfrak{g}\tilde{z})^{+}\mathrm{u}\mathrm{a}\mathrm{u}\mathrm{t}(\mathfrak{g}\tilde{z})^{-})/\mathrm{i}\mathrm{n}\mathrm{t}(\mathfrak{g}\tilde{z})^{+} を満たす \tilde{z}\in W:=\{A\in \mathfrak{a} \forall $\alpha$\in $\Pi$ $\alpha$(a)\geq 0\} が存在する 2 $\gamma$(a)=1 なる任意の A\in W に対して H_{A}:=C_{G}(A) $\sigma$_{a}:=\mathrm{a}_{\exp^{\sqrt{-1}} $\pi$ A} とおく ここで A_{a} は a\in G による G の内部自己同型写像を表す 加えて B_{\mathfrak{g}} _{[A\mathfrak{g}]\times[A\mathfrak{g}]} \mathrm{a}\mathrm{d}_{[a\mathrm{g}]}a の G 不変拡張を それぞれ g_{a} 為と定める このとき (GlHA $\sigma$_{a}i_{a} g_{a} ) はパラエルミート対称空間で Isom (G/H_{A} g_{a})/\mathrm{i}\mathrm{s}\mathrm{o}\mathrm{m}(g/h_{a} g_{a})_{0}\cong(\mathrm{a}\mathrm{u}\mathrm{t}(\mathrm{g}a)^{+}\mathrm{u}\mathrm{a}\mathrm{u}\mathrm{t}(\mathrm{g}a)^{-})/\mathrm{i}\mathrm{n}\mathrm{t}(\mathfrak{g}a)^{+} 注意 4 本定理のカルタン対合 $\xi$ は $\sigma$ との可換性を求めた $\theta$ でなく 勝手な カルタン対合でよい そのため ( 記号は同一だが ) \mathfrak{k} や \mathrm{p} は命題 1のそれらとは別物である また カルタン対合だけでなく極大可換部分空間 a も 勝手に 選んでよい この両者の任意性が重要になる 本研究の目的を達成するためには 定理 3により各複素単純リー代数の実形 \mathfrak{g} に対して $\gamma$(a)=1 なる任意の A\in W を求め (\mathrm{a}\mathrm{u}\mathrm{t}(\mathfrak{g}a)^{+}\mathrm{u}\mathrm{a}\mathrm{u}\mathrm{t}(\mathrm{g}a)^{-})/\mathrm{i}\mathrm{n}\mathrm{t}(\mathfrak{g}a)^{+} の各代表元とそれらの代数的関係を調べれば十分であることがわかる ここで実際にこの定理 3を用いた等長変換群の計算例を挙げよう 例 2 (GlH $\sigma$ Ig) G/H=SL(n\mathbb{R})/S(GL(k\mathbb{R})\times GL(n-k\mathrm{R})) を例 1と同様にして得られるパラエ ) レミート 対称空間とする ただし n\geq 2 1\leq k\leq n-1 は単純である G のリー代数 \mathfrak{g}=\mathfrak{s}\mathrm{i}(n\mathbb{r}) に対して その複素化 9\mathrm{c}=\mathfrak{s}\mathrm{I}(n \mathbb{c}) *2 この仮定は本質的ではない 実際今の状況下では G の中心 Z(G) が自明であるか否かに関係なく G/H\cong(G/Z(G))/(H/Z(G)) となっ ている
5 146 さて \mathfrak{g} の勝手なカルタン対合 $\xi$ として $\xi$(x):=-tx for X\in \mathrm{g} を選ぼう すると 1-1 固有空間はそれぞれ \mathfrak{k}=\mathfrak{s}\mathrm{o}(n):=\{x\in \mathfrak{g} {}^{\mathrm{t}}x=-x\} \mathrm{p}=\{x\in \mathfrak{g} ^{t}x=x\} となる そこで \mathfrak{p} 内の勝手な極大可換部分空間 \mathfrak{a} として次 を選ぶ : \displaystyle \mathfrak{a}:=\{\left(\begin{array}{lll}x_{1} & 0 & 0\\0 & x_{2} & 0\\\vdots & & \\0 & 0 & x_{n}\end{array}\right) \displaystyle \sum_{i=1}^{n}x_{i}=0\} すると (\mathfrak{g} \mathfrak{a}) に関する ) レート系 $\Delta$ は $\Delta$:=\{\pm(e_{i^{-e}j)} 1\leq i<j\leq n} 基本系 $\Pi$ は $\Pi$=\{$\alpha$_{i}:=e_{i}-e_{i+1} 1\leq j\leq n-1\} 最大ルート $\gamma$ は $\gamma$=$\alpha$_{1}+$\alpha$_{2}+\cdots+$\alpha$_{n-1} として得られる : $\alpha$_{1} $\alpha$_{2} $\alpha$_{n-1} このとき G/H に対する定理 3 内の 2 は 条件 $\gamma$(\tilde{z})=1 および \tilde{z}\in W:=\{A\in \mathfrak{a} \forall $\alpha$\in $\Pi$ $\alpha$(a)\geq 0\} により Zl Z2 る双対基である : Z_{n-1} の n-1 個のいずれかである ここで Zl Z2 Z_{i}=\displaystyle \frac{1}{n}\left((n & -i)e_{i}o & O-iE_{n-i}\right)(1\displaystyle \leq i\leq n-1) いま 各乙に対して \mathrm{a}\mathrm{d}z_{i} による \mathrm{g} の固有空間分解は次のようになる : Z_{n-1} は $\Pi$=\{$\alpha$_{1} $\alpha$_{2} $\alpha$_{n-1}\} の $\alpha$ i(zi) = $\delta$ りな El は l 次単位行列 行列 \mathfrak{g}_{-1}=\{\left(\begin{array}{ll}o & O\\X_{n-ii} & O\end{array}\right) X_{n-ii}:(n-i)\times i \} 行 \mathrm{g}_{1}=\{\left(\begin{array}{ll}o & X_{in-i}\\O & O\end{array}\right) X_{in-i}:i\times(n-i) \mathrm{f}^{1}\mathrm{j}\} X_{i}:i\times i \mathfrak{h}=\mathrm{g}_{0}=\{\left(\begin{array}{ll}x_{i} & O\\O & X_{n-i}\end{array}\right) \mathrm{t}\mathrm{r}(x_{i}+x_{n-i})=0x_{n-i}:(n-i)\mathrm{x}(n-i) \cong \mathfrak{s}1(i\mathbb{r})\oplus \mathfrak{s}\mathrm{i}(n-i \mathbb{r})\oplus \mathbb{r} 行列 従って 求める2は姦だけである 簡単のため n が偶数のときのみを考えることにすると M Takeuchi [Ta]^{*3} により \mathrm{a}\mathrm{u}\mathrm{t}(\mathrm{g})/\mathrm{i}\mathrm{n}\mathrm{t}(\mathfrak{g})= {[idg] [ $\xi$] [Ad I_{1n-1}] [ $\xi$\circ Ad I_{1n-1}] } \cong \mathbb{z}_{q}\oplus \mathbb{z}_{2} \} である ここで I_{1n-\downarrow=}\left(\begin{array}{ll}-\mathrm{l} & 0\\0 & E_{n-1}\end{array}\right) このとき $\xi$(z_{k})=-z_{k} Ad I_{1n-1}(Z_{k})=Z_{k} Int (\mathrm{g}z_{k})^{-}=\mathrm{a}\mathrm{u}\mathrm{t}(\mathfrak{g} Z)^{-}\cap \mathrm{i}\mathrm{n}\mathrm{t}(\mathrm{g})=\emptyset となることが示されるため (\mathrm{a}\mathrm{u}\mathrm{t}(\mathfrak{g}z_{k})^{+}\mathrm{u}\mathrm{a}\mathrm{u}\mathrm{t}(\mathfrak{g}z_{k})^{-})/\mathrm{i}\mathrm{n}\mathrm{t}(\mathfrak{g}z_{k})^{+}=\{[\mathrm{i}(\mathrm{h}] [ $\xi$] [ \mathrm{a}\mathrm{d} I_{1n-1} ] [ $\xi$\circ \mathrm{a}\mathrm{d} I_{1n-1} ] \}\cong \mathbb{z}_{q}\oplus \mathbb{z}_{ $\Omega$} となる 定理 23の同型関係を紐解くと 実は次のような具体的な記述も可能である : Isom(GlH g) /\mathrm{i}\mathrm{s}\mathrm{o}\mathrm{m}(g/h g)_{0}=\{[\mathrm{i}\mathrm{d}_{c/h}] [ $\Phi$] \circ $\Phi$]\}\cong \mathbb{z}_{2}\oplus \mathbb{z}_{2} ただし --(ah):={}^{t}a^{-1}h $\Phi$(aH):=I_{1n-1}aI_{1}{}_{n-1}H for a\in G *3 正確には田 ] では n\geq 3 である しかし 簡単な確認により n=2 でも成立することがわかる
6 147 余談 2 アフィン対称空間には標準アフィン接続というものが考えられる 定理 3 における条件の場合 それは gf_{\sim}^{\rightarrow} よるレビチビタ接続と一致する 標準アフィン接続 ( レビチビタ接続 ) に関するアフィン変換群は 実は 等長変換群 Isom(GlH g) と完全に一致し : 今回の等長変換群の決定は標準アフィン接続 ( レビチビタ接続 ) に 関するアフィン変換群の決定とも言える またこの等長変換群とアフィン変換群との同一性から 実は G/H の 相似変換は必ず等長変換となる すなわち 相似 と 等長 は同一の概念となる 謝辞本研究に際し 終始ご指導ご鞭燵を賜りました坊向伸隆先生に深謝申し上げます また本研究集会において 様々なご支援頂きました佐藤隆夫先生 発表の場を設けて下さった世話人の藤田亮介先生に御礼申し上げますと共に 本講演をお聞き下さった方々に感謝致します 参考文献 [Ka Koz] S Kaneyuki and M Kozai Paracomplex structures and affine symmetric spaces Tokyo J Math 8 (1985) no [Koh] S S Koh On affine symmetric spaces Amer Math Soc 119 (1965) [Sh Su] T Shimokawa and K Sugimoto On the groups of isometries of simple para Hermitian symmetric spaces preprint [St] N Steenrod Topology of fibre bundles Princeton Univ Press Princeton 1951 [Ta] M Takeuchi On the fundamental group and the group of isometries of a symmetric space J Fac Sci Univ Tokyo Sect I 10 (1964)
PowerPoint Presentation
 付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
Microsoft PowerPoint - 10.pptx
 m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
Microsoft PowerPoint - 9.pptx
 9/7/8( 水 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 拡大とスカラー倍 行列演算と写像 ( 次変換 拡大後 k 倍 k 倍 k 倍拡大の関係は スカラー倍を用いて次のように表現できる p = (, ' = k ' 拡大前 p ' = ( ', ' = ( k, k 拡大 4 拡大と行列の積 拡大後 k 倍
9/7/8( 水 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 拡大とスカラー倍 行列演算と写像 ( 次変換 拡大後 k 倍 k 倍 k 倍拡大の関係は スカラー倍を用いて次のように表現できる p = (, ' = k ' 拡大前 p ' = ( ', ' = ( k, k 拡大 4 拡大と行列の積 拡大後 k 倍
航空機の運動方程式
 可制御性 可観測性. 可制御性システムの状態を, 適切な操作によって, 有限時間内に, 任意の状態から別の任意の状態に移動させることができるか否かという特性を可制御性という. 可制御性を有するシステムに対し, システムは可制御である, 可制御なシステム という言い方をする. 状態方程式, 出力方程式が以下で表されるn 次元 m 入力 r 出力線形時不変システム x Ax u y x Du () に対し,
可制御性 可観測性. 可制御性システムの状態を, 適切な操作によって, 有限時間内に, 任意の状態から別の任意の状態に移動させることができるか否かという特性を可制御性という. 可制御性を有するシステムに対し, システムは可制御である, 可制御なシステム という言い方をする. 状態方程式, 出力方程式が以下で表されるn 次元 m 入力 r 出力線形時不変システム x Ax u y x Du () に対し,
Microsoft Word - thesis.doc
 剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
DVIOUT-17syoze
 平面の合同変換と相似変換 岩瀬順一 要約 : 平面の合同変換と相似変換を論じる いま大学で行列を学び始めている大学一年生を念頭に置いている 高等学校で行列や一次変換を学んでいなくてもよい 1. 写像 定義 1.1 X, Y を集合とする X の各元 x に対し Y のただ一つの元 y を対応させる規則 f を写像とよび,f : X! Y のように書く f によって x に対応する Y の元を f(x)
平面の合同変換と相似変換 岩瀬順一 要約 : 平面の合同変換と相似変換を論じる いま大学で行列を学び始めている大学一年生を念頭に置いている 高等学校で行列や一次変換を学んでいなくてもよい 1. 写像 定義 1.1 X, Y を集合とする X の各元 x に対し Y のただ一つの元 y を対応させる規則 f を写像とよび,f : X! Y のように書く f によって x に対応する Y の元を f(x)
曲面上の正則閉曲線の回転数について (新しい変換群論とその周辺)
 数理解析研究所講究録第 2016 巻 2017 年 168-174 168 曲面上の正則閉曲線の回転数について On Rotation Numbers of Regular on Surfaces Closed Curves 岡山理科大学 理学部山崎正之 Masayuki Yamasaki Faculty of Science, Okayama University of Science 1 序 論文
数理解析研究所講究録第 2016 巻 2017 年 168-174 168 曲面上の正則閉曲線の回転数について On Rotation Numbers of Regular on Surfaces Closed Curves 岡山理科大学 理学部山崎正之 Masayuki Yamasaki Faculty of Science, Okayama University of Science 1 序 論文
<4D F736F F D E4F8E9F82C982A882AF82E98D7397F1>
 3 三次における行列 要旨高校では ほとんど 2 2 の正方行列しか扱ってなく 三次の正方行列について考えてみたかったため 数 C で学んだ定理を三次の正方行列に応用して 自分たちで仮説を立てて求めていったら 空間における回転移動を表す行列 三次のケーリー ハミルトンの定理 三次における逆行列を求めたり 仮説をたてることができた. 目的 数 C で学んだ定理を三次の正方行列に応用する 2. 概要目的の到達点として
3 三次における行列 要旨高校では ほとんど 2 2 の正方行列しか扱ってなく 三次の正方行列について考えてみたかったため 数 C で学んだ定理を三次の正方行列に応用して 自分たちで仮説を立てて求めていったら 空間における回転移動を表す行列 三次のケーリー ハミルトンの定理 三次における逆行列を求めたり 仮説をたてることができた. 目的 数 C で学んだ定理を三次の正方行列に応用する 2. 概要目的の到達点として
以下 変数の上のドットは時間に関する微分を表わしている (ex. 2 dx d x x, x 2 dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-1) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( x や x, x などがすべて 1 次で なおかつ
 以下 変数の上のドットは時間に関する微分を表わしている (e. d d, dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( や, などがすべて 次で なおかつそれらの係数が定数であるような微分方程式 ) に対して安定性の解析を行ってきた しかしながら 実際には非線形の微分方程式で記述される現象も多く存在する
以下 変数の上のドットは時間に関する微分を表わしている (e. d d, dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( や, などがすべて 次で なおかつそれらの係数が定数であるような微分方程式 ) に対して安定性の解析を行ってきた しかしながら 実際には非線形の微分方程式で記述される現象も多く存在する
Microsoft PowerPoint - 第3回2.ppt
 講義内容 講義内容 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 ベクトルの直交性 3
講義内容 講義内容 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 ベクトルの直交性 3
Dehn 手術による 3 次元多様体の構成 Lickorish-Wallace の定理 B 久家正樹指導教員古宇田悠哉広島大学理学部数学科卒業論文 2017 年 2 月 10 日
 Dehn 手術による 3 次元多様体の構成 Lickorish-Wallace の定理 B132209 久家正樹指導教員古宇田悠哉広島大学理学部数学科卒業論文 2017 年 2 月 10 日 まえがき 3 次元多様体論を 1 年間学んできた過程で, 全ての閉曲面が完全に分類できるという定理に出会い, さらに 1 つ上の次元の 3 次元多様体の分類について興味を持った. 3 次元多様体に対するこの問題は,
Dehn 手術による 3 次元多様体の構成 Lickorish-Wallace の定理 B132209 久家正樹指導教員古宇田悠哉広島大学理学部数学科卒業論文 2017 年 2 月 10 日 まえがき 3 次元多様体論を 1 年間学んできた過程で, 全ての閉曲面が完全に分類できるという定理に出会い, さらに 1 つ上の次元の 3 次元多様体の分類について興味を持った. 3 次元多様体に対するこの問題は,
Microsoft PowerPoint - H22制御工学I-2回.ppt
 制御工学 I 第二回ラプラス変換 平成 年 4 月 9 日 /4/9 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
制御工学 I 第二回ラプラス変換 平成 年 4 月 9 日 /4/9 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
Microsoft PowerPoint - H21生物計算化学2.ppt
 演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
第 6 章超ゲージ対称性 2002 年 1/12 第 6 章超ゲージ対称性 Non-abelian ゲージ群 第 1 章場の変換性と演算子 - 変数 X が同じとき より T a を generators にもつ Non-abelian 群の下で に注意して カイラル超場 F が = W = ( )
 第 6 章超ゲージ対称性 00 年 / 第 6 章超ゲージ対称性 o-el ゲージ群 第 章場の変換性と演算子 - 変数 X が同じとき より T を geetos にもつ o-el 群の下で に注意して カイラル超場 F が = W = W = ( ) ( gk T ) ˆ j ( gk T ) ( gk t ) ˆ j j U ˆ j U ˆ wth U ep T & ep t Ü ep - ep
第 6 章超ゲージ対称性 00 年 / 第 6 章超ゲージ対称性 o-el ゲージ群 第 章場の変換性と演算子 - 変数 X が同じとき より T を geetos にもつ o-el 群の下で に注意して カイラル超場 F が = W = W = ( ) ( gk T ) ˆ j ( gk T ) ( gk t ) ˆ j j U ˆ j U ˆ wth U ep T & ep t Ü ep - ep
2 α 2 A α 1 α 5 α 3 α 4 1.2: A 3 π n 4 n 3 n = 3 n 3 n = 2 1 α A 4π α/2π A = 4π α 2π = 2α n = 2 α α 1.3: 2 n = 3,, R 3 α, β, γ S 2,, R,, R 2, R 2 T T
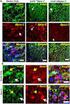 1 I: 1.1 3 1 S 2 = {(x, y, z) : x 2 + y 2 + z 2 = 1} O S 2 S 2 n n O (a) (b) 3 1.1: 3 n A α 1,, α n n α j = (n 2)π + A j=1 n (n 2)π 2 α 2 A α 1 α 5 α 3 α 4 1.2: A 3 π n 4 n 3 n = 3 n 3 n = 2 1 α A 4π α/2π
1 I: 1.1 3 1 S 2 = {(x, y, z) : x 2 + y 2 + z 2 = 1} O S 2 S 2 n n O (a) (b) 3 1.1: 3 n A α 1,, α n n α j = (n 2)π + A j=1 n (n 2)π 2 α 2 A α 1 α 5 α 3 α 4 1.2: A 3 π n 4 n 3 n = 3 n 3 n = 2 1 α A 4π α/2π
2018年度 筑波大・理系数学
 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ < < とする 放物線 上に 点 (, ), A (ta, ta ), B( - ta, ta ) をとる 三角形 AB の内心の 座標を p とし, 外心の 座標を q とする また, 正の実数 a に対して, 直線 a と放物線 で囲まれた図形の面積を S( a) で表す () p, q を cos を用いて表せ S( p) () S(
筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ < < とする 放物線 上に 点 (, ), A (ta, ta ), B( - ta, ta ) をとる 三角形 AB の内心の 座標を p とし, 外心の 座標を q とする また, 正の実数 a に対して, 直線 a と放物線 で囲まれた図形の面積を S( a) で表す () p, q を cos を用いて表せ S( p) () S(
vecrot
 1. ベクトル ベクトル : 方向を持つ量 ベクトルには 1 方向 2 大きさ ( 長さ ) という 2 つの属性がある ベクトルの例 : 物体の移動速度 移動量電場 磁場の強さ風速力トルクなど 2. ベクトルの表現 2.1 矢印で表現される 矢印の長さ : ベクトルの大きさ 矢印の向き : ベクトルの方向 2.2 2 個の点を用いて表現する 始点 () と終点 () を結ぶ半直線の向き : ベクトルの方向
1. ベクトル ベクトル : 方向を持つ量 ベクトルには 1 方向 2 大きさ ( 長さ ) という 2 つの属性がある ベクトルの例 : 物体の移動速度 移動量電場 磁場の強さ風速力トルクなど 2. ベクトルの表現 2.1 矢印で表現される 矢印の長さ : ベクトルの大きさ 矢印の向き : ベクトルの方向 2.2 2 個の点を用いて表現する 始点 () と終点 () を結ぶ半直線の向き : ベクトルの方向
2010年度 筑波大・理系数学
 00 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ f( x) x ax とおく ただしa>0 とする () f( ) f() となるa の範囲を求めよ () f(x) の極小値が f ( ) 以下になる a の範囲を求めよ () x における f(x) の最小値をa を用いて表せ -- 00 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ つの曲線 C : y six ( 0
00 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ f( x) x ax とおく ただしa>0 とする () f( ) f() となるa の範囲を求めよ () f(x) の極小値が f ( ) 以下になる a の範囲を求めよ () x における f(x) の最小値をa を用いて表せ -- 00 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ つの曲線 C : y six ( 0
2011年度 筑波大・理系数学
 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ O を原点とするy 平面において, 直線 y= の を満たす部分をC とする () C 上に点 A( t, ) をとるとき, 線分 OA の垂直二等分線の方程式を求めよ () 点 A が C 全体を動くとき, 線分 OA の垂直二等分線が通過する範囲を求め, それ を図示せよ -- 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ
0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ O を原点とするy 平面において, 直線 y= の を満たす部分をC とする () C 上に点 A( t, ) をとるとき, 線分 OA の垂直二等分線の方程式を求めよ () 点 A が C 全体を動くとき, 線分 OA の垂直二等分線が通過する範囲を求め, それ を図示せよ -- 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ
ポンスレの定理
 ポンスレの定理. qution Section 定理 有本彰雄 東京都市大学 平成 年 月 4 日 定義. n 角形 P とは 平面上にあるn 個の点の順序列 ( p, p,, pn - ) のことである 各 pk は P の頂点と呼ばれる 記号法を簡単にするため便宜的に p n とする また 線分 p i i pp, i,,,, n - を P の辺と呼ぶ 定義. すべての頂点 p k が曲線 C
ポンスレの定理. qution Section 定理 有本彰雄 東京都市大学 平成 年 月 4 日 定義. n 角形 P とは 平面上にあるn 個の点の順序列 ( p, p,, pn - ) のことである 各 pk は P の頂点と呼ばれる 記号法を簡単にするため便宜的に p n とする また 線分 p i i pp, i,,,, n - を P の辺と呼ぶ 定義. すべての頂点 p k が曲線 C
経済数学演習問題 2018 年 5 月 29 日 I a, b, c R n に対して a + b + c 2 = a 2 + b 2 + c 2 + 2( a, b) + 2( b, c) + 2( a, c) が成立することを示しましょう.( 線型代数学 教科書 13 ページ 演習 1.17)
 経済数学演習問題 8 年 月 9 日 I a, b, c R n に対して a + b + c a + b + c + a, b + b, c + a, c が成立することを示しましょう. 線型代数学 教科書 ページ 演習.7 II a R n がすべての x R n に対して垂直, すなわち a, x x R n が成立するとします. このとき a となることを示しましょう. 線型代数学 教科書
経済数学演習問題 8 年 月 9 日 I a, b, c R n に対して a + b + c a + b + c + a, b + b, c + a, c が成立することを示しましょう. 線型代数学 教科書 ページ 演習.7 II a R n がすべての x R n に対して垂直, すなわち a, x x R n が成立するとします. このとき a となることを示しましょう. 線型代数学 教科書
Microsoft Word - K-ピタゴラス数.doc
 - ピタゴラス数の代数と幾何学 津山工業高等専門学校 菅原孝慈 ( 情報工学科 年 ) 野山由貴 ( 情報工学科 年 ) 草地弘幸 ( 電子制御工学科 年 ) もくじ * 第 章ピタゴラス数の幾何学 * 第 章ピタゴラス数の代数学 * 第 3 章代数的極小元の幾何学の考察 * 第 章ピタゴラス数の幾何学的研究の動機 交点に注目すると, つの曲線が直交しているようにみえる. これらは本当に直交しているのだろうか.
- ピタゴラス数の代数と幾何学 津山工業高等専門学校 菅原孝慈 ( 情報工学科 年 ) 野山由貴 ( 情報工学科 年 ) 草地弘幸 ( 電子制御工学科 年 ) もくじ * 第 章ピタゴラス数の幾何学 * 第 章ピタゴラス数の代数学 * 第 3 章代数的極小元の幾何学の考察 * 第 章ピタゴラス数の幾何学的研究の動機 交点に注目すると, つの曲線が直交しているようにみえる. これらは本当に直交しているのだろうか.
Microsoft PowerPoint - mp11-02.pptx
 数理計画法第 2 回 塩浦昭義情報科学研究科准教授 [email protected] http://www.dais.is.tohoku.ac.jp/~shioura/teaching 前回の復習 数理計画とは? 数理計画 ( 復習 ) 数理計画問題とは? 狭義には : 数理 ( 数学 ) を使って計画を立てるための問題 広義には : 与えられた評価尺度に関して最も良い解を求める問題
数理計画法第 2 回 塩浦昭義情報科学研究科准教授 [email protected] http://www.dais.is.tohoku.ac.jp/~shioura/teaching 前回の復習 数理計画とは? 数理計画 ( 復習 ) 数理計画問題とは? 狭義には : 数理 ( 数学 ) を使って計画を立てるための問題 広義には : 与えられた評価尺度に関して最も良い解を求める問題
2018年度 東京大・理系数学
 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ関数 f ( ) = + cos (0 < < ) の増減表をつくり, + 0, 0 のと sin きの極限を調べよ 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ n+ 数列 a, a, を, Cn a n = ( n =,, ) で定める n! an qn () n とする を既約分数 an p として表したときの分母
08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ関数 f ( ) = + cos (0 < < ) の増減表をつくり, + 0, 0 のと sin きの極限を調べよ 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ n+ 数列 a, a, を, Cn a n = ( n =,, ) で定める n! an qn () n とする を既約分数 an p として表したときの分母
補足 中学で学習したフレミング左手の法則 ( 電 磁 力 ) と関連付けると覚えやすい 電磁力は電流と磁界の外積で表される 力 F 磁 電磁力 F li 右ねじの回転の向き電 li ( l は導線の長さ ) 補足 有向線分とベクトル有向線分 : 矢印の位
 http://totemt.sur.ne.p 外積 ( ベクトル積 ) の活用 ( 面積, 法線ベクトル, 平面の方程式 ) 3 次元空間の つのベクトルの積が つのベクトルを与えるようなベクトルの掛け算 ベクトルの積がベクトルを与えることからベクトル積とも呼ばれる これに対し内積は符号と大きさをもつ量 ( スカラー量 ) を与えるので, スカラー積とも呼ばれる 外積を使うと, 平行四辺形や三角形の面積,
http://totemt.sur.ne.p 外積 ( ベクトル積 ) の活用 ( 面積, 法線ベクトル, 平面の方程式 ) 3 次元空間の つのベクトルの積が つのベクトルを与えるようなベクトルの掛け算 ベクトルの積がベクトルを与えることからベクトル積とも呼ばれる これに対し内積は符号と大きさをもつ量 ( スカラー量 ) を与えるので, スカラー積とも呼ばれる 外積を使うと, 平行四辺形や三角形の面積,
2014年度 筑波大・理系数学
 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ f ( x) = x x とする y = f ( x ) のグラフに点 P(, ) から引いた接線は 本あるとする つの接点 A (, f ( )), B(, f ( )), C(, f ( )) を頂点とする三角形の 重心を G とする () + +, + + および を, を用いて表せ () 点 G の座標を, を用いて表せ () 点 G
筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ f ( x) = x x とする y = f ( x ) のグラフに点 P(, ) から引いた接線は 本あるとする つの接点 A (, f ( )), B(, f ( )), C(, f ( )) を頂点とする三角形の 重心を G とする () + +, + + および を, を用いて表せ () 点 G の座標を, を用いて表せ () 点 G
微分方程式による現象記述と解きかた
 微分方程式による現象記述と解きかた 土木工学 : 公共諸施設 構造物の有用目的にむけた合理的な実現をはかる方法 ( 技術 ) に関する学 橋梁 トンネル ダム 道路 港湾 治水利水施設 安全化 利便化 快適化 合法則的 経済的 自然および人口素材によって作られた 質量保存則 構造物の自然的な性質 作用 ( 外力による応答 ) エネルギー則 の解明 社会的諸現象のうち マスとしての移動 流通 運動量則
微分方程式による現象記述と解きかた 土木工学 : 公共諸施設 構造物の有用目的にむけた合理的な実現をはかる方法 ( 技術 ) に関する学 橋梁 トンネル ダム 道路 港湾 治水利水施設 安全化 利便化 快適化 合法則的 経済的 自然および人口素材によって作られた 質量保存則 構造物の自然的な性質 作用 ( 外力による応答 ) エネルギー則 の解明 社会的諸現象のうち マスとしての移動 流通 運動量則
オートマトン 形式言語及び演習 3. 正規表現 酒井正彦 正規表現とは 正規表現 ( 正則表現, Regular Expression) オートマトン : 言語を定義する機械正規表現 : 言語
 オートマトン 形式言語及び演習 3. 酒井正彦 www.trs.css.i.nagoya-u.ac.jp/~sakai/lecture/automata/ とは ( 正則表現, Regular Expression) オートマトン : 言語を定義する機械 : 言語を記号列で定義 - 記述しやすい ( ユーザフレンドリ ) 例 :01 + 10 - UNIX の grep コマンド - UNIX の
オートマトン 形式言語及び演習 3. 酒井正彦 www.trs.css.i.nagoya-u.ac.jp/~sakai/lecture/automata/ とは ( 正則表現, Regular Expression) オートマトン : 言語を定義する機械 : 言語を記号列で定義 - 記述しやすい ( ユーザフレンドリ ) 例 :01 + 10 - UNIX の grep コマンド - UNIX の
千葉大学 ゲーム論II
 千葉大学ゲーム論 II 第五, 六回 担当 上條良夫 千葉大学ゲーム論 II 第五 六回上條良夫 本日の講義内容 前回宿題の問題 3 の解答 Nash の交渉問題 Nash 解とその公理的特徴づけ 千葉大学ゲーム論 II 第五 六回上條良夫 宿題の問題 3 の解答 ホワイトボードでやる 千葉大学ゲーム論 II 第五 六回上條良夫 3 Nash の二人交渉問題 Nash の二人交渉問題は以下の二つから構成される
千葉大学ゲーム論 II 第五, 六回 担当 上條良夫 千葉大学ゲーム論 II 第五 六回上條良夫 本日の講義内容 前回宿題の問題 3 の解答 Nash の交渉問題 Nash 解とその公理的特徴づけ 千葉大学ゲーム論 II 第五 六回上條良夫 宿題の問題 3 の解答 ホワイトボードでやる 千葉大学ゲーム論 II 第五 六回上條良夫 3 Nash の二人交渉問題 Nash の二人交渉問題は以下の二つから構成される
Microsoft Word - 付録1誘導機の2軸理論.doc
 NAOSIE: Nagaaki Univity' Ac itl パワーエレクトロニクスと電動機制御入門 Autho( 辻, 峰男 Citation パワーエレクトロニクスと電動機制御入門 ; 15 Iu Dat 15 U http://hl.hanl.nt/169/55 ight hi ocumnt i ownloa http://naoit.lb.nagaaki-u.ac.jp 付録 1 誘導機の
NAOSIE: Nagaaki Univity' Ac itl パワーエレクトロニクスと電動機制御入門 Autho( 辻, 峰男 Citation パワーエレクトロニクスと電動機制御入門 ; 15 Iu Dat 15 U http://hl.hanl.nt/169/55 ight hi ocumnt i ownloa http://naoit.lb.nagaaki-u.ac.jp 付録 1 誘導機の
DVIOUT-SS_Ma
 第 章 微分方程式 ニュートンはリンゴが落ちるのを見て万有引力を発見した という有名な逸話があります 無重力の宇宙船の中ではリンゴは落ちないで静止していることを考えると 重力が働くと始め静止しているものが動き出して そのスピードはどんどん大きくなる つまり速度の変化が現れることがわかります 速度は一般に時間と共に変化します 速度の瞬間的変化の割合を加速度といい で定義しましょう 速度が変化する, つまり加速度がでなくなるためにはその原因があり
第 章 微分方程式 ニュートンはリンゴが落ちるのを見て万有引力を発見した という有名な逸話があります 無重力の宇宙船の中ではリンゴは落ちないで静止していることを考えると 重力が働くと始め静止しているものが動き出して そのスピードはどんどん大きくなる つまり速度の変化が現れることがわかります 速度は一般に時間と共に変化します 速度の瞬間的変化の割合を加速度といい で定義しましょう 速度が変化する, つまり加速度がでなくなるためにはその原因があり
Matrix and summation convention Kronecker delta δ ij 1 = 0 ( i = j) ( i j) permutation symbol e ijk = (even permutation) (odd permutation) (othe
 Matr ad summato covto Krockr dlta δ ( ) ( ) prmutato symbol k (v prmutato) (odd prmutato) (othrs) gvalu dtrmat dt 6 k rst r s kt opyrght s rsrvd. No part of ths documt may b rproducd for proft. 行列 行 正方行列
Matr ad summato covto Krockr dlta δ ( ) ( ) prmutato symbol k (v prmutato) (odd prmutato) (othrs) gvalu dtrmat dt 6 k rst r s kt opyrght s rsrvd. No part of ths documt may b rproducd for proft. 行列 行 正方行列
航空機の運動方程式
 オブザーバ 状態フィードバックにはすべての状態変数の値が必要であった. しかしながら, システムの外部から観測できるのは出力だけであり, すべての状態変数が観測できるとは限らない. そこで, 制御対象システムの状態変数を, システムのモデルに基づいてその入出力信号から推定する方法を考える.. オブザーバとは 次元 m 入力 r 出力線形時不変システム x Ax Bu y Cx () の状態変数ベクトル
オブザーバ 状態フィードバックにはすべての状態変数の値が必要であった. しかしながら, システムの外部から観測できるのは出力だけであり, すべての状態変数が観測できるとは限らない. そこで, 制御対象システムの状態変数を, システムのモデルに基づいてその入出力信号から推定する方法を考える.. オブザーバとは 次元 m 入力 r 出力線形時不変システム x Ax Bu y Cx () の状態変数ベクトル
2015-2017年度 2次数学セレクション(複素数)解答解説
 05 次数学セレクション解答解説 [ 筑波大 ] ( + より, 0 となり, + から, ( (,, よって, の描く図形 C は, 点 を中心とし半径が の円である すなわち, 原 点を通る円となる ( は虚数, は正の実数より, である さて, w ( ( とおくと, ( ( ( w ( ( ( ここで, w は純虚数より, は純虚数となる すると, の描く図形 L は, 点 を通り, 点 と点
05 次数学セレクション解答解説 [ 筑波大 ] ( + より, 0 となり, + から, ( (,, よって, の描く図形 C は, 点 を中心とし半径が の円である すなわち, 原 点を通る円となる ( は虚数, は正の実数より, である さて, w ( ( とおくと, ( ( ( w ( ( ( ここで, w は純虚数より, は純虚数となる すると, の描く図形 L は, 点 を通り, 点 と点
1/10 平成 29 年 3 月 24 日午後 1 時 37 分第 5 章ローレンツ変換と回転 第 5 章ローレンツ変換と回転 Ⅰ. 回転 第 3 章光速度不変の原理とローレンツ変換 では 時間の遅れをローレンツ変換 ct 移動 v相対 v相対 ct - x x - ct = c, x c 2 移動
 / 平成 9 年 3 月 4 日午後 時 37 分第 5 章ローレンツ変換と回転 第 5 章ローレンツ変換と回転 Ⅰ. 回転 第 3 章光速度不変の原理とローレンツ変換 では 時間の遅れをローレンツ変換 t t - x x - t, x 静止静止静止静止 を導いた これを 図の場合に当てはめると t - x x - t t, x t + x x + t t, x (5.) (5.) (5.3) を得る
/ 平成 9 年 3 月 4 日午後 時 37 分第 5 章ローレンツ変換と回転 第 5 章ローレンツ変換と回転 Ⅰ. 回転 第 3 章光速度不変の原理とローレンツ変換 では 時間の遅れをローレンツ変換 t t - x x - t, x 静止静止静止静止 を導いた これを 図の場合に当てはめると t - x x - t t, x t + x x + t t, x (5.) (5.) (5.3) を得る
例 e 指数関数的に減衰する信号を h( a < + a a すると, それらのラプラス変換は, H ( ) { e } e インパルス応答が h( a < ( ただし a >, U( ) { } となるシステムにステップ信号 ( y( のラプラス変換 Y () は, Y ( ) H ( ) X (
 第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
チュートリアル:ノンパラメトリックベイズ
 { x,x, L, xn} 2 p( θ, θ, θ, θ, θ, } { 2 3 4 5 θ6 p( p( { x,x, L, N} 2 x { θ, θ2, θ3, θ4, θ5, θ6} K n p( θ θ n N n θ x N + { x,x, L, N} 2 x { θ, θ2, θ3, θ4, θ5, θ6} log p( 6 n logθ F 6 log p( + λ θ F θ
{ x,x, L, xn} 2 p( θ, θ, θ, θ, θ, } { 2 3 4 5 θ6 p( p( { x,x, L, N} 2 x { θ, θ2, θ3, θ4, θ5, θ6} K n p( θ θ n N n θ x N + { x,x, L, N} 2 x { θ, θ2, θ3, θ4, θ5, θ6} log p( 6 n logθ F 6 log p( + λ θ F θ
Microsoft PowerPoint - H22制御工学I-10回.ppt
 制御工学 I 第 回 安定性 ラウス, フルビッツの安定判別 平成 年 6 月 日 /6/ 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
制御工学 I 第 回 安定性 ラウス, フルビッツの安定判別 平成 年 6 月 日 /6/ 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
線型代数試験前最後の 3 日間 できるようになっておきたい計算問題 ( 特に注意 まぁ注意 ) シュミットの直交化とその行列表示 (P5) ユニタリ行列による行列の対角化 (P8) 数列, 微分方程式の解法 対角可能な条件もおさえておきたい とりあえず次の問題を ( まだやっていない人は ) やって
 線型代数試験前最後の 日間 できるようになっておきたい計算問題 特に注意 まぁ注意 シュミットの直交化とその行列表示 P ユニタリ行列による行列の対角化 P8 数列 微分方程式の解法 対角可能な条件もおさえておきたい とりあえず次の問題を まだやっていない人は やってください 8 年 月 日 理二三 組の線型代数担当志甫先生の過去問から持ってきました 結構計算が大変だったと思います これが難なくできる人は以下の総復習編はさらっと目を通すだけで
線型代数試験前最後の 日間 できるようになっておきたい計算問題 特に注意 まぁ注意 シュミットの直交化とその行列表示 P ユニタリ行列による行列の対角化 P8 数列 微分方程式の解法 対角可能な条件もおさえておきたい とりあえず次の問題を まだやっていない人は やってください 8 年 月 日 理二三 組の線型代数担当志甫先生の過去問から持ってきました 結構計算が大変だったと思います これが難なくできる人は以下の総復習編はさらっと目を通すだけで
DVIOUT
 第 章 離散フーリエ変換 離散フーリエ変換 これまで 私たちは連続関数に対するフーリエ変換およびフーリエ積分 ( 逆フーリエ変換 ) について学んできました この節では フーリエ変換を離散化した離散フーリエ変換について学びましょう 自然現象 ( 音声 ) などを観測して得られる波 ( 信号値 ; 観測値 ) は 通常 電気信号による連続的な波として観測機器から出力されます しかしながら コンピュータはこの様な連続的な波を直接扱うことができないため
第 章 離散フーリエ変換 離散フーリエ変換 これまで 私たちは連続関数に対するフーリエ変換およびフーリエ積分 ( 逆フーリエ変換 ) について学んできました この節では フーリエ変換を離散化した離散フーリエ変換について学びましょう 自然現象 ( 音声 ) などを観測して得られる波 ( 信号値 ; 観測値 ) は 通常 電気信号による連続的な波として観測機器から出力されます しかしながら コンピュータはこの様な連続的な波を直接扱うことができないため
数学の学び方のヒント
 数学 Ⅱ における微分単元の 指導法の改善に関する研究 2017 年 10 月北数教旭川大会で発表した内容です 北海道札幌国際情報高等学校和田文興 1 Ⅰ. 研究の動機と背景 高校では極限を厳密に定義できず, 曖昧でわかりにくい. 私自身は, はじめて微分と出会ったとき, 極限の考え方等が納得できなかった. y () a h 接線 a 傾き (a) 2 Ⅰ. 研究の動機と背景 微分の指導改善に関する優れた先行研究がいくつかあるが,
数学 Ⅱ における微分単元の 指導法の改善に関する研究 2017 年 10 月北数教旭川大会で発表した内容です 北海道札幌国際情報高等学校和田文興 1 Ⅰ. 研究の動機と背景 高校では極限を厳密に定義できず, 曖昧でわかりにくい. 私自身は, はじめて微分と出会ったとき, 極限の考え方等が納得できなかった. y () a h 接線 a 傾き (a) 2 Ⅰ. 研究の動機と背景 微分の指導改善に関する優れた先行研究がいくつかあるが,
代数 幾何 < ベクトル > 1 ベクトルの演算 和 差 実数倍については 文字の計算と同様 2 ベクトルの成分表示 平面ベクトル : a x e y e x, ) ( 1 y1 空間ベクトル : a x e y e z e x, y, ) ( 1 1 z1
 代数 幾何 < ベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル :, 空間ベクトル : z,, z 成分での計算ができるようにすること ベクトルの内積 : os 平面ベクトル :,, 空間ベクトル :,,,, z z zz 4 ベクトルの大きさ 平面上 : 空間上 : z は 良く用いられる 5 m: に分ける点 : m m 図形への応用
代数 幾何 < ベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル :, 空間ベクトル : z,, z 成分での計算ができるようにすること ベクトルの内積 : os 平面ベクトル :,, 空間ベクトル :,,,, z z zz 4 ベクトルの大きさ 平面上 : 空間上 : z は 良く用いられる 5 m: に分ける点 : m m 図形への応用
数学の世界
 東京女子大学文理学部数学の世界 (2002 年度 ) 永島孝 17 6 行列式の基本法則と効率的な計算法 基本法則 三次以上の行列式についても, 二次の場合と同様な法則がなりたつ ここには三次の場合を例示するが, 四次以上でも同様である 1 単位行列の行列式の値は 1 である すなわち 1 0 0 0 1 0 1 0 0 1 2 二つの列を入れ替えると行列式の値は 1 倍になる 例えば a 13 a
東京女子大学文理学部数学の世界 (2002 年度 ) 永島孝 17 6 行列式の基本法則と効率的な計算法 基本法則 三次以上の行列式についても, 二次の場合と同様な法則がなりたつ ここには三次の場合を例示するが, 四次以上でも同様である 1 単位行列の行列式の値は 1 である すなわち 1 0 0 0 1 0 1 0 0 1 2 二つの列を入れ替えると行列式の値は 1 倍になる 例えば a 13 a
Microsoft PowerPoint - ce07-09b.ppt
 6. フィードバック系の内部安定性キーワード : 内部安定性, 特性多項式 6. ナイキストの安定判別法キーワード : ナイキストの安定判別法 復習 G u u u 制御対象コントローラ u T 閉ループ伝達関数フィードバック制御系 T 相補感度関数 S S T L 開ループ伝達関数 L いま考えているのは どの伝達関数,, T, L? フィードバック系の内部安定性 u 内部安定性 T G だけでは不十分
6. フィードバック系の内部安定性キーワード : 内部安定性, 特性多項式 6. ナイキストの安定判別法キーワード : ナイキストの安定判別法 復習 G u u u 制御対象コントローラ u T 閉ループ伝達関数フィードバック制御系 T 相補感度関数 S S T L 開ループ伝達関数 L いま考えているのは どの伝達関数,, T, L? フィードバック系の内部安定性 u 内部安定性 T G だけでは不十分
曲線 = f () は を媒介変数とする自然な媒介変数表示 =,= f () をもつので, これを利用して説明する 以下,f () は定義域で連続であると仮定する 例えば, 直線 =c が曲線 = f () の漸近線になるとする 曲線 = f () 上の点 P(,f ()) が直線 =c に近づくこ
 伊伊伊伊伊伊伊伊伊伊 伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊 漸近線の求め方に関する考察 たまい玉井 かつき克樹 伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊 伊伊伊伊伊伊伊伊伊伊. 漸近線についての生徒からの質問 数学において図を使って直感的な説明を与えることは, 理解を深めるのに大いに役立つ
伊伊伊伊伊伊伊伊伊伊 伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊 漸近線の求め方に関する考察 たまい玉井 かつき克樹 伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊伊 伊伊伊伊伊伊伊伊伊伊. 漸近線についての生徒からの質問 数学において図を使って直感的な説明を与えることは, 理解を深めるのに大いに役立つ
2011年度 大阪大・理系数学
 0 大阪大学 ( 理系 ) 前期日程問題 解答解説のページへ a a を自然数とする O を原点とする座標平面上で行列 A= a の表す 次変換 を f とする cosθ siθ () >0 および0θ
0 大阪大学 ( 理系 ) 前期日程問題 解答解説のページへ a a を自然数とする O を原点とする座標平面上で行列 A= a の表す 次変換 を f とする cosθ siθ () >0 および0θ
線形代数とは
 線形代数とは 第一回ベクトル 教科書 エクササイズ線形代数 立花俊一 成田清正著 共立出版 必要最低限のことに限る 得意な人には物足りないかもしれません 線形代数とは何をするもの? 線形関係 y 直線 yもも 次式で登場する (( 次の形 ) 線形 ただし 次元の話世の中は 3 次元 [4[ 次元 ] 次元 3 次元 4 次元 はどうやって直線を表すの? ベクトルや行列の概念 y A ベクトルを使うと
線形代数とは 第一回ベクトル 教科書 エクササイズ線形代数 立花俊一 成田清正著 共立出版 必要最低限のことに限る 得意な人には物足りないかもしれません 線形代数とは何をするもの? 線形関係 y 直線 yもも 次式で登場する (( 次の形 ) 線形 ただし 次元の話世の中は 3 次元 [4[ 次元 ] 次元 3 次元 4 次元 はどうやって直線を表すの? ベクトルや行列の概念 y A ベクトルを使うと
Microsoft Word - 201hyouka-tangen-1.doc
 数学 Ⅰ 評価規準の作成 ( 単元ごと ) 数学 Ⅰ の目標及び図形と計量について理解させ 基礎的な知識の習得と技能の習熟を図り それらを的確に活用する機能を伸ばすとともに 数学的な見方や考え方のよさを認識できるようにする 評価の観点の趣旨 式と不等式 二次関数及び図形と計量における考え方に関 心をもつとともに 数学的な見方や考え方のよさを認識し それらを事象の考察に活用しようとする 式と不等式 二次関数及び図形と計量における数学的な見
数学 Ⅰ 評価規準の作成 ( 単元ごと ) 数学 Ⅰ の目標及び図形と計量について理解させ 基礎的な知識の習得と技能の習熟を図り それらを的確に活用する機能を伸ばすとともに 数学的な見方や考え方のよさを認識できるようにする 評価の観点の趣旨 式と不等式 二次関数及び図形と計量における考え方に関 心をもつとともに 数学的な見方や考え方のよさを認識し それらを事象の考察に活用しようとする 式と不等式 二次関数及び図形と計量における数学的な見
2014年度 名古屋大・理系数学
 04 名古屋大学 ( 理系 ) 前期日程問題 解答解説のページへ空間内にある半径 の球 ( 内部を含む ) を B とする 直線 と B が交わっており, その交わりは長さ の線分である () B の中心と との距離を求めよ () のまわりに B を 回転してできる立体の体積を求めよ 04 名古屋大学 ( 理系 ) 前期日程問題 解答解説のページへ 実数 t に対して 点 P( t, t ), Q(
04 名古屋大学 ( 理系 ) 前期日程問題 解答解説のページへ空間内にある半径 の球 ( 内部を含む ) を B とする 直線 と B が交わっており, その交わりは長さ の線分である () B の中心と との距離を求めよ () のまわりに B を 回転してできる立体の体積を求めよ 04 名古屋大学 ( 理系 ) 前期日程問題 解答解説のページへ 実数 t に対して 点 P( t, t ), Q(
離散数学
 離散数学 ブール代数 落合秀也 前回の復習 : 命題計算 キーワード 文 複合文 結合子 命題 恒真 矛盾 論理同値 条件文 重条件文 論法 論理含意 記号 P(p,q,r, ),,,,,,, 2 今日のテーマ : ブール代数 ブール代数 ブール代数と束 そして 順序 加法標準形とカルノー図 3 今日のテーマ : ブール代数 ブール代数 ブール代数と束 そして 順序 加法標準形とカルノー図 4 ブール代数の法則
離散数学 ブール代数 落合秀也 前回の復習 : 命題計算 キーワード 文 複合文 結合子 命題 恒真 矛盾 論理同値 条件文 重条件文 論法 論理含意 記号 P(p,q,r, ),,,,,,, 2 今日のテーマ : ブール代数 ブール代数 ブール代数と束 そして 順序 加法標準形とカルノー図 3 今日のテーマ : ブール代数 ブール代数 ブール代数と束 そして 順序 加法標準形とカルノー図 4 ブール代数の法則
画像類似度測定の初歩的な手法の検証
 画像類似度測定の初歩的な手法の検証 島根大学総合理工学部数理 情報システム学科 計算機科学講座田中研究室 S539 森瀧昌志 1 目次 第 1 章序論第 章画像間類似度測定の初歩的な手法について.1 A. 画素値の平均を用いる手法.. 画素値のヒストグラムを用いる手法.3 C. 相関係数を用いる手法.4 D. 解像度を合わせる手法.5 E. 振れ幅のヒストグラムを用いる手法.6 F. 周波数ごとの振れ幅を比較する手法第
画像類似度測定の初歩的な手法の検証 島根大学総合理工学部数理 情報システム学科 計算機科学講座田中研究室 S539 森瀧昌志 1 目次 第 1 章序論第 章画像間類似度測定の初歩的な手法について.1 A. 画素値の平均を用いる手法.. 画素値のヒストグラムを用いる手法.3 C. 相関係数を用いる手法.4 D. 解像度を合わせる手法.5 E. 振れ幅のヒストグラムを用いる手法.6 F. 周波数ごとの振れ幅を比較する手法第
<4D F736F F F696E74202D2091E6824F82538FCD8CEB82E88C9F8F6F814592F990B382CC8CB4979D82BB82CC82505F D E95848D8682CC90B69
 第 章 誤り検出 訂正の原理 その ブロック符号とその復号 安達文幸 目次 誤り訂正符号化を用いる伝送系誤り検出符号誤り検出 訂正符号 7, ハミング符号, ハミング符号生成行列, パリティ検査行列の一般形符号の生成行列符号の生成行列とパリティ検査行列の関係符号の訂正能力符号多項式 安達 : コミュニケーション符号理論 安達 : コミュニケーション符号理論 誤り訂正符号化を用いる伝送系 伝送システム
第 章 誤り検出 訂正の原理 その ブロック符号とその復号 安達文幸 目次 誤り訂正符号化を用いる伝送系誤り検出符号誤り検出 訂正符号 7, ハミング符号, ハミング符号生成行列, パリティ検査行列の一般形符号の生成行列符号の生成行列とパリティ検査行列の関係符号の訂正能力符号多項式 安達 : コミュニケーション符号理論 安達 : コミュニケーション符号理論 誤り訂正符号化を用いる伝送系 伝送システム
2019年度 千葉大・理系数学
 9 千葉大学 ( 理系 ) 前期日程問題 解答解説のページへ a, a とし, のとき, a+ a + a - として数列 { a } () のとき a+ a a a - が成り立つことを証明せよ () åai aaa + が成り立つような自然数 を求めよ i を定める -- 9 千葉大学 ( 理系 ) 前期日程問題 解答解説のページへ 三角形 ABC は AB+ AC BCを満たしている また,
9 千葉大学 ( 理系 ) 前期日程問題 解答解説のページへ a, a とし, のとき, a+ a + a - として数列 { a } () のとき a+ a a a - が成り立つことを証明せよ () åai aaa + が成り立つような自然数 を求めよ i を定める -- 9 千葉大学 ( 理系 ) 前期日程問題 解答解説のページへ 三角形 ABC は AB+ AC BCを満たしている また,
様々なミクロ計量モデル†
 担当 : 長倉大輔 ( ながくらだいすけ ) この資料は私の講義において使用するために作成した資料です WEB ページ上で公開しており 自由に参照して頂いて構いません ただし 内容について 一応検証してありますが もし間違いがあった場合でもそれによって生じるいかなる損害 不利益について責任を負いかねますのでご了承ください 間違いは発見次第 継続的に直していますが まだ存在する可能性があります 1 カウントデータモデル
担当 : 長倉大輔 ( ながくらだいすけ ) この資料は私の講義において使用するために作成した資料です WEB ページ上で公開しており 自由に参照して頂いて構いません ただし 内容について 一応検証してありますが もし間違いがあった場合でもそれによって生じるいかなる損害 不利益について責任を負いかねますのでご了承ください 間違いは発見次第 継続的に直していますが まだ存在する可能性があります 1 カウントデータモデル
CAPELLI (T\^o $\mathrm{r}\mathrm{u}$ UMEDA) MATHEMATICS, KYOTO UNIVERSITY DEPARTMENT $\mathrm{o}\mathrm{p}$ $0$:, Cape i,.,.,,,,.,,,.
 1508 2006 1-11 1 CAPELLI (T\^o $\mathrm{r}\mathrm{u}$ UMEDA) MATHEMATICS KYOTO UNIVERSITY DEPARTMENT $\mathrm{o}\mathrm{p}$ $0$: Cape i Capelli 1991 ( ) (1994 ; 1998 ) 100 Capelli Capelli Capelli ( ) (
1508 2006 1-11 1 CAPELLI (T\^o $\mathrm{r}\mathrm{u}$ UMEDA) MATHEMATICS KYOTO UNIVERSITY DEPARTMENT $\mathrm{o}\mathrm{p}$ $0$: Cape i Capelli 1991 ( ) (1994 ; 1998 ) 100 Capelli Capelli Capelli ( ) (
2015年度 2次数学セレクション(整数と数列)
 05 次数学セレクション問題 [ 千葉大 文 ] k, m, を自然数とする 以下の問いに答えよ () k を 7 で割った余りが 4 であるとする このとき, k を 3 で割った余りは であることを示せ () 4m+ 5が 3 で割り切れるとする このとき, m を 7 で割った余りは 4 ではないことを示せ -- 05 次数学セレクション問題 [ 九州大 理 ] 以下の問いに答えよ () が正の偶数のとき,
05 次数学セレクション問題 [ 千葉大 文 ] k, m, を自然数とする 以下の問いに答えよ () k を 7 で割った余りが 4 であるとする このとき, k を 3 で割った余りは であることを示せ () 4m+ 5が 3 で割り切れるとする このとき, m を 7 で割った余りは 4 ではないことを示せ -- 05 次数学セレクション問題 [ 九州大 理 ] 以下の問いに答えよ () が正の偶数のとき,
2015年度 信州大・医系数学
 05 信州大学 ( 医系 ) 前期日程問題 解答解説のページへ 放物線 y = a + b + c ( a > 0) を C とし, 直線 y = -を l とする () 放物線 C が点 (, ) で直線 l と接し, かつ 軸と共有点をもつための a, b, c が満 たす必要十分条件を求めよ () a = 8 のとき, () の条件のもとで, 放物線 C と直線 l および 軸とで囲まれた部
05 信州大学 ( 医系 ) 前期日程問題 解答解説のページへ 放物線 y = a + b + c ( a > 0) を C とし, 直線 y = -を l とする () 放物線 C が点 (, ) で直線 l と接し, かつ 軸と共有点をもつための a, b, c が満 たす必要十分条件を求めよ () a = 8 のとき, () の条件のもとで, 放物線 C と直線 l および 軸とで囲まれた部
パソコンシミュレータの現状
 第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
2015年度 金沢大・理系数学
 05 金沢大学 ( 理系 ) 前期日程問題 解答解説のページへ四面体 OABC において, 3 つのベクトル OA, OB, OC はどの つも互いに垂直で あり, h > 0 に対して, OA, OB, OC h とする 3 点 O, A, B を通る平面上の点 P は, CP が CA と CB のどちらとも垂直となる点であるとする 次の問いに答えよ () OP OA + OB とするとき, と
05 金沢大学 ( 理系 ) 前期日程問題 解答解説のページへ四面体 OABC において, 3 つのベクトル OA, OB, OC はどの つも互いに垂直で あり, h > 0 に対して, OA, OB, OC h とする 3 点 O, A, B を通る平面上の点 P は, CP が CA と CB のどちらとも垂直となる点であるとする 次の問いに答えよ () OP OA + OB とするとき, と
複素数平面への誘い
 いざな複素数平面への誘い GRS による複素数平面の表現 複素数平面への第一歩 - 複素数モード - 点と複素数 -3 複素数の四則演算 -4 絶対値と偏角, 共役複素数 -5 絶対値と偏角による複素数の表現 複素数平面の変換 4 - 回転移動と相似拡大 - 直線 に関する対称変換 -3 単位円に関する反転変換 -4 複素数平面の変換と曲線 3 入試問題に挑戦 6 3- 陰関数を利用した図形の表示
いざな複素数平面への誘い GRS による複素数平面の表現 複素数平面への第一歩 - 複素数モード - 点と複素数 -3 複素数の四則演算 -4 絶対値と偏角, 共役複素数 -5 絶対値と偏角による複素数の表現 複素数平面の変換 4 - 回転移動と相似拡大 - 直線 に関する対称変換 -3 単位円に関する反転変換 -4 複素数平面の変換と曲線 3 入試問題に挑戦 6 3- 陰関数を利用した図形の表示
ディジタル信号処理
 ディジタルフィルタの設計法. 逆フィルター. 直線位相 FIR フィルタの設計. 窓関数法による FIR フィルタの設計.5 時間領域での FIR フィルタの設計 3. アナログフィルタを基にしたディジタル IIR フィルタの設計法 I 4. アナログフィルタを基にしたディジタル IIR フィルタの設計法 II 5. 双 次フィルタ LI 離散時間システムの基礎式の証明 [ ] 4. ] [ ]*
ディジタルフィルタの設計法. 逆フィルター. 直線位相 FIR フィルタの設計. 窓関数法による FIR フィルタの設計.5 時間領域での FIR フィルタの設計 3. アナログフィルタを基にしたディジタル IIR フィルタの設計法 I 4. アナログフィルタを基にしたディジタル IIR フィルタの設計法 II 5. 双 次フィルタ LI 離散時間システムの基礎式の証明 [ ] 4. ] [ ]*
Microsoft Word - NumericalComputation.docx
 数値計算入門 武尾英哉. 離散数学と数値計算 数学的解法の中には理論計算では求められないものもある. 例えば, 定積分は, まずは積分 ( 被積分関数の原始関数をみつけること できなければ値を得ることはできない. また, ある関数の所定の値における微分値を得るには, まずその関数の微分ができなければならない. さらに代数方程式の解を得るためには, 解析的に代数方程式を解く必要がある. ところが, これらは必ずしも解析的に導けるとは限らない.
数値計算入門 武尾英哉. 離散数学と数値計算 数学的解法の中には理論計算では求められないものもある. 例えば, 定積分は, まずは積分 ( 被積分関数の原始関数をみつけること できなければ値を得ることはできない. また, ある関数の所定の値における微分値を得るには, まずその関数の微分ができなければならない. さらに代数方程式の解を得るためには, 解析的に代数方程式を解く必要がある. ところが, これらは必ずしも解析的に導けるとは限らない.




