|
|
|
- ふさこ ちとく
- 9 years ago
- Views:
Transcription
1 Landau
2 hyperbolic sin, hyperbolic cos, hyperbolic tan
3 sin θ a c, cos θ b c, tan θ b a cosec θ sin θ, sec θ cos θ, cot θ tan θ inverse arcsin θ sin θ, arccos θ cos θ, arctan θ tan θ. sin θ + cos θ sin sin θ sin θ, cos cos θ cos θ tan tan θ tan θ π sin θ sin θ ± πn, cos θ cos θ ± πn, tan θ tan θ ± πn [ π, π] 4 sin π + θ sin θ sin θ sin π θ cos π + θ cos θ cos θ cos π θ tan π + θ tan θ tan θ tan π θ π sin θ cos θ 3
4 sin 3 cos 4 tan. sin α ± β sin α cos β ± cos α sin β cos α ± β cos α cos β sin α sin β sin θ sin θ cos θ cos θ cos θ sin θ sin θ cos θ sin θ cos θ cos θ + cos θ.3 A sin θ + B cos θ A + B sin θ + φ cos φ A A +B, sin φ B A +B, tan φ B A θ A sin ωt + B sin ωt + θ A + B + AB cos θ sin ωt + φ 4
5 cos φ A+B cos θ, sin φ B sin θ B sin θ, tan φ A +B +AB cos θ A +B +AB cos θ A+B cos θ A sin ωt + B sin ωt + θ A sin ωt + B sin ωt cos θ + B cos ωt sin θ A + B cos θ sin ωt + B sin θ cos ωt sin ωt + θ + sin ωt + φ sin sin ωt + θ sin ωt + φ cos cos ωt + θ + cos ωt + φ cos cos ωt + θ cos ωt + φ sin α ωt + θ, β ωt + φ ωt + θ + φ ωt + θ + φ ωt + θ + φ ωt + θ + φ cos sin θ φ θ φ θ φ θ φ cos sin sin ωt + θ + sin ωt + φ sin α + sin β A α+β, B α β sin α + sin β sin A + B + sin A B sin A cos B + cos A sin B + sin A cos B cos A sin B sin A cos B sin α+β cos α β sin ωt + θ+φ cos θ φ log a b log a b log c b log c a ln b ln a a e t t ln a 5
6 3 3. f a ε >, δ >, a > δ f f a < ε ε δ a δ < < a + δ f a f ε : a M M f [a, b] f a α, f b β α < γ < β γ f c γ a < c < b c Rolle f f a f b f c a < c < b a, b f [a, b] C C f f c f b f a b a a < c < b c a, f a b, f b [a, b] C Cauchy C f, g c f c f b f a g c g b g a a < c < b C m : m C : 6
7 C f, y y f y f 3. Landau lim a u u a v lim v u v o u v u a u v lim v u v O u a u 3.3 f f + f y lim lim 3.4 c u c u u ± v u ± v u v u v + u v u v u v u v u v w u v w + u v w + u v w v Leibniz f, g C m n f g n nc k f n k g k k f g f g + f g f g + f g + f g f g 3 f 3 g + 3 f g + 3 f g + f g 3 7
8 3.5 d sin cos d d cos sin d d d tan cos sec d sin d d cos d d tan d d d e e d d a ln a a d d log a d d ln d d ln f f f ln ln a ln a 8
9 3.7 f, y,, y, : f f +, y, f, y, }{{} : Chain rule d f f f d + dy + y, y, z t t, y t, z t 3 d f f d f dy f dz dt dt + y dt + z dt d dt, dy dt, dz dt t f, y, z a, b, c f a, b, c n, f a, b, c, y f a, b, c z a, b, c t t, y t, z t f t, y t, z t. t a, b, c a, y b, z c. t d f dt f d dt + f y dy dt + f z dz dt t f 9
10 3.8 d f f d d d f f g d dg dg d y f f y d dy dy d y f y d f dy dy d d f dy / t t, y t y dy dy d dyt dt dt d dt y t dy dt dy d d dy dt d dy / dt d dt F, y y y f s F dy d F y df F + F d + F dy y F dy dy y d d : F / F y
11 y f g y f y f, f, f, g y y, g yy y, g yyy y, y f y g f g f f g f f + g f f g f f f f + g f f g f gy f g f f f + g f f g f f f + f f g f f f f 3 g f f f f 3 + 3g f f f f + g f f 3 g f f f f 3 3 f f + f f g f f f f f 5 f f 4 3 g f f f f f 4 + 6g f f f f f + g f f 3 f + 4 f f + g f f g f f f f f f 3 f 3 f f f + f f g f f f f 5 f 3 f 7 + f f f 6 f f 5, y
12 F, y, y, y df F F d + y dy F d + F y dy d y, d d dy dy d F y F, d dy F F y d F F d + F y dy F F dy F + F y d d F y Fy d + F yy dy F yy F y dy F y + F yy d F y F y F df d F, df y d F y d d dy d F y d d F F y d d F y F Fy + F yy dy d F dy yf F yy d F dy + F y F + F y F y d F yf + F yy F dy F + F y F + F y d F F y F F + F y F F F y F y F y F F F yf + F yy F y + F y F F y F y y F F y F + F yy F y F + F y F F Fy Fy F F 3, y d y d F F y F + F yy F + Fy Fy d dy F F y F 3 F + F yy F + F y F 3 y Fy
13 3.9 O O s P r s τ s d r ds s r P t χ s d τ ds d r ds χ χ s d τ ds d r ds R R P s t v s t v s : const v t d r dt d r ds ds dt v s τ a t d v dt v s d τ dt v s d τ ds ds dt v s χ v s v τ, a χ τ s d r ds ds dr ds dr P R R 3 χ cs 3
14 y f dy d y R d d dy + d f f + f F, y { } R F + F y F F y F + F y Fy F + Fy F + Fy v c P, y t d v dt, dy dt d + dt dy dt y f y dy dt dy d d dt d + dt dy d d dt + dy d + f g f f t y y t f t t d a dt, d y dt d dt d d d d g dt dt dt dt d d g g d d g g d f d d d f g g f dg d f f f f f + f + f 3 + f 4
15 d y dt d dt dy d d dt dt dt dy d d d d f dt + g dt d f d dt g f d d dt g f + g dt f d f dt + g f d + dt d y dt d + f dt + g f f f + f + f + f + f /R f f f + f + + f + f f f + f + f f f + f R f f + f dy d + dy d d y d dy d F y F, d y d F F y F + F yy F + F y F 3 Fy R + F y F + F y F F F y F + F yy F + F y Fy F + F y { } F F y F + F yy F + F F + Fy y Fy F 3 5
16 λ λ, y y λ, z z λ R λ + y λ + z λ λλ + y λλ + z λλ λ λλ + y λ y λλ + z λ z λλ λ + y λ + 3 λ z v c P, y, z t d + dt dy + dt dz dt dλ dt d + dλ dy + dλ dz dλ dλ dt d + dy dλ dλ + dz dλ G λ : G λ d + dλ λ λ t P λ d dλ, dλ dt λ + y λ + z λ d λ dt d dλ d dt dt dt d dt d dt dy + dλ dz dλ G, G λ + y λ + z λ, G λ λ λλ + y λ y λλ + z λ z λλ G dλ d dt dλ G G G λ G 3 G λ G λ λλ + y λ y λλ + z λ z λλ λ + y λ + λ z d dt d dλ d dt dt dλ λ λ + dλ d dt dt dt dt λ d λ dt λ + dλ dλ dt dt λλ d λ dt λ + dλ λλ dt λ λλ + y λ y λλ + z λ z λλ λ + y λ + z λ λ λλ λ + y λ + z λ λλ λ λλ + y λ y λλ + z λ z λλ λ λ + y λ + z λ λ + y λ + A λ B λλ B z λ d y dt Ay λ By λλ B, d z dt Az λ Bz λλ B R d + dt d y + dt A B A B + B λλ + y λλ + y λλ B 4 d z A λ + y λ + y λ AB λ λλ + y λ y λλ + z λ z λλ + B λλ + y λλ + λλ y dt B 4 λ + y λ + z λ A + B λλ + y λλ + λλ y λ λλ + y λ y λλ + z λ z λλ + B 3 λ + y λ + 3 λ z λλ + y λλ + y λλ 6
17 3. f d a n d n+ an+ + C n d ln a + C a f d ln f + C f e d e + C a d ln a a + C + a d ln + a + C + a d a tan a + C 3. m d n m n m n m n + n n m n i f f f d ln f + C f n n i d ln + + C + + d ln + + C d ln C 7
18 i f m f m f f m d m + f m+ + C i d C 3 m d + + d / + 4 d + C d C 8
19 ii-a n : n n a n n a + a + + a n n n n n n n n n i n + c i i n c i i d c i ln i + C ii-a d ln + + ln + C d ln + ln + C ii-b n : n p p n p n a n p n n n a p k k a k + n k + a p k p k a k + + p n k n k + + a n a n n k p n k n n k i p i a i j { n n n i j a i i i } n i p i 3 n g Taylor b n n g g i + g i i + g i! b + b i + b i + + b n i n i + + gn i n! i n 9
20 3 j { n b b a i i j a i i j + i + + b j j i + b } j + b j + b j+ i + + b n i n j i 3 j m i a i m i a i j n i j c c i p + i i + + c p i + c p i + c p i i pi + c pi + i + + c n i n i }{{} }{{} group.b group.a group.a c i i p d p + c i i p+ + C cpi i d c pi ln i + C group.b ii-b d ln f f a + b + + c g + f a g + b g + + c g + a /6, b /6, c /4 g g 57 g 9 g g 7 g 6 g g 78 g 3 g 4 + g 6 g g 4 g g
21 iii : + d tan + C d : unknown 3 + d : unknown / d ln tan + C / { } ln + 4 ln + + tan + C + +
22 f f a n a + a + + a n n n k a k k a k a k k k k k }{{} k n n k l eclude llk a b c a a b a c + b a b b c + c a c b c b p p p n p n l a,l p + l l a,l p n + + l l a n,l n l n p k k l a k,l k l a k,l a b a a b + b a a a b + b a b a 3 b a 3 a b + b a a a b + b a a a b + b a 3 b a b a a b + b a a a b + b a b a b + b a b a b c a a b a c + b a + c a + b a b b c + c a c b c a a b a c 3. sin a d cos a + C a
23 cos a d sin a + C a tan a d ln cos a + C a cot a d ln sin a + C a cos a d sin a d cos a d sin a d sec a d tan a + C a cosec a d cot a + C a sec a d cosec a d ln d ln + C a ln + sin a cos a + C a ln tan a + C a d a sin + C a cos + C π/ ± a d ln + ± a + C a d a + a sin + C a ± a d { ± a ± a ln + ± a } + C 3.3 a φ α b φ β b a f d β α f φ t φ t dt 3.4 f g I C I a, b b a f g d [ f g ] b a b a f g d 3
24 3.5 sin m cos n d e sin d e e cos d e e sin a d e cos a d sin cos + C sin + cos + C e a sin a cos + C a + e a sin + a cos + C a + m n n sin m sin n + m cos m cos n + C m n 4m cos m + C m n sin m cos n d + cos m sin n d sin m + n d cos m + n + C m + n 3.6 β α β α α β d β α3 6 α m β n d n m!n! β αm+n+ m + n +! n β α αm β n d n β n α m+ n m+ m+n m+n αm+n d [ ] β n n m+ n n m!n! m+n+! m+ β αm+n+ m+n m+n α m+n+ m+n+ α 4
25 Bete B p, q p q d p! q! p + q! B, B p, B, p p B p, p p! p! p! B n, B, n n d [ n n n ] n Bete q : B p, q q p B p +, q p : B p, q p q B p, q + Bete B p, q B q, p y B p, q π/ sin p θ cos q θdθ sin θ 5
26 Gamma Γ s s! e s d Γ e d Γ Γ 3 Γ 4 Γ 5 e d e d 3 e d 6 4 e d 4 Γ π Γ e d e t t t dt t e dt t e t dt y e t dt e +y ddy z e +y y z e +y e r r ln z z πr dz r ln z π ln zdz π [z z ln z] π Gamma Γ s + s Γ s Gamma Γ s e r r s dr 3 e r3 r 3s dr r, r 3, 6
27 Gamma Bete B s, t Γ s Γ t Γ s + t Γ s Γ t 4 r e s d π/ θ e y y t dy 4 e +y s y t ddy e r r s+t cos s θ sin t θ drdθ Γ s + t B s, t Gamma Bete π/ cos m θ sin n θ dθ m + B, n + Γ m+ Γ n+ Γ m+ + n+ π/ Γ n + n + n + + π sin n θ dθ case n π/ cos n θ dθ π/ π sin θ dθ Γ n+ Γ n+ π/ cos θ dθ case n π/ sin θ dθ π/ cos θ dθ π 4 case n 3 Fourier π/ sin 3 θ dθ π/ cos 3 θ dθ 3 π π π π cos n d cos n d π π π π sin n d sin n d π π π π π sin n sin m d sin n cos m d π π cos n cos m d δ nm π 7
28 3.7 u, v, y u, v, y u, v u, v J u y u v y v, y f, y ddy f u, v, y u, v J dudv, y Jacobian J u, v d u du + dv dy v y du + u y dv v u, v, u, v ddy d, dy d dy u v y u y u 5 u, v, w, y, z u, v, w, y u, v, w, z u, v, w u, v, w f ddydz f J dudvdw J J u y u z u v y v z v w y w z w, y, z u, v, w 8
29 u v y y, y, J u v.... u, v,, y, z d du + u v dv + dv dy w y du + u y dv + v y dv w d, dy, dz du, dv, dw ddydz d, d u v w dy, dz dy dz y y y u v w z u z v z w y z u u + v v + w w + u y u z u + v y v + w y w + u + v z v + w z w +. f u, v, w du, dv, dw, y, z f u u u u d + dy + y z dz + f u u + f v v + f w w + f, y, z OK d f f u du + f v dv + f w dw + + f v v v d + dy + v y z dz + + f w f u d+ u y + f v v y + f w w y + d f f d + f y dy + f z dz + w f dy+ u w w d + dy + y z dz + + u z + f v v z + f w w z + dz+ 9
30 r cos ϕ y r sin ϕ r + y ϕ π z z ϕ tan y r r + ϕ ϕ cos ϕ r sin ϕ r ϕ y r y r + ϕ y ϕ sin ϕ r + cos ϕ r ϕ, y r, ϕ det cos ϕ r sin ϕ sin ϕ r cos ϕ r + y + z r + r r + r ϕ + z r sin θ cos φ y r sin θ sin φ z r cos θ r + y + z θ tan + y z φ tan y θ π, φ π y z r r + θ θ + φ φ r y r + θ y θ + φ y φ r z r + θ z θ + φ z φ sin θ cos φ cos θ cos φ + r r θ sin φ r sin θ φ sin θ sin φ cos θ sin φ + r r θ + cos φ r sin θ φ cos θ r sin θ r θ + y + z, y, z r, θ, φ r sin θ r + r r r r sin θ sin θ + θ θ r sin θ φ 3
31 r, θ, φ, r y, θ y, φ y, r z, θ z, φ z r + y + z, tan θ + y z, tan φ y, y, z J r r y r z θ θ y θ z φ φ y φ z sin θ cos φ sin θ sin φ cos θ cos θ cos φ r cos θ sin φ r sin θ r sin φ r sin θ cos φ r sin θ OK 3
32 4 4. f, y z 3 y, y f +, y + f, y + f y, y y + { f, y + f y, y y + f yy, y y } z f, y, y : n : f f y : f y f y f, f y, f + fy + : f y, f, : f, f y, f + f y : f + f y a,, f, b, y, f y y α, β p α a + β b i j k f y a b f f y y y f y y y // f f y α a + β b z α f + β f y y α, β y, f y y, f y, f, f y,c C f f + f y f y 6 3
33 4. f, f y y, y A f, y B f y, y C f yy, y X, Y y F X, Y f, y + f y, y y + f yy, y y X, Y A X + B XY + C Y i D AC B < F A X αy X βy Y X/α Y X/β F F f, y ii D AC B F A X αy Y X/α A F f iii D AC B > X, Y, 7 F A C F > f A C F < f 33
34 Hessian f, y, y H f, y f, y f y, y f y, y f yy, y det [ H f, y ] [ f f yy f y ],y i det [ H f, y ] < ii det [ H f, y ] iii det [ H f, y ] > iii- f > iii- f < F H f X, Y A X + B XY + C Y X Y [ ] A B X X Y X H B C Y f Y det H f λ, µ α α γ H f λ, H β β f δ γ µ δ α γ α γ H f β δ β δ λ H f T µ λ µ T T H f T λ µ α γ T β δ λ T H f T µ H f H t f H f T t T λ µ t T H f T t T t H t f T t T t H f T t 34 :
35 X T Y u T v T X Y u v T t X Y u v X Y T u v F X λ H T T µ Y X H f X Y λ X T T Y µ Y u v λ u λu µ v + µv F H f λ, µ λµ Hessian f, y, z, r, y, z, H f r i f r f y r f z r f y r f yy r f yz r f z r f zy r f zz r.... f r ii f r iii f r iv 35
36 5 5. a n a < a < a 3 < : a a a 3 : a n ε >, N >, n > N a n α < ε ε N N n a n α ε Cauchy a n ε >, N >, p, q > N a p a q < ε N a n Cauchy Cauchy Cauchy : f lim a f ε >, δ >, < α a < δ, < β b < δ L Hopital f α f β < ε f f a g a f f lim a g c c lim a g c f a g a 5. sin θ tan θ lim lim θ θ 36
37 log cos lim cos log lim lim + lim ln + f ln ln t / f ln/t t + t ln t t ln t t ln t < t ln t t ln t lim t t < lim t lim t ln t t < t f ln + lim lim lim e e t t a ln a 5.3 a f b f a + f a b a + f a! R n+ f n+ a + θ b a n! f f + f + f! b a + + f n a n! b a n+, < θ < + + f n n + R n+ n! b a n + R n+ R n+ f n+ θ n+, < θ < n! 37
38 D i i i i Dy j y j j y j }{{} i }{{} i y y y }{{} y y y j }{{} j D i D j D i+ j D i yd j y D i+ j y D i D j y D j yd i i y j i i j y j f f + }{{} y y y }{{} i }{{} y y y j }{{} i j f +! n f + n! Dn f n n n! n n f [ f, y f, + + y ] f, + y! f, y n [ + y y + [ 3 3 3! y y + ] 3y 3 + y3 f, + y y 3 n n f, y n! n n n [ n ] D + D y f, n! n n n! n n m m n m ] + y f, y y m m m! y m f, n y m n+m n!m! n f, ym n!m! Dn D m y f, f,,, i n n n i n [ D + D + D n ] i f,,, n! n!n! n i! Dn D n D n i i f,,, 38
39 n n! α + βn n m n!m! αn β m n n! α + β + γ + + ωn n m l ω n!m! w! αn β m ω w n n! α + βn n n! n n! k! n k! αk β n k k case : n + α + β case : n + α + αβ + β case : n + α 3 + 3α β + 3αβ + β 3 case : n 3 + α a β b a, b C a,b α a β b C a,b a b k a n k b n a + b case 5.4 C a,b a + b! a + b! a!b! a!b! + α + α + e ! n! n + sin 3! 3 + 5! 5 7! n cos! + 4! 4 6! n n n! + n n! + ln n n < n α α + α α α 3 α α α n < 3! n! 5.5 e iθ cos θ + i sin θ 39
40 5.6 n e ik k n n cos k + i sin k k k + e i + e i + + e ni sin + sin n + sin + i cos cos n + sin n cos k + cos + cos + + cos n k sin + sin n + sin sin n + sin + n sin k + sin + sin + + sin n k cos cos n + sin cos n + sin cos sin n e ik k sin { n + } } sin { sin n n sin Laue S + e i + e i + + e n e i S e i + e i + + e n + e n+i e i S e n+i S en+i e i eni e i e i eni e i/ e i/ e i/ e i/ cos n + i sin n cos + i sin cos i sin cos + i sin cos i sin 4
41 cos n + i sin cos n cos sin n sin cos + i sin n cos + cos n sin + sin i sin cos + sin n + sin + sin sin + sin n + sin + i cos cos n + sin n cos k, k n sin k k n cos k, k S n e ik k sin + sin n + sin + cos { sin + sin sin n + } { + sin n + + cos cos 4 sin cos n + cos n + cos n+ + sin n+ n k 4 sin sin sin n sin k k cos k + cos + cos + + cos n + e cos n + sin cos n + + cos n + sin n+ sin sin n+ sin + e i + e i S e ni + + e i + e + e i + e ni + e i + e i } + + e ni + e ni S en+i e ni e i e i S e n i + + e n+i eni e i/ e ni e i/ e i/ e i/ sin n + sin S sin n + sin + S n sin k sin + sin + + sin n e i + e i k i + e i + e i i is e ni e i + e i + + e ni e i is e n i e + e i + + e n+i is en+i e i e + e ni e i en+i + e ni e i ei + e e i eni e i/ + e ni e i/ e i/ e i/ cos n + cos S cos n + + cos i sin i sin sin sin + + e ni + e ni i ei/ + e i/ e i/ e i/ 4
42 5.7 hyperbolic sin, hyperbolic cos, hyperbolic tan sinh e e, cosh e + e, tanh sinh cosh e + e e e cosech, sech, coth sinh + 3 3! + 5 5! + 7 7! i sin i, sinh i i sin 9! cosh +! + 4 4! + 6 6! cos i, cosh i cos 8! e cosh + sinh cos i + i sin i e cosh sinh cos i i sin i cosh sinh sinh cosh cosh sinh sinh α + β sinh α cosh β + cosh α sinh β cosh α + β cosh α cosh β + sinh α sinh β arcsinh sinh ln + + arccosh cosh ± ln + d + arcsinh + C e i cos + i sin e cosh + sinh 4
43 sinh cosh. tanh sinh 9 cosh tanh sinl ln ln + ln + ln + cosl ln + ln + ln ln tanl sinl ln ln + ln cosl ln + ln + ln + + ln + ln + sinl d cosl d ln : sinl + cosl sinl cosl sinl + cosl + cosl sinl? d d d 43
44 3 sinl - ln - + ln + /.5..5 cosl -ln - - ln + / sinl cosl sinl+cosl -ln tanl -ln - - ln + / -ln - + ln sinl cosl 4 tanl 5.8 : a, d : a, r : a n nr n a n a + n d, S n n a + a n na + a n a r n, S n a r n r r S n r + r + 3r 3 + 4r 4 + nr n n n d 44
45 r { n + r n + nr n+} r rs n r + r 3 + 3r 4 + 4r n r n + nr n+ S n rs n r + r + r 3 + r 4 + r r n nr n+ r rn r nrn+ r r r r { { rn n r r n } r n nr n + nr n+} r S n { r r + n r n + nr n+} r n n + r n n + n + 6 { } r 3 n n + r r + 3 n n + n +, r r + r + n n + n + n r r + r + { r r r + r + + r r + r + r + 3} 4 r r + n n odd even + n n n π 6 n n n n n n π 4 π π 8 45
46 f z u, y + i v, y : f f z f z z lim z z z z u v y, v u y u / v v, y / u y 46
47 7 7. L f f a + n a n cos nπ L a L f d L L + b n sin nπ L a n L f cos nπ L L L d b n L f sin nπ L L L d f cos sin cos sin 5 L/n cos 6 L/n sin f a, a n, b n OK 47
48 : π π d π π π cos d π π sin d π π cos sin d cos sin π π cos n cos m d π π sin n sin m d π π cos cos d π π sin sin d π L L cos mπ L L L cos mπ L mπ L cos L d L mπ sin L d sin mπ L mπ sin L d L m n m n 48
49 49
50 cos n + m d cos n cos md sin n sin md [ π, π] π π π cos n cos md π sin n sin md sin n cos n cos md cos md n [ ] sin n sin n cos m cos m d n n [ ] sin n cos m + m sin n sin md n n [ π, π] π π cos n cos md m n π π sin n sin md n m π π cos n cos md π π sin n sin md n m π π cos n d π π sin n d π cos.5 7 cos 5
51 f 4 π sin 3 sin 5 sin 7 sin f 4 π cos 3 cos 5 cos 7 cos
52 f 4 π sin sin 3 sin 4 sin 5 sin f 4 sin + π sin sin sin
53 f 4 π cos cos 3 cos 4 cos 5 cos δ f + cos + cos + cos 3 + cos 4 + cos 5 + π 7 δ f + sin + sin + sin 3 + sin 4 + sin 5 + π 53
54 8 f f f π 4 π cos 3 cos 5 cos 7 cos π 8 9 f f 4 π cos 3 cos 5 cos 7 cos
55 f 4 π cos cos 3 cos 4 cos 5 cos 6 cos f 4 π sin sin 3 sin 4 sin 5 sin 6 sin
56 y f π π f π cos cos 3 cos 4 cos 5 cos 6 cos π 6 56
57 7.3 [ L, L] f f α n ep i nπ L n α n L f ep L L i nπ L d cos nπ L nπ e L i + e nπ i L sin nπ L i e nπ L i + e nπ L i [ L, L] f g n ep i nπ L f α n g n n f f, α, α, α,, α n, g n n g n,,,,,, g n f L L g n f d α n f f f f f L L f f d Ψ α n α n n 57
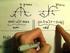
sin cos No. sine, cosine : trigonometric function π : π = 3.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin : odd cos = cos : even.
 08 No. : No. : No.3 : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No.0 : No. : sin cos No. sine, cosine : trigonometric function π : π = 3.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin
08 No. : No. : No.3 : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No.0 : No. : sin cos No. sine, cosine : trigonometric function π : π = 3.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin
I No. sin cos sine, cosine : trigonometric function π : π =.4 : n =, ±, ±, sin + nπ = sin cos + nπ = cos sin = sin : cos = cos :. sin. sin. sin + π si
 I 8 No. : No. : No. : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No. : I No. sin cos sine, cosine : trigonometric function π : π =.4 : n =, ±, ±, sin + nπ = sin cos + nπ = cos sin = sin : cos = cos :. sin.
I 8 No. : No. : No. : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No. : I No. sin cos sine, cosine : trigonometric function π : π =.4 : n =, ±, ±, sin + nπ = sin cos + nπ = cos sin = sin : cos = cos :. sin.
I No. sin cos sine, cosine : trigonometric function π : π =.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin : odd cos = cos : even.
 I 0 No. : No. : No. : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No.0 : I No. sin cos sine, cosine : trigonometric function π : π =.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin : odd
I 0 No. : No. : No. : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No.0 : I No. sin cos sine, cosine : trigonometric function π : π =.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin : odd
(1) (2) (3) (4) HB B ( ) (5) (6) (7) 40 (8) (9) (10)
 2017 12 9 4 1 30 4 10 3 1 30 3 30 2 1 30 2 50 1 1 30 2 10 (1) (2) (3) (4) HB B ( ) (5) (6) (7) 40 (8) (9) (10) (1) i 23 c 23 0 1 2 3 4 5 6 7 8 9 a b d e f g h i (2) 23 23 (3) 23 ( 23 ) 23 x 1 x 2 23 x
2017 12 9 4 1 30 4 10 3 1 30 3 30 2 1 30 2 50 1 1 30 2 10 (1) (2) (3) (4) HB B ( ) (5) (6) (7) 40 (8) (9) (10) (1) i 23 c 23 0 1 2 3 4 5 6 7 8 9 a b d e f g h i (2) 23 23 (3) 23 ( 23 ) 23 x 1 x 2 23 x
= M + M + M + M M + =.,. f = < ρ, > ρ ρ. ρ f. = ρ = = ± = log 4 = = = ± f = k k ρ. k
 7 b f n f} d = b f n f d,. 5,. [ ] ɛ >, n ɛ + + n < ɛ. m. n m log + < n m. n lim sin kπ sin kπ } k π sin = n n n. k= 4 f, y = r + s, y = rs f rs = f + r + sf y + rsf yy + f y. f = f =, f = sin. 5 f f =.
7 b f n f} d = b f n f d,. 5,. [ ] ɛ >, n ɛ + + n < ɛ. m. n m log + < n m. n lim sin kπ sin kπ } k π sin = n n n. k= 4 f, y = r + s, y = rs f rs = f + r + sf y + rsf yy + f y. f = f =, f = sin. 5 f f =.
http://www2.math.kyushu-u.ac.jp/~hara/lectures/lectures-j.html 2 N(ε 1 ) N(ε 2 ) ε 1 ε 2 α ε ε 2 1 n N(ɛ) N ɛ ɛ- (1.1.3) n > N(ɛ) a n α < ɛ n N(ɛ) a n
 http://www2.math.kyushu-u.ac.jp/~hara/lectures/lectures-j.html 1 1 1.1 ɛ-n 1 ɛ-n lim n a n = α n a n α 2 lim a n = 1 n a k n n k=1 1.1.7 ɛ-n 1.1.1 a n α a n n α lim n a n = α ɛ N(ɛ) n > N(ɛ) a n α < ɛ
http://www2.math.kyushu-u.ac.jp/~hara/lectures/lectures-j.html 1 1 1.1 ɛ-n 1 ɛ-n lim n a n = α n a n α 2 lim a n = 1 n a k n n k=1 1.1.7 ɛ-n 1.1.1 a n α a n n α lim n a n = α ɛ N(ɛ) n > N(ɛ) a n α < ɛ
24.15章.微分方程式
 m d y dt = F m d y = mg dt V y = dy dt d y dt = d dy dt dt = dv y dt dv y dt = g dv y dt = g dt dt dv y = g dt V y ( t) = gt + C V y ( ) = V y ( ) = C = V y t ( ) = gt V y ( t) = dy dt = gt dy = g t dt
m d y dt = F m d y = mg dt V y = dy dt d y dt = d dy dt dt = dv y dt dv y dt = g dv y dt = g dt dt dv y = g dt V y ( t) = gt + C V y ( ) = V y ( ) = C = V y t ( ) = gt V y ( t) = dy dt = gt dy = g t dt
0.,,., m Euclid m m. 2.., M., M R 2 ψ. ψ,, R 2 M.,, (x 1 (),, x m ()) R m. 2 M, R f. M (x 1,, x m ), f (x 1,, x m ) f(x 1,, x m ). f ( ). x i : M R.,,
 2012 10 13 1,,,.,,.,.,,. 2?.,,. 1,, 1. (θ, φ), θ, φ (0, π),, (0, 2π). 1 0.,,., m Euclid m m. 2.., M., M R 2 ψ. ψ,, R 2 M.,, (x 1 (),, x m ()) R m. 2 M, R f. M (x 1,, x m ), f (x 1,, x m ) f(x 1,, x m ).
2012 10 13 1,,,.,,.,.,,. 2?.,,. 1,, 1. (θ, φ), θ, φ (0, π),, (0, 2π). 1 0.,,., m Euclid m m. 2.., M., M R 2 ψ. ψ,, R 2 M.,, (x 1 (),, x m ()) R m. 2 M, R f. M (x 1,, x m ), f (x 1,, x m ) f(x 1,, x m ).
( ) sin 1 x, cos 1 x, tan 1 x sin x, cos x, tan x, arcsin x, arccos x, arctan x. π 2 sin 1 x π 2, 0 cos 1 x π, π 2 < tan 1 x < π 2 1 (1) (
 6 20 ( ) sin, cos, tan sin, cos, tan, arcsin, arccos, arctan. π 2 sin π 2, 0 cos π, π 2 < tan < π 2 () ( 2 2 lim 2 ( 2 ) ) 2 = 3 sin (2) lim 5 0 = 2 2 0 0 2 2 3 3 4 5 5 2 5 6 3 5 7 4 5 8 4 9 3 4 a 3 b
6 20 ( ) sin, cos, tan sin, cos, tan, arcsin, arccos, arctan. π 2 sin π 2, 0 cos π, π 2 < tan < π 2 () ( 2 2 lim 2 ( 2 ) ) 2 = 3 sin (2) lim 5 0 = 2 2 0 0 2 2 3 3 4 5 5 2 5 6 3 5 7 4 5 8 4 9 3 4 a 3 b
. sinh x sinh x) = e x e x = ex e x = sinh x 3) y = cosh x, y = sinh x y = e x, y = e x 6 sinhx) coshx) 4 y-axis x-axis : y = cosh x, y = s
 . 00 3 9 [] sinh x = ex e x, cosh x = ex + e x ) sinh cosh 4 hyperbolic) hyperbola) = 3 cosh x cosh x) = e x + e x = cosh x ) . sinh x sinh x) = e x e x = ex e x = sinh x 3) y = cosh x, y = sinh x y =
. 00 3 9 [] sinh x = ex e x, cosh x = ex + e x ) sinh cosh 4 hyperbolic) hyperbola) = 3 cosh x cosh x) = e x + e x = cosh x ) . sinh x sinh x) = e x e x = ex e x = sinh x 3) y = cosh x, y = sinh x y =
応力とひずみ.ppt
 in [email protected] 2 3 4 5 x 2 6 Continuum) 7 8 9 F F 10 F L L F L 1 L F L F L F 11 F L F F L F L L L 1 L 2 12 F L F! A A! S! = F S 13 F L L F F n = F " cos# F t = F " sin# S $ = S cos# S S
in [email protected] 2 3 4 5 x 2 6 Continuum) 7 8 9 F F 10 F L L F L 1 L F L F L F 11 F L F F L F L L L 1 L 2 12 F L F! A A! S! = F S 13 F L L F F n = F " cos# F t = F " sin# S $ = S cos# S S
5.. z = f(x, y) y y = b f x x g(x) f(x, b) g x ( ) A = lim h g(a + h) g(a) h g(x) a A = g (a) = f x (a, b)............................................
 5 partial differentiation (total) differentiation 5. z = f(x, y) (a, b) A = lim h f(a + h, b) f(a, b) h........................................................... ( ) f(x, y) (a, b) x A (a, b) x (a, b)
5 partial differentiation (total) differentiation 5. z = f(x, y) (a, b) A = lim h f(a + h, b) f(a, b) h........................................................... ( ) f(x, y) (a, b) x A (a, b) x (a, b)
I.2 z x, y i z = x + iy. x, y z (real part), (imaginary part), x = Re(z), y = Im(z). () i. (2) 2 z = x + iy, z 2 = x 2 + iy 2,, z ± z 2 = (x ± x 2 ) +
 I..... z 2 x, y z = x + iy (i ). 2 (x, y). 2.,,.,,. (), ( 2 ),,. II ( ).. z, w = f(z). z f(z), w. z = x + iy, f(z) 2 x, y. f(z) u(x, y), v(x, y), w = f(x + iy) = u(x, y) + iv(x, y).,. 2. z z, w w. D, D.
I..... z 2 x, y z = x + iy (i ). 2 (x, y). 2.,,.,,. (), ( 2 ),,. II ( ).. z, w = f(z). z f(z), w. z = x + iy, f(z) 2 x, y. f(z) u(x, y), v(x, y), w = f(x + iy) = u(x, y) + iv(x, y).,. 2. z z, w w. D, D.
untitled
 10 log 10 W W 10 L W = 10 log 10 W 10 12 10 log 10 I I 0 I 0 =10 12 I = P2 ρc = ρcv2 L p = 10 log 10 p 2 p 0 2 = 20 log 10 p p = 20 log p 10 0 2 10 5 L 3 = 10 log 10 10 L 1 /10 +10 L 2 ( /10 ) L 1 =10
10 log 10 W W 10 L W = 10 log 10 W 10 12 10 log 10 I I 0 I 0 =10 12 I = P2 ρc = ρcv2 L p = 10 log 10 p 2 p 0 2 = 20 log 10 p p = 20 log p 10 0 2 10 5 L 3 = 10 log 10 10 L 1 /10 +10 L 2 ( /10 ) L 1 =10
 211 [email protected] 1 R *1 n n R n *2 R n = {(x 1,..., x n ) x 1,..., x n R}. R R 2 R 3 R n R n R n D D R n *3 ) (x 1,..., x n ) f(x 1,..., x n ) f D *4 n 2 n = 1 ( ) 1 f D R n f : D R 1.1. (x,
211 [email protected] 1 R *1 n n R n *2 R n = {(x 1,..., x n ) x 1,..., x n R}. R R 2 R 3 R n R n R n D D R n *3 ) (x 1,..., x n ) f(x 1,..., x n ) f D *4 n 2 n = 1 ( ) 1 f D R n f : D R 1.1. (x,
[ ] 0.1 lim x 0 e 3x 1 x IC ( 11) ( s114901) 0.2 (1) y = e 2x (x 2 + 1) (2) y = x/(x 2 + 1) 0.3 dx (1) 1 4x 2 (2) e x sin 2xdx (3) sin 2 xdx ( 11) ( s
![[ ] 0.1 lim x 0 e 3x 1 x IC ( 11) ( s114901) 0.2 (1) y = e 2x (x 2 + 1) (2) y = x/(x 2 + 1) 0.3 dx (1) 1 4x 2 (2) e x sin 2xdx (3) sin 2 xdx ( 11) ( s [ ] 0.1 lim x 0 e 3x 1 x IC ( 11) ( s114901) 0.2 (1) y = e 2x (x 2 + 1) (2) y = x/(x 2 + 1) 0.3 dx (1) 1 4x 2 (2) e x sin 2xdx (3) sin 2 xdx ( 11) ( s](/thumbs/94/118579915.jpg) [ ]. lim e 3 IC ) s49). y = e + ) ) y = / + ).3 d 4 ) e sin d 3) sin d ) s49) s493).4 z = y z z y s494).5 + y = 4 =.6 s495) dy = 3e ) d dy d = y s496).7 lim ) lim e s49).8 y = e sin ) y = sin e 3) y =
[ ]. lim e 3 IC ) s49). y = e + ) ) y = / + ).3 d 4 ) e sin d 3) sin d ) s49) s493).4 z = y z z y s494).5 + y = 4 =.6 s495) dy = 3e ) d dy d = y s496).7 lim ) lim e s49).8 y = e sin ) y = sin e 3) y =
di-problem.dvi
 005/05/05 by. I : : : : : : : : : : : : : : : : : : : : : : : : :. II : : : : : : : : : : : : : : : : : : : : : : : : : 3 3. III : : : : : : : : : : : : : : : : : : : : : : : : 4 4. : : : : : : : : : :
005/05/05 by. I : : : : : : : : : : : : : : : : : : : : : : : : :. II : : : : : : : : : : : : : : : : : : : : : : : : : 3 3. III : : : : : : : : : : : : : : : : : : : : : : : : 4 4. : : : : : : : : : :
( ) a, b c a 2 + b 2 = c 2. 2 1 2 2 : 2 2 = p q, p, q 2q 2 = p 2. p 2 p 2 2 2 q 2 p, q (QED)
 rational number p, p, (q ) q ratio 3.14 = 3 + 1 10 + 4 100 ( ) a, b c a 2 + b 2 = c 2. 2 1 2 2 : 2 2 = p q, p, q 2q 2 = p 2. p 2 p 2 2 2 q 2 p, q (QED) ( a) ( b) a > b > 0 a < nb n A A B B A A, B B A =
rational number p, p, (q ) q ratio 3.14 = 3 + 1 10 + 4 100 ( ) a, b c a 2 + b 2 = c 2. 2 1 2 2 : 2 2 = p q, p, q 2q 2 = p 2. p 2 p 2 2 2 q 2 p, q (QED) ( a) ( b) a > b > 0 a < nb n A A B B A A, B B A =
S I. dy fx x fx y fx + C 3 C dy fx 4 x, y dy v C xt y C v e kt k > xt yt gt [ v dt dt v e kt xt v e kt + C k x v + C C k xt v k 3 r r + dr e kt S dt d
 S I.. http://ayapin.film.s.dendai.ac.jp/~matuda /TeX/lecture.html PDF PS.................................... 3.3.................... 9.4................5.............. 3 5. Laplace................. 5....
S I.. http://ayapin.film.s.dendai.ac.jp/~matuda /TeX/lecture.html PDF PS.................................... 3.3.................... 9.4................5.............. 3 5. Laplace................. 5....
0104.pages
 bit 8, 6, 3 bit byte = 8 bit, char CBYTEFORTRAN) 055, -87 word = 6 bit int (C) INTEGER (FORTRAN) -37683767 unsgined int (C) 065535 double word = 3 bit, longint C -4748364847483647 CD-audio 6 bit, 44. kbpsch74
bit 8, 6, 3 bit byte = 8 bit, char CBYTEFORTRAN) 055, -87 word = 6 bit int (C) INTEGER (FORTRAN) -37683767 unsgined int (C) 065535 double word = 3 bit, longint C -4748364847483647 CD-audio 6 bit, 44. kbpsch74
i 18 2H 2 + O 2 2H 2 + ( ) 3K
 i 18 2H 2 + O 2 2H 2 + ( ) 3K ii 1 1 1.1.................................. 1 1.2........................................ 3 1.3......................................... 3 1.4....................................
i 18 2H 2 + O 2 2H 2 + ( ) 3K ii 1 1 1.1.................................. 1 1.2........................................ 3 1.3......................................... 3 1.4....................................
A B 5 C 9 3.4 7 mm, 89 mm 7/89 = 3.4. π 3 6 π 6 6 = 6 π > 6, π > 3 : π > 3
 π 9 3 7 4. π 3................................................. 3.3........................ 3.4 π.................... 4.5..................... 4 7...................... 7..................... 9 3 3. p
π 9 3 7 4. π 3................................................. 3.3........................ 3.4 π.................... 4.5..................... 4 7...................... 7..................... 9 3 3. p
.5 z = a + b + c n.6 = a sin t y = b cos t dy d a e e b e + e c e e e + e 3 s36 3 a + y = a, b > b 3 s363.7 y = + 3 y = + 3 s364.8 cos a 3 s365.9 y =,
 [ ] IC. r, θ r, θ π, y y = 3 3 = r cos θ r sin θ D D = {, y ; y }, y D r, θ ep y yddy D D 9 s96. d y dt + 3dy + y = cos t dt t = y = e π + e π +. t = π y =.9 s6.3 d y d + dy d + y = y =, dy d = 3 a, b
[ ] IC. r, θ r, θ π, y y = 3 3 = r cos θ r sin θ D D = {, y ; y }, y D r, θ ep y yddy D D 9 s96. d y dt + 3dy + y = cos t dt t = y = e π + e π +. t = π y =.9 s6.3 d y d + dy d + y = y =, dy d = 3 a, b
f (x) f (x) f (x) f (x) f (x) 2 f (x) f (x) f (x) f (x) 2 n f (x) n f (n) (x) dn f f (x) dx n dn dx n D n f (x) n C n C f (x) x = a 1 f (x) x = a x >
 5.1 1. x = a f (x) a x h f (a + h) f (a) h (5.1) h 0 f (x) x = a f +(a) f (a + h) f (a) = lim h +0 h (5.2) x h h 0 f (a) f (a + h) f (a) f (a h) f (a) = lim = lim h 0 h h 0 h (5.3) f (x) x = a f (a) =
5.1 1. x = a f (x) a x h f (a + h) f (a) h (5.1) h 0 f (x) x = a f +(a) f (a + h) f (a) = lim h +0 h (5.2) x h h 0 f (a) f (a + h) f (a) f (a h) f (a) = lim = lim h 0 h h 0 h (5.3) f (x) x = a f (a) =
grad φ(p ) φ P grad φ(p ) p P p φ P p l t φ l t = 0 g (0) g (0) (31) grad φ(p ) p grad φ φ (P, φ(p )) xy (x, y) = (ξ(t), η(t)) ( )
 2 9 2 5 2.2.3 grad φ(p ) φ P grad φ(p ) p P p φ P p l t φ l t = g () g () (3) grad φ(p ) p grad φ φ (P, φ(p )) y (, y) = (ξ(t), η(t)) ( ) ξ (t) (t) := η (t) grad f(ξ(t), η(t)) (t) g(t) := f(ξ(t), η(t))
2 9 2 5 2.2.3 grad φ(p ) φ P grad φ(p ) p P p φ P p l t φ l t = g () g () (3) grad φ(p ) p grad φ φ (P, φ(p )) y (, y) = (ξ(t), η(t)) ( ) ξ (t) (t) := η (t) grad f(ξ(t), η(t)) (t) g(t) := f(ξ(t), η(t))
S I. dy fx x fx y fx + C 3 C vt dy fx 4 x, y dy yt gt + Ct + C dt v e kt xt v e kt + C k x v k + C C xt v k 3 r r + dr e kt S Sr πr dt d v } dt k e kt
 S I. x yx y y, y,. F x, y, y, y,, y n http://ayapin.film.s.dendai.ac.jp/~matuda n /TeX/lecture.html PDF PS yx.................................... 3.3.................... 9.4................5..............
S I. x yx y y, y,. F x, y, y, y,, y n http://ayapin.film.s.dendai.ac.jp/~matuda n /TeX/lecture.html PDF PS yx.................................... 3.3.................... 9.4................5..............
 A 2008 10 (2010 4 ) 1 1 1.1................................. 1 1.2..................................... 1 1.3............................ 3 1.3.1............................. 3 1.3.2..................................
A 2008 10 (2010 4 ) 1 1 1.1................................. 1 1.2..................................... 1 1.3............................ 3 1.3.1............................. 3 1.3.2..................................
0104.pages
 0 5 9 07 0 bit 8, 6, 3 bit byte = 8 bit, char (C )BYTEFORTRAN) 055, -87 word = 6 bit int (C) INTEGER (FORTRAN) -3,7683,767 unsgined int (C) 065,535 double word = 3 bit, longint (C )-,47,483,648,47,483,647
0 5 9 07 0 bit 8, 6, 3 bit byte = 8 bit, char (C )BYTEFORTRAN) 055, -87 word = 6 bit int (C) INTEGER (FORTRAN) -3,7683,767 unsgined int (C) 065,535 double word = 3 bit, longint (C )-,47,483,648,47,483,647
i 0 1 0.1 I................................................ 1 0.2.................................................. 2 0.2.1...........................
 2008 II 21 1 31 i 0 1 0.1 I................................................ 1 0.2.................................................. 2 0.2.1............................................. 2 0.2.2.............................................
2008 II 21 1 31 i 0 1 0.1 I................................................ 1 0.2.................................................. 2 0.2.1............................................. 2 0.2.2.............................................
7 9 7..................................... 9 7................................ 3 7.3...................................... 3 A A. ω ν = ω/π E = hω. E
 B 8.9.4, : : MIT I,II A.P. E.F.,, 993 I,,, 999, 7 I,II, 95 A A........................... A........................... 3.3 A.............................. 4.4....................................... 5 6..............................
B 8.9.4, : : MIT I,II A.P. E.F.,, 993 I,,, 999, 7 I,II, 95 A A........................... A........................... 3.3 A.............................. 4.4....................................... 5 6..............................
( 4) ( ) (Poincaré) (Poincaré disk) 1 2 (hyperboloid) [1] [2, 3, 4] 1 [1] 1 y = 0 L (hyperboloid) K (Klein disk) J (hemisphere) I (P
![( 4) ( ) (Poincaré) (Poincaré disk) 1 2 (hyperboloid) [1] [2, 3, 4] 1 [1] 1 y = 0 L (hyperboloid) K (Klein disk) J (hemisphere) I (P ( 4) ( ) (Poincaré) (Poincaré disk) 1 2 (hyperboloid) [1] [2, 3, 4] 1 [1] 1 y = 0 L (hyperboloid) K (Klein disk) J (hemisphere) I (P](/thumbs/94/121424413.jpg) 4) 07.3.7 ) Poincaré) Poincaré disk) hyperboloid) [] [, 3, 4] [] y 0 L hyperboloid) K Klein disk) J hemisphere) I Poincaré disk) : hyperboloid) L Klein disk) K hemisphere) J Poincaré) I y 0 x + y z 0 z
4) 07.3.7 ) Poincaré) Poincaré disk) hyperboloid) [] [, 3, 4] [] y 0 L hyperboloid) K Klein disk) J hemisphere) I Poincaré disk) : hyperboloid) L Klein disk) K hemisphere) J Poincaré) I y 0 x + y z 0 z
330
 330 331 332 333 334 t t P 335 t R t t i R +(P P ) P =i t P = R + P 1+i t 336 uc R=uc P 337 338 339 340 341 342 343 π π β τ τ (1+π ) (1 βτ )(1 τ ) (1+π ) (1 βτ ) (1 τ ) (1+π ) (1 τ ) (1 τ ) 344 (1 βτ )(1
330 331 332 333 334 t t P 335 t R t t i R +(P P ) P =i t P = R + P 1+i t 336 uc R=uc P 337 338 339 340 341 342 343 π π β τ τ (1+π ) (1 βτ )(1 τ ) (1+π ) (1 βτ ) (1 τ ) (1+π ) (1 τ ) (1 τ ) 344 (1 βτ )(1
5.. z = f(x, y) y y = b f x x g(x) f(x, b) g x ( ) A = lim h 0 g(a + h) g(a) h g(x) a A = g (a) = f x (a, b)
 5 partial differentiation (total) differentiation 5. z = f(x, y) (a, b) A = lim h 0 f(a + h, b) f(a, b) h............................................................... ( ) f(x, y) (a, b) x A (a, b) x
5 partial differentiation (total) differentiation 5. z = f(x, y) (a, b) A = lim h 0 f(a + h, b) f(a, b) h............................................................... ( ) f(x, y) (a, b) x A (a, b) x
2009 I 2 II III 14, 15, α β α β l 0 l l l l γ (1) γ = αβ (2) α β n n cos 2k n n π sin 2k n π k=1 k=1 3. a 0, a 1,..., a n α a
 009 I II III 4, 5, 6 4 30. 0 α β α β l 0 l l l l γ ) γ αβ ) α β. n n cos k n n π sin k n π k k 3. a 0, a,..., a n α a 0 + a x + a x + + a n x n 0 ᾱ 4. [a, b] f y fx) y x 5. ) Arcsin 4) Arccos ) ) Arcsin
009 I II III 4, 5, 6 4 30. 0 α β α β l 0 l l l l γ ) γ αβ ) α β. n n cos k n n π sin k n π k k 3. a 0, a,..., a n α a 0 + a x + a x + + a n x n 0 ᾱ 4. [a, b] f y fx) y x 5. ) Arcsin 4) Arccos ) ) Arcsin
II No.01 [n/2] [1]H n (x) H n (x) = ( 1) r n! r!(n 2r)! (2x)n 2r. r=0 [2]H n (x) n,, H n ( x) = ( 1) n H n (x). [3] H n (x) = ( 1) n dn x2 e dx n e x2
![II No.01 [n/2] [1]H n (x) H n (x) = ( 1) r n! r!(n 2r)! (2x)n 2r. r=0 [2]H n (x) n,, H n ( x) = ( 1) n H n (x). [3] H n (x) = ( 1) n dn x2 e dx n e x2 II No.01 [n/2] [1]H n (x) H n (x) = ( 1) r n! r!(n 2r)! (2x)n 2r. r=0 [2]H n (x) n,, H n ( x) = ( 1) n H n (x). [3] H n (x) = ( 1) n dn x2 e dx n e x2](/thumbs/101/149159646.jpg) II No.1 [n/] [1]H n x) H n x) = 1) r n! r!n r)! x)n r r= []H n x) n,, H n x) = 1) n H n x) [3] H n x) = 1) n dn x e dx n e x [4] H n+1 x) = xh n x) nh n 1 x) ) d dx x H n x) = H n+1 x) d dx H nx) = nh
II No.1 [n/] [1]H n x) H n x) = 1) r n! r!n r)! x)n r r= []H n x) n,, H n x) = 1) n H n x) [3] H n x) = 1) n dn x e dx n e x [4] H n+1 x) = xh n x) nh n 1 x) ) d dx x H n x) = H n+1 x) d dx H nx) = nh
, x R, f (x),, df dx : R R,, f : R R, f(x) ( ).,, f (a) d f dx (a), f (a) d3 f dx 3 (a),, f (n) (a) dn f dx n (a), f d f dx, f d3 f dx 3,, f (n) dn f
 ,,,,.,,,. R f : R R R a R, f(a + ) f(a) lim 0 (), df dx (a) f (a), f(x) x a, f (a), f(x) x a ( ). y f(a + ) y f(x) f(a+) f(a) f(a + ) f(a) f(a) x a 0 a a + x 0 a a + x y y f(x) 0 : 0, f(a+) f(a)., f(x)
,,,,.,,,. R f : R R R a R, f(a + ) f(a) lim 0 (), df dx (a) f (a), f(x) x a, f (a), f(x) x a ( ). y f(a + ) y f(x) f(a+) f(a) f(a + ) f(a) f(a) x a 0 a a + x 0 a a + x y y f(x) 0 : 0, f(a+) f(a)., f(x)
Part. 4. () 4.. () 4.. 3 5. 5 5.. 5 5.. 6 5.3. 7 Part 3. 8 6. 8 6.. 8 6.. 8 7. 8 7.. 8 7.. 3 8. 3 9., 34 9.. 34 9.. 37 9.3. 39. 4.. 4.. 43. 46.. 46..
 Cotets 6 6 : 6 6 6 6 6 6 7 7 7 Part. 8. 8.. 8.. 9..... 3. 3 3.. 3 3.. 7 3.3. 8 Part. 4. () 4.. () 4.. 3 5. 5 5.. 5 5.. 6 5.3. 7 Part 3. 8 6. 8 6.. 8 6.. 8 7. 8 7.. 8 7.. 3 8. 3 9., 34 9.. 34 9.. 37 9.3.
Cotets 6 6 : 6 6 6 6 6 6 7 7 7 Part. 8. 8.. 8.. 9..... 3. 3 3.. 3 3.. 7 3.3. 8 Part. 4. () 4.. () 4.. 3 5. 5 5.. 5 5.. 6 5.3. 7 Part 3. 8 6. 8 6.. 8 6.. 8 7. 8 7.. 8 7.. 3 8. 3 9., 34 9.. 34 9.. 37 9.3.
1 I p2/30
 I I p1/30 1 I p2/30 1 ( ) I p3/30 1 ( ), y = y() d = f() g(y) ( g(y) = f()d) (1) I p4/30 1 ( ), y = y() d = f() g(y) ( g(y) = f()d) (1) g(y) = f()d I p4/30 1 ( ), y = y() d = f() g(y) ( g(y) = f()d) (1)
I I p1/30 1 I p2/30 1 ( ) I p3/30 1 ( ), y = y() d = f() g(y) ( g(y) = f()d) (1) I p4/30 1 ( ), y = y() d = f() g(y) ( g(y) = f()d) (1) g(y) = f()d I p4/30 1 ( ), y = y() d = f() g(y) ( g(y) = f()d) (1)
(ii) (iii) z a = z a =2 z a =6 sin z z a dz. cosh z z a dz. e z dz. (, a b > 6.) (z a)(z b) 52.. (a) dz, ( a = /6.), (b) z =6 az (c) z a =2 53. f n (z
 B 4 24 7 9 ( ) :,..,,.,. 4 4. f(z): D C: D a C, 2πi C f(z) dz = f(a). z a a C, ( ). (ii), a D, a U a,r D f. f(z) = A n (z a) n, z U a,r, n= A n := 2πi C f(ζ) dζ, n =,,..., (ζ a) n+, C a D. (iii) U a,r
B 4 24 7 9 ( ) :,..,,.,. 4 4. f(z): D C: D a C, 2πi C f(z) dz = f(a). z a a C, ( ). (ii), a D, a U a,r D f. f(z) = A n (z a) n, z U a,r, n= A n := 2πi C f(ζ) dζ, n =,,..., (ζ a) n+, C a D. (iii) U a,r
KENZOU
 KENZOU 2008 8 2 3 2 3 2 2 4 2 4............................................... 2 4.2............................... 3 4.2........................................... 4 4.3..............................
KENZOU 2008 8 2 3 2 3 2 2 4 2 4............................................... 2 4.2............................... 3 4.2........................................... 4 4.3..............................
96 7 1m =2 10 7 N 1A 7.1 7.2 a C (1) I (2) A C I A A a A a A A a C C C 7.2: C A C A = = µ 0 2π (1) A C 7.2 AC C A 3 3 µ0 I 2 = 2πa. (2) A C C 7.2 A A
 7 Lorentz 7.1 Ampère I 1 I 2 I 2 I 1 L I 1 I 2 21 12 L r 21 = 12 = µ 0 2π I 1 I 2 r L. (7.1) 7.1 µ 0 =4π 10 7 N A 2 (7.2) magnetic permiability I 1 I 2 I 1 I 2 12 21 12 21 7.1: 1m 95 96 7 1m =2 10 7 N
7 Lorentz 7.1 Ampère I 1 I 2 I 2 I 1 L I 1 I 2 21 12 L r 21 = 12 = µ 0 2π I 1 I 2 r L. (7.1) 7.1 µ 0 =4π 10 7 N A 2 (7.2) magnetic permiability I 1 I 2 I 1 I 2 12 21 12 21 7.1: 1m 95 96 7 1m =2 10 7 N
 ( 12 ( ( ( ( Levi-Civita grad div rot ( ( = 4 : 6 3 1 1.1 f(x n f (n (x, d n f(x (1.1 dxn f (2 (x f (x 1.1 f(x = e x f (n (x = e x d dx (fg = f g + fg (1.2 d dx d 2 dx (fg = f g + 2f g + fg 2... d n n
( 12 ( ( ( ( Levi-Civita grad div rot ( ( = 4 : 6 3 1 1.1 f(x n f (n (x, d n f(x (1.1 dxn f (2 (x f (x 1.1 f(x = e x f (n (x = e x d dx (fg = f g + fg (1.2 d dx d 2 dx (fg = f g + 2f g + fg 2... d n n
I, II 1, A = A 4 : 6 = max{ A, } A A 10 10%
 1 2006.4.17. A 3-312 tel: 092-726-4774, e-mail: [email protected], http://www.math.kyushu-u.ac.jp/ hara/lectures/lectures-j.html Office hours: B A I ɛ-δ ɛ-δ 1. 2. A 1. 1. 2. 3. 4. 5. 2. ɛ-δ 1. ɛ-n
1 2006.4.17. A 3-312 tel: 092-726-4774, e-mail: [email protected], http://www.math.kyushu-u.ac.jp/ hara/lectures/lectures-j.html Office hours: B A I ɛ-δ ɛ-δ 1. 2. A 1. 1. 2. 3. 4. 5. 2. ɛ-δ 1. ɛ-n
M3 x y f(x, y) (= x) (= y) x + y f(x, y) = x + y + *. f(x, y) π y f(x, y) x f(x + x, y) f(x, y) lim x x () f(x,y) x 3 -
 M3............................................................................................ 3.3................................................... 3 6........................................... 6..........................................
M3............................................................................................ 3.3................................................... 3 6........................................... 6..........................................
第85 回日本感染症学会総会学術集会後抄録(III)
 β β α α α µ µ µ µ α α α α γ αβ α γ α α γ α γ µ µ β β β β β β β β β µ β α µ µ µ β β µ µ µ µ µ µ γ γ γ γ γ γ µ α β γ β β µ µ µ µ µ β β µ β β µ α β β µ µµ β µ µ µ µ µ µ λ µ µ β µ µ µ µ µ µ µ µ
β β α α α µ µ µ µ α α α α γ αβ α γ α α γ α γ µ µ β β β β β β β β β µ β α µ µ µ β β µ µ µ µ µ µ γ γ γ γ γ γ µ α β γ β β µ µ µ µ µ β β µ β β µ α β β µ µµ β µ µ µ µ µ µ λ µ µ β µ µ µ µ µ µ µ µ
() x + y + y + x dy dx = 0 () dy + xy = x dx y + x y ( 5) ( s55906) 0.7. (). 5 (). ( 6) ( s6590) 0.8 m n. 0.9 n n A. ( 6) ( s6590) f A (λ) = det(a λi)
 0. A A = 4 IC () det A () A () x + y + z = x y z X Y Z = A x y z ( 5) ( s5590) 0. a + b + c b c () a a + b + c c a b a + b + c 0 a b c () a 0 c b b c 0 a c b a 0 0. A A = 7 5 4 5 0 ( 5) ( s5590) () A ()
0. A A = 4 IC () det A () A () x + y + z = x y z X Y Z = A x y z ( 5) ( s5590) 0. a + b + c b c () a a + b + c c a b a + b + c 0 a b c () a 0 c b b c 0 a c b a 0 0. A A = 7 5 4 5 0 ( 5) ( s5590) () A ()
0 1-4. 1-5. (1) + b = b +, (2) b = b, (3) + 0 =, (4) 1 =, (5) ( + b) + c = + (b + c), (6) ( b) c = (b c), (7) (b + c) = b + c, (8) ( + b)c = c + bc (9
 1-1. 1, 2, 3, 4, 5, 6, 7,, 100,, 1000, n, m m m n n 0 n, m m n 1-2. 0 m n m n 0 2 = 1.41421356 π = 3.141516 1-3. 1 0 1-4. 1-5. (1) + b = b +, (2) b = b, (3) + 0 =, (4) 1 =, (5) ( + b) + c = + (b + c),
1-1. 1, 2, 3, 4, 5, 6, 7,, 100,, 1000, n, m m m n n 0 n, m m n 1-2. 0 m n m n 0 2 = 1.41421356 π = 3.141516 1-3. 1 0 1-4. 1-5. (1) + b = b +, (2) b = b, (3) + 0 =, (4) 1 =, (5) ( + b) + c = + (b + c),
z z x = y = /x lim y = + x + lim y = x (x a ) a (x a+) lim z z f(z) = A, lim z z g(z) = B () lim z z {f(z) ± g(z)} = A ± B (2) lim {f(z) g(z)} = AB z
 Tips KENZOU 28 6 29 sin 2 x + cos 2 x = cos 2 z + sin 2 z = OK... z < z z < R w = f(z) z z w w f(z) w lim z z f(z) = w x x 2 2 f(x) x = a lim f(x) = lim f(x) x a+ x a z z x = y = /x lim y = + x + lim y
Tips KENZOU 28 6 29 sin 2 x + cos 2 x = cos 2 z + sin 2 z = OK... z < z z < R w = f(z) z z w w f(z) w lim z z f(z) = w x x 2 2 f(x) x = a lim f(x) = lim f(x) x a+ x a z z x = y = /x lim y = + x + lim y
 4 5.............................................. 5............................................ 6.............................................. 7......................................... 8.3.................................................4.........................................4..............................................4................................................4.3...............................................
4 5.............................................. 5............................................ 6.............................................. 7......................................... 8.3.................................................4.........................................4..............................................4................................................4.3...............................................
6. Euler x
 ...............................................................................3......................................... 4.4................................... 5.5......................................
...............................................................................3......................................... 4.4................................... 5.5......................................
1 1 x y = y(x) y, y,..., y (n) : n y F (x, y, y,..., y (n) ) = 0 n F (x, y, y ) = 0 1 y(x) y y = G(x, y) y, y y + p(x)y = q(x) 1 p(x) q(
 1 1 y = y() y, y,..., y (n) : n y F (, y, y,..., y (n) ) = 0 n F (, y, y ) = 0 1 y() 1.1 1 y y = G(, y) 1.1.1 1 y, y y + p()y = q() 1 p() q() (q() = 0) y + p()y = 0 y y + py = 0 y y = p (log y) = p log
1 1 y = y() y, y,..., y (n) : n y F (, y, y,..., y (n) ) = 0 n F (, y, y ) = 0 1 y() 1.1 1 y y = G(, y) 1.1.1 1 y, y y + p()y = q() 1 p() q() (q() = 0) y + p()y = 0 y y + py = 0 y y = p (log y) = p log
1 913 10301200 A B C D E F G H J K L M 1A1030 10 : 45 1A1045 11 : 00 1A1100 11 : 15 1A1115 11 : 30 1A1130 11 : 45 1A1145 12 : 00 1B1030 1B1045 1C1030
 1 913 9001030 A B C D E F G H J K L M 9:00 1A0900 9:15 1A0915 9:30 1A0930 9:45 1A0945 10 : 00 1A1000 10 : 15 1B0900 1B0915 1B0930 1B0945 1B1000 1C0900 1C0915 1D0915 1C0930 1C0945 1C1000 1D0930 1D0945 1D1000
1 913 9001030 A B C D E F G H J K L M 9:00 1A0900 9:15 1A0915 9:30 1A0930 9:45 1A0945 10 : 00 1A1000 10 : 15 1B0900 1B0915 1B0930 1B0945 1B1000 1C0900 1C0915 1D0915 1C0930 1C0945 1C1000 1D0930 1D0945 1D1000
z f(z) f(z) x, y, u, v, r, θ r > 0 z = x + iy, f = u + iv C γ D f(z) f(z) D f(z) f(z) z, Rm z, z 1.1 z = x + iy = re iθ = r (cos θ + i sin θ) z = x iy
 z fz fz x, y, u, v, r, θ r > z = x + iy, f = u + iv γ D fz fz D fz fz z, Rm z, z. z = x + iy = re iθ = r cos θ + i sin θ z = x iy = re iθ = r cos θ i sin θ x = z + z = Re z, y = z z = Im z i r = z = z
z fz fz x, y, u, v, r, θ r > z = x + iy, f = u + iv γ D fz fz D fz fz z, Rm z, z. z = x + iy = re iθ = r cos θ + i sin θ z = x iy = re iθ = r cos θ i sin θ x = z + z = Re z, y = z z = Im z i r = z = z
Note.tex 2008/09/19( )
 1 20 9 19 2 1 5 1.1........................ 5 1.2............................. 8 2 9 2.1............................. 9 2.2.............................. 10 3 13 3.1.............................. 13 3.2..................................
1 20 9 19 2 1 5 1.1........................ 5 1.2............................. 8 2 9 2.1............................. 9 2.2.............................. 10 3 13 3.1.............................. 13 3.2..................................
2011de.dvi
 211 ( 4 2 1. 3 1.1............................... 3 1.2 1- -......................... 13 1.3 2-1 -................... 19 1.4 3- -......................... 29 2. 37 2.1................................ 37
211 ( 4 2 1. 3 1.1............................... 3 1.2 1- -......................... 13 1.3 2-1 -................... 19 1.4 3- -......................... 29 2. 37 2.1................................ 37
1 No.1 5 C 1 I III F 1 F 2 F 1 F 2 2 Φ 2 (t) = Φ 1 (t) Φ 1 (t t). = Φ 1(t) t = ( 1.5e 0.5t 2.4e 4t 2e 10t ) τ < 0 t > τ Φ 2 (t) < 0 lim t Φ 2 (t) = 0
 1 No.1 5 C 1 I III F 1 F 2 F 1 F 2 2 Φ 2 (t) = Φ 1 (t) Φ 1 (t t). = Φ 1(t) t = ( 1.5e 0.5t 2.4e 4t 2e 10t ) τ < 0 t > τ Φ 2 (t) < 0 lim t Φ 2 (t) = 0 0 < t < τ I II 0 No.2 2 C x y x y > 0 x 0 x > b a dx
1 No.1 5 C 1 I III F 1 F 2 F 1 F 2 2 Φ 2 (t) = Φ 1 (t) Φ 1 (t t). = Φ 1(t) t = ( 1.5e 0.5t 2.4e 4t 2e 10t ) τ < 0 t > τ Φ 2 (t) < 0 lim t Φ 2 (t) = 0 0 < t < τ I II 0 No.2 2 C x y x y > 0 x 0 x > b a dx
K E N Z OU
 K E N Z OU 11 1 1 1.1..................................... 1.1.1............................ 1.1..................................................................................... 4 1.........................................
K E N Z OU 11 1 1 1.1..................................... 1.1.1............................ 1.1..................................................................................... 4 1.........................................
1 8, : 8.1 1, 2 z = ax + by + c ax by + z c = a b +1 x y z c = 0, (0, 0, c), n = ( a, b, 1). f = n i=1 a ii x 2 i + i<j 2a ij x i x j = ( x, A x), f =
 1 8, : 8.1 1, z = ax + by + c ax by + z c = a b +1 x y z c = 0, (0, 0, c), n = ( a, b, 1). f = a ii x i + i
1 8, : 8.1 1, z = ax + by + c ax by + z c = a b +1 x y z c = 0, (0, 0, c), n = ( a, b, 1). f = a ii x i + i
II 2 II
 II 2 II 2005 [email protected] 2005 4 1 1 2 5 2.1.................................... 5 2.2................................. 6 2.3............................. 6 2.4.................................
II 2 II 2005 [email protected] 2005 4 1 1 2 5 2.1.................................... 5 2.2................................. 6 2.3............................. 6 2.4.................................
2009 IA 5 I 22, 23, 24, 25, 26, (1) Arcsin 1 ( 2 (4) Arccos 1 ) 2 3 (2) Arcsin( 1) (3) Arccos 2 (5) Arctan 1 (6) Arctan ( 3 ) 3 2. n (1) ta
 009 IA 5 I, 3, 4, 5, 6, 7 6 3. () Arcsin ( (4) Arccos ) 3 () Arcsin( ) (3) Arccos (5) Arctan (6) Arctan ( 3 ) 3. n () tan x (nπ π/, nπ + π/) f n (x) f n (x) fn (x) Arctan x () sin x [nπ π/, nπ +π/] g n
009 IA 5 I, 3, 4, 5, 6, 7 6 3. () Arcsin ( (4) Arccos ) 3 () Arcsin( ) (3) Arccos (5) Arctan (6) Arctan ( 3 ) 3. n () tan x (nπ π/, nπ + π/) f n (x) f n (x) fn (x) Arctan x () sin x [nπ π/, nπ +π/] g n
1 (Berry,1975) 2-6 p (S πr 2 )p πr 2 p 2πRγ p p = 2γ R (2.5).1-1 : : : : ( ).2 α, β α, β () X S = X X α X β (.1) 1 2
 2005 9/8-11 2 2.2 ( 2-5) γ ( ) γ cos θ 2πr πρhr 2 g h = 2γ cos θ ρgr (2.1) γ = ρgrh (2.2) 2 cos θ θ cos θ = 1 (2.2) γ = 1 ρgrh (2.) 2 2. p p ρgh p ( ) p p = p ρgh (2.) h p p = 2γ r 1 1 (Berry,1975) 2-6
2005 9/8-11 2 2.2 ( 2-5) γ ( ) γ cos θ 2πr πρhr 2 g h = 2γ cos θ ρgr (2.1) γ = ρgrh (2.2) 2 cos θ θ cos θ = 1 (2.2) γ = 1 ρgrh (2.) 2 2. p p ρgh p ( ) p p = p ρgh (2.) h p p = 2γ r 1 1 (Berry,1975) 2-6
 1 1 1 1 1 1 2 f z 2 C 1, C 2 f 2 C 1, C 2 f(c 2 ) C 2 f(c 1 ) z C 1 f f(z) xy uv ( u v ) = ( a b c d ) ( x y ) + ( p q ) (p + b, q + d) 1 (p + a, q + c) 1 (p, q) 1 1 (b, d) (a, c) 2 3 2 3 a = d, c = b
1 1 1 1 1 1 2 f z 2 C 1, C 2 f 2 C 1, C 2 f(c 2 ) C 2 f(c 1 ) z C 1 f f(z) xy uv ( u v ) = ( a b c d ) ( x y ) + ( p q ) (p + b, q + d) 1 (p + a, q + c) 1 (p, q) 1 1 (b, d) (a, c) 2 3 2 3 a = d, c = b
() (, y) E(, y) () E(, y) (3) q ( ) () E(, y) = k q q (, y) () E(, y) = k r r (3).3 [.7 ] f y = f y () f(, y) = y () f(, y) = tan y y ( ) () f y = f y
![() (, y) E(, y) () E(, y) (3) q ( ) () E(, y) = k q q (, y) () E(, y) = k r r (3).3 [.7 ] f y = f y () f(, y) = y () f(, y) = tan y y ( ) () f y = f y () (, y) E(, y) () E(, y) (3) q ( ) () E(, y) = k q q (, y) () E(, y) = k r r (3).3 [.7 ] f y = f y () f(, y) = y () f(, y) = tan y y ( ) () f y = f y](/thumbs/85/92979039.jpg) 5. [. ] z = f(, y) () z = 3 4 y + y + 3y () z = y (3) z = sin( y) (4) z = cos y (5) z = 4y (6) z = tan y (7) z = log( + y ) (8) z = tan y + + y ( ) () z = 3 8y + y z y = 4 + + 6y () z = y z y = (3) z =
5. [. ] z = f(, y) () z = 3 4 y + y + 3y () z = y (3) z = sin( y) (4) z = cos y (5) z = 4y (6) z = tan y (7) z = log( + y ) (8) z = tan y + + y ( ) () z = 3 8y + y z y = 4 + + 6y () z = y z y = (3) z =
第86回日本感染症学会総会学術集会後抄録(II)
 χ μ μ μ μ β β μ μ μ μ β μ μ μ β β β α β β β λ Ι β μ μ β Δ Δ Δ Δ Δ μ μ α φ φ φ α γ φ φ γ φ φ γ γδ φ γδ γ φ φ φ φ φ φ φ φ φ φ φ φ φ α γ γ γ α α α α α γ γ γ γ γ γ γ α γ α γ γ μ μ κ κ α α α β α
χ μ μ μ μ β β μ μ μ μ β μ μ μ β β β α β β β λ Ι β μ μ β Δ Δ Δ Δ Δ μ μ α φ φ φ α γ φ φ γ φ φ γ γδ φ γδ γ φ φ φ φ φ φ φ φ φ φ φ φ φ α γ γ γ α α α α α γ γ γ γ γ γ γ α γ α γ γ μ μ κ κ α α α β α
a n a n ( ) (1) a m a n = a m+n (2) (a m ) n = a mn (3) (ab) n = a n b n (4) a m a n = a m n ( m > n ) m n 4 ( ) 552
 3 3.0 a n a n ( ) () a m a n = a m+n () (a m ) n = a mn (3) (ab) n = a n b n (4) a m a n = a m n ( m > n ) m n 4 ( ) 55 3. (n ) a n n a n a n 3 4 = 8 8 3 ( 3) 4 = 8 3 8 ( ) ( ) 3 = 8 8 ( ) 3 n n 4 n n
3 3.0 a n a n ( ) () a m a n = a m+n () (a m ) n = a mn (3) (ab) n = a n b n (4) a m a n = a m n ( m > n ) m n 4 ( ) 55 3. (n ) a n n a n a n 3 4 = 8 8 3 ( 3) 4 = 8 3 8 ( ) ( ) 3 = 8 8 ( ) 3 n n 4 n n
F S S S S S S S 32 S S S 32: S S rot F ds = F d l (63) S S S 0 F rot F ds = 0 S (63) S rot F S S S S S rot F F (63)
 211 12 1 19 2.9 F 32 32: rot F d = F d l (63) F rot F d = 2.9.1 (63) rot F rot F F (63) 12 2 F F F (63) 33 33: (63) rot 2.9.2 (63) I = [, 1] [, 1] 12 3 34: = 1 2 1 2 1 1 = C 1 + C C 2 2 2 = C 2 + ( C )
211 12 1 19 2.9 F 32 32: rot F d = F d l (63) F rot F d = 2.9.1 (63) rot F rot F F (63) 12 2 F F F (63) 33 33: (63) rot 2.9.2 (63) I = [, 1] [, 1] 12 3 34: = 1 2 1 2 1 1 = C 1 + C C 2 2 2 = C 2 + ( C )
 4................................. 4................................. 4 6................................. 6................................. 9.................................................... 3..3..........................
4................................. 4................................. 4 6................................. 6................................. 9.................................................... 3..3..........................
i
 i 3 4 4 7 5 6 3 ( ).. () 3 () (3) (4) /. 3. 4/3 7. /e 8. a > a, a = /, > a >. () a >, a =, > a > () a > b, a = b, a < b. c c n a n + b n + c n 3c n..... () /3 () + (3) / (4) /4 (5) m > n, a b >, m > n,
i 3 4 4 7 5 6 3 ( ).. () 3 () (3) (4) /. 3. 4/3 7. /e 8. a > a, a = /, > a >. () a >, a =, > a > () a > b, a = b, a < b. c c n a n + b n + c n 3c n..... () /3 () + (3) / (4) /4 (5) m > n, a b >, m > n,
 20 4 20 i 1 1 1.1............................ 1 1.2............................ 4 2 11 2.1................... 11 2.2......................... 11 2.3....................... 19 3 25 3.1.............................
20 4 20 i 1 1 1.1............................ 1 1.2............................ 4 2 11 2.1................... 11 2.2......................... 11 2.3....................... 19 3 25 3.1.............................
i ( ) PDF http://moodle.sci.u-toyama.ac.jp/kyozai/ I +α II II III A: IV B: V C: III V I, II III IV V III IV 8 5 6 [email protected]
 8 5 6 i ( ) PDF http://moodle.sci.u-toyama.ac.jp/kyozai/ I +α II II III A: IV B: V C: III V I, II III IV V III IV 8 5 6 [email protected] ii I +α 3.....................................................
8 5 6 i ( ) PDF http://moodle.sci.u-toyama.ac.jp/kyozai/ I +α II II III A: IV B: V C: III V I, II III IV V III IV 8 5 6 [email protected] ii I +α 3.....................................................
(3) (2),,. ( 20) ( s200103) 0.7 x C,, x 2 + y 2 + ax = 0 a.. D,. D, y C, C (x, y) (y 0) C m. (2) D y = y(x) (x ± y 0), (x, y) D, m, m = 1., D. (x 2 y
 [ ] 7 0.1 2 2 + y = t sin t IC ( 9) ( s090101) 0.2 y = d2 y 2, y = x 3 y + y 2 = 0 (2) y + 2y 3y = e 2x 0.3 1 ( y ) = f x C u = y x ( 15) ( s150102) [ ] y/x du x = Cexp f(u) u (2) x y = xey/x ( 16) ( s160101)
[ ] 7 0.1 2 2 + y = t sin t IC ( 9) ( s090101) 0.2 y = d2 y 2, y = x 3 y + y 2 = 0 (2) y + 2y 3y = e 2x 0.3 1 ( y ) = f x C u = y x ( 15) ( s150102) [ ] y/x du x = Cexp f(u) u (2) x y = xey/x ( 16) ( s160101)
ma22-9 u ( v w) = u v w sin θê = v w sin θ u cos φ = = 2.3 ( a b) ( c d) = ( a c)( b d) ( a d)( b c) ( a b) ( c d) = (a 2 b 3 a 3 b 2 )(c 2 d 3 c 3 d
 A 2. x F (t) =f sin ωt x(0) = ẋ(0) = 0 ω θ sin θ θ 3! θ3 v = f mω cos ωt x = f mω (t sin ωt) ω t 0 = f ( cos ωt) mω x ma2-2 t ω x f (t mω ω (ωt ) 6 (ωt)3 = f 6m ωt3 2.2 u ( v w) = v ( w u) = w ( u v) ma22-9
A 2. x F (t) =f sin ωt x(0) = ẋ(0) = 0 ω θ sin θ θ 3! θ3 v = f mω cos ωt x = f mω (t sin ωt) ω t 0 = f ( cos ωt) mω x ma2-2 t ω x f (t mω ω (ωt ) 6 (ωt)3 = f 6m ωt3 2.2 u ( v w) = v ( w u) = w ( u v) ma22-9
30
 3 ............................................2 2...........................................2....................................2.2...................................2.3..............................
3 ............................................2 2...........................................2....................................2.2...................................2.3..............................
NumRu::GPhys::EP Flux 2 2 NumRu::GPhys::EP Flux 3 2.................................. 3 2.2 EP............................. 4 2.3.....................
 NumRu::GPhys::EP Flux 7 2 9 NumRu::GPhys::EP Flux 2 2 NumRu::GPhys::EP Flux 3 2.................................. 3 2.2 EP............................. 4 2.3................................. 5 2.4.............................
NumRu::GPhys::EP Flux 7 2 9 NumRu::GPhys::EP Flux 2 2 NumRu::GPhys::EP Flux 3 2.................................. 3 2.2 EP............................. 4 2.3................................. 5 2.4.............................
 1 B64653 1 1 3.1....................................... 3.......................... 3..1.............................. 4................................ 4..3.............................. 5..4..............................
1 B64653 1 1 3.1....................................... 3.......................... 3..1.............................. 4................................ 4..3.............................. 5..4..............................
36 3 D f(z) D z f(z) z Taylor z D C f(z) z C C f (z) C f(z) f (z) f(z) D C D D z C C 3.: f(z) 3. f (z) f 2 (z) D D D D D f (z) f 2 (z) D D f (z) f 2 (
 3 3. D f(z) D D D D D D D D f(z) D f (z) f (z) f(z) D (i) (ii) (iii) f(z) = ( ) n z n = z + z 2 z 3 + n= z < z < z > f (z) = e t(+z) dt Re z> Re z> [ ] f (z) = e t(+z) = (Rez> ) +z +z t= z < f(z) Taylor
3 3. D f(z) D D D D D D D D f(z) D f (z) f (z) f(z) D (i) (ii) (iii) f(z) = ( ) n z n = z + z 2 z 3 + n= z < z < z > f (z) = e t(+z) dt Re z> Re z> [ ] f (z) = e t(+z) = (Rez> ) +z +z t= z < f(z) Taylor
b3e2003.dvi
 15 II 5 5.1 (1) p, q p = (x + 2y, xy, 1), q = (x 2 + 3y 2, xyz, ) (i) p rotq (ii) p gradq D (2) a, b rot(a b) div [11, p.75] (3) (i) f f grad f = 1 2 grad( f 2) (ii) f f gradf 1 2 grad ( f 2) rotf 5.2
15 II 5 5.1 (1) p, q p = (x + 2y, xy, 1), q = (x 2 + 3y 2, xyz, ) (i) p rotq (ii) p gradq D (2) a, b rot(a b) div [11, p.75] (3) (i) f f grad f = 1 2 grad( f 2) (ii) f f gradf 1 2 grad ( f 2) rotf 5.2
No δs δs = r + δr r = δr (3) δs δs = r r = δr + u(r + δr, t) u(r, t) (4) δr = (δx, δy, δz) u i (r + δr, t) u i (r, t) = u i x j δx j (5) δs 2
 No.2 1 2 2 δs δs = r + δr r = δr (3) δs δs = r r = δr + u(r + δr, t) u(r, t) (4) δr = (δx, δy, δz) u i (r + δr, t) u i (r, t) = u i δx j (5) δs 2 = δx i δx i + 2 u i δx i δx j = δs 2 + 2s ij δx i δx j
No.2 1 2 2 δs δs = r + δr r = δr (3) δs δs = r r = δr + u(r + δr, t) u(r, t) (4) δr = (δx, δy, δz) u i (r + δr, t) u i (r, t) = u i δx j (5) δs 2 = δx i δx i + 2 u i δx i δx j = δs 2 + 2s ij δx i δx j
 21 2 26 i 1 1 1.1............................ 1 1.2............................ 3 2 9 2.1................... 9 2.2.......... 9 2.3................... 11 2.4....................... 12 3 15 3.1..........
21 2 26 i 1 1 1.1............................ 1 1.2............................ 3 2 9 2.1................... 9 2.2.......... 9 2.3................... 11 2.4....................... 12 3 15 3.1..........
C:/KENAR/0p1.dvi
 2{3. 53 2{3 [ ] 4 2 1 2 10,15 m 10,10 m 2 2 54 2 III 1{I U 2.4 U r (2.16 F U F =, du dt du dr > 0 du dr < 0 O r 0 r 2.4: 1 m =1:00 10 kg 1:20 10 kgf 8:0 kgf g =9:8 m=s 2 (a) x N mg 2.5: N 2{3. 55 (b) x
2{3. 53 2{3 [ ] 4 2 1 2 10,15 m 10,10 m 2 2 54 2 III 1{I U 2.4 U r (2.16 F U F =, du dt du dr > 0 du dr < 0 O r 0 r 2.4: 1 m =1:00 10 kg 1:20 10 kgf 8:0 kgf g =9:8 m=s 2 (a) x N mg 2.5: N 2{3. 55 (b) x
120 9 I I 1 I 2 I 1 I 2 ( a) ( b) ( c ) I I 2 I 1 I ( d) ( e) ( f ) 9.1: Ampère (c) (d) (e) S I 1 I 2 B ds = µ 0 ( I 1 I 2 ) I 1 I 2 B ds =0. I 1 I 2
 9 E B 9.1 9.1.1 Ampère Ampère Ampère s law B S µ 0 B ds = µ 0 j ds (9.1) S rot B = µ 0 j (9.2) S Ampère Biot-Savart oulomb Gauss Ampère rot B 0 Ampère µ 0 9.1 (a) (b) I B ds = µ 0 I. I 1 I 2 B ds = µ 0
9 E B 9.1 9.1.1 Ampère Ampère Ampère s law B S µ 0 B ds = µ 0 j ds (9.1) S rot B = µ 0 j (9.2) S Ampère Biot-Savart oulomb Gauss Ampère rot B 0 Ampère µ 0 9.1 (a) (b) I B ds = µ 0 I. I 1 I 2 B ds = µ 0
 (yx4) 1887-1945 741936 50 1995 1 31 http://kenboushoten.web.fc.com/ OCR TeX 50 yx4 e-mail: [email protected] i Jacobi 1751 1 3 Euler Fagnano 187 9 0 Abel iii 1 1...................................
(yx4) 1887-1945 741936 50 1995 1 31 http://kenboushoten.web.fc.com/ OCR TeX 50 yx4 e-mail: [email protected] i Jacobi 1751 1 3 Euler Fagnano 187 9 0 Abel iii 1 1...................................




