II
|
|
|
- ひでき かいじ
- 5 years ago
- Views:
Transcription
1 II 9 7 8
2 HP lecture 017 II 6/13 7/18 I I 0 (004) L. D. Landau and E. M. Lifshitz, Quantum Mechanics Pergamon Press (1991) Steven Weinberg Lectures on Quantum Mechanics Cambridge University Press (015) 016
3 Hellmann-Feynmann
4
5
6
7 e 1 0, e 1, e 3 0, (1.1) (e 1 ) t = (1, 0, 0) (e ) t = (0, 1, 0) (e 3 ) t = (0, 0, 1) i=1,,3 (e i ) t e j = δ ij (1.) e i (e i ) t = Î (1.3) 1 {x n} lim m,n xm xn = 0
8 8 1 {e i } {e i } A A = ÎA = i=1,,3 e i (e i ) t A = i=1,,3 A i e i (1.4) A i := (e i ) t A A ( i ) e i e i (e i ) t e i (1.) e i e j = δ ij (1.5) (1.3) d e i e i = Î (1.6) i=1 d x dx x x = Î (1.7) (Hilbert space) ψ ψ : ψ = 0 ψ ψ > 0 ϕ (a ψ 1 + b ψ ) = a ϕ ψ 1 + b ϕ ψ : ϕ ψ = ψ ϕ θ ψ e iθ ψ (ray ψ ψ := ψ ψ { x } { p } Ψ(x, t)
9 (1.4) Ψ (1.7) Ψ = Î Ψ = dx x x Ψ (1.8) { x } x Ψ { x } Ψ Ψ(x) := x Ψ (1.9) { p } Ψ = dp p p Ψ (1.10) πħ p Ψ Ψ(p) Ψ(p) := p Ψ (1.11) (1.10) πħ dp p p = Î (1.1) πħ p ˆp = (ħ/i)d/dx ˆp p = p p x x ˆp p = ħ i d x p = p x p (1.13) dx x p = ( p x ) = e i ħ px (1.14) x p (transformation function) x Ψ ( ) x Ψ
10 10 1 x (1.1) (1.14) dp dp x = πħ p p x = πħ p e i ħ px (1.15) (1.15) dp x = πħ p e i ħ px (1.16) Ψ(t) dp Ψ(x, t) = x Ψ(t) = πħ p Ψ(t) e i ħ px = dp πħ Ψ(p, t)e i ħ px (1.17) (ray) θ ψ e iθ ψ a ϕ + b ψ a ϕ + e iθ b ψ 1.3. Ô Ô ϕ Ô ψ = ψ Ô ϕ (1.18) Ô = Ô ϕ Ô ψ = ψ Ô ϕ = ϕ Ô ψ (1.19)
11 ϕ = ψ Ô D(Ô) Ô D(Ô ) Ôϕ ψ = ϕ Ôψ (1.0) D(Ô) = D(Ô ) Ô Ô Ô = n O n P n, P n = n n (1.1) P n P m P n = δ mn P m (1.) iħ ψ(t) = Ĥ(t) ψ(t) (1.3) t iħ ψ(x, t) = Ĥ(t)ψ(x, t) (1.4) t ψ 1 ψ aψ 1 + bψ (1.3) ψ(t) = Û(t, t 0) ψ(t 0 ), U(t, t 0 ) = exp ( i ) ħĥ(t t 0) (1.5)
12 1 1 t t t 0 = n t ψ(t) = e i ħ Ĥ(t 0+(n 1) t) t e i ħ Ĥ(t 0+ t) t e i ħ Ĥ(t 0) t ψ(t 0 ) (1.6) ψ(t) = Û(t, t 0) ψ(t 0 ), U(t, t 0 ) = T exp ( i ħ t t 0 ) Ĥdt (1.7) T U(t, t ) Û (t, t 0 ) = Û 1 (t, t 0 ) (1.8) (Uα ψ = α U ψ ) ψ Ô O n Prob(O n ) = P n ψ = ψ P n ψ = n ψ (1.9) ψ n = P n ψ P n ψ (1.30) O n Prob(O n ) Ô = n Prob(O n )O n = n O n ψ P n ψ = ψ Ô ψ (1.31) ψ ψ n
13 (1.9) (1.30) µ(a) = Tr(ρP a ) 3 ρ P a a (positive operator valued measure) ( ( 3 Bell-Kochen-Specker (corollary) ) A B H A, H B AB H A H B ϕ A, ψ B ϕ A ψ B ϕ A ψ B ÔA ÔB ÔA H A ÔB H B (ÔA ÔB) ϕ A ψ B = (ÔA ϕ A )(ÔB ψ B ) (1.3) 3 A. M. Gleason, J. Math. Mech. 6, 885 (1957) 4 P. Bush, Phys. Rev. Lett. 91, (003)
14 Ô O mn = ψ môψ ndx = ψ m, Ôψ n (1.33) Ô Omn t := O nm = ψ nôψ mdx = ψ n, Ôψ m (1.34) Ô (Ô ) mn = Onm = ψ n Ô ψmdx = ψ n, Ôψ m (1.35) (1.33) Ô = Ô 5 ψ, ϕ = ϕ, ψ (1.35) (Ô ) mn = ψ n, Ôψ m = Ôψ m, ψ n (1.36) (Ô ) mn = ψ m, Ô ψ n ΨÔt Φdx = ψ m, Ô ψ n = Ôψ m, ψ n (1.37) ΦÔΨdx (1.38) Ψ Ô t Φ dx = Φ (ÔΨ) dx = (ÔΨ) Φ dx (1.39) Φ Φ Ψ Ô t Φdx = (1.37) (ÔΨ) Φdx = ÔΨ, Φ (1.40) Ψ, Ô Φ = ÔΨ, Φ (1.41) 5 (P) (T) PT
15 Ψ(x, y) x y Ôs x Ô Ô = = Ψ (x, y)ô(x)ψ(x, y)dxdy [ ] dx Ô(x) dyψ (x, y)ψ(x, y) x =x (1.4) [ ] x =x Ô(x) x x ρ(x, x ) := Ψ(x, y)ψ (x, y)dy (1.43) Ō = [Ô(x)ρ(x, x )] x =xdx (1.44) Ψ(x, y) = x y Ψ ρ(x, x ) = x y Ψ Ψ y x dy (1.45) ρ(x, x ) := x ˆρ x (1.46) ˆρ = y Ψ Ψ y dy (1.47) (1.43) ρ(x, x ) ρ(x, x ) = ρ (x, x) (1.48)
16 16 1 (1.43) ρ(x, x) = Ψ(x, y) dy (1.49) x Ψ (pure state) ˆρ = ψ ψ (1.50) ˆρ = ˆρ (1.51) (idenpotency condition) { n } n p n ˆρ = n p n n n (1.5) ˆρ = n p n n n (1.53) ψ ψ ρ ψ < ψ ρ ψ (mixed state) ˆρ n (1.5) p n = n ˆρ n (1.54) 1 p n = n ˆρ n Trˆρ = 1 (1.55) n n Tr (trace) Ô TrÔ n n Ô n (1.56)
17 { n } { n } Ô Ô n p n n Ô n = Tr(ˆρÔ) (1.57) n, ρ = ρ p n 0 (1.55) (1.5) (1.5) { ψ k } { χ k } ˆρ = n p n ( k ψ k ψ k ) n n ( l χ l χ l ) = k,l w kl ψ k χ l (1.58) w kl = n p n ψ k n n χ l = n ψ k ˆρn n χ l = ψ k ˆρ χ l (1.59) ψ k = χ k ˆρ w kl (w kl = w k δ kl ) ˆρ ˆρ = n w k ψ k ψ k (1.60) (1.5) { 0, 1 } ˆρ = p (1 p) 1 1, (0 p 1) (1.61) ˆρ
18 A B ˆρ A+B ˆρ A+B ˆρ A+B = n p n ψ n AA ψ n χ n BB χ n (1.6) A B A Tr( χ n BB χ n ) = m B m χ n BB χ n m B = B χ n m m B m χ n B = B χ n χ n B = 1 (1.63) ˆρ A Tr B (ˆρ A+B ) = n p n ψ n AA ψ n (1.64) Tr B B ˆρ A A (reduced density operator) A ÔA ˆρ A ˆρ Tr A (ˆρ A Ô A) ( = Tr ˆρÔA) (1.65) 1.5. ρ(x, x ) ρ(x, x ; t) = a mn ψn(x, t)ψ m (x, t) m,n = m,n ψ n(x )ψ m (x)e i ħ (Em En)t (1.66)
19 A, B Ψ AB H A H B H A H B n A n B Ψ AB = n pn n A n B, p n > 0 (1.67) (Schmidt decomposition) Ψ AB Ψ AB = n n AA n Ψ AB = n n AA ñ B (1.68) ñ B := A n Ψ AB (1.69) { n A } ρ A ρ A = n p n n AA n (1.70) (1.68) A ρ A = Tr B ( Ψ ABAB Ψ ) = n AA n Tr B ( n BB n ) n,n = n,n n AA n B n n B (1.71) (1.70) (1.67) B n n B = p n δ nn (1.7) n B = p n n B (1.73) (1.67) Ψ AB Ψ AB Φ AB
20 0 1 3 ρ B = Tr A ρ AB = n p n n BB n (1.74) ρ A ρ B n A e iθ n A n B e iθ n B n A n B P si AB A B Ψ AB = ab Ψ ab a A b B (1.75) n A = a a A (U A ) an, n B = b b B (U B ) bn (1.76) (1.67) Ψ AB = pn a A (U A ) an b B (U B ) bn n ab = (U A ) an pn (UB T ) nb a A b B (1.77) ab n (1.75) Ψ ab = n (U A ) an pn (U T B ) nb (1.78) (Ψ ab ) (1.67) (1.78) (singular value decomposition) p n (singular value)
21 P si AB (separable) Ψ AB = ϕ A ψ B (1.79) ρ A = ϕ AA ϕ, ρ B = ψ BB ψ (1.80) U A U B Ψ AB Ψ AB A B U AB ħ A B A ( ) B ( ) z Ψ = 1 ( A B A B ) (1.81) A B 1 ( )
22 1 A B (1.81) A Ψ A B Ψ B Ψ A Ψ B (nonseparability) (entangled state) A B (nonlocal correlation) (Einstein-Podolsky-Rosen correlation) EPR (EPR correlation) 6 (1.81) EPR (EPR pair) A B (hidden variable theory) 7 x x + A B z + = 1 ( + ), = 1 ( ) (1.8) = 1 ( + + ), = 1 ( + ) (1.83) (1.81) Ψ = 1 ( A + B + A B ) (1.84) 6 A. Einstein, B. Podolsky, and N. Rosen, Phys. Rev. 47 (1935) D. Bohm (Phys. Rev. 85 (195) 166, 180)
23 A x ( ) B ( ) EPR (delayed choice) 8 EPR 8 W. Tittel, J. Brendel, B. Gisin, T. Herzog, H. Zbinden, and N. Gisin, Phys. Rev. A 57 (1998) 330
24
25 5.1 Ψ(t)/ t Ψ(t) iħ Ψ t = ĤΨ (.1) Ĥ iħ Ĥ ( ) d Ψ Ψ Ψ dx = Ψ + Ψ dx = 0 (.) dt t t (.1) i ħ ( (Ĥ Ψ )Ψ Ψ ĤΨ) dx = i ħ = i ħ Ψ (Ĥ t Ĥ)Ψdx Ψ (Ĥ Ĥ)Ψdx = 0 (.3) Ψ Ĥ = Ĥ Ĥ Ĥ Ψ = Ae i ħ S (.4) (.1) ħ 0 (S/ħ) A A iħ Ψ t = S t Ψ (.5)
26 6 S/ t Ĥ. ˆf = d Ψ ˆfΨdx dt ( Ψ = ˆfΨ + Ψ ˆf ) t t Ψ + Ψ Ψ ˆf dx (.6) t (.1) ( i = ħ (Ĥ Ψ ) ˆfΨ + Ψ ˆf ) t Ψ i ħ Ψ ˆfĤΨ dx ( ) = Ψ i ħ (Ĥ ˆf ˆf ˆfĤ) + Ψdx t ( = Ψ i ħ [Ĥ, ˆf] + ˆf ) Ψdx (.7) t [Ĥ, ˆf] := Ĥ ˆf ˆfĤ ˆf ˆf = Ψ ˆfΨdx (.8) ˆf ˆf (.7) (.8) d dt ˆf = i ħ [Ĥ, ˆf] + ˆf t (.9) ˆf ( ˆf/ t = 0) ˆf = 0 ˆf
27 ( Ĥ/ t = 0) (.9) d dtĥ = 0 (.10) E n Ψ n iħ Ψ n t = ĤΨ n = E n Ψ n (.11) Ψ n (x, t) = e i ħ Ent ψ n (x) (.1) ψ Ĥψ = Eψ (.13) Ψ(x) ψ n (x) Ψ(x) = n a n ψ n (x) (.14) (.1) Ψ(x, t) = e i ħ Ĥt Ψ(x) = n a n e i ħ Ent ψ n (x) (.15) ψ(r) ) ( ħ m + U(r) ψ(r) = Eψ(r) (.16) ψ (r) ψ(r) ψ (r)
28 8.4 Ĥ Ψ m, Ψ n ĤΨ m = E m Ψ m, ĤΨ n = E n Ψ n (.17) Ψ n, Ψ m Ψ nĥψ mdr = E m Ψ nψ m dr (.18) Ψ mĥψ ndr = E n Ψ mψ n dr (.19) (.18) Ĥ = Ĥ Ψ nĥ Ψ m dr = (ĤΨ n) Ψ m dr = E m Ψ nψ m dr (.0) Ψ mĥψ ndr = E m Ψ mψ n dr (.1) (.19) 0 = (E m E n ) Ψ mψ n dr (.) E m E n Ψ mψ n dr = 0 (E m E n ) (.3) 1.5 ˆP, ˆQ ([ ˆP, ˆQ] = 0) ˆP ˆQ = ˆQ ˆP P mk Q kn = Q mk ˆPkn (.4) k k
29 .6. Hellmann-Feynmann 9 (.4) ˆP ψ n P mk = P mm δ mk P mm Q mn = Q mn P nn Q mn (P mm P nn ) = 0 (.5) m n P mm P nn Q mn = 0 ψ n ˆQ ˆP ψ m, ψ n P mm = P nn Q mn 0 ψ m, ψ n Q mn.6 Hellmann-Feynmann Ĥ λ ( ) Ĥ = E n λ λ nn (.6) (Ĥ E n)ψ n = 0 λ ψn ( ) ψn(ĥ E n) ψ n λ = E n ψ n λ Ĥ ψ n (.7) λ ψn(ĥ E n) ψ n λ dx = ψ n ( ) E n λ Ĥ ψ n dx (.8) λ (1.41) ψn = λ (Ĥt E n )ψndx ψn = λ [(Ĥ E n)ψ n ] dx = 0 (.9) 0 (.6) (.9) n ψ n n λ E(λ) = n E n ψ n (λ) (.30)
30 30 λ ψ(λ) Ĥ λ ψ(λ) = ( ) Ĥ ψ n (λ) (.31) λ n ψ(λ) Ĥ λ ψ(λ) nn = E(λ) λ Hellmann-Feynmann (.3).7 Ō(g) = Ψ (x, t)ôψ(x, t)dx (.33) (.1) Ψ(x, t) = e i ħ Ĥt Ψ(x, 0) = ÛΨ(x, 0), Û = e i ħ Ĥt (.34) Ĥ Û Û = Û 1 (.35) (.33) = (Û Ψ (x, 0))ÔÛΨ(x, 0)dx = Ψ (x, 0)Û ÔÛΨ(x, 0)dx (.36) Ô(t) := Û (t)ôû(t) (.37) d dtô(t) = i [Ĥ, Ô(t)] (.38) ħ
31 Ĥ ψ(x) a ψ(x + a) ψ(x) Ĥψ(x)dx = ψ(x + a) Ĥψ(x + a)dx (.39) ψ(x + a) = ψ(x) + a d a ψ(x) + dx! dx ψ(x) + = ψ(x) + ia ħ d ħ i dx ψ(x) + 1 ( ) ia ( ) ħ d ψ(x) +! ħ i dx = ψ(x) + ia ħ ˆpψ(x) + 1 ( ) ia! ħ ˆp + ψ(x) + ( = 1 + ia ħ ˆp + 1 ( ) ) ia! ħ ˆp + ψ(x) ( ) i = exp ħ aˆp ψ(x) (.40) (.39) d e i ħ aˆp Ĥe i ħ ˆpa = Ĥ (.41) a a e i ħ aˆp i ħ [Ĥ, ˆp]e i ħ ˆpa = 0 (.4) [Ĥ, ˆp] = 0 (.43).9 (xˆp ˆpx)ψ = iħx ψ x + iħ (xψ) = iħψ (.44) x
32 3 ψ 3 [x, ˆp] = iħ (.45) [x i, ˆp j ] = iħδ ij (.46) (.45) x p ħ (.47) Kennard-Robertson x p ħ/ x (.47) 1 t 1 016)
33 p E k ω (p, E) (k, ω) 1 p = ħk, E = ħω (3.1) (Einstein-de Broglie formulae) (3.1) ħ h π = J s (3.) (Planck constant) 1 (p, E) (k, ω) E = ħω ω ħω p = ħk λ π k = h p (3.3) 1
34 34 3 p λ = h/ p λ λ p = h/λ (3.3) (de Broglie relation) Ψ(x, t) = e i(kx ωt) (3.4) (3.1) pψ = ħkψ = ħke i(kx ωt) = ħ i x ei(kx ωt) = ħ i x Ψ (3.5) EΨ = ħωψ = ħωe i(kx ωt) = iħ t ei(kx ωt) = iħ t Ψ (3.6) p E Ψ (ˆ) ˆp = ħ i x, Ê = iħ t (3.7) 3.3 iħ Ψ = ĤΨ (3.8) t Ĥ Ĥ = 1 m (ˆp x + ˆp y + ˆp z) (3.9)
35 ˆp x = iħ x, ˆp y = iħ y, ˆp z = iħ z (3.10) (3.9) ( ) Ĥ = ħ m x + y + z = ħ m (3.11) U(x, y, z) Ĥ = ˆp ħ + U(x, y, z) = + U(x, y, z) (3.1) m m (3.8) iħ ( ) t ψ = ħ + U(x, y, z) ψ (3.13) m ψ(x, y, z, t) = e i ħ Et ψ 0 (x, y, z) (3.14) ) ( ħ + U(x, y, z) ψ 0 = Eψ 0 (3.15) m (i.e., U = 0) (3.15) c ψ 0 (r) = ce i ħ p r (3.16) E = p /(m) ψ(r, t) = ce i ħ (p r Et) (3.17) k = p/ħ ω = E/ħ
36 K K v r = r + vt p = p + mv (3.18) E = E + v p + m v t = t (3.17) ψ(r, t) = c i ħ[(p +mv)(r +vt) (E +v p + m v )t] = ce i ħ (p r E t)+ i ħ(mv r + m v t) = ψ(r, t)e i ħ(mv r + m v t) = ψ(r vt)e i ħ(mv r m v t) ψ(r, t) = ψ(r vt)e i ħ(mv r m v t) (3.19) (3.13) a S t + iħ a t ψ = Ae i ħ S (3.0) = a m ( S) iħ m a S iħ S a m ħ a + Ua (3.1) m a S (3.1) S t = 1 m ( S) + U ħ a ma (3.) a t = a m S 1 S a m (3.3)
37 (3.) (3.3) E = S/ t p = S (3.) Hamilton-Jacobi ħ (quantum pressure term) (3.3) a a t = a m S a S a ( m = a S ) m (3.4) a S/m = p/m =: v quantum pressure term) 3.4 U(x, y, z) U = 0 p /m = E < 0 (Bohr-Sommerfeld ) E > 0 ψ dr E < U E < U E > U
38 38 3 U = c r s (c > 0) (3.5) r = 0 r p ħ/ r ( p) /m ħ /m( r) c/( r) s E = ħ m( r) c ( r) s (3.6) s > r E r = 0 s < r (3.6) (s = 1) r 0 r E = ħ m( r) c r s 0 (3.7) r/r 0 =: k 1 r 0 E = ħ ( 1 ck mr0 r s ) k 0 (3.8) s < E r 0 > (1/(ck )) 1/( s) k r 0 E < 0 s > E < 0 k 0 r v (.9) ˆv = dtˆr d = i [Ĥ,ˆr] (3.9) ħ
39 Ĥ (3.1) ˆv = ˆp m (3.30) d dt ˆv = i [Ĥ, ˆv] = i ħ [Ĥ, ˆp] = i mħ mħ [U, ˆp] = 1 U (3.31) m m d ˆv = U (3.3) dt V ( ) d ψ ψ ψ dr = ψ + ψ dr dt t t = i ħ [(Ĥ ψ )ψ ψ Ĥψ]dr (3.33) Ĥ = Ĥ = ħ m + U (3.34) d dt ψ dr = iħ m = iħ m [( ψ )ψ ψ ψ]dr [( ψ )ψ ψ ψ]dr (3.35) d ψ dr = divjdr (3.36) dt V V j : = iħ m [( ψ )ψ ψ ψ] = 1 m [( ˆpψ) ψ + ψ ˆpψ] (3.37) (3.36) V ψ = divj (3.38) t
40 40 3 (3.36) V S d ψ dr = j ds (3.39) dt V j 1 ψ = 1 v e i ħ (p r Et) (3.40) (3.37) j = 1 mv p (3.41) 3.6 ψ 0 x = x 0 ψ(x) ψ(x 0 ) + c(x x 0 ) (3.4) ψ (x) ( ħ d ) m dx ψ(x) = 0 (3.43) ψ(x) x 0 (3.43) ψ 0, ψ 0 cψ 0 + c ψ 0 c, c R. Courant and D. Hilbert, Methods of Mathematical Physics, Vol. I, Chap. VI, Sec.6 (Interscience, New York, 1953)
41 U x U = U 1 (x) + U (y) + U 3 (z) 1 d ψ dx + m [E U(x)]ψ = 0 (3.44) ħ E ψ 1, ψ (3.44) ψ 1 = ψ = m (U E) (3.45) ψ 1 ψ ħ ψ 1 ψ ψ 1 ψ = (ψ 1 ψ ψ 1 ψ ) = 0 ψ 1 ψ ψ 1 ψ = ψ 1 = ψ = 0 ψ 1 ψ 1 = ψ ψ (3.46) ψ 1 ψ ray (n + 1) ψ n (x) n E 1 < E < E 3 < n n + 1 ψ n, ψ n+1 ψ n + m ħ (E n U)ψ n = 0 (3.47) ψ n+1 + m ħ (E n+1 U)ψ n+1 = 0 (3.48)
42 4 3 (3.47) ψ n+1 (3.48) ψ n ψ n α, β ψ n(β)ψ n+1 (β) ψ n(α)ψ n+1 (α) = m ħ (E n+1 E n ) β α ψ n ψ n+1 dx(3.49) (α, β) ψ n > 0 ψ n(α) > 0, ψ n(β) < 0 ψ n+1 ψ n+1 ψ n+1 1 U( ) = 0 U( ) = U 0 > 0 E E < 0 (3.50) U min E > U min U( ) = 0, U( ) > 0 0 < E < U 0 (x = + ) x = =0 U = 0 x d ψ dx + m ħ Eψ =: d ψ dx + k ψ = 0, k := me ħ (3.51) ψ = a cos(kx + δ) (3.5) a, δ x d ψ dx m ħ (U 0 E)ψ =: d ψ dx κ ψ = 0, κ := m(u0 E) ħ (3.53) ψ = be κx (3.54) b E > U 0 x = ±
43 ψ(x, t) iħ ( ) t ψ(x, t) = ħ m + U(x) ψ(x, t) (3.55) iħ ) t ψ (x, t) = ( ħ m + U(x) ψ (x, t) (3.56) t t iħ ) t ψ (x, t) = ( ħ m + U(x) ψ (x, t) (3.57) ψ(x, t) ψ (x, t) ψ rev (x, t) = ψ (x, t) (3.58)
44
45 O {A, B} = A B q p B A q p (4.1) do dt = {O, H} + O t (4.) (.9) O O {O, H} 4. Ĥ d dtĥ = 0 (4.3)
46 46 4 iħ Ψ(t) = Ĥ Ψ(t) (4.4) t Ĥ Ψ(t) = e i ħ Ĥt Ψ(0) (4.5) Û(t) := e i ħ Ĥt (4.6) Û (t) = Û 1 (t) = Û( t) (4.7) Ĥ k = 1,, Ψ(t) Ĥk Ψ(t) = Ψ(0) e i ħ Ĥt Ĥ k e i ħ Ĥt Ψ(0) = Ψ(0) Ĥk Ψ(0) (4.8) (time-translation symmetry) 4.3 Ψ(x) x a Ψ(x a) x ( Ψ(x a) = 1 + ( a) d dx + ( a) d )! dx + Ψ(x) = e a d dx Ψ(x) = e i ħ ˆpa Ψ(x) (4.9) ˆp = iħd/dx ˆT (a) = e i ħ ˆpa (4.10)
47 (generator) Ψ(x a) Ĥ Ψ(x) (space-translational symmetry) Ψ (x)ĥψ(x)dx = (4.9) Ψ (x)ĥψ(x)dx = = Ψ (x a)ĥψ(x a)dx (4.11) (e i ħ ˆpa Ψ(x)) Ĥe i ħ ˆpa Ψ(x)dx ( ˆT (a)ψ(x)) Ĥ ˆT (a)ψ(x)dx ˆT Ψ (x)ĥψ(x)dx = Ψ(x) ˆT (a)ĥ ˆT (a)ψ(x)dx = Ψ (x)e i ħ ˆpa Ĥe i ħ ˆpa Ψ(x)dx (4.1) Ψ(x) Ĥ = e i ħ ˆpa Ĥe i ħ ˆpa (4.13) a Ĥ = Ĥ + i ħ [ˆp, Ĥ]a + O(a ) (4.14) O(a ) a (4.14) [ˆp, Ĥ] = 0 (4.15) dˆp dt = i [Ĥ, ˆp] (4.16) ħ (4.15)
48 z ϕ Ψ(x, y, z) Ψ (x, y, z) Ψ (x, y, z) = Ψ(x cos ϕ + y sin ϕ, y cos ϕ x sin ϕ, z) (4.17) ϕ 1 ϕ 1 Ψ (x, y, z) = Ψ(x + yϕ, y xϕ, z) [ ( = 1 + ϕ y x x )] Ψ(x, y, z) y [ = 1 i ] ħ ϕ (xˆp y yˆp x ) Ψ(x, y, z) = (1 iħ ) ϕˆl z Ψ(x, y, z) (4.18) z (orbital angular momentum) z ˆL z xˆp y yˆp x (4.19) ϕ N N N ( Ψ (x, y, z) = lim 1 i N ħ ) ϕ N N ˆL z Ψ(x, y, z) = e i ħ ϕˆl z Ψ(x, y, z) (4.0) z ϕ ˆR z (ϕ) = e i ħ ˆL zϕ (4.1) 1 ˆL z z x y x y ˆL x yˆp z z ˆp y, ˆLy z ˆp x xˆp z (4.) 1 e i ħ ˆL zθ
49 θ ˆR x (ϕ) = e i ħ ˆL xϕ, ˆRy (ϕ) = e i ħ ˆL yϕ (4.3) Ψ(x, y, z) Ψ (x, y, z) Ĥ = e i ħ ˆL zϕ Ĥe i ħ ˆL zϕ (4.4) θ Ĥ = Ĥ + i ħ [ˆL z, Ĥ]ϕ + O(ϕ ) (4.5) ϕ [ˆL z, Ĥ] = 0 (4.6) ˆL z dˆl z dt = i ħ [Ĥ, ˆL z ] (4.7) (4.6) z ˆL = iħ ψ (r )ψdr (4.8).3 (4.8) ˆL = U( x) = U(x) (4.9)
50 50 4 (x x) ψ(x) ψ( x) (1 c ψ( x) = cψ(x) x x ψ(x) = cψ( x) = c ψ(x) (4.30) c = ±1 (ψ( x) = ψ(x)) (ψ( x) = ψ(x)) ψ(x) 4.5. a (discrete symmetry) (4.13) x 0 = na (n ) ˆT (na) = ( ˆT (a)) n [Ĥ, ( ˆT (a)) n ] = 0 (4.31) Ĥ ( ˆT (a)) n ˆT (a) ( ˆT (a)) n e inθ θ = ka Ψ k,e (x) (4.9) (4.3) e i ħ ˆpna Ψ k,e (x) = e ikan Ψ k,e (x) (4.3) ĤΨ k,e (x) = EΨ k,e (x) (4.33) e i ħ ˆpna Ψ k,e (x) = Ψ k,e (x + na) Ψ k,e (x + na) = e ikna Ψ k,e (x) (4.34) Û Ô Û = eiô θ e iθ
51 (4.34) e ikx a u k,e (x) Ψ k,e (x) = e ikx u k,e (x), u k,e (x + a) = u k,e (x) (4.35) (4.35) 4.6 Ĥ ˆP ˆQ [Ĥ, ˆP ] = 0 (4.36) [Ĥ, ˆQ] = 0 (4.37) ˆP ˆQ [ ˆP, ˆQ] 0 (4.38) (4.36) Ĥ ˆP { E i, p i } Ĥ E i, p i = E i E i, p i, ˆP E1, p i = p i E i, p i (4.38) i( i = 1 ) ˆQ E 1, p 1 = c E 1, p 1 (4.39) (c ) i ˆQ E i, p i = c E i, p i ˆP ˆQ E i, p i = c ˆP E i, p i = cp i E i, p i ˆQ ˆP E i, p i = p i ˆQ Ei, p i = cp i E i, p i ˆP ˆQ (4.37) Ĥ ˆQ E 1, p 1 = ˆQĤ E 1, p 1 = E 1 ˆQ E1, p 1 E 1, p 1 ˆQ E 1, p 1 E 1 Ĥ (4.39)
52
53 (4.19) (4.) ˆL x ˆL x ˆL x [ˆL x, ˆL y ] = iħˆl z, [ˆL y, ˆL z ] = iħˆl x, [ˆL z, ˆL x ] = iħˆl y (5.1) ˆL x, ˆL y, ˆL z ˆL := ˆL x + ˆL y + ˆL z (5.) [ ˆL, ˆL x ] = 0, [ ˆL, ˆL y ] = 0, [ ˆL, ˆL z ] = 0 (5.3) [Â ˆB, Ĉ] = Â ˆBĈ ĈÂ ˆB (5.3) [ ˆL, ˆL x ] = [ˆL y + ˆL z, ˆL x ] = Â( ˆBĈ Ĉ ˆB) + (ÂĈ ĈÂ) ˆB = Â[ ˆB, Ĉ] + [Â, Ĉ] ˆB (5.4) = ˆL y [ˆL y, ˆL x ] + [ˆL y, ˆL x ]ˆL y + ˆL z [ˆL z, ˆL x ] + [ˆL z, ˆL x ]ˆL z = iħ( ˆL y ˆLz ˆL z ˆLy + ˆL z ˆLy + ˆL y ˆLz ) = 0 ˆL 1
54 54 5 ˆL ˆL z L, M ˆL L, M = ħ f(l) L, M, ˆLz L, M = ħm L, M (5.5) M ˆL z ˆL ħ f(l) ˆL z ˆL x ˆL y ˆL z (raising and lowering operators) ˆL + ˆL x + iˆl y, ˆL ˆL x iˆl y (5.6) (5.1) [ˆL z, ˆL + ] = ħˆl +, [ˆL z, ˆL ] = ħˆl, [ˆL +, ˆL ] = ħˆl z (5.7) ˆL ˆL = ˆL ˆL+ + ˆL z + ħˆl z (5.8) = ˆL + ˆL + ˆL z ħˆl z (5.9) (5.7) ˆL z ˆL+ = ˆL + (ˆL z + ħ) (5.10) L, M ˆL z (ˆL + L, M ) = ˆL + (ˆL z + ħ) L, M = ħ(m + 1)ˆL + L, M (5.11) ˆL + L, M ˆL z M + 1 ˆL + L, M L, M + 1 (5.1) (5.7) ˆL z ˆL = ˆL (ˆL z ħ) (5.13)
55 ˆL M 1 ˆL z (ˆL L, M ) = ˆL + (ˆL z ħ) L, M = ħ(m 1)ˆL L, M (5.14) ˆL L, M L, M 1 (5.15) (5.5) ħ (f(l) M ) = L, M ˆL ˆL z L, M = L, M ˆL x + ˆL y L, M 0 (5.16) L M M max M min ˆL + L, M max = 0 (5.17) ˆL L, M min = 0 (5.18) (5.17) ˆL (5.8) ˆL ˆL+ = ˆL ˆL z ħˆl z f(l) = ħ M max (M max + 1) (5.19) (5.18) ˆL + (5.9) ˆL + ˆL = ˆL ˆL z + ħˆl z f(l) = ħ M min (M min 1) (5.0) (5.19) (5.0) M max = M min M max = L f(l) = L(L + 1) (5.1) ˆL ħ L ħ L(L + 1) ˆL ˆL z ˆL L, M = ħ L(L + 1) L, M (5.) ˆL z L, M = ħm L, M, (M = L, L 1,, L) (5.3)
56 56 5 L L L 0, 1, 1, 3,, (5.4) π (single-valuedness of the wave function) (4.0) ϕ = π L L = 0, 1,, (5.5) (5.4) (5.1) 5.1. L L=0 M= L L, M L, M = Î (5.6) Î L, M L, M = δ L,L δ M,M (5.7) L (5.8) ˆL ˆL+ = ˆL ˆL z ħˆl z L, M ˆL ˆL+ L, M = L, M + 1 ˆL + L, M = ħ (L M)(L + M + 1) (5.8) ˆL ˆL + (5.6) (5.1) (5.15) L, M + 1 ˆL + L, M = ħ (L M)(L + M + 1) (5.9)
57 ˆL + ˆL = ˆL ˆL z + ħˆl z L, M ˆL + ˆL L, M = L, M 1 ˆL L, M = ħ (L + M)(L M + 1) (5.30) L, M 1 ˆL L, M = ħ (L + M)(L M + 1) (5.31) (5.9) (5.31) ˆL x, ˆL y L, M ˆL x L, M 1 = L, M 1 ˆL x L, M = 1 (L + M)(L M + 1) (5.3) L, M ˆL y L, M 1 = L, M 1 ˆL x L, M = i (L + M)(L M + 1) (5.33) ˆL x, ˆL y ˆL z x, y ˆL z ˆL z L, M ˆL z L, M = δ M,M ħm (5.34) (5.7) dω θ, ϕ θ, ϕ = Î, dω = sin θdθdϕ (0 θ π, 0 ϕ < π) (5.35) θ ϕ x = r sin θ cos ϕ, y = r sin θ sin ϕ, z = r cos θ (5.36) dω dω L, M θ, ϕ θ, ϕ L, M = dωyl M (θ, ϕ)y M (θ, ϕ) = δ L,L δ M,M (5.37) L
58 58 5 Y M L (θ, ϕ) θ, ϕ L, M (5.38) ˆL Y M L (θ, ϕ) = ħ L(L + 1)Y M L (θ, ϕ) (5.39) ˆL z Y M L (θ, ϕ) = ħmy M L (θ, ϕ) (M = L, L 1,, L) (5.40) M L L L L + 1 YL M (θ, ϕ) M (θ, ϕ) (5.39) (5.40) Y M L (5.36) x, y, z x = sin θ cos ϕ cos θ cos ϕ + r r θ sin ϕ r sin θ ϕ = sin θ sin ϕ cos θ sin ϕ + y r r θ + cos ϕ r sin θ ϕ = cos θ z r sin θ r ϕ ( ˆL z = iħ x y y ) x = iħ ϕ (5.41) (5.4) (5.40) ϕ Y M L (θ, ϕ) e imϕ (5.43) M z ( ϕ ϕ + π) ˆL x, ˆL y ( ˆL x = iħ ˆL y = iħ ) + cot θ cos ϕ ϕ sin ϕ θ ( cos ϕ + cot θ sin ϕ θ ϕ ) (5.44) (5.45)
59 ˆL ± ( L + = ħe iϕ θ + i cot θ ) ϕ ( L = ħe iϕ θ i cot θ ) ϕ (5.9) ˆL = ˆL + ˆL + ˆL z ħˆl z [ ( 1 ˆL = ħ sin θ ) + 1 ] sin θ θ θ sin θ ϕ = 1 ( r r ) + 1 [ ( 1 r r r sin θ sin θ θ θ ) + 1 sin θ ] ϕ (5.46) (5.47) (5.48) (5.49) (5.48) (5.39) Y M L (θ, ϕ) = AM L (θ)eimϕ A M L [ 1 sin θ θ ( sin θ ) M ] θ sin A M L = L(L + 1)A M L (5.50) θ A M L θ, ϕ ˆL L, L = 0 ( θ i cot θ ) θ, ϕ L, L = 0 (5.51) ϕ θ, ϕ L, L = A L L e ilϕ da L L dθ L cot θa L L = 0 (5.5) A L L = c(sin θ)l (5.53) c Y L L 1 dω Y L L (θ, ϕ) = π 0 π dϕ 0 dθ sin θ A L L (θ) π = πc (sin θ) L+1 dθ 0 = 4πc L (L!) (L + 1)! = 1 (5.54)
60 60 5 c = 1 (L + 1)! L L! 4π (5.53) (5.55) A M L A L L = 1 (L + 1)! L (sin θ) L (5.56) L! 4π (5.9) 1 L, M = ħ ˆL + L, M 1 (5.57) (L M + 1)(L + M) θ, ϕ (5.46) A M L (θ)e imϕ = = e iϕ (L M + 1)(L + M) ( θ + i cot θ ) ϕ e imϕ (L M + 1)(L + M) ( ) (M 1) cot θ θ e imϕ A M 1 L (θ)e i(m 1)ϕ A M 1 L (θ) = (sin θ) M (L M + 1)(L + M) d d(cos θ) [(sin θ) (M 1) A M 1 L (θ)] (5.58) y M := (sin θ) M A M L ym y M = 1 d (L M + 1)(L + M) d(cos θ) ym 1 (5.59) L + M y M = ( 1) L+M (L M)! 1 d L+M (L)! (L + M)! d(cos θ) L+M y L (5.60) A M L = ( 1) L+M (L M)! (L)! 1 (L + M)! dl+m d(cos θ) L+M [(sin θ)l A L L ] (5.61)
61 (5.56) A M L = ( 1)L+M L L! (sin θ) M L + 1 (L M)! 4π (L + M)! d L+M d(cos θ) L+M [(sin θ)l ] (5.6) YL M (θ, ϕ) = θ, ϕ L, M = ( 1)L+M L + 1 (L M)! L L! 4π (L + M)! e imϕ (sin θ) M d L+M d(cos θ) L+M (sin θ)l (5.63) θ, ϕ ˆL + L, L = 0 (5.46) A L L = ( 1)L L L! (L + 1)! (sin θ) L (5.64) 4π ( 1) L (5.6) (5.64) YL M (θ, ϕ) = ( 1)L L + 1 (L + M)! L L! 4π (L M)! e imϕ (sin θ) M d L M d(cos θ) L M (sin θ)l (5.65) (5.63) A M L A M L (5.50) x = cos θ (1 x ) d A M L dx x dam L [L(L dx + + 1) M ] 1 x A M L = 0 ( 1 x 1) (5.66) L M 1 M L 1 x 1 P M L (x) = (1 x ) M L L! d L+M dx L+M (x 1) L ( L M L) (5.67)
62 6 5 PL 0 (x) d L P L (x) = 1 L L! dx L (x 1) L (5.68) P M L A M L (θ) P L M (x) (cos θ) 0 Y M L Y M L e x x M PL M (x)pl M (L + M)! (x)dx = δ L,L (5.69) L! (5.37) (θ, ϕ) = ( 1) M+ M L + 1 (L M )! 4π (L + M )! P M L (cos θ)eimϕ (5.70) Y M L M = 0 Y M L (θ, ϕ) = ( 1) M [Y M L (θ, ϕ)] (5.71) Y 0 L (θ, ϕ) = L L=0 M= L [Y M L (θ, ϕ)] Y M L (θ, ϕ ) = L + 1 4π P L(cos θ) (5.7) 1 sin θ δ(θ θ )δ(ϕ ϕ ) =: δ(ω Ω ) (5.73) sin θdθdϕ 1 Y 0 0 = 1 4π 3 8π sin θe±iϕ, Y Y 1 ±1 = 1 = 4π cos θ 15 Y ± = 3π sin θe ±iϕ, Y ±1 = 8π sin θ cos θe±iϕ, 5 Y 0 = 16π (3 cos θ 1) (5.74)
63 ħs (spin angular momentum) ħl ħ 0 L S G. Uhlenbeck S.Goudsmit 197 Pauli ħs S = 0, 1, 1, 3,, (5.75) ħs S + 1 M = S, S 1,, S ħ/ ħ/ 1 0 [Ŝx, Ŝy] = iħŝz, [Ŝy, Ŝz] = iħŝx, [Ŝz, Ŝx] = iħŝy (5.76) 5.1 (5.9) (5.31) (5.34) S, M + 1 Ŝ+ S, M = ħ (S M)(S + M + 1) (5.77) S, M 1 Ŝ S, M = ħ (S + M)(S M + 1) (5.78) S, M Ŝz S, M = ħm (5.79) S, M + 1 Ŝx S, M = ħ (S M)(S + M + 1) (5.80) S, M 1 Ŝy S, M = i ħ (S + M)(S M + 1) (5.81) 1
64 64 5 S ψ S (M) := S, M ψ (5.8) i = x, y, z Ŝ i ψ S (M) := S, M Ŝi ψ = S, M Ŝi S, M S, M ψ M = S i,mm ψ S (M ) (5.83) M S imm (5.77)-(5.81) 1/ Ŝ i = ħ ˆσ i, (i = x, y, z) (5.84) ˆσ i (Pauli matrices) [ˆσ x, ˆσ y ] = iˆσ z, [ˆσ y, ˆσ z ] = iˆσ x, [ˆσ z, ˆσ x ] = iˆσ y (5.85) (5.77)-(5.79) ˆσ x = ( ), ˆσ y = ( 0 i i 0 ), ˆσ z = ( ) (5.86) ˆσ x = ˆσ y = ˆσ z = ˆ1 (5.87) ˆ1 ( ) 1 0 ˆ1 = 0 1 (5.88) (5.85) (anticommutation relation) {ˆσ x, ˆσ y } = 0, {ˆσ y, ˆσ z } = 0, {ˆσ z, ˆσ x } = 0 (5.89) {Â, ˆB} Â ˆB + ˆBÂ (5.87) (5.89) ˆσ iˆσ j + ˆσ j ˆσ i = δ ij (5.90)
65 ˆσ x, ˆσ y, ˆσ z ˆ1 ˆσ xˆσ y = iˆσ z, ˆσ y ˆσ z = iˆσ x, ˆσ z ˆσ x = iˆσ y (5.91) (5.87) (5.91) ˆσ iˆσ j = ˆ1δ i,j + iϵ ijkˆσ k (5.9) ϵ ijk (i, j, k) (x, y, z) 1-1 ( i, j, k ) 0 A, B 3 (ˆσ A)(ˆσ B) = A B + iˆσ (A B) (5.93) ˆσ A = σ x A x + σ y A y + σ z A z (5.9) = ˆσ iˆσ j A i B j = (ˆ1δ i,j + iϵ ijkˆσ k )A i B j i,j=x,y,z = i=x,y,z A i B i + i k=x,y,z = ( ) i,j=x,y,z ˆσ k (A B) k e i θˆσ i = ˆ1 cos θ iˆσ i sin θ, (i = x, y, z) (5.94) ˆσ = ˆ1 e i θˆσ i = = ˆ1 n=0 ( 1 i ) n (n)! θ ˆσ n n=0 ( 1) n (n)! ( θ = ˆ1 cos θ iˆσ i sin θ i + n=0 ) n + ( i)ˆσ i ( 1 i ) n+1 (n + 1)! θ ˆσ i n+1 n=0 ( 1) n (n + 1)! ( ) θ n+1
66 66 5 (5.94) χ i = x, y, z π e i (π)ˆσ i χ = χ (5.95) 1/ θ ±e i θˆσ i χ (double valued) π π 5.3 Ĵ1 Ĵ Ĵ = Ĵ1 + Ĵ (5.96) Ĵ1 Ĵ Ĵ [Ĵx, Ĵy] = iħĵz, [Ĵy, Ĵz] = iħĵx, [Ĵz, ˆL x ] = iħĵy (5.97) Ĵ 1 = ħ J 1 (J 1 + 1), Ĵ1z, Ĵ = ħ J (J + 1), Ĵz J 1, M 1 ; J, M M 1, M ħm 1 ħm Ĵ1z Ĵz Ĵ = ħ J(J + 1) Ĵ 1, Ĵ Ĵ z Ĵ z = Ĵ1z + Ĵz (5.98) J, M; J 1, J J, M ħm Ĵz (5.98) M = M 1 + M (5.99) J (5.96) Ĵ = Ĵ 1 + Ĵ + Ĵ1Ĵ = ħ J 1 (J 1 + 1) + ħ J (J + 1) + Ĵ1+Ĵ + Ĵ1 Ĵ+ +Ĵ1zĴz (5.100)
67 Ĵ i± Ĵix ± iĵiy, (i = 1, ) (5.101) (5.100) M 1 = J 1, M = J Ĵ J 1, J = ħ (J 1 + J )(J 1 + J + 1) J 1, J (5.10) J 1, J J = J 1 + J J = J 1 + J, M = J 1 + J = M 1 = J 1, M = J (5.103) Ĵ = Ĵ1 + Ĵ (J1 + J ) J 1 + J, J 1 + J 1 = J 1 J 1 1, J + J J 1, J 1 J 1 + J, J 1 + J 1 = J1 J 1 1, J J 1 + J J + J 1, J 1 (5.104) J 1 + J (5.104) Ĵ = Ĵ1 + Ĵ J 1 + J J 1 + J J 1 + J, J 1 + J = 1 (J1 + J )(J 1 + J 1) [ J1 (J 1 1) J 1, J + J 1 J J 1 1, J 1 + ] J (J 1) J 1, J (5.105) J 1 + J J 1 + J 1 (5.104) J 1 + J 1, J 1 + J 1 = J1 J 1, J 1 J 1 + J J J 1 1, J (5.106) J 1 + J
68 68 5 (5.100) J 1 + J 1 (5.106) Ĵ = Ĵ1 + Ĵ J 1 + J 1, J 1 + J = 1 (J1 + J )(J 1 + J 3) [ J1 (J 1) J 1, J + (J 1 J ) J 1 1, J 1 ] J (J 1 1) J 1, J (5.107) (5.107) Ĵ = Ĵ1 + Ĵ J 1 + J 1 J 1 + J (5.105) (5.107) 1 J > J 1 J J 1 J 1 J J 1 + J, J 1 + J 1,, J 1 J (5.108) (5.108) Ĵ1 Ĵ J J + 1 J 1 +J J= J 1 J (J + 1) = (J 1 + 1)(J + 1) (5.109) J 1, M 1 ; J, M 1/ 1 0 1, 1 = 1, 1 1, 0 = 1 ( 1, 1 + 1, 1 ) 1, 1 = 1, 1 0, 0 = 1 ( 1, 1 1, 1 )
69 / 3 3/ 1/ 3, 3 = 1, 1, 1 3, 1 = 1 3 ( 1, 1, 1 + 1, 1, 1 + 1, 1, 1 ) 3, 1 = 1 3 ( 1, 1, 1 + 1, 1, 1 + 1, 1, 1 ) 3, 3 = 1, 1, 1 3, 1 α 1, 1, 1 + β 1, 1, 1 + γ 1, 1, 1 (5.110) 3, 1 α + β + γ = 0 α + β + γ = 1 ( ) 1/ (α, β, γ) ( α, 1 [ α + 3α ], 1 [α + ) 3α ] ( α, 1 [α + 3α ], 1 [ α + ) 3α ] α α / J, M; J 1, J := J, M J 1, M 1 ; J, M := M 1, M J, M = J 1 M 1 = J 1 J 1 M 1 = J 1 J M = J M 1 ; M M 1 ; M = Î (5.111) J M = J M 1 ; M M 1 ; M J, M (5.11)
70 70 5 C(J 1 J J; M 1 M M) := J 1, M 1 ; J, M J, M; J 1, J (5.113) (5.113) M = M 1 + M (5.114) J, M J, M = δ JJ δ MM M 1,M C(J 1 J J; M 1 M M)C(J 1 J J ; M 1 M M) = δ JJ δ MM (5.115) M 1, M M 1, M = δ M 1 M 1 δ M M C(J 1 J J; M 1 M M)C(J 1 J J; M 1M M) = δ M1 M 1 δ M M J,M (5.116) ( J = M = 0) (5.108) J 1 = J := j (5.114) M 1 = M := m (5.11) 0, 0 = j m= j m; m m; m 0, 0 (5.117) j 0 = Ĵ+ 0, 0 = (Ĵ1+ + Ĵ+) m; m m; m 0, 0 = m= j j [ (j m)(j + m + 1) m + 1; m m= j + (j + m)(j m + 1) m, m + 1 ] m; m 0, 0 (5.118) m m + 1 j 0 = (j m)(j + m + 1) m= j ( m; m 0, 0 + m + 1, m 1 0, 0 ) m + 1, m (5.119)
71 C(jj0; m, m, 0) = C(jj0; m + 1, m 1, 0 (5.10) m = j C(jj0; m, m, 0) = ( 1) j m c j (5.115) C(jj0; m, m, 0) = ( 1)j m j + 1 (5.11) 5.4 r r ([Ĥ, ˆP ] = 0) ˆP ψ(r) = ψ( r) (5.1) P ˆP P = P = ±1 (5.13) P = 1 P = 1 ˆL = ˆr ˆp ([ ˆP, ˆL] = 0) L, M, P ˆP ˆL ± L M ψ g ψ u g, u gerade, ungerade ˆf f ug = ψu ˆfψ g dr (5.14) f ug = f ug = 0
72 7 5 g g, u u g u, u g (5.15) g u, u g g g, u u (5.16) L YL M(θ, ϕ) P L M(cos θ)eimϕ r r, θ π θ, ϕ ϕ + π (5.17) e im(ϕ+π) = ( 1) M e imϕ PL M ( cos θ) = ( 1) L+M PL M (cos θ) (5.18) ((5.67) ) l P = ( 1) L (5.19) L L L ± 1 L L (5.130) 5.5 iħ [ ] t ψ(r, t) = ħ m + V (r) ψ(r, t) (5.131)
73 t t iħ ] t ψ (r, t) = [ ħ m + V (r) ψ (r, t) (5.13) ψ(r, t) ψ (r, t) Θ Θψ(r, t) = ψ (r, t) (5.133) (Θψ, Θϕ) = (ϕ, ψ) = (ψ, ϕ) (5.134) Θ(aψ + bϕ) = a Θψ + b Θϕ (5.135) U Θ = UK, Θ 1 = KU 1 = KU (5.136) K Θ 1 rθ = r (5.137) Θ 1 pθ = p (5.138) p = iħ i (5.137) (5.138) Θ = K (U = 1) 1/ Θ 1 σ i Θ = σ i (i = x, y, z) (5.139) σ y Θ = K σ x, σ z K Θ = σ y Θ = iσ y K, Θ 1 = ikσ y (5.140)
74 74 5 (σy 1 = σ y ) i Kσ y = σ y Θ = 1 (5.141) (1 ) 1/ 4 π x π n Θ = ( iσ y (1) ) ( iσ y (n) )K (5.14) Θ = ( 1) n Kramers : ψ Θ ψ Θ ψ = c ψ Θ Θc = c Θ ψ = c ψ Θ = 1 ψ, Θψ Θ ψ Θψ = ( Θψ ψ ) = ψ Θψ Θ = 1 ψ Θψ = ψ Θψ = 0 ψ Θψ ( )
75 m ω 1 Ĥ = ˆp m + mωˆx (6.1) [ˆx, ˆp] = iħ (6.) ħω p m = ħω mω x = ħω p 0 = mħω (6.3) ħ x 0 = mω (6.4) (6.1) (6.3) (6.4) â â â = 1 mħω (mωˆx + iˆp), â = 1 mħω (mωˆx iˆp) (6.5)
76 76 6 (6.) [â, â ] = 1 (6.6) (6.5) ħ mħω ˆx = mω (â + â), ˆp = i (â â) (6.7) (6.1) (6.6) ( Ĥ = ħω â â + 1 ) (6.8) â (creation operator) â (annihilation operator) Ĥ E n n Ĥ n = E n n (6.9) â (6.6) (ââ 1 {}}{ = â Ĥ n = ħωâ = ħω = E n â n ) n â â + 1 ) (â â â â + 1â n = Ĥâ n ħωâ n Ĥâ n = (E n + ħω)â n (6.10) â n E n + ħω Ĥ â ħω 1 â Ĥâ n = (E n ħω)â n â ħω 1
77 â 0 = 0 (6.11) ( Ĥ 0 = ħω â â + 1 ) 0 = 1 ħω 0 (6.1) E 0 = 1 ħω 0 (6.6) [â, â ] = 1 E E Ĥ = ˆp m + mω ˆx (6.13) ˆx = 0, ˆp = 0 ˆx = (ˆx ˆx ) ( x) ˆp = (ˆp ˆp ) ( p) (6.13) E = ( p) m + mω ( x) (6.14) ( p) mω E ( x) m = ω p x (6.15) p x ħ/ ħω/ (6.) (6.6) (6.10) â ħω 0 â n n E n Ĥ n = E n n, ( E n = ħω n + 1 ) (n = 0, 1,, ) (6.16) ħω ( ) ˆn â â (6.17)
78 78 6 (number operator) n n (Fock state) (6.16) ˆn n = â â n = n n. (6.18) â 1 â n n 1 â n = c n 1, (6.19) c n â = c n 1 (6.19) n â â n }{{} n n n =n = c n 1 n 1 = c c = ne iφ = n 1 ( n n = 1) φ 0 â 1 â n n + 1 n ââ n }{{} n ââ + 1 n = n + 1 â n = α n + 1 (6.0) = α n + 1 n + 1 = α α = n + 1 â n = n n 1 (6.1) â n = n + 1 n + 1 (6.) (6.) n = 1 n! (â ) n 0 (6.3) 6.1. â(t) = e i ħ Ĥt ae i ħ Ĥt (6.4) â (t) = e i ħ Ĥt a e i ħ Ĥt (6.5)
79 ( Ĥ = ħω â â + 1 ) (6.6) â(t) â(t) (.38) d d = iωâ(t), dtâ(t) dtâ (t) = iωâ (t) (6.7) â(t) = âe iωt, â (t) = â e iωt (6.8) n e i ħ Ĥt n = e i(n+1/)ωt n (6.9) n ϕ n (x) (6.9) (6.1) ( ˆp m + mωˆx x x ˆp = ħ i ) n = E n n (6.30) d x (6.31) dx ϕ n (x) x n ϕ n (x) ( ħ d m dx + mωˆx ) ϕ n (x) = E n ϕ n (x) (6.3) ϕ n (x) ϕ n=0 (x) â 0 = 0 â = (mωˆx + iˆp)/ mħω x â 0 = 1 (mωx + ħ d ) x 0 = 0 (6.33) mħω dx
80 80 6 ϕ 0 (x) x 0 = ( mω ) 1 4 e mω ħ x (6.34) πħ ϕ 0(x)dx = 1 n (6.3) (6.5) ϕ n (x) = x n = x (â ) n n! 0 = 1 n (mωx ħ d n!(mħω) dx )n ϕ 0 (x) (6.35) mωx ħ d mω = e ħ x dx d dx e mω ħ x (6.36) ξ x mω/ħ (6.35) ϕ n (x) = ( 1)n n n! 1 = n n! ( mω ħ ( mω πħ ) 1 4 e ξ d n dξ n e ξ ) 1 4 e ξ Hn (ξ) (6.37) dn H n (ξ) = ( 1) n e ξ dξ n e ξ (6.38) H 0 (ξ) = 1, H 1 (ξ) = ξ, H (ξ) = 4ξ, H 3 (ξ) = 8ξ 3 1ξ (6.39) ϕ n (x) a ħ/mω n=0 ϕ n (x)ϕ n (y) = 1 x +y πa e a n=0 1 n n! H n(x/a)h n (y/a) (6.40)
81 n=0 z n n n! H n(x)h n (y) = [ 1 exp 1 z ] xyz (x + y )z 1 z (6.41) n=0 1 n n! H n(x/a)h n (y/a) [ 1 = lim exp xyz (x + y )z z 1 1 z (1 z )a ] (6.4) ϕ n (x)ϕ n (y) = n=0 1 lim 1 πa z 1 1 z [ ] exp x + y 1 + z a 1 z + xyz (1 z )a (6.43) z = 1 ϵ lim ϵ 0 1 (x y) πa e a ϵ = δ(x y) (6.44) ϵ ϕ n (x)ϕ n (y) = δ(x y) (6.45) n= (coherent state) k λ k λ â â (displacement operator) ˆD(α) e αâ α â (6.46)
82 8 6 α (α ) ˆD (α)â ˆD(α) = â + α (6.47) ˆD (α)â ˆD(α) = â + α (6.48) α α α (6.47) α α [ ˆD (α)â ˆD(α)] = ˆD (α)[â, â ] ˆD(α) = ˆD (α) ˆD(α) = 1 (6.49) α 0 α (6.47) (6.48) α α ˆD(α) 0 (6.50) â α = ˆD(α) ˆD (α)α ˆD(α) 0 = ˆD(α)(â + α) 0 = α ˆD(α) 0 = α α â α = α α (6.51) ˆD(α) ˆD (α) = 1 â 0 = 0 eâ+ ˆB = eâe ˆBe 1 [Â, ˆB] (6.5) ˆD(α) ˆD(α) = e 1 α e αâ e α â (6.53) e α â 0 = 0 α α = e α e αâ 0 = e α n=0 α n n! (â ) n 0 = e α n=0 α n n! n (6.54) n P (n) P (n) = n α n nn = e n! (6.55)
83 n α ( n) n n = n (6.56) α = α e iϕ (6.54) α = P (n)(e iϕ ) n n (6.57) n=0 n P (n) 1 e iϕ 6. Ĥ = ( ) ˆp x m + mω x ˆx + ( ˆp y m + mω y ŷ ) (6.58) [ˆx, ˆp x ] = [ŷ, ˆp y ] = iħ, 0 (6.59) 1 (6.5) x y â x = 1 mħωx (mω xˆx + iˆp x ), â y = 1 mħωy (mω y ŷ + iˆp y ) (6.60) [â x, â x] = [â y, â y] = 1, 0 (6.61) ( Ĥ = ħω x â xâ x + 1 ) ( + ħω y â yâ y + 1 ) (6.6)
84 84 6 ω x = ω y =: ω ˆL z := ˆxˆp y ŷˆp x (6.63) â x, â y ˆL z = iħ(â x â y â xâ y ) (6.64) [Ĥ, ˆL z ] = 0 (6.65) â + = 1 (â x iâ y ), â = 1 (â x + iâ y ) (6.66) â x = 1 (â + + â ), â y = i (â + â ) (6.67) â + â, â [â +, â ] = [â +, â ] = 0 (6.68) Ĥ = ħω(â +â+ + â â + 1) (6.69) ˆL z = ħ(â +â+ â â ) (6.70) Ĥ ˆL z â +â+ â â n + n n := min(n +, n ) m := n + n E L z E = ħω(n + + n + 1) = ħω(n + m + 1) (6.71) L z = n + n = m (6.7) m, n N := E ħω (6.73) 6.1
85 : N = E/ħω n, m g N n + m n m g ±1 3 0 ± ±3 4 1 ± (6.71) (6.7) n +, n = (a + )n + n+! (a )n 0, 0 (6.74) n! a + = 1 (a x + ia y) = [ = 1 mω (x + iy) ħ a = 1 (a x ia y) = [ = 1 mω (x iy) ħ ħ l ho = mω 1 4mħω [mω(x + iy) i(p x + ip y )] ( ħ mω x + i ) ] (6.75) y 1 4mħω [mω(x iy) + i(p x ip y )] ( ħ mω x i ) ] (6.76) y a + = 1 [ ( (x + iy) x + i )] y a = 1 [ ( (x iy) x i )] y (6.77) (6.78) (6.79) z := x + iy, x = z + z, y = z z i (6.80)
86 86 6 x, y z, z z a + = 1 ( x iy + x i ) = z y + z = z e z e z (6.81) a + = 1 ( x + iy x i ) = z y z z = e z z e (6.8) a = 1 ( x + iy + x + i ) = z y + z = z e z e z (6.83) a = 1 ( x iy x + i ) = z y z z = e z z e (6.84) ψ 0 a + ϕ 0 = a ϕ 0 = 0 (6.85) (6.81) (6.83) ψ 0 = const.e z 1 ψ 0 (z, z ) = 1 e z, d z ψ 0 (z, z ) = 1, d z := dxdy (6.86) π (6.74) ψ n+,n (z, z ) = 1 n+!n! (a + )n + (a )n ψ 0 (z, z ) (6.87) (6.8) (6.84) ψ n+,n (z, z ) = ( 1)n ++n ( πn+!n! e z z min(n +,n ) n+!n! = π k=0 = ( 1) k n! π(n + m )! z m e L (m) n (x) = ) n+ ( ) n e z ψ0 (z, z ) z ( 1) k k!(n + k)!(n k)! zn + k z n k e z z L ( m ) n ( z )e imϕ (6.88) n ( 1) k (m + n)! k!(m + k)!(n k)! xk (m > 1) (6.89) k=0
87 n = min(n +, n ) m = n + n r = z ϕ = argz ψ n,m (r, ϕ) : = ψ n+,n (z, z ) = ( 1) n n! π(n + m )! r m e r L ( m ) n (r )e imϕ (6.90) 0 e x L (m) n (x)l (m) n (x)dx = δ nn Γ(m + 1) m+n C n (6.91) H = α=x,y,z ( ) p α m + mω q α (6.9) q α, p α [q α, p β ] = iħδ αβ (6.93) m, ω, ħ ħ/(mω), mħω q k, p k ħ q α mω q α, p α mħωp α (6.94) H = q α, p α α=x,y,z ħω ( p α + q α) (6.95) [q α, p α ] = iδ αβ (6.96) q x = r sin θ cos ϕ, q y = r sin θ sin ϕ, q z = r cos θ (6.97)
88 88 6 α=x,y,z α=x,y,z q α = r (6.98) p α = = 1 r = 1 r r r 1 [ 1 r sin θ ( sin θ ) + 1 θ θ sin θ ] ϕ r r + ˆL ħ r (6.99) ˆL 3 ( 1 r r r + ˆL ) ħ r + r ψ = E ħω ψ (6.100) ˆL ((5.39) ) ħ l(l + 1) (6.100) (6.100) [ ( d l + 1 dr + r ψ = 1 r u l(r)y m l (θ, ϕ) (6.101) [ d l(l + 1) dr r r + E ] u l (r) = 0 (6.10) ħω ρ = r ( [ρ d dρ + l + 3 ) d ρ dρ 1 u l (r) = r l+1 e r vl (r) (6.103) ) ( d r dr l + 3 E )] v l (r) = 0 (6.104) ħω ( l + 3 E ħω )] v l (r) = 0 (6.105) (6.115) v l (r) = 1 F 1 (a, b; ρ), a = 1 ( l + 3 E ), b = l + 3 ħω (6.106)
89 c nl a n a = n ( E = ħω n + l + 3 ), n, l = 0, 1,, (6.107) ψ nlm = c nl r l e r 1F 1 ( n, l + 3/; r )Y m l (θ, ϕ) m = l, l 1,, l (6.108) (6.10) ψ nlm = c nl r l e r L (l+1/) n (r )Yl m (θ, ϕ) (6.109) π π r dr sin θdθ ϕψnlm (r, θ, ϕ)ψ n l m (r, θ, ϕ) = δ nn δ ll δ mm (6.110) 0 dru nl (r)u n l(r) = δ ll (6.111) u nl (r) = ( 1) n Γ(n + 1) Γ(n + l + 3/) rl+1 L (l+1/) n (r )e r (6.11) (6.107) N = n + l N N/ N : l = N n, n = 0, 1,,, K = (N 1)/ N : (6.113) ħω(n + 3/) D N D N = K (l + 1) = n=0 K n=0 [(N n) + 1] = 1 (N + 1)(N + ) (6.114) n x, n y, n z 0 n x + n y + n z = N (n x, n y, n z ) N+ C (6.110)
90 [z d dz + (b z) d ] dz a w(z) = 0 (6.115) a z = 0 w(z) = c n z n (6.116) n=0 [z d dz + (b z) d ] dz a w(z) = [n(n + 1)c n+1 + b(n + 1)c n+1 (n + a)c n ] z n = 0 (6.117) n=0 c n+1 = 1 a + n n + 1 b + n c n = c 0 = 1 1 a(a + 1) (a + n) (n + 1)! b(b + 1) (b + n) c 0 (6.118) 1F 1 (a, b; z) = 1 + =: 1 + n=1 n=1 a(a + 1) (a + n 1) z n b(b + 1) (b + n 1) n! (a) n z n (b) n n! (6.119) a J m (z) = L (m) n (z) = m+n C n 1 F 1 ( n, m + 1 : z) (6.10) z m m Γ(m + 1) e iz 1F 1 (m + 1/, m + 1; iz) (6.11)
91 (6.10) (6.115) a = n, b = m + 1 [z d dz + (m + 1 z) d ] dz + n L (m) n (z) = 0 (6.1) Wikipedia Wilhelm Magnus Formulas and theorems for the special functions of mathematical physics (Springer-Verlag, New York 1966) p.4 I p.150, (5.107) (6.1) n n m L (m) n L (m) n Landau-Lifshitz L (m) n+m L (l+1) n l 1 L(l+1) n+l
92
93 m 1 m U(r) r := r 1 r H = ħ 1 ħ + U(r) (7.1) m 1 m r R r := r r 1, R := m 1r 1 + m r m 1 + m (7.) ħ H = (m 1 + m ) R ħ + U(r) (7.3) m R m := m 1m m 1 + m (7.4) ψ(r 1, r ) ϕ(r) ψ(r) ) ( ħ m + U(r) ψ(r) = Eψ(r) (7.5) = 1 r r r ˆL ħ r (7.6) [ ] ħ mr r r ˆL mr + U(r) ψ(r) = Eψ(r) (7.7)
94 94 7 l m ψ = R(r)Y m l (θ, ϕ) (7.8) ˆL Yl m = ħ l(l + 1)Yl m [ ħ ] mr r r ħ l(l + 1) mr + U(r) R(r) = ER(r) (7.9) R(r) = χ(r) r (7.10) d [ ] χ m dr + l(l + 1) (E U(r)) ħ r χ = 0 (7.11) ħ l(l + 1) mr (7.1) 1 χ(0) = 0 (7.13) (7.11) 1 Yl m (θ, ϕ) E, l, m l n = 0 n = 0, 1,, n r = 0 r l = 0, 1,, 3, 4, 5, 6, 7 s, p, d, f, g, h, i, k, 1 l l l
95 U(r) lim r 0 r U(r) = 0 (7.14) R(r) r s (7.9) (7.13) (7.14) s = l R(r) r l (7.15) 7. p E = p /m ψ e i ħ p r l m U(r) = 0) E k := me/ħ ψ klm = R kl (r)y m l (θ, ϕ) (7.16) π π r dr sin θdθ dϕψk l m ψ klm = πδ(k k )δ ll δ mm (7.17) r d 0 dr (rr kl) + r drr k lr kl = πδ(k k ) (7.18) [ k ] l(l + 1) r R kl = 0 (7.19) l = 0 (7.13) (7.19) sin kr R k0 (r) = r (7.0) l 0 R kl (r) = r l χ kl (7.1)
96 96 7 r d 3 χ kl dr 3 + l + 1 r d χ kl dr + l + 1 r dχ kl dr + k χ kl = 0 (7.) d ( χ kl dr + k l + 1 ) dχkl r dr = 0 (7.3) d ( ) 1 dχ kl dr + l + ( ) d 1 dχ kl + k 1 dχ kl r dr r dr r dr r dr = 0 (7.4) (7.) χ kl+1 = 1 r dχ kl dr (7.5) χ kl = (7.0) ( ) 1 d l χ k0 (7.6) r dr ( ) R kl = ( 1) l rl 1 d l sin kr k l r dr r (7.7) ( 1) l k l (7.19) x = kr y = R kl d [ 1 1 x dr (xy) + l(l + 1) x ] y = 0 (7.8) j l (x) n l (x) ( ) 1 j l (x) = ( x) l d l sin x π x dx x = ( ) 1 n l (x) = ( x) l d l cos x π x dx x = x J l+ 1 (x) (7.9) x N l+ 1 (x) (7.30) (7.9) (7.30) j l
97 (7.7) πk R kl = kj l (kr) = r J l+ 1 (kr) (7.31) r 1/r n (n ) sin(kr lπ/) R kl r (7.3) (7.7) sin kr r r 0 ( ) 1 d l sin kr r dr r ( 1) l ( 1 r = ( 1) l k l+1 (l + 1)!! ) d l k l+1 r l dr (l + 1)! (7.33) R kl = (7.15) kl+1 (l + 1)!! rl (7.34) (7.9) (7.30) ( ) 1 n (x) := j n (x) + in n (x) = i( x) n d n e ix x dx x π = x H(1) n+ 1 ( ) 1 n (x) := j n (x) in n (x) = i( x) n d n e ix x dx x π = x H() n+ 1 h (1) h () (7.35) (7.36) h (1) n h () n l = 0 R ± k0 = A r e±ikr (7.37)
98 98 7 l R ± kl := ( 1) l A rl = ±ia k l πk r ( ) 1 d l e ±ikr r dr r r H(1,) (kr) (7.38) l+ 1 R ± kl Ae±i(kr lπ/) r (7.39) R ± kl A(l 1)!! k l r l 1 (7.40) 1 v = ħk/m j = v ψ r 1 dω r dωj = r v R + k0 = A v = 1 A = 1 v (7.41) 1/r (7.19) 1 d (rr kl ) r dr + k R kl = 0 (7.4) R kl = r sin(kr lπ/ + δ l(k)) (7.43) δ l (k) l 7.3 U = α r (α > 0) (7.44)
99 (7.9) 1 d (rr) r dr l(l + 1) r R + m (E ħ + α ) R = 0 (7.45) r m, ħ /(mα), ħ 3 /(mα ) m ( ) = mα ħ (7.46) (7.45) 1 d ( (rr) l(l + 1) r dr r R + E + 1 ) R = 0 (7.47) r n = 1 E, ρ = r n (7.48) (7.47) 1 d [ (ρr) l(l + 1) ρ dρ + ρ n ] R = 0 (7.49) ρ R ρ l ρ (7.49) d R dρ 1 4 R = 0 (7.50) R e 1 ρ w(ρ) R = ρ l e 1 ρ w(ρ) (7.51) [ρ d dρ + (l + ρ) d ] (l + 1 n) w = 0 (7.5) dρ (6.115) w(ρ) = 1 F 1 (l + 1 n, l + ; ρ) 1 = (ρ) (7.53) L (l+1) n l 1 n+lc l+1
100 100 7 (6.10) L (l+1) n l 1 L(l+1) n+l (6.4 ) 6.4 l + 1 n n l + 1 n l + 1, n (7.54) R nl = const.ρ l e ρ 1F 1 (l + 1 n, l + ; ρ) (7.55) R nl = (7.48) 0 R nl r dr = 1 (7.56) (n + l)! n l+ (l + 1)! (n l 1)! (r)l e r n 1 F 1 (l + 1 n, l + ; ρ) (7.57) E = 1, n = 1,, (7.58) n mα /ħ E = mα ħ, n = 1,, (7.59) n n = 1,, n l = 0, 1,, n 1 (7.60) (7.56) l m l m l + 1 l n n 1 (l + 1) = n (7.61) l=0 l
101 H = p m e 4πϵ 0 r (7.6) L i (i = 1,, 3) H L i H 4.6 L 3 m n l = 0, 1,, l max = n 1 (n ) l l + 1 n n 1 (l + 1) = n (7.63) l=0 (accidental degeneracy) SO(4) m n m l l R R = L p p L m + e r. (7.64) 4πϵ 0 r 1/r (dynamical symmetry) - R i = 1 m ϵ ijk(l j p k p j L k ) + k x i r, k e 4πϵ 0 (7.65) ϵ ijk i, j, k 1,, Eddington Levi-Civita
102 10 7 R i H [L i, x j ] = iħϵ ijk x k (7.66) [L i, p j = iħϵ ijk p k (7.67) [ L i, 1 ] = 0 (7.68) r [ ] 1 r, p i = iħ x i r 3 (7.69) [ ] 1 r, R i = 1 [ ] 1 m ϵ ijk r, L jp k p j L k = 1 ( [ ] [ ] ) 1 1 m ϵ ijk L j r, p k r, p j L k = iħ ( m ϵ x k ijk L j r 3 x ) j r 3 L k = iħ ( m ϵ x k ijk ϵ jlm x l p m r 3 x ) j r 3 ϵ klmx l p m = iħ [( 1 p i m r + 1 ) r p i 1 ] r 3 (p kx k x i + x i x k p k ) (7.70) [ ] p 1 l, R i = iħk [(p i r + 1 ) r p i 1 ] r 3 (p kx k x i + x i x k p k ) (7.71) [H, R i ] = 0 (7.7) R R 1/r R i [R i, R j ] = iħ m ϵ ijkl k H (7.73) [L i, R j ] = iħϵ ijk R k (7.74) (4.6 )
103 L (R x, R y, R z ) R i L l R p L + L p = iħp (7.75) R = e 4πϵ 0 [ r r c(p L iħp) ] = e 4πϵ 0 [ r r + c(l p iħp) ] (7.76) c = 4πϵ 0 /(me ) [ r ] [ r ] R (mc) = r + c(l p iħp) r c(p L iħp) [ r ] = 1 c r (p L iħp) (L p iħp)r r +c [ (L p)(p L) + iħ(l p)p + iħp(p L) + ħ p ] = 1 c 1 r (L + ħ ) + c p (L + ħ ) ( = 1 + c p ) 1 (L + ħ ) c r = 1 + mc H(L + ħ ) (7.77) ( ) e R = + 4πϵ 0 m H(L + ħ ) (7.78) 4 SO(4) (V. A. Fock, 1935) H L i R i E E < 0 A i := (7.73) (7.74) m E R i (7.79) [A i, A j ] = iħϵ ijk L k, [L i, A j ] = iħϵ ijk A k (7.80)
104 104 7 [L i, L j ] = iħϵ ijk L k (7.81) L i (7.79) A i L x, L y, L z yz, zx, xy w 4 4 A x, A y, A z wx, wy, wz A x, A y xw, yw ( A x = xp w wp x = iħ A y = yp w wp y = iħ w, w y ) x w w x ( y w w y A x, A y ([ [A x, A y ] = ħ x ] ( = ħ x y y x ) ) [ w x, y w ]) (7.8) (7.83) = iħl z (7.84) (7.80) L i, A j 4 1/r (7.80) (W. Pauli, 196) M i := L i + A i, N i := L i A i (7.85) (7.80) [M i, M j ] = iħϵ ijk M k, [N i, N j ] = iħϵ ijk N k, [M i, N j ] = 0 (7.86) {M 1, M, M 3 } {N 1, N, N 3 } M, N M(M + 1), N(N + 1) (M, N = 0, 1/, 1, 3/, )
105 (7.86) M, M 3, N, N 3 M = ħ a(a + 1) (a = 0, 1/, 1, 3/, ) M 3 = ħµ (µ = a, a 1,, a) (7.87) N = ħ b(b + 1) (b = 0, 1/, 1, 3/, ) N 3 = ħν (ν = b, b 1,, b) (7.88) R L R R L = L R = 0 (7.89) M = N = 1 4 (L + A ) (7.90) a = b (7.78) ( e ) (7.91) A = m E R = (L + ħ ) m E 4πϵ 0 [ 1 4 (L + A ) = 1 ħ + m ( ) e ] = ħ a(a + 1) (7.9) 4 E 4πϵ 0 ((7.90) ) E = m ( ) e ħ n (7.93) 4πϵ 0 n := a + 1 = 1,, 7.5 III (7.86) SU() SU() SU() SU() SO(4) so(4) = so(3) + so(3)
106 106 7 SO(3) SO(4) 6 L ij = 1 ħ ϵ ijkl k (i, j, k = 1,, 3) (7.94) L 4i = 1 ħ A i (i = 1,, 3) (7.95) a (7.85) SU() SU() (a + 1) = n L i = M i + N i (7.96) L SU() M N l a b l a + b a = b l = 0, 1,, a = n 1 N = (N x, N y, N z ) N ±1 1 = N x ± in y, N 0 1 = N z. (7.97) N 1 1 H ([H, N 1 1] = 0) N 1 1 n, l, l N N 1 1 n, l, l = c n, l + 1, l + 1 (7.98) N 1 1 n l n, l + k, l + k L l m n n 1 (l + 1) = n (7.99) l=0 1/r SO(4) M N 4 4 C =6
107 SO(3,1) 3 3 M. Bander and C. Itzykson, Rev. Mod. Phys. 38, 330 (1966); Rev. Mod. Phys. 38, 346 (1966)
108
109 H H 0 V H = H 0 + V (8.1) H 0 V (H 0 + V ) ψ = E ψ (8.) m E 0m H 0 m = E 0m m (8.3) { m } ψ ψ = n c m m (8.4) (8.) (8.3) c m (E 0m + V ) m = E c m m (8.5) m m
110 110 8 k m ( k m = δ km ) V km c m = (E E 0k )c k (8.6) m V km := k V m = ψ (0) k V ψ (0) m dx, ψ (0) m (x) := x m (8.7) dx n d n x ˆV Ĥ0 (8.6) H n E n ψ n c n E = E (0) + E (1) + E () + (8.8) c m = c (0) n δ mn + c (1) m + c () m + (8.9) ψ n = n (8.9) δ mn E (k), c (k) m V k O(V k ) (8.6) V km (c n (0) δ mn + c (1) m + c () m + ) = (E (0) E 0k + E (1) + E () + ) m V (c (0) n δ kn + c (1) k + c () k + ) (8.10) (8.10) V 0 k = n 0 = (E (0) E 0k )c (0) n δ kn (8.11) E (0) = E 0n (8.1) 0 c (0) n = 1 (8.13) ψ (0) n = n (8.14)
111 V kn c (0) n = (E (0) E 0k )c (1) k + E (1) c (0) n δ kn (8.15) (8.1) (8.13) k = n E (1) = V nn (8.16) E n (0) 1 n V k = n c (1) k = V kn E 0n E 0k (k n) (8.17) ψ (1) n = (1 + c (1) n ) n + k c (1) k k (8.18) k = n c (1) n V 1 1 c (1) k = O(V ) ψ (1) n ψ (1) n = 1 + c (1) n + O(V ) (8.19) O(V ) 1 c (1) n = E = E 0n + V nn (8.0) ψ (1) n = n + k V kn E 0n E 0k k (8.1) V V kn E 0n E 0k 1 O O mn := ψ (1) m O ψ (1) n (8.) 1 v V c (1) n = iv n 1 + c (1) n = 1 + vn V 1 1
112 11 8 (8.19) O(V ) O mn = O mn (0) + [ (1 δ km ) V km O(0) kn + (1 δ kn ) V ] kno (0) mk (8.3) E 0m E 0k E 0n E 0k k c (0) n = 1, c (1) n = 0, E (0) = E 0n, E (1) = V nn V km c (1) m = (E 0n E 0k )c () k + V nn c (1) k + E () δ kn (8.4) m m = n k = n E () = m V nm c (1) m V nn c (1) n = m V nm c (1) m (8.5) (8.17) E () = m V nm E 0n E 0m (8.6) (n = 0) E () 00 < E() 0m (m > 0) k n V km c (1) m = (E 0n E 0k )c () k + V nn c (1) k (8.7) m c () k = = ( 1 δ kn E 0n E 0k m ( 1 δ kn E 0n E 0k m ψ = (1 + c () n ) n + k V km c (1) m V nn c (1) k V km V mn E 0n E 0m c (1) k k + k ) V nnv kn E 0n E 0k ) (8.8) c () k k (8.9) c () n O(V ) 1 (8.9) ψ ψ = 1 + Rec () n + k V kn (E 0n E 0k ) = 1 (8.30)
113 c () n = 1 k V kn (E 0n E 0k ) (8.31) ( ) ψ = 1 1 V kn (E 0n E 0k ) n + V kn k E 0n E 0k k k + ( ) 1 V km V mn V nnv kn k (8.3) E 0n E 0k E k m 0n E 0m E 0n E 0k 8. H 0 s E 0n n i (i = 1,,, s) (H 0 + V ) ψ = E ψ (8.33) ψ = s j=1 E = E 0n + E (1) s c nj (E 0n + V ) n j = E 0n + E (1) ) j=1 E 0n s c nj V n j = E (1) j=1 n i c (0) n j n j (8.34) s c nj n j (8.35) j=1 s c nj n j (8.36) j=1 s (V ni n j E (1) δ nj n j )c nj = 0 (8.37) j=1
114 114 8 V ni n j := n i V n j det(v ni n j E (1) δ nj n j ) = 0 (8.38) s = (8.38) E (1) ± = 1 (V 11 + V ± ħω) (8.39) ω = 1 ħ (V11 V ) + 4 V 1 (8.40) (8.37) ψ ± = c (0) 1± n 1 + c (0) ± n ( c (0) 1± = V 1 1 ± V ) 11 V (8.41) V 1 ħω ( c (0) ± = ± V 1 1 V ) 11 V (8.4) V 1 ħω ψ ± n 1, ( ψ + ψ ) = ( c (0) 1+ c(0) + c (0) 1 c(0) ) ( n 1 n ) =: M M ( ) ( ) n 1 =: M 1 ψ + n ψ ( n 1 n ) (8.43) (8.44) ψ ± E ± := E 0n +E (1) ± t = 0 n 1, n n 1 (t), n (t) ( ) ( ) n 1 (t) = M 1 e i ħ E +t ψ + n (t) e i ħ E t ψ = M 1 ( = M 1 ( e i ħ E +t 0 0 e i ħ E t e i ħ E +t 0 0 e i ħ E t )( ) ) ψ + ψ ( ) M n 1 n (8.45)
115 M n 1 (t), n (t) t = 0 n 1 t n n n 1 (t) = (e i ħ E +t e i ħ E t )c (0) + c(0) c (0) 1+ c(0) c(0) 1 c(0) + (8.46) (8.39) (8.40) (8.41) (8.4) w 1 = n n 1 (t) = V 1 (1 cos ωt) (8.47) (ħω) E (1) + E() = ħω ω m V ni m ψ = s j=1 c (0) n j n j + m (8.33) s j=1 = E (1) s c (0) n j V n j + m j=1 c (1) m m (8.48) c (1) m (E 0m + V ) m c (0) n j n j + (E 0n + E (1) ) m n i n i m = 0 s j=1 c (0) n j V ni n j + m c (1) m m (8.49) c (1) m V ni m = E (1) c (0) n i (8.50) (8.49) m V mm c (1) m E 0m = (E n + E (1) )c (1) m (8.51) c (1) m = j V mn j c (0) n j E 0n E 0m (8.5)
116 116 8 (8.50) ( V nj n j + ) V nj mv mnj E (1) δ nj n E m 0n E j c (0) n j = 0 (8.53) 0m j H = H 0 + V (t) (8.54) iħ t ψ(t) = (H 0 + V (t)) ψ(t) (8.55) iħ t ψ 0(t) = H 0 ψ 0 (t) (8.56) ψ 0n (t) = n e i ħ E 0nt (8.57) H 0 n = E 0n n (8.58) H 0 { ψ 0k (t) } t (8.55) ψ(t) = n a n (t) ψ 0n (t) = n a n (t) n e i ħ E 0nt (8.59) (8.55) (8.58) iħ n da n dt n e i ħ E 0nt = n V (t)a n (t) n e i ħ E 0nt (8.60)
117 m { n } iħ da m(t) dt = n = n m V (t) n a n (t)e i ħ (E 0m E 0n )t m V (t) n a n (t)e iωmnt (8.61) ω mn = 1 ħ (E 0m E 0n ) (8.6) m n t = 0 n t m a m (t) = δ mn + a (1) mn(t), a (1) mn(0) = 0 (8.63) a (1) mn(t) n n (8.61) a (1) mn O(V ) V iħ da(1) mn(t) dt = m V (t) n e iωmnt + O(V ) (8.64) a (1) mn(0) = 0 a (1) mn(t) = i ħ t (8.65) a (1) mn(t) = i ħ t 0 0 dt m V (t ) n e iωmnt (8.65) V (t) = V e iωt + V e iωt (8.66) dt [ m V n e i(ωmn ω)t + m V n e i(ωmn+ω)t ] = V mn e i(ωmn ω)t 1 ħ(ω mn ω) Vnm e i(ωmn+ω)t 1 ħ(ω mn + ω) (8.67) ω mn ±ω a (1) mn (8.59) n V 1 ψ n (t) = n e i ħ E 0mt + m a (1) mn(t) m e i ħ E 0nt (8.68)
118 118 8 O V 1 (8.68) = O mn (t) = ψ m (t) O ψ n (t) ( m e i ħ E 0mt + k a (1) km k e i ħ E 0kt ) O ( n e i ħ E 0nt + k a (1) kn e i ħ E 0kt k ) = O (0) mne iωmnt + O (1) mn(t) (8.69) O (0) mn = m O n (8.70) O (1) mn = k ( a (1) km (t) O (0) kn eiω knt + a (1) kn (t)o(0) mk eiω mkt ) (8.71) (8.67) {[ O mn(t) (1) = k [ + = e iωmnt k [ + V km e i(ω km ω)t 1 ħ(ω km ω) e i(ωkn ω)t 1 V kn + Vnk ħ(ω kn ω) {[ O (0) mk V nk O (0) mk V kn 1 e i(ω+ω kn)t ħ(ω kn + ω) ] e i(ωkm+ω)t 1 + V mk ħ(ω km + ω) ] } e i(ωkn+ω)t 1 O (0) ħ(ω kn + ω) mk eiω mkt 1 e i(ω ω kn)t ħ(ω kn ω) O (0) kn eiω knt + O (0) kn V 1 e i(ω+ω km)t mk ħ(ω km + ω) + O (0) kn V km 1 e i(ω ω km)t ħ(ω km ω) ] e iωt } ] e iωt (8.7) 8.4 (8.66) ω m n E 0m E 0n E 0m E 0n = ħ(ω + ϵ), ϵ/ω 1 (8.73) ϵ (8.67) (8.61)
119 (8.73) m, n (8.61) m, n iħ da m dt iħ da n dt m V (t) n a n e iωmnt V mn e iϵt a n (8.74) n V (t) m a m e iωmnt V mne iϵt a m (8.75) (8.66) v := V mn /ħ da m = ive iϵt a n dt (8.76) da n = iv e iωmnt a m dt (8.77) ( d dt iϵ d ) dt + v a m = 0 (8.78) ( d dt + iϵ d ) dt + v a n = 0 (8.79) (8.78) a m = e iχt χ ϵχ v = 0 (8.80) χ = ϵ ± Ω, Ω := 1 ϵ + 4 v (8.81) t = 0 a m (0) = 1, a n (0) = 0 a m (t) = e i ϵt (cos Ωt + A sin Ωt) (8.8) (8.76) t = 0 da m dt = i ϵ + ΩA = 0 (8.83) t=0 A = iϵ/(ω) ( a m (t) = e i ϵt cos Ωt i ϵ ) Ω sin Ωt (8.84) (8.76) a n (t) = i v Ω e i ϵt sin Ωt (8.85)
120 10 8 ψ(t) = a m (t) m + a n (t) n (8.86) t n w nm (t) = n ψ(t) = v (1 cos Ωt) (8.87) Ω Ω v/ω 1 (ϵ = 0) w nm (t) = 1 (1 cos v t) (8.88) 1 m n T = π/ v 8.5 H 0 t = i V (t) t f ψ(t) = f a fi (t) f (8.89) (8.65) a fi (t) = δ fi i ħ t dt f V (t ) i e iω fit (8.90) t = w fi = 1 ħ dt f V (t) i e iω fit (8.91) t (f i) (8.90) t a fi (t) = i dt f V (t ) i e iω fit ħ = f V (t ) i e iiω t t fit ħω fi + dt f V (t ) i t e iωfit ħω fi (8.9)
121 t V (t ) (8.1) V (t ) 1 w fi = (ħω fi ) dt f V (t) i t e iω fit (8.93) V (t) ω fi w fi 0 V = H H 0 ( ω fi ) i H ψ f H 0 i = E (0) i i, H ψ f = E f ψ f (8.94) (E f E (0) i ) ψ f i = ψ f H H 0 i = ψ f V i (8.95) E f E (0) f ψ f f ψ f i = 1 ħω fi f V i (8.96) w fi = ψ f i = 1 (ħω) f V i (8.97) (8.93) e iω fit 8.6 E < E min E > E min t = 0 E 0i V (t) = V e iωt + V e iωt, ħω > E min E 0i (8.98)
122 1 8 E 0f a fi ħω E 0f E 0i (8.67) a fi = V fi e i(ω fi ω)t 1 ħ(ω fi ω) (8.99) a fi = 4 V fi sin (ω fi ω)t ħ (ω fi ω) (8.100) sin αt lim t tα = πδ(α) (8.101) w fi = a fi lim t t = π V fi δ(ω fi ω) = π ħ V fi δ(e 0f E 0i ħω) (8.10) 8.10) ω = 0 E 0i = E 0f 8.7 (Ê = iħ / t) [Ê, t] = iħ E t ħ/ (8.103) (8.103) α 0 1 t t > 0 sin αt tα dα = sin x dx = π x t πδ(α)
123 Ψ(x, t) t = t t x p ħ/ (8.103) t E E ħ/( t) t ħ/( t) (8.103) Ĥ Ĥ t = 0 t = 0 ˆV t = t 0 (> 0) Ĥ = Ĥ + Ĥ + ˆV Ĥ0 + ˆV (8.104) iħ t Ψ(x, t) = (Ĥ0 + ˆV )Ψ(x, t) (8.105) Ψ(x, t) = e i ħ Ĥ0t Ψ I (x, t) (8.106) (8.105) iħ t Ψ I(x, t) = ˆV I (t)ψ I (x, t), ˆVI (t) e i ħ Ĥ0t ˆV e i ħ Ĥ0t (8.107) (8.107) ( Ψ I (x, t) = 1 i t0 ) V I (t)dt Ψ I (x, 0) (8.108) ħ 0 Ψ I (x, 0) = Ψ(x, 0) Ψ i (x) Ψ i Ψ f a fi a fi = Ψ f (x)ψ I(x, t)dx Ψ f (x)ψ i(x)dx i ħ t0 dx dtψ ˆV f I (t)ψ i (8.109) 0
124 14 8 E i E f Ĥ0 dxψ ˆV f I (t)ψ i = dxψ f e i ħ Ĥ0t ˆV e i ħ Ĥ0t Ψ i = e i ħ (E f E i )t dxψ ˆV f Ψ i e i ħ (E f E i )t f ˆV i a fi 1 t0 f ˆV i ħ dte i ħ (E f E i )t ) 0 = 4 f ˆV i sin (E f E i )t 0 ħ (E f E i ) (8.110) E f E i (8.110) t 0 E f E i ħ/t 0 E f(i) ħ/t 0 δ(α) = lim t sin αt πα t (8.111) i f w fi a fi w fi lim t t = π ħ f ˆV i δ(e f E i ) (8.11) (8.11)
125 ) ( ħ m + U ψ = Eψ (9.1) ψ = e i ħ S (9.) 1 m ( S) iħ S = E U (9.3) m (9.3) (9.1) S π ħ S = S 0 + ħ i S 1 + ( ) ħ S + (9.4) i (9.3) S 0, S 1, Wentzel, Kramers, Brillouin WKB (9.3) 1 m ( ) ds iħ dx m d S = E U(x) (9.5) dx 0 S = S 0 ħ 1 m ( ) ds0 = E U(x) (9.6) dx
4. ϵ(ν, T ) = c 4 u(ν, T ) ϵ(ν, T ) T ν π4 Planck dx = 0 e x 1 15 U(T ) x 3 U(T ) = σt 4 Stefan-Boltzmann σ 2π5 k 4 15c 2 h 3 = W m 2 K 4 5.
 A 1. Boltzmann Planck u(ν, T )dν = 8πh ν 3 c 3 kt 1 dν h 6.63 10 34 J s Planck k 1.38 10 23 J K 1 Boltzmann u(ν, T ) T ν e hν c = 3 10 8 m s 1 2. Planck λ = c/ν Rayleigh-Jeans u(ν, T )dν = 8πν2 kt dν c
A 1. Boltzmann Planck u(ν, T )dν = 8πh ν 3 c 3 kt 1 dν h 6.63 10 34 J s Planck k 1.38 10 23 J K 1 Boltzmann u(ν, T ) T ν e hν c = 3 10 8 m s 1 2. Planck λ = c/ν Rayleigh-Jeans u(ν, T )dν = 8πν2 kt dν c
II No.01 [n/2] [1]H n (x) H n (x) = ( 1) r n! r!(n 2r)! (2x)n 2r. r=0 [2]H n (x) n,, H n ( x) = ( 1) n H n (x). [3] H n (x) = ( 1) n dn x2 e dx n e x2
![II No.01 [n/2] [1]H n (x) H n (x) = ( 1) r n! r!(n 2r)! (2x)n 2r. r=0 [2]H n (x) n,, H n ( x) = ( 1) n H n (x). [3] H n (x) = ( 1) n dn x2 e dx n e x2 II No.01 [n/2] [1]H n (x) H n (x) = ( 1) r n! r!(n 2r)! (2x)n 2r. r=0 [2]H n (x) n,, H n ( x) = ( 1) n H n (x). [3] H n (x) = ( 1) n dn x2 e dx n e x2](/thumbs/101/149159646.jpg) II No.1 [n/] [1]H n x) H n x) = 1) r n! r!n r)! x)n r r= []H n x) n,, H n x) = 1) n H n x) [3] H n x) = 1) n dn x e dx n e x [4] H n+1 x) = xh n x) nh n 1 x) ) d dx x H n x) = H n+1 x) d dx H nx) = nh
II No.1 [n/] [1]H n x) H n x) = 1) r n! r!n r)! x)n r r= []H n x) n,, H n x) = 1) n H n x) [3] H n x) = 1) n dn x e dx n e x [4] H n+1 x) = xh n x) nh n 1 x) ) d dx x H n x) = H n+1 x) d dx H nx) = nh
ii p ϕ x, t = C ϕ xe i ħ E t +C ϕ xe i ħ E t ψ x,t ψ x,t p79 やは時間変化しないことに注意 振動 粒子はだいたい このあたりにいる 粒子はだいたい このあたりにいる p35 D.3 Aψ Cϕdx = aψ ψ C Aϕ dx
 i B5 7.8. p89 4. ψ x, tψx, t = ψ R x, t iψ I x, t ψ R x, t + iψ I x, t = ψ R x, t + ψ I x, t p 5.8 π π π F e ix + F e ix + F 3 e 3ix F e ix + F e ix + F 3 e 3ix dx πψ x πψx p39 7. AX = X A [ a b c d x
i B5 7.8. p89 4. ψ x, tψx, t = ψ R x, t iψ I x, t ψ R x, t + iψ I x, t = ψ R x, t + ψ I x, t p 5.8 π π π F e ix + F e ix + F 3 e 3ix F e ix + F e ix + F 3 e 3ix dx πψ x πψx p39 7. AX = X A [ a b c d x
量子力学 問題
 3 : 203 : 0. H = 0 0 2 6 0 () = 6, 2 = 2, 3 = 3 3 H 6 2 3 ϵ,2,3 (2) ψ = (, 2, 3 ) ψ Hψ H (3) P i = i i P P 2 = P 2 P 3 = P 3 P = O, P 2 i = P i (4) P + P 2 + P 3 = E 3 (5) i ϵ ip i H 0 0 (6) R = 0 0 [H,
3 : 203 : 0. H = 0 0 2 6 0 () = 6, 2 = 2, 3 = 3 3 H 6 2 3 ϵ,2,3 (2) ψ = (, 2, 3 ) ψ Hψ H (3) P i = i i P P 2 = P 2 P 3 = P 3 P = O, P 2 i = P i (4) P + P 2 + P 3 = E 3 (5) i ϵ ip i H 0 0 (6) R = 0 0 [H,
I ( ) 1 de Broglie 1 (de Broglie) p λ k h Planck ( Js) p = h λ = k (1) h 2π : Dirac k B Boltzmann ( J/K) T U = 3 2 k BT
 I (008 4 0 de Broglie (de Broglie p λ k h Planck ( 6.63 0 34 Js p = h λ = k ( h π : Dirac k B Boltzmann (.38 0 3 J/K T U = 3 k BT ( = λ m k B T h m = 0.067m 0 m 0 = 9. 0 3 kg GaAs( a T = 300 K 3 fg 07345
I (008 4 0 de Broglie (de Broglie p λ k h Planck ( 6.63 0 34 Js p = h λ = k ( h π : Dirac k B Boltzmann (.38 0 3 J/K T U = 3 k BT ( = λ m k B T h m = 0.067m 0 m 0 = 9. 0 3 kg GaAs( a T = 300 K 3 fg 07345
) ] [ h m x + y + + V x) φ = Eφ 1) z E = i h t 13) x << 1) N n n= = N N + 1) 14) N n n= = N N + 1)N + 1) 6 15) N n 3 n= = 1 4 N N + 1) 16) N n 4
![) ] [ h m x + y + + V x) φ = Eφ 1) z E = i h t 13) x << 1) N n n= = N N + 1) 14) N n n= = N N + 1)N + 1) 6 15) N n 3 n= = 1 4 N N + 1) 16) N n 4 ) ] [ h m x + y + + V x) φ = Eφ 1) z E = i h t 13) x << 1) N n n= = N N + 1) 14) N n n= = N N + 1)N + 1) 6 15) N n 3 n= = 1 4 N N + 1) 16) N n 4](/thumbs/92/107866707.jpg) 1. k λ ν ω T v p v g k = π λ ω = πν = π T v p = λν = ω k v g = dω dk 1) ) 3) 4). p = hk = h λ 5) E = hν = hω 6) h = h π 7) h =6.6618 1 34 J sec) hc=197.3 MeV fm = 197.3 kev pm= 197.3 ev nm = 1.97 1 3 ev
1. k λ ν ω T v p v g k = π λ ω = πν = π T v p = λν = ω k v g = dω dk 1) ) 3) 4). p = hk = h λ 5) E = hν = hω 6) h = h π 7) h =6.6618 1 34 J sec) hc=197.3 MeV fm = 197.3 kev pm= 197.3 ev nm = 1.97 1 3 ev
( )
 7..-8..8.......................................................................... 4.................................... 3...................................... 3..3.................................. 4.3....................................
7..-8..8.......................................................................... 4.................................... 3...................................... 3..3.................................. 4.3....................................
IA
 IA 31 4 11 1 1 4 1.1 Planck.............................. 4 1. Bohr.................................... 5 1.3..................................... 6 8.1................................... 8....................................
IA 31 4 11 1 1 4 1.1 Planck.............................. 4 1. Bohr.................................... 5 1.3..................................... 6 8.1................................... 8....................................
SO(3) 7 = = 1 ( r ) + 1 r r r r ( l ) (5.17) l = 1 ( sin θ ) + sin θ θ θ ϕ (5.18) χ(r)ψ(θ, ϕ) l ψ = αψ (5.19) l 1 = i(sin ϕ θ l = i( cos ϕ θ l 3 = i ϕ
 SO(3) 71 5.7 5.7.1 1 ħ L k l k l k = iϵ kij x i j (5.117) l k SO(3) l z l ± = l 1 ± il = i(y z z y ) ± (z x x z ) = ( x iy) z ± z( x ± i y ) = X ± z ± z (5.118) l z = i(x y y x ) = 1 [(x + iy)( x i y )
SO(3) 71 5.7 5.7.1 1 ħ L k l k l k = iϵ kij x i j (5.117) l k SO(3) l z l ± = l 1 ± il = i(y z z y ) ± (z x x z ) = ( x iy) z ± z( x ± i y ) = X ± z ± z (5.118) l z = i(x y y x ) = 1 [(x + iy)( x i y )
Hanbury-Brown Twiss (ver. 2.0) van Cittert - Zernike mutual coherence
 Hanbury-Brown Twiss (ver. 2.) 25 4 4 1 2 2 2 2.1 van Cittert - Zernike..................................... 2 2.2 mutual coherence................................. 4 3 Hanbury-Brown Twiss ( ) 5 3.1............................................
Hanbury-Brown Twiss (ver. 2.) 25 4 4 1 2 2 2 2.1 van Cittert - Zernike..................................... 2 2.2 mutual coherence................................. 4 3 Hanbury-Brown Twiss ( ) 5 3.1............................................
3 filename=quantum-3dim110705a.tex ,2 [1],[2],[3] [3] U(x, y, z; t), p x ˆp x = h i x, p y ˆp y = h i y, p z ˆp z = h
![3 filename=quantum-3dim110705a.tex ,2 [1],[2],[3] [3] U(x, y, z; t), p x ˆp x = h i x, p y ˆp y = h i y, p z ˆp z = h 3 filename=quantum-3dim110705a.tex ,2 [1],[2],[3] [3] U(x, y, z; t), p x ˆp x = h i x, p y ˆp y = h i y, p z ˆp z = h](/thumbs/102/156509212.jpg) filename=quantum-dim110705a.tex 1 1. 1, [1],[],[]. 1980 []..1 U(x, y, z; t), p x ˆp x = h i x, p y ˆp y = h i y, p z ˆp z = h i z (.1) Ĥ ( ) Ĥ = h m x + y + + U(x, y, z; t) (.) z (U(x, y, z; t)) (U(x,
filename=quantum-dim110705a.tex 1 1. 1, [1],[],[]. 1980 []..1 U(x, y, z; t), p x ˆp x = h i x, p y ˆp y = h i y, p z ˆp z = h i z (.1) Ĥ ( ) Ĥ = h m x + y + + U(x, y, z; t) (.) z (U(x, y, z; t)) (U(x,
9 1. (Ti:Al 2 O 3 ) (DCM) (Cr:Al 2 O 3 ) (Cr:BeAl 2 O 4 ) Ĥ0 ψ n (r) ω n Schrödinger Ĥ 0 ψ n (r) = ω n ψ n (r), (1) ω i ψ (r, t) = [Ĥ0 + Ĥint (
 9 1. (Ti:Al 2 O 3 ) (DCM) (Cr:Al 2 O 3 ) (Cr:BeAl 2 O 4 ) 2. 2.1 Ĥ ψ n (r) ω n Schrödinger Ĥ ψ n (r) = ω n ψ n (r), (1) ω i ψ (r, t) = [Ĥ + Ĥint (t)] ψ (r, t), (2) Ĥ int (t) = eˆxe cos ωt ˆdE cos ωt, (3)
9 1. (Ti:Al 2 O 3 ) (DCM) (Cr:Al 2 O 3 ) (Cr:BeAl 2 O 4 ) 2. 2.1 Ĥ ψ n (r) ω n Schrödinger Ĥ ψ n (r) = ω n ψ n (r), (1) ω i ψ (r, t) = [Ĥ + Ĥint (t)] ψ (r, t), (2) Ĥ int (t) = eˆxe cos ωt ˆdE cos ωt, (3)
 006 11 8 0 3 1 5 1.1..................... 5 1......................... 6 1.3.................... 6 1.4.................. 8 1.5................... 8 1.6................... 10 1.6.1......................
006 11 8 0 3 1 5 1.1..................... 5 1......................... 6 1.3.................... 6 1.4.................. 8 1.5................... 8 1.6................... 10 1.6.1......................
 0 3 1 5 1.1.............................. 5 1. 3.................. 6 1.3.......................... 7 1.4.............................. 8 1.5.............................. 10 1.6.................................
0 3 1 5 1.1.............................. 5 1. 3.................. 6 1.3.......................... 7 1.4.............................. 8 1.5.............................. 10 1.6.................................
SO(3) 49 u = Ru (6.9), i u iv i = i u iv i (C ) π π : G Hom(V, V ) : g D(g). π : R 3 V : i 1. : u u = u 1 u 2 u 3 (6.10) 6.2 i R α (1) = 0 cos α
 SO(3) 48 6 SO(3) t 6.1 u, v u = u 1 1 + u 2 2 + u 3 3 = u 1 e 1 + u 2 e 2 + u 3 e 3, v = v 1 1 + v 2 2 + v 3 3 = v 1 e 1 + v 2 e 2 + v 3 e 3 (6.1) i (e i ) e i e j = i j = δ ij (6.2) ( u, v ) = u v = ij
SO(3) 48 6 SO(3) t 6.1 u, v u = u 1 1 + u 2 2 + u 3 3 = u 1 e 1 + u 2 e 2 + u 3 e 3, v = v 1 1 + v 2 2 + v 3 3 = v 1 e 1 + v 2 e 2 + v 3 e 3 (6.1) i (e i ) e i e j = i j = δ ij (6.2) ( u, v ) = u v = ij
6 6.1 L r p hl = r p (6.1) 1, 2, 3 r =(x, y, z )=(r 1,r 2,r 3 ), p =(p x,p y,p z )=(p 1,p 2,p 3 ) (6.2) hl i = jk ɛ ijk r j p k (6.3) ɛ ijk Levi Civit
 6 6.1 L r p hl = r p (6.1) 1, 2, 3 r =(x, y, z )=(r 1,r 2,r 3 ), p =(p x,p y,p z )=(p 1,p 2,p 3 ) (6.2) hl i = jk ɛ ijk r j p k (6.3) ɛ ijk Levi Civita ɛ 123 =1 0 r p = 2 2 = (6.4) Planck h L p = h ( h
6 6.1 L r p hl = r p (6.1) 1, 2, 3 r =(x, y, z )=(r 1,r 2,r 3 ), p =(p x,p y,p z )=(p 1,p 2,p 3 ) (6.2) hl i = jk ɛ ijk r j p k (6.3) ɛ ijk Levi Civita ɛ 123 =1 0 r p = 2 2 = (6.4) Planck h L p = h ( h
 25 7 18 1 1 1.1 v.s............................. 1 1.1.1.................................. 1 1.1.2................................. 1 1.1.3.................................. 3 1.2................... 3
25 7 18 1 1 1.1 v.s............................. 1 1.1.1.................................. 1 1.1.2................................. 1 1.1.3.................................. 3 1.2................... 3
simx simxdx, cosxdx, sixdx 6.3 px m m + pxfxdx = pxf x p xf xdx = pxf x p xf x + p xf xdx 7.4 a m.5 fx simxdx 8 fx fx simxdx = πb m 9 a fxdx = πa a =
 II 6 ishimori@phys.titech.ac.jp 6.. 5.4.. f Rx = f Lx = fx fx + lim = lim x x + x x f c = f x + x < c < x x x + lim x x fx fx x x = lim x x f c = f x x < c < x cosmx cosxdx = {cosm x + cosm + x} dx = [
II 6 ishimori@phys.titech.ac.jp 6.. 5.4.. f Rx = f Lx = fx fx + lim = lim x x + x x f c = f x + x < c < x x x + lim x x fx fx x x = lim x x f c = f x x < c < x cosmx cosxdx = {cosm x + cosm + x} dx = [
30
 3 ............................................2 2...........................................2....................................2.2...................................2.3..............................
3 ............................................2 2...........................................2....................................2.2...................................2.3..............................
W u = u(x, t) u tt = a 2 u xx, a > 0 (1) D := {(x, t) : 0 x l, t 0} u (0, t) = 0, u (l, t) = 0, t 0 (2)
 3 215 4 27 1 1 u u(x, t) u tt a 2 u xx, a > (1) D : {(x, t) : x, t } u (, t), u (, t), t (2) u(x, ) f(x), u(x, ) t 2, x (3) u(x, t) X(x)T (t) u (1) 1 T (t) a 2 T (t) X (x) X(x) α (2) T (t) αa 2 T (t) (4)
3 215 4 27 1 1 u u(x, t) u tt a 2 u xx, a > (1) D : {(x, t) : x, t } u (, t), u (, t), t (2) u(x, ) f(x), u(x, ) t 2, x (3) u(x, t) X(x)T (t) u (1) 1 T (t) a 2 T (t) X (x) X(x) α (2) T (t) αa 2 T (t) (4)
( ) ) ) ) 5) 1 J = σe 2 6) ) 9) 1955 Statistical-Mechanical Theory of Irreversible Processes )
 ( 3 7 4 ) 2 2 ) 8 2 954 2) 955 3) 5) J = σe 2 6) 955 7) 9) 955 Statistical-Mechanical Theory of Irreversible Processes 957 ) 3 4 2 A B H (t) = Ae iωt B(t) = B(ω)e iωt B(ω) = [ Φ R (ω) Φ R () ] iω Φ R (t)
( 3 7 4 ) 2 2 ) 8 2 954 2) 955 3) 5) J = σe 2 6) 955 7) 9) 955 Statistical-Mechanical Theory of Irreversible Processes 957 ) 3 4 2 A B H (t) = Ae iωt B(t) = B(ω)e iωt B(ω) = [ Φ R (ω) Φ R () ] iω Φ R (t)
2 G(k) e ikx = (ik) n x n n! n=0 (k ) ( ) X n = ( i) n n k n G(k) k=0 F (k) ln G(k) = ln e ikx n κ n F (k) = F (k) (ik) n n= n! κ n κ n = ( i) n n k n
 . X {x, x 2, x 3,... x n } X X {, 2, 3, 4, 5, 6} X x i P i. 0 P i 2. n P i = 3. P (i ω) = i ω P i P 3 {x, x 2, x 3,... x n } ω P i = 6 X f(x) f(x) X n n f(x i )P i n x n i P i X n 2 G(k) e ikx = (ik) n
. X {x, x 2, x 3,... x n } X X {, 2, 3, 4, 5, 6} X x i P i. 0 P i 2. n P i = 3. P (i ω) = i ω P i P 3 {x, x 2, x 3,... x n } ω P i = 6 X f(x) f(x) X n n f(x i )P i n x n i P i X n 2 G(k) e ikx = (ik) n
 2019 1 5 0 3 1 4 1.1.................... 4 1.1.1......................... 4 1.1.2........................ 5 1.1.3................... 5 1.1.4........................ 6 1.1.5......................... 6 1.2..........................
2019 1 5 0 3 1 4 1.1.................... 4 1.1.1......................... 4 1.1.2........................ 5 1.1.3................... 5 1.1.4........................ 6 1.1.5......................... 6 1.2..........................
B ver B
 B ver. 2017.02.24 B Contents 1 11 1.1....................... 11 1.1.1............. 11 1.1.2.......................... 12 1.2............................. 14 1.2.1................ 14 1.2.2.......................
B ver. 2017.02.24 B Contents 1 11 1.1....................... 11 1.1.1............. 11 1.1.2.......................... 12 1.2............................. 14 1.2.1................ 14 1.2.2.......................
Part () () Γ Part ,
 Contents a 6 6 6 6 6 6 6 7 7. 8.. 8.. 8.3. 8 Part. 9. 9.. 9.. 3. 3.. 3.. 3 4. 5 4.. 5 4.. 9 4.3. 3 Part. 6 5. () 6 5.. () 7 5.. 9 5.3. Γ 3 6. 3 6.. 3 6.. 3 6.3. 33 Part 3. 34 7. 34 7.. 34 7.. 34 8. 35
Contents a 6 6 6 6 6 6 6 7 7. 8.. 8.. 8.3. 8 Part. 9. 9.. 9.. 3. 3.. 3.. 3 4. 5 4.. 5 4.. 9 4.3. 3 Part. 6 5. () 6 5.. () 7 5.. 9 5.3. Γ 3 6. 3 6.. 3 6.. 3 6.3. 33 Part 3. 34 7. 34 7.. 34 7.. 34 8. 35
V(x) m e V 0 cos x π x π V(x) = x < π, x > π V 0 (i) x = 0 (V(x) V 0 (1 x 2 /2)) n n d 2 f dξ 2ξ d f 2 dξ + 2n f = 0 H n (ξ) (ii) H
 199 1 1 199 1 1. Vx) m e V cos x π x π Vx) = x < π, x > π V i) x = Vx) V 1 x /)) n n d f dξ ξ d f dξ + n f = H n ξ) ii) H n ξ) = 1) n expξ ) dn dξ n exp ξ )) H n ξ)h m ξ) exp ξ )dξ = π n n!δ n,m x = Vx)
199 1 1 199 1 1. Vx) m e V cos x π x π Vx) = x < π, x > π V i) x = Vx) V 1 x /)) n n d f dξ ξ d f dξ + n f = H n ξ) ii) H n ξ) = 1) n expξ ) dn dξ n exp ξ )) H n ξ)h m ξ) exp ξ )dξ = π n n!δ n,m x = Vx)
0 4/
 04 II 6 7 5 0 4/8 0............................. 0.... 0.3............................ 0.4................... 5 0.5.................... 5 7.......................... 7............................ 7........................
04 II 6 7 5 0 4/8 0............................. 0.... 0.3............................ 0.4................... 5 0.5.................... 5 7.......................... 7............................ 7........................
1 filename=mathformula tex 1 ax 2 + bx + c = 0, x = b ± b 2 4ac, (1.1) 2a x 1 + x 2 = b a, x 1x 2 = c a, (1.2) ax 2 + 2b x + c = 0, x = b ± b 2
 filename=mathformula58.tex ax + bx + c =, x = b ± b 4ac, (.) a x + x = b a, x x = c a, (.) ax + b x + c =, x = b ± b ac. a (.3). sin(a ± B) = sin A cos B ± cos A sin B, (.) cos(a ± B) = cos A cos B sin
filename=mathformula58.tex ax + bx + c =, x = b ± b 4ac, (.) a x + x = b a, x x = c a, (.) ax + b x + c =, x = b ± b ac. a (.3). sin(a ± B) = sin A cos B ± cos A sin B, (.) cos(a ± B) = cos A cos B sin
kawa (Spin-Orbit Tomography: Kawahara and Fujii 21,Kawahara and Fujii 211,Fujii & Kawahara submitted) 2 van Cittert-Zernike Appendix A V 2
 Hanbury-Brown Twiss (ver. 1.) 24 2 1 1 1 2 2 2.1 van Cittert - Zernike..................................... 2 2.2 mutual coherence................................. 3 3 Hanbury-Brown Twiss ( ) 4 3.1............................................
Hanbury-Brown Twiss (ver. 1.) 24 2 1 1 1 2 2 2.1 van Cittert - Zernike..................................... 2 2.2 mutual coherence................................. 3 3 Hanbury-Brown Twiss ( ) 4 3.1............................................
18 I ( ) (1) I-1,I-2,I-3 (2) (3) I-1 ( ) (100 ) θ ϕ θ ϕ m m l l θ ϕ θ ϕ 2 g (1) (2) 0 (3) θ ϕ (4) (3) θ(t) = A 1 cos(ω 1 t + α 1 ) + A 2 cos(ω 2 t + α
 18 I ( ) (1) I-1,I-2,I-3 (2) (3) I-1 ( ) (100 ) θ ϕ θ ϕ m m l l θ ϕ θ ϕ 2 g (1) (2) 0 (3) θ ϕ (4) (3) θ(t) = A 1 cos(ω 1 t + α 1 ) + A 2 cos(ω 2 t + α 2 ), ϕ(t) = B 1 cos(ω 1 t + α 1 ) + B 2 cos(ω 2 t
18 I ( ) (1) I-1,I-2,I-3 (2) (3) I-1 ( ) (100 ) θ ϕ θ ϕ m m l l θ ϕ θ ϕ 2 g (1) (2) 0 (3) θ ϕ (4) (3) θ(t) = A 1 cos(ω 1 t + α 1 ) + A 2 cos(ω 2 t + α 2 ), ϕ(t) = B 1 cos(ω 1 t + α 1 ) + B 2 cos(ω 2 t
.2 ρ dv dt = ρk grad p + 3 η grad (divv) + η 2 v.3 divh = 0, rote + c H t = 0 dive = ρ, H = 0, E = ρ, roth c E t = c ρv E + H c t = 0 H c E t = c ρv T
 NHK 204 2 0 203 2 24 ( ) 7 00 7 50 203 2 25 ( ) 7 00 7 50 203 2 26 ( ) 7 00 7 50 203 2 27 ( ) 7 00 7 50 I. ( ν R n 2 ) m 2 n m, R = e 2 8πε 0 hca B =.09737 0 7 m ( ν = ) λ a B = 4πε 0ħ 2 m e e 2 = 5.2977
NHK 204 2 0 203 2 24 ( ) 7 00 7 50 203 2 25 ( ) 7 00 7 50 203 2 26 ( ) 7 00 7 50 203 2 27 ( ) 7 00 7 50 I. ( ν R n 2 ) m 2 n m, R = e 2 8πε 0 hca B =.09737 0 7 m ( ν = ) λ a B = 4πε 0ħ 2 m e e 2 = 5.2977
. ev=,604k m 3 Debye ɛ 0 kt e λ D = n e n e Ze 4 ln Λ ν ei = 5.6π / ɛ 0 m/ e kt e /3 ν ei v e H + +e H ev Saha x x = 3/ πme kt g i g e n
 003...............................3 Debye................. 3.4................ 3 3 3 3. Larmor Cyclotron... 3 3................ 4 3.3.......... 4 3.3............ 4 3.3...... 4 3.3.3............ 5 3.4.........
003...............................3 Debye................. 3.4................ 3 3 3 3. Larmor Cyclotron... 3 3................ 4 3.3.......... 4 3.3............ 4 3.3...... 4 3.3.3............ 5 3.4.........
 n ξ n,i, i = 1,, n S n ξ n,i n 0 R 1,.. σ 1 σ i .10.14.15 0 1 0 1 1 3.14 3.18 3.19 3.14 3.14,. ii 1 1 1.1..................................... 1 1............................... 3 1.3.........................
n ξ n,i, i = 1,, n S n ξ n,i n 0 R 1,.. σ 1 σ i .10.14.15 0 1 0 1 1 3.14 3.18 3.19 3.14 3.14,. ii 1 1 1.1..................................... 1 1............................... 3 1.3.........................
1
 016 017 6 16 1 1 5 1.1............................................... 5 1................................................... 5 1.3................................................ 5 1.4...............................................
016 017 6 16 1 1 5 1.1............................................... 5 1................................................... 5 1.3................................................ 5 1.4...............................................
( ) ( 40 )+( 60 ) Schrödinger 3. (a) (b) (c) yoshioka/education-09.html pdf 1
 2009 1 ( ) ( 40 )+( 60 ) 1 1. 2. Schrödinger 3. (a) (b) (c) http://goofy.phys.nara-wu.ac.jp/ yoshioka/education-09.html pdf 1 1. ( photon) ν λ = c ν (c = 3.0 108 /m : ) ɛ = hν (1) p = hν/c = h/λ (2) h
2009 1 ( ) ( 40 )+( 60 ) 1 1. 2. Schrödinger 3. (a) (b) (c) http://goofy.phys.nara-wu.ac.jp/ yoshioka/education-09.html pdf 1 1. ( photon) ν λ = c ν (c = 3.0 108 /m : ) ɛ = hν (1) p = hν/c = h/λ (2) h
DVIOUT-fujin
 2005 Limit Distribution of Quantum Walks and Weyl Equation 2006 3 2 1 2 2 4 2.1...................... 4 2.2......................... 5 2.3..................... 6 3 8 3.1........... 8 3.2..........................
2005 Limit Distribution of Quantum Walks and Weyl Equation 2006 3 2 1 2 2 4 2.1...................... 4 2.2......................... 5 2.3..................... 6 3 8 3.1........... 8 3.2..........................
,. Black-Scholes u t t, x c u 0 t, x x u t t, x c u t, x x u t t, x + σ x u t, x + rx ut, x rux, t 0 x x,,.,. Step 3, 7,,, Step 6., Step 4,. Step 5,,.
 9 α ν β Ξ ξ Γ γ o δ Π π ε ρ ζ Σ σ η τ Θ θ Υ υ ι Φ φ κ χ Λ λ Ψ ψ µ Ω ω Def, Prop, Th, Lem, Note, Remark, Ex,, Proof, R, N, Q, C [a, b {x R : a x b} : a, b {x R : a < x < b} : [a, b {x R : a x < b} : a,
9 α ν β Ξ ξ Γ γ o δ Π π ε ρ ζ Σ σ η τ Θ θ Υ υ ι Φ φ κ χ Λ λ Ψ ψ µ Ω ω Def, Prop, Th, Lem, Note, Remark, Ex,, Proof, R, N, Q, C [a, b {x R : a x b} : a, b {x R : a < x < b} : [a, b {x R : a x < b} : a,
p = mv p x > h/4π λ = h p m v Ψ 2 Ψ
 II p = mv p x > h/4π λ = h p m v Ψ 2 Ψ Ψ Ψ 2 0 x P'(x) m d 2 x = mω 2 x = kx = F(x) dt 2 x = cos(ωt + φ) mω 2 = k ω = m k v = dx = -ωsin(ωt + φ) dt = d 2 x dt 2 0 y v θ P(x,y) θ = ωt + φ ν = ω [Hz] 2π
II p = mv p x > h/4π λ = h p m v Ψ 2 Ψ Ψ Ψ 2 0 x P'(x) m d 2 x = mω 2 x = kx = F(x) dt 2 x = cos(ωt + φ) mω 2 = k ω = m k v = dx = -ωsin(ωt + φ) dt = d 2 x dt 2 0 y v θ P(x,y) θ = ωt + φ ν = ω [Hz] 2π
Planck Bohr
 I 30 7 11 1 1 5 1.1 Planck.............................. 5 1. Bohr.................................... 6 1.3..................................... 7 9.1................................... 9....................................
I 30 7 11 1 1 5 1.1 Planck.............................. 5 1. Bohr.................................... 6 1.3..................................... 7 9.1................................... 9....................................
v v = v 1 v 2 v 3 (1) R = (R ij ) (2) R (R 1 ) ij = R ji (3) 3 R ij R ik = δ jk (4) i=1 δ ij Kronecker δ ij = { 1 (i = j) 0 (i
 1. 1 1.1 1.1.1 1.1.1.1 v v = v 1 v 2 v 3 (1) R = (R ij ) (2) R (R 1 ) ij = R ji (3) R ij R ik = δ jk (4) δ ij Kronecker δ ij = { 1 (i = j) 0 (i j) (5) 1 1.1. v1.1 2011/04/10 1. 1 2 v i = R ij v j (6) [
1. 1 1.1 1.1.1 1.1.1.1 v v = v 1 v 2 v 3 (1) R = (R ij ) (2) R (R 1 ) ij = R ji (3) R ij R ik = δ jk (4) δ ij Kronecker δ ij = { 1 (i = j) 0 (i j) (5) 1 1.1. v1.1 2011/04/10 1. 1 2 v i = R ij v j (6) [
6kg 1.1m 1.m.1m.1 l λ ϵ λ l + λ l l l dl dl + dλ ϵ dλ dl dl + dλ dl dl 3 1. JIS 1 6kg 1% 66kg 1 13 σ a1 σ m σ a1 σ m σ m σ a1 f f σ a1 σ a1 σ m f 4
 35-8585 7 8 1 I I 1 1.1 6kg 1m P σ σ P 1 l l λ λ l 1.m 1 6kg 1.1m 1.m.1m.1 l λ ϵ λ l + λ l l l dl dl + dλ ϵ dλ dl dl + dλ dl dl 3 1. JIS 1 6kg 1% 66kg 1 13 σ a1 σ m σ a1 σ m σ m σ a1 f f σ a1 σ a1 σ m
35-8585 7 8 1 I I 1 1.1 6kg 1m P σ σ P 1 l l λ λ l 1.m 1 6kg 1.1m 1.m.1m.1 l λ ϵ λ l + λ l l l dl dl + dλ ϵ dλ dl dl + dλ dl dl 3 1. JIS 1 6kg 1% 66kg 1 13 σ a1 σ m σ a1 σ m σ m σ a1 f f σ a1 σ a1 σ m
 http://www1.doshisha.ac.jp/ bukka/qc.html 1. 107 2. 116 3. 1 119 4. 2 126 5. 132 6. 136 7. 1 140 8. 146 9. 2 150 10. 153 11. 157 12. π Hückel 159 13. 163 A-1. Laguerre 165 A-2. Hermite 167 A-3. 170 A-4.
http://www1.doshisha.ac.jp/ bukka/qc.html 1. 107 2. 116 3. 1 119 4. 2 126 5. 132 6. 136 7. 1 140 8. 146 9. 2 150 10. 153 11. 157 12. π Hückel 159 13. 163 A-1. Laguerre 165 A-2. Hermite 167 A-3. 170 A-4.
Dirac 38 5 Dirac 4 4 γ µ p µ p µ + m 2 = ( p µ γ µ + m)(p ν γ ν + m) (5.1) γ = p µ p ν γ µ γ ν p µ γ µ m + mp ν γ ν + m 2 = 1 2 p µp ν {γ µ, γ ν } + m
 Dirac 38 5 Dirac 4 4 γ µ p µ p µ + m 2 p µ γ µ + mp ν γ ν + m 5.1 γ p µ p ν γ µ γ ν p µ γ µ m + mp ν γ ν + m 2 1 2 p µp ν {γ µ, γ ν } + m 2 5.2 p m p p µ γ µ {, } 10 γ {γ µ, γ ν } 2η µν 5.3 p µ γ µ + mp
Dirac 38 5 Dirac 4 4 γ µ p µ p µ + m 2 p µ γ µ + mp ν γ ν + m 5.1 γ p µ p ν γ µ γ ν p µ γ µ m + mp ν γ ν + m 2 1 2 p µp ν {γ µ, γ ν } + m 2 5.2 p m p p µ γ µ {, } 10 γ {γ µ, γ ν } 2η µν 5.3 p µ γ µ + mp
2000年度『数学展望 I』講義録
 2000 I I IV I II 2000 I I IV I-IV. i ii 3.10 (http://www.math.nagoya-u.ac.jp/ kanai/) 2000 A....1 B....4 C....10 D....13 E....17 Brouwer A....21 B....26 C....33 D....39 E. Sperner...45 F....48 A....53
2000 I I IV I II 2000 I I IV I-IV. i ii 3.10 (http://www.math.nagoya-u.ac.jp/ kanai/) 2000 A....1 B....4 C....10 D....13 E....17 Brouwer A....21 B....26 C....33 D....39 E. Sperner...45 F....48 A....53
 30 I .............................................2........................................3................................................4.......................................... 2.5..........................................
30 I .............................................2........................................3................................................4.......................................... 2.5..........................................
振動と波動
 Report JS0.5 J Simplicity February 4, 2012 1 J Simplicity HOME http://www.jsimplicity.com/ Preface 2 Report 2 Contents I 5 1 6 1.1..................................... 6 1.2 1 1:................ 7 1.3
Report JS0.5 J Simplicity February 4, 2012 1 J Simplicity HOME http://www.jsimplicity.com/ Preface 2 Report 2 Contents I 5 1 6 1.1..................................... 6 1.2 1 1:................ 7 1.3
QMI_10.dvi
 ... black body radiation black body black body radiation Gustav Kirchhoff 859 895 W. Wien O.R. Lummer cavity radiation ν ν +dν f T (ν) f T (ν)dν = 8πν2 c 3 kt dν (Rayleigh Jeans) (.) f T (ν) spectral energy
... black body radiation black body black body radiation Gustav Kirchhoff 859 895 W. Wien O.R. Lummer cavity radiation ν ν +dν f T (ν) f T (ν)dν = 8πν2 c 3 kt dν (Rayleigh Jeans) (.) f T (ν) spectral energy
S I. dy fx x fx y fx + C 3 C dy fx 4 x, y dy v C xt y C v e kt k > xt yt gt [ v dt dt v e kt xt v e kt + C k x v + C C k xt v k 3 r r + dr e kt S dt d
 S I.. http://ayapin.film.s.dendai.ac.jp/~matuda /TeX/lecture.html PDF PS.................................... 3.3.................... 9.4................5.............. 3 5. Laplace................. 5....
S I.. http://ayapin.film.s.dendai.ac.jp/~matuda /TeX/lecture.html PDF PS.................................... 3.3.................... 9.4................5.............. 3 5. Laplace................. 5....
構造と連続体の力学基礎
 II 37 Wabash Avenue Bridge, Illinois 州 Winnipeg にある歩道橋 Esplanade Riel 橋6 6 斜張橋である必要は多分無いと思われる すぐ横に道路用桁橋有り しかも塔基部のレストランは 8 年には営業していなかった 9 9. 9.. () 97 [3] [5] k 9. m w(t) f (t) = f (t) + mg k w(t) Newton
II 37 Wabash Avenue Bridge, Illinois 州 Winnipeg にある歩道橋 Esplanade Riel 橋6 6 斜張橋である必要は多分無いと思われる すぐ横に道路用桁橋有り しかも塔基部のレストランは 8 年には営業していなかった 9 9. 9.. () 97 [3] [5] k 9. m w(t) f (t) = f (t) + mg k w(t) Newton
note1.dvi
 (1) 1996 11 7 1 (1) 1. 1 dx dy d x τ xx x x, stress x + dx x τ xx x+dx dyd x x τ xx x dyd y τ xx x τ xx x+dx d dx y x dy 1. dx dy d x τ xy x τ x ρdxdyd x dx dy d ρdxdyd u x t = τ xx x+dx dyd τ xx x dyd
(1) 1996 11 7 1 (1) 1. 1 dx dy d x τ xx x x, stress x + dx x τ xx x+dx dyd x x τ xx x dyd y τ xx x τ xx x+dx d dx y x dy 1. dx dy d x τ xy x τ x ρdxdyd x dx dy d ρdxdyd u x t = τ xx x+dx dyd τ xx x dyd
S I. dy fx x fx y fx + C 3 C vt dy fx 4 x, y dy yt gt + Ct + C dt v e kt xt v e kt + C k x v k + C C xt v k 3 r r + dr e kt S Sr πr dt d v } dt k e kt
 S I. x yx y y, y,. F x, y, y, y,, y n http://ayapin.film.s.dendai.ac.jp/~matuda n /TeX/lecture.html PDF PS yx.................................... 3.3.................... 9.4................5..............
S I. x yx y y, y,. F x, y, y, y,, y n http://ayapin.film.s.dendai.ac.jp/~matuda n /TeX/lecture.html PDF PS yx.................................... 3.3.................... 9.4................5..............
 215 11 13 1 2 1.1....................... 2 1.2.................... 2 1.3..................... 2 1.4...................... 3 1.5............... 3 1.6........................... 4 1.7.................. 4
215 11 13 1 2 1.1....................... 2 1.2.................... 2 1.3..................... 2 1.4...................... 3 1.5............... 3 1.6........................... 4 1.7.................. 4
phs.dvi
 483F 3 6.........3... 6.4... 7 7.... 7.... 9.5 N (... 3.6 N (... 5.7... 5 3 6 3.... 6 3.... 7 3.3... 9 3.4... 3 4 7 4.... 7 4.... 9 4.3... 3 4.4... 34 4.4.... 34 4.4.... 35 4.5... 38 4.6... 39 5 4 5....
483F 3 6.........3... 6.4... 7 7.... 7.... 9.5 N (... 3.6 N (... 5.7... 5 3 6 3.... 6 3.... 7 3.3... 9 3.4... 3 4 7 4.... 7 4.... 9 4.3... 3 4.4... 34 4.4.... 34 4.4.... 35 4.5... 38 4.6... 39 5 4 5....
微分積分 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. このサンプルページの内容は, 初版 1 刷発行時のものです.
 微分積分 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. ttp://www.morikita.co.jp/books/mid/00571 このサンプルページの内容は, 初版 1 刷発行時のものです. i ii 014 10 iii [note] 1 3 iv 4 5 3 6 4 x 0 sin x x 1 5 6 z = f(x, y) 1 y = f(x)
微分積分 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. ttp://www.morikita.co.jp/books/mid/00571 このサンプルページの内容は, 初版 1 刷発行時のものです. i ii 014 10 iii [note] 1 3 iv 4 5 3 6 4 x 0 sin x x 1 5 6 z = f(x, y) 1 y = f(x)
II A A441 : October 02, 2014 Version : Kawahira, Tomoki TA (Kondo, Hirotaka )
 II 214-1 : October 2, 214 Version : 1.1 Kawahira, Tomoki TA (Kondo, Hirotaka ) http://www.math.nagoya-u.ac.jp/~kawahira/courses/14w-biseki.html pdf 1 2 1 9 1 16 1 23 1 3 11 6 11 13 11 2 11 27 12 4 12 11
II 214-1 : October 2, 214 Version : 1.1 Kawahira, Tomoki TA (Kondo, Hirotaka ) http://www.math.nagoya-u.ac.jp/~kawahira/courses/14w-biseki.html pdf 1 2 1 9 1 16 1 23 1 3 11 6 11 13 11 2 11 27 12 4 12 11
i
 009 I 1 8 5 i 0 1 0.1..................................... 1 0.................................................. 1 0.3................................. 0.4........................................... 3
009 I 1 8 5 i 0 1 0.1..................................... 1 0.................................................. 1 0.3................................. 0.4........................................... 3
1 (Contents) (1) Beginning of the Universe, Dark Energy and Dark Matter Noboru NAKANISHI 2 2. Problem of Heat Exchanger (1) Kenji
 8 4 2018 6 2018 6 7 1 (Contents) 1. 2 2. (1) 22 3. 31 1. Beginning of the Universe, Dark Energy and Dark Matter Noboru NAKANISHI 2 2. Problem of Heat Exchanger (1) Kenji SETO 22 3. Editorial Comments Tadashi
8 4 2018 6 2018 6 7 1 (Contents) 1. 2 2. (1) 22 3. 31 1. Beginning of the Universe, Dark Energy and Dark Matter Noboru NAKANISHI 2 2. Problem of Heat Exchanger (1) Kenji SETO 22 3. Editorial Comments Tadashi
Hilbert, von Neuman [1, p.86] kt 2 1 [1, 2] 2 2
![Hilbert, von Neuman [1, p.86] kt 2 1 [1, 2] 2 2 Hilbert, von Neuman [1, p.86] kt 2 1 [1, 2] 2 2](/thumbs/91/105692760.jpg) hara@math.kyushu-u.ac.jp 1 1 1.1............................................... 2 1.2............................................. 3 2 3 3 5 3.1............................................. 6 3.2...................................
hara@math.kyushu-u.ac.jp 1 1 1.1............................................... 2 1.2............................................. 3 2 3 3 5 3.1............................................. 6 3.2...................................
 http://www.ns.kogakuin.ac.jp/~ft13389/lecture/physics1a2b/ pdf I 1 1 1.1 ( ) 1. 30 m µm 2. 20 cm km 3. 10 m 2 cm 2 4. 5 cm 3 km 3 5. 1 6. 1 7. 1 1.2 ( ) 1. 1 m + 10 cm 2. 1 hr + 6400 sec 3. 3.0 10 5 kg
http://www.ns.kogakuin.ac.jp/~ft13389/lecture/physics1a2b/ pdf I 1 1 1.1 ( ) 1. 30 m µm 2. 20 cm km 3. 10 m 2 cm 2 4. 5 cm 3 km 3 5. 1 6. 1 7. 1 1.2 ( ) 1. 1 m + 10 cm 2. 1 hr + 6400 sec 3. 3.0 10 5 kg
eto-vol2.prepri.dvi
 ( 2) 3.4 5 (b),(c) [ 5 (a)] [ 5 (b)] [ 5 (c)] (extrinsic) skew scattering side jump [] [2, 3] (intrinsic) 2 Sinova 2 heavy-hole light-hole ( [4, 5, 6] ) Sinova Sinova 3. () 3 3 Ṽ = V (r)+ σ [p V (r)] λ
( 2) 3.4 5 (b),(c) [ 5 (a)] [ 5 (b)] [ 5 (c)] (extrinsic) skew scattering side jump [] [2, 3] (intrinsic) 2 Sinova 2 heavy-hole light-hole ( [4, 5, 6] ) Sinova Sinova 3. () 3 3 Ṽ = V (r)+ σ [p V (r)] λ
TOP URL 1
 TOP URL http://amonphys.web.fc.com/ 1 19 3 19.1................... 3 19.............................. 4 19.3............................... 6 19.4.............................. 8 19.5.............................
TOP URL http://amonphys.web.fc.com/ 1 19 3 19.1................... 3 19.............................. 4 19.3............................... 6 19.4.............................. 8 19.5.............................
 IA hara@math.kyushu-u.ac.jp Last updated: January,......................................................................................................................................................................................
IA hara@math.kyushu-u.ac.jp Last updated: January,......................................................................................................................................................................................
..3. Ω, Ω F, P Ω, F, P ). ) F a) A, A,..., A i,... F A i F. b) A F A c F c) Ω F. ) A F A P A),. a) 0 P A) b) P Ω) c) [ ] A, A,..., A i,... F i j A i A
![..3. Ω, Ω F, P Ω, F, P ). ) F a) A, A,..., A i,... F A i F. b) A F A c F c) Ω F. ) A F A P A),. a) 0 P A) b) P Ω) c) [ ] A, A,..., A i,... F i j A i A ..3. Ω, Ω F, P Ω, F, P ). ) F a) A, A,..., A i,... F A i F. b) A F A c F c) Ω F. ) A F A P A),. a) 0 P A) b) P Ω) c) [ ] A, A,..., A i,... F i j A i A](/thumbs/93/112175219.jpg) .. Laplace ). A... i),. ω i i ). {ω,..., ω } Ω,. ii) Ω. Ω. A ) r, A P A) P A) r... ).. Ω {,, 3, 4, 5, 6}. i i 6). A {, 4, 6} P A) P A) 3 6. ).. i, j i, j) ) Ω {i, j) i 6, j 6}., 36. A. A {i, j) i j }.
.. Laplace ). A... i),. ω i i ). {ω,..., ω } Ω,. ii) Ω. Ω. A ) r, A P A) P A) r... ).. Ω {,, 3, 4, 5, 6}. i i 6). A {, 4, 6} P A) P A) 3 6. ).. i, j i, j) ) Ω {i, j) i 6, j 6}., 36. A. A {i, j) i j }.
 23 7 28 i i 1 1 1.1................................... 2 1.2............................... 3 1.2.1.................................... 3 1.2.2............................... 4 1.2.3 SI..............................
23 7 28 i i 1 1 1.1................................... 2 1.2............................... 3 1.2.1.................................... 3 1.2.2............................... 4 1.2.3 SI..............................
6 2 T γ T B (6.4) (6.1) [( d nm + 3 ] 2 nt B )a 3 + nt B da 3 = 0 (6.9) na 3 = T B V 3/2 = T B V γ 1 = const. or T B a 2 = const. (6.10) H 2 = 8π kc2
![6 2 T γ T B (6.4) (6.1) [( d nm + 3 ] 2 nt B )a 3 + nt B da 3 = 0 (6.9) na 3 = T B V 3/2 = T B V γ 1 = const. or T B a 2 = const. (6.10) H 2 = 8π kc2 6 2 T γ T B (6.4) (6.1) [( d nm + 3 ] 2 nt B )a 3 + nt B da 3 = 0 (6.9) na 3 = T B V 3/2 = T B V γ 1 = const. or T B a 2 = const. (6.10) H 2 = 8π kc2](/thumbs/92/109118076.jpg) 1 6 6.1 (??) (P = ρ rad /3) ρ rad T 4 d(ρv ) + PdV = 0 (6.1) dρ rad ρ rad + 4 da a = 0 (6.2) dt T + da a = 0 T 1 a (6.3) ( ) n ρ m = n (m + 12 ) m v2 = n (m + 32 ) T, P = nt (6.4) (6.1) d [(nm + 32 ] )a
1 6 6.1 (??) (P = ρ rad /3) ρ rad T 4 d(ρv ) + PdV = 0 (6.1) dρ rad ρ rad + 4 da a = 0 (6.2) dt T + da a = 0 T 1 a (6.3) ( ) n ρ m = n (m + 12 ) m v2 = n (m + 32 ) T, P = nt (6.4) (6.1) d [(nm + 32 ] )a
Maxwell
 I 2018 12 13 0 4 1 6 1.1............................ 6 1.2 Maxwell......................... 8 1.3.......................... 9 1.4..................... 11 1.5..................... 12 2 13 2.1...................
I 2018 12 13 0 4 1 6 1.1............................ 6 1.2 Maxwell......................... 8 1.3.......................... 9 1.4..................... 11 1.5..................... 12 2 13 2.1...................
July 28, H H 0 H int = H H 0 H int = H int (x)d 3 x Schrödinger Picture Ψ(t) S =e iht Ψ H O S Heisenberg Picture Ψ H O H (t) =e iht O S e i
 July 8, 4. H H H int H H H int H int (x)d 3 x Schrödinger Picture Ψ(t) S e iht Ψ H O S Heisenberg Picture Ψ H O H (t) e iht O S e iht Interaction Picture Ψ(t) D e iht Ψ(t) S O D (t) e iht O S e ih t (Dirac
July 8, 4. H H H int H H H int H int (x)d 3 x Schrödinger Picture Ψ(t) S e iht Ψ H O S Heisenberg Picture Ψ H O H (t) e iht O S e iht Interaction Picture Ψ(t) D e iht Ψ(t) S O D (t) e iht O S e ih t (Dirac
液晶の物理1:連続体理論(弾性,粘性)
 The Physics of Liquid Crystals P. G. de Gennes and J. Prost (Oxford University Press, 1993) Liquid crystals are beautiful and mysterious; I am fond of them for both reasons. My hope is that some readers
The Physics of Liquid Crystals P. G. de Gennes and J. Prost (Oxford University Press, 1993) Liquid crystals are beautiful and mysterious; I am fond of them for both reasons. My hope is that some readers
I A A441 : April 15, 2013 Version : 1.1 I Kawahira, Tomoki TA (Shigehiro, Yoshida )
 I013 00-1 : April 15, 013 Version : 1.1 I Kawahira, Tomoki TA (Shigehiro, Yoshida) http://www.math.nagoya-u.ac.jp/~kawahira/courses/13s-tenbou.html pdf * 4 15 4 5 13 e πi = 1 5 0 5 7 3 4 6 3 6 10 6 17
I013 00-1 : April 15, 013 Version : 1.1 I Kawahira, Tomoki TA (Shigehiro, Yoshida) http://www.math.nagoya-u.ac.jp/~kawahira/courses/13s-tenbou.html pdf * 4 15 4 5 13 e πi = 1 5 0 5 7 3 4 6 3 6 10 6 17
(3) (2),,. ( 20) ( s200103) 0.7 x C,, x 2 + y 2 + ax = 0 a.. D,. D, y C, C (x, y) (y 0) C m. (2) D y = y(x) (x ± y 0), (x, y) D, m, m = 1., D. (x 2 y
 [ ] 7 0.1 2 2 + y = t sin t IC ( 9) ( s090101) 0.2 y = d2 y 2, y = x 3 y + y 2 = 0 (2) y + 2y 3y = e 2x 0.3 1 ( y ) = f x C u = y x ( 15) ( s150102) [ ] y/x du x = Cexp f(u) u (2) x y = xey/x ( 16) ( s160101)
[ ] 7 0.1 2 2 + y = t sin t IC ( 9) ( s090101) 0.2 y = d2 y 2, y = x 3 y + y 2 = 0 (2) y + 2y 3y = e 2x 0.3 1 ( y ) = f x C u = y x ( 15) ( s150102) [ ] y/x du x = Cexp f(u) u (2) x y = xey/x ( 16) ( s160101)
1. 2 P 2 (x, y) 2 x y (0, 0) R 2 = {(x, y) x, y R} x, y R P = (x, y) O = (0, 0) OP ( ) OP x x, y y ( ) x v = y ( ) x 2 1 v = P = (x, y) y ( x y ) 2 (x
 . P (, (0, 0 R {(,, R}, R P (, O (0, 0 OP OP, v v P (, ( (, (, { R, R} v (, (, (,, z 3 w z R 3,, z R z n R n.,..., n R n n w, t w ( z z Ke Words:. A P 3 0 B P 0 a. A P b B P 3. A π/90 B a + b c π/ 3. +
. P (, (0, 0 R {(,, R}, R P (, O (0, 0 OP OP, v v P (, ( (, (, { R, R} v (, (, (,, z 3 w z R 3,, z R z n R n.,..., n R n n w, t w ( z z Ke Words:. A P 3 0 B P 0 a. A P b B P 3. A π/90 B a + b c π/ 3. +
80 4 r ˆρ i (r, t) δ(r x i (t)) (4.1) x i (t) ρ i ˆρ i t = 0 i r 0 t(> 0) j r 0 + r < δ(r 0 x i (0))δ(r 0 + r x j (t)) > (4.2) r r 0 G i j (r, t) dr 0
 79 4 4.1 4.1.1 x i (t) x j (t) O O r 0 + r r r 0 x i (0) r 0 x i (0) 4.1 L. van. Hove 1954 space-time correlation function V N 4.1 ρ 0 = N/V i t 80 4 r ˆρ i (r, t) δ(r x i (t)) (4.1) x i (t) ρ i ˆρ i t
79 4 4.1 4.1.1 x i (t) x j (t) O O r 0 + r r r 0 x i (0) r 0 x i (0) 4.1 L. van. Hove 1954 space-time correlation function V N 4.1 ρ 0 = N/V i t 80 4 r ˆρ i (r, t) δ(r x i (t)) (4.1) x i (t) ρ i ˆρ i t
sec13.dvi
 13 13.1 O r F R = m d 2 r dt 2 m r m = F = m r M M d2 R dt 2 = m d 2 r dt 2 = F = F (13.1) F O L = r p = m r ṙ dl dt = m ṙ ṙ + m r r = r (m r ) = r F N. (13.2) N N = R F 13.2 O ˆn ω L O r u u = ω r 1 1:
13 13.1 O r F R = m d 2 r dt 2 m r m = F = m r M M d2 R dt 2 = m d 2 r dt 2 = F = F (13.1) F O L = r p = m r ṙ dl dt = m ṙ ṙ + m r r = r (m r ) = r F N. (13.2) N N = R F 13.2 O ˆn ω L O r u u = ω r 1 1:
 27 1 21 19 i WKB ii i 1 1 1.1................................. 1 1.2......................................... 1 1.2.1.................................. 1 1.2.2.................................. 3 1.3........................................
27 1 21 19 i WKB ii i 1 1 1.1................................. 1 1.2......................................... 1 1.2.1.................................. 1 1.2.2.................................. 3 1.3........................................
50 2 I SI MKSA r q r q F F = 1 qq 4πε 0 r r 2 r r r r (2.2 ε 0 = 1 c 2 µ 0 c = m/s q 2.1 r q' F r = 0 µ 0 = 4π 10 7 N/A 2 k = 1/(4πε 0 qq
 49 2 I II 2.1 3 e e = 1.602 10 19 A s (2.1 50 2 I SI MKSA 2.1.1 r q r q F F = 1 qq 4πε 0 r r 2 r r r r (2.2 ε 0 = 1 c 2 µ 0 c = 3 10 8 m/s q 2.1 r q' F r = 0 µ 0 = 4π 10 7 N/A 2 k = 1/(4πε 0 qq F = k r
49 2 I II 2.1 3 e e = 1.602 10 19 A s (2.1 50 2 I SI MKSA 2.1.1 r q r q F F = 1 qq 4πε 0 r r 2 r r r r (2.2 ε 0 = 1 c 2 µ 0 c = 3 10 8 m/s q 2.1 r q' F r = 0 µ 0 = 4π 10 7 N/A 2 k = 1/(4πε 0 qq F = k r
A
 A 2563 15 4 21 1 3 1.1................................................ 3 1.2............................................. 3 2 3 2.1......................................... 3 2.2............................................
A 2563 15 4 21 1 3 1.1................................................ 3 1.2............................................. 3 2 3 2.1......................................... 3 2.2............................................
Z: Q: R: C:
 0 Z: Q: R: C: 3 4 4 4................................ 4 4.................................. 7 5 3 5...................... 3 5......................... 40 5.3 snz) z)........................... 4 6 46 x
0 Z: Q: R: C: 3 4 4 4................................ 4 4.................................. 7 5 3 5...................... 3 5......................... 40 5.3 snz) z)........................... 4 6 46 x
1990 IMO 1990/1/15 1:00-4:00 1 N N N 1, N 1 N 2, N 2 N 3 N 3 2 x x + 52 = 3 x x , A, B, C 3,, A B, C 2,,,, 7, A, B, C
 0 9 (1990 1999 ) 10 (2000 ) 1900 1994 1995 1999 2 SAT ACT 1 1990 IMO 1990/1/15 1:00-4:00 1 N 1990 9 N N 1, N 1 N 2, N 2 N 3 N 3 2 x 2 + 25x + 52 = 3 x 2 + 25x + 80 3 2, 3 0 4 A, B, C 3,, A B, C 2,,,, 7,
0 9 (1990 1999 ) 10 (2000 ) 1900 1994 1995 1999 2 SAT ACT 1 1990 IMO 1990/1/15 1:00-4:00 1 N 1990 9 N N 1, N 1 N 2, N 2 N 3 N 3 2 x 2 + 25x + 52 = 3 x 2 + 25x + 80 3 2, 3 0 4 A, B, C 3,, A B, C 2,,,, 7,
December 28, 2018
 e-mail : kigami@i.kyoto-u.ac.jp December 28, 28 Contents 2............................. 3.2......................... 7.3..................... 9.4................ 4.5............. 2.6.... 22 2 36 2..........................
e-mail : kigami@i.kyoto-u.ac.jp December 28, 28 Contents 2............................. 3.2......................... 7.3..................... 9.4................ 4.5............. 2.6.... 22 2 36 2..........................
( ) s n (n = 0, 1,...) n n = δ nn n n = I n=0 ψ = n C n n (1) C n = n ψ α = e 1 2 α 2 n=0 α, β α n n! n (2) β α = e 1 2 α 2 1
 (3.5 3.8) 03032s 2006.7.0 n (n = 0,,...) n n = δ nn n n = I n=0 ψ = n C n n () C n = n ψ α = e 2 α 2 n=0 α, β α n n (2) β α = e 2 α 2 2 β 2 n=0 =0 = e 2 α 2 β n α 2 β 2 n=0 = e 2 α 2 2 β 2 +β α β n α!
(3.5 3.8) 03032s 2006.7.0 n (n = 0,,...) n n = δ nn n n = I n=0 ψ = n C n n () C n = n ψ α = e 2 α 2 n=0 α, β α n n (2) β α = e 2 α 2 2 β 2 n=0 =0 = e 2 α 2 β n α 2 β 2 n=0 = e 2 α 2 2 β 2 +β α β n α!
Note.tex 2008/09/19( )
 1 20 9 19 2 1 5 1.1........................ 5 1.2............................. 8 2 9 2.1............................. 9 2.2.............................. 10 3 13 3.1.............................. 13 3.2..................................
1 20 9 19 2 1 5 1.1........................ 5 1.2............................. 8 2 9 2.1............................. 9 2.2.............................. 10 3 13 3.1.............................. 13 3.2..................................
x (x, ) x y (, y) iy x y z = x + iy (x, y) (r, θ) r = x + y, θ = tan ( y ), π < θ π x r = z, θ = arg z z = x + iy = r cos θ + ir sin θ = r(cos θ + i s
 ... x, y z = x + iy x z y z x = Rez, y = Imz z = x + iy x iy z z () z + z = (z + z )() z z = (z z )(3) z z = ( z z )(4)z z = z z = x + y z = x + iy ()Rez = (z + z), Imz = (z z) i () z z z + z z + z.. z
... x, y z = x + iy x z y z x = Rez, y = Imz z = x + iy x iy z z () z + z = (z + z )() z z = (z z )(3) z z = ( z z )(4)z z = z z = x + y z = x + iy ()Rez = (z + z), Imz = (z z) i () z z z + z z + z.. z
i
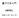 18 16 i 1 1 1.1....................................... 1 1.................................. 3 1.3............................. 5 1.4........................................... 6 7.1..................................
18 16 i 1 1 1.1....................................... 1 1.................................. 3 1.3............................. 5 1.4........................................... 6 7.1..................................
 211 kotaro@math.titech.ac.jp 1 R *1 n n R n *2 R n = {(x 1,..., x n ) x 1,..., x n R}. R R 2 R 3 R n R n R n D D R n *3 ) (x 1,..., x n ) f(x 1,..., x n ) f D *4 n 2 n = 1 ( ) 1 f D R n f : D R 1.1. (x,
211 kotaro@math.titech.ac.jp 1 R *1 n n R n *2 R n = {(x 1,..., x n ) x 1,..., x n R}. R R 2 R 3 R n R n R n D D R n *3 ) (x 1,..., x n ) f(x 1,..., x n ) f D *4 n 2 n = 1 ( ) 1 f D R n f : D R 1.1. (x,
1 1.1 H = µc i c i + c i t ijc j + 1 c i c j V ijklc k c l (1) V ijkl = V jikl = V ijlk = V jilk () t ij = t ji, V ijkl = V lkji (3) (1) V 0 H mf = µc
 013 6 30 BCS 1 1.1........................ 1................................ 3 1.3............................ 3 1.4............................... 5 1.5.................................... 5 6 3 7 4 8
013 6 30 BCS 1 1.1........................ 1................................ 3 1.3............................ 3 1.4............................... 5 1.5.................................... 5 6 3 7 4 8
dynamics-solution2.dvi
 1 1. (1) a + b = i +3i + k () a b =5i 5j +3k (3) a b =1 (4) a b = 7i j +1k. a = 14 l =/ 14, m=1/ 14, n=3/ 14 3. 4. 5. df (t) d [a(t)e(t)] =ti +9t j +4k, = d a(t) d[a(t)e(t)] e(t)+ da(t) d f (t) =i +18tj
1 1. (1) a + b = i +3i + k () a b =5i 5j +3k (3) a b =1 (4) a b = 7i j +1k. a = 14 l =/ 14, m=1/ 14, n=3/ 14 3. 4. 5. df (t) d [a(t)e(t)] =ti +9t j +4k, = d a(t) d[a(t)e(t)] e(t)+ da(t) d f (t) =i +18tj
δ ij δ ij ˆx ˆx ŷ ŷ ẑ ẑ 0, ˆx ŷ ŷ ˆx ẑ, ŷ ẑ ẑ ŷ ẑ, ẑ ˆx ˆx ẑ ŷ, a b a x ˆx + a y ŷ + a z ẑ b x ˆx + b
 23 2 2.1 n n r x, y, z ˆx ŷ ẑ 1 a a x ˆx + a y ŷ + a z ẑ 2.1.1 3 a iˆx i. 2.1.2 i1 i j k e x e y e z 3 a b a i b i i 1, 2, 3 x y z ˆx i ˆx j δ ij, 2.1.3 n a b a i b i a i b i a x b x + a y b y + a z b
23 2 2.1 n n r x, y, z ˆx ŷ ẑ 1 a a x ˆx + a y ŷ + a z ẑ 2.1.1 3 a iˆx i. 2.1.2 i1 i j k e x e y e z 3 a b a i b i i 1, 2, 3 x y z ˆx i ˆx j δ ij, 2.1.3 n a b a i b i a i b i a x b x + a y b y + a z b
Radiation from moving charges#1 Liénard-Wiechert potential Yuji Chinone 1 Maxwell Maxwell MKS E (x, t) + B (x, t) t = 0 (1) B (x, t) = 0 (2) B (x, t)
 Radiation from moving harges# Liénard-Wiehert potential Yuji Chinone Maxwell Maxwell MKS E x, t + B x, t = B x, t = B x, t E x, t = µ j x, t 3 E x, t = ε ρ x, t 4 ε µ ε µ = E B ρ j A x, t φ x, t A x, t
Radiation from moving harges# Liénard-Wiehert potential Yuji Chinone Maxwell Maxwell MKS E x, t + B x, t = B x, t = B x, t E x, t = µ j x, t 3 E x, t = ε ρ x, t 4 ε µ ε µ = E B ρ j A x, t φ x, t A x, t
(1.2) T D = 0 T = D = 30 kn 1.2 (1.4) 2F W = 0 F = W/2 = 300 kn/2 = 150 kn 1.3 (1.9) R = W 1 + W 2 = = 1100 N. (1.9) W 2 b W 1 a = 0
 1 1 1.1 1.) T D = T = D = kn 1. 1.4) F W = F = W/ = kn/ = 15 kn 1. 1.9) R = W 1 + W = 6 + 5 = 11 N. 1.9) W b W 1 a = a = W /W 1 )b = 5/6) = 5 cm 1.4 AB AC P 1, P x, y x, y y x 1.4.) P sin 6 + P 1 sin 45
1 1 1.1 1.) T D = T = D = kn 1. 1.4) F W = F = W/ = kn/ = 15 kn 1. 1.9) R = W 1 + W = 6 + 5 = 11 N. 1.9) W b W 1 a = a = W /W 1 )b = 5/6) = 5 cm 1.4 AB AC P 1, P x, y x, y y x 1.4.) P sin 6 + P 1 sin 45
I ( ) 2019
 I ( ) 2019 i 1 I,, III,, 1,,,, III,,,, (1 ) (,,, ), :...,, : NHK... NHK, (YouTube ),!!, manaba http://pen.envr.tsukuba.ac.jp/lec/physics/,, Richard Feynman Lectures on Physics Addison-Wesley,,,, x χ,
I ( ) 2019 i 1 I,, III,, 1,,,, III,,,, (1 ) (,,, ), :...,, : NHK... NHK, (YouTube ),!!, manaba http://pen.envr.tsukuba.ac.jp/lec/physics/,, Richard Feynman Lectures on Physics Addison-Wesley,,,, x χ,
量子力学3-2013
 ( 3 ) 5 8 5 03 Email: hatsugai.yasuhiro.ge@u.tsukuba.ac.jp 3 5.............................. 5........................ 5........................ 6.............................. 8.......................
( 3 ) 5 8 5 03 Email: hatsugai.yasuhiro.ge@u.tsukuba.ac.jp 3 5.............................. 5........................ 5........................ 6.............................. 8.......................
 ( 12 ( ( ( ( Levi-Civita grad div rot ( ( = 4 : 6 3 1 1.1 f(x n f (n (x, d n f(x (1.1 dxn f (2 (x f (x 1.1 f(x = e x f (n (x = e x d dx (fg = f g + fg (1.2 d dx d 2 dx (fg = f g + 2f g + fg 2... d n n
( 12 ( ( ( ( Levi-Civita grad div rot ( ( = 4 : 6 3 1 1.1 f(x n f (n (x, d n f(x (1.1 dxn f (2 (x f (x 1.1 f(x = e x f (n (x = e x d dx (fg = f g + fg (1.2 d dx d 2 dx (fg = f g + 2f g + fg 2... d n n
 K E N Z U 2012 7 16 HP M. 1 1 4 1.1 3.......................... 4 1.2................................... 4 1.2.1..................................... 4 1.2.2.................................... 5................................
K E N Z U 2012 7 16 HP M. 1 1 4 1.1 3.......................... 4 1.2................................... 4 1.2.1..................................... 4 1.2.2.................................... 5................................
x, y x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = 15 xy (x y) (x + y) xy (x y) (x y) ( x 2 + xy + y 2) = 15 (x y)
 x, y x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = 15 1 1977 x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = 15 xy (x y) (x + y) xy (x y) (x y) ( x 2 + xy + y 2) = 15 (x y) ( x 2 y + xy 2 x 2 2xy y 2) = 15 (x y) (x + y) (xy
x, y x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = 15 1 1977 x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = 15 xy (x y) (x + y) xy (x y) (x y) ( x 2 + xy + y 2) = 15 (x y) ( x 2 y + xy 2 x 2 2xy y 2) = 15 (x y) (x + y) (xy
( ; ) C. H. Scholz, The Mechanics of Earthquakes and Faulting : - ( ) σ = σ t sin 2π(r a) λ dσ d(r a) =
 1 9 8 1 1 1 ; 1 11 16 C. H. Scholz, The Mechanics of Earthquakes and Faulting 1. 1.1 1.1.1 : - σ = σ t sin πr a λ dσ dr a = E a = π λ σ πr a t cos λ 1 r a/λ 1 cos 1 E: σ t = Eλ πa a λ E/π γ : λ/ 3 γ =
1 9 8 1 1 1 ; 1 11 16 C. H. Scholz, The Mechanics of Earthquakes and Faulting 1. 1.1 1.1.1 : - σ = σ t sin πr a λ dσ dr a = E a = π λ σ πr a t cos λ 1 r a/λ 1 cos 1 E: σ t = Eλ πa a λ E/π γ : λ/ 3 γ =
2011de.dvi
 211 ( 4 2 1. 3 1.1............................... 3 1.2 1- -......................... 13 1.3 2-1 -................... 19 1.4 3- -......................... 29 2. 37 2.1................................ 37
211 ( 4 2 1. 3 1.1............................... 3 1.2 1- -......................... 13 1.3 2-1 -................... 19 1.4 3- -......................... 29 2. 37 2.1................................ 37
 20 9 19 1 3 11 1 3 111 3 112 1 4 12 6 121 6 122 7 13 7 131 8 132 10 133 10 134 12 14 13 141 13 142 13 143 15 144 16 145 17 15 19 151 1 19 152 20 2 21 21 21 211 21 212 1 23 213 1 23 214 25 215 31 22 33
20 9 19 1 3 11 1 3 111 3 112 1 4 12 6 121 6 122 7 13 7 131 8 132 10 133 10 134 12 14 13 141 13 142 13 143 15 144 16 145 17 15 19 151 1 19 152 20 2 21 21 21 211 21 212 1 23 213 1 23 214 25 215 31 22 33
第5章 偏微分方程式の境界値問題
 October 5, 2018 1 / 113 4 ( ) 2 / 113 Poisson 5.1 Poisson ( A.7.1) Poisson Poisson 1 (A.6 ) Γ p p N u D Γ D b 5.1.1: = Γ D Γ N 3 / 113 Poisson 5.1.1 d {2, 3} Lipschitz (A.5 ) Γ D Γ N = \ Γ D Γ p Γ N Γ
October 5, 2018 1 / 113 4 ( ) 2 / 113 Poisson 5.1 Poisson ( A.7.1) Poisson Poisson 1 (A.6 ) Γ p p N u D Γ D b 5.1.1: = Γ D Γ N 3 / 113 Poisson 5.1.1 d {2, 3} Lipschitz (A.5 ) Γ D Γ N = \ Γ D Γ p Γ N Γ
医系の統計入門第 2 版 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. このサンプルページの内容は, 第 2 版 1 刷発行時のものです.
 医系の統計入門第 2 版 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/009192 このサンプルページの内容は, 第 2 版 1 刷発行時のものです. i 2 t 1. 2. 3 2 3. 6 4. 7 5. n 2 ν 6. 2 7. 2003 ii 2 2013 10 iii 1987
医系の統計入門第 2 版 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/009192 このサンプルページの内容は, 第 2 版 1 刷発行時のものです. i 2 t 1. 2. 3 2 3. 6 4. 7 5. n 2 ν 6. 2 7. 2003 ii 2 2013 10 iii 1987
 A 2008 10 (2010 4 ) 1 1 1.1................................. 1 1.2..................................... 1 1.3............................ 3 1.3.1............................. 3 1.3.2..................................
A 2008 10 (2010 4 ) 1 1 1.1................................. 1 1.2..................................... 1 1.3............................ 3 1.3.1............................. 3 1.3.2..................................
