マイクロ波領域の誘電緩和で何がわかるか
|
|
|
- みいか さどひら
- 5 years ago
- Views:
Transcription
1
2 TDR(time domain reflectometry) Cole-Cole plot Debye Cole-Cole Davidson-Cole Havriliak-Negami KWW
3 Rocard Equation itinerant oscillator model A KWW 42 42
4 /τ ω ω 1.1: Böttcher[1] 3
5 1.1 4 (2.17) 10 1/τ ω 0 ω e τ GHz MHz (H 2 0 MW=18) 25GHz CH 3 OH MW=32 3GHz (C 2 H 5 OH MW=46) 1GHz 0 2.4GHz GHz (CCl 4 ) 1.1
6 1.1 5
7 2 2.1 p 0 (a) ( E = 0) < p 0 >=0 (b) ( E 0) 2.1: 2.1(a) p 0 0 P 2.1(b) P 0 2.1(a) P 2.2 P 6
8 2.2 7 V Q C C = Q V (2.1) C C = εk (2.2) ε ε 0 K C = εk C 0 ε 0 K = ε (2.3) ε 0 ε r = ε ε 0 (2.4) E 1 P P o : 1 (rise transient) (decay transient) [2]
9 2.2 8 P o P 0 P o P o P s P o P o P s dp o = P s P P o (2.5) dt τ 1/τ d(p s P P o ) P s P P o = dt τ (2.6) ln(p s P P o )= t τ + C (2.7) C t =0 P o =0 C = ln(p s P ) { ( P o (t) =(P s P ) 1 exp t )} (2.8) τ P o P s t =0 P P s dp s dt = P s τ ln P o = C t τ (2.9) (2.10) t =0 P o = P s P P o (t) =(P P ) exp ( t ) τ (2.11) dp o (t) = 1 dt τ P o(t) (2.12) ( P o (t) =P o (0) exp t ) τ (2.13) step response function ( Φ or P (t) =exp t ) τ (2.14)
10 2.2 9 τ pulse response function ( φ or P (t) = Φ or P (t) =1 τ exp t ) τ (2.15) ε (ω) =ε +(ε S ε ) 1 τ 0 e iωt φ or P (t)dt (2.16) ε (ω) =ε + ε S ε 1+iωτ (2.17) ε ε S (ω 0) ε = ε S ε (2.17) Debye Debye 4.1 6
11 3 3.1 Hz electric wave microwave Brillouin light visible light Raman scattering IR absorption radiation neutron(inelastic incoherent) NMR TDR LCR meter impedance material analyzer network analyzer photon correlation Fabry-Perot interferometry grating cable waveguide 3.1: LCR TDR 10
12 3.2 TDR(time domain reflectometry) GHz TDR 10 GHz THz THz TDR(time domain reflectometry) TDR (a) Z Z = 3.2(b) Z V 0 Z 0 Time Domain Reflectometry(TDR) TDR ISBN
13 3.2 TDR(time domain reflectometry) 12 (a) S V i Z V r (b) voltage V0 reference plane time (c) 0.45 Voltage (V) R s R x Time (sec.) 40 50x : Time Domain Reflectometry 3.2(b) TDR 3.2(c) TDR ε x (ω) ε s(ω) ε x(ω) = 1+{(cf s)/[jω(γd)ε s(ω)]}ρ f x (3.1) 1+{[jω(γd)ε s(ω)]/(cf s )}ρ f s ρ = V s(ω) V x (ω) V s (ω)+v x (ω) (3.2) f i (z) =z i cot(z i ) z i =(ωd/c)ε(ω) 1/2 d γd V s (ω) R s (t) V x (ω) R x (t) ω c
14 3.2 TDR(time domain reflectometry) 13 R s (t) R x (t) ε s(ω) 3.1 ε x (ω) ε x(ω) γd HP54121T,Hewlett- Packard (HP54120B) (HP54121A) Power Macintosh8100, Apple Computer) GPIB SCSI (MacAdios488s, GW Instruments, Inc.) TDR 200 mv [3][4][5] Hz d=1.0 mm d=2.0 mm Hz d=0.01 mm d
15 (a) (b) 3.3: 3.3 SMAjack-jack 50 Ω mv 200 mv NaCl [6] R s Voltage (V) R s2 R X Time (sec.) x :
16 R S1 R x R S2 NaCl R S2 R x 3.5 3x Voltage (V) x10-9 Time (sec.) 3.5: σ/(iω) (3.2) 3.5 NaCl (3.2) NaCl NaCl TDR TDR TDR
17 3.3 16
18 4 4.1 (2.17) Debye Debye Debye (2.14) Φ or P (t) = ( g k exp t ) (4.1) τ k k (2.15) ( φ or P (t) = g k exp t ) τ k τ k k (4.2) ε (ω) =ε +(ε S ε ) k g k 1+iωτ k (4.3) τ k Debye Debye (4.3) τ k (g k,τ k ) 4.3 τ k Debye 17
19 4.2 Cole-Cole plot Cole-Cole plot Debye Debye ε (ω) =ε + ε S ε 1+iωτ (4.4) 4.1(a) τ ω ε s ε =1 ε =0.1 ωτ = τ ε', ε'' ε" log(f) Hz ε' (a) Debye (b) Debye Cole-Cole plot 4.1: Debye Cole-Cole plot Debye ε (ω) ε (ω) Cole-Cole plot Debye 4.1(b)
20 4.2 Cole-Cole plot Cole-Cole Cole Cole Debye ε Debye [7] ε (ω) =ε + ε S ε 1+(iωτ) β (4.5) β 0 <β 1 β =1 β (4.5) Cole-Cole ε', ε'' β=0.8 β=0.6 β=0.4 β=0.2 β=1.0 ε" β=1.0 β=0.8 β=0.6 β=0.4 β= log(f) Hz ε' (a) Cole-Cole (b) Cole-Cole Cole-Cole plot 4.2: Cole-Cole Debye Cole-Cole Cole-Cole plot Cole-Cole τ Davidson-Cole Davidson Cole [8, 9] ε (ω) =ε + ε S ε (1 + iωτ) α (4.6) α 0 <α 1 α =1 α (4.6) Davidson-Cole
21 4.2 Cole-Cole plot ε', ε'' α=1.0 α=0.8 α=0.6 α=0.4 ε" α=1.0 α=0.8 α=0.6 α= α= α= log(f) Hz ε' (a) Davidson-Cole (b) Davidson-Cole Cole-Cole plot 4.3: Davidson-Cole Havriliak-Negami Havriliak Negami Cole-Cole Davidson-Cole ε (ω) =ε + ε S ε (4.7) (1 + (iωτ) β ) α [10, 11] α 0 <α 1 β 0 <β 1 Havriliak-Negami α β [12] Cole-Cole Davidson-Cole Havriliak-Negami Debye Havriliak-Negami ( ) β(1 α) τ sin βθ G(ln τ) = 1 π { ( τ τ 0 ) 2(1 α) ( τ +2 ) (1 α) cos π(1 α)+1} β 2 (4.8) τ 0 sin π(1 α) θ = arctan τ (4.9) + cos π(1 α) τ 0 [1] α =1 β =1 Cole-Cole Davidson-Cole τ 0
22 4.2 Cole-Cole plot 21 (4.8) α β (4.7) Debye ε S ε τ α β ε', ε'' α,β=1.0 α,β=0.8 α,β=0.6 α,β=0.4 α,β=0.2 ε" α,β=1.0 α,β=0.8 α,β=0.6 α,β=0.4 α,β= log(f) Hz ε' (a) Havriliak-Negami (b) Havriliak-Negami Cole-Cole plot 4.4: Havriliak-Negami ωτ =1 (4.6) (4.8) ω ωτ =1 τ KWW ( ) βkww t Φ or P (t) =exp, 0 <β KWW 1 (4.10) τ 0 (4.10) Kohraush function stretched exponential
23 A KWW ε', ε'' β KWW =1.0 β KWW =0.8 β KWW =0.6 β KWW =0.4 β KWW =0.2 ε" β KWW =1.0 β KWW =0.8 β KWW =0.6 β KWW =0.4 β KWW = log(f) Hz ε' (a) KWW (b) KWW Cole-Cole plot 4.5: KWW β KWW Debye KWW β KWW Ngai 4.10 [13] Cole-Cole Davidson-Cole Havriliak-Negami KWW 4.3 Debye Cole-Cole Davidson-Cole KWW Havriliak-Negami Debye Debye [14] Debye Debye
24 Debye 500kHz 10GHz [15, 16] KHz MHz MHz GHz Debye Cole-Cole Davidson-Cole Havriliak-Negami KWW [17] 4.4 Havriliak Havriliak-Negami α β [12] 4.6
25 HN(α=2.5,β=1) Debye DHO ε', ε'' log(f) Hz 4.6: HN α>1 4.6 Debye Havriliak- Negami α =2.5,β =1 Havriliak-Negami β α β Havriliak-Negami 6 Havriliak-Negami α β Havriliak-Negami Debye Havriliak-Negami 4.6
26 GHz ps ps [18] 4.7
27 : [19] Mashimo TDR [20] Mashimo TDR Havriliak-Negami log(τ) 0.8 α 0.8 Eyring τ τ = h kt exp ( G RT ) (4.11)
28 h k T R G G mix = x G 1 +(1 x) G 2 (4.12) G mix G 1 G 2 x 1 τ mix = h ( ) kt exp Gmix = τ1 x τ (1 x) 2 (4.13) RT log τ mix = x log τ 1 +(1 x) log τ 2 (4.14) Mashimo x =0.83 m m 1 x w G =[x w (m 1)(1 x w )] G w +(1 x w ) G c = m[x w (m 1)/m] G w +(1 x w ) G c (4.15) G G w G c log τ = m[x w (m 1)/m] log τ w +(1 x w ) log τ c (4.16) m =5.9 ± 0.3 (4.16) Sato TDR 300MHz 25GHz 20 C 22.5 C 25 C [21] Davidson-Cole Havriliak-Negami X X >0.4 Cole-Cole Debye 0 <X 4 Cole-Cole
29 Eyring τ τ = h ( ) G kt exp = h RT kt exp ( H RT ) exp ( ) S R (4.17) H S G = H TδS [ ( )] h G = RT ln τ 1 ln (4.18) kt H = ( G/T ) (1/T ) [ ] ln τ1 = R RT (4.19) (1/T ) T S = H G (4.20) G H S X =0.18 H S H S Cole-Cole β X 0.42
30 5 5.1 C 0 ω =2Πf V (t) =V 0 e iωt 90 I(t)=iωC 0 V (t) ω δ δ (a) (b) 5.1: I c = iωcv I l = GV R =1/G I =(iωc + G)V (5.1) ε C = ε C 0 δ tan δ = I l I C = G ωc (5.2) I I =(iωε C 0 + ωε tan δ) V (5.3) 29
31 ε = ε iε tan δ ε ε (5.4) 1 I =(iωε + ωε ) C 0 V = iωε C 0 V (5.5) W W (ω) = 1 2 R(IV )=1 2 ωε (ω)c 0 V 2 0 (5.6) 5.2 (5.6) ωε (ω) ε χ 2 ε ω ω
32 ωε"(ω) ε"(ω) plateau ωε"(ω) ε"(ω) log(f) Hz 5.2: Debye GHz 25GHz 25GHz 5.3 [14, 22] GHz THz
33 Dielectric loss ε" GHz loss peak Barthel Hasted water at room temperature far infrared intermolecular vibration 300 µm 30 µm Absorption coefficient α" (arb. units) water at room temperature micreowave oven far infrared Barthel Hasted Frequency (Hz) Frequency (Hz) (a) (b) 5.3: [14, 22] 5.2 plateau Debye plateau (2.17) ω 1 ωε (ω) 6 ωε (ω) ε (ω)
34 5.3 33
35 Debye [23, 24] dipole moment µ µ u = µ(t)/ µ u d u dt = ω(t) u(t) (6.1) ω(t) ω(t) I d u(t) dt + ζ ω(t) =λ(t)+ µ(t) E(t) (6.2) I zeta ω(t) λ(t) (6.2) λ(t) =0 (6.3) λ i (t)λ j (t ) =2kT ij δ(t t ) (6.4) δ i, j x, y, z I 0 ζ
36 ω(t) = λ(t) ζ + µ(t) E(t) ζ (6.5) (6.5) (6.4) narrowing limit (6.2) (6.5) overdamped limit (THz) (6.5) (6.1) d µ(t) dt = λ(t) ζ + µ(t)+ µ2 E(t) ζ µ[ µ E(t)] ζ (6.6) J d J d = W v (6.7) v = u W (θ, φ, t) dipole moment u u x = sin θ cos φ, u y = sin θ sin φ, u z = cos φ E drift current (6.6) (6.7) E(t) = gradv = V θ e θ 1 V sin θ φ e φ (6.8) = E θ e θ + E φ e φ (6.9) J d = 1 ζ [ V θ e θ + 1 ] V sin θ φ e φ J d J diff W (θ, φ) (6.10) J = J d + J diff J diff = DgradW (6.11)
37 [ W J θ = ζ J φ = ] V θ + D W θ V φ + D sin θ [ W ζ sin θ ] W φ (6.12) (6.13) W t + div J =0 (6.14) divj = 1 [ sin θ θ (J θ sin θ)+ J ] φ φ (6.15) (6.12) (6.15) Fokker-Plank W t [ ( 1 = D sin θw sin θ θ + 1 [ 1 ζ sin θ θ W theta + 1 ( sin θw V θ + 1 sin 2 θ )] 2 W sin 2 θ φ ( 2 W V ))] φ φ (6.16) W t =0 W Maxwell-Boltzmann W 0 = Ae V (θ,φ) k B T (6.17) (6.16) D = k BT ζ Debye relaxation time τ D τ D (6.16) 2τ D W t = + 1 sin θ θ 1 k B T τ D = ( sin θ W θ [ 1 sin θ θ ζ 2k B T ) + 1 sin 2 θ ) ( sin θw V θ 2 W φ sin 2 θ ( W V )] φ φ (6.18) (6.19) (6.20) z V (θ, φ) =V (θ) = µe cos θ (6.20) W(θ, t) = 1 [ ( kb T W(θ, t) sin θ + µe )] t sin θ θ ζ θ ζ sin θw(θ, t) (6.21)
38 6.2 Rocard Equation 37 (6.21) W (θ, t) = a n (t)p n (cos θ), n =1, 2, (6.22) n=0 P n (cos θ) E = E 0 t =0 (after effect solution) W (θ, t) =A(1 + µe 0 g(t) cos θ) (6.23) k B T (6.23) (6.21) ( W (θ, t) =A 1+ µe ) 0 k B T e (2k Bt/ζ)t cos θ dipole moment 2π π 0 0 2π π 0 0 2k B T t ζ µ cos θ = µw cos θ sin θdθdφ W sin θdθdφ = µ2 E 0 e 3k B T (6.24) (6.25) GHz Debye ω 1 ω 3 THz (6.2) 6.2 Rocard Equation t =0 t =0 f(θ, 0) Maxwell-Boltzmann I θ(t)+ζ θ(t)+µe sin θ(t) = λ(t) (t<0) (6.26) I θ(t)+ζ θ(t) = λ(t) (t>0) (6.27)
39 6.2 Rocard Equation 38 λ(t) λ(t)λ(t ) =2kTζδ(t t ) θ(t) Gaussian random variable cos θ(0) cos θ(t) cos 2 θ(0) cos θ(t 1 ) cos θ(t 2 ) = cos θ(t 1 ) cos[θ(t 1 )+ θ] (6.28) θ = θ(t 2 ) θ(t 1 ) cos θ(t 1 ) cos θ(t 2 ) = 1 2 { cos θ + cos [ θ +2θ(t 1)] } = 1 2 R{ exp i θ + exp [i θ +2θ(t 1)] } (6.29) R θ(t 1 ),θ(t 2 ) Gaussian random variable θ Gaussian random variable X { exp ix = exp i X 1 [ X 2 X 2]} (6.30) 2 (6.29) cos θ(t 1 ) cos θ(t 2 ) = 1 { (exp 2 R i θ 1 [ ( θ) 2 θ 2]} 2 { + exp i θ +2θ(t 1 ) 1 }) 2 [ θ +2θ(t 1)] 2 [ θ +2θ(t 1 )] (6.31) θ (6.31) t 2 t 1 cos θ(t 1 ) cos θ(t 2 ) = 1 [ {exp 2 R i θ 1 ( ( θ) 2 θ 2)]} (6.32) 2 θ =0 (6.32) cos θ(t 1 ) cos θ(t 2 ) = 1 2 [ 1 ] 2 ( θ)2 (6.33) mẍ(t) = ζẋ(t)+λ(t) ( x) 2 = 2k ( ) BTm ζ ζ ζ 2 m t 1+e m t ([23], pp ) { [ ( )]} cos θ(0) cos θ(t) kb TI ζt R(t) = = exp cos 2 θ(0) ζ 2 I ζ 1+e I t (6.34) ε[s] ε [0] =1 s 0 e st R(t)dt, s = iω (6.35)
40 6.3 itinerant oscillator model 39 ε[s] ε [0] = 1 s s + γβ [ 1+ γ = k BT Iβ 2,βγ = 1 τ D γ (s/β)+γ +1 + ε [s] ε [0] =1 s β β s + (6.37) ] γ [(s/β)+γ + 1][(s/β)+γ +2] + (6.36) 1 γ 1+ β s + 2γ 2+ β s + 3γ ε[s] ε[0] = 1 1+sτ 3+ β s... ε[s] ε[0] = γβ 2 (s + γβ)(s + β) 1 1+sτ + s 2 τ/β (6.37) (6.38) (6.39) Rocard equation Rocard equation (6.39) CH 3 Cl THz ([25] p.247, [2] p.382) 6.3 itinerant oscillator model itinerant oscillator(io) model dipole µ 1 I 1 dipole µ 2 I 2 cage φ 1,φ 2 cage V (φ 1 φ 2 ) [23] ( I 1 φ1 (t)+ζ 1 φ1 (t) φ ) 1 (t) + V (φ 1 (t) φ 2 (t)) = λ 1 (t) (6.40) ( I 2 φ2 (t)+ζ 1 φ2 (t) φ ) 1 (t) ζ 2 φ2 (t) V (φ 1 (t) φ 2 (t)) = λ 1 (t)+λ 2 (t) (6.41)
41 6.3 itinerant oscillator model 40 1 V (φ 1 φ 2 )=2V 0 sin(φ 1 φ 2 ) (6.42) λ 1 (t),λ 2 (t) λ i (t)λ i (t ) =2k B Tζ i δ ij δ(t t ) (6.43) α [ ] µ 1 (ω) α µ 1 (0) = ωβ2 x y(2ˆαˆγi 1 ˆα2 r ω 2 ) imaginary part x 2 + y 2 α [ ] µ 1 (ω) x(2ˆαˆγi 1 α µ 1 (0) =ˆα2 r ω 2 (6.44) )+ωβ 1 y real part x 2 + y 2 ˆα = ( kt I 1 ) 1 2 (6.45) ˆγ = V 0 I 1 ˆα (6.46) β 1 = ζ 1 /I 1 (6.47) β 2 = ζ 2 /I 2 (6.48) Ω 2 0 = I 1 ω0 2 i 2 (6.49) I r = I 2 /I 1 (6.50) b = β 1 /β 2 (6.51) x 1 = ˆα 2 Ir 1 β 2 (1 + bir 1 ) = K 2 (6.52) x 2 = β 2 (1 + b) (6.53) x 3 = 2ˆαˆγ(1 + Ir 1 )+β2 2 b (6.54) x 4 = 2β 2 ˆαˆγ(1 + bir 1 ) (6.55) x = ω 2 (ω 2 x 3 )+x 1 (x 4 x 2 ω 2 ) (6.56) y = ω [ x 4 + x 1 (x 3 ω 2 ) x 2 ω 2] (6.57) ε (ω) = ε +(ε S ε ) α µ 1 (ω) α µ 1 (0), ε (ω) = (ε S ε ) α µ 1 (ω) α µ 1 (0) (6.58) 1 dipole moment single friction model itinerant oscillator model ([23]pp )
42 6.3 itinerant oscillator model 41 (6.44) I r,b,ˆα, ˆβ, ˆγ [26, 23]
43 A KWW [27] 1 ε = ε (ω) iε (ω) ε (ε) ε ε 0 ε = 0 [ ] dφ (t) exp ( iωt) dt (1.1) dt λ = τ β 0 s = λ 0 + iω λ 0 0 ε (ε) ε ε 0 ε = βλ 0 [exp ( st)] [ exp ( λt β)] t β 1 dt (1.2) ε (ε) ε ε 0 ε = n=1 ( 1) n 1 1 Γ(nβ +1) [ cos nβ π (ωτ) nβ Γ(n +1) 2 i sin nβ π ] 2 (1.3) 0 <β log ωτ <β<1.0 1 log ωτ 0 4 ε (ε) ε = ( 1) n 1 (ωτ 0 ) n 1 ( ) n + β 1 [ Γ cos (n 1) π ε 0 ε Γ(n) β 2 + i sin (n 1) π ] 2 n=1 (1.4) 1.4 t 0 t β 1, (0 <β<1) singularity x = λt β ε (ε) ε ε 0 ε = 0 [exp ( x)] [ exp ( iωτ 0 x 1/β)] (1.5) Macintosh Igor Pro 1 (?) [1] KWW 42
44 [1] C. J. F. Böttcher and P. Bordewijk, Theory of electric polarization, vol. II. Elsevier, second ed., , 20, 42 [2] M. W. Evans, Simulation and symmetry in molecular diffusion and spectroscopy, Adv. Chem. Phys., vol. 81, pp , , 39 [3] Y.-Z. Wei and S. Sridhar, Radiation-corrected open-ended coax line technique for dielectric measurements of liquids up to 20 ghz, IEEE Trans. Microwave Theor. Tech.s, vol. 39, no. 3, pp , [4] T. W. Athey, M. A. Stuchly, and S. S. Stuchly, Measurement of radio frequency permittivity of biological tissues with an open-ended coaxial line: Part i, IEEE Trans. Microwave Theor. Tech.s, vol. MTT-30, no. 1, pp , [5] M. A. Stuchly, T. W. Athey, G. M. Samaras, and G. E. Taylor, Measurement of radio frequency permittivity of biological tissues with an open-ended coaxial line: Part ii-experimental results, IEEE Trans. Microwave Theor. Tech.s, vol. MTT-30, no. 1, pp , [6] S. Mashimo, T. Umehara, S. Kuwabara, and S. Yagihara, Dielectric study on dynamics and structure of water bound to dna using a frequency range hz, J. Phys. Chem., vol. 93, no. 12, pp , [7] K. S. Cole and R. H. Cole, Dispersion and absorption in dielectrics, J. Chem. Phys., vol. 9, pp , [8] D. W. Davidson and R. H. Cole J. Chem. Phys., vol. 18, p. 1417, [9] D. W. Davidson and R. H. Cole J. Chem. Phys., vol. 19, p. 1484, [10] S. Havriliak and S. Negami J. Polymer Sci., vol. C14, p. 99, [11] S. Havriliak and S. Negami Polymer, vol. 8, p. 161, [12] J. Havriliak, Stephen and S. J. Havriliak, Dielectric and mechanical relaxation in materials : analysis, interpretation, and application to polymers. Hanser Publishers, , 23 43
45 44 [13] R. Richert and A. Blumen, Disorder Effects on Relaxational Processes Glasses, Polymers, Proteins. New York: Springer-Verlag, [14] J. BARTHEL, K. BACHHUBER, R. BUCHNER, and H. HETZENAUER, Dielectric spectra of some common solvents in the microwave region. water and lower alcohols, Chem. Phys. Lett., vol. 165, no. 4, pp , , 31, 32 [15] S. Bone and B. Zaba, Bioelectronics. Wiley, [16] N. Miura, N. Asaka, N. Shinyashiki, and S. Mashimo, Microwave dielectric study on bound water of globule proteins in aqueous solution, Biopolymers,vol. 34, pp , [17] N. Shinyashiki, S. Sudo, W. Abe, and S. Yagihara, Shape of dielectric relaxation curve of ethylene glycol oligomer-water mixtures, J. Phys. Chem., vol. 109, no. 22, pp , [18] I. Ohmine, Liquid water dynamics: Collective motions, fluctuation, and relaxation, J. Phys. Chem., vol. 99, pp , [19],., :, [20] S. Mashimo, T. Umehara, and H. Redlin, Structures of water and primary alcohol studied by microwave dielectric analyses, J. Chem. Phys., vol. 95, no. 9, pp , [21] T. Sato, A. Chiba, and R. Nozaki, Dynamical aspects of mixing schemesin ethanolwater mixtures in terms of the excess partial molar activation free energy, enthalpy, and entropy of the dielectric relaxation process, J. Chem. Phys., vol. 110, no. 5, pp , [22] J. B. Hasted, S. K. Husain, F. A. M. Frescura, and J. R. Birch, Far-infrared absorption in liquid water, Chem. Phys. Lett., vol. 118, no. 6, pp , , 32 [23] W. T. Coffey, Y. P. Kalmykov, and J. T. Waldron, The Langevin Equation With Applications in Physics, Chemistry and Electrical Engineering, vol. 10 of World Scientific Seriesin Contemporary Chemical Physics. Singapore: World Scientific, , 38, 39, 40, 41 [24] V. I. Gaiduk, DIELECTRIC RELAXATION AND DYNAMICS OF POLAR MOLECULES, vol. 8 of World Scientific Series in Contemporary Chemical Physics. Singapole: World Scientific,
46 45 [25] J. McConnell, Rotational Brownian Motion and Dielectric Theory. London: Academic Press, [26] M. Evans, G. H. Evans, W. T. Coffey, and P. Grigolini, Molecular Dynamics and Theory of Broad Band Spectroscopy. New York: Wiley, [27] G. Williams and D. C. Watts, Further cosiderations of non symmetrical dielectric relaxation behabiour arising from a simple empirical decay function, Trans. Faraday Soc., vol. 67, pp ,
1 2 2 (Dielecrics) Maxwell ( ) D H
 2003.02.13 1 2 2 (Dielecrics) 4 2.1... 4 2.2... 5 2.3... 6 2.4... 6 3 Maxwell ( ) 9 3.1... 9 3.2 D H... 11 3.3... 13 4 14 4.1... 14 4.2... 14 4.3... 17 4.4... 19 5 22 6 THz 24 6.1... 24 6.2... 25 7 26
2003.02.13 1 2 2 (Dielecrics) 4 2.1... 4 2.2... 5 2.3... 6 2.4... 6 3 Maxwell ( ) 9 3.1... 9 3.2 D H... 11 3.3... 13 4 14 4.1... 14 4.2... 14 4.3... 17 4.4... 19 5 22 6 THz 24 6.1... 24 6.2... 25 7 26
01-C08244-食品の物性 indd
 , Vol. 9, No. 3, pp. 123-134, Sep. 2008 Physical Properties of Foods and the Effect of Water on Them II Electrical Properties and Dielectric Relaxation Hitoshi KUMAGAI Department of Food Science and Nutrition,
, Vol. 9, No. 3, pp. 123-134, Sep. 2008 Physical Properties of Foods and the Effect of Water on Them II Electrical Properties and Dielectric Relaxation Hitoshi KUMAGAI Department of Food Science and Nutrition,
磁性物理学 - 遷移金属化合物磁性のスピンゆらぎ理論
 email: takahash@sci.u-hyogo.ac.jp May 14, 2009 Outline 1. 2. 3. 4. 5. 6. 2 / 262 Today s Lecture: Mode-mode Coupling Theory 100 / 262 Part I Effects of Non-linear Mode-Mode Coupling Effects of Non-linear
email: takahash@sci.u-hyogo.ac.jp May 14, 2009 Outline 1. 2. 3. 4. 5. 6. 2 / 262 Today s Lecture: Mode-mode Coupling Theory 100 / 262 Part I Effects of Non-linear Mode-Mode Coupling Effects of Non-linear
SFGÇÃÉXÉyÉNÉgÉãå`.pdf
 SFG 1 SFG SFG I SFG (ω) χ SFG (ω). SFG χ χ SFG (ω) = χ NR e iϕ +. ω ω + iγ SFG φ = ±π/, χ φ = ±π 3 χ SFG χ SFG = χ NR + χ (ω ω ) + Γ + χ NR χ (ω ω ) (ω ω ) + Γ cosϕ χ NR χ Γ (ω ω ) + Γ sinϕ. 3 (θ) 180
SFG 1 SFG SFG I SFG (ω) χ SFG (ω). SFG χ χ SFG (ω) = χ NR e iϕ +. ω ω + iγ SFG φ = ±π/, χ φ = ±π 3 χ SFG χ SFG = χ NR + χ (ω ω ) + Γ + χ NR χ (ω ω ) (ω ω ) + Γ cosϕ χ NR χ Γ (ω ω ) + Γ sinϕ. 3 (θ) 180
ver.1 / c /(13)
 1 -- 11 1 c 2010 1/(13) 1 -- 11 -- 1 1--1 1--1--1 2009 3 t R x R n 1 ẋ = f(t, x) f = ( f 1,, f n ) f x(t) = ϕ(x 0, t) x(0) = x 0 n f f t 1--1--2 2009 3 q = (q 1,..., q m ), p = (p 1,..., p m ) x = (q,
1 -- 11 1 c 2010 1/(13) 1 -- 11 -- 1 1--1 1--1--1 2009 3 t R x R n 1 ẋ = f(t, x) f = ( f 1,, f n ) f x(t) = ϕ(x 0, t) x(0) = x 0 n f f t 1--1--2 2009 3 q = (q 1,..., q m ), p = (p 1,..., p m ) x = (q,
基礎数学I
 I & II ii ii........... 22................. 25 12............... 28.................. 28.................... 31............. 32.................. 34 3 1 9.................... 1....................... 1............
I & II ii ii........... 22................. 25 12............... 28.................. 28.................... 31............. 32.................. 34 3 1 9.................... 1....................... 1............
LCR e ix LC AM m k x m x x > 0 x < 0 F x > 0 x < 0 F = k x (k > 0) k x = x(t)
 338 7 7.3 LCR 2.4.3 e ix LC AM 7.3.1 7.3.1.1 m k x m x x > 0 x < 0 F x > 0 x < 0 F = k x k > 0 k 5.3.1.1 x = xt 7.3 339 m 2 x t 2 = k x 2 x t 2 = ω 2 0 x ω0 = k m ω 0 1.4.4.3 2 +α 14.9.3.1 5.3.2.1 2 x
338 7 7.3 LCR 2.4.3 e ix LC AM 7.3.1 7.3.1.1 m k x m x x > 0 x < 0 F x > 0 x < 0 F = k x k > 0 k 5.3.1.1 x = xt 7.3 339 m 2 x t 2 = k x 2 x t 2 = ω 2 0 x ω0 = k m ω 0 1.4.4.3 2 +α 14.9.3.1 5.3.2.1 2 x
Nosé Hoover 1.2 ( 1) (a) (b) 1:
 1 watanabe@cc.u-tokyo.ac.jp 1 1.1 Nosé Hoover 1. ( 1) (a) (b) 1: T ( f(p x, p y, p z ) exp p x + p y + p ) z (1) mk B T p x p y p = = z = 1 m m m k BT () k B T = 1.3 0.04 0.03 0.0 0.01 0-5 -4-3 - -1 0
1 watanabe@cc.u-tokyo.ac.jp 1 1.1 Nosé Hoover 1. ( 1) (a) (b) 1: T ( f(p x, p y, p z ) exp p x + p y + p ) z (1) mk B T p x p y p = = z = 1 m m m k BT () k B T = 1.3 0.04 0.03 0.0 0.01 0-5 -4-3 - -1 0
The Physics of Atmospheres CAPTER :
 The Physics of Atmospheres CAPTER 4 1 4 2 41 : 2 42 14 43 17 44 25 45 27 46 3 47 31 48 32 49 34 41 35 411 36 maintex 23/11/28 The Physics of Atmospheres CAPTER 4 2 4 41 : 2 1 σ 2 (21) (22) k I = I exp(
The Physics of Atmospheres CAPTER 4 1 4 2 41 : 2 42 14 43 17 44 25 45 27 46 3 47 31 48 32 49 34 41 35 411 36 maintex 23/11/28 The Physics of Atmospheres CAPTER 4 2 4 41 : 2 1 σ 2 (21) (22) k I = I exp(
JIS Z803: (substitution method) 3 LCR LCR GPIB
 LCR NMIJ 003 Agilent 8A 500 ppm JIS Z803:000 50 (substitution method) 3 LCR LCR GPIB Taylor 5 LCR LCR meter (Agilent 8A: Basic accuracy 500 ppm) V D z o I V DUT Z 3 V 3 I A Z V = I V = 0 3 6 V, A LCR meter
LCR NMIJ 003 Agilent 8A 500 ppm JIS Z803:000 50 (substitution method) 3 LCR LCR GPIB Taylor 5 LCR LCR meter (Agilent 8A: Basic accuracy 500 ppm) V D z o I V DUT Z 3 V 3 I A Z V = I V = 0 3 6 V, A LCR meter
医系の統計入門第 2 版 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. このサンプルページの内容は, 第 2 版 1 刷発行時のものです.
 医系の統計入門第 2 版 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/009192 このサンプルページの内容は, 第 2 版 1 刷発行時のものです. i 2 t 1. 2. 3 2 3. 6 4. 7 5. n 2 ν 6. 2 7. 2003 ii 2 2013 10 iii 1987
医系の統計入門第 2 版 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/009192 このサンプルページの内容は, 第 2 版 1 刷発行時のものです. i 2 t 1. 2. 3 2 3. 6 4. 7 5. n 2 ν 6. 2 7. 2003 ii 2 2013 10 iii 1987
磁性物理学 - 遷移金属化合物磁性のスピンゆらぎ理論
 email: takahash@sci.u-hyogo.ac.jp April 30, 2009 Outline 1. 2. 3. 4. 5. 6. 2 / 260 Today s Lecture: Itinerant Magnetism 60 / 260 Multiplets of Single Atom System HC HSO : L = i l i, S = i s i, J = L +
email: takahash@sci.u-hyogo.ac.jp April 30, 2009 Outline 1. 2. 3. 4. 5. 6. 2 / 260 Today s Lecture: Itinerant Magnetism 60 / 260 Multiplets of Single Atom System HC HSO : L = i l i, S = i s i, J = L +
( ) ,
 II 2007 4 0. 0 1 0 2 ( ) 0 3 1 2 3 4, - 5 6 7 1 1 1 1 1) 2) 3) 4) ( ) () H 2.79 10 10 He 2.72 10 9 C 1.01 10 7 N 3.13 10 6 O 2.38 10 7 Ne 3.44 10 6 Mg 1.076 10 6 Si 1 10 6 S 5.15 10 5 Ar 1.01 10 5 Fe 9.00
II 2007 4 0. 0 1 0 2 ( ) 0 3 1 2 3 4, - 5 6 7 1 1 1 1 1) 2) 3) 4) ( ) () H 2.79 10 10 He 2.72 10 9 C 1.01 10 7 N 3.13 10 6 O 2.38 10 7 Ne 3.44 10 6 Mg 1.076 10 6 Si 1 10 6 S 5.15 10 5 Ar 1.01 10 5 Fe 9.00
LLG-R8.Nisus.pdf
 d M d t = γ M H + α M d M d t M γ [ 1/ ( Oe sec) ] α γ γ = gµ B h g g µ B h / π γ g = γ = 1.76 10 [ 7 1/ ( Oe sec) ] α α = λ γ λ λ λ α γ α α H α = γ H ω ω H α α H K K H K / M 1 1 > 0 α 1 M > 0 γ α γ =
d M d t = γ M H + α M d M d t M γ [ 1/ ( Oe sec) ] α γ γ = gµ B h g g µ B h / π γ g = γ = 1.76 10 [ 7 1/ ( Oe sec) ] α α = λ γ λ λ λ α γ α α H α = γ H ω ω H α α H K K H K / M 1 1 > 0 α 1 M > 0 γ α γ =
5 H Boltzmann Einstein Brown 5.1 Onsager [ ] Tr Tr Tr = dγ (5.1) A(p, q) Â 0 = Tr Âe βĥ0 Tr e βĥ0 = dγ e βh 0(p,q) A(p, q) dγ e βh 0(p,q) (5.2) e βĥ0
![5 H Boltzmann Einstein Brown 5.1 Onsager [ ] Tr Tr Tr = dγ (5.1) A(p, q) Â 0 = Tr Âe βĥ0 Tr e βĥ0 = dγ e βh 0(p,q) A(p, q) dγ e βh 0(p,q) (5.2) e βĥ0 5 H Boltzmann Einstein Brown 5.1 Onsager [ ] Tr Tr Tr = dγ (5.1) A(p, q) Â 0 = Tr Âe βĥ0 Tr e βĥ0 = dγ e βh 0(p,q) A(p, q) dγ e βh 0(p,q) (5.2) e βĥ0](/thumbs/99/141438380.jpg) 5 H Boltzmann Einstein Brown 5.1 Onsager [ ] Tr Tr Tr = dγ (5.1) A(p, q) Â = Tr Âe βĥ Tr e βĥ = dγ e βh (p,q) A(p, q) dγ e βh (p,q) (5.2) e βĥ A(p, q) p q Â(t) = Tr Â(t)e βĥ Tr e βĥ = dγ() e βĥ(p(),q())
5 H Boltzmann Einstein Brown 5.1 Onsager [ ] Tr Tr Tr = dγ (5.1) A(p, q) Â = Tr Âe βĥ Tr e βĥ = dγ e βh (p,q) A(p, q) dγ e βh (p,q) (5.2) e βĥ A(p, q) p q Â(t) = Tr Â(t)e βĥ Tr e βĥ = dγ() e βĥ(p(),q())
OHO.dvi
 1 Coil D-shaped electrodes ( [1] ) Vacuum chamber Ion source Oscillator 1.1 m e v B F = evb (1) r m v2 = evb r v = erb (2) m r T = 2πr v = 2πm (3) eb v
1 Coil D-shaped electrodes ( [1] ) Vacuum chamber Ion source Oscillator 1.1 m e v B F = evb (1) r m v2 = evb r v = erb (2) m r T = 2πr v = 2πm (3) eb v
m(ẍ + γẋ + ω 0 x) = ee (2.118) e iωt P(ω) = χ(ω)e = ex = e2 E(ω) m ω0 2 ω2 iωγ (2.119) Z N ϵ(ω) ϵ 0 = 1 + Ne2 m j f j ω 2 j ω2 iωγ j (2.120)
 2.6 2.6.1 mẍ + γẋ + ω 0 x) = ee 2.118) e iωt Pω) = χω)e = ex = e2 Eω) m ω0 2 ω2 iωγ 2.119) Z N ϵω) ϵ 0 = 1 + Ne2 m j f j ω 2 j ω2 iωγ j 2.120) Z ω ω j γ j f j f j f j sum j f j = Z 2.120 ω ω j, γ ϵω) ϵ
2.6 2.6.1 mẍ + γẋ + ω 0 x) = ee 2.118) e iωt Pω) = χω)e = ex = e2 Eω) m ω0 2 ω2 iωγ 2.119) Z N ϵω) ϵ 0 = 1 + Ne2 m j f j ω 2 j ω2 iωγ j 2.120) Z ω ω j γ j f j f j f j sum j f j = Z 2.120 ω ω j, γ ϵω) ϵ
From Evans Application Notes
 3 From Evans Application Notes http://www.eaglabs.com From Evans Application Notes http://www.eaglabs.com XPS AES ISS SSIMS ATR-IR 1-10keV µ 1 V() r = kx 2 = 2π µν x mm 1 2 µ= m + m 1 2 1 k ν = OSC 2
3 From Evans Application Notes http://www.eaglabs.com From Evans Application Notes http://www.eaglabs.com XPS AES ISS SSIMS ATR-IR 1-10keV µ 1 V() r = kx 2 = 2π µν x mm 1 2 µ= m + m 1 2 1 k ν = OSC 2
2 (March 13, 2010) N Λ a = i,j=1 x i ( d (a) i,j x j ), Λ h = N i,j=1 x i ( d (h) i,j x j ) B a B h B a = N i,j=1 ν i d (a) i,j, B h = x j N i,j=1 ν i
 1. A. M. Turing [18] 60 Turing A. Gierer H. Meinhardt [1] : (GM) ) a t = D a a xx µa + ρ (c a2 h + ρ 0 (0 < x < l, t > 0) h t = D h h xx νh + c ρ a 2 (0 < x < l, t > 0) a x = h x = 0 (x = 0, l) a = a(x,
1. A. M. Turing [18] 60 Turing A. Gierer H. Meinhardt [1] : (GM) ) a t = D a a xx µa + ρ (c a2 h + ρ 0 (0 < x < l, t > 0) h t = D h h xx νh + c ρ a 2 (0 < x < l, t > 0) a x = h x = 0 (x = 0, l) a = a(x,
Mott散乱によるParity対称性の破れを検証
 Mott Parity P2 Mott target Mott Parity Parity Γ = 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 t P P ),,, ( 3 2 1 0 1 γ γ γ γ γ γ ν ν µ µ = = Γ 1 : : : Γ P P P P x x P ν ν µ µ vector axial vector ν ν µ µ γ γ Γ ν γ
Mott Parity P2 Mott target Mott Parity Parity Γ = 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 t P P ),,, ( 3 2 1 0 1 γ γ γ γ γ γ ν ν µ µ = = Γ 1 : : : Γ P P P P x x P ν ν µ µ vector axial vector ν ν µ µ γ γ Γ ν γ
(Compton Scattering) Beaming 1 exp [i (k x ωt)] k λ k = 2π/λ ω = 2πν k = ω/c k x ωt ( ω ) k α c, k k x ωt η αβ k α x β diag( + ++) x β = (ct, x) O O x
![(Compton Scattering) Beaming 1 exp [i (k x ωt)] k λ k = 2π/λ ω = 2πν k = ω/c k x ωt ( ω ) k α c, k k x ωt η αβ k α x β diag( + ++) x β = (ct, x) O O x (Compton Scattering) Beaming 1 exp [i (k x ωt)] k λ k = 2π/λ ω = 2πν k = ω/c k x ωt ( ω ) k α c, k k x ωt η αβ k α x β diag( + ++) x β = (ct, x) O O x](/thumbs/104/162595168.jpg) Compton Scattering Beaming exp [i k x ωt] k λ k π/λ ω πν k ω/c k x ωt ω k α c, k k x ωt η αβ k α x β diag + ++ x β ct, x O O x O O v k α k α β, γ k γ k βk, k γ k + βk k γ k k, k γ k + βk 3 k k 4 k 3 k
Compton Scattering Beaming exp [i k x ωt] k λ k π/λ ω πν k ω/c k x ωt ω k α c, k k x ωt η αβ k α x β diag + ++ x β ct, x O O x O O v k α k α β, γ k γ k βk, k γ k + βk k γ k k, k γ k + βk 3 k k 4 k 3 k
 2007 5 iii 1 1 1.1.................... 1 2 5 2.1 (shear stress) (shear strain)...... 5 2.1.1...................... 6 2.1.2.................... 6 2.2....................... 7 2.2.1........................
2007 5 iii 1 1 1.1.................... 1 2 5 2.1 (shear stress) (shear strain)...... 5 2.1.1...................... 6 2.1.2.................... 6 2.2....................... 7 2.2.1........................
 K E N Z U 01 7 16 HP M. 1 1 4 1.1 3.......................... 4 1.................................... 4 1..1..................................... 4 1...................................... 5................................
K E N Z U 01 7 16 HP M. 1 1 4 1.1 3.......................... 4 1.................................... 4 1..1..................................... 4 1...................................... 5................................
1. (8) (1) (x + y) + (x + y) = 0 () (x + y ) 5xy = 0 (3) (x y + 3y 3 ) (x 3 + xy ) = 0 (4) x tan y x y + x = 0 (5) x = y + x + y (6) = x + y 1 x y 3 (
 1 1.1 (1) (1 + x) + (1 + y) = 0 () x + y = 0 (3) xy = x (4) x(y + 3) + y(y + 3) = 0 (5) (a + y ) = x ax a (6) x y 1 + y x 1 = 0 (7) cos x + sin x cos y = 0 (8) = tan y tan x (9) = (y 1) tan x (10) (1 +
1 1.1 (1) (1 + x) + (1 + y) = 0 () x + y = 0 (3) xy = x (4) x(y + 3) + y(y + 3) = 0 (5) (a + y ) = x ax a (6) x y 1 + y x 1 = 0 (7) cos x + sin x cos y = 0 (8) = tan y tan x (9) = (y 1) tan x (10) (1 +
, 1.,,,.,., (Lin, 1955).,.,.,.,. f, 2,. main.tex 2011/08/13( )
 81 4 2 4.1, 1.,,,.,., (Lin, 1955).,.,.,.,. f, 2,. 82 4.2. ζ t + V (ζ + βy) = 0 (4.2.1), V = 0 (4.2.2). (4.2.1), (3.3.66) R 1 Φ / Z, Γ., F 1 ( 3.2 ). 7,., ( )., (4.2.1) 500 hpa., 500 hpa (4.2.1) 1949,.,
81 4 2 4.1, 1.,,,.,., (Lin, 1955).,.,.,.,. f, 2,. 82 4.2. ζ t + V (ζ + βy) = 0 (4.2.1), V = 0 (4.2.2). (4.2.1), (3.3.66) R 1 Φ / Z, Γ., F 1 ( 3.2 ). 7,., ( )., (4.2.1) 500 hpa., 500 hpa (4.2.1) 1949,.,
 1 1 1 1-1 1 1-9 1-3 1-1 13-17 -3 6-4 6 3 3-1 35 3-37 3-3 38 4 4-1 39 4- Fe C TEM 41 4-3 C TEM 44 4-4 Fe TEM 46 4-5 5 4-6 5 5 51 6 5 1 1-1 1991 1,1 multiwall nanotube 1993 singlewall nanotube ( 1,) sp 7.4eV
1 1 1 1-1 1 1-9 1-3 1-1 13-17 -3 6-4 6 3 3-1 35 3-37 3-3 38 4 4-1 39 4- Fe C TEM 41 4-3 C TEM 44 4-4 Fe TEM 46 4-5 5 4-6 5 5 51 6 5 1 1-1 1991 1,1 multiwall nanotube 1993 singlewall nanotube ( 1,) sp 7.4eV
I
 I 6 4 10 1 1 1.1............... 1 1................ 1 1.3.................... 1.4............... 1.4.1.............. 1.4................. 1.4.3........... 3 1.4.4.. 3 1.5.......... 3 1.5.1..............
I 6 4 10 1 1 1.1............... 1 1................ 1 1.3.................... 1.4............... 1.4.1.............. 1.4................. 1.4.3........... 3 1.4.4.. 3 1.5.......... 3 1.5.1..............
ω 0 m(ẍ + γẋ + ω0x) 2 = ee (2.118) e iωt x = e 1 m ω0 2 E(ω). (2.119) ω2 iωγ Z N P(ω) = χ(ω)e = exzn (2.120) ϵ = ϵ 0 (1 + χ) ϵ(ω) ϵ 0 = 1 +
 2.6 2.6.1 ω 0 m(ẍ + γẋ + ω0x) 2 = ee (2.118) e iωt x = e 1 m ω0 2 E(ω). (2.119) ω2 iωγ Z N P(ω) = χ(ω)e = exzn (2.120) ϵ = ϵ 0 (1 + χ) ϵ(ω) ϵ 0 = 1 + Ne2 m j f j ω 2 j ω2 iωγ j (2.121) Z ω ω j γ j f j
2.6 2.6.1 ω 0 m(ẍ + γẋ + ω0x) 2 = ee (2.118) e iωt x = e 1 m ω0 2 E(ω). (2.119) ω2 iωγ Z N P(ω) = χ(ω)e = exzn (2.120) ϵ = ϵ 0 (1 + χ) ϵ(ω) ϵ 0 = 1 + Ne2 m j f j ω 2 j ω2 iωγ j (2.121) Z ω ω j γ j f j
吸収分光.PDF
 3 Rb 1 1 4 1.1 4 1. 4 5.1 5. 5 3 8 3.1 8 4 1 4.1 External Cavity Laser Diode: ECLD 1 4. 1 4.3 Polarization Beam Splitter: PBS 13 4.4 Photo Diode: PD 13 4.5 13 4.6 13 5 Rb 14 6 15 6.1 ECLD 15 6. 15 6.3
3 Rb 1 1 4 1.1 4 1. 4 5.1 5. 5 3 8 3.1 8 4 1 4.1 External Cavity Laser Diode: ECLD 1 4. 1 4.3 Polarization Beam Splitter: PBS 13 4.4 Photo Diode: PD 13 4.5 13 4.6 13 5 Rb 14 6 15 6.1 ECLD 15 6. 15 6.3
 B 1 B.1.......................... 1 B.1.1................. 1 B.1.2................. 2 B.2........................... 5 B.2.1.......................... 5 B.2.2.................. 6 B.2.3..................
B 1 B.1.......................... 1 B.1.1................. 1 B.1.2................. 2 B.2........................... 5 B.2.1.......................... 5 B.2.2.................. 6 B.2.3..................
1 1 sin cos P (primary) S (secondly) 2 P S A sin(ω2πt + α) A ω 1 ω α V T m T m 1 100Hz m 2 36km 500Hz. 36km 1
 sin cos P (primary) S (secondly) 2 P S A sin(ω2πt + α) A ω ω α 3 3 2 2V 3 33+.6T m T 5 34m Hz. 34 3.4m 2 36km 5Hz. 36km m 34 m 5 34 + m 5 33 5 =.66m 34m 34 x =.66 55Hz, 35 5 =.7 485.7Hz 2 V 5Hz.5V.5V V
sin cos P (primary) S (secondly) 2 P S A sin(ω2πt + α) A ω ω α 3 3 2 2V 3 33+.6T m T 5 34m Hz. 34 3.4m 2 36km 5Hz. 36km m 34 m 5 34 + m 5 33 5 =.66m 34m 34 x =.66 55Hz, 35 5 =.7 485.7Hz 2 V 5Hz.5V.5V V
<4D F736F F D B B83578B6594BB2D834A836F815B82D082C88C60202E646F63>
 マイクロメカトロニクス サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/077331 このサンプルページの内容は, 初版 1 刷発行当時のものです. 1984.10 1986.7 1995 60 1991 Piezoelectric Actuators and Ultrasonic Motors
マイクロメカトロニクス サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/077331 このサンプルページの内容は, 初版 1 刷発行当時のものです. 1984.10 1986.7 1995 60 1991 Piezoelectric Actuators and Ultrasonic Motors
 006 11 8 0 3 1 5 1.1..................... 5 1......................... 6 1.3.................... 6 1.4.................. 8 1.5................... 8 1.6................... 10 1.6.1......................
006 11 8 0 3 1 5 1.1..................... 5 1......................... 6 1.3.................... 6 1.4.................. 8 1.5................... 8 1.6................... 10 1.6.1......................
δf = δn I [ ( FI (N I ) N I ) T,V δn I [ ( FI N I ( ) F N T,V ( ) FII (N N I ) + N I ) ( ) FII T,V N II T,V T,V ] ] = 0 = 0 (8.2) = µ (8.3) G
![δf = δn I [ ( FI (N I ) N I ) T,V δn I [ ( FI N I ( ) F N T,V ( ) FII (N N I ) + N I ) ( ) FII T,V N II T,V T,V ] ] = 0 = 0 (8.2) = µ (8.3) G δf = δn I [ ( FI (N I ) N I ) T,V δn I [ ( FI N I ( ) F N T,V ( ) FII (N N I ) + N I ) ( ) FII T,V N II T,V T,V ] ] = 0 = 0 (8.2) = µ (8.3) G](/thumbs/91/106215968.jpg) 8 ( ) 8. 1 ( ) F F = F I (N I, T, V I ) + F II (N II, T, V II ) (8.1) F δf = δn I [ ( FI (N I ) N I 8. 1 111 ) T,V δn I [ ( FI N I ( ) F N T,V ( ) FII (N N I ) + N I ) ( ) FII T,V N II T,V T,V ] ] = 0
8 ( ) 8. 1 ( ) F F = F I (N I, T, V I ) + F II (N II, T, V II ) (8.1) F δf = δn I [ ( FI (N I ) N I 8. 1 111 ) T,V δn I [ ( FI N I ( ) F N T,V ( ) FII (N N I ) + N I ) ( ) FII T,V N II T,V T,V ] ] = 0
m dv = mg + kv2 dt m dv dt = mg k v v m dv dt = mg + kv2 α = mg k v = α 1 e rt 1 + e rt m dv dt = mg + kv2 dv mg + kv 2 = dt m dv α 2 + v 2 = k m dt d
 m v = mg + kv m v = mg k v v m v = mg + kv α = mg k v = α e rt + e rt m v = mg + kv v mg + kv = m v α + v = k m v (v α (v + α = k m ˆ ( v α ˆ αk v = m v + α ln v α v + α = αk m t + C v α v + α = e αk m
m v = mg + kv m v = mg k v v m v = mg + kv α = mg k v = α e rt + e rt m v = mg + kv v mg + kv = m v α + v = k m v (v α (v + α = k m ˆ ( v α ˆ αk v = m v + α ln v α v + α = αk m t + C v α v + α = e αk m
1).1-5) - 9 -
 - 8 - 1).1-5) - 9 - ε = ε xx 0 0 0 ε xx 0 0 0 ε xx (.1 ) z z 1 z ε = ε xx ε x y 0 - ε x y ε xx 0 0 0 ε zz (. ) 3 xy ) ε xx, ε zz» ε x y (.3 ) ε ij = ε ij ^ (.4 ) 6) xx, xy ε xx = ε xx + i ε xx ε xy = ε
- 8 - 1).1-5) - 9 - ε = ε xx 0 0 0 ε xx 0 0 0 ε xx (.1 ) z z 1 z ε = ε xx ε x y 0 - ε x y ε xx 0 0 0 ε zz (. ) 3 xy ) ε xx, ε zz» ε x y (.3 ) ε ij = ε ij ^ (.4 ) 6) xx, xy ε xx = ε xx + i ε xx ε xy = ε
1. ( ) 1.1 t + t [m]{ü(t + t)} + [c]{ u(t + t)} + [k]{u(t + t)} = {f(t + t)} (1) m ü f c u k u 1.2 Newmark β (1) (2) ( [m] + t ) 2 [c] + β( t)2
![1. ( ) 1.1 t + t [m]{ü(t + t)} + [c]{ u(t + t)} + [k]{u(t + t)} = {f(t + t)} (1) m ü f c u k u 1.2 Newmark β (1) (2) ( [m] + t ) 2 [c] + β( t)2 1. ( ) 1.1 t + t [m]{ü(t + t)} + [c]{ u(t + t)} + [k]{u(t + t)} = {f(t + t)} (1) m ü f c u k u 1.2 Newmark β (1) (2) ( [m] + t ) 2 [c] + β( t)2](/thumbs/80/80934335.jpg) 212 1 6 1. (212.8.14) 1 1.1............................................. 1 1.2 Newmark β....................... 1 1.3.................................... 2 1.4 (212.8.19)..................................
212 1 6 1. (212.8.14) 1 1.1............................................. 1 1.2 Newmark β....................... 1 1.3.................................... 2 1.4 (212.8.19)..................................
Black-Scholes [1] Nelson [2] Schrödinger 1 Black Scholes [1] Black-Scholes Nelson [2][3][4] Schrödinger Nelson Parisi Wu [5] Nelson Parisi-W
![Black-Scholes [1] Nelson [2] Schrödinger 1 Black Scholes [1] Black-Scholes Nelson [2][3][4] Schrödinger Nelson Parisi Wu [5] Nelson Parisi-W Black-Scholes [1] Nelson [2] Schrödinger 1 Black Scholes [1] Black-Scholes Nelson [2][3][4] Schrödinger Nelson Parisi Wu [5] Nelson Parisi-W](/thumbs/97/132191371.jpg) 003 7 14 Black-Scholes [1] Nelson [] Schrödinger 1 Black Scholes [1] Black-Scholes Nelson [][3][4] Schrödinger Nelson Parisi Wu [5] Nelson Parisi-Wu Nelson e-mail: takatoshi-tasaki@nifty.com kabutaro@mocha.freemail.ne.jp
003 7 14 Black-Scholes [1] Nelson [] Schrödinger 1 Black Scholes [1] Black-Scholes Nelson [][3][4] Schrödinger Nelson Parisi Wu [5] Nelson Parisi-Wu Nelson e-mail: takatoshi-tasaki@nifty.com kabutaro@mocha.freemail.ne.jp
数学の基礎訓練I
 I 9 6 13 1 1 1.1............... 1 1................ 1 1.3.................... 1.4............... 1.4.1.............. 1.4................. 3 1.4.3........... 3 1.4.4.. 3 1.5.......... 3 1.5.1..............
I 9 6 13 1 1 1.1............... 1 1................ 1 1.3.................... 1.4............... 1.4.1.............. 1.4................. 3 1.4.3........... 3 1.4.4.. 3 1.5.......... 3 1.5.1..............
MUFFIN3
 MUFFIN - MUltiFarious FIeld simulator for Non-equilibrium system - ( ) MUFFIN WG3 - - JCII, - ( ) - ( ) - ( ) - (JSR) - - MUFFIN sec -3 msec -6 sec GOURMET SUSHI MUFFIN -9 nsec PASTA -1 psec -15 fsec COGNAC
MUFFIN - MUltiFarious FIeld simulator for Non-equilibrium system - ( ) MUFFIN WG3 - - JCII, - ( ) - ( ) - ( ) - (JSR) - - MUFFIN sec -3 msec -6 sec GOURMET SUSHI MUFFIN -9 nsec PASTA -1 psec -15 fsec COGNAC
遍歴電子磁性とスピン揺らぎ理論 - 京都大学大学院理学研究科 集中講義
 email: takahash@sci.u-hyogo.ac.jp August 3, 2009 Title of Lecture: SCR Spin Fluctuation Theory 2 / 179 Part I Introduction Introduction Stoner-Wohlfarth Theory Stoner-Wohlfarth Theory Hatree Fock Approximation
email: takahash@sci.u-hyogo.ac.jp August 3, 2009 Title of Lecture: SCR Spin Fluctuation Theory 2 / 179 Part I Introduction Introduction Stoner-Wohlfarth Theory Stoner-Wohlfarth Theory Hatree Fock Approximation
液晶の物理1:連続体理論(弾性,粘性)
 The Physics of Liquid Crystals P. G. de Gennes and J. Prost (Oxford University Press, 1993) Liquid crystals are beautiful and mysterious; I am fond of them for both reasons. My hope is that some readers
The Physics of Liquid Crystals P. G. de Gennes and J. Prost (Oxford University Press, 1993) Liquid crystals are beautiful and mysterious; I am fond of them for both reasons. My hope is that some readers
MS#sugaku(ver.2).dvi
 1 1,,,.,,,,,.,.,,,.,, Computer-Aided Design).,,, Boltzmann,, [1]., Anderson, []., Anderson, Schrödinger [3],[4]., nm,,.,,,.,, Schrödinger.,, [5],[6].,,.,,, 1 .,, -. -, -., -,,,. Wigner-Boltzmann Schrödinger,
1 1,,,.,,,,,.,.,,,.,, Computer-Aided Design).,,, Boltzmann,, [1]., Anderson, []., Anderson, Schrödinger [3],[4]., nm,,.,,,.,, Schrödinger.,, [5],[6].,,.,,, 1 .,, -. -, -., -,,,. Wigner-Boltzmann Schrödinger,
Venkatram and Wyngaard, Lectures on Air Pollution Modeling, m km 6.2 Stull, An Introduction to Boundary Layer Meteorology,
 65 6 6.1 No.4 1982 1 1981 J. C. Kaimal 1993 1994 Turbulence and Diffusion in the Atmosphere : Lectures in Environmental Sciences, by A. K. Blackadar, Springer, 1998 An Introduction to Boundary Layer Meteorology,
65 6 6.1 No.4 1982 1 1981 J. C. Kaimal 1993 1994 Turbulence and Diffusion in the Atmosphere : Lectures in Environmental Sciences, by A. K. Blackadar, Springer, 1998 An Introduction to Boundary Layer Meteorology,
1 (Berry,1975) 2-6 p (S πr 2 )p πr 2 p 2πRγ p p = 2γ R (2.5).1-1 : : : : ( ).2 α, β α, β () X S = X X α X β (.1) 1 2
 2005 9/8-11 2 2.2 ( 2-5) γ ( ) γ cos θ 2πr πρhr 2 g h = 2γ cos θ ρgr (2.1) γ = ρgrh (2.2) 2 cos θ θ cos θ = 1 (2.2) γ = 1 ρgrh (2.) 2 2. p p ρgh p ( ) p p = p ρgh (2.) h p p = 2γ r 1 1 (Berry,1975) 2-6
2005 9/8-11 2 2.2 ( 2-5) γ ( ) γ cos θ 2πr πρhr 2 g h = 2γ cos θ ρgr (2.1) γ = ρgrh (2.2) 2 cos θ θ cos θ = 1 (2.2) γ = 1 ρgrh (2.) 2 2. p p ρgh p ( ) p p = p ρgh (2.) h p p = 2γ r 1 1 (Berry,1975) 2-6
LD
 989935 1 1 3 3 4 4 LD 6 7 10 1 3 13 13 16 0 4 5 30 31 33 33 35 35 37 38 5 40 FFT 40 40 4 4 4 44 47 48 49 51 51 5 53 54 55 56 Abstract [1] HDD (LaserDopplerVibrometer; LDV) [] HDD IC 1 4 LDV LDV He-Ne Acousto-optic
989935 1 1 3 3 4 4 LD 6 7 10 1 3 13 13 16 0 4 5 30 31 33 33 35 35 37 38 5 40 FFT 40 40 4 4 4 44 47 48 49 51 51 5 53 54 55 56 Abstract [1] HDD (LaserDopplerVibrometer; LDV) [] HDD IC 1 4 LDV LDV He-Ne Acousto-optic
 ( ) 1 1.1? ( ) ( ) ( ) 1.1(a) T m ( ) 1.1(a) T g ( ) T g T g 500 74% ( ) T K ( 1.1(b) 15 T g T g 10 13 T g T g T g [ ] A ( ) exp (1.1) T T 0 Vogel-Fulcher T 0 T 0 T K T K Ortho-Terphenil (OTP) SiO 2 (1.1)
( ) 1 1.1? ( ) ( ) ( ) 1.1(a) T m ( ) 1.1(a) T g ( ) T g T g 500 74% ( ) T K ( 1.1(b) 15 T g T g 10 13 T g T g T g [ ] A ( ) exp (1.1) T T 0 Vogel-Fulcher T 0 T 0 T K T K Ortho-Terphenil (OTP) SiO 2 (1.1)
master.dvi
 4 Maxwell- Boltzmann N 1 4.1 T R R 5 R (Heat Reservor) S E R 20 E 4.2 E E R E t = E + E R E R Ω R (E R ) S R (E R ) Ω R (E R ) = exp[s R (E R )/k] E, E E, E E t E E t E exps R (E t E) exp S R (E t E )
4 Maxwell- Boltzmann N 1 4.1 T R R 5 R (Heat Reservor) S E R 20 E 4.2 E E R E t = E + E R E R Ω R (E R ) S R (E R ) Ω R (E R ) = exp[s R (E R )/k] E, E E, E E t E E t E exps R (E t E) exp S R (E t E )
19 σ = P/A o σ B Maximum tensile strength σ % 0.2% proof stress σ EL Elastic limit Work hardening coefficient failure necking σ PL Proportional
 19 σ = P/A o σ B Maximum tensile strength σ 0. 0.% 0.% proof stress σ EL Elastic limit Work hardening coefficient failure necking σ PL Proportional limit ε p = 0.% ε e = σ 0. /E plastic strain ε = ε e
19 σ = P/A o σ B Maximum tensile strength σ 0. 0.% 0.% proof stress σ EL Elastic limit Work hardening coefficient failure necking σ PL Proportional limit ε p = 0.% ε e = σ 0. /E plastic strain ε = ε e
L L L L C C C C (a) (b) (c) 4.4 (a) (b) (a) RG59/U 6.2mm ( ) 73Ω web page (c) 4 4 dx 4 J V dx dj Ydx Zdx dv Z,Y dv = JZdx, dj = VYdx (4.8) d 2 J dx 2
 8 ( ) 2014 11 23 OP h g m r d 4 ( ) 4.2 + (lumped constant circuit) 4.2.1 3 (Poynting ) (strip line) (waveguide) (coaxial cable) GHz 4.4(a) dj dx dv Zdx Ydx ( ) (distributed constatn circuit) *1 4.4(c)
8 ( ) 2014 11 23 OP h g m r d 4 ( ) 4.2 + (lumped constant circuit) 4.2.1 3 (Poynting ) (strip line) (waveguide) (coaxial cable) GHz 4.4(a) dj dx dv Zdx Ydx ( ) (distributed constatn circuit) *1 4.4(c)
untitled
 MRR Physical Basis( 1.8.4) METEK MRR 1 MRR 1.1 MRR 24GHz FM-CW(frequency module continuous wave) 30 r+ r f+ f 1.2 1 4 MRR 24GHz 1.3 50mW 1 rf- (waveguide) (horn) 60cm ( monostatic radar) (continuous wave)
MRR Physical Basis( 1.8.4) METEK MRR 1 MRR 1.1 MRR 24GHz FM-CW(frequency module continuous wave) 30 r+ r f+ f 1.2 1 4 MRR 24GHz 1.3 50mW 1 rf- (waveguide) (horn) 60cm ( monostatic radar) (continuous wave)
4. ϵ(ν, T ) = c 4 u(ν, T ) ϵ(ν, T ) T ν π4 Planck dx = 0 e x 1 15 U(T ) x 3 U(T ) = σt 4 Stefan-Boltzmann σ 2π5 k 4 15c 2 h 3 = W m 2 K 4 5.
 A 1. Boltzmann Planck u(ν, T )dν = 8πh ν 3 c 3 kt 1 dν h 6.63 10 34 J s Planck k 1.38 10 23 J K 1 Boltzmann u(ν, T ) T ν e hν c = 3 10 8 m s 1 2. Planck λ = c/ν Rayleigh-Jeans u(ν, T )dν = 8πν2 kt dν c
A 1. Boltzmann Planck u(ν, T )dν = 8πh ν 3 c 3 kt 1 dν h 6.63 10 34 J s Planck k 1.38 10 23 J K 1 Boltzmann u(ν, T ) T ν e hν c = 3 10 8 m s 1 2. Planck λ = c/ν Rayleigh-Jeans u(ν, T )dν = 8πν2 kt dν c
5 1.2, 2, d a V a = M (1.2.1), M, a,,,,, Ω, V a V, V a = V + Ω r. (1.2.2), r i 1, i 2, i 3, i 1, i 2, i 3, A 2, A = 3 A n i n = n=1 da = 3 = n=1 3 n=1
 4 1 1.1 ( ) 5 1.2, 2, d a V a = M (1.2.1), M, a,,,,, Ω, V a V, V a = V + Ω r. (1.2.2), r i 1, i 2, i 3, i 1, i 2, i 3, A 2, A = 3 A n i n = n=1 da = 3 = n=1 3 n=1 da n i n da n i n + 3 A ni n n=1 3 n=1
4 1 1.1 ( ) 5 1.2, 2, d a V a = M (1.2.1), M, a,,,,, Ω, V a V, V a = V + Ω r. (1.2.2), r i 1, i 2, i 3, i 1, i 2, i 3, A 2, A = 3 A n i n = n=1 da = 3 = n=1 3 n=1 da n i n da n i n + 3 A ni n n=1 3 n=1
. ev=,604k m 3 Debye ɛ 0 kt e λ D = n e n e Ze 4 ln Λ ν ei = 5.6π / ɛ 0 m/ e kt e /3 ν ei v e H + +e H ev Saha x x = 3/ πme kt g i g e n
 003...............................3 Debye................. 3.4................ 3 3 3 3. Larmor Cyclotron... 3 3................ 4 3.3.......... 4 3.3............ 4 3.3...... 4 3.3.3............ 5 3.4.........
003...............................3 Debye................. 3.4................ 3 3 3 3. Larmor Cyclotron... 3 3................ 4 3.3.......... 4 3.3............ 4 3.3...... 4 3.3.3............ 5 3.4.........
18 I ( ) (1) I-1,I-2,I-3 (2) (3) I-1 ( ) (100 ) θ ϕ θ ϕ m m l l θ ϕ θ ϕ 2 g (1) (2) 0 (3) θ ϕ (4) (3) θ(t) = A 1 cos(ω 1 t + α 1 ) + A 2 cos(ω 2 t + α
 18 I ( ) (1) I-1,I-2,I-3 (2) (3) I-1 ( ) (100 ) θ ϕ θ ϕ m m l l θ ϕ θ ϕ 2 g (1) (2) 0 (3) θ ϕ (4) (3) θ(t) = A 1 cos(ω 1 t + α 1 ) + A 2 cos(ω 2 t + α 2 ), ϕ(t) = B 1 cos(ω 1 t + α 1 ) + B 2 cos(ω 2 t
18 I ( ) (1) I-1,I-2,I-3 (2) (3) I-1 ( ) (100 ) θ ϕ θ ϕ m m l l θ ϕ θ ϕ 2 g (1) (2) 0 (3) θ ϕ (4) (3) θ(t) = A 1 cos(ω 1 t + α 1 ) + A 2 cos(ω 2 t + α 2 ), ϕ(t) = B 1 cos(ω 1 t + α 1 ) + B 2 cos(ω 2 t
keisoku01.dvi
 2.,, Mon, 2006, 401, SAGA, JAPAN Dept. of Mechanical Engineering, Saga Univ., JAPAN 4 Mon, 2006, 401, SAGA, JAPAN Dept. of Mechanical Engineering, Saga Univ., JAPAN 5 Mon, 2006, 401, SAGA, JAPAN Dept.
2.,, Mon, 2006, 401, SAGA, JAPAN Dept. of Mechanical Engineering, Saga Univ., JAPAN 4 Mon, 2006, 401, SAGA, JAPAN Dept. of Mechanical Engineering, Saga Univ., JAPAN 5 Mon, 2006, 401, SAGA, JAPAN Dept.
untitled
 1 Physical Chemistry I (Basic Chemical Thermodynamics) [I] [II] [III] [IV] Introduction Energy(The First Law of Thermodynamics) Work Heat Capacity C p and C v Adiabatic Change Exact(=Perfect) Differential
1 Physical Chemistry I (Basic Chemical Thermodynamics) [I] [II] [III] [IV] Introduction Energy(The First Law of Thermodynamics) Work Heat Capacity C p and C v Adiabatic Change Exact(=Perfect) Differential
( ) Note (e ) (µ ) (τ ) ( (ν e,e ) e- (ν µ, µ ) µ- (ν τ,τ ) τ- ) ( ) ( ) (SU(2) ) (W +,Z 0,W ) * 1) 3 * 2) [ ] [ ] [ ] ν e ν µ ν τ e
![( ) Note (e ) (µ ) (τ ) ( (ν e,e ) e- (ν µ, µ ) µ- (ν τ,τ ) τ- ) ( ) ( ) (SU(2) ) (W +,Z 0,W ) * 1) 3 * 2) [ ] [ ] [ ] ν e ν µ ν τ e ( ) Note (e ) (µ ) (τ ) ( (ν e,e ) e- (ν µ, µ ) µ- (ν τ,τ ) τ- ) ( ) ( ) (SU(2) ) (W +,Z 0,W ) * 1) 3 * 2) [ ] [ ] [ ] ν e ν µ ν τ e](/thumbs/98/136160482.jpg) ( ) Note 3 19 12 13 8 8.1 (e ) (µ ) (τ ) ( (ν e,e ) e- (ν µ, µ ) µ- (ν τ,τ ) τ- ) ( ) ( ) (SU(2) ) (W +,Z 0,W ) * 1) 3 * 2) [ ] [ ] [ ] ν e ν µ ν τ e µ τ, e R, µ R, τ R (1a) L ( ) ) * 3) W Z 1/2 ( - )
( ) Note 3 19 12 13 8 8.1 (e ) (µ ) (τ ) ( (ν e,e ) e- (ν µ, µ ) µ- (ν τ,τ ) τ- ) ( ) ( ) (SU(2) ) (W +,Z 0,W ) * 1) 3 * 2) [ ] [ ] [ ] ν e ν µ ν τ e µ τ, e R, µ R, τ R (1a) L ( ) ) * 3) W Z 1/2 ( - )
64 3 g=9.85 m/s 2 g=9.791 m/s 2 36, km ( ) 1 () 2 () m/s : : a) b) kg/m kg/m k
 63 3 Section 3.1 g 3.1 3.1: : 64 3 g=9.85 m/s 2 g=9.791 m/s 2 36, km ( ) 1 () 2 () 3 9.8 m/s 2 3.2 3.2: : a) b) 5 15 4 1 1. 1 3 14. 1 3 kg/m 3 2 3.3 1 3 5.8 1 3 kg/m 3 3 2.65 1 3 kg/m 3 4 6 m 3.1. 65 5
63 3 Section 3.1 g 3.1 3.1: : 64 3 g=9.85 m/s 2 g=9.791 m/s 2 36, km ( ) 1 () 2 () 3 9.8 m/s 2 3.2 3.2: : a) b) 5 15 4 1 1. 1 3 14. 1 3 kg/m 3 2 3.3 1 3 5.8 1 3 kg/m 3 3 2.65 1 3 kg/m 3 4 6 m 3.1. 65 5
80 4 r ˆρ i (r, t) δ(r x i (t)) (4.1) x i (t) ρ i ˆρ i t = 0 i r 0 t(> 0) j r 0 + r < δ(r 0 x i (0))δ(r 0 + r x j (t)) > (4.2) r r 0 G i j (r, t) dr 0
 79 4 4.1 4.1.1 x i (t) x j (t) O O r 0 + r r r 0 x i (0) r 0 x i (0) 4.1 L. van. Hove 1954 space-time correlation function V N 4.1 ρ 0 = N/V i t 80 4 r ˆρ i (r, t) δ(r x i (t)) (4.1) x i (t) ρ i ˆρ i t
79 4 4.1 4.1.1 x i (t) x j (t) O O r 0 + r r r 0 x i (0) r 0 x i (0) 4.1 L. van. Hove 1954 space-time correlation function V N 4.1 ρ 0 = N/V i t 80 4 r ˆρ i (r, t) δ(r x i (t)) (4.1) x i (t) ρ i ˆρ i t
(Blackbody Radiation) (Stefan-Boltzmann s Law) (Wien s Displacement Law)
 ( ) ( ) 2002.11 1 1 1.1 (Blackbody Radiation).............................. 1 1.2 (Stefan-Boltzmann s Law)................ 1 1.3 (Wien s Displacement Law)....................... 2 1.4 (Kirchhoff s Law)...........................
( ) ( ) 2002.11 1 1 1.1 (Blackbody Radiation).............................. 1 1.2 (Stefan-Boltzmann s Law)................ 1 1.3 (Wien s Displacement Law)....................... 2 1.4 (Kirchhoff s Law)...........................
N cos s s cos ψ e e e e 3 3 e e 3 e 3 e
 3 3 5 5 5 3 3 7 5 33 5 33 9 5 8 > e > f U f U u u > u ue u e u ue u ue u e u e u u e u u e u N cos s s cos ψ e e e e 3 3 e e 3 e 3 e 3 > A A > A E A f A A f A [ ] f A A e > > A e[ ] > f A E A < < f ; >
3 3 5 5 5 3 3 7 5 33 5 33 9 5 8 > e > f U f U u u > u ue u e u ue u ue u e u e u u e u u e u N cos s s cos ψ e e e e 3 3 e e 3 e 3 e 3 > A A > A E A f A A f A [ ] f A A e > > A e[ ] > f A E A < < f ; >
NMRの信号がはじめて観測されてから47年になる。その後、NMRは1960年前半までPhys. Rev.等の物理学誌上を賑わせた。1960年代後半、物理学者の間では”NMRはもう死んだ”とささやかれたということであるが(1)、しかし、これほど発展した構造、物性の
 8. CW-NR Bloch[]Z (longitudinal relaxation timexy (transversal relaxation timebloembergen [] Bloch Bloembergen Bloch (3.. d d d x z = ( ω ω = ωz + ( ω ω x = ω ( z x (8..a (8..b (8..c = z = z θ = ω t (
8. CW-NR Bloch[]Z (longitudinal relaxation timexy (transversal relaxation timebloembergen [] Bloch Bloembergen Bloch (3.. d d d x z = ( ω ω = ωz + ( ω ω x = ω ( z x (8..a (8..b (8..c = z = z θ = ω t (
Microsoft Word - 学士論文(表紙).doc
 GHz 18 2 1 1 3 1.1....................................... 3 1.2....................................... 3 1.3................................... 3 2 (LDV) 5 2.1................................ 5 2.2.......................
GHz 18 2 1 1 3 1.1....................................... 3 1.2....................................... 3 1.3................................... 3 2 (LDV) 5 2.1................................ 5 2.2.......................
Keysight Technologies 誘電体測定の基礎
 Keysight Technologies Application Note LCR1.1 THz (MUT) 1. PCB PCB SAR RAM IC 3 Keysight - Application Note... 2... 4... 4... 7... 8... 1... 11... 11... 12 Debye... 12 Cole-Cole... 13... 13... 14... 15...
Keysight Technologies Application Note LCR1.1 THz (MUT) 1. PCB PCB SAR RAM IC 3 Keysight - Application Note... 2... 4... 4... 7... 8... 1... 11... 11... 12 Debye... 12 Cole-Cole... 13... 13... 14... 15...
S I. dy fx x fx y fx + C 3 C dy fx 4 x, y dy v C xt y C v e kt k > xt yt gt [ v dt dt v e kt xt v e kt + C k x v + C C k xt v k 3 r r + dr e kt S dt d
 S I.. http://ayapin.film.s.dendai.ac.jp/~matuda /TeX/lecture.html PDF PS.................................... 3.3.................... 9.4................5.............. 3 5. Laplace................. 5....
S I.. http://ayapin.film.s.dendai.ac.jp/~matuda /TeX/lecture.html PDF PS.................................... 3.3.................... 9.4................5.............. 3 5. Laplace................. 5....
1 No.1 5 C 1 I III F 1 F 2 F 1 F 2 2 Φ 2 (t) = Φ 1 (t) Φ 1 (t t). = Φ 1(t) t = ( 1.5e 0.5t 2.4e 4t 2e 10t ) τ < 0 t > τ Φ 2 (t) < 0 lim t Φ 2 (t) = 0
 1 No.1 5 C 1 I III F 1 F 2 F 1 F 2 2 Φ 2 (t) = Φ 1 (t) Φ 1 (t t). = Φ 1(t) t = ( 1.5e 0.5t 2.4e 4t 2e 10t ) τ < 0 t > τ Φ 2 (t) < 0 lim t Φ 2 (t) = 0 0 < t < τ I II 0 No.2 2 C x y x y > 0 x 0 x > b a dx
1 No.1 5 C 1 I III F 1 F 2 F 1 F 2 2 Φ 2 (t) = Φ 1 (t) Φ 1 (t t). = Φ 1(t) t = ( 1.5e 0.5t 2.4e 4t 2e 10t ) τ < 0 t > τ Φ 2 (t) < 0 lim t Φ 2 (t) = 0 0 < t < τ I II 0 No.2 2 C x y x y > 0 x 0 x > b a dx
i
 009 I 1 8 5 i 0 1 0.1..................................... 1 0.................................................. 1 0.3................................. 0.4........................................... 3
009 I 1 8 5 i 0 1 0.1..................................... 1 0.................................................. 1 0.3................................. 0.4........................................... 3
I-2 (100 ) (1) y(x) y dy dx y d2 y dx 2 (a) y + 2y 3y = 9e 2x (b) x 2 y 6y = 5x 4 (2) Bernoulli B n (n = 0, 1, 2,...) x e x 1 = n=0 B 0 B 1 B 2 (3) co
 16 I ( ) (1) I-1 I-2 I-3 (2) I-1 ( ) (100 ) 2l x x = 0 y t y(x, t) y(±l, t) = 0 m T g y(x, t) l y(x, t) c = 2 y(x, t) c 2 2 y(x, t) = g (A) t 2 x 2 T/m (1) y 0 (x) y 0 (x) = g c 2 (l2 x 2 ) (B) (2) (1)
16 I ( ) (1) I-1 I-2 I-3 (2) I-1 ( ) (100 ) 2l x x = 0 y t y(x, t) y(±l, t) = 0 m T g y(x, t) l y(x, t) c = 2 y(x, t) c 2 2 y(x, t) = g (A) t 2 x 2 T/m (1) y 0 (x) y 0 (x) = g c 2 (l2 x 2 ) (B) (2) (1)
.2 ρ dv dt = ρk grad p + 3 η grad (divv) + η 2 v.3 divh = 0, rote + c H t = 0 dive = ρ, H = 0, E = ρ, roth c E t = c ρv E + H c t = 0 H c E t = c ρv T
 NHK 204 2 0 203 2 24 ( ) 7 00 7 50 203 2 25 ( ) 7 00 7 50 203 2 26 ( ) 7 00 7 50 203 2 27 ( ) 7 00 7 50 I. ( ν R n 2 ) m 2 n m, R = e 2 8πε 0 hca B =.09737 0 7 m ( ν = ) λ a B = 4πε 0ħ 2 m e e 2 = 5.2977
NHK 204 2 0 203 2 24 ( ) 7 00 7 50 203 2 25 ( ) 7 00 7 50 203 2 26 ( ) 7 00 7 50 203 2 27 ( ) 7 00 7 50 I. ( ν R n 2 ) m 2 n m, R = e 2 8πε 0 hca B =.09737 0 7 m ( ν = ) λ a B = 4πε 0ħ 2 m e e 2 = 5.2977
O x y z O ( O ) O (O ) 3 x y z O O x v t = t = 0 ( 1 ) O t = 0 c t r = ct P (x, y, z) r 2 = x 2 + y 2 + z 2 (t, x, y, z) (ct) 2 x 2 y 2 z 2 = 0
 9 O y O ( O ) O (O ) 3 y O O v t = t = 0 ( ) O t = 0 t r = t P (, y, ) r = + y + (t,, y, ) (t) y = 0 () ( )O O t (t ) y = 0 () (t) y = (t ) y = 0 (3) O O v O O v O O O y y O O v P(, y,, t) t (, y,, t )
9 O y O ( O ) O (O ) 3 y O O v t = t = 0 ( ) O t = 0 t r = t P (, y, ) r = + y + (t,, y, ) (t) y = 0 () ( )O O t (t ) y = 0 () (t) y = (t ) y = 0 (3) O O v O O v O O O y y O O v P(, y,, t) t (, y,, t )
x A Aω ẋ ẋ 2 + ω 2 x 2 = ω 2 A 2. (ẋ, ωx) ζ ẋ + iωx ζ ζ dζ = ẍ + iωẋ = ẍ + iω(ζ iωx) dt dζ dt iωζ = ẍ + ω2 x (2.1) ζ ζ = Aωe iωt = Aω cos ωt + iaω sin
 2 2.1 F (t) 2.1.1 mẍ + kx = F (t). m ẍ + ω 2 x = F (t)/m ω = k/m. 1 : (ẋ, x) x = A sin ωt, ẋ = Aω cos ωt 1 2-1 x A Aω ẋ ẋ 2 + ω 2 x 2 = ω 2 A 2. (ẋ, ωx) ζ ẋ + iωx ζ ζ dζ = ẍ + iωẋ = ẍ + iω(ζ iωx) dt dζ
2 2.1 F (t) 2.1.1 mẍ + kx = F (t). m ẍ + ω 2 x = F (t)/m ω = k/m. 1 : (ẋ, x) x = A sin ωt, ẋ = Aω cos ωt 1 2-1 x A Aω ẋ ẋ 2 + ω 2 x 2 = ω 2 A 2. (ẋ, ωx) ζ ẋ + iωx ζ ζ dζ = ẍ + iωẋ = ẍ + iω(ζ iωx) dt dζ
I ( ) 1 de Broglie 1 (de Broglie) p λ k h Planck ( Js) p = h λ = k (1) h 2π : Dirac k B Boltzmann ( J/K) T U = 3 2 k BT
 I (008 4 0 de Broglie (de Broglie p λ k h Planck ( 6.63 0 34 Js p = h λ = k ( h π : Dirac k B Boltzmann (.38 0 3 J/K T U = 3 k BT ( = λ m k B T h m = 0.067m 0 m 0 = 9. 0 3 kg GaAs( a T = 300 K 3 fg 07345
I (008 4 0 de Broglie (de Broglie p λ k h Planck ( 6.63 0 34 Js p = h λ = k ( h π : Dirac k B Boltzmann (.38 0 3 J/K T U = 3 k BT ( = λ m k B T h m = 0.067m 0 m 0 = 9. 0 3 kg GaAs( a T = 300 K 3 fg 07345
* 1 1 (i) (ii) Brückner-Hartree-Fock (iii) (HF, BCS, HFB) (iv) (TDHF,TDHFB) (RPA) (QRPA) (v) (vi) *
 * 1 1 (i) (ii) Brückner-Hartree-Fock (iii) (HF, BCS, HFB) (iv) (TDHF,TDHFB) (RPA) (QRPA) (v) (vi) *1 2004 1 1 ( ) ( ) 1.1 140 MeV 1.2 ( ) ( ) 1.3 2.6 10 8 s 7.6 10 17 s? Λ 2.5 10 10 s 6 10 24 s 1.4 ( m
* 1 1 (i) (ii) Brückner-Hartree-Fock (iii) (HF, BCS, HFB) (iv) (TDHF,TDHFB) (RPA) (QRPA) (v) (vi) *1 2004 1 1 ( ) ( ) 1.1 140 MeV 1.2 ( ) ( ) 1.3 2.6 10 8 s 7.6 10 17 s? Λ 2.5 10 10 s 6 10 24 s 1.4 ( m
(1.2) T D = 0 T = D = 30 kn 1.2 (1.4) 2F W = 0 F = W/2 = 300 kn/2 = 150 kn 1.3 (1.9) R = W 1 + W 2 = = 1100 N. (1.9) W 2 b W 1 a = 0
 1 1 1.1 1.) T D = T = D = kn 1. 1.4) F W = F = W/ = kn/ = 15 kn 1. 1.9) R = W 1 + W = 6 + 5 = 11 N. 1.9) W b W 1 a = a = W /W 1 )b = 5/6) = 5 cm 1.4 AB AC P 1, P x, y x, y y x 1.4.) P sin 6 + P 1 sin 45
1 1 1.1 1.) T D = T = D = kn 1. 1.4) F W = F = W/ = kn/ = 15 kn 1. 1.9) R = W 1 + W = 6 + 5 = 11 N. 1.9) W b W 1 a = a = W /W 1 )b = 5/6) = 5 cm 1.4 AB AC P 1, P x, y x, y y x 1.4.) P sin 6 + P 1 sin 45
TOP URL 1
 TOP URL http://amonphys.web.fc.com/ 1 19 3 19.1................... 3 19.............................. 4 19.3............................... 6 19.4.............................. 8 19.5.............................
TOP URL http://amonphys.web.fc.com/ 1 19 3 19.1................... 3 19.............................. 4 19.3............................... 6 19.4.............................. 8 19.5.............................
4.6 (E i = ε, ε + ) T Z F Z = e βε + e β(ε+ ) = e βε (1 + e β ) F = kt log Z = kt log[e βε (1 + e β )] = ε kt ln(1 + e β ) (4.18) F (T ) S = T = k = k
![4.6 (E i = ε, ε + ) T Z F Z = e βε + e β(ε+ ) = e βε (1 + e β ) F = kt log Z = kt log[e βε (1 + e β )] = ε kt ln(1 + e β ) (4.18) F (T ) S = T = k = k 4.6 (E i = ε, ε + ) T Z F Z = e βε + e β(ε+ ) = e βε (1 + e β ) F = kt log Z = kt log[e βε (1 + e β )] = ε kt ln(1 + e β ) (4.18) F (T ) S = T = k = k](/thumbs/94/119235351.jpg) 4.6 (E i = ε, ε + ) T Z F Z = e ε + e (ε+ ) = e ε ( + e ) F = kt log Z = kt loge ε ( + e ) = ε kt ln( + e ) (4.8) F (T ) S = T = k = k ln( + e ) + kt e + e kt 2 + e ln( + e ) + kt (4.20) /kt T 0 = /k (4.20)
4.6 (E i = ε, ε + ) T Z F Z = e ε + e (ε+ ) = e ε ( + e ) F = kt log Z = kt loge ε ( + e ) = ε kt ln( + e ) (4.8) F (T ) S = T = k = k ln( + e ) + kt e + e kt 2 + e ln( + e ) + kt (4.20) /kt T 0 = /k (4.20)
) a + b = i + 6 b c = 6i j ) a = 0 b = c = 0 ) â = i + j 0 ˆb = 4) a b = b c = j + ) cos α = cos β = 6) a ˆb = b ĉ = 0 7) a b = 6i j b c = i + 6j + 8)
 4 4 ) a + b = i + 6 b c = 6i j ) a = 0 b = c = 0 ) â = i + j 0 ˆb = 4) a b = b c = j + ) cos α = cos β = 6) a ˆb = b ĉ = 0 7) a b = 6i j b c = i + 6j + 8) a b a b = 6i j 4 b c b c 9) a b = 4 a b) c = 7
4 4 ) a + b = i + 6 b c = 6i j ) a = 0 b = c = 0 ) â = i + j 0 ˆb = 4) a b = b c = j + ) cos α = cos β = 6) a ˆb = b ĉ = 0 7) a b = 6i j b c = i + 6j + 8) a b a b = 6i j 4 b c b c 9) a b = 4 a b) c = 7
pp * Yw; Mq 1. 1L 20 cc [1] Sonoluminescence: Light emission from acoustic cavitation bubble. Pak-Kon Choi (Departm
![pp * Yw; Mq 1. 1L 20 cc [1] Sonoluminescence: Light emission from acoustic cavitation bubble. Pak-Kon Choi (Departm pp * Yw; Mq 1. 1L 20 cc [1] Sonoluminescence: Light emission from acoustic cavitation bubble. Pak-Kon Choi (Departm](/thumbs/94/118261255.jpg) 73 7 2017 pp. 447 454 447 * 43.25.Yw; 78.60.Mq 1. 1L 20 cc [1] Sonoluminescence: Light emission from acoustic cavitation bubble. Pak-Kon Choi (Department of Physics, Meiji University, Kawasaki, 214 8571)
73 7 2017 pp. 447 454 447 * 43.25.Yw; 78.60.Mq 1. 1L 20 cc [1] Sonoluminescence: Light emission from acoustic cavitation bubble. Pak-Kon Choi (Department of Physics, Meiji University, Kawasaki, 214 8571)
Anderson ( ) Anderson / 14
 Anderson 2008 12 ( ) Anderson 2008 12 1 / 14 Anderson ( ) Anderson 2008 12 2 / 14 Anderson P.W.Anderson 1958 ( ) Anderson 2008 12 3 / 14 Anderson tight binding Anderson tight binding Z d u (x) = V i u
Anderson 2008 12 ( ) Anderson 2008 12 1 / 14 Anderson ( ) Anderson 2008 12 2 / 14 Anderson P.W.Anderson 1958 ( ) Anderson 2008 12 3 / 14 Anderson tight binding Anderson tight binding Z d u (x) = V i u
( ) ) ) ) 5) 1 J = σe 2 6) ) 9) 1955 Statistical-Mechanical Theory of Irreversible Processes )
 ( 3 7 4 ) 2 2 ) 8 2 954 2) 955 3) 5) J = σe 2 6) 955 7) 9) 955 Statistical-Mechanical Theory of Irreversible Processes 957 ) 3 4 2 A B H (t) = Ae iωt B(t) = B(ω)e iωt B(ω) = [ Φ R (ω) Φ R () ] iω Φ R (t)
( 3 7 4 ) 2 2 ) 8 2 954 2) 955 3) 5) J = σe 2 6) 955 7) 9) 955 Statistical-Mechanical Theory of Irreversible Processes 957 ) 3 4 2 A B H (t) = Ae iωt B(t) = B(ω)e iωt B(ω) = [ Φ R (ω) Φ R () ] iω Φ R (t)
V(x) m e V 0 cos x π x π V(x) = x < π, x > π V 0 (i) x = 0 (V(x) V 0 (1 x 2 /2)) n n d 2 f dξ 2ξ d f 2 dξ + 2n f = 0 H n (ξ) (ii) H
 199 1 1 199 1 1. Vx) m e V cos x π x π Vx) = x < π, x > π V i) x = Vx) V 1 x /)) n n d f dξ ξ d f dξ + n f = H n ξ) ii) H n ξ) = 1) n expξ ) dn dξ n exp ξ )) H n ξ)h m ξ) exp ξ )dξ = π n n!δ n,m x = Vx)
199 1 1 199 1 1. Vx) m e V cos x π x π Vx) = x < π, x > π V i) x = Vx) V 1 x /)) n n d f dξ ξ d f dξ + n f = H n ξ) ii) H n ξ) = 1) n expξ ) dn dξ n exp ξ )) H n ξ)h m ξ) exp ξ )dξ = π n n!δ n,m x = Vx)
,, 2. Matlab Simulink 2018 PC Matlab Scilab 2
 (2018 ) ( -1) TA Email : ohki@i.kyoto-u.ac.jp, ske.ta@bode.amp.i.kyoto-u.ac.jp : 411 : 10 308 1 1 2 2 2.1............................................ 2 2.2..................................................
(2018 ) ( -1) TA Email : ohki@i.kyoto-u.ac.jp, ske.ta@bode.amp.i.kyoto-u.ac.jp : 411 : 10 308 1 1 2 2 2.1............................................ 2 2.2..................................................
SO(3) 7 = = 1 ( r ) + 1 r r r r ( l ) (5.17) l = 1 ( sin θ ) + sin θ θ θ ϕ (5.18) χ(r)ψ(θ, ϕ) l ψ = αψ (5.19) l 1 = i(sin ϕ θ l = i( cos ϕ θ l 3 = i ϕ
 SO(3) 71 5.7 5.7.1 1 ħ L k l k l k = iϵ kij x i j (5.117) l k SO(3) l z l ± = l 1 ± il = i(y z z y ) ± (z x x z ) = ( x iy) z ± z( x ± i y ) = X ± z ± z (5.118) l z = i(x y y x ) = 1 [(x + iy)( x i y )
SO(3) 71 5.7 5.7.1 1 ħ L k l k l k = iϵ kij x i j (5.117) l k SO(3) l z l ± = l 1 ± il = i(y z z y ) ± (z x x z ) = ( x iy) z ± z( x ± i y ) = X ± z ± z (5.118) l z = i(x y y x ) = 1 [(x + iy)( x i y )
1 9 v.0.1 c (2016/10/07) Minoru Suzuki T µ 1 (7.108) f(e ) = 1 e β(e µ) 1 E 1 f(e ) (Bose-Einstein distribution function) *1 (8.1) (9.1)
 1 9 v..1 c (216/1/7) Minoru Suzuki 1 1 9.1 9.1.1 T µ 1 (7.18) f(e ) = 1 e β(e µ) 1 E 1 f(e ) (Bose-Einstein distribution function) *1 (8.1) (9.1) E E µ = E f(e ) E µ (9.1) µ (9.2) µ 1 e β(e µ) 1 f(e )
1 9 v..1 c (216/1/7) Minoru Suzuki 1 1 9.1 9.1.1 T µ 1 (7.18) f(e ) = 1 e β(e µ) 1 E 1 f(e ) (Bose-Einstein distribution function) *1 (8.1) (9.1) E E µ = E f(e ) E µ (9.1) µ (9.2) µ 1 e β(e µ) 1 f(e )
I A A441 : April 15, 2013 Version : 1.1 I Kawahira, Tomoki TA (Shigehiro, Yoshida )
 I013 00-1 : April 15, 013 Version : 1.1 I Kawahira, Tomoki TA (Shigehiro, Yoshida) http://www.math.nagoya-u.ac.jp/~kawahira/courses/13s-tenbou.html pdf * 4 15 4 5 13 e πi = 1 5 0 5 7 3 4 6 3 6 10 6 17
I013 00-1 : April 15, 013 Version : 1.1 I Kawahira, Tomoki TA (Shigehiro, Yoshida) http://www.math.nagoya-u.ac.jp/~kawahira/courses/13s-tenbou.html pdf * 4 15 4 5 13 e πi = 1 5 0 5 7 3 4 6 3 6 10 6 17
S I. dy fx x fx y fx + C 3 C vt dy fx 4 x, y dy yt gt + Ct + C dt v e kt xt v e kt + C k x v k + C C xt v k 3 r r + dr e kt S Sr πr dt d v } dt k e kt
 S I. x yx y y, y,. F x, y, y, y,, y n http://ayapin.film.s.dendai.ac.jp/~matuda n /TeX/lecture.html PDF PS yx.................................... 3.3.................... 9.4................5..............
S I. x yx y y, y,. F x, y, y, y,, y n http://ayapin.film.s.dendai.ac.jp/~matuda n /TeX/lecture.html PDF PS yx.................................... 3.3.................... 9.4................5..............
 K E N Z U 2012 7 16 HP M. 1 1 4 1.1 3.......................... 4 1.2................................... 4 1.2.1..................................... 4 1.2.2.................................... 5................................
K E N Z U 2012 7 16 HP M. 1 1 4 1.1 3.......................... 4 1.2................................... 4 1.2.1..................................... 4 1.2.2.................................... 5................................
gr09.dvi
 .1, θ, ϕ d = A, t dt + B, t dtd + C, t d + D, t dθ +in θdϕ.1.1 t { = f1,t t = f,t { D, t = B, t =.1. t A, tdt e φ,t dt, C, td e λ,t d.1.3,t, t d = e φ,t dt + e λ,t d + dθ +in θdϕ.1.4 { = f1,t t = f,t {
.1, θ, ϕ d = A, t dt + B, t dtd + C, t d + D, t dθ +in θdϕ.1.1 t { = f1,t t = f,t { D, t = B, t =.1. t A, tdt e φ,t dt, C, td e λ,t d.1.3,t, t d = e φ,t dt + e λ,t d + dθ +in θdϕ.1.4 { = f1,t t = f,t {
NMRの信号がはじめて観測されてから47年になる。その後、NMRは1960年前半までPhys. Rev.等の物理学誌上を賑わせた。1960年代後半、物理学者の間では”NMRはもう死んだ”とささやかれたということであるが(1)、しかし、これほど発展した構造、物性の
 9. I S H0 = ωii + ωss ( (9.. H A ( q (0 A = a ( os θ (9..a r ( ± ± i A =± a sinθosθe ϕ r (9..b A a sin e r ( ± ± iϕ = θ (9.. µ 0 γ I γ S a = (9..d 4π A ( q q ( q * = ( A ( q (9..e (0 = { IS ( I+ S + I
9. I S H0 = ωii + ωss ( (9.. H A ( q (0 A = a ( os θ (9..a r ( ± ± i A =± a sinθosθe ϕ r (9..b A a sin e r ( ± ± iϕ = θ (9.. µ 0 γ I γ S a = (9..d 4π A ( q q ( q * = ( A ( q (9..e (0 = { IS ( I+ S + I
 http://www.ike-dyn.ritsumei.ac.jp/ hyoo/wave.html 1 1, 5 3 1.1 1..................................... 3 1.2 5.1................................... 4 1.3.......................... 5 1.4 5.2, 5.3....................
http://www.ike-dyn.ritsumei.ac.jp/ hyoo/wave.html 1 1, 5 3 1.1 1..................................... 3 1.2 5.1................................... 4 1.3.......................... 5 1.4 5.2, 5.3....................
03.Œk’ì
 HRS KG NG-HRS NG-KG AIC Fama 1965 Mandelbrot Blattberg Gonedes t t Kariya, et. al. Nagahara ARCH EngleGARCH Bollerslev EGARCH Nelson GARCH Heynen, et. al. r n r n =σ n w n logσ n =α +βlogσ n 1 + v n w
HRS KG NG-HRS NG-KG AIC Fama 1965 Mandelbrot Blattberg Gonedes t t Kariya, et. al. Nagahara ARCH EngleGARCH Bollerslev EGARCH Nelson GARCH Heynen, et. al. r n r n =σ n w n logσ n =α +βlogσ n 1 + v n w
/ Christopher Essex Radiation and the Violation of Bilinearity in the Thermodynamics of Irreversible Processes, Planet.Space Sci.32 (1984) 1035 Radiat
 / Christopher Essex Radiation and the Violation of Bilinearity in the Thermodynamics of Irreversible Processes, Planet.Space Sci.32 (1984) 1035 Radiation and the Continuing Failure of the Bilinear Formalism,
/ Christopher Essex Radiation and the Violation of Bilinearity in the Thermodynamics of Irreversible Processes, Planet.Space Sci.32 (1984) 1035 Radiation and the Continuing Failure of the Bilinear Formalism,
positron 1930 Dirac 1933 Anderson m 22Na(hl=2.6years), 58Co(hl=71days), 64Cu(hl=12hour) 68Ge(hl=288days) MeV : thermalization m psec 100
 positron 1930 Dirac 1933 Anderson m 22Na(hl=2.6years), 58Co(hl=71days), 64Cu(hl=12hour) 68Ge(hl=288days) 0.5 1.5MeV : thermalization 10 100 m psec 100psec nsec E total = 2mc 2 + E e + + E e Ee+ Ee-c mc
positron 1930 Dirac 1933 Anderson m 22Na(hl=2.6years), 58Co(hl=71days), 64Cu(hl=12hour) 68Ge(hl=288days) 0.5 1.5MeV : thermalization 10 100 m psec 100psec nsec E total = 2mc 2 + E e + + E e Ee+ Ee-c mc
3 3.1 R r r + R R r Rr [ ] ˆn(r) = ˆn(r + R) (3.1) R R = r ˆn(r) = ˆn(0) r 0 R = r C nn (r, r ) = C nn (r + R, r + R) = C nn (r r, 0) (3.2) ( 2.2 ) C
![3 3.1 R r r + R R r Rr [ ] ˆn(r) = ˆn(r + R) (3.1) R R = r ˆn(r) = ˆn(0) r 0 R = r C nn (r, r ) = C nn (r + R, r + R) = C nn (r r, 0) (3.2) ( 2.2 ) C 3 3.1 R r r + R R r Rr [ ] ˆn(r) = ˆn(r + R) (3.1) R R = r ˆn(r) = ˆn(0) r 0 R = r C nn (r, r ) = C nn (r + R, r + R) = C nn (r r, 0) (3.2) ( 2.2 ) C](/thumbs/94/119172213.jpg) 3 3.1 R r r + R R r Rr [ ] ˆn(r) = ˆn(r + R) (3.1) R R = r ˆn(r) = ˆn(0) r 0 R = r C nn (r, r ) = C nn (r + R, r + R) = C nn (r r, 0) (3.2) ( 2.2 ) C nn (r r ) = C nn (R(r r )) [2 ] 2 g(r, r ) ˆn(r) ˆn(r
3 3.1 R r r + R R r Rr [ ] ˆn(r) = ˆn(r + R) (3.1) R R = r ˆn(r) = ˆn(0) r 0 R = r C nn (r, r ) = C nn (r + R, r + R) = C nn (r r, 0) (3.2) ( 2.2 ) C nn (r r ) = C nn (R(r r )) [2 ] 2 g(r, r ) ˆn(r) ˆn(r
Microsoft PowerPoint - 山形大高野send ppt [互換モード]
![Microsoft PowerPoint - 山形大高野send ppt [互換モード] Microsoft PowerPoint - 山形大高野send ppt [互換モード]](/thumbs/96/127884904.jpg) , 2012 10 SCOPE, 2012 10 2 CDMA OFDMA OFDM SCOPE, 2012 10 OFDM 0-20 Relative Optical Power [db] -40-60 10 Gbps NRZ BPSK-SSB 36dB -80-20 -10 0 10 20 Relative Frequency [GHz] SSB SSB OFDM SSB SSB OFDM OFDM
, 2012 10 SCOPE, 2012 10 2 CDMA OFDMA OFDM SCOPE, 2012 10 OFDM 0-20 Relative Optical Power [db] -40-60 10 Gbps NRZ BPSK-SSB 36dB -80-20 -10 0 10 20 Relative Frequency [GHz] SSB SSB OFDM SSB SSB OFDM OFDM
untitled
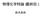 D nucleation 3 3D nucleation Glucose isomerase 10 V / nm s -1 5 0 0 5 10 C - C e / mg ml -1 kinetics µ R K kt kinetics kinetics kinetics r β π µ π r a r s + a s : β: µ πβ µ β s c s c a a r, & exp exp
D nucleation 3 3D nucleation Glucose isomerase 10 V / nm s -1 5 0 0 5 10 C - C e / mg ml -1 kinetics µ R K kt kinetics kinetics kinetics r β π µ π r a r s + a s : β: µ πβ µ β s c s c a a r, & exp exp
iBookBob:Users:bob:Documents:CurrentData:flMŠÍ…e…L…X…g:Statistics.dvi
 4 4 9............................................... 3.3......................... 4.4................. 5.5............................ 7 9..................... 9.............................3................................4..........................5.............................6...........................
4 4 9............................................... 3.3......................... 4.4................. 5.5............................ 7 9..................... 9.............................3................................4..........................5.............................6...........................
q π =0 Ez,t =ε σ {e ikz ωt e ikz ωt } i/ = ε σ sinkz ωt 5.6 x σ σ *105 q π =1 Ez,t = 1 ε σ + ε π {e ikz ωt e ikz ωt } i/ = 1 ε σ + ε π sinkz ωt 5.7 σ
 H k r,t= η 5 Stokes X k, k, ε, ε σ π X Stokes 5.1 5.1.1 Maxwell H = A A *10 A = 1 c A t 5.1 A kη r,t=ε η e ik r ωt 5. k ω ε η k η = σ, π ε σ, ε π σ π A k r,t= q η A kη r,t+qηa kηr,t 5.3 η q η E = 1 c A
H k r,t= η 5 Stokes X k, k, ε, ε σ π X Stokes 5.1 5.1.1 Maxwell H = A A *10 A = 1 c A t 5.1 A kη r,t=ε η e ik r ωt 5. k ω ε η k η = σ, π ε σ, ε π σ π A k r,t= q η A kη r,t+qηa kηr,t 5.3 η q η E = 1 c A
( ) ) AGD 2) 7) 1
 ( 9 5 6 ) ) AGD ) 7) S. ψ (r, t) ψ(r, t) (r, t) Ĥ ψ(r, t) = e iĥt/ħ ψ(r, )e iĥt/ħ ˆn(r, t) = ψ (r, t)ψ(r, t) () : ψ(r, t)ψ (r, t) ψ (r, t)ψ(r, t) = δ(r r ) () ψ(r, t)ψ(r, t) ψ(r, t)ψ(r, t) = (3) ψ (r,
( 9 5 6 ) ) AGD ) 7) S. ψ (r, t) ψ(r, t) (r, t) Ĥ ψ(r, t) = e iĥt/ħ ψ(r, )e iĥt/ħ ˆn(r, t) = ψ (r, t)ψ(r, t) () : ψ(r, t)ψ (r, t) ψ (r, t)ψ(r, t) = δ(r r ) () ψ(r, t)ψ(r, t) ψ(r, t)ψ(r, t) = (3) ψ (r,
