untitled
|
|
|
- やすもり かくはり
- 7 years ago
- Views:
Transcription
1 1 Physical Chemistry I (Basic Chemical Thermodynamics) [I] [II] [III] [IV] Introduction Energy(The First Law of Thermodynamics) Work Heat Capacity C p and C v Adiabatic Change Exact(=Perfect) Differential Heat of Chemical Reaction Entropy (The Second Law of Thermodynamics) Spontaneous Change Reversible Change and Irreversible Change Entropy 1) Randomness 2) Exact(=Perfect) Differential ds Calculation of Entropy Change 1) Adsorbed Heat by Reversible Change 2) Entropy Change accompany with Volume Change 3) S= f (T,P) Entropy of Mixing ΔS mix The Third Law Free Energy and Chemical Potential Helmholtz Free Energy and Gibbs Free Energy Exact(=Perfect) Differential da and dg Gibbs-Helmholtz Equation Properties of Mixtures; Partial Molar Quantities Partial Molar Free Energy; Chemical Potential a) Chemical Equilibrium b) Phase Equilibrium Thermodynamic Formulas Fundamental Relationship
2 2 A) 1 1mol A (A) B) 10 B (B) (A) (B) Isothermal compression, (B) (A) Isothermal expansion 0 (A) (B) (B) (A) 0
3 3 4 Heat of Solution ( ) 1 C 2 H 5 OH(l) +9H 2 O C 2 H 5 OH 9H 2 O 1mol 9mol 10%mol ΔH 1 = kj/mol 2 C 2 H 5 OH(l) +4H 2 O C 2 H 5 OH 4H 2 O 1mol 9mol 20%mol ΔH 2 = kj/mol ΔH 3) C 2 H 5 OH(4H 2 O) +5H 2 O C 2 H 5 OH 9H 2 O 20%mol 10%mol ΔH = ΔH 1 ΔH 2 = ( 7.021) ( 3.757) = kj/mol 10%mol 20%mol 20%mol 10%mol EtOH ( ΔH) n w /n a = n H2O /n alc=etoh ΔH ΔH= ΔH (Integral Heat of Solution) (Diffrential Heat of Solution) H 2 O n w = n H2O >>0, EtOH 1mol EtOH
4 J (A) 0 1atm, 22.4l (B) 0 10atm, 2.24l (A) (B) (A) 10atm 1atm W W =10 ( )=201.6(l atm) = = (kj) =1 ( )= 20.16(l atm) = = (kj) (kj) { (kj)}= (kj) J(=80Cal 4.184) 1g A B (A) 10atm 1atm (kj) J 54.9g AB (A)
5 5 Δs 10atm (A) (B) entropy Ideal gas R= (dm 3 atm K -1 mol -1 ) = (J K -1 mol -1 ) A 0 1atm, 22.4 dm 3 (B) 0 10atm, 2.24 dm 3 ( ) Δs = nc V In( T 2 T 1 ) + nrin( V 2 V 1 ) (III-32) 1-a: Δs gas = nrin( V 2 V 1 )= log(2.24/22.4) =19.15 (-1)=-19.15(J K -1 ) (A) (B) entropy V B 1-b: W = PdV = nrt ( 1 V )dv = nrtin V B V A = log(2.24/22.4) = 5218 ( 1)= +5218(kJ) ( ) V B V A V A
6 6 1-c: V B W = PdV = nrt ( 1 V )dv = nrtin V B V A V B V A V A U 1 =Q 1 + W 1 U 2 =Q 2 + W 2 ΔU=ΔQ ΔW ΔU =0 Q= W= PdV Δs gas = Q nrtin T = T V B V A = nrin V B V A = (J K -1 ) Δs gas =( W)/T= ( 5238)/(273.2)= 19.15(J K -1 ) () J 10atm W= PdV= 10 ( )= = (J) =+20.43(kJ) ΔU= J Δs ice =Δs surr =( W)/T= (+20430)/(273.2)= 74.8(J K -1 ) entropy 20430J J Δ s total = Δs gas + Δs surr = =+55.6(J K -1 )
7 7 U = Q+W du = TdS-PdV H = U+PV dh = TdS+VdP A = U-TS da = -SdT-PdV (IV-8) G = H-TS dg = -SdT + VdP (IV-12) Euler s relationship T V T P S V S P S S T T = P S = V S = P T P V = V T V P Maxwell s relationship (IV-16) (IV-17) (III-30) (III-39) Maxwell equation du = TdS-PdV U V U V T T = T S V = T P T V V P = T P T P V P (III-29) H P H P T T dh = TdS+VdP = T S P T = T V T + V = T V T P P + V + V (III-30) da = -SdT-PdV dg = -SdT + VdP (IV-8) (IV-12) A V A T G P G T T V T P = P = S = V = S da = -SdT-PdV (IV-8) dg = -SdT + VdP (IV-12) (IV-18) (IV-19) (IV-20) (IV-21)
8 8 U S U V H S H T V S T S = T = P = T = V du = TdS-PdV dh = TdS+VdP 1) x =f (y, z) 2) 3) dx = x y 1 y x x y z z Z = x y y z dy + x z x z z x y y = 1 dz (S-1) (II-32) (S-2) 4) dx = Kdy + Ldz K z y = L y z Eulers reciprocity relation (II-24) U T H T 1 V V P V T C V C P P 1 V V P α T β α : thermal expansion coefficient β : compressibility (II-14) (II-15) (S-3) (S-4) Gibbs-Helmholtz Equation ΔA =ΔU TΔS ΔG =ΔH TΔS P ΔG/T T ( ) ΔA =ΔU + T ΔA T ( ) ΔG =ΔH + T ΔG T (IV-24) (IV-25)
9 9 ΔG T T ( ) ΔG = 1 T ΔG + 1 T ( ΔG) 2 T T = T ΔG T 2 = ΔH T 2 Properties of Mixtures; Partial Molar Quantities X (V, U, H, S, A, G) X = f (T,P, n 1, n 2, n i ) (IV-26) dx = X dt + X dp + X T P, n 1, n 2, P dn T, n 1, n 2, n X 1 n i T, P, n 2, T, P, n j, dn i +... (IV-27) where n j ; n i n X X n i (IV-28) i T, P, n j T, P dx = X 1 dn 1 + X 2 dn X i dn i +... (IV-29) X = X 1 n 1 + X 2 n X i n i +... (IV-30) X = V; V i = V (IV-31) n i T, P, n j X = S; S i = S n i T, P, n j (IV-32) X = H; H i = H n i T, P, n j (IV-33) X = G; G i = G n i T, P, n j (IV-34) Partial Molar Enthalpy Change
10 10 ( ) ΔH i = ΔH n i T, P, n j Partial Molar Free Energy ; Chemical Potential G i = G μ n i i dg = -SdT+VdP+μ 1 dn 1 + μ 2 dn μ i dn i (IV-35) (IV-36) G = μ 1 n 1 + μ 2 n μ i n i (IV-37) a) (Chemical Equilibrium) ( μ 1,n i ) react ( ) = μ 1,n i aa + bb+.. react Ideal Gas Mixture productt ll + mm+.. Product eq. (III-42) ΔS MIX = R n i InX i 2 (n 1, n 2 ) S 0 1,S 0 2 ; ΔS MIX = ( n 1 S 1 + n 2 S 2 ) n 1 S ( 1 + n 2 S 2 )= n 1 ( S 1 S 1 )+ n 2 ( S 2 S 2 ) ( ) S 1 S 0 1 =ΔS 1 = ΔS MIX n 1 ( ) S 2 S 0 2 =ΔS 2 = ΔS MIX n 2 T, P, n 2 T, P, n 1 ΔH MIX = 0 ΔG MIX =ΔH MIX TΔS MIX (IV-38) (IV-39) ΔG MIX = - TΔS MIX ΔG MIX = TΔS MIX = T( R n i InX i )= RT n i InX i (IV-40)
11 11 ΔG 1 = G 1 G 0 1 = G MIX n 1 ΔG 2 = G 2 G 0 2 = G MIX n 2 = RTInX 1 T, P, n 2 = RTInX 2 T, P, n 1 (IV-41) (IV-41) μ 1 = μ RTInX 1 μ 2 = μ RTInX 2 (IV-42) Dolton X 1 = P 1 P X 2 = P 2 P P 1, P 2 P = P 1 = 1atm 1atm 0 μ = μ μ 0 : μ i = μ i 0 + RTInX i μ i = μ i 0 + RTInP i
12 12 Clapeyron-Clausius equation / G 1 = G 2 dg 1 = dg 2 dg = VdP SdT dg 1 = V 1 dp S 1 dt dg 2 = V 2 dp S 2 dt V 1 dp S 1 dt = = V 2 dp S 2 dt T (K), H b dp dt = S 2 S 1 V 2 V 1 S 2 S 1 =ΔS = H b T dp dt = H b ( ) TV 2 V 1 Clapeyron equation V 2 >>V 1 V 2 V 1 V dp dt = H b TV 2 = PH b RT 2 dp P 1 dt = H b RT 2 dinp dt = H b RT 2 Clapeyron-Clausius equation H b H b (A) InP = H b RT + const. (P 1, T 1 ) (P 2, T 2 ) In P 2 = H b 1 1 P 1 R T 2 T 1 (B) (C)
13 13 (Phase Rule) C α, β, γ, P (C - 1) P (C - 1)P μ α 1 = μ β p 1 == μ 1 μ α 2 = μ β p 2 == μ 2 C C μ α c = μ β p c == μ c P : C : P μ A = μ 0 A +RTInC A (P - 1) C F = 2+ (C 1)P (P 1)C = 2 + C P 1) C = 1, 2 P = 2 F = 2 + C P F = 1
14 14 2) C = 2, P = 2 F = 2 + C P F = 2 3) α- β C = 1, 2 P = 2 F = 2 + C P F = ) 3 C = 1, P = 3 F = 2 + C P F = (273.16K) 0.006atm 71 c t b x t : b t : c t : t : x t : b t : c t : t : x
15 15 U(S,V) c U = U(S,V,n 1,n 2,,n c ) U(S,V,n i ) n i i U du = U ds + U dv + S V, n i V S, n i = TdS PdV + μ i dn i c i =1 c i =1 U dn n i = TdS PdV + i S, V, n j i c i =1 U dn n i i S, V, n j i μ i chemical potential μ i = U n i S, V, n j i dn i 2 IV.1
16 16 2 IV.2 IV.3 IV T(X g ) (X l ) *X g X 2 X 2 X l X 2 T 1 T 2 2 T T 2 X 2 2 2
17 17 IV.4 (critical solution temperature) (a)(b) (c) (a) (b) (c) IV.5 [G/(n 1 +n 2 )] (X B, X B ) IV.4(a) 2 y, z y, z (tie line)2 2 2 IV
18 18 IV.6 IV.7 b 50 (E, eutectic point) (e) 2 (solid solution) Ni-Cu 2 IV.8 IV.3 IV.6 IV.8
19 19 (S 1,S 2 ) 2 (S A,S B ) IV.9 2 IV.6 2 IV (congruent melting compound, C ) 2 (congruent melting point) 2 3 ( r = 1)
20 20 2 / ( ) 2 X 2 n g, n l P 2 (n g + n l )X 2 = n g X g 2 + n l l X 2 X 2 X 2 g X 2 l X 2 = n l n g Gas P Liquid g l 0 X 2 X 2 X 2 2
21 21 entropy eq.(iii-37) T2 C T2 Δ = P S dt = C Pd ln T T1 T T g100 60g entropy t 80 (t 20) = 60 (100 t) t = 54.3 = K =Cal/g K=4.184J/g K 1mol C p = =75.3J K 1 mol 1 80g 327.5K entropy T ΔS1 = nc P ln = ln = log T J [J] = = = [K][mol] [K] 60g 100 =373.2K 327.5K entropy T ΔS 2 = nc P ln = ln = log T = entropy Δ 2 S over all = ΔS 1 + ΔS = = 4.23 [J/K] > 0 ΔS > 0
22 22 [IV] Free Energy and Chemical Potential Helmholtz Free Energy and Gibbs Free Energy [Energy or (Enthalpy) and Entropy] U or H ( ), S ( ) A U TS Helmholtz Free energy at constant volume G H TS Gibbs Free energy at constant pressure (IV-1) (IV-2) A or G: ΔA=ΔU TΔS (IV-3) ΔG=ΔH TΔS (IV-4) H (ΔH<0) G (ΔG<0) S (ΔS>0) G G ΔG = 0 Available capacity U A H, S G
23 23 ΔA = A 2 A 1 ΔG = G 2 G 1 (ΔA) T,V = 0 (ΔG) T,P = 0 (Equilibrium) ΔU = Q + W = TΔS+ W ΔH = ΔU + PΔV = TΔS+ W + PΔV ΔS (IV-3) ΔA=ΔU TΔS ΔA=ΔU TΔS = TΔS+ W TΔS = W (IV-4) : ΔG = ΔH TΔS ΔG = ΔH TΔS = TΔS+ W + PΔV TΔS = W + PΔV (IV-5) (IV-6) (IV-5) A ; Work function (Energy Dimension ) (IV-6) G ; Thermodynamic function ( G ) (Free energy) G 1 = G 2 (ΔG) T,P = 0 ΔG = ΔH TΔS ΔH > 0 = TΔS ΔH ΔG<0 eq. (IV-6) ΔG = W + PΔV W : PΔV : = ΔG<0, ΔG = 0 ΔG = ΔH TΔS
24 24 = Cell emf (electromotive force) Cell Chemical Reaction Voltaic cell (reversible cell ) Zn electrode 1 Cu electrode dil. H 2 SO 4 Daniell Cell = Reversible cell Zn ZnSO 4 aq. CuSO 4 aq. Cu Cu Zn, emf = 1.1V Zn + Cu 2+ Zn 2+ + Cu 1.1V Zn + Cu 2+ Zn 2+ + Cu 1.1V Cu 2+ Zn + Cu 2+ Zn 2+ + Cu Zn Zn 1.1V 1.1V emf W= ΔG = nfε
25 25 F = N A e = (mol 1 ) (C) = (C mol 1 ) Where: F: Faraday constant N A : Avogadro constant e: elementary charge () electric element 1[VC] =1[J] ΔG = nfε (IV-7) = (mol 1 )(C) 1.1(V)= = (kj/mol) 1.1V emf Daniell Cell 213.4(kJ/mol) Zn + Cu (kJ/mol) Zn 2+ + Cu 213.4(kJ/mol) Daniell Cell 1M CuSO 4 Zn ΔH = 218(kJ/mol) Zn + Cu 2+ Zn 2+ + Cu ΔG = 213.4(kJ/mol) at 25 ΔG = ΔH TΔS cell ΔS cell = (ΔH ΔG )/T=[ 218 ( 213.4)]/298.2 = (kJ/K)= 19.1 (J/K mol) 218kJ ΔH = 218 kj mol ΔS sur =ΔH/T= /298.2=731.1(J/K mol) ΔS total = ΔS cell +ΔS sur = =712(J/K mol) > 0
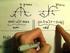
3.2 [ ]< 86, 87 > ( ) T = U V,N,, du = TdS PdV + µdn +, (3) P = U V S,N,, µ = U N. (4) S,V,, ( ) ds = 1 T du + P T dv µ dn +, (5) T 1 T = P U V,N,, T
![3.2 [ ]< 86, 87 > ( ) T = U V,N,, du = TdS PdV + µdn +, (3) P = U V S,N,, µ = U N. (4) S,V,, ( ) ds = 1 T du + P T dv µ dn +, (5) T 1 T = P U V,N,, T](/thumbs/82/86676506.jpg "3.2 [ ]< 86, 87 > ( ) T = U V,N,, du = TdS PdV + µdn +, (3) P = U V S,N,, µ = U N. (4) S,V,, ( ) ds = 1 T du + P T dv µ dn +, (5) T 1 T = P U V,N,, T")
3 3.1 [ ]< 85, 86 > ( ) ds > 0. (1) dt ds dt =0, S = S max. (2) ( δq 1 = TdS 1 =0) (δw 1 < 0) (du 1 < 0) (δq 2 > 0) (ds = ds 2 = TδQ 2 > 0) 39 3.2 [ ]< 86, 87 > ( ) T = U V,N,, du = TdS PdV + µdn +, (3)
September 25, ( ) pv = nrt (T = t( )) T: ( : (K)) : : ( ) e.g. ( ) ( ): 1
September 25, 2017 1 1.1 1.2 p = nr = 273.15 + t : : K : 1.3 1.3.1 : e.g. 1.3.2 : 1 intensive variable e.g. extensive variable e.g. 1.3.3 Equation of State e.g. p = nr X = A 2 2.1 2.1.1 Quantity of Heat
現代物理化学 1-1(4)16.ppt
(pdf) pdf pdf http://www1.doshisha.ac.jp/~bukka/lecture/index.html http://www.doshisha.ac.jp/ Duet -1-1-1 2-a. 1-1-2 EU E = K E + P E + U ΔE K E = 0P E ΔE = ΔU U U = εn ΔU ΔU = Q + W, du = d 'Q + d 'W
// //( ) (Helmholtz, Hermann Ludwig Ferdinand von: ) [ ]< 35, 36 > δq =0 du
![// //( ) (Helmholtz, Hermann Ludwig Ferdinand von: ) [ ]< 35, 36 > δq =0 du](/thumbs/91/105254510.jpg "// //( ) (Helmholtz, Hermann Ludwig Ferdinand von: ) [ ]< 35, 36 > δq =0 du")
2 2.1 1 [ 1 ]< 33, 34 > 1 (the first law of thermodynamics) U du = δw + δq (1) (internal energy)u (work)w δw rev = PdV (2) P (heat)q 1 1. U ( U ) 2. 1 (perpetuum mobile) 3. du 21 // //( ) (Helmholtz, Hermann
6 6.1 B A: Γ d Q S(B) S(A) = S (6.1) T (e) Γ (6.2) : Γ B A R (reversible) 6-1
6 6.1 B A: Γ d Q S(B) S(A) = S (6.1) (e) Γ (6.2) : Γ B A R (reversible) 6-1 (e) = Clausius 0 = B A: Γ B A: Γ d Q A + d Q (e) B: R d Q + S(A) S(B) (6.3) (e) // 6.2 B A: Γ d Q S(B) S(A) = S (6.4) (e) Γ (6.5)
P F ext 1: F ext P F ext (Count Rumford, ) H 2 O H 2 O 2 F ext F ext N 2 O 2 2
1 1 2 2 2 1 1 P F ext 1: F ext P F ext (Count Rumford, 1753 1814) 0 100 H 2 O H 2 O 2 F ext F ext N 2 O 2 2 P F S F = P S (1) ( 1 ) F ext x W ext W ext = F ext x (2) F ext P S W ext = P S x (3) S x V V
m d2 x = kx αẋ α > 0 (3.5 dt2 ( de dt = d dt ( 1 2 mẋ kx2 = mẍẋ + kxẋ = (mẍ + kxẋ = αẋẋ = αẋ 2 < 0 (3.6 Joule Joule 1843 Joule ( A B (> A ( 3-2
3 3.1 ( 1 m d2 x(t dt 2 = kx(t k = (3.1 d 2 x dt 2 = ω2 x, ω = x(t = 0, ẋ(0 = v 0 k m (3.2 x = v 0 ω sin ωt (ẋ = v 0 cos ωt (3.3 E = 1 2 mẋ2 + 1 2 kx2 = 1 2 mv2 0 cos 2 ωt + 1 2 k v2 0 ω 2 sin2 ωt = 1
1 (Berry,1975) 2-6 p (S πr 2 )p πr 2 p 2πRγ p p = 2γ R (2.5).1-1 : : : : ( ).2 α, β α, β () X S = X X α X β (.1) 1 2
2005 9/8-11 2 2.2 ( 2-5) γ ( ) γ cos θ 2πr πρhr 2 g h = 2γ cos θ ρgr (2.1) γ = ρgrh (2.2) 2 cos θ θ cos θ = 1 (2.2) γ = 1 ρgrh (2.) 2 2. p p ρgh p ( ) p p = p ρgh (2.) h p p = 2γ r 1 1 (Berry,1975) 2-6
A solution to Problems（物理化学II）Problem５
A solution to roblems( 物理化学 II)roblem 5 ) Q 0, W 0, Δ 0, ΔU0, nr dg - Sd d より, G - 8.345 298 2.303log(6/) - 4440(J/mol) da - Sd d A - 8.345 298 2.303log(6/) - 4440(J/mol) 2) da - Sd d A ΔA da d, ΔG d R
5 1.2, 2, d a V a = M (1.2.1), M, a,,,,, Ω, V a V, V a = V + Ω r. (1.2.2), r i 1, i 2, i 3, i 1, i 2, i 3, A 2, A = 3 A n i n = n=1 da = 3 = n=1 3 n=1
4 1 1.1 ( ) 5 1.2, 2, d a V a = M (1.2.1), M, a,,,,, Ω, V a V, V a = V + Ω r. (1.2.2), r i 1, i 2, i 3, i 1, i 2, i 3, A 2, A = 3 A n i n = n=1 da = 3 = n=1 3 n=1 da n i n da n i n + 3 A ni n n=1 3 n=1
i 18 2H 2 + O 2 2H 2 + ( ) 3K
i 18 2H 2 + O 2 2H 2 + ( ) 3K ii 1 1 1.1.................................. 1 1.2........................................ 3 1.3......................................... 3 1.4....................................
2007 5 iii 1 1 1.1.................... 1 2 5 2.1 (shear stress) (shear strain)...... 5 2.1.1...................... 6 2.1.2.................... 6 2.2....................... 7 2.2.1........................
3章 問題・略解
S S W R S O( l) O( ) c Jg g J Jg S R J 7. K.9 JK S W S R S JK S S R J 7. K.9JK 4 (a) -Tice 7.K T ice T N 77 K S R.9 JK 4. JK T T ice N.6JK S W S R S JK S S.6JK R (b) S R JK S.6 JK T T ice N 6 O( c) O(
1
I II II 1 dw = pd = 0 1 U = Q (4.10) 1K (heat capacity) (mole heat capacity) ( dq / d ) = ( du d C = / ) (4.11) du = C d U = C d (4.1) 1 1 du = dq + dw dw = pd dq = du + pd (4.13) p dq = d( U + p ) p (4.14)
1.5.1 SI kg, m, s ,,
0 9 0.1............................ 9 0.2.............. 10 0.3.................................. 13 0.4 (A2).................... 14 1, 0, 16 1.0.1..... 16 1.1............................. 16 1.1.1 (system)...........................
(A2) , 0,
0 10 0.1............................ 10 0.2.............. 11 0.3.................................. 14 0.4 (A2).................... 15 1, 0, 17 1.0.1..... 17 1.1............................. 17 1.1.1 (system)...........................
H21環境地球化学6_雲と雨_ ppt
1 2 3 40 13 (0.001%) 71 24,000 (1.7%) 385 425 111 1,350,000 (97%) 125 (0.009%) 40 10,000 (0.7%) 25 (0.002%) 10 3 km 3 10 3 km 3 /y 4 +1.3 +5.8 (21) () ( ) 5 HNO 3, SO 2 etc 6 7 2009年度 環境地球化学 大河内 10種雲形と発生高度
30
3 ............................................2 2...........................................2....................................2.2...................................2.3..............................
理想気体ideal gasの熱力学的基本関係式
the equipartition law of energy ( )kt k Boltzmann constant 5 Longman Dictionary of Physics (/)kt q Bq (/)kt equipartition law of energy mol (3/)kT (3/)RT (3/)R (5/)R 3R kt - equipartition of energy The
H22環境地球化学4_化学平衡III_ ppt
1 2 3 2009年度 環境地球化学 大河内 温度上昇による炭酸水の発泡 気泡 温度が高くなると 溶けきれなくなった 二酸化炭素が気泡として出てくる 4 2009年度 環境地球化学 圧力上昇による炭酸水の発泡 栓を開けると 瓶の中の圧力が急激に 小さくなるので 発泡する 大河内 5 CO 2 K H CO 2 H 2 O K H + 1 HCO 3- K 2 H + CO 3 2- (M) [CO
Microsoft Word - 11問題表紙（選択）.docx
A B A.70g/cm 3 B.74g/cm 3 B C 70at% %A C B at% 80at% %B 350 C γ δ y=00 x-y ρ l S ρ C p k C p ρ C p T ρ l t l S S ξ S t = ( k T ) ξ ( ) S = ( k T) ( ) t y ξ S ξ / t S v T T / t = v T / y 00 x v S dy dx
2009 June 8 toki/thermodynamics.pdf ) 1
2009 June 8 http://www.rcnp.osaka-u.ac.jp/ toki/thermodynamics.pdf 1 6 10 23 ) 1 H download 2 http://www.rcnp.osaka-u.ac.jp/ toki/thermodynamics.pdf 2 2.1 [1] [2] [3] Q = mc (1) C gr Q C = 1cal/gr deg
sin cos No. sine, cosine : trigonometric function π : π = 3.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin : odd cos = cos : even.
08 No. : No. : No.3 : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No.0 : No. : sin cos No. sine, cosine : trigonometric function π : π = 3.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin
r 1 m A r/m i) t ii) m i) t B(t; m) ( B(t; m) = A 1 + r ) mt m ii) B(t; m) ( B(t; m) = A 1 + r ) mt m { ( = A 1 + r ) m } rt r m n = m r m n B
1 1.1 1 r 1 m A r/m i) t ii) m i) t Bt; m) Bt; m) = A 1 + r ) mt m ii) Bt; m) Bt; m) = A 1 + r ) mt m { = A 1 + r ) m } rt r m n = m r m n Bt; m) Aert e lim 1 + 1 n 1.1) n!1 n) e a 1, a 2, a 3,... {a n
物理化学I-第12回(13).ppt
I- 12-1 11 11.1 2Mg(s) + O 2 (g) 2MgO(s) [Mg 2+ O 2 ] Zn(s) + Cu 2+ (aq) Zn 2+ (aq) + Cu(s) - 2Mg(s) 2Mg 2+ (s) + 4e +) O 2 (g) + 4e 2O 2 (s) 2Mg(s) + O 2 (g) 2MgO(s) Zn(s) Zn 2+ (aq) + 2e +) Cu 2+ (aq)
09 II 09/12/ (3D ) f(, y) = 2 + y 2 3D- 1 f(0, 0) = 2 f(1, 0) = 3 f(0, 1) = 4 f(1, 1) = 5 f( 1, 2) = 6 f(0, 1) = z y (3D ) f(, y) = 2 + y
09 II 09/12/21 1 1 7 1.1 I 2D II 3D f() = 3 6 2 + 9 2 f(, y) = 2 2 + 2y + y 2 6 4y f(1) = 1 3 6 1 2 9 1 2 = 2 y = f() f(3, 2) = 2 3 2 + 2 3 2 + 2 2 6 3 4 2 = 8 z = f(, y) y 2 1 z 8 3 2 y 1 ( y ) 1 (0,
<4D F736F F D B B83578B6594BB2D834A836F815B82D082C88C60202E646F63>
基礎からの冷凍空調 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/067311 このサンプルページの内容は, 初版 1 刷発行当時のものです. http://www.morikita.co.jp/support. 03-3817-5670FAX 03-3815-8199 i () () Q&A
I No. sin cos sine, cosine : trigonometric function π : π =.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin : odd cos = cos : even.
I 0 No. : No. : No. : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No.0 : I No. sin cos sine, cosine : trigonometric function π : π =.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin : odd
( ) Loewner SLE 13 February
( ) Loewner SLE 3 February 00 G. F. Lawler, Conformally Invariant Processes in the Plane, (American Mathematical Society, 005)., Summer School 009 (009 8 7-9 ) . d- (BES d ) d B t = (Bt, B t,, Bd t ) (d
211 [email protected] 1 R *1 n n R n *2 R n = {(x 1,..., x n ) x 1,..., x n R}. R R 2 R 3 R n R n R n D D R n *3 ) (x 1,..., x n ) f(x 1,..., x n ) f D *4 n 2 n = 1 ( ) 1 f D R n f : D R 1.1. (x,
I No. sin cos sine, cosine : trigonometric function π : π =.4 : n =, ±, ±, sin + nπ = sin cos + nπ = cos sin = sin : cos = cos :. sin. sin. sin + π si
I 8 No. : No. : No. : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No. : I No. sin cos sine, cosine : trigonometric function π : π =.4 : n =, ±, ±, sin + nπ = sin cos + nπ = cos sin = sin : cos = cos :. sin.
Part () () Γ Part ,
Contents a 6 6 6 6 6 6 6 7 7. 8.. 8.. 8.3. 8 Part. 9. 9.. 9.. 3. 3.. 3.. 3 4. 5 4.. 5 4.. 9 4.3. 3 Part. 6 5. () 6 5.. () 7 5.. 9 5.3. Γ 3 6. 3 6.. 3 6.. 3 6.3. 33 Part 3. 34 7. 34 7.. 34 7.. 34 8. 35
meiji_resume_1.PDF
β β β (q 1,q,..., q n ; p 1, p,..., p n ) H(q 1,q,..., q n ; p 1, p,..., p n ) Hψ = εψ ε k = k +1/ ε k = k(k 1) (x, y, z; p x, p y, p z ) (r; p r ), (θ; p θ ), (ϕ; p ϕ ) ε k = 1/ k p i dq i E total = E
.1 z = e x +xy y z y 1 1 x 0 1 z x y α β γ z = αx + βy + γ (.1) ax + by + cz = d (.1') a, b, c, d x-y-z (a, b, c). x-y-z 3 (0,
.1.1 Y K L Y = K 1 3 L 3 L K K (K + ) 1 1 3 L 3 K 3 L 3 K 0 (K + K) 1 3 L 3 K 1 3 L 3 lim K 0 K = L (K + K) 1 3 K 1 3 3 lim K 0 K = 1 3 K 3 L 3 z = f(x, y) x y z x-y-z.1 z = e x +xy y 3 x-y ( ) z 0 f(x,
18 I ( ) (1) I-1,I-2,I-3 (2) (3) I-1 ( ) (100 ) θ ϕ θ ϕ m m l l θ ϕ θ ϕ 2 g (1) (2) 0 (3) θ ϕ (4) (3) θ(t) = A 1 cos(ω 1 t + α 1 ) + A 2 cos(ω 2 t + α
18 I ( ) (1) I-1,I-2,I-3 (2) (3) I-1 ( ) (100 ) θ ϕ θ ϕ m m l l θ ϕ θ ϕ 2 g (1) (2) 0 (3) θ ϕ (4) (3) θ(t) = A 1 cos(ω 1 t + α 1 ) + A 2 cos(ω 2 t + α 2 ), ϕ(t) = B 1 cos(ω 1 t + α 1 ) + B 2 cos(ω 2 t
ma22-9 u ( v w) = u v w sin θê = v w sin θ u cos φ = = 2.3 ( a b) ( c d) = ( a c)( b d) ( a d)( b c) ( a b) ( c d) = (a 2 b 3 a 3 b 2 )(c 2 d 3 c 3 d
A 2. x F (t) =f sin ωt x(0) = ẋ(0) = 0 ω θ sin θ θ 3! θ3 v = f mω cos ωt x = f mω (t sin ωt) ω t 0 = f ( cos ωt) mω x ma2-2 t ω x f (t mω ω (ωt ) 6 (ωt)3 = f 6m ωt3 2.2 u ( v w) = v ( w u) = w ( u v) ma22-9
2 p T, Q
270 C, 6000 C, 2 p T, Q p: : p = N/ m 2 N/ m 2 Pa : pdv p S F Q 1 g 1 1 g 1 14.5 C 15.5 1 1 cal = 4.1855 J du = Q pdv U ( ) Q pdv 2 : z = f(x, y). z = f(x, y) (x 0, y 0 ) y y = y 0 z = f(x, y 0 ) x x =
untitled
SPring-8 RFgun JASRI/SPring-8 6..7 Contents.. 3.. 5. 6. 7. 8. . 3 cavity γ E A = er 3 πε γ vb r B = v E c r c A B A ( ) F = e E + v B A A A A B dp e( v B+ E) = = m d dt dt ( γ v) dv e ( ) dt v B E v E
25 7 18 1 1 1.1 v.s............................. 1 1.1.1.................................. 1 1.1.2................................. 1 1.1.3.................................. 3 1.2................... 3
入試の軌跡
4 y O x 4 Typed by L A TEX ε ) ) ) 6 4 ) 4 75 ) http://kumamoto.s.xrea.com/plan/.. PDF) Ctrl +L) Ctrl +) Ctrl + Ctrl + ) ) Alt + ) Alt + ) ESC. http://kumamoto.s.xrea.com/nyusi/kumadai kiseki ri i.pdf
( ) ( )
20 21 2 8 1 2 2 3 21 3 22 3 23 4 24 5 25 5 26 6 27 8 28 ( ) 9 3 10 31 10 32 ( ) 12 4 13 41 0 13 42 14 43 0 15 44 17 5 18 6 18 1 1 2 2 1 2 1 0 2 0 3 0 4 0 2 2 21 t (x(t) y(t)) 2 x(t) y(t) γ(t) (x(t) y(t))
genron-3
" ( K p( pasals! ( kg / m 3 " ( K! v M V! M / V v V / M! 3 ( kg / m v ( v "! v p v # v v pd v ( J / kg p ( $ 3! % S $ ( pv" 3 ( ( 5 pv" pv R" p R!" R " ( K ( 6 ( 7 " pv pv % p % w ' p% S & $ p% v ( J /
,. Black-Scholes u t t, x c u 0 t, x x u t t, x c u t, x x u t t, x + σ x u t, x + rx ut, x rux, t 0 x x,,.,. Step 3, 7,,, Step 6., Step 4,. Step 5,,.
9 α ν β Ξ ξ Γ γ o δ Π π ε ρ ζ Σ σ η τ Θ θ Υ υ ι Φ φ κ χ Λ λ Ψ ψ µ Ω ω Def, Prop, Th, Lem, Note, Remark, Ex,, Proof, R, N, Q, C [a, b {x R : a x b} : a, b {x R : a < x < b} : [a, b {x R : a x < b} : a,
1 12 ( )150 ( ( ) ) x M x 0 1 M 2 5x 2 + 4x + 3 x 2 1 M x M 2 1 M x (x + 1) 2 (1) x 2 + x + 1 M (2) 1 3 M (3) x 4 +
( )5 ( ( ) ) 4 6 7 9 M M 5 + 4 + M + M M + ( + ) () + + M () M () 4 + + M a b y = a + b a > () a b () y V a () V a b V n f() = n k= k k () < f() = log( ) t dt log () n+ (i) dt t (n + ) (ii) < t dt n+ n
1) K. J. Laidler, "Reaction Kinetics", Vol. II, Pergamon Press, New York (1963) Chap. 1 ; P. G. Ashmore, "Catalysis and Inhibition of Chemical Reactio
1) K. J. Laidler, "Reaction Kinetics", Vol. II, Pergamon Press, New York (1963) Chap. 1 ; P. G. Ashmore, "Catalysis and Inhibition of Chemical Reactions", Butterworths, London (1963) Chap. 7, p. 185. 2)
(a) (b) X Ag + + X AgX F < Cl < Br < I Li + + X LiX F > Cl > Br > I (a) (b) (c)
( 13 : 30 16 : 00 ) (a) (b) X Ag + + X AgX F < Cl < Br < I Li + + X LiX F > Cl > Br > I (a) (b) (c) (a) CH 3 -Br (b) (c),2,4- (d) CH 3 O-CH=CH-CH 2 (a) NH 2 CH 3 H 3 C NH 2 H CH 3 CH 3 NH 2 H 3 C CH 3
I-2 (100 ) (1) y(x) y dy dx y d2 y dx 2 (a) y + 2y 3y = 9e 2x (b) x 2 y 6y = 5x 4 (2) Bernoulli B n (n = 0, 1, 2,...) x e x 1 = n=0 B 0 B 1 B 2 (3) co
16 I ( ) (1) I-1 I-2 I-3 (2) I-1 ( ) (100 ) 2l x x = 0 y t y(x, t) y(±l, t) = 0 m T g y(x, t) l y(x, t) c = 2 y(x, t) c 2 2 y(x, t) = g (A) t 2 x 2 T/m (1) y 0 (x) y 0 (x) = g c 2 (l2 x 2 ) (B) (2) (1)
<4D F736F F D B B83578B6594BB2D834A836F815B82D082C88C60202D B202D B202D
わかりやすい熱力学第 3 版 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/060013 このサンプルページの内容は, 第 3 版発行時のものです. i ii 49 7 iii 3 38 40 90 3 2012 9 iv 1 1 2 4 2.1 4 2.2 5 2.3 6 2.4 7 2.5
KENZOU
KENZOU 2008 8 2 3 2 3 2 2 4 2 4............................................... 2 4.2............................... 3 4.2........................................... 4 4.3..............................
D v D F v/d F v D F η v D (3.2) (a) F=0 (b) v=const. D F v Newtonian fluid σ ė σ = ηė (2.2) ė kl σ ij = D ijkl ė kl D ijkl (2.14) ė ij (3.3) µ η visco
post glacial rebound 3.1 Viscosity and Newtonian fluid f i = kx i σ ij e kl ideal fluid (1.9) irreversible process e ij u k strain rate tensor (3.1) v i u i / t e ij v F 23 D v D F v/d F v D F η v D (3.2)
「産業上利用することができる発明」の審査の運用指針（案）
1 1.... 2 1.1... 2 2.... 4 2.1... 4 3.... 6 4.... 6 1 1 29 1 29 1 1 1. 2 1 1.1 (1) (2) (3) 1 (4) 2 4 1 2 2 3 4 31 12 5 7 2.2 (5) ( a ) ( b ) 1 3 2 ( c ) (6) 2. 2.1 2.1 (1) 4 ( i ) ( ii ) ( iii ) ( iv)
Note.tex 2008/09/19( )
1 20 9 19 2 1 5 1.1........................ 5 1.2............................. 8 2 9 2.1............................. 9 2.2.............................. 10 3 13 3.1.............................. 13 3.2..................................
.2 ρ dv dt = ρk grad p + 3 η grad (divv) + η 2 v.3 divh = 0, rote + c H t = 0 dive = ρ, H = 0, E = ρ, roth c E t = c ρv E + H c t = 0 H c E t = c ρv T
NHK 204 2 0 203 2 24 ( ) 7 00 7 50 203 2 25 ( ) 7 00 7 50 203 2 26 ( ) 7 00 7 50 203 2 27 ( ) 7 00 7 50 I. ( ν R n 2 ) m 2 n m, R = e 2 8πε 0 hca B =.09737 0 7 m ( ν = ) λ a B = 4πε 0ħ 2 m e e 2 = 5.2977
1
1 1 7 1.1.................................. 11 2 13 2.1............................ 13 2.2............................ 17 2.3.................................. 19 3 21 3.1.............................
研修コーナー
l l l l l l l l l l l α α β l µ l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l
120 9 I I 1 I 2 I 1 I 2 ( a) ( b) ( c ) I I 2 I 1 I ( d) ( e) ( f ) 9.1: Ampère (c) (d) (e) S I 1 I 2 B ds = µ 0 ( I 1 I 2 ) I 1 I 2 B ds =0. I 1 I 2
9 E B 9.1 9.1.1 Ampère Ampère Ampère s law B S µ 0 B ds = µ 0 j ds (9.1) S rot B = µ 0 j (9.2) S Ampère Biot-Savart oulomb Gauss Ampère rot B 0 Ampère µ 0 9.1 (a) (b) I B ds = µ 0 I. I 1 I 2 B ds = µ 0
1
1 2 3 4 5 6 7 8 9 10 A I A I d d d+a 11 12 57 c 1 NIHONN 2 i 3 c 13 14 < 15 16 < 17 18 NS-TB2N NS-TBR1D 19 -21BR -70-21 -70-22 20 21 22 23 24 d+ a 25 26 w qa e a a 27 28 -21 29 w w q q q w 30 r w q!5 y
[ ] (Ising model) 2 i S i S i = 1 (up spin : ) = 1 (down spin : ) (4.38) s z = ±1 4 H 0 = J zn/2 i,j S i S j (4.39) i, j z 5 2 z = 4 z = 6 3
![[ ] (Ising model) 2 i S i S i = 1 (up spin : ) = 1 (down spin : ) (4.38) s z = ±1 4 H 0 = J zn/2 i,j S i S j (4.39) i, j z 5 2 z = 4 z = 6 3](/thumbs/103/161261933.jpg "[ ] (Ising model) 2 i S i S i = 1 (up spin : ) = 1 (down spin : ) (4.38) s z = ±1 4 H 0 = J zn/2 i,j S i S j (4.39) i, j z 5 2 z = 4 z = 6 3")
4.2 4.2.1 [ ] (Ising model) 2 i S i S i = 1 (up spin : ) = 1 (down spin : ) (4.38) s z = ±1 4 H 0 = J zn/2 S i S j (4.39) i, j z 5 2 z = 4 z = 6 3 z = 6 z = 8 zn/2 1 2 N i z nearest neighbors of i j=1
Microsoft PowerPoint - 熱力学Ⅱ2FreeEnergy2012HP.ppt [互換モード]
![Microsoft PowerPoint - 熱力学Ⅱ2FreeEnergy2012HP.ppt [互換モード]](/thumbs/79/80168709.jpg "Microsoft PowerPoint - 熱力学Ⅱ2FreeEnergy2012HP.ppt [互換モード]")
熱力学 Ⅱ 第 章自由エネルギー システム情報工学研究科 構造エネルギー工学専攻 金子暁子 問題 ( 解答 ). 熱量 Q をある系に与えたところ, 系の体積は膨張し, 温度は上昇した. () 熱量 Q は何に変化したか. () またこのとき系の体積がV よりV に変化した.( 圧力は変化無し.) 内部エネルギーはどのように表されるか. また, このときのp-V 線図を示しなさい.. 不可逆過程の例を
24 I ( ) 1. R 3 (i) C : x 2 + y 2 1 = 0 (ii) C : y = ± 1 x 2 ( 1 x 1) (iii) C : x = cos t, y = sin t (0 t 2π) 1.1. γ : [a, b] R n ; t γ(t) = (x
![24 I ( ) 1. R 3 (i) C : x 2 + y 2 1 = 0 (ii) C : y = ± 1 x 2 ( 1 x 1) (iii) C : x = cos t, y = sin t (0 t 2π) 1.1. γ : [a, b] R n ; t γ(t) = (x](/thumbs/94/118744578.jpg "24 I ( ) 1. R 3 (i) C : x 2 + y 2 1 = 0 (ii) C : y = ± 1 x 2 ( 1 x 1) (iii) C : x = cos t, y = sin t (0 t 2π) 1.1. γ : [a, b] R n ; t γ(t) = (x")
24 I 1.1.. ( ) 1. R 3 (i) C : x 2 + y 2 1 = 0 (ii) C : y = ± 1 x 2 ( 1 x 1) (iii) C : x = cos t, y = sin t (0 t 2π) 1.1. γ : [a, b] R n ; t γ(t) = (x 1 (t), x 2 (t),, x n (t)) ( ) ( ), γ : (i) x 1 (t),
i
mailto: tomita@physhkyoto-uacjp 2000 3 2000 8 2001 7 2002 9 2003 9 2000 2002 9 i 1 1 11 { : : : : : : : : : : : : : : : : : : : : : : : : 1 12 : : : : : : : : : : : : : : : : : : : : : : : : : : : : 3