|
|
|
- やすはる やすもと
- 5 years ago
- Views:
Transcription
1 九州大学学術情報リポジトリ Kyushu University Institutional Repository 大規模電力系統の故障計算手法に関する研究 田中, 和幸 出版情報 :Kyushu University, 1996, 博士 ( 工学 ), 論文博士バージョン :published 権利関係 :
2
3 大規模電力系統の故障計算手法に関する研究 田中和幸
4 フ犬二支見本莫霊亘プフヨミ乏充 α 古まと陸註言十主宰弓三才去じこ隠司す一る石井ラ宅 まえがき 1. 故障計算の概要と用途一一 一一一一一一一一一一一一一一一一一一一一一一一 大規模系統の故障計算に求められる要件 1.2 対称座標法 1.3 故障計算の基本的方法一一一一一一一一一一一一一一一一一一一一一一一一 一安定度解析計算における位置付け一一一一一一一一一一一一一一一一一一 短絡容量計算における位置付け一一一一一一一一一一一一一一一一一一一一 各種故障の統一的定式化手法の開発一一一一一 一一一一一一一一一一一一一 地絡故障 一一ー一一一一一一一一一一一一一一一一一一一一一一一一一一 線間短絡故障ー一一一一一一一一一一一一一一一一一一一一一一一一一一一 ブランチ断線 遮断一一一一一一一一一一一一一一一一一一一一一一一一 -- 3 は 2. 一一一一一一一一一一一一一一一一一一一一一 - - 件直列コンデンサの短絡故障 各種故障計算式の統一的表現一一一一一一一一一一一一一一一一一一一一 任意の多点故障計算手法の開発一一一一一一一一一一一一一一一一一一一一 多点故障の基本方程式ー一一一一一一一一一一一 一 ー一一一一一一一一一札 故障数に制約のない計算法一一一一一一一一一一一一一一一一一一一一一 非基準相故障の場合の計算法ー一一一一一一一一一一一一一一一一 一一 - - 一 零相回線開影響の効率的計算法一一一一一一一一一一一一一一一一一一一一 3.5 ブランチ中間点故障の効率的計算法一一一一一一一一一一一一一一一一一 零相分や逆相分電源を考慮する場合の計算法一一一一一一一一一一一一一一 5 切 故障計算プログラムの開発一一一一一一一一一一一一一一一一一一一一一一一 プログラム構成と機能の概要 一一一一一一一一一一一一一一一一一一一一 は.2 単純モデル系統に対する試算例 一一一一一一一一一一一一一一一一一一一一 小規模モデル系統に対する試算例一一一 一一一一一一一一一一一一一一一一 72 件.4 大規模モデル系統に対する試算例 一ーー一一一一一一一一一一一一一一一一 85 一一一一一一 5. 過渡安定度解析計算への適用一一一一一一一一一一一一一一一 プログラム機能の概要 ー一一一一一一一一一一一一一一一一一一一一一一一 シミュレータ実験との対比例 一一一一一一一一一一一一一一一一一一一一一 大規模モデル系統に対する試算例 5.4 各種故障が安定度に及ぼす影響の考察 1
5 6. 短絡容量計算への適用一一一 6. 1 短絡容量計算の基本式一一 一一一一一一一一一一一一一一一一一一一一一 ー一一一一一一一一一一一一一一一一一一一一 Z 行列特定要素の効率的な修正法一一一一一一一一一一一一一一一一一一 プログラム構成と機能の概要一一一一一一一一一一一一一一一一一一一一 大規模モデル系統に対する試算例一一一一一一一一一一一一一一一一一一 短絡容量とその計算条件に関する考察一一 一一一一一一一一一一一一一一 あとがき一一一一一一一一一一一一一一一一一一一一一一一一一一一一 一一一一 1 比 3 参考文献 - 一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一 付録 -- 一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一ー 1 件 9 1. Y 行列に基づく電圧 電流計算法一一一一一一一一一一一一一一一一一一 2. Z 行列の特定要素の計算法一一一一一一一 149 一一一一一一一一一一一一一一 日
6 まえがき 我が圏内外を問わず 長距離 大電力の輸送を担う基幹電力系統のほとんどは架空送電線で構成されている これらの送電線は地理的に大きな拡がりを持ち また空間的に無防備な状態にさらされているため 落雷など外部からの影響 ( 系統外乱 ) を受ける危険が避けられない ( 表 1 参照 ) この系統外乱は 一般に送電線への地絡故障や短絡故障として多く現れ これに対する電力系統側からの対応の如何によっては 最悪の場合 停電を招きかねない ことにこれが電力系統の広範囲に及ぶ場合には 電気の途絶による社会的な影響は甚大なものとなる 電力系統の故障計算は 起こるであろう故障に対しても電力系統の健全性を保持するための すなわち電力供給の安定性を維持するための各種方策の検討に必須の基礎的計算と言うことができる 電力系統の安定性を維持するための主要な検討項目には 次のようなものがある 1 保護継電方式の検討計算 ( 故障の検出 除去方法の選定に関する計算 ) 2 過渡安定度解析計算 ( 故障に伴う発電機群の同期運転継続の可否に関する計算 ) 3 短絡容量計算 ( 遮断器の遮断容量の選定や電磁誘導障害の有無に関する計算 言うまでもなく 故障計算はこれら全てに必要となる 故障計算のための基本論理には 対称座標法やクラーク座標法があり また近年では相座標法と呼ばれる新しい論理も提案されている3)o このうち 前 2 者の論理には大差がなく 実態として研究教育の場や電気事業等の実務で長年 対称座標法が広く用いられていることは周知の事実である また相座標法は 前 2 者とは異なり計算回路を現実そのままの3 相で表現して扱うものであるが 直観的に見てもその分だけ計算労力が多大になることは避けられない 蛇足になるが 故障計算の歴史的経緯をみると そもそも3 相そのものを扱う複雑な計算を容易にするために前 2 者が考案されたと見るのが自然 であり 近年改めて相座標法が注視され始めているのは多分に今日に至る計算機能力の飛躍的進歩と無縁ではない このように 故障計算の基本論理として最も馴染みが深く 使用実績もまた長いのが対称座標法であり 本論文で述べる故障計算もこの対称座標法に基づく さて 上記 3 種類の解析計算を念頭に置いた場合 対象とすべき故障種類は 送変電線での平衡や不平衡の地絡故障 短絡故障 断線故障 直列コンデンサの保護ギャップ放電故障といったいわゆる故障の他に 系統側からの制御動作である遮断器の遮断計算も含めて考えなければならない 最後に挙げた遮断計算は手法面では断線計算と等価である しかし適用面からは 断線は通常 1つの地点を前提とすれば済むのに対し 制御動作である遮断計算では1つの故障ごとに少なくとも送電線の両端 2ヵ所での計算が必要となるという相違点がある 後述するように 本研究に着手した大きな理由のひとつに 複数地点での同時遮断計算の実現化という目的があった 従来 故障計算の上記各種解析計算への適用にあたっては たとえば過渡安定度解析で
7 は3 線 3 相地絡故障 /3 相遮断 (3LG/3LO) に代表されるいわゆる平衡故障が主として用いられていたため 故障条件に係わる問題はそれ程には深刻ではなかった 一方 保護の検討計算では異地点での同時不平衡故障など比較的複雑な現象計算も行われていたものの 計算にあたっては故障地点から遠方の系統は集約した単純化モデル系統が用いられていた この背景には 計算精度よりは計算効率重視といった実務上の理由もあるがそもそも計算手法面での制約から数百母線といった大規模モデル系統の計算が困難であったことの方が大きい しかしながら 近年における電力系統の故障の実態を考えると 表 1 からも分かるよう に従来の代表的な故障条件である3LG 故障よりは むしろ1L Gなど不平衡故障の発止頻度が相対的に大きくなってきている また こうした故障実態の変化に関連し 故障に対する電力供給の信頼度向上のため 送電線故障時に故障相のみを選択遮断し再接続する多相再開路システムという高度な系統制御 保護方策が広範囲に導入されている 更に 電力系統の広域にわたる連系の強化など電気的結合の拡大が進み 計算精度を保つ上から より大規模な電力系統モデルに対する計算の必要性が増している こうした要件を満たすには 以下のような故障計算機能の実現が不可欠となる (1) 計算対象系統が大規模であっても効率良く計算でき (2) かっ 故障の種類や数ならびに発生位置が自由に選択できることこれらの機能は 具体的には (1) については千母線オーダーの大規模モデル系統に対しでも効率的に計算可能なことを指す (2) については たとえば図 1に例示するような複雑な故障状態に対しでも高効率かっ高精度で模擬できることを意味する しかしながら これまで これらの要件を満たし得る手法が確立されているとは言えなかった 筆者は これらの問題解決を目的として 過去 1 0 年余にわたり新しい故障計算手法の開発研究に携わってきた49-59) 本論文はこの間の成果を取りまとめたものであり 内容の大略は上記の機能を満足する新しい故障計算法と その過渡安定度解析計算や短絡容量計算への効果的な適用方法 ならびに大規模モデル系統に対する検証結果から成る 以下 大規模モデル系統の故障計算を目的として開発した各種手法について順次述べるが まず第 1 章では序論として開発した手法の要点や対称座標法について概説し 更に安定度解析計算や短絡容量計算における故障計算の位置付けや適用時の特徴などについても概観する 次の第 2 3 章では新たに開発した故障計算手法について 続く第 4,...,6 章では開発手法の具体化として上記 1~3の解析計算のために開発した計算機プログラムの概要ならびに大小の電力系統モデ ルへの適用例について記述する まず第 2 章では 地絡や短絡故障 断線故障など各々の故障を統一的に1つの計算式で表す新しい定式化手法を述べる 本手法の主な特徴は2つに大別できる ひとつは 各種の故障条件式をひとつの統一的な形で定式化したことにより 故障種別による分類を不安とした点にある このことが 多数の地点での同時故障計算の実現につながった 特徴のあとひとつは 特に断線 ( あるいは遮断 ) 計算について回路網の構造を変更しないですむ - 2 -
8 求解式を導いたという点にある 第 1 章で詳述するが 大規模モデル系統 すなわち大規模回路網の変更計算は一般に極めて煩雑な演算手 )1 債を必要とする したがって この同路網の構造が変更不要という利点により 大規模モデル系統に対する計算が格段に容易かっ効率的に行えるようになった 次いで第 3 章では 任意の故障種別から成る多地点での同時放障を効率的に計算する手法 - 多点故障計算手法ーについて述べる 多点故障計算にあたっての最大の課題は 任意の組合せ故障をどのように定式化するかという点にある 一般的な方法でこれを行うとすれば膨大な数の求解式が必要となる このため 従来の方法ではせいぜい2 地点までの同時故障が限界であった 本論文では 第 2 章で述べた統一的定式化に基づき 単に1 つの方程式のみで任意の数の組合せ故障を計算できる手法を開発した この他 多点故障計算に不可欠な幾つかの問題を指摘できる まず 一般に指定される故障が常に基準相 すなわち1 線故障ならばa 相であり また2 線故障ならばb c 相とは限らない 多点故障を計算する場合 故障種別に加え こうした故障相の相違をどのように定式化するかが問題となる また 想定される故障位置が常に母線 ( ノード ) とも限らない 仮に故障位置がノードであれば 計算に必要となる故障点電圧や電流は計算を行う際の直接の状態変数であるノードの値を利用することができる しかし 故障位置が送電線 ( ブランチ ) 上の場合には直接的に状態量が得られないため 問題となる これを行うために一時的に架空のノードを追加する方策も考えられるが その都度複雑な計算回路網の計算が必要となるため 現実的とは言えない 更にまた 対象系統に多回線からなる並行送電線を含む場合 故障に伴って流れる零相電流に起因する回線聞の影響の計算も問題となる ちなみに我が国の基幹系統は 一般に 2 回線以上の並行送電線で構成されている この回線間影響の計算方法としては 対称座標法における二相回路理論が良く知られているが しかしながらこの理論は計算対象が2 回線のみの単純系統の場合には利点があるものの 本論文で扱うような多回線送電線を & む大規模系統に対しては有効な手段を提供し得ない 本論文では これら諸問題に対しても複雑な計算回路が一切不要で かっ効率的に計算するこのとできる新しい手法をそれぞれ開発した この詳細を第 3 章で記述する 続く第 4'""-'6 章では 開発した手法に基づき作成した官頭 1~3の項目ごとの個々の計算機プログラムの概要と大小の電力系統モデルを用いた検証例 ならびに故障に関連した電力系統の諸特徴についての考察結果等について 順次記述する 第 4 章では 作成した故障計算プログラムの機能と構成について述べるとともに 木プログラムを大小のモデル系統に適用することにより 開発した故障計算手法の機能検証を行った結果について述べる すなわち 任意の多地点での同時故障計算機能 多回線並行送電線における故障計算機能 更に大規模モデル系統への適用性の検証結果等で ある 第 5 章では 開発した故障計算手法の過渡安定度計算への適用結果について述べる 本章では 電力系統模擬シミュレータ実験との対比に基づく過渡安定度計算における故障計算精度の検証結果 大規模モデル系統への適用性の検証結果について述べる 更に モデ -3 一
9 ル系統試算に基づき 種々の故障条件が過渡安定度に及ぼす影響の差異についての考察を記述する 最後の第 6 章では 開発した故障計算手法の短絡容量計算への適用結果について述べる すなわち 短絡容量の効率計算のために開発したノード分割や結合時の計算手法と これを大規模モデル系統の試算を通じて検証した結果について述べる また 計算に用いられる送変電線のインピーダンス定数の精組が短絡容量計算結果に及ぼす影響の試算と この結果に基づく考察を記述する 開発した各々のプログラムの扱い得る系統規模は ノード数 1500 ブランチ数 1800 発電機数件 00である これらのプログラムは 側 ) 電力中央研究所が開発した 電力系統解析システムcll ( 図 2 ) の機能高度化の一環として追加し 既に電気事業の実務ならびに研究用途で広く活用されている - 4 -
10 表 1 187kV 以上の 2 回線送電線の雷事故実績 (1980 年 4 月 年 3 月 電力 1 0 社 ) 事故様相 を匠旨ヨ事故 相数地絡数件数割合 (%) 1ゆ 1 L G L G ゆ 2LG (8) L G LG 中 3 L G (1) I 4LG LG LG メ o 入目十 ( 注 ) 1. L G : 地絡故障 (Line Ground) の略記 2. ( ) 内は 2 回線にまたがる事故件数 大規模電力系統モデル... 寸トー / イト一一 \シ こ斗 a 相 ì 1 b 相 } 回 c 相 J 線 a 相 ì 1 b 相 } 回 C 相 j 線 a' 相 ì 2 寸 b' 相ト巨 x-l c' 相 j 線 (a) 断線を伴う線路地絡の状態 (b) 並行送電線の多相再開路状態 図 1. 複雑な故障の例 - 5 -
11 う一々ノ一一一一一Jデ一一f灯一一Lふqu一/一刀牛一正ん旬月一/ L( 注 ) 1. Pro.: 計算機プログラム 2. 口 : 開発した機能 ( i 法は故障計 1 算部分を開発 j 図 2. 電力系統解析システム -6 一
12 ,,E 各変数は全て直角座標表示の複素数 また添字 (1 ) は正相分を表し ここに 4 't' 4,B,B,,,1. 故障計算の概要と用途本章では 序論として とくに大規模電力系統モデルの故障計算において求められる要件や本論文で述べる故障計算の基礎とした対称座標法の概要について述べるとともに 安定度解析計算など故障計算の代表的な適用分野における計算面での位置付けや役割等について概説する なお 以下では送電線 変圧器とブランチ 母線とノードの用語を必要に応じて使い分 ける また 用いる英字記号は特に断らない限り全て複素数を表すものとする 1.1 大規模系統の故障計算に求められる要件故障計算では 故障条件が特定されさえすれば すなわち同時故障数の数 ならびに各々の故障の種類 故障相 発生位置の全てが指定されさえすれば 原理的には既存の方法であってもこれら指定条件に基づく求解手順を示すことができる しかしながら現実的な観点 からは 原理的に可能であるということが必ずしも実現可能ということには結びつか ない ことに千母線オーダーといった大規模モデル系統の計算を可能とするためには 次 のような要件を満たすことが不可欠となる ( 1 ) 今日では大規模系統モデルの計算に適した効率的な演算手順が広く採用されているが 故障計算機能を付加しでも この利点を大幅に損なわないこと (2) 故障の数や種類 発生位置などの故障条件設定上の制約が少ないこと (3) 多回線並行送電線であっても その零相回線開影響が計算できることこれらに関する計算手法については次章以下で詳述するが 本節ではその理解を助ける上から以下 上記 3 点に係わる一般的な計算方法について概説する ( 1 ) 効率的な故障計算手法本項目の理解のためには上述の 大規模系統モデルの計算に適した効率的な演算手順 " の内容についてある程度の知見が必要であるので 若干冗長にはなるがまずこの手順の概略について記述しておく 上述した系統モデルの計算とは ここでは電力系統を表す回路網計算 すなわち回路網の各地点に現れる電圧あるいは各地点を流れる電流分布を計算することを指す 具体的に は ノード数 N から成る次の多元連立の線形方程式を解くことに等しい y ( 1 ) E ( 1 ) = 1 (l) o E : N 次元のノード電圧ベクトル ( 未知変数 ) Y: (NXN) 次元のノードアドミタンス行列 ( 既知変数 ) o 1 : N 次元のノード注入電流源ベクトル ( 既知変数 ) 上式の変数の添字 (l) は 故障を含まない系統解析計算では省略されることが多いが 本論文では以降逆相分 (2) や零相分 (0) の状態変数も出現するため それらと区別するために添字を振った この式の左辺のノードアドミタンス行列 Yは通常 単にY 行列と呼ばれ その行列要素 YiJは次式で表される - 7 -
13 ( Yi1=ZF1J (1.2) YiJ=-YiJ (i=fj) ここに 右辺の Y i J (i 手 j) はノード i と j の聞の正相ブランチアドミタンス Y i i はノー ド i の正相対地アドミタンスを意味している Y 行列の非対角要素である Y i J (i 手 j) は ブランチが送電線や変圧器の場合にはY i j= Y j iである ブランチi-j が移相変圧器である場合のみ Y i J 学 Y j iとなる しかし 我が国の電力系統には移相変圧器はほとんど設置されていないので Y 行列は一般に対称行列とみなしてよい (1. 1 ) 式では通常 ノード注入電流 Iを既知としてノード電圧 Eを求めることが目的となる ちなみに 良く知られている潮流計算でも この (1.1) 式の計算が主体となる 潮流計算では (1.1) 式の次元が2Nになり Y 行列がヤコビアン行列 Iが電力ミスマッチ Eが電圧修正分で構成される行列となり 更にこうした行列計算を繰り返し行うという特徴があるのみであり 潮流計算であっても計算の大半が (1. 1 ) 式のような多元方程式の計算であることに変わりはない Eを得るにはY 行列の逆行列 Z=y-1を計算し E=ZIによるのが最も手っとり早い しかし 一般に逆行列計算のための労力はおおよそN3 に比例するため 行列の次元 Nが大きくなるとZの計算には多大の労力を要することになる また (1.2) 式の行列要素かり成る電力回路ではZ 行列要素は全て非ゼロとなる特徴があるため 実際に計算を行う上での必要メモリーの点での欠点も無視できない 歴史を振り返ると 1960 年代まではこうしたZ 行列ベースの計算に依存していたため 大規模系統モデルに対する計算は極めて困難であった しかしながら今日では 以下に述べるようにY 行列から直接的にEを求める技法が広く用いられている まず Y 行列の構造に注目すると Y 行列はその要素中にゼロが多いという特徴を有する すなわち Y 行列は疎行列である その疎性の程度を概略推定すると まずY 行列のその非対角要素 Y,j(i=Fj) は ( 1.2) 式からノードiとjの間にブランチがある場合にのみ非ゼロの値を持つ こうした非ゼロ要素の数は ブランチ数をBとすれば 2 Bとなる また 対角要素 Yjiは全て非ゼロなので その数はNである すると Y 行列中に非ゼロ要素が占める割合をαとすれば αは α= (N + 2 B) /N2 と書ける ところで 回路理論の示すところによれば NとBとの聞には2を独立したループの数とするときB=N+Q-lの関係が成立するため 上式はさらに α= (3N+2 Q-2) /N2 となる ここで 電力系統を表す回路はよく知られているように 回路構成としては極めて単純な部類に属する すなわち Nが数百の値を持つような場合でもdの値は極めて小さい そこで 上式はおおむね α ー 3N/N2 = 3/N ( 1.3) と表現できる (1. 3) 式は一般に Y 行列が極めて疎であり そうした特徴は N が大きいほど すなわち - 8 -
14 系統が大規模であるほど顕著になることを示している たとえばNが1 00であれば疎な割合は3% 500 であれば0.6% でしかない こうした特徴を活かす観点から (1 1. ) 式の電圧 Eの計算にあたっては 今日ではYfÏ 列の疎性を活かした効率的な演算技法一一 Y 行列の三角化行列への分解手順に基づく計 算法一ーが広く用いられている ) 歴史的に見ると 電力系統の解析にこの技法か導入されたことにより 系統解析で取り扱える系統規模が飛躍的に増大したことは論をまたない 参考までにこの方法の具体的な計算手順を付録 1. に示すが この一連の計算はおおよそ苅 1.1に示すような3つの計算ステップに分けることができる すなわち 最初に回路構成を確定してまずノードの順序付け操作を行い 次いで回路インピーダンスを用いてY 行列の三角化行列への分解計算を行い その後にノードへの注入電流条件の下で回路電圧の計算を行う という3 段階の計算ステップを踏む このうち 計算労力は初期のステップが最も厳しい たとえば 各ステップの演算時間比率は100ノード以上の大規模モデルではおおよそ6 : 2 : 1である このように全体の計算を分離する理由は 一般にY 行列演算を繰り返し計算する必要がある場合でも 最初のステップだけはあらかじめ一度だけ計算しておばよいことが多し1からである 先に触れた潮流計算がこれに該当する好例であり この計算ではY 行列と類似の特徴を持つヤコビアン行列に対する収数計算が必須となるが その収数のループはステップ2と3で足りるので 図 1.1のように全体の計算を分離しておくことで全体としての計算の高速化を図ることができることになる 以上 前置きが長くなったが 述べたようなY 行列演算に基づきたとえば図 1で例示したような複雑な故障計算を行うことを考える この場合 従来の方法では遮断についてはいったん遮断点を開放する必要があり またブランチ上の地絡等については故障点に対応する架空ノードを追加する必要がある こうした変更はY 行列の次元拡大を含む変更計算を行うことに等しく これを上記 Y 行列演算プロセスに則して言えば その初期ステップに戻って再計算する必要があるということになる すなわち Y 行列の煩雑な再計算が必要となる 加えて 1.4 節で述べる安定度解析への適用を考えた場合には 故障様相 ( 故障の数や種別 ) が時系列的に様々に移り変わるような条件指定が行われることを念頭に置く必要が あり これら諸点を考えると を得ない 従来の方法に基づく故障計算は困難を究めると判断せざる これまで 述べたような複雑な計算の労力軽減を主目的とした種々の提案が行われている29 38) しかしながら それらの全ては多少なりともY 行列の変更を伴うという点で本論文で扱う大規模系統モデルの計算を容易に行い得るとは言えない 本論文では 図 1.2に示すように遮断 ( 断線 ) 計算についてもY 行列の再計算を一切必要としない新しい計算法を開発した これにより 大規模系統モデルに対しても効率的な故障計算が可能となった これは第 2 章で詳述する - 9 -
15 STEP 1 o ノード番号の順序付け Y 行列の三角化分解時に新たな非 ゼロ要素出現を抑制するため行う STEP 2 y 行列の三角化分解計算 Y 行列を 3 つの行列の積 ( 印 LT) で表したときの各行列要素計算 STEP 3 回路網の電圧 電流計算 行列 LDLT を用いて Y の逆行列が 不要な手順によるノード電圧計算 次ケース有り? Y N 図 1.1 Y 行列演算の一般的な手順ハU
16 対称分回路 l 断線点 "'-- I \ 一 _.u, 一ノ (sトベt ) ゲー( r) -...J( I 変数 = 故障電流 ( I ) (a) 従来の方法 ( 回路変更必要 ) 変数 = 断線開電位差 (E) (b) 開発した方法 ( 回路不変 ) 図 1.2 断線 遮断計算方法 (2) 故障数や故障位置に制約のない故障計算手法故障の代表的なものは地絡 短絡ならびに遮断 ( あるいは断線 ) である 通常 これらの計算式は各々異なる形の方程式で記述される したがって 故障解を記述する方程式の数も3 種類となる 他方 故障には1 線 2 線および3 線故障の計 3ケースがある これらの計算式もまた 通常は各々異なる3 種類の方程式で表される ( 厳密には短絡では1 線故障は考えられないが簡単のためここでは存在するものとして考える ) そこでたとえば同時に発生する故障数 Mが1つの場合には 3 x 3 = 9パターンの定式化を行い 対応する計算式を用意すれば故障計算を行い得る 実際上は更に 1 線と2 線故障についてはどの相が故障相かという分類が加わるが 議論を簡単化するためここでは考えない では こうした従来の計算手順に準拠し 故障数 Mを複数に拡張することを考える たとえばM 豆 2が必要となる場合を考える この場合 M=2ではそれぞれの故障相数の組合せが3 線 - 3 線 3 線 - 2 線 3 線 -1 線 2 線 -2 線 2 線 - 1 線 および1 線 -1 線の6ケースが考えられる これらのうち たとえば2 線 -2 線では地絡一地絡 地絡 - 短絡 地絡 - 遮断 短絡 - 短絡 短絡 - 遮断 遮断一遮断の計 6ケースの故障組合せが加わる また3 線 -2 線では上の6ケースに加え 短絡一地絡 遮断一地絡 遮断一短絡を加えた計 9ケースの故障組合せが更に加わる このようにして M=2の場合に必要となる定式化数を全て数え上げると45ケースとなる したがってM 豆 2の場合には この45ケースにM=lでの9ケースを加えた計 54ケースについて定式化を行わなければならない 更にM 三五 3の場合には 全体のケース数が優に100を越えることになることは言うまでもない このことから推察されるように Mの増加に伴い必要定式化数は級数的に増える 現実的な観点 からは こうした数多くの求解式を導くための多大の労苦に加え そもそもMか 5あるいは6 以上の高次の場合に求解可能な形を導出できるかどうかも疑わしい 述べたような理由から 従来の方法で計算し得る同時故障の数 Mは実質的に2つが限界であった 無論 実際上は5つや6つもの故障が同時に発生するような計算を行わなければならな いような必要性はほとんどないと言ってよい しかしながら このことは故障を地絡や短
17 絡といった本来の故障を指す場合にのみ妥当性を持つに過ぎない すなわち 手法上は遮断 ( 断線 ) も故障のひとつとして数え上げられることから たとえば故障相のみをブランチ両端で遮断する多相再開路模擬を含む計算を行いたい場合には 多数の地点での同時故障計算の必要性が現実味を帯びてくる たとえばまえがき図 1(b) で例示した状態を実現するには 遮断数 4 地絡数 1の計 5つから成る同時故障計算が必要となる 本論文では 故障種別や故障相による分類が一切不要な故障計算の新しい定式化論理をすなわち故障数が複数から成るどのような組合せ故障であっても必要な求解式が単にlつで済む求解手法を開発した 本開発により Mの数に一切制約がなく しかも効率的な故障計算が可能となった 一方 故障位置について考えると 現実的には多くの故障が送電線の母線端 すなわちノードで発生する訳ではなく むしろ送電線上である確率が大であるのは当然 である しかしながら従来 故障計算では多くの場合に故障位置はノードに限定されるか あるいは一時的に架空のノードを追加するという方策が用いられていた これは ノード故障であれば計算が容易という理由による 言うまでもなく 故障計算を行うには故障点の電圧や故障電流などの状態量が必要となる 故障位置がノードであれば 故障点電圧は回路網計算の直接の計算結果として得ることができ また故障電流はノードの注入電流として容易に設定できるので 計算上好都合であった しかし 故障位置がブランチ上の場合には 特に故障電流の設定をし1かに行うかという問題を生じる 本論文では 故障位置がブランチ上の任意の地点であっても 従来から行われているノード故障の計算に若干の追加的処置を施すだけで計算できる手法を開発した これらの詳細については第 3 章で記述する (3) 多回線並行送電線の零相回線間影響の計算手法送電ルートが1 回線構成ではなく 2 回線送電線など白線と並行した送電線を有する場合 正相分や逆相分と異なり 零相分では他回線を流れる電流からの影響 ( 電磁誘導 ) カご無視できないため これを考慮する必要がある 従来 回線開影響を計算する代表的な方法として 二相回路理論 等価回路構成法の2 つが良く知られている 二相回路理論は 図 1.3(a) に示すような2 回線並行送電線での故障計算方法として最も一般的なものである ) この方法では 故障区間を零相の第 1 回路と第 2 回路とに分離することを基本として計算するものであり 系統構成上の一 定の条件が成立していれば計算が容易という利点を持つ ここで言う一定の条件とは 2 ヌべk _.' ーの \ (a) 並行 2 回線送電線 ( 注 ) - -- : 追加ブランチ +: 追加ノード k 三1今, 金 1ご 活字? のご (b) 従来の計算手法 (k と t の 2 地点故障 ) 図 1.3 零相回線問影響 ム
18 回線ブランチで構成され かっ全てのブランチにおいてその両端ノードが共通ということを指す 換言すれば 仮に1つでもこれに該当しないブランチ ( この典型例が並行多回線ブランチやπ 分岐ブランチ等であり現実の系統に少なからず存在する ) が含まれれば この方法を用いることはできない 一方 等価回路構成法は送電ルート内の電気的関係が等価となるような計算回路を構成して計算するものである5 ) この方法では 前者と異なり系統構成上の制約はないという利点がある反面 同図 (b) に示すようなブランチ上での故障では計算するための回路要素を多く増やさざるを得ないという難点がある これらの欠点を改善するために 計算回路の簡易化を目的とした提案 33) や 回路要素追加に伴うY 行列演算時の疎性悪化を低減させる提案 39) 等が行われている しかしながら いずれの方法も正相あるいは逆相回路とは異なる構造の零相回路を計算する必要があるという点での非効率性が免れない また より複雑な構造の回路の必要性は 必要メモリーや総合演算性等で現行の長所を著しく回害する 事実 これまで多くの場合 安定度解析などで簡略的に正相回路と同じ構造の零相回路が用いられてきたのは このことと無縁ではない そこで本論文では 零相計算回路の構造が正相や逆相回路と全く同等のままで 多回線ブランチ聞の回線間影響を計算できる新しい手法を開発した これについては 第 3 章で記述する 1.2 対称座標法 今日 対称座標法は国内外を問わず 最も一般的な故障計算論理である 後述するように 故障計算論理には他に2 3の方法があるが いずれも研究教育の場や電気事業における活用の度合し から見て対称座標法には遠く及ばない 振り返れば この対称座標法は長年の歴史を有する この理論を最初に考案したのは米 国の Dr.C.L.Fortescue 氏で 1918 年のことである 当時の米国電気学会に投稿された論 文名は Method of Symmetrical Co-ordinates Applied to the Solution of Polyphase Networks" である これを直訳すれば 多相回路の計算のための対称座標法 " となる 多 相回路は電力系統では3 相回路を指す 対称座標法 " という名でこの理論を我が国に紹介した最初の技術者は 当時の逓信省電気試験所に所属していた別宮貞俊氏である 1925 年 11 月の電気学会誌においてである 題名は 封稀座標法とその送電線問題に於ける臆用 " という ちなみに この別宮氏は当時電力系統の保護 継電関係に従事していた技術者であり この論文の冒頭に対称座標法に出会って大変に感激したとの記述がある 確かに 対称座標法の基本概念 はその考案時点で既に確立していた感はある なお この対称座標法の英語での呼称は 今日では原文の Symmetrical Co-ordinates ではなく Symmetrical Components と称される場合が多い その理由は 数学的な厳密さ からは 座標変換というよりは変数分解と呼ぶ方が適切であるという理由によるものであ円ぺU
19 \'ろう 我が国でも 過去に対称分法と意訳した研究者が一部にあった しかし 対称分法 という名前の持つ漠然としたイメージに抵抗を持たれたせし か広まることがなく ム は原題の直訳そのままの対称座標法という呼称が広く定着するに至っている さて対称座標法に関しては その基本原理や適用等についての書籍は極めて多く 電力 系統工学を扱っている著書であれば必ず記述されているといってよい そこで ここで改 めてくどく説明することは割愛し その要点だけを以下に述べることとする で ( 1 ) 正相分変数 (1. 1 ) 式で注釈をしないまま正相分という用語を用いた 潮流計算を始めとする電力系 統の種々の解析計算では通常 この正相分変数が用いられる 以下に この変数の特徴に ついて述べる 図 1.4 に示すように そもそも電力系統は 3 相交流の電圧 電流で構成されている し たがって 基本的には電力系統の解析は 3 相そのままで取り扱うべきである 図 1.4 の例 で Vaa, =Va-Va, (Vbb' や V c c' も同様 ) と表すとき この 3 相電圧 電流の関係を示 せば次式となる Z a b V a a' Z aa Z ac Zb c 〆'i 4 l', V b b' V c c' Z b a Z c 且 Z bb Z c b Z c c hh,,, Z88 Z b b Z c c a b c 相回路の自己インピーダンス o Z a b Z a c 一一一 : 各相閣の相互インピーダンス しかし それぞれの送変電線に対して逐一 3 相回路のままで定式化を行うのは極めて煩雑 な手順を必要とし また求解のための計算労力も多大となる そこでいま 基幹系統の通 ( 前提 1.: 各相イン日ンスは完全に平衡した値を持つ ( 対称 3 相回路 ) 常の運用状態で十分に成立しうる次の事項を前提としてみる 前提 2. : 各相電圧 電流は完全に平衡した状態にある (3 相平衡電力 ) ( 前提 1.: Z aa =Zbb=Z c これを数式的に表現すれば 演算子 a=1.0 ど 120 を用いて Zab=Z8C=. 前提 2. : V b = a 2 V a V c = a V a Ib =a2 Ia 1 c = a 1 11 となる これらの諸条件を (1.4) 式に代入して整理すれば次式を得る Va Vb Vc Z b b Z C C kz--一ー a〆't,e t-,'-一'l一--一ワ'bab U一一ワ 'k-u''l'-一,'''一--一且一lu--仰し u 戸一,一Pνn-ノ. 一 1 i..ft\,-司'e,,l',,ワ'心ワluaaap回初c--)a一一z'z88 図 1.43 相送電線の回路 Z一/ t一e'国\,,ノvb スJ亀 J巳 -14-
20 1ptiti-E,Jv 1一1Etl'tE 一 E1vv/ ワむワluー ノ1 rill11111(1.5) すなわち (1.4) 式と異なり a 相電圧は a 相電流のみに依存し また b 相電圧は b 相電 流のみに依存するというように 3 相が完全に分離した式を得る 更に 分離されたこれ ら 3 つの式は全て等しいので 実際にはこれら各相全てについて計算する必要がない 代 表的に a 相分だけの状態のみを求めさえすれば 残りの相の状態は前提 2. から容易に知る ことができる このことから 電力系統の状態を解析するにあたって上記の 2 つの前提が妥当性を持つ ような場合には 3 相回路を扱う必要はないため 代表的に a 相分の変数だけを取り出した 単相ベースでの計算が行われる よく知られている電力潮流計算は これに該当する好例 である なお (1.5) 式で Zaa-Zab を正相インピーダンスと呼ぶ このことから (1. 1 ) 式の正相分方程式は暗に上記 2 つの前提が成立する範囲での計算 式を意味していることになる したがって故障計算でいえば もし対象とする故障が 3 相 地絡故障や 3 相遮断などの 3 相平衡故障であれば (1. 1 ) 式により正確に計算しうる これを逆にいえば もし 1 線地絡など不平衡の故障をも対象とする場合には (1.1 ) 式の みに頼ることができないことになる うちの前提 2. が明らかに成立しなし からである 何故ならば 不平衡の故障では上記の 2 つの前提の (2) 対称分変数そこで 不平衡故障も計算対象に含めたい場合は 改めて (1.4) 式に戻って前提 2. を除いた定式化を試みる必要がある いま 不平衡故障の場合でも前提 1. は成立するとみてよ いので このときの (1.4) 式を記述すると次式を得る Vaa, ì (Zna Zab ZabÎ (1 a Vbb' 1 =1 Zab Zaa Zab I I 1 b V b b' ) l Z a b Z a b Z a a ) l 1 c しかし この式は単に右辺のインピーダンス定数の種類が減少しているだけに過ぎない すなわちa-b-c 相それぞれの変数が相互に結合していることに変わりはなく 電圧 電流の関係式の複雑さは基本的に解消されていない この複雑な関係式を 3 相が分離された別の変数に変換して計算する論理が対称座標法である 対称座標法の基本原理は lín 次元の任意のベクトルは独立したn 本の対称ベクトルの和に分解することができる に基づく 本問題の場合にはn=3であることから ベクトル分解のための変換行列 Tは次式で表される 1 ( I 1 T = - a a2 I 3 l 1 a2 a) l 1 a a2 (1.6) T - 1 = 1 1 a2 a 1 (1.7) ここに a は (1.5) 式の上方で 述べた演算子 1.0 ど 120 である この a には 1 + a +a2 三 O およびa3 三 1の関係がある -15-
21 具体的に分解の手 JI 闘を述べると いま (1.6) 式のベクトル変数 V 列 Tを乗じた新しい変数を次式で定義する Voo V a a' I にそれぞれこの行 Vll I=T I V h b' 11 1= T I 1 b ( 1.8) V 22 V b b 次いで この (1.8) 式で導入した新しい変数を用いて (1.6) 式を表せば次式を得る Voo' Vll V 22 2 a 8 2!I b 2 a b =T I 2ab 2 R a Z a b T 1 2 ß b 2 B h 2 fl fl 2 a a b Z 角 a Z a b Zaa-Zab r : Z o 0 222) li2 (1.9) すなわち 新しい変数の下では 3 相が完全に分離された式となる このことを概念的に示 すと図 1.5 のようである このように 対称座標法では電力系統に生じ ao",,- /9a ' る 3 相不平衡な現象を 3 つの独立した単相回路 上で計算することができる この特徴が対称座 標法の最大かっ唯一の利点 である もし 最終 b ど?で戸 ぷxミ\ lt 'U C 的な計算結果が a-b-c 座標で必要とされる場合 (a)a-b-c 座標系 行列 T 00 っ 0 ' q Cコ 行列 T-1 2 ひ 1 0 つ 1 ' っ 2 ' (b) 座標系 は 単に 座標の値を (1.7) 式の変換行列図 1.5 座標変換による変数分離 を用いて逆変換するだけでよい ちなみに 節冒頭で対称座標法という呼称について言及したが (1. 7) 式の変数操作を適切に言い てる呼び名としては 座標変換というよりは変数分解といった方が適切のようではある 本 (1. 9) 式で 添字 O に関する変数を零相分 添字 1 に関する変数を正相分 添字 2 に関 する変数を逆相分と呼ぶ このうち 正相分の関係式が (1.5) 式に等しいことの説明は不 要であろう 各対称分変数の特徴を図的に表せば図 1.6 のようである ところで 電力系統の通常の運用状態では前提 1. に加え 前提 2. もまた成立すると考え V bb 正相分 図 相電圧の対称分電圧 逆相分
22 nu,,,てよい すなわち 通常の運用状態では正相分のみが系統に存在し 零相分と逆相分成分 は系統に存在しない このことを電圧を例に数式的に確かめると 前提 2. の条件を (1.8) 式に代入することにより Voo Vl1 1 (1 1 1 ì ( V 88 ' 1 a a 2 I I a 2 V 88' V 88',,, -a', V 22 ) 3 l 1 a 2 a) l a V 8 a ) l 0 aeee'のように容易に確かめることができる (1.10) 式は 物理的には発電機の出力や負荷など 広い意味での電源全てが 3 相バランスしていると見なしていることを意味している (3) 対称分インピーダンス (1. 9) 式右辺のZ00 Z11 Z22の各対称分インピーダンスは (1.9) 式の意味するところから それぞれ図 1.6のような対称分電圧 電流を系統に想定したときのインピーダンスに相当することは明らかである このうち 正相分と逆相分インピーダンスは 送変電線では (1.9) 式の例示でZ11とZ22が共にZ88-Z8bと等しいように ブランチインピーダンスとして等しい値を持つ ただし 回転機である発電機のリアクタンスについては 逆相分は2 倍周期の成分を含むことから 両者は異なる値となる したがって電力回路全体でみた場合でも 正相分と逆相分は相異なる値となる ただ 実際の計算ではその差異は少ないと見なして同値として扱う場合も少なくない 一方 3 相同相電流に基づく零相分インピーダンスは 送変電線であっても上記 2 成分とは異なり しかも大きな値を持つことはい.9) 式からも明らかである この零相分インピーダンスに関し まず送電線について述べると その算定は大地帰路電流が前提となるので簡単ではない たとえばい.9) 式で示した値 Z8 a +2 Z 8 bは 大地表面が完全導体と仮定したときの理想的な数値であり 実際には帰路電流の線路としての大地の扱い方に応じて もっと大きな値となる このように 零相分の値は導線の形状や鉄塔配置だけでは決まらず たとえば平野部か山間部かなど送電ルート下の大地の電導性に少なからず依存したものとなる また 送電ルートが1 回線構成ではなく 2 回線送電線など白線と並行した送電線を有する場合 正相分や逆相分と異なり 零相分では他回線からの影響 ( 電磁誘導 ) を考慮する必要が生じてくる いま 図 1.4を並行多回線送電線のひとつと見なし そこを流れる各対称分の電流による別回線への影響度合いを考えるものとする このうち 正相分と逆相分電流については回線単位 (3 相一括 ) で見て常にゼロであるため 実際の電線配置グ電気的に幾分は不均衡ではあるものの 計算上は回線同士の相互影響は無視できる しかし 零相分電流については各相同相電流というその性質上 回線単位で常にゼロと見なす訳にはいかないため 回線同士の相互影響を考慮に入れる必要がある こうした計算を行うにあたり用いられる定数が回線問零相インピーダンスである この値は 他回線に零相分の単位電流が流れたときに自回線 a 相の単位区間に現れる誘導電圧に等しい 変圧器の零相分インピーダンスもまた異なる この相違のあり様は 上記送電線とは異なり 変圧器自身が2 巻線であるか3 巻線か あるいはまた変圧器の中性点の接地方式な
23 ,,どに依存する これらの選定は故障検出の容易性あるいは故障による設備保護などの観ハ から決定されるが たとえば ある送電線を流れる零相分電流の終点がスター結線の変 器であり この時その変圧器の中性点が非接地であれば 結果的にこの系統に零相分電流 は流れ得ない し 1 からである 何故ならばこの場合 同相の 3 相電流は変圧器端に流れ込むことができな 逆に接地されていれば 接地抵抗に依存した電流が流れる したがって 変圧器の零相分等価回路も 1 次 2 次間での回路の分離 あるいはインピ ーダンス接続 片端のみの接地など様々な表現で構成される 1.3 故障計算の基本的方法本節では 対称座標法に基づく故障計算の基本的方法について概説する なお 故障計算に用いられる論理としては他にクラーク座標法や相座標法がある しカし クラーク座標法は (1.7) 式の形式とは異なる変数変換を行う点が異なるのみであり 基本的な考え方は対称座標法と大差ない 一方 相座標法は a-b-c 座標の (1.4 ) 式を直接 そのままの形で解く方法である したがって 理論的には仮に多重故障であっても計算は容易といえる3)O しかし 一般の大規模系統への適用を念頭に置いた場合 控えめに見ても前 2 者の3 倍の計算機メモリーと計算労力が必要であるということ また適用先が本論文のように線路インピーダンス等の3 相対称を前提とした安定度解析や短絡容量計算であるということ などの点から見て利点があるかどうかは議論の余地があろう (1 ) 対称座標法の一般式への展開 ここでは図 1.4 のような 1 つの送電線に対してではなく 図 1.7 に示すように系統の任 意の地点 kにおける故障を考える いま 故障が発生する直前のk 点電圧をEa Eb E c とする この状態で故障が発生し このときk 点から系統の外に流れ出る故障電流が 1 a 1b 1 c そのときのk 点電圧がVa Vb Vc になるものとすれば これらの変数の間に次の関係が成立することは明らかである Va E 白 Zaa Zab Zab,,E 縄E縄E E 4a,.,Zab Zaa Zab l 1 1 b EE -Vb 1=1 Eb 1-1 Vc E c Zab Zab Zlln この式の右辺のインピーダンス行列は (1.6) 式と同形である ただし Z 要素の持つ意味は異なる すなわち (1.6) 式は単に1 本の送電線インピーダンスに対するものであるが この (1.11) 式の各要素は図 1.7からも分かるようにk 点から系統内部を覗いたときの一括したインピーダンスを表している この (1.11) 式の各変数に対して (1.7)--- 換を施す すなわち (1.11) 式の両辺に左側から行列 T を乗じて Va E a Znll Zab Zab (1.9) 式で行ったと同様な 座標への変 T I Vb I=TIEb I -T I Zab Zaa ZablT 1 T 1 1 b (1. 12a) Vc E c ZlIb Zab Za8 --aaoau
24 -Z k 点 E a / VR a 平目 Eb\ b 相 c ( 故障前 ) Ec\ c 相 電力系統 と表す この式で T が掛かった各ベクトルはそれぞれ (1.8) 式で定義した対称分ベクト ルで記述することができる すなわち V k (0) Va Vk(1) I =T I V b V k(z) Vc ム 1 k (0) ム 1 k(l) I = T ム 1 k (Z) 免UYE'AYE ALU( 1.12b) VE-APLWここに ム 1 k (n ) (n =0, 1,2) は各対称分回路のk 点故障電流 またV k(n) は故障時のk} 対称分電圧に相当する また (1.12a) 式の右辺第 l 項のEa E b E c は故障前の電圧であり (1.10) 式で述べたように正相電圧のみから成る 更に 第 2 項のインピーダンス行列は (1. 9) 式の形に等しい したがってい.12) 式は V k (0) ì (0 Z (O} kk V k(l) Ea Z k ム 1 k (0) ム 1 k (1) V k (Z)) l 0 ) l 0 0 Z パ Z)) l ム 1 k (Z) 1: ー k O) ム1 k (0) のように表すことができる ここで便宜上 k 点の a 相電圧 EIl を E k と表して V k (1) = - Z k 1) ム 1 k(l) + E k (1.13) を得る この式が k 点 を故障点とする故障計算の基本式である 図的に示せば図 1.8 のよ うである この (1.13) 式で 右辺の z dn} は (1.11) 式の下方で述べたことから明らかなよ うに それぞれ各対称分回路の k 点から回路内部を覗いたときの一括した対称分インピー ダンスとなる したがってこの (1.13) 式は いわば全系の特性をひとつのノード k に縮約 して表現したものとも言える そこで 故障時の系統状態を故障点 k のみならず系統全体について求めるという観点か ら (1.13) 式を全系統を対称とする表現形式で示すと 便宜上 対称分 Z 行列を用いて次の ( =-Z 形式の方程式を得ることができる } ム 1 (0) V (1 )= - z (1). ム 1 (1)+ E 4 a'hh坤 1Ja,E'a',,I -
25 o v(n) 故障時の対称分電圧ベクトル 図 1.8 故障計算の基本回路 o Z (n). 対称分 Z 行列 ム1 (n): 要素 kのみに (1.13) 式のム1 k (n) を持ち 他要素は全てゼロのベクトル o E 故障前の正相分電圧ベクトルであり (1.1 ) 式の解 E(1) に等しい 当然だが この式でk 行の式だけを取り出して記述すれば (1.13) 式を得る さて EはY 行列ベースで表した (1.1 ) 式の解に等しいので (1.1 4) 式についてもY 行列ベースの関係式で表現しておくと 次式を得る y ( O) 刊二一ム1 (0) y(1) V( l )= - ム1 (1) + 1 (1) (1.1 5) この (1.1 5) 式あるいは先の (1.1 4) 式から明らかなように 故障時の系統状態は故障電流ベクトルム1 (n) を得さえすれば容易に計算することができる したがって 地絡や短絡などの故障種別 およびそれぞれの故障に与えられる故障相を故障条件として それらを満たすようなム1 k (n) を求めることが故障計算の基本的な目的となる (2) 具体的な計算方法 ここでは 上記ム 1 k (n) の求解例として k 点における a 相 1 線地絡 (1 L G ) 場合を示す 故障の この場合 k 点 では図 1.7 で a 相電圧は 0 また b 相と c 相では外部に流れ出る故障電 流は O でなければならない すなわち この故障で満たされるべき制約条件は a-b-c 座標 系で Va = 0 および Ib =Ic =0 である そこで この条件を (1. 12b) 式を用いて O -1-2 座標系に変換すれば 次式を得る ( VUO +VUI}+VP=o ム 1 k (0) - ム 1 k ( 1) ム 1 k (Z) (1.1 6) 次いで この (1.16) 式の関係を (1.13) 式に代入して Vk( 川を消去して整理すれば 次のよ うにム 1 k( 川を求めることができる ム 1 k(o) = ム I K {1) = ム 1 k (Z) = E k / (Z k 0) + Z k 1) + Z k Z) ) (1. 17) 故障時の系統状態は この値を (1.1 4) 式あるいは (1.1 5) 式に代入することにより簡単に得 ることができる ここで 解である (1.1 7) 式のム 1 k (n) が故障前の k 点電圧 Ek の関数となっていること
26 に 奇異を感じられるかも知れない 何故ならば E k はいったん (1. 1 ) 式の故障前系統計算を行わなければ知れ得なし1からである したがって上記の計算手順では 本方法では故障時の電圧分布を得るためにまず (1.1) 式の計算を行ってEk を得て 次いでこのE k から計算される (1.17) 式のム1 k (n) を (1.15) 式に代入計算して最終解を求める というこ度手聞を要するように見れる しかし次章で述べるように 実際の計算ではこうした負伊を要しない効率的な計算手順により解を求めることができる さて 故障時の系統計算の基本式は上述のように (1.13) ---(1.15) 式で与えられる 次章以下では これらの基本式に基づく新しい故障計算法について述べるが ここでこれらの式から導かれる故障の系統計算の別な方法について触れておく その方法とは 正相回路上で故障点に故障インピーダンスを挿入して計算する方法である たとえば1 線地絡故障では (1.13) の正相分基本式と (1.17) の両式に含まれるEk を 消去して次式を得る Vk(l)_ (Zk O)+Zk Z)) ム 1 k ( l) この関係式から 1 線地絡故障は図 1.9 に示すように正相回 (1. 18) 路のノード k からインピーダンス (Z k 0) + Z k Z) ) を対地 に接続することにより表現できることが分かる この1 線地絡故障を含め 一般に故障がひとつだけの単純故障であれば どのような故障種別であれ正相回路において故障点へ故障インピーダンスを挿入することにより故障を模 擬することができる この手順は 単に (1. 1 ) 式の正相分行 図 1.9 故障点抵抗の接続 安 IJ y(l) の一部の要素に変更を要するのみである すなわち 故障計算を行う方法には大別して次の2つがある ( 1 ) 故障条件に応じて各対称分の故障電流値を求め 注入電流として計算する方法 ( 吟故障点への故障等価電流の注入 ) (2) 故障条件に応じて正相 Y 行列要素を変更する方法 ( ゆ故障点への故障等価インピーダンスの挿入 ) 一般の電力系統解析に用いる故障計算方法として両者を比較すると 故障が単純故障であってかっ正相分のみに関する系統諸量が得られれば十分な場合は後者が扱い易く 事実長年にわたり多用されている たとえば電力各社の実務で電力系統の安定度が検討される場合 現状では想定される故障の多くは単純故障である また安定度上からは その安定 不安定を支配する諸量は主として正相分である ( 発電機の同期運転の可否はほぼ正相分で決まる ) そこで こうした計算に限られる場合には 後者の故障インピーダンス挿入法が適用し易い 安定度関連の専門書籍で 故障の表現方法としてこの故障インピーダンス挿入法が記述されることがほとんどであるのも 系統故障と安定度との因果関係についての物理的な説明が容易であるという面も含め こうした背景によるものと考えてよい しかし このように単純故障では後者が計算し易いとはいっても これにまったく欠点 -21-
27 ムがないわけではない 最も分かりやすい事例を示すと 後者の故障インピーダンス挿入法 では最も多用される 3 相 3 線地絡 (3L G) 故障が厳密には計算できない 3LG 故障を 表現するには 基本的に当該ノードに抵抗ゼロの接地ブランチを接続すれば事は足りるが 回路網計算の特徴から抵抗ゼロのブランチ表現は厳密には不可能であるからである ( 低抗 ゼロを指定することは逆に抵抗がない すなわち開放を指すことになる ) したがって実 際上は小さな低抗で接地するしかないが これにより生じる誤差は避けることができない また インピーダンス挿入による回路定数の変更はそのインピーダンスの値によっては Y 行列演算の過程でいわゆる丸め誤差を生じる恐れがある しかしながら むしろ後者の計算法の最大の欠点は 不平衡故障を含む多重故障につい てはこれを後者の方法で計算するのは実質的に不可能であるということである たとえば k 点と 2 点での 2 点同時故障の場合 もしいずれもが不平衡故障であれば (1.18) 式に相当 する関係式は次のような形で表される ωvzワム一一z7uv(1. 19) なお この式では簡単化のために正相分添字 (1) は省いた この式は k 点と 2 点との聞に 相互インピーダンス成分 Z k I Z I k が存在することを表している 一般に k 点と 2 点とは 同一系統上にあるので相互インピーダンスがゼロとなることはなく この相互関係を後者 の方法によりインピーダンス挿入的に計算することは容易ではない 何故ならば こうし た関係を実現するためにはノードやブランチの追加操作が必要となるが これを Y 行列ベ ースで行うことは計算効率を著しく阻害するからである (1.19) 式のような関係式の次数は同時故障の数に等しい したがって 同時故障の数カご さらに多くなれば故障点間の相互インピーダンスも級数的に増加する すなわち 後者に よる計算は実質的に不可能といってよい 一方 注入電流 61 を用いる前者であれば ム I をどうやって求めるかという問題はあ るものの いったんム I を得さえすれば 故障時の電圧分布はこれを (1.14) 式あるいは (1. 15) 式へ代入計算するだけで求まる 特に Y 行列ベースの (1.15) 式を用いる場合 その計 算は故障数に依存せず極めて効率的であるという利点がある また 注入電流法では原理 的にインピーダンス挿入法に見られるような演算上の誤差を生じる欠点がなく 常に厳密な計算を行うことができる 更に 故障時の系統各部におけるa-b-c 座標での各相の電圧 電流諸量を得たい場合は 基本的に注入電流法を用いる他ない 1.4 安定度解析計算における位置付け本節および次節では 安定度解析計算ならびに短絡容量計算の目的と計算法 またその中で故障計算がどのような位置付けにあるかを各々概括しておくこととする さて 電力系統の拡充計画や運用計画にあたっては 経済性と信頼性の協調を保つ目的 から 設備構成あるいは運用に係わる指針が設定されている この指針は 具体的にはあ -22-
28 る一定の厳しさまでの系統外乱を受けても供給支障を生じないというものであり この一 準となる系統外乱は一般に想定故障条件と呼ばれている 想定故障に起因する技術的検討には 潮流過負荷や定態安定度 過渡安定度 電圧安定 性などがあるが これらの中で広域な連系により大規模系統を構成している我が国におい ては過渡安定度が輸送力を制限する最大要因となっている なお 電力系統の過渡安定度解析においては 特に実用用途では発電機などに備わって いる安定度維持 向上用の各種制御機器 (A VR GOV 等 ) の応動を含んだ詳細な解析 が不可欠となっている 8 9) この場合 一般には動特性安定度解析と呼ばれることが多い が 本論文では安定度解析そのものは主対象でないため 以下 過渡安定度解析と呼ぶ ( 1 ) 過渡安定度解析計算の概略フロー 電力系統の過渡安定度解析の計算式は 一般に次の多元連立式で表される 1) ( dx/d t=f(x y u) (12ω g (x, y, u) = 0 ( 1. 20b) ここで X, Y および u はそれぞれ電力系統の状態変数ベクトルである X は 発電機の 相差角や回転数ならびに磁束など あるいは発電機制御系のそれぞれの状態変数から構成 される また y は系統や発電機などの電圧 電流変数である u は 発電機制御系や系 統電圧ならびに潮流などの初期設定値である (1.20a) 式で記述される微分方程式は 主として発電機を含む発電プラントの動特性を表 すものであり 状態 x の多くは取りうる値にハード上の制約 ( リミッタ ) あるいは飽和な どの非線形特性を有する特徴がある 一方 (1.20b) 式で記述される代数式は 主として系統各部の電圧や電流の関係を表す ものである この計算はいわゆる潮流計算に相当するが 計算要素に発電機や負荷の特性 および本論文の主題である故障計算などを含むことから 通常の潮流計算とは異なる求解 法が用いられる この (1.20b) 式の計算を 通常 過渡時系統計算と呼ぶ ついては次項で改めて述べる この計算法に (1.20) 式の各変数の時間変化は とくに多機系の場合 これを解析的に解くのはほとん ど不可能であり 図 の概略フローに示すようにシミュレーションにより時間を追って 数値的に解くしかない すなわち 数値積分解法を用いる他ない この解法には種々の手 法があるが たとえば Y 法プログラム ( 電力中央研究所が所有している過渡安定度解析計 算プログラムの略称 詳細は文献 7 ) では 4 次のルンゲクッタ (Runge-Ku 七回 ) 法を採用し ている なお 図の左上の部分は シミュレーション解析の対象となる初期潮流断面を作成する 部分である 電気事業の実務などでは たとえば年間の最大電力が発生する夏季潮流断面 など特定のひとつの潮流断面に対して多数回のシミュレーション解析が行われることが多 い そこで この図のように潮流計算部分を分割しておくことにより 全体の解析効率の 向上を図ることができる 円tun,,ん
29 図 1.10 中央のシミュレーション部で 2 番目のブロックB2 に記述している状態変更には発電機の運転条件の変更 あるいは送変電線の接続切り換えなど段々なものが想定対象となるが 中でも最も頻繁に用いられるのが系統故障である これらの変更は (1.20b) ずでの関係式の変更として表される 関係式の変更は 発電機の電圧や電流変数の変化をもたらし この変化は (1.20a) 式における計算条件の設定変更となる これにより (1.20a) 式の各状態に変化が現れる すなわち系統動揺現象が模擬されることになる 更にこのずの状態変化の一部は 次の時間断面での (1.20b) 式に対する計算条件として渡される このように 動特性シミュレーション解析では (1.20) 式の2つの式が時系列的に交互に解かれる Y 法では 数値積分解法として上述のように4 次のルンゲクッタ法を採用して マ 81 マ 82 f g 83 x u を用いて系統の方程式 g (x y u) = 0 を解き yを求める 84 上記 y を用いて動特性方程式 dx/dt=f (x y u) を解き 新しい x を求める 図 1.10 過渡安定度解析計算の流れ いるので 時閣を1 単位だけ進めるために (1.20) 式の交互計算が4 回繰り返される ただし ほとんどの場合はそれぞれの繰り返しの中でさらに収数計算を要するので 時間を進めるための繰り返し回数は実際はもっと多い ちなみに 時間を1 単位だけ進めるための時間幅 すなわち刻み時間はY 法では0.01 秒が標準となっている (2) 過渡時系統計算 さて シミュレーションの各時間断面ごとに系統のノード電圧やブランチ電流を計算す
30 る過渡時系統計算は (1.1 ) 式による 再掲すると y(1) E (1)= 1 (1) (1.1 再 ) である なお 前項で述べた安定度プログラムの呼称である Y 法はこの Y 行列の Y に由来する o Y 法の前身は Z 法であった z という記号名は (1. 1 ) 式の E(1) を求める計算にノードイン ピーダンス行列 (Z 行列 ) を用いていたことに由来する しかし この Z 行列は数多くの メモリーを必要とする基本的欠点があり そのため取り扱える系統規模に限りがあった そこで 系統規模の拡大を目的として Z 行列に代わって Y 行列が導入され その際に呼名 も Y 法と変わったのである この更新により 動特性解析の基本論理が変わったわけでは 無論ない ちなみに現在 Y 法プログラムで計算しうる系統規模は ノード数 ( 負荷数 )1500 ブ ランチ数 1800 ならびに発電機数 400である これらの値はメモリー上の限界で設定されているものでなく 電気事業における解析実務面からの必要性によるものに過ぎない さて 前項末尾で 述べたように (1.20) 式の2つの式は連立して解かれるが 求解にあたってこの2つの式を結び付ける状態変数は具体的には発電機の背後電圧 Egどe gとそのリアクタンスxgである 背後電圧は (1.1 ) 式における発電機接続ノードの等価電流源として 極めて簡単に表現することができる すなわち図 1. 11のようである なお この図からも明らかなように この等価電流源は (1.1) 式の計算にのみ使われる便宜的なものに過ぎず 物理的な意味を持ついわゆる発電機電流とは異なることに注意を要する (1. 1 ) 式は系統を表すので 負荷もこれに含まれる ノード負荷は もし消費電力が電圧の2 乗に比例するものとすれば (1.2) 式で述べたノードの正相対地アドミタンスyの一部 ( 定インピーダンス負荷 ) として簡単に表現できる すなわち Y 行列の要素として表現することができる したがって もし全ての負荷が定インピーダンス特性であれば このときの系統電圧 EωはベクトルIωの発電機接続ノード要素だけに所与の等価電流源を設定してい.1) 式から簡単に得ることができる なお 上述した発電機の背後電圧やリアクタンスは 実際の計算では発電機モデルの精 疎に応じて異なる値が採用される 1-9) このとき 詳細なモデルではベクトル I の設定時 に背後電圧値の座標変換 すなわち個々の発電機におけるd-q 座標軸基準での電圧 電流値を系統座標軸基準に変換する操作などが必要となる しかしい.1) 式の過渡時系統計算を主体とする場合には単に電流源の数値が変わるだけであり したがって発電機モデルの相違にかかわらず計算手順は基本的に変わらない また負荷についても 定インピーダンス特性でなく 定電流や定電力特性などの様々な非線型特性負荷が あるいはまた負荷の周波数依存特性が考慮されることが少なくない しかし こうした場合は電流源で扱えば計算できる ただし その電流値は電圧の関数となることから (1.1) 式が収数計算の対象となるだけである 故障計算はこの (1.1 ) 式に含まれて計算され その具体的な方法は前節で述べたとおり である 安定度解析における故障計算の最大の特徴は 故障様相 ( 故障の数や種別 ) が時
31 系列的に様々に移り変わるような条件指定が行われる得ることである またこのとき 必 要に応じて各地点での a-b-c 座標ベースでの状態量が求められることも考えておかなけれ ばならない こうした点から見ると 前節で述べたように 安定度解析における従来から献発納g系統ーか図 背後電圧の等価変換 の一般的方法である正相 Y 行列要素を変更して計算する方法よりは 故障電流ム I をあら かじめ求めておき これを電流源 I に加えて計算する方法が 計算効率や必要メモリーな ど多くの面で利点があると判断せざるを得ない 1.5 短絡容量計算における位置付け (, ) 短絡容量地絡や短絡などの系統故障は 前節で述べた系統安定度の維持 向上を図る目的から できる限り速やかに除去することが望ましい 故障発生から除去までの具体的手順を述べると まず故障区聞を検出しなければならない この責務は保護リレーが担う 故障は何時 何処で発生するか分からない そのため標準的な保護リレー ( 電流差動リレー ) では常時 送電線の両端での電気情報を互いにやり取りし 比較しており これにより当該送電線で故障が発生した場合の故障様相 ( 故障種類と故障相 ) を迅速に検出一一これに要する時間は基幹系で2,. 3サイクルーーする構造を有している 次に この異常検出に基づいて故障の除去が行われる 故障除去は 保護リレーからの動作指令により送電線両端に設置しである遮断器を開放一一これに要する時間もまた基幹系で2,. 3サイクルーーすることで達せられる この動作は一般に主保護遮断と呼ばれる この時 故障継続中に送電線を流れる電流は常時に比べて十分に大きいことから 遮断器には故障電流を確実に遮断できる機能を持たせておく必要がある でないと 最悪の場合には遮断器接点聞の溶着を招き 故障が永久に続くことになる ( 実際には 仮に遮断失敗となっても後備保護リレーと連動したパックアップ用の遮断器等が動作するので このような最悪の事態はまず考えられなしリ 遮断器が故障電流を確実に遮断できるか否かは 遮断器の遮断容量に依存する 遮断器の遮断容量は 後述するように定格電圧と定格遮断電流の積 [MVA] によって定まる 遮断 器は 定格電圧の運用条件の下でその定格遮断電流を越えない値までの電流であれば こ noりム
32 VA短絡容量はこの遮断容量と深い関係にある 短絡容量の値は故障想定点における故障前運転電圧と3 相短絡 ( 地絡 ) 電流の積 [MVA] によって定義される43) 短絡容量の特徴を2 3 述量れを確実に遮断できる機能を有している べると 上述の定義から短絡容量はは地点によ って異なり その最大のものを最大短絡容量と 呼ぶが これは図 1.12 に例示するように概ね系 統容量の拡大に比例して増加する 短絡容量は 一方 電圧維持能力の目安としてもよく用いら れ 短絡容量が大なる地点程 電圧変動が少な いと判断できる 遮断器の選定にあたっては 上述の遮断機能 との関連から分かるように ごく大雑把に言っ て 遮断容量 孟 その地点での短絡容量 な る性能のものを選択する必要がある 20 また 上述のように系統増強等の系統拡大に伴って 各地点の短絡容量は必ず増大するので その際には既存の遮断器についても上の不等号の 関係が満たされているかをチェックする必要もある 近年における遮断容量の運用上の上限は電流値で約 60kA (500kV 系統 ) である が 電力系統の拡大に伴って短絡電流がこの上限値に近づきつつある 短絡容量 ( 短絡電 流 ) の抑制対策は後述する計算式から分かるように高インピーダンス化が基本であり こ れには 1 より高い電圧階級の導入 2 直流分割 3 母線分離 などがある しかし 12 は系統拡充の基本構想といった施策的大問題に係わると同時に多大な経済的負担をも要す ることから その実現は容易ではない o 5 一一+系統容量 (103MVA) また 3 は比較的実施に移しやすいものの一般に 安定度や供給信頼度の悪化要因となることから その実施にあたっては細心の配慮が必要 となる 系統短,,aE 唱EAnu図 僧aM絡容4Ill ,,5,10 最大短絡容量と系統容量の関係 (2) 短絡容量計算 図 1. 13に示すように 電力系統のある地点 kで3 相地絡故障 ( これは3 相短絡に等しい 以下 3 L Sと略称 ) が発生したときの故障電流 および故障点近傍を流れる故障電流を計算することを短絡容量計算と言う 上述したように その主たる目的は遮断器の遮断電流 のチェックである 通常 地点 kは母線 ( ノード ) に 限られる 短絡容量計算における故障計算には 前項の安定度解析におけるそれとは異なる演算技法が用いられる 図 初ヲ 短絡電流の分布
33 何故ならば この計算では安定度解析のように特定のノードについての故障のみが対象ではなく 一般に全てのノードについての故障電流を一挙に計算することが求められるからである その代わり 故障時の状態分布としては図 1. 13のように故障点近傍のみが得られればよいとされるのは 上述の目的から当然 と言えよう 一般に 短絡容量計算では上記 3 L S 故障に加えて1 線地絡故障 ( 以下 1 L G) も同時 に計算されることが多い llg 計算の主な目的は 故障時の近傍通信線等への電磁誘 L 障害の有無のチェックにある なお 短絡時の故障電流として 本論文では交流分 1 11 Cのみを対象としていることを注記しておく 良く知られているように 実際の故障電流は発生時から完全な交流を形成せず 交流分実効値 1 R C ( いわゆる対称短絡電流 ) に故障発生時の諸条件による直流分電流 1 d cを含んだものとなる このうち1 d cは後述するように時間の経過と共に減衰するものの 実際の遮断時間における1 d cの値が無視できないような場合には 故障電流としてこの成分をも考慮する必要があることは当然である このような場合の補正方法については 文献日で交流分電流 1 D Cに基づく推奨式が提案されているので 詳しくはその文献を参照されたい ここでは簡単に直流分による影響に触れておく 短絡瞬時 ( 正確には短絡後の半サイクル後 ) の直流分電流の理論的上限は交流分波高値である したがって 直流分を含めた非対称の最大短絡電流の上限は 交流分波高値の2 倍となる この内 直流分は故障点での系統のX/Rに比例して減衰する 基幹系統におけるX/Rは大きいと考えられるので 直流分は極めて早く減衰する ( たとえば文献切の試算ではO.1 秒後には5% 程度以下 ) と推定され したがって問題となることは一般に少ないと考えられる 言葉を変えれば X/Rの値が小さい傾向にある発電端などでは時に注意する必要があろう さて 各ノードk (k=1,2, 一一 N) の短絡電流を一挙に計算する方法については第 6 章で詳述するが 基本的にこの計算で必要となるのは (1.1) 式のY 行列の逆行列であるZ 行列である より厳密には Z 行列のN 個の対角要素 Zk l) ならびに非対角要素の一部 ( その数はブランチ数 ) さえあれば図 1.13の送電線分流を含む故障電流が容易に計算できる このとき 故障後のどの時点での値を求めるかにより Y 行列を構成する際の発電機インピーダンスとしてXd" Xd' あるいはXdのいずれかが選択される 通常は遮断電流のチェック用途が多いため 遮断時間付近の状態を代表するXd" が用いられることが多い いずれにせよ 短絡容量計算は前項の安定度解析とは異なり 系統解析の分野では簡単な部類に属する しかしながら (1.3) 式の上方で述べたように Z 行列はどのような回路であっても全ての要素が必ず非ゼロの密行列であり 計算が簡単とは言えどもZ 行列をそのまま扱うのでは計算機メモリーや計算速度の面で大規模系統の計算には適さない したがって 短絡容量計算における手法上の主眼は 短絡電流の計算に必要な特定のZ 行列要素のみをし かに効率的に求めるかという点 に絞られる このように 前項で述べた安定度解析計算と短絡容量計算とでは故障計算を適用する際の視点が大きく異なる -28-
34 (3) Z 行列要素の計算前章で述べたように 短絡容量計算では個々のノードにおける3 相短絡 ( 3 L S) 電流を一挙に計算することを基本的な目的とする それ故 同じ故障計算でも前項の安定度解析におけるそれとは異なる演算技法が必要となる ノード k における 3 L S 故障時の故障電流ム 1 k ( l) は (1.13) 式から容易に得ることがで きる すなわち ノード k が 3 L S 故障時の正相電圧は Vk(l) = 0 であるので この条件 を (1.13) 式に代入して故障電流 ム 1 k ( 1) =Ek /Zk l) (1.21 ) を得る ここで 第 6 章で詳述するように我が国においては一般に故障前系統は無負荷 すなわち E k ム 1 k ( 1) と概略表現できる =1. 0 を前提として計算されているので 上式は更に - 1 / Z k 1) (1.22 ) このように k 点での短絡電流を計算するには Z 行列の対角要素 Z KA 1 のみがあればよ い なお 一般には短絡電流に加え 故障ノード k に接続する各ブランチ ( 相手先ノード j ) から流入する短絡電流の分流ム I kj1} も併せて計算される場合が多い このム 1 kj 1) は次式で表すことができる ム 1 kj 1) = ム 1 k (1) ( Z k 1) - Z kp)) / x kj ここに 右辺の X kjl) はブランチ k-j の正相インピーダンスである (1. 22 ) (1.23) 式から分かるように k=1,2, 1) (1. 23) N の全ノードを対象とする短絡容量計 算で必要となる値は 基本的に正相分 Z 行列の N 個の対角要素 Zk 1 ) ( k= 1,2, びにブランチ数だけの非対角要素 Zk)l) のみであることが分かる N) なら これらの値さえ計算で きれば 短絡電流の具体的数値は上記の各式から簡単に求めることができる しかも Z 行 列全体の要素数と比べたこれら必要要素数の数の割合は (1.3) 式で示したように対象系 統が大規模になるほど顕著になる そこで短絡容量計算における手法上の要点は これら 特定の Z 行列要素のみをいかに効率的に求めるかという点に絞られる なお 1 L G 計算が 加わる場合には 逆相分と零相分について正相分と同様の追加的計算が必要となるのみで あり この場合にも上述した基本的特徴は変わらない さて Z 行列要素を得る一般的な方法には以下のようなものがある 1Z 行列の組立て法 2Y 行列計算の繰り返しによる方法 3Z 行列の特定要素の計算法 短絡容量計算への適用という点で これらの長短を見ると概略つぎのようである まず 1 の方法は Z 行列の次元を 1,2,3 一一ー と増やしながら組み立てていく方法であ る 歴史的に見ると 付録 1. で述べた Y 行列による直接演算法が登場するまではこの方法 に頼るしかなかった しかし この方法ではノード N のおおよそ 3 乗に比例して計算時聞 が増大する上に 計算手順の上から Z 行列の全要素を記憶しておく必要がある欠点を有す るため大規模モデルの計算には適さず 今日では実務上はほとんど使われていない -29-
35 次に 2 の方法は Y 行列による直接演算法を単純に繰り返し利用するものである この 方法の概要を示すと いま Y 行列ベースの次式で y. v= 1 (1.24) 右辺のベクトル I の最初の要素のみに 1.0 他は 0.0 と設定して V を計算する すると こうして得られる V は Z 行列の 1 列目のベクトルに相当することは明らかである そこで 次はベクトル I の 2 番目の要素のみにし O を設定して同様な計算を行い 更に次は 3 番 というような計算を継続することにより すなわち (1. 24) 式の計算をノード数 N だ け繰り返せば最終的に Z 行列が構成できる このように この方法では計算が容易であり かつ各計算で 得られる Z 行列ベクトルの全てを記憶する必要もないため 前述 1 の方法よ りは機能面で優る しかし 短絡容量計算に不要なものも含めた全ての Z 行列要素を計算 する必要があるという点での欠点 は拭えない 最後の 3 が本論文で用いる方法であり 第 6 章で述べるように この方法では基本的に 短絡容量計算に必要な Z 行列の特定要素のみを必要最小限の手順で計算できるという優れ た特徴を有する比 0)
36 2. 各種故障の統一的定式化手法の開発 本章と次章では 新しく開発した故障計算手法について述べる 開発した故障計算手法 の内容は次の 2 つに大別できる ひとつは 大規模電力系統モデルに対する多地点での故 障計算という観点から これを実現するには種類の異なる各々の故障をどのように定式化 すべきかという問題に対するものであり まずこれを本章で述べる あとひとつは 各 の組合せ故障の求解式をし 1 かに導出するかという問題であり これについては本章での定 式化を受けて次章で詳述する さて 前章 3 節において故障計算の基本的方法を述べたが 要点は (1.14) 式に集約され る 再掲すると l (0). ニー Z 1 (0) V( 1 ) = - Z( 1 ). 1 ( 1 ) + E (2.1) である なお (1.14) 式の61 川 (n=o,1,2) は この (2.1) 式以降 以下簡素化して単に I 川で表すこととする (2.1) 式中の各記号について改めて注釈すると V 川は故障時の対称分電圧ベクトル z( 川は対称分 Z 行列 1(1) は故障ノードk だけに故障電流 1 k( 川を持つベクトルである また Eは故障前の状態における正相分電圧ベクトルである 行列 Z (n) は対称分回路に相当する 実際の計算にZ 行列ベースのこの (2.1) 式を用いることはないが便宜上 本章ではこの表記に基づくこととする 本論文における目的はこの式で 全ての故障に対してI 川のみによる求解式を導くことである 1(n) のみによる ということは行列 Z 川には一切変更を加えないことを意味し Z (n) 不変ということはとくに大規模モデルが計算対象となる場合に重要となる 何故ならば Z(n) が変更不要であることは対称分回路を変更しないで済むということを意味し これは実際にY 行列ベースでの故障計算を行う上でY 行列の煩雑な変更計算を一切行わないで済むことに通じるからである しかしながらこれまで こうしたI のみによる求解を探る試みは行われてはいなかった もしくは成し得なかったといって良し かも知れない まえがきで述べたように 本論文で対象としている故障種別は送電線の地絡故障 短絡故障 断線故障 ( あるいは遮断 ) ならびに直列コンデンサの保護ギャップ放電故障の4 種類である これらの中で 送電線断線 ( 遮断 ) を除く故障については長年の研究成果から基本的に1(n) だけによる定式化が可能となっている25. 26) しかし 遮断についてはいったん対称分回路の変更計算を行うことが不可避とされてきた このことが従来 大規模モデルに対する故障計算が困難であった理由のひとつである 一方 仮に全ての故障についてI 川のみによる定式化が可能となったとしても もしそれぞれの故障種別ごとの定式の形が互いに異なれば 多点故障計算を行うことは極めて困難となる 何故ならば 最終的には故障数だけの大きさのベクトルとしてのI 川の求解エ1 を求める必要があるが もし故障種別ごとに式の形が異なれば 第 1. 1 節で述べたように考えられる全ての故障組合せケース数に対応したI 川の計算式を用意しなければならない
37 -Z (2.4a)ワ臼からである そこで本章では 多点故障計算の基本的要件となる上記 2 点 すなわち送電線遮断についてはY 行列の変更計算を伴わない定式化 また4 種類それぞれの故障計算式についてはそれらを全て同形式の方程式で すなわち統一的な表現とすることを念頭に記述することとする なお 本章では以下とくに断らない限り 故障地点はノード また故障相はいわゆる基 準相 (1 線故障では a 相 2 線故障では b c 相 ) と仮定する また も考えないこととする これらは次章で取り扱う 零相分の回線開影響 2. 1 地絡故障 i k k 点での地絡故障の基本計算式は (1.13) 式で述べたとおりであり 再掲すると =-zd} I K {} Vk(l) =- Zk l) 1 k(l) +Ek (2.2) (n) は z d n とE k の関数として定である この式で k 点での故障相が指定されれば1 k 式化できる たとえばa 相 1 線故障についてはい.17) 式で記述したように 1 k(o) -1 k(l) 1 k(2) =Ek / (Zk O) +Zk l) +Zk 2)) (2.3a) と得ることができる また b c 相 2 線地絡故障の場合には a-b-c 座標系での故障条件はVb =Vc =0 ( V K {O}=V K 1)=V K {Z} および 1 8 = 0 であり この条件は 座標系では次となる そこで 1 k (0) + 1 k (1) + 1 k (2) = 0 ( ー k 2) / A E 上式と (2.2) 式とから Vk(n) を消去することにより次式を得る 1 k(l) = (Zk O) +Zk 2)) /A. Ek 1 k (2) = - Z k 0) / A Ek (2.3b) ( I 同様な手順により K { =O 3 線故障の場合には 1 k (1) - 1 / Z k 1) E k (2.3c) 以上 必要な 1 k (n) が全て求まった したがって この値を (2.1) 式に代入すれば故障 時における系統各部の電圧 電流分布を得ることができる ここで 後の便利のために (2.3) 式を導いた際の制約式をまとめて記述しておくと 次 のようである o 1 線地絡 : 一 ( V k(o) + V k(l) + V k(2) -0 l 1 k (0) -1 k (1) -1 k (2) ηδ
38 o 2 線地絡 : ( V k (0) = V k (1) = V k (Z) l 1 k(o) + 1 k(1) + 1 k(z) 0 (2.4b) o 3 線地絡 : Vk(O)=Vk(l)=Vk(Z)=O (2.4c) さて ここで k 点地絡故障時における電圧分布 Vi{ 川の具体的な計算法について述べて ( i おく いま 行列である (2.1) 式をその要素 i について記述すると次式を得る =-Zii} I K {} Vi (1 ) =-Zi l) 1 k(1) +Ei (2.5a) したがって 故障点が確定した時点においてZ 行列のk 列ベクトル要素 Z ip を計算することにより これを上の (2.3)---(2.5) 式に代入して地絡故障時の電圧分布を得ることができる すなわち 故障時の回路網計算を改めて行う必要はない この手順は次節以降の 他の故障についても同様である Z 行列の k :7IJ ベクトル要素 Zi n) は Y 行列ベー スの (1.15) 式で要素 k だけに 1.0 を設定して計算し たときの電圧解として容易に求めることができる 回路的にいえば 図 2.1 に示すように各対称分回路のノードkに単位電流源を注入したときにノードi に現れる電圧がベクトル要素 Zip} に相当する なお 実際上は図 2.1 の計算の際に同時にブランチ諸量 y.; ωも得ておけば これを用いて故障時の ブランチjの電流についても簡単に次式により計算 ( ーでき 都合がよい -y j 0) 1 k (0) C.i (1) = -Y.i 1) 1 k (1) + F j 当ぐ 1 [A] 主ム 図 2.1 地絡 短絡故障計算 における Z と Y ベクトル要素 (2.5b) ここに C ジ n) は故障時にブランチ j を流れる対称分の電流であり また Fj は故障前の 状態においてブランチ j を流れていた正相分電流である 2.2 線間短絡故障 線間短絡故障の基本計算式は 地絡故障と同じ (2.2) 式で与えられる また 短絡相数に対応する制約条件は次となる o 2 線短絡 : ( V k (1) = V k (Z) l 1 k (1) + 1 k (Z) = 0 1 k (0) = 0 (2.6a) o 3 線短絡 Vk(1) = V k(z) ニ O 1 k(o) = 0 (2.6b) この (2.6) 式の特徴は (2.4) 式で記述した地絡故障の条件式で単に零相成分を無視したも のに等しいという点 である したがって 短絡計算は後述するように地絡故障の定式化に 含めて取り扱うことができる n Un U
39 (z 2.3ブランチ断線 遮断上述した地絡 短絡故障の計算方法は既に確立している方法である 同様にブランチの断線や遮断計算についても 従来より用いられている一般的な方法がある しかし 従来の方法は極めて煩わしい計算手順を要する そこで ここではそれに代わる新しい計算法について述べる なお 断線と遮断は計算する上では同一であるので 以下断線と総称する ただし両者の適用上の相違点として 断線はいわゆる故障のひとつであり 発生位置は一般にブランチ上という特徴があるのに比べ 遮断は遮断器の開放という制御動作であり 指定位置は常にブランチ端に限られる まず これまでの断線計算方法を示す いま 図 2.2(a) に示すブランチs-rのs 端でブ ランチ断線を計算する場合 従来の方法ではいったん断線点を開放する必要がある この [H= 一 s 0) + Z tf 0) ) 回路を対象に 断線計算に関する従来の基本式は次式で表される H k - (1) C k (0) ( Z s 1) + Z tf 1) ) Ck(1) +Ek (2.7) o H k (n) 断線時のノード s t 聞の電位差 C k(n) 断線時に断線点を流れる電流 o Z s n) Z tfn) それぞれノードsおよびノードtから対称分回路を覗いたときのインピーダンス o E k 断線点を単に開放したときのノードs t 閣の電位差断線時の系統電圧 電流分布は この (2.7) 式のCk(n) を既述の地絡故障と同様な手順で求め その電流値を図 2.2(a) のノードsから取り出し 同じ電流をノードtに注入することにより得ることができる しかし こうした従来の方法では 断線点の開放に伴い新しいノードtを追加する回路変更が必要となる 回路変更は すなわちY 行列の変更を意味する 第 1. 1 節で述べたように 一般にY 行列の構造変更は極めて煩わしい手順を伴う そこで以下では Y 行列の変更計算を必要としない すなわちY 行列は常に元のままで断線計算を行うことのできる新しい方法について述べる 対称分回路合くH k (n) [ V J ィ マ (k) ヂコ :;i;gj 対称分回路 (a) 従来の方法 ( 回路変更必要 ) (b) 新しい方法 ( 回路変更不要 ) 図 2.2 断線 遮断の計算方法
40 (k=-m/(zp+zj) 新しい方法では まず (2.7) 式を次のように表現し直す C k (1) = -H k (1) / (Z s l) + Z tf.1 )) + E k / (Z s 1) + Z tf.l) ) (2.8) するとこの式で 右辺のH k (n) にかかる係数は 対称分回路の断線点から直列に回路を覗 = いた全体のアドミタンスyk n), こ等しいことは明らかである すなわち Y k n) 1 / (Z s ω+ Z tf. n) ) (2.9a) また正相分方程式の右辺第 2 項は 断線前の状態において k 点を流れていた電流 F k に等 しい すなわち F k = E k / (Z s 1 ) + Z tf.l)) = E k / y k 1 ) (2.9b) この (2.9b) 式の等価性について注釈すると いま図 2.2(a) で断線点聞の電位差が E k であ るとするとき この電位差がゼロとなるようにノード s から t に向かつて電流を流すもの とする するとこの時 k 点から正相分回路を除いたときのインピーダンスは 1 /Y k l) あるので 電位差をゼロとする電流値はキルヒホッフ則から E k / Y k 1) でなければなら ない この電流を流したときの回路の電圧 電流分布は 断線点を開く前の状態に等しい すなわち E k / Y k 1) は断線前の状態において k 点を流れていた電流 F k に等しい こ とが分かる さて (2.9) 式を (2.8) 式に代入して次式を得る (CK =-yi} 日 C k ( 1) -Y k 1) Hk(l) + F k = (2.10) この式が ブランチ断線計算のための新しい計算式である56-57)0 新しい計算法では (2.7) 式との対比から分かるように 最終的に得るべき未知変数として断線時に断線点聞を通過する電流 Ck( 川ではなく 断線時の電位差 H k(n) として定式化している このH k(n) は 図 2.2(b) に示すように 元の回路における断線点 kでの電圧源として表現することができる このような電圧源は よく知られているように当該ブランチの両端ノードsとrでの注入電流源 (Nortonの電流源 図 2.3) として等価計算することができる したがって 新しい計算法では電圧源 H k( 川による断線計算を行うためにY 行列を変更する必要は一切ない このことを図 1.1 のY 行列の計算フローに即して言えば断線計算であっても単にステップ3のみを繰り返すだけでよい また (2.10) 式のアドミタンスYAn についても これは図 2.4に示すように元の回路の断線点 kに単位電圧源を挿入 ( 図 2.2(b) とは向きが異なることに注意 ) したときの通過電流として簡単に得ることができる 具体的な計算では 上記 YAn} を計算する際に得られる他の諸量 ノード電圧 z dn} お よびブランチ電流 Y JF} を記憶しておけば 地絡故障の項で述べたように故障時の回路網 計算を省略で き 効率的な計算が可能となる すなわち いったん (2.10) 式の解 H k(n) が -35-
41 -y 三副 Jぃ 二 与等価表現 1 [ 品主 治よもこ 示 7ム 図 2.3 Norton の電流源図 2.4 ブランチ断線 遮断計算 における Z と Y ベクトル要素 求まりさえすれば (2.5) 式と同様に k 点断線時の電圧 電流分布はこの H k(n) を次式に 代入するだけで簡単に得ることができる ( i一 一=一一一 Viジ(1 ) _ 一 Z ij41υ) H kピ( 1υ) + E i ( ー j 0) H k (0) Viジ(Z) _ 一 Z i Z幻) H kピ(z) (2.11a) (2.11b) ここで (2.10) 式に対して断線相が指定された場合の制約式をまとめて記述すれば o 1 線断線 : o 2 線断線 : ( C k (0) + C k (1) + C k (Z) = 0 l Hk(O) =Hk(l) =Hk(Z) ( Ck(O) =Ck(l) =ck(z) l Hk(O) +Hk(l) +Hk(Z) = 0 (2.12a) (2. 12b) o 3 線断線 Ck(O) =Ck(1) =ck(z) - 0 (2.12c) となる 以上述べた (2.10)---(2.12) 式の新しい基本式は 地絡故障のそれである (2.2)--- (2.4) 式と全く同形となっている 後述するように 基本式が同形というこの特徴が多点故障の効率的な計算を可能とすることになる 2.4 直列コンデンサの短絡故障 我が国では 基幹系統の輸送能力はおおむね安定度で制限されている よく知られてい るように 安定度は送受端聞のリアクタンスの大きさに反比例する そこで 送電線に直 列にコンデンサ SrC を接続することにより送受端聞のリアクタンスを減少させ これによ り安定度向上を図る方策が考えられる 現在 我が国では SrC はごく一部の系統にのみ実 用されている状況にある さて この SrC には構造的に図 2.5 に示すように SrC 自身との並列回路が設けられてい るのが通常である この並列回路は 通常の運用状態ではギャップを挟んで電気的に開い た開放状態にあるが 地絡故障等により SrC に大電流が流れると その電流による SrC 損 円 Uno
42 図 2.5Src の構造 図 2.6Src 短絡計算における Z と Y ベクトル 傷防止のために該当相のギャップが放電して回路が閉じる機能となっている 並列回路が閉じたときのSrCの受端聞の電位差はゼ口 すなわちSrcはシステムとして短絡と等価な状態となる この現象をSrCの短絡故障という SrC 短絡の引き金は上述のように大電流であり したがって一般にSrCの短絡故障は単独では発生せず 地絡など他の故障の発 t による波及現象として現れる いま図 2.5で 保護ギャップのある並列回路に 1 k ( n) なる電流が流れたとき SrC 送受 端 s-r 聞に電位差 VsJ n} が現れるものと仮定する すると これらの変数の聞には次の関 [ s 係が成立する =-zk IK } Vsf1) =-Zk(l) 1 k(1) +Esr (2.13) Zk(n) 図 2.6 に示すようにノード r から単位電流を取り出しノード s に注入し たときに得られるノード s-r 聞の電位差 o E s r 故障前の s-r 聞の電位差 この (2.13) 式で SrC の場合には指定された短絡相の電位差 V s r はゼロであるので こ れに基づく制約式を記述すれば o 1 線短絡 : ー o 2 線短絡 : イー ( V sf 0 ) + V sf 1) + V sf Z) -0 l 1 k(o) 1 k(1) - 1 k(z) ( V sf 0) = V sf 1) = V sf Z) l 1 k ( 0) +1 k (1) +1 k (Z) = 0 (2.14a) (2.14b) o 3 線短絡 : V sjo} ニ Vsf 1) = V sf Z) = 0 (2. 14c) となる (2.13) 式と (2.14) 式から短絡電流 1 k (n) が求まれば SrC 短絡時の電圧 電流分布は 図 2.6の計算時に同時に得られるノード電圧 Z Jn} およびブランチ電流 y j n) を用いて 1 k ( n) を次式に代入することにより簡単に得ることができる (Vi =-zr IK( Vi(1)=-Zi 1) Ik(1)+Ei (2.15a)ηinペU
43 (C }= 一 一 C j f {l} = 一 Yj 1) Ikμ(1) + F j (2. 15b) 以上述べた (2.13)---(2.15) 式の基本式もまた 地絡故障のそれである (2.2)--- (2. 4)Jj と全く同形となっている 2.5 各種故障計算式の統一的表現上述の4 種類の故障の求解式をまとめて表すと 表 2.1となる 同表で それぞれの故 障計算の基本式 故障の制約条件 および故障時の系統分布の計算式の全ては全て同形と なっている 無論 計算の対象となる対称分回路も元のままの同じ回路である この特徴 は 特に多地点での故障計算を行うにあたって大きな利点となる 何故ならば 同形であ ることは 上記 4つの故障の求解の定式化をそれぞれ個別に行う必要がないことを意味す るからである すなわち 単に故障数や故障相による定式化を図れば足りる その定式化については次章で述べることとし ここではそのための基本計算式をまとめ て記述しておく すなわち それぞれの故障の基本式は 表 2.1の右欄に示すように代表 変数 Uk とWk を用いることにより 故障の種類には無関係に次式により統一的に表現で l ーきる5Q) 0 - (0) U k (1) = - X k 1) W k (1) + S k (2. 16) 無論 この式に現れるx dn} およびS k は既述のようにそれぞれ故障種類に応じて異なるので それぞれの値を具体的に設定する際に注意する必要がある なお 本章冒頭で故障計算の目的は (2.1) 式の1 (n) を用いて求解の定式化を行うことであると述べたが その基本目的はこの (2.16) 式ではWk( 川として表されている Wk(n) の物理的意味が図 2.7に示すように故障種別に応じて異なることは これまでの記述から当然 である さて 故障相を表す制約式についても 表 2.1 ' ØIJ 示しているようにそれぞれの故障ごとに個別に表現する必要はない 何故ならば 地絡故障についての (2.4) 式 短絡故障に ( 注 ) いずれも対称分回路を示す (a) 地絡故障 ( 短絡故障 ) (b) ブランチ断線 遮断 図 2.7 故障計算方法の概略 (c) Src 短絡故障 -38-
44 表 2. 1 故障計算式の統一的表現 S r C 短絡故障基 lf V K{O)=-zdO I H (O 本 I V k (1) = -Z k 1) 1 k (l) + E 祉計 l l V H(Z =-zdz I K(Z 算 I V k : 故障点電圧式 I 1 k : 地絡電流 ( 短絡電流 ) 線路断線 遮断 ( c r = 一山 k{o C k (1) = - y k 1) H k (1) + F k C k(z) = - Y k Z) H k(z) C k : 断線点通過電流 Hk : 断線点電位差 ( 小一 Zk(O) 1 k(o) V sfl) = -Z k ( 1) 1 k (1) + E s r V sfz) = -Z k (Z) 1 k (Z) V s r: SrC f げ電位差 (Vs-Vr) 1 k : 泣 C t げ通過電流 コ巳ο llg 故障 (a 相 ) 故 I (V k (0) + V k (1) + V k (2) = 0 障 I l 1 k(o) = 1 k(l) = 1 k(z) 条 12LG (2L8) 故障 (b,c 相 ) 件 I (Vk(O)=Vk(l)=Vk(Z) 伊 ij I l 1 k(o) + 1 k(o 十 1 k (Z) = 0 G 1 k (0) 1 k (1) 1 k (Z) を求める卜\J地絡故統一化した表現ザ 00め一一一一求Z幻Z幻を-KKHK幻CHCHピ+一一一一+Hυυuunuv JKK1jkuυ相CH相CHピa+=ρ=+Hf - hu}}凸vau〆't nuhu O{k{kOピピωLCHLCHE-KIf-L2flLH1 L f,1 放電 (a 相 ( v sjo}+vsji +Vsj~o 1 k(o) = 1 k(1) = 1 k(2) 2 L f げ放電 (b,c 相 ( VsjO =VsjI}=VsJZ 1 k(o) + 1 k(o + 1 k(z) = 0 G 1 k(o) 1 k (1) 1 k (2) を求める故 I (V i (0) = -Z i 0) 1 k (0) 障 イ V i(l) =- Z i l) 1 k(l) + E i 状 I l V i (2) =-Z i Z) 1 k (Z) 台邑計算式廿ム+nuv a.,ゐuah民uaye-tiveinv,. ゐ{-K U且{反-唱Ju--u JWYYY一一一一一一一一一nv a 号ゐ.,d.噌J P upupuflit--j 21111t ( Vi{O} 一 } 日 V i(1) =- Z i 1) H k(1) + E i V i ( 幻 =-Zi Z)Hk(Z) 廿ム+のu' 92 b民uhbhhhhhuv'a勾'u, ba, br, U凪YYY一一一一一一一一白v,.,- upupufl-'l,くli-- E+n日v'AqL uhbabryebate-ムγase6012, bn,. ihrr un.,aa--& 唱ムワlU7U7u一一一一一一一一一nv-a勿'M-唱ゐ 噌'a 噌 -vvvrbild--lkf+hu--. ゐbnbhbnマBaa-?'EAYEBAhu--. b, brr unr UA-唱Aw--d.,uYYY一一一一一一一一一のυ 且今& 4.,u 4 FUFUPUf-- lll備 短絡故障では零相成分を無視 Zk =Zsk-Zrk E i Fì はそれぞれ故障前の正相 i 点電圧 j 点通過電流 考 V i{n C /n ) (n=o, 1,2) はそれぞれ故障時の対称分 i 点電圧 j 点通過電流 ( 日 川 (0) U k (1) = - X k 1) W k (1) + 8 k U k (Z) = -X k Z) W k (Z) U k : 故障点状態変数 W 包 : 故障点未知変数 1 L 故障は相 ) ( UK{O +UK{1}+Uj~o Wk(O) =Wk(l) =Wk(Z) 2 L 故障 (b,c 相 ) ( UK{O)=UJ=UK Z Wk(O) +Wk(1) +Wk(Z) = 0 G Wk(O) Wk(l) WkCZ) を求める ( Vi O} 寸 0)Wk(O) Vi(1) =-Zi 1)Wk(l) +Ei V i (Z) = - Z i Z) W k (Z) ( C J fo} ー 0)W k (0) C /1) = - Y j l) W k(l) + F j C /Z) = -Y j Z) W k (2)
45 ついての (2.6) 式 ブランチ断線 遮断についての (2.12) 式 およびSrC 短絡についての (2. 山 ) 式のそれぞれの故障制約式もまた 上式と同様に互いに同形 ( ただし短絡故障の場合は零相成分を無視する ) となっているからである すなわち 制約式についても (2.16) 式で導入した変数 Uk と W k を用いて 次のように統一的に表すことができる 1 線故障 : ( U k (0) + U k (1) + U k (Z) = 0 i l W k <O) =W k(t) =W k(z) (2.17a) 2 線故障 : ( Uk(O) =Uk(l) =Uk(Z) i l Wk(O) +Wk(l) +Wk(Z) = 0 (2.17b) 3 線故障 Uk(O) =Uk(l) =Uk(Z) -0 (2.17c) 更に 故障時の電圧 電流分布の計算式も上記同様に互いに同形 ( (2.5) 式 (2.11) エ 1 および (2.15) 式 ) である これについても統ーした計算式を示しておけば (Vi ー )W k(o) V i (1) = - 2 i 1) \九Tk(t)+Ei 1 一一一 (0) V i(z) =-2i Z)Wk(Z) (2.18a) (2.18b) となる 無論 この式の右辺の係数 Z i in} y j n ) もまた 既述のように故障種類によって異なる その求解の方法をここでまとめて示しておくと それぞれ図 2.8 の計算によって得られるノードiの電圧がZ ir\ ブランチjの電流がY An} である すなわち 地絡あるいは短絡故障の場合のxdn はZ kin} として ブランチ遮断 遮断の場合はY kdn と k して さらにSrC 短絡の場合はZ (n) s - Z r k ( 川 ( これは (2.13) 式右辺のZ k( n ) に相当 ) と して得ることができる 無論 Wk<n ) 求解のベースとなる (2.16) 式右辺の係数 xdn} は 当然ながらこれら Z i n ) と Y din} の一部の要素から得ることができる 次章では これら (2.16) (2.18) 式の統一式表記に基づき 多点故障計算のための定式化や求解方法等を述べる 注 ) いずれも対称分回路を示す (a) 地絡故障 ( 短絡故障 ) (b) ブランチ断線 遮断 (c) SrC 短絡故障 図 2.8 故障種別ごとのインピーダンス定数 (2 と y) の算出方法 -40 一
Microsoft PowerPoint - 電力回路h ppt
 電力回路 対称座標法 平成 年 6 月 日 単位値から実値への変換 単位値は, 実値をベース値で割って得る 実値は, 単位値にベース値を掛けて求まる 電流 ( A) 電流 ( p. u.) ベース電流 ( A) 電圧 ( ) 電圧 ( p. u.) ベース電圧 ( ) インピーダンス( Ω) インピーダンス( p. u.) ベースインピーダンス( Ω) 三相電力回路 三相一回線送電線の回路 回路図
電力回路 対称座標法 平成 年 6 月 日 単位値から実値への変換 単位値は, 実値をベース値で割って得る 実値は, 単位値にベース値を掛けて求まる 電流 ( A) 電流 ( p. u.) ベース電流 ( A) 電圧 ( ) 電圧 ( p. u.) ベース電圧 ( ) インピーダンス( Ω) インピーダンス( p. u.) ベースインピーダンス( Ω) 三相電力回路 三相一回線送電線の回路 回路図
Microsoft Word - thesis.doc
 剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
Microsoft Word _3.2.1−î‚bfiI”Œ“•.doc
 3. 電圧安定性に関する解析例 3.. 電圧安定性の基礎的事項 近年, 電力設備の立地難や環境問題などから電源の遠隔化 偏在化や送電線の大容量化の趨勢が顕著になって来ており, 電力系統の安定運用のために従来にも増して高度な技術が必要となっている 最近, なかでも電力系統の電圧不安定化現象は広く注目を集めており, 海外では CIGRE や IEEE において, また国内では電気協同研究会において幅広い検討が行われてきた
3. 電圧安定性に関する解析例 3.. 電圧安定性の基礎的事項 近年, 電力設備の立地難や環境問題などから電源の遠隔化 偏在化や送電線の大容量化の趨勢が顕著になって来ており, 電力系統の安定運用のために従来にも増して高度な技術が必要となっている 最近, なかでも電力系統の電圧不安定化現象は広く注目を集めており, 海外では CIGRE や IEEE において, また国内では電気協同研究会において幅広い検討が行われてきた
パソコンシミュレータの現状
 第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
(3) E-I 特性の傾きが出力コンダクタンス である 添え字 は utput( 出力 ) を意味する (4) E-BE 特性の傾きが電圧帰還率 r である 添え字 r は rrs( 逆 ) を表す 定数の値は, トランジスタの種類によって異なるばかりでなく, 同一のトランジスタでも,I, E, 周
 トランジスタ増幅回路設計入門 pyrgt y Km Ksaka 005..06. 等価回路についてトランジスタの動作は図 のように非線形なので, その動作を簡単な数式で表すことができない しかし, アナログ信号を扱う回路では, 特性グラフのの直線部分に動作点を置くので線形のパラメータにより, その動作を簡単な数式 ( 一次式 ) で表すことができる 図. パラメータトランジスタの各静特性の直線部分の傾きを数値として特性を表したものが
トランジスタ増幅回路設計入門 pyrgt y Km Ksaka 005..06. 等価回路についてトランジスタの動作は図 のように非線形なので, その動作を簡単な数式で表すことができない しかし, アナログ信号を扱う回路では, 特性グラフのの直線部分に動作点を置くので線形のパラメータにより, その動作を簡単な数式 ( 一次式 ) で表すことができる 図. パラメータトランジスタの各静特性の直線部分の傾きを数値として特性を表したものが
Microsoft Word - 2_0421
 電気工学講義資料 直流回路計算の基礎 ( オームの法則 抵抗の直並列接続 キルヒホッフの法則 テブナンの定理 ) オームの法則 ( 復習 ) 図 に示すような物体に電圧 V (V) の直流電源を接続すると物体には電流が流れる 物体を流れる電流 (A) は 物体に加えられる電圧の大きさに比例し 次式のように表すことができる V () これをオームの法則 ( 実験式 ) といい このときの は比例定数であり
電気工学講義資料 直流回路計算の基礎 ( オームの法則 抵抗の直並列接続 キルヒホッフの法則 テブナンの定理 ) オームの法則 ( 復習 ) 図 に示すような物体に電圧 V (V) の直流電源を接続すると物体には電流が流れる 物体を流れる電流 (A) は 物体に加えられる電圧の大きさに比例し 次式のように表すことができる V () これをオームの法則 ( 実験式 ) といい このときの は比例定数であり
例 e 指数関数的に減衰する信号を h( a < + a a すると, それらのラプラス変換は, H ( ) { e } e インパルス応答が h( a < ( ただし a >, U( ) { } となるシステムにステップ信号 ( y( のラプラス変換 Y () は, Y ( ) H ( ) X (
 第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
Microsoft Word - 付録1誘導機の2軸理論.doc
 NAOSIE: Nagaaki Univity' Ac itl パワーエレクトロニクスと電動機制御入門 Autho( 辻, 峰男 Citation パワーエレクトロニクスと電動機制御入門 ; 15 Iu Dat 15 U http://hl.hanl.nt/169/55 ight hi ocumnt i ownloa http://naoit.lb.nagaaki-u.ac.jp 付録 1 誘導機の
NAOSIE: Nagaaki Univity' Ac itl パワーエレクトロニクスと電動機制御入門 Autho( 辻, 峰男 Citation パワーエレクトロニクスと電動機制御入門 ; 15 Iu Dat 15 U http://hl.hanl.nt/169/55 ight hi ocumnt i ownloa http://naoit.lb.nagaaki-u.ac.jp 付録 1 誘導機の
Microsoft Word - 補論3.2
 補論 3. 多変量 GARC モデル 07//6 新谷元嗣 藪友良 対数尤度関数 3 章 7 節では 変量の対数尤度を求めた ここでは多変量の場合 とくに 変量について対数尤度を求める 誤差項 は平均 0 で 次元の正規分布に従うとする 単純化のため 分散と共分散は時間を通じて一定としよう ( この仮定は後で変更される ) したがって ij から添え字 を除くことができる このとき と の尤度関数は
補論 3. 多変量 GARC モデル 07//6 新谷元嗣 藪友良 対数尤度関数 3 章 7 節では 変量の対数尤度を求めた ここでは多変量の場合 とくに 変量について対数尤度を求める 誤差項 は平均 0 で 次元の正規分布に従うとする 単純化のため 分散と共分散は時間を通じて一定としよう ( この仮定は後で変更される ) したがって ij から添え字 を除くことができる このとき と の尤度関数は
行列、ベクトル
 行列 (Mtri) と行列式 (Determinnt). 行列 (Mtri) の演算. 和 差 積.. 行列とは.. 行列の和差 ( 加減算 ).. 行列の積 ( 乗算 ). 転置行列 対称行列 正方行列. 単位行列. 行列式 (Determinnt) と逆行列. 行列式. 逆行列. 多元一次連立方程式のコンピュータによる解法. コンピュータによる逆行列の計算.. 定数項の異なる複数の方程式.. 逆行列の計算
行列 (Mtri) と行列式 (Determinnt). 行列 (Mtri) の演算. 和 差 積.. 行列とは.. 行列の和差 ( 加減算 ).. 行列の積 ( 乗算 ). 転置行列 対称行列 正方行列. 単位行列. 行列式 (Determinnt) と逆行列. 行列式. 逆行列. 多元一次連立方程式のコンピュータによる解法. コンピュータによる逆行列の計算.. 定数項の異なる複数の方程式.. 逆行列の計算
Microsoft PowerPoint - 10.pptx
 m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
Microsoft Word - Chap17
 第 7 章化学反応に対する磁場効果における三重項機構 その 7.. 節の訂正 年 7 月 日. 節 章の9ページ の赤枠に記載した説明は間違いであった事に気付いた 以下に訂正する しかし.. 式は 結果的には正しいので安心して下さい 磁場 の存在下でのT 状態のハミルトニアン は ゼーマン項 と時間に依存するスピン-スピン相互作用の項 との和となる..=7.. g S = g S z = S z g
第 7 章化学反応に対する磁場効果における三重項機構 その 7.. 節の訂正 年 7 月 日. 節 章の9ページ の赤枠に記載した説明は間違いであった事に気付いた 以下に訂正する しかし.. 式は 結果的には正しいので安心して下さい 磁場 の存在下でのT 状態のハミルトニアン は ゼーマン項 と時間に依存するスピン-スピン相互作用の項 との和となる..=7.. g S = g S z = S z g
Microsoft Word - NumericalComputation.docx
 数値計算入門 武尾英哉. 離散数学と数値計算 数学的解法の中には理論計算では求められないものもある. 例えば, 定積分は, まずは積分 ( 被積分関数の原始関数をみつけること できなければ値を得ることはできない. また, ある関数の所定の値における微分値を得るには, まずその関数の微分ができなければならない. さらに代数方程式の解を得るためには, 解析的に代数方程式を解く必要がある. ところが, これらは必ずしも解析的に導けるとは限らない.
数値計算入門 武尾英哉. 離散数学と数値計算 数学的解法の中には理論計算では求められないものもある. 例えば, 定積分は, まずは積分 ( 被積分関数の原始関数をみつけること できなければ値を得ることはできない. また, ある関数の所定の値における微分値を得るには, まずその関数の微分ができなければならない. さらに代数方程式の解を得るためには, 解析的に代数方程式を解く必要がある. ところが, これらは必ずしも解析的に導けるとは限らない.
Microsoft PowerPoint - パワエレH20第4回.ppt
 パワーエレトクロニクス ( 舟木担当分 ) 第 4 回 サイリスタ変換器 ( 相ブリッジ ) 自励式変換器 平成 年 7 月 7 日月曜日 限目 位相制御単相全波整流回路 転流重なり角 これまでの解析は交流電源の内部インピーダンスを無視 考慮したらどうなるか? 電源インピーダンスを含まない回路図 点弧時に交流電流は瞬時に反転» 概念図 電源インピーダンスを含んだ回路図 点弧時に交流電流は瞬時に反転できない»
パワーエレトクロニクス ( 舟木担当分 ) 第 4 回 サイリスタ変換器 ( 相ブリッジ ) 自励式変換器 平成 年 7 月 7 日月曜日 限目 位相制御単相全波整流回路 転流重なり角 これまでの解析は交流電源の内部インピーダンスを無視 考慮したらどうなるか? 電源インピーダンスを含まない回路図 点弧時に交流電流は瞬時に反転» 概念図 電源インピーダンスを含んだ回路図 点弧時に交流電流は瞬時に反転できない»
PowerPoint Presentation
 付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
横浜市環境科学研究所
 周期時系列の統計解析 単回帰分析 io 8 年 3 日 周期時系列に季節調整を行わないで単回帰分析を適用すると, 回帰係数には周期成分の影響が加わる. ここでは, 周期時系列をコサイン関数モデルで近似し単回帰分析によりモデルの回帰係数を求め, 周期成分の影響を検討した. また, その結果を気温時系列に当てはめ, 課題等について考察した. 気温時系列とコサイン関数モデル第 報の結果を利用するので, その一部を再掲する.
周期時系列の統計解析 単回帰分析 io 8 年 3 日 周期時系列に季節調整を行わないで単回帰分析を適用すると, 回帰係数には周期成分の影響が加わる. ここでは, 周期時系列をコサイン関数モデルで近似し単回帰分析によりモデルの回帰係数を求め, 周期成分の影響を検討した. また, その結果を気温時系列に当てはめ, 課題等について考察した. 気温時系列とコサイン関数モデル第 報の結果を利用するので, その一部を再掲する.
Microsoft PowerPoint - H22制御工学I-2回.ppt
 制御工学 I 第二回ラプラス変換 平成 年 4 月 9 日 /4/9 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
制御工学 I 第二回ラプラス変換 平成 年 4 月 9 日 /4/9 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
トランスの利用率の話 トランスの利用率の話をします この書き込みをお読みの方は トランスの容量が下記の様に示される事はご存じだと思います ( ご存じでない方は 下図を見て納得して下さい ) 単相 2 線式トランスの容量を P[VA] とすれば 単相負荷は P[VA] 接続できます この単相トランスを
![トランスの利用率の話 トランスの利用率の話をします この書き込みをお読みの方は トランスの容量が下記の様に示される事はご存じだと思います ( ご存じでない方は 下図を見て納得して下さい ) 単相 2 線式トランスの容量を P[VA] とすれば 単相負荷は P[VA] 接続できます この単相トランスを トランスの利用率の話 トランスの利用率の話をします この書き込みをお読みの方は トランスの容量が下記の様に示される事はご存じだと思います ( ご存じでない方は 下図を見て納得して下さい ) 単相 2 線式トランスの容量を P[VA] とすれば 単相負荷は P[VA] 接続できます この単相トランスを](/thumbs/99/142050544.jpg) トランスの利用率の話 トランスの利用率の話をします この書き込みをお読みの方は トランスの容量が下記の様に示される事はご存じだと思います ( ご存じでない方は 下図を見て納得して下さい ) 単相 2 線式トランスの容量を P[VA] とすれば は P[VA] 接続できます この単相トランスを 3 台組み合わせて三相トランスとした場合 当然三相容量は 3P[VA] 接続出来ます この単相トランスを 2
トランスの利用率の話 トランスの利用率の話をします この書き込みをお読みの方は トランスの容量が下記の様に示される事はご存じだと思います ( ご存じでない方は 下図を見て納得して下さい ) 単相 2 線式トランスの容量を P[VA] とすれば は P[VA] 接続できます この単相トランスを 3 台組み合わせて三相トランスとした場合 当然三相容量は 3P[VA] 接続出来ます この単相トランスを 2
Microsoft PowerPoint - H22パワエレ第3回.ppt
 パワーエレトクロニクス ( 舟木担当分 ) 第三回サイリスタ位相制御回路逆変換動作 平成 年 月 日月曜日 限目 誘導負荷 位相制御単相全波整流回路 導通期間 ( 点弧角, 消弧角 β) ~β( 正の半波について ) ~ β( 負の半波について ) β> となる時に連続導通となる» この時, 正の半波の導通期間は~» ダイオードでは常に連続導通 連続導通と不連続導通の境界を求める オン状態の微分方程式
パワーエレトクロニクス ( 舟木担当分 ) 第三回サイリスタ位相制御回路逆変換動作 平成 年 月 日月曜日 限目 誘導負荷 位相制御単相全波整流回路 導通期間 ( 点弧角, 消弧角 β) ~β( 正の半波について ) ~ β( 負の半波について ) β> となる時に連続導通となる» この時, 正の半波の導通期間は~» ダイオードでは常に連続導通 連続導通と不連続導通の境界を求める オン状態の微分方程式
RMS(Root Mean Square value 実効値 ) 実効値は AC の電圧と電流両方の値を規定する 最も一般的で便利な値です AC 波形の実効値はその波形から得られる パワーのレベルを示すものであり AC 信号の最も重要な属性となります 実効値の計算は AC の電流波形と それによって
 入門書 最近の数多くの AC 電源アプリケーションに伴う複雑な電流 / 電圧波形のため さまざまな測定上の課題が発生しています このような問題に対処する場合 基本的な測定 使用される用語 それらの関係について理解することが重要になります このアプリケーションノートではパワー測定の基本的な考え方やパワー測定において重要な 以下の用語の明確に定義します RMS(Root Mean Square value
入門書 最近の数多くの AC 電源アプリケーションに伴う複雑な電流 / 電圧波形のため さまざまな測定上の課題が発生しています このような問題に対処する場合 基本的な測定 使用される用語 それらの関係について理解することが重要になります このアプリケーションノートではパワー測定の基本的な考え方やパワー測定において重要な 以下の用語の明確に定義します RMS(Root Mean Square value
以下 変数の上のドットは時間に関する微分を表わしている (ex. 2 dx d x x, x 2 dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-1) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( x や x, x などがすべて 1 次で なおかつ
 以下 変数の上のドットは時間に関する微分を表わしている (e. d d, dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( や, などがすべて 次で なおかつそれらの係数が定数であるような微分方程式 ) に対して安定性の解析を行ってきた しかしながら 実際には非線形の微分方程式で記述される現象も多く存在する
以下 変数の上のドットは時間に関する微分を表わしている (e. d d, dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( や, などがすべて 次で なおかつそれらの係数が定数であるような微分方程式 ) に対して安定性の解析を行ってきた しかしながら 実際には非線形の微分方程式で記述される現象も多く存在する
s とは何か 2011 年 2 月 5 日目次へ戻る 1 正弦波の微分 y=v m sin ωt を時間 t で微分します V m は正弦波の最大値です 合成関数の微分法を用い y=v m sin u u=ωt と置きますと dy dt dy du du dt d du V m sin u d dt
 とは何か 0 年 月 5 日目次へ戻る 正弦波の微分 y= in を時間 で微分します は正弦波の最大値です 合成関数の微分法を用い y= in u u= と置きますと y y in u in u (co u co になります in u の は定数なので 微分後も残ります 合成関数の微分法ですので 最後に u を に戻しています 0[ra] の co 値は [ra] の in 値と同じです その先の角
とは何か 0 年 月 5 日目次へ戻る 正弦波の微分 y= in を時間 で微分します は正弦波の最大値です 合成関数の微分法を用い y= in u u= と置きますと y y in u in u (co u co になります in u の は定数なので 微分後も残ります 合成関数の微分法ですので 最後に u を に戻しています 0[ra] の co 値は [ra] の in 値と同じです その先の角
<4D F736F F D E4F8E9F82C982A882AF82E98D7397F1>
 3 三次における行列 要旨高校では ほとんど 2 2 の正方行列しか扱ってなく 三次の正方行列について考えてみたかったため 数 C で学んだ定理を三次の正方行列に応用して 自分たちで仮説を立てて求めていったら 空間における回転移動を表す行列 三次のケーリー ハミルトンの定理 三次における逆行列を求めたり 仮説をたてることができた. 目的 数 C で学んだ定理を三次の正方行列に応用する 2. 概要目的の到達点として
3 三次における行列 要旨高校では ほとんど 2 2 の正方行列しか扱ってなく 三次の正方行列について考えてみたかったため 数 C で学んだ定理を三次の正方行列に応用して 自分たちで仮説を立てて求めていったら 空間における回転移動を表す行列 三次のケーリー ハミルトンの定理 三次における逆行列を求めたり 仮説をたてることができた. 目的 数 C で学んだ定理を三次の正方行列に応用する 2. 概要目的の到達点として
RLC 共振回路 概要 RLC 回路は, ラジオや通信工学, 発信器などに広く使われる. この回路の目的は, 特定の周波数のときに大きな電流を得ることである. 使い方には, 周波数を設定し外へ発する, 外部からの周波数に合わせて同調する, がある. このように, 周波数を扱うことから, 交流を考える
 共振回路 概要 回路は ラジオや通信工学 などに広く使われる この回路の目的は 特定の周波数のときに大きな電流を得ることである 使い方には 周波数を設定し外へ発する 外部からの周波数に合わせて同調する がある このように 周波数を扱うことから 交流を考える 特に ( キャパシタ ) と ( インダクタ ) のそれぞれが 周波数によってインピーダンス *) が変わることが回路解釈の鍵になることに注目する
共振回路 概要 回路は ラジオや通信工学 などに広く使われる この回路の目的は 特定の周波数のときに大きな電流を得ることである 使い方には 周波数を設定し外へ発する 外部からの周波数に合わせて同調する がある このように 周波数を扱うことから 交流を考える 特に ( キャパシタ ) と ( インダクタ ) のそれぞれが 周波数によってインピーダンス *) が変わることが回路解釈の鍵になることに注目する
Microsoft PowerPoint - H21生物計算化学2.ppt
 演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
memo
 数理情報工学特論第一 機械学習とデータマイニング 4 章 : 教師なし学習 3 かしまひさし 鹿島久嗣 ( 数理 6 研 ) kashima@mist.i.~ DEPARTMENT OF MATHEMATICAL INFORMATICS 1 グラフィカルモデルについて学びます グラフィカルモデル グラフィカルラッソ グラフィカルラッソの推定アルゴリズム 2 グラフィカルモデル 3 教師なし学習の主要タスクは
数理情報工学特論第一 機械学習とデータマイニング 4 章 : 教師なし学習 3 かしまひさし 鹿島久嗣 ( 数理 6 研 ) kashima@mist.i.~ DEPARTMENT OF MATHEMATICAL INFORMATICS 1 グラフィカルモデルについて学びます グラフィカルモデル グラフィカルラッソ グラフィカルラッソの推定アルゴリズム 2 グラフィカルモデル 3 教師なし学習の主要タスクは
 PA3-145 213-214 Kodensy.Co.Ltd.KDS 励磁突入電流発生のメカニズムとその抑制のためのアルゴリズム. 励磁突入電流抑制のアルゴリズム 弊社特許方式 変圧器の励磁突入電流の原因となる残留磁束とは変圧器の解列瞬時の鉄心内磁束ではありません 一般に 変圧器の 2次側 負荷側 開放で励磁課電中の変圧器を 1 次側 高圧側 遮断器の開操作で解列する時 その遮断直後は 変圧器鉄心
PA3-145 213-214 Kodensy.Co.Ltd.KDS 励磁突入電流発生のメカニズムとその抑制のためのアルゴリズム. 励磁突入電流抑制のアルゴリズム 弊社特許方式 変圧器の励磁突入電流の原因となる残留磁束とは変圧器の解列瞬時の鉄心内磁束ではありません 一般に 変圧器の 2次側 負荷側 開放で励磁課電中の変圧器を 1 次側 高圧側 遮断器の開操作で解列する時 その遮断直後は 変圧器鉄心
Taro-F25理論 印刷原稿
 第 種理論 A 問題 ( 配点は 問題当たり小問各 点, 計 0 点 ) 問 次の文章は, 真空中の静電界に関する諸法則の微分形に関する記述である 文中の に当てはまるものを解答群の中から選びなさい 図のように, 直交座標系において電界の z 軸成分が零となるような電界について, y 平面の二次元で電位や電界を考える ここで,4 点 (h,0),(0,h), (- h,0),(0,-h) の電位がそれぞれ
第 種理論 A 問題 ( 配点は 問題当たり小問各 点, 計 0 点 ) 問 次の文章は, 真空中の静電界に関する諸法則の微分形に関する記述である 文中の に当てはまるものを解答群の中から選びなさい 図のように, 直交座標系において電界の z 軸成分が零となるような電界について, y 平面の二次元で電位や電界を考える ここで,4 点 (h,0),(0,h), (- h,0),(0,-h) の電位がそれぞれ
喨微勃挹稉弑
 == 全微分方程式 == 全微分とは 変数の関数 z=f(, ) について,, の増分を Δ, Δ とするとき, z の増分 Δz は Δz z Δ+ z Δ で表されます. この式において, Δ 0, Δ 0 となる極限を形式的に dz= z d+ z d (1) で表し, dz を z の全微分といいます. z は z の に関する偏導関数で, を定数と見なし て, で微分したものを表し, 方向の傾きに対応します.
== 全微分方程式 == 全微分とは 変数の関数 z=f(, ) について,, の増分を Δ, Δ とするとき, z の増分 Δz は Δz z Δ+ z Δ で表されます. この式において, Δ 0, Δ 0 となる極限を形式的に dz= z d+ z d (1) で表し, dz を z の全微分といいます. z は z の に関する偏導関数で, を定数と見なし て, で微分したものを表し, 方向の傾きに対応します.
DVIOUT
 最適レギュレータ 松尾研究室資料 第 最適レギュレータ 節時不変型無限時間最適レギュレータ 状態フィードバックの可能な場合の無限時間問題における最適レギュレータについて確定系について説明する. ここで, レギュレータとは状態量をゼロにするようなコントローラのことである. なぜ, 無限時間問題のみを述べるかという理由は以下のとおりである. 有限時間の最適レギュレータ問題の場合の最適フィードバックゲインは微分方程式の解から構成される時間関数として表現される.
最適レギュレータ 松尾研究室資料 第 最適レギュレータ 節時不変型無限時間最適レギュレータ 状態フィードバックの可能な場合の無限時間問題における最適レギュレータについて確定系について説明する. ここで, レギュレータとは状態量をゼロにするようなコントローラのことである. なぜ, 無限時間問題のみを述べるかという理由は以下のとおりである. 有限時間の最適レギュレータ問題の場合の最適フィードバックゲインは微分方程式の解から構成される時間関数として表現される.
Microsoft PowerPoint - H22制御工学I-10回.ppt
 制御工学 I 第 回 安定性 ラウス, フルビッツの安定判別 平成 年 6 月 日 /6/ 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
制御工学 I 第 回 安定性 ラウス, フルビッツの安定判別 平成 年 6 月 日 /6/ 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
<4D F736F F D2097CD8A7793FC96E582BD82ED82DD8A E6318FCD2E646F63>
 - 第 章たわみ角法の基本式 ポイント : たわみ角法の基本式を理解する たわみ角法の基本式を梁の微分方程式より求める 本章では たわみ角法の基本式を導くことにする 基本式の誘導法は各種あるが ここでは 梁の微分方程式を解いて基本式を求める方法を採用する この本で使用する座標系は 右手 右ネジの法則に従った座標を用いる また ひとつの部材では 図 - に示すように部材の左端の 点を原点とし 軸線を
- 第 章たわみ角法の基本式 ポイント : たわみ角法の基本式を理解する たわみ角法の基本式を梁の微分方程式より求める 本章では たわみ角法の基本式を導くことにする 基本式の誘導法は各種あるが ここでは 梁の微分方程式を解いて基本式を求める方法を採用する この本で使用する座標系は 右手 右ネジの法則に従った座標を用いる また ひとつの部材では 図 - に示すように部材の左端の 点を原点とし 軸線を
数学の世界
 東京女子大学文理学部数学の世界 (2002 年度 ) 永島孝 17 6 行列式の基本法則と効率的な計算法 基本法則 三次以上の行列式についても, 二次の場合と同様な法則がなりたつ ここには三次の場合を例示するが, 四次以上でも同様である 1 単位行列の行列式の値は 1 である すなわち 1 0 0 0 1 0 1 0 0 1 2 二つの列を入れ替えると行列式の値は 1 倍になる 例えば a 13 a
東京女子大学文理学部数学の世界 (2002 年度 ) 永島孝 17 6 行列式の基本法則と効率的な計算法 基本法則 三次以上の行列式についても, 二次の場合と同様な法則がなりたつ ここには三次の場合を例示するが, 四次以上でも同様である 1 単位行列の行列式の値は 1 である すなわち 1 0 0 0 1 0 1 0 0 1 2 二つの列を入れ替えると行列式の値は 1 倍になる 例えば a 13 a
PowerPoint Presentation
 応用数学 Ⅱ (7) 7 連立微分方程式の立て方と解法. 高階微分方程式による解法. ベクトル微分方程式による解法 3. 演算子による解法 連立微分方程式 未知数が複数個あり, 未知数の数だけ微分方程式が与えられている場合, これらを連立微分方程式という. d d 解法 () 高階微分方程式化による解法 つの方程式から つの未知数を消去して, 未知数が つの方程式に変換 のみの方程式にするために,
応用数学 Ⅱ (7) 7 連立微分方程式の立て方と解法. 高階微分方程式による解法. ベクトル微分方程式による解法 3. 演算子による解法 連立微分方程式 未知数が複数個あり, 未知数の数だけ微分方程式が与えられている場合, これらを連立微分方程式という. d d 解法 () 高階微分方程式化による解法 つの方程式から つの未知数を消去して, 未知数が つの方程式に変換 のみの方程式にするために,
線積分.indd
 線積分 線積分 ( n, n, n ) (ξ n, η n, ζ n ) ( n-, n-, n- ) (ξ k, η k, ζ k ) ( k, k, k ) ( k-, k-, k- ) 物体に力 を作用させて位置ベクトル A の点 A から位置ベクトル の点 まで曲線 に沿って物体を移動させたときの仕事 W は 次式で計算された A, A, W : d 6 d+ d+ d@,,, d+ d+
線積分 線積分 ( n, n, n ) (ξ n, η n, ζ n ) ( n-, n-, n- ) (ξ k, η k, ζ k ) ( k, k, k ) ( k-, k-, k- ) 物体に力 を作用させて位置ベクトル A の点 A から位置ベクトル の点 まで曲線 に沿って物体を移動させたときの仕事 W は 次式で計算された A, A, W : d 6 d+ d+ d@,,, d+ d+
Microsoft PowerPoint - mp11-02.pptx
 数理計画法第 2 回 塩浦昭義情報科学研究科准教授 shioura@dais.is.tohoku.ac.jp http://www.dais.is.tohoku.ac.jp/~shioura/teaching 前回の復習 数理計画とは? 数理計画 ( 復習 ) 数理計画問題とは? 狭義には : 数理 ( 数学 ) を使って計画を立てるための問題 広義には : 与えられた評価尺度に関して最も良い解を求める問題
数理計画法第 2 回 塩浦昭義情報科学研究科准教授 shioura@dais.is.tohoku.ac.jp http://www.dais.is.tohoku.ac.jp/~shioura/teaching 前回の復習 数理計画とは? 数理計画 ( 復習 ) 数理計画問題とは? 狭義には : 数理 ( 数学 ) を使って計画を立てるための問題 広義には : 与えられた評価尺度に関して最も良い解を求める問題
航空機の運動方程式
 可制御性 可観測性. 可制御性システムの状態を, 適切な操作によって, 有限時間内に, 任意の状態から別の任意の状態に移動させることができるか否かという特性を可制御性という. 可制御性を有するシステムに対し, システムは可制御である, 可制御なシステム という言い方をする. 状態方程式, 出力方程式が以下で表されるn 次元 m 入力 r 出力線形時不変システム x Ax u y x Du () に対し,
可制御性 可観測性. 可制御性システムの状態を, 適切な操作によって, 有限時間内に, 任意の状態から別の任意の状態に移動させることができるか否かという特性を可制御性という. 可制御性を有するシステムに対し, システムは可制御である, 可制御なシステム という言い方をする. 状態方程式, 出力方程式が以下で表されるn 次元 m 入力 r 出力線形時不変システム x Ax u y x Du () に対し,
微分方程式による現象記述と解きかた
 微分方程式による現象記述と解きかた 土木工学 : 公共諸施設 構造物の有用目的にむけた合理的な実現をはかる方法 ( 技術 ) に関する学 橋梁 トンネル ダム 道路 港湾 治水利水施設 安全化 利便化 快適化 合法則的 経済的 自然および人口素材によって作られた 質量保存則 構造物の自然的な性質 作用 ( 外力による応答 ) エネルギー則 の解明 社会的諸現象のうち マスとしての移動 流通 運動量則
微分方程式による現象記述と解きかた 土木工学 : 公共諸施設 構造物の有用目的にむけた合理的な実現をはかる方法 ( 技術 ) に関する学 橋梁 トンネル ダム 道路 港湾 治水利水施設 安全化 利便化 快適化 合法則的 経済的 自然および人口素材によって作られた 質量保存則 構造物の自然的な性質 作用 ( 外力による応答 ) エネルギー則 の解明 社会的諸現象のうち マスとしての移動 流通 運動量則
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生
 0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
Probit , Mixed logit
 Probit, Mixed logit 2016/5/16 スタートアップゼミ #5 B4 後藤祥孝 1 0. 目次 Probit モデルについて 1. モデル概要 2. 定式化と理解 3. 推定 Mixed logit モデルについて 4. モデル概要 5. 定式化と理解 6. 推定 2 1.Probit 概要 プロビットモデルとは. 効用関数の誤差項に多変量正規分布を仮定したもの. 誤差項には様々な要因が存在するため,
Probit, Mixed logit 2016/5/16 スタートアップゼミ #5 B4 後藤祥孝 1 0. 目次 Probit モデルについて 1. モデル概要 2. 定式化と理解 3. 推定 Mixed logit モデルについて 4. モデル概要 5. 定式化と理解 6. 推定 2 1.Probit 概要 プロビットモデルとは. 効用関数の誤差項に多変量正規分布を仮定したもの. 誤差項には様々な要因が存在するため,
周期時系列の統計解析 (3) 移動平均とフーリエ変換 nino 2017 年 12 月 18 日 移動平均は, 周期時系列における特定の周期成分の消去や不規則変動 ( ノイズ ) の低減に汎用されている統計手法である. ここでは, 周期時系列をコサイン関数で近似し, その移動平均により周期成分の振幅
 周期時系列の統計解析 3 移動平均とフーリエ変換 io 07 年 月 8 日 移動平均は, 周期時系列における特定の周期成分の消去や不規則変動 ノイズ の低減に汎用されている統計手法である. ここでは, 周期時系列をコサイン関数で近似し, その移動平均により周期成分のがどのように変化するのか等について検討する. また, 気温の実測値に移動平均を適用した結果についてフーリエ変換も併用して考察する. 単純移動平均の計算式移動平均には,
周期時系列の統計解析 3 移動平均とフーリエ変換 io 07 年 月 8 日 移動平均は, 周期時系列における特定の周期成分の消去や不規則変動 ノイズ の低減に汎用されている統計手法である. ここでは, 周期時系列をコサイン関数で近似し, その移動平均により周期成分のがどのように変化するのか等について検討する. また, 気温の実測値に移動平均を適用した結果についてフーリエ変換も併用して考察する. 単純移動平均の計算式移動平均には,
Microsoft PowerPoint pptx
 4.2 小信号パラメータ 1 電圧利得をどのように求めるか 電圧ー電流変換 入力信号の変化 dv BE I I e 1 v be の振幅から i b を求めるのは難しい? 電流増幅 電流ー電圧変換 di B di C h FE 電流と電圧の関係が指数関数になっているのが問題 (-RC), ただし RL がない場合 dv CE 出力信号の変化 2 pn 接合の非線形性への対処 I B 直流バイアスに対する抵抗
4.2 小信号パラメータ 1 電圧利得をどのように求めるか 電圧ー電流変換 入力信号の変化 dv BE I I e 1 v be の振幅から i b を求めるのは難しい? 電流増幅 電流ー電圧変換 di B di C h FE 電流と電圧の関係が指数関数になっているのが問題 (-RC), ただし RL がない場合 dv CE 出力信号の変化 2 pn 接合の非線形性への対処 I B 直流バイアスに対する抵抗
Microsoft PowerPoint - 10.pptx
 0. 固有値とその応用 固有値と固有ベクトル 2 行列による写像から固有ベクトルへ m n A : m n n m 行列によって線形写像 f R R A が表せることを見てきた ここでは 2 次元平面の行列による写像を調べる 2 = 2 A 2 2 とし 写像 まず 単位ベクトルの像を求める u 2 x = v 2 y f : R A R を考える u 2 2 u, 2 2 0 = = v 2 0
0. 固有値とその応用 固有値と固有ベクトル 2 行列による写像から固有ベクトルへ m n A : m n n m 行列によって線形写像 f R R A が表せることを見てきた ここでは 2 次元平面の行列による写像を調べる 2 = 2 A 2 2 とし 写像 まず 単位ベクトルの像を求める u 2 x = v 2 y f : R A R を考える u 2 2 u, 2 2 0 = = v 2 0
問 の標準解答 () 遮へい失敗事故 : 雷が電力線を直撃してアークホーンにフラッシオーバが発生する 逆フラッシオーバ事故 : 架空地線あるいは鉄塔への雷撃によって架空地線あるいは鉄塔の電位が上昇し, 架空地線と導体間, 又はアークホーンにフラッシオーバが発生する () 架空地線の弛度を電力線のそれ
 平成 4 年度第二種電気主任技術者二次試験標準解答 配点 : 一題当たり 3 点 電力 管理科目 4 題 3 点 = 点 機械 制御科目 題 3 点 = 6 点 < 電力 管理科目 > 問 の標準解答 () 電動機出力 ( ポンプ入力 )= 電動機入力 電動機効率なので, A P M = P Mi h M B 又はC P Mi = M f M D 又はE P G = G f G 3 () G M なので,
平成 4 年度第二種電気主任技術者二次試験標準解答 配点 : 一題当たり 3 点 電力 管理科目 4 題 3 点 = 点 機械 制御科目 題 3 点 = 6 点 < 電力 管理科目 > 問 の標準解答 () 電動機出力 ( ポンプ入力 )= 電動機入力 電動機効率なので, A P M = P Mi h M B 又はC P Mi = M f M D 又はE P G = G f G 3 () G M なので,
3.5 トランジスタ基本増幅回路 ベース接地基本増幅回路 C 1 C n n 2 R E p v V 2 v R E p 1 v EE 0 VCC 結合コンデンサ ベース接地基本増幅回路 V EE =0, V CC =0として交流分の回路 (C 1, C 2 により短絡 ) トランジスタ
 3.4 の特性を表す諸量 入力 i 2 出力 負荷抵抗 4 端子 (2 端子対 ) 回路としての の動作量 (i) 入力インピーダンス : Z i = (ii) 電圧利得 : A v = (iii) 電流利得 : A i = (iv) 電力利得 : A p = i 2 v2 i 2 i 2 =i 2 (v) 出力インピーダンス : Z o = i 2 = 0 i 2 入力 出力 出力インピーダンスの求め方
3.4 の特性を表す諸量 入力 i 2 出力 負荷抵抗 4 端子 (2 端子対 ) 回路としての の動作量 (i) 入力インピーダンス : Z i = (ii) 電圧利得 : A v = (iii) 電流利得 : A i = (iv) 電力利得 : A p = i 2 v2 i 2 i 2 =i 2 (v) 出力インピーダンス : Z o = i 2 = 0 i 2 入力 出力 出力インピーダンスの求め方
untitled
 に, 月次モデルの場合でも四半期モデルの場合でも, シミュレーション期間とは無関係に一様に RMSPE を最小にするバンドの設定法は存在しないということである 第 2 は, 表で与えた 2 つの期間及びすべての内生変数を見渡して, 全般的にパフォーマンスのよいバンドの設定法は, 最適固定バンドと最適可変バンドのうちの M 2, Q2 である いずれにしても, 以上述べた 3 つのバンド設定法は若干便宜的なものと言わざるを得ない
に, 月次モデルの場合でも四半期モデルの場合でも, シミュレーション期間とは無関係に一様に RMSPE を最小にするバンドの設定法は存在しないということである 第 2 は, 表で与えた 2 つの期間及びすべての内生変数を見渡して, 全般的にパフォーマンスのよいバンドの設定法は, 最適固定バンドと最適可変バンドのうちの M 2, Q2 である いずれにしても, 以上述べた 3 つのバンド設定法は若干便宜的なものと言わざるを得ない
s と Z(s) の関係 2019 年 3 月 22 日目次へ戻る s が虚軸を含む複素平面右半面の値の時 X(s) も虚軸を含む複素平面右半面の値でなけれ ばなりません その訳を探ります 本章では 受動回路をインピーダンス Z(s) にしていま す リアクタンス回路の駆動点リアクタンス X(s)
 と Z の関係 9 年 3 月 日目次へ戻る が虚軸を含む複素平面右半面の値の時 X も虚軸を含む複素平面右半面の値でなけれ ばなりません その訳を探ります 本章では 受動回路をインピーダンス Z にしていま す リアクタンス回路の駆動点リアクタンス X も Z に含まれます Z に正弦波電流を入れた時最大値 抵抗 コイル コンデンサーで作られた受動回路の ラプラスの世界でのインピーダンスを Z とします
と Z の関係 9 年 3 月 日目次へ戻る が虚軸を含む複素平面右半面の値の時 X も虚軸を含む複素平面右半面の値でなけれ ばなりません その訳を探ります 本章では 受動回路をインピーダンス Z にしていま す リアクタンス回路の駆動点リアクタンス X も Z に含まれます Z に正弦波電流を入れた時最大値 抵抗 コイル コンデンサーで作られた受動回路の ラプラスの世界でのインピーダンスを Z とします
<4D F736F F D208CF68BA48C6F8DCF8A C30342C CFA90B68C6F8DCF8A7782CC8AEE967B92E8979D32288F4390B394C529332E646F63>
 2. 厚生経済学の ( 第 ) 基本定理 2 203 年 4 月 7 日 ( 水曜 3 限 )/8 本章では 純粋交換経済において厚生経済学の ( 第 ) 基本定理 が成立することを示す なお より一般的な生産技術のケースについては 4.5 補論 2 で議論する 2. 予算集合と最適消費点 ( 完全 ) 競争市場で達成される資源配分がパレート効率的であることを示すための準備として 個人の最適化行動を検討する
2. 厚生経済学の ( 第 ) 基本定理 2 203 年 4 月 7 日 ( 水曜 3 限 )/8 本章では 純粋交換経済において厚生経済学の ( 第 ) 基本定理 が成立することを示す なお より一般的な生産技術のケースについては 4.5 補論 2 で議論する 2. 予算集合と最適消費点 ( 完全 ) 競争市場で達成される資源配分がパレート効率的であることを示すための準備として 個人の最適化行動を検討する
三相の誘導電動機をスターデルタ始動した場合の電流の話です 皆様ご承知の様に スターデルタ始動はよく用いられる始動方法です この始動方式を用いた場合の 始動電流及び始動トルクの関係は次の様に説明されています 説明その 1 始動電流は全電圧始動の 1/3 になり 始動トルクは 1/3 になる 説明その
 三相のをスターデルタ始動した場合の電流の話です 皆様ご承知の様に スターデルタ始動はよく用いられる始動方法です この始動方式を用いた場合の 始動電流及び始動トルクの関係は次の様に説明されています 説明その 1 始動電流は全電圧始動の 1/3 になり 始動トルクは 1/3 になる 説明その 2 始動電流は全電圧始動の 1/ 3 になり 始動トルクは 1/3 になる 一つの事項に対する説明が 2 種類ある場合
三相のをスターデルタ始動した場合の電流の話です 皆様ご承知の様に スターデルタ始動はよく用いられる始動方法です この始動方式を用いた場合の 始動電流及び始動トルクの関係は次の様に説明されています 説明その 1 始動電流は全電圧始動の 1/3 になり 始動トルクは 1/3 になる 説明その 2 始動電流は全電圧始動の 1/ 3 になり 始動トルクは 1/3 になる 一つの事項に対する説明が 2 種類ある場合
09.pptx
 講義内容 数値解析 第 9 回 5 年 6 月 7 日 水 理学部物理学科情報理学コース. 非線形方程式の数値解法. はじめに. 分法. 補間法.4 ニュートン法.4. 多変数問題への応用.4. ニュートン法の収束性. 連立 次方程式の解法. 序論と行列計算の基礎. ガウスの消去法. 重対角行列の場合の解法項目を変更しました.4 LU 分解法.5 特異値分解法.6 共役勾配法.7 反復法.7. ヤコビ法.7.
講義内容 数値解析 第 9 回 5 年 6 月 7 日 水 理学部物理学科情報理学コース. 非線形方程式の数値解法. はじめに. 分法. 補間法.4 ニュートン法.4. 多変数問題への応用.4. ニュートン法の収束性. 連立 次方程式の解法. 序論と行列計算の基礎. ガウスの消去法. 重対角行列の場合の解法項目を変更しました.4 LU 分解法.5 特異値分解法.6 共役勾配法.7 反復法.7. ヤコビ法.7.
受信機時計誤差項の が残ったままであるが これをも消去するのが 重位相差である. 重位相差ある時刻に 衛星 から送られてくる搬送波位相データを 台の受信機 でそれぞれ測定する このとき各受信機で測定された衛星 からの搬送波位相データを Φ Φ とし 同様に衛星 からの搬送波位相データを Φ Φ とす
 RTK-GPS 測位計算アルゴリズム -FLOT 解 - 東京海洋大学冨永貴樹. はじめに GPS 測量を行う際 実時間で測位結果を得ることが出来るのは今のところ RTK-GPS 測位のみである GPS 測量では GPS 衛星からの搬送波位相データを使用するため 整数値バイアスを決定しなければならず これが測位計算を複雑にしている所以である この整数値バイアスを決定するためのつの方法として FLOT
RTK-GPS 測位計算アルゴリズム -FLOT 解 - 東京海洋大学冨永貴樹. はじめに GPS 測量を行う際 実時間で測位結果を得ることが出来るのは今のところ RTK-GPS 測位のみである GPS 測量では GPS 衛星からの搬送波位相データを使用するため 整数値バイアスを決定しなければならず これが測位計算を複雑にしている所以である この整数値バイアスを決定するためのつの方法として FLOT
7 章問題解答 7-1 予習 1. 長方形断面であるため, 断面積 A と潤辺 S は, 水深 h, 水路幅 B を用い以下で表される A = Bh, S = B + 2h 径深 R の算定式に代入すると以下のようになる A Bh h R = = = S B + 2 h 1+ 2( h B) 分母の
 7 章問題解答 7- 予習. 長方形断面であるため, 断面積 と潤辺 S は, 水深, 水路幅 B を用い以下で表される B, S B + 径深 R の算定式に代入すると以下のようになる B R S B + ( B) 分母の /B は河幅が水深に対して十分に広ければ, 非常に小さな値となるため, 上式は R ( B) となり, 径深 R は水深 で近似できる. マニングの式の水深 を等流水深 0 と置き換えると,
7 章問題解答 7- 予習. 長方形断面であるため, 断面積 と潤辺 S は, 水深, 水路幅 B を用い以下で表される B, S B + 径深 R の算定式に代入すると以下のようになる B R S B + ( B) 分母の /B は河幅が水深に対して十分に広ければ, 非常に小さな値となるため, 上式は R ( B) となり, 径深 R は水深 で近似できる. マニングの式の水深 を等流水深 0 と置き換えると,
<4D F736F F D2094F795AA95FB92F68EAE82CC89F082AB95FB E646F63>
 力学 A 金曜 限 : 松田 微分方程式の解き方 微分方程式の解き方のところが分からなかったという声が多いので プリントにまとめます 数学的に厳密な話はしていないので 詳しくは数学の常微分方程式を扱っているテキストを参照してください また os s は既知とします. 微分方程式の分類 常微分方程式とは 独立変数 と その関数 その有限次の導関数 がみたす方程式 F,,, = のことです 次までの導関数を含む方程式を
力学 A 金曜 限 : 松田 微分方程式の解き方 微分方程式の解き方のところが分からなかったという声が多いので プリントにまとめます 数学的に厳密な話はしていないので 詳しくは数学の常微分方程式を扱っているテキストを参照してください また os s は既知とします. 微分方程式の分類 常微分方程式とは 独立変数 と その関数 その有限次の導関数 がみたす方程式 F,,, = のことです 次までの導関数を含む方程式を
1/17 平成 29 年 3 月 25 日 ( 土 ) 午前 11 時 1 分量子力学とクライン ゴルドン方程式 ( 学部 3 年次秋学期向 ) 量子力学とクライン ゴルドン方程式 素粒子の満たす場 y ( x,t) の運動方程式 : クライン ゴルドン方程式 : æ 3 ö ç å è m= 0
 /7 平成 9 年 月 5 日 ( 土 午前 時 分量子力学とクライン ゴルドン方程式 ( 学部 年次秋学期向 量子力学とクライン ゴルドン方程式 素粒子の満たす場 (,t の運動方程式 : クライン ゴルドン方程式 : æ ö ç å è = 0 c + ( t =, 0 (. = 0 ì æ = = = ö æ ö æ ö ç ì =,,,,,,, ç 0 = ç Ñ 0 = ç Ñ 0 Ñ Ñ
/7 平成 9 年 月 5 日 ( 土 午前 時 分量子力学とクライン ゴルドン方程式 ( 学部 年次秋学期向 量子力学とクライン ゴルドン方程式 素粒子の満たす場 (,t の運動方程式 : クライン ゴルドン方程式 : æ ö ç å è = 0 c + ( t =, 0 (. = 0 ì æ = = = ö æ ö æ ö ç ì =,,,,,,, ç 0 = ç Ñ 0 = ç Ñ 0 Ñ Ñ
1
 半剛節が部材上の任意点にある部材剛性方程式 米子高専 川端康洋 稲田祐二. ピン半剛節を有する部材の解析の歴史 ()940 二見秀雄材の途中にピン接合点を有するラーメン材の算式とその応用建築学会論文集 つのピン節を含む部材の撓角法基本式と荷重項ピン節を含む部材の撓角法基本式と荷重項が求められている 以降 固定モーメント法や異形ラーメンの解法への応用が研究された 戦後には 関連する論文は見当たらない
半剛節が部材上の任意点にある部材剛性方程式 米子高専 川端康洋 稲田祐二. ピン半剛節を有する部材の解析の歴史 ()940 二見秀雄材の途中にピン接合点を有するラーメン材の算式とその応用建築学会論文集 つのピン節を含む部材の撓角法基本式と荷重項ピン節を含む部材の撓角法基本式と荷重項が求められている 以降 固定モーメント法や異形ラーメンの解法への応用が研究された 戦後には 関連する論文は見当たらない
<4D F736F F D FCD B90DB93AE96402E646F63>
 7 章摂動法講義のメモ 式が複雑なので 黒板を何度も修正したし 間違ったことも書いたので メモを置きます 摂動論の式の導出無摂動系 先ず 厳密に解けている Schrödiger 方程式を考える,,,3,... 3,,,3,... は状態を区別する整数であり 状態 はエネルギー順に並んでいる 即ち は基底状態 は励起状態である { m } は相互に規格直交条件が成立する k m k mdx km k
7 章摂動法講義のメモ 式が複雑なので 黒板を何度も修正したし 間違ったことも書いたので メモを置きます 摂動論の式の導出無摂動系 先ず 厳密に解けている Schrödiger 方程式を考える,,,3,... 3,,,3,... は状態を区別する整数であり 状態 はエネルギー順に並んでいる 即ち は基底状態 は励起状態である { m } は相互に規格直交条件が成立する k m k mdx km k
1.民営化
 参考資料 最小二乗法 数学的性質 経済統計分析 3 年度秋学期 回帰分析と最小二乗法 被説明変数 の動きを説明変数 の動きで説明 = 回帰分析 説明変数がつ 単回帰 説明変数がつ以上 重回帰 被説明変数 従属変数 係数 定数項傾き 説明変数 独立変数 残差... で説明できる部分 説明できない部分 説明できない部分が小さくなるように回帰式の係数 を推定する有力な方法 = 最小二乗法 最小二乗法による回帰の考え方
参考資料 最小二乗法 数学的性質 経済統計分析 3 年度秋学期 回帰分析と最小二乗法 被説明変数 の動きを説明変数 の動きで説明 = 回帰分析 説明変数がつ 単回帰 説明変数がつ以上 重回帰 被説明変数 従属変数 係数 定数項傾き 説明変数 独立変数 残差... で説明できる部分 説明できない部分 説明できない部分が小さくなるように回帰式の係数 を推定する有力な方法 = 最小二乗法 最小二乗法による回帰の考え方
Microsoft Word - 8章(CI).doc
 8 章配置間相互作用法 : Configuration Interaction () etho [] 化学的精度化学反応の精密な解析をするためには エネルギー誤差は数 ~ kcal/mol 程度に抑えたいものである この程度の誤差内に治まる精度を 化学的精度 と呼ぶことがある He 原子のエネルギーをシュレーディンガー方程式と分子軌道法で計算した結果を示そう He 原子のエネルギー Hartree-Fock
8 章配置間相互作用法 : Configuration Interaction () etho [] 化学的精度化学反応の精密な解析をするためには エネルギー誤差は数 ~ kcal/mol 程度に抑えたいものである この程度の誤差内に治まる精度を 化学的精度 と呼ぶことがある He 原子のエネルギーをシュレーディンガー方程式と分子軌道法で計算した結果を示そう He 原子のエネルギー Hartree-Fock
第1章 様々な運動
 自己誘導と相互誘導 自己誘導 自己誘導起電力 ( 逆起電力 ) 図のように起電力 V V の電池, 抵抗値 R Ω の抵抗, スイッチS, コイルを直列につないだ回路を考える. コイルに電流が流れると, コイル自身が作る磁場による磁束がコイルを貫く. コイルに流れる電流が変化すると, コイルを貫く磁束も変化するのでコイルにはこの変化を妨げる方向に誘導起電力が生じる. この現象を自己誘導という. 自己誘導による起電力は電流変化を妨げる方向に生じるので逆起電力とも呼ばれる.
自己誘導と相互誘導 自己誘導 自己誘導起電力 ( 逆起電力 ) 図のように起電力 V V の電池, 抵抗値 R Ω の抵抗, スイッチS, コイルを直列につないだ回路を考える. コイルに電流が流れると, コイル自身が作る磁場による磁束がコイルを貫く. コイルに流れる電流が変化すると, コイルを貫く磁束も変化するのでコイルにはこの変化を妨げる方向に誘導起電力が生じる. この現象を自己誘導という. 自己誘導による起電力は電流変化を妨げる方向に生じるので逆起電力とも呼ばれる.
フィードバック ~ 様々な電子回路の性質 ~ 実験 (1) 目的実験 (1) では 非反転増幅器の増幅率や位相差が 回路を構成する抵抗値や入力信号の周波数によってどのように変わるのかを調べる 実験方法 図 1 のような自由振動回路を組み オペアンプの + 入力端子を接地したときの出力電圧 が 0 と
 フィードバック ~ 様々な電子回路の性質 ~ 実験 (1) 目的実験 (1) では 非反転増幅器の増幅率や位相差が 回路を構成する抵抗値や入力信号の周波数によってどのように変わるのかを調べる 実験方法 図 1 のような自由振動回路を組み オペアンプの + 入力端子を接地したときの出力電圧 が 0 となるように半固定抵抗器を調整する ( ゼロ点調整のため ) 図 1 非反転増幅器 2010 年度版物理工学実験法
フィードバック ~ 様々な電子回路の性質 ~ 実験 (1) 目的実験 (1) では 非反転増幅器の増幅率や位相差が 回路を構成する抵抗値や入力信号の周波数によってどのように変わるのかを調べる 実験方法 図 1 のような自由振動回路を組み オペアンプの + 入力端子を接地したときの出力電圧 が 0 となるように半固定抵抗器を調整する ( ゼロ点調整のため ) 図 1 非反転増幅器 2010 年度版物理工学実験法
代数 幾何 < ベクトル > 1 ベクトルの演算 和 差 実数倍については 文字の計算と同様 2 ベクトルの成分表示 平面ベクトル : a x e y e x, ) ( 1 y1 空間ベクトル : a x e y e z e x, y, ) ( 1 1 z1
 代数 幾何 < ベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル :, 空間ベクトル : z,, z 成分での計算ができるようにすること ベクトルの内積 : os 平面ベクトル :,, 空間ベクトル :,,,, z z zz 4 ベクトルの大きさ 平面上 : 空間上 : z は 良く用いられる 5 m: に分ける点 : m m 図形への応用
代数 幾何 < ベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル :, 空間ベクトル : z,, z 成分での計算ができるようにすること ベクトルの内積 : os 平面ベクトル :,, 空間ベクトル :,,,, z z zz 4 ベクトルの大きさ 平面上 : 空間上 : z は 良く用いられる 5 m: に分ける点 : m m 図形への応用
Microsoft PowerPoint - 6.PID制御.pptx
 プロセス制御工学 6.PID 制御 京都大学 加納学 Division of Process Control & Process Systems Engineering Department of Chemical Engineering, Kyoto University manabu@cheme.kyoto-u.ac.jp http://www-pse.cheme.kyoto-u.ac.jp/~kano/
プロセス制御工学 6.PID 制御 京都大学 加納学 Division of Process Control & Process Systems Engineering Department of Chemical Engineering, Kyoto University manabu@cheme.kyoto-u.ac.jp http://www-pse.cheme.kyoto-u.ac.jp/~kano/
<4D F736F F D208D5C91A297CD8A7793FC96E591E631308FCD2E646F63>
 第 1 章モールの定理による静定梁のたわみ 1-1 第 1 章モールの定理による静定梁のたわみ ポイント : モールの定理を用いて 静定梁のたわみを求める 断面力の釣合と梁の微分方程式は良く似ている 前章では 梁の微分方程式を直接積分する方法で 静定梁の断面力と変形状態を求めた 本章では 梁の微分方程式と断面力による力の釣合式が類似していることを利用して 微分方程式を直接解析的に解くのではなく 力の釣合より梁のたわみを求める方法を学ぶ
第 1 章モールの定理による静定梁のたわみ 1-1 第 1 章モールの定理による静定梁のたわみ ポイント : モールの定理を用いて 静定梁のたわみを求める 断面力の釣合と梁の微分方程式は良く似ている 前章では 梁の微分方程式を直接積分する方法で 静定梁の断面力と変形状態を求めた 本章では 梁の微分方程式と断面力による力の釣合式が類似していることを利用して 微分方程式を直接解析的に解くのではなく 力の釣合より梁のたわみを求める方法を学ぶ
<4D F736F F D B4389F D985F F4B89DB91E88250>
 電気回路理論 II 演習課題 H30.0.5. 図 の回路で =0 で SW を on 接続 とする時 >0 での i, 並びに を求め 図示しなさい ただし 0 での i, 並びに を求めなさい ただし 0 とする 3. 図 3の回路で =0 で SW を下向きに瞬時に切り替える時 >0 での i,
電気回路理論 II 演習課題 H30.0.5. 図 の回路で =0 で SW を on 接続 とする時 >0 での i, 並びに を求め 図示しなさい ただし 0 での i, 並びに を求めなさい ただし 0 とする 3. 図 3の回路で =0 で SW を下向きに瞬時に切り替える時 >0 での i,
PowerPoint プレゼンテーション
 復習 ) 時系列のモデリング ~a. 離散時間モデル ~ y k + a 1 z 1 y k + + a na z n ay k = b 0 u k + b 1 z 1 u k + + b nb z n bu k y k = G z 1 u k = B(z 1 ) A(z 1 u k ) ARMA モデル A z 1 B z 1 = 1 + a 1 z 1 + + a na z n a = b 0
復習 ) 時系列のモデリング ~a. 離散時間モデル ~ y k + a 1 z 1 y k + + a na z n ay k = b 0 u k + b 1 z 1 u k + + b nb z n bu k y k = G z 1 u k = B(z 1 ) A(z 1 u k ) ARMA モデル A z 1 B z 1 = 1 + a 1 z 1 + + a na z n a = b 0
多変量解析 ~ 重回帰分析 ~ 2006 年 4 月 21 日 ( 金 ) 南慶典
 多変量解析 ~ 重回帰分析 ~ 2006 年 4 月 21 日 ( 金 ) 南慶典 重回帰分析とは? 重回帰分析とは複数の説明変数から目的変数との関係性を予測 評価説明変数 ( 数量データ ) は目的変数を説明するのに有効であるか得られた関係性より未知のデータの妥当性を判断する これを重回帰分析という つまり どんなことをするのか? 1 最小 2 乗法により重回帰モデルを想定 2 自由度調整済寄与率を求め
多変量解析 ~ 重回帰分析 ~ 2006 年 4 月 21 日 ( 金 ) 南慶典 重回帰分析とは? 重回帰分析とは複数の説明変数から目的変数との関係性を予測 評価説明変数 ( 数量データ ) は目的変数を説明するのに有効であるか得られた関係性より未知のデータの妥当性を判断する これを重回帰分析という つまり どんなことをするのか? 1 最小 2 乗法により重回帰モデルを想定 2 自由度調整済寄与率を求め
技術者のための構造力学 2014/06/11 1. はじめに 資料 2 節点座標系による傾斜支持節点節点の処理 三好崇夫加藤久人 従来, マトリックス変位法に基づく骨組解析を紹介する教科書においては, 全体座標系に対して傾斜 した斜面上の支持条件を考慮する処理方法として, 一旦, 傾斜支持を無視した
 . はじめに 資料 節点座標系による傾斜支持節点節点の処理 三好崇夫加藤久人 従来, マトリックス変位法に基づく骨組解析を紹介する教科書においては, 全体座標系に対して傾斜 した斜面上の支持条件を考慮する処理方法として, 一旦, 傾斜支持を無視した全体座標系に関する構造 全体の剛性マトリックスを組み立てた後に, 傾斜支持する節点に関して対応する剛性成分を座標変換に よって傾斜方向に回転処理し, その後は通常の全体座標系に対して傾斜していない支持点に対するのと
. はじめに 資料 節点座標系による傾斜支持節点節点の処理 三好崇夫加藤久人 従来, マトリックス変位法に基づく骨組解析を紹介する教科書においては, 全体座標系に対して傾斜 した斜面上の支持条件を考慮する処理方法として, 一旦, 傾斜支持を無視した全体座標系に関する構造 全体の剛性マトリックスを組み立てた後に, 傾斜支持する節点に関して対応する剛性成分を座標変換に よって傾斜方向に回転処理し, その後は通常の全体座標系に対して傾斜していない支持点に対するのと
数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュ
 数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュレーションによって計算してみる 4.1 放物運動一様な重力場における放物運動を考える 一般に質量の物体に作用する力をとすると運動方程式は
数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュレーションによって計算してみる 4.1 放物運動一様な重力場における放物運動を考える 一般に質量の物体に作用する力をとすると運動方程式は
Microsoft PowerPoint - ›žŠpfidŠÍŁÏ−·“H−w5›ñŒÚ.ppt
 応用電力変換工学舟木剛 第 5 回本日のテーマ交流 - 直流変換半端整流回路 平成 6 年 月 7 日 整流器 (cfr) とは 交流を直流に変換する 半波整流器は 交直変換半波整流回路 小電力用途 入力電源側の平均電流が零にならない あんまり使われていない 全波整流回路の基本回路 変圧器が直流偏磁しやすい 変圧器の負荷電流に直流分を含むと その直流分により 鉄心が一方向に磁化する これにより 鉄心の磁束密度の増大
応用電力変換工学舟木剛 第 5 回本日のテーマ交流 - 直流変換半端整流回路 平成 6 年 月 7 日 整流器 (cfr) とは 交流を直流に変換する 半波整流器は 交直変換半波整流回路 小電力用途 入力電源側の平均電流が零にならない あんまり使われていない 全波整流回路の基本回路 変圧器が直流偏磁しやすい 変圧器の負荷電流に直流分を含むと その直流分により 鉄心が一方向に磁化する これにより 鉄心の磁束密度の増大
第 4 週コンボリューションその 2, 正弦波による分解 教科書 p. 16~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問 1. 以下の図にならって,1 と 2 の δ 関数を図示せよ δ (t) 2
 第 4 週コンボリューションその, 正弦波による分解 教科書 p. 6~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問. 以下の図にならって, と の δ 関数を図示せよ. - - - δ () δ ( ) - - - 図 δ 関数の図示の例 δ ( ) δ ( ) δ ( ) δ ( ) δ ( ) - - - - - - - -
第 4 週コンボリューションその, 正弦波による分解 教科書 p. 6~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問. 以下の図にならって, と の δ 関数を図示せよ. - - - δ () δ ( ) - - - 図 δ 関数の図示の例 δ ( ) δ ( ) δ ( ) δ ( ) δ ( ) - - - - - - - -
技術資料(5) 各種ケーブルのインピーダンス 表 V CVD 600V CVT 及びEM 600V CED/F EM 600V CET/Fのインピーダンス 公称 cosθ=1 cosθ=0.9 cosθ=0.8 cosθ=1 cosθ=0.9 cosθ=
 技2. 電圧降下術資料(1) 電圧降下計算式 1 基本計算式 (CV VV は この計算式を使用 ) -3 Vd =Ku I L Z 10 Vd= 電圧降下 (V) I = 電流 (A) L = 亘長 (m) Z =インピーダンス =Rcosθ+Xsinθ R = 交流導体抵抗 X =リアクタンス cosθ = 力率 sinθ = 1-cos 2 θ 力率が不明は場合は 次式によりインピーダンスを求める
技2. 電圧降下術資料(1) 電圧降下計算式 1 基本計算式 (CV VV は この計算式を使用 ) -3 Vd =Ku I L Z 10 Vd= 電圧降下 (V) I = 電流 (A) L = 亘長 (m) Z =インピーダンス =Rcosθ+Xsinθ R = 交流導体抵抗 X =リアクタンス cosθ = 力率 sinθ = 1-cos 2 θ 力率が不明は場合は 次式によりインピーダンスを求める
Microsoft Word - 5章摂動法.doc
 5 章摂動法 ( 次の Moller-Plesset (MP) 法のために ) // 水素原子など 電子系を除いては 原子系の Schrödiger 方程式を解析的に解くことはできない 分子系の Schrödiger 方程式の正確な数値解を求めることも困難である そこで Hartree-Fock(H-F) 法を導入した H-F 法は Schrödiger 方程式が与える全エネルギーの 99% を再現することができる優れた近似方法である
5 章摂動法 ( 次の Moller-Plesset (MP) 法のために ) // 水素原子など 電子系を除いては 原子系の Schrödiger 方程式を解析的に解くことはできない 分子系の Schrödiger 方程式の正確な数値解を求めることも困難である そこで Hartree-Fock(H-F) 法を導入した H-F 法は Schrödiger 方程式が与える全エネルギーの 99% を再現することができる優れた近似方法である
ボルツマンマシンの高速化
 1. はじめに ボルツマン学習と平均場近似 山梨大学工学部宗久研究室 G04MK016 鳥居圭太 ボルツマンマシンは学習可能な相互結合型ネットワー クの代表的なものである. ボルツマンマシンには, 学習のための統計平均を取る必要があり, 結果を求めるまでに長い時間がかかってしまうという欠点がある. そこで, 学習の高速化のために, 統計を取る2つのステップについて, 以下のことを行う. まず1つ目のステップでは,
1. はじめに ボルツマン学習と平均場近似 山梨大学工学部宗久研究室 G04MK016 鳥居圭太 ボルツマンマシンは学習可能な相互結合型ネットワー クの代表的なものである. ボルツマンマシンには, 学習のための統計平均を取る必要があり, 結果を求めるまでに長い時間がかかってしまうという欠点がある. そこで, 学習の高速化のために, 統計を取る2つのステップについて, 以下のことを行う. まず1つ目のステップでは,
3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x0 = f x= x0 t f c x f =0 [1] c f 0 x= x 0 x 0 f x= x0 x 2 x 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考
![3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x0 = f x= x0 t f c x f =0 [1] c f 0 x= x 0 x 0 f x= x0 x 2 x 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考 3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x0 = f x= x0 t f c x f =0 [1] c f 0 x= x 0 x 0 f x= x0 x 2 x 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考](/thumbs/103/158269281.jpg) 3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x = f x= x t f c x f = [1] c f x= x f x= x 2 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考える まず 初期時刻 t=t に f =R f exp [ik x ] [3] のような波動を与えたとき どのように時間変化するか調べる
3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x = f x= x t f c x f = [1] c f x= x f x= x 2 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考える まず 初期時刻 t=t に f =R f exp [ik x ] [3] のような波動を与えたとき どのように時間変化するか調べる
ビジネス統計 統計基礎とエクセル分析 正誤表
 ビジネス統計統計基礎とエクセル分析 ビジネス統計スペシャリスト エクセル分析スペシャリスト 公式テキスト正誤表と学習用データ更新履歴 平成 30 年 5 月 14 日現在 公式テキスト正誤表 頁場所誤正修正 6 知識編第 章 -3-3 最頻値の解説内容 たとえば, 表.1 のデータであれば, 最頻値は 167.5cm というたとえば, 表.1 のデータであれば, 最頻値は 165.0cm ということになります
ビジネス統計統計基礎とエクセル分析 ビジネス統計スペシャリスト エクセル分析スペシャリスト 公式テキスト正誤表と学習用データ更新履歴 平成 30 年 5 月 14 日現在 公式テキスト正誤表 頁場所誤正修正 6 知識編第 章 -3-3 最頻値の解説内容 たとえば, 表.1 のデータであれば, 最頻値は 167.5cm というたとえば, 表.1 のデータであれば, 最頻値は 165.0cm ということになります
モデリングとは
 コンピュータグラフィックス基礎 第 5 回曲線 曲面の表現 ベジェ曲線 金森由博 学習の目標 滑らかな曲線を扱う方法を学習する パラメトリック曲線について理解する 広く一般的に使われているベジェ曲線を理解する 制御点を入力することで ベジェ曲線を描画するアプリケーションの開発を行えるようになる C++ 言語の便利な機能を使えるようになる 要素数が可変な配列としての std::vector の活用 計算機による曲線の表現
コンピュータグラフィックス基礎 第 5 回曲線 曲面の表現 ベジェ曲線 金森由博 学習の目標 滑らかな曲線を扱う方法を学習する パラメトリック曲線について理解する 広く一般的に使われているベジェ曲線を理解する 制御点を入力することで ベジェ曲線を描画するアプリケーションの開発を行えるようになる C++ 言語の便利な機能を使えるようになる 要素数が可変な配列としての std::vector の活用 計算機による曲線の表現
Matrix and summation convention Kronecker delta δ ij 1 = 0 ( i = j) ( i j) permutation symbol e ijk = (even permutation) (odd permutation) (othe
 Matr ad summato covto Krockr dlta δ ( ) ( ) prmutato symbol k (v prmutato) (odd prmutato) (othrs) gvalu dtrmat dt 6 k rst r s kt opyrght s rsrvd. No part of ths documt may b rproducd for proft. 行列 行 正方行列
Matr ad summato covto Krockr dlta δ ( ) ( ) prmutato symbol k (v prmutato) (odd prmutato) (othrs) gvalu dtrmat dt 6 k rst r s kt opyrght s rsrvd. No part of ths documt may b rproducd for proft. 行列 行 正方行列
Microsoft Word - 第2章 ブロック線図.doc
 NAOSIE: Nagaaki Univriy' Ac il ディジタル制御システム Auhor() 辻, 峰男 Ciaion ディジタル制御システム ; 06 Iu Da 06 URL hp://hdl.handl.n/0069/3686 Righ hi documn i downloadd hp://naoi.lb.nagaaki-u.ac.jp 第 章ブロック線図. インパルス列を用いた z
NAOSIE: Nagaaki Univriy' Ac il ディジタル制御システム Auhor() 辻, 峰男 Ciaion ディジタル制御システム ; 06 Iu Da 06 URL hp://hdl.handl.n/0069/3686 Righ hi documn i downloadd hp://naoi.lb.nagaaki-u.ac.jp 第 章ブロック線図. インパルス列を用いた z
様々なミクロ計量モデル†
 担当 : 長倉大輔 ( ながくらだいすけ ) この資料は私の講義において使用するために作成した資料です WEB ページ上で公開しており 自由に参照して頂いて構いません ただし 内容について 一応検証してありますが もし間違いがあった場合でもそれによって生じるいかなる損害 不利益について責任を負いかねますのでご了承ください 間違いは発見次第 継続的に直していますが まだ存在する可能性があります 1 カウントデータモデル
担当 : 長倉大輔 ( ながくらだいすけ ) この資料は私の講義において使用するために作成した資料です WEB ページ上で公開しており 自由に参照して頂いて構いません ただし 内容について 一応検証してありますが もし間違いがあった場合でもそれによって生じるいかなる損害 不利益について責任を負いかねますのでご了承ください 間違いは発見次第 継続的に直していますが まだ存在する可能性があります 1 カウントデータモデル
Microsoft Word - Chap11
 第 章 次元回転群とそのリー代数. SO のリー代数. 節でリー代数を定義したが 以下にその定義を再録する なお 多くの教科書に従って本章以降は ep t A の代わりに ep t と書くこととする 定義.. G を 次の線型リー群とすると 任意の実数 t に対して ep t G となる gl C の全体をGのリー代数 またはリー環 という 例えば ep t が 次の特殊直交群 SO の元であれば
第 章 次元回転群とそのリー代数. SO のリー代数. 節でリー代数を定義したが 以下にその定義を再録する なお 多くの教科書に従って本章以降は ep t A の代わりに ep t と書くこととする 定義.. G を 次の線型リー群とすると 任意の実数 t に対して ep t G となる gl C の全体をGのリー代数 またはリー環 という 例えば ep t が 次の特殊直交群 SO の元であれば
計算機シミュレーション
 . 運動方程式の数値解法.. ニュートン方程式の近似速度は, 位置座標 の時間微分で, d と定義されます. これを成分で書くと, d d li li とかけます. 本来は が の極限をとらなければいけませんが, 有限の小さな値とすると 秒後の位置座標は速度を用いて, と近似できます. 同様にして, 加速度は, 速度 の時間微分で, d と定義されます. これを成分で書くと, d d li li とかけます.
. 運動方程式の数値解法.. ニュートン方程式の近似速度は, 位置座標 の時間微分で, d と定義されます. これを成分で書くと, d d li li とかけます. 本来は が の極限をとらなければいけませんが, 有限の小さな値とすると 秒後の位置座標は速度を用いて, と近似できます. 同様にして, 加速度は, 速度 の時間微分で, d と定義されます. これを成分で書くと, d d li li とかけます.
ベクトル公式.rtf
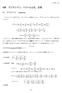 6 章ラプラシアン, ベクトル公式, 定理 6.1 ラプラシアン Laplacian φ はベクトル量である. そこでさらに発散をとると, φ はどういう形になるであろうか? φ = a + a + a φ a + a φ + a φ = φ + φ + φ = 2 φ + 2 φ 2 + 2 φ 2 2 φ = 2 φ 2 + 2 φ 2 + 2 φ 2 = 2 φ したがって,2 階の偏微分演算となる.
6 章ラプラシアン, ベクトル公式, 定理 6.1 ラプラシアン Laplacian φ はベクトル量である. そこでさらに発散をとると, φ はどういう形になるであろうか? φ = a + a + a φ a + a φ + a φ = φ + φ + φ = 2 φ + 2 φ 2 + 2 φ 2 2 φ = 2 φ 2 + 2 φ 2 + 2 φ 2 = 2 φ したがって,2 階の偏微分演算となる.
相対性理論入門 1 Lorentz 変換 光がどのような座標系に対しても同一の速さ c で進むことから導かれる座標の一次変換である. (x, y, z, t ) の座標系が (x, y, z, t) の座標系に対して x 軸方向に w の速度で進んでいる場合, 座標系が一次変換で関係づけられるとする
 相対性理論入門 Lorentz 変換 光がどのような座標系に対しても同一の速さ で進むことから導かれる座標の一次変換である. x, y, z, t ) の座標系が x, y, z, t) の座標系に対して x 軸方向に w の速度で進んでいる場合, 座標系が一次変換で関係づけられるとすると, x A x wt) y y z z t Bx + Dt 弨弱弩弨弲弩弨弳弩弨弴弩 が成立する. 図 : 相対速度
相対性理論入門 Lorentz 変換 光がどのような座標系に対しても同一の速さ で進むことから導かれる座標の一次変換である. x, y, z, t ) の座標系が x, y, z, t) の座標系に対して x 軸方向に w の速度で進んでいる場合, 座標系が一次変換で関係づけられるとすると, x A x wt) y y z z t Bx + Dt 弨弱弩弨弲弩弨弳弩弨弴弩 が成立する. 図 : 相対速度
1/30 平成 29 年 3 月 24 日 ( 金 ) 午前 11 時 25 分第三章フェルミ量子場 : スピノール場 ( 次元あり ) 第三章フェルミ量子場 : スピノール場 フェルミ型 ボーズ量子場のエネルギーは 第二章ボーズ量子場 : スカラー場 の (2.18) より ˆ dp 1 1 =
 / 平成 9 年 月 日 ( 金 午前 時 5 分第三章フェルミ量子場 : スピノール場 ( 次元あり 第三章フェルミ量子場 : スピノール場 フェルミ型 ボーズ量子場のエネルギーは 第二章ボーズ量子場 : スカラー場 の (.8 より ˆ ( ( ( q -, ( ( c ( H c c ë é ù û - Ü + c ( ( - に限る (. である 一方 フェルミ型は 成分をもち その成分を,,,,
/ 平成 9 年 月 日 ( 金 午前 時 5 分第三章フェルミ量子場 : スピノール場 ( 次元あり 第三章フェルミ量子場 : スピノール場 フェルミ型 ボーズ量子場のエネルギーは 第二章ボーズ量子場 : スカラー場 の (.8 より ˆ ( ( ( q -, ( ( c ( H c c ë é ù û - Ü + c ( ( - に限る (. である 一方 フェルミ型は 成分をもち その成分を,,,,
DVIOUT-SS_Ma
 第 章 微分方程式 ニュートンはリンゴが落ちるのを見て万有引力を発見した という有名な逸話があります 無重力の宇宙船の中ではリンゴは落ちないで静止していることを考えると 重力が働くと始め静止しているものが動き出して そのスピードはどんどん大きくなる つまり速度の変化が現れることがわかります 速度は一般に時間と共に変化します 速度の瞬間的変化の割合を加速度といい で定義しましょう 速度が変化する, つまり加速度がでなくなるためにはその原因があり
第 章 微分方程式 ニュートンはリンゴが落ちるのを見て万有引力を発見した という有名な逸話があります 無重力の宇宙船の中ではリンゴは落ちないで静止していることを考えると 重力が働くと始め静止しているものが動き出して そのスピードはどんどん大きくなる つまり速度の変化が現れることがわかります 速度は一般に時間と共に変化します 速度の瞬間的変化の割合を加速度といい で定義しましょう 速度が変化する, つまり加速度がでなくなるためにはその原因があり
2018年度 東京大・理系数学
 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ関数 f ( ) = + cos (0 < < ) の増減表をつくり, + 0, 0 のと sin きの極限を調べよ 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ n+ 数列 a, a, を, Cn a n = ( n =,, ) で定める n! an qn () n とする を既約分数 an p として表したときの分母
08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ関数 f ( ) = + cos (0 < < ) の増減表をつくり, + 0, 0 のと sin きの極限を調べよ 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ n+ 数列 a, a, を, Cn a n = ( n =,, ) で定める n! an qn () n とする を既約分数 an p として表したときの分母
Microsoft Word - t30_西_修正__ doc
 反応速度と化学平衡 金沢工業大学基礎教育部西誠 ねらい 化学反応とは分子を構成している原子が組み換り 新しい分子構造を持つことといえます この化学反応がどのように起こるのか どのような速さでどの程度の分子が組み換るのかは 反応の種類や 濃度 温度などの条件で決まってきます そして このような反応の進行方向や速度を正確に予測するために いろいろな数学 物理的な考え方を取り入れて化学反応の理論体系が作られています
反応速度と化学平衡 金沢工業大学基礎教育部西誠 ねらい 化学反応とは分子を構成している原子が組み換り 新しい分子構造を持つことといえます この化学反応がどのように起こるのか どのような速さでどの程度の分子が組み換るのかは 反応の種類や 濃度 温度などの条件で決まってきます そして このような反応の進行方向や速度を正確に予測するために いろいろな数学 物理的な考え方を取り入れて化学反応の理論体系が作られています
経営統計学
 5 章基本統計量 3.5 節で量的データの集計方法について簡単に触れ 前章でデータの分布について学びましたが データの特徴をつの数値で示すこともよく行なわれます これは統計量と呼ばれ 主に分布の中心や拡がりなどを表わします この章ではよく利用される分布の統計量を特徴で分類して説明します 数式表示を統一的に行なうために データの個数を 個とし それらを,,, と表わすことにします ここで学ぶ統計量は統計分析の基礎となっており
5 章基本統計量 3.5 節で量的データの集計方法について簡単に触れ 前章でデータの分布について学びましたが データの特徴をつの数値で示すこともよく行なわれます これは統計量と呼ばれ 主に分布の中心や拡がりなどを表わします この章ではよく利用される分布の統計量を特徴で分類して説明します 数式表示を統一的に行なうために データの個数を 個とし それらを,,, と表わすことにします ここで学ぶ統計量は統計分析の基礎となっており
降圧コンバータIC のスナバ回路 : パワーマネジメント
 スイッチングレギュレータシリーズ 降圧コンバータ IC では スイッチノードで多くの高周波ノイズが発生します これらの高調波ノイズを除去する手段の一つとしてスナバ回路があります このアプリケーションノートでは RC スナバ回路の設定方法について説明しています RC スナバ回路 スイッチングの 1 サイクルで合計 の損失が抵抗で発生し スイッチングの回数だけ損失が発生するので 発生する損失は となります
スイッチングレギュレータシリーズ 降圧コンバータ IC では スイッチノードで多くの高周波ノイズが発生します これらの高調波ノイズを除去する手段の一つとしてスナバ回路があります このアプリケーションノートでは RC スナバ回路の設定方法について説明しています RC スナバ回路 スイッチングの 1 サイクルで合計 の損失が抵抗で発生し スイッチングの回数だけ損失が発生するので 発生する損失は となります
第1章 単 位
 H. Hamano,. 長柱の座屈 - 長柱の座屈 長い柱は圧縮荷重によって折れてしまう場合がある. この現象を座屈といい, 座屈するときの荷重を座屈荷重という.. 換算長 長さ の柱に荷重が作用する場合, その支持方法によって, 柱の理論上の長さ L が異なる. 長柱の計算は, この L を用いて行うと都合がよい. この L を換算長 ( あるいは有効長さという ) という. 座屈荷重は一般に,
H. Hamano,. 長柱の座屈 - 長柱の座屈 長い柱は圧縮荷重によって折れてしまう場合がある. この現象を座屈といい, 座屈するときの荷重を座屈荷重という.. 換算長 長さ の柱に荷重が作用する場合, その支持方法によって, 柱の理論上の長さ L が異なる. 長柱の計算は, この L を用いて行うと都合がよい. この L を換算長 ( あるいは有効長さという ) という. 座屈荷重は一般に,
特殊なケースでの定式化技法
 特殊なケースでの定式化技法 株式会社数理システム. はじめに 本稿は, 特殊な数理計画問題を線形計画問題 (Lear Programmg:LP) ないしは混合整数計画問題 (Med Ieger Programmg:MIP) に置き換える為の, 幾つかの代表的な手法についてまとめたものである. 具体的には以下の話題を扱った. LP による定式化 絶対値最小化問題 最大値最小化問題 ノルム最小化問題 MIP
特殊なケースでの定式化技法 株式会社数理システム. はじめに 本稿は, 特殊な数理計画問題を線形計画問題 (Lear Programmg:LP) ないしは混合整数計画問題 (Med Ieger Programmg:MIP) に置き換える為の, 幾つかの代表的な手法についてまとめたものである. 具体的には以下の話題を扱った. LP による定式化 絶対値最小化問題 最大値最小化問題 ノルム最小化問題 MIP
ギリシャ文字の読み方を教えてください
 埼玉工業大学機械工学学習支援セミナー ( 小西克享 ) 行列と行列式の意味 -1/6 テーマ B15: 行列と行列式の意味 線形代数と呼ばれる分野では, 必ず, 行列と行列式が出てきます. これらがどのような 意味を持ち, またその違いは何なのかについて解説します. 1. 連立方程式と行列次の例題を考えてみましょう. 例題リンゴ 2 個とミカン 3 個買うと代金は 350 円になり. リンゴ 5 個とミカン
埼玉工業大学機械工学学習支援セミナー ( 小西克享 ) 行列と行列式の意味 -1/6 テーマ B15: 行列と行列式の意味 線形代数と呼ばれる分野では, 必ず, 行列と行列式が出てきます. これらがどのような 意味を持ち, またその違いは何なのかについて解説します. 1. 連立方程式と行列次の例題を考えてみましょう. 例題リンゴ 2 個とミカン 3 個買うと代金は 350 円になり. リンゴ 5 個とミカン
Kumamoto University Center for Multimedia and Information Technologies Lab. 熊本大学アプリケーション実験 ~ 実環境における無線 LAN 受信電波強度を用いた位置推定手法の検討 ~ InKIAI 宮崎県美郷
 熊本大学アプリケーション実験 ~ 実環境における無線 LAN 受信電波強度を用いた位置推定手法の検討 ~ InKIAI プロジェクト @ 宮崎県美郷町 熊本大学副島慶人川村諒 1 実験の目的 従来 信号の受信電波強度 (RSSI:RecevedSgnal StrengthIndcator) により 対象の位置を推定する手法として 無線 LAN の AP(AccessPont) から受信する信号の減衰量をもとに位置を推定する手法が多く検討されている
熊本大学アプリケーション実験 ~ 実環境における無線 LAN 受信電波強度を用いた位置推定手法の検討 ~ InKIAI プロジェクト @ 宮崎県美郷町 熊本大学副島慶人川村諒 1 実験の目的 従来 信号の受信電波強度 (RSSI:RecevedSgnal StrengthIndcator) により 対象の位置を推定する手法として 無線 LAN の AP(AccessPont) から受信する信号の減衰量をもとに位置を推定する手法が多く検討されている
Microsoft PowerPoint - 9.pptx
 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 行列演算と写像 ( 次変換 3 拡大とスカラー倍 p ' = ( ', ' = ( k, kk p = (, k 倍 k 倍 拡大後 k 倍拡大の関係は スカラー倍を用いて次のように表現できる ' = k ' 拡大前 拡大 4 拡大と行列の積 p ' = ( ', '
9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 行列演算と写像 ( 次変換 3 拡大とスカラー倍 p ' = ( ', ' = ( k, kk p = (, k 倍 k 倍 拡大後 k 倍拡大の関係は スカラー倍を用いて次のように表現できる ' = k ' 拡大前 拡大 4 拡大と行列の積 p ' = ( ', '
Microsoft Word - mathtext8.doc
 8 章偏微分と重積分 8. 偏微分とは これまで微分を考える際 関数は f という形で 関数値がつの変数 に依存している場合のみを扱ってきました しかし一般に変数はつとは決まっておらず f のように 複数の変数を持つ関数も考えなければなりません そ こでこの節では今まで学んできた微分を一般化させ 複数の変数に対応した偏微分と呼ばれるものについて説明します これまでの微分を偏微分と区別したいとき 常微分という呼び方を用います
8 章偏微分と重積分 8. 偏微分とは これまで微分を考える際 関数は f という形で 関数値がつの変数 に依存している場合のみを扱ってきました しかし一般に変数はつとは決まっておらず f のように 複数の変数を持つ関数も考えなければなりません そ こでこの節では今まで学んできた微分を一般化させ 複数の変数に対応した偏微分と呼ばれるものについて説明します これまでの微分を偏微分と区別したいとき 常微分という呼び方を用います
超入門対称座標法 皆様こん は今回の御題は 対称座標法 です この解析手法を解説したものは沢山有りますが ヨクワカラン! というものが多いと思います そこで毎度の事ですが 骨流トンデモ解説擬き を作りました この記載が何かの参考になる事を期待します サイタマ ドズニーランド 大学 SDU 学長鹿の骨
 超入門対称座標法 皆様こん は今回の御題は 対称座標法 です この解析手法を解説したものは沢山有りますが ヨクワカラン! というものが多いと思います そこで毎度の事ですが 骨流トンデモ解説擬き を作りました この記載が何かの参考になる事を期待します サイタマ ドズニーランド 大学 SDU 学長鹿の骨記平成鹿年骨月吉日一説に依ると SDU はさいたまドスケベ大学ではないか? と言う話が有るが あながち間違いでは無い
超入門対称座標法 皆様こん は今回の御題は 対称座標法 です この解析手法を解説したものは沢山有りますが ヨクワカラン! というものが多いと思います そこで毎度の事ですが 骨流トンデモ解説擬き を作りました この記載が何かの参考になる事を期待します サイタマ ドズニーランド 大学 SDU 学長鹿の骨記平成鹿年骨月吉日一説に依ると SDU はさいたまドスケベ大学ではないか? と言う話が有るが あながち間違いでは無い
電気電子発送配変電二次練習問題
 Copy Rght (c) 008 宮田明則技術士事務所 . ()() () n n 60 f f f 50, 60503000rp(n - ) f 60, 66060300rp(n - ) f 50, 060500300rp(n - ) f 50, 46050500rp(n - ) N N N (6) N () Copy Rght (c) 008 宮田明則技術士事務所 . r a, r a a a
Copy Rght (c) 008 宮田明則技術士事務所 . ()() () n n 60 f f f 50, 60503000rp(n - ) f 60, 66060300rp(n - ) f 50, 060500300rp(n - ) f 50, 46050500rp(n - ) N N N (6) N () Copy Rght (c) 008 宮田明則技術士事務所 . r a, r a a a
ディジタル信号処理
 ディジタルフィルタの設計法. 逆フィルター. 直線位相 FIR フィルタの設計. 窓関数法による FIR フィルタの設計.5 時間領域での FIR フィルタの設計 3. アナログフィルタを基にしたディジタル IIR フィルタの設計法 I 4. アナログフィルタを基にしたディジタル IIR フィルタの設計法 II 5. 双 次フィルタ LI 離散時間システムの基礎式の証明 [ ] 4. ] [ ]*
ディジタルフィルタの設計法. 逆フィルター. 直線位相 FIR フィルタの設計. 窓関数法による FIR フィルタの設計.5 時間領域での FIR フィルタの設計 3. アナログフィルタを基にしたディジタル IIR フィルタの設計法 I 4. アナログフィルタを基にしたディジタル IIR フィルタの設計法 II 5. 双 次フィルタ LI 離散時間システムの基礎式の証明 [ ] 4. ] [ ]*
Microsoft PowerPoint - 三次元座標測定 ppt
 冗長座標測定機 ()( 三次元座標計測 ( 第 9 回 ) 5 年度大学院講義 6 年 月 7 日 冗長性を持つ 次元座標測定機 次元 辺測量 : 冗長性を出すために つのレーザトラッカを配置し, キャッツアイまでの距離から座標を測定する つのカメラ ( 次元的なカメラ ) とレーザスキャナ : つの角度測定システムによる座標測定 つの回転関節による 次元 自由度多関節機構 高増潔東京大学工学系研究科精密機械工学専攻
冗長座標測定機 ()( 三次元座標計測 ( 第 9 回 ) 5 年度大学院講義 6 年 月 7 日 冗長性を持つ 次元座標測定機 次元 辺測量 : 冗長性を出すために つのレーザトラッカを配置し, キャッツアイまでの距離から座標を測定する つのカメラ ( 次元的なカメラ ) とレーザスキャナ : つの角度測定システムによる座標測定 つの回転関節による 次元 自由度多関節機構 高増潔東京大学工学系研究科精密機械工学専攻
布に従う しかし サイコロが均質でなく偏っていて の出る確率がひとつひとつ異なっているならば 二項分布でなくなる そこで このような場合に の出る確率が同じであるサイコロをもっている対象者をひとつのグループにまとめてしまえば このグループの中では回数分布は二項分布になる 全グループの合計の分布を求め
 < 解説 > 広告媒体の到達率推定モデル 株式会社ビデオリサーチ常務取締役木戸茂 広告媒体計画の評価指標として広告業界では 有効リーチ あるいは 有効フリークエンシー の概念が一般に用いられている 広告の到達回数分布 Frequency Distribution の推定が重視される背景としては Krugan97977 の3ヒット セオリー Threeexosuretheory を根拠とした 3リーチ
< 解説 > 広告媒体の到達率推定モデル 株式会社ビデオリサーチ常務取締役木戸茂 広告媒体計画の評価指標として広告業界では 有効リーチ あるいは 有効フリークエンシー の概念が一般に用いられている 広告の到達回数分布 Frequency Distribution の推定が重視される背景としては Krugan97977 の3ヒット セオリー Threeexosuretheory を根拠とした 3リーチ
