[, + f : f = [, +, f 4 = =. 3 f 5 =,. f 3, f 4, f 5 R, {, }, {, } 3 R.3. I = π, π tn f I R f R f = f { R } =,, +, +.4. f 3, f 4,
|
|
|
- あいり うえや
- 5 years ago
- Views:
Transcription
1 865.. f f f f f f f f 3 R 4 X X R X X 5 Y X Y X 6 7 Y X Y X * /3 8 4 : function; :the domin; : the rnge; : the imge. 3 set; 4 : rel numbers; : the set of rel numbers; R R R 5 : n element; : subset; X Y Y 6 Y X Y X Y X X X 7 A B A B A B A if nd onl if B A is equivlent to B R, b = { R < < b}, [, b] = { R b},, = { R < },, + = { R > },, + = R,, b] = { R < b}, [, b = { R < b},, ] = { R }, [, + = { R }, [, ] = {}., b < b, b [, b] 8.. f f R R f : R R f f :, f = f f f =, f = 4, f =, fs = s, f =. f 9 f [, + 8 : n intervl; n open intervl; : closed intervl., b ], b[ ±, + ] 9 : nonnegtive rel number; the set of nonnegtive rel numbers [, + the set of positive rel numbers, + the set of nonpositive negtive rel numbers, ],,.
2 [, + f : f = [, +, f 4 = =. 3 f 5 =,. f 3, f 4, f 5 R, {, }, {, } 3 R.3. I = π, π tn f I R f R f = f { R } =,, +, +.4. f 3, f 4, f 5 R sin f 3 = +, =. the union A B = { A B} 4 I f : I R {, f I } f..3,.4 f f 5. 5 cosine, sine, tngent. cot := cos, sec :=, csc := sin cos sin. : rtionl number; : n irrtionl number. 3 f 3 R 4 f : the grph of function f. 5 rtionl function; rdicl root; the squre root; the cubic root; n- the n-th root the eponentil function; the logrithmic function; the trigonometric functions, the circulr functions.
3 = cos, π = Cos Π Π 4 Π 4 Π f = tn b f = c f 3.4 d f 4.4 e f ,.4 f 5 cotngent, secnt, cosecnt d d tn = + tn = sec, d d sec = sec tn, d tn d = log cos, d d cot = + cot, csc = csc cot, d cot d = log sin. - sec d = + sin log sin = log + tn tn,.3 csc d = cos tn log + cos = log. 6 cosec sec = cos cos 7 := 8 = Cos = cos π. = sin, π π = Sin = Sin = sin π π. = tn, π < < π = Tn = Tn = tn π < < π. Cos, Sin, Tn 9 Cos = π 6 + 3, Sin 4.7. Cos + Sin = π = 5 π, Tn = π 8. sin π Cos = cos Cos = Cos π π π Cos π Sin = π Cos Tn + Tn 3 = π 4, 4 Tn 5 Tn 39 = π 4. α = Tn, β = Tn 3 tn α = tn β = 3 tnα + β = Tn 9 rc cosine; rc sine; : rc tngent; inverse trigonometric functions. rccos, rcsin, rctn, cos, sin, tn
4 7 865 < β < α = Tn < Tn = π 4. < α + β < π α + β = Tn = π d d Cos =, d d Tn = +. d d Sin =, = Cos = cos d d = d/d = sin. π sin sin = cos =.7 Tn.5-3 Cos, Sin = ±.4 d.5 + = Tn, d = Sin Tn =, Sin =.6 Tn = dt + t, Sin = dt t.7 Mchin α C cosh = e + e, sinh = e e, tnh = sinh cosh = e e e + e = e e cosh sinh = 67 cosh + = cosh cosh + sinh sinh, sinh + = sinh cosh + cosh sinh, tnh + = tnh + tnh + tnh tnh. elementr functions. 3 n α { > } 4 hperbolic cosine; hperbolic sine; hperbolic tngent; hperbolic functions. 5 cosh t ht cos ht 6 cosh cosh 7 t, t = cosh t, sinh t =
5 d d cosh = sinh, sinh = cosh, d d d d tnh = tnh. cosh d = sinh, tnh d = log cosh. t, t sinh d = cosh, t + t 4 + N t N = t N+ = + t + t N+ t N+ + t t =.6 Tn = R N = R N = dt + t = N t N+ + t dt t N+ + t dt N + N+ + R N R N = t N+ dt = N+3 N + 3 N+ t N+ + t dt t N+ + dt = N+3 N Tn = N N + N+ + R N N k k+ = + R N, k + k= N+3 N R N N+3 N lim RN = N.8 Tn = = k k+ k + k=..8 =, π.9 4 = R N 3 N π = N + 3 R N, N + 3 R 4 N N + 3 R N N 3 N α = /5, β = /39. π = 4 M k= 4 k α k+ k + N j= j β j+ + R M,N, j + R M,N 6αM+3 M βN+3 N + 3 R M,N M =, N = = =5 8 TSUBAME Pet flops 5
6 865 4 = tn 5 = tn π, π - -3.,.4-4 cosh, < tnh < cosh sinh, tnh 3 = cosh, = sinh, = tnh t = tnh u cosh u, sinh u t 7 A, B A cos t + B sin t r cost + α, r sint + β 8 = cosh = Cosh Cosh = log + Sinh, Tnh Sinh = log + +, Tnh = log M =, N = -6 log = log log Cos, Sin, Tn -7 n I n = π/ I n = n n I n m π/ I n = cos n m m 3 m... π d = m m + m m... 3 cos n d n n = m, n = m + m sin n = sin θ u = + -9 f = + /f -, b / + b b =, / b > 3 b < / + u -.3 t = tn t cos = cos sin u = sin 3 = cosh u cos - / + d = log + + = Sinh / + = tn θ 3 = sinh u -4, 4, R R R
7 R = R. n n R n R n = {,..., n,..., n R}. R = {,, R} = {,, } R 3 = {,, z,, z } R R R 3 R n R n R n,..., n f,..., n f n f n. f R n R f : R..., R f, = + f R 3 f : R R f : R, f, = + R f, =, f, =, f, = * / : the number line; : the coordinte plne, the Crtesin plne; : the coordinte spce; : point. R n R,, f,.. f, f, f, =.3. f p, f p, 4 f : R R R 3 { },, f,, f f R 3 f : R c R {, f, = c} f c 4 f c z = c f c 3 n f : R n R c {,,..., n, f,..., n,..., n } R n+, {,,..., n f,..., n = c } R n f c.4. R f, = + [, + c, + {, f, = c} 4 : the contour, the level curve, the level set.
8 f b f..4 c f c c f z. R f, = R c {, f, = c} c =. b I I R f f + h f. lim h h f. f f 7 I f f : I f R f f = f f = d d f f f f f f f = f n f n = dn d n f = f.,.3 f R f R R f :, f, R, b f f + h, b f, b, b = lim, h h f f, b + k f, b, b = lim k k 5 : sclr field. 6 7 : differentible; : the differentil coefficient; : the derivtive; f : f-prime dsh. 8 : the second derivtive; 3 : the third derivtive; n : the n-th derivtive. 9 domin 3
9 7 865 f, b f f, b, b f, b f f f :,, R f f f.5. d f = f, f = f f f, f,,..3 f f, f f, f, f, f, 4 f, f,, f, f = f = f, f = f = f, f = f = f, f = f = f f.6. f, = f, = 3 + 6, f, = 3 +. f = 6 + 6, f = 6, f = 6, f =..7. R = {, } f, = Tn.8 f, = + / = f, = + / = + / + / = = + +, f = +, f = f = + +, f = +..6,.7 f f f f 3-9 f f 3 f f, 3 3 f = f, 3 f = f, 3 f = f,... : prtill differentible; : the prtil derivtive with respect to. : the second prtil derivtives. : the commuttivit of prtil differentils.
10 f 3, 3 f, 3 f, 3 f 3 4 n f,..., n i i =,..., n f i f = f k, l n. k l l k ut... 3 ut.8. A t A ut ut du.4 dt = λu k.5 ut = ke λt λ m t t 5 k k > ρ d ρ > t dt 3 n ordinr differentil eqution : Hooke s Lw; Hooke, Robert, , En. 865 t.6 m d dt + ρ d dt + k = = t u = u,, 3 w = w,, z u = u + u, w = w + w + w z 7 u = w = u w 8 w = ρ ρ = ρ,, z,, z w = ρ ρ 9.. t ut, u u.7 t = c u c.8 u t, = πct ep 4ct {t, t > } R B t 6 prtil differentil eqution. 7 the Lplcin; Lplce, Pierre-Simon , F 8 hrmonic function. 9 the Poisson equiton; Poisson, Siméon enis 78 84, F. the het eqution.
11 u.5, u., u.5, u., u.5, u.3, u.35, u.4, u.45, u.5,. c = u., u., u.3, u.4, u.5,.. t ut, u. u t = c u c 3 ut, = F + ct + G ct F, G - 4 u tt = c u u.6, u.7, u.8, u.9, u.,.3.9 c = u t, ct ct u t, d = πct ep d = 4ct t lim ut, = t + { = t = t >. { f = >.9 ut, = u t, f d ut,.7 t f.3 - I R f R f , f,, F f, = F + f f f 7 3 the wve eqution. 4
12 ,, f, = +, =, -4 f, f + f = + f + f + f + f : f,, f,, f,, f, 3. f, 4, f3, 6, f4, 8. f, m m,. f 3 f -7 n -8 n m -9,, f, = +, =, f 5 f, = log + + +, g, = log cos cos, h, = Tn. -5 θ e iθ = cos θ + i sin θ i z = + i, e z = e +i = e cos + i sin, e z Re e z Im e z, z = + i fz = z m m Re fz Im fz,, m =, 3, 4 m ut, = sin + qt + b sin qt, b, q., b, q - f, = log +, g, = Tn., 3-3 F t f,, z = F + + z 3 f F 5 : miniml surfce.
13 I R f I lim f = f f I f I {, f = =. lim f = lim + f f = lim f = f = f = { cos, =. n = nπ, n = n+π n =,, 3... { n}, { n } lim f n =, lim f n = n n lim f f lim f f = lim f f = lim f + h f h f + h f f + h f = lim h = lim lim h h h h h h = f =. * / : continuous; : continuous function. f f 3. f = f = f = 3. f = 3 R f fh f h = 3 + h h f sin f = + = R sin f = cos + = f 3 C k - I f I C - 4 I C - I f I C k - k > f k f k I C - k C k - 3 : the squeeze theorem. 4 C - : of clss C ; C r - : of clss C r ; C - : of clss C C-infinit.
14 f R C - 3. f C - n { > } 3. n n > R 5 R 6 {, R + < r }, {, R < < b, c < < d} r,, b, c, d r >, < b, c < d f A 3. lim f, = A f, A,,b,, b 7,, b f, A 8 + h, b + k, b h, k, 3. lim f, = lim f + h, b + k.,,b h,k, 3.6. α, β, f lim αh, k =, lim h,k, βh, k =, lim h,k, f, = A,,b lim f + αh, k, b + βh, k = A. h,k, 5 : domin; 6 : n open disc; : n open rectngle rectngulr domin. 7,, b f, b the limit {h n }, {k n } 9 lim n f + h n, b + k n = A. 3. {f + h n, b + k n } A {h n }, {k n } 3.8. R,, f, = +, =, -6 h n = /n, k n = /n, k n = /n 3 {h n }, {k n }, {k n} lim fh n, k n =, lim fh n, k n = n n 3.7,, f, f,,, f, lim f, = lim = lim lim + f, =, lim f, = lim = lim lim f, =. + f, = / +,, lim lim f, =, lim lim f, =. 3 f, = / +,, r > θ = r cos θ, = r sin θ 9 : rbitrr; X P : P holds for n rbitrr X.
15 ,, r = + f, = fr cos θ, r sin θ = r cos θ sin θcos θ sin θ = r sin θ cos θ = 4 r sin 4θ sin 4θ r R f, b lim f, = f, b,,b f f f, f, = f, = -9, 3.8 3,, f, = +, =,, R f,, b A, B h, k, 3.3 f + h, b + k f, b = Ah + Bk + εh, k h + k εh, k lim εh, k =. h,k, f,, b f, b 3.3 A, B A = f, b, B = f, b 3.3 k = f + h, b f, b h εh, εh, h h = Ah + εh, h h = A + εh, h h εh, h εh, f + h, b f, b A = lim = f, b. h h h = B = f, b R f,, b f, b 3.4 lim εh, k = h,k, εh, k := f + h, b + k f, b f, bh f, bk h + k 3.4. f, b, b 3.3 h, k, f, f f, f f 35
16 sin,, f, = +, =,, f, f 3.8. R f f, f, f = f C k - R f C - C - f, f C - f f, f, f, f C k - k f k C - k C k R f C C k m C m - C k - 4 C - f = f df P f P, f,, f, df f f 3.6 df =, f. 3.. φ, =, ψ, = dφ =,, dψ =, d =,, d =, df = f f d + d h, k, h + k h, k,, 3.8 f f f, b +, b, f := f +, b + f, b I t, t t, t I R γ : I t γt = t, t R. t, t γ 3.3 f, P =, b f f 3.5 df P =, b,, b, - 4 ; row vector column vector; totl differentil; differentil. curve; prmetric representtion of the curve. γ γt = t sin t, cos t ccloid C - t = nπ nπ, n =, ±, ±,...
17 γt = t, t γt = dγ dt t = ẋt, ẏt d d = t, dt dt t t, t 3 t b+v b+v b v P v O s coss,sins t O s t +t, t +t γt t γt O v +v +v γt t v = v, v P =, b γt = + tv, b + tv t = P v P v 3. s σs = cos s, sin s π < s < π, 4 sin s, cos s 3. 3, t σt := + t, t + t < t <. t = tn s 3. f, γt = t, t 3.9 F t = f t, t f, γt = t, t 3.9 df f d f d t = t, t t + t, t dt dt dt t. t δ hδ, kδ hδ := t + δ t, kδ := t + δ t 3 the velocit vector; the speed. 4 line; circle , δ hδ, kδ t + δ t ε δ := ẋt = hδ ẋt, ε δ := kδ ẏt δ δ δ t, t δ ε δ, ε δ f F t + δ F t = f t + δ, t + δ f t, t = f t + hδ, t + kδ f t, t = f f t, t hδ + t, t kδ + ε hδ, kδ hδ + kδ εh, k h, k, F t + δ F t δ = f ẋt t, t + ε δ + f ẏt t, t + ε δ + ε hδ, kδ δ ẋt + ε δ + ẏt + ε δ. δ δ ε j δ, j =, hδ, kδ, εhδ, kδ δ /δ = F F t + δ F t t = lim = f ẋt f ẏt t, t + t, t δ δ
18 I = [, b], γt = t, t t b R γ γb γ,. R P, Q P Q γ : [, b] R γt t b. R P =, b ε U εp := {, R + b < ε } R R P ε. R 5 P U εp ε. F : R R {, R F, > } R. R f I I + h I h θ f + h f = f + θhh < θ <. 3.6, b h, k 3.4 εh, k k F h := f + h, b + k f, b + k f F h F h = f + h, b + k, F = F F h = F h F = F θhh = f + θh, b + kh < θ < θ Gk = f, b + k f, b k Gk = G δkk = f, b + δkk < δ < δ εh, k = F h + Gk f, bh f, bk h + k 5 : n open set; : connected set; : disc disk. 6 : the men vlue theorem = f + θh, b + k f, b h h + k + f, b + δk f, b k h + k θh < h, δk < k h/ h + k, k/ h + k h, k, 3.8, b f, b = f, b f + h, b + k f, b + k f + h, b + f, b V = V h, k := hk h, k V = F h F F t := f + t, b + k f + t, b k h F t = f + t, b + k f + t, b V = k F θ h = k f + θ h, b + k f + θ h, b = k Fk F F t := f + θ h, b + t θ, F t = f + θ h, b + t θ, θ V = f + θ h, b + θ k θ, θ,. V = Gk G/hk Gt := f + h, b + t f, b + t V = f + φ h, b + φ k φ, φ, φ, φ f, f, h, k, f, b = f, b , 3.8, 3., C - f, = +, 3-3 f, = e cos + sin f., f. γt t 3.9
19 n n n,,,,, 3, = = t,, t =,. t , = +,,, 3 3 = = t A * / vector, mtri, mtrices. sclr; row vector; column vector. 3 trnsposition. 4 squre mtri A = =, = = α α α =, α =,, = A A 4., ξ α A =, ξa = ξ, ξ. α A B α AB = b α b α A =, B = b α b α b α, b. A 4. AA = A A = E E := A A A A E 5 ξ, A 4.3 E =, ξe = ξ, EA = AE = A. 4. A 4.4 det A := det A A 6 A det A A 4.5 A =. det A 5 regulr mtri; the inverse mtri; the identit mtri. 6 : determinnt.
20 f, = t, f = f, 7 3. P = t, b v = t v, v γt γt = P + tv = t + v t, b + v t. 4.. R f P =, b v = t v, v F t := f + v t, b + v t = fp + tv t = F f P v 8 v v f P R f P =, b f P v 4.6 df P v = f, bv + f, bv v = t v, v. P f f grd f P :=, b = t dfp f, b f P df P v = grd f P v grd f P P f the directionl derivtive. 9 the grdient vector f, = ξ, η, = ξ, η fξ, η = f ξ, η, ξ, η f ξ f η f f ξ, η = ξ, η, ξ, η ξ, η + ξ, η, ξ, η ξ, η ξ ξ f f ξ, η = ξ, η, ξ, η ξ, η + ξ, η, ξ, η ξ, η. η η fξ, η f, f fξ, η 4.3 f ξ = f ξ + f ξ, f η = f η + f η z = f, = f ξ, η, ξ, η = fξ, η z ξ = z ξ + z ξ, z η = z η + z η. R R R F : R, R F, F, R ξ, η ξ, η, F : R R the chin rule. ξ: i; η: et. ξ, η, ζ zet,, z
21 R 4.7 F : R, ξ,, η, R. ξ,, η, F ξ = F ξ = ξ, η, =, F = ξ, η: R R C k - 3 ξ, η C k R C - F = ξ, η: R n ξ ξ ξ ξ df = = η η F 4, U R F : R G: U R =, F U η η G F : R G F R G F : R R F G F, G C - dg F = dg df, dg F = dg F df R id : id = 6 R U R F : mp : components. 3 C k - 4 the differentil the Jcobin mtri Jcobi, Crl Gustv Jcob 84 85,. 5 the composition. 6 the identit mp id id U G F = id, F G = id U G: U G F G = F { = r, θ R r >, π < θ < π }, U = {, R > } F : r, θ F r, θ = r cos θ, r sin θ U, G: U, G, = +, Tn G = F, F = G, r, θ π < θ < π Tn tn θ = θ.6 r > G F r, θ = Gr cos θ, r sin θ = r cos θ + r sin θ, Tn r sin θ r cos θ = r, Tn tn θ = r, θ = id r, θ. θ = Tn / π < θ < π cos θ > > cos Tn = cos θ = + tn θ = + tn Tn = + = +, sin Tn = sin θ = cos θ tn θ = F G, = F + +, Tn = + = +. =, = id U,. 4.8., 4.7 r, θ = G,, r, θ, 8 7 the inverse mp; F : the inverse of F /F -inverse; 8 the polr coordinte sstem; the orthognonl cooridnte sstem; the Crtesin coordinte sstem; : escrtes, René Rentus Crtesius;
22 , = {r, θ r >, π < θ < π}, Ũ = {, > } h: Ũ R Tn h, := Tn + π Tn π 9 >, >, < F : r, θ F r, θ = r cos θ, r sin θ Ũ, G: Ũ, G, = +, h, F = G, G = F, r, θ = G,, 4.9. F : R U R G = F F F C - df = df df F = df E F F = id 4.6 df df = E, F F = id U 4.6 df df = E df df = r, θ = r cos θ, = r, θ = r sin θ. F : r, θ, 4.5 r θ cos θ r sin θ 4.9 df = =, sin θ r cos θ r θ 9 h,,, C Fortrn tn, G = F r r cos θ sin θ 4. dg = = df = θ θ r sin θ r cos θ 4. = cos θ r r sin θ θ, = sin θ r + r cos θ θ. C - f, 4. z = f = f + f. f, 4.8 r, θ f f r, θ 4. f = cos θf rr r cos θ sin θf rθ + r sin θf θθ + r sin θf r + r sin θ cos θf θ f = sin θf rr + r cos θ sin θf rθ + r cos θf θθ + r cos θf r r sin θ cos θf θ 4.3 f = f + f = f rr + r f r + r f θθ. 4.4 R F, F, = F, = = φ. F, = = φ = φ 4.. F, = 3+5 F, = = 3 +5 = 3 5 F, = + F, = n implicit function.
23 F U := {, R > }, U F, = = < < U := {, R < } = {, > } F, = = f, = 4.. R C k - F : R F, =, F, P U R I C k - φ: I R, U F, = I = φ. I F, φ =. P F, = 4. F P P F, = 4.3. R 3 3 F,, z := + + z C - P =,, F P = F z P = U := {,, z R 3 z > } V := {, R + < } F,, z =,, z U z =, V F,, z = z {,, z R 3 F,, z = } R 3 z sphere; bll the Northern Hemisphere R C - F C = {, F, = } P C P R U C U C - C P C 4.4. C = {, R + = } 3 P C U := {, > }, U := {, < }, U 3 := {, > }, U 4 := {, < } j =,, 3, 4 C U j C - < < R C - F C := {, F, = } P C df P, C 4.6. F, := + df, = 4, df, =,, =,,,,, F ±, F, = C = {, F, = }, = F, = = φ dφ d = F / F,, = φ. smooth curve. 3 circle; the circle centered t the origin with rdius. 4 the lemniscte.
24 F, φ = = d d F, φ = F d, φ d + F = F F dφ, +, d., φ dφ d 4. F 4.7 d d = F. F F, = = ψ F dψ d = F, F, 4-4. = ψ 4 d d = F F. 4-, f, = P =, b f P df P, f P v df P v v grd f P v 4-4 P =, b f P df P, P f γt = t, t γ = P t = γ γ grd f P 4-5 c ξ = + ct, η = ct t, ξ, η C - ft, f t c f = 4c f ξ η f tt c f = C - f C - F, G ft, = F + ct + G ct f tt = c f f,, z f = f + f + f zz -3 = r cos θ cos φ, = r sin θ cos φ, z = r sin φ r >, π < θ < π, π < φ < π r r r z cos θ cos φ sin θ cos φ sin φ θ θ θ z = sin θ cos θ r cos φ r cos φ φ φ φ z cos θ sin φ sin θ sin φ cos φ r r r f = f rr + r f r +. r cos φ f θθ + r f φφ r tn φf φ 4-7 F, = 3 F, = R C = {, R F, = } P =, F P C = φ d d = φ = F F F F F + F F. F, φ 4-9 F, = +, C = {, R F, = } C = φ φ C 4- R 3 C 3 F,, z F,, z = P =, b, c F P = F, b, c = P F, F, F z P F,, z =,, z F,, z = = ξ, z, = ηz,, z = ζ,. P F,, z = ξ, z η z z, ζ 5 d Alembert, Jen Le Rond , F. F 3 z, z = z =
25 [, b] = {,,,..., N } = < < < N = b := m{,,..., N N }. I = [, b] f I = {,,..., N } N N 5. S f := f j j, S f := f j j, j= j= j = j j f j := [ j, j ] f, f j := [ j, j ] f. 5.. I f I 3 I S f, S f I f 4 b f d = f d. I * / m{,..., N },..., N f [ j, j ] the superimum the infinimum integrble; I f the integrl of f on the intervl I. 4 < b [, ] f = 5 = {,,..., N } [ j, j ] N N S f = j j = N =, S f = j j =, j= j= f [, ] 5.3. [, ] = f = [, ] = {,..., N } k = k [ k, k ] f [ k, k ] f S f = k k k = k, S f =. < k k S f f [, ] f I = [, b] 5. f d := f d, f d := f d I b I f I = [, b] f, g f g b f d 5 6 the definite integrl. g d.
26 f, g [, b] f + g, αf α [, b] b f + g d = f d + αf d = α f d. 7 g d, 5.6., b, c f f d = c f d + c f d [, b] [n] : = [n] < [n] < < [n] N n = b n =,,... lim n [n] = n j =,,..., N n [n] j ξ [n] j f [, b] 5.3 f d = lim n N n j= ξ [n] j [ [n] j, [n] j fξ [n] j [n] j [n] j S n S [n]f S n S [n]f ]. f [n] n f [, b] I = [, b] f I I 8 I α lim α f = fα 5.4 α { n } lim n f n = fα I = [, b] f I I f fα, f fβ α, β I 5.9. I = [, b] f I f f 5.. f I = [, b] f f d f d. f f 5.9 f f f I = [, b] f F = ft dt b F I F = f 8 continuous, continuous function. 7 c [, b] [, c] [c, b] [, b], b, c < c < b 5. 9
27 [, b] + h [, b] h 5.6 F + h F = = +h ft dt ft dt + +h ft dt ft dt 5.5, 5. F + h F f h = +h h ft dt = +h { } h ft f dt h +h ft dt = +h +h ft dt. f dt ft f dt. {h n } + h n [, b] t gt := ft f I n := [, + h n ] gt n = ft n f gt t I n t n I n t n I n n t n 5.4 F + h F h f h +h gt n dt = h gtn = gtn. h n g gt n g = F + h F lim f =. h h F = f F f I f F, G G = F + { G F } = G F = f f = G F I I f 5.. I f I F = 5.3. e the primitive ft dt e t dt f F F = f d 5.4. I f F I, b f d = F b F [, b] C - f + {f } d [, b] = {,,..., N }, f,, f,..., N, f N N fj f j I = + j j j j j= f j f j j j = f ξ j j < ξ j < j ξ j N I = + f ξ j j j j = j j j= f C - + f 5.7 I 5.6. t γt = t, t t b C - d + dt +C d dt dt
28 [, b] [c, d] [, b] [c, d] = {, [, b], [c, d]} = {, b, c d} R [, b] [c, d] 3 R [, b] [c, d] 5.5 = < < < m = b, c = < < < n = d I = [, b] [c, d] mn I = [, b] [c, d] = jk, jk = [ j, j ] [ k, k ] j =,..., m k =,..., n 4 := m{,,..., m m,,..., n n } R 3 5 f,..., f n { R f,..., f n } R R R I I R I = [, b] [c, d] f I 5.5 m m fξ jk, η jk j+ j k+ k j= k= ξ jk [ j, j ], η jk [ k, k ] ξ jk, η jk f I I f 7 8 f, d d. I R f I f,, f, =, I f f f, d d = f, d d I f 9 R f, = 5.6 := d d 3 the Crtesin product; rectngle. 4 t lest t most 5 closed set the comlement. 6 bounded set; : compct set. R n 7 double integrl; multiple integrl. 8 9 I mesurble set; re.
29 R f Ω f f 5.7. R f 5.8. I = [, b] [c, d] R I = b d c 5.9. [, b] φ, ψ φ ψ b := {, R φ ψ, b} R 5.7 f, d d = [ ] ψ f, d d. φ d ψ φ f, d. 5.9 [, b] = < < < m = b [ j, j ] j := {, [ j, j]} f [ ] ψj f j, d j j = j j φ j j n iterted integrl [, b] [c, d] R f, I f, d d = d d c f, d = d c d f, d. 5.. = {, + } f, = = {,, } 5.9 d d = = = [ d ] d = 4 [ ] d = d d {,, d d = = [ d 3 ] d = 3 d = 4 d = π 4. } [ ] d d 3 d = π 3 4. R 3 R m [, b] ρ b kg/m ρ d kg, ρ, kg/m ρ, d d kg,, z ρ,, z kg/m 3 ρ,, z d d dz kg.
30 f F f d = F b F 5- E : + = > b > b E πb E π 4 k sin b t dt, k = km, km 5-3 = P =, O =,, A =, OA, OP, AP t/ P, t 5-4 = 5-5 γt = t sin t, cos t t π { } + +, d d, =,,, d d, = {,, 4}, { } π, d d, =, sin { },, d d, =,, + { } + + z,, z d d dz, =,, z. + + z R I = [, b] [c, d] C - F F d d = F b, d F, d F b, c + F, c I 5-9 R 3 d d dz R 4, R , b, c {,, z } { + b + z c,,, z } + b + z4 c 4 5- R = {, R + } C - F, G G, F, d d = π F cos t, sin t sin t + Gcos t, sin t cos t dt C : t, t t b F, G F, d + G, d C := F t, t d dt + G t, t d dt dt C F d + G d C G, F, d d = F, d + G, d 5. C 5-7 R r ρ = ρrkg/m 3 ρ ρ [, R]
31 R 6.. = {, } R := {, 3 + 3,, } = 4 = d d = 3π/ d d = [ 3 3 ] d = 3π 3. R f Ω f := {,, z,, z f, } R 3 R 3 f, [, + ] [, + ] f, f, * 8 5 /5 f, d d. 6.. f, = b,b f, { =, } + b f, d d = b d d = 3 πb R 3 Ω Ω 6.3. = {,, z z 4, } = {, } = d d dz = d d dz = 4 d d = = 3 5. z = f,, R f C - [, + ] [, + ] 3 P =,, f,, Q = +,, f +,, R =, +, f, + P Q, P R volume; R 3 R
32 P Q P R =,, f +, f,,, f, + f, f +, f, f, + f, = + + f f +, +, 6. + f + f d d 6.4. f, = + = {,, } d d = d + + d log π 8 6. = [, b] f [α, β] C - φ φα =, φβ = b 6. 3 f d = β α f φu φ u du integrtion b substitution. 3 φ C = u = φu 6. β α f u d du du [α, β] : α = u < u < < u N = β j = φu j j =,,..., N φ : < < < N [, b] [u j, u j ] φ φ η j, η j [u j, u j ] 5.4 j j = φu j φu j = j j φ η j u j u j uj u j φ u du φ η j u j u j, 6.3 φ η j u j u j j j φ η j u j u j u j u j j j : φ φ [u j, u j] gu := f φu φ u, ξ j = φη j, ξ j = φη j gη j u j u j = fξ j φ η j u j u j fξ j j j, gη j u j u j = fξ j φ η j u j u j fξ j j j. S g N fξ j j j, j= S g N fξ j j j 6.3 f, g g, f j=
33 φ [, b] [α, β] φ 6.3 R 4. R R L A : R X = A R A R 4 A 38 L A 6.7. L A L A p = L A q Ap = Aq A p = q 6.8. L A R L A P, Q R l P, Q p, q l l L A l = { tp + tq t R} L A tp + tq = tap + taq l = { t p + t q t R} p = Ap, q = Aq OP = p, OQ = q P, Q P Q l P, Q P = Q l P L A L A R L A 6.. l P, Q l R, S l det P R, P Q det P S, P Q R det 38 t, b = P Q n = t b, det P Q, v = v, n R n l l R l n P R n P R, n > 6.. L A R R L A L A P QRS p = OP, q = OQ P Q { tp + tq t } P, Q P, Q L A P, Q P QRS det, b = P Q, b = P R, b θ 6.4 b sin θ = b b cos θ = b, b., b, b = t,, b = t b, b liner trnsformtion.
34 L A det A = P QRS P, Q, R p, q, r = P Q = q p, b = P R = r p P, Q, R L A P, Q, R P Q = Aq Ap = Aq p = A, P R = Ab = deta, Ab = det A, b = det A det, b = det A. R C - F : R u, v F u, v = u, v, u, v R F + h, b + k u, b v, b h = F, b + + h + k εh, k u, b v, b k εh, k h, k, t h, k F df 4.5 h, k u, b v, b h 6.5 Φh, k := F + h, b + k F, b u, b v, b k 5 3. u, v, u, v, ε, ε ε = t ε, ε , u, v = det u v u, v uv-, b, + u, b,, b + v, + u, b + v F u, v = u, v, u, v u, b,, b,, b + u, b u,, b + u, b u,, b + v, b v,, b + v, b v,, b + u, b u + v, b v,, b + u, b u + v, b v, u, v u v v R C - u, v u, v, u, v uv E f f, d d = f u, v, u, v, u, v du dv 6 the Jcobin. E
35 d d + + := {, +, } 5 6.6, = r cos θ, r sin θ E := { r, θ r, π θ π } r, θ, r, θ = det r θ cos θ r sin θ = det = r sin θ r cos θ 6.5 d d + + = E r θ [ r dr dθ π/ ] + r = r dr π/ + r dθ = π log 3 := {, + }, := {, + } 6.6 E := {r, θ r, π θ π}, E := {r, θ r, π θ π}, d d + + = j E j r dr dθ + r j =, R n C - u,..., u n u,..., u n,..., n u,..., u n R n E f f,..., n d... d n =... f u,..., u n,..., n u,..., u n J du du... du n E J := u... un,..., n u,..., u n = det n u... n un 6-6 Ω := {,, z +, + z } R 3 6- R > S R = {,, z + + z = R } N =,, R S R P P N P N P r N r N r C r C r C r L r r 3 C r S R N A r r < r < πr/ L r 4 lim r + πr, lim A r r + πr.
36 {, > } π d d d d, d d = d d 6-4 = f b π f + f d [, b] f > 6-5 C C : γt = t, t t b t, t t C - [, b] t > C = r cos θ, = r sin θ. = uv, = v. 3 = u, = v sin u. 4 = r cos θ, = r sin θ. 5 = r cos θ cos φ, = r sin θ cos φ, z = r sin φ ,, z = r cos θ cos φ, r sin θ cos φ, r sin φ 6-8 C - φ φ = φ = φ u du u = t t φ = ψ ψ π C L d t + dt d dt dt d d b d t + dt, t + dt dt dt d d L = + dt dt d dt dt dt
37 , b] f lim f d ε + +ε f [, b [, f M lim f d M + f d f d f d f d 7.. ε, ε d = [ ] ε = ε ε +, ] ε, ε d =. d = [log ] ε = log log ε = log ε + ε + * 8 6 5/6 improper integrl, ] 3 M M d. e d = [ e ] M = e M M + [, + 4 M M e d =. d = [log ]M = log M + M + [, + d α α d α > β β d β < 3 e d > 7.3.
38 k, k 7. d ε, ε k sin ε d = k sin t dt = sin t [, π ] ε + k d = π k sin t dt. f, b [ + ε, b ε ] ε, ε +, + f d = lim ε,ε, ε +ε f d 7.4. ε, ε, ε [ +ε d = ] ε log +ε [ ] ε = log + log + +ε = log ε + log ε log ε log ε ε + d ε, ε, ε = ε = ε + ε +ε d = 5. [ ] ε log + log + = +ε d = 7.5. I =, b] f, g I f, g f g I, f d g d m m m!e m f m = m!e m m f m e = e e 4 e e =. f k f k f k+ = kf k f k+ f k+ f k+ = m! 7.7. p p Me M = [p] +! [p] p > p [p]+ m = [p] < f f f
39 p lim + p e =. p p p e e, +. p 7.6 / p 7. p [p] +!e / p p e [p] +!e / p p e d p e e / > [, p p e d. [, ] [, + e e p e p e 7.9 [, p = e d = e d + e d = e d 5 7. π 5 the Gussin integrl; Guss Guß, Crl Friedlich , G s > Γ s = e s d e s d s > 7.3. p, q Bp, q = p q d e d = π, e d = π. 7., 7. e M I M := M M M 7.5 I M = e d = R e = M e M e d M e d e d d = e d E M e d d E M := [, M] [, M] R { } 7.6 J R := d d, R :=, R + R,, 6 B b β
40 M M M M E M Π Θ M M E M 7.6. µ σ µ e σ d =, πσ µ e σ d = µ, πσ µ µ e σ d = σ. πσ M 7. r, θ = r cos θ, = r sin θ R { R := r, θ r R, θ π } [ = [, R], π ], / r, θ = r π 7.7 J R = e r R r dr dθ = re r dr dθ R R dr = π e r M M dθ = π e R M M E M M 7. π e M = J M I M J 4 M = π e M, 4 e d = lim M + I M = π r u = µ/ σ M, M M µ e σ d = e u du α j := Mj + µ, j =, M πσ π σ M j + j + j =, M, M M M M µ e σ d = πσ µ M πσ = = σ π σ π µ e σ σu + µ e u du π ue u µ du + π e u du e e + µ π e u d = σ u e u π [ = σ ue u] + e u π du du µ, +. σ du = π u e u du Γ = π. 7.3 u Γ = e d = e u du = π. 7., 7.3 Γ pγ q 7.7. p, q > Bp, q = Γ p + q.
41 v Iε, M e u u p+q v p v q du dv = M ε e u u p+q du M M+ε ε M+ε v p v q dv Iε, M e u u p+q v p v q du dv M ε ε = e u u p+q du v p v q dv. ε ε, Ε Ε M u ε +, M + Γ p + qbp, q p, q ε < /4 M > Iε, M := e p e q d d ε,m M M = e p d e q d ε,m = [ε, M] [ε, M] ε lim ε + M + ε Iε, M = Γ pγ q. = uv, = u v ε,m uv { := u, v ε u v M u, M u v ε } u 7., / u, v = u u > Iε, M = e u u p+q v p v q du dv := [ ε, M ε ] [ ε, [ ε], := [ε, M] 7. ε M + ε, ] M M + ε X X = k C k / X j p j > j p j = µ := p j j, σ := p j j µ µ X σ σ 7, b X b P,b P,b = ρ d ρ ρ P,b 7. ρ d =, ρ 7 stochstic vrible, rndom vrible, probbilit distribution, the binomil distribution, the men, the vrince, the stndrd devition, probbilit densit function.
42 ρ µ := ρ d, σ := µ σ ρ := πσ µ e σ µ ρ d ρ 7. ρ µ, σ 5-9 n R R n R 9 B n R := {,..., n R n n R } R n V nr := d d... d n B n R α n := V n j = R j j =,..., n V n R = R n α n α = π, α 3 = 4 π 3 n π 7.8. α n = Γ n +. f,..., n := e n n 7.3 n d d... d n = e dt t = π n. R n e r = + + n f = e r r r + r f fr r r + r = fr V n r + r V n r = frα n r + r n r n = frα n nr n r + r... 8 the norml distribution. 9 bll. sphere , 5 f R n r r f,..., n d d... d n = nα n e r r n dr R n r = u nα n e u u n du = n n n α nγ = α n Γ , ] [, s Γ s + = sγ s n Γ n = n! [, + ft * ˆfs := e st ft dt s ˆf f ft = * s > ˆfs = /s ft = t * s > ˆfs = /s 3 ft = t k k * s > ˆfs = k!/s k+ 4 ft = e t * s > ˆfs = /s 5 ft = cos ωt ω * s > ˆfs = s/s + ω 6 ft = sin ωt ω * s > ˆfs = ω/s + ω r = + s
43 - Yes; No; 3 Yes, = No; 4 No; 5 Yes. - cos Π Π Π Π sin Π Π tn Π 4 Π 4 = Cos = Sin = Tn sec Π Π Π Π csc Π Π Π Π Π cot = sec = csc = cot -3 cos, sin -4 cosh tnh tnh = e e e + e = e e + = e + = + e e +. Π Π f = f f f = f 3 cosh sinh tnh = cosh = sinh = tnh 4, 5 6 cosh u = +t t, sinh u = t t, tnh u = t +t. 7 A > B ± A B cosh + α, α = Tnh B/A A A < B B A sinh+α, α = Tnh A/B. A = B 8 = cosh Y = e Y -5 α = Tn 5, β = Tn tn4α β = 39 4α β = π 4 + nπ n Tn < 4α β < 4 Tn = 5 π n = Sin = Sin -7 cos n = sin cos n -8 + Sin log + 4 log + 5 log /, +b = α, β α β log α β 3 Tn A A. A = b. + b = + b = A A + /A. -4 Tn + 4 log +, 6 log Tn log + 3, 3 3 log ++log + + Tn + Tn mm. R + R Tn R+. R 4 R 8 /πm Tn.8 N =
44 ; z z = F z -6,, 4/5, 3/5; 4/5, 4/5, 4/5; m/ + m. m m m/ + m 3 fh, f, f, = lim = lim h h h h = f, = +,,, =,, f, = +,,, =,. nn+ -7 : n -8 : n m n H m = n+m! m!n! nm -9 f, = f, = f, = f, = f, = f, = ,,, =,, ,,, =,, ,, 3, =,, ,, 3, =,, { ,,, =,, + 3,,, =,. { : f, = b c + d + p + q + m., b, c, d, p, q, m -3 f f,, z = r F r, r = + + z f,, z = r F r + r F r r 3 f + f + f zz = F r r + F r. F F r = /r + b, b -4 f {, + > }, g {, cos cos > }, h {, > } -5 Re e z = e cos, Im e z = e sin m = Re fz =, Im fz =, m = 3 Re fz = 3 3, Im fz = 3 3, m = 3 Re fz = , Im fz = m γs = cos s, sin s F s := f γs = + sin s F s = cos s s π/4, π/4, 3π/4, π, π, 3π/4 3π/4, π/4, π/4, 3π/4 4-3 df P v = grd f P v v = grd f P df P v grd f P v = kgrd f P k > 4-4 γt P f f f t, t = t fξ, η = f ξ+η, ξ η c f ξη = f ξ η f ξ ξ, η = Hξ ξ fξ, η = Hξ dξ + Gη Gη η - q = ±c;, b
45 4-6 r, θ, φ,, z r θ φ cos θ cos φ r cos φ sin θ r cos θ sin φ r θ φ = cos φ sin θ r cos θ cos φ r sin θ sin φ z r z θ z φ sin φ r cos φ,, z r θ φ,, z = rcos θ sin φ, sin θ sin φ, cos φ 4-7 df =, 3 C := {, F, = }, C C > < = 3 = /3 b, b b, b, b, b ; > C = φ φ = + + φ = = + = φ = 3 = =, ± +3 3 < < 4 = C, b C = φ φ = φ [, b φ = φ = F, φ /F, φ d d F, φ = F, φ + F, φ φ φ F, = 4 + C = C = {,,, } < { {, [ b, b ] [b, b ]} < < C {, [ b, b ] b = +, b =. C = ±b, ±b > = F = C = φ F = ψ C 4-3 = 5 59 ξ = F F, η z = F z F, ζ = F F z = b / b [ ] d = 4b u du = 4b u u + sin u., = cos t, b sin t π t π
46 π/ π/ 4 sin t + b cos t dt = 4 π/ = 4 cos t + b cos t dt π/ π/ = 4 k cos t dt = 4 t = π u 3 k π/ 4 k sin t dt 4 π/ sin t + b cos t dt k sin u du. k π sin t dt = 4 k 8 π., b k = km 5-3 = + + u du + = log + + = sinh 5-4 = sinh t, = + = cosh t. P = cosh t, sinh t log π, 8 = f π π d = d dt = 3π. dt = t = t sin t 5-6 /6, 8 log 6, R 5-7 4πr ρr dr. 4 ππ 3, /45, / [, R] = r < r < < r N = R [r j, r j ] r j r j 4 3 πr3 j r3 j ρr j 4 3 πρr j r j r j r j + r j r j + rj 4 3 πρr j3r j r j r j = 4πr j ρr j r j r j = r j r j. [, R] ρ m [, R] : = r < r < < r N = R I j := [r j, r j ] r j r j ρ ρ j ρ j = ρξ j, r j ξ j r j ξ j I j M j M j 4 3 π ρ jr 3 j r3 j = 4 3 πρξ jr j r j r j + r jr j + r j = 4 3 πρξ j3ξ j r j r j + µ j µ j := 4 3 πr j r j ρξ j r j + r jr j + r j 3ξ j µ j 4 3 πr j r j Mr j ξ j 4 3 πr j r j Mr j r j = 4πm 3 r j r j r j + r j 8πmR r j r j 3 8πmR r j r j 3 n µ j j= 8πmR n r j r j = 8πmR. 3 3 j= fr := 4πr ρr f j I j f 4 3 πρξ j3ξ j r j r j f j r j r j N N M j S f + µ j j= j= S f + 8πmR. 3 f R fr dr M r M 4πr ρr dr. M j ρ r M 4πr ρr dr.
47 5-8 d [ F, d d = d F, d = F, ] =d =c d c = F, d d F, c d = [ F, d ] =b = [ F, c ] =b = = F b, d F, d F b, c + F, c /4π, π /, 8π /5, /3bcπ, 8/5bcπ. 6- π r R πr sin r R. 3 4πR sin r R. f, = R + πr sinr/r 6. 4 r r 6-3,, +, + + π + π = π + π 5- G, d d = d G, d = [G, ] = d = = G, d G, d =, d d m,..., m n n,..., n = sin t π t π, = sin u π u 3π π/ 3π/ = Gcos t, sin t dt + Gcos u, sin u du π/ π/ 3π/ π = Gcos t, sin t dt = Gcos t, sin t dt. π/ π F [ ] d dz d = 4 d = 6 3, [ z ] d d dz z [ z ] = 8 d d dz = 6 3. m + + m n n m + + m n k, l, k + k, l + l m kl := k l kl := k, l m kl = k l d d =, k,l k,l m kl kl = k k l, l k l k,l kl kl d d, d d -
48 6-4 + z = f b z > z = F, = f =, := {, b, f } 6. S S = F F d d = [ b f = f + f f = π f + f d. f + f f ] d d f d d 6-5 [, b] C = f ẋ = C I = [, b ] C = f 6-4 π b f + df d d = π t ẋ + ẏ dt = d/dt = t t = f t [, b ] ẋ = ẏ π b = π = π d dt dt = π ẏ dt = π ẏ dt ẋ + ẏ dt ẋ =, > ẏ C [, b] m j, j m j = t j, j = t j, t j π/ /cos θ+sin θ r 3 dr dθ = dθ r 3 dr = 6, { = r, θ rcos θ + sin θ, θ π }. 4 u uv du dv = u du v dv 4 u 4 u 4 4 u + u du v dv + u du v dv = 8 log 6, u { = u, v v, u v 4 u, v } u. π 3 u v sin u du dv = u sin u du v dv = 4 ππ 3, = {u, v u π, v }. π/ cos θ sin θr cos θ+ sin θ 4 dr dθ = cos θ sin θ dθ r dr { } = 45, = r, θ θ π, r cos θ + sin θ 5 r 4 cos φ dr dθ dφ π π cos θ cos φ+sin θ cos φ+sin φ = dθ dφ r 4 cos φ dr =, { = r, θ, φ θ, φ π }, rcos θ cos φ + sin θ cos φ + sin φ. 6-7 r cos φ, { = r, θ, φ r R, π θ π, π φ π } ρr d d dz = ρrr cos φ dr dθ dφ π π R R = dθ cos φ dφ r ρr dr = π r ρr dr. π π 6-8 φ = φ u du = φ t dt = φ t dt
49 ψ := φ t dt ψ ε α d = ε { α+ ε α+ α log ε α = ε + α + > M M β d = { β+ M β+ β log M β = M + β + < 3 M { M e d = e M M = M + > 7- [, ] e e s s. s > 7., ] 7.5 e s d [, Γ = M M M e s d = e s d = [ e s] M M + s e s d M = e M M s + s e s d M Γ s+ = sγ s n 7-4, ] q M, M = { q q < q < p q M p <. p > 7., /] 7.5 / p q d t p q d / s > ˆfs = e st dt = lim e sm = M + s s. 7.9 = + s s. 3 ˆfs = te st dt = [ s ] t= te st + e st dt t= s ˆfs = te st dt = [ s ] t= tk e st + k t k e st dt t= s = k t k e st dt s s < ˆfs = e st dt Γ n = n Γ n = = n n... Γ = n!.
50 5 ω = ω M M M sin ωt e st cos ωt dt = e st dt ω [ ] M = ω e st sin ω t + s M e st sin ωt dt ω = ω e sm sin ωm s M cos ωt e st dt ω ω = ω e sm sin ωm s ω e st cos ωm s M ω e st cos ωt dt. s + ω M ω e st cos ωt dt = ω e sm sin ωm s ω e st cos ωm e sm e sm sin ω e sm, e sm e sm cos ω e sm s > M + e sm cos ωm, e sm sin ωm 6 5 s + ω ω e st cos ωt dt = s ω M M cos ωt e st sin ωt dt = e st dt ω [ ] = ω e st cos ωt s e st cos ωt dt ω = ω s ωs + ω = ω s + ω.
[, + f : f = [, +, f 4 = =. 3 f 5 =,. f 3, f 4, f 5 R, {, }, {, } 3 R.3. I = π, π tn f I R f R f = f { R } =,, +, +.4. f 3, f 4,
 473.. f f f f f f f f 3 R 4 X X R X X 5 Y X Y X 6 7 Y X Y X * 4 4 9 3 4 9 : function; :the domin; : the rnge; : the imge. 3 set; 4 : rel numbers; R R R 5 : n element; : subset; X Y Y 6 Y X Y X X X 7 A
473.. f f f f f f f f 3 R 4 X X R X X 5 Y X Y X 6 7 Y X Y X * 4 4 9 3 4 9 : function; :the domin; : the rnge; : the imge. 3 set; 4 : rel numbers; R R R 5 : n element; : subset; X Y Y 6 Y X Y X X X 7 A
 211 kotaro@math.titech.ac.jp 1 R *1 n n R n *2 R n = {(x 1,..., x n ) x 1,..., x n R}. R R 2 R 3 R n R n R n D D R n *3 ) (x 1,..., x n ) f(x 1,..., x n ) f D *4 n 2 n = 1 ( ) 1 f D R n f : D R 1.1. (x,
211 kotaro@math.titech.ac.jp 1 R *1 n n R n *2 R n = {(x 1,..., x n ) x 1,..., x n R}. R R 2 R 3 R n R n R n D D R n *3 ) (x 1,..., x n ) f(x 1,..., x n ) f D *4 n 2 n = 1 ( ) 1 f D R n f : D R 1.1. (x,
IA September 25, 2017 ( ) I = [a, b], f (x) I = (a 0 = a < a 1 < < a m = b) I ( ) (partition) S (, f (x)) = w (I k ) I k a k a k 1 S (, f (x)) = I k 2
![IA September 25, 2017 ( ) I = [a, b], f (x) I = (a 0 = a < a 1 < < a m = b) I ( ) (partition) S (, f (x)) = w (I k ) I k a k a k 1 S (, f (x)) = I k 2 IA September 25, 2017 ( ) I = [a, b], f (x) I = (a 0 = a < a 1 < < a m = b) I ( ) (partition) S (, f (x)) = w (I k ) I k a k a k 1 S (, f (x)) = I k 2](/thumbs/97/133729157.jpg) IA September 5, 7 I [, b], f x I < < < m b I prtition S, f x w I k I k k k S, f x I k I k [ k, k ] I I I m I k I j m inf f x w I k x I k k m k sup f x w I k x I k inf f x w I S, f x S, f x sup f x w I
IA September 5, 7 I [, b], f x I < < < m b I prtition S, f x w I k I k k k S, f x I k I k [ k, k ] I I I m I k I j m inf f x w I k x I k k m k sup f x w I k x I k inf f x w I S, f x S, f x sup f x w I
2. 2 P M A 2 F = mmg AP AP 2 AP (G > : ) AP/ AP A P P j M j F = n j=1 mm j G AP j AP j 2 AP j 3 P ψ(p) j ψ(p j ) j (P j j ) A F = n j=1 mgψ(p j ) j AP
 1. 1 213 1 6 1 3 1: ( ) 2: 3: SF 1 2 3 1: 3 2 A m 2. 2 P M A 2 F = mmg AP AP 2 AP (G > : ) AP/ AP A P P j M j F = n j=1 mm j G AP j AP j 2 AP j 3 P ψ(p) j ψ(p j ) j (P j j ) A F = n j=1 mgψ(p j ) j AP
1. 1 213 1 6 1 3 1: ( ) 2: 3: SF 1 2 3 1: 3 2 A m 2. 2 P M A 2 F = mmg AP AP 2 AP (G > : ) AP/ AP A P P j M j F = n j=1 mm j G AP j AP j 2 AP j 3 P ψ(p) j ψ(p j ) j (P j j ) A F = n j=1 mgψ(p j ) j AP
Note.tex 2008/09/19( )
 1 20 9 19 2 1 5 1.1........................ 5 1.2............................. 8 2 9 2.1............................. 9 2.2.............................. 10 3 13 3.1.............................. 13 3.2..................................
1 20 9 19 2 1 5 1.1........................ 5 1.2............................. 8 2 9 2.1............................. 9 2.2.............................. 10 3 13 3.1.............................. 13 3.2..................................
D = [a, b] [c, d] D ij P ij (ξ ij, η ij ) f S(f,, {P ij }) S(f,, {P ij }) = = k m i=1 j=1 m n f(ξ ij, η ij )(x i x i 1 )(y j y j 1 ) = i=1 j
![D = [a, b] [c, d] D ij P ij (ξ ij, η ij ) f S(f,, {P ij }) S(f,, {P ij }) = = k m i=1 j=1 m n f(ξ ij, η ij )(x i x i 1 )(y j y j 1 ) = i=1 j D = [a, b] [c, d] D ij P ij (ξ ij, η ij ) f S(f,, {P ij }) S(f,, {P ij }) = = k m i=1 j=1 m n f(ξ ij, η ij )(x i x i 1 )(y j y j 1 ) = i=1 j](/thumbs/103/158001152.jpg) 6 6.. [, b] [, d] ij P ij ξ ij, η ij f Sf,, {P ij } Sf,, {P ij } k m i j m fξ ij, η ij i i j j i j i m i j k i i j j m i i j j k i i j j kb d {P ij } lim Sf,, {P ij} kb d f, k [, b] [, d] f, d kb d 6..
6 6.. [, b] [, d] ij P ij ξ ij, η ij f Sf,, {P ij } Sf,, {P ij } k m i j m fξ ij, η ij i i j j i j i m i j k i i j j m i i j j k i i j j kb d {P ij } lim Sf,, {P ij} kb d f, k [, b] [, d] f, d kb d 6..
 4................................. 4................................. 4 6................................. 6................................. 9.................................................... 3..3..........................
4................................. 4................................. 4 6................................. 6................................. 9.................................................... 3..3..........................
untitled
 0. =. =. (999). 3(983). (980). (985). (966). 3. := :=. A A. A A. := := 4 5 A B A B A B. A = B A B A B B A. A B A B, A B, B. AP { A, P } = { : A, P } = { A P }. A = {0, }, A, {0, }, {0}, {}, A {0}, {}.
0. =. =. (999). 3(983). (980). (985). (966). 3. := :=. A A. A A. := := 4 5 A B A B A B. A = B A B A B B A. A B A B, A B, B. AP { A, P } = { : A, P } = { A P }. A = {0, }, A, {0, }, {0}, {}, A {0}, {}.
(1) (2) (3) (4) 1
 8 3 4 3.................................... 3........................ 6.3 B [, ].......................... 8.4........................... 9........................................... 9.................................
8 3 4 3.................................... 3........................ 6.3 B [, ].......................... 8.4........................... 9........................................... 9.................................
 20 6 4 1 4 1.1 1.................................... 4 1.1.1.................................... 4 1.1.2 1................................ 5 1.2................................... 7 1.2.1....................................
20 6 4 1 4 1.1 1.................................... 4 1.1.1.................................... 4 1.1.2 1................................ 5 1.2................................... 7 1.2.1....................................
II No.01 [n/2] [1]H n (x) H n (x) = ( 1) r n! r!(n 2r)! (2x)n 2r. r=0 [2]H n (x) n,, H n ( x) = ( 1) n H n (x). [3] H n (x) = ( 1) n dn x2 e dx n e x2
![II No.01 [n/2] [1]H n (x) H n (x) = ( 1) r n! r!(n 2r)! (2x)n 2r. r=0 [2]H n (x) n,, H n ( x) = ( 1) n H n (x). [3] H n (x) = ( 1) n dn x2 e dx n e x2 II No.01 [n/2] [1]H n (x) H n (x) = ( 1) r n! r!(n 2r)! (2x)n 2r. r=0 [2]H n (x) n,, H n ( x) = ( 1) n H n (x). [3] H n (x) = ( 1) n dn x2 e dx n e x2](/thumbs/101/149159646.jpg) II No.1 [n/] [1]H n x) H n x) = 1) r n! r!n r)! x)n r r= []H n x) n,, H n x) = 1) n H n x) [3] H n x) = 1) n dn x e dx n e x [4] H n+1 x) = xh n x) nh n 1 x) ) d dx x H n x) = H n+1 x) d dx H nx) = nh
II No.1 [n/] [1]H n x) H n x) = 1) r n! r!n r)! x)n r r= []H n x) n,, H n x) = 1) n H n x) [3] H n x) = 1) n dn x e dx n e x [4] H n+1 x) = xh n x) nh n 1 x) ) d dx x H n x) = H n+1 x) d dx H nx) = nh
 X G P G (X) G BG [X, BG] S 2 2 2 S 2 2 S 2 = { (x 1, x 2, x 3 ) R 3 x 2 1 + x 2 2 + x 2 3 = 1 } R 3 S 2 S 2 v x S 2 x x v(x) T x S 2 T x S 2 S 2 x T x S 2 = { ξ R 3 x ξ } R 3 T x S 2 S 2 x x T x S 2
X G P G (X) G BG [X, BG] S 2 2 2 S 2 2 S 2 = { (x 1, x 2, x 3 ) R 3 x 2 1 + x 2 2 + x 2 3 = 1 } R 3 S 2 S 2 v x S 2 x x v(x) T x S 2 T x S 2 S 2 x T x S 2 = { ξ R 3 x ξ } R 3 T x S 2 S 2 x x T x S 2
Z: Q: R: C: sin 6 5 ζ a, b
 Z: Q: R: C: 3 3 7 4 sin 6 5 ζ 9 6 6............................... 6............................... 6.3......................... 4 7 6 8 8 9 3 33 a, b a bc c b a a b 5 3 5 3 5 5 3 a a a a p > p p p, 3,
Z: Q: R: C: 3 3 7 4 sin 6 5 ζ 9 6 6............................... 6............................... 6.3......................... 4 7 6 8 8 9 3 33 a, b a bc c b a a b 5 3 5 3 5 5 3 a a a a p > p p p, 3,
W u = u(x, t) u tt = a 2 u xx, a > 0 (1) D := {(x, t) : 0 x l, t 0} u (0, t) = 0, u (l, t) = 0, t 0 (2)
 3 215 4 27 1 1 u u(x, t) u tt a 2 u xx, a > (1) D : {(x, t) : x, t } u (, t), u (, t), t (2) u(x, ) f(x), u(x, ) t 2, x (3) u(x, t) X(x)T (t) u (1) 1 T (t) a 2 T (t) X (x) X(x) α (2) T (t) αa 2 T (t) (4)
3 215 4 27 1 1 u u(x, t) u tt a 2 u xx, a > (1) D : {(x, t) : x, t } u (, t), u (, t), t (2) u(x, ) f(x), u(x, ) t 2, x (3) u(x, t) X(x)T (t) u (1) 1 T (t) a 2 T (t) X (x) X(x) α (2) T (t) αa 2 T (t) (4)
1 (Berry,1975) 2-6 p (S πr 2 )p πr 2 p 2πRγ p p = 2γ R (2.5).1-1 : : : : ( ).2 α, β α, β () X S = X X α X β (.1) 1 2
 2005 9/8-11 2 2.2 ( 2-5) γ ( ) γ cos θ 2πr πρhr 2 g h = 2γ cos θ ρgr (2.1) γ = ρgrh (2.2) 2 cos θ θ cos θ = 1 (2.2) γ = 1 ρgrh (2.) 2 2. p p ρgh p ( ) p p = p ρgh (2.) h p p = 2γ r 1 1 (Berry,1975) 2-6
2005 9/8-11 2 2.2 ( 2-5) γ ( ) γ cos θ 2πr πρhr 2 g h = 2γ cos θ ρgr (2.1) γ = ρgrh (2.2) 2 cos θ θ cos θ = 1 (2.2) γ = 1 ρgrh (2.) 2 2. p p ρgh p ( ) p p = p ρgh (2.) h p p = 2γ r 1 1 (Berry,1975) 2-6
I No. sin cos sine, cosine : trigonometric function π : π =.4 : n =, ±, ±, sin + nπ = sin cos + nπ = cos sin = sin : cos = cos :. sin. sin. sin + π si
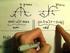 I 8 No. : No. : No. : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No. : I No. sin cos sine, cosine : trigonometric function π : π =.4 : n =, ±, ±, sin + nπ = sin cos + nπ = cos sin = sin : cos = cos :. sin.
I 8 No. : No. : No. : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No. : I No. sin cos sine, cosine : trigonometric function π : π =.4 : n =, ±, ±, sin + nπ = sin cos + nπ = cos sin = sin : cos = cos :. sin.
数学の基礎訓練I
 I 9 6 13 1 1 1.1............... 1 1................ 1 1.3.................... 1.4............... 1.4.1.............. 1.4................. 3 1.4.3........... 3 1.4.4.. 3 1.5.......... 3 1.5.1..............
I 9 6 13 1 1 1.1............... 1 1................ 1 1.3.................... 1.4............... 1.4.1.............. 1.4................. 3 1.4.3........... 3 1.4.4.. 3 1.5.......... 3 1.5.1..............
 K E N Z U 2012 7 16 HP M. 1 1 4 1.1 3.......................... 4 1.2................................... 4 1.2.1..................................... 4 1.2.2.................................... 5................................
K E N Z U 2012 7 16 HP M. 1 1 4 1.1 3.......................... 4 1.2................................... 4 1.2.1..................................... 4 1.2.2.................................... 5................................
No δs δs = r + δr r = δr (3) δs δs = r r = δr + u(r + δr, t) u(r, t) (4) δr = (δx, δy, δz) u i (r + δr, t) u i (r, t) = u i x j δx j (5) δs 2
 No.2 1 2 2 δs δs = r + δr r = δr (3) δs δs = r r = δr + u(r + δr, t) u(r, t) (4) δr = (δx, δy, δz) u i (r + δr, t) u i (r, t) = u i δx j (5) δs 2 = δx i δx i + 2 u i δx i δx j = δs 2 + 2s ij δx i δx j
No.2 1 2 2 δs δs = r + δr r = δr (3) δs δs = r r = δr + u(r + δr, t) u(r, t) (4) δr = (δx, δy, δz) u i (r + δr, t) u i (r, t) = u i δx j (5) δs 2 = δx i δx i + 2 u i δx i δx j = δs 2 + 2s ij δx i δx j
I
 I 6 4 10 1 1 1.1............... 1 1................ 1 1.3.................... 1.4............... 1.4.1.............. 1.4................. 1.4.3........... 3 1.4.4.. 3 1.5.......... 3 1.5.1..............
I 6 4 10 1 1 1.1............... 1 1................ 1 1.3.................... 1.4............... 1.4.1.............. 1.4................. 1.4.3........... 3 1.4.4.. 3 1.5.......... 3 1.5.1..............
sin cos No. sine, cosine : trigonometric function π : π = 3.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin : odd cos = cos : even.
 08 No. : No. : No.3 : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No.0 : No. : sin cos No. sine, cosine : trigonometric function π : π = 3.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin
08 No. : No. : No.3 : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No.0 : No. : sin cos No. sine, cosine : trigonometric function π : π = 3.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin
1 R n (x (k) = (x (k) 1,, x(k) n )) k 1 lim k,l x(k) x (l) = 0 (x (k) ) 1.1. (i) R n U U, r > 0, r () U (ii) R n F F F (iii) R n S S S = { R n ; r > 0
 III 2018 11 7 1 2 2 3 3 6 4 8 5 10 ϵ-δ http://www.mth.ngoy-u.c.jp/ ymgmi/teching/set2018.pdf http://www.mth.ngoy-u.c.jp/ ymgmi/teching/rel2018.pdf n x = (x 1,, x n ) n R n x 0 = (0,, 0) x = (x 1 ) 2 +
III 2018 11 7 1 2 2 3 3 6 4 8 5 10 ϵ-δ http://www.mth.ngoy-u.c.jp/ ymgmi/teching/set2018.pdf http://www.mth.ngoy-u.c.jp/ ymgmi/teching/rel2018.pdf n x = (x 1,, x n ) n R n x 0 = (0,, 0) x = (x 1 ) 2 +
= M + M + M + M M + =.,. f = < ρ, > ρ ρ. ρ f. = ρ = = ± = log 4 = = = ± f = k k ρ. k
 7 b f n f} d = b f n f d,. 5,. [ ] ɛ >, n ɛ + + n < ɛ. m. n m log + < n m. n lim sin kπ sin kπ } k π sin = n n n. k= 4 f, y = r + s, y = rs f rs = f + r + sf y + rsf yy + f y. f = f =, f = sin. 5 f f =.
7 b f n f} d = b f n f d,. 5,. [ ] ɛ >, n ɛ + + n < ɛ. m. n m log + < n m. n lim sin kπ sin kπ } k π sin = n n n. k= 4 f, y = r + s, y = rs f rs = f + r + sf y + rsf yy + f y. f = f =, f = sin. 5 f f =.
I No. sin cos sine, cosine : trigonometric function π : π =.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin : odd cos = cos : even.
 I 0 No. : No. : No. : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No.0 : I No. sin cos sine, cosine : trigonometric function π : π =.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin : odd
I 0 No. : No. : No. : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No.0 : I No. sin cos sine, cosine : trigonometric function π : π =.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin : odd
Part () () Γ Part ,
 Contents a 6 6 6 6 6 6 6 7 7. 8.. 8.. 8.3. 8 Part. 9. 9.. 9.. 3. 3.. 3.. 3 4. 5 4.. 5 4.. 9 4.3. 3 Part. 6 5. () 6 5.. () 7 5.. 9 5.3. Γ 3 6. 3 6.. 3 6.. 3 6.3. 33 Part 3. 34 7. 34 7.. 34 7.. 34 8. 35
Contents a 6 6 6 6 6 6 6 7 7. 8.. 8.. 8.3. 8 Part. 9. 9.. 9.. 3. 3.. 3.. 3 4. 5 4.. 5 4.. 9 4.3. 3 Part. 6 5. () 6 5.. () 7 5.. 9 5.3. Γ 3 6. 3 6.. 3 6.. 3 6.3. 33 Part 3. 34 7. 34 7.. 34 7.. 34 8. 35
構造と連続体の力学基礎
 II 37 Wabash Avenue Bridge, Illinois 州 Winnipeg にある歩道橋 Esplanade Riel 橋6 6 斜張橋である必要は多分無いと思われる すぐ横に道路用桁橋有り しかも塔基部のレストランは 8 年には営業していなかった 9 9. 9.. () 97 [3] [5] k 9. m w(t) f (t) = f (t) + mg k w(t) Newton
II 37 Wabash Avenue Bridge, Illinois 州 Winnipeg にある歩道橋 Esplanade Riel 橋6 6 斜張橋である必要は多分無いと思われる すぐ横に道路用桁橋有り しかも塔基部のレストランは 8 年には営業していなかった 9 9. 9.. () 97 [3] [5] k 9. m w(t) f (t) = f (t) + mg k w(t) Newton
2000年度『数学展望 I』講義録
 2000 I I IV I II 2000 I I IV I-IV. i ii 3.10 (http://www.math.nagoya-u.ac.jp/ kanai/) 2000 A....1 B....4 C....10 D....13 E....17 Brouwer A....21 B....26 C....33 D....39 E. Sperner...45 F....48 A....53
2000 I I IV I II 2000 I I IV I-IV. i ii 3.10 (http://www.math.nagoya-u.ac.jp/ kanai/) 2000 A....1 B....4 C....10 D....13 E....17 Brouwer A....21 B....26 C....33 D....39 E. Sperner...45 F....48 A....53
A (1) = 4 A( 1, 4) 1 A 4 () = tan A(0, 0) π A π
 4 4.1 4.1.1 A = f() = f() = a f (a) = f() (a, f(a)) = f() (a, f(a)) f(a) = f 0 (a)( a) 4.1 (4, ) = f() = f () = 1 = f (4) = 1 4 4 (4, ) = 1 ( 4) 4 = 1 4 + 1 17 18 4 4.1 A (1) = 4 A( 1, 4) 1 A 4 () = tan
4 4.1 4.1.1 A = f() = f() = a f (a) = f() (a, f(a)) = f() (a, f(a)) f(a) = f 0 (a)( a) 4.1 (4, ) = f() = f () = 1 = f (4) = 1 4 4 (4, ) = 1 ( 4) 4 = 1 4 + 1 17 18 4 4.1 A (1) = 4 A( 1, 4) 1 A 4 () = tan
S I. dy fx x fx y fx + C 3 C dy fx 4 x, y dy v C xt y C v e kt k > xt yt gt [ v dt dt v e kt xt v e kt + C k x v + C C k xt v k 3 r r + dr e kt S dt d
 S I.. http://ayapin.film.s.dendai.ac.jp/~matuda /TeX/lecture.html PDF PS.................................... 3.3.................... 9.4................5.............. 3 5. Laplace................. 5....
S I.. http://ayapin.film.s.dendai.ac.jp/~matuda /TeX/lecture.html PDF PS.................................... 3.3.................... 9.4................5.............. 3 5. Laplace................. 5....
 K E N Z U 01 7 16 HP M. 1 1 4 1.1 3.......................... 4 1.................................... 4 1..1..................................... 4 1...................................... 5................................
K E N Z U 01 7 16 HP M. 1 1 4 1.1 3.......................... 4 1.................................... 4 1..1..................................... 4 1...................................... 5................................
S I. dy fx x fx y fx + C 3 C vt dy fx 4 x, y dy yt gt + Ct + C dt v e kt xt v e kt + C k x v k + C C xt v k 3 r r + dr e kt S Sr πr dt d v } dt k e kt
 S I. x yx y y, y,. F x, y, y, y,, y n http://ayapin.film.s.dendai.ac.jp/~matuda n /TeX/lecture.html PDF PS yx.................................... 3.3.................... 9.4................5..............
S I. x yx y y, y,. F x, y, y, y,, y n http://ayapin.film.s.dendai.ac.jp/~matuda n /TeX/lecture.html PDF PS yx.................................... 3.3.................... 9.4................5..............
数学Ⅱ演習(足助・09夏)
 II I 9/4/4 9/4/2 z C z z z z, z 2 z, w C zw z w 3 z, w C z + w z + w 4 t R t C t t t t t z z z 2 z C re z z + z z z, im z 2 2 3 z C e z + z + 2 z2 + 3! z3 + z!, I 4 x R e x cos x + sin x 2 z, w C e z+w
II I 9/4/4 9/4/2 z C z z z z, z 2 z, w C zw z w 3 z, w C z + w z + w 4 t R t C t t t t t z z z 2 z C re z z + z z z, im z 2 2 3 z C e z + z + 2 z2 + 3! z3 + z!, I 4 x R e x cos x + sin x 2 z, w C e z+w
 http://www.ike-dyn.ritsumei.ac.jp/ hyoo/wave.html 1 1, 5 3 1.1 1..................................... 3 1.2 5.1................................... 4 1.3.......................... 5 1.4 5.2, 5.3....................
http://www.ike-dyn.ritsumei.ac.jp/ hyoo/wave.html 1 1, 5 3 1.1 1..................................... 3 1.2 5.1................................... 4 1.3.......................... 5 1.4 5.2, 5.3....................
 20 9 19 1 3 11 1 3 111 3 112 1 4 12 6 121 6 122 7 13 7 131 8 132 10 133 10 134 12 14 13 141 13 142 13 143 15 144 16 145 17 15 19 151 1 19 152 20 2 21 21 21 211 21 212 1 23 213 1 23 214 25 215 31 22 33
20 9 19 1 3 11 1 3 111 3 112 1 4 12 6 121 6 122 7 13 7 131 8 132 10 133 10 134 12 14 13 141 13 142 13 143 15 144 16 145 17 15 19 151 1 19 152 20 2 21 21 21 211 21 212 1 23 213 1 23 214 25 215 31 22 33
N cos s s cos ψ e e e e 3 3 e e 3 e 3 e
 3 3 5 5 5 3 3 7 5 33 5 33 9 5 8 > e > f U f U u u > u ue u e u ue u ue u e u e u u e u u e u N cos s s cos ψ e e e e 3 3 e e 3 e 3 e 3 > A A > A E A f A A f A [ ] f A A e > > A e[ ] > f A E A < < f ; >
3 3 5 5 5 3 3 7 5 33 5 33 9 5 8 > e > f U f U u u > u ue u e u ue u ue u e u e u u e u u e u N cos s s cos ψ e e e e 3 3 e e 3 e 3 e 3 > A A > A E A f A A f A [ ] f A A e > > A e[ ] > f A E A < < f ; >
I, II 1, A = A 4 : 6 = max{ A, } A A 10 10%
 1 2006.4.17. A 3-312 tel: 092-726-4774, e-mail: hara@math.kyushu-u.ac.jp, http://www.math.kyushu-u.ac.jp/ hara/lectures/lectures-j.html Office hours: B A I ɛ-δ ɛ-δ 1. 2. A 1. 1. 2. 3. 4. 5. 2. ɛ-δ 1. ɛ-n
1 2006.4.17. A 3-312 tel: 092-726-4774, e-mail: hara@math.kyushu-u.ac.jp, http://www.math.kyushu-u.ac.jp/ hara/lectures/lectures-j.html Office hours: B A I ɛ-δ ɛ-δ 1. 2. A 1. 1. 2. 3. 4. 5. 2. ɛ-δ 1. ɛ-n
( ; ) C. H. Scholz, The Mechanics of Earthquakes and Faulting : - ( ) σ = σ t sin 2π(r a) λ dσ d(r a) =
 1 9 8 1 1 1 ; 1 11 16 C. H. Scholz, The Mechanics of Earthquakes and Faulting 1. 1.1 1.1.1 : - σ = σ t sin πr a λ dσ dr a = E a = π λ σ πr a t cos λ 1 r a/λ 1 cos 1 E: σ t = Eλ πa a λ E/π γ : λ/ 3 γ =
1 9 8 1 1 1 ; 1 11 16 C. H. Scholz, The Mechanics of Earthquakes and Faulting 1. 1.1 1.1.1 : - σ = σ t sin πr a λ dσ dr a = E a = π λ σ πr a t cos λ 1 r a/λ 1 cos 1 E: σ t = Eλ πa a λ E/π γ : λ/ 3 γ =
f : R R f(x, y) = x + y axy f = 0, x + y axy = 0 y 直線 x+y+a=0 に漸近し 原点で交叉する美しい形をしている x +y axy=0 X+Y+a=0 o x t x = at 1 + t, y = at (a > 0) 1 + t f(x, y
 017 8 10 f : R R f(x) = x n + x n 1 + 1, f(x) = sin 1, log x x n m :f : R n R m z = f(x, y) R R R R, R R R n R m R n R m R n R m f : R R f (x) = lim h 0 f(x + h) f(x) h f : R n R m m n M Jacobi( ) m n
017 8 10 f : R R f(x) = x n + x n 1 + 1, f(x) = sin 1, log x x n m :f : R n R m z = f(x, y) R R R R, R R R n R m R n R m R n R m f : R R f (x) = lim h 0 f(x + h) f(x) h f : R n R m m n M Jacobi( ) m n
) ] [ h m x + y + + V x) φ = Eφ 1) z E = i h t 13) x << 1) N n n= = N N + 1) 14) N n n= = N N + 1)N + 1) 6 15) N n 3 n= = 1 4 N N + 1) 16) N n 4
![) ] [ h m x + y + + V x) φ = Eφ 1) z E = i h t 13) x << 1) N n n= = N N + 1) 14) N n n= = N N + 1)N + 1) 6 15) N n 3 n= = 1 4 N N + 1) 16) N n 4 ) ] [ h m x + y + + V x) φ = Eφ 1) z E = i h t 13) x << 1) N n n= = N N + 1) 14) N n n= = N N + 1)N + 1) 6 15) N n 3 n= = 1 4 N N + 1) 16) N n 4](/thumbs/92/107866707.jpg) 1. k λ ν ω T v p v g k = π λ ω = πν = π T v p = λν = ω k v g = dω dk 1) ) 3) 4). p = hk = h λ 5) E = hν = hω 6) h = h π 7) h =6.6618 1 34 J sec) hc=197.3 MeV fm = 197.3 kev pm= 197.3 ev nm = 1.97 1 3 ev
1. k λ ν ω T v p v g k = π λ ω = πν = π T v p = λν = ω k v g = dω dk 1) ) 3) 4). p = hk = h λ 5) E = hν = hω 6) h = h π 7) h =6.6618 1 34 J sec) hc=197.3 MeV fm = 197.3 kev pm= 197.3 ev nm = 1.97 1 3 ev
(3) (2),,. ( 20) ( s200103) 0.7 x C,, x 2 + y 2 + ax = 0 a.. D,. D, y C, C (x, y) (y 0) C m. (2) D y = y(x) (x ± y 0), (x, y) D, m, m = 1., D. (x 2 y
 [ ] 7 0.1 2 2 + y = t sin t IC ( 9) ( s090101) 0.2 y = d2 y 2, y = x 3 y + y 2 = 0 (2) y + 2y 3y = e 2x 0.3 1 ( y ) = f x C u = y x ( 15) ( s150102) [ ] y/x du x = Cexp f(u) u (2) x y = xey/x ( 16) ( s160101)
[ ] 7 0.1 2 2 + y = t sin t IC ( 9) ( s090101) 0.2 y = d2 y 2, y = x 3 y + y 2 = 0 (2) y + 2y 3y = e 2x 0.3 1 ( y ) = f x C u = y x ( 15) ( s150102) [ ] y/x du x = Cexp f(u) u (2) x y = xey/x ( 16) ( s160101)
I A A441 : April 21, 2014 Version : Kawahira, Tomoki TA (Kondo, Hirotaka ) Google
 I4 - : April, 4 Version :. Kwhir, Tomoki TA (Kondo, Hirotk) Google http://www.mth.ngoy-u.c.jp/~kwhir/courses/4s-biseki.html pdf 4 4 4 4 8 e 5 5 9 etc. 5 6 6 6 9 n etc. 6 6 6 3 6 3 7 7 etc 7 4 7 7 8 5 59
I4 - : April, 4 Version :. Kwhir, Tomoki TA (Kondo, Hirotk) Google http://www.mth.ngoy-u.c.jp/~kwhir/courses/4s-biseki.html pdf 4 4 4 4 8 e 5 5 9 etc. 5 6 6 6 9 n etc. 6 6 6 3 6 3 7 7 etc 7 4 7 7 8 5 59
入試の軌跡
 4 y O x 4 Typed by L A TEX ε ) ) ) 6 4 ) 4 75 ) http://kumamoto.s.xrea.com/plan/.. PDF) Ctrl +L) Ctrl +) Ctrl + Ctrl + ) ) Alt + ) Alt + ) ESC. http://kumamoto.s.xrea.com/nyusi/kumadai kiseki ri i.pdf
4 y O x 4 Typed by L A TEX ε ) ) ) 6 4 ) 4 75 ) http://kumamoto.s.xrea.com/plan/.. PDF) Ctrl +L) Ctrl +) Ctrl + Ctrl + ) ) Alt + ) Alt + ) ESC. http://kumamoto.s.xrea.com/nyusi/kumadai kiseki ri i.pdf
( ) ( )
 20 21 2 8 1 2 2 3 21 3 22 3 23 4 24 5 25 5 26 6 27 8 28 ( ) 9 3 10 31 10 32 ( ) 12 4 13 41 0 13 42 14 43 0 15 44 17 5 18 6 18 1 1 2 2 1 2 1 0 2 0 3 0 4 0 2 2 21 t (x(t) y(t)) 2 x(t) y(t) γ(t) (x(t) y(t))
20 21 2 8 1 2 2 3 21 3 22 3 23 4 24 5 25 5 26 6 27 8 28 ( ) 9 3 10 31 10 32 ( ) 12 4 13 41 0 13 42 14 43 0 15 44 17 5 18 6 18 1 1 2 2 1 2 1 0 2 0 3 0 4 0 2 2 21 t (x(t) y(t)) 2 x(t) y(t) γ(t) (x(t) y(t))
[ ] 0.1 lim x 0 e 3x 1 x IC ( 11) ( s114901) 0.2 (1) y = e 2x (x 2 + 1) (2) y = x/(x 2 + 1) 0.3 dx (1) 1 4x 2 (2) e x sin 2xdx (3) sin 2 xdx ( 11) ( s
![[ ] 0.1 lim x 0 e 3x 1 x IC ( 11) ( s114901) 0.2 (1) y = e 2x (x 2 + 1) (2) y = x/(x 2 + 1) 0.3 dx (1) 1 4x 2 (2) e x sin 2xdx (3) sin 2 xdx ( 11) ( s [ ] 0.1 lim x 0 e 3x 1 x IC ( 11) ( s114901) 0.2 (1) y = e 2x (x 2 + 1) (2) y = x/(x 2 + 1) 0.3 dx (1) 1 4x 2 (2) e x sin 2xdx (3) sin 2 xdx ( 11) ( s](/thumbs/94/118579915.jpg) [ ]. lim e 3 IC ) s49). y = e + ) ) y = / + ).3 d 4 ) e sin d 3) sin d ) s49) s493).4 z = y z z y s494).5 + y = 4 =.6 s495) dy = 3e ) d dy d = y s496).7 lim ) lim e s49).8 y = e sin ) y = sin e 3) y =
[ ]. lim e 3 IC ) s49). y = e + ) ) y = / + ).3 d 4 ) e sin d 3) sin d ) s49) s493).4 z = y z z y s494).5 + y = 4 =.6 s495) dy = 3e ) d dy d = y s496).7 lim ) lim e s49).8 y = e sin ) y = sin e 3) y =
SFGÇÃÉXÉyÉNÉgÉãå`.pdf
 SFG 1 SFG SFG I SFG (ω) χ SFG (ω). SFG χ χ SFG (ω) = χ NR e iϕ +. ω ω + iγ SFG φ = ±π/, χ φ = ±π 3 χ SFG χ SFG = χ NR + χ (ω ω ) + Γ + χ NR χ (ω ω ) (ω ω ) + Γ cosϕ χ NR χ Γ (ω ω ) + Γ sinϕ. 3 (θ) 180
SFG 1 SFG SFG I SFG (ω) χ SFG (ω). SFG χ χ SFG (ω) = χ NR e iϕ +. ω ω + iγ SFG φ = ±π/, χ φ = ±π 3 χ SFG χ SFG = χ NR + χ (ω ω ) + Γ + χ NR χ (ω ω ) (ω ω ) + Γ cosϕ χ NR χ Γ (ω ω ) + Γ sinϕ. 3 (θ) 180
meiji_resume_1.PDF
 β β β (q 1,q,..., q n ; p 1, p,..., p n ) H(q 1,q,..., q n ; p 1, p,..., p n ) Hψ = εψ ε k = k +1/ ε k = k(k 1) (x, y, z; p x, p y, p z ) (r; p r ), (θ; p θ ), (ϕ; p ϕ ) ε k = 1/ k p i dq i E total = E
β β β (q 1,q,..., q n ; p 1, p,..., p n ) H(q 1,q,..., q n ; p 1, p,..., p n ) Hψ = εψ ε k = k +1/ ε k = k(k 1) (x, y, z; p x, p y, p z ) (r; p r ), (θ; p θ ), (ϕ; p ϕ ) ε k = 1/ k p i dq i E total = E
2011de.dvi
 211 ( 4 2 1. 3 1.1............................... 3 1.2 1- -......................... 13 1.3 2-1 -................... 19 1.4 3- -......................... 29 2. 37 2.1................................ 37
211 ( 4 2 1. 3 1.1............................... 3 1.2 1- -......................... 13 1.3 2-1 -................... 19 1.4 3- -......................... 29 2. 37 2.1................................ 37
量子力学 問題
 3 : 203 : 0. H = 0 0 2 6 0 () = 6, 2 = 2, 3 = 3 3 H 6 2 3 ϵ,2,3 (2) ψ = (, 2, 3 ) ψ Hψ H (3) P i = i i P P 2 = P 2 P 3 = P 3 P = O, P 2 i = P i (4) P + P 2 + P 3 = E 3 (5) i ϵ ip i H 0 0 (6) R = 0 0 [H,
3 : 203 : 0. H = 0 0 2 6 0 () = 6, 2 = 2, 3 = 3 3 H 6 2 3 ϵ,2,3 (2) ψ = (, 2, 3 ) ψ Hψ H (3) P i = i i P P 2 = P 2 P 3 = P 3 P = O, P 2 i = P i (4) P + P 2 + P 3 = E 3 (5) i ϵ ip i H 0 0 (6) R = 0 0 [H,
(Bessel) (Legendre).. (Hankel). (Laplace) V = (x, y, z) n (r, θ, ϕ) r n f n (θ, ϕ). f n (θ, ϕ) n f n (θ, ϕ) z = cos θ z θ ϕ n ν. P ν (z), Q ν (z) (Fou
 (Bessel) (Legendre).. (Hankel). (Laplace) V = (x, y, z) n (r, θ, ϕ) r n f n (θ, ϕ). f n (θ, ϕ) n f n (θ, ϕ) z = cos θ z θ ϕ n ν. P ν (z), Q ν (z) (Fourier) (Fourier Bessel).. V ρ(x, y, z) V = 4πGρ G :.
(Bessel) (Legendre).. (Hankel). (Laplace) V = (x, y, z) n (r, θ, ϕ) r n f n (θ, ϕ). f n (θ, ϕ) n f n (θ, ϕ) z = cos θ z θ ϕ n ν. P ν (z), Q ν (z) (Fourier) (Fourier Bessel).. V ρ(x, y, z) V = 4πGρ G :.
1 8, : 8.1 1, 2 z = ax + by + c ax by + z c = a b +1 x y z c = 0, (0, 0, c), n = ( a, b, 1). f = n i=1 a ii x 2 i + i<j 2a ij x i x j = ( x, A x), f =
 1 8, : 8.1 1, z = ax + by + c ax by + z c = a b +1 x y z c = 0, (0, 0, c), n = ( a, b, 1). f = a ii x i + i
1 8, : 8.1 1, z = ax + by + c ax by + z c = a b +1 x y z c = 0, (0, 0, c), n = ( a, b, 1). f = a ii x i + i
y = f(x) y = f( + h) f(), x = h dy dx f () f (derivtive) (differentition) (velocity) p(t) =(x(t),y(t),z(t)) ( dp dx dt = dt, dy dt, dz ) dt f () > f x
 I 5 2 6 3 8 4 Riemnn 9 5 Tylor 8 6 26 7 3 8 34 f(x) x = A = h f( + h) f() h A (differentil coefficient) f f () y = f(x) y = f( + h) f(), x = h dy dx f () f (derivtive) (differentition) (velocity) p(t)
I 5 2 6 3 8 4 Riemnn 9 5 Tylor 8 6 26 7 3 8 34 f(x) x = A = h f( + h) f() h A (differentil coefficient) f f () y = f(x) y = f( + h) f(), x = h dy dx f () f (derivtive) (differentition) (velocity) p(t)
 n ξ n,i, i = 1,, n S n ξ n,i n 0 R 1,.. σ 1 σ i .10.14.15 0 1 0 1 1 3.14 3.18 3.19 3.14 3.14,. ii 1 1 1.1..................................... 1 1............................... 3 1.3.........................
n ξ n,i, i = 1,, n S n ξ n,i n 0 R 1,.. σ 1 σ i .10.14.15 0 1 0 1 1 3.14 3.18 3.19 3.14 3.14,. ii 1 1 1.1..................................... 1 1............................... 3 1.3.........................
A = A x x + A y y + A, B = B x x + B y y + B, C = C x x + C y y + C..6 x y A B C = A x x + A y y + A B x B y B C x C y C { B = A x x + A y y + A y B B
 9 7 A = A x x + A y y + A, B = B x x + B y y + B, C = C x x + C y y + C..6 x y A B C = A x x + A y y + A B x B y B C x C y C { B = A x x + A y y + A y B B x x B } B C y C y + x B y C x C C x C y B = A
9 7 A = A x x + A y y + A, B = B x x + B y y + B, C = C x x + C y y + C..6 x y A B C = A x x + A y y + A B x B y B C x C y C { B = A x x + A y y + A y B B x x B } B C y C y + x B y C x C C x C y B = A
 2019 1 5 0 3 1 4 1.1.................... 4 1.1.1......................... 4 1.1.2........................ 5 1.1.3................... 5 1.1.4........................ 6 1.1.5......................... 6 1.2..........................
2019 1 5 0 3 1 4 1.1.................... 4 1.1.1......................... 4 1.1.2........................ 5 1.1.3................... 5 1.1.4........................ 6 1.1.5......................... 6 1.2..........................
64 3 g=9.85 m/s 2 g=9.791 m/s 2 36, km ( ) 1 () 2 () m/s : : a) b) kg/m kg/m k
 63 3 Section 3.1 g 3.1 3.1: : 64 3 g=9.85 m/s 2 g=9.791 m/s 2 36, km ( ) 1 () 2 () 3 9.8 m/s 2 3.2 3.2: : a) b) 5 15 4 1 1. 1 3 14. 1 3 kg/m 3 2 3.3 1 3 5.8 1 3 kg/m 3 3 2.65 1 3 kg/m 3 4 6 m 3.1. 65 5
63 3 Section 3.1 g 3.1 3.1: : 64 3 g=9.85 m/s 2 g=9.791 m/s 2 36, km ( ) 1 () 2 () 3 9.8 m/s 2 3.2 3.2: : a) b) 5 15 4 1 1. 1 3 14. 1 3 kg/m 3 2 3.3 1 3 5.8 1 3 kg/m 3 3 2.65 1 3 kg/m 3 4 6 m 3.1. 65 5
 http://www.ns.kogakuin.ac.jp/~ft13389/lecture/physics1a2b/ pdf I 1 1 1.1 ( ) 1. 30 m µm 2. 20 cm km 3. 10 m 2 cm 2 4. 5 cm 3 km 3 5. 1 6. 1 7. 1 1.2 ( ) 1. 1 m + 10 cm 2. 1 hr + 6400 sec 3. 3.0 10 5 kg
http://www.ns.kogakuin.ac.jp/~ft13389/lecture/physics1a2b/ pdf I 1 1 1.1 ( ) 1. 30 m µm 2. 20 cm km 3. 10 m 2 cm 2 4. 5 cm 3 km 3 5. 1 6. 1 7. 1 1.2 ( ) 1. 1 m + 10 cm 2. 1 hr + 6400 sec 3. 3.0 10 5 kg
December 28, 2018
 e-mail : kigami@i.kyoto-u.ac.jp December 28, 28 Contents 2............................. 3.2......................... 7.3..................... 9.4................ 4.5............. 2.6.... 22 2 36 2..........................
e-mail : kigami@i.kyoto-u.ac.jp December 28, 28 Contents 2............................. 3.2......................... 7.3..................... 9.4................ 4.5............. 2.6.... 22 2 36 2..........................
II 1 II 2012 II Gauss-Bonnet II
 II 1 II 212 II Gauss-Bonnet II 1 1 1.1......................................... 1 1.2............................................ 2 1.3.................................. 3 1.4.............................................
II 1 II 212 II Gauss-Bonnet II 1 1 1.1......................................... 1 1.2............................................ 2 1.3.................................. 3 1.4.............................................
18 2 F 12 r 2 r 1 (3) Coulomb km Coulomb M = kg F G = ( ) ( ) ( ) 2 = [N]. Coulomb
![18 2 F 12 r 2 r 1 (3) Coulomb km Coulomb M = kg F G = ( ) ( ) ( ) 2 = [N]. Coulomb 18 2 F 12 r 2 r 1 (3) Coulomb km Coulomb M = kg F G = ( ) ( ) ( ) 2 = [N]. Coulomb](/thumbs/93/114079295.jpg) r 1 r 2 r 1 r 2 2 Coulomb Gauss Coulomb 2.1 Coulomb 1 2 r 1 r 2 1 2 F 12 2 1 F 21 F 12 = F 21 = 1 4πε 0 1 2 r 1 r 2 2 r 1 r 2 r 1 r 2 (2.1) Coulomb ε 0 = 107 4πc 2 =8.854 187 817 10 12 C 2 N 1 m 2 (2.2)
r 1 r 2 r 1 r 2 2 Coulomb Gauss Coulomb 2.1 Coulomb 1 2 r 1 r 2 1 2 F 12 2 1 F 21 F 12 = F 21 = 1 4πε 0 1 2 r 1 r 2 2 r 1 r 2 r 1 r 2 (2.1) Coulomb ε 0 = 107 4πc 2 =8.854 187 817 10 12 C 2 N 1 m 2 (2.2)
 25 7 18 1 1 1.1 v.s............................. 1 1.1.1.................................. 1 1.1.2................................. 1 1.1.3.................................. 3 1.2................... 3
25 7 18 1 1 1.1 v.s............................. 1 1.1.1.................................. 1 1.1.2................................. 1 1.1.3.................................. 3 1.2................... 3
II (10 4 ) 1. p (x, y) (a, b) ε(x, y; a, b) 0 f (x, y) f (a, b) A, B (6.5) y = b f (x, b) f (a, b) x a = A + ε(x, b; a, b) x a 2 x a 0 A = f x (
 II (1 4 ) 1. p.13 1 (x, y) (a, b) ε(x, y; a, b) f (x, y) f (a, b) A, B (6.5) y = b f (x, b) f (a, b) x a = A + ε(x, b; a, b) x a x a A = f x (a, b) y x 3 3y 3 (x, y) (, ) f (x, y) = x + y (x, y) = (, )
II (1 4 ) 1. p.13 1 (x, y) (a, b) ε(x, y; a, b) f (x, y) f (a, b) A, B (6.5) y = b f (x, b) f (a, b) x a = A + ε(x, b; a, b) x a x a A = f x (a, b) y x 3 3y 3 (x, y) (, ) f (x, y) = x + y (x, y) = (, )
 1 3 1.1.......................... 3 1............................... 3 1.3....................... 5 1.4.......................... 6 1.5........................ 7 8.1......................... 8..............................
1 3 1.1.......................... 3 1............................... 3 1.3....................... 5 1.4.......................... 6 1.5........................ 7 8.1......................... 8..............................
) a + b = i + 6 b c = 6i j ) a = 0 b = c = 0 ) â = i + j 0 ˆb = 4) a b = b c = j + ) cos α = cos β = 6) a ˆb = b ĉ = 0 7) a b = 6i j b c = i + 6j + 8)
 4 4 ) a + b = i + 6 b c = 6i j ) a = 0 b = c = 0 ) â = i + j 0 ˆb = 4) a b = b c = j + ) cos α = cos β = 6) a ˆb = b ĉ = 0 7) a b = 6i j b c = i + 6j + 8) a b a b = 6i j 4 b c b c 9) a b = 4 a b) c = 7
4 4 ) a + b = i + 6 b c = 6i j ) a = 0 b = c = 0 ) â = i + j 0 ˆb = 4) a b = b c = j + ) cos α = cos β = 6) a ˆb = b ĉ = 0 7) a b = 6i j b c = i + 6j + 8) a b a b = 6i j 4 b c b c 9) a b = 4 a b) c = 7
V(x) m e V 0 cos x π x π V(x) = x < π, x > π V 0 (i) x = 0 (V(x) V 0 (1 x 2 /2)) n n d 2 f dξ 2ξ d f 2 dξ + 2n f = 0 H n (ξ) (ii) H
 199 1 1 199 1 1. Vx) m e V cos x π x π Vx) = x < π, x > π V i) x = Vx) V 1 x /)) n n d f dξ ξ d f dξ + n f = H n ξ) ii) H n ξ) = 1) n expξ ) dn dξ n exp ξ )) H n ξ)h m ξ) exp ξ )dξ = π n n!δ n,m x = Vx)
199 1 1 199 1 1. Vx) m e V cos x π x π Vx) = x < π, x > π V i) x = Vx) V 1 x /)) n n d f dξ ξ d f dξ + n f = H n ξ) ii) H n ξ) = 1) n expξ ) dn dξ n exp ξ )) H n ξ)h m ξ) exp ξ )dξ = π n n!δ n,m x = Vx)
July 28, H H 0 H int = H H 0 H int = H int (x)d 3 x Schrödinger Picture Ψ(t) S =e iht Ψ H O S Heisenberg Picture Ψ H O H (t) =e iht O S e i
 July 8, 4. H H H int H H H int H int (x)d 3 x Schrödinger Picture Ψ(t) S e iht Ψ H O S Heisenberg Picture Ψ H O H (t) e iht O S e iht Interaction Picture Ψ(t) D e iht Ψ(t) S O D (t) e iht O S e ih t (Dirac
July 8, 4. H H H int H H H int H int (x)d 3 x Schrödinger Picture Ψ(t) S e iht Ψ H O S Heisenberg Picture Ψ H O H (t) e iht O S e iht Interaction Picture Ψ(t) D e iht Ψ(t) S O D (t) e iht O S e ih t (Dirac
TOP URL 1
 TOP URL http://amonphys.web.fc.com/ 1 19 3 19.1................... 3 19.............................. 4 19.3............................... 6 19.4.............................. 8 19.5.............................
TOP URL http://amonphys.web.fc.com/ 1 19 3 19.1................... 3 19.............................. 4 19.3............................... 6 19.4.............................. 8 19.5.............................
TOP URL 1
 TOP URL http://amonphys.web.fc.com/ 3.............................. 3.............................. 4.3 4................... 5.4........................ 6.5........................ 8.6...........................7
TOP URL http://amonphys.web.fc.com/ 3.............................. 3.............................. 4.3 4................... 5.4........................ 6.5........................ 8.6...........................7
: , 2.0, 3.0, 2.0, (%) ( 2.
 2017 1 2 1.1...................................... 2 1.2......................................... 4 1.3........................................... 10 1.4................................. 14 1.5..........................................
2017 1 2 1.1...................................... 2 1.2......................................... 4 1.3........................................... 10 1.4................................. 14 1.5..........................................
() x + y + y + x dy dx = 0 () dy + xy = x dx y + x y ( 5) ( s55906) 0.7. (). 5 (). ( 6) ( s6590) 0.8 m n. 0.9 n n A. ( 6) ( s6590) f A (λ) = det(a λi)
 0. A A = 4 IC () det A () A () x + y + z = x y z X Y Z = A x y z ( 5) ( s5590) 0. a + b + c b c () a a + b + c c a b a + b + c 0 a b c () a 0 c b b c 0 a c b a 0 0. A A = 7 5 4 5 0 ( 5) ( s5590) () A ()
0. A A = 4 IC () det A () A () x + y + z = x y z X Y Z = A x y z ( 5) ( s5590) 0. a + b + c b c () a a + b + c c a b a + b + c 0 a b c () a 0 c b b c 0 a c b a 0 0. A A = 7 5 4 5 0 ( 5) ( s5590) () A ()
9 5 ( α+ ) = (α + ) α (log ) = α d = α C d = log + C C 5. () d = 4 d = C = C = 3 + C 3 () d = d = C = C = 3 + C 3 =
 5 5. 5.. A II f() f() F () f() F () = f() C (F () + C) = F () = f() F () + C f() F () G() f() G () = F () 39 G() = F () + C C f() F () f() F () + C C f() f() d f() f() C f() f() F () = f() f() f() d =
5 5. 5.. A II f() f() F () f() F () = f() C (F () + C) = F () = f() F () + C f() F () G() f() G () = F () 39 G() = F () + C C f() F () f() F () + C C f() f() d f() f() C f() f() F () = f() f() f() d =
( ) ) ) ) 5) 1 J = σe 2 6) ) 9) 1955 Statistical-Mechanical Theory of Irreversible Processes )
 ( 3 7 4 ) 2 2 ) 8 2 954 2) 955 3) 5) J = σe 2 6) 955 7) 9) 955 Statistical-Mechanical Theory of Irreversible Processes 957 ) 3 4 2 A B H (t) = Ae iωt B(t) = B(ω)e iωt B(ω) = [ Φ R (ω) Φ R () ] iω Φ R (t)
( 3 7 4 ) 2 2 ) 8 2 954 2) 955 3) 5) J = σe 2 6) 955 7) 9) 955 Statistical-Mechanical Theory of Irreversible Processes 957 ) 3 4 2 A B H (t) = Ae iωt B(t) = B(ω)e iωt B(ω) = [ Φ R (ω) Φ R () ] iω Φ R (t)
M3 x y f(x, y) (= x) (= y) x + y f(x, y) = x + y + *. f(x, y) π y f(x, y) x f(x + x, y) f(x, y) lim x x () f(x,y) x 3 -
 M3............................................................................................ 3.3................................................... 3 6........................................... 6..........................................
M3............................................................................................ 3.3................................................... 3 6........................................... 6..........................................
chap9.dvi
 9 AR (i) (ii) MA (iii) (iv) (v) 9.1 2 1 AR 1 9.1.1 S S y j = (α i + β i j) D ij + η j, η j = ρ S η j S + ε j (j =1,,T) (1) i=1 {ε j } i.i.d(,σ 2 ) η j (j ) D ij j i S 1 S =1 D ij =1 S>1 S =4 (1) y j =
9 AR (i) (ii) MA (iii) (iv) (v) 9.1 2 1 AR 1 9.1.1 S S y j = (α i + β i j) D ij + η j, η j = ρ S η j S + ε j (j =1,,T) (1) i=1 {ε j } i.i.d(,σ 2 ) η j (j ) D ij j i S 1 S =1 D ij =1 S>1 S =4 (1) y j =
chap1.dvi
 1 1 007 1 e iθ = cos θ + isin θ 1) θ = π e iπ + 1 = 0 1 ) 3 11 f 0 r 1 1 ) k f k = 1 + r) k f 0 f k k = 01) f k+1 = 1 + r)f k ) f k+1 f k = rf k 3) 1 ) ) ) 1+r/)f 0 1 1 + r/) f 0 = 1 + r + r /4)f 0 1 f
1 1 007 1 e iθ = cos θ + isin θ 1) θ = π e iπ + 1 = 0 1 ) 3 11 f 0 r 1 1 ) k f k = 1 + r) k f 0 f k k = 01) f k+1 = 1 + r)f k ) f k+1 f k = rf k 3) 1 ) ) ) 1+r/)f 0 1 1 + r/) f 0 = 1 + r + r /4)f 0 1 f
18 I ( ) (1) I-1,I-2,I-3 (2) (3) I-1 ( ) (100 ) θ ϕ θ ϕ m m l l θ ϕ θ ϕ 2 g (1) (2) 0 (3) θ ϕ (4) (3) θ(t) = A 1 cos(ω 1 t + α 1 ) + A 2 cos(ω 2 t + α
 18 I ( ) (1) I-1,I-2,I-3 (2) (3) I-1 ( ) (100 ) θ ϕ θ ϕ m m l l θ ϕ θ ϕ 2 g (1) (2) 0 (3) θ ϕ (4) (3) θ(t) = A 1 cos(ω 1 t + α 1 ) + A 2 cos(ω 2 t + α 2 ), ϕ(t) = B 1 cos(ω 1 t + α 1 ) + B 2 cos(ω 2 t
18 I ( ) (1) I-1,I-2,I-3 (2) (3) I-1 ( ) (100 ) θ ϕ θ ϕ m m l l θ ϕ θ ϕ 2 g (1) (2) 0 (3) θ ϕ (4) (3) θ(t) = A 1 cos(ω 1 t + α 1 ) + A 2 cos(ω 2 t + α 2 ), ϕ(t) = B 1 cos(ω 1 t + α 1 ) + B 2 cos(ω 2 t
I A A441 : April 15, 2013 Version : 1.1 I Kawahira, Tomoki TA (Shigehiro, Yoshida )
 I013 00-1 : April 15, 013 Version : 1.1 I Kawahira, Tomoki TA (Shigehiro, Yoshida) http://www.math.nagoya-u.ac.jp/~kawahira/courses/13s-tenbou.html pdf * 4 15 4 5 13 e πi = 1 5 0 5 7 3 4 6 3 6 10 6 17
I013 00-1 : April 15, 013 Version : 1.1 I Kawahira, Tomoki TA (Shigehiro, Yoshida) http://www.math.nagoya-u.ac.jp/~kawahira/courses/13s-tenbou.html pdf * 4 15 4 5 13 e πi = 1 5 0 5 7 3 4 6 3 6 10 6 17
v v = v 1 v 2 v 3 (1) R = (R ij ) (2) R (R 1 ) ij = R ji (3) 3 R ij R ik = δ jk (4) i=1 δ ij Kronecker δ ij = { 1 (i = j) 0 (i
 1. 1 1.1 1.1.1 1.1.1.1 v v = v 1 v 2 v 3 (1) R = (R ij ) (2) R (R 1 ) ij = R ji (3) R ij R ik = δ jk (4) δ ij Kronecker δ ij = { 1 (i = j) 0 (i j) (5) 1 1.1. v1.1 2011/04/10 1. 1 2 v i = R ij v j (6) [
1. 1 1.1 1.1.1 1.1.1.1 v v = v 1 v 2 v 3 (1) R = (R ij ) (2) R (R 1 ) ij = R ji (3) R ij R ik = δ jk (4) δ ij Kronecker δ ij = { 1 (i = j) 0 (i j) (5) 1 1.1. v1.1 2011/04/10 1. 1 2 v i = R ij v j (6) [
I 1
 I 1 1 1.1 1. 3 m = 3 1 7 µm. cm = 1 4 km 3. 1 m = 1 1 5 cm 4. 5 cm 3 = 5 1 15 km 3 5. 1 = 36 6. 1 = 8.64 1 4 7. 1 = 3.15 1 7 1 =3 1 7 1 3 π 1. 1. 1 m + 1 cm = 1.1 m. 1 hr + 64 sec = 1 4 sec 3. 3. 1 5 kg
I 1 1 1.1 1. 3 m = 3 1 7 µm. cm = 1 4 km 3. 1 m = 1 1 5 cm 4. 5 cm 3 = 5 1 15 km 3 5. 1 = 36 6. 1 = 8.64 1 4 7. 1 = 3.15 1 7 1 =3 1 7 1 3 π 1. 1. 1 m + 1 cm = 1.1 m. 1 hr + 64 sec = 1 4 sec 3. 3. 1 5 kg
II A A441 : October 02, 2014 Version : Kawahira, Tomoki TA (Kondo, Hirotaka )
 II 214-1 : October 2, 214 Version : 1.1 Kawahira, Tomoki TA (Kondo, Hirotaka ) http://www.math.nagoya-u.ac.jp/~kawahira/courses/14w-biseki.html pdf 1 2 1 9 1 16 1 23 1 3 11 6 11 13 11 2 11 27 12 4 12 11
II 214-1 : October 2, 214 Version : 1.1 Kawahira, Tomoki TA (Kondo, Hirotaka ) http://www.math.nagoya-u.ac.jp/~kawahira/courses/14w-biseki.html pdf 1 2 1 9 1 16 1 23 1 3 11 6 11 13 11 2 11 27 12 4 12 11
( ) sin 1 x, cos 1 x, tan 1 x sin x, cos x, tan x, arcsin x, arccos x, arctan x. π 2 sin 1 x π 2, 0 cos 1 x π, π 2 < tan 1 x < π 2 1 (1) (
 6 20 ( ) sin, cos, tan sin, cos, tan, arcsin, arccos, arctan. π 2 sin π 2, 0 cos π, π 2 < tan < π 2 () ( 2 2 lim 2 ( 2 ) ) 2 = 3 sin (2) lim 5 0 = 2 2 0 0 2 2 3 3 4 5 5 2 5 6 3 5 7 4 5 8 4 9 3 4 a 3 b
6 20 ( ) sin, cos, tan sin, cos, tan, arcsin, arccos, arctan. π 2 sin π 2, 0 cos π, π 2 < tan < π 2 () ( 2 2 lim 2 ( 2 ) ) 2 = 3 sin (2) lim 5 0 = 2 2 0 0 2 2 3 3 4 5 5 2 5 6 3 5 7 4 5 8 4 9 3 4 a 3 b
高校生の就職への数学II
 II O Tped b L A TEX ε . II. 3. 4. 5. http://www.ocn.ne.jp/ oboetene/plan/ 7 9 i .......................................................................................... 3..3...............................
II O Tped b L A TEX ε . II. 3. 4. 5. http://www.ocn.ne.jp/ oboetene/plan/ 7 9 i .......................................................................................... 3..3...............................
i
 i 3 4 4 7 5 6 3 ( ).. () 3 () (3) (4) /. 3. 4/3 7. /e 8. a > a, a = /, > a >. () a >, a =, > a > () a > b, a = b, a < b. c c n a n + b n + c n 3c n..... () /3 () + (3) / (4) /4 (5) m > n, a b >, m > n,
i 3 4 4 7 5 6 3 ( ).. () 3 () (3) (4) /. 3. 4/3 7. /e 8. a > a, a = /, > a >. () a >, a =, > a > () a > b, a = b, a < b. c c n a n + b n + c n 3c n..... () /3 () + (3) / (4) /4 (5) m > n, a b >, m > n,
t = h x z z = h z = t (x, z) (v x (x, z, t), v z (x, z, t)) ρ v x x + v z z = 0 (1) 2-2. (v x, v z ) φ(x, z, t) v x = φ x, v z
 I 1 m 2 l k 2 x = 0 x 1 x 1 2 x 2 g x x 2 x 1 m k m 1-1. L x 1, x 2, ẋ 1, ẋ 2 ẋ 1 x = 0 1-2. 2 Q = x 1 + x 2 2 q = x 2 x 1 l L Q, q, Q, q M = 2m µ = m 2 1-3. Q q 1-4. 2 x 2 = h 1 x 1 t = 0 2 1 t x 1 (t)
I 1 m 2 l k 2 x = 0 x 1 x 1 2 x 2 g x x 2 x 1 m k m 1-1. L x 1, x 2, ẋ 1, ẋ 2 ẋ 1 x = 0 1-2. 2 Q = x 1 + x 2 2 q = x 2 x 1 l L Q, q, Q, q M = 2m µ = m 2 1-3. Q q 1-4. 2 x 2 = h 1 x 1 t = 0 2 1 t x 1 (t)
#A A A F, F d F P + F P = d P F, F y P F F x A.1 ( α, 0), (α, 0) α > 0) (x, y) (x + α) 2 + y 2, (x α) 2 + y 2 d (x + α)2 + y 2 + (x α) 2 + y 2 =
 #A A A. F, F d F P + F P = d P F, F P F F A. α, 0, α, 0 α > 0, + α +, α + d + α + + α + = d d F, F 0 < α < d + α + = d α + + α + = d d α + + α + d α + = d 4 4d α + = d 4 8d + 6 http://mth.cs.kitmi-it.c.jp/
#A A A. F, F d F P + F P = d P F, F P F F A. α, 0, α, 0 α > 0, + α +, α + d + α + + α + = d d F, F 0 < α < d + α + = d α + + α + = d d α + + α + d α + = d 4 4d α + = d 4 8d + 6 http://mth.cs.kitmi-it.c.jp/
4. ϵ(ν, T ) = c 4 u(ν, T ) ϵ(ν, T ) T ν π4 Planck dx = 0 e x 1 15 U(T ) x 3 U(T ) = σt 4 Stefan-Boltzmann σ 2π5 k 4 15c 2 h 3 = W m 2 K 4 5.
 A 1. Boltzmann Planck u(ν, T )dν = 8πh ν 3 c 3 kt 1 dν h 6.63 10 34 J s Planck k 1.38 10 23 J K 1 Boltzmann u(ν, T ) T ν e hν c = 3 10 8 m s 1 2. Planck λ = c/ν Rayleigh-Jeans u(ν, T )dν = 8πν2 kt dν c
A 1. Boltzmann Planck u(ν, T )dν = 8πh ν 3 c 3 kt 1 dν h 6.63 10 34 J s Planck k 1.38 10 23 J K 1 Boltzmann u(ν, T ) T ν e hν c = 3 10 8 m s 1 2. Planck λ = c/ν Rayleigh-Jeans u(ν, T )dν = 8πν2 kt dν c
Hanbury-Brown Twiss (ver. 2.0) van Cittert - Zernike mutual coherence
 Hanbury-Brown Twiss (ver. 2.) 25 4 4 1 2 2 2 2.1 van Cittert - Zernike..................................... 2 2.2 mutual coherence................................. 4 3 Hanbury-Brown Twiss ( ) 5 3.1............................................
Hanbury-Brown Twiss (ver. 2.) 25 4 4 1 2 2 2 2.1 van Cittert - Zernike..................................... 2 2.2 mutual coherence................................. 4 3 Hanbury-Brown Twiss ( ) 5 3.1............................................
K E N Z OU
 K E N Z OU 11 1 1 1.1..................................... 1.1.1............................ 1.1..................................................................................... 4 1.........................................
K E N Z OU 11 1 1 1.1..................................... 1.1.1............................ 1.1..................................................................................... 4 1.........................................
7. y fx, z gy z gfx dz dx dz dy dy dx. g f a g bf a b fa 7., chain ule Ω, D R n, R m a Ω, f : Ω R m, g : D R l, fω D, b fa, f a g b g f a g f a g bf a
 9 203 6 7 WWW http://www.math.meiji.ac.jp/~mk/lectue/tahensuu-203/ 2 8 8 7. 7 7. y fx, z gy z gfx dz dx dz dy dy dx. g f a g bf a b fa 7., chain ule Ω, D R n, R m a Ω, f : Ω R m, g : D R l, fω D, b fa,
9 203 6 7 WWW http://www.math.meiji.ac.jp/~mk/lectue/tahensuu-203/ 2 8 8 7. 7 7. y fx, z gy z gfx dz dx dz dy dy dx. g f a g bf a b fa 7., chain ule Ω, D R n, R m a Ω, f : Ω R m, g : D R l, fω D, b fa,
xyz,, uvw,, Bernoulli-Euler u c c c v, w θ x c c c dv ( x) dw uxyz (,, ) = u( x) y z + ω( yz, ) φ dx dx c vxyz (,, ) = v( x) zθ x ( x) c wxyz (,, ) =
 ,, uvw,, Bernoull-Euler u v, w θ dv ( ) dw u (,, ) u( ) ω(, ) φ d d v (,, ) v( ) θ ( ) w (,, ) w( ) θ ( ) (11.1) ω φ φ dθ / dφ v v θ u w u w 11.1 θ θ θ 11. vw, (11.1) u du d v d w ε d d d u v ω γ φ w u
,, uvw,, Bernoull-Euler u v, w θ dv ( ) dw u (,, ) u( ) ω(, ) φ d d v (,, ) v( ) θ ( ) w (,, ) w( ) θ ( ) (11.1) ω φ φ dθ / dφ v v θ u w u w 11.1 θ θ θ 11. vw, (11.1) u du d v d w ε d d d u v ω γ φ w u
 Sgr.A 2 saida@daido-it.a.jp Sgr.A 1 3 1.1 2............................................. 3 1.2.............................. 4 2 1 6 2.1................................. 6 2.2...................................
Sgr.A 2 saida@daido-it.a.jp Sgr.A 1 3 1.1 2............................................. 3 1.2.............................. 4 2 1 6 2.1................................. 6 2.2...................................
.5 z = a + b + c n.6 = a sin t y = b cos t dy d a e e b e + e c e e e + e 3 s36 3 a + y = a, b > b 3 s363.7 y = + 3 y = + 3 s364.8 cos a 3 s365.9 y =,
 [ ] IC. r, θ r, θ π, y y = 3 3 = r cos θ r sin θ D D = {, y ; y }, y D r, θ ep y yddy D D 9 s96. d y dt + 3dy + y = cos t dt t = y = e π + e π +. t = π y =.9 s6.3 d y d + dy d + y = y =, dy d = 3 a, b
[ ] IC. r, θ r, θ π, y y = 3 3 = r cos θ r sin θ D D = {, y ; y }, y D r, θ ep y yddy D D 9 s96. d y dt + 3dy + y = cos t dt t = y = e π + e π +. t = π y =.9 s6.3 d y d + dy d + y = y =, dy d = 3 a, b
z f(z) f(z) x, y, u, v, r, θ r > 0 z = x + iy, f = u + iv C γ D f(z) f(z) D f(z) f(z) z, Rm z, z 1.1 z = x + iy = re iθ = r (cos θ + i sin θ) z = x iy
 z fz fz x, y, u, v, r, θ r > z = x + iy, f = u + iv γ D fz fz D fz fz z, Rm z, z. z = x + iy = re iθ = r cos θ + i sin θ z = x iy = re iθ = r cos θ i sin θ x = z + z = Re z, y = z z = Im z i r = z = z
z fz fz x, y, u, v, r, θ r > z = x + iy, f = u + iv γ D fz fz D fz fz z, Rm z, z. z = x + iy = re iθ = r cos θ + i sin θ z = x iy = re iθ = r cos θ i sin θ x = z + z = Re z, y = z z = Im z i r = z = z
 i 6 3 ii 3 7 8 9 3 6 iii 5 8 5 3 7 8 v...................................................... 5.3....................... 7 3........................ 3.................3.......................... 8 3 35
i 6 3 ii 3 7 8 9 3 6 iii 5 8 5 3 7 8 v...................................................... 5.3....................... 7 3........................ 3.................3.......................... 8 3 35
液晶の物理1:連続体理論(弾性,粘性)
 The Physics of Liquid Crystals P. G. de Gennes and J. Prost (Oxford University Press, 1993) Liquid crystals are beautiful and mysterious; I am fond of them for both reasons. My hope is that some readers
The Physics of Liquid Crystals P. G. de Gennes and J. Prost (Oxford University Press, 1993) Liquid crystals are beautiful and mysterious; I am fond of them for both reasons. My hope is that some readers
1 1 3 ABCD ABD AC BD E E BD 1 : 2 (1) AB = AD =, AB AD = (2) AE = AB + (3) A F AD AE 2 = AF = AB + AD AF AE = t AC = t AE AC FC = t = (4) ABD ABCD 1 1
 ABCD ABD AC BD E E BD : () AB = AD =, AB AD = () AE = AB + () A F AD AE = AF = AB + AD AF AE = t AC = t AE AC FC = t = (4) ABD ABCD AB + AD AB + 7 9 AD AB + AD AB + 9 7 4 9 AD () AB sin π = AB = ABD AD
ABCD ABD AC BD E E BD : () AB = AD =, AB AD = () AE = AB + () A F AD AE = AF = AB + AD AF AE = t AC = t AE AC FC = t = (4) ABD ABCD AB + AD AB + 7 9 AD AB + AD AB + 9 7 4 9 AD () AB sin π = AB = ABD AD
all.dvi
 29 4 Green-Lagrange,,.,,,,,,.,,,,,,,,,, E, σ, ε σ = Eε,,.. 4.1? l, l 1 (l 1 l) ε ε = l 1 l l (4.1) F l l 1 F 30 4 Green-Lagrange Δz Δδ γ = Δδ (4.2) Δz π/2 φ γ = π 2 φ (4.3) γ tan γ γ,sin γ γ ( π ) γ tan
29 4 Green-Lagrange,,.,,,,,,.,,,,,,,,,, E, σ, ε σ = Eε,,.. 4.1? l, l 1 (l 1 l) ε ε = l 1 l l (4.1) F l l 1 F 30 4 Green-Lagrange Δz Δδ γ = Δδ (4.2) Δz π/2 φ γ = π 2 φ (4.3) γ tan γ γ,sin γ γ ( π ) γ tan
2 1 κ c(t) = (x(t), y(t)) ( ) det(c (t), c x (t)) = det (t) x (t) y (t) y = x (t)y (t) x (t)y (t), (t) c (t) = (x (t)) 2 + (y (t)) 2. c (t) =
 1 1 1.1 I R 1.1.1 c : I R 2 (i) c C (ii) t I c (t) (0, 0) c (t) c(i) c c(t) 1.1.2 (1) (2) (3) (1) r > 0 c : R R 2 : t (r cos t, r sin t) (2) C f : I R c : I R 2 : t (t, f(t)) (3) y = x c : R R 2 : t (t,
1 1 1.1 I R 1.1.1 c : I R 2 (i) c C (ii) t I c (t) (0, 0) c (t) c(i) c c(t) 1.1.2 (1) (2) (3) (1) r > 0 c : R R 2 : t (r cos t, r sin t) (2) C f : I R c : I R 2 : t (t, f(t)) (3) y = x c : R R 2 : t (t,
I II
 I II I I 8 I I 5 I 5 9 I 6 6 I 7 7 I 8 87 I 9 96 I 7 I 8 I 9 I 7 I 95 I 5 I 6 II 7 6 II 8 II 9 59 II 67 II 76 II II 9 II 8 II 5 8 II 6 58 II 7 6 II 8 8 I.., < b, b, c, k, m. k + m + c + c b + k + m log
I II I I 8 I I 5 I 5 9 I 6 6 I 7 7 I 8 87 I 9 96 I 7 I 8 I 9 I 7 I 95 I 5 I 6 II 7 6 II 8 II 9 59 II 67 II 76 II II 9 II 8 II 5 8 II 6 58 II 7 6 II 8 8 I.., < b, b, c, k, m. k + m + c + c b + k + m log
ma22-9 u ( v w) = u v w sin θê = v w sin θ u cos φ = = 2.3 ( a b) ( c d) = ( a c)( b d) ( a d)( b c) ( a b) ( c d) = (a 2 b 3 a 3 b 2 )(c 2 d 3 c 3 d
 A 2. x F (t) =f sin ωt x(0) = ẋ(0) = 0 ω θ sin θ θ 3! θ3 v = f mω cos ωt x = f mω (t sin ωt) ω t 0 = f ( cos ωt) mω x ma2-2 t ω x f (t mω ω (ωt ) 6 (ωt)3 = f 6m ωt3 2.2 u ( v w) = v ( w u) = w ( u v) ma22-9
A 2. x F (t) =f sin ωt x(0) = ẋ(0) = 0 ω θ sin θ θ 3! θ3 v = f mω cos ωt x = f mω (t sin ωt) ω t 0 = f ( cos ωt) mω x ma2-2 t ω x f (t mω ω (ωt ) 6 (ωt)3 = f 6m ωt3 2.2 u ( v w) = v ( w u) = w ( u v) ma22-9
50 2 I SI MKSA r q r q F F = 1 qq 4πε 0 r r 2 r r r r (2.2 ε 0 = 1 c 2 µ 0 c = m/s q 2.1 r q' F r = 0 µ 0 = 4π 10 7 N/A 2 k = 1/(4πε 0 qq
 49 2 I II 2.1 3 e e = 1.602 10 19 A s (2.1 50 2 I SI MKSA 2.1.1 r q r q F F = 1 qq 4πε 0 r r 2 r r r r (2.2 ε 0 = 1 c 2 µ 0 c = 3 10 8 m/s q 2.1 r q' F r = 0 µ 0 = 4π 10 7 N/A 2 k = 1/(4πε 0 qq F = k r
49 2 I II 2.1 3 e e = 1.602 10 19 A s (2.1 50 2 I SI MKSA 2.1.1 r q r q F F = 1 qq 4πε 0 r r 2 r r r r (2.2 ε 0 = 1 c 2 µ 0 c = 3 10 8 m/s q 2.1 r q' F r = 0 µ 0 = 4π 10 7 N/A 2 k = 1/(4πε 0 qq F = k r
