<4D F736F F D F385F322089E6919C8DC48D5C90AC82CC8AEE B CC8CB4979D815B>
|
|
|
- わんど さわなか
- 5 years ago
- Views:
Transcription
1 画像再構成の基礎 1-FBP 法の原理 - Basic of Image Reconstruction 1-Fundamentals of FBP method- 首都大学東京篠原広行 Shinohara Hiroyuki はじめに画像再構成は被写体の積分変換 ( 投影 ) から被写体を求める逆問題であり, 解析的方法と逐次近似法に大別される. フィルタ補正逆投影 (filtered back projection: FBP) 法は解析的方法であり, CT,MRI,SPECT,PET など医用イメージングの画像再構成に広く用いられる. 被写体は線減弱係数分布, 水素原子分布, 放射濃度分布などであり, 次元画像再構成はそれら断面の投影から元の分布を復元する. これに対し 3 次元画像再構成はボリュームデータの投影から 3 次元被写体を復元する. 投影の計測法には 次元では平行ビームとファンビームがあり,3 次元では平行ビームとコーンビームがある. 本稿では, それら投影からの FBP 法による画像再構成 1,) について解説する. 1. 次元ラドン変換 Fig. 1(a) は固定座標系 (x, y) とそれに対し半時計回りに θ 回転した回転座標系 (s, t) を示す. 両者の関係は次式で表される. s xcos ysin, t xsin ycos (1) 固定座標系は被写体の座標を回転座標系は検出器の座標を表す. (a) のように 次元関数 f(x,y) を直線 L 上で積分することを線積分という. s 軸は x 軸から θ 傾いており, 原点から直線 L に下ろした垂線の座標が s である. sに平行な直線を検出器の並びとし, 線積分の値が s 上に測定される様子を示している. 次元ラドン変換 p(s, θ) は被写体の線積分であり次式で表される p(, s ) f( scos tsin, ssin tcos ) dt f ( xy, ) ( xcos ysin sdxdy ) () はデルタ関数を表す. 次元ラドン変換を投影と呼ぶ.θ は投影角度を示す. (b) は矩形内の強度が一定値 A の断面 ( 矩形画像 )f(x,y) の周囲を検出器が回転し, 平行ビーム投影 p(s, θ) を収集する様子を示す. CT では入射強度を透過強度で除し対数をとることで f(x,y) と p(s, θ) の関係が積分変換で表される. 平行ビーム投影は検出器に垂直な垂線上の f(x,y) を線積分したものなので,θ = 0 度から 360 度の投影角度によって矩形, 台形, 三角形の繰り返しとなる. () 1
2 . 投影切断面定理平行ビーム投影には投影切断面定理が成り立つ.Fig. 1 の f(x,y) の 次元フーリエ変換 F(u,v) は次式で表される. 4a Asin( au) sin( av) Fuv (, ) au av (3) 投影角度 30 度の投影は台形となり, この 1 次元フーリエ変換は周波数を k とし 4a Asin( 3 ak) sin( ak) Pk (, /6) 3 ak ak (4) となる 3).θ = π/6 にして 3k k u kcos( / 6), v ksin( / 6) (5) を (3) 式に代入すると (4) 式に等しくなる. すなわち矩形画像の 次元フーリエ変換の 30 度方向の成分は,30 度の投影の 1 次元フーリエ変換から得られる. このことは他の投影角度についても成り立ち, 投影の 1 次元フーリエ変換と被写体の 次元フーリエ変換の関係を投影切断面定理 ( 中央断面定理 ) という. 平行ビーム投影からの画像再構成は, 投影切断面定理を利用したフーリエ変換法で行える. 投影は極座標で得られるので, フーリエ逆変換するには直交座標に並び換える必要がある. この際, 補間処理による誤差を生じる.FBP 法はこの補間誤差を回避するために, フィルタ補正した投影を逆投影し再構成像を得る方法である.FBP 法の式はフーリエ変換法の式を変形すると導かれる. 3. 次元画像再構成 3.1 平行ビーム Fig. (a) は Fig. 1(a) の被写体の断面について横に座標 s, 縦に投影角度 θ をとり投影を並べたものでサイノグラムと呼ばれる. 上部の 0 度の位置から矩形, 台形, 三角形となる様子が観察される. 投影が三角形となる 45 度,135 度の投影角度で値が最大となる.(b) は FBP 法の Ramp フィルタ (Fig. 6(b)) を実空間で表した Ram-Lak フィルタ 4), (c) はフィルタ補正した投影を示す. 投影は積分変換であるから必ず正であるが,(c) は (a) と異なり, フィルタ補正した投影は大きな負の値を持つ.FBP 法はフィルタ補正した投影の値を投影線に沿って空白な画面に書き込み ( 逆投影 ), 重なった部分を足し算し再構成像を得る方法である.Fig. 3 は 180 度について,4,6,1,30,60 方向からの逆投影の様子を示す. 次元被写体の投影は θ を固定すると s の 1 次元関数であるが, それを逆投影すると 次元画像になる. 単純な逆投影では矩形内の領域で値が一定, 矩形外ではゼロの画像とはならないが, 被写体のおおまかな形状を類推できるぼけた画像が得られる.Fig. 4 は Ramp フィルタによって投影に負の成分を持た
3 せ逆投影した画像である. フィルタ補正した投影を逆投影し足し算していくと, 負の成分の寄与でぼけが除去され被写体に近い矩形画像が得られる. FBP 法の Ramp フィルタは逆投影で生じるぼけを除く働きがある. 線形性と位置非依存性を満たすシステム ( 線形 非位置依存性システム ) では, 入力 ( 被写体 ), 応答関数 ( 画像再構成の点広がり関数 h(x,y)), 出力 ( 再構成像 ) の関係は畳み込みで表される. 線形 非位置依存性システムの点広がり関数は位置に依存しないので, 被写体を点線源の集まりとみなすと各点線源の強度を点広がり関数に掛け足し算したものが逆投影の再構成像となる. そして, 逆投影の点広がり関数は次式のように距離に逆比例する強度を持つことが導かれる. hxy (, ) 1 1 x y r (6) h(x,y) のフーリエ変換 H(u,v) は次式で表される. i ( ux vy) 1 1 Huv (, ) hxye (, ) dxdy u v (7) k 分解能の劣化がない理想的な点広がり関数はデルタ関数 ( フーリエ変換の振幅が周波数に関係なく 1) であるが,H(u,v) は高周波数成分が弱められている. この減衰分を補うため, 投影のフーリエ変換 P(k, θ) に k で表される Ramp フィルタを掛ける. i ks f ( x, y) P( k, ) k e dk d 0 (8) 続いてフーリエ逆変換し,Fig. (c) のような負の成分を持つ投影に作り換え逆投影することで, ぼけのない Fig. 4 の再構成像が得られる.Fig. (b) の Ram-Lak フィルタの離散式は画素の幅を a として次式で表される. 1/4a m 0 h( ma) 1/( ma) m : odd 0 m: even (9) フーリエ変換の性質から (8) 式の周波数空間における投影とフィルタの掛け算は, 実空間では畳み込みになり, フィルタ補正した投影 q(s,θ) を逆投影し再構成像が得られる. qs (, ) ps ( ', ) hs ( s') ds' (10) f ( xy, ) qs (, ) d (11) 0 FBP 法のフィルタ補正を実空間で実行する方法は重畳積分法と呼ばれる. 3
4 3. ラドン逆変換平行ビーム投影からのラドン逆変換による画像再構成は次式で表される 5). f ( x, y) 1 ps (, )/ s dsd (1) x y s 0 cos sin (1) 式は変数 s に着目すれば (10) 式の畳み込みの式になっている.Fig. 5(a) は Fig. (a) の矩形画像の投影を s で微分した投影,(b) は微分した投影とフィルタ (1 / s) の畳み込み,(c) はそれを逆投影した再構成像を示す 6).(1) 式は FBP 法の (8) 式における投影と Ramp フィルタの掛け算に関し, フーリエ変換の性質とヒルベルト変換を用い実空間で行う形に書き直したものである. 1 k 0 1 Hk ( ) k i k sgn( k), sgn( k) 0 k0 i 1 k 0 (13) ヒルベルト変換 { f ( x)} は次式で表される. 1 f( x') { f ( x)} dx' (14) x x ' 3.3 一様吸収体のラドン逆変換ラドン変換が吸収の影響を含むとき吸収を受けたラドン変換という. 線減弱係数 が一定の一様吸収体を仮定すると, 吸収を受けたラドン変換からの画像再構成には Fig. 6 (a) のフィルタが用いられる. (b) の吸収の影響がない場合の Ramp フィルタと異なり, フィルタは k / の区間でゼロである.SPECT における吸収の影響を周波数空間で考えると, 吸収がない場合に比べ周波数の推移が生じ, その結果, フィルタは (a) のように修正される. 画像再構成ははじめに (c) に示すように, 吸収を受けた投影 p(s, θ) に s 軸から被写体の輪郭までの距離 d(s, θ) を用いスケーリングした投影 ˆ( ps, ) を作る. t d( s, ) pˆ( s, ) f(, x y) e dt e p(, s ) (15) 次に 3. 節のラドン逆変換のように投影を微分し, 次式でフィルタ補正して逆投影する 5). 1 ( xsinycos ) cos( ( s xcos ysin )) pˆ ( s, ) f ( xy, ) e dsd 4 0 (16) sxcos ysin s 積分内の指数関数は (c) の s 軸からの被写体 ( 線源 ) までの距離 t に関係し, t ( xcos ysin ) (1) 式から e e である. 一様吸収体に対する解析的吸収補正法には 3 つの方法があり, それらの数学的な関係が工藤ら 7) によって明らかにされた. その 1 つである Inoue の方法 8,9) は線減弱係数を虚数の周波数という概念で捉えることによって, 投影切断面定理を吸収の影響を受けたラドン変換にも適用で 4
5 きるように複素数に拡張した. 解析的吸収補正法を用いた SPECT による放射濃度の定量性について報告されている 10). 3.4 ファンビーム Fig. 7 は検出器が直線状に並んだファンビーム投影の幾何学的配置を示す. この画像再構成には, 本来の検出器の位置から拡大率 (1 画素の長さで換算する ) を考慮し, 原点を通る X 座標軸上に投影を持ってくる. 線源からファンビームの回転中心 ( 原点 ) までの距離を D, 線源から実際の検出器までの距離を D0, 実際の検出器の標本間隔 ( 検出器 1 つの幅, 投影の 1 画素の幅としている ) を Δd としたとき,X 軸上での標本間隔 ΔX は X ( D/ D0 ) d となる. ファンビーム投影を p'( X, ) とすると画像再構成は次式で表される. 1 1 X max D f ( x, y) { p'( X, )} h( X ' X ) dxd (17) 0 X L max D X t sin( ) D cos( ) L, X ' t (18) D L Lは線源から原点までの距離 D と f(x,y) から投影の中心線に垂線を下ろした点 C までの距離の比である.X 軸上の点 X ' は (18) 式で表される.Fig.8 の 1 行はファンビームの逆投影, 行は Ramp フィルタで補正した投影の逆投影を示し, 平行ビームと異なり投影線の経路は扇状になる. 4.3 次元画像再構成 4.1 平行線積分による 次元投影 PET には Fig. 9(a) の 次元 PET(D PET) や (b) のように斜め方向にも投影を収集する 3 次元 PET (3D PET) がある. 被写体に Fig. 1 の 次元ラドン変換の線積分を断面ごとに行うと, 平行な線積分からなる (a) や (b) の 次元投影が得られる. (c) は半径 1 の単位球を表しベクトル μ は xy 平面から θ 傾いた線積 11) 分の投影方向ベクトルを表す ( このような単位球を Orlov の球という ). 投影方向ベクトルの終点を Orlov の球上にプロットしたものを投影領域 とする. 次元検出器は μ に垂直な平面とする.θ = 0 の投影領域 0 の場合には, 次元検出器が z 軸に平行に被写体の回りを回転する SPECT や D PET の投影となる. Orlov によると 次元投影から画像再構成できる十分条件は, 投影方向領域が Orlov の球のあらゆる大円 ( 単位球を横切る円にはいろいろあるが, 円周の長さが π の円を大円という ) と交差すること である. z 軸回りの回転角度を とするとき, における 次元投影の 次元フーリエ変換は,3 次元投影切断面定理によって被写体の 3 次元フーリエ変換の原点を通る角度 の成分に等しい. したがって,(c) の θ = 0 の場合には を 360 度の範囲に変化させ投影を収集す 5
6 れば,3 次元フーリエ変換が完全に求められる. それをフーリエ逆変換すると再構成像が得られる. 一方,3D PET では画像再構成に必要な θ = 0 以外の投影も収集することで, 投影の冗長性を利用し信号対雑音比を高めている. (d) は投影方向領域が太線の帯状内にあるときの ( max max ) を示す. ここで はこの帯を大円が横切る長さ, は周波数空間のベクトル ν の極角 ( / ν cos ) である. 平行線積分による 次元投影からの 3 次元画像再構成では, 次式の Colsher の 次元フィルタ 13) HC ( u, v, ) が用いられる. z Huv (,, ) u v u v / sin sin / 4 arcsin(sin / sin ) sin sin max max max (19) 帯を横切る長さ は (c) や (d) のとき π,(f) のときは (19) 式の 行の分母で表される. これら帯の長さでフィルタが重み付けされる.3 次元 FBP 法は Colsher の 次元フィルタで補正した投影 p'( x, y,, ) を次式で 3 次元逆投影する ( 低域通過フィルタ処理も併用される ) 1). f( x, y, z) f( x, y, z) (cos ) p'( x, y,, ) (0) 4. 面積分による 1 次元投影 Fig. 10(a) は原点を始点とする方向ベクトル μ が z 軸となす角を θ, μ の xy 平面に下した垂線が x 軸となす角を とし, μ に直交する平面上での 3 次元被写体の面積分を p(s, μ ) としている. ここで s は原点から平面までの距離である. この p(s, μ ) を 3 次元ラドン変換といい,3 次元被写体の 1 次元への投影になる. ラドン逆変換は次式で表される 14). 1 ps (, μ) s sμr f ( xyz,, ) sin dd (1) μ (sin cos,sinsin,cos ) () ここで, μ r はベクトルの内積を表す. フーリエ変換の性質から 3),(1) 式の投影の s に関する 階微分は, 周波数空間で投影 Pk (,, ) に Ramp フィルタを 乗した k フィルタを掛け, フーリエ逆変換して得られる投影 qs (,, ) に等しい. 1 i ks qs (,, ) Pk (,, ) ke dk (3) (b) は 3 次元被写体と 3 次元ラドン変換の 3 つの変数の関係を示す.Fig. 11 は (a) 0 の投影 ps (,, 0),(b) k フィルタ補正した投影 qs (,, 0),(c) (b) の FBP 法の再構成像 ( 次元投影 ) pxz (,, 0),(d) 0の投影 ps (, 0, ),(e) Ramp フィルタ補正した投影 qs (, 0, ),(f) (e) の FBP 法による再構成像 ( 次元投影 ) pxy (,, 0) をそれぞれ示す.(c) と (f) は (1), (3) 式の画像再構成に直接関係ないが,1 次元投影と 次元投影の関係を示すために載せた.Fig.1 は 6
7 Shepp-Logan ファントムと 3 次元ラドン逆変換による再構成像を示す 6). 内部の腫瘍 ( 画像中央の円 ) を見やすくするため,Shepp の論文 14) よりも腫瘍の強度を大きくし鼻や耳の強度と同じにしている.(1) 式の微分と積分の順序を入れ換えると 3 次元ラドン逆変換は次式で表される. 1 f ( xyz,, ) p(, )sin d d 8 x y z 0 0 μ r μ (4) (4) 式ははじめに 3 次元逆投影を行い, その後に画像処理でよく知られている 次微分 ( ラプラシアン ) 処理を行う形である. 4.3 コーンビームコーンビーム投影では 次元ファンビームの傾いた投影が得られるとみなし画像再構成を行う 15). 計算機によるコーンビーム投影の作り方は文献 16) に詳しく紹介されている. 傾いた投影は回転すると別の断面の線積分となるため, 正確な画像再構成ができない. 傾きが大きくなるほど画像再構成の誤差は大きくなる. しかし, 近似的ではあるがそれなりの画像が再構成されるので,3 次元コーンビームではこの Feldkamp 法 17) が用いられている. フィルタには (9) 式の Ram- Lak フィルタが用いられる.Fig. 13 は単位ベクトル i, j, k を用いコーンビームの座標系を示す. コーンビーム投影を p'( X, Z, ) として画像再構成は次式で表される. 1 1 X max D f ( xyz,, ) { '(,, )} ( ' ) 0 p XZ hx X dxd L Xmax D X Z (5) L はファンビームの (18) 式と同じである. p'( X, Z, ) の X が 次元検出器の横方向,Z が 次元検出器の縦方向に相当する. は 次元検出器の回転角を示す. Fig. 14 は (a) 楕円体を並べた Defries ファントムの横断面,(b) 冠状断面, (c) 矢状断面,(d) 0 における 次元検出器への投影 pxz (,, 0),(e) Z 0 における 1 次元投影 px (,, Z 0), (f) 0 における逆投影の横断面 bxyz (,, 0),(g) 0 における逆投影の冠状断面 bxzy (,, 0),(h) 0 における逆投影の矢状断面 byzx (,, 0),(i) 再構成像 f( y, z, x 0) をそれぞれ示す. (f) から横断面 (xy 平面 ) ではファンビームに,(h) から矢状断面 (yz 平面 ) ではコーンビームになっている様子がわかる. ファントムの強度は同じであるが, z = 0 の原点 ( 中央 ) から遠くなるほど, コーン角の影響で楕円体の強度が低下し周辺部がぼける.Feldkamp 法は円柱内の強度が一定な 3 次元被写体に対し正確な画像再構成となる.Fedkamp 法は実用的なコーンビーム画像再構成であり, コーン角が小さければ誤差が小さく, 放射線治療装置に装備されているフラットパネル検出器の CT に応用されている.Fig. 15 は (a) Shepp-Logan ファントムのコーンビームによる 次元投影 pxz (,, 0),(b) フィルタ補正した 次元投 7
8 影 qxz (,, 0),(c) Z 0 におけるフィルタ補正した 1 次元投影 qx (,, Z 0), (d) 横断面,(e) 冠状断面,(f) 矢状断面の再構成像を示す.(d)-(f) の再構成像は表示範囲を (0.98, 1.05) の狭い範囲に限定し, 線状のアーチファクトの様子をわかりやすくしている. ファントムの口, 耳, 鼻など強度が大きく変化する部分ではアーチファクトが発生し, コーンビーム画像再構成法の評価では強度変化の小さい領域のみからなる Shepp-Logan ファントムが通常用いられる. このような強度範囲であれば,Fig. 15 に強調して表示したアーチファクトは観察されない. FBP 法による 次元画像再構成においても同様である. Fig. 16 は Feldkamp 法を用いたヘリカルコーンビームの投影とフィルタ補正した投影を示す 18). これは線源と 次元検出器が回転しながら体軸方向に移動し, 4 回転し 1440 度の投影を収集する様子の一部を示している.Feldkamp 法によるヘリカルコーンビーム再構成像には角度依存性のあるアーチファクトが見られるが,Feldkamp 法による単一円軌道のコーンビームの再構成像に近い画像が得られる. コーンビームのより正確な画像再構成法は,Defries 19),Kudo 0) らによって報告されている. Figure Captions 8
9 Fig.1 矩形内で値が一定の断面の投影 Fig. FBP 法による画像再構成 Fig.3 逆投影 Fig.4 フィルタ補正逆投影 Fig.5 次元ラドン逆変換公式による画像再構成 Fig.6 一様吸収体に対する再構成フィルタ Fig.7 ファンビームの幾何学的配置 Fig.8 ファンビームの逆投影 Fig.9 平行線積分による 次元投影 Fig.10 面積分による 1 次元投影 (3 次元ラドン変換 ) Fig.11 3 次元ラドン逆変換公式による画像再構成 Fig.1 3 次元ラドン逆変換公式による再構成像 Fig.13 コーンビームの幾何学的配置 Fig.14 コーンビームの投影と逆投影 Fig.15 コーンビームの再構成像 Fig.16 ヘリカルコーンビームの投影 参考文献 9
10 1) 橋本雄幸, 篠原広行 :C 言語による画像再構成の基礎. 医療科学社, 東京, 006: ) 篠原広行, 坂口和也, 橋本雄幸 :Excel による画像再構成入門. 医療科学社, 東京,007: ) 篠原広行, 橋本雄幸 :MRI とフーリエ変換. 医療科学社, 東京, 01: ) Ramachandran GN, Lakshminarayanan AV: Three-dimensional reconstruction from radiographs and electron micrographs: application of convolutions instead of Fourier transforms. Pro Natl Acad Sci 68: 36-40, ) Zeng GL: Medical Image Reconstruction. A Conceptual Tutorial, Springer, New York, 010: 5-4, ) 篠原広行, 梶原宏則, 中世古和真, 他 :C 言語による画像再構成入門 -トモシンセシスから 3 次元ラドン逆変換まで-. 医療科学社,014 年,9 月発刊予定. 7) 工藤博幸, 斎藤恒雄 :SPECT における解析的画像再構成法の体系化と雑音伝搬特性. 電子情報通信学会誌 J79-D-II: , ) Inoue T, Kose K, Hasegawa A: Image reconstruction algorithm for SPECT with uniform attenuation. Phys Med Biol 34: , ) 橋本雄幸, 横井孝司, 篠原広行 :SPECT 画像再構成の基礎. 医療科学社, 東京, 006: ) Shinohara H, Yamamoto T, Kuniyasu Y, et al.: Implementation and quantitative evaluation of analytical methods for attenuation correction in SPECT: a phantom study. Phys Med Biol 44: , ) Orlov SS: Theory of three-dimensional image reconstruction: I Conditions for a complete set of projections. Soviet Physics Crystallography 0: , ) 市原隆, 飯田秀博監訳 :3D PET の理論と実践,Bendriem B, Townsend D eds: The Theory and Practice of 3D PET. 東芝メディカルシステムズ, 東京, 005: ) Colsher JG: Fully three-dimensional positron emission tomography. Phys Med Biol 5: , ) Shepp LA: Computerized tomography and nuclear magnetic resonance. J Comput Assist Tomogr 1: 1-43, ) Kak AC, Slaney M: Principles of Computerized Tomographic Imaging. IEEE press, New York, 1988: ) 中世古和真, 梶原宏則, 渡邊裕之, 他 : コーンビームによる頭部単純撮影用コンピュータ支援学習プログラムの開発. 医学物理 3: -11, 01 10
11 17) Feldkamp LA, Davis LC, Kress JW: Practical cone-beam algorithm. J Opt Soc Am A1:61-619, ) 篠原広行, 中世古和真, 陳欣胤, 他 : コーンビーム CT 画像再構成の基礎. 医療科学社, 東京,013: ) Defries M, Coack R: A cone-beam reconstruction algorithm using shift-variant filtering and cone-beam backprojection. IEEE Trans Med Imaging 13: , ) Kudo H, Saito T: Fast and stable cone-beam filtered backprojection method for nonplanar orbits. Phys Med Biol 43: ,
連続講座 断層映像法の基礎第 29 回 : 篠原広行 他 断層映像法の基礎第 29 回 2 次元ファンビームの投影と画像再構成 篠原広行 II 梶原宏則 II 中世古和真 1 ) 橘篤志 II 橋本雄幸 2) 首都大学東京人間健康科学研究科放射線科学域 21 横浜愈 l 英短期大学情報学科 はじめに
 連続講座 断層映像法の基礎第 29 回 : 篠原広行 他 断層映像法の基礎第 29 回 2 次元ファンビームの投影と画像再構成 篠原広行 II 梶原宏則 II 中世古和真 1 ) 橘篤志 II 橋本雄幸 2) 首都大学東京人間健康科学研究科放射線科学域 21 横浜愈 l 英短期大学情報学科 はじめに第 28 固までで レジストレーションについてその基本から非剛体レジストレーションまで解説してきた 今回から直接
連続講座 断層映像法の基礎第 29 回 : 篠原広行 他 断層映像法の基礎第 29 回 2 次元ファンビームの投影と画像再構成 篠原広行 II 梶原宏則 II 中世古和真 1 ) 橘篤志 II 橋本雄幸 2) 首都大学東京人間健康科学研究科放射線科学域 21 横浜愈 l 英短期大学情報学科 はじめに第 28 固までで レジストレーションについてその基本から非剛体レジストレーションまで解説してきた 今回から直接
連続講座 断層映像法の基礎第 34 回 : 篠原 広行 他 放射状に 線を照射し 対面に検出器の列を置いておき 一度に 1 つの角度データを取得する 後は全体を 1 回転しながら次々と角度データを取得することで計測を終了する この計測で得られる投影はとなる ここで l はファンビームのファンに沿った
 連続講座 断層映像法の基礎第 34 回 : 篠原広行 他 篠原 広行 桑山 潤 小川 亙 中世古 和真 断層映像法の基礎第 34 回スパイラルスキャン CT 1) 軽部修平 2) 橋本雄幸 1) 小島慎也 1) 藤堂幸宏 1) 3) 首都大学東京人間健康科学研究科放射線科学域 2) 東邦大学医療センター大橋病院 3) 横浜創英短期大学情報学科 1) はじめに第 33 回では検出確率 C ij の関係を行列とベクトルの計算式に置き換えて解を求める最小二乗法を利用した方法について解説した
連続講座 断層映像法の基礎第 34 回 : 篠原広行 他 篠原 広行 桑山 潤 小川 亙 中世古 和真 断層映像法の基礎第 34 回スパイラルスキャン CT 1) 軽部修平 2) 橋本雄幸 1) 小島慎也 1) 藤堂幸宏 1) 3) 首都大学東京人間健康科学研究科放射線科学域 2) 東邦大学医療センター大橋病院 3) 横浜創英短期大学情報学科 1) はじめに第 33 回では検出確率 C ij の関係を行列とベクトルの計算式に置き換えて解を求める最小二乗法を利用した方法について解説した
連続講座 画像再構成 : 臨床医のための解説第 2 回 : 篠原 広行 他 ラムと呼ばれる 上部の 度の位置から矩形 台形 三角形となる様子が観察される 投影が三角形と なる 5 度 35 度の投影角度で値が最大となる 図 2 は空白の画面に投影を得た方向に投影の値 を戻し重なった部分を足し算する逆
 連続講座 画像再構成 : 臨床医のための解説第 2 回 : 篠原広行 他 画像再構成 : 臨床医のための解説第 2 回逐次近似画像再構成法 篠原 広行 ) 小島慎也 2) 橋本雄幸 3) 2) 上野惠子 2) ) 首都大学東京東京女子医科大学東医療センター放射線科 3) 横浜創英大学こども教育学部 はじめに 画像再構成は被写体の積分変換 ( 投影 ) から被 写体を求める逆問題であり 解析的方法と逐次近似
連続講座 画像再構成 : 臨床医のための解説第 2 回 : 篠原広行 他 画像再構成 : 臨床医のための解説第 2 回逐次近似画像再構成法 篠原 広行 ) 小島慎也 2) 橋本雄幸 3) 2) 上野惠子 2) ) 首都大学東京東京女子医科大学東医療センター放射線科 3) 横浜創英大学こども教育学部 はじめに 画像再構成は被写体の積分変換 ( 投影 ) から被 写体を求める逆問題であり 解析的方法と逐次近似
福島県立医科大学総合科学教育研究センター紀要 Vol. 4, 1-10, 2015 原著論文 CT 2 ( ) CT 2 Received 2 October 2015, Accepted 16 October CT 2 f 0 (x, y) Radon f 0 2 f (x, y)
 福島県立医科大学総合科学教育研究センター紀要 Vol. 4, -, 5 原著論文 CT () CT Received October 5, Accepted 6 October 5 CT f (x, y) Radon f f (x, y) (FBP) Fourier Fourier (Bracewell & Riddle, 967 () ; Ramachangran & Lakshminarayanan,
福島県立医科大学総合科学教育研究センター紀要 Vol. 4, -, 5 原著論文 CT () CT Received October 5, Accepted 6 October 5 CT f (x, y) Radon f f (x, y) (FBP) Fourier Fourier (Bracewell & Riddle, 967 () ; Ramachangran & Lakshminarayanan,
連続講座 画像再構成 : 臨床医のための解説第 2 回 : 篠原広行 他 画像再構成 : 臨床医のための解説第 2 回逐次近似画像再構成法 篠原 広行 1) 小島慎也 2) 橋本雄幸 3) 2) 上野惠子 2) 1) 首都大学東京東京女子医科大学東医療センター放射線科 3) 横浜創英大学こども教育学
 連続講座 画像再構成 : 臨床医のための解説第 回 : 篠原 画像再構成 : 臨床医のための解説第 回逐次近似画像再構成法 篠原 広行 ) 小島慎也 ) 橋本雄幸 3) ) 上野惠子 ) ) 首都大学東京東京女子医科大学東医療センター放射線科 3) 横浜創英大学こども教育学部 はじめに 画像再構成は被写体の積分変換 ( 投影 ) から被 写体を求める逆問題であり 解析的方法と逐次近似 法に大別される
連続講座 画像再構成 : 臨床医のための解説第 回 : 篠原 画像再構成 : 臨床医のための解説第 回逐次近似画像再構成法 篠原 広行 ) 小島慎也 ) 橋本雄幸 3) ) 上野惠子 ) ) 首都大学東京東京女子医科大学東医療センター放射線科 3) 横浜創英大学こども教育学部 はじめに 画像再構成は被写体の積分変換 ( 投影 ) から被 写体を求める逆問題であり 解析的方法と逐次近似 法に大別される
連続講座 断層映像法の基礎第 32 回 : 篠原広行 他 断層映像法の基礎 第 32 回 ML-EM 法と OS-EM 法 篠原広行 1) 桑山潤 1) 小川亙 1) 2) 橋本雄幸 1) 首都大学東京人間健康科学研究科放射線科学域 2) 横浜創英短期大学情報学科 はじめに第 31 回では繰り返しを
 断層映像法の基礎 第 32 回 ML-EM 法と OS-EM 法 篠原広行 1) 桑山潤 1) 小川亙 1) 2) 橋本雄幸 1) 首都大学東京人間健康科学研究科放射線科学域 2) 横浜創英短期大学情報学科 はじめに第 31 回では繰り返しを利用して徐々に解に近づけていく方法を紹介した 本稿ではその繰り返しを使った方法で最も多く使われている ML-EM 法と OS-EM 法について解説する また その方法を利用した数値シミュレーションの結果についても紹介する
断層映像法の基礎 第 32 回 ML-EM 法と OS-EM 法 篠原広行 1) 桑山潤 1) 小川亙 1) 2) 橋本雄幸 1) 首都大学東京人間健康科学研究科放射線科学域 2) 横浜創英短期大学情報学科 はじめに第 31 回では繰り返しを利用して徐々に解に近づけていく方法を紹介した 本稿ではその繰り返しを使った方法で最も多く使われている ML-EM 法と OS-EM 法について解説する また その方法を利用した数値シミュレーションの結果についても紹介する
Microsoft PowerPoint - 第3回2.ppt
 講義内容 講義内容 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 ベクトルの直交性 3
講義内容 講義内容 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 ベクトルの直交性 3
臨床画像技術学Ⅱ
 核医学機器工学概論 2 断層画像 CT( Computed Tomography) を得る方法 1. フィルタ重畳逆投影法 FBP ( Filtered Back Projection ) 2. 逐次近似再構成法 Iterative Reconstruction MLEM (Maximum Likelihood Expectation Maximization) OSEM ( Ordered Subsets
核医学機器工学概論 2 断層画像 CT( Computed Tomography) を得る方法 1. フィルタ重畳逆投影法 FBP ( Filtered Back Projection ) 2. 逐次近似再構成法 Iterative Reconstruction MLEM (Maximum Likelihood Expectation Maximization) OSEM ( Ordered Subsets
例 e 指数関数的に減衰する信号を h( a < + a a すると, それらのラプラス変換は, H ( ) { e } e インパルス応答が h( a < ( ただし a >, U( ) { } となるシステムにステップ信号 ( y( のラプラス変換 Y () は, Y ( ) H ( ) X (
 第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
Microsoft PowerPoint - ip02_01.ppt [互換モード]
![Microsoft PowerPoint - ip02_01.ppt [互換モード] Microsoft PowerPoint - ip02_01.ppt [互換モード]](/thumbs/96/127250376.jpg) 空間周波数 周波数領域での処理 空間周波数 (spatial frquncy) とは 単位長さ当たりの正弦波状の濃淡変化の繰り返し回数を表したもの 正弦波 : y sin( t) 周期 : 周波数 : T f / T 角周波数 : f 画像処理 空間周波数 周波数領域での処理 波形が違うと 周波数も違う 画像処理 空間周波数 周波数領域での処理 画像処理 3 周波数領域での処理 周波数は一つしかない?-
空間周波数 周波数領域での処理 空間周波数 (spatial frquncy) とは 単位長さ当たりの正弦波状の濃淡変化の繰り返し回数を表したもの 正弦波 : y sin( t) 周期 : 周波数 : T f / T 角周波数 : f 画像処理 空間周波数 周波数領域での処理 波形が違うと 周波数も違う 画像処理 空間周波数 周波数領域での処理 画像処理 3 周波数領域での処理 周波数は一つしかない?-
Microsoft PowerPoint - SPECTPETtheory.ppt [互換モード]
![Microsoft PowerPoint - SPECTPETtheory.ppt [互換モード] Microsoft PowerPoint - SPECTPETtheory.ppt [互換モード]](/thumbs/92/110123396.jpg) SPECT( Single Photon Emission CT ) PET( Positron Emission CT ) の原理 断層画像を得る方法 フィルタ重畳逆投影法 FBP ( Filtered Back Projection ) 逐次近似再構成法 Iterative Reconstruction MLEM ( Maximun Likelihood Expectation ti Maximization
SPECT( Single Photon Emission CT ) PET( Positron Emission CT ) の原理 断層画像を得る方法 フィルタ重畳逆投影法 FBP ( Filtered Back Projection ) 逐次近似再構成法 Iterative Reconstruction MLEM ( Maximun Likelihood Expectation ti Maximization
逐次近似法の基礎と各種補正方法
 逐次近似法の基礎と各種補正方法 横浜創英大学橋本雄幸 画像再構成における逐次近似法の歴史は長く,X 線 CT においても解析的方法が見つかる前は, 逐次近似法を用いて画像を再構成していた. 解析的方法が見つかってからは, 計算時間の長さから逐次近似法はあまり使われなくなった. しかし, コンピュータの発展に伴い, 繰り返しても計算時間がそれほどかからなくなったこともあり, 解析的方法が確立できない
逐次近似法の基礎と各種補正方法 横浜創英大学橋本雄幸 画像再構成における逐次近似法の歴史は長く,X 線 CT においても解析的方法が見つかる前は, 逐次近似法を用いて画像を再構成していた. 解析的方法が見つかってからは, 計算時間の長さから逐次近似法はあまり使われなくなった. しかし, コンピュータの発展に伴い, 繰り返しても計算時間がそれほどかからなくなったこともあり, 解析的方法が確立できない
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生
 0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
PowerPoint Presentation
 付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
スライド タイトルなし
 次元フーリエ変換 講義内容 空間周波数の概念 次元フーリエ変換代表的な 次元フーリエ変換対 次元離散フーリエ変換 フーリエ変換と逆変換 F.T. j F } ep{ 連続系離散系 } / ep{ N N N j N F F I. F.T. F ただし ここでは絶対値をとって画像化 } / ep{ N N N j F N 順変換逆変換 3 次元フーリエ変換の具体的なイメージ } / ep{ N N N
次元フーリエ変換 講義内容 空間周波数の概念 次元フーリエ変換代表的な 次元フーリエ変換対 次元離散フーリエ変換 フーリエ変換と逆変換 F.T. j F } ep{ 連続系離散系 } / ep{ N N N j N F F I. F.T. F ただし ここでは絶対値をとって画像化 } / ep{ N N N j F N 順変換逆変換 3 次元フーリエ変換の具体的なイメージ } / ep{ N N N
第 4 週コンボリューションその 2, 正弦波による分解 教科書 p. 16~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問 1. 以下の図にならって,1 と 2 の δ 関数を図示せよ δ (t) 2
 第 4 週コンボリューションその, 正弦波による分解 教科書 p. 6~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問. 以下の図にならって, と の δ 関数を図示せよ. - - - δ () δ ( ) - - - 図 δ 関数の図示の例 δ ( ) δ ( ) δ ( ) δ ( ) δ ( ) - - - - - - - -
第 4 週コンボリューションその, 正弦波による分解 教科書 p. 6~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問. 以下の図にならって, と の δ 関数を図示せよ. - - - δ () δ ( ) - - - 図 δ 関数の図示の例 δ ( ) δ ( ) δ ( ) δ ( ) δ ( ) - - - - - - - -
ディジタル信号処理
 ディジタルフィルタの設計法. 逆フィルター. 直線位相 FIR フィルタの設計. 窓関数法による FIR フィルタの設計.5 時間領域での FIR フィルタの設計 3. アナログフィルタを基にしたディジタル IIR フィルタの設計法 I 4. アナログフィルタを基にしたディジタル IIR フィルタの設計法 II 5. 双 次フィルタ LI 離散時間システムの基礎式の証明 [ ] 4. ] [ ]*
ディジタルフィルタの設計法. 逆フィルター. 直線位相 FIR フィルタの設計. 窓関数法による FIR フィルタの設計.5 時間領域での FIR フィルタの設計 3. アナログフィルタを基にしたディジタル IIR フィルタの設計法 I 4. アナログフィルタを基にしたディジタル IIR フィルタの設計法 II 5. 双 次フィルタ LI 離散時間システムの基礎式の証明 [ ] 4. ] [ ]*
Microsoft PowerPoint - SPECTPETの原理2012.ppt [互換モード]
![Microsoft PowerPoint - SPECTPETの原理2012.ppt [互換モード] Microsoft PowerPoint - SPECTPETの原理2012.ppt [互換モード]](/thumbs/94/121508518.jpg) 22 年国家試験解答 1,5 フーリエ変換は線形変換 FFT はデータ数に 2 の累乗数を要求するが DFT は任意のデータ数に対応 123I-IMP Brain SPECT FBP with Ramp filter 123I-IMP Brain SPECT FBP with Shepp&Logan filter 99mTc-MIBI Myocardial SPECT における ストリークアーチファクト
22 年国家試験解答 1,5 フーリエ変換は線形変換 FFT はデータ数に 2 の累乗数を要求するが DFT は任意のデータ数に対応 123I-IMP Brain SPECT FBP with Ramp filter 123I-IMP Brain SPECT FBP with Shepp&Logan filter 99mTc-MIBI Myocardial SPECT における ストリークアーチファクト
スライド 1
 5.5.2 画像の間引き 5.1 線形変換 5.2 アフィン変換 5.3 同次座標 5.4 平面射影変換 5.5 再標本化 1. 画素数の減少による表現能力の低下 画像の縮小 変形を行う際 結果画像の 画素数 < 入力画像の 画素数 ( 画素の密度 ) ( 画素の密度 ) になることがある この場合 結果画像の表現力 < 入力画像の表現力 ( 情報量 ) ( 情報量 ) 結果的に 情報の損失が生じる!
5.5.2 画像の間引き 5.1 線形変換 5.2 アフィン変換 5.3 同次座標 5.4 平面射影変換 5.5 再標本化 1. 画素数の減少による表現能力の低下 画像の縮小 変形を行う際 結果画像の 画素数 < 入力画像の 画素数 ( 画素の密度 ) ( 画素の密度 ) になることがある この場合 結果画像の表現力 < 入力画像の表現力 ( 情報量 ) ( 情報量 ) 結果的に 情報の損失が生じる!
スライド 1
 断層画像 (CT,SPECT,PET) を得るためのフィルタは 2 種類ある Pre-filter 前処理フィルタ 断層画像の元になるプロジェクション像の雑音除去 Butterworth, Wiener フィルタなど Reconstruction filter 再構成フィルタ FBP( フィルタ畳重逆投影法 ) で断層画像を作成する場合に フーリエ空間 ( 周波数空間 ) で行う処理と同じ計算結果を得る実空間フィルタ
断層画像 (CT,SPECT,PET) を得るためのフィルタは 2 種類ある Pre-filter 前処理フィルタ 断層画像の元になるプロジェクション像の雑音除去 Butterworth, Wiener フィルタなど Reconstruction filter 再構成フィルタ FBP( フィルタ畳重逆投影法 ) で断層画像を作成する場合に フーリエ空間 ( 周波数空間 ) で行う処理と同じ計算結果を得る実空間フィルタ
数学 t t t t t 加法定理 t t t 倍角公式加法定理で α=β と置く. 三角関数
 . 三角関数 基本関係 t cot c sc c cot sc t 還元公式 t t t t t t cot t cot t 数学 数学 t t t t t 加法定理 t t t 倍角公式加法定理で α=β と置く. 三角関数 数学. 三角関数 5 積和公式 6 和積公式 数学. 三角関数 7 合成 t V v t V v t V V V V VV V V V t V v v 8 べき乗 5 6 6
. 三角関数 基本関係 t cot c sc c cot sc t 還元公式 t t t t t t cot t cot t 数学 数学 t t t t t 加法定理 t t t 倍角公式加法定理で α=β と置く. 三角関数 数学. 三角関数 5 積和公式 6 和積公式 数学. 三角関数 7 合成 t V v t V v t V V V V VV V V V t V v v 8 べき乗 5 6 6
<4D F736F F D20824F E B82CC90FC90CF95AA2E646F63>
 1/1 平成 3 年 6 月 11 日午前 1 時 3 分 4 ベクトルの線積分 4 ベクトルの線積分 Ⅰ. 積分の種類 通常の物理で使う積分には 3 種類あります 積分変数の数に応じて 線積分 ( 記号 横(1 重 d, dy, dz d ( ine: 面積分 ( 記号 縦 横 ( 重 線 4 ベクトルの線積分 重積分記号 ddy, dydz, dzdz ds ( Surface: 1 重積分記号
1/1 平成 3 年 6 月 11 日午前 1 時 3 分 4 ベクトルの線積分 4 ベクトルの線積分 Ⅰ. 積分の種類 通常の物理で使う積分には 3 種類あります 積分変数の数に応じて 線積分 ( 記号 横(1 重 d, dy, dz d ( ine: 面積分 ( 記号 縦 横 ( 重 線 4 ベクトルの線積分 重積分記号 ddy, dydz, dzdz ds ( Surface: 1 重積分記号
画像処理工学
 画像処理工学 画像の空間周波数解析とテクスチャ特徴 フーリエ変換の基本概念 信号波形のフーリエ変換 信号波形を周波数の異なる三角関数 ( 正弦波など ) に分解する 逆に, 周波数の異なる三角関数を重ねあわせることにより, 任意の信号波形を合成できる 正弦波の重ね合わせによる矩形波の表現 フーリエ変換の基本概念 フーリエ変換 次元信号 f (t) のフーリエ変換 変換 ( ω) ( ) ωt F f
画像処理工学 画像の空間周波数解析とテクスチャ特徴 フーリエ変換の基本概念 信号波形のフーリエ変換 信号波形を周波数の異なる三角関数 ( 正弦波など ) に分解する 逆に, 周波数の異なる三角関数を重ねあわせることにより, 任意の信号波形を合成できる 正弦波の重ね合わせによる矩形波の表現 フーリエ変換の基本概念 フーリエ変換 次元信号 f (t) のフーリエ変換 変換 ( ω) ( ) ωt F f
Microsoft Word - NumericalComputation.docx
 数値計算入門 武尾英哉. 離散数学と数値計算 数学的解法の中には理論計算では求められないものもある. 例えば, 定積分は, まずは積分 ( 被積分関数の原始関数をみつけること できなければ値を得ることはできない. また, ある関数の所定の値における微分値を得るには, まずその関数の微分ができなければならない. さらに代数方程式の解を得るためには, 解析的に代数方程式を解く必要がある. ところが, これらは必ずしも解析的に導けるとは限らない.
数値計算入門 武尾英哉. 離散数学と数値計算 数学的解法の中には理論計算では求められないものもある. 例えば, 定積分は, まずは積分 ( 被積分関数の原始関数をみつけること できなければ値を得ることはできない. また, ある関数の所定の値における微分値を得るには, まずその関数の微分ができなければならない. さらに代数方程式の解を得るためには, 解析的に代数方程式を解く必要がある. ところが, これらは必ずしも解析的に導けるとは限らない.
Chap2.key
 . f( ) V (V V ) V e + V e V V V V ( ) V V ( ) E. - () V (0 ) () V (0 ) () V (0 ) (4) V ( ) E. - () V (0 ) () V (0 ) O r θ ( ) ( ) : (r θ) : { r cos θ r sn θ { r + () V (0 ) (4) V ( ) θ θ arg( ) : π π
. f( ) V (V V ) V e + V e V V V V ( ) V V ( ) E. - () V (0 ) () V (0 ) () V (0 ) (4) V ( ) E. - () V (0 ) () V (0 ) O r θ ( ) ( ) : (r θ) : { r cos θ r sn θ { r + () V (0 ) (4) V ( ) θ θ arg( ) : π π
Microsoft Word - 1B2011.doc
 第 14 回モールの定理 ( 単純梁の場合 ) ( モールの定理とは何か?p.11) 例題 下記に示す単純梁の C 点のたわみ角 θ C と, たわみ δ C を求めよ ただし, 部材の曲げ 剛性は材軸に沿って一様で とする C D kn B 1.5m 0.5m 1.0m 解答 1 曲げモーメント図を描く,B 点の反力を求める kn kn 4 kn 曲げモーメント図を描く knm 先に得られた曲げモーメントの値を
第 14 回モールの定理 ( 単純梁の場合 ) ( モールの定理とは何か?p.11) 例題 下記に示す単純梁の C 点のたわみ角 θ C と, たわみ δ C を求めよ ただし, 部材の曲げ 剛性は材軸に沿って一様で とする C D kn B 1.5m 0.5m 1.0m 解答 1 曲げモーメント図を描く,B 点の反力を求める kn kn 4 kn 曲げモーメント図を描く knm 先に得られた曲げモーメントの値を
Microsoft PowerPoint - CSA_B3_EX2.pptx
 Computer Science A Hardware Design Excise 2 Handout V2.01 May 27 th.,2019 CSAHW Computer Science A, Meiji University CSA_B3_EX2.pptx 32 Slides Renji Mikami 1 CSAHW2 ハード演習内容 2.1 二次元空間でのベクトルの直交 2.2 Reserved
Computer Science A Hardware Design Excise 2 Handout V2.01 May 27 th.,2019 CSAHW Computer Science A, Meiji University CSA_B3_EX2.pptx 32 Slides Renji Mikami 1 CSAHW2 ハード演習内容 2.1 二次元空間でのベクトルの直交 2.2 Reserved
画像解析論(2) 講義内容
 画像解析論 画像解析論 東京工業大学長橋宏 主な講義内容 信号処理と画像処理 二次元システムとその表現 二次元システムの特性解析 各種の画像フィルタ 信号処理と画像処理 画像解析論 処理の応答 記憶域 入出力の流れ 信号処理系 実時間性が求められる メモリ容量に対する制限が厳しい オンラインでの対応が厳しく求められる 画像処理系 ある程度の処理時間が許容される 大容量のメモリ使用が容認され易い オフラインでの対応が容認され易い
画像解析論 画像解析論 東京工業大学長橋宏 主な講義内容 信号処理と画像処理 二次元システムとその表現 二次元システムの特性解析 各種の画像フィルタ 信号処理と画像処理 画像解析論 処理の応答 記憶域 入出力の流れ 信号処理系 実時間性が求められる メモリ容量に対する制限が厳しい オンラインでの対応が厳しく求められる 画像処理系 ある程度の処理時間が許容される 大容量のメモリ使用が容認され易い オフラインでの対応が容認され易い
vecrot
 1. ベクトル ベクトル : 方向を持つ量 ベクトルには 1 方向 2 大きさ ( 長さ ) という 2 つの属性がある ベクトルの例 : 物体の移動速度 移動量電場 磁場の強さ風速力トルクなど 2. ベクトルの表現 2.1 矢印で表現される 矢印の長さ : ベクトルの大きさ 矢印の向き : ベクトルの方向 2.2 2 個の点を用いて表現する 始点 () と終点 () を結ぶ半直線の向き : ベクトルの方向
1. ベクトル ベクトル : 方向を持つ量 ベクトルには 1 方向 2 大きさ ( 長さ ) という 2 つの属性がある ベクトルの例 : 物体の移動速度 移動量電場 磁場の強さ風速力トルクなど 2. ベクトルの表現 2.1 矢印で表現される 矢印の長さ : ベクトルの大きさ 矢印の向き : ベクトルの方向 2.2 2 個の点を用いて表現する 始点 () と終点 () を結ぶ半直線の向き : ベクトルの方向
DVIOUT
 第 章 離散フーリエ変換 離散フーリエ変換 これまで 私たちは連続関数に対するフーリエ変換およびフーリエ積分 ( 逆フーリエ変換 ) について学んできました この節では フーリエ変換を離散化した離散フーリエ変換について学びましょう 自然現象 ( 音声 ) などを観測して得られる波 ( 信号値 ; 観測値 ) は 通常 電気信号による連続的な波として観測機器から出力されます しかしながら コンピュータはこの様な連続的な波を直接扱うことができないため
第 章 離散フーリエ変換 離散フーリエ変換 これまで 私たちは連続関数に対するフーリエ変換およびフーリエ積分 ( 逆フーリエ変換 ) について学んできました この節では フーリエ変換を離散化した離散フーリエ変換について学びましょう 自然現象 ( 音声 ) などを観測して得られる波 ( 信号値 ; 観測値 ) は 通常 電気信号による連続的な波として観測機器から出力されます しかしながら コンピュータはこの様な連続的な波を直接扱うことができないため
2009 年 11 月 16 日版 ( 久家 ) 遠地 P 波の変位波形の作成 遠地 P 波の変位波形 ( 変位の時間関数 ) は 波線理論をもとに P U () t = S()* t E()* t P() t で近似的に計算できる * は畳み込み積分 (convolution) を表す ( 付録
 遠地 波の変位波形の作成 遠地 波の変位波形 ( 変位の時間関数 ) は 波線理論をもとに U () t S() t E() t () t で近似的に計算できる は畳み込み積分 (convolution) を表す ( 付録 参照 ) ここで St () は地震の断層運動によって決まる時間関数 1 E() t は地下構造によって生じる種々の波の到着を与える時間関数 ( ここでは 直達 波とともに 震源そばの地表での反射波や変換波を与える時間関数
遠地 波の変位波形の作成 遠地 波の変位波形 ( 変位の時間関数 ) は 波線理論をもとに U () t S() t E() t () t で近似的に計算できる は畳み込み積分 (convolution) を表す ( 付録 参照 ) ここで St () は地震の断層運動によって決まる時間関数 1 E() t は地下構造によって生じる種々の波の到着を与える時間関数 ( ここでは 直達 波とともに 震源そばの地表での反射波や変換波を与える時間関数
20~22.prt
 [ 三クリア W] 辺が等しいことの証明 ( 円周角と弦の関係利用 ) の の二等分線がこの三角形の外接円と交わる点をそれぞれ とするとき 60 ならば であることを証明せよ 60 + + 0 + 0 80-60 60 から ゆえに 等しい長さの弧に対する弦の長さは等しいから [ 三クリア ] 方べきの定理 接線と弦のなす角と円周角を利用 線分 を直径とする円 があり 右の図のように の延長上の点
[ 三クリア W] 辺が等しいことの証明 ( 円周角と弦の関係利用 ) の の二等分線がこの三角形の外接円と交わる点をそれぞれ とするとき 60 ならば であることを証明せよ 60 + + 0 + 0 80-60 60 から ゆえに 等しい長さの弧に対する弦の長さは等しいから [ 三クリア ] 方べきの定理 接線と弦のなす角と円周角を利用 線分 を直径とする円 があり 右の図のように の延長上の点
スライド 1
 暫定版修正 加筆の可能性あり ( 付録 ) デルタ関数. ローレンツ関数. ガウス関数 3. Sinc 関数 4. Sinc 関数 5. 指数関数 6. 量子力学 : デルタ関数 7. プレメリの公式 8. 電磁気学 : デルタ関数 9. デルタ関数 : スケール 微分 デルタ関数 (delta function) ( ) δ ( ) ( ), δ ( ), δ ( ), δ ( ) f x x dx
暫定版修正 加筆の可能性あり ( 付録 ) デルタ関数. ローレンツ関数. ガウス関数 3. Sinc 関数 4. Sinc 関数 5. 指数関数 6. 量子力学 : デルタ関数 7. プレメリの公式 8. 電磁気学 : デルタ関数 9. デルタ関数 : スケール 微分 デルタ関数 (delta function) ( ) δ ( ) ( ), δ ( ), δ ( ), δ ( ) f x x dx
<4D F736F F F696E74202D2091E6824F82518FCD E838B C68CEB82E894AD90B B2E >
 目次 参考文献安達著 : 通信システム工学, 朝倉書店,7 年. ディジタル変調. ディジタル伝送系モデル 3. 符号判定誤り確率 4. 元対称通信路 安達 : コミュニケーション符号理論 安達 : コミュニケーション符号理論 変調とは?. ディジタル変調 基底帯域 ( ベースバンド ) 伝送の信号波形は零周波数付近のスペクトルを持っている. しかし, 現実の大部分の通信路は零周波数付近を殆ど伝送することができない帯域通信路とみなされる.
目次 参考文献安達著 : 通信システム工学, 朝倉書店,7 年. ディジタル変調. ディジタル伝送系モデル 3. 符号判定誤り確率 4. 元対称通信路 安達 : コミュニケーション符号理論 安達 : コミュニケーション符号理論 変調とは?. ディジタル変調 基底帯域 ( ベースバンド ) 伝送の信号波形は零周波数付近のスペクトルを持っている. しかし, 現実の大部分の通信路は零周波数付近を殆ど伝送することができない帯域通信路とみなされる.
Microsoft PowerPoint - 画像工学 print
 教室 : 14-22 画像工学 28 年度版 Imaging Science and Technology 画像工学 28 年度版 2 慶応義塾大学理工学部 教授 慶応義塾大学理工学部 准教授 中島真人青木義満 ( 例 ) 画像システムとしてのカメラ y 入力 f(x,y) x ( 紙に書かれた文字 ) カメラ ( フィルムカメラ デジタルカメラ どちらでも OK ) (u,v) ) SYSTEM
教室 : 14-22 画像工学 28 年度版 Imaging Science and Technology 画像工学 28 年度版 2 慶応義塾大学理工学部 教授 慶応義塾大学理工学部 准教授 中島真人青木義満 ( 例 ) 画像システムとしてのカメラ y 入力 f(x,y) x ( 紙に書かれた文字 ) カメラ ( フィルムカメラ デジタルカメラ どちらでも OK ) (u,v) ) SYSTEM
代数 幾何 < ベクトル > 1 ベクトルの演算 和 差 実数倍については 文字の計算と同様 2 ベクトルの成分表示 平面ベクトル : a x e y e x, ) ( 1 y1 空間ベクトル : a x e y e z e x, y, ) ( 1 1 z1
 代数 幾何 < ベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル :, 空間ベクトル : z,, z 成分での計算ができるようにすること ベクトルの内積 : os 平面ベクトル :,, 空間ベクトル :,,,, z z zz 4 ベクトルの大きさ 平面上 : 空間上 : z は 良く用いられる 5 m: に分ける点 : m m 図形への応用
代数 幾何 < ベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル :, 空間ベクトル : z,, z 成分での計算ができるようにすること ベクトルの内積 : os 平面ベクトル :,, 空間ベクトル :,,,, z z zz 4 ベクトルの大きさ 平面上 : 空間上 : z は 良く用いられる 5 m: に分ける点 : m m 図形への応用
線形システム応答 Linear System response
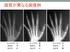 画質が異なる画像例 コントラスト劣 コントラスト優 コントラスト普 鮮鋭性 普 鮮鋭性 優 鮮鋭性 劣 粒状性 普 粒状性 劣 粒状性 優 医用画像の画質 コントラスト, 鮮鋭性, 粒状性の要因が互いに密接に関わり合って形成されている. 比 鮮鋭性 コントラスト 反 反 粒状性 増感紙 - フィルム系での 3 要因の関係 ディジタル画像処理系でもおよそ成り立つ WS u MTFu 画質に影響する因子
画質が異なる画像例 コントラスト劣 コントラスト優 コントラスト普 鮮鋭性 普 鮮鋭性 優 鮮鋭性 劣 粒状性 普 粒状性 劣 粒状性 優 医用画像の画質 コントラスト, 鮮鋭性, 粒状性の要因が互いに密接に関わり合って形成されている. 比 鮮鋭性 コントラスト 反 反 粒状性 増感紙 - フィルム系での 3 要因の関係 ディジタル画像処理系でもおよそ成り立つ WS u MTFu 画質に影響する因子
点におけるひずみの定義 ( その1)-(ε, ε,γ ) の定義ひずみは 構造物の中で変化しているのが一般的である このために 応力と同様に 構造物内の任意の点で定義できるようにした方がよい また 応力と同様に 一つの点に注目しても ひずみは向きによって値が異なる これらを勘案し あ
 3. 変位とひずみ 3.1 変位関数構造物は外力の作用の下で変形する いま この変形により構造物内の任意の点 P(,,z) が P (',',z') に移動したものとする ( 図 3.1 参照 ) (,,z) は変形前の点 Pの座標 (',', z') は変形後の座標である このとき 次式で示される変形前後の座標の差 u ='- u ='- u z =z'-z (3.1) を変位成分と呼ぶ 変位 (
3. 変位とひずみ 3.1 変位関数構造物は外力の作用の下で変形する いま この変形により構造物内の任意の点 P(,,z) が P (',',z') に移動したものとする ( 図 3.1 参照 ) (,,z) は変形前の点 Pの座標 (',', z') は変形後の座標である このとき 次式で示される変形前後の座標の差 u ='- u ='- u z =z'-z (3.1) を変位成分と呼ぶ 変位 (
パソコンシミュレータの現状
 第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
<4D F736F F D20824F B CC92E8979D814696CA90CF95AA82C691CC90CF95AA2E646F63>
 1/1 平成 23 年 3 月 24 日午後 6 時 52 分 6 ガウスの定理 : 面積分と体積分 6 ガウスの定理 : 面積分と体積分 Ⅰ. 直交座標系 ガウスの定理は 微分して すぐに積分すると元に戻るというルールを 3 次元積分に適用した定理になります よく知っているのは 簡単化のため 変数が1つの場合は dj ( d ( ににします全微分 = 偏微分 d = d = J ( + C d です
1/1 平成 23 年 3 月 24 日午後 6 時 52 分 6 ガウスの定理 : 面積分と体積分 6 ガウスの定理 : 面積分と体積分 Ⅰ. 直交座標系 ガウスの定理は 微分して すぐに積分すると元に戻るというルールを 3 次元積分に適用した定理になります よく知っているのは 簡単化のため 変数が1つの場合は dj ( d ( ににします全微分 = 偏微分 d = d = J ( + C d です
<4D F736F F D A CF95AA B B82CC90CF95AA8CF68EAE2E646F63>
 /8 平成 年 月 日午後 時 6 分 複素積分 : コーシーの積分公式 複素積分 : コーシーの積分公式 Ⅰ. 閉じた積分経路と円周 積分しなくても線積分の結果が分かる場合の第 弾です それは ( ( π d は正則関数 d! d 積分経路は を囲む (. になります これを コーシーの積分公式といいます 複素積分 : コーシーの積分定理 -Ⅰ. 線積分の実技での線積分では 半径 r の円 周上の閉じた経路
/8 平成 年 月 日午後 時 6 分 複素積分 : コーシーの積分公式 複素積分 : コーシーの積分公式 Ⅰ. 閉じた積分経路と円周 積分しなくても線積分の結果が分かる場合の第 弾です それは ( ( π d は正則関数 d! d 積分経路は を囲む (. になります これを コーシーの積分公式といいます 複素積分 : コーシーの積分定理 -Ⅰ. 線積分の実技での線積分では 半径 r の円 周上の閉じた経路
2014年度 千葉大・医系数学
 04 千葉大学 ( 医系 ) 前期日程問題 解答解説のページへ 袋の中に, 赤玉が 3 個, 白玉が 7 個が入っている 袋から玉を無作為に つ取り出し, 色を確認してから, 再び袋に戻すという試行を行う この試行を N 回繰り返したときに, 赤玉を A 回 ( ただし 0 A N) 取り出す確率を p( N, A) とする このとき, 以下の問いに答えよ () 確率 p( N, A) を N と
04 千葉大学 ( 医系 ) 前期日程問題 解答解説のページへ 袋の中に, 赤玉が 3 個, 白玉が 7 個が入っている 袋から玉を無作為に つ取り出し, 色を確認してから, 再び袋に戻すという試行を行う この試行を N 回繰り返したときに, 赤玉を A 回 ( ただし 0 A N) 取り出す確率を p( N, A) とする このとき, 以下の問いに答えよ () 確率 p( N, A) を N と
Microsoft PowerPoint - Robotics_13_review_1short.pptx
 東北文化学園大学 科学技術学部知能情報システム学科 費 仙鳳 ロボットの概要 数学的基礎 座標変換 同次変換 オイラー角 ロールピッチヨウ角 座標系設定 リンクパラメータ 腕型ロボットの構造 腕型ロボットの順運動学 腕型ロボットの逆運動学 腕型ロボットのヤコビアン 速度 特異姿勢 1 2 3 4 1 三角関数 ベクトルと行列 並進変換と回転変換 同次変換行列の導入 オイラー角 (Z-Y-Z) ロール
東北文化学園大学 科学技術学部知能情報システム学科 費 仙鳳 ロボットの概要 数学的基礎 座標変換 同次変換 オイラー角 ロールピッチヨウ角 座標系設定 リンクパラメータ 腕型ロボットの構造 腕型ロボットの順運動学 腕型ロボットの逆運動学 腕型ロボットのヤコビアン 速度 特異姿勢 1 2 3 4 1 三角関数 ベクトルと行列 並進変換と回転変換 同次変換行列の導入 オイラー角 (Z-Y-Z) ロール
p tn tn したがって, 点 の 座標は p p tn tn tn また, 直線 l と直線 p の交点 の 座標は p p tn p tn よって, 点 の座標 (, ) は p p, tn tn と表され p 4p p 4p 4p tn tn tn より, 点 は放物線 4 p 上を動くこと
 567_ 次曲線の三角関数による媒介変数表示 次曲線の三角関数による媒介変数表示 次曲線 ( 放物線 楕円 双曲線 ) の標準形の, についての方程式と, 三角関数による媒介変数表示は次のように対応している.. 放物線 () 4 p (, ) ( ptn, ptn ) (). 楕円. 双曲線 () () (, p p ), tn tn (, ) ( cos, sin ) (, ), tn cos (,
567_ 次曲線の三角関数による媒介変数表示 次曲線の三角関数による媒介変数表示 次曲線 ( 放物線 楕円 双曲線 ) の標準形の, についての方程式と, 三角関数による媒介変数表示は次のように対応している.. 放物線 () 4 p (, ) ( ptn, ptn ) (). 楕円. 双曲線 () () (, p p ), tn tn (, ) ( cos, sin ) (, ), tn cos (,
例題1 転がり摩擦
 重心 5.. 重心問題解法虎の巻. 半円 分円. 円弧. 扇形. 半球殻 5. 半球体 6. 厚みのある半球殻 7. 三角形 8. 円錐 9. 円錐台. 穴あき板. 空洞のある半球ボール 重心問題解法虎の巻 関西大学工学部物理学教室 齊藤正 重心を求める場合 質点系の重心の求め方が基本 実際の物体では連続体であるので 積分形式で求める場合が多い これらの式は 次元のベクトル形式で書かれている通り つの式は実際には
重心 5.. 重心問題解法虎の巻. 半円 分円. 円弧. 扇形. 半球殻 5. 半球体 6. 厚みのある半球殻 7. 三角形 8. 円錐 9. 円錐台. 穴あき板. 空洞のある半球ボール 重心問題解法虎の巻 関西大学工学部物理学教室 齊藤正 重心を求める場合 質点系の重心の求め方が基本 実際の物体では連続体であるので 積分形式で求める場合が多い これらの式は 次元のベクトル形式で書かれている通り つの式は実際には
PowerPoint プレゼンテーション
 空間フィルタリング (spatal lterng) 入力画像の対応する画素値だけではなく その周囲 ( 近傍領域 ) の画素も含めた領域内の画素値を用いて 出力画像の対応する画素値を計算する処理 入力画像出力画像入力画像出力画像 画素ごとの濃淡変換 ( 階調処理 ) 領域に基づく濃淡変換 ( 空間フィルタリング ) 空間フィルタ (spatal lter) 線形フィルタ (lnear lter) w
空間フィルタリング (spatal lterng) 入力画像の対応する画素値だけではなく その周囲 ( 近傍領域 ) の画素も含めた領域内の画素値を用いて 出力画像の対応する画素値を計算する処理 入力画像出力画像入力画像出力画像 画素ごとの濃淡変換 ( 階調処理 ) 領域に基づく濃淡変換 ( 空間フィルタリング ) 空間フィルタ (spatal lter) 線形フィルタ (lnear lter) w
Microsoft PowerPoint - zairiki_3
 材料力学講義 (3) 応力と変形 Ⅲ ( 曲げモーメント, 垂直応力度, 曲率 ) 今回は, 曲げモーメントに関する, 断面力 - 応力度 - 変形 - 変位の関係について学びます 1 曲げモーメント 曲げモーメント M 静定力学で求めた曲げモーメントも, 仮想的に断面を切ることによって現れる内力です 軸方向力は断面に働く力 曲げモーメント M は断面力 曲げモーメントも, 一つのモーメントとして表しますが,
材料力学講義 (3) 応力と変形 Ⅲ ( 曲げモーメント, 垂直応力度, 曲率 ) 今回は, 曲げモーメントに関する, 断面力 - 応力度 - 変形 - 変位の関係について学びます 1 曲げモーメント 曲げモーメント M 静定力学で求めた曲げモーメントも, 仮想的に断面を切ることによって現れる内力です 軸方向力は断面に働く力 曲げモーメント M は断面力 曲げモーメントも, 一つのモーメントとして表しますが,
PowerPoint プレゼンテーション
 電磁波工学 第 5 回平面波の媒質への垂直および射入射と透過 柴田幸司 Bounda Plan Rgon ε μ Rgon Mdum ( ガラスなど ε μ z 平面波の反射と透過 垂直入射の場合 左図に示す様に 平面波が境界面に対して垂直に入射する場合を考える この時の入射波を とすると 入射波は境界において 透過波 と とに分解される この時の透過量を 反射量を Γ とおくと 領域 における媒質の誘電率に対して透過量
電磁波工学 第 5 回平面波の媒質への垂直および射入射と透過 柴田幸司 Bounda Plan Rgon ε μ Rgon Mdum ( ガラスなど ε μ z 平面波の反射と透過 垂直入射の場合 左図に示す様に 平面波が境界面に対して垂直に入射する場合を考える この時の入射波を とすると 入射波は境界において 透過波 と とに分解される この時の透過量を 反射量を Γ とおくと 領域 における媒質の誘電率に対して透過量
<4D F736F F D20824F F6490CF95AA82C696CA90CF95AA2E646F63>
 1/15 平成 3 年 3 月 4 日午後 6 時 49 分 5 ベクトルの 重積分と面積分 5 重積分と面積分 Ⅰ. 重積分 と で 回積分することを 重積分 といいます この 重積分は何を意味しているのでしょう? 通常の積分 (1 重積分 ) では C d 図 1a 1 f d (5.1) 1 f d f ( ) は 図形的には図 1a のように面積を表しています つまり 1 f ( ) を高さとしてプロットすると図
1/15 平成 3 年 3 月 4 日午後 6 時 49 分 5 ベクトルの 重積分と面積分 5 重積分と面積分 Ⅰ. 重積分 と で 回積分することを 重積分 といいます この 重積分は何を意味しているのでしょう? 通常の積分 (1 重積分 ) では C d 図 1a 1 f d (5.1) 1 f d f ( ) は 図形的には図 1a のように面積を表しています つまり 1 f ( ) を高さとしてプロットすると図
2 Hermite-Gaussian モード 2-1 Hermite-Gaussian モード 自由空間を伝搬するレーザ光は次のような Hermite-gaussian Modes を持つ光波として扱う ことができる ここで U lm (x, y, z) U l (x, z)u m (y, z) e
 Wavefront Sensor 法による三角共振器のミスアラインメント検出 齊藤高大 新潟大学大学院自然科学研究科電気情報工学専攻博士後期課程 2 年 214 年 8 月 6 日 1 はじめに Input Mode Cleaner(IMC) は Fig.1 に示すような三角共振器である 懸架鏡の共振などにより IMC を構成する各ミラーが角度変化を起こすと 入射光軸と共振器軸との間にずれが生じる
Wavefront Sensor 法による三角共振器のミスアラインメント検出 齊藤高大 新潟大学大学院自然科学研究科電気情報工学専攻博士後期課程 2 年 214 年 8 月 6 日 1 はじめに Input Mode Cleaner(IMC) は Fig.1 に示すような三角共振器である 懸架鏡の共振などにより IMC を構成する各ミラーが角度変化を起こすと 入射光軸と共振器軸との間にずれが生じる
Microsoft PowerPoint - 物情数学C(2012)(フーリエ前半)_up
 年度物理情報工学科 年生秋学期 物理情報数学 C フーリエ解析 (Fourier lysis) 年 月 5 日 フーリエ ( フランス ) (768~83: ナポレオンの時代 ) 歳で Ecole Polyechique ( フランス国立理工科大学 ) の教授 ナポレオンのエジプト遠征に従軍 (798) 87: 任意の関数は三角関数によって級数展開できる という フーリエ級数 の概念を提唱 ( 論文を提出
年度物理情報工学科 年生秋学期 物理情報数学 C フーリエ解析 (Fourier lysis) 年 月 5 日 フーリエ ( フランス ) (768~83: ナポレオンの時代 ) 歳で Ecole Polyechique ( フランス国立理工科大学 ) の教授 ナポレオンのエジプト遠征に従軍 (798) 87: 任意の関数は三角関数によって級数展開できる という フーリエ級数 の概念を提唱 ( 論文を提出
応用数学A
 応用数学 A 米田 戸倉川月 7 限 1930~2100 西 5-109 V を :x 2 + y 2 + z 2 = 4 で囲まれる内部とする F = ye x xe y + ze z FdV = V e x e y e z F = = 2e z 2e z dv = 2e z 3 23 = 64π 3 e z y x z 4π V n Fd = 1 F nd 2 F nd 法線ベクトル n g x,
応用数学 A 米田 戸倉川月 7 限 1930~2100 西 5-109 V を :x 2 + y 2 + z 2 = 4 で囲まれる内部とする F = ye x xe y + ze z FdV = V e x e y e z F = = 2e z 2e z dv = 2e z 3 23 = 64π 3 e z y x z 4π V n Fd = 1 F nd 2 F nd 法線ベクトル n g x,
学習指導要領
 (1) いろいろな式 学習指導要領紅葉川高校学力スタンダードア式と証明展開の公式を用いて 3 乗に関わる式を展開すること ( ア ) 整式の乗法 除法 分数式の計算ができるようにする 三次の乗法公式及び因数分解の公式を理解し そ 3 次の因数分解の公式を理解し それらを用いて因数れらを用いて式の展開や因数分解をすること また 分解することができるようにする 整式の除法や分数式の四則計算について理解し
(1) いろいろな式 学習指導要領紅葉川高校学力スタンダードア式と証明展開の公式を用いて 3 乗に関わる式を展開すること ( ア ) 整式の乗法 除法 分数式の計算ができるようにする 三次の乗法公式及び因数分解の公式を理解し そ 3 次の因数分解の公式を理解し それらを用いて因数れらを用いて式の展開や因数分解をすること また 分解することができるようにする 整式の除法や分数式の四則計算について理解し
DVIOUT
 3 第 2 章フーリエ級数 23 フーリエ級数展開 これまで 関数 f(x) のフーリエ級数展開に関して 関数の定義区間やフーリエ級数の積分区間を断りなく [, ] に取ってきました これは フーリエ級数を構成する三角関数が基本周期 2 を持つためです すなわち フーリエ級数の各項 cos nx および sin nx (n =1, 2, 3, 4, ) の周期は それぞれ 2, 2 2, 2 3,
3 第 2 章フーリエ級数 23 フーリエ級数展開 これまで 関数 f(x) のフーリエ級数展開に関して 関数の定義区間やフーリエ級数の積分区間を断りなく [, ] に取ってきました これは フーリエ級数を構成する三角関数が基本周期 2 を持つためです すなわち フーリエ級数の各項 cos nx および sin nx (n =1, 2, 3, 4, ) の周期は それぞれ 2, 2 2, 2 3,
2018年度 筑波大・理系数学
 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ < < とする 放物線 上に 点 (, ), A (ta, ta ), B( - ta, ta ) をとる 三角形 AB の内心の 座標を p とし, 外心の 座標を q とする また, 正の実数 a に対して, 直線 a と放物線 で囲まれた図形の面積を S( a) で表す () p, q を cos を用いて表せ S( p) () S(
筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ < < とする 放物線 上に 点 (, ), A (ta, ta ), B( - ta, ta ) をとる 三角形 AB の内心の 座標を p とし, 外心の 座標を q とする また, 正の実数 a に対して, 直線 a と放物線 で囲まれた図形の面積を S( a) で表す () p, q を cos を用いて表せ S( p) () S(
構造力学Ⅰ第12回
 第 回材の座屈 (0 章 ) p.5~ ( 復習 ) モールの定理 ( 手順 ) 座屈とは 荷重により梁に生じた曲げモーメントをで除して仮想荷重と考える 座屈荷重 偏心荷重 ( 曲げと軸力 ) 断面の核 この仮想荷重に対するある点でのせん断力 たわみ角に相当する曲げモーメント たわみに相当する ( 例 ) 単純梁の支点のたわみ角 : は 図 を仮想荷重と考えたときの 点の支点反力 B は 図 を仮想荷重と考えたときのB
第 回材の座屈 (0 章 ) p.5~ ( 復習 ) モールの定理 ( 手順 ) 座屈とは 荷重により梁に生じた曲げモーメントをで除して仮想荷重と考える 座屈荷重 偏心荷重 ( 曲げと軸力 ) 断面の核 この仮想荷重に対するある点でのせん断力 たわみ角に相当する曲げモーメント たわみに相当する ( 例 ) 単純梁の支点のたわみ角 : は 図 を仮想荷重と考えたときの 点の支点反力 B は 図 を仮想荷重と考えたときのB
重要例題113
 04_ 高校 数学 Ⅱ 必須基本公式 定理集 数学 Ⅱ 第 章式の計算と方程式 0 商と余り についての整式 A をについての整式 B で割ったときの商を Q, 余りを R とすると, ABQ+R (R の次数 ) > 0
04_ 高校 数学 Ⅱ 必須基本公式 定理集 数学 Ⅱ 第 章式の計算と方程式 0 商と余り についての整式 A をについての整式 B で割ったときの商を Q, 余りを R とすると, ABQ+R (R の次数 ) > 0
Microsoft PowerPoint - DigitalMedia2_3b.pptx
 Contents デジタルメディア処理 2 の概要 フーリエ級数展開と 離散とその性質 周波数フィルタリング 担当 : 井尻敬 とは ( ) FourierSound.py とは ( ) FourierSound.py 横軸が時間の関数を 横軸が周波数の関数に変換する 法 声周波数 周波数 ( 係数番号 ) 後の関数は元信号に含まれる正弦波の量を す 中央に近いほど低周波, 外ほどが 周波 中央 (
Contents デジタルメディア処理 2 の概要 フーリエ級数展開と 離散とその性質 周波数フィルタリング 担当 : 井尻敬 とは ( ) FourierSound.py とは ( ) FourierSound.py 横軸が時間の関数を 横軸が周波数の関数に変換する 法 声周波数 周波数 ( 係数番号 ) 後の関数は元信号に含まれる正弦波の量を す 中央に近いほど低周波, 外ほどが 周波 中央 (
画像類似度測定の初歩的な手法の検証
 画像類似度測定の初歩的な手法の検証 島根大学総合理工学部数理 情報システム学科 計算機科学講座田中研究室 S539 森瀧昌志 1 目次 第 1 章序論第 章画像間類似度測定の初歩的な手法について.1 A. 画素値の平均を用いる手法.. 画素値のヒストグラムを用いる手法.3 C. 相関係数を用いる手法.4 D. 解像度を合わせる手法.5 E. 振れ幅のヒストグラムを用いる手法.6 F. 周波数ごとの振れ幅を比較する手法第
画像類似度測定の初歩的な手法の検証 島根大学総合理工学部数理 情報システム学科 計算機科学講座田中研究室 S539 森瀧昌志 1 目次 第 1 章序論第 章画像間類似度測定の初歩的な手法について.1 A. 画素値の平均を用いる手法.. 画素値のヒストグラムを用いる手法.3 C. 相関係数を用いる手法.4 D. 解像度を合わせる手法.5 E. 振れ幅のヒストグラムを用いる手法.6 F. 周波数ごとの振れ幅を比較する手法第
2018年度 神戸大・理系数学
 8 神戸大学 ( 理系 ) 前期日程問題 解答解説のページへ t を < t < を満たす実数とする OABC を 辺の長さが の正四面体とする 辺 OA を -t : tに内分する点を P, 辺 OB を t :-tに内分する点を Q, 辺 BC の中点を R とする また a = OA, b = OB, c = OC とする 以下の問いに答えよ () QP と QR をt, a, b, c を用いて表せ
8 神戸大学 ( 理系 ) 前期日程問題 解答解説のページへ t を < t < を満たす実数とする OABC を 辺の長さが の正四面体とする 辺 OA を -t : tに内分する点を P, 辺 OB を t :-tに内分する点を Q, 辺 BC の中点を R とする また a = OA, b = OB, c = OC とする 以下の問いに答えよ () QP と QR をt, a, b, c を用いて表せ
HPC pdf
 GPU 1 1 2 2 1 1024 3 GPUGraphics Unit1024 3 GPU GPU GPU GPU 1024 3 Tesla S1070-400 1 GPU 2.6 Accelerating Out-of-core Cone Beam Reconstruction Using GPU Yusuke Okitsu, 1 Fumihiko Ino, 1 Taketo Kishi, 2
GPU 1 1 2 2 1 1024 3 GPUGraphics Unit1024 3 GPU GPU GPU GPU 1024 3 Tesla S1070-400 1 GPU 2.6 Accelerating Out-of-core Cone Beam Reconstruction Using GPU Yusuke Okitsu, 1 Fumihiko Ino, 1 Taketo Kishi, 2
Math-Aquarium 例題 図形と計量 図形と計量 1 直角三角形と三角比 P 木の先端を P, 根元を Q とする A 地点の目の位置 A' から 木の先端への仰角が 30,A から 7m 離れた AQB=90 と なる B 地点の目の位置 B' から木の先端への仰角が 45 であ るとき,
 図形と計量 直角三角形と三角比 P 木の先端を P, 根元を Q とする 地点の目の位置 ' から 木の先端への仰角が 0, から 7m 離れた Q=90 と なる 地点の目の位置 ' から木の先端への仰角が であ るとき, 木の高さを求めよ ただし, 目の高さを.m とし, Q' を右の図のように定める ' 0 Q' '.m Q 7m 要点 PQ PQ PQ' =x とおき,' Q',' Q' を
図形と計量 直角三角形と三角比 P 木の先端を P, 根元を Q とする 地点の目の位置 ' から 木の先端への仰角が 0, から 7m 離れた Q=90 と なる 地点の目の位置 ' から木の先端への仰角が であ るとき, 木の高さを求めよ ただし, 目の高さを.m とし, Q' を右の図のように定める ' 0 Q' '.m Q 7m 要点 PQ PQ PQ' =x とおき,' Q',' Q' を
2014年度 名古屋大・理系数学
 04 名古屋大学 ( 理系 ) 前期日程問題 解答解説のページへ空間内にある半径 の球 ( 内部を含む ) を B とする 直線 と B が交わっており, その交わりは長さ の線分である () B の中心と との距離を求めよ () のまわりに B を 回転してできる立体の体積を求めよ 04 名古屋大学 ( 理系 ) 前期日程問題 解答解説のページへ 実数 t に対して 点 P( t, t ), Q(
04 名古屋大学 ( 理系 ) 前期日程問題 解答解説のページへ空間内にある半径 の球 ( 内部を含む ) を B とする 直線 と B が交わっており, その交わりは長さ の線分である () B の中心と との距離を求めよ () のまわりに B を 回転してできる立体の体積を求めよ 04 名古屋大学 ( 理系 ) 前期日程問題 解答解説のページへ 実数 t に対して 点 P( t, t ), Q(
Microsoft PowerPoint - 10.pptx
 m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
座標系.rtf
 2 章座標系 場 空間は3 次元なので, ベクトルを表現するには少なくとも3 成分を指定する必要がある. そのために座標系が必要となる. 座標系として最も一般的なものは,,, 成分を使った直角座標系である. しかし, 他にも円柱座標, 球座標, だ円座標, 放物線座標など様々なものがある. 現在までに3 成分で変数分離可能な座標系は11 個あるといわれている (Moon & Spencer, Field
2 章座標系 場 空間は3 次元なので, ベクトルを表現するには少なくとも3 成分を指定する必要がある. そのために座標系が必要となる. 座標系として最も一般的なものは,,, 成分を使った直角座標系である. しかし, 他にも円柱座標, 球座標, だ円座標, 放物線座標など様々なものがある. 現在までに3 成分で変数分離可能な座標系は11 個あるといわれている (Moon & Spencer, Field
2015-2017年度 2次数学セレクション(複素数)解答解説
 05 次数学セレクション解答解説 [ 筑波大 ] ( + より, 0 となり, + から, ( (,, よって, の描く図形 C は, 点 を中心とし半径が の円である すなわち, 原 点を通る円となる ( は虚数, は正の実数より, である さて, w ( ( とおくと, ( ( ( w ( ( ( ここで, w は純虚数より, は純虚数となる すると, の描く図形 L は, 点 を通り, 点 と点
05 次数学セレクション解答解説 [ 筑波大 ] ( + より, 0 となり, + から, ( (,, よって, の描く図形 C は, 点 を中心とし半径が の円である すなわち, 原 点を通る円となる ( は虚数, は正の実数より, である さて, w ( ( とおくと, ( ( ( w ( ( ( ここで, w は純虚数より, は純虚数となる すると, の描く図形 L は, 点 を通り, 点 と点
平成 年 月 7 日 ( 土 第 75 回数学教育実践研究会アスティ 45 ビル F セミナールーム A 札幌医科大学 年 P ab, を正の定数とする 平面上において ( a, を中心とする円 Q 4 C と (, b を中心とする円 C が 原点 O で外接している また P を円 C 上の点と
 平成 年 月 7 日 ( 土 第 75 回数学教育実践研究会アスティ 45 ビル F セミナールーム 微分積分の拡張 変数関数問題へのアプローチ 予選決勝優勝法からラグランジュ未定乗数法 松本睦郎 ( 札幌北高等学校 変数関数の最大値 最小値に関する問題には多様なアプローチ法がある 文字を固定した 予選決勝優勝法, 計算のみで解法する 文字消去法, 微分積分を利用した ラグランジュ未定乗数法 がある
平成 年 月 7 日 ( 土 第 75 回数学教育実践研究会アスティ 45 ビル F セミナールーム 微分積分の拡張 変数関数問題へのアプローチ 予選決勝優勝法からラグランジュ未定乗数法 松本睦郎 ( 札幌北高等学校 変数関数の最大値 最小値に関する問題には多様なアプローチ法がある 文字を固定した 予選決勝優勝法, 計算のみで解法する 文字消去法, 微分積分を利用した ラグランジュ未定乗数法 がある
<4D F736F F F696E74202D20836F CC8A C58B858B4F93B982A882E682D1978E89BA814091B28BC68CA48B E >
 バットの角度 打球軌道および落下地点の関係 T999 和田真迪 担当教員 飯田晋司 目次 1. はじめに. ボールとバットの衝突 -1 座標系 -ボールとバットの衝突の前後でのボールの速度 3. ボールの軌道の計算 4. おわりに参考文献 はじめに この研究テーマにした理由は 好きな野球での小さい頃からの疑問であるバッテングについて 角度が変わればどう打球に変化が起こるのかが大学で学んだ物理と数学んだ物理と数学を使って判明できると思ったから
バットの角度 打球軌道および落下地点の関係 T999 和田真迪 担当教員 飯田晋司 目次 1. はじめに. ボールとバットの衝突 -1 座標系 -ボールとバットの衝突の前後でのボールの速度 3. ボールの軌道の計算 4. おわりに参考文献 はじめに この研究テーマにした理由は 好きな野球での小さい頃からの疑問であるバッテングについて 角度が変わればどう打球に変化が起こるのかが大学で学んだ物理と数学んだ物理と数学を使って判明できると思ったから
2 図微小要素の流体の流入出 方向の断面の流体の流入出の収支断面 Ⅰ から微小要素に流入出する流体の流量 Q 断面 Ⅰ は 以下のように定式化できる Q 断面 Ⅰ 流量 密度 流速 断面 Ⅰ の面積 微小要素の断面 Ⅰ から だけ移動した断面 Ⅱ を流入出する流体の流量 Q 断面 Ⅱ は以下のように
 3 章 Web に Link 解説 連続式 微分表示 の誘導.64 *4. 連続式連続式は ある領域の内部にある流体の質量の収支が その表面からの流入出の合計と等しくなることを定式化したものであり 流体における質量保存則を示したものである 2. 連続式 微分表示 の誘導図のような微小要素 コントロールボリューム の領域内の流体の増減と外部からの流体の流入出を考えることで定式化できる 微小要素 流入
3 章 Web に Link 解説 連続式 微分表示 の誘導.64 *4. 連続式連続式は ある領域の内部にある流体の質量の収支が その表面からの流入出の合計と等しくなることを定式化したものであり 流体における質量保存則を示したものである 2. 連続式 微分表示 の誘導図のような微小要素 コントロールボリューム の領域内の流体の増減と外部からの流体の流入出を考えることで定式化できる 微小要素 流入
2017年度 長崎大・医系数学
 07 長崎大学 ( 医系 ) 前期日程問題 解答解説のページへ 以下の問いに答えよ () 0 のとき, si + cos の最大値と最小値, およびそのときの の値 をそれぞれ求めよ () e を自然対数の底とする > eの範囲において, 関数 y を考える この両 辺の対数を について微分することにより, y は減少関数であることを示せ また, e< < bのとき, () 数列 { } b の一般項が,
07 長崎大学 ( 医系 ) 前期日程問題 解答解説のページへ 以下の問いに答えよ () 0 のとき, si + cos の最大値と最小値, およびそのときの の値 をそれぞれ求めよ () e を自然対数の底とする > eの範囲において, 関数 y を考える この両 辺の対数を について微分することにより, y は減少関数であることを示せ また, e< < bのとき, () 数列 { } b の一般項が,
相対性理論入門 1 Lorentz 変換 光がどのような座標系に対しても同一の速さ c で進むことから導かれる座標の一次変換である. (x, y, z, t ) の座標系が (x, y, z, t) の座標系に対して x 軸方向に w の速度で進んでいる場合, 座標系が一次変換で関係づけられるとする
 相対性理論入門 Lorentz 変換 光がどのような座標系に対しても同一の速さ で進むことから導かれる座標の一次変換である. x, y, z, t ) の座標系が x, y, z, t) の座標系に対して x 軸方向に w の速度で進んでいる場合, 座標系が一次変換で関係づけられるとすると, x A x wt) y y z z t Bx + Dt 弨弱弩弨弲弩弨弳弩弨弴弩 が成立する. 図 : 相対速度
相対性理論入門 Lorentz 変換 光がどのような座標系に対しても同一の速さ で進むことから導かれる座標の一次変換である. x, y, z, t ) の座標系が x, y, z, t) の座標系に対して x 軸方向に w の速度で進んでいる場合, 座標系が一次変換で関係づけられるとすると, x A x wt) y y z z t Bx + Dt 弨弱弩弨弲弩弨弳弩弨弴弩 が成立する. 図 : 相対速度
<4D F736F F D F385F322089E6919C8DC48D5C90AC82CC8AEE B92808E9F8BDF8E CC8CB4979D815B>
 画像再構成の基礎 - 逐次近似法の原理 - Basic of Image Reconstruction -Fundamentals of iterative method- 首都大学東京篠原広行 Shinohara Hiroyuki はじめに解析的画像再構成法のフィルタ補正逆投影法 (FBP 法 ) の特徴は, 回の計算で解 ( 再構成像 ) が求まることである. 一方, 反復計算によって解を求める画像再構成法は逐次近似法と呼ばれる.
画像再構成の基礎 - 逐次近似法の原理 - Basic of Image Reconstruction -Fundamentals of iterative method- 首都大学東京篠原広行 Shinohara Hiroyuki はじめに解析的画像再構成法のフィルタ補正逆投影法 (FBP 法 ) の特徴は, 回の計算で解 ( 再構成像 ) が求まることである. 一方, 反復計算によって解を求める画像再構成法は逐次近似法と呼ばれる.
Microsoft PowerPoint - 第5回電磁気学I
 1 年 11 月 8 日 ( 月 ) 1:-1: Y 平成 年度工 系 ( 社会環境工学科 ) 第 5 回電磁気学 Ⅰ 天野浩 項目 電界と電束密度 ガウスの発散定理とガウスの法則の積分形と微分形 * ファラデーの電気力線の使い方をマスターします * 電界と電束密度を定義します * ガウスの発散定理を用いて ガウスの法則の積分形から微分形をガウスの法則の積分形から微分形を導出します * ガウスの法則を用いて
1 年 11 月 8 日 ( 月 ) 1:-1: Y 平成 年度工 系 ( 社会環境工学科 ) 第 5 回電磁気学 Ⅰ 天野浩 項目 電界と電束密度 ガウスの発散定理とガウスの法則の積分形と微分形 * ファラデーの電気力線の使い方をマスターします * 電界と電束密度を定義します * ガウスの発散定理を用いて ガウスの法則の積分形から微分形をガウスの法則の積分形から微分形を導出します * ガウスの法則を用いて
Microsoft Word - 断面諸量
 応用力学 Ⅱ 講義資料 / 断面諸量 断面諸量 断面 次 次モーメントの定義 図 - に示すような形状を有する横断面を考え その全断面積を とする いま任意に定めた直交座標軸 O-, をとり また図中の斜線部の微小面積要素を d とするとき d, d () で定義される, をそれぞれ与えられた横断面の 軸, 軸に関する断面 次モーメント (geometrcal moment of area) という
応用力学 Ⅱ 講義資料 / 断面諸量 断面諸量 断面 次 次モーメントの定義 図 - に示すような形状を有する横断面を考え その全断面積を とする いま任意に定めた直交座標軸 O-, をとり また図中の斜線部の微小面積要素を d とするとき d, d () で定義される, をそれぞれ与えられた横断面の 軸, 軸に関する断面 次モーメント (geometrcal moment of area) という
2013年度 九州大・理系数学
 九州大学 ( 理系 ) 前期日程問題 解答解説のページへ a> とし, つの曲線 y= ( ), y= a ( > ) を順にC, C とする また, C とC の交点 P におけるC の接線をl とする 以下 の問いに答えよ () 曲線 C とy 軸および直線 l で囲まれた部分の面積をa を用いて表せ () 点 P におけるC の接線と直線 l のなす角を ( a) とき, limasin θ(
九州大学 ( 理系 ) 前期日程問題 解答解説のページへ a> とし, つの曲線 y= ( ), y= a ( > ) を順にC, C とする また, C とC の交点 P におけるC の接線をl とする 以下 の問いに答えよ () 曲線 C とy 軸および直線 l で囲まれた部分の面積をa を用いて表せ () 点 P におけるC の接線と直線 l のなす角を ( a) とき, limasin θ(
線形代数とは
 線形代数とは 第一回ベクトル 教科書 エクササイズ線形代数 立花俊一 成田清正著 共立出版 必要最低限のことに限る 得意な人には物足りないかもしれません 線形代数とは何をするもの? 線形関係 y 直線 yもも 次式で登場する (( 次の形 ) 線形 ただし 次元の話世の中は 3 次元 [4[ 次元 ] 次元 3 次元 4 次元 はどうやって直線を表すの? ベクトルや行列の概念 y A ベクトルを使うと
線形代数とは 第一回ベクトル 教科書 エクササイズ線形代数 立花俊一 成田清正著 共立出版 必要最低限のことに限る 得意な人には物足りないかもしれません 線形代数とは何をするもの? 線形関係 y 直線 yもも 次式で登場する (( 次の形 ) 線形 ただし 次元の話世の中は 3 次元 [4[ 次元 ] 次元 3 次元 4 次元 はどうやって直線を表すの? ベクトルや行列の概念 y A ベクトルを使うと
数学 ⅡB < 公理 > 公理を論拠に定義を用いて定理を証明する 1 大小関係の公理 順序 (a > b, a = b, a > b 1 つ成立 a > b, b > c a > c 成立 ) 順序と演算 (a > b a + c > b + c (a > b, c > 0 ac > bc) 2 図
 数学 Ⅱ < 公理 > 公理を論拠に定義を用いて定理を証明する 大小関係の公理 順序 >, =, > つ成立 >, > > 成立 順序と演算 > + > + >, > > 図形の公理 平行線の性質 錯角 同位角 三角形の合同条件 三角形の合同相似 量の公理 角の大きさ 線分の長さ < 空間における座漂とベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル
数学 Ⅱ < 公理 > 公理を論拠に定義を用いて定理を証明する 大小関係の公理 順序 >, =, > つ成立 >, > > 成立 順序と演算 > + > + >, > > 図形の公理 平行線の性質 錯角 同位角 三角形の合同条件 三角形の合同相似 量の公理 角の大きさ 線分の長さ < 空間における座漂とベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル
公式集 数学 Ⅱ B 頭に入っていますか? 8 和積の公式 A + B A B si A + si B si os A + B A B si A si B os si A + B A B os A + os B os os A + B A B os A os B si si 9 三角関数の合成 si
 公式集 数学 Ⅱ B 頭に入っていますか? < 図形と方程式 > 点間の距離 A x, B x, のとき x x + : に分ける点 A x, B x, のとき 線分 AB を:に分ける点 æ x + x + ö は ç, è + + ø 注 < のとき外分点 直線の方程式 傾き で 点 x, を通る : x 点 x, x, を通る : x 注 分母が のとき は座標軸と平行な直線 x x 4 直線の位置関係
公式集 数学 Ⅱ B 頭に入っていますか? < 図形と方程式 > 点間の距離 A x, B x, のとき x x + : に分ける点 A x, B x, のとき 線分 AB を:に分ける点 æ x + x + ö は ç, è + + ø 注 < のとき外分点 直線の方程式 傾き で 点 x, を通る : x 点 x, x, を通る : x 注 分母が のとき は座標軸と平行な直線 x x 4 直線の位置関係
2011年度 大阪大・理系数学
 0 大阪大学 ( 理系 ) 前期日程問題 解答解説のページへ a a を自然数とする O を原点とする座標平面上で行列 A= a の表す 次変換 を f とする cosθ siθ () >0 および0θ
0 大阪大学 ( 理系 ) 前期日程問題 解答解説のページへ a a を自然数とする O を原点とする座標平面上で行列 A= a の表す 次変換 を f とする cosθ siθ () >0 および0θ
座標軸以外の直線のまわりの回転体の体積 ( バウムクーヘン分割公式 ) の問題の解答 立体の体積の求め方 図 1 の立体の体積 V を求める方法を考えてみる 図 1 図 1 のように 軸の から までの長さを 等分する そして とおく とすると となる 図 1 のように のときの 軸に垂直な平面 に
 立体の体積の求め方 図 1 の立体の体積 V を求める方法を考えてみる 図 1 図 1 のように 軸の から までの長さを 等分する そして とおく とすると となる 図 1 のように のときの 軸に垂直な平面 による立体の断面積を とする 図 1の から までの斜線部分の立体 の体積を とすると, 図 2のように は 底面積 高さ の角柱の体積とみなせる よって 図 2 と表せる ただし とすると,
立体の体積の求め方 図 1 の立体の体積 V を求める方法を考えてみる 図 1 図 1 のように 軸の から までの長さを 等分する そして とおく とすると となる 図 1 のように のときの 軸に垂直な平面 による立体の断面積を とする 図 1の から までの斜線部分の立体 の体積を とすると, 図 2のように は 底面積 高さ の角柱の体積とみなせる よって 図 2 と表せる ただし とすると,
3-2 PET ( : CYRIC ) ( 0 ) (3-1 ) PET PET [min] 11 C 13 N 15 O 18 F 68 Ga [MeV] [mm] [MeV]
![3-2 PET ( : CYRIC ) ( 0 ) (3-1 ) PET PET [min] 11 C 13 N 15 O 18 F 68 Ga [MeV] [mm] [MeV] 3-2 PET ( : CYRIC ) ( 0 ) (3-1 ) PET PET [min] 11 C 13 N 15 O 18 F 68 Ga [MeV] [mm] [MeV]](/thumbs/91/106519999.jpg) 3 PET 3-1 PET 3-1-1 PET PET 1-1 X CT MRI(Magnetic Resonance Imaging) X CT MRI PET 3-1 PET [1] H1 D2 11 C-doxepin 11 C-raclopride PET H1 D2 3-2 PET 0 0 H1 D2 3-1 PET 3-2 PET ( : CYRIC ) ( 0 ) 3-1-2 (3-1
3 PET 3-1 PET 3-1-1 PET PET 1-1 X CT MRI(Magnetic Resonance Imaging) X CT MRI PET 3-1 PET [1] H1 D2 11 C-doxepin 11 C-raclopride PET H1 D2 3-2 PET 0 0 H1 D2 3-1 PET 3-2 PET ( : CYRIC ) ( 0 ) 3-1-2 (3-1
<4D F736F F D EBF97CD8A B7982D189898F4B A95748E9197BF4E6F31312E646F63>
 土質力学 Ⅰ 及び演習 (B 班 : 小高担当 ) 配付資料 N.11 (6.1.1) モールの応力円 (1) モールの応力円を使う上での3つの約束 1 垂直応力は圧縮を正とし, 軸の右側を正の方向とする 反時計まわりのモーメントを起こさせるせん断応力 の組を正とする 3 物体内で着目する面が,θ だけ回転すると, モールの応力円上では θ 回転する 1とは物理的な実際の作用面とモールの応力円上との回転の方向を一致させるために都合の良い約束である
土質力学 Ⅰ 及び演習 (B 班 : 小高担当 ) 配付資料 N.11 (6.1.1) モールの応力円 (1) モールの応力円を使う上での3つの約束 1 垂直応力は圧縮を正とし, 軸の右側を正の方向とする 反時計まわりのモーメントを起こさせるせん断応力 の組を正とする 3 物体内で着目する面が,θ だけ回転すると, モールの応力円上では θ 回転する 1とは物理的な実際の作用面とモールの応力円上との回転の方向を一致させるために都合の良い約束である
Microsoft Word - 卒業論文.doc
 006 年度卒業研究 画像補間法を用いた拡大画像の比較 岡山理科大学総合情報学部情報科学科 澤見研究室 I03I04 兼安俊治 I03I050 境永 目次 はじめに ラスタ画像 3 画像補間法 3. ニアレストネイバー法 3. バイリニア法 3.3 バイキュービック法 4 DCT を用いた拡大画像手法 5 FIR 法 6 評価 6. SNR 6. PSNR 7 実験 7. 主観評価 7. 客観評価
006 年度卒業研究 画像補間法を用いた拡大画像の比較 岡山理科大学総合情報学部情報科学科 澤見研究室 I03I04 兼安俊治 I03I050 境永 目次 はじめに ラスタ画像 3 画像補間法 3. ニアレストネイバー法 3. バイリニア法 3.3 バイキュービック法 4 DCT を用いた拡大画像手法 5 FIR 法 6 評価 6. SNR 6. PSNR 7 実験 7. 主観評価 7. 客観評価
コンピュータグラフィックス第8回
 コンピュータグラフィックス 第 8 回 レンダリング技法 1 ~ 基礎と概要, 隠面消去 ~ 理工学部 兼任講師藤堂英樹 レポート提出状況 課題 1 の選択が多い (STAND BY ME ドラえもん ) 体験演習型 ( 課題 3, 課題 4) の選択も多い 内訳 課題 1 課題 2 課題 3 課題 4 課題 5 2014/11/24 コンピュータグラフィックス 2 次回レポートの体験演習型 メタセコイア,
コンピュータグラフィックス 第 8 回 レンダリング技法 1 ~ 基礎と概要, 隠面消去 ~ 理工学部 兼任講師藤堂英樹 レポート提出状況 課題 1 の選択が多い (STAND BY ME ドラえもん ) 体験演習型 ( 課題 3, 課題 4) の選択も多い 内訳 課題 1 課題 2 課題 3 課題 4 課題 5 2014/11/24 コンピュータグラフィックス 2 次回レポートの体験演習型 メタセコイア,
<4D F736F F D208D5C91A297CD8A7793FC96E591E631308FCD2E646F63>
 第 1 章モールの定理による静定梁のたわみ 1-1 第 1 章モールの定理による静定梁のたわみ ポイント : モールの定理を用いて 静定梁のたわみを求める 断面力の釣合と梁の微分方程式は良く似ている 前章では 梁の微分方程式を直接積分する方法で 静定梁の断面力と変形状態を求めた 本章では 梁の微分方程式と断面力による力の釣合式が類似していることを利用して 微分方程式を直接解析的に解くのではなく 力の釣合より梁のたわみを求める方法を学ぶ
第 1 章モールの定理による静定梁のたわみ 1-1 第 1 章モールの定理による静定梁のたわみ ポイント : モールの定理を用いて 静定梁のたわみを求める 断面力の釣合と梁の微分方程式は良く似ている 前章では 梁の微分方程式を直接積分する方法で 静定梁の断面力と変形状態を求めた 本章では 梁の微分方程式と断面力による力の釣合式が類似していることを利用して 微分方程式を直接解析的に解くのではなく 力の釣合より梁のたわみを求める方法を学ぶ
反射係数
 平面波の反射と透過 電磁波の性質として, 反射と透過は最も基礎的な現象である. 我々の生活している空間は, 各種の形状を持った媒質で構成されている. 人間から見れば, 空気, 水, 木, 土, 火, 金属, プラスチックなど, 全く異なるものに見えるが, 電磁波からすると誘電率, 透磁率, 導電率が異なるだけである. 磁性体を除く媒質は比透磁率がで, ほとんど媒質に当てはまるので, 実質的に我々の身の回りの媒質で,
平面波の反射と透過 電磁波の性質として, 反射と透過は最も基礎的な現象である. 我々の生活している空間は, 各種の形状を持った媒質で構成されている. 人間から見れば, 空気, 水, 木, 土, 火, 金属, プラスチックなど, 全く異なるものに見えるが, 電磁波からすると誘電率, 透磁率, 導電率が異なるだけである. 磁性体を除く媒質は比透磁率がで, ほとんど媒質に当てはまるので, 実質的に我々の身の回りの媒質で,
横浜市環境科学研究所
 周期時系列の統計解析 単回帰分析 io 8 年 3 日 周期時系列に季節調整を行わないで単回帰分析を適用すると, 回帰係数には周期成分の影響が加わる. ここでは, 周期時系列をコサイン関数モデルで近似し単回帰分析によりモデルの回帰係数を求め, 周期成分の影響を検討した. また, その結果を気温時系列に当てはめ, 課題等について考察した. 気温時系列とコサイン関数モデル第 報の結果を利用するので, その一部を再掲する.
周期時系列の統計解析 単回帰分析 io 8 年 3 日 周期時系列に季節調整を行わないで単回帰分析を適用すると, 回帰係数には周期成分の影響が加わる. ここでは, 周期時系列をコサイン関数モデルで近似し単回帰分析によりモデルの回帰係数を求め, 周期成分の影響を検討した. また, その結果を気温時系列に当てはめ, 課題等について考察した. 気温時系列とコサイン関数モデル第 報の結果を利用するので, その一部を再掲する.
2011年度 筑波大・理系数学
 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ O を原点とするy 平面において, 直線 y= の を満たす部分をC とする () C 上に点 A( t, ) をとるとき, 線分 OA の垂直二等分線の方程式を求めよ () 点 A が C 全体を動くとき, 線分 OA の垂直二等分線が通過する範囲を求め, それ を図示せよ -- 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ
0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ O を原点とするy 平面において, 直線 y= の を満たす部分をC とする () C 上に点 A( t, ) をとるとき, 線分 OA の垂直二等分線の方程式を求めよ () 点 A が C 全体を動くとき, 線分 OA の垂直二等分線が通過する範囲を求め, それ を図示せよ -- 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ
“Hfi¡.book
 MEDICAL IMAGING TECHNOLOGY Vol.23 No.1 January 2005 23 特集論文 / 3D / 4D イメージングの最前線 逐次近似法を用いた CT 画像再構成法の考え方と驚異 Iterative Methods for Tomographic Image Reconstruction: Foundations and Surprizing Examples 工藤博幸
MEDICAL IMAGING TECHNOLOGY Vol.23 No.1 January 2005 23 特集論文 / 3D / 4D イメージングの最前線 逐次近似法を用いた CT 画像再構成法の考え方と驚異 Iterative Methods for Tomographic Image Reconstruction: Foundations and Surprizing Examples 工藤博幸
数学 IB まとめ ( 教科書とノートの復習 ) IB ということで計算に関する話題中心にまとめました 理論を知りたい方はのみっちー IA のシケプリを参考にするとよいと思います 河澄教授いわく テストはまんべんなく出すらしいです でも 重積分 ( 特に変数変換使うもの ) 線積分とグリーンの定理は
 数学 IB まとめ ( 教科書とノートの復習 ) IB ということで計算に関する話題中心にまとめました 理論を知りたい方はのみっちー IA のシケプリを参考にするとよいと思います 河澄教授いわく テストはまんべんなく出すらしいです でも 重積分 ( 特に変数変換使うもの ) 線積分とグリーンの定理はほぼ間違いなく出ると思うんで 時間がない人はこのあたりに絞ってやるとよいと思います 多分 前にも書きましたが
数学 IB まとめ ( 教科書とノートの復習 ) IB ということで計算に関する話題中心にまとめました 理論を知りたい方はのみっちー IA のシケプリを参考にするとよいと思います 河澄教授いわく テストはまんべんなく出すらしいです でも 重積分 ( 特に変数変換使うもの ) 線積分とグリーンの定理はほぼ間違いなく出ると思うんで 時間がない人はこのあたりに絞ってやるとよいと思います 多分 前にも書きましたが
2014年度 センター試験・数学ⅡB
 第 問 解答解説のページへ [] O を原点とする座標平面において, 点 P(, q) を中心とする円 C が, 方程式 y 4 x で表される直線 l に接しているとする () 円 C の半径 r を求めよう 点 P を通り直線 l に垂直な直線の方程式は, y - ア ( x- ) + qなので, P イ から l に引いた垂線と l の交点 Q の座標は ( ( ウ + エ q ), 4 (
第 問 解答解説のページへ [] O を原点とする座標平面において, 点 P(, q) を中心とする円 C が, 方程式 y 4 x で表される直線 l に接しているとする () 円 C の半径 r を求めよう 点 P を通り直線 l に垂直な直線の方程式は, y - ア ( x- ) + qなので, P イ から l に引いた垂線と l の交点 Q の座標は ( ( ウ + エ q ), 4 (
2016年度 筑波大・理系数学
 06 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ k を実数とする y 平面の曲線 C : y とC : y- + k+ -k が異なる共 有点 P, Q をもつとする ただし点 P, Q の 座標は正であるとする また, 原点を O とする () k のとりうる値の範囲を求めよ () k が () の範囲を動くとき, OPQ の重心 G の軌跡を求めよ () OPQ の面積を S とするとき,
06 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ k を実数とする y 平面の曲線 C : y とC : y- + k+ -k が異なる共 有点 P, Q をもつとする ただし点 P, Q の 座標は正であるとする また, 原点を O とする () k のとりうる値の範囲を求めよ () k が () の範囲を動くとき, OPQ の重心 G の軌跡を求めよ () OPQ の面積を S とするとき,
Microsoft PowerPoint - dm1_5.pptx
 デジタルメディア処理 1 017( 後期 ) 09/6 イントロダクション1 : デジタル画像とは, 量 化と標本化,Dynamic Range 10/03 イントロダクション : デジタルカメラ, 間の視覚, 表 系 10/10 フィルタ処理 1 : トーンカーブ, 線形フィルタ デジタルメディア処理 1 担当 : 井尻敬 10/17 フィルタ処理 : 線形フィルタ, ハーフトーニング 10/4
デジタルメディア処理 1 017( 後期 ) 09/6 イントロダクション1 : デジタル画像とは, 量 化と標本化,Dynamic Range 10/03 イントロダクション : デジタルカメラ, 間の視覚, 表 系 10/10 フィルタ処理 1 : トーンカーブ, 線形フィルタ デジタルメディア処理 1 担当 : 井尻敬 10/17 フィルタ処理 : 線形フィルタ, ハーフトーニング 10/4
スライド 1
 OSEM ( Ordered Subsets Expectation Maximization ) OSEM フォルダ内の OSEM.exe を起動する Contribution Ratio ボタンを押すと 逐次近似法における確率分布の計算を行う ( やや時間がかかる場合がある ) Contribution Ratio による処理を行い画像が表示された後 Read Sino ボタンを押し 脳 PET
OSEM ( Ordered Subsets Expectation Maximization ) OSEM フォルダ内の OSEM.exe を起動する Contribution Ratio ボタンを押すと 逐次近似法における確率分布の計算を行う ( やや時間がかかる場合がある ) Contribution Ratio による処理を行い画像が表示された後 Read Sino ボタンを押し 脳 PET
1/17 平成 29 年 3 月 25 日 ( 土 ) 午前 11 時 1 分量子力学とクライン ゴルドン方程式 ( 学部 3 年次秋学期向 ) 量子力学とクライン ゴルドン方程式 素粒子の満たす場 y ( x,t) の運動方程式 : クライン ゴルドン方程式 : æ 3 ö ç å è m= 0
 /7 平成 9 年 月 5 日 ( 土 午前 時 分量子力学とクライン ゴルドン方程式 ( 学部 年次秋学期向 量子力学とクライン ゴルドン方程式 素粒子の満たす場 (,t の運動方程式 : クライン ゴルドン方程式 : æ ö ç å è = 0 c + ( t =, 0 (. = 0 ì æ = = = ö æ ö æ ö ç ì =,,,,,,, ç 0 = ç Ñ 0 = ç Ñ 0 Ñ Ñ
/7 平成 9 年 月 5 日 ( 土 午前 時 分量子力学とクライン ゴルドン方程式 ( 学部 年次秋学期向 量子力学とクライン ゴルドン方程式 素粒子の満たす場 (,t の運動方程式 : クライン ゴルドン方程式 : æ ö ç å è = 0 c + ( t =, 0 (. = 0 ì æ = = = ö æ ö æ ö ç ì =,,,,,,, ç 0 = ç Ñ 0 = ç Ñ 0 Ñ Ñ
2014年度 筑波大・理系数学
 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ f ( x) = x x とする y = f ( x ) のグラフに点 P(, ) から引いた接線は 本あるとする つの接点 A (, f ( )), B(, f ( )), C(, f ( )) を頂点とする三角形の 重心を G とする () + +, + + および を, を用いて表せ () 点 G の座標を, を用いて表せ () 点 G
筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ f ( x) = x x とする y = f ( x ) のグラフに点 P(, ) から引いた接線は 本あるとする つの接点 A (, f ( )), B(, f ( )), C(, f ( )) を頂点とする三角形の 重心を G とする () + +, + + および を, を用いて表せ () 点 G の座標を, を用いて表せ () 点 G
PoincareDisk-3.doc
 3. ポアンカレ円盤上の 次分数変換この節以降では, 単に双曲的直線, 双曲的円などといえば, 全てポアンカレ円盤上の基本図形とします. また, 点 と点 B のポアンカレ円盤上での双曲的距離を,[,B] と表します. 3. 双曲的垂直 等分線 ユークリッドの原論 において 円 双曲的円, 直線 双曲的直線 の置き換えを行うだけで, 双曲的垂直 等分線, 双曲的内心, 双曲的外心などを 機械的に (
3. ポアンカレ円盤上の 次分数変換この節以降では, 単に双曲的直線, 双曲的円などといえば, 全てポアンカレ円盤上の基本図形とします. また, 点 と点 B のポアンカレ円盤上での双曲的距離を,[,B] と表します. 3. 双曲的垂直 等分線 ユークリッドの原論 において 円 双曲的円, 直線 双曲的直線 の置き換えを行うだけで, 双曲的垂直 等分線, 双曲的内心, 双曲的外心などを 機械的に (
学習指導要領
 (1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 絶対値の意味を理解し適切な処理することができる 例題 1-3 の絶対値をはずせ 展開公式 ( a + b ) ( a - b ) = a 2 - b 2 を利用して根号を含む分数の分母を有理化することができる 例題 5 5 + 2 の分母を有理化せよ 実数の整数部分と小数部分の表し方を理解している
(1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 絶対値の意味を理解し適切な処理することができる 例題 1-3 の絶対値をはずせ 展開公式 ( a + b ) ( a - b ) = a 2 - b 2 を利用して根号を含む分数の分母を有理化することができる 例題 5 5 + 2 の分母を有理化せよ 実数の整数部分と小数部分の表し方を理解している
DVIOUT
 第 3 章 フーリエ変換 3.1 フーリエ積分とフーリエ変換 第 章では 周期を持つ関数のフーリエ級数について学びました この章では 最初に 周期を持つ関数のフーリエ級数を拡張し 周期を持たない ( 一般的な ) 関数のフーリエ級数を導きましょう 具体的には 関数 f(x) を区間 L x L で考え この L を限りなく大きくするというアプローチを取ります (L ) なお ここで扱う関数 f(x)
第 3 章 フーリエ変換 3.1 フーリエ積分とフーリエ変換 第 章では 周期を持つ関数のフーリエ級数について学びました この章では 最初に 周期を持つ関数のフーリエ級数を拡張し 周期を持たない ( 一般的な ) 関数のフーリエ級数を導きましょう 具体的には 関数 f(x) を区間 L x L で考え この L を限りなく大きくするというアプローチを取ります (L ) なお ここで扱う関数 f(x)
多次元レーザー分光で探る凝縮分子系の超高速動力学
 波動方程式と量子力学 谷村吉隆 京都大学理学研究科化学専攻 http:theochem.kuchem.kyoto-u.ac.jp TA: 岩元佑樹 iwamoto.y@kuchem.kyoto-u.ac.jp ベクトルと行列の作法 A 列ベクトル c = c c 行ベクトル A = [ c c c ] 転置ベクトル T A = [ c c c ] AA 内積 c AA = [ c c c ] c =
波動方程式と量子力学 谷村吉隆 京都大学理学研究科化学専攻 http:theochem.kuchem.kyoto-u.ac.jp TA: 岩元佑樹 iwamoto.y@kuchem.kyoto-u.ac.jp ベクトルと行列の作法 A 列ベクトル c = c c 行ベクトル A = [ c c c ] 転置ベクトル T A = [ c c c ] AA 内積 c AA = [ c c c ] c =
