図 1 3 次元単純立方ブラベ 格子 図 2 体心立方ブラベー格子の格子点 図 3 体心立方ブラベー格子の 3 個の基本 ベクトル 点 P は P=-a 1 -a 2 +2a 3 図 4 体心立方ブラベー格子の基本ベクト ル点 P は P=2a 1 +a 2 +a 3 第 2 節 逆格子 前節で定義
|
|
|
- かつかげ あきます
- 5 years ago
- Views:
Transcription
1 バンドでみる固体の中の電子 岡山大学理学部物理学科 4 回生 上村直樹 バンド理論 は 1920 年代における量子力学の完成以降 量子力学の固体結晶系への応用を目指して繰り広げられた理論研究分野である 固体中電子に対する現代的な理論の基礎をなすものであり それは結晶構造の周期性に関する考察から始まる この周期性がバンドの形成へとつながるのである その際に根底にある仮定は 電子間相互作用のすべてが 独立な電子近似によって説明されうるとすることである すなわち 1つの電子と他のすべての電子との相互作用は ある平均された有効周期ポテンシャルで近似できると考えるのである つまり 独立電子近似をする際に無視されたエネルギーと比較して 結晶の周期性に起因する周期的なポテンシャル エネルギーの方がずっと重要なのである 今回は バンド理論を通して 金属中の電子の様子をみていく 第 1 章周期性 第 1 節 並進対称性 固体結晶は ある変位ベクトル R n だけ座標を移動させると元の結晶とすべてが全く同じく重なるような性質をもっている これを並進対称性といい 変位ベクトルの集まり {R n } は格子ベクトルとよばれ そのベクトルが示す座標の集まりを格子点という 3 次元空間での格子点 R n は 一般に3 個の整数 n=(n 1 n 2 n 3 ) により表現される R n =n 1 a 1 +n 2 a 2 +n 3 a 3 (1.1) この基本並進ベクトル すなわち3 次元結晶の格子は14 種類に分類されブラベー格子とよばれている 3つの基本並進ベクトルa 1 a 2 a 3 が作る平行六面体は 3 次元空間を隙間なく埋める単位胞 ( ユニットセル ) とよばれている その単位胞の体積はΩ 0 =a 1 ( a 2 a 3 ) で与えられる 体心立方格子 (bcc) や面心立方格子 (fcc) などのように単位胞に一つの原子だけが含まれている場合は ある原子とその周辺の原子とを結ぶ線分の2 等分面から作られる最小体積がやはり単位胞である これは ウィグナー サイツセルとよばれ 原子の周りの点群の回転操作に対して不変な形状をもっている 1
2 図 1 3 次元単純立方ブラベ 格子 図 2 体心立方ブラベー格子の格子点 図 3 体心立方ブラベー格子の 3 個の基本 ベクトル 点 P は P=-a 1 -a 2 +2a 3 図 4 体心立方ブラベー格子の基本ベクト ル点 P は P=2a 1 +a 2 +a 3 第 2 節 逆格子 前節で定義した格子ベクトル {R n } に対応して K m R n =2πI mn (1.2) の関係を満たす格子点 {K m } を考えてみよう ここで I mn は整数である このベクトル の次元は 長さの逆数の次元をもっていることから 逆格子空間での格子ベクトル もし くは単に逆格子ベクトルという 実空間での格子の基本並進ベクトル {t i }( i=1 2 2
3 3) と b j a i =2πδ ij (1.3) の関係にあるベクトル {b j }( j=1 2 3) を新たに定義すると 任意の整数組 m= (m 1 m 2 m 3 ) に対して 逆格子ベクトル {K m } が K m =m 1 b 1 +m 2 b 2 +m 3 b 3 (1.4) のように書き下せていれば,(1.2) は満たされることが分かる ここで (1.3) を与えるため には {b j } は b 1 =2π a 2 a 3 a 1 (a 2 a 3 ) (1.5) b 2 =2π a 3 a 1 a 1 (a 2 a 3 ) (1.6) b 3 =2π a 1 a 2 a 1 (a 2 a 3 ) (1.7) であればよい この {b j } は (1.4) から分かるように逆格子の基本並進ベクトルになって いる この 3 つの基本並進ベクトルがつくる逆格子の単位胞の体積は b 1 (b 2 b 3 )= (2π)3 Ω 0 (1.8) である さて (1.3) で定義された逆格子ベクトル {K m } は大変重要な性質をもっている ある任意の逆格子ベクトル K m を波数とする平面波 exp(ik m r) を考え 実格子の並進操作 ( 実格子ベクトル分だけ座標を移動させる操作 r r+r n のこと また rは3 次元ベクトルである ) を作用させると次のようになる exp[ik m (r+r n )]=exp[ik m r] exp[ik m R n ] =exp[ik m r] exp[2πii mn ] =exp[ik m r] (1.9) 3
4 すなわち 逆格子ベクトルを波数にもつ平面波は格子の並進操作に対して不変である 第 3 節 ブロッホの定理 結晶中の電子に関する 1 つの基本的な定理が 1928 年にブロッホによって証明された こ れは結晶中の電子の波動関数は次のようなブロッホ型をしているという主張である ψ k (r)=u k (r)exp(ik r) (1.10) ここでuk (r) は結晶格子の周期性 uk (r)=uk (r+r) をもつ関数である この関数は一般には波数ベクトルkに依存する ブロッホ関数は自由電子の波動関数 exp(ik r) が 結晶格子の対称性をもつ関数で変調を受けた形をしている つまり 変調された平面波であるといえる 1 次元の場合のブロッホの定理の証明 長さ a をもった基本単位格子 N 個からなる長さ L=Na の 1 次元的な結晶を考える こ のとき波動方程式は ħ2 2m d2 ψ x dx 2 + V(x)ψ x = Eψ x (1.11) となる ただし 周期ポテンシャルV(x) の中を運動する電子を考えるので V(x)=V (x +a) を満たす 周期境界条件からψ(x)=ψ(x+L) が要請され 電荷密度はx+aでもx +maでもxでの値と同じである つまり ψ(x+ma) 2 = ψ(x) 2 である ( ここでmは任意の整数 ) 以上から ψ(x+a)=aψ(x) (1.12) ψ(x+ma)=a m ψ(x) (1.13) 係数 AはA * A=1を満たす複素数である ( 電荷密度はψ * ψに比例する ) N 回繰り返せば次式を得る ψ(x+na)=a N ψ(x)=ψ(x) (1.14) A N =1 (1.15) A=exp(2πim/N) (m=0 ±1 ±2 ) (1.16) 4
5 式 (1.15) は A が式 (1.16) で表される 1 の N 乗根のうちの 1 つであることを示している す なわち 波動関数は次のような形でなければならない ψ(x+a)=exp( 2πim )ψ(x) (1.17) N これを波動関数のブロッホ条件という この条件を満たす関数は並進対称性から必要とされる条件 ( つまり 並進操作に対して不変という条件 ) を満たしている この結果が示唆しているのは 電子の波動関数 ( つまり式 (1.11) を満たす関数 ) を求めたければ まずは変調された自由電子の波動関数 ψ(x)=exp(ikx)u(x) を試してみて その関数がブロッホ条件式 (1.17) を満足するように条件を定めればよい ということである この変調された平面波を式 (1.17) の両辺に代入すると k=2πm/(na) (1.18) u(x+a)=u(x) (1.19) であれば等式が成り立つことがわかる もし u(x) が定数であれば k の値に同じ条件がつ けられた自由電子の波動関数がえられる したがって 結晶格子の周期性をもつ波動方程 式 (1.11) の解は 1 次元の場合次の形に書ける ψ(x)=exp(ikx)u k (x) (1.20) k の値は m を任意の整数として式 (1.18) で与えられ u(x) は結晶格子の周期性をもつ こ れは 1 次元の場合のブロッホの定理の証明を与えている 第 2 章結晶の中の電子 第 1 節 エネルギーバンド 固体中での電子は大きく二種類に分けて考えることが出来る 一つは内殻電子と呼ばれ, 原子核の周りの比較的内側の電子軌道にいて 原子核に強く結合し その原子核の周辺にのみとどまっている電子である 二つ目は外側の電子軌道で原子核とはあまり強く結合していない電子である 固体中ではこの電子は特定の原子に属していると言うことは出来ない 物質の性質を決めているのはこの電子である 電子のエネルギーの観点からいえば 固体中でも電子には存在できるエネルギー状態と存在できないエネルギー状態があり 存 5
6 在できるエネルギー領域をエネルギーバンドと呼び 存在できない状態をバンド ギャッ プと呼ぶ それぞれのバンドは受け入れられる電子の数が決まっており 電子は原子での 場合と同様にエネルギーの低い状態から先に埋まっていく 図 5. 絶縁体と金属と 2 種類の半導体のそれぞれのエネ ルギーバンドが電子によって占められている様子を模型 的に示す 第 2 節 ほとんど自由な電子の模型 この節では固体のエネルギーバンド構造を ほとんど自由な電子の模型と 強結合模型 によって考察する この 2 つの模型は エネルギーバンドの異なる 2 つの極限に対応して おり 現実の結晶のエネルギーバンドでは両方の中間的な特徴を示すことが多い 完全に自由な電子の状態とは一様なポテンシャル場の中にいる電子の状態をいうのであるが このとき電子の波動関数は平面波 あるいは大きさの等しい波数ベクトルの平面波の重ね合わせで記述される 一方 ほとんど自由な電子の状態は 波数が互いに逆格子ベクトルだけ異なるごく少数の平面波から構成される状態で ポテンシャル場の変動が小さい周期場で実現される すなわち 電子の感じる結晶場のポテンシャルは逆格子 {K m } により V(r)= v K (K m )exp(ik m r) m (2.1) と展開されるのであるが 一様でないポテンシャルの成分 vk (K m )(K m 0) は運動エネ ルギーに比べ小さいと仮定する 一方 電子の波動関数 すなわちブロッホ関数 ψ(r)=exp(i k r)u k (r) の u k (r) は結晶の並進対称性をもつ関数なので 同じように 6
7 u K (r)= C(K m )exp(ik m r) m (2.2) と展開することができる (2.1) (2.2) の m についての和は すべての逆格子ベクトルにつ いての和である これらの展開形を結晶の 3 次元のシュレーディンガー方程式 ħ2 + V(r) ψ r = Eψ r (2.3) 2m に代入し 波数ベクトル k+k m の平面波成分に注目すれば ħ 2 2m k+k m 2 E(k) C Km + v(k m K n ) n C K n = 0 (2.4) の関係が成立することがわかる エネルギーの一番低い状態については u k (r) の展開係数の中で C(K m ) は 運動エネルギーが最も小さい項に対応するものが大きく C(0) C(K m 0) が成り立つ そのため (2.4) の左辺第 2 項の中で K n =0の項が圧倒的に大きい そこで その項だけを残して他を無視すれば C K m v(k m )C 0 E(k) ħ2 2m k+k m 2 (2.5) が得られる この関係式を (2.4) で K m =0 の場合の式に代入すると エネルギー E(k) に ついて 次の結果をえられる E(k) ħ2 k 2 n 0 (2.6) + v K n v K n 2m E(k) ħ2 2m k+k 2 n v(k n ) は小さい量であるから その2 乗のオーダーとなる第 2 項は分母が特に小さくならない限り第 1 項に比べ小さい 第 1 項は自由電子のエネルギーなので (2.6) で決まるエネルギーバンドは大部分のk 空間の領域で 自由電子とほとんど同じように振舞う したがって この模型をほとんど自由な電子の模型という 1 次元結晶の場合について ほとんど自由な電子の模型のエネルギーバンドを図示すると 図 2のようになる すなわち 各逆格子点を中心として放物線を成して上昇するエネルギーバンドは電子波に対応するのであるが それらの交点ではエネルギーバンドは互いに反発し合い バンドギャップとよばれるエネルギーバンドのない領域を形成する 7
8 図 6 1 次元結晶における種々の平面波のエネルギーとエネルギーバンドの関係 第 3 節 強結合模型 前節では電子の振舞が自由電子とそれほど違わないほとんど自由な電子の模型について述べたが 強結合模型はこれと逆の極限になっている すなわち この模型では電子はどれかの原子に強く束縛させているが 全体としては結晶内の全ての原子を巡り歩いている これを記述する波動関数は 電子を束縛している原子の付近では その原子の軌道で記述されるが 原子の存在する位置に応じて平面因子が掛かる すなわち この模型では電子の波動関数は ψ r = 1 N R ϕ n r R exp ik R (2.7) のように表される ここで φ n (r-r) は R に位置する原子の n 番目の原子軌道関数であ る また N は 結晶中の格子点の数である もっと正確には 電子の波動関数は何種類か の原子軌道の重ね合わせとして ψ r = 1 N R C nk ϕ n r R exp ik R (2.8) 8
9 のように書かれる さて (2.7) または (2.8) のように書かれる波動関数はブロッホ和と呼ば れるが これらがブロッホの条件を満たすことは容易に示せる すなわち これらの式に おいて ψ r = U k (r)exp ik R (2.9) U k r = 1 N R ϕ n r R exp ik r R (2.10) とおくと Uk (r) が結晶格子の並進対称性を満たすからである このようにブロッホ和で波動関数が表わされるとき それに対応するエネルギーバンドE(k) はどのようなものであろうか これは (2.7) または (2.8) で表わされる状態について ハミルトニアンの期待値をとればよい (2.7) の場合 E k = ψ r H ψ r = ϕ n r H ϕ n r + d ϕ n r H ϕ n r R exp ik d (2.11) である 右辺の第 2 項は異なる格子位置にある原子軌道の間の行列要素であるが 格子点同士を結ぶベクトルdが大きくなると dについて指数関数的に小さくなる そこで通常は 第 2 項は最近接格子点にわたる和だけをとることが多い すなわち この場合のエネルギーバンドは E k =ε n + J d exp ik d (2.12) と表わされる ただし ε n = ϕ n r H ϕ n r (2.13) は n 番目の原子軌道のエネルギー準位に近いが 結晶中での他の原子のポテンシャルの 影響を受けて多少の変化をしたものである また J = ϕ n r H ϕ n r R (2.14) は電子 d だけ隔たった格子点上の軌道に飛び移る確率に比例するので ホッピング積分ま たはトランスファー積分とよばれる ( 共鳴積分とよばれることもある ) 現実の結晶のエネルギーバンドは 強結合模型によるものと ほとんど自由な電子の模 9
10 型によるものと どちらに近いだろうか これは 考えているエネルギーの領域によって違ってくる 結晶の中でも原子の中心にごく近ければ そこでは結晶中のポテンシャルは原子のポテンシャルとほぼ等しく 非常に深く鋭くなっている したがって その中心付近に束縛された電子軌道 ( これを内殻状態という ) はこの原子の周りに強く局在しており 隣の原子との間のホッピング積分も小さく バンド幅は狭い そのため エネルギーが低い軌道にある電子については 強結合模型の方がほとんど自由な電子の模型よりも良い描像を与える 内殻状態よりエネルギーの高い状態は価電子状態とよばれる 価電子状態のエネルギーは結晶中のポテンシャル ( 結晶ポテンシャル ) の最大値の付近となるので 波動関数は個々の原子に局在するのではなく 結晶全体に広がった波として表す方が現実に近くなる 結晶ポテンシャルの最大値よりエネルギーの高い領域では ほとんど自由な電子の模型の方が良い近似になる 図 7 結晶中のポテンシャルとエネルギーバンドの概念図 参考資料 [ 固体の電子論 ( 訳 ) 長尾辰哉 米沢富美子 澤田昭勝 小島誠治 中村輝太郎 東海大学出版 1991 年 ] [ 固体物理学 ( 著 ) 鹿児島誠一, 裳華房 2002 年 ] [ 物性物理学 ( 著 ) 塚田捷 裳華房 2007 年 ] [ バンド理論物質科学の基礎として ( 著 ) 小口多美夫 内田老鶴圃 1999 年 ] [ 固体物理の基礎 ( 著 ) アシュクロフト マーミン 1981 年 ] [KEK キッズサイエンティスト ( 10
Microsoft PowerPoint - H21生物計算化学2.ppt
 演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
Microsoft PowerPoint _量子力学短大.pptx
 . エネルギーギャップとrllouゾーン ブリルアン領域,t_8.. 周期ポテンシャル中の電子とエネルギーギャップ 簡単のため 次元に間隔 で原子が並んでいる結晶を考える 右方向に進行している電子の波は 間隔 で規則正しく並んでいる原子が作る格子によって散乱され 左向きに進行する波となる 波長 λ が の時 r の反射条件 式を満たし 両者の波が互いに強め合い 定在波を作る つまり 式 式を満たす波は
. エネルギーギャップとrllouゾーン ブリルアン領域,t_8.. 周期ポテンシャル中の電子とエネルギーギャップ 簡単のため 次元に間隔 で原子が並んでいる結晶を考える 右方向に進行している電子の波は 間隔 で規則正しく並んでいる原子が作る格子によって散乱され 左向きに進行する波となる 波長 λ が の時 r の反射条件 式を満たし 両者の波が互いに強め合い 定在波を作る つまり 式 式を満たす波は
<4D F736F F F696E74202D2095A890AB95A8979D91E682528FCD B8CDD8AB B83685D>
 3. 回折現象と逆格子 3.1 逆格子とは 簡単な例で 逆格子が何かを示そう 逆格子は物性工学を理解する上で 非常に重要である 逆格子は ブラべー格子をフーリエ空間に移したものであり 次のよう に定義される まず 平面波が e ik r で与えられることを思い出して欲 しい この平面波がブラべー格子の周期性を持つとすると R をブラべ ー格子ベクトルとして ik r+r e = e ik r (3-1)
3. 回折現象と逆格子 3.1 逆格子とは 簡単な例で 逆格子が何かを示そう 逆格子は物性工学を理解する上で 非常に重要である 逆格子は ブラべー格子をフーリエ空間に移したものであり 次のよう に定義される まず 平面波が e ik r で与えられることを思い出して欲 しい この平面波がブラべー格子の周期性を持つとすると R をブラべ ー格子ベクトルとして ik r+r e = e ik r (3-1)
ハートレー近似(Hartree aproximation)
 ハートリー近似 ( 量子多体系の平均場近似 1) 0. ハミルトニアンの期待値の変分がシュレディンガー方程式と等価であること 1. 独立粒子近似という考え方. 電子系におけるハートリー近似 3.3 電子系におけるハートリー近似 Mde by R. Okmoto (Kyushu Institute of Technology) filenme=rtree080609.ppt (0) ハミルトニアンの期待値の変分と
ハートリー近似 ( 量子多体系の平均場近似 1) 0. ハミルトニアンの期待値の変分がシュレディンガー方程式と等価であること 1. 独立粒子近似という考え方. 電子系におけるハートリー近似 3.3 電子系におけるハートリー近似 Mde by R. Okmoto (Kyushu Institute of Technology) filenme=rtree080609.ppt (0) ハミルトニアンの期待値の変分と
2018/6/12 表面の電子状態 表面に局在する電子状態 表面電子状態表面準位 1. ショックレー状態 ( 準位 ) 2. タム状態 ( 準位 ) 3. 鏡像状態 ( 準位 ) 4. 表面バンドのナローイング 5. 吸着子の状態密度 鏡像力によるポテンシャル 表面からzの位置の電子に働く力とポテン
 表面の電子状態 表面に局在する電子状態 表面電子状態表面準位. ショックレー状態 ( 準位. タム状態 ( 準位 3. 鏡像状態 ( 準位 4. 表面バンドのナローイング 5. 吸着子の状態密度 鏡像力によるポテンシャル 表面からzの位置の電子に働く力とポテンシャル e F z ( z z e V ( z ( Fz dz 4z e V ( z 4z ( z > ( z < のときの電子の運動を考える
表面の電子状態 表面に局在する電子状態 表面電子状態表面準位. ショックレー状態 ( 準位. タム状態 ( 準位 3. 鏡像状態 ( 準位 4. 表面バンドのナローイング 5. 吸着子の状態密度 鏡像力によるポテンシャル 表面からzの位置の電子に働く力とポテンシャル e F z ( z z e V ( z ( Fz dz 4z e V ( z 4z ( z > ( z < のときの電子の運動を考える
H AB φ A,1s (r r A )Hφ B,1s (r r B )dr (9) S AB φ A,1s (r r A )φ B,1s (r r B )dr (10) とした (S AA = S BB = 1). なお,H ij は共鳴積分 (resonance integra),s ij は重
 半経験量子計算法 : Tight-binding( 強結合近似 ) 計算の基礎 1. 基礎 Tight-binding 近似 ( 強結合近似, TB 近似あるいは TB 法などとも呼ばれる ) とは, 電子が強く拘束されており隣り合う軌道へ自由に移動できない, とする近似であり, 自由電子近似とは対極にある. 但し, 軌道間はわずかに重なり合っているので, 全く飛び移れないわけではない. Tight-binding
半経験量子計算法 : Tight-binding( 強結合近似 ) 計算の基礎 1. 基礎 Tight-binding 近似 ( 強結合近似, TB 近似あるいは TB 法などとも呼ばれる ) とは, 電子が強く拘束されており隣り合う軌道へ自由に移動できない, とする近似であり, 自由電子近似とは対極にある. 但し, 軌道間はわずかに重なり合っているので, 全く飛び移れないわけではない. Tight-binding
Microsoft PowerPoint - 10.pptx
 m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
<4D F736F F F696E74202D2091E688EA8CB4979D8C768E5A B8CDD8AB B83685D>
 第一原理計算法の基礎 固体物理からのアプローチを中心に 第一原理計算法とは 原子レベルやナノスケールレベルにおける物質の基本法則である量子力学 ( 第一原理 ) に基づいて, 原子番号だけを入力パラメーターとして, 非経験的に物理機構の解明や物性予測を行う計算手法である. 計算可能な物性値 第一原理計算により, 計算セル ( 原子番号と空間座標既知の原子を含むモデル ) の全エネルギーと電子のエネルギーバンド構造が求まる.
第一原理計算法の基礎 固体物理からのアプローチを中心に 第一原理計算法とは 原子レベルやナノスケールレベルにおける物質の基本法則である量子力学 ( 第一原理 ) に基づいて, 原子番号だけを入力パラメーターとして, 非経験的に物理機構の解明や物性予測を行う計算手法である. 計算可能な物性値 第一原理計算により, 計算セル ( 原子番号と空間座標既知の原子を含むモデル ) の全エネルギーと電子のエネルギーバンド構造が求まる.
<4D F736F F D FCD B90DB93AE96402E646F63>
 7 章摂動法講義のメモ 式が複雑なので 黒板を何度も修正したし 間違ったことも書いたので メモを置きます 摂動論の式の導出無摂動系 先ず 厳密に解けている Schrödiger 方程式を考える,,,3,... 3,,,3,... は状態を区別する整数であり 状態 はエネルギー順に並んでいる 即ち は基底状態 は励起状態である { m } は相互に規格直交条件が成立する k m k mdx km k
7 章摂動法講義のメモ 式が複雑なので 黒板を何度も修正したし 間違ったことも書いたので メモを置きます 摂動論の式の導出無摂動系 先ず 厳密に解けている Schrödiger 方程式を考える,,,3,... 3,,,3,... は状態を区別する整数であり 状態 はエネルギー順に並んでいる 即ち は基底状態 は励起状態である { m } は相互に規格直交条件が成立する k m k mdx km k
Microsoft Word - thesis.doc
 剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
線積分.indd
 線積分 線積分 ( n, n, n ) (ξ n, η n, ζ n ) ( n-, n-, n- ) (ξ k, η k, ζ k ) ( k, k, k ) ( k-, k-, k- ) 物体に力 を作用させて位置ベクトル A の点 A から位置ベクトル の点 まで曲線 に沿って物体を移動させたときの仕事 W は 次式で計算された A, A, W : d 6 d+ d+ d@,,, d+ d+
線積分 線積分 ( n, n, n ) (ξ n, η n, ζ n ) ( n-, n-, n- ) (ξ k, η k, ζ k ) ( k, k, k ) ( k-, k-, k- ) 物体に力 を作用させて位置ベクトル A の点 A から位置ベクトル の点 まで曲線 に沿って物体を移動させたときの仕事 W は 次式で計算された A, A, W : d 6 d+ d+ d@,,, d+ d+
Microsoft Word - 固体の電子論第2講.doc
 第 講 - エネルギーバンドとブリルアンゾーン - はじめに前回は一様なポテンシャル中を運動する電子の振る舞いをポテンシャル 0(V(r)=0) の下でシュレーディンガー波動方程式を解くことによって明らかにした その結果 電子の波動関数は平面波 ( r) A exp( ir) で記述され そのエネルギーは 3 V m 状態密度は D m で与えられ 体積 V の中に N 個の電子があるとき フェルミ
第 講 - エネルギーバンドとブリルアンゾーン - はじめに前回は一様なポテンシャル中を運動する電子の振る舞いをポテンシャル 0(V(r)=0) の下でシュレーディンガー波動方程式を解くことによって明らかにした その結果 電子の波動関数は平面波 ( r) A exp( ir) で記述され そのエネルギーは 3 V m 状態密度は D m で与えられ 体積 V の中に N 個の電子があるとき フェルミ
2014年度 名古屋大・理系数学
 04 名古屋大学 ( 理系 ) 前期日程問題 解答解説のページへ空間内にある半径 の球 ( 内部を含む ) を B とする 直線 と B が交わっており, その交わりは長さ の線分である () B の中心と との距離を求めよ () のまわりに B を 回転してできる立体の体積を求めよ 04 名古屋大学 ( 理系 ) 前期日程問題 解答解説のページへ 実数 t に対して 点 P( t, t ), Q(
04 名古屋大学 ( 理系 ) 前期日程問題 解答解説のページへ空間内にある半径 の球 ( 内部を含む ) を B とする 直線 と B が交わっており, その交わりは長さ の線分である () B の中心と との距離を求めよ () のまわりに B を 回転してできる立体の体積を求めよ 04 名古屋大学 ( 理系 ) 前期日程問題 解答解説のページへ 実数 t に対して 点 P( t, t ), Q(
以下 変数の上のドットは時間に関する微分を表わしている (ex. 2 dx d x x, x 2 dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-1) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( x や x, x などがすべて 1 次で なおかつ
 以下 変数の上のドットは時間に関する微分を表わしている (e. d d, dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( や, などがすべて 次で なおかつそれらの係数が定数であるような微分方程式 ) に対して安定性の解析を行ってきた しかしながら 実際には非線形の微分方程式で記述される現象も多く存在する
以下 変数の上のドットは時間に関する微分を表わしている (e. d d, dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( や, などがすべて 次で なおかつそれらの係数が定数であるような微分方程式 ) に対して安定性の解析を行ってきた しかしながら 実際には非線形の微分方程式で記述される現象も多く存在する
Microsoft PowerPoint - 第3回2.ppt
 講義内容 講義内容 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 ベクトルの直交性 3
講義内容 講義内容 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 ベクトルの直交性 3
Microsoft Word - 5章摂動法.doc
 5 章摂動法 ( 次の Moller-Plesset (MP) 法のために ) // 水素原子など 電子系を除いては 原子系の Schrödiger 方程式を解析的に解くことはできない 分子系の Schrödiger 方程式の正確な数値解を求めることも困難である そこで Hartree-Fock(H-F) 法を導入した H-F 法は Schrödiger 方程式が与える全エネルギーの 99% を再現することができる優れた近似方法である
5 章摂動法 ( 次の Moller-Plesset (MP) 法のために ) // 水素原子など 電子系を除いては 原子系の Schrödiger 方程式を解析的に解くことはできない 分子系の Schrödiger 方程式の正確な数値解を求めることも困難である そこで Hartree-Fock(H-F) 法を導入した H-F 法は Schrödiger 方程式が与える全エネルギーの 99% を再現することができる優れた近似方法である
3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x0 = f x= x0 t f c x f =0 [1] c f 0 x= x 0 x 0 f x= x0 x 2 x 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考
![3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x0 = f x= x0 t f c x f =0 [1] c f 0 x= x 0 x 0 f x= x0 x 2 x 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考 3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x0 = f x= x0 t f c x f =0 [1] c f 0 x= x 0 x 0 f x= x0 x 2 x 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考](/thumbs/103/158269281.jpg) 3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x = f x= x t f c x f = [1] c f x= x f x= x 2 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考える まず 初期時刻 t=t に f =R f exp [ik x ] [3] のような波動を与えたとき どのように時間変化するか調べる
3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x = f x= x t f c x f = [1] c f x= x f x= x 2 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考える まず 初期時刻 t=t に f =R f exp [ik x ] [3] のような波動を与えたとき どのように時間変化するか調べる
パソコンシミュレータの現状
 第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
ベクトル公式.rtf
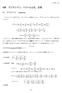 6 章ラプラシアン, ベクトル公式, 定理 6.1 ラプラシアン Laplacian φ はベクトル量である. そこでさらに発散をとると, φ はどういう形になるであろうか? φ = a + a + a φ a + a φ + a φ = φ + φ + φ = 2 φ + 2 φ 2 + 2 φ 2 2 φ = 2 φ 2 + 2 φ 2 + 2 φ 2 = 2 φ したがって,2 階の偏微分演算となる.
6 章ラプラシアン, ベクトル公式, 定理 6.1 ラプラシアン Laplacian φ はベクトル量である. そこでさらに発散をとると, φ はどういう形になるであろうか? φ = a + a + a φ a + a φ + a φ = φ + φ + φ = 2 φ + 2 φ 2 + 2 φ 2 2 φ = 2 φ 2 + 2 φ 2 + 2 φ 2 = 2 φ したがって,2 階の偏微分演算となる.
PowerPoint Presentation
 付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
2011年度 大阪大・理系数学
 0 大阪大学 ( 理系 ) 前期日程問題 解答解説のページへ a a を自然数とする O を原点とする座標平面上で行列 A= a の表す 次変換 を f とする cosθ siθ () >0 および0θ
0 大阪大学 ( 理系 ) 前期日程問題 解答解説のページへ a a を自然数とする O を原点とする座標平面上で行列 A= a の表す 次変換 を f とする cosθ siθ () >0 および0θ
vecrot
 1. ベクトル ベクトル : 方向を持つ量 ベクトルには 1 方向 2 大きさ ( 長さ ) という 2 つの属性がある ベクトルの例 : 物体の移動速度 移動量電場 磁場の強さ風速力トルクなど 2. ベクトルの表現 2.1 矢印で表現される 矢印の長さ : ベクトルの大きさ 矢印の向き : ベクトルの方向 2.2 2 個の点を用いて表現する 始点 () と終点 () を結ぶ半直線の向き : ベクトルの方向
1. ベクトル ベクトル : 方向を持つ量 ベクトルには 1 方向 2 大きさ ( 長さ ) という 2 つの属性がある ベクトルの例 : 物体の移動速度 移動量電場 磁場の強さ風速力トルクなど 2. ベクトルの表現 2.1 矢印で表現される 矢印の長さ : ベクトルの大きさ 矢印の向き : ベクトルの方向 2.2 2 個の点を用いて表現する 始点 () と終点 () を結ぶ半直線の向き : ベクトルの方向
Microsoft Word - 素粒子物理学I.doc
 6. 自発的対称性の破れとヒッグス機構 : 素粒子の標準模型 Dc 方程式.5 を導くラグランジアンは ϕ ϕ mϕϕ 6. である [H] Eu-nn 方程式 を使って 6. のラグランジア ンから Dc 方程式が導かれることを示せ 6. ゲージ対称性 6.. U 対称性 :QED ディラック粒子の複素場 ψに対する位相変換 ϕ ϕ 6. に対して ラグランジアンが不変であることを要請する これは簡単に示せる
6. 自発的対称性の破れとヒッグス機構 : 素粒子の標準模型 Dc 方程式.5 を導くラグランジアンは ϕ ϕ mϕϕ 6. である [H] Eu-nn 方程式 を使って 6. のラグランジア ンから Dc 方程式が導かれることを示せ 6. ゲージ対称性 6.. U 対称性 :QED ディラック粒子の複素場 ψに対する位相変換 ϕ ϕ 6. に対して ラグランジアンが不変であることを要請する これは簡単に示せる
2011年度 筑波大・理系数学
 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ O を原点とするy 平面において, 直線 y= の を満たす部分をC とする () C 上に点 A( t, ) をとるとき, 線分 OA の垂直二等分線の方程式を求めよ () 点 A が C 全体を動くとき, 線分 OA の垂直二等分線が通過する範囲を求め, それ を図示せよ -- 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ
0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ O を原点とするy 平面において, 直線 y= の を満たす部分をC とする () C 上に点 A( t, ) をとるとき, 線分 OA の垂直二等分線の方程式を求めよ () 点 A が C 全体を動くとき, 線分 OA の垂直二等分線が通過する範囲を求め, それ を図示せよ -- 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ
Microsoft PowerPoint - 卒業論文 pptx
 時間に依存するポテンシャルによる 量子状態の変化 龍谷大学理工学部数理情報学科 T966 二正寺章指導教員飯田晋司 目次 はじめに 次元のシュレーディンガー方程式 3 井戸型ポテンシャルの固有エネルギーと固有関数 4 4 中央に障壁のある井戸型ポテンシャルの固有エネルギーと固有関数 3 5 障壁が時間によって変化する場合 7 6 まとめ 5 一次元のシュレディンガー方程式量子力学の基本方程式 ψ (
時間に依存するポテンシャルによる 量子状態の変化 龍谷大学理工学部数理情報学科 T966 二正寺章指導教員飯田晋司 目次 はじめに 次元のシュレーディンガー方程式 3 井戸型ポテンシャルの固有エネルギーと固有関数 4 4 中央に障壁のある井戸型ポテンシャルの固有エネルギーと固有関数 3 5 障壁が時間によって変化する場合 7 6 まとめ 5 一次元のシュレディンガー方程式量子力学の基本方程式 ψ (
PowerPoint Presentation
 Non-linea factue mechanics き裂先端付近の塑性変形 塑性域 R 破壊進行領域応カ特異場 Ω R R Hutchinson, Rice and Rosengen 全ひずみ塑性理論に基づいた解析 現段階のひずみは 除荷がないとすると現段階の応力で一義的に決まる 単純引張り時の応カーひずみ関係 ( 構成方程式 ): ( ) ( ) n () y y y ここで α,n 定数, /
Non-linea factue mechanics き裂先端付近の塑性変形 塑性域 R 破壊進行領域応カ特異場 Ω R R Hutchinson, Rice and Rosengen 全ひずみ塑性理論に基づいた解析 現段階のひずみは 除荷がないとすると現段階の応力で一義的に決まる 単純引張り時の応カーひずみ関係 ( 構成方程式 ): ( ) ( ) n () y y y ここで α,n 定数, /
微分方程式による現象記述と解きかた
 微分方程式による現象記述と解きかた 土木工学 : 公共諸施設 構造物の有用目的にむけた合理的な実現をはかる方法 ( 技術 ) に関する学 橋梁 トンネル ダム 道路 港湾 治水利水施設 安全化 利便化 快適化 合法則的 経済的 自然および人口素材によって作られた 質量保存則 構造物の自然的な性質 作用 ( 外力による応答 ) エネルギー則 の解明 社会的諸現象のうち マスとしての移動 流通 運動量則
微分方程式による現象記述と解きかた 土木工学 : 公共諸施設 構造物の有用目的にむけた合理的な実現をはかる方法 ( 技術 ) に関する学 橋梁 トンネル ダム 道路 港湾 治水利水施設 安全化 利便化 快適化 合法則的 経済的 自然および人口素材によって作られた 質量保存則 構造物の自然的な性質 作用 ( 外力による応答 ) エネルギー則 の解明 社会的諸現象のうち マスとしての移動 流通 運動量則
20~22.prt
 [ 三クリア W] 辺が等しいことの証明 ( 円周角と弦の関係利用 ) の の二等分線がこの三角形の外接円と交わる点をそれぞれ とするとき 60 ならば であることを証明せよ 60 + + 0 + 0 80-60 60 から ゆえに 等しい長さの弧に対する弦の長さは等しいから [ 三クリア ] 方べきの定理 接線と弦のなす角と円周角を利用 線分 を直径とする円 があり 右の図のように の延長上の点
[ 三クリア W] 辺が等しいことの証明 ( 円周角と弦の関係利用 ) の の二等分線がこの三角形の外接円と交わる点をそれぞれ とするとき 60 ならば であることを証明せよ 60 + + 0 + 0 80-60 60 から ゆえに 等しい長さの弧に対する弦の長さは等しいから [ 三クリア ] 方べきの定理 接線と弦のなす角と円周角を利用 線分 を直径とする円 があり 右の図のように の延長上の点
固体物理学固体物理学固体物理学固体物理学 B ここではフェルミ球内における電子の総和を考えているから 次元極形式の積分により si (.) となるから は以下のようになる 8 (.) 単位体積当たりの電子数 つまり電子密度 / を用いると フェルミ波数 は以下のように求められる. / (.) が求め
 固体物理学 B. 金属の Sorfl 理論 [] 金属の 次元 Sorfl モデル金属中の電子を量子力学的に扱う. 最初に絶対零度 (TK) における場合を考える. 金属を その中に電子が閉じこめられている体積 の箱と考える. 電子は箱の中では自由に運動できるが 箱の外には出られない ( 箱の外に電子は存在しない ). このようなモデルを金属の Sorfl モデルという. 箱の中の電子のシュレーディンガー方程式は以下のようになる.
固体物理学 B. 金属の Sorfl 理論 [] 金属の 次元 Sorfl モデル金属中の電子を量子力学的に扱う. 最初に絶対零度 (TK) における場合を考える. 金属を その中に電子が閉じこめられている体積 の箱と考える. 電子は箱の中では自由に運動できるが 箱の外には出られない ( 箱の外に電子は存在しない ). このようなモデルを金属の Sorfl モデルという. 箱の中の電子のシュレーディンガー方程式は以下のようになる.
ଗȨɍɫȮĘർǻ 図 : a)3 次元自由粒子の波数空間におけるエネルギー固有値の分布の様子 b) マクロなサイズの系 L ) における W E) と ΩE) の対応 として与えられる 周期境界条件を満たす波数 kn は kn = πn, L n = 0, ±, ±, 7) となる 長さ L の有限
 : Email: mizushima@mp.es.osaka-u.ac.jp, D38 0 08 5 S = k B ln W ) W n [] [] 5 N. 6 d h m dx ϕ nx) = E n ϕ n x) ) L 5 ϕ n x = 0) = ϕ n x = L) = 0, N k n ϕ n = N sink n x), E n = h k n m 3) k n = nπ, n =,,
: Email: mizushima@mp.es.osaka-u.ac.jp, D38 0 08 5 S = k B ln W ) W n [] [] 5 N. 6 d h m dx ϕ nx) = E n ϕ n x) ) L 5 ϕ n x = 0) = ϕ n x = L) = 0, N k n ϕ n = N sink n x), E n = h k n m 3) k n = nπ, n =,,
Microsoft Word - Chap17
 第 7 章化学反応に対する磁場効果における三重項機構 その 7.. 節の訂正 年 7 月 日. 節 章の9ページ の赤枠に記載した説明は間違いであった事に気付いた 以下に訂正する しかし.. 式は 結果的には正しいので安心して下さい 磁場 の存在下でのT 状態のハミルトニアン は ゼーマン項 と時間に依存するスピン-スピン相互作用の項 との和となる..=7.. g S = g S z = S z g
第 7 章化学反応に対する磁場効果における三重項機構 その 7.. 節の訂正 年 7 月 日. 節 章の9ページ の赤枠に記載した説明は間違いであった事に気付いた 以下に訂正する しかし.. 式は 結果的には正しいので安心して下さい 磁場 の存在下でのT 状態のハミルトニアン は ゼーマン項 と時間に依存するスピン-スピン相互作用の項 との和となる..=7.. g S = g S z = S z g
Microsoft PowerPoint - 第2回半導体工学
 17 年 1 月 16 日 月 1 限 8:5~1:15 IB15 第 回半導体工学 * バンド構造と遷移確率 天野浩 項目 1 章量子論入門 何故 Si は光らず GN は良く光るのか? *MOSFET ゲート SiO / チャネル Si 界面の量子輸送過程 MOSFET には どのようなゲート材料が必要なのか? http://www.iue.tuwien.c.t/ph/vsicek/noe3.html
17 年 1 月 16 日 月 1 限 8:5~1:15 IB15 第 回半導体工学 * バンド構造と遷移確率 天野浩 項目 1 章量子論入門 何故 Si は光らず GN は良く光るのか? *MOSFET ゲート SiO / チャネル Si 界面の量子輸送過程 MOSFET には どのようなゲート材料が必要なのか? http://www.iue.tuwien.c.t/ph/vsicek/noe3.html
1/30 平成 29 年 3 月 24 日 ( 金 ) 午前 11 時 25 分第三章フェルミ量子場 : スピノール場 ( 次元あり ) 第三章フェルミ量子場 : スピノール場 フェルミ型 ボーズ量子場のエネルギーは 第二章ボーズ量子場 : スカラー場 の (2.18) より ˆ dp 1 1 =
 / 平成 9 年 月 日 ( 金 午前 時 5 分第三章フェルミ量子場 : スピノール場 ( 次元あり 第三章フェルミ量子場 : スピノール場 フェルミ型 ボーズ量子場のエネルギーは 第二章ボーズ量子場 : スカラー場 の (.8 より ˆ ( ( ( q -, ( ( c ( H c c ë é ù û - Ü + c ( ( - に限る (. である 一方 フェルミ型は 成分をもち その成分を,,,,
/ 平成 9 年 月 日 ( 金 午前 時 5 分第三章フェルミ量子場 : スピノール場 ( 次元あり 第三章フェルミ量子場 : スピノール場 フェルミ型 ボーズ量子場のエネルギーは 第二章ボーズ量子場 : スカラー場 の (.8 より ˆ ( ( ( q -, ( ( c ( H c c ë é ù û - Ü + c ( ( - に限る (. である 一方 フェルミ型は 成分をもち その成分を,,,,
プランクの公式と量子化
 Planck の公式と量子化 埼玉大学理学部物理学科 久保宗弘 序論 一般に 量子力学 と表現すると Schrödinger の量子力学などの 後期量子力学 を指すことが多い 本当の量子概念 には どうアプローチ? 何故 エネルギーが量子化されるか という根本的な問いにどうこたえるか? どのように 量子 の扉は叩かれたのか? 序論 統計力学 熱力学 がことの始まり 総括的な動き を表現するための学問である
Planck の公式と量子化 埼玉大学理学部物理学科 久保宗弘 序論 一般に 量子力学 と表現すると Schrödinger の量子力学などの 後期量子力学 を指すことが多い 本当の量子概念 には どうアプローチ? 何故 エネルギーが量子化されるか という根本的な問いにどうこたえるか? どのように 量子 の扉は叩かれたのか? 序論 統計力学 熱力学 がことの始まり 総括的な動き を表現するための学問である
OCW-iダランベールの原理
 講義名連続体力学配布資料 OCW- 第 2 回ダランベールの原理 無機材料工学科准教授安田公一 1 はじめに今回の講義では, まず, 前半でダランベールの原理について説明する これを用いると, 動力学の問題を静力学の問題として解くことができ, さらに, 前回の仮想仕事の原理を適用すると動力学問題も簡単に解くことができるようになる また, 後半では, ダランベールの原理の応用として ラグランジュ方程式の導出を示す
講義名連続体力学配布資料 OCW- 第 2 回ダランベールの原理 無機材料工学科准教授安田公一 1 はじめに今回の講義では, まず, 前半でダランベールの原理について説明する これを用いると, 動力学の問題を静力学の問題として解くことができ, さらに, 前回の仮想仕事の原理を適用すると動力学問題も簡単に解くことができるようになる また, 後半では, ダランベールの原理の応用として ラグランジュ方程式の導出を示す
Microsoft PowerPoint - 10.pptx
 0. 固有値とその応用 固有値と固有ベクトル 2 行列による写像から固有ベクトルへ m n A : m n n m 行列によって線形写像 f R R A が表せることを見てきた ここでは 2 次元平面の行列による写像を調べる 2 = 2 A 2 2 とし 写像 まず 単位ベクトルの像を求める u 2 x = v 2 y f : R A R を考える u 2 2 u, 2 2 0 = = v 2 0
0. 固有値とその応用 固有値と固有ベクトル 2 行列による写像から固有ベクトルへ m n A : m n n m 行列によって線形写像 f R R A が表せることを見てきた ここでは 2 次元平面の行列による写像を調べる 2 = 2 A 2 2 とし 写像 まず 単位ベクトルの像を求める u 2 x = v 2 y f : R A R を考える u 2 2 u, 2 2 0 = = v 2 0
2011年度 東京大・文系数学
 東京大学 ( 文系 ) 前期日程問題 解答解説のページへ x の 次関数 f( x) = x + x + cx+ d が, つの条件 f () =, f ( ) =, ( x + cx+ d) dx= をすべて満たしているとする このような f( x) の中で定積分 I = { f ( x) } dx を最小にするものを求め, そのときの I の値を求めよ ただし, f ( x) は f ( x)
東京大学 ( 文系 ) 前期日程問題 解答解説のページへ x の 次関数 f( x) = x + x + cx+ d が, つの条件 f () =, f ( ) =, ( x + cx+ d) dx= をすべて満たしているとする このような f( x) の中で定積分 I = { f ( x) } dx を最小にするものを求め, そのときの I の値を求めよ ただし, f ( x) は f ( x)
<8D828D5A838A817C A77425F91E6318FCD2E6D6364>
 4 1 平面上のベクトル 1 ベクトルとその演算 例題 1 ベクトルの相等 次の問いに答えよ. ⑴ 右の図 1 は平行四辺形 である., と等しいベクトルをいえ. ⑵ 右の図 2 の中で互いに等しいベクトルをいえ. ただし, すべてのマス目は正方形である. 解 ⑴,= より, =,= より, = ⑵ 大きさと向きの等しいものを調べる. a =d, c = f d e f 1 右の図の長方形 において,
4 1 平面上のベクトル 1 ベクトルとその演算 例題 1 ベクトルの相等 次の問いに答えよ. ⑴ 右の図 1 は平行四辺形 である., と等しいベクトルをいえ. ⑵ 右の図 2 の中で互いに等しいベクトルをいえ. ただし, すべてのマス目は正方形である. 解 ⑴,= より, =,= より, = ⑵ 大きさと向きの等しいものを調べる. a =d, c = f d e f 1 右の図の長方形 において,
Microsoft Word - 8章(CI).doc
 8 章配置間相互作用法 : Configuration Interaction () etho [] 化学的精度化学反応の精密な解析をするためには エネルギー誤差は数 ~ kcal/mol 程度に抑えたいものである この程度の誤差内に治まる精度を 化学的精度 と呼ぶことがある He 原子のエネルギーをシュレーディンガー方程式と分子軌道法で計算した結果を示そう He 原子のエネルギー Hartree-Fock
8 章配置間相互作用法 : Configuration Interaction () etho [] 化学的精度化学反応の精密な解析をするためには エネルギー誤差は数 ~ kcal/mol 程度に抑えたいものである この程度の誤差内に治まる精度を 化学的精度 と呼ぶことがある He 原子のエネルギーをシュレーディンガー方程式と分子軌道法で計算した結果を示そう He 原子のエネルギー Hartree-Fock
2018年度 筑波大・理系数学
 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ < < とする 放物線 上に 点 (, ), A (ta, ta ), B( - ta, ta ) をとる 三角形 AB の内心の 座標を p とし, 外心の 座標を q とする また, 正の実数 a に対して, 直線 a と放物線 で囲まれた図形の面積を S( a) で表す () p, q を cos を用いて表せ S( p) () S(
筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ < < とする 放物線 上に 点 (, ), A (ta, ta ), B( - ta, ta ) をとる 三角形 AB の内心の 座標を p とし, 外心の 座標を q とする また, 正の実数 a に対して, 直線 a と放物線 で囲まれた図形の面積を S( a) で表す () p, q を cos を用いて表せ S( p) () S(
ニュートン重力理論.pptx
 3 ニュートン重力理論 1. ニュートン重力理論の基本 : 慣性系とガリレイ変換不変性 2. ニュートン重力理論の定式化 3. 等価原理 4. 流体力学方程式とその基礎 3.1 ニュートン重力理論の基本 u ニュートンの第一法則 = 力がかからなければ 等速直線運動を続ける u 等速直線運動に見える系を 慣性系 と呼ぶ ² 直線とはどんな空間の直線か? ニュートン理論では 3 次元ユークリッド空間
3 ニュートン重力理論 1. ニュートン重力理論の基本 : 慣性系とガリレイ変換不変性 2. ニュートン重力理論の定式化 3. 等価原理 4. 流体力学方程式とその基礎 3.1 ニュートン重力理論の基本 u ニュートンの第一法則 = 力がかからなければ 等速直線運動を続ける u 等速直線運動に見える系を 慣性系 と呼ぶ ² 直線とはどんな空間の直線か? ニュートン理論では 3 次元ユークリッド空間
~5 セメナノサイエンス基礎 A 1~ 結晶 結晶と非晶質結晶 : 原子配列が規則的非晶質 : 原子配列が不規則的 単結晶と多結晶単結晶 : 巨視的に見て原子配列が規則的な結晶多結晶 : 単結晶が集まったもの いろいろな操作によって 結晶格子を自分自身に重ね合わすことができる操作をまとめて点群操作と
 A ~ 結晶 結晶と非晶質結晶 : 原子配列が規則的非晶質 : 原子配列が不規則的 単結晶と多結晶単結晶 : 巨視的に見て原子配列が規則的な結晶多結晶 : 単結晶が集まったもの いろいろな操作によって 結晶格子を自分自身に重ね合わすことができる操作をまとめて点群操作という 点群操作には 回転操作 鏡映操作および反転操作がある 結晶系 次元格子を 5 種類示す つの明確な格子型を示すときに その基となる格子をブラベブラベ格子
A ~ 結晶 結晶と非晶質結晶 : 原子配列が規則的非晶質 : 原子配列が不規則的 単結晶と多結晶単結晶 : 巨視的に見て原子配列が規則的な結晶多結晶 : 単結晶が集まったもの いろいろな操作によって 結晶格子を自分自身に重ね合わすことができる操作をまとめて点群操作という 点群操作には 回転操作 鏡映操作および反転操作がある 結晶系 次元格子を 5 種類示す つの明確な格子型を示すときに その基となる格子をブラベブラベ格子
多次元レーザー分光で探る凝縮分子系の超高速動力学
 波動方程式と量子力学 谷村吉隆 京都大学理学研究科化学専攻 http:theochem.kuchem.kyoto-u.ac.jp TA: 岩元佑樹 iwamoto.y@kuchem.kyoto-u.ac.jp ベクトルと行列の作法 A 列ベクトル c = c c 行ベクトル A = [ c c c ] 転置ベクトル T A = [ c c c ] AA 内積 c AA = [ c c c ] c =
波動方程式と量子力学 谷村吉隆 京都大学理学研究科化学専攻 http:theochem.kuchem.kyoto-u.ac.jp TA: 岩元佑樹 iwamoto.y@kuchem.kyoto-u.ac.jp ベクトルと行列の作法 A 列ベクトル c = c c 行ベクトル A = [ c c c ] 転置ベクトル T A = [ c c c ] AA 内積 c AA = [ c c c ] c =
反射係数
 平面波の反射と透過 電磁波の性質として, 反射と透過は最も基礎的な現象である. 我々の生活している空間は, 各種の形状を持った媒質で構成されている. 人間から見れば, 空気, 水, 木, 土, 火, 金属, プラスチックなど, 全く異なるものに見えるが, 電磁波からすると誘電率, 透磁率, 導電率が異なるだけである. 磁性体を除く媒質は比透磁率がで, ほとんど媒質に当てはまるので, 実質的に我々の身の回りの媒質で,
平面波の反射と透過 電磁波の性質として, 反射と透過は最も基礎的な現象である. 我々の生活している空間は, 各種の形状を持った媒質で構成されている. 人間から見れば, 空気, 水, 木, 土, 火, 金属, プラスチックなど, 全く異なるものに見えるが, 電磁波からすると誘電率, 透磁率, 導電率が異なるだけである. 磁性体を除く媒質は比透磁率がで, ほとんど媒質に当てはまるので, 実質的に我々の身の回りの媒質で,
2016年度 京都大・文系数学
 06 京都大学 ( 文系 ) 前期日程問題 解答解説のページへ xy 平面内の領域の面積を求めよ x + y, x で, 曲線 C : y= x + x -xの上側にある部分 -- 06 京都大学 ( 文系 ) 前期日程問題 解答解説のページへ ボタンを押すと あたり か はずれ のいずれかが表示される装置がある あたり の表示される確率は毎回同じであるとする この装置のボタンを 0 回押したとき,
06 京都大学 ( 文系 ) 前期日程問題 解答解説のページへ xy 平面内の領域の面積を求めよ x + y, x で, 曲線 C : y= x + x -xの上側にある部分 -- 06 京都大学 ( 文系 ) 前期日程問題 解答解説のページへ ボタンを押すと あたり か はずれ のいずれかが表示される装置がある あたり の表示される確率は毎回同じであるとする この装置のボタンを 0 回押したとき,
Microsoft Word - 補論3.2
 補論 3. 多変量 GARC モデル 07//6 新谷元嗣 藪友良 対数尤度関数 3 章 7 節では 変量の対数尤度を求めた ここでは多変量の場合 とくに 変量について対数尤度を求める 誤差項 は平均 0 で 次元の正規分布に従うとする 単純化のため 分散と共分散は時間を通じて一定としよう ( この仮定は後で変更される ) したがって ij から添え字 を除くことができる このとき と の尤度関数は
補論 3. 多変量 GARC モデル 07//6 新谷元嗣 藪友良 対数尤度関数 3 章 7 節では 変量の対数尤度を求めた ここでは多変量の場合 とくに 変量について対数尤度を求める 誤差項 は平均 0 で 次元の正規分布に従うとする 単純化のため 分散と共分散は時間を通じて一定としよう ( この仮定は後で変更される ) したがって ij から添え字 を除くことができる このとき と の尤度関数は
2017年度 長崎大・医系数学
 07 長崎大学 ( 医系 ) 前期日程問題 解答解説のページへ 以下の問いに答えよ () 0 のとき, si + cos の最大値と最小値, およびそのときの の値 をそれぞれ求めよ () e を自然対数の底とする > eの範囲において, 関数 y を考える この両 辺の対数を について微分することにより, y は減少関数であることを示せ また, e< < bのとき, () 数列 { } b の一般項が,
07 長崎大学 ( 医系 ) 前期日程問題 解答解説のページへ 以下の問いに答えよ () 0 のとき, si + cos の最大値と最小値, およびそのときの の値 をそれぞれ求めよ () e を自然対数の底とする > eの範囲において, 関数 y を考える この両 辺の対数を について微分することにより, y は減少関数であることを示せ また, e< < bのとき, () 数列 { } b の一般項が,
横浜市環境科学研究所
 周期時系列の統計解析 単回帰分析 io 8 年 3 日 周期時系列に季節調整を行わないで単回帰分析を適用すると, 回帰係数には周期成分の影響が加わる. ここでは, 周期時系列をコサイン関数モデルで近似し単回帰分析によりモデルの回帰係数を求め, 周期成分の影響を検討した. また, その結果を気温時系列に当てはめ, 課題等について考察した. 気温時系列とコサイン関数モデル第 報の結果を利用するので, その一部を再掲する.
周期時系列の統計解析 単回帰分析 io 8 年 3 日 周期時系列に季節調整を行わないで単回帰分析を適用すると, 回帰係数には周期成分の影響が加わる. ここでは, 周期時系列をコサイン関数モデルで近似し単回帰分析によりモデルの回帰係数を求め, 周期成分の影響を検討した. また, その結果を気温時系列に当てはめ, 課題等について考察した. 気温時系列とコサイン関数モデル第 報の結果を利用するので, その一部を再掲する.
第 4 週コンボリューションその 2, 正弦波による分解 教科書 p. 16~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問 1. 以下の図にならって,1 と 2 の δ 関数を図示せよ δ (t) 2
 第 4 週コンボリューションその, 正弦波による分解 教科書 p. 6~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問. 以下の図にならって, と の δ 関数を図示せよ. - - - δ () δ ( ) - - - 図 δ 関数の図示の例 δ ( ) δ ( ) δ ( ) δ ( ) δ ( ) - - - - - - - -
第 4 週コンボリューションその, 正弦波による分解 教科書 p. 6~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問. 以下の図にならって, と の δ 関数を図示せよ. - - - δ () δ ( ) - - - 図 δ 関数の図示の例 δ ( ) δ ( ) δ ( ) δ ( ) δ ( ) - - - - - - - -
2018年度 神戸大・理系数学
 8 神戸大学 ( 理系 ) 前期日程問題 解答解説のページへ t を < t < を満たす実数とする OABC を 辺の長さが の正四面体とする 辺 OA を -t : tに内分する点を P, 辺 OB を t :-tに内分する点を Q, 辺 BC の中点を R とする また a = OA, b = OB, c = OC とする 以下の問いに答えよ () QP と QR をt, a, b, c を用いて表せ
8 神戸大学 ( 理系 ) 前期日程問題 解答解説のページへ t を < t < を満たす実数とする OABC を 辺の長さが の正四面体とする 辺 OA を -t : tに内分する点を P, 辺 OB を t :-tに内分する点を Q, 辺 BC の中点を R とする また a = OA, b = OB, c = OC とする 以下の問いに答えよ () QP と QR をt, a, b, c を用いて表せ
航空機の運動方程式
 可制御性 可観測性. 可制御性システムの状態を, 適切な操作によって, 有限時間内に, 任意の状態から別の任意の状態に移動させることができるか否かという特性を可制御性という. 可制御性を有するシステムに対し, システムは可制御である, 可制御なシステム という言い方をする. 状態方程式, 出力方程式が以下で表されるn 次元 m 入力 r 出力線形時不変システム x Ax u y x Du () に対し,
可制御性 可観測性. 可制御性システムの状態を, 適切な操作によって, 有限時間内に, 任意の状態から別の任意の状態に移動させることができるか否かという特性を可制御性という. 可制御性を有するシステムに対し, システムは可制御である, 可制御なシステム という言い方をする. 状態方程式, 出力方程式が以下で表されるn 次元 m 入力 r 出力線形時不変システム x Ax u y x Du () に対し,
Microsoft Word - 1B2011.doc
 第 14 回モールの定理 ( 単純梁の場合 ) ( モールの定理とは何か?p.11) 例題 下記に示す単純梁の C 点のたわみ角 θ C と, たわみ δ C を求めよ ただし, 部材の曲げ 剛性は材軸に沿って一様で とする C D kn B 1.5m 0.5m 1.0m 解答 1 曲げモーメント図を描く,B 点の反力を求める kn kn 4 kn 曲げモーメント図を描く knm 先に得られた曲げモーメントの値を
第 14 回モールの定理 ( 単純梁の場合 ) ( モールの定理とは何か?p.11) 例題 下記に示す単純梁の C 点のたわみ角 θ C と, たわみ δ C を求めよ ただし, 部材の曲げ 剛性は材軸に沿って一様で とする C D kn B 1.5m 0.5m 1.0m 解答 1 曲げモーメント図を描く,B 点の反力を求める kn kn 4 kn 曲げモーメント図を描く knm 先に得られた曲げモーメントの値を
例 e 指数関数的に減衰する信号を h( a < + a a すると, それらのラプラス変換は, H ( ) { e } e インパルス応答が h( a < ( ただし a >, U( ) { } となるシステムにステップ信号 ( y( のラプラス変換 Y () は, Y ( ) H ( ) X (
 第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
2017年度 金沢大・理系数学
 07 金沢大学 ( 理系 前期日程問題 解答解説のページへ 次の問いに答えよ ( 6 z + 7 = 0 を満たす複素数 z をすべて求め, それらを表す点を複素数平面上に図 示せよ ( ( で求めた複素数 z を偏角が小さい方から順に z, z, とするとき, z, z と 積 zz を表す 点が複素数平面上で一直線上にあることを示せ ただし, 偏角は 0 以上 未満とする -- 07 金沢大学
07 金沢大学 ( 理系 前期日程問題 解答解説のページへ 次の問いに答えよ ( 6 z + 7 = 0 を満たす複素数 z をすべて求め, それらを表す点を複素数平面上に図 示せよ ( ( で求めた複素数 z を偏角が小さい方から順に z, z, とするとき, z, z と 積 zz を表す 点が複素数平面上で一直線上にあることを示せ ただし, 偏角は 0 以上 未満とする -- 07 金沢大学
(Microsoft Word - 10ta320a_\220U\223\256\212w\223\301\230__6\217\315\221O\224\274\203\214\203W\203\201.docx)
 6 章スペクトルの平滑化 スペクトルの平滑化とはフーリエスペクトルやパワ スペクトルのギザギザを取り除き 滑らかにする操作のことをいう ただし 波のもっている本質的なものをゆがめてはいけない 図 6-7 パワ スペクトルの平滑化 6. 合積のフーリエ変換スペクトルの平滑化を学ぶ前に 合積とそのフーリエ変換について説明する 6. データ ウィンドウデータ ウィンドウの定義と特徴について説明する 6.3
6 章スペクトルの平滑化 スペクトルの平滑化とはフーリエスペクトルやパワ スペクトルのギザギザを取り除き 滑らかにする操作のことをいう ただし 波のもっている本質的なものをゆがめてはいけない 図 6-7 パワ スペクトルの平滑化 6. 合積のフーリエ変換スペクトルの平滑化を学ぶ前に 合積とそのフーリエ変換について説明する 6. データ ウィンドウデータ ウィンドウの定義と特徴について説明する 6.3
数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュ
 数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュレーションによって計算してみる 4.1 放物運動一様な重力場における放物運動を考える 一般に質量の物体に作用する力をとすると運動方程式は
数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュレーションによって計算してみる 4.1 放物運動一様な重力場における放物運動を考える 一般に質量の物体に作用する力をとすると運動方程式は
2016年度 筑波大・理系数学
 06 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ k を実数とする y 平面の曲線 C : y とC : y- + k+ -k が異なる共 有点 P, Q をもつとする ただし点 P, Q の 座標は正であるとする また, 原点を O とする () k のとりうる値の範囲を求めよ () k が () の範囲を動くとき, OPQ の重心 G の軌跡を求めよ () OPQ の面積を S とするとき,
06 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ k を実数とする y 平面の曲線 C : y とC : y- + k+ -k が異なる共 有点 P, Q をもつとする ただし点 P, Q の 座標は正であるとする また, 原点を O とする () k のとりうる値の範囲を求めよ () k が () の範囲を動くとき, OPQ の重心 G の軌跡を求めよ () OPQ の面積を S とするとき,
補足 中学で学習したフレミング左手の法則 ( 電 磁 力 ) と関連付けると覚えやすい 電磁力は電流と磁界の外積で表される 力 F 磁 電磁力 F li 右ねじの回転の向き電 li ( l は導線の長さ ) 補足 有向線分とベクトル有向線分 : 矢印の位
 http://totemt.sur.ne.p 外積 ( ベクトル積 ) の活用 ( 面積, 法線ベクトル, 平面の方程式 ) 3 次元空間の つのベクトルの積が つのベクトルを与えるようなベクトルの掛け算 ベクトルの積がベクトルを与えることからベクトル積とも呼ばれる これに対し内積は符号と大きさをもつ量 ( スカラー量 ) を与えるので, スカラー積とも呼ばれる 外積を使うと, 平行四辺形や三角形の面積,
http://totemt.sur.ne.p 外積 ( ベクトル積 ) の活用 ( 面積, 法線ベクトル, 平面の方程式 ) 3 次元空間の つのベクトルの積が つのベクトルを与えるようなベクトルの掛け算 ベクトルの積がベクトルを与えることからベクトル積とも呼ばれる これに対し内積は符号と大きさをもつ量 ( スカラー量 ) を与えるので, スカラー積とも呼ばれる 外積を使うと, 平行四辺形や三角形の面積,
三重大学工学部
 反応理論化学 ( その 軌道相互作用 複数の原子が相互作用して分子が形成される複数の原子軌道 ( または混成軌道 が混合して分子軌道が形成される原子軌道 ( または混成軌道 が混合して分子軌道に変化すると軌道エネルギーも変化する. 原子軌道 原子軌道は3つの量子数 ( nlm,, の組合せにより指定される量子数の取り得る値の範囲 n の値が定まる l の範囲は n の値に依存して定まる m の範囲は
反応理論化学 ( その 軌道相互作用 複数の原子が相互作用して分子が形成される複数の原子軌道 ( または混成軌道 が混合して分子軌道が形成される原子軌道 ( または混成軌道 が混合して分子軌道に変化すると軌道エネルギーも変化する. 原子軌道 原子軌道は3つの量子数 ( nlm,, の組合せにより指定される量子数の取り得る値の範囲 n の値が定まる l の範囲は n の値に依存して定まる m の範囲は
s ss s ss = ε = = s ss s (3) と表される s の要素における s s = κ = κ, =,, (4) jωε jω s は複素比誘電率に相当する物理量であり ここで PML 媒質定数を次のように定義する すなわち κξ をPML 媒質の等価比誘電率 ξ をPML 媒質の
 FDTD 解析法 (Matlab 版 2 次元 PML) プログラム解説 v2.11 1. 概要 FDTD 解析における吸収境界である完全整合層 (Perfectl Matched Laer, PML) の定式化とプログラミングを2 次元 TE 波について解説する PMLは異方性の損失をもつ仮想的な物質であり 侵入して来る電磁波を逃さず吸収する 通常の物質と接する界面でインピーダンスが整合しており
FDTD 解析法 (Matlab 版 2 次元 PML) プログラム解説 v2.11 1. 概要 FDTD 解析における吸収境界である完全整合層 (Perfectl Matched Laer, PML) の定式化とプログラミングを2 次元 TE 波について解説する PMLは異方性の損失をもつ仮想的な物質であり 侵入して来る電磁波を逃さず吸収する 通常の物質と接する界面でインピーダンスが整合しており
Microsoft PowerPoint - mp11-02.pptx
 数理計画法第 2 回 塩浦昭義情報科学研究科准教授 shioura@dais.is.tohoku.ac.jp http://www.dais.is.tohoku.ac.jp/~shioura/teaching 前回の復習 数理計画とは? 数理計画 ( 復習 ) 数理計画問題とは? 狭義には : 数理 ( 数学 ) を使って計画を立てるための問題 広義には : 与えられた評価尺度に関して最も良い解を求める問題
数理計画法第 2 回 塩浦昭義情報科学研究科准教授 shioura@dais.is.tohoku.ac.jp http://www.dais.is.tohoku.ac.jp/~shioura/teaching 前回の復習 数理計画とは? 数理計画 ( 復習 ) 数理計画問題とは? 狭義には : 数理 ( 数学 ) を使って計画を立てるための問題 広義には : 与えられた評価尺度に関して最も良い解を求める問題
ギリシャ文字の読み方を教えてください
 埼玉工業大学機械工学学習支援セミナー ( 小西克享 ) 慣性モーメント -1/6 テーマ 01: 慣性モーメント (Momet of ietia) コマ回しをすると, 長い時間回転させるには重くて大きなコマを選ぶことや, ひもを早く引くことが重要であることが経験的にわかります. 遊びを通して, 回転の運動エネルギーを増やせば, 回転の勢いが増すことを学習できるので, 機械系の学生にとってコマ回しも大切な体験学習のひとつと言えます.
埼玉工業大学機械工学学習支援セミナー ( 小西克享 ) 慣性モーメント -1/6 テーマ 01: 慣性モーメント (Momet of ietia) コマ回しをすると, 長い時間回転させるには重くて大きなコマを選ぶことや, ひもを早く引くことが重要であることが経験的にわかります. 遊びを通して, 回転の運動エネルギーを増やせば, 回転の勢いが増すことを学習できるので, 機械系の学生にとってコマ回しも大切な体験学習のひとつと言えます.
木村の理論化学小ネタ 体心立方構造 面心立方構造 六方最密構造 剛球の並べ方と最密構造剛球を平面上に の向きに整列させるのに次の 2 つの方法がある 図より,B の方が A より密であることがわかる A B 1
 体心立方構造 面心立方構造 六方最密構造 剛球の並べ方と最密構造剛球を平面上に の向きに整列させるのに次の 2 つの方法がある 図より,B の方が A より密であることがわかる A B 1 体心立方構造 A を土台に剛球を積み重ねる 1 段目 2 2 段目 3 3 段目 他と色で区別した部分は上から見た最小繰り返し単位構造 ( 体心立方構造 ) 4 つまり,1 段目,2 段目,3 段目と順に重ねることにより,
体心立方構造 面心立方構造 六方最密構造 剛球の並べ方と最密構造剛球を平面上に の向きに整列させるのに次の 2 つの方法がある 図より,B の方が A より密であることがわかる A B 1 体心立方構造 A を土台に剛球を積み重ねる 1 段目 2 2 段目 3 3 段目 他と色で区別した部分は上から見た最小繰り返し単位構造 ( 体心立方構造 ) 4 つまり,1 段目,2 段目,3 段目と順に重ねることにより,
diode_revise
 2.3 pn 接合の整流作用 c 大豆生田利章 2015 1 2.3 pn 接合の整流作用 2.2 節では外部から電圧を加えないときの pn 接合について述べた. ここでは, 外部か らバイアス電圧を加えるとどのようにして電流が流れるかを電子の移動を中心に説明す る. 2.2 節では熱エネルギーの存在を考慮していなかったが, 実際には半導体のキャリアは 周囲から熱エネルギーを受け取る その結果 半導体のキャリヤのエネルギーは一定でな
2.3 pn 接合の整流作用 c 大豆生田利章 2015 1 2.3 pn 接合の整流作用 2.2 節では外部から電圧を加えないときの pn 接合について述べた. ここでは, 外部か らバイアス電圧を加えるとどのようにして電流が流れるかを電子の移動を中心に説明す る. 2.2 節では熱エネルギーの存在を考慮していなかったが, 実際には半導体のキャリアは 周囲から熱エネルギーを受け取る その結果 半導体のキャリヤのエネルギーは一定でな
DVIOUT-SS_Ma
 第 章 微分方程式 ニュートンはリンゴが落ちるのを見て万有引力を発見した という有名な逸話があります 無重力の宇宙船の中ではリンゴは落ちないで静止していることを考えると 重力が働くと始め静止しているものが動き出して そのスピードはどんどん大きくなる つまり速度の変化が現れることがわかります 速度は一般に時間と共に変化します 速度の瞬間的変化の割合を加速度といい で定義しましょう 速度が変化する, つまり加速度がでなくなるためにはその原因があり
第 章 微分方程式 ニュートンはリンゴが落ちるのを見て万有引力を発見した という有名な逸話があります 無重力の宇宙船の中ではリンゴは落ちないで静止していることを考えると 重力が働くと始め静止しているものが動き出して そのスピードはどんどん大きくなる つまり速度の変化が現れることがわかります 速度は一般に時間と共に変化します 速度の瞬間的変化の割合を加速度といい で定義しましょう 速度が変化する, つまり加速度がでなくなるためにはその原因があり
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生
 0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
電気電子工学CH-2_1017_v2済
 i-perc 電気通信 学 基礎電 学 CH-2 曽我部 東 電気通信 学 i- パワードエネルギーシステム研究センター (i-perc) 先週の OUTLINE: 2 体輻射 量 論の誕 光量 論 量 論 電 の古典 学特性 原 構造における電 の早期量 論 電 波とは何? 量 論 今週の概要 : 3 電 波 不確定性原理 量 論 円運動の方程式 量 学 複素数表現の導入 シュレーディンガー方程式の導き
i-perc 電気通信 学 基礎電 学 CH-2 曽我部 東 電気通信 学 i- パワードエネルギーシステム研究センター (i-perc) 先週の OUTLINE: 2 体輻射 量 論の誕 光量 論 量 論 電 の古典 学特性 原 構造における電 の早期量 論 電 波とは何? 量 論 今週の概要 : 3 電 波 不確定性原理 量 論 円運動の方程式 量 学 複素数表現の導入 シュレーディンガー方程式の導き
7 渦度方程式 総観規模あるいは全球規模の大気の運動を考える このような大きな空間スケールでの大気の運動においては 鉛直方向の運動よりも水平方向の運動のほうがずっと大きい しかも 水平方向の運動の中でも 収束 発散成分は相対的に小さく 低気圧や高気圧などで見られるような渦 つまり回転成分のほうが卓越
 7 渦度方程式 総観規模あるいは全球規模の大気の運動を考える このような大きな空間スケールでの大気の運動においては 鉛直方向の運動よりも水平方向の運動のほうがずっと大きい しかも 水平方向の運動の中でも 収束 発散成分は相対的に小さく 低気圧や高気圧などで見られるような渦 つまり回転成分のほうが卓越している そこで 回転成分に着目して大気の運動を論じる 7.1 渦度 大気の回転成分を定量化する方法を考えてみる
7 渦度方程式 総観規模あるいは全球規模の大気の運動を考える このような大きな空間スケールでの大気の運動においては 鉛直方向の運動よりも水平方向の運動のほうがずっと大きい しかも 水平方向の運動の中でも 収束 発散成分は相対的に小さく 低気圧や高気圧などで見られるような渦 つまり回転成分のほうが卓越している そこで 回転成分に着目して大気の運動を論じる 7.1 渦度 大気の回転成分を定量化する方法を考えてみる
木村の物理小ネタ ケプラーの第 2 法則と角運動量保存則 A. 面積速度面積速度とは平面内に定点 O と動点 P があるとき, 定点 O と動点 P を結ぶ線分 OP( 動径 OP という) が単位時間に描く面積を 動点 P の定点 O に
 ケプラーの第 法則と角運動量保存則 A. 面積速度面積速度とは平面内に定点 O と動点 P があるとき, 定点 O と動点 P を結ぶ線分 OP( 動径 OP という が単位時間に描く面積を 動点 P の定点 O に関する面積速度の大きさ という 定点 O まわりを回る面積速度の導き方導き方 A ( x( + D, y( + D v ( q r ( A ( x (, y( 動点 P が xy 座標平面上を時刻
ケプラーの第 法則と角運動量保存則 A. 面積速度面積速度とは平面内に定点 O と動点 P があるとき, 定点 O と動点 P を結ぶ線分 OP( 動径 OP という が単位時間に描く面積を 動点 P の定点 O に関する面積速度の大きさ という 定点 O まわりを回る面積速度の導き方導き方 A ( x( + D, y( + D v ( q r ( A ( x (, y( 動点 P が xy 座標平面上を時刻
<4D F736F F F696E74202D2091E6824F82538FCD8CEB82E88C9F8F6F814592F990B382CC8CB4979D82BB82CC82505F D E95848D8682CC90B69
 第 章 誤り検出 訂正の原理 その ブロック符号とその復号 安達文幸 目次 誤り訂正符号化を用いる伝送系誤り検出符号誤り検出 訂正符号 7, ハミング符号, ハミング符号生成行列, パリティ検査行列の一般形符号の生成行列符号の生成行列とパリティ検査行列の関係符号の訂正能力符号多項式 安達 : コミュニケーション符号理論 安達 : コミュニケーション符号理論 誤り訂正符号化を用いる伝送系 伝送システム
第 章 誤り検出 訂正の原理 その ブロック符号とその復号 安達文幸 目次 誤り訂正符号化を用いる伝送系誤り検出符号誤り検出 訂正符号 7, ハミング符号, ハミング符号生成行列, パリティ検査行列の一般形符号の生成行列符号の生成行列とパリティ検査行列の関係符号の訂正能力符号多項式 安達 : コミュニケーション符号理論 安達 : コミュニケーション符号理論 誤り訂正符号化を用いる伝送系 伝送システム
<4D F736F F D E4F8E9F82C982A882AF82E98D7397F1>
 3 三次における行列 要旨高校では ほとんど 2 2 の正方行列しか扱ってなく 三次の正方行列について考えてみたかったため 数 C で学んだ定理を三次の正方行列に応用して 自分たちで仮説を立てて求めていったら 空間における回転移動を表す行列 三次のケーリー ハミルトンの定理 三次における逆行列を求めたり 仮説をたてることができた. 目的 数 C で学んだ定理を三次の正方行列に応用する 2. 概要目的の到達点として
3 三次における行列 要旨高校では ほとんど 2 2 の正方行列しか扱ってなく 三次の正方行列について考えてみたかったため 数 C で学んだ定理を三次の正方行列に応用して 自分たちで仮説を立てて求めていったら 空間における回転移動を表す行列 三次のケーリー ハミルトンの定理 三次における逆行列を求めたり 仮説をたてることができた. 目的 数 C で学んだ定理を三次の正方行列に応用する 2. 概要目的の到達点として
線形代数とは
 線形代数とは 第一回ベクトル 教科書 エクササイズ線形代数 立花俊一 成田清正著 共立出版 必要最低限のことに限る 得意な人には物足りないかもしれません 線形代数とは何をするもの? 線形関係 y 直線 yもも 次式で登場する (( 次の形 ) 線形 ただし 次元の話世の中は 3 次元 [4[ 次元 ] 次元 3 次元 4 次元 はどうやって直線を表すの? ベクトルや行列の概念 y A ベクトルを使うと
線形代数とは 第一回ベクトル 教科書 エクササイズ線形代数 立花俊一 成田清正著 共立出版 必要最低限のことに限る 得意な人には物足りないかもしれません 線形代数とは何をするもの? 線形関係 y 直線 yもも 次式で登場する (( 次の形 ) 線形 ただし 次元の話世の中は 3 次元 [4[ 次元 ] 次元 3 次元 4 次元 はどうやって直線を表すの? ベクトルや行列の概念 y A ベクトルを使うと
振動学特論火曜 1 限 TA332J 藤井康介 6 章スペクトルの平滑化 スペクトルの平滑化とはギザギザした地震波のフーリエ スペクトルやパワ スペクトルでは正確にスペクトルの山がどこにあるかはよく分からない このようなスペクトルから不純なものを取り去って 本当の性質を浮き彫
 6 章スペクトルの平滑化 スペクトルの平滑化とはギザギザした地震波のフーリエ スペクトルやパワ スペクトルでは正確にスペクトルの山がどこにあるかはよく分からない このようなスペクトルから不純なものを取り去って 本当の性質を浮き彫りにするために スペクトルを滑らかにする操作のことをいう 6.1 合積のフーリエ変換スペクトルの平滑化を行う際に必要な 合積とそのフーリエ変換について説明する 6.2 データ
6 章スペクトルの平滑化 スペクトルの平滑化とはギザギザした地震波のフーリエ スペクトルやパワ スペクトルでは正確にスペクトルの山がどこにあるかはよく分からない このようなスペクトルから不純なものを取り去って 本当の性質を浮き彫りにするために スペクトルを滑らかにする操作のことをいう 6.1 合積のフーリエ変換スペクトルの平滑化を行う際に必要な 合積とそのフーリエ変換について説明する 6.2 データ
人間科学部研究年報平成 24 年 (1) (2) (3) (4) 式 (1) は, クーロン (Coulomb) の法則とも呼ばれる.ρは電荷密度を表し,ε 0 は真空の誘電率と呼ばれる定数である. 式 (2) は, 磁荷が存在しないことを表す式である. 式 (3) はファラデー (Faraday)
 複素振幅をもつ球面波の人間科学部研究年報 Maxwell 平成 24 方程式年 複素振幅をもつ球面波の Maxwell 方程式 Maxwell Equation of Spherical Wave with Complex Amplitude 戸上良弘 Yoshihiro TOGAMI Abstract 複素振幅をもつ球面波に関して, マクスウェル (Maxwell) 方程式との関係を考察した. 電気的な球面波としてのスカラーポテンシャルが与えられたとき,
複素振幅をもつ球面波の人間科学部研究年報 Maxwell 平成 24 方程式年 複素振幅をもつ球面波の Maxwell 方程式 Maxwell Equation of Spherical Wave with Complex Amplitude 戸上良弘 Yoshihiro TOGAMI Abstract 複素振幅をもつ球面波に関して, マクスウェル (Maxwell) 方程式との関係を考察した. 電気的な球面波としてのスカラーポテンシャルが与えられたとき,
<4D F736F F D20824F B CC92E8979D814696CA90CF95AA82C691CC90CF95AA2E646F63>
 1/1 平成 23 年 3 月 24 日午後 6 時 52 分 6 ガウスの定理 : 面積分と体積分 6 ガウスの定理 : 面積分と体積分 Ⅰ. 直交座標系 ガウスの定理は 微分して すぐに積分すると元に戻るというルールを 3 次元積分に適用した定理になります よく知っているのは 簡単化のため 変数が1つの場合は dj ( d ( ににします全微分 = 偏微分 d = d = J ( + C d です
1/1 平成 23 年 3 月 24 日午後 6 時 52 分 6 ガウスの定理 : 面積分と体積分 6 ガウスの定理 : 面積分と体積分 Ⅰ. 直交座標系 ガウスの定理は 微分して すぐに積分すると元に戻るというルールを 3 次元積分に適用した定理になります よく知っているのは 簡単化のため 変数が1つの場合は dj ( d ( ににします全微分 = 偏微分 d = d = J ( + C d です
2018年度 東京大・理系数学
 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ関数 f ( ) = + cos (0 < < ) の増減表をつくり, + 0, 0 のと sin きの極限を調べよ 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ n+ 数列 a, a, を, Cn a n = ( n =,, ) で定める n! an qn () n とする を既約分数 an p として表したときの分母
08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ関数 f ( ) = + cos (0 < < ) の増減表をつくり, + 0, 0 のと sin きの極限を調べよ 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ n+ 数列 a, a, を, Cn a n = ( n =,, ) で定める n! an qn () n とする を既約分数 an p として表したときの分母
< BD96CA E B816989A B A>
 数 Ⅱ 平面ベクトル ( 黄色チャート ) () () ~ () " 図 # () () () - - () - () - - () % から %- から - -,- 略 () 求めるベクトルを とする S であるから,k となる実数 k がある このとき k k, であるから k すなわち k$, 求めるベクトルは --,- - -7- - -, から また ',' 7 (),,-,, -, -,
数 Ⅱ 平面ベクトル ( 黄色チャート ) () () ~ () " 図 # () () () - - () - () - - () % から %- から - -,- 略 () 求めるベクトルを とする S であるから,k となる実数 k がある このとき k k, であるから k すなわち k$, 求めるベクトルは --,- - -7- - -, から また ',' 7 (),,-,, -, -,
Microsoft PowerPoint - 10JUL13.ppt
 無機化学 03 年 4 月 ~03 年 8 月 水曜日 時間目 4M 講義室第 3 回 7 月 0 日ミラー指数面の間隔 X 線回折ブラッグの法則 (0 章材料 : 固体 ) 結晶構造 担当教員 : 福井大学大学院工学研究科生物応用化学専攻教授前田史郎 E-mil:sme@u-fukui.c.jp URL:http://cbio.cbio.u-fukui.c.jp/phychem/me/kougi
無機化学 03 年 4 月 ~03 年 8 月 水曜日 時間目 4M 講義室第 3 回 7 月 0 日ミラー指数面の間隔 X 線回折ブラッグの法則 (0 章材料 : 固体 ) 結晶構造 担当教員 : 福井大学大学院工学研究科生物応用化学専攻教授前田史郎 E-mil:sme@u-fukui.c.jp URL:http://cbio.cbio.u-fukui.c.jp/phychem/me/kougi
相対性理論入門 1 Lorentz 変換 光がどのような座標系に対しても同一の速さ c で進むことから導かれる座標の一次変換である. (x, y, z, t ) の座標系が (x, y, z, t) の座標系に対して x 軸方向に w の速度で進んでいる場合, 座標系が一次変換で関係づけられるとする
 相対性理論入門 Lorentz 変換 光がどのような座標系に対しても同一の速さ で進むことから導かれる座標の一次変換である. x, y, z, t ) の座標系が x, y, z, t) の座標系に対して x 軸方向に w の速度で進んでいる場合, 座標系が一次変換で関係づけられるとすると, x A x wt) y y z z t Bx + Dt 弨弱弩弨弲弩弨弳弩弨弴弩 が成立する. 図 : 相対速度
相対性理論入門 Lorentz 変換 光がどのような座標系に対しても同一の速さ で進むことから導かれる座標の一次変換である. x, y, z, t ) の座標系が x, y, z, t) の座標系に対して x 軸方向に w の速度で進んでいる場合, 座標系が一次変換で関係づけられるとすると, x A x wt) y y z z t Bx + Dt 弨弱弩弨弲弩弨弳弩弨弴弩 が成立する. 図 : 相対速度
2014年度 筑波大・理系数学
 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ f ( x) = x x とする y = f ( x ) のグラフに点 P(, ) から引いた接線は 本あるとする つの接点 A (, f ( )), B(, f ( )), C(, f ( )) を頂点とする三角形の 重心を G とする () + +, + + および を, を用いて表せ () 点 G の座標を, を用いて表せ () 点 G
筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ f ( x) = x x とする y = f ( x ) のグラフに点 P(, ) から引いた接線は 本あるとする つの接点 A (, f ( )), B(, f ( )), C(, f ( )) を頂点とする三角形の 重心を G とする () + +, + + および を, を用いて表せ () 点 G の座標を, を用いて表せ () 点 G
Microsoft Word - note02.doc
 年度 物理化学 Ⅱ 講義ノート. 二原子分子の振動. 調和振動子近似 モデル 分子 = 理想的なバネでつながった原子 r : 核間距離, r e : 平衡核間距離, : 変位 ( = r r e ), k f : 力の定数ポテンシャルエネルギー ( ) k V = f (.) 古典運動方程式 [ 振動数 ] 3.3 d kf (.) dt μ : 換算質量 (m, m : 原子, の質量 ) mm
年度 物理化学 Ⅱ 講義ノート. 二原子分子の振動. 調和振動子近似 モデル 分子 = 理想的なバネでつながった原子 r : 核間距離, r e : 平衡核間距離, : 変位 ( = r r e ), k f : 力の定数ポテンシャルエネルギー ( ) k V = f (.) 古典運動方程式 [ 振動数 ] 3.3 d kf (.) dt μ : 換算質量 (m, m : 原子, の質量 ) mm
重要例題113
 04_ 高校 数学 Ⅱ 必須基本公式 定理集 数学 Ⅱ 第 章式の計算と方程式 0 商と余り についての整式 A をについての整式 B で割ったときの商を Q, 余りを R とすると, ABQ+R (R の次数 ) > 0
04_ 高校 数学 Ⅱ 必須基本公式 定理集 数学 Ⅱ 第 章式の計算と方程式 0 商と余り についての整式 A をについての整式 B で割ったときの商を Q, 余りを R とすると, ABQ+R (R の次数 ) > 0
物性物理学I_2.pptx
 The University of Tokyo, Komaba Graduate School of Arts and Sciences I 凝縮系 固体 をデザインする 銅()面上の鉄原子の 量子珊瑚礁 IBM Almaden 許可を得て掲載 www.almaden.ibm.com/vis/stm/imagesstm5.jpg&imgrefurl=http://www.almaden.ibm.com/vis/
The University of Tokyo, Komaba Graduate School of Arts and Sciences I 凝縮系 固体 をデザインする 銅()面上の鉄原子の 量子珊瑚礁 IBM Almaden 許可を得て掲載 www.almaden.ibm.com/vis/stm/imagesstm5.jpg&imgrefurl=http://www.almaden.ibm.com/vis/
<4D F736F F D2097CD8A7793FC96E582BD82ED82DD8A E6318FCD2E646F63>
 - 第 章たわみ角法の基本式 ポイント : たわみ角法の基本式を理解する たわみ角法の基本式を梁の微分方程式より求める 本章では たわみ角法の基本式を導くことにする 基本式の誘導法は各種あるが ここでは 梁の微分方程式を解いて基本式を求める方法を採用する この本で使用する座標系は 右手 右ネジの法則に従った座標を用いる また ひとつの部材では 図 - に示すように部材の左端の 点を原点とし 軸線を
- 第 章たわみ角法の基本式 ポイント : たわみ角法の基本式を理解する たわみ角法の基本式を梁の微分方程式より求める 本章では たわみ角法の基本式を導くことにする 基本式の誘導法は各種あるが ここでは 梁の微分方程式を解いて基本式を求める方法を採用する この本で使用する座標系は 右手 右ネジの法則に従った座標を用いる また ひとつの部材では 図 - に示すように部材の左端の 点を原点とし 軸線を
PowerPoint プレゼンテーション
 第 6 回新電極触媒 宿泊セミナー 触媒解析技術の進展と FC ビジネスへの期待 金属の電子構造 触媒作用の理解のために 東京農工大学名誉教授 ( 独 ) 科学技術振興機構 佐藤勝昭 はじめに 触媒には 金属触媒 分子 ( 金属錯体 ) 触媒 半導体光触媒があります いずれも 触媒表面で 反応物の吸着 表面反応 生成物の脱離が起きています このとき 触媒と反応物との間に化学結合が起きます 化学結合は
第 6 回新電極触媒 宿泊セミナー 触媒解析技術の進展と FC ビジネスへの期待 金属の電子構造 触媒作用の理解のために 東京農工大学名誉教授 ( 独 ) 科学技術振興機構 佐藤勝昭 はじめに 触媒には 金属触媒 分子 ( 金属錯体 ) 触媒 半導体光触媒があります いずれも 触媒表面で 反応物の吸着 表面反応 生成物の脱離が起きています このとき 触媒と反応物との間に化学結合が起きます 化学結合は
2015-2017年度 2次数学セレクション(複素数)解答解説
 05 次数学セレクション解答解説 [ 筑波大 ] ( + より, 0 となり, + から, ( (,, よって, の描く図形 C は, 点 を中心とし半径が の円である すなわち, 原 点を通る円となる ( は虚数, は正の実数より, である さて, w ( ( とおくと, ( ( ( w ( ( ( ここで, w は純虚数より, は純虚数となる すると, の描く図形 L は, 点 を通り, 点 と点
05 次数学セレクション解答解説 [ 筑波大 ] ( + より, 0 となり, + から, ( (,, よって, の描く図形 C は, 点 を中心とし半径が の円である すなわち, 原 点を通る円となる ( は虚数, は正の実数より, である さて, w ( ( とおくと, ( ( ( w ( ( ( ここで, w は純虚数より, は純虚数となる すると, の描く図形 L は, 点 を通り, 点 と点
PowerPoint プレゼンテーション
 電磁波工学 第 5 回平面波の媒質への垂直および射入射と透過 柴田幸司 Bounda Plan Rgon ε μ Rgon Mdum ( ガラスなど ε μ z 平面波の反射と透過 垂直入射の場合 左図に示す様に 平面波が境界面に対して垂直に入射する場合を考える この時の入射波を とすると 入射波は境界において 透過波 と とに分解される この時の透過量を 反射量を Γ とおくと 領域 における媒質の誘電率に対して透過量
電磁波工学 第 5 回平面波の媒質への垂直および射入射と透過 柴田幸司 Bounda Plan Rgon ε μ Rgon Mdum ( ガラスなど ε μ z 平面波の反射と透過 垂直入射の場合 左図に示す様に 平面波が境界面に対して垂直に入射する場合を考える この時の入射波を とすると 入射波は境界において 透過波 と とに分解される この時の透過量を 反射量を Γ とおくと 領域 における媒質の誘電率に対して透過量
. 角の二等分線と調和平均 平面上に点 を端点とする線分 と を重ならないようにとる, とし とする の二等分線が線分 と交わる点を とし 点 から に垂直に引いた直線が線分 と交わる点 とする 線分 の長さを求めてみよう 点 から に垂直な直線と および との交点をそれぞれ, Dとする つの直角三
 角の二等分線で開くいろいろな平均 札幌旭丘高校中村文則 0. 数直線上に現れるいろいろな平均下図は 数 (, ) の調和平均 相乗平均 相加平均 二乗平均を数直線上に置いたものである, とし 直径 中心 である円を用いていろいろな平均の大小関係を表現するもっとも美しい配置方法であり その証明も容易である Q D E F < 相加平均 > (0), ( ), ( とすると 線分 ) の中点 の座標はである
角の二等分線で開くいろいろな平均 札幌旭丘高校中村文則 0. 数直線上に現れるいろいろな平均下図は 数 (, ) の調和平均 相乗平均 相加平均 二乗平均を数直線上に置いたものである, とし 直径 中心 である円を用いていろいろな平均の大小関係を表現するもっとも美しい配置方法であり その証明も容易である Q D E F < 相加平均 > (0), ( ), ( とすると 線分 ) の中点 の座標はである
予定 (川口担当分)
 予定 ( 川口担当分 ) (1)4 月 13 日 量子力学 固体の性質の復習 (2)4 月 20 日 自由電子モデル (3)4 月 27 日 結晶中の電子 (4)5 月 11 日 半導体 (5)5 月 18 日 輸送現象 金属絶縁体転移 (6)5 月 25 日 磁性の基礎 (7)6 月 1 日 物性におけるトポロジー 今日 (5/11) の内容 ブロッホ電子の運動 電磁場中の運動 ランダウ量子化 半導体
予定 ( 川口担当分 ) (1)4 月 13 日 量子力学 固体の性質の復習 (2)4 月 20 日 自由電子モデル (3)4 月 27 日 結晶中の電子 (4)5 月 11 日 半導体 (5)5 月 18 日 輸送現象 金属絶縁体転移 (6)5 月 25 日 磁性の基礎 (7)6 月 1 日 物性におけるトポロジー 今日 (5/11) の内容 ブロッホ電子の運動 電磁場中の運動 ランダウ量子化 半導体
物性基礎
 水素様原子 水素原子 水素様原子 エネルギー固有値 波動関数 主量子数 角運動量 方位量子数 磁気量子数 原子核 + 電子 個 F p F = V = 水素様原子 古典力学 水素様原子 量子力学 角運動量 L p F p L 運動方程式 d dt p = d d d p p = p + dt dt dt = p p = d dt L = 角運動量の保存則 ポテンシャルエネルギー V = 4πε =
水素様原子 水素原子 水素様原子 エネルギー固有値 波動関数 主量子数 角運動量 方位量子数 磁気量子数 原子核 + 電子 個 F p F = V = 水素様原子 古典力学 水素様原子 量子力学 角運動量 L p F p L 運動方程式 d dt p = d d d p p = p + dt dt dt = p p = d dt L = 角運動量の保存則 ポテンシャルエネルギー V = 4πε =
行列、ベクトル
 行列 (Mtri) と行列式 (Determinnt). 行列 (Mtri) の演算. 和 差 積.. 行列とは.. 行列の和差 ( 加減算 ).. 行列の積 ( 乗算 ). 転置行列 対称行列 正方行列. 単位行列. 行列式 (Determinnt) と逆行列. 行列式. 逆行列. 多元一次連立方程式のコンピュータによる解法. コンピュータによる逆行列の計算.. 定数項の異なる複数の方程式.. 逆行列の計算
行列 (Mtri) と行列式 (Determinnt). 行列 (Mtri) の演算. 和 差 積.. 行列とは.. 行列の和差 ( 加減算 ).. 行列の積 ( 乗算 ). 転置行列 対称行列 正方行列. 単位行列. 行列式 (Determinnt) と逆行列. 行列式. 逆行列. 多元一次連立方程式のコンピュータによる解法. コンピュータによる逆行列の計算.. 定数項の異なる複数の方程式.. 逆行列の計算
喨微勃挹稉弑
 == 全微分方程式 == 全微分とは 変数の関数 z=f(, ) について,, の増分を Δ, Δ とするとき, z の増分 Δz は Δz z Δ+ z Δ で表されます. この式において, Δ 0, Δ 0 となる極限を形式的に dz= z d+ z d (1) で表し, dz を z の全微分といいます. z は z の に関する偏導関数で, を定数と見なし て, で微分したものを表し, 方向の傾きに対応します.
== 全微分方程式 == 全微分とは 変数の関数 z=f(, ) について,, の増分を Δ, Δ とするとき, z の増分 Δz は Δz z Δ+ z Δ で表されます. この式において, Δ 0, Δ 0 となる極限を形式的に dz= z d+ z d (1) で表し, dz を z の全微分といいます. z は z の に関する偏導関数で, を定数と見なし て, で微分したものを表し, 方向の傾きに対応します.
<4D F736F F D2097CA8E718CF889CA F E F E2E646F63>
 量子効果デバイス第 11 回 前澤宏一 トンネル効果とフラッシュメモリ デバイスサイズの縮小縮小とトンネルトンネル効果 Si-CMOS はサイズの縮小を続けることによってその性能を伸ばしてきた チャネル長や ゲート絶縁膜の厚さ ソース ドレイン領域の深さ 電源電圧をあるルール ( これをスケーリング則という ) に従って縮小することで 高速化 低消費電力化が可能となる 集積回路の誕生以来 スケーリング側にしたがって縮小されてきたデバイスサイズは
量子効果デバイス第 11 回 前澤宏一 トンネル効果とフラッシュメモリ デバイスサイズの縮小縮小とトンネルトンネル効果 Si-CMOS はサイズの縮小を続けることによってその性能を伸ばしてきた チャネル長や ゲート絶縁膜の厚さ ソース ドレイン領域の深さ 電源電圧をあるルール ( これをスケーリング則という ) に従って縮小することで 高速化 低消費電力化が可能となる 集積回路の誕生以来 スケーリング側にしたがって縮小されてきたデバイスサイズは
静的弾性問題の有限要素法解析アルゴリズム
 概要 基礎理論. 応力とひずみおよび平衡方程式. 降伏条件式. 構成式 ( 応力 - ひずみ関係式 ) 有限要素法. 有限要素法の概要. 仮想仕事の原理式と変分原理. 平面ひずみ弾性有限要素法定式化 FEM の基礎方程式平衡方程式. G G G ひずみ - 変位関係式 w w w. kl jkl j D 構成式応力 - ひずみ関係式 ) (. 変位の境界条件力の境界条件境界条件式 t S on V
概要 基礎理論. 応力とひずみおよび平衡方程式. 降伏条件式. 構成式 ( 応力 - ひずみ関係式 ) 有限要素法. 有限要素法の概要. 仮想仕事の原理式と変分原理. 平面ひずみ弾性有限要素法定式化 FEM の基礎方程式平衡方程式. G G G ひずみ - 変位関係式 w w w. kl jkl j D 構成式応力 - ひずみ関係式 ) (. 変位の境界条件力の境界条件境界条件式 t S on V
工業数学F2-04(ウェブ用).pptx
 工業数学 F2 #4 フーリエ級数を極める 京都大学加納学 京都大学大学院情報学研究科システム科学専攻 Human Systems Lab., Dept. of Systems Science Graduate School of Informatics, Kyoto University 復習 1: 複素フーリエ級数 2 周期 2π の周期関数 f(x) の複素フーリエ級数展開 複素フーリエ係数
工業数学 F2 #4 フーリエ級数を極める 京都大学加納学 京都大学大学院情報学研究科システム科学専攻 Human Systems Lab., Dept. of Systems Science Graduate School of Informatics, Kyoto University 復習 1: 複素フーリエ級数 2 周期 2π の周期関数 f(x) の複素フーリエ級数展開 複素フーリエ係数
Microsoft Word - 9章(分子物性).doc
 1/1/6 9 章分子物性 1 節電気双極子モーメント (Electric Dipole Moment) 電子双極子モーメント とは 微小な距離 a だけ離れて点電荷 q が存在する状態 絶対値は aq で 負電荷 q から正電荷 q へ向かうベクトルである 例えば 水分子は下右図のような向きの電気双極子モーメントをもち その大きさは約 1.85D である このように元々から持っている双極子モーメントを
1/1/6 9 章分子物性 1 節電気双極子モーメント (Electric Dipole Moment) 電子双極子モーメント とは 微小な距離 a だけ離れて点電荷 q が存在する状態 絶対値は aq で 負電荷 q から正電荷 q へ向かうベクトルである 例えば 水分子は下右図のような向きの電気双極子モーメントをもち その大きさは約 1.85D である このように元々から持っている双極子モーメントを
1999年度 センター試験・数学ⅡB
 99 センター試験数学 Ⅱ 数学 B 問題 第 問 ( 必答問題 ) [] 関数 y cos3x の周期のうち正で最小のものはアイウ 解答解説のページへ 0 x 360 のとき, 関数 y cos3x において, y となる x はエ個, y となる x はオ 個ある また, y sin x と y cos3x のグラフより, 方程式 sin x cos3x は 0 x 360のときカ個の解をもつことがわかる
99 センター試験数学 Ⅱ 数学 B 問題 第 問 ( 必答問題 ) [] 関数 y cos3x の周期のうち正で最小のものはアイウ 解答解説のページへ 0 x 360 のとき, 関数 y cos3x において, y となる x はエ個, y となる x はオ 個ある また, y sin x と y cos3x のグラフより, 方程式 sin x cos3x は 0 x 360のときカ個の解をもつことがわかる
14 化学実験法 II( 吉村 ( 洋 mmol/l の半分だったから さんの測定値は くんの測定値の 4 倍の重みがあり 推定値 としては 0.68 mmol/l その標準偏差は mmol/l 程度ということになる 測定値を 特徴づけるパラメータ t を推定するこの手
 14 化学実験法 II( 吉村 ( 洋 014.6.1. 最小 乗法のはなし 014.6.1. 内容 最小 乗法のはなし...1 最小 乗法の考え方...1 最小 乗法によるパラメータの決定... パラメータの信頼区間...3 重みの異なるデータの取扱い...4 相関係数 決定係数 ( 最小 乗法を語るもう一つの立場...5 実験条件の誤差の影響...5 問題...6 最小 乗法の考え方 飲料水中のカルシウム濃度を
14 化学実験法 II( 吉村 ( 洋 014.6.1. 最小 乗法のはなし 014.6.1. 内容 最小 乗法のはなし...1 最小 乗法の考え方...1 最小 乗法によるパラメータの決定... パラメータの信頼区間...3 重みの異なるデータの取扱い...4 相関係数 決定係数 ( 最小 乗法を語るもう一つの立場...5 実験条件の誤差の影響...5 問題...6 最小 乗法の考え方 飲料水中のカルシウム濃度を
2014年度 センター試験・数学ⅡB
 第 問 解答解説のページへ [] O を原点とする座標平面において, 点 P(, q) を中心とする円 C が, 方程式 y 4 x で表される直線 l に接しているとする () 円 C の半径 r を求めよう 点 P を通り直線 l に垂直な直線の方程式は, y - ア ( x- ) + qなので, P イ から l に引いた垂線と l の交点 Q の座標は ( ( ウ + エ q ), 4 (
第 問 解答解説のページへ [] O を原点とする座標平面において, 点 P(, q) を中心とする円 C が, 方程式 y 4 x で表される直線 l に接しているとする () 円 C の半径 r を求めよう 点 P を通り直線 l に垂直な直線の方程式は, y - ア ( x- ) + qなので, P イ から l に引いた垂線と l の交点 Q の座標は ( ( ウ + エ q ), 4 (
有限密度での非一様なカイラル凝縮と クォーク質量による影響
 空間的に非一様なカイラル凝縮に対する current quark mass の影響 東京高専 前段眞治 東京理科大学セミナー 2010.9.6 1 1.Introduction 低温 高密度における QCD の振る舞い 中性子星 compact star クォーク物質の理解に重要 T 0 での QCD の基底状態 カイラル対称性の破れた相 カラー超伝導相 μ 2 有限密度において fermionic
空間的に非一様なカイラル凝縮に対する current quark mass の影響 東京高専 前段眞治 東京理科大学セミナー 2010.9.6 1 1.Introduction 低温 高密度における QCD の振る舞い 中性子星 compact star クォーク物質の理解に重要 T 0 での QCD の基底状態 カイラル対称性の破れた相 カラー超伝導相 μ 2 有限密度において fermionic
