Microsoft PowerPoint - H17-5時限(パターン認識).ppt
|
|
|
- はるまさ すえがら
- 7 years ago
- Views:
Transcription
1 パターン認識早稲田大学講義 平成 7 年度 独 産業技術総合研究所栗田多喜夫 赤穂昭太郎 統計的特徴抽出
2 パターン認識過程 特徴抽出 認識対象から何らかの特徴量を計測 抽出 する必要がある 認識に有効な情報 特徴 を抽出し 次元を縮小した効率の良い空間を構成する過程 文字認識 : スキャナ等で取り込んだ画像から文字の識別に必要な本質的な特徴のみを抽出 例 文字線の傾き 曲率 面積など 識別 与えられた未知の対象を 特徴とクラスの関係に関する知識に基づいて どのクラスに属するかを決定 判定 する過程 パターン空間 特徴抽出識別,,, M C,, C, C 概念空間 識別に有効な特徴の抽出 パターンを計測して得られる特徴は 必ずしも識別に有効とは限らない > 識別に有効な特徴を取り出すには? 有効な特徴を抽出する方法 方法 : 統計的特徴抽出法 重回帰分析 主成分分析 判別分析 方法 : 特徴選択法
3 統計的特徴抽出 パターンの変形 実際のパターンは不規則な変形を伴っている また 観測にノイズが混入することもある > 内の理想的な点の回りの確率的な散らばり 分布 となる 統計的特徴抽出 で特徴ベクトルの確率統計的な構造を利用して パターンを識別するのに有効な特徴を抽出する過程 Ψ から認識に有効なより低次元の判別への最適な写像は での良さを表す評価基準とでのパターンの確率統計的構造に依存して決まる パターン空間 特徴抽出 Ψ 判別空間 C,, C, C 概念空間 線形多変量データ解析手法 線形特徴抽出 Ψ b 多変量データ解析手法 線形判別分析 線形重回帰分析 主成分分析など 多変量を線形結合した新変量に関する評価基準として 平均 乗誤差最小 分散最大などの 次の統計量に基づく評価基準を考える データの空間 の確率統計的構造が 次までの統計量 平均ベクトル 相関行列 共分散行列など に要約され 線形代数の範囲で最適解が陽に求まる 3
4 線形重回帰分析 線形回帰による直線の当てはめ 個のデータ モデル 評価基準 平均 乗誤差最小,,,, + b + ε b ε ε b 4
5 5 最適解 直線の当てはめ 最適なパラメータ 最適な直線 r b r * * r + 達成される平均 乗誤差 この時 達成される平均 乗誤差 ρ ε r r
6 訓練データ 線形重回帰分析,,,, 線形写像 Ψ 予測空間 教師 平均 乗誤差基準 入力と望みの出力の対が学習データとして与えられている時 線形モデルの出力と望みの出力との平均 乗誤差が最小となるような係数行列を求める ε 線形重回帰分析の最適解 最適解 R XX R XY R R XX XY 達成される平均 乗誤差 ε tr R YY tr R XY R XX R XY 6
7 最小 乗線形判別写像 理想出力を各クラスの代表ベクトルとする 平均 乗誤差 ε t ω 最適な係数行列 R XX ω μ e 最適写像 最小 乗線形判別写像 j C e j ω μ R XX e 教師 e 判別空間 主成分分析 7
8 8 主成分分析 訓練データ 与えられたデータの変動を最もよく表す新たな特徴量を求める 新特徴の統計量 { } X,, b b M j j j + + X b b + + 分散最大主成分空間 評価基準 新特徴の分散最大 制約条件 最適化問題 Lgrnge 乗数 主成分分析 導出 M j j X X Q λ λ
9 主成分分析 導出 Q のパラメータに関する偏微分 Q X λ 0 これから X の分散共分散行列の固有値問題が得られる X λ 最適なパラメータは Xの分散共分散行列の最大固有値として求まる ただし その大きさについては 制約条件を満たす必要がある M j j 直線の当てはめ 重回帰分析 ε 主成分分析 b ε d, r 0 9
10 主成分分析 多次元の場合 主成分分析 Prncpl Component nlss 多変量の計測値から変量間の相関を無くし しかも より低次元の変量によって元の計測値の特性を記述 最適な係数行列 最小二乗近似 ~ Λ, I X ~ ˆ~ ε, ˆ~ ~ 分散最大 主成分空間 最小 乗近似 主成分分析と最小 乗近似 ˆ~ ε ~ ˆ~ ~ 主成分空間 ˆ~ 0
11 固有顔による顔画像の認識 主成分分析 Prncpl Component nlss 多変量の計測値から変量間の相関を無くし しかも より低次元の変量によって元の計測値の特性を記述 ~ Λ, I 固有顔 Egen Fce X 最小二乗近似 ~ ˆ~, ˆ~ ε ~ ~ 各画像を画素の値をならべたベクトルとして表現し 画像集合を主成分分析して得られる固有ベクトル 主成分スコア間の距離 ˆ~ ˆ~ ~ ~ 線形判別分析
12 線形判別分析 歴史 英国の統計学者フィシャーが 多くの変量に基づく クラスの判別問題に対して 線形モデルによる解析的な手法を提案 936 年 次の統計量に基づく判別基準を最大化 フィシャーの線形判別分析 Lner Dscrmnnt nlss LD 確率分布を仮定しないノンパラメトリックな統計手法としての多変量データ解析の誕生 線形判別写像 Ψ 判別空間 線形判別分析 次元の場合 訓練データ <, l >,, 各クラスの分離度 判別基準 が最大となる新たな特徴量を求める 新特徴の統計量 { } l C l C 0 判別基準最大 主成分空間
13 3 線形判別分析 次元の場合 新特徴の統計量 平均クラス間分散 平均クラス内分散 C l C l 判別基準最大化 等価な問題 制約条件 最大化 最適化問題 Lgrnge 乗数 線形判別分析 導出 η Q λ λ
14 線形判別分析 導出 Q のパラメータに関する偏微分 Q λ 0 これから 一般化固有値問題が得られる λ 最適なパラメータは Xの分散共分散行列の最大固有値として求まる ただし その大きさについては 制約条件を満たす必要がある 線形判別分析 多次元の場合 判別基準 同じクラスに属す点はなるべく近く 異なるクラスに属す点は離れる ただし J [ ] tr Ψ Y Y : 平均クラス内共分散行列 : 平均クラス間共分散行列 Y, 最適解 最適な係数行列は 固有値問題, Y Λ, I の最大 n 個の固有値に対応する固有ベクトルを列とする行列として求められる ただし Yの次元 nは行列のランクの関係から n mn, m 4
15 線形判別分析の例 アヤメのデータの場合 Fsher のアヤメのデータ 3 種類のアヤメの花から 4 種類の特徴を測定 4 次元の特徴ベクトル 各種類 50 個のサンプル ここまでのまとめ ベイズ識別の理論 事後確率が重要 事後確率最大のクラスに識別すればよい そのためには 確率密度関数の推定が必要 パラメトリックモデル ノンパラメトリックな手法 セミパラメトリック 各クラスの条件付確率が正規分布の場合 事後確率の対数をとると 特徴量に関して 次の関数 識別関数 クラスの分散共分散行列が等しい場合には 次 線形 の識別関数 線形識別関数の学習 訓練データから直接識別関数のパラメータを求める パーセプトロン 最小 乗判別関数の学習 ロジスティック回帰 多層パーセプトロン 汎化性能 訓練データに対する識別性能ではなく 未学習データに対する性能が重要 汎化性能の評価 Cross-Vldton ブートストラップ 情報量基準 汎化性能の向上 Shrnge 法 ノイズの付加 変数選択 統計的特長抽出 最小 乗判別関数 主成分分析 判別分析 5
16 質問等 電子メール ホームページ 連絡先 茨城県つくば市梅園 -- つくば中央第 産業技術総合研究所栗田多喜夫 電話 FX 電話 FX 限目終了 6
0 部分的最小二乗回帰 Partial Least Squares Regression PLS 明治大学理 学部応用化学科 データ化学 学研究室 弘昌
 0 部分的最小二乗回帰 Parial Leas Squares Regressio PLS 明治大学理 学部応用化学科 データ化学 学研究室 弘昌 部分的最小二乗回帰 (PLS) とは? 部分的最小二乗回帰 (Parial Leas Squares Regressio, PLS) 線形の回帰分析手法の つ 説明変数 ( 記述 ) の数がサンプルの数より多くても計算可能 回帰式を作るときにノイズの影響を受けにくい
0 部分的最小二乗回帰 Parial Leas Squares Regressio PLS 明治大学理 学部応用化学科 データ化学 学研究室 弘昌 部分的最小二乗回帰 (PLS) とは? 部分的最小二乗回帰 (Parial Leas Squares Regressio, PLS) 線形の回帰分析手法の つ 説明変数 ( 記述 ) の数がサンプルの数より多くても計算可能 回帰式を作るときにノイズの影響を受けにくい
PowerPoint Presentation
 . カーネル法への招待 正定値カーネルによるデータ解析 - カーネル法の基礎と展開 - 福水健次統計数理研究所 / 総合研究大学院大学 統計数理研究所公開講座 0 年 月 34 日 概要 カーネル法の基本 線形データ解析と非線形データ解析 カーネル法の原理 カーネル法の つの例 カーネル主成分分析 : PCA の非線形拡張 リッジ回帰とそのカーネル化 概要 カーネル法の基本 線形データ解析と非線形データ解析
. カーネル法への招待 正定値カーネルによるデータ解析 - カーネル法の基礎と展開 - 福水健次統計数理研究所 / 総合研究大学院大学 統計数理研究所公開講座 0 年 月 34 日 概要 カーネル法の基本 線形データ解析と非線形データ解析 カーネル法の原理 カーネル法の つの例 カーネル主成分分析 : PCA の非線形拡張 リッジ回帰とそのカーネル化 概要 カーネル法の基本 線形データ解析と非線形データ解析
ベイズ統計入門
 ベイズ統計入門 条件付確率 事象 F が起こったことが既知であるという条件の下で E が起こる確率を条件付確率 (codtoal probablt) という P ( E F ) P ( E F ) P( F ) 定義式を変形すると 確率の乗法公式となる ( E F ) P( F ) P( E F ) P( E) P( F E) P 事象の独立 ある事象の生起する確率が 他のある事象が生起するかどうかによって変化しないとき
ベイズ統計入門 条件付確率 事象 F が起こったことが既知であるという条件の下で E が起こる確率を条件付確率 (codtoal probablt) という P ( E F ) P ( E F ) P( F ) 定義式を変形すると 確率の乗法公式となる ( E F ) P( F ) P( E F ) P( E) P( F E) P 事象の独立 ある事象の生起する確率が 他のある事象が生起するかどうかによって変化しないとき
Microsoft PowerPoint - 資料04 重回帰分析.ppt
 04. 重回帰分析 京都大学 加納学 Division of Process Control & Process Sstems Engineering Department of Chemical Engineering, Koto Universit [email protected] http://www-pse.cheme.koto-u.ac.jp/~kano/ Outline
04. 重回帰分析 京都大学 加納学 Division of Process Control & Process Sstems Engineering Department of Chemical Engineering, Koto Universit [email protected] http://www-pse.cheme.koto-u.ac.jp/~kano/ Outline
多変量解析 ~ 重回帰分析 ~ 2006 年 4 月 21 日 ( 金 ) 南慶典
 多変量解析 ~ 重回帰分析 ~ 2006 年 4 月 21 日 ( 金 ) 南慶典 重回帰分析とは? 重回帰分析とは複数の説明変数から目的変数との関係性を予測 評価説明変数 ( 数量データ ) は目的変数を説明するのに有効であるか得られた関係性より未知のデータの妥当性を判断する これを重回帰分析という つまり どんなことをするのか? 1 最小 2 乗法により重回帰モデルを想定 2 自由度調整済寄与率を求め
多変量解析 ~ 重回帰分析 ~ 2006 年 4 月 21 日 ( 金 ) 南慶典 重回帰分析とは? 重回帰分析とは複数の説明変数から目的変数との関係性を予測 評価説明変数 ( 数量データ ) は目的変数を説明するのに有効であるか得られた関係性より未知のデータの妥当性を判断する これを重回帰分析という つまり どんなことをするのか? 1 最小 2 乗法により重回帰モデルを想定 2 自由度調整済寄与率を求め
Microsoft PowerPoint - e-stat(OLS).pptx
 経済統計学 ( 補足 ) 最小二乗法について 担当 : 小塚匡文 2015 年 11 月 19 日 ( 改訂版 ) 神戸大学経済学部 2015 年度後期開講授業 補足 : 最小二乗法 ( 単回帰分析 ) 1.( 単純 ) 回帰分析とは? 標本サイズTの2 変数 ( ここではXとY) のデータが存在 YをXで説明する回帰方程式を推定するための方法 Y: 被説明変数 ( または従属変数 ) X: 説明変数
経済統計学 ( 補足 ) 最小二乗法について 担当 : 小塚匡文 2015 年 11 月 19 日 ( 改訂版 ) 神戸大学経済学部 2015 年度後期開講授業 補足 : 最小二乗法 ( 単回帰分析 ) 1.( 単純 ) 回帰分析とは? 標本サイズTの2 変数 ( ここではXとY) のデータが存在 YをXで説明する回帰方程式を推定するための方法 Y: 被説明変数 ( または従属変数 ) X: 説明変数
Probit , Mixed logit
 Probit, Mixed logit 2016/5/16 スタートアップゼミ #5 B4 後藤祥孝 1 0. 目次 Probit モデルについて 1. モデル概要 2. 定式化と理解 3. 推定 Mixed logit モデルについて 4. モデル概要 5. 定式化と理解 6. 推定 2 1.Probit 概要 プロビットモデルとは. 効用関数の誤差項に多変量正規分布を仮定したもの. 誤差項には様々な要因が存在するため,
Probit, Mixed logit 2016/5/16 スタートアップゼミ #5 B4 後藤祥孝 1 0. 目次 Probit モデルについて 1. モデル概要 2. 定式化と理解 3. 推定 Mixed logit モデルについて 4. モデル概要 5. 定式化と理解 6. 推定 2 1.Probit 概要 プロビットモデルとは. 効用関数の誤差項に多変量正規分布を仮定したもの. 誤差項には様々な要因が存在するため,
1. 多変量解析の基本的な概念 1. 多変量解析の基本的な概念 1.1 多変量解析の目的 人間のデータは多変量データが多いので多変量解析が有用 特性概括評価特性概括評価 症 例 主 治 医 の 主 観 症 例 主 治 医 の 主 観 単変量解析 客観的規準のある要約多変量解析 要約値 客観的規準のな
 1.1 多変量解析の目的 人間のデータは多変量データが多いので多変量解析が有用 特性概括評価特性概括評価 症 例 治 医 の 観 症 例 治 医 の 観 単変量解析 客観的規準のある要約多変量解析 要約値 客観的規準のない要約知識 直感 知識 直感 総合的評価 考察 総合的評価 考察 単変量解析の場合 多変量解析の場合 < 表 1.1 脂質異常症患者の TC と TG と重症度 > 症例 No. TC
1.1 多変量解析の目的 人間のデータは多変量データが多いので多変量解析が有用 特性概括評価特性概括評価 症 例 治 医 の 観 症 例 治 医 の 観 単変量解析 客観的規準のある要約多変量解析 要約値 客観的規準のない要約知識 直感 知識 直感 総合的評価 考察 総合的評価 考察 単変量解析の場合 多変量解析の場合 < 表 1.1 脂質異常症患者の TC と TG と重症度 > 症例 No. TC
スライド 1
 データ解析特論第 10 回 ( 全 15 回 ) 2012 年 12 月 11 日 ( 火 ) 情報エレクトロニクス専攻横田孝義 1 終了 11/13 11/20 重回帰分析をしばらくやります 12/4 12/11 12/18 2 前回から回帰分析について学習しています 3 ( 単 ) 回帰分析 単回帰分析では一つの従属変数 ( 目的変数 ) を 一つの独立変数 ( 説明変数 ) で予測する事を考える
データ解析特論第 10 回 ( 全 15 回 ) 2012 年 12 月 11 日 ( 火 ) 情報エレクトロニクス専攻横田孝義 1 終了 11/13 11/20 重回帰分析をしばらくやります 12/4 12/11 12/18 2 前回から回帰分析について学習しています 3 ( 単 ) 回帰分析 単回帰分析では一つの従属変数 ( 目的変数 ) を 一つの独立変数 ( 説明変数 ) で予測する事を考える
統計的データ解析
 統計的データ解析 011 011.11.9 林田清 ( 大阪大学大学院理学研究科 ) 連続確率分布の平均値 分散 比較のため P(c ) c 分布 自由度 の ( カイ c 平均値 0, 標準偏差 1の正規分布 に従う変数 xの自乗和 c x =1 が従う分布を自由度 の分布と呼ぶ 一般に自由度の分布は f /1 c / / ( c ) {( c ) e }/ ( / ) 期待値 二乗 ) 分布 c
統計的データ解析 011 011.11.9 林田清 ( 大阪大学大学院理学研究科 ) 連続確率分布の平均値 分散 比較のため P(c ) c 分布 自由度 の ( カイ c 平均値 0, 標準偏差 1の正規分布 に従う変数 xの自乗和 c x =1 が従う分布を自由度 の分布と呼ぶ 一般に自由度の分布は f /1 c / / ( c ) {( c ) e }/ ( / ) 期待値 二乗 ) 分布 c
14 化学実験法 II( 吉村 ( 洋 mmol/l の半分だったから さんの測定値は くんの測定値の 4 倍の重みがあり 推定値 としては 0.68 mmol/l その標準偏差は mmol/l 程度ということになる 測定値を 特徴づけるパラメータ t を推定するこの手
 14 化学実験法 II( 吉村 ( 洋 014.6.1. 最小 乗法のはなし 014.6.1. 内容 最小 乗法のはなし...1 最小 乗法の考え方...1 最小 乗法によるパラメータの決定... パラメータの信頼区間...3 重みの異なるデータの取扱い...4 相関係数 決定係数 ( 最小 乗法を語るもう一つの立場...5 実験条件の誤差の影響...5 問題...6 最小 乗法の考え方 飲料水中のカルシウム濃度を
14 化学実験法 II( 吉村 ( 洋 014.6.1. 最小 乗法のはなし 014.6.1. 内容 最小 乗法のはなし...1 最小 乗法の考え方...1 最小 乗法によるパラメータの決定... パラメータの信頼区間...3 重みの異なるデータの取扱い...4 相関係数 決定係数 ( 最小 乗法を語るもう一つの立場...5 実験条件の誤差の影響...5 問題...6 最小 乗法の考え方 飲料水中のカルシウム濃度を
Microsoft PowerPoint - H18早稲田大学講義.ppt
 統計的パターン認識とニューラルネット 汎化性能の高い非線形識別器の学習と画像認識への応用 産業技術総合研究所副研究部門長筑波大学大学院システム情報工学研究科教授 連携 栗田多喜夫 [email protected] 006 年度早稲田大学集中講義 ニューラルネットワーク 産業技術総合研究所 講演内容 パターン認識とベイズ識別 パターン認識とは ベイズ決定理論 密度関数の推定 線形識別関数の学習 線形識別関数の性質
統計的パターン認識とニューラルネット 汎化性能の高い非線形識別器の学習と画像認識への応用 産業技術総合研究所副研究部門長筑波大学大学院システム情報工学研究科教授 連携 栗田多喜夫 [email protected] 006 年度早稲田大学集中講義 ニューラルネットワーク 産業技術総合研究所 講演内容 パターン認識とベイズ識別 パターン認識とは ベイズ決定理論 密度関数の推定 線形識別関数の学習 線形識別関数の性質
スライド 1
 データ解析特論重回帰分析編 2017 年 7 月 10 日 ( 月 )~ 情報エレクトロニクスコース横田孝義 1 ( 単 ) 回帰分析 単回帰分析では一つの従属変数 ( 目的変数 ) を 一つの独立変数 ( 説明変数 ) で予測する事を考える 具体的には y = a + bx という回帰直線 ( モデル ) でデータを代表させる このためにデータからこの回帰直線の切片 (a) と傾き (b) を最小
データ解析特論重回帰分析編 2017 年 7 月 10 日 ( 月 )~ 情報エレクトロニクスコース横田孝義 1 ( 単 ) 回帰分析 単回帰分析では一つの従属変数 ( 目的変数 ) を 一つの独立変数 ( 説明変数 ) で予測する事を考える 具体的には y = a + bx という回帰直線 ( モデル ) でデータを代表させる このためにデータからこの回帰直線の切片 (a) と傾き (b) を最小
Microsoft Word - 補論3.2
 補論 3. 多変量 GARC モデル 07//6 新谷元嗣 藪友良 対数尤度関数 3 章 7 節では 変量の対数尤度を求めた ここでは多変量の場合 とくに 変量について対数尤度を求める 誤差項 は平均 0 で 次元の正規分布に従うとする 単純化のため 分散と共分散は時間を通じて一定としよう ( この仮定は後で変更される ) したがって ij から添え字 を除くことができる このとき と の尤度関数は
補論 3. 多変量 GARC モデル 07//6 新谷元嗣 藪友良 対数尤度関数 3 章 7 節では 変量の対数尤度を求めた ここでは多変量の場合 とくに 変量について対数尤度を求める 誤差項 は平均 0 で 次元の正規分布に従うとする 単純化のため 分散と共分散は時間を通じて一定としよう ( この仮定は後で変更される ) したがって ij から添え字 を除くことができる このとき と の尤度関数は
ビジネス統計 統計基礎とエクセル分析 正誤表
 ビジネス統計統計基礎とエクセル分析 ビジネス統計スペシャリスト エクセル分析スペシャリスト 公式テキスト正誤表と学習用データ更新履歴 平成 30 年 5 月 14 日現在 公式テキスト正誤表 頁場所誤正修正 6 知識編第 章 -3-3 最頻値の解説内容 たとえば, 表.1 のデータであれば, 最頻値は 167.5cm というたとえば, 表.1 のデータであれば, 最頻値は 165.0cm ということになります
ビジネス統計統計基礎とエクセル分析 ビジネス統計スペシャリスト エクセル分析スペシャリスト 公式テキスト正誤表と学習用データ更新履歴 平成 30 年 5 月 14 日現在 公式テキスト正誤表 頁場所誤正修正 6 知識編第 章 -3-3 最頻値の解説内容 たとえば, 表.1 のデータであれば, 最頻値は 167.5cm というたとえば, 表.1 のデータであれば, 最頻値は 165.0cm ということになります
1.民営化
 参考資料 最小二乗法 数学的性質 経済統計分析 3 年度秋学期 回帰分析と最小二乗法 被説明変数 の動きを説明変数 の動きで説明 = 回帰分析 説明変数がつ 単回帰 説明変数がつ以上 重回帰 被説明変数 従属変数 係数 定数項傾き 説明変数 独立変数 残差... で説明できる部分 説明できない部分 説明できない部分が小さくなるように回帰式の係数 を推定する有力な方法 = 最小二乗法 最小二乗法による回帰の考え方
参考資料 最小二乗法 数学的性質 経済統計分析 3 年度秋学期 回帰分析と最小二乗法 被説明変数 の動きを説明変数 の動きで説明 = 回帰分析 説明変数がつ 単回帰 説明変数がつ以上 重回帰 被説明変数 従属変数 係数 定数項傾き 説明変数 独立変数 残差... で説明できる部分 説明できない部分 説明できない部分が小さくなるように回帰式の係数 を推定する有力な方法 = 最小二乗法 最小二乗法による回帰の考え方
Kumamoto University Center for Multimedia and Information Technologies Lab. 熊本大学アプリケーション実験 ~ 実環境における無線 LAN 受信電波強度を用いた位置推定手法の検討 ~ InKIAI 宮崎県美郷
 熊本大学アプリケーション実験 ~ 実環境における無線 LAN 受信電波強度を用いた位置推定手法の検討 ~ InKIAI プロジェクト @ 宮崎県美郷町 熊本大学副島慶人川村諒 1 実験の目的 従来 信号の受信電波強度 (RSSI:RecevedSgnal StrengthIndcator) により 対象の位置を推定する手法として 無線 LAN の AP(AccessPont) から受信する信号の減衰量をもとに位置を推定する手法が多く検討されている
熊本大学アプリケーション実験 ~ 実環境における無線 LAN 受信電波強度を用いた位置推定手法の検討 ~ InKIAI プロジェクト @ 宮崎県美郷町 熊本大学副島慶人川村諒 1 実験の目的 従来 信号の受信電波強度 (RSSI:RecevedSgnal StrengthIndcator) により 対象の位置を推定する手法として 無線 LAN の AP(AccessPont) から受信する信号の減衰量をもとに位置を推定する手法が多く検討されている
Microsoft PowerPoint - 統計科学研究所_R_主成分分析.ppt
 主成分分析 1 内容 主成分分析 主成分分析について 成績データの解析 R で主成分分析 相関行列による主成分分析 寄与率 累積寄与率 因子負荷量 主成分得点 2 主成分分析 3 次元の縮小と主成分分析 主成分分析 次元の縮小に関する手法 次元の縮小 国語 数学 理科 社会 英語の総合点 5 次元データから1 次元データへの縮約 体形評価 : BMI (Body Mass Index) 判定肥満度の判定方法の1つで
主成分分析 1 内容 主成分分析 主成分分析について 成績データの解析 R で主成分分析 相関行列による主成分分析 寄与率 累積寄与率 因子負荷量 主成分得点 2 主成分分析 3 次元の縮小と主成分分析 主成分分析 次元の縮小に関する手法 次元の縮小 国語 数学 理科 社会 英語の総合点 5 次元データから1 次元データへの縮約 体形評価 : BMI (Body Mass Index) 判定肥満度の判定方法の1つで
PowerPoint プレゼンテーション
 復習 ) 時系列のモデリング ~a. 離散時間モデル ~ y k + a 1 z 1 y k + + a na z n ay k = b 0 u k + b 1 z 1 u k + + b nb z n bu k y k = G z 1 u k = B(z 1 ) A(z 1 u k ) ARMA モデル A z 1 B z 1 = 1 + a 1 z 1 + + a na z n a = b 0
復習 ) 時系列のモデリング ~a. 離散時間モデル ~ y k + a 1 z 1 y k + + a na z n ay k = b 0 u k + b 1 z 1 u k + + b nb z n bu k y k = G z 1 u k = B(z 1 ) A(z 1 u k ) ARMA モデル A z 1 B z 1 = 1 + a 1 z 1 + + a na z n a = b 0
講義「○○○○」
 講義 信頼度の推定と立証 内容. 点推定と区間推定. 指数分布の点推定 区間推定 3. 指数分布 正規分布の信頼度推定 担当 : 倉敷哲生 ( ビジネスエンジニアリング専攻 ) 統計的推測 標本から得られる情報を基に 母集団に関する結論の導出が目的 測定値 x x x 3 : x 母集団 (populaio) 母集団の特性値 統計的推測 標本 (sample) 標本の特性値 分布のパラメータ ( 母数
講義 信頼度の推定と立証 内容. 点推定と区間推定. 指数分布の点推定 区間推定 3. 指数分布 正規分布の信頼度推定 担当 : 倉敷哲生 ( ビジネスエンジニアリング専攻 ) 統計的推測 標本から得られる情報を基に 母集団に関する結論の導出が目的 測定値 x x x 3 : x 母集団 (populaio) 母集団の特性値 統計的推測 標本 (sample) 標本の特性値 分布のパラメータ ( 母数
横浜市環境科学研究所
 周期時系列の統計解析 単回帰分析 io 8 年 3 日 周期時系列に季節調整を行わないで単回帰分析を適用すると, 回帰係数には周期成分の影響が加わる. ここでは, 周期時系列をコサイン関数モデルで近似し単回帰分析によりモデルの回帰係数を求め, 周期成分の影響を検討した. また, その結果を気温時系列に当てはめ, 課題等について考察した. 気温時系列とコサイン関数モデル第 報の結果を利用するので, その一部を再掲する.
周期時系列の統計解析 単回帰分析 io 8 年 3 日 周期時系列に季節調整を行わないで単回帰分析を適用すると, 回帰係数には周期成分の影響が加わる. ここでは, 周期時系列をコサイン関数モデルで近似し単回帰分析によりモデルの回帰係数を求め, 周期成分の影響を検討した. また, その結果を気温時系列に当てはめ, 課題等について考察した. 気温時系列とコサイン関数モデル第 報の結果を利用するので, その一部を再掲する.
ファイナンスのための数学基礎 第1回 オリエンテーション、ベクトル
 時系列分析 変量時系列モデルとその性質 担当 : 長倉大輔 ( ながくらだいすけ 時系列モデル 時系列モデルとは時系列データを生み出すメカニズムとなるものである これは実際には未知である 私たちにできるのは観測された時系列データからその背後にある時系列モデルを推測 推定するだけである 以下ではいくつかの代表的な時系列モデルを考察する 自己回帰モデル (Auoregressive Model もっとも頻繁に使われる時系列モデルは自己回帰モデル
時系列分析 変量時系列モデルとその性質 担当 : 長倉大輔 ( ながくらだいすけ 時系列モデル 時系列モデルとは時系列データを生み出すメカニズムとなるものである これは実際には未知である 私たちにできるのは観測された時系列データからその背後にある時系列モデルを推測 推定するだけである 以下ではいくつかの代表的な時系列モデルを考察する 自己回帰モデル (Auoregressive Model もっとも頻繁に使われる時系列モデルは自己回帰モデル
Microsoft PowerPoint - 10.pptx
 m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
Microsoft PowerPoint - 統計科学研究所_R_重回帰分析_変数選択_2.ppt
 重回帰分析 残差分析 変数選択 1 内容 重回帰分析 残差分析 歯の咬耗度データの分析 R で変数選択 ~ step 関数 ~ 2 重回帰分析と単回帰分析 体重を予測する問題 分析 1 身長 のみから体重を予測 分析 2 身長 と ウエスト の両方を用いて体重を予測 分析 1 と比べて大きな改善 体重 に関する推測では 身長 だけでは不十分 重回帰分析における問題 ~ モデルの構築 ~ 適切なモデルで分析しているか?
重回帰分析 残差分析 変数選択 1 内容 重回帰分析 残差分析 歯の咬耗度データの分析 R で変数選択 ~ step 関数 ~ 2 重回帰分析と単回帰分析 体重を予測する問題 分析 1 身長 のみから体重を予測 分析 2 身長 と ウエスト の両方を用いて体重を予測 分析 1 と比べて大きな改善 体重 に関する推測では 身長 だけでは不十分 重回帰分析における問題 ~ モデルの構築 ~ 適切なモデルで分析しているか?
memo
 数理情報工学特論第一 機械学習とデータマイニング 4 章 : 教師なし学習 3 かしまひさし 鹿島久嗣 ( 数理 6 研 ) [email protected].~ DEPARTMENT OF MATHEMATICAL INFORMATICS 1 グラフィカルモデルについて学びます グラフィカルモデル グラフィカルラッソ グラフィカルラッソの推定アルゴリズム 2 グラフィカルモデル 3 教師なし学習の主要タスクは
数理情報工学特論第一 機械学習とデータマイニング 4 章 : 教師なし学習 3 かしまひさし 鹿島久嗣 ( 数理 6 研 ) [email protected].~ DEPARTMENT OF MATHEMATICAL INFORMATICS 1 グラフィカルモデルについて学びます グラフィカルモデル グラフィカルラッソ グラフィカルラッソの推定アルゴリズム 2 グラフィカルモデル 3 教師なし学習の主要タスクは
データサイエンス講座第 3 回機械学習その 2 ロジスティクス回帰 カーネル法とサポートベクターマシン アンサンブル学習
 データサイエンス講座第 3 回機械学習その 2 ロジスティクス回帰 カーネル法とサポートベクターマシン アンサンブル学習 ロジスティクス回帰 基本的には重回帰分析のモデルと考え方は似ている = 1 1+ ( ) 目的変数 = 係数 説明変数 + 定数 この式をグラフ化すると y は 0 1 に収まる ( シグモイド関数 ) トレーニングデータから確率を最大となる地点をもとめ それぞれの係数を求める
データサイエンス講座第 3 回機械学習その 2 ロジスティクス回帰 カーネル法とサポートベクターマシン アンサンブル学習 ロジスティクス回帰 基本的には重回帰分析のモデルと考え方は似ている = 1 1+ ( ) 目的変数 = 係数 説明変数 + 定数 この式をグラフ化すると y は 0 1 に収まる ( シグモイド関数 ) トレーニングデータから確率を最大となる地点をもとめ それぞれの係数を求める
SAP11_03
 第 3 回 音声音響信号処理 ( 線形予測分析と自己回帰モデル ) 亀岡弘和 東京大学大学院情報理工学系研究科日本電信電話株式会社 NTT コミュニケーション科学基礎研究所 講義内容 ( キーワード ) 信号処理 符号化 標準化の実用システム例の紹介情報通信の基本 ( 誤り検出 訂正符号 変調 IP) 符号化技術の基本 ( 量子化 予測 変換 圧縮 ) 音声分析 合成 認識 強調 音楽信号処理統計的信号処理の基礎
第 3 回 音声音響信号処理 ( 線形予測分析と自己回帰モデル ) 亀岡弘和 東京大学大学院情報理工学系研究科日本電信電話株式会社 NTT コミュニケーション科学基礎研究所 講義内容 ( キーワード ) 信号処理 符号化 標準化の実用システム例の紹介情報通信の基本 ( 誤り検出 訂正符号 変調 IP) 符号化技術の基本 ( 量子化 予測 変換 圧縮 ) 音声分析 合成 認識 強調 音楽信号処理統計的信号処理の基礎
Microsoft PowerPoint - 三次元座標測定 ppt
 冗長座標測定機 ()( 三次元座標計測 ( 第 9 回 ) 5 年度大学院講義 6 年 月 7 日 冗長性を持つ 次元座標測定機 次元 辺測量 : 冗長性を出すために つのレーザトラッカを配置し, キャッツアイまでの距離から座標を測定する つのカメラ ( 次元的なカメラ ) とレーザスキャナ : つの角度測定システムによる座標測定 つの回転関節による 次元 自由度多関節機構 高増潔東京大学工学系研究科精密機械工学専攻
冗長座標測定機 ()( 三次元座標計測 ( 第 9 回 ) 5 年度大学院講義 6 年 月 7 日 冗長性を持つ 次元座標測定機 次元 辺測量 : 冗長性を出すために つのレーザトラッカを配置し, キャッツアイまでの距離から座標を測定する つのカメラ ( 次元的なカメラ ) とレーザスキャナ : つの角度測定システムによる座標測定 つの回転関節による 次元 自由度多関節機構 高増潔東京大学工学系研究科精密機械工学専攻
Microsoft PowerPoint - H21生物計算化学2.ppt
 演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
PowerPoint プレゼンテーション
 非線形カルマンフィルタ ~a. 問題設定 ~ 離散時間非線形状態空間表現 x k + 1 = f x k y k = h x k + bv k + w k f : ベクトル値をとるx k の非線形関数 h : スカラ値をとるx k の非線形関数 v k システム雑音 ( 平均値 0, 分散 σ v 2 k ) x k + 1 = f x k,v k w k 観測雑音 ( 平均値 0, 分散 σ w
非線形カルマンフィルタ ~a. 問題設定 ~ 離散時間非線形状態空間表現 x k + 1 = f x k y k = h x k + bv k + w k f : ベクトル値をとるx k の非線形関数 h : スカラ値をとるx k の非線形関数 v k システム雑音 ( 平均値 0, 分散 σ v 2 k ) x k + 1 = f x k,v k w k 観測雑音 ( 平均値 0, 分散 σ w
様々なミクロ計量モデル†
 担当 : 長倉大輔 ( ながくらだいすけ ) この資料は私の講義において使用するために作成した資料です WEB ページ上で公開しており 自由に参照して頂いて構いません ただし 内容について 一応検証してありますが もし間違いがあった場合でもそれによって生じるいかなる損害 不利益について責任を負いかねますのでご了承ください 間違いは発見次第 継続的に直していますが まだ存在する可能性があります 1 カウントデータモデル
担当 : 長倉大輔 ( ながくらだいすけ ) この資料は私の講義において使用するために作成した資料です WEB ページ上で公開しており 自由に参照して頂いて構いません ただし 内容について 一応検証してありますが もし間違いがあった場合でもそれによって生じるいかなる損害 不利益について責任を負いかねますのでご了承ください 間違いは発見次第 継続的に直していますが まだ存在する可能性があります 1 カウントデータモデル
パソコンシミュレータの現状
 第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
Microsoft Word doc
 . 正規線形モデルのベイズ推定翠川 大竹距離減衰式 (PGA(Midorikawa, S., and Ohtake, Y. (, Attenuation relationships of peak ground acceleration and velocity considering attenuation characteristics for shallow and deeper earthquakes,
. 正規線形モデルのベイズ推定翠川 大竹距離減衰式 (PGA(Midorikawa, S., and Ohtake, Y. (, Attenuation relationships of peak ground acceleration and velocity considering attenuation characteristics for shallow and deeper earthquakes,
回帰分析の用途・実験計画法の意義・グラフィカルモデリングの活用 | 永田 靖教授(早稲田大学)
 回帰分析の用途 実験計画法の意義 グラフィカルモデリングの活用 早稲田大学創造理工学部 経営システム工学科 永田靖, The Institute of JUSE. All Rights Reserved. 内容. 回帰分析の結果の解釈の仕方. 回帰分析による要因効果の把握の困難さ. 実験計画法の意義 4. グラフィカルモデリング 参考文献 : 統計的品質管理 ( 永田靖, 朝倉書店,9) 入門実験計画法
回帰分析の用途 実験計画法の意義 グラフィカルモデリングの活用 早稲田大学創造理工学部 経営システム工学科 永田靖, The Institute of JUSE. All Rights Reserved. 内容. 回帰分析の結果の解釈の仕方. 回帰分析による要因効果の把握の困難さ. 実験計画法の意義 4. グラフィカルモデリング 参考文献 : 統計的品質管理 ( 永田靖, 朝倉書店,9) 入門実験計画法
スライド 1
 計測工学第 12 回以降 測定値の誤差と精度編 2014 年 7 月 2 日 ( 水 )~7 月 16 日 ( 水 ) 知能情報工学科 横田孝義 1 授業計画 4/9 4/16 4/23 5/7 5/14 5/21 5/28 6/4 6/11 6/18 6/25 7/2 7/9 7/16 7/23 2 誤差とその取扱い 3 誤差 = 測定値 真の値 相対誤差 = 誤差 / 真の値 4 誤差 (error)
計測工学第 12 回以降 測定値の誤差と精度編 2014 年 7 月 2 日 ( 水 )~7 月 16 日 ( 水 ) 知能情報工学科 横田孝義 1 授業計画 4/9 4/16 4/23 5/7 5/14 5/21 5/28 6/4 6/11 6/18 6/25 7/2 7/9 7/16 7/23 2 誤差とその取扱い 3 誤差 = 測定値 真の値 相対誤差 = 誤差 / 真の値 4 誤差 (error)
09.pptx
 講義内容 数値解析 第 9 回 5 年 6 月 7 日 水 理学部物理学科情報理学コース. 非線形方程式の数値解法. はじめに. 分法. 補間法.4 ニュートン法.4. 多変数問題への応用.4. ニュートン法の収束性. 連立 次方程式の解法. 序論と行列計算の基礎. ガウスの消去法. 重対角行列の場合の解法項目を変更しました.4 LU 分解法.5 特異値分解法.6 共役勾配法.7 反復法.7. ヤコビ法.7.
講義内容 数値解析 第 9 回 5 年 6 月 7 日 水 理学部物理学科情報理学コース. 非線形方程式の数値解法. はじめに. 分法. 補間法.4 ニュートン法.4. 多変数問題への応用.4. ニュートン法の収束性. 連立 次方程式の解法. 序論と行列計算の基礎. ガウスの消去法. 重対角行列の場合の解法項目を変更しました.4 LU 分解法.5 特異値分解法.6 共役勾配法.7 反復法.7. ヤコビ法.7.
PowerPoint Presentation
 付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
PowerPoint プレゼンテーション
 20150528 信号処理システム特論 本日の内容 適応フィルタ ( 時間領域 ) 適応アルゴリズム (LMS,NLMS,RLS) 適応フィルタの応用例 適応処理 非適応処理 : 状況によらずいつでも同じ処理 適応処理 : 状況に応じた適切な処理 高度な適応処理の例 雑音抑圧, 音響エコーキャンセラ, 騒音制御など 時間領域の適応フィルタ 誤差信号 与えられた手順に従ってフィルタ係数を更新し 自動的に所望の信号を得るフィルタ
20150528 信号処理システム特論 本日の内容 適応フィルタ ( 時間領域 ) 適応アルゴリズム (LMS,NLMS,RLS) 適応フィルタの応用例 適応処理 非適応処理 : 状況によらずいつでも同じ処理 適応処理 : 状況に応じた適切な処理 高度な適応処理の例 雑音抑圧, 音響エコーキャンセラ, 騒音制御など 時間領域の適応フィルタ 誤差信号 与えられた手順に従ってフィルタ係数を更新し 自動的に所望の信号を得るフィルタ
13章 回帰分析
 単回帰分析 つ以上の変数についての関係を見る つの 目的 被説明 変数を その他の 説明 変数を使って 予測しようというものである 因果関係とは限らない ここで勉強すること 最小 乗法と回帰直線 決定係数とは何か? 最小 乗法と回帰直線 これまで 変数の間の関係の深さについて考えてきた 相関係数 ここでは 変数に役割を与え 一方の 説明 変数を用いて他方の 目的 被説明 変数を説明することを考える
単回帰分析 つ以上の変数についての関係を見る つの 目的 被説明 変数を その他の 説明 変数を使って 予測しようというものである 因果関係とは限らない ここで勉強すること 最小 乗法と回帰直線 決定係数とは何か? 最小 乗法と回帰直線 これまで 変数の間の関係の深さについて考えてきた 相関係数 ここでは 変数に役割を与え 一方の 説明 変数を用いて他方の 目的 被説明 変数を説明することを考える
カイ二乗フィット検定、パラメータの誤差
 統計的データ解析 008 008.. 林田清 ( 大阪大学大学院理学研究科 ) 問題 C (, ) ( x xˆ) ( y yˆ) σ x πσ σ y y Pabx (, ;,,, ) ˆ y σx σ y = dx exp exp πσx ただし xy ˆ ˆ はyˆ = axˆ+ bであらわされる直線モデル上の点 ( ˆ) ( ˆ ) ( ) x x y ax b y ax b Pabx (,
統計的データ解析 008 008.. 林田清 ( 大阪大学大学院理学研究科 ) 問題 C (, ) ( x xˆ) ( y yˆ) σ x πσ σ y y Pabx (, ;,,, ) ˆ y σx σ y = dx exp exp πσx ただし xy ˆ ˆ はyˆ = axˆ+ bであらわされる直線モデル上の点 ( ˆ) ( ˆ ) ( ) x x y ax b y ax b Pabx (,
Microsoft Word - mstattext02.docx
 章重回帰分析 複数の変数で 1つの変数を予測するような手法を 重回帰分析 といいます 前の巻でところで述べた回帰分析は 1つの説明変数で目的変数を予測 ( 説明 ) する手法でしたが この説明変数が複数個になったと考えればよいでしょう 重回帰分析はこの予測式を与える分析手法です 以下の例を見て下さい 例 以下のデータ (Samples 重回帰分析 1.txt) をもとに体重を身長と胸囲の1 次関数で
章重回帰分析 複数の変数で 1つの変数を予測するような手法を 重回帰分析 といいます 前の巻でところで述べた回帰分析は 1つの説明変数で目的変数を予測 ( 説明 ) する手法でしたが この説明変数が複数個になったと考えればよいでしょう 重回帰分析はこの予測式を与える分析手法です 以下の例を見て下さい 例 以下のデータ (Samples 重回帰分析 1.txt) をもとに体重を身長と胸囲の1 次関数で
Microsoft PowerPoint - S11_1 2010Econometrics [互換モード]
![Microsoft PowerPoint - S11_1 2010Econometrics [互換モード] Microsoft PowerPoint - S11_1 2010Econometrics [互換モード]](/thumbs/79/79771572.jpg) S11_1 計量経済学 一般化古典的回帰モデル -3 1 図 7-3 不均一分散の検定と想定の誤り 想定の誤りと不均一分散均一分散を棄却 3つの可能性 1. 不均一分散がある. 不均一分散はないがモデルの想定に誤り 3. 両者が同時に起きている 想定に誤り不均一分散を 検出 したら散布図に戻り関数形の想定や説明変数の選択を再検討 残差 残差 Y 真の関係 e e 線形回帰 X X 1 実行可能な一般化最小二乗法
S11_1 計量経済学 一般化古典的回帰モデル -3 1 図 7-3 不均一分散の検定と想定の誤り 想定の誤りと不均一分散均一分散を棄却 3つの可能性 1. 不均一分散がある. 不均一分散はないがモデルの想定に誤り 3. 両者が同時に起きている 想定に誤り不均一分散を 検出 したら散布図に戻り関数形の想定や説明変数の選択を再検討 残差 残差 Y 真の関係 e e 線形回帰 X X 1 実行可能な一般化最小二乗法
ボルツマンマシンの高速化
 1. はじめに ボルツマン学習と平均場近似 山梨大学工学部宗久研究室 G04MK016 鳥居圭太 ボルツマンマシンは学習可能な相互結合型ネットワー クの代表的なものである. ボルツマンマシンには, 学習のための統計平均を取る必要があり, 結果を求めるまでに長い時間がかかってしまうという欠点がある. そこで, 学習の高速化のために, 統計を取る2つのステップについて, 以下のことを行う. まず1つ目のステップでは,
1. はじめに ボルツマン学習と平均場近似 山梨大学工学部宗久研究室 G04MK016 鳥居圭太 ボルツマンマシンは学習可能な相互結合型ネットワー クの代表的なものである. ボルツマンマシンには, 学習のための統計平均を取る必要があり, 結果を求めるまでに長い時間がかかってしまうという欠点がある. そこで, 学習の高速化のために, 統計を取る2つのステップについて, 以下のことを行う. まず1つ目のステップでは,
 Ecel 演習問題 Work Shee 解答 第 章 Ecel 演習問題 WorkShee 解答 問題 - 4 8 7 転置行列 4 8 7 TRANSPOSE( ) 問題 - X.6 4 4.8 8 4.9 6. 7 48 8. X 転置行列 4 8 7 4 6 48 TRANSPOSE( ).6 4.8.9. 8. 問題 -.6 4 4.8 8 y.9. 7 8. 転置行列 4 8 7 TRANSPOSE(
Ecel 演習問題 Work Shee 解答 第 章 Ecel 演習問題 WorkShee 解答 問題 - 4 8 7 転置行列 4 8 7 TRANSPOSE( ) 問題 - X.6 4 4.8 8 4.9 6. 7 48 8. X 転置行列 4 8 7 4 6 48 TRANSPOSE( ).6 4.8.9. 8. 問題 -.6 4 4.8 8 y.9. 7 8. 転置行列 4 8 7 TRANSPOSE(
PowerPoint プレゼンテーション
 データ解析 第 7 回 : 時系列分析 渡辺澄夫 過去から未来を予測する 観測データ 回帰 判別分析 解析方法 主成分 因子 クラスタ分析 時系列予測 時系列を予測する 無限個の確率変数 ( 確率変数が作る無限数列 ){X(t) ; t は整数 } を生成する情報源を考える {X(t)} を確率過程という 確率過程に ついて過去の値から未来を予測するにはどうしたらよいだろうか X(t-K),X(t-K+1),,X(t-1)
データ解析 第 7 回 : 時系列分析 渡辺澄夫 過去から未来を予測する 観測データ 回帰 判別分析 解析方法 主成分 因子 クラスタ分析 時系列予測 時系列を予測する 無限個の確率変数 ( 確率変数が作る無限数列 ){X(t) ; t は整数 } を生成する情報源を考える {X(t)} を確率過程という 確率過程に ついて過去の値から未来を予測するにはどうしたらよいだろうか X(t-K),X(t-K+1),,X(t-1)
統計学 - 社会統計の基礎 - 正規分布 標準正規分布累積分布関数の逆関数 t 分布正規分布に従うサンプルの平均の信頼区間 担当 : 岸 康人 資料ページ :
 統計学 - 社会統計の基礎 - 正規分布 標準正規分布累積分布関数の逆関数 t 分布正規分布に従うサンプルの平均の信頼区間 担当 : 岸 康人 資料ページ : https://goo.gl/qw1djw 正規分布 ( 復習 ) 正規分布 (Normal Distribution)N (μ, σ 2 ) 別名 : ガウス分布 (Gaussian Distribution) 密度関数 Excel:= NORM.DIST
統計学 - 社会統計の基礎 - 正規分布 標準正規分布累積分布関数の逆関数 t 分布正規分布に従うサンプルの平均の信頼区間 担当 : 岸 康人 資料ページ : https://goo.gl/qw1djw 正規分布 ( 復習 ) 正規分布 (Normal Distribution)N (μ, σ 2 ) 別名 : ガウス分布 (Gaussian Distribution) 密度関数 Excel:= NORM.DIST
Microsoft PowerPoint - 測量学.ppt [互換モード]
![Microsoft PowerPoint - 測量学.ppt [互換モード] Microsoft PowerPoint - 測量学.ppt [互換モード]](/thumbs/92/109082022.jpg) 8/5/ 誤差理論 測定の分類 性格による分類 独立 ( な ) 測定 : 測定値がある条件を満たさなければならないなどの拘束や制約を持たないで独立して行う測定 条件 ( 付き ) 測定 : 三角形の 3 つの内角の和のように, 個々の測定値間に満たすべき条件式が存在する場合の測定 方法による分類 直接測定 : 距離や角度などを機器を用いて直接行う測定 間接測定 : 求めるべき量を直接測定するのではなく,
8/5/ 誤差理論 測定の分類 性格による分類 独立 ( な ) 測定 : 測定値がある条件を満たさなければならないなどの拘束や制約を持たないで独立して行う測定 条件 ( 付き ) 測定 : 三角形の 3 つの内角の和のように, 個々の測定値間に満たすべき条件式が存在する場合の測定 方法による分類 直接測定 : 距離や角度などを機器を用いて直接行う測定 間接測定 : 求めるべき量を直接測定するのではなく,
スライド 1
 データ解析特論第 1 回 ~( 全 15 回 ) 2014 年 4 月 10 日 ( 木 ) 情報エレクトロニクス専攻横田孝義 1 を先に集中してやります 2 を勉強します 3 データマイニングの分野ではマクロ ( 巨視的 ) な視点で全体を捉える能力が求められる 1. コンピュータは数値の集合として全体を把握していますので 意味ある情報として全体を見ることが不得意 2. 逆に人間には もともと空間的に全体像を捉える能力が得意
データ解析特論第 1 回 ~( 全 15 回 ) 2014 年 4 月 10 日 ( 木 ) 情報エレクトロニクス専攻横田孝義 1 を先に集中してやります 2 を勉強します 3 データマイニングの分野ではマクロ ( 巨視的 ) な視点で全体を捉える能力が求められる 1. コンピュータは数値の集合として全体を把握していますので 意味ある情報として全体を見ることが不得意 2. 逆に人間には もともと空間的に全体像を捉える能力が得意
線形システム応答 Linear System response
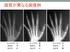 画質が異なる画像例 コントラスト劣 コントラスト優 コントラスト普 鮮鋭性 普 鮮鋭性 優 鮮鋭性 劣 粒状性 普 粒状性 劣 粒状性 優 医用画像の画質 コントラスト, 鮮鋭性, 粒状性の要因が互いに密接に関わり合って形成されている. 比 鮮鋭性 コントラスト 反 反 粒状性 増感紙 - フィルム系での 3 要因の関係 ディジタル画像処理系でもおよそ成り立つ WS u MTFu 画質に影響する因子
画質が異なる画像例 コントラスト劣 コントラスト優 コントラスト普 鮮鋭性 普 鮮鋭性 優 鮮鋭性 劣 粒状性 普 粒状性 劣 粒状性 優 医用画像の画質 コントラスト, 鮮鋭性, 粒状性の要因が互いに密接に関わり合って形成されている. 比 鮮鋭性 コントラスト 反 反 粒状性 増感紙 - フィルム系での 3 要因の関係 ディジタル画像処理系でもおよそ成り立つ WS u MTFu 画質に影響する因子
0 スペクトル 時系列データの前処理 法 平滑化 ( スムージング ) と微分 明治大学理 学部応用化学科 データ化学 学研究室 弘昌
 0 スペクトル 時系列データの前処理 法 平滑化 ( スムージング ) と微分 明治大学理 学部応用化学科 データ化学 学研究室 弘昌 スペクトルデータの特徴 1 波 ( 波数 ) が近いと 吸光度 ( 強度 ) の値も似ている ノイズが含まれる 吸光度 ( 強度 ) の極大値 ( ピーク ) 以外のデータも重要 時系列データの特徴 2 時刻が近いと プロセス変数の値も似ている ノイズが含まれる プロセス変数の極大値
0 スペクトル 時系列データの前処理 法 平滑化 ( スムージング ) と微分 明治大学理 学部応用化学科 データ化学 学研究室 弘昌 スペクトルデータの特徴 1 波 ( 波数 ) が近いと 吸光度 ( 強度 ) の値も似ている ノイズが含まれる 吸光度 ( 強度 ) の極大値 ( ピーク ) 以外のデータも重要 時系列データの特徴 2 時刻が近いと プロセス変数の値も似ている ノイズが含まれる プロセス変数の極大値
基礎統計
 基礎統計 第 11 回講義資料 6.4.2 標本平均の差の標本分布 母平均の差 標本平均の差をみれば良い ただし, 母分散に依存するため場合分けをする 1 2 3 分散が既知分散が未知であるが等しい分散が未知であり等しいとは限らない 1 母分散が既知のとき が既知 標準化変量 2 母分散が未知であり, 等しいとき 分散が未知であるが, 等しいということは分かっているとき 標準化変量 自由度 の t
基礎統計 第 11 回講義資料 6.4.2 標本平均の差の標本分布 母平均の差 標本平均の差をみれば良い ただし, 母分散に依存するため場合分けをする 1 2 3 分散が既知分散が未知であるが等しい分散が未知であり等しいとは限らない 1 母分散が既知のとき が既知 標準化変量 2 母分散が未知であり, 等しいとき 分散が未知であるが, 等しいということは分かっているとき 標準化変量 自由度 の t
集中理論談話会 #9 Bhat, C.R., Sidharthan, R.: A simulation evaluation of the maximum approximate composite marginal likelihood (MACML) estimator for mixed mu
 集中理論談話会 #9 Bhat, C.R., Sidharthan, R.: A simulation evaluation of the maximum approximate composite marginal likelihood (MACML) estimator for mixed multinomial probit models, Transportation Research Part
集中理論談話会 #9 Bhat, C.R., Sidharthan, R.: A simulation evaluation of the maximum approximate composite marginal likelihood (MACML) estimator for mixed multinomial probit models, Transportation Research Part
構造方程式モデリング Structural Equation Modeling (SEM)
 時間でだいたいわかる 構造方程式モデリング Structural Equaton Modlng (SEM) 構造方程式モデリングとは何か 構造方程式モデリング (Structural Equaton Modlng, SEM) とは : 別名 共分散構造分析 (coaranc structural analyss) 構成概念やの性質を調べるために集めた多くのを同時に分析するための統計的方法 本来 構造方程式モデリングは主に以下の3つを含みます
時間でだいたいわかる 構造方程式モデリング Structural Equaton Modlng (SEM) 構造方程式モデリングとは何か 構造方程式モデリング (Structural Equaton Modlng, SEM) とは : 別名 共分散構造分析 (coaranc structural analyss) 構成概念やの性質を調べるために集めた多くのを同時に分析するための統計的方法 本来 構造方程式モデリングは主に以下の3つを含みます
Medical3
 Chapter 1 1.4.1 1 元配置分散分析と多重比較の実行 3つの治療法による測定値に有意な差が認められるかどうかを分散分析で調べます この例では 因子が1つだけ含まれるため1 元配置分散分析 one-way ANOVA の適用になります また 多重比較法 multiple comparison procedure を用いて 具体的のどの治療法の間に有意差が認められるかを検定します 1. 分析メニュー
Chapter 1 1.4.1 1 元配置分散分析と多重比較の実行 3つの治療法による測定値に有意な差が認められるかどうかを分散分析で調べます この例では 因子が1つだけ含まれるため1 元配置分散分析 one-way ANOVA の適用になります また 多重比較法 multiple comparison procedure を用いて 具体的のどの治療法の間に有意差が認められるかを検定します 1. 分析メニュー
Presentation Title
 データの本質を読み解くための機械学習 MATLAB でデータ解析の課題に立ち向かう MathWorks Japan アプリケーションエンジニア部アプリケーションエンジニア井原瑞希 2016 The MathWorks, Inc. 1 Buzzwords IoT 人工知能 / AI データ解析 ビッグデータ 2 データ解析ワークフロー データへのアクセスと探索 データの前処理 予測モデルの構築 システムへの統合
データの本質を読み解くための機械学習 MATLAB でデータ解析の課題に立ち向かう MathWorks Japan アプリケーションエンジニア部アプリケーションエンジニア井原瑞希 2016 The MathWorks, Inc. 1 Buzzwords IoT 人工知能 / AI データ解析 ビッグデータ 2 データ解析ワークフロー データへのアクセスと探索 データの前処理 予測モデルの構築 システムへの統合
Microsoft PowerPoint - Statistics[B]
![Microsoft PowerPoint - Statistics[B] Microsoft PowerPoint - Statistics[B]](/thumbs/101/151482563.jpg) 講義の目的 サンプルサイズの大きい標本比率の分布は正規分布で近似できることを理解します 科目コード 130509, 130609, 110225 統計学講義第 19/20 回 2019 年 6 月 25 日 ( 火 )6/7 限 担当教員 : 唐渡広志 ( からと こうじ ) 研究室 : email: website: 経済学研究棟 4 階 432 号室 [email protected]
講義の目的 サンプルサイズの大きい標本比率の分布は正規分布で近似できることを理解します 科目コード 130509, 130609, 110225 統計学講義第 19/20 回 2019 年 6 月 25 日 ( 火 )6/7 限 担当教員 : 唐渡広志 ( からと こうじ ) 研究室 : email: website: 経済学研究棟 4 階 432 号室 [email protected]
第6章 実験モード解析
 第 6 章実験モード解析 6. 実験モード解析とは 6. 有限自由度系の実験モード解析 6.3 連続体の実験モード解析 6. 実験モード解析とは 実験モード解析とは加振実験によって測定された外力と応答を用いてモードパラメータ ( 固有振動数, モード減衰比, 正規固有モードなど ) を求める ( 同定する ) 方法である. 力計 試験体 変位計 / 加速度計 実験モード解析の概念 時間領域データを利用する方法
第 6 章実験モード解析 6. 実験モード解析とは 6. 有限自由度系の実験モード解析 6.3 連続体の実験モード解析 6. 実験モード解析とは 実験モード解析とは加振実験によって測定された外力と応答を用いてモードパラメータ ( 固有振動数, モード減衰比, 正規固有モードなど ) を求める ( 同定する ) 方法である. 力計 試験体 変位計 / 加速度計 実験モード解析の概念 時間領域データを利用する方法
相関分析・偏相関分析
 相関分析 偏相関分析 教育学研究科修士課程 1 回生 田中友香理 MENU 相関とは 相関分析とは ' パラメトリックな手法 ( Pearsonの相関係数について SPSSによる相関係数 偏相関係数 SPSSによる偏相関係数 順位相関係数とは ' ノンパラメトリックな手法 ( SPSS による順位相関係数 おまけ ' 時間があれば ( 回帰分析で2 変数間の関係を出す 曲線回帰分析を行う 相関とは
相関分析 偏相関分析 教育学研究科修士課程 1 回生 田中友香理 MENU 相関とは 相関分析とは ' パラメトリックな手法 ( Pearsonの相関係数について SPSSによる相関係数 偏相関係数 SPSSによる偏相関係数 順位相関係数とは ' ノンパラメトリックな手法 ( SPSS による順位相関係数 おまけ ' 時間があれば ( 回帰分析で2 変数間の関係を出す 曲線回帰分析を行う 相関とは
Microsoft PowerPoint - LectureB1_17woAN.pptx
 本講義の範囲 都市防災工学 後半第 回 : 導入 確率過程の基礎 千葉大学大学院工学研究院都市環境システムコース岡野創 http://oko-lb.tu.chib-u.c.jp/oshibousi/. ランダム振動論 地震動を不規則波形 ( 確率過程 ) と捉えて, 構造物の地震応答を評価する理論. 震源モデルによる地震動評価 断層の動きを仮定して, 断層から発せられる地震動を評価する方法 ( 運動学的モデル
本講義の範囲 都市防災工学 後半第 回 : 導入 確率過程の基礎 千葉大学大学院工学研究院都市環境システムコース岡野創 http://oko-lb.tu.chib-u.c.jp/oshibousi/. ランダム振動論 地震動を不規則波形 ( 確率過程 ) と捉えて, 構造物の地震応答を評価する理論. 震源モデルによる地震動評価 断層の動きを仮定して, 断層から発せられる地震動を評価する方法 ( 運動学的モデル
画像解析論(2) 講義内容
 画像解析論 画像解析論 東京工業大学長橋宏 主な講義内容 信号処理と画像処理 二次元システムとその表現 二次元システムの特性解析 各種の画像フィルタ 信号処理と画像処理 画像解析論 処理の応答 記憶域 入出力の流れ 信号処理系 実時間性が求められる メモリ容量に対する制限が厳しい オンラインでの対応が厳しく求められる 画像処理系 ある程度の処理時間が許容される 大容量のメモリ使用が容認され易い オフラインでの対応が容認され易い
画像解析論 画像解析論 東京工業大学長橋宏 主な講義内容 信号処理と画像処理 二次元システムとその表現 二次元システムの特性解析 各種の画像フィルタ 信号処理と画像処理 画像解析論 処理の応答 記憶域 入出力の流れ 信号処理系 実時間性が求められる メモリ容量に対する制限が厳しい オンラインでの対応が厳しく求められる 画像処理系 ある程度の処理時間が許容される 大容量のメモリ使用が容認され易い オフラインでの対応が容認され易い
多次元レーザー分光で探る凝縮分子系の超高速動力学
 波動方程式と量子力学 谷村吉隆 京都大学理学研究科化学専攻 http:theochem.kuchem.kyoto-u.ac.jp TA: 岩元佑樹 [email protected] ベクトルと行列の作法 A 列ベクトル c = c c 行ベクトル A = [ c c c ] 転置ベクトル T A = [ c c c ] AA 内積 c AA = [ c c c ] c =
波動方程式と量子力学 谷村吉隆 京都大学理学研究科化学専攻 http:theochem.kuchem.kyoto-u.ac.jp TA: 岩元佑樹 [email protected] ベクトルと行列の作法 A 列ベクトル c = c c 行ベクトル A = [ c c c ] 転置ベクトル T A = [ c c c ] AA 内積 c AA = [ c c c ] c =
航空機の運動方程式
 オブザーバ 状態フィードバックにはすべての状態変数の値が必要であった. しかしながら, システムの外部から観測できるのは出力だけであり, すべての状態変数が観測できるとは限らない. そこで, 制御対象システムの状態変数を, システムのモデルに基づいてその入出力信号から推定する方法を考える.. オブザーバとは 次元 m 入力 r 出力線形時不変システム x Ax Bu y Cx () の状態変数ベクトル
オブザーバ 状態フィードバックにはすべての状態変数の値が必要であった. しかしながら, システムの外部から観測できるのは出力だけであり, すべての状態変数が観測できるとは限らない. そこで, 制御対象システムの状態変数を, システムのモデルに基づいてその入出力信号から推定する方法を考える.. オブザーバとは 次元 m 入力 r 出力線形時不変システム x Ax Bu y Cx () の状態変数ベクトル
主成分分析 -因子分析との比較-
 主成分分析 - 因子分析との比較 - 2013.7.10. 心理データ解析演習 M1 枡田恵 主成分分析とは 主成分分析は 多変量データに共通な成分を探って 一種の合成変数 ( 主成分 ) を作り出すもの * 主成分はデータを新しい視点でみるための新しい軸 主成分分析の目的 : 情報を縮約すること ( データを合成変数 ( 主成分 ) に総合化 ) 因子分析の目的 : 共通因子を見つけること ( データを潜在因子に分解
主成分分析 - 因子分析との比較 - 2013.7.10. 心理データ解析演習 M1 枡田恵 主成分分析とは 主成分分析は 多変量データに共通な成分を探って 一種の合成変数 ( 主成分 ) を作り出すもの * 主成分はデータを新しい視点でみるための新しい軸 主成分分析の目的 : 情報を縮約すること ( データを合成変数 ( 主成分 ) に総合化 ) 因子分析の目的 : 共通因子を見つけること ( データを潜在因子に分解
<4D F736F F F696E74202D E738A5889BB8BE688E68A4F82CC926E89BF908492E882C98AD682B782E98CA48B862E707074>
 市街化区域外の地価推定に関する研究 不動産 空間計量研究室 筑波大学第三学群社会工学類都市計画主専攻宮下将尚筑波大学大学院システム情報工学研究科社会システム工学専攻高野哲司 背景 日本の国土の区域区分 都市計画区域 市街化区域 市街化を促進する区域 市街化調整区域 市街化を抑制する区域 非線引都市計画区域 上記に属さない区域 非線引き市街化調整区域市街化区域 都市計画区域 本研究での対象区域 都市計画区域外
市街化区域外の地価推定に関する研究 不動産 空間計量研究室 筑波大学第三学群社会工学類都市計画主専攻宮下将尚筑波大学大学院システム情報工学研究科社会システム工学専攻高野哲司 背景 日本の国土の区域区分 都市計画区域 市街化区域 市街化を促進する区域 市街化調整区域 市街化を抑制する区域 非線引都市計画区域 上記に属さない区域 非線引き市街化調整区域市街化区域 都市計画区域 本研究での対象区域 都市計画区域外
画像工学入門
 セグメンテーション 講義内容 閾値法,k-mean 法 領域拡張法 SNAK 法 P タイル法 モード法 P タイル法 画像内で対象物の占める面積 (P パーセント ) があらかじめわかっているとき, 濃度ヒストグラムを作成し, 濃度値の累積分布が全体の P パーセントとなる濃度値を見つけ, この値を閾値とする. モード法 画像の輝度ヒストグラムを調べ その分布のモード ( 頻値輝度 ) 間の谷をしきい値とする
セグメンテーション 講義内容 閾値法,k-mean 法 領域拡張法 SNAK 法 P タイル法 モード法 P タイル法 画像内で対象物の占める面積 (P パーセント ) があらかじめわかっているとき, 濃度ヒストグラムを作成し, 濃度値の累積分布が全体の P パーセントとなる濃度値を見つけ, この値を閾値とする. モード法 画像の輝度ヒストグラムを調べ その分布のモード ( 頻値輝度 ) 間の谷をしきい値とする
ii 3.,. 4. F. (), ,,. 8.,. 1. (75% ) (25% ) =9 7, =9 8 (. ). 1.,, (). 3.,. 1. ( ).,.,.,.,.,. ( ) (1 2 )., ( ), 0. 2., 1., 0,.
 23(2011) (1 C104) 5 11 (2 C206) 5 12 http://www.math.is.tohoku.ac.jp/~obata,.,,,.. 1. 2. 3. 4. 5. 6. 7.,,. 1., 2007 ( ). 2. P. G. Hoel, 1995. 3... 1... 2.,,. ii 3.,. 4. F. (),.. 5.. 6.. 7.,,. 8.,. 1. (75%
23(2011) (1 C104) 5 11 (2 C206) 5 12 http://www.math.is.tohoku.ac.jp/~obata,.,,,.. 1. 2. 3. 4. 5. 6. 7.,,. 1., 2007 ( ). 2. P. G. Hoel, 1995. 3... 1... 2.,,. ii 3.,. 4. F. (),.. 5.. 6.. 7.,,. 8.,. 1. (75%
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生
 0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
因子分析
 因子分析 心理データ解析演習 M1 枡田恵 2013.6.5. 1 因子分析とは 因子分析とは ある観測された変数 ( 質問項目への回答など ) が どのような潜在的な変数 ( 観測されない 仮定された変数 ) から影響を受けているかを探る手法 多変量解析の手法の一つ 複数の変数の関係性をもとにした構造を探る際によく用いられる 2 因子分析とは 探索的因子分析 - 多くの観測変数間に見られる複雑な相関関係が
因子分析 心理データ解析演習 M1 枡田恵 2013.6.5. 1 因子分析とは 因子分析とは ある観測された変数 ( 質問項目への回答など ) が どのような潜在的な変数 ( 観測されない 仮定された変数 ) から影響を受けているかを探る手法 多変量解析の手法の一つ 複数の変数の関係性をもとにした構造を探る際によく用いられる 2 因子分析とは 探索的因子分析 - 多くの観測変数間に見られる複雑な相関関係が
Microsoft PowerPoint - 基礎・経済統計6.ppt
 . 確率変数 基礎 経済統計 6 確率分布 事象を数値化したもの ( 事象ー > 数値 の関数 自然に数値されている場合 さいころの目 量的尺度 数値化が必要な場合 質的尺度, 順序的尺度 それらの尺度に数値を割り当てる 例えば, コインの表が出たら, 裏なら 0. 離散確率変数と連続確率変数 確率変数の値 連続値をとるもの 身長, 体重, 実質 GDP など とびとびの値 離散値をとるもの 新生児の性別
. 確率変数 基礎 経済統計 6 確率分布 事象を数値化したもの ( 事象ー > 数値 の関数 自然に数値されている場合 さいころの目 量的尺度 数値化が必要な場合 質的尺度, 順序的尺度 それらの尺度に数値を割り当てる 例えば, コインの表が出たら, 裏なら 0. 離散確率変数と連続確率変数 確率変数の値 連続値をとるもの 身長, 体重, 実質 GDP など とびとびの値 離散値をとるもの 新生児の性別
目次 ガウス過程 (Gaussian Process; GP) 序論 GPによる回帰 GPによる識別 GP 状態空間モデル 概括 GP 状態空間モデルによる音楽ムードの推定
 公開講座 : ガウス過程の基礎と応用 05/3/3 ガウス過程の基礎 統計数理研究所 松井知子 目次 ガウス過程 (Gaussian Process; GP) 序論 GPによる回帰 GPによる識別 GP 状態空間モデル 概括 GP 状態空間モデルによる音楽ムードの推定 GP 序論 ノンパラメトリック予測 カーネル法の利用 参照文献 : C. E. Rasmussen and C. K. I. Williams
公開講座 : ガウス過程の基礎と応用 05/3/3 ガウス過程の基礎 統計数理研究所 松井知子 目次 ガウス過程 (Gaussian Process; GP) 序論 GPによる回帰 GPによる識別 GP 状態空間モデル 概括 GP 状態空間モデルによる音楽ムードの推定 GP 序論 ノンパラメトリック予測 カーネル法の利用 参照文献 : C. E. Rasmussen and C. K. I. Williams
【補足資料】確率・統計の基礎知識
 補足資料 確率 統計の基礎知識 2011 年 5 月 日本銀行金融機構局 金融高度化センター 1 目 次 1. 基本統計量 (1 変量 ) - 平均 分散 標準偏差 パーセント点 2. 基本統計量 (2 変量 ) - 散布図 共分散 相関係数 相関行列 3. 確率変数 - 確率変数 確率分布 期待値 独立 4. 推定と検定 - 記述統計と推測統計 推定 検定 (2 項検定 ) 5. 線形回帰分析 -
補足資料 確率 統計の基礎知識 2011 年 5 月 日本銀行金融機構局 金融高度化センター 1 目 次 1. 基本統計量 (1 変量 ) - 平均 分散 標準偏差 パーセント点 2. 基本統計量 (2 変量 ) - 散布図 共分散 相関係数 相関行列 3. 確率変数 - 確率変数 確率分布 期待値 独立 4. 推定と検定 - 記述統計と推測統計 推定 検定 (2 項検定 ) 5. 線形回帰分析 -
Microsoft PowerPoint - データ解析発表2用パワポ
 7/3 教育学研究科 M1 藤田弥世 SEM とは structural equation model の略 ; 構造方程式モデル ( 別名. 共分散構造分析 ) 多変量解析の色々な手法を統合したモデル 相関行列や共分散行列を利用して 多くの変数間の関係を総合的に分析する手法 共分散 ( 相関係数 ) の観点から 相関係数で関連の大小を評価することができるデータすべてに適用可能 パス解析との違い 前回の授業の修正点
7/3 教育学研究科 M1 藤田弥世 SEM とは structural equation model の略 ; 構造方程式モデル ( 別名. 共分散構造分析 ) 多変量解析の色々な手法を統合したモデル 相関行列や共分散行列を利用して 多くの変数間の関係を総合的に分析する手法 共分散 ( 相関係数 ) の観点から 相関係数で関連の大小を評価することができるデータすべてに適用可能 パス解析との違い 前回の授業の修正点
ハートレー近似(Hartree aproximation)
 ハートリー近似 ( 量子多体系の平均場近似 1) 0. ハミルトニアンの期待値の変分がシュレディンガー方程式と等価であること 1. 独立粒子近似という考え方. 電子系におけるハートリー近似 3.3 電子系におけるハートリー近似 Mde by R. Okmoto (Kyushu Institute of Technology) filenme=rtree080609.ppt (0) ハミルトニアンの期待値の変分と
ハートリー近似 ( 量子多体系の平均場近似 1) 0. ハミルトニアンの期待値の変分がシュレディンガー方程式と等価であること 1. 独立粒子近似という考え方. 電子系におけるハートリー近似 3.3 電子系におけるハートリー近似 Mde by R. Okmoto (Kyushu Institute of Technology) filenme=rtree080609.ppt (0) ハミルトニアンの期待値の変分と
