<4D F736F F D2091E6318FCD E B82CC89898E5A82C688D396A12E646F63>
|
|
|
- まな わたぬき
- 4 years ago
- Views:
Transcription
1 NOITE: Nagasak Uverst's c Ttle 電気回路から見た電磁気学 uthor(s) 辻, 峰男 tato 電気回路から見た電磁気学 ; 19 Issue Date 19-3 URL Rght Ths documet s dowloaded
2 第 1 章ベクトルの演算と意味 この章では, 電磁気を学ぶときに必要となる数学をまとめて示しておく 一般にはベクトル解析と呼ばれる分野の公式である 高校までの微分と積分の知識で理解できるように書いたつもりで, 最初から順に読んでいけば見かけほどは難しくない 電磁気学を考えるときには, 常にスカラ場やベクトル場を思っていなければならない スカラ場とベクトル場 ばばまず, スカラ場とベクトル場について話そう 空気中の温度の分布は, 場所によって値 ( 負になることもある ) が異なり, スカラ場の一例である 風速は場所 ( 高さも含め ) によって大きさが異なると同時に, その向きも違うのでベクトル場の一例である このように, 空間の至る所にスカラ量 (1 つの実数値 ), ベクトル量 (3 つの実数値 ) が各点ごとに値を持って分布しているとき, それぞれスカラ場 (scalar feld), ベクトル場 (vector feld) という 電磁気学で学ぶ電界や磁界は, 大き さだけでなく向きをもつので, ベクトル場を作る 3 次元空間を直角座標系で考えると, 座標 (,, ) の点 P に存在するベクトル量は, 図 1-1 に示すように ˆ ˆ ˆ (,, ) (1-1) と表すことができる,, の目盛 ( 単位 ) と,, の目盛 ( 単位 m) は違う ここで, ˆ, ˆ, ˆ はそれぞれ,, の増える向きの単位ベクトル ( 大きさ 1) である,, はそれぞれ実数で 負になることもある ベクトル の大きさを次式で表す (1-) ˆ ẑ O ŷ P ˆ ˆ ˆ,, は負になることもある 点のベクトル量が ẑ ˆ O ŷ 同じ と書いても値は違う 図 1-1 点 P (,, ) にある図 1- ベクトル場 (3 次元空間 ) ベクトル量の表現電磁気ではこの図をいつもイメージしよう! 1
3 ベクトル について, 以下のことを知っておこう 1 ベクトルは大きさと向きで決るから,(1-1) のように 3 つの成分で表すことができる 各 成分はスカラ量であり, 正負がある 1 つのベクトル量は 3 つのスカラ量からなる ベクトル は, 電磁気の場合,P 点の座標 (, ), と時間 t の関数になり (, t,, ) ( t,,, ) ˆ ( t,,, ) ˆ ( t,,, ) ˆ (1-3) と書くことがある つまり, 場所によって, また時間によって値が違う また,P 点の位置ベクトル r ˆ ˆ ˆ を用いて (,) r t (,) r t ˆ (,) r t ˆ (,) r t ˆ (1-4) と書くこともある 簡単のため, あるいは注目しない r やt を省くこともある 3 は空間に分布してベクトル場を作るが, 大きさ や成分 などは 1 つの量なのでスカラ場を作る 4 のベクトル場を視覚的に表現する方法として, 図 1- の様に 3 次元空間に適当に間引 いて矢印を書く方法と, 図 1-3 の様に力線を描く方法がある 矢印を書く方法で, は場所と時間によって値が異なるが, 区別して書くのは面倒だから, 普通は同じ記号で と書いている ベクトル場の矢印は実際の向きを表す 回路で電圧や電流 ( いずれもス カラ量 ) に付ける矢印は測定の向きを示し, 意味が違う 図 1- はイメージを得るため のもので, 正式に書くなら, ある断面の 次元平面で格子点ごとに矢印を書く 力線については, 以下に述べる (1) 力線の接線方向が の方向で, 曲線につけた矢印で の向きを表す ベクトル場は 3 次元なので力線も 3 次元空間に書くべきであるが, 複雑になるから, ある断面を考えて 次元で表示するのが一般的である () 力線の密度 ( 混み具合 ) で の大きさを表す このあたり 小さい このあたり 大きい 力線の向き 図 1-3 力線によるベクトル場 の表現例 基本的なベクトル演算の定義及び定理 必要に応じて, 以下のベクトルを用いる 電磁気の場合は場所の関数だから動かさない ˆ ˆ ˆ
4 ˆ ˆ ˆ ˆ ˆ ˆ (1) 加法, 減法, スカラとベクトルの乗法 ( ) ˆ ( ) ˆ ( ) ˆ (1-5) a a ˆ a ˆ a ˆ (1-6) ただし, a はスカラ は定義を表す 電磁気の場合, 通常同じ点 P でのベクトルを加えないと意味がない () 内積またはスカラ積 (scalar product) cos (1-7) ただし, は, のなす角である もちろん は /以上でも構わない このとき内積は負となる, が直交する必要十分条件は, /だから である 内積には以下の性質がある (1-8) (1-9) (1-1) ( ) (1-11) a( ) ( a) ( a ) (1-1) (3) 外積またはベクトル積 (vector product) ( s ) e ( ) ˆ ( ) ˆ ( ) ˆ (1-13) ただし, は, のなす角で とする また, e は, を回転させて に重ねると き, 右ねじの進む向きをもつ単位ベクトルである P e 1 e は面 に垂直 e ˆ ˆ ˆ (1-14) と書くこともある つのベクトル, の作る平行四辺形の面積 は, 絶対値をとって 3
5 s (1-15) である また, と が平行であるための必要十分条件は だから となる 外積については以下の性質がある (1-16) (1-17) ( ) (1-18) a( ) ( a) ( a ) (1-19) ( ) ( ) ( ) ( 左へ移動可能 ) (1-) (4) スカラとベクトルの偏微分ベクトル は, 電磁気の場合, 座標 (, ), と時間 t の関数で,(1-3),(1-4) に示した このと き, ベクトル の偏微分は, 各成分の偏微分として定義される 例えば, ˆ ˆ ˆ (1-1) ˆ ˆ ˆ (1-) スカラの偏微分は, 例えば次式のように定義されている ( デルタ ) は微小変動を表す ( t,,, ) ( t,,, ) ( t,,, ) lm (1-3) つまり, 偏微分する変数以外は一定値と考えて微分すればよい 階偏微分については ( ) と考えればよい 例 1 なら,, (1-4) スカラ場として, 空気中の温度分布 f ( t,,, ) がある 偏微分は微分する変数の向きの変化の割合を示すから, 例えば f / は, わずかに 方向にずれたら, 温度 f がどれくらい変化するかを考えている 点 P では, 図中のような正, 負の値になるだろう 当然, 点ごとに値は異なる f / t も考えられる この値は, 同じ P 点で時間がわずかに経過したときの温度変化の割合を表す P f f f 点では 氷 P 炎 温度 f ( t,,, ) スカラ場である 氷 方向には温度は高くなる 図 1-4 偏微分の意味 4
6 偏微分を用いたテイラーの定理を示しておく スカラ関数 f (,, ) について, 任意の点 P (,, ) の近くの点 Q (,, ) における関数の値は,P 点の値で近似できる 近似と言うと嫌いな人もいるだろうが,Q 点が非常に近いなら実質的に等号でよい f f f f (,, ) f (,, ) (1-5) Q (,, ) P f ( ) 接線 f ( ) の近似 P (,, ) 関数 f は各点で値をもつ 正のとき 図 1-5 P, Q 点図 1-6 関数の接線 (1 変数 ) ( デルタ ) は点 P からの小さな変動を意味する,, は負でもよい 時間 t についても同様に考えてよいが,(1-5) では, ある瞬間を考え t とした 右辺の第, 3, 4 項はそれぞれ f (,, ) を,, で偏微分した後,,, を代入して求める つまり,P 点での偏微分の値である f (,, )/ と書くと, 一定値の偏微分で になる 点 P の近くの点では, 関数 f は,P 点の値に,,, の各向きの傾きに変動分をそれぞれ掛けた変化分 ( 負になることもある ) を全部加えたものになる P 点の座標を (,, ) として f f f f (,, ) f(,, ) (1-6) f f f 全微分 d f d d d (1-7) と書くことも多い f (,, ) を偏微分した後,,, を代入するので, 簡単な表現になる (1-6) で とすると,(1-3) の偏微分の定義式に対応していることが判る 変数が だけなら d としてよく, とおくと,(1-5) より次式が得られる df( ) f ( ) f( ) ( ) d これは, 高校で習う接線の方程式である つまり, 元の関数は,P 点の近くでは P 点における接線の値で近似できるのである ( 図 1-6 参照 ) (1-5) は, それが 3 変数になっただけである (1-5), (1-6) はいろいろの場合に利用される重要な公式である (4) 勾配 5
7 スカラ場 f (,, ) の点 (,, ) における勾配 (gradet) は grad f f f f f ˆ ˆ ˆ (1-8) で表される ここで, ( ナブラと読む ) は演算子で, 次式で与えられる ˆ + ˆ + ˆ (1-9) 例えば, 部屋の温度 f (,, ) の分布はスカラ場を作る ある点 P (,, ) で 方向にどれだけ温度が変化するか, その変化の割合 ( 傾き, 勾配 ) が f / であった ベクトル gradf は, 変化の割合が大きい向きを向く grad( f g) gradf gradg である 例スカラ場 f (,, ) の点 (,1,1) における勾配を求めよ grad f (4 ) ˆ ˆ ˆ7 ˆ ˆ ˆ 点 (,1,1) から 軸の向きに進むと急に f が増え, 軸の向きに進むと f が減る (5) 発散 ベクトル場 (,, ) に対して dv (1-3) を点 (,, ) における発散 (dvergece) という dv( ) dvdv である 例ベクトル場 ( ) ˆ ( ) ˆ ( ) ˆ のとき, 点 (1, 1,1) における発散を求めよ dv (6) 回転 ベクトル場 (,, ) に対して ˆ ˆ ˆ rot ( ) ˆ ( ) ˆ ( ) ˆ (1-31) を点 (,, ) における回転 (rotato) という rot( ) rotrot である 例ベクトル場 ˆ ˆ ˆ のとき, 点 (1,1,1) における回転を求めよ ˆ ˆ ˆ rot ( ) ˆ ( ) ˆ4 ˆ 3 ˆ 6
8 線積分, 面積分, 体積分 (1) 線積分 図 1-7(a) の様に 点, を結ぶ曲線 に沿って, 点 から図った長さを l, 点 ではl L( 線の長さ ) とする 上の各点でスカラ関数 f (,, ) が与えられているとき, f (,, ) の曲線 に沿っての線積分 (le tegral) は次式で定義される L 1 f (,, ) dl f(,, ) dl lm f l (1-3) ここで, f f(,, ), l L/ 右辺の意味は, 点, 間を 等分し, 各区間での関数の値 f と微小長さ l ( 正 ) を掛けて, それらを加え合わせる そのとき, として分割数を十分大きくし, その分 は十分小さ く取る から の道 の上にお金が落ちていて ( ある点ではお金を落としてマイナス ), か ら出発し に着くまでに集めたお金の総額が線積分のイメージである l l f l l L P(,, ) l L f l l P(,, ) l l (a) の線積分 (b) の線積分図 1-7 スカラ場の線積分 図 (b) では, 点 から図った長さを l としている 今度は から出発して までお金を集めるということである 微小長さ は正で変らない よって, l f ( dl,, ) f( dl,, ) (1-33) が成り立ち積分値は変わらない もし, f(,, ) 1なら, 線積分の値は道の長さ L になる 高校で習う積分 1 b b a f ( d ) lm f( ) a ここで, (1-34) は, 軸上で値が f ( ) であるとき,a から b までの線積分と考えることができる しかし, は b aなら正であるが,b aなら負となる この結果 7
9 b a a b f ( d ) f( d ) (1-35) となる この点は が常に正で,(1-33) が成り立つ線積分と異なる l 例点 (,,) から点 (1,1,1) に至る直線を経路 として, から までの線積分 dl を求めよ f (,, ) である 次に, から までの線積分を求めよ ( 解 ) 間の距離は 3 である から経路 に沿った長さ l に対し l/ 3 である 故に 3 dl l l dl 3 3 から測った長さ l に対し 1 ( l/ 3) である よって 3 l l 3 3 dl (1 ) dl l (1,1,1) 次にベクトル場の線積分について述べる 図 1-8(a) に示すように, 空間の各点で値が異なるベクトル場 がある 経路 に対し, の線積分を次式で定義する 図 1-8 の dlは図 1-7 のように l と書くのが厳密だが, 次式との対応が判りやすいので, dlと書いた もともと dlは極めて小さいから図には書けないだろう L t dl または t dl (1-36) ここで, t は経路 と同じ向きの単位接線ベクトルである ( t 1) t は内積で, スカラである よって, t f (,, ) とおけば,(1-3) の定義はそのまま使える 接線は taget だから t とする l t dl l L l L t dl l ' (a) の線積分 (b) の線積分図 1-8 ベクトル場の線積分 8
10 この場合, の線積分と の線積分は値が異なる 図に示すように,(a) の場合, t cos だが,(b) の場合, t cos( ) cos となる 従って, tdl t dl (1-37) ' となる t の向きが逆になるので, スカラ関数の値の符号が変わる ベクトルの線積分と言っても, 内積を取るので, 実はスカラの線積分である 図 1-8 で物体に力 を加え, から まで動かしたとき, 線積分はこの力がする仕事を表す 図 1-9 を使って単位接線ベクトル t の公式を導いておく 積分路 上の任意の点 P は, 点 から測った長さ l の点である この点の位置ベクトルは,l だけの関数として r() l () l ˆ () l ˆ () l ˆ (1-38) と書ける つまり 上の点の座標 (,, ) は l で表されるということ 点 P から少し l が増えると, その分, 座標も変化する 点 P で, それぞれの座標を l で微分したベクトル dr() l d() l d() l d() l t() l ˆ ˆ ˆ (1-39) dl dl dl dl は, 点 P での曲線 の単位接線ベクトルとなる なぜなら, まず図 1-9 より d r () l ( l l) () l lm r r (1-4) dl l l は の接線方向を向いている 次に, 大きさについては d d d ( d) ( d) ( d) ˆ ˆ ˆ 1 (1-41) dl dl dl dl が成り立つ l r() l P l l l t r( l l) l L r() l r( l l) r( l) r( l l) l が厳密だが dl と書くこともある 図 1-9 単位接線ベクトル t (1-39) より, 次式が成り立つ tdldr dˆ d ˆ d ˆ (1-4) また, tdl dl と置いて,(1-36) の線積分を tdl dr あるいは tdl dl (1-43) 9
11 と書いた本も多い 本テキストでは, 線積分の意味がはっきりわかるように (1-36) のように書く () 面積分 スカラ場の面積分 図 1-1 に示すように, スカラ場 f (,, ) の中に滑らかな曲面 がある この曲面を 分割して, 番目の小片上に任意の点 P をとる 点 P でのスカラ場の値 f (P ) と小片の面積 ( 正 ) を用いて, 面積分 (surface tegral) を次式で定義する f (P ) f(,, ) である 1 f ( d,, ) lm f(p) (1-44) とするのは, 分割数を十分大きくし, は十分小さく取るということである 十分小 さくとるので, 小片の形に制限はない 畑 の上にお金が落ちていて ( ある点ではお金を落と して ), 畑で集めたお金の総額が面積分のイメージである 畑やベレー帽は面のイメージのた めで, ボールのような閉曲面であっても構わない f 1なら面積分は の面積になる P 図 1-1 スカラ場の面積分 図 1-11 ベクトル場の面積分 ベクトル場の面積分図 1-11 に示すように, 空間の各点で値が異なるベクトル場 (,, ) がある いま曲面 があり, 曲面上にある ( ベクトル場 の一部 ) の面積分を次式で定義する d lm (1-45) 1 ここで, は曲面 の向きを決める単位法線ベクトル ( は に垂直 ) である は内積で, スカラである よって, f (P ) とおけば,(1-44) と同じである d d と置いて d d (1-46) と書く本もある は, ベクトル のうちで面を の向きに通過する量のイメージである と のなす角が /なら は となり, 面を通過する量が ということである /以上になると値が負になり, と逆向きに通過することを意味する ベクトルの面積分と言っても, 内積を取るので, 実はスカラの面積分である 本テキストでは が見えたほうが良いので (1-45) の様に書く 1
12 (3) 体積分スカラ場 f (,, ) の中にボールのような閉曲面 で囲まれた領域 V がある この領域を 分割して, 番目の小立体内に任意の点 P をとる 点 P でのスカラ場の値 f (P ) と小立体の体積 V を用いて, 体積分 (volume tegral) を次式で定義する f ( dv,, ) lm f(p) V (1-47) V 1 は, 分割数を十分大きくし, V は十分小さく取るということである 貯金箱の中 V に 各種のお金が入っていて, 全部を集めたお金の総額が体積分のイメージである f 1のとき 体積分は V の体積となる V V P 図 1-1 スカラ場の体積分 線積分, 面積分, 体積分の定理 (1) ストークスの定理図 1-13 に示すように, ベクトル場 の中に開曲面 を考える 開曲面 上で面に垂直な単位法線ベクトルを とする もちろん, は場所によって異なる ( は面の上だけではない ) の 向く側を の表という 境界 の向きは の表を左に見て進む向きにとるものとする t は の 向きの単位接線ベクトルである このとき, 次式が成立する (rot ) d t d l (1-48) これをストークスの定理 (tokes' theorem) という の回転である rot の面に垂直な成分を開曲面 上で集めた値と, 境界 上で の接線方向成分を 1 周回って集めた値は等しいことを意味する : 上の単位法線ベクトルベレー帽の ような曲面 と の向きその縁 t 右ねじの関係 t t : 上の単位 接線ベクトル, t, は同じ記号で書いて いるが場所で異なる 図 1-13 ストークスの定理 11
13 以下, 回転の定義, ストークスの定理の証明,(1-31) の導出に関して説明しよう 図 1-14 に示すように, 曲面を 分割し, つのループ 1, を考える 1 周する 1 と の線積分の和を考えると,, 間は向きが反対なので,(1-37) より打ち消し tdl tdl t dl (1-49) 1 となる は外側の境界を 1 周している 単位接線ベクトル t は 1,, ごとに一部異なる t t 1 t t (a) 開曲面 ( ベレー帽 ) の 分割 (b) 開曲面 ( ベレー帽 ) の多分割図 1-14 線積分の和 ( ベレー帽を真上から見た図 ) rot P t 図 1-15 rot の定義 rot rot 図 1-14 (b) のように開曲面を小片 ( 形に制限はない ) に 分割した場合,(1-49) の考え方を何度も使うと内側の線積分は消えて, 一番外側 の線積分だけが残る よって, tdl t dl (1-5) 1 が成り立つ いま, 図 1-15 に示す小片の境界での線積分を面積 で割って, 小片での ( 極限では点と考えてよい ) rot を次式で定義する は面に垂直な単位法線ベクトルである t dl (rot ) lm (1-51) 分りにくい定義の仕方であるが, 以下の様に解釈しよう ベクトル場 について, ある点で, うずを巻いている量を定義したい このために, ある点 P を含む小さな面を考え, その境界 で線積分を計算する これが大きければ経路 に沿って強いうずを巻いていると考えられる なぜなら線積分は P の回りを 1 周する の向きで の経路方向成分を集めたものだから ところが, ある点 P を含む小さな面は角度を変えればいろいろある 全部試してみて最も大きな線積分が得 1
14 られた面の法線の向きを rot の向きと定義する rot の大きさはそのときの線積分の値としたいところであるが, それだと面の大きさで値が異なるから, で割っている lm は, が極めて小さいなら, 省いて考えてよい 適当に決めた経路 は, 線積分が最も大きくなるとは限らず, rot の向きとのずれの分だけ小さくなる それが (1-51) 左辺で内積をとる理由である たまたま線積分が最も大きくなるなら, rot と の向きは一致し, 右辺が rot の大きさとなる 小さな水車を点 P において, 角度をいろいろと試し, 水車が最も速く回るときの水車の軸が rot の向きで, 水車の速さが rot の大きさに対応すると考えるとイメージしやすい (1-51) で は十分小さいとして lm を省き, 図 1-14(b) の場合について 個分加え合わせると (rot ) t dl (1-5) 1 1 となる 分割数を多くし としたときの左辺を (1-45) の面積分の定義で (rot ) d と書くので, 右辺に (1-5) を用いて,(1-48) のストークスの定理が証明できた 最後に,(1-31) の導出を行う 図 1-16 のような, 微小な長方形の経路 を考える 軸は紙面に対し手前を向いている 点 1 (,, ) の を成分表示すると (,, ) (,, ) ˆ (,, ) ˆ (,, ) ˆ と書ける 点 3 の を成分表示すると (,, ) (,, ) ˆ (,, ) ˆ (,, ) ˆ と書ける テイラーの定理を用いると,(1-6) より次式を得る (,, ) (,, ) (,, ) (,, ) 点 は, 上式の を, 点 4 は上式の を とすればよい ẑ ŷ (,, ) 4 3 (,, ) ˆ 1 (,, ) (,, ) 図 1-16 一定の - 平面にとった積分路 13
15 次に, 経路 での の線積分を考える 例えば,1 への積分では, t ˆ であるから tdl tdl tdl tdl t dl ˆdl ˆdl ˆdl ˆdl (1-53) dl dl dl dl 各線積分を, 例えば1 の場合は点 1 と点 の の平均値に長さを掛けて求めると 1 ( (,, ) (,, ) dl ) 1 1 ( (,, ) (,, ) ) 3 dl 1 ( (,, ) (,, ) ) 3 4 dl 1 ( (,, ) (,, )) 4 1 dl これらを (1-53) に代入して, t dl( ) (1-51) より dl (rot ) lm t (1-54) ここで, は経路 と右ねじの関係で決まるから, ˆ で (rot ) ˆ は rot の 軸方向成分である これで, rot の 成分が求まった,, と順に入れ替えることで, rot の 成分が求まる,, と順に入れ替えることで,rot の 成分が求まる 以上で, (1-31) が導出できた () ガウスの定理図 1-17 に示すように, ベクトル場 の中に例えばボールのような閉曲面 とその中の領域 V を考える 閉曲面 上で面に垂直な外向きの単位法線ベクトルを とする もちろん, は場所によって異なる このとき, 次式が成立する V dvdv d (1-55) これをガウスの定理 (Gauss' theorem) という の発散である dv を領域 V で集めた体積分と, 面 上で の外向き成分を集めた面積分とは等しいことを意味する dv は水の源泉で, 領域 V の中の湧き水を全て集めると, 境界面から出て行く水の量 ( 方向成分 ) と等しいというイメージである 14
16 V : 図 1-17 ガウスの定理 以下, 発散の定義, ガウスの定理の証明,(1-3) の導出に関して説明しよう 図 1-18(a) に示すように, ボールのような閉曲面を 分割し, つの閉曲面 + と + を作る 境界面 は共通の断面である 閉曲面上でのベクトル場 の面積分を考える 曲面 上の同じ点では, 単位法線ベクトル であり, 面積分について次式が成り立つ d d (1-56) したがって, 境界面 上の面積分は打ち消すので となる d d d d (1-57) 図 1-18(b) のように閉曲面内を小閉曲面 ( 形に制限はない ) に 分割した場合, 共通の面 ( 小 立体中の面 ) の面積分が打ち消すので, この考え方を繰り返し用いることで 1 d d (1-58) が成り立つ は面 に垂直な単位法線ベクトルである 結局一番外の面積分しか残らない 面 面 境界面 P V V P (a) 閉曲面の 分割図 1-18 面積分の和 (b) 閉曲面の多分割 15
17 いま, 図 1-18(b) に示す小閉曲面の面上での面積分をその体積 よい ) dv を次式で定義する V で割って ( 極限では点と考えて d dv lm (1-59) V V lm は, V が極めて小さいとして, 省いて考えてもよい dv は極めて小さい閉曲面 ( 点とみなせる ) から が外に出る量を集めたものである が面に垂直な部分では最も外に出る 図 1-18(b) の場合について考えると, 定義 (1-59) より dvv d (1-6) 1 1 となる とし, 十分小さく分割したときの左辺を体積分の定義 (1-47) で dv dv V と書くので,(1-58) であるから, ガウスの定理が証明できた 最後に,(1-3) の導出を行う 図 1-19 のように, ベクトル場 の中に座標軸に平行な辺の極小の直方体を考え,6 つの面上で面積分を考えていく ẑ ˆ (,, ) 5 ŷ (,, ) 7,, 6 (,, ) 図 1-19 dv の公式の証明 点 1 (,, ) の を成分表示して (,, ) (,, ) ˆ (,, ) ˆ (,, ) ˆ とする まず, 面 134 と面 5678 について考える 面 134 の中心の を成分表示すると (,, ) ( (,, ), (,, ), (,, )) と書ける テイラーの定理を用いると, 成分について次式を得る (,, ) (,, ) (1-61) 16
18 同様に, 面 5678 の中心の の 成分は, テイラーの定理を用いると, 次式で表せる (,, ) (,, ) (1-6) 次に, 面 134 と面 5678 での面積分を考える (1-61),(1-6) を用い, 面積分を面の中心の値 面積と近似すると d d ˆd ˆd d d 1 1 ( (,, ) ) 1 1 ( (,, ) ) (1-63) V であるから, (1-59) より, V で割って, これらの面に関しては / となる 他の, 軸方向についても同様に求まり, これらの和として (1-3) が得られる 以上は, 直角座標系 (,, ) で考えたが, 円柱座標系 (, r, ) や球座標系 (, r, ) を考えることもある 定義は当然同じであるが,dv, grad, rot などの得られる公式については, 付録を参照願いたい 数学の公式は恐れることなく使ってみよう 複雑な式は覚える必要もない また, 導かなくても, 3 冊以上の版を重ねた本に同じ公式が載っていて本文中でも利用されていたら, 正しいと信じて良いだろう 17
補足 中学で学習したフレミング左手の法則 ( 電 磁 力 ) と関連付けると覚えやすい 電磁力は電流と磁界の外積で表される 力 F 磁 電磁力 F li 右ねじの回転の向き電 li ( l は導線の長さ ) 補足 有向線分とベクトル有向線分 : 矢印の位
 http://totemt.sur.ne.p 外積 ( ベクトル積 ) の活用 ( 面積, 法線ベクトル, 平面の方程式 ) 3 次元空間の つのベクトルの積が つのベクトルを与えるようなベクトルの掛け算 ベクトルの積がベクトルを与えることからベクトル積とも呼ばれる これに対し内積は符号と大きさをもつ量 ( スカラー量 ) を与えるので, スカラー積とも呼ばれる 外積を使うと, 平行四辺形や三角形の面積,
http://totemt.sur.ne.p 外積 ( ベクトル積 ) の活用 ( 面積, 法線ベクトル, 平面の方程式 ) 3 次元空間の つのベクトルの積が つのベクトルを与えるようなベクトルの掛け算 ベクトルの積がベクトルを与えることからベクトル積とも呼ばれる これに対し内積は符号と大きさをもつ量 ( スカラー量 ) を与えるので, スカラー積とも呼ばれる 外積を使うと, 平行四辺形や三角形の面積,
線積分.indd
 線積分 線積分 ( n, n, n ) (ξ n, η n, ζ n ) ( n-, n-, n- ) (ξ k, η k, ζ k ) ( k, k, k ) ( k-, k-, k- ) 物体に力 を作用させて位置ベクトル A の点 A から位置ベクトル の点 まで曲線 に沿って物体を移動させたときの仕事 W は 次式で計算された A, A, W : d 6 d+ d+ d@,,, d+ d+
線積分 線積分 ( n, n, n ) (ξ n, η n, ζ n ) ( n-, n-, n- ) (ξ k, η k, ζ k ) ( k, k, k ) ( k-, k-, k- ) 物体に力 を作用させて位置ベクトル A の点 A から位置ベクトル の点 まで曲線 に沿って物体を移動させたときの仕事 W は 次式で計算された A, A, W : d 6 d+ d+ d@,,, d+ d+
ベクトル公式.rtf
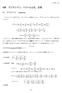 6 章ラプラシアン, ベクトル公式, 定理 6.1 ラプラシアン Laplacian φ はベクトル量である. そこでさらに発散をとると, φ はどういう形になるであろうか? φ = a + a + a φ a + a φ + a φ = φ + φ + φ = 2 φ + 2 φ 2 + 2 φ 2 2 φ = 2 φ 2 + 2 φ 2 + 2 φ 2 = 2 φ したがって,2 階の偏微分演算となる.
6 章ラプラシアン, ベクトル公式, 定理 6.1 ラプラシアン Laplacian φ はベクトル量である. そこでさらに発散をとると, φ はどういう形になるであろうか? φ = a + a + a φ a + a φ + a φ = φ + φ + φ = 2 φ + 2 φ 2 + 2 φ 2 2 φ = 2 φ 2 + 2 φ 2 + 2 φ 2 = 2 φ したがって,2 階の偏微分演算となる.
回転.rtf
 ベクトルの回転の定義は A A rot A ΔS 0 n ΔS (5.) : ounter dl 図 5. ベクトルの回転 であり, 回転量を調べる演算子である. ローテーションA, カールA,Aの回転とも読む. 図 5.のように, 閉曲線 に沿ってベクトル Aの線積分を行うものとする. 線積分はベクトル Aと線素 dl の内積だから, ある大きさ ( スカラー量 ) が得られる. その大きさをもち,
ベクトルの回転の定義は A A rot A ΔS 0 n ΔS (5.) : ounter dl 図 5. ベクトルの回転 であり, 回転量を調べる演算子である. ローテーションA, カールA,Aの回転とも読む. 図 5.のように, 閉曲線 に沿ってベクトル Aの線積分を行うものとする. 線積分はベクトル Aと線素 dl の内積だから, ある大きさ ( スカラー量 ) が得られる. その大きさをもち,
座標系.rtf
 2 章座標系 場 空間は3 次元なので, ベクトルを表現するには少なくとも3 成分を指定する必要がある. そのために座標系が必要となる. 座標系として最も一般的なものは,,, 成分を使った直角座標系である. しかし, 他にも円柱座標, 球座標, だ円座標, 放物線座標など様々なものがある. 現在までに3 成分で変数分離可能な座標系は11 個あるといわれている (Moon & Spencer, Field
2 章座標系 場 空間は3 次元なので, ベクトルを表現するには少なくとも3 成分を指定する必要がある. そのために座標系が必要となる. 座標系として最も一般的なものは,,, 成分を使った直角座標系である. しかし, 他にも円柱座標, 球座標, だ円座標, 放物線座標など様々なものがある. 現在までに3 成分で変数分離可能な座標系は11 個あるといわれている (Moon & Spencer, Field
Microsoft PowerPoint - 第5回電磁気学I
 1 年 11 月 8 日 ( 月 ) 1:-1: Y 平成 年度工 系 ( 社会環境工学科 ) 第 5 回電磁気学 Ⅰ 天野浩 項目 電界と電束密度 ガウスの発散定理とガウスの法則の積分形と微分形 * ファラデーの電気力線の使い方をマスターします * 電界と電束密度を定義します * ガウスの発散定理を用いて ガウスの法則の積分形から微分形をガウスの法則の積分形から微分形を導出します * ガウスの法則を用いて
1 年 11 月 8 日 ( 月 ) 1:-1: Y 平成 年度工 系 ( 社会環境工学科 ) 第 5 回電磁気学 Ⅰ 天野浩 項目 電界と電束密度 ガウスの発散定理とガウスの法則の積分形と微分形 * ファラデーの電気力線の使い方をマスターします * 電界と電束密度を定義します * ガウスの発散定理を用いて ガウスの法則の積分形から微分形をガウスの法則の積分形から微分形を導出します * ガウスの法則を用いて
<4D F736F F D20824F B834E835882CC92E8979D814690FC90CF95AA82C696CA90CF95AA2E646F63>
 1/10 平成 23 年 6 月 1 日午後 4 時 33 分 07 ストークスの定理 : 線積分と面積分 07 ストークスの定理 : 線積分と面積分 ストークスの定理はガウスの定理とともに 非常に重要な定理であり 線積分と面積分の関係を表します つまり ガウスの定理 : 面積分と体積分 ( 体積を囲む閉じた面 = 表面 ) の関係 ストークスの定理 : 線積分と面積分 ( 面積を囲む外周の線 )
1/10 平成 23 年 6 月 1 日午後 4 時 33 分 07 ストークスの定理 : 線積分と面積分 07 ストークスの定理 : 線積分と面積分 ストークスの定理はガウスの定理とともに 非常に重要な定理であり 線積分と面積分の関係を表します つまり ガウスの定理 : 面積分と体積分 ( 体積を囲む閉じた面 = 表面 ) の関係 ストークスの定理 : 線積分と面積分 ( 面積を囲む外周の線 )
応用数学A
 応用数学 A 米田 戸倉川月 7 限 1930~2100 西 5-109 V を :x 2 + y 2 + z 2 = 4 で囲まれる内部とする F = ye x xe y + ze z FdV = V e x e y e z F = = 2e z 2e z dv = 2e z 3 23 = 64π 3 e z y x z 4π V n Fd = 1 F nd 2 F nd 法線ベクトル n g x,
応用数学 A 米田 戸倉川月 7 限 1930~2100 西 5-109 V を :x 2 + y 2 + z 2 = 4 で囲まれる内部とする F = ye x xe y + ze z FdV = V e x e y e z F = = 2e z 2e z dv = 2e z 3 23 = 64π 3 e z y x z 4π V n Fd = 1 F nd 2 F nd 法線ベクトル n g x,
発散.rtf
 4 章発散 発散は重要なベクトル演算の一つであり, 定義は A =diva = lim Δv 0 Δv A d (4.) である.Divergence( ダイバージェンス ) ともいう. この意味は, 微小体積 vを取り囲む全表面 ( 閉曲面という ) 上で, 外向きのベクトル法線成分をすべて加えあわせ, 全体としての量を調べるものである. ベクトルAはどのような向きでもかまわないが, 面ベクトルとの内積
4 章発散 発散は重要なベクトル演算の一つであり, 定義は A =diva = lim Δv 0 Δv A d (4.) である.Divergence( ダイバージェンス ) ともいう. この意味は, 微小体積 vを取り囲む全表面 ( 閉曲面という ) 上で, 外向きのベクトル法線成分をすべて加えあわせ, 全体としての量を調べるものである. ベクトルAはどのような向きでもかまわないが, 面ベクトルとの内積
座標軸以外の直線のまわりの回転体の体積 ( バウムクーヘン分割公式 ) の問題の解答 立体の体積の求め方 図 1 の立体の体積 V を求める方法を考えてみる 図 1 図 1 のように 軸の から までの長さを 等分する そして とおく とすると となる 図 1 のように のときの 軸に垂直な平面 に
 立体の体積の求め方 図 1 の立体の体積 V を求める方法を考えてみる 図 1 図 1 のように 軸の から までの長さを 等分する そして とおく とすると となる 図 1 のように のときの 軸に垂直な平面 による立体の断面積を とする 図 1の から までの斜線部分の立体 の体積を とすると, 図 2のように は 底面積 高さ の角柱の体積とみなせる よって 図 2 と表せる ただし とすると,
立体の体積の求め方 図 1 の立体の体積 V を求める方法を考えてみる 図 1 図 1 のように 軸の から までの長さを 等分する そして とおく とすると となる 図 1 のように のときの 軸に垂直な平面 による立体の断面積を とする 図 1の から までの斜線部分の立体 の体積を とすると, 図 2のように は 底面積 高さ の角柱の体積とみなせる よって 図 2 と表せる ただし とすると,
<4D F736F F D20824F B CC92E8979D814696CA90CF95AA82C691CC90CF95AA2E646F63>
 1/1 平成 23 年 3 月 24 日午後 6 時 52 分 6 ガウスの定理 : 面積分と体積分 6 ガウスの定理 : 面積分と体積分 Ⅰ. 直交座標系 ガウスの定理は 微分して すぐに積分すると元に戻るというルールを 3 次元積分に適用した定理になります よく知っているのは 簡単化のため 変数が1つの場合は dj ( d ( ににします全微分 = 偏微分 d = d = J ( + C d です
1/1 平成 23 年 3 月 24 日午後 6 時 52 分 6 ガウスの定理 : 面積分と体積分 6 ガウスの定理 : 面積分と体積分 Ⅰ. 直交座標系 ガウスの定理は 微分して すぐに積分すると元に戻るというルールを 3 次元積分に適用した定理になります よく知っているのは 簡単化のため 変数が1つの場合は dj ( d ( ににします全微分 = 偏微分 d = d = J ( + C d です
vecrot
 1. ベクトル ベクトル : 方向を持つ量 ベクトルには 1 方向 2 大きさ ( 長さ ) という 2 つの属性がある ベクトルの例 : 物体の移動速度 移動量電場 磁場の強さ風速力トルクなど 2. ベクトルの表現 2.1 矢印で表現される 矢印の長さ : ベクトルの大きさ 矢印の向き : ベクトルの方向 2.2 2 個の点を用いて表現する 始点 () と終点 () を結ぶ半直線の向き : ベクトルの方向
1. ベクトル ベクトル : 方向を持つ量 ベクトルには 1 方向 2 大きさ ( 長さ ) という 2 つの属性がある ベクトルの例 : 物体の移動速度 移動量電場 磁場の強さ風速力トルクなど 2. ベクトルの表現 2.1 矢印で表現される 矢印の長さ : ベクトルの大きさ 矢印の向き : ベクトルの方向 2.2 2 個の点を用いて表現する 始点 () と終点 () を結ぶ半直線の向き : ベクトルの方向
<4D F736F F D20824F F6490CF95AA82C696CA90CF95AA2E646F63>
 1/15 平成 3 年 3 月 4 日午後 6 時 49 分 5 ベクトルの 重積分と面積分 5 重積分と面積分 Ⅰ. 重積分 と で 回積分することを 重積分 といいます この 重積分は何を意味しているのでしょう? 通常の積分 (1 重積分 ) では C d 図 1a 1 f d (5.1) 1 f d f ( ) は 図形的には図 1a のように面積を表しています つまり 1 f ( ) を高さとしてプロットすると図
1/15 平成 3 年 3 月 4 日午後 6 時 49 分 5 ベクトルの 重積分と面積分 5 重積分と面積分 Ⅰ. 重積分 と で 回積分することを 重積分 といいます この 重積分は何を意味しているのでしょう? 通常の積分 (1 重積分 ) では C d 図 1a 1 f d (5.1) 1 f d f ( ) は 図形的には図 1a のように面積を表しています つまり 1 f ( ) を高さとしてプロットすると図
パソコンシミュレータの現状
 第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
ベクトルの基礎.rtf
 章ベクトルの表現方法 ベクトルは大きさと方向を持つ量である. 図.に示すように始点 Pから終点 Qに向かう有向線分として で表現する. 大きさは矢印の長さに対応している. Q P 図. ベクトルの表現方法 文字を使ったベクトルの表記方法として, あるいは の表記が用いられるが, このテキストでは太字表示 を採用する. 専門書では太字で書く の表記が一般的であり, 矢印を付ける表記は用いない. なお,
章ベクトルの表現方法 ベクトルは大きさと方向を持つ量である. 図.に示すように始点 Pから終点 Qに向かう有向線分として で表現する. 大きさは矢印の長さに対応している. Q P 図. ベクトルの表現方法 文字を使ったベクトルの表記方法として, あるいは の表記が用いられるが, このテキストでは太字表示 を採用する. 専門書では太字で書く の表記が一般的であり, 矢印を付ける表記は用いない. なお,
PowerPoint プレゼンテーション
 電磁波工学 第 5 回平面波の媒質への垂直および射入射と透過 柴田幸司 Bounda Plan Rgon ε μ Rgon Mdum ( ガラスなど ε μ z 平面波の反射と透過 垂直入射の場合 左図に示す様に 平面波が境界面に対して垂直に入射する場合を考える この時の入射波を とすると 入射波は境界において 透過波 と とに分解される この時の透過量を 反射量を Γ とおくと 領域 における媒質の誘電率に対して透過量
電磁波工学 第 5 回平面波の媒質への垂直および射入射と透過 柴田幸司 Bounda Plan Rgon ε μ Rgon Mdum ( ガラスなど ε μ z 平面波の反射と透過 垂直入射の場合 左図に示す様に 平面波が境界面に対して垂直に入射する場合を考える この時の入射波を とすると 入射波は境界において 透過波 と とに分解される この時の透過量を 反射量を Γ とおくと 領域 における媒質の誘電率に対して透過量
Microsoft PowerPoint - 応用数学8回目.pptx
 8- 次の 標 : 複素関数 ( 正則関数 ) の積分 8- 実関数 : 定積分 講義内容 名城 学理 学部材料機能 学科岩 素顕 複素関数の積分について学ぶ 複素関数の積分 複素積分の性質 周回積分の解法 コーシーの積分定理 コーシーの積分公式 グルサーの公式 - 定義 複素関数の積分 : 線積分 今後の内容 区分的に滑らかな曲線に沿って複素関数の積分を計算する 複素関数の積分の性質に関して議論する
8- 次の 標 : 複素関数 ( 正則関数 ) の積分 8- 実関数 : 定積分 講義内容 名城 学理 学部材料機能 学科岩 素顕 複素関数の積分について学ぶ 複素関数の積分 複素積分の性質 周回積分の解法 コーシーの積分定理 コーシーの積分公式 グルサーの公式 - 定義 複素関数の積分 : 線積分 今後の内容 区分的に滑らかな曲線に沿って複素関数の積分を計算する 複素関数の積分の性質に関して議論する
数学 ⅡB < 公理 > 公理を論拠に定義を用いて定理を証明する 1 大小関係の公理 順序 (a > b, a = b, a > b 1 つ成立 a > b, b > c a > c 成立 ) 順序と演算 (a > b a + c > b + c (a > b, c > 0 ac > bc) 2 図
 数学 Ⅱ < 公理 > 公理を論拠に定義を用いて定理を証明する 大小関係の公理 順序 >, =, > つ成立 >, > > 成立 順序と演算 > + > + >, > > 図形の公理 平行線の性質 錯角 同位角 三角形の合同条件 三角形の合同相似 量の公理 角の大きさ 線分の長さ < 空間における座漂とベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル
数学 Ⅱ < 公理 > 公理を論拠に定義を用いて定理を証明する 大小関係の公理 順序 >, =, > つ成立 >, > > 成立 順序と演算 > + > + >, > > 図形の公理 平行線の性質 錯角 同位角 三角形の合同条件 三角形の合同相似 量の公理 角の大きさ 線分の長さ < 空間における座漂とベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル
Chap3.key
 区分求積法. 面積 ( )/ f () > n + n, S 長方形の和集合で近似 n f (n ) リーマン和 f (n ) 区分求積法 リーマン和 S S n n / n n f ()d リーマン積分 ( + ) + S (, f ( )) 微分の心 Zoom In して局所的な性質を調べる 積分の心 Zoom Ou して大域的な性質を調べる 曲線の長さ 領域の面積や体積 ある領域に含まれる物質の質量
区分求積法. 面積 ( )/ f () > n + n, S 長方形の和集合で近似 n f (n ) リーマン和 f (n ) 区分求積法 リーマン和 S S n n / n n f ()d リーマン積分 ( + ) + S (, f ( )) 微分の心 Zoom In して局所的な性質を調べる 積分の心 Zoom Ou して大域的な性質を調べる 曲線の長さ 領域の面積や体積 ある領域に含まれる物質の質量
Microsoft Word - thesis.doc
 剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
平成 年 月 7 日 ( 土 第 75 回数学教育実践研究会アスティ 45 ビル F セミナールーム A 札幌医科大学 年 P ab, を正の定数とする 平面上において ( a, を中心とする円 Q 4 C と (, b を中心とする円 C が 原点 O で外接している また P を円 C 上の点と
 平成 年 月 7 日 ( 土 第 75 回数学教育実践研究会アスティ 45 ビル F セミナールーム 微分積分の拡張 変数関数問題へのアプローチ 予選決勝優勝法からラグランジュ未定乗数法 松本睦郎 ( 札幌北高等学校 変数関数の最大値 最小値に関する問題には多様なアプローチ法がある 文字を固定した 予選決勝優勝法, 計算のみで解法する 文字消去法, 微分積分を利用した ラグランジュ未定乗数法 がある
平成 年 月 7 日 ( 土 第 75 回数学教育実践研究会アスティ 45 ビル F セミナールーム 微分積分の拡張 変数関数問題へのアプローチ 予選決勝優勝法からラグランジュ未定乗数法 松本睦郎 ( 札幌北高等学校 変数関数の最大値 最小値に関する問題には多様なアプローチ法がある 文字を固定した 予選決勝優勝法, 計算のみで解法する 文字消去法, 微分積分を利用した ラグランジュ未定乗数法 がある
Microsoft PowerPoint - A1_vector_intro_slide.pptx
 v3.9 Ma.2018 1 ベクトル解析が必要な理由 2 ベクトル解析の基礎 - 内積と外積 回転と発散 - 1 st 2011/04/01 L st 2018/05/06 1. 電磁場 ( 電界と磁界 ) がベクトル量 ( 大きさだけでなく方向を有する物理量 ) であるため 2. 電磁界は自然法則 = マクスウェルの方程式で記述されるため 方程式を解くための計算において 重ね合わせや微分積分が出てくる
v3.9 Ma.2018 1 ベクトル解析が必要な理由 2 ベクトル解析の基礎 - 内積と外積 回転と発散 - 1 st 2011/04/01 L st 2018/05/06 1. 電磁場 ( 電界と磁界 ) がベクトル量 ( 大きさだけでなく方向を有する物理量 ) であるため 2. 電磁界は自然法則 = マクスウェルの方程式で記述されるため 方程式を解くための計算において 重ね合わせや微分積分が出てくる
木村の物理小ネタ ケプラーの第 2 法則と角運動量保存則 A. 面積速度面積速度とは平面内に定点 O と動点 P があるとき, 定点 O と動点 P を結ぶ線分 OP( 動径 OP という) が単位時間に描く面積を 動点 P の定点 O に
 ケプラーの第 法則と角運動量保存則 A. 面積速度面積速度とは平面内に定点 O と動点 P があるとき, 定点 O と動点 P を結ぶ線分 OP( 動径 OP という が単位時間に描く面積を 動点 P の定点 O に関する面積速度の大きさ という 定点 O まわりを回る面積速度の導き方導き方 A ( x( + D, y( + D v ( q r ( A ( x (, y( 動点 P が xy 座標平面上を時刻
ケプラーの第 法則と角運動量保存則 A. 面積速度面積速度とは平面内に定点 O と動点 P があるとき, 定点 O と動点 P を結ぶ線分 OP( 動径 OP という が単位時間に描く面積を 動点 P の定点 O に関する面積速度の大きさ という 定点 O まわりを回る面積速度の導き方導き方 A ( x( + D, y( + D v ( q r ( A ( x (, y( 動点 P が xy 座標平面上を時刻
応用数学Ⅱ 偏微分方程式(2) 波動方程式(12/13)
 偏微分方程式. 偏微分方程式の形 偏微分 偏導関数 つの独立変数 をもつ関数 があるとき 変数 が一定値をとって だけが変化したとす ると は だけの関数となる このとき を について微分して得られる関数を 関数 の に関する 偏微分係数 略して偏微分 あるいは偏導関数 pil deiie といい 次のように表される についても同様な偏微分を定義できる あるいは あるいは - あるいは あるいは -
偏微分方程式. 偏微分方程式の形 偏微分 偏導関数 つの独立変数 をもつ関数 があるとき 変数 が一定値をとって だけが変化したとす ると は だけの関数となる このとき を について微分して得られる関数を 関数 の に関する 偏微分係数 略して偏微分 あるいは偏導関数 pil deiie といい 次のように表される についても同様な偏微分を定義できる あるいは あるいは - あるいは あるいは -
PowerPoint Presentation
 付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
数学 t t t t t 加法定理 t t t 倍角公式加法定理で α=β と置く. 三角関数
 . 三角関数 基本関係 t cot c sc c cot sc t 還元公式 t t t t t t cot t cot t 数学 数学 t t t t t 加法定理 t t t 倍角公式加法定理で α=β と置く. 三角関数 数学. 三角関数 5 積和公式 6 和積公式 数学. 三角関数 7 合成 t V v t V v t V V V V VV V V V t V v v 8 べき乗 5 6 6
. 三角関数 基本関係 t cot c sc c cot sc t 還元公式 t t t t t t cot t cot t 数学 数学 t t t t t 加法定理 t t t 倍角公式加法定理で α=β と置く. 三角関数 数学. 三角関数 5 積和公式 6 和積公式 数学. 三角関数 7 合成 t V v t V v t V V V V VV V V V t V v v 8 べき乗 5 6 6
テンソル ( その ) テンソル ( その ) スカラー ( 階のテンソル ) スカラー ( 階のテンソル ) 階数 ベクトル ( 階のテンソル ) ベクトル ( 階のテンソル ) 行列表現 シンボリック表現 [ ]
![テンソル ( その ) テンソル ( その ) スカラー ( 階のテンソル ) スカラー ( 階のテンソル ) 階数 ベクトル ( 階のテンソル ) ベクトル ( 階のテンソル ) 行列表現 シンボリック表現 [ ] テンソル ( その ) テンソル ( その ) スカラー ( 階のテンソル ) スカラー ( 階のテンソル ) 階数 ベクトル ( 階のテンソル ) ベクトル ( 階のテンソル ) 行列表現 シンボリック表現 [ ]](/thumbs/93/113587990.jpg) Tsor th-ordr tsor by dcl xprsso m m Lm m k m k L mk kk quott rul by symbolc xprsso Lk X thrd-ordr tsor cotrcto j j Copyrght s rsrvd. No prt of ths documt my b rproducd for proft. テンソル ( その ) テンソル ( その
Tsor th-ordr tsor by dcl xprsso m m Lm m k m k L mk kk quott rul by symbolc xprsso Lk X thrd-ordr tsor cotrcto j j Copyrght s rsrvd. No prt of ths documt my b rproducd for proft. テンソル ( その ) テンソル ( その
重要例題113
 04_ 高校 数学 Ⅱ 必須基本公式 定理集 数学 Ⅱ 第 章式の計算と方程式 0 商と余り についての整式 A をについての整式 B で割ったときの商を Q, 余りを R とすると, ABQ+R (R の次数 ) > 0
04_ 高校 数学 Ⅱ 必須基本公式 定理集 数学 Ⅱ 第 章式の計算と方程式 0 商と余り についての整式 A をについての整式 B で割ったときの商を Q, 余りを R とすると, ABQ+R (R の次数 ) > 0
<4D F736F F F696E74202D2095A8979D90948A CE394BC A2E707074>
 物理数学 1B( 後半部 ) 担当教員 : 山本貴博 講義内容 : ベクトル場における積分定理 第 1 回目講義 : 平面におけるグリーンの定理 ( 線積分 2 重積分 ) (12 月 11 日 ) 第 2 回目講義 : ガウスの定理 ( 面積分 体積分 ) (12 月 18 日 ) 第 3 回目講義 : ストークスの定理 ( 線積分 面積分 ) (1 月 15 日 ) 第 1 回目講義 : 平面におけるグリーンの定理
物理数学 1B( 後半部 ) 担当教員 : 山本貴博 講義内容 : ベクトル場における積分定理 第 1 回目講義 : 平面におけるグリーンの定理 ( 線積分 2 重積分 ) (12 月 11 日 ) 第 2 回目講義 : ガウスの定理 ( 面積分 体積分 ) (12 月 18 日 ) 第 3 回目講義 : ストークスの定理 ( 線積分 面積分 ) (1 月 15 日 ) 第 1 回目講義 : 平面におけるグリーンの定理
<4D F736F F D20824F E B82CC90FC90CF95AA2E646F63>
 1/1 平成 3 年 6 月 11 日午前 1 時 3 分 4 ベクトルの線積分 4 ベクトルの線積分 Ⅰ. 積分の種類 通常の物理で使う積分には 3 種類あります 積分変数の数に応じて 線積分 ( 記号 横(1 重 d, dy, dz d ( ine: 面積分 ( 記号 縦 横 ( 重 線 4 ベクトルの線積分 重積分記号 ddy, dydz, dzdz ds ( Surface: 1 重積分記号
1/1 平成 3 年 6 月 11 日午前 1 時 3 分 4 ベクトルの線積分 4 ベクトルの線積分 Ⅰ. 積分の種類 通常の物理で使う積分には 3 種類あります 積分変数の数に応じて 線積分 ( 記号 横(1 重 d, dy, dz d ( ine: 面積分 ( 記号 縦 横 ( 重 線 4 ベクトルの線積分 重積分記号 ddy, dydz, dzdz ds ( Surface: 1 重積分記号
Microsoft Word - 1B2011.doc
 第 14 回モールの定理 ( 単純梁の場合 ) ( モールの定理とは何か?p.11) 例題 下記に示す単純梁の C 点のたわみ角 θ C と, たわみ δ C を求めよ ただし, 部材の曲げ 剛性は材軸に沿って一様で とする C D kn B 1.5m 0.5m 1.0m 解答 1 曲げモーメント図を描く,B 点の反力を求める kn kn 4 kn 曲げモーメント図を描く knm 先に得られた曲げモーメントの値を
第 14 回モールの定理 ( 単純梁の場合 ) ( モールの定理とは何か?p.11) 例題 下記に示す単純梁の C 点のたわみ角 θ C と, たわみ δ C を求めよ ただし, 部材の曲げ 剛性は材軸に沿って一様で とする C D kn B 1.5m 0.5m 1.0m 解答 1 曲げモーメント図を描く,B 点の反力を求める kn kn 4 kn 曲げモーメント図を描く knm 先に得られた曲げモーメントの値を
Microsoft Word - NumericalComputation.docx
 数値計算入門 武尾英哉. 離散数学と数値計算 数学的解法の中には理論計算では求められないものもある. 例えば, 定積分は, まずは積分 ( 被積分関数の原始関数をみつけること できなければ値を得ることはできない. また, ある関数の所定の値における微分値を得るには, まずその関数の微分ができなければならない. さらに代数方程式の解を得るためには, 解析的に代数方程式を解く必要がある. ところが, これらは必ずしも解析的に導けるとは限らない.
数値計算入門 武尾英哉. 離散数学と数値計算 数学的解法の中には理論計算では求められないものもある. 例えば, 定積分は, まずは積分 ( 被積分関数の原始関数をみつけること できなければ値を得ることはできない. また, ある関数の所定の値における微分値を得るには, まずその関数の微分ができなければならない. さらに代数方程式の解を得るためには, 解析的に代数方程式を解く必要がある. ところが, これらは必ずしも解析的に導けるとは限らない.
Microsoft Word - mathtext8.doc
 8 章偏微分と重積分 8. 偏微分とは これまで微分を考える際 関数は f という形で 関数値がつの変数 に依存している場合のみを扱ってきました しかし一般に変数はつとは決まっておらず f のように 複数の変数を持つ関数も考えなければなりません そ こでこの節では今まで学んできた微分を一般化させ 複数の変数に対応した偏微分と呼ばれるものについて説明します これまでの微分を偏微分と区別したいとき 常微分という呼び方を用います
8 章偏微分と重積分 8. 偏微分とは これまで微分を考える際 関数は f という形で 関数値がつの変数 に依存している場合のみを扱ってきました しかし一般に変数はつとは決まっておらず f のように 複数の変数を持つ関数も考えなければなりません そ こでこの節では今まで学んできた微分を一般化させ 複数の変数に対応した偏微分と呼ばれるものについて説明します これまでの微分を偏微分と区別したいとき 常微分という呼び方を用います
2015-2017年度 2次数学セレクション(複素数)解答解説
 05 次数学セレクション解答解説 [ 筑波大 ] ( + より, 0 となり, + から, ( (,, よって, の描く図形 C は, 点 を中心とし半径が の円である すなわち, 原 点を通る円となる ( は虚数, は正の実数より, である さて, w ( ( とおくと, ( ( ( w ( ( ( ここで, w は純虚数より, は純虚数となる すると, の描く図形 L は, 点 を通り, 点 と点
05 次数学セレクション解答解説 [ 筑波大 ] ( + より, 0 となり, + から, ( (,, よって, の描く図形 C は, 点 を中心とし半径が の円である すなわち, 原 点を通る円となる ( は虚数, は正の実数より, である さて, w ( ( とおくと, ( ( ( w ( ( ( ここで, w は純虚数より, は純虚数となる すると, の描く図形 L は, 点 を通り, 点 と点
Microsoft PowerPoint - H21生物計算化学2.ppt
 演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
2018年度 筑波大・理系数学
 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ < < とする 放物線 上に 点 (, ), A (ta, ta ), B( - ta, ta ) をとる 三角形 AB の内心の 座標を p とし, 外心の 座標を q とする また, 正の実数 a に対して, 直線 a と放物線 で囲まれた図形の面積を S( a) で表す () p, q を cos を用いて表せ S( p) () S(
筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ < < とする 放物線 上に 点 (, ), A (ta, ta ), B( - ta, ta ) をとる 三角形 AB の内心の 座標を p とし, 外心の 座標を q とする また, 正の実数 a に対して, 直線 a と放物線 で囲まれた図形の面積を S( a) で表す () p, q を cos を用いて表せ S( p) () S(
Chap2.key
 . f( ) V (V V ) V e + V e V V V V ( ) V V ( ) E. - () V (0 ) () V (0 ) () V (0 ) (4) V ( ) E. - () V (0 ) () V (0 ) O r θ ( ) ( ) : (r θ) : { r cos θ r sn θ { r + () V (0 ) (4) V ( ) θ θ arg( ) : π π
. f( ) V (V V ) V e + V e V V V V ( ) V V ( ) E. - () V (0 ) () V (0 ) () V (0 ) (4) V ( ) E. - () V (0 ) () V (0 ) O r θ ( ) ( ) : (r θ) : { r cos θ r sn θ { r + () V (0 ) (4) V ( ) θ θ arg( ) : π π
<4D F736F F D A CF95AA B B82CC90CF95AA8CF68EAE2E646F63>
 /8 平成 年 月 日午後 時 6 分 複素積分 : コーシーの積分公式 複素積分 : コーシーの積分公式 Ⅰ. 閉じた積分経路と円周 積分しなくても線積分の結果が分かる場合の第 弾です それは ( ( π d は正則関数 d! d 積分経路は を囲む (. になります これを コーシーの積分公式といいます 複素積分 : コーシーの積分定理 -Ⅰ. 線積分の実技での線積分では 半径 r の円 周上の閉じた経路
/8 平成 年 月 日午後 時 6 分 複素積分 : コーシーの積分公式 複素積分 : コーシーの積分公式 Ⅰ. 閉じた積分経路と円周 積分しなくても線積分の結果が分かる場合の第 弾です それは ( ( π d は正則関数 d! d 積分経路は を囲む (. になります これを コーシーの積分公式といいます 複素積分 : コーシーの積分定理 -Ⅰ. 線積分の実技での線積分では 半径 r の円 周上の閉じた経路
Microsoft Word - 付録1誘導機の2軸理論.doc
 NAOSIE: Nagaaki Univity' Ac itl パワーエレクトロニクスと電動機制御入門 Autho( 辻, 峰男 Citation パワーエレクトロニクスと電動機制御入門 ; 15 Iu Dat 15 U http://hl.hanl.nt/169/55 ight hi ocumnt i ownloa http://naoit.lb.nagaaki-u.ac.jp 付録 1 誘導機の
NAOSIE: Nagaaki Univity' Ac itl パワーエレクトロニクスと電動機制御入門 Autho( 辻, 峰男 Citation パワーエレクトロニクスと電動機制御入門 ; 15 Iu Dat 15 U http://hl.hanl.nt/169/55 ight hi ocumnt i ownloa http://naoit.lb.nagaaki-u.ac.jp 付録 1 誘導機の
代数 幾何 < ベクトル > 1 ベクトルの演算 和 差 実数倍については 文字の計算と同様 2 ベクトルの成分表示 平面ベクトル : a x e y e x, ) ( 1 y1 空間ベクトル : a x e y e z e x, y, ) ( 1 1 z1
 代数 幾何 < ベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル :, 空間ベクトル : z,, z 成分での計算ができるようにすること ベクトルの内積 : os 平面ベクトル :,, 空間ベクトル :,,,, z z zz 4 ベクトルの大きさ 平面上 : 空間上 : z は 良く用いられる 5 m: に分ける点 : m m 図形への応用
代数 幾何 < ベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル :, 空間ベクトル : z,, z 成分での計算ができるようにすること ベクトルの内積 : os 平面ベクトル :,, 空間ベクトル :,,,, z z zz 4 ベクトルの大きさ 平面上 : 空間上 : z は 良く用いられる 5 m: に分ける点 : m m 図形への応用
Microsoft PowerPoint - 第9回電磁気学
 017 年 1 月 04 日 ( 月 ) 13:00-14:30 C13 平成 9 年度工 V 系 ( 社会環境工学科 ) 第 9 回電磁気学 Ⅰ 天野浩 mno@nuee.ngoy-u.c.jp 9 1 月 04 日 第 5 章 電流の間に働く力 磁場 微分形で表したア ンペールの法則 ビオ サバールの法則 第 5 章電流の作る場 http://www.ntt-est.co.jp/business/mgzine/netwok_histoy/0/
017 年 1 月 04 日 ( 月 ) 13:00-14:30 C13 平成 9 年度工 V 系 ( 社会環境工学科 ) 第 9 回電磁気学 Ⅰ 天野浩 mno@nuee.ngoy-u.c.jp 9 1 月 04 日 第 5 章 電流の間に働く力 磁場 微分形で表したア ンペールの法則 ビオ サバールの法則 第 5 章電流の作る場 http://www.ntt-est.co.jp/business/mgzine/netwok_histoy/0/
20~22.prt
 [ 三クリア W] 辺が等しいことの証明 ( 円周角と弦の関係利用 ) の の二等分線がこの三角形の外接円と交わる点をそれぞれ とするとき 60 ならば であることを証明せよ 60 + + 0 + 0 80-60 60 から ゆえに 等しい長さの弧に対する弦の長さは等しいから [ 三クリア ] 方べきの定理 接線と弦のなす角と円周角を利用 線分 を直径とする円 があり 右の図のように の延長上の点
[ 三クリア W] 辺が等しいことの証明 ( 円周角と弦の関係利用 ) の の二等分線がこの三角形の外接円と交わる点をそれぞれ とするとき 60 ならば であることを証明せよ 60 + + 0 + 0 80-60 60 から ゆえに 等しい長さの弧に対する弦の長さは等しいから [ 三クリア ] 方べきの定理 接線と弦のなす角と円周角を利用 線分 を直径とする円 があり 右の図のように の延長上の点
<4D F736F F D2094F795AA8C608EAE8E478B4C92A08250>
 微分形式雑記帳 1 ベクトルの内積と外積 次元ベクトルを A a, a, a, B b, b, b とする A a, a, a の長さを A a a a と定義する AB A B cos を A と B の内積とよぶ ただ し はベクトル A と B がなす角度である e1 1, 0, 0, e 0,1, 0, e 0, 0,1 は互いに直交しているので e 1 e 0, e 1 e 0 であり e
微分形式雑記帳 1 ベクトルの内積と外積 次元ベクトルを A a, a, a, B b, b, b とする A a, a, a の長さを A a a a と定義する AB A B cos を A と B の内積とよぶ ただ し はベクトル A と B がなす角度である e1 1, 0, 0, e 0,1, 0, e 0, 0,1 は互いに直交しているので e 1 e 0, e 1 e 0 であり e
OCW-iダランベールの原理
 講義名連続体力学配布資料 OCW- 第 2 回ダランベールの原理 無機材料工学科准教授安田公一 1 はじめに今回の講義では, まず, 前半でダランベールの原理について説明する これを用いると, 動力学の問題を静力学の問題として解くことができ, さらに, 前回の仮想仕事の原理を適用すると動力学問題も簡単に解くことができるようになる また, 後半では, ダランベールの原理の応用として ラグランジュ方程式の導出を示す
講義名連続体力学配布資料 OCW- 第 2 回ダランベールの原理 無機材料工学科准教授安田公一 1 はじめに今回の講義では, まず, 前半でダランベールの原理について説明する これを用いると, 動力学の問題を静力学の問題として解くことができ, さらに, 前回の仮想仕事の原理を適用すると動力学問題も簡単に解くことができるようになる また, 後半では, ダランベールの原理の応用として ラグランジュ方程式の導出を示す
DVIOUT-SS_Ma
 第 章 微分方程式 ニュートンはリンゴが落ちるのを見て万有引力を発見した という有名な逸話があります 無重力の宇宙船の中ではリンゴは落ちないで静止していることを考えると 重力が働くと始め静止しているものが動き出して そのスピードはどんどん大きくなる つまり速度の変化が現れることがわかります 速度は一般に時間と共に変化します 速度の瞬間的変化の割合を加速度といい で定義しましょう 速度が変化する, つまり加速度がでなくなるためにはその原因があり
第 章 微分方程式 ニュートンはリンゴが落ちるのを見て万有引力を発見した という有名な逸話があります 無重力の宇宙船の中ではリンゴは落ちないで静止していることを考えると 重力が働くと始め静止しているものが動き出して そのスピードはどんどん大きくなる つまり速度の変化が現れることがわかります 速度は一般に時間と共に変化します 速度の瞬間的変化の割合を加速度といい で定義しましょう 速度が変化する, つまり加速度がでなくなるためにはその原因があり
Microsoft PowerPoint - 第3回2.ppt
 講義内容 講義内容 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 ベクトルの直交性 3
講義内容 講義内容 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 ベクトルの直交性 3
5-仮想仕事式と種々の応力.ppt
 1 以上, 運動の変数についての話を終える. 次は再び力の変数に戻る. その前に, まず次の話が唐突と思われないように 以下は前置き. 先に, 力の変数と運動の変数には対応関係があって, 適当な内積演算によって仕事量を表す ことを述べた. 実は,Cauchy 応力と速度勾配テンソル ( あるいは変位勾配テンソル ) を用いると, それらの内積は内部仮想仕事を表していて, そして, それは外力がなす仮想仕事に等しいという
1 以上, 運動の変数についての話を終える. 次は再び力の変数に戻る. その前に, まず次の話が唐突と思われないように 以下は前置き. 先に, 力の変数と運動の変数には対応関係があって, 適当な内積演算によって仕事量を表す ことを述べた. 実は,Cauchy 応力と速度勾配テンソル ( あるいは変位勾配テンソル ) を用いると, それらの内積は内部仮想仕事を表していて, そして, それは外力がなす仮想仕事に等しいという
2011年度 筑波大・理系数学
 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ O を原点とするy 平面において, 直線 y= の を満たす部分をC とする () C 上に点 A( t, ) をとるとき, 線分 OA の垂直二等分線の方程式を求めよ () 点 A が C 全体を動くとき, 線分 OA の垂直二等分線が通過する範囲を求め, それ を図示せよ -- 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ
0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ O を原点とするy 平面において, 直線 y= の を満たす部分をC とする () C 上に点 A( t, ) をとるとき, 線分 OA の垂直二等分線の方程式を求めよ () 点 A が C 全体を動くとき, 線分 OA の垂直二等分線が通過する範囲を求め, それ を図示せよ -- 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ
公式集 数学 Ⅱ B 頭に入っていますか? 8 和積の公式 A + B A B si A + si B si os A + B A B si A si B os si A + B A B os A + os B os os A + B A B os A os B si si 9 三角関数の合成 si
 公式集 数学 Ⅱ B 頭に入っていますか? < 図形と方程式 > 点間の距離 A x, B x, のとき x x + : に分ける点 A x, B x, のとき 線分 AB を:に分ける点 æ x + x + ö は ç, è + + ø 注 < のとき外分点 直線の方程式 傾き で 点 x, を通る : x 点 x, x, を通る : x 注 分母が のとき は座標軸と平行な直線 x x 4 直線の位置関係
公式集 数学 Ⅱ B 頭に入っていますか? < 図形と方程式 > 点間の距離 A x, B x, のとき x x + : に分ける点 A x, B x, のとき 線分 AB を:に分ける点 æ x + x + ö は ç, è + + ø 注 < のとき外分点 直線の方程式 傾き で 点 x, を通る : x 点 x, x, を通る : x 注 分母が のとき は座標軸と平行な直線 x x 4 直線の位置関係
2011年度 大阪大・理系数学
 0 大阪大学 ( 理系 ) 前期日程問題 解答解説のページへ a a を自然数とする O を原点とする座標平面上で行列 A= a の表す 次変換 を f とする cosθ siθ () >0 および0θ
0 大阪大学 ( 理系 ) 前期日程問題 解答解説のページへ a a を自然数とする O を原点とする座標平面上で行列 A= a の表す 次変換 を f とする cosθ siθ () >0 および0θ
喨微勃挹稉弑
 == 全微分方程式 == 全微分とは 変数の関数 z=f(, ) について,, の増分を Δ, Δ とするとき, z の増分 Δz は Δz z Δ+ z Δ で表されます. この式において, Δ 0, Δ 0 となる極限を形式的に dz= z d+ z d (1) で表し, dz を z の全微分といいます. z は z の に関する偏導関数で, を定数と見なし て, で微分したものを表し, 方向の傾きに対応します.
== 全微分方程式 == 全微分とは 変数の関数 z=f(, ) について,, の増分を Δ, Δ とするとき, z の増分 Δz は Δz z Δ+ z Δ で表されます. この式において, Δ 0, Δ 0 となる極限を形式的に dz= z d+ z d (1) で表し, dz を z の全微分といいます. z は z の に関する偏導関数で, を定数と見なし て, で微分したものを表し, 方向の傾きに対応します.
1 対 1 対応の演習例題を解いてみた 微分法とその応用 例題 1 極限 微分係数の定義 (2) 関数 f ( x) は任意の実数 x について微分可能なのは明らか f ( 1, f ( 1) ) と ( 1 + h, f ( 1 + h)
 微分法とその応用 例題 1 極限 微分係数の定義 () 関数 ( x) は任意の実数 x について微分可能なのは明らか ( 1, ( 1) ) と ( 1 + h, ( 1 + h) ) の傾き= ( 1 + h ) - ( 1 ) ( 1 + ) - ( 1) = ( 1 + h) - 1 h ( 1) = lim h ( 1 + h) - ( 1) h ( 1, ( 1) ) と ( 1 - h,
微分法とその応用 例題 1 極限 微分係数の定義 () 関数 ( x) は任意の実数 x について微分可能なのは明らか ( 1, ( 1) ) と ( 1 + h, ( 1 + h) ) の傾き= ( 1 + h ) - ( 1 ) ( 1 + ) - ( 1) = ( 1 + h) - 1 h ( 1) = lim h ( 1 + h) - ( 1) h ( 1, ( 1) ) と ( 1 - h,
PowerPoint プレゼンテーション
 工業数学 Ⅰ 第 7 章多変数関数の微分 2. 実多変数の実数値関数 千葉大学工学部機械工学科担当者武居昌宏 教科書 工科系の数学 (4) [ 単行本 ] マイベルク ファヘンアウア著 及川正行訳 出版社 : サイエンス社 (1996/12) ISBN-10: 4781907814 第 7 章多変数関数の微分 2. 実多変数の実数値関数 2.1 基礎 多変数の実数値関数変数が2つ以上の n 変数関数定義域がn
工業数学 Ⅰ 第 7 章多変数関数の微分 2. 実多変数の実数値関数 千葉大学工学部機械工学科担当者武居昌宏 教科書 工科系の数学 (4) [ 単行本 ] マイベルク ファヘンアウア著 及川正行訳 出版社 : サイエンス社 (1996/12) ISBN-10: 4781907814 第 7 章多変数関数の微分 2. 実多変数の実数値関数 2.1 基礎 多変数の実数値関数変数が2つ以上の n 変数関数定義域がn
<4D F736F F D FCD B90DB93AE96402E646F63>
 7 章摂動法講義のメモ 式が複雑なので 黒板を何度も修正したし 間違ったことも書いたので メモを置きます 摂動論の式の導出無摂動系 先ず 厳密に解けている Schrödiger 方程式を考える,,,3,... 3,,,3,... は状態を区別する整数であり 状態 はエネルギー順に並んでいる 即ち は基底状態 は励起状態である { m } は相互に規格直交条件が成立する k m k mdx km k
7 章摂動法講義のメモ 式が複雑なので 黒板を何度も修正したし 間違ったことも書いたので メモを置きます 摂動論の式の導出無摂動系 先ず 厳密に解けている Schrödiger 方程式を考える,,,3,... 3,,,3,... は状態を区別する整数であり 状態 はエネルギー順に並んでいる 即ち は基底状態 は励起状態である { m } は相互に規格直交条件が成立する k m k mdx km k
例題1 転がり摩擦
 重心 5.. 重心問題解法虎の巻. 半円 分円. 円弧. 扇形. 半球殻 5. 半球体 6. 厚みのある半球殻 7. 三角形 8. 円錐 9. 円錐台. 穴あき板. 空洞のある半球ボール 重心問題解法虎の巻 関西大学工学部物理学教室 齊藤正 重心を求める場合 質点系の重心の求め方が基本 実際の物体では連続体であるので 積分形式で求める場合が多い これらの式は 次元のベクトル形式で書かれている通り つの式は実際には
重心 5.. 重心問題解法虎の巻. 半円 分円. 円弧. 扇形. 半球殻 5. 半球体 6. 厚みのある半球殻 7. 三角形 8. 円錐 9. 円錐台. 穴あき板. 空洞のある半球ボール 重心問題解法虎の巻 関西大学工学部物理学教室 齊藤正 重心を求める場合 質点系の重心の求め方が基本 実際の物体では連続体であるので 積分形式で求める場合が多い これらの式は 次元のベクトル形式で書かれている通り つの式は実際には
<4D F736F F D2094F795AA95FB92F68EAE82CC89F082AB95FB E646F63>
 力学 A 金曜 限 : 松田 微分方程式の解き方 微分方程式の解き方のところが分からなかったという声が多いので プリントにまとめます 数学的に厳密な話はしていないので 詳しくは数学の常微分方程式を扱っているテキストを参照してください また os s は既知とします. 微分方程式の分類 常微分方程式とは 独立変数 と その関数 その有限次の導関数 がみたす方程式 F,,, = のことです 次までの導関数を含む方程式を
力学 A 金曜 限 : 松田 微分方程式の解き方 微分方程式の解き方のところが分からなかったという声が多いので プリントにまとめます 数学的に厳密な話はしていないので 詳しくは数学の常微分方程式を扱っているテキストを参照してください また os s は既知とします. 微分方程式の分類 常微分方程式とは 独立変数 と その関数 その有限次の導関数 がみたす方程式 F,,, = のことです 次までの導関数を含む方程式を
p tn tn したがって, 点 の 座標は p p tn tn tn また, 直線 l と直線 p の交点 の 座標は p p tn p tn よって, 点 の座標 (, ) は p p, tn tn と表され p 4p p 4p 4p tn tn tn より, 点 は放物線 4 p 上を動くこと
 567_ 次曲線の三角関数による媒介変数表示 次曲線の三角関数による媒介変数表示 次曲線 ( 放物線 楕円 双曲線 ) の標準形の, についての方程式と, 三角関数による媒介変数表示は次のように対応している.. 放物線 () 4 p (, ) ( ptn, ptn ) (). 楕円. 双曲線 () () (, p p ), tn tn (, ) ( cos, sin ) (, ), tn cos (,
567_ 次曲線の三角関数による媒介変数表示 次曲線の三角関数による媒介変数表示 次曲線 ( 放物線 楕円 双曲線 ) の標準形の, についての方程式と, 三角関数による媒介変数表示は次のように対応している.. 放物線 () 4 p (, ) ( ptn, ptn ) (). 楕円. 双曲線 () () (, p p ), tn tn (, ) ( cos, sin ) (, ), tn cos (,
<8D828D5A838A817C A77425F91E6318FCD2E6D6364>
 4 1 平面上のベクトル 1 ベクトルとその演算 例題 1 ベクトルの相等 次の問いに答えよ. ⑴ 右の図 1 は平行四辺形 である., と等しいベクトルをいえ. ⑵ 右の図 2 の中で互いに等しいベクトルをいえ. ただし, すべてのマス目は正方形である. 解 ⑴,= より, =,= より, = ⑵ 大きさと向きの等しいものを調べる. a =d, c = f d e f 1 右の図の長方形 において,
4 1 平面上のベクトル 1 ベクトルとその演算 例題 1 ベクトルの相等 次の問いに答えよ. ⑴ 右の図 1 は平行四辺形 である., と等しいベクトルをいえ. ⑵ 右の図 2 の中で互いに等しいベクトルをいえ. ただし, すべてのマス目は正方形である. 解 ⑴,= より, =,= より, = ⑵ 大きさと向きの等しいものを調べる. a =d, c = f d e f 1 右の図の長方形 において,
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生
 0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
2014年度 センター試験・数学ⅡB
 第 問 解答解説のページへ [] O を原点とする座標平面において, 点 P(, q) を中心とする円 C が, 方程式 y 4 x で表される直線 l に接しているとする () 円 C の半径 r を求めよう 点 P を通り直線 l に垂直な直線の方程式は, y - ア ( x- ) + qなので, P イ から l に引いた垂線と l の交点 Q の座標は ( ( ウ + エ q ), 4 (
第 問 解答解説のページへ [] O を原点とする座標平面において, 点 P(, q) を中心とする円 C が, 方程式 y 4 x で表される直線 l に接しているとする () 円 C の半径 r を求めよう 点 P を通り直線 l に垂直な直線の方程式は, y - ア ( x- ) + qなので, P イ から l に引いた垂線と l の交点 Q の座標は ( ( ウ + エ q ), 4 (
2 図微小要素の流体の流入出 方向の断面の流体の流入出の収支断面 Ⅰ から微小要素に流入出する流体の流量 Q 断面 Ⅰ は 以下のように定式化できる Q 断面 Ⅰ 流量 密度 流速 断面 Ⅰ の面積 微小要素の断面 Ⅰ から だけ移動した断面 Ⅱ を流入出する流体の流量 Q 断面 Ⅱ は以下のように
 3 章 Web に Link 解説 連続式 微分表示 の誘導.64 *4. 連続式連続式は ある領域の内部にある流体の質量の収支が その表面からの流入出の合計と等しくなることを定式化したものであり 流体における質量保存則を示したものである 2. 連続式 微分表示 の誘導図のような微小要素 コントロールボリューム の領域内の流体の増減と外部からの流体の流入出を考えることで定式化できる 微小要素 流入
3 章 Web に Link 解説 連続式 微分表示 の誘導.64 *4. 連続式連続式は ある領域の内部にある流体の質量の収支が その表面からの流入出の合計と等しくなることを定式化したものであり 流体における質量保存則を示したものである 2. 連続式 微分表示 の誘導図のような微小要素 コントロールボリューム の領域内の流体の増減と外部からの流体の流入出を考えることで定式化できる 微小要素 流入
数学 Ⅲ 微分法の応用 大学入試問題 ( 教科書程度 ) 1 問 1 (1) 次の各問に答えよ (ⅰ) 極限 を求めよ 年会津大学 ( 前期 ) (ⅱ) 極限値 を求めよ 年愛媛大学 ( 前期 ) (ⅲ) 無限等比級数 が収束するような実数 の範囲と そのときの和を求めよ 年広島市立大学 ( 前期
 数学 Ⅲ 微分法の応用 大学入試問題 ( 教科書程度 )1 問 1 (1) 次の各問に答えよ (ⅰ) 極限 を求めよ 年会津大学 ( 前期 ) (ⅱ) 極限値 を求めよ 年愛媛大学 ( 前期 ) (ⅲ) 無限等比級数 が収束するような実数 の範囲と そのときの和を求めよ 年広島市立大学 ( 前期 ) (2) 次の関数を微分せよ (ⅰ) を正の定数とする (ⅱ) (ⅳ) (ⅵ) ( 解答 )(1) 年群馬大学
数学 Ⅲ 微分法の応用 大学入試問題 ( 教科書程度 )1 問 1 (1) 次の各問に答えよ (ⅰ) 極限 を求めよ 年会津大学 ( 前期 ) (ⅱ) 極限値 を求めよ 年愛媛大学 ( 前期 ) (ⅲ) 無限等比級数 が収束するような実数 の範囲と そのときの和を求めよ 年広島市立大学 ( 前期 ) (2) 次の関数を微分せよ (ⅰ) を正の定数とする (ⅱ) (ⅳ) (ⅵ) ( 解答 )(1) 年群馬大学
物性物理学 I( 平山 ) 補足資料 No.6 ( 量子ポイントコンタクト ) 右図のように 2つ物質が非常に小さな接点を介して接触している状況を考えましょう 物質中の電子の平均自由行程に比べて 接点のサイズが非常に小さな場合 この接点を量子ポイントコンタクトと呼ぶことがあります この系で左右の2つ
 物性物理学 I( 平山 ) 補足資料 No.6 ( 量子ポイントコンタクト ) 右図のように つ物質が非常に小さな接点を介して接触している状況を考えましょう 物質中の電子の平均自由行程に比べて 接点のサイズが非常に小さな場合 この接点を量子ポイントコンタクトと呼ぶことがあります この系で左右のつの物質の間に電位差を設けて左から右に向かって電流を流すことを行った場合に接点を通って流れる電流を求めるためには
物性物理学 I( 平山 ) 補足資料 No.6 ( 量子ポイントコンタクト ) 右図のように つ物質が非常に小さな接点を介して接触している状況を考えましょう 物質中の電子の平均自由行程に比べて 接点のサイズが非常に小さな場合 この接点を量子ポイントコンタクトと呼ぶことがあります この系で左右のつの物質の間に電位差を設けて左から右に向かって電流を流すことを行った場合に接点を通って流れる電流を求めるためには
Microsoft Word - 中村工大連携教材(最終 ).doc
 音速について考えてみよう! 金沢工業大学 中村晃 ねらい 私たちの身の回りにはいろいろな種類の波が存在する. 体感できる波もあれば, できない波もある. その中で音は体感できる最も身近な波である. 遠くで雷が光ってから雷鳴が届くまで数秒間時間がかかることにより, 音の方が光より伝わるのに時間がかかることも経験していると思う. 高校の物理の授業で音の伝わる速さ ( 音速 ) は約 m/s で, 詳しく述べると
音速について考えてみよう! 金沢工業大学 中村晃 ねらい 私たちの身の回りにはいろいろな種類の波が存在する. 体感できる波もあれば, できない波もある. その中で音は体感できる最も身近な波である. 遠くで雷が光ってから雷鳴が届くまで数秒間時間がかかることにより, 音の方が光より伝わるのに時間がかかることも経験していると思う. 高校の物理の授業で音の伝わる速さ ( 音速 ) は約 m/s で, 詳しく述べると
2018年度 東京大・理系数学
 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ関数 f ( ) = + cos (0 < < ) の増減表をつくり, + 0, 0 のと sin きの極限を調べよ 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ n+ 数列 a, a, を, Cn a n = ( n =,, ) で定める n! an qn () n とする を既約分数 an p として表したときの分母
08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ関数 f ( ) = + cos (0 < < ) の増減表をつくり, + 0, 0 のと sin きの極限を調べよ 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ n+ 数列 a, a, を, Cn a n = ( n =,, ) で定める n! an qn () n とする を既約分数 an p として表したときの分母
<4D F736F F F696E74202D20836F CC8A C58B858B4F93B982A882E682D1978E89BA814091B28BC68CA48B E >
 バットの角度 打球軌道および落下地点の関係 T999 和田真迪 担当教員 飯田晋司 目次 1. はじめに. ボールとバットの衝突 -1 座標系 -ボールとバットの衝突の前後でのボールの速度 3. ボールの軌道の計算 4. おわりに参考文献 はじめに この研究テーマにした理由は 好きな野球での小さい頃からの疑問であるバッテングについて 角度が変わればどう打球に変化が起こるのかが大学で学んだ物理と数学んだ物理と数学を使って判明できると思ったから
バットの角度 打球軌道および落下地点の関係 T999 和田真迪 担当教員 飯田晋司 目次 1. はじめに. ボールとバットの衝突 -1 座標系 -ボールとバットの衝突の前後でのボールの速度 3. ボールの軌道の計算 4. おわりに参考文献 はじめに この研究テーマにした理由は 好きな野球での小さい頃からの疑問であるバッテングについて 角度が変わればどう打球に変化が起こるのかが大学で学んだ物理と数学んだ物理と数学を使って判明できると思ったから
Microsoft Word - 201hyouka-tangen-1.doc
 数学 Ⅰ 評価規準の作成 ( 単元ごと ) 数学 Ⅰ の目標及び図形と計量について理解させ 基礎的な知識の習得と技能の習熟を図り それらを的確に活用する機能を伸ばすとともに 数学的な見方や考え方のよさを認識できるようにする 評価の観点の趣旨 式と不等式 二次関数及び図形と計量における考え方に関 心をもつとともに 数学的な見方や考え方のよさを認識し それらを事象の考察に活用しようとする 式と不等式 二次関数及び図形と計量における数学的な見
数学 Ⅰ 評価規準の作成 ( 単元ごと ) 数学 Ⅰ の目標及び図形と計量について理解させ 基礎的な知識の習得と技能の習熟を図り それらを的確に活用する機能を伸ばすとともに 数学的な見方や考え方のよさを認識できるようにする 評価の観点の趣旨 式と不等式 二次関数及び図形と計量における考え方に関 心をもつとともに 数学的な見方や考え方のよさを認識し それらを事象の考察に活用しようとする 式と不等式 二次関数及び図形と計量における数学的な見
Taro-F25理論 印刷原稿
 第 種理論 A 問題 ( 配点は 問題当たり小問各 点, 計 0 点 ) 問 次の文章は, 真空中の静電界に関する諸法則の微分形に関する記述である 文中の に当てはまるものを解答群の中から選びなさい 図のように, 直交座標系において電界の z 軸成分が零となるような電界について, y 平面の二次元で電位や電界を考える ここで,4 点 (h,0),(0,h), (- h,0),(0,-h) の電位がそれぞれ
第 種理論 A 問題 ( 配点は 問題当たり小問各 点, 計 0 点 ) 問 次の文章は, 真空中の静電界に関する諸法則の微分形に関する記述である 文中の に当てはまるものを解答群の中から選びなさい 図のように, 直交座標系において電界の z 軸成分が零となるような電界について, y 平面の二次元で電位や電界を考える ここで,4 点 (h,0),(0,h), (- h,0),(0,-h) の電位がそれぞれ
スライド 1
 電流と磁場 目次 0. はじめにー物質の磁気的性質と磁場ー 1. 磁石と磁場 2. 電流のつくる磁場 (1) 3. 磁場中の運動する荷電粒子に働く磁気力 ( ローレンツ力 ) 4. 磁場中の電流に働く力 ( アンペアの力 ) 5. 平行または反平行電流の間に働く磁気力 6. 電流のつくる磁場 (2)- ビオ サバールの法則 7. アンペアの法則 ( アンペアの回路定理 ) 8. 磁場 に対するガウスの法則付録
電流と磁場 目次 0. はじめにー物質の磁気的性質と磁場ー 1. 磁石と磁場 2. 電流のつくる磁場 (1) 3. 磁場中の運動する荷電粒子に働く磁気力 ( ローレンツ力 ) 4. 磁場中の電流に働く力 ( アンペアの力 ) 5. 平行または反平行電流の間に働く磁気力 6. 電流のつくる磁場 (2)- ビオ サバールの法則 7. アンペアの法則 ( アンペアの回路定理 ) 8. 磁場 に対するガウスの法則付録
点におけるひずみの定義 ( その1)-(ε, ε,γ ) の定義ひずみは 構造物の中で変化しているのが一般的である このために 応力と同様に 構造物内の任意の点で定義できるようにした方がよい また 応力と同様に 一つの点に注目しても ひずみは向きによって値が異なる これらを勘案し あ
 3. 変位とひずみ 3.1 変位関数構造物は外力の作用の下で変形する いま この変形により構造物内の任意の点 P(,,z) が P (',',z') に移動したものとする ( 図 3.1 参照 ) (,,z) は変形前の点 Pの座標 (',', z') は変形後の座標である このとき 次式で示される変形前後の座標の差 u ='- u ='- u z =z'-z (3.1) を変位成分と呼ぶ 変位 (
3. 変位とひずみ 3.1 変位関数構造物は外力の作用の下で変形する いま この変形により構造物内の任意の点 P(,,z) が P (',',z') に移動したものとする ( 図 3.1 参照 ) (,,z) は変形前の点 Pの座標 (',', z') は変形後の座標である このとき 次式で示される変形前後の座標の差 u ='- u ='- u z =z'-z (3.1) を変位成分と呼ぶ 変位 (
1/17 平成 29 年 3 月 25 日 ( 土 ) 午前 11 時 1 分量子力学とクライン ゴルドン方程式 ( 学部 3 年次秋学期向 ) 量子力学とクライン ゴルドン方程式 素粒子の満たす場 y ( x,t) の運動方程式 : クライン ゴルドン方程式 : æ 3 ö ç å è m= 0
 /7 平成 9 年 月 5 日 ( 土 午前 時 分量子力学とクライン ゴルドン方程式 ( 学部 年次秋学期向 量子力学とクライン ゴルドン方程式 素粒子の満たす場 (,t の運動方程式 : クライン ゴルドン方程式 : æ ö ç å è = 0 c + ( t =, 0 (. = 0 ì æ = = = ö æ ö æ ö ç ì =,,,,,,, ç 0 = ç Ñ 0 = ç Ñ 0 Ñ Ñ
/7 平成 9 年 月 5 日 ( 土 午前 時 分量子力学とクライン ゴルドン方程式 ( 学部 年次秋学期向 量子力学とクライン ゴルドン方程式 素粒子の満たす場 (,t の運動方程式 : クライン ゴルドン方程式 : æ ö ç å è = 0 c + ( t =, 0 (. = 0 ì æ = = = ö æ ö æ ö ç ì =,,,,,,, ç 0 = ç Ñ 0 = ç Ñ 0 Ñ Ñ
1/30 平成 29 年 3 月 24 日 ( 金 ) 午前 11 時 25 分第三章フェルミ量子場 : スピノール場 ( 次元あり ) 第三章フェルミ量子場 : スピノール場 フェルミ型 ボーズ量子場のエネルギーは 第二章ボーズ量子場 : スカラー場 の (2.18) より ˆ dp 1 1 =
 / 平成 9 年 月 日 ( 金 午前 時 5 分第三章フェルミ量子場 : スピノール場 ( 次元あり 第三章フェルミ量子場 : スピノール場 フェルミ型 ボーズ量子場のエネルギーは 第二章ボーズ量子場 : スカラー場 の (.8 より ˆ ( ( ( q -, ( ( c ( H c c ë é ù û - Ü + c ( ( - に限る (. である 一方 フェルミ型は 成分をもち その成分を,,,,
/ 平成 9 年 月 日 ( 金 午前 時 5 分第三章フェルミ量子場 : スピノール場 ( 次元あり 第三章フェルミ量子場 : スピノール場 フェルミ型 ボーズ量子場のエネルギーは 第二章ボーズ量子場 : スカラー場 の (.8 より ˆ ( ( ( q -, ( ( c ( H c c ë é ù û - Ü + c ( ( - に限る (. である 一方 フェルミ型は 成分をもち その成分を,,,,
物理演習問題
 < 物理 > =0 問 ビルの高さを, ある速さ ( 初速 をとおく,において等加速度運動の公式より (- : -= t - t : -=- t - t (-, 式よりを消去すると t - t =- t - t ( + - ( + ( - =0 0 t t t t t t ( t + t - ( t - =0 t=t t=t t - 地面 ( t - t t +t 0 より, = 3 図 問 が最高点では速度が
< 物理 > =0 問 ビルの高さを, ある速さ ( 初速 をとおく,において等加速度運動の公式より (- : -= t - t : -=- t - t (-, 式よりを消去すると t - t =- t - t ( + - ( + ( - =0 0 t t t t t t ( t + t - ( t - =0 t=t t=t t - 地面 ( t - t t +t 0 より, = 3 図 問 が最高点では速度が
<4D F736F F D20837D834E B95FB92F68EAE>
 マクスウエルの方程式 Akio Arimoto, Monday, November, 7. イントロ長野 []p.4 に証明抜きで以下のような解説がある 次節以下これを証明していきたいと思う grad f «df d dx =,, rot «( i i), [ ] div «d ( dx dx + dx dx + dx dx ) æ f f f æ f f f rot grad f = rot( df
マクスウエルの方程式 Akio Arimoto, Monday, November, 7. イントロ長野 []p.4 に証明抜きで以下のような解説がある 次節以下これを証明していきたいと思う grad f «df d dx =,, rot «( i i), [ ] div «d ( dx dx + dx dx + dx dx ) æ f f f æ f f f rot grad f = rot( df
Microsoft Word - Chap17
 第 7 章化学反応に対する磁場効果における三重項機構 その 7.. 節の訂正 年 7 月 日. 節 章の9ページ の赤枠に記載した説明は間違いであった事に気付いた 以下に訂正する しかし.. 式は 結果的には正しいので安心して下さい 磁場 の存在下でのT 状態のハミルトニアン は ゼーマン項 と時間に依存するスピン-スピン相互作用の項 との和となる..=7.. g S = g S z = S z g
第 7 章化学反応に対する磁場効果における三重項機構 その 7.. 節の訂正 年 7 月 日. 節 章の9ページ の赤枠に記載した説明は間違いであった事に気付いた 以下に訂正する しかし.. 式は 結果的には正しいので安心して下さい 磁場 の存在下でのT 状態のハミルトニアン は ゼーマン項 と時間に依存するスピン-スピン相互作用の項 との和となる..=7.. g S = g S z = S z g
数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュ
 数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュレーションによって計算してみる 4.1 放物運動一様な重力場における放物運動を考える 一般に質量の物体に作用する力をとすると運動方程式は
数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュレーションによって計算してみる 4.1 放物運動一様な重力場における放物運動を考える 一般に質量の物体に作用する力をとすると運動方程式は
Microsoft Word - 微分入門.doc
 基本公式 例題 0 定義式 f( ) 数 Ⅲ 微分入門 = の導関数を定義式にもとづいて計算しなさい 基本事項 ( f( ), g( ) が微分可能ならば ) y= f( ) g( ) のとき, y = y= f( ) g( ) h( ) のとき, y = ( f( ), g( ) が微分可能で, g( ) 0 ならば ) f( ) y = のとき, y = g ( ) とくに, y = のとき,
基本公式 例題 0 定義式 f( ) 数 Ⅲ 微分入門 = の導関数を定義式にもとづいて計算しなさい 基本事項 ( f( ), g( ) が微分可能ならば ) y= f( ) g( ) のとき, y = y= f( ) g( ) h( ) のとき, y = ( f( ), g( ) が微分可能で, g( ) 0 ならば ) f( ) y = のとき, y = g ( ) とくに, y = のとき,
中学 1 年生 e ライブラリ数学教材一覧 学校図書 ( 株 ) 中学 1 年 数学 文字式式の計算 項と係数 中学 1 年 数学 次式 中学 1 年 数学 項のまとめ方 中学 1 年 数学 次式の加法 中学 1 年 数学 77
 中学 1 年生 e ライブラリ数学教材一覧 学校図書 ( 株 ) 中学 1 年 数学 1 14-20 正の数 負の数正の数 負の数 14- ある基準から考えた量の表現 中学 1 年 数学 14- 正の数 中学 1 年 数学 14- 負の数 中学 1 年 数学 14- 量の基準を表す数 中学 1 年 数学 15- 反対の性質をもつ量の表現 中学 1 年 数学 17- 数直線 中学 1 年 数学 18-19
中学 1 年生 e ライブラリ数学教材一覧 学校図書 ( 株 ) 中学 1 年 数学 1 14-20 正の数 負の数正の数 負の数 14- ある基準から考えた量の表現 中学 1 年 数学 14- 正の数 中学 1 年 数学 14- 負の数 中学 1 年 数学 14- 量の基準を表す数 中学 1 年 数学 15- 反対の性質をもつ量の表現 中学 1 年 数学 17- 数直線 中学 1 年 数学 18-19
学習指導要領
 (1) 数と式 学習指導要領 数と式 (1) 式の計算二次の乗法公式及び因数分解の公式の理解を深め 式を多面的にみたり目的に応じて式を適切に変形したりすること 東京都立町田高等学校学力スタンダード 整式の加法 減法 乗法展開の公式を利用できる 式を1 つの文字におき換えることによって, 式の計算を簡略化することができる 式の形の特徴に着目して変形し, 展開の公式が適用できるようにすることができる 因数分解因数分解の公式を利用できる
(1) 数と式 学習指導要領 数と式 (1) 式の計算二次の乗法公式及び因数分解の公式の理解を深め 式を多面的にみたり目的に応じて式を適切に変形したりすること 東京都立町田高等学校学力スタンダード 整式の加法 減法 乗法展開の公式を利用できる 式を1 つの文字におき換えることによって, 式の計算を簡略化することができる 式の形の特徴に着目して変形し, 展開の公式が適用できるようにすることができる 因数分解因数分解の公式を利用できる
Microsoft Word - 断面諸量
 応用力学 Ⅱ 講義資料 / 断面諸量 断面諸量 断面 次 次モーメントの定義 図 - に示すような形状を有する横断面を考え その全断面積を とする いま任意に定めた直交座標軸 O-, をとり また図中の斜線部の微小面積要素を d とするとき d, d () で定義される, をそれぞれ与えられた横断面の 軸, 軸に関する断面 次モーメント (geometrcal moment of area) という
応用力学 Ⅱ 講義資料 / 断面諸量 断面諸量 断面 次 次モーメントの定義 図 - に示すような形状を有する横断面を考え その全断面積を とする いま任意に定めた直交座標軸 O-, をとり また図中の斜線部の微小面積要素を d とするとき d, d () で定義される, をそれぞれ与えられた横断面の 軸, 軸に関する断面 次モーメント (geometrcal moment of area) という
例 e 指数関数的に減衰する信号を h( a < + a a すると, それらのラプラス変換は, H ( ) { e } e インパルス応答が h( a < ( ただし a >, U( ) { } となるシステムにステップ信号 ( y( のラプラス変換 Y () は, Y ( ) H ( ) X (
 第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
線形代数とは
 線形代数とは 第一回ベクトル 教科書 エクササイズ線形代数 立花俊一 成田清正著 共立出版 必要最低限のことに限る 得意な人には物足りないかもしれません 線形代数とは何をするもの? 線形関係 y 直線 yもも 次式で登場する (( 次の形 ) 線形 ただし 次元の話世の中は 3 次元 [4[ 次元 ] 次元 3 次元 4 次元 はどうやって直線を表すの? ベクトルや行列の概念 y A ベクトルを使うと
線形代数とは 第一回ベクトル 教科書 エクササイズ線形代数 立花俊一 成田清正著 共立出版 必要最低限のことに限る 得意な人には物足りないかもしれません 線形代数とは何をするもの? 線形関係 y 直線 yもも 次式で登場する (( 次の形 ) 線形 ただし 次元の話世の中は 3 次元 [4[ 次元 ] 次元 3 次元 4 次元 はどうやって直線を表すの? ベクトルや行列の概念 y A ベクトルを使うと
Phys1_03.key
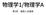 物理学1/物理学A 第3回 速度と加速度 速度 加速度 関数の話 やりたいこと : 物体の運動を調べる 物体の位置と速度を調べる これらを時間の関数として表したい 関数とは? ある された変数に対して, 出 の値が決まる対応関係のこと inpu 関数 ( 函数 ) oupu 例 : y(x)=x 2 x=2 を inpu すると y=4 が得られる 時々刻々と変化していく物体の位置 をその時刻とともに記録する
物理学1/物理学A 第3回 速度と加速度 速度 加速度 関数の話 やりたいこと : 物体の運動を調べる 物体の位置と速度を調べる これらを時間の関数として表したい 関数とは? ある された変数に対して, 出 の値が決まる対応関係のこと inpu 関数 ( 函数 ) oupu 例 : y(x)=x 2 x=2 を inpu すると y=4 が得られる 時々刻々と変化していく物体の位置 をその時刻とともに記録する
Microsoft Word - 第2章 ブロック線図.doc
 NAOSIE: Nagaaki Univriy' Ac il ディジタル制御システム Auhor() 辻, 峰男 Ciaion ディジタル制御システム ; 06 Iu Da 06 URL hp://hdl.handl.n/0069/3686 Righ hi documn i downloadd hp://naoi.lb.nagaaki-u.ac.jp 第 章ブロック線図. インパルス列を用いた z
NAOSIE: Nagaaki Univriy' Ac il ディジタル制御システム Auhor() 辻, 峰男 Ciaion ディジタル制御システム ; 06 Iu Da 06 URL hp://hdl.handl.n/0069/3686 Righ hi documn i downloadd hp://naoi.lb.nagaaki-u.ac.jp 第 章ブロック線図. インパルス列を用いた z
ポンスレの定理
 ポンスレの定理. qution Section 定理 有本彰雄 東京都市大学 平成 年 月 4 日 定義. n 角形 P とは 平面上にあるn 個の点の順序列 ( p, p,, pn - ) のことである 各 pk は P の頂点と呼ばれる 記号法を簡単にするため便宜的に p n とする また 線分 p i i pp, i,,,, n - を P の辺と呼ぶ 定義. すべての頂点 p k が曲線 C
ポンスレの定理. qution Section 定理 有本彰雄 東京都市大学 平成 年 月 4 日 定義. n 角形 P とは 平面上にあるn 個の点の順序列 ( p, p,, pn - ) のことである 各 pk は P の頂点と呼ばれる 記号法を簡単にするため便宜的に p n とする また 線分 p i i pp, i,,,, n - を P の辺と呼ぶ 定義. すべての頂点 p k が曲線 C
数学の学び方のヒント
 数学 Ⅱ における微分単元の 指導法の改善に関する研究 2017 年 10 月北数教旭川大会で発表した内容です 北海道札幌国際情報高等学校和田文興 1 Ⅰ. 研究の動機と背景 高校では極限を厳密に定義できず, 曖昧でわかりにくい. 私自身は, はじめて微分と出会ったとき, 極限の考え方等が納得できなかった. y () a h 接線 a 傾き (a) 2 Ⅰ. 研究の動機と背景 微分の指導改善に関する優れた先行研究がいくつかあるが,
数学 Ⅱ における微分単元の 指導法の改善に関する研究 2017 年 10 月北数教旭川大会で発表した内容です 北海道札幌国際情報高等学校和田文興 1 Ⅰ. 研究の動機と背景 高校では極限を厳密に定義できず, 曖昧でわかりにくい. 私自身は, はじめて微分と出会ったとき, 極限の考え方等が納得できなかった. y () a h 接線 a 傾き (a) 2 Ⅰ. 研究の動機と背景 微分の指導改善に関する優れた先行研究がいくつかあるが,
<4D F736F F D2097CD8A7793FC96E582BD82ED82DD8A E6318FCD2E646F63>
 - 第 章たわみ角法の基本式 ポイント : たわみ角法の基本式を理解する たわみ角法の基本式を梁の微分方程式より求める 本章では たわみ角法の基本式を導くことにする 基本式の誘導法は各種あるが ここでは 梁の微分方程式を解いて基本式を求める方法を採用する この本で使用する座標系は 右手 右ネジの法則に従った座標を用いる また ひとつの部材では 図 - に示すように部材の左端の 点を原点とし 軸線を
- 第 章たわみ角法の基本式 ポイント : たわみ角法の基本式を理解する たわみ角法の基本式を梁の微分方程式より求める 本章では たわみ角法の基本式を導くことにする 基本式の誘導法は各種あるが ここでは 梁の微分方程式を解いて基本式を求める方法を採用する この本で使用する座標系は 右手 右ネジの法則に従った座標を用いる また ひとつの部材では 図 - に示すように部材の左端の 点を原点とし 軸線を
< BD96CA E B816989A B A>
 数 Ⅱ 平面ベクトル ( 黄色チャート ) () () ~ () " 図 # () () () - - () - () - - () % から %- から - -,- 略 () 求めるベクトルを とする S であるから,k となる実数 k がある このとき k k, であるから k すなわち k$, 求めるベクトルは --,- - -7- - -, から また ',' 7 (),,-,, -, -,
数 Ⅱ 平面ベクトル ( 黄色チャート ) () () ~ () " 図 # () () () - - () - () - - () % から %- から - -,- 略 () 求めるベクトルを とする S であるから,k となる実数 k がある このとき k k, であるから k すなわち k$, 求めるベクトルは --,- - -7- - -, から また ',' 7 (),,-,, -, -,
2016年度 筑波大・理系数学
 06 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ k を実数とする y 平面の曲線 C : y とC : y- + k+ -k が異なる共 有点 P, Q をもつとする ただし点 P, Q の 座標は正であるとする また, 原点を O とする () k のとりうる値の範囲を求めよ () k が () の範囲を動くとき, OPQ の重心 G の軌跡を求めよ () OPQ の面積を S とするとき,
06 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ k を実数とする y 平面の曲線 C : y とC : y- + k+ -k が異なる共 有点 P, Q をもつとする ただし点 P, Q の 座標は正であるとする また, 原点を O とする () k のとりうる値の範囲を求めよ () k が () の範囲を動くとき, OPQ の重心 G の軌跡を求めよ () OPQ の面積を S とするとき,
測量試補 重要事項
 用地測量面積計算 < 試験合格へのポイント > 座標法による面積計算に関する問題は その出題回数からも定番問題と言えるが 計算自体はさほど難しいものではなく 計算表を作成しその中に数値を当てはめていくことで答えを導くことができる 過去問をしっかりとこなし 計算手順を覚えれば点の取りやすい問題と言える 士補試験に出題される問題は過去の例を見ても 座標が簡単な数値に置き換えることができるようになっている
用地測量面積計算 < 試験合格へのポイント > 座標法による面積計算に関する問題は その出題回数からも定番問題と言えるが 計算自体はさほど難しいものではなく 計算表を作成しその中に数値を当てはめていくことで答えを導くことができる 過去問をしっかりとこなし 計算手順を覚えれば点の取りやすい問題と言える 士補試験に出題される問題は過去の例を見ても 座標が簡単な数値に置き換えることができるようになっている
スライド 1
 暫定版修正 加筆の可能性あり ( 付録 ) マクスウェルの方程式 : 真空中 () 1. 電磁波 ( 光波 ) の姿 : 真空中. エネルギー密度 3. ポインティング ベクトル 4. 絵解き : ポインティング ベクトル 5. ポインティング ベクトル : 再確認 6. 両者の関係 7. 付録 : ベクトル解析 注意 1. 本付録 : マクスウェルの方程式: 微分型 を使用. マクスウェルの方程式を数学的に取扱います
暫定版修正 加筆の可能性あり ( 付録 ) マクスウェルの方程式 : 真空中 () 1. 電磁波 ( 光波 ) の姿 : 真空中. エネルギー密度 3. ポインティング ベクトル 4. 絵解き : ポインティング ベクトル 5. ポインティング ベクトル : 再確認 6. 両者の関係 7. 付録 : ベクトル解析 注意 1. 本付録 : マクスウェルの方程式: 微分型 を使用. マクスウェルの方程式を数学的に取扱います
2014年度 筑波大・理系数学
 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ f ( x) = x x とする y = f ( x ) のグラフに点 P(, ) から引いた接線は 本あるとする つの接点 A (, f ( )), B(, f ( )), C(, f ( )) を頂点とする三角形の 重心を G とする () + +, + + および を, を用いて表せ () 点 G の座標を, を用いて表せ () 点 G
筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ f ( x) = x x とする y = f ( x ) のグラフに点 P(, ) から引いた接線は 本あるとする つの接点 A (, f ( )), B(, f ( )), C(, f ( )) を頂点とする三角形の 重心を G とする () + +, + + および を, を用いて表せ () 点 G の座標を, を用いて表せ () 点 G
学習指導要領
 (1) いろいろな式 学習指導要領紅葉川高校学力スタンダードア式と証明展開の公式を用いて 3 乗に関わる式を展開すること ( ア ) 整式の乗法 除法 分数式の計算ができるようにする 三次の乗法公式及び因数分解の公式を理解し そ 3 次の因数分解の公式を理解し それらを用いて因数れらを用いて式の展開や因数分解をすること また 分解することができるようにする 整式の除法や分数式の四則計算について理解し
(1) いろいろな式 学習指導要領紅葉川高校学力スタンダードア式と証明展開の公式を用いて 3 乗に関わる式を展開すること ( ア ) 整式の乗法 除法 分数式の計算ができるようにする 三次の乗法公式及び因数分解の公式を理解し そ 3 次の因数分解の公式を理解し それらを用いて因数れらを用いて式の展開や因数分解をすること また 分解することができるようにする 整式の除法や分数式の四則計算について理解し
反射係数
 平面波の反射と透過 電磁波の性質として, 反射と透過は最も基礎的な現象である. 我々の生活している空間は, 各種の形状を持った媒質で構成されている. 人間から見れば, 空気, 水, 木, 土, 火, 金属, プラスチックなど, 全く異なるものに見えるが, 電磁波からすると誘電率, 透磁率, 導電率が異なるだけである. 磁性体を除く媒質は比透磁率がで, ほとんど媒質に当てはまるので, 実質的に我々の身の回りの媒質で,
平面波の反射と透過 電磁波の性質として, 反射と透過は最も基礎的な現象である. 我々の生活している空間は, 各種の形状を持った媒質で構成されている. 人間から見れば, 空気, 水, 木, 土, 火, 金属, プラスチックなど, 全く異なるものに見えるが, 電磁波からすると誘電率, 透磁率, 導電率が異なるだけである. 磁性体を除く媒質は比透磁率がで, ほとんど媒質に当てはまるので, 実質的に我々の身の回りの媒質で,
<4D F736F F D F2095A F795AA B B A815B837D839382CC95FB92F68EAE2E646F63>
 1/8 平成 3 年 3 月 4 日午後 6 時 11 分 10 複素微分 : コーシー リーマンの方程式 10 複素微分 : コーシー リーマンの方程式 9 複素微分 : 正則関数 で 正則性は複素数 z の関数 f ( z) の性質として導き出しまし た 複素数 z は つの実数, で表され z i 数 u, v で表され f ( z) u i 複素数 z と つの実数, : z + i + です
1/8 平成 3 年 3 月 4 日午後 6 時 11 分 10 複素微分 : コーシー リーマンの方程式 10 複素微分 : コーシー リーマンの方程式 9 複素微分 : 正則関数 で 正則性は複素数 z の関数 f ( z) の性質として導き出しまし た 複素数 z は つの実数, で表され z i 数 u, v で表され f ( z) u i 複素数 z と つの実数, : z + i + です
05 年度センター試験数学 ⅡB () において,cos q 0 であるから,P ( cos q, sin q) より, 直線 OP を表す方程式は y sin q sin q x cos q cos q x すなわち, (sin q) x - (cos q) y 0 ( ) ク 点 O,P,Q が
 05 年度大学入試センター試験解説 数学 ⅡB 第 問 []() 点間の距離の公式から, OP ( cos q ) + ( sin q ) ( cos q + sin q ) ア PQ { ( cos q + cos 7q ) - cos q } + { ( sin q + sin 7q ) - sin q } cos q + sin q 7 7 イ である また, OQ ( cos q + cos
05 年度大学入試センター試験解説 数学 ⅡB 第 問 []() 点間の距離の公式から, OP ( cos q ) + ( sin q ) ( cos q + sin q ) ア PQ { ( cos q + cos 7q ) - cos q } + { ( sin q + sin 7q ) - sin q } cos q + sin q 7 7 イ である また, OQ ( cos q + cos
7 渦度方程式 総観規模あるいは全球規模の大気の運動を考える このような大きな空間スケールでの大気の運動においては 鉛直方向の運動よりも水平方向の運動のほうがずっと大きい しかも 水平方向の運動の中でも 収束 発散成分は相対的に小さく 低気圧や高気圧などで見られるような渦 つまり回転成分のほうが卓越
 7 渦度方程式 総観規模あるいは全球規模の大気の運動を考える このような大きな空間スケールでの大気の運動においては 鉛直方向の運動よりも水平方向の運動のほうがずっと大きい しかも 水平方向の運動の中でも 収束 発散成分は相対的に小さく 低気圧や高気圧などで見られるような渦 つまり回転成分のほうが卓越している そこで 回転成分に着目して大気の運動を論じる 7.1 渦度 大気の回転成分を定量化する方法を考えてみる
7 渦度方程式 総観規模あるいは全球規模の大気の運動を考える このような大きな空間スケールでの大気の運動においては 鉛直方向の運動よりも水平方向の運動のほうがずっと大きい しかも 水平方向の運動の中でも 収束 発散成分は相対的に小さく 低気圧や高気圧などで見られるような渦 つまり回転成分のほうが卓越している そこで 回転成分に着目して大気の運動を論じる 7.1 渦度 大気の回転成分を定量化する方法を考えてみる
2013年度 九州大・理系数学
 九州大学 ( 理系 ) 前期日程問題 解答解説のページへ a> とし, つの曲線 y= ( ), y= a ( > ) を順にC, C とする また, C とC の交点 P におけるC の接線をl とする 以下 の問いに答えよ () 曲線 C とy 軸および直線 l で囲まれた部分の面積をa を用いて表せ () 点 P におけるC の接線と直線 l のなす角を ( a) とき, limasin θ(
九州大学 ( 理系 ) 前期日程問題 解答解説のページへ a> とし, つの曲線 y= ( ), y= a ( > ) を順にC, C とする また, C とC の交点 P におけるC の接線をl とする 以下 の問いに答えよ () 曲線 C とy 軸および直線 l で囲まれた部分の面積をa を用いて表せ () 点 P におけるC の接線と直線 l のなす角を ( a) とき, limasin θ(
木村の物理小ネタ 単振動と単振動の力学的エネルギー 1. 弾性力と単振動 弾性力も単振動も力は F = -Kx の形で表されるが, x = 0 の位置は, 弾性力の場合, 弾性体の自然状態の位置 単振動の場合, 振動する物体に働く力のつり合
 単振動と単振動の力学的エネルギー. 弾性力と単振動 弾性力も単振動も力は F = -x の形で表されるが, x = の位置は, 弾性力の場合, 弾性体の自然状態の位置 単振動の場合, 振動する物体に働く力のつり合いの位置 である たとえば, おもりをつるしたばねについて, ばねの弾性力を考えるときは, ばねの自然長を x = とし, おもりの単振動で考える場合は, おもりに働く力がつり合った位置を
単振動と単振動の力学的エネルギー. 弾性力と単振動 弾性力も単振動も力は F = -x の形で表されるが, x = の位置は, 弾性力の場合, 弾性体の自然状態の位置 単振動の場合, 振動する物体に働く力のつり合いの位置 である たとえば, おもりをつるしたばねについて, ばねの弾性力を考えるときは, ばねの自然長を x = とし, おもりの単振動で考える場合は, おもりに働く力がつり合った位置を
以下 変数の上のドットは時間に関する微分を表わしている (ex. 2 dx d x x, x 2 dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-1) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( x や x, x などがすべて 1 次で なおかつ
 以下 変数の上のドットは時間に関する微分を表わしている (e. d d, dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( や, などがすべて 次で なおかつそれらの係数が定数であるような微分方程式 ) に対して安定性の解析を行ってきた しかしながら 実際には非線形の微分方程式で記述される現象も多く存在する
以下 変数の上のドットは時間に関する微分を表わしている (e. d d, dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( や, などがすべて 次で なおかつそれらの係数が定数であるような微分方程式 ) に対して安定性の解析を行ってきた しかしながら 実際には非線形の微分方程式で記述される現象も多く存在する
