Microsoft Word - main.doc
|
|
|
- ゆりか ふじつぐ
- 6 years ago
- Views:
Transcription
1 電磁界解析のための有限要素法 FE 入門 電磁界解析のための有限要素法 FE 入門 平野拓一 目次. はじめに.... 有限要素法の特徴.... 座標変換と基底関数.... 座標変換と面積座標..... 次の変換.... スカラー基底関数...7. 次要素...7. ベクトル基底関数 次要素...8. ノードベース有限要素法...9. 問題の設定 微分方程式 境界条件...9. 有限要素法の適用..... メッシュと基底関数..... 基底関数による展開..... 要素行列..... 系行列 境界条件の適用 固有値問題を解く まとめ.... 系行列生成例.... ノードベース有限要素法 ガラーキン法.... 問題の設定 微分方程式 境界条件.... 重み付け残差法と弱形式 エッジベース有限要素法 問題の設定 微分方程式 境界条件 重み付け残差法と弱形式 離散化 系行列の組み立てと解法.... 面分岐回路の解析.... 問題の設定 微分方程式 境界条件.... 重み付け残差法と弱形式.... 離散化...
2 電磁界解析のための有限要素法 FE 入門. 付録...7. ヘルムホルツの方程式の導出 導波管のベクトルヘルムホルツ方程式 導波管のスカラーヘルムホルツ方程式.... 汎関数 変分 変分原理.... 重み付け モーメント...8. マクスウェルの方程式と境界条件 マイクロストリップ線路の準 E モード...5. 物理定数 電気媒質定数 ベクトル公式...5. はじめに有限要素法 FE F El hod は微分方程式をある境界条件の下で解く数値計算手法の一つである 歴史的には航空機や建築物の強度解析に使われ始めたのが有限要素法の始まりであり 95 年の論文 [] が有限要素法の始まりであると言われる 例えば航空機 図 を設計する際には 主翼に着目して見た場合 主翼自身の重さで主翼の胴体との付け根部分に大きな力が加わる 他にも大きな力が加わる場所を考慮しておく必要があるので航空機の任意の場所に加わる応力 ある点に加わるねじる力 を求める必要がある 応力を求めるには微分方程式を与えられた境界条件の下で解く必要がある 有限要素法は構造物を要素と呼ばれる小さな多角形の集合で表す 有限要素法という名前の理由である ので 複雑な形状の構造物に対しても簡単に適用でき 数値的に微分方程式を与えられた境界条件の下で解いたことになる このようにして任意の場所の応力が求まれば大きな力が加わるところには丈夫な材料を使ったり構造を工夫したりして丈夫に設計する 翼の幅を厚くして丈夫にしようとしても自重が増加してかえって逆効果になってしまったり 航空力学 rods 的条件を満たさなかったりして苦労することが予想できる しかし 有限要素法を使うとこのように構造物の任意の場所に働く応力を実験に依らず計算で求めることができ 試行錯誤で設計することも可能となり 構造物の設計に関して革命的な影響を与えたことは言うまでもない その後 建築土木などの他の構造解析を必要とする分野に使われ始めた 巨大な建築物や橋は地震や風などの影響で揺れる 全ての構造物はその構造と使う材料の重さなどで決まるエネルギーを吸収しやすい共振周波数がある 有限要素法を勉強すればわかる 地震や風が影響無いと思える程小さな規模でもその構造物の共振周波数が地震や風などの外力の共振周波数と一致するといとも簡単に構造物が崩壊することがある 例えば 9 年 月 7 日にアメリカ ワシントン州で起きたタコマ橋落下事故 図 は有名であり 同年 7 月に開通してわずか ヶ月後 風速 9 s という弱い風で落下してしまった 計算上は風速 s まで耐えられるようにしてあったつもりらしいが 共振現象を考慮していなかったようである ただし 風の強さが周期的に変化す
3 電磁界解析のための有限要素法 FE 入門 る訳ではなく 一定の強さの風が橋に当たっているだけでも 橋の風下側に不規則な渦 カルマン渦 が発生し それが周期的に橋に外力を与えることになる それがタコマ橋のねじれ共振の周波数と一致し ブランコをこぐ場合のようにエネルギーを溜めていってケーブルが振動による引っ張られる力に耐えられなくなって落下した よって現在では風による外力も考えて流体力学的にも安定した構造を設計するようである 地震によるビルの崩壊も 地震の周波数をビルの共振周波数と一致させないように設計すると崩壊を防ぐことができる 地震の多い日本においては特に重要な技術である このように構造力学については有限要素法は中心的役割を果たし実用化されていたが 電磁界解析で有限要素法が使われ始めたのは有限要素法の歴史の中ではかなり最近のことであり 9 年代後半から 97 年以降である 文献 [] にそれらの経緯が記されている 有限要素法が行うことは基本的には 微分方程式をある境界条件の下で解く ということであり 工学 経済学など多くの分野の問題に適用できる それでも電磁界解析において有限要素法の発達が遅れていたのは 応力を求める問題の場合には未知数がスカラー量で良かったが 電磁界を求めるにはベクトル量を求める必要があり スカラーのポテンシャルを未知数として有限要素法を適用しても得られる解には 物理的には出てくるはずがない非物理解 スプリアス解と言う が出てきてしまうことが原因であった しかしベクトル基底関数が開発され スカラー基底関数を使うノード ベース有限要素法からベクトル基底関数を使うエッジ ベース有限要素法へと発展し 有限要素法の電磁界解析問題への適用は成功してきた 現在では市販の 次元構造を有限要素法で解析する汎用電磁界シミュレータ FSSso 社と gl holog 社版がある 最初は gl 社が so 社に委託していたようだが 喧嘩別れしてしまったらしい があり 様々な研究機関 企業等で使われている 図 og77- hp:
4 電磁界解析のための有限要素法 FE 入門 図 タコマ橋落下事故 hp:oud..os-ou..p~sopldo.hl. 有限要素法の特徴 要素に分けてメッシュを作って行列を解く問題に直す 微分方程式を直接数値的に解くのではなく 一度積分するので数値的に安定である 数学的には変分原理で説明される 周波数領域の解析法である. 座標変換と基底関数 ここでは 次元の三角要素を扱う 変換の次数を高くすると曲辺を扱うことができる. 座標変換と面積座標.. 次の変換
5 有限要素法の基底関数 5 η O P η ξ ς P P ξ O P P η ξ ς P η ξ pl ξ η pl 図 面積座標 次元有限要素法では 解析領域を三角要素に分割する 要素行列の要素を計算する場合 その各領域内で面積分を行う必要がある まともに積分しても積分できるが 場合分けが面倒な上 全ての要素について個別に積分しなければならない そこで 図 左の一般の三角形 三角要素 を右のように決まった三角形に座標変換し 変換された座標で面積分を行うと場合分けをする必要がなく さらに座標変換を全ての要素に対して行えば積分の値も使いまわしができて計算速度 が向上する また 基底関数を作るときも 決まった ξ η 平面で作成しておき それを座標変換 すればいいので楽になる 図 の座標変換においてξ η 平面は面積座標と呼ばれる 平面上の三角形をξ η 平面に移すことを考えると図に示されるように三角形内の各面積の比がξ η ς となっているからである この考え方がわかりにくい場合は単に頂点 P P P を P P P に座標変換したと思えばよい この座標変換は 一次変換 拡大 縮小 回転 平行移動 なので アフィン変換である ξ η ξ η ς ξ η ς ξ η ς ξ η ς ξ η ξ η 変数変換 ξ η に伴うヤコビアンを J とすると
6 有限要素法の基底関数 J η ξ η ξ ただし は 平面上の三角形の面積である 意味を考えると ヤコビアンは変数変換の変化率を意味するし はベクトル P P と P P の外積になっているから P P と P P を辺とする平行四辺形の面積となって 三角形の面積の 倍になることが理解できる η ξ ς η ξ ここで 積分公式 ξ ξ η η ξ η ξ η ξ d Jd dd S!!!! l l dd S l ς η ξ ここで S は三角要素が存在する範囲 は三角要素の面積である
7 有限要素法の基底関数 7. スカラー基底関数 図 一次スカラー形状関数 有限要素法の三角要素内で使う基底関数はスカラー場解析の場合図 のようなつの基底関数がよく使われる これは一次要素基底関数と言う さらに 各頂点 においてつの基底関数だけが値を持ち 他のつはになっている この性質は方程式を作るとき非常に便利であり 各基底関数の展開係数は解こうとしている未知関数の頂点の値を意味することになる あるサンプリング点で他の基底関数の値がになるので このような基底関数を使う要素をラグランジュ要素 Lgrg ls と言う ラグランジュ基底関数という名前はラグランジュの補間多項式に由来している. 次要素一次要素なので 平面の形状関数を作る よって 補間関数は次のように仮定できる ϕ ξ η ξ η P P P ϕ ϕ ϕ での値を とすると ϕ ϕ ϕ ϕ ϕ ϕ ϕ ϕ ϕ ϕ ϕ 5 式 に式 5 を代入する ϕ ξ η ϕ ϕ ϕ ξ ϕ ϕ η ξϕ ηϕ ξ η ϕ ϕ ϕ ϕ を変数として内部の値が補間されていることがわかる これは点 で ϕ 点 で ϕ 点 でϕ の値を取る平面である また 各頂点ではつの基底関数のみが値を持つので 頂点 だけで値を持つ基底関数 ξ を求めるときには ϕ ϕ ϕ と おいて ξ η ξ η となる 同様にして他の つの基底関数も次のように求まる
8 有限要素法の基底関数 8 ξ η ξ ξ η η ξ η ξ η 実は 今の作業は ϕ ξ η を ϕ ϕ ϕ について整理して ϕ ϕ ϕ の係数を読み取るだけで が求まる はまた 形状関数 shp uo とも呼ばれる これを式 を用いて座標変換すれば容易に全ての三角要素に対して基底関数が作れる しかし 実際には式 で座標変換して の例を示す ξ η 平面で面積分するのでその必要はない 図 にこの基底関数. ベクトル基底関数.. 次要素 図 5 ベクトル基底関数一次要素 まず 基底関数の性質として次の性質を要求する w はエッジ 上でのみ一様な接線成分を持つ 他の 辺上では接線成分はであり 法線成分は持っても構わない この条件を満たすように基底関数を作ると次のようになる w l ξη ηξ w l ης ςη w l ςξ ξς ここで は に関する微分演算子である これらのベクトル基底関数のフィールドを図 5 に示す w の条件と構成法について説明する エッジ とエッジ 上ではフィールドの接線成分がである η に掛かっているξ はエッジ 上でη の寄与を無くすためである η はη が増えていく 方向を表すから 辺 P P 上ではフィールドが垂直になっているのがわかる
9 有限要素法の基底関数 9 ξ η に付いている負号はフィールドの向きを揃えるためである l はエッジ上でフィールドの接線成分を に規格化するための係数である [ 基底関数を η ξ 座標で表す ] { } { } { } ξ ζ ξ ζ ζ η ζ η η ξ η ξ l l l w w w [ 基底関数を 座標で表す ] C C C { } C l w. ノードベース有限要素法. 問題の設定 微分方程式 境界条件 有限要素法で解析する航空 土木 建築 電磁界などの工学の問題は数学の問題として共通部分を抽出すれば 微分方程式を与えられた境界条件の下で解く という問題を解いているだけである
10 電磁界解析のための有限要素法 FE 入門 u v 図 次元問題本稿では電磁界解析を目的としているので例として図 に示すような導波路問題を考え モード関数を求める問題を考える その場合の未知数は各モードの断面の電磁界分布と伝搬定数 位相定数 である この問題に対する微分方程式は付録.. の式 より次のヘルムホルツ方程式である 7 上の微分方程式を次の境界条件の下で解く v u v w u u 上での境界条件は境界上で関数 の値を直接指定しており これを第一種境界条件 またはディリクレ条件と呼ばれる v 上での境界条件は第三種境界条件 または混合境界条件と呼ばれる 特に w のとき 関数 の境界垂直方向の微係数を指定しており これを第二種境界条件 またはノイマン条件と呼ばれる 上の問題に対する生成汎関数 変分問題が微分方程式を解くのと等価になる汎関数 は次のようになる 汎関数 変分などについては付録. 参照 今はどうやってこの汎関数を上の微分方程式から作ったのか納得できないかもしれないが とりあえず変分して確認してほしい [ ] v d w v dd F 8 [ ] v d w v dd F δ δ δ δ δ δ
11 電磁界解析のための有限要素法 FE 入門 v d w v dd ] [ δ δ δ δ δ δ δ δ δ 二次の微小変化を無視すると [ ] [ ] v d w v dd F F δ δ δ δ δ δ ここで δ を δ で表現したいから面積分に 次元版のガウスの定理を適用する 次元で言う部分積分 δ δ δ δ δ δ δ δ δ δ δ δ δ δ [ ] [ ] v d w v dd F F δ δ δ δ δ v d w v d dd δ δ δ v d w v d dd δ δ δ
12 電磁界解析のための有限要素法 FE 入門 { } u δd v δdd v w δd さて 関数 の微小変化 δ に対する汎関数 F[ ] の変化が となるような条件を上の式から求 めてみる δ という関数は任意に選ぶことができる しかし境界 上はディリクレ条件であり 問題を解くときにこちらで値を指定するから微小変化量 δ は 上では のものを用いる する と上の式の 上の線積分は となる ディリクレ条件は問題を解くと強制的に値を指定するので u 強制境界条件とも言われる また v 上の線積分は混合境界条件から となり 汎関数で組み込んでいる もし v w ならば汎関数に線積分の項を組み込む必要も無く楽である 実際の応用上はそのような境界条件がよく使われるため 境界条件は何も考えなくても汎関数に組み込まれることになる 汎関数に境界条件が組み込まれていて 後で何も特別な処理をする必要がないので 混合境界条件は自然境界条件とも言われる この章では微分方程式を与えられた境界条件の下で解く問題と 汎関数の極小値を求める問題が等価であることを説明した u u. 有限要素法の適用 図 7 方形導波管
13 電磁界解析のための有限要素法 FE 入門 図 8 全域関数と局所関数.. メッシュと基底関数問題の例として簡単のために図 7に示すような方形導波管の E モード解析を取り上げる 付 録.. より E モードの場合 E E なので すべての導波管壁面上 で の境界条件となり 式 8 の線積分の項が消えて次のようになる F[ ] dd 9 この汎関数に変分原理を適用して未知の関数 を求める方法を説明する まず 未知の関数 を既知の基底関数の線形和として展開する 基底関数の選び方には図 8に示すように全域 基底関数で展開する方法と局所基底関数で展開する方法がある この問題の場合には構造が簡単だから前者でもいいが 一般に複雑な断面形状を有する導波路の解析を行いたいので 有限要素法では後者の局所基底関数の和として未知関数を展開する それが 有限要素法 と言う名前の由来でもある 値が要素内では急激に変化しない程度に細かく要素分割するので 要素内では簡単な基底関数の和で十分いい精度で未知関数を近似できる また 要素に分割する場合 次元の場合には三角形や四角形などのいろいろな多角形が考えられる 実際に三角形も四角形も要素として使われているが 複雑な構造に対して要素分割する場合 三角形は多角形を構成する最小単位なので柔軟性が高く 一番多く使われている 図 8の右上のように要素分割された要素の集合をメッシュ sh と言う
14 電磁界解析のための有限要素法 FE 入門.. 基底関数による展開 図 9 要素分割 今 領域内を 個の三角要素に分割し 各要素内で定義される 個の基底関数を用いて未知スカラー関数 を次のように表す 基底関数についての詳しいことは別の章を参照 は要素 内の 番目の節点の基底関数である はその基底関数に対する重みである は図 9の右に示されるように要素内の節点 のみで の値を持ち 他のつの節点では の値を取る つまり はその節点での未知数 の値そのものである.. 要素行列式 を式 9 に代入すると F [ ] F dd また 異なる要素の基底関数は互いに定義域が重なることはなく 異なる要素の基底関数同士を掛け算したら になるので 要素に対する和は 乗の外 さらに積分の外に出すことができる また 積分範囲は各要素内 に限定できる
15 電磁界解析のための有限要素法 FE 入門 5 dd F dd dd ここで 変分原理を適用する すでに未知関数 を既知の基底関数で展開しているので 汎関数 F の極小値を求めるには F を全ての で微分して になる条件式の連立一次方程式を作る このように離散化する方法をリッツ R 法と言う [] 要素 内の変数について行うと F より [ 参考 計算方法 ] とする { } { } { } L L L { } { } { } L L L { } { } ] [ dd dd
16 電磁界解析のための有限要素法 FE 入門 整理すると ここで dd dd 同様に F F を計算すると要素 に関して次の連立方程式を得る F F F 上の行列表現は要素 に対して汎関数が極小値を持つための条件であり 要素方程式と呼ばれる を要素行列 l r と言う [ 要素行列の計算 ] 点 P P P を頂点とする三角形の要素行列を計算する P P P は三角形を左に回るような頂点とする dd dd d d d Jd dd ξ ξ η ξ ξ η η ξ η ξ は三角形 P P P の面積であり は基底関数の章の式 で説明されている座標変換パラメータである
17 電磁界解析のための有限要素法 FE 入門 7.. 系行列 図 ローカル基底関数 図 グローバル基底関数 構造全体の問題を解くためには要素行列を結合して構造固有の系行列を作る必要がある そのための条件として節点での未知数の値の連続条件を用いる 各節点は図 9の左に示す の節点のようにいくつかの要素によって同じ節点が共有される このようにメッシュ全体を見たときに のように一意に節点に番号を振るとき その頂点の番号をグローバル節点番号と言う ここで 境界上の節点に対しても今のところはグローバル番号を振っておいて統一的に扱い 後でその境界条件を考慮する それに対して 要素内で と示されているように要素内だけで節点に番号を振るとき その節点の番号をローカル節点番号という 今 系のグローバル節点数を とする グローバル節点番号はいくつかの要素のローカル節点番号で共有される よって 式 で異 なる要素の は共有される節点において同じ値になるように 未知関数 は連続だから 拘束される 図 9 の左の を考えてみると
18 電磁界解析のための有限要素法 FE 入門 8 となる における未知関数の値を と置いた この関係で 局所的な要素が解析領域全体では繋がっているのである 方形導波管断面の例で説明すると 図 のように各要素内で自由に定義されているローカル基底関数が節点での関数の連続条件で拘束されて図 のようなグローバル基底関数となる 具体的には 新たにグローバル節点番号上の展開係数 それを節点とする要素の基底関数の共通の重み係数 を未知数とする行列方程式を立てる L L L L L L L L L L このようにして全体の構造が考慮された系行列が作成される 図 9 の例では例えば となる まとめると次のようになる g g g をグローバル節点番号に対応する展開係数とし ローカル節点番号 の未知数 が g g g のように対応するとする 要素行列 をそれぞれ系行列 g g g g に足す の操作を全要素に対して行う 今の操作をプログラムリスト風に書くとつぎのようになる do l do do g g g g g g g g d do d do d do
19 電磁界解析のための有限要素法 FE 入門 9 この系行列の作成過程が理解しにくい場合は 式 の展開に最初から式 を適用して行列方程式を作ってみるとわかりやすい そのとき と表現される は節点 で重み係数 がかかる 番目の要素基底関数である 節点 を共 有する要素は 個ある ある の部分は図 に示される節点 のグローバル基底関数で..5 境界条件の適用周囲上の境界条件を考慮する ディリクレ条件ディリクレ条件である境界上のグローバル節点 に対しては その節点の値が指定されているので は最初から未知数ではない そこで 系方程式の中の を取り外す 具体的には系行列の 行と 列を取り除いてよりサイズのつ小さな行列を作ればよい この操作を全てのディリクレ条件境界上の節点に対して行う 混合境界条件 ノイマン条件ノイマン条件は式 8 に周回積分として組み込まれているので何もする必要はない 周回積分はノ イマン条件の境界壁に接する辺を持つ要素内のみで行う 特に 上記の例題のように の ときは線積分の評価も行う必要がない.. 固有値問題を解く 出来上がった行列方程式は未知係数ベクトル [ ] と波数 を未知数とするので固有値問題 gvlu prol となる 各固有値に対応してモードが求まる 波数の 乗 が固有値 gvlu として モード関数を決定するための重みベクトルが固有ベクトル gvor として求まる 橋やビルや航空機の共振周波数を求める問題もこのように決定される なお この問題の場合波源 力学では外力に相当する がなかったので固有値問題となったが 波源がある場合は連立一次方程式を解いてフィールドを決定する問題となる 要素分割数を増やせばより精度の高い結果が得られる また 要素分割するときには極端に細長くメッシュを切ったら精度が落ちる []p.-7 また なるべく扁平率の小さな三角形で自動的にメッシュを生成するアダプティブメッシュ生成アルゴリズムもいくつか存在する
20 .. まとめ 電磁界解析のための有限要素法 FE 入門
21 電磁界解析のための有限要素法 FE 入門. 系行列生成例 5 5 l: l ur lu: lol od ur Rd: glol od ur 図 例題メッシュここでは 記号の簡単化のため U U とおく 要素行列 U U U U U U U U U U U U U U U U U U 要素行列 行列
22 電磁界解析のための有限要素法 FE 入門 ここで 節点 においては なので それらに対応する行と列を取り除く U 行列についても同様の操作を行い 固有値問題を解く. ノードベース有限要素法 ガラーキン法. 問題の設定 微分方程式 境界条件. 節と全く同じ例題を用いる 上の微分方程式を次の境界条件の下で解く v u v w u. 重み付け残差法と弱形式与えられた微分方程式に対して式 8 のような汎関数を作る方法についてはまだ説明していなかった 式 8 は変分して生成汎関数となっていることを確認したが 実はその汎関数は変分演算に慣れた人が予想して作ったのである 一般には微分方程式に対する汎関数は存在しないことがある これは変分演算が微分演算に似ていることを考えると 一般の関数は必ずしも積分できる訳ではない という事実に似ている 一般の関数が積分できない理由は 任意関数の和については線形性から積分公式が確実に存在するが 積については積分公式 部分積分はそれに近いが十
23 電磁界解析のための有限要素法 FE 入門 分ではない が存在しないからである 一般の関数は必ずしも積分できる訳ではない という事実はガロア理論によって証明されている ガロア理論は 5 次以上の方程式に対する解の公式は存在しない ということを証明したことで有名である 例えば 電磁波問題の有限要素法解析では 損失がある場合の問題を支配する微分方程式の汎関数は存在しない これでは一般の解析ができず 気分が悪い しかし 変分原理を用いなくてもこれから説明する重み付け残差法 付録. 参照 の特殊な場合であるガラーキン法を用いると一般の微分方程式の問題を有限要素法で解析できる ガラーキン法を用いると 汎関数が存在する問題に対してはガラーキン法を使った場合も全く同じ行列方程式が得られる つまり ガラーキン法は変分原理をより一般の問題に拡張できるようにした手法と考えてよい さて 式 は領域 の至る所で成立することを要求している そのために 次のような操作を考える 今 W を領域 内で定義される任意の関数とする すると 式 が領域 内で常に成り立つならば任意の関数 W に対して常に次の式を満たさなければならない W ds 5 左辺は残差 Rsdul と呼ばれ 微分方程式の誤差量に関数 W で重み付けをして積分した値である W は重み関数 wghg uo または試験関数 rl uo などと呼ばれる 数値計算 で の近似値を求めた場合 誤差量の積分値は当然 に近いのが望ましい が厳密に微分方程 式を満たすならば残差は完全にになる 式 5 を変形すると W ds ベクトル公式 V V V を使って変形すると { W W W} ds [ W W] ds W ds ガウスの公式を使うと [ W W] ds W d [ W W ] ds W d ここで. 節の方形導波管の解析に限定すると である PEC 境界上では磁界の接線成分の境界法線方向への変化率が ノイマン条件 である 付録. 参照 よって
24 電磁界解析のための有限要素法 FE 入門 [ W W ] ds を式 と同様に展開する [ W W ] ds ここで W L を上の方程式につずつ代入し 個の連立一次方程式を得る [ ] ds L ここで異なる要素内の基底関数はオーバーラップしないので となったときだけ積分は値を持つ [ ] ds L この方程式は変分原理を適用して得た要素方程式と全く同じである 系行列の作成も要素境界の連続条件から同様に作成すると 変分原理のときと全く同様の方程式が得られる 5. エッジベース有限要素法ノードベース有限要素法 od-sd FE ではスカラー基底関数を用いた しかし ベクトルを求める問題でスカラー基底関数を使うとスプリアス 非物理 解が発生してしまうという問題があった そこで エッジベース Edg-sd FE 基底関数が考案され ベクトル基底関数を用いて直接ベクトル界を求める 5. 問題の設定 微分方程式 境界条件 図 に示すノードベース有限要素法の例と同じ例題を考える 今回はベクトル基底関数を使うので微分方程式はベクトルバージョン 付録. を用いる E E 境界条件は 周囲の導体壁上で電界の接線成分が である 5. 重み付け残差法と弱形式任意のベクトル重み関数を W として式 に重み付け残差法を適用する
25 電磁界解析のための有限要素法 FE 入門 5 E E ds W 7 式 7 では ベクトル関数 W との内積の積分値を求めているが 別にスカラー関数との積を取ってベクトルになるような方程式を立てても構わない どちらでもいいのだが次のように変形できるし 数値計算上便利だから式 7 のように定義している モーメント法でもベクトル基底関数を使う際の重み付けで内積を取るが それは接線成分を抜き出すという意味もある ベクトル公式 を使って式 7 を変形すると [ W E { W E } W E] ds [ W E W E] ds { W E } ds ガウスの定理を用いて [ W E W E] ds { W E } dl ベクトル公式 C C C を用いて線積分の項を変形すると [ E W E] ds { W E } dl W 8 式 8 の重み関数 W はどのように選んでもよいが 精度が良く 変分原理から安定性が保証されているのでガラーキン法を用いる 電界 E は展開する際もディリクレ境界条件を満たすような基底関数で展開しており かならずディリクレ条件を境界上で満足する W は E と同じにするので W も境界上で E と同じディリクレ条件を満たす よって W なので 線積分の項は消え る [ E W E] ds W 9 E 波の解析 ここで E 波の解析を行う E なので γ E E E E E E とすると E E γ
26 電磁界解析のための有限要素法 FE 入門 γ E γe γ γ E E γ γ E E ここで E と定義すると γ E E E γ [ γe γe E ] E W W W W W γ γ [ γw γw W ] W ここで 電界 E は複素数なので ガラーキン法を用いるとき必ず正数になるように 付 * 録. 参照 重み関数を W E と選ぶのがよい しかし 基底関数として最初から実数のものを用いたら W E としても同じことになる 最初から実数の基底関数を用いることにするので後で W E とする よって これらを式 9 に代入すると [ γw γw W γe γe E W W E E ] ds [{ γ WE γ WE W E } WE WE ] ds [{ γ W E W E } W E ] ds [ W E γ ] W E ds [ E W E ] ds W ここで γ γ が実数 α のとき γ が純虚数 β のとき α β E 波の解析
27 電磁界解析のための有限要素法 FE 入門 7 [ W ] { W ds W } dl ベクトル公式 C C C を用いて線積分の項を変形すると [ W W ] ds W { } dl [ W W ] ds W { ωε E } dl 電界は境界 上で境界条件 E を満たすので 線積分の項は消える [ W W ] ds 磁界の境界 上の接線成分は依然として未知数である しかし 境界上の線積分の項が消えたので 境界 上に隣接する要素に対しても何も特別な処理を行う必要がなく 内部にある要素と同じように評価すればよい 5. 離散化 式 の離散化を行う * W E ds W * E ds
28 電磁界解析のための有限要素法 FE 入門 8 図 離散化 今 例として図 に示すように方形導波管の断面をつの三角要素に分割し 角要素内の電界をつの基底関数の和で表す 付録. より 波源や電荷がないとき 電界 磁界の接線成分は異なる媒質の境界でも連続になる 電束と磁束は垂直成分が連続 今 エッジベース基底関数を用いると 要素の辺 エッジ 上で電界の接線成分が連続になるという条件を簡単に表現することができる エッジベースのベクトル基底関数はすでにつの辺上で接線成分が一定になり 他のつの辺上では接線成分がになるように作られている よってエッジベース基底関数を使うと非常に容易に電磁界を展開できる 今 導波管断面の電界を次のように展開する l E w ここで l は要素数 図 の例では w は要素 内のエッジ で接線成分を持つベクトル基底関数で はその基底関数に対する重みである 金属上で電界の接線成分は なの で であるが これは後で考慮する また 各ベクトル基底関数はその要素内だけで定義されるものであり 違う要素の基底関数がオーバーラップすることはないということを強く意識しておく必要がある 式 を式 に代入すると l l * W w ds W * w ds
29 電磁界解析のための有限要素法 FE 入門 9 重み付け W としては E と同じ境界条件を満たす関数ならば 線積分の項が消えるから 何でも良いので W として w を選ぶ 本当は PEC 境界上では接線成分を持つ電界の基底関数を使ってはいけないので 後から取り除く ds ds l l w w w w l L 展開関数は l 個あり また l 個の関数で重み付けを行って l 個の方程式を得たので l 文字 l 元連立一次方程式となる も未知数だから固有値問題となる 式 を行列表現すると次のようになる l l l l l l l l l l l l L L O O L L l l l l l l l l l l l l L L O O L L ここで ds w w
30 電磁界解析のための有限要素法 FE 入門 w w ds 行列の対角以外の成分が になっているのは違う要素の基底関数は互いにオーバーラップしないからである 行列内にが多いというのはそのような行列を解くのに特化した数値計算サブルー チンを使えば計算速度が速くなる 明らかに となる [ 次三角要素の要素行列の計算 ] l l l l [ C C C C l l dd dd dd dd ここで C は式 で与えられる また積分は次のようになる dd dd dd dd dd ] 5. 系行列の組み立てと解法前節では各要素内で離散化を行った この節ではさらに全体の構造を一意に表すための条件を適用する 界の連続条件の適用同じ媒質内では当然界は連続である また違う媒質境界でもその境界に波源や電荷が無いときは電界と磁界の接線成分は連続となる 付録. 幸い 意図的に この問題でも電界を未知数としているので各要素境界において接線成分は連続である ベクトル基底関数の辺上の接線成分の大きさは に規格化されているので 図 の例では
31 電磁界解析のための有限要素法 FE 入門 5 となる ここで 構造全体のエッジの数を dg とすると L dg はエッジ番号 に対応する基底関数の重み係数であり その辺を有するつの三角要素内の基底関数の共通の重み係数となる ここで 注意しなければならないことは ベクトルの向きも一意に揃えなければいけないので片方の係数に負号が付いている この界の連続条件を適用すると未知数が減る その分方程式の数も減って正方行列を保つようにする訳だが どうするかと言うと の重みが掛かるつの要素のつの基底関数をペアとして つの基底関数と見なす 境界にある辺だけはペアとならないが問題ない こうするとエッジに基底関数が対応しているようになり 多少近くの基底関数と定義域がオーバーラップするようになるが 依然としての多い行列である 未知数の順番をうまく入れ替えれば対角付近にのみ値をもつ帯構造の行列にすることができ 特化したサブルーチンを使うと高速に計算できる つの基底関数がペアとなった基底関数は電界を磁流に対応させたとき モーメント法のルーフトップ関数 [] と一致する 実際にモーメント法と有限要素法を組み合わせるときの相性がよく モーメント法と有限要素法を組み合わせたハイブリッド計算が行われている [] しかし この要素内で定義された最初の基底関数をペアの基底関数に置き換えて計算し直すのは少し煩雑なので より簡単な系行列の作成法を紹介する まず 各要素で要素行列を作成する or l or or l l と対応するとする or は要素 の基底関数を系行列に組み込むときに向きを揃えるための符号である そのままの向きでいいときは 反転させる必要があるときには- となっている このとき全体の系行列は dg L dg L dg O O L dg L dg dg dg dgdg dg の要素に対して do l do do
32 電磁界解析のための有限要素法 FE 入門 d do d do d do l l l l or or l l l l or or というように足していけばよい こうすると うまく周りの基底関数からの重み付けの効果が足されていく この操作で図 の例に対する行列としては次のような行列が出来る 7 L O L L O L 有限要素法のプログラムでは各要素内で積分を行い を計算したら後はいかに変換テーブ ルを駆使して作成 使用するかである また各要素内の積分も座標変換して決まった位置で行うのでやはり変換テーブルを作ったり読んだりする操作が基本となる 境界条件 ディリクレ条件 の適用次に 境界条件を適用する 導体上で電界の接線成分はとならなければいけないので 図 の例ではグローバルエッジ 7 に配置された基底関数の重みはにしなければならない 7 重みがということは値が既知であり 未知数ではないからグローバルエッジ が金属境界上ならば であり 行列の 行と 列を取り除き よりサイズの小さな行列とする 列を取り除くのは が既知だからであり 行を取り除くのは境界条件を満たす重み付け関数を使わなければならなかったから重み付けを元々行わなかったという意味合いにしたいからである E モードを解析で 磁界のヘルムホルツ方程式を使ったときの境界条件では. 節で述べたように何もする必要はなく境界条件が満足される 図 の例に対する最終的な系行列は次のようになる これはベクトル [ ] 5 と実数 を未知数とする固有値問題である ベクトル [ ] 5 が固有ベクトル が固有値である また特につの行列が対称行列になっているので これを一般化固有値問題と言い この問題に特化した多くの数値計算サブルーチンが存在する この行列は実対称行列なので 固有値はすべて実数となる よって 固有ベクトルも実ベクトルとなる [] [] []
33 電磁界解析のための有限要素法 FE 入門 この固有値問題を解くとモード毎に分離されて各モードのカットオフ波数 が固有値として モード関数の界分布のための重み係数ベクトル [ ] 5 が固有ベクトルとして求まる. 面分岐回路の解析 por por E dlr por 図 面分岐回路 この章では図 に示すような 面分岐回路の有限要素解析法 [5] について説明する また この例題を通してポートという概念とその取り扱いについて説明する ポート por とは導波管 同軸ケーブル マイクロストリップ線路 並行 本線路などの二次元構造をもつ 線路の軸方向には変化がない 線路の断面である マイクロ波回路などの応用例ではよく二次元構造をもつ線路からアンテナやマイクロ波回路などに電力を送りこみ その反射特性を知りたいという問題がよくある 例えば 携帯電話の例では 発信機で発信されたキャリアを変調し それをアンプに送って増幅する その増幅された信号は二次元構造の線路を通ってアンテナに伝わるが ここで反射が無いように設計をしたいことがよくある 実験ではネットワークアナライザを用いて反射 散乱特性を S パラメータで測定する. 問題の設定 微分方程式 境界条件 今回はスカラー基底関数を使ことにするので微分方程式はスカラーバージョン 付録.. を用いる
34 電磁界解析のための有限要素法 FE 入門 oudr odo E suppos E E ssr odo ẑ E E E 図 5 電磁波成分考察モデル また E E なので E だけで全電磁界を表現できる その理由は 付録.5 の説明による 電界が境界面に垂直な成分を持つとき 必然的に電界は境界面の進行方向接線成分をもたなければならない しかし 垂直成分が最初からないならば進行方向接線成分を持たなくても境界条件は満たす よって 図 が 面分岐回路として使われる場合 電界は 成分しかもたない すると 波なので つのスカラーポテンシャルだけで電磁界を完全に表現することができる E 面分岐回路について図 5 のモデルで考える 誘電体と空気層の境界条件を考える の境界条件を考えると E が存在するならば E を持たなければならない また E の境界条件を考えたとき が存在するならば を持たなければならない 今 E 面分岐回路を考えているので を持つことを前提としている 逆もまた真なので を持つならば を持たなければならない するとマクスウェルの方程式から E も存在してしまう ここでは 面分岐回路を扱うので E だけで完全に電磁界を表現できる E E 境界条件は 周囲の導体壁上で電界の接線成分が である. 重み付け残差法と弱形式 W E E ds ベクトル公式 5 V V V を使って式 7 を変形すると E WdS WE ds WE ds
35 電磁界解析のための有限要素法 FE 入門 5 E WdS dl WEdS WE E E WdS WEdS W dl ガラーキン法を用いるので 後でW E と選ぶことを考えると 線積分の項は境界上では消える ポート上では寄与が残るので次のようになる E E WdS l WEdS W d E E WdS WEdS W d ここで ポート上の電磁を次のように入射波と反射波のモードの和で表す ポート が基本モー で励振されているとすると L を高次モードの電界の 成分として ド E δ p β p β 7 また E モードの規格化モード関数 電力が W になっている は η π s β である β は位相定数である π の遮断モードでは が負になると減衰するようにしている はE モードのカットオフ波数である 次元の有限要素法解析を行う場合 伝送線路の断面は 次元となる その断面が方形導波管だけでなく 任意形状の場合でもモード関数と伝搬定数は 章 章のように二次元有限要素法解析で求めることができるからプログラムは複雑になるが可能である 問題を考える場合 反射波についてはマイクロ波回路からポートまでの距離を十分長くとっておけば高次モードは減衰するので 基本モードのみを考えればよい 式 7 を式 8 に代入して
36 電磁界解析のための有限要素法 FE 入門 [ ] p p d W ds WE WdS E β β β δ β d W d W ds WE WdS E p p β δ β β β. 離散化 l E E と展開する [ ] l d W d W ds W WdS E p p β δ β β β E と が未知数である 図 FE メッシュ
37 電磁界解析のための有限要素法 FE 入門 7 図 7 ポート上での重み付けこの式に対して l L で重み付けを行うと [ ] l d d ds ds E p p β δ β β β E L 8 ここで ds ds d L p β β d p β δ β 式 8 は決定問題であり 連立一次方程式を解くと未知数 E が求まる 入射波として用いる規格化固有モード関数の電力は定義から W なので 入射ポートが だけのときは はそのまま反射係数となる 入射ポートが 以外のときは は透過係数となる. 付録
38 電磁界解析のための有限要素法 FE 入門 8. ヘルムホルツの方程式の導出マクスウェルの方程式 wll s quo は波源からの放射問題を考えるとき 電界と磁界を未知数とする 元連立微分方程式であり つの未知数が混在しているため数値的に計算しにくい そこで つの方程式から 文字 電界または磁界 消去して電界だけ または磁界だけを未知数とするつの微分方程式を作り その微分方程式を解くことに集中する つの連立微分方程式から 文字消去したつの微分方程式は解が波動を表すヘルムホルツの方程式 lhol quo となる 次のマクスウェルの方程式からヘルムホルツの方程式を導出する J ωεe E ωµ wll s quo ここで ε ε r ε µ µ rµ であり µ 一般には場所の関数である ε はそれぞれ真空中の誘電率と透磁率である ε µ は 磁界のヘルムホルツ方程式 より ε r J ε r ε r J ε r ωε E ωε ωµ これを整理すると J µ r 磁界のヘルムホルツ方程式 9 ε r η ε r となる ただし η は真空中の界インピーダンスである 電界のヘルムホルツ方程式 より µ r
39 電磁界解析のための有限要素法 FE 入門 9 E µ r µ r µ r ωµ E ωµ J ωεe これを整理すると E ε re η J µ r µ r 電界のヘルムホルツ方程式 となる 式 9 は空間の至る所で成り立つ微分方程式である.. 導波管のベクトルヘルムホルツ方程式 図 8 導波管 波源が無く 導波管内が真空 ε のとき 式 のヘルムホルツ方程式は次のようになる E E r µ r ここで 第一項はベクトルラプラシアン を用いて次のように表される E E E 電荷がないから E E よって 波動方程式は E E となり 直角 カルテシアン 座標系では次のようになる E E E E
40 電磁界解析のための有限要素法 FE 入門 E 波の解析ここで E 波 波 の解析を考える 図 8 のような導波管を考えたとき E 波は電界の 成分を持たない また 上のヘルムホルツ方程式を変数分離法で解くことを考えると 方向には無限に長く 一様な構造をしているので各成分に共通の 成分依存項 Z p γ p γ が現れる その理由は フレネルの反射 透過係数を導出する際の位相整合条件と同じで そうならなければ境界条件を満足できないからである 反射波がなく 進行波だけが存在する状態を 考えると γ とおける 条件をまとめると E E 波を扱うから γ 方向に一様な構造をしているから E E E E E E として 電界の断面成分 E に対して次の方程式が成り立つ 電界の管軸方向成分は E 波なので 当然 である E γ E E E ここで γ であり をカットオフ波数 o wvur と言う その理由は γ ± だから α β を実数として ± α γ ± β > < であり 導波管内の電界が E E p γ で表されることを考えると が よりも大きくなると減衰せずに伝搬可能になるからであ
41 電磁界解析のための有限要素法 FE 入門 る カットオフ周波数 o rqu π λ π の計算はγ となるとき つまり π として求まる 周波数がカットオフ周波数を超えるとそのモードは伝搬可能となる 式 で 未知数は E と のつである よって これは固有値問題 gvlu prol であり が固有値 gvlu として E が固有関数 guo として求まる 離散化された各固有値に対する電磁界分布をモード od 姿態 と言う 有限要素法では式 の電磁界の導波管断面成分を導波管断面の管壁などの境界条件の下で解くことになる 式 の方程式は導波管だけではなく 方向に一様ならばどんな構造のものでも適用できるため 同軸ケーブルや平行 本線路 フィーダ などの 導体系の解析もできる そのときはカットオフ波数 の直流から伝搬するモード E 波 が存在する カットオフ波数 ということは式 のヘルムホルツの方程式はラプラスの方程式となる それが 同軸線路や平行 本線路の解析を行うときに断面成分を静電界で求め 進行方向成分を p γ として掛け算して線路上の電磁界分布を求めることができる理由である.. 導波管のスカラーヘルムホルツ方程式文献 [7] p. -7 より E 波に対しては磁界の 成分 だけを未知数とするスカラーヘルムホルツ方程式 波に対しては電界の 成分 E だけを未知数とするスカラーヘルムホルツ方程式 E E E を解き 簡単な計算で電磁界の断面成分も から求めることができる E E は次式で与えられる E E E ωµ γ γ E ωµ γ γ E ωε γ γ E ωε γ γ
42 電磁界解析のための有限要素法 FE 入門. 汎関数 変分 変分原理 汎関数汎関数 uol とは関数をパラメータ 変数 引数 とする関数である 関数よりもより上位のものとして見ているので汎関数と呼ばれる L δl LδL 図 9 汎関数と変分の説明 例えば 図 9 のような関数 を考える それをギターなどの弦を指で引っ張ったときの変位 と考える その弦の変位によるエネルギーのようなものを考え 次のように F[ ] で表す 汎関数 であることを強調するために引数には大括弧 [ ] を使う F [ ] { } d すると そのエネルギーらしき F はある値となり 関数 の形によって値が変わる つまり 関数 の関数になっており その意味で F は汎関数であると言う 図 汎関数の写像による説明 また 図 に示すように汎関数を写像により説明する 普通の関数はあるスカラー量 図中では複素数 C の集合を考えている を別のスカラー量に対応させるものであるが 汎関数はある関
43 電磁界解析のための有限要素法 FE 入門 数形をあるスカラー量に対応させるものであると考えることができる 変分図 9 に示すように関数 の形が δ 一般に微小変化を扱う だけ変わり δ となったときに汎関数の値はどれだけ δ F 変わるか言うのが変分 vro である 汎関数の変分は関数の微分に相当する量である 定義は微分と同じようなものであり 次のように定義してみる [ δ ] F[ ] F δf δ l δ δ 分子第 項の δ というのはつの関数の和 δ を意味することになる この定義は関数の微分と同じ定義になっているので 変分も関数 を文字と見なして関数と同様に微分する ことができる δ は関数のノルムである 変分の意味より変分の意味が明確になるように次のように定義してみる [ εg] F[ ] F δf ε l 5 ε ε ε はスカラーであり g は任意波形の関数である よって g の関数形 微小変化の与え方 に よって変分の値は変わる もし g ならば式 は式 5 の定義と一致する つまり 式 の定義では関数 を一様に上下に変化させようとしたときの変化量だと言える 関数と同様の微分公式を使って微分したら全体を上下に一様に変化させたときの変分を求めたことになるから なるべく式 5 の定義に従って微分するのが望ましい また 関数と同様の微分公式を使わなければ式 の定義に従って変分しても式 5 と同様の操作をしているので式 5 の定義に従って変分しているのと同じことになる より意味がわかりやすいような表現にするにはパラメータの関数 を δ だけ変化させて δ 量 δf を調べればよい としたときの汎関数の値 F[ δ ] から元の値 F[ ] δ F F [ δ ] F[ ] を引いて汎関数のδ による微小変化 例題 汎関数 F [ ] { } d を一様に変化させたときの変分を求めよ 解答一様に変化させるのであるから関数のように微分すればよい
44 電磁界解析のための有限要素法 FE 入門 δf δ d δ F δ 数値例 d のとき F [] δf δ F [.5]. 75 [.5] F F.5. F δ F から微小に変化させて F.5 にしたとき F δf とよく一致するからδF は変分であるという意味がよくわかる のとき F [ ] 8. δf 8δ F [.] F[.] F δ F 例題 次の汎関数の変分を求めよ F d [ ] d d 解答一様に変化させるとは言われていないし 微分があるので 定義に従って変分した方が楽である F F [ δ] [ δ] F[ ] d dδ δ d d d d d dδ dδ d d d d d dδ dδ d d d δ d δ d ここで 次の微小量は無視する δ が に比べて微小ならば d δ d も微小である なぜならば 図 9 に示すように振幅が小さく よって微係数も小さくなるからである
45 電磁界解析のための有限要素法 FE 入門 5 F [ δ] F[ ] あえてこの表現で止めておく d dδ δ d d d d dδ d δ d d d d d δ δ d δ d d d d d δd δ d d 変分原理微分方程式 D を解いて未知関数 を求める問題を考える ある汎関数 F[ ] が極値 変分が になるところ になるような 求めるとそれは D の解の と全く同じものになることがあ F の極値を求めることは微分方程式 D を解くのと全く等価になることがある そのようなとき 汎関数を変分して極値を求め 汎関数の極値問題と等価な微分方程式を求めることを変分原理 vrol prpl を適用すると言う 汎関数に変分原理を適用して得られる微分方程式はオイラーの微分方程式と呼ばれる ただし 極小値を求めるときには放物曲面のよ うに極小値はただつでなければならない δ F > 峰や鞍のような停留点があってもいけない 変分原理を適用して微分方程式を得る過程は電磁気学の分野でポテンシャルを微分してフィールドを求めたり 確率 統計の分野で積率母関数 o grg uo を微分してモーメント 積率 を求めたりするのに似ている 変分原理が使われている問題は数多く存在する 特に物理学の分野の一つである解析力学で汎関数や変分原理が多用される [8] ラグランジアン ハミルトニアンなどがあり 微分方程式を生成するので生成汎関数と呼ばれる 電磁界理論のモーメント法もガラーキン法を適用したら電流分布の微小変化に対して入力インピーダンスが変分表現になっており 安定な解を与えることが証明されている ICIprovd Cr hor[9] でも入力インピーダンスは電流分布の変分表現になっていることを利用して 変分原理を適用してアンテナ上の電流分布を求めている 変分原理は物理学では 系全体のエネルギー 汎関数 が最小になるように物理量 フィールドや温度 が分布する というエントロピー増大の原理のような最小エネルギー原理として解釈することができる フェルマー Fr の原理として知られる 屈折率が場所によって異なる媒質中の 点間を光が通るときの光路は 点間を光が通るのに要する時間を最小にする路である は 変分原理から来ている 屈折角はフレネルの反射 透過係数を求めるときに位相整合条件を適用して導出されるが 変分原理を用いてフェルマーの原理として解釈することもできる どちらの解釈も正しいのだが 慣れないうちは誰でも変分原理の考え方は理解しにくいのではないだろうか 筆者も変分原理による解釈は天下り的な感じがしてちょっと腑に落ちない る つまり 汎関数 [ ]
46 電磁界解析のための有限要素法 FE 入門 例題 次の微分方程式を解け d d ただし 境界条件 解答 d C d C C 境界条件を適用して積分定数を求めると C 9 C C よって 例題 例題 の汎関数に変分原理を適用し オイラーの微分方程式を導け ただし 例題 のときのように の値が で強制されている ディリクレ条件 とする 解答例題 の解答より F d d δd δ d d [ δ] F[ ] ここで の値が で強制されているので 微小変化させる関数 δ も の値を動かすことはできない よってδ δ となるような微小変化関数 δ を用いるので F d [ δ] F[ ] d δd これがいかなる関数 δ に対しても となるためには d d を満たす必要がある よって この汎関数の極値問題を解いて を求めればそれは上のオイラーの微分方程式の解である
47 電磁界解析のための有限要素法 FE 入門 7
48 電磁界解析のための有限要素法 FE 入門 8. 重み付け モーメント 図 区間 [] が図 上のように区間 [ ] で定義されている を区間 [ ] 全域で満たすようにしたい場合 その条件を書くとすれば例えば図 下に示されるような離散的な点で を満足するような条件を書く L は正かも知れないし負かもしれないが { } の条件式群をまとめて次のように書くことができる { } は絶対に正数なので 式 7 しかし 式 7 もまだ離散的な点でしか の条件を満足しないので 全区間で満たすようにするには 次のように離散点の間隔を無限に小さくする 図 区分求積
49 電磁界解析のための有限要素法 FE 入門 9 l { } これは区分求積 リーマン積分の定義 であり 次のように表現される { } d が式 8 を満たすとき は区間 [ ] 内の至る所で であり 目的の条件と等価になる ここで 式 8 は次のモーメントの定義 g d の特殊な場合である g を重み関数 wghg uo または試験関数 rl uo と言う 8 9 g 図 モーメント 式 9 の表現では図 に示されるように g の形によっては 区間 [ ] 内で が満たされるとは限らない しかし g と選び 式 8 の表現にすると式 8 を満たすことと 区間 [ ] 内で となることは等価となる g と選ぶ重み付けの方法はガラーキン法 Glr s hod と呼ばれ 数値的に安定した解を与える 有限要素法だけでなく モーメント法 o hod o os o hod でもよく使われる手法である. マクスウェルの方程式と境界条件 マクスウェルの方程式基礎方程式
50 電磁界解析のための有限要素法 FE 入門 5 ρ ρ ω ω D J D E 物性方程式 E D µ ε 等方性のとき J E E ωε ωµ 境界条件 s s s s ρ ρ D D J E E 上と下の条件式は同時に満たす 左右の条件式も同時に満たす 電気壁 PECPr Elr Coduor E ただし は境界法線方向の軸 は磁界の法線成分 は磁界の接線方向ベクトルである 証明 平面を境界面と考えて の証明をする E ωε
51 電磁界解析のための有限要素法 FE 入門 5 磁気壁 PCPr g Coduor E E
52 電磁界解析のための有限要素法 FE 入門 5.5 マイクロストリップ線路の準 E モード ε µ ε ε µ r h ε µ ε ε µ r h 図 マイクロストリップ線路 h 平面での境界条件から図 左に示すマイクロストリップ線路では E 波が存在しないことを示す 右のモデルで考察 h 平面での境界条件 : E と は連続 E ωµ E E r dlr E E r E E dlr 空気中でも誘電体中でも 方向の伝搬定数は同一 E r E dlr γ γ γ E E r dlr ε E E r ε E r dlr dlr dlr γ E は恒等的ににはなりえない 同様に よって E 波ではありえない 周波数が低いときは 成分はすごく小さいので準 E 波と呼ばれる
53 電磁界解析のための有限要素法 FE 入門 5. 物理定数 [ 参考 ] 理科年表 丸善 ε 9 真空の誘電率 prv 8.85 [F ] π 7 真空の透磁率 prl µ π [ ] 真空の波動インピーダンス η µ ε 7.7 π [ ] 8 真空中の光速 µ ε.998 [ ] 9 素電荷. [ C] s 電子の質量 9.9 [ g] 7 陽子の質量.7 [ g] 万有引力定数 G.7 [ g ] プランク定数 h. [ J s] p h h π.5 [ J s] 9 ボルツマン定数.8 [ J ] π
54 電磁界解析のための有限要素法 FE 入門 5.7 電気媒質定数 [ 参考 ] so FSS Vr.8 導体 実際には導電率は温度によって変化する の値を下の表に示す 媒質名 比誘電率 ε r 比透磁率 µ r 導電率 σ 7 S アルミニウム..8 真鍮.5 青銅. 銅 コバルト 5. クロム.7 金 グラファイト.7 鉄. 鉛 ニッケル.5 白金.9 銀 はんだ.7 ステンレス. チタン.8. タングステン.8 亜鉛.7 パラジウム.8.9
55 電磁界解析のための有限要素法 FE 入門 55 誘電体 実際には誘電率は温度 周波数によって変化する また 誘電体の分極は電子分極 原子分極 配向分極 界面分極などの複数の分極によって構成されており それらの分極が印加電界の周波数に追従できなくなり 急激に誘電率が変化する周波数がある 媒質名 比誘電率 ε r 比透磁率 µ r 導電率 σ S 真空 空気. テフロン. ダイアモンド.5. ダイアモンド 高圧 5.7 ガリウムヒ素.9 ガラス 5.5. ゴム 硬い. 5 サファイア シリコン.9 石英ガラス SO その他 周波数によって 誘電体と導体のどちらの性質が支配的となるかが変わる 媒質名 比誘電率 ε r 比透磁率 µ r 導電率 σ S フェライト. 蒸留水 水 綺麗 海水
56 電磁界解析のための有限要素法 FE 入門 5.8 ベクトル公式 θ os θ : と の間の角 θ s u û : から の方に回転する右ねじの進む方向の単位ベクトル C C C C C C 5 u 方向の単位ベクトル 7 8 V 9 V V V ここで V V V V V ラプラシアン 5 ベクトル ラプラシアン ϕ θ θ θ ρ ϕ ρ ϕ ρ ρ V r V r V r V V V V V V V s θ θ
57 電磁界解析のための有限要素法 FE 入門 57 7 ϕ θ θ θ θ ϕ ρ ρ ρ ρ ϕ θ ϕ ρ r r r r r r s s s 8 ϕ θ ϕ ρ θ ϕ θ θϕ θ θ ρ ϕ ρ ρϕ ρ ρ r r r r r r r r s s s 9 C S d d l S ストークスの定理 S V d dv S ガウスの発散定理 Gr の定理 Gr の第一公式 { } S V dv g g ds g Gr の第二公式 { } S V dv g g ds g g ここで は S の内部から外側に向かう S に垂直方向の座標である V S ds ds dl C S S V
58 電磁界解析のための有限要素法 FE 入門 58 Rr []. J. urr R. W. Clough. C. r d J. L. opp Sss d dlo lss o opl srurs Jourl o roul Ss vol. pp []. V.. Chr d P. P. Slvsr F Els Elrl d g Fld Prols Joh Wl & Sos 98. [] 小柴正則 高周波電磁界における有限要素法の基礎と実用例 電子情報通信学会 アンテナ 伝播研究専門委員会 ワークショップ第 回 年 月 日 [] 寺沢寛一 自然科学者のための数学概論応用編 岩波書店 995. [5] J. L. Vols F El hod or Elrogs IEEE Prss []. Slr-Pl l. Irv d Sl-dpv F-Els Elrog odlg rh ous 998. [7] 中島将光 マイクロ波工学基礎と原理 森北出版 998. [8] 杉田勝実 岡本良夫 関根松夫 経路積分と量子電磁気学 森北出版 998. [9]. Ig Iprovd Cr hor o ull IEEE rs. s d Propg. Vol. P-7 o. r. 99. [] S.. Ro D. R. Wlo. W. Glsso Elrog Srg Surs o rrr Shp IEEE rs o s d Propgo Vol. P- o []. ro J. row. do hod o os lss o wvgud rossd slo usg h god ss uos drvd h dg-sd -l hod IEE Prodgs rowv s d Propgo. Vol. 7 o. 5 pp.9-5 O.. [] 寺田文行 線形代数 サイエンスライブラリ理工系の数学 [] 笠原晧司 線形代数学 サイエンスライブラリ [] ギルバート ストラング 著 井上昭 翻訳 線形代数とその応用 産業図書 [5] Guspp Plos Roro Cool So Sllr Qu F Els or Elrog Wvs rh ous Lrr
59 電磁界解析のための有限要素法 FE 入門 59
パソコンシミュレータの現状
 第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
PowerPoint プレゼンテーション
 電磁波工学 第 5 回平面波の媒質への垂直および射入射と透過 柴田幸司 Bounda Plan Rgon ε μ Rgon Mdum ( ガラスなど ε μ z 平面波の反射と透過 垂直入射の場合 左図に示す様に 平面波が境界面に対して垂直に入射する場合を考える この時の入射波を とすると 入射波は境界において 透過波 と とに分解される この時の透過量を 反射量を Γ とおくと 領域 における媒質の誘電率に対して透過量
電磁波工学 第 5 回平面波の媒質への垂直および射入射と透過 柴田幸司 Bounda Plan Rgon ε μ Rgon Mdum ( ガラスなど ε μ z 平面波の反射と透過 垂直入射の場合 左図に示す様に 平面波が境界面に対して垂直に入射する場合を考える この時の入射波を とすると 入射波は境界において 透過波 と とに分解される この時の透過量を 反射量を Γ とおくと 領域 における媒質の誘電率に対して透過量
Microsoft PowerPoint - H21生物計算化学2.ppt
 演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
Microsoft Word - thesis.doc
 剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
PowerPoint Presentation
 付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
FEM原理講座 (サンプルテキスト)
 サンプルテキスト FEM 原理講座 サイバネットシステム株式会社 8 年 月 9 日作成 サンプルテキストについて 各講師が 講義の内容が伝わりやすいページ を選びました テキストのページは必ずしも連続していません 一部を抜粋しています 幾何光学講座については 実物のテキストではなくガイダンスを掲載いたします 対象とする構造系 物理モデル 連続体 固体 弾性体 / 弾塑性体 / 粘弾性体 / 固体
サンプルテキスト FEM 原理講座 サイバネットシステム株式会社 8 年 月 9 日作成 サンプルテキストについて 各講師が 講義の内容が伝わりやすいページ を選びました テキストのページは必ずしも連続していません 一部を抜粋しています 幾何光学講座については 実物のテキストではなくガイダンスを掲載いたします 対象とする構造系 物理モデル 連続体 固体 弾性体 / 弾塑性体 / 粘弾性体 / 固体
PowerPoint プレゼンテーション
 電磁波工学 第 6 回境界条件と伝送線路 柴田幸司 伝送線路とは 伝送線路とは光速で進む電磁波を構造体の中に閉じ込めて低損失にて伝送させるための線路であり 伝搬方向 断面方向に電磁波を閉じ込めるためには金属条件や誘電体の境界条件を利用する必要がある 開放型 TM 型 平行 線 誘電体型 誘電体線路 光ファイバ 閉鎖型 TM 型 同軸線路 導波路型 導波管 おのおのの伝送線路の形状に対する管内断面の電磁波の姿体の導出
電磁波工学 第 6 回境界条件と伝送線路 柴田幸司 伝送線路とは 伝送線路とは光速で進む電磁波を構造体の中に閉じ込めて低損失にて伝送させるための線路であり 伝搬方向 断面方向に電磁波を閉じ込めるためには金属条件や誘電体の境界条件を利用する必要がある 開放型 TM 型 平行 線 誘電体型 誘電体線路 光ファイバ 閉鎖型 TM 型 同軸線路 導波路型 導波管 おのおのの伝送線路の形状に対する管内断面の電磁波の姿体の導出
s ss s ss = ε = = s ss s (3) と表される s の要素における s s = κ = κ, =,, (4) jωε jω s は複素比誘電率に相当する物理量であり ここで PML 媒質定数を次のように定義する すなわち κξ をPML 媒質の等価比誘電率 ξ をPML 媒質の
 FDTD 解析法 (Matlab 版 2 次元 PML) プログラム解説 v2.11 1. 概要 FDTD 解析における吸収境界である完全整合層 (Perfectl Matched Laer, PML) の定式化とプログラミングを2 次元 TE 波について解説する PMLは異方性の損失をもつ仮想的な物質であり 侵入して来る電磁波を逃さず吸収する 通常の物質と接する界面でインピーダンスが整合しており
FDTD 解析法 (Matlab 版 2 次元 PML) プログラム解説 v2.11 1. 概要 FDTD 解析における吸収境界である完全整合層 (Perfectl Matched Laer, PML) の定式化とプログラミングを2 次元 TE 波について解説する PMLは異方性の損失をもつ仮想的な物質であり 侵入して来る電磁波を逃さず吸収する 通常の物質と接する界面でインピーダンスが整合しており
(Microsoft PowerPoint - \221\34613\211\361)
 計算力学 ~ 第 回弾性問題の有限要素解析 (Ⅱ)~ 修士 年後期 ( 選択科目 ) 担当 : 岩佐貴史 講義の概要 全 5 講義. 計算力学概論, ガイダンス. 自然現象の数理モデル化. 行列 場とその演算. 数値計算法 (Ⅰ) 5. 数値計算法 (Ⅱ) 6. 初期値 境界値問題 (Ⅰ) 7. 初期値 境界値問題 (Ⅱ) 8. マトリックス変位法による構造解析 9. トラス構造の有限要素解析. 重み付き残差法と古典的近似解法.
計算力学 ~ 第 回弾性問題の有限要素解析 (Ⅱ)~ 修士 年後期 ( 選択科目 ) 担当 : 岩佐貴史 講義の概要 全 5 講義. 計算力学概論, ガイダンス. 自然現象の数理モデル化. 行列 場とその演算. 数値計算法 (Ⅰ) 5. 数値計算法 (Ⅱ) 6. 初期値 境界値問題 (Ⅰ) 7. 初期値 境界値問題 (Ⅱ) 8. マトリックス変位法による構造解析 9. トラス構造の有限要素解析. 重み付き残差法と古典的近似解法.
反射係数
 平面波の反射と透過 電磁波の性質として, 反射と透過は最も基礎的な現象である. 我々の生活している空間は, 各種の形状を持った媒質で構成されている. 人間から見れば, 空気, 水, 木, 土, 火, 金属, プラスチックなど, 全く異なるものに見えるが, 電磁波からすると誘電率, 透磁率, 導電率が異なるだけである. 磁性体を除く媒質は比透磁率がで, ほとんど媒質に当てはまるので, 実質的に我々の身の回りの媒質で,
平面波の反射と透過 電磁波の性質として, 反射と透過は最も基礎的な現象である. 我々の生活している空間は, 各種の形状を持った媒質で構成されている. 人間から見れば, 空気, 水, 木, 土, 火, 金属, プラスチックなど, 全く異なるものに見えるが, 電磁波からすると誘電率, 透磁率, 導電率が異なるだけである. 磁性体を除く媒質は比透磁率がで, ほとんど媒質に当てはまるので, 実質的に我々の身の回りの媒質で,
例 e 指数関数的に減衰する信号を h( a < + a a すると, それらのラプラス変換は, H ( ) { e } e インパルス応答が h( a < ( ただし a >, U( ) { } となるシステムにステップ信号 ( y( のラプラス変換 Y () は, Y ( ) H ( ) X (
 第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
Microsoft PowerPoint - 10.pptx
 m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
平面波
 平面波 図.に示すように, 波源 ( 送信アンテナあるいは散乱点 ) から遠い位置で, 観測点 Pにおける波の状態を考えてみる. 遠いとは, 波長 λ に比べて距離 が十分大きいことを意味しており, 観測点 Pの近くでは, 等位相面が平面とみなせる状態にある. 平面波とは波の等位相面が平面になっている波のことである. 通信や計測を行うとき, 遠方における波の振舞いは平面波で近似できる. したがって平面波の性質を理解することが最も重要である.
平面波 図.に示すように, 波源 ( 送信アンテナあるいは散乱点 ) から遠い位置で, 観測点 Pにおける波の状態を考えてみる. 遠いとは, 波長 λ に比べて距離 が十分大きいことを意味しており, 観測点 Pの近くでは, 等位相面が平面とみなせる状態にある. 平面波とは波の等位相面が平面になっている波のことである. 通信や計測を行うとき, 遠方における波の振舞いは平面波で近似できる. したがって平面波の性質を理解することが最も重要である.
Microsoft PowerPoint - 第3回2.ppt
 講義内容 講義内容 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 ベクトルの直交性 3
講義内容 講義内容 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 ベクトルの直交性 3
多次元レーザー分光で探る凝縮分子系の超高速動力学
 波動方程式と量子力学 谷村吉隆 京都大学理学研究科化学専攻 http:theochem.kuchem.kyoto-u.ac.jp TA: 岩元佑樹 iwamoto.y@kuchem.kyoto-u.ac.jp ベクトルと行列の作法 A 列ベクトル c = c c 行ベクトル A = [ c c c ] 転置ベクトル T A = [ c c c ] AA 内積 c AA = [ c c c ] c =
波動方程式と量子力学 谷村吉隆 京都大学理学研究科化学専攻 http:theochem.kuchem.kyoto-u.ac.jp TA: 岩元佑樹 iwamoto.y@kuchem.kyoto-u.ac.jp ベクトルと行列の作法 A 列ベクトル c = c c 行ベクトル A = [ c c c ] 転置ベクトル T A = [ c c c ] AA 内積 c AA = [ c c c ] c =
DVIOUT-SS_Ma
 第 章 微分方程式 ニュートンはリンゴが落ちるのを見て万有引力を発見した という有名な逸話があります 無重力の宇宙船の中ではリンゴは落ちないで静止していることを考えると 重力が働くと始め静止しているものが動き出して そのスピードはどんどん大きくなる つまり速度の変化が現れることがわかります 速度は一般に時間と共に変化します 速度の瞬間的変化の割合を加速度といい で定義しましょう 速度が変化する, つまり加速度がでなくなるためにはその原因があり
第 章 微分方程式 ニュートンはリンゴが落ちるのを見て万有引力を発見した という有名な逸話があります 無重力の宇宙船の中ではリンゴは落ちないで静止していることを考えると 重力が働くと始め静止しているものが動き出して そのスピードはどんどん大きくなる つまり速度の変化が現れることがわかります 速度は一般に時間と共に変化します 速度の瞬間的変化の割合を加速度といい で定義しましょう 速度が変化する, つまり加速度がでなくなるためにはその原因があり
補足 中学で学習したフレミング左手の法則 ( 電 磁 力 ) と関連付けると覚えやすい 電磁力は電流と磁界の外積で表される 力 F 磁 電磁力 F li 右ねじの回転の向き電 li ( l は導線の長さ ) 補足 有向線分とベクトル有向線分 : 矢印の位
 http://totemt.sur.ne.p 外積 ( ベクトル積 ) の活用 ( 面積, 法線ベクトル, 平面の方程式 ) 3 次元空間の つのベクトルの積が つのベクトルを与えるようなベクトルの掛け算 ベクトルの積がベクトルを与えることからベクトル積とも呼ばれる これに対し内積は符号と大きさをもつ量 ( スカラー量 ) を与えるので, スカラー積とも呼ばれる 外積を使うと, 平行四辺形や三角形の面積,
http://totemt.sur.ne.p 外積 ( ベクトル積 ) の活用 ( 面積, 法線ベクトル, 平面の方程式 ) 3 次元空間の つのベクトルの積が つのベクトルを与えるようなベクトルの掛け算 ベクトルの積がベクトルを与えることからベクトル積とも呼ばれる これに対し内積は符号と大きさをもつ量 ( スカラー量 ) を与えるので, スカラー積とも呼ばれる 外積を使うと, 平行四辺形や三角形の面積,
テンソル ( その ) テンソル ( その ) スカラー ( 階のテンソル ) スカラー ( 階のテンソル ) 階数 ベクトル ( 階のテンソル ) ベクトル ( 階のテンソル ) 行列表現 シンボリック表現 [ ]
![テンソル ( その ) テンソル ( その ) スカラー ( 階のテンソル ) スカラー ( 階のテンソル ) 階数 ベクトル ( 階のテンソル ) ベクトル ( 階のテンソル ) 行列表現 シンボリック表現 [ ] テンソル ( その ) テンソル ( その ) スカラー ( 階のテンソル ) スカラー ( 階のテンソル ) 階数 ベクトル ( 階のテンソル ) ベクトル ( 階のテンソル ) 行列表現 シンボリック表現 [ ]](/thumbs/93/113587990.jpg) Tsor th-ordr tsor by dcl xprsso m m Lm m k m k L mk kk quott rul by symbolc xprsso Lk X thrd-ordr tsor cotrcto j j Copyrght s rsrvd. No prt of ths documt my b rproducd for proft. テンソル ( その ) テンソル ( その
Tsor th-ordr tsor by dcl xprsso m m Lm m k m k L mk kk quott rul by symbolc xprsso Lk X thrd-ordr tsor cotrcto j j Copyrght s rsrvd. No prt of ths documt my b rproducd for proft. テンソル ( その ) テンソル ( その
代数 幾何 < ベクトル > 1 ベクトルの演算 和 差 実数倍については 文字の計算と同様 2 ベクトルの成分表示 平面ベクトル : a x e y e x, ) ( 1 y1 空間ベクトル : a x e y e z e x, y, ) ( 1 1 z1
 代数 幾何 < ベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル :, 空間ベクトル : z,, z 成分での計算ができるようにすること ベクトルの内積 : os 平面ベクトル :,, 空間ベクトル :,,,, z z zz 4 ベクトルの大きさ 平面上 : 空間上 : z は 良く用いられる 5 m: に分ける点 : m m 図形への応用
代数 幾何 < ベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル :, 空間ベクトル : z,, z 成分での計算ができるようにすること ベクトルの内積 : os 平面ベクトル :,, 空間ベクトル :,,,, z z zz 4 ベクトルの大きさ 平面上 : 空間上 : z は 良く用いられる 5 m: に分ける点 : m m 図形への応用
Microsoft PowerPoint - em01.pptx
 No. 基礎 ~ マクスウェルの方程式 ~ t t D H B E d t d d d t d D l H B l E 微分形積分形 電磁気学の知識からマクスウェルの方程式を導く No. ファラデーの法則 V d dt E dl t B d ストークスの定理を使って E d E ファラデー : 近接作用 界の概念を提唱 B t t B d アンペアの法則 I H rh I H dl d r dl V
No. 基礎 ~ マクスウェルの方程式 ~ t t D H B E d t d d d t d D l H B l E 微分形積分形 電磁気学の知識からマクスウェルの方程式を導く No. ファラデーの法則 V d dt E dl t B d ストークスの定理を使って E d E ファラデー : 近接作用 界の概念を提唱 B t t B d アンペアの法則 I H rh I H dl d r dl V
数学 ⅡB < 公理 > 公理を論拠に定義を用いて定理を証明する 1 大小関係の公理 順序 (a > b, a = b, a > b 1 つ成立 a > b, b > c a > c 成立 ) 順序と演算 (a > b a + c > b + c (a > b, c > 0 ac > bc) 2 図
 数学 Ⅱ < 公理 > 公理を論拠に定義を用いて定理を証明する 大小関係の公理 順序 >, =, > つ成立 >, > > 成立 順序と演算 > + > + >, > > 図形の公理 平行線の性質 錯角 同位角 三角形の合同条件 三角形の合同相似 量の公理 角の大きさ 線分の長さ < 空間における座漂とベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル
数学 Ⅱ < 公理 > 公理を論拠に定義を用いて定理を証明する 大小関係の公理 順序 >, =, > つ成立 >, > > 成立 順序と演算 > + > + >, > > 図形の公理 平行線の性質 錯角 同位角 三角形の合同条件 三角形の合同相似 量の公理 角の大きさ 線分の長さ < 空間における座漂とベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル
Microsoft PowerPoint - 第5回電磁気学I
 1 年 11 月 8 日 ( 月 ) 1:-1: Y 平成 年度工 系 ( 社会環境工学科 ) 第 5 回電磁気学 Ⅰ 天野浩 項目 電界と電束密度 ガウスの発散定理とガウスの法則の積分形と微分形 * ファラデーの電気力線の使い方をマスターします * 電界と電束密度を定義します * ガウスの発散定理を用いて ガウスの法則の積分形から微分形をガウスの法則の積分形から微分形を導出します * ガウスの法則を用いて
1 年 11 月 8 日 ( 月 ) 1:-1: Y 平成 年度工 系 ( 社会環境工学科 ) 第 5 回電磁気学 Ⅰ 天野浩 項目 電界と電束密度 ガウスの発散定理とガウスの法則の積分形と微分形 * ファラデーの電気力線の使い方をマスターします * 電界と電束密度を定義します * ガウスの発散定理を用いて ガウスの法則の積分形から微分形をガウスの法則の積分形から微分形を導出します * ガウスの法則を用いて
Microsoft PowerPoint - H22制御工学I-2回.ppt
 制御工学 I 第二回ラプラス変換 平成 年 4 月 9 日 /4/9 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
制御工学 I 第二回ラプラス変換 平成 年 4 月 9 日 /4/9 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
Microsoft PowerPoint - シミュレーション工学-2010-第1回.ppt
 シミュレーション工学 ( 後半 ) 東京大学人工物工学研究センター 鈴木克幸 CA( Compter Aded geerg ) r. Jaso Lemo (SC, 98) 設計者が解析ツールを使いこなすことにより 設計の評価 設計の質の向上を図る geerg の本質の 計算機による支援 (CA CAM などより広い名前 ) 様々な汎用ソフトの登場 工業製品の設計に不可欠のツール 構造解析 流体解析
シミュレーション工学 ( 後半 ) 東京大学人工物工学研究センター 鈴木克幸 CA( Compter Aded geerg ) r. Jaso Lemo (SC, 98) 設計者が解析ツールを使いこなすことにより 設計の評価 設計の質の向上を図る geerg の本質の 計算機による支援 (CA CAM などより広い名前 ) 様々な汎用ソフトの登場 工業製品の設計に不可欠のツール 構造解析 流体解析
<4D F736F F D20824F B CC92E8979D814696CA90CF95AA82C691CC90CF95AA2E646F63>
 1/1 平成 23 年 3 月 24 日午後 6 時 52 分 6 ガウスの定理 : 面積分と体積分 6 ガウスの定理 : 面積分と体積分 Ⅰ. 直交座標系 ガウスの定理は 微分して すぐに積分すると元に戻るというルールを 3 次元積分に適用した定理になります よく知っているのは 簡単化のため 変数が1つの場合は dj ( d ( ににします全微分 = 偏微分 d = d = J ( + C d です
1/1 平成 23 年 3 月 24 日午後 6 時 52 分 6 ガウスの定理 : 面積分と体積分 6 ガウスの定理 : 面積分と体積分 Ⅰ. 直交座標系 ガウスの定理は 微分して すぐに積分すると元に戻るというルールを 3 次元積分に適用した定理になります よく知っているのは 簡単化のため 変数が1つの場合は dj ( d ( ににします全微分 = 偏微分 d = d = J ( + C d です
vecrot
 1. ベクトル ベクトル : 方向を持つ量 ベクトルには 1 方向 2 大きさ ( 長さ ) という 2 つの属性がある ベクトルの例 : 物体の移動速度 移動量電場 磁場の強さ風速力トルクなど 2. ベクトルの表現 2.1 矢印で表現される 矢印の長さ : ベクトルの大きさ 矢印の向き : ベクトルの方向 2.2 2 個の点を用いて表現する 始点 () と終点 () を結ぶ半直線の向き : ベクトルの方向
1. ベクトル ベクトル : 方向を持つ量 ベクトルには 1 方向 2 大きさ ( 長さ ) という 2 つの属性がある ベクトルの例 : 物体の移動速度 移動量電場 磁場の強さ風速力トルクなど 2. ベクトルの表現 2.1 矢印で表現される 矢印の長さ : ベクトルの大きさ 矢印の向き : ベクトルの方向 2.2 2 個の点を用いて表現する 始点 () と終点 () を結ぶ半直線の向き : ベクトルの方向
以下 変数の上のドットは時間に関する微分を表わしている (ex. 2 dx d x x, x 2 dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-1) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( x や x, x などがすべて 1 次で なおかつ
 以下 変数の上のドットは時間に関する微分を表わしている (e. d d, dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( や, などがすべて 次で なおかつそれらの係数が定数であるような微分方程式 ) に対して安定性の解析を行ってきた しかしながら 実際には非線形の微分方程式で記述される現象も多く存在する
以下 変数の上のドットは時間に関する微分を表わしている (e. d d, dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( や, などがすべて 次で なおかつそれらの係数が定数であるような微分方程式 ) に対して安定性の解析を行ってきた しかしながら 実際には非線形の微分方程式で記述される現象も多く存在する
ベクトル公式.rtf
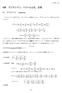 6 章ラプラシアン, ベクトル公式, 定理 6.1 ラプラシアン Laplacian φ はベクトル量である. そこでさらに発散をとると, φ はどういう形になるであろうか? φ = a + a + a φ a + a φ + a φ = φ + φ + φ = 2 φ + 2 φ 2 + 2 φ 2 2 φ = 2 φ 2 + 2 φ 2 + 2 φ 2 = 2 φ したがって,2 階の偏微分演算となる.
6 章ラプラシアン, ベクトル公式, 定理 6.1 ラプラシアン Laplacian φ はベクトル量である. そこでさらに発散をとると, φ はどういう形になるであろうか? φ = a + a + a φ a + a φ + a φ = φ + φ + φ = 2 φ + 2 φ 2 + 2 φ 2 2 φ = 2 φ 2 + 2 φ 2 + 2 φ 2 = 2 φ したがって,2 階の偏微分演算となる.
数学の世界
 東京女子大学文理学部数学の世界 (2002 年度 ) 永島孝 17 6 行列式の基本法則と効率的な計算法 基本法則 三次以上の行列式についても, 二次の場合と同様な法則がなりたつ ここには三次の場合を例示するが, 四次以上でも同様である 1 単位行列の行列式の値は 1 である すなわち 1 0 0 0 1 0 1 0 0 1 2 二つの列を入れ替えると行列式の値は 1 倍になる 例えば a 13 a
東京女子大学文理学部数学の世界 (2002 年度 ) 永島孝 17 6 行列式の基本法則と効率的な計算法 基本法則 三次以上の行列式についても, 二次の場合と同様な法則がなりたつ ここには三次の場合を例示するが, 四次以上でも同様である 1 単位行列の行列式の値は 1 である すなわち 1 0 0 0 1 0 1 0 0 1 2 二つの列を入れ替えると行列式の値は 1 倍になる 例えば a 13 a
Microsoft Word - 断面諸量
 応用力学 Ⅱ 講義資料 / 断面諸量 断面諸量 断面 次 次モーメントの定義 図 - に示すような形状を有する横断面を考え その全断面積を とする いま任意に定めた直交座標軸 O-, をとり また図中の斜線部の微小面積要素を d とするとき d, d () で定義される, をそれぞれ与えられた横断面の 軸, 軸に関する断面 次モーメント (geometrcal moment of area) という
応用力学 Ⅱ 講義資料 / 断面諸量 断面諸量 断面 次 次モーメントの定義 図 - に示すような形状を有する横断面を考え その全断面積を とする いま任意に定めた直交座標軸 O-, をとり また図中の斜線部の微小面積要素を d とするとき d, d () で定義される, をそれぞれ与えられた横断面の 軸, 軸に関する断面 次モーメント (geometrcal moment of area) という
Microsoft Word - NumericalComputation.docx
 数値計算入門 武尾英哉. 離散数学と数値計算 数学的解法の中には理論計算では求められないものもある. 例えば, 定積分は, まずは積分 ( 被積分関数の原始関数をみつけること できなければ値を得ることはできない. また, ある関数の所定の値における微分値を得るには, まずその関数の微分ができなければならない. さらに代数方程式の解を得るためには, 解析的に代数方程式を解く必要がある. ところが, これらは必ずしも解析的に導けるとは限らない.
数値計算入門 武尾英哉. 離散数学と数値計算 数学的解法の中には理論計算では求められないものもある. 例えば, 定積分は, まずは積分 ( 被積分関数の原始関数をみつけること できなければ値を得ることはできない. また, ある関数の所定の値における微分値を得るには, まずその関数の微分ができなければならない. さらに代数方程式の解を得るためには, 解析的に代数方程式を解く必要がある. ところが, これらは必ずしも解析的に導けるとは限らない.
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生
 0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
Microsoft PowerPoint - 9.pptx
 9/7/8( 水 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 拡大とスカラー倍 行列演算と写像 ( 次変換 拡大後 k 倍 k 倍 k 倍拡大の関係は スカラー倍を用いて次のように表現できる p = (, ' = k ' 拡大前 p ' = ( ', ' = ( k, k 拡大 4 拡大と行列の積 拡大後 k 倍
9/7/8( 水 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 拡大とスカラー倍 行列演算と写像 ( 次変換 拡大後 k 倍 k 倍 k 倍拡大の関係は スカラー倍を用いて次のように表現できる p = (, ' = k ' 拡大前 p ' = ( ', ' = ( k, k 拡大 4 拡大と行列の積 拡大後 k 倍
OCW-iダランベールの原理
 講義名連続体力学配布資料 OCW- 第 2 回ダランベールの原理 無機材料工学科准教授安田公一 1 はじめに今回の講義では, まず, 前半でダランベールの原理について説明する これを用いると, 動力学の問題を静力学の問題として解くことができ, さらに, 前回の仮想仕事の原理を適用すると動力学問題も簡単に解くことができるようになる また, 後半では, ダランベールの原理の応用として ラグランジュ方程式の導出を示す
講義名連続体力学配布資料 OCW- 第 2 回ダランベールの原理 無機材料工学科准教授安田公一 1 はじめに今回の講義では, まず, 前半でダランベールの原理について説明する これを用いると, 動力学の問題を静力学の問題として解くことができ, さらに, 前回の仮想仕事の原理を適用すると動力学問題も簡単に解くことができるようになる また, 後半では, ダランベールの原理の応用として ラグランジュ方程式の導出を示す
DVIOUT
 第 章 離散フーリエ変換 離散フーリエ変換 これまで 私たちは連続関数に対するフーリエ変換およびフーリエ積分 ( 逆フーリエ変換 ) について学んできました この節では フーリエ変換を離散化した離散フーリエ変換について学びましょう 自然現象 ( 音声 ) などを観測して得られる波 ( 信号値 ; 観測値 ) は 通常 電気信号による連続的な波として観測機器から出力されます しかしながら コンピュータはこの様な連続的な波を直接扱うことができないため
第 章 離散フーリエ変換 離散フーリエ変換 これまで 私たちは連続関数に対するフーリエ変換およびフーリエ積分 ( 逆フーリエ変換 ) について学んできました この節では フーリエ変換を離散化した離散フーリエ変換について学びましょう 自然現象 ( 音声 ) などを観測して得られる波 ( 信号値 ; 観測値 ) は 通常 電気信号による連続的な波として観測機器から出力されます しかしながら コンピュータはこの様な連続的な波を直接扱うことができないため
<4D F736F F F696E74202D20906C8D488AC28BAB90DD8C7689F090CD8D488A D91E F1>
 人工環境設計解析工学構造力学と有限要素法 ( 第 回 ) 東京大学新領域創成科学研究科 鈴木克幸 固体力学の基礎方程式 変位 - ひずみの関係 適合条件式 ひずみ - 応力の関係 構成方程式 応力 - 外力の関係 平衡方程式 境界条件 変位規定境界 反力規定境界 境界条件 荷重応力ひずみ変形 場の方程式 Γ t Γ t 平衡方程式構成方程式適合条件式 構造力学の基礎式 ひずみ 一軸 荷重応力ひずみ変形
人工環境設計解析工学構造力学と有限要素法 ( 第 回 ) 東京大学新領域創成科学研究科 鈴木克幸 固体力学の基礎方程式 変位 - ひずみの関係 適合条件式 ひずみ - 応力の関係 構成方程式 応力 - 外力の関係 平衡方程式 境界条件 変位規定境界 反力規定境界 境界条件 荷重応力ひずみ変形 場の方程式 Γ t Γ t 平衡方程式構成方程式適合条件式 構造力学の基礎式 ひずみ 一軸 荷重応力ひずみ変形
線形代数とは
 線形代数とは 第一回ベクトル 教科書 エクササイズ線形代数 立花俊一 成田清正著 共立出版 必要最低限のことに限る 得意な人には物足りないかもしれません 線形代数とは何をするもの? 線形関係 y 直線 yもも 次式で登場する (( 次の形 ) 線形 ただし 次元の話世の中は 3 次元 [4[ 次元 ] 次元 3 次元 4 次元 はどうやって直線を表すの? ベクトルや行列の概念 y A ベクトルを使うと
線形代数とは 第一回ベクトル 教科書 エクササイズ線形代数 立花俊一 成田清正著 共立出版 必要最低限のことに限る 得意な人には物足りないかもしれません 線形代数とは何をするもの? 線形関係 y 直線 yもも 次式で登場する (( 次の形 ) 線形 ただし 次元の話世の中は 3 次元 [4[ 次元 ] 次元 3 次元 4 次元 はどうやって直線を表すの? ベクトルや行列の概念 y A ベクトルを使うと
Microsoft PowerPoint - 9.pptx
 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 行列演算と写像 ( 次変換 3 拡大とスカラー倍 p ' = ( ', ' = ( k, kk p = (, k 倍 k 倍 拡大後 k 倍拡大の関係は スカラー倍を用いて次のように表現できる ' = k ' 拡大前 拡大 4 拡大と行列の積 p ' = ( ', '
9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 行列演算と写像 ( 次変換 3 拡大とスカラー倍 p ' = ( ', ' = ( k, kk p = (, k 倍 k 倍 拡大後 k 倍拡大の関係は スカラー倍を用いて次のように表現できる ' = k ' 拡大前 拡大 4 拡大と行列の積 p ' = ( ', '
H AB φ A,1s (r r A )Hφ B,1s (r r B )dr (9) S AB φ A,1s (r r A )φ B,1s (r r B )dr (10) とした (S AA = S BB = 1). なお,H ij は共鳴積分 (resonance integra),s ij は重
 半経験量子計算法 : Tight-binding( 強結合近似 ) 計算の基礎 1. 基礎 Tight-binding 近似 ( 強結合近似, TB 近似あるいは TB 法などとも呼ばれる ) とは, 電子が強く拘束されており隣り合う軌道へ自由に移動できない, とする近似であり, 自由電子近似とは対極にある. 但し, 軌道間はわずかに重なり合っているので, 全く飛び移れないわけではない. Tight-binding
半経験量子計算法 : Tight-binding( 強結合近似 ) 計算の基礎 1. 基礎 Tight-binding 近似 ( 強結合近似, TB 近似あるいは TB 法などとも呼ばれる ) とは, 電子が強く拘束されており隣り合う軌道へ自由に移動できない, とする近似であり, 自由電子近似とは対極にある. 但し, 軌道間はわずかに重なり合っているので, 全く飛び移れないわけではない. Tight-binding
電磁波解析入門セミナー 説明資料 All Rights Reserved, Copyright c Murata Software Co., Ltd. 1
 電磁波解析入門セミナー 説明資料 1 もくじ 1. 電磁波解析の概要 2. 電磁波解析の機能 設定の紹介 2 もくじ 1. 電磁波解析の概要 Femtet の3つの電磁界ソルバ... 4 電磁波解析の3つの種類... 5 調和解析... 6 導波路解析... 7 共振解析... 8 2. 電磁波解析の機能 設定の紹介 3 Femtet の 3 つの電磁界ソルバ Femtet には 3 つの電磁界ソルバがあります
電磁波解析入門セミナー 説明資料 1 もくじ 1. 電磁波解析の概要 2. 電磁波解析の機能 設定の紹介 2 もくじ 1. 電磁波解析の概要 Femtet の3つの電磁界ソルバ... 4 電磁波解析の3つの種類... 5 調和解析... 6 導波路解析... 7 共振解析... 8 2. 電磁波解析の機能 設定の紹介 3 Femtet の 3 つの電磁界ソルバ Femtet には 3 つの電磁界ソルバがあります
1/17 平成 29 年 3 月 25 日 ( 土 ) 午前 11 時 1 分量子力学とクライン ゴルドン方程式 ( 学部 3 年次秋学期向 ) 量子力学とクライン ゴルドン方程式 素粒子の満たす場 y ( x,t) の運動方程式 : クライン ゴルドン方程式 : æ 3 ö ç å è m= 0
 /7 平成 9 年 月 5 日 ( 土 午前 時 分量子力学とクライン ゴルドン方程式 ( 学部 年次秋学期向 量子力学とクライン ゴルドン方程式 素粒子の満たす場 (,t の運動方程式 : クライン ゴルドン方程式 : æ ö ç å è = 0 c + ( t =, 0 (. = 0 ì æ = = = ö æ ö æ ö ç ì =,,,,,,, ç 0 = ç Ñ 0 = ç Ñ 0 Ñ Ñ
/7 平成 9 年 月 5 日 ( 土 午前 時 分量子力学とクライン ゴルドン方程式 ( 学部 年次秋学期向 量子力学とクライン ゴルドン方程式 素粒子の満たす場 (,t の運動方程式 : クライン ゴルドン方程式 : æ ö ç å è = 0 c + ( t =, 0 (. = 0 ì æ = = = ö æ ö æ ö ç ì =,,,,,,, ç 0 = ç Ñ 0 = ç Ñ 0 Ñ Ñ
2009 年 11 月 16 日版 ( 久家 ) 遠地 P 波の変位波形の作成 遠地 P 波の変位波形 ( 変位の時間関数 ) は 波線理論をもとに P U () t = S()* t E()* t P() t で近似的に計算できる * は畳み込み積分 (convolution) を表す ( 付録
 遠地 波の変位波形の作成 遠地 波の変位波形 ( 変位の時間関数 ) は 波線理論をもとに U () t S() t E() t () t で近似的に計算できる は畳み込み積分 (convolution) を表す ( 付録 参照 ) ここで St () は地震の断層運動によって決まる時間関数 1 E() t は地下構造によって生じる種々の波の到着を与える時間関数 ( ここでは 直達 波とともに 震源そばの地表での反射波や変換波を与える時間関数
遠地 波の変位波形の作成 遠地 波の変位波形 ( 変位の時間関数 ) は 波線理論をもとに U () t S() t E() t () t で近似的に計算できる は畳み込み積分 (convolution) を表す ( 付録 参照 ) ここで St () は地震の断層運動によって決まる時間関数 1 E() t は地下構造によって生じる種々の波の到着を与える時間関数 ( ここでは 直達 波とともに 震源そばの地表での反射波や変換波を与える時間関数
線積分.indd
 線積分 線積分 ( n, n, n ) (ξ n, η n, ζ n ) ( n-, n-, n- ) (ξ k, η k, ζ k ) ( k, k, k ) ( k-, k-, k- ) 物体に力 を作用させて位置ベクトル A の点 A から位置ベクトル の点 まで曲線 に沿って物体を移動させたときの仕事 W は 次式で計算された A, A, W : d 6 d+ d+ d@,,, d+ d+
線積分 線積分 ( n, n, n ) (ξ n, η n, ζ n ) ( n-, n-, n- ) (ξ k, η k, ζ k ) ( k, k, k ) ( k-, k-, k- ) 物体に力 を作用させて位置ベクトル A の点 A から位置ベクトル の点 まで曲線 に沿って物体を移動させたときの仕事 W は 次式で計算された A, A, W : d 6 d+ d+ d@,,, d+ d+
Microsoft PowerPoint - 10.pptx
 0. 固有値とその応用 固有値と固有ベクトル 2 行列による写像から固有ベクトルへ m n A : m n n m 行列によって線形写像 f R R A が表せることを見てきた ここでは 2 次元平面の行列による写像を調べる 2 = 2 A 2 2 とし 写像 まず 単位ベクトルの像を求める u 2 x = v 2 y f : R A R を考える u 2 2 u, 2 2 0 = = v 2 0
0. 固有値とその応用 固有値と固有ベクトル 2 行列による写像から固有ベクトルへ m n A : m n n m 行列によって線形写像 f R R A が表せることを見てきた ここでは 2 次元平面の行列による写像を調べる 2 = 2 A 2 2 とし 写像 まず 単位ベクトルの像を求める u 2 x = v 2 y f : R A R を考える u 2 2 u, 2 2 0 = = v 2 0
<4D F736F F D20824F B834E835882CC92E8979D814690FC90CF95AA82C696CA90CF95AA2E646F63>
 1/10 平成 23 年 6 月 1 日午後 4 時 33 分 07 ストークスの定理 : 線積分と面積分 07 ストークスの定理 : 線積分と面積分 ストークスの定理はガウスの定理とともに 非常に重要な定理であり 線積分と面積分の関係を表します つまり ガウスの定理 : 面積分と体積分 ( 体積を囲む閉じた面 = 表面 ) の関係 ストークスの定理 : 線積分と面積分 ( 面積を囲む外周の線 )
1/10 平成 23 年 6 月 1 日午後 4 時 33 分 07 ストークスの定理 : 線積分と面積分 07 ストークスの定理 : 線積分と面積分 ストークスの定理はガウスの定理とともに 非常に重要な定理であり 線積分と面積分の関係を表します つまり ガウスの定理 : 面積分と体積分 ( 体積を囲む閉じた面 = 表面 ) の関係 ストークスの定理 : 線積分と面積分 ( 面積を囲む外周の線 )
数学 t t t t t 加法定理 t t t 倍角公式加法定理で α=β と置く. 三角関数
 . 三角関数 基本関係 t cot c sc c cot sc t 還元公式 t t t t t t cot t cot t 数学 数学 t t t t t 加法定理 t t t 倍角公式加法定理で α=β と置く. 三角関数 数学. 三角関数 5 積和公式 6 和積公式 数学. 三角関数 7 合成 t V v t V v t V V V V VV V V V t V v v 8 べき乗 5 6 6
. 三角関数 基本関係 t cot c sc c cot sc t 還元公式 t t t t t t cot t cot t 数学 数学 t t t t t 加法定理 t t t 倍角公式加法定理で α=β と置く. 三角関数 数学. 三角関数 5 積和公式 6 和積公式 数学. 三角関数 7 合成 t V v t V v t V V V V VV V V V t V v v 8 べき乗 5 6 6
2011年度 大阪大・理系数学
 0 大阪大学 ( 理系 ) 前期日程問題 解答解説のページへ a a を自然数とする O を原点とする座標平面上で行列 A= a の表す 次変換 を f とする cosθ siθ () >0 および0θ
0 大阪大学 ( 理系 ) 前期日程問題 解答解説のページへ a a を自然数とする O を原点とする座標平面上で行列 A= a の表す 次変換 を f とする cosθ siθ () >0 および0θ
ディジタル信号処理
 ディジタルフィルタの設計法. 逆フィルター. 直線位相 FIR フィルタの設計. 窓関数法による FIR フィルタの設計.5 時間領域での FIR フィルタの設計 3. アナログフィルタを基にしたディジタル IIR フィルタの設計法 I 4. アナログフィルタを基にしたディジタル IIR フィルタの設計法 II 5. 双 次フィルタ LI 離散時間システムの基礎式の証明 [ ] 4. ] [ ]*
ディジタルフィルタの設計法. 逆フィルター. 直線位相 FIR フィルタの設計. 窓関数法による FIR フィルタの設計.5 時間領域での FIR フィルタの設計 3. アナログフィルタを基にしたディジタル IIR フィルタの設計法 I 4. アナログフィルタを基にしたディジタル IIR フィルタの設計法 II 5. 双 次フィルタ LI 離散時間システムの基礎式の証明 [ ] 4. ] [ ]*
物性物理学 I( 平山 ) 補足資料 No.6 ( 量子ポイントコンタクト ) 右図のように 2つ物質が非常に小さな接点を介して接触している状況を考えましょう 物質中の電子の平均自由行程に比べて 接点のサイズが非常に小さな場合 この接点を量子ポイントコンタクトと呼ぶことがあります この系で左右の2つ
 物性物理学 I( 平山 ) 補足資料 No.6 ( 量子ポイントコンタクト ) 右図のように つ物質が非常に小さな接点を介して接触している状況を考えましょう 物質中の電子の平均自由行程に比べて 接点のサイズが非常に小さな場合 この接点を量子ポイントコンタクトと呼ぶことがあります この系で左右のつの物質の間に電位差を設けて左から右に向かって電流を流すことを行った場合に接点を通って流れる電流を求めるためには
物性物理学 I( 平山 ) 補足資料 No.6 ( 量子ポイントコンタクト ) 右図のように つ物質が非常に小さな接点を介して接触している状況を考えましょう 物質中の電子の平均自由行程に比べて 接点のサイズが非常に小さな場合 この接点を量子ポイントコンタクトと呼ぶことがあります この系で左右のつの物質の間に電位差を設けて左から右に向かって電流を流すことを行った場合に接点を通って流れる電流を求めるためには
2018年度 東京大・理系数学
 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ関数 f ( ) = + cos (0 < < ) の増減表をつくり, + 0, 0 のと sin きの極限を調べよ 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ n+ 数列 a, a, を, Cn a n = ( n =,, ) で定める n! an qn () n とする を既約分数 an p として表したときの分母
08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ関数 f ( ) = + cos (0 < < ) の増減表をつくり, + 0, 0 のと sin きの極限を調べよ 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ n+ 数列 a, a, を, Cn a n = ( n =,, ) で定める n! an qn () n とする を既約分数 an p として表したときの分母
横浜市環境科学研究所
 周期時系列の統計解析 単回帰分析 io 8 年 3 日 周期時系列に季節調整を行わないで単回帰分析を適用すると, 回帰係数には周期成分の影響が加わる. ここでは, 周期時系列をコサイン関数モデルで近似し単回帰分析によりモデルの回帰係数を求め, 周期成分の影響を検討した. また, その結果を気温時系列に当てはめ, 課題等について考察した. 気温時系列とコサイン関数モデル第 報の結果を利用するので, その一部を再掲する.
周期時系列の統計解析 単回帰分析 io 8 年 3 日 周期時系列に季節調整を行わないで単回帰分析を適用すると, 回帰係数には周期成分の影響が加わる. ここでは, 周期時系列をコサイン関数モデルで近似し単回帰分析によりモデルの回帰係数を求め, 周期成分の影響を検討した. また, その結果を気温時系列に当てはめ, 課題等について考察した. 気温時系列とコサイン関数モデル第 報の結果を利用するので, その一部を再掲する.
Microsoft Word - Chap17
 第 7 章化学反応に対する磁場効果における三重項機構 その 7.. 節の訂正 年 7 月 日. 節 章の9ページ の赤枠に記載した説明は間違いであった事に気付いた 以下に訂正する しかし.. 式は 結果的には正しいので安心して下さい 磁場 の存在下でのT 状態のハミルトニアン は ゼーマン項 と時間に依存するスピン-スピン相互作用の項 との和となる..=7.. g S = g S z = S z g
第 7 章化学反応に対する磁場効果における三重項機構 その 7.. 節の訂正 年 7 月 日. 節 章の9ページ の赤枠に記載した説明は間違いであった事に気付いた 以下に訂正する しかし.. 式は 結果的には正しいので安心して下さい 磁場 の存在下でのT 状態のハミルトニアン は ゼーマン項 と時間に依存するスピン-スピン相互作用の項 との和となる..=7.. g S = g S z = S z g
Microsoft Word - 微分入門.doc
 基本公式 例題 0 定義式 f( ) 数 Ⅲ 微分入門 = の導関数を定義式にもとづいて計算しなさい 基本事項 ( f( ), g( ) が微分可能ならば ) y= f( ) g( ) のとき, y = y= f( ) g( ) h( ) のとき, y = ( f( ), g( ) が微分可能で, g( ) 0 ならば ) f( ) y = のとき, y = g ( ) とくに, y = のとき,
基本公式 例題 0 定義式 f( ) 数 Ⅲ 微分入門 = の導関数を定義式にもとづいて計算しなさい 基本事項 ( f( ), g( ) が微分可能ならば ) y= f( ) g( ) のとき, y = y= f( ) g( ) h( ) のとき, y = ( f( ), g( ) が微分可能で, g( ) 0 ならば ) f( ) y = のとき, y = g ( ) とくに, y = のとき,
人間科学部研究年報平成 24 年 (1) (2) (3) (4) 式 (1) は, クーロン (Coulomb) の法則とも呼ばれる.ρは電荷密度を表し,ε 0 は真空の誘電率と呼ばれる定数である. 式 (2) は, 磁荷が存在しないことを表す式である. 式 (3) はファラデー (Faraday)
 複素振幅をもつ球面波の人間科学部研究年報 Maxwell 平成 24 方程式年 複素振幅をもつ球面波の Maxwell 方程式 Maxwell Equation of Spherical Wave with Complex Amplitude 戸上良弘 Yoshihiro TOGAMI Abstract 複素振幅をもつ球面波に関して, マクスウェル (Maxwell) 方程式との関係を考察した. 電気的な球面波としてのスカラーポテンシャルが与えられたとき,
複素振幅をもつ球面波の人間科学部研究年報 Maxwell 平成 24 方程式年 複素振幅をもつ球面波の Maxwell 方程式 Maxwell Equation of Spherical Wave with Complex Amplitude 戸上良弘 Yoshihiro TOGAMI Abstract 複素振幅をもつ球面波に関して, マクスウェル (Maxwell) 方程式との関係を考察した. 電気的な球面波としてのスカラーポテンシャルが与えられたとき,
構造力学Ⅰ第12回
 第 回材の座屈 (0 章 ) p.5~ ( 復習 ) モールの定理 ( 手順 ) 座屈とは 荷重により梁に生じた曲げモーメントをで除して仮想荷重と考える 座屈荷重 偏心荷重 ( 曲げと軸力 ) 断面の核 この仮想荷重に対するある点でのせん断力 たわみ角に相当する曲げモーメント たわみに相当する ( 例 ) 単純梁の支点のたわみ角 : は 図 を仮想荷重と考えたときの 点の支点反力 B は 図 を仮想荷重と考えたときのB
第 回材の座屈 (0 章 ) p.5~ ( 復習 ) モールの定理 ( 手順 ) 座屈とは 荷重により梁に生じた曲げモーメントをで除して仮想荷重と考える 座屈荷重 偏心荷重 ( 曲げと軸力 ) 断面の核 この仮想荷重に対するある点でのせん断力 たわみ角に相当する曲げモーメント たわみに相当する ( 例 ) 単純梁の支点のたわみ角 : は 図 を仮想荷重と考えたときの 点の支点反力 B は 図 を仮想荷重と考えたときのB
Laplace2.rtf
 =0 ラプラスの方程式は 階の微分方程式で, 一般的に3つの座標変数をもつ. ここでは, 直角座標系, 円筒座標系, 球座標系におけるラプラスの方程式の解き方を説明しよう. 座標変数ごとに方程式を分離し, それを解いていく方法は変数分離法と呼ばれる. 変数分離解と固有関数展開法. 直角座標系における 3 次元の偏微分方程式 = x + y + z =0 (.) を解くために,x, y, z について互いに独立な関数の積で成り立っていると考え,
=0 ラプラスの方程式は 階の微分方程式で, 一般的に3つの座標変数をもつ. ここでは, 直角座標系, 円筒座標系, 球座標系におけるラプラスの方程式の解き方を説明しよう. 座標変数ごとに方程式を分離し, それを解いていく方法は変数分離法と呼ばれる. 変数分離解と固有関数展開法. 直角座標系における 3 次元の偏微分方程式 = x + y + z =0 (.) を解くために,x, y, z について互いに独立な関数の積で成り立っていると考え,
Microsoft PowerPoint - 夏の学校(CFD).pptx
 /9/5 FD( 計算流体力学 ) の基礎理論 性能 運動分野 夏の学校 神戸大学大学院海事科学研究科勝井辰博 流体の質量保存 流体要素内の質量の増加率 [ 単位時間当たりの増加量 ] 単位時間に流体要素に流入する質量 流体要素 Fl lm (orol olm) v ( ) ガウスの定理 v( ) /9/5 = =( ) b=b =(b b b ) b= b = b + b + b アインシュタイン表記
/9/5 FD( 計算流体力学 ) の基礎理論 性能 運動分野 夏の学校 神戸大学大学院海事科学研究科勝井辰博 流体の質量保存 流体要素内の質量の増加率 [ 単位時間当たりの増加量 ] 単位時間に流体要素に流入する質量 流体要素 Fl lm (orol olm) v ( ) ガウスの定理 v( ) /9/5 = =( ) b=b =(b b b ) b= b = b + b + b アインシュタイン表記
Microsoft PowerPoint - H22制御工学I-10回.ppt
 制御工学 I 第 回 安定性 ラウス, フルビッツの安定判別 平成 年 6 月 日 /6/ 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
制御工学 I 第 回 安定性 ラウス, フルビッツの安定判別 平成 年 6 月 日 /6/ 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
Microsoft Word ã‡»ã…«ã‡ªã…¼ã…‹ã…žã…‹ã…³ã†¨åłºæœ›å•¤(佒芤喋çfl�)
 Cellulr uo nd heir eigenlues 東洋大学総合情報学部 佐藤忠一 Tdzu So Depren o Inorion Siene nd rs Toyo Uniersiy. まえがき 一次元セルオ-トマトンは数学的には記号列上の行列の固有値問題である 固有値問題の行列はふつう複素数体上の行列である 量子力学における固有値問題も無限次元ではあるが関数環上の行列でその成分は可換環である
Cellulr uo nd heir eigenlues 東洋大学総合情報学部 佐藤忠一 Tdzu So Depren o Inorion Siene nd rs Toyo Uniersiy. まえがき 一次元セルオ-トマトンは数学的には記号列上の行列の固有値問題である 固有値問題の行列はふつう複素数体上の行列である 量子力学における固有値問題も無限次元ではあるが関数環上の行列でその成分は可換環である
Microsoft Word - 5章摂動法.doc
 5 章摂動法 ( 次の Moller-Plesset (MP) 法のために ) // 水素原子など 電子系を除いては 原子系の Schrödiger 方程式を解析的に解くことはできない 分子系の Schrödiger 方程式の正確な数値解を求めることも困難である そこで Hartree-Fock(H-F) 法を導入した H-F 法は Schrödiger 方程式が与える全エネルギーの 99% を再現することができる優れた近似方法である
5 章摂動法 ( 次の Moller-Plesset (MP) 法のために ) // 水素原子など 電子系を除いては 原子系の Schrödiger 方程式を解析的に解くことはできない 分子系の Schrödiger 方程式の正確な数値解を求めることも困難である そこで Hartree-Fock(H-F) 法を導入した H-F 法は Schrödiger 方程式が与える全エネルギーの 99% を再現することができる優れた近似方法である
Microsoft PowerPoint EM2_15.ppt
 ( 第 5 回 ) 鹿間信介摂南大学理工学部電気電子工学科 後半部 (4~5 章 ) のまとめ 4. 導体 4.3 誘電体 5. 磁性体 5. 電気抵抗 演習 導体表面の電界強度 () 外部電界があっても導体内部の電界は ( ゼロ ) になる () 導体の電位は一定 () 導体表面は等電位面 (3) 導体表面の電界は導体に垂直 導体表面と平行な成分があると, 導体表面の電子が移動 導体表面の電界は不連続
( 第 5 回 ) 鹿間信介摂南大学理工学部電気電子工学科 後半部 (4~5 章 ) のまとめ 4. 導体 4.3 誘電体 5. 磁性体 5. 電気抵抗 演習 導体表面の電界強度 () 外部電界があっても導体内部の電界は ( ゼロ ) になる () 導体の電位は一定 () 導体表面は等電位面 (3) 導体表面の電界は導体に垂直 導体表面と平行な成分があると, 導体表面の電子が移動 導体表面の電界は不連続
ハートレー近似(Hartree aproximation)
 ハートリー近似 ( 量子多体系の平均場近似 1) 0. ハミルトニアンの期待値の変分がシュレディンガー方程式と等価であること 1. 独立粒子近似という考え方. 電子系におけるハートリー近似 3.3 電子系におけるハートリー近似 Mde by R. Okmoto (Kyushu Institute of Technology) filenme=rtree080609.ppt (0) ハミルトニアンの期待値の変分と
ハートリー近似 ( 量子多体系の平均場近似 1) 0. ハミルトニアンの期待値の変分がシュレディンガー方程式と等価であること 1. 独立粒子近似という考え方. 電子系におけるハートリー近似 3.3 電子系におけるハートリー近似 Mde by R. Okmoto (Kyushu Institute of Technology) filenme=rtree080609.ppt (0) ハミルトニアンの期待値の変分と
様々なミクロ計量モデル†
 担当 : 長倉大輔 ( ながくらだいすけ ) この資料は私の講義において使用するために作成した資料です WEB ページ上で公開しており 自由に参照して頂いて構いません ただし 内容について 一応検証してありますが もし間違いがあった場合でもそれによって生じるいかなる損害 不利益について責任を負いかねますのでご了承ください 間違いは発見次第 継続的に直していますが まだ存在する可能性があります 1 カウントデータモデル
担当 : 長倉大輔 ( ながくらだいすけ ) この資料は私の講義において使用するために作成した資料です WEB ページ上で公開しており 自由に参照して頂いて構いません ただし 内容について 一応検証してありますが もし間違いがあった場合でもそれによって生じるいかなる損害 不利益について責任を負いかねますのでご了承ください 間違いは発見次第 継続的に直していますが まだ存在する可能性があります 1 カウントデータモデル
PowerPoint Presentation
 応用数学 Ⅱ (7) 7 連立微分方程式の立て方と解法. 高階微分方程式による解法. ベクトル微分方程式による解法 3. 演算子による解法 連立微分方程式 未知数が複数個あり, 未知数の数だけ微分方程式が与えられている場合, これらを連立微分方程式という. d d 解法 () 高階微分方程式化による解法 つの方程式から つの未知数を消去して, 未知数が つの方程式に変換 のみの方程式にするために,
応用数学 Ⅱ (7) 7 連立微分方程式の立て方と解法. 高階微分方程式による解法. ベクトル微分方程式による解法 3. 演算子による解法 連立微分方程式 未知数が複数個あり, 未知数の数だけ微分方程式が与えられている場合, これらを連立微分方程式という. d d 解法 () 高階微分方程式化による解法 つの方程式から つの未知数を消去して, 未知数が つの方程式に変換 のみの方程式にするために,
第1章 単 位
 H. Hamano,. 長柱の座屈 - 長柱の座屈 長い柱は圧縮荷重によって折れてしまう場合がある. この現象を座屈といい, 座屈するときの荷重を座屈荷重という.. 換算長 長さ の柱に荷重が作用する場合, その支持方法によって, 柱の理論上の長さ L が異なる. 長柱の計算は, この L を用いて行うと都合がよい. この L を換算長 ( あるいは有効長さという ) という. 座屈荷重は一般に,
H. Hamano,. 長柱の座屈 - 長柱の座屈 長い柱は圧縮荷重によって折れてしまう場合がある. この現象を座屈といい, 座屈するときの荷重を座屈荷重という.. 換算長 長さ の柱に荷重が作用する場合, その支持方法によって, 柱の理論上の長さ L が異なる. 長柱の計算は, この L を用いて行うと都合がよい. この L を換算長 ( あるいは有効長さという ) という. 座屈荷重は一般に,
平成 年 月 7 日 ( 土 第 75 回数学教育実践研究会アスティ 45 ビル F セミナールーム A 札幌医科大学 年 P ab, を正の定数とする 平面上において ( a, を中心とする円 Q 4 C と (, b を中心とする円 C が 原点 O で外接している また P を円 C 上の点と
 平成 年 月 7 日 ( 土 第 75 回数学教育実践研究会アスティ 45 ビル F セミナールーム 微分積分の拡張 変数関数問題へのアプローチ 予選決勝優勝法からラグランジュ未定乗数法 松本睦郎 ( 札幌北高等学校 変数関数の最大値 最小値に関する問題には多様なアプローチ法がある 文字を固定した 予選決勝優勝法, 計算のみで解法する 文字消去法, 微分積分を利用した ラグランジュ未定乗数法 がある
平成 年 月 7 日 ( 土 第 75 回数学教育実践研究会アスティ 45 ビル F セミナールーム 微分積分の拡張 変数関数問題へのアプローチ 予選決勝優勝法からラグランジュ未定乗数法 松本睦郎 ( 札幌北高等学校 変数関数の最大値 最小値に関する問題には多様なアプローチ法がある 文字を固定した 予選決勝優勝法, 計算のみで解法する 文字消去法, 微分積分を利用した ラグランジュ未定乗数法 がある
<4D F736F F D E4F8E9F82C982A882AF82E98D7397F1>
 3 三次における行列 要旨高校では ほとんど 2 2 の正方行列しか扱ってなく 三次の正方行列について考えてみたかったため 数 C で学んだ定理を三次の正方行列に応用して 自分たちで仮説を立てて求めていったら 空間における回転移動を表す行列 三次のケーリー ハミルトンの定理 三次における逆行列を求めたり 仮説をたてることができた. 目的 数 C で学んだ定理を三次の正方行列に応用する 2. 概要目的の到達点として
3 三次における行列 要旨高校では ほとんど 2 2 の正方行列しか扱ってなく 三次の正方行列について考えてみたかったため 数 C で学んだ定理を三次の正方行列に応用して 自分たちで仮説を立てて求めていったら 空間における回転移動を表す行列 三次のケーリー ハミルトンの定理 三次における逆行列を求めたり 仮説をたてることができた. 目的 数 C で学んだ定理を三次の正方行列に応用する 2. 概要目的の到達点として
スライド 1
 暫定版修正 加筆の可能性あり ( 付録 ) 屈折率と誘電率 : 金属. 復習. 電気伝導度 3. アンペールの法則の修正 4. 表皮効果 表皮深さ 5. 鏡の反射 6. 整理 : 電子振動子模型 注意 : 整理しましょう! 前回 : 付録 (4) のアプローチ. 屈折率と損失について記述するために分極振動 ( 電気双極子の集団運動 ) による電気双極子放射を考慮. 誘電率は 真空中の値 を採用 オリジナル光
暫定版修正 加筆の可能性あり ( 付録 ) 屈折率と誘電率 : 金属. 復習. 電気伝導度 3. アンペールの法則の修正 4. 表皮効果 表皮深さ 5. 鏡の反射 6. 整理 : 電子振動子模型 注意 : 整理しましょう! 前回 : 付録 (4) のアプローチ. 屈折率と損失について記述するために分極振動 ( 電気双極子の集団運動 ) による電気双極子放射を考慮. 誘電率は 真空中の値 を採用 オリジナル光
Microsoft Word - 素粒子物理学I.doc
 6. 自発的対称性の破れとヒッグス機構 : 素粒子の標準模型 Dc 方程式.5 を導くラグランジアンは ϕ ϕ mϕϕ 6. である [H] Eu-nn 方程式 を使って 6. のラグランジア ンから Dc 方程式が導かれることを示せ 6. ゲージ対称性 6.. U 対称性 :QED ディラック粒子の複素場 ψに対する位相変換 ϕ ϕ 6. に対して ラグランジアンが不変であることを要請する これは簡単に示せる
6. 自発的対称性の破れとヒッグス機構 : 素粒子の標準模型 Dc 方程式.5 を導くラグランジアンは ϕ ϕ mϕϕ 6. である [H] Eu-nn 方程式 を使って 6. のラグランジア ンから Dc 方程式が導かれることを示せ 6. ゲージ対称性 6.. U 対称性 :QED ディラック粒子の複素場 ψに対する位相変換 ϕ ϕ 6. に対して ラグランジアンが不変であることを要請する これは簡単に示せる
座標系.rtf
 2 章座標系 場 空間は3 次元なので, ベクトルを表現するには少なくとも3 成分を指定する必要がある. そのために座標系が必要となる. 座標系として最も一般的なものは,,, 成分を使った直角座標系である. しかし, 他にも円柱座標, 球座標, だ円座標, 放物線座標など様々なものがある. 現在までに3 成分で変数分離可能な座標系は11 個あるといわれている (Moon & Spencer, Field
2 章座標系 場 空間は3 次元なので, ベクトルを表現するには少なくとも3 成分を指定する必要がある. そのために座標系が必要となる. 座標系として最も一般的なものは,,, 成分を使った直角座標系である. しかし, 他にも円柱座標, 球座標, だ円座標, 放物線座標など様々なものがある. 現在までに3 成分で変数分離可能な座標系は11 個あるといわれている (Moon & Spencer, Field
Microsoft Word - 1B2011.doc
 第 14 回モールの定理 ( 単純梁の場合 ) ( モールの定理とは何か?p.11) 例題 下記に示す単純梁の C 点のたわみ角 θ C と, たわみ δ C を求めよ ただし, 部材の曲げ 剛性は材軸に沿って一様で とする C D kn B 1.5m 0.5m 1.0m 解答 1 曲げモーメント図を描く,B 点の反力を求める kn kn 4 kn 曲げモーメント図を描く knm 先に得られた曲げモーメントの値を
第 14 回モールの定理 ( 単純梁の場合 ) ( モールの定理とは何か?p.11) 例題 下記に示す単純梁の C 点のたわみ角 θ C と, たわみ δ C を求めよ ただし, 部材の曲げ 剛性は材軸に沿って一様で とする C D kn B 1.5m 0.5m 1.0m 解答 1 曲げモーメント図を描く,B 点の反力を求める kn kn 4 kn 曲げモーメント図を描く knm 先に得られた曲げモーメントの値を
ニュートン重力理論.pptx
 3 ニュートン重力理論 1. ニュートン重力理論の基本 : 慣性系とガリレイ変換不変性 2. ニュートン重力理論の定式化 3. 等価原理 4. 流体力学方程式とその基礎 3.1 ニュートン重力理論の基本 u ニュートンの第一法則 = 力がかからなければ 等速直線運動を続ける u 等速直線運動に見える系を 慣性系 と呼ぶ ² 直線とはどんな空間の直線か? ニュートン理論では 3 次元ユークリッド空間
3 ニュートン重力理論 1. ニュートン重力理論の基本 : 慣性系とガリレイ変換不変性 2. ニュートン重力理論の定式化 3. 等価原理 4. 流体力学方程式とその基礎 3.1 ニュートン重力理論の基本 u ニュートンの第一法則 = 力がかからなければ 等速直線運動を続ける u 等速直線運動に見える系を 慣性系 と呼ぶ ² 直線とはどんな空間の直線か? ニュートン理論では 3 次元ユークリッド空間
領域シンポ発表
 1 次元の減衰運動の中の強制振動 ) ( f d d d d d e f e ce ) ( si ) ( 1 ) ( cos ω =ω -γ とおくと 一般解は 外力 f()=f siω の場合 f d d d d si f ce f ce si ) cos( cos si ) cos( この一般解は 1 φ は外力と変位との間の位相差で a 時間が経つと 第 1 項は無視できる この場合の振幅を
1 次元の減衰運動の中の強制振動 ) ( f d d d d d e f e ce ) ( si ) ( 1 ) ( cos ω =ω -γ とおくと 一般解は 外力 f()=f siω の場合 f d d d d si f ce f ce si ) cos( cos si ) cos( この一般解は 1 φ は外力と変位との間の位相差で a 時間が経つと 第 1 項は無視できる この場合の振幅を
Microsoft Word - 201hyouka-tangen-1.doc
 数学 Ⅰ 評価規準の作成 ( 単元ごと ) 数学 Ⅰ の目標及び図形と計量について理解させ 基礎的な知識の習得と技能の習熟を図り それらを的確に活用する機能を伸ばすとともに 数学的な見方や考え方のよさを認識できるようにする 評価の観点の趣旨 式と不等式 二次関数及び図形と計量における考え方に関 心をもつとともに 数学的な見方や考え方のよさを認識し それらを事象の考察に活用しようとする 式と不等式 二次関数及び図形と計量における数学的な見
数学 Ⅰ 評価規準の作成 ( 単元ごと ) 数学 Ⅰ の目標及び図形と計量について理解させ 基礎的な知識の習得と技能の習熟を図り それらを的確に活用する機能を伸ばすとともに 数学的な見方や考え方のよさを認識できるようにする 評価の観点の趣旨 式と不等式 二次関数及び図形と計量における考え方に関 心をもつとともに 数学的な見方や考え方のよさを認識し それらを事象の考察に活用しようとする 式と不等式 二次関数及び図形と計量における数学的な見
微分方程式による現象記述と解きかた
 微分方程式による現象記述と解きかた 土木工学 : 公共諸施設 構造物の有用目的にむけた合理的な実現をはかる方法 ( 技術 ) に関する学 橋梁 トンネル ダム 道路 港湾 治水利水施設 安全化 利便化 快適化 合法則的 経済的 自然および人口素材によって作られた 質量保存則 構造物の自然的な性質 作用 ( 外力による応答 ) エネルギー則 の解明 社会的諸現象のうち マスとしての移動 流通 運動量則
微分方程式による現象記述と解きかた 土木工学 : 公共諸施設 構造物の有用目的にむけた合理的な実現をはかる方法 ( 技術 ) に関する学 橋梁 トンネル ダム 道路 港湾 治水利水施設 安全化 利便化 快適化 合法則的 経済的 自然および人口素材によって作られた 質量保存則 構造物の自然的な性質 作用 ( 外力による応答 ) エネルギー則 の解明 社会的諸現象のうち マスとしての移動 流通 運動量則
2018年度 2次数学セレクション(微分と積分)
 08 次数学セレクション問題 [ 東京大 ] > 0 とし, f = x - x とおく () x で f ( x ) が単調に増加するための, についての条件を求めよ () 次の 条件を満たす点 (, b) の動きうる範囲を求め, 座標平面上に図示せよ 条件 : 方程式 f = bは相異なる 実数解をもつ 条件 : さらに, 方程式 f = bの解を < < とすると > である -- 08 次数学セレクション問題
08 次数学セレクション問題 [ 東京大 ] > 0 とし, f = x - x とおく () x で f ( x ) が単調に増加するための, についての条件を求めよ () 次の 条件を満たす点 (, b) の動きうる範囲を求め, 座標平面上に図示せよ 条件 : 方程式 f = bは相異なる 実数解をもつ 条件 : さらに, 方程式 f = bの解を < < とすると > である -- 08 次数学セレクション問題
破壊の予測
 本日の講義内容 前提 : 微分積分 線形代数が何をしているかはうろ覚え 材料力学は勉強したけど ちょっと 弾性および塑性学は勉強したことが無い ー > ですので 解らないときは質問してください モールの応力円を理解するとともに 応力を 3 次元的に考える FM( 有限要素法 の概略 内部では何を計算しているのか? 3 物が壊れる条件を考える 特に 変形 ( 塑性変形 が発生する条件としてのミーゼス応力とはどのような応力か?
本日の講義内容 前提 : 微分積分 線形代数が何をしているかはうろ覚え 材料力学は勉強したけど ちょっと 弾性および塑性学は勉強したことが無い ー > ですので 解らないときは質問してください モールの応力円を理解するとともに 応力を 3 次元的に考える FM( 有限要素法 の概略 内部では何を計算しているのか? 3 物が壊れる条件を考える 特に 変形 ( 塑性変形 が発生する条件としてのミーゼス応力とはどのような応力か?
3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x0 = f x= x0 t f c x f =0 [1] c f 0 x= x 0 x 0 f x= x0 x 2 x 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考
![3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x0 = f x= x0 t f c x f =0 [1] c f 0 x= x 0 x 0 f x= x0 x 2 x 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考 3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x0 = f x= x0 t f c x f =0 [1] c f 0 x= x 0 x 0 f x= x0 x 2 x 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考](/thumbs/103/158269281.jpg) 3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x = f x= x t f c x f = [1] c f x= x f x= x 2 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考える まず 初期時刻 t=t に f =R f exp [ik x ] [3] のような波動を与えたとき どのように時間変化するか調べる
3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x = f x= x t f c x f = [1] c f x= x f x= x 2 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考える まず 初期時刻 t=t に f =R f exp [ik x ] [3] のような波動を与えたとき どのように時間変化するか調べる
1/30 平成 29 年 3 月 24 日 ( 金 ) 午前 11 時 25 分第三章フェルミ量子場 : スピノール場 ( 次元あり ) 第三章フェルミ量子場 : スピノール場 フェルミ型 ボーズ量子場のエネルギーは 第二章ボーズ量子場 : スカラー場 の (2.18) より ˆ dp 1 1 =
 / 平成 9 年 月 日 ( 金 午前 時 5 分第三章フェルミ量子場 : スピノール場 ( 次元あり 第三章フェルミ量子場 : スピノール場 フェルミ型 ボーズ量子場のエネルギーは 第二章ボーズ量子場 : スカラー場 の (.8 より ˆ ( ( ( q -, ( ( c ( H c c ë é ù û - Ü + c ( ( - に限る (. である 一方 フェルミ型は 成分をもち その成分を,,,,
/ 平成 9 年 月 日 ( 金 午前 時 5 分第三章フェルミ量子場 : スピノール場 ( 次元あり 第三章フェルミ量子場 : スピノール場 フェルミ型 ボーズ量子場のエネルギーは 第二章ボーズ量子場 : スカラー場 の (.8 より ˆ ( ( ( q -, ( ( c ( H c c ë é ù û - Ü + c ( ( - に限る (. である 一方 フェルミ型は 成分をもち その成分を,,,,
OpenFOAM(R) ソースコード入門 pt1 熱伝導方程式の解法から有限体積法の実装について考える 前編 : 有限体積法の基礎確認 2013/11/17 オープンCAE 富山富山県立大学中川慎二
 OpenFOAM(R) ソースコード入門 pt1 熱伝導方程式の解法から有限体積法の実装について考える 前編 : 有限体積法の基礎確認 2013/11/17 オープンCAE 勉強会 @ 富山富山県立大学中川慎二 * OpenFOAM のソースコードでは, 基礎式を偏微分方程式の形で記述する.OpenFOAM 内部では, 有限体積法を使ってこの微分方程式を解いている. どのようにして, 有限体積法に基づく離散化が実現されているのか,
OpenFOAM(R) ソースコード入門 pt1 熱伝導方程式の解法から有限体積法の実装について考える 前編 : 有限体積法の基礎確認 2013/11/17 オープンCAE 勉強会 @ 富山富山県立大学中川慎二 * OpenFOAM のソースコードでは, 基礎式を偏微分方程式の形で記述する.OpenFOAM 内部では, 有限体積法を使ってこの微分方程式を解いている. どのようにして, 有限体積法に基づく離散化が実現されているのか,
Microsoft PowerPoint - 物情数学C(2012)(フーリエ前半)_up
 年度物理情報工学科 年生秋学期 物理情報数学 C フーリエ解析 (Fourier lysis) 年 月 5 日 フーリエ ( フランス ) (768~83: ナポレオンの時代 ) 歳で Ecole Polyechique ( フランス国立理工科大学 ) の教授 ナポレオンのエジプト遠征に従軍 (798) 87: 任意の関数は三角関数によって級数展開できる という フーリエ級数 の概念を提唱 ( 論文を提出
年度物理情報工学科 年生秋学期 物理情報数学 C フーリエ解析 (Fourier lysis) 年 月 5 日 フーリエ ( フランス ) (768~83: ナポレオンの時代 ) 歳で Ecole Polyechique ( フランス国立理工科大学 ) の教授 ナポレオンのエジプト遠征に従軍 (798) 87: 任意の関数は三角関数によって級数展開できる という フーリエ級数 の概念を提唱 ( 論文を提出
Microsoft PowerPoint _量子力学短大.pptx
 . エネルギーギャップとrllouゾーン ブリルアン領域,t_8.. 周期ポテンシャル中の電子とエネルギーギャップ 簡単のため 次元に間隔 で原子が並んでいる結晶を考える 右方向に進行している電子の波は 間隔 で規則正しく並んでいる原子が作る格子によって散乱され 左向きに進行する波となる 波長 λ が の時 r の反射条件 式を満たし 両者の波が互いに強め合い 定在波を作る つまり 式 式を満たす波は
. エネルギーギャップとrllouゾーン ブリルアン領域,t_8.. 周期ポテンシャル中の電子とエネルギーギャップ 簡単のため 次元に間隔 で原子が並んでいる結晶を考える 右方向に進行している電子の波は 間隔 で規則正しく並んでいる原子が作る格子によって散乱され 左向きに進行する波となる 波長 λ が の時 r の反射条件 式を満たし 両者の波が互いに強め合い 定在波を作る つまり 式 式を満たす波は
Chap3.key
 区分求積法. 面積 ( )/ f () > n + n, S 長方形の和集合で近似 n f (n ) リーマン和 f (n ) 区分求積法 リーマン和 S S n n / n n f ()d リーマン積分 ( + ) + S (, f ( )) 微分の心 Zoom In して局所的な性質を調べる 積分の心 Zoom Ou して大域的な性質を調べる 曲線の長さ 領域の面積や体積 ある領域に含まれる物質の質量
区分求積法. 面積 ( )/ f () > n + n, S 長方形の和集合で近似 n f (n ) リーマン和 f (n ) 区分求積法 リーマン和 S S n n / n n f ()d リーマン積分 ( + ) + S (, f ( )) 微分の心 Zoom In して局所的な性質を調べる 積分の心 Zoom Ou して大域的な性質を調べる 曲線の長さ 領域の面積や体積 ある領域に含まれる物質の質量
解析力学B - 第11回: 正準変換
 解析力学 B 第 11 回 : 正準変換 神戸大 : 陰山聡 ホームページ ( 第 6 回から今回までの講義ノート ) http://tinyurl.com/kage2010 2011.01.27 正準変換 バネ問題 ( あえて下手に座標をとった ) ハミルトニアンを考える q 正準方程式は H = p2 2m + k 2 (q l 0) 2 q = H p = p m ṗ = H q = k(q
解析力学 B 第 11 回 : 正準変換 神戸大 : 陰山聡 ホームページ ( 第 6 回から今回までの講義ノート ) http://tinyurl.com/kage2010 2011.01.27 正準変換 バネ問題 ( あえて下手に座標をとった ) ハミルトニアンを考える q 正準方程式は H = p2 2m + k 2 (q l 0) 2 q = H p = p m ṗ = H q = k(q
Microsoft Word - 中村工大連携教材(最終 ).doc
 音速について考えてみよう! 金沢工業大学 中村晃 ねらい 私たちの身の回りにはいろいろな種類の波が存在する. 体感できる波もあれば, できない波もある. その中で音は体感できる最も身近な波である. 遠くで雷が光ってから雷鳴が届くまで数秒間時間がかかることにより, 音の方が光より伝わるのに時間がかかることも経験していると思う. 高校の物理の授業で音の伝わる速さ ( 音速 ) は約 m/s で, 詳しく述べると
音速について考えてみよう! 金沢工業大学 中村晃 ねらい 私たちの身の回りにはいろいろな種類の波が存在する. 体感できる波もあれば, できない波もある. その中で音は体感できる最も身近な波である. 遠くで雷が光ってから雷鳴が届くまで数秒間時間がかかることにより, 音の方が光より伝わるのに時間がかかることも経験していると思う. 高校の物理の授業で音の伝わる速さ ( 音速 ) は約 m/s で, 詳しく述べると
Microsoft PowerPoint - CSA_B3_EX2.pptx
 Computer Science A Hardware Design Excise 2 Handout V2.01 May 27 th.,2019 CSAHW Computer Science A, Meiji University CSA_B3_EX2.pptx 32 Slides Renji Mikami 1 CSAHW2 ハード演習内容 2.1 二次元空間でのベクトルの直交 2.2 Reserved
Computer Science A Hardware Design Excise 2 Handout V2.01 May 27 th.,2019 CSAHW Computer Science A, Meiji University CSA_B3_EX2.pptx 32 Slides Renji Mikami 1 CSAHW2 ハード演習内容 2.1 二次元空間でのベクトルの直交 2.2 Reserved
Microsoft PowerPoint - mp11-02.pptx
 数理計画法第 2 回 塩浦昭義情報科学研究科准教授 shioura@dais.is.tohoku.ac.jp http://www.dais.is.tohoku.ac.jp/~shioura/teaching 前回の復習 数理計画とは? 数理計画 ( 復習 ) 数理計画問題とは? 狭義には : 数理 ( 数学 ) を使って計画を立てるための問題 広義には : 与えられた評価尺度に関して最も良い解を求める問題
数理計画法第 2 回 塩浦昭義情報科学研究科准教授 shioura@dais.is.tohoku.ac.jp http://www.dais.is.tohoku.ac.jp/~shioura/teaching 前回の復習 数理計画とは? 数理計画 ( 復習 ) 数理計画問題とは? 狭義には : 数理 ( 数学 ) を使って計画を立てるための問題 広義には : 与えられた評価尺度に関して最も良い解を求める問題
応用数学Ⅱ 偏微分方程式(2) 波動方程式(12/13)
 偏微分方程式. 偏微分方程式の形 偏微分 偏導関数 つの独立変数 をもつ関数 があるとき 変数 が一定値をとって だけが変化したとす ると は だけの関数となる このとき を について微分して得られる関数を 関数 の に関する 偏微分係数 略して偏微分 あるいは偏導関数 pil deiie といい 次のように表される についても同様な偏微分を定義できる あるいは あるいは - あるいは あるいは -
偏微分方程式. 偏微分方程式の形 偏微分 偏導関数 つの独立変数 をもつ関数 があるとき 変数 が一定値をとって だけが変化したとす ると は だけの関数となる このとき を について微分して得られる関数を 関数 の に関する 偏微分係数 略して偏微分 あるいは偏導関数 pil deiie といい 次のように表される についても同様な偏微分を定義できる あるいは あるいは - あるいは あるいは -
Microsoft Word - 補論3.2
 補論 3. 多変量 GARC モデル 07//6 新谷元嗣 藪友良 対数尤度関数 3 章 7 節では 変量の対数尤度を求めた ここでは多変量の場合 とくに 変量について対数尤度を求める 誤差項 は平均 0 で 次元の正規分布に従うとする 単純化のため 分散と共分散は時間を通じて一定としよう ( この仮定は後で変更される ) したがって ij から添え字 を除くことができる このとき と の尤度関数は
補論 3. 多変量 GARC モデル 07//6 新谷元嗣 藪友良 対数尤度関数 3 章 7 節では 変量の対数尤度を求めた ここでは多変量の場合 とくに 変量について対数尤度を求める 誤差項 は平均 0 で 次元の正規分布に従うとする 単純化のため 分散と共分散は時間を通じて一定としよう ( この仮定は後で変更される ) したがって ij から添え字 を除くことができる このとき と の尤度関数は
DVIOUT
 最適レギュレータ 松尾研究室資料 第 最適レギュレータ 節時不変型無限時間最適レギュレータ 状態フィードバックの可能な場合の無限時間問題における最適レギュレータについて確定系について説明する. ここで, レギュレータとは状態量をゼロにするようなコントローラのことである. なぜ, 無限時間問題のみを述べるかという理由は以下のとおりである. 有限時間の最適レギュレータ問題の場合の最適フィードバックゲインは微分方程式の解から構成される時間関数として表現される.
最適レギュレータ 松尾研究室資料 第 最適レギュレータ 節時不変型無限時間最適レギュレータ 状態フィードバックの可能な場合の無限時間問題における最適レギュレータについて確定系について説明する. ここで, レギュレータとは状態量をゼロにするようなコントローラのことである. なぜ, 無限時間問題のみを述べるかという理由は以下のとおりである. 有限時間の最適レギュレータ問題の場合の最適フィードバックゲインは微分方程式の解から構成される時間関数として表現される.
第 4 週コンボリューションその 2, 正弦波による分解 教科書 p. 16~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問 1. 以下の図にならって,1 と 2 の δ 関数を図示せよ δ (t) 2
 第 4 週コンボリューションその, 正弦波による分解 教科書 p. 6~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問. 以下の図にならって, と の δ 関数を図示せよ. - - - δ () δ ( ) - - - 図 δ 関数の図示の例 δ ( ) δ ( ) δ ( ) δ ( ) δ ( ) - - - - - - - -
第 4 週コンボリューションその, 正弦波による分解 教科書 p. 6~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問. 以下の図にならって, と の δ 関数を図示せよ. - - - δ () δ ( ) - - - 図 δ 関数の図示の例 δ ( ) δ ( ) δ ( ) δ ( ) δ ( ) - - - - - - - -
PowerPoint Presentation
 Non-linea factue mechanics き裂先端付近の塑性変形 塑性域 R 破壊進行領域応カ特異場 Ω R R Hutchinson, Rice and Rosengen 全ひずみ塑性理論に基づいた解析 現段階のひずみは 除荷がないとすると現段階の応力で一義的に決まる 単純引張り時の応カーひずみ関係 ( 構成方程式 ): ( ) ( ) n () y y y ここで α,n 定数, /
Non-linea factue mechanics き裂先端付近の塑性変形 塑性域 R 破壊進行領域応カ特異場 Ω R R Hutchinson, Rice and Rosengen 全ひずみ塑性理論に基づいた解析 現段階のひずみは 除荷がないとすると現段階の応力で一義的に決まる 単純引張り時の応カーひずみ関係 ( 構成方程式 ): ( ) ( ) n () y y y ここで α,n 定数, /
第6章 実験モード解析
 第 6 章実験モード解析 6. 実験モード解析とは 6. 有限自由度系の実験モード解析 6.3 連続体の実験モード解析 6. 実験モード解析とは 実験モード解析とは加振実験によって測定された外力と応答を用いてモードパラメータ ( 固有振動数, モード減衰比, 正規固有モードなど ) を求める ( 同定する ) 方法である. 力計 試験体 変位計 / 加速度計 実験モード解析の概念 時間領域データを利用する方法
第 6 章実験モード解析 6. 実験モード解析とは 6. 有限自由度系の実験モード解析 6.3 連続体の実験モード解析 6. 実験モード解析とは 実験モード解析とは加振実験によって測定された外力と応答を用いてモードパラメータ ( 固有振動数, モード減衰比, 正規固有モードなど ) を求める ( 同定する ) 方法である. 力計 試験体 変位計 / 加速度計 実験モード解析の概念 時間領域データを利用する方法
電磁気学 IV 第 7 回導体内の電磁界 表皮効果 ( 電磁気ノート19 章を参照 ) 工学部電気電子工学科松嶋徹 授業のスケジュール ( 順番変更 ) 6 月 12 日 ( 第 1 回 ) 電磁気学的な量 一般直交座標におけるベクトル演算 6 月 14 日 ( 第 2 回 )
 電磁気学 IV 08.07.03 第 7 回導体内の電磁界 表皮効果 ( 電磁気ノート9 章を参照 ) 工学部電気電子工学科松嶋徹 授業のスケジュール ( 順番変更 ) 6 月 日 ( 第 回 ) 電磁気学的な量 一般直交座標におけるベクトル演算 6 月 4 日 ( 第 回 ) 時間的に変化がない場 静電界 静磁界 定常電流界 6 月 9 日 ( 第 3 回 ) 定常的な場のシミュレーション 6 月
電磁気学 IV 08.07.03 第 7 回導体内の電磁界 表皮効果 ( 電磁気ノート9 章を参照 ) 工学部電気電子工学科松嶋徹 授業のスケジュール ( 順番変更 ) 6 月 日 ( 第 回 ) 電磁気学的な量 一般直交座標におけるベクトル演算 6 月 4 日 ( 第 回 ) 時間的に変化がない場 静電界 静磁界 定常電流界 6 月 9 日 ( 第 3 回 ) 定常的な場のシミュレーション 6 月
2011年度 筑波大・理系数学
 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ O を原点とするy 平面において, 直線 y= の を満たす部分をC とする () C 上に点 A( t, ) をとるとき, 線分 OA の垂直二等分線の方程式を求めよ () 点 A が C 全体を動くとき, 線分 OA の垂直二等分線が通過する範囲を求め, それ を図示せよ -- 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ
0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ O を原点とするy 平面において, 直線 y= の を満たす部分をC とする () C 上に点 A( t, ) をとるとき, 線分 OA の垂直二等分線の方程式を求めよ () 点 A が C 全体を動くとき, 線分 OA の垂直二等分線が通過する範囲を求め, それ を図示せよ -- 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ
2 図微小要素の流体の流入出 方向の断面の流体の流入出の収支断面 Ⅰ から微小要素に流入出する流体の流量 Q 断面 Ⅰ は 以下のように定式化できる Q 断面 Ⅰ 流量 密度 流速 断面 Ⅰ の面積 微小要素の断面 Ⅰ から だけ移動した断面 Ⅱ を流入出する流体の流量 Q 断面 Ⅱ は以下のように
 3 章 Web に Link 解説 連続式 微分表示 の誘導.64 *4. 連続式連続式は ある領域の内部にある流体の質量の収支が その表面からの流入出の合計と等しくなることを定式化したものであり 流体における質量保存則を示したものである 2. 連続式 微分表示 の誘導図のような微小要素 コントロールボリューム の領域内の流体の増減と外部からの流体の流入出を考えることで定式化できる 微小要素 流入
3 章 Web に Link 解説 連続式 微分表示 の誘導.64 *4. 連続式連続式は ある領域の内部にある流体の質量の収支が その表面からの流入出の合計と等しくなることを定式化したものであり 流体における質量保存則を示したものである 2. 連続式 微分表示 の誘導図のような微小要素 コントロールボリューム の領域内の流体の増減と外部からの流体の流入出を考えることで定式化できる 微小要素 流入
<4D F736F F D2097CD8A7793FC96E582BD82ED82DD8A E6318FCD2E646F63>
 - 第 章たわみ角法の基本式 ポイント : たわみ角法の基本式を理解する たわみ角法の基本式を梁の微分方程式より求める 本章では たわみ角法の基本式を導くことにする 基本式の誘導法は各種あるが ここでは 梁の微分方程式を解いて基本式を求める方法を採用する この本で使用する座標系は 右手 右ネジの法則に従った座標を用いる また ひとつの部材では 図 - に示すように部材の左端の 点を原点とし 軸線を
- 第 章たわみ角法の基本式 ポイント : たわみ角法の基本式を理解する たわみ角法の基本式を梁の微分方程式より求める 本章では たわみ角法の基本式を導くことにする 基本式の誘導法は各種あるが ここでは 梁の微分方程式を解いて基本式を求める方法を採用する この本で使用する座標系は 右手 右ネジの法則に従った座標を用いる また ひとつの部材では 図 - に示すように部材の左端の 点を原点とし 軸線を
memo
 数理情報工学特論第一 機械学習とデータマイニング 4 章 : 教師なし学習 3 かしまひさし 鹿島久嗣 ( 数理 6 研 ) kashima@mist.i.~ DEPARTMENT OF MATHEMATICAL INFORMATICS 1 グラフィカルモデルについて学びます グラフィカルモデル グラフィカルラッソ グラフィカルラッソの推定アルゴリズム 2 グラフィカルモデル 3 教師なし学習の主要タスクは
数理情報工学特論第一 機械学習とデータマイニング 4 章 : 教師なし学習 3 かしまひさし 鹿島久嗣 ( 数理 6 研 ) kashima@mist.i.~ DEPARTMENT OF MATHEMATICAL INFORMATICS 1 グラフィカルモデルについて学びます グラフィカルモデル グラフィカルラッソ グラフィカルラッソの推定アルゴリズム 2 グラフィカルモデル 3 教師なし学習の主要タスクは
計算機シミュレーション
 . 運動方程式の数値解法.. ニュートン方程式の近似速度は, 位置座標 の時間微分で, d と定義されます. これを成分で書くと, d d li li とかけます. 本来は が の極限をとらなければいけませんが, 有限の小さな値とすると 秒後の位置座標は速度を用いて, と近似できます. 同様にして, 加速度は, 速度 の時間微分で, d と定義されます. これを成分で書くと, d d li li とかけます.
. 運動方程式の数値解法.. ニュートン方程式の近似速度は, 位置座標 の時間微分で, d と定義されます. これを成分で書くと, d d li li とかけます. 本来は が の極限をとらなければいけませんが, 有限の小さな値とすると 秒後の位置座標は速度を用いて, と近似できます. 同様にして, 加速度は, 速度 の時間微分で, d と定義されます. これを成分で書くと, d d li li とかけます.
数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュ
 数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュレーションによって計算してみる 4.1 放物運動一様な重力場における放物運動を考える 一般に質量の物体に作用する力をとすると運動方程式は
数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュレーションによって計算してみる 4.1 放物運動一様な重力場における放物運動を考える 一般に質量の物体に作用する力をとすると運動方程式は
