<4D F736F F D F91E595AA8D8290EA8B D2082D082B882DD C838B834D815B82C6895E93AE C838B834D815B82F08E C682B582BD8D5C91A295948DDE82CC8EA AE82CC955D89BF82C982C282A282C45F8AAE90A
|
|
|
- りえ にかどり
- 5 years ago
- Views:
Transcription
1 大分工業高等専門学校紀要第 50 号 ( 平成 5 年 11 月 ) ひずみエネルギーと運動エネルギーを指標とした 構造部材の自由振動の評価について 清成康平 1 名木野晴暢 水澤富作 3 三上隆 4 1 九州大学大学院 本校都市 環境工学科 3 大同大学 4 北海道大学 構造物の自由振動特性は固有値問題を解くことで得られる固有円振動数とこれに対応する固有振動モードによって評価されるが これらの情報のみでは構造物の自由振動における支配的な変形成分とそれらの割合などを定量的に把握することが難しい. よって 構造物の動力学的挙動を把握 解明する上で 構造物の自由振動状態を定量的に評価することができる指標の存在は重要である. 本稿では 基本的な構造部材である矩形板の自由振動問題を例に取り ひずみエネルギーと運動エネルギーを指標とした矩形板の自由振動状態の定量的な評価について検討し その有用性や効果性について明らかにした. キーワード : 矩形板 自由振動 ひずみエネルギー 運動エネルギー 三次元弾性論 1. まえがき w v 自然災害の影響を大きく受ける我が国の構造物は 地震 台風 波浪や落石などの周波数特性を有する動的荷重を受ける. したがって これらの動的荷重を受ける構造物の精確な動力学的挙動を把握することは 構造物の合理的かつ安全な設計 維持管理に不可欠である. 構造物の動力学的挙動の把握において 基礎的な情報を提供してくれるものが固有円振動数と固有振動モードである. これらは構造物の時間依存性の運動方程式から調和振動の仮定により 時間依存性を排除した空間のみに関する連立偏微分方程式の境界値問題 いわゆる自由振動問題 ( 固有値問題 )を解くことによって得ることができる. また 固有円振動数と固有振動モードは 構造物の運動方程式の余解に相当するため その完全解を知る上で必要不可欠なものである. さて 何らかの離散化手法によれば 減衰の影響を無視した構造物の自由振動問題は 一般的に次式のような一般固有値問題で表される. ([K] w [M]){ } {0} - D = (1) ただし (rd / sec)は固有円振動数 ( 固有値 )[K]は構造物の剛性マトリックス [M]は構造物の質量マトリックスであり {}は固有円振動数 に対応する固有振動モード ( 固有ベクトル )である. この式 (1) を解けば 構造物の固有円振動数 (rd / sec) 固有周期 T (sec) 固有振動数 f (H) とこれらに対応する固有振動モードが求められる. しかし 固有円振動数と固有振動モードの情報のみでは 構造物の o 図 -1 矩形板と直交座標系 自由振動における支配的な変形成分やその割合などの振動状態を把握することが難しい. したがって 構造物の自由振動状態を定量的に評価できる指標の存在は重要であり これは構造物の自由振動特性および動力学的挙動の把握 理解の手助けになるであろう. 本稿では 基本的な構造部材である矩形板の自由振動問題を例に取り ひずみエネルギーと運動エネルギーを指標とした矩形板の自由振動状態の定量的な評価について検討し その有用性や効果性について明らかにした.. 解析モデル (1) 解析モデルと解析仮定 図 -1 に 矩形板 直交座標系および変位方向の定義を示す. ここで は矩形板の長さ は幅であり は板 u 58
2 大分工業高等専門学校紀要第 50 号 ( 平成 5 年 11 月 ) 厚である. また 矩形板の下面 ( = 0)および上面 ( = ) は自由面とする. なお 方向の時間依存性の変位成分は時間変数を として それぞれ u ( ) v ( ) w ( ) ( 以下 u v w)で表す. 等質 等方な材料からなる矩形板は微小変形かつ線形弾性であるとし 三次元弾性論に基づいて解析する. また その運動は調和振動を仮定する. () 基礎方程式と境界条件三次元弾性論に基づく矩形板の運動方程式は 次のように表される 1). 1 e r u u + = 1- n G 1 e r v v + = 1- n G 1 e r w w + =. () 1- n G ここで = + + e = e + e + e E G = (1 + n) (3) であり は Lplce の演算子 e は体積ひずみ は後述するひずみ成分 G はせん断弾性係数 E は縦弾性係数 はポアソン比でありは密度である. 三次元弾性論に基づく矩形板のひずみ成分は 次式のように表される 1). u v w u v e = e = e = g = + v w g = + w u g = +. (4) また 応力成分は 次式のように表される 1). s = le + me s = le + me s = le + me = mg mg ここで = = mg. (5) n l = m m = G (6) 1 - n であり とは Lmé の定数である. 調和振動する矩形板の変位成分 u v w は 振幅変位 u v w を用いて 次のように表すことができる. e rw v + + v = 0 1- n G 1 e rw w + + w = 0. (8) 1- n G ここで 1 e = e + e + e (9) であり e は時間依存性を排除した体積ひずみである. なお 時間依存性を排除したひずみ成分および応力成分は それぞれ 次のように表される. u v w u v e = e = e = g = + g v w = + w u g = +. (10) s = le + me s = le + me s = le + me = mg mg = = mg. (11) 矩形板の周面 ( = 0 および = 0 )における境界条件は 次のように定義される. () 単純支持面 () 固定面 (c) 自由面 v = w = 0 s = 0 ( = 0 ) u = w = 0 s = 0 ( = 0 ). (1) u = v = w = 0 ( = 0 ) u = v = w = 0 ( = 0 ). (13) s = = = 0 ( = 0 ) s = = = 0 ( = 0 ). (14) よって 式 (8) で表される基礎方程式を式 (1) 式 (13) および式 (14) で与えられる境界条件の下で解けば 固有円振動数 とこれに対応する固有振動モード( 振幅変位 u v w ) が求められる. i u () ue () - w = i v () ve () - w = 3. エネルギー解析 i w () we () - w =. (7) ただし は固有円振動数であり i = 1は虚数単位である. よって 式 (7) を式 () に代入すれば 時間依存性を排除した空間のみに関する基礎方程式が得られる. e rw u + + u = 0 1- n G 1 ここでは ひずみエネルギーと運動エネルギーを指標とした矩形板の自由振動状態の評価方法について述べる. 矩形板のひずみエネルギー は 次のように与えられる. 1 = ( se se se g g g )dv. òòò V (15) 59
3 大分工業高等専門学校紀要第 50 号 ( 平成 5 年 11 月 ) ただし V は体積を意味する. また 矩形板の運動エネルギー T は 次のように与えられる. r óóó ìïæ ö æ ö æ ö üï u v w T = ôôô ï ï í + + ýdv. ç ç ç õõõ è ø è ø è ø Vïî ïþ (16) ここで 式 (7) を式 (15) と式 (16) に代入すれば 時間依存性を排除した最大ひずみエネルギー m と最大運動エネルギー T m は それぞれ 次のように表される. m 1 = ( ò0 ò0 ò se + se + se + g + g 0 + g )ddd. rw Tm = ( u + v + w )ddd ここで (17) ò ò ò. (18) 1 = se ddd ( i = ) ii i i ò ò ò 1 = g ddd ( i j = ; i ¹ j) ij ij ij ò ò ò rw T u ddd = ò ò ò rw TVV v ddd = ò ò ò rw TWW w ddd と置けば 次のように表すことができる. = ò ò ò (19) m = (0) Tm = T + TVV + TWW. (1) 例として矩形板の曲げ振動を対象とすれば は曲げ変形 は面外伸縮変形 は面外せん断変形に関するひずみエネルギーを意味し これらの値は矩形板の自由振動状態におけるそれぞれの変形成分の割合を表していると解釈できる. 同様に考えれば T T VV は面 内変位 T WW は面外変位に関する運動エネルギーを意味し これらの値は矩形板の自由振動状態における面内慣性と面外慣性の影響の割合を表していると解釈できよう. これより 各ひずみエネルギー成分や各運動エネルギー成分の値を比較したり 値の変化を調べたりすることで 矩形板の自由振動状態を定量的に評価することができる. なお 式 (19) で定義される各ひずみエネルギー成分および各運動エネルギー成分の値の計算には Guss-Legendre の数値積分を用いた. 式 (19) から明らかなように 矩形板の各ひずみエネルギー成分および各運動エネルギー成分の値を求めるためには 矩形板の固有円振動数とこれに対応する固有振動モードが既知でなければならない. これらは 式 (8) で表される基礎方程式を式 (1) 式 (13) および式 (14) で与えられる境界条件の下で解くことで得られるが 任意の支持条件を有する矩形板では厳密解を得ることが困難になり また解析解は支持条件に制限を受ける. そこで 本稿では 任意の支 ) 持条件を有する矩形板の自由振動問題をB-spline Ri 法 により解析することとした. これによれば 任意の支持条件を有する薄板から厚板までの低次から高次までの固有円振動数と固有振動モードを高い解析精度で求めることが可能である.B-spline Ri 法による矩形板の自由振動問題の解析については 文献 )を参考にされたい. 4. 数値計算例および考察 ここでは ひずみエネルギーと運動エネルギーを指標とした矩形板の自由振動状態の定量的な評価について検討し その有用性や効果性を明らかにする. 本稿では 板厚と辺長を表す無次元量を それぞれ 板厚比 辺長比 / と定義し 固有円振動数は次式の振動数パラメータとして表す. r W= w () E 表 -1 周面単純支持矩形薄板の基本振動の振動数パラメータと各エネルギー成分の収束性および精度比較 m m m 1s T WW CPT CPT
4 大分工業高等専門学校紀要第 50 号 ( 平成 5 年 11 月 ) (i) = 0.1 (ii) = () 対称曲げ振動の振動数パラメータ (iii) = 0.5 () 対称曲げ振動の振動モード 図 - 周面単純支持矩形板の対称曲げ振動の振動数パラメータと振動モードに与える板厚比の影響 Srin energies 0. s Kineic energies 0. T () 運動エネルギー 図 -3 周面単純支持矩形板の対称曲げ振動のひずみエネルギーと運動エネルギーに与える板厚比の影響 数値計算には personl compuer(windows 7 Professionl 64 i)を用い Forrn( インテル Visul Forrn Composer XE インテル M Kernel Lirr)の倍精度計算で行った. また 振動数パラメータ 各ひずみエネルギー成分および各運動エネルギー成分の値は有効数字四桁で整理した. なお 数値計算例では 特に断りがない限り 正方形板 ( / = 1)とし ポアソン比 = 0.3 を用い 方向の spline 次数 (k 1) (k 1) (k 1)は 応力 ひずみ場までが連続なることを考慮し また 文献 )を参考にして 板厚比 5 である薄板の問題では spline 次数 (k 1) (k 1) (k 1) = 4 4 板厚比 > 5 である中等厚板から厚板の問題では spline 次数 (k 1) (k 1) (k 1) = 4 4 3に設定した. (1) 数値解の収束性および妥当性表 -1 には 周面単純支持矩形薄板の基本振動 ( 最低次 ) の振動数パラメータ 1s ひずみエネルギー成分および運 表 - 周面単純支持矩形板の対称曲げ振動状態 s + + T 動エネルギー成分の収束性と精度比較が示してある. ここで 板厚は = 01 1 に設定した. また 板厚方向の区分点の数 m は 5 に固定し 面内方向の区分点の数 m m を から まで変化させて 数値解の収束状態を調べた. さらに 数値解の妥当性を確認するために 周辺単純支持の条件を満足する固有関数を仮定し 古典薄板理論 (CPT) 3) 4) の時間依存性を排除した空間のみに関する基礎方程式を解析的に解いて求めた振動数パラメ 61
5 大分工業高等専門学校紀要第 50 号 ( 平成 5 年 11 月 ) (i) = 0.1 (ii) = () 逆対称曲げ振動の振動数パラメータ (iii) = 0.5 () 逆対称曲げ振動の振動モード 図 -4 周面単純支持矩形板の逆対称曲げ振動の振動数パラメータと振動モードに与える板厚比の影響 Srin energies 0. s Kineic energies 0. T () 運動エネルギー 図 -5 周面単純支持矩形板の逆対称曲げ振動のひずみエネルギーと運動エネルギーに与える板厚比の影響 ータ 1s ひずみエネルギー成分 および運動エネルギー成分 T WW の値も併記してある. これより B-spline Ri 法により求めた数値解は 面内方向の区分点の数 m m の増大にともなって一定の値に収束し 有効数字四桁での収束値を得る. また その収束 3) 4) 値は古典薄板理論に基づく解析解と良い一致を示している. さらに 基本振動以外の振動次数 異なる板厚比 や支持条件でも検討を行っているが 同様の結果を得ている. 加えて 全ての数値計算において 常に m = T m の関係を満足していることを確認している. 以上の結果から B-spline Ri 法による数値解の妥当性は十分にあり また エネルギー成分に対しても高い解析精度を有していると判断できよう. () ひずみエネルギーと運動エネルギーを指標とした種々の支持条件を有する矩形板の自由振動の評価ここでは ひずみエネルギーと運動エネルギーを指標とした矩形板の自由振動状態の評価について検討する. まず 表 -3 周面単純支持矩形板の逆対称曲げ振動状態 s + + T 式 (19) で定義した矩形板のひずみエネルギー成分と運動エネルギー成分を次のように置いて評価する. = + = s = + =. (3) = T + TVV T = TWW. (4) ただし は曲げ変形成分または面内伸縮変形成分 6
6 大分工業高等専門学校紀要第 50 号 ( 平成 5 年 11 月 ) (i) = 0.1 (ii) = Srin energies () 面内振動の振動数パラメータ (iii) = 0.5 () 面内振動の振動モード 図 -6 周面単純支持矩形板の面内振動の振動数パラメータと振動モードに与える板厚比の影響 s Kineic energies () 運動エネルギー 図 -7 周面単純支持矩形板の面内振動のひずみエネルギーと運動エネルギーに与える板厚比の影響 T は面内せん断変形成分 ( 曲げ変形成分またはねじれ変形成分 ) s は面外せん断変形成分 は面外伸縮変形成分 は面内慣性成分 T は面外慣性成分を意味する. これより 矩形板の最大ひずみエネルギー m と最大運動エネルギー T m には 次の関係式が成立する. m = + + s +. (5) Tm = + T. (6) 本稿では m = T m = 1 になるようにエネルギーの値を正規化した. したがって s のそれぞれの値は最大ひずみエネルギー m = 1( 自由振動による変形全体 )に対するそれぞれの変形成分の割合を T のそれぞれの値は最大運動エネルギー T m = 1( 自由振動による慣性全体 )に対するそれぞれの慣性成分の割合を定量的に表している. 図 - は 周面単純支持矩形板の対称曲げ振動の振動数 表 -4 周面単純支持矩形板の面内振動状態 s + + T パラメータとその振動モードに与える板厚比 の影響を示したものである. ここで 板厚比 は 0.1( 中等厚板 )から 0.5( 厚板 )まで変化させた. これより 周面単純支持矩形板の対称曲げ振動の振動数パラメータは 板厚の増大にともなって曲線的に増加する. また 振動モードに着目すると 板厚の増大にともなって断面の歪みが認められる. これらの原因は 板厚が大きくなることによる面外せん断変形の影響であることは 63
7 大分工業高等専門学校紀要第 50 号 ( 平成 5 年 11 月 ) (i) = 0.1 (ii) = () 曲げ振動の振動数パラメータ (iii) = 0.5 () 曲げ振動の振動モード 図 -8 片持矩形板の曲げ振動の振動数パラメータと振動モードに与える板厚比の影響 Srin energies 0. s Kineic energies 0. T () 運動エネルギー 図 -9 片持矩形板の曲げ振動のひずみエネルギーと運動エネルギーに与える板厚比の影響 周知の通りであるが 図 - のみではこの影響を定量的に評価することは難しい. そこで 矩形板のひずみエネルギーと運動エネルギーを指標としてみる. 図 -3 は 周面単純支持矩形板の対称曲げ振動のひずみエネルギーと運動エネルギーに与える板厚比 の影響を示したものである. ここで 板厚比 は 図 - と同様にして 0.1 から 0.5 まで変化させている. これより 周面単純支持矩形板の曲げ変形に関係する成分である と は板厚比 の増大にともなって減少するが 面外せん断変形成分である s は板厚の増大にともなって大きくなる. これは 板厚が大きくなると 面外せん断変形の影響が表れることを意味している. また 面外慣性に関係する成分 T は板厚が大きくなると僅かに減少するが 面内慣性に関係する成分 は面外慣性成分 T が減少した分だけ増加することがわかる. これは 板厚の増大にともなって 面内慣性の影響が表れることを意味している. さらに ひずみエネルギーと運動エネルギーを指標 表 -5 片持矩形板の曲げ振動状態 s T とした周面単純支持矩形板の対称曲げ振動状態の定量的な評価の一例として 曲げ変形に関する成分 ( + )を基準とした時の面外せん断変形成分 s の割合 曲げ変形に関する成分 ( + )を基準とした時の面外伸縮変形成分 の割合および面外慣性に関係する成分 T を基準とした時の面内慣性に関係する成分 の割合を表 - に示した. これより 板厚比 に係らず 曲げ変形に対する面外伸縮変形の割合と面外慣性に対する面内慣性の割合は極 64
8 大分工業高等専門学校紀要第 50 号 ( 平成 5 年 11 月 ) (i) = 0.1 (ii) = () ねじれ振動の振動数パラメータ (iii) = 0.5 () ねじれ振動の振動モード 図 -10 片持矩形板のねじれ振動の振動数パラメータと振動モードに与える板厚比の影響 Srin energies 0. s Kineic energies 0. T () 運動エネルギー 図 -11 片持矩形板のねじれ振動のひずみエネルギーと運動エネルギーに与える板厚比の影響 めて小さく 周面単純支持矩形板の対称曲げ振動状態に影響を与えない. しかし 曲げ変形に対する面外せん断変形の割合は = 0.1 の時に約 1 割程度 = 0.3 の時に約 4 割程度であり = 0.5 の時には曲げ変形と面外せん断変形の割合が同程度になる. 図 -4 に周面単純支持矩形板の逆対称曲げ振動の振動数パラメータとその振動モードに与える板厚比 の影響を 図 -5 に周面単純支持矩形板の逆対称曲げ振動のひずみエネルギーと運動エネルギーに与える板厚比 の影響を示す. ここで 板厚比 は 0.1 から 0.5 まで変化させた. また 表 -3 には周面単純支持矩形板の逆対称曲げ振動状態の定量的な評価を示した. これらより 板厚の増大にともなう周面単純支持矩形板の逆対称曲げ振動の振動数パラメータの曲線的な増加は面外せん断応力 および面外せん断ひずみ による変形 ( 面外せん断変形や面外ねじれ変形 )の影響が大きいことがわかる. また 周面単純支持矩形板の逆対称曲 表 -6 片持矩形板のねじれ振動状態 s T げ振動は その対称曲げ振動と比較すると面外せん断応力 および面外せん断ひずみ による変形が生じ易 5) いため 一次せん断変形理論である Mindlin 理論による矩形厚板の自由振動問題の二次元解析では 理論誤差が生じる可能性がある. 図 -6 には周面単純支持矩形板の面内振動の振動数パラメータとその振動モードに与える板厚比 の影響を 図 -7 には周面単純支持矩形板の面内振動のひずみエネル 65
9 大分工業高等専門学校紀要第 50 号 ( 平成 5 年 11 月 ) ギーと運動エネルギーに与える板厚比 の影響を示してある. ここで 板厚比 は 0.1 から 0.5 まで変化させた. また 表 -4 には周面単純支持矩形板の面内振動状態の定量的な評価を示した. これらより 周面単純支持矩形板の面内振動の振動数パラメータの値は板厚によらず一定であるため 面内に動的荷重が作用する場合 その周波数成分には十分に注意する必要がある. また 周面単純支持矩形板の面内振動は面外変位 w の影響を受けず 面内変位 u v のみによって生じる自由振動状態であることもわかる. 図 -8 に片持矩形板の曲げ振動の振動数パラメータとその振動モードに与える板厚比 の影響を 図 -9 に片持矩形板の曲げ振動のひずみエネルギーと運動エネルギーに与える板厚比 の影響を示す. ここで 板厚比 は 0.1 から 0.5 まで変化させている. また 表 -5 には片持矩形板の曲げ振動状態の定量的な評価を示した. ただし / は曲げ変形成分 を基準とした時の面内せん断変形成分 の割合 s / は曲げ変形成分 を基準とした時の面外せん断変形成分 の割合および / T は面外慣性成分 T を基準とした時の面内慣性成分 の割合を意味する. なお 曲げ変形成分 を基準とした時の面外伸縮変形成分 の割合である / はほぼ零であったので省略してある. これらより 片持矩形板の曲げ振動の振動数パラメータ は 板厚の増大にともなってほぼ直線的に増加する. ここで ひずみエネルギー成分および運動エネルギー成分と板厚の関係を見てみると 片持矩形板の曲げ振動は 曲げ変形成分 と面外せん断変形成分 s によって構成されているが 板厚に係らず曲げ変形成分 が支配的であることがわかる. また 面外慣性成分 T の影響が支配的であり 面内慣性成分 の影響はほとんど見られない. 最後に 図 -10 に片持矩形板のねじれ振動の振動数パラメータとその振動モードに与える板厚比 の影響を 図 -11 に片持矩形板のねじれ振動のひずみエネルギーと運動エネルギーに与える板厚比 の影響を示した. ここで 板厚比 は 0.1 から 0.5 まで変化させている. また 表 -5 と同様にして 表 -6 は片持矩形板のねじれ振動状態の定量的な評価を示したものである. これらより 片持矩形板のねじれ振動の振動数パラメータは 片持矩形板の曲げ振動の振動数パラメータと異なり 板厚の増大にともなって曲線的に増加する. また 片持矩形板のねじれ振動は 板厚が大きくなると曲げ変形成分 よりも面内せん断変形成分 ( ねじれ変形成分 ) および面外せん断変形成分 s の影響が大きくなる. さらに 板厚の増大にともない 面内慣性成分 の影響が最大で 割程度表れている. したがって 片持矩形板のねじれ振動の振動数パラメータの曲線的な増加は 面内せん断変形成分 ( ねじれ変形成分 ) 面外せん断変形成分 s および 面内慣性成分 の影響であると考えられる. このようにひずみエネルギーと運動エネルギーを指標として評価することにより 矩形板の自由振動状態や卓越する変形成分とそれらの割合を定量的に把握することが可能である. また 面外せん断変形成分や面内慣性成分の値に着目すれば 各種せん断変形理論の適用範囲の検討に関する指標にもなるであろう. さらに この評価の考え方は簡易かつ単純であるので 誰もが容易に取り扱うことができる. よって 本評価方法は構造部材の自由振動特性の把握 理解に有用かつ効果的である. また 幾つかの構造部材から構成される構造物を対象としても同様の評価が可能であることは容易に理解でき 本評価方法は構造物の動力学的挙動を把握するための指標に十分成り得ると判断できよう. 5. あとがき 本稿では 基本的な構造部材である矩形板を例に取り ひずみエネルギーと運動エネルギーを指標とした矩形板の自由振動の状態の定量的な評価について検討した. その結果 ひずみエネルギーと運動エネルギーを指標とすることにより 矩形板の自由振動における支配的な変形成分および変形成分の割合を定量的に把握することができることを明らかにした. また 面外せん断変形成分や面内慣性成分の値に着目すれば 各種せん断変形理論の適用範囲の検討に関する指標にも成り得る. さらに この考え方は簡易かつ単純であるので 誰もが容易に取り扱うことができる. よって 本評価方法は構造部材 構造物の自由振動特性や動力学的挙動の把握 理解に有用かつ効果的である. 参考文献 1) 小林繁夫 近藤恭平 : 工学基礎講座 7 弾性力学 培風館 pp ) Hrunou Ngino Tksi Mikmi Tomisku Miusw: Tree-dimensionl free virion nlsis of isoropic recngulr ples using e B-spline Ri meod Journl of Sound nd Virion Vol.317 pp ) Leiss A.W.: Virion of Ples Acousicl Socie of Americ ) Wng C.M. Redd J.N. nd Lee K.H.: Ser deformle ems nd ples Relionsip wi clssicl soluions Elsevier ) Mindlin R.D.: Influence of roor ineri nd ser on fleurl moions of isoropic elsic ples ASEM Journl of Applied Mecnics Vol.18 pp ( 受付 ) 66
第 5 章 構造振動学 棒の振動を縦振動, 捩り振動, 曲げ振動に分けて考える. 5.1 棒の縦振動と捩り振動 まっすぐな棒の縦振動の固有振動数 f[ Hz] f = l 2pL である. ただし, L [ 単位 m] は棒の長さ, [ 2 N / m ] 3 r[ 単位 Kg / m ] E r
![第 5 章 構造振動学 棒の振動を縦振動, 捩り振動, 曲げ振動に分けて考える. 5.1 棒の縦振動と捩り振動 まっすぐな棒の縦振動の固有振動数 f[ Hz] f = l 2pL である. ただし, L [ 単位 m] は棒の長さ, [ 2 N / m ] 3 r[ 単位 Kg / m ] E r 第 5 章 構造振動学 棒の振動を縦振動, 捩り振動, 曲げ振動に分けて考える. 5.1 棒の縦振動と捩り振動 まっすぐな棒の縦振動の固有振動数 f[ Hz] f = l 2pL である. ただし, L [ 単位 m] は棒の長さ, [ 2 N / m ] 3 r[ 単位 Kg / m ] E r](/thumbs/94/120041361.jpg) 第 5 章 構造振動学 棒の振動を縦振動, 捩り振動, 曲げ振動に分けて考える 5 棒の縦振動と捩り振動 まっすぐな棒の縦振動の固有振動数 f[ Hz] f l pl である ただし, L [ 単位 m] は棒の長さ, [ N / m ] [ 単位 Kg / m ] E は (5) E 単位は棒の材料の縦弾性係数 ( ヤング率 ) は棒の材料の単位体積当りの質量である l は境界条件と振動モードによって決まる無
第 5 章 構造振動学 棒の振動を縦振動, 捩り振動, 曲げ振動に分けて考える 5 棒の縦振動と捩り振動 まっすぐな棒の縦振動の固有振動数 f[ Hz] f l pl である ただし, L [ 単位 m] は棒の長さ, [ N / m ] [ 単位 Kg / m ] E は (5) E 単位は棒の材料の縦弾性係数 ( ヤング率 ) は棒の材料の単位体積当りの質量である l は境界条件と振動モードによって決まる無
大分工業高等専門学校紀要第 号 ( 平成 6 年 月 ) h 図 - 部分等分布荷重を受ける Winkler 基礎上の矩形板と直交座標系 b z, w o o. 解析モデル d d a c a c, v 図 - 板上面に作用する局所荷重 図 - には, 部分等分布荷重を受けるWinkler 基礎上に
 大分工業高等専門学校紀要第 号 ( 平成 6 年 月 ) 局所的な表 を受ける Winkler 基礎上の周 単純 持矩形板 の静的曲げ変形問題における三次元弾性論と板理論との 較 局所的な表 の載荷幅が板の辺 の半分の場合 志賀有人 名木野晴暢 足立忠晴 3 水澤富作 4 三上隆 ショーボンド建設株式会社, 都市 環境工学科, 3 豊橋技術科学大学, 4 大同大学, 北海道大学 本稿では局所的な表面力を受けるWinkler
大分工業高等専門学校紀要第 号 ( 平成 6 年 月 ) 局所的な表 を受ける Winkler 基礎上の周 単純 持矩形板 の静的曲げ変形問題における三次元弾性論と板理論との 較 局所的な表 の載荷幅が板の辺 の半分の場合 志賀有人 名木野晴暢 足立忠晴 3 水澤富作 4 三上隆 ショーボンド建設株式会社, 都市 環境工学科, 3 豊橋技術科学大学, 4 大同大学, 北海道大学 本稿では局所的な表面力を受けるWinkler
パソコンシミュレータの現状
 第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
FEM原理講座 (サンプルテキスト)
 サンプルテキスト FEM 原理講座 サイバネットシステム株式会社 8 年 月 9 日作成 サンプルテキストについて 各講師が 講義の内容が伝わりやすいページ を選びました テキストのページは必ずしも連続していません 一部を抜粋しています 幾何光学講座については 実物のテキストではなくガイダンスを掲載いたします 対象とする構造系 物理モデル 連続体 固体 弾性体 / 弾塑性体 / 粘弾性体 / 固体
サンプルテキスト FEM 原理講座 サイバネットシステム株式会社 8 年 月 9 日作成 サンプルテキストについて 各講師が 講義の内容が伝わりやすいページ を選びました テキストのページは必ずしも連続していません 一部を抜粋しています 幾何光学講座については 実物のテキストではなくガイダンスを掲載いたします 対象とする構造系 物理モデル 連続体 固体 弾性体 / 弾塑性体 / 粘弾性体 / 固体
Microsoft Word - 1B2011.doc
 第 14 回モールの定理 ( 単純梁の場合 ) ( モールの定理とは何か?p.11) 例題 下記に示す単純梁の C 点のたわみ角 θ C と, たわみ δ C を求めよ ただし, 部材の曲げ 剛性は材軸に沿って一様で とする C D kn B 1.5m 0.5m 1.0m 解答 1 曲げモーメント図を描く,B 点の反力を求める kn kn 4 kn 曲げモーメント図を描く knm 先に得られた曲げモーメントの値を
第 14 回モールの定理 ( 単純梁の場合 ) ( モールの定理とは何か?p.11) 例題 下記に示す単純梁の C 点のたわみ角 θ C と, たわみ δ C を求めよ ただし, 部材の曲げ 剛性は材軸に沿って一様で とする C D kn B 1.5m 0.5m 1.0m 解答 1 曲げモーメント図を描く,B 点の反力を求める kn kn 4 kn 曲げモーメント図を描く knm 先に得られた曲げモーメントの値を
静的弾性問題の有限要素法解析アルゴリズム
 概要 基礎理論. 応力とひずみおよび平衡方程式. 降伏条件式. 構成式 ( 応力 - ひずみ関係式 ) 有限要素法. 有限要素法の概要. 仮想仕事の原理式と変分原理. 平面ひずみ弾性有限要素法定式化 FEM の基礎方程式平衡方程式. G G G ひずみ - 変位関係式 w w w. kl jkl j D 構成式応力 - ひずみ関係式 ) (. 変位の境界条件力の境界条件境界条件式 t S on V
概要 基礎理論. 応力とひずみおよび平衡方程式. 降伏条件式. 構成式 ( 応力 - ひずみ関係式 ) 有限要素法. 有限要素法の概要. 仮想仕事の原理式と変分原理. 平面ひずみ弾性有限要素法定式化 FEM の基礎方程式平衡方程式. G G G ひずみ - 変位関係式 w w w. kl jkl j D 構成式応力 - ひずみ関係式 ) (. 変位の境界条件力の境界条件境界条件式 t S on V
PowerPoint Presentation
 Non-linea factue mechanics き裂先端付近の塑性変形 塑性域 R 破壊進行領域応カ特異場 Ω R R Hutchinson, Rice and Rosengen 全ひずみ塑性理論に基づいた解析 現段階のひずみは 除荷がないとすると現段階の応力で一義的に決まる 単純引張り時の応カーひずみ関係 ( 構成方程式 ): ( ) ( ) n () y y y ここで α,n 定数, /
Non-linea factue mechanics き裂先端付近の塑性変形 塑性域 R 破壊進行領域応カ特異場 Ω R R Hutchinson, Rice and Rosengen 全ひずみ塑性理論に基づいた解析 現段階のひずみは 除荷がないとすると現段階の応力で一義的に決まる 単純引張り時の応カーひずみ関係 ( 構成方程式 ): ( ) ( ) n () y y y ここで α,n 定数, /
以下 変数の上のドットは時間に関する微分を表わしている (ex. 2 dx d x x, x 2 dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-1) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( x や x, x などがすべて 1 次で なおかつ
 以下 変数の上のドットは時間に関する微分を表わしている (e. d d, dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( や, などがすべて 次で なおかつそれらの係数が定数であるような微分方程式 ) に対して安定性の解析を行ってきた しかしながら 実際には非線形の微分方程式で記述される現象も多く存在する
以下 変数の上のドットは時間に関する微分を表わしている (e. d d, dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( や, などがすべて 次で なおかつそれらの係数が定数であるような微分方程式 ) に対して安定性の解析を行ってきた しかしながら 実際には非線形の微分方程式で記述される現象も多く存在する
(Microsoft PowerPoint - \221\34613\211\361)
 計算力学 ~ 第 回弾性問題の有限要素解析 (Ⅱ)~ 修士 年後期 ( 選択科目 ) 担当 : 岩佐貴史 講義の概要 全 5 講義. 計算力学概論, ガイダンス. 自然現象の数理モデル化. 行列 場とその演算. 数値計算法 (Ⅰ) 5. 数値計算法 (Ⅱ) 6. 初期値 境界値問題 (Ⅰ) 7. 初期値 境界値問題 (Ⅱ) 8. マトリックス変位法による構造解析 9. トラス構造の有限要素解析. 重み付き残差法と古典的近似解法.
計算力学 ~ 第 回弾性問題の有限要素解析 (Ⅱ)~ 修士 年後期 ( 選択科目 ) 担当 : 岩佐貴史 講義の概要 全 5 講義. 計算力学概論, ガイダンス. 自然現象の数理モデル化. 行列 場とその演算. 数値計算法 (Ⅰ) 5. 数値計算法 (Ⅱ) 6. 初期値 境界値問題 (Ⅰ) 7. 初期値 境界値問題 (Ⅱ) 8. マトリックス変位法による構造解析 9. トラス構造の有限要素解析. 重み付き残差法と古典的近似解法.
<4D F736F F F696E74202D20906C8D488AC28BAB90DD8C7689F090CD8D488A D91E F1>
 人工環境設計解析工学構造力学と有限要素法 ( 第 回 ) 東京大学新領域創成科学研究科 鈴木克幸 固体力学の基礎方程式 変位 - ひずみの関係 適合条件式 ひずみ - 応力の関係 構成方程式 応力 - 外力の関係 平衡方程式 境界条件 変位規定境界 反力規定境界 境界条件 荷重応力ひずみ変形 場の方程式 Γ t Γ t 平衡方程式構成方程式適合条件式 構造力学の基礎式 ひずみ 一軸 荷重応力ひずみ変形
人工環境設計解析工学構造力学と有限要素法 ( 第 回 ) 東京大学新領域創成科学研究科 鈴木克幸 固体力学の基礎方程式 変位 - ひずみの関係 適合条件式 ひずみ - 応力の関係 構成方程式 応力 - 外力の関係 平衡方程式 境界条件 変位規定境界 反力規定境界 境界条件 荷重応力ひずみ変形 場の方程式 Γ t Γ t 平衡方程式構成方程式適合条件式 構造力学の基礎式 ひずみ 一軸 荷重応力ひずみ変形
Microsoft PowerPoint - zairiki_3
 材料力学講義 (3) 応力と変形 Ⅲ ( 曲げモーメント, 垂直応力度, 曲率 ) 今回は, 曲げモーメントに関する, 断面力 - 応力度 - 変形 - 変位の関係について学びます 1 曲げモーメント 曲げモーメント M 静定力学で求めた曲げモーメントも, 仮想的に断面を切ることによって現れる内力です 軸方向力は断面に働く力 曲げモーメント M は断面力 曲げモーメントも, 一つのモーメントとして表しますが,
材料力学講義 (3) 応力と変形 Ⅲ ( 曲げモーメント, 垂直応力度, 曲率 ) 今回は, 曲げモーメントに関する, 断面力 - 応力度 - 変形 - 変位の関係について学びます 1 曲げモーメント 曲げモーメント M 静定力学で求めた曲げモーメントも, 仮想的に断面を切ることによって現れる内力です 軸方向力は断面に働く力 曲げモーメント M は断面力 曲げモーメントも, 一つのモーメントとして表しますが,
<4D F736F F D208D5C91A297CD8A7793FC96E591E631308FCD2E646F63>
 第 1 章モールの定理による静定梁のたわみ 1-1 第 1 章モールの定理による静定梁のたわみ ポイント : モールの定理を用いて 静定梁のたわみを求める 断面力の釣合と梁の微分方程式は良く似ている 前章では 梁の微分方程式を直接積分する方法で 静定梁の断面力と変形状態を求めた 本章では 梁の微分方程式と断面力による力の釣合式が類似していることを利用して 微分方程式を直接解析的に解くのではなく 力の釣合より梁のたわみを求める方法を学ぶ
第 1 章モールの定理による静定梁のたわみ 1-1 第 1 章モールの定理による静定梁のたわみ ポイント : モールの定理を用いて 静定梁のたわみを求める 断面力の釣合と梁の微分方程式は良く似ている 前章では 梁の微分方程式を直接積分する方法で 静定梁の断面力と変形状態を求めた 本章では 梁の微分方程式と断面力による力の釣合式が類似していることを利用して 微分方程式を直接解析的に解くのではなく 力の釣合より梁のたわみを求める方法を学ぶ
構造力学Ⅰ第12回
 第 回材の座屈 (0 章 ) p.5~ ( 復習 ) モールの定理 ( 手順 ) 座屈とは 荷重により梁に生じた曲げモーメントをで除して仮想荷重と考える 座屈荷重 偏心荷重 ( 曲げと軸力 ) 断面の核 この仮想荷重に対するある点でのせん断力 たわみ角に相当する曲げモーメント たわみに相当する ( 例 ) 単純梁の支点のたわみ角 : は 図 を仮想荷重と考えたときの 点の支点反力 B は 図 を仮想荷重と考えたときのB
第 回材の座屈 (0 章 ) p.5~ ( 復習 ) モールの定理 ( 手順 ) 座屈とは 荷重により梁に生じた曲げモーメントをで除して仮想荷重と考える 座屈荷重 偏心荷重 ( 曲げと軸力 ) 断面の核 この仮想荷重に対するある点でのせん断力 たわみ角に相当する曲げモーメント たわみに相当する ( 例 ) 単純梁の支点のたわみ角 : は 図 を仮想荷重と考えたときの 点の支点反力 B は 図 を仮想荷重と考えたときのB
Microsoft PowerPoint - シミュレーション工学-2010-第1回.ppt
 シミュレーション工学 ( 後半 ) 東京大学人工物工学研究センター 鈴木克幸 CA( Compter Aded geerg ) r. Jaso Lemo (SC, 98) 設計者が解析ツールを使いこなすことにより 設計の評価 設計の質の向上を図る geerg の本質の 計算機による支援 (CA CAM などより広い名前 ) 様々な汎用ソフトの登場 工業製品の設計に不可欠のツール 構造解析 流体解析
シミュレーション工学 ( 後半 ) 東京大学人工物工学研究センター 鈴木克幸 CA( Compter Aded geerg ) r. Jaso Lemo (SC, 98) 設計者が解析ツールを使いこなすことにより 設計の評価 設計の質の向上を図る geerg の本質の 計算機による支援 (CA CAM などより広い名前 ) 様々な汎用ソフトの登場 工業製品の設計に不可欠のツール 構造解析 流体解析
1 対 1 対応の演習例題を解いてみた 微分法とその応用 例題 1 極限 微分係数の定義 (2) 関数 f ( x) は任意の実数 x について微分可能なのは明らか f ( 1, f ( 1) ) と ( 1 + h, f ( 1 + h)
 微分法とその応用 例題 1 極限 微分係数の定義 () 関数 ( x) は任意の実数 x について微分可能なのは明らか ( 1, ( 1) ) と ( 1 + h, ( 1 + h) ) の傾き= ( 1 + h ) - ( 1 ) ( 1 + ) - ( 1) = ( 1 + h) - 1 h ( 1) = lim h ( 1 + h) - ( 1) h ( 1, ( 1) ) と ( 1 - h,
微分法とその応用 例題 1 極限 微分係数の定義 () 関数 ( x) は任意の実数 x について微分可能なのは明らか ( 1, ( 1) ) と ( 1 + h, ( 1 + h) ) の傾き= ( 1 + h ) - ( 1 ) ( 1 + ) - ( 1) = ( 1 + h) - 1 h ( 1) = lim h ( 1 + h) - ( 1) h ( 1, ( 1) ) と ( 1 - h,
第3章 ひずみ
 第 4 章 応力とひずみの関係 4. 単軸応力を受ける弾性体の応力とひずみの関係 温度一定の下で, 負荷による変形が徐荷によって完全に回復する場合を広義の弾性というが, 狭義の弾 性では, 負荷過程と徐荷過程で応力 - ひずみ関係が一致しない場合は含めず ( 図 - 参照 ), 与えられたひ ずみ状態に対して応力が一意に定まる, つまり応力がひずみの関数と して表される. このような物体を狭義の弾性体
第 4 章 応力とひずみの関係 4. 単軸応力を受ける弾性体の応力とひずみの関係 温度一定の下で, 負荷による変形が徐荷によって完全に回復する場合を広義の弾性というが, 狭義の弾 性では, 負荷過程と徐荷過程で応力 - ひずみ関係が一致しない場合は含めず ( 図 - 参照 ), 与えられたひ ずみ状態に対して応力が一意に定まる, つまり応力がひずみの関数と して表される. このような物体を狭義の弾性体
木村の物理小ネタ ケプラーの第 2 法則と角運動量保存則 A. 面積速度面積速度とは平面内に定点 O と動点 P があるとき, 定点 O と動点 P を結ぶ線分 OP( 動径 OP という) が単位時間に描く面積を 動点 P の定点 O に
 ケプラーの第 法則と角運動量保存則 A. 面積速度面積速度とは平面内に定点 O と動点 P があるとき, 定点 O と動点 P を結ぶ線分 OP( 動径 OP という が単位時間に描く面積を 動点 P の定点 O に関する面積速度の大きさ という 定点 O まわりを回る面積速度の導き方導き方 A ( x( + D, y( + D v ( q r ( A ( x (, y( 動点 P が xy 座標平面上を時刻
ケプラーの第 法則と角運動量保存則 A. 面積速度面積速度とは平面内に定点 O と動点 P があるとき, 定点 O と動点 P を結ぶ線分 OP( 動径 OP という が単位時間に描く面積を 動点 P の定点 O に関する面積速度の大きさ という 定点 O まわりを回る面積速度の導き方導き方 A ( x( + D, y( + D v ( q r ( A ( x (, y( 動点 P が xy 座標平面上を時刻
Microsoft Word - 付録A,Bとその図
 付録 A 1 自由度系 ( 自由振動 ) の解法 はじめに振動現象を解明するのに基本となる 1 自由度不減衰系 ( 自由振動 ) の運動方程式の作成方法とその微分 ( あるいは偏微分 ) 方程式の解法を説明する. 1 自由度系モデルには, 単振動のばね 質量モデルと数学振子を用いる. A.1 運動方程式 ( 微分方程式 ) を立てる A.1.1 ばね 質量の場合 ( 1) 単振動の運動から運動方程式を求める
付録 A 1 自由度系 ( 自由振動 ) の解法 はじめに振動現象を解明するのに基本となる 1 自由度不減衰系 ( 自由振動 ) の運動方程式の作成方法とその微分 ( あるいは偏微分 ) 方程式の解法を説明する. 1 自由度系モデルには, 単振動のばね 質量モデルと数学振子を用いる. A.1 運動方程式 ( 微分方程式 ) を立てる A.1.1 ばね 質量の場合 ( 1) 単振動の運動から運動方程式を求める
<4D F736F F D2097CD8A7793FC96E582BD82ED82DD8A E6318FCD2E646F63>
 - 第 章たわみ角法の基本式 ポイント : たわみ角法の基本式を理解する たわみ角法の基本式を梁の微分方程式より求める 本章では たわみ角法の基本式を導くことにする 基本式の誘導法は各種あるが ここでは 梁の微分方程式を解いて基本式を求める方法を採用する この本で使用する座標系は 右手 右ネジの法則に従った座標を用いる また ひとつの部材では 図 - に示すように部材の左端の 点を原点とし 軸線を
- 第 章たわみ角法の基本式 ポイント : たわみ角法の基本式を理解する たわみ角法の基本式を梁の微分方程式より求める 本章では たわみ角法の基本式を導くことにする 基本式の誘導法は各種あるが ここでは 梁の微分方程式を解いて基本式を求める方法を採用する この本で使用する座標系は 右手 右ネジの法則に従った座標を用いる また ひとつの部材では 図 - に示すように部材の左端の 点を原点とし 軸線を
Microsoft PowerPoint - elast.ppt [互換モード]
![Microsoft PowerPoint - elast.ppt [互換モード] Microsoft PowerPoint - elast.ppt [互換モード]](/thumbs/82/86104681.jpg) 弾性力学入門 年夏学期 中島研吾 科学技術計算 Ⅰ(48-7) コンピュータ科学特別講義 Ⅰ(48-4) elast 弾性力学 弾性力学の対象 応力 弾性力学の支配方程式 elast 3 弾性力学 連続体力学 (Continuum Mechanics) 固体力学 (Solid Mechanics) の一部 弾性体 (lastic Material) を対象 弾性論 (Theor of lasticit)
弾性力学入門 年夏学期 中島研吾 科学技術計算 Ⅰ(48-7) コンピュータ科学特別講義 Ⅰ(48-4) elast 弾性力学 弾性力学の対象 応力 弾性力学の支配方程式 elast 3 弾性力学 連続体力学 (Continuum Mechanics) 固体力学 (Solid Mechanics) の一部 弾性体 (lastic Material) を対象 弾性論 (Theor of lasticit)
OCW-iダランベールの原理
 講義名連続体力学配布資料 OCW- 第 2 回ダランベールの原理 無機材料工学科准教授安田公一 1 はじめに今回の講義では, まず, 前半でダランベールの原理について説明する これを用いると, 動力学の問題を静力学の問題として解くことができ, さらに, 前回の仮想仕事の原理を適用すると動力学問題も簡単に解くことができるようになる また, 後半では, ダランベールの原理の応用として ラグランジュ方程式の導出を示す
講義名連続体力学配布資料 OCW- 第 2 回ダランベールの原理 無機材料工学科准教授安田公一 1 はじめに今回の講義では, まず, 前半でダランベールの原理について説明する これを用いると, 動力学の問題を静力学の問題として解くことができ, さらに, 前回の仮想仕事の原理を適用すると動力学問題も簡単に解くことができるようになる また, 後半では, ダランベールの原理の応用として ラグランジュ方程式の導出を示す
技術者のための構造力学 2014/06/11 1. はじめに 資料 2 節点座標系による傾斜支持節点節点の処理 三好崇夫加藤久人 従来, マトリックス変位法に基づく骨組解析を紹介する教科書においては, 全体座標系に対して傾斜 した斜面上の支持条件を考慮する処理方法として, 一旦, 傾斜支持を無視した
 . はじめに 資料 節点座標系による傾斜支持節点節点の処理 三好崇夫加藤久人 従来, マトリックス変位法に基づく骨組解析を紹介する教科書においては, 全体座標系に対して傾斜 した斜面上の支持条件を考慮する処理方法として, 一旦, 傾斜支持を無視した全体座標系に関する構造 全体の剛性マトリックスを組み立てた後に, 傾斜支持する節点に関して対応する剛性成分を座標変換に よって傾斜方向に回転処理し, その後は通常の全体座標系に対して傾斜していない支持点に対するのと
. はじめに 資料 節点座標系による傾斜支持節点節点の処理 三好崇夫加藤久人 従来, マトリックス変位法に基づく骨組解析を紹介する教科書においては, 全体座標系に対して傾斜 した斜面上の支持条件を考慮する処理方法として, 一旦, 傾斜支持を無視した全体座標系に関する構造 全体の剛性マトリックスを組み立てた後に, 傾斜支持する節点に関して対応する剛性成分を座標変換に よって傾斜方向に回転処理し, その後は通常の全体座標系に対して傾斜していない支持点に対するのと
<4D F736F F D208D5C91A297CD8A7793FC96E591E6328FCD2E646F63>
 -1 ポイント : 材料の応力とひずみの関係を知る 断面内の応力とひずみ 本章では 建築構造で多く用いられる材料の力学的特性について学ぶ 最初に 応力とひずみの関係 次に弾性と塑性 また 弾性範囲における縦弾性係数 ( ヤング係数 ) について 建築構造用材料として代表的な鋼を例にして解説する さらに 梁理論で使用される軸方向応力と軸方向ひずみ あるいは せん断応力とせん断ひずみについて さらにポアソン比についても説明する
-1 ポイント : 材料の応力とひずみの関係を知る 断面内の応力とひずみ 本章では 建築構造で多く用いられる材料の力学的特性について学ぶ 最初に 応力とひずみの関係 次に弾性と塑性 また 弾性範囲における縦弾性係数 ( ヤング係数 ) について 建築構造用材料として代表的な鋼を例にして解説する さらに 梁理論で使用される軸方向応力と軸方向ひずみ あるいは せん断応力とせん断ひずみについて さらにポアソン比についても説明する
1/17 平成 29 年 3 月 25 日 ( 土 ) 午前 11 時 1 分量子力学とクライン ゴルドン方程式 ( 学部 3 年次秋学期向 ) 量子力学とクライン ゴルドン方程式 素粒子の満たす場 y ( x,t) の運動方程式 : クライン ゴルドン方程式 : æ 3 ö ç å è m= 0
 /7 平成 9 年 月 5 日 ( 土 午前 時 分量子力学とクライン ゴルドン方程式 ( 学部 年次秋学期向 量子力学とクライン ゴルドン方程式 素粒子の満たす場 (,t の運動方程式 : クライン ゴルドン方程式 : æ ö ç å è = 0 c + ( t =, 0 (. = 0 ì æ = = = ö æ ö æ ö ç ì =,,,,,,, ç 0 = ç Ñ 0 = ç Ñ 0 Ñ Ñ
/7 平成 9 年 月 5 日 ( 土 午前 時 分量子力学とクライン ゴルドン方程式 ( 学部 年次秋学期向 量子力学とクライン ゴルドン方程式 素粒子の満たす場 (,t の運動方程式 : クライン ゴルドン方程式 : æ ö ç å è = 0 c + ( t =, 0 (. = 0 ì æ = = = ö æ ö æ ö ç ì =,,,,,,, ç 0 = ç Ñ 0 = ç Ñ 0 Ñ Ñ
<4D F736F F D208D5C91A297CD8A7793FC96E591E6398FCD2E646F63>
 9-1 第 9 章静定梁のたわみ ポイント : 梁の微分方程式を用いて梁のたわみを求める 静定梁のたわみを計算 前章では 梁の微分方程式を導き 等分布荷重を受ける単純梁の解析を行った 本節では 導いた梁の微分方程式を利用し さらに多くの静定構造物の解析を行い 梁の最大たわみや変形状態を求めることにする さらに を用いて課題で解析した構造を数値計算し 解析結果を比較 検討しよう 9.1 はじめに キーワード梁の微分方程式単純梁の応力解析片持ち梁の応力解析
9-1 第 9 章静定梁のたわみ ポイント : 梁の微分方程式を用いて梁のたわみを求める 静定梁のたわみを計算 前章では 梁の微分方程式を導き 等分布荷重を受ける単純梁の解析を行った 本節では 導いた梁の微分方程式を利用し さらに多くの静定構造物の解析を行い 梁の最大たわみや変形状態を求めることにする さらに を用いて課題で解析した構造を数値計算し 解析結果を比較 検討しよう 9.1 はじめに キーワード梁の微分方程式単純梁の応力解析片持ち梁の応力解析
< B795FB8C6094C28F6F97CD97E12E786477>
 長方形板の計算システム Ver3.0 適用基準 級数解法 ( 理論解析 ) 構造力学公式集( 土木学会発行 /S61.6) 板とシェルの理論( チモシェンコ ヴォアノフスキークリ ガー共著 / 長谷川節訳 ) 有限要素法解析 参考文献 マトリックス構造解析法(J.L. ミーク著, 奥村敏恵, 西野文雄, 西岡隆訳 /S50.8) 薄板構造解析( 川井忠彦, 川島矩郎, 三本木茂夫 / 培風館 S48.6)
長方形板の計算システム Ver3.0 適用基準 級数解法 ( 理論解析 ) 構造力学公式集( 土木学会発行 /S61.6) 板とシェルの理論( チモシェンコ ヴォアノフスキークリ ガー共著 / 長谷川節訳 ) 有限要素法解析 参考文献 マトリックス構造解析法(J.L. ミーク著, 奥村敏恵, 西野文雄, 西岡隆訳 /S50.8) 薄板構造解析( 川井忠彦, 川島矩郎, 三本木茂夫 / 培風館 S48.6)
Microsoft Word - thesis.doc
 剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
線積分.indd
 線積分 線積分 ( n, n, n ) (ξ n, η n, ζ n ) ( n-, n-, n- ) (ξ k, η k, ζ k ) ( k, k, k ) ( k-, k-, k- ) 物体に力 を作用させて位置ベクトル A の点 A から位置ベクトル の点 まで曲線 に沿って物体を移動させたときの仕事 W は 次式で計算された A, A, W : d 6 d+ d+ d@,,, d+ d+
線積分 線積分 ( n, n, n ) (ξ n, η n, ζ n ) ( n-, n-, n- ) (ξ k, η k, ζ k ) ( k, k, k ) ( k-, k-, k- ) 物体に力 を作用させて位置ベクトル A の点 A から位置ベクトル の点 まで曲線 に沿って物体を移動させたときの仕事 W は 次式で計算された A, A, W : d 6 d+ d+ d@,,, d+ d+
Microsoft PowerPoint - H21生物計算化学2.ppt
 演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
<4D F736F F D208D5C91A297CD8A7793FC96E591E631318FCD2E646F63>
 11-1 第 11 章不静定梁のたわみ ポイント : 基本的な不静定梁のたわみ 梁部材の断面力とたわみ 本章では 不静定構造物として 最も単純でしかも最も大切な両端固定梁の応力解析を行う ここでは 梁の微分方程式を用いて解くわけであるが 前章とは異なり 不静定構造物であるため力の釣合から先に断面力を決定することができない そのため 梁のたわみ曲線と同時に断面力を求めることになる この両端固定梁のたわみ曲線や断面力分布は
11-1 第 11 章不静定梁のたわみ ポイント : 基本的な不静定梁のたわみ 梁部材の断面力とたわみ 本章では 不静定構造物として 最も単純でしかも最も大切な両端固定梁の応力解析を行う ここでは 梁の微分方程式を用いて解くわけであるが 前章とは異なり 不静定構造物であるため力の釣合から先に断面力を決定することができない そのため 梁のたわみ曲線と同時に断面力を求めることになる この両端固定梁のたわみ曲線や断面力分布は
<4D F736F F D208D7E959A82A882E682D18F498BC78BC882B B BE98C60816A2E646F63>
 降伏時および終局時曲げモーメントの誘導 矩形断面 日中コンサルタント耐震解析部松原勝己. 降伏時の耐力と変形 複鉄筋の矩形断面を仮定する また コンクリートの応力ひずみ関係を非線形 放物線型 とする さらに 引張鉄筋がちょうど降伏ひずみに達しているものとし コンクリート引張応力は無視する ⅰ 圧縮縁のひずみ
降伏時および終局時曲げモーメントの誘導 矩形断面 日中コンサルタント耐震解析部松原勝己. 降伏時の耐力と変形 複鉄筋の矩形断面を仮定する また コンクリートの応力ひずみ関係を非線形 放物線型 とする さらに 引張鉄筋がちょうど降伏ひずみに達しているものとし コンクリート引張応力は無視する ⅰ 圧縮縁のひずみ
微分方程式による現象記述と解きかた
 微分方程式による現象記述と解きかた 土木工学 : 公共諸施設 構造物の有用目的にむけた合理的な実現をはかる方法 ( 技術 ) に関する学 橋梁 トンネル ダム 道路 港湾 治水利水施設 安全化 利便化 快適化 合法則的 経済的 自然および人口素材によって作られた 質量保存則 構造物の自然的な性質 作用 ( 外力による応答 ) エネルギー則 の解明 社会的諸現象のうち マスとしての移動 流通 運動量則
微分方程式による現象記述と解きかた 土木工学 : 公共諸施設 構造物の有用目的にむけた合理的な実現をはかる方法 ( 技術 ) に関する学 橋梁 トンネル ダム 道路 港湾 治水利水施設 安全化 利便化 快適化 合法則的 経済的 自然および人口素材によって作られた 質量保存則 構造物の自然的な性質 作用 ( 外力による応答 ) エネルギー則 の解明 社会的諸現象のうち マスとしての移動 流通 運動量則
1/30 平成 29 年 3 月 24 日 ( 金 ) 午前 11 時 25 分第三章フェルミ量子場 : スピノール場 ( 次元あり ) 第三章フェルミ量子場 : スピノール場 フェルミ型 ボーズ量子場のエネルギーは 第二章ボーズ量子場 : スカラー場 の (2.18) より ˆ dp 1 1 =
 / 平成 9 年 月 日 ( 金 午前 時 5 分第三章フェルミ量子場 : スピノール場 ( 次元あり 第三章フェルミ量子場 : スピノール場 フェルミ型 ボーズ量子場のエネルギーは 第二章ボーズ量子場 : スカラー場 の (.8 より ˆ ( ( ( q -, ( ( c ( H c c ë é ù û - Ü + c ( ( - に限る (. である 一方 フェルミ型は 成分をもち その成分を,,,,
/ 平成 9 年 月 日 ( 金 午前 時 5 分第三章フェルミ量子場 : スピノール場 ( 次元あり 第三章フェルミ量子場 : スピノール場 フェルミ型 ボーズ量子場のエネルギーは 第二章ボーズ量子場 : スカラー場 の (.8 より ˆ ( ( ( q -, ( ( c ( H c c ë é ù û - Ü + c ( ( - に限る (. である 一方 フェルミ型は 成分をもち その成分を,,,,
応用数学Ⅱ 偏微分方程式(2) 波動方程式(12/13)
 偏微分方程式. 偏微分方程式の形 偏微分 偏導関数 つの独立変数 をもつ関数 があるとき 変数 が一定値をとって だけが変化したとす ると は だけの関数となる このとき を について微分して得られる関数を 関数 の に関する 偏微分係数 略して偏微分 あるいは偏導関数 pil deiie といい 次のように表される についても同様な偏微分を定義できる あるいは あるいは - あるいは あるいは -
偏微分方程式. 偏微分方程式の形 偏微分 偏導関数 つの独立変数 をもつ関数 があるとき 変数 が一定値をとって だけが変化したとす ると は だけの関数となる このとき を について微分して得られる関数を 関数 の に関する 偏微分係数 略して偏微分 あるいは偏導関数 pil deiie といい 次のように表される についても同様な偏微分を定義できる あるいは あるいは - あるいは あるいは -
DVIOUT-SS_Ma
 第 章 微分方程式 ニュートンはリンゴが落ちるのを見て万有引力を発見した という有名な逸話があります 無重力の宇宙船の中ではリンゴは落ちないで静止していることを考えると 重力が働くと始め静止しているものが動き出して そのスピードはどんどん大きくなる つまり速度の変化が現れることがわかります 速度は一般に時間と共に変化します 速度の瞬間的変化の割合を加速度といい で定義しましょう 速度が変化する, つまり加速度がでなくなるためにはその原因があり
第 章 微分方程式 ニュートンはリンゴが落ちるのを見て万有引力を発見した という有名な逸話があります 無重力の宇宙船の中ではリンゴは落ちないで静止していることを考えると 重力が働くと始め静止しているものが動き出して そのスピードはどんどん大きくなる つまり速度の変化が現れることがわかります 速度は一般に時間と共に変化します 速度の瞬間的変化の割合を加速度といい で定義しましょう 速度が変化する, つまり加速度がでなくなるためにはその原因があり
NumericalProg09
 数値解析および プログラミング演習 [08 第 9 回目 ] の解法 - 4. Ruge-Kua( ルンゲ クッタ 法 Ruge-Kua-Gill( ルンゲ クッタ ジル / ギル 法 5. 多段解法 解法の対象 常微分方程式 d( d 初期値条件 (, の変化に応じて変化する の値を求める. ( 0 ( 0 と 0 は,give 0 常微分方程式の初期値問題 と言う. 3 Ruge-Kua 法の導出
数値解析および プログラミング演習 [08 第 9 回目 ] の解法 - 4. Ruge-Kua( ルンゲ クッタ 法 Ruge-Kua-Gill( ルンゲ クッタ ジル / ギル 法 5. 多段解法 解法の対象 常微分方程式 d( d 初期値条件 (, の変化に応じて変化する の値を求める. ( 0 ( 0 と 0 は,give 0 常微分方程式の初期値問題 と言う. 3 Ruge-Kua 法の導出
2 図微小要素の流体の流入出 方向の断面の流体の流入出の収支断面 Ⅰ から微小要素に流入出する流体の流量 Q 断面 Ⅰ は 以下のように定式化できる Q 断面 Ⅰ 流量 密度 流速 断面 Ⅰ の面積 微小要素の断面 Ⅰ から だけ移動した断面 Ⅱ を流入出する流体の流量 Q 断面 Ⅱ は以下のように
 3 章 Web に Link 解説 連続式 微分表示 の誘導.64 *4. 連続式連続式は ある領域の内部にある流体の質量の収支が その表面からの流入出の合計と等しくなることを定式化したものであり 流体における質量保存則を示したものである 2. 連続式 微分表示 の誘導図のような微小要素 コントロールボリューム の領域内の流体の増減と外部からの流体の流入出を考えることで定式化できる 微小要素 流入
3 章 Web に Link 解説 連続式 微分表示 の誘導.64 *4. 連続式連続式は ある領域の内部にある流体の質量の収支が その表面からの流入出の合計と等しくなることを定式化したものであり 流体における質量保存則を示したものである 2. 連続式 微分表示 の誘導図のような微小要素 コントロールボリューム の領域内の流体の増減と外部からの流体の流入出を考えることで定式化できる 微小要素 流入
問題-1.indd
 科目名学科 学年 組学籍番号氏名採点結果 016 年度材料力学 Ⅲ 問題 1 1 3 次元的に外力負荷を受ける物体を考える際にデカルト直交座標 - を採る 物体 内のある点 を取り囲む微小六面体上に働く応力 が v =- 40, = 60 =- 30 v = 0 = 10 v = 60 である 図 1 の 面上にこれらの応力 の作用方向を矢印で記入し その脇にその矢印が示す応力成分を記入しなさい 図
科目名学科 学年 組学籍番号氏名採点結果 016 年度材料力学 Ⅲ 問題 1 1 3 次元的に外力負荷を受ける物体を考える際にデカルト直交座標 - を採る 物体 内のある点 を取り囲む微小六面体上に働く応力 が v =- 40, = 60 =- 30 v = 0 = 10 v = 60 である 図 1 の 面上にこれらの応力 の作用方向を矢印で記入し その脇にその矢印が示す応力成分を記入しなさい 図
Microsoft PowerPoint - H22制御工学I-2回.ppt
 制御工学 I 第二回ラプラス変換 平成 年 4 月 9 日 /4/9 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
制御工学 I 第二回ラプラス変換 平成 年 4 月 9 日 /4/9 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
Microsoft PowerPoint - fuseitei_6
 不静定力学 Ⅱ 骨組の崩壊荷重の計算 不静定力学 Ⅱ では, 最後の問題となりますが, 骨組の崩壊荷重の計算法について学びます 1 参考書 松本慎也著 よくわかる構造力学の基本, 秀和システム このスライドの説明には, 主にこの参考書の説明を引用しています 2 崩壊荷重 構造物に作用する荷重が徐々に増大すると, 構造物内に発生する応力は増加し, やがて, 構造物は荷重に耐えられなくなる そのときの荷重を崩壊荷重あるいは終局荷重という
不静定力学 Ⅱ 骨組の崩壊荷重の計算 不静定力学 Ⅱ では, 最後の問題となりますが, 骨組の崩壊荷重の計算法について学びます 1 参考書 松本慎也著 よくわかる構造力学の基本, 秀和システム このスライドの説明には, 主にこの参考書の説明を引用しています 2 崩壊荷重 構造物に作用する荷重が徐々に増大すると, 構造物内に発生する応力は増加し, やがて, 構造物は荷重に耐えられなくなる そのときの荷重を崩壊荷重あるいは終局荷重という
PowerPoint Presentation
 応用数学 Ⅱ (7) 7 連立微分方程式の立て方と解法. 高階微分方程式による解法. ベクトル微分方程式による解法 3. 演算子による解法 連立微分方程式 未知数が複数個あり, 未知数の数だけ微分方程式が与えられている場合, これらを連立微分方程式という. d d 解法 () 高階微分方程式化による解法 つの方程式から つの未知数を消去して, 未知数が つの方程式に変換 のみの方程式にするために,
応用数学 Ⅱ (7) 7 連立微分方程式の立て方と解法. 高階微分方程式による解法. ベクトル微分方程式による解法 3. 演算子による解法 連立微分方程式 未知数が複数個あり, 未知数の数だけ微分方程式が与えられている場合, これらを連立微分方程式という. d d 解法 () 高階微分方程式化による解法 つの方程式から つの未知数を消去して, 未知数が つの方程式に変換 のみの方程式にするために,
<4D F736F F F696E74202D AB97CD8A E631318FCD5F AB8D5C90AC8EAE816A2E B8CDD8AB B83685D>
 弾塑性構成式 弾塑性応力 ひずみ解析における基礎式 応力の平衡方程式 ひずみの適合条件式 構成式 (), 全ひずみ理論 () 硬化則 () 塑性ポテンシャル理論の概要 ひずみ 応力の増分, 速度 弾性丸棒の引張変形を考える ( 簡単のため 公称 で考える ). 時間増分 dt 時刻 t 0 du u 時刻 t t 時刻 t t のひずみ, 応力 u, 微小な時間増分 dt におけるひずみ増分, 応力増分
弾塑性構成式 弾塑性応力 ひずみ解析における基礎式 応力の平衡方程式 ひずみの適合条件式 構成式 (), 全ひずみ理論 () 硬化則 () 塑性ポテンシャル理論の概要 ひずみ 応力の増分, 速度 弾性丸棒の引張変形を考える ( 簡単のため 公称 で考える ). 時間増分 dt 時刻 t 0 du u 時刻 t t 時刻 t t のひずみ, 応力 u, 微小な時間増分 dt におけるひずみ増分, 応力増分
第6章 実験モード解析
 第 6 章実験モード解析 6. 実験モード解析とは 6. 有限自由度系の実験モード解析 6.3 連続体の実験モード解析 6. 実験モード解析とは 実験モード解析とは加振実験によって測定された外力と応答を用いてモードパラメータ ( 固有振動数, モード減衰比, 正規固有モードなど ) を求める ( 同定する ) 方法である. 力計 試験体 変位計 / 加速度計 実験モード解析の概念 時間領域データを利用する方法
第 6 章実験モード解析 6. 実験モード解析とは 6. 有限自由度系の実験モード解析 6.3 連続体の実験モード解析 6. 実験モード解析とは 実験モード解析とは加振実験によって測定された外力と応答を用いてモードパラメータ ( 固有振動数, モード減衰比, 正規固有モードなど ) を求める ( 同定する ) 方法である. 力計 試験体 変位計 / 加速度計 実験モード解析の概念 時間領域データを利用する方法
Microsoft PowerPoint - suta.ppt [互換モード]
![Microsoft PowerPoint - suta.ppt [互換モード] Microsoft PowerPoint - suta.ppt [互換モード]](/thumbs/92/108124831.jpg) 弾塑性不飽和土構成モデルの一般化と土 / 水連成解析への適用 研究の背景 不飽和状態にある土構造物の弾塑性挙動 ロックフィルダム 道路盛土 長期的に正確な予測 不飽和土弾塑性構成モデル 水頭変動 雨水の浸潤 乾湿の繰り返し 土構造物の品質変化 不飽和土の特徴的な力学特性 不飽和土の特性 サクション サクション s w C 飽和度が低い状態 飽和度が高い状態 サクションの効果 空気侵入値 B. サクション増加
弾塑性不飽和土構成モデルの一般化と土 / 水連成解析への適用 研究の背景 不飽和状態にある土構造物の弾塑性挙動 ロックフィルダム 道路盛土 長期的に正確な予測 不飽和土弾塑性構成モデル 水頭変動 雨水の浸潤 乾湿の繰り返し 土構造物の品質変化 不飽和土の特徴的な力学特性 不飽和土の特性 サクション サクション s w C 飽和度が低い状態 飽和度が高い状態 サクションの効果 空気侵入値 B. サクション増加
Microsoft PowerPoint - 10.pptx
 m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
1/12 平成 29 年 3 月 24 日午後 1 時 1 分第 3 章測地線 第 3 章測地線 Ⅰ. 変分法と運動方程式最小作用の原理に基づくラグランジュの方法により 重力場中の粒子の運動方程式が求められる これは 力が未知の時に有効な方法であり 今のような 一般相対性理論における力を求めるのに使
 / 平成 9 年 3 月 4 日午後 時 分第 3 章測地線 第 3 章測地線 Ⅰ. 変分法と運動方程式最小作用の原理に基づくラグランジュの方法により 重力場中の粒子の運動方程式が求められる これは 力が未知の時に有効な方法であり 今のような 一般相対性理論における力を求めるのに使う事ができる 最小作用の原理 : 粒子が時刻 から の間に移動したとき 位置 と速度 v = するのが ラグランジュ関数
/ 平成 9 年 3 月 4 日午後 時 分第 3 章測地線 第 3 章測地線 Ⅰ. 変分法と運動方程式最小作用の原理に基づくラグランジュの方法により 重力場中の粒子の運動方程式が求められる これは 力が未知の時に有効な方法であり 今のような 一般相対性理論における力を求めるのに使う事ができる 最小作用の原理 : 粒子が時刻 から の間に移動したとき 位置 と速度 v = するのが ラグランジュ関数
木村の物理小ネタ 単振動と単振動の力学的エネルギー 1. 弾性力と単振動 弾性力も単振動も力は F = -Kx の形で表されるが, x = 0 の位置は, 弾性力の場合, 弾性体の自然状態の位置 単振動の場合, 振動する物体に働く力のつり合
 単振動と単振動の力学的エネルギー. 弾性力と単振動 弾性力も単振動も力は F = -x の形で表されるが, x = の位置は, 弾性力の場合, 弾性体の自然状態の位置 単振動の場合, 振動する物体に働く力のつり合いの位置 である たとえば, おもりをつるしたばねについて, ばねの弾性力を考えるときは, ばねの自然長を x = とし, おもりの単振動で考える場合は, おもりに働く力がつり合った位置を
単振動と単振動の力学的エネルギー. 弾性力と単振動 弾性力も単振動も力は F = -x の形で表されるが, x = の位置は, 弾性力の場合, 弾性体の自然状態の位置 単振動の場合, 振動する物体に働く力のつり合いの位置 である たとえば, おもりをつるしたばねについて, ばねの弾性力を考えるときは, ばねの自然長を x = とし, おもりの単振動で考える場合は, おもりに働く力がつり合った位置を
第1章 単 位
 H. Hamano,. 長柱の座屈 - 長柱の座屈 長い柱は圧縮荷重によって折れてしまう場合がある. この現象を座屈といい, 座屈するときの荷重を座屈荷重という.. 換算長 長さ の柱に荷重が作用する場合, その支持方法によって, 柱の理論上の長さ L が異なる. 長柱の計算は, この L を用いて行うと都合がよい. この L を換算長 ( あるいは有効長さという ) という. 座屈荷重は一般に,
H. Hamano,. 長柱の座屈 - 長柱の座屈 長い柱は圧縮荷重によって折れてしまう場合がある. この現象を座屈といい, 座屈するときの荷重を座屈荷重という.. 換算長 長さ の柱に荷重が作用する場合, その支持方法によって, 柱の理論上の長さ L が異なる. 長柱の計算は, この L を用いて行うと都合がよい. この L を換算長 ( あるいは有効長さという ) という. 座屈荷重は一般に,
2014年度 筑波大・理系数学
 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ f ( x) = x x とする y = f ( x ) のグラフに点 P(, ) から引いた接線は 本あるとする つの接点 A (, f ( )), B(, f ( )), C(, f ( )) を頂点とする三角形の 重心を G とする () + +, + + および を, を用いて表せ () 点 G の座標を, を用いて表せ () 点 G
筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ f ( x) = x x とする y = f ( x ) のグラフに点 P(, ) から引いた接線は 本あるとする つの接点 A (, f ( )), B(, f ( )), C(, f ( )) を頂点とする三角形の 重心を G とする () + +, + + および を, を用いて表せ () 点 G の座標を, を用いて表せ () 点 G
PowerPoint Presentation
 付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
材料の力学解答集
 材料の力学 ( 第 章 ) 解答集 ------------------------------------------------------------------------------- 各種応力の計算問題 (No1) 1. 断面積 1mm の材料に 18N の引張荷重が働くとき, 断面に生じる応力はどれほどか ( 18(N/mm ) または 18(MP)) P 18( N) 18 N /
材料の力学 ( 第 章 ) 解答集 ------------------------------------------------------------------------------- 各種応力の計算問題 (No1) 1. 断面積 1mm の材料に 18N の引張荷重が働くとき, 断面に生じる応力はどれほどか ( 18(N/mm ) または 18(MP)) P 18( N) 18 N /
数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュ
 数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュレーションによって計算してみる 4.1 放物運動一様な重力場における放物運動を考える 一般に質量の物体に作用する力をとすると運動方程式は
数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュレーションによって計算してみる 4.1 放物運動一様な重力場における放物運動を考える 一般に質量の物体に作用する力をとすると運動方程式は
Microsoft PowerPoint - 夏の学校(CFD).pptx
 /9/5 FD( 計算流体力学 ) の基礎理論 性能 運動分野 夏の学校 神戸大学大学院海事科学研究科勝井辰博 流体の質量保存 流体要素内の質量の増加率 [ 単位時間当たりの増加量 ] 単位時間に流体要素に流入する質量 流体要素 Fl lm (orol olm) v ( ) ガウスの定理 v( ) /9/5 = =( ) b=b =(b b b ) b= b = b + b + b アインシュタイン表記
/9/5 FD( 計算流体力学 ) の基礎理論 性能 運動分野 夏の学校 神戸大学大学院海事科学研究科勝井辰博 流体の質量保存 流体要素内の質量の増加率 [ 単位時間当たりの増加量 ] 単位時間に流体要素に流入する質量 流体要素 Fl lm (orol olm) v ( ) ガウスの定理 v( ) /9/5 = =( ) b=b =(b b b ) b= b = b + b + b アインシュタイン表記
Microsoft Word - 4_構造特性係数の設定方法に関する検討.doc
 第 4 章 構造特性係数の設定方法に関する検討 4. はじめに 平成 年度 年度の時刻歴応答解析を実施した結果 課題として以下の点が指摘 された * ) 脆性壁の評価法の問題 時刻歴応答解析により 初期剛性が高く脆性的な壁については現在の構造特性係数 Ds 評価が危険であることが判明した 脆性壁では.5 倍程度必要保有耐力が大きくなる * ) 併用構造の Ds の設定の問題 異なる荷重変形関係を持つ壁の
第 4 章 構造特性係数の設定方法に関する検討 4. はじめに 平成 年度 年度の時刻歴応答解析を実施した結果 課題として以下の点が指摘 された * ) 脆性壁の評価法の問題 時刻歴応答解析により 初期剛性が高く脆性的な壁については現在の構造特性係数 Ds 評価が危険であることが判明した 脆性壁では.5 倍程度必要保有耐力が大きくなる * ) 併用構造の Ds の設定の問題 異なる荷重変形関係を持つ壁の
耳桁の剛性の考慮分配係数の計算条件は 主桁本数 n 格子剛度 zです 通常の並列鋼桁橋では 主桁はすべて同じ断面を使います しかし 分配の効率を上げる場合 耳桁 ( 幅員端側の桁 ) の断面を大きくすることがあります 最近の桁橋では 上下線を別橋梁とすることがあり また 防音壁などの敷設が片側に有る
 格子桁の分配係数の計算 ( デモ版 ) 理論と解析の背景主桁を並列した鋼単純桁の設計では 幅員方向の横桁の剛性を考えて 複数の主桁が協力して活荷重を分担する効果を計算します これを 単純な (1,0) 分配に対して格子分配と言います レオンハルト (F.Leonhardt,1909-1999) が 1950 年初頭に発表した論文が元になっていて 理論仮定 記号などの使い方は その論文を踏襲して設計に応用しています
格子桁の分配係数の計算 ( デモ版 ) 理論と解析の背景主桁を並列した鋼単純桁の設計では 幅員方向の横桁の剛性を考えて 複数の主桁が協力して活荷重を分担する効果を計算します これを 単純な (1,0) 分配に対して格子分配と言います レオンハルト (F.Leonhardt,1909-1999) が 1950 年初頭に発表した論文が元になっていて 理論仮定 記号などの使い方は その論文を踏襲して設計に応用しています
Microsoft Word - NumericalComputation.docx
 数値計算入門 武尾英哉. 離散数学と数値計算 数学的解法の中には理論計算では求められないものもある. 例えば, 定積分は, まずは積分 ( 被積分関数の原始関数をみつけること できなければ値を得ることはできない. また, ある関数の所定の値における微分値を得るには, まずその関数の微分ができなければならない. さらに代数方程式の解を得るためには, 解析的に代数方程式を解く必要がある. ところが, これらは必ずしも解析的に導けるとは限らない.
数値計算入門 武尾英哉. 離散数学と数値計算 数学的解法の中には理論計算では求められないものもある. 例えば, 定積分は, まずは積分 ( 被積分関数の原始関数をみつけること できなければ値を得ることはできない. また, ある関数の所定の値における微分値を得るには, まずその関数の微分ができなければならない. さらに代数方程式の解を得るためには, 解析的に代数方程式を解く必要がある. ところが, これらは必ずしも解析的に導けるとは限らない.
平板曲げ理論による部材の等分布荷重または節点の集中荷重を受ける薄板のたわみと断面力の計算ソフト 鉄筋コンクリート床版や鋼板などの平板 ( 薄板 ) の等分布や集中荷重による作用曲げモーメント等の算出方法は 下記の平板の曲げ解析法一覧表より [1 平板曲げ理論による解析 ( 理論解 ) による方法 ]
![平板曲げ理論による部材の等分布荷重または節点の集中荷重を受ける薄板のたわみと断面力の計算ソフト 鉄筋コンクリート床版や鋼板などの平板 ( 薄板 ) の等分布や集中荷重による作用曲げモーメント等の算出方法は 下記の平板の曲げ解析法一覧表より [1 平板曲げ理論による解析 ( 理論解 ) による方法 ] 平板曲げ理論による部材の等分布荷重または節点の集中荷重を受ける薄板のたわみと断面力の計算ソフト 鉄筋コンクリート床版や鋼板などの平板 ( 薄板 ) の等分布や集中荷重による作用曲げモーメント等の算出方法は 下記の平板の曲げ解析法一覧表より [1 平板曲げ理論による解析 ( 理論解 ) による方法 ]](/thumbs/97/131337752.jpg) 平板曲げ理論による部材の等分布荷重または節点の集中荷重を受ける薄板のたわみと断面力の計算ソフト 鉄筋コンクリート床版や鋼板などの平板 ( 薄板 ) の等分布や集中荷重による作用曲げモーメント等の算出方法は 下記の平板の曲げ解析法一覧表より [1 平板曲げ理論による解析 ( 理論解 ) による方法 ] と [2 格子モデルによる微小変位理論 ( 棒部材の簡易格子モデル )] および [3 簡易算出式による方法
平板曲げ理論による部材の等分布荷重または節点の集中荷重を受ける薄板のたわみと断面力の計算ソフト 鉄筋コンクリート床版や鋼板などの平板 ( 薄板 ) の等分布や集中荷重による作用曲げモーメント等の算出方法は 下記の平板の曲げ解析法一覧表より [1 平板曲げ理論による解析 ( 理論解 ) による方法 ] と [2 格子モデルによる微小変位理論 ( 棒部材の簡易格子モデル )] および [3 簡易算出式による方法
上式を整理すると d df - N = 両辺を で割れば df d - N = (5) となる ところで
 長柱の座屈 断面寸法に対して非常に長い柱に圧縮荷重を加えると 初期段階においては一様圧縮変形を生ずるが ある荷重に達すると急に横方向にたわむことがある このように長柱が軸圧縮荷重を受けていて突然横方向にたわむ現象を座屈といい この現象を示す荷重を座屈荷重 cr このときの応力を座屈応力 s cr という 図 に示すように一端を鉛直な剛性壁に固定された長柱が自 図 曲げと圧縮を受けるはり + 由端に圧縮力
長柱の座屈 断面寸法に対して非常に長い柱に圧縮荷重を加えると 初期段階においては一様圧縮変形を生ずるが ある荷重に達すると急に横方向にたわむことがある このように長柱が軸圧縮荷重を受けていて突然横方向にたわむ現象を座屈といい この現象を示す荷重を座屈荷重 cr このときの応力を座屈応力 s cr という 図 に示すように一端を鉛直な剛性壁に固定された長柱が自 図 曲げと圧縮を受けるはり + 由端に圧縮力
喨微勃挹稉弑
 == 全微分方程式 == 全微分とは 変数の関数 z=f(, ) について,, の増分を Δ, Δ とするとき, z の増分 Δz は Δz z Δ+ z Δ で表されます. この式において, Δ 0, Δ 0 となる極限を形式的に dz= z d+ z d (1) で表し, dz を z の全微分といいます. z は z の に関する偏導関数で, を定数と見なし て, で微分したものを表し, 方向の傾きに対応します.
== 全微分方程式 == 全微分とは 変数の関数 z=f(, ) について,, の増分を Δ, Δ とするとき, z の増分 Δz は Δz z Δ+ z Δ で表されます. この式において, Δ 0, Δ 0 となる極限を形式的に dz= z d+ z d (1) で表し, dz を z の全微分といいます. z は z の に関する偏導関数で, を定数と見なし て, で微分したものを表し, 方向の傾きに対応します.
1/10 平成 29 年 3 月 24 日午後 1 時 37 分第 5 章ローレンツ変換と回転 第 5 章ローレンツ変換と回転 Ⅰ. 回転 第 3 章光速度不変の原理とローレンツ変換 では 時間の遅れをローレンツ変換 ct 移動 v相対 v相対 ct - x x - ct = c, x c 2 移動
 / 平成 9 年 3 月 4 日午後 時 37 分第 5 章ローレンツ変換と回転 第 5 章ローレンツ変換と回転 Ⅰ. 回転 第 3 章光速度不変の原理とローレンツ変換 では 時間の遅れをローレンツ変換 t t - x x - t, x 静止静止静止静止 を導いた これを 図の場合に当てはめると t - x x - t t, x t + x x + t t, x (5.) (5.) (5.3) を得る
/ 平成 9 年 3 月 4 日午後 時 37 分第 5 章ローレンツ変換と回転 第 5 章ローレンツ変換と回転 Ⅰ. 回転 第 3 章光速度不変の原理とローレンツ変換 では 時間の遅れをローレンツ変換 t t - x x - t, x 静止静止静止静止 を導いた これを 図の場合に当てはめると t - x x - t t, x t + x x + t t, x (5.) (5.) (5.3) を得る
宇宙機工学 演習問題
 宇宙システム工学演習 重力傾度トルク関連. 図に示すように地球回りの円軌道上を周回する宇宙機の運動 を考察する 地球中心座標系を 系 { } 軌道面基準回転系を 系 { } 機体固定系を 系 { } とする 特に次の右手直交系 : 地心方向単位ベクトル 軌道面内 : 進行方向単位ベクトル 軌道面内 : 面外方向単位ベクトル 軌道面外 を取る 特に この { } Lol Horiotl frme と呼ぶ
宇宙システム工学演習 重力傾度トルク関連. 図に示すように地球回りの円軌道上を周回する宇宙機の運動 を考察する 地球中心座標系を 系 { } 軌道面基準回転系を 系 { } 機体固定系を 系 { } とする 特に次の右手直交系 : 地心方向単位ベクトル 軌道面内 : 進行方向単位ベクトル 軌道面内 : 面外方向単位ベクトル 軌道面外 を取る 特に この { } Lol Horiotl frme と呼ぶ
Microsoft Word - 5章摂動法.doc
 5 章摂動法 ( 次の Moller-Plesset (MP) 法のために ) // 水素原子など 電子系を除いては 原子系の Schrödiger 方程式を解析的に解くことはできない 分子系の Schrödiger 方程式の正確な数値解を求めることも困難である そこで Hartree-Fock(H-F) 法を導入した H-F 法は Schrödiger 方程式が与える全エネルギーの 99% を再現することができる優れた近似方法である
5 章摂動法 ( 次の Moller-Plesset (MP) 法のために ) // 水素原子など 電子系を除いては 原子系の Schrödiger 方程式を解析的に解くことはできない 分子系の Schrödiger 方程式の正確な数値解を求めることも困難である そこで Hartree-Fock(H-F) 法を導入した H-F 法は Schrödiger 方程式が与える全エネルギーの 99% を再現することができる優れた近似方法である
新日本技研 ( 株 ) 技術報告 弾性横桁で支持された床版の断面力式 仙台支店 設計部高橋眞太郎 本社 顧問倉方慶夫 元本社 顧問高尾孝二 要旨 橋梁形式は 公共事業費抑制の要求を受けてコスト縮減を図ることができる合理化形式の採用が多くなっている この流れを受けて鈑桁形式では少数鈑桁橋
 新日本技研 ( 株 技術報告 - 弾性横桁で支持された床版の断面力式 仙台支店 設計部高橋眞太郎 本社 顧問倉方慶夫 元本社 顧問高尾孝二 要旨 橋梁形式は 公共事業費抑制の要求を受けてコスト縮減を図ることができる合理化形式の採用が多くなっている この流れを受けて鈑桁形式では少数鈑桁橋の採用が多くなっている この形式はおよそ 年前に 日本道路公団が欧州の少数鈑桁橋を参考にPC 床版を有する少数鈑桁橋の検討を始め
新日本技研 ( 株 技術報告 - 弾性横桁で支持された床版の断面力式 仙台支店 設計部高橋眞太郎 本社 顧問倉方慶夫 元本社 顧問高尾孝二 要旨 橋梁形式は 公共事業費抑制の要求を受けてコスト縮減を図ることができる合理化形式の採用が多くなっている この流れを受けて鈑桁形式では少数鈑桁橋の採用が多くなっている この形式はおよそ 年前に 日本道路公団が欧州の少数鈑桁橋を参考にPC 床版を有する少数鈑桁橋の検討を始め
スライド 1
 H25 創造設計演習 ~ 振動設計演習 1~ 1 ゆれない片持ち梁の設計 振動設計演習全体 HP(2011 年度まで使用 今は閲覧のみ ): http://hockey.t.u-tokyo.ac.jp/shindousekkei/index.html M4 取付ネジ 2 Xin 加振器 50mm 幅 30mm 材料 :A2017または ABS 樹脂 計測点 :Xout 2mm? Hz CAD 所望の特性になるまで繰り返す?
H25 創造設計演習 ~ 振動設計演習 1~ 1 ゆれない片持ち梁の設計 振動設計演習全体 HP(2011 年度まで使用 今は閲覧のみ ): http://hockey.t.u-tokyo.ac.jp/shindousekkei/index.html M4 取付ネジ 2 Xin 加振器 50mm 幅 30mm 材料 :A2017または ABS 樹脂 計測点 :Xout 2mm? Hz CAD 所望の特性になるまで繰り返す?
例 e 指数関数的に減衰する信号を h( a < + a a すると, それらのラプラス変換は, H ( ) { e } e インパルス応答が h( a < ( ただし a >, U( ) { } となるシステムにステップ信号 ( y( のラプラス変換 Y () は, Y ( ) H ( ) X (
 第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
横浜市環境科学研究所
 周期時系列の統計解析 単回帰分析 io 8 年 3 日 周期時系列に季節調整を行わないで単回帰分析を適用すると, 回帰係数には周期成分の影響が加わる. ここでは, 周期時系列をコサイン関数モデルで近似し単回帰分析によりモデルの回帰係数を求め, 周期成分の影響を検討した. また, その結果を気温時系列に当てはめ, 課題等について考察した. 気温時系列とコサイン関数モデル第 報の結果を利用するので, その一部を再掲する.
周期時系列の統計解析 単回帰分析 io 8 年 3 日 周期時系列に季節調整を行わないで単回帰分析を適用すると, 回帰係数には周期成分の影響が加わる. ここでは, 周期時系列をコサイン関数モデルで近似し単回帰分析によりモデルの回帰係数を求め, 周期成分の影響を検討した. また, その結果を気温時系列に当てはめ, 課題等について考察した. 気温時系列とコサイン関数モデル第 報の結果を利用するので, その一部を再掲する.
第1章 単 位
 H. Hmno 問題解答 問題解答. 力の釣合い [ 問題.] V : sin. H :.cos. 7 V : sin sin H : cos cos cos 上第 式より これと第 式より.. cos V : sin sin H : coscos cos 上第 式より これと第 式より.98. cos [ 問題.] :. V :. : 9 9. V :. : sin V : sin 8.78 H
H. Hmno 問題解答 問題解答. 力の釣合い [ 問題.] V : sin. H :.cos. 7 V : sin sin H : cos cos cos 上第 式より これと第 式より.. cos V : sin sin H : coscos cos 上第 式より これと第 式より.98. cos [ 問題.] :. V :. : 9 9. V :. : sin V : sin 8.78 H
2014年度 名古屋大・理系数学
 04 名古屋大学 ( 理系 ) 前期日程問題 解答解説のページへ空間内にある半径 の球 ( 内部を含む ) を B とする 直線 と B が交わっており, その交わりは長さ の線分である () B の中心と との距離を求めよ () のまわりに B を 回転してできる立体の体積を求めよ 04 名古屋大学 ( 理系 ) 前期日程問題 解答解説のページへ 実数 t に対して 点 P( t, t ), Q(
04 名古屋大学 ( 理系 ) 前期日程問題 解答解説のページへ空間内にある半径 の球 ( 内部を含む ) を B とする 直線 と B が交わっており, その交わりは長さ の線分である () B の中心と との距離を求めよ () のまわりに B を 回転してできる立体の体積を求めよ 04 名古屋大学 ( 理系 ) 前期日程問題 解答解説のページへ 実数 t に対して 点 P( t, t ), Q(
SPACEstJ User's Manual
 6-1 第 6 章部材の断面力計算 ポイント : 部材断面力の計算 両端の変位より両端外力を計算する 本章では 両端の変位を用いて部材両端の材端力を求め 断面内の応力との釣合より 断面力を求める方法を学ぶ ここでは 部材荷重は等分布荷重を考慮しているため 基本応力と節点荷重による断面力を重ね合わせて 実際の部材断面力を求める 6.1 はじめに キーワード 部材断面力の計算部材座標系の変位等分布荷重による基本応力
6-1 第 6 章部材の断面力計算 ポイント : 部材断面力の計算 両端の変位より両端外力を計算する 本章では 両端の変位を用いて部材両端の材端力を求め 断面内の応力との釣合より 断面力を求める方法を学ぶ ここでは 部材荷重は等分布荷重を考慮しているため 基本応力と節点荷重による断面力を重ね合わせて 実際の部材断面力を求める 6.1 はじめに キーワード 部材断面力の計算部材座標系の変位等分布荷重による基本応力
<4D F736F F F696E74202D E94D58B9393AE82F AC82B782E982BD82DF82CC8AEE E707074>
 地盤数値解析学特論 防災環境地盤工学研究室村上哲 Mrakam, Satoh. 地盤挙動を把握するための基礎. 変位とひずみ. 力と応力. 地盤の変形と応力. 変位とひずみ 変形勾配テンソルひずみテンソル ひずみテンソル : 材料線素の長さの 乗の変化量の尺度 Green-Lagrange のひずみテンソルと Alman のひずみテンソル 微小変形状態でのひずみテンソル ひずみテンソルの物理的な意味
地盤数値解析学特論 防災環境地盤工学研究室村上哲 Mrakam, Satoh. 地盤挙動を把握するための基礎. 変位とひずみ. 力と応力. 地盤の変形と応力. 変位とひずみ 変形勾配テンソルひずみテンソル ひずみテンソル : 材料線素の長さの 乗の変化量の尺度 Green-Lagrange のひずみテンソルと Alman のひずみテンソル 微小変形状態でのひずみテンソル ひずみテンソルの物理的な意味
材料強度試験 ( 曲げ試験 ) [1] 概要 実験 実習 Ⅰ の引張り試験に引続き, 曲げ試験による機械特性評価法を実施する. 材料力学で学ぶ梁 の曲げおよびたわみの基礎式の理解, 材料への理解を深めることが目的である. [2] 材料の変形抵抗変形抵抗は, 外力が付与された時の変形に対する各材料固有
![材料強度試験 ( 曲げ試験 ) [1] 概要 実験 実習 Ⅰ の引張り試験に引続き, 曲げ試験による機械特性評価法を実施する. 材料力学で学ぶ梁 の曲げおよびたわみの基礎式の理解, 材料への理解を深めることが目的である. [2] 材料の変形抵抗変形抵抗は, 外力が付与された時の変形に対する各材料固有 材料強度試験 ( 曲げ試験 ) [1] 概要 実験 実習 Ⅰ の引張り試験に引続き, 曲げ試験による機械特性評価法を実施する. 材料力学で学ぶ梁 の曲げおよびたわみの基礎式の理解, 材料への理解を深めることが目的である. [2] 材料の変形抵抗変形抵抗は, 外力が付与された時の変形に対する各材料固有](/thumbs/97/134628245.jpg) 材料強度試験 ( 曲げ試験 [] 概要 実験 実習 Ⅰ の引張り試験に引続き, 曲げ試験による機械特性評価法を実施する. 材料力学で学ぶ梁 の曲げおよびたわみの基礎式の理解, 材料への理解を深めることが目的である. [] 材料の変形抵抗変形抵抗は, 外力が付与された時の変形に対する各材料固有の抵抗値のことであり, 一般に素材の真応力 - 真塑性ひずみ曲線で表される. 多くの金属材料は加工硬化するため,
材料強度試験 ( 曲げ試験 [] 概要 実験 実習 Ⅰ の引張り試験に引続き, 曲げ試験による機械特性評価法を実施する. 材料力学で学ぶ梁 の曲げおよびたわみの基礎式の理解, 材料への理解を深めることが目的である. [] 材料の変形抵抗変形抵抗は, 外力が付与された時の変形に対する各材料固有の抵抗値のことであり, 一般に素材の真応力 - 真塑性ひずみ曲線で表される. 多くの金属材料は加工硬化するため,
第 4 週コンボリューションその 2, 正弦波による分解 教科書 p. 16~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問 1. 以下の図にならって,1 と 2 の δ 関数を図示せよ δ (t) 2
 第 4 週コンボリューションその, 正弦波による分解 教科書 p. 6~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問. 以下の図にならって, と の δ 関数を図示せよ. - - - δ () δ ( ) - - - 図 δ 関数の図示の例 δ ( ) δ ( ) δ ( ) δ ( ) δ ( ) - - - - - - - -
第 4 週コンボリューションその, 正弦波による分解 教科書 p. 6~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問. 以下の図にならって, と の δ 関数を図示せよ. - - - δ () δ ( ) - - - 図 δ 関数の図示の例 δ ( ) δ ( ) δ ( ) δ ( ) δ ( ) - - - - - - - -
公式集 数学 Ⅱ B 頭に入っていますか? 8 和積の公式 A + B A B si A + si B si os A + B A B si A si B os si A + B A B os A + os B os os A + B A B os A os B si si 9 三角関数の合成 si
 公式集 数学 Ⅱ B 頭に入っていますか? < 図形と方程式 > 点間の距離 A x, B x, のとき x x + : に分ける点 A x, B x, のとき 線分 AB を:に分ける点 æ x + x + ö は ç, è + + ø 注 < のとき外分点 直線の方程式 傾き で 点 x, を通る : x 点 x, x, を通る : x 注 分母が のとき は座標軸と平行な直線 x x 4 直線の位置関係
公式集 数学 Ⅱ B 頭に入っていますか? < 図形と方程式 > 点間の距離 A x, B x, のとき x x + : に分ける点 A x, B x, のとき 線分 AB を:に分ける点 æ x + x + ö は ç, è + + ø 注 < のとき外分点 直線の方程式 傾き で 点 x, を通る : x 点 x, x, を通る : x 注 分母が のとき は座標軸と平行な直線 x x 4 直線の位置関係
航空機の運動方程式
 可制御性 可観測性. 可制御性システムの状態を, 適切な操作によって, 有限時間内に, 任意の状態から別の任意の状態に移動させることができるか否かという特性を可制御性という. 可制御性を有するシステムに対し, システムは可制御である, 可制御なシステム という言い方をする. 状態方程式, 出力方程式が以下で表されるn 次元 m 入力 r 出力線形時不変システム x Ax u y x Du () に対し,
可制御性 可観測性. 可制御性システムの状態を, 適切な操作によって, 有限時間内に, 任意の状態から別の任意の状態に移動させることができるか否かという特性を可制御性という. 可制御性を有するシステムに対し, システムは可制御である, 可制御なシステム という言い方をする. 状態方程式, 出力方程式が以下で表されるn 次元 m 入力 r 出力線形時不変システム x Ax u y x Du () に対し,
ベクトル公式.rtf
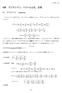 6 章ラプラシアン, ベクトル公式, 定理 6.1 ラプラシアン Laplacian φ はベクトル量である. そこでさらに発散をとると, φ はどういう形になるであろうか? φ = a + a + a φ a + a φ + a φ = φ + φ + φ = 2 φ + 2 φ 2 + 2 φ 2 2 φ = 2 φ 2 + 2 φ 2 + 2 φ 2 = 2 φ したがって,2 階の偏微分演算となる.
6 章ラプラシアン, ベクトル公式, 定理 6.1 ラプラシアン Laplacian φ はベクトル量である. そこでさらに発散をとると, φ はどういう形になるであろうか? φ = a + a + a φ a + a φ + a φ = φ + φ + φ = 2 φ + 2 φ 2 + 2 φ 2 2 φ = 2 φ 2 + 2 φ 2 + 2 φ 2 = 2 φ したがって,2 階の偏微分演算となる.
4.3 材料試験 材料試験とは材料の応力 -ひずみの関係や強度を明らかにするために その材料で作成した供試体( 試験体 ) に荷重を負荷し そのときのひずみ挙動や強度を調べる作業を材料試験という 材料試験では 供試体に一様な応力が発生することが望ましい 一様な応力 とは 至るところ ある
 4. 均質 等方弾性体の応力とひずみの関係 ( 構成方程式 ) およびひずみエネルギ 4.1 はじめに材料が応力を受けると それに応じてひずみが発生する この応力とひずみの関係は 応力 -ひずみの関係または構成方程式と呼ばれ 一般に材料によって異なる しかも同一の材料でも 応力やひずみを負荷する速度によって発生するひずみ ( または応力 ) の大きさが異なる すなわち ゆっくりと負荷すれば 粘性的な性質が強く現れ
4. 均質 等方弾性体の応力とひずみの関係 ( 構成方程式 ) およびひずみエネルギ 4.1 はじめに材料が応力を受けると それに応じてひずみが発生する この応力とひずみの関係は 応力 -ひずみの関係または構成方程式と呼ばれ 一般に材料によって異なる しかも同一の材料でも 応力やひずみを負荷する速度によって発生するひずみ ( または応力 ) の大きさが異なる すなわち ゆっくりと負荷すれば 粘性的な性質が強く現れ
1/15 平成 29 年 3 月 24 日午前 11 時 48 分第八章ニュートリノ質量行列 第八章 フレーバーニュートリノ ( e, m, t ) 換で結びつく (5.12) の ( e, m ) ニュートリノ質量行列 3 種混合 n n n と質量固有状態のニュートリノ ( n1, n 2, n
 /5 平成 9 年 月 4 日午前 時 48 分第八章ニュートリノ質量行列 第八章 フレーバーニュートリノ ( t ) 換で結びつく (5.) の ( ) ニュートリノ質量行列 種混合 と質量固有状態のニュートリノ ( ) と ( ) の場合の は ユニタリー変 æ æ cosq siq æ ø -siq cosq ø ø (8.) 以外に æ æ cosq siq æ -siq cosq t ø
/5 平成 9 年 月 4 日午前 時 48 分第八章ニュートリノ質量行列 第八章 フレーバーニュートリノ ( t ) 換で結びつく (5.) の ( ) ニュートリノ質量行列 種混合 と質量固有状態のニュートリノ ( ) と ( ) の場合の は ユニタリー変 æ æ cosq siq æ ø -siq cosq ø ø (8.) 以外に æ æ cosq siq æ -siq cosq t ø
<4D F736F F D E682568FCD CC82B982F192668BAD9378>
 7. 組み合わせ応力 7.7. 応力の座標変換載荷 ( 要素 の上方右側にずれている位置での載荷を想定 図 ( この場合正 ( この場合負 応力の座標変換の知識は なぜ必要か? 例 土の二つの基本的せん断変形モード : - 三軸圧縮変形 - 単純せん断変形 一面せん断変形両者でのせん断強度の関連を理解するためには 応力の座標変換を理解する必要がある 例 粘着力のない土 ( 代表例 乾燥した砂 のせん断破壊は
7. 組み合わせ応力 7.7. 応力の座標変換載荷 ( 要素 の上方右側にずれている位置での載荷を想定 図 ( この場合正 ( この場合負 応力の座標変換の知識は なぜ必要か? 例 土の二つの基本的せん断変形モード : - 三軸圧縮変形 - 単純せん断変形 一面せん断変形両者でのせん断強度の関連を理解するためには 応力の座標変換を理解する必要がある 例 粘着力のない土 ( 代表例 乾燥した砂 のせん断破壊は
2018年度 東京大・理系数学
 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ関数 f ( ) = + cos (0 < < ) の増減表をつくり, + 0, 0 のと sin きの極限を調べよ 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ n+ 数列 a, a, を, Cn a n = ( n =,, ) で定める n! an qn () n とする を既約分数 an p として表したときの分母
08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ関数 f ( ) = + cos (0 < < ) の増減表をつくり, + 0, 0 のと sin きの極限を調べよ 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ n+ 数列 a, a, を, Cn a n = ( n =,, ) で定める n! an qn () n とする を既約分数 an p として表したときの分母
前期募集 令和 2 年度山梨大学大学院医工農学総合教育部修士課程工学専攻 入学試験問題 No.1/2 コース等 メカトロニクス工学コース 試験科目 数学 問 1 図 1 は, 原点 O の直交座標系 x,y,z に関して, 線分 OA,OB,OC を 3 辺にもつ平行六面体を示す. ここで, 点 A
 No.1/2 数学 問 1 図 1 は, 原点 O の直交座標系 x,y,z に関して, 線分 OA,OB,OC を 3 辺にもつ平行六面体を示す. ここで, 点 A,B,C の座標はそれぞれ A (,6,-2), B (4,-5,3),C (-5.1,4.9,.9) である. 次の問いに答えよ. (1) を求めよ. (2) および の向きを解答用紙の図 1 に描け. (3) 図 1 の平行六面体の体積
No.1/2 数学 問 1 図 1 は, 原点 O の直交座標系 x,y,z に関して, 線分 OA,OB,OC を 3 辺にもつ平行六面体を示す. ここで, 点 A,B,C の座標はそれぞれ A (,6,-2), B (4,-5,3),C (-5.1,4.9,.9) である. 次の問いに答えよ. (1) を求めよ. (2) および の向きを解答用紙の図 1 に描け. (3) 図 1 の平行六面体の体積
2011年度 大阪大・理系数学
 0 大阪大学 ( 理系 ) 前期日程問題 解答解説のページへ a a を自然数とする O を原点とする座標平面上で行列 A= a の表す 次変換 を f とする cosθ siθ () >0 および0θ
0 大阪大学 ( 理系 ) 前期日程問題 解答解説のページへ a a を自然数とする O を原点とする座標平面上で行列 A= a の表す 次変換 を f とする cosθ siθ () >0 および0θ
2016年度 筑波大・理系数学
 06 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ k を実数とする y 平面の曲線 C : y とC : y- + k+ -k が異なる共 有点 P, Q をもつとする ただし点 P, Q の 座標は正であるとする また, 原点を O とする () k のとりうる値の範囲を求めよ () k が () の範囲を動くとき, OPQ の重心 G の軌跡を求めよ () OPQ の面積を S とするとき,
06 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ k を実数とする y 平面の曲線 C : y とC : y- + k+ -k が異なる共 有点 P, Q をもつとする ただし点 P, Q の 座標は正であるとする また, 原点を O とする () k のとりうる値の範囲を求めよ () k が () の範囲を動くとき, OPQ の重心 G の軌跡を求めよ () OPQ の面積を S とするとき,
2013年度 信州大・医系数学
 03 信州大学 ( 医系 ) 前期日程問題 解答解説のページへ () 式 + + a a a3 を満たす自然数の組 ( a, a, a3) で, a a a3とな るものをすべて求めよ () r を正の有理数とする 式 r + + a a a を満たす自然数の組 ( a, a, a3) で, 3 a a a3となるものは有限個しかないことを証明せよ ただし, そのよう な組が存在しない場合は 0 個とし,
03 信州大学 ( 医系 ) 前期日程問題 解答解説のページへ () 式 + + a a a3 を満たす自然数の組 ( a, a, a3) で, a a a3とな るものをすべて求めよ () r を正の有理数とする 式 r + + a a a を満たす自然数の組 ( a, a, a3) で, 3 a a a3となるものは有限個しかないことを証明せよ ただし, そのよう な組が存在しない場合は 0 個とし,
様々なミクロ計量モデル†
 担当 : 長倉大輔 ( ながくらだいすけ ) この資料は私の講義において使用するために作成した資料です WEB ページ上で公開しており 自由に参照して頂いて構いません ただし 内容について 一応検証してありますが もし間違いがあった場合でもそれによって生じるいかなる損害 不利益について責任を負いかねますのでご了承ください 間違いは発見次第 継続的に直していますが まだ存在する可能性があります 1 カウントデータモデル
担当 : 長倉大輔 ( ながくらだいすけ ) この資料は私の講義において使用するために作成した資料です WEB ページ上で公開しており 自由に参照して頂いて構いません ただし 内容について 一応検証してありますが もし間違いがあった場合でもそれによって生じるいかなる損害 不利益について責任を負いかねますのでご了承ください 間違いは発見次第 継続的に直していますが まだ存在する可能性があります 1 カウントデータモデル
Microsoft PowerPoint - 知財報告会H20kobayakawa.ppt [互換モード]
![Microsoft PowerPoint - 知財報告会H20kobayakawa.ppt [互換モード] Microsoft PowerPoint - 知財報告会H20kobayakawa.ppt [互換モード]](/thumbs/91/106644305.jpg) 亀裂の変形特性を考慮した数値解析による岩盤物性評価法 地球工学研究所地圏科学領域小早川博亮 1 岩盤構造物の安定性評価 ( 斜面の例 ) 代表要素 代表要素の応力ひずみ関係 変形: 弾性体の場合 :E,ν 強度: モールクーロン破壊規準 :c,φ Rock Mech. Rock Engng. (2007) 40 (4), 363 382 原位置試験 せん断試験, 平板載荷試験 原位置三軸試験 室内試験
亀裂の変形特性を考慮した数値解析による岩盤物性評価法 地球工学研究所地圏科学領域小早川博亮 1 岩盤構造物の安定性評価 ( 斜面の例 ) 代表要素 代表要素の応力ひずみ関係 変形: 弾性体の場合 :E,ν 強度: モールクーロン破壊規準 :c,φ Rock Mech. Rock Engng. (2007) 40 (4), 363 382 原位置試験 せん断試験, 平板載荷試験 原位置三軸試験 室内試験
3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x0 = f x= x0 t f c x f =0 [1] c f 0 x= x 0 x 0 f x= x0 x 2 x 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考
![3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x0 = f x= x0 t f c x f =0 [1] c f 0 x= x 0 x 0 f x= x0 x 2 x 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考 3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x0 = f x= x0 t f c x f =0 [1] c f 0 x= x 0 x 0 f x= x0 x 2 x 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考](/thumbs/103/158269281.jpg) 3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x = f x= x t f c x f = [1] c f x= x f x= x 2 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考える まず 初期時刻 t=t に f =R f exp [ik x ] [3] のような波動を与えたとき どのように時間変化するか調べる
3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x = f x= x t f c x f = [1] c f x= x f x= x 2 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考える まず 初期時刻 t=t に f =R f exp [ik x ] [3] のような波動を与えたとき どのように時間変化するか調べる
Microsoft PowerPoint - 2_FrontISTRと利用可能なソフトウェア.pptx
 東京大学本郷キャンパス 工学部8号館2階222中会議室 13:30-14:00 FrontISTRと利用可能なソフトウェア 2017年4月28日 第35回FrontISTR研究会 FrontISTRの並列計算ハンズオン 精度検証から並列性能評価まで 観測された物理現象 物理モデル ( 支配方程式 ) 連続体の運動を支配する偏微分方程式 離散化手法 ( 有限要素法, 差分法など ) 代数的な数理モデル
東京大学本郷キャンパス 工学部8号館2階222中会議室 13:30-14:00 FrontISTRと利用可能なソフトウェア 2017年4月28日 第35回FrontISTR研究会 FrontISTRの並列計算ハンズオン 精度検証から並列性能評価まで 観測された物理現象 物理モデル ( 支配方程式 ) 連続体の運動を支配する偏微分方程式 離散化手法 ( 有限要素法, 差分法など ) 代数的な数理モデル
補足 中学で学習したフレミング左手の法則 ( 電 磁 力 ) と関連付けると覚えやすい 電磁力は電流と磁界の外積で表される 力 F 磁 電磁力 F li 右ねじの回転の向き電 li ( l は導線の長さ ) 補足 有向線分とベクトル有向線分 : 矢印の位
 http://totemt.sur.ne.p 外積 ( ベクトル積 ) の活用 ( 面積, 法線ベクトル, 平面の方程式 ) 3 次元空間の つのベクトルの積が つのベクトルを与えるようなベクトルの掛け算 ベクトルの積がベクトルを与えることからベクトル積とも呼ばれる これに対し内積は符号と大きさをもつ量 ( スカラー量 ) を与えるので, スカラー積とも呼ばれる 外積を使うと, 平行四辺形や三角形の面積,
http://totemt.sur.ne.p 外積 ( ベクトル積 ) の活用 ( 面積, 法線ベクトル, 平面の方程式 ) 3 次元空間の つのベクトルの積が つのベクトルを与えるようなベクトルの掛け算 ベクトルの積がベクトルを与えることからベクトル積とも呼ばれる これに対し内積は符号と大きさをもつ量 ( スカラー量 ) を与えるので, スカラー積とも呼ばれる 外積を使うと, 平行四辺形や三角形の面積,
杭の事前打ち込み解析
 杭の事前打ち込み解析 株式会社シーズエンジニアリング はじめに杭の事前打込み解析 ( : Pile Driving Prediction) は, ハンマー打撃時の杭の挙動と地盤抵抗をシミュレートする解析方法である 打ち込み工法の妥当性を検討する方法で, 杭施工に最適なハンマー, 杭の肉厚 材質等の仕様等を決めることができる < 特徴 > 杭施工に最適なハンマーを選定することができる 杭の肉厚 材質等の仕様を選定することができる
杭の事前打ち込み解析 株式会社シーズエンジニアリング はじめに杭の事前打込み解析 ( : Pile Driving Prediction) は, ハンマー打撃時の杭の挙動と地盤抵抗をシミュレートする解析方法である 打ち込み工法の妥当性を検討する方法で, 杭施工に最適なハンマー, 杭の肉厚 材質等の仕様等を決めることができる < 特徴 > 杭施工に最適なハンマーを選定することができる 杭の肉厚 材質等の仕様を選定することができる
2014年度 信州大・医系数学
 4 信州大学 ( 医系 ) 前期日程問題 解答解説のページへ 3 個の玉が横に 列に並んでいる コインを 回投げて, それが表であれば, そのときに中央にある玉とその左にある玉とを入れ替える また, それが裏であれば, そのときに中央にある玉とその右にある玉とを入れ替える この操作を繰り返す () 最初に中央にあったものが 回後に中央にある確率を求めよ () 最初に右端にあったものが 回後に右端にある確率を求めよ
4 信州大学 ( 医系 ) 前期日程問題 解答解説のページへ 3 個の玉が横に 列に並んでいる コインを 回投げて, それが表であれば, そのときに中央にある玉とその左にある玉とを入れ替える また, それが裏であれば, そのときに中央にある玉とその右にある玉とを入れ替える この操作を繰り返す () 最初に中央にあったものが 回後に中央にある確率を求めよ () 最初に右端にあったものが 回後に右端にある確率を求めよ
<4D F736F F D FCD B90DB93AE96402E646F63>
 7 章摂動法講義のメモ 式が複雑なので 黒板を何度も修正したし 間違ったことも書いたので メモを置きます 摂動論の式の導出無摂動系 先ず 厳密に解けている Schrödiger 方程式を考える,,,3,... 3,,,3,... は状態を区別する整数であり 状態 はエネルギー順に並んでいる 即ち は基底状態 は励起状態である { m } は相互に規格直交条件が成立する k m k mdx km k
7 章摂動法講義のメモ 式が複雑なので 黒板を何度も修正したし 間違ったことも書いたので メモを置きます 摂動論の式の導出無摂動系 先ず 厳密に解けている Schrödiger 方程式を考える,,,3,... 3,,,3,... は状態を区別する整数であり 状態 はエネルギー順に並んでいる 即ち は基底状態 は励起状態である { m } は相互に規格直交条件が成立する k m k mdx km k
Microsoft PowerPoint - NA03-09black.ppt
 きょうの講義 数値 記号処理 2003.2.6 櫻井彰人 NumSymbol@soft.ae.keo.ac.jp http://www.sakura.comp.ae.keo.ac.jp/ 数値計算手法の定石 多項式近似 ( 復習 )» 誤差と手間の解析も 漸化式» 非線型方程式の求解 数値演算上の誤差 数値計算上の誤差 打ち切り誤差 (truncaton error)» 使う公式を有限項で打ち切る
きょうの講義 数値 記号処理 2003.2.6 櫻井彰人 NumSymbol@soft.ae.keo.ac.jp http://www.sakura.comp.ae.keo.ac.jp/ 数値計算手法の定石 多項式近似 ( 復習 )» 誤差と手間の解析も 漸化式» 非線型方程式の求解 数値演算上の誤差 数値計算上の誤差 打ち切り誤差 (truncaton error)» 使う公式を有限項で打ち切る
Laplace2.rtf
 =0 ラプラスの方程式は 階の微分方程式で, 一般的に3つの座標変数をもつ. ここでは, 直角座標系, 円筒座標系, 球座標系におけるラプラスの方程式の解き方を説明しよう. 座標変数ごとに方程式を分離し, それを解いていく方法は変数分離法と呼ばれる. 変数分離解と固有関数展開法. 直角座標系における 3 次元の偏微分方程式 = x + y + z =0 (.) を解くために,x, y, z について互いに独立な関数の積で成り立っていると考え,
=0 ラプラスの方程式は 階の微分方程式で, 一般的に3つの座標変数をもつ. ここでは, 直角座標系, 円筒座標系, 球座標系におけるラプラスの方程式の解き方を説明しよう. 座標変数ごとに方程式を分離し, それを解いていく方法は変数分離法と呼ばれる. 変数分離解と固有関数展開法. 直角座標系における 3 次元の偏微分方程式 = x + y + z =0 (.) を解くために,x, y, z について互いに独立な関数の積で成り立っていると考え,
<4D F736F F D20824F B CC92E8979D814696CA90CF95AA82C691CC90CF95AA2E646F63>
 1/1 平成 23 年 3 月 24 日午後 6 時 52 分 6 ガウスの定理 : 面積分と体積分 6 ガウスの定理 : 面積分と体積分 Ⅰ. 直交座標系 ガウスの定理は 微分して すぐに積分すると元に戻るというルールを 3 次元積分に適用した定理になります よく知っているのは 簡単化のため 変数が1つの場合は dj ( d ( ににします全微分 = 偏微分 d = d = J ( + C d です
1/1 平成 23 年 3 月 24 日午後 6 時 52 分 6 ガウスの定理 : 面積分と体積分 6 ガウスの定理 : 面積分と体積分 Ⅰ. 直交座標系 ガウスの定理は 微分して すぐに積分すると元に戻るというルールを 3 次元積分に適用した定理になります よく知っているのは 簡単化のため 変数が1つの場合は dj ( d ( ににします全微分 = 偏微分 d = d = J ( + C d です
< B837B B835E82C982A882AF82E991CF905593AE90AB8CFC8FE382C98AD682B782E988EA8D6C8E40>
 1 / 4 SANYO DENKI TECHNICAL REPORT No.10 November-2000 一般論文 日置洋 Hiroshi Hioki 清水明 Akira Shimizu 石井秀幸 Hideyuki Ishii 小野寺悟 Satoru Onodera 1. まえがき サーボモータを使用する機械の小型軽量化と高応答化への要求に伴い サーボモータは振動の大きな環境で使用される用途が多くなってきた
1 / 4 SANYO DENKI TECHNICAL REPORT No.10 November-2000 一般論文 日置洋 Hiroshi Hioki 清水明 Akira Shimizu 石井秀幸 Hideyuki Ishii 小野寺悟 Satoru Onodera 1. まえがき サーボモータを使用する機械の小型軽量化と高応答化への要求に伴い サーボモータは振動の大きな環境で使用される用途が多くなってきた
PowerPoint プレゼンテーション
 電磁波工学 第 6 回境界条件と伝送線路 柴田幸司 伝送線路とは 伝送線路とは光速で進む電磁波を構造体の中に閉じ込めて低損失にて伝送させるための線路であり 伝搬方向 断面方向に電磁波を閉じ込めるためには金属条件や誘電体の境界条件を利用する必要がある 開放型 TM 型 平行 線 誘電体型 誘電体線路 光ファイバ 閉鎖型 TM 型 同軸線路 導波路型 導波管 おのおのの伝送線路の形状に対する管内断面の電磁波の姿体の導出
電磁波工学 第 6 回境界条件と伝送線路 柴田幸司 伝送線路とは 伝送線路とは光速で進む電磁波を構造体の中に閉じ込めて低損失にて伝送させるための線路であり 伝搬方向 断面方向に電磁波を閉じ込めるためには金属条件や誘電体の境界条件を利用する必要がある 開放型 TM 型 平行 線 誘電体型 誘電体線路 光ファイバ 閉鎖型 TM 型 同軸線路 導波路型 導波管 おのおのの伝送線路の形状に対する管内断面の電磁波の姿体の導出
線形弾性体 線形弾性体 応力テンソル とひずみテンソルソル の各成分が線形関係を有する固体. kl 応力テンソル O kl ひずみテンソル
 Constitutive equation of elasti solid Hooke s law λδ μ kk Lame s onstant λ μ ( )( ) ( ) linear elasti solid kl kl Copyright is reserved. No part of this doument may be reprodued for profit. 線形弾性体 線形弾性体
Constitutive equation of elasti solid Hooke s law λδ μ kk Lame s onstant λ μ ( )( ) ( ) linear elasti solid kl kl Copyright is reserved. No part of this doument may be reprodued for profit. 線形弾性体 線形弾性体
ギリシャ文字の読み方を教えてください
 埼玉工業大学機械工学学習支援セミナー ( 小西克享 ) 慣性モーメント -1/6 テーマ 01: 慣性モーメント (Momet of ietia) コマ回しをすると, 長い時間回転させるには重くて大きなコマを選ぶことや, ひもを早く引くことが重要であることが経験的にわかります. 遊びを通して, 回転の運動エネルギーを増やせば, 回転の勢いが増すことを学習できるので, 機械系の学生にとってコマ回しも大切な体験学習のひとつと言えます.
埼玉工業大学機械工学学習支援セミナー ( 小西克享 ) 慣性モーメント -1/6 テーマ 01: 慣性モーメント (Momet of ietia) コマ回しをすると, 長い時間回転させるには重くて大きなコマを選ぶことや, ひもを早く引くことが重要であることが経験的にわかります. 遊びを通して, 回転の運動エネルギーを増やせば, 回転の勢いが増すことを学習できるので, 機械系の学生にとってコマ回しも大切な体験学習のひとつと言えます.
を入れて,,, について解けば ( ) ( ) 得る. よって となるが ( / ( ) ( ) と無次元化している ), これを { N ( ) } { d} と表現して内部変位 と節点変位 { d} とを結びつける { } { ( ) ( ) } (.) (.) 節点での F と M は図. の
 第 章有限要素法 ( その ). 梁要素 有限要素法においては外力も境界条件も節点で考える. もちろん分布荷重は考慮でき るが, 要素上の分布荷重は適当に節点への等価は集中荷重として置き換える. こう考える と梁の曲げの方程式 (.8) において分布荷重無し (p()) の d d (.) である. この一般解は先に解いたように (.) となる. 梁の有限要素の長さを とすると, その両端, にて境界条件を導入して解い
第 章有限要素法 ( その ). 梁要素 有限要素法においては外力も境界条件も節点で考える. もちろん分布荷重は考慮でき るが, 要素上の分布荷重は適当に節点への等価は集中荷重として置き換える. こう考える と梁の曲げの方程式 (.8) において分布荷重無し (p()) の d d (.) である. この一般解は先に解いたように (.) となる. 梁の有限要素の長さを とすると, その両端, にて境界条件を導入して解い
2016年度 九州大・理系数学
 0 九州大学 ( 理系 ) 前期日程問題 解答解説のページへ 座標平面上の曲線 C, C をそれぞれ C : y logx ( x > 0), C : y ( x-)( x- a) とする ただし, a は実数である を自然数とするとき, 曲線 C, C が 点 P, Q で交わり, P, Q の x 座標はそれぞれ, + となっている また, 曲線 C と直線 PQ で囲まれた領域の面積を S,
0 九州大学 ( 理系 ) 前期日程問題 解答解説のページへ 座標平面上の曲線 C, C をそれぞれ C : y logx ( x > 0), C : y ( x-)( x- a) とする ただし, a は実数である を自然数とするとき, 曲線 C, C が 点 P, Q で交わり, P, Q の x 座標はそれぞれ, + となっている また, 曲線 C と直線 PQ で囲まれた領域の面積を S,
