PowerPoint プレゼンテーション
|
|
|
- ともみ ほうねん
- 9 years ago
- Views:
Transcription
1 REDD+ Reducing Emission from Deforestation and Forest Degradation-plus 平成 24 年度 応用講習 2 第 1 章 地上調査の設計 一般社団法人日本森林技術協会金森匡彦 1
2 目次 1. REDD+ における地上調査 2. 標本調査の基礎 3. 標本数と標本の形状 大きさ 4. 地上調査の設計 計画 実施 5. 実習 2
3 REDD+ における地上調査 3
4 森林を計測する様々な方法 上空からの間接的な計測 衛星や空中写真 ( リモートセンシング ) 樹幹解析 (1 本の木を正確に計測する ) 破壊的調査 地上調査 ( プロット調査等 ) 地上における直接計測 ( 樹木やその他生物 ) 4
5 基本の式 : 活動量データ 排出係数 = 炭素量 Forest area change (unit:ha) Mean carbon stock (unit:ct/ha) 引用 :Referrence Emission Levels Indonesia - Ruandha Sugardiman MRV Meeting Mexico. 5
6 Activity data Emission factor Satellite Imageries Classification Developing National forest Inventory System 1. Above ground biomass(agb) 2. Dead wood 3. Litter 4. Belowground biomass 5. Soil Organic Carbon Sampling Sampling Forest Type maps Partitioned for branch, leaf, steam individually Digs up root using shovel car Measurement of dead woods Forest Area Change Detection 500 y = ln(x) R² = Measurement of weight Laboratory experiment Measurement of weight Measurement of tree high and DBH Merchantable Volume by forest types Measurement of litter Average stock by each forest types Taking samples of Soil and Organic matter Development of Biomass conversion and expansion parameter(bcef) Laboratory experiment Laboratory experiment (AGB=Merchantable volume BCEF) Activity data Emission factor Forest types change in the past 1. Above Ground Biomass 4. Below Ground Biomass 2. Dead Wood 3. Litter 5. Soil Organic Carbon 6
7 固定調査地における地上調査 固定調査地における調査 森林を直接地上で計測する方法 成立する樹木の樹種 大きさ ( 胸高直径や樹高 ) 個体数を記録 標本調査として行われる場合が多い 固定調査地の特徴 同じ調査地を繰り返し調査する 時系列的な変化を正確に知ることができる 暫定調査 は1 回限りの調査プロット ( 調査のたびにサンプリングをし直す ) 固定調査地であることを明確化することにより 森林管理にバイアスが生じる可能性 隠しプロット にする場合も 7
8 樹木をモデル化して蓄積やバイオマスを把握する 計測値を材積 バイオマス 炭素量に変換するために必要な様々な情報 BEF 樹幹材積 総バイオマス 胸高直径 樹高 R < 幹材積からの変換 > 樹幹のモデル化 : 既存の材積式 材積表を利用 ( 胸高直径 樹高を調べることにより計算 ) バイオマスへの拡張 : 幹材積を基準として 幹以外の部分 ( 枝 葉 根 ) の構成比を調べることによりバイオマス量に換算する < 計測値からの直接変換 > アロメトリー式 ( 相対生長式 ) 胸高直径等から直接バイオマス量や炭素量に変換する 8
9 計測結果のバイオマス 炭素量への変換 幹材積から変換するアプローチ 立木幹材積 現実の立木を単純な幾何学的なモデルで近似し 材積を計算する 材積 =f( 直径, 樹高, 幹形 ) 材積表 ( 材積式 ) ( 地域 樹種別に ) 胸高直径 樹高等と立木材積の関係を示した表 ( 式 ) 一変数 ( 胸高直径のみ ) 二変数 ( 胸高直径と樹高 ) バイオマス拡大係数 (BEF) 幹重量とそれ以外の地上部分 ( 枝 葉 ) を含めた全体のバイオマス重量との比 ( 樹種別 成育段階別 ) 例 : スギ 1.23 ヒノキ 1.24 アカマツ 1.23 ブナ 1.32( いずれも林齢 20 年以上 ) 容積密度 幹の比重 ( 単位材積当たりの重さ ) 例 : スギ ヒノキ アカマツ ブナ 地下 / 地上バイオマス比 (R) 地下部 ( 根 ) の総バイオマスと地上の総バイオマスの比 例 : スギ 0.25 ヒノキ 0.26 アカマツ 0.27 ブナ
10 調査結果のバイオマス 炭素量への変換 アロメトリ式による直接推定 生物の個体の部分の大きさと他の部分の大きさの間には関係がある 相対生長関係 ( アロメトリ ) 個体の計測しやすい一部 ( 胸高直径など ) を調べることにより 実測が困難な部分 ( 樹木全体のバイオマスなど ) を推定することができる 汎用式と個別の樹種 森林タイプ別に調整された式 REDD+CookBook 10
11 標本調査の基礎 11
12 標本調査とは? 統計調査の目的調べたい対象全体 ( 母集団 ) に関する情報 ( 知識 ) を得ること母集団を構成する要素 ( 個体 :unit) を調べて観測値を取得する全数調査 ( センサス ) 母集団を構成するすべての要素から観測値を得る調査費用や実務上の問題から 一般的には実施困難国勢調査は代表的な全数調査標本調査 ( サンプリング ) 母集団から 一部の要素を抽出して調査 観測値を得て その情報をもとに母集団の傾向を 推測 する 12
13 標本調査に基づく統計的推測母集団から標本を取り出し観測値を得て 標本の情報から母集団の傾向を推測することを統計的推測という 母集団 統計的推測 標本 標本抽出 13
14 標本調査と誤差 正確度 (accuracy) と精度 (precision) 正確度は 真の値からどの程度離れているか 精度はどれほど標本が集中しているかを示す 偏り (bias) とランダム誤差 (random error) 偏りは調査方法の誤りなどにより系統的に発生する誤差 ( この値が小さいほど正確性が高い ) ランダム誤差は標本抽出において確率的に発生する誤差 ( この値が小さいほど精度が高い ) 正確度 : 高精度 : 低 正確度 : 低精度 : 高 正確度 : 高精度 : 高 GOFC-GOLD Source Book より GOFC-GOLD ホームページ 14
15 森林を対象としたサンプリング調査 森林調査におけるサンプリング調査の適用標本調査の目的は 最小の費用 ( コスト ) で最良の推定結果を得ること測定対象として見た場合の森林の特徴 1 形状が複雑で正確に計測するのが難しい モデル化して考える必要 2 大量に存在する 統計的方法の必要 3 山に生えており動かすことができない 測定に労力が必要 4 時間と共に成長する 変化を知るためには繰り返し計測する必要 5 高価なものではない 測定に掛けられるコストに制限 15
16 標本調査の基礎 単純無作為抽出最も基本的な標本抽出法 実務上はランダムに標本を得ることは困難な場合が多い 基本的な定理 ( 有限母集団 非復元抽出 ) N 1 母平均 µ = θ = θ 標本平均 x = i N i= 1 1 n n i= 1 x i 母分散 N θi σ 2 N 1 = ( θi θ ) N i= 1 : 母集団の大きさ n : 標本数 x i 2 標本分散 : 母集団の i 番目の値 : 標本の i 番目の値 s 2 n 1 = ( x n 1 i= 1 i x) 2 16
17 標本平均と標本分散標本平均の期待値は 母平均に一致する ( 不偏推定量 ) 標本平均の分散は 非復元抽出の場合 (N-n)/(N-1) という因子 ( 有限母集団修正 ) が掛かるが 一般には n に対して N が十分大きいので これを 1 とみなして無視しても問題ない 標本平均の期待値 標本平均の分散 E(x) V ( x) = = µ E( x E( x) 区間推定標本平均 標本数 標準分散の値から 母平均を一定の信頼区間で推定することができる 2 ) 2 = σ n 2 N N n 1 σ n 2 x t σ n 2 µ x + t σ n 2 17
18 系統抽出法 (Systematic sampling) 無作為抽出法の課題無作為に標本を取り出すのは 実際は大変森林調査など空間的な広がりのある対象からサンプリングする場合 地域的な偏りが生じる可能性もある標本を一定の間隔で取り出すことにすれば 上記の問題を解決できる N 個の要素からなる母集団に 1~N の番号を付けておき n 個の標本を取り出すことを考える ( ここで d=n/n を抽出間隔 f=n/n を抽出率という ) 1~d までの番号の中からランダムに番号を選び その番号を開始位置として d 個ごとに標本を取り出していくと n 個の標本が抽出される 系統抽出法の課題厳密には無作為抽出に比べて精度が下がるとされている 母集団の値に空間的な規則性がある場合 標本の取り方によって偏りのある推定結果が得られる可能性がある 18
19 系統抽出法の実施面積 Aの対象地域において n 個の標本を取り出す場合 d = A n となるように格子点を設定する (dが端数になる場合は 切りのいい値に切り下げる) 対象地域内にランダムに任意の1 点を抽出し そこを原点としてXY 方向に間隔 dの方眼を描き その交点を抽出プロットとする より簡易には 切りのいい経緯度等を基準として設定する FAOのNFMAマニュアルでは 少なくとも経緯度 1 度の間隔で格子点を設定することを推奨 実際には層化多段抽出法との組合せが多い 国 層区分 標本抽出区域 ( トラクト ) の数 分 ( 緯度 経度 ) 抽出間隔 km( 緯度 経度 ) レバノン なし 226 4' 4' 約 7 6km フィリピン なし ' 15' 約 25 25km カメルーン ' 15' 約 50 25km ' 30' 約 50 50km 計 236 グァテマラ ' 30' 約 28 54km ' 15' 約 28 28km ' 30' 約 28 54km 計 108 (FAO,NFMA Working paper No.37/E, 2008) 19
20 母集ンプルREDD+ Reducing Emission from Deforestation and Forest Degradation-plus 層化抽出法 (Stratified sampling) 母集団が 相異なる部分集団 ( 部分集団内は同質 ) で構成されていることが事前にわかっている場合 それぞれの部分集団を基準として標本抽出を行うことで より少ないサンプル数で推定精度を上げることができる これを層化抽出法という N 1 層 1 n 1 層 3 N 2 団サ層 2 n 2 N 3 n 3 N L 層 L n L 20
21 FAO ホームページ 21
22 層化抽出法におけるサンプルの割当 ( 比例配分 ) 層化抽出法では より少ないサンプル数で精度の高い推計結果を得るために 層ごとに適切にサンプル数を割り当てる必要がある 各層の母集団に対する比率 ( ウェイト ) がわかっている場合 これに標本総数を掛けることにより 各層に標本数を割り当てることができる こ れを比例配分という L N = Ni = N1 + N2 + + i= 1 N L w N N i = ( 層 iのウェイト ) i 全体で n の標本を抽出する場合 層 i からサイズ n i の標本を抽出するものとすると 下記のとおり 層ごとのウェイトを掛けて比例配分する n i = Ni n N 層 i から観測値 x を得るものとするとその平均は x i = xi ni 22
23 母集団の平均 μは 各層の標本平均にウェイトを掛けた和により推定されるの分散は下記で与えられる µˆ L ˆµ = w i xi V ˆ) µ = i= 1 1 ( σ n 層化抽出法におけるサンプルの割当 ( ネイマン配分 ) あらかじめ予備調査等により 各層のばらつき ( 分散 ) がわかっている場合 それも考慮に入れて全体の分散を最小にするようにサンプルの 割当数を決定する方法をネイマン配分といい 下記の式により割当を行う このときの分散をとすると V (µ ˆ ) L w i i= 1 2 i µˆ n i n = L wσ i= 1 i i i wσ i L L V ( ˆ µ ) = w iσ i wiσ i n i= 1 N i=
24 比例配分とネイマン配分の比較 ここで 母分散と各層の分散との間には下記の関係が成り立つことがわかっている σ 2 L L 2 = σ + i i= 1 i= 1 w i w ( θ i µ) i 2 2 σ : 母分散 µ : 母平均 θ i : 各層の平均 上式で 第 2 項は 0 以上であることが明らかであるので 第 2 項を無視すれば σ n 2 1 n L i= 1 wσ 2 i i = V ( ˆ) µ となり 単純無作為抽出法より比例配分の方が分散が小さくなる ( 精度が高い ) また 比例配分の分散とネイマン配分の分散を比較すると 以下の関係が成り立つ ( 各層が十分に大きく かつ各層のサンプル数が小さい場合 ) L N V ( ˆ) µ V ( ˆ µ ) N i ( σ i σ ) n i= 1 よって 一般的に下記のような関係が成り立ち また層間のばらつきが大きいほど 比例配分よりネイマン配分の方が精度が高くなる 単純無作為抽出法の分散 比例配分の分散 ネイマン配分の分散 2 σ : 各層の標準偏差の加重平均 24
25 比例配分とネイマン配分の比較 階層 層化抽出法による層別抽出個数の計算 ( ネイマン配分 ) 各層の全各層の標面積に対準偏差 Si 面積 (ha) Wi Si する比率 ( 予備調 Wi 査による ) 抽出個数 比例配分の場合 Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ 計 1, 条件 1:95% 信頼係数を2 誤差率 10% とする 条件 2: 予備調査時のプロット当たり平均材積を7.559とする ( 山田 村松,1971を参考) n 抽出率
26 コストを考慮した層化抽出の例 全体の必要プロット数 層ごとのサンプル数 26 = = = L h h h h L h h h h C s W C W s E t n = = L h h h h h h h h C S W C W S n n 1 N h N N N W h h = E t C h s h n 母集団全体の大きさ層 h の大きさ層 h のウェイト 95% 信頼度係数 L 層の数層 h の標準偏差目標誤差率層 h のプロットあたりの調査コスト
27 適切な層化 層化サンプリングの目的 :1 推定精度を高めること 2 サンプル数を少なくして調査コストを低減させること 効率的な層化のためには 森林タイプと森林の状態の 2 軸で構成された 層化マトリックス を利用することが有効と考えられる ( 事前の情報収集 予備調査が非常に重要 ) REDD+CookBook 27
28 多段抽出法 (multi-stage sampling, cluster sampling) 全国規模の調査など 母集団が非常に大きく 無作為抽出法や単純な系統抽出法による調査の実施に多大なコストが掛かることが想定される場合等に 多段抽出法が行われる 多段抽出法は 母集団からの標本抽出を段階的に行うものである 多段抽出法の実施母集団をいくつかのサブ集団 ( 第 1 次抽出単位 集落ともいう ) に分け ( 例 : 全国を都道府県に分割する場合等 ) 分割された集団から標本抽出する さらに 抽出された第 1 次抽出単位を母集団として標本抽出を行う ( 第 2 次抽出単位 ) 第 1 次抽出単位のことを集落 ( クラスター cluster) ともいう 多段抽出法に系統抽出法と層化抽出法を効果的に組み合わせることにより 調査に係る労力を大幅に軽減することが可能である 28
29 多段抽出法のイメージ ( ここでは 2 段抽出 ) 第 1 段階の集落の選び方は 等確率抽出の場合と集落の大きさの違いを考慮した比例抽出の 2 通りがある 2 段階の標本抽出場合 同一の標本数とする場合と 集落の大きさによってサンプリング数を変える場合がある 第 1 次抽出単位 ( 集落 ) 第 2 次抽出単位 ( 標本 ) 母集団 29
30 多段抽出法における不偏推定量と分散 母集団が M 個の集落で構成され そこから m 個の集落を抽出して調査したとする a 番目の集落からn a 個のサンプルを取り出したときの観測値を X ii とする (i: 抽出された集落の番号 j:iから取り出したサンプルの番号 ) 母平均をμとしたときμの不偏推定量 µˆ は 各集落毎の標本平均を X とし 各集落のサイズを N i i すれば m n M N ˆµ = i 1 j 母平均の不偏推定量 X ここで X i i = X m N n 分散は ここで θ V a = M N i= 1 σ M M a a 2 ( ˆ) µ = 2 + σ 2 e mn a= 1 nan mn N a b= 1 θ ab σ 1 2 = a N N ( ) 2 θab θa Na a a= 1 M σ 1 2 = e M a= 1 i j= 1 ij ( ) 2 θ Nµ M a 30
31 FAO の NFMA(2008) における層化多段抽出法の適用例 地域内を 2 層に区分 1km 四方の第 1 次抽出単位 (SU) から 4 個の帯状プロット (20 250m) 12 個の長方形サブプロット (10 20m) 12 個の円形サブプロット ( 半径 3.99m) をそれぞれ抽出する FAO ホームページ 31
32 標本数 標本の形状 大きさ 32
33 標本数標本調査を行う場合 どの程度の標本数を抽出すればよいかについては 慎重に検討される必要がある 許容すべき誤差が定まった場合 標本数 標本平均 標本標準偏差の間には以下の関係が成り立つ 2 t0.05cν x N 0, e =, Cν = e x N0 x : 必要な標本数 x : 標本平均 : 許容誤差 t s x :95% 信頼度係数 (=2) e : 目標誤差率 C v : 変動係数 : 標本標準偏差 s 33
34 標本数 ( つづき ) 前記の式において 注目すべき点としては 変動係数 ( 標準偏差 / 標本平均 ) と目標誤差率が決まれば 対象面積の大きさに依存せず 標本数が自動的に定まることにある すなわち 対象面積が広くても狭くても ( 変動係数が等しければ ) 必要な標本数は変わらないということを意味する 必要な標本の数は同じ 大きさは異なるが変動係数は等しいと仮定した 2 つの母集団 34
35 標本数 ( つづき ) 1961 年に日本で実施された 全国森林資源標本調査においては 許容誤差率 E を 3% 95% 信頼度係数を 2 層材積の変動係数を過去の調査結果より 150% として 以下のとおり必要なプロット数を 10,000 と定めた N 2 0 = ,000 材積の変動係数に関しては 事前の予備調査や過去の経験に基づき事前に得ておく必要がある 35
36 標本 ( プロット ) の大きさ一般にプロット面積が大きいほど 測定値のばらつきは少なくなる 一方 プロット面積が大きいほど 調査に要する経費は多くなるので 両者を考慮して決定する 少なくともプロットあたり 20~30 本の立木が含まれるようにする 森林を対象とした場合の問題等確率抽出の原則から 抽出するプロットの大きさは同一サイズにするのが原則である すなわち水平投影面積が同じになることを考慮したプロット設定が必要森林は 大小様々な立木で構成されていることから 例えば胸高直径の測定に着目すると 同一サイズプロットでは 小径木林では測定対象木が大量に発生し 大径木林では測定本数が少なくなるおそれがある このような場合 例えば直径階をグループ分けして 直径階グループごとにプロットサイズを変えるといったことが行われる これは一種の集落サンプリングを行っているとも考えられる 36
37 大円中円小円 0.10ha 0.04ha 0.01ha 測定対象に応じて プロットの大きさを変える例 ( 日本の森林生態系多様性基礎調査 ) r1 r2 r3 調査項目小円中円大円 立木 (DBH) 伐根 ( 直径 ) 1.0cm 以上 5.0cm 以上 5.0cm 以上 18.0c m 以上 18.0c m 以上 θ 倒木 ( 中央径 長さ ) 5.0cm 以上 計測しない 37
38 標本 (= プロット ) の形状プロットの形状には 円形 方形 長方形等がある 長方形の特殊な場合としては帯状プロットもある 林縁効果の問題小さいプロットでは 林縁部分の 1 本の木が入るか否かが大きな影響を及ぼす ( 例 :0.01ha のプロットで 1m 3 の立木が入るか否かは 1ha 当たりでは 100m 3 の差となる ) 大きなプロットでは 相対的に林縁木の影響は少なくなる 林縁効果を少なくするためには プロットを大きくする 林縁長ができるだけ短かくなるようにすることが望ましい すなわち 同じ面積であれば 長方形よりは方形が望ましい 円形のプロットが設定できるのであれば 上記の条件を最も満足する 38
39 円形プロット長所 : 理論上は林縁効果を最も少なくできる 周囲測量をする必要がない すなわち 中心位置が定まれば周囲に一定長の竿などを用いてプロット内に入る立木であるか否かを簡単に特定できる ( バーテックスを用いれば 効率的に in/out を確認することができる ) 傾斜によりプロット半径を変えることにより 水平投影面積を一定の大きさにできる短所 : 外周部は曲線 ( 円弧 ) となるため 上記のように 1 本ごとに in/out の確認を行わない場合は 林縁木の見落としが生じやすい : プロット原点 : 設定方向 39
40 方形プロット a 長所 : 外周部は直線となり 目視での林縁木のin/outの判断がしやすい 左図のaタイプについては プロット設定の効率は円形プロットに勝る ( あまり大きなプロットは設定できない ) 短所 : bタイプのプロットでは 周囲測量をする必要があり 初回調査時のプロット設定の効率は下がる 円形プロットに比べ 理論上は林縁効果が大きい c b : プロット原点 : 設定方向 40
41 地上調査の設計 41
42 1 調査の企画調査の対象地域を決めるサンプルを抽出する対象を明確にすることが重要である 森林面積の変化をモニターするのであれば 森林以外の部分も対象として考慮する必要がある 基礎資料を収集 整理する対象地域の地形図 空中写真 衛星画像等を準備する 既存の森林分布図や資源調査結果の有無も確認する 蓄積量やバイオマス量を推定するのに必要なパラメータ ( 材積式等 ) の状況も確認しておく 予備調査の実施対象地域の森林の状態について得られる事前情報が少ない場合には 予備的調査を行うことにより 調査設計の参考資料とする 42
43 2 調査の設計調査方法の決定事前情報と予備調査の結果により サンプリング手法 ( 系統抽出 層化抽出 多段抽出 ) を決定する また 暫定調査地とするか 固定調査地の継続調査とするか モニタリングの時間間隔についても検討する プロットの設計目標とする調査精度 予算等を考慮し プロットの大きさ 抽出個数 サンプルの配置 プロットの形状等を決定する 調査項目の決定目標精度と予備調査結果に基づき 必要な調査項目を決定する 具体的には 樹種区分をどの程度細分するか 計測対象範囲をどのようにするか ( 最小胸高直径等 ) を明確にしておく必要がある 43
44 2 調査の設計 ( つづき ) 調査野帳 調査マニュアルの作成決定した調査項目に基づいて 調査野帳と調査マニュアルを作成する 適切な野帳とマニュアルの作成は 調査の効率化するとともに調査漏れを軽減し 調査精度を高精度かつ一定のレベルに保つことにつながることから 非常に重要である 実行体制の検討 整備調査精度は 調査員の資質に大きく依存する 調査精度を高いレベルに保つためには 訓練された専従の調査員による調査チームを組織することが望ましい 44
45 森林生態系多様性基礎調査野帳 ( 林野庁 ) より 45
46 森林生態系多様性基礎調査簡易マニュアル ( 林野庁 ) より 46
47 47
48 3 現地調査の準備プロット位置情報の整理地図上に抽出した格子点の位置と番号を記載し プロット原図を作成する 可能であれば 衛星画像や空中写真にプロット位置を記載したものも準備する 調査計画の作成調査行程 ( プロットまでの到達時間 プロット設定に掛かる時間 計測に掛かる時間及び必要人員 ) を検討し 調査計画を立てる 工程 時間 備考 徒歩移動 ( 駐車場所からプロ 90 分杭の探索時間も見込む ットまで ) プロット設営 60 分必要に応じ杭の交換 立木調査 120 分人工林 調査対象立木本数 120 本 立木調査総括表 下層植生調査土壌侵食調査 (30 分 ) 立木調査と並行して実施 終了次第 立木調査を実施 伐根調査 倒木調査 30 分調査対象伐根 倒木の有無による 撤収 20 分巻尺 すずらんテープ回収 プロットから駐車場所まで 50 分必要に応じマーキングしながら 合計 370 分 日本の森林生態系多様性基礎調査で想定している標準的な調査行程 48
49 3 現地調査の準備 ( つづき ) 調査器材の準備調査目的に応じ 必要な器材を準備する資材の例 : 地図 空中写真 野帳 ( 耐水紙が望ましい ) GPS 杭 ( 中心杭の他 必要に応じ準備 ) ポケットコンパス 斜距離換算表 巻尺 輪尺もしくは直径巻尺 測高器 ( ブルーメライス バーテックス ) チョーク ナンバーテープ 測量用ポール 49
50 d u n v o m l q p s h b b w j k i c g a r x t e f e 50
51 現地到達情報 ( プロットへの到達経路図 ) 次回調査のためにもっとも重要な情報 計画上の位置と実際の位置 (GPS 情報 事情により計画位置に設定できない場合がある ) ルート上の GPS 情報 ( 車を降りた位置からプロットまで ) ルート上の写真 ルート上の情報 ( 歩道の有無 路面の情報 目印となる地物 分岐点 ) スケッチの方がわかりやすい場合もある もし調査チームが前回の調査地を発見できなかったら 元の計画上の位置にプロットを再設定する 51
52 プロットの設定 効率的な設定方法を工夫する必要 円形プロットの場合は 傾斜により半径の補正を行うので 正確な傾斜測定を行う必要がある ( バーテックスを使用すれば 効率的に設定可能 ) 方形のプロットの場合はコンパス等により測量して設定する ( 林縁木のin/outは 測量時に決定できる ) 帯状プロットの場合は 中心線を測量 通常は中心杭を設置 ( 固定調査地とする場合は 次回調査までの耐久性を考慮 ) 必要に応じ周辺杭 調査の効率性を確保するための暫定杭を設置 52
53 立木調査 胸高直径 必ず赤白ポール等で毎木胸高位置を確認すること 1.2m (1.3m) 基本は山側地際から 1.3m - 平坦地では 例えば中心杭に向かった方向に立って測るというように ルールを決めておく - 基本は直径巻尺で測定 1.2m (1.3m) 1.2m (1.3m) 斜立している場合は 幹軸に沿わせる 森林生態系多様性基礎調査マニュアル ( 林野庁 ) より 53
54 立木調査 様々なケースでの胸高直径の測定 二股木 こぶ 合体木 板根 タケ 1.2m (1.3m) 1.2m (1.3m) 1.2m (1.3m) 板根 0.2m マーキング 1.3m 1.2m (1.3m) つる巻き 根上がり 個々の樹幹の測定困難な場合 ( ガジュマルなど ) は 樹種の記録のみで計測の必要なし 1.2m (1.3m) 1.2m (1.3m) ツル 根 1.2m (1.3m) マーキング 森林生態系多様性基礎調査マニュアル ( 林野庁 ) より 54
55 立木調査樹高 毎木もしくは標準木を何本か選択して実測 ( 樹高未測定木は測定木の値より回帰推定 ) 樹幹長を計測 ( 垂直高ではないことに留意 ) 測定機器 : バーテックス ブルーメライスを使用梢端 低い樹木は測かんも使用可 機器の誤使用に注意 トランスポンダー 1.2m(1.3m) 最適な手法 斜立木の傾きを真横から見通す位置に立ち バーテックスで梢端を見通す トランスポンダーは山側地際位置の 1.2m(1.3m) 高さに設置 垂直高 h 樹高以上の水平距離をとる 斜面下部から見上げてはならない 森林生態系多様性基礎調査マニュアル ( 林野庁 ) より 55
56 56
57 林分情報の記載必要に応じて作成 立木位置図林相写真 中心杭からの方位別 天空写真 地況 林分構造等 斜面傾斜 局所地形 林分構造 優占樹種 ( 相観 ) 人為の影響程度 病虫害等の有無 災害の歴史 57
58 品質管理を考慮に入れたインベントリー調査の設計 PDCA サイクルの中で品質管理を考える PLAN 情報に基づく改善策 ACT 改善に必要な情報 森林情報に基づく計画 目標 : 持続可能な森林管理の実現 CHECK DO 森林管理に必要な情報 58
59 QA/QC のための調査 目的 PDCA サイクルによる精度の向上 (QA/QC) 計測誤差や傾向を確認する 客観的にデータの精度を確認する データの透明性 信頼性の確保 設計 ( 森林生態系多様性基礎調査の場合 ) 再測定 : 3% の点を抽出 (110 点 / 年 ) 本体調査チームが調査終了後速やかに (1 月以内 ) コントロールチームが同一プロットを再測定 エラーの修正は行わない 立会 : 本体調査チームとコントロールチームがともに同じ調査プロットに行き コントロール調査チームは 本体調査チームの実施状況を確認する ( 正しい機器の使い方等 ) 問題があれば その場で指摘 エラーの修正も行う 研修的意味合い 59
60 調査員の育成 研修 目的 設計 調査精度 ( データの信頼性 ) の向上チーム間の情報交換調査チームの技術レベルを平準化 講義 : 調査の目的を理解させ データ分析結果を説明することにより 調査員のモチベーションを維持 各調査項目の意味と重要性の説明 ( 測定値の少しの誤差が全体に大きく影響する場合等 ) マニュアルの理解 野帳の正しい使い方等現地研修 : 調査道具の適切な使い方 プロット設定等効率的な実施方法のノウハウ 精度確保の面では できるだけ少ない数の専門技術者が継続的に計測する体制が構築されることが望ましい 60
PowerPoint プレゼンテーション
 REDD+ Reducing Emission from Deforestation and Forest Degradation-plus 第 4 章 森林炭素モニタリングの基礎 森林の地上計測手法 一般社団法人日本森林技術協会金森匡彦 1 森林の地上計測の基礎 森林を計測することの困難さ 木の形状は複雑である 正確に計測するのが困難 ( モデル化の歴史 ) 時間によって変化する ( 樹木の成長その他
REDD+ Reducing Emission from Deforestation and Forest Degradation-plus 第 4 章 森林炭素モニタリングの基礎 森林の地上計測手法 一般社団法人日本森林技術協会金森匡彦 1 森林の地上計測の基礎 森林を計測することの困難さ 木の形状は複雑である 正確に計測するのが困難 ( モデル化の歴史 ) 時間によって変化する ( 樹木の成長その他
EBNと疫学
 推定と検定 57 ( 復習 ) 記述統計と推測統計 統計解析は大きく 2 つに分けられる 記述統計 推測統計 記述統計 観察集団の特性を示すもの 代表値 ( 平均値や中央値 ) や ばらつきの指標 ( 標準偏差など ) 図表を効果的に使う 推測統計 観察集団のデータから母集団の特性を 推定 する 平均 / 分散 / 係数値などの推定 ( 点推定 ) 点推定値のばらつきを調べる ( 区間推定 ) 検定統計量を用いた検定
推定と検定 57 ( 復習 ) 記述統計と推測統計 統計解析は大きく 2 つに分けられる 記述統計 推測統計 記述統計 観察集団の特性を示すもの 代表値 ( 平均値や中央値 ) や ばらつきの指標 ( 標準偏差など ) 図表を効果的に使う 推測統計 観察集団のデータから母集団の特性を 推定 する 平均 / 分散 / 係数値などの推定 ( 点推定 ) 点推定値のばらつきを調べる ( 区間推定 ) 検定統計量を用いた検定
スライド 1
 計測工学第 12 回以降 測定値の誤差と精度編 2014 年 7 月 2 日 ( 水 )~7 月 16 日 ( 水 ) 知能情報工学科 横田孝義 1 授業計画 4/9 4/16 4/23 5/7 5/14 5/21 5/28 6/4 6/11 6/18 6/25 7/2 7/9 7/16 7/23 2 誤差とその取扱い 3 誤差 = 測定値 真の値 相対誤差 = 誤差 / 真の値 4 誤差 (error)
計測工学第 12 回以降 測定値の誤差と精度編 2014 年 7 月 2 日 ( 水 )~7 月 16 日 ( 水 ) 知能情報工学科 横田孝義 1 授業計画 4/9 4/16 4/23 5/7 5/14 5/21 5/28 6/4 6/11 6/18 6/25 7/2 7/9 7/16 7/23 2 誤差とその取扱い 3 誤差 = 測定値 真の値 相対誤差 = 誤差 / 真の値 4 誤差 (error)
基礎統計
 基礎統計 第 11 回講義資料 6.4.2 標本平均の差の標本分布 母平均の差 標本平均の差をみれば良い ただし, 母分散に依存するため場合分けをする 1 2 3 分散が既知分散が未知であるが等しい分散が未知であり等しいとは限らない 1 母分散が既知のとき が既知 標準化変量 2 母分散が未知であり, 等しいとき 分散が未知であるが, 等しいということは分かっているとき 標準化変量 自由度 の t
基礎統計 第 11 回講義資料 6.4.2 標本平均の差の標本分布 母平均の差 標本平均の差をみれば良い ただし, 母分散に依存するため場合分けをする 1 2 3 分散が既知分散が未知であるが等しい分散が未知であり等しいとは限らない 1 母分散が既知のとき が既知 標準化変量 2 母分散が未知であり, 等しいとき 分散が未知であるが, 等しいということは分かっているとき 標準化変量 自由度 の t
<4D F736F F D208EC08CB18C7689E68A E F AA957A82C682948C9F92E82E646F63>
 第 7 回 t 分布と t 検定 実験計画学 A.t 分布 ( 小標本に関する平均の推定と検定 ) 前々回と前回の授業では, 標本が十分に大きいあるいは母分散が既知であることを条件に正規分布を用いて推定 検定した. しかし, 母集団が正規分布し, 標本が小さい場合には, 標本分散から母分散を推定するときの不確実さを加味したt 分布を用いて推定 検定しなければならない. t 分布は標本分散の自由度 f(
第 7 回 t 分布と t 検定 実験計画学 A.t 分布 ( 小標本に関する平均の推定と検定 ) 前々回と前回の授業では, 標本が十分に大きいあるいは母分散が既知であることを条件に正規分布を用いて推定 検定した. しかし, 母集団が正規分布し, 標本が小さい場合には, 標本分散から母分散を推定するときの不確実さを加味したt 分布を用いて推定 検定しなければならない. t 分布は標本分散の自由度 f(
統計的データ解析
 統計的データ解析 011 011.11.9 林田清 ( 大阪大学大学院理学研究科 ) 連続確率分布の平均値 分散 比較のため P(c ) c 分布 自由度 の ( カイ c 平均値 0, 標準偏差 1の正規分布 に従う変数 xの自乗和 c x =1 が従う分布を自由度 の分布と呼ぶ 一般に自由度の分布は f /1 c / / ( c ) {( c ) e }/ ( / ) 期待値 二乗 ) 分布 c
統計的データ解析 011 011.11.9 林田清 ( 大阪大学大学院理学研究科 ) 連続確率分布の平均値 分散 比較のため P(c ) c 分布 自由度 の ( カイ c 平均値 0, 標準偏差 1の正規分布 に従う変数 xの自乗和 c x =1 が従う分布を自由度 の分布と呼ぶ 一般に自由度の分布は f /1 c / / ( c ) {( c ) e }/ ( / ) 期待値 二乗 ) 分布 c
Microsoft PowerPoint - 測量学.ppt [互換モード]
![Microsoft PowerPoint - 測量学.ppt [互換モード] Microsoft PowerPoint - 測量学.ppt [互換モード]](/thumbs/92/109082022.jpg) 8/5/ 誤差理論 測定の分類 性格による分類 独立 ( な ) 測定 : 測定値がある条件を満たさなければならないなどの拘束や制約を持たないで独立して行う測定 条件 ( 付き ) 測定 : 三角形の 3 つの内角の和のように, 個々の測定値間に満たすべき条件式が存在する場合の測定 方法による分類 直接測定 : 距離や角度などを機器を用いて直接行う測定 間接測定 : 求めるべき量を直接測定するのではなく,
8/5/ 誤差理論 測定の分類 性格による分類 独立 ( な ) 測定 : 測定値がある条件を満たさなければならないなどの拘束や制約を持たないで独立して行う測定 条件 ( 付き ) 測定 : 三角形の 3 つの内角の和のように, 個々の測定値間に満たすべき条件式が存在する場合の測定 方法による分類 直接測定 : 距離や角度などを機器を用いて直接行う測定 間接測定 : 求めるべき量を直接測定するのではなく,
不偏推定量
 不偏推定量 情報科学の補足資料 018 年 6 月 7 日藤本祥二 統計的推定 (statistical estimatio) 確率分布が理論的に分かっている標本統計量を利用する 確率分布の期待値の値をそのまま推定値とするのが点推定 ( 信頼度 0%) 点推定に ± で幅を持たせて信頼度を上げたものが区間推定 持たせた幅のことを誤差 (error) と呼ぶ 信頼度 (cofidece level)
不偏推定量 情報科学の補足資料 018 年 6 月 7 日藤本祥二 統計的推定 (statistical estimatio) 確率分布が理論的に分かっている標本統計量を利用する 確率分布の期待値の値をそのまま推定値とするのが点推定 ( 信頼度 0%) 点推定に ± で幅を持たせて信頼度を上げたものが区間推定 持たせた幅のことを誤差 (error) と呼ぶ 信頼度 (cofidece level)
講義「○○○○」
 講義 信頼度の推定と立証 内容. 点推定と区間推定. 指数分布の点推定 区間推定 3. 指数分布 正規分布の信頼度推定 担当 : 倉敷哲生 ( ビジネスエンジニアリング専攻 ) 統計的推測 標本から得られる情報を基に 母集団に関する結論の導出が目的 測定値 x x x 3 : x 母集団 (populaio) 母集団の特性値 統計的推測 標本 (sample) 標本の特性値 分布のパラメータ ( 母数
講義 信頼度の推定と立証 内容. 点推定と区間推定. 指数分布の点推定 区間推定 3. 指数分布 正規分布の信頼度推定 担当 : 倉敷哲生 ( ビジネスエンジニアリング専攻 ) 統計的推測 標本から得られる情報を基に 母集団に関する結論の導出が目的 測定値 x x x 3 : x 母集団 (populaio) 母集団の特性値 統計的推測 標本 (sample) 標本の特性値 分布のパラメータ ( 母数
<4D F736F F D208EC08CB18C7689E68A E F193F18D8095AA957A C C839395AA957A814590B38B4B95AA957A2E646F63>
 第 4 回二項分布, ポアソン分布, 正規分布 実験計画学 009 年 月 0 日 A. 代表的な分布. 離散分布 二項分布大きさ n の標本で, 事象 Eの起こる確率を p とするとき, そのうち x 個にEが起こる確率 P(x) は二項分布に従う. 例さいころを 0 回振ったときに の出る回数 x の確率分布は二項分布に従う. この場合, n = 0, p = 6 の二項分布になる さいころを
第 4 回二項分布, ポアソン分布, 正規分布 実験計画学 009 年 月 0 日 A. 代表的な分布. 離散分布 二項分布大きさ n の標本で, 事象 Eの起こる確率を p とするとき, そのうち x 個にEが起こる確率 P(x) は二項分布に従う. 例さいころを 0 回振ったときに の出る回数 x の確率分布は二項分布に従う. この場合, n = 0, p = 6 の二項分布になる さいころを
横浜市環境科学研究所
 周期時系列の統計解析 単回帰分析 io 8 年 3 日 周期時系列に季節調整を行わないで単回帰分析を適用すると, 回帰係数には周期成分の影響が加わる. ここでは, 周期時系列をコサイン関数モデルで近似し単回帰分析によりモデルの回帰係数を求め, 周期成分の影響を検討した. また, その結果を気温時系列に当てはめ, 課題等について考察した. 気温時系列とコサイン関数モデル第 報の結果を利用するので, その一部を再掲する.
周期時系列の統計解析 単回帰分析 io 8 年 3 日 周期時系列に季節調整を行わないで単回帰分析を適用すると, 回帰係数には周期成分の影響が加わる. ここでは, 周期時系列をコサイン関数モデルで近似し単回帰分析によりモデルの回帰係数を求め, 周期成分の影響を検討した. また, その結果を気温時系列に当てはめ, 課題等について考察した. 気温時系列とコサイン関数モデル第 報の結果を利用するので, その一部を再掲する.
ビジネス統計 統計基礎とエクセル分析 正誤表
 ビジネス統計統計基礎とエクセル分析 ビジネス統計スペシャリスト エクセル分析スペシャリスト 公式テキスト正誤表と学習用データ更新履歴 平成 30 年 5 月 14 日現在 公式テキスト正誤表 頁場所誤正修正 6 知識編第 章 -3-3 最頻値の解説内容 たとえば, 表.1 のデータであれば, 最頻値は 167.5cm というたとえば, 表.1 のデータであれば, 最頻値は 165.0cm ということになります
ビジネス統計統計基礎とエクセル分析 ビジネス統計スペシャリスト エクセル分析スペシャリスト 公式テキスト正誤表と学習用データ更新履歴 平成 30 年 5 月 14 日現在 公式テキスト正誤表 頁場所誤正修正 6 知識編第 章 -3-3 最頻値の解説内容 たとえば, 表.1 のデータであれば, 最頻値は 167.5cm というたとえば, 表.1 のデータであれば, 最頻値は 165.0cm ということになります
多変量解析 ~ 重回帰分析 ~ 2006 年 4 月 21 日 ( 金 ) 南慶典
 多変量解析 ~ 重回帰分析 ~ 2006 年 4 月 21 日 ( 金 ) 南慶典 重回帰分析とは? 重回帰分析とは複数の説明変数から目的変数との関係性を予測 評価説明変数 ( 数量データ ) は目的変数を説明するのに有効であるか得られた関係性より未知のデータの妥当性を判断する これを重回帰分析という つまり どんなことをするのか? 1 最小 2 乗法により重回帰モデルを想定 2 自由度調整済寄与率を求め
多変量解析 ~ 重回帰分析 ~ 2006 年 4 月 21 日 ( 金 ) 南慶典 重回帰分析とは? 重回帰分析とは複数の説明変数から目的変数との関係性を予測 評価説明変数 ( 数量データ ) は目的変数を説明するのに有効であるか得られた関係性より未知のデータの妥当性を判断する これを重回帰分析という つまり どんなことをするのか? 1 最小 2 乗法により重回帰モデルを想定 2 自由度調整済寄与率を求め
スライド 1
 データ解析特論第 10 回 ( 全 15 回 ) 2012 年 12 月 11 日 ( 火 ) 情報エレクトロニクス専攻横田孝義 1 終了 11/13 11/20 重回帰分析をしばらくやります 12/4 12/11 12/18 2 前回から回帰分析について学習しています 3 ( 単 ) 回帰分析 単回帰分析では一つの従属変数 ( 目的変数 ) を 一つの独立変数 ( 説明変数 ) で予測する事を考える
データ解析特論第 10 回 ( 全 15 回 ) 2012 年 12 月 11 日 ( 火 ) 情報エレクトロニクス専攻横田孝義 1 終了 11/13 11/20 重回帰分析をしばらくやります 12/4 12/11 12/18 2 前回から回帰分析について学習しています 3 ( 単 ) 回帰分析 単回帰分析では一つの従属変数 ( 目的変数 ) を 一つの独立変数 ( 説明変数 ) で予測する事を考える
14 化学実験法 II( 吉村 ( 洋 mmol/l の半分だったから さんの測定値は くんの測定値の 4 倍の重みがあり 推定値 としては 0.68 mmol/l その標準偏差は mmol/l 程度ということになる 測定値を 特徴づけるパラメータ t を推定するこの手
 14 化学実験法 II( 吉村 ( 洋 014.6.1. 最小 乗法のはなし 014.6.1. 内容 最小 乗法のはなし...1 最小 乗法の考え方...1 最小 乗法によるパラメータの決定... パラメータの信頼区間...3 重みの異なるデータの取扱い...4 相関係数 決定係数 ( 最小 乗法を語るもう一つの立場...5 実験条件の誤差の影響...5 問題...6 最小 乗法の考え方 飲料水中のカルシウム濃度を
14 化学実験法 II( 吉村 ( 洋 014.6.1. 最小 乗法のはなし 014.6.1. 内容 最小 乗法のはなし...1 最小 乗法の考え方...1 最小 乗法によるパラメータの決定... パラメータの信頼区間...3 重みの異なるデータの取扱い...4 相関係数 決定係数 ( 最小 乗法を語るもう一つの立場...5 実験条件の誤差の影響...5 問題...6 最小 乗法の考え方 飲料水中のカルシウム濃度を
統計学の基礎から学ぶ実験計画法ー1
 第 部統計学の基礎と. 統計学とは. 統計学の基本. 母集団とサンプル ( 標本 ). データ (data) 3. 集団の特性を示す統計量 基本的な解析手法 3. 統計量 (statistic) とは 3. 集団を代表する統計量 - 平均値など 3.3 集団のばらつきを表す値 - 平方和 分散 標準偏差 4. ばらつき ( 分布 ) を表す関数 4. 確率密度関数 4. 最も重要な正規分布 4.3
第 部統計学の基礎と. 統計学とは. 統計学の基本. 母集団とサンプル ( 標本 ). データ (data) 3. 集団の特性を示す統計量 基本的な解析手法 3. 統計量 (statistic) とは 3. 集団を代表する統計量 - 平均値など 3.3 集団のばらつきを表す値 - 平方和 分散 標準偏差 4. ばらつき ( 分布 ) を表す関数 4. 確率密度関数 4. 最も重要な正規分布 4.3
航空レーザ計測による効率的な森林資源の把握
 発表 1 航空レーザ計測による効率的な森林資源の把握 北海道森林管理局計画課佐々木貢 アジア航測株式会社空間情報事業部大野勝正 森林の適切な管理経営のため 森林資源の把握は重要 森林調査簿等のデータベース 森林計画等の策定 間伐等の事業発注 調査 研究 その他 夏のパイロット フォレスト 新たな森林調査の手法を導入 航空レーザ計測技術の活用 これまでは 必要の都度 人手による森林調査を実施 主として標準地等によるサンプル調査
発表 1 航空レーザ計測による効率的な森林資源の把握 北海道森林管理局計画課佐々木貢 アジア航測株式会社空間情報事業部大野勝正 森林の適切な管理経営のため 森林資源の把握は重要 森林調査簿等のデータベース 森林計画等の策定 間伐等の事業発注 調査 研究 その他 夏のパイロット フォレスト 新たな森林調査の手法を導入 航空レーザ計測技術の活用 これまでは 必要の都度 人手による森林調査を実施 主として標準地等によるサンプル調査
Kumamoto University Center for Multimedia and Information Technologies Lab. 熊本大学アプリケーション実験 ~ 実環境における無線 LAN 受信電波強度を用いた位置推定手法の検討 ~ InKIAI 宮崎県美郷
 熊本大学アプリケーション実験 ~ 実環境における無線 LAN 受信電波強度を用いた位置推定手法の検討 ~ InKIAI プロジェクト @ 宮崎県美郷町 熊本大学副島慶人川村諒 1 実験の目的 従来 信号の受信電波強度 (RSSI:RecevedSgnal StrengthIndcator) により 対象の位置を推定する手法として 無線 LAN の AP(AccessPont) から受信する信号の減衰量をもとに位置を推定する手法が多く検討されている
熊本大学アプリケーション実験 ~ 実環境における無線 LAN 受信電波強度を用いた位置推定手法の検討 ~ InKIAI プロジェクト @ 宮崎県美郷町 熊本大学副島慶人川村諒 1 実験の目的 従来 信号の受信電波強度 (RSSI:RecevedSgnal StrengthIndcator) により 対象の位置を推定する手法として 無線 LAN の AP(AccessPont) から受信する信号の減衰量をもとに位置を推定する手法が多く検討されている
13章 回帰分析
 単回帰分析 つ以上の変数についての関係を見る つの 目的 被説明 変数を その他の 説明 変数を使って 予測しようというものである 因果関係とは限らない ここで勉強すること 最小 乗法と回帰直線 決定係数とは何か? 最小 乗法と回帰直線 これまで 変数の間の関係の深さについて考えてきた 相関係数 ここでは 変数に役割を与え 一方の 説明 変数を用いて他方の 目的 被説明 変数を説明することを考える
単回帰分析 つ以上の変数についての関係を見る つの 目的 被説明 変数を その他の 説明 変数を使って 予測しようというものである 因果関係とは限らない ここで勉強すること 最小 乗法と回帰直線 決定係数とは何か? 最小 乗法と回帰直線 これまで 変数の間の関係の深さについて考えてきた 相関係数 ここでは 変数に役割を与え 一方の 説明 変数を用いて他方の 目的 被説明 変数を説明することを考える
データ解析
 データ解析 ( 前期 ) 最小二乗法 向井厚志 005 年度テキスト 0 データ解析 - 最小二乗法 - 目次 第 回 Σ の計算 第 回ヒストグラム 第 3 回平均と標準偏差 6 第 回誤差の伝播 8 第 5 回正規分布 0 第 6 回最尤性原理 第 7 回正規分布の 分布の幅 第 8 回最小二乗法 6 第 9 回最小二乗法の練習 8 第 0 回最小二乗法の推定誤差 0 第 回推定誤差の計算 第
データ解析 ( 前期 ) 最小二乗法 向井厚志 005 年度テキスト 0 データ解析 - 最小二乗法 - 目次 第 回 Σ の計算 第 回ヒストグラム 第 3 回平均と標準偏差 6 第 回誤差の伝播 8 第 5 回正規分布 0 第 6 回最尤性原理 第 7 回正規分布の 分布の幅 第 8 回最小二乗法 6 第 9 回最小二乗法の練習 8 第 0 回最小二乗法の推定誤差 0 第 回推定誤差の計算 第
と 測定を繰り返した時のばらつき の和が 全体のばらつき () に対して どれくらいの割合となるかがわかり 測定システムを評価することができる MSA 第 4 版スタディガイド ジャパン プレクサス (010)p.104 では % GRR の値が10% 未満であれば 一般に受容れられる測定システムと
 .5 Gage R&R による解析.5.1 Gage R&Rとは Gage R&R(Gage Repeatability and Reproducibility ) とは 測定システム分析 (MSA: Measurement System Analysis) ともいわれ 測定プロセスを管理または審査するための手法である MSAでは ばらつきの大きさを 変動 という尺度で表し 測定システムのどこに原因があるのか
.5 Gage R&R による解析.5.1 Gage R&Rとは Gage R&R(Gage Repeatability and Reproducibility ) とは 測定システム分析 (MSA: Measurement System Analysis) ともいわれ 測定プロセスを管理または審査するための手法である MSAでは ばらつきの大きさを 変動 という尺度で表し 測定システムのどこに原因があるのか
スライド 1
 データ解析特論重回帰分析編 2017 年 7 月 10 日 ( 月 )~ 情報エレクトロニクスコース横田孝義 1 ( 単 ) 回帰分析 単回帰分析では一つの従属変数 ( 目的変数 ) を 一つの独立変数 ( 説明変数 ) で予測する事を考える 具体的には y = a + bx という回帰直線 ( モデル ) でデータを代表させる このためにデータからこの回帰直線の切片 (a) と傾き (b) を最小
データ解析特論重回帰分析編 2017 年 7 月 10 日 ( 月 )~ 情報エレクトロニクスコース横田孝義 1 ( 単 ) 回帰分析 単回帰分析では一つの従属変数 ( 目的変数 ) を 一つの独立変数 ( 説明変数 ) で予測する事を考える 具体的には y = a + bx という回帰直線 ( モデル ) でデータを代表させる このためにデータからこの回帰直線の切片 (a) と傾き (b) を最小
PowerPoint プレゼンテーション
 REDD+ Reducing Emission from Deforestation and Forest Degradation-plus 第 5 章 森林炭素量の把握 ベトナム国 DienBien 省におけるバイオマス関連データの開発の事例 一般社団法人日本森林技術協会金森匡彦 1 REDD+CookBook より 2 各森林被覆タイプ この時間の講習 森林被覆の時系列変化 リモートセンシングによる森林被覆の時系列変化の把握
REDD+ Reducing Emission from Deforestation and Forest Degradation-plus 第 5 章 森林炭素量の把握 ベトナム国 DienBien 省におけるバイオマス関連データの開発の事例 一般社団法人日本森林技術協会金森匡彦 1 REDD+CookBook より 2 各森林被覆タイプ この時間の講習 森林被覆の時系列変化 リモートセンシングによる森林被覆の時系列変化の把握
Medical3
 Chapter 1 1.4.1 1 元配置分散分析と多重比較の実行 3つの治療法による測定値に有意な差が認められるかどうかを分散分析で調べます この例では 因子が1つだけ含まれるため1 元配置分散分析 one-way ANOVA の適用になります また 多重比較法 multiple comparison procedure を用いて 具体的のどの治療法の間に有意差が認められるかを検定します 1. 分析メニュー
Chapter 1 1.4.1 1 元配置分散分析と多重比較の実行 3つの治療法による測定値に有意な差が認められるかどうかを分散分析で調べます この例では 因子が1つだけ含まれるため1 元配置分散分析 one-way ANOVA の適用になります また 多重比較法 multiple comparison procedure を用いて 具体的のどの治療法の間に有意差が認められるかを検定します 1. 分析メニュー
Microsoft PowerPoint - statistics pptx
 統計学 第 16 回 講義 母平均の区間推定 Part-1 016 年 6 10 ( ) 1 限 担当教員 : 唐渡 広志 ( からと こうじ ) 研究室 : 経済学研究棟 4 階 43 号室 email: [email protected] website: http://www3.u-toyama.ac.jp/kkarato/ 1 講義の目的 標本平均は正規分布に従うという性質を
統計学 第 16 回 講義 母平均の区間推定 Part-1 016 年 6 10 ( ) 1 限 担当教員 : 唐渡 広志 ( からと こうじ ) 研究室 : 経済学研究棟 4 階 43 号室 email: [email protected] website: http://www3.u-toyama.ac.jp/kkarato/ 1 講義の目的 標本平均は正規分布に従うという性質を
第 3 回講義の項目と概要 統計的手法入門 : 品質のばらつきを解析する 平均と標準偏差 (P30) a) データは平均を見ただけではわからない 平均が同じだからといって 同一視してはいけない b) データのばらつきを示す 標準偏差 にも注目しよう c) 平均
 第 3 回講義の項目と概要 016.8.9 1.3 統計的手法入門 : 品質のばらつきを解析する 1.3.1 平均と標準偏差 (P30) a) データは平均を見ただけではわからない 平均が同じだからといって 同一視してはいけない b) データのばらつきを示す 標準偏差 にも注目しよう c) 平均 :AVERAGE 関数, 標準偏差 :STDEVP 関数とSTDEVという関数 1 取得したデータそのものの標準偏差
第 3 回講義の項目と概要 016.8.9 1.3 統計的手法入門 : 品質のばらつきを解析する 1.3.1 平均と標準偏差 (P30) a) データは平均を見ただけではわからない 平均が同じだからといって 同一視してはいけない b) データのばらつきを示す 標準偏差 にも注目しよう c) 平均 :AVERAGE 関数, 標準偏差 :STDEVP 関数とSTDEVという関数 1 取得したデータそのものの標準偏差
Microsoft PowerPoint - e-stat(OLS).pptx
 経済統計学 ( 補足 ) 最小二乗法について 担当 : 小塚匡文 2015 年 11 月 19 日 ( 改訂版 ) 神戸大学経済学部 2015 年度後期開講授業 補足 : 最小二乗法 ( 単回帰分析 ) 1.( 単純 ) 回帰分析とは? 標本サイズTの2 変数 ( ここではXとY) のデータが存在 YをXで説明する回帰方程式を推定するための方法 Y: 被説明変数 ( または従属変数 ) X: 説明変数
経済統計学 ( 補足 ) 最小二乗法について 担当 : 小塚匡文 2015 年 11 月 19 日 ( 改訂版 ) 神戸大学経済学部 2015 年度後期開講授業 補足 : 最小二乗法 ( 単回帰分析 ) 1.( 単純 ) 回帰分析とは? 標本サイズTの2 変数 ( ここではXとY) のデータが存在 YをXで説明する回帰方程式を推定するための方法 Y: 被説明変数 ( または従属変数 ) X: 説明変数
Microsoft PowerPoint - stat-2014-[9] pptx
![Microsoft PowerPoint - stat-2014-[9] pptx Microsoft PowerPoint - stat-2014-[9] pptx](/thumbs/49/25555771.jpg) 統計学 第 17 回 講義 母平均の区間推定 Part-1 014 年 6 17 ( )6-7 限 担当教員 : 唐渡 広志 ( からと こうじ ) 研究室 : 経済学研究棟 4 階 43 号室 email: [email protected] website: htt://www3.u-toyama.ac.j/kkarato/ 1 講義の目的 標本平均は正規分布に従うという性質を
統計学 第 17 回 講義 母平均の区間推定 Part-1 014 年 6 17 ( )6-7 限 担当教員 : 唐渡 広志 ( からと こうじ ) 研究室 : 経済学研究棟 4 階 43 号室 email: [email protected] website: htt://www3.u-toyama.ac.j/kkarato/ 1 講義の目的 標本平均は正規分布に従うという性質を
Probit , Mixed logit
 Probit, Mixed logit 2016/5/16 スタートアップゼミ #5 B4 後藤祥孝 1 0. 目次 Probit モデルについて 1. モデル概要 2. 定式化と理解 3. 推定 Mixed logit モデルについて 4. モデル概要 5. 定式化と理解 6. 推定 2 1.Probit 概要 プロビットモデルとは. 効用関数の誤差項に多変量正規分布を仮定したもの. 誤差項には様々な要因が存在するため,
Probit, Mixed logit 2016/5/16 スタートアップゼミ #5 B4 後藤祥孝 1 0. 目次 Probit モデルについて 1. モデル概要 2. 定式化と理解 3. 推定 Mixed logit モデルについて 4. モデル概要 5. 定式化と理解 6. 推定 2 1.Probit 概要 プロビットモデルとは. 効用関数の誤差項に多変量正規分布を仮定したもの. 誤差項には様々な要因が存在するため,
カイ二乗フィット検定、パラメータの誤差
 統計的データ解析 008 008.. 林田清 ( 大阪大学大学院理学研究科 ) 問題 C (, ) ( x xˆ) ( y yˆ) σ x πσ σ y y Pabx (, ;,,, ) ˆ y σx σ y = dx exp exp πσx ただし xy ˆ ˆ はyˆ = axˆ+ bであらわされる直線モデル上の点 ( ˆ) ( ˆ ) ( ) x x y ax b y ax b Pabx (,
統計的データ解析 008 008.. 林田清 ( 大阪大学大学院理学研究科 ) 問題 C (, ) ( x xˆ) ( y yˆ) σ x πσ σ y y Pabx (, ;,,, ) ˆ y σx σ y = dx exp exp πσx ただし xy ˆ ˆ はyˆ = axˆ+ bであらわされる直線モデル上の点 ( ˆ) ( ˆ ) ( ) x x y ax b y ax b Pabx (,
Excelによる統計分析検定_知識編_小塚明_1_4章.indd
 第1章 母集団と統計データ 本章では, ビジネスのさまざまな場面において統計データを扱ううえで, もっとも基本的事項となる母集団の概念と統計データの種類についてまとめています 母集団の統計的性質を調べるためにとても重要な概念であるサンプリングについて述べるとともに, ランダムサンプリングの重要性についても説明します 統計分析の考え方 ビジネスの多くの場面において, 統計分析は重要です この場合の統計分析とは,
第1章 母集団と統計データ 本章では, ビジネスのさまざまな場面において統計データを扱ううえで, もっとも基本的事項となる母集団の概念と統計データの種類についてまとめています 母集団の統計的性質を調べるためにとても重要な概念であるサンプリングについて述べるとともに, ランダムサンプリングの重要性についても説明します 統計分析の考え方 ビジネスの多くの場面において, 統計分析は重要です この場合の統計分析とは,
Microsoft PowerPoint - statistics pptx
 統計学 第 回 講義 仮説検定 Part-3 06 年 6 8 ( )3 限 担当教員 唐渡 広志 ( からと こうじ ) 研究室 経済学研究棟 4 階 43 号室 email [email protected] webite htt://www3.u-toyama.ac.j/kkarato/ 講義の目的 つの 集団の平均 ( 率 ) に差があるかどうかを検定する 法を理解します keyword:
統計学 第 回 講義 仮説検定 Part-3 06 年 6 8 ( )3 限 担当教員 唐渡 広志 ( からと こうじ ) 研究室 経済学研究棟 4 階 43 号室 email [email protected] webite htt://www3.u-toyama.ac.j/kkarato/ 講義の目的 つの 集団の平均 ( 率 ) に差があるかどうかを検定する 法を理解します keyword:
1. 多変量解析の基本的な概念 1. 多変量解析の基本的な概念 1.1 多変量解析の目的 人間のデータは多変量データが多いので多変量解析が有用 特性概括評価特性概括評価 症 例 主 治 医 の 主 観 症 例 主 治 医 の 主 観 単変量解析 客観的規準のある要約多変量解析 要約値 客観的規準のな
 1.1 多変量解析の目的 人間のデータは多変量データが多いので多変量解析が有用 特性概括評価特性概括評価 症 例 治 医 の 観 症 例 治 医 の 観 単変量解析 客観的規準のある要約多変量解析 要約値 客観的規準のない要約知識 直感 知識 直感 総合的評価 考察 総合的評価 考察 単変量解析の場合 多変量解析の場合 < 表 1.1 脂質異常症患者の TC と TG と重症度 > 症例 No. TC
1.1 多変量解析の目的 人間のデータは多変量データが多いので多変量解析が有用 特性概括評価特性概括評価 症 例 治 医 の 観 症 例 治 医 の 観 単変量解析 客観的規準のある要約多変量解析 要約値 客観的規準のない要約知識 直感 知識 直感 総合的評価 考察 総合的評価 考察 単変量解析の場合 多変量解析の場合 < 表 1.1 脂質異常症患者の TC と TG と重症度 > 症例 No. TC
(4) 横断面形調査要領では メッシュの中心点と 中心点を通る等高線が内接円に交わる 2 点を結んだ 2 直線の山麓側の角度 ( メッシュの中心点を通る等高線がない場合は 中心点に最も近接している等高線から類推する角度 ) を計測し 10 度括約で求める とされている 横断面形の概念図を図 4.4
 (4) 横断面形調査要領では メッシュの中心点と 中心点を通る等高線が内接円に交わる 2 点を結んだ 2 直線の山麓側の角度 ( メッシュの中心点を通る等高線がない場合は 中心点に最も近接している等高線から類推する角度 ) を計測し 10 度括約で求める とされている 横断面形の概念図を図 4.4 に示す 凹地形 (~150 ) 等斉斜面 (151 ~210 ) 凸地形 (211 ~) 図 4.4
(4) 横断面形調査要領では メッシュの中心点と 中心点を通る等高線が内接円に交わる 2 点を結んだ 2 直線の山麓側の角度 ( メッシュの中心点を通る等高線がない場合は 中心点に最も近接している等高線から類推する角度 ) を計測し 10 度括約で求める とされている 横断面形の概念図を図 4.4 に示す 凹地形 (~150 ) 等斉斜面 (151 ~210 ) 凸地形 (211 ~) 図 4.4
したがって ばらつきを表すには 偏差の符号をなくしてから平均化する必要がある そのひとつの方法は 1 偏差の絶対値を用いることである 偏差の絶対値の算術平均を 平均偏差 という ( )/5=10.8 偏差の符号を取るもうひとつの方法は 2それを2 乗することです 偏差の2 乗の算
 統計学テキストの69ページに 平均偏差 分散 標準偏差 変動係数 標準誤差 信頼区間に関する記述がある 分布を考える分布の中心の位置 ( 例 ) 65 53 44 78 50 の数値の算術平均は (65+53+44+78+50)/5=58 である 此れだけでは 分布の状態がわからない ばらつきの程度を表すには最大値と最小値との差 (78-44)=34 これをレンジ ( 範囲 ) と言う しかし 両端の数字だけでは
統計学テキストの69ページに 平均偏差 分散 標準偏差 変動係数 標準誤差 信頼区間に関する記述がある 分布を考える分布の中心の位置 ( 例 ) 65 53 44 78 50 の数値の算術平均は (65+53+44+78+50)/5=58 である 此れだけでは 分布の状態がわからない ばらつきの程度を表すには最大値と最小値との差 (78-44)=34 これをレンジ ( 範囲 ) と言う しかし 両端の数字だけでは
Microsoft PowerPoint - 奈良井国有林での収穫調査へのICTドローン活用Ver1
 奈良井国有林での収穫調査の ICT ドローン活用 林野庁中部森林管理局中信森林管理署 岩塚伸人 中部森林管理局の概要 中部森林管理局は 富山県 長野県 岐阜県 愛知県の 4 県にまたがる国有林を管理しています 国有林の管轄面積は 65 万 6 千 ha におよび 太平洋側の海岸縁から 日本の屋根 と言われる日本アルプスの山岳地帯まで分布し その多くは地形が急峻な脊梁山脈や河川の源流域に分布しています
奈良井国有林での収穫調査の ICT ドローン活用 林野庁中部森林管理局中信森林管理署 岩塚伸人 中部森林管理局の概要 中部森林管理局は 富山県 長野県 岐阜県 愛知県の 4 県にまたがる国有林を管理しています 国有林の管轄面積は 65 万 6 千 ha におよび 太平洋側の海岸縁から 日本の屋根 と言われる日本アルプスの山岳地帯まで分布し その多くは地形が急峻な脊梁山脈や河川の源流域に分布しています
Microsoft PowerPoint - Statistics[B]
![Microsoft PowerPoint - Statistics[B] Microsoft PowerPoint - Statistics[B]](/thumbs/101/151482563.jpg) 講義の目的 サンプルサイズの大きい標本比率の分布は正規分布で近似できることを理解します 科目コード 130509, 130609, 110225 統計学講義第 19/20 回 2019 年 6 月 25 日 ( 火 )6/7 限 担当教員 : 唐渡広志 ( からと こうじ ) 研究室 : email: website: 経済学研究棟 4 階 432 号室 [email protected]
講義の目的 サンプルサイズの大きい標本比率の分布は正規分布で近似できることを理解します 科目コード 130509, 130609, 110225 統計学講義第 19/20 回 2019 年 6 月 25 日 ( 火 )6/7 限 担当教員 : 唐渡広志 ( からと こうじ ) 研究室 : email: website: 経済学研究棟 4 階 432 号室 [email protected]
Microsoft Word - NumericalComputation.docx
 数値計算入門 武尾英哉. 離散数学と数値計算 数学的解法の中には理論計算では求められないものもある. 例えば, 定積分は, まずは積分 ( 被積分関数の原始関数をみつけること できなければ値を得ることはできない. また, ある関数の所定の値における微分値を得るには, まずその関数の微分ができなければならない. さらに代数方程式の解を得るためには, 解析的に代数方程式を解く必要がある. ところが, これらは必ずしも解析的に導けるとは限らない.
数値計算入門 武尾英哉. 離散数学と数値計算 数学的解法の中には理論計算では求められないものもある. 例えば, 定積分は, まずは積分 ( 被積分関数の原始関数をみつけること できなければ値を得ることはできない. また, ある関数の所定の値における微分値を得るには, まずその関数の微分ができなければならない. さらに代数方程式の解を得るためには, 解析的に代数方程式を解く必要がある. ところが, これらは必ずしも解析的に導けるとは限らない.
Microsoft PowerPoint - 資料04 重回帰分析.ppt
 04. 重回帰分析 京都大学 加納学 Division of Process Control & Process Sstems Engineering Department of Chemical Engineering, Koto Universit [email protected] http://www-pse.cheme.koto-u.ac.jp/~kano/ Outline
04. 重回帰分析 京都大学 加納学 Division of Process Control & Process Sstems Engineering Department of Chemical Engineering, Koto Universit [email protected] http://www-pse.cheme.koto-u.ac.jp/~kano/ Outline
周期時系列の統計解析 (3) 移動平均とフーリエ変換 nino 2017 年 12 月 18 日 移動平均は, 周期時系列における特定の周期成分の消去や不規則変動 ( ノイズ ) の低減に汎用されている統計手法である. ここでは, 周期時系列をコサイン関数で近似し, その移動平均により周期成分の振幅
 周期時系列の統計解析 3 移動平均とフーリエ変換 io 07 年 月 8 日 移動平均は, 周期時系列における特定の周期成分の消去や不規則変動 ノイズ の低減に汎用されている統計手法である. ここでは, 周期時系列をコサイン関数で近似し, その移動平均により周期成分のがどのように変化するのか等について検討する. また, 気温の実測値に移動平均を適用した結果についてフーリエ変換も併用して考察する. 単純移動平均の計算式移動平均には,
周期時系列の統計解析 3 移動平均とフーリエ変換 io 07 年 月 8 日 移動平均は, 周期時系列における特定の周期成分の消去や不規則変動 ノイズ の低減に汎用されている統計手法である. ここでは, 周期時系列をコサイン関数で近似し, その移動平均により周期成分のがどのように変化するのか等について検討する. また, 気温の実測値に移動平均を適用した結果についてフーリエ変換も併用して考察する. 単純移動平均の計算式移動平均には,
森林水文 水資源学 2 2. 水文統計 豪雨があった時, 新聞やテレビのニュースで 50 年に一度の大雨だった などと報告されることがある. 今争点となっている川辺川ダムは,80 年に 1 回の洪水を想定して治水計画が立てられている. 畑地かんがいでは,10 年に 1 回の渇水を対象として計画が立て
 . 水文統計 豪雨があった時, 新聞やテレビのニュースで 50 年に一度の大雨だった などと報告されることがある. 今争点となっている川辺川ダムは,80 年に 回の洪水を想定して治水計画が立てられている. 畑地かんがいでは,0 年に 回の渇水を対象として計画が立てられる. このように, 水利構造物の設計や, 治水や利水の計画などでは, 年に 回起こるような降雨事象 ( 最大降雨強度, 最大連続干天日数など
. 水文統計 豪雨があった時, 新聞やテレビのニュースで 50 年に一度の大雨だった などと報告されることがある. 今争点となっている川辺川ダムは,80 年に 回の洪水を想定して治水計画が立てられている. 畑地かんがいでは,0 年に 回の渇水を対象として計画が立てられる. このように, 水利構造物の設計や, 治水や利水の計画などでは, 年に 回起こるような降雨事象 ( 最大降雨強度, 最大連続干天日数など
Microsoft Word - 補論3.2
 補論 3. 多変量 GARC モデル 07//6 新谷元嗣 藪友良 対数尤度関数 3 章 7 節では 変量の対数尤度を求めた ここでは多変量の場合 とくに 変量について対数尤度を求める 誤差項 は平均 0 で 次元の正規分布に従うとする 単純化のため 分散と共分散は時間を通じて一定としよう ( この仮定は後で変更される ) したがって ij から添え字 を除くことができる このとき と の尤度関数は
補論 3. 多変量 GARC モデル 07//6 新谷元嗣 藪友良 対数尤度関数 3 章 7 節では 変量の対数尤度を求めた ここでは多変量の場合 とくに 変量について対数尤度を求める 誤差項 は平均 0 で 次元の正規分布に従うとする 単純化のため 分散と共分散は時間を通じて一定としよう ( この仮定は後で変更される ) したがって ij から添え字 を除くことができる このとき と の尤度関数は
Microsoft PowerPoint - mp11-06.pptx
 数理計画法第 6 回 塩浦昭義情報科学研究科准教授 [email protected] http://www.dais.is.tohoku.ac.jp/~shioura/teaching 第 5 章組合せ計画 5.2 分枝限定法 組合せ計画問題 組合せ計画問題とは : 有限個の もの の組合せの中から, 目的関数を最小または最大にする組合せを見つける問題 例 1: 整数計画問題全般
数理計画法第 6 回 塩浦昭義情報科学研究科准教授 [email protected] http://www.dais.is.tohoku.ac.jp/~shioura/teaching 第 5 章組合せ計画 5.2 分枝限定法 組合せ計画問題 組合せ計画問題とは : 有限個の もの の組合せの中から, 目的関数を最小または最大にする組合せを見つける問題 例 1: 整数計画問題全般
1.民営化
 参考資料 最小二乗法 数学的性質 経済統計分析 3 年度秋学期 回帰分析と最小二乗法 被説明変数 の動きを説明変数 の動きで説明 = 回帰分析 説明変数がつ 単回帰 説明変数がつ以上 重回帰 被説明変数 従属変数 係数 定数項傾き 説明変数 独立変数 残差... で説明できる部分 説明できない部分 説明できない部分が小さくなるように回帰式の係数 を推定する有力な方法 = 最小二乗法 最小二乗法による回帰の考え方
参考資料 最小二乗法 数学的性質 経済統計分析 3 年度秋学期 回帰分析と最小二乗法 被説明変数 の動きを説明変数 の動きで説明 = 回帰分析 説明変数がつ 単回帰 説明変数がつ以上 重回帰 被説明変数 従属変数 係数 定数項傾き 説明変数 独立変数 残差... で説明できる部分 説明できない部分 説明できない部分が小さくなるように回帰式の係数 を推定する有力な方法 = 最小二乗法 最小二乗法による回帰の考え方
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生
 0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
青焼 1章[15-52].indd
![青焼 1章[15-52].indd 青焼 1章[15-52].indd](/thumbs/86/94313777.jpg) 1 第 1 章統計の基礎知識 1 1 なぜ統計解析が必要なのか? 人間は自分自身の経験にもとづいて 感覚的にものごとを判断しがちである 例えばある疾患に対する標準治療薬の有効率が 50% であったとする そこに新薬が登場し ある医師がその新薬を 5 人の患者に使ったところ 4 人が有効と判定されたとしたら 多くの医師はこれまでの標準治療薬よりも新薬のほうが有効性が高そうだと感じることだろう しかし
1 第 1 章統計の基礎知識 1 1 なぜ統計解析が必要なのか? 人間は自分自身の経験にもとづいて 感覚的にものごとを判断しがちである 例えばある疾患に対する標準治療薬の有効率が 50% であったとする そこに新薬が登場し ある医師がその新薬を 5 人の患者に使ったところ 4 人が有効と判定されたとしたら 多くの医師はこれまでの標準治療薬よりも新薬のほうが有効性が高そうだと感じることだろう しかし
経済統計分析1 イントロダクション
 1 経済統計分析 9 分散分析 今日のおはなし. 検定 statistical test のいろいろ 2 変数の関係を調べる手段のひとつ適合度検定独立性検定分散分析 今日のタネ 吉田耕作.2006. 直感的統計学. 日経 BP. 中村隆英ほか.1984. 統計入門. 東大出版会. 2 仮説検定の手続き 仮説検定のロジック もし帰無仮説が正しければ, 検定統計量が既知の分布に従う 計算された検定統計量の値から,
1 経済統計分析 9 分散分析 今日のおはなし. 検定 statistical test のいろいろ 2 変数の関係を調べる手段のひとつ適合度検定独立性検定分散分析 今日のタネ 吉田耕作.2006. 直感的統計学. 日経 BP. 中村隆英ほか.1984. 統計入門. 東大出版会. 2 仮説検定の手続き 仮説検定のロジック もし帰無仮説が正しければ, 検定統計量が既知の分布に従う 計算された検定統計量の値から,
相関係数と偏差ベクトル
 相関係数と偏差ベクトル 経営統計演習の補足資料 07 年 月 9 日金沢学院大学経営情報学部藤本祥二 相関係数の復習 r = s xy s x s y = = n σ n i= σn i= n σ n i= n σ i= x i xҧ y i തy x i xҧ n σ n i= y i തy x i xҧ x i xҧ y i തy σn i= y i തy 式が長くなるので u, v の文字で偏差を表すことにする
相関係数と偏差ベクトル 経営統計演習の補足資料 07 年 月 9 日金沢学院大学経営情報学部藤本祥二 相関係数の復習 r = s xy s x s y = = n σ n i= σn i= n σ n i= n σ i= x i xҧ y i തy x i xҧ n σ n i= y i തy x i xҧ x i xҧ y i തy σn i= y i തy 式が長くなるので u, v の文字で偏差を表すことにする
解析センターを知っていただく キャンペーン
 005..5 SAS 問題設定 目的 PKパラメータ (AUC,Cmax,Tmaxなど) の推定 PKパラメータの群間比較 PKパラメータのバラツキの評価! データの特徴 非反復測定値 個体につき 個の測定値しか得られない plasma concentration 非反復測定値のイメージ図 測定時点間で個体の対応がない 着目する状況 plasma concentration 経時反復測定値のイメージ図
005..5 SAS 問題設定 目的 PKパラメータ (AUC,Cmax,Tmaxなど) の推定 PKパラメータの群間比較 PKパラメータのバラツキの評価! データの特徴 非反復測定値 個体につき 個の測定値しか得られない plasma concentration 非反復測定値のイメージ図 測定時点間で個体の対応がない 着目する状況 plasma concentration 経時反復測定値のイメージ図
資料3-5 モニタリング方法ガイドライン(森林管理プロジェクト用)(案)
 ステップ 2-1: 対象となる森林に傾斜がある場合のプロット設定方法 図 Ⅱ-4 プロジェクト対象地に傾斜がある場合のプロット設定方法 赤部は設定したプロットを示す プロジェクト対象の森林に傾斜がある場合は 斜面の中腹に調査プロットを設置する ステップ 2-2: 対象となる森林が 平地に立地している場合のプロット設定方法 図 Ⅱ-5 プロジェクト対象地に傾斜がない場合のプロット設定方法 ( 森林の平面図
ステップ 2-1: 対象となる森林に傾斜がある場合のプロット設定方法 図 Ⅱ-4 プロジェクト対象地に傾斜がある場合のプロット設定方法 赤部は設定したプロットを示す プロジェクト対象の森林に傾斜がある場合は 斜面の中腹に調査プロットを設置する ステップ 2-2: 対象となる森林が 平地に立地している場合のプロット設定方法 図 Ⅱ-5 プロジェクト対象地に傾斜がない場合のプロット設定方法 ( 森林の平面図
ファイナンスのための数学基礎 第1回 オリエンテーション、ベクトル
 時系列分析 変量時系列モデルとその性質 担当 : 長倉大輔 ( ながくらだいすけ 時系列モデル 時系列モデルとは時系列データを生み出すメカニズムとなるものである これは実際には未知である 私たちにできるのは観測された時系列データからその背後にある時系列モデルを推測 推定するだけである 以下ではいくつかの代表的な時系列モデルを考察する 自己回帰モデル (Auoregressive Model もっとも頻繁に使われる時系列モデルは自己回帰モデル
時系列分析 変量時系列モデルとその性質 担当 : 長倉大輔 ( ながくらだいすけ 時系列モデル 時系列モデルとは時系列データを生み出すメカニズムとなるものである これは実際には未知である 私たちにできるのは観測された時系列データからその背後にある時系列モデルを推測 推定するだけである 以下ではいくつかの代表的な時系列モデルを考察する 自己回帰モデル (Auoregressive Model もっとも頻繁に使われる時系列モデルは自己回帰モデル
JUSE-StatWorks/V5 活用ガイドブック
 4.6 薄膜金属材料の表面加工 ( 直積法 ) 直積法では, 内側に直交配列表または要因配置計画の M 個の実験, 外側に直交配列表または要因配置計画の N 個の実験をわりつけ, その組み合わせの M N のデータを解析します. 直積法を用いることにより, 内側計画の各列と全ての外側因子との交互作用を求めることができます. よって, 環境条件や使用条件のように制御が難しい ( 水準を指定できない )
4.6 薄膜金属材料の表面加工 ( 直積法 ) 直積法では, 内側に直交配列表または要因配置計画の M 個の実験, 外側に直交配列表または要因配置計画の N 個の実験をわりつけ, その組み合わせの M N のデータを解析します. 直積法を用いることにより, 内側計画の各列と全ての外側因子との交互作用を求めることができます. よって, 環境条件や使用条件のように制御が難しい ( 水準を指定できない )
ダンゴムシの 交替性転向反応に 関する研究 3A15 今野直輝
 ダンゴムシの 交替性転向反応に 関する研究 3A15 今野直輝 1. 研究の動機 ダンゴムシには 右に曲がった後は左に 左に曲がった後は右に曲がる という交替性転向反応という習性がある 数多くの生物において この習性は見受けられるのだが なかでもダンゴムシやその仲間のワラジムシは その行動が特に顕著であるとして有名である そのため図 1のような道をダンゴムシに歩かせると 前の突き当りでどちらの方向に曲がったかを見ることによって
ダンゴムシの 交替性転向反応に 関する研究 3A15 今野直輝 1. 研究の動機 ダンゴムシには 右に曲がった後は左に 左に曲がった後は右に曲がる という交替性転向反応という習性がある 数多くの生物において この習性は見受けられるのだが なかでもダンゴムシやその仲間のワラジムシは その行動が特に顕著であるとして有名である そのため図 1のような道をダンゴムシに歩かせると 前の突き当りでどちらの方向に曲がったかを見ることによって
Microsoft PowerPoint - 基礎・経済統計6.ppt
 . 確率変数 基礎 経済統計 6 確率分布 事象を数値化したもの ( 事象ー > 数値 の関数 自然に数値されている場合 さいころの目 量的尺度 数値化が必要な場合 質的尺度, 順序的尺度 それらの尺度に数値を割り当てる 例えば, コインの表が出たら, 裏なら 0. 離散確率変数と連続確率変数 確率変数の値 連続値をとるもの 身長, 体重, 実質 GDP など とびとびの値 離散値をとるもの 新生児の性別
. 確率変数 基礎 経済統計 6 確率分布 事象を数値化したもの ( 事象ー > 数値 の関数 自然に数値されている場合 さいころの目 量的尺度 数値化が必要な場合 質的尺度, 順序的尺度 それらの尺度に数値を割り当てる 例えば, コインの表が出たら, 裏なら 0. 離散確率変数と連続確率変数 確率変数の値 連続値をとるもの 身長, 体重, 実質 GDP など とびとびの値 離散値をとるもの 新生児の性別
Excelによる統計分析検定_知識編_小塚明_5_9章.indd
 第7章57766 検定と推定 サンプリングによって得られた標本から, 母集団の統計的性質に対して推測を行うことを統計的推測といいます 本章では, 推測統計の根幹をなす仮説検定と推定の基本的な考え方について説明します 前章までの知識を用いて, 具体的な分析を行います 本章以降の知識は操作編での操作に直接関連していますので, 少し聞きなれない言葉ですが, 帰無仮説 有意水準 棄却域 などの意味を理解して,
第7章57766 検定と推定 サンプリングによって得られた標本から, 母集団の統計的性質に対して推測を行うことを統計的推測といいます 本章では, 推測統計の根幹をなす仮説検定と推定の基本的な考え方について説明します 前章までの知識を用いて, 具体的な分析を行います 本章以降の知識は操作編での操作に直接関連していますので, 少し聞きなれない言葉ですが, 帰無仮説 有意水準 棄却域 などの意味を理解して,
モジュール1のまとめ
 数理統計学 第 0 回 復習 標本分散と ( 標本 ) 不偏分散両方とも 分散 というのが実情 二乗偏差計標本分散 = データ数 (0ページ) ( 標本 ) 不偏分散 = (03 ページ ) 二乗偏差計 データ数 - 分析ではこちらをとることが多い 復習 ここまで 実験結果 ( 万回 ) 平均 50Kg 標準偏差 0Kg 0 人 全体に小さすぎる > mea(jkke) [] 89.4373 標準偏差
数理統計学 第 0 回 復習 標本分散と ( 標本 ) 不偏分散両方とも 分散 というのが実情 二乗偏差計標本分散 = データ数 (0ページ) ( 標本 ) 不偏分散 = (03 ページ ) 二乗偏差計 データ数 - 分析ではこちらをとることが多い 復習 ここまで 実験結果 ( 万回 ) 平均 50Kg 標準偏差 0Kg 0 人 全体に小さすぎる > mea(jkke) [] 89.4373 標準偏差
PowerPoint プレゼンテーション
 1/X Chapter 9: Linear correlation Cohen, B. H. (2007). In B. H. Cohen (Ed.), Explaining Psychological Statistics (3rd ed.) (pp. 255-285). NJ: Wiley. 概要 2/X 相関係数とは何か 相関係数の数式 検定 注意点 フィッシャーのZ 変換 信頼区間 相関係数の差の検定
1/X Chapter 9: Linear correlation Cohen, B. H. (2007). In B. H. Cohen (Ed.), Explaining Psychological Statistics (3rd ed.) (pp. 255-285). NJ: Wiley. 概要 2/X 相関係数とは何か 相関係数の数式 検定 注意点 フィッシャーのZ 変換 信頼区間 相関係数の差の検定
Microsoft PowerPoint - H24全国大会_発表資料.ppt [互換モード]
![Microsoft PowerPoint - H24全国大会_発表資料.ppt [互換モード] Microsoft PowerPoint - H24全国大会_発表資料.ppt [互換モード]](/thumbs/94/118755799.jpg) 第 47 回地盤工学研究発表会 モアレを利用した変位計測システムの開発 ( 計測原理と画像解析 ) 平成 24 年 7 月 15 日 山形設計 ( 株 ) 技術部長堀内宏信 1. はじめに ひびわれ計測の必要性 高度成長期に建設された社会基盤の多くが老朽化を迎え, また近年多発している地震などの災害により, 何らかの損傷を有する構造物は膨大な数に上ると想定される 老朽化による劣化や外的要因による損傷などが生じた構造物の適切な維持管理による健全性の確保と長寿命化のためには,
第 47 回地盤工学研究発表会 モアレを利用した変位計測システムの開発 ( 計測原理と画像解析 ) 平成 24 年 7 月 15 日 山形設計 ( 株 ) 技術部長堀内宏信 1. はじめに ひびわれ計測の必要性 高度成長期に建設された社会基盤の多くが老朽化を迎え, また近年多発している地震などの災害により, 何らかの損傷を有する構造物は膨大な数に上ると想定される 老朽化による劣化や外的要因による損傷などが生じた構造物の適切な維持管理による健全性の確保と長寿命化のためには,
統計学 - 社会統計の基礎 - 正規分布 標準正規分布累積分布関数の逆関数 t 分布正規分布に従うサンプルの平均の信頼区間 担当 : 岸 康人 資料ページ :
 統計学 - 社会統計の基礎 - 正規分布 標準正規分布累積分布関数の逆関数 t 分布正規分布に従うサンプルの平均の信頼区間 担当 : 岸 康人 資料ページ : https://goo.gl/qw1djw 正規分布 ( 復習 ) 正規分布 (Normal Distribution)N (μ, σ 2 ) 別名 : ガウス分布 (Gaussian Distribution) 密度関数 Excel:= NORM.DIST
統計学 - 社会統計の基礎 - 正規分布 標準正規分布累積分布関数の逆関数 t 分布正規分布に従うサンプルの平均の信頼区間 担当 : 岸 康人 資料ページ : https://goo.gl/qw1djw 正規分布 ( 復習 ) 正規分布 (Normal Distribution)N (μ, σ 2 ) 別名 : ガウス分布 (Gaussian Distribution) 密度関数 Excel:= NORM.DIST
Microsoft PowerPoint - H17-5時限(パターン認識).ppt
 パターン認識早稲田大学講義 平成 7 年度 独 産業技術総合研究所栗田多喜夫 赤穂昭太郎 統計的特徴抽出 パターン認識過程 特徴抽出 認識対象から何らかの特徴量を計測 抽出 する必要がある 認識に有効な情報 特徴 を抽出し 次元を縮小した効率の良い空間を構成する過程 文字認識 : スキャナ等で取り込んだ画像から文字の識別に必要な本質的な特徴のみを抽出 例 文字線の傾き 曲率 面積など 識別 与えられた未知の対象を
パターン認識早稲田大学講義 平成 7 年度 独 産業技術総合研究所栗田多喜夫 赤穂昭太郎 統計的特徴抽出 パターン認識過程 特徴抽出 認識対象から何らかの特徴量を計測 抽出 する必要がある 認識に有効な情報 特徴 を抽出し 次元を縮小した効率の良い空間を構成する過程 文字認識 : スキャナ等で取り込んだ画像から文字の識別に必要な本質的な特徴のみを抽出 例 文字線の傾き 曲率 面積など 識別 与えられた未知の対象を
Microsoft PowerPoint - Inoue-statistics [互換モード]
![Microsoft PowerPoint - Inoue-statistics [互換モード] Microsoft PowerPoint - Inoue-statistics [互換モード]](/thumbs/92/107910528.jpg) 誤差論 神戸大学大学院農学研究科 井上一哉 (Kazuya INOUE) 誤差論 2011 年度前期火曜クラス 1 講義内容 誤差と有効数字 (Slide No.2~8 Text p.76~78) 誤差の分布と標準偏差 (Slide No.9~18 Text p.78~80) 最確値とその誤差 (Slide No.19~25 Text p.80~81) 誤差の伝播 (Slide No.26~32 Text
誤差論 神戸大学大学院農学研究科 井上一哉 (Kazuya INOUE) 誤差論 2011 年度前期火曜クラス 1 講義内容 誤差と有効数字 (Slide No.2~8 Text p.76~78) 誤差の分布と標準偏差 (Slide No.9~18 Text p.78~80) 最確値とその誤差 (Slide No.19~25 Text p.80~81) 誤差の伝播 (Slide No.26~32 Text
はじめに Excel における計算式の入力方法の基礎 Excel では計算式を入力することで様々な計算を行うことができる 例えば はセルに =SQRT((4^2)/3+3*5-2) と入力することで算出される ( 答え ) どのような数式が使えるかは 数式
 統計演習 統計 とはバラツキのあるデータから数値上の性質や規則性あるいは不規則性を 客観的に分析 評価する手法のことである 統計的手法には様々なものが含まれるが 今回はそのなかから 記述統計と統計学的推測について簡単にふれる 記述統計 : 収集した標本の平均や分散 標準偏差などを計算し データの示す傾向や性質を要約して把握する手法のこと 求められた値を記述統計量 ( または要約統計量 ) と言う 平均値
統計演習 統計 とはバラツキのあるデータから数値上の性質や規則性あるいは不規則性を 客観的に分析 評価する手法のことである 統計的手法には様々なものが含まれるが 今回はそのなかから 記述統計と統計学的推測について簡単にふれる 記述統計 : 収集した標本の平均や分散 標準偏差などを計算し データの示す傾向や性質を要約して把握する手法のこと 求められた値を記述統計量 ( または要約統計量 ) と言う 平均値
Microsoft PowerPoint - SPECTPETの原理2012.ppt [互換モード]
![Microsoft PowerPoint - SPECTPETの原理2012.ppt [互換モード] Microsoft PowerPoint - SPECTPETの原理2012.ppt [互換モード]](/thumbs/94/121508518.jpg) 22 年国家試験解答 1,5 フーリエ変換は線形変換 FFT はデータ数に 2 の累乗数を要求するが DFT は任意のデータ数に対応 123I-IMP Brain SPECT FBP with Ramp filter 123I-IMP Brain SPECT FBP with Shepp&Logan filter 99mTc-MIBI Myocardial SPECT における ストリークアーチファクト
22 年国家試験解答 1,5 フーリエ変換は線形変換 FFT はデータ数に 2 の累乗数を要求するが DFT は任意のデータ数に対応 123I-IMP Brain SPECT FBP with Ramp filter 123I-IMP Brain SPECT FBP with Shepp&Logan filter 99mTc-MIBI Myocardial SPECT における ストリークアーチファクト
ファイナンスのための数学基礎 第1回 オリエンテーション、ベクトル
 春学期統計学 I 記述統計と推測統計 担当 : 長倉大輔 ( ながくらだいすけ ) 1 本日の予定 本日はまず記述統計と推測統計の違い 推測統計学の基本的な構造について説明します 2 記述統計と推測統計 統計学とは? 与えられたデータの背後にある 特性 法則 を 検証 発見 分析 するための手法の開発 その応用などに関わる学問の事です 3 記述統計と推測統計 データの種類 データの種類はおおまかに
春学期統計学 I 記述統計と推測統計 担当 : 長倉大輔 ( ながくらだいすけ ) 1 本日の予定 本日はまず記述統計と推測統計の違い 推測統計学の基本的な構造について説明します 2 記述統計と推測統計 統計学とは? 与えられたデータの背後にある 特性 法則 を 検証 発見 分析 するための手法の開発 その応用などに関わる学問の事です 3 記述統計と推測統計 データの種類 データの種類はおおまかに
Python-statistics5 Python で統計学を学ぶ (5) この内容は山田 杉澤 村井 (2008) R によるやさしい統計学 (
 http://localhost:8888/notebooks/... Python で統計学を学ぶ (5) この内容は山田 杉澤 村井 (2008) R によるやさしい統計学 (http://shop.ohmsha.co.jp/shop /shopdetail.html?brandcode=000000001781&search=978-4-274-06710-5&sort=) を参考にしています
http://localhost:8888/notebooks/... Python で統計学を学ぶ (5) この内容は山田 杉澤 村井 (2008) R によるやさしい統計学 (http://shop.ohmsha.co.jp/shop /shopdetail.html?brandcode=000000001781&search=978-4-274-06710-5&sort=) を参考にしています
workshop.pdf
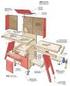 01 02 03 04 05 06 07 08 09 2 樹木の高さ 樹高 を測る 木の高さは どうやって知ることができるのでしょうか 名人は この木が自分のところへ倒れてきたときも安全だと思った場所まではなれると その位置と樹 木までの距離が だいたい木の高さと同じになるのだそうです でも 私たちはなかなか名人にはなれ ません 図5 ブルーメライスでは木までの距離を 15m 20m 30mと変えて測
01 02 03 04 05 06 07 08 09 2 樹木の高さ 樹高 を測る 木の高さは どうやって知ることができるのでしょうか 名人は この木が自分のところへ倒れてきたときも安全だと思った場所まではなれると その位置と樹 木までの距離が だいたい木の高さと同じになるのだそうです でも 私たちはなかなか名人にはなれ ません 図5 ブルーメライスでは木までの距離を 15m 20m 30mと変えて測
Microsoft PowerPoint - データ解析基礎2.ppt
 データ解析基礎. 度数分布と特性値 keyword データの要約 度数分布表, ヒストグラム 分布の中心を表す基本統計量 平均, 最頻値, 中央値 分布のばらつきを表す統計量 分散, 標準偏差 統計データの構造 - データ解析の目的 具体的な対象 ( 母集団 ) についての調査結果 ( 標本をどう加工 処理し, 有益な情報を引き出すかである. 加工 処理するための調査結果として, データ ( 観測データ
データ解析基礎. 度数分布と特性値 keyword データの要約 度数分布表, ヒストグラム 分布の中心を表す基本統計量 平均, 最頻値, 中央値 分布のばらつきを表す統計量 分散, 標準偏差 統計データの構造 - データ解析の目的 具体的な対象 ( 母集団 ) についての調査結果 ( 標本をどう加工 処理し, 有益な情報を引き出すかである. 加工 処理するための調査結果として, データ ( 観測データ
2017年度 千葉大・理系数学
 017 千葉大学 ( 理系 ) 前期日程問題 1 解答解説のページへ n を 4 以上の整数とする 座標平面上で正 n 角形 A1A A n は点 O を中心とする半径 1 の円に内接している a = OA 1, b = OA, c = OA 3, d = OA4 とし, k = cos とおく そして, 線分 A1A3 と線分 AA4 との交点 P は線分 A1A3 を n :1に内分するとする
017 千葉大学 ( 理系 ) 前期日程問題 1 解答解説のページへ n を 4 以上の整数とする 座標平面上で正 n 角形 A1A A n は点 O を中心とする半径 1 の円に内接している a = OA 1, b = OA, c = OA 3, d = OA4 とし, k = cos とおく そして, 線分 A1A3 と線分 AA4 との交点 P は線分 A1A3 を n :1に内分するとする
Microsoft Word doc
 . 正規線形モデルのベイズ推定翠川 大竹距離減衰式 (PGA(Midorikawa, S., and Ohtake, Y. (, Attenuation relationships of peak ground acceleration and velocity considering attenuation characteristics for shallow and deeper earthquakes,
. 正規線形モデルのベイズ推定翠川 大竹距離減衰式 (PGA(Midorikawa, S., and Ohtake, Y. (, Attenuation relationships of peak ground acceleration and velocity considering attenuation characteristics for shallow and deeper earthquakes,
PowerPoint Presentation
 Non-linea factue mechanics き裂先端付近の塑性変形 塑性域 R 破壊進行領域応カ特異場 Ω R R Hutchinson, Rice and Rosengen 全ひずみ塑性理論に基づいた解析 現段階のひずみは 除荷がないとすると現段階の応力で一義的に決まる 単純引張り時の応カーひずみ関係 ( 構成方程式 ): ( ) ( ) n () y y y ここで α,n 定数, /
Non-linea factue mechanics き裂先端付近の塑性変形 塑性域 R 破壊進行領域応カ特異場 Ω R R Hutchinson, Rice and Rosengen 全ひずみ塑性理論に基づいた解析 現段階のひずみは 除荷がないとすると現段階の応力で一義的に決まる 単純引張り時の応カーひずみ関係 ( 構成方程式 ): ( ) ( ) n () y y y ここで α,n 定数, /
学習指導要領
 (1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 絶対値の意味を理解し適切な処理することができる 例題 1-3 の絶対値をはずせ 展開公式 ( a + b ) ( a - b ) = a 2 - b 2 を利用して根号を含む分数の分母を有理化することができる 例題 5 5 + 2 の分母を有理化せよ 実数の整数部分と小数部分の表し方を理解している
(1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 絶対値の意味を理解し適切な処理することができる 例題 1-3 の絶対値をはずせ 展開公式 ( a + b ) ( a - b ) = a 2 - b 2 を利用して根号を含む分数の分母を有理化することができる 例題 5 5 + 2 の分母を有理化せよ 実数の整数部分と小数部分の表し方を理解している
異文化言語教育評価論 ⅠA 第 4 章分散分析 (3 グループ以上の平均を比較する ) 平成 26 年 5 月 14 日 報告者 :D.M. K.S. 4-1 分散分析とは 検定の多重性 t 検定 2 群の平均値を比較する場合の手法分散分析 3 群以上の平均を比較する場合の手法 t 検定
 異文化言語教育評価論 ⅠA 第 4 章分散分析 (3 グループ以上の平均を比較する ) 平成 26 年 5 月 14 日 報告者 :D.M. K.S. 4-1 分散分析とは 4-1-1 検定の多重性 t 検定 2 群の平均値を比較する場合の手法分散分析 3 群以上の平均を比較する場合の手法 t 検定の反復 (e.g., A, B, C の 3 群の比較を A-B 間 B-C 間 A-C 間の t 検定で行う
異文化言語教育評価論 ⅠA 第 4 章分散分析 (3 グループ以上の平均を比較する ) 平成 26 年 5 月 14 日 報告者 :D.M. K.S. 4-1 分散分析とは 4-1-1 検定の多重性 t 検定 2 群の平均値を比較する場合の手法分散分析 3 群以上の平均を比較する場合の手法 t 検定の反復 (e.g., A, B, C の 3 群の比較を A-B 間 B-C 間 A-C 間の t 検定で行う
