2 Part Part
|
|
|
- ただきよ たつざわ
- 6 years ago
- Views:
Transcription
1 Contents 7 7 Part Part Part Date:. 1
2 2 Part Part Part Part 7. 63
3 Part Part Part
4 Part G CW (fibration) BG,EG Hurewicz Part
5 σ Part
6 Part References 189
7 7 yosihiro math.kyoto u.ac.jp (1) (2) (3) f θ (1) (2) (3)
8 8 Part 1. (1) (a) 100 one million (2) (a) 10 one billion (3) (a) thirteen point zero seven five (4) 0.36 (a) 0 36 zero point three six (5) 1.5 (a) 1 5 one point five (6) 2.7 (a) 2 7 two point seven (7) 0.48 (a) 48 (i) zero point four eight (ii) point four eight (8) (a) fifteen point zero three seven 1. (9) 3 8 (a) 8 3 three eighths (10) (a) (i) two and one fifth (ii) two and a fifth (11) = 7 (a) (i) Three and four makes seven. (ii) Three and four make seven. (iii) Three plus four equals seven. (iv) Three plus four equal seven. (v) Three plus four is seven. (vi) Three plus four are seven. (vii) Three and four is seven. (viii) Three and four are seven. (12) 7 4 = 3 (a) (i) Seven from four is three. (ii) Seven from four leaves three. (iii) Seven minus four is three.
9 (24) 5 2 (a) (iv) Seven minus four equals three. (13) 3 2 = 6 (a) (i) Three times two is six. (ii) Three times two equals six. (iii) Three by two is six. (iv) Three by two equals six. (v) Three multiplied by two is six. (vi) Three multiplied by two equals six. (14) 12 3 = 4 (a) (i) Twelve devided by three equals four. (ii) Twelve devided by three is four. (iii) Twelve into three is four. (iv) Twelve into three goes four. (15) 1 2 (a) 2 1 one half (16) 1 3 (a) 3 1 one third (17) 2 3 (a) 3 2 two thirds (18) 1 4 (a) 4 1 one quarter (19) 2 4 (a) 4 2 two quarters (20) 3 4 (a) 4 3 (i) three quarters (ii) three fourths (21) 1 5 (a) 5 1 one fifth (22) 2 5 (a) 5 2 two fifths (23) 3 2 (a) 2 3
10 10 (25) 2 5 (a) 5 2 minus two over five (26) (a) two and three seventh (27) 843 (a) 843 (28) (i) four forty-three (ii) four hundred forty-three (a) (29) (a) (30) (a) (31) (a) (32) (a) (i) thirty two over four hundred and forty five (ii) thirty two over four hundred forty five
11 11 (1) a = b (a) a equals b (2) a def = b, a := b, a b (a) ( ) a is defined as b (3) a < b (a) (i) a is smaller than b (ii) a is less than b (iii) a less than b (iv) a is strictly smaller than b (v) a is strictly less than b (vi) a strictly less than b 2. (4) a b, a b (a) a is less than or equal to b 1 (5) a > b (a) (i) a is greater than b (ii) a is strictly greater than b (6) a b, a b (a) a is greater than or equal to b 1 (7) a b, a b (a) (i) a is bounded by a constant multiple of b (ii) a bounds a constant multiple of b C > 0 a Cb, a Cb (8) a p b, a p b (a) p p (i) a is p-bounded by a constant multiple of b (ii) a p-bounds a constant multiple of b p C > 0 a Cb, a Cb (9) a p,q b, a p,q b (a) p, q p, q (i) a is p, q-bounded by a constant multiple of b (ii) a p, q-bounds a constant multiple of b p, q C > 0 a Cb, a Cb (10) a < x < b (a) (i) a is smaller than x is smaller than b (ii) a is strictly smaller than x is strictly smaller than b x = a, x = b (11) a < x b
12 12 (a) (i) a is smaller than x is smaller than or equal to b (ii) a is strictly smaller than x is smaller than or equal to b x = b x = a (12) [a, b] (a) (i) closed interval a, b (ii) closed interval from a to b a, b (13) [a, b) (a) (i) right-open interval a, b (ii) right-open interval from a to b a (14) (a, b] (a) (i) left-open interval a, b (ii) left-open interval from a to b b (15) (a, b) (a) (i) open interval a, b (ii) open interval from a to b (16) (0, ) (a) open interval zero infinity (17) x [a, b] (a) (i) x is a member of the closed interval a, b (ii) x is a member of the closed interval from a to b a x b
13 13 Part (1) α, A alpha (2) β, B beta (3) γ, Γ gamma (4) δ,, delta (5) ϵ, ε epsilon (6) ζ, Z zeta (7) η, H eta (8) θ, Θ theta (9) ι, I iota (10) κ, K kappa (11) λ, Λ lambda (12) µ, M mu (13) ν, N nu (14) ξ, Ξ xi (15) o, O o (16) π, Π pi (17) ρ, P rho (18) σ,, sigma (19) τ, T tau (20) υ, Υ upsilon (21) ϕ, φ, Φ phi (22) χ, X chi (23) ψ, Ψ psi (24) ω, Ω omega
14 (1) A, a (2) B, b (3) C, c (4) D, d (5) E, e (6) F, f (7) G, g (8) H, h (9) I, i (10) J, j (11) K, k (12) L, l (13) M, m (14) N, n (15) O, o (16) P, p (17) Q, q (18) R, r (19) S, s (20) T, t (21) U, u (22) V, v (23) W, w (24) X, x (25) Y, y (26) Z, z
15 15 (1) a 0 (a) a zero a 0 (2) a n (a) a n a n (3) a λ (a) a lambda (4) a (a) a prime (5) ã (a) tilde a (6) a (a) (i) a star (ii) a sup star (7) a (a) (i) a star (ii) a sub star (8) a (a) a double star (9) (a) (10) (a) (11) (a) (12) (a) 4.
16 16 (1) A = B (a) A implies B (2) A B (a) A is equivalent to B (3) A = B (a) A follows from B 5.
17 17 Part (1) 30 (a) 30 degree angle (2) ABC (a) angle A B C (3) ABC (a) triangle A B C (4) AB (a) (i) line segment A B (ii) distance A B ( ) ( ) (5) ABCD (a) A B C D (6) AB//CD AB// CD (a) ( ) ( ) (i) AB is parallel to CD (ii) vector AB is parallel to vector CD (7) AB CD (a) AB is orthogonal to CD (8) S T (a) S is congruent to T (9) ABC DEF (a) ABC is congruent to DEF (10) ABC DEF (a) ABC is similar to DEF
18 (1) a (a) vector a (2) AB (a) vector A B 1 (3) A (a) the magnitude of vector A (4) AB (a) (i) the magnitude of A B (ii) the magnitude of vector A B A B AB = BA (5) a// b (a) (i) a is parallel to b (ii) vector a is parallel to vector b (6) a b (a) (i) a is perpendicular to b (ii) vector a is perpendicular to vector b
19 (1) P (a) (a) P a 1 (2) P (a, b) (a) P of a, b 2, ( ) (3) P (a, b, c) (a) P of a, b, c 3, ( ) (4) R, (R 1 ) (a) (i) R one (ii) real numbers 1 (5) R 2 (a) 2 R two 2 (6) R 3 (a) 3 R three 3 (7) C (a) (i) C (ii) complex numbers 1 ( ) (8) R n (a) R n n (9) C n (a) C n n (10) S n (a) n-dimensional sphere n x x x n 2 = 1
20 (1) ax + b (a) a x plus b (2) ax 2 + bx + c (a) 2 ( ) a x squared plus b x plus c (3) ax 3 + bx 2 + cx + d (a) 3 2 ( ) a x cubed plus b x squared plus c x plus d (4) ax 4 + bx 3 + cx 2 + dx + e (a) ( ) (i) a x to the fourth plus b x cubed plus c x squared plus d x plus e (ii) a x to the fourth power plus b x cubed plus c x squared plus d x plus e (iii) a x raised to the fourth power plus b x cubed plus c x squared plus d x plus e (5) ax + by + c (a) a x plus b y plus c (6) ax 2 + 2bxy + cy 2 + 2dx + 2ey + f (a) a x squared plus two b y plus c y squared plus two d x plus two e y plus f x, y 2 (7) ax + by + cz + d (a) a x plus b y plus c z plus d x, y, z 1 (8) ax 2 + 2bxy + cy 2 + 2dxz + 2eyz + fz 2 (a) a x squared plus two b y plus c y squared plus two d x z plus two e y z plus f z squared x, y, z 2
21 (1) (a + b)(c + d) = ac + ad + bc + bd (a) (i) a plus b times c plus d equals a c plus a d plus b c plus b d (ii) a plus b in parentheses times c plus d in parentheses equals a c plus a d plus b c plus b d 2 (2) (x + a)(x + b) = x 2 + (a + b)x + ab (a) 2 x plus a times x plus b equals x squared plus a plus b times x plus a b (3) (x + a) 2 = x 2 + 2ax + a 2 (a) x plus a squared equals x squared plus two a x plus a squared (4) (x a) 2 = x 2 2ax + a 2 (a) x minus a squared equals x squared minus two a x plus a squared (5) (x + a)(x a) = x 2 a 2 (a) 2 2 x plus a times x minus a equals x squared minus a squared (6) (x + a) 3 = x 3 + 3ax 2 + 3a 2 x + a 3 (a) x plus a cubed equals x cubed plus three a x squared plus three a squared x plus a squared (7) (x a) 3 = x 3 3ax 2 + 3a 2 x a 3 (a) x minus a cubed equals x cubed minus three a x squared plus three a squared x minus a squared (8) (x a)(x 2 + ax + a 2 ) = x 3 a 3 (a) x minus a times x squared plus a x plus a squared equals x cubed minus a cubed (9) (x + a)(x 2 ax + a 2 ) = x 3 + a 3 (a) x plus a x squared minus a x plus a squared equals x cubed plus a cubed (10) (x + a) 4 = x 4 + 4ax 3 + 6a 2 x 2 + 4a 3 x + a 4 (a) x plus a to four equals x to four plus four a x cubed plus six a squared x squared plus four a cubed x plus x to the power four (11) (x + a) 5 = x 5 + 5ax a 2 x a 3 x 2 + 5a 4 x + a 5
22 22 (a) x plus a in parenthesis to fifth equals x to fifth plus five a x to fourth plus ten a squared x cubed plus ten a cubed x squared plus five a to the power four x plus a to the power five (12) (x + y + z)(x 2 + y 2 + z 2 xy yz zx) = x 3 + y 3 + z 3 3xyz (a) x plus y plus z in parenthesis times x squared plus y squared plus x squared minus x y minus y z minus z x in parenthesis equals x cubed plus y cubed plus z cubed minus three x y z
23 (1) x 2 + (a + b)x + ab = (x + a)(x + b) (a) 2 x squared plus a plus b x plus a b equals x plus a x plus b (2) x 2 + 2ax + a 2 = (x + a) 2 (a) x squared plus two a x plus a squared equals x plus a squared (3) x 2 2ax + a 2 = (x a) 2 (a) x squared minus two a x plus a squared equals x minus a squared (4) x 2 a 2 = (x + a)(x a) (a) 2 2 x squared minus a squared equals x plus a x minus a (5) x 3 + 3ax 2 + 3a 2 x + a 3 = (x + a) 3 (a) x cubed plus three a x squared plus three a squared x plus a cubed equals x plus a cubed (6) x 3 3ax 2 + 3a 2 x a 3 = (x a) 3 (a) x cubed minus three a x squared plus three a squared x minus a cubed (7) x 3 + a 3 = (x + a)(x 2 ax + a 2 ) (a) x cubed plus a cubed equals x plus a x squared minus a x plus a squared (8) x 3 a 3 = (x a)(x 2 + ax + a 2 ) (a) x cubed minus a cubed equals x minus a times x squared plus a x plus a squared (9) x 4 + x = (x 2 + x + 1)(x 2 x + 1) (a) x to fourth plus x squared plus one equals x squared plus x plus one times x squared minus x plus one (10) x 3 + y 3 + z 3 3xyz = (x + y + z)(x 2 + y 2 + z 2 xy yz zx) (a) x cubed plus y cubed plus z cubed minus three x y z equals x plus y plus z in parenthesis times x squared plus y squared plus x squared minus x y minus y z minus z x in parenthesis (11) z 5 = (z 1)(z cos 72 i sin 72 )(z cos 144 i sin 144 )(z cos 216 i sin 216 )(z cos 288 i sin 288 )
24 24 (a) z to the five minus 1 equals z minus 1 times z minus cosine 72 degree angle minus i sine 72 degree angle times z minus cosine 144 degree angle minus i sine 144 degree angle times z minus cosine 216 degree angle minus i sine 216 degree angle times z minus cosine 288 degree angle minus i sine 288 degree angle
25 (1) a 0 x n + a 1 x n a n (a) n 1 n 1 n (i) a n x to the power n plus a n minus one x to the power n minus one plus dot dot dot plus a zero (ii) a sub n x to the power n plus a sub n minus one x to the power n minus one plus dot dot dot plus a sub zero sub dot dot dot (2) a n x n + a n 1 x n a 0 (a) n n 1 (3) (4) (i) a n x to the power n plus a n minus one x to the power n minus one plus dot dot dot plus a zero (ii) a sup n x to the power n plus a sup n minus one x to the power n minus one plus dot dot dot plus a sup zero sup dot dot dot n a k x k k=0 (a) k (i) summation from zero to n a k x to n (ii) summation k runs from zero to n a k x to n (iii) summation k moves from zero to n a k x to n n a k x k a 0 + a 1 x + a 2 x a n x n k=0 n a n k x k k=0 (a) k (i) summation from zero to n a n minus k x to n (ii) summation k runs from zero to n a n minus k x to n (iii) summation k moves from zero to n a n minus k x to n n a n k x k a n + a n 1 x + a n 2 x a 0 x n (5) k n a k k=0 (a) k n summation for k less than n a k k (6) λ Λ a λ (7) (a) ( ) summation of a lambda over (lower case) lambda belonging to capital lambda n j=1 a j (a) 1 product j runs from one to n a j
26 26 n a j a 1 a 2 a n j=1
27 27 Part (1) a n (a) a n (2) {a n } n=1 (a) 1 (i) a n with n equals one to infinity (ii) sequence a n with n equals one to infinity sequence (3) (a n ) n=1 (a) 1 (i) a n with n equals one to infinity (ii) sequence a n with n equals one to infinity sequence (4) a n + b n (a) a n plus b n (a + b) n, a + b n (5) a n+1 (a) 1 a n plus one (6) a n + 1 (a) 1 a n plus one a n+1 a n + 1 (7) (8) (9) (10) n k=1 a k (a) 1 (i) summation from k equal one to n a k (ii) summation of a k over one through n n=1 a n (a) 1 (i) summation from n equal one to infinity a n (ii) summation of a n over one through infinity 40 a n n=2 (a) 2 40 (i) summation from n equal two to forty a n (ii) summation of a n over two through forty 1 n 2 n=1 (a) (i) summation from n one to infinity one over n squared (ii) summation of one over n squared where n moves from one to infinity
28 28 summation of one over n squared over one through over 1 over n 2 = π2 6 n=1 (11) a n b n (n ) (a) (i) (ii) a sub n {a n } n=1, {b n } n=1 a a n n b n (n ) lim = 1 n b n
29 (1) n k,j=1 a jk = n n k=1 j=1 a jk (a) j k 1 n a j k k 1 n j 1 n a j k (i) summation j and k run from one to n a j k equals summation k runs from one to n of summation j runs from one to n of a sub j k in parenthesis (ii) the sum from j and k equal one to n of a sub j k equals the sum from k equals one to n of the sum from j equals one to n of a sub j k 2
30 30 Part (1) a 2 (a) 2 a squared (2) 2a 1 (a) 2 1 (i) double a minus one (ii) twice a minus one (3) 3a 4 (a) 3 4 triple a minus 4 (4) a 3 (a) 3 a cubed (5) a 4 (a) 4 (i) a to the fourth power (ii) a raised to the fourth power (6) (a + b) n (a) (i) a plus b to the n-th power (ii) a plus b in parenthesis to the n-th power (7) ab n (a) a b to the power n (8) a d (a) a devided by d (9) a (a) (i) the absolute value of a (ii) the modulus of a
31 (1) 2 (a) 2 (i) square root two (ii) square root of two of (2) 3 2 (a) 3 2 cube root of 2 of (3) (a) (i) two to two thirds (ii) two to the two thirds (iii) two to two over three (4) a b (a) a to the power b (5) (a + b) n/2 (a) 2 2 (i) a + b to n over 2 (ii) a + b in parenthesis to n over 2 n halves (6) n a (a) n-th root of a n a n a (7) log a R (a) (i) log a R (ii) log a of R (iii) log to the base a R (iv) log to the base a of R b = log a R a b = R
32 (1) Re(z) (a) the real part of z (2) Im(z) (a) the imaginary part of z (3) z (a) (i) the absolute value of z (ii) the modulus of z (4) log z (a) (i) log z (ii) natural logarithm of z (5) ln z (a) l n z (6) e z (a) e to z
33 (1) π (a) pi (2) sin x (a) sine x (3) cos x (a) cosine x (4) tan x (a) tangent x (5) cot x = 1 tan x (a) 1 cotangent x equals one over tangent x cot (6) sec x = 1 cos x (a) 1 secant x equals one over cosine x sec (d) (7) cosec x = 1 sin x (a) 1 cosecant x equals one over sine x (8) sin 2 x + cos 2 x = 1 (a) sine theta squared plus cosine theta squared equals one cosine squared theta argument cosine cubed cos 5 θ cosine theta to the ( fifth power θ π ) (9) sin 2 θ = cos θ (a) 2 ( sine of pi over two minus theta equals cosine theta π ) (10) cos 2 θ = sin θ (a) 2 cosine of pi over two minus theta equals sine theta ( π ) (11) tan 2 θ = 1 tan θ (a) 2 1 (i) tangent pi over two minus theta equals one over tangent theta (ii) tangent of pi over two minus theta equals one over tangent theta
34 (1) cos(α + β) = cos α cos β sin α sin β (a) cosine alpha plus beta equals cosine alpha times cosine beta minus sine alpha times sine beta (2) sin(α + β) = sin α cos β + cos α sin β (a) sine alpha plus beta equals sine alpha times cosine beta plus cosine alpha times sine beta tan α + tan β (3) tan(α + β) = 1 tan α tan β (a) 1 (i) tangent alpha plus beta equals tangent alpha plus tangent beta over one minus tangent alpha times tangent beta (ii) tangent alpha plus beta equals tangent alpha plus tangent beta devided by one minus tangent alpha times tangent beta (4) cos(α β) = cos α cos β + sin α sin β (a) cosine alpha minus beta equals cosine alpha times cosine beta plus sine alpha times sine beta (5) sin(α β) = sin α cos β cos α sin β (a) sine alpha minus beta equals sine alpha times cos beta minus cosine alpha times sine beta tan α tan β (6) tan(α β) = 1 + tan α tan β (a) 1 (i) tangent alpha minus beta equals tangent alpha minus tangent beta devided by one plus tangent alpha times tangent beta (ii) tangent alpha minus beta equals tangent alpha minus tangent beta over one plus tangent alpha times tangent beta (7) sin α + sin β = 2 sin α + β cos α β 2 2 (a) (i) sine alpha plus sine beta equals two sine alpha plus beta over two times cosine alpha minus beta over two (ii) sine alpha plus sine beta equals two times sine alpha plus beta over two times cosine alpha minus beta over two cos α + β 2 (8) sin α sin β = 2 sin α β 2 (a) 2 2 2
35 35 (i) sine alpha minus sine beta equals two sine alpha minus beta over two times cosine alpha plus beta over two (ii) sine alpha minus sine beta equals two times sine alpha minus beta over two times cosine alpha plus beta over two (9) cos α + cos β = 2 cos α + β cos α β 2 2 (a) (i) cosine alpha plus cosine beta equals two cosine alpha plus beta over two times cosine alpha minus beta over two (ii) cosine alpha plus cosine beta equals two times cosine alpha plus beta over two times cosine alpha minus beta over two (10) cos α cos β = 2 sin α + β sin α β 2 2 (a) (i) cosine alpha minus cosine beta equals minus two sine alpha plus beta over two times sine alpha minus beta over two (ii) cosine alpha minus cosine beta equals minus two times sine alpha plus beta over two times sine alpha minus beta over two (11) sin 2θ = 2 sin θ cos θ (a) 2 2 sine two theeta equals 2 times sine theta times cosine theta (12) cos 2θ = cos 2 θ sin 2 θ (a) cosine two theta equals cosine theta squared minus sine theta squared (13) sin 3θ = 3 sin θ 4 sin 3 θ (a) sine three theta equals three times sine theta minus four times sin theta cubed (14) cos 3θ = 4 cos 3 θ 3 cos θ (a) cosine three theta equals four times cosine theta cubed minus three cosine theta
36 (1) sin z (a) sine z sin z = eiz e iz 2i (2) cos z (a) cosine z cos z = eiz + e iz 2 (3) tan z (a) tangent z tan z = sin z cos z (4) arc tan z (a) arctangent of z (5) arc sin z (a) arcsine of z (6) arc cos z (a) arccosine of z (7) sinh z (a) (i) sintsh z (ii) hyperbolic sine of z sinh z ez e z 2 (8) cosh z (a) cosh z, hyperbolic cosine of z cosh z ez + e z 2 (9) tanh z (a) hyperbolic tangent of z tanh z ez e z e z + e z (10) Arc sinh z (a) Arc hyperbolic sine z Arc sinh z log(z + z 2 + 1) (11) Arc cosh z (a) Arc hyperbolic cosine z Arc cosh z log(z + z 2 1) (12) Arc tanh z (a) Arc hyperbolic tangent z
37 ( ) z + 1 Arc cosh z log z 1 (13) tan 1 z (a) tangent inverse z (14) sin 1 z (a) sine inverse z (15) cos 1 z (a) cosine inverse z 37
38 sin x (1) lim x 0 x = 1 (a) (i) 0 1 (ii) 0 1 (i) limit of sine x over x as x goes to zero equals one (ii) limit as x goes to zero of sine x over x equals one sin x lim = sin x 0 x tan x (2) lim = 1 x 0 x (a) (i) 0 1 (ii) 0 1 (i) limit of tangent x over x as x goes to zero equals one (ii) limit as x goes to zero of tangent x over x equals one tan x lim = tan x 0 x 1 cos x (3) lim x 0 x 2 = 1 2 (a) (i) (ii) (i) limit of one minus cosine x over x squared as x goes to zero equals one half (ii) limit as x goes to zero of one minus cosine x over x squared equals one half n k (4) lim n a n = 0 (a) (i) 0 (ii) 0 (i) limit of n to k over a to n as n goes to infinity equals zero (ii) limit as n goes to infinity of n to k over a to n equals zero a > 1 k R n k (5) lim n n! = 0 (a) (i) 0 (ii) 0 (i) limit of n to k over n factorial as n goes to infinity equals zero (ii) limit as n goes to infinity of n factorial over a to n equals zero k R (6) lim n (a) log n n k = 0 (i) 0
39 39 (ii) 0 (i) limit of log n over n to k as n goes to infinity equals zero (ii) limit as n goes to infinity of log n over n to k equals zero k > 0 (7) (a) (8) (a)
40 (1) supp(f) (a) support of f f 0 f ( ) (2) χ E (a) (i) indicator function of the set E (ii) indicator E (iii) indicator of E x E χ E (x) = 1 x / E χ E (x) = 0 (3) 1 E (a) 1 indicator function of the set E x E 1 E (x) = 1 x / E 1 E (x) = 0 (4) I E (a) indicator function of the set E x E I E (x) = 1 x / E I E (x) = 0 (5) f E (a) f E f restricted to the set E f E
41 (1) x a (a) (i) x tends to a (ii) x goes to a (iii) x approaches a (2) x, y (a) (i) Delta x (ii) Delta y (3) y (a) y prime y dash (4) dy dx (a) d y d x (5) f (x) (a) f prime of x (6) f (x) (a) (i) f double prime of x (ii) second derivative of f at x at evaluated at (7) y (x) (a) (i) y double prime of x (ii) second derivative of y at x at evaluated at (8) y (4) (a) 4 fourth derivative of y y 4 y four (9) y (4) (x) (a) 4 fourth derivative of y at x y 4 y four (of,at) x (10) y (n) (a) n-th derivative of y y n (11) d dx f(x) (a) d d x (of) f at x (12) df(x) dx
42 42 (a) (i) d f d x at x (ii) d f of x d x (13) d2 f(x) dx 2 (a) 2 2 second derivative of f at x (14) dn f(x) dx n (a) n n n-th derivative of f at x (15) df dx (x) (a) d dx (of) f at x (16) d2 f dx 2 (x) (a) 2 2 second derivative of f at x (17) dn f dx n (x) (a) n ( n-th derivative of f at x dx (18) dt, dy ) dt (a) d x d t and d y d t (19) v (a) (i) length of v (ii) magnitude of v (iii) modulus of v (iv) absolute value of v ( ) v (20) α (a) (i) length of α (ii) magnitude of α (iii) modulus of α (iv) absolute value of α ( ) α (21) v x, v y (a) partial derivative of v in x, partial derivative of v in y (22) f g (a) f composed with g g : C A f : A B g, f C (23) D 2 f (a) Hessian matrix of f
43 43 f Ω C 2 - D 2 f = { i j f} n i,j=1 (24) Jf (a) Jacobian of f f Ω C 2 - Jf = det{ i j f} n i,j=1
44 (1) I (a) (i) (ii) the length of I I = [a, b] I = b a (2) f(x) dx (3) (a) integral of f b a f(x) dx (a) ( ) (i) integral of f from a to b (ii) integral from a to b of f (4) [F (x)] b a (a) difference of F evaluated at b and a [F (x)] b a = F F (a) (5) Ω (a) integral over Omega Ω (6) f(x) dx (a) ( ) ( ) (i) integral of f from minus infinity to infinity (ii) integral from minus infinity to infinity of f (7) f(x) dx E f(x) dx = lim R,S (a) integral of f over E (8) B (a) B the mean over B f(x) dx = 1 f(x) dx B B B (9) f(x) dx B R S f(x) dx (a) the mean of f over B f(x) dx = 1 f(x) dx B B B (10) = {x j } N j=0 (a) {x j } N j=0 [a, b] a = x 0 < x 1 < < x N = b
45 45 (11) (a) [a, b] = {x j } N j=0 = max x j x j 1 1 j N (12) S f (a) Capital S sub delta f f (13) s f (a) s sub delta f f (14) (15) b a f(x) dx (a) a b the upper integral from a to b of f of x d x lim S f = 0 b a f(x) dx b a f(x) dx (a) a b the lower integral from a to b of f of x d x lim s f = f(x) dx 0 a x2 (16) + 1 dx = 1 ( x x log(x + ) x 2 + 1) + C (a) integral of square root of x squared plus 1 d x equals 1 over 2 x square root of x squared plus 1 plus log x plus square root of x squared plus 1 plus C x2 (17) 1 dx = 1 ( x x log x + ) x C (a) integral of square root of x squared minus 1 d x equals 1 over 2 x square root of x squared minus 1 minus log x plus square root of x squared minus 1 plus C dx (18) x2 + 1 = log(x + x 2 + 1) + C (19) (a) integral of d x over square root of x squared plus 1 equals log x plus square root of x squared plus 1 plus C dx x2 1 = log x + x C (a) integral of d x over square root of x squared minus 1 equals log the absolute value of x plus square root of x squared minus 1 plus C b
46 46 (20) (21) dx 1 x 2 = sin 1 x + C (a) integral of d x over square root of 1 minus x squared equals sine inverse x plus C 1 x2 dx = 1 ( x ) 1 x sin 1 x + C (a) integral square root of 1 minus x squared d x equals 1 over 2 times x square root of 1 minus x squared plus sine inverse x plus C
47 (1) f(x, y) x (a) (i) (ii) partial derivative of f in x (evaluated) at x, y y x x (2) f (x, y) y (a) (3) (i) (ii) partial derivative of f in y (evaluated) at x, y x y y 2 f(x, y) x2 (a) (i) 2 2 (ii) 2 2 second (order) partial derivative of f in x (evaluated) at x, y y x 2 x 2 (4) 2 f (x, y) x2 (a) (5) (6) (i) 2 2 (ii) 2 2 second (order) partial derivative of f in x (evaluated) at x, y y x 2 x 2 2 f(x, y) x y (a) (i) 2 (ii) 2 (i) mixed derivative of f in x and y at x, y (ii) mixed second order derivative of f in x and y at x, y (iii) mixed partial derivative of f in x and y at x, y (iv) mixed second order partial derivative of f in x and y at x, y (v) mixed derivative in x and y of f at x, y (vi) mixed second order derivative in x and y of f at x, y (vii) mixed partial derivative in x and y of f at x, y (viii) mixed second order partial derivative in x and y of f at x, y x y y x 2 f(x, y) y x (a) (i) 2 (ii) 2 (i) mixed derivative of f in x and y at x, y (ii) mixed second order derivative of f in x and y at x, y (iii) mixed partial derivative of f in x and y at x, y (iv) mixed second order partial derivative of f in x and y at x, y (v) mixed derivative in x and y of f at x, y (vi) mixed second order derivative in x and y of f at x, y
48 48 (7) (vii) mixed partial derivative in x and y of f at x, y (viii) mixed second order partial derivative in x and y of f at x, y y x x y 2 f (x, y) x y (a) (i) 2 (ii) 2 (i) mixed derivative of f in x and y at x, y (ii) mixed second order derivative of f in x and y at x, y (iii) mixed partial derivative of f in x and y at x, y (iv) mixed second order partial derivative of f in x and y at x, y (v) mixed derivative in x and y of f at x, y (vi) mixed second order derivative in x and y of f at x, y (vii) mixed partial derivative in x and y of f at x, y (viii) mixed second order partial derivative in x and y of f at x, y
49 (1) [a,b] [c,d] f(x, y) dx dy (a) (i) integration over a, b, cross c, d of f d x d y (ii) integration integral over a, b, cross c, d of f d x d y (iii) integral of f over a, b cross c, d (iv) integral of f over a, b times c, d (v) intergation of f over a, b cross c, d (vi) intergation of f over a, b times c, d 2 (2) f(x) dx E (a) E (i) integral of f over E (ii) integration of f over E (iii) integral over E of f x d x (iv) integral over E of f of x d x (v) integration over E of f x d x (vi) integration over E of f of x d x, dx (3) Q (a) Q integral average over Q Q Q (4) f(x) dx (5) Q (a) Q integral average over Q Q Q f(x, y) dx dy E (a) E (i) integral of f over E (ii) integral of f in x, y over E (iii) integration of f over E (iv) integration of f in x, y over E (v) double integral of f over E (vi) double integral of f in x, y over E (vii) double integration of f over E (viii) double integration of f in x, y over E E (6) f(x, y) dx [a,b] [c,d] (a) (i) integral of f over a, b cross c, d (ii) integral of f in x, y over a, b cross c, d (iii) integration of f over a, b cross c, d
50 50 (iv) integration of f in x, y over a, b cross c, d (v) double integral of f over a, b cross c, d (vi) double integral of f in x, y over a, b cross c, d (vii) double integration of f over a, b cross c, d (viii) double integration of f in x, y over a, b cross c, d dx( ) dx dy( )
51 51 Part 6. (1) x A (a) (i) x is an element in A (ii) x in A (iii) x belonging to A 13. (2) {x} (a) (1 ) the set with element x x {x} x {x} (3) {a, b, c} (a) a, b, c the set with elements a, b, c a, b, c 3 (4) {x R : 1 < x 3}, {x R : 1 < x 3} (a) 1 3 (i) the set of x in R such that minus one less than x less than or equal to 3 (ii) the set of of x in R between one and three : ; R : (5) A c (a) (i) The complement of the subset A (ii) The complement of A A (6) A (a) (i) The complement of the subset A (ii) The complement of A A (7) A B (a) (i) subset A of B, (ii) A, a subset of B B A (8) A B (a) A contains B B A (9) A B (a) (i) intersection of A and B (ii) A intersected with B (iii) A cap B A, B intersection A intersection B (10) A B (a) (i) A union B
52 52 (ii) union of A and B (iii) A cup B A, B (11) A \ B (a) A minus B, A B (12) A B, A B (a) the symmetric difference of A and B A, B (13) A B (a) (i) A times B (ii) A cross B A B A a B b (a, b) (14) (15) j=1 A j (a) j = 1 ( )( ) union of A j over j equal one to infinity A 1, A 2,, A j, j=1 A j (a) j = 1 ( )( ) intersection of A j over j equal one to infinity A 1, A 2,, A j, (16) λ Λ A λ (a) ( ) (i) union of A lambda over lambda in lambda (ii) union of A lambda for lambda in lambda (iii) union of A lambda over lambda belonging to lambda (iv) union of A lambda over lambda in capital lambda (v) union of A lambda for lambda in capital lambda (vi) union of A lambda over lambda belonging to capital lambda A λ capital (17) λ Λ A λ (a) ( ) (i) intersection of A lambda over lambda in lambda (ii) intersection of A lambda for lambda in lambda (iii) intersection of A lambda over lambda belonging to lambda (iv) intersection of A lambda over lambda in capital lambda (v) intersection of A lambda for lambda in capital lambda (vi) intersection of A lambda over lambda belonging to capital lambda A λ (18) 2 A (a) 2
53 53 (i) power set of A (ii) two to A A A, A 2 A A a 2 A 2 a (19) χ E (a) (i) indicator function of the set E (ii) indicator E (iii) indicator of E x E χ E (x) = 1 x / E χ E (x) = 0
54 (1) max A (a) (i) max A (ii) maximum of A 14. max A A A a b A b a max A (2) min A (a) (i) min A (ii) minimum of A min A A A a b A b a min A (3) max{1, 2, 3, 4} (a) (i) max of one, two, three, four (ii) max of one, two, three, four (iii) maximum of one, two, three, four (iv) maximum of one, two, three, four (v) max over one, two, three, and four (vi) max over one, two, three, and four (vii) maximum over one, two, three, and four (viii) maximum over one, two, three, and four max{1, 2, 3, 4} = 4 (4) min{1, 2, 3, 4} (a) (i) min of one, two, three, four (ii) min of one, two, three, four (iii) min over one, two, three, and four (iv) min over one, two, three, and four (v) minimum of one, two, three, four (vi) minimum of one, two, three, four (vii) minimum over one, two, three, and four (viii) minimum over one, two, three, and four min{1, 2, 3, 4} = 1 (5) max x A f(x) (a) max (of) f (of) x, maximum of f (of) x for/over x in A, maximum of f (of) x over A A f : A R max f(a) = max {f(a) : a A} a A (6) min f(x) x A (a) (i) minimum of f x for x in A (ii) minimum of f x over x in A (iii) minimum of f of x for x in A
55 55 (iv) minimum of f of x over x in A (v) minimum of f x over A (vi) minimum of f of x over A (vii) min f x (viii) min f of x (ix) min of f x (x) min of f of x A f : A R (7) sup A (a) (i) sup A (ii) sup of A (iii) supremum of A min f(a) = min {f(a) : a A} a A A M M of (i) M a A a M (ii) M M M < M a > M a A M sup A supremum A of (8) inf A (a) (9) sup n N (i) inf A (ii) inf of A (iii) infimum of A A m m of (i) m a A a m (ii) m m m > m a < m a A m inf A infimum A of a n (a) (i) sup a n (ii) sup of a n (iii) supremum of a n over n in N (iv) supremum of a n for n in N (v) supremum of a n over natural numbers N {a n } n=1 sup a n = sup {a n : n = 1, 2, } n N (10) sup n=1,2, a n (a) 1 2 (i) sup a n (ii) sup of a n (iii) supremum of a n for n equal to one, two, dot dot dot.
56 56 (iv) supremum of a n as n moves from one, two, and so on. {a n } n=1 sup a n = sup {a n : n = 1, 2, } n=1,2, (11) inf a n n N (a) (i) inf a n (ii) inf of a n (iii) infimum of a n for n in N (iv) infimum of a n over n in N (v) infimum of a n over natural numbers N {a n } n=1 inf a n = inf {a n : n = 1, 2, } n N (12) inf n=1,2, an (a) 1 2 (i) inf a n (ii) inf of a n (iii) infimum of a n for n equal to one, two, dot dot dot. (iv) infimum of a n as n moves from one, two, and so on. {a n } n=1 inf n=1,2, an = inf {a n : n = 1, 2, } (13) sup f(a) a A (a) (i) sup f a (ii) sup of f a (iii) sup f of a (iv) sup of f of a (v) supremum of f of a over a in A (vi) supremum of f of a for a in A (vii) supremum of f of a over a belonging to A (viii) supremum of f of a for a belonging to A (ix) supremum of f a over a in A (x) supremum of f a for a in A (xi) supremum of f a over a belonging to A (xii) supremum of f a for a belonging to A A f : A R sup f(a) = sup {f(a) : a A} a A (14) inf f(a) a A (a) (i) inf f a (ii) inf of f a (iii) inf f of a
57 57 (iv) inf of f of a (v) infimum of f of a over a in A (vi) infimum of f of a for a in A (vii) infimum of f of a over a belonging to A (viii) infimum of f of a for a belonging to A (ix) infimum of f a over a in A (x) infimum of f a for a in A (xi) infimum of f a over a belonging to A (xii) infimum of f a for a belonging to A A f : A R inf f(a) = inf {f(a) : a A} a A
58 (1) n (a) (i) n goes to infinity (ii) n tends to infinity (2) n + (a) (i) n goes to infinity (ii) n tends to infinity (iii) n goes to plus infinity (iv) n tends to plus infinity + (3) n (a) (i) n goes to minus infinity (4) lim sup n (a) (ii) n tends to minus infinity a n (i) (ii) lim sup of a n (as n goes to infinity), lim sup (as n goes to infinity) of a n, limit supremum of a n {a n } n=1 (5) lim inf a n n (a) lim sup a n := inf n k N ( ) sup a n = inf n k { sup a n : k N n k (i) (ii) lim inf of a n (as n goes to infinity), lim inf (as n goes to infinity) of a n, limit infimum of a n {a n } n=1 lim inf n a n := sup k N ( inf n k a n ) } { } = sup inf a n : k N n k (6) lim a n n (a) (i) (ii) limit of a n as n goes to infinity, limit as n goes to infinity of a n lim sup a n = lim inf a n R {± } lim a n = lim sup n n n n (7) x a (a) (i) x tends to a (ii) x tending to a (8) lim f(x) x a (a) (i) (ii) a n = lim inf n a n
59 59 limit of f (of) x as x goes to a, limit as x goes to a of f (of) x (9) (i) lim f(x) (ii) lim f(x) x a x a 0 (a) (i), (ii) (i) right limit of f x as x goes to a (ii) right limit of f x as x goes to a from the right (iii) right limit of f of x as x goes to a (iv) right limit of f of x as x goes to a from the right (v) limit from the right of f x as x goes to a (vi) limit from the right of f of x as x goes to a (vii) limit of f x as x goes to a from the right (viii) limit of f of x as x goes to a from the right (ix) one-sided limit of f x as x goes to a from the right (x) one-sided limit of f of x as x goes to a from the right (xi) limit of f x as x goes to a from below (xii) limit of f of x as x goes to a from below (xiii) one-sided limit of f x as x goes to a from below (xiv) one-sided limit of f of x as x goes to a from below (xv) limit of f x as x decreases to a (xvi) limit of f of x as x decreases to a x > a (10) lim f(x), lim f(x) x a x a+ (a) (i) (ii) (i) left limit of f x as x goes to a (ii) left limit of f x as x goes to a from the left (iii) left limit of f of x as x goes to a (iv) left limit of f of x as x goes to a from the left (v) limit from the left of f x as x goes to a (vi) limit from the left of f of x as x goes to a (vii) limit of f x as x goes to a from the left (viii) limit of f of x as x goes to a from the left (ix) one-sided limit of f x as x goes to a from the left (x) one-sided limit of f of x as x goes to a from the left (xi) limit of f x as x goes to a from above (xii) limit of f of x as x goes to a from above (xiii) one-sided limit of f x as x goes to a from above (xiv) one-sided limit of f of x as x goes to a from above (xv) limit of f x as x increases to a (xvi) limit of f of x as x increases to a lim f(x) lim f(x) x a x a+0
60 60 (1) f : A B (a) (i) f mapping from A to B (ii) f mapping from A into B 15. f A B A B (2) f(x) (a) (i) f x (ii) f of x f x f(x) (3) A B (a) (i) A to B (ii) collection of functions from A to B B A A B B b A a A B a b (4) f g (a) f composed with g g : C A f : A B g, f C (5) f g(x) (a) (i) f composed with g or evaluated at x (ii) f composed with g of x (iii) f g x (iv) f g of x f g(x) f(g(x)) (6) f 1 (a) (i) f inverse (ii) inverse of f x y f(x) f(y) (7) f 1 (x) (a) (i) f inverse at x (ii) f inverse of x 2 (i) f 1 f 1 x (ii) f 1 f 1 (x) f x (8) f 1 (A) (a) f inverse of A f 1 f 1 (A) f A at A (9) λ Λ A λ (a) ( ) ( )
61 61 product of a lambda over lambda in capital lambda λ A λ (10) z v(z, ω) (a) z to v of z omega z v(z, ω) (11) u 1 (a) 1 u 1
62 (1) O X (a) O sub X (2) E F, E F (a) E is homeomorphic to F (3) Int(E), E, E int (a) interior of E E X x X x A x Int(E) x U U E Int(E) (4) Ext(E), E ext (a) exterior of E E X x X x A x Ext(E) x U U E c Ext(E) (5) E (a) closure of E E X E = X \ E ext (6) E (a) boundary of E E X E E E = {x X : U O X x A U E, U E c } (7) V U, V U (a) (i) V is compactly contained in U (ii) V is deeply contained in U U, V X V U V U V U V (8) V f W (a) A V, A W f : A A f(a) = a (a, a ) V W V f W
63 63 Part ( ) a b (1) A = c d (a) abcd (i) A equals a, b, c, d (ii) A equals matrix a, b, c, d ( 2 2 ) (2) A = (a) 1, 4, 5, 2, 6, 8 A equals matrix one, four, five, two, six, eight (3) A = (a) 1, 4, 5, 2, 3, 9, 2, 6, 8 A equals matrix one, four, five, two, three, nine, two, six, eight (4) {a ij } n i,j=1 (a) 1 The n by n matrix a sub i j from i j equal to n. n n n n 1 2 n 1 n 2 3 n n + 1 (5) A = n n + 1 2n 2 2n 1 (a) A equals one, two, dot, dot, dot, n minus one, n, two, three, dot, dot, dot, n, n plus one, dot, dot, dot, n, n + 1, dot, dot, dot two n minus two, two n minus one 1, 2,, n 1, n, 2, 3,, n, n + 1, n, n + 1,, 2n 2, 2n 1 n n (6) det(a) (a) determinant of A (7) det 2 3 9, (a) 1, 4, 5, 2, 3, 9, 2, 6, 8, 1, 4, 5, 2, 3, 9, 2, 6, 8 (i) determinant of one, four, five, two, three, nine, two, six, eight (ii) determinant of matrix one, four, five, two, three, nine, two, six, eight det =
64 64 t (8) t 2 3 9, (a) 1, 4, 5, 2, 3, 9, 2, 6, 8 (i) transpose of one, four, five, two, three, nine, two, six, eight (ii) transpose of matrix one, four, five, two, three, nine, two, six, eight t = i 5 + 3i (9) 2 3i 3 9i i (a) (i) adjoint of one, four plus two i, five plus three i, two minus three i, three minus nine i, nine, two, six, eight plus three i (ii) adjoint of matrix one, four plus two i, five plus three i, two minus three i, three minus nine i, nine, two, six, eight plus three i i 5 + 3i 2 3i 3 9i 9 = 4 2i 2 + 3i 3 + 9i i 5 3i 9 8 3i ( ) A B (10) A 0 = C D (a) 0 (i) A zero equals A, B, C, D (ii) A zero equals matrix A, B, C, D (11) A 1 (a) The inverse of A A ( ) 1 a b (12) c d (a) ( The inverse ) of the two by two matrix, a, b, c, d a b c d
65 (1) k x (a) k dot x, dot product of k and x k x (2) x + y (a) x plus y (3) 0 (a) ( ) zero 0 0 (4) f : V W (a) (i) f from V to W (ii) f from V to W (iii) f mapping from V into W (iv) f mapping from V into W f V f W (5) f V (a) f restricted to V V V V f f V (6) f(k x) = k f(x) (a) (i) f of k dot x equals k dot f of x (ii) f of k dot x equals k dot f x (iii) f of k x equals k f of x (iv) f of k x equals k f x (7) f(x + y) = f(x) + f(y) (a) (i) f of x plus y equals f of x plus f of y (ii) f of x plus y equals f x plus f y
66 (1) V W (a) (i) V plus W (ii) direct sum of V and W V W V W 0 (2) V + W (a) V plus W V W + V W 0 (3) V W (a) (i) V times W (ii) direct product of V and W V v W w (v, w) V W V W (4) V/W (a) V quotiented by W V W V V/W (5) Imf, Im(f), imf, im(f) (a) image of f f (6) Ranf, Ran(f), ranf, ran(f) (a) range of f f (7) Kerf, Ker(f), kerf, ker(f) (a) kernel of f f 0 (8) Nullf, Null(f), nullf, null(f) (a) null space of f f 0 (9) A B (a) the direct sum of A and B A B = {0} A + B (10) dimv (a) dimension of V V (11) dim R V (a) dimension of V over R
67 67 V R- (12) V (a) dual of V V R/C (13) V 1 V 2 (a) 1 2 tensor product of V one and V two V 1 V 2 ( ) (14) n i=1v i (a) 1 tensor product of V i for i from one to n V 1,, V n (15) n V (a) n-th tensor power of V V i = V, i = 1, 2,, n n i=1v i = n V (16) x y (a) tensor product of x and y V W x y (17) V V (a) wedge product of V and V x y y x V V V V (18) x y (a) wedge product of x and y x y V V V V (19) n V (a) n-th wedge power of V n V n V
68 (1), (a) (i) inner product (ii) dot product (iii) scalar product ( ) x, αy = α x, y Dot (2) x, y (a) inner product of x and y (3) V (a) (i) V perp (ii) orthogonal complement of V V perp perpendicular
69 (1) V = {v 1, v 2,, v k } (a) 1 2 k V equals the set of the elements v sub one, v sub two, and so on, v sub k. ( ) (2) Span(V) = {a 1 v 1 + a 2 v a k v k : t (a 1, a 2,, a k ) } [V] = {a 1 v 1 + a 2 v a k v k : t (a 1, a 2,, a k ) } (a) k k t (a 1, a 2,, a k ) The linear span of V equals the set of a sub one v sub one plus a sub one v sub one plus, and so on, plus a sub k v sub k for scalers a sub one, a sub two, and so on, a sub k V = {v 1, v 2,, v k } (3) p = p 1 p 2 p 3 (a) p equals the three by one matrix p sub one, p sub two, p sub tree. 3 (4) p = (5) p 1 p 2. p n (a) 1 2 n p equals the three by one matrix p sub one, p sub two, and so on, p sub n. n α α 01 α 02 α 0n 0 α 11 α 12 α 1n 0 α 21 α 22 α 2n α n 1 1 α n 1 2 α n 1 n 0 α n1 α n2 α nn (a) n n n n 0 n1 n2 nn The n plus one by n plus one matrix, alpha, alpha sub zero one, alpha sub zero two, and so on, alpha sub zero n, zero, alpha sub one one, alpha sub one two, and so on, alpha sub one n, zero, alpha sub two one, alpha sub two two, and so on, alpha sub two n, and so on, and so on, and so on, and so on, and so on, alpha sub n minus one one, alpha sub n minus one two, and so on, alpha sub n minus one n, alpha sub n one, alpha sub n two, and so on, alpha sub n n.
70 70 a 00 a 01 a 02 a 0n 1 a 0n 0 a 11 a 12 a 1n 1 a 1n 0 0 a 22 a 2n 1 a 2n (6) A = a n 1 n 1 a n 1 n a nn (a) n 1 0n n 1 1n n 1 2n n nn A equals the n plus one by n plus one matrix, a sub zero zero, a sub zero one, a sub zero two, and so on, a sub zero n minus one, a sub zero n, zero, a sub one one, a sub one two, and so on, a sub one n minus one, a sub one n, zero, zero, a sub two two, and so on, a sub two n minus one, a sub two n, and so on, and so on, and so on, and so on, and so on, and so on, zero, zero, zero, and so on, a sub n minus one n minus one, a sub n minus one n, zero, zero, zero, and so on, zero, a sub n n. (7) V n (A, α) (a) V sub n of A alpha n V n (A, α) V n (A, α) = {x C n : (A αi) n x = 0} (8) E(A, α) (a) E of A alpha V 1 (A, α) (9) V (A, α) (a) V of A alpha V (A, α) = V n (A, α) = { x C n : k (A αi) k x = 0 } n=1 (10) C n = V (A, α 1 ) V (A, α 2 ) V (A, α r ) (a) 1 2 r bold capital C equals the direct sum of V of A alpha sub one, V of A alpha sub two, and so on, V of A alpha sub n. ( )n n A α 1,, α r C n = V (A, α 1 ) V (A, α 2 ) V (A, α r ) (11) φ A (t) (a) ( ) phi sub A of t A P (A) = 0 0 P (t) A φ A (t) (12) Φ A (t) (a) ( ) Capital phi sub A of t Φ A (t) (13) P 1 AP (a) The inverse of P A P
71 71 A P 1 AP β β (14) 0 0 β β n (a) The n times n matrix, beta sub one, zero, zero, and so on, zero, zero, beta sub two, zero, and so on, zero, zero, zero, beta sub three, and so on, zero, and so on, and so on, and so on, and so on, and so on, zero, zero, zero, and so on, beta sub n. (15) A 1 A 2 A N (a) 1 2 N A sub one, A sub two, and so on, A sub N.?? A 1 A 2 (16)... AN (a) 1 2 N The direct sum of A sub one, A sub two, and so on, A sub N equals A sub one, A sub two, and so on, A sub N.?? A 1, A 2,, A N A 1 A 2 A N A 1 A 2 A 1 A 2 A N =... AN 0 (17) J(α, n) = αe + {δ i,j 1 } i,j=1,2,,n (a) 1 1, 2 n J of alpha n equals alpha E plus the (18) P 1 AP = J(α 1, n 1 ) J(α 2, n 2 ) J(α k, n k ) (a) The inverse of P A P equals the direct sum of J of alpha sub one n sub one, J of alpha sub two n sub two, and so on, and J of alpha sub k n sub k.
72 (1) x 2 + y 2 = a 2 (a) x squared plus y squared equals a squared (0, 0) a (2) (x x 0 ) 2 + (y y 0 ) 2 = a 2 (a) x minus x sub zero squared plus y minus y sub zero squared equals a squared. (x 0, y 0 ) a (3) xy = a (a) x y equals a a > 0 a < 0 (4) x + y = b (a) The square root of x plus the square root of y equals b. (5) x2 a 2 + y2 b 2 = 1 (a) x squared over a squared plus y squared over b squared equals one (6) x2 a 2 y2 b 2 = 1 (a) x squared over a squared minus y squared over b squared equals one (±a, 0) (0, ±b) (7) y = ax 2 (a) 2 y equals a x squared. (8) x 3 + y 3 3axy = 0 (a) x cubed plus y cubed minus three a x y equals 0 (9) ax + by + cz = d (a) a x plus b y plus c z equals d. (10) x2 a 2 + y2 b 2 + z2 c 2 = 1 (a) x squared over a squared plus y squared over b squared plus z squared over c squared equals one (11) x2 a 2 + y2 b 2 z2 c 2 = 1
73 73 (a) x squared over a squared plus y squared over b squared minus z squared over c squared equals one 1 b 2 z2 c 2 = 1 (12) x2 a 2 y2 (a) x squared over a squared minus y squared over b squared minus z squared over c squared equals one 2 (13) z = x2 a 2 + y2 b 2 (a) z equals x squared over a squared plus y squared over b squared. (14) z = x2 a 2 y2 b 2 (a) z equals x squared over a squared minus y squared over b squared. (15) M G (a)?? m e G = m, (m g 1 ) g 2 = m (g 1 g 2 ) M G M ( )
74 74 Part (1) 3! (a) 3 the factorial of 3 3! = (2) n! (a) n the factorial of n n! = n (n 1) (n 2) 2 1 (3) n!! (a) n 2 the double factorial of n n = 0, 1, 2, 1 (n = 0 ) (20.1) n!! = n (n 2) 3 1 (n ) n (n 2) 4 2 (n ) (4) n C r (a) (i) n choose r (ii) n C r (iii) combination of choosing k objects out of n (iv) combination of k objects out of n (5) n P r (a) (i) n P r (ii) permutation of choosing r objects out of n (iii) permutation of r objects out of n n choose r
75 (1) (a) (i) empty set (ii) null set (2) n(a) (a) n A A (3) A (a) (i) the number of the set A (ii) the number of A n(a) (4) a A (a) (i) a is in A (ii) a in A (iii) a belongs to A (iv) a belonging to A a A (5) a / A (a) a is not in A, a not in A, a does not belong to A, a not belonging to A a A (6) A B (a) A intersection B, intersection of A and B, A cap B A B (7) A B C (a) (i) A intersection B intersection C (ii) intersection of A, B, and C (iii) A cap B cap C A B C (8) A B (a) (i) A union B (ii) union of A and B (iii) A cup B A B ( ) (9) A B C (a) (i) A union B union C (ii) union of A, B, and C (iii) A cup B cup C A B C ( ) (10) A B (a) (i) (ii)
76 76 (iii) (i) A contained in B (ii) A implies B A B (11) A B (a) A includes B B A (12) A (a) (i) A bar (ii) complement of A A (13) A c (a) complement of A A A c (14) A B (a) A times B A B (15) P (A) (a) (i) probability of A (ii) probability A (iii) probability of the event A (iv) probability of an event A A (16) P (A B) (a) probability of A union B A B
77 (1) E[X], E(X) (a) (i) expectation of X (ii) E X X (2) V [X], V (X) (a) (i) variance of x (ii) V x X (3) σ[x], σ(x) (a) (i) standard deviation of x (ii) sigma x X (4) σ XY (a) (i) covariance of X and Y (ii) sigma X Y σ XY = E[(X E[X])(Y E[Y ])] (5) r xy (a) (i) correlation (coefficient) of x and y (ii) r x y (6) B(n, p) (a) (i) binomial distribution with paramters n and p (ii) B n p p n 2 (7) N(m, σ 2 ) (a) 2 (i) normal distribution with mean m and variance sigma squared (ii) N m sigma suqared m σ (8) χ 2 - (a) chi square distribution X 1, X 2,, X n X X X n 2 n χ 2 - (9) Po(λ) (a) the poisson distribution with parameter lambda Z + X P (X = n) = λn n! e λ λ
78 78 Part (1) y = f(x, y) (a) (i) y prime equals f x y (ii) y prime equals f of x y 1 (2) y = f(x)g(y) (a) (i) y prime equals f x times g y (ii) y prime equals f of x times g of y (3) y = y (a) y prime equals y y = Ce x C (4) y = a(x)y (a) (i) y prime equals a x times y (ii) y prime equals a of x times y ( y = C exp ) a(x) dx (5) f (x) = f(x) (a) (i) f prime of x equal f of x (ii) f prime of x equal f x y = y (6) y + ay + by = 0 (a) (i) y double prime plus a y prime plus b y equals zero (ii) second derivative of y plus a derivative of y plus b y equals zero (iii) the second derivative of y plus a the derivative of y plus b y equals zero a, b 2 (7) y + ay = 0 (a) (i) y double prime plus a y equals zero (ii) second derivative of y plus a derivative of y equals zero (iii) the second derivative of y plus a the derivative of y equals zero b = 0 y = C 1 + C 2 e ax (8) y + ay + by + cy = 0 (a) (i) third derivative of y plus a y double prime plus b y prime plus c y equals zero
79 79 (9) (ii) the third derivative of y plus a y double prime plus b y prime plus c y equals zero (iii) third derivative of y plus a second derivative of y plus b derivative of y plus b y equals zero (iv) the third derivative of y plus a the second derivative of y plus b the derivative of y plus b y equals zero a, b, c 3 ( y ) ( ( ) y triple prime d x a b x = dt y c d) y (a) d d t (time derivative of (vector) x y equals (matrix) a b c d times (vector) x y ( x y ) = exp ( t ( )) ( ) a b x(0) c d y(0)
80 (1) Lf (a) (i) Laplace trnasform of f (ii) The Laplace transform of f (iii) The Laplace transform for f (iv) L f (2) L 1 F (a) (i) inverse Laplace transform of f (ii) The Laplace transform of f (iii) The Laplace transform for f (iv) L inverse f (3) Lf(t) (a) (i) Laplace trnasform of f at t (ii) The Laplace transform of f of t (iii) The Laplace transform for f of t (iv) L f of t Lf(t) = 0 f(p)e tp dp (4) L 1 F (t) (a) inverse Laplace transform of f (at t)/ The Laplace transform of F of t/ The Laplace transform for F of t/ L inverse F of t
基礎数学I
 I & II ii ii........... 22................. 25 12............... 28.................. 28.................... 31............. 32.................. 34 3 1 9.................... 1....................... 1............
I & II ii ii........... 22................. 25 12............... 28.................. 28.................... 31............. 32.................. 34 3 1 9.................... 1....................... 1............
I
 I 6 4 10 1 1 1.1............... 1 1................ 1 1.3.................... 1.4............... 1.4.1.............. 1.4................. 1.4.3........... 3 1.4.4.. 3 1.5.......... 3 1.5.1..............
I 6 4 10 1 1 1.1............... 1 1................ 1 1.3.................... 1.4............... 1.4.1.............. 1.4................. 1.4.3........... 3 1.4.4.. 3 1.5.......... 3 1.5.1..............
数学の基礎訓練I
 I 9 6 13 1 1 1.1............... 1 1................ 1 1.3.................... 1.4............... 1.4.1.............. 1.4................. 3 1.4.3........... 3 1.4.4.. 3 1.5.......... 3 1.5.1..............
I 9 6 13 1 1 1.1............... 1 1................ 1 1.3.................... 1.4............... 1.4.1.............. 1.4................. 3 1.4.3........... 3 1.4.4.. 3 1.5.......... 3 1.5.1..............
IA 2013 : :10722 : 2 : :2 :761 :1 (23-27) : : ( / ) (1 /, ) / e.g. (Taylar ) e x = 1 + x + x xn n! +... sin x = x x3 6 + x5 x2n+1 + (
 IA 2013 : :10722 : 2 : :2 :761 :1 23-27) : : 1 1.1 / ) 1 /, ) / e.g. Taylar ) e x = 1 + x + x2 2 +... + xn n! +... sin x = x x3 6 + x5 x2n+1 + 1)n 5! 2n + 1)! 2 2.1 = 1 e.g. 0 = 0.00..., π = 3.14..., 1
IA 2013 : :10722 : 2 : :2 :761 :1 23-27) : : 1 1.1 / ) 1 /, ) / e.g. Taylar ) e x = 1 + x + x2 2 +... + xn n! +... sin x = x x3 6 + x5 x2n+1 + 1)n 5! 2n + 1)! 2 2.1 = 1 e.g. 0 = 0.00..., π = 3.14..., 1
確率論と統計学の資料
 5 June 015 ii........................ 1 1 1.1...................... 1 1........................... 3 1.3... 4 6.1........................... 6................... 7 ii ii.3.................. 8.4..........................
5 June 015 ii........................ 1 1 1.1...................... 1 1........................... 3 1.3... 4 6.1........................... 6................... 7 ii ii.3.................. 8.4..........................
I, II 1, A = A 4 : 6 = max{ A, } A A 10 10%
 1 2006.4.17. A 3-312 tel: 092-726-4774, e-mail: hara@math.kyushu-u.ac.jp, http://www.math.kyushu-u.ac.jp/ hara/lectures/lectures-j.html Office hours: B A I ɛ-δ ɛ-δ 1. 2. A 1. 1. 2. 3. 4. 5. 2. ɛ-δ 1. ɛ-n
1 2006.4.17. A 3-312 tel: 092-726-4774, e-mail: hara@math.kyushu-u.ac.jp, http://www.math.kyushu-u.ac.jp/ hara/lectures/lectures-j.html Office hours: B A I ɛ-δ ɛ-δ 1. 2. A 1. 1. 2. 3. 4. 5. 2. ɛ-δ 1. ɛ-n
1 I
 1 I 3 1 1.1 R x, y R x + y R x y R x, y, z, a, b R (1.1) (x + y) + z = x + (y + z) (1.2) x + y = y + x (1.3) 0 R : 0 + x = x x R (1.4) x R, 1 ( x) R : x + ( x) = 0 (1.5) (x y) z = x (y z) (1.6) x y =
1 I 3 1 1.1 R x, y R x + y R x y R x, y, z, a, b R (1.1) (x + y) + z = x + (y + z) (1.2) x + y = y + x (1.3) 0 R : 0 + x = x x R (1.4) x R, 1 ( x) R : x + ( x) = 0 (1.5) (x y) z = x (y z) (1.6) x y =
 211 kotaro@math.titech.ac.jp 1 R *1 n n R n *2 R n = {(x 1,..., x n ) x 1,..., x n R}. R R 2 R 3 R n R n R n D D R n *3 ) (x 1,..., x n ) f(x 1,..., x n ) f D *4 n 2 n = 1 ( ) 1 f D R n f : D R 1.1. (x,
211 kotaro@math.titech.ac.jp 1 R *1 n n R n *2 R n = {(x 1,..., x n ) x 1,..., x n R}. R R 2 R 3 R n R n R n D D R n *3 ) (x 1,..., x n ) f(x 1,..., x n ) f D *4 n 2 n = 1 ( ) 1 f D R n f : D R 1.1. (x,
( ) ± = 2018
 30 ( 3 ) ( ) 2018 ( ) ± = 2018 (PDF ), PDF PDF. PDF, ( ), ( ),,,,., PDF,,. , 7., 14 (SSH).,,,.,,,.,., 1.. 2.,,. 3.,,. 4...,, 14 16, 17 21, 22 26, 27( ), 28 32 SSH,,,, ( 7 9 ), ( 14 16 SSH ), ( 17 21, 22
30 ( 3 ) ( ) 2018 ( ) ± = 2018 (PDF ), PDF PDF. PDF, ( ), ( ),,,,., PDF,,. , 7., 14 (SSH).,,,.,,,.,., 1.. 2.,,. 3.,,. 4...,, 14 16, 17 21, 22 26, 27( ), 28 32 SSH,,,, ( 7 9 ), ( 14 16 SSH ), ( 17 21, 22
Basic Math. 1 0 [ N Z Q Q c R C] 1, 2, 3,... natural numbers, N Def.(Definition) N (1) 1 N, (2) n N = n +1 N, (3) N (1), (2), n N n N (element). n/ N.
![Basic Math. 1 0 [ N Z Q Q c R C] 1, 2, 3,... natural numbers, N Def.(Definition) N (1) 1 N, (2) n N = n +1 N, (3) N (1), (2), n N n N (element). n/ N. Basic Math. 1 0 [ N Z Q Q c R C] 1, 2, 3,... natural numbers, N Def.(Definition) N (1) 1 N, (2) n N = n +1 N, (3) N (1), (2), n N n N (element). n/ N.](/thumbs/93/113887245.jpg) Basic Mathematics 16 4 16 3-4 (10:40-12:10) 0 1 1 2 2 2 3 (mapping) 5 4 ε-δ (ε-δ Logic) 6 5 (Potency) 9 6 (Equivalence Relation and Order) 13 7 Zorn (Axiom of Choice, Zorn s Lemma) 14 8 (Set and Topology)
Basic Mathematics 16 4 16 3-4 (10:40-12:10) 0 1 1 2 2 2 3 (mapping) 5 4 ε-δ (ε-δ Logic) 6 5 (Potency) 9 6 (Equivalence Relation and Order) 13 7 Zorn (Axiom of Choice, Zorn s Lemma) 14 8 (Set and Topology)
医系の統計入門第 2 版 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. このサンプルページの内容は, 第 2 版 1 刷発行時のものです.
 医系の統計入門第 2 版 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/009192 このサンプルページの内容は, 第 2 版 1 刷発行時のものです. i 2 t 1. 2. 3 2 3. 6 4. 7 5. n 2 ν 6. 2 7. 2003 ii 2 2013 10 iii 1987
医系の統計入門第 2 版 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/009192 このサンプルページの内容は, 第 2 版 1 刷発行時のものです. i 2 t 1. 2. 3 2 3. 6 4. 7 5. n 2 ν 6. 2 7. 2003 ii 2 2013 10 iii 1987
I No. sin cos sine, cosine : trigonometric function π : π =.4 : n =, ±, ±, sin + nπ = sin cos + nπ = cos sin = sin : cos = cos :. sin. sin. sin + π si
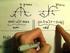 I 8 No. : No. : No. : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No. : I No. sin cos sine, cosine : trigonometric function π : π =.4 : n =, ±, ±, sin + nπ = sin cos + nπ = cos sin = sin : cos = cos :. sin.
I 8 No. : No. : No. : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No. : I No. sin cos sine, cosine : trigonometric function π : π =.4 : n =, ±, ±, sin + nπ = sin cos + nπ = cos sin = sin : cos = cos :. sin.
Note.tex 2008/09/19( )
 1 20 9 19 2 1 5 1.1........................ 5 1.2............................. 8 2 9 2.1............................. 9 2.2.............................. 10 3 13 3.1.............................. 13 3.2..................................
1 20 9 19 2 1 5 1.1........................ 5 1.2............................. 8 2 9 2.1............................. 9 2.2.............................. 10 3 13 3.1.............................. 13 3.2..................................
微分積分 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. このサンプルページの内容は, 初版 1 刷発行時のものです.
 微分積分 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. ttp://www.morikita.co.jp/books/mid/00571 このサンプルページの内容は, 初版 1 刷発行時のものです. i ii 014 10 iii [note] 1 3 iv 4 5 3 6 4 x 0 sin x x 1 5 6 z = f(x, y) 1 y = f(x)
微分積分 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. ttp://www.morikita.co.jp/books/mid/00571 このサンプルページの内容は, 初版 1 刷発行時のものです. i ii 014 10 iii [note] 1 3 iv 4 5 3 6 4 x 0 sin x x 1 5 6 z = f(x, y) 1 y = f(x)
x () g(x) = f(t) dt f(x), F (x) 3x () g(x) g (x) f(x), F (x) (3) h(x) = x 3x tf(t) dt.9 = {(x, y) ; x, y, x + y } f(x, y) = xy( x y). h (x) f(x), F (x
 [ ] IC. f(x) = e x () f(x) f (x) () lim f(x) lim f(x) x + x (3) lim f(x) lim f(x) x + x (4) y = f(x) ( ) ( s46). < a < () a () lim a log xdx a log xdx ( ) n (3) lim log k log n n n k=.3 z = log(x + y ),
[ ] IC. f(x) = e x () f(x) f (x) () lim f(x) lim f(x) x + x (3) lim f(x) lim f(x) x + x (4) y = f(x) ( ) ( s46). < a < () a () lim a log xdx a log xdx ( ) n (3) lim log k log n n n k=.3 z = log(x + y ),
I A A441 : April 15, 2013 Version : 1.1 I Kawahira, Tomoki TA (Shigehiro, Yoshida )
 I013 00-1 : April 15, 013 Version : 1.1 I Kawahira, Tomoki TA (Shigehiro, Yoshida) http://www.math.nagoya-u.ac.jp/~kawahira/courses/13s-tenbou.html pdf * 4 15 4 5 13 e πi = 1 5 0 5 7 3 4 6 3 6 10 6 17
I013 00-1 : April 15, 013 Version : 1.1 I Kawahira, Tomoki TA (Shigehiro, Yoshida) http://www.math.nagoya-u.ac.jp/~kawahira/courses/13s-tenbou.html pdf * 4 15 4 5 13 e πi = 1 5 0 5 7 3 4 6 3 6 10 6 17
sin cos No. sine, cosine : trigonometric function π : π = 3.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin : odd cos = cos : even.
 08 No. : No. : No.3 : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No.0 : No. : sin cos No. sine, cosine : trigonometric function π : π = 3.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin
08 No. : No. : No.3 : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No.0 : No. : sin cos No. sine, cosine : trigonometric function π : π = 3.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin
基礎から学ぶトラヒック理論 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. このサンプルページの内容は, 初版 1 刷発行時のものです.
 基礎から学ぶトラヒック理論 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/085221 このサンプルページの内容は, 初版 1 刷発行時のものです. i +α 3 1 2 4 5 1 2 ii 3 4 5 6 7 8 9 9.3 2014 6 iii 1 1 2 5 2.1 5 2.2 7
基礎から学ぶトラヒック理論 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/085221 このサンプルページの内容は, 初版 1 刷発行時のものです. i +α 3 1 2 4 5 1 2 ii 3 4 5 6 7 8 9 9.3 2014 6 iii 1 1 2 5 2.1 5 2.2 7
I No. sin cos sine, cosine : trigonometric function π : π =.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin : odd cos = cos : even.
 I 0 No. : No. : No. : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No.0 : I No. sin cos sine, cosine : trigonometric function π : π =.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin : odd
I 0 No. : No. : No. : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No.0 : I No. sin cos sine, cosine : trigonometric function π : π =.4 : n = 0, ±, ±, sin + nπ = sin cos + nπ = cos : parity sin = sin : odd
¿ô³Ø³Ø½øÏÀ¥Î¡¼¥È
 2011 i N Z Q R C A def B, A B. ii..,.,.. (, ), ( ),.?????????,. iii 04-13 04-20 04-27 05-04 [ ] 05-11 05-18 05-25 06-01 06-08 06-15 06-22 06-29 07-06 07-13 07-20 07-27 08-03 10-05 10-12 10-19 [ ] 10-26
2011 i N Z Q R C A def B, A B. ii..,.,.. (, ), ( ),.?????????,. iii 04-13 04-20 04-27 05-04 [ ] 05-11 05-18 05-25 06-01 06-08 06-15 06-22 06-29 07-06 07-13 07-20 07-27 08-03 10-05 10-12 10-19 [ ] 10-26
() x + y + y + x dy dx = 0 () dy + xy = x dx y + x y ( 5) ( s55906) 0.7. (). 5 (). ( 6) ( s6590) 0.8 m n. 0.9 n n A. ( 6) ( s6590) f A (λ) = det(a λi)
 0. A A = 4 IC () det A () A () x + y + z = x y z X Y Z = A x y z ( 5) ( s5590) 0. a + b + c b c () a a + b + c c a b a + b + c 0 a b c () a 0 c b b c 0 a c b a 0 0. A A = 7 5 4 5 0 ( 5) ( s5590) () A ()
0. A A = 4 IC () det A () A () x + y + z = x y z X Y Z = A x y z ( 5) ( s5590) 0. a + b + c b c () a a + b + c c a b a + b + c 0 a b c () a 0 c b b c 0 a c b a 0 0. A A = 7 5 4 5 0 ( 5) ( s5590) () A ()
Part () () Γ Part ,
 Contents a 6 6 6 6 6 6 6 7 7. 8.. 8.. 8.3. 8 Part. 9. 9.. 9.. 3. 3.. 3.. 3 4. 5 4.. 5 4.. 9 4.3. 3 Part. 6 5. () 6 5.. () 7 5.. 9 5.3. Γ 3 6. 3 6.. 3 6.. 3 6.3. 33 Part 3. 34 7. 34 7.. 34 7.. 34 8. 35
Contents a 6 6 6 6 6 6 6 7 7. 8.. 8.. 8.3. 8 Part. 9. 9.. 9.. 3. 3.. 3.. 3 4. 5 4.. 5 4.. 9 4.3. 3 Part. 6 5. () 6 5.. () 7 5.. 9 5.3. Γ 3 6. 3 6.. 3 6.. 3 6.3. 33 Part 3. 34 7. 34 7.. 34 7.. 34 8. 35
: , 2.0, 3.0, 2.0, (%) ( 2.
 2017 1 2 1.1...................................... 2 1.2......................................... 4 1.3........................................... 10 1.4................................. 14 1.5..........................................
2017 1 2 1.1...................................... 2 1.2......................................... 4 1.3........................................... 10 1.4................................. 14 1.5..........................................
ベクトル B Vector Vector B ベクトルエー ベクトルエービー Scalar スカラー エー Magnitude of vector 長 さベクトルエー B Magnitude of vector B 長 さベクトルエービー B B dot B ; Dot product of vec
 機 械 工 学 で 使 う 数 式 公 式 の 読 み 方 (2013.11.05) S. Miwa English (US) 分 数 小 数 数 の 読 み 方 (Decimal, Fraction) Japanese 2 3 Two-thirds Two over three 3 分 の2 1 One and a sixth 1と6 分 の1 1 6 One and one over sixth
機 械 工 学 で 使 う 数 式 公 式 の 読 み 方 (2013.11.05) S. Miwa English (US) 分 数 小 数 数 の 読 み 方 (Decimal, Fraction) Japanese 2 3 Two-thirds Two over three 3 分 の2 1 One and a sixth 1と6 分 の1 1 6 One and one over sixth
 A 2008 10 (2010 4 ) 1 1 1.1................................. 1 1.2..................................... 1 1.3............................ 3 1.3.1............................. 3 1.3.2..................................
A 2008 10 (2010 4 ) 1 1 1.1................................. 1 1.2..................................... 1 1.3............................ 3 1.3.1............................. 3 1.3.2..................................
L A TEX ver L A TEX LATEX 1.1 L A TEX L A TEX tex 1.1 1) latex mkdir latex 2) latex sample1 sample2 mkdir latex/sample1 mkdir latex/sampl
 L A TEX ver.2004.11.18 1 L A TEX LATEX 1.1 L A TEX L A TEX tex 1.1 1) latex mkdir latex 2) latex sample1 sample2 mkdir latex/sample1 mkdir latex/sample2 3) /staff/kaede work/www/math/takase sample1.tex
L A TEX ver.2004.11.18 1 L A TEX LATEX 1.1 L A TEX L A TEX tex 1.1 1) latex mkdir latex 2) latex sample1 sample2 mkdir latex/sample1 mkdir latex/sample2 3) /staff/kaede work/www/math/takase sample1.tex
/02/18
 3 09/0/8 i III,,,, III,?,,,,,,,,,,,,,,,,,,,,?,?,,,,,,,,,,,,,,!!!,? 3,,,, ii,,,!,,,, OK! :!,,,, :!,,,,,, 3:!,, 4:!,,,, 5:!,,! 7:!,,,,, 8:!,! 9:!,,,,,,,,, ( ),, :, ( ), ( ), 6:!,,, :... : 3 ( )... iii,,
3 09/0/8 i III,,,, III,?,,,,,,,,,,,,,,,,,,,,?,?,,,,,,,,,,,,,,!!!,? 3,,,, ii,,,!,,,, OK! :!,,,, :!,,,,,, 3:!,, 4:!,,,, 5:!,,! 7:!,,,,, 8:!,! 9:!,,,,,,,,, ( ),, :, ( ), ( ), 6:!,,, :... : 3 ( )... iii,,
II A A441 : October 02, 2014 Version : Kawahira, Tomoki TA (Kondo, Hirotaka )
 II 214-1 : October 2, 214 Version : 1.1 Kawahira, Tomoki TA (Kondo, Hirotaka ) http://www.math.nagoya-u.ac.jp/~kawahira/courses/14w-biseki.html pdf 1 2 1 9 1 16 1 23 1 3 11 6 11 13 11 2 11 27 12 4 12 11
II 214-1 : October 2, 214 Version : 1.1 Kawahira, Tomoki TA (Kondo, Hirotaka ) http://www.math.nagoya-u.ac.jp/~kawahira/courses/14w-biseki.html pdf 1 2 1 9 1 16 1 23 1 3 11 6 11 13 11 2 11 27 12 4 12 11
b3e2003.dvi
 15 II 5 5.1 (1) p, q p = (x + 2y, xy, 1), q = (x 2 + 3y 2, xyz, ) (i) p rotq (ii) p gradq D (2) a, b rot(a b) div [11, p.75] (3) (i) f f grad f = 1 2 grad( f 2) (ii) f f gradf 1 2 grad ( f 2) rotf 5.2
15 II 5 5.1 (1) p, q p = (x + 2y, xy, 1), q = (x 2 + 3y 2, xyz, ) (i) p rotq (ii) p gradq D (2) a, b rot(a b) div [11, p.75] (3) (i) f f grad f = 1 2 grad( f 2) (ii) f f gradf 1 2 grad ( f 2) rotf 5.2
III 1 (X, d) d U d X (X, d). 1. (X, d).. (i) d(x, y) d(z, y) d(x, z) (ii) d(x, y) d(z, w) d(x, z) + d(y, w) 2. (X, d). F X.. (1), X F, (2) F 1, F 2 F
 III 1 (X, d) d U d X (X, d). 1. (X, d).. (i) d(x, y) d(z, y) d(x, z) (ii) d(x, y) d(z, w) d(x, z) + d(y, w) 2. (X, d). F X.. (1), X F, (2) F 1, F 2 F F 1 F 2 F, (3) F λ F λ F λ F. 3., A λ λ A λ. B λ λ
III 1 (X, d) d U d X (X, d). 1. (X, d).. (i) d(x, y) d(z, y) d(x, z) (ii) d(x, y) d(z, w) d(x, z) + d(y, w) 2. (X, d). F X.. (1), X F, (2) F 1, F 2 F F 1 F 2 F, (3) F λ F λ F λ F. 3., A λ λ A λ. B λ λ
1 = = = (set) (element) a A a A a A a A a A {2, 5, (0, 1)}, [ 1, 1] = {x; 1 x 1}. (proposition) A = {x; P (x)} P (x) x x a A a A Remark. (i) {2, 0, 0,
![1 = = = (set) (element) a A a A a A a A a A {2, 5, (0, 1)}, [ 1, 1] = {x; 1 x 1}. (proposition) A = {x; P (x)} P (x) x x a A a A Remark. (i) {2, 0, 0, 1 = = = (set) (element) a A a A a A a A a A {2, 5, (0, 1)}, [ 1, 1] = {x; 1 x 1}. (proposition) A = {x; P (x)} P (x) x x a A a A Remark. (i) {2, 0, 0,](/thumbs/91/105754557.jpg) 2005 4 1 1 2 2 6 3 8 4 11 5 14 6 18 7 20 8 22 9 24 10 26 11 27 http://matcmadison.edu/alehnen/weblogic/logset.htm 1 1 = = = (set) (element) a A a A a A a A a A {2, 5, (0, 1)}, [ 1, 1] = {x; 1 x 1}. (proposition)
2005 4 1 1 2 2 6 3 8 4 11 5 14 6 18 7 20 8 22 9 24 10 26 11 27 http://matcmadison.edu/alehnen/weblogic/logset.htm 1 1 = = = (set) (element) a A a A a A a A a A {2, 5, (0, 1)}, [ 1, 1] = {x; 1 x 1}. (proposition)
 20 9 19 1 3 11 1 3 111 3 112 1 4 12 6 121 6 122 7 13 7 131 8 132 10 133 10 134 12 14 13 141 13 142 13 143 15 144 16 145 17 15 19 151 1 19 152 20 2 21 21 21 211 21 212 1 23 213 1 23 214 25 215 31 22 33
20 9 19 1 3 11 1 3 111 3 112 1 4 12 6 121 6 122 7 13 7 131 8 132 10 133 10 134 12 14 13 141 13 142 13 143 15 144 16 145 17 15 19 151 1 19 152 20 2 21 21 21 211 21 212 1 23 213 1 23 214 25 215 31 22 33
5 36 5................................................... 36 5................................................... 36 5.3..............................
 9 8 3............................................. 3.......................................... 4.3............................................ 4 5 3 6 3..................................................
9 8 3............................................. 3.......................................... 4.3............................................ 4 5 3 6 3..................................................
2 7 V 7 {fx fx 3 } 8 P 3 {fx fx 3 } 9 V 9 {fx fx f x 2fx } V {fx fx f x 2fx + } V {{a n } {a n } a n+2 a n+ + a n n } 2 V 2 {{a n } {a n } a n+2 a n+
 R 3 R n C n V??,?? k, l K x, y, z K n, i x + y + z x + y + z iv x V, x + x o x V v kx + y kx + ky vi k + lx kx + lx vii klx klx viii x x ii x + y y + x, V iii o K n, x K n, x + o x iv x K n, x + x o x
R 3 R n C n V??,?? k, l K x, y, z K n, i x + y + z x + y + z iv x V, x + x o x V v kx + y kx + ky vi k + lx kx + lx vii klx klx viii x x ii x + y y + x, V iii o K n, x K n, x + o x iv x K n, x + x o x
(, Goo Ishikawa, Go-o Ishikawa) ( ) 1
 (, Goo Ishikawa, Go-o Ishikawa) ( ) 1 ( ) ( ) ( ) G7( ) ( ) ( ) () ( ) BD = 1 DC CE EA AF FB 0 0 BD DC CE EA AF FB =1 ( ) 2 (geometry) ( ) ( ) 3 (?) (Topology) ( ) DNA ( ) 4 ( ) ( ) 5 ( ) H. 1 : 1+ 5 2
(, Goo Ishikawa, Go-o Ishikawa) ( ) 1 ( ) ( ) ( ) G7( ) ( ) ( ) () ( ) BD = 1 DC CE EA AF FB 0 0 BD DC CE EA AF FB =1 ( ) 2 (geometry) ( ) ( ) 3 (?) (Topology) ( ) DNA ( ) 4 ( ) ( ) 5 ( ) H. 1 : 1+ 5 2
 n ξ n,i, i = 1,, n S n ξ n,i n 0 R 1,.. σ 1 σ i .10.14.15 0 1 0 1 1 3.14 3.18 3.19 3.14 3.14,. ii 1 1 1.1..................................... 1 1............................... 3 1.3.........................
n ξ n,i, i = 1,, n S n ξ n,i n 0 R 1,.. σ 1 σ i .10.14.15 0 1 0 1 1 3.14 3.18 3.19 3.14 3.14,. ii 1 1 1.1..................................... 1 1............................... 3 1.3.........................
,. Black-Scholes u t t, x c u 0 t, x x u t t, x c u t, x x u t t, x + σ x u t, x + rx ut, x rux, t 0 x x,,.,. Step 3, 7,,, Step 6., Step 4,. Step 5,,.
 9 α ν β Ξ ξ Γ γ o δ Π π ε ρ ζ Σ σ η τ Θ θ Υ υ ι Φ φ κ χ Λ λ Ψ ψ µ Ω ω Def, Prop, Th, Lem, Note, Remark, Ex,, Proof, R, N, Q, C [a, b {x R : a x b} : a, b {x R : a < x < b} : [a, b {x R : a x < b} : a,
9 α ν β Ξ ξ Γ γ o δ Π π ε ρ ζ Σ σ η τ Θ θ Υ υ ι Φ φ κ χ Λ λ Ψ ψ µ Ω ω Def, Prop, Th, Lem, Note, Remark, Ex,, Proof, R, N, Q, C [a, b {x R : a x b} : a, b {x R : a < x < b} : [a, b {x R : a x < b} : a,
1 8, : 8.1 1, 2 z = ax + by + c ax by + z c = a b +1 x y z c = 0, (0, 0, c), n = ( a, b, 1). f = n i=1 a ii x 2 i + i<j 2a ij x i x j = ( x, A x), f =
 1 8, : 8.1 1, z = ax + by + c ax by + z c = a b +1 x y z c = 0, (0, 0, c), n = ( a, b, 1). f = a ii x i + i
1 8, : 8.1 1, z = ax + by + c ax by + z c = a b +1 x y z c = 0, (0, 0, c), n = ( a, b, 1). f = a ii x i + i
December 28, 2018
 e-mail : kigami@i.kyoto-u.ac.jp December 28, 28 Contents 2............................. 3.2......................... 7.3..................... 9.4................ 4.5............. 2.6.... 22 2 36 2..........................
e-mail : kigami@i.kyoto-u.ac.jp December 28, 28 Contents 2............................. 3.2......................... 7.3..................... 9.4................ 4.5............. 2.6.... 22 2 36 2..........................
II 2 II
 II 2 II 2005 yugami@cc.utsunomiya-u.ac.jp 2005 4 1 1 2 5 2.1.................................... 5 2.2................................. 6 2.3............................. 6 2.4.................................
II 2 II 2005 yugami@cc.utsunomiya-u.ac.jp 2005 4 1 1 2 5 2.1.................................... 5 2.2................................. 6 2.3............................. 6 2.4.................................
S I. dy fx x fx y fx + C 3 C dy fx 4 x, y dy v C xt y C v e kt k > xt yt gt [ v dt dt v e kt xt v e kt + C k x v + C C k xt v k 3 r r + dr e kt S dt d
 S I.. http://ayapin.film.s.dendai.ac.jp/~matuda /TeX/lecture.html PDF PS.................................... 3.3.................... 9.4................5.............. 3 5. Laplace................. 5....
S I.. http://ayapin.film.s.dendai.ac.jp/~matuda /TeX/lecture.html PDF PS.................................... 3.3.................... 9.4................5.............. 3 5. Laplace................. 5....
I A A441 : April 21, 2014 Version : Kawahira, Tomoki TA (Kondo, Hirotaka ) Google
 I4 - : April, 4 Version :. Kwhir, Tomoki TA (Kondo, Hirotk) Google http://www.mth.ngoy-u.c.jp/~kwhir/courses/4s-biseki.html pdf 4 4 4 4 8 e 5 5 9 etc. 5 6 6 6 9 n etc. 6 6 6 3 6 3 7 7 etc 7 4 7 7 8 5 59
I4 - : April, 4 Version :. Kwhir, Tomoki TA (Kondo, Hirotk) Google http://www.mth.ngoy-u.c.jp/~kwhir/courses/4s-biseki.html pdf 4 4 4 4 8 e 5 5 9 etc. 5 6 6 6 9 n etc. 6 6 6 3 6 3 7 7 etc 7 4 7 7 8 5 59
No δs δs = r + δr r = δr (3) δs δs = r r = δr + u(r + δr, t) u(r, t) (4) δr = (δx, δy, δz) u i (r + δr, t) u i (r, t) = u i x j δx j (5) δs 2
 No.2 1 2 2 δs δs = r + δr r = δr (3) δs δs = r r = δr + u(r + δr, t) u(r, t) (4) δr = (δx, δy, δz) u i (r + δr, t) u i (r, t) = u i δx j (5) δs 2 = δx i δx i + 2 u i δx i δx j = δs 2 + 2s ij δx i δx j
No.2 1 2 2 δs δs = r + δr r = δr (3) δs δs = r r = δr + u(r + δr, t) u(r, t) (4) δr = (δx, δy, δz) u i (r + δr, t) u i (r, t) = u i δx j (5) δs 2 = δx i δx i + 2 u i δx i δx j = δs 2 + 2s ij δx i δx j
 IA hara@math.kyushu-u.ac.jp Last updated: January,......................................................................................................................................................................................
IA hara@math.kyushu-u.ac.jp Last updated: January,......................................................................................................................................................................................
A S hara/lectures/lectures-j.html ϵ-n 1 ϵ-n lim n a n = α n a n α 2 lim a n = 0 1 n a k n n k= ϵ
 A S1-20 http://www2.mth.kyushu-u.c.jp/ hr/lectures/lectures-j.html 1 1 1.1 ϵ-n 1 ϵ-n lim n n = α n n α 2 lim n = 0 1 n k n n k=1 0 1.1.7 ϵ-n 1.1.1 n α n n α lim n n = α ϵ N(ϵ) n > N(ϵ) n α < ϵ (1.1.1)
A S1-20 http://www2.mth.kyushu-u.c.jp/ hr/lectures/lectures-j.html 1 1 1.1 ϵ-n 1 ϵ-n lim n n = α n n α 2 lim n = 0 1 n k n n k=1 0 1.1.7 ϵ-n 1.1.1 n α n n α lim n n = α ϵ N(ϵ) n > N(ϵ) n α < ϵ (1.1.1)
(3) (2),,. ( 20) ( s200103) 0.7 x C,, x 2 + y 2 + ax = 0 a.. D,. D, y C, C (x, y) (y 0) C m. (2) D y = y(x) (x ± y 0), (x, y) D, m, m = 1., D. (x 2 y
 [ ] 7 0.1 2 2 + y = t sin t IC ( 9) ( s090101) 0.2 y = d2 y 2, y = x 3 y + y 2 = 0 (2) y + 2y 3y = e 2x 0.3 1 ( y ) = f x C u = y x ( 15) ( s150102) [ ] y/x du x = Cexp f(u) u (2) x y = xey/x ( 16) ( s160101)
[ ] 7 0.1 2 2 + y = t sin t IC ( 9) ( s090101) 0.2 y = d2 y 2, y = x 3 y + y 2 = 0 (2) y + 2y 3y = e 2x 0.3 1 ( y ) = f x C u = y x ( 15) ( s150102) [ ] y/x du x = Cexp f(u) u (2) x y = xey/x ( 16) ( s160101)
[ ] 0.1 lim x 0 e 3x 1 x IC ( 11) ( s114901) 0.2 (1) y = e 2x (x 2 + 1) (2) y = x/(x 2 + 1) 0.3 dx (1) 1 4x 2 (2) e x sin 2xdx (3) sin 2 xdx ( 11) ( s
![[ ] 0.1 lim x 0 e 3x 1 x IC ( 11) ( s114901) 0.2 (1) y = e 2x (x 2 + 1) (2) y = x/(x 2 + 1) 0.3 dx (1) 1 4x 2 (2) e x sin 2xdx (3) sin 2 xdx ( 11) ( s [ ] 0.1 lim x 0 e 3x 1 x IC ( 11) ( s114901) 0.2 (1) y = e 2x (x 2 + 1) (2) y = x/(x 2 + 1) 0.3 dx (1) 1 4x 2 (2) e x sin 2xdx (3) sin 2 xdx ( 11) ( s](/thumbs/94/118579915.jpg) [ ]. lim e 3 IC ) s49). y = e + ) ) y = / + ).3 d 4 ) e sin d 3) sin d ) s49) s493).4 z = y z z y s494).5 + y = 4 =.6 s495) dy = 3e ) d dy d = y s496).7 lim ) lim e s49).8 y = e sin ) y = sin e 3) y =
[ ]. lim e 3 IC ) s49). y = e + ) ) y = / + ).3 d 4 ) e sin d 3) sin d ) s49) s493).4 z = y z z y s494).5 + y = 4 =.6 s495) dy = 3e ) d dy d = y s496).7 lim ) lim e s49).8 y = e sin ) y = sin e 3) y =
III ϵ-n ϵ-n lim n a n = α n a n α 1 lim a n = 0 1 n a k n n k= ϵ-n 1.1
 III http://www2.mth.kyushu-u.c.jp/~hr/lectures/lectures-j.html 1 1 1.1 ϵ-n ϵ-n lim n = α n n α 1 lim n = 0 1 n k n k=1 0 1.1.7 ϵ-n 1.1.1 n α n n α lim n = α ϵ Nϵ n > Nϵ n α < ϵ 1.1.1 ϵ n > Nϵ n α < ϵ 1.1.2
III http://www2.mth.kyushu-u.c.jp/~hr/lectures/lectures-j.html 1 1 1.1 ϵ-n ϵ-n lim n = α n n α 1 lim n = 0 1 n k n k=1 0 1.1.7 ϵ-n 1.1.1 n α n n α lim n = α ϵ Nϵ n > Nϵ n α < ϵ 1.1.1 ϵ n > Nϵ n α < ϵ 1.1.2
 20 6 4 1 4 1.1 1.................................... 4 1.1.1.................................... 4 1.1.2 1................................ 5 1.2................................... 7 1.2.1....................................
20 6 4 1 4 1.1 1.................................... 4 1.1.1.................................... 4 1.1.2 1................................ 5 1.2................................... 7 1.2.1....................................
(1.2) T D = 0 T = D = 30 kn 1.2 (1.4) 2F W = 0 F = W/2 = 300 kn/2 = 150 kn 1.3 (1.9) R = W 1 + W 2 = = 1100 N. (1.9) W 2 b W 1 a = 0
 1 1 1.1 1.) T D = T = D = kn 1. 1.4) F W = F = W/ = kn/ = 15 kn 1. 1.9) R = W 1 + W = 6 + 5 = 11 N. 1.9) W b W 1 a = a = W /W 1 )b = 5/6) = 5 cm 1.4 AB AC P 1, P x, y x, y y x 1.4.) P sin 6 + P 1 sin 45
1 1 1.1 1.) T D = T = D = kn 1. 1.4) F W = F = W/ = kn/ = 15 kn 1. 1.9) R = W 1 + W = 6 + 5 = 11 N. 1.9) W b W 1 a = a = W /W 1 )b = 5/6) = 5 cm 1.4 AB AC P 1, P x, y x, y y x 1.4.) P sin 6 + P 1 sin 45
 ( 12 ( ( ( ( Levi-Civita grad div rot ( ( = 4 : 6 3 1 1.1 f(x n f (n (x, d n f(x (1.1 dxn f (2 (x f (x 1.1 f(x = e x f (n (x = e x d dx (fg = f g + fg (1.2 d dx d 2 dx (fg = f g + 2f g + fg 2... d n n
( 12 ( ( ( ( Levi-Civita grad div rot ( ( = 4 : 6 3 1 1.1 f(x n f (n (x, d n f(x (1.1 dxn f (2 (x f (x 1.1 f(x = e x f (n (x = e x d dx (fg = f g + fg (1.2 d dx d 2 dx (fg = f g + 2f g + fg 2... d n n
 21 2 26 i 1 1 1.1............................ 1 1.2............................ 3 2 9 2.1................... 9 2.2.......... 9 2.3................... 11 2.4....................... 12 3 15 3.1..........
21 2 26 i 1 1 1.1............................ 1 1.2............................ 3 2 9 2.1................... 9 2.2.......... 9 2.3................... 11 2.4....................... 12 3 15 3.1..........
 1 1 1.1...................................... 1 1.2................................... 5 1.3................................... 7 1.4............................. 9 1.5....................................
1 1 1.1...................................... 1 1.2................................... 5 1.3................................... 7 1.4............................. 9 1.5....................................
I, II 1, 2 ɛ-δ 100 A = A 4 : 6 = max{ A, } A A 10
 1 2007.4.13. A 3-312 tel: 092-726-4774, e-mail: hara@math.kyushu-u.ac.jp, http://www.math.kyushu-u.ac.jp/ hara/lectures/lectures-j.html Office hours: B A I ɛ-δ ɛ-δ 1. 2. A 0. 1. 1. 2. 3. 2. ɛ-δ 1. ɛ-n
1 2007.4.13. A 3-312 tel: 092-726-4774, e-mail: hara@math.kyushu-u.ac.jp, http://www.math.kyushu-u.ac.jp/ hara/lectures/lectures-j.html Office hours: B A I ɛ-δ ɛ-δ 1. 2. A 0. 1. 1. 2. 3. 2. ɛ-δ 1. ɛ-n
ルベーグ積分 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. このサンプルページの内容は, 初版 1 刷発行時のものです.
 ルベーグ積分 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/005431 このサンプルページの内容は, 初版 1 刷発行時のものです. Lebesgue 1 2 4 4 1 2 5 6 λ a
ルベーグ積分 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/005431 このサンプルページの内容は, 初版 1 刷発行時のものです. Lebesgue 1 2 4 4 1 2 5 6 λ a
untitled
 2 : n =1, 2,, 10000 0.5125 0.51 0.5075 0.505 0.5025 0.5 0.4975 0.495 0 2000 4000 6000 8000 10000 2 weak law of large numbers 1. X 1,X 2,,X n 2. µ = E(X i ),i=1, 2,,n 3. σi 2 = V (X i ) σ 2,i=1, 2,,n ɛ>0
2 : n =1, 2,, 10000 0.5125 0.51 0.5075 0.505 0.5025 0.5 0.4975 0.495 0 2000 4000 6000 8000 10000 2 weak law of large numbers 1. X 1,X 2,,X n 2. µ = E(X i ),i=1, 2,,n 3. σi 2 = V (X i ) σ 2,i=1, 2,,n ɛ>0
1 No.1 5 C 1 I III F 1 F 2 F 1 F 2 2 Φ 2 (t) = Φ 1 (t) Φ 1 (t t). = Φ 1(t) t = ( 1.5e 0.5t 2.4e 4t 2e 10t ) τ < 0 t > τ Φ 2 (t) < 0 lim t Φ 2 (t) = 0
 1 No.1 5 C 1 I III F 1 F 2 F 1 F 2 2 Φ 2 (t) = Φ 1 (t) Φ 1 (t t). = Φ 1(t) t = ( 1.5e 0.5t 2.4e 4t 2e 10t ) τ < 0 t > τ Φ 2 (t) < 0 lim t Φ 2 (t) = 0 0 < t < τ I II 0 No.2 2 C x y x y > 0 x 0 x > b a dx
1 No.1 5 C 1 I III F 1 F 2 F 1 F 2 2 Φ 2 (t) = Φ 1 (t) Φ 1 (t t). = Φ 1(t) t = ( 1.5e 0.5t 2.4e 4t 2e 10t ) τ < 0 t > τ Φ 2 (t) < 0 lim t Φ 2 (t) = 0 0 < t < τ I II 0 No.2 2 C x y x y > 0 x 0 x > b a dx
ii 3.,. 4. F. ( ), ,,. 8.,. 1. (75% ) (25% ) =7 24, =7 25, =7 26 (. ). 1.,, ( ). 3.,...,.,.,.,.,. ( ) (1 2 )., ( ), 0., 1., 0,.
 (1 C205) 4 10 (2 C206) 4 11 (2 B202) 4 12 25(2013) http://www.math.is.tohoku.ac.jp/~obata,.,,,..,,. 1. 2. 3. 4. 5. 6. 7. 8. 1., 2007 ( ).,. 2. P. G., 1995. 3. J. C., 1988. 1... 2.,,. ii 3.,. 4. F. ( ),..
(1 C205) 4 10 (2 C206) 4 11 (2 B202) 4 12 25(2013) http://www.math.is.tohoku.ac.jp/~obata,.,,,..,,. 1. 2. 3. 4. 5. 6. 7. 8. 1., 2007 ( ).,. 2. P. G., 1995. 3. J. C., 1988. 1... 2.,,. ii 3.,. 4. F. ( ),..
. sinh x sinh x) = e x e x = ex e x = sinh x 3) y = cosh x, y = sinh x y = e x, y = e x 6 sinhx) coshx) 4 y-axis x-axis : y = cosh x, y = s
 . 00 3 9 [] sinh x = ex e x, cosh x = ex + e x ) sinh cosh 4 hyperbolic) hyperbola) = 3 cosh x cosh x) = e x + e x = cosh x ) . sinh x sinh x) = e x e x = ex e x = sinh x 3) y = cosh x, y = sinh x y =
. 00 3 9 [] sinh x = ex e x, cosh x = ex + e x ) sinh cosh 4 hyperbolic) hyperbola) = 3 cosh x cosh x) = e x + e x = cosh x ) . sinh x sinh x) = e x e x = ex e x = sinh x 3) y = cosh x, y = sinh x y =
( ) sin 1 x, cos 1 x, tan 1 x sin x, cos x, tan x, arcsin x, arccos x, arctan x. π 2 sin 1 x π 2, 0 cos 1 x π, π 2 < tan 1 x < π 2 1 (1) (
 6 20 ( ) sin, cos, tan sin, cos, tan, arcsin, arccos, arctan. π 2 sin π 2, 0 cos π, π 2 < tan < π 2 () ( 2 2 lim 2 ( 2 ) ) 2 = 3 sin (2) lim 5 0 = 2 2 0 0 2 2 3 3 4 5 5 2 5 6 3 5 7 4 5 8 4 9 3 4 a 3 b
6 20 ( ) sin, cos, tan sin, cos, tan, arcsin, arccos, arctan. π 2 sin π 2, 0 cos π, π 2 < tan < π 2 () ( 2 2 lim 2 ( 2 ) ) 2 = 3 sin (2) lim 5 0 = 2 2 0 0 2 2 3 3 4 5 5 2 5 6 3 5 7 4 5 8 4 9 3 4 a 3 b
S I. dy fx x fx y fx + C 3 C vt dy fx 4 x, y dy yt gt + Ct + C dt v e kt xt v e kt + C k x v k + C C xt v k 3 r r + dr e kt S Sr πr dt d v } dt k e kt
 S I. x yx y y, y,. F x, y, y, y,, y n http://ayapin.film.s.dendai.ac.jp/~matuda n /TeX/lecture.html PDF PS yx.................................... 3.3.................... 9.4................5..............
S I. x yx y y, y,. F x, y, y, y,, y n http://ayapin.film.s.dendai.ac.jp/~matuda n /TeX/lecture.html PDF PS yx.................................... 3.3.................... 9.4................5..............
2 1 κ c(t) = (x(t), y(t)) ( ) det(c (t), c x (t)) = det (t) x (t) y (t) y = x (t)y (t) x (t)y (t), (t) c (t) = (x (t)) 2 + (y (t)) 2. c (t) =
 1 1 1.1 I R 1.1.1 c : I R 2 (i) c C (ii) t I c (t) (0, 0) c (t) c(i) c c(t) 1.1.2 (1) (2) (3) (1) r > 0 c : R R 2 : t (r cos t, r sin t) (2) C f : I R c : I R 2 : t (t, f(t)) (3) y = x c : R R 2 : t (t,
1 1 1.1 I R 1.1.1 c : I R 2 (i) c C (ii) t I c (t) (0, 0) c (t) c(i) c c(t) 1.1.2 (1) (2) (3) (1) r > 0 c : R R 2 : t (r cos t, r sin t) (2) C f : I R c : I R 2 : t (t, f(t)) (3) y = x c : R R 2 : t (t,
1990 IMO 1990/1/15 1:00-4:00 1 N N N 1, N 1 N 2, N 2 N 3 N 3 2 x x + 52 = 3 x x , A, B, C 3,, A B, C 2,,,, 7, A, B, C
 0 9 (1990 1999 ) 10 (2000 ) 1900 1994 1995 1999 2 SAT ACT 1 1990 IMO 1990/1/15 1:00-4:00 1 N 1990 9 N N 1, N 1 N 2, N 2 N 3 N 3 2 x 2 + 25x + 52 = 3 x 2 + 25x + 80 3 2, 3 0 4 A, B, C 3,, A B, C 2,,,, 7,
0 9 (1990 1999 ) 10 (2000 ) 1900 1994 1995 1999 2 SAT ACT 1 1990 IMO 1990/1/15 1:00-4:00 1 N 1990 9 N N 1, N 1 N 2, N 2 N 3 N 3 2 x 2 + 25x + 52 = 3 x 2 + 25x + 80 3 2, 3 0 4 A, B, C 3,, A B, C 2,,,, 7,
e a b a b b a a a 1 a a 1 = a 1 a = e G G G : x ( x =, 8, 1 ) x 1,, 60 θ, ϕ ψ θ G G H H G x. n n 1 n 1 n σ = (σ 1, σ,..., σ N ) i σ i i n S n n = 1,,
 01 10 18 ( ) 1 6 6 1 8 8 1 6 1 0 0 0 0 1 Table 1: 10 0 8 180 1 1 1. ( : 60 60 ) : 1. 1 e a b a b b a a a 1 a a 1 = a 1 a = e G G G : x ( x =, 8, 1 ) x 1,, 60 θ, ϕ ψ θ G G H H G x. n n 1 n 1 n σ = (σ 1,
01 10 18 ( ) 1 6 6 1 8 8 1 6 1 0 0 0 0 1 Table 1: 10 0 8 180 1 1 1. ( : 60 60 ) : 1. 1 e a b a b b a a a 1 a a 1 = a 1 a = e G G G : x ( x =, 8, 1 ) x 1,, 60 θ, ϕ ψ θ G G H H G x. n n 1 n 1 n σ = (σ 1,
y π π O π x 9 s94.5 y dy dx. y = x + 3 y = x logx + 9 s9.6 z z x, z y. z = xy + y 3 z = sinx y 9 s x dx π x cos xdx 9 s93.8 a, fx = e x ax,. a =
 [ ] 9 IC. dx = 3x 4y dt dy dt = x y u xt = expλt u yt λ u u t = u u u + u = xt yt 6 3. u = x, y, z = x + y + z u u 9 s9 grad u ux, y, z = c c : grad u = u x i + u y j + u k i, j, k z x, y, z grad u v =
[ ] 9 IC. dx = 3x 4y dt dy dt = x y u xt = expλt u yt λ u u t = u u u + u = xt yt 6 3. u = x, y, z = x + y + z u u 9 s9 grad u ux, y, z = c c : grad u = u x i + u y j + u k i, j, k z x, y, z grad u v =
6kg 1.1m 1.m.1m.1 l λ ϵ λ l + λ l l l dl dl + dλ ϵ dλ dl dl + dλ dl dl 3 1. JIS 1 6kg 1% 66kg 1 13 σ a1 σ m σ a1 σ m σ m σ a1 f f σ a1 σ a1 σ m f 4
 35-8585 7 8 1 I I 1 1.1 6kg 1m P σ σ P 1 l l λ λ l 1.m 1 6kg 1.1m 1.m.1m.1 l λ ϵ λ l + λ l l l dl dl + dλ ϵ dλ dl dl + dλ dl dl 3 1. JIS 1 6kg 1% 66kg 1 13 σ a1 σ m σ a1 σ m σ m σ a1 f f σ a1 σ a1 σ m
35-8585 7 8 1 I I 1 1.1 6kg 1m P σ σ P 1 l l λ λ l 1.m 1 6kg 1.1m 1.m.1m.1 l λ ϵ λ l + λ l l l dl dl + dλ ϵ dλ dl dl + dλ dl dl 3 1. JIS 1 6kg 1% 66kg 1 13 σ a1 σ m σ a1 σ m σ m σ a1 f f σ a1 σ a1 σ m
di-problem.dvi
 005/05/05 by. I : : : : : : : : : : : : : : : : : : : : : : : : :. II : : : : : : : : : : : : : : : : : : : : : : : : : 3 3. III : : : : : : : : : : : : : : : : : : : : : : : : 4 4. : : : : : : : : : :
005/05/05 by. I : : : : : : : : : : : : : : : : : : : : : : : : :. II : : : : : : : : : : : : : : : : : : : : : : : : : 3 3. III : : : : : : : : : : : : : : : : : : : : : : : : 4 4. : : : : : : : : : :
n ( (
 1 2 27 6 1 1 m-mat@mathscihiroshima-uacjp 2 http://wwwmathscihiroshima-uacjp/~m-mat/teach/teachhtml 2 1 3 11 3 111 3 112 4 113 n 4 114 5 115 5 12 7 121 7 122 9 123 11 124 11 125 12 126 2 2 13 127 15 128
1 2 27 6 1 1 m-mat@mathscihiroshima-uacjp 2 http://wwwmathscihiroshima-uacjp/~m-mat/teach/teachhtml 2 1 3 11 3 111 3 112 4 113 n 4 114 5 115 5 12 7 121 7 122 9 123 11 124 11 125 12 126 2 2 13 127 15 128
(1) (2) (3) (4) HB B ( ) (5) (6) (7) 40 (8) (9) (10)
 2017 12 9 4 1 30 4 10 3 1 30 3 30 2 1 30 2 50 1 1 30 2 10 (1) (2) (3) (4) HB B ( ) (5) (6) (7) 40 (8) (9) (10) (1) i 23 c 23 0 1 2 3 4 5 6 7 8 9 a b d e f g h i (2) 23 23 (3) 23 ( 23 ) 23 x 1 x 2 23 x
2017 12 9 4 1 30 4 10 3 1 30 3 30 2 1 30 2 50 1 1 30 2 10 (1) (2) (3) (4) HB B ( ) (5) (6) (7) 40 (8) (9) (10) (1) i 23 c 23 0 1 2 3 4 5 6 7 8 9 a b d e f g h i (2) 23 23 (3) 23 ( 23 ) 23 x 1 x 2 23 x
 8 i, III,,,, III,, :!,,,, :!,,,,, 4:!,,,,,,!,,,, OK! 5:!,,,,,,,,,, OK 6:!, 0, 3:!,,,,! 7:!,,,,,, ii,,,,,, ( ),, :, ( ), ( ), :... : 3 ( )...,, () : ( )..., :,,, ( ), (,,, ),, (ϵ δ ), ( ), (ˆ ˆ;),,,,,,!,,,,.,,
8 i, III,,,, III,, :!,,,, :!,,,,, 4:!,,,,,,!,,,, OK! 5:!,,,,,,,,,, OK 6:!, 0, 3:!,,,,! 7:!,,,,,, ii,,,,,, ( ),, :, ( ), ( ), :... : 3 ( )...,, () : ( )..., :,,, ( ), (,,, ),, (ϵ δ ), ( ), (ˆ ˆ;),,,,,,!,,,,.,,
1 1.1 ( ). z = a + bi, a, b R 0 a, b 0 a 2 + b 2 0 z = a + bi = ( ) a 2 + b 2 a a 2 + b + b 2 a 2 + b i 2 r = a 2 + b 2 θ cos θ = a a 2 + b 2, sin θ =
 1 1.1 ( ). z = + bi,, b R 0, b 0 2 + b 2 0 z = + bi = ( ) 2 + b 2 2 + b + b 2 2 + b i 2 r = 2 + b 2 θ cos θ = 2 + b 2, sin θ = b 2 + b 2 2π z = r(cos θ + i sin θ) 1.2 (, ). 1. < 2. > 3. ±,, 1.3 ( ). A
1 1.1 ( ). z = + bi,, b R 0, b 0 2 + b 2 0 z = + bi = ( ) 2 + b 2 2 + b + b 2 2 + b i 2 r = 2 + b 2 θ cos θ = 2 + b 2, sin θ = b 2 + b 2 2π z = r(cos θ + i sin θ) 1.2 (, ). 1. < 2. > 3. ±,, 1.3 ( ). A
 ( ) 2002 1 1 1 1.1....................................... 1 1.1.1................................. 1 1.1.2................................. 1 1.1.3................... 3 1.1.4......................................
( ) 2002 1 1 1 1.1....................................... 1 1.1.1................................. 1 1.1.2................................. 1 1.1.3................... 3 1.1.4......................................
( )/2 hara/lectures/lectures-j.html 2, {H} {T } S = {H, T } {(H, H), (H, T )} {(H, T ), (T, T )} {(H, H), (T, T )} {1
 ( )/2 http://www2.math.kyushu-u.ac.jp/ hara/lectures/lectures-j.html 1 2011 ( )/2 2 2011 4 1 2 1.1 1 2 1 2 3 4 5 1.1.1 sample space S S = {H, T } H T T H S = {(H, H), (H, T ), (T, H), (T, T )} (T, H) S
( )/2 http://www2.math.kyushu-u.ac.jp/ hara/lectures/lectures-j.html 1 2011 ( )/2 2 2011 4 1 2 1.1 1 2 1 2 3 4 5 1.1.1 sample space S S = {H, T } H T T H S = {(H, H), (H, T ), (T, H), (T, T )} (T, H) S
January 27, 2015
 e-mail : kigami@i.kyoto-u.ac.jp January 27, 205 Contents 2........................ 2.2....................... 3.3....................... 6.4......................... 2 6 2........................... 6
e-mail : kigami@i.kyoto-u.ac.jp January 27, 205 Contents 2........................ 2.2....................... 3.3....................... 6.4......................... 2 6 2........................... 6
II 2 3.,, A(B + C) = AB + AC, (A + B)C = AC + BC. 4. m m A, m m B,, m m B, AB = BA, A,, I. 5. m m A, m n B, AB = B, A I E, 4 4 I, J, K
 II. () 7 F 7 = { 0,, 2, 3, 4, 5, 6 }., F 7 a, b F 7, a b, F 7,. (a) a, b,,. (b) 7., 4 5 = 20 = 2 7 + 6, 4 5 = 6 F 7., F 7,., 0 a F 7, ab = F 7 b F 7. (2) 7, 6 F 6 = { 0,, 2, 3, 4, 5 },,., F 6., 0 0 a F
II. () 7 F 7 = { 0,, 2, 3, 4, 5, 6 }., F 7 a, b F 7, a b, F 7,. (a) a, b,,. (b) 7., 4 5 = 20 = 2 7 + 6, 4 5 = 6 F 7., F 7,., 0 a F 7, ab = F 7 b F 7. (2) 7, 6 F 6 = { 0,, 2, 3, 4, 5 },,., F 6., 0 0 a F
( ; ) C. H. Scholz, The Mechanics of Earthquakes and Faulting : - ( ) σ = σ t sin 2π(r a) λ dσ d(r a) =
 1 9 8 1 1 1 ; 1 11 16 C. H. Scholz, The Mechanics of Earthquakes and Faulting 1. 1.1 1.1.1 : - σ = σ t sin πr a λ dσ dr a = E a = π λ σ πr a t cos λ 1 r a/λ 1 cos 1 E: σ t = Eλ πa a λ E/π γ : λ/ 3 γ =
1 9 8 1 1 1 ; 1 11 16 C. H. Scholz, The Mechanics of Earthquakes and Faulting 1. 1.1 1.1.1 : - σ = σ t sin πr a λ dσ dr a = E a = π λ σ πr a t cos λ 1 r a/λ 1 cos 1 E: σ t = Eλ πa a λ E/π γ : λ/ 3 γ =
main.dvi
 SGC - 70 2, 3 23 ɛ-δ 2.12.8 3 2.92.13 4 2 3 1 2.1 2.102.12 [8][14] [1],[2] [4][7] 2 [4] 1 2009 8 1 1 1.1... 1 1.2... 4 1.3 1... 8 1.4 2... 9 1.5... 12 1.6 1... 16 1.7... 18 1.8... 21 1.9... 23 2 27 2.1
SGC - 70 2, 3 23 ɛ-δ 2.12.8 3 2.92.13 4 2 3 1 2.1 2.102.12 [8][14] [1],[2] [4][7] 2 [4] 1 2009 8 1 1 1.1... 1 1.2... 4 1.3 1... 8 1.4 2... 9 1.5... 12 1.6 1... 16 1.7... 18 1.8... 21 1.9... 23 2 27 2.1
2000年度『数学展望 I』講義録
 2000 I I IV I II 2000 I I IV I-IV. i ii 3.10 (http://www.math.nagoya-u.ac.jp/ kanai/) 2000 A....1 B....4 C....10 D....13 E....17 Brouwer A....21 B....26 C....33 D....39 E. Sperner...45 F....48 A....53
2000 I I IV I II 2000 I I IV I-IV. i ii 3.10 (http://www.math.nagoya-u.ac.jp/ kanai/) 2000 A....1 B....4 C....10 D....13 E....17 Brouwer A....21 B....26 C....33 D....39 E. Sperner...45 F....48 A....53
agora04.dvi
 Workbook E-mail: kawahira@math.nagoya-u.ac.jp 2004 8 9, 10, 11 1 2 1 2 a n+1 = pa n + q x = px + q a n better 2 a n+1 = aan+b ca n+d 1 (a, b, c, d) =(p, q, 0, 1) 1 = 0 3 2 2 2 f(z) =z 2 + c a n+1 = a 2
Workbook E-mail: kawahira@math.nagoya-u.ac.jp 2004 8 9, 10, 11 1 2 1 2 a n+1 = pa n + q x = px + q a n better 2 a n+1 = aan+b ca n+d 1 (a, b, c, d) =(p, q, 0, 1) 1 = 0 3 2 2 2 f(z) =z 2 + c a n+1 = a 2
(ii) (iii) z a = z a =2 z a =6 sin z z a dz. cosh z z a dz. e z dz. (, a b > 6.) (z a)(z b) 52.. (a) dz, ( a = /6.), (b) z =6 az (c) z a =2 53. f n (z
 B 4 24 7 9 ( ) :,..,,.,. 4 4. f(z): D C: D a C, 2πi C f(z) dz = f(a). z a a C, ( ). (ii), a D, a U a,r D f. f(z) = A n (z a) n, z U a,r, n= A n := 2πi C f(ζ) dζ, n =,,..., (ζ a) n+, C a D. (iii) U a,r
B 4 24 7 9 ( ) :,..,,.,. 4 4. f(z): D C: D a C, 2πi C f(z) dz = f(a). z a a C, ( ). (ii), a D, a U a,r D f. f(z) = A n (z a) n, z U a,r, n= A n := 2πi C f(ζ) dζ, n =,,..., (ζ a) n+, C a D. (iii) U a,r
ii th-note
 4 I alpha α nu N ν beta B β i Ξ ξ gamma Γ γ omicron o delta δ pi Π π, ϖ epsilon E ϵ, ε rho P ρ, ϱ zeta Z ζ sigma Σ σ, ς eta H η tau T τ theta Θ θ, ϑ upsilon Υ υ iota I ι phi Φ ϕ, φ kappa K κ chi X χ lambda
4 I alpha α nu N ν beta B β i Ξ ξ gamma Γ γ omicron o delta δ pi Π π, ϖ epsilon E ϵ, ε rho P ρ, ϱ zeta Z ζ sigma Σ σ, ς eta H η tau T τ theta Θ θ, ϑ upsilon Υ υ iota I ι phi Φ ϕ, φ kappa K κ chi X χ lambda
 i I II I II II IC IIC I II ii 5 8 5 3 7 8 iii I 3........................... 5......................... 7........................... 4........................ 8.3......................... 33.4...................
i I II I II II IC IIC I II ii 5 8 5 3 7 8 iii I 3........................... 5......................... 7........................... 4........................ 8.3......................... 33.4...................
 2016 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 1 16 2 1 () X O 3 (O1) X O, O (O2) O O (O3) O O O X (X, O) O X X (O1), (O2), (O3) (O2) (O3) n (O2) U 1,..., U n O U k O k=1 (O3) U λ O( λ Λ) λ Λ U λ O 0 X 0 (O2) n =
2016 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 1 16 2 1 () X O 3 (O1) X O, O (O2) O O (O3) O O O X (X, O) O X X (O1), (O2), (O3) (O2) (O3) n (O2) U 1,..., U n O U k O k=1 (O3) U λ O( λ Λ) λ Λ U λ O 0 X 0 (O2) n =
.3. (x, x = (, u = = 4 (, x x = 4 x, x 0 x = 0 x = 4 x.4. ( z + z = 8 z, z 0 (z, z = (0, 8, (,, (8, 0 3 (0, 8, (,, (8, 0 z = z 4 z (g f(x = g(
 06 5.. ( y = x x y 5 y 5 = (x y = x + ( y = x + y = x y.. ( Y = C + I = 50 + 0.5Y + 50 r r = 00 0.5Y ( L = M Y r = 00 r = 0.5Y 50 (3 00 0.5Y = 0.5Y 50 Y = 50, r = 5 .3. (x, x = (, u = = 4 (, x x = 4 x,
06 5.. ( y = x x y 5 y 5 = (x y = x + ( y = x + y = x y.. ( Y = C + I = 50 + 0.5Y + 50 r r = 00 0.5Y ( L = M Y r = 00 r = 0.5Y 50 (3 00 0.5Y = 0.5Y 50 Y = 50, r = 5 .3. (x, x = (, u = = 4 (, x x = 4 x,
2
 p1 i 2 = 1 i 2 x, y x + iy 2 (x + iy) + (γ + iδ) = (x + γ) + i(y + δ) (x + iy)(γ + iδ) = (xγ yδ) + i(xδ + yγ) i 2 = 1 γ + iδ 0 x + iy γ + iδ xγ + yδ xδ = γ 2 + iyγ + δ2 γ 2 + δ 2 p7 = x 2 +y 2 z z p13
p1 i 2 = 1 i 2 x, y x + iy 2 (x + iy) + (γ + iδ) = (x + γ) + i(y + δ) (x + iy)(γ + iδ) = (xγ yδ) + i(xδ + yγ) i 2 = 1 γ + iδ 0 x + iy γ + iδ xγ + yδ xδ = γ 2 + iyγ + δ2 γ 2 + δ 2 p7 = x 2 +y 2 z z p13
 7 i 7 1 2 3 4 5 6 ii 7 8 9 10 11 1 12 13 14 iii.......................................... iv................................................ 21... 1 v 3 6 7 3 vi vii viii ix x xi xii xiii xiv xv 26 27
7 i 7 1 2 3 4 5 6 ii 7 8 9 10 11 1 12 13 14 iii.......................................... iv................................................ 21... 1 v 3 6 7 3 vi vii viii ix x xi xii xiii xiv xv 26 27
 9 i 9 1 2 3 4 5 6 ii 7 8 9 10 11 12 .......................................... iii ... 1... 1........................................ 9 iv... v 3 8 9 3 vi vii viii ix x xi xii xiii xiv 34 35 22 1 2 1
9 i 9 1 2 3 4 5 6 ii 7 8 9 10 11 12 .......................................... iii ... 1... 1........................................ 9 iv... v 3 8 9 3 vi vii viii ix x xi xii xiii xiv 34 35 22 1 2 1
 i ii iii iv v vi vii viii ix x xi xii xiii xiv xv xvi 2 3 4 5 6 7 $ 8 9 10 11 12 13 14 15 16 17 $ $ $ 18 19 $ 20 21 22 23 24 25 26 27 $$ 28 29 30 31 $ $ $ 32 33 34 $ 35 $ 36 $ 37 38 39 40 $ 41 42 43 44
i ii iii iv v vi vii viii ix x xi xii xiii xiv xv xvi 2 3 4 5 6 7 $ 8 9 10 11 12 13 14 15 16 17 $ $ $ 18 19 $ 20 21 22 23 24 25 26 27 $$ 28 29 30 31 $ $ $ 32 33 34 $ 35 $ 36 $ 37 38 39 40 $ 41 42 43 44
2S III IV K A4 12:00-13:30 Cafe David 1 2 TA 1 appointment Cafe David K2-2S04-00 : C
 2S III IV K200 : April 16, 2004 Version : 1.1 TA M2 TA 1 10 2 n 1 ɛ-δ 5 15 20 20 45 K2-2S04-00 : C 2S III IV K200 60 60 74 75 89 90 1 email 3 4 30 A4 12:00-13:30 Cafe David 1 2 TA 1 email appointment Cafe
2S III IV K200 : April 16, 2004 Version : 1.1 TA M2 TA 1 10 2 n 1 ɛ-δ 5 15 20 20 45 K2-2S04-00 : C 2S III IV K200 60 60 74 75 89 90 1 email 3 4 30 A4 12:00-13:30 Cafe David 1 2 TA 1 email appointment Cafe
meiji_resume_1.PDF
 β β β (q 1,q,..., q n ; p 1, p,..., p n ) H(q 1,q,..., q n ; p 1, p,..., p n ) Hψ = εψ ε k = k +1/ ε k = k(k 1) (x, y, z; p x, p y, p z ) (r; p r ), (θ; p θ ), (ϕ; p ϕ ) ε k = 1/ k p i dq i E total = E
β β β (q 1,q,..., q n ; p 1, p,..., p n ) H(q 1,q,..., q n ; p 1, p,..., p n ) Hψ = εψ ε k = k +1/ ε k = k(k 1) (x, y, z; p x, p y, p z ) (r; p r ), (θ; p θ ), (ϕ; p ϕ ) ε k = 1/ k p i dq i E total = E
201711grade1ouyou.pdf
 2017 11 26 1 2 52 3 12 13 22 23 32 33 42 3 5 3 4 90 5 6 A 1 2 Web Web 3 4 1 2... 5 6 7 7 44 8 9 1 2 3 1 p p >2 2 A 1 2 0.6 0.4 0.52... (a) 0.6 0.4...... B 1 2 0.8-0.2 0.52..... (b) 0.6 0.52.... 1 A B 2
2017 11 26 1 2 52 3 12 13 22 23 32 33 42 3 5 3 4 90 5 6 A 1 2 Web Web 3 4 1 2... 5 6 7 7 44 8 9 1 2 3 1 p p >2 2 A 1 2 0.6 0.4 0.52... (a) 0.6 0.4...... B 1 2 0.8-0.2 0.52..... (b) 0.6 0.52.... 1 A B 2
 Ver.2.2 20.07.2 3 200 6 2 4 ) 2) 3) 4) 5) (S45 9 ) ( 4) III 6) 7) 8) 9) ) 2) 3) 4) BASIC 5) 6) 7) 8) 9) ..2 3.2. 3.2.2 4.2.3 5.2.4 6.3 8.3. 8.3.2 8.3.3 9.4 2.5 3.6 5 2.6. 5.6.2 6.6.3 9.6.4 20.6.5 2.6.6
Ver.2.2 20.07.2 3 200 6 2 4 ) 2) 3) 4) 5) (S45 9 ) ( 4) III 6) 7) 8) 9) ) 2) 3) 4) BASIC 5) 6) 7) 8) 9) ..2 3.2. 3.2.2 4.2.3 5.2.4 6.3 8.3. 8.3.2 8.3.3 9.4 2.5 3.6 5 2.6. 5.6.2 6.6.3 9.6.4 20.6.5 2.6.6
x, y x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = 15 xy (x y) (x + y) xy (x y) (x y) ( x 2 + xy + y 2) = 15 (x y)
 x, y x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = 15 1 1977 x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = 15 xy (x y) (x + y) xy (x y) (x y) ( x 2 + xy + y 2) = 15 (x y) ( x 2 y + xy 2 x 2 2xy y 2) = 15 (x y) (x + y) (xy
x, y x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = 15 1 1977 x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = 15 xy (x y) (x + y) xy (x y) (x y) ( x 2 + xy + y 2) = 15 (x y) ( x 2 y + xy 2 x 2 2xy y 2) = 15 (x y) (x + y) (xy
18 ( ) I II III A B C(100 ) 1, 2, 3, 5 I II A B (100 ) 1, 2, 3 I II A B (80 ) 6 8 I II III A B C(80 ) 1 n (1 + x) n (1) n C 1 + n C
 8 ( ) 8 5 4 I II III A B C( ),,, 5 I II A B ( ),, I II A B (8 ) 6 8 I II III A B C(8 ) n ( + x) n () n C + n C + + n C n = 7 n () 7 9 C : y = x x A(, 6) () A C () C P AP Q () () () 4 A(,, ) B(,, ) C(,,
8 ( ) 8 5 4 I II III A B C( ),,, 5 I II A B ( ),, I II A B (8 ) 6 8 I II III A B C(8 ) n ( + x) n () n C + n C + + n C n = 7 n () 7 9 C : y = x x A(, 6) () A C () C P AP Q () () () 4 A(,, ) B(,, ) C(,,
.5 z = a + b + c n.6 = a sin t y = b cos t dy d a e e b e + e c e e e + e 3 s36 3 a + y = a, b > b 3 s363.7 y = + 3 y = + 3 s364.8 cos a 3 s365.9 y =,
 [ ] IC. r, θ r, θ π, y y = 3 3 = r cos θ r sin θ D D = {, y ; y }, y D r, θ ep y yddy D D 9 s96. d y dt + 3dy + y = cos t dt t = y = e π + e π +. t = π y =.9 s6.3 d y d + dy d + y = y =, dy d = 3 a, b
[ ] IC. r, θ r, θ π, y y = 3 3 = r cos θ r sin θ D D = {, y ; y }, y D r, θ ep y yddy D D 9 s96. d y dt + 3dy + y = cos t dt t = y = e π + e π +. t = π y =.9 s6.3 d y d + dy d + y = y =, dy d = 3 a, b
..3. Ω, Ω F, P Ω, F, P ). ) F a) A, A,..., A i,... F A i F. b) A F A c F c) Ω F. ) A F A P A),. a) 0 P A) b) P Ω) c) [ ] A, A,..., A i,... F i j A i A
![..3. Ω, Ω F, P Ω, F, P ). ) F a) A, A,..., A i,... F A i F. b) A F A c F c) Ω F. ) A F A P A),. a) 0 P A) b) P Ω) c) [ ] A, A,..., A i,... F i j A i A ..3. Ω, Ω F, P Ω, F, P ). ) F a) A, A,..., A i,... F A i F. b) A F A c F c) Ω F. ) A F A P A),. a) 0 P A) b) P Ω) c) [ ] A, A,..., A i,... F i j A i A](/thumbs/93/112175219.jpg) .. Laplace ). A... i),. ω i i ). {ω,..., ω } Ω,. ii) Ω. Ω. A ) r, A P A) P A) r... ).. Ω {,, 3, 4, 5, 6}. i i 6). A {, 4, 6} P A) P A) 3 6. ).. i, j i, j) ) Ω {i, j) i 6, j 6}., 36. A. A {i, j) i j }.
.. Laplace ). A... i),. ω i i ). {ω,..., ω } Ω,. ii) Ω. Ω. A ) r, A P A) P A) r... ).. Ω {,, 3, 4, 5, 6}. i i 6). A {, 4, 6} P A) P A) 3 6. ).. i, j i, j) ) Ω {i, j) i 6, j 6}., 36. A. A {i, j) i j }.
³ÎΨÏÀ
 2017 12 12 Makoto Nakashima 2017 12 12 1 / 22 2.1. C, D π- C, D. A 1, A 2 C A 1 A 2 C A 3, A 4 D A 1 A 2 D Makoto Nakashima 2017 12 12 2 / 22 . (,, L p - ). Makoto Nakashima 2017 12 12 3 / 22 . (,, L p
2017 12 12 Makoto Nakashima 2017 12 12 1 / 22 2.1. C, D π- C, D. A 1, A 2 C A 1 A 2 C A 3, A 4 D A 1 A 2 D Makoto Nakashima 2017 12 12 2 / 22 . (,, L p - ). Makoto Nakashima 2017 12 12 3 / 22 . (,, L p
0104.pages
 bit 8, 6, 3 bit byte = 8 bit, char CBYTEFORTRAN) 055, -87 word = 6 bit int (C) INTEGER (FORTRAN) -37683767 unsgined int (C) 065535 double word = 3 bit, longint C -4748364847483647 CD-audio 6 bit, 44. kbpsch74
bit 8, 6, 3 bit byte = 8 bit, char CBYTEFORTRAN) 055, -87 word = 6 bit int (C) INTEGER (FORTRAN) -37683767 unsgined int (C) 065535 double word = 3 bit, longint C -4748364847483647 CD-audio 6 bit, 44. kbpsch74
1 Abstract 2 3 n a ax 2 + bx + c = 0 (a 0) (1) ( x + b ) 2 = b2 4ac 2a 4a 2 D = b 2 4ac > 0 (1) 2 D = 0 D < 0 x + b 2a = ± b2 4ac 2a b ± b 2
 1 Abstract n 1 1.1 a ax + bx + c = 0 (a 0) (1) ( x + b ) = b 4ac a 4a D = b 4ac > 0 (1) D = 0 D < 0 x + b a = ± b 4ac a b ± b 4ac a b a b ± 4ac b i a D (1) ax + bx + c D 0 () () (015 8 1 ) 1. D = b 4ac
1 Abstract n 1 1.1 a ax + bx + c = 0 (a 0) (1) ( x + b ) = b 4ac a 4a D = b 4ac > 0 (1) D = 0 D < 0 x + b a = ± b 4ac a b ± b 4ac a b a b ± 4ac b i a D (1) ax + bx + c D 0 () () (015 8 1 ) 1. D = b 4ac
28
 y i = Z i δ i +ε i ε i δ X y i = X Z i δ i + X ε i [ ] 1 δ ˆ i = Z i X( X X) 1 X Z i [ ] 1 σ ˆ 2 Z i X( X X) 1 X Z i Z i X( X X) 1 X y i σ ˆ 2 ˆ σ 2 = [ ] y i Z ˆ [ i δ i ] 1 y N p i Z i δ ˆ i i RSTAT
y i = Z i δ i +ε i ε i δ X y i = X Z i δ i + X ε i [ ] 1 δ ˆ i = Z i X( X X) 1 X Z i [ ] 1 σ ˆ 2 Z i X( X X) 1 X Z i Z i X( X X) 1 X y i σ ˆ 2 ˆ σ 2 = [ ] y i Z ˆ [ i δ i ] 1 y N p i Z i δ ˆ i i RSTAT
