入門講座
|
|
|
- さあしゃ ひろなが
- 5 years ago
- Views:
Transcription
1 第 7 章弾性歪エネルギー評価法 7- はじめに本稿では相分解組織の有する弾性歪エネルギーの定式化について説明する 基本的には整合相分解における弾性歪エネルギ - をマイクロメカニクス - に基づき定式化する この種の理論では 理論式の変形に応用数学を多用するために 結構 式の導出が長く複雑になり 何が既知量で どの法則を利用して 何を導こうとしているのかが不明確になる場合が多い しかし マイクロメカニクスの論理は非常に洗練された体系を持っており やっていることは至極単純である つまり ign 歪 の空間分布が与えられた時に 平衡方程式 力の釣り合い方程式 とフックの法則を用いて 応力場 歪場 および弾性歪エネルギー場を計算しているだけである 以下では まず Eshlby サイクルについて説明し 続いて秩序変数が濃度場のみの場合を例に取り 析出相が薄い板状である特殊な場合について 弾性歪エネルギーの計算方法を説明する 7- Eshlby サイクル γ 相内にα 相がマルテンサイト変態によって形成される場合を考えよう γ α 変態によって 格子は膨張すると仮定する この時の ign 歪をε と置く 図 7- が Eshlby サイクルの説明図である 求めたい量は γ 相母相内にα 相が存在する時に材料内にため込まれている弾性歪エネルギー E str である 図 7- の Eshlby サイクルに従い E str を計算する方法について定性的に説明する Estr = ε ε ε c a γ + b E = E E str εε C εε c = C ε ε ε c + α c ε d + E εε f γ α c ε E εε c 図 7- Eshlby サイクルの説明図 積分記号は省略している まず初期状態はγ 単相状態 a である この状態から中央の部分を切り出す b この切り出した領域がマルテンサイト変態によってα 相に変化する c α 相に変態することによって 格子が膨張すると仮定したので 図のようにα 相のサイズは切り出したγ 相よりも大きくなる さらにこの場合 切り出した状態でのマルテンサイト変態であるので α 相の周囲に拘束はない 次にこの変 態したα 相に外力を加えて ign 歪 ε 分だけ変形させ 元のγ 相のサイズに戻す d この変形に要 する弾性歪エネルギーを E とすると E は 7-
2 E = Cεε dv V C にて与えられる は弾性定数である 図 d の応力のかかった状態を維持しながらγ 相の切り出した穴にα 相を入れる 最後にかけていた外力を取り去るf 外力を取り去ったので α 相は図 c のサイズに向かって膨張しようとするが 今度は周囲にγ 相が存在するので c のサイズまでは膨張できずに途中で止まる この時のα 相がγ 相へなした歪が全歪 拘束歪 ε である この時の 仕事 E は 反作用の応力 C ε で c ε だけ歪ませたのであるから c c E = Cεε dv V と表現できる 結局 最終的に材料に蓄えられている弾性歪エネルギー E str は E だけ拘束して E だけ緩和した後の残量に対応するので E = E E εε dv C εε dv = C ε ε εdv c c str V V V と与えられることになる 特に最終的な応力場は ε ε c l c となる ε = ε ε が弾性歪である ので E str は E = ε dv str V となる 通常 弾性歪エネルギーは E ε ε dv ε ε ε ε l l c c str V V = ε ε V c = ε dv V dv ε dv c V dv にて表現されるが この右辺第 項をガウスの発散定理を用いて変形すると ε dv = u n ds u dv = c i j, j i V S V を得る ここで 平衡方程式 =, j 体積力は考慮していない と 物体表面における力の釣り 合い n = 物体表面には圧力などの外力は と仮定している を用いた したがって Estr は j 7-
3 E = ε dv str V となり Eshlby サイクルの帰結と一致する 図 7- ではマルテンサイト変態を想定したが 整合における拡散相分解においても同様の式となる 切り出した領域内の原子数は固定されるので 図 7- の状態は 整合における拡散相分解では 析出相の格子定数が濃度変化に伴い大きくなる場合に対応していることになる なお拡散相変態で 界面が非整合である場合は 切り出した領域内の原子数は固定されず 最終的に物体全体が膨張 収縮 する 拡散相変態であるので原子は動ける ことによって 弾性歪エネルギーが緩和される 7- Cahn のスピノ-ダル分解理論おける弾性歪エネルギ- ここでは Cahn のスピノ-ダル分解理論 にて用いられている弾性歪エネルギーにおける弾性定数の関数 Y < h> を 斜方晶について導出してみよう 整合析出物の形状を h 面上にのった非常に薄い板形状と仮定し 結晶構造は斜方晶とする ign 歪場は純膨張 収縮 pur dilatation とし ign 歪の値をε と置く 以上の仮定から 歪テンソルは以下のように与えられる ε ε = ε ε ε は濃度 ca-b 元系を想定し B 成分の濃度 の関数で 格子定数にベガード則が成立する場合 ε = ηcc にて与えられる η は格子ミスマッチで c は合金の平均 B 成分濃度である 本来 ign 歪の基準は純物質の格子定数が基準となるが ここでは基準を組成 の固溶体にしている これは 物体全体の応力の総和がになるように鏡像応力を考慮することによって 弾性歪の基準が純物質から組成の固溶体に移行するためである つまり組成 c の固溶体を歪の基準に取らな c くては 全応力の積分が にならない また弾性定数は斜方晶を想定して以下のように置く c C C C C C C C * C C C C C * * C C C C = * * * C C C * * * * C C * * * * * C C C C C C C C C C C = C C = C C C C55 C C 66 C C C C C C 先の場合と同様 図 7- で示した Eshlby サイクルの考え方に基づき弾性歪エネルギ - を計算する なお図 7- ではわかりやすいように板状析出物をかなり厚く表現している A の状態は相分離前の固溶体で B は A より これから析出相となる板状部分を切り抜いた状態である 図は板状析出物の断面を表示している C は相分離が生じて板状析出相の格子定数が大きくなり 格子定数は濃度の関数で 析出相の格子定数の方が母相の格子定数よりも大きいとする 析出相全体が 7-
4 str - 膨張した状態を示している この時の歪が ign 歪 ε である 特にこの場合は純膨張になるので ign 歪テンソルは 式 のようにε = δε と表現される δ はクロネッカーのデルタで i = jの時 δ = およびi jの時 δ = である D は析出相に外から外力をかけて ign 歪分だけ弾性収縮させて元のサイズにもどす操作である これに要する弾性歪エネルギ- E は 式 と より以下のように計算される なお添え字に関して総和規約を採用している A E E E = x c ε E E B C D E ε 図 7- Eshlby サイクルの説明図 板状物の場合 E εε εε + Cεε + Cεε + C ε ε + C ε ε + C ε ε + C ε ε + C ε ε + C ε ε = C + C + C + C + C + C ε D の状態の析出物を左の母相にもどした状態が E である いま非常に薄い板状析出物を想定しているので E の状態から矢印で示した外力を取り去ると 板面に垂直方向にのみ応力の緩和が生じる 面内は母相の格子定数に完全に一致する この緩和後の状態を表した図が である この板面に垂直方向を x 方向 参照 とし その方向を表すミラ- 指数を < h > としよう h 面は板状析出物の板面 また x 方向に垂直な 方向 つまり板面内 を y および z とし xyz 座 標系における弾性定数と応力をそれぞれ C および とする 完全拘束状態 E における応力は ε = C + C + C ε = C + C + C ε = C + C + C ε = C + C + C ε = C + C + C ε = C + C + C ε = C + C + C ε = = = にて与えられる xyz および xyz 両座標間の方向余弦をとすると 応力における座標変換 の公式 = l l を用いて ip jq pq l = l l = l l + l l + l l = n + n + n p q pq を得る ここで l n, l n, l n と置いた これより x 方向への 反作用の 応力 は次式にて与えられる 7-
5 = n + n + n = ε{ n C + C + C + n C + C + C + n C + C + C } さて の応力が加わって x 方向にのみ歪の緩和が生じた場合 その時の緩和による歪量 ε + C + C ε ε ε は 応力の釣合い条件から以下のように導かれる すなわち ε ε ε y および z 方向に歪の緩和は生じないと仮定したので = = および式 より ε ε{ n C + C + C + n C + C + C + n C + C + C } = = C C 5 である これより ε の応力緩和による弾性歪エネルギ-の減少量 E は次式にて与えられる E { n C + C + C + n C + C + C + n C + C + C } = ε = ε C 6 結局 始め E 分だけエネルギ- 的に拘束し その後 E 分だけエネルギ- 緩和したのであるから 状態において まだ析出物に蓄えられているエネルギ-は E E であり これが析出相の弾 性歪エネルギ - となる したがって 式 と 6 から弾性歪エネルギ - E str は次式に与えられる E = E E str = C + C + C + C + C + C ε { n C + C + C + n C + C + C + n C + C + C } ε C C + C + C + C + C + C = ε { n C C C n C C C n C C C } C 7 以上が Eshlby サイクルにて弾性歪エネルギーを計算する時の基本的な考え方である ここで C をC, C, C, C, C, C, C, C, C を用いて書き直そう 座標変換の公式 C = lipljql km l ln C pqmn を用いて 7-5
6 C = l C p q m n pqmn = l C + l C + l C + l C + l C + l C + l C + l C + l C + l C + l C + l C + l C + l C + l C + l C + l C + llllc + llllc + llllc + llllc = l C + l C + l C + l l C + l l C + l l C l l C + l l C + l l C = nc + nc + nc = n C + nc + nc + nnc + nnc を得る 式 8 を式 7 に代入して 最終的に弾性歪エネルギ - として次式を得る C + C + C + C + C + C Estr = ε { } n C + C + C + n C + C + C + n C + C + C nc + nc + nc + nnc + nnc これより Y < h> は C + C + C + C + C + C Y< h> = { } n C + C + C + n C + C + C + n C + C + C nc + nc + nc + nnc + nnc と与えられる またε はベガード則が仮定できる場合には ε = ηc c と表現できるので 結局 弾性歪エネルギ-は E c = Y c c str η < h > にて与えられる η は格子ミスマッチ c は局所的な濃度 および c は合金組成である 以上は斜方晶系における定式化であるが 立方晶 正方晶 および六方晶への変換は弾性定数マトリックスを 立方晶 C C C C C C C C C C C C C C C C C C = C C C55 C C 66 C 7-6
7 正方晶 C C C C C C C C C C C C C C C C C C = C C C55 C C C 六方晶 C C C C C C C C C C C C C C C C C C = C C C C55 C C C 66 とすればよい 正方晶と六方晶については z 方向を c 軸としている 例えば式 を立方晶について書き下すと C + C + C + C + C + C Y< h> = { } n C + C + C + n C + C + C + n C + C + C nc + nc + nc + nnc + nnc C + 6C = { n C + C + n C + C + n C + C } C n n n C nn nn nn C nn nn nn C + C = C C + C{ n n + n n + n n } + C n n + n n + n n + C nn + nn + nn C + C C + C = C + C C + C nn + nn + nn となり 従来の結果に一致している なおここで n + n + n = n + n + n n n + n n + n n = n n + n n + n n を用いた なお n, n, n はミラー指数 h,, を用いて h k l h k + k l + l h n n n n n n n n n h + k + l h + k + l h + k + l h + k + l =, =, = + + = と表される 特に < h >=< > および < h >=< > では それぞれ 7-7
8 Y < > = C + C C C 6C C C, Y + < > = C C + C + C と計算される また式 において [ ] 内の分母にある C C + C の正負によって 弾性的にソフトな方向 Y < > が最小となる方向 が変化する C C + C > の時には < > 方 h 向がソフトとなり C C + C < の時には < > 方向がソフトとなる これを反映して立方晶における弾性異方性パラメ-タは通常 A C / C C にて定義される Y < h > Y < hkil> また六方晶ではをと書き直し A C + C + C + C + C + C Y< hkil> = { } n C + C + C + n C + C + C + n C + C + C nc + nc + nc + nnc + nnc を得る 六方晶でc 軸に垂直な面 最密面 は < hkil >=< > で n, n, n =,, である したがって C + C + C Y< > = C + C + C + C + C + C C となる 六方晶で a 軸に垂直な面は < hkil >=< > で n, n, n =,, であるので C + C + C Y C C C C C < > C となる n i は斜方晶における直交座標系での単位ベクトルであるので注意 さて以上から Cahnのスピノ-ダル分解理論にて用いられている弾性歪エネルギ-において 非常に大きな仮定がなされていることがわかる すなわちこの弾性歪エネルギ-は 非常に薄い板状析出物以外には厳密には適用できない またスピノ-ダル分解における変調構造のように 板状析出相が周期的に配列している場合であっても 以上の定式化においては析出相間の弾性相互作用が考慮されていないために やはり厳密ではない 式 では 弾性歪エネルギーがつの単純な式で陽に与えられるので 定性的な考察を行うには非常に有用であるが 実際の材料の相分解に伴う弾性場について定量的な議論が必要である場合には 式 の弾性歪エネルギ-では不十分である 一般形状を有する析出相が分散した組織の弾性歪エネルギ-は hachaturyanの弾性歪エネルギ- 評価法 内容的にはマイクロメカニクスと等価であるが 任意の組織形態の弾性場の数値計算に便利な形式に定式化されている を用いて かなり正確に計算することができるので これについては次章にて説明する 参考文献 森勉, 村外志夫 : マイクロメカニクス, 培風館, 976 T.Mura; "Micromchanics of Dfcts in Solids", nd Rv. Ed., luwr Acadmic, 99. A.hachaturyan:"Thory of Structural Transformations in Solids.", Wily, Nw York, NY, 98.E.illiard: "Phas Transformation", d. by..aaronson, ASM, Mtals Park, Ohio, 97, 97. ************************************ 参考 *************************************** 弾性定数の対称性について. 弾性定数の定義広義のフックの法則を式 にて定義する 7-8
9 = C 弾性定数には 式 の関係が成立する C, C, C ji lk これより 独立な弾性定数に基づき 式 を書き下すと以下のようになる C C C C C C * C C C C C * * C C C C = * * * C C C * * * * C C * * * * * C なお * はマトリックスの対称要素を表す したがって 独立な弾性定数は 最大 個である 次に結晶の対称性による独立な弾性定数の決定方法について考察する. 独立な弾性定数の決定まず 結晶の対称性を数式的に扱うために直交座標の回転による座標変換公式を導く 旧直角座標系におけるベクトル P の成分を x, x, x とし 変換後の新座標系におけるベクトル P の成分 を x, x, x と置く また両座標系の原点は一致させるものとする この両座標系間の関係を導くために 方向余弦 l を以下のように定義する x x x = x x x 方向余弦の意味は以下のように理解することができる いま Px, x, x が与えられて P x, x, x を導く場合を考える 旧座標系において x, x, x を成分とするベクトル P は当然ながら x,,,, x, および,, x の和である これらつのベクトルは旧座標系ではその座標軸上に存在するが 新座標系では必ずしも座標軸上に存在するとは限らない したがって x,,,, x, および,, x を さらにそれぞれ新座標系成分に分解してやらなくてはならない 旧座標系 x 軸上のベクトル x,, を 新座標系で見た場合の成分は xcos θ, xcos θ, x cos θ にて与えられる θ は旧座標系 x j 軸と新座標系 x i 軸との間の角度である 同様に, x, および,, x の新座標成分は x cos θ, x cos θ, xcos θ および x cos θ, x cos θ, x cos θ にて与えられる 以上を行列を用いて表記すると以下のようになる x x x = x cos θ + x cos θ + x cos θ x cos θ + x cos θ + x cos θ x cos θ + x cos θ + x cos θ = cos θ cos θ cos θ cos θ cos θ cos θ cos θ cos θ cos θ 式 と式 5 を比較することにより 方向余弦 l は式 6 にて与えられる x x x 5 7-9
10 = cos θ cos θ cos θ cos θ cos θ cos θ cos θ cos θ cos θ 6 式 6 右辺の θ の添え字は 前が新座標系の軸を 後が旧座標系の軸を表す これより 方向余弦 l には 内積の定義から次の性質が存在する l l ik ik l l = i j ik l l jk ki ki l l = i j ki kj = = 7 ll i i = ll + ll + ll = 例 : l l = l l + l l + l l + l l + l l + l l = i j この方向余弦 l を用いることによて 歪および応力成分の座標変換公式は それぞれ式 8 および式 9 にて与えられる 例 : = l l ik jl = l l k l = l l + l l + l l + l l + l l + l l + l l + l l + l l = l ik l jl 8 9 以上の歪および応力成分の座標変換公式を用いることにより 結晶の対称性による独立な弾性定数は以下のように計算することができる. 斜方晶における独立な弾性定数の導き方斜方晶は直方体対称性を有する したがって x x, x x, および x x 面に対する座標変換において 弾性体の応力および歪は不変である この条件により 斜方晶における独立な弾性定数が導くことが出来る - x x 面における対称性 この対称性は x = x, x = x, x = xと変換した場合 弾性定数 C が不変であることを意味する この場合の方向余弦 l は次式にて与えられる = = cos θ cos θ cos θ cos θ cos θ cos θ cos θ cos θ cos θ cos cos 9 cos 9 cos 9 cos cos 9 = cos 9 cos 9 cos 8 これより 歪および応力成分の座標変換公式 89 を用いることによって 以下の関係式を得る 7-
11 = l l = l l = k l = l l = l l = k l = l l = l l = k l = l l = l l = k l = l l = l l = k l = l l = l l = k l = l l = l l = k l = l l = l l = k l = l l = l l = k l = l l = l l = k l = l l = l l = k l = l l = l l = k l 新座標系においても フックの法則は成立するので より 次式を得る = + C + C + C + C + C + C + C + C に式 と を代入することに + C + C + C + C + C + C + C + C + C + C + C + C + C + C + C + C これより C =, C = となる 同様に C =, C =, C =, C =, C =, C = が得られる また = + C + C + C + C + C + C + C + C + C + C + C + C + C + C + C + C = C + C + C + C + C + C + C + C + C より C =, C =, C =, C =, C = となる 同様に C =, C =, C =, C =, C = である 以上をまとめると となる弾性定数は以下のようになる C =, C =, C =, C =, C =, C =, C =, C = これより 独立な弾性定数は 個となり 式 は次式にて与えられる 7-
12 C C C C * C C C * * C C = * * * C C * * * * C * * * * * C - x x 面における対称性 この対称性は x = x, x = x, x = x と変換した場合 弾性定数 C が不変であることを意味する この場合の方向余弦 l は次式にて与えられる = = cos θ cos θ cos θ cos θ cos θ cos θ cos θ cos θ cos θ cos 8 cos 9 cos 9 cos 9 cos cos 9 = cos 9 cos 9 cos これより 歪および応力成分の座標変換公式 89 を用いることによって 以下の関係式を得る 5 = l l = l l = k l = l l = l l = k l = l l = l l = k l = l l = l l = k l = l l = l l = k l = l l = l l = k l = l l = l l = k l = l l = l l = k l = l l = l l = k l = l l = l l = k l = l l = l l = k l = l l = l l = k l 6 7 新座標系においても フックの法則は成立するので より 次式を得る に式 6 と 7 を代入することに 7-
13 = + C + C + C + C + C + C + C + C + C + C + C + C + C + C + C + C + C + C + C + C + C + C + C + C これより C =, C = となる 同様に C =, C =, C =, C =, C =, C = が得られる また = + C + C + C + C + C + C + C + C + C + C + C + C + C + C + C + C = C + C + C + C + C + C + C + C + C より C =, C =, C =, C =, C = となる 同様に C =, C =, C =, C =, C = である 以上をまとめると となる弾性定数は以下のようになる C =, C =, C =, C =, C =, C =, C =, C = 8 これより 独立な弾性定数は 個となり 式 は次式にて与えられる C C C C * C C C * * C C = * * * C * * * * C C * * * * * C 9 - x x 面における対称性 この対称性は x = x, x = x, x = xと変換した場合 弾性定数 C が不変であることを意味する この場合の方向余弦 l は次式にて与えられる = cos cos 9 cos 9 = cos 9 cos 8 cos 9 = cos 9 cos 9 cos cos θ cos θ cos θ cos θ cos θ cos θ cos θ cos θ cos θ これより 歪および応力成分の座標変換公式 89 を用いることによって 以下の関係式を得る 7-
14 = l l = l l = k l = l l = l l = k l = l l = l l = k l = l l = l l = k l = l l = l l = k l = l l = l l = k l = l l = l l = k l = l l = l l = k l = l l = l l = k l = l l = l l = k l = l l = l l = k l = l l = l l = k l 新座標系においても フックの法則は成立するので より 次式を得る = + C + C + C + C + C + C + C + C に式 と を代入することに + C + C + C + C + C + C + C + C + C + C + C + C + C + C + C + C これより C =, C = となる 同様に C =, C =, C =, C =, C =, C = が得られる また = + C + C + C + C + C + C + C + C + C + C + C + C + C + C + C + C = C + C + C + C + C + C + C + C + C より C =, C =, C =, C =, C = となる 同様に C =, C =, C =, C =, C = である 以上をまとめると となる弾性定数は以下のようになる C =, C =, C =, C =, C =, C =, C =, C = これより 独立な弾性定数は 個となり 式 は次式にて与えられる 7-
15 C C C C * C C C * * C C = * * * C C * * * * C * * * * * C 以上より 式 9 を総合することにより 斜方晶の弾性定数は次式にて与えられる C C C * C C * * C = * * * C * * * * C * * * * * C 5. 立方晶の弾性定数の導出立方晶は 斜方晶の対称性に加え 回転対称性も有する つまり 座標変換 x = x, x = x, x = x x = x, x = x, x = x および x = x, x = x, x = x において応力 歪状態は不変である - x = x, x = x, x = x における独立な弾性定数の決定まず 方向余弦 l は次式にて与えられる = = cos θ cos θ cos θ cos θ cos θ cos θ cos θ cos θ cos θ cos 9 cos cos 9 cos 8 cos 9 cos 9 = cos 9 cos 9 cos 6 これより 歪および応力成分の座標変換公式 89 を用いることによって 以下の関係式を得る = l l = l l = k l = l l = l l = k l = l l = l l = k l = l l = l l = k l = l l = l l = k l = l l = l l = k l 7 7-5
16 = l l = l l = k l = l l = l l = k l = l l = l l = k l = l l = l l = k l = l l = l l = k l = l l = l l = k l 8 新座標系においても フックの法則は成立するので に式 7 と 8 を代入することに より 次式を得る なお斜方晶において既に となっている弾性定数成分は とおいた = + C + C + C + C + C + C + C + C これより C, C また = + C + C + C + C + C + C + C + C これより C, C また = + C + C + C + C + C + C + C + C これより C また 7-6
17 = C = = =C また = これより C また =C == =C これより C である 弾性定数に関する関係式は以下のようになる C, C, C 9 これより 独立な弾性定数は次式にて与えられる C C C * C C * * C = * * * C * * * * C * * * * * C 式 の条件は正方晶に対応するので 正方晶における独立な弾性定数は 6 個になり 正方晶の弾性率は式 にて与えられる C C C * C C * * C = * * * C * * * * C * * * * * C
18 - x = x, x = x, x = xにおける独立な弾性定数の決定この条件は - 節において,, とした場合に等しい したがって 式 9 において 添え字を,, のように変換すればよい すなわち C, C, C これより 独立な弾性定数は 次式にて与えられる C C C * C C * * C = * * * C * * * * C * * * * * C - x = x, x = x, x = x における独立な弾性定数の決定この条件は - 節において,, とした場合に等しい したがって 式 9 において 添え字を,, のように変換すればよい すなわち C, C, C これより 独立な弾性定数は 次式にて与えられる C C C * C C * * C = * * * C * * * * C * * * * * C 5 以上より 立方晶の弾性定数は次式にて与えられる C C C * C C * * C = * * * C * * * * C * * * * * C 6 5. 正方晶の弾性定数式 5 より 正方晶軸 回転軸 によって 弾性定数は以下の 種類が存在する 正方晶軸 x 方向 7-8
19 C C C * C C * * C = * * * C * * * * C * * * * * C 66 7 正方晶軸 x 方向 C C C C C C * C C * C C * * C * * C = = * * * C * * * C66 * * * * C55 * * * * C * * * * * C 55 * * * * * C 正方晶軸 x 方向 C C C C C C * C C * C C * * C * * C = = * * * C66 * * * C * * * * C55 * * * * C66 * * * * * C 66 * * * * * C 六方晶の弾性定数 xy 平面上における 6 回転における独立な弾性定数の決定まず 方向余弦 l は次式にて与えられる = = cos θ cos θ cos θ cos θ cos θ cos θ cos θ cos θ cos θ cos 6 cos cos 9 cos 5 cos 6 cos 9 = cos 9 cos 9 cos / / / / これより 歪および応力成分の座標変換公式 89 を用いることによって 以下の関係式を得る 7-9
20 = l l = l l + l l + l l + l l = = l l = l l + l l + l l + l l = + = l l = l l = k l = ll = ll + ll = + = l l = l l + l l = + = l l = l l + l l + l l + l l = + + k l = l l = l l + l l + l l + l l = = l l = l l + l l + l l + l l = + = l l = l l = k l = ll = ll + ll = + = l l = l l + l l = + = l l = l l + l l + l l + l l = + + 新座標系においても フックの法則は成立するので に式 と を代入することに より 次式を得る なお斜方晶において既に となっている弾性定数成分は とおいた = C + C L = M O P L + M O C C + P + C N Q N b g b g b g + C + C C + C + C + C bc C Cg C C + C + C + C = = bc + C g + C + bc + C g + bc + C g これより C, C, C C また b g b g Q 7-
21 = C C + C = + b g b g b = C + C + C C + C + C + C + C b g b g b g = C C C + C + C + C C これより C C, C C, C また = + + C + C これより C 以上より 弾性定数に関する関係式は以下のようになる C, C, C, C C したがって 独立な弾性定数は次式にて与えられる g C C C * C C * * C = * * * C * * * * C C C * * * * * これより 六方晶における独立な弾性定数は 5 個になり 六方晶の弾性率は最終的に式 5 にて与えられる 7-
22 C C C * C C * * C = * * * C * * * * C C C * * * * * 5 7-
入門講座
 第 8 章弾性歪エネルギー評価法 () () 8- Khhtun の弾性歪エネルギ- 評価ここでも簡単のため A-B 元系における不規則相の整合相分離を考え この相分解組織の弾性歪エネルギーを評価する 手順は ステップ ) まず位置 の関数として与えられる濃度場 () を用いて egen 歪場 ε () を定義する ステップ ) 次に全歪場 ε () を均一全歪 ε とそこからの変動量 δε ()
第 8 章弾性歪エネルギー評価法 () () 8- Khhtun の弾性歪エネルギ- 評価ここでも簡単のため A-B 元系における不規則相の整合相分離を考え この相分解組織の弾性歪エネルギーを評価する 手順は ステップ ) まず位置 の関数として与えられる濃度場 () を用いて egen 歪場 ε () を定義する ステップ ) 次に全歪場 ε () を均一全歪 ε とそこからの変動量 δε ()
パソコンシミュレータの現状
 第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
線形弾性体 線形弾性体 応力テンソル とひずみテンソルソル の各成分が線形関係を有する固体. kl 応力テンソル O kl ひずみテンソル
 Constitutive equation of elasti solid Hooke s law λδ μ kk Lame s onstant λ μ ( )( ) ( ) linear elasti solid kl kl Copyright is reserved. No part of this doument may be reprodued for profit. 線形弾性体 線形弾性体
Constitutive equation of elasti solid Hooke s law λδ μ kk Lame s onstant λ μ ( )( ) ( ) linear elasti solid kl kl Copyright is reserved. No part of this doument may be reprodued for profit. 線形弾性体 線形弾性体
Microsoft Word - thesis.doc
 剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
2 図微小要素の流体の流入出 方向の断面の流体の流入出の収支断面 Ⅰ から微小要素に流入出する流体の流量 Q 断面 Ⅰ は 以下のように定式化できる Q 断面 Ⅰ 流量 密度 流速 断面 Ⅰ の面積 微小要素の断面 Ⅰ から だけ移動した断面 Ⅱ を流入出する流体の流量 Q 断面 Ⅱ は以下のように
 3 章 Web に Link 解説 連続式 微分表示 の誘導.64 *4. 連続式連続式は ある領域の内部にある流体の質量の収支が その表面からの流入出の合計と等しくなることを定式化したものであり 流体における質量保存則を示したものである 2. 連続式 微分表示 の誘導図のような微小要素 コントロールボリューム の領域内の流体の増減と外部からの流体の流入出を考えることで定式化できる 微小要素 流入
3 章 Web に Link 解説 連続式 微分表示 の誘導.64 *4. 連続式連続式は ある領域の内部にある流体の質量の収支が その表面からの流入出の合計と等しくなることを定式化したものであり 流体における質量保存則を示したものである 2. 連続式 微分表示 の誘導図のような微小要素 コントロールボリューム の領域内の流体の増減と外部からの流体の流入出を考えることで定式化できる 微小要素 流入
テンソル ( その ) テンソル ( その ) スカラー ( 階のテンソル ) スカラー ( 階のテンソル ) 階数 ベクトル ( 階のテンソル ) ベクトル ( 階のテンソル ) 行列表現 シンボリック表現 [ ]
![テンソル ( その ) テンソル ( その ) スカラー ( 階のテンソル ) スカラー ( 階のテンソル ) 階数 ベクトル ( 階のテンソル ) ベクトル ( 階のテンソル ) 行列表現 シンボリック表現 [ ] テンソル ( その ) テンソル ( その ) スカラー ( 階のテンソル ) スカラー ( 階のテンソル ) 階数 ベクトル ( 階のテンソル ) ベクトル ( 階のテンソル ) 行列表現 シンボリック表現 [ ]](/thumbs/93/113587990.jpg) Tsor th-ordr tsor by dcl xprsso m m Lm m k m k L mk kk quott rul by symbolc xprsso Lk X thrd-ordr tsor cotrcto j j Copyrght s rsrvd. No prt of ths documt my b rproducd for proft. テンソル ( その ) テンソル ( その
Tsor th-ordr tsor by dcl xprsso m m Lm m k m k L mk kk quott rul by symbolc xprsso Lk X thrd-ordr tsor cotrcto j j Copyrght s rsrvd. No prt of ths documt my b rproducd for proft. テンソル ( その ) テンソル ( その
vecrot
 1. ベクトル ベクトル : 方向を持つ量 ベクトルには 1 方向 2 大きさ ( 長さ ) という 2 つの属性がある ベクトルの例 : 物体の移動速度 移動量電場 磁場の強さ風速力トルクなど 2. ベクトルの表現 2.1 矢印で表現される 矢印の長さ : ベクトルの大きさ 矢印の向き : ベクトルの方向 2.2 2 個の点を用いて表現する 始点 () と終点 () を結ぶ半直線の向き : ベクトルの方向
1. ベクトル ベクトル : 方向を持つ量 ベクトルには 1 方向 2 大きさ ( 長さ ) という 2 つの属性がある ベクトルの例 : 物体の移動速度 移動量電場 磁場の強さ風速力トルクなど 2. ベクトルの表現 2.1 矢印で表現される 矢印の長さ : ベクトルの大きさ 矢印の向き : ベクトルの方向 2.2 2 個の点を用いて表現する 始点 () と終点 () を結ぶ半直線の向き : ベクトルの方向
PowerPoint Presentation
 付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
ベクトル公式.rtf
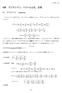 6 章ラプラシアン, ベクトル公式, 定理 6.1 ラプラシアン Laplacian φ はベクトル量である. そこでさらに発散をとると, φ はどういう形になるであろうか? φ = a + a + a φ a + a φ + a φ = φ + φ + φ = 2 φ + 2 φ 2 + 2 φ 2 2 φ = 2 φ 2 + 2 φ 2 + 2 φ 2 = 2 φ したがって,2 階の偏微分演算となる.
6 章ラプラシアン, ベクトル公式, 定理 6.1 ラプラシアン Laplacian φ はベクトル量である. そこでさらに発散をとると, φ はどういう形になるであろうか? φ = a + a + a φ a + a φ + a φ = φ + φ + φ = 2 φ + 2 φ 2 + 2 φ 2 2 φ = 2 φ 2 + 2 φ 2 + 2 φ 2 = 2 φ したがって,2 階の偏微分演算となる.
静的弾性問題の有限要素法解析アルゴリズム
 概要 基礎理論. 応力とひずみおよび平衡方程式. 降伏条件式. 構成式 ( 応力 - ひずみ関係式 ) 有限要素法. 有限要素法の概要. 仮想仕事の原理式と変分原理. 平面ひずみ弾性有限要素法定式化 FEM の基礎方程式平衡方程式. G G G ひずみ - 変位関係式 w w w. kl jkl j D 構成式応力 - ひずみ関係式 ) (. 変位の境界条件力の境界条件境界条件式 t S on V
概要 基礎理論. 応力とひずみおよび平衡方程式. 降伏条件式. 構成式 ( 応力 - ひずみ関係式 ) 有限要素法. 有限要素法の概要. 仮想仕事の原理式と変分原理. 平面ひずみ弾性有限要素法定式化 FEM の基礎方程式平衡方程式. G G G ひずみ - 変位関係式 w w w. kl jkl j D 構成式応力 - ひずみ関係式 ) (. 変位の境界条件力の境界条件境界条件式 t S on V
PowerPoint プレゼンテーション
 電磁波工学 第 5 回平面波の媒質への垂直および射入射と透過 柴田幸司 Bounda Plan Rgon ε μ Rgon Mdum ( ガラスなど ε μ z 平面波の反射と透過 垂直入射の場合 左図に示す様に 平面波が境界面に対して垂直に入射する場合を考える この時の入射波を とすると 入射波は境界において 透過波 と とに分解される この時の透過量を 反射量を Γ とおくと 領域 における媒質の誘電率に対して透過量
電磁波工学 第 5 回平面波の媒質への垂直および射入射と透過 柴田幸司 Bounda Plan Rgon ε μ Rgon Mdum ( ガラスなど ε μ z 平面波の反射と透過 垂直入射の場合 左図に示す様に 平面波が境界面に対して垂直に入射する場合を考える この時の入射波を とすると 入射波は境界において 透過波 と とに分解される この時の透過量を 反射量を Γ とおくと 領域 における媒質の誘電率に対して透過量
Phase field法を用いた材料組織形成過程の計算機シミュレ-ション
 Cahn-Hilliard Cahn-Hilliard 4 Cahn-Hilliard 5 x F (x F v F µ x (- µ v (- v M F M µ (- M F J v (- J v M µ (- Fik (-4 (- (-5 J D D µ M (-4 (-5 µ µ + RT ln a γ a γ (-5 (-6 D D * (ln γ * (ln γ D D +, D D +
Cahn-Hilliard Cahn-Hilliard 4 Cahn-Hilliard 5 x F (x F v F µ x (- µ v (- v M F M µ (- M F J v (- J v M µ (- Fik (-4 (- (-5 J D D µ M (-4 (-5 µ µ + RT ln a γ a γ (-5 (-6 D D * (ln γ * (ln γ D D +, D D +
Microsoft Word - 1B2011.doc
 第 14 回モールの定理 ( 単純梁の場合 ) ( モールの定理とは何か?p.11) 例題 下記に示す単純梁の C 点のたわみ角 θ C と, たわみ δ C を求めよ ただし, 部材の曲げ 剛性は材軸に沿って一様で とする C D kn B 1.5m 0.5m 1.0m 解答 1 曲げモーメント図を描く,B 点の反力を求める kn kn 4 kn 曲げモーメント図を描く knm 先に得られた曲げモーメントの値を
第 14 回モールの定理 ( 単純梁の場合 ) ( モールの定理とは何か?p.11) 例題 下記に示す単純梁の C 点のたわみ角 θ C と, たわみ δ C を求めよ ただし, 部材の曲げ 剛性は材軸に沿って一様で とする C D kn B 1.5m 0.5m 1.0m 解答 1 曲げモーメント図を描く,B 点の反力を求める kn kn 4 kn 曲げモーメント図を描く knm 先に得られた曲げモーメントの値を
線積分.indd
 線積分 線積分 ( n, n, n ) (ξ n, η n, ζ n ) ( n-, n-, n- ) (ξ k, η k, ζ k ) ( k, k, k ) ( k-, k-, k- ) 物体に力 を作用させて位置ベクトル A の点 A から位置ベクトル の点 まで曲線 に沿って物体を移動させたときの仕事 W は 次式で計算された A, A, W : d 6 d+ d+ d@,,, d+ d+
線積分 線積分 ( n, n, n ) (ξ n, η n, ζ n ) ( n-, n-, n- ) (ξ k, η k, ζ k ) ( k, k, k ) ( k-, k-, k- ) 物体に力 を作用させて位置ベクトル A の点 A から位置ベクトル の点 まで曲線 に沿って物体を移動させたときの仕事 W は 次式で計算された A, A, W : d 6 d+ d+ d@,,, d+ d+
点におけるひずみの定義 ( その1)-(ε, ε,γ ) の定義ひずみは 構造物の中で変化しているのが一般的である このために 応力と同様に 構造物内の任意の点で定義できるようにした方がよい また 応力と同様に 一つの点に注目しても ひずみは向きによって値が異なる これらを勘案し あ
 3. 変位とひずみ 3.1 変位関数構造物は外力の作用の下で変形する いま この変形により構造物内の任意の点 P(,,z) が P (',',z') に移動したものとする ( 図 3.1 参照 ) (,,z) は変形前の点 Pの座標 (',', z') は変形後の座標である このとき 次式で示される変形前後の座標の差 u ='- u ='- u z =z'-z (3.1) を変位成分と呼ぶ 変位 (
3. 変位とひずみ 3.1 変位関数構造物は外力の作用の下で変形する いま この変形により構造物内の任意の点 P(,,z) が P (',',z') に移動したものとする ( 図 3.1 参照 ) (,,z) は変形前の点 Pの座標 (',', z') は変形後の座標である このとき 次式で示される変形前後の座標の差 u ='- u ='- u z =z'-z (3.1) を変位成分と呼ぶ 変位 (
ニュートン重力理論.pptx
 3 ニュートン重力理論 1. ニュートン重力理論の基本 : 慣性系とガリレイ変換不変性 2. ニュートン重力理論の定式化 3. 等価原理 4. 流体力学方程式とその基礎 3.1 ニュートン重力理論の基本 u ニュートンの第一法則 = 力がかからなければ 等速直線運動を続ける u 等速直線運動に見える系を 慣性系 と呼ぶ ² 直線とはどんな空間の直線か? ニュートン理論では 3 次元ユークリッド空間
3 ニュートン重力理論 1. ニュートン重力理論の基本 : 慣性系とガリレイ変換不変性 2. ニュートン重力理論の定式化 3. 等価原理 4. 流体力学方程式とその基礎 3.1 ニュートン重力理論の基本 u ニュートンの第一法則 = 力がかからなければ 等速直線運動を続ける u 等速直線運動に見える系を 慣性系 と呼ぶ ² 直線とはどんな空間の直線か? ニュートン理論では 3 次元ユークリッド空間
相対性理論入門 1 Lorentz 変換 光がどのような座標系に対しても同一の速さ c で進むことから導かれる座標の一次変換である. (x, y, z, t ) の座標系が (x, y, z, t) の座標系に対して x 軸方向に w の速度で進んでいる場合, 座標系が一次変換で関係づけられるとする
 相対性理論入門 Lorentz 変換 光がどのような座標系に対しても同一の速さ で進むことから導かれる座標の一次変換である. x, y, z, t ) の座標系が x, y, z, t) の座標系に対して x 軸方向に w の速度で進んでいる場合, 座標系が一次変換で関係づけられるとすると, x A x wt) y y z z t Bx + Dt 弨弱弩弨弲弩弨弳弩弨弴弩 が成立する. 図 : 相対速度
相対性理論入門 Lorentz 変換 光がどのような座標系に対しても同一の速さ で進むことから導かれる座標の一次変換である. x, y, z, t ) の座標系が x, y, z, t) の座標系に対して x 軸方向に w の速度で進んでいる場合, 座標系が一次変換で関係づけられるとすると, x A x wt) y y z z t Bx + Dt 弨弱弩弨弲弩弨弳弩弨弴弩 が成立する. 図 : 相対速度
合金の凝固
 合金の一方向凝固 ( 古典論 by T.Koyama (-3 分配係数平衡分配係数は, と定義される 凝固において基本的にベースとなる独立変数は液相の濃度である 状態図の局所平衡を仮定することにより から が決まる つまり は従属変数となり 特に が定数である場合 は上記の式から簡単に計算できる 融点をT とし 液相線の温度 T と固相線の温度 T をそれぞれ m T Tm α, T Tm α とすると
合金の一方向凝固 ( 古典論 by T.Koyama (-3 分配係数平衡分配係数は, と定義される 凝固において基本的にベースとなる独立変数は液相の濃度である 状態図の局所平衡を仮定することにより から が決まる つまり は従属変数となり 特に が定数である場合 は上記の式から簡単に計算できる 融点をT とし 液相線の温度 T と固相線の温度 T をそれぞれ m T Tm α, T Tm α とすると
微分方程式による現象記述と解きかた
 微分方程式による現象記述と解きかた 土木工学 : 公共諸施設 構造物の有用目的にむけた合理的な実現をはかる方法 ( 技術 ) に関する学 橋梁 トンネル ダム 道路 港湾 治水利水施設 安全化 利便化 快適化 合法則的 経済的 自然および人口素材によって作られた 質量保存則 構造物の自然的な性質 作用 ( 外力による応答 ) エネルギー則 の解明 社会的諸現象のうち マスとしての移動 流通 運動量則
微分方程式による現象記述と解きかた 土木工学 : 公共諸施設 構造物の有用目的にむけた合理的な実現をはかる方法 ( 技術 ) に関する学 橋梁 トンネル ダム 道路 港湾 治水利水施設 安全化 利便化 快適化 合法則的 経済的 自然および人口素材によって作られた 質量保存則 構造物の自然的な性質 作用 ( 外力による応答 ) エネルギー則 の解明 社会的諸現象のうち マスとしての移動 流通 運動量則
弾性定数の対称性について
 () by T. oyama () ij C ij = () () C, C, C () ij ji ij ijlk ij ij () C C C C C C * C C C C C * * C C C C = * * * C C C * * * * C C * * * * * C () * P (,, ) P (,, ) lij = () P (,, ) P(,, ) (,, ) P (, 00,
() by T. oyama () ij C ij = () () C, C, C () ij ji ij ijlk ij ij () C C C C C C * C C C C C * * C C C C = * * * C C C * * * * C C * * * * * C () * P (,, ) P (,, ) lij = () P (,, ) P(,, ) (,, ) P (, 00,
<4D F736F F D20824F B CC92E8979D814696CA90CF95AA82C691CC90CF95AA2E646F63>
 1/1 平成 23 年 3 月 24 日午後 6 時 52 分 6 ガウスの定理 : 面積分と体積分 6 ガウスの定理 : 面積分と体積分 Ⅰ. 直交座標系 ガウスの定理は 微分して すぐに積分すると元に戻るというルールを 3 次元積分に適用した定理になります よく知っているのは 簡単化のため 変数が1つの場合は dj ( d ( ににします全微分 = 偏微分 d = d = J ( + C d です
1/1 平成 23 年 3 月 24 日午後 6 時 52 分 6 ガウスの定理 : 面積分と体積分 6 ガウスの定理 : 面積分と体積分 Ⅰ. 直交座標系 ガウスの定理は 微分して すぐに積分すると元に戻るというルールを 3 次元積分に適用した定理になります よく知っているのは 簡単化のため 変数が1つの場合は dj ( d ( ににします全微分 = 偏微分 d = d = J ( + C d です
Microsoft Word - 断面諸量
 応用力学 Ⅱ 講義資料 / 断面諸量 断面諸量 断面 次 次モーメントの定義 図 - に示すような形状を有する横断面を考え その全断面積を とする いま任意に定めた直交座標軸 O-, をとり また図中の斜線部の微小面積要素を d とするとき d, d () で定義される, をそれぞれ与えられた横断面の 軸, 軸に関する断面 次モーメント (geometrcal moment of area) という
応用力学 Ⅱ 講義資料 / 断面諸量 断面諸量 断面 次 次モーメントの定義 図 - に示すような形状を有する横断面を考え その全断面積を とする いま任意に定めた直交座標軸 O-, をとり また図中の斜線部の微小面積要素を d とするとき d, d () で定義される, をそれぞれ与えられた横断面の 軸, 軸に関する断面 次モーメント (geometrcal moment of area) という
Microsoft PowerPoint - 夏の学校(CFD).pptx
 /9/5 FD( 計算流体力学 ) の基礎理論 性能 運動分野 夏の学校 神戸大学大学院海事科学研究科勝井辰博 流体の質量保存 流体要素内の質量の増加率 [ 単位時間当たりの増加量 ] 単位時間に流体要素に流入する質量 流体要素 Fl lm (orol olm) v ( ) ガウスの定理 v( ) /9/5 = =( ) b=b =(b b b ) b= b = b + b + b アインシュタイン表記
/9/5 FD( 計算流体力学 ) の基礎理論 性能 運動分野 夏の学校 神戸大学大学院海事科学研究科勝井辰博 流体の質量保存 流体要素内の質量の増加率 [ 単位時間当たりの増加量 ] 単位時間に流体要素に流入する質量 流体要素 Fl lm (orol olm) v ( ) ガウスの定理 v( ) /9/5 = =( ) b=b =(b b b ) b= b = b + b + b アインシュタイン表記
補足 中学で学習したフレミング左手の法則 ( 電 磁 力 ) と関連付けると覚えやすい 電磁力は電流と磁界の外積で表される 力 F 磁 電磁力 F li 右ねじの回転の向き電 li ( l は導線の長さ ) 補足 有向線分とベクトル有向線分 : 矢印の位
 http://totemt.sur.ne.p 外積 ( ベクトル積 ) の活用 ( 面積, 法線ベクトル, 平面の方程式 ) 3 次元空間の つのベクトルの積が つのベクトルを与えるようなベクトルの掛け算 ベクトルの積がベクトルを与えることからベクトル積とも呼ばれる これに対し内積は符号と大きさをもつ量 ( スカラー量 ) を与えるので, スカラー積とも呼ばれる 外積を使うと, 平行四辺形や三角形の面積,
http://totemt.sur.ne.p 外積 ( ベクトル積 ) の活用 ( 面積, 法線ベクトル, 平面の方程式 ) 3 次元空間の つのベクトルの積が つのベクトルを与えるようなベクトルの掛け算 ベクトルの積がベクトルを与えることからベクトル積とも呼ばれる これに対し内積は符号と大きさをもつ量 ( スカラー量 ) を与えるので, スカラー積とも呼ばれる 外積を使うと, 平行四辺形や三角形の面積,
<4D F736F F D2097CD8A7793FC96E582BD82ED82DD8A E6318FCD2E646F63>
 - 第 章たわみ角法の基本式 ポイント : たわみ角法の基本式を理解する たわみ角法の基本式を梁の微分方程式より求める 本章では たわみ角法の基本式を導くことにする 基本式の誘導法は各種あるが ここでは 梁の微分方程式を解いて基本式を求める方法を採用する この本で使用する座標系は 右手 右ネジの法則に従った座標を用いる また ひとつの部材では 図 - に示すように部材の左端の 点を原点とし 軸線を
- 第 章たわみ角法の基本式 ポイント : たわみ角法の基本式を理解する たわみ角法の基本式を梁の微分方程式より求める 本章では たわみ角法の基本式を導くことにする 基本式の誘導法は各種あるが ここでは 梁の微分方程式を解いて基本式を求める方法を採用する この本で使用する座標系は 右手 右ネジの法則に従った座標を用いる また ひとつの部材では 図 - に示すように部材の左端の 点を原点とし 軸線を
Microsoft Word - 201hyouka-tangen-1.doc
 数学 Ⅰ 評価規準の作成 ( 単元ごと ) 数学 Ⅰ の目標及び図形と計量について理解させ 基礎的な知識の習得と技能の習熟を図り それらを的確に活用する機能を伸ばすとともに 数学的な見方や考え方のよさを認識できるようにする 評価の観点の趣旨 式と不等式 二次関数及び図形と計量における考え方に関 心をもつとともに 数学的な見方や考え方のよさを認識し それらを事象の考察に活用しようとする 式と不等式 二次関数及び図形と計量における数学的な見
数学 Ⅰ 評価規準の作成 ( 単元ごと ) 数学 Ⅰ の目標及び図形と計量について理解させ 基礎的な知識の習得と技能の習熟を図り それらを的確に活用する機能を伸ばすとともに 数学的な見方や考え方のよさを認識できるようにする 評価の観点の趣旨 式と不等式 二次関数及び図形と計量における考え方に関 心をもつとともに 数学的な見方や考え方のよさを認識し それらを事象の考察に活用しようとする 式と不等式 二次関数及び図形と計量における数学的な見
<4D F736F F D E4F8E9F82C982A882AF82E98D7397F1>
 3 三次における行列 要旨高校では ほとんど 2 2 の正方行列しか扱ってなく 三次の正方行列について考えてみたかったため 数 C で学んだ定理を三次の正方行列に応用して 自分たちで仮説を立てて求めていったら 空間における回転移動を表す行列 三次のケーリー ハミルトンの定理 三次における逆行列を求めたり 仮説をたてることができた. 目的 数 C で学んだ定理を三次の正方行列に応用する 2. 概要目的の到達点として
3 三次における行列 要旨高校では ほとんど 2 2 の正方行列しか扱ってなく 三次の正方行列について考えてみたかったため 数 C で学んだ定理を三次の正方行列に応用して 自分たちで仮説を立てて求めていったら 空間における回転移動を表す行列 三次のケーリー ハミルトンの定理 三次における逆行列を求めたり 仮説をたてることができた. 目的 数 C で学んだ定理を三次の正方行列に応用する 2. 概要目的の到達点として
PowerPoint Presentation
 Non-linea factue mechanics き裂先端付近の塑性変形 塑性域 R 破壊進行領域応カ特異場 Ω R R Hutchinson, Rice and Rosengen 全ひずみ塑性理論に基づいた解析 現段階のひずみは 除荷がないとすると現段階の応力で一義的に決まる 単純引張り時の応カーひずみ関係 ( 構成方程式 ): ( ) ( ) n () y y y ここで α,n 定数, /
Non-linea factue mechanics き裂先端付近の塑性変形 塑性域 R 破壊進行領域応カ特異場 Ω R R Hutchinson, Rice and Rosengen 全ひずみ塑性理論に基づいた解析 現段階のひずみは 除荷がないとすると現段階の応力で一義的に決まる 単純引張り時の応カーひずみ関係 ( 構成方程式 ): ( ) ( ) n () y y y ここで α,n 定数, /
Microsoft Word - 補論3.2
 補論 3. 多変量 GARC モデル 07//6 新谷元嗣 藪友良 対数尤度関数 3 章 7 節では 変量の対数尤度を求めた ここでは多変量の場合 とくに 変量について対数尤度を求める 誤差項 は平均 0 で 次元の正規分布に従うとする 単純化のため 分散と共分散は時間を通じて一定としよう ( この仮定は後で変更される ) したがって ij から添え字 を除くことができる このとき と の尤度関数は
補論 3. 多変量 GARC モデル 07//6 新谷元嗣 藪友良 対数尤度関数 3 章 7 節では 変量の対数尤度を求めた ここでは多変量の場合 とくに 変量について対数尤度を求める 誤差項 は平均 0 で 次元の正規分布に従うとする 単純化のため 分散と共分散は時間を通じて一定としよう ( この仮定は後で変更される ) したがって ij から添え字 を除くことができる このとき と の尤度関数は
Microsoft PowerPoint - 10.pptx
 m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
OCW-iダランベールの原理
 講義名連続体力学配布資料 OCW- 第 2 回ダランベールの原理 無機材料工学科准教授安田公一 1 はじめに今回の講義では, まず, 前半でダランベールの原理について説明する これを用いると, 動力学の問題を静力学の問題として解くことができ, さらに, 前回の仮想仕事の原理を適用すると動力学問題も簡単に解くことができるようになる また, 後半では, ダランベールの原理の応用として ラグランジュ方程式の導出を示す
講義名連続体力学配布資料 OCW- 第 2 回ダランベールの原理 無機材料工学科准教授安田公一 1 はじめに今回の講義では, まず, 前半でダランベールの原理について説明する これを用いると, 動力学の問題を静力学の問題として解くことができ, さらに, 前回の仮想仕事の原理を適用すると動力学問題も簡単に解くことができるようになる また, 後半では, ダランベールの原理の応用として ラグランジュ方程式の導出を示す
Chap2.key
 . f( ) V (V V ) V e + V e V V V V ( ) V V ( ) E. - () V (0 ) () V (0 ) () V (0 ) (4) V ( ) E. - () V (0 ) () V (0 ) O r θ ( ) ( ) : (r θ) : { r cos θ r sn θ { r + () V (0 ) (4) V ( ) θ θ arg( ) : π π
. f( ) V (V V ) V e + V e V V V V ( ) V V ( ) E. - () V (0 ) () V (0 ) () V (0 ) (4) V ( ) E. - () V (0 ) () V (0 ) O r θ ( ) ( ) : (r θ) : { r cos θ r sn θ { r + () V (0 ) (4) V ( ) θ θ arg( ) : π π
例 e 指数関数的に減衰する信号を h( a < + a a すると, それらのラプラス変換は, H ( ) { e } e インパルス応答が h( a < ( ただし a >, U( ) { } となるシステムにステップ信号 ( y( のラプラス変換 Y () は, Y ( ) H ( ) X (
 第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
Microsoft Word - 中村工大連携教材(最終 ).doc
 音速について考えてみよう! 金沢工業大学 中村晃 ねらい 私たちの身の回りにはいろいろな種類の波が存在する. 体感できる波もあれば, できない波もある. その中で音は体感できる最も身近な波である. 遠くで雷が光ってから雷鳴が届くまで数秒間時間がかかることにより, 音の方が光より伝わるのに時間がかかることも経験していると思う. 高校の物理の授業で音の伝わる速さ ( 音速 ) は約 m/s で, 詳しく述べると
音速について考えてみよう! 金沢工業大学 中村晃 ねらい 私たちの身の回りにはいろいろな種類の波が存在する. 体感できる波もあれば, できない波もある. その中で音は体感できる最も身近な波である. 遠くで雷が光ってから雷鳴が届くまで数秒間時間がかかることにより, 音の方が光より伝わるのに時間がかかることも経験していると思う. 高校の物理の授業で音の伝わる速さ ( 音速 ) は約 m/s で, 詳しく述べると
1/17 平成 29 年 3 月 25 日 ( 土 ) 午前 11 時 1 分量子力学とクライン ゴルドン方程式 ( 学部 3 年次秋学期向 ) 量子力学とクライン ゴルドン方程式 素粒子の満たす場 y ( x,t) の運動方程式 : クライン ゴルドン方程式 : æ 3 ö ç å è m= 0
 /7 平成 9 年 月 5 日 ( 土 午前 時 分量子力学とクライン ゴルドン方程式 ( 学部 年次秋学期向 量子力学とクライン ゴルドン方程式 素粒子の満たす場 (,t の運動方程式 : クライン ゴルドン方程式 : æ ö ç å è = 0 c + ( t =, 0 (. = 0 ì æ = = = ö æ ö æ ö ç ì =,,,,,,, ç 0 = ç Ñ 0 = ç Ñ 0 Ñ Ñ
/7 平成 9 年 月 5 日 ( 土 午前 時 分量子力学とクライン ゴルドン方程式 ( 学部 年次秋学期向 量子力学とクライン ゴルドン方程式 素粒子の満たす場 (,t の運動方程式 : クライン ゴルドン方程式 : æ ö ç å è = 0 c + ( t =, 0 (. = 0 ì æ = = = ö æ ö æ ö ç ì =,,,,,,, ç 0 = ç Ñ 0 = ç Ñ 0 Ñ Ñ
第3章 ひずみ
 第 4 章 応力とひずみの関係 4. 単軸応力を受ける弾性体の応力とひずみの関係 温度一定の下で, 負荷による変形が徐荷によって完全に回復する場合を広義の弾性というが, 狭義の弾 性では, 負荷過程と徐荷過程で応力 - ひずみ関係が一致しない場合は含めず ( 図 - 参照 ), 与えられたひ ずみ状態に対して応力が一意に定まる, つまり応力がひずみの関数と して表される. このような物体を狭義の弾性体
第 4 章 応力とひずみの関係 4. 単軸応力を受ける弾性体の応力とひずみの関係 温度一定の下で, 負荷による変形が徐荷によって完全に回復する場合を広義の弾性というが, 狭義の弾 性では, 負荷過程と徐荷過程で応力 - ひずみ関係が一致しない場合は含めず ( 図 - 参照 ), 与えられたひ ずみ状態に対して応力が一意に定まる, つまり応力がひずみの関数と して表される. このような物体を狭義の弾性体
数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュ
 数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュレーションによって計算してみる 4.1 放物運動一様な重力場における放物運動を考える 一般に質量の物体に作用する力をとすると運動方程式は
数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュレーションによって計算してみる 4.1 放物運動一様な重力場における放物運動を考える 一般に質量の物体に作用する力をとすると運動方程式は
Microsoft PowerPoint - H21生物計算化学2.ppt
 演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
平成 年 月 7 日 ( 土 第 75 回数学教育実践研究会アスティ 45 ビル F セミナールーム A 札幌医科大学 年 P ab, を正の定数とする 平面上において ( a, を中心とする円 Q 4 C と (, b を中心とする円 C が 原点 O で外接している また P を円 C 上の点と
 平成 年 月 7 日 ( 土 第 75 回数学教育実践研究会アスティ 45 ビル F セミナールーム 微分積分の拡張 変数関数問題へのアプローチ 予選決勝優勝法からラグランジュ未定乗数法 松本睦郎 ( 札幌北高等学校 変数関数の最大値 最小値に関する問題には多様なアプローチ法がある 文字を固定した 予選決勝優勝法, 計算のみで解法する 文字消去法, 微分積分を利用した ラグランジュ未定乗数法 がある
平成 年 月 7 日 ( 土 第 75 回数学教育実践研究会アスティ 45 ビル F セミナールーム 微分積分の拡張 変数関数問題へのアプローチ 予選決勝優勝法からラグランジュ未定乗数法 松本睦郎 ( 札幌北高等学校 変数関数の最大値 最小値に関する問題には多様なアプローチ法がある 文字を固定した 予選決勝優勝法, 計算のみで解法する 文字消去法, 微分積分を利用した ラグランジュ未定乗数法 がある
<4D F736F F F696E74202D E94D58B9393AE82F AC82B782E982BD82DF82CC8AEE E707074>
 地盤数値解析学特論 防災環境地盤工学研究室村上哲 Mrakam, Satoh. 地盤挙動を把握するための基礎. 変位とひずみ. 力と応力. 地盤の変形と応力. 変位とひずみ 変形勾配テンソルひずみテンソル ひずみテンソル : 材料線素の長さの 乗の変化量の尺度 Green-Lagrange のひずみテンソルと Alman のひずみテンソル 微小変形状態でのひずみテンソル ひずみテンソルの物理的な意味
地盤数値解析学特論 防災環境地盤工学研究室村上哲 Mrakam, Satoh. 地盤挙動を把握するための基礎. 変位とひずみ. 力と応力. 地盤の変形と応力. 変位とひずみ 変形勾配テンソルひずみテンソル ひずみテンソル : 材料線素の長さの 乗の変化量の尺度 Green-Lagrange のひずみテンソルと Alman のひずみテンソル 微小変形状態でのひずみテンソル ひずみテンソルの物理的な意味
構造力学Ⅰ第12回
 第 回材の座屈 (0 章 ) p.5~ ( 復習 ) モールの定理 ( 手順 ) 座屈とは 荷重により梁に生じた曲げモーメントをで除して仮想荷重と考える 座屈荷重 偏心荷重 ( 曲げと軸力 ) 断面の核 この仮想荷重に対するある点でのせん断力 たわみ角に相当する曲げモーメント たわみに相当する ( 例 ) 単純梁の支点のたわみ角 : は 図 を仮想荷重と考えたときの 点の支点反力 B は 図 を仮想荷重と考えたときのB
第 回材の座屈 (0 章 ) p.5~ ( 復習 ) モールの定理 ( 手順 ) 座屈とは 荷重により梁に生じた曲げモーメントをで除して仮想荷重と考える 座屈荷重 偏心荷重 ( 曲げと軸力 ) 断面の核 この仮想荷重に対するある点でのせん断力 たわみ角に相当する曲げモーメント たわみに相当する ( 例 ) 単純梁の支点のたわみ角 : は 図 を仮想荷重と考えたときの 点の支点反力 B は 図 を仮想荷重と考えたときのB
<4D F736F F D20824F F6490CF95AA82C696CA90CF95AA2E646F63>
 1/15 平成 3 年 3 月 4 日午後 6 時 49 分 5 ベクトルの 重積分と面積分 5 重積分と面積分 Ⅰ. 重積分 と で 回積分することを 重積分 といいます この 重積分は何を意味しているのでしょう? 通常の積分 (1 重積分 ) では C d 図 1a 1 f d (5.1) 1 f d f ( ) は 図形的には図 1a のように面積を表しています つまり 1 f ( ) を高さとしてプロットすると図
1/15 平成 3 年 3 月 4 日午後 6 時 49 分 5 ベクトルの 重積分と面積分 5 重積分と面積分 Ⅰ. 重積分 と で 回積分することを 重積分 といいます この 重積分は何を意味しているのでしょう? 通常の積分 (1 重積分 ) では C d 図 1a 1 f d (5.1) 1 f d f ( ) は 図形的には図 1a のように面積を表しています つまり 1 f ( ) を高さとしてプロットすると図
DVIOUT
 最適レギュレータ 松尾研究室資料 第 最適レギュレータ 節時不変型無限時間最適レギュレータ 状態フィードバックの可能な場合の無限時間問題における最適レギュレータについて確定系について説明する. ここで, レギュレータとは状態量をゼロにするようなコントローラのことである. なぜ, 無限時間問題のみを述べるかという理由は以下のとおりである. 有限時間の最適レギュレータ問題の場合の最適フィードバックゲインは微分方程式の解から構成される時間関数として表現される.
最適レギュレータ 松尾研究室資料 第 最適レギュレータ 節時不変型無限時間最適レギュレータ 状態フィードバックの可能な場合の無限時間問題における最適レギュレータについて確定系について説明する. ここで, レギュレータとは状態量をゼロにするようなコントローラのことである. なぜ, 無限時間問題のみを述べるかという理由は以下のとおりである. 有限時間の最適レギュレータ問題の場合の最適フィードバックゲインは微分方程式の解から構成される時間関数として表現される.
例題1 転がり摩擦
 重心 5.. 重心問題解法虎の巻. 半円 分円. 円弧. 扇形. 半球殻 5. 半球体 6. 厚みのある半球殻 7. 三角形 8. 円錐 9. 円錐台. 穴あき板. 空洞のある半球ボール 重心問題解法虎の巻 関西大学工学部物理学教室 齊藤正 重心を求める場合 質点系の重心の求め方が基本 実際の物体では連続体であるので 積分形式で求める場合が多い これらの式は 次元のベクトル形式で書かれている通り つの式は実際には
重心 5.. 重心問題解法虎の巻. 半円 分円. 円弧. 扇形. 半球殻 5. 半球体 6. 厚みのある半球殻 7. 三角形 8. 円錐 9. 円錐台. 穴あき板. 空洞のある半球ボール 重心問題解法虎の巻 関西大学工学部物理学教室 齊藤正 重心を求める場合 質点系の重心の求め方が基本 実際の物体では連続体であるので 積分形式で求める場合が多い これらの式は 次元のベクトル形式で書かれている通り つの式は実際には
Microsoft PowerPoint - 第3回2.ppt
 講義内容 講義内容 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 ベクトルの直交性 3
講義内容 講義内容 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 ベクトルの直交性 3
座標系.rtf
 2 章座標系 場 空間は3 次元なので, ベクトルを表現するには少なくとも3 成分を指定する必要がある. そのために座標系が必要となる. 座標系として最も一般的なものは,,, 成分を使った直角座標系である. しかし, 他にも円柱座標, 球座標, だ円座標, 放物線座標など様々なものがある. 現在までに3 成分で変数分離可能な座標系は11 個あるといわれている (Moon & Spencer, Field
2 章座標系 場 空間は3 次元なので, ベクトルを表現するには少なくとも3 成分を指定する必要がある. そのために座標系が必要となる. 座標系として最も一般的なものは,,, 成分を使った直角座標系である. しかし, 他にも円柱座標, 球座標, だ円座標, 放物線座標など様々なものがある. 現在までに3 成分で変数分離可能な座標系は11 個あるといわれている (Moon & Spencer, Field
学習指導要領
 (1) 数と式 学習指導要領 数と式 (1) 式の計算二次の乗法公式及び因数分解の公式の理解を深め 式を多面的にみたり目的に応じて式を適切に変形したりすること 東京都立町田高等学校学力スタンダード 整式の加法 減法 乗法展開の公式を利用できる 式を1 つの文字におき換えることによって, 式の計算を簡略化することができる 式の形の特徴に着目して変形し, 展開の公式が適用できるようにすることができる 因数分解因数分解の公式を利用できる
(1) 数と式 学習指導要領 数と式 (1) 式の計算二次の乗法公式及び因数分解の公式の理解を深め 式を多面的にみたり目的に応じて式を適切に変形したりすること 東京都立町田高等学校学力スタンダード 整式の加法 減法 乗法展開の公式を利用できる 式を1 つの文字におき換えることによって, 式の計算を簡略化することができる 式の形の特徴に着目して変形し, 展開の公式が適用できるようにすることができる 因数分解因数分解の公式を利用できる
技術者のための構造力学 2014/06/11 1. はじめに 資料 2 節点座標系による傾斜支持節点節点の処理 三好崇夫加藤久人 従来, マトリックス変位法に基づく骨組解析を紹介する教科書においては, 全体座標系に対して傾斜 した斜面上の支持条件を考慮する処理方法として, 一旦, 傾斜支持を無視した
 . はじめに 資料 節点座標系による傾斜支持節点節点の処理 三好崇夫加藤久人 従来, マトリックス変位法に基づく骨組解析を紹介する教科書においては, 全体座標系に対して傾斜 した斜面上の支持条件を考慮する処理方法として, 一旦, 傾斜支持を無視した全体座標系に関する構造 全体の剛性マトリックスを組み立てた後に, 傾斜支持する節点に関して対応する剛性成分を座標変換に よって傾斜方向に回転処理し, その後は通常の全体座標系に対して傾斜していない支持点に対するのと
. はじめに 資料 節点座標系による傾斜支持節点節点の処理 三好崇夫加藤久人 従来, マトリックス変位法に基づく骨組解析を紹介する教科書においては, 全体座標系に対して傾斜 した斜面上の支持条件を考慮する処理方法として, 一旦, 傾斜支持を無視した全体座標系に関する構造 全体の剛性マトリックスを組み立てた後に, 傾斜支持する節点に関して対応する剛性成分を座標変換に よって傾斜方向に回転処理し, その後は通常の全体座標系に対して傾斜していない支持点に対するのと
2011年度 大阪大・理系数学
 0 大阪大学 ( 理系 ) 前期日程問題 解答解説のページへ a a を自然数とする O を原点とする座標平面上で行列 A= a の表す 次変換 を f とする cosθ siθ () >0 および0θ
0 大阪大学 ( 理系 ) 前期日程問題 解答解説のページへ a a を自然数とする O を原点とする座標平面上で行列 A= a の表す 次変換 を f とする cosθ siθ () >0 および0θ
FEM原理講座 (サンプルテキスト)
 サンプルテキスト FEM 原理講座 サイバネットシステム株式会社 8 年 月 9 日作成 サンプルテキストについて 各講師が 講義の内容が伝わりやすいページ を選びました テキストのページは必ずしも連続していません 一部を抜粋しています 幾何光学講座については 実物のテキストではなくガイダンスを掲載いたします 対象とする構造系 物理モデル 連続体 固体 弾性体 / 弾塑性体 / 粘弾性体 / 固体
サンプルテキスト FEM 原理講座 サイバネットシステム株式会社 8 年 月 9 日作成 サンプルテキストについて 各講師が 講義の内容が伝わりやすいページ を選びました テキストのページは必ずしも連続していません 一部を抜粋しています 幾何光学講座については 実物のテキストではなくガイダンスを掲載いたします 対象とする構造系 物理モデル 連続体 固体 弾性体 / 弾塑性体 / 粘弾性体 / 固体
Microsoft PowerPoint - シミュレーション工学-2010-第1回.ppt
 シミュレーション工学 ( 後半 ) 東京大学人工物工学研究センター 鈴木克幸 CA( Compter Aded geerg ) r. Jaso Lemo (SC, 98) 設計者が解析ツールを使いこなすことにより 設計の評価 設計の質の向上を図る geerg の本質の 計算機による支援 (CA CAM などより広い名前 ) 様々な汎用ソフトの登場 工業製品の設計に不可欠のツール 構造解析 流体解析
シミュレーション工学 ( 後半 ) 東京大学人工物工学研究センター 鈴木克幸 CA( Compter Aded geerg ) r. Jaso Lemo (SC, 98) 設計者が解析ツールを使いこなすことにより 設計の評価 設計の質の向上を図る geerg の本質の 計算機による支援 (CA CAM などより広い名前 ) 様々な汎用ソフトの登場 工業製品の設計に不可欠のツール 構造解析 流体解析
Microsoft Word - 町田・全 H30学力スタ 別紙1 1年 数学Ⅰ.doc
 (1) 数と式 学習指導要領 都立町田高校 学力スタンダード ア 数と集合 ( ア ) 実数 根号を含む式の計算 数を実数まで拡張する意義を理解し 簡単な 循環小数を表す記号を用いて, 分数を循環小数で表 無理数の四則計算をすること すことができる 今まで学習してきた数の体系について整理し, 考察 しようとする 絶対値の意味と記号表示を理解している 根号を含む式の加法, 減法, 乗法の計算ができる
(1) 数と式 学習指導要領 都立町田高校 学力スタンダード ア 数と集合 ( ア ) 実数 根号を含む式の計算 数を実数まで拡張する意義を理解し 簡単な 循環小数を表す記号を用いて, 分数を循環小数で表 無理数の四則計算をすること すことができる 今まで学習してきた数の体系について整理し, 考察 しようとする 絶対値の意味と記号表示を理解している 根号を含む式の加法, 減法, 乗法の計算ができる
学習指導要領
 (1) 数と式 学習指導要領ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 第 1 章第 節実数 東高校学力スタンダード 4 実数 (P.3~7) 自然数 整数 有理数 無理数 実数のそれぞれの集 合について 四則演算の可能性について判断できる ( 例 ) 下の表において, それぞれの数の範囲で四則計算を考えるとき, 計算がその範囲で常にできる場合には
(1) 数と式 学習指導要領ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 第 1 章第 節実数 東高校学力スタンダード 4 実数 (P.3~7) 自然数 整数 有理数 無理数 実数のそれぞれの集 合について 四則演算の可能性について判断できる ( 例 ) 下の表において, それぞれの数の範囲で四則計算を考えるとき, 計算がその範囲で常にできる場合には
破壊の予測
 本日の講義内容 前提 : 微分積分 線形代数が何をしているかはうろ覚え 材料力学は勉強したけど ちょっと 弾性および塑性学は勉強したことが無い ー > ですので 解らないときは質問してください モールの応力円を理解するとともに 応力を 3 次元的に考える FM( 有限要素法 の概略 内部では何を計算しているのか? 3 物が壊れる条件を考える 特に 変形 ( 塑性変形 が発生する条件としてのミーゼス応力とはどのような応力か?
本日の講義内容 前提 : 微分積分 線形代数が何をしているかはうろ覚え 材料力学は勉強したけど ちょっと 弾性および塑性学は勉強したことが無い ー > ですので 解らないときは質問してください モールの応力円を理解するとともに 応力を 3 次元的に考える FM( 有限要素法 の概略 内部では何を計算しているのか? 3 物が壊れる条件を考える 特に 変形 ( 塑性変形 が発生する条件としてのミーゼス応力とはどのような応力か?
<4D F736F F F696E74202D D488A778AEE B4F93B982CC8AEE A2E707074>
 宇宙工学基礎 ( 軌道の基礎 松永三郎 機械宇宙学科 機械宇宙システム専攻 ニュートンの法則 第 法則 力が作用作用しないしない限り 質点質点は静止静止ないしはないしは一定速度一定速度で運動するする ( 慣性の法則 慣性空間 慣性座標系慣性座標系の定義第 法則 慣性座標系におけるにおける質点質点の運動 p F ( pɺ t ( F: 全作用力, pmv: 並進運動量 ( 質量と速度速度の積 慣性系を規準規準としてとして時間微分時間微分を行うことにことに注意第
宇宙工学基礎 ( 軌道の基礎 松永三郎 機械宇宙学科 機械宇宙システム専攻 ニュートンの法則 第 法則 力が作用作用しないしない限り 質点質点は静止静止ないしはないしは一定速度一定速度で運動するする ( 慣性の法則 慣性空間 慣性座標系慣性座標系の定義第 法則 慣性座標系におけるにおける質点質点の運動 p F ( pɺ t ( F: 全作用力, pmv: 並進運動量 ( 質量と速度速度の積 慣性系を規準規準としてとして時間微分時間微分を行うことにことに注意第
<4D F736F F D208D5C91A297CD8A7793FC96E591E631308FCD2E646F63>
 第 1 章モールの定理による静定梁のたわみ 1-1 第 1 章モールの定理による静定梁のたわみ ポイント : モールの定理を用いて 静定梁のたわみを求める 断面力の釣合と梁の微分方程式は良く似ている 前章では 梁の微分方程式を直接積分する方法で 静定梁の断面力と変形状態を求めた 本章では 梁の微分方程式と断面力による力の釣合式が類似していることを利用して 微分方程式を直接解析的に解くのではなく 力の釣合より梁のたわみを求める方法を学ぶ
第 1 章モールの定理による静定梁のたわみ 1-1 第 1 章モールの定理による静定梁のたわみ ポイント : モールの定理を用いて 静定梁のたわみを求める 断面力の釣合と梁の微分方程式は良く似ている 前章では 梁の微分方程式を直接積分する方法で 静定梁の断面力と変形状態を求めた 本章では 梁の微分方程式と断面力による力の釣合式が類似していることを利用して 微分方程式を直接解析的に解くのではなく 力の釣合より梁のたわみを求める方法を学ぶ
学習指導要領
 (1 ) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 自然数 整数 有理数 無理数の包含関係など 実 数の構成を理解する ( 例 ) 次の空欄に適当な言葉をいれて, 数の集合を表しなさい 実数の絶対値が実数と対応する点と原点との距離で あることを理解する ( 例 ) 次の値を求めよ (1) () 6 置き換えなどを利用して 三項の無理数の乗法の計
(1 ) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 自然数 整数 有理数 無理数の包含関係など 実 数の構成を理解する ( 例 ) 次の空欄に適当な言葉をいれて, 数の集合を表しなさい 実数の絶対値が実数と対応する点と原点との距離で あることを理解する ( 例 ) 次の値を求めよ (1) () 6 置き換えなどを利用して 三項の無理数の乗法の計
耳桁の剛性の考慮分配係数の計算条件は 主桁本数 n 格子剛度 zです 通常の並列鋼桁橋では 主桁はすべて同じ断面を使います しかし 分配の効率を上げる場合 耳桁 ( 幅員端側の桁 ) の断面を大きくすることがあります 最近の桁橋では 上下線を別橋梁とすることがあり また 防音壁などの敷設が片側に有る
 格子桁の分配係数の計算 ( デモ版 ) 理論と解析の背景主桁を並列した鋼単純桁の設計では 幅員方向の横桁の剛性を考えて 複数の主桁が協力して活荷重を分担する効果を計算します これを 単純な (1,0) 分配に対して格子分配と言います レオンハルト (F.Leonhardt,1909-1999) が 1950 年初頭に発表した論文が元になっていて 理論仮定 記号などの使い方は その論文を踏襲して設計に応用しています
格子桁の分配係数の計算 ( デモ版 ) 理論と解析の背景主桁を並列した鋼単純桁の設計では 幅員方向の横桁の剛性を考えて 複数の主桁が協力して活荷重を分担する効果を計算します これを 単純な (1,0) 分配に対して格子分配と言います レオンハルト (F.Leonhardt,1909-1999) が 1950 年初頭に発表した論文が元になっていて 理論仮定 記号などの使い方は その論文を踏襲して設計に応用しています
学習指導要領
 (1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 絶対値の意味を理解し適切な処理することができる 例題 1-3 の絶対値をはずせ 展開公式 ( a + b ) ( a - b ) = a 2 - b 2 を利用して根号を含む分数の分母を有理化することができる 例題 5 5 + 2 の分母を有理化せよ 実数の整数部分と小数部分の表し方を理解している
(1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 絶対値の意味を理解し適切な処理することができる 例題 1-3 の絶対値をはずせ 展開公式 ( a + b ) ( a - b ) = a 2 - b 2 を利用して根号を含む分数の分母を有理化することができる 例題 5 5 + 2 の分母を有理化せよ 実数の整数部分と小数部分の表し方を理解している
第1章 序論
 第 章 応力とその性質. 応力.. 垂直応力とせん断応力物体が外力 (external force) を受けているとき, 物体内部では断面に内力 (internal force) が働き, その断面で分離しないように抵抗している. つまり内力は断面を結合する力である. 断面に垂直な内力が働く場合, その単位面積当たりの値を垂直応力 (normal stress) という. 例えば図 -(a) に示すように,
第 章 応力とその性質. 応力.. 垂直応力とせん断応力物体が外力 (external force) を受けているとき, 物体内部では断面に内力 (internal force) が働き, その断面で分離しないように抵抗している. つまり内力は断面を結合する力である. 断面に垂直な内力が働く場合, その単位面積当たりの値を垂直応力 (normal stress) という. 例えば図 -(a) に示すように,
s ss s ss = ε = = s ss s (3) と表される s の要素における s s = κ = κ, =,, (4) jωε jω s は複素比誘電率に相当する物理量であり ここで PML 媒質定数を次のように定義する すなわち κξ をPML 媒質の等価比誘電率 ξ をPML 媒質の
 FDTD 解析法 (Matlab 版 2 次元 PML) プログラム解説 v2.11 1. 概要 FDTD 解析における吸収境界である完全整合層 (Perfectl Matched Laer, PML) の定式化とプログラミングを2 次元 TE 波について解説する PMLは異方性の損失をもつ仮想的な物質であり 侵入して来る電磁波を逃さず吸収する 通常の物質と接する界面でインピーダンスが整合しており
FDTD 解析法 (Matlab 版 2 次元 PML) プログラム解説 v2.11 1. 概要 FDTD 解析における吸収境界である完全整合層 (Perfectl Matched Laer, PML) の定式化とプログラミングを2 次元 TE 波について解説する PMLは異方性の損失をもつ仮想的な物質であり 侵入して来る電磁波を逃さず吸収する 通常の物質と接する界面でインピーダンスが整合しており
木村の物理小ネタ ケプラーの第 2 法則と角運動量保存則 A. 面積速度面積速度とは平面内に定点 O と動点 P があるとき, 定点 O と動点 P を結ぶ線分 OP( 動径 OP という) が単位時間に描く面積を 動点 P の定点 O に
 ケプラーの第 法則と角運動量保存則 A. 面積速度面積速度とは平面内に定点 O と動点 P があるとき, 定点 O と動点 P を結ぶ線分 OP( 動径 OP という が単位時間に描く面積を 動点 P の定点 O に関する面積速度の大きさ という 定点 O まわりを回る面積速度の導き方導き方 A ( x( + D, y( + D v ( q r ( A ( x (, y( 動点 P が xy 座標平面上を時刻
ケプラーの第 法則と角運動量保存則 A. 面積速度面積速度とは平面内に定点 O と動点 P があるとき, 定点 O と動点 P を結ぶ線分 OP( 動径 OP という が単位時間に描く面積を 動点 P の定点 O に関する面積速度の大きさ という 定点 O まわりを回る面積速度の導き方導き方 A ( x( + D, y( + D v ( q r ( A ( x (, y( 動点 P が xy 座標平面上を時刻
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生
 0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
木村の物理小ネタ 単振動と単振動の力学的エネルギー 1. 弾性力と単振動 弾性力も単振動も力は F = -Kx の形で表されるが, x = 0 の位置は, 弾性力の場合, 弾性体の自然状態の位置 単振動の場合, 振動する物体に働く力のつり合
 単振動と単振動の力学的エネルギー. 弾性力と単振動 弾性力も単振動も力は F = -x の形で表されるが, x = の位置は, 弾性力の場合, 弾性体の自然状態の位置 単振動の場合, 振動する物体に働く力のつり合いの位置 である たとえば, おもりをつるしたばねについて, ばねの弾性力を考えるときは, ばねの自然長を x = とし, おもりの単振動で考える場合は, おもりに働く力がつり合った位置を
単振動と単振動の力学的エネルギー. 弾性力と単振動 弾性力も単振動も力は F = -x の形で表されるが, x = の位置は, 弾性力の場合, 弾性体の自然状態の位置 単振動の場合, 振動する物体に働く力のつり合いの位置 である たとえば, おもりをつるしたばねについて, ばねの弾性力を考えるときは, ばねの自然長を x = とし, おもりの単振動で考える場合は, おもりに働く力がつり合った位置を
<4D F736F F F696E74202D20906C8D488AC28BAB90DD8C7689F090CD8D488A D91E F1>
 人工環境設計解析工学構造力学と有限要素法 ( 第 回 ) 東京大学新領域創成科学研究科 鈴木克幸 固体力学の基礎方程式 変位 - ひずみの関係 適合条件式 ひずみ - 応力の関係 構成方程式 応力 - 外力の関係 平衡方程式 境界条件 変位規定境界 反力規定境界 境界条件 荷重応力ひずみ変形 場の方程式 Γ t Γ t 平衡方程式構成方程式適合条件式 構造力学の基礎式 ひずみ 一軸 荷重応力ひずみ変形
人工環境設計解析工学構造力学と有限要素法 ( 第 回 ) 東京大学新領域創成科学研究科 鈴木克幸 固体力学の基礎方程式 変位 - ひずみの関係 適合条件式 ひずみ - 応力の関係 構成方程式 応力 - 外力の関係 平衡方程式 境界条件 変位規定境界 反力規定境界 境界条件 荷重応力ひずみ変形 場の方程式 Γ t Γ t 平衡方程式構成方程式適合条件式 構造力学の基礎式 ひずみ 一軸 荷重応力ひずみ変形
5-仮想仕事式と種々の応力.ppt
 1 以上, 運動の変数についての話を終える. 次は再び力の変数に戻る. その前に, まず次の話が唐突と思われないように 以下は前置き. 先に, 力の変数と運動の変数には対応関係があって, 適当な内積演算によって仕事量を表す ことを述べた. 実は,Cauchy 応力と速度勾配テンソル ( あるいは変位勾配テンソル ) を用いると, それらの内積は内部仮想仕事を表していて, そして, それは外力がなす仮想仕事に等しいという
1 以上, 運動の変数についての話を終える. 次は再び力の変数に戻る. その前に, まず次の話が唐突と思われないように 以下は前置き. 先に, 力の変数と運動の変数には対応関係があって, 適当な内積演算によって仕事量を表す ことを述べた. 実は,Cauchy 応力と速度勾配テンソル ( あるいは変位勾配テンソル ) を用いると, それらの内積は内部仮想仕事を表していて, そして, それは外力がなす仮想仕事に等しいという
<4D F736F F D20824F E B82CC90FC90CF95AA2E646F63>
 1/1 平成 3 年 6 月 11 日午前 1 時 3 分 4 ベクトルの線積分 4 ベクトルの線積分 Ⅰ. 積分の種類 通常の物理で使う積分には 3 種類あります 積分変数の数に応じて 線積分 ( 記号 横(1 重 d, dy, dz d ( ine: 面積分 ( 記号 縦 横 ( 重 線 4 ベクトルの線積分 重積分記号 ddy, dydz, dzdz ds ( Surface: 1 重積分記号
1/1 平成 3 年 6 月 11 日午前 1 時 3 分 4 ベクトルの線積分 4 ベクトルの線積分 Ⅰ. 積分の種類 通常の物理で使う積分には 3 種類あります 積分変数の数に応じて 線積分 ( 記号 横(1 重 d, dy, dz d ( ine: 面積分 ( 記号 縦 横 ( 重 線 4 ベクトルの線積分 重積分記号 ddy, dydz, dzdz ds ( Surface: 1 重積分記号
学習指導要領
 (1) いろいろな式 学習指導要領紅葉川高校学力スタンダードア式と証明展開の公式を用いて 3 乗に関わる式を展開すること ( ア ) 整式の乗法 除法 分数式の計算ができるようにする 三次の乗法公式及び因数分解の公式を理解し そ 3 次の因数分解の公式を理解し それらを用いて因数れらを用いて式の展開や因数分解をすること また 分解することができるようにする 整式の除法や分数式の四則計算について理解し
(1) いろいろな式 学習指導要領紅葉川高校学力スタンダードア式と証明展開の公式を用いて 3 乗に関わる式を展開すること ( ア ) 整式の乗法 除法 分数式の計算ができるようにする 三次の乗法公式及び因数分解の公式を理解し そ 3 次の因数分解の公式を理解し それらを用いて因数れらを用いて式の展開や因数分解をすること また 分解することができるようにする 整式の除法や分数式の四則計算について理解し
Microsoft PowerPoint - fuseitei_6
 不静定力学 Ⅱ 骨組の崩壊荷重の計算 不静定力学 Ⅱ では, 最後の問題となりますが, 骨組の崩壊荷重の計算法について学びます 1 参考書 松本慎也著 よくわかる構造力学の基本, 秀和システム このスライドの説明には, 主にこの参考書の説明を引用しています 2 崩壊荷重 構造物に作用する荷重が徐々に増大すると, 構造物内に発生する応力は増加し, やがて, 構造物は荷重に耐えられなくなる そのときの荷重を崩壊荷重あるいは終局荷重という
不静定力学 Ⅱ 骨組の崩壊荷重の計算 不静定力学 Ⅱ では, 最後の問題となりますが, 骨組の崩壊荷重の計算法について学びます 1 参考書 松本慎也著 よくわかる構造力学の基本, 秀和システム このスライドの説明には, 主にこの参考書の説明を引用しています 2 崩壊荷重 構造物に作用する荷重が徐々に増大すると, 構造物内に発生する応力は増加し, やがて, 構造物は荷重に耐えられなくなる そのときの荷重を崩壊荷重あるいは終局荷重という
多次元レーザー分光で探る凝縮分子系の超高速動力学
 波動方程式と量子力学 谷村吉隆 京都大学理学研究科化学専攻 http:theochem.kuchem.kyoto-u.ac.jp TA: 岩元佑樹 iwamoto.y@kuchem.kyoto-u.ac.jp ベクトルと行列の作法 A 列ベクトル c = c c 行ベクトル A = [ c c c ] 転置ベクトル T A = [ c c c ] AA 内積 c AA = [ c c c ] c =
波動方程式と量子力学 谷村吉隆 京都大学理学研究科化学専攻 http:theochem.kuchem.kyoto-u.ac.jp TA: 岩元佑樹 iwamoto.y@kuchem.kyoto-u.ac.jp ベクトルと行列の作法 A 列ベクトル c = c c 行ベクトル A = [ c c c ] 転置ベクトル T A = [ c c c ] AA 内積 c AA = [ c c c ] c =
Microsoft Word - 素粒子物理学I.doc
 6. 自発的対称性の破れとヒッグス機構 : 素粒子の標準模型 Dc 方程式.5 を導くラグランジアンは ϕ ϕ mϕϕ 6. である [H] Eu-nn 方程式 を使って 6. のラグランジア ンから Dc 方程式が導かれることを示せ 6. ゲージ対称性 6.. U 対称性 :QED ディラック粒子の複素場 ψに対する位相変換 ϕ ϕ 6. に対して ラグランジアンが不変であることを要請する これは簡単に示せる
6. 自発的対称性の破れとヒッグス機構 : 素粒子の標準模型 Dc 方程式.5 を導くラグランジアンは ϕ ϕ mϕϕ 6. である [H] Eu-nn 方程式 を使って 6. のラグランジア ンから Dc 方程式が導かれることを示せ 6. ゲージ対称性 6.. U 対称性 :QED ディラック粒子の複素場 ψに対する位相変換 ϕ ϕ 6. に対して ラグランジアンが不変であることを要請する これは簡単に示せる
1.民営化
 参考資料 最小二乗法 数学的性質 経済統計分析 3 年度秋学期 回帰分析と最小二乗法 被説明変数 の動きを説明変数 の動きで説明 = 回帰分析 説明変数がつ 単回帰 説明変数がつ以上 重回帰 被説明変数 従属変数 係数 定数項傾き 説明変数 独立変数 残差... で説明できる部分 説明できない部分 説明できない部分が小さくなるように回帰式の係数 を推定する有力な方法 = 最小二乗法 最小二乗法による回帰の考え方
参考資料 最小二乗法 数学的性質 経済統計分析 3 年度秋学期 回帰分析と最小二乗法 被説明変数 の動きを説明変数 の動きで説明 = 回帰分析 説明変数がつ 単回帰 説明変数がつ以上 重回帰 被説明変数 従属変数 係数 定数項傾き 説明変数 独立変数 残差... で説明できる部分 説明できない部分 説明できない部分が小さくなるように回帰式の係数 を推定する有力な方法 = 最小二乗法 最小二乗法による回帰の考え方
ギリシャ文字の読み方を教えてください
 埼玉工業大学機械工学学習支援セミナー ( 小西克享 ) 慣性モーメント -1/6 テーマ 01: 慣性モーメント (Momet of ietia) コマ回しをすると, 長い時間回転させるには重くて大きなコマを選ぶことや, ひもを早く引くことが重要であることが経験的にわかります. 遊びを通して, 回転の運動エネルギーを増やせば, 回転の勢いが増すことを学習できるので, 機械系の学生にとってコマ回しも大切な体験学習のひとつと言えます.
埼玉工業大学機械工学学習支援セミナー ( 小西克享 ) 慣性モーメント -1/6 テーマ 01: 慣性モーメント (Momet of ietia) コマ回しをすると, 長い時間回転させるには重くて大きなコマを選ぶことや, ひもを早く引くことが重要であることが経験的にわかります. 遊びを通して, 回転の運動エネルギーを増やせば, 回転の勢いが増すことを学習できるので, 機械系の学生にとってコマ回しも大切な体験学習のひとつと言えます.
学力スタンダード(様式1)
 (1) 数と式 学習指導要領ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 稔ヶ丘高校学力スタンダード 有理数 無理数の定義や実数の分類について理解し ている 絶対値の意味と記号表示を理解している 実数と直線上の点が一対一対応であることを理解 し 実数を数直線上に示すことができる 例 実数 (1) -.5 () π (3) 数直線上の点はどれか答えよ
(1) 数と式 学習指導要領ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 稔ヶ丘高校学力スタンダード 有理数 無理数の定義や実数の分類について理解し ている 絶対値の意味と記号表示を理解している 実数と直線上の点が一対一対応であることを理解 し 実数を数直線上に示すことができる 例 実数 (1) -.5 () π (3) 数直線上の点はどれか答えよ
2018年度 筑波大・理系数学
 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ < < とする 放物線 上に 点 (, ), A (ta, ta ), B( - ta, ta ) をとる 三角形 AB の内心の 座標を p とし, 外心の 座標を q とする また, 正の実数 a に対して, 直線 a と放物線 で囲まれた図形の面積を S( a) で表す () p, q を cos を用いて表せ S( p) () S(
筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ < < とする 放物線 上に 点 (, ), A (ta, ta ), B( - ta, ta ) をとる 三角形 AB の内心の 座標を p とし, 外心の 座標を q とする また, 正の実数 a に対して, 直線 a と放物線 で囲まれた図形の面積を S( a) で表す () p, q を cos を用いて表せ S( p) () S(
発散.rtf
 4 章発散 発散は重要なベクトル演算の一つであり, 定義は A =diva = lim Δv 0 Δv A d (4.) である.Divergence( ダイバージェンス ) ともいう. この意味は, 微小体積 vを取り囲む全表面 ( 閉曲面という ) 上で, 外向きのベクトル法線成分をすべて加えあわせ, 全体としての量を調べるものである. ベクトルAはどのような向きでもかまわないが, 面ベクトルとの内積
4 章発散 発散は重要なベクトル演算の一つであり, 定義は A =diva = lim Δv 0 Δv A d (4.) である.Divergence( ダイバージェンス ) ともいう. この意味は, 微小体積 vを取り囲む全表面 ( 閉曲面という ) 上で, 外向きのベクトル法線成分をすべて加えあわせ, 全体としての量を調べるものである. ベクトルAはどのような向きでもかまわないが, 面ベクトルとの内積
行列、ベクトル
 行列 (Mtri) と行列式 (Determinnt). 行列 (Mtri) の演算. 和 差 積.. 行列とは.. 行列の和差 ( 加減算 ).. 行列の積 ( 乗算 ). 転置行列 対称行列 正方行列. 単位行列. 行列式 (Determinnt) と逆行列. 行列式. 逆行列. 多元一次連立方程式のコンピュータによる解法. コンピュータによる逆行列の計算.. 定数項の異なる複数の方程式.. 逆行列の計算
行列 (Mtri) と行列式 (Determinnt). 行列 (Mtri) の演算. 和 差 積.. 行列とは.. 行列の和差 ( 加減算 ).. 行列の積 ( 乗算 ). 転置行列 対称行列 正方行列. 単位行列. 行列式 (Determinnt) と逆行列. 行列式. 逆行列. 多元一次連立方程式のコンピュータによる解法. コンピュータによる逆行列の計算.. 定数項の異なる複数の方程式.. 逆行列の計算
Microsoft PowerPoint - 9.pptx
 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 行列演算と写像 ( 次変換 3 拡大とスカラー倍 p ' = ( ', ' = ( k, kk p = (, k 倍 k 倍 拡大後 k 倍拡大の関係は スカラー倍を用いて次のように表現できる ' = k ' 拡大前 拡大 4 拡大と行列の積 p ' = ( ', '
9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 行列演算と写像 ( 次変換 3 拡大とスカラー倍 p ' = ( ', ' = ( k, kk p = (, k 倍 k 倍 拡大後 k 倍拡大の関係は スカラー倍を用いて次のように表現できる ' = k ' 拡大前 拡大 4 拡大と行列の積 p ' = ( ', '
学習指導要領
 (1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 自然数 整数 有理数 無理数 実数のそれぞれの集 合について 四則演算の可能性について判断できる ( 例 ) 下の表において それぞれの数の範囲で四則計算を考えるとき 計算がその範囲で常にできる場合には を 常にできるとは限らない場合には を付けよ ただし 除法では 0 で割ることは考えない
(1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 自然数 整数 有理数 無理数 実数のそれぞれの集 合について 四則演算の可能性について判断できる ( 例 ) 下の表において それぞれの数の範囲で四則計算を考えるとき 計算がその範囲で常にできる場合には を 常にできるとは限らない場合には を付けよ ただし 除法では 0 で割ることは考えない
Microsoft PowerPoint - 9.pptx
 9/7/8( 水 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 拡大とスカラー倍 行列演算と写像 ( 次変換 拡大後 k 倍 k 倍 k 倍拡大の関係は スカラー倍を用いて次のように表現できる p = (, ' = k ' 拡大前 p ' = ( ', ' = ( k, k 拡大 4 拡大と行列の積 拡大後 k 倍
9/7/8( 水 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 拡大とスカラー倍 行列演算と写像 ( 次変換 拡大後 k 倍 k 倍 k 倍拡大の関係は スカラー倍を用いて次のように表現できる p = (, ' = k ' 拡大前 p ' = ( ', ' = ( k, k 拡大 4 拡大と行列の積 拡大後 k 倍
物理演習問題
 < 物理 > =0 問 ビルの高さを, ある速さ ( 初速 をとおく,において等加速度運動の公式より (- : -= t - t : -=- t - t (-, 式よりを消去すると t - t =- t - t ( + - ( + ( - =0 0 t t t t t t ( t + t - ( t - =0 t=t t=t t - 地面 ( t - t t +t 0 より, = 3 図 問 が最高点では速度が
< 物理 > =0 問 ビルの高さを, ある速さ ( 初速 をとおく,において等加速度運動の公式より (- : -= t - t : -=- t - t (-, 式よりを消去すると t - t =- t - t ( + - ( + ( - =0 0 t t t t t t ( t + t - ( t - =0 t=t t=t t - 地面 ( t - t t +t 0 より, = 3 図 問 が最高点では速度が
20~22.prt
 [ 三クリア W] 辺が等しいことの証明 ( 円周角と弦の関係利用 ) の の二等分線がこの三角形の外接円と交わる点をそれぞれ とするとき 60 ならば であることを証明せよ 60 + + 0 + 0 80-60 60 から ゆえに 等しい長さの弧に対する弦の長さは等しいから [ 三クリア ] 方べきの定理 接線と弦のなす角と円周角を利用 線分 を直径とする円 があり 右の図のように の延長上の点
[ 三クリア W] 辺が等しいことの証明 ( 円周角と弦の関係利用 ) の の二等分線がこの三角形の外接円と交わる点をそれぞれ とするとき 60 ならば であることを証明せよ 60 + + 0 + 0 80-60 60 から ゆえに 等しい長さの弧に対する弦の長さは等しいから [ 三クリア ] 方べきの定理 接線と弦のなす角と円周角を利用 線分 を直径とする円 があり 右の図のように の延長上の点
数学の世界
 東京女子大学文理学部数学の世界 (2002 年度 ) 永島孝 17 6 行列式の基本法則と効率的な計算法 基本法則 三次以上の行列式についても, 二次の場合と同様な法則がなりたつ ここには三次の場合を例示するが, 四次以上でも同様である 1 単位行列の行列式の値は 1 である すなわち 1 0 0 0 1 0 1 0 0 1 2 二つの列を入れ替えると行列式の値は 1 倍になる 例えば a 13 a
東京女子大学文理学部数学の世界 (2002 年度 ) 永島孝 17 6 行列式の基本法則と効率的な計算法 基本法則 三次以上の行列式についても, 二次の場合と同様な法則がなりたつ ここには三次の場合を例示するが, 四次以上でも同様である 1 単位行列の行列式の値は 1 である すなわち 1 0 0 0 1 0 1 0 0 1 2 二つの列を入れ替えると行列式の値は 1 倍になる 例えば a 13 a
応用数学Ⅱ 偏微分方程式(2) 波動方程式(12/13)
 偏微分方程式. 偏微分方程式の形 偏微分 偏導関数 つの独立変数 をもつ関数 があるとき 変数 が一定値をとって だけが変化したとす ると は だけの関数となる このとき を について微分して得られる関数を 関数 の に関する 偏微分係数 略して偏微分 あるいは偏導関数 pil deiie といい 次のように表される についても同様な偏微分を定義できる あるいは あるいは - あるいは あるいは -
偏微分方程式. 偏微分方程式の形 偏微分 偏導関数 つの独立変数 をもつ関数 があるとき 変数 が一定値をとって だけが変化したとす ると は だけの関数となる このとき を について微分して得られる関数を 関数 の に関する 偏微分係数 略して偏微分 あるいは偏導関数 pil deiie といい 次のように表される についても同様な偏微分を定義できる あるいは あるいは - あるいは あるいは -
Microsoft PowerPoint - 2.ppt [互換モード]
![Microsoft PowerPoint - 2.ppt [互換モード] Microsoft PowerPoint - 2.ppt [互換モード]](/thumbs/74/70606453.jpg) 0 章数学基礎 1 大学では 高校より厳密に議論を行う そのために 議論の議論の対象を明確にする必要がある 集合 ( 定義 ) 集合 物の集まりである集合 X に対して X を構成している物を X の要素または元という 集合については 3 セメスタ開講の 離散数学 で詳しく扱う 2 集合の表現 1. 要素を明示する表現 ( 外延的表現 ) 中括弧で 囲う X = {0,1, 2,3} 慣用的に 英大文字を用いる
0 章数学基礎 1 大学では 高校より厳密に議論を行う そのために 議論の議論の対象を明確にする必要がある 集合 ( 定義 ) 集合 物の集まりである集合 X に対して X を構成している物を X の要素または元という 集合については 3 セメスタ開講の 離散数学 で詳しく扱う 2 集合の表現 1. 要素を明示する表現 ( 外延的表現 ) 中括弧で 囲う X = {0,1, 2,3} 慣用的に 英大文字を用いる
重要例題113
 04_ 高校 数学 Ⅱ 必須基本公式 定理集 数学 Ⅱ 第 章式の計算と方程式 0 商と余り についての整式 A をについての整式 B で割ったときの商を Q, 余りを R とすると, ABQ+R (R の次数 ) > 0
04_ 高校 数学 Ⅱ 必須基本公式 定理集 数学 Ⅱ 第 章式の計算と方程式 0 商と余り についての整式 A をについての整式 B で割ったときの商を Q, 余りを R とすると, ABQ+R (R の次数 ) > 0
Microsoft PowerPoint - 熱力学Ⅱ2FreeEnergy2012HP.ppt [互換モード]
![Microsoft PowerPoint - 熱力学Ⅱ2FreeEnergy2012HP.ppt [互換モード] Microsoft PowerPoint - 熱力学Ⅱ2FreeEnergy2012HP.ppt [互換モード]](/thumbs/79/80168709.jpg) 熱力学 Ⅱ 第 章自由エネルギー システム情報工学研究科 構造エネルギー工学専攻 金子暁子 問題 ( 解答 ). 熱量 Q をある系に与えたところ, 系の体積は膨張し, 温度は上昇した. () 熱量 Q は何に変化したか. () またこのとき系の体積がV よりV に変化した.( 圧力は変化無し.) 内部エネルギーはどのように表されるか. また, このときのp-V 線図を示しなさい.. 不可逆過程の例を
熱力学 Ⅱ 第 章自由エネルギー システム情報工学研究科 構造エネルギー工学専攻 金子暁子 問題 ( 解答 ). 熱量 Q をある系に与えたところ, 系の体積は膨張し, 温度は上昇した. () 熱量 Q は何に変化したか. () またこのとき系の体積がV よりV に変化した.( 圧力は変化無し.) 内部エネルギーはどのように表されるか. また, このときのp-V 線図を示しなさい.. 不可逆過程の例を
<4D F736F F D E682568FCD CC82B982F192668BAD9378>
 7. 組み合わせ応力 7.7. 応力の座標変換載荷 ( 要素 の上方右側にずれている位置での載荷を想定 図 ( この場合正 ( この場合負 応力の座標変換の知識は なぜ必要か? 例 土の二つの基本的せん断変形モード : - 三軸圧縮変形 - 単純せん断変形 一面せん断変形両者でのせん断強度の関連を理解するためには 応力の座標変換を理解する必要がある 例 粘着力のない土 ( 代表例 乾燥した砂 のせん断破壊は
7. 組み合わせ応力 7.7. 応力の座標変換載荷 ( 要素 の上方右側にずれている位置での載荷を想定 図 ( この場合正 ( この場合負 応力の座標変換の知識は なぜ必要か? 例 土の二つの基本的せん断変形モード : - 三軸圧縮変形 - 単純せん断変形 一面せん断変形両者でのせん断強度の関連を理解するためには 応力の座標変換を理解する必要がある 例 粘着力のない土 ( 代表例 乾燥した砂 のせん断破壊は
Microsoft PowerPoint - 10.pptx
 0. 固有値とその応用 固有値と固有ベクトル 2 行列による写像から固有ベクトルへ m n A : m n n m 行列によって線形写像 f R R A が表せることを見てきた ここでは 2 次元平面の行列による写像を調べる 2 = 2 A 2 2 とし 写像 まず 単位ベクトルの像を求める u 2 x = v 2 y f : R A R を考える u 2 2 u, 2 2 0 = = v 2 0
0. 固有値とその応用 固有値と固有ベクトル 2 行列による写像から固有ベクトルへ m n A : m n n m 行列によって線形写像 f R R A が表せることを見てきた ここでは 2 次元平面の行列による写像を調べる 2 = 2 A 2 2 とし 写像 まず 単位ベクトルの像を求める u 2 x = v 2 y f : R A R を考える u 2 2 u, 2 2 0 = = v 2 0
学習指導要領
 (1) 数と式 学習指導要領ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 千早高校学力スタンダード 自然数 整数 有理数 無理数の用語の意味を理解す る ( 例 ) 次の数の中から自然数 整数 有理 数 無理数に分類せよ 3 3,, 0.7, 3,,-, 4 (1) 自然数 () 整数 (3) 有理数 (4) 無理数 自然数 整数 有理数 無理数の包含関係など
(1) 数と式 学習指導要領ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 千早高校学力スタンダード 自然数 整数 有理数 無理数の用語の意味を理解す る ( 例 ) 次の数の中から自然数 整数 有理 数 無理数に分類せよ 3 3,, 0.7, 3,,-, 4 (1) 自然数 () 整数 (3) 有理数 (4) 無理数 自然数 整数 有理数 無理数の包含関係など
第1章 単 位
 H. Hmno 問題解答 問題解答. 力の釣合い [ 問題.] V : sin. H :.cos. 7 V : sin sin H : cos cos cos 上第 式より これと第 式より.. cos V : sin sin H : coscos cos 上第 式より これと第 式より.98. cos [ 問題.] :. V :. : 9 9. V :. : sin V : sin 8.78 H
H. Hmno 問題解答 問題解答. 力の釣合い [ 問題.] V : sin. H :.cos. 7 V : sin sin H : cos cos cos 上第 式より これと第 式より.. cos V : sin sin H : coscos cos 上第 式より これと第 式より.98. cos [ 問題.] :. V :. : 9 9. V :. : sin V : sin 8.78 H
Microsoft Word - cavitation.doc
 音響キャビテーション ヤング ラプラスの式 A B dl g C ヤングは 二つの流体の境界に厚さの無視できる架空の膜が存在し しかもこの膜には張力が作用するというモデルを考えた. すなわち 図に示すように 気泡表面と交わる平面 ABC を考えたとき 表面の接線方向の単位長さ dl 当たり g の力が作用していると考え この力を表面張力とよんだ. 次元は [N/m][J/m] となる. 気相と液相が接する界面には表面張力が働く
音響キャビテーション ヤング ラプラスの式 A B dl g C ヤングは 二つの流体の境界に厚さの無視できる架空の膜が存在し しかもこの膜には張力が作用するというモデルを考えた. すなわち 図に示すように 気泡表面と交わる平面 ABC を考えたとき 表面の接線方向の単位長さ dl 当たり g の力が作用していると考え この力を表面張力とよんだ. 次元は [N/m][J/m] となる. 気相と液相が接する界面には表面張力が働く
Microsoft PowerPoint - 構造力学Ⅰ第03回.pptx
 分布荷重の合力 ( 効果 ) 前回の復習 ( 第 回 ) p. 分布荷重は平行な力が連続して分布していると考えられる 例 : 三角形分布 l dx P=ql/ q l qx q l 大きさ P dx x 位置 Px 0 x x 0 l ql 0 : 面積に等しい 0 l l 重心に等しいモーメントの釣合より ( バリノンの定理 ) l qx l qx ql q 3 l ql l xdx x0 xdx
分布荷重の合力 ( 効果 ) 前回の復習 ( 第 回 ) p. 分布荷重は平行な力が連続して分布していると考えられる 例 : 三角形分布 l dx P=ql/ q l qx q l 大きさ P dx x 位置 Px 0 x x 0 l ql 0 : 面積に等しい 0 l l 重心に等しいモーメントの釣合より ( バリノンの定理 ) l qx l qx ql q 3 l ql l xdx x0 xdx
Matrix and summation convention Kronecker delta δ ij 1 = 0 ( i = j) ( i j) permutation symbol e ijk = (even permutation) (odd permutation) (othe
 Matr ad summato covto Krockr dlta δ ( ) ( ) prmutato symbol k (v prmutato) (odd prmutato) (othrs) gvalu dtrmat dt 6 k rst r s kt opyrght s rsrvd. No part of ths documt may b rproducd for proft. 行列 行 正方行列
Matr ad summato covto Krockr dlta δ ( ) ( ) prmutato symbol k (v prmutato) (odd prmutato) (othrs) gvalu dtrmat dt 6 k rst r s kt opyrght s rsrvd. No part of ths documt may b rproducd for proft. 行列 行 正方行列
(Microsoft PowerPoint - \221\34613\211\361)
 計算力学 ~ 第 回弾性問題の有限要素解析 (Ⅱ)~ 修士 年後期 ( 選択科目 ) 担当 : 岩佐貴史 講義の概要 全 5 講義. 計算力学概論, ガイダンス. 自然現象の数理モデル化. 行列 場とその演算. 数値計算法 (Ⅰ) 5. 数値計算法 (Ⅱ) 6. 初期値 境界値問題 (Ⅰ) 7. 初期値 境界値問題 (Ⅱ) 8. マトリックス変位法による構造解析 9. トラス構造の有限要素解析. 重み付き残差法と古典的近似解法.
計算力学 ~ 第 回弾性問題の有限要素解析 (Ⅱ)~ 修士 年後期 ( 選択科目 ) 担当 : 岩佐貴史 講義の概要 全 5 講義. 計算力学概論, ガイダンス. 自然現象の数理モデル化. 行列 場とその演算. 数値計算法 (Ⅰ) 5. 数値計算法 (Ⅱ) 6. 初期値 境界値問題 (Ⅰ) 7. 初期値 境界値問題 (Ⅱ) 8. マトリックス変位法による構造解析 9. トラス構造の有限要素解析. 重み付き残差法と古典的近似解法.
線形代数とは
 線形代数とは 第一回ベクトル 教科書 エクササイズ線形代数 立花俊一 成田清正著 共立出版 必要最低限のことに限る 得意な人には物足りないかもしれません 線形代数とは何をするもの? 線形関係 y 直線 yもも 次式で登場する (( 次の形 ) 線形 ただし 次元の話世の中は 3 次元 [4[ 次元 ] 次元 3 次元 4 次元 はどうやって直線を表すの? ベクトルや行列の概念 y A ベクトルを使うと
線形代数とは 第一回ベクトル 教科書 エクササイズ線形代数 立花俊一 成田清正著 共立出版 必要最低限のことに限る 得意な人には物足りないかもしれません 線形代数とは何をするもの? 線形関係 y 直線 yもも 次式で登場する (( 次の形 ) 線形 ただし 次元の話世の中は 3 次元 [4[ 次元 ] 次元 3 次元 4 次元 はどうやって直線を表すの? ベクトルや行列の概念 y A ベクトルを使うと
<4D F736F F D208C51985F82CD82B682DF82CC88EA95E A>
 群論はじめの一歩 (6) 6. 指数 2の定理と2 面体群 命題 H を群 G の部分群とする そして 左剰余類全体 G/ H 右剰 余類全体 \ H G ともに指数 G: H 2 と仮定する このとき H は群 G の正規部分群である すなわち H 注意 ) 集合 A と B があるとき A から B を引いた差集合は A \ B と書かれるが ここで書いた H \ Gは差集合ではなく右剰余類の集合の意味である
群論はじめの一歩 (6) 6. 指数 2の定理と2 面体群 命題 H を群 G の部分群とする そして 左剰余類全体 G/ H 右剰 余類全体 \ H G ともに指数 G: H 2 と仮定する このとき H は群 G の正規部分群である すなわち H 注意 ) 集合 A と B があるとき A から B を引いた差集合は A \ B と書かれるが ここで書いた H \ Gは差集合ではなく右剰余類の集合の意味である
学習指導要領
 (1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 自然数 整数 有理数 無理数の包含関係など 実数 の構成を理解する ( 例 ) 次の空欄に適当な言葉をいれて, 数の集合を表しなさい ア イ 無理数 整数 ウ 無理数の加法及び減法 乗法公式などを利用した計 算ができる また 分母だけが二項である無理数の 分母の有理化ができる ( 例 1)
(1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 自然数 整数 有理数 無理数の包含関係など 実数 の構成を理解する ( 例 ) 次の空欄に適当な言葉をいれて, 数の集合を表しなさい ア イ 無理数 整数 ウ 無理数の加法及び減法 乗法公式などを利用した計 算ができる また 分母だけが二項である無理数の 分母の有理化ができる ( 例 1)
7 章問題解答 7-1 予習 1. 長方形断面であるため, 断面積 A と潤辺 S は, 水深 h, 水路幅 B を用い以下で表される A = Bh, S = B + 2h 径深 R の算定式に代入すると以下のようになる A Bh h R = = = S B + 2 h 1+ 2( h B) 分母の
 7 章問題解答 7- 予習. 長方形断面であるため, 断面積 と潤辺 S は, 水深, 水路幅 B を用い以下で表される B, S B + 径深 R の算定式に代入すると以下のようになる B R S B + ( B) 分母の /B は河幅が水深に対して十分に広ければ, 非常に小さな値となるため, 上式は R ( B) となり, 径深 R は水深 で近似できる. マニングの式の水深 を等流水深 0 と置き換えると,
7 章問題解答 7- 予習. 長方形断面であるため, 断面積 と潤辺 S は, 水深, 水路幅 B を用い以下で表される B, S B + 径深 R の算定式に代入すると以下のようになる B R S B + ( B) 分母の /B は河幅が水深に対して十分に広ければ, 非常に小さな値となるため, 上式は R ( B) となり, 径深 R は水深 で近似できる. マニングの式の水深 を等流水深 0 と置き換えると,
Laplace2.rtf
 =0 ラプラスの方程式は 階の微分方程式で, 一般的に3つの座標変数をもつ. ここでは, 直角座標系, 円筒座標系, 球座標系におけるラプラスの方程式の解き方を説明しよう. 座標変数ごとに方程式を分離し, それを解いていく方法は変数分離法と呼ばれる. 変数分離解と固有関数展開法. 直角座標系における 3 次元の偏微分方程式 = x + y + z =0 (.) を解くために,x, y, z について互いに独立な関数の積で成り立っていると考え,
=0 ラプラスの方程式は 階の微分方程式で, 一般的に3つの座標変数をもつ. ここでは, 直角座標系, 円筒座標系, 球座標系におけるラプラスの方程式の解き方を説明しよう. 座標変数ごとに方程式を分離し, それを解いていく方法は変数分離法と呼ばれる. 変数分離解と固有関数展開法. 直角座標系における 3 次元の偏微分方程式 = x + y + z =0 (.) を解くために,x, y, z について互いに独立な関数の積で成り立っていると考え,
