21世紀の統計科学 <Vol. III>
|
|
|
- よいかず ふじした
- 7 years ago
- Views:
Transcription
1 21 III HP, ( ),.,,.,,. 1 uchida@sigmath.es.osaa-u.ac.jp 168
2 1, (stochastic differential equation, SDE) 1 X. dx t = b(x t,α)dt + σ(x t,β)dw t, t [,T], X = x., b : R Θ α R, σ : R Θ β R w 1 Wiener, x. b, σ. α β ( ), b σ., Θ α Θ β, R., X T := {X t } t [,T ] X n := {X hn } =,1,...,n, nh n = T,.,,.,.,,. Yoshida [31] h n, nh n nh 3 n,, α β,., α β. Kessler [14] h n, nh n nh l n (l 2), Ito-Taylor, α β,. [,T], h n = T/n, α,.,,., SDE 1. dx t = b(x t,α)dt + εσ(x t,β)dw t, t [,T], ε (, 1], X = x, ε., Genon-Catalot [4] Laredo [21] β, α 169
3 . Sørensen and Uchida [28] α β,.,,., 1, 1,. 2,,. 3,. 4,., 5.., 2, 3, (Ω, F,P; {F t } t ), 1 F t - Wiener {w t } t., , 1 X. dx t = b(x t,α)dt + σ(x t,β)dw t, t [,T], X = x, (2.1), b : R Θ α R, σ : R Θ β R, w 1 Wiener, x., θ := (α, β) Θ:=Θ α Θ β R 2, Θ. θ =(α,β ) SDE (2.1), θ Int(Θ). 1. (Ornstein-Uhlenbec ). b(x, α) = αx, σ(x, β) =β, dx t = αx t dt + βdw t, t [,T], X = x, (2.2) α>, β>. 17
4 2. (The hyperbolic diffusion process). b(x, α) = α x 1+x 2, σ(x, β) =β, X t dx t = α dt + βdw t, t [,T], X = x, (2.3) 1+X 2 t α>, β>. 2.2 SDE (2.1) θ = θ dx t = b(x t,α )dt + σ(x t,β )dw t, t [,T], X = x (2.4) t n = h n,( =, 1,...,n)., t n n = nh n = T, h n., X n = {X t n } =,1,...,n. 3. (i) (nh n = T h n ). (ii) (h n =Δ nh n = nδ =T ). (iii), (h n nh n = T ). (i),. (ii),. (iii) ( (i)) ( (ii)),. 2, (iii)., n, h n T = nh n. 3. (1985/1/1 24/12/31 2 ). T = 2, h n = T/n = 2/(1461 5) = 2/ nh 2 n = Th n 2.27 = (2/1/1 24/12/31 6 ). T =6, h n = T/n =6/ (i) nh 2 n = Th n 6.32 = (ii) nh 3 n = Th 2 n (1985/1/1 24/12/31 2 ). T = 2, h n = T/n =2/ (i) nh 2 n = Th n 2.83 = (ii) nh 3 n = Th 2 n (iii) nh 4 n = Th 3 n
5 (T h n ), T. 4, T =5( ).,, h n. 3 : Th n = nh 2 n. 4 : Th 2 n = nh 3 n. 5 : Th 3 n = nh 4 n. 2.3 (simulation) SDE (2.1) X = {X t } t [,T ] ( )., T., α,β. t>s, X t X s = t s b(x u,α )du + t s σ(x u,β )dw u, X = x. X t, X (n) t. X (n) t n X (n) t n X (n) t n = b(x (n) t n,α )(t n t n )+σ(x (n) t n,β )(w t n w t n ), = x.., h n = t n tn, ΔW t n := w t n w t n N(,h n ), =1,...,n, X (n) t n = x t n + b(x t n,α )h n + σ(x t n,β )ΔW t n, X (n) t n = x t, X X (n) = {X (n) t n,x(n) t n,...,x(n) 1 t }., ΔW n t n, ΔW t n,...δw 1 t n. X (n) T = X (n) t n, [ ] (Kloeden and Platen [15]) c> XT, E X (n) c h n. T 6. (Ornstein-Uhlenbec ) dx t = αx t dt + βdw t, X = x, t [,T]. 7-1 ( ) x =6, α =1, β =2, T =2, h n =1/1., 1/2. 172
6 6 7-1: , X = {X t } t [,T ], ,,, ( ). 2.4 SDE (2.1) X (state space) (, ). X θ = θ, μ θ, f(x) μ θ (dx) < f, T, 1 T f(x t )dt f(x)μ θ (dx) 1., μ θ θ = θ X,, t> 1 B, μ θ (B) = P x(x t B)μ θ (dx)., P x x X.. 173
7 X scale measure s(x, θ)dx speed measure ξ(x, θ)dx. x R, θ Θ, { x } 2b(y, α) s(x, θ) := exp σ 2 (y, β) dy, { 1 x } ξ(x, θ) := σ 2 (x, β) exp 2b(y, α) σ 2 (y, β) dy 1 = σ 2 (x, β)s(x, θ). x = / x, δ α = / α, δ β = / β. R Θ f(x, θ), δ θ f(x, θ) =(δ α f(x, θ),δ β f(x, θ)).. C,l (R Θ α) f : (i)f(x, α) R Θ α, x, n =, 1,...,, C>, x, sup α x n f(x, α) C(1 + x ) C. (ii) n =, 1,...,, x n f(x, α) α l, ν =, 1,...,l, C>, x sup α δα ν x n f(x, α) C(1 + x ) C. 2 2 (Fisher ) I(θ ) ( ) I b (θ ) I(θ )= I σ (θ )., I b (θ ) = I σ (θ ) = 2 ( ) 2 δα b(x, α ) μ θ(dx), σ(x, β ) ( ) 2 δβ σ(x, β ) μ θ(dx). σ(x, β ) P θ SDE(2.1) X, E θ P θ. p d P θ.. A1 θ Θ, s(x, θ)dx =, s(x, θ)dx =, 174
8 Ξ(θ) = ξ(x, θ)dx <. A2 (i) L>, x, y R, θ Θ b(x, α) b(y, α) + σ(x, β) σ(y, β) L x y. (ii) b(x, α) C 2,3 (R Θ α). (iii) σ(x, β) C 2,3 (R Θ β),, inf x,β σ 2 (x, β) >. (v) p, sup t E θ [ X t p ] <. A3 (i) I(θ ). (ii) x, b(x, α) =b(x, α )= α = α. x, σ 2 (x, β) =σ 2 (x, β )= β = β., (, Kutoyants [19]). 1. A1, A2-(i), x, β, σ 2 (x, β) >., X., μ θ (x) ξ(x, θ)/ξ(θ). A2-(i) SDE(2.1) (5 6). A3-(ii) (identifiability condition),. 7. (Ornstein-Uhlenbec ) scale measure s(x, θ)dx speed measure ξ(x, θ)dx { } α s(x, θ) = exp β 2 x2, ξ(x, θ) = 1 { β exp α } 2 β 2 x2, α, β > { α exp Ξ(θ) = β 2 x2 } dx =, 1 β 2 exp { α exp { αβ 2 x2 } dx = β 2 x2 } dx =, π αβ 2 <., 1 Ornstein-Uhlenbec ( 1), μ θ { } ξ(x, θ) μ θ (dx) = Ξ(θ) dx = 1 πβ2 /α exp x2 dx β 2 /α,, β 2 /(2α). 175
9 8. (Ornstein-Uhlenbec ) SDE(2.2), t ) X t = e (X αt + βe αs dw s. (2.5), X t, (5 5),. f(t, v) =e αt v, V t = X + t βeαs dw s,, X t = f(t, V t )=V α = X α t X s ds + t t e αs V s ds + βdw s. t e αs βe αs dw s, X t E θ [X t ] V θ [X t ] (2.5) 5 4, E θ [X t ] = x e αt, V θ [X t ] = β 2 1 e 2αt. 2α X t, p sup t E θ [ X t p ] <. 9. (Ornstein-Uhlenbec Fisher ) 7, μ θ N(,β 2 /(2α)). I(θ ) = ( 1 β 2 x2 μ θ (dx) 2 β 2 α,β >, det(i(θ )) = 1 α β 2. ) = ( 1 2α 2 β 2 ). 2.5 (2.1), X t = x X t y p(h n,x,y; θ). X n =(X t n,x t n 1,...,X t n ) (X t n = x ) f Xt n,x t n 1,...,X t n n (x t,x t1,...,x tn ; θ) = n p(h n,x t,x t ; θ) =1 176
10 , l n (θ) = n log p(h n,x t n,x t n ; θ) =1. ˆθ (ML) n l n (ˆθ (ML) n )=supl n (θ) θ. p,,. l n (θ) θ, S n (θ) :=δ θ l n (θ) = n δ θ p(h n,x t n,x t n ; θ) =1 p(h n,x t n,x t n ; θ) R ˆθ (ML) n, S n (ˆθ n (ML) )=. F n {X t n } =,1,...,n σ-,, F n = σ(x t n,x t n 1,...,X t n ),, [ ] δθ p(h n,x t n E θ [S n (θ) S (θ) F ] = E,X t n ; θ) θ p(h n,x t n,x t n ; θ) X t n δ θ p(h n,x t n =,y; θ) p(h n,x t n,y; θ) p(h n,x t n,y; θ)dy = R = δ θ δ θ p(h n,x t n,y; θ)dy R p(h n,x t n,y; θ)dy =., S n (θ) F n -.,,, h n nh n, (ML) ˆθ n., m(x, θ) :=E θ [X t n X t n = x], v(x, θ) :=V θ [X t n X t n = x]. 1. (Ornstein-Uhlenbec ) 8, t X t = x e αt + βe αt e αs dw s. 177
11 t eαs dw s Wiener,, t e2αs ds = 1 2α (e2αt 1)., { 1 p(t, x, y; θ) = πβ2 (1 e 2αt )/α exp (y } e αt x) 2. β 2 (1 e 2αt )/α, X = x X t L(X t X = x) ( ) L(X t X = x) N e αt x, β2 (1 e 2αt ) 2α, l n (θ) = 1 2 n =1 { log(2π) + log + (X t n } e αhn X t n ) 2 β 2 (1 e 2αh n )/(2α) ( β 2 (1 e 2αh n ) ) 2α (2.6)., m(x, θ) v(x, θ), L(X t n m(x, θ) = e αh n x, v(x, θ) = β2 (1 e 2αhn ) 2α X t n = x) N (m(x, θ),v(x, θ)), (2.6),. { l n (θ) = 1 n log(2π) + log v(x t n 2,θ)+ (X t n m(x } t n,θ))2. v(x t n,θ) =1 1, Ornstein-Uhlenbec p (ML), ˆθ n., Ornstein- (ML) Uhlenbec, h n nh n, ˆθ n., SDE (2.1) X., SDE 178
12 ,., 1, L(X t n X t n = x) m(x, θ), v(x, θ). U n (θ) = n U(X t n,x t n,θ), (2.7) =1 U(x, y, θ) = 1 2 (y m(x, θ))2 log(2πv(x, θ)). (2.8) 2v(x, θ) U n (θ),., (M) U n (θ). ˆθ n U n (ˆθ n (M) )=supu n (θ)., U n (θ) θ, θ ( ) ( ) M n (α) (θ) δ α U n (θ) M n (θ) = := = (θ) δ β U n (θ) M (β) n M-.,, M n (θ) = n δ θ m(x t n,θ) =1 v(x t n,θ) n δ θ v(x t n,θ) =1 v 2 (X t n,θ) θ [ ] X t n m(x t n,θ) [ ] (X t n m(x t n,θ)) 2 v(x t n,θ). E θ [M n (θ) M (θ) F ] = δ θm(x t n,θ) v(x t n,θ) E θ[(x t n n m(x t n,θ) X t n ] = δ θ v(x t n,θ) v 2 (X t n,θ) E θ[(x t n n m(x t n,θ)) 2 v(x t n,θ) X t n ], M n (θ) F n -. M n (θ). U n (θ) 179
13 l n (θ), M n (θ) S n (θ). m(x, θ) v(x, θ) SDE, U n (θ) M n (θ).,,, M-., m(x, θ) v(x, θ)., 2 SDE m(x, θ) v(x, θ). SDE,,,., SDE,. 2.6, (2.7)-(2.8)., 2.3. Z t n := X (n) t n, Z t n = Z t n + b(z t n,α)h n + σ(z t n,β)(w t n w t n ), Z = x., w t n w t n, h n, L(Z t n Z t n = z), L(Z t n Z t n = z) N(z + b(z,α)h n,σ 2 (z,β)h n ).,., A2. E θ [X t n X t n ] = X t n + h n b(x t n,α)+o p (h 2 n), V θ [X t n X t n ] = h n σ 2 (X t n,α)+o p (h 2 n).,, (2.7)-(2.8) h n., g n. n g n (θ) = g(x t n,x t n,θ), (2.9) =1 g(x, y, θ) = 1 2 log(σ2 (x, β)) (y x h nb(x, α)) 2. (2.1) 2h n σ 2 (x, β) 18
14 , (2.7)-(2.8), (2.1) log(2πh nσ 2 (x, β)), θ, (2.1). ˆθ n =(ˆα n, ˆβ n ) g n (ˆθ n )=supg n (θ) θ., Kessler [14]. 1. A1-A3, nh 2 n, ( ) nhn (ˆα n α ) d N(,I 1 (θ )). n( ˆβn β ) g n, h n nh n, 1, nh 2 n., (2.7)-(2.8) h n. 1 3 (nh 2 n ), 4-5. nh 2 n,. Kessler [14] Ito-Taylor,,. 1,.,., (iii),. 1 ˆθ n,,. Gobet [8],, u, v R, P θ, l n (α + u/ nh n,β + v/ n) l n (α,β ) d ( u v ) Z 1 2 ( ) u I(θ ) v., Z, I(θ ) 2. (Local Asymptotic Normality, LAN). I(θ ), I(θ ) 1. 1 ˆθ n. ( u v ) 181
15 3, 1. dx ε t = b(x ε t,α)dt + εσ(x ε t,β)dw t,t [,T], ε (, 1], X ε = x, (3.1) ε, SDE (2.1). ε, SDE (3.1) X ε t dx t = b(x t,α)dt, t [,T], X = x X t. SDE (2.1), SDE (3.1)., SDE (3.1) Xt ε., (Yoshida [33], Kunitomo and Taahashi [16])). 2,. Xt SDE (3.1) ε = : dxt = b(xt,α )dt, X = x. C,l (R Θ α ) f : (i)f(x, α) R Θ α, x, n, C>, x, sup α x n f(x, α) C(1 + x ) C. (ii) n, x n f(x, α) α l, ν =, 1,...,l, C>, x sup α δα ν x n f(x, α) C(1 + x ) C. 2 2 (Fisher ) I(θ ) ( ) I b (θ ) I(θ )= I σ (θ )., I b (θ ) = I σ (θ ) = 2 ( ) δα b(xs 2,α ) ds, σ(xs,β ) ( ) δβ σ(xs 2,β ) ds. σ(xs,β ) 182
16 11. ( ) dxt ε = (Xt ε β +(Xt ε ) α)dt + ε 2 1+(Xt ε ) dw t, t [,T], ε (, 1], X ε 2 = x., α, β >. ε =,, X t = x e t + α(1 e t ). 7-2 x =1.5, α =2, β =1, T =5, ε =.25, ε =.15, ε =.5, ε =, h n =1/1 Xt ε. ε, Xt ε, X t ( ) : , [,T], T =1., [, 1]., X ε n = {Xt ε } =,1,...,n, t = /n. X ε n α β., ε n. 2 (iii), t n = h n, h n, t n n = nh n, (i). 183
17 3.1 SDE (3.1),., T =1. B1 (i) C>, x, y R,θ Θ, b(x, α) b(y, α) + σ(x, β) σ(y, β) C x y. (ii) b(x, α) C,3 (R Θ α ). (iii) σ(x, β) C,3 (R Θ β ),, inf x,β σ 2 (x, β) >. B2 (i) I(θ ). (ii) α α t [, 1], b(x t,α) b(x t,α ). β β t [, 1], σ 2 (X t,β) σ 2 (X t,β ).,. { } G ε,n (θ) = 1 n log σ 2 (Xt ε 2,β)+ n (Xt ε Xt ε 1 n b(xε t,α)) 2. ε 2 σ 2 (Xt ε β) =1 2.6 (2.9)-(2.1). ˆθ ε,n =(ˆα ε,n, ˆβ ε,n ) G ε,n (ˆθ ε,n )=supg ε,n (θ). θ Θ., ˆθ ε,n (Sørensen and Uchida [28])). 2. B1-B2, (ε n) 1 = O(1), ( ε 1 ) (ˆα ε,n α ) d N (, I(θ ) 1). n( ˆβε,n β ) (ε n) 1, ˆβ ε,n ˆα ε,n., ε n, ε n,, ε := ε n (n ),,. 2, n ε, n := n ε (ε ). 184
18 4,,, Praasa Rao [24, 25]., Genon-Catalot and Jacod [5, 6] (i) β,., (i), α,. Bibby and Sørensen [1] (ii). α β,. Uchida [29],,. Uchida [3], α M-,.,,., Kutoyants [17] Ibragimov and Has minsii [1], Küchler and Sørensen [2]. 1, Kutoyants [18, 19], Praasa Rao [25].,.,.,, [35], Ieda and Watanabe [11], Karatzas and Shreve [13], [3], [23],, Freidlin and Wentzell [2],, Jacod and Shiryaev [12],, Kloeden and Platen [15].,, ( [9]).,, Shimizu and Yoshida [27] Masuda [22],., Yoshida [32], 185
19 ,,., [34], Saamoto and Yoshida [26]., 1,,.,. 5,. ( [35], Ieda and Watanabe [11], Karatzas and Shreve [13], [3], [23]),,. 5.1 Wiener 1. (Ω, F,P). (i) {X t } t 1. (ii) 1 {X t } t. P ({ω Ω [, ) t X t (ω) R }) =1. 2. (Ω, F,P). {F t } t, (i) t, F t σ-. (ii) s<t, F s F t F. (Ω, F,P; {F t } t ).,. 3. {X t } t 1. (i) t, X t F t -, {X t } t F t. 186
20 (ii) t, (s, ω) [,t] Ω X s (ω) R B([,t]) F t, {X t } t F t {w t } t (i)-(iv), 1 F t - Wiener. (i) {w t } t F t. (ii) P (w =)=1. (iii) t>s, w t w s F s,, t s 1. (iv) {w t } t F t - Wiener {w t } t,. (i) p =1, 2,..., E[w 2p t ]=(2p 1)!!t p, E[w 2p 1 t ]=. (ii) a.s. ω, w t (ω) t,. (iii) w t (ω) t 2. (iv) a.s. ω, w t (ω) t. 5. p 1. 1 X = {X t } t F t - L p (i)-(iv). (i) t, E[ X t p ] <. (ii) X = {X t } t F t. (iii) t>s, E[X t F s ]=X s a.s. (iv) {X t } t. 1 F t - Wiener {w t } t F t - L p. 187
21 5.2 (Ω, F,P; {F t } t ) (i)-(iii),. (i)(ω, F,P),, M N F P (N) = M F. (ii) F t,, t F t = s>t F s. (iii) F P -,, N := {A Ω B F A B,P(B) =} F., (Ω, F,P; {F t } t )), 1 F t - Wiener {w t } t. w t a.s. ω, t ( 3-(iv)), f t (ω)dw t (ω) (5.1) ω Lebesgue-Stieltjes., Wiener w, L 2 loc (F t) f Wiener w (5.1)., L 2 loc (F t)={{f t } t 1 F t, T, P( } T f 2 t (ω)dt < ) =1., [35] [23]. L 2 (F t )={{f t } t 1 F t, T, E[ } T f 2 t (ω)dt] <. L 2 (F t ) L 2 loc (F t). 4. f L 2 (F t ). (i) { t f sdw s }t F t - L 2. (ii) T, [ ] E f t dw t [ ( ) 2 ] E f t dw t =, [ = E ] ft 2 dt. L 1 loc (F t)={{f t } t 1 F t, T, P ( } T f t(ω) dt < ) =1. 188
22 5 ( ). X F -, b L 1 loc (F t), σ L 2 loc (F t). 1 ( ) X T = X + b t dt +., f C 2 (R), f(x T ) = f(x )+ + f x (X t)b t dt f x (X t)σ t dw t σ t dw t 2 f x 2 (X t)σ 2 t dt., (t, x) f(t, x) x 2, t 1, (t, x),. f(t,x T ) = f(,x )+ + + f t (t, X t)dt f x (t, X t)b t dt f x (t, X t)σ t dw t 2 f x 2 (t, X t)σ 2 t dt 5.3 (Ω, F,P; {F t } t ), 1 F t - Wiener {w t } t. b, σ R R Borel. 6. X t (ω) :[, ) Ω R x dx t = b(x t )dt + σ(x t )dw t, X = x (5.2),. (i) X = {X t } t F t, T ( { P b(xt ) + σ 2 (X t ) } ) dt < =1. 189
23 (ii) P (X = x )=1, (iii) X t = X + t b(x s)dt + t σ(x s)dw t, t (Lipschitz) L>, x, y R b(x) b(y) + σ(x) σ(y) L x y., (5.2) X = {X t } t., : X Y (5.2), P (X t = Y t, t ) = 1. [1] Bibby, B. M. and Sørensen, M. (1995). Martingale estimating functions for discretely observed diffusion processes. Bernoulli 1, [2] Freidlin M. I. and Wentzell A. D. (1998). Random perturbations of dynamical systems, second edition. Springer-Verlag, New Yor. [3] (1997)... [4] Genon-Catalot, V. (199). Maximum contrast estimation for diffusion processes from discrete observations. Statistics 21, [5] Genon-Catalot, V. and Jacod, J. (1993). On the estimation of the diffusion coefficient for multidimensional diffusion processes. Ann. Inst. Henri Poincaré Probab. Statist. 29, [6] Genon-Catalot, V. and Jacod, J. (1994). Estimation of the diffusion coefficient for diffusion processes: random sampling. Scand. J. Statist. 21, [7] Gobet, E. (21). Local asymptotic mixed normality property for elliptic diffusion: a Malliavin calculus approach. Bernoulli 7, [8] Gobet, E. (22). LAN property for ergodic diffusions with discrete observations. Ann. Inst. H. Poincare Probab. Statist. 38, [9] (28).. 21 I:, 1,. 19
24 [1] Ibragimov, I. A. and Has minsii, R. Z. (1981). Statistical estimation. Springer Verlag, New Yor. [11] Ieda, N. and Watanabe, S. (1989). Stochastic differential equations and diffusion processes, second edition. North-Holland/Kodansha, Toyo. [12] Jacod, J. and Shiryaev, A. N. (1987). Limit theorems for stochastic processes. Springer, Heidelberg. [13] Karatzas, I. and Shreve, S. E. (1991). Brownian motion and stochastic calculus, second edition. Springer-Verlag, New Yor. [14] Kessler, M. (1997). Estimation of an ergodic diffusion from discrete observations. Scand. J. Statist. 24, [15] Kloeden, P. E. and Platen, E. (1992). Numerical solution of stochastic differential equations. Springer-Verlag, New Yor. [16] Kunitomo, N. and Taahashi, A. (21). The asymptotic expansion approach to the valuation of interest rate contingent claims. Mathematical Finance, 11, (21) [17] Kutoyants, Yu. A. (1984). Parameter estimation for stochastic processes. Praasa Rao, B.L.S. (ed.) Heldermann, Berlin. [18] Kutoyants, Yu. A. (1994). Identification of dynamical systems with small noise. Kluwer, Dordrecht. [19] Kutoyants, Yu. A. (24). Statistical inference for ergodic diffusion processes. Springer-Verlag, London. [2] Küchler, U. and Sørensen, M. (1997). Exponential families of stochastic processes. Springer, New Yor. [21] Laredo, C. F. (199). A sufficient condition for asymptotic sufficiency of incomplete observations of a diffusion process. Ann. Statist. 18, [22] Masuda, H. (27). Ergodicity and exponential β-mixing bound for multidimensional diffusions with jumps. Stochastic Processes Appl, 117, [23] (1999)
25 [24] Praasa Rao, B. L. S. (1999a). Statistical inference for diffusion type processes. London, Arnold. [25] Praasa Rao, B. L. S. (1999b). Semimartingales and their statistical inference. Chapman & Hall/CRC. [26] Saamoto, Y. and Yoshida, N. (24). Asymptotic expansion formulas for functionals of ɛ-marov processes with a mixing property. Ann. Inst. Statist. Math. 56, [27] Shimizu, Y. and Yoshida, N. (26). Estimation of parameters for diffusion processes with jumps from discrete observations. Statist. Infer. Stochast. Process., 9, [28] Sørensen, M. and Uchida, M. (23). Small diffusion asymptotics for discretely sampled stochastic differential equations. Bernoulli 9, [29] Uchida, M. (23). Estimation for dynamical systems with small noise from discrete observations. J. Japan Statist. Soc., 33, [3] Uchida, M. (24). Estimation for discretely observed small diffusions based on approximate martingale estimating functions. Scand. J. Statist. 31, [31] Yoshida, N. (1992a). Estimation for diffusion processes from discrete observation. J. Multivariate Anal. 41, [32] Yoshida, N. (1992b). Asymptotic expansion of maximum lielihood estimators for small diffusions via the theory of Malliavin-Watanabe. Probab. Theory Relat. Fields 92, [33] Yoshida, N. (1992c). Asymptotic expansion for statistics related to small diffusions. J. Japan Statist. Soc. 22, [34] (23). Malliavin,, 55, [35] (1975)
 43433 8 3 . Stochastic exponentials...................................... 3. Girsanov s theorem......................................... 4 On the martingale property of stochastic exponentials 5. Gronwall
43433 8 3 . Stochastic exponentials...................................... 3. Girsanov s theorem......................................... 4 On the martingale property of stochastic exponentials 5. Gronwall
untitled
 3 3. (stochastic differential equations) { dx(t) =f(t, X)dt + G(t, X)dW (t), t [,T], (3.) X( )=X X(t) : [,T] R d (d ) f(t, X) : [,T] R d R d (drift term) G(t, X) : [,T] R d R d m (diffusion term) W (t)
3 3. (stochastic differential equations) { dx(t) =f(t, X)dt + G(t, X)dW (t), t [,T], (3.) X( )=X X(t) : [,T] R d (d ) f(t, X) : [,T] R d R d (drift term) G(t, X) : [,T] R d R d m (diffusion term) W (t)
( ) Loewner SLE 13 February
 ( ) Loewner SLE 3 February 00 G. F. Lawler, Conformally Invariant Processes in the Plane, (American Mathematical Society, 005)., Summer School 009 (009 8 7-9 ) . d- (BES d ) d B t = (Bt, B t,, Bd t ) (d
( ) Loewner SLE 3 February 00 G. F. Lawler, Conformally Invariant Processes in the Plane, (American Mathematical Society, 005)., Summer School 009 (009 8 7-9 ) . d- (BES d ) d B t = (Bt, B t,, Bd t ) (d
,,,17,,, ( ),, E Q [S T F t ] < S t, t [, T ],,,,,,,,
![,,,17,,, ( ),, E Q [S T F t ] < S t, t [, T ],,,,,,,, ,,,17,,, ( ),, E Q [S T F t ] < S t, t [, T ],,,,,,,,](/thumbs/91/105754403.jpg) 14 5 1 ,,,17,,,194 1 4 ( ),, E Q [S T F t ] < S t, t [, T ],,,,,,,, 1 4 1.1........................................ 4 5.1........................................ 5.........................................
14 5 1 ,,,17,,,194 1 4 ( ),, E Q [S T F t ] < S t, t [, T ],,,,,,,, 1 4 1.1........................................ 4 5.1........................................ 5.........................................
mf.dvi
 21 9 29 1 2 3....................................... 3 :......................... 3....................................... 4................................ 4..................................... 5................................
21 9 29 1 2 3....................................... 3 :......................... 3....................................... 4................................ 4..................................... 5................................
Part. 4. () 4.. () 4.. 3 5. 5 5.. 5 5.. 6 5.3. 7 Part 3. 8 6. 8 6.. 8 6.. 8 7. 8 7.. 8 7.. 3 8. 3 9., 34 9.. 34 9.. 37 9.3. 39. 4.. 4.. 43. 46.. 46..
 Cotets 6 6 : 6 6 6 6 6 6 7 7 7 Part. 8. 8.. 8.. 9..... 3. 3 3.. 3 3.. 7 3.3. 8 Part. 4. () 4.. () 4.. 3 5. 5 5.. 5 5.. 6 5.3. 7 Part 3. 8 6. 8 6.. 8 6.. 8 7. 8 7.. 8 7.. 3 8. 3 9., 34 9.. 34 9.. 37 9.3.
Cotets 6 6 : 6 6 6 6 6 6 7 7 7 Part. 8. 8.. 8.. 9..... 3. 3 3.. 3 3.. 7 3.3. 8 Part. 4. () 4.. () 4.. 3 5. 5 5.. 5 5.. 6 5.3. 7 Part 3. 8 6. 8 6.. 8 6.. 8 7. 8 7.. 8 7.. 3 8. 3 9., 34 9.. 34 9.. 37 9.3.
untitled
 2 : n =1, 2,, 10000 0.5125 0.51 0.5075 0.505 0.5025 0.5 0.4975 0.495 0 2000 4000 6000 8000 10000 2 weak law of large numbers 1. X 1,X 2,,X n 2. µ = E(X i ),i=1, 2,,n 3. σi 2 = V (X i ) σ 2,i=1, 2,,n ɛ>0
2 : n =1, 2,, 10000 0.5125 0.51 0.5075 0.505 0.5025 0.5 0.4975 0.495 0 2000 4000 6000 8000 10000 2 weak law of large numbers 1. X 1,X 2,,X n 2. µ = E(X i ),i=1, 2,,n 3. σi 2 = V (X i ) σ 2,i=1, 2,,n ɛ>0
boost_sine1_iter4.eps
 3 (, 3D ) 2. 2 3.. 3D 3D....,,. a + b = f, a, f. b a (.) b a.: b f (.2), b f., f.2. 2 Y y Q(X,Y,Z) O f o q(x,y) Z X x image plane.2:.2, O, z,. O..2 (X, Y, Z) 3D Q..2 O f, x, y X, Y. Q OQ q, q (x, y). x
3 (, 3D ) 2. 2 3.. 3D 3D....,,. a + b = f, a, f. b a (.) b a.: b f (.2), b f., f.2. 2 Y y Q(X,Y,Z) O f o q(x,y) Z X x image plane.2:.2, O, z,. O..2 (X, Y, Z) 3D Q..2 O f, x, y X, Y. Q OQ q, q (x, y). x
[1][2] [3] *1 Defnton 1.1. W () = σ 2 dt [2] Defnton 1.2. W (t ) Defnton 1.3. W () = E[W (t)] = Cov[W (t), W (s)] = E[W (t)w (s)] = σ 2 mn{s, t} Propo
![[1][2] [3] *1 Defnton 1.1. W () = σ 2 dt [2] Defnton 1.2. W (t ) Defnton 1.3. W () = E[W (t)] = Cov[W (t), W (s)] = E[W (t)w (s)] = σ 2 mn{s, t} Propo [1][2] [3] *1 Defnton 1.1. W () = σ 2 dt [2] Defnton 1.2. W (t ) Defnton 1.3. W () = E[W (t)] = Cov[W (t), W (s)] = E[W (t)w (s)] = σ 2 mn{s, t} Propo](/thumbs/93/114156950.jpg) @phykm 218 7 12 [2] [2] [1] ([4] ) 1 Ω = 2 N {Π n =1 A { 1, 1} N n N, A {{ 1, 1}, { 1}, {1}, }} B : Ω { 1, 1} P (Π n =1 A 2 N ) = 2 #{ A={ 1},{1}} X = j=1 B j B X +k X V[X ] = 1 ( ) 1 1 dt dx W (t) = t/dt
@phykm 218 7 12 [2] [2] [1] ([4] ) 1 Ω = 2 N {Π n =1 A { 1, 1} N n N, A {{ 1, 1}, { 1}, {1}, }} B : Ω { 1, 1} P (Π n =1 A 2 N ) = 2 #{ A={ 1},{1}} X = j=1 B j B X +k X V[X ] = 1 ( ) 1 1 dt dx W (t) = t/dt
24.15章.微分方程式
 m d y dt = F m d y = mg dt V y = dy dt d y dt = d dy dt dt = dv y dt dv y dt = g dv y dt = g dt dt dv y = g dt V y ( t) = gt + C V y ( ) = V y ( ) = C = V y t ( ) = gt V y ( t) = dy dt = gt dy = g t dt
m d y dt = F m d y = mg dt V y = dy dt d y dt = d dy dt dt = dv y dt dv y dt = g dv y dt = g dt dt dv y = g dt V y ( t) = gt + C V y ( ) = V y ( ) = C = V y t ( ) = gt V y ( t) = dy dt = gt dy = g t dt
Grushin 2MA16039T
 Grushin 2MA1639T 3 2 2 R d Borel α i k (x, bi (x, 1 i d, 1 k N d N α R d b α = α(x := (αk(x i 1 i d, 1 k N b = b(x := (b i (x 1 i d X = (X t t x R d dx t = α(x t db t + b(x t dt ( 3 u t = Au + V u, u(,
Grushin 2MA1639T 3 2 2 R d Borel α i k (x, bi (x, 1 i d, 1 k N d N α R d b α = α(x := (αk(x i 1 i d, 1 k N b = b(x := (b i (x 1 i d X = (X t t x R d dx t = α(x t db t + b(x t dt ( 3 u t = Au + V u, u(,
6. Euler x
 ...............................................................................3......................................... 4.4................................... 5.5......................................
...............................................................................3......................................... 4.4................................... 5.5......................................
Green
 28 6/-3 2 ax, bx R, L = d2 ax 2 dx 2 + bx d dx 2 L X = {Xt, t }. σ y = inf{t > ; Xt = y} t Xt L y = sup{t > ; Xt = y} 2. Gauss Gamma 3. tree 4. t Black-Scholes Madan-Roynette-Yor [6] σ y E x [exp λσ y
28 6/-3 2 ax, bx R, L = d2 ax 2 dx 2 + bx d dx 2 L X = {Xt, t }. σ y = inf{t > ; Xt = y} t Xt L y = sup{t > ; Xt = y} 2. Gauss Gamma 3. tree 4. t Black-Scholes Madan-Roynette-Yor [6] σ y E x [exp λσ y
 Recent Developments and Perspectives of Statistical Time Series Analysis /ta) : t"i,,t Q) w (^ - p) dp *+*ffi t 1 ] Abraham, B. and Ledolter, J. (1986). Forecast functions implied by autoregressive
Recent Developments and Perspectives of Statistical Time Series Analysis /ta) : t"i,,t Q) w (^ - p) dp *+*ffi t 1 ] Abraham, B. and Ledolter, J. (1986). Forecast functions implied by autoregressive
r 1 m A r/m i) t ii) m i) t B(t; m) ( B(t; m) = A 1 + r ) mt m ii) B(t; m) ( B(t; m) = A 1 + r ) mt m { ( = A 1 + r ) m } rt r m n = m r m n B
 1 1.1 1 r 1 m A r/m i) t ii) m i) t Bt; m) Bt; m) = A 1 + r ) mt m ii) Bt; m) Bt; m) = A 1 + r ) mt m { = A 1 + r ) m } rt r m n = m r m n Bt; m) Aert e lim 1 + 1 n 1.1) n!1 n) e a 1, a 2, a 3,... {a n
1 1.1 1 r 1 m A r/m i) t ii) m i) t Bt; m) Bt; m) = A 1 + r ) mt m ii) Bt; m) Bt; m) = A 1 + r ) mt m { = A 1 + r ) m } rt r m n = m r m n Bt; m) Aert e lim 1 + 1 n 1.1) n!1 n) e a 1, a 2, a 3,... {a n
5.. z = f(x, y) y y = b f x x g(x) f(x, b) g x ( ) A = lim h g(a + h) g(a) h g(x) a A = g (a) = f x (a, b)............................................
 5 partial differentiation (total) differentiation 5. z = f(x, y) (a, b) A = lim h f(a + h, b) f(a, b) h........................................................... ( ) f(x, y) (a, b) x A (a, b) x (a, b)
5 partial differentiation (total) differentiation 5. z = f(x, y) (a, b) A = lim h f(a + h, b) f(a, b) h........................................................... ( ) f(x, y) (a, b) x A (a, b) x (a, b)
 Design of highly accurate formulas for numerical integration in weighted Hardy spaces with the aid of potential theory 1 Ken ichiro Tanaka 1 Ω R m F I = F (t) dt (1.1) Ω m m 1 m = 1 1 Newton-Cotes Gauss
Design of highly accurate formulas for numerical integration in weighted Hardy spaces with the aid of potential theory 1 Ken ichiro Tanaka 1 Ω R m F I = F (t) dt (1.1) Ω m m 1 m = 1 1 Newton-Cotes Gauss
0 1-4. 1-5. (1) + b = b +, (2) b = b, (3) + 0 =, (4) 1 =, (5) ( + b) + c = + (b + c), (6) ( b) c = (b c), (7) (b + c) = b + c, (8) ( + b)c = c + bc (9
 1-1. 1, 2, 3, 4, 5, 6, 7,, 100,, 1000, n, m m m n n 0 n, m m n 1-2. 0 m n m n 0 2 = 1.41421356 π = 3.141516 1-3. 1 0 1-4. 1-5. (1) + b = b +, (2) b = b, (3) + 0 =, (4) 1 =, (5) ( + b) + c = + (b + c),
1-1. 1, 2, 3, 4, 5, 6, 7,, 100,, 1000, n, m m m n n 0 n, m m n 1-2. 0 m n m n 0 2 = 1.41421356 π = 3.141516 1-3. 1 0 1-4. 1-5. (1) + b = b +, (2) b = b, (3) + 0 =, (4) 1 =, (5) ( + b) + c = + (b + c),
II Brown Brown
 II 16 12 5 1 Brown 3 1.1..................................... 3 1.2 Brown............................... 5 1.3................................... 8 1.4 Markov.................................... 1 1.5
II 16 12 5 1 Brown 3 1.1..................................... 3 1.2 Brown............................... 5 1.3................................... 8 1.4 Markov.................................... 1 1.5
untitled
 II(c) 1 October. 21, 2009 1 CS53 yamamoto@cs.kobe-u.ac.jp 3 1 7 1.1 : : : : : : : : : : : : : : : : : : : : : : 7 1.2 : : : : : : : : : : : : : : : : 8 1.2.1 : : : : : : : : : : : : : : : : : : : 8 1.2.2
II(c) 1 October. 21, 2009 1 CS53 yamamoto@cs.kobe-u.ac.jp 3 1 7 1.1 : : : : : : : : : : : : : : : : : : : : : : 7 1.2 : : : : : : : : : : : : : : : : 8 1.2.1 : : : : : : : : : : : : : : : : : : : 8 1.2.2
Black-Scholes [1] Nelson [2] Schrödinger 1 Black Scholes [1] Black-Scholes Nelson [2][3][4] Schrödinger Nelson Parisi Wu [5] Nelson Parisi-W
![Black-Scholes [1] Nelson [2] Schrödinger 1 Black Scholes [1] Black-Scholes Nelson [2][3][4] Schrödinger Nelson Parisi Wu [5] Nelson Parisi-W Black-Scholes [1] Nelson [2] Schrödinger 1 Black Scholes [1] Black-Scholes Nelson [2][3][4] Schrödinger Nelson Parisi Wu [5] Nelson Parisi-W](/thumbs/97/132191371.jpg) 003 7 14 Black-Scholes [1] Nelson [] Schrödinger 1 Black Scholes [1] Black-Scholes Nelson [][3][4] Schrödinger Nelson Parisi Wu [5] Nelson Parisi-Wu Nelson e-mail: takatoshi-tasaki@nifty.com kabutaro@mocha.freemail.ne.jp
003 7 14 Black-Scholes [1] Nelson [] Schrödinger 1 Black Scholes [1] Black-Scholes Nelson [][3][4] Schrödinger Nelson Parisi Wu [5] Nelson Parisi-Wu Nelson e-mail: takatoshi-tasaki@nifty.com kabutaro@mocha.freemail.ne.jp
7) ẋt) =iaω expiωt) ibω exp iωt) 9) ẋ0) = iωa b) = 0 0) a = b a = b = A/ xt) = A expiωt) + exp iωt)) = A cosωt) ) ) vt) = Aω sinωt) ) ) 9) ) 9) E = mv
 - - m k F = kx ) kxt) =m d xt) dt ) ω = k/m ) ) d dt + ω xt) = 0 3) ) ) d d dt iω dt + iω xt) = 0 4) ω d/dt iω) d/dt + iω) 4) ) d dt iω xt) = 0 5) ) d dt + iω xt) = 0 6) 5) 6) a expiωt) b exp iωt) ) )
- - m k F = kx ) kxt) =m d xt) dt ) ω = k/m ) ) d dt + ω xt) = 0 3) ) ) d d dt iω dt + iω xt) = 0 4) ω d/dt iω) d/dt + iω) 4) ) d dt iω xt) = 0 5) ) d dt + iω xt) = 0 6) 5) 6) a expiωt) b exp iωt) ) )
5 36 5................................................... 36 5................................................... 36 5.3..............................
 9 8 3............................................. 3.......................................... 4.3............................................ 4 5 3 6 3..................................................
9 8 3............................................. 3.......................................... 4.3............................................ 4 5 3 6 3..................................................
(interval estimation) 3 (confidence coefficient) µ σ/sqrt(n) 4 P ( (X - µ) / (σ sqrt N < a) = α a α X α µ a σ sqrt N X µ a σ sqrt N 2
 7 2 1 (interval estimation) 3 (confidence coefficient) µ σ/sqrt(n) 4 P ( (X - µ) / (σ sqrt N < a) = α a α X α µ a σ sqrt N X µ a σ sqrt N 2 (confidence interval) 5 X a σ sqrt N µ X a σ sqrt N - 6 P ( X
7 2 1 (interval estimation) 3 (confidence coefficient) µ σ/sqrt(n) 4 P ( (X - µ) / (σ sqrt N < a) = α a α X α µ a σ sqrt N X µ a σ sqrt N 2 (confidence interval) 5 X a σ sqrt N µ X a σ sqrt N - 6 P ( X
2011de.dvi
 211 ( 4 2 1. 3 1.1............................... 3 1.2 1- -......................... 13 1.3 2-1 -................... 19 1.4 3- -......................... 29 2. 37 2.1................................ 37
211 ( 4 2 1. 3 1.1............................... 3 1.2 1- -......................... 13 1.3 2-1 -................... 19 1.4 3- -......................... 29 2. 37 2.1................................ 37
1 No.1 5 C 1 I III F 1 F 2 F 1 F 2 2 Φ 2 (t) = Φ 1 (t) Φ 1 (t t). = Φ 1(t) t = ( 1.5e 0.5t 2.4e 4t 2e 10t ) τ < 0 t > τ Φ 2 (t) < 0 lim t Φ 2 (t) = 0
 1 No.1 5 C 1 I III F 1 F 2 F 1 F 2 2 Φ 2 (t) = Φ 1 (t) Φ 1 (t t). = Φ 1(t) t = ( 1.5e 0.5t 2.4e 4t 2e 10t ) τ < 0 t > τ Φ 2 (t) < 0 lim t Φ 2 (t) = 0 0 < t < τ I II 0 No.2 2 C x y x y > 0 x 0 x > b a dx
1 No.1 5 C 1 I III F 1 F 2 F 1 F 2 2 Φ 2 (t) = Φ 1 (t) Φ 1 (t t). = Φ 1(t) t = ( 1.5e 0.5t 2.4e 4t 2e 10t ) τ < 0 t > τ Φ 2 (t) < 0 lim t Φ 2 (t) = 0 0 < t < τ I II 0 No.2 2 C x y x y > 0 x 0 x > b a dx
2 (March 13, 2010) N Λ a = i,j=1 x i ( d (a) i,j x j ), Λ h = N i,j=1 x i ( d (h) i,j x j ) B a B h B a = N i,j=1 ν i d (a) i,j, B h = x j N i,j=1 ν i
 1. A. M. Turing [18] 60 Turing A. Gierer H. Meinhardt [1] : (GM) ) a t = D a a xx µa + ρ (c a2 h + ρ 0 (0 < x < l, t > 0) h t = D h h xx νh + c ρ a 2 (0 < x < l, t > 0) a x = h x = 0 (x = 0, l) a = a(x,
1. A. M. Turing [18] 60 Turing A. Gierer H. Meinhardt [1] : (GM) ) a t = D a a xx µa + ρ (c a2 h + ρ 0 (0 < x < l, t > 0) h t = D h h xx νh + c ρ a 2 (0 < x < l, t > 0) a x = h x = 0 (x = 0, l) a = a(x,
18 ( ) I II III A B C(100 ) 1, 2, 3, 5 I II A B (100 ) 1, 2, 3 I II A B (80 ) 6 8 I II III A B C(80 ) 1 n (1 + x) n (1) n C 1 + n C
 8 ( ) 8 5 4 I II III A B C( ),,, 5 I II A B ( ),, I II A B (8 ) 6 8 I II III A B C(8 ) n ( + x) n () n C + n C + + n C n = 7 n () 7 9 C : y = x x A(, 6) () A C () C P AP Q () () () 4 A(,, ) B(,, ) C(,,
8 ( ) 8 5 4 I II III A B C( ),,, 5 I II A B ( ),, I II A B (8 ) 6 8 I II III A B C(8 ) n ( + x) n () n C + n C + + n C n = 7 n () 7 9 C : y = x x A(, 6) () A C () C P AP Q () () () 4 A(,, ) B(,, ) C(,,
ばらつき抑制のための確率最適制御
 ( ) http://wwwhayanuemnagoya-uacjp/ fujimoto/ 2011 3 9 11 ( ) 2011/03/09-11 1 / 46 Outline 1 2 3 4 5 ( ) 2011/03/09-11 2 / 46 Outline 1 2 3 4 5 ( ) 2011/03/09-11 3 / 46 (1/2) r + Controller - u Plant y
( ) http://wwwhayanuemnagoya-uacjp/ fujimoto/ 2011 3 9 11 ( ) 2011/03/09-11 1 / 46 Outline 1 2 3 4 5 ( ) 2011/03/09-11 2 / 46 Outline 1 2 3 4 5 ( ) 2011/03/09-11 3 / 46 (1/2) r + Controller - u Plant y
1
 1 1 7 1.1.................................. 11 2 13 2.1............................ 13 2.2............................ 17 2.3.................................. 19 3 21 3.1.............................
1 1 7 1.1.................................. 11 2 13 2.1............................ 13 2.2............................ 17 2.3.................................. 19 3 21 3.1.............................
基礎数学I
 I & II ii ii........... 22................. 25 12............... 28.................. 28.................... 31............. 32.................. 34 3 1 9.................... 1....................... 1............
I & II ii ii........... 22................. 25 12............... 28.................. 28.................... 31............. 32.................. 34 3 1 9.................... 1....................... 1............
<4D F736F F D B B83578B6594BB2D834A836F815B82D082C88C60202E646F63>
 常微分方程式の局所漸近解析 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/007651 このサンプルページの内容は, 初版 1 刷発行当時のものです. i Leibniz ydy = y 2 /2 1675 11 11 [6] 100 Bernoulli Riccati 19 Fuchs
常微分方程式の局所漸近解析 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/007651 このサンプルページの内容は, 初版 1 刷発行当時のものです. i Leibniz ydy = y 2 /2 1675 11 11 [6] 100 Bernoulli Riccati 19 Fuchs
4 4 4 a b c d a b A c d A a da ad bce O E O n A n O ad bc a d n A n O 5 {a n } S n a k n a n + k S n a a n+ S n n S n n log x x {xy } x, y x + y 7 fx
 4 4 5 4 I II III A B C, 5 7 I II A B,, 8, 9 I II A B O A,, Bb, b, Cc, c, c b c b b c c c OA BC P BC OP BC P AP BC n f n x xn e x! e n! n f n x f n x f n x f k x k 4 e > f n x dx k k! fx sin x cos x tan
4 4 5 4 I II III A B C, 5 7 I II A B,, 8, 9 I II A B O A,, Bb, b, Cc, c, c b c b b c c c OA BC P BC OP BC P AP BC n f n x xn e x! e n! n f n x f n x f n x f k x k 4 e > f n x dx k k! fx sin x cos x tan
 , 26 1 1 3 1 5 1.1.............................. 5 1.2,........................ 6 1.3......................... 16 2 Poisson Lévy 19 2.1 Poisson Poisson................. 19 2.1.1........................
, 26 1 1 3 1 5 1.1.............................. 5 1.2,........................ 6 1.3......................... 16 2 Poisson Lévy 19 2.1 Poisson Poisson................. 19 2.1.1........................
3
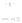 - { } / f ( ) e nπ + f( ) = Cne n= nπ / Eucld r e (= N) j = j e e = δj, δj = 0 j r e ( =, < N) r r r { } ε ε = r r r = Ce = r r r e ε = = C = r C r e + CC e j e j e = = ε = r ( r e ) + r e C C 0 r e =
- { } / f ( ) e nπ + f( ) = Cne n= nπ / Eucld r e (= N) j = j e e = δj, δj = 0 j r e ( =, < N) r r r { } ε ε = r r r = Ce = r r r e ε = = C = r C r e + CC e j e j e = = ε = r ( r e ) + r e C C 0 r e =
5. [1 ] 1 [], u(x, t) t c u(x, t) x (5.3) ξ x + ct, η x ct (5.4),u(x, t) ξ, η u(ξ, η), ξ t,, ( u(ξ,η) ξ η u(x, t) t ) u(x, t) { ( u(ξ, η) c t ξ ξ { (
![5. [1 ] 1 [], u(x, t) t c u(x, t) x (5.3) ξ x + ct, η x ct (5.4),u(x, t) ξ, η u(ξ, η), ξ t,, ( u(ξ,η) ξ η u(x, t) t ) u(x, t) { ( u(ξ, η) c t ξ ξ { ( 5. [1 ] 1 [], u(x, t) t c u(x, t) x (5.3) ξ x + ct, η x ct (5.4),u(x, t) ξ, η u(ξ, η), ξ t,, ( u(ξ,η) ξ η u(x, t) t ) u(x, t) { ( u(ξ, η) c t ξ ξ { (](/thumbs/92/107866626.jpg) 5 5.1 [ ] ) d f(t) + a d f(t) + bf(t) : f(t) 1 dt dt ) u(x, t) c u(x, t) : u(x, t) t x : ( ) ) 1 : y + ay, : y + ay + by : ( ) 1 ) : y + ay, : yy + ay 3 ( ): ( ) ) : y + ay, : y + ay b [],,, [ ] au xx
5 5.1 [ ] ) d f(t) + a d f(t) + bf(t) : f(t) 1 dt dt ) u(x, t) c u(x, t) : u(x, t) t x : ( ) ) 1 : y + ay, : y + ay + by : ( ) 1 ) : y + ay, : yy + ay 3 ( ): ( ) ) : y + ay, : y + ay b [],,, [ ] au xx
CALCULUS II (Hiroshi SUZUKI ) f(x, y) A(a, b) 1. P (x, y) A(a, b) A(a, b) f(x, y) c f(x, y) A(a, b) c f(x, y) c f(x, y) c (x a, y b)
 CALCULUS II (Hiroshi SUZUKI ) 16 1 1 1.1 1.1 f(x, y) A(a, b) 1. P (x, y) A(a, b) A(a, b) f(x, y) c f(x, y) A(a, b) c f(x, y) c f(x, y) c (x a, y b) lim f(x, y) = lim f(x, y) = lim f(x, y) = c. x a, y b
CALCULUS II (Hiroshi SUZUKI ) 16 1 1 1.1 1.1 f(x, y) A(a, b) 1. P (x, y) A(a, b) A(a, b) f(x, y) c f(x, y) A(a, b) c f(x, y) c f(x, y) c (x a, y b) lim f(x, y) = lim f(x, y) = lim f(x, y) = c. x a, y b
f(x) = x (1) f (1) (2) f (2) f(x) x = a y y = f(x) f (a) y = f(x) A(a, f(a)) f(a + h) f(x) = A f(a) A x (3, 3) O a a + h x 1 f(x) x = a
 3 3.1 3.1.1 A f(a + h) f(a) f(x) lim f(x) x = a h 0 h f(x) x = a f 0 (a) f 0 (a) = lim h!0 f(a + h) f(a) h = lim x!a f(x) f(a) x a a + h = x h = x a h 0 x a 3.1 f(x) = x x = 3 f 0 (3) f (3) = lim h 0 (
3 3.1 3.1.1 A f(a + h) f(a) f(x) lim f(x) x = a h 0 h f(x) x = a f 0 (a) f 0 (a) = lim h!0 f(a + h) f(a) h = lim x!a f(x) f(a) x a a + h = x h = x a h 0 x a 3.1 f(x) = x x = 3 f 0 (3) f (3) = lim h 0 (
名古屋工業大の数学 2000 年 ~2015 年 大学入試数学動画解説サイト
 名古屋工業大の数学 年 ~5 年 大学入試数学動画解説サイト http://mathroom.jugem.jp/ 68 i 4 3 III III 3 5 3 ii 5 6 45 99 5 4 3. () r \= S n = r + r + 3r 3 + + nr n () x > f n (x) = e x + e x + 3e 3x + + ne nx f(x) = lim f n(x) lim
名古屋工業大の数学 年 ~5 年 大学入試数学動画解説サイト http://mathroom.jugem.jp/ 68 i 4 3 III III 3 5 3 ii 5 6 45 99 5 4 3. () r \= S n = r + r + 3r 3 + + nr n () x > f n (x) = e x + e x + 3e 3x + + ne nx f(x) = lim f n(x) lim
= π2 6, ( ) = π 4, ( ). 1 ( ( 5) ) ( 9 1 ( ( ) ) (
 + + 3 + 4 +... π 6, ( ) 3 + 5 7 +... π 4, ( ). ( 3 + ( 5) + 7 + ) ( 9 ( ( + 3) 5 + ) ( 7 + 9 + + 3 ) +... log( + ), ) +... π. ) ( 3 + 5 e x dx π.......................................................................
+ + 3 + 4 +... π 6, ( ) 3 + 5 7 +... π 4, ( ). ( 3 + ( 5) + 7 + ) ( 9 ( ( + 3) 5 + ) ( 7 + 9 + + 3 ) +... log( + ), ) +... π. ) ( 3 + 5 e x dx π.......................................................................
a. How to start: b. How to continue: c. How to stop: b EAP 2. EAP EAP (expected a posteriori) (posteriori distribution) (θ) MAP (maximum a posteriori)
 LET 2015 7 (pp. 25 39) EAP EAP (, 2013) (, 2014) PROX (, 2015) (computer-adaptive testing) EAP (expected a posteriori) Keywords: EAP 1. (, 1996, p. 273; Thissen & Mislevy, 2000, p. 101) 25 a. How to start:
LET 2015 7 (pp. 25 39) EAP EAP (, 2013) (, 2014) PROX (, 2015) (computer-adaptive testing) EAP (expected a posteriori) Keywords: EAP 1. (, 1996, p. 273; Thissen & Mislevy, 2000, p. 101) 25 a. How to start:
f(x) = f(x ) + α(x)(x x ) α(x) x = x. x = f (y), x = f (y ) y = f f (y) = f f (y ) + α(f (y))(f (y) f (y )) f (y) = f (y ) + α(f (y)) (y y ) ( (2) ) f
 22 A 3,4 No.3 () (2) (3) (4), (5) (6) (7) (8) () n x = (x,, x n ), = (,, n ), x = ( (x i i ) 2 ) /2 f(x) R n f(x) = f() + i α i (x ) i + o( x ) α,, α n g(x) = o( x )) lim x g(x) x = y = f() + i α i(x )
22 A 3,4 No.3 () (2) (3) (4), (5) (6) (7) (8) () n x = (x,, x n ), = (,, n ), x = ( (x i i ) 2 ) /2 f(x) R n f(x) = f() + i α i (x ) i + o( x ) α,, α n g(x) = o( x )) lim x g(x) x = y = f() + i α i(x )
I, II 1, A = A 4 : 6 = max{ A, } A A 10 10%
 1 2006.4.17. A 3-312 tel: 092-726-4774, e-mail: hara@math.kyushu-u.ac.jp, http://www.math.kyushu-u.ac.jp/ hara/lectures/lectures-j.html Office hours: B A I ɛ-δ ɛ-δ 1. 2. A 1. 1. 2. 3. 4. 5. 2. ɛ-δ 1. ɛ-n
1 2006.4.17. A 3-312 tel: 092-726-4774, e-mail: hara@math.kyushu-u.ac.jp, http://www.math.kyushu-u.ac.jp/ hara/lectures/lectures-j.html Office hours: B A I ɛ-δ ɛ-δ 1. 2. A 1. 1. 2. 3. 4. 5. 2. ɛ-δ 1. ɛ-n
untitled
 Y = Y () x i c C = i + c = ( x ) x π (x) π ( x ) = Y ( ){1 + ( x )}( 1 x ) Y ( )(1 + C ) ( 1 x) x π ( x) = 0 = ( x ) R R R R Y = (Y ) CS () CS ( ) = Y ( ) 0 ( Y ) dy Y ( ) A() * S( π ), S( CS) S( π ) =
Y = Y () x i c C = i + c = ( x ) x π (x) π ( x ) = Y ( ){1 + ( x )}( 1 x ) Y ( )(1 + C ) ( 1 x) x π ( x) = 0 = ( x ) R R R R Y = (Y ) CS () CS ( ) = Y ( ) 0 ( Y ) dy Y ( ) A() * S( π ), S( CS) S( π ) =
163 KdV KP Lax pair L, B L L L 1/2 W 1 LW = ( / x W t 1, t 2, t 3, ψ t n ψ/ t n = B nψ (KdV B n = L n/2 KP B n = L n KdV KP Lax W Lax τ KP L ψ τ τ Cha
 63 KdV KP Lax pair L, B L L L / W LW / x W t, t, t 3, ψ t n / B nψ KdV B n L n/ KP B n L n KdV KP Lax W Lax τ KP L ψ τ τ Chapter 7 An Introduction to the Sato Theory Masayui OIKAWA, Faculty of Engneering,
63 KdV KP Lax pair L, B L L L / W LW / x W t, t, t 3, ψ t n / B nψ KdV B n L n/ KP B n L n KdV KP Lax W Lax τ KP L ψ τ τ Chapter 7 An Introduction to the Sato Theory Masayui OIKAWA, Faculty of Engneering,
xia2.dvi
 Journal of Differential Equations 96 (992), 70-84 Melnikov method and transversal homoclinic points in the restricted three-body problem Zhihong Xia Department of Mathematics, Harvard University Cambridge,
Journal of Differential Equations 96 (992), 70-84 Melnikov method and transversal homoclinic points in the restricted three-body problem Zhihong Xia Department of Mathematics, Harvard University Cambridge,
II 2014 2 (1) log(1 + r/100) n = log 2 n log(1 + r/100) = log 2 n = log 2 log(1 + r/100) (2) y = f(x) = log(1 + x) x = 0 1 f (x) = 1/(1 + x) f (0) = 1
 II 2014 1 1 I 1.1 72 r 2 72 8 72/8 = 9 9 2 a 0 1 a 1 a 1 = a 0 (1+r/100) 2 a 2 a 2 = a 1 (1 + r/100) = a 0 (1 + r/100) 2 n a n = a 0 (1 + r/100) n a n a 0 2 n a 0 (1 + r/100) n = 2a 0 (1 + r/100) n = 2
II 2014 1 1 I 1.1 72 r 2 72 8 72/8 = 9 9 2 a 0 1 a 1 a 1 = a 0 (1+r/100) 2 a 2 a 2 = a 1 (1 + r/100) = a 0 (1 + r/100) 2 n a n = a 0 (1 + r/100) n a n a 0 2 n a 0 (1 + r/100) n = 2a 0 (1 + r/100) n = 2
チュートリアル:ノンパラメトリックベイズ
 { x,x, L, xn} 2 p( θ, θ, θ, θ, θ, } { 2 3 4 5 θ6 p( p( { x,x, L, N} 2 x { θ, θ2, θ3, θ4, θ5, θ6} K n p( θ θ n N n θ x N + { x,x, L, N} 2 x { θ, θ2, θ3, θ4, θ5, θ6} log p( 6 n logθ F 6 log p( + λ θ F θ
{ x,x, L, xn} 2 p( θ, θ, θ, θ, θ, } { 2 3 4 5 θ6 p( p( { x,x, L, N} 2 x { θ, θ2, θ3, θ4, θ5, θ6} K n p( θ θ n N n θ x N + { x,x, L, N} 2 x { θ, θ2, θ3, θ4, θ5, θ6} log p( 6 n logθ F 6 log p( + λ θ F θ
http://www2.math.kyushu-u.ac.jp/~hara/lectures/lectures-j.html 2 N(ε 1 ) N(ε 2 ) ε 1 ε 2 α ε ε 2 1 n N(ɛ) N ɛ ɛ- (1.1.3) n > N(ɛ) a n α < ɛ n N(ɛ) a n
 http://www2.math.kyushu-u.ac.jp/~hara/lectures/lectures-j.html 1 1 1.1 ɛ-n 1 ɛ-n lim n a n = α n a n α 2 lim a n = 1 n a k n n k=1 1.1.7 ɛ-n 1.1.1 a n α a n n α lim n a n = α ɛ N(ɛ) n > N(ɛ) a n α < ɛ
http://www2.math.kyushu-u.ac.jp/~hara/lectures/lectures-j.html 1 1 1.1 ɛ-n 1 ɛ-n lim n a n = α n a n α 2 lim a n = 1 n a k n n k=1 1.1.7 ɛ-n 1.1.1 a n α a n n α lim n a n = α ɛ N(ɛ) n > N(ɛ) a n α < ɛ
I.2 z x, y i z = x + iy. x, y z (real part), (imaginary part), x = Re(z), y = Im(z). () i. (2) 2 z = x + iy, z 2 = x 2 + iy 2,, z ± z 2 = (x ± x 2 ) +
 I..... z 2 x, y z = x + iy (i ). 2 (x, y). 2.,,.,,. (), ( 2 ),,. II ( ).. z, w = f(z). z f(z), w. z = x + iy, f(z) 2 x, y. f(z) u(x, y), v(x, y), w = f(x + iy) = u(x, y) + iv(x, y).,. 2. z z, w w. D, D.
I..... z 2 x, y z = x + iy (i ). 2 (x, y). 2.,,.,,. (), ( 2 ),,. II ( ).. z, w = f(z). z f(z), w. z = x + iy, f(z) 2 x, y. f(z) u(x, y), v(x, y), w = f(x + iy) = u(x, y) + iv(x, y).,. 2. z z, w w. D, D.
21世紀の統計科学 <Vol. I>
 21 I HP, 2011 10 3 10 ( ) ( ) 21 1,,. (,, (realized volatility), (.,.,, [33] (.,,,,. 1, 18 ( : ), 19 ( (C), : 19530186, :, B), : 19340021,, COE ( : 15 19, :.. 245 1 1.1 (high-frequency data),,,, ( ).,
21 I HP, 2011 10 3 10 ( ) ( ) 21 1,,. (,, (realized volatility), (.,.,, [33] (.,,,,. 1, 18 ( : ), 19 ( (C), : 19530186, :, B), : 19340021,, COE ( : 15 19, :.. 245 1 1.1 (high-frequency data),,,, ( ).,
(1) (2) (3) (4) HB B ( ) (5) (6) (7) 40 (8) (9) (10)
 2017 12 9 4 1 30 4 10 3 1 30 3 30 2 1 30 2 50 1 1 30 2 10 (1) (2) (3) (4) HB B ( ) (5) (6) (7) 40 (8) (9) (10) (1) i 23 c 23 0 1 2 3 4 5 6 7 8 9 a b d e f g h i (2) 23 23 (3) 23 ( 23 ) 23 x 1 x 2 23 x
2017 12 9 4 1 30 4 10 3 1 30 3 30 2 1 30 2 50 1 1 30 2 10 (1) (2) (3) (4) HB B ( ) (5) (6) (7) 40 (8) (9) (10) (1) i 23 c 23 0 1 2 3 4 5 6 7 8 9 a b d e f g h i (2) 23 23 (3) 23 ( 23 ) 23 x 1 x 2 23 x
確率論と統計学の資料
 5 June 015 ii........................ 1 1 1.1...................... 1 1........................... 3 1.3... 4 6.1........................... 6................... 7 ii ii.3.................. 8.4..........................
5 June 015 ii........................ 1 1 1.1...................... 1 1........................... 3 1.3... 4 6.1........................... 6................... 7 ii ii.3.................. 8.4..........................
y = f(x) y = f( + h) f(), x = h dy dx f () f (derivtive) (differentition) (velocity) p(t) =(x(t),y(t),z(t)) ( dp dx dt = dt, dy dt, dz ) dt f () > f x
 I 5 2 6 3 8 4 Riemnn 9 5 Tylor 8 6 26 7 3 8 34 f(x) x = A = h f( + h) f() h A (differentil coefficient) f f () y = f(x) y = f( + h) f(), x = h dy dx f () f (derivtive) (differentition) (velocity) p(t)
I 5 2 6 3 8 4 Riemnn 9 5 Tylor 8 6 26 7 3 8 34 f(x) x = A = h f( + h) f() h A (differentil coefficient) f f () y = f(x) y = f( + h) f(), x = h dy dx f () f (derivtive) (differentition) (velocity) p(t)
Feynman Encounter with Mathematics 52, [1] N. Kumano-go, Feynman path integrals as analysis on path space by time slicing approximation. Bull
![Feynman Encounter with Mathematics 52, [1] N. Kumano-go, Feynman path integrals as analysis on path space by time slicing approximation. Bull Feynman Encounter with Mathematics 52, [1] N. Kumano-go, Feynman path integrals as analysis on path space by time slicing approximation. Bull](/thumbs/94/118365979.jpg) Feynman Encounter with Mathematics 52, 200 9 [] N. Kumano-go, Feynman path integrals as analysis on path space by time slicing approximation. Bull. Sci. Math. vol. 28 (2004) 97 25. [2] D. Fujiwara and
Feynman Encounter with Mathematics 52, 200 9 [] N. Kumano-go, Feynman path integrals as analysis on path space by time slicing approximation. Bull. Sci. Math. vol. 28 (2004) 97 25. [2] D. Fujiwara and
 211 kotaro@math.titech.ac.jp 1 R *1 n n R n *2 R n = {(x 1,..., x n ) x 1,..., x n R}. R R 2 R 3 R n R n R n D D R n *3 ) (x 1,..., x n ) f(x 1,..., x n ) f D *4 n 2 n = 1 ( ) 1 f D R n f : D R 1.1. (x,
211 kotaro@math.titech.ac.jp 1 R *1 n n R n *2 R n = {(x 1,..., x n ) x 1,..., x n R}. R R 2 R 3 R n R n R n D D R n *3 ) (x 1,..., x n ) f(x 1,..., x n ) f D *4 n 2 n = 1 ( ) 1 f D R n f : D R 1.1. (x,
z z x = y = /x lim y = + x + lim y = x (x a ) a (x a+) lim z z f(z) = A, lim z z g(z) = B () lim z z {f(z) ± g(z)} = A ± B (2) lim {f(z) g(z)} = AB z
 Tips KENZOU 28 6 29 sin 2 x + cos 2 x = cos 2 z + sin 2 z = OK... z < z z < R w = f(z) z z w w f(z) w lim z z f(z) = w x x 2 2 f(x) x = a lim f(x) = lim f(x) x a+ x a z z x = y = /x lim y = + x + lim y
Tips KENZOU 28 6 29 sin 2 x + cos 2 x = cos 2 z + sin 2 z = OK... z < z z < R w = f(z) z z w w f(z) w lim z z f(z) = w x x 2 2 f(x) x = a lim f(x) = lim f(x) x a+ x a z z x = y = /x lim y = + x + lim y
2015/4/13 10: C C C C John C. Hull,, Steven E. Shreve, (1), Peter E. Kloeden, Eckhard Platen Num
 2015/4/13 10:56 0 0.1 http://cm.hit-u.ac.jp/~kobayashi/lecture/ 0.2 C C C C John C. Hull,, Steven E. Shreve, (1, Peter E. Kloeden, Eckhard Platen Numerical Solution of Stochastic Differential Equations,
2015/4/13 10:56 0 0.1 http://cm.hit-u.ac.jp/~kobayashi/lecture/ 0.2 C C C C John C. Hull,, Steven E. Shreve, (1, Peter E. Kloeden, Eckhard Platen Numerical Solution of Stochastic Differential Equations,
1 1.1 ( ). z = a + bi, a, b R 0 a, b 0 a 2 + b 2 0 z = a + bi = ( ) a 2 + b 2 a a 2 + b + b 2 a 2 + b i 2 r = a 2 + b 2 θ cos θ = a a 2 + b 2, sin θ =
 1 1.1 ( ). z = + bi,, b R 0, b 0 2 + b 2 0 z = + bi = ( ) 2 + b 2 2 + b + b 2 2 + b i 2 r = 2 + b 2 θ cos θ = 2 + b 2, sin θ = b 2 + b 2 2π z = r(cos θ + i sin θ) 1.2 (, ). 1. < 2. > 3. ±,, 1.3 ( ). A
1 1.1 ( ). z = + bi,, b R 0, b 0 2 + b 2 0 z = + bi = ( ) 2 + b 2 2 + b + b 2 2 + b i 2 r = 2 + b 2 θ cos θ = 2 + b 2, sin θ = b 2 + b 2 2π z = r(cos θ + i sin θ) 1.2 (, ). 1. < 2. > 3. ±,, 1.3 ( ). A
takei.dvi
 0 Newton Leibniz ( ) α1 ( ) αn (1) a α1,...,α n (x) u(x) = f(x) x 1 x n α 1 + +α n m 1957 Hans Lewy Lewy 1970 1 1.1 Example 1.1. (2) d 2 u dx 2 Q(x)u = f(x), u(0) = a, 1 du (0) = b. dx Q(x), f(x) x = 0
0 Newton Leibniz ( ) α1 ( ) αn (1) a α1,...,α n (x) u(x) = f(x) x 1 x n α 1 + +α n m 1957 Hans Lewy Lewy 1970 1 1.1 Example 1.1. (2) d 2 u dx 2 Q(x)u = f(x), u(0) = a, 1 du (0) = b. dx Q(x), f(x) x = 0
() n C + n C + n C + + n C n n (3) n C + n C + n C 4 + n C + n C 3 + n C 5 + (5) (6 ) n C + nc + 3 nc n nc n (7 ) n C + nc + 3 nc n nc n (
 3 n nc k+ k + 3 () n C r n C n r nc r C r + C r ( r n ) () n C + n C + n C + + n C n n (3) n C + n C + n C 4 + n C + n C 3 + n C 5 + (4) n C n n C + n C + n C + + n C n (5) k k n C k n C k (6) n C + nc
3 n nc k+ k + 3 () n C r n C n r nc r C r + C r ( r n ) () n C + n C + n C + + n C n n (3) n C + n C + n C 4 + n C + n C 3 + n C 5 + (4) n C n n C + n C + n C + + n C n (5) k k n C k n C k (6) n C + nc
example2_time.eps
 Google (20/08/2 ) ( ) Random Walk & Google Page Rank Agora on Aug. 20 / 67 Introduction ( ) Random Walk & Google Page Rank Agora on Aug. 20 2 / 67 Introduction Google ( ) Random Walk & Google Page Rank
Google (20/08/2 ) ( ) Random Walk & Google Page Rank Agora on Aug. 20 / 67 Introduction ( ) Random Walk & Google Page Rank Agora on Aug. 20 2 / 67 Introduction Google ( ) Random Walk & Google Page Rank
基礎から学ぶトラヒック理論 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. このサンプルページの内容は, 初版 1 刷発行時のものです.
 基礎から学ぶトラヒック理論 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/085221 このサンプルページの内容は, 初版 1 刷発行時のものです. i +α 3 1 2 4 5 1 2 ii 3 4 5 6 7 8 9 9.3 2014 6 iii 1 1 2 5 2.1 5 2.2 7
基礎から学ぶトラヒック理論 サンプルページ この本の定価 判型などは, 以下の URL からご覧いただけます. http://www.morikita.co.jp/books/mid/085221 このサンプルページの内容は, 初版 1 刷発行時のものです. i +α 3 1 2 4 5 1 2 ii 3 4 5 6 7 8 9 9.3 2014 6 iii 1 1 2 5 2.1 5 2.2 7
II A A441 : October 02, 2014 Version : Kawahira, Tomoki TA (Kondo, Hirotaka )
 II 214-1 : October 2, 214 Version : 1.1 Kawahira, Tomoki TA (Kondo, Hirotaka ) http://www.math.nagoya-u.ac.jp/~kawahira/courses/14w-biseki.html pdf 1 2 1 9 1 16 1 23 1 3 11 6 11 13 11 2 11 27 12 4 12 11
II 214-1 : October 2, 214 Version : 1.1 Kawahira, Tomoki TA (Kondo, Hirotaka ) http://www.math.nagoya-u.ac.jp/~kawahira/courses/14w-biseki.html pdf 1 2 1 9 1 16 1 23 1 3 11 6 11 13 11 2 11 27 12 4 12 11
2 1 17 1.1 1.1.1 1650
 1 3 5 1 1 2 0 0 1 2 I II III J. 2 1 17 1.1 1.1.1 1650 1.1 3 3 6 10 3 5 1 3/5 1 2 + 1 10 ( = 6 ) 10 1/10 2000 19 17 60 2 1 1 3 10 25 33221 73 13111 0. 31 11 11 60 11/60 2 111111 3 60 + 3 332221 27 x y xy
1 3 5 1 1 2 0 0 1 2 I II III J. 2 1 17 1.1 1.1.1 1650 1.1 3 3 6 10 3 5 1 3/5 1 2 + 1 10 ( = 6 ) 10 1/10 2000 19 17 60 2 1 1 3 10 25 33221 73 13111 0. 31 11 11 60 11/60 2 111111 3 60 + 3 332221 27 x y xy
Global phase portraits of planar autonomous half-linear systems (Masakazu Onitsuka) (Aya Yamaguchi) (Jitsuro Sugie) Department of M
 1445 2005 88-98 88 Global phase portraits of planar autonomous half-linear systems (Masakazu Onitsuka) (Aya Yamaguchi) (Jitsuro Sugie) Department of Mathematics Shimane University 1 2 $(\mathit{4}_{p}(\dot{x}))^{\circ}+\alpha\phi_{p}(\dot{x})+\beta\phi_{p}(x)=0$
1445 2005 88-98 88 Global phase portraits of planar autonomous half-linear systems (Masakazu Onitsuka) (Aya Yamaguchi) (Jitsuro Sugie) Department of Mathematics Shimane University 1 2 $(\mathit{4}_{p}(\dot{x}))^{\circ}+\alpha\phi_{p}(\dot{x})+\beta\phi_{p}(x)=0$
tokei01.dvi
 2. :,,,. :.... Apr. - Jul., 26FY Dept. of Mechanical Engineering, Saga Univ., JAPAN 4 3. (probability),, 1. : : n, α A, A a/n. :, p, p Apr. - Jul., 26FY Dept. of Mechanical Engineering, Saga Univ., JAPAN
2. :,,,. :.... Apr. - Jul., 26FY Dept. of Mechanical Engineering, Saga Univ., JAPAN 4 3. (probability),, 1. : : n, α A, A a/n. :, p, p Apr. - Jul., 26FY Dept. of Mechanical Engineering, Saga Univ., JAPAN
入試の軌跡
 4 y O x 4 Typed by L A TEX ε ) ) ) 6 4 ) 4 75 ) http://kumamoto.s.xrea.com/plan/.. PDF) Ctrl +L) Ctrl +) Ctrl + Ctrl + ) ) Alt + ) Alt + ) ESC. http://kumamoto.s.xrea.com/nyusi/kumadai kiseki ri i.pdf
4 y O x 4 Typed by L A TEX ε ) ) ) 6 4 ) 4 75 ) http://kumamoto.s.xrea.com/plan/.. PDF) Ctrl +L) Ctrl +) Ctrl + Ctrl + ) ) Alt + ) Alt + ) ESC. http://kumamoto.s.xrea.com/nyusi/kumadai kiseki ri i.pdf
 June 2016 i (statistics) F Excel Numbers, OpenOffice/LibreOffice Calc ii *1 VAR STDEV 1 SPSS SAS R *2 R R R R *1 Excel, Numbers, Microsoft Office, Apple iwork, *2 R GNU GNU R iii URL http://ruby.kyoto-wu.ac.jp/statistics/training/
June 2016 i (statistics) F Excel Numbers, OpenOffice/LibreOffice Calc ii *1 VAR STDEV 1 SPSS SAS R *2 R R R R *1 Excel, Numbers, Microsoft Office, Apple iwork, *2 R GNU GNU R iii URL http://ruby.kyoto-wu.ac.jp/statistics/training/
 n ξ n,i, i = 1,, n S n ξ n,i n 0 R 1,.. σ 1 σ i .10.14.15 0 1 0 1 1 3.14 3.18 3.19 3.14 3.14,. ii 1 1 1.1..................................... 1 1............................... 3 1.3.........................
n ξ n,i, i = 1,, n S n ξ n,i n 0 R 1,.. σ 1 σ i .10.14.15 0 1 0 1 1 3.14 3.18 3.19 3.14 3.14,. ii 1 1 1.1..................................... 1 1............................... 3 1.3.........................
診療ガイドライン外来編2014(A4)/FUJGG2014‐01(大扉)
 !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
³ÎΨÏÀ
 2017 12 12 Makoto Nakashima 2017 12 12 1 / 22 2.1. C, D π- C, D. A 1, A 2 C A 1 A 2 C A 3, A 4 D A 1 A 2 D Makoto Nakashima 2017 12 12 2 / 22 . (,, L p - ). Makoto Nakashima 2017 12 12 3 / 22 . (,, L p
2017 12 12 Makoto Nakashima 2017 12 12 1 / 22 2.1. C, D π- C, D. A 1, A 2 C A 1 A 2 C A 3, A 4 D A 1 A 2 D Makoto Nakashima 2017 12 12 2 / 22 . (,, L p - ). Makoto Nakashima 2017 12 12 3 / 22 . (,, L p
日本糖尿病学会誌第58巻第1号
 α β β β β β β α α β α β α l l α l μ l β l α β β Wfs1 β β l l l l μ l l μ μ l μ l Δ l μ μ l μ l l ll l l l l l l l l μ l l l l μ μ l l l l μ l l l l l l l l l l μ l l l μ l μ l l l l l l l l l μ l l l l
α β β β β β β α α β α β α l l α l μ l β l α β β Wfs1 β β l l l l μ l l μ μ l μ l Δ l μ μ l μ l l ll l l l l l l l l μ l l l l μ μ l l l l μ l l l l l l l l l l μ l l l μ l μ l l l l l l l l l μ l l l l
1 4 1 ( ) ( ) ( ) ( ) () 1 4 2
 7 1995, 2017 7 21 1 2 2 3 3 4 4 6 (1).................................... 6 (2)..................................... 6 (3) t................. 9 5 11 (1)......................................... 11 (2)
7 1995, 2017 7 21 1 2 2 3 3 4 4 6 (1).................................... 6 (2)..................................... 6 (3) t................. 9 5 11 (1)......................................... 11 (2)
ver.1 / c /(13)
 1 -- 11 1 c 2010 1/(13) 1 -- 11 -- 1 1--1 1--1--1 2009 3 t R x R n 1 ẋ = f(t, x) f = ( f 1,, f n ) f x(t) = ϕ(x 0, t) x(0) = x 0 n f f t 1--1--2 2009 3 q = (q 1,..., q m ), p = (p 1,..., p m ) x = (q,
1 -- 11 1 c 2010 1/(13) 1 -- 11 -- 1 1--1 1--1--1 2009 3 t R x R n 1 ẋ = f(t, x) f = ( f 1,, f n ) f x(t) = ϕ(x 0, t) x(0) = x 0 n f f t 1--1--2 2009 3 q = (q 1,..., q m ), p = (p 1,..., p m ) x = (q,
() Remrk I = [0, ] [x i, x i ]. (x : ) f(x) = 0 (x : ) ξ i, (f) = f(ξ i )(x i x i ) = (x i x i ) = ξ i, (f) = f(ξ i )(x i x i ) = 0 (f) 0.
![() Remrk I = [0, ] [x i, x i ]. (x : ) f(x) = 0 (x : ) ξ i, (f) = f(ξ i )(x i x i ) = (x i x i ) = ξ i, (f) = f(ξ i )(x i x i ) = 0 (f) 0. () Remrk I = [0, ] [x i, x i ]. (x : ) f(x) = 0 (x : ) ξ i, (f) = f(ξ i )(x i x i ) = (x i x i ) = ξ i, (f) = f(ξ i )(x i x i ) = 0 (f) 0.](/thumbs/89/98384840.jpg) () 6 f(x) [, b] 6. Riemnn [, b] f(x) S f(x) [, b] (Riemnn) = x 0 < x < x < < x n = b. I = [, b] = {x,, x n } mx(x i x i ) =. i [x i, x i ] ξ i n (f) = f(ξ i )(x i x i ) i=. (ξ i ) (f) 0( ), ξ i, S, ε >
() 6 f(x) [, b] 6. Riemnn [, b] f(x) S f(x) [, b] (Riemnn) = x 0 < x < x < < x n = b. I = [, b] = {x,, x n } mx(x i x i ) =. i [x i, x i ] ξ i n (f) = f(ξ i )(x i x i ) i=. (ξ i ) (f) 0( ), ξ i, S, ε >
x (x, ) x y (, y) iy x y z = x + iy (x, y) (r, θ) r = x + y, θ = tan ( y ), π < θ π x r = z, θ = arg z z = x + iy = r cos θ + ir sin θ = r(cos θ + i s
 ... x, y z = x + iy x z y z x = Rez, y = Imz z = x + iy x iy z z () z + z = (z + z )() z z = (z z )(3) z z = ( z z )(4)z z = z z = x + y z = x + iy ()Rez = (z + z), Imz = (z z) i () z z z + z z + z.. z
... x, y z = x + iy x z y z x = Rez, y = Imz z = x + iy x iy z z () z + z = (z + z )() z z = (z z )(3) z z = ( z z )(4)z z = z z = x + y z = x + iy ()Rez = (z + z), Imz = (z z) i () z z z + z z + z.. z
1.1 ft t 2 ft = t 2 ft+ t = t+ t 2 1.1 d t 2 t + t 2 t 2 = lim t 0 t = lim t 0 = lim t 0 t 2 + 2t t + t 2 t 2 t + t 2 t 2t t + t 2 t 2t + t = lim t 0
 A c 2008 by Kuniaki Nakamitsu 1 1.1 t 2 sin t, cos t t ft t t vt t xt t + t xt + t xt + t xt t vt = xt + t xt t t t vt xt + t xt vt = lim t 0 t lim t 0 t 0 vt = dxt ft dft dft ft + t ft = lim t 0 t 1.1
A c 2008 by Kuniaki Nakamitsu 1 1.1 t 2 sin t, cos t t ft t t vt t xt t + t xt + t xt + t xt t vt = xt + t xt t t t vt xt + t xt vt = lim t 0 t lim t 0 t 0 vt = dxt ft dft dft ft + t ft = lim t 0 t 1.1
Title 二重指数関数型変数変換を用いたSinc 関数近似 ( 科学技術における数値計算の理論と応用 II) Author(s) 杉原, 正顯 Citation 数理解析研究所講究録 (1997), 990: Issue Date URL
 Title 二重指数関数型変数変換を用いたSinc 関数近似 ( 科学技術における数値計算の理論と応用 II) Author(s) 杉原 正顯 Citation 数理解析研究所講究録 (1997) 990 125-134 Issue Date 1997-04 URL http//hdlhandlenet/2433/61094 Right Type Departmental Bulletin Paper
Title 二重指数関数型変数変換を用いたSinc 関数近似 ( 科学技術における数値計算の理論と応用 II) Author(s) 杉原 正顯 Citation 数理解析研究所講究録 (1997) 990 125-134 Issue Date 1997-04 URL http//hdlhandlenet/2433/61094 Right Type Departmental Bulletin Paper
December 28, 2018
 e-mail : kigami@i.kyoto-u.ac.jp December 28, 28 Contents 2............................. 3.2......................... 7.3..................... 9.4................ 4.5............. 2.6.... 22 2 36 2..........................
e-mail : kigami@i.kyoto-u.ac.jp December 28, 28 Contents 2............................. 3.2......................... 7.3..................... 9.4................ 4.5............. 2.6.... 22 2 36 2..........................
CEV(Constant Elasticity of Variance) FE 1
 23 6 1 CEV(Consan Elasiciy of Variance) FE 1 1 (Karazas and Shreve[1998] Carr, Jarrow and Myneni[1992] J. Huang, Subrahmanyam and Yu[1996] ) S 1 ds =(r δ)s d + σ(s )dw,s = x(> ) r δ K T sup E[e rτ (K S
23 6 1 CEV(Consan Elasiciy of Variance) FE 1 1 (Karazas and Shreve[1998] Carr, Jarrow and Myneni[1992] J. Huang, Subrahmanyam and Yu[1996] ) S 1 ds =(r δ)s d + σ(s )dw,s = x(> ) r δ K T sup E[e rτ (K S
( 年 2 回発行 ) Vol. 65, No. 1 編集委員長加藤昇吾編集委員足立淳小山慎介武田朗子野間久史南和宏特集担当編集委員川崎能典荻原哲平 編集室 池田 広樹 長嶋 昭子 脇地直子 渡邉百合子 統計数理 は, 統計数理研究所における研究成果を掲載する統計数理研究所 彙報 として 1953
 第 65 1 ( 通巻 125 号 ) PROCEEDINGS OF THE INSTITUTE OF STATISTICAL MATHEMATICS 目次 特集 高頻度金融データに基づく統計的推測とモデリング Vol.65, No.1 PROCEEDINGS OF THE INSTITUTE OF STATISTICAL MATHEMATICS 特集高頻度金融データに基づく統計的推測とモデリング
第 65 1 ( 通巻 125 号 ) PROCEEDINGS OF THE INSTITUTE OF STATISTICAL MATHEMATICS 目次 特集 高頻度金融データに基づく統計的推測とモデリング Vol.65, No.1 PROCEEDINGS OF THE INSTITUTE OF STATISTICAL MATHEMATICS 特集高頻度金融データに基づく統計的推測とモデリング
4 4. A p X A 1 X X A 1 A 4.3 X p X p X S(X) = E ((X p) ) X = X E(X) = E(X) p p 4.3p < p < 1 X X p f(i) = P (X = i) = p(1 p) i 1, i = 1,,... 1 + r + r
 4 1 4 4.1 X P (X = 1) =.4, P (X = ) =.3, P (X = 1) =., P (X = ) =.1 E(X) = 1.4 +.3 + 1. +.1 = 4. X Y = X P (X = ) = P (X = 1) = P (X = ) = P (X = 1) = P (X = ) =. Y P (Y = ) = P (X = ) =., P (Y = 1) =
4 1 4 4.1 X P (X = 1) =.4, P (X = ) =.3, P (X = 1) =., P (X = ) =.1 E(X) = 1.4 +.3 + 1. +.1 = 4. X Y = X P (X = ) = P (X = 1) = P (X = ) = P (X = 1) = P (X = ) =. Y P (Y = ) = P (X = ) =., P (Y = 1) =
x i [, b], (i 0, 1, 2,, n),, [, b], [, b] [x 0, x 1 ] [x 1, x 2 ] [x n 1, x n ] ( 2 ). x 0 x 1 x 2 x 3 x n 1 x n b 2: [, b].,, (1) x 0, x 1, x 2,, x n
![x i [, b], (i 0, 1, 2,, n),, [, b], [, b] [x 0, x 1 ] [x 1, x 2 ] [x n 1, x n ] ( 2 ). x 0 x 1 x 2 x 3 x n 1 x n b 2: [, b].,, (1) x 0, x 1, x 2,, x n x i [, b], (i 0, 1, 2,, n),, [, b], [, b] [x 0, x 1 ] [x 1, x 2 ] [x n 1, x n ] ( 2 ). x 0 x 1 x 2 x 3 x n 1 x n b 2: [, b].,, (1) x 0, x 1, x 2,, x n](/thumbs/92/108343288.jpg) 1, R f : R R,.,, b R < b, f(x) [, b] f(x)dx,, [, b] f(x) x ( ) ( 1 ). y y f(x) f(x)dx b x 1: f(x)dx, [, b] f(x) x ( ).,,,,,., f(x)dx,,,, f(x)dx. 1.1 Riemnn,, [, b] f(x) x., x 0 < x 1 < x 2 < < x n 1
1, R f : R R,.,, b R < b, f(x) [, b] f(x)dx,, [, b] f(x) x ( ) ( 1 ). y y f(x) f(x)dx b x 1: f(x)dx, [, b] f(x) x ( ).,,,,,., f(x)dx,,,, f(x)dx. 1.1 Riemnn,, [, b] f(x) x., x 0 < x 1 < x 2 < < x n 1
S I. dy fx x fx y fx + C 3 C dy fx 4 x, y dy v C xt y C v e kt k > xt yt gt [ v dt dt v e kt xt v e kt + C k x v + C C k xt v k 3 r r + dr e kt S dt d
 S I.. http://ayapin.film.s.dendai.ac.jp/~matuda /TeX/lecture.html PDF PS.................................... 3.3.................... 9.4................5.............. 3 5. Laplace................. 5....
S I.. http://ayapin.film.s.dendai.ac.jp/~matuda /TeX/lecture.html PDF PS.................................... 3.3.................... 9.4................5.............. 3 5. Laplace................. 5....
1 913 10301200 A B C D E F G H J K L M 1A1030 10 : 45 1A1045 11 : 00 1A1100 11 : 15 1A1115 11 : 30 1A1130 11 : 45 1A1145 12 : 00 1B1030 1B1045 1C1030
 1 913 9001030 A B C D E F G H J K L M 9:00 1A0900 9:15 1A0915 9:30 1A0930 9:45 1A0945 10 : 00 1A1000 10 : 15 1B0900 1B0915 1B0930 1B0945 1B1000 1C0900 1C0915 1D0915 1C0930 1C0945 1C1000 1D0930 1D0945 1D1000
1 913 9001030 A B C D E F G H J K L M 9:00 1A0900 9:15 1A0915 9:30 1A0930 9:45 1A0945 10 : 00 1A1000 10 : 15 1B0900 1B0915 1B0930 1B0945 1B1000 1C0900 1C0915 1D0915 1C0930 1C0945 1C1000 1D0930 1D0945 1D1000
2009 IA I 22, 23, 24, 25, 26, a h f(x) x x a h
 009 IA I, 3, 4, 5, 6, 7 7 7 4 5 h fx) x x h 4 5 4 5 1 3 1.1........................... 3 1........................... 4 1.3..................................... 6 1.4.............................. 8 1.4.1..............................
009 IA I, 3, 4, 5, 6, 7 7 7 4 5 h fx) x x h 4 5 4 5 1 3 1.1........................... 3 1........................... 4 1.3..................................... 6 1.4.............................. 8 1.4.1..............................
Note5.dvi
 12 2011 7 4 2.2.2 Feynman ( ) S M N S M + N S Ai Ao t ij (i Ai, j Ao) N M G = 2e2 t ij 2 (8.28) h i μ 1 μ 2 J 12 J 12 / μ 2 μ 1 (8.28) S S (8.28) (8.28) 2 ( ) (collapse) j 12-1 2.3 2.3.1 Onsager S B S(B)
12 2011 7 4 2.2.2 Feynman ( ) S M N S M + N S Ai Ao t ij (i Ai, j Ao) N M G = 2e2 t ij 2 (8.28) h i μ 1 μ 2 J 12 J 12 / μ 2 μ 1 (8.28) S S (8.28) (8.28) 2 ( ) (collapse) j 12-1 2.3 2.3.1 Onsager S B S(B)
II No.01 [n/2] [1]H n (x) H n (x) = ( 1) r n! r!(n 2r)! (2x)n 2r. r=0 [2]H n (x) n,, H n ( x) = ( 1) n H n (x). [3] H n (x) = ( 1) n dn x2 e dx n e x2
![II No.01 [n/2] [1]H n (x) H n (x) = ( 1) r n! r!(n 2r)! (2x)n 2r. r=0 [2]H n (x) n,, H n ( x) = ( 1) n H n (x). [3] H n (x) = ( 1) n dn x2 e dx n e x2 II No.01 [n/2] [1]H n (x) H n (x) = ( 1) r n! r!(n 2r)! (2x)n 2r. r=0 [2]H n (x) n,, H n ( x) = ( 1) n H n (x). [3] H n (x) = ( 1) n dn x2 e dx n e x2](/thumbs/101/149159646.jpg) II No.1 [n/] [1]H n x) H n x) = 1) r n! r!n r)! x)n r r= []H n x) n,, H n x) = 1) n H n x) [3] H n x) = 1) n dn x e dx n e x [4] H n+1 x) = xh n x) nh n 1 x) ) d dx x H n x) = H n+1 x) d dx H nx) = nh
II No.1 [n/] [1]H n x) H n x) = 1) r n! r!n r)! x)n r r= []H n x) n,, H n x) = 1) n H n x) [3] H n x) = 1) n dn x e dx n e x [4] H n+1 x) = xh n x) nh n 1 x) ) d dx x H n x) = H n+1 x) d dx H nx) = nh
,. Black-Scholes u t t, x c u 0 t, x x u t t, x c u t, x x u t t, x + σ x u t, x + rx ut, x rux, t 0 x x,,.,. Step 3, 7,,, Step 6., Step 4,. Step 5,,.
 9 α ν β Ξ ξ Γ γ o δ Π π ε ρ ζ Σ σ η τ Θ θ Υ υ ι Φ φ κ χ Λ λ Ψ ψ µ Ω ω Def, Prop, Th, Lem, Note, Remark, Ex,, Proof, R, N, Q, C [a, b {x R : a x b} : a, b {x R : a < x < b} : [a, b {x R : a x < b} : a,
9 α ν β Ξ ξ Γ γ o δ Π π ε ρ ζ Σ σ η τ Θ θ Υ υ ι Φ φ κ χ Λ λ Ψ ψ µ Ω ω Def, Prop, Th, Lem, Note, Remark, Ex,, Proof, R, N, Q, C [a, b {x R : a x b} : a, b {x R : a < x < b} : [a, b {x R : a x < b} : a,
2 A A 3 A 2. A [2] A A A A 4 [3]
![2 A A 3 A 2. A [2] A A A A 4 [3] 2 A A 3 A 2. A [2] A A A A 4 [3]](/thumbs/40/20588263.jpg) 1 2 A A 1. ([1]3 3[ ]) 2 A A 3 A 2. A [2] A A A A 4 [3] Xi 1 1 2 1 () () 1 n () 1 n 0 i i = 1 1 S = S +! X S ( ) 02 n 1 2 Xi 1 0 2 ( ) ( 2) n ( 2) n 0 i i = 1 2 S = S +! X 0 k Xip 1 (1-p) 1 ( ) n n k Pr
1 2 A A 1. ([1]3 3[ ]) 2 A A 3 A 2. A [2] A A A A 4 [3] Xi 1 1 2 1 () () 1 n () 1 n 0 i i = 1 1 S = S +! X S ( ) 02 n 1 2 Xi 1 0 2 ( ) ( 2) n ( 2) n 0 i i = 1 2 S = S +! X 0 k Xip 1 (1-p) 1 ( ) n n k Pr
untitled
 B2 3 2005 (10:30 12:00) 201 2005/10/04 10/04 10/11 9, 15 10/18 10/25 11/01 17 20 11/08 11/15 22 11/22 11/29 ( ) 12/06 12/13 L p L p Hölder 12/20 1/10 1/17 ( ) URL: http://www.math.tohoku.ac.jp/ hattori/hattori.htm
B2 3 2005 (10:30 12:00) 201 2005/10/04 10/04 10/11 9, 15 10/18 10/25 11/01 17 20 11/08 11/15 22 11/22 11/29 ( ) 12/06 12/13 L p L p Hölder 12/20 1/10 1/17 ( ) URL: http://www.math.tohoku.ac.jp/ hattori/hattori.htm
80 X 1, X 2,, X n ( λ ) λ P(X = x) = f (x; λ) = λx e λ, x = 0, 1, 2, x! l(λ) = n f (x i ; λ) = i=1 i=1 n λ x i e λ i=1 x i! = λ n i=1 x i e nλ n i=1 x
 80 X 1, X 2,, X n ( λ ) λ P(X = x) = f (x; λ) = λx e λ, x = 0, 1, 2, x! l(λ) = n f (x i ; λ) = n λ x i e λ x i! = λ n x i e nλ n x i! n n log l(λ) = log(λ) x i nλ log( x i!) log l(λ) λ = 1 λ n x i n =
80 X 1, X 2,, X n ( λ ) λ P(X = x) = f (x; λ) = λx e λ, x = 0, 1, 2, x! l(λ) = n f (x i ; λ) = n λ x i e λ x i! = λ n x i e nλ n x i! n n log l(λ) = log(λ) x i nλ log( x i!) log l(λ) λ = 1 λ n x i n =
(3) (2),,. ( 20) ( s200103) 0.7 x C,, x 2 + y 2 + ax = 0 a.. D,. D, y C, C (x, y) (y 0) C m. (2) D y = y(x) (x ± y 0), (x, y) D, m, m = 1., D. (x 2 y
 [ ] 7 0.1 2 2 + y = t sin t IC ( 9) ( s090101) 0.2 y = d2 y 2, y = x 3 y + y 2 = 0 (2) y + 2y 3y = e 2x 0.3 1 ( y ) = f x C u = y x ( 15) ( s150102) [ ] y/x du x = Cexp f(u) u (2) x y = xey/x ( 16) ( s160101)
[ ] 7 0.1 2 2 + y = t sin t IC ( 9) ( s090101) 0.2 y = d2 y 2, y = x 3 y + y 2 = 0 (2) y + 2y 3y = e 2x 0.3 1 ( y ) = f x C u = y x ( 15) ( s150102) [ ] y/x du x = Cexp f(u) u (2) x y = xey/x ( 16) ( s160101)
8.1 Fubini 8.2 Fubini 9 (0%) 10 (50%) 10.1 10.2 Carathéodory 10.3 Fubini 1 Introduction [1],, [2],, [3],, [4],, [5],, [6],, [7],, [8],, [1, 2, 3] 1980
![8.1 Fubini 8.2 Fubini 9 (0%) 10 (50%) 10.1 10.2 Carathéodory 10.3 Fubini 1 Introduction [1],, [2],, [3],, [4],, [5],, [6],, [7],, [8],, [1, 2, 3] 1980 8.1 Fubini 8.2 Fubini 9 (0%) 10 (50%) 10.1 10.2 Carathéodory 10.3 Fubini 1 Introduction [1],, [2],, [3],, [4],, [5],, [6],, [7],, [8],, [1, 2, 3] 1980](/thumbs/39/20489863.jpg) % 100% 1 Introduction 2 (100%) 2.1 2.2 2.3 3 (100%) 3.1 3.2 σ- 4 (100%) 4.1 4.2 5 (100%) 5.1 5.2 5.3 6 (100%) 7 (40%) 8 Fubini (90%) 2006.11.20 1 8.1 Fubini 8.2 Fubini 9 (0%) 10 (50%) 10.1 10.2 Carathéodory
% 100% 1 Introduction 2 (100%) 2.1 2.2 2.3 3 (100%) 3.1 3.2 σ- 4 (100%) 4.1 4.2 5 (100%) 5.1 5.2 5.3 6 (100%) 7 (40%) 8 Fubini (90%) 2006.11.20 1 8.1 Fubini 8.2 Fubini 9 (0%) 10 (50%) 10.1 10.2 Carathéodory
4 41 01, ARMAP, Q) CARMAP, Q) DARMAp, q) CARMAP, Q) CARMAP, Q) DARMAp, q) DARMAp, q), CARMAP, Q) CARMAP, Q) Chan and Tong 1987), He and Wang 1989), Br
 41,, 01 3 41 444 ARMA Can We Have Correspondence between Discrete-Time ARM A Process and Continuous-Time ARM A Process? Mituaki Huzii ARMA Huzii 006) Huzii 006) ARMA3, ) We assume that a time series is
41,, 01 3 41 444 ARMA Can We Have Correspondence between Discrete-Time ARM A Process and Continuous-Time ARM A Process? Mituaki Huzii ARMA Huzii 006) Huzii 006) ARMA3, ) We assume that a time series is
.1 z = e x +xy y z y 1 1 x 0 1 z x y α β γ z = αx + βy + γ (.1) ax + by + cz = d (.1') a, b, c, d x-y-z (a, b, c). x-y-z 3 (0,
 .1.1 Y K L Y = K 1 3 L 3 L K K (K + ) 1 1 3 L 3 K 3 L 3 K 0 (K + K) 1 3 L 3 K 1 3 L 3 lim K 0 K = L (K + K) 1 3 K 1 3 3 lim K 0 K = 1 3 K 3 L 3 z = f(x, y) x y z x-y-z.1 z = e x +xy y 3 x-y ( ) z 0 f(x,
.1.1 Y K L Y = K 1 3 L 3 L K K (K + ) 1 1 3 L 3 K 3 L 3 K 0 (K + K) 1 3 L 3 K 1 3 L 3 lim K 0 K = L (K + K) 1 3 K 1 3 3 lim K 0 K = 1 3 K 3 L 3 z = f(x, y) x y z x-y-z.1 z = e x +xy y 3 x-y ( ) z 0 f(x,
untitled
 Amazon.co.jp 2008.09.02 START Amazon.co.jp Amazon.co.jp Amazon.co.jp Amazon Internet retailers are extremely hesitant about releasing specific sales data 1( ) ranking 500,000 100,000 Jan.1 Mar.1 Jun.1
Amazon.co.jp 2008.09.02 START Amazon.co.jp Amazon.co.jp Amazon.co.jp Amazon Internet retailers are extremely hesitant about releasing specific sales data 1( ) ranking 500,000 100,000 Jan.1 Mar.1 Jun.1
untitled
 3,,, 2 3.1 3.1.1,, A4 1mm 10 1, 21.06cm, 21.06cm?, 10 1,,,, i),, ),, ),, x best ± δx 1) ii), x best ), δx, e,, e =1.602176462 ± 0.000000063) 10 19 [C] 2) i) ii), 1) x best δx
3,,, 2 3.1 3.1.1,, A4 1mm 10 1, 21.06cm, 21.06cm?, 10 1,,,, i),, ),, ),, x best ± δx 1) ii), x best ), δx, e,, e =1.602176462 ± 0.000000063) 10 19 [C] 2) i) ii), 1) x best δx

