exp z =
|
|
|
- わんど いちぞの
- 7 years ago
- Views:
Transcription
1
2 exp z = Jordan Weierstrass M / z, / z Cauchy-Riemann
3 3.4 Cauchy Green Cauchy () ( ) (residue theorem) e iax f(x) dx x α (log x) n (log x) n f(x)e iax dx π r(cos θ, sin θ)dθ x α f(x)dx f(x) dx g(x)(log x) n dx f(x)(log x) n dx ( ) ,4 ( )
4 Cauchy Goursat Morera Schwarz Poisson Schwarz (Schwarz reflection principle) Rouché Mittag-Leffler Runge Jordan Poisson Ascoli-Arzelra Laplace Dirichlet A 5 A A.., a a A A..3 a a A.2 arg z, log z A.2. arg z A.2.2 log z A.2.3 z α A A A.4 cot z A
5 A A.4.3 cot z = cos z/ sin z A.5 tan z B 63 B B C C. 8, C.. arg z, log z C.2 9, C C.3, C C C.4 2, C.4. (analytic continuation) C
6 . R, C R +, +, 3 = +.2 {a n } n N {a n } n N n N inf k n a k = inf{a k ; k n} {a k ; k } {a k ; k 2} {a k ; k 3} inf a k inf a k inf a k. k k 2 k 3 { } inf a k k n n N sup inf a k (, ] k n n N {a n } n N n N {a k ; k n} inf k n a k =. sup inf a k =. k n n N lim sup n {a n } {a n } n N a a n := sup inf a k [, ] k n n N lim a n = a n 5
7 (a) ( ε > ) ( n N) ( n N: n n ) a n < a + ε (b) ε > k N ( n N: n k) a n > a ε lim n a n = a ε > n a ε < a n < a+ε n a n < a+ε a ε < a n n a {a n }.3.3. n N, {a j } n j= C n, a, f(z) = a z n + a z n + + a n z + a n ( < ε < )( R R)( z C : z R) ( ε) a z n f(z) ( + ε) a z n. f(z) ( z R), lim f(z) =. z A := max{ a, a 2,..., a n } a z n + + a n z + a n a z n + + a n z + a n A ( z n + + z + ). z z j z n (j =,,..., n 2) a z n + + a n z + a n na z n ( z ). { } na R := max ε a, na ε a R a z n + + a n z + a n ε a R z n ( z ). a z n + + a n z + a n ε a R z n ε a z n ( z R). f(z) a z n + a z n + + a n z + a n a z n + ε a z n = ( + ε) a z n, f(z) a z n a z n + + a n z + a n a z n ε a z n = ( ε) a z n. 6
8 ( ) z f(z) z n = a + a z + a 2 z a n z n. m N f(z) ( z ) lim zm z z n ε >, R R s.t. lim z f(z) a z n =. ε f(z) a z n + ε ( z R). = a..3. n N, {a j } n j= C n+, a, f(z) = a z n + a z n + + a n z + a n ( M R)( M R)( R R)( z C : z R) M z n f(z) M z n..3. ε = /2 2 a z n f(z) 3 2 a z n ( z R). M := a /2, M := 3 a /2.4 exp z =.4. C exp z = z = 2nπi (n Z). i z = x + iy (x, y R) exp z = e x (cos y + i sin y) exp z = e x. exp z = e x = and cos y + i sin y = x = and n Z s.t. y = 2nπ n Z s.t. z = 2nπi. sin z = n Z s.t. z = nπ 7
9 .5 Jordan R 2 Jordan C ( ) C C R 2 \ C Ω i, Ω e Ω i Ω e C.6 k N {} c f ( ) k f(z) = (z c) k g(z), g(c) c g f(c) = f (c) = = f (k ) (c) =, f (k) (c) k N c f k f(z) = g(z) (z c) k, g(c) c g k k c f k Z c g l Z c f g k + l.7 Abraham de Moivre 667 (Virty-le-Fran ois, France) 754 (London) Brook Taylor 685 (Edmonton, Middlesex) 73 (Somerset Ho Johann Carl Friedrich Gauss 777 (Brunswick) 855 (Göttingen) Augustin Louis Cauchy 789 (Paris) 857 (Sceaux) Joseph Liouville 89 (Saint-Omer) 882 (Paris) Pierre Alphonse Laurent 83 (Paris) 854 (Paris) Karl Theodor Wilhelm Weierstrass 85 (Ostenfelde) 897 (Berlin) Georg Friedrich Bernhard Riemann 826(Breselenz) 866(Selasca) Felice Casorati 835(Pavia, Italy) 89(Casteggio, Italy) Charles Emile Picard 856 (Paris) 94 (Paris) [] ( ) E. T.,,, I, II, III, NF, (23). 8
10 [2],,, (995)..8 ().,, (98) 2., 3, (96) , II, (985) IX ( ) 4. L. V.,,, (982) A 5., 2, (965).9 (8 2 8 ) dx (Gelehrter Anzeiger) [ li(x) = log x ] (Ueberbein) a + b = a + bi 9
11 [ ] li(a + bi) x = a + bi φ(x)dx x ( α + βi ) x = a + bi φ(x) dx [] x a + bi [ ] : φ(x) dx φx = φ(x) x φx = φ(x) dx φ(x) dx x φ(x) = log x x dx x = +2πi 2πi log x φx x φ(x) = ex x e x dx x x : x + 4 x2 + 8 x x4 + etc. [ ] 88
12
13 Weierstrass M ( a n (z c) n dz = C n= n= C a n (z c) n dz ( ) Weierstrass M Weierstrass 9 Cauchy Weierstrass M-test ) 2.. ( ) {a n } n N a n a n k= n, m N, m > n m n a k a k = k= k= m k=n+ a k m k=n+ m a k = a k k= n a k. n n a k Cauchy a k Cauchy C n a k k= k= k= a n a n a n (absolutely convergent) 2
14 Proposition 2.. ( ) {a n } n N, {b n } n N (2.) a n b n (n N) b n a n n, m N, m n m m a k a k = m k= k= k=n+ a k = m k=n+ a k m k=n+ b k = m b k k= n b k. n b k Cauchy s n := k= Cauchy C a n (2.) b n k= n a k k= a n (majorant, majorant series, dominant series, dominating series) Ω ( ) n N f n : Ω C {f n } n N Ω z Ω {f n (z)} n N lim f n(z) n Ω Ω z f(z) := lim n f n(z) f : Ω z f(z) = lim n f n(z) C {f n } n N Ω f f lim f n n f n z Ω () f n (z) Ω Ω z S(z) := f n (z) = lim S : Ω z S(z) = n k= n f k (z) f n (z) C f n Ω (S ) ( ) S n := n k= f k {S n } n N S S f n 3
15 2.. Ω {f n } n N Ω () f : Ω C {f n } n N Ω f ({f n } is uniformly convergent to f on Ω) lim f(z) f n (z) = sup n z Ω (2) S : Ω C f n Ω S lim sup n n S(z) f k (z) = z Ω k= Ω f Ω f Example 2.. Ω := R, n N (x < /n) f n (x) := nx ( x /n) (x > /n), f(x) := (x < ) (x = ) (x > ) {f n } R f x R lim f n(x) = f(x) n {f n } R f sup f(x) f n (x) = x R lim sup f(x) f n (x) =. n x R f n f Proposition 2..2 () Ω C, Ω, {f n } n N Ω f : Ω C {f n } Ω f f Ω z, z Ω, N N f(z ) f(z ) f(z ) f N (z ) + f N (z ) f N (z ) + f N (z ) f(z ) sup z Ω f(z) f N (z) + f N (z ) f N (z ) + sup f(z) f N (z) z Ω = 2 sup f(z) f N (z) + f N (z ) f N (z ). z Ω 4
16 z Ω ε > {f n } f N N s.t. n N = sup f(z) f n (z) < ε z Ω 3. sup f(z) f N (z) < ε z Ω 3. f N z δ > s.t. z z < δ = f N (z ) f N (z ) < ε 3. z z < δ = f(z ) f(z ) < 2 ε 3 + ε 3 = ε. f z f n (z) = lim n ( ) lim f n(z), n ( ) f n (z) = f n (z) ( ) Example 2..2 ( ) (x < x > 2/n) f n (x) = n 2 x ( x /n) 2n n 2 x (/n x 2/n), f(x) = (x R) ( 2/n, n ) {f n } f 2 f(x) dx =, 2 f n (x) dx = 2 2 n n = 2 lim n f n (x) dx = = 2 f(x) dx. f n, f x R lim f n(x) = n Proposition 2..3 () Ω C C Ω C {f n } Ω f : Ω C {f n } Ω f lim n C f n (z) dz = C f(z) dz. 5
17 C z = φ(t) (t [α, β]) C f(z) dz C β β f n (z) dz = f (φ(t)) φ (t) dt f n (φ(t)) φ (t) dt α α β = (f (φ(t)) f n (φ(t))) φ (t) dt α β α (f (φ(t)) fn (φ(t))) φ (t) dt sup f(z) f n (z) z Ω = sup z Ω β α φ (t) dt f(z) f n (z) (C ). (Ω C {φ(t); t [α, β]} ) Proposition 2..4 (Weierstrass M (the Weierstrass M-test)) Ω, Ω {f n } n N M n n N, z Ω f n (z) M n f n (z) Ω (converges absolutely and uniformly on Ω) z Ω f n (z) (z ) ε >, N N s.t. n N, z Ω f k (z) k= n f k (z) ε. f n (z) z Ω ε >, N N s.t. f n (x) k= n f n (z) ε. k= z Ω f n (z) ( 2..) m > n m f k (z) k= n f k (z) = k= m k=n+ m f k (z) m n M k = M k M k M k k=n+ k= k= k= k= n M k. 6
18 M n m ( ) f k (z) k= n f k (z) M k k= sup f k (z) z Ω k= k= n M k. k= n f k (z) M k k= k= n M k. n f n (z) k= 2.. {a n } n c C a n (z c) n (z C) n= (power series) 2..2 ( ) 2.. {a n } n c C (2.2) a n (z c) n n= z = z ( c) < r < z c r (2.2) z D(c; r) (2.2) z D(c; z c ) ( : z z c > z c z ) n= a n (z c) n lim n a n(z c) n =. M R s.t. a n (z c) n M (n =,, 2,... ). < r < z c z D(c; r) a n (z c) n a n (z c) n z c n z c M M n= ( ) r n (n =,, 2,... ). z c ( ) r n Weierstrass z c M (2.2) D(c; r) 7
19 2..2 {a n } n c C a n (z c) n n= (i), (ii), (iii) (i) z c (ii) ρ (, ) s.t. z D(c; ρ) z {z C; z c > ρ} (iii) z C (i) (iii) (ii) C := {z C; }, D := {z C; }, ρ := sup{ z c ; z C} < ρ <, {z C; z c < ρ} C, {z C; z c > ρ} D C D = C, c C C (i) z C \ {c}. ρ = sup{ z c ; z C} z c >. (iii) z D. 2.. z C, z 2 D = z c z 2 c z 2 = z z C ρ z c. ρ <. z c < ρ z C s.t. z c < z c. 2.. z C. z c > ρ z C. z D. (i) ρ =, (iii) ρ = (i),(ii),(iii) {z C; z c < ρ} {z C; z c > ρ} 2 ρ [, ] (2.2) (radius of convergence) {z C; z c < ρ} (2.2) (circle of convergence) ( = ) ( = ) 2..3 f (z) = z + z z n +..., f (z) = z + z zn n +..., f 2 (z) = z 2 + z zn n z > z n, z n n, z n n 2 ( ) z < z n n 2 z n n zn = z n 2 ρ = {z C; z c < ρ} =, ρ = {z C; z c < ρ} = C, {z C; z c > ρ} = 8
20 z n 2.. () f (z), f (z), f 2 (z) z = z f (z) z n f 2 (z) z n /n 2 z n = n 2 n () n2 f (z) z = ( = ) z =, z z n t n := + z + + z n = n z k (n =,, 2,... ) k= t n = z n+ z + z n+ z /k n k= 2 z ( k ) = k + n + f (z) Abel 3 n k= z k k = n k= n = k= k (t k t k ) = t k ( k k + {t n } n t n n n t k k= ( k ) sup k + k k= n t k n k k= k= ) + t n n t n t k k=. t k k n = k= = n k= n t k k t k k + k= t k ( k k + ) + t n n. ( k ) 2 k + z = 2 z < n ( n t k k ) n k + [3] 75 n k= z k k 3 Abel summation, Abel s transformation, Abel s partial summation A n := n k= a k n k= a kb k = A n b n + n k= A k(b k b k+ ) 9
21 2.. (Abel (Abel s transformation)) {α n } n, {β n } n n (2.3) ( M R)( n N {}) α k M, (2.4) n= k= β n β n+ <, lim n β n = S = α n β n n= S A B, k=m+ α k β k A m+ B m+ n A m := sup α n m k, B m := β k β k+. k=m k=m {α n } {β n } {β n } (2.3) A m 2M < n n m n m α k = α k α k α k + α k M + M = 2M k=m k= k= k= k= A m 2M. n S n := α k β k, σ n := k= n α k S n Abel k= S n = α β + = σ β + n α k β k = σ β + k= n k= n (σ k σ k )β k k= n σ k β k σ k β k+ = k= n = σ k (β k β k+ ) + σ n β n. k= n k= n σ k β k σ k β k+ σ n β n = σ n β n A β n (n ). k= n n σ k β k β k+ A β k β k+ A B <. k= k= S = lim n S n S A B. 2
22 k = m + S m+,n := n k=m+ k=m+ α k β k, σ m+,n := α k β k A m+ B m+ n k=m+ k m + 2 α k = σ m+,k σ m+,k, α m+ = σ m+,m+. S m+,n = σ m+,m+ β m+ + = σ m+,m+ β m+ + = = n k=m+ n k=m+ σ m+,k β k n k=m+2 n k=m+2 n k=m+ α k (σ m+,k σ m+,k ) β k σ m+,k β k σ m+,k β k σ m+,k (β k β k ) + σ m+,n β n. n k=m+ σ m+,k β k σ m+,n β n A m+ β n, n k=m+ σ m+,k (β k β k ) lim n S m+,n n k=m+ k=m+ A m+ β k β k lim S m+,n A m+ B m+. n A m+ β k β k = A m+ B m+ 2.. (Abel ( 2..) ) a f(x)g(x) dx F (x) := a x a f(x)g(x)dx sup x [a, ) f(t) dt x a f(t) dt F (x) = f(x) F, M := a (x [a, )) sup F (x) < x [a, ) 2 g (x) dx
23 a g (x) dx <, lim g(x) = x F (a) = R a a a f(x)g(x) dx = R a R F (x)g(x) dx = [F (x)g(x)] R a F (x)g (x) dx = F (R)g(R) R a F (x)g (x) dx. F (R)g(R) M g(r) (R ), F (x)g (x) M g (x), f(x)g(x) dx f(x)g(x) dx M g (x) dx = a R a sup x [a, ) c [a, ) f(x)g(x) dx sup x f(t)dt c x [c, ) c a g (x) dx < x a c f(t) dt a g (x) dx. g (x) dx {β n } α n = ( ) n α n = e inθ (θ 2πZ) f(z) b z b f(z) f(b) Abel 2..2 (Abel (Abel s continuity theorem)) f(z) = a n z n z = R (R > ) K { } z/r Ω K := z C; z < R, z /R K f Ω K {R} f Ω K {R} n= lim f(x) = f(r). x [,R) x R f n (z) := n a k z k k= 22
24 k= sup f(z) f n (z) (n ) z Ω K {R} z = R lim f n(r) = f(r) ( n z ) n z Ω K α n := a n R n, β n := R n n α k = a k R k = f n (R) (n =,, 2,... ) k= β n β n+ = n= n= ( ) z n z R R = Abel n N A n+ = z R z R K. f(z) f n (z) A n+ B n+ A n+ B KA n+ (z Ω K ). sup m n+ m k=n+ f(z) f n (z) K α k = sup m n+ m k=n+ a k R k = sup f m (R) f n (R) m n+ sup f m (R) f n (R) (z Ω K, n N). m n+ { } sup z Ω K {R} f(z) f n (z) max K sup m n+ f m (R) f n (R), f(r) f n (R). n f n (R) f(r) {f n (R)} n Cauchy n {f n } n N Ω K {R} f α (, π/2) arg (z ) π < α z Stolz K := 2 sec α z z < K D z z = re iθ θ < α, cos θ > cos α, r = z < cos α z r ( + z ) = z z 2 = 2..5 r ( + z ) ( 2r cos θ + r 2 ) < 2 2 cos θ r < 2 = 2 sec α. 2 cos α cos α tan x = x x3 3 + x5 x2n + ( )n + ( x < ) 5 2n 23
25 x = Abel tan = π 4 π 4 = ( )n 2n +. log 2 = ( )n n 2..6 (Cauchy-Hadamard ) =, = ( ) 2..7 ρ = +. a n (z c) n ρ [, ] n= ( ) n lim sup an. n a n (z c) n n= lim n a n a n+ lim n a n a n+ = ( ) 24
26 2..8 (2 ) {a n } n c C f(z) := a n (z c) n r (, ] n= g(z) := na n (z c) n = (n + )a n+ (z c) n n= r f D(c; r) f (z) = g(z) (z D(c; r)) f D(c; r) a n = f (n) (c) n! (n =,,... ) B 2n e z z z e z + z 2 = + ( ) n B 2n (2n)! z2n B 2 = 6, B 4 = 3, B 6 = 42, B 8 = 3, B = 5 66, B 2 = , B 4 = 6 7, B 6 = 367 5, B 8 = , B 2 = , ( B 2k+ = (k =, 2, 3,... ) B B = 2 ( Bernoulli) B = 2 () ) (2.5) z cot z = n B 2n z 2n. (2n)!
27 tan z = 2 2n (2 2n )B 2n z 2n. (2n)! Mathematica BernoulliB[n], Maple bernoulli(n) Bernoulli BASIC (exp, cos, sin, ( + x) α, log( + x) ) Taylor tan Taylor tan Taylor 2 ( Bernoulli ) Taylor,2 ( f(x) = tan x f (n) () OK BASIC ) cos z, sin z C cos z ( z < π/2) z < π 2 F (z) := tan z = sin z cos z F (z) = c n z n ( z < π 2 ) n= Taylor (n c n ) ( ) F (z) = g(z) f(z) f(z) = a n z n, g(z) = n= (2.6) c = b a, c n = b n z n, F (z) = n= c n z n n= ( f() ) b n n a k c n k k= a (n N) g(z) = f(z)f (z) (A + A + A 2 + ) (B + B + B 2 + ) = A B + (A B + A B ) + (A B 2 + A B + A 2 B ) + ( ) ( ) ( n ) A n B n = A k B n k n= n= n= k= 26
28 ( ) ( ) ( n ) f(z)f (z) = a n z n c n z n = a k c n k z n. n= n= n= k= g(z) = b n z n n= b = a c, b = a c + a c, b 2 = a c 2 + a c + a 2 c,.. n b n = a c n + a k c n k (n N) k= c = b a, c = b a c a, c 2 = b 2 a c a 2 c a,, c n = b n n a k c n k k= a (n N). (2.6) cos, sin Taylor cos z = n= ( ) n (2n)! z2n, sin z = n= ( ) n (2n + )! z2n+ (z C) tan z Taylor BASIC OPTION ARITHMETIC RATIONAL cos, sin Taylor ^ FACT() tan z = z + 3 z z z7 + tan z 27
29 cotangent.bas OPTION ARITHMETIC RATIONAL DECLARE EXTERNAL SUB INverse DECLARE EXTERNAL SUB conv LET maxn=2 OPTION BASE DIM c( TO maxn),s( TO maxn),is( TO maxn),cotangent( TO maxn) FOR n= TO maxn LET c(n)= LET s(n)= NEXT n FOR j= TO maxn/2 LET c(2*j)=(-)^j/fact(2*j) LET s(2*j)=(-)^j/fact(2*j+) NEXT j PRINT "z/sin(z)" CALL INverse(s,IS,maxn) CALL PRINTc(IS,maxn) PRINT "z cos(z)/sin(z)" CALL CONv(IS,c,cotangent,maxn) CALL printc(cotangent,maxn) END REM EXTERNAL SUB printc(a(),maxn) OPTION ARITHMETIC RATIONAL FOR n= TO maxn PRINT a(n) NEXT n END SUB REM EXTERNAL SUB INverse(a(),b(),maxn) OPTION ARITHMETIC RATIONAL LET b()=/a() FOR TO maxn LET s= FOR k= TO n LET s=s+a(k)*b(n-k) NEXT k LET b(n)=-s/a() NEXT n END sub REM EXTERNAL SUB conv(a(),b(),c(),maxn) OPTION ARITHMETIC RATIONAL FOR n= TO maxn LET s= FOR j= TO n LET s=s+a(j)*b(n-j) NEXT j LET c(n)=s next n END sub 28
30 OPTION ARITHMETIC RATIONAL LET maxn=4 DIM a( TO maxn+),b( TO maxn) REM sin(z) FOR n= TO maxn+ LET a(n)= NEXT n FOR j= TO maxn/2 LET a(2*j+)=(-)^j/fact(2*j+) NEXT j REM f(z)=sin(z)/z FOR j= TO maxn+ LET a(j-)=a(j) NEXT j REM /f(z) LET b()=/a() FOR TO maxn LET s= FOR k= TO n LET s=s+a(k)*b(n-k) NEXT k LET b(n)=-s/a() NEXT n FOR n= TO maxn PRINT b(n) NEXT n END 29
31 / z, / z Cauchy-Riemann C Ω f : Ω C (3.) (3.2) Ω := {(x, y) R 2 ; x + yi Ω}, u(x, y) := Re f(x + iy), v(x, y) := Im f(x + iy) ((x, y) Ω) f Ω u x = v y, u y = v x ((x, y) Ω). Cauchy-Riemann (the Cauchy-Riemann equations), Cauchy-Riemann (the Cauchy-Riemann differential equations), Cauchy-Riemann (the Cauchy- Riemann relations) 3.2. (, ) ( ) f : Ω C f(z) R (z Ω) (3.), (3.2) Ω, u, v v(x, y) = ((x, y) Ω). v x (x, y) = v y (x, y) = ((x, y) Ω). Cauchy-Riemann u x (x, y) = u y (x, y) = ((x, y) Ω). C R s.t. u = C on Ω. f(x + iy) = u(x, y) + iv(x, y) = C + i = C. 3
32 3.2.2 ( ) f f f ( ) C R s.t. f(z) = C (z Ω) C = f(z) = (z Ω) f C > (3.), (3.2) Ω, u, v Cauchy-Riemann = x C2 = x = y C2 = y ( u 2 + v 2) = 2uu x + 2vv x = 2(uu x vu y ), ( u 2 + v 2) = 2uu y + 2vv y = 2(uu y + vu x ) ( u v v u ) ( ) ux = u y ( ). u u ( v) v = u 2 + v 2 = C 2 > u x = u y =. Cauchy-Riemann v x = v y =. u v f(x + iy) = u(x, y) + iv(x, y) Cauchy 3.4. Green Cauchy
33 4 (24 22 ) ( ) : D(c; R), D(c; R), z a = r z = a + re iθ (θ [, 2π]) ( Cauchy ) Ω C f : Ω C c C, R >, Ω D(c; R) z D(c; R) (4.) f(z) = f(ζ) 2πi ζ c =R ζ z dζ. ζ z = ε D(c; R) ε > ζ z = ε, ζ c = R ζ f(ζ) Cauchy ( ζ z ) f(ζ) (4.2) 2πi ζ c =R ζ z dζ = f(ζ) 2πi ζ z =ε ζ z dζ. ζ = z + εe iθ (θ [, 2π]) f(ζ) 2πi ζ z =ε ζ z dζ = 2π f(z + εe iθ )dθ 2π ε f(z) 2π f(z + εe iθ )dθ f(z) 2π = 2π [ ] f(z + εe iθ ) f(z) 2π 2π f(z + εe iθ ) f(z) dθ 2π max θ [,2π] f(z + εe iθ ) f(z) dθ (ε ). f(ζ) dζ = f(z). 2πi ζ c =R ζ z 32
34 4..2 (, =, 4.3, 4.4 ) c C, R >, f : D(c; R) C z D(c; R) (4.3) 2πi ζ c =R f(ζ) ζ z dζ = n= a n (z c) n, a n := 2πi ζ c =R f(ζ) dζ (n ). (ζ c) n+ f ( 4.. ) (4.4) f(z) = a n (z c) n n= (z D(c; R)). (4.5) f (n) (z) = n! 2πi ζ c =R f(ζ) dζ (n =,,... ). (ζ z) n+ ((4.) ) Weierstrass M < r < R z c r z ζ c = R ζ z c z c ζ c = ζ c r R. r/r ζ z = ζ c (z c) = ζ c z c ζ c = ζ c n= ( ) z c n = ζ c n= (z c) n (ζ c) n+. (4. ) f(ζ) ζ z = n= f(ζ)(z c) n (ζ c) n+. ζ c = R ζ M := n= M R ( r R f(ζ)(z c) n (ζ c) n+ M ( r n R R) max ζ c =R f(ζ) ) n Weierstrass M test (4. ) ζ c = R ζ c =R f(ζ) ζ z dζ = n= ζ c =R f(ζ)(z c) n dζ. (ζ c) n+ 2πi (4.3) 4.. (4.4) ζ c = R ζ f(ζ) 33
35 (4.5) ζ c = R ζ z = R 4..3 Taylor f(z) = n= f (n) (c) (z c) n n! 4..5 (Cauchy ( )) Ω C f : Ω C D D = D D Ω D (4.6) f(z) = 2πi D f(ζ) ζ z dζ (z D). (4.7) f (n) (z) = n! f(ζ) dζ 2πi D (ζ z) n+ (z D). z D D(z ; R) D R > z D(z ; R) f(ζ) f(ζ) dζ = dζ 2πi D (ζ z) n+ 2πi ζ z =R (ζ z) n+ (n =,, 2, ) 4..2 f(ζ) 2πi (ζ z) n+ dζ = f (n) (z). n! D ( (the mean-value property)) Ω C f : Ω C c Ω D(c; r) Ω r > f(c) = 2π ( f c + re iθ) dθ. 2π ( z c = r f ) Cauchy z = c f(c) = f(ζ) 2πi ζ c dζ. ζ c =r ζ = c + re iθ (θ [, 2π]) f(ζ) 2πi ζ c dζ = 2π f(c + re iθ ) 2πi re iθ ire iθ dθ = 2π ζ c =r 2π f ( c + re iθ) dθ. 34
36 4.2. ( ) u = u(x) = u(x,..., x n ) (n = ) u u = (u ) u u (x) = u. u(a + r) + u(a r) a u(a) a ± r 2 f u, v (f(x + iy) = u(x, y) + iv(x, y)) u = v = ( ) Proposition 4.2. (() (the maximum principle, maximum-modulus theorem)) Ω C f : Ω C z Ω, z Ω f(z) f(z ) ( f(z ) f ) C C s.t. z Ω f(z) = C. ( ) (( ) ) c C, R >, f : D(c; R) C D(c; R) f z f(z) D(c; R) 4.2. ( ) ( ) 2 [] max f(ζ) max ζ D(c;R) ) ζ D(c;R) [2] max ζ D(c;R) f(ζ) z D(c; R) f(z) = z D(c; R) f(z) < f(ζ) ( max ζ D(c;R) max f(ζ) () ζ D(c;R) f(ζ) 2 [] [2] [] ( z D(c; R) f(z ) = z D(c; R) f(z) = max f(ζ). ζ D(c;R) max f(ζ) f(z ) = ζ D(c;R) [] ) [2] max ζ D(c;R) max f(ζ) < ζ D(c;R) max ζ D(c;R) max f(ζ) ζ D(c;R) f(ζ) f(ζ) f [] 2 35
37 M := f(z ) Ω ε > s.t. D(z ; ε) Ω. ρ := ε/2 D(z ; ρ) Ω. < r ρ r f(z ) = 2π ( f z + re iθ) dθ. 2π M = f(z ) 2π ( f z + re iθ) 2π dθ M dθ = M. 2π 2π 3 2π 2π ( f z + re iθ) 2π dθ = M dθ. 2π f(z + re iθ ) M θ f ( z + re iθ) r ( f z + re iθ) = M (θ [, 2π]) i.e. f(z) = M ( z z = r). f(z) = M ( z z ρ) (p. 3, ( p. 56, 3., ) f D(z ; ρ) : C C s.t. f = C on D(z ; ρ). (identity theorem, p. 4, 2.38) Ω f = C. ( ) z Lemma 4.2. ( ) n N, {a j } n j= Cn+, a, f(z) = a z n +a z n + + a n z + a n ( < ε < )( R R)( z C : z R) ( ε) a z n f(z) ( + ε) a z n. f(z) ( z R), n lim f(z) =. z z f(z) a z n = + a a z + a 2 a z a n a z n. m N f(z) ( z ) lim =. zm z a zn lim z f(z) a z n =. 3 f g on [a, b] b f(x) dx b a a ( ) b f(x) dx = a a g(x) dx. f g x [a, b] f(x ) < g(x ) b f(x) dx < b a a b g(x) dx f g. 36 g(x) dx. f g
38 ε >, R R, ( z C: z R) f(z) a z n f(z) < ε, i.e. ε a z n + ε ( (fundamental theorem of algebra) ) ( ) P (z) n P (z) z C P (z) f(z) := f P (z) Lemma 4.2.(p. 36) R R M >, R R, ( z C : z R ) P (z) M z n. (4. ) ( z C : z R) f(z) M z n MR n. f D(; R) z = R (4. ) MR n f(z) (z C). R f(z) =. MRn f(z) ( ) p. 8 ( ) (R M R R M > ) Liouville Definition 4.2. () C (entire function) Example 4.2. ( ) exp z, cos z, sin z tan z, log z, + z (Liouville (, Liouville s theorem)) f : C C M R s.t. f(z) M (z C) f Taylor f(z) = a n z n z C n N n= a n = R > a n = f (n) () = f(ζ) dζ = n! 2πi ζn+ 2πi ζ =R Cauchy a n 2π 2π 2π f(re iθ ) (Re iθ ) n+ ireiθ dθ = 2π f(re iθ ) 2π R n e inθ dθ. f(re iθ ) R n dθ 2π M 2π R n dθ = M R n 37
39 4 R a n = (n N). f(z) = a ( z C). Example ( ( )) P (z) n P (z) z C P (z) f(z) := P (z) Lemma 4.2.(p. 36) M >, R R, ( z C : z R) P (z) M z n f(z) M z n MR n ( z R). D(; R) = {z C; z R} f M R, z D(; R) : f(z) M. { } f(z) max MR n, M (z C). Liouville f P n 5 Example f(z) := z, g(z) := (z )(z 2) C \ {}, C \ {, 2} f g z < h := f + g z < h z < 2 g(z) g(z) = z + z 2 Taylor Ω C f : Ω C c Ω R := {R > ; f D(c; R) } f c Taylor ρ sup R 4 : ) n ( R) ratio test Cauchy-Hadamard n ( z R Cauchy 5 a z n + a z n + + a n z + a n (a, n ) a z n + a z n a n ( )a n = a n 2 = = a = a = a 6 n= a n (z c) n R = lim n ( a n n R (ratio test), R = lim sup an ) a n+ n R (Cauchy-Hadamard) {a n } (a n = a n ) a n (z c) n = (a(z c)) n z c < / a z c > / a R = / a. n= n= 38
40 4.2.3 ( ) R f D(c; R) D(c; R) Ω (f D(c; R) ) D(c; R) Ω f : D(c; R) C s.t. f = f in D(c; R) Ω (R D(c; R) Ω ) (2 ) f : D(c; R) C s.t. f = f in D(c; R) Ω sup R c f ( f f ) ρ R ρ sup R. R R, < ε < R f c Taylor D(c; R ε) 7 ( 4..2) R ε ρ. ε R ρ. sup R ρ. ρ = sup R. Example ( Taylor ) f(z) = Q(z) (P (z), Q(z) C[z], P (z) P (z) Q(z) ) P (z) α, α 2,..., α n Ω := C \ {α j ; j n} z f(z) c Ω f c Taylor min α j c j n ( p.8) 2.29 ( pp.33 34) (Bernoulli ) f(z) g(z) := + z 2! + z2 3! + = z n (n + )! z C g : C C g(z) = ez z n= (z C \ {}) g(z) = (z e z = ) n Z \ {} s.t. z = 2nπi. g(z) f(z) : f(z) := g(z). Ω := C \ {2nπi; n Z \ {}} (Ω ) D(; 2π) Taylor B n Bernoulli f(z) = z 2 + ( ) n B 2n (2n)! z2n ( pp.33 34) B 2 = 6, B 4 = 3, B 6 = 42,. 7 ε Taylor D(c; R) 4..2 R ε 39
41 2π 8 f z < 2π f R > 2π R z < R sup R = 2π () f Taylor Mathematica Series[z/(Exp[z]-),{z,,}] Maple taylor(z/(exp(z)-),z=,) f(z) = z 2 + z2 2 z z6 324 z z exp z = n Z s.t. z = 2nπi (p.7 ) sin z = ( p.8) f(x) := + x 2 R ( x R f x : r >, {a n } n s.t. f(x) = a n (x x n ) (x r < x < x + r)) x = Taylor n= f(x) = x 2 + x 4 x 6 + = ( ) n x 2n < x < ( ) f(z) = z 2 + = (z + i)(z i) z < z = ±i z < R ( R > ) R sup R = n= () ( ) (Taylor ) ( 4.) ( ) Laurent ( 4.3.4) b n (z c) n ( ) 8 ratio test Hadamard 4
42 Example 4.3. ( Laurent ) f(z) := C \ {3} z 3 c = D(; 2) (Taylor ) f(z) = z 3 = (z ) 2 = ( 2 z ) 2 = ( ) z n (z ) n = n+ (z D(; 2)). n= f D(; 2) D := {z C; z > 2} n= f(z) = z 3 = (z ) 2 = ( (z ) 2 ) z = ( ) 2 n 2 n = z z (z ) n+ n= n= 2 n = (z ) n ( 2 z < z > 2). ( z 3 ) 4.2 Prop ( (Lemma 4.3.) ( )) Lemma 4.3. ( ( )) a n (z c) n 3 n= (i) z C < ρ < z c ρ (ii) < ρ < s.t. z c < ρ z c > ρ < ρ < ρ z c ρ (iii) z C \ {c} 4
43 Proposition 4.3. () b n 3 (z c) n (i) z C \ {c} < R < z c R (ii) < R < s.t. z c > R z c < R R < R < z c R (iii) z C \ {c} z c z c = ζ b n (z c) n = b nζ n. b n ζ n Lemma 4.3. (i) b n ζ n b n ζ C z C \ {c} (z c) n < R < ρ = /R b n ζ n ζ ρ b n (z c) n z c R (ii) < ρ < s.t. b n ζ n ζ < ρ ζ > ρ b n R := /ρ (z c) n z c > R z c < R R < R < R /R < /R = ρ b n ζ n ζ /R b n (z c) n z c R (iii) b n ζ n b n ζ z c (z c) n (i) R =, (iii) R = ( ) Prop R s.t. b n (z c) n z c > R z c < R R < R < b n (z c) n z c R a n (z c) n a n + (z c) n n= 42
44 Theorem 4.3. (Laurent ) a n (z c) n a n + (z c) n ρ n= ρ s.t. ρ < z c < ρ (ρ = ρ ) z c < ρ z c > ρ ρ < R < R < ρ R, R R z c R 4.3. ( ) 4.3. c f (isolated singularity) R > s.t. f < z c < R ( {z; < z c < R} ) f c c c 3 (i) f c (ii) f c c (iii) f c c ( f z c < R ) (iii) c f ( f D(c; ε) ) Ω f Ω f f (f < z < ) (a) f(z) := sin z z (b) f(z) := z(z 2 ) ( R < z < R ) ( < z < ) (c) f(z) := exp z ( R < z < R ) Example ( ) f(z) = { } sin C\ nπ ; n Z z z = (n Z) c = R > f < z c < R nπ c = f ( ) ( p.82) f(z) = Q(z) (P (z), Q(z) C[z]) P (z) P (z) n P (z) n n P (z) f f 43
45 c f c (c ) ( ) c f [4] c ( < z c < R) c (annulus) A(c; R, R 2 ) := {z C; R < z c < R 2 } R = c ( Laurent ) c C R, R 2 R < R 2 (R R 2 R ) f R < z c < R 2 {a n } n Z s.t. (4.8) f(z) = a n (z c) n a n + (z c) n = n= n= a n (z c) n (R < z c < R 2 ). (4.8) R < r < r 2 < R 2 r, r 2 r z c r 2 ( ) () (4.8) R < r < R 2 r (4.9) a n = f(z) dz 2πi z c =r (z c) n+ (n Z). () m Z (4.8) (z c) m+ f(z) (z c) m+ = n= a n (z c) n m R < r < R 2 r z c = r f(z) dz = 2πi z c =r (z c) m+ 2πi z c =r = = n= n= 2πi a n n= z c =r a n (z c) n m dz 2πi a n 2πiδ nm = a m. (z c) n m dz (4.9) ( ) R < z c < R 2 z R < r < z c < r 2 < R 2 r, r 2 C : ζ c = r, C 2 : ζ c = r 2, C := C 2 C C D = {ζ; r < ζ c < r 2 } D D = {ζ C; r ζ c r 2 } R < ζ c < R 2 f Cauchy f(z) = 2πi = 2πi C f(ζ) ζ z dζ = f(ζ) 2πi C 2 f(ζ) ζ z dζ 2πi ζ c =r 2 ζ z dζ 2πi ζ c =r C f(ζ) ζ z dζ. f(ζ) ζ z dζ 44
46 : S(ζ) := f(ζ) ζ z = f(ζ) ζ c z c ζ c S N (ζ) := f(ζ) ζ c ζ c = r 2 ζ S(ζ) S N (ζ) max f(ζ) ζ c =r 2 ζ c N n= = f(ζ) ζ c n= ( ) z c n = f(ζ) ζ c ζ c S(ζ) S N (ζ) = f(ζ) ζ c z c N ζ c z c = ζ c ( ) z c N ζ c z c ζ c max f(ζ) ζ c =r 2 r 2 {ζ C; ζ c = r 2 } f(ζ) ζ z = f(ζ) (ζ c) (z c) = f(ζ) z c = f(ζ) n= (ζ c) n (z c) n+ = f(ζ) ζ c z c (ζ c) n (z c) n ( ) z c n. ζ c ( ) z c N ζ c z c ζ c ( z c r 2 = f(ζ) z c ) N z c r 2 n= ( z c = const. ( ) ζ c n z c {ζ C; ζ c = r } ( ζ c z c r z c < ) f(z) = = a n := 2πi (z c) n 2πi a n (z c) n + n= n= ζ c =r 2 ζ c =R 2 f(ζ) (ζ c) n+ dζ + a n (z c) n. (z c) n f(ζ) (ζ c) n+ dζ (n =,, ), a n := 2πi ζ c =r R < r < R 2 r a n = f(ζ) dζ (n Z). 2πi (ζ c) n+ ζ c =r 45 r 2 ) N f(ζ)(ζ c) n dζ 2πi ζ c =R f(ζ) dζ (n =, 2, ). (ζ c) n+
47 r ζ c r 2 Lemma 4.3., Prop ( self-contained ) {a n } (4.9) R < ρ < ρ 2 < R 2 ρ, ρ 2 f(z) = a n (z c) n a n + (z c) n (ρ z c ρ 2 ) n= R < r < ρ < ρ 2 < r 2 < R 2 r, r 2 C : ζ c = r, C 2 : ζ c = r 2, C := C 2 C, D := A(c; r, r 2 ), Ω := A(c; R, R 2 ), M := max f(ζ), M 2 := max f(ζ) ζ c =r ζ c =r 2 D = C ( ), D Ω Cauchy (4.) f(z) = f(ζ) 2πi ζ z dζ = f(ζ) 2πi ζ z dζ f(ζ) 2πi ζ z dζ (z D). C C 2 z A(c; ρ, ρ 2 ) (4.) ζ C2 ζ c = r 2, z c ρ 2 z c ζ c ρ 2 <. r 2 C ζ z = (ζ c) (z c) = ζ c z c ζ c = ζ c n= ( ) z c n ζ c (4.) f(ζ) ζ z = n= f(ζ)(z c) n (ζ c) n+ (ζ C 2 ). f(ζ)(z c) n (ζ c) n+ M 2 ρ n 2 r2 n+ = M 2 r 2 ( ρ2 r 2 ) n, n= M 2 r 2 ( ρ2 r 2 ) n = M 2 r 2 ( ρ 2 /r 2 ) < (4.) ζ C 2 2πi C 2 f(ζ) ζ z dζ = 2πi C 2 f(ζ)(z c) n (ζ c) n+ dζ = (z c) n 2πi n= n= C 2 f(ζ) dζ. (ζ c) n+ (4.) 2 ζ C ζ c = r, z c ρ ζ c z c r <. ρ ζ z = (ζ c) (z c) = z c ζ c z c = z c n= ( ) ζ c n = z c (ζ c) n (z c) n 46
48 (4.2) f(ζ) ζ z = f(ζ)(ζ c) n (z c) n (ζ C ). f(ζ)(ζ c) n (z c) n M r n r ρ n = M r ( r ρ ) n, M r ( r ρ ) n = M r ( r /ρ ) < (4.2) ζ C 2πi C f(z) = n= a n = 2πi f(ζ) ζ z dζ = 2πi C a n (z c) n + f(ζ)(ζ c) n (z c) n dζ = a n (z c) n (z A(c; r, r 2 )), a n = 2πi C 2 C f(ζ)(ζ c) n dζ (n =, 2,... ). n= (z c) n f(ζ)(ζ c) n dζ. 2πi C f(ζ) dζ (n =,,... ), (ζ c) n+ 2 Weierstrass M-test a n (z c) n = f(ζ)(z c) 2πi C2 n dζ (ζ c) n+ ( ) n ( ) n 2π 2πr 2 M2 ρ2 ρ2 = M 2 (n =,, ), r 2 r 2 r 2 a n (z c) n = f(ζ)(ζ c) 2πi C n (z c) n dζ ( ) n ( ) n 2π 2πr M r r = M (n =, 2, ), r ρ ρ ( ) n ρ2 M 2 ( ) n r M r M 2 = <, M = r 2 ρ 2 /r 2 ρ ρ ( r /ρ ) <. C, C 2 ζ c = r (R < r < R 2 ) a n = f(ζ) dζ (n Z). 2πi (ζ c) n+ ζ c =r 4.3. ( n= ) S = a n n= k=n a k n k= n S = lim S = a n + a n = lim n= m k= m a k + lim n k= n a k, S = lim n m k=m k= n a k 47
49 ( a lim R R 2 f(x) dx + R2 a f(x) dx = lim R 2 R2 a f(x) dx = lim f(x) dx + lim R R f(x) dx ) n m R a R ε >, N N, M N, ( n N : n N), ( m N : m M) R f(x)dx R f(x) dx, f(x) dx = f(x) dx = ε-n S m k= n a k < ε, ε >, N N, ( n N : n N), ( m N : m N) S m k= n a k < ε, () (4.8) f R < z c < R 2 (Laurent expansion, Laurent series) R = c ( c ) Example () Laurent Taylor (c Taylor Laurent ) Taylor f(z) = a n (z c) n, n= a n = f (n) (c) n! (n =,, 2,... ) a n = f(ζ) 2πi n+ dζ (ζ c) ζ c =r a n () f(z) = n Z a n (z c) n (R < z c < R 2 ) {a n } Laurent 3 f(z) = Laurent (z ) 2 {a n } f(z) = a 2 := 3, a n := (n Z \ { 2}) n= a n (z ) n ( < z < ) 48
50 Taylor sin z z 2 = exp z = n= n= exp z = n! sin z = n= ( ) n = + z n= n! zn (z C) n! z n ( ) n (2n + )! z2n+ (z C) ( < z < ). ( ) n (2n + )! z2n = z + ( ) n (2n + )! z2n ( < z < ) : Laurent 4.3. f (z a) n Laurent f Laurent n = z a r = r n ( r < ) Laurent Laurent z a = a( z/a) = a ( z n = a) z n a n+ n= n= n= ( z/a < z < a ). a < z a < Laurent z a = z( a/z) = ( a ) n = z z n= n= a n z n+ = a n z n ( a/z < a < z < ). c C Laurent z a = z c (a c) = a c (z c)/(a c) = a c = n= n= ( ) z c n a c (z c) n (a c) n+ ( (z c)/(a c) < z c < a c ). a c < z c < Laurent z a = z c (a c) = z c (a c)/(z c) = z c = n= ( ) a c n = z c (a c) n (z c) n ( (a c)/(z c) < a c < z c < ). n= (a c) n (z c) n+ 49
51 4.3.2 f c ( R < z c < R 2 ) Laurent (z c) a n (z c) n f (, principal part) ( p.84) cos z () z 2 sin z (z = ) () z 2 (z 2 (z = ) ) 3 Definition 4.3. ( ( ) ) Ω C f : Ω C, c C f ( ) R R s.t. f < z c < R R =, R 2 = R {a n } n Z s.t. f(z) = a n (z c) n n= ( < z c < R). (a) c f (removable singularity) (f c ) n N a n = 9 f c (b) c f (pole) (f c ) k N a k [ n > k a n = ] f c k c c k (c) c f ( ) (isolated essential singularity) k N n > k a n f c 4.3. X ( ) X (a) c f {n N; a n } = ( ) 5
52 (b) c f {n N; a n } < ( ) (c) c f {n N; a n } = () Example f(z) = sin z (z C \ {}) f z Laurent ( ) n sin z (2n + )! z2n+ n= ( ) n = = z z (2n + )! z2n = z2 3! + z4 5! z6 + ( < z < ) 7! Example f(z) = n= 2 (z C \ {3}) 3 4 (z 3) 4 f(z) = 2 (z 3) 4 3 Laurent (a 4 = 2, a n = (n Z \ { 4}) f(z) = n Z a n (z 3) n ) 2 Laurent (z 3) 4 Example f(z) = exp z Laurent f(z) = (z C \ {}) f n= n! ( ) n = + z n! z n ( < z < ) f Laurent = n! z n Proposition ( ) c f (), (2) () lim f(z) ( ) z c z c (2) R (, ], f : D(c; R) C s.t. f(z) = f(z) ( < z c < R). f c c f R > s.t. f < z c < R {a n } s.t. f(z) = a n (z c) n a n + (z c) n ( < z c < R). n= 5
53 c f f(z) = n N a n =. a n (z c) n n= z = c ( a ) f(z) := ( < z c < R). a n (z c) n ( z c < R) n= f : D(c; R) C ( ) z = c lim z c z c f(z) = lim z c z c f(z) = f(c) = a c f f D(c; R) f f f(z) ( < z c < R) f(z) := f(z) (z = c) lim z c z c c f k {a n } n k, R > s.t. k a j f(z) = (z c) j + a n (z c) n ( < z c < R) j= n= Laurent a k+n = n! lim z c z c ( ) d n [ (z c) f(z)] k dz (n =,, 2,... ) Proposition ( ) c f lim f(z) =. z c z c c f R >, {a n } s.t. f(z) = a n (z c) n a n + (z c) n ( < z c < R). n= k a k ( n N: n > k) a n = f(z) = a n (z c) n + n= k a n (z c) n ( < z c < R). 52
54 ζ = z c lim z c z c a n (z c) n = a. n= z c, z c ζ k a n k (z c) n = a n ζ n. Lemma 4.2. lim ζ k a n ζ n =. lim f(z) = a + =. z c z c Lemma (Riemann) f < z c < R c f lim f(z) c f z c z c f < z c < R {a n } s.t. f(z) = a n (z c) n a n + (z c) n ( < z c < R). n= a n (n Z) < r < R r a n = 2πi ζ c =r f(ζ) 2π dζ = (ζ c) n+ 2πi f(c + re iθ ) r n+ e i(n+)θ ireiθ dθ = 2π 2πr n f(c + re iθ )e inθ dθ. f M R s.t. f(z) M ( < z c < R). a n 2π 2πr n f(c + re iθ )e inθ 2π dθ 2πr n Mdθ = 2πM 2πr n = M r n. a n M = Mrn (n r n N). r a n = (n N). f c c f ( ) f A(c;, R) { (z c) g(z) := 2 f(z) ( < z c < R) (z = c) Riemann Liouville Cauchy 53
55 g < z c < R g g(z) g(c) (z c) 2 f(z) (c) = lim = lim = lim(z c)f(z) = z c z c z c z c z c ( f ) g c z c < R : {a n } n s.t. g(z) = a n (z c) n n= ( z c < R). g(c) =, g (c) = a = a =. g(z) = a n (z c) n = (z c) 2 a n (z c) n 2 = (z c) 2 n=2 n=2 n= a n+2 (z c) n ( z c < R). f(z) = a n+2 (z c) n n= c f ( < z c < R). Theorem (Casorati-Weierstrass) c f β C, {z n } n N s.t. z n c ( n N), lim z n = c, lim f(z n) = β. n n ( β = ) f < z c < R β C ε >, r (, R), z A(c;, r) s.t. f(z) β < ε. n =, 2, ε = r = n {z n} n N s.t. n N z n B(c; /n), f(z n ) β < n. lim z n = c, n lim f(z n) = β. n 2 ε > r > z A(c;, r) f(z) β ε. g(z) := f(z) β (z A(c;, r)) ( ) g A(c;, r) c g g(z) ε (z A(c;, r)) ε-δ 2 (proof by contradiction, reductio ad absurdum) 54
56 Riemann c g B(c; r) g(z) (z A(c;, r)) f(z) = β + g(z) = βg(z) + g(z) c f (c g c f, c g k c f k ) c f Corollary 4.3. ( lim ) c f (), (2), (3) () c f lim f(z) z c z c (2) c f lim f(z) = z c z c (3) c f lim f(z) lim f(z) = z c z c z c z c Example f(z) := exp ( z ) 2 f z f(z) lim f(x) =, x R x lim f(iy) = y R y Casorati-Weierstrass Theorem (Picard ) c f e C, ( U: c ) v C \ {e}, z U s.t. f(z) = v. c ( Ahlfors [5] ) Picard [6] 2 ( p.85) f(z) = exp z z n () f(z) (2) f(z n ) (3) α f(z n ) α. (), (2), (3) () a C \ {}, ε >, z A(;, ε) s.t. exp z = a. (2) {z n } n N s.t. lim n z n = lim n exp z n =. 55
57 (3) {z n } n N s.t. lim n z n = lim n exp z n =. ( : a = re iθ (r >, θ [, 2π)) exp z = a = reiθ n Z s.t. z = log r + i(θ + 2nπ) n Z s.t. z = log r + i(θ + 2nπ) n (2), (3) w n = /z n w n ) () lim f(z) z c z c ( ) f(z) = (z c) n g(z) ( < z c < r), n Z, g z c < r, g(c) n c 3 n < c n ( p.85) f a a f (f(z) := sin(/z) z = ) (multifunction, multi-valued function) (transcendental branch point) 3 f(z) = Log ( z) z =. ( ) () f(z) = cos z z 2 (2) f(z) = sin(z3 ) z( cos z) (3) r > A(c; ; r) f c f def. R > s.t. f A(c;, R) := {z C; < z c < R} f A(c; ; R) 3 n > lim z c 4 lim z c z c z c f(z) =, n = lim f(z) = g(c) z c z c f(z) = 56
58 c f = R >, {a n } s.t. f(z) = n= a n (z c) n (z A(c;, R)) ( a n a n = f (n) (c) = f(z) 2πi z c =r (z c) n+ dz ( < r < R), < r < r 2 < R A(c; r, r 2 ) = {z C; r z c r 2 } ) c f def. f c = c f lim f(z) z c z c c f = f(z) f(z) (z A(c;, r)) := f(z) (z = c) D(c; r) lim z c a c c f k def. f c k a n (z c) n, a k c f def. k N s.t. c f k c f lim f(z) = z c z c c f def. f c ( ) ( {n N; a n } = ) : f(z) 5 ( ) Proposition (k ) f(z) C[z], c C, k N 3 (i) c f(z) k ( f(z) (z c) k k = ) (ii) g(z) C[z] s.t. f(z) = (z c) k g(z) g(c). (iii) f(c) = f (c) = = f (k ) (c) = f (k) (c). f c C f(z) 5 f(z) = a n (z α j ) f(z) α j (j =, 2,..., n) j= f(z) ( f(z) = ) (root) α f(z) = f(α) = α f(z) α f(z) = 57
59 Proposition (k ) c C, f c U k N 2 (i) U g f(z) = (z c) k g(z) (z U) g(c). (ii) f(c) = f (c) = = f (k ) (c) = f (k) (c). k (i) (ii) (i) = (ii) f(z) = (z c) k g(z), g(c) h(z) := (z c) k f(z) = g(z)h(z). m k Leibniz m ( ) m f (m) (z) = h (r) (z)g (m r) (z). r r= r k h (r) (c) = m k h (r) (c) = ( r m) h (k) (z) k! f (m) (c) = f (k) (c) = m ( m r ) k!g(c) = k!g(c). r= ( k k ) g (m r) (c) = ( m k ), (ii) = (i) f c c Taylor R >, {a n } s.t. f(z) = a n (z c) n ( z c < R). n= a n = f (n) (c) a = a = = a k =, a k. n! f(z) = a n (z c) n = (z c) k a n (z c) n k = (z c) k a n+k (z c) n. n=k g(z) := n=k z c < R ( Prop. ) f(c) = f a n+k (z c) n n= f(z) = (z c) k g(z), g(c) = a k. n= f(c) = f (c) = = f (k ) (c) = f (k) (c) k N n N {} f (n) (c) = c f(x) = n= f (n) (c) (z c) n = n! f 58 n= n! (z c)n =
60 Definition (, ) c C, f c () c f (zero) f(c) = (2) c f f ( ) f(c) = f (c) = = f (k ) (c) = f (k) (c) k N f c (oredr) Example f(z) ( ) Example (a) f(z) = sin z kπ (k Z) f(kπ) = sin kπ =, f (kπ) = cos kπ = ( ) k kπ f Taylor sin z = ( ) k sin(z kπ) = ( ) k n= sin z = (z kπ)g(z), g(z) := ( ) k g() = ( ) k (b) f(z) = cos z 2kπ (k Z) 2 ( ) n (z kπ)2n+ (2n + )! n= f(2kπ) = cos 2kπ = =, f (z) = sin z, f (2kπ) = sin 2kπ =, ( ) n (z kπ)2n (2n + )! f (z) = cos z, f (2kπ) = cos 2kπ = 2kπ (k Z) 2 Taylor cos z = cos(z 2kπ) = n= ( ) n (z 2kπ)2n (2n)! cos z = (z kπ) 2 g(z), g(z) := ( ) n (z 2kπ)2(n ) (2n)! g(2kπ) = 2 2: Laurent Laurent 59
61 Proposition (ii) = (i) Laurent Taylor ( ) Laurent Proposition () c f, k N (i), (ii) (i) c f k (ii) c U g f(z) = g(z) (z c) k (z U \ {c}), g(c). c f c Laurent R (, ], {a n } n Z s.t. f(z) = a n (z c) n ( < z c < R). n= (i) = (ii) c f k f(z) = n= k a n (z c) n a k ( n N : n > k) a n =. = a k (z c) k + + a z c + a + a (z c) + a 2 (z c) 2 + ( < z c < R) (z c) k f(z) = a k + a k+ (z c) + = a n k (z c) n n= ( < z c < R). ( < z c < R ) R g(z) := g D(c; R) f(z) = a n k (z c) n ( z c < R) n= (z c) k f(z) = g(z) ( < z c < R). g(z) (z c) k ( < z c < R) g(c) = n= k a n k (c c) n = a k. (ii)= (i) (ii) R >, g : D(c; R) C s.t. g f(z) = g(z) (z c) k ( < z c < R), g(c). 6
62 g D(c; R) Taylor {a n } n s.t. g(z) = a n (z c) n = a + a (z c) + a 2 (z c) 2 + n= ( z c < R). < z c < R z f(z) = g(z) (z c) k = a (z c) k + + a k z c + a k + a k+ (z c) + a k+2 (z c) 2 + k = a n+k (z c) n a k n + (z c) n. n= a = g(c) c f k ( ) Proposition c f k f(z) = (z c) k g(z) ( z c < R), g(c) g : D(c; R) C Proposition c f k f(z) = g(z) (z c) k ( < z c < R), g(c) g : D(c; R) C Example 4.3. f(z) = z 2 f 2 ( f(z) = z 2 f ) f(z) = sin z f z ( ) n sin z = (2n + )! z2n+ = z z3 3! + z5 5! z7 + (z C) 7! n= sin z z = n= ( ) n (2n + )! z2n = z2 3! + z4 5! z6 + ( < z < ) 7! f exp z = n! z n = + z + 2!z 2 + 3!z 3 + n= exp z n! z n = z + 2 z 2 + 3! z 3 + exp z 6
63 Corollary P Q c c P k Q(c) c f := Q P k c P k c R P (z) = (z c) k R(z), R(c). g(z) := Q(z) Q(c) g c g(c) =, f(z) = g(z) R(z) R(c) (z c) k (c ) Proposition c f k k N, c C, f c c f k c f 4.3. f(z) := sinh z sin z ( ) Q(z) := sinh z, P (z) := sin z C (sinh z = (exp z exp( z))/2, sin z = (exp(iz) exp( iz))/(2i) Taylor ) c C P (c) = sin c = n Z s.t. c = nπ. P (c) = cos nπ = ( ) n c = nπ P (i) n Q(nπ) = sinh nπ (sinh nπ > ) Cor. nπ f = Q/P (ii) P P s.t. P (C OK) P (z) = zp (z), P (z) ( < z < ). Q Q s.t. Q (C OK) Q(z) = zq (z). ( < z < ) f(z) = Q(z) P (z) = zq (z) zp (z) = Q (z) P (z). z < f f (residue theorem) ( ) c f f c Laurent n= a n (z c) n a f c (residue) Res(f; c) Res f(z) dz : Res(f; c) = Res z=c f(z) dz := a. z=c Laurent ( ) Laurent 62
64 Example 4.3. f(z) = (z C\{}) f Laurent z (a =, a n = (n ) f(z) = a n z n ( < z < )) Res(f; ) =. n= Example f(z) := exp z (z C \ {}) f(z) = n= n! ( ) n = + z z + 2! z 2 + 3! z 3 + Res(f; ) =. Res (zf(z); ) = 2, Res(z2 f(z); ) = 3! = 6. f < z c < R 4.6 ( Laurent ) a n = f(ζ) dζ (n Z, < r < R) 2πi ζ c =r (ζ c) n+ ( ) Res(f; c) = a = 2πi ζ c =r f(ζ)dζ ( < r < R). a (f(ζ)/(ζ c) n+ ) f { (z c) n 2πi (n = ) dz = (n ) z c =R f ( f ) Res(f; c) = a (Res(f; c) f ) () Res(f(z) + cos z; c) (2) Res(3f(z); c) ( (the residue theorem)) C C D C Ω D Ω {c j } N j= D f : Ω\{c,..., c N } C N f(z) dz = 2πi Res(f; c j ). C j= C (C D ) () j c j r j C j C := C C C 2 C N, D := D \ N D(c j ; r j ) j= 63
65 D = C ( ), D Ω \ {c,, c n } 3.2 (Cauchy ) N f(z) dz = f(z) dz. C C j (f C j ) ( ) f(z) dz = f(z) dz = 2πi Res(f; c j ). C j z c j =r j j= C N f(z) dz = 2πi Res(f; c j ). j= () (2) (3) (4) (5) C D D (6) Example z = C C C D = {z C; z < } D = {z C; z } Ω := C C f(z) := z Ω \ {} N =, c = dz = 2πi Res(f; ) = 2πi = 2πi. z z = Mathematica, Maple Maple series(/(z*sin(z)),z=,) Laurent z z z z6 + Mathematica Series[/(z Sin[z]),{z=,}] Res(f; c) = a f(z) = a n (z c) n f n= a n = f(z) dz 2πi (z c) n+ z c =r Res(f; c) 64 z c =r f(z) dz
66 a n = f (n) (c) n! Cf. Taylor ( ) f(z) = a n (z c) n = a + a (z c) + a 2 (z c) 2 + a 3 (z c) 3 + n= ( z c < R). z = c f(c) = a. z = c f (c) = a. f (z) = a + 2a 2 (z c) + 3a 3 (z c) 2 +. f (z) = 2a a 3 (z c) + 4 3a 4 (z c) 2 +. z = c f (c) = 2a 2. a 2 = f (c) 2. f (z) = 3 2a a 4 (z c) a 5 (z c) 2 +. z = c f (c) = 3!a 3. a 3 = f (c). 3! f (n) (z) = n(n ) 2 a n + (n + )n(n ) 2a n+ (z c) + = k(k ) (k n + )a k (z c) k n k! = (k n)! a k(z c) k n = k= m= (n + m)! a n+m (z c) m m! f (n) (c) = n!a n. a n = f (n) (c). n! c f k f(z) = a k (z c) k + a (k ) (z c) k + + a z c + a n (z c) n ( < z c < R) n= (z c) k f(z) = a k + a (k ) (z c) + a (k 2) (z c) 2 + = k=n a n k (z c) n b n := a n k, g(z) := b n = g(n) (c) n! = lim z c z c n= ( ) d n [ (z c) f(z)] k. n! dz 65 ( < z c < R). b n (z c) n n=
67 (4.3) a n = b n+k = lim z c z c ( ) d n+k [ (z c) f(z)] k. (n + k)! dz a = lim z c z c ( ) d k [ (z c) f(z)] k. (k )! dz c c f R, {a n } s.t. f(z) = n= a n (z c) n + a z c ( < z c < R). (z c) (z c)f(z) = a + a (z c) + a (z c) 2 + ( < z c < R) Res(f; c) = a z = c z c Proposition c f (4.4) Res(f; c) = lim(z c)f(z). z c 2 c f (4.4) ( ) f f = Q/P (P, Q c ) c P (Q ) c f c f f Example f(z) = z 2 + Res(f; i) f(z) = (z + i)(z i) i f Res(f; i) = lim(z i)f(z) = lim z i z i z + i = z + i = z=i 2i = i 2. Proposition f(z) = Q(z), P (z) Q(z) c c P (z) P (z) (P (c) = P (c) ), Q(c) c f (4.5) Res(f; c) = Q(c) P (c). 66
68 c P g s.t. g c P (z) = (z c)g(z), g(c). f(z) = Q(z) P (z) = Q(z) (z c)g(z) = h(z) z c, Q(z) h(z) := g(z). h c h(c) = Q(c) g(c) (4.6) Res(f; c) = lim z c z c c f Prop (z c)q(z) (z c)f(z) = lim = lim z c P (z) z c z c Q(z) P (z) P (c) z c = Q(c) P (c). P (c) = f = Q/P, P Q c c P c f Res(f; c) = Q(c) P. c P Prop (x) Example f(z) = z 4 Res(f; i) ( ) f(z) = i (z )(z + )(z + i)(z i) Res(f; i) = (z 4 ) = z=i 4i 3 = i 4i 4 = i n N, f(z) = z n. z = ωk (ω := exp 2πi, k =,,, n ) n z n ( ( ω k) n = ) Res(f; ω k ) = (z n ) = z z=ω nz n = ωk k n. z=ω k c k c f k f(z) = a k (z c) k + + a z c + a + a (z c) + ( < z c < R). (z c) k f(z) = a k + a (k ) (z c) + + a (z c) k + a (z c) k + a (z c) k+ + a k ( ) d k [ (z c) f(z)] k = (k )!a + k! dz! a (k + )! (z c) + a (z c) ! 4.3. c f k Res(f; c) = lim z c z c ( ) d k [ (z c) f(z)] k. (k )! dz ( k ) 67
69 Example f(z) = 3 f 2 z (z 3) 2 (z + ) ( ) d 2 [ Res(f; 3) = lim (z 3) 2 f(z) ] ( ) z (z + ) z = lim = lim z 3 (2 )! dz z 3 z + z 3 (z + ) 2 = lim z 3 (z + ) 2 = (3 + ) 2 = f(z) =. z = 2 Laurent z sin z f(z) = z Res(f; ) =. f f < z < ρ f( z) = f(z) ( < z < ρ) Res(f; ) = c f Res(f; c) = a φ c Res(φ(z)f(z); c) 4.3. () f(z) = π cot πz ( ) (Prop ) P (z) := sin πz, Q(z) := π cos πz f(z) = Q(z) P (z). P (z) = n Z s.t. z = n. P (z) = Q(z) Q(n) = P (n) = π cos nπ = π( ) n. n f ( 2: p.88 ) 4.3. ( pp.88 89) f(z) = Res(f; n) = Q(n) P (n) =. 8z 2 2z 68
70 Mathematica, Maple Mathematica Residue[,{, }] Series[,{,, }] Infinity Apart[ ] Residue[z/((z-2)(z-)^3),{z,}] Series[z/((z-2)(z-)^3),{z,,}] Maple residue(z/((z-2)*(z-)^3)),z= residue(z/((z-2)*(z-)^3)),z=, c f or f c (c f ) = Res(f; c) = c f k = Res(f; c) = ( (k )! lim d ) k [ z c dz (z c) k f(z) ]. z c f = Q P, P (c) =, P (c) Res(f; c) = Q(c) P (c) c f = 4.4 2t sin x x dx = π, e x2 /4t e ixy dx = e ty2 ( ) 9C Cauchy (Cauchy ) ( ) 2 [7], [8], [9], Bak and Newman [] ( Ahlfors [5] ) [8] 69
71 4.4., Cauchy I C ( ) f(x) dx B lim f(x) dx = I, A,B + A ( ε > ) ( R R) ( A R : A R) ( B R : B R) B I f(x) dx < ε A ( ) A lim f(x) dx = I A A ( ) ( ) ( ) Cauchy p.v. f(x) dx v.p. f(x) dx Example 4.4. f(x) := p.v. dx + x 2 = π. x ( x ) ( x < ) f(x) dx = f(x) dx ( ) Cauchy f c c (a, b) b a f(x) dx c f ( ) Cauchy 7
72 f [a, b] C c (a, b) ( c ε lim ε + a f(x) b x c dx + c+ε ) f(x) x c dx b p.v. c a Cauchy f(x) b dx p.v. x c a f(x) x c dx f(x) dx Proposition 4.4. f(x) = Q(x), P (z), Q(z) C[z], deg P (z) deg Q(z)+2, x R P (x) P (x) f(x) dx = 2πi Res(f; c). ( Im c> Im c> f c ) 4.4. ( ) C Ĉ := C { } Ĉ n := deg P (z), m := deg Q(z) P (z) = a z n + a z n + + a n (a ), Q(z) = b z m + b z m + + b m (b ) R [, ) ( z C : z R ) P (z) a 2 z n, Q(z) 3 b 2 z m. P (z) z < R n m + 2 ( ) f(z) = Q(z) P (z) 3 2 b z m 3 b = 2 a z n a z n m M z 2 ( z R ), M := 3 b a. P (x) (x R) f R R f(x) dx = lim f(x) dx R R Γ R : z = x (x [ R, R]), C R : z = Re iθ (θ [, π]), γ R := Γ R + C R f(x) dx 7
73 R R f(x) dx = f(z) dz. Γ R ( ) R > R π f(z) dz = f(re iθ ) ire iθ dθ max C R θ [,π] f ( lim f(z) dz =. R C R Re iθ) M Mπ R π πr = R2 R P (z) z < R f(z) f ( c j γ R ) γ R f(z) dz = 2πi Res(f; c) = 2πi Res(f; c). γ R c Γ R Im c> 2πi Im c> R Res(f; c) f(x) dx = R f(z) dz γ R f(z) dz = Γ R f(z) dz C R (R ). f(x) dx = 2πi Im c> Res(f; c). f Prop πi Im c< Res(f; c) ( p.76) Example I := x 2 dx. Prop f(z) := + z 2 + z2 + c = ±i Im c > i I = 2πi Res(f; c) = 2πi Res(f; i). i f Im c> Res(f; i) = lim z i z i (z i)f(z) = lim z i z i z + i = 2i. I = 2πi 2i = π Mathematica Integrate[/(x^2+),{x,-Infinity,Infinity}] Maple int(/(x^2+),x=-infinity..infinity) 72
74 4.4. f Example (Ahlfors [5] p.73) I := x 2 f(x) dx = 2 I = 2 f(x) dx (, ) x 2 x 4 + 5x 2 dx. + 6 x 2 x 4 + 5x dx. f(x) := x 4 + 5x 2 + 6, P (z) := z4 + 5z 2 + 6, Q(z) := z 2 f(x) = Q(x), deg P = deg Q + 2, P (x) P (z) = (z 2 + 2)(z 2 + 3) = (z + 2i)(z 2i)(z + 3i)(z 3i), x R P (x) I = 2 2πi ( ( Res (f; c) = πi Res f; ) ( 2i + Res f; )) 3i. Im c> ( Res f; ) 2i = Q ( 2i ) P ( 2i ) = z 2 4z 3 + z = z= 2i 4z 3 + z = z= 3i ( Res f; ) 3i = Q ( 3i ) P ( 3i ) = z 2 z 2i 2i 4z 2 + = z= 2i 8 + = 2, z 3i 3i 4z 2 + = z= 3i 2 + = 2. 2i 3i 3 2 I = πi = π. 2 2 ( Mathematica Maple ) 4.4. ( pp.89 9 ) I := dx + x 4. f(x) := + x 4, P (z) := z4 +, Q(z) := f = Q, deg P deg Q + 2, x R P (x). P P (z) = z = c c = exp ( πi 4 + k 2πi ) ± ± i 4 (k =,, 2, 3) c = ( ). 2 c = + i, + i, i, i ( P (z) = z 4 + 2z 2 + 2z 2 = (z 2 + ) 2 ( 2z ) 2 = (z 2 + 2z + )(z 2 2z + ) c = 2 ± ± 2 4, 2 2 = ± i, ± i i. P (z) c c 4 = 2 Res(f; c) = Q(c) P (c) = 4z 3 I = 2πi = 2πi Im c> = z=c ) + i 2 z 4z 4 z=c = c 4 ( ) = c 4 ( ( Res(f; c) = 2πi Res f; + i ) ( + Res f; + i )) 2 2 ( ) ( + i + + i ) = π
75 4.4.3 Mathematica Integrate[/(x^4+), {x,-infinity,infinity}] Maple int(/(x^4+),x=-infinity..infinity) 4.4. n N I = dx + x 2n = π n sin π. 2n Maple assume(n::integer, n>) int(/(x^(2n)+),x=-infinity..infinity) Mathematica n N I := dx (2n )!! ( + x 2 = π. ) n+ (2n)!! ( ) Mathematica Integrate[/(+x^2)^(n+), {x,-infinity,infinity}, Assumptions-> n>] Maple assume(n::integer, ( n>) ) int ( + x 2, x = infinity..infinity ) n+ ( πγ n + ) 2 I = Γ (n + ) Γ (x) = xγ (x ) ( Γ n + ) ( = n ) ( n 3 ) Γ (/2) = (2n )!! = π, 2 n I = Γ (n + ) = n! = (2n)!! 2 n π (2n )!! π/2 n (2n)!!/2 n = ( n 2 π(2n )!!. (2n)!! ) ( n 3 ) 2 π 2 () a I = (2) a I = dx x 2 + a 2. ( : π a ) dx x 4 + a 4 dx. ( : π a 3 2 ) 74
76 (3) a I = (4) a I = (5) a I = (6) a I = (7) a, n I = (8) a, n I = dx (x 2 + a 2 ) 2. ( : π 2a 3 ) dx x 6 + a 6 dx. ( : 2π 3a 5 ) x 4 (x 2 + a 2 ) 4 dx. ( : π 6a 3 ) x 2 (x 4 + a 4 ) 5 2π dx. ( : 3 64a 9 ) dx (x 2 + a 2 ) n. ( : π(2n 3)!! a 2n (2n 2)!! ) dx x 2n + a 2n. ( : π na 2n sin π ) 2n Maple assume(n::integer, n>) assume(a>) f:= n-> int(/(x^2+a^2)^n,x=-infinity..infinity) f(n) (a 2 ) n a πγ (n /2) Γ (n) seq(f(j),j=..) = πγ (n /2) a 2n (n )! = π a, π 2a 3, 3π 8a 5, 5π 6a 7, 35π 28a 9, dx x 2n + a 2n = π π(2n 3)!!/2 n a 2n (2n 2)!!/2 n = 63π 256a, 23π 24a 3, π na 2n sin π 2n. 429π 248a 5. π(2n 3)!! a 2n (2n 2)!!. () x 2 (Ahlfors p.73) ( ) () π( 3 2) 2 x 4 + 5x 2 dx (2) + 6 (2) 5π 2 (3) π 6 a 3 x 2 x + 2 x 2 x 4 + x 2 dx (3) + 9 (x 2 + a 2 ) 3 dx, a R Cauchy P (z), Q(z) C[z], deg P (z) deg Q(z) +, x R P (x) c R Q(x) p.v. dx = πiq(c) (x c)p (x) P (c) + 2πi ( ) Q(z) Res (z c)p (z) ; ζ. Im ζ> 75
77 p.72 f(x) dx e iax Fourier Fourier (F) f(y) := 2π f(x)e iax dx f(x)e ixy dx (y R) (F ) g(x) := 2π g(y)e ixy dy (x R) Fourier (F) y < a = y y f(x) x R f(x) R f(x) cos(ax) dx = Re f(x)e iax dx, f(x) sin(ax) dx = Im f(x)e iax dx Proposition f(x) = Q(x), P (z), Q(z) C[z], deg P (z) deg Q(z)+, x R P (x), P (x) a > (4.7) f(x)e iax dx = 2πi Res(f(z)e iaz ; c). Im c> (4.7) f(z)e iaz ( f ) c Im c> ( ) M R, R [, ) s.t. f(z) P (z) z < R f(z) M z ( z R ). ( ) A, B [R, ) C : z = x (x [ A, B]), C 2 : z = B + iy (y [, A + B]), C 3 : z = x + i(a + B) (x [ A, B]), C 4 : z = A + iy (y [, A + B]), C A,B := C + C 2 + C 3 + C 4 76
78 P (z) z < R f(z)e iaz f(z)e iaz Im c > c C A,B f(z)e iaz dz = 2πi Res(f(z)e iaz ; c) = 2πi Res(f(z)e iaz ; c). C A,B C B A c C A,B C f(z)e iaz dz = B A f(x)e iax dx. f(z)e iaz dz = f(z)e iaz dz = C f(z)e iaz dz C A,B = 2πi Im c> Res(f(z)e iaz ; c) 4 j=2 Im c> 4 j=2 C j f(z)e iaz dz. C j f(z)e iaz dz C 2 z C 2 z = z(y) = B + iy (y [, A + B]) dz = i dy, z = B 2 + y 2 B R, f(z) M z M B, Re (iaz) = a Re (iz) = a Im z = ay, e iaz = e Re(iaz) = e ay f(z)e iaz dz f(z) e iaz M dz C 2 C 2 B A+B e ay dy M B e ay dy = M ab. C 3 C 3 z = z(x) = x + (A + B)i (x [ A, B]) dz = dx, z = (A + B) 2 + x 2 A + B R, f(z) M z M A + B, Re (iaz) = a Re (iz) = a Im z = a(a + B), f(z) dz f(z) e iaz dz C 3 C 3 e iaz = e Re(iaz) = e a(a+b) M B A + B e a(a+b) dx = Me a(a+b). A C 4 C 4 z = z(y) = A + iy (y [, A + B]) dz = i dy, z = A 2 + y 2 A R, f(z) M z M A, Re (iaz) = a Re (iz) = a Im z = ay, e iaz = e Re(eiaz ) = e ay 77
z z x = y = /x lim y = + x + lim y = x (x a ) a (x a+) lim z z f(z) = A, lim z z g(z) = B () lim z z {f(z) ± g(z)} = A ± B (2) lim {f(z) g(z)} = AB z
 Tips KENZOU 28 6 29 sin 2 x + cos 2 x = cos 2 z + sin 2 z = OK... z < z z < R w = f(z) z z w w f(z) w lim z z f(z) = w x x 2 2 f(x) x = a lim f(x) = lim f(x) x a+ x a z z x = y = /x lim y = + x + lim y
Tips KENZOU 28 6 29 sin 2 x + cos 2 x = cos 2 z + sin 2 z = OK... z < z z < R w = f(z) z z w w f(z) w lim z z f(z) = w x x 2 2 f(x) x = a lim f(x) = lim f(x) x a+ x a z z x = y = /x lim y = + x + lim y
I.2 z x, y i z = x + iy. x, y z (real part), (imaginary part), x = Re(z), y = Im(z). () i. (2) 2 z = x + iy, z 2 = x 2 + iy 2,, z ± z 2 = (x ± x 2 ) +
 I..... z 2 x, y z = x + iy (i ). 2 (x, y). 2.,,.,,. (), ( 2 ),,. II ( ).. z, w = f(z). z f(z), w. z = x + iy, f(z) 2 x, y. f(z) u(x, y), v(x, y), w = f(x + iy) = u(x, y) + iv(x, y).,. 2. z z, w w. D, D.
I..... z 2 x, y z = x + iy (i ). 2 (x, y). 2.,,.,,. (), ( 2 ),,. II ( ).. z, w = f(z). z f(z), w. z = x + iy, f(z) 2 x, y. f(z) u(x, y), v(x, y), w = f(x + iy) = u(x, y) + iv(x, y).,. 2. z z, w w. D, D.
No. No. 4 No f(z) z = z z n n sin x x dx = π, π n sin(mπ/n) x m + x n dx = m, n m < n e z, sin z, cos z, log z, z α 4 4 9
 4 4 No. pdf pdf II Fourier No. No. 4 No. 4 4 38 f(z) z = z z n n sin x x dx = π, π n sin(mπ/n) x m + x n dx = m, n m < n e z, sin z, cos z, log z, z α 4 4 9 4 9 i = imaginary unit z = x + iy x, y R x real
4 4 No. pdf pdf II Fourier No. No. 4 No. 4 4 38 f(z) z = z z n n sin x x dx = π, π n sin(mπ/n) x m + x n dx = m, n m < n e z, sin z, cos z, log z, z α 4 4 9 4 9 i = imaginary unit z = x + iy x, y R x real
, ( ) 2 (312), 3 (402) Cardano
 214 9 21, 215 4 21 ( ) 2 (312), 3 (42) 5.1.......... 5.2......................................... 6.2.1 Cardano................................... 6.2.2 Bombelli................................... 6.2.3
214 9 21, 215 4 21 ( ) 2 (312), 3 (42) 5.1.......... 5.2......................................... 6.2.1 Cardano................................... 6.2.2 Bombelli................................... 6.2.3
z f(z) f(z) x, y, u, v, r, θ r > 0 z = x + iy, f = u + iv C γ D f(z) f(z) D f(z) f(z) z, Rm z, z 1.1 z = x + iy = re iθ = r (cos θ + i sin θ) z = x iy
 z fz fz x, y, u, v, r, θ r > z = x + iy, f = u + iv γ D fz fz D fz fz z, Rm z, z. z = x + iy = re iθ = r cos θ + i sin θ z = x iy = re iθ = r cos θ i sin θ x = z + z = Re z, y = z z = Im z i r = z = z
z fz fz x, y, u, v, r, θ r > z = x + iy, f = u + iv γ D fz fz D fz fz z, Rm z, z. z = x + iy = re iθ = r cos θ + i sin θ z = x iy = re iθ = r cos θ i sin θ x = z + z = Re z, y = z z = Im z i r = z = z
36 3 D f(z) D z f(z) z Taylor z D C f(z) z C C f (z) C f(z) f (z) f(z) D C D D z C C 3.: f(z) 3. f (z) f 2 (z) D D D D D f (z) f 2 (z) D D f (z) f 2 (
 3 3. D f(z) D D D D D D D D f(z) D f (z) f (z) f(z) D (i) (ii) (iii) f(z) = ( ) n z n = z + z 2 z 3 + n= z < z < z > f (z) = e t(+z) dt Re z> Re z> [ ] f (z) = e t(+z) = (Rez> ) +z +z t= z < f(z) Taylor
3 3. D f(z) D D D D D D D D f(z) D f (z) f (z) f(z) D (i) (ii) (iii) f(z) = ( ) n z n = z + z 2 z 3 + n= z < z < z > f (z) = e t(+z) dt Re z> Re z> [ ] f (z) = e t(+z) = (Rez> ) +z +z t= z < f(z) Taylor
5 36 5................................................... 36 5................................................... 36 5.3..............................
 9 8 3............................................. 3.......................................... 4.3............................................ 4 5 3 6 3..................................................
9 8 3............................................. 3.......................................... 4.3............................................ 4 5 3 6 3..................................................
 1 1 1 1 1 1 2 f z 2 C 1, C 2 f 2 C 1, C 2 f(c 2 ) C 2 f(c 1 ) z C 1 f f(z) xy uv ( u v ) = ( a b c d ) ( x y ) + ( p q ) (p + b, q + d) 1 (p + a, q + c) 1 (p, q) 1 1 (b, d) (a, c) 2 3 2 3 a = d, c = b
1 1 1 1 1 1 2 f z 2 C 1, C 2 f 2 C 1, C 2 f(c 2 ) C 2 f(c 1 ) z C 1 f f(z) xy uv ( u v ) = ( a b c d ) ( x y ) + ( p q ) (p + b, q + d) 1 (p + a, q + c) 1 (p, q) 1 1 (b, d) (a, c) 2 3 2 3 a = d, c = b
(ii) (iii) z a = z a =2 z a =6 sin z z a dz. cosh z z a dz. e z dz. (, a b > 6.) (z a)(z b) 52.. (a) dz, ( a = /6.), (b) z =6 az (c) z a =2 53. f n (z
 B 4 24 7 9 ( ) :,..,,.,. 4 4. f(z): D C: D a C, 2πi C f(z) dz = f(a). z a a C, ( ). (ii), a D, a U a,r D f. f(z) = A n (z a) n, z U a,r, n= A n := 2πi C f(ζ) dζ, n =,,..., (ζ a) n+, C a D. (iii) U a,r
B 4 24 7 9 ( ) :,..,,.,. 4 4. f(z): D C: D a C, 2πi C f(z) dz = f(a). z a a C, ( ). (ii), a D, a U a,r D f. f(z) = A n (z a) n, z U a,r, n= A n := 2πi C f(ζ) dζ, n =,,..., (ζ a) n+, C a D. (iii) U a,r
x (x, ) x y (, y) iy x y z = x + iy (x, y) (r, θ) r = x + y, θ = tan ( y ), π < θ π x r = z, θ = arg z z = x + iy = r cos θ + ir sin θ = r(cos θ + i s
 ... x, y z = x + iy x z y z x = Rez, y = Imz z = x + iy x iy z z () z + z = (z + z )() z z = (z z )(3) z z = ( z z )(4)z z = z z = x + y z = x + iy ()Rez = (z + z), Imz = (z z) i () z z z + z z + z.. z
... x, y z = x + iy x z y z x = Rez, y = Imz z = x + iy x iy z z () z + z = (z + z )() z z = (z z )(3) z z = ( z z )(4)z z = z z = x + y z = x + iy ()Rez = (z + z), Imz = (z z) i () z z z + z z + z.. z
Z: Q: R: C:
 0 Z: Q: R: C: 3 4 4 4................................ 4 4.................................. 7 5 3 5...................... 3 5......................... 40 5.3 snz) z)........................... 4 6 46 x
0 Z: Q: R: C: 3 4 4 4................................ 4 4.................................. 7 5 3 5...................... 3 5......................... 40 5.3 snz) z)........................... 4 6 46 x
http://www2.math.kyushu-u.ac.jp/~hara/lectures/lectures-j.html 2 N(ε 1 ) N(ε 2 ) ε 1 ε 2 α ε ε 2 1 n N(ɛ) N ɛ ɛ- (1.1.3) n > N(ɛ) a n α < ɛ n N(ɛ) a n
 http://www2.math.kyushu-u.ac.jp/~hara/lectures/lectures-j.html 1 1 1.1 ɛ-n 1 ɛ-n lim n a n = α n a n α 2 lim a n = 1 n a k n n k=1 1.1.7 ɛ-n 1.1.1 a n α a n n α lim n a n = α ɛ N(ɛ) n > N(ɛ) a n α < ɛ
http://www2.math.kyushu-u.ac.jp/~hara/lectures/lectures-j.html 1 1 1.1 ɛ-n 1 ɛ-n lim n a n = α n a n α 2 lim a n = 1 n a k n n k=1 1.1.7 ɛ-n 1.1.1 a n α a n n α lim n a n = α ɛ N(ɛ) n > N(ɛ) a n α < ɛ
 Email: kawahiraamath.titech.ac.jp (A=@) 27 2 25 . 2. 3. 4. 5. 3 4 5 ii 5 50 () : (2) R: (3) Q: (4) Z: (5) N: (6) : () α: (2) β: (3) γ, Γ: (4) δ, : (5) ϵ: (6) ζ: (7) η: (8) θ, Θ: (9) ι: (0) κ: () λ, Λ:
Email: kawahiraamath.titech.ac.jp (A=@) 27 2 25 . 2. 3. 4. 5. 3 4 5 ii 5 50 () : (2) R: (3) Q: (4) Z: (5) N: (6) : () α: (2) β: (3) γ, Γ: (4) δ, : (5) ϵ: (6) ζ: (7) η: (8) θ, Θ: (9) ι: (0) κ: () λ, Λ:
Z: Q: R: C: 3. Green Cauchy
 7 Z: Q: R: C: 3. Green.............................. 3.............................. 5.3................................. 6.4 Cauchy..................... 6.5 Taylor..........................6...............................
7 Z: Q: R: C: 3. Green.............................. 3.............................. 5.3................................. 6.4 Cauchy..................... 6.5 Taylor..........................6...............................
z f(z) f(z) x, y, u, v, r, θ r > 0 z = x + iy, f = u + iv C γ D f(z) f(z) D f(z) f(z) z, Rm z, z 1.1 z = x + iy = re iθ = r (cos θ + i sin θ) z = x iy
 f f x, y, u, v, r, θ r > = x + iy, f = u + iv C γ D f f D f f, Rm,. = x + iy = re iθ = r cos θ + i sin θ = x iy = re iθ = r cos θ i sin θ x = + = Re, y = = Im i r = = = x + y θ = arg = arctan y x e i =
f f x, y, u, v, r, θ r > = x + iy, f = u + iv C γ D f f D f f, Rm,. = x + iy = re iθ = r cos θ + i sin θ = x iy = re iθ = r cos θ i sin θ x = + = Re, y = = Im i r = = = x + y θ = arg = arctan y x e i =
1 : f(z = re iθ ) = u(r, θ) + iv(r, θ). (re iθ ) 2 = r 2 e 2iθ = r 2 cos 2θ + ir 2 sin 2θ r f(z = x + iy) = u(x, y) + iv(x, y). (x + iy) 2 = x 2 y 2 +
 1.3 1.4. (pp.14-27) 1 1 : f(z = re iθ ) = u(r, θ) + iv(r, θ). (re iθ ) 2 = r 2 e 2iθ = r 2 cos 2θ + ir 2 sin 2θ r f(z = x + iy) = u(x, y) + iv(x, y). (x + iy) 2 = x 2 y 2 + i2xy x = 1 y (1 + iy) 2 = 1
1.3 1.4. (pp.14-27) 1 1 : f(z = re iθ ) = u(r, θ) + iv(r, θ). (re iθ ) 2 = r 2 e 2iθ = r 2 cos 2θ + ir 2 sin 2θ r f(z = x + iy) = u(x, y) + iv(x, y). (x + iy) 2 = x 2 y 2 + i2xy x = 1 y (1 + iy) 2 = 1
Tips KENZOU PC no problem 2 1 w = f(z) z 1 w w z w = (z z 0 ) b b w = log (z z 0 ) z = z 0 2π 2 z = z 0 w = z 1/2 z = re iθ θ (z = 0) 0 2π 0
 Tips KENZOU 28 7 6 P no problem 2 w = f(z) z w w z w = (z z ) b b w = log (z z ) z = z 2π 2 z = z w = z /2 z = re iθ θ (z = ) 2π 4π 2 θ θ 2π 4π z r re iθ re i2π = r re i4π = r w r re iθ/2 re iπ = r re
Tips KENZOU 28 7 6 P no problem 2 w = f(z) z w w z w = (z z ) b b w = log (z z ) z = z 2π 2 z = z w = z /2 z = re iθ θ (z = ) 2π 4π 2 θ θ 2π 4π z r re iθ re i2π = r re i4π = r w r re iθ/2 re iπ = r re
Z[i] Z[i] π 4,1 (x) π 4,3 (x) 1 x (x ) 2 log x π m,a (x) 1 x ϕ(m) log x 1.1 ( ). π(x) x (a, m) = 1 π m,a (x) x modm a 1 π m,a (x) 1 ϕ(m) π(x)
![Z[i] Z[i] π 4,1 (x) π 4,3 (x) 1 x (x ) 2 log x π m,a (x) 1 x ϕ(m) log x 1.1 ( ). π(x) x (a, m) = 1 π m,a (x) x modm a 1 π m,a (x) 1 ϕ(m) π(x) Z[i] Z[i] π 4,1 (x) π 4,3 (x) 1 x (x ) 2 log x π m,a (x) 1 x ϕ(m) log x 1.1 ( ). π(x) x (a, m) = 1 π m,a (x) x modm a 1 π m,a (x) 1 ϕ(m) π(x)](/thumbs/94/118373946.jpg) 3 3 22 Z[i] Z[i] π 4, (x) π 4,3 (x) x (x ) 2 log x π m,a (x) x ϕ(m) log x. ( ). π(x) x (a, m) = π m,a (x) x modm a π m,a (x) ϕ(m) π(x) ϕ(m) x log x ϕ(m) m f(x) g(x) (x α) lim f(x)/g(x) = x α mod m (a,
3 3 22 Z[i] Z[i] π 4, (x) π 4,3 (x) x (x ) 2 log x π m,a (x) x ϕ(m) log x. ( ). π(x) x (a, m) = π m,a (x) x modm a π m,a (x) ϕ(m) π(x) ϕ(m) x log x ϕ(m) m f(x) g(x) (x α) lim f(x)/g(x) = x α mod m (a,
prime number theorem
 For Tutor MeBio ζ Eite by kamei MeBio 7.8.3 : Bernoulli Bernoulli 4 Bernoulli....................................................................................... 4 Bernoulli............................................................................
For Tutor MeBio ζ Eite by kamei MeBio 7.8.3 : Bernoulli Bernoulli 4 Bernoulli....................................................................................... 4 Bernoulli............................................................................
4 R f(x)dx = f(z) f(z) R f(z) = lim R f(x) p(x) q(x) f(x) = p(x) q(x) = [ q(x) [ p(x) + p(x) [ q(x) dx =πi Res(z ) + Res(z )+ + Res(z n ) Res(z k ) k
 f(x) f(z) z = x + i f(z). x f(x) + R f(x)dx = lim f(x)dx. R + f(x)dx = = lim R f(x)dx + f(x)dx f(x)dx + lim R R f(x)dx Im z R Re z.: +R. R f(z) = R f(x)dx + f(z) 3 4 R f(x)dx = f(z) f(z) R f(z) = lim R
f(x) f(z) z = x + i f(z). x f(x) + R f(x)dx = lim f(x)dx. R + f(x)dx = = lim R f(x)dx + f(x)dx f(x)dx + lim R R f(x)dx Im z R Re z.: +R. R f(z) = R f(x)dx + f(z) 3 4 R f(x)dx = f(z) f(z) R f(z) = lim R
1 I
 1 I 3 1 1.1 R x, y R x + y R x y R x, y, z, a, b R (1.1) (x + y) + z = x + (y + z) (1.2) x + y = y + x (1.3) 0 R : 0 + x = x x R (1.4) x R, 1 ( x) R : x + ( x) = 0 (1.5) (x y) z = x (y z) (1.6) x y =
1 I 3 1 1.1 R x, y R x + y R x y R x, y, z, a, b R (1.1) (x + y) + z = x + (y + z) (1.2) x + y = y + x (1.3) 0 R : 0 + x = x x R (1.4) x R, 1 ( x) R : x + ( x) = 0 (1.5) (x y) z = x (y z) (1.6) x y =
CIII CIII : October 4, 2013 Version : 1.1 A A441 Kawahira, Tomoki TA (Takahiro, Wakasa 3 )
 III203 00- III : October 4, 203 Version :. Kawahira, Tomoki TA (Takahiro, Wakasa 3 ) http://www.math.nagoya-u.ac.jp/~kawahira/courses/3w-kansuron.html pdf 0 4 0 0 8 2 0 25 8 5 22 2 6 2 3 2 20 0 7 24 3
III203 00- III : October 4, 203 Version :. Kawahira, Tomoki TA (Takahiro, Wakasa 3 ) http://www.math.nagoya-u.ac.jp/~kawahira/courses/3w-kansuron.html pdf 0 4 0 0 8 2 0 25 8 5 22 2 6 2 3 2 20 0 7 24 3
() Remrk I = [0, ] [x i, x i ]. (x : ) f(x) = 0 (x : ) ξ i, (f) = f(ξ i )(x i x i ) = (x i x i ) = ξ i, (f) = f(ξ i )(x i x i ) = 0 (f) 0.
![() Remrk I = [0, ] [x i, x i ]. (x : ) f(x) = 0 (x : ) ξ i, (f) = f(ξ i )(x i x i ) = (x i x i ) = ξ i, (f) = f(ξ i )(x i x i ) = 0 (f) 0. () Remrk I = [0, ] [x i, x i ]. (x : ) f(x) = 0 (x : ) ξ i, (f) = f(ξ i )(x i x i ) = (x i x i ) = ξ i, (f) = f(ξ i )(x i x i ) = 0 (f) 0.](/thumbs/89/98384840.jpg) () 6 f(x) [, b] 6. Riemnn [, b] f(x) S f(x) [, b] (Riemnn) = x 0 < x < x < < x n = b. I = [, b] = {x,, x n } mx(x i x i ) =. i [x i, x i ] ξ i n (f) = f(ξ i )(x i x i ) i=. (ξ i ) (f) 0( ), ξ i, S, ε >
() 6 f(x) [, b] 6. Riemnn [, b] f(x) S f(x) [, b] (Riemnn) = x 0 < x < x < < x n = b. I = [, b] = {x,, x n } mx(x i x i ) =. i [x i, x i ] ξ i n (f) = f(ξ i )(x i x i ) i=. (ξ i ) (f) 0( ), ξ i, S, ε >
main.dvi
 7 f(z) H f(z)dz = f(z), f (z)dz = 9 3 4 7 7.. 7. 7.. 3 f(z) D D z 7. f(z) = f () d (7.) z f(z) - =( z) = z = z Res(z) =lim!z ( z) z = f(z): (7.) 7. (7.) f(z) 7. 5 7.. f(z) z = a jz aj = r z = a r Ref(a)
7 f(z) H f(z)dz = f(z), f (z)dz = 9 3 4 7 7.. 7. 7.. 3 f(z) D D z 7. f(z) = f () d (7.) z f(z) - =( z) = z = z Res(z) =lim!z ( z) z = f(z): (7.) 7. (7.) f(z) 7. 5 7.. f(z) z = a jz aj = r z = a r Ref(a)
I, II 1, A = A 4 : 6 = max{ A, } A A 10 10%
 1 2006.4.17. A 3-312 tel: 092-726-4774, e-mail: hara@math.kyushu-u.ac.jp, http://www.math.kyushu-u.ac.jp/ hara/lectures/lectures-j.html Office hours: B A I ɛ-δ ɛ-δ 1. 2. A 1. 1. 2. 3. 4. 5. 2. ɛ-δ 1. ɛ-n
1 2006.4.17. A 3-312 tel: 092-726-4774, e-mail: hara@math.kyushu-u.ac.jp, http://www.math.kyushu-u.ac.jp/ hara/lectures/lectures-j.html Office hours: B A I ɛ-δ ɛ-δ 1. 2. A 1. 1. 2. 3. 4. 5. 2. ɛ-δ 1. ɛ-n
(Bessel) (Legendre).. (Hankel). (Laplace) V = (x, y, z) n (r, θ, ϕ) r n f n (θ, ϕ). f n (θ, ϕ) n f n (θ, ϕ) z = cos θ z θ ϕ n ν. P ν (z), Q ν (z) (Fou
 (Bessel) (Legendre).. (Hankel). (Laplace) V = (x, y, z) n (r, θ, ϕ) r n f n (θ, ϕ). f n (θ, ϕ) n f n (θ, ϕ) z = cos θ z θ ϕ n ν. P ν (z), Q ν (z) (Fourier) (Fourier Bessel).. V ρ(x, y, z) V = 4πGρ G :.
(Bessel) (Legendre).. (Hankel). (Laplace) V = (x, y, z) n (r, θ, ϕ) r n f n (θ, ϕ). f n (θ, ϕ) n f n (θ, ϕ) z = cos θ z θ ϕ n ν. P ν (z), Q ν (z) (Fourier) (Fourier Bessel).. V ρ(x, y, z) V = 4πGρ G :.
Part () () Γ Part ,
 Contents a 6 6 6 6 6 6 6 7 7. 8.. 8.. 8.3. 8 Part. 9. 9.. 9.. 3. 3.. 3.. 3 4. 5 4.. 5 4.. 9 4.3. 3 Part. 6 5. () 6 5.. () 7 5.. 9 5.3. Γ 3 6. 3 6.. 3 6.. 3 6.3. 33 Part 3. 34 7. 34 7.. 34 7.. 34 8. 35
Contents a 6 6 6 6 6 6 6 7 7. 8.. 8.. 8.3. 8 Part. 9. 9.. 9.. 3. 3.. 3.. 3 4. 5 4.. 5 4.. 9 4.3. 3 Part. 6 5. () 6 5.. () 7 5.. 9 5.3. Γ 3 6. 3 6.. 3 6.. 3 6.3. 33 Part 3. 34 7. 34 7.. 34 7.. 34 8. 35
(2 X Poisso P (λ ϕ X (t = E[e itx ] = k= itk λk e k! e λ = (e it λ k e λ = e eitλ e λ = e λ(eit 1. k! k= 6.7 X N(, 1 ϕ X (t = e 1 2 t2 : Cauchy ϕ X (t
![(2 X Poisso P (λ ϕ X (t = E[e itx ] = k= itk λk e k! e λ = (e it λ k e λ = e eitλ e λ = e λ(eit 1. k! k= 6.7 X N(, 1 ϕ X (t = e 1 2 t2 : Cauchy ϕ X (t (2 X Poisso P (λ ϕ X (t = E[e itx ] = k= itk λk e k! e λ = (e it λ k e λ = e eitλ e λ = e λ(eit 1. k! k= 6.7 X N(, 1 ϕ X (t = e 1 2 t2 : Cauchy ϕ X (t](/thumbs/67/56612994.jpg) 6 6.1 6.1 (1 Z ( X = e Z, Y = Im Z ( Z = X + iy, i = 1 (2 Z E[ e Z ] < E[ Im Z ] < Z E[Z] = E[e Z] + ie[im Z] 6.2 Z E[Z] E[ Z ] : E[ Z ] < e Z Z, Im Z Z E[Z] α = E[Z], Z = Z Z 1 {Z } E[Z] = α = α [ α ]
6 6.1 6.1 (1 Z ( X = e Z, Y = Im Z ( Z = X + iy, i = 1 (2 Z E[ e Z ] < E[ Im Z ] < Z E[Z] = E[e Z] + ie[im Z] 6.2 Z E[Z] E[ Z ] : E[ Z ] < e Z Z, Im Z Z E[Z] α = E[Z], Z = Z Z 1 {Z } E[Z] = α = α [ α ]
0 1-4. 1-5. (1) + b = b +, (2) b = b, (3) + 0 =, (4) 1 =, (5) ( + b) + c = + (b + c), (6) ( b) c = (b c), (7) (b + c) = b + c, (8) ( + b)c = c + bc (9
 1-1. 1, 2, 3, 4, 5, 6, 7,, 100,, 1000, n, m m m n n 0 n, m m n 1-2. 0 m n m n 0 2 = 1.41421356 π = 3.141516 1-3. 1 0 1-4. 1-5. (1) + b = b +, (2) b = b, (3) + 0 =, (4) 1 =, (5) ( + b) + c = + (b + c),
1-1. 1, 2, 3, 4, 5, 6, 7,, 100,, 1000, n, m m m n n 0 n, m m n 1-2. 0 m n m n 0 2 = 1.41421356 π = 3.141516 1-3. 1 0 1-4. 1-5. (1) + b = b +, (2) b = b, (3) + 0 =, (4) 1 =, (5) ( + b) + c = + (b + c),
A B 5 C 9 3.4 7 mm, 89 mm 7/89 = 3.4. π 3 6 π 6 6 = 6 π > 6, π > 3 : π > 3
 π 9 3 7 4. π 3................................................. 3.3........................ 3.4 π.................... 4.5..................... 4 7...................... 7..................... 9 3 3. p
π 9 3 7 4. π 3................................................. 3.3........................ 3.4 π.................... 4.5..................... 4 7...................... 7..................... 9 3 3. p
y π π O π x 9 s94.5 y dy dx. y = x + 3 y = x logx + 9 s9.6 z z x, z y. z = xy + y 3 z = sinx y 9 s x dx π x cos xdx 9 s93.8 a, fx = e x ax,. a =
 [ ] 9 IC. dx = 3x 4y dt dy dt = x y u xt = expλt u yt λ u u t = u u u + u = xt yt 6 3. u = x, y, z = x + y + z u u 9 s9 grad u ux, y, z = c c : grad u = u x i + u y j + u k i, j, k z x, y, z grad u v =
[ ] 9 IC. dx = 3x 4y dt dy dt = x y u xt = expλt u yt λ u u t = u u u + u = xt yt 6 3. u = x, y, z = x + y + z u u 9 s9 grad u ux, y, z = c c : grad u = u x i + u y j + u k i, j, k z x, y, z grad u v =
2 1 17 1.1 1.1.1 1650
 1 3 5 1 1 2 0 0 1 2 I II III J. 2 1 17 1.1 1.1.1 1650 1.1 3 3 6 10 3 5 1 3/5 1 2 + 1 10 ( = 6 ) 10 1/10 2000 19 17 60 2 1 1 3 10 25 33221 73 13111 0. 31 11 11 60 11/60 2 111111 3 60 + 3 332221 27 x y xy
1 3 5 1 1 2 0 0 1 2 I II III J. 2 1 17 1.1 1.1.1 1650 1.1 3 3 6 10 3 5 1 3/5 1 2 + 1 10 ( = 6 ) 10 1/10 2000 19 17 60 2 1 1 3 10 25 33221 73 13111 0. 31 11 11 60 11/60 2 111111 3 60 + 3 332221 27 x y xy
Jacobi, Stieltjes, Gauss : :
 Jacobi, Stieltjes, Gauss : : 28 2 0 894 T. J. Stieltjes [St94a] Recherches sur les fractions continues Stieltjes 0 f(u)du, z + u f(u) > 0, z C z + + a a 2 z + a 3 +..., a p > 0 (a) Vitali (a) Stieltjes
Jacobi, Stieltjes, Gauss : : 28 2 0 894 T. J. Stieltjes [St94a] Recherches sur les fractions continues Stieltjes 0 f(u)du, z + u f(u) > 0, z C z + + a a 2 z + a 3 +..., a p > 0 (a) Vitali (a) Stieltjes
¿ô³Ø³Ø½øÏÀ¥Î¡¼¥È
 2011 i N Z Q R C A def B, A B. ii..,.,.. (, ), ( ),.?????????,. iii 04-13 04-20 04-27 05-04 [ ] 05-11 05-18 05-25 06-01 06-08 06-15 06-22 06-29 07-06 07-13 07-20 07-27 08-03 10-05 10-12 10-19 [ ] 10-26
2011 i N Z Q R C A def B, A B. ii..,.,.. (, ), ( ),.?????????,. iii 04-13 04-20 04-27 05-04 [ ] 05-11 05-18 05-25 06-01 06-08 06-15 06-22 06-29 07-06 07-13 07-20 07-27 08-03 10-05 10-12 10-19 [ ] 10-26
y = f(x) (x, y : ) w = f(z) (w, z : ) df(x) df(z), f(x)dx dx dz f(z)dz : e iωt = cos(ωt) + i sin(ωt) [ ] : y = f(t) f(ω) = 1 2π f(t)e iωt d
![y = f(x) (x, y : ) w = f(z) (w, z : ) df(x) df(z), f(x)dx dx dz f(z)dz : e iωt = cos(ωt) + i sin(ωt) [ ] : y = f(t) f(ω) = 1 2π f(t)e iωt d y = f(x) (x, y : ) w = f(z) (w, z : ) df(x) df(z), f(x)dx dx dz f(z)dz : e iωt = cos(ωt) + i sin(ωt) [ ] : y = f(t) f(ω) = 1 2π f(t)e iωt d](/thumbs/104/162030620.jpg) 8. y = f(x) (x, y : ) w = f(z) (w, z : ) df(x) df(z), f(x)dx dx dz f(z)dz : e iωt = cos(ωt) + i sin(ωt) [ ] : y = f(t) f(ω) = π f(t)e iωt dt. : ϕ(x, y) x + ϕ(x, y) y = ( ).. . : 3. (z p, e z, sin z, sinh
8. y = f(x) (x, y : ) w = f(z) (w, z : ) df(x) df(z), f(x)dx dx dz f(z)dz : e iωt = cos(ωt) + i sin(ωt) [ ] : y = f(t) f(ω) = π f(t)e iωt dt. : ϕ(x, y) x + ϕ(x, y) y = ( ).. . : 3. (z p, e z, sin z, sinh
3 0407).3. I f x sin fx) = x + x x 0) 0 x = 0). f x sin f x) = x cos x + x 0) x = 0) x n = /nπ) n = 0,,... ) x n 0 n ) fx n ) = f 0 lim f x n ) = f 0)
 0407).. I ) f ) a I 3).) lim x a fx) = fa) a.) 4)5) lim fx) = fa) x a+0 lim x a 0 fx) = fa)). I f I I I I f I a 6) fx) fa) lim x a x a f a f a) I I 7) *) 03 0 8 ) an interval; ) an open a closed) interval.
0407).. I ) f ) a I 3).) lim x a fx) = fa) a.) 4)5) lim fx) = fa) x a+0 lim x a 0 fx) = fa)). I f I I I I f I a 6) fx) fa) lim x a x a f a f a) I I 7) *) 03 0 8 ) an interval; ) an open a closed) interval.
4 9, ( ) (3), 3 (3) 7 ( ) Cardano Bombelli de Moivre Euler Gauss Cauchy Abel,
 (7 ) 8 (8 ) http://nalab.mind.meiji.ac.jp/~mk/lecture/complex-function-8/complex8. pdf 4 9, 8 6 7 ( ) (3), 3 (3) 7 ( ) 7.... 7.... 7.3... 8.3. Cardano... 8.3. Bombelli....3.3 de Moivre....3.4 Euler....3.5
(7 ) 8 (8 ) http://nalab.mind.meiji.ac.jp/~mk/lecture/complex-function-8/complex8. pdf 4 9, 8 6 7 ( ) (3), 3 (3) 7 ( ) 7.... 7.... 7.3... 8.3. Cardano... 8.3. Bombelli....3.3 de Moivre....3.4 Euler....3.5
x (0, 6, N x 2 (4 + 2(4 + 3 < 6 2 3, a 2 + a 2+ > 0. x (0, 6 si x > 0. (2 cos [0, 6] (0, 6 (cos si < 0. ( 5.4.6 (2 (3 cos 0, cos 3 < 0. cos 0 cos cos
![x (0, 6, N x 2 (4 + 2(4 + 3 < 6 2 3, a 2 + a 2+ > 0. x (0, 6 si x > 0. (2 cos [0, 6] (0, 6 (cos si < 0. ( 5.4.6 (2 (3 cos 0, cos 3 < 0. cos 0 cos cos x (0, 6, N x 2 (4 + 2(4 + 3 < 6 2 3, a 2 + a 2+ > 0. x (0, 6 si x > 0. (2 cos [0, 6] (0, 6 (cos si < 0. ( 5.4.6 (2 (3 cos 0, cos 3 < 0. cos 0 cos cos](/thumbs/39/20131394.jpg) 6 II 3 6. π 3.459... ( /( π 33 π 00 π 34 6.. ( (a cos π 2 0 π (0, 2 3 π (b z C, m, Z ( ( cos z + π 2 (, si z + π 2 (cos z, si z, 4m, ( si z, cos z, 4m +, (cos z, si z, 4m + 2, (si z, cos z, 4m + 3. (6.
6 II 3 6. π 3.459... ( /( π 33 π 00 π 34 6.. ( (a cos π 2 0 π (0, 2 3 π (b z C, m, Z ( ( cos z + π 2 (, si z + π 2 (cos z, si z, 4m, ( si z, cos z, 4m +, (cos z, si z, 4m + 2, (si z, cos z, 4m + 3. (6.
2S III IV K A4 12:00-13:30 Cafe David 1 2 TA 1 appointment Cafe David K2-2S04-00 : C
 2S III IV K200 : April 16, 2004 Version : 1.1 TA M2 TA 1 10 2 n 1 ɛ-δ 5 15 20 20 45 K2-2S04-00 : C 2S III IV K200 60 60 74 75 89 90 1 email 3 4 30 A4 12:00-13:30 Cafe David 1 2 TA 1 email appointment Cafe
2S III IV K200 : April 16, 2004 Version : 1.1 TA M2 TA 1 10 2 n 1 ɛ-δ 5 15 20 20 45 K2-2S04-00 : C 2S III IV K200 60 60 74 75 89 90 1 email 3 4 30 A4 12:00-13:30 Cafe David 1 2 TA 1 email appointment Cafe
( ) a, b c a 2 + b 2 = c 2. 2 1 2 2 : 2 2 = p q, p, q 2q 2 = p 2. p 2 p 2 2 2 q 2 p, q (QED)
 rational number p, p, (q ) q ratio 3.14 = 3 + 1 10 + 4 100 ( ) a, b c a 2 + b 2 = c 2. 2 1 2 2 : 2 2 = p q, p, q 2q 2 = p 2. p 2 p 2 2 2 q 2 p, q (QED) ( a) ( b) a > b > 0 a < nb n A A B B A A, B B A =
rational number p, p, (q ) q ratio 3.14 = 3 + 1 10 + 4 100 ( ) a, b c a 2 + b 2 = c 2. 2 1 2 2 : 2 2 = p q, p, q 2q 2 = p 2. p 2 p 2 2 2 q 2 p, q (QED) ( a) ( b) a > b > 0 a < nb n A A B B A A, B B A =
I, II 1, 2 ɛ-δ 100 A = A 4 : 6 = max{ A, } A A 10
 1 2007.4.13. A 3-312 tel: 092-726-4774, e-mail: hara@math.kyushu-u.ac.jp, http://www.math.kyushu-u.ac.jp/ hara/lectures/lectures-j.html Office hours: B A I ɛ-δ ɛ-δ 1. 2. A 0. 1. 1. 2. 3. 2. ɛ-δ 1. ɛ-n
1 2007.4.13. A 3-312 tel: 092-726-4774, e-mail: hara@math.kyushu-u.ac.jp, http://www.math.kyushu-u.ac.jp/ hara/lectures/lectures-j.html Office hours: B A I ɛ-δ ɛ-δ 1. 2. A 0. 1. 1. 2. 3. 2. ɛ-δ 1. ɛ-n
example2_time.eps
 Google (20/08/2 ) ( ) Random Walk & Google Page Rank Agora on Aug. 20 / 67 Introduction ( ) Random Walk & Google Page Rank Agora on Aug. 20 2 / 67 Introduction Google ( ) Random Walk & Google Page Rank
Google (20/08/2 ) ( ) Random Walk & Google Page Rank Agora on Aug. 20 / 67 Introduction ( ) Random Walk & Google Page Rank Agora on Aug. 20 2 / 67 Introduction Google ( ) Random Walk & Google Page Rank
Fourier (a) C, (b) C, (c) f 2 (a), (b) (c) (L 2 ) (a) C x : f(x) = a 0 2 + (a n cos nx + b n sin nx). ( N ) a 0 f(x) = lim N 2 + (a n cos nx + b n sin
 ( ) 205 6 Fourier f : R C () (2) f(x) = a 0 2 + (a n cos nx + b n sin nx), n= a n = f(x) cos nx dx, b n = π π f(x) sin nx dx a n, b n f Fourier, (3) f Fourier or No. ) 5, Fourier (3) (4) f(x) = c n = n=
( ) 205 6 Fourier f : R C () (2) f(x) = a 0 2 + (a n cos nx + b n sin nx), n= a n = f(x) cos nx dx, b n = π π f(x) sin nx dx a n, b n f Fourier, (3) f Fourier or No. ) 5, Fourier (3) (4) f(x) = c n = n=
I A A441 : April 15, 2013 Version : 1.1 I Kawahira, Tomoki TA (Shigehiro, Yoshida )
 I013 00-1 : April 15, 013 Version : 1.1 I Kawahira, Tomoki TA (Shigehiro, Yoshida) http://www.math.nagoya-u.ac.jp/~kawahira/courses/13s-tenbou.html pdf * 4 15 4 5 13 e πi = 1 5 0 5 7 3 4 6 3 6 10 6 17
I013 00-1 : April 15, 013 Version : 1.1 I Kawahira, Tomoki TA (Shigehiro, Yoshida) http://www.math.nagoya-u.ac.jp/~kawahira/courses/13s-tenbou.html pdf * 4 15 4 5 13 e πi = 1 5 0 5 7 3 4 6 3 6 10 6 17
(1) (2) (3) (4) HB B ( ) (5) (6) (7) 40 (8) (9) (10)
 2017 12 9 4 1 30 4 10 3 1 30 3 30 2 1 30 2 50 1 1 30 2 10 (1) (2) (3) (4) HB B ( ) (5) (6) (7) 40 (8) (9) (10) (1) i 23 c 23 0 1 2 3 4 5 6 7 8 9 a b d e f g h i (2) 23 23 (3) 23 ( 23 ) 23 x 1 x 2 23 x
2017 12 9 4 1 30 4 10 3 1 30 3 30 2 1 30 2 50 1 1 30 2 10 (1) (2) (3) (4) HB B ( ) (5) (6) (7) 40 (8) (9) (10) (1) i 23 c 23 0 1 2 3 4 5 6 7 8 9 a b d e f g h i (2) 23 23 (3) 23 ( 23 ) 23 x 1 x 2 23 x
1 1 sin cos P (primary) S (secondly) 2 P S A sin(ω2πt + α) A ω 1 ω α V T m T m 1 100Hz m 2 36km 500Hz. 36km 1
 sin cos P (primary) S (secondly) 2 P S A sin(ω2πt + α) A ω ω α 3 3 2 2V 3 33+.6T m T 5 34m Hz. 34 3.4m 2 36km 5Hz. 36km m 34 m 5 34 + m 5 33 5 =.66m 34m 34 x =.66 55Hz, 35 5 =.7 485.7Hz 2 V 5Hz.5V.5V V
sin cos P (primary) S (secondly) 2 P S A sin(ω2πt + α) A ω ω α 3 3 2 2V 3 33+.6T m T 5 34m Hz. 34 3.4m 2 36km 5Hz. 36km m 34 m 5 34 + m 5 33 5 =.66m 34m 34 x =.66 55Hz, 35 5 =.7 485.7Hz 2 V 5Hz.5V.5V V
B2 ( 19 ) Lebesgue ( ) ( ) 0 This note is c 2007 by Setsuo Taniguchi. It may be used for personal or classroom purposes, but not for commercia
 B2 ( 19) Lebesgue ( ) ( 19 7 12 ) 0 This note is c 2007 by Setsuo Taniguchi. It may be used for personal or classroom purposes, but not for commercial purposes. i Riemann f n : [0, 1] R 1, x = k (1 m
B2 ( 19) Lebesgue ( ) ( 19 7 12 ) 0 This note is c 2007 by Setsuo Taniguchi. It may be used for personal or classroom purposes, but not for commercial purposes. i Riemann f n : [0, 1] R 1, x = k (1 m
x, y x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = 15 xy (x y) (x + y) xy (x y) (x y) ( x 2 + xy + y 2) = 15 (x y)
 x, y x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = 15 1 1977 x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = 15 xy (x y) (x + y) xy (x y) (x y) ( x 2 + xy + y 2) = 15 (x y) ( x 2 y + xy 2 x 2 2xy y 2) = 15 (x y) (x + y) (xy
x, y x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = 15 1 1977 x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = 15 xy (x y) (x + y) xy (x y) (x y) ( x 2 + xy + y 2) = 15 (x y) ( x 2 y + xy 2 x 2 2xy y 2) = 15 (x y) (x + y) (xy
(iii) 0 V, x V, x + 0 = x. 0. (iv) x V, y V, x + y = 0., y x, y = x. (v) 1x = x. (vii) (α + β)x = αx + βx. (viii) (αβ)x = α(βx)., V, C.,,., (1)
 1. 1.1...,. 1.1.1 V, V x, y, x y x + y x + y V,, V x α, αx αx V,, (i) (viii) : x, y, z V, α, β C, (i) x + y = y + x. (ii) (x + y) + z = x + (y + z). 1 (iii) 0 V, x V, x + 0 = x. 0. (iv) x V, y V, x + y
1. 1.1...,. 1.1.1 V, V x, y, x y x + y x + y V,, V x α, αx αx V,, (i) (viii) : x, y, z V, α, β C, (i) x + y = y + x. (ii) (x + y) + z = x + (y + z). 1 (iii) 0 V, x V, x + 0 = x. 0. (iv) x V, y V, x + y
Z: Q: R: C: sin 6 5 ζ a, b
 Z: Q: R: C: 3 3 7 4 sin 6 5 ζ 9 6 6............................... 6............................... 6.3......................... 4 7 6 8 8 9 3 33 a, b a bc c b a a b 5 3 5 3 5 5 3 a a a a p > p p p, 3,
Z: Q: R: C: 3 3 7 4 sin 6 5 ζ 9 6 6............................... 6............................... 6.3......................... 4 7 6 8 8 9 3 33 a, b a bc c b a a b 5 3 5 3 5 5 3 a a a a p > p p p, 3,
1 filename=mathformula tex 1 ax 2 + bx + c = 0, x = b ± b 2 4ac, (1.1) 2a x 1 + x 2 = b a, x 1x 2 = c a, (1.2) ax 2 + 2b x + c = 0, x = b ± b 2
 filename=mathformula58.tex ax + bx + c =, x = b ± b 4ac, (.) a x + x = b a, x x = c a, (.) ax + b x + c =, x = b ± b ac. a (.3). sin(a ± B) = sin A cos B ± cos A sin B, (.) cos(a ± B) = cos A cos B sin
filename=mathformula58.tex ax + bx + c =, x = b ± b 4ac, (.) a x + x = b a, x x = c a, (.) ax + b x + c =, x = b ± b ac. a (.3). sin(a ± B) = sin A cos B ± cos A sin B, (.) cos(a ± B) = cos A cos B sin
Lebesgue Fubini L p Banach, Hilbert Höld
 II (Analysis II) Lebesgue (Applications of Lebesgue Integral Theory) 1 (Seiji HIABA) 1 ( ),,, ( ) 1 1 1.1 1 Lebesgue........................ 1 1.2 2 Fubini...................... 2 2 L p 5 2.1 Banach, Hilbert..............................
II (Analysis II) Lebesgue (Applications of Lebesgue Integral Theory) 1 (Seiji HIABA) 1 ( ),,, ( ) 1 1 1.1 1 Lebesgue........................ 1 1.2 2 Fubini...................... 2 2 L p 5 2.1 Banach, Hilbert..............................
29
 9 .,,, 3 () C k k C k C + C + C + + C 8 + C 9 + C k C + C + C + C 3 + C 4 + C 5 + + 45 + + + 5 + + 9 + 4 + 4 + 5 4 C k k k ( + ) 4 C k k ( k) 3 n( ) n n n ( ) n ( ) n 3 ( ) 3 3 3 n 4 ( ) 4 4 4 ( ) n n
9 .,,, 3 () C k k C k C + C + C + + C 8 + C 9 + C k C + C + C + C 3 + C 4 + C 5 + + 45 + + + 5 + + 9 + 4 + 4 + 5 4 C k k k ( + ) 4 C k k ( k) 3 n( ) n n n ( ) n ( ) n 3 ( ) 3 3 3 n 4 ( ) 4 4 4 ( ) n n
 4................................. 4................................. 4 6................................. 6................................. 9.................................................... 3..3..........................
4................................. 4................................. 4 6................................. 6................................. 9.................................................... 3..3..........................
) ] [ h m x + y + + V x) φ = Eφ 1) z E = i h t 13) x << 1) N n n= = N N + 1) 14) N n n= = N N + 1)N + 1) 6 15) N n 3 n= = 1 4 N N + 1) 16) N n 4
![) ] [ h m x + y + + V x) φ = Eφ 1) z E = i h t 13) x << 1) N n n= = N N + 1) 14) N n n= = N N + 1)N + 1) 6 15) N n 3 n= = 1 4 N N + 1) 16) N n 4 ) ] [ h m x + y + + V x) φ = Eφ 1) z E = i h t 13) x << 1) N n n= = N N + 1) 14) N n n= = N N + 1)N + 1) 6 15) N n 3 n= = 1 4 N N + 1) 16) N n 4](/thumbs/92/107866707.jpg) 1. k λ ν ω T v p v g k = π λ ω = πν = π T v p = λν = ω k v g = dω dk 1) ) 3) 4). p = hk = h λ 5) E = hν = hω 6) h = h π 7) h =6.6618 1 34 J sec) hc=197.3 MeV fm = 197.3 kev pm= 197.3 ev nm = 1.97 1 3 ev
1. k λ ν ω T v p v g k = π λ ω = πν = π T v p = λν = ω k v g = dω dk 1) ) 3) 4). p = hk = h λ 5) E = hν = hω 6) h = h π 7) h =6.6618 1 34 J sec) hc=197.3 MeV fm = 197.3 kev pm= 197.3 ev nm = 1.97 1 3 ev
8.1 Fubini 8.2 Fubini 9 (0%) 10 (50%) 10.1 10.2 Carathéodory 10.3 Fubini 1 Introduction [1],, [2],, [3],, [4],, [5],, [6],, [7],, [8],, [1, 2, 3] 1980
![8.1 Fubini 8.2 Fubini 9 (0%) 10 (50%) 10.1 10.2 Carathéodory 10.3 Fubini 1 Introduction [1],, [2],, [3],, [4],, [5],, [6],, [7],, [8],, [1, 2, 3] 1980 8.1 Fubini 8.2 Fubini 9 (0%) 10 (50%) 10.1 10.2 Carathéodory 10.3 Fubini 1 Introduction [1],, [2],, [3],, [4],, [5],, [6],, [7],, [8],, [1, 2, 3] 1980](/thumbs/39/20489863.jpg) % 100% 1 Introduction 2 (100%) 2.1 2.2 2.3 3 (100%) 3.1 3.2 σ- 4 (100%) 4.1 4.2 5 (100%) 5.1 5.2 5.3 6 (100%) 7 (40%) 8 Fubini (90%) 2006.11.20 1 8.1 Fubini 8.2 Fubini 9 (0%) 10 (50%) 10.1 10.2 Carathéodory
% 100% 1 Introduction 2 (100%) 2.1 2.2 2.3 3 (100%) 3.1 3.2 σ- 4 (100%) 4.1 4.2 5 (100%) 5.1 5.2 5.3 6 (100%) 7 (40%) 8 Fubini (90%) 2006.11.20 1 8.1 Fubini 8.2 Fubini 9 (0%) 10 (50%) 10.1 10.2 Carathéodory
II No.01 [n/2] [1]H n (x) H n (x) = ( 1) r n! r!(n 2r)! (2x)n 2r. r=0 [2]H n (x) n,, H n ( x) = ( 1) n H n (x). [3] H n (x) = ( 1) n dn x2 e dx n e x2
![II No.01 [n/2] [1]H n (x) H n (x) = ( 1) r n! r!(n 2r)! (2x)n 2r. r=0 [2]H n (x) n,, H n ( x) = ( 1) n H n (x). [3] H n (x) = ( 1) n dn x2 e dx n e x2 II No.01 [n/2] [1]H n (x) H n (x) = ( 1) r n! r!(n 2r)! (2x)n 2r. r=0 [2]H n (x) n,, H n ( x) = ( 1) n H n (x). [3] H n (x) = ( 1) n dn x2 e dx n e x2](/thumbs/101/149159646.jpg) II No.1 [n/] [1]H n x) H n x) = 1) r n! r!n r)! x)n r r= []H n x) n,, H n x) = 1) n H n x) [3] H n x) = 1) n dn x e dx n e x [4] H n+1 x) = xh n x) nh n 1 x) ) d dx x H n x) = H n+1 x) d dx H nx) = nh
II No.1 [n/] [1]H n x) H n x) = 1) r n! r!n r)! x)n r r= []H n x) n,, H n x) = 1) n H n x) [3] H n x) = 1) n dn x e dx n e x [4] H n+1 x) = xh n x) nh n 1 x) ) d dx x H n x) = H n+1 x) d dx H nx) = nh
1 1.1 ( ). z = a + bi, a, b R 0 a, b 0 a 2 + b 2 0 z = a + bi = ( ) a 2 + b 2 a a 2 + b + b 2 a 2 + b i 2 r = a 2 + b 2 θ cos θ = a a 2 + b 2, sin θ =
 1 1.1 ( ). z = + bi,, b R 0, b 0 2 + b 2 0 z = + bi = ( ) 2 + b 2 2 + b + b 2 2 + b i 2 r = 2 + b 2 θ cos θ = 2 + b 2, sin θ = b 2 + b 2 2π z = r(cos θ + i sin θ) 1.2 (, ). 1. < 2. > 3. ±,, 1.3 ( ). A
1 1.1 ( ). z = + bi,, b R 0, b 0 2 + b 2 0 z = + bi = ( ) 2 + b 2 2 + b + b 2 2 + b i 2 r = 2 + b 2 θ cos θ = 2 + b 2, sin θ = b 2 + b 2 2π z = r(cos θ + i sin θ) 1.2 (, ). 1. < 2. > 3. ±,, 1.3 ( ). A
 211 kotaro@math.titech.ac.jp 1 R *1 n n R n *2 R n = {(x 1,..., x n ) x 1,..., x n R}. R R 2 R 3 R n R n R n D D R n *3 ) (x 1,..., x n ) f(x 1,..., x n ) f D *4 n 2 n = 1 ( ) 1 f D R n f : D R 1.1. (x,
211 kotaro@math.titech.ac.jp 1 R *1 n n R n *2 R n = {(x 1,..., x n ) x 1,..., x n R}. R R 2 R 3 R n R n R n D D R n *3 ) (x 1,..., x n ) f(x 1,..., x n ) f D *4 n 2 n = 1 ( ) 1 f D R n f : D R 1.1. (x,
2000年度『数学展望 I』講義録
 2000 I I IV I II 2000 I I IV I-IV. i ii 3.10 (http://www.math.nagoya-u.ac.jp/ kanai/) 2000 A....1 B....4 C....10 D....13 E....17 Brouwer A....21 B....26 C....33 D....39 E. Sperner...45 F....48 A....53
2000 I I IV I II 2000 I I IV I-IV. i ii 3.10 (http://www.math.nagoya-u.ac.jp/ kanai/) 2000 A....1 B....4 C....10 D....13 E....17 Brouwer A....21 B....26 C....33 D....39 E. Sperner...45 F....48 A....53
III 1 (X, d) d U d X (X, d). 1. (X, d).. (i) d(x, y) d(z, y) d(x, z) (ii) d(x, y) d(z, w) d(x, z) + d(y, w) 2. (X, d). F X.. (1), X F, (2) F 1, F 2 F
 III 1 (X, d) d U d X (X, d). 1. (X, d).. (i) d(x, y) d(z, y) d(x, z) (ii) d(x, y) d(z, w) d(x, z) + d(y, w) 2. (X, d). F X.. (1), X F, (2) F 1, F 2 F F 1 F 2 F, (3) F λ F λ F λ F. 3., A λ λ A λ. B λ λ
III 1 (X, d) d U d X (X, d). 1. (X, d).. (i) d(x, y) d(z, y) d(x, z) (ii) d(x, y) d(z, w) d(x, z) + d(y, w) 2. (X, d). F X.. (1), X F, (2) F 1, F 2 F F 1 F 2 F, (3) F λ F λ F λ F. 3., A λ λ A λ. B λ λ
7 9 7..................................... 9 7................................ 3 7.3...................................... 3 A A. ω ν = ω/π E = hω. E
 B 8.9.4, : : MIT I,II A.P. E.F.,, 993 I,,, 999, 7 I,II, 95 A A........................... A........................... 3.3 A.............................. 4.4....................................... 5 6..............................
B 8.9.4, : : MIT I,II A.P. E.F.,, 993 I,,, 999, 7 I,II, 95 A A........................... A........................... 3.3 A.............................. 4.4....................................... 5 6..............................
n=1 1 n 2 = π = π f(z) f(z) 2 f(z) = u(z) + iv(z) *1 f (z) u(x, y), v(x, y) f(z) f (z) = f/ x u x = v y, u y = v x
 n= n 2 = π2 6 3 2 28 + 4 + 9 + = π2 6 2 f(z) f(z) 2 f(z) = u(z) + iv(z) * f (z) u(x, y), v(x, y) f(z) f (z) = f/ x u x = v y, u y = v x f x = i f y * u, v 3 3. 3 f(t) = u(t) + v(t) [, b] f(t)dt = u(t)dt
n= n 2 = π2 6 3 2 28 + 4 + 9 + = π2 6 2 f(z) f(z) 2 f(z) = u(z) + iv(z) * f (z) u(x, y), v(x, y) f(z) f (z) = f/ x u x = v y, u y = v x f x = i f y * u, v 3 3. 3 f(t) = u(t) + v(t) [, b] f(t)dt = u(t)dt
x () g(x) = f(t) dt f(x), F (x) 3x () g(x) g (x) f(x), F (x) (3) h(x) = x 3x tf(t) dt.9 = {(x, y) ; x, y, x + y } f(x, y) = xy( x y). h (x) f(x), F (x
 [ ] IC. f(x) = e x () f(x) f (x) () lim f(x) lim f(x) x + x (3) lim f(x) lim f(x) x + x (4) y = f(x) ( ) ( s46). < a < () a () lim a log xdx a log xdx ( ) n (3) lim log k log n n n k=.3 z = log(x + y ),
[ ] IC. f(x) = e x () f(x) f (x) () lim f(x) lim f(x) x + x (3) lim f(x) lim f(x) x + x (4) y = f(x) ( ) ( s46). < a < () a () lim a log xdx a log xdx ( ) n (3) lim log k log n n n k=.3 z = log(x + y ),
2012 IA 8 I p.3, 2 p.19, 3 p.19, 4 p.22, 5 p.27, 6 p.27, 7 p
 2012 IA 8 I 1 10 10 29 1. [0, 1] n x = 1 (n = 1, 2, 3,...) 2 f(x) = n 0 [0, 1] 2. 1 x = 1 (n = 1, 2, 3,...) 2 f(x) = n 0 [0, 1] 1 0 f(x)dx 3. < b < c [, c] b [, c] 4. [, b] f(x) 1 f(x) 1 f(x) [, b] 5.
2012 IA 8 I 1 10 10 29 1. [0, 1] n x = 1 (n = 1, 2, 3,...) 2 f(x) = n 0 [0, 1] 2. 1 x = 1 (n = 1, 2, 3,...) 2 f(x) = n 0 [0, 1] 1 0 f(x)dx 3. < b < c [, c] b [, c] 4. [, b] f(x) 1 f(x) 1 f(x) [, b] 5.
6. Euler x
 ...............................................................................3......................................... 4.4................................... 5.5......................................
...............................................................................3......................................... 4.4................................... 5.5......................................
 A 2008 10 (2010 4 ) 1 1 1.1................................. 1 1.2..................................... 1 1.3............................ 3 1.3.1............................. 3 1.3.2..................................
A 2008 10 (2010 4 ) 1 1 1.1................................. 1 1.2..................................... 1 1.3............................ 3 1.3.1............................. 3 1.3.2..................................
() n C + n C + n C + + n C n n (3) n C + n C + n C 4 + n C + n C 3 + n C 5 + (5) (6 ) n C + nc + 3 nc n nc n (7 ) n C + nc + 3 nc n nc n (
 3 n nc k+ k + 3 () n C r n C n r nc r C r + C r ( r n ) () n C + n C + n C + + n C n n (3) n C + n C + n C 4 + n C + n C 3 + n C 5 + (4) n C n n C + n C + n C + + n C n (5) k k n C k n C k (6) n C + nc
3 n nc k+ k + 3 () n C r n C n r nc r C r + C r ( r n ) () n C + n C + n C + + n C n n (3) n C + n C + n C 4 + n C + n C 3 + n C 5 + (4) n C n n C + n C + n C + + n C n (5) k k n C k n C k (6) n C + nc
5.. z = f(x, y) y y = b f x x g(x) f(x, b) g x ( ) A = lim h g(a + h) g(a) h g(x) a A = g (a) = f x (a, b)............................................
 5 partial differentiation (total) differentiation 5. z = f(x, y) (a, b) A = lim h f(a + h, b) f(a, b) h........................................................... ( ) f(x, y) (a, b) x A (a, b) x (a, b)
5 partial differentiation (total) differentiation 5. z = f(x, y) (a, b) A = lim h f(a + h, b) f(a, b) h........................................................... ( ) f(x, y) (a, b) x A (a, b) x (a, b)
4 4 4 a b c d a b A c d A a da ad bce O E O n A n O ad bc a d n A n O 5 {a n } S n a k n a n + k S n a a n+ S n n S n n log x x {xy } x, y x + y 7 fx
 4 4 5 4 I II III A B C, 5 7 I II A B,, 8, 9 I II A B O A,, Bb, b, Cc, c, c b c b b c c c OA BC P BC OP BC P AP BC n f n x xn e x! e n! n f n x f n x f n x f k x k 4 e > f n x dx k k! fx sin x cos x tan
4 4 5 4 I II III A B C, 5 7 I II A B,, 8, 9 I II A B O A,, Bb, b, Cc, c, c b c b b c c c OA BC P BC OP BC P AP BC n f n x xn e x! e n! n f n x f n x f n x f k x k 4 e > f n x dx k k! fx sin x cos x tan
2 2 ( Riemann ( 2 ( ( 2 ( (.8.4 (PDF 2
 2 ( 28 8 (http://nalab.mind.meiji.ac.jp/~mk/lecture/tahensuu2/ 2 2 ( Riemann ( 2 ( ( 2 ( (.8.4 (PDF http://nalab.mind.meiji.ac.jp/~mk/lecture/tahensuu2/ http://nalab.mind.meiji.ac.jp/~mk/lecture/tahensuu/
2 ( 28 8 (http://nalab.mind.meiji.ac.jp/~mk/lecture/tahensuu2/ 2 2 ( Riemann ( 2 ( ( 2 ( (.8.4 (PDF http://nalab.mind.meiji.ac.jp/~mk/lecture/tahensuu2/ http://nalab.mind.meiji.ac.jp/~mk/lecture/tahensuu/
18 ( ) I II III A B C(100 ) 1, 2, 3, 5 I II A B (100 ) 1, 2, 3 I II A B (80 ) 6 8 I II III A B C(80 ) 1 n (1 + x) n (1) n C 1 + n C
 8 ( ) 8 5 4 I II III A B C( ),,, 5 I II A B ( ),, I II A B (8 ) 6 8 I II III A B C(8 ) n ( + x) n () n C + n C + + n C n = 7 n () 7 9 C : y = x x A(, 6) () A C () C P AP Q () () () 4 A(,, ) B(,, ) C(,,
8 ( ) 8 5 4 I II III A B C( ),,, 5 I II A B ( ),, I II A B (8 ) 6 8 I II III A B C(8 ) n ( + x) n () n C + n C + + n C n = 7 n () 7 9 C : y = x x A(, 6) () A C () C P AP Q () () () 4 A(,, ) B(,, ) C(,,
E F 06 00- H0 A.F. Beardon Iterations of rational functions. Springer. Q Q Q Q 6 45 8 45 H3/4 URL: http://www.math.titech.ac.jp/ kawahira/courses/5s-k
 E F 06 00- H0 : 06 4 5 Version :. Kawahira, Tomoki http://www.math.titech.ac.jp/~kawahira/courses/6s-tokuron.html pdf 4 E F E F Q E 4 5 4 Beltrami 4 9 4 6 Beltrami 5 0 Beltrami 5 7 Beltrami 3 5 4 (5 3
E F 06 00- H0 : 06 4 5 Version :. Kawahira, Tomoki http://www.math.titech.ac.jp/~kawahira/courses/6s-tokuron.html pdf 4 E F E F Q E 4 5 4 Beltrami 4 9 4 6 Beltrami 5 0 Beltrami 5 7 Beltrami 3 5 4 (5 3
 (yx4) 1887-1945 741936 50 1995 1 31 http://kenboushoten.web.fc.com/ OCR TeX 50 yx4 e-mail: yx4.aydx5@gmail.com i Jacobi 1751 1 3 Euler Fagnano 187 9 0 Abel iii 1 1...................................
(yx4) 1887-1945 741936 50 1995 1 31 http://kenboushoten.web.fc.com/ OCR TeX 50 yx4 e-mail: yx4.aydx5@gmail.com i Jacobi 1751 1 3 Euler Fagnano 187 9 0 Abel iii 1 1...................................
IA 2013 : :10722 : 2 : :2 :761 :1 (23-27) : : ( / ) (1 /, ) / e.g. (Taylar ) e x = 1 + x + x xn n! +... sin x = x x3 6 + x5 x2n+1 + (
 IA 2013 : :10722 : 2 : :2 :761 :1 23-27) : : 1 1.1 / ) 1 /, ) / e.g. Taylar ) e x = 1 + x + x2 2 +... + xn n! +... sin x = x x3 6 + x5 x2n+1 + 1)n 5! 2n + 1)! 2 2.1 = 1 e.g. 0 = 0.00..., π = 3.14..., 1
IA 2013 : :10722 : 2 : :2 :761 :1 23-27) : : 1 1.1 / ) 1 /, ) / e.g. Taylar ) e x = 1 + x + x2 2 +... + xn n! +... sin x = x x3 6 + x5 x2n+1 + 1)n 5! 2n + 1)! 2 2.1 = 1 e.g. 0 = 0.00..., π = 3.14..., 1
koji07-02.dvi
 007 I II III 1,, 3, 4, 5, 6, 7 5 4 1 ε-n 1 ε-n ε-n ε-n. {a } =1 a ε N N a a N= a a
007 I II III 1,, 3, 4, 5, 6, 7 5 4 1 ε-n 1 ε-n ε-n ε-n. {a } =1 a ε N N a a N= a a
2 8 BASIC (4) WWW Taylor BASIC 1 2 ( ) 2 ( ) ( ) ( ) (A.2.1 ) 1
 2 8 BASIC (4) 203 6 5 WWW http://www.math.meiji.ac.jp/~mk/syori2-203/ Taylor BASIC 2 ( ) 2 ( ) ( ) ( ) 2 (A.2. ) 6B 2 2. f a f(x) = f (n) (a) n! (x a) n = f(a)+f (a)(x a)+ f (a) 2 (x a) 2 + + f (n) (a)
2 8 BASIC (4) 203 6 5 WWW http://www.math.meiji.ac.jp/~mk/syori2-203/ Taylor BASIC 2 ( ) 2 ( ) ( ) ( ) 2 (A.2. ) 6B 2 2. f a f(x) = f (n) (a) n! (x a) n = f(a)+f (a)(x a)+ f (a) 2 (x a) 2 + + f (n) (a)
1 = = = (set) (element) a A a A a A a A a A {2, 5, (0, 1)}, [ 1, 1] = {x; 1 x 1}. (proposition) A = {x; P (x)} P (x) x x a A a A Remark. (i) {2, 0, 0,
![1 = = = (set) (element) a A a A a A a A a A {2, 5, (0, 1)}, [ 1, 1] = {x; 1 x 1}. (proposition) A = {x; P (x)} P (x) x x a A a A Remark. (i) {2, 0, 0, 1 = = = (set) (element) a A a A a A a A a A {2, 5, (0, 1)}, [ 1, 1] = {x; 1 x 1}. (proposition) A = {x; P (x)} P (x) x x a A a A Remark. (i) {2, 0, 0,](/thumbs/91/105754557.jpg) 2005 4 1 1 2 2 6 3 8 4 11 5 14 6 18 7 20 8 22 9 24 10 26 11 27 http://matcmadison.edu/alehnen/weblogic/logset.htm 1 1 = = = (set) (element) a A a A a A a A a A {2, 5, (0, 1)}, [ 1, 1] = {x; 1 x 1}. (proposition)
2005 4 1 1 2 2 6 3 8 4 11 5 14 6 18 7 20 8 22 9 24 10 26 11 27 http://matcmadison.edu/alehnen/weblogic/logset.htm 1 1 = = = (set) (element) a A a A a A a A a A {2, 5, (0, 1)}, [ 1, 1] = {x; 1 x 1}. (proposition)
2 2 L 5 2. L L L L k.....
 L 528 206 2 9 2 2 L 5 2. L........................... 5 2.2 L................................... 7 2............................... 9. L..................2 L k........................ 2 4 I 5 4. I...................................
L 528 206 2 9 2 2 L 5 2. L........................... 5 2.2 L................................... 7 2............................... 9. L..................2 L k........................ 2 4 I 5 4. I...................................
S I. dy fx x fx y fx + C 3 C dy fx 4 x, y dy v C xt y C v e kt k > xt yt gt [ v dt dt v e kt xt v e kt + C k x v + C C k xt v k 3 r r + dr e kt S dt d
 S I.. http://ayapin.film.s.dendai.ac.jp/~matuda /TeX/lecture.html PDF PS.................................... 3.3.................... 9.4................5.............. 3 5. Laplace................. 5....
S I.. http://ayapin.film.s.dendai.ac.jp/~matuda /TeX/lecture.html PDF PS.................................... 3.3.................... 9.4................5.............. 3 5. Laplace................. 5....
Part. 4. () 4.. () 4.. 3 5. 5 5.. 5 5.. 6 5.3. 7 Part 3. 8 6. 8 6.. 8 6.. 8 7. 8 7.. 8 7.. 3 8. 3 9., 34 9.. 34 9.. 37 9.3. 39. 4.. 4.. 43. 46.. 46..
 Cotets 6 6 : 6 6 6 6 6 6 7 7 7 Part. 8. 8.. 8.. 9..... 3. 3 3.. 3 3.. 7 3.3. 8 Part. 4. () 4.. () 4.. 3 5. 5 5.. 5 5.. 6 5.3. 7 Part 3. 8 6. 8 6.. 8 6.. 8 7. 8 7.. 8 7.. 3 8. 3 9., 34 9.. 34 9.. 37 9.3.
Cotets 6 6 : 6 6 6 6 6 6 7 7 7 Part. 8. 8.. 8.. 9..... 3. 3 3.. 3 3.. 7 3.3. 8 Part. 4. () 4.. () 4.. 3 5. 5 5.. 5 5.. 6 5.3. 7 Part 3. 8 6. 8 6.. 8 6.. 8 7. 8 7.. 8 7.. 3 8. 3 9., 34 9.. 34 9.. 37 9.3.
I No. sin cos sine, cosine : trigonometric function π : π =.4 : n =, ±, ±, sin + nπ = sin cos + nπ = cos sin = sin : cos = cos :. sin. sin. sin + π si
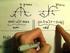 I 8 No. : No. : No. : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No. : I No. sin cos sine, cosine : trigonometric function π : π =.4 : n =, ±, ±, sin + nπ = sin cos + nπ = cos sin = sin : cos = cos :. sin.
I 8 No. : No. : No. : No.4 : No.5 : No.6 : No.7 : No.8 : No.9 : No. : I No. sin cos sine, cosine : trigonometric function π : π =.4 : n =, ±, ±, sin + nπ = sin cos + nπ = cos sin = sin : cos = cos :. sin.
() x + y + y + x dy dx = 0 () dy + xy = x dx y + x y ( 5) ( s55906) 0.7. (). 5 (). ( 6) ( s6590) 0.8 m n. 0.9 n n A. ( 6) ( s6590) f A (λ) = det(a λi)
 0. A A = 4 IC () det A () A () x + y + z = x y z X Y Z = A x y z ( 5) ( s5590) 0. a + b + c b c () a a + b + c c a b a + b + c 0 a b c () a 0 c b b c 0 a c b a 0 0. A A = 7 5 4 5 0 ( 5) ( s5590) () A ()
0. A A = 4 IC () det A () A () x + y + z = x y z X Y Z = A x y z ( 5) ( s5590) 0. a + b + c b c () a a + b + c c a b a + b + c 0 a b c () a 0 c b b c 0 a c b a 0 0. A A = 7 5 4 5 0 ( 5) ( s5590) () A ()
main.dvi
 2 f(z) 0 f(z 0 ) lim z!z 0 z 0 z 0 z z 1z = z 0 z 0 1z z z 0 1z 21 22 2 2 (1642-1727) (1646-1716) (1777-1855) (1789-1857) (1826-1866) 18 19 2.1 2.1.1 12 z w w = f (z) (2.1) f(z) z w = f(z) z z 0 w w 0
2 f(z) 0 f(z 0 ) lim z!z 0 z 0 z 0 z z 1z = z 0 z 0 1z z z 0 1z 21 22 2 2 (1642-1727) (1646-1716) (1777-1855) (1789-1857) (1826-1866) 18 19 2.1 2.1.1 12 z w w = f (z) (2.1) f(z) z w = f(z) z z 0 w w 0
[ ] x f(x) F = f(x) F(x) f(x) f(x) f(x)dx A p.2/29
![[ ] x f(x) F = f(x) F(x) f(x) f(x) f(x)dx A p.2/29 [ ] x f(x) F = f(x) F(x) f(x) f(x) f(x)dx A p.2/29](/thumbs/93/114156928.jpg) A p./29 [ ] x f(x) F = f(x) F(x) f(x) f(x) f(x)dx A p.2/29 [ ] x f(x) F = f(x) F(x) f(x) f(x) f(x)dx [ ] F(x) f(x) C F(x) + C f(x) A p.2/29 [ ] x f(x) F = f(x) F(x) f(x) f(x) f(x)dx [ ] F(x) f(x) C F(x)
A p./29 [ ] x f(x) F = f(x) F(x) f(x) f(x) f(x)dx A p.2/29 [ ] x f(x) F = f(x) F(x) f(x) f(x) f(x)dx [ ] F(x) f(x) C F(x) + C f(x) A p.2/29 [ ] x f(x) F = f(x) F(x) f(x) f(x) f(x)dx [ ] F(x) f(x) C F(x)
.1 1,... ( )
 1 δ( ε )δ 2 f(b) f(a) slope f (c) = f(b) f(a) b a a c b 1 213 3 21. 2 [e-mail] nobuo@math.kyoto-u.ac.jp, [URL] http://www.math.kyoto-u.ac.jp/ nobuo 1 .1 1,... ( ) 2.1....................................
1 δ( ε )δ 2 f(b) f(a) slope f (c) = f(b) f(a) b a a c b 1 213 3 21. 2 [e-mail] nobuo@math.kyoto-u.ac.jp, [URL] http://www.math.kyoto-u.ac.jp/ nobuo 1 .1 1,... ( ) 2.1....................................
untitled
 2 : n =1, 2,, 10000 0.5125 0.51 0.5075 0.505 0.5025 0.5 0.4975 0.495 0 2000 4000 6000 8000 10000 2 weak law of large numbers 1. X 1,X 2,,X n 2. µ = E(X i ),i=1, 2,,n 3. σi 2 = V (X i ) σ 2,i=1, 2,,n ɛ>0
2 : n =1, 2,, 10000 0.5125 0.51 0.5075 0.505 0.5025 0.5 0.4975 0.495 0 2000 4000 6000 8000 10000 2 weak law of large numbers 1. X 1,X 2,,X n 2. µ = E(X i ),i=1, 2,,n 3. σi 2 = V (X i ) σ 2,i=1, 2,,n ɛ>0
f(x) = f(x ) + α(x)(x x ) α(x) x = x. x = f (y), x = f (y ) y = f f (y) = f f (y ) + α(f (y))(f (y) f (y )) f (y) = f (y ) + α(f (y)) (y y ) ( (2) ) f
 22 A 3,4 No.3 () (2) (3) (4), (5) (6) (7) (8) () n x = (x,, x n ), = (,, n ), x = ( (x i i ) 2 ) /2 f(x) R n f(x) = f() + i α i (x ) i + o( x ) α,, α n g(x) = o( x )) lim x g(x) x = y = f() + i α i(x )
22 A 3,4 No.3 () (2) (3) (4), (5) (6) (7) (8) () n x = (x,, x n ), = (,, n ), x = ( (x i i ) 2 ) /2 f(x) R n f(x) = f() + i α i (x ) i + o( x ) α,, α n g(x) = o( x )) lim x g(x) x = y = f() + i α i(x )
24.15章.微分方程式
 m d y dt = F m d y = mg dt V y = dy dt d y dt = d dy dt dt = dv y dt dv y dt = g dv y dt = g dt dt dv y = g dt V y ( t) = gt + C V y ( ) = V y ( ) = C = V y t ( ) = gt V y ( t) = dy dt = gt dy = g t dt
m d y dt = F m d y = mg dt V y = dy dt d y dt = d dy dt dt = dv y dt dv y dt = g dv y dt = g dt dt dv y = g dt V y ( t) = gt + C V y ( ) = V y ( ) = C = V y t ( ) = gt V y ( t) = dy dt = gt dy = g t dt
数学の基礎訓練I
 I 9 6 13 1 1 1.1............... 1 1................ 1 1.3.................... 1.4............... 1.4.1.............. 1.4................. 3 1.4.3........... 3 1.4.4.. 3 1.5.......... 3 1.5.1..............
I 9 6 13 1 1 1.1............... 1 1................ 1 1.3.................... 1.4............... 1.4.1.............. 1.4................. 3 1.4.3........... 3 1.4.4.. 3 1.5.......... 3 1.5.1..............
確率論と統計学の資料
 5 June 015 ii........................ 1 1 1.1...................... 1 1........................... 3 1.3... 4 6.1........................... 6................... 7 ii ii.3.................. 8.4..........................
5 June 015 ii........................ 1 1 1.1...................... 1 1........................... 3 1.3... 4 6.1........................... 6................... 7 ii ii.3.................. 8.4..........................
8.1 Fubini 8.2 Fubini 9 (0%) 10 (50%) Carathéodory 10.3 Fubini 1 Introduction 1 (1) (2) {f n (x)} n=1 [a, b] K > 0 n, x f n (x) K < ( ) x [a
![8.1 Fubini 8.2 Fubini 9 (0%) 10 (50%) Carathéodory 10.3 Fubini 1 Introduction 1 (1) (2) {f n (x)} n=1 [a, b] K > 0 n, x f n (x) K < ( ) x [a 8.1 Fubini 8.2 Fubini 9 (0%) 10 (50%) Carathéodory 10.3 Fubini 1 Introduction 1 (1) (2) {f n (x)} n=1 [a, b] K > 0 n, x f n (x) K < ( ) x [a](/thumbs/92/108011076.jpg) % 100% 1 Introduction 2 (100%) 2.1 2.2 2.3 3 (100%) 3.1 3.2 σ- 4 (100%) 4.1 4.2 5 (100%) 5.1 5.2 5.3 6 (100%) 7 (40%) 8 Fubini (90%) 2007.11.5 1 8.1 Fubini 8.2 Fubini 9 (0%) 10 (50%) 10.1 10.2 Carathéodory
% 100% 1 Introduction 2 (100%) 2.1 2.2 2.3 3 (100%) 3.1 3.2 σ- 4 (100%) 4.1 4.2 5 (100%) 5.1 5.2 5.3 6 (100%) 7 (40%) 8 Fubini (90%) 2007.11.5 1 8.1 Fubini 8.2 Fubini 9 (0%) 10 (50%) 10.1 10.2 Carathéodory
SAMA- SUKU-RU Contents p-adic families of Eisenstein series (modular form) Hecke Eisenstein Eisenstein p T
 SAMA- SUKU-RU Contents 1. 1 2. 7.1. p-adic families of Eisenstein series 3 2.1. modular form Hecke 3 2.2. Eisenstein 5 2.3. Eisenstein p 7 3. 7.2. The projection to the ordinary part 9 3.1. The ordinary
SAMA- SUKU-RU Contents 1. 1 2. 7.1. p-adic families of Eisenstein series 3 2.1. modular form Hecke 3 2.2. Eisenstein 5 2.3. Eisenstein p 7 3. 7.2. The projection to the ordinary part 9 3.1. The ordinary
基礎数学I
 I & II ii ii........... 22................. 25 12............... 28.................. 28.................... 31............. 32.................. 34 3 1 9.................... 1....................... 1............
I & II ii ii........... 22................. 25 12............... 28.................. 28.................... 31............. 32.................. 34 3 1 9.................... 1....................... 1............
takei.dvi
 0 Newton Leibniz ( ) α1 ( ) αn (1) a α1,...,α n (x) u(x) = f(x) x 1 x n α 1 + +α n m 1957 Hans Lewy Lewy 1970 1 1.1 Example 1.1. (2) d 2 u dx 2 Q(x)u = f(x), u(0) = a, 1 du (0) = b. dx Q(x), f(x) x = 0
0 Newton Leibniz ( ) α1 ( ) αn (1) a α1,...,α n (x) u(x) = f(x) x 1 x n α 1 + +α n m 1957 Hans Lewy Lewy 1970 1 1.1 Example 1.1. (2) d 2 u dx 2 Q(x)u = f(x), u(0) = a, 1 du (0) = b. dx Q(x), f(x) x = 0
- II
 - II- - -.................................................................................................... 3.3.............................................. 4 6...........................................
- II- - -.................................................................................................... 3.3.............................................. 4 6...........................................
,..,,.,,.,.,..,,.,,..,,,. 2
 A.A. (1906) (1907). 2008.7.4 1.,.,.,,.,,,.,..,,,.,,.,, R.J.,.,.,,,..,.,. 1 ,..,,.,,.,.,..,,.,,..,,,. 2 1, 2, 2., 1,,,.,, 2, n, n 2 (, n 2 0 ).,,.,, n ( 2, ), 2 n.,,,,.,,,,..,,. 3 x 1, x 2,..., x n,...,,
A.A. (1906) (1907). 2008.7.4 1.,.,.,,.,,,.,..,,,.,,.,, R.J.,.,.,,,..,.,. 1 ,..,,.,,.,.,..,,.,,..,,,. 2 1, 2, 2., 1,,,.,, 2, n, n 2 (, n 2 0 ).,,.,, n ( 2, ), 2 n.,,,,.,,,,..,,. 3 x 1, x 2,..., x n,...,,
1990 IMO 1990/1/15 1:00-4:00 1 N N N 1, N 1 N 2, N 2 N 3 N 3 2 x x + 52 = 3 x x , A, B, C 3,, A B, C 2,,,, 7, A, B, C
 0 9 (1990 1999 ) 10 (2000 ) 1900 1994 1995 1999 2 SAT ACT 1 1990 IMO 1990/1/15 1:00-4:00 1 N 1990 9 N N 1, N 1 N 2, N 2 N 3 N 3 2 x 2 + 25x + 52 = 3 x 2 + 25x + 80 3 2, 3 0 4 A, B, C 3,, A B, C 2,,,, 7,
0 9 (1990 1999 ) 10 (2000 ) 1900 1994 1995 1999 2 SAT ACT 1 1990 IMO 1990/1/15 1:00-4:00 1 N 1990 9 N N 1, N 1 N 2, N 2 N 3 N 3 2 x 2 + 25x + 52 = 3 x 2 + 25x + 80 3 2, 3 0 4 A, B, C 3,, A B, C 2,,,, 7,
di-problem.dvi
 III 005/06/6 by. : : : : : : : : : : : : : : : : : : : : :. : : : : : : : : : : : : : : : : : : : : : : : : : : 3 3. : : : : : : : : : : : : : : 4 4. : : : : : : : : : : : : : : : : : : : : : : 5 5. :
III 005/06/6 by. : : : : : : : : : : : : : : : : : : : : :. : : : : : : : : : : : : : : : : : : : : : : : : : : 3 3. : : : : : : : : : : : : : : 4 4. : : : : : : : : : : : : : : : : : : : : : : 5 5. :

 IV 1 IV ] shib@mth.hiroshim-u.c.jp [] 1. z 0 ε δ := ε z 0 z
IV 1 IV ] shib@mth.hiroshim-u.c.jp [] 1. z 0 ε δ := ε z 0 z