1 flux flux Plumb (1985) flux F s Plumb (1985) Karoly et al. (1989) flux flux Plumb (1985) Plumb (1986) Trenberth (1986) Andrews (1983) review flux Pl
|
|
|
- きみかず たかひ
- 5 years ago
- Views:
Transcription
1 wave-activity flux flux flux ( ) takaya@jamstec.go.jp 1 Introduction ( ) (e.g., Nakamura et al. 1997) storm track cyclogenesis downstream development (e.g., Chang 1993) wave-activity ( ) flux ( ) A F flux A t + F = D, (1) D 0 C g F = C g A F flux sources and sinks, A F ( ) 1 flux Eliassen-Palm (E-P) flux (e.g., Andrews and McIntyre 1976; Edmon et al. 1980; McIntyre 198; Andrews et al. 1987) flux ( ) flux Hoskins et al. (1983) Trenberth (1986) Plumb (1986) flux flux 1
2 1 flux flux Plumb (1985) flux F s Plumb (1985) Karoly et al. (1989) flux flux Plumb (1985) Plumb (1986) Trenberth (1986) Andrews (1983) review flux Plumb (1985) F s Plumb (1985) Plumb (1985) straightforward flux Takaya and Nakamura (1997) Takaya and Nakamura (000) 1
3 wave-activity flux wave-activity flux feedback ( TEM ).1 wave-activity flux: EP flux (x, y, z) β [A] t + 1 ρ 0 F = D () 0 F = ρ 0 [u v ] (3) f[v θ ]/θ 0z [U] t + f 0 v = 1 ρ 0 F (4) v [A] A. Trenberth (1986) flux F = ρ 0 (v u )/ u v f[v θ ]/θ 0z (5) du dt + f 0v = 1 ρ 0 F (6) A A flux.3 Plumb (1986) flux A t + 1 ρ 0 M T = D (7) M T = UA + M R (8) {U(v e) V u v } M R = ρ 0 { Uu v + V (u e)} (9) u f {Uv θ θ + V u θ } 0z TEM V 0 du dt + f 0v = 1 ρ 0 M R (10) 3
4 flux flux Trenberth (1986) flux.4 Plumb (1985) flux F s = ρ 0 A s t + 1 ρ 0 F s = C s (11) ( ψ ) ψ ψ ψ ( ψ ) z ψ ( f N ( ψ z ψ )) 3 wave-activity flux flux Plumb (1985) flux Plumb (1985) feedback ( ) (1) 4
5 3 p- β potential vorticity equation u = ( ψ, ψ, 0) q t + u q = 0 (13) q = f 0 + βy + ψ + ψ + p ( f S ψ p ) (14) (S ) ψ ψ = Ψ + ψ U potential vorticity eq. q t + U q + v = 0 (15) Q potential vorticity q potential vorticity q = ψ + ψ + p ( f S p ) (16) ψ = ψ 0 exp{i(kx + ly + mp ωt)} (15) (16) ω = ku x C x C x = U k k + l + (f/s) m (17) k + l + (f/s) m (18) C gx = U + k l (f/s) m {k + l + (f/s) m } ( ) (19) C gy = C gp = kl {k + l + (f/s) m } ( ) (0) ( f S )km {k + l + (f/s) m } ( ) (1) (18) (C x = 0) K = (k, l, ( f S )m) U = ( )/ K 5
6 C g = U K k kl ( f S )km = ( ) K 4 k kl ( f S )km () U = (U, V ) potential vorticity eq. q t + U q + V q + u + v = 0 (3) ψ = ψ 0 exp{i(kx + ly + mp ωt)} ω = ku + lv + ( l k)/ K (4) C gx = U + (k l (f/s) m )( ) kl( ) K 4 (5) C gy = V + (k l + (f/s) m )( ) + kl( ) K 4 (6) C gp = km( ) lm( ) K 4 (7) C g = 1 K (Appendix ) k U + klv klu + l V (kmu + mlv ) f S (8) 4 flux U flux vorticity eq. = β ζ t + U ζ + βv = 0 6
7 ψ ψ t ζ + Uψ ζ + βψ ψ = 0 ζ = ψ + ψ ψ t ψ = (ψ t ψ ) t {1 ( ψ ) } ψ ψ = (ψ ψ ) {1 ( ψ ) } e t + U e ( ψ + ( t ψ ( t + U + U ) 1 βψ ) e flux F ) = 0 (9) e = 1 {( ψ ) + ( ψ ) } = 1 (u + v ) (30) F = ( Ue ψ ( t v g + U v g) 1 βψ ψ ( t u g + U u g) u g = ψ, v g = ψ ) (31) t e + F = 0 (3) ψ = ψ 0 sin(kx + ly ωt) (17) ω = kc x U C x = β/ K 1 ( K = (k, l)) (3) ( 1 1 t 4 K ψ0 + 4 U K ψ0 1 (k β/ K )ψ0 1 4 βψ 0 1 (klβ/ K )ψ0 ) = 0 (33) ( 1 4 U K ψ0 1 (k β/ K )ψ0 1 ) ( 1 4 βψ 0 1 (klβ/ K )ψ0 = 4 U K ψ0 1 4 (k l ( f S m) )β/ K )ψ0 ) 1 (klβ/ K )ψ0 ( U + (k l ( f = S m) )β/ K 4 ) 1 klβ/ K 4 4 K ψ0 = C g ē overbar 1 7
8 t ē + F = 0, F = Cg ē (34) vorticity eq. u t + U u fv = Φ v t + U v + fu = Φ e ( t ē + F 0 = 0, F 0 Ue + ua Φ = v a Φ ) (35) (36) (37) (u a, v a ) ageostrophic flux F 0 (3) flux F (31) (35) (36) u = u g + u a u g t + U u g (f 0 + βy)(v g + v a ) = Φ v g t + U v g + (f 0 + βy)(u g + u a ) = Φ (38) (39) (31) F = ( Ue + ua Φ ( 1 βyψ ) v a Φ + ( 1 βyψ ) ) (38) (39) (40) F F 0 F = F 0 + ( ( 1 βyψ ) + ( 1 βyψ ) F = F 0 F = F 0 F 0 C g C g F flux C g C g ) 8
9 5 wave activity flux U U wave activity density potential vorticity eq. q t + U q + v = s (41) s Sources and/or sinks q enstrophy Eq. 1 t q + 1 U q + v q = s q (4) v q = v { v u + p ( f S p )} = v v = = B (R) u u u v 1 (v u ( f S p ) ) u v v e u v f S f S p p u v + p ( ψ f S p ) 1 { f S p } (43) y t (4) A t + U A + B(R) = C (44) A = 1 q /( ) (45) wave activity Density U = (U, 0, 0) B (T ) = B (R) + UA (46) A t + B(T ) = C (47) B (T ) 9
10 ( ) 5.1 : Plumb (1986) V = 0 B (T ) ψ = ψ 0 sin(kx + ly + mp ωt) overbar K = (k, l, f S m) Ā = q B (T ) = = K 4 4 ψ0, Ue + v e u v f S p ē = 1 {u + v + ( f S p ) } = K 4 ψ 0 = U + {k l ( f S m) } / K 4 kl /K 4 K 4 ( f S ) km 4 ψ0 / K 4 = C g Ā (48) Ā t + B(T ) = C, B (T ) = C g Ā (49) 5. : Plumb (1985) B (T ) Plumb(1985) B (T ) flux G(i.e. G = 0) F s = B (T ) + G (50) F s A t + F s = C s (51) C s = C + G 10
11 G = 1 4 ψ + p ( f ) S p ψ r q / ψ f S p ψ r r = s s = 0 G = 0 F s F s = 1 ( ψ ) ψ ψ f ( ψ S + ψ q + [(Uq r q )/ p ψ ( ψ ) ψ ( p ψ )) (5) (41) t = 0 U q + ψ = s (Uq + ψ r ) = 0 Uq + ψ q r q = 0 F s F s = 1 f ( ψ S ( ψ p ) ψ ψ ψ ( ψ ) ψ ( p ψ )) ] (53) (54) 1 order ψ = ψ 0 sin(kx + ly + mp ωt) F s k F s ψ 0 kl (55) f km/s ( C g = ) k K 4 kl (56) ( f )km S 11
12 F s = ( 1 4 K 4 ψ0 )C g (57) (57) F s = C g A WKB limit A K = /U A s 1 (A + e U ) = 1 K 4 ψ0 4 (58) WKB limit A s t + F s = C s (59) F s = C g A s (60) 6 U,V wave activity flux: Plumb (1986) Plumb(1986) U = (U, V, 0) wave activity flux β potential vorticity eq. q t + U q + V q + u + v = s (61) q enstrophy Eq. q t + U q + V q + u q + v q = s q (6) u q = u { v u + p ( f S p } = u v + v u + v v u u ψ p ( f S p } 1
13 = u v + (1 (v u )) p ( f S u v = 1 (v u + f ( ψ S p ) ) = f S u v e u f S p p p } + ( f S ( ψ p ) ) enstrophy Eq. q t + U q + V q + ( ) u v e u f S p + ( ) v e u v f S p = s q (63) wave activity density A = q H Q ( H = (,, 0) ) 1 A t + 1 H Q Uq u v v e 1 V q + H Q e u + H Q u v = D (64) 0 1 H Q H Q H Q 1 Uq 1 V q 0 u v e u f S p v e u v f S p f S p 1 { H Q { { H Q H Q 1 Uq 1 V q 0 u v e u f S p v e u v f S p f S p } (65) } (66) } (67) (65) enstrophy potential vorticity (66) (67) potential vorticity flux U + V 0 H Q u U 13 u V
14 ( u = (U, V, 0)) (64) M T = A t + M T = D (68) UA + 1 u {U(v e) V u v } V A + 1 u { Uu v + V (u e)} f ψ {U S u p + V ψ p } (69) ψ = ψ 0 sin(kx + ly + mp ωt) A = K 4 ψ 0 4 H Q M T = C g A (70) 7 pseudoenergy : Andrews (1983) pseudoenergy Andrews(1983) wave activity flux potential vorticity eq. U + V = 0 (71) q t + U q + V q + u + v = s (71) U = (U, V, 0) = ( ψ q t + U q + u 0 Q = 0 (7), ψ, 0) Q Q = Q( ψ; p) Λ( ψ; p) = ψ (73) U Λ = U( ψ Λ ψ Λ ) + V ( ψ ψ ) = 0 (74) 14
15 (7) u 0 Q = Λu 0 ψ = Λ( ψ ψ + ψ ψ ) = ΛU ψ f = ɛ S = U (Λψ ) (75) q t = U (q Λψ ) (76) q = ψ + ψ + p (ɛ ψ p ) (77) ψ q t = 1 t {( ψ ) + ( ψ ) + ɛ( ψ p ) } + (ψ t ) + (ψ t ) + p (ɛψ t p ) (78) (78) Λ 1 q q t = 1 t (q /Λ) 1 t {( ψ ) + ( ψ ) + ɛ( ψ p ) + q /Λ} + ( ψ t ) + ( ψ t ) + p ( ɛψ t p ) 1 q = Λ t (q Λψ ) (79) (76) 1 q Λ t (q Λψ ) = (Λ) 1 U (q Λψ) = U [(q Λψ ) /Λ] = [U(q Λψ ) /Λ] (80) α t + I = 0 (81) 15
16 α = 1 t {( ψ ) + ( ψ ) + ɛ( ψ p ) + q /Λ} (8) ψ ( t ) + U Λ (q Λψ ) I = ψ ( t ) + V Λ (q Λψ ) (83) ɛψ ( t p ) Pseudoenergy overbar 1 I = C g ᾱ (84) V = 0 Λ = /U (83) ψ ( t I = ) U ψ ( t ɛψ ( t (q + Q ) p ) Q U ψ ) α = e UA (86) (85) 8 flux (ψ ) (PV) A E A (pseudomomentum) ( Andrews and McIntyre 1976) E Uryu (1974) ( ) ( ) M (A + E)/ 16
17 log-p β- PV (q) q t + u q + v q = s; q = f 0 + βy + ψ + ψ + f 0 p ( ) p ψ z N. (87) z (u, v) T = u = ( ψ y, ψ x ) T s f = f 0 + βy z = H ln p p =(pressure/1000hpa) H N = R ap κ θ H z θ R a κ R a U = (U, V, 0) T ɛ u = U(x, y, z) + u, v = V (x, y, z) + v, ψ = Ψ(x, y, z) + ψ, q = Q(x, y, z) + q (88) O(ɛ ) PV q q t + U Hq + u H Q = s ; q = ψ + ψ + f 0 p ( p ) z N, (89) z H gradient operator ( U C P energy e = ψ x + ψ y + (f 0 ψ z/s) ) / A E A pq /( H Q ) E pe/( U C P ) C U U x- y- C U = C P U U = ( U U C P, V U C P, 0) T (90) U C P zonal U ( H Q) 0 n PV n H Q/ H Q γ( V, U, 0) T / U γ = 1 pseudoeastward (Andrews 1984, Plumb 1986) WKB ( ) H Q, U n C P U (89) pq / H Q A [ A U t + p H q ] + n u 0 q = D 1, (91) H Q D 1 = ps q / H Q WKB A A t + (E + C UA) + N (1) = D 1. (9) 17
18 N (1) E N (1) (U C U )A, pn u 0 q E = p U U(ψ x e) + V ψ xψ y Uψ xψ y + V (ψ y e) f 0 N {Uψ xψ z + V ψ yψ z} (93) (V = 0) WKB (9) A (9) Plumb (1986) (.19) (89) pψ /( U C P ) E pe/( U C P ) E t p (k Hψ ) (ψ H Q) U C P ( U pψ H q U + C U U C P ) + R(1) U C P = D (94) D = ps ψ /( U C P ) k ( R (1) = p ψ ψ xt, ψ ψ yt, f ) 0 T ψ N ψ zt A E H t E + (H + C UE) + N () R = D +, (95) U C P p U U (ψ H q ) pnψ (k H q ) H = p U U(e ψ ψ xx) V ψ ψ xy V (e Uψ ψ xy) V ψ ψ yy f 0 N {Uψ ψ xz + V ψ ψ yz} (96) (94) p (k Hψ ) (ψ H Q) N () = (k HQ)ψ U C P ( U C P ) R R = p ( e t + U U C e P + V U C P U H Q ψ = U ( U C P ) ) ( e q + pψ t + U U C q P + V U C P C P R = 0 (95) M 1 (A + E) = p q ) (97) (98) ( ) q H Q + e. (99) U C P M ψ = ψ 0 exp(z/h)sin(kx+ ly + mz ωt) M M K 4 ψ 0 4 H Q (100) 18
19 K = (k, l, (f 0 S 1 )m) T H 1 m M (pseudomomentum) M M (9) (95) M t + W = D N + R ( U C P ), (101) D = (D 1 + D )/ D 0 s, N = (N (1) + N () )/, W = (E + H)/ + C U M W N N (1) N () N = p U 4 U ( q H Q ψ ) [ ( U C P )q + H Q ψ ]. (10) U C P (89) r 0 U [ ( U CP )q + H Q ψ ] s, (103) U (10) N = 1 r0 D 0 D 0 (101) ( ) N (s = 0) N = 0 D T = D N = (D 0 r 0 r 0 D 0 )/ C p R = 0 M M t + W = D T. (104) W W s (E + H)/ W = W s + C U M W = p U U(ψ x ψ ψ xx) + V (ψ xψ y ψ ψ xy) U(ψ xψ y ψ ψ xy) + V (ψ y ψ ψ yy) f 0 N {U(ψ xψ z ψ ψ xz) + V (ψ yψ z ψ ψ yz)} + C UM. (105) (104) (105) W W C P ( C P = 0 ) C U M W s Takaya and Nakamura (1997) wave-activity flux ( W ) V = 0 D T = (D 0 r 0 r 0 D 0 )/ W D T M 19
20 (U = U(y, p)) (104) C P = 0 W F s (Plumb, 1985) (104) C g (100) W = C g M W ( ) 9 W W C g W Plumb (1985) F s ( ) transformed Eulerian-mean (TEM) (V = 0) W s Plumb (1985) F s v t + U v + f(u + u (a) ) = φ, (106) u (a) ( ) β- c (U c) v + f 0u (a) + βyu = 0 (107) ψ xx = v x f 0 u (a) /(U c) ψ xy = u x f 0 v (a) /(U c) f 0 Θ z ψ xz/n = θ x Θ z w (a) /(U c) v (a) w (a) U > c ( ψ ψ xx, ψ ψ xy, f 0 N ψ ψ xz) T (Φ u (a), Φ v (a), Φ w (a) ) T /(U c) Φ F s ( W s ) C g (Figs. 1a 1b) ( ψ ψ xx, ψ ψ xy, f 0 ψ N ψ xz) T C g F s ( W s ) v (Fig. 1c) ψ - 0
21 (v ) ψ - F s (W s ) u v (Fig. 1c) F s (W s ) v θ (Fig. 1b) F s ψ - flux W ( W s ) ψ = ψ 0 sin(kx + ly + mz ωt) ψ - F s W Plumb (1986) O(ɛ ) D (0) U () Dt fv () + Φ() = u u v = ψ ψ yy ψ ψ xy, (108) () D (0) U () /Dt U () / t + (U )U () + (U () )U (108) D (0) U () Dt fv () + Φ() = 1 ( u + ψ ψ yy) 1 (u v + ψ ψ xy) (109) (109) ( ) (109) D (0) U () Dt fv () + Φ() = 1 (ψ xq ψ q x) 1
22 1 [ ] (ψ x ψ ψ xx) + (ψ y ψ ψ yy) 1 [ ] f p z p 0 N (ψ xψ z ψ ψ xz). D (0) U () fk U Dt (a) = G + X, (110) D (0) Θ () + W dθ (a) Dt dz = Q, (111) X Q TEM (110) G G = p k (u0 q ψ k H q ) p k P (11) (110) Ua U (a) = (U (a), V (a), W (a) )T = U () (a) + 1 pr, (113) p () (a) = (U(a), V () (a), W () (a) )T Euler (113) R R = 1 (v θ ψ θ x)/θ z (u θ + ψ θ [ y)/θ z ]. (114) (v ψ ψ xx) + (u ψ ψ yy) /f U () (110), (111), (11), (113), (114) Plumb (1986) (4.3), (4.4), (4.5) (4.6) Plumb (1986) PV ( H Q) s s k n G G = p [(P n)s (P s)n]. (115) (93), (96) W s (E + H)/ β- W s p n (u0 q ψ k H q ) = p P n (116) (115) W s Plumb (1986) W s PV
23 10 W Enomoto and Matsuda (1999) [40 N, 90 E] (Fig. a) Fig. b 14 ψ W C P = 0 (Fig. c) W flux W ψ W 3 Plumb (1985) F s W F s F s Figs. 1c 1d W W W NCEP/NCAR 8 W p Fig.3 flux plot W 300-hPa, 600-hPa W W U C P 3 Enomoto and Matsuda (1999) 3
24 11 flux W flux flux A E M M W ψ - flux W W flux W W flux W Takaya and Nakamura (000) W W W 4
25 Appendix: Rossby potential vorticity eq. q t + U q + V q + u + v = 0 (A1) ψ = ψ 0 exp{i(kx + ly + mp ωt)} K = k + l + f 0 N m ω = ku + lv + l K k K = k(u / K ) + l(v + / K ) (A) U + V = 0 (A3) (A) (A3) ω = k(u / K ) + l(v V U / K ) = k(u / K ) + l V (U U / K ) = (k + l V )(U U / K ) (A4) ω = ( U V k + l)(v + / K ) ω = 0 (U / K ) = 0, k l = V U (V + / K ) = 0 (A6) ( 1) (A7) ( ) (A5) (A6) (A7) 5
26 ( ) (A1) ( ) ( Q contour ) ( 1) ( 1) (U / K ) = 0, (A) (V + / K ) = 0 (A8) C gx = U + (k l (f/s) m )( ) kl( ) K 4 C gy = V + (k l + (f/s) m )( ) + kl( ) K 4 (A9) (A10) C gp = km( ) lm( ) K 4 (A11) (A8) C g = 1 K k U + klv klu + l V (kmu + mlv ) f S (A1) 6
27 ( wave-activity flux ) Andrews, D. G., 1983: A conservation law for small-amplitude quasigeostrophic disturbances on a zonally asymmetric basic flow. J.Atmos.Sci., 40, , 1984: On the existence of nonzonal flows satisfying sufficient conditions for instability. Geophys. Astrophys. Fluid Dyn., 8, , and M. E. McIntyre, 1976: Planetary waves in horizontal and vertical shear: The generalized Eliassen-Palm relation and the mean zonal acceleration. J. Atmos. Sci., 33, , J.R. Holton, and C.B. Leovy, 1987: Middle Atmosphere Dynamics., Academic press, 489pp. Chang, E. -K. M., 1993: Downstream development of baroclinic waves as inferred from regression analysis. J. Atmos. Sci., 50, , I. Orlanski, 1994: On energy flux and group velocity of waves in baroclinic flows. J.Atmos.Sci., 51, Edmon, H. J., B. J. Hoskins and M. E. McIntyre, 1980: Eliassen-Palm cross sections for the troposphere. J. Atmos. Sci., 37, [See also Corrigendum, 1981: J. Atmos. Sci., 38, 1115, especially nd last item]. Enomoto, T., and Y. Matsuda, 1999: Rossby wavepacket propagation in a zonally-varying basic flow. Tellus in press. Hoskins, B. J., I. N. James, and G. H. White, 1983: The shape, propagation and mean-flow interaction of large-scale weather system. J. Atmos. Sci., 40, Karoly, D.J., R.A. Plumb, and M. Ting, 1989: Examples of the horizontal propagation of quasi-stationary waves, J. Atmos. Sci., 46, Longuet-Higgins, M. S., 1964: On group velocity and energy flux in planetary wave motions. Deep-Sea Res., 11, McIntyre, M. E., 198: How well do we understand the dynamics of stratospheric warmings? J. Meteor. Soc. Japan., 60, Nakamura, H., M. Nakamura, and J.L. Anderson, 1997: The role of high- and low-frequency dynamics in the blocking formation, Mon. Wea. Rev., 15, Orlanski, I., J. Sheldon, 1993: A case of downstream baroclinic development over western north america. Mon.Wea.Rev., 11, Pedlosky, J., 1987: Geophysical Fluid Dynamics. nd ed. Springer-Verlag, 710pp. Plumb, R. A., 1985: On the three-dimensional propagation of stationary waves. J. Atmos. Sci., 4, 17-9., 1985: An alternative form of Andrews conservation law for quasi-geostrophic waves on a steady,nonuniform flow. J.Atmos.Sci., 4, , 1986: Three-dimensional propagation of transient quasi-geostrophic eddies and its relationship with the eddy forcing of the time-mean flow, J. Atmos. Sci., 43, Takaya, K., and H. Nakamura, 1997: A formulation of a wave-activity flux for stationary Rossby waves on a zonally varying basic flow. Geophys. Res. Lett., 4,
28 and, 000: A formulation of a phase-independent wave-activity flux for stationary and migratory quasi-geostrophic eddies on a zonally-varying basic flow. J. Atmos. Sci., submitted. Trenberth, K. E., 1986: An assessment of the impact of transient eddies on the zonal flow during a blocking episode using localized Eliassen-Palm flux diagnostics. J. Atmos. Sci., 43, Uryu, M., 1974: Mean zonal flows induced by a vertically propagating Rossby wave packet. J. Meteor. Soc. Japan., 56,
2012専門分科会_new_4.pptx
 d dt L L = 0 q i q i d dt L L = 0 r i i r i r r + Δr Δr δl = 0 dl dt = d dt i L L q i q i + q i i q i = q d L L i + q i i dt q i i q i = i L L q i L = 0, H = q q i L = E i q i i d dt L q q i i L = L(q
d dt L L = 0 q i q i d dt L L = 0 r i i r i r r + Δr Δr δl = 0 dl dt = d dt i L L q i q i + q i i q i = q d L L i + q i i dt q i i q i = i L L q i L = 0, H = q q i L = E i q i i d dt L q q i i L = L(q
, 1.,,,.,., (Lin, 1955).,.,.,.,. f, 2,. main.tex 2011/08/13( )
 81 4 2 4.1, 1.,,,.,., (Lin, 1955).,.,.,.,. f, 2,. 82 4.2. ζ t + V (ζ + βy) = 0 (4.2.1), V = 0 (4.2.2). (4.2.1), (3.3.66) R 1 Φ / Z, Γ., F 1 ( 3.2 ). 7,., ( )., (4.2.1) 500 hpa., 500 hpa (4.2.1) 1949,.,
81 4 2 4.1, 1.,,,.,., (Lin, 1955).,.,.,.,. f, 2,. 82 4.2. ζ t + V (ζ + βy) = 0 (4.2.1), V = 0 (4.2.2). (4.2.1), (3.3.66) R 1 Φ / Z, Γ., F 1 ( 3.2 ). 7,., ( )., (4.2.1) 500 hpa., 500 hpa (4.2.1) 1949,.,
No pp The Relationship between Southeast Asian Summer Monsoon and Upper Atmospheric Field over Eurasia Takeshi MORI and Shuji YAMAKAWA
 No.42 2007 pp.159 166 The Relationship between Southeast Asian Summer Monsoon and Upper Atmospheric Field over Eurasia Takeshi MORI and Shuji YAMAKAWA Received September 30, 2006 Using Southeast Asian
No.42 2007 pp.159 166 The Relationship between Southeast Asian Summer Monsoon and Upper Atmospheric Field over Eurasia Takeshi MORI and Shuji YAMAKAWA Received September 30, 2006 Using Southeast Asian
63 3.2,.,.,. (2.6.38a), (2.6.38b), V + V V + Φ + fk V = 0 (3.2.1)., Φ = gh, f.,. (2.6.40), Φ + V Φ + Φ V = 0 (3.2.2). T = L/C (3.2.3), C. C V, T = L/V
 62 3 3.1,,.,. J. Charney, 1948., Burger(1958) Phillips(1963),.,. L : ( 1/4) T : ( 1/4) V :,. v x u x V L, etc, u V T,,.,., ( )., 2.1.1. 63 3.2,.,.,. (2.6.38a), (2.6.38b), V + V V + Φ + fk V = 0 (3.2.1).,
62 3 3.1,,.,. J. Charney, 1948., Burger(1958) Phillips(1963),.,. L : ( 1/4) T : ( 1/4) V :,. v x u x V L, etc, u V T,,.,., ( )., 2.1.1. 63 3.2,.,.,. (2.6.38a), (2.6.38b), V + V V + Φ + fk V = 0 (3.2.1).,
5 1.2, 2, d a V a = M (1.2.1), M, a,,,,, Ω, V a V, V a = V + Ω r. (1.2.2), r i 1, i 2, i 3, i 1, i 2, i 3, A 2, A = 3 A n i n = n=1 da = 3 = n=1 3 n=1
 4 1 1.1 ( ) 5 1.2, 2, d a V a = M (1.2.1), M, a,,,,, Ω, V a V, V a = V + Ω r. (1.2.2), r i 1, i 2, i 3, i 1, i 2, i 3, A 2, A = 3 A n i n = n=1 da = 3 = n=1 3 n=1 da n i n da n i n + 3 A ni n n=1 3 n=1
4 1 1.1 ( ) 5 1.2, 2, d a V a = M (1.2.1), M, a,,,,, Ω, V a V, V a = V + Ω r. (1.2.2), r i 1, i 2, i 3, i 1, i 2, i 3, A 2, A = 3 A n i n = n=1 da = 3 = n=1 3 n=1 da n i n da n i n + 3 A ni n n=1 3 n=1
hPa ( ) hPa
 200520241 19 1 18 1993 850hPa 6 7 6 27 7 3 6 29 ( ) 250 200hPa i iii 1 1 1.1...................................... 1 1.1.1................................. 1 1.1.2......................... 1 1.1.3...........
200520241 19 1 18 1993 850hPa 6 7 6 27 7 3 6 29 ( ) 250 200hPa i iii 1 1 1.1...................................... 1 1.1.1................................. 1 1.1.2......................... 1 1.1.3...........
Holton semigeostrophic semigeostrophic,.., Φ(x, y, z, t) = (p p 0 )/ρ 0, Θ = θ θ 0,,., p 0 (z), θ 0 (z).,,,, Du Dt fv + Φ x Dv Φ + fu +
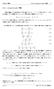 Holton 9.2.2 semigeostrophic 1 9.2.2 semigeostrophic,.., Φ(x, y, z, t) = (p p 0 )/ρ 0, Θ = θ θ 0,,., p 0 (z), θ 0 (z).,,,, Du Dt fv + Φ x Dv Φ + fu + Dt DΘ Dt + w dθ 0 dz = 0, (9.2) = 0, (9.3) = 0, (9.4)
Holton 9.2.2 semigeostrophic 1 9.2.2 semigeostrophic,.., Φ(x, y, z, t) = (p p 0 )/ρ 0, Θ = θ θ 0,,., p 0 (z), θ 0 (z).,,,, Du Dt fv + Φ x Dv Φ + fu + Dt DΘ Dt + w dθ 0 dz = 0, (9.2) = 0, (9.3) = 0, (9.4)
note1.dvi
 (1) 1996 11 7 1 (1) 1. 1 dx dy d x τ xx x x, stress x + dx x τ xx x+dx dyd x x τ xx x dyd y τ xx x τ xx x+dx d dx y x dy 1. dx dy d x τ xy x τ x ρdxdyd x dx dy d ρdxdyd u x t = τ xx x+dx dyd τ xx x dyd
(1) 1996 11 7 1 (1) 1. 1 dx dy d x τ xx x x, stress x + dx x τ xx x+dx dyd x x τ xx x dyd y τ xx x τ xx x+dx d dx y x dy 1. dx dy d x τ xy x τ x ρdxdyd x dx dy d ρdxdyd u x t = τ xx x+dx dyd τ xx x dyd
II A A441 : October 02, 2014 Version : Kawahira, Tomoki TA (Kondo, Hirotaka )
 II 214-1 : October 2, 214 Version : 1.1 Kawahira, Tomoki TA (Kondo, Hirotaka ) http://www.math.nagoya-u.ac.jp/~kawahira/courses/14w-biseki.html pdf 1 2 1 9 1 16 1 23 1 3 11 6 11 13 11 2 11 27 12 4 12 11
II 214-1 : October 2, 214 Version : 1.1 Kawahira, Tomoki TA (Kondo, Hirotaka ) http://www.math.nagoya-u.ac.jp/~kawahira/courses/14w-biseki.html pdf 1 2 1 9 1 16 1 23 1 3 11 6 11 13 11 2 11 27 12 4 12 11
QMI_09.dvi
 25 3 19 Erwin Schrödinger 1925 3.1 3.1.1 3.1.2 σ τ 2 2 ux, t) = ux, t) 3.1) 2 x2 ux, t) σ τ 2 u/ 2 m p E E = p2 3.2) E ν ω E = hν = hω. 3.3) k p k = p h. 3.4) 26 3 hω = E = p2 = h2 k 2 ψkx ωt) ψ 3.5) h
25 3 19 Erwin Schrödinger 1925 3.1 3.1.1 3.1.2 σ τ 2 2 ux, t) = ux, t) 3.1) 2 x2 ux, t) σ τ 2 u/ 2 m p E E = p2 3.2) E ν ω E = hν = hω. 3.3) k p k = p h. 3.4) 26 3 hω = E = p2 = h2 k 2 ψkx ωt) ψ 3.5) h
QMI_10.dvi
 25 3 19 Erwin Schrödinger 1925 3.1 3.1.1 σ τ x u u x t ux, t) u 3.1 t x P ux, t) Q θ P Q Δx x + Δx Q P ux + Δx, t) Q θ P u+δu x u x σ τ P x) Q x+δx) P Q x 3.1: θ P θ Q P Q equation of motion P τ Q τ σδx
25 3 19 Erwin Schrödinger 1925 3.1 3.1.1 σ τ x u u x t ux, t) u 3.1 t x P ux, t) Q θ P Q Δx x + Δx Q P ux + Δx, t) Q θ P u+δu x u x σ τ P x) Q x+δx) P Q x 3.1: θ P θ Q P Q equation of motion P τ Q τ σδx
untitled
 1. [IPCC, 2001] ( ) [UNEP, 1997] [Yatagai and Yasunari, 1995] 1990 1999 2002 [Iwao and Takahashi, 2006] 4 [Morinaga and Shinoda, 2003] [Kurosaki and Mikami, 2003] Iwao and Takahashi [2006] [Enomoto et
1. [IPCC, 2001] ( ) [UNEP, 1997] [Yatagai and Yasunari, 1995] 1990 1999 2002 [Iwao and Takahashi, 2006] 4 [Morinaga and Shinoda, 2003] [Kurosaki and Mikami, 2003] Iwao and Takahashi [2006] [Enomoto et
* Meso- -scale Features of the Tokai Heavy Rainfall in September 2000 Shin-ichi SUZUKI Disaster Prevention Research Group, National R
 38 2002 7 2000 9 * Meso- -scale Features of the Tokai Heavy Rainfall in September 2000 Shin-ichi SUZUKI Disaster Prevention Research Group, National Research Institute for Earth Science and Disaster Prevention,
38 2002 7 2000 9 * Meso- -scale Features of the Tokai Heavy Rainfall in September 2000 Shin-ichi SUZUKI Disaster Prevention Research Group, National Research Institute for Earth Science and Disaster Prevention,
24 I ( ) 1. R 3 (i) C : x 2 + y 2 1 = 0 (ii) C : y = ± 1 x 2 ( 1 x 1) (iii) C : x = cos t, y = sin t (0 t 2π) 1.1. γ : [a, b] R n ; t γ(t) = (x
![24 I ( ) 1. R 3 (i) C : x 2 + y 2 1 = 0 (ii) C : y = ± 1 x 2 ( 1 x 1) (iii) C : x = cos t, y = sin t (0 t 2π) 1.1. γ : [a, b] R n ; t γ(t) = (x 24 I ( ) 1. R 3 (i) C : x 2 + y 2 1 = 0 (ii) C : y = ± 1 x 2 ( 1 x 1) (iii) C : x = cos t, y = sin t (0 t 2π) 1.1. γ : [a, b] R n ; t γ(t) = (x](/thumbs/94/118744578.jpg) 24 I 1.1.. ( ) 1. R 3 (i) C : x 2 + y 2 1 = 0 (ii) C : y = ± 1 x 2 ( 1 x 1) (iii) C : x = cos t, y = sin t (0 t 2π) 1.1. γ : [a, b] R n ; t γ(t) = (x 1 (t), x 2 (t),, x n (t)) ( ) ( ), γ : (i) x 1 (t),
24 I 1.1.. ( ) 1. R 3 (i) C : x 2 + y 2 1 = 0 (ii) C : y = ± 1 x 2 ( 1 x 1) (iii) C : x = cos t, y = sin t (0 t 2π) 1.1. γ : [a, b] R n ; t γ(t) = (x 1 (t), x 2 (t),, x n (t)) ( ) ( ), γ : (i) x 1 (t),
( ) ( )
 20 21 2 8 1 2 2 3 21 3 22 3 23 4 24 5 25 5 26 6 27 8 28 ( ) 9 3 10 31 10 32 ( ) 12 4 13 41 0 13 42 14 43 0 15 44 17 5 18 6 18 1 1 2 2 1 2 1 0 2 0 3 0 4 0 2 2 21 t (x(t) y(t)) 2 x(t) y(t) γ(t) (x(t) y(t))
20 21 2 8 1 2 2 3 21 3 22 3 23 4 24 5 25 5 26 6 27 8 28 ( ) 9 3 10 31 10 32 ( ) 12 4 13 41 0 13 42 14 43 0 15 44 17 5 18 6 18 1 1 2 2 1 2 1 0 2 0 3 0 4 0 2 2 21 t (x(t) y(t)) 2 x(t) y(t) γ(t) (x(t) y(t))
(2005) (2005) 1 2 ( 1 ) 20km 2 4km 20km 40km 400km 10 1km 2km Ruscher and Deardroff (1982) Dempsey and Rotunno (1988) Smolarkiewcz et al. (1988) Smola
 (2005) (2005) 1 2 ( 1 ) 20km 2 4km 20km 40km 400km 10 1km 2km Ruscher and Deardroff (1982) Dempsey and Rotunno (1988) Smolarkiewcz et al. (1988) Smolarkiwicz and Rotunno (1989) F r = 0.15 0.5 ( F r = u/nh,
(2005) (2005) 1 2 ( 1 ) 20km 2 4km 20km 40km 400km 10 1km 2km Ruscher and Deardroff (1982) Dempsey and Rotunno (1988) Smolarkiewcz et al. (1988) Smolarkiwicz and Rotunno (1989) F r = 0.15 0.5 ( F r = u/nh,
mains.dvi
 8 Λ MRI.COM 8.1 Mellor and Yamada (198) level.5 8. Noh and Kim (1999) 8.3 Large et al. (1994) K-profile parameterization 8.1 8.1: (MRI.COM ) Mellor and Yamada Noh and Kim KPP (avdsl) K H K B K x (avm)
8 Λ MRI.COM 8.1 Mellor and Yamada (198) level.5 8. Noh and Kim (1999) 8.3 Large et al. (1994) K-profile parameterization 8.1 8.1: (MRI.COM ) Mellor and Yamada Noh and Kim KPP (avdsl) K H K B K x (avm)
KENZOU Karman) x
 KENZO 8 8 31 8 1 3 4 5 6 Karman) 7 3 8 x 8 1 1.1.............................. 3 1............................................. 5 1.3................................... 5 1.4 /.........................
KENZO 8 8 31 8 1 3 4 5 6 Karman) 7 3 8 x 8 1 1.1.............................. 3 1............................................. 5 1.3................................... 5 1.4 /.........................
Venkatram and Wyngaard, Lectures on Air Pollution Modeling, m km 6.2 Stull, An Introduction to Boundary Layer Meteorology,
 65 6 6.1 No.4 1982 1 1981 J. C. Kaimal 1993 1994 Turbulence and Diffusion in the Atmosphere : Lectures in Environmental Sciences, by A. K. Blackadar, Springer, 1998 An Introduction to Boundary Layer Meteorology,
65 6 6.1 No.4 1982 1 1981 J. C. Kaimal 1993 1994 Turbulence and Diffusion in the Atmosphere : Lectures in Environmental Sciences, by A. K. Blackadar, Springer, 1998 An Introduction to Boundary Layer Meteorology,
II 1 II 2012 II Gauss-Bonnet II
 II 1 II 212 II Gauss-Bonnet II 1 1 1.1......................................... 1 1.2............................................ 2 1.3.................................. 3 1.4.............................................
II 1 II 212 II Gauss-Bonnet II 1 1 1.1......................................... 1 1.2............................................ 2 1.3.................................. 3 1.4.............................................
K E N Z OU
 K E N Z OU 11 1 1 1.1..................................... 1.1.1............................ 1.1..................................................................................... 4 1.........................................
K E N Z OU 11 1 1 1.1..................................... 1.1.1............................ 1.1..................................................................................... 4 1.........................................
k m m d2 x i dt 2 = f i = kx i (i = 1, 2, 3 or x, y, z) f i σ ij x i e ij = 2.1 Hooke s law and elastic constants (a) x i (2.1) k m σ A σ σ σ σ f i x
 k m m d2 x i dt 2 = f i = kx i (i = 1, 2, 3 or x, y, z) f i ij x i e ij = 2.1 Hooke s law and elastic constants (a) x i (2.1) k m A f i x i B e e e e 0 e* e e (2.1) e (b) A e = 0 B = 0 (c) (2.1) (d) e
k m m d2 x i dt 2 = f i = kx i (i = 1, 2, 3 or x, y, z) f i ij x i e ij = 2.1 Hooke s law and elastic constants (a) x i (2.1) k m A f i x i B e e e e 0 e* e e (2.1) e (b) A e = 0 B = 0 (c) (2.1) (d) e
II (10 4 ) 1. p (x, y) (a, b) ε(x, y; a, b) 0 f (x, y) f (a, b) A, B (6.5) y = b f (x, b) f (a, b) x a = A + ε(x, b; a, b) x a 2 x a 0 A = f x (
 II (1 4 ) 1. p.13 1 (x, y) (a, b) ε(x, y; a, b) f (x, y) f (a, b) A, B (6.5) y = b f (x, b) f (a, b) x a = A + ε(x, b; a, b) x a x a A = f x (a, b) y x 3 3y 3 (x, y) (, ) f (x, y) = x + y (x, y) = (, )
II (1 4 ) 1. p.13 1 (x, y) (a, b) ε(x, y; a, b) f (x, y) f (a, b) A, B (6.5) y = b f (x, b) f (a, b) x a = A + ε(x, b; a, b) x a x a A = f x (a, b) y x 3 3y 3 (x, y) (, ) f (x, y) = x + y (x, y) = (, )
x,, z v = (, b, c) v v 2 + b 2 + c 2 x,, z 1 i = (1, 0, 0), j = (0, 1, 0), k = (0, 0, 1) v 1 = ( 1, b 1, c 1 ), v 2 = ( 2, b 2, c 2 ) v
 12 -- 1 4 2009 9 4-1 4-2 4-3 4-4 4-5 4-6 4-7 4-8 4-9 4-10 c 2011 1/(13) 4--1 2009 9 3 x,, z v = (, b, c) v v 2 + b 2 + c 2 x,, z 1 i = (1, 0, 0), j = (0, 1, 0), k = (0, 0, 1) v 1 = ( 1, b 1, c 1 ), v 2
12 -- 1 4 2009 9 4-1 4-2 4-3 4-4 4-5 4-6 4-7 4-8 4-9 4-10 c 2011 1/(13) 4--1 2009 9 3 x,, z v = (, b, c) v v 2 + b 2 + c 2 x,, z 1 i = (1, 0, 0), j = (0, 1, 0), k = (0, 0, 1) v 1 = ( 1, b 1, c 1 ), v 2
B ver B
 B ver. 2017.02.24 B Contents 1 11 1.1....................... 11 1.1.1............. 11 1.1.2.......................... 12 1.2............................. 14 1.2.1................ 14 1.2.2.......................
B ver. 2017.02.24 B Contents 1 11 1.1....................... 11 1.1.1............. 11 1.1.2.......................... 12 1.2............................. 14 1.2.1................ 14 1.2.2.......................
1 Tokyo Daily Rainfall (mm) Days (mm)
 ( ) r-taka@maritime.kobe-u.ac.jp 1 Tokyo Daily Rainfall (mm) 0 100 200 300 0 10000 20000 30000 40000 50000 Days (mm) 1876 1 1 2013 12 31 Tokyo, 1876 Daily Rainfall (mm) 0 50 100 150 0 100 200 300 Tokyo,
( ) r-taka@maritime.kobe-u.ac.jp 1 Tokyo Daily Rainfall (mm) 0 100 200 300 0 10000 20000 30000 40000 50000 Days (mm) 1876 1 1 2013 12 31 Tokyo, 1876 Daily Rainfall (mm) 0 50 100 150 0 100 200 300 Tokyo,
No δs δs = r + δr r = δr (3) δs δs = r r = δr + u(r + δr, t) u(r, t) (4) δr = (δx, δy, δz) u i (r + δr, t) u i (r, t) = u i x j δx j (5) δs 2
 No.2 1 2 2 δs δs = r + δr r = δr (3) δs δs = r r = δr + u(r + δr, t) u(r, t) (4) δr = (δx, δy, δz) u i (r + δr, t) u i (r, t) = u i δx j (5) δs 2 = δx i δx i + 2 u i δx i δx j = δs 2 + 2s ij δx i δx j
No.2 1 2 2 δs δs = r + δr r = δr (3) δs δs = r r = δr + u(r + δr, t) u(r, t) (4) δr = (δx, δy, δz) u i (r + δr, t) u i (r, t) = u i δx j (5) δs 2 = δx i δx i + 2 u i δx i δx j = δs 2 + 2s ij δx i δx j
= M + M + M + M M + =.,. f = < ρ, > ρ ρ. ρ f. = ρ = = ± = log 4 = = = ± f = k k ρ. k
 7 b f n f} d = b f n f d,. 5,. [ ] ɛ >, n ɛ + + n < ɛ. m. n m log + < n m. n lim sin kπ sin kπ } k π sin = n n n. k= 4 f, y = r + s, y = rs f rs = f + r + sf y + rsf yy + f y. f = f =, f = sin. 5 f f =.
7 b f n f} d = b f n f d,. 5,. [ ] ɛ >, n ɛ + + n < ɛ. m. n m log + < n m. n lim sin kπ sin kπ } k π sin = n n n. k= 4 f, y = r + s, y = rs f rs = f + r + sf y + rsf yy + f y. f = f =, f = sin. 5 f f =.
.1 z = e x +xy y z y 1 1 x 0 1 z x y α β γ z = αx + βy + γ (.1) ax + by + cz = d (.1') a, b, c, d x-y-z (a, b, c). x-y-z 3 (0,
 .1.1 Y K L Y = K 1 3 L 3 L K K (K + ) 1 1 3 L 3 K 3 L 3 K 0 (K + K) 1 3 L 3 K 1 3 L 3 lim K 0 K = L (K + K) 1 3 K 1 3 3 lim K 0 K = 1 3 K 3 L 3 z = f(x, y) x y z x-y-z.1 z = e x +xy y 3 x-y ( ) z 0 f(x,
.1.1 Y K L Y = K 1 3 L 3 L K K (K + ) 1 1 3 L 3 K 3 L 3 K 0 (K + K) 1 3 L 3 K 1 3 L 3 lim K 0 K = L (K + K) 1 3 K 1 3 3 lim K 0 K = 1 3 K 3 L 3 z = f(x, y) x y z x-y-z.1 z = e x +xy y 3 x-y ( ) z 0 f(x,
2 (March 13, 2010) N Λ a = i,j=1 x i ( d (a) i,j x j ), Λ h = N i,j=1 x i ( d (h) i,j x j ) B a B h B a = N i,j=1 ν i d (a) i,j, B h = x j N i,j=1 ν i
 1. A. M. Turing [18] 60 Turing A. Gierer H. Meinhardt [1] : (GM) ) a t = D a a xx µa + ρ (c a2 h + ρ 0 (0 < x < l, t > 0) h t = D h h xx νh + c ρ a 2 (0 < x < l, t > 0) a x = h x = 0 (x = 0, l) a = a(x,
1. A. M. Turing [18] 60 Turing A. Gierer H. Meinhardt [1] : (GM) ) a t = D a a xx µa + ρ (c a2 h + ρ 0 (0 < x < l, t > 0) h t = D h h xx νh + c ρ a 2 (0 < x < l, t > 0) a x = h x = 0 (x = 0, l) a = a(x,
gr09.dvi
 .1, θ, ϕ d = A, t dt + B, t dtd + C, t d + D, t dθ +in θdϕ.1.1 t { = f1,t t = f,t { D, t = B, t =.1. t A, tdt e φ,t dt, C, td e λ,t d.1.3,t, t d = e φ,t dt + e λ,t d + dθ +in θdϕ.1.4 { = f1,t t = f,t {
.1, θ, ϕ d = A, t dt + B, t dtd + C, t d + D, t dθ +in θdϕ.1.1 t { = f1,t t = f,t { D, t = B, t =.1. t A, tdt e φ,t dt, C, td e λ,t d.1.3,t, t d = e φ,t dt + e λ,t d + dθ +in θdϕ.1.4 { = f1,t t = f,t {
/ Christopher Essex Radiation and the Violation of Bilinearity in the Thermodynamics of Irreversible Processes, Planet.Space Sci.32 (1984) 1035 Radiat
 / Christopher Essex Radiation and the Violation of Bilinearity in the Thermodynamics of Irreversible Processes, Planet.Space Sci.32 (1984) 1035 Radiation and the Continuing Failure of the Bilinear Formalism,
/ Christopher Essex Radiation and the Violation of Bilinearity in the Thermodynamics of Irreversible Processes, Planet.Space Sci.32 (1984) 1035 Radiation and the Continuing Failure of the Bilinear Formalism,
I ( ) 1 de Broglie 1 (de Broglie) p λ k h Planck ( Js) p = h λ = k (1) h 2π : Dirac k B Boltzmann ( J/K) T U = 3 2 k BT
 I (008 4 0 de Broglie (de Broglie p λ k h Planck ( 6.63 0 34 Js p = h λ = k ( h π : Dirac k B Boltzmann (.38 0 3 J/K T U = 3 k BT ( = λ m k B T h m = 0.067m 0 m 0 = 9. 0 3 kg GaAs( a T = 300 K 3 fg 07345
I (008 4 0 de Broglie (de Broglie p λ k h Planck ( 6.63 0 34 Js p = h λ = k ( h π : Dirac k B Boltzmann (.38 0 3 J/K T U = 3 k BT ( = λ m k B T h m = 0.067m 0 m 0 = 9. 0 3 kg GaAs( a T = 300 K 3 fg 07345
D v D F v/d F v D F η v D (3.2) (a) F=0 (b) v=const. D F v Newtonian fluid σ ė σ = ηė (2.2) ė kl σ ij = D ijkl ė kl D ijkl (2.14) ė ij (3.3) µ η visco
 post glacial rebound 3.1 Viscosity and Newtonian fluid f i = kx i σ ij e kl ideal fluid (1.9) irreversible process e ij u k strain rate tensor (3.1) v i u i / t e ij v F 23 D v D F v/d F v D F η v D (3.2)
post glacial rebound 3.1 Viscosity and Newtonian fluid f i = kx i σ ij e kl ideal fluid (1.9) irreversible process e ij u k strain rate tensor (3.1) v i u i / t e ij v F 23 D v D F v/d F v D F η v D (3.2)
(3) (2),,. ( 20) ( s200103) 0.7 x C,, x 2 + y 2 + ax = 0 a.. D,. D, y C, C (x, y) (y 0) C m. (2) D y = y(x) (x ± y 0), (x, y) D, m, m = 1., D. (x 2 y
 [ ] 7 0.1 2 2 + y = t sin t IC ( 9) ( s090101) 0.2 y = d2 y 2, y = x 3 y + y 2 = 0 (2) y + 2y 3y = e 2x 0.3 1 ( y ) = f x C u = y x ( 15) ( s150102) [ ] y/x du x = Cexp f(u) u (2) x y = xey/x ( 16) ( s160101)
[ ] 7 0.1 2 2 + y = t sin t IC ( 9) ( s090101) 0.2 y = d2 y 2, y = x 3 y + y 2 = 0 (2) y + 2y 3y = e 2x 0.3 1 ( y ) = f x C u = y x ( 15) ( s150102) [ ] y/x du x = Cexp f(u) u (2) x y = xey/x ( 16) ( s160101)
Note.tex 2008/09/19( )
 1 20 9 19 2 1 5 1.1........................ 5 1.2............................. 8 2 9 2.1............................. 9 2.2.............................. 10 3 13 3.1.............................. 13 3.2..................................
1 20 9 19 2 1 5 1.1........................ 5 1.2............................. 8 2 9 2.1............................. 9 2.2.............................. 10 3 13 3.1.............................. 13 3.2..................................
 II 1 3 2 5 3 7 4 8 5 11 6 13 7 16 8 18 2 1 1. x 2 + xy x y (1 lim (x,y (1,1 x 1 x 3 + y 3 (2 lim (x,y (, x 2 + y 2 x 2 (3 lim (x,y (, x 2 + y 2 xy (4 lim (x,y (, x 2 + y 2 x y (5 lim (x,y (, x + y x 3y
II 1 3 2 5 3 7 4 8 5 11 6 13 7 16 8 18 2 1 1. x 2 + xy x y (1 lim (x,y (1,1 x 1 x 3 + y 3 (2 lim (x,y (, x 2 + y 2 x 2 (3 lim (x,y (, x 2 + y 2 xy (4 lim (x,y (, x 2 + y 2 x y (5 lim (x,y (, x + y x 3y
,., 5., ,. 2.2,., x z. y,.,,,. du dt + α p x = 0 dw dt + α p z + g = 0 α dp dt + pγ dα dt = 0 α V dα dt = 0 (2.2.1), γ = c p /c
 29 2 1 2.1 2.1.1.,., 5.,. 2.1.1,. 2.2,., x z. y,.,,,. du dt + α p x = 0 dw dt + α p z + g = 0 α dp dt + pγ dα dt = 0 α V dα dt = 0 (2.2.1), γ = c p /c v., V = (u, w), = ( / x, / z). 30 2.1.1: 31., U p(z),
29 2 1 2.1 2.1.1.,., 5.,. 2.1.1,. 2.2,., x z. y,.,,,. du dt + α p x = 0 dw dt + α p z + g = 0 α dp dt + pγ dα dt = 0 α V dα dt = 0 (2.2.1), γ = c p /c v., V = (u, w), = ( / x, / z). 30 2.1.1: 31., U p(z),
1 nakayama/print/ Def (Definition ) Thm (Theorem ) Prop (Proposition ) Lem (Lemma ) Cor (Corollary ) 1. (1) A, B (2) ABC
 1 http://www.gem.aoyama.ac.jp/ nakayama/print/ Def (Definition ) Thm (Theorem ) Prop (Proposition ) Lem (Lemma ) Cor (Corollary ) 1. (1) A, B (2) ABC r 1 A B B C C A (1),(2),, (8) A, B, C A,B,C 2 1 ABC
1 http://www.gem.aoyama.ac.jp/ nakayama/print/ Def (Definition ) Thm (Theorem ) Prop (Proposition ) Lem (Lemma ) Cor (Corollary ) 1. (1) A, B (2) ABC r 1 A B B C C A (1),(2),, (8) A, B, C A,B,C 2 1 ABC
B 38 1 (x, y), (x, y, z) (x 1, x 2 ) (x 1, x 2, x 3 ) 2 : x 2 + y 2 = 1. (parameter) x = cos t, y = sin t. y = f(x) r(t) = (x(t), y(t), z(t)), a t b.
 2009 7 9 1 2 2 2 3 6 4 9 5 14 6 18 7 23 8 25 9 26 10 29 11 32 12 35 A 37 1 B 38 1 (x, y), (x, y, z) (x 1, x 2 ) (x 1, x 2, x 3 ) 2 : x 2 + y 2 = 1. (parameter) x = cos t, y = sin t. y = f(x) r(t) = (x(t),
2009 7 9 1 2 2 2 3 6 4 9 5 14 6 18 7 23 8 25 9 26 10 29 11 32 12 35 A 37 1 B 38 1 (x, y), (x, y, z) (x 1, x 2 ) (x 1, x 2, x 3 ) 2 : x 2 + y 2 = 1. (parameter) x = cos t, y = sin t. y = f(x) r(t) = (x(t),
2 1 κ c(t) = (x(t), y(t)) ( ) det(c (t), c x (t)) = det (t) x (t) y (t) y = x (t)y (t) x (t)y (t), (t) c (t) = (x (t)) 2 + (y (t)) 2. c (t) =
 1 1 1.1 I R 1.1.1 c : I R 2 (i) c C (ii) t I c (t) (0, 0) c (t) c(i) c c(t) 1.1.2 (1) (2) (3) (1) r > 0 c : R R 2 : t (r cos t, r sin t) (2) C f : I R c : I R 2 : t (t, f(t)) (3) y = x c : R R 2 : t (t,
1 1 1.1 I R 1.1.1 c : I R 2 (i) c C (ii) t I c (t) (0, 0) c (t) c(i) c c(t) 1.1.2 (1) (2) (3) (1) r > 0 c : R R 2 : t (r cos t, r sin t) (2) C f : I R c : I R 2 : t (t, f(t)) (3) y = x c : R R 2 : t (t,
I, II 1, A = A 4 : 6 = max{ A, } A A 10 10%
 1 2006.4.17. A 3-312 tel: 092-726-4774, e-mail: hara@math.kyushu-u.ac.jp, http://www.math.kyushu-u.ac.jp/ hara/lectures/lectures-j.html Office hours: B A I ɛ-δ ɛ-δ 1. 2. A 1. 1. 2. 3. 4. 5. 2. ɛ-δ 1. ɛ-n
1 2006.4.17. A 3-312 tel: 092-726-4774, e-mail: hara@math.kyushu-u.ac.jp, http://www.math.kyushu-u.ac.jp/ hara/lectures/lectures-j.html Office hours: B A I ɛ-δ ɛ-δ 1. 2. A 1. 1. 2. 3. 4. 5. 2. ɛ-δ 1. ɛ-n
V 0 = + r pv (H) + qv (T ) = + r ps (H) + qs (T ) = S 0 X n+ (T ) = n S n+ (T ) + ( + r)(x n n S n ) = ( + r)x n + n (d r)s n = ( + r)v n + V n+(h) V
 I (..2) (0 < d < + r < u) X 0, X X = 0 S + ( + r)(x 0 0 S 0 ) () X 0 = 0, P (X 0) =, P (X > 0) > 0 0 H, T () X 0 = 0, X (H) = 0 us 0 ( + r) 0 S 0 = 0 S 0 (u r) X (T ) = 0 ds 0 ( + r) 0 S 0 = 0 S 0 (d r)
I (..2) (0 < d < + r < u) X 0, X X = 0 S + ( + r)(x 0 0 S 0 ) () X 0 = 0, P (X 0) =, P (X > 0) > 0 0 H, T () X 0 = 0, X (H) = 0 us 0 ( + r) 0 S 0 = 0 S 0 (u r) X (T ) = 0 ds 0 ( + r) 0 S 0 = 0 S 0 (d r)
I A A441 : April 21, 2014 Version : Kawahira, Tomoki TA (Kondo, Hirotaka ) Google
 I4 - : April, 4 Version :. Kwhir, Tomoki TA (Kondo, Hirotk) Google http://www.mth.ngoy-u.c.jp/~kwhir/courses/4s-biseki.html pdf 4 4 4 4 8 e 5 5 9 etc. 5 6 6 6 9 n etc. 6 6 6 3 6 3 7 7 etc 7 4 7 7 8 5 59
I4 - : April, 4 Version :. Kwhir, Tomoki TA (Kondo, Hirotk) Google http://www.mth.ngoy-u.c.jp/~kwhir/courses/4s-biseki.html pdf 4 4 4 4 8 e 5 5 9 etc. 5 6 6 6 9 n etc. 6 6 6 3 6 3 7 7 etc 7 4 7 7 8 5 59
 2019 1 5 0 3 1 4 1.1.................... 4 1.1.1......................... 4 1.1.2........................ 5 1.1.3................... 5 1.1.4........................ 6 1.1.5......................... 6 1.2..........................
2019 1 5 0 3 1 4 1.1.................... 4 1.1.1......................... 4 1.1.2........................ 5 1.1.3................... 5 1.1.4........................ 6 1.1.5......................... 6 1.2..........................
NumRu::GPhys::EP Flux 2 2 NumRu::GPhys::EP Flux 3 2.................................. 3 2.2 EP............................. 4 2.3.....................
 NumRu::GPhys::EP Flux 7 2 9 NumRu::GPhys::EP Flux 2 2 NumRu::GPhys::EP Flux 3 2.................................. 3 2.2 EP............................. 4 2.3................................. 5 2.4.............................
NumRu::GPhys::EP Flux 7 2 9 NumRu::GPhys::EP Flux 2 2 NumRu::GPhys::EP Flux 3 2.................................. 3 2.2 EP............................. 4 2.3................................. 5 2.4.............................
 n ξ n,i, i = 1,, n S n ξ n,i n 0 R 1,.. σ 1 σ i .10.14.15 0 1 0 1 1 3.14 3.18 3.19 3.14 3.14,. ii 1 1 1.1..................................... 1 1............................... 3 1.3.........................
n ξ n,i, i = 1,, n S n ξ n,i n 0 R 1,.. σ 1 σ i .10.14.15 0 1 0 1 1 3.14 3.18 3.19 3.14 3.14,. ii 1 1 1.1..................................... 1 1............................... 3 1.3.........................
x = a 1 f (a r, a + r) f(a) r a f f(a) 2 2. (a, b) 2 f (a, b) r f(a, b) r (a, b) f f(a, b)
 2011 I 2 II III 17, 18, 19 7 7 1 2 2 2 1 2 1 1 1.1.............................. 2 1.2 : 1.................... 4 1.2.1 2............................... 5 1.3 : 2.................... 5 1.3.1 2.....................................
2011 I 2 II III 17, 18, 19 7 7 1 2 2 2 1 2 1 1 1.1.............................. 2 1.2 : 1.................... 4 1.2.1 2............................... 5 1.3 : 2.................... 5 1.3.1 2.....................................
(1.2) T D = 0 T = D = 30 kn 1.2 (1.4) 2F W = 0 F = W/2 = 300 kn/2 = 150 kn 1.3 (1.9) R = W 1 + W 2 = = 1100 N. (1.9) W 2 b W 1 a = 0
 1 1 1.1 1.) T D = T = D = kn 1. 1.4) F W = F = W/ = kn/ = 15 kn 1. 1.9) R = W 1 + W = 6 + 5 = 11 N. 1.9) W b W 1 a = a = W /W 1 )b = 5/6) = 5 cm 1.4 AB AC P 1, P x, y x, y y x 1.4.) P sin 6 + P 1 sin 45
1 1 1.1 1.) T D = T = D = kn 1. 1.4) F W = F = W/ = kn/ = 15 kn 1. 1.9) R = W 1 + W = 6 + 5 = 11 N. 1.9) W b W 1 a = a = W /W 1 )b = 5/6) = 5 cm 1.4 AB AC P 1, P x, y x, y y x 1.4.) P sin 6 + P 1 sin 45
DVIOUT
 A. A. A-- [ ] f(x) x = f 00 (x) f 0 () =0 f 00 () > 0= f(x) x = f 00 () < 0= f(x) x = A--2 [ ] f(x) D f 00 (x) > 0= y = f(x) f 00 (x) < 0= y = f(x) P (, f()) f 00 () =0 A--3 [ ] y = f(x) [, b] x = f (y)
A. A. A-- [ ] f(x) x = f 00 (x) f 0 () =0 f 00 () > 0= f(x) x = f 00 () < 0= f(x) x = A--2 [ ] f(x) D f 00 (x) > 0= y = f(x) f 00 (x) < 0= y = f(x) P (, f()) f 00 () =0 A--3 [ ] y = f(x) [, b] x = f (y)
 211 kotaro@math.titech.ac.jp 1 R *1 n n R n *2 R n = {(x 1,..., x n ) x 1,..., x n R}. R R 2 R 3 R n R n R n D D R n *3 ) (x 1,..., x n ) f(x 1,..., x n ) f D *4 n 2 n = 1 ( ) 1 f D R n f : D R 1.1. (x,
211 kotaro@math.titech.ac.jp 1 R *1 n n R n *2 R n = {(x 1,..., x n ) x 1,..., x n R}. R R 2 R 3 R n R n R n D D R n *3 ) (x 1,..., x n ) f(x 1,..., x n ) f D *4 n 2 n = 1 ( ) 1 f D R n f : D R 1.1. (x,
x () g(x) = f(t) dt f(x), F (x) 3x () g(x) g (x) f(x), F (x) (3) h(x) = x 3x tf(t) dt.9 = {(x, y) ; x, y, x + y } f(x, y) = xy( x y). h (x) f(x), F (x
 [ ] IC. f(x) = e x () f(x) f (x) () lim f(x) lim f(x) x + x (3) lim f(x) lim f(x) x + x (4) y = f(x) ( ) ( s46). < a < () a () lim a log xdx a log xdx ( ) n (3) lim log k log n n n k=.3 z = log(x + y ),
[ ] IC. f(x) = e x () f(x) f (x) () lim f(x) lim f(x) x + x (3) lim f(x) lim f(x) x + x (4) y = f(x) ( ) ( s46). < a < () a () lim a log xdx a log xdx ( ) n (3) lim log k log n n n k=.3 z = log(x + y ),
Untitled
 II 14 14-7-8 8/4 II (http://www.damp.tottori-u.ac.jp/~ooshida/edu/fluid/) [ (3.4)] Navier Stokes [ 6/ ] Navier Stokes 3 [ ] Reynolds [ (4.6), (45.8)] [ p.186] Navier Stokes I 1 balance law t (ρv i )+ j
II 14 14-7-8 8/4 II (http://www.damp.tottori-u.ac.jp/~ooshida/edu/fluid/) [ (3.4)] Navier Stokes [ 6/ ] Navier Stokes 3 [ ] Reynolds [ (4.6), (45.8)] [ p.186] Navier Stokes I 1 balance law t (ρv i )+ j
,.,. 2, R 2, ( )., I R. c : I R 2, : (1) c C -, (2) t I, c (t) (0, 0). c(i). c (t)., c(t) = (x(t), y(t)) c (t) = (x (t), y (t)) : (1)
 ( ) 1., : ;, ;, ; =. ( ).,.,,,., 2.,.,,.,.,,., y = f(x), f ( ).,,.,.,., U R m, F : U R n, M, f : M R p M, p,, R m,,, R m. 2009 A tamaru math.sci.hiroshima-u.ac.jp 1 ,.,. 2, R 2, ( ).,. 2.1 2.1. I R. c
( ) 1., : ;, ;, ; =. ( ).,.,,,., 2.,.,,.,.,,., y = f(x), f ( ).,,.,.,., U R m, F : U R n, M, f : M R p M, p,, R m,,, R m. 2009 A tamaru math.sci.hiroshima-u.ac.jp 1 ,.,. 2, R 2, ( ).,. 2.1 2.1. I R. c
,. Black-Scholes u t t, x c u 0 t, x x u t t, x c u t, x x u t t, x + σ x u t, x + rx ut, x rux, t 0 x x,,.,. Step 3, 7,,, Step 6., Step 4,. Step 5,,.
 9 α ν β Ξ ξ Γ γ o δ Π π ε ρ ζ Σ σ η τ Θ θ Υ υ ι Φ φ κ χ Λ λ Ψ ψ µ Ω ω Def, Prop, Th, Lem, Note, Remark, Ex,, Proof, R, N, Q, C [a, b {x R : a x b} : a, b {x R : a < x < b} : [a, b {x R : a x < b} : a,
9 α ν β Ξ ξ Γ γ o δ Π π ε ρ ζ Σ σ η τ Θ θ Υ υ ι Φ φ κ χ Λ λ Ψ ψ µ Ω ω Def, Prop, Th, Lem, Note, Remark, Ex,, Proof, R, N, Q, C [a, b {x R : a x b} : a, b {x R : a < x < b} : [a, b {x R : a x < b} : a,
砂浜砕波帯における流れと地形変化
 47 * Currents and Morphological Changes in the Surf Zone on a Sandy Beach Yoshiaki KURIYAMA, Littoral Drift Division, Port and Airport Research Institute 1 1 1) ρd M M x y 2 + + = (1) t x y 2.1 M x UM
47 * Currents and Morphological Changes in the Surf Zone on a Sandy Beach Yoshiaki KURIYAMA, Littoral Drift Division, Port and Airport Research Institute 1 1 1) ρd M M x y 2 + + = (1) t x y 2.1 M x UM
 2016 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 1 16 2 1 () X O 3 (O1) X O, O (O2) O O (O3) O O O X (X, O) O X X (O1), (O2), (O3) (O2) (O3) n (O2) U 1,..., U n O U k O k=1 (O3) U λ O( λ Λ) λ Λ U λ O 0 X 0 (O2) n =
2016 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 1 16 2 1 () X O 3 (O1) X O, O (O2) O O (O3) O O O X (X, O) O X X (O1), (O2), (O3) (O2) (O3) n (O2) U 1,..., U n O U k O k=1 (O3) U λ O( λ Λ) λ Λ U λ O 0 X 0 (O2) n =
sikepuri.dvi
 2009 2 2 2. 2.. F(s) G(s) H(s) G(s) F(s) H(s) F(s),G(s) H(s) : V (s) Z(s)I(s) I(s) Y (s)v (s) Z(s): Y (s): 2: ( ( V V 2 I I 2 ) ( ) ( Z Z 2 Z 2 Z 22 ) ( ) ( Y Y 2 Y 2 Y 22 ( ) ( ) Z Z 2 Y Y 2 : : Z 2 Z
2009 2 2 2. 2.. F(s) G(s) H(s) G(s) F(s) H(s) F(s),G(s) H(s) : V (s) Z(s)I(s) I(s) Y (s)v (s) Z(s): Y (s): 2: ( ( V V 2 I I 2 ) ( ) ( Z Z 2 Z 2 Z 22 ) ( ) ( Y Y 2 Y 2 Y 22 ( ) ( ) Z Z 2 Y Y 2 : : Z 2 Z
 4 5.............................................. 5............................................ 6.............................................. 7......................................... 8.3.................................................4.........................................4..............................................4................................................4.3...............................................
4 5.............................................. 5............................................ 6.............................................. 7......................................... 8.3.................................................4.........................................4..............................................4................................................4.3...............................................
S I. dy fx x fx y fx + C 3 C dy fx 4 x, y dy v C xt y C v e kt k > xt yt gt [ v dt dt v e kt xt v e kt + C k x v + C C k xt v k 3 r r + dr e kt S dt d
 S I.. http://ayapin.film.s.dendai.ac.jp/~matuda /TeX/lecture.html PDF PS.................................... 3.3.................... 9.4................5.............. 3 5. Laplace................. 5....
S I.. http://ayapin.film.s.dendai.ac.jp/~matuda /TeX/lecture.html PDF PS.................................... 3.3.................... 9.4................5.............. 3 5. Laplace................. 5....
x, y x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = 15 xy (x y) (x + y) xy (x y) (x y) ( x 2 + xy + y 2) = 15 (x y)
 x, y x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = 15 1 1977 x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = 15 xy (x y) (x + y) xy (x y) (x y) ( x 2 + xy + y 2) = 15 (x y) ( x 2 y + xy 2 x 2 2xy y 2) = 15 (x y) (x + y) (xy
x, y x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = 15 1 1977 x 3 y xy 3 x 2 y + xy 2 x 3 + y 3 = 15 xy (x y) (x + y) xy (x y) (x y) ( x 2 + xy + y 2) = 15 (x y) ( x 2 y + xy 2 x 2 2xy y 2) = 15 (x y) (x + y) (xy
201711grade1ouyou.pdf
 2017 11 26 1 2 52 3 12 13 22 23 32 33 42 3 5 3 4 90 5 6 A 1 2 Web Web 3 4 1 2... 5 6 7 7 44 8 9 1 2 3 1 p p >2 2 A 1 2 0.6 0.4 0.52... (a) 0.6 0.4...... B 1 2 0.8-0.2 0.52..... (b) 0.6 0.52.... 1 A B 2
2017 11 26 1 2 52 3 12 13 22 23 32 33 42 3 5 3 4 90 5 6 A 1 2 Web Web 3 4 1 2... 5 6 7 7 44 8 9 1 2 3 1 p p >2 2 A 1 2 0.6 0.4 0.52... (a) 0.6 0.4...... B 1 2 0.8-0.2 0.52..... (b) 0.6 0.52.... 1 A B 2
5. [1 ] 1 [], u(x, t) t c u(x, t) x (5.3) ξ x + ct, η x ct (5.4),u(x, t) ξ, η u(ξ, η), ξ t,, ( u(ξ,η) ξ η u(x, t) t ) u(x, t) { ( u(ξ, η) c t ξ ξ { (
![5. [1 ] 1 [], u(x, t) t c u(x, t) x (5.3) ξ x + ct, η x ct (5.4),u(x, t) ξ, η u(ξ, η), ξ t,, ( u(ξ,η) ξ η u(x, t) t ) u(x, t) { ( u(ξ, η) c t ξ ξ { ( 5. [1 ] 1 [], u(x, t) t c u(x, t) x (5.3) ξ x + ct, η x ct (5.4),u(x, t) ξ, η u(ξ, η), ξ t,, ( u(ξ,η) ξ η u(x, t) t ) u(x, t) { ( u(ξ, η) c t ξ ξ { (](/thumbs/92/107866626.jpg) 5 5.1 [ ] ) d f(t) + a d f(t) + bf(t) : f(t) 1 dt dt ) u(x, t) c u(x, t) : u(x, t) t x : ( ) ) 1 : y + ay, : y + ay + by : ( ) 1 ) : y + ay, : yy + ay 3 ( ): ( ) ) : y + ay, : y + ay b [],,, [ ] au xx
5 5.1 [ ] ) d f(t) + a d f(t) + bf(t) : f(t) 1 dt dt ) u(x, t) c u(x, t) : u(x, t) t x : ( ) ) 1 : y + ay, : y + ay + by : ( ) 1 ) : y + ay, : yy + ay 3 ( ): ( ) ) : y + ay, : y + ay b [],,, [ ] au xx
 1 B () Ver 2014 0 2014/10 2015/1 http://www-cr.scphys.kyoto-u.ac.jp/member/tsuru/lecture/... 1. ( ) 2. 3. 3 1 7 1.1..................................................... 7 1.2.............................................
1 B () Ver 2014 0 2014/10 2015/1 http://www-cr.scphys.kyoto-u.ac.jp/member/tsuru/lecture/... 1. ( ) 2. 3. 3 1 7 1.1..................................................... 7 1.2.............................................
CALCULUS II (Hiroshi SUZUKI ) f(x, y) A(a, b) 1. P (x, y) A(a, b) A(a, b) f(x, y) c f(x, y) A(a, b) c f(x, y) c f(x, y) c (x a, y b)
 CALCULUS II (Hiroshi SUZUKI ) 16 1 1 1.1 1.1 f(x, y) A(a, b) 1. P (x, y) A(a, b) A(a, b) f(x, y) c f(x, y) A(a, b) c f(x, y) c f(x, y) c (x a, y b) lim f(x, y) = lim f(x, y) = lim f(x, y) = c. x a, y b
CALCULUS II (Hiroshi SUZUKI ) 16 1 1 1.1 1.1 f(x, y) A(a, b) 1. P (x, y) A(a, b) A(a, b) f(x, y) c f(x, y) A(a, b) c f(x, y) c f(x, y) c (x a, y b) lim f(x, y) = lim f(x, y) = lim f(x, y) = c. x a, y b
() n C + n C + n C + + n C n n (3) n C + n C + n C 4 + n C + n C 3 + n C 5 + (5) (6 ) n C + nc + 3 nc n nc n (7 ) n C + nc + 3 nc n nc n (
 3 n nc k+ k + 3 () n C r n C n r nc r C r + C r ( r n ) () n C + n C + n C + + n C n n (3) n C + n C + n C 4 + n C + n C 3 + n C 5 + (4) n C n n C + n C + n C + + n C n (5) k k n C k n C k (6) n C + nc
3 n nc k+ k + 3 () n C r n C n r nc r C r + C r ( r n ) () n C + n C + n C + + n C n n (3) n C + n C + n C 4 + n C + n C 3 + n C 5 + (4) n C n n C + n C + n C + + n C n (5) k k n C k n C k (6) n C + nc
変 位 変位とは 物体中のある点が変形後に 別の点に異動したときの位置の変化で あり ベクトル量である 変位には 物体の変形の他に剛体運動 剛体変位 が含まれている 剛体変位 P(x, y, z) 平行移動と回転 P! (x + u, y + v, z + w) Q(x + d x, y + dy,
 変 位 変位とは 物体中のある点が変形後に 別の点に異動したときの位置の変化で あり ベクトル量である 変位には 物体の変形の他に剛体運動 剛体変位 が含まれている 剛体変位 P(x, y, z) 平行移動と回転 P! (x + u, y + v, z + w) Q(x + d x, y + dy, z + dz) Q! (x + d x + u + du, y + dy + v + dv, z +
変 位 変位とは 物体中のある点が変形後に 別の点に異動したときの位置の変化で あり ベクトル量である 変位には 物体の変形の他に剛体運動 剛体変位 が含まれている 剛体変位 P(x, y, z) 平行移動と回転 P! (x + u, y + v, z + w) Q(x + d x, y + dy, z + dz) Q! (x + d x + u + du, y + dy + v + dv, z +
untitled
 BELLE TOP 12 1 3 2 BELLE 4 2.1 BELLE........................... 4 2.1.1......................... 4 2.1.2 B B........................ 7 2.1.3 B CP............... 8 2.2 BELLE...................... 9 2.3
BELLE TOP 12 1 3 2 BELLE 4 2.1 BELLE........................... 4 2.1.1......................... 4 2.1.2 B B........................ 7 2.1.3 B CP............... 8 2.2 BELLE...................... 9 2.3
08-Note2-web
 r(t) t r(t) O v(t) = dr(t) dt a(t) = dv(t) dt = d2 r(t) dt 2 r(t), v(t), a(t) t dr(t) dt r(t) =(x(t),y(t),z(t)) = d 2 r(t) dt 2 = ( dx(t) dt ( d 2 x(t) dt 2, dy(t), dz(t) dt dt ), d2 y(t) dt 2, d2 z(t)
r(t) t r(t) O v(t) = dr(t) dt a(t) = dv(t) dt = d2 r(t) dt 2 r(t), v(t), a(t) t dr(t) dt r(t) =(x(t),y(t),z(t)) = d 2 r(t) dt 2 = ( dx(t) dt ( d 2 x(t) dt 2, dy(t), dz(t) dt dt ), d2 y(t) dt 2, d2 z(t)
2011de.dvi
 211 ( 4 2 1. 3 1.1............................... 3 1.2 1- -......................... 13 1.3 2-1 -................... 19 1.4 3- -......................... 29 2. 37 2.1................................ 37
211 ( 4 2 1. 3 1.1............................... 3 1.2 1- -......................... 13 1.3 2-1 -................... 19 1.4 3- -......................... 29 2. 37 2.1................................ 37
Richard J. Greatbatch
 https://www.gfd-dennou.org/seminars/gfdsemi/ 2013 @ Lecture note for the 2013 Summer Seminar in Geophysical Fluid Dynamics Lagrange Development of Lagrangean mean theories for baroclinic eddies and wind
https://www.gfd-dennou.org/seminars/gfdsemi/ 2013 @ Lecture note for the 2013 Summer Seminar in Geophysical Fluid Dynamics Lagrange Development of Lagrangean mean theories for baroclinic eddies and wind
液晶の物理1:連続体理論(弾性,粘性)
 The Physics of Liquid Crystals P. G. de Gennes and J. Prost (Oxford University Press, 1993) Liquid crystals are beautiful and mysterious; I am fond of them for both reasons. My hope is that some readers
The Physics of Liquid Crystals P. G. de Gennes and J. Prost (Oxford University Press, 1993) Liquid crystals are beautiful and mysterious; I am fond of them for both reasons. My hope is that some readers
 X G P G (X) G BG [X, BG] S 2 2 2 S 2 2 S 2 = { (x 1, x 2, x 3 ) R 3 x 2 1 + x 2 2 + x 2 3 = 1 } R 3 S 2 S 2 v x S 2 x x v(x) T x S 2 T x S 2 S 2 x T x S 2 = { ξ R 3 x ξ } R 3 T x S 2 S 2 x x T x S 2
X G P G (X) G BG [X, BG] S 2 2 2 S 2 2 S 2 = { (x 1, x 2, x 3 ) R 3 x 2 1 + x 2 2 + x 2 3 = 1 } R 3 S 2 S 2 v x S 2 x x v(x) T x S 2 T x S 2 S 2 x T x S 2 = { ξ R 3 x ξ } R 3 T x S 2 S 2 x x T x S 2
Feynman Encounter with Mathematics 52, [1] N. Kumano-go, Feynman path integrals as analysis on path space by time slicing approximation. Bull
![Feynman Encounter with Mathematics 52, [1] N. Kumano-go, Feynman path integrals as analysis on path space by time slicing approximation. Bull Feynman Encounter with Mathematics 52, [1] N. Kumano-go, Feynman path integrals as analysis on path space by time slicing approximation. Bull](/thumbs/94/118365979.jpg) Feynman Encounter with Mathematics 52, 200 9 [] N. Kumano-go, Feynman path integrals as analysis on path space by time slicing approximation. Bull. Sci. Math. vol. 28 (2004) 97 25. [2] D. Fujiwara and
Feynman Encounter with Mathematics 52, 200 9 [] N. Kumano-go, Feynman path integrals as analysis on path space by time slicing approximation. Bull. Sci. Math. vol. 28 (2004) 97 25. [2] D. Fujiwara and
Akito Tsuboi June 22, T ϕ T M M ϕ M M ϕ T ϕ 2 Definition 1 X, Y, Z,... 1
 Akito Tsuboi June 22, 2006 1 T ϕ T M M ϕ M M ϕ T ϕ 2 Definition 1 X, Y, Z,... 1 1. X, Y, Z,... 2. A, B (A), (A) (B), (A) (B), (A) (B) Exercise 2 1. (X) (Y ) 2. ((X) (Y )) (Z) 3. (((X) (Y )) (Z)) Exercise
Akito Tsuboi June 22, 2006 1 T ϕ T M M ϕ M M ϕ T ϕ 2 Definition 1 X, Y, Z,... 1 1. X, Y, Z,... 2. A, B (A), (A) (B), (A) (B), (A) (B) Exercise 2 1. (X) (Y ) 2. ((X) (Y )) (Z) 3. (((X) (Y )) (Z)) Exercise
by ( ) ( ) ( FORTRAN routines for computation of Special Functions [
 by (kubok@ees.hokudai.ac.jp) ( ) 2009 12 7 9 ( ) ( FORTRAN routines for computation of Special Functions [http://jin.ece.uiuc.edu/routines/routines.html] ) (2010 2 19 ) Chapter 1 1 1 2 3 4 β 5 3 Chapter
by (kubok@ees.hokudai.ac.jp) ( ) 2009 12 7 9 ( ) ( FORTRAN routines for computation of Special Functions [http://jin.ece.uiuc.edu/routines/routines.html] ) (2010 2 19 ) Chapter 1 1 1 2 3 4 β 5 3 Chapter
1 (Berry,1975) 2-6 p (S πr 2 )p πr 2 p 2πRγ p p = 2γ R (2.5).1-1 : : : : ( ).2 α, β α, β () X S = X X α X β (.1) 1 2
 2005 9/8-11 2 2.2 ( 2-5) γ ( ) γ cos θ 2πr πρhr 2 g h = 2γ cos θ ρgr (2.1) γ = ρgrh (2.2) 2 cos θ θ cos θ = 1 (2.2) γ = 1 ρgrh (2.) 2 2. p p ρgh p ( ) p p = p ρgh (2.) h p p = 2γ r 1 1 (Berry,1975) 2-6
2005 9/8-11 2 2.2 ( 2-5) γ ( ) γ cos θ 2πr πρhr 2 g h = 2γ cos θ ρgr (2.1) γ = ρgrh (2.2) 2 cos θ θ cos θ = 1 (2.2) γ = 1 ρgrh (2.) 2 2. p p ρgh p ( ) p p = p ρgh (2.) h p p = 2γ r 1 1 (Berry,1975) 2-6
80 4 r ˆρ i (r, t) δ(r x i (t)) (4.1) x i (t) ρ i ˆρ i t = 0 i r 0 t(> 0) j r 0 + r < δ(r 0 x i (0))δ(r 0 + r x j (t)) > (4.2) r r 0 G i j (r, t) dr 0
 79 4 4.1 4.1.1 x i (t) x j (t) O O r 0 + r r r 0 x i (0) r 0 x i (0) 4.1 L. van. Hove 1954 space-time correlation function V N 4.1 ρ 0 = N/V i t 80 4 r ˆρ i (r, t) δ(r x i (t)) (4.1) x i (t) ρ i ˆρ i t
79 4 4.1 4.1.1 x i (t) x j (t) O O r 0 + r r r 0 x i (0) r 0 x i (0) 4.1 L. van. Hove 1954 space-time correlation function V N 4.1 ρ 0 = N/V i t 80 4 r ˆρ i (r, t) δ(r x i (t)) (4.1) x i (t) ρ i ˆρ i t
A
 A 2563 15 4 21 1 3 1.1................................................ 3 1.2............................................. 3 2 3 2.1......................................... 3 2.2............................................
A 2563 15 4 21 1 3 1.1................................................ 3 1.2............................................. 3 2 3 2.1......................................... 3 2.2............................................
PowerPoint Presentation
 2010 KEK (Japan) (Japan) (Japan) Cheoun, Myun -ki Soongsil (Korea) Ryu,, Chung-Yoe Soongsil (Korea) 1. S.Reddy, M.Prakash and J.M. Lattimer, P.R.D58 #013009 (1998) Magnetar : ~ 10 15 G ~ 10 17 19 G (?)
2010 KEK (Japan) (Japan) (Japan) Cheoun, Myun -ki Soongsil (Korea) Ryu,, Chung-Yoe Soongsil (Korea) 1. S.Reddy, M.Prakash and J.M. Lattimer, P.R.D58 #013009 (1998) Magnetar : ~ 10 15 G ~ 10 17 19 G (?)
2 1 1 (1) 1 (2) (3) Lax : (4) Bäcklund : (5) (6) 1.1 d 2 q n dt 2 = e q n 1 q n e q n q n+1 (1.1) 1 m q n n ( ) r n = q n q n 1 r ϕ(r) ϕ (r)
 ( ( (3 Lax : (4 Bäcklud : (5 (6 d q = e q q e q q + ( m q ( r = q q r ϕ(r ϕ (r 0 5 0 q q q + 5 3 4 5 m d q = ϕ (r + ϕ (r + ( Hooke ϕ(r = κr (κ > 0 ( d q = κ(q q + κ(q + q = κ(q + + q q (3 ϕ(r = a b e br
( ( (3 Lax : (4 Bäcklud : (5 (6 d q = e q q e q q + ( m q ( r = q q r ϕ(r ϕ (r 0 5 0 q q q + 5 3 4 5 m d q = ϕ (r + ϕ (r + ( Hooke ϕ(r = κr (κ > 0 ( d q = κ(q q + κ(q + q = κ(q + + q q (3 ϕ(r = a b e br
December 28, 2018
 e-mail : kigami@i.kyoto-u.ac.jp December 28, 28 Contents 2............................. 3.2......................... 7.3..................... 9.4................ 4.5............. 2.6.... 22 2 36 2..........................
e-mail : kigami@i.kyoto-u.ac.jp December 28, 28 Contents 2............................. 3.2......................... 7.3..................... 9.4................ 4.5............. 2.6.... 22 2 36 2..........................
. ev=,604k m 3 Debye ɛ 0 kt e λ D = n e n e Ze 4 ln Λ ν ei = 5.6π / ɛ 0 m/ e kt e /3 ν ei v e H + +e H ev Saha x x = 3/ πme kt g i g e n
 003...............................3 Debye................. 3.4................ 3 3 3 3. Larmor Cyclotron... 3 3................ 4 3.3.......... 4 3.3............ 4 3.3...... 4 3.3.3............ 5 3.4.........
003...............................3 Debye................. 3.4................ 3 3 3 3. Larmor Cyclotron... 3 3................ 4 3.3.......... 4 3.3............ 4 3.3...... 4 3.3.3............ 5 3.4.........
MUFFIN3
 MUFFIN - MUltiFarious FIeld simulator for Non-equilibrium system - ( ) MUFFIN WG3 - - JCII, - ( ) - ( ) - ( ) - (JSR) - - MUFFIN sec -3 msec -6 sec GOURMET SUSHI MUFFIN -9 nsec PASTA -1 psec -15 fsec COGNAC
MUFFIN - MUltiFarious FIeld simulator for Non-equilibrium system - ( ) MUFFIN WG3 - - JCII, - ( ) - ( ) - ( ) - (JSR) - - MUFFIN sec -3 msec -6 sec GOURMET SUSHI MUFFIN -9 nsec PASTA -1 psec -15 fsec COGNAC
( ; ) C. H. Scholz, The Mechanics of Earthquakes and Faulting : - ( ) σ = σ t sin 2π(r a) λ dσ d(r a) =
 1 9 8 1 1 1 ; 1 11 16 C. H. Scholz, The Mechanics of Earthquakes and Faulting 1. 1.1 1.1.1 : - σ = σ t sin πr a λ dσ dr a = E a = π λ σ πr a t cos λ 1 r a/λ 1 cos 1 E: σ t = Eλ πa a λ E/π γ : λ/ 3 γ =
1 9 8 1 1 1 ; 1 11 16 C. H. Scholz, The Mechanics of Earthquakes and Faulting 1. 1.1 1.1.1 : - σ = σ t sin πr a λ dσ dr a = E a = π λ σ πr a t cos λ 1 r a/λ 1 cos 1 E: σ t = Eλ πa a λ E/π γ : λ/ 3 γ =
68 JAXA-RR r v m Ó e ε 0 E = - Ó/ r f f 0 f 1 f = f 0 + f 1 x k f 1 = f k e ikx Ó = Ó k e ikx Ó k 3
 67 1 Landau Damping and RF Current Drive Kazuya UEHARA* 1 Abstract The current drive due to the rf travelling wave has been available to sustain the plasma current of tokamaks aiming the stational operation.
67 1 Landau Damping and RF Current Drive Kazuya UEHARA* 1 Abstract The current drive due to the rf travelling wave has been available to sustain the plasma current of tokamaks aiming the stational operation.
 21 2 26 i 1 1 1.1............................ 1 1.2............................ 3 2 9 2.1................... 9 2.2.......... 9 2.3................... 11 2.4....................... 12 3 15 3.1..........
21 2 26 i 1 1 1.1............................ 1 1.2............................ 3 2 9 2.1................... 9 2.2.......... 9 2.3................... 11 2.4....................... 12 3 15 3.1..........
ii
 ii iii 1 1 1.1..................................... 1 1.2................................... 3 1.3........................... 4 2 9 2.1.................................. 9 2.2...............................
ii iii 1 1 1.1..................................... 1 1.2................................... 3 1.3........................... 4 2 9 2.1.................................. 9 2.2...............................
 IA hara@math.kyushu-u.ac.jp Last updated: January,......................................................................................................................................................................................
IA hara@math.kyushu-u.ac.jp Last updated: January,......................................................................................................................................................................................
1. (8) (1) (x + y) + (x + y) = 0 () (x + y ) 5xy = 0 (3) (x y + 3y 3 ) (x 3 + xy ) = 0 (4) x tan y x y + x = 0 (5) x = y + x + y (6) = x + y 1 x y 3 (
 1 1.1 (1) (1 + x) + (1 + y) = 0 () x + y = 0 (3) xy = x (4) x(y + 3) + y(y + 3) = 0 (5) (a + y ) = x ax a (6) x y 1 + y x 1 = 0 (7) cos x + sin x cos y = 0 (8) = tan y tan x (9) = (y 1) tan x (10) (1 +
1 1.1 (1) (1 + x) + (1 + y) = 0 () x + y = 0 (3) xy = x (4) x(y + 3) + y(y + 3) = 0 (5) (a + y ) = x ax a (6) x y 1 + y x 1 = 0 (7) cos x + sin x cos y = 0 (8) = tan y tan x (9) = (y 1) tan x (10) (1 +
: (1:, 2:, 3:, 4: ) 1 (Stratospheric Sudden Warming; SSW),, 1 (Displacement), 2 (Splitting) 2 (Charlton and Polvani 2007)., (Mi
 : 2009 1 1 2 3 3 4 3 3 3 (1:, 2:, 3:, 4: ) 1 (Stratospheric Sudden Warming; SSW),, 1 (Displacement), 2 (Splitting) 2 (Charlton and Polvani 2007)., (Mitchell et al. 2013),. SSW,, (Labitzke 1965),, SSW,,
: 2009 1 1 2 3 3 4 3 3 3 (1:, 2:, 3:, 4: ) 1 (Stratospheric Sudden Warming; SSW),, 1 (Displacement), 2 (Splitting) 2 (Charlton and Polvani 2007)., (Mitchell et al. 2013),. SSW,, (Labitzke 1965),, SSW,,
1 Ricci V, V i, W f : V W f f(v ) = Imf W ( ) f : V 1 V k W 1
 1 Ricci V, V i, W f : V W f f(v = Imf W ( f : V 1 V k W 1 {f(v 1,, v k v i V i } W < Imf > < > f W V, V i, W f : U V L(U; V f : V 1 V r W L(V 1,, V r ; W L(V 1,, V r ; W (f + g(v 1,, v r = f(v 1,, v r
1 Ricci V, V i, W f : V W f f(v = Imf W ( f : V 1 V k W 1 {f(v 1,, v k v i V i } W < Imf > < > f W V, V i, W f : U V L(U; V f : V 1 V r W L(V 1,, V r ; W L(V 1,, V r ; W (f + g(v 1,, v r = f(v 1,, v r
v v = v 1 v 2 v 3 (1) R = (R ij ) (2) R (R 1 ) ij = R ji (3) 3 R ij R ik = δ jk (4) i=1 δ ij Kronecker δ ij = { 1 (i = j) 0 (i
 1. 1 1.1 1.1.1 1.1.1.1 v v = v 1 v 2 v 3 (1) R = (R ij ) (2) R (R 1 ) ij = R ji (3) R ij R ik = δ jk (4) δ ij Kronecker δ ij = { 1 (i = j) 0 (i j) (5) 1 1.1. v1.1 2011/04/10 1. 1 2 v i = R ij v j (6) [
1. 1 1.1 1.1.1 1.1.1.1 v v = v 1 v 2 v 3 (1) R = (R ij ) (2) R (R 1 ) ij = R ji (3) R ij R ik = δ jk (4) δ ij Kronecker δ ij = { 1 (i = j) 0 (i j) (5) 1 1.1. v1.1 2011/04/10 1. 1 2 v i = R ij v j (6) [
 http://www.ns.kogakuin.ac.jp/~ft13389/lecture/physics1a2b/ pdf I 1 1 1.1 ( ) 1. 30 m µm 2. 20 cm km 3. 10 m 2 cm 2 4. 5 cm 3 km 3 5. 1 6. 1 7. 1 1.2 ( ) 1. 1 m + 10 cm 2. 1 hr + 6400 sec 3. 3.0 10 5 kg
http://www.ns.kogakuin.ac.jp/~ft13389/lecture/physics1a2b/ pdf I 1 1 1.1 ( ) 1. 30 m µm 2. 20 cm km 3. 10 m 2 cm 2 4. 5 cm 3 km 3 5. 1 6. 1 7. 1 1.2 ( ) 1. 1 m + 10 cm 2. 1 hr + 6400 sec 3. 3.0 10 5 kg
φ 4 Minimal subtraction scheme 2-loop ε 2008 (University of Tokyo) (Atsuo Kuniba) version 21/Apr/ Formulas Γ( n + ɛ) = ( 1)n (1 n! ɛ + ψ(n + 1)
 φ 4 Minimal subtraction scheme 2-loop ε 28 University of Tokyo Atsuo Kuniba version 2/Apr/28 Formulas Γ n + ɛ = n n! ɛ + ψn + + Oɛ n =,, 2, ψn + = + 2 + + γ, 2 n ψ = γ =.5772... Euler const, log + ax x
φ 4 Minimal subtraction scheme 2-loop ε 28 University of Tokyo Atsuo Kuniba version 2/Apr/28 Formulas Γ n + ɛ = n n! ɛ + ψn + + Oɛ n =,, 2, ψn + = + 2 + + γ, 2 n ψ = γ =.5772... Euler const, log + ax x
 4................................. 4................................. 4 6................................. 6................................. 9.................................................... 3..3..........................
4................................. 4................................. 4 6................................. 6................................. 9.................................................... 3..3..........................
I-2 (100 ) (1) y(x) y dy dx y d2 y dx 2 (a) y + 2y 3y = 9e 2x (b) x 2 y 6y = 5x 4 (2) Bernoulli B n (n = 0, 1, 2,...) x e x 1 = n=0 B 0 B 1 B 2 (3) co
 16 I ( ) (1) I-1 I-2 I-3 (2) I-1 ( ) (100 ) 2l x x = 0 y t y(x, t) y(±l, t) = 0 m T g y(x, t) l y(x, t) c = 2 y(x, t) c 2 2 y(x, t) = g (A) t 2 x 2 T/m (1) y 0 (x) y 0 (x) = g c 2 (l2 x 2 ) (B) (2) (1)
16 I ( ) (1) I-1 I-2 I-3 (2) I-1 ( ) (100 ) 2l x x = 0 y t y(x, t) y(±l, t) = 0 m T g y(x, t) l y(x, t) c = 2 y(x, t) c 2 2 y(x, t) = g (A) t 2 x 2 T/m (1) y 0 (x) y 0 (x) = g c 2 (l2 x 2 ) (B) (2) (1)
simx simxdx, cosxdx, sixdx 6.3 px m m + pxfxdx = pxf x p xf xdx = pxf x p xf x + p xf xdx 7.4 a m.5 fx simxdx 8 fx fx simxdx = πb m 9 a fxdx = πa a =
 II 6 ishimori@phys.titech.ac.jp 6.. 5.4.. f Rx = f Lx = fx fx + lim = lim x x + x x f c = f x + x < c < x x x + lim x x fx fx x x = lim x x f c = f x x < c < x cosmx cosxdx = {cosm x + cosm + x} dx = [
II 6 ishimori@phys.titech.ac.jp 6.. 5.4.. f Rx = f Lx = fx fx + lim = lim x x + x x f c = f x + x < c < x x x + lim x x fx fx x x = lim x x f c = f x x < c < x cosmx cosxdx = {cosm x + cosm + x} dx = [


